§1.3.1 二项式定理习题课(三)
1.3.1 二项式定理 课件(人教A选修2-3)
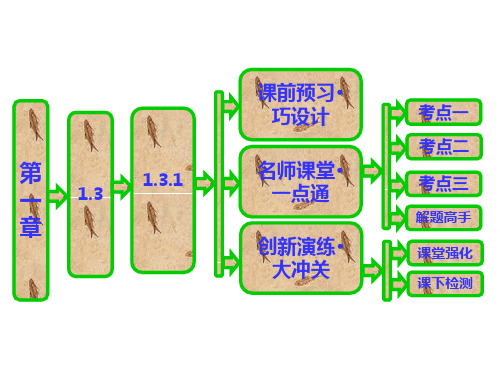
(2)求展开式中的常数项.
解:(1)x2+2
1
10
x
的展开式的第
5
项为
T5=C410·(x2)6·21 x4=C410·124·x12· 1x4=1805x10.
(2)设第 k+1 项为常数项,
则
Tk
+
1
=
C
k 10
2.相关概念
(1)公式右边的多项式叫做(a+b)n 的二项展开式. (2)各项的系数 Ckn(k∈{0,1,2,…,n}) 叫做二项式系数. (3)展开式中的 Cknan-kbk 叫做二项展开式的通项,记作 Tk+1 , 它表示展开式的第 k+1 项.
(4)在二项式定理中,如果设 a=1,b=x,则得到公式 (1+x)n= C0n+C1nx+C2nx2+…+Cknxk+…+Cnnxn.
()
A.10
B.-10
C.40
D.-40
解析:二项式(2x2-1x)5 展开式的第 r+1 项为 Tr+1=Cr5(2x2)5
-r(-1x)r=Cr5·25-r×(-1)rx10-3r,当 r=3 时,含有 x,其系数
为 C35·22×(-1)3=-40. 答案:D
4.已知二项式x2+21 x10. (1)求展开式中的第 5 项;
+C44·( 1x)4 =81x2+108x+54+1x2+x12.
法二:(3 x+ 1x)4=3x+ x2 14 =x12(81x4+108x3+54x2+12x+1) =81x2+108x+54+1x2+x12. (2)原式=C05(x-1)5+C15(x-1)4+C25(x-1)3+C35(x-1)2 +C45(x-1)+C55(x-1)0-1 =[(x-1)+1]5-1=x5-1.
高二数学 第一章1.3.1 二项式定理

本
解析 依题意 C57a2+C37a4=2C74a3.
课
时 由于 a≠0,整理得 5a2-10a+3=0,
栏
目 开 关
解得
a=1±
10 5.
练一练·当堂检测、目标达成落实处
1.3.1
4.求2
x-
1 6 x
的展开式.
解 先将原式化简,再展开,得
本
2 x- 1x6=2x-x 16=x13(2x-1)6
开 关
(a+b)在相乘时都有两种选择:选 a 或选 b,而且每个(a+b)
中的 a 或 b 都选定后,才能得到展开式的一项.由分步乘法
计数原理,在合并同类项之前,(a+b)2 展开式共有 2×2=
22 项,而且 a2-kbk 相当于从 2 个(a+b)中取 k 个 b 的组合数
Ck2,即 a2-kbk 的系数是 Ck2.
பைடு நூலகம்
当 9-2r=5 时,解得 r=2,所以系数为 36.
所以展开式中,不含 x6 项,含有 x5 项,系数为 36.
研一研·问题探究、课堂更高效
1.3.1
探究点三 综合应用
例3
已知
x- 2
1 4
x
n
的展开式中,前三项系数的绝对值依次
成等差数列.
本
(1)证明:展开式中没有常数项;
课
时
(2)求展开式中所有的有理项.
栏 目 开 关
(即1)证n2-明9n+由8题=意0,得:2Cn1·12=1+Cn2·122,
∴n=8 (n=1 舍去).
∴Tk+1=Ck8(
x)8-k·-241
xk=-12k·Ck8x
8-k 2
·x-4k =
高中数学 第1章 计数原理 1.3 二项式定理 1.3.1 二项式定理 新人教B版选修2-3

(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
解 原式=C05(x-1)5+C15(x-1)4+C25(x-1)3+C35(x-1)2 +C45(x-1)+C55-1
=[(x-1)+1]5-1=x5-1.
规律方法 运用二项式定理展开二项式,要记准展开式的 通项公式,对于较复杂的二项式,有时先化简再展开更简 捷;要搞清楚二项展开式中的项以及该项的系数与二项式 系数的区别.逆用二项式定理可将多项式化简,对于这类问 题的求解,要熟悉公式的特点、项数、各项幂指数的规律 以及各项的系数.
要点二 二项展开式通项的应用 例2 若 ( x+ 1 )n展开式中前三项系数成等差数列,求:
4 2x (1)展开式中含x的一次项; 解 由已知可得 C0n+C2n·212=2C1n·12, 即n2-9n+8=0, 解得n=8,或n=1(舍去).
Tr+1=Cr8(
x)8-r·(
1
4
)r=Cr8·2-r·x 4-34r,
+
C
2 2n+1
×142n
-
1×52
-
…
+
C22nn+1×14×52n-C22nn+ +11×52n+1+52n+1
=
14(142n
-
C
1 2n+1
×142n
-
1×5
+
C
22n+1×142n
-
2×52
-
…
+
C22nn+1×52n).
上式是14的倍数,能被14整除,所以34n+2+52n+1能被14整除 .
10-2r 令 3 =2,得
r=12(10-6)=2.
故 x2 项的系数为 C210(-3)2=405.
高中数学 1.3.1二项式定理课件 新人教A版选修23[1]
![高中数学 1.3.1二项式定理课件 新人教A版选修23[1]](https://img.taocdn.com/s3/m/669c5843fd0a79563d1e725d.png)
二项式定理(dìnglǐ) 思维导航 1.我们已知(a+b)2=a2+2ab+b2,展开式中有3项;运 用多项式乘法可以求得(a+b)3、(a+b)4的展开式,并且它们分 别(fēnbié)有4项、5项,你能用类比归纳的方法得出(a+b)n(n≥2) 的展开式吗?
第八页,共38页。
新知导学 1.二项展开式的推导:(a+b)n(n∈N*)是 n 个因式(a+b) 的积,按多项式乘以多项式的法则,可知确定乘积展开式中的 每一项,需要看有多少个因式(a+b)中取 a,多少个因式(a+b) 中取 b,如果从 k 个因式中选取 b,则就有__n_-__k____个因式中 选 a.∴积式为 an-kbk(k=0、1、2、…、n)的形式的项共有__C_nk___ 个.合并同类项后为 _____C_nk_a_n-_k_b_k__________.因此(a +b)n= _C_0n_a_n+__C__1na_n_-_1b_+__…__+__C__rna_n_-_rb_r_+__…__+__C_nn_-_1a_b_n_-_1_+__C_nn_b_n__这个公式 叫做二项式定理.
D.-40
[解析] Tr+1=Cr5(x2)5-r(-x23)r=Cr5x10-2r·(-2)r·x-3r =C5r (-2)r·x10-5r. 令 10-5r=0,∴r=2,常数项为 C25×4=40.
第二十页,共38页。
若
x+ 1 4
2
n x
展开式中前三项系数依次成等差
数列.求:
(1)展开式中含 x 的一次幂的项;
第三十一页,共38页。
[方法规律总结] 二项式系数与项的系数是两个不同的概 念,前者仅与二项式的指数及项数有关(yǒuguān),与二项式的 构成无关,后者与二项式的构成、二项式的指数及项数均有关 (yǒuguān).
1.3.1二项式定理课件-高二数学人教A版选修2-3

2 x
6
的展开式的常数项是
240
2.
1
1 x
10的展开式中含
1 x3 项的系数是
120
五、课堂小结
思想共鸣 经验共享
你
1.二项式定理
学
到
了
a b n Cn0an Cn1an1b Cnk ankbk Cnnbn n N *
什
么
2.二项展开式的通项
Tk1 Cnk ankbk,k 0,1, 2,…, n
C
0 3
a
3
C
1a
3
2b
C 32ab 2
C
3 3
b
3
思想共鸣 经验共享
请同学们类比 (a+b)2 ,(a+b)3的展开式的特
征及方法,你能直接写出 (a+b)4 的展开式
吗?
第 二
( ( a a+ b ) b4 ) = 2( a + Cb ) 20( a a+ 2 b ) ( Ca + 21ab ( b) a + Cb 2) 2b2
恰有1个括号取b的情况有C21种,则ab前的系数为C21
恰有2个括号取b的情况有C22 种,则b2前的系数为C22
(a+b)2 = C20 a2 + C21 ab+ C22 b2 = a2 +2ab+b2
对(a+b)3展开式的分析:
(a b)3 (a b)(a b)(a b)
项的形式: a 3 a 2b ab2 b3
探
(a b)3= C 4 0 Ca 4 30+ aC 3 4 1 a 3 Cb + 31aC 24 2 ba 2 b 2 C+ 3C 2a4 3 a bb 23 + C C4 4 3b 3b4 3
高中数学 1.3.1《二项式定理》课件 新人教A版选修2-3

1 5 1、求(2 x − ) 的展开式 x 2、求( + 2 x) 7的展开式第4项的系数 1 1 7 3、求(x − ) 的展开式中x 3的系数 x
破解疑惑: 破解疑惑: 今天是星期五,再过2 天后是星期几, 今天是星期五,再过22007 天后是星期几, 你知道吗? 你知道吗?
解: = 8670 × 2 22011 = 2(7 +1)670
0 1 669 670 = 2(C670767010 + C670766911 + ...+ C670 711669 + C670 701670)
发现被7整除余 ,故相当过2天后是星期几是一样的 天后是星期几是一样的。 发现被 整除余2,故相当过 天后是星期几是一样的。 整除余 故是周日
拓 展 提 高 (x2+3x+2)5展开式中 的系数为 展开式中x的系数为 _____. 方法1 方法 (x2+3x+2)5=[(x2+2)+3x]5
在展开式中只有 C 1 (x 2 + 2)4 ⋅ 3x才存在 x的项 , 5 其系数为 5C 4 2 4 ⋅ 3 = 240 4
方法2 方法 (x2+3x+2)5=[x(x+3)+2]5
在展开式中只有 C 1 x(x + 3) ⋅ 2 4 才存在 x的项 , 5 其系数为 C 1 ⋅ 3 ⋅ 2 4 = 240 5
1 x
)10 的展开式中是否包含常数项? 的展开式中是否包含常数项?
分析:取通项来分析, 分析:取通项来分析, 常数项即 x 项.
0
Tr +1 = C ⋅ ( 3 x
r 10
2
)
课件1:1.3 二项式定理(习题课)

(三)展开式中各项系数和
例4.(2x2-1)n的展开式的各项系数和为……( D)
A.2n+1
B.2n
C.0
D.1
分析:设(2x2-1)n=a0x2n+a1x2(n-1)+…+an,
展开式各项系数和为a0+a1+a2+…+an
∵上式是恒等式,所以当且仅当x=1时(2-1)n=a0+a1+a2+…+an
数相等.
2.如果二项式的幂指数是偶数,中间一项的二项式系数最大;
如果二项式的幂指数是奇数,中间两项的二项式系数相等并且
最大.
n
2
3.在二项展开式中,所有二项式系数的和等于
;奇数项的
二项式系数的和等于偶数项的二项式系数的和,都等于 2 n 1.
(一)通项公式的应用
例1、(1)如果 (
1
+ )2 的展开式中,第四项与第六项的系
第一章 计数原理
§1.3二项式定理复习
高中数学选修2-3·同步课件
概念复习
n
0 n
1 n 1
r nr r
n n
(
a
b
)
C
a
C
a
b
C
a
b
C
b
n
n
n
n
1、二项式定理:
通项(第r+1项):Tr 1 C nr a nr b r
2、二项式系数的性质:
1.在二项展开式中,与首末两端“等距离”的两项的二项式系
数相等,求展开式中的常数项;
人教版高中数学选修2-3教案:1.3.1二项式定理

§1.3.1 二项式定理【教学目标】1.理解二项式定理及推导方法,识记二项展开式的有关特征,能对二项式定理进行简单应用;2.通过对二项式定理内容的研究,体验特殊到一般的发现规律,一般到特殊指导实践的认识事物过程。
【教学重难点】教学重点:二项式定理的内容及归纳过程;教学难点:在二项式展开的过程中,发现各项及各项系数的规律。
【教学过程】一、设置情景,引入课题引入:二项式定理研究的是(a+b)n的展开式。
如(a+b)2=a2+2ab+b2, (a+b)3=?,(a+b)4=?,那么(a+b)n的展开式是什么呢?二、引导探究,发现规律1、多项式乘法的再认识问题1:(a1+ b1)(a2+b2) (a3+ b3)展开式中每一项是怎样构成的?展开式有几项?2、(a+b)3展开式的再认识问题2:将上式中,若令a1=a2=a3=a, b1=b2= b3=b,则展开式又是什么?合作探究1:合并同类项后,为什么a2b的系数是3?教师引导:可以发现a2b是从(a+b)(a+b)(a+b)这三个括号中的任意两个中选a,剩下的一个括号中选b;利用组合知识可以得到a2b应该出现了C23· C11=3次,所以a2b的系数是3。
问题3:(a+b)4的展开式又是什么呢?可以对(a+b)4按a或按b进行分类:(1)四个括号中全都取a,得:C44a4(2)四个括号中有3个取a,剩下的1个取b,得:C34a3· C11b(3)四个括号中有2个取a,剩下的2个取b,得:C24a2· C22b2(4)四个括号中有1个取a,剩下的3个取b,得:C14a· C33b3(5)四个括号中全都取b,得:C44b4小结:对于展开式,只要按一个字母分类就可以了,可以按a分类,也可以按b分类,再如:(1)不取b:C04a4;(2)取1个b:C14a3b;(3)取2个b:C24a2b2;(4)取3个b:C34a b3;(5)取4个b:C44b4,然后将上面各式相加得到展开式。
高中数学 第一章 计数原理 1.3 二项式定理 1.3.3 二项式定理习题课教案 3数学教案

1.3.3 二项式定理习题课教学目标知识与技能1.能熟练地掌握二项式定理的展开式及其有关概念.2.会用二项式定理解决与二项展开式有关的简单问题.3.能熟练掌握杨辉三角及二项式系数的有关性质.4.会用二项式系数的性质解决一些简单问题,并能熟练地使用赋值法.过程与方法1.能解决二项展开式的有关概念问题:项、二项式系数、系数、有理项、无理项、常数项、整数项等.2.能用二项式定理解决诸如整除、近似值、求和等有关问题.3.能用二项式系数的有关性质,解决诸如:最值、二项式系数和、系数和等问题.情感、态度与价值观1.培养学生对整个数学知识的驾驭能力,能在一定高度上进行数学知识的应用.2.培养学生观察、归纳的能力以及分析问题与解决问题的能力.3.进一步提升学生学好数学用好数学的积极性,进一步提升学生学习数学的兴趣.重点难点教学重点:掌握二项展开式,掌握二项式系数的有关性质,掌握解决二项式定理性质等有关问题的方法.教学难点:利用二项式定理解决有关问题,利用二项式系数的性质解决有关问题.教学过程复习巩顾前面我们学习了二项式定理,请回顾:1.(a+b)n=________________(n∈N*),这个公式表示的定理叫做二项式定理,公式右边的多项式叫做(a+b)n的______________,其中C r n(r=0,1,2,…,n)叫做______________,通项是指展开式的第__________________项,共有____________项.其中二项式系数是____________,系数是____________.2.二项式系数的四个性质(杨辉三角的规律) (1)对称性:____________________. (2)性质2:______________________.(3)二项式系数的最大值________________________.(4)二项式系数之和____________________,所用方法是____________________. 答案:1.(a +b)n=C 0n a n+C 1n an -1b +C 2n an -2b 2+…+C r n an -r b r+…+C n n b n(n∈N )、展开式、二项式系数、r +1、n +1、C rn 、变量前的常数2.(1)C mn =Cn -mn (2)C rn +1=C r -1n +C rn(3)当n 是偶数时,中间的一项取得最大值,即C n2n 最大;当n 是奇数时,中间的两项相等,且同时取得最大值,即C n -12n =C n +12n 最大(4)C 0n +C 1n +C 2n +…+C rn +…+C nn =2n赋值法典型示例类型一:二项展开式的有关概念 例1试求:(1)(x 3-2x 2)5的展开式中x 5的系数;(2)(2x 2-1x)6的展开式中的常数项;(3)在(3x +32)100的展开式中,系数为有理数的项的个数.思路分析:理解二项展开式的有关概念,什么是二项式系数,什么是系数,什么是项,什么是常数项、有理项、无理项等,其实都是由通项入手,根据变量的系数、指数进行判断,当指数为0时是常数项,当指数是整数时是有理项,当指数是分数时是无理项.解:(1)T r +1=C r5(x 3)5-r(-2x2)r =(-2)r C r 5x 15-5r ,依题意15-5r =5,解得r =2.故(-2)2C 25=40为所求x 5的系数.(2)T r +1=C r 6(2x 2)6-r(-1x)r =(-1)r ·26-r ·C r 6x 12-3r ,依题意12-3r =0,解得r =4.故(-1)4·22C 26=60为所求的常数项.(3)T r +1=C r 100(3x)100-r(32)r =C r100·350-r 2·2r 3x 100-r ,要使x 的系数为有理数,指数50-r 2与r 3都必须是整数,因此r 应是6的倍数,即r =6k(k∈Z ),又0≤6k≤100,解得0≤k≤1623(k∈Z ),∴x 的系数为有理数的项共有17项.点评:求二项展开式中具有某特定性质的项,关键是确定r 的值或取值范围.应当注意的是二项式系数与二项展开式中各项的系数不是同一概念,要加以区分.【巩固练习】试求:(1)(x +2)10(x 2-1)的展开式中x 10的系数;(2)(|x|+1|x|-2)3的展开式中的常数项.解:(1)∵(x+2)10=x 10+20x 9+180x 8+…,∴(x+2)10(x 2-1)的展开式中x 10的系数是-1+180=179.(2)∵(|x|+1|x|-2)3=(|x|-1|x|)6,∴所求展开式中的常数项是-C 36=-20.类型二:二项展开式的有关应用——简单应用例2求(x -1)-(x -1)2+(x -1)3-(x -1)4+(x -1)5的展开式中x 2的系数. 解:∵(x-1)-(x -1)2+(x -1)3-(x -1)4+(x -1)5=x -1{1-[-x -1]5}1-[-x -1]=x -1+x -16x ,∴所求展开式中x 2的系数就是(x -1)6的展开式中x 3的系数-C 36=-20.点评:这是一组将一个二项式扩展为若干个二项式相乘或相加,或扩展为简单的三项展开式的问题,求解的关键在于转化为二项展开式的问题,转化时要注意分析题目中式子的结构特征.能够最大限度地考查学生对知识的把握程度.【巩固练习】(1-x)5+(1-x)6+(1-x)7+(1-x)8的展开式中x 3项的系数是( ) A .74 B .121 C .-74 D .-121解析:先求和:(1-x)5+(1-x)6+(1-x)7+(1-x)8=1-x 5[1-1-x4]1-1-x=1-x5[4x -6x 2+4x 3-x 4]x,分子的展开式中x 4的系数,即为原式的展开式中x 3项的系数,(-1)×1+4×(-C 15)-6C 25+4×(-C 35)=-1-20-60-40=-121,所以选D.答案:D类型三:二项展开式的有关应用:整除、不等式、近似值等问题 例3证明:(1)2≤(1+1n)n <3,其中n∈N *;(2)证明:对任意非负整数n,33n-26n -1可被676整除.思路分析:对于二项式中的不等式,通过展开式,分析其中的特殊项,可以证明一些简单的不等式问题;对于整除问题同样如此,关键是把二项式拆成676的形式;对于比较麻烦的数列问题,我们经常采用的方法就是数学归纳法,本题也不例外.证明:(1)(1+1n )n =1+C 1n ·1n +C 2n (1n )2+…≥2(当且仅当n =1时取等号).当n =1时,(1+1n)n=2<3显然成立;当n≥2时,(1+1n )n =C 0n +C 1n ·1n +C 2n ·1n 2+…+C nn ·1n n =2+n(n -1)2!1n 2+n(n -1)(n -2)3!1n 3+…+n(n -1)…2·1n !1n n =2+12!n n n -1n +13!n n n -1n n -2n +…+1n !n n n -1n …2n 1n <2+12!+13!+…1n !<2+11×2+12×3+…+1n(n -1)=2+(1-12)+(12-13)+…+(1n -1-1n )=3-1n <3.综上所述:2≤(1+1n)n <3,其中n∈N *.(2)当n =0,n =1时33n-26n -1=0,显然33n-26n -1可被676整除.当n≥2时,33n-26n -1=27n-26n -1=(1+26)n-26n -1=1+26n +C 2n ·262+…+C nn ·26n-26n -1=C 2n ·262+C 3n ·263+…+C nn 26n=676(C 2n +26C 3n +…+26n -2C nn).综上所述:对任意非负整数n,33n-26n -1可被676整除.点评:用二项式定理解决整除问题是二项式定理的一大特色,这是二项展开式的一种基本应用,通过对二项式的拆解,我们可以解决一些看似很难但易解决的问题.【巩固练习】已知m ,n 是正整数,f(x)=(1+x)m+(1+x)n的展开式中x 的系数为7,(1)试求f(x)中的x 2的系数的最小值;(2)对于使f(x)中的x 2的系数为最小的m ,n ,求出此时x 3的系数; (3)利用上述结果,求f(0.003)的近似值(精确到0.01). 解:根据题意得:C 1m +C 1n =7,即m +n =7.(*)(1)x 2的系数为C 2m+C 2n=m(m -1)2+n(n -1)2=m 2+n 2-m -n2.将(*)变形为n =7-m 代入上式得:x 2的系数为m 2-7m +21=(m -72)2+354.故当m =3或4时,x 2的系数的最小值为9.(2)当m =3,n =4或m =4,n =3时,x 3的系数为C 33+C 34=5. (3)f(0.003)≈2.02.类型四:二项式系数的最大值、系数的最大值问题 例4求(x -1)9的展开式中系数最大的项.思路分析:二项式系数最大的项我们可以根据公式求解,但是系数最大的项怎么求呢?观察本题中二项式系数与系数之间的关系,我们发现它们只不过相差一个负号而已,所以可以通过二项式系数的大小反映系数的大小,只不过要注意正负号.解:T r +1=(-1)r C r 9x 9-r .∵C 49=C 59=126,而(-1)4=1,(-1)5=-1,∴T 5=126x 5是所求系数最大的项.点评:此类问题仍然是利用二项展开式的通项公式来求解,但在解题过程中要注意一些常用方法和数学思想的应用.【巩固练习】 求(x +124x)8展开式中系数最大的项.解:记第r 项系数为T r ,设第k 项系数最大,则有⎩⎪⎨⎪⎧T k ≥T k -1,T k ≥T k +1,又T r =C r -182-r +1,那么有⎩⎪⎨⎪⎧C k -182-k +1≥C k -282-k +2,C k -182-k +1≥C k 82-k,即⎩⎪⎨⎪⎧8!(k -1)!(9-k)!≥8!(k -2)!(10-k)!×2,8!(k -1)!(9-k)!×2≥8!k !(8-k)!,∴⎩⎪⎨⎪⎧1k -1≥2k -2,29-k ≥1k .解得3≤k≤4,∴系数最大的项为第3项T 3=7x 52和第4项T 4=7x 72.类型五:二项式系数之和、系数之和等问题例5若(2x +3)4=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4,则(a 0+a 2+a 4)2-(a 1+a 3)2的值等于__________;思路分析:注意到与系数的和差有关,所以可以用赋值法求得奇数项的系数之和与偶数项的系数之和,注意使用平方差公式.解:令x =1,得a 0+a 1+a 2+a 3+a 4=(2+3)4,令x =-1,得a 0-a 1+a 2-a 3+a 4=(3-2)4,由此可得(a 0+a 2+a 4)2-(a 1+a 3)2=(a 0+a 1+a 2+a 3+a 4)(a 0-a 1+a 2-a 3+a 4)=[(3+2)(3-2)]4=1.点评:在二项式系数的性质应用中,尤其是系数和的问题,我们经常使用赋值法,这是一种奇妙的方法,可以帮助我们在不用计算每一个系数的前提下,求出各个系数的和.【巩固练习】已知(1-2x)7=a 0+a 1x +a 2x 2+…+a 7x 7, 求(1)a 0+a 1+…+a 7的值;(2)a 0+a 2+a 4+a 6及a 1+a 3+a 5+a 7的值; (3)各项二项式系数和.解:(1)令x =1,则a 0+a 1+…+a 7=-1.(2)令x =-1,则a 0-a 1+a 2-a 3+…+a 6-a 7=2 187. 则a 1+a 3+a 5+a 7=-1 094;a 0+a 2+a 4+a 6=1 093. (3)各项二项式系数和C 07+C 17+…+C 77=27=128. 【拓展实例】例1(1+3x)6(1+14x)10的展开式中的常数项为( )A .1B .46C .4 245D .4 246思路分析:对于非一般的二项式问题,要注意转化成二项式问题解决.本题虽然有两个式子相乘,只要我们写出整个式子的通项,令指数为0,即可求得常数项.解:先求(1+3x)6的展开式中的通项.T r +1=C r 6(x 13)r =C r 6x r3,r =0,1,2,3,4,5,6.再求(1+14x )10的展开式中的通项.T k +1=C k10(x -14)k =C k 10x -k 4,k =0,1,2,3,4,…,10.两通项相乘得:C r 6x r 3C k10x -k 4=C r 6C k 10x r 3-k 4,令r 3-k 4=0,得4r =3k ,这样一来,(r ,k)只有三组:(0,0),(3,4),(6,8)满足要求.故常数项为:1+C 36C 410+C 66C 810=4 246.点评:对于乘积的式子或者三项的式子的展开问题,我们可以通过化归思想,将其转化成二项展开式问题.要注意本题中,常数项的位置有三处.【巩固练习】已知(1+x +x 2)(x +1x 3)n 的展开式中没有..常数项,n∈N *,且2≤n≤8,则n =______. 解析:依题意(x +1x 3)n ,对n∈N *,且2≤n≤8中,只有n =5时,其展开式既不出现常数项,也不会出现与x 、x 2乘积为常数的项.故填5.答案:5 【变练演编】(1)对于9100你能编出什么样的整除问题? 如9100被________整除的余数是________.(2)(2x 2-1x )6的展开式中的常数项是第____________项,整数项是第______________项,x 的最高次项是第______________项,二项式系数之和是______________,系数之和是______________.将你能得到的所有正确的答案一一列举出来.答案:(1)这是一个开放性的问题,学生可以有多种答案,比如说9100被8整除的余数是1,9100被80整除的余数是1等等.(2)T r +1=C r6(2x 2)6-r(-1x)r =(-1)r ·26-r ·C r 6x 12-3r .依题意12-3r =0,解得r =4,所以常数项是第5项;整数项是第1,2,3,4,5项;x 的最高次项是第1项;二项式系数之和为64;系数之和为1.设计意图:变练演编——这种开放性的设计,能够有效地提高学生学习的积极性,使得编题不仅仅是老师的专利,学生在编题解题的过程中,领悟知识,提高能力,增长兴趣,增强信心,不仅有助于训练同学们的常规思维,还能培养同学们的逆向思维,最终提高学生的数学成绩.【达标检测】1)12展开式中的常数项为( )1.(x-3xA.-1 320 B.1 320 C.-220 D.2202.(1-x)6(1+x)4的展开式中x的系数是( )A.-4 B.-3 C.3 D.43.若(1-2x)2 005=a0+a1x+a2x2+…+a2 005x2 005(x∈R),则(a0+a1)+(a0+a2)+(a0+a3)+…+(a0+a2 005)=________(用数字作答).答案:1.C 2.B 3.2 003反考老师:即由学生出题,教师现场解答(约8分钟).(活动设计:请学生到黑板板书题目,要求别太烦琐,且与本节习题课内容相符.一般不多于3道题,教师尽可能全部解答,具体解答数目视题目难度和时间而定.教师要边做边讲,以向学生现场展示解题思路的发现过程和解题能力.做完后,请学生给“阅卷”)课堂小结活动设计:先给学生1~2分钟的时间默写本节的主要基础知识、方法,例题、题目类型、解题规律等;然后用精练的、精确的语言概括本节的知识脉络,思想方法,解题规律等.活动成果:(板书)1.知识收获:二项式定理、二项展开式、二项式系数的性质.2.方法收获:利用二项式定理解决有关问题,利用二项式系数的性质解决有关问题.3.思维收获:合作意识,创新精神,增加了学习数学的积极性,提升学习数学的兴趣.设计意图:通过学生自己总结所学、所识、所想,不但能充分体现新课程的理念,还能充分发挥学生在课堂上的“主人翁”精神,真正体现了学生的主体地位.不仅可以使学生更好地掌握本节所学,而且还能提高学生学习的主动性,提高学生学习数学的兴趣,久而久之,学生的数学水平与数学素养必定会得到长足的提高!补充练习【基础练习】1.计算1-3C 1n +9C 2n -27C 3n +…+(-1)n 3n C nn . 2.(x +1x -2)3的展开式中,常数项是________.3.已知(3x -13x2)n ,n∈N *的展开式中各项系数和为128,则展开式中1x3的系数是( )A .7B .-7C .21D .-21 4.求(x -13x)10的展开式中有理项共有________项.1.解:原式=C 0n +C 1n (-3)1+C 2n (-3)2+C 3n (-3)3+…+C 3n (-3)n=(1-3)n=(-2)n. 2.解析:(x +1x -2)3=[(x -1)2x ]3=(x -1)6x 3. 上述式子展开后常数项只有一项C 36x3-13x3,即-20.3.解析:由已知条件可得:(3-1)n=128,n =7. ∵T r +1=(-1)r C r7(3x)7-r(13x2)r =(-1)r C r 737-rx7-53r.令7-5r3=-3,则有:r =6.所以二项展开式中1x 3的系数是:T 7=(-1)6C 6737-6=21,故选C.4.解析:∵T r +1=C r10(x)10-r(-13x)r =C r 10(-1)rx5-56r.∴当r =0,6时,所对应的项是有理项.故展开式中有理项有2项. 【拓展练习】5.已知(1+kx 2)6(k 是正整数)的展开式中,x 8的系数小于120,则k =____________. 6.设n∈N ,则C 1n +C 2n 6+C 3n 62+…+C n n 6n -1=____________.5.解析:(1+kx 2)6按二项式定理展开的通项为T r +1=C r 6(kx 2)r =C r 6k r x 2r,我们知道x 8的系数为C 46k 4=15k 4,即15k 4<120,也即k 4<8,而k 是正整数,故k 只能取1.6.解:C 1n +C 2n 6+C 3n 62+…+C n n 6n -1=16C 0n +C 1n +C 2n 6+…+C n n 6n -1-16C 0n =16(C 0n +C 1n 6+C 2n 62+…+C n n 6n -1)=16[(1+6)n-1]=16(7n -1).设计说明二项式定理的内容,是各地高考中经常要考查的内容之一,其形式主要是选择题和填空题,题型往往相对稳定,思路方法常常是利用二项展开式的通项公式、二项式系数的有关性质等.常见的二项式问题有:求二项展开式中某一项或某一项的系数,求所有项系数的和或奇(偶)数项系数和,求展开式的项数,求常数项,求近似值,证明不等式等.实际教学的过程中,要努力把表现的机会让给学生,以发挥他们的自主精神;尽量创造让学生活动的机会,以让学生在直接体验中建构自己的知识体系;尽量引导学生发挥其创造意识,以使他们能在创造的氛围中学习.二项式定理是初中学习的多项式乘法的继续,它所研究的是一种特殊的多项式——二项式的乘方的展开式.二项式定理既是排列组合的直接应用,又与概率理论中的三大概率分布之一的二项分布有着密切联系.掌握好二项式定理既可对初中学习的多项式的变形起到很好的复习、深化作用,又可以为进一步学习概率统计做好必要的知识储备.所以有必要掌握好二项式定理的相关内容.备课资料 二项式定理 同步练习选择题1.已知C 7n +1-C 7n =C 8n ,那么n 等于( )A .14B .12C .13D .15 2.C 0n +3C 1n +9C 2n …+3n C nn 的值等于( )A .4nB .3·4nC.4n3-1 D .4n-133.C 111+C 311+…+C 911的值为( )A .2 048B .1 024C .1 023D .5124.(x +1)(2x +1)(3x +1)……(nx+1)展开式中x 的一次项系数为( )A .C n -1nB .C 2nC .C 2n +1D .不能用组合数表示5.设(1+x +x 2)n =a 0+a 1x +a 2x 2+…a 2n x 2n ,则a 0+a 1+a 2+…+a 2n 等于 …( )A .22nB .3n C.3n -12 D.3n +12 6.若n 是正奇数,则7n +C 1n 7n -1+C 2n 7n -2+…C n -1n 7被9除的余数为( ) A .2 B .5 C .7 D .87.(1+x)2+(1+x)3+…+(1+x)10展开式中x 4的系数为( )A .C 511B .C 411 C .C 510D .C 410填空题8.(a +b)n 展开式中第r 项为__________.9.11100-1的末位连续零的个数为__________.参考答案1.A 2.A 3.C 4.C 5.B 6.C 7.A5.提示:令x =1即可.8.T r =C r -1n an +1-r b r -1 9.3。
原创1:1.3 二项式定理(习题课)

(1)求n; (2)求含x2的项的系数; (3)求展开式中所有的有理项.
例2.已知 ( 3 x x2 )2n 的展开式的二项式系数和比 (3x 1)n 的展开式的二项式系数和大992,求 (2x 1 )2n的展开式中:
x
(1)二项式系数最大的项; (2)系数的绝对值最大的项.
变式:已知 10 M 1 (n∈N*)的展开式中第五项的系数与第三项的系
整除或余数问题 例5 .求:112004被10除的余数.
(10 1)2004 C20004102004 C21004102003
C2200004310
C 2004 2004
10 M 1
变式: 1.求证:5555+1能被8整除; 证:5555+1=(56−1)55+1=56·M−1+1=56·M,所以5555+1能被8整除.
是 Tr 1 Cnr anrbr.
3. 对称性:Cnr =
C nr n
= 聚合性:Cnr
C r1 n
Cr n1
知识回顾
二项式系数的性质
(1)对称性:
C
r n
C nr n
(2)增减性即最大值
f
(r)
C
r n
在[0,
n 2
]上是增函数
;
在[
n 2
,
n]上是减函数。
当n为偶数时,f (r)max
n
f
第一章 计数原理
§1.3二项式定理(习题课)
高中数学选修2-3·精品课件
知识回顾
1.(a+b)n= Cn0an Cn1an1b Cn2a b n2 2 Cnnbn 展开式共有 n+1 项,其中C(nr r=0,1,2,……,n)
高中数学选修2-3课时作业9:1.3.1二项式定理

1.3.1二项式定理一、选择题 1.(1+1x)4等于( )A .1+3x +6x 2+3x 3+1x 4B .1+4x +6x 2+4x 3+1x 4C .1+4x +5x 2+6x 3+1x 4D .1+6x +5x 2+4x 3+1x42.在⎝⎛⎭⎪⎫x 2-2x 6的二项展开式中,x 2的系数为( )A .-154 B.154C .-38 D.383.(x -2y )10的展开式中x 6y 4项的系数是( )A .840B .-840C .210D .-210 4.(x -13x )10的展开式中含x 的正整数指数幂的项数是( )A .1B .2C .4D .6 5.若(3x -132x)n 的展开式中含有非零常数项,则这样的正整数n 的最小值是( )A .3B .4C .5D .66.若(1+x )n 的展开式中x 2项的系数为a n ,则1a 2+1a 3+…+1a n的值( )A .大于2B .小于2C .等于2D .大于32二、填空题7.在(x -a )10的展开式中,x 7的系数是15,则实数a =________. 8.已知a =⎠⎛0π(sin x +cos x )d x ,则二项式(a x -1x)6展开式中含x 2项的系数是________. 9.设二项式(x -ax)(a >0)的展开式中x 3的系数为A,常数项为B.若B =4A,则a 的值是________. 三、解答题10.已知在(3x -33x)n 的展开式中,第6项为常数项.(1)求n ;(2)求含x 2的项的系数; (3)求展开式中所有的有理项.11.求证:32n +2-8n -9(n ∈N *)能被64整除.12.求(1+x+x2)8的展开式中x5的系数.——★参考答案★——一、选择题1[答案]B[解析]由(1+1x )4=C 04+C 141x +C 24(1x )2+C 34(1x )3+C 44(1x )4=1+4x +6x 2+4x 3+1x 4. 2[答案]C [解析]T r +1=C r 6(x 2)6-r ·(-2x)r =(-1)r 22r -6C r 6x 3-r,令3-r =2,则r =1,所以x 2的系数为(-1)1×2-4×C 16=-38,故选C . 3.[答案]A[解析]方法一:设二项展开式中的第(r +1)项为x 6y 4,则T r +1=C r 10x 10-r ·(-2y )r =(-1)r ·(2)r ·C r 10·x 10-r ·y r ,∴10-r =6.∴r =4.∴该项系数为(-1)4·(2)4·C 410=840.方法二:(x -2y )10可以看作是由10个括号形成的连乘积,而x 6y 4是10项中取6个x 、4个y ,∴系数是C 610x 6·C 44·(-2y )4中的系数.∴系数为C 610·22=840. 4.[答案]A[解析]展开式通项为T r +1=C r 10(x )10-r (-13x)r = C r 10(-13)r x 10-3r 2,若展开式中含x 的正整数指数幂,即5-32r ∈N *,且0≤r ≤10,r ∈N , 所以r =2,即含x 的正整数指数幂的项只有一项. 5.[答案]B[解析]T r +1=C r n (3x )n -r(-132x)r=C r n (3)n -r (-1)r (132)r ·x n -r ·x -r 3=C r n (3)n -r(-132)r xn -4r3,令n -43r =0,得n =43r .∴n 取最小值为4.6.[答案]B[解析]由题意知a n =C 2n =nn -12,∴1a n =2nn -1=2(1n -1-1n),从而1a 2+1a 3+…+1a n =2(1-12+12-13+…+1n -1-1n )=2(1-1n )<2.二、填空题7.[答案]-12[解析]T 4=C 310x 7(-a )3,则C 310(-a )3=15,解得a =-12. 8.[答案]-192[解析]由题意知,a =(-cos x +sin x )|π0=2,则展开式中x 2的系数为C 16·25·(-1)=-192.9.[答案]2[解析]展开式的通项为T k +1=C k 6x 6-k ·(-a )k x -k 2 =(-a )k C k 6x 6-3k2 ,故A =(-a )2C 26,B =(-a )4C 46,由B =4A ,得a 2=4,又a >0,故a =2. 三、解答题10.[解析](1)通项公式为T k +1=C k n x n -k 3(-3)k x ―k 3=C k n (-3)k xn -2k 3.∵第6项为常数项,∴k =5时有n -2k 3=0,即n =10.(2)令n -2k 3=2,得k =12(n -6)=2,∴所求的系数为C 210(-3)2=405. (3)根据通项公式,由题意得⎩⎪⎨⎪⎧10-2k3∈Z0≤k ≤10k ∈Z ,令10-2k3=R (R ∈Z),则10-2k =3R ,即k =5-32R .∵k ∈Z ,∴R 应为偶数.∴R 可取2,0,-2,即k 可取2,5,8. ∴第3项,第6项与第9项为有理项,它们分别为C 210(-3)2x 2,C 510(-3)5,C 810(-3)8x -2.11.证明:32n +2-8n -9=(8+1)n +1-8n -9=C 0n +18n +1+C 1n +18n +…+C n +1n +1-8n -9=C 0n +18n +1+C 1n +18n +…+C n -1n +1·82+8(n +1)+1-8n -9=C 0n +18n +1+C 1n +18n +…+C n -1n +182,该式每一项都含因式82,故能被64整除. 12.解:方法一:(1+x +x 2)8=[1+(x +x 2)]8, 所以T r +1=C r8·(x +x 2)r ,则x 5的系数由(x +x 2)r 来决定,T′k +1=C k r ·x r -k ·x 2k =C k r xr +k , 令r +k =5,由r ≥k ,解得⎩⎪⎨⎪⎧ r =5k =0或⎩⎪⎨⎪⎧ r =4k =1或⎩⎪⎨⎪⎧r =3k =2,∴含x 5的项的系数为C 58·C 05+C 48·C 14+C 38·C 23=504.方法二:(1+x +x 2)8=[(1+x )+x 2]8=C 08(1+x )8+C 18·(1+x )7·x 2+C 28·(1+x )6·(x 2)2+C 38·(1+x )5·(x 2)3+…+C 78(1+x )(x 2)7+C 88(x 2)8,则展开式中含x 5的项的系数为C 08·C 58+C 18·C 37+C 28·C 16=504.方法三:(1+x +x 2)8=(1+x +x 2)(1+x +x 2)…(1+x +x 2)(共8个),这8个因式的乘积的展开式中形成x 5的来源有三种.(1)有2个括号各出1个x 2,其余6个括号恰有1个括号出1个x ,这种方式共有C 28·C 16种; (2)有1个括号出1个x 2,其余7个括号中恰有3个括号出1个x ,共有C 18·C 37种; (3)没有1个括号出x 2,恰有5个括号各给出1个x ,共有C 58种;∴x 5的系数为:C 28·C 16+C 18·C 37+C 58=504.。
新课标高中数学人教版选修2-3精品课件-【数学】1.3.1《二项式定理习题课》课件(新人教A版选修2-3)
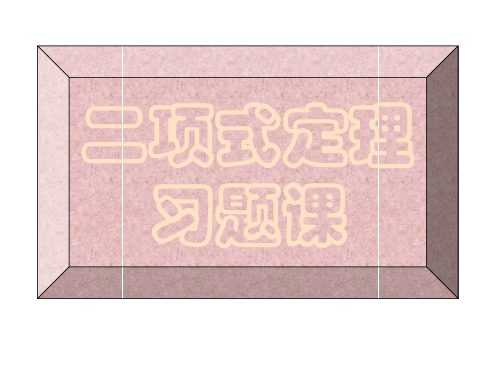
(3)Cn1 2Cn2 3Cn3 ... nCnn
(4)Cn0
1 2
Cn1
1 3
Cn2
...
1 n
1
Cnn
6、(1-2x)6 a0 a1x a2 x2 a3x3 ... a6x6, 则 a0 a1 a2 ... a6 的值为( ) A.1 B.64 C.243 D.729
⑷“第一盒中恰有三球”的概率。
P A
24 34
16 81
PB
C41 23 34
32 81
PC
C42 22 34
24 81
P
D
C43 34
2
8 81
如何产生[a,b]区间上均匀随机数呢?
利用计算器或计算机产生[0,1]上的均匀随机数
x=RAND,然后利用伸缩和变换,x x1 *(b a) a
7、若(2x 3)4 a0 a1x a2x2 a3x3 a4x4 , 则(a0 +a2 +a4 )2 (a1 a3 )2的值为( ) A.1 B.-1 C.0 D.2
8、(2x3
+
1 x2
)n
(n
N
* )的展开式中,若存在
常数项,则n的最小值是( )
A.3 B.5 C.8 D.10
i=1
s=0
s=0
i<=100? 否 输出s
结束
i=i+1
是
s=s+i
WHILE i<=100 s=s+i i=i+1
课件2:1.3 二项式定理(习题课)

则 10-2r=3k,即 r=5-23k, ∵r∈Z,∴k 应为偶数.∴k 可取 2,0,-2,即 r 可取 2,5,8. 所以第 3 项,第 6 项与第 9 项为有理项,它们分别为
C210(-21)2x2,C510(-21)5,C180(-12)8x-2.
[变式 1] (1)(1+3 x)6(1+ 1 )10 的展开式中的常数项为( D )
解 由题(2x-3y)10=C010(2x)10(-3y)0+C110(2x)9(-3y)+…+C1100(2x)0(-3y)10. (1)二项式系数和为 C010+C110+…+C1100=210. (2)在二项式展开式子中,令 x=y=1,得各项系数和为(2-3)10=1. (3)奇数项的二项式系数和为 C100+C210+…+C1100=29,偶数项的二项式 系数和为 C110+C130+…+C910=29.
变式 3 (2014·琼海一模)已知(3 x+x2)2n 的展开式的二项式系数和比(3x-1)n 的展开式的二项式系数和大 992,求(2x-1x)2n 的展开式中: (1)二项式系数最大的项; (2)系数的绝对值最大的项.
解:由题意知,22n-2n=992,即(2n-32)(2n+31)=0,∴2n=32,解得 n=5. (1)由二项式系数的性质知,(2x-1x)10 的展开式中第 6 项的二项式系数最大.即 C510=252. ∴T6=C510(2x)5(-1x)5=-8064.
(4)(2x-3y)10=a0x10+a1x9y+a2x8y2+…+a10y10, 令 x=1,y=1,得 1=a0+a1+a2+…+a10. ① 当 x=1,y=-1,得 510=a0-a1+a2-…+a10. ② ①+②得 2(a0+a2+a4+…+a10)=510+1, ∴奇数项系数和为5102+1. ①-②得 2(a1+a3+…+a9)=1-510. ∴偶数项系数和为1-2510.
高中数学2-3第一章1.3.1《二项式定理》【练习】(教师版)

1。
3。
1 二项式定理一、选择题1.在(x-错误!)10的展开式中,x6的系数是( )A.-27C错误!B.27C错误!C.-9C错误!D.9C错误!【答案】D【解析】∵T r+1=C错误!x10-r(-错误!)r。
令10-r =6,解得r=4。
∴系数为(-错误!)4C错误!=9C错误!.2.在错误!n(n∈N*)的展开式中,若存在常数项,则n的最小值是( )A.3 B.5 C.8D.10【答案】B【解析】T r+1=C错误!(2x3)n-r错误!r=2n-r·C错误! x3n-5r。
令3n-5r=0,∵0≤r≤n,r、n∈Z。
∴n的最小值为5。
3.在错误!n的展开式中,常数项为15,则n的一个值可以是( )A .3B .4C .5D .6来源:学*科*网]【答案】 D【解析】 通项T r +1=C r ,10(x 2)n -r (-1x)r =(-1)r C 错误!x 2n -3r ,常数项是15,则2n =3r ,且C 错误!=15,验证n =6时,r =4合题意,故选D 。
4.(x +错误!)5(x ∈R )展开式中x 3的系数为10,则实数a 等于( )[来源:学科网ZXXK]A .-1 B.错误! C .1 D .2【答案】 D【解析】 C 错误!·x r (错误!)5-r =C 错误!·a 5-r x 2r -5,令2r -5=3,∴r =4,由C 45·a =10,得a =2。
5.若(1+2x )6的展开式中的第2项大于它的相邻两项,则x 的取值范围是( )A.错误!<x <错误!B.错误!<x <错误! C 。
错误!<x <错误! D.错误!<x <错误!【答案】 A【解析】由错误!得错误!∴错误!<x<错误!。
6.在错误!20的展开式中,系数是有理数的项共有( )A.4项B.5项C.6项D.7项【答案】A【解析】T r+1=C错误!(错误!x)20-r错误!r=错误! r·(错误!)20-r C错误!·x20-r,∵系数为有理数,∴(2)r与2错误!均为有理数,∴r能被2整除,且20-r能被3整除,故r为偶数,20-r是3的倍数,0≤r≤20.∴r=2,8,14,20.二、填空题7.若错误!6的二项展开式中x3的系数为错误!,则a=________(用数字作答).【答案】2【解析】C错误!(x2)3·错误!3=错误!x3=错误!x3,∴a =2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1.3.1 二项式定理习题课(三) 学习目标
1. 进一步熟悉二项式定理及其二项式系数的性质;
2. 熟练掌握二项式系数各项和的推导方法;
3.会把二项式定理推广到两个以上二项式展开式的情况. 重点难点
学习重点:进一步熟悉二项式定理及其二项式系数的性质;
学习难点:.会把二项式定理推广到两个以上二项式展开式的情况 教学过程: ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ______________________________________________________________________________ 知识链接
复习1:⑴ n b a )(+= 展开式中r n C 叫做第 项的 系数,
通项公式是 ,展开式中共有 项.
⑵ 二项式系数的三个性质:
对称性是指
增减性:当r 满足 时,r n C 是增函数;
最值:当n 是偶数时,展开式中间项是第 项,它的二项式系数有最 值
为 ;当n 是奇数时,展开式中间项是第 项,它的二项式系数有
最 值为 ;
复习2:求91()x x -
的展开式中3x 的系数及它的二项式系数,并求展开式中二项式系数最大的项和系数最大的项.
合作探究:整除性问题,余数问题
问题:2008101除以100的余数是多少?
新知:整除性问题,余数问题,主要根据二项式定理的特点,进行添项或减项,凑成能整除
的结构,展开后观察前几项或后几项,再分析整除性或余数。
这是解此类问题的最常用技巧,余数要为正整数.
试试: 20098除以7的余数是 ;996除以7的余数是 。
典型例题
例1 用二项式定理证明:()11-+n
n 能被2n 整除.
变式:证明10099能被1000整除.
例2 求
()()56121-+x x 展开式中6x 系数.
变式:求()()4
53121x x +-展开式中按x 的升幂排列的第3项.
例3
()100323+x 展开式是关于x 的多项式,问展开式中共有多少个有理项?
变式:已知
n
-的展开式中,前三项系数的绝对值依次成等差数列, (1)证明展开式中没有常数项;(2)求展开式中所有的有理项
学习小结
1. 利用二项式定理解决有关余数以及整除问题;
2. 掌握二项式定理在两项以上项展开式中的应用,并会求有理项问题.
应用转化
1. ()n
x 21-展开式中各项系数的和是 2. 今天是星期三,再过20098是星期 3. 10211⎪⎭⎫ ⎝⎛-x 展开式的5x 系数是
4. 已知()()2611-+ax x 展开式中3x 系数是56,则实数a 的值为
5. 812221221=+⋅⋅⋅+++n n n n n C C C ,则n n n n C C C +⋅⋅⋅++21= .
6.求42)43(-+x x 的展开式中x 的系数.
7.(05湖南).()()()()6
321111x x x x ++⋅⋅⋅++++++展开式中2x 的系数
课后作业 1. 求()()10
211x x x -++展开式中的4x 的系数.
2. 用二项式定理证明95555+能被8整除.
课后反思:。
