概统2-1
2-1 M 基础统计

利用MINITAB计算基础统计量
利用MINITAB,计算中心倾向及分散性倾向的指标 (文件名称 : Statistics_Normal.MTW ) Stat > Basic Statistics > Graphical Summary
Confidence Level (置信区间) 一般设定为 95%
30
40
50
60
70
( xi x )
xi
x
样本标准差是分散的平方根。 样本标准偏差: s
Proprietary to Samsung Electronics Company
2 x x i i 1
n
(n 1)
Rev 7.0
基础统计- 13
分散性倾向的指标
- 范围(Range)
平方的理由
如果,从 xi 点开始到
x
点为止的均值为 ( xi x )2 的话,
分散即为平均平方值(统计上要求子集并非 n,而用 n-1来定义) 样本方差 : s 2 xi x (n 1)
2 i 1 n
● ● ● ● ● ● ● ● ● ● ●●● ● ● ● ●●● ●●●
那么,你是 第一次碰到 这种热天 啦。。。
听说今年的38度是 19年以来第一次。。
决定某些对策时,起到基本信息的作用。
比起1980年,
人均电消耗量
已经增加了3倍
是吗? 看来得多建几 个 发电厂啊!
什么叫统计呢? 把事实(情况)用一些数据表示。
Proprietary to Samsung Electronics Company
数据中最大值与最小值之差,用R表示
R = 最大值 – 最小值
概率论2-1-优质课件

(2)除了初等数学的方法,还要引入高等数学 的方法来研究随机试验。
例1 一报童卖报,每份0.15元,其成本为0.10元. 报馆每天给报童1000份报,并规定他不得把卖不
出的报纸退回. 设X为报童每天卖出的报纸份数,
X1
pk 95
100
0
5 100
2பைடு நூலகம்二项分布
在贝努利试验中,事件A在n次试验中恰好出现k 次的概率:
Pn (k) Cnk pk (1 p)nk , 0 k n. 其中:p P(A), 1 p P(A).
设X为事件A在n次试验中出现的次数,则:
P{ X
k}
C
k n
pk (1
例3 有一繁忙的汽车站, 每天有大量汽车通过, 设每辆汽车,在一天的某段时间内出事故的概率 为0.0001,在每天的该段时间内有1000 辆汽车通 过,问出事故的次数不小于2的概率是多少?
解
设1000 辆车通过,
出事故的次数为 X , 则
X ~ B(1000, 0.0001),
实例1 抛掷骰子,观察出现的点数. 则有
S={1,2,3,4,5,6} 样本点本身就是数量 X (e) e 恒等变换
X (1) 1, X (2) 2, X (3) 3, X (4) 4, X (5) 5, X (6) 6,
且有
P{ X i} 1 , (i 1,2,3,4,5,6). 6
二、随机变量的概念
1.定义 根据随机试验的结果而确定取某一个数
值的变量,称为一维随机变量。
由两个一维随机变量所确定的有序数组, 称为二维随机变量。
概率2-1

二、几种常见的离散型随机变量 1.(0-1)分布 1.(0-1)分布 (0
如果随机变量X只能取0,1两个值,其分布律为 如果随机变量 只能取0,1两个值,其分布律为 只能取0,1两个值 P{X =1}=p, P{X =0}=1(0<p<1) <1), P{ =1}= , P{ =0}=1- p (0< <1), X 即: pk 1-p p 0 1
分 类
取有限个或可数个值) 离散型随机变量(取有限个或可数个值) ,它与 随机变量是定义在样本空间上的实值集函数, 随机变量是定义在样本空间上的实值集函数
的概念在概率论与数理统计中既是基本的, 随机变量的概念在概率论与数理统计中既是基本的 , 普通的实函数有本质的区别.一方面它的取值是随机的, 普通的实函数有本质的区别.一方面它的取值是随机的, -----连续型随机变量 连续型随机变量. 非离散型的随机变量 -----连续型随机变量. , 又是非常重要的.后面将会看到,由于引入了随机变量, 又是非常重要的.后面将会看到,由于引入了随机变量 而它取每一个可能值都有一定的概率;另一方面, 而它取每一个可能值都有一定的概率;另一方面,它的 高等数学的方法就可用来研究随机现象了. 高等数学的方法就可用来研究随机现象了. 的方法就可用来研究随机现象了 定义域是样本空间S 不一定是实数集. 定义域是样本空间S,而S不一定是实数集. e S X(e) R
设有20台机床,独立地各加工一件齿轮, 20台机床 例3 设有20台机床,独立地各加工一件齿轮,若各机床加 工的废品率都是0.2 0.2, 20件齿轮产品中的废品数的分布律 件齿轮产品中的废品数的分布律? 工的废品率都是0.2,求20件齿轮产品中的废品数的分布律? 本题可看作是20 20次重复独立试验 解 本题可看作是20次重复独立试验 表示20件齿轮产品中的废品个数, 设X表示20件齿轮产品中的废品个数,则X~b(20, 0.2) 表示20件齿轮产品中的废品个数 ~ (20, 故
概论论与数理统计 第2章_PPT课件

1 2
分别表示两事件
发生的概率.
一般地,对任意实数集 I ,随机变量 X 在 I 上取值常写成 {X I} ,
它表示事件 {e | X (e) I} ,此时有
P{X I} P{e | X (e) I} .
§2.2 离散型随机变量及其分布
定 义 2.3 设 离 散 型 随 机 变 量 X 所 有 可 能 取 值 为 xi (i 1, 2, ) ,则称 X 取 xi 的概率
X ~ P() . 显然有下式成立:
(1) P{X k} 0 ( k 0,1, 2, );
(2) P{X k 0
k}
e
k 0
k
k!
e k
k0 k !
e
e
1.
定理 2.1(泊松定理)对二项分布 b(n, p) ,设 np , 0 ,
则
lim
n
Ckn
pk
(1
p)nk
k e (k
系.设一个随机试验只有两个结果 A 和 A ,且 P(A) p ,
现将试验独立进行 n 次,记 X 为 n 次试验中 A 出现的次
数,则 X ~ b(n, p) ,记 Xi 为第 i 次试验中 A 出现的次数,
1, 第i次试验中A 出现即Xi Nhomakorabea0,
第i次试验中A
不出现
,i
1, 2,
, n ,则 Xi ~ b(1, p) ,
对应数.这样随机试验的结果就是随机变化的变量,把随机试
验的结果数量化,便于应用数学知识研究随机现象,使对随机
现象的研究更深入和简单.
▪
例2.1 抛掷一枚硬币两次,观察出现正面(记为 H )
和反面 (记为T )的情况.
概统知识点

概统知识点概统(概率和统计学)是一门关于随机现象的数学分支,主要研究随机变量、概率分布、统计推断等内容。
它在各个领域中都起到了重要的作用,例如在科学研究、金融分析、医学统计等方面。
本文将以“概统知识点”为标题,分步骤介绍一些概率和统计学的基础知识点。
1. 随机变量随机变量是概统中的重要概念。
它可以看作是对可能的结果进行数值化的方式。
随机变量可以分为离散型和连续型两种。
离散型随机变量的取值是有限个或可数个,例如扔一枚硬币的结果可以是正面或反面。
而连续型随机变量的取值可以是任意的实数,例如人的身高。
2. 概率分布概率分布描述了随机变量的取值以及每个取值的概率。
常见的概率分布包括离散型的二项分布、泊松分布以及连续型的正态分布等。
其中,二项分布用于描述有两种可能结果的试验,泊松分布用于描述单位时间或单位空间内某一事件发生的次数,正态分布在自然界中广泛出现。
3. 统计推断统计推断是根据样本数据对总体进行推断的过程。
它包括估计和假设检验两个主要步骤。
估计是利用样本数据来估计总体参数的值,例如利用样本平均值来估计总体均值。
假设检验是对总体参数进行假设的检验,例如判断某一总体均值是否等于某个特定值。
4. 相关和回归分析相关分析用于研究两个变量之间的关系,回归分析则是用一个变量来预测另一个变量。
相关系数可以用来衡量两个变量之间的相关程度,其取值范围从-1到1。
回归分析可以通过找到最佳拟合线来建立变量之间的函数关系。
5. 抽样与抽样分布抽样是从总体中获取样本的过程。
在统计学中,通过对样本数据进行分析来得到总体的统计特征。
抽样分布是指统计量在多次抽样中的分布情况。
中心极限定理是抽样分布的重要结果,它表明对于足够大的样本,样本均值的分布会接近正态分布。
6. 参数估计与假设检验参数估计是利用样本数据推断总体参数的过程。
点估计是用单个值来估计总体参数,例如样本均值。
区间估计是利用一个区间来估计总体参数,例如置信区间。
假设检验是对总体参数的某个假设进行检验,例如判断两个总体均值是否相等。
概率统计2-1

5
随机变量的分类
按随机变量的取值情况,可将其分为两类:
(1) 离散型随机变量:取值为有限个或无限可 列个值。 (2) 非离散型随机变量:所有可能取值不能一 一列举出来
而非离散型随机变量中最常用的为连续型随机
变量(它的值域是一个或若干个区间)。 今后我们主要研究离散型和连续型随机变量。
xn pn
… …
一般所说的离散性随机变量的分布就是指它 的概率函数或概率分布表.
对于集合{xn , n=1,2,…}中的任何一个子集A,事 件“X在A中取值”即“XA”的概率为
P{ X A}
xn A
p
n
介绍几个分布之两点分布(2)
8
两点分布
两点分布: 只有两个可能取值的随机变量X所服 从的分布, 称为两点分布。其概率函数为: P(X=xk)=pk (k=1,2)。亦称X服从两点分布。 概率分布表为:
概率密度函数的性质(3)
21
概率密度函数的两个性质
连续型的概率非负性和概率完备性表现为
(1)非负性 :f(x) 0,(- <x< +); (2)归一性: f(x)
-
f ( x )dx=1.
-
f ( x )dx 1
P ( a X b ) f ( x )dx
举例(1)
4
一些随机变量的例子
(1) 一个射手对目标进行射击, 击中目标记为1分,
未中目标记为0分. 如果用X表示射手在一次射击 中的得分, 则它是一个随机变量, 可以取0和1两个 可能的值. (2) 某段时间内候车室的旅客数目记为X, 它是一 个随机变量, 可以取0及一切不大于M的自然数, M为候车室的最大容量. (3) 单位面积上某农作物的产量X是一个随机变 量, 它可以取一个区间内的一切实数值, 即 x[0,T], T是一个常数.
高中数学选修2-1第一章复习课件

或
简单的逻辑联结词
并集
交集 补集 全称量词 存在量词 运算
且 非或
全称量词与存在量词
量词
含有一个量词的否定
一、命题:
可以判断真假的语句叫命题;
一个符号
二、 四 种 命 题
条件P的否定,记作“P”。读作“非 P”。
原命题: 若p 则q 逆命题: 若q 则p
否命题:若 p 则 q
逆否命题:若 q 则 p
特称命题的否定是全称命题.
题型一:命题
例 1. 写出由下述各命题构成的“p 或 q”, “p 且 q ” , “非 p”形式的复合命题,并指出复合命题的真假。 (1)p:9 是 144 的约数,q:9 是 225 的约数。 (2)p:方程 x2-1=0 的解是 x=1, q:方程 x2-1=0 的解是 x=-1; (3)p:实数的平方是正数,q:实数的平方是 0.
“p 或 q”形式复合命题的真假可以用 下表表示: p 真 真 假 假 q 真 假 真 假 p或q 真 真 真 假
短语”对所有的””对任意一 个”在逻辑中通常叫做全称量词, ”表示.含有全称 并用符号 “ 量词的命题,叫做全称命题. ,
常见的全称量词还有: “对所有的”,”对任意一个”,”对一 切”,”对每一个”,”任给”,”所有的” 等.
命题及其关系简单的逻辑联结词全称量词与存在量词四种命题充分条件与必要条件量词全称量词存在量词含有一个量词的否定运算除地下室外的相邻两个防火分区当防火墙上有防火门连通且两个防火分区建筑面积之和不超过规范规定的一个防火分区面积的14倍可设一个安全出口
知识网络
四种命题
命题及其关系
充分条件与必要条件
用常 语用 逻 辑
x 1 (4)设集合 A={x| < 0} , x 1
1.2-1概率论

P ( A) P (ei1 ei 2 ... eik ) P (eij ) k / n
j 1
k
A中包含的基本事件数 S中基本事件的总数
从 n 个不同的元素中, 任取 k ( n ) 个元素, 按 照一定的顺序排成一列,全部排列个数为
k An
n ! n(n 1) (n k 1) (n k )!
基本概念
1o 随机试验E的所有可能结果组成的集合称 为样本空间,记为 S. 2o 样本空间的元素 ,即试验E 的每一个结果, 称 为样本点.
3o 随机试验 E 的样本空间 S 的子集称为 E
的随机事件, 简称事件.
重要的随机事件
基本事件 必然事件 由一个样本点组成的单点集. 随机试验中必然会出现的结果.
当 k n 时,称为全排列,计算公式为 n 取数与次序有关 An n! 从 n 个不同的元素中, 任取 k ( n ) 个元素并成 一组 ,全部组合数为
k A n n! k Cn k Ak k !(n k )! n(n 1) (n k 1) k!
取数与次序无关
50 设 A 是 A 的对立事件, 则 P ( A) 1 P ( A).
60 (加法公式) 对于任意两事件 A, B 有 P ( A B ) P ( A) P ( B ) P ( AB ).
n 个事件和的情况
P ( A1 A2 An ) P ( Ai )
S
(2) A等于B 若事件 A 包含事件 B , 而且事件 B 包含事件
A, 则称事件 A 与事件 B 相等,记作 A=B. (3) 事件A与B的并(和事件)
事件 A B { x x A或x B}称为事件 A与 事件B的和事件.
概率统计二级结论-概述说明以及解释

概率统计二级结论-概述说明以及解释1.引言1.1 概述概述部分的内容可以从以下角度进行展开:概率统计是一门研究随机现象规律的学科,它是数学的一个重要分支,也是现代科学领域中不可或缺的一部分。
其主要研究对象为随机事件的出现规律和概率分布以及基于概率的推断和决策方法。
通过统计概率,我们可以揭示自然界和社会现象中的客观规律,并为科学研究提供重要的工具和方法。
概率统计的发展可以追溯到17世纪,伽利略和费马等伟大科学家对概率问题进行了初步研究,随后由拉普拉斯、贝叶斯等人的贡献,使概率统计学逐渐形成独立的理论体系,并在各个学科领域中得到广泛应用。
概率统计通过建立数学模型来描述和分析随机现象,通过收集样本数据进行推断和预测,从而对不确定性进行量化和控制。
在概率统计的研究中,我们普遍使用统计模型、概率分布和统计方法等工具来分析和解决实际问题。
通过对概率统计的学习和应用,我们可以了解和理解事件发生的可能性,并通过样本数据的收集和分析,得出结论并做出决策。
概率统计的应用广泛涉及自然科学、社会科学、工程技术等众多领域,如风险管理、市场调查、质量控制等。
本文主要围绕概率统计的二级结论展开,通过引言给读者提供一个全面而清晰的概述,介绍概率统计的基本概念、历史发展以及应用领域,为读者提供一个全面理解概率统计的基础。
接下来的章节将分析和总结概率统计的关键要点,并给出相应的结论,以进一步巩固读者对概率统计的理解和应用能力。
通过本文的阅读,我们将能够更深入地了解概率统计的核心观点和方法,为我们在实际问题中的决策和推断提供一种科学且可靠的工具。
最后,本文还将总结概率统计的核心要点,并展望它在未来的发展前景。
1.2文章结构文章结构是指文章的组织和安排方式,它是整篇文章的骨架和框架,决定了文章内容的展开和发展。
良好的文章结构能够使读者更好地理解作者的观点和思路。
本文的结构包括引言、正文和结论三个部分。
引言部分主要是对文章主题进行概述,从宏观角度对读者进行引导和导入,使其了解文章的目的和意义。
2-1概率论

k 0,1,...,6
(2) P{ X 5} P{ X 5} P{ X 6}
13 1 2 1 C 3 3 3 729
(3)各次试验相互独立; (4)试验共进行了n次.
例:有放回抽取产品50次,已知每次抽到正品 的概率为0.8, X表示抽取到正品的件数. 求抽取到20件正品的概率?
在n重伯努利试验中,以X表示事件A发生的次数, 则称随机变量X服从参数为n , p的二项分布. 记作X ~ b(n, p).分布律为
P{X k} C p (1 p)
1.(0-1)分布:若随机试验的结果只有两个,X=1
表示一个结果,X=0表示另一个结果,则X服从(01)分布,分布律为:
X pk
0 1 p
1 p
其中0< p <1.
或
P{ X k } pk (1 p)1 k (k 0, 1)
说明: (0-1)分布是最简单的一种分布,任何一 个只有两种可能结果的随机现象,都可用(0-1)分 布来描述.比如新生婴儿是男还是女、产品是正 品还是次品、明天是否下雨、种籽是否发芽等.
因此 P { X 2} 1 P { X 0} P { X 1}
1 (0.98)400 400(0.02)(0.98)399 0.9972.
这个结果很接近于1,在实际中具有两方面的意义: (1)一个事件尽管在一次试验中发生的概率 很小,但当试验次数很多且独立进行时,那么这一 事件的发生是肯定的,所以不能轻视小概率事件. (2)小概率事件在一次试验中几乎是不可能 发生的(通常称为实际推断原理或小概率事件). 定理1(泊松定理) 设 pn
数学选修2-1知识点总结

数学选修2-1知识点总结第一章:命题与逻辑构造知识点:1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.真命题:判断为真的语句.假命题:判断为假的语句.2、“假设p ,那么q 〞形式的命题中的p 称为命题的条件,q 称为命题的结论.3、对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题.其中一个命题称为原命题,另一个称为原命题的逆命题。
假设原命题为“假设p ,那么q 〞,它的逆命题为“假设q ,那么p 〞.4、对于两个命题,如果一个命题的条件和结论恰好是另一个命题的条件的否认和结论的否认,那么这两个命题称为互否命题.中一个命题称为原命题,另一个称为原命题的否命题.假设原命题为“假设p ,那么q 〞,那么它的否命题为“假设p ⌝,那么q ⌝〞.5、对于两个命题,如果一个命题的条件和结论恰好是另一个命题的结论的否认和条件的否认,那么这两个命题称为互为逆否命题。
其中一个命题称为原命题,另一个称为原命题的逆否命题。
假设原命题为“假设p ,那么q 〞,那么它的否命题为“假设q ⌝,那么p ⌝〞。
6、四种命题的真假性: 原命题 逆命题 否命题 逆否命题真 真 真 真 真 假 假 真 假 真 真 假 假假假假()1两个命题互为逆否命题,它们有一样的真假性;()2两个命题为互逆命题或互否命题,它们的真假性没有关系.7、假设p q ⇒,那么p 是q 的充分条件,q 是p 的必要条件.假设p q ⇔,那么p 是q 的充要条件〔充分必要条件〕.8、用联结词“且〞把命题p 和命题q 联结起来,得到一个新命题,记作p q ∧. 当p 、q 都是真命题时,p q ∧是真命题;当p 、q 两个命题中有一个命题是假命题时,p q ∧是假命题.用联结词“或〞把命题p 和命题q 联结起来,得到一个新命题,记作p q ∨.当p 、q 两个命题中有一个命题是真命题时,p q ∨是真命题;当p 、q 两个命题都是假命题时,p q ∨是假命题.对一个命题p 全盘否认,得到一个新命题,记作p ⌝.假设p 是真命题,那么p ⌝必是假命题;假设p是假命题,那么p ⌝必是真命题.9、短语“对所有的〞、“对任意一个〞在逻辑中通常称为全称量词,用“∀〞表示.含有全称量词的命题称为全称命题. 全称命题“对M 中任意一个x ,有()p x 成立〞,记作“x ∀∈M ,()p x 〞.短语“存在一个〞、“至少有一个〞在逻辑中通常称为存在量词,用“∃〞表示.含有存在量词的命题称为特称命题.特称命题“存在M 中的一个x ,使()p x 成立〞,记作“x ∃∈M ,()p x 〞.10、全称命题p :x ∀∈M ,()p x ,它的否认p ⌝:x ∃∈M ,()p x ⌝。
新概念2 L12

Text
He will be in his small boat, Topsail.
be+副词构成的表语 动词be如与不同的副词连用意义不同,意思 主要由副词的意义决定 be in 在家 be back 回来 be out 出去 be away 离开 be on 上映 be over 结束 be up to胜任
1.你打算什么时候起程? When are you going to set out on your trip?
2.他们两周前便动身去北京了
They set out/off for Beijing two weeks ago.
3.船长动身去参加一场重要的比赛。
The captain set out to take part in an important race.
Summary writing
We shall meet our neighbor, Captain Charles Alison,at Portsmouth Harbor early tomorrow morning.He will be in his small boat,Topsail.He will leave at eight o’clock.We shall say goodbye to him.He will take part in an important race across the Atlantic.
Captain Alison will set out at eight o’clock.
1.to leave a place and begin a journey 2.To begin a job, task, etc. with a particular aim or goal =set out /start out/ start off/ leave
经济数学基础第三册《概率统计》一、二、三章知识点总结

第一章 随机事件与概率1、事件间的关系与运算关系:事件的包含与相等;事件的和(并);事件的积(交);事件的差; 互不相容事件(互斥);对立事件(逆事件);完备事件组。
运算: BAAB A B B A == )交换律(1)()()2(C B A C B A C B A C B A ==)()结合律())(()()()()分配律(C A B A BC A BC AC C B A ==)3(BA B A C B A ABC CB AC B A B A AB ==== )对偶律(42、概率的性质10=Ω=Φ)()(①P P ∑=∑==ni i ni i n A P A P A A A 1121,,,)()(为互不相容事件:② )()()(有,为两个互不相容事件与特别的:B P A P B A P B A +=+121=∑ii n A P A A A )(,则有构成一个完备事件组,,,,③ )()(率有特别的:对立事件的概A P A P -=1)()()(有,如果④B P A P B A P B A -=-⊃)()()()(有,与对于任意两个事件⑤AB P B P A P B A P B A -+=+()1()()(2111111nn nk j i k j i ni nj i j i i ni i A A A P A A A P A A P A P A P-≤<<≤=≤<≤=-+∑-+∑∑-=∑)()(件的情形推广:对任意有限个事3、古典概型⎩⎨⎧等可能性有限性试验的基本事件总数的基本事件数有利于A n m A P ==)(4、条件概率)()()(A P AB P A B P =乘法公式)()()()()()()()()(AB C P A B P A P ABC P B A P B P A B P A P AB P ===5、独立事件 )()()(B P A P AB p =)()()()(B P A B P A P B A P ==或或6、全概率公式有则对任一事件构成完备事件组,,,2,1,0)(,,,,21B n i A P A A A i n =>)()()()()()()()()(22111n n ni i i A B P A P A B P A P A B P A P A B P A P B P +++=∑== 7、贝叶斯公式 有若则对任一事件构成完备事件组,0)(,,,2,1,0)(,,,,21>=>B P B n i A P A A A i n nm A BP A P A B P A P B A P ni i im m m,,2,1)()()()()(1==∑=1.概率分布(X 的所有取值及其相应概率),2,1}{,===i p x X P i i 1x X 2x 3x … nx … P1p 2p 3p …np …分布律2、分布函数 F(x) =P(X ≤x)∑=≤=≤xi x ip x X P x F )()(3、随机变量函数 Y=g(X) 的概率分布(1)写出函数的对应取值(2)抄写相应的概率(相同函数值的要合并,对应概率相加) ∑=iii p x EX 22)(EX EX DX -=?2=EX ∑==ii i p x g EY X g Y })()({∑=iii p x EX 221、概率密度: ),(,)(+∞-∞∈x xf ⎰=<<ba dxx f b X a P )()(})(,)()({)(3的值域)是的反函数,(是为零。
概论与统计ch1-2-1随机事件的概率

件 关 系
事件A与事件B相等
(
事件A与B至少有一个发生 (和,并) 事件A与事件B同时发生 (积,交)
文 氏 图
事件A的对立事件
(逆) )
事件A发生而B不发生
(差)
事件A与B互不相容
(互斥)
样本空间的划分 (完备事件组)
若 1 Ai Aj ,i j,i, j 1,2, ,n
n
小测验 Tests
向指定目标射击三枪,分别用 A1、A2、A3 表示第一、第二、第三枪击中目标,试用它们 表示以下事件:
(1)只有第一枪击中; (2)至少有一枪击中; (3)至少有两枪击中; (4)三枪都未击中
Great minds think alike.
——英雄所见略同
答案
解 设 Ai 表示第 i 枪击中目标
第一章 随机事件及其概率
Chapter 1 Random Events and Probability
§ 1.2 随机事件的概率
Probability of Random Events
教学要求 1.理解概率的四 种定义
Requests
2.掌握概率的基本性质 3.会计算古典型、几何型概率
主要内容
Contents
在古典概型的随机试验中,
P( A) 1 P( A)
(√ )
AA , A A
例1 (掷硬币问题)
把一枚质地均匀的硬币连掷两次,设事件 A={出现两个反面}, B={出现两个面相同}
求 P( A),P(B)
A (BC) (A B)(A C)
A(B C) AB AC
4.对偶律: A B A B, AB A B
第一章 随机事件及其概率
Chapter 1 Random Events and Probability
概论第二章课件

解 (1) 设 需要配备 N 个维修工人,设 X 为90 台
设备中发生故障的台数,则 X ~ B( 90, 0.01)
90
P( X N ) C9k0 (0.01)k (0.99)Nk
k N 1
令 90 0.01 0.9
2.3 随机变量的分布函数
一、分布函数的概念.
定义 设X是随机变量,对任意实数x,事件{Xx}的 概率P{Xx}称为随机变量X的分布函数。 记为F(x),即
F(x)=P {Xx}. 易知,对任意实数a, b (a<b),
P {a<Xb}=P{Xb}-P{Xa}= F(b)-F(a).
二、分布函数的性质 1、单调不减性:若x1<x2, 则F(x1)F(x2); 2、归一 性:对任意实数x,0F(x)1,且
事件{收到不少于1次呼叫} { X 1}
{没有收到呼叫} {X= 0}
可见,随机事件这个概念实际上是包 容在随机变量这个更广的概念内. 也可以 说,随机事件是从静态的观点来研究随机 现象,而随机变量则是一种动态的观点, 就象数学分析中常量与变量的区别那样.
随机变量概念的产生是概率论发展 史上的重大事件. 引入随机变量后,对 随机现象统计规律的研究,就由对事件 及事件概率的研究扩大为对随机变量及 其取值规律的研究.
一旦我们实际选定了一个 学生并量了他的身高之后, 我们就得到X的一个具体的 值,记作x.
这时,要么x≥1.7米,要么x <1.7米, 再去求P(x ≥1.7米)就没有什么意义了.
二、引入随机变量的意义 有了随机变量,随机试验中的各种事件, 就可以通过随机变量的关系式表达出来. 如:单位时间内某电话交换台收到的呼 叫次数用X表示,它是一个随机变量.
2-1概率论与数理统计
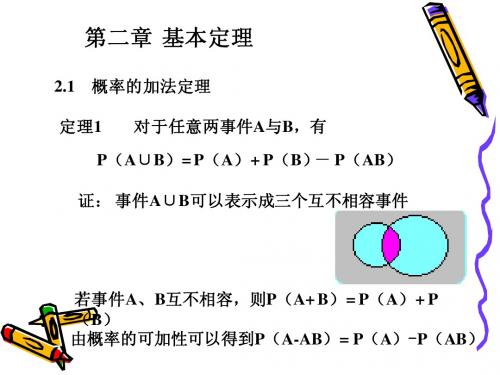
某商店经销的某种商品100 100件 经理声称其中只有5 例10 某商店经销的某种商品100件,经理声称其中只有5件带 有不影响使用效果的小缺陷,工商部门对这批商品进行抽检时, 有不影响使用效果的小缺陷,工商部门对这批商品进行抽检时, 采用有放回每次抽一件检查的重复抽样检查法, 采用有放回每次抽一件检查的重复抽样检查法,试问接连抽检 两件这种商品时“第一件查出带缺陷” 第二件查出带缺陷” 两件这种商品时“第一件查出带缺陷”与“第二件查出带缺陷” 这两个事件是否独立? 这两个事件是否独立?被抽检的这两件产品皆是有缺陷的商品 的概率是多少? 的概率是多少?
本例也可以直接由古典概型算出,大家自己动手算一下! 本例也可以直接由古典概型算出,大家自己动手算一下! 直接 概型算出 自己动手
2.2.3
定义2 定义
独立事件
对事件A、 , 对事件 、B,若P(AB)=P(A)P(B) ( ) ( ) ( ) 则称事件A与事件 是相互独立的,简称独立的。 则称事件 与事件B是相互独立的,简称独立的。 与事件
这是个小概率事件,若恰好遇到, 这是个小概率事件,若恰好遇到,则有理由怀疑经理 小概率事件 的谎报,可以采取更进一步的行动了。 的谎报,可以采取更进一步的行动了。
定义 1.5 如果 n(n≥2)个事件: A , A ,..., A 中任意两个事件均相互独立, 1 2 n 即对任意 1≤ i <
j ≤ n ,均有 P(AAj ) = P(Ai )P(Aj ) 则称这 n 个事件两两独立。 i
件是合格品, 件是次品, 例 1 一批产品 50 件,其中 45 件是合格品,5 件是次品,今从中抽取 件中至少有一件是次品的概率是多少? 3 件,求这 3 件中至少有一件是次品的概率是多少?
概论概要统计第二章节答案

第二章课后习题参考答案P56 10 有甲乙两种味道和颜色都极为相似的名酒各4杯。
如果从中挑4杯,能将甲种酒全部挑出来,算是试验成功一次。
(1)某人随机地去猜,问他试验成功一次的概率是多少?(2)某人声称他通过品尝能区分两种酒。
他连续试验10次,成功3次。
试推断他是猜对的,还是他确有区分的能力。
(各次试验是相互独立的)解 (1)某人随机去猜,从8杯中挑取4杯共有4870C =种取法,其中只有一种是正确的。
故若某人随机去猜,试验成功一次的概率是170p =(2)为判断某人是否有区分能力,先假设:“某人无区分能力”,由(1)他猜对一次的概率为1/70,连续试验10次,则猜对次数(10,1/70)Xb3741011{3}1 3.161037070P X -⎛⎫⎛⎫⎛⎫==-=⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭ 不仅如此10224001011{3}1{}11 3.24107070kkk k P X P X k k --==⎛⎫⎛⎫⎛⎫≥=-==--=⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭∑∑即试验10次,他猜对的次数大于等于3的概率也仅为万分之三。
今事件{3}X ≥ 竟然发生了,按实际推断原理,应否定原假设“某人无区分能力”,而认为他确有区分能力。
P57 16 有一繁忙的汽车站, 每天有大量汽车通过,设每辆汽车,在一天的某段时间内出事故的概率为0.0001,在每天的该段时间内有1000 辆汽车通过,问出事故的次数不小于2的概率是多少?解 设1000 辆车通过,出事故的次数为 X , 则~(1000,0.0001),X b 所求概率为1000999{2}1{0}{1}100010.99990.00010.99991P X P X P X ≥=-=-=⎛⎫=--⋅⋅ ⎪⎝⎭ 利用泊松定理,10000.00010.1,λ=⨯= 所以0.10.1e 0.1e {2}10.0047.0!1!P X --⋅≥≈--=X 的分布函数为0,0()1,011,1x F x p x x <⎧⎪=-≤<⎨⎪≥⎩()F x 的图像如下X 的分布函数为0,31,3410()4,45101,5x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩ P57 20、解(1)(2)(2)ln 2,(03)(3)(0)(3)(0)15555(2)()(2)()(2)ln2224X X X X X P X F P X P X P XF F P X P X P X F F <==<≤=≤-≤=-=<<=<-≤=-=(2)概率密度函数为1,1()()0,X Xx e f x F x x others⎧≤<⎪'==⎨⎪⎩ 27、某地区18岁女青年的血压服从2(110,12)N 分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P{a ≤ X ≤ b} = F (b) − F (a − 0), P{ X > a} = 1 − F (a )
x → x0 + 0
10
例5 若 P { X ≤ x2 } = 0.6, P { X > x1} = 0.6 , 且 x1 < x2 ,求
取值为2({ X
的样本点构成的子集为
A = {HHT , HTH , THH },
7
故 P{ X = 2} = P( A) = 3 / 8, 类似有
P{ X ≤ 1} = P{HTT , THT , TTH , TTT } = 4 / 8.
常见的两类随机变量
离散型
连续型
取值可数 收到的信息条数 骰子出现的点数
9
分布函数的性质 (1) 0 ≤ F ( x) ≤ 1 (2) F ( x) 为单增右连续的函数,即若 x1 < x2 ,则 为单增右连续的函数,
F ( x1 ) ≤ F ( x2 ), lim F ( x) = F ( x0 )
(3) lim F ( x) = 0, lim F ( x) = 1 , 分别记为F (−∞) = 0, F (+∞) = 1 x →−∞ x →+∞ (4) P{ X ≤ a} = F (a)
取值无穷多, 取值无穷多,不可一一 列举, 列举,充满某一区间 电视机的寿命 一地区男子的身高
8
二 分布函数 定义 称 F ( x) = P { X ≤ x} , x ∈ (−∞, +∞) 为 数(简记为d . f ),其中事件 简记为 ,
X
的分布函
{ X ≤ x} = {e X (e) ≤ x}
P { x1 < X ≤ x2 }
随机变量不是高等数学中的普通函数, 注 随机变量不是高等数学中的普通函数,而分 布函数则是高等数学中的普通函数, 布函数则是高等数学中的普通函数,因而可借用微 积分的方法来研究概率论. 积分的方法来研究概率论
11
► 例1 ► 例1 ► 例1 ► 例1
(1) { X ≥ 4} (2) {1000 ≤ X ≤ 2000} (3) {10 ≤ X ≤ 15} (4) { X ≥ 2}
5
特征
(1)随试验结果而变, (1)随试验结果而变,事先只知其取值 随试验结果而变 范围,而不知取何值. 范围,而不知取何值. (2)取值和每个确定范围内的取值有一 (2)取值和每个确定范围内的取值有一 定概率性. 定概率性.
掷一颗骰子, 例1 (1)设试验 E :掷一颗骰子, :骰子朝上之面的 ) 掷一颗骰子 X 骰子朝上之面的 点数, 为随机变量, 出现大点数” 点数,则 X 为随机变量,“出现大点数”可以表示为 (2)设试验 E :观察某网站某时间段内收到的信 ) 观察某网站某时间段内收到的信 X 信息条数 信息条数, 为随机变量.“ 息, :信息条数,则 X 为随机变量 “收到的信息条 数在1000-2000之间”可以表示为 之间” 数在 之间 观察炮弹落点, 射程( (3)设试验 E :观察炮弹落点, :射程(公里), ) 观察炮弹落点 X 射程 公里), 为随机变量. 射程在10-15公里之间”可以表 公里之间” 则 X 为随机变量 “射程在 公里之间 示为
从数值上看 F ( x) 表示随机变量 X 落入区间( −∞, x ] 的 概率. 概率 袋中有6个球 标号为-1,1,1,2,2,2 ,任取一球, 个球, 任取一球, 例3 袋中有 个球,标号为 X X 设随机变量 表示取到的球的标号,求 的分布函数. 表示取到的球的标号 求 的分布函数 随机投点, 落点刻度 落点刻度, 例4 向 [a, b] 随机投点, :落点刻度,求 的分布函数. 的分布函数
12
例3解 由分布函数 F ( x)的定义及古典概率可计算得 解
0 1 6 F ( x) = P { X ≤ x} = 3 6 1 , x < −1 , −1 ≤ x < 1 ,1 ≤ x < 2 ,x ≥ 2
13
例4解 由分布函数 F ( x)的定义及几何概率可计算得 解
= 0.6 − 1 + 0.6 = 0.2.
Ω = {HHH , HHT , HTH ,THH , HTT ,THT ,TTH ,TTT };
出
记每次试验出现正面 的总次数 为随机变量 , 则 作为样本空间 Ω 上的函数定义为
e X HHH 3 HHT 2 HTH 2
= 2})
THH 2
HTT 1
THT 1
TTH 1
TTT 0
易见, 易见 使
0 x − a F ( x) = b − a 1 ,x < a ,a ≤ x < b ,x ≥b
14
例5解 P { x1 < X ≤ x2 } = P { X ≤ x2 } − P { X ≤ x1} 解
= P { X ≤ x2 } − 1 − P { X > x1}
2
第二章
一维随机变量及其分布
随机变量及其分布函数 离散型随机变量 连续型随机变量 随机变量的函数及其分布
3
第一节
随机变量及其分布函数
随机变量 分布函数
4
一 随机变量
随机试验结果
e
数量化
随机变量
X = f (e)
Ω
随机变量
实值函数
定义 设随机试验 E 下样本空间为Ω = {e} ,若对任 为一个随机 意e ∈ Ω ,对应唯一个实数X (e) 元钱任买一张彩票, 奖金, (4)设试验 E :用2元钱任买一张彩票, :奖金,则 ) 用 元钱任买一张彩票 X 奖金 X 为随机变量 “不赔钱”可以表示为 为随机变量. 不赔钱” 在将一枚硬币抛掷三次, 例2 在将一枚硬币抛掷三次 观察正面 、反面 现情况的试验中, 现情况的试验中 其样本空间
