南通市初中数学四边形经典测试题
新初中数学四边形经典测试题附答案

新初中数学四边形经典测试题附答案一、选择题1.一个多边形的每一个外角都是72°,那么这个多边形的内角和为() A.540 °B. 720 °C. 900 °D. 1080 °【答案】 A【分析】【详解】解:∵多边形的每一个外角都是72°,∴多边形的边数为:3605 ,72∴该多边形的内角和为:(5-2)×180=540°°.应选 A.【点睛】外角和是 360°,除以一个外角度数即为多边形的边数.依据多边形的内角和公式可求得该多边形的内角和.2.如图,若的坐标为(A.(4,1)【答案】 B 【分析】【剖析】Y OABC的极点O,A,C的坐标分别为(0,0),(4,0),(1,3),则极点B)B.(5,3)C.(4,3)D.(5, 4)依据平行四边形的性质,以及点的平移性质,即可求出点B的坐标 .【详解】解:∵四边形 OABC是平行四边形,∴OC∥ AB, OA∥ BC,∴点 B 的纵坐标为 3,∵点 O 向右平移 1 个单位,向上平移 3 个单位获得点C,∴点 A 向右平移 1 个单位,向上平移 3 个单位获得点B,∴点 B 的坐标为:( 5, 3);应选: B.【点睛】本题考察了平行四边形的性质,点坐标平移的性质,解题的重点是娴熟掌握平行四边形的性质进行解题 .3.若菱形的对角线分别为6 和 8 ,则这个菱形的周长为()A .10B . 20C . 40D . 48【答案】 B【分析】【剖析】依据菱形的对角线相互垂直均分的性质,利用对角线的一半,依据勾股定理求出菱形的边长,再依据菱形的四条边相等求出周长即可.【详解】以下图,依据题意得 AO= 1 × 8=4, BO= 1× 6=3,2 2∵四边形 ABCD 是菱形,∴ A B=BC=CD=DA , AC ⊥ BD ,∴△ AOB 是直角三角形,∴AB=AO 2 BO 216 9 =5,∴此菱形的周长为: 5×4=20. 应选: B . 【点睛】本题考察菱形的性质,利用勾股定理求出菱形的边长是解题的重点.4.如图 1,点 F 从菱形 ABCD 的项点 A 出发,沿 A - D - B 以 1cm/ s 的速度匀速运动到点B .图 2 是点 F 运动时, △FBC 的面积 y (m 2)随时间 x (s)变化的关系图象,则a 的值为 ( )A .5B . 2C .5 D .2 52【答案】 C【分析】【剖析】过点 D 作DEBC 于点 E 由图象可知,点 F 由点 A 到点 D 用时为 as , FBC 的面积为acm2.求出 DE=2,再由图像得 BD5 ,从而求出 BE=1,再在 Rt △ DEC 依据勾股定理结构方程,即可求解.【详解】解:过点 D作DE BC于点 E由图象可知,点 F 由点 A 到点D用时为as,FBC 的面积为acm2.AD BC a1D E gAD a2DE 2由图像得,当点 F 从 D 到B时,用5sBD5RtVDBE 中,BE BD 2DE 2( 5)2 2 21∵四边形 ABCD 是菱形,EC a 1, DC aRt △DEC 中,a222(a1)2解得 a 5 2应选: C.【点睛】本题综合考察了菱形性质和一次函数图象性质,要注意函数图象变化与动点地点之间的关系,解答本题重点依据图像重点点确立菱形的有关数据.5.如图,AB∥EF,ABP 1EFP1FCD 60 ,则ABC,EFC ,已知33P 的度数为()A.60B.80C.90D.100【答案】 B【分析】【剖析】延伸 BC 、 EF 交于点 G ,依据平行线的性质得 ∠ABG ∠ BGE 180 ,再依据三角形外角的性质和平角的性质得∠ EFC ∠ FCD ∠ BGE 60∠ BGE ,∠ BCF 180 ∠ FCD 120 ,最后依据四边形内角和定理求解即可.【详解】延伸 BC 、 EF 交于点 G ∵ AB//EF∴ ∠ ABG ∠ BGE 180 ∵ FCD 60∴∠ EFC ∠FCD ∠ BGE60 ∠ BGE ,∠ BCF 180 ∠ FCD 120 ∵ ABP1 EFP1ABC ,EFC33∴ ∠ P 360 ∠ PBC ∠BCF ∠PFC3602∠ABG2∠EFC120333602 2 60 ∠ BGE 120∠ ABG333602∠ABG 402∠BGE 120332002∠ABG ∠ BGE 32200180 380故答案为: B .【点睛】本题考察了平行线的角度问题,掌握平行线的性质、三角形外角的性质、平角的性质、四边形内角和定理是解题的重点.6.设四边形的内角和等于 ,五边形的外角和等于,则与的关系是 ( ). . .. 180 oABCD【答案】 B【分析】【剖析】依据多边形的内角和定理与多边形外角的关系即可得出结论.【详解】解:∵四边形的内角和等于a,∴a=( 4-2) ?180°=360°.∵五边形的外角和等于,∴=360 °,∴a= .应选 B.【点睛】本题考察的是多边形的内角与外角,熟知多边形的内角和定理是解答本题的重点.7.如图,在菱形ABCD 中,ABC60 ,AB 1 ,点P 是这个菱形内部或边上的一点,若以点P ,B ,C为极点的三角形是等腰三角形,则P,D(P, D 两点不重合)两点间的最短距离为()1A.B.1C.3D.31 2【答案】 D【分析】【剖析】分三种情况议论①若以边 BC为底.②若以边 PC为底.③若以边 PB为底.分别求出 PD 的最小值,即可判断.【详解】解:在菱形 ABCD中,∵∠ ABC=60°, AB=1,∴△ ABC,△ACD 都是等边三角形,①若以边 BC为底,则 BC 垂直均分线上(在菱形的边及其内部)的点知足题意,此时就转化为了“直线外一点与直线上全部点连线的线段中垂线段最短“,即当点 P 与点 A 重合时,PD 值最小,最小值为 1 ;②若以边 PC为底,∠ PBC为顶角时,以点 B 为圆心, BC长为半径作圆,与 BD 订交于一点,则弧 AC(除点 C 外)上的全部点都知足△PBC是等腰三角形,当点P在 BD上时, PD 最小,最小值为31③若以边 PB 为底,∠ PCB为顶角,以点 C 为圆心, BC 为半径作圆,则弧BD上的点 A 与点 D 均知足△PBC为等腰三角形,当P 与点D 重合时,PD 最小,明显不知足题意,故此点种状况不存在;上所述, PD的最小值为31应选 D.【点睛】本题考察菱形的性质、等边三角形的性质、等腰三角形的判断和性质等知识,解题的重点是学会用分类议论的思想思虑问题,属于中考常考题型.DG8.如图,四边形ABCD 和四边形AEFG均为正方形,连结CF, DG,则()CF2233 A.B.C.D.3232【答案】 B【分析】【剖析】连结 AC 和 AF,证明△DAG∽△ CAF可得DG的值.CF【详解】连结 AC 和 AF,则 AD AG 2 ,AC AF2∵∠ DAG=45°-∠ GAC,∠ CAF=45°-GAC,∴∠ DAG=∠ CAF.∴△ DAG∽△ CAF.∴DG AD2.CF AC2故答案为: B.【点睛】本题主要考察了正方形的性质、相像三角形的判断和性质,解题的重点是结构相像三角形.9.如图,正方形 ABCD的边长为 9,将正方形折叠,使极点 D 落在 BC 边上的点 E 处,折痕为GH,若 BE:EC=2:1,则线段 CH 的长是()A.3B.4C.5D.6【答案】 B【分析】试题剖析:设 CH= x,由于 BE: EC= 2: 1, BC=9,因此, EC= 3,由折叠知, EH= DH =9-x,在 Rt△ECH中,由勾股定理,得:(9 x)232x2,解得:x=4,即CH=4考点:( 1)图形的折叠;( 2)勾股定理10.如图,在矩形△PAB=1S矩形 ABCD,则点P到ABCD中, AB=5 ,AD= 3,动点 P 知足 S3A、 B 两点距离之和PA+PB的最小值为()A.29B.34C.52D.41【答案】 D【分析】解:设△ABP 中 AB 边上的高是h.∵ S△PAB= 1S 矩形ABCD,∴1AB?h=1AB?AD,∴3232h= AD=2,∴动点P 在与 AB 平行且与AB 的距离是 2 的直线 l 上,如图,作 A 对于直线l 3的对称点E,连结 AE,连结 BE,则 BE 就是所求的最短距离.在 Rt△ABE中,∵ AB=5, AE=2+2=4,∴ BE= AB2AE2 = 5242 = 41,即 PA+PB 的最小值为41.应选 D.11.在四边形 ABCD中, AD∥ BC,要使四边形ABCD是平行四边形,可增添的条件不正确的是()A. AB∥ CD B.∠ B=∠ D C. AD= BC D. AB= CD【答案】 D【分析】【剖析】依据平行四边形的判断解答即可.【详解】∵AD∥ BC, AB∥ CD,∴四边形ABCD是平行四边形,故 A 正确;∵AD∥ BC, AD=BC,∴四边形ABCD是平行四边形,故 C 正确;∵AD∥ BC,∴∠ D+∠ C=180°,∵∠ B=∠D,∴∠ B+C=180°,∴AB∥ CD,∴四边形ABCD是平行四边形,故 B 正确;应选: D.【点睛】本题考察平行四边形的判断,解题重点是依据平行四边形的判断解答.12.如图,菱形 ABCD中,对角线 AC= 6, BD= 8,M 、 N 分别是 BC、 CD 上的动点, P 是线段 BD 上的一个动点,则 PM+ PN 的最小值是()A .9 12 16 24B .5C .D .555【答案】 D【分析】【剖析】作 M 对于 BD 的对称点 Q ,连结 NQ ,交 BD 于 P ,连结 MP ,此时 MP+NP=NQ 最小, NQ 为所求,当 NQ ⊥ AB 时, NQ 最小,既而利用面积法求出 NQ 长即可得答案 .【详解】作 M 对于 BD 的对称点 Q ,连结 NQ ,交 BD 于 P ,连结 MP ,此时 MP+NP=NQ 最小, NQ 为所求,当 NQ ⊥ AB 时, NQ 最小,∵四边形 ABCD 是菱形, AC=6,DB=8,∴ O A=3,OB=4, AC ⊥ BD ,在 Rt △AOB 中, AB= OA 2 OB 2 =5,∵S 菱形 ABCD = 1AC gBDABgNQ ,2∴18 6 5NQ ,2∴NQ=24,5∴PM+PN 的最小值为24 ,5应选 D.【点睛】本题考察了菱形的性质,轴对称确立最短路线问题,熟记菱形的轴对称性和利用轴对称确立最短路线的方法是解题的重点.13. 如图,在 Y ABCD 中, AC 8, BD 6, AD 5 ,则 Y ABCD 的面积为 ( )A .6B . 12C . 24D . 48【答案】 C 【分析】 【剖析】由勾股定理的逆定理得出 AOD90o ,即 ACBD ,得出 Y ABCD 是菱形,由菱形面积公式即可得出结果. 【详解】∵四边形 ABCD 是平行四边形,∴ OCOC1AC4, OBOD1BD 3 ,22∴ OA 2 OD 225 AD 2,∴ AOD 90o ,即 AC BD ,∴ Y ABCD 是菱形,∴ Y ABCD 的面积1 1 AC BD86 24;22应选 C .【点睛】本题考察平行四边形的性质、勾股定理的逆定理、菱形的判断与性质,娴熟掌握平行四边形的性质,证明四边形 ABCD 是菱形是解题的重点.14. 如图,四边形 ABCD 的对角线为 AC 、 BD ,且 AC=BD ,则以下条件能判断四边形 ABCD 为矩形的是( )A . BA=BCB . AC 、 BD 相互均分 C . AC ⊥ BD D . AB ∥ CD 【答案】 B【分析】试题剖析:依据矩形的判断方法解答.解:能判断四边形ABCD 是矩形的条件为 AC 、 BD 相互均分.原因以下:∵ AC、 BD 相互均分,∴四边形ABCD是平行四边形,∵AC=BD,∴? ABCD是矩形.其余三个条件再加上AC=BD均不可以判断四边形ABCD是矩形.应选 B.考点:矩形的判断.15.如图,△ABC中, AB=4, AC=3, AD、 AE 分别是其角均分线和中线,过点 C 作 CG⊥ AD 于 F,交 AB 于 G,连结 EF,则线段EF的长为()A.1321 B.C.D.432【答案】 D【分析】【剖析】由等腰三角形的判断方法可知△AGC是等腰三角形,因此 F 为 GC 中点,再由已知条件可得EF 为△CBG的中位线,利用中位线的性质即可求出线段EF的长.【详解】∵AD 是△ABC 角均分线, CG⊥AD 于 F,∴△ AGC是等腰三角形,∴AG=AC=3, GF=CF,∵AB=4, AC=3,∴B G=1,∵AE 是△ABC 中线,∴B E=CE,∴E F 为△CBG的中位线,∴E F=1BG=1,22应选: D.【点睛】本题考察等腰三角形的判断和性质、三角形的中位线性质定理,解题重点在于掌握三角形的中位线平行于第三边,而且等于第三边的一半.16.如图,四边形ABCD 和 EFGH 都是正方形,点E,H 在 AD, CD 边上,点F,G在对角线 AC 上,若 AB 6 ,则 EFGH 的面积是()A.6B.8C.9D.12【答案】 B【分析】【剖析】依据正方形的性质获得∠DAC=∠ ACD= 45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是获得DE=2EH=2EF, EF=2AE,即可获得结论.222【详解】解:∵在正方形ABCD中,∠ D=90°,AD= CD= AB,∴∠ DAC=∠ DCA= 45°,∵四边形EFGH为正方形,∴EH= EF,∠ AFE=∠ FEH= 90°,∴∠ AEF=∠ DEH=45°,∴A F= EF, DE= DH,∵在 Rt△AEF中, AF2+EF2=AE2,∴A F= EF=2AE,2同理可得: DH= DE=2EH 2又∵ EH=EF,∴DE=2EF=2×2AE=1AE,2222∵AD= AB=6,∴DE=2, AE= 4,∴EH= 2 DE=2∴EFGH 的面积为2,EH2=( 22)2=8,应选: B .【点睛】本题考察了正方形的性质,等腰直角三角形的判断及性质以及勾股定理的应用,娴熟掌握图形的性质及勾股定理是解决本题的重点.17. 如图,在矩形 ABCD 中, AD=2AB ,点 M 、 N 分别在边 AD 、 BC 上,连结 BM 、 DN .若四边形 MBND 是菱形,则AM等于( )MDA .35B .233 C .8D .45【答案】 A【分析】试题剖析:设 AB=a,依据题意知 AD=2a ,由四边形 BM=MD=2a-b. 在 Rt △ABM 中,由勾股定理即可求值试题分析:∵四边形MBND 是菱形,BMDN .是菱形知BM=MD ,设AM=b, 则∴MD=MB .∵四边形 ABCD 是矩形,∴∠ A=90°.设 AB=a , AM=b ,则 MB=2a-b ,( a 、 b 均为正数).在 Rt △ABM 中, AB 2+AM 2=BM 2,即 a 2 +b 2=( 2a-b ) 2,4解得 a=b ,∴MD=MB=2a-b= 5b ,3 AMb 3∴MD5 5.b3应选 A.考点: 1.矩形的性质; 2.勾股定理; 3.菱形的性质.18. 以下结论正确的选项是()A .平行四边形是轴对称图形B .平行四边形的对角线相等C .平行四边形的对边平行且相等D .平行四边形的对角互补,邻角相等【答案】 C【分析】【剖析】分别利用平行四边形的性质和判断逐项判断即可.【详解】A、平行四边形不必定是轴对称图形,故 A 错误;B、平行四边形的对角线不相等,故 B 错误;C、平行四边形的对边平行且相等,故C正确;D 错误.D、平行四边形的对角相等,邻角互补,故应选: C.【点睛】本题考察平行四边形的性质,掌握特别平行四边形与一般平行四边形的差别是解题的重点.19.如图,在□ ABCD中,延伸CD到 E,使 DE= CD,连结 BE 交 AD 于点 F,交 AC于点G.以下结论中:① DE=DF;② AG=GF;③ AF=DF;④ BG=GC;⑤ BF=EF,此中正确的有()A.1 个B.2 个C.3 个D.4 个【答案】 B【分析】【剖析】由 AAS证明△ABF≌△ DEF,得出对应边相等 AF=DF, BF=EF,即可得出结论,对于①②④不必定正确.【详解】解:∵四边形 ABCD是平行四边形,∴AB∥CD,AB=CD,即AB∥CE,∴∠ ABF=∠ E,∵DE=CD,∴AB=DE,在△ABF 和△DEF中,ABF=E∵AFB= DFE ,AB=DE∴△ ABF≌△ DEF( AAS),∴A F=DF, BF=EF;可得③⑤ 正确,应选: B.【点睛】本题考察平行四边形的性质、全等三角形的判断与性质、平行线的性质;娴熟掌握平行四边形的性质,证明三角形全等是解题的重点.20.在平面直角坐标系中, A, B, C 三点坐标分别是( 0, 0),( 4, 0),( 3, 2),以A,B,C三点为极点画平行四边形,则第四个极点不行能在() .A.第一象限B.第二象限C.第三象限D.第四象限【答案】 C【分析】A 点在原点上,B 点在横轴上,C 点在第一象限,依据平行四边形的性质:两组对边分别平行,可知第四个极点可能在第一、二、四象限,不行能在第三象限,应选C。
初中数学经典四边形习题50道(附答案)

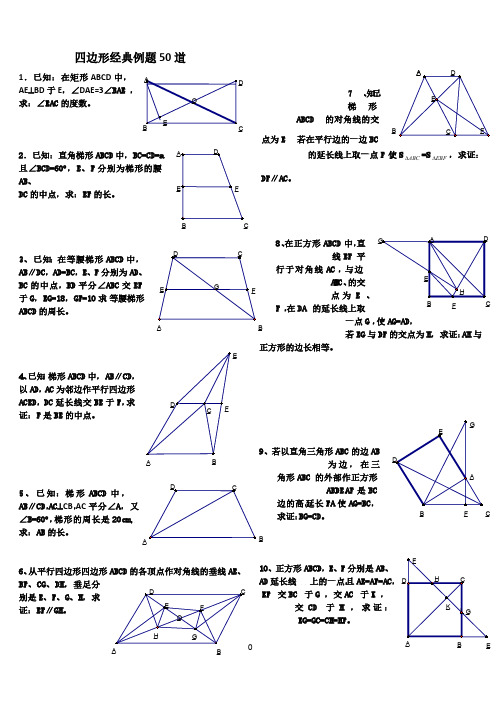
1.已知:在矩形ABCD 中,AE ⊥BD 于E , ∠DAE=3∠BAE ,求:∠EAC 的度数。
2.已知:直角梯形ABCD 中,BC=CD=a 且∠BCD=60︒,E 、F 分别为梯形的腰AB 、 DC 的中点,求:EF 的长。
3、已知:在等腰梯形ABCD 中,AB ∥DC ,AD=BC ,E 、F 分别为AD 、BC 的中点,BD 平分∠ABC 交EF 于G ,EG=18,GF=10 求:等腰梯形ABCD 的周长。
4、已知:梯形ABCD 中,AB ∥CD ,以AD , AC 为邻边作平行四边形ACED ,DC 延长线交BE 于F ,求证:F 是BE 的中点。
5、已知:梯形ABCD 中,AB ∥CD ,AC ⊥CB , AC 平分∠A ,又∠B=60︒,梯形的周长是 20cm, 求:AB 的长。
6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ,垂足分别是E 、F 、G 、H ,求证:EF ∥GH 。
7、已知:梯形ABCD 的对角线的交点为E_ D_ C_B _ C_ A _ B_ A_ B_ E _A_ B_ A_ B若在平行边的一边BC 的延长线上取一点F , 使S ABC ∆=S EBF ∆,求证:DF ∥AC 。
8、在正方形ABCD 中,直线EF 平行于 对角线AC ,与边AB 、BC 的交点为E 、F , 在DA 的延长线上取一点G ,使AG=AD , 若EG 与DF 的交点为H ,求证:AH 与正方形的边长相等。
9、若以直角三角形ABC 的边AB 为边,在三角形ABC 的外部作正方形ABDE ,AF 是BC 边的高,延长FA 使AG=BC ,求证:BG=CD 。
10、正方形ABCD ,E 、F 分别是AB 、AD 延长线上的一点,且AE=AF=AC ,EF 交BC 于G ,交AC于K ,交CD 于H ,求证:EG=GC=CH=HF 。
11、在正方形ABCD 的对角线BD 上,取BE=AB ,若过E 作BD 的垂线EF 交CD 于F ,求证:CF=ED 。
(2021年整理)初中数学经典四边形习题50道(附答案)

初中数学经典四边形习题50道(附答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初中数学经典四边形习题50道(附答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初中数学经典四边形习题50道(附答案)的全部内容。
经典四边形习题50道(附答案)1.已知:在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE ,求:∠EAC的度数。
2.已知:直角梯形ABCD中,BC=CD=a且∠BCD=60度,E、F分别为梯形的腰AB、DC的中点,求:EF的长。
3、已知:在等腰梯形ABCD中,AB∥DC,AD=BC,E、F分别为AD、BC的中点,BD 平分∠ABC交EF于G,EG=18,GF=10求:等腰梯形ABCD的周长.4、已知:梯形ABCD中,AB∥CD,以AD,AC为邻边作平行四边形ACED,DC延长线交BE于F,求证:F是BE的中点。
_D_C_B_C_A_B_A_B_E5、已知:梯形ABCD 中,AB ∥CD ,AC ⊥CB, AC 平分∠A ,又∠B=60度,梯形的周长是 20cm, 求:AB 的长.6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH,垂足分别是E 、F 、G 、H ,求证:EF ∥GH 。
7、已知:梯形ABCD 的对角线的交点为E 若在平行边的一边BC 的延长线上取一点F , 使S ABC ∆=S EBF ∆,求证:DF ∥AC.8、在正方形ABCD 中,直线EF 平行于 对角线AC ,与边AB 、BC 的交点为E 、F, 在DA 的延长线上取一点G,使AG=AD , 若EG 与DF 的交点为H ,求证:AH 与正方形的边长相等。
初二数学经典四边形习题50道(附答案)

1.已知:在矩形ABCD 中,AE BD 于E , ∠DAE=3∠BAE ,求:∠EAC 的度数。
2.已知:直角梯形ABCD 中,BC=CD=a 且∠BCD=60,E 、F 分别为梯形的腰AB 、 DC 的中点,求:EF 的长。
3、已知:在等腰梯形ABCD 中,AB ∥DC , AD=BC ,E 、F 分别为AD 、BC 的中点,BD 平分∠ABC 交EF 于G ,EG=18,GF=10 求:等腰梯形ABCD 的周长。
4、已知:梯形ABCD 中,AB ∥CD ,以AD , AC 为邻边作平行四边形ACED ,DC 延长线 交BE 于F ,求证:F 是BE 的中点。
5、已知:梯形ABCD 中,AB ∥CD ,AC CB , AC 平分∠A ,又∠B=60,梯形的周长是 20cm, 求:AB 的长。
6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ,垂足分别是E 、F 、G 、H ,求证:EF ∥GH 。
_O_A_D_C_E_F_B _D_C_G _A _B_D _C_E _F _D _A _B _C_E _F _A_B_D _C _O_D _C_H _F _G_E7、已知:梯形ABCD 的对角线的交点为E 若在平行边的一边BC 的延长线上取一点F , 使S ABC ∆=S EBF ∆,求证:DF ∥AC 。
8、在正方形ABCD 中,直线EF 平行于 对角线AC ,与边AB 、BC 的交点为E 、F , 在DA 的延长线上取一点G ,使AG=AD , 若EG 与DF 的交点为H ,求证:AH 与正方形的边长相等。
9、若以直角三角形ABC 的边AB 为边, 在三角形ABC 的外部作正方形ABDE ,AF 是BC 边的高,延长FA 使AG=BC ,求证:BG=CD 。
10、正方形ABCD ,E 、F 分别是AB 、AD 延长线 上的一点,且AE=AF=AC ,EF 交BC 于G ,交AC 于K ,交CD 于H ,求证:EG=GC=CH=HF 。
初中数学经典四边形习题50道(附答案)

四边形经典例题50道1.已知:在矩形 ABCD 中, AE BD 于 E, Z DAE=3 / BAE 求:/ EAC 的度数。
平行边的一边 S ABC =S EBFD8、在正方形 ABCD 中,G 线EF 平行于对角线AC ,与边 AB 、BC 的交点为E 、F,在DA 长线上取一点 G,使AG=AD , 若EG 与DF 的交点为H,求证: 正方形的边长相等。
的 延AHB F3、已知:在等腰梯形 ABCD 中, AB // DC, AD=BC , E 、F 分另 U 为 AD 、 BC 的中点,BD 平分Z ABC 交EF 于 G, EG=18, GF=10求:等腰梯形 ABCD 的周长。
A4、已知:梯形ABCD 中,AB II CD,以AD , AC 为邻边作平行四边形 ACED, DC 延 线交BE 于F,求证:F 是BE 的中点。
长AB9、若以直角三角形 ABC 的边 边,在三角形ABC 的外部作- ABDE , AF 是BC&的高,延 使 AG=BC ,求证:BG=CD 。
BF C6、从平行四边形四边形 AE 、BF 、CG 、DH ,垂足分另U 是 5、已知:梯形 ABCD 中,AB // CD, AC CB, AC 平分 Z A ,又 Z B=60 , 梯形的周长是 20cm,求:AB 的 长。
10、正方形ABCD , E 、F 分别是 AD 延长线 上的一点,且AE=AF=AC , EF 交 BC 于 G,交 K , 交CD 于 H , 求证: EG=GC=CH=HF 。
ABCD 的各顶点作对角线的垂线E 、F 、G 、H ,求证:EF//GH 。
7、已知:梯形 对角线的交点为 B11、 在正方形ABCD 的对角线BD 上,取BE=AB ,若过E 作BD 的垂 线EF 交CD 于F,求证:CF=ED 。
12、 平行四边形ABCD 中,/ A 、AE 、DE 与 DC 、AB 延长线交于 G 、F,求证:AD=DG=GF=FA 。
江苏省南通市历年中考数学试题分类解析专题10:四边形
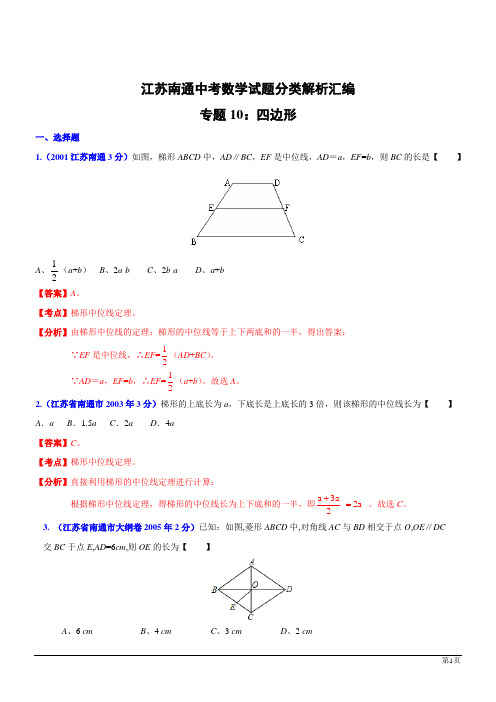
江苏南通中考数学试题分类解析汇编专题10:四边形一、选择题1.(2001江苏南通3分)如图,梯形ABCD 中,AD ∥BC ,EF 是中位线,AD =a ,EF =b ,则BC 的长是【 】A 、21(a +b ) B 、2a -b C 、2b -a D 、a +b 【答案】A 。
【考点】梯形中位线定理。
【分析】由梯形中位线的定理:梯形的中位线等于上下两底和的一半,得出答案:∵EF 是中位线,∴EF =12(AD +BC )。
∵AD =a ,EF =b ,∴EF =12(a +b )。
故选A 。
2.(江苏省南通市2003年3分)梯形的上底长为a ,下底长是上底长的3倍,则该梯形的中位线长为【 】 A .a B .1.5a C .2a D .4a 【答案】C 。
【考点】梯形中位线定理。
【分析】直接利用梯形的中位线定理进行计算:根据梯形中位线定理,得梯形的中位线长为上下底和的一半,即a 3a2a 2+= 。
故选C 。
3. (江苏省南通市大纲卷2005年2分)已知:如图,菱形ABCD 中,对角线AC 与BD 相交于点O ,OE ∥DC 交BC 于点E ,AD =6cm ,则OE 的长为【 】A 、6 cmB 、4 cmC 、3 cmD 、2 cm【答案】C。
【考点】菱形的性质,相似三角形的判定和性质【分析】利用菱形的四边都相等的性质结合三角形相似求解:∵四边形ABCD是菱形,∴AB=AD=6cm,OC=OA=12 AC。
∵OE∥DC,∴△ABC∽△OEC,则OC OEAC AB=,即1OE26=。
∴OE=3(cm)。
故选C。
4. (江苏省南通市大纲卷2006年3分)如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为【】A、6cmB、12cmC、4cmD、8cm【答案】D。
【考点】平行四边形的性质。
【分析】根据平行四边形对边相等的性质可知:∵ ABCD的周长是28cm,∴AB+BC=14cm。
初中数学四边形经典测试题含答案

初中数学四边形经典测试题含答案一、选择题1.如图,平行四边形 ABCD 的周长是26cm,对角线AC 与BD 交于点O,AC AB, E 是 BC 中点,4AOD 的周长比VAOB 的周长多 X ° £ C A. 3cm B. 4cm ( 【答案】B 【解析】 【分析】 根据题意,由平行四边形的周长得到 AB AD 3cm,则AE 的长度为() :5cm D. 8cm )13,由4AOD 的周长比VAOB 的周长 多3cm,则AD AB 3,求出AD 的长度,即可求出 AE 的长度. 【详解】 解:.••平行四边形 ABCD 的周长是26cm, 1 ••• AB AD - 26 13, 2 • •,BD 是平行四边形的对角线,则 BO=DO, • •• AAOD 的周长比VAOB 的周长多3cm, ..(AO OD AD) (AO OB AB) AD AB 3,AB 5, AD 8, BC AD 8, • •• AC AB,点E 是BC 中点, 1 - 1 ••• AE — BC - 8 4 ; 2 2 故选:B. 【点睛】 本题考查了平行四边形的性质,直角三角形斜边上的中线等于斜边的一半 熟练掌握平行四边形的性质进行解题. 2.如图,足球图片正中的黑色正五边形的内角和是 (). ,解题的关键是A. 180°B. 360°C. 540°D. 720 °【答案】C 【解析】 【分析】根据多边形内角和公式 (n 2) 180即可求出结果. 【详解】解:黑色正五边形的内角和为: (5 2) 180 540 ,故选:C. 【点睛】本题考查了多边形的内角和公式,解题关键是牢记多边形的内角和公式.3 .在平面直角坐标系中, A, B, C 三点坐标分别是(0, 0) , ( 4, 0) , (3, 2),以A, B, C 三点为顶点画平行四边形,则第四个顶点不可能在( ).A.第一象限B.第二象限C.第三象限D.第四象限【答案】C 【解析】A 点在原点上,B 点在横轴上,C 点在第一象限,根据平行四边形的性质:两组对边分别平行,可知第四个顶点可能在第一、二、四象限,不可能在第三象限,故选 C4 .如图,矩形 ABCD 的对角线 AC BD 相交于点 行四边形是菱形即可判断四边形OBEC 是菱形,则 OE 与BC 垂直平分,易得 EF=1x,2CF=x 再由锐角三角函数定义作答即可.【详解】解:•••矩形 ABCD 的对角线 AC 、BD 相交于点 O, AB: BC= 2: 1 ,• .BC= AD,设 AB=2x,贝U BC= x.O, AB: BC= 2: 1 ,且 BE// AC, CE//C.D.3 10过点E 作EFL 直线DC 交线段DC 延长线于点F,连接OE 交BC 于点G.根据邻边相等的平【答案】B如图,过点E作EH直线DC交线段DC延长线于点F,连接OE交BC于点G.•. BE//AC, CE// BD,••・四边形BOCE是平行四边形,•••四边形ABCD是矩形,.•.OB=OC,••・四边形BOCE是菱形.••・OE与BC垂直平分,1 1 —一・ EF= -AD= — x,OE// AB,2 2••・四边形AOEB是平行四边形,.-.OE=AB= 2x,一1 一•• CF—— OE= x.2【点睛】本题考查矩形的性质、平行四边形的判定与性质、菱形的判定与性质以及解直角三角形, 解题的关键是熟练掌握矩形的性质和菱形的判定与性质,属于中考常考题型.5.如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论不正确的是()/ _____________ Q______________ E--- 1cA. AAOB0△ BOCB. ABO必△ EODC. AAOg△ EODD. AAOg△ BOC【答案】A【解析】根据矩形的性质和全等三角形的性质找出全等三角形应用排它法求欠妥即可:•. AD=DE, DO// AB, • . OD 为AABE的中位线.「. OD=OC•.在RtAAOD和RtAEOD 中,AD=DE, OD=OD, . .△AODZ△ EOD (HL.).•.在RtAAOD和RtABOC中,AD=BC, OD=OC, . .△AOg△ BOC (HL.). . BO® △ EOD.综上所述,B、C D均正确.故选A.6.如图,菱形 ABCD 中,点P 是CD 的中点,/ BCD=60。
四边形测试题(通用8篇)

四边形测试题〔通用8篇〕篇1:数学四边形测试题数学四边形测试题一、选择题(每题3分,共30分)。
1、顺次连结四边形各边的中点,所成的四边形必定是A等腰梯形B直角梯形C矩形D平行四边形2、如图1:等腰梯形ABCD中,AD∥BC,对角线AC、BD 相交于点O,那么图中的全等三角形共有A1对B2对C3对D4对3、如图2,在矩形ABCD中,AD∥BC,AC与BD交于点O,那么图中面积相等的三角形有A4对B5对C6对D8对4、不能断定四边形ABCD为平行四边形的命题是AAB∥CD且AB=CDBAB=AD、BC=CDCAB=CD,AD=BCD∠A=∠C,∠B=∠D5、以下命题中,真命题是A一组对边平行,另一组对边相等的'四边形是平行四边形B有一组对边和一组对角分别相等的四边形是平行四边形C两组对角分别相等的四边形是平行四边形D两条对角线互相垂直且相等的四边形是平行四边形6、正方形具有而菱形不一定具有的性质是A对角线相等B对角线互相垂直且平分C四条边都相等D对角线平分一组对角篇2:初中数学四边形单元测试题参考初中数学四边形单元测试题参考一、精心选一选,相信你一定能选对!(每题3分,共30分)1.如图1,用两个完全一样的直角三角板,不能拼成以下图形的是( ).A.平行四边形B.矩形C.等腰三角形D.梯形2.以下说法中,正确的选项是( ).A.等腰梯形的对角线互相垂直B.菱形的对角线相等C.矩形的对角线互相垂直;D.正方形的对角线互相垂直且相等3.四边形ABCD是平行四边形,以下结论中,错误的选项是( ).A.AB=CD;B.AC=BD;C.当AC⊥BD时,它是菱形;D.当∠ABC =90°时,它是矩形4.如图2,将一张矩形纸片ABCD那样折起,使顶点C落在C′处,其中AB=4,假设∠C ′ED=30°,那么折痕ED的长为( ) .A.4B.4C.5D.85.如图3,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影局部的面积是矩形面积的( ).A. B. C. D.6.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①, ②两局部,将①展开后得到的平面图形是( ).A.三角形B.矩形C.菱形D.梯形7. 等腰梯形ABCD的中位线EF的长为6,腰AD的长为5,那么等腰梯形的周长为(• ).A.11B.16C.17D.228.顺次连结菱形各边中点所围成的四边形是( ).A.一般的平行四边形B.矩形C.菱形D.等腰梯形9.如图4是一块电脑主板的示意图,每一转角处都是直角,数据如图所示,•那么该主板的周长是( ).A.88mmB.96mmC.80mmD.84mm10.如图5,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,那么DN+MN的最小值为( ).A.8B.8C.2D.10二、细心填一填,相信你填得又快又准!(每题2分,共16分)11. ABCD两邻角∠A:∠B=1:2,那么∠C=_ ____度.12.如图6,在 ABCD中,E、F和G、H分别是AD和BC的三等分点,那么图中平行四边形的个数共有______个.13., ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD 于E,那么DE=_____cm.14.如图,在长方形ABCD中,AB=3,BC=2,E为BC的中点,F在AB上,且BF=2AF,那么四边形AFEC的面积为________.15.如图,矩形纸片ABCD中,AB=6cm,AD=9cm,再按以下步骤折叠:①将∠BAD对折,使AB落在AD上,得折痕AF(如图2);②将△AFB沿BF折叠,AF与CD交于点G(如图3),•那么CG的长等于_______c m.16.过边长为1的正方形的中心O引两条互相垂直的射线,分别与正方形的边交于A、B两点,那么线段 AB长的取值范围是_______.17.菱形ABCD的边长为6,∠A=60°,假如点P是菱形内一点,且PB=PD=2 ,那么AP的长为_______.18.下面图1的梯形符合_______条件时,可以经过旋转和翻折成图案三、耐心选一选,千万别漏选!(每题4分,共8分,错选一项得0分,•对而不全酌情给分)19.如图,在等腰梯形ABCD中,AD∥BC,AC与BD相交于点O.下面结论正确的选项是( ).A.AC=BDB.∠DAO=∠DBCC.S△BOC= S梯形ABCDD.△AOB≌△DOC20.如图,把两个边长为3的正方形叠放在一起,假设∠BCF=30°,•那么下面结论正确的选项是( ).A.∠DCG=30°B.∠AHF与∠BCF互余C.DH=FHD.DH=四、用心做一做,展示你的证明才能!21.如图,在矩形ABCD中,点E、F在BC边上,且BE=CF,AF、DE交于点M.求证:AM=DM.(6分)22.如图,等腰梯形ABCD中,AD∥BC,AB =CD,DE⊥BC 于E,AE=BE.BF⊥AE于F,请你判断线段BF与图中的哪条线段相等,先写出你的猜测,再加以证明.(6分)(1)猜测:BF=______.(2)证明:23.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD=BF,以AD•为边作等边△ADE.(1)求证:△ACD≌△CBF;(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且∠DEF=30°?•证明你的结论.(8分)五、仔细想一想,相信你一定行!24.如图,以△ABC的各边向同侧作正△ABD,BCF,ACE.(1)求证:四边形AEFD是平行四边形;(2)当△ABC是______三角形时,四边形AEFD是菱形;(3)当∠BAC=_____时,四边形AEFD是矩形;(4)当∠BAC=_______时,以A、E、F、D 为顶点的四边形不存在.(8分)25.矩形,菱形由于其特殊的性质,为拼图提供了方便,因此墙面瓷砖一般设计为矩形,图案也以菱形居多.如图,是一种长30cm,宽20cm的矩形瓷砖,E、F、G、H•分别是矩形各边的中点,阴影局部为淡黄色,中间局部为白色,现有一面长4.2m,宽2.8m的墙壁准备贴瓷砖.问:(1)这面墙壁最少要贴这种瓷砖多少块?(2)全部贴满瓷砖后,这面墙壁最多会出现多少个面积相等的菱形?•其中淡黄色的菱形有多少个?六、动脑想一想,展示你的设计才能!26.在劳技课上,老师请同学们在一张长为17cm,宽为16cm的长方形纸板上,剪下一个腰长为10cm的等腰三角形(•要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边长上).•请你帮助同学们计算剪下的'等腰三角形的面积.(6分)27.蓝天希望学校准备建一个多媒体教室,方案做长120cm,宽30cm的长方形桌面,现只有长80cm,宽45cm的木板,请你为该校设计不同的拼接方案,使拼起来的桌面符合要求.(只要求画出裁剪,拼接图形,并标上尺寸)(6分)七、理论与探究,展示你的创新才能!28.设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…….(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4, ……,an,恳求出a2,a3,a4的值.(2)根据以上规律写出an的表达式.(8分)29.在△ABC中,借助作图工具可以作出中位线EF,沿着中位线EF一刀剪切后,•用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP,剪切线与拼图如下图1.仿照上述的方法,按要求完成以下操作设计,并在规定位置画出图示.(1)在△ABC中,增加条件:_________,沿着_______一刀剪切后可以拼成矩形,剪切线与拼图画在图示2的位置上.(2)在△ABC中,增加条件:_________,沿着_______一刀剪切后可以拼成菱形,剪切线与拼图画在图示3的位置上.(3)在△ABC中,增加条件:_________,沿着_______一刀剪切后可以拼成正方形,剪切线与拼图画在图示4的位置上.(4)在△ABC中(AB≠AC),一刀剪切后也可以拼成等腰梯形,首先要确定剪切线,•其操作过程(剪切线的作法)是:___________,然后,沿着剪切线一刀剪切后可以拼成等腰梯形,剪切线与拼图画在图示5的位置上.(10分)篇3:四边形四边形有关概念四边形内角和例1十、随堂练习教材P122中1、2、3.篇4:四边形性质探究的测试题(有答案) 一、选择题(每题3分,共30分)1.以下各组图形中有可能不相似的是A.各有一个角是45°的两个等腰三角形B.各有一个角是60°的两个等腰三角形C.各有一个角是105°的两个等腰三角形D.两个等腰直角三角形2.以下说法①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的等腰三角形相似;④有一个角为60o的两个直角三角形相似,其中正确的说法是A.①③B.②④C.①②④D.②③④3.△ABC和△DEF满足以下条件,其中使△ABC和△DEF不相似的是A.∠A=∠D=45°,∠C=27°,∠E=108°B.AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=16C.BC=a,AC=b,AB=c,DE=,EF=,DF=D.AB=AC,DE=DF,∠A=∠D=40o,4.如下图,给出以下条件:①; ②;③; ④.其中单独可以断定的个数为A.1B.2C.3D.45.假如一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值A.只有1个B.可以有2个C.有2个以上但有限D.有无数个6.如图,△ABC中,EF∥BC,DG∥AB,EF和DG相交于点H,那么图中与△ABC相似的三角形共有A.1个B.2个C.3个D.4个7.△ABC中,D是AB上一固定点。
中考复习——初中数学经典四边形习题50道(附答案)
1.已知:在矩形 ABCD 中, _A
AEBD 于 E,∠DAE=3∠BAE ,
求:∠EAC 的度数。
_O
_E _B
2.已知:直角梯形 ABCD 中,BC=CD=a _A
且∠BCD=60,E、F 分别为梯形的腰
AB、
_E
DC 的中点,求:EF 的长。
_D
_C _D
_F
_A
_D
_E
证:ADEF 是平行四边形。
_D
_E
_B
_C _F
_F
_A
_A
14、在四边形 ABCD 中,AB=CD,
_P
P、Q 分别是 AD、BC 中点,M、N
_D
_B
_C
分别是对角线 AC、BD 的中点,
求证:PQMN。
_N
_M
_B
_Q
19、M、N 为ABC 的边 AB、AC 的中点,E、F 为边 AC 的
G,BG= 4 2 ,则ΔCEF 的周长为( )
A.8 B.9.5
C.10
D.11.5
正确的
A.③② B.③④ C.①④② D.②③④
例 4.13.在下列命题中,是真命题的是( )
A.两条对角线相等的四边形是矩形 B.两条对角线互相垂
直的四边形是菱形 C.两条对角线互相平分的四边形是平行
四边形 D.两条对角线互相垂直且相等的四边形是正方形
_D _E
_A
_C
8 、在正方形 ABCD 中,直 _G
_A
_D
_C
线 EF 平
行 于 对 角 线 AC ,与 边
_G
_F
ABBC 、的交 点为 E 、
初二数学经典四边形习题50道(附答案)

1.已知:在矩形ABCD 中,AE ⊥BD 于E , ∠DAE=3∠BAE ,求:∠EAC 的度数。
2.已知:直角梯形ABCD 中,BC=CD=a 且∠BCD=60︒,E 、F 分别为梯形的腰AB 、 DC 的中点,求:EF 的长。
3、已知:在等腰梯形ABCD 中,AB ∥DC , AD=BC ,E 、F 分别为AD 、BC 的中点,BD 平分∠ABC 交EF 于G ,EG=18,GF=10 求:等腰梯形ABCD 的周长。
4、已知:梯形ABCD 中,AB ∥CD ,以AD , AC 为邻边作平行四边形ACED ,DC 延长线 交BE 于F ,求证:F 是BE 的中点。
5、已知:梯形ABCD 中,AB ∥CD ,AC ⊥CB , AC 平分∠A ,又∠B=60︒,梯形的周长是 20cm, 求:AB 的长。
6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ,垂足分别是E 、F 、G 、H ,求证:EF ∥GH 。
_ D_ C_ B _ C_ A _ B_ A _ B_ E _A_ B7、已知:梯形ABCD 的对角线的交点为E 若在平行边的一边BC 的延长线上取一点F , 使S ABC ∆=S EBF ∆,求证:DF ∥AC 。
8、在正方形ABCD 中,直线EF 平行于 对角线AC ,与边AB 、BC 的交点为E 、F , 在DA 的延长线上取一点G ,使AG=AD , 若EG 与DF 的交点为H ,求证:AH 与正方形的边长相等。
9、若以直角三角形ABC 的边AB 为边, 在三角形ABC 的外部作正方形ABDE , AF 是BC 边的高,延长FA 使AG=BC ,求证:BG=CD 。
10、正方形ABCD ,E 、F 分别是AB 、AD 延长线上的一点,且AE=AF=AC ,EF 交BC 于G ,交AC 于K ,交CD 于H ,求证:EG=GC=CH=HF 。
11、在正方形ABCD 的对角线BD 上,取BE=AB ,若过E 作BD 的垂线EF 交CD 于F ,求证:CF=ED 。
初中数学四边形专题训练50题含答案

中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.平行四边形不一定具有的性质是( )A .对角线互相垂直B .对边平行且相等C .对角线互相平分D .对角相等 2.如图,在MON ∠的两边.上分别截取,OA OB ,使OA OB =;分别以点A ,B 为圆心,OA 长为半径作弧,两弧交于点C ;连接,,,AC BC AB OC .若2AB =,四边形OACB 的面积为4.则OC 的长为( )A .2B .3C .4D .5 3.在ABCD 中,下列结论错误的是( )A .//AB CD B .B D ∠=∠C .AC BD =D .180C D ∠+∠=︒ 4.如图,在平行四边形ABCD 中,E 是AB 延长线上的一点,若∠A=60°,则∠1的度数为( )A .120°B .60°C .45°D .30° 5.若平行四边形中两个内角的度数比为1∠2,则其中较大的内角是( ) A .100° B .60° C .120° D .90° 6.如图,正方形OABC 与正方形ODEF 是位似图形,点O 为位似中心,位似比为2:3,点B 、E 在第一象限.若点A 的坐标为()1,0,则点E 的坐标是( )A .0)B .33,22⎛⎫ ⎪⎝⎭C .D .(2,2) 7.四边形ABCD 中,对角线AC ,BD 交于点O ,AD//BC ,为了判定四边形是平行四边形,还需一个条件,其中错误..的是( ) A .AB//CD B .∠A=∠C C .AB=CD D .AO=CO 8.一个多边形的内角和等于外角和,则这个多边形的边数为( )A .10B .8C .6D .49.顺次连接等腰梯形各边中点所围成的四边形是( )A .平行四边形B .矩形C .菱形D .正方形 10.已知平行四边形ABCD 的周长为32,AB =4,则BC 的长为( )A .4B .12C .24D .48 11.如图,四边形ABCD 是矩形,,把矩形沿直线AC 折叠,点B 落在点E处,连结DE,则的值是( )A .B .C .8D .7:25 12.如图,在平行四边形ABCD 中,AB=4,CE 平分∠BCD 交AD 边于点E ,且AE=3,则BC 的长为( )A .4B .6C .7D .813.如图,在矩形ABCD ,对角线AC 与BD 相交于点O ,EO AC ⊥于点O ,交BC 于点E ,若ABE ∆的周长为8,3AB =,则AD 的长为 ( )A .2B .5.5C .5D .414.如图,矩形ABCD 中,4AB =,2BC =.点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则BE 的长是( )A .B C .2.5 D .1.5 15.如图,在平行四边形ABCD 中,过点P 作直线EF 、GH 分别平行于AB 、BC ,那么图中共有( )平行四边形.A .4个B .5个C .8个D .9个 16.如图,已知直线PQ CD ⊥于点P ,B 是CPQ ∠内部一点,过点B 作BA PQ ⊥于点A ,BC CD ⊥于点C ,四边形PABC 是边长为8cm 的正方形,N 是AB 的中点,动点M 从点P 出发,以2cm/s 的速度,沿P A B C →→→方向运动,到达点C 停止运动,设运动时间为()s t ,当CM PN =时,t 等于( )A .2B .4C .2或4D .2或617.如图,在菱形中,,,是的中点.过点作,垂足为.将沿点到点的方向平移,得到.设、分别是、的中点,当点与点重合时,四边形的面积为A .B .C .D . 18.如图,点EF 、分别是菱形ABCD 的边AD 、DC 的中点,如果阴影部分的面积和是10,则菱形对角线AC 与BD 的乘积AC BD ⋅等于( )A .10B .32C .20D .1619.如图,在正方形1ABCB 中,AB =AB 与直线l 所夹锐角为60,延长1CB 交直线l 于点1A ,作正方形1112A B C B ,延长12C B 交直线l 于点2A ,作正方形2223A B C B ,延长23C B 交直线l 于点3A ,作正方形3334A B C B ⋯,依次规律,则线段20212022A A =( )A .20192⨯⎝⎭B .20202⨯⎝⎭C .20212⨯⎝⎭D .20222⨯⎝⎭20.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,添加一个条件使平行四边形ABCD 为矩形的是( )A .AD AB = B .AB AD ⊥C .AB AC =D .CA BD ⊥二、填空题21.如图,这个图案是用形状、大小完全相同的等腰梯形密铺而成的,则这个图案中的等腰梯形的底角(指锐角)是_________度.22.如图,点E 在矩形ABCD 的对角线BD 上,EF BC ⊥于点F ,连接AF ,若5BC =,2EF =,则ABF △的面积为_________.23.已知菱形的两条对角线长分别为3和4,则菱形的面积为______.24.有一个边长为50cm 的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为_____.25.如图,Rt ABC 中,90C BC AC ∠=︒>,,以AB BC AC ,,三边为边长的三个正方形面积分别为1S ,2S ,3S .若ABC 的面积为7,140S =,则32S S -的值等于______.26.如图,将长方形ABCD沿AE折叠,已知50∠=︒,则BADCED'∠'的大小是_____27.如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为CC',则图中阴影部分的面积为__.28.用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是______.29.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为_____.30.如图,将四边形ABCD沿BD、AC剪开,得到四个全等的直角三角形,已知,OA =4,OB=3,AB=5将这四个直角三角形拼为一个没有重叠和缝隙的四边形,则重新拼成的四边形的周长为_____.31.在长方形ABCD中,10AB=,将长方形ABCD折叠,折痕为EF.AD=,8(1)如图1,当A'与B重合时,EF=_______;(2)如图1,当直线EF过点D时,点A的对应点A'落在线段BC上,则线段EF的长为______.32.如图,P 是▱ABCD 内的任意一点,连接P A 、PB 、PC 、PD ,得到△P AB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论:∠S 1+S 3=S 2+S 4,∠若S 3=2S 1,则S 2=2S 4,∠若S 1+S 3=5,则ABCD 的面积为10;∠S 1+S 2=S 3+S 4.其中正确的结论的序号是____________(把所有正确结论的序号都填在横线上).33.如图, 直线l 是四边形ABCD 的对称轴,若AB CD =,有下面的结论:∠AB BC ⊥;∠AC BD ⊥;∠//AB CD ;∠AO OC =.其中正确的结论有__.34.如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形,恰好能拼成这样一个“勾股圆方图”,则该矩形与拼成的正方形的周长之比为________.35.如图,平行四边形ABCD 中,45B ∠=︒,7BC =,CD =E ,F 分别是边AB ,BC 的中点,连接CE ,DF ,取CE ,DF 的中点G ,H ,连接GH ,则GH 的长度为__________.36.如图,正方形ABCD的边长为1,AC,BD是对角线,将∠DCB绕着点D顺时针旋转45°得到∠DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:∠DE平分∠ADB;∠BE∠四边形AEGF是菱形;∠BC+FG=1.5.其中结论正确的序号是_______.37.如图,点E、F是平行四边形ABCD的边AB、DC上的点,F与DE相交于点P,BF与CE相交于点Q若S△APD=14cm2,S△BCQ=16cm2,四边形PEQF的面积为______.38.如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为_____.39.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为__________.三、解答题40.□ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F ,四边形AFCE 是否是菱形?为什么?41.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,延长CD 到E ,使DE CD =,连接AE .(1)求证:四边形ABDE 是平行四边形;(2)连接OE ,若60ABC ∠=︒,且8AD DE ==,求OE 的长.42.如图,点E 、F 分别在ABCD 的边AB 、CD 的延长线上,且BE =DF ,连接AC 、EF 、AF 、CE ,AC 与EF 交于点O .(1)求证:AC 、EF 互相平分;(2)若EF 平分∠AEC ,判断四边形AECF 的形状并证明.43.正方形ABCD 的对角线交点为O ,连AE 交BC 于E ,交OB 于F ,2EC FO =,求证:AE 平分BAC ∠.44.如图,在三角形ABC 中,90C ∠=︒,四边形DEFC 是边长为4的正方形,且D 、E 、F 分别在边AC AB BC 、、上.把三角形ADE 绕点E 逆时针旋转一定的角度.(1)当点D 与点F 重合时,点A 的对应点G 落在边BC 上,此时四边形ACGE 的面积为___________;(2)当点D 的对应点1D 落在线段BE 上时,点A 的对应点为点1A ,在旋转过程中点A 经过的路程为1l ,点D 经过的路程为2l ,且12:3:2l l =,求线段1AD 的长. 45.如图所示,已知四边形ABCD 是平行四边形,在AB 的延长线上截取BE=AB ,BF=BD ,连接CE ,DF ,相交于点M .求证:CD=CM .46.如图,在直角梯形ABCD 中,AD ∠BC ,AD ∠CD ,M 为腰AB 上一动点,联结MC 、MD ,AD =10,BC =15,cot B 512=.(1)求线段CD 的长.(2)设线段BM 的长为x ,∠CDM 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域.47.在Rt ABC 与Rt BDE 中,90ABC DBE ∠=∠=︒,AB BC =,BD BE =.(1)如图1,若点D ,B ,C 在同一直线上,连接AD ,CE ,则AD 与CE 的关系为_________;(2)如果将图1中的BDE △绕点B 在平面内顺时针旋转到如图2的位置,那么请你判断AD 与CE 的关系,并说明理由;(3)如图3,若6AB =,2BD =,连接AE ,分别取DE ,AE ,AC 的中点M ,P ,N ,连接MP ,NP ,MN ,将BDE △绕点B 在平面内顺时针旋转一周,请直接写出旋转过程中MPN△面积的最小值和最大值.48.如图,在矩形ABCD中,AD=4,CD=3,点E为AD的中点.连接CE,将∠CDE 沿CE折叠得∠CFE,CE交BD于点G,交BA的延长线于点M,延长CF交AB于点N.(1)求DG的长;(2)求MN的长.49.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED 的边长;如果不存在,请说明理由.参考答案:1.A【分析】结合平行四边形的性质即可判定.【详解】结合平行四边形的性质可知选项B、C、D均正确,但平行四边形的对角线不垂直,则A不正确.故选A.【点睛】本题考查了平行四边形的性质,熟练掌握平行四边形的性质是正确解题的关键.2.C【分析】根据作法判定出四边形OACB是菱形,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.【详解】解:根据作图,AC=BC=OA,∠OA=OB,∠OA=OB=BC=AC,∠四边形OACB是菱形,∠AB=2,四边形OACB的面积为4,∠12AB•OC=12×2×OC=4,解得OC=4.故选:C.【点睛】本题主要考查菱形的性质与判定,熟练掌握菱形的性质与判定是解题的关键.3.C【分析】根据平行四边形的性质逐项判断即可.【详解】解:A、由平行四边形行两组对边分别平行可得//AB CD,故A正确;B、由平行四边形对角相等可得B D∠=∠,故B正确;C、AC、BD为平行四边形对角线,平行四边形对角线互相平分,但不一定相等,故C错误;D、由平行四边形行两组对边分别平行可得//AD BC,两直线平行同旁内角互补,可得180C D∠+∠=︒,故D正确.故选:C.【点睛】本题主要考查平行四边形的性质及其推论,熟练掌握平行四边形的性质是解题关键.4.B【详解】解:∠四边形ABCD 是平行四边形,∠AD∠BC ,∠∠1=∠A=60°.故选B .5.C【分析】据平行四边形的性质得出AB //CD ,推出∠B +∠C =180°,根据∠B :∠C =1:2,求出∠C 即可.【详解】解:∠四边形ABCD 是平行四边形∠AB //CD ,∠∠B +∠C =180°,∠∠B :∠C =1:2,∠∠C =23×180°=120°,故选:C .【点睛】本题考查了平行线的性质和平行四边形的性质的应用,能熟练地运用性质进行计算是解此题的关键,题目比较典型,难度不大.6.B【分析】由题意可得:2:3OA OD =,又由点A 的坐标为()1,0,即可求得OD 的长,又由正方形的性质,即可求得E 点的坐标.【详解】解:∠正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为2:3, ∠:2:3OA OD =,∠点A 的坐标为()1,0,即1OA =, ∠32OD =, ∠四边形ODEF 是正方形,∠32 DE OD==.∠E点的坐标为:33,22⎛⎫ ⎪⎝⎭.故选:B.【点睛】此题考查了位似变换的性质与正方形的性质.此题比较简单,注意理解位似变换与相似比的定义是解此题的关键.7.C【分析】根据平行四边形的判定定理逐项判断即可.【详解】解:A.根据两组对边分别平行可判定是平行四边形,不符合题意;B.根据平行线性质可得另一对内角相等,根据两组对角分别相等可判定是平行四边形,不符合题意;C.不能判定是平行四边形,可能是等腰梯形,符合题意;D.可通过全等证对角线互相平分,能判定是平行四边形,不符合题意;故选:C.【点睛】本题考查了平行四边形的判定,解题关键是熟知平行四边形的判定定理,准确进行判断.8.D【分析】设这个多边形的边数为n,根据内角和等于外角和列方程解答即可.【详解】解:设这个多边形的边数为n,则()2180360n-⨯︒=︒,解得4n=,故选:D.【点睛】此题考查了多边形内角和与外角和的计算,熟练掌握多边形内角和公式及外角和是解题的关键.9.C【分析】由E、F、G、H分别为AB、BC、CD、DA的中点,得出EF,HG,FG,EH是中位线,再得出四条边相等,根据“四条边都相等的四边形是菱形”进行证明.【详解】解:如图所示,因为E、F、G、H分别为AB、BC、CD、DA的中点,连接AC、BD,因为E、F分别是AB、BC的中点,所以EF=12AC ,且EF∠AC同理可得HG=12AC ,且HG∠AC , FG=12BD ,且FG∠BD , EH=12BD ,且EH∠BD , ∠EF∠HG ,HE ∠FG ,∠四边形EFGH 是平行四边形,又因为等腰梯形的对角线相等,即AC=BD ,因此有EF=FG=GH=HE ,所以连接等腰梯形各中点所得四边形为菱形.故选:C【点睛】此题考查三角形中位线的性质,解题的关键是掌握三角形的中位线定理及菱形的判定.10.B【详解】由题意得:2()32,4,12AB BC AB BC +===得: .故选B.11.D【详解】试题分析:从D,E 处向AC 作高DF,EH .设AB=4k,AD=3k,则AC=5k .由∠AEC的面积=4k×3k=5k×EH,得EH=95k k;根据勾股定理得CH=,∠四边形ACED是等腰梯形,∠CH=AF=95 k,所以DE=5k﹣95k×2=75k.所以DE:AC=75k:5k=7:25.故选D.考点:翻折变换.12.C【分析】由平行四边形的性质可得AD∠BC,且AD=BC,结合角平分线的性质可求得DE=DC=AB=4,则可求得AD的长,可求得答案.【详解】解:∠四边形ABCD为平行四边形,∠AB=CD=4,AD∠BC,AD=BC,∠∠DEC=∠BCE.∠CE平分∠BCD,∠∠DCE=∠BCE,∠∠DEC=∠DCE,∠DE=DC=4.∠AE=3,∠AD=BC=3+4=7.故选C.【点睛】本题主要考查平行四边形的性质,利用平行线的性质及角平分线的性质求得DE=DC是解题的关键.13.C【分析】由矩形的性质可得AO=CO,由线段垂直平分线的性质可得AE=EC,即可求解.【详解】解:∵四边形ABCD是矩形,∴AO=CO,BC=AD,∵EO⊥AC,∴AE=EC,∵△ABE的周长为8,∴AB+AE+BE=8,∴3+BC=8,∴AD =BC =5,故选:C .【点睛】本题考查了矩形的性质,线段垂直平分线的性质,掌握矩形的性质是本题的关键.14.D【分析】由矩形ABCD 中,四边形EGFH 是菱形,易证得()COF AOE AAS ≌,即可得OA OC =,然后由勾股定理求得AC 的长,继而求得OA 的长,又由AOE ABC ∽△△,利用相似三角形的对应边成比例,即可求得答案.【详解】解:如图,连接EF ,交AC 于O ,∠四边形EHFG 是菱形,EF AC OE OF ∴⊥=,,∠四边形ABCD 是矩形,90B D ∴∠=∠=︒,AB CD ∥,ACD CAB ∴∠=∠,在COF 与AOE △中,FCO OAE FOC AOE OF OE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()COF AOE AAS ∴≌,AO CO ∴=,AC AB ==12AO AC ∴==, 90CAB CAB AOE B ∠=∠∠=∠=︒,,AOE ABC ∴∽,∠AO AE AB AC=,=, 2.5AE ∴=,1.5BE ∴=,故选:D .【点睛】本题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质,准确作出辅助线是解此题的关键.15.D【详解】∠AD∠BC 、AB∠CD ,EF∠AB ,GH∠BC ,∠AB∠EF∠DC ,AD∠GH∠BC ,∠共有9个平行四边形,如平行四边形AGPE ,平行四边形BGPF ,平行四边形PEDH ,平行四边形PFCH ,平行四边形ABFE ,平行四边形EFCD ,平行四边形AGHD ,平行四边形BGHC ,平行四边形ABCD ,故选D.16.D【分析】分点M 是AP 的中点和点M 与点N 重合两种情况讨论,由全等三角形的性质和正方形的性质即可求解.【详解】解:当点M 是AP 的中点时,∵四边形P ABC 是正方形,∴PC =P A =AB ,∠CP A =∠P AN =90°,∵N 是AB 的中点,点M 是AP 的中点,∴PM =AN =4,在△CPM 和△P AN 中,PA CP CPA PAN PM AN =⎧⎪∠=∠⎨⎪=⎩∴△CPM ≌△P AN (SAS ),∴PN =CM ,∴t 42==2, 当点M 与点N 重合时,由正方形的对称性可得PN =CM ,∴t842+==6,故选:D【点睛】本题考查了正方形的性质,全等三角形的性质,利用分类讨论思想解决问题是解题的关键.17.A【详解】试题分析:作在菱形中,,,是的中点是的中点,故答案选A.考点:平行四边形的面积,三角函数.18.B【分析】设EF交BD于G,AC交BD于O,由三角形中位线的性质可得EF=12AC,EF//AC,可得EG为∠AOD的中位线,可得DG=12OD,根据菱形的性质可得BG=34BD,根据菱形的面积公式列方程即可得答案.【详解】设EF交BD于G,AC交BD于O,∠点E F 、分别是菱形ABCD 的边AD 、DC 的中点, ∠EF=12AC ,EF//AC ,∠EG 为∠AOD 的中位线, ∠OG=12OD ,∠四边形ABCD 是菱形, ∠OD=OB=12BD ,BD∠AC , ∠BG=34BD ,BG∠EF , ∠S 菱形ABCD =S 阴影+S △BEF ,阴影部分的面积和是10, ∠12AC·BD=10+12EF·BG=10+12·12AC·34BD , 解得:AC·BD=32.故选:B【点睛】本题考查菱形的性质、三角形中位线的性质及菱形的面积公式,菱形的对角线互相垂直且平分;菱形的面积等于两条对角线乘积的一半;三角形的中位线平行于第三边且等于第三边的一半;熟练掌握相关性质及公式是解题关键.19.C【分析】利用特殊角的三角函数值分别求出11A B 、22A B 、33A B ,以此类推找到规律求出20222022A B ,最后根据202120222022Rt A A B 中20212022202290A B A ∠=︒,20222021202230A A B ∠=︒,即可求解.【详解】解:∠AB 与直线l 所夹锐角为60︒,且1BAB ∠是正方形1ABCB 的一个顶角, ∠11180609030B AA ∠=︒-︒-︒=︒,又∠1190AB A ∠=︒,∠在11Rt AB A △中,11111tan A B AB A AB =⨯∠,∠正方形1ABCB 的边长AB∠11111tan A B AB A AB =⨯∠同理可求得: 222A B =⎝⎭,333A B =⎝⎭,以此类推可知: 20222021202120222022A B ===⎝⎭⎝⎭⎝⎭,∠202120222022Rt A A B 中20212022202290A B A ∠=︒,20222021202230A A B ∠=︒,∠2021202120222022202222A A A B ==⨯⎝⎭,故C 正确.故选:C . 【点睛】本题主要考查了正方形的性质、含特殊角的锐角三角函数等知识,含30°的直角三角形的性质.利用从特殊到一般寻找规律是解题的关键.20.B【分析】根据矩形的判定和平行四边形的性质分别对各个选项进行判断即可.【详解】解: A 、AD AB =时,平行四边形ABCD 是菱形,故选项A 不符合题意; B 、AB AD ⊥时,∠BAD =90°,则平行四边形ABCD 是矩形,故选项B 符合题意; C 、AB AC =时,平行四边形ABCD 不一定是矩形,故选项C 不符合题意;D 、CA BD ⊥时,平行四边形ABCD 是菱形,故选项D 不符合题意;故选:B .【点睛】此题考查的是平行四边形的性质、矩形的判定以及等腰三角形的判定等知识;熟练掌握矩形的判定和平行四边形的性质是解答此题的关键.21.60°【分析】根据图案的特点,可知密铺的一个顶点处的周角,由3个完全相同的等腰梯形的较大内角组成,即可求出等腰梯形的较大内角的度数,进而即可得到答案.【详解】由图案可知:密铺的一个顶点处的周角,由3个完全相同的等腰梯形的较大内角组成,∠等腰梯形的较大内角为360°÷3=120°,∠等腰梯形的两底平行,∠等腰梯形的底角(指锐角)是:180°-120°=60°.故答案是:60°.【点睛】本题主要考查等腰梯形的性质以及平面镶嵌,掌握平面镶嵌的性质是解题的关键.22.5【分析】证明∠BEF∠∠BCD,由相似三角形的性质求得BF•CD,即求得BF•AB,进而由三角形的面积公式求得结果.【详解】解:∠四边形ABCD是矩形,∠AB=CD,∠ABC=∠BCD=90°,∠EF∠BC,∠EF∠CD,∠∠BEF∠∠BDC,∠BF EF BC CD=,∠BC=5,EF=2,∠BF•CD=BC•EF=5×2=10,∠BF•AB=10,∠∠ABF的面积=12BF•AB=5,故答案为:5.【点睛】本题主要考查了矩形的性质,相似三角形的判定与性质,三角形的面积计算,关键是由相似三角形求得BF•AB的值.23.6【分析】根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.【详解】解:∠菱形的两条对角线长分别为3和4,∠菱形的面积为134=6 2⨯⨯故答案为:6【点睛】本题考查了菱形的性质,菱形的面积通常有两种求法,可以用底乘以高,也可以用对角线乘积的一半求解,计算时要根据具体情况灵活运用.24.【分析】根据圆与其内切正方形的关系,易得圆盖的直径至少应为正方形的对角线的长,已知正方形边长为50cm,进而由勾股定理可得答案.【详解】解:根据题意,知圆盖的直径至少应为正方形的对角线的长;再根据勾股定理,50故答案为:.【点睛】题主要考查正多边形和圆的相关知识;注意:熟记等腰直角三角形的斜边是直角边的 倍,可以给解决此题带来方便.25.【分析】结合正方形面积公式,平方差公式,勾股定理,三角形面积公式,可知()()2223S S BC AC BC AC BC AC -=-=+-,2240BC AC +=,14BC AC ⋅=,然后运用完全平方公式()2222a b a b ab ±=+±求解即可.【详解】解:根据题意,2140S AB ==,22S BC =,23S AC = ∠()()2223S S BC AC BC AC BC AC -=-=+-在Rt ABC 中,根据勾股定理,222BC AC AB +=∠2240BC AC +=∠7Rt ABC S = ∠172BC AC ⋅⋅= ∠14BC AC ⋅=∠BC AC +==BC AC -====∠()()BC AC BC AC +-==即23S S -=故答案为:【点睛】本题考查勾股定理与三角形、正方形的面积,完全平方公式与平方差公式的灵活应用,掌握并熟练应用勾股定理和各类公式是解题的关键.26.40【详解】试题分析:先根据折叠的性质求得、的度数,即可求得、的度数,再根据长方形的性质求解即可.∠50CED ∠='︒,AE 为折痕∠∠∠BAD ∠'. 考点:折叠的性质点评:折叠的性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.27.342π+【分析】根据菱形的性质以及旋转角为30°,连接CD ′和BC ',可得A 、D′、C 及A 、B 、C′分别共线,求出扇形的面积,再根据AAS 证得两个小三角形全等,求得面积,最后根据扇形ACC '的面积-两个小的三角形的面积即可.【详解】解:连接CD ′和BC '∠∠DAB =60°∠30DAC CAB ∠=∠=︒∠30C AB ∠''=︒∠A 、D′、C 及A 、B 、C′分别共线∠AC =∠扇形ACC′的面积为:2303604ππ⨯=∠AC =AC ′,AD′=AB在OCD OC B ''和中CD BC ACD AC D COD C OB '='⎧⎪∠=∠''⎨⎪∠'=∠'⎩∠()OCD OC B AAS ''≌∠OB =OD′,CO =C′O又∠60,30CBC BC O ︒∠'∠=='︒∠90BOC ∠'=︒在Rt BOC '中,())22211BO BO +-=解得13,22BO C O ='=∠S △OCB=12BO C O '⨯⨯=,∠322442C B AC OC S S Sππ''=-=-=+阴影扇形 故答案为:342π+ 【点睛】本题考查了旋转的性质,菱形的性质,扇形的面积公式,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.28.18或16【分析】首先由直角边分别为3和4,求得其斜边,然后分别从以边长为3,4,5的边为对角线拼成一个平行四边形(非矩形),去分析求解即可求得答案. 【详解】解:直角边分别为3和4,∴5=,若以边长为3的边为对角线,则所得的平行四边形的周长是:2(54)18⨯+=; 若以边长为4的边为对角线,则所得的平行四边形的周长是:2(53)16⨯+=;若以边长为5的边为对角线,则所得的平行四边形的周长是:2(34)14⨯+=(此时是矩形,舍去);综上可得:所得的平行四边形的周长是:16或18.故答案为:16或18.【点睛】此题考查了平行四边形的性质以及勾股定理.注意掌握分类讨论思想的应用是解此题的关键.29【分析】如图,连接BD交AC于E,由四边形ABCD是菱形,推出AC∠BD,AE=EC,在Rt△EOD中,利用勾股定理求出DE,在Rt△ADE中利用勾股定理求出AD即可.【详解】如图,连接BD交AC于E.∠四边形ABCD是菱形,∠AC∠BD,AE=EC,∠OA=2OC,AC=3,∠CO=DO=2EO=1,AE=32,∠EO=12,DE=EB==,∠AD=【点睛】本题考查菱形的性质、勾股定理等知识,解题的关键是灵活应用勾股定理解决问题.30.20,22,26,28【分析】以直角三角形边长相等的边为公共边,拼接四边形,再计算周长;【详解】解:∠如图周长=20;∠如图周长=22;∠如图周长=26;∠如图周长=28;∠如图周长=22;∠四边形的周长为:20,22,26,28;故答案为:20,22,26,28.【点睛】本题考查了图形的拼接,四边形的周长;作出拼接图形是解题关键.31.10【分析】(1)根据题意结合图形直接写出答案即可解决问题;(2)根据勾股定理首先求出A C'的长度;再次利用勾股定理求出AE的长度,即可解决问题.【详解】解:(1)如图1,当A'与B重合时,EF=10;(2)如图2,设AE=x,则BE=8-x;∠四边形ABCD为矩形,∠BC=AD=10,DC=AB=8;∠B=∠C=90°;由题意得:=A D AD '=10;由勾股定理得:222A C A D DC 1006436''=-=-=∠A C 6BA 1064''==-=, ,在Rt∠A BE '中,由勾股定理得:222(8)4x x =-+解得:x=5,由勾股定理得:222EF =10+5=125∠EF =【点睛】该命题主要考查了翻折变换及其应用问题;能根据翻折变换的性质准确找出命题图形中隐含的等量关系是解题的关键.32.∠∠【分析】根据平行四边形的的性质可以得到AB =CD ,AD =BC ,设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4,然后利用三角形的面积公式列式整理判断即可得到答案.【详解】解:∠四边形ABCD 是平行四边形,∠AB =CD ,AD =BC ,设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4,hAB 、hBC 分别为平行四边形的AB 边和BC 边的高则S 1=12AB •h 1,S 2=12BC •h 2,S 3=12CD •h 3,S 4=12AD •h 4,hAB = h 1+h 3,hBC =h 2+h 4 ∠12AB •h 1+12CD •h 3=12AB •hAB ,12BC •h 2+12AD •h 4=12BC •hBC ,又∠S 平行四边形ABCD =AB •hAB =BC •hBC ,∠S 2+S 4=S 1+S 3,故∠正确;根据S 3=2S 1只能判断h 3=2h 1,不能判断h 2=2h 4,即不能得出S 2=2S 4,故∠错误; 根据S 1+S 3=S 2+S 4,S 1+S 3=5,能得出ABCD 的面积为5×2=10,故∠正确;由题意只能得到S 2+S 4=S 1+S 3无法得到S 1+S 2=S 3+S 4,故∠错误;故答案为:∠∠.【点睛】本题主要考查了平行四边形的性质,三角形的面积,用平行四边形的面积表示出相对的两个三角形的面积是解题的关键.33.∠∠∠【分析】根据轴对称的性质得到直线l 垂直平分BD ,则根据线段垂直平分线的性质得AB AD =,CD CB =,由于AB=CD ,则AB BC CD BC ===,于是可判断四边形ABCD 为菱形,然后根据菱形的性质对4个结论进行判断.【详解】证明:∠直线l 是四边形ABCD 的对称轴,∴直线l 垂直平分BD ,AB AD ∴=,CD CB =,AB CD =,AB BC CD BC ∴===,∴四边形ABCD 为菱形,AC BD ∴⊥,//AB CD ,OA OC =,所以∠∠∠正确 .故答案为∠∠∠.【点睛】本题考查了轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.也考查了菱形的判定与性质.34.35)【分析】设图2的矩形分割成四个全等三角形的两直角边为a 、b (a >b ),由图1与图2的两个小正方形相同,得出a 与b 的关系,再求出矩形的边长和大正方形的边长,应用周长公式求得其周长,最后便可求得其比值.【详解】解:设图2的矩形分割成四个全等三角形的两直角边为a 、b (a >b ),小正方形的边长为a-b ,矩形的长为2a+a-b=3a-b ,宽为b ,∠矩形的周长为:2(3a-b+b )=6a ,由图2知,中间小正方形的边长为b ,∠a-b=b ,∠a=2b ,∠大正方形的周长为,==∠该矩形与拼成的正方形的周长之比:=故答案为:3:5).【点睛】本题主要考查了勾股定理,矩形的性质,正方形的性质,关键是根据图形求得全等直角三角形的两直角边与矩形和大正方形的边长的关系.35.134【分析】连接DG 并延长,交于AB 延长线于点M ,过点M 作MN ∠CB ,交于CB 延长线于点N ,首先根据平行四边形的性质证明(),CGD EGM AAS ≅得出,DG GM =即可得出1,2HG FM =再利用勾股定理求出FM ,即可求得答案. 【详解】连接DG 并延长,交于AB 延长线于点M ,过点M 作MN ∠CB ,交于CB 延长线于点N ,如图,∠四边形ABCD 为平行四边形,∠CD ∠AB,AB CD ==∠CDG EMG ∠=∠又∠G 为CE 中点,∠,CG GE =在CGD △和EGM 中∠CDG EMG DGC MGE CG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩∠(),CGD EGM AAS ≅∠,DG GM = ,CD EM = ∠1,2HG FM = AB EM =, ∠,AE BM =∠点E 为AB 的中点,∠1,2AE EB AB ==∠12EB BM AB ===, 又∠45,B ∠=︒∠45,MBN ∠=︒∠,BN MN =设,BN MN x ==在Rt BMN 中,∠222,BN MN BM +=∠222x x +=, 解得,5,2x = 即5,2BN MN == ∠点F 为BC 的中点, ∠17,22BF BC == ∠75622FN BF BN =+=+=, 在Rt MNF △中,∠222,NF MN MF +=∠13,2MF = ∠113,24HG FM == 故填:134. 【点睛】本题考查平行四边形的性质,全等三角形的判定与性质,三角形中位线定理,勾股定理,解题关键是熟练掌握平行四边形的性质和三角形中位线定理.36.∠∠∠【分析】根据旋转的性质可知,∠DGH ∠∠DCB ,进而得知DH =DB ,∠H =∠CBD =45°,∠DGH =∠DCB =90°,DG =DC =AD ,之后可证∠ADF ∠∠GDF ,四边形AEGF 是菱形,再根据勾股定理可知AE 的长度,进而可以一一判断选出答案.【详解】解:根据旋转的性质可知,∠DGH ∠∠DCB ,∠DH =DB ,∠H =∠CBD =45°,∠DGH =∠DCB =90°,DG =DC =AD ,在Rt ∠AED 与Rt ∠GED 中,AD =DG ,ED =ED∠Rt ∠AED ∠Rt ∠GED (HL )∠∠ADE =∠GDE ,即DE 平分∠ADB ,故∠正确;在∠ADF 和∠GDF 中,AD =DG ,∠ADF =∠GDF ,DF =DF ,∠∠ADF ∠∠GDF (SAS )∠AF =GF ,∠DAF =∠DGF =45°又∠∠ABD =45°∠FG ∠AE∠∠DAC =45°,∠∠DAC =∠H ,∠AF ∠EG∠四边形AEGF 是平行四边形,又∠AF =GF∠平行四边形AEGF 是菱形,故∠正确;∠∠H =45°,∠HAE =90°∠AE =AH∠AE =AF =HD -AD =BD -AD∠正方形ABCD 的边长为1,根据勾股定理可知BD ==即HD∠AE 1∠BE =)11=2-∠正确; ∠四边形AEGF 是菱形∠FG =AE 1∠BC +FG =1∠错误;综上答案为:∠∠∠.【点睛】本题考查的是正方形的性质,菱形的判定与性质,勾股定理和直角三角形的性质,是一道综合性较强的题,能够充分调动所学知识是解题的关键.37.30cm 2。
初二数学经典四边形习题50道(附答案)

初二数学经典四边形习题50道(附答案)1.在矩形ABCD中,已知AE垂直于BD于点E,且角DAE是角BAE的三倍。
求角EAC的度数。
2.在直角梯形ABCD中,BC=CD=a,且角BCD为60度。
点E和F分别为梯形的腰AB和DC的中点。
求EF的长度。
3.在等腰梯形ABCD中,AB平行于DC,AD=BC,E和F分别为AD和BC的中点。
BD平分角ABC,与EF交于点G,且EG=18,GF=10.求等腰梯形ABCD的周长。
4.在梯形ABCD中,AB平行于CD,以AD和EAC为邻边作平行四边形ACED。
DC的延长线交于BE于点F。
证明:F是BE的中点。
5.在梯形ABCD中,AB平行于CD,AC垂直于CB,AC平分角A,且角B为60度。
已知梯形的周长为20厘米。
求AB的长度。
6.从平行四边形ABCD的各顶点作对角线的垂线AE、BF、CG、DH,垂足分别是E、F、G、H。
证明:EF平行于GH。
7.在梯形ABCD中,对角线交点为E。
在平行边的一边BC的延长线上取一点F,使得三角形ABC和三角形EBF的面积相等。
证明:DF平行于AC。
8.在正方形ABCD中,直线EF平行于对角线AC,与边AB和BC相交于点E和F。
在DA的延长线上取一点G,使AG等于AD。
若EG与DF相交于点H,证明:AH等于正方形的边长。
9.以直角三角形ABC的边AB为边,在三角形ABC的外部作正方形ABDE。
AF是BC边的高,延长FA使AG等于BC。
证明:BG等于CD。
10.在正方形ABCD中,E和F分别是AB和AD延长线上的一点,且AE、AF和AC相等。
EF交BC于点G,交AC于点K,交CD于点H。
证明:EG等于GC等于CH等于HF。
11.在正方形ABCD的对角线BD上,取BE等于AB。
过点E作BD的垂线EF,与CD相交于点F。
证明:CF等于ED。
12.在平行四边形ABCD中,角A和角D的平分线相交于点XXX与DC和AB的延长线交于点G和F。
中考数学四边形专题训练50题(含答案)

中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.若正多边形的一个外角是24°,则这个正多边形( )A .正十二边形B .正十五边形C .正十八边形D .正二十边形 2.若平行四边形中两个相邻内角的度数比为1:2,则其中较小的内角是( ) A .120︒ B .90︒ C .60︒ D .45︒ 3.如图,四边形ABCD ∽四边形EFGH ,80E ∠=︒,90G ∠=︒,120D ∠=︒,则B ∠等于( )A .50︒B .60︒C .70︒D .80︒ 4.已知三角形的3条中位线分别为3cm 、4cm 、6cm ,则这个三角形的周长是( )A .13cmB .26cmC .24cmD .65cm 5.如图,正方形ABCD 中,E ,F 分别在边AD ,CD 上,AF ,BE 相交于G ,若34AE ED =,DF CF =,则AG GF 的值是( )A .59B .611C .713D .1115 6.在平行四边形ABCD 中,∠B =60°,那么下列各式中,不能成立的是( ) A .∠D =60° B .∠A =120° C .∠C +∠D =180° D .∠C +∠A =180°7.下列说法中,不正确的是()A.对角线互相平分的四边形是平行四边形B.对角线相等的四边形是矩形C.对角线互相垂直的矩形是正方形D.对角线互相垂直的平行四边形是菱形8.对角线互相平分且相等的四边形是()A.菱形B.矩形C.正方形D.等腰梯形9.如图,过O外一点P作O的两条切线PD、PB,切点分别为D、B,作直径∠的度数为()AB,连接AD、BD,若80P∠=︒,则AA.50°B.60°C.70°D.80°10.如图,在∠ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE∠AB于E,PF∠AC于F,M为EF中点,则AM的最小值为()A.1B.1.3C.1.2D.1.5∠=︒,11.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处,若148∠=︒,则B232∠的度数为().A.124°B.114°C.104°D.56°12.下列说法正确的是()A.矩形的对角线相互垂直B.菱形的对角线相等C.平行四边形是轴对称图形D.等腰梯形的对角线相等13.如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE 对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:∠△EAG=45°:∠CE=3DE;∠AG∠CF;∠S△FGC=725,其中正确结论的个数是()A.1个B.2个C.3个D.4个14.如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为()A.8B.10C.12D.1415.如图,在四边形ABCD中,∠A=90°,AB=AD=3,M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),E、F分别为D M,MN的中点,则EF长度的最大值为() .A.4B.3C.D.16.下列说法错误的是()A.菱形的面积等于两条对角线乘积的一半B.矩形的对角线相等C.对角线互相垂直的平行四边形是矩形D.对角线相等的菱形是正方形17.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠COF的度数是()A.86°B.84°C.76°D.74°18.如图,在矩形ABCD中,点E、F分别在边AD、DC上,ABE DEF,AB=,26DF=,则BE的长是()DE=,3D.A.12B.15C.19.如图,在一张矩形纸片ABCD中4BC=,点E,F分别在AD,BC上,AB=,8将纸片ABCD沿直线EF折叠,点C落在AD上的点H处,点D落在点G处,连接CE,CH.有以下四个结论:∠四边形CFHE是菱形;∠CE平分∠DCH;∠线段BF的EF=.以上结论中,其中正确结取值范围为34BF≤≤;∠当点H与点A重合时,5论的个数有()A.1个B.2个C.3个D.4个二、填空题=,连接AE交CD于F,那么20.四边形ABCD是正方形,延长BC至E,使CE AC∠的度数为________.AFC21.M为矩形ABCD中AD的中点,P为BC上一点,PE∠MC,PF∠MB,当AB、BC 满足_________时,四边形PEMF为矩形.22.如图,在矩形ABCD中,E,F分别是边AB,BC上的点.将∠A,∠B,∠C按如图所示的方式向内翻折,EQ ,EF ,DF 为折痕.若A ,B ,C 恰好都落在同一点P 上,AE =1,则ED =___.23.如图,△ABC 内接于∠O ,∠BAC =120°,AB =AC ,BD 为∠O 的直径,CD =8,OA 交 BC 于点 E ,则 AE 的长度是________.24.如图,在正五边形ABCDE 中,AC 为对角线,以点A 为圆心,AE 为半径画圆弧交AC 于点F ,连结EF ,则∠1的度数为__.25.如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD 内,装饰图中的三角形顶点E ,F 分别在边AB ,BC 上,三角形∠的边GD 在边AD 上,若图1正方形中MN=1,则CD=____.26.如图,在正方形ABCD 中,点E ,F 分别是BC ,CD 上的点,连接AE ,EF ,AF ,若DF BE EF +=,则EAF ∠=______︒.27.如图,已知抛物线24=-+的顶点为D,与y轴交于点C,过点C作x轴的y x x c平行线AC交抛物线于点A,过点A作y轴的平行线AB交射线OD于点B,若OA OB=,则c的值为_____________.28.如图,点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点,且HG 与EF交于点I,连接HE、FG,若AB=7,BC=6,EF//AD,HG//AB,则HE+FG的最小值是______.29.在□ABCD中,∠A:∠B=2:3,则∠B=____,∠C=_____,∠D=____.30.如图,菱形ABCD中,∠BCD=50°,BC的垂直平分线交对角线AC于点F,垂足为E,连接BF、DF,则∠DFC的度数是_____.'沿对角线AC折叠,得到如图所示的图形.若∠BAO=34°,则31.把长方形AB CD∠BAC的大小为_______.32.如图,M 是▭ABCD 的AB 的中点,CM 交BD 于E ,则图中阴影部分的面积与▱ABCD 的面积之比为_____.33.如图,矩形ABCD 中,AD=6,P 为边AD 上一点,且AP=2,在对角线BD 上寻找一点M ,使AM+PM 最小,则AM+PM 的最小值为_____.34.如图,在▱ABCD 中,BE 、CE 分别平分∠ABC 、∠BCD ,E 在AD 上,BE=12cm ,CE=5cm .则▱ABCD 的周长为_____,面积为_____.35.在平面直角坐标系中,对于不在坐标轴上的任意一点(),P x y ,我们把点11,Q y x ⎛⎫ ⎪⎝⎭称为点P 的“逆倒数点”.如图,在矩形OABC 中,点B 的坐标为(48),,反比例函数()0k y x x =>的图象经过矩形对角线交点M .点D 是该反比例函数图象上的点,点E 是对角线上的一点,且点E 是点D 的“逆倒数点”,点E 的坐标为______.36.如图,正方形ABCD 的对角线AC ,BD 交于点O ,M 是边AD 上一点,连接OM ,过点O 作ON ∠OM ,交CD 于点N .若四边形MOND 的面积是1,则AB 的长为 _____.37.如图,点E 为正方形ABCD 外一点,且ED CD =,连接AE ,交BD 于点F .若40CDE ∠=,则∠DCF 的度数为_______.38.如图,在矩形ABCD 中,5,3AB BC ==,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ,点A 落在矩形ABCD 的边CD 上,连接CE ,则CE 的长是 _____ .39.如图,点E 、F 分别为正方形ABCD 的边AB 、BC 上的点,满足∠EDF =45°.连接DE 、DF 分别交正方形对角线AC 于点H 、G ,再连接EG ,有如下结论:∠AE CF EF +>;∠ED 始终平分∠AEF ;∠∠AEH ∠∠DGH ;∠DE ;∠14DGH DEF S S =△△.在上述结论中,正确的有______.(请填正确的序号)三、解答题40.如图,方格纸中每个小正方形的边长均为1,ABC 的顶点和线段的端点均在小正方形的顶点上.(利用格点和没有刻度的直尺作图,保留作图痕迹)(1)在方格纸1中画出ADC △,使ADC △与ABC 关于直线AC 对称;(2)在方格纸2中画出以EF 线段为一边的平行四边形(点G ,点H 均在小正方形的顶点上),且平行四边形面积为4;(3)在方格纸3中,连接FM ,在FM 上确定一点P ,使得点P 为FM 中点. 41.如图,在平行四边形ABCD 中,∠BAD 的平分线交CD 于点E ,连接BE 并延长交AD 延长线于点F ,若AB =AF .(1)求证:点D 是AF 的中点;(2)若∠F =60︒,CD =6,求∠ABF 的面积.42.如图1,在等腰ABO 中,AB AO =,分别延长AO 、BO 至点C 、点D ,使得CO AO =、DO BO =,连接AD 、BC .()1如图1,求证:AD BC =;()2如图2,分别取边AD 、CO 、BO 的中点E 、F 、H ,猜想EFH 的形状,并说明理由.43.如图,在矩形ABCD 中,M ,N 分别是AD ,BC 的中点,E ,F 分别是线段BM ,CM 的中点,若AB=8,AD=12,则四边形ENFM 的周长是多少?44.如图∠,在矩形OACB 中,点A 在x 轴正半轴上,点B 在y 轴正半轴上,点C 在第一象限,8OA =,6OB =.(1)直接写出点C 的坐标:________;(2)如图∠,点G 在BC 边上,连接AG ,将ACG 沿AG 折叠,点C 恰好与线段AB 上一点C '重合,求线段CG 的长度;(3)如图∠,P 是直线26y x =-上一点,PD PB ⊥交线段AC 于D .若P 在第一象限,且PB PD =,试求符合条件的所有点P 的坐标.45.直线443y x =-+与x 轴交于点A ,与y 轴交于点B ,菱形ABCD 如图放置在平面直角坐标系中,其中点D 在x 轴负半轴上,直线y =x +m 经过点C ,交x 轴于点E .(1)请直接写出点C ,点D 的坐标,并求出m 的值;(2)点P (0,t )是线段OB 上的一个动点(点P 不与O 、B 重合),经过点P 且平行于x 轴的直线交AB 于M ,交CE 于N .当四边形NEDM 是平行四边形时,求点P 的坐标;(3)点P (0,t )是y 轴正半轴上的一个动点,Q 是平面内任意一点,t 为何值时,以点C 、D 、P 、Q 为顶点的四边形是菱形?46.如图,在Rt ∠ABC 中,∠C =90°,AC =8,BC =6.动点P 从点A 出发,沿AB 以每秒5个单位长度的速度向终点B 运动.当点P 不与点A 重合时,过点P 作PD ∠AC 于点D ,以AP ,AD 为边作▱APED .设点P 的运动时间为t 秒.(1)线段AD的长为(用含t的代数式表示).(2)当点E落在BC边上时,求t的值.(3)连结BE,当tan∠CBE=13时,求t的值.(4)若线段PE的中点为Q,当点Q落在∠ABC一边垂直平分线上时,直接写出t的值.47.如图,BC为∠O的直径,BD平分∠ABC交∠O于点D,DA∠AB于点A.(1)求证:AD是∠O的切线;(2)∠O交AB于点E,若AD=2AE,求sin ABC∠的值.48.如图1,已知在四边形ABCD中,AB//CD,90ABC∠=︒,8BC=,6CD=,1tan2A=.动点P从点D DA方向运动,到A点结束;点Q同时从点A出发,以3个单位的速度沿射线AB运动,点P停止运动后,点Q 也随之停止.以AP,AQ为边作平行四边形AQGP.设运动时间为t.(1)求AB的长;(2)连接GC 、GB ,当CGB △为等腰三角形时,求t 的值;(3)如图2,以PQ 为直径作圆与AD 、PG 分别交于点M 、N ,连接MQ 交PG 于点F ,连接NQ 、DG ,∠当点N 为弧MQ 的中点时,求PMQPNQ S S △△的值;∠当PQM CDG ∠=∠时,求PQ =______(请直接写出答案).49.思维启迪:(1)如图1,A ,B 两点分别位于一个池塘的两端,小亮想用绳子测量A ,B 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B 点的点C ,连接BC ,取BC 的中点P (点P 可以直接到达A 点),利用工具过点C 作CD∠AB 交AP 的延长线于点D ,此时测得CD =100米,那么A ,B 间的距离是_____米.思维探索:(2)在∠ABC 和∠ADE 中,AC =BC ,AE =DE ,且AE <AC ,∠ACB =∠AED =90°,将∠ADE 绕点A 逆时针方向旋转,把点E 在AC 边上时∠ADE 的位置作为起始位置(此时点B 和点D 位于AC 的两侧),设旋转角为α,连接BD ,点M 是线段BD 的中点,连接MC ,ME .∠如图2,当∠ADE 在起始位置时,猜想:MC 与ME 的数量关系和位置关系分别是______;∠如图3,当α=90°时,点D 落在AB 边上,请判断MC 与ME 的数量关系和位置关系,并证明你的结论;参考答案:1.B【详解】分析:利用任意凸多边形的外角和均为360°,正多边形的每个外角相等即可求出答案.详解:∠多边形的每个外角相等,且其和为360°,∠这个正多边形的边形为3602415o o ÷=,∠这个正多边形是正十五边形.故选B.点睛:考查了正多边形外角和的知识,正多边形的每个外角相等,且其和为360°,用360除以一个外角的度数,结果即为正多边形的边形.2.C【分析】根据平行四边形的性质来解答即可.【详解】解:∠平行四边形,∠两个相邻内角互补,又∠两个相邻内角的度数比为1:2,∠两个相邻的内角为60°、120°,∠较小的内角为60°.故选:C .【点睛】本题考查平行四边形的性质,熟练掌握平行四边形的相关性质是解题的关键. 3.C【分析】根据相似多边形的对应角相等以及四边形的内角和为360︒解答即可.【详解】解:∠四边形ABCD ∽四边形EFGH∠120H D ∠=∠=︒∠360()70B F E G H ∠=∠=︒-∠+∠+∠=︒故选:C .【点睛】本题考查了相似多边形的性质、多边形的内角和;理解相似多边形的对应角相等是解题的关键.4.B【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出三角形的三边,再求解即可.【详解】解:∠三角形的三条中位线分别为3cm、4cm、6cm,∠三角形的三边分别为6cm,8cm,12cm,∠这个三角形的周长=6+8+12=26cm.故选:B.【点睛】本题考查了三角形中位线的性质,解题的关键是熟记三角形中位线的性质定理.5.B【分析】延长AF交BC的延长线于点H,证明∠ADF∠∠HCF,得到CH=AD,设AE=3x,则DE=4x,AD=7x,证得∠AEG∠∠HBG,得到AE AGBH HG==314,即可求出AGGF【详解】解:延长AF交BC的延长线于点H,∠四边形ABCD是正方形,∠∠D=∠DCH=90°,AD∥BC,∠∠DAF=∠H,∠DF CF=,∠∠ADF∠∠HCF(AAS),∠CH=AD,设AE=3x,则DE=4x,AD=7x,∠CH=AD=BC=7x,∠AD∥BC,∠∠AEG∠∠HBG,∠AE AGBH HG==314,∠AGGF =6 11,故选:B.【点睛】此题考查了正方形的性质,相似三角形的性质,全等三角形的判定及性质,熟记各定理是解题的关键.6.D【详解】解:∠四边形ABCD是平行四边形,∠∠D=∠B=60°.故A成立;∠AD△BC,∠∠A+∠B=180°,∠∠A=180°-∠B=120°,故B成立;∠AD△BC,∠∠C+∠D=180°,故C成立;∠四边形ABCD是平行四边形,∠∠C=∠A=120°,故D不成立,故选D.7.B【分析】根据各四边形的性质对各个选项进行分析从而得出最后答案.【详解】解:A、对角线互相平分的四边形是平行四边形,正确;B、错误,对角线相等的四边形不一定是矩形,对角线相等的平行四边形才是矩形;C、对角线互相垂直的矩形是正方形,正确;D、对角线互相垂直的平行四边形是菱形,正确.故选:B.【点睛】本题主要考查了正方形、平行四边形、菱形的判定方法.解决此题的关键是熟练掌握运用这些判定.8.B【分析】根据平行四边形的判定与矩形的判定定理,即可求得答案.【详解】∠对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形,∠对角线相等且互相平分的四边形一定是矩形.故选B.【点睛】此题考查了平行四边形,矩形,菱形以及等腰梯形的判定定理.此题比较简单,解题的关键是熟记定理.9.A【分析】如图,连接OD ,可得90ODP OBP ∠=∠=︒,再利用四边形的内角和定理求解BOD ∠,从而可得答案.【详解】解:如图,连接OD ,∠过O 外一点P 作O 的两条切线PD 、PB ,∠90ODP OBP ∠=∠=︒,∠80P ∠=︒,∠360909080100DOB ∠=︒-︒-︒-︒=︒, ∠1502A DOB ∠=∠=︒, 故选A .【点睛】本题考查的是切线的性质,四边形的内角和定理的应用,圆周角定理的应用,作出过切点的半径是解本题的关键.10.C【分析】首先证明四边形AEPF 为矩形,可得AM =12AP ,最后利用垂线段最短确定AP 的位置,利用面积相等求出AP 的长,即可得AM .【详解】在△ABC 中,因为AB 2+AC 2=BC 2,所以△ABC 为直角三角形,∠A =90°,又因为PE ∠AB ,PF ∠AC ,故四边形AEPF 为矩形,因为M 为 EF 中点,所以M 也是 AP 中点,即AM =12AP ,故当AP ∠BC 时,AP 有最小值,此时AM 最小, 由1122ABC S AB AC BC AP ∆=⨯⨯=⨯⨯,可得AP =125,AM =12AP =6 1.25= 故本题正确答案为C.【点睛】本题考查了矩形的判定和性质,确定出AP ∠BC 时AM 最小是解题关键.11.A【分析】根据折叠、平行四边形的性质,三角形的内角和定理,即可求出答案.【详解】解:由折叠得,45∠=∠,∠四边形ABCD 是平行四边形,∠AB CD ,∠53∠=∠,∠3=4∠∠,又∠13448∠=∠+∠=︒, ∠154348242∠=∠=∠=⨯︒=︒, 在ABC 中,180521802432124B ∠=︒-∠-∠=︒-︒-︒=︒,故选:A .【点睛】本题考查折叠的性质、平行四边形的性质,三角形的内角和定理等知识,由图形直观得出各个角之间的关系是正确解答的关键.12.D【分析】根据矩形、菱形、平行四边形、等腰梯形的性质进行逐一分析解答即可.【详解】A 、错误,矩形的对角线相等;B 、错误,菱形的对角线相互垂直;C 、错误,平行四边形是中心对称图形;D 、正确,等腰梯形的对角线相等.故选D . 【点睛】此题考查命题与定理,解题关键在于掌握正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉其性质定理.13.C【分析】∠由正方形的性质和翻折的性质可证明Rt△ABG∠Rt△AFG(HL),推出∠BAG=∠F AG,根据∠DAE=∠F AE,可得∠EAG=12∠BAD=45°;∠由题意得EF=DE,GB=CG=GF=6,设DE=EF=x,则CE=12-x,在Rt△ECG中,(12-x)2+36=(x+6)2,求出x,则可得到CE=2DE;∠由CG=BG,BG=GF,可得CG=GF,则∠GFC=∠GCF,因为∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,可推出∠AGB=∠GCF,则AG∠CF;∠由S△GCE=12×GC×CE,又因为△GFC和△FCE等高,可得S△GFC:S△FEC=3:2,S△GFC=3 5×24=725.【详解】解:∠∠正方形ABCD,∠AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,由折叠的性质可得,AF=AD,∠AFE=∠D=90°,∠∠AFG=90°=∠B,AB=AF,又∠AG=AG,∠Rt△ABG∠Rt△AFG(HL),∠∠BAG=∠F AG,∠∠DAE=∠F AE,∠∠EAG=12∠BAD=45°,故∠正确;∠由题意得EF=DE,GB=CG=GF=6,设DE=EF=x,则CE=12-x,在Rt∠ECG中,(12-x)2+62=(x+6)2,∠x=4,∠DE=4,CE=8,∠CE=2DE,故∠错误;∠∠CG=BG,BG=GF,∠CG=GF,∠∠GFC=∠GCF,∠Rt∠ABG∠Rt∠AFG,∠∠AGB=∠AGF,∠∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,∠∠AGB=∠GCF,∠AG∠CF,故∠正确;∠∠S△GCE=12×GC×CE=12×6×8=24,又∠GF=6,EF=4,∠GFC和∠FCE等高,∠S△GFC:S△FEC=3:2,∠S△GFC=35×24=725,故∠正确;综上,正确的是∠∠∠,共3个.故选:C.【点睛】本题考查翻折变换的性质、正方形的性质,本题综合性很强,熟练掌握全等三角形的判定和性质,勾股定理,三角形面积的计算方法是解题的关键.14.B【详解】试题分析:根据平行四边形的性质可知AB=CD,AD∠BC,AD=BC,然后根据平行线的性质和角平分线的性质可知AB=AF,DE=CD,因此可知AF+DE=AD+EF=2AB=12,解得AD=BC=12-2=10.故选B.点睛:此题主要考查了平行四边形的性质和等腰三角形的性质,解题关键是把所求线段转化为题目中已知的线段,根据等量代换可求解.15.B【分析】根据三角形的中位线定理得出EF=12DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN=DB=6,从而求得EF的最大值为3.【详解】解:∠ED=EM,MF=FN,∠EF=12DN,∠DN最大时,EF最大,∠N与B重合时DN最大,此时DN=DB=6,∠EF的最大值为3.故选:B.【点睛】本题考查了三角形中位线定理,勾股定理的应用,熟练掌握定理是解题的关键.16.C【分析】根据有关的定理和定义找到错误的命题即可得到答案;【详解】A、菱形的面积等于对角线乘积的一半,故正确,不符合题意;B、矩形的对角线相等,正确,不符合题意;C、对角线平分且相等的平行四边形是矩形,错误,符合题意;D、对角线相等的菱形是正方形,正确,不符合题意;故选C.【点睛】考查了命题与定理的知识,在判断一个命题正误的时候可以举出反例.17.B【分析】利用正多边形的性质求出∠EOF,∠BOC,∠BOE即可解决问题.【详解】解:由题意:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,∠∠BOE=180°﹣72°﹣60°=48°,∠∠COF=360°﹣108°﹣48°﹣120°=84°,故选:B.【点睛】本题考查正多边形,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于常考题型.18.C【分析】利用相似三角形的性质求出AE的长,再利用勾股定理求解即可.【详解】解:∠ABE DEF,∠AB AE DE DF,∠623AE =,∠9AE=,∠矩形ABCD中,90A∠=︒,∠BE故选:C.【点睛】本题考查了矩形的性质、相似三角形的性质、勾股定理,解题关键是求出AE的长后利用勾股定理求解.19.B【分析】先根据翻折的性质可得CF=FH,∠HFE=∠CFE,可证∠FEH是等腰三角形,可得HE=HF=FC,判断出四边形CFHE是平行四边形,然后根据邻边相等的平行四边形是菱形证明,判断出∠正确;根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时CE平分∠DCH,判断出∠错误;过点F作FM∠AD于M,点H与点A 重合时,设BF=x,表示出AF=FC=8﹣x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=FM=MD=CD,求出BF=4,然后写出BF的取值范围,判断出∠正确;求出ME,再利用勾股定理列式求解得到EF,判断出∠正确.【详解】解:∠将纸片ABCD沿直线EF折叠,∠FC=FH,∠HFE=∠CFE,∠AD△BC,∠∠HEF=∠EFC=∠HFE,HE△FC,∠∠HFE为等腰三角形,∠HE=HF=FC,∠EH与CF都是矩形ABCD的对边AD、BC的一部分,∠EH△CF,且HE=FC,∠四边形CFHE是平行四边形,∠FC=FH,∠四边形CFHE是菱形,故∠正确;∠HC为菱形的对角线,∠∠BCH=∠ECH,∠BCD=90°,∠只有∠DCE=30°时CE平分∠DCH,故∠错误;过点F作FM∠AD于M,点H与点A重合时,BF最小,设BF=x,则AF=FC=8﹣x,在Rt∠ABF中,AB2+BF2=AF2,即42+x2=(8﹣x)2,解得:x=3,点G与点D重合时,点H与点M重合,BF最大,CF=FM=DM=CD=4,∠BF=4,∠线段BF的取值范围为3≤BF≤4,故∠正确;当点H与点A重合时,由∠中BF=3,∠AF=AE=CF=EC=8-3=5,则ME=5﹣3=2,由勾股定理得,EF=∠错误;综上所述,结论正确的有∠∠共2个,故B正确.故选:B.【点睛】本题考查矩形折叠性质,等腰三角形的判定,菱形的判定与性质,勾股定理,掌握矩形折叠性质,菱形的判定与性质,勾股定理是解题关键.20.112.5【分析】根据正方形的性质有∠ACD=∠ACB=45°=∠CAE+∠AEC,根据CE=AC就可以求出∠CAE=22.5°,在△AFC中由三角形的内角和就可以得出∠AFC的度数.【详解】解:∠四边形ABCD是正方形,∠∠ACD=∠ACB=45°.∠∠ACB═∠CAE+∠AEC,∠∠CAE+∠AEC=45°.∠CE=AC,∠∠CAE=∠AEC,∠∠CAE=22.5°.∠∠CAE+∠ACD+∠AFC=180°,∠∠AFC=180°-22.5°-45°=112.5°.故答案为112.5°.【点睛】本题考查了正方形的性质的运用,等腰三角形的性质的运用,三角形的外角与内角的关系的运用及三角形内角和定理的运用.21.12AB BC =##2BC AB =【详解】∠在矩形ABCD 中,M 为AD 边的中点,AB=12BC ,∠AB =DC =AM =MD ,∠A =∠D =90°,∠∠ABM =∠MCD =45°,∠∠BMC =90°,又∠PE ∠MC ,PF ∠MB ,∠∠PFM =△PEM =90°,∠四边形PEMF 是矩形.故答案为:AB =12BC .22.3【分析】连接,EP DP ,根据折叠的性质得出三角形全等,根据三角形全等的性质得出对应边相等,由ED EP PD =+,利用等量代换分别求出,EP PD .【详解】解:连接,EP DP 如下图所示:根据A ,B ,C 恰好都落在同一点P 上及折叠的性质,有,,AQE PQE EBF EPF FPD FCD ≌≌≌,1,1,AE PE EB EP CD PD ∴=====,2AB AE EB =+=,根据正方形的性质得:2AB DC ==,2PD ∴=,ED EP PD =+,123ED ∴=+=,故答案是:3.【点睛】本题考查了翻折的性质,三角形全等的性质,解题的关键是添加辅助线,通过等量代换的思想进行解答.23.4【分析】证明△OAB 是等边三角形,OA ∠BC 即可推出OE =AE ,再利用三角形中位线定理即可解决问题.【详解】解:∠AB =AC ,∠AB AC =,∠OA ∠BC ,BE =EC ,AB =AC∠∠ABC 是等腰三角形∠∠BAE =∠CAE =12∠BAC =60°,∠OA =OB ,∠∠OAB 是等边三角形,∠BE ∠OA ,∠OE =AE ,∠OB =OD ,BE =EC ,∠ OE是△BCD的中位线∠OE=AE=12CD=4.故答案为:4.【点睛】本题考查三角形的外接圆与外心,圆周角定理,垂径定理,三角形的中位线定理,等边三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.54°【分析】根据五边形的内角和公式求出∠ABC,根据等腰三角形的性质,三角形内角和的定理计算∠BAC,再求∠EAF,利用圆的性质得AE=AF,最后求出∠1即可.【详解】解:∠五边形ABCDE是正五边形,∠∠EAB=∠ABC=()5-21805⨯︒=108°,∠BA=BC,∠∠BAC=∠BCA=180-1082︒︒=36°,∠∠EAF=108°﹣36°=72°,∠以点A为圆心,AE为半径画圆弧交AC于点F,∠AE=AF,∠∠1=180-722︒︒=54°.故答案为:54°.【点睛】本题考查了正多边形的内角与圆,熟练掌握正多边形的内角的计算公式、和圆的性质,等腰三角形的性质是解题的关键.25122【分析】根据七巧板中图形分别是等腰直角三角形和正方形计算PH的长,即FF'的长,作高线GG',根据直角三角形斜边中线的性质可得GG'的长,即AE的长,可得结论.【详解】解:如图:∠四边形MNQK是正方形,且MN=1,∠∠MNK=45°,在Rt△MNO中,OM=ON∠NL=PL=OL∠PN=12,∠PQ=12,∠∠PQH是等腰直角三角形,∠PH=FF'BE,过G作GG'∠EF',∠GG'=AE=12MN=12,∠CD=AB=AE+BE=12122.故答案为122.【点睛】本题主要考查了正方形的性质、七巧板、等腰直角三角形的性质及勾股定理等知识.熟悉七巧板是由七块板组成的,完整图案为一正方形:五块等腰直角三角形(两块小形三角形、一块中形三角形和两块大形三角形)、一块正方形和一块平行四边.26.45【分析】延长CB到G,使BG=DF,根据正方形的性质得到AD=AB,∠D=∠ABE=90°,求得∠ABG=∠D=90°,根据全等三角形的性质得到AG=AF,∠GAB=∠DAF,求得GE=EF,推出∠AGE∠∠AFE(SSS),根据全等三角形的性质得到∠GAE=∠EAF,根据全等三角形的性质即可得到结论.【详解】解:延长CB到G,使BG=DF,∠四边形ABCD是正方形,∠AD=AB,∠D=∠ABE=90°,∠∠ABG =∠D =90°,在∠ADF 与∠ABG 中,AB AD ABG D BG DF =⎧⎪∠=∠⎨⎪=⎩,∠∠ADF ∠∠ABG (SAS ),∠AG =AF ,∠GAB =∠DAF ,∠DF +BE =EF ,EG =BG +BE =DF +BE ,∠GE =EF ,在∠AGE 与∠AFE 中,AG AF AE AE GE EF =⎧⎪=⎨⎪=⎩,∠∠AGE ∠∠AFE (SSS ),∠∠GAE =∠EAF ,∠∠GAE =∠GAB +∠BAE =∠DAF +∠BAE =∠EAF ,∠∠BAD =90°,∠∠EAF =45°,故答案为:45.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.27.83【分析】根据抛物线的解析式求得4DH c =-,BF AF OC c ===,然后根据三角形中位线定理得到142c c -=,解得即可. 【详解】解:作抛物线的对称轴,交OA 于E ,交x 轴于H ,∠224()42y x x c x c =-+=-+-,∠顶点为(2)4c -,,∠4DH c =-,∠AC x ∥轴,∠AF OC c AB x ==⊥,轴,∠OA OB =,∠AF BF c ==,∠OH FH =, ∠12DH BF =, ∠142c c -= ∠83c =, 故答案为:83. 【点睛】本题考查了二次函数与几何的综合运用,熟练掌握三角形的中位线定理是解决本题的关键.28【分析】由EF ∠AD ,HG ∠AB ,结合矩形的性质可得四边形AHIE 和四边形IFCG 为矩形,然后根据矩形的性质可的HE +FG 的长度即为AI +CI 的长度,最后利用两点之间,线段最短,求出AC 的长即可.【详解】解:如图所示,连接AI ,CI ,AC ,在矩形ABCD 中,∠BAD =∠BCD =∠B =90°,AB ∠CD ,AD ∠BC ,又∠EF ∠AD ,HG ∠AB ,∠四边形AHIE和四边形IFCG为矩形,∠HE=AI,FG=CI,∠HE+FG的长度即为AI+CI的长度,又∠AI+CI≥AC,∠当A,I,C三点共线时,AI+CI最小值等于AC的长度,在Rt∠ABC中,AC∠HE+FG【点睛】本题考查矩形的判定和性质以及两点之间,线段最短的运用,正确判定四边形AHIE和四边形IFCG为矩形,运用矩形的对角线相等是解题的关键.29.108º,72º,108º【详解】解:∠平行四边形ABCD中,∠A+∠B=180°,又∠∠A:∠B=2:3,∠∠A=72°,∠B=108°,∠∠D=∠B=108°,∠C=∠A=72°.故答案为108º,72º,108º.30.130°【分析】首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB即可解决问题.【详解】∠四边形ABCD是菱形,∠BCD=25°,∠∠ACD=∠ACB=12∠EF垂直平分线段BC,∠FB=FC,∠∠FBC=∠FCB=25°,∠∠CFB=180°﹣25°﹣25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故答案为130°.【点睛】本题考查菱形的性质、线段的垂直平分线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.31.62°【分析】先利用AAS 证明∠AOB∠∠COD ,得出∠BAO=∠DCO=34°,∠B′CO=68°,结合折叠的性质得出∠B′CA=∠BCA=34°,则∠BAC=∠B′AC=56°.【详解】由题意,得∠B′CA∠∠BCA ,∠AB′=AB ,∠B′CA=∠BCA ,∠B′AC=∠BAC .∠长方形AB′CD 中,AB′=CD ,∠AB=CD .在∠AOB 与∠COD 中,90B D AOB COD AB CD ∠∠︒⎧⎪∠∠⎨⎪⎩==== , ∠∠AOB∠∠COD (AAS ),∠∠BAO=∠DCO=34°,∠∠B′CO=90°-∠DCO=56°,∠∠B′CA=∠BCA=28°,∠∠B′AC=90°-∠B′CA=62°,∠∠BAC=∠B′AC=62°.【点睛】考查了折叠的性质、矩形的性质和全等三角形的判定与性质,解题关键是证明∠AOB∠∠COD ,得出∠BAO=∠DCO=34°是解题的关键.32.1:3【详解】试题解析:设平行四边形的面积为1,∠四边形ABCD 是平行四边形, ∠12DAB ABCD S S =,又∠M 是ABCD 的AB 的中点, 则1124DAM DAB ABCD S S S ==,1,2BE MB DE CD == ∠EMB △上的高线与DAB 上的高线比为1.3BE BD ==∠1113212 EMB DABS S=⨯=,∠143 DEC MEBS S,==S阴影面积1111141233 =---=,则阴影部分的面积与▱ABCD的面积比为13.故填空答案:13.33.【详解】分析:作DH平分∠BDC交BC于H.连接AH交BD于M.首先证明P、H关于BD对称,连接AH交BD于M,则AM+PM的值最小,最小值=AH.详解:作DH平分∠BDC交BC于H.连接AH交BD于M.∠四边形ABCD是矩形,∠∠C=∠BAD=∠ADC=90°,∠tan∠ADB=ABAD∠∠ADB=30°,∠∠BDC=60°,∠∠CDH=30°,∠CD∠CH2,△DH=2CH=4,∠DP=DH,∠∠MDP=∠MDH,∠P、H关于BD对称,连接AH交BD于M,则AM+PM的值最小,最小值=AH=点睛:本题考查了矩形的性质,解直角三角形,勾股定理,含30º角的直角三角形的性质,轴对称的性质,作DH平分∠BDC交BC于H.连接AH交BD于M.说明P和H关于BD成轴对称是解答本题的关键.34.39cm60cm2【分析】根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13cm,根据等腰三角形的性质得到AB=CD=12AD=12CD=6.5cm,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.【详解】∠BE、CE分别平分∠ABC、∠BCD,∠∠1=∠3=12∠ABC,∠DCE=∠BCE=12∠BCD,在▱ABCD中,AB=CD,AD=BC,AD∠BC,AB∠CD,∠AD∠BC,AB∠CD,∠∠2=∠3,∠BCE=∠CED,∠ABC+∠BCD=180°,∠∠1=∠2,∠DCE=∠CED,∠3+∠BCE=90°,∠AB=AE,CD=DE,∠BEC=90°,在Rt△BCE中,根据勾股定理得:BC=13cm,∠平行四边形的周长等于:AB+BC+CD+AD=6.5+13+6.5+13=39cm;作EF∠BC于F,根据直角三角形的面积公式得:EF=·6013BE CEBC=cm,∠平行四边形ABCD的面积=BC·EF=601313⨯=60cm2,故答案为39cm,60cm2.【点睛】本题考查了平行四边形的性质、等腰三角形的判定与性质、勾股定理等,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.。
初中数学四边形专题训练50题含参考答案

初中数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1.如果从某个多边形的一个顶点出发,可以作2条对角线,则这个多边形的边数是( )A .4B .5C .6D .7 2.如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC ,BD 就可以判断,其推理依据是( )A .矩形的对角线相等B .矩形的四个角是直角C .对角线相等的四边形是矩形D .对角线相等的平行四边形是矩形3.在Rt ABC 中,90,30,4,C A BC D E ∠=︒∠=︒=、分别为AC AB 、边上的中点,连接DE 到F ,使得2EF ED =,连接BF ,则BF 长为( )A .2B .C .4D .4.一个多边形的内角和是外角和的5倍,这个多边形边数为( ) A .14 B .12 C .10 D .8 5.在平面直角坐标系中,矩形ABCD 的位置如图所示,其中(1,1)B --,点A 在第二象限,//AB y 轴,3,4AB BC ==,则顶点D 的坐标为( )A.(3,2)B.(2,2)C.(3,3)D.(2,3)6.下列选项中,能判定四边形ABCD是平行四边形的是()A.AB//CD,AD=BC B.∠A=∠D,∠B=∠CC.AB//CD,∠A+∠B=180°D.∠A=∠C,∠B+∠D=180°7.下列命题正确的是()A.同一边上两个角相等的梯形是等腰梯形B.一组对边平行,一组对边相等的四边形是平行四边形C.如果顺次连接一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形D.对角线互相垂直的四边形面积等于对角线乘积的一半8.下列命题中,正确的是()A.梯形的对角线相等B.菱形的对角线不相等C.矩形的对角线不能互相垂直D.平行四边形的对角线可以互相垂直9.如图,已知点D、E分别是△ABC的边AB、CB的中点,若AB=8,CE=6,AC=10,则△BDE的周长为()A.12B.15C.19D.2410.一个正多边形的每个外角都等于36°,那么它是()A.正五边形B.正六边形C.正八边形D.正十边形11.如图,将一边长AB为4的矩形纸片折叠,使点D与点B重合,折痕为EF,若EF=)A .32B .28C .30D .36 12.将如图甲所示的长方形沿着虚线剪开得到两个全等三角形,现拼成如图乙所示的图形,取BC 的中点O ,连接OA ,OD ,AD ,若22.5ACB ∠=︒,4BC =,则AOD △的周长是( )A .4B .C .4D .4+13.如图,ABD △是等边三角形,CBD △是等腰三角形,且BC DC =,点E 是边AD 上的一点,满足//CE AB ,如果8AB =,6CE =,那么BC 的长是( )A .6B .CD .14.如图,在矩形ABCD 中,3AB =,6BC =,点O 为对角线AC 和BD 的交点,延长BA 至E ,使AE AB =,以AE 为边向右侧作矩形AEFG ,点G 在AD 上,若4AG =,过点O 的一条直线平分该组合图形的面积,并分别交EF 、BC 于点P 、Q ,则2PQ 的值为( )A .39B .40C .41D .42 15.凸n 边形恰好只有三个内角是钝角,这样的多边形边数n 的最大值是( ) A .7 B .6 C .5 D .4 16.如图,点E 为菱形ABCD 边上的一个动点,并沿A →B →C →D 的路径移动,设点E 经过的路径长为x ,∠ADE 的面积为y ,则下列图象能大致反映y 与x 的函数关系的是( )A .B .C .D .17.如图,AB CD =,AD BC =,4=AD ,6BE =,DCE △的面积为3,则四边形ABCD 的面积为( )A .10B .12C .15D .2018.如图,在矩形纸片ABCD 中,5AB =,3BC =,将BCD △沿BD 折叠到BED 位置,DE 交AB 于点F ,则cos ADF ∠的值为( )A .817B .715C .1517D .815 19.如图,矩形ABCD 中,2AB =,4BC =.点E ,G 分别在边BC ,AD 上,点F ,H 在对角线AC 上.若四边形EFGH 是菱形,则AG 的长是( )A .2BC .52D 20.如图,矩形ABCD 中,6,8AB BC ==.点E 、F 分别为边BC 、AD 上一点,连接EF ,将矩形ABCD 沿着EF 折叠,使得点A 落到边CD 上的点A '处,且2DA A C '=',则折痕EF 的长度为( )A .B .C D二、填空题21.▱ABCD 中,AC 、BD 交于点O ,已知6AB =,8AC =,10BD =,则DOC 的周长为______.22.如图,平行四边形OABC 的边OA 在x 轴上,顶点C 在反比例函数y =k x的图象上,BC 与y 轴相交于点D ,且D 为BC 的中点,若平行四边形OABC 的面积为6,则k =_____.23.四边形具有不稳定性.如图,矩形ABCD 按箭头方向变形成平行四边形A B C D '''',当变形后图形面积是原图形面积的一半时,则A '∠=________.24.如图,ABCD 的对角线交于点O .点M ,N ,P ,Q 分别是ABCD 四条边上不重合的点.下列条件能判定四边形MNPQ 是平行四边形的有_____(填序号). ∠,AQ CN AM CP ==;∠,MP NQ 均经过点O :∠NQ 经过点O ,AQ CN =.25.如图,DE 为ABC ∆的中位线,点F 在DE 上,且AFC ∠为直角,若6AC cm =,8BC cm =,则DF 的长为__________cm .26.在ABCD 中,3AD =,2AB =,则ABCD 的周长是______.27.如图,在▱ABCD 中,对角线 AC 、BD 相交于 O ,E 为 DC 边的中点,如果▱ABCD 的周长为 24, 且12AB BC =,则 OE 的长为_______.28.矩形纸片ABCD ,长8cm AD =,宽4cm AB =,折叠纸片,使折痕经过点B ,交AD 边于点E ,点A 落在点A '处,展平后得到折痕BE ,同时得到线段BA ',EA ',不再添加其它线段,当图中存在30角时,AE 的长为__________厘米.29.如图,将边长为4的正方形ABCD 沿着折痕EF 折叠,使点B 落在边AD 的中点G 处,则BE 的长为________.30.各角都相等的十五边形的每个内角的度数是_____度.31.如图,在Rt ABC 中,90ACB ∠=︒,以斜边AB 为边向下作正方形ADEB ,过点E 作EF BC ∥交AC 于点F ,过点C 作CG BE ∥交EF 于点G ,连接DG ,若3AF =,15DE =,则四边形CGEB 的面积为______.32.如图,矩形ABCD的两条对角线相交于点O,CD=A为圆心,AD长为半径画弧,此弧恰好经过点O,并与AB交于点E,则图中阴影部分的面积为_____.33.如图,在平行四边形ABCD中,AD=5,AB=3,BE平分∠ABC,则DE=_____.34.在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于A、B,在AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,则此正方形落在x轴正半轴的顶点坐标为_____.35.如图,在矩形ABCD中,点E在BC上,连接AE、DE,若2==,AD DE∠=︒,则CE的长为______________.BAE15AE=,四边形ABCD是平行四边形,且顶点A、B、36.如图,在半圆O中,直径10C在半圆上,点D在直径AE上,连接CE,若8AD=,则CE长为________.37.如图,正方形ABCD内接于圆O,点E为BC上一点,连接BE,若15∠=,CBE5BE =,则正方形ABCD 的边长为________,BE 的长为________.38.如图,ABCD 的顶点A 、B 的坐标分别是()1,0-、()0,2-,顶点C 、D 均在函数(0,0)k y k x x =>>的图象上,AD 交y 轴于点E ,若612ABE ABCD S S ==四边形,则k 的值为_____________.39.如图,将边长为4的正方形ABCD 纸片沿EF 折叠,点C 落在AB 边上的点G 处,点D 与点H 重合, CG 与EF 交于点P ,取GH 的中点Q ,连接PQ ,则GPQ 的周长最小值是__________.40.在ABC 中,已知45ABC ∠=,BD AC ⊥于D ,2CD =,3AD =,则BD 的长为________.三、解答题41.如图,二次函数2y x bx c =-++的图像经过()0A 1,,()03B -,两点.(1)求这个抛物线的解析式及顶点坐标;(2)在抛物线的对称轴上是否存在一点P ,使得O 、B 、C 、P 四点为顶点的四边形是平行四边形?若存在,请直接写出P 点坐标;若不存在,请说明理由.42.如图,点A 在双曲线y=(x >0)上,点B 在双曲线y=﹣(x <0)上,且AB 平行于x 轴,BC∠AO 交x 轴于点C ,交双曲线y=﹣(x <0)于点D ,连接AD . (1)设点A 的纵坐标为n ,用n 表示AB 的长为_________;(2)当OC=3时,求点D 的坐标.43.已知:如图,四边形DEBF 是平行四边形,且AE CF =.求证:四边形ABCD 是平行四边形.44.已知:点D 是ABC ∆的边BC 的中点,DE AB ⊥,DF AC ⊥,垂足分别为E 、F ,且BE CF =.(1)如图1,求证:AE AF =;(2)如图2,若90BAC ︒∠=,连接AD 交EF 于M ,连接BM 、CM ,在不添加任何辅助线的情况下,直接写出图中所有与AEF ∆面积相等的等腰三角形.45.已知:如图,已知∠O 的半径为1,菱形ABCD 的三个顶点A 、B 、D 在∠O 上,且CD 与∠O 相切.(1)求证:BC 与∠O 相切;(2)求阴影部分面积.46.在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.【动手操作】某数学小组对图1的矩形纸片ABCD 进行如下折叠操作:第一步:如图2,把矩形纸片ABCD 对折,使AD 与BC 重合,得到折痕MN ,然后把纸片展开;第二步:如图3,将图2中的矩形纸片沿过点B 的直线折叠,使得点A 落在MN 上的点A '处,折痕与AD 交于点E ,然后展开纸片,连接AA ',BA ',EA .【问题解决】(1)观察猜想:A BC '∠=______度(2)请判断图3中ABA '△的形状,并说明理由;(3)如图4,折痕BE 与MN 交于点F ,BA '的延长线交直线CD 于点P ,若1MF =,7BC =,请求出PD 的长.47.如图,在矩形ABCD 中,E 是对角线AC 上一点(不与A 、C 重合),过点E 作EF //CD ,且EF =DC ,连接DE 、BF 、CF .(1)如图1,若AE=AB,求证:四边形ABFE是菱形.DE∠AC时,求线段BF的长.(2)如图2,若AB=2,BC48.已知:ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点.(1)如图∠,求证:DF=BE;(2)如图∠,连接DE、BF,求证:四边形DEBF是平行四边形.49.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP∠AB交边CD于点P,连接NM,NP.(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;(2)求证:NM=NP;(3)当∠NPC为等腰三角形时,求∠B的度数.参考答案:1.B【分析】根据n 边形从一个顶点出发可引出()3n -条对角线,得出32n -=,求出n 即可.【详解】解:设这个多边形的边数是n ,由题意得32n -=,解得5n =.故选:B .【点睛】本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.掌握n 边形从一个顶点出发可引出()3n -条对角线是解题的关键.2.D【分析】根据矩形的判定定理:对角线相等的平行四边形是矩形即可判定.【详解】解:这种做法的依据是对角线相等的平行四边形为矩形,故选D .【点睛】本题主要考查对矩形的性质和判定的理解和掌握,能熟练地运用矩形的性质解决实际问题是解此题的关键.3.C【分析】根据直角三角形的性质求出AB ,进而求出AE 、EB ,根据三角形中位线定理得到DE ∠BC ,得到∠AED =∠AED =60°,根据等边三角形的判定定理和性质定理解答即可.【详解】解:在Rt ∠ABC 中,∠C =90°,∠A =30°,BC =4,∠AB =2BC =8,∠ABC =60°,∠E 为AB 边上的中点,∠AE =EB =4,∠D 、E 分别为A C 、AB 边上的中点,∠DE ∠BC ,∠∠AED =∠AED =60°,∠∠BEF =∠ABC =60°,在Rt ∠AED 中,∠A =30°,∠AE =2DE ,∠EF =2DE ,∠AE =EF ,∠∠BEF 为等边三角形,∠BF =BE =4,故选:C .【点睛】本题考查的是三角形中位线定理、等边三角形的判定和性质、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键. 4.B【分析】设这个多边形有n 条边,根据内角和是它的外角和的5倍,列出方程,然后解方程即可.【详解】解:设这个多边形有n 条边.由题意得:(2)1803605n -⨯︒=︒⨯,解得n =12.故这个多边形的边数是12.故选B【点睛】此题主要考查了多边形的外角和,内角和公式,做题的关键是正确把握多边形的内角和公式为:2180()n -⨯︒,外角和为360°.5.A【分析】由矩形的性质可得3AB CD ==,4CB AD ==,////AD BC x 轴,////AB CD y 轴,则可求点D 坐标. 【详解】解:四边形ABCD 是矩形3AB CD ∴==,4CB AD ==,//AD BC ,//AB CD ,且//AB y 轴,////AD BC x ∴轴,////AB CD y 轴,(1,1)B --,3AB =,4BC =,∴点C 横坐标为3,点A 纵坐标为2,∴点D 坐标为(3,2),故选:A .【点睛】本题考查了矩形的性质,坐标与图形性质,熟练运用矩形的性质是本题的关键. 6.C【分析】平行四边形的判定定理:(1)两组对边分别平行的四边形是平行四边形(2)两组对边分别相等的四边形是平行四边形(3)一组对边平行且相等的四边形是平行四边形(4)两组对角分别相等的四边形是平行四边形(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定定理逐个分析即可解答.【详解】解:A、AB//CD,AD=BC不能判定四边形ABCD是平行四边形,故此选项错误;B、∠A=∠D,∠B=∠C不能判定四边形ABCD是平行四边形,故此选项错误;C、因为∠A+∠B=180°,所以AD//BC,又因为AB//CD,所以四边形ABCD是平行四边形,故此选项正确;D、∠A=∠C,∠B+∠D=180°不能判定四边形ABCD是平行四边形,故此选项错误;故选C.【点睛】本题主要考查平行四边形的判定定理,解决本题的关键是要熟练掌握平行四边形的判定定理.7.D【详解】试题分析:A、同一底上两个角相等的梯形可能是等腰梯形也可能是直角梯形,故A选项错误;B、一组对边平行且相等的四边形不一定是平行四边形,故B选项错误;C、如果顺次连接一个四边形各边中点得到的是一个正方形,那么原四边形对角线相等且互相垂直,不是任意的四边形,故C选项错误;D、对角线互相垂直的四边形面积等于对角线乘积的一半,故D选项正确.故选D.考点:1.等腰梯形的判定;2.平行四边形的判定;3.正方形的判定.8.D【详解】试题分析:根据特殊四边形的性质逐一作出判断:A .梯形的对角线不一定相等,命题错误;B.当菱形满足一个角是直角,即为正方形时,菱形的对角线相等,命题错误;C.当矩形满足一组邻边相等,即为正方形时,矩形的对角线互相垂直,命题错误;D.当平行四边形满足一组邻边相等,即为菱形时,平行四边形的对角线可以互相垂直,命题正确.故选D.考点:特殊四边形的性质.9.B【分析】根据三角形中位线定理得到DE=12AC=5,根据中点定义可得BE=CE=6,BD=12AB=4,再根据三角形的周长公式得到BD+BE+DE,计算即可.【详解】解:∠点D、E分别是△ABC的边AB、CB的中点,∠DE=12AC=5,BE=CE=6,BD=12AB=4,∠△BDE的周长=BD+BE+DE=4+6+5=15,故选:B.【点睛】本题考查三角形中位线性质,熟练掌握三角形中位线性质是解题的关键.10.D【详解】试题分析:正多边形的边数=外角和÷每个外角的度数.考点:多边形的外角11.A【分析】连接BD交EF于O,由折叠的性质可推出BD∠EF,BO=DO,然后证明∠EDO∠∠FBO,得到OE=OF,设BC=x,利用勾股定理求BO,再根据∠BOF∠∠BCD,列出比例式求出x,即可求矩形面积.【详解】解:连接BD交EF于O,如图所示:∠折叠纸片使点D与点B重合,折痕为EF,∠BD∠EF,BO=DO,∠四边形ABCD是矩形,∠AD∠BC∠∠EDO=∠FBO在∠EDO和∠FBO中,∠∠EDO=∠FBO,DO=BO,∠EOD=∠FOB=90°∠∠EDO∠∠FBO(ASA)∠OE =OF =12EF ∠四边形ABCD 是矩形,∠AB =CD =4,∠BCD =90°,设BC =x ,BD∠BO , ∠∠BOF =∠C =90°,∠CBD =∠OBF ,∠∠BOF ∠∠BCD , ∠OB BC =OF CD,即:2x 解得:x =8,∠BC =8,∠S 矩形ABCD =AB •BC =4×8=32,故选:A .【点睛】本题考查矩形的折叠问题,熟练掌握折叠的性质,全等三角形的判定,以及相似三角形的判定与性质是解题的关键.12.D【分析】根据直角三角形斜边的中线等于斜边的一半可得AOC 和BOD 均为等腰三角形,由22.5ACB ∠=︒,可得:45AOB DOC ∠=∠=︒,证得AOD △为等腰直角三角形,根据勾股定理求得AD =【详解】解:由题意可知ABC 与DBC △全等,且都为直角三角形,∠点O 是BC 的中点, ∠122OA OD BC BO CO =====, ∠AOC 和BOD 均为等腰三角形,∠22.5ACB ∠=︒,∠22.5OAC ∠=︒,∠45AOB OAC ACB ∠=∠+∠=︒,同理可得:45DOC ∠=︒,∠18090AOD AOB COD ∠=︒-∠-∠=︒,在Rt AOD 中,AD∠AOD △的周长是224AD OA OD ++=+=+故选:D .【点睛】本题考查了矩形的性质,全等三角形的性质,直角三角形斜边的中线,勾股定理等知识,根据题意证出AOD △为等腰直角三角形是解题的关键.13.B【分析】连结AC ,过E 作EF ∠AB 于F ,过C 作CG ∠AB 于G ,先确定AC 为对称轴,得到∠BAC =∠DAC ,∠ACB =∠ACD ,由CE∥AB ,可得∠ECA =∠BAC =∠EAC ,得等腰三角形AE =CE =6,求出AF =AE cos60°=3,EF =AE sin60°=EFGC 为矩形,求出GB = AF +FG -AB =1,在Rt △BCG 中,由勾股定理BC【详解】解:连结AC ,过E 作EF ∠AB 于F ,过C 作CG ∠AB 于G ,∠△ABC 为等边三角形,△BCD 为等腰三角形,AC 为对称轴,∠∠BAC =∠DAC ,∠ACB =∠ACD ,∠CE∥AB ,∠∠ECA =∠BAC =∠EAC ,∠AE =CE =6,∠AF =AE cos60°=61=32⨯,∠EF =AE sin60°=6 ∠CE∥AB ,EF ∠AB , CG ∠AB ,∠FE ∠EC ,CG ∠EC ,∠∠EFG =∠FEC =∠CGF =90°∠四边形EFGC 为矩形,∠EF =CG CE =FG =6,∠GB = AF +FG -AB =3+6-8=1,在Rt ∠BCG 中,由勾股定理BC =故选择:B .【点睛】本题考查等边三角形性质,等腰三角形判定与性质,锐角三角函数,矩形判定与性质,勾股定理,掌握等边三角形性质,等腰三角形判定与性质,锐角三角函数,矩形判定与性质,勾股定理是解题关键.14.B【分析】根据题意可得PQ 必过矩形EFGA 的对角线交点,连接AF ,EG 交于点H ,取AE 的中点M ,AB 的中点N ,连接HM ,ON ,过点H 作HT ∠ON 于T ,设PQ 与AD 的交点为S ,根据三角形中位线定理可得133,22ON BC AN ===,∠ANO =∠ABC =90°,32,2NH AM ==,∠AMH =90°,再由勾股定理可得OH 的长,再证明∠ASO ∠∠CQO ,可得SO =OQ ,即可求解.【详解】解:∠过点O 的一条直线平分该组合图形的面积,∠PQ 必过矩形EFGA 的对角线交点,连接AF ,EG 交于点H ,取AE 的中点M ,AB 的中点N ,连接HM ,ON ,过点H 作HT ∠ON 于T ,设PQ 与AD 的交点为S ,∠四边形ABCD 是矩形,∠AO =CO ,又∠点N 是AB 的中点,∠133,22ON BC AN ===,ON ∠BC , ∠∠ANO =∠ABC =90°,同理:32,2NH AM ==,∠AMH =90°,∠HT∠NO,∠四边形MHTN为矩形,∠MH=NT=2,MT=MN=3,∠TO=1,∠HO=∠AD∠BC,∠∠DAC=∠BCA,∠ASO=∠CQO,在∠ASO和∠CQO中,∠DAC ACBASO CQOAO CO∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠ASO∠∠CQO(AAS),∠SO=OQ,同理PH=SH,∠2PQ HO==∠240PQ=.故选:B【点睛】本题考查了矩形的性质,三角形中位线定理,全等三角形的判定和性质,勾股定理,灵活运用这些性质解决问题是本题的关键.15.B【分析】由题意知在n边形的外角中恰好有3个锐角,则其余(n-3)个外角是直角或钝角,而n个外角中最多只能有4个直角或3个钝角,而4个直角已不可能,所以n-3≤3,由此即得答案.【详解】解:因为n 边形恰好只有三个内角是钝角,所以在n 边形的外角中恰好有3个锐角,所以其余(n -3)个外角是直角或钝角,又由于n 边形的外角和是360°,其n 个外角中最多只能有4个直角或3个钝角,而4个直角显然已不可能,所以n -3≤3,解得n ≤6,即n 的最大值为6.故选B.【点睛】本题考查了多边形的内角、外角的概念与外角和,从多边形的外角的角度入手分析是解题的关键.16.D【分析】分三段来考虑点E 沿A→B 运动,∠ADE 的面积逐渐变大;点E 沿B→C 移动,∠ADE 的面积不变;点E 沿C→D 的路径移动,∠ADE 的面积逐渐减小,据此选择即可.【详解】解:点E 沿A →B 运动,∠ADE 的面积逐渐变大,设菱形的边长为a ,∠A =β, ∠AE 边上的高为AB sinβ=a •sinβ,∠y =12•a •sinβ,点E 沿B →C 移动,∠ADE 的面积不变;点E 沿C →D 的路径移动,y =12(3a ﹣x )•sinβ,∠ADE 的面积逐渐减小.故选:D .【点睛】本题考查了动点问题的函数图像,分析判断几何动点问题的函数图象的题目一般有两种类型:(1)观察型(函数的图象有明显的增减性差异):根据题目描述,只需确定函数值在每段函数图象上随自变量的增减情况或变化的快慢即可得解.(2)计算型:先根据自变量的取值范围对函数进行分段,再求出每段函数的解析式,最后由每段函数的解析式确定每段函数的图象.17.B【分析】根据两组对边分别相等的四边形是平行四边形证明四边形ABCD 是平行四边形,再根据DCE △的面积为3计算出DH ,最后根据平行四边形的面积公式即可得到答案.【详解】解:过点D 作DH CE ⊥,垂足为H ,∠AB CD =,AD BC =,∠四边形ABCD 是平行四边形,∠2CE BE BC BE AD =-=-=, ∠112322DCE S CE DH DH =⨯=⨯⨯=, ∠3DH =,∠4312ABCD S BC DH =⨯=⨯=,故选:B .【点睛】本题考查平行四边形的判断,解题的关键是熟知两组对边分别相等的四边形是平行四边形.18.C【分析】先根据矩形的性质和折叠的性质,利用“AAS”证明AFD EFB ∆∆≌,得出AF EF =,DF BF =,设AF EF x ==,则5BF x =-,根据勾股定理列出关于x 的方程,解方程得出x 的值,最后根据余弦函数的定义求出结果即可.【详解】解:∠四边形ABCD 为矩形,∠CD =AB =5,AB =BC =3,90A C ∠=∠=︒,根据折叠可知,3BE BC ==,5DE DE ==,90∠=∠=︒E C ,∠在∠AFD 和∠EFB 中903A E AFD EFB AD BE ∠=∠=︒⎧⎪∠=∠⎨⎪==⎩,∠AFD EFB ∆∆≌(AAS ),∠AF EF =,DF BF =,设AF EF x ==,则5BF x =-,在Rt BEF ∆中,222BF EF BE =+,即()22253x x -=+, 解得:85x =,则817555DF BF ==-=, ∠315cos 17175AD ADF DF ∠===,故C 正确.故选:C .【点睛】本题主要考查了矩形的折叠问题,三角形全等的判定和性质,勾股定理,三角函数的定义,根据题意证明AFD EFB ∆∆≌,是解题的关键.【分析】连接EG 交AC 于O ,根据菱形和矩形的性质证明∠CEO ∠∠AGO ,推出AO=CO ,由勾股定理求出AC 得到AO ,再证明∠AOG ∠∠ADC ,得到AG AO AC AD=,代入数值即可求出AG .【详解】解:连接EG 交AC 于O ,∠四边形EFGH 是菱形,∠EG ∠FH ,OE=OG ,∠四边形ABCD 是矩形,∠∠B =∠D =90°,AD BC ∥,∠∠ACB =∠CAD ,∠∠CEO ∠∠AGO ,∠AO=CO ,∠AC ==∠12AO AC == ∠∠AOG =∠D =90°,∠OAG =∠CAD ,∠∠AOG ∠∠ADC , ∠AG AO AC AD=,=, ∠AG =52故选:C .【点睛】此题考查了菱形的性质,矩形的性质,勾股定理,全等三角形的判定及性质,相似三角形的判定及性质,是图形类的综合题,熟练掌握各知识点是解题的关键.【分析】由2DA A C '=',6DC =,可求出DA ',A C '的长,再根据折叠和勾股定理可求出DF 和FA ',依据三角形相似可求出NC 、NA ',进而求出MF ,最后根据勾股定理求出EF .【详解】解:如图,过点E 作EM AD ⊥,垂足为M ,2DA A C ''=,6DC =, 243DA DC '==,123A C DC '==, 由折叠得,AF FA =',6AB A B =''=,设DF x =,则8FA FA x ='=-,在Rt DFA ∆'中,由勾股定理得,2224(8)x x +=-,解得3x =,即3DF =,835FA FA ∴='=-=,1809090NAC DA F ∠'+∠'=︒-︒=︒,90NAC A NC ∠'+∠'=︒,DA F A NC ∴∠'=∠',90C D ∴∠=∠=︒,∴∠A NC '∽∠FA D ',∴A C NC A N FD A D FA ''=='',即2345NC A N '==, 解得83NC =,103A N '=, 108633B N A B A N NC ∴'=''-'=-==, ∴∠()A CN ENB AAS '≅∆',103EN A N ∴='=, 108633EC EN NC MD ∴=+=+==, 633MF ∴=-=,在Rt EFM ∆中,EF故选:A .【点睛】本题考查矩形的性质、折叠轴对称、相似三角形、全等三角形以及勾股定理等知识,掌握折叠的性质和直角三角形的边角关系是得出答案的前提,建立图形中线段之间的关系是解决问题的关键.21.15【分析】根据平行四边形的对角线互相平分,求得OC 与OD 的长,继而可求得答案. 【详解】解:四边形ABCD 是平行四边形,142OC AC ∴==,152OD BD ==,6CD AB ==, OCD ∴△的周长为:64515CD OC OD ++=++=.故答案为:15.【点睛】本题重点考查了平行四边形的性质,并利用性质解题.平行四边形基本性质:∠平行四边形两组对边分别平行;∠平行四边形的两组对边分别相等;∠平行四边形的两组对角分别相等;∠平行四边形的对角线互相平分.22.3-【分析】由D 为BC 的中点,平行四边形OABC 的面积为6,可得∠OCD 的面积为平行四边形OABC 的面积的14,再根据反比例函数系数k 的几何意义即可求出答案. 【详解】解:∠D 为BC 的中点,平行四边形OABC 的面积为6,∠∠OCD 的面积为6×14=1.5, ∠12|k |=1.5, ∠k <0,∠3k =-.故答案为:3-.【点睛】本题考查了反比例函数k 的几何意义,平行四边形的性质,求得∠OCD 的面积是解题的关键.23.30︒【分析】根据矩形和平行四边形的面积公式可知,平行四边形A 'B 'C 'D '的底边A D ''边上的高等于A B ''的一半,据此可得∠A '为30°.【详解】解:如图,过点B '作B E A D '⊥''于点E .设矩形ABCD 的边AD 长为a ,AB 长为b ,B E '长为c ,则ABCD S ab =矩形,A B C D Sac ''''=. ∠12A B C D ABCDS S ''''=矩形, ∠12ac ab =, ∠12c b =, ∠sin A '12c b ==, ∠30A ∠'=︒.【点睛】本题主要考查了四边形的不稳定性、矩形与平行四边形的面积公式、解直角三角形等相关知识,熟记特殊角的三角函数值是解答本题的关键.24.∠∠##∠∠【分析】∠根据平行四边形的性质结合已知条件,证明AMQ CPN ≌,DQP BNM ≌,可得MQ NP =,MN PQ =,根据两组对边相等的四边形是平行四边形,即可判断∠,∠根据平行四边形是中心对称图形,即可判断∠,根据已知条件不能判断∠.【详解】解:∠四边形ABCD 是平行四边形A C ∴∠=∠,B D ∠=∠,,AD BC AB CD == ∠,AQ CN AM CP ==∠AMQ CPN ≌∠MQ NP =,AQ CN AM CP ==∴,DQ BN DP BM ==又B D ∠=∠DQP BNM ∴≌MN PQ ∴=∴四边形MNPQ 是平行四边形故∠正确 ∠四边形ABCD 的对角线交于点O ,,MP NQ 均经过点O :,OQ ON OM OP ∴==∴四边形MNPQ 是平行四边形故∠正确∠NQ 经过点O ,AQ CN =,,M P 的位置未知,不能判断四边形MNPQ 是平行四边形 故∠不正确故答案为:∠∠【点睛】本题考查了平行四边形的性质与判定,掌握平行四边形的性质与判定是解题的关键.25.1【分析】根据三角形中位线定理求出DE ,根据直角三角形的性质求出EF ,结合图形计算即可.【详解】∠DE 为△ABC 的中位线, ∠DE=12BC=4(cm), ∠∠AFC 为直角,E 为AC 的中点, ∠FE=12AC=3(cm),∠DF=DE−FE=1(cm),故答案为1cm.【点睛】此题考查三角形中位线定理,解题关键在于掌握其性质定义.26.10【分析】平行四边形的两组对边相等,以此便可求解.【详解】解:如图:平行四边形ABCD 的周长为:2()2(32)10AD AB +=⨯+=.故答案是:10.【点睛】本题考查平行四边形两组对边相等的性质,解题的关键是掌握其性质. 27.4【分析】直接利用三角形中位线的性质,证明EO =AB ,然后根据平行四边形的性质列方程得出答案.【详解】解:∠四边形ABCD 是平行四边形,∠AB =DC ,BO =DO ,又∠E 为DC 边的中点,∠EO 是△DBC 的中位线,∠EO =12BC , ∠EO =AB∠▱ABCD 的周长为24,∠设AB =x ,则BC =2x ,则2(x +2x )=24,解得:x =4,故EO =4.故答案为4.【点睛】此题主要考查了平行四边形的性质、三角形中位线的性质等,正确得出EO 是△DBC 的中位线是解题关键.28 8-【分析】分∠ABE=30°或∠AEB=30°或∠ABA′=30°时三种情况,利用锐角三角函数进行求解即可.【详解】解:当∠ABE=30°时,∠AB=4cm ,∠A=90°,; 当∠AEB=30°时,则∠ABE=60°,∠AB=4cm ,∠A=90°,∠AE=AB·tan60°=;当∠ABE=15°时,∠ABA′=30°,延长BA′交AD 于F ,如下图所示,设AE=x ,则EA′=x ,sin 60x EF ==︒∠x +=∠8x =-∠8AE =-cm .8- 【点睛】本题考查了矩形与折叠,以及分类讨论的数学思想,分类讨论是解答本题的关键.29.2.5【分析】由折叠的性质可得CF=HF ,BE=GE ,设BE=GE=x ,则AE=4-x ,在Rt △AEG 中利用勾股定理求出x 的值.【详解】解:由题意,点C 与点H ,点B 与点G 分别关于直线EF 对称,∠CF=HF ,BE=GE ,设BE=GE=x ,则AE=4-x ,∠四边形ABCD 是正方形,∠∠A=90°,∠AE 2+AG 2=EG 2,∠B 落在边AD 的中点G 处,∠AG=2,∠(4-x )2+22=x 2,解得:x=2.5,∠BE=2.5.故答案为:2.5.【点睛】本题考查了折叠问题与勾股定理以及正方形的性质,掌握翻折的性质是解题的关键.30.156【分析】根据多边形的内角和公式即可得出结果.【详解】解:∠十五边形的内角和=(15﹣2)•180°=2340°,又∠十五边形的每个内角都相等,∠每个内角的度数=2340°÷15=156°.故答案为156.【点睛】本题考查了多边形的内角和计算公式.多边形内角和定理:多边形内角和等于(n ﹣2)•180°.31.81【分析】先证明四边形CGBE 是平行四边形, 然后证明CGF BAC ≌,再解直角三角形即可求得BH 的长度,进而根据BE BH ⨯即可求得答案.【详解】如图,设,AB CG 交于点H ,四边形ADEB 是正方形,15AB BE ∴==,EF BC ∥,CG BE ∥,∴四边形CGBE 是平行四边形,15CG BE AB ∴===,BE AB ⊥,CG AB ∴⊥,90ABC HCB ∴∠+∠=︒,90ACB ∠=︒,∴90ABC CAB ∠+∠=︒,HCB CAB ∴∠=∠,EF BC ∥,HCB CGF ∴∠=∠,90GFC ACB ∠=∠=︒,CGF BAC ∴∠=∠,∴CGF BAC ≌,CB FC ∴=,设CB x =,则3AC AF FC x =+=+,Rt ABC 中,222AB AC BC =+,即()222153x x =++,解得9x =或12x =-(舍), 9312,9AC BC ∴=+==,93cos 155BC CBA AB ∴∠===, 327cos 955HB BC CBA ∴=⋅∠=⨯=, ∴平行四边形CGEB 的面积为BE BH ⨯2715815BE BH =⨯=⨯=, 故答案为:81.【点睛】本题考查了正方形的性质,平行四边形的判定,全等三角形的性质与判定,勾股定理,解直角三角形等知识,熟练掌握知识间的联系,是解答本题的关键.32.43π 【分析】根据题意得到ADO ∆是等边三角形,从而得到角度,再结合特殊角的直角三角形三边关系得到4=AD ,8AC =,分别求出ACD S ∆=83AOD S π=扇形,43AOE S π=扇形,最后根据图形得到=ACD AOD AOE S S S S ∆-+阴影扇形扇形,代值求解即可. 【详解】解:矩形ABCD 的两条对角线相交于点O ,OA OB OC OD ∴===,以点A 为圆心,AD 长为半径画弧,此弧恰好经过点O ,AO AD OD ∴==,即ADO ∆是等边三角形,60DAO ∴∠=︒,30OAE ∠=︒,在Rt ACD ∆中,30ACD OAE ∠=∠=︒,90ADC ∠=︒,CD =4=AD ,8AC =, 11422ACD S AD CD ∆∴==⨯⨯ 260843603AOD S ππ︒=⨯⨯=︒扇形, 230443603AOE S ππ︒=⨯⨯=︒扇形, 844=333ACD AOD AOE S S S S πππ∆∴-+=+=阴影扇形扇形,故答案为:43π 【点睛】本题考查阴影图形面积,对于不规则图形面积求解,我们要根据题中图形转化为规则图形面积间接表示出来,在求解此题过程中涉及到矩形的性质、等边三角形的判定与性质、特殊角度的直角三角形三边关系、三角形面积公式和扇形面积公式,将阴影部分面积转化为常见图形面积来间接求解是解决问题的关键.33.2【分析】根据平行四边形性质求出AD∠BC ,由平行线的性质可得∠AEB=∠CBE ,然后由角平分线的定义知∠ABE=∠AEB ,所以∠ABE=∠AEB ,即可得AB=AE ,由此即可求出DE 的长.【详解】∠四边形ABCD 是平行四边形,∠AD∠BC ,∠∠AEB=∠CBE .∠BE 平分∠ABC ,∠∠ABE=∠CBE ,∠∠ABE=∠AEB ,∠AB=AE=3,∠DE=AD-AE=5-3=2.故答案是:2.【点睛】本题考查了平行四边形性质、三角形的角平分线的定义,平行线的性质的应用,证得AB=AE 是解题的关键.34.(1.5,0)或(1,0).。
(专题精选)初中数学四边形经典测试题及答案解析

(专题精选)初中数学四边形经典测试题及答案解析一、选择题1.在四边形ABCD 中,两对角线交于点O ,若OA =OB =OC =OD ,则这个四边形( ) A .可能不是平行四边形B .一定是菱形C .一定是正方形D .一定是矩形【答案】D【解析】【分析】根据OA=OC, OB=OD ,判断四边形ABCD 是平行四边形.然后根据AC=BD ,判定四边形ABCD 是矩形.【详解】解:这个四边形是矩形,理由如下:∵对角线AC 、BD 交于点O ,OA= OC, OB=OD ,∴四边形ABCD 是平行四边形,又∵OA=OC=OD=OB ,∴AC=BD ,∴四边形ABCD 是矩形.故选D .【点睛】本题考查了矩形的判断,熟记矩形的各种判定方法是解题的关键.2.如图,□ABCD 的对角线AC 与BD 相交于点O ,AB ⊥AC .若4AB =,6AC =,则BD 的长为( )A .11B .10C .9D .8 【答案】B【解析】【分析】根据勾股定理先求出BO 的长,再根据平行四边形的性质即可求解.【详解】∵6AC =,∵AB ⊥AC ,∴BO=2234+=5∴BD=2BO=10,故选B.【点睛】此题主要考查平行四边形的性质,解题的关键是熟知勾股定理的应用.3.如图,在菱形ABCD 中,点E 在边AD 上,30BE ADBCE ⊥∠=︒,.若2AE =,则边BC 的长为( )A 5B 6C 7D .22【答案】B【解析】【分析】 由菱形的性质得出AD ∥BC ,BC=AB=AD ,由直角三角形的性质得出3,在Rt △ABE 中,由勾股定理得:BE 2+22=3)2,解得:2,即可得出结果. 【详解】∵四边形ABCD 是菱形,∴AD BC BC AB =,∥.∵BE AD ⊥.∴BE BC ⊥.∴30BCE ∠=︒,∴2EC BE =, ∴223AB BC EC BE BE ==-=.在Rt ABE △中,由勾股定理得)22223BE BE +=, 解得2BE =,∴36BC BE ==故选B.【点睛】 此题考查菱形的性质,含30°角的直角三角形的性质,勾股定理,熟练掌握菱形的性质,由勾股定理得出方程是解题的关键.4.正九边形的内角和比外角和多( )A .720︒B .900︒C .1080︒D .1260︒【答案】B【分析】根据多边形的内角和公式求出正九边形的内角和,减去外角和360°即可.【详解】∵正九边形的内角和是(92)1801260-⨯=o o,∴1260360-=o o 900︒,故选:B.【点睛】此题考查多边形的内角和公式、外角和,熟记公式是解题的关键.5.如图,在矩形ABCD 中, 4,6,AB BC ==点E 是AD 的中点,点F 在DC 上,且1,CF =若在此矩形上存在一点P ,使得PEF V 是等腰三角形,则点P 的个数是( )A .3B .4C .5D .6【答案】D【解析】【分析】 根据等腰三角形的定义,分三种情况讨论:①当EF 为腰,E 为顶角顶点时,②当EF 为腰,F 为顶角顶点时,③当EF 为底,P 为顶角顶点时,分别确定点P 的位置,即可得到答案.【详解】∵在矩形ABCD 中,461AB BC CF ===,,,点E 是AD 的中点,32184EF ∴==>.∴PEF V 是等腰三角形,存在三种情况:①当EF 为腰,E 为顶角顶点时,根据矩形的轴对称性,可知:在BC 上存在两个点P ,在AB 上存在一个点P ,共3个,使PEF V 是等腰三角形;②当EF 为腰,F 为顶角顶点时,186,Q∴在BC 上存在一个点P ,使PEF V 是等腰三角形;③当EF 为底,P 为顶角顶点时,点P 一定在EF 的垂直平分线上,∴EF 的垂直平分线与矩形的交点,即为点P ,存在两个点.综上所述,满足题意的点P 的个数是6.故选D .【点睛】本题主要考查等腰三角形的定义,矩形的性质,熟练掌握等腰三角形的定义和矩形的性质,学会分类讨论思想,是解题的关键.6.如图,四边形ABCD和四边形AEFG均为正方形,连接CF,DG,则DGCF=()A.23B.22C.33D.32【答案】B 【解析】【分析】连接AC和AF,证明△DAG∽△CAF可得DGCF的值.【详解】连接AC和AF,则22 AD AGAC AF==,∵∠DAG=45°-∠GAC,∠CAF=45°-GAC,∴∠DAG=∠CAF.∴△DAG∽△CAF.∴22 DG ADCF AC==.故答案为:B.【点睛】本题主要考查了正方形的性质、相似三角形的判定和性质,解题的关键是构造相似三角形.7.如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F,设BP=x,EF=y,则能反映y与x之间关系的图象是()A.B.C.D.【答案】C【解析】【分析】【详解】图象是函数关系的直观表现,因此须先求出函数关系式.分两段求:当P在BO上和P在OD上,分别求出两函数解析式,根据函数解析式的性质即可得出函数图象.解:设AC与BD交于O点,当P在BO上时,∵EF∥AC,∴EF BPAC BO=即43y x=,∴43y x =;当P在OD上时,有643 DP EF y x DO AC-==即,∴y=483x -+.故选C .8.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是( )A .8B .9C .10D .12【答案】A【解析】试题分析:设这个多边形的外角为x°,则内角为3x°,根据多边形的相邻的内角与外角互补可的方程x+3x=180,解可得外角的度数,再用外角和除以外角度数即可得到边数. 解:设这个多边形的外角为x°,则内角为3x°,由题意得:x+3x=180,解得x=45,这个多边形的边数:360°÷45°=8,故选A .考点:多边形内角与外角.9.如图,四边形ABCD 是菱形,30ACD ∠=︒,2BD =,则AC 的长度为( )A .3B .2C .4D .2【答案】A【解析】【分析】 由菱形的性质,得到AC ⊥BD ,由直角三角形的性质,得到BO=1,BC=2,根据勾股定理求出CO ,即可求出AC 的长度.【详解】解,如图,∵四边形ABCD 是菱形,∴AC ⊥BD ,AO=CO ,BO=DO ,∵2BD =,∴BO=1,在Rt △OBC 中,30BCO ACD ∠=∠=︒,∴BC=2, ∴22213CO =-=; ∴23AC =;故选:A.【点睛】本题考查了菱形的性质,勾股定理解直角三角形,解题的关键是熟练掌握菱形的性质,利用勾股定理求出OC 的长度.10.如图,在矩形ABCD 中,AB m =,6BC =,点E 在边CD 上,且23CE m =.连接BE ,将BCE V 沿BE 折叠,点C 的对应点C '恰好落在边AD 上,则m =( )A .33B .3C 3D .4【答案】A【解析】【分析】设AC′=x ,在直角三角形ABC′和直角三角形DEC′中分别利用勾股定理列出关于x 和m 的关系式,再进行求解,即可得出m 的值.【详解】解:设AC′=x ,∵AB=m ,BC=6,23CE m =, 根据折叠的性质可得:BC′=6,EC′=23CE m =, ∴C ′D=6-x ,DE=13m ,在△ABC ′中,AB 2+AC′2=BC′2,即2226x m +=,在△DEC ′中,C′D 2+DE 2=C′E 2,即()22212633x m m ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭, 化简得:()2236x m -=,代入2226x m +=中,得:()222366x x -=-,解得:x=3或x=6,代入2226x m +=,可得:当x=3时,m=33或33-(舍),当x=6时,m=0(舍),故m 的值为33,故选A.【点睛】本题考查了折叠的性质,勾股定理,解一元二次方程,有一定难度,解题的关键是根据折叠的性质运用勾股定理求解.11.如图,在矩形ABCD 中,AD=2AB ,点M 、N 分别在边AD 、BC 上,连接BM 、DN .若四边形MBND 是菱形,则AM MD等于( )A .35B .23C .38D .45【答案】A【解析】试题分析:设AB=a,根据题意知AD=2a ,由四边形BMDN 是菱形知BM=MD ,设AM=b,则BM=MD=2a-b.在Rt △ABM 中,由勾股定理即可求值.试题解析:∵四边形MBND 是菱形,∴MD=MB .∵四边形ABCD是矩形,∴∠A=90°.设AB=a,AM=b,则MB=2a-b,(a、b均为正数).在Rt△ABM中,AB2+AM2=BM2,即a2+b2=(2a-b)2,解得a=4b3,∴MD=MB=2a-b=53b,∴3553AM bMD b==.故选A.考点:1.矩形的性质;2.勾股定理;3.菱形的性质.12.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点()5,3D在边AB上,以C为中心,把CDB△旋转90︒,则旋转后点D的对应点'D的坐标是( )A.()2,10B.()2,0-C.()2,10或()2,0-D.()10, 2或()2,0-【答案】C【解析】【分析】先根据正方形的性质求出BD、BC的长,再分逆时针旋转和顺时针旋转两种情况,然后分别根据旋转的性质求解即可得.【详解】Q四边形OABC是正方形,(5,3)D5,3,2,90BC OC AB OA AD BD AB AD B∴======-=∠=︒由题意,分以下两种情况:(1)如图,把CDB△逆时针旋转90︒,此时旋转后点B的对应点B'落在y轴上,旋转后点D的对应点D¢落在第一象限由旋转的性质得:2,5,90B D BD BC BC CBD B'''''====∠=∠=︒10OB OC B C''∴=+=∴点D¢的坐标为(2,10)(2)如图,把CDB △顺时针旋转90︒,此时旋转后点B 的对应点B ''与原点O 重合,旋转后点D 的对应点D ''落在x 轴负半轴上由旋转的性质得:2,5,90B D BD B C BC CB D B ''''''''''====∠=∠=︒∴点D ''的坐标为(2,0)-综上,旋转后点D 的对应点D ¢的坐标为(2,10)或(2,0)-故选:C .【点睛】本题考查了正方形的性质、旋转的性质等知识点,依据题意,正确分两种情况讨论是解题关键.13.如图,ABCD Y 的对角线AC 与BD 相交于点O ,AD BD ⊥,30ABD ∠=︒,若23AD =.则OC 的长为( )A .3B .3C 21D .6【答案】C【解析】【分析】 先根据勾股定理解Rt ABD △求得6BD =,再根据平行四边形的性质求得3OD =,然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得21OC OA ==【详解】解:∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中,30ABD ∠=︒,23AD =∴243AB AD ==∴226BD AB AD =-= ∵四边形ABCD 是平行四边形∴132OB OD BD ===,12OA OC AC == ∴在Rt AOD △中,23AD =,3OD =∴2221OA AD OD =+=∴21OC OA ==. 故选:C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.14.将一个边长为4的正方形ABCD 分割成如图所示的9部分,其中ABE △,BCF V ,CDG V ,DAH V 全等,AEH △,BEF V ,CFG △,DGH V 也全等,中间小正方形EFGH 的面积与ABE △面积相等,且ABE △是以AB 为底的等腰三角形,则AEH △的面积为( )A .2B .169C .32D .2【答案】C【解析】【分析】【详解】 解:如图,连结EG 并向两端延长分别交AB 、CD 于点M 、N ,连结HF ,∵四边形EFGH 为正方形,∴EG FH =,∵ABE △是以AB 为底的等腰三角形,∴AE BE =,则点E 在AB 的垂直平分线上,∵ABE △≌CDG V ,∴CDG V 为等腰三角形,∴CG DG =,则点G 在CD 的垂直平分线上,∵四边形ABCD 为正方形,∴AB 的垂直平分线与CD 的垂直平分线重合,∴MN 即为AB 或CD 的垂直平分线,则,EM AB GN CD ^^,EM GN =,∵正方形ABCD 的边长为4,即4AB CD AD BC ====,∴4MN =,设EM GN x ==,则42EG FH x ==-,∵正方形EFGH 的面积与ABE △面积相等, 即2114(42)22x x ?-,解得:121,4x x ==, ∵4x =不符合题意,故舍去,∴1x =,则S 正方形EFGH 14122==⨯⨯=V ABE S , ∵ABE △,BCF V ,CDG V ,DAH V 全等,∴2====V V V V ABE BCF CDG DAH S S S S ,∵正方形ABCD 的面积4416=⨯=,AEH △,BEF V ,CFG △,DGH V 也全等, ∴1(4=V AEH S S 正方形ABCD − S 正方形EFGH 134)(16242)42-=⨯--⨯=V ABE S , 故选:C .【点睛】本题考查了正方形的性质、全等三角形的性质和等腰三角形的性质,解题的关键是求得ABE △的面积.15.如图,在□ABCD 中,E 、F 分别是边BC 、CD 的中点,AE 、AF 分别交BD 于点G 、H ,则图中阴影部分图形的面积与□ABCD 的面积之比为( )A .7 : 12B .7 : 24C .13 : 36D .13 : 72【答案】B【解析】【分析】根据已知条件想办法证明BG=GH=DH ,即可解决问题;【详解】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC ,AB=CD ,AD=BC ,∵DF=CF ,BE=CE , ∴12DH DF HB AB ==,12BG BE DG AD ==, ∴13DH BG BD BD ==, ∴BG=GH=DH ,∴S △ABG =S △AGH =S △ADH ,∴S 平行四边形ABCD =6 S △AGH ,∴S △AGH :ABCD S 平行四边形=1:6,∵E 、F 分别是边BC 、CD 的中点, ∴12EF BD =, ∴14EFC BCDD S S =V V , ∴18EFCABCD S S =V 四边形, ∴1176824AGH EFC ABCD S S S +=+=V V 四边形=7∶24, 故选B.【点睛】本题考查了平行四边形的性质、平行线分线段成比例定理、等底同高的三角形面积性质,题目的综合性很强,难度中等.16.如图,点E F G H 、、、分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点.则下列说法:①若AC BD =,则四边形EFGH 为矩形;②若AC BD ⊥,则四边形EFGH 为菱形;③若四边形EFGH 是平行四边形,则AC 与BD 互相平分;④若四边形EFGH 是正方形,则AC 与BD 互相垂直且相等.其中正确的个数是( )A .1B .2C .3D .4【答案】A【解析】【分析】 因为一般四边形的中点四边形是平行四边形,当对角线BD=AC 时,中点四边形是菱形,当对角线AC ⊥BD 时,中点四边形是矩形,当对角线AC=BD ,且AC ⊥BD 时,中点四边形是正方形.【详解】因为一般四边形的中点四边形是平行四边形,当对角线BD=AC 时,中点四边形是菱形,当对角线AC ⊥BD 时,中点四边形是矩形,当对角线AC=BD ,且AC ⊥BD 时,中点四边形是正方形,故④选项正确,故选A .【点睛】本题考查中点四边形、平行四边形、矩形、菱形的判定等知识,解题的关键是记住一般四边形的中点四边形是平行四边形,当对角线BD=AC 时,中点四边形是菱形,当对角线AC ⊥BD 时,中点四边形是矩形,当对角线AC=BD ,且AC ⊥BD 时,中点四边形是正方形.17.如图,四边形ABCD 和EFGH 都是正方形,点E H ,在ADCD ,边上,点F G ,在对角线AC 上,若6AB ,则EFGH 的面积是( )A .6B .8C .9D .12【解析】【分析】根据正方形的性质得到∠DAC=∠ACD=45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是得到DE=22EH=22EF,EF=22AE,即可得到结论.【详解】解:∵在正方形ABCD中,∠D=90°,AD=CD=AB,∴∠DAC=∠DCA=45°,∵四边形EFGH为正方形,∴EH=EF,∠AFE=∠FEH=90°,∴∠AEF=∠DEH=45°,∴AF=EF,DE=DH,∵在Rt△AEF中,AF2+EF2=AE2,∴AF=EF=22AE,同理可得:DH=DE=22EH又∵EH=EF,∴DE=2EF=2×2AE=12AE,∵AD=AB=6,∴DE=2,AE=4,∴EH=2DE=22,∴EFGH的面积为EH2=(22)2=8,故选:B.【点睛】本题考查了正方形的性质,等腰直角三角形的判定及性质以及勾股定理的应用,熟练掌握图形的性质及勾股定理是解决本题的关键.18.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD 于点F,若BF=12,AB=10,则AE的长为()A.13 B.14 C.15 D.16【答案】D【解析】先证明四边形ABEF 是平行四边形,再证明邻边相等即可得出四边形ABEF 是菱形,得出AE ⊥BF ,OA=OE ,OB=OF=12BF=6,由勾股定理求出OA ,即可得出AE 的长. 【详解】如图所示:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠DAE=∠AEB ,∵∠BAD 的平分线交BC 于点E ,∴∠DAE=∠BAE ,∴∠BAE=∠BEA ,∴AB=BE ,同理可得AB=AF ,∴AF=BE ,∴四边形ABEF 是平行四边形,∵AB=AF ,∴四边形ABEF 是菱形,∴AE ⊥BF ,OA=OE ,OB=OF=12BF=6, ∴2222=106AB OB --=8,∴AE=2OA=16.故选D .【点睛】本题考查平行四边形的性质与判定、等腰三角形的判定、菱形的判定和性质、勾股定理等知识;熟练掌握平行四边形的性质,证明四边形ABEF 是菱形是解决问题的关键.19.如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB ,CD 交于点E ,F ,连结BF ,交AC 于点M ,连结DE ,BO .若∠BOC =60°,FO =FC ,则下列结论:①AE =CF ;②BF 垂直平分线段OC ;③△EOB ≌△CMB ;④四边形是BFDE 菱形.其中正确结论的个数是( )A.1个B.2个C.3个D.4个【答案】C【解析】【分析】利用ASA定理证明△AOE≌△COF,从而判断①;利用线段垂直平分线的性质的逆定理可得结论②;在△EOB和△CMB中,对应直角边不相等,则两三角形不全等,从而判断③;连接BD,先证得BO=DO, OE=OF,进而证得OB⊥EF,因为BD、EF互相垂直平分,即可证得四边形EBFD是菱形,从而判断④.【详解】解:∵矩形ABCD中,O为AC中点∴∠DCA=∠BAC,OA=OC,∠AOE=∠COF∴△AOE≌△COF∴AE=CF,故①正确∵矩形ABCD中,O为AC中点,∴OB=OC,∵∠COB=60°,∴△OBC是等边三角形,∴OB=BC,∵FO=FC,∴FB垂直平分OC,故②正确;∵△BOC为等边三角形,FO=FC,∴BO⊥EF,BF⊥OC,∴∠CMB=∠EOB=90°,∴BO≠BM,∴△EOB与△CMB不全等;故③错误;连接BD,∵四边形ABCD是矩形,∴AC=BD,AC、BD互相平分,∵O为AC中点,∴BD也过O点,且BO=DO由①可知△AOE≌△COF,∴OE=OF∴四边形EBFD是平行四边形由②可知,OB=CB,OF=FC又∵BF=BF∴△OBF≌△OCF∴BD⊥EF∴平行四边形EBFD是菱形,故④正确所以其中正确结论的个数为3个;故选:C.【点睛】本题考查了矩形的性质,菱形的判定和性质,全等三角形的判定和性质,等边三角形的判定和性质以及三角函数等的知识.20.一个多边形的每一个外角都是72°,那么这个多边形的内角和为( )A.540°B.720°C.900°D.1080°【答案】A【解析】【详解】解:∵多边形的每一个外角都是72°,∴多边形的边数为:3605 72,∴该多边形的内角和为:(5-2)×180°=540°.故选A.【点睛】外角和是360°,除以一个外角度数即为多边形的边数.根据多边形的内角和公式可求得该多边形的内角和.。
中考数学试题分类10 四边形(部分题含答案)

8.(南通市) 如图,菱形ABCD 中,AB = 5,∠BCD = 120°,则对角线AC 的长是 A .20 B .15 C .10D .59.(南通市)如图,已知□ABCD 的对角线BD =4cm ,将□ABCD 绕其对称中心O 旋转180°,则点D 所转过的路径长为 A .4π cmB .3π cmC .2π cmD .π cm6.(盐城市)如图所示,在菱形ABCD 中,两条对角线AC =6,BD =8,则此菱形 的边长为 A .5 B .6 C .8 D .1016.(南通市)如图,小章利用一张左、右两边已经破损的长方形纸片ABCD 做折纸游戏,他将纸片沿EF 折叠后,D 、C 两点分别落在D ′、C ′的位 置,并利用量角器量得∠EFB =65°,则∠AED ′等于 ▲ 度.17.(南通市)如图,正方形ABCD 的边长为4,点M 在边DC 上,M 、N 两点关于对角线AC 对称,若DM =1,则tan ∠ADN = ▲ .17.(盐城市)小明尝试着将矩形纸片ABCD(如图①,AD >CD )沿过A 点的直线折叠,使得B 点落在AD 边上的点F 处,折痕为AE (如图②);再沿过D 点的直线折叠,使得C 点落在DA 边上的点N 处,E 点落在AE 边上的点M 处,折痕为DG (如图③).如果第二次折叠后,M 点正好在∠NDG 的平分线上,那么矩形ABCD长与宽的比值为 ▲ .11. (兰州市)如图所示,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,sin A=53,则下列结论正确的个数有①cm DE 3= ②cm BE 1= ③菱形的面积为215cm ④cm BD 102= A . 1个 B . 2个 C . 3个 D . 4个17. (兰州市)如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD = 2,将腰CD 以D 为中心逆时针旋转90°至DE ,连接AE 、CE ,△ADE 的面积为3,则BC 的长为 .①②D③ BACD(第8题)(第9题)ABCDOA (第17题)B D M NC· ·21. (青岛市)已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1)求证:BE = DF ;(2)连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.21.(本小题满分8分)证明:(1)∵四边形ABCD 是正方形,∴AB =AD ,∠B = ∠D = 90°.∵AE = AF ,∴Rt Rt ABE ADF △≌△.∴BE =DF . (2)四边形AEMF 是菱形. ∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC .∵BE =DF ,∴BC -BE = DC -DF . 即CE CF =. ∴OE OF =. ∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.13.(青岛市)把一张矩形纸片(矩形ABCD )按如图方式折叠,使顶点B 和点D 重合,折痕为EF .若AB = 3 cm ,BC = 5 cm ,则重叠部分△DEF 的面积是 cm 2.22.(8分)(济宁市)数学课上,李老师出示了这样一道题目:如图1,正方形ABCD 的边长为12,P 为边BC 延长线上的一点,E 为DP 的中点,DP 的垂直平分线交边DC 于M ,交边AB 的延长线于N .当6CP =时,EM 与EN 的比值是多少?经过思考,小明展示了一种正确的解题思路:过E 作直线平行于BC 交DC ,AB 分别于F ,G ,如图2,则可得:DF DEFC EP=,因为DE EP =,所以DF FC =.可求出EF 和EG 的值,进而可求得EM 与EN 的比值. (1) 请按照小明的思路写出求解过程.(2) 小东又对此题作了进一步探究,得出了DP MN =的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.HDEMAABCE'A 第13题图('B )D A DB E F OCM 第21题图22.(1)解:过E 作直线平行于BC 交DC ,AB 分别于点F ,G ,则DF DE FC EP =,EM EFEN EG=,12GF BC ==. ∵DE EP =,∴DF FC =.····························································· 2分∴116322EF CP ==⨯=,12315EG GF EF =+=+=. ∴31155EM EF EN EG ===. ································································· 4分 (2)证明:作MH ∥BC 交AB 于点H , ······················································ 5分则MH CB CD ==,90MHN ∠=︒. ∵1809090DCP ∠=︒-︒=︒, ∴DCP MHN ∠=∠.∵90MNH CMN DME CDP ∠=∠=∠=︒-∠,90DPC CDP ∠=︒-∠, ∴DPC MNH ∠=∠.∴DPC MNH ∆≅∆. ········································ 7分 ∴DP MN =. ············································································ 8分22.(盐城市)(本题满分8分)如图,在梯形ABCD 中,AD ∥BC ,AB =CD =AD ,BD ⊥CD .(1)求sin ∠DBC 的值;(2)若BC 长度为4cm ,求梯形ABCD 的面积.22.解:(1)∵AD =AB ∴∠ADB =∠ABD∵AD ∥CB ∴∠DBC = ∠ADB =∠ABD ……………(1分) ∵在梯形ABCD 中,AB =CD ,∴∠ABD +∠DBC =∠C =2∠DBC ∵BD ⊥CD ∴3∠DBC =90º ∴∠DBC =30º ……(3分) B AC D B A CD (第22题图)∴sin ∠DBC =12……………………(4分)(2)过D 作DF ⊥BC 于F …………………………(5分) 在Rt △CDB 中,BD =BC ×c os ∠DBC =2 3 (cm ) …………………(6分) 在Rt △BDF 中,DF =BD ×sin ∠DBC = 3 (cm ) …………………(7分)∴S 梯=12(2+4)·3 =3 3 (cm 2)………………………………………(8分)27. (兰州市)(本题满分10分)已知平行四边形ABCD 中,对角线AC 和BD 相交于点O ,AC=10,BD=8.(1)若AC ⊥BD ,试求四边形ABCD 的面积 ;(2)若AC 与BD 的夹角∠AOD=60,求四边形ABCD 的面积;(3)试讨论:若把题目中“平行四边形ABCD ”改为“四边形ABCD ”,且∠AOD=θAC=a ,BD=b ,试求四边形ABCD 的面积(用含θ,a ,b 的代数式表示).27. (本题满分10分) 解:(1)∵AC ⊥BD∴四边形ABCD 的面积(2)过点A分别作AE ⊥BD ,垂足为E ∵四边形ABCD 为平行四边形521===AC CO AO 421===BD DO BO在Rt ⊿AOE 中,AO AEAOE =∠sin ∴ 23523560sin sin =⨯=⨯=∠∙=o AO AOE AO AE∴3552342121=⨯⨯⨯=∙=∆AE OD S AOD∴四边形ABCD 的面积 3204==∆AOD S S(3)如图所示过点A,C 分别作AE ⊥BD ,CF ⊥BD ,垂足分别为E,F在Rt ⊿AOE 中,AO AE AOE =∠sin ∴θsin sin ⨯=∠∙=AO AOE AO AE同理可得 θsin sin ⨯=∠∙=CO COF CO CF∴四边形ABCD 的面积θθ1sin 21)(sin 212121AC BD CO AO BD CF BD AE BD S S S CBD ABD ∙=+=∙+∙=+=∆∆27.(盐城市)(本题满分12分)如图1所示,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,∠DCB =75º,以CD为一边的等边△DCE 的另一顶点E 在腰AB 上. (1)求∠AED 的度数; (2)求证:AB =BC ;(3)如图2所示,若F 为线段CD 上一点,∠FBC =30º.求DFFC 的值.27.解:(1)∵∠BCD =75º,AD ∥BC ∴∠ADC =105º …………………………………(1分) 由等边△DCE 可知:∠CDE =60º,故∠ADE =45º由AB ⊥BC ,AD ∥BC 可得:∠DAB =90º , ∴∠AED =45º…………………(3分)(2)方法一:由(1)知:∠AED =45º,∴AD =AE ,故点A 在线段DE 的垂直平分线上.由△DCE 是等边三角形得:CD =CE ,故点C 也在线段DE 的垂直平分线上. ∴AC 就是线段DE 的垂直平分线,即AC ⊥DE …………………(5分) 连接AC ,∵∠AED =45º,∴∠BAC =45º,又AB ⊥BC ∴BA =BC .…………(7分) 方法二:过D 点作DF ⊥BC ,交BC 于点 ………………(4分) 可证得:△DFC ≌△CBE 则DF=BC ……………………(6分) 从而:AB =CB ………………………………………………(7分) (3)∵∠FBC =30º,∴∠ABF =60º连接AF ,BF 、AD 的延长线相交于点G ,∵∠FBC =30º,∠DCB =75º,∴∠BFC =75º,故BC =BF 由(2)知:BA =BC ,故BA =BF ,∵∠ABF =60º,∴AB =BF =F A ,又∵AD ∥BC ,AB ⊥BC ,∴∠F AG =∠G =30º∴FG =F A = FB ……………………………(10分) ∵∠G =∠FBC =30º,∠DFG =∠CFB ,FB =FG∴△BCF ≌△GDF ………………………(11分) ∴DF =CF ,即点F 是线段CD 的中点.∴DFFC =1………………………………………(12分)AB C DE 图1A B CDEF 图2 A B CD EF 图1A BCDE F 图2G13.(连云港市)一只自由飞行的小鸟,将随意地落在如图所示方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为___________.2.(常德市)如图2,四边形ABCD 中,AB ∥CD ,要使四边形ABCD 为平行四边形,则可添加的条件为_____________________.(填一个即可)18.(连云港市)矩形纸片ABCD 中,AB =3,AD =4,将纸片折叠,使点B 落在边CD 上的B ’处,折痕为AE .在折痕AE 上存在一点P 到边CD 的距离与到点B 的距离相等,则此相等距离为________.5.(淮安市)若一个多边形的内角和小于其外角和,则这个多边形的边数是 A .3 B .4 C .5 D .6题17图 题18图 18.(淮安市)已知菱形ABCD 中,对角线AC=8cm ,BD=6cm ,在菱形内部(包括边界)任取一点P ,使△A CP 的面积大于6 cm 2的概率为 . 26.(淮安市)(本小题满分10分) (1)观察发现如题26(a)图,若点A ,B 在直线l 同侧,在直线l 上找一点P ,使AP+BP 的值最小. 做法如下:作点B 关于直线l 的对称点B ',连接AB ',与直线l 的交点就是所求的点P再如题26(b)图,在等边三角形ABC 中,AB=2,点E 是AB 的中点,AD 是高,在AD 上找一点P ,使BP+PE 的值最小.做法如下:作点B 关于AD 的对称点,恰好与点C 重合,连接CE 交AD 于一点,则这 点就是所求的点P ,故BP+PE 的最小值为 .题26(a)图 题26(b)图(2)实践运用如题26(c)图,已知⊙O 的直径CD 为4,AD 的度数为60°,点B 是AD 的中点,在直径CD 上找一点P ,使BP+AP 的值最小,并求BP+AP 的最小值.DABC图2A 第24题BCDO题26(c)图 题26(d)图(3)拓展延伸如题26(d)图,在四边形ABCD 的对角线AC 上找一点P ,使∠APB=∠APD .保留 作图痕迹,不必写出作法.24.(连云港市)(本题满分10分)如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD 的四个顶点都在格点上,O 为AD 边的中点,若把四边形ABCD 绕着点O 顺时针旋转,试解决下列问题: (1)画出四边形ABCD 旋转后的图形; (2)求点C 旋转过程事所经过的路径长;(3)设点B 旋转后的对应点为B ’,求tan ∠DAB ’的值.7.(连云港市)如图,四边形ABCD 的对角线AC 、BD 互相垂直,则下列条件能判定四边形ABCD 为菱形的是( )A .BA =BCB .AC 、BD 互相平分 C .AC =BD9.(常德市)四边形的内角和为( )A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南通市初中数学四边形经典测试题一、选择题1.如图,在▱ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为()A.33°B.34°C.35°D.36°【答案】B【解析】【分析】由平行四边形的性质可得∠D=∠B,由折叠的性质可得∠D'=∠D,根据三角形的内角和定理可得∠DEC,即为∠D'EC,而∠AEC易求,进而可得∠D'EA的度数.【详解】解:∵四边形ABCD是平行四边形,∴∠D=∠B=48°,由折叠的性质得:∠D'=∠D=48°,∠D'EC=∠DEC=180°﹣∠D﹣∠ECD=107°,∴∠AEC=180°﹣∠DEC=180°﹣107°=73°,∴∠D'EA=∠D'EC﹣∠AEC=107°﹣73°=34°.故选:B.【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的内角和定理等知识,属于常考题型,熟练掌握上述基本知识是解题关键.∠=()2.如图,把矩形ABCD沿EF对折后使两部分重合,若150∠=o,则AEFA.110°B.115°C.120°D.130°【答案】B【解析】【分析】根据翻折的性质可得∠2=∠3,再求出∠3,然后根据两直线平行,同旁内角互补列式计算即可得解.【详解】∠=o,∵矩形ABCD沿EF对折后两部分重合,150∴∠3=∠2=180-502︒︒=65°, ∵矩形对边AD ∥BC , ∴∠AEF=180°-∠3=180°-65°=115°.故选:B .【点睛】本题考查了矩形中翻折的性质,两直线平行的性质,平角的定义,掌握翻折的性质是解题的关键.3.如图,在矩形ABCD 中,6AB =,8BC =,若P 是BD 上的一个动点,则PB PC PD ++的最小值是( )A .16B .15.2C .15D .14.8【答案】D【解析】【分析】 根据题意,当PC ⊥BD 时,PB PC PD ++有最小值,由勾股定理求出BD 的长度,由三角形的面积公式求出PC 的长度,即可求出最小值.【详解】解:如图,当PC ⊥BD 时,PB PC PD BD PC ++=+有最小值,在矩形ABCD 中,∠A=∠BCD=90°,AB=CD=6,AD=BC=8,由勾股定理,得226810BD +=,∴=10PB PD BD +=,在△BCD 中,由三角形的面积公式,得11=22BD PC BC CD ••, 即1110=8622PC ⨯⨯⨯⨯, 解得: 4.8PC =, ∴PB PC PD ++的最小值是:10 4.814.8PB PC PD BD PC ++=+=+=; 故选:D.【点睛】本题考查了勾股定理解直角三角形,最短路径问题,垂线段最短,以及三角形的面积公式,解题的关键是熟练掌握勾股定理,正确确定点P 的位置,得到PC 最短.4.下列命题错误的是( )A .平行四边形的对角线互相平分B .两直线平行,内错角相等C .等腰三角形的两个底角相等D .若两实数的平方相等,则这两个实数相等【答案】D【解析】【分析】根据平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,分别进行判断,即可得到答案.【详解】解:A 、平行四边形的对角线互相平分,正确;B 、两直线平行,内错角相等,正确;C 、等腰三角形的两个底角相等,正确;D 、若两实数的平方相等,则这两个实数相等或互为相反数,故D 错误;故选:D.【点睛】本题考查了判断命题的真假,以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,解题的关键是熟练掌握所学的性质进行解题.5.如图,已知AD 是三角形纸片ABC 的高,将纸片沿直线EF 折叠,使点A 与点D 重合,给出下列判断:①EF 是ABC V 的中位线;②DEF V 的周长等于ABC V 周长的一半:③若四边形AEDF 是菱形,则AB AC =;④若BAC ∠是直角,则四边形AEDF 是矩形.其中正确的是( )A .①②③B .①②④C .②④D .①③④ 【答案】A【解析】【分析】根据折叠可得EF 是AD 的垂直平分线,再加上条件AD 是三角形纸片ABC 的高可以证明EF ∥BC ,进而可得△AEF ∽△ABC ,从而得12AE AF AO AB AC AD ===,进而得到EF 是△ABC 的中位线;再根据三角形的中位线定理可判断出△AEF 的周长是△ABC 的一半,进而得到△DEF 的周长等于△ABC 周长的一半;根据三角形中位线定理可得AE=12AB ,AF=12AC ,若四边形AEDF 是菱形则AE=AF ,即可得到AB=AC .【详解】解:∵AD 是△ABC 的高,∴AD ⊥BC ,∴∠ADC=90°,根据折叠可得:EF 是AD 的垂直平分线,∴AO=DO=12AD ,AD ⊥EF , ∴∠AOF=90°,∴∠AOF=∠ADC=90°,∴EF ∥BC ,∴△AEF ∽△ABC , 12AE AF AO AB AC AD ===, ∴EF 是△ABC 的中位线,故①正确;∵EF 是△ABC 的中位线,∴△AEF 的周长是△ABC 的一半,根据折叠可得△AEF ≌△DEF ,∴△DEF的周长等于△ABC周长的一半,故②正确;∵EF是△ABC的中位线,∴AE=12AB,AF=12AC,若四边形AEDF是菱形,则AE=AF,∴AB=AC,故③正确;根据折叠只能证明∠BAC=∠EDF=90°,不能确定∠AED和∠AFD的度数,故④错误;故选:A.【点睛】此题主要考查了图形的翻折变换,以及三角形中位线的性质,关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.6.如图,在平行四边形ABCD中,2=AD AB,CE平分BCD∠交AD于点E,且8BC=,则AB的长为()A.4 B.3 C.52D.2【答案】A【解析】【分析】利用平行四边形的对边相等且互相平行,进而得出AE=DE=AB即可得出答案.【详解】∵CE平分∠BCD交AD边于点E,∴∠ECD=∠ECB,∵在平行四边形ABCD中,AD∥BC,AB=CD,∴∠DEC=∠ECB,∠DEC=∠DCE,∴DE=DC,∵AD=2AB,∴AD=2CD ,∴AE=DE=AB .∵8AD BC ==,2=AD AB∴AB=4,故选:A .【点睛】此题考查了平行四边形的性质,得出∠DEC=∠DCE 是解题关键.7.如图,在矩形ABCD 中,AB m =,6BC =,点E 在边CD 上,且23CE m =.连接BE ,将BCE V 沿BE 折叠,点C 的对应点C '恰好落在边AD 上,则m =( )A .33B .3C 3D .4【答案】A【解析】【分析】设AC′=x ,在直角三角形ABC′和直角三角形DEC′中分别利用勾股定理列出关于x 和m 的关系式,再进行求解,即可得出m 的值.【详解】解:设AC′=x ,∵AB=m ,BC=6,23CE m =, 根据折叠的性质可得:BC′=6,EC′=23CE m =, ∴C ′D=6-x ,DE=13m ,在△ABC ′中,AB 2+AC′2=BC′2,即2226x m +=,在△DEC ′中,C′D 2+DE 2=C′E 2,即()22212633x m m ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭, 化简得:()2236x m -=,代入2226x m +=中,得:()222366x x -=-,解得:x=3或x=6,代入2226x m +=,可得:当x=3时,m=33或33-(舍),当x=6时,m=0(舍),故m 的值为33, 故选A.【点睛】本题考查了折叠的性质,勾股定理,解一元二次方程,有一定难度,解题的关键是根据折叠的性质运用勾股定理求解.8.如图,在边长为8的菱形ABCD 中,∠DAB =60°,以点D 为圆心,菱形的高DF 为半径画弧,交AD 于点E ,交CD 于点G ,则图中阴影部分的面积是 ( )A .183π-B .183πC .32316πD .1839π-【答案】C【解析】【分析】 由菱形的性质得出AD=AB=8,∠ADC=120°,由三角函数求出菱形的高DF ,图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积,根据面积公式计算即可.【详解】解:∵四边形ABCD 是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°-60°=120°,∵DF 是菱形的高,∴DF ⊥AB ,∴DF=AD •sin60°=383= ∴图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积=2120(43)84332316360ππ⨯⨯=. 故选:C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.9.已知,如图,在ABC V 中,90ACB ∠=︒,30A ∠=︒,求证:12BC AB =.在证明该结论时,需添加辅助线,则作法不正确的是( )A .延长BC 至点D ,使CD BC =,连接ADB .在ACB ∠中作BCE B ∠=∠,CE 交AB 于点EC .取AB 的中点P ,连接CPD .作ACB ∠的平分线CM ,交AB 于点M【答案】D【解析】【分析】 分别根据各选项的要求进行证明,推出正确结论,则问题可解.【详解】解:选项A : 如图,由辅助线可知,ABC ADC ≅V ;,则有AB=AD ,再由90ACB ∠=︒,由30BAC ∠=︒,则60B ∠=︒,∴ABD △是等边三角形∴1122BC DB AB == 故选项A 正确;选项B:如图,由辅助线可知,EBD △是等边三角形则60BEC EAC ECA ∠=∠+∠=︒,BE=EC∵30A ∠=︒∴30ECA A ∠=∠=︒∴AE=EC ∴12BC AB =故选项B 正确选项C 如图,有辅助线可知,CP 为直角三角形斜边上的中线∴AP=CP=BP∵30A ∠=︒∴60B ∠=︒∴PBC V 是等边三角形∴12BC BP AB ==综上可知选项D 错误故应选D【点睛】 此题主要考查了全等三角形的判定,等边三角形的判定与性质的综合应用,根据条件选择正确的证明方法是解题的关键.10.四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,DH ⊥AB 于H ,连接OH ,∠DHO =20°,则∠CAD 的度数是().A .25°B .20°C .30°D .40°【答案】B【解析】 ∵四边形ABCD 是菱形,∴OB=OD ,AC ⊥BD ,∵DH ⊥AB ,∴OH=OB=12BD , ∵∠DHO=20°, ∴∠OHB=90°-∠DHO=70°,∴∠ABD=∠OHB=70°,∴∠CAD=∠CAB=90°-∠ABD=20°.故选A .11.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,将边长为4的菱形OBCD 的边OB 固定在x 轴上,开始时30DOB ∠=︒,现把菱形向左推,使点D 落在y 轴正半轴上的点D ¢处,则下列说法中错误的是( )A .点C '的坐标为()4,4B .60CBC '∠=︒ C .点D 移动的路径长度为4个单位长度D .CD 垂直平分BC '【答案】C【解析】【分析】 先证明四边形OBC′D′是正方形,且边长=4,即可判断A ;由平行线的性质得∠OBC 的度数,进而得到60CBC '∠=︒,即可判断B ;根据弧长公式,求出点D 移动的路径长度,即可判断C ;证明CD ⊥BC ′,BC′=BC=2BE ,即可判断D .【详解】∵四边形OBCD 是菱形,∴OB=BC=CD=OD ,∴OB=BC ′=C ′D ′=OD ′,∵∠BOD′=90°,∴四边形OBC′D′是正方形,且边长=4,∴点C '的坐标为()4,4,故A 不符合题意.∵30DOB ∠=︒,OD ∥BC ,∴∠OBC=180°-30°=150°,∵∠OBC ′=90°,∴60CBC '∠=︒,故B 不符合题意.∵点D 移动的路径是以OD 长为半径,圆心角为∠DOD ′=90°-30°=60°的弧长,∴点D 移动的路径长度=604180π⨯=43π,故C 符合题意. 设CD 与BC′交于点E ,∵在菱形OBCD 中,∠C=30DOB ∠=︒,∵60CBC '∠=︒,∴∠BEC=180°-60°-30°=90°,即CD ⊥BC ′,∴BC′=BC=2BE ,∴CD 垂直平分BC ',故D 不符合题意.故先C .【点睛】本题主要考查菱形的性质,正方形的判定和性质以及点的坐标,熟练掌握菱形的性质和正方形性质,含30°角的直角三角形的性质,是解题的关键.12.如图1,在△ABC 中,∠B =90°,∠C =30°,动点P 从点B 开始沿边BA 、AC 向点C 以恒定的速度移动,动点Q 从点B 开始沿边BC 向点C 以恒定的速度移动,两点同时到达点C ,设△BPQ 的面积为y (cm 2).运动时间为x (s ),y 与x 之间关系如图2所示,当点P 恰好为AC 的中点时,PQ 的长为( )A .2B .4C .3D .3【答案】C【解析】【分析】点P、Q的速度比为3:3,根据x=2,y=63,确定P、Q运动的速度,即可求解.【详解】解:设AB=a,∠C=30°,则AC=2a,BC=3a,设P、Q同时到达的时间为T,则点P的速度为3aT,点Q的速度为3a,故点P、Q的速度比为3:3,故设点P、Q的速度分别为:3v、3v,由图2知,当x=2时,y=63,此时点P到达点A的位置,即AB=2×3v=6v,BQ=2×3v=23v,y=12⨯AB×BQ=12⨯6v×23v=63,解得:v=1,故点P、Q的速度分别为:3,3,AB=6v=6=a,则AC=12,BC=63,如图当点P在AC的中点时,PC=6,此时点P运动的距离为AB+AP=12,需要的时间为12÷3=4,则BQ=3x=43,CQ=BC﹣BQ=63﹣43=23,过点P作PH⊥BC于点H,PC=6,则PH=PC sin C=6×12=3,同理CH=3,则HQ=CH﹣CQ=333,PQ22PH HQ+39+3,故选:C.【点睛】本题考查的是动点图象问题,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.13.如图,在□ABCD中,E、F分别是边BC、CD的中点,AE、AF分别交BD于点G、H,则图中阴影部分图形的面积与□ABCD的面积之比为()A .7 : 12B .7 : 24C .13 : 36D .13 : 72【答案】B【解析】【分析】 根据已知条件想办法证明BG=GH=DH ,即可解决问题;【详解】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC ,AB=CD ,AD=BC ,∵DF=CF ,BE=CE , ∴12DH DF HB AB ==,12BG BE DG AD ==, ∴13DH BG BD BD ==, ∴BG=GH=DH ,∴S △ABG =S △AGH =S △ADH ,∴S 平行四边形ABCD =6 S △AGH ,∴S △AGH :ABCD S 平行四边形=1:6,∵E 、F 分别是边BC 、CD 的中点, ∴12EF BD =, ∴14EFC BCDD S S =V V , ∴18EFCABCD S S =V 四边形, ∴1176824AGH EFC ABCD S S S +=+=V V 四边形=7∶24, 故选B.【点睛】本题考查了平行四边形的性质、平行线分线段成比例定理、等底同高的三角形面积性质,题目的综合性很强,难度中等.14.如图,△ABC 中,AB=4,AC=3,AD 、AE 分别是其角平分线和中线,过点C 作CG ⊥AD 于F ,交AB 于G ,连接EF ,则线段EF 的长为( )A .1B .34C .23D .12【答案】D【解析】【分析】 由等腰三角形的判定方法可知△AGC 是等腰三角形,所以F 为GC 中点,再由已知条件可得EF 为△CBG 的中位线,利用中位线的性质即可求出线段EF 的长.【详解】∵AD 是△ABC 角平分线,CG ⊥AD 于F ,∴△AGC 是等腰三角形,∴AG=AC=3,GF=CF ,∵AB=4,AC=3,∴BG=1,∵AE 是△ABC 中线,∴BE=CE ,∴EF 为△CBG 的中位线,∴EF=12BG=12, 故选:D .【点睛】 此题考查等腰三角形的判定和性质、三角形的中位线性质定理,解题关键在于掌握三角形的中位线平行于第三边,并且等于第三边的一半.15.已知ABCD Y (AB BC >),用尺规在ABCD 内作菱形,下列作法错误的是( )A .如图1所示,作对角线AC 的垂直平分线EF ,则四边形AECF 为所求B .如图2所示,在AB DC ,上截取AE AD DF DA ==,,则四边形AEFD 为所求 C .如图3所示,作ADC ABC ∠∠、的平分线DE BF ,,则四边形DEBF 为所求 D .如图4所示,作BDE BDC DBF DBA ∠=∠∠=∠,,则四边形DEBF 为所求【答案】C【解析】【分析】根据平行四边形的性质及判定、菱形的判定逐个判断即可.【详解】解:A、根据线段的垂直平分线的性质可知AB=AD,一组邻边相等的平行四边形是菱形;符合题意;B、根据四条边相等的四边形是菱形,符合题意;C、根据两组对边分别平行四边形是平行四边形,不符合题意;D、根据一组邻边相等的平行四边形是菱形,符合题意.故选:C.【点睛】本题考查了复杂作图,解决本题的关键是利用平行四边形的性质及判定、菱形的判定.16.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则AMMD等于()A.35B.23C.38D.45【答案】A【解析】试题分析:设AB=a,根据题意知AD=2a,由四边形BMDN是菱形知BM=MD,设AM=b,则BM=MD=2a-b.在Rt△ABM中,由勾股定理即可求值.试题解析:∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=a,AM=b,则MB=2a-b,(a、b均为正数).在Rt△ABM中,AB2+AM2=BM2,即a2+b2=(2a-b)2,解得a=4b3,∴MD=MB=2a-b=53 b,∴3553AM bMD b==.故选A.考点:1.矩形的性质;2.勾股定理;3.菱形的性质.17.如图,在菱形ABCD 中,点A 在x 轴上,点B 的坐标轴为()4,1, 点D 的坐标为()0,1, 则菱形ABCD 的周长等于( )A .5B .43C .45D .20【答案】C【解析】【分析】 如下图,先求得点A 的坐标,然后根据点A 、D 的坐标刻碟AD 的长,进而得出菱形ABCD 的周长.【详解】如下图,连接AC 、BD ,交于点E∵四边形ABCD 是菱形,∴DB ⊥AC ,且DE=EB 又∵B ()4,1,D ()0,1∴E(2,1)∴A(2,0)∴()()2220015-+-=∴菱形ABCD 的周长为:5故选:C【点睛】本题在直角坐标系中考查菱形的性质,解题关键是利用菱形的性质得出点A 的坐标,从而求得菱形周长.18.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD 上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.3cm D.2cm【答案】D【解析】分析:根据翻折的性质可得∠B=∠AB1E=90°,AB=AB1,然后求出四边形ABEB1是正方形,再根据正方形的性质可得BE=AB,然后根据CE=BC-BE,代入数据进行计算即可得解.详解:∵沿AE对折点B落在边AD上的点B1处,∴∠B=∠AB1E=90°,AB=AB1,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC-BE=8-6=2cm.故选:D.点睛:本题考查了矩形的性质,正方形的判定与性质,翻折变换的性质,判断出四边形ABEB1是正方形是解题的关键.19.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是()A.110°B.120°C.140°D.150°【答案】B【解析】【详解】解:∵AD∥BC,∴∠DEF=∠EFB=20°,图b中∠GFC=180°-2∠EFG=140°,在图c中∠CFE=∠GFC-∠EFG=120°,故选B.20.一个多边形的每个内角均为108º,则这个多边形是()A.七边形 B.六边形 C.五边形 D.四边形【答案】C【解析】试题分析:因为这个多边形的每个内角都为108°,所以它的每一个外角都为72°,所以它的边数=360÷72=5(边).考点:⒈多边形的内角和;⒉多边形的外角和.。
