da2013年高考数学试卷答案 江苏
2013江苏省高考数学真题含答案清晰版

2013高考数学试卷参考公式: 样本数据12,,,n x x x 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑。
棱锥的体积公式:13V Sh =,其中S 是锥体的底面积,h 为高。
棱柱的体积公式:V Sh =,其中S 是柱体的底面积,h 为高。
一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置上。
DE AB AC λλ=+(λ、11、已知()f x 是定义在R12n n a a a a ++>的最大正整数内作答,解答时应写出文字说明、证明或演.(本小题满分14分)已知向量(cos ,sin ),(cos ,sin ),0a b ααββ==(1)若||2a b -=,求证:a b ⊥;(2)设(0,1)c =,若a b c +=,求βα,的值。
16、(本小题满分14分)如图,在三棱锥S-ABC 中,平面⊥SAB 平面SBC,BC AB ⊥,AS=AB 。
过A 作SB AF ⊥,垂足为F ,点E 、G 分别为线段SA 、SC 的中点。
求证:(1)平面EFG//平面ABC ;(2)BC SA ⊥。
如图,在平面直角坐标系xoy 中,点A(0,3),直线42:-=x y l ,设圆C 的半径为1,圆心在直线l 上。
(1)若圆心C 也在直线1-=x y 上,过点A 作圆C 的切线,求切线的方程;(2)若圆C 上存在点M ,使MA=2MO ,求圆心C 的横坐标a 的取值范围。
18、(本小题满分16分)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径。
一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C 。
现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50米/分钟。
在甲出发2分钟后,乙从A 乘坐缆车到B ,在B 处停留1分钟后,再从B 匀速步行到C 。
假设缆车速度为130米/分钟,山路AC 的长为1260米,经测量,123cos ,cos 135A C ==。
2013年高考真题——数学(江苏卷)解析版

2013年普通高等学校招生全国统一考试 (江苏卷)数学Ⅰ 注意事项绝密★启用前考生在答题前请认真阅读本注意事项及各题答题要求:1.本试卷共4页,均为非选择题(第1题~第20题,共20题).本卷满分为160分.考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请您务必将自己的姓名、考试证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符. 4.作答试题必须用0.5毫米黑色墨水的签字笔在答题卡的指定位置作答,在其它位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置.......上.. 1.函数)42sin(3π-=x y 的最小正周期为 ▲ .2.设2)2(i z -=(i 为虚数单位),则复数z 的模为 ▲ .YN 输出n 1a 2n ←←,1n n ←+32a a ←+20a <结束(第5题)3.双曲线191622=-y x 的两条渐近线的方程为 ▲ .4.集合{}1,0,1-共有 ▲ 个子集.5.右图是一个算法的流程图,则输出的n 的值是 ▲6.抽样统计甲,乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为▲.7.现有某类病毒记作n m Y X ,其中正整数)9,7(,≤≤n m n m 可以任意选取,则n m ,都取到奇数的概率为 ▲ .8.抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界).若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是 ▲ .9.抛物线2y x =在1x =处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界) 。
2013年江苏高考数学试题及答案解析版1_(word版)

2013年普通高等学校统一考试试题(江苏卷)一、填空题:本大题共14小题,每小题5分,共计70分。
请把答案填写在答题卡相印位置上。
.6则成绩较为稳定(方差较小)的那位运动员成绩的方差为 【答案】2 7.现在某类病毒记作n m Y X ,其中正整数m ,n (7≤m ,9≤n )可以任意选取,则n m , 都取到奇数的概率为 .63208.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V .1:249.抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界) .若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是 .[—2,12 ]10.设E D ,分别是ABC ∆的边BC AB ,上的点,AB AD 21=,BC BE 32=, 若AC AB DE 21λλ+=(21λλ,为实数),则21λλ+的值为 .1211.已知)(x f 是定义在R 上的奇函数。
当0>x 时,x x x f 4)(2-=,则不等式x x f >)( 的解集用区间表示为 .(﹣5,0) ∪(5,﹢∞)12.在平面直角坐标系xOy 中,椭圆C 的标准方程为)0,0(12222>>=+b a by a x ,右焦点为F ,右准线为l ,短轴的一个端点为B ,设原点到直线BF 的距离为1d ,F 到l 的距离为2d ,若126d d =,则椭圆C 的离心率为 .3313.在平面直角坐标系xOy 中,设定点),(a a A ,P 是函数xy 1=(0>x )图象上一动点,若点A P ,之间的最短距离为22,则满足条件的实数a 的所值为 .1或1014.在正项等比数列}{n a 中,215=a ,376=+a a ,则满足n n a a a a a a 2121>+++的最大正整数n 的值为 .12二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分) 已知)sin ,(cos )sin ,(cos ββαα=b a ,=,παβ<<<0.(1)若2||=-b a ,求证:b a ⊥;(2)设)1,0(=c ,若c b a =+,求βα,的值. 解:(1)a -b =(cosα-cosβ,sin α-sin β),|a -b |2=(cosα-cosβ)2+(sin α-sin β)2=2-2(cosα·cosβ+sin α·sin β)=2, 所以,cosα·cosβ+sin α·sin β=0,所以,b a ⊥. (2)⎩⎨⎧=+=+②1sin sin ①0cos cos βαβα,①2+②2得:cos(α-β)=-12 .所以,α-β=π32,α=π32+β,带入②得:sin(π32+β)+sin β=23cosβ+12 sin β=sin(3π+β)=1, 所以,3π+β=2π. 所以,α=65π,β=6π.16.(本小题满分14分)如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证: (1)平面//EFG 平面ABC ;(2)SA BC ⊥. 证:(1)因为SA =AB 且AF ⊥SB , 所以F 为SB 的中点. 又E ,G 分别为SA ,SC 的中点, 所以,EF ∥AB ,EG ∥AC .又AB ∩AC =A ,AB ⊂面SBC ,AC ⊂面ABC , 所以,平面//EFG 平面ABC . (2)因为平面SAB ⊥平面SBC ,平面SAB ∩平面SBC =BC ,AF ⊂平面ASB ,AF ⊥SB .所以,AF ⊥平面SBC .又BC ⊂平面SBC , 所以,AF ⊥BC .又AB ⊥BC ,AF ∩AB =A , 所以,BC ⊥平面SAB .又SA ⊂平面SAB , 所以,SA BC ⊥.17.(本小题满分14分)如图,在平面直角坐标系xOy 中,点)3,0(A ,直线42:-=x y l .设圆C 的半径为1,圆心在l 上. (1)若圆心C 也在直线1-=x y 上,过点A 作圆C 的切线, 求切线的方程;A BSG F E(2)若圆C 上存在点M ,使MO MA 2=,求圆心C 的横坐 标a 的取值范围.解:(1)联立:⎩⎨⎧-=-=421x y x y ,得圆心为:C (3,2).设切线为:3+=kx y ,d =11|233|2==+-+r k k ,得:430-==k or k .故所求切线为:343+-==x y or y .(2)设点M (x ,y ),由MO MA 2=,知:22222)3(y x y x +=-+,化简得:4)1(22=++y x ,即:点M 的轨迹为以(0,1)为圆心,2为半径的圆,可记为圆D . 又因为点M 在圆C 上,故圆C 圆D 的关系为相交或相切. 故:1≤|CD |≤3,其中22)32(-+=a a CD .解之得:0≤a ≤125 .18.(本小题满分16分)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径。
2013年江苏省高考数学试卷及答案(Word解析版)

2013年江苏省高考数学试卷及答案(Word解析版)2013年普通高等学校统一考试试题(江苏卷)一、填空题:本大题共14小题,每小题5分,共计70分。
请把答案填写在答题卡相印位置上。
1.函数)42sin(3π+=x y 的最小正周期为.【答案】π【解析】T =|2πω |=|2π2 |=π.2.设2)2(i z -=(i 为虚数单位),则复数z 的模为.【答案】5【解析】z =3-4i ,i 2=-1,| z |==5.3.双曲线191622=-y x 的两条渐近线的方程为.【答案】x y 43±= 【解析】令:091622=-y x ,得x x y 431692±=±=. 4.集合}1,0,1{-共有个子集.【答案】8【解析】23=8.5.右图是一个算法的流程图,则输出的n 的值是.【答案】3【解析】n =1,a =2,a =4,n =2;a =10,n =3;a =28,n =4. 6则成绩较为稳定(方差较小)的那位运动员成绩的方差为.【答案】2【解析】易得乙较为稳定,乙的平均值为:9059288919089=++++=x .方差为:25)9092()9088()9091()9090()9089(222222=-+-+-+-+-=S . 7.现在某类病毒记作n m Y X ,其中正整数m ,n (7≤m ,9≤n )可以任意选取,则n m ,都取到奇数的概率为.【答案】6320 【解析】m 取到奇数的有1,3,5,7共4种情况;n 取到奇数的有1,3,5,7,9共5种情况,则n m ,8.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V .【答案】1:24【解析】三棱锥ADE F -与三棱锥ABC A -1的相似比为1:2,故体积之比为1:8.又因三棱锥ABC A -1与三棱柱ABC C B A -111的体积之比为1:3.所以,三棱锥ADE F -与三棱柱ABC C B A -111的体积之比为1:24.9.抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界) .若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是.【答案】[—2,12 ]【解析】抛物线2x y =在1=x 处的切线易得为y =2x —1,令z =y x 2+,y =—12 x +z2 .画出可行域如下,易得过点(0,—1)时,z min =—2,过点(12 ,0)时,z max =12 .10.设E D ,分别是ABC ?的边BC AB ,上的点,AB AD 21= ,BC BE 32=,若AC AB DE 21λλ+=(21λλ,为实数),则21λλ+的值为.【答案】12【解析】)(32213221++=+=+= 213261λλ+=+-=所以,611-=λ,322=λ,=+21λλ12 .11.已知)(x f 是定义在R 上的奇函数。
2013年江苏高考数学试题和答案(含理科附加)
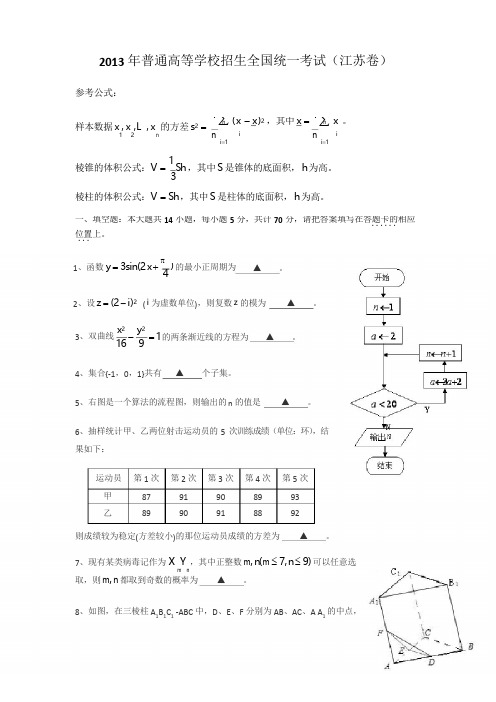
1∑(x-x)2,其中x= n 1∑x。
n一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应...4)的最小正周期为2013年普通高等学校招生全国统一考试(江苏卷)参考公式:样本数据x,x,L,x的方差s2=12nni=1ini=1i棱锥的体积公式:V=1Sh,其中S是锥体的底面积,h为高。
3棱柱的体积公式:V=Sh,其中S是柱体的底面积,h为高。
......位置上。
1、函数y=3sin(2x+π▲。
2、设z=(2-i)2(i为虚数单位),则复数z的模为▲。
3、双曲线x2y2-=1的两条渐近线的方程为▲。
1694、集合{-1,0,1}共有▲个子集。
5、右图是一个算法的流程图,则输出的n的值是▲。
6、抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:运动员第1次第2次第3次第4次第5次甲乙87899190909189889392则成绩较为稳定(方差较小)的那位运动员成绩的方差为▲。
7、现有某类病毒记作为X Y,其中正整数m,n(m≤7,n≤9)可以任意选m n取,则m,n都取到奇数的概率为▲。
8、如图,在三棱柱A1B1C1-ABC中,D、E、F分别为AB、AC、A A1的中点,uuur uuur uuur2 F }中, a = , a + a =3 ,则满足a + a + L + a > a a L a 的2二、解答题:本大题共 6 小题,共计 90 分,请在答题卡指定区域内作答,解答时应写出文字说设三棱锥 F -ADE 的体积为V 1 ,三棱柱 A 1B 1C 1 -ABC 的体积为V 2 ,则V 1 : V 2 =▲。
9、抛物线 y = x 2 在 x = 1 处的切线与坐标轴围成三角形区域为 D(包含三角形内部与边界)。
若点 P(x ,y)是区域 D 内的任意一点,则 x + 2 y 的取值范围是▲。
1 210 、 设 D 、 E 分 别 是 △ ABC 的 边 AB 、 BC 上 的 点 , 且 AD = AB, BE = BC 。
2013年江苏省高考数学试卷及答案(Word解析版)

2013年普通高等学校统一考试试题【江苏卷】一、填空题:本大题共14小题,每小题5分,共计70分。
请把答案填写在答题卡相印位置上。
1、函数)42sin(3π+=x y 的最小正周期为 、【答案】π【解析】T =|2πω |=|2π2 |=π、2、设2)2(i z -=【i 为虚数单位】,则复数z 的模为 、 【答案】5【解析】z =3-4i ,i 2=-1,| z |==5、3、双曲线191622=-y x 的两条渐近线的方程为 、 【答案】x y 43±= 【解析】令:091622=-y x ,得x x y 431692±=±=、 4、集合}1,0,1{-共有 个子集、【答案】8【解析】23=8、5、右图是一个算法的流程图,则输出的n 的值是 、 【答案】3【解析】n =1,a =2,a =4,n =2;a =10,n =3;a =28,n =4、 6则成绩较为稳定【方差较小】的那位运动员成绩的方差为 、 【答案】2【解析】易得乙较为稳定,乙的平均值为:9059288919089=++++=x 、方差为:25)9092()9088()9091()9090()9089(222222=-+-+-+-+-=S 、 7、现在某类病毒记作n m Y X ,其中正整数m ,n 【7≤m ,9≤n 】可以任意选取,则n m , 都取到奇数的概率为 、【答案】6320 【解析】m 取到奇数的有1,3,5,7共4种情况;n 取到奇数的有1,3,5,7,9共5种情况,则n m ,都取到奇数的概率为63209754=⨯⨯、 8、如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V 、【答案】1:24【解析】三棱锥ADE F -与三棱锥ABC A -1的相似比为1:2,故体积之比为1:8、又因三棱锥ABC A -1与三棱柱ABC C B A -111的体积之比为1:3、所以,三棱锥ADE F -与三棱柱ABC C B A -111的体积之比为1:24、9、抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界) 、若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是 、 【答案】[—2,12 ]【解析】抛物线2x y =在1=x 处的切线易得为y =2x —1,令z =y x 2+,y =—12 x +z 2 、 画出可行域如下,易得过点(0,—1)时,z min =—2,过点(12 ,0)时,z max =12 、10、设E D ,分别是ABC ∆的边BC AB ,上的点,AB AD 21=,BC BE 32=, 若21λλ+=【21λλ,为实数】,则21λλ+的值为 、 【答案】12【解析】)(32213221AC BA AB BC AB BE DB DE ++=+=+=xAB C1A DE F1B 1CAC AB AC AB 213261λλ+=+-= 所以,611-=λ,322=λ,=+21λλ12 、 11、已知)(x f 是定义在R 上的奇函数。
2013年江苏高考数学试题和答案(含理科附加)
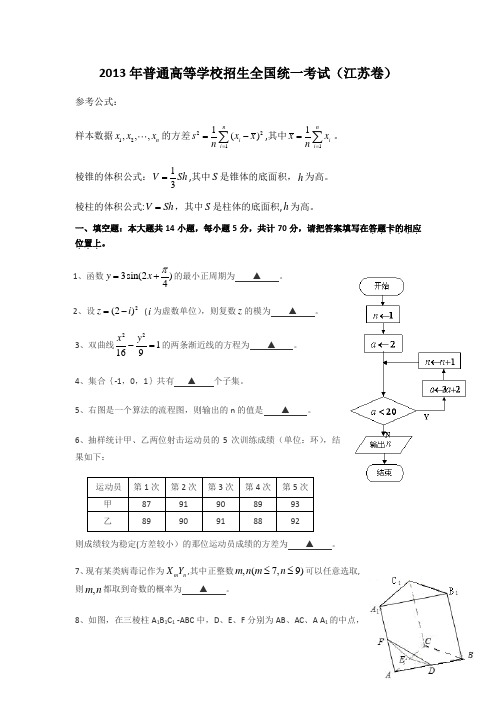
2013年普通高等学校招生全国统一考试(江苏卷)参考公式:样本数据12,,,n x x x 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑。
棱锥的体积公式:13V Sh =,其中S 是锥体的底面积,h 为高。
棱柱的体积公式:V Sh =,其中S 是柱体的底面积,h 为高。
一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应......位置上...。
1、函数3sin(2)4y x π=+的最小正周期为 ▲ 。
2、设2(2)z i =- (i 为虚数单位),则复数z 的模为 ▲ 。
3、双曲线221169x y -=的两条渐近线的方程为 ▲ 。
4、集合{-1,0,1}共有 ▲ 个子集。
5、右图是一个算法的流程图,则输出的n 的值是 ▲ 。
6、抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为 ▲ 。
7、现有某类病毒记作为m n X Y ,其中正整数,(7,9)m n m n ≤≤可以任意选取,则,m n 都取到奇数的概率为 ▲ 。
8、如图,在三棱柱A 1B 1C 1 -ABC 中,D 、E 、F 分别为AB 、AC 、A A 1的中点,运动员 第1次 第2次 第3次 第4次 第5次 甲 87 91 90 89 93 乙899091889210、设D 、E 分别是△ABC 12DE AB AC λλ=+(1λ、11、已知()f x 是定义在R 上的奇函数。
解集用区间表示为 ▲ 12、在平面直角坐标系xoy 12n n a a a a ++>的二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明或演算步骤. 15、(本小题满分14分)已知向量(cos ,sin ),(cos ,sin ),0a b ααβββαπ==<<<。
2013年江苏高考数学试题及参考答案

2013年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ(必做题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求:1.本试卷共4页,均为非选择题(第1题~第20题,共20题).本卷满分为160分.考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请您务必将自己的姓名、考试证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符. 4.作答试题必须用0.5毫米黑色墨水的签字笔在答题卡的指定位置作答,在其它位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗. 一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.函数)42sin(3π+=x y 的最小正周期为 .2.设2)2(i z -=(i 为虚数单位),则复数z 的模为 .3.双曲线191622=-y x 的两条渐近线的方程为 .4.集合}1,0,1{-共有 个子集.5.下图是一个算法的流程图,则输出的n 的值是 .6.抽样统计甲、乙两位设计运动员的5此训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为 .7.现在某类病毒记作n m Y X ,其中正整数m ,n (7≤m ,9≤n )可以任意选取,则n m ,都取到奇数的概率为 .8.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V . 9.抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包含三角形内部与边界)。
若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是 .10.设E D ,分别是ABC ∆的边BC AB ,上的点,AB AD 21=,BC BE 32=,若21λλ+= (21λλ,为实数),则21λλ+的值为 .11.已知)(x f 是定义在R 上的奇函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年普通高等学校统一考试试题(江苏卷)答案一、填空题1、π2、53、34y x =±4、85、46、27、2063 8、1249、1[2,]2-10、1211、(5,0)(5,)-⋃+∞12 13、1,3- 14、12二、解答题15、(1)略 (2)5,66ππαβ==16、证:(1)SA BA =,AF SB ⊥,SF BF ∴=,由题SE EA =,//EF AB ∴,EF ⊄平面ABCAB ⊂平面ABC ,//EF ∴平面ABC ,同理//EG 平面ABC ,EF 与EG 为平面EFG 内的两条相交直线,∴平面//EFG 平面ABC ,(2)平面⊥SAB 平面SBC 于SB ,AF ⊂平面SAB ,AF ∴⊥平面SBC ,AF BC ∴⊥, 又BC AB ⊥且AB 与AF 为平面SAB 内的两条相交直线,BC SA ∴⊥。
17、解:(1)由题设点(,24)C a a -,又C 也在直线1-=x y 上,241,3a a a ∴-=-∴= 22:(3)(2)1C x y ∴-+-=,由题,过A 点切线方程可设为3y kx =+,即30kx y -+=,1=,解得:30,4k =-,∴所求切线为3y =或334y x =-+(2)设点(,24)C a a -,00(,)M x y ,2MA MO =,)3,0(A ,(0,0)O ,22220000(3)4()x y x y ∴+-=+,即2200032x y y +=-,又点M 在圆C 上,2200()(24)1x a y a ∴-+-+=,两式相减得2005(23)(89)02a ax a y a +---+=,由题以上两式有公共点,21≤整理得:25|63|2a a -+≤,即222(5126)4(5129)a a a a -+≤-+,令25126t a a =-+,则24(3)t t ≤+,解得:26t -≤≤,2251266a a ∴-≤-+≤,解得:1205a ≤≤. 18、解:(1)在ABC ∆中,1312cos =A ,53cos =C ,5sin 13A ∴=,4sin 5C =, 63sin sin()sin cos cos sin 65B A C A C A C ∴=+=+=,sin sin AB ACC B=,5651260463AB ⨯∴=, 1040AB ∴=.答:索道AB 的长为1040m .(2)设乙出发min t 到点P ,则甲出发(2)min t +到点Q ,130AP t =,50(2)AQ t =+,在APQ ∆中,222222122cos (130)50(2)213050(2)13PQ AP AQ APAQ A t t t t =+-=++-⨯⨯+⨯, 2222222100[(13)5(2)120(2)]100[16925(2)120(2)]PQ t t t t t t t t ∴=++-+=++-+ 22100(74140100)PQ t t ∴=-+,当且仅当35min 37t =时,PQ 最小. 答:乙出发3537分钟后,乙在缆车上与甲的距离最短. (3)甲走完长为m 1260的山路AC ,共需126025.250=分钟,设乙总用时为min t ,乙步行的速度为/min vm ,则22.228.2t ≤≤,由题104021130BCt v=+++,在ABC ∆中,由正弦定理求得500BC =,50011[22.2,28.2]t v ∴=+∈,500[11.2,17.2]v ∴∈,11[,]50017.211.2v ∴∈,500500[,]17.211.2v ∴∈,500500[,]17.211.2v ∴∈,50005000[,]172112v ∴∈,50005000[,]172112v ∴∈,39[29,44]4314v ∴∈答:为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制329/min43m 到944/min 14m 内.19、证明:(1)若0=c ,则n n S b n =,*N n ∈,又由题(1)2n n n dS na -=+,12n n S n b a d n -∴==+,112n n b b d +∴-=,{}n b ∴是等差数列,首项为a ,公差为2d,)0(≠d ,又421b b b ,,成等比数列, 2214b b b ∴=,23()()22d da a a ∴+=+,23()42d d ad a ∴+=,0d ≠,2d a ∴=,2n S n a ∴=,222222(),nk k S nk a n k a n S n k a ∴===,2nk k S n S ∴=(*,N n k ∈). (2)由题c n nS b n n +=2,*N n ∈,22[2(1)]2()n n a n d b n c +-=+,若}{n b 是等差数列,则可设n b x yn =+,,x y 是常数,22[2(1)]2()n a n d x yn n c +-=++关于*N n ∈恒成立.整理得:32(2)(22)220d y n a d x n cyn cx -+----=关于*N n ∈恒成立.20,220,20,20d y a d x cy cx ∴-=--===,20,22,0,0d y a x d cy cx ∴=≠-===0c ∴=。
20、解:(1)由题1'()0f x a x =-≤在),1(+∞上恒成立,1a x∴≥在),1(+∞上恒成立,1a ∴≥;'()x g x e a =-若0a ≤,则'()0xg x e a =->在),1(+∞上恒成立,)(x g 在),1(+∞上递增,()g x ∴在),1(+∞上没有最小值,0a ∴>, 当ln x a =时,'()0g x =,由于'()x g x e a =-在),1(+∞递增,ln x a ∴>时'()0g x >,)(x g 递增,ln x a <时'()0g x <,)(x g 递减,从而ln x a=为)(x g 的可疑极小点,由题ln 1a >,a e ∴>, 综上a 的取值范围为a e >.(2)由题'()0xg x e a =-≥在(1,)-+∞上恒成立,x e a ∴≥在(1,)-+∞上恒成立,1a e∴≤, 由()ln 0,(0)f x x ax x =-=>得 ln ,(0)x a x x =>,令ln (),(0)xh x x x=>,则21ln '(),(0)xh x x x -=>, 当0x e <<时,'()0h x >,ln (),(0)xh x x x=>递增,当x e >时,'()0h x <,ln (),(0)xh x x x=>递减, x e ∴=时,ln (),(0)x h x x x =>最大值为1e,又01x <<时,ln ()0x h x x =<,1x >时,ln ()0x h x x=>,据此作出ln (),(0)xh x x x=>的大致图象,由图知:当0a ≤或1a e =时,)(x f 的零点有1个, 当10a e <<时,)(x f 的零点有2个,21.A 证明:连接OD,∵AB 与BC 分别与圆O 相切于点D 与C∴090=∠=∠ACB ADO ,又∵A A ∠=∠ ∴ADO RT ∆~ACB RT ∆ ∴ADACOD BC = 又∵BC=2OC=2OD ∴AC=2ADB 解:设矩阵A 的逆矩阵为⎥⎦⎤⎢⎣⎡d c b a ,则⎥⎦⎤⎢⎣⎡-2001 ⎥⎦⎤⎢⎣⎡d c b a =⎥⎦⎤⎢⎣⎡1001 ,即⎥⎦⎤⎢⎣⎡--d c b a 22 =⎥⎦⎤⎢⎣⎡1001 , 故a=-1,b=0,c=0,d=21∴矩阵A 的逆矩阵为⎥⎥⎦⎤⎢⎢⎣⎡⋅-=-210011 A ,∴B A 1-=⎥⎥⎦⎤⎢⎢⎣⎡⋅-21001 ⎥⎦⎤⎢⎣⎡6021 =⎥⎦⎤⎢⎣⎡⋅⋅--3021 . C 解:∵直线l 的参数方程为⎩⎨⎧=+=t y t x 21∴消去参数t 后得直线的普通方程为022=--y x ①同理得曲线C 的普通方程为x y 22= ②①②联立方程组解得它们公共点的坐标为)2,2(,)1,21(-. D 证明: ∵=---b a ab b a 223322()=---)(223223b b a ab a())(22222b a b b a a ---())2)()(()2(22b a b a b a b a b a --+=--=又∵b a ≥>0,∴b a +>0,0≥-b a 02≥-b a , ∴0)2)()((≥--+b a b a b a ∴0222233≥---b a ab b a ∴b a ab b a 223322-≥-22.答案:解:(1)以{}1,,AA AC AB 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=A ,)4,1,1(1--=A∴10103182018,cos 11==>=<C A ∴异面直线B A 1与D C 1所成角的余弦值为10103(2))0,2,0(= 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x m =,∵)0,1,1(=AD ,)4,2,0(1=AC由1,AC m AD m ⊥⊥∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-= 设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为3523.(1)由数列{}n a 的定义得123456781,2,2,3,3,3,4,4,a a a a a a a a ==-=-====-=-910114,4,5,a a a =-=-=所以12345671,1,3,0,3,6,2,S S S S S S S ==-=-==== 8910112,6,10,5,S S S S =-=-=-=-从而114,0,S a S a S a==⨯=,6611112,S a S a ==-,所以集合11P 中元素的个数为5.(2)先证: (21)(21)()i i S i i i *+=-+∈N .事实上,①当1i =时,(21)33,(21)3i i S S i i +==--+=-,故原等式成立;②假设i m=时成立,即(21)(21),m m S m m +=-+则1i m =+时,22(1)(23)(21)(21)(22)m m m m S S m m +++=++-+=(21)43m m m -+--=2(253)m m -++=(1)(23).m m -++综合①②可得,(21)(21).i i S i i +=-+于是22(1)(21)(21)(21)(21)(21)(21)(1)i i i i S S i i i i i i +++=++=-+++=++. 由上可知(21)i i S +是21i +的倍数,而(21)21(1,2,,21)i i ja i j i ++=+=+,所以(21)(21)(21)i i j i i S S j i +++=++是(21)(1,2,,21)i i j a j i ++=+的倍数.又(1)(21)(1)(21)i i S i i ++=++不是22i +的倍数,而(1)(21)(22)(1,2,,22)i i j a i j i +++=-+=+,所以(1)(21)(1(22)(21)(1i i j i i S S j ii i j i +++++=-+=++-+不是(1)(2(1,2,,22)i i j a j i +++=+的倍数,故当(21)l i i =+时,集合l P 中元素的个数为213(21)i i +++-=,于是,当(21)(121)l i i j j i =++≤≤+时,集合l P 中元素的个数为2i j +.又200031(2311)47=⨯⨯++,故集合2000P 中元素的个数为231471008+=.。
