清华大学-理论力学-习题解答-5-48
大学教材课后习题答案免费下载链接下部

大学教材课后习题答案免费下载链接(上中下)190-290本资料由上网购返利网分享汽车理论习题答案(考研_作业).pdf→→/s/1zobam汽车理论第五版_课后习题答案(正确).pdf→→/s/1o67DaHk波动习题答案.pdf→→/s/1pJDGFyj泵与风机课后习题答案.pdf→→/s/1gdBph3H 流体力学习题解答李晓燕吴邦喜.pdf→→/s/1qWM2gAo液压与气压传动习题答案.pdf→→/s/1bnksUmV物理化学第五版习题解答(上下册).pdf→→/s/1sjvvFPj物理学教程第二版马文蔚下册课后答案完整版_cropped.pdf→→/s/1sj98Mct物理学第五版上册习题答案.pdf→→/s/1jG1F9NS王勖成《有限单元法》1-5章课后习题答案.pdf→→/s/1nt8vc3B理论力学教程_第三版_周衍柏_课后习题答案_总汇(1).pdf→→理论力学教程_第三版_周衍柏_课后习题答案_总汇.pdf→→/s/1eQABmxW电力系统分析课后习题答案.pdf→→/s/1bngpktD电动力学习题答案chapter5.pdf→→/s/1pJ7AZ5x电子商务法律与法规综合复习题与答案.pdf→→/s/1c0nEFUo电子测量技术基础课后习题答案上1,2,5,6,7,8.pdf→→/s/1hq3f7Is电子线路习题答案梁明理版.pdf→→/s/1bn5rEIr电工学简明教程(第二版)学习辅导与习题解答.pdf→→/s/1mgHQ6xi电机与拖动基础第三版李发海答案(全).pdf→→/s/1dD25KyP电气测试技术第三版_课后习题答案%28林德杰%29.pdf→→/s/1jGwVRE2电磁场与电磁波习题答案 (6).pdf→→/s/1bnrK3pX电磁场与电磁波习题答案 (7).pdf→→电磁场与电磁波习题答案 (8).pdf→→/s/1mgLUqCC电磁场与电磁波习题答案 .pdf→→/s/1hqsqmX2电磁场与电磁波习题答案2.pdf→→/s/1pJDGF0n电路(第五版)_课后习题答案(全)].邱关源_罗先觉_高等教育出版社.pdf→→/s/1sjtZPBR电路与电子学模拟复习题答案.pdf→→/s/1pJvzN6r电路第五版课后习题答案上册.pdf→→/s/1jG3bA30电路第五版课后习题答案下册.pdf→→/s/1jGn22Ke病理学试题库及答案.pdf→→/s/1hqp80wW 看完包过江苏材料员习题和答案——本人亲自考过.pdf→→/s/1qWyL8IS离散数学课后习题答案_屈婉玲(高等教育出版社).pdf→→/s/1gdghe9t算法导论课后习题与思考题答案合集.pdf→→/s/1pJqaiQf粤教版高中物理必修一课后习题答案(1~4章).pdf→→/s/1gdoU5qF线性代数习题册答案(理).pdf→→/s/1dD5n9ZV线性代数习题解答.pdf→→/s/1i3JY7PV线性规划习题答案.pdf→→/s/1hqiMQ00组合数学课后习题答案.pdf→→/s/1hqwuajE 组合逻辑电路课后习题答案.pdf→→/s/1bnnaNwF经典国外教材atkins物理化学第七版课后习题答案.pdf→→/s/1i39jobj经济学原理习题解答第五版%28微观、宏观).pdf→→/s/1sjm8rKT经济应用数学(三)概率论与数理统计修订版(袁荫棠编)习题答案.pdf →→/s/1ntsgiBR结构力学上龙驭求包世华课后习题答案.pdf→→/s/1eQiQVAU结构力学答案(全).pdf→→/s/1qW2Pud2结构力学课后习题答案.pdf→→/s/1kTKA1sN 结构力学龙驭球习题解答(ch2~ch3).pdf→→/s/1eQ676WM结构化学基础第四版习题答案.pdf→→/s/1jGkKEDw罗默《高级宏观经济学》课后习题答案中文版(金圣才主编).pdf→→/s/1c0h9fxe考研数学一历年真题答案(2002-2011).pdf→→/s/1qWoCltU胡寿松《自动控制原理》(第四版)课件_习题答案.pdf→→/s/1o6qcjqy自动控制原理习题解答(第二版)(余成波_张莲_胡.pdf→→/s/1pJsHZ0R自动控制原理习题解答.pdf→→/s/1bn3VJPH 船舶结构力学—课后习题答案.pdf→→/s/1lBC6西安理工大学_供电技术习题答案_机械工业出版社_第四版.pdf→→/s/1kTyVJSz西方经济学简明教程(第七版)习题参考答案.pdf→→/s/1bnmuORd计算机组成原理习题答案.pdf→→/s/1pJAYQQv计算机组成原理课后习题答案.pdf→→/s/1o68tfcA计算机编译原理课后习题答案第三版张幸儿.pdf→→/s/1eQikYlW计算机网络(第4版)习题答案(中文版).pdf→→/s/1dDcNuTj计算机网络(第五版)习题答案_谢希仁.pdf→→/s/1dDmWLJb计算机网络第四版习题答案(第五版上的很多题在这都能找到答案).pdf→→/s/1qWnqs0G计量经济学习题与解答于俊年主编对外经济贸易大学出版社.pdf→→/s/1i3hyUTv证券交易习题大全与答案.pdf→→/s/1o6NSibo证券投资基金章节习题及答案.pdf→→/s/1mgFiKWS课后习题答案(叶见曙主编结构设计原理1-9章).pdf→→/s/1pJ6Vfp5贾俊平_统计学_第四版_习题答案.pdf→→/s/1jG9hn0M软件工程导论(第五版)_(张海藩_着)_清华大学出版社_课后习题答案.pdf→→/s/1kT8zkz1软件工程导论-第五版_课后习题答案%28清华大学出版社%29张海藩著.pdf→→/s/1qWtvU9m软件工程导论_张海藩_第五版课后习题答案.pdf→→/s/1mgK802G运筹学基础及应用第五版胡运权主编课后练习答案.pdf→→/s/1o6K4t8e近代物理复习题答案.pdf→→/s/1bnzmbTl 通信原理_李晓峰_课后习题答案.pdf→→/s/1pJ2lyXX通信原理习题及答案(第六版)_樊昌信_曹丽娜_编著__国防工业出版社.pdf→→/s/1jGDQUJ8通信电子线路习题解答(严国萍版).pdf→→/s/1ntjs7hf逻辑代数基础课后习题答案.pdf→→/s/1o6ufVGe重点推荐---《数值分析》课后习题答案.pdf→→/s/1eQ456QQ量子力学习题解答-第3章.pdf→→/s/1sjoAeID量子力学练习题答案.pdf→→/s/1eQqsylG 金属材料学习题答案(曹志强老师的).pdf→→/s/1gdwvZFl钢结构基础(第二版)课后习题答案.pdf→→/s/1sjlSrut铁道社单片机习题参考答案.pdf→→/s/1o6qIbSA随机过程习题解答.pdf→→/s/1o6G0618集成电子技术基础教程(上)习题解答.pdf→→/s/1i3mO3fn雷达原理习题解答1.pdf→→/s/13XQ6U高一数学期末复习题及答案.pdf→→/s/1ntlu7g9高中物理必修1、必修2课后习题答案(人教版).pdf→→/s/1jGFSIME高二数列复习题答案.pdf→→/s/1o6lY2nC 高电压技术习题与答案.pdf→→/s/1sjEY8pB 高等代数北大第三版习题全解王萼芳石生明修订.pdf→→/s/1gdn87ZX高等代数_北大第三版_习题答案.pdf.pdf→→/s/1o6lYx6M高等土力学(李广信)1-5章部分习题答案(最新版).pdf→→/s/1jGC4XGa高等教育出版社离散数学课后习题完整答案.pdf→→/s/1dDy2aTb高考数学填空题解答策略.pdf→→/s/1vQmF8 高频电子线路习题答案_张肃文__第五版.pdf→→/s/1nt7Ff1v高鸿业版宏观经济学课后习题答案_%28第十二章到二十三章%29第五版全.pdf→→/s/1sjBAEq5王镜岩生物化学课后习题答案.pdf→→/s/1hqn649e《国际金融学》习题与答案→→/s/1eQ1NKe2 黄达《金融学》精编版(第二版)课后习题答案→→/s/1pJFI9j92014年江南大学微生物学教程(第二版周德庆)考研资料及历年真题答案→→/s/1hq7Pxfm中南大学土木工程材料课后习题及答案→→/s/1o64psNo本资料分上,中,下部三份,欢迎查阅下载建筑装修用花岗岩石材友情赞助。
理论力学答案完整版(清华大学出版社)1

本章要点:
一、 三个概念:力、力矩和力偶 1 力: 力的定义、力的三要素、集中力、分布力;
力的投影:直接投影法和二次投影法;力在平行轴上的投影都相等; 力的合成:平行四边形法则、三角形法则、多边形法则; 合力投影定理 2 力矩:力对点之矩的定义、力对点之矩的三要素、对点的合力矩定理; 力对轴之矩的定义、力对轴之矩和对点之矩的关系、对轴的合力矩定理; 3 力偶:力偶的定义、力偶的三要素、力偶的等效条件; 力偶系的合力偶等于分力偶的矢量和.
解:ξ 轴与 y 轴的交点为 B,合力对 B 点的力矩为 M B = FRx 3k − FRz 3i ;
ξ 轴方向的单位向量为:ξˆ = 1 (3i − 2k )。
13
利用力对点吱矩与力对轴之矩的关系有:
Mξ = M B ⋅ξˆ = −513.4 (N) 。
1-4 图示平面 Π 在各坐标轴上的截矩分别为 a,b, c ,且 a = b 。计算图示力 F 和力偶 M
解:(a)图示三铰拱,BC 半拱为二力构件,约束力一定是沿 BC 连线作用,铰链 A 处的约 束力方向由三力平衡汇交定理确定。
题 1-7(a)图 (b)图示三铰拱,铰链 A、B 和 C 三处的约束力方向都不能确定,因此用两个分力力表示。
3
题 1-7(b)图 (c)图示三铰拱,BC 半拱为二力构件,约束力一定是沿 BC 连线作用,AC 半拱上除约束 力外仅有力偶作用,因力偶只能与力偶平衡,因此 A、C 处的约束力必互相平行并组成力偶。
题 1-9(d力的大小为:
其中: cosϕ1
=
3 13 13
, cosγ 2
=
22 11
;ϕ2
=
45o
。
FR = FR2x + FR2y + FR2z = 645 (N) ;
理论力学习题解答

b
F1
2 3 3 22 3 F 0 F F 2 3 6
' FRy F1 y F2 y F3 y
b
2 3 3 22 3 0 F F F 2 3 6
b o F2 y
' FRz F1 z F2 z F3 z
2 x 2 y 2 z
40 arccos 39.7 o 52
105.2o
54.8o
1-4 已知:F1= 100N,F2=10√5N, b= 0.3m , c= 0.4m , d= 0.2m , e= 0.1m 。 求:力系的主矢和对O点的主矩。 z ' FRx F1 x F2 x 解: c b e b F
M
D
0
B
M Oy
0.3 1 2 100 0.3 10 5 0.2 10 5 0.2 0.5 5 5 6 Nm
1-4 已知:F1= 100N,F2=10√5N, b= 0.3m , c= 0.4m , d= 0.2m , e= 0.1m 。 求:力系的主矢和对O点的主矩。 z
1-4 已知:F1= 100N,F2=10√5N, b= 0.3m , c= 0.4m , d= 0.2m , e= 0.1m 。 求:力系的主矢和对O点的主矩。 z
M Oy M y
b d x
F1
c e
b b c e
2 2
F1d F2d F2 b e
O F2 y
e2 d 2 d e2 d 2
FAy B 30° FB 0.8kN
选AB为研究对象
M A 0
0.2FB 0.1 1 0.3 0.8 sin30o 0
理论力学(周衍柏第三版)习题答案

⑦--⑧
对⑦⑧俩式分别作如下处理:⑦ cos ,⑧ sin
即得
xcos ysin
ar ar
cos a sin cos sin a sin cos
⑨--⑩
⑨+⑩得
ar xcos ysin ⑾
把④⑥代入 ⑾得
ar r r2
3h 4
即午后 45 分钟时两船相距最近最近距离
1.3 解 1 如题 1.3.2 图
smin
15
3 2
15
3
15
3 2
km
4 4
2
y
A
r
a C
aB
O
x
第1.3题图
y
A r
O
C a B x
题1.3.2图
由题分析可知,点 C 的坐标为
v0
s t1
1 2
at1
a
2st2 t1t2 t1
t1 t2
1.2 解 由题可知,以灯塔为坐标原点建立直角坐标如题 1.2.1 图.
AO
B 题1.2.1图
设
ห้องสมุดไป่ตู้
A 船经过 t0
小时向东经过灯塔,则向北行驶的
B
船经
过
t
0
1 1 2
小时经过灯塔任意时刻
A
船的坐标
即
1 1 t cot
此即质点的速度随时间而变化的规律.
v v0 r
1.12 证 由题 1.11 可知质点运动有关系式
所以 dv dv d dv ,联立①②,有 dt d dt d
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
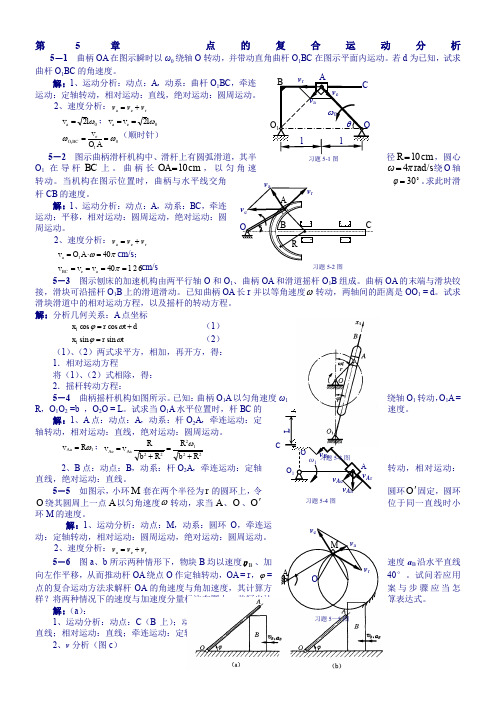
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
理论力学答案完整版(清华大学出版社)3

之差称为静不定次数。这类问题需要补充与静不定次数相同数量的变形协调方程才能求解。 未知约束力分量的数目小于独立平衡方程的数目,这类平衡问题是不存在的。 解题要领:
为自锁。反之,主动力的合力作用线位于摩擦锥外时,不论这个力多小,物体总不平衡。
1 滚动摩擦
维持滚动体平衡的滚阻力偶 M f 的值只能在零和 M f ,max 之间,即 0 ≤ M f ≤ M f ,max . 最大滚阻力偶 M f ,max 与正压力 FN 成正比,即
M f ,max = δFN 。
(a) 解:以 AB 以梁为研究对象,画受力图,列平衡方程
∑ Fx = 0 , FC cos 60o + F1 cos 60o = 0 ,
FC = −F1 = −30 kN
∑ mB = 0,
−
FA
×8
−
M
−
FC
sin
60o
×3+
F1
sin 60o
×8
,
+ F2 × 4 + q × 3×1.5 = 0
平面力偶系:
∑mz = 0
∑my ≡ 0
平面平行力系:
∑ Fz = 0 ∑mx = 0
解题要领: 1 解平衡问题的三部曲:确定研究对象、画受力图、列平衡方程; 2 通常先以整体为研究对象,再以部分为研究对象; 3 平衡方程的两种形式:投影式和对轴的力矩式,两者都与轴有关,选择合适的坐标轴可
避免解联立方程。 4 做一定数量的习题是掌握平衡问题的关键。
清华理论力学课后答案5

第五章点的合成运动习题解答5-1在图a 、b 所示的两种机构中,已知20021==a O O mm ,31=ωrad/s 。
求图示位置时杆A O 2的角速度。
解:(1)取杆A O 1上的A 点为动点,杆A O 2为动系。
1a ωa v =,由r e a v v v +=作速度平行四边形(如题5-1图a 所示),得a v v 1a e 2330cos ω==�,rad/s 5.1212e 2===ωωA O v ,(逆时针)(2)取滑块A 为动点,杆A O 1为动系,1e ωa v =,由r e a v v v +=作速度平行四边形(如题5-1图b 所示),得1ea 3230cos ωa v v ==�,rad/s 23212a 2===ωωA O v .(逆时针)5-2图示曲柄滑道机构中,杆BC 为水平,杆DE 保持铅直。
曲柄长10.OA =m ,并以匀角速度20=ωrad/s 绕O 轴转动,通过滑块A 使杆BC 作往复运动。
求当曲柄水平线的交角分别为0=ϕ、�30、�90时杆BC 的速度。
解:取滑块A 为动点,动系为BCE 杆。
m/s 2OA a =⋅=ϕ̇v .由r e a v v v +=得ϕsin a e v v =当�0=ϕ时,0e =v ;当�30=ϕ时,m/s 1e =v ;当90=ϕ时,m/s 2e =v .5-3图示曲柄滑道机构中,曲柄长r OA =,并以匀角速度ω饶O 轴转动。
装在水平杆上的滑槽DE 与水平线成�60角。
求当曲柄与水平线交角0=ϕ、�30、�60时,杆BC 的速度。
解:取滑块A 为动点,动系为杆BC ,ωωr v =⋅=OA a .作速度矢量图如图示。
题5-2图(a)(b)题5-1图课后答案网ww w.kh da w .c o m题5-3图由正弦定理)30-sin()60-sin(180ea ���ϕv v =,解得)30-sin(32-e �ϕω⋅=r v .当�0=ϕ时,e v r =;当30o ϕ=时,0=e v ;当60o ϕ=时,e v r =(向右).5-4如图所示,瓦特离心调速器以角速度ω绕铅垂轴转动。
理论力学答案完整版(清华大学出版社)9

F1 = F1(sinϑ i − cosϑ j) , F2 = F2i
点 A 和 B 的坐标及其变分为
rA = −(l1 − l2 )cosϑ i + (l1 + l2 )sinϑ j
,
rB = −2l1 cosϑ i
δrA = (l1 − l2 )sinϑ ⋅δϑ i + (l1 + l2 )cosϑ ⋅δϑ j ,
Fδ re − G1δ ra = 0 按速度合成定理,虚位移存在如下关系:δ ra = δ re tan β ,于是
(a)
题 9-9 图
导出 F = G1 tan β .
(2)水平面有摩擦时,当水平力 F 较小,斜面 D 有向左运动趋势,此时摩擦力方向向右,
临界平衡时,虚功方程为
(F + ) Fmax δ re − G1δ ra = 0 , 其中 Fmax = (G1 + G2 ) f 。求得: F ≥ G1 tan β − (G1 + G2 ) f .
i =1
解题要领 1) 对于自由度不为零的系统,求其平衡时主动力满足的关系可用虚功原理. 2) 对于自由度为零的系统,为求其约束力,可以依次解除一个约束,使自由度为 1,即将
此约束力作为主动力应用虚功原理. 3) 独立的坐标变分个数与系统的自由度相同,可以用解析或虚速度的方法建立不独立的坐
标变分满足的关系.
三 广义坐标表示的虚位移原理
广义坐标:确定质点系位形的独立坐标。
虚功原理的广义坐标表述:受理想约束的质点系,其平衡的充分必要条件是系统所有与广义
坐标对应的广义力为零
Qj = 0 ( j = 1,2,L, m)
∑ 其中
Qj
=
清华大学-理论力学-习题解答-2-28

2-28 图示机构中,主动件的角速度或速度已经标明,欲求从动件的速度或角速度,试选择动点和动系,分析三个运动,并按图示位置分析三个速度。
解:
(a) 以折杆为动系,曲柄末端为动点,则牵连运动和相对运动都是直线运动,绝对运动是定轴转动。
(b) 以滑槽为动系, 曲柄末端为动点,牵连运动为直线运动,相对运动为沿滑槽的曲线运动,绝对运动为定轴转动。
(c) 以曲柄为动系,直杆末端点为动点,则牵连运动为定轴转动,相对运动和绝对运动都是直线运动。
(d) 以曲柄为动系,销钉为动点,则绝对运动和相对运动是直线运动,牵连运动是定轴转动。
(e) 以曲柄为动系,半圆的圆心为动点。
则绝对运动和相对运动都是直线运动,牵连运动是定轴转动。
(f) 以曲柄为动系,铰结点为动点,则绝对运动为定轴转动,相对运动为直线运动,牵连运动为定轴转动。
(g) 以曲柄为动系,销钉为动点,则相对运动为直线运动,绝对运动为定轴转动,牵连运动也为定轴转动。
(h) 以较长的曲柄为动系,滑块铰结点为动点,分别讨论联立求解。
第一组,绝对运动为定轴转动,第二组绝对运动为直线运动。
相对运动都为直线运动,牵连运动为定轴转动。
平面运动,牵连运动为定轴转动。
平面运动,牵连运动为定轴转动。
很全的大学课本课后答案及往年考试练习你们懂的

新视野大学英语课后习题答案1-4册全集&tid=6423&fromuid=562806《毛泽东思想和中国特色社会主义理论体系概论》有史以来最全面的复习资料!!!&tid=5900&fromuid=562806中国近现代史纲要课后题答案&tid=5310&fromuid=562806新视野大学英语第四册答案(第二版)&tid=5161&fromuid=562806新视野大学英语视听说第三册答案&tid=2647&fromuid=562806《物理化学》习题解答(天津大学, 第四版,106张)&tid=2531&fromuid=562806新视野大学英语听说教程1听力原文及答案下载&tid=2006&fromuid=562806西方宏观经济高鸿业第四版课后答案&tid=1282&fromuid=562806大学英语综合教程 1-4册练习答案&tid=1275&fromuid=562806新视野大学英语课本详解(四册全)&tid=805&fromuid=562806新视野大学英语读写教程3册的课后习题答案&tid=514&fromuid=562806毛邓三全部课后思考题答案(高教版)/毛邓三课后答案&tid=384&fromuid=562806《宏观经济学》资料包集合(PPT讲稿+案例+课后答案)[主用教材:N·格里高利·曼昆的]&tid=305&fromuid=562806《会计学原理》同步练习题答案&tid=304&fromuid=562806《管理学》课后答案(周三多)&tid=301&fromuid=562806《成本会计》习题及答案(自学推荐,23页)&tid=300&fromuid=562806《成本会计》配套习题集参考答案&tid=294&fromuid=562806《现代西方经济学(微观经济学)》笔记与课后习题详解(第3版,宋承先)&tid=290&fromuid=562806《国际贸易》课后习题答案(海闻 P.林德特王新奎)&tid=289&fromuid=562806《西方经济学》习题答案(第三版,高鸿业)可直接打印&tid=283&fromuid=562806《微观经济学》课后答案(高鸿业版)&tid=280&fromuid=562806《管理学》经典笔记(周三多,第二版)&tid=277&fromuid=562806《教育心理学》课后习题答案(皮连生版)&tid=268&fromuid=562806《信号与系统》习题答案(第四版,吴大正)&tid=262&fromuid=562806《计算机操作系统》习题答案(汤子瀛版,完整版)&tid=260&fromuid=562806高等数学习题答案及提示&tid=258&fromuid=562806《生物化学》复习资料大全(3套试卷及答案+各章习题集)&tid=249&fromuid=562806《概率论与数理统计》8套习题及习题答案(自学推荐)&tid=244&fromuid=562806《线性代数》9套习题+9套相应答案(自学,复习推荐)&tid=236&fromuid=562806《高分子化学》课后习题答案(第四版,潘祖仁主编)&tid=232&fromuid=562806《电工学》课后习题答案(第六版,上册,秦曾煌主编)&tid=217&fromuid=562806《大学物理》完整习题答案&tid=203&fromuid=562806《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)&tid=195&fromuid=562806《化工原理答案》课后习题答案(高教出版社,王志魁主编,第三版)&tid=191&fromuid=562806《工程力学》课后习题答案(梅凤翔主编)&tid=186&fromuid=562806《中国近代史纲要》课后习题答案&tid=182&fromuid=562806《概率论与数理统计》优秀学习资料&tid=181&fromuid=562806《中国近现代史》选择题全集(共含250道题目和答案)&tid=178&fromuid=562806《概率论与数理统计及其应用》课后答案(浙江大学盛骤谢式千编著)&tid=174&fromuid=562806《数字信号处理——基于计算机的方法》习题答案(第二版)&tid=173&fromuid=562806《数据结构习题集》答案(C版,清华大学,严蔚敏)&tid=172&fromuid=562806《大学物理基础教程》课后习题答案(第二版,等教育出版社)&tid=170&fromuid=562806C语言资料大全(有课后答案,自学资料,C程序等)&tid=168&fromuid=562806《新编大学英语》课后答案(第三册)&tid=164&fromuid=562806《电力电子技术》习题答案(第四版,王兆安,王俊主编)&tid=163&fromuid=562806《中级财务会计》习题答案(第二版,刘永泽)&tid=162&fromuid=562806《常微分方程》习题解答(王高雄版)&tid=161&fromuid=562806《C++程序设计》课后习题答案(第2版,吴乃陵,高教版)&tid=158&fromuid=562806《机械制图》习题册答案(近机类、非机类,清华大学出版社)&tid=143&fromuid=562806《物理化学》习题答案(南大,第五版)&tid=142&fromuid=562806《高频电子线路》习题参考答案(第四版)&tid=138&fromuid=562806《宏观经济学》课后答案(曼昆,中文版)&tid=137&fromuid=562806《电路》习题答案上(邱关源,第五版)&tid=136&fromuid=562806《信息论与编码》辅导PPT及部分习题答案(曹雪虹,张宗橙,北京邮电大学出版社)&tid=122&fromuid=562806《分析化学》课后习题答案(第五版,高教版)&tid=112&fromuid=562806《电工学》习题答案(第六版,秦曾煌)&tid=102&fromuid=562806《离散数学》习题答案(高等教育出版社)&tid=96&fromuid=562806《机械设计》课后习题答案(高教版,第八版,西北工业大学)&tid=90&fromuid=562806《数字电子技术基础》习题答案(阎石,第五版)&tid=85&fromuid=562806曼昆《经济学原理》课后习题解答&tid=83&fromuid=562806《流体力学》习题答案&tid=81&fromuid=562806《中国近代史纲要》完整课后答案(高教版)&tid=78&fromuid=562806《全新版大学英语综合教程》(第四册)练习答案及课文译文&tid=77&fromuid=562806《全新版大学英语综合教程》(第三册)练习答案及课文译文&tid=76&fromuid=562806《全新版大学英语综合教程》(第二册)练习答案及课文译文&tid=75&fromuid=562806《全新版大学英语综合教程》(第一册)练习答案及课文译文&tid=74&fromuid=562806《信号与线性系统分析》习题答案及辅导参考(吴大正版)&tid=69&fromuid=562806《有机化学》习题答案(汪小兰主编)&tid=66&fromuid=562806高等数学上下《习题PPT》&tid=63&fromuid=562806思想道德修养与法律基础课后习题答案&tid=61&fromuid=562806新编大学英语4(外研版)课后练习答案&tid=60&fromuid=562806西方经济学(高鸿业版)教材详细答案&tid=59&fromuid=562806《c语言程序与设计》习题答案(谭浩强,第三版)&tid=58&fromuid=562806《数字信号处理》课后答案及详细辅导(丁美玉,第二版)&tid=57&fromuid=562806《概率论与数理统计》习题答案&tid=55&fromuid=562806《理论力学》课后习题答案&tid=52&fromuid=562806《自动控制原理》课后题答案(胡寿松,第四版)&tid=50&fromuid=562806《物理学》习题分析与解答(马文蔚主编,清华大学,第五版)&tid=48&fromuid=562806《毛泽东思想和中国特色社会主义理论体系概论》习题答案(2008年修订版的)&tid=47&fromuid=562806完整的英文原版曼昆宏观、微观经济学答案&tid=46&fromuid=562806离散数学习题解答(第四版)清华大学出版社&tid=45&fromuid=562806《电机与拖动基础》课后习题答案(第四版,机械工业出版社,顾绳谷主编)&tid=44&fromuid=562806《现代通信原理》习题答案(曹志刚版)&tid=43&fromuid=562806《土力学》习题解答/课后答案&tid=42&fromuid=562806《模拟电子技术基础》详细习题答案(童诗白,华成英版,高教版)&tid=41&fromuid=562806《模拟电子技术基础简明教程》课后习题答案(杨素行第三版)&tid=38&fromuid=562806《数学物理方法》习题解答案详细版(梁昆淼,第二版)&tid=37&fromuid=562806《马克思主义基本原理概论》新版完整答案&tid=36&fromuid=562806《单片机原理及应用》课后习题答案(张毅刚主编,高教版)&tid=35&fromuid=562806机械设计课程设计——二级斜齿圆柱齿轮减速器(WORD+原图)&tid=34&fromuid=562806《管理运筹学》第二版习题答案(韩伯棠教授)&tid=31&fromuid=562806《材料力学》详细辅导及课后答案(PDF格式,共642页)&tid=29&fromuid=562806《统计学》课后答案(第二版,贾俊平版)&tid=28&fromuid=562806谢希仁《计算机网络教程》(第五版)习题参考答案(共48页)&tid=25&fromuid=562806《大学基础物理学》课后答案(共16个单元)&tid=23&fromuid=562806机械设计基础(第五版)习题答案[杨可桢等主编]&tid=22&fromuid=562806流体力学课后答案(高教版,张也影,第二版)&tid=21&fromuid=562806《模拟电子技术基础》课后习题答案(共10章)&tid=20&fromuid=562806《液压传动》第2版思考题和习题解答(共36页)&tid=18&fromuid=562806高等数学(同济第五版)课后答案(PDF格式,共527页)&tid=17&fromuid=562806《线性代数》(同济第四版)课后习题答案(完整版)&tid=16&fromuid=562806《新视野大学英语读写教程(第二版)第三册》课后答案&tid=15&fromuid=562806《新视野大学英语读写教程(第二版)第二册》课后答案&tid=14&fromuid=562806新视野大学英语读写教程(第二版)第一册》课后答案&tid=13&fromuid=562806统计学原理作业及参考答案&tid=9&fromuid=562806大学英语精读第3册答案(外教社)&tid=8&fromuid=562806大学数学基础教程课后答案(微积分)&tid=7&fromuid=56280621世纪大学英语读写教程(第四册)课后答案&tid=6&fromuid=56280621世纪大学英语读写教程(第三册)课文翻译&tid=5&fromuid=56280621世纪大学英语读写教程(第三册)参考答案&tid=4&fromuid=56280621世纪大学实用英语综合教程(第一册)课后答案及课文翻译&tid=3&fromuid=562806程守洙、江之永主编《普通物理学》(第五版)详细解答及辅导更多资料可以进入【】下载。
清华大学理论力学课后习题答案大全

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R yt r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度=12 rad/s ,=30,=60,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
习题6-1图A BCv 0h习题6-2图 P ABv CA BCv o h习题6-2解图习题6-3解图习题6-3图 v A = vv B = v习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
清华大学-理论力学-习题解答-8-14

9 mg sin ϕ − ( R + r ) mg sin ϕ = − mgr sin ϕ 2
33 2 9 ! + 3θ! 2 − 3ϕθ ! ! + mgr sin ϕ L = T − V = mr 2 ϕ 4 2
d ∂L 33 2 ∂L 9 ∂L 33 2 !! !! − 3mr 2θ ! − 3mr 2θ! , = mgr cos ϕ, = mr ϕ ! = mr ϕ ! 2 dt ∂ϕ 2 ∂ϕ 2 ∂ϕ ∂L ∂L d ∂L 2 !! 2 !! !, = 0, = 6mr 2θ! − 3mr 2ϕ = 6mr θ − 3mr ϕ ∂θ dt ∂θ! ∂θ!
将以上各式代入拉氏方程,得:
!! − 9 g cos ϕ = 0 33rϕ !! − 6rθ !! !! = 0 2θ − 3ϕ
即为系统得运动微分方程。
系统的所有主动力都为有势力,且拉格朗日函数不显含 θ ,所以有循环积分:
! =C 6mr 2θ! − 3以有广义能量积分:
θ! ϕ
x
y
系统的动能为:
T= 1 !2 1 1 1 2 2 ! 2 + mB vB J Aθ + J ABϕ + J Bω B 2 2 2 2
(1)
! = 3rϕ ! 。取杆 AB 为动系,即 ω e = ϕ ! ,则有: 其中, vB = ( R + r ) ϕ !,ω Br = − ω Ar = 2 (ϕ ! − θ! ) ω Ar = θ! − ϕ ! = 3ϕ ! − 2θ! 。又有: 所以 ω B = ω Br + ϕ
1 1 2 J AB = m ( R + r ) = 3mr 2,J A = 4mr 2,J B = mr 2 3 2
理论力学答案完整版(清华大学出版社)10

子 C 沿水平轨道滚动而不滑动,试求重物 A 的加速度。
解: 取整个系统为研究对象,自由度为 1。设重物速度为 vA ,则轮
题 10-9 图
的角速度 ω = vA ,轮心速度为 R−r
vO
=
R
r −
r
vA 。系统的动能为
( ) T
拉格朗日方程的普遍形式
d dt
∂L ∂q& j
− ∂L ∂q j
= Q′j
( j = 1,2,..., m)
式中 Q′j 为非有势力对应的广义力。
矢量方法
动量法:动量定理
动量矩定理 质心运动定理 定轴转动微分方程 平面运动微分方程
质点系统动力学
动静法
动能定理
能量方法
拉格朗日方程
3 保守系统拉格朗日方程的初积分
10-3 质量为 m1 的匀质杆,长为 l,一端放在水平面上, 另一端与质量为 m2、半径为 r 的匀质圆盘在圆盘中心 O 点 铰接。圆盘在地面上作纯滚动,圆心速度为 v。求系统在此
题 10-3 图
位置的动能。
解:杆作平移,动能为
T1
=
1 2
m1v2
;
圆盘作纯滚动,动能为
T2
=
1 2
m2v2
+
1 2
mivi
⋅ vi
,
其中 n 为系统中的质点数目,可以是有限或无穷,mi 和 vi 分别为各质点的质量和速度。 平
移刚体的动能 T = 1 mv2 , 2
其中 m 为平移刚体的质量。
定轴转动刚体的动能
T
=
1 2
理论力学习题解答

问题: 质点M沿椭圆轨道匀 速率运动,如何确定其加速 度的大小和方向?
例:已知点的运动方程,求点任意时刻的速度、 加速度的大小和运动轨迹的曲率半径。
运动方程: x R cost, y R sin t, z Ct
解: vx x vy y
vz
z
解: 是共面力系的
0
平衡问题
第
0
三
章
Fx 0
N1 cos(90 0 ) f 0
Fy 0 Mz 0
N1 sin(90 0 ) N2 P 0
Pl cos0
N1
h
sin 0
0
f N2
解出
0
f
N2
第
h
l sin 2 0 cos 0 l sin 0 cos2 0
例:已知图示瞬时动点A的速度和加速度, 求该瞬时动点A
的 x, y, x, y, 。 已知:v 10m/s, a 10m/s2
yv
300
A(x,y)
解: x vx 10cos300 (m/s) y vy 10sin 300 (m/s)
a
O
x
vx x vy y
23 3
R
第
O
B
vB
三(1)速度瞬心可以位于平面运动刚体之上,也可以位于其延展体上。
章
(2)当 =90º时,滑块B的速度及连
杆AB的角速度为多少?
研究连杆AB:该瞬时,连杆AB的 vA A
P?
速度瞬心P在无穷远处,AB 0
A为基点,杆AB上任一点M的速度
vM
M
理论力学(周衍柏第三版)习题答案

vx
dv y dv y dv x v v dv x v v x v y v v y x y x y dt dt dt dt
d 15t 0 15t
2
1 15 t 0 1 15t 2
2
- - 1- -
1 2 450t 2 900t 0 675t 225t 0 225 t 0 1 2
2
d
2 对时间 t 求导
d d2 900t 900t 0 675 dt
1.4 解 如题 1.4.1 图所示,
L A
d O
第1.4题图
x
C
B
OL 绕 O 点以匀角速度转动, C 在 AB 上滑动,因此 C 点有一个垂直杆的速度分量
v OC d 2 x 2
C 点速度
v
v d 2 x2 v sec d sec 2 cos d
又因为 所以 C 点加速度
a
2 2 2 dv 2d 2 sec 2 tan 2 x d x d 2 sec sec tan dt d2
1.5 解 由题可知,变加速度表示为 由加速度的微分形式我们可知 代入得 对等式两边同时积分 可得 :
对两边分别求导
r cos 2a cos
2
所以
r cos r 2 2 cos 2 2 2 V x y r sin 2 cos sin 4
r 2 cos
清华大学-理论力学-习题解答-8-13

! 2 + 4mR 2 ϕ !ϕ ! 2 − 6mR 2θ ! (1 + sin ϕ ) + 2mgR sin ϕ L = 18mR 2θ
d ∂L ∂L ( )− =0 ! ∂θ d t ∂θ d ∂L ∂L ( )− =0 ! ∂ϕ d t ∂ϕ d ∂L ∂L = 0 ,由 (1)′ 得: ( ) = 0 因 L 中不显含 θ ,即 d t ∂θ! ∂θ ∂L = const . , 积分得: ∂θ! ! − 6mR 2ϕ ! (1 + sin ϕ ) = C 即: 36mR 2θ
代入拉氏方程,得:
!! − 6mR 2 ϕ !!(1 + sin ϕ ) − 6mR 2 ϕ ! 2 cos ϕ = 0 36mR 2θ !!(1 + sin ϕ ) − 2mgR cos ϕ = 0 !! − 6mR 2θ 8mR 2 ϕ !! − ϕ !!(1 + sin ϕ ) − ϕ ! 2 cos ϕ = 0 6θ !!(1 + sin ϕ ) − g cos ϕ = 0 !! − 3θ 4ϕ R
V = −2mgR sin ϕ
系统的动能由两部分合成
2 m 2 J O1 2 m m vO1 + ω1 = 3Rθ! + (3R )2θ! 2 = 9mR 2θ! 2 2 2 2 2 J O2 2 m 2 T小 = vO + ω2 2 2 2 ! ,v + v O2 O1 , vO = 3Rθ O2 O1 = 2 Rϕ
清华大学理论力学习题解答67
[ ρ × mve ]z = mρ 2ω
x
[ ρ × mvr ]z = mv0 cosϕ ⋅ (l + r cosϕ ) + mv0 sinϕ ⋅ r sinϕ
= mv0 (l cosϕ + r)
《理论力学》习题解答
由 LO1 = LO2 得:
m(l + r)v0 = J zω + mρ 2ω + mv0 (l cosϕ + r)
《理论力学》习题解答
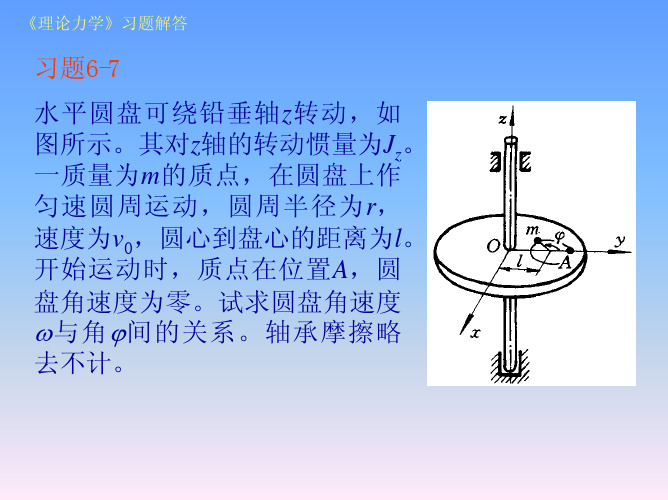
习题6-7
水平圆盘可绕铅垂轴z转动,如 图所示。其对z轴的转动惯量为Jz。 一质量为m的质点,在圆盘上作 匀速圆周运动,圆周半径为r, 速度为v0,圆心到盘心的距离为l。 开始运动时,质点在位置A,圆 盘角速度为零。试求圆盘角速度
ω与角ϕ间的关。轴承摩擦略
去不计。
《理论力学》习题解答
∴
ω
=
JZ
+
mv0l(1 − cosϕ ) m(l 2 + r 2 + 2rl cosϕ )
解:取圆盘连同其上的质点作为一个系统,此系统 对于z轴动量矩守恒。
系统在初始时刻对z轴的动量矩为: Lo1 = m(l + r)v0
系统在任意时刻对z轴的动量矩为:
Lo2 = J zω + [ ρ × m(ve + vr )]z
其中:ve = ρω,vr = v0
O
vrve
ρ
m
ϕ
y
ρ = l 2 + r 2 + 2lr cosϕ
理论力学作业解答
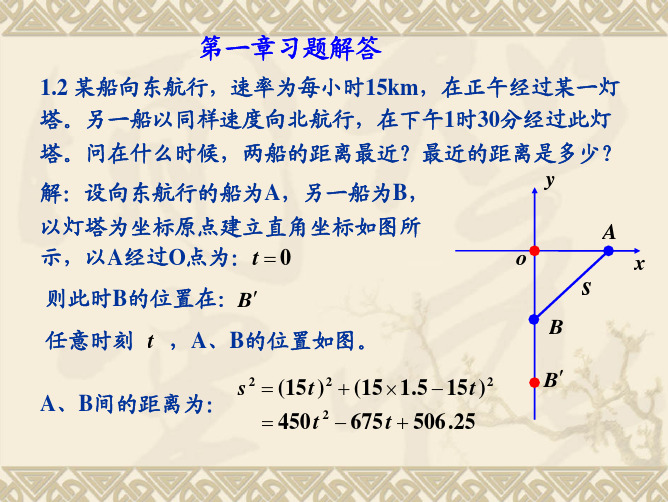
1.2 某船向东航行,速率为每小时15km,在正午经过某一灯 塔。另一船以同样速度向北航行,在下午1时30分经过此灯 塔。问在什么时候,两船的距离最近?最近的距离是多少? y 解:设向东航行的船为A,另一船为B, 以灯塔为坐标原点建立直角坐标如图所 示,以A经过O点为:t = 0 则此时B的位置在:B′ 任意时刻 t ,A、B的位置如图。 A、B间的距离为:
d ( − kv 0 cos α tg θ ) 1 dt = k ( g + kv 0 cos α tg α ) − kv 0 cos α tg θ
对上式积分可得:
1 ∫0 dt = k
t
∫α
−α
d ( − kv 0 cos α tg θ ) ( g + kv 0 cos α tg α ) − kv 0 cos α tg θ
v v0
α
v mg
θ
x
α v v
dv m = − mkv − mg sin θ (1) dt v2 m = mg cos θ ( 2)
随着质点运动,切线方 向与 x 轴夹角减少,故有:
ρ
ds ρ =− dθ
(3)
dv m = − mkv − mg sin θ (1) dt v2 m = mg cos θ ( 2)
s 2 = (15 t ) 2 + (15 × 1 .5 − 15 t ) 2 = 450 t 2 − 675 t + 506 .25
A
o
s
B B′
x
s = 450 t − 675 t + 506 .25
2 2
y
A
当 A、B相距最近时有: d (s2 ) = 900 t − 675 = 0 dt 可得:
