15-工程光学公式表+-+副本
工程光学复习资料

一、n·sin I'=nsinI。
sinI m=n'/n。
发生全反射的条件:①光线从光密介质向光疏介质入射,②入射角大于临界角。
光程s=n l=ct(l是介质中传播的几何路程)完善成像条件:入射光为同心光束,出射光也为同心光束。
通过物点和光轴的截面称为子午面。
i=(l-r)*u/r i'=n*i/n'u'=u+i-i'l'=r(1+i'/u')n'/l'—n/l=(n'—n)/r ,β=y'/y=n l'/n'l,α=(n'/n)*β2,γ=(n/n')/β,α*γ=βnuy=n'u'y',1/l+1/l'=2/r ,l i+1=l i'—d i二、每个物点对应于唯一的一个像点,称作“共轭”。
物方主平面和像方主平面是一对共轭面。
牛顿公式(以焦点为坐标原点):xx'=ff′,β=—f/x=—x'/f'高斯公式(以主点为坐标原点):f'/l'+f/l=1 ,β=—f l'/f'l物像空间介质相同时,f'=—f ,有1/l'—1/l=1/f',β=l'/l多光组系统:l i=l i-1'—d i-1,x i=x i-1—△i-1,△i=d i—f i'+f i+1理想光学系统两焦距之间关系f'/f=—n'/n理想光学系统的放大率α=—x'/x=(—f'/f)*β2=(n'/n)*β 2 ,γ=(n'/n)/β理想光学系统的组合焦距f'=—(f1'f2')/△,f=(f1f2)/△。
△为第一个系统的像方焦点到第二个系统物方焦点的距离。
通常用Φ表示像方焦距的倒数,Φ=1/f',称为光焦度。
三、平面镜的旋转特性:平面镜转动α,反射光线转动θ,θ=2α。
y=f'tan2θ≈2f'θ,tanθ≈θ=x/a→y=(2f'/a)*x=K*x双平面镜成像:出射光线和入射光线夹角β=2α,α为双平面镜夹角。
平行平板近轴区内的轴向位移为△l'=d(1-1/l).平行平板不改变光线方向,平行平板不会使物体放大或缩小,对光束既不发散也不会聚,表明它是一个无焦元件,在光学系统中对光焦度无贡献,物体经平板成正立像,物像始终位于平板的同侧,且虚实相反。
高中物理中的光学中的重要公式

高中物理中的光学中的重要公式在高中物理学习中,光学是一个重要的分支,其中包含了许多重要的公式。
本文将介绍几个在高中物理光学中必须了解和掌握的重要公式,帮助读者更好地理解和应用光学知识。
一、折射定律光的折射定律描述了光线在不同介质中传播时发生的折射现象。
它可以通过下面的公式来表示:n1*sinθ1 = n2*sinθ2其中,n1和n2分别表示两个介质的折射率,θ1和θ2分别表示入射角和折射角。
该公式常被用来计算光线在不同介质中传播的方向。
二、薄透镜公式薄透镜公式用于计算透镜成像的位置和放大率。
对于凸透镜和凹透镜,薄透镜公式可以分别表示为:1/f = 1/v - 1/u和1/f = 1/u - 1/v其中,f表示透镜的焦距,u和v分别表示物体距离透镜的距离和像距。
三、光的直线传播公式光在直线上传播是光学中的基本性质。
当光线从一个点向另一个点传播时,可以使用以下公式计算光线的传播距离:s = c*t其中,s表示光线的传播距离,c表示光在真空中的光速,t表示时间。
四、光的光程差公式光程差是光线传播过程中两条光线之间的路径差。
光的光程差公式可以表示为:ΔL = n*d其中,ΔL表示光程差,n表示介质的折射率,d表示光线传播的路径长度。
五、光的干涉和衍射公式光的干涉和衍射是光学中重要的现象,可以通过一些公式来描述。
例如,双缝干涉的干涉条纹间距d可以由以下公式计算:λ = dsinθ其中,λ表示光的波长,d表示双缝间距,θ表示干涉条纹的角度。
六、光的反射角和入射角关系公式当光线从一个介质界面到达另一个介质时,发生反射现象。
根据光的反射定律,反射角和入射角之间存在以下关系:θi = θr其中,θi表示入射角,θr表示反射角。
以上是高中物理光学中的一些重要公式。
通过掌握并应用这些公式,我们可以更好地理解和解决与光学相关的问题。
在学习过程中,我们也应该注意理论与实际的结合,通过实验来验证和加深对这些公式的理解。
只有将理论和实践相结合,我们才能真正掌握高中物理光学知识,提升学习水平。
工程光学基础

17
全反射应用例:
18
6. 矢量形式的折射定律和反射定律
有时在光路计算中,用矢量形式的折射
定律和反射定律是比较方便的。
设
NAA00'0为为为入折折射射射光面光线入线的射的单点单位处位矢的矢量单量;位;法矢量;
30
等光程面的例子: (1)椭球面
椭球面对 A、 A'这一对
特殊点来说是等光程面,故 是完善成像。
(2)抛物面
反射镜等光程面是以 A为
焦点的抛物面。无穷远物 点相应于平行光,全交于 (或完善成像于)抛物面 焦点。
31
四、物、像的虚实
实际光线相交所形成的点为实物点或实像点 光线的延长线相交所形成的点为虚物点或虚像点
光线经过单个折射球面的情况如图所示。
包含光轴和物点的平面称为含轴面(纸面)或子午面。 计算的目的:光从何处来,经何处到哪里去(由此得出 由物点发出的光线经过系统后能否交到一点完善成像)? 首要问题:用什么量(怎样)来决定光线在空间中的位 置?
我们用两个量来表示一条光线: (1)A到O的距离OA,记作L,称为截距。 (2)光轴到光线的夹角,记作U,称为孔径角。
沿光轴方向线段(如 L( L')、r)
光线传播由左向右,以折(反)射面顶点 为原点(起点), 顺光线传播方向为正; 逆光线传播方向为负。
垂轴线段 光轴以上为正; 光轴以下为负。
40
(2)角度
孔径角 U、U '
从光轴起算,光轴转向光线(按锐角方向), 顺时针为正,逆时针为负。
入射角、折射角 从光线起算,光线转向法线(按锐角方向), 顺时针为正,逆时针为负。
工程光学基础

9
反射定律归结为:
(1)反射光线位于由入射光线和法线所 决定的平面内;
(2)反射光线和入射光线位于法线的两 侧,且反射角与入射角的绝对值相等,符号 相反,即:
I" I
(1-2)
折射定律归结为:
12
5. 全反射现象 光线入射到两种介质的分界面时,通常 都会发生折射与反射。但在一定条件下,入 射到介质上的光会全部反射回原来的介质中, 没有折射光产生,这种现象称为光的全反射 现象。下面就来研究产生全反射的条件。
13
通常,我们把分界面两边折射率较高的 介质称为光密介质,而把折射率较低的介质 称为光疏介质。当光从光密介质射向光疏介
第一章 几何光学基本定律与 成像概念
几何光学主要是以光线为模型来研究光 在介质中的传播规律及光学系统的成像特性。
本章主要介绍: 1.几何光学的几本定律 2.成像的概念和完善成像的条件 3.光路计算和近轴光学系统
1
第一节 几何光学的基本定律
一、基本概念
光线:在几何光学中,通常将发光点发 出的光抽象为许许多多携带能量并带有方向 的几何线,即光线。光线的方向代表光的传 播方向。光线的传播途径称为光路。
36
L、U 两量唯一地确定了一条光线在子午面 内(纸内)的位置。
计算的目的:
就是已知 L、U(光线从何处来)
经过已知的r、n 、n',求出像方截距 L' 、 像方孔径角 U(' 光线到何处去)
37
正负号规定: 为什么要规定正负号? 如果r=100,则可能是
也可能是 所以应该规定正负号
38
大学物理光学部分必须熟记的公式(很容易混淆哦)及大学物理公式总结

大学物理光学部分有关于明暗的公式及其结论1.获得相干光的方法 杨氏实验.......,2,1022,,=⋅±==k k D xd λδ 此时P 点的光强极大,会出现明条纹。
......,2,102)12(,,=⋅+±==k k D xd λδ此时的光强极小,会出现暗条纹。
或者,dD kx 22λ±= 此时出现明条纹 dD k x 2)12(λ+±= 此时出现暗条纹。
屏上相邻明条纹或者暗条纹的间距为:dD x λ=∆。
洛埃镜。
半波损失。
2.薄膜等厚干涉。
○1根据光程差的定义有: ⎪⎪⎩⎪⎪⎨⎧=⋅+=⋅=+=相消干涉。
相长干涉。
,...2,1,2)12(,.....2,1,22222k k k k d n λλλδ○2劈尖干涉:暗条纹。
明条纹。
,...2,1,0,2)12(22,...2,1,2222=⋅+=+==⋅=+=k k d k k d λλδλλδ相邻明条纹或者暗条纹对应的空气层厚度差都等于2λ即:21λ=-+k k d d 。
则设劈尖的夹角为θ,相邻明纹或者暗纹的间距 a 应满足关系式:2sin λθ=a○3牛顿环: 直接根据实验结果的出结论为:⎪⎭⎪⎬⎫===⋅-=暗条纹明条纹,...3,2,1,0,R ,...3,2,1,2)12(k k r k R k r λλ3.单缝的夫琅禾费衍射关键词:半波带。
注意:半波带的数目可以是整数也可以是非整数。
结论:光源是平行光的单缝夫琅禾费衍射的条纹明暗条件为:明条纹,)(暗条纹,...3,2,10,212sin ,...3,2,1,22sin =⋅+±==⋅±=k k a k k a λϕλϕ特殊地当ϕ=0时,有:,中央明条纹中心0sin =ϕa当将单缝换做圆孔时,得到中心的明亮光斑为艾里斑,且其半角宽度0ϕ为:Dλϕϕ22.1sin 00=≈ 这一角度也是我们在天文望远镜中的最小分辨角。
工程光学上篇

3.掌握四种不同条件下光波叠加后形成的物理现象、合 成波表达式及其性质(见表)
第十二章 光的干涉和干涉系统
1.干涉及干涉条件
1)什么是干涉?
2)干涉条件(3条)
2.杨氏双缝干涉
1)干涉性质:分波前的干涉 2)实验装置
22
第十二章 光的干涉和干涉系统
3)干涉公式及条纹性质
I I 1 I 2 2 I 1 I 2 cos 设I 1 I 2 I 0 则:I 4 I 0 cos2
2
第一章 几何光学的基本定律与成像概念
图1-10 光线经过单个折射面的折射 3. 应用光学中的符号规则(6条) 4. 单个折射球面的光线光路计算公式(近轴、远轴)
lr i u r i n i n u u i i i l r ( 1 ) u
12
第三章 平面和平面系统
4.反射棱镜的种类(4种)、基本用途、成像 方向判别。
5.折射棱镜的作用?其最小偏向角公式及应用
m sin n sin 2 2
6.光楔的偏向角公式及其应用(测小角度和 微位移) (n 1)
13
第三章 平面和平面系统
7.棱镜色散、色散曲线、白光光谱的概念。
1)定义及公式
K (IM Im ) (IM Im )
I ( I1 I 2 )(1 K cos )
2)条纹可见度的影响因素:(两相干光束的振 幅比、光源大小、光源单色性)
24
第十二章 光的干涉和干涉系统
4. 平行平板的双光束干涉
1)定域面位置
2)干涉装置(图11-14)
25
7
第二章 理想光学系统
3. 无限远的轴上(外)像点的对应物点是什 么?(主点,主平面) 4. 物(像)方焦距的计算公式为何?
工程光学复习(完整)

轴外光束的渐晕——轴上点与轴外物点成像光束大小不 同的现象。 轴外物点<轴上点
§5.3 渐晕光阑及场镜的应用
一、渐晕光阑:
一个系统可以有0~2个渐晕光阑
线渐晕系数KD,指轴外物点通过系统的光束直径Dω与轴上 物点通过系统的光束直径D0之比,即KD =Dω/ D0
视场光阑
△h’=4.6 h12=4.6 △h
二、场镜的应用
在物镜一次实像面处加一正透
镜——场镜。
场镜能够改变成像光束的位置,
对系统特性、方向无影响。
长光路连续成像系统中,场镜
的作用:光瞳衔接,降低主光 线在其后面系统的投射高度, 减小光学零件的口径。
二、场镜的应用
在物镜一次实像面处加一透镜,以降低主光线在其后面系 统的投射高度,减小光学零件的口径 ;
4
场镜
组合多章出题,如: 摄影系统、望远系统
§5 光学系统中的光束限制
一、基本概念
孔径光阑、入瞳和出瞳的判定方法 视场光阑、入窗和出窗的判定方法
孔径光阑、视场光阑的设置原则
孔径光阑和视场光阑的区别
二、渐晕及其计算
入窗和物平面不重合产生的渐晕
• 消除渐晕的方法是采用物平面与入窗平面重合。
1 2 L k 12 L k 1 2 L k
A
B P22例2.2
§3 理想光学系统
§3.1 ~§3.2
§3.3 理想光学系统的物像关系 一、图解法求像 二、解析法求像 1、物像位置计算:牛顿公式、高斯公式 2、理想光学系统的放大率 3、理想光学系统两焦距之间的关系
D 1477 f' F#
0.61 1.22 NA D f
工程光学

R
B
SQ n( AQ QB )
延长AQ交N于R点,并连接RB。由于椭圆上的点与两 焦点间线段长度之和为定值,即总有AP+PB=AR+RB,
因此有,
S P n( AR RB ) n AQ (QR RB ) n( AQ QB ) SQ
得到物像距公式, 且像点位置L'与d无关, 这表明物点A在傍轴条件下完 善成像于像点A'.
习题: 例1:物体放在凹面反射镜的何处,可产生大小与物体相等 的倒立实像?
解:由反射镜放大率公式
=y’/y=-l’/l=-1,
求得像距l’=l。代入反射镜成像公式求得
1 1 2 l r l' l r
在傍轴近似下, d<<l, l'和 r, 进行泰勒展开并略去二阶无穷小量,有
(l r ) AE l 1 d 2 l
(l ' r ) EA ' l ' 1 d l '2
成立, 即
由物象之间的等光程性, 有 S ( AEA ') S ( AOA ')
2 n1 d12 x 2 n2 d 2 ( L x)2
根据费马原理,光程应取极值,即
dS x Lx n1 n2 0 2 2 2 2 dx d1 x d 2 ( L x)
如图定义入射角和折射角,则光程取极值必有
即折射定律
dS n1 sin 1 n2 sin 2 0 dx
例4:设光导纤维玻璃芯和外包层的折射率分别为n1和n2(n1>n2), 垂直端面外的媒质的折射率为n0。试证明:能使光线在纤芯内发生 全反射的入射光束的最大孔径角满足
工程光学第六讲
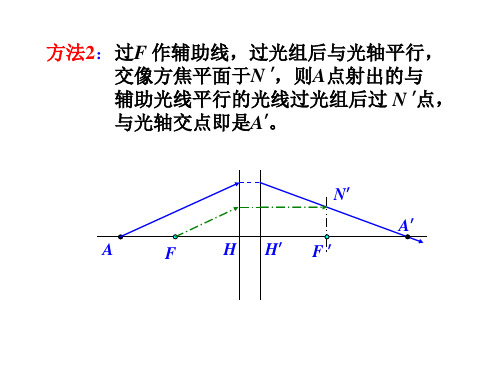
x—以物方焦点为原
点的物距。称为焦物 距。
以F为起始点, x方 向与光线方向一致为
正。(图中为-)
B
Q
Q'
y
A
F
H H'
F'
A'
R R'
-x -f
f'
-y' B'
x'
-l
l'
x’—以像方焦点为原点的像距。称为焦像距。
以F ’为起始点, x’方向与光线方向一致为正。(图 中为+)
B
Q
Q'
y
A
F
H H'
lk=l’k-1- dk-1 xk=x’k-1-Δk-1 Δk=dk - f ’k+fk+1
Δk—(焦点间隔或光学间隔): 表示第 k个光组的像方焦点与第k+1个光组物方焦点的距离;
dk— 两光组间距离。
系统的垂轴放大率:
yk' y1
y1' y2' yk' y1 y2 yk
1 2 k
四、理想光学系统两焦距之间的关系
l2’=25mm
结论:物距相同而焦距不同时,焦距短的光组对 光束会聚的能力强些。
如何计算光焦度:
利用
f ' n'
f
n
将高斯公式
f f 1 l l
写成
n' n n' n
l l f '
f
令: ' n' ; n ; n' n
l'
l
f'
f
则上式可写成: '
光学公式

第一章 几何光学1.基本规律光程费马原理.sin n sin n ,i i 2211θθ='-=2. 成像 ①单球面折射()()()()⎥⎦⎤⎢⎣⎡'-''++⎪⎭⎫ ⎝⎛-='-'''-+r s n r s n sin r r s n s r s n s 2222222221124ϕ 保持同心性物像点:()()()().r s n r s n ,r s n s r s n s 011022222222='-''++='-'''-+榜轴条件:②球面镜成像.n n -='③薄透镜.r n n r n n n f ,r n n r n n nf LL LL 2121-'+-'='-'+-=n n ='④密接透镜组⑤望远镜第二章 光的干涉一.光波基本描述s m c 800100.31⨯==με,rr n με=.2.单色波①电场 ()()()p t p E E ϕω-=cos 0磁场 ()()()p t p B B ϕω-=cos 0Eof f M -≡②单色平面波其中R为r在k方向上的投影.③单色球面波3.光强度是电磁波能流密度.谱密度()λλλddIi=,(λdI是λ~λλd+之间光强).()⎰⎰∞∞==λλλdidII4.二、线性叠加原理(弱光情况下成立):1.()()().t,pEt,pEt,pE21++=同方向光振动叠加:()()().t ,p E t ,p E t ,p E 21 ++=2.同频率、同振向波的叠加()()()()p t cos p E t ,p E 1101ϕω-=, ()()()()p t cos p E t ,p E 2202ϕω-=()()().t cos p E t ,p E ϕω-=0()()()()()()[]()p E p p cos p E p E p E p E 202110210201202+-+=ϕϕ ()()()()()()()()().p cos p E p cos p E p sin p E p sin p E p tg 220110220110ϕϕϕϕϕ++=三、光的干涉和相干条件 1. 相干条件 ①位相差判据同位相),称为干涉极大,对应亮纹;反位相),称为干涉极小,对应暗纹.②光程差判据其中().r n r n p l 2211-=∆四、杨氏实验1.光程差sin d r r l θ≈-=∆212.3.4.光强分布实验中, ,I I I 021=≈.x D d cos I 4D x d 2cos 1I 2I 02000⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+=λπλπ 5.6.光源S 沿x 方向移动s δ,干涉条纹的移动.s lDx δδ-≈7.扩展光源●临界宽度.dl b c λ=干涉口径角,l d ≡β扩展光源干涉条件为.b βλ<●横向相干宽度.bl d c λ≡●光场的空间相干性:,d d c <即ld cc =<ββ内两点源都是相干点源.●.b c λβ=五、薄膜干涉 1.光程差2.等倾干涉从中心向外数第N 个亮环附近相邻两亮环间的角距离为()1=∆N .N2Nt n n 1N ∆λθ∆'=第N 个亮环半径.tnN n f f r N N λθ'=≈相邻两亮环间的径向距离为.t n 2fn f r N2N N θλθ∆∆'=≈ 3.等厚干涉 ①楔形②牛顿环m m .N r r R 2m 2N mλ'-'=+4.透射光()t r 0I I I +=5.薄膜厚度要求6.7.迈克尔逊干涉仪 六、光场的时间相干性:.0τ<t 光波的相干长度,L L max c λλ∆=∆=2相干时间.0cL c ≡τ第三章 光的衍射一、惠更斯-菲涅耳原理()()()().,~~00∑=⎰⎰∑d re F Q E k P E ikr θθ基尔霍夫公式()()()().~2cos cos ~000∑+-=⎰⎰∑d re Q E i P E ikr θθλ 傍轴条件下,即00,0r r ≈≈≈θθ()()().~~000∑-=⎰⎰∑d e Q E r i P E ikr λ 二、巴俾涅原理几何像点之外,()()(),0~~~0==+P E P E P E b a()()()().,~~P I P a a I P E P E b a =⇒=∴ 三、菲涅耳圆孔衍射和圆屏衍射平行光入射圆孔,则∞→R ,3.4.5.波带片∙遮住偶数带,轴上P 点的振幅为()()()()().P E P E P E P E n P E 1025030100+∆∆∆∆=+++∙遮住奇数带,轴上P 点的振幅为()()()()()().026040200P E P E P E P E P E n ∆+∆+∆+∆-=∙半波带半径.bR Rb ,k +==λρρρ11∙透镜作用:.112kk b R ρλ=⎪⎭⎫ ⎝⎛+四、夫琅禾费衍射 1. 单缝 ①光强()()().sin P E ~P E ~ααθ000=(),sin I I 20⎪⎭⎫ ⎝⎛=ααθ其中0I 为衍射场中心光强度,()2sin ⎪⎭⎫⎝⎛αα为单缝衍射因子. ②次极强 ,67.3,46.2,43.1sin aa a λλλθ±±±=③④零级2. 圆孔中心角半径:.2,22.1610.0a D Da=≈=λλθ3.光栅 ①光强●()()()()().P I sin N sin sin P A 2202220⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛=δδααθ ●().sin A N I MAX2220⎪⎭⎫ ⎝⎛=αα.d k MAXλ= ●极小:.sin d N m k λθ⎪⎭⎫ ⎝⎛+=()N ,m .N ,,m 0121≠-=●●主极大缺级:主极大 ,3,2,1,0,sin ±±±==k k d λθ 单缝极小 ,3,2,1,sin ±±±==n n a λθ当a n d k λλθ==sin 时,. ②光谱●●瑞利判据 :最小分辨角θδ'等于光谱线的半角宽度,●③闪耀光栅k 级最亮. 同时,d a ≈,()k B B k a λθ=2sin 也成立,即其它干涉级均成为缺级.第四章 全息照相1.全息感光片记录●物光波和参考光在该平面上的复振幅分布为()()()[]y x i y x O y x E o ,exp ,,~0ϕ=, ()()()[]y x i y x R y x E R R ,exp ,,~ϕ=.()()()()[]()[].i exp RO i xp Re O R O E ~E ~E ~E ~E ~E ~E ~E ~E ~E ~E ~E ~y ,x I e o e o *RR *R *O R *O *R*O R ϕϕϕϕ--+-++=+++=++=∙22000●透射系数.~~~12E E t = ()()[]()[].i exp RO i xp Re O R O y ,x I t ~R o R o ϕϕϕϕ--+-++==222.物光波前的再现()()()()[][][][].i exp O i exp R i exp OR i xp Re R O y ,x t ~y ,x E ~y ,x E ~o R o R R D ϕϕϕϕ-+++==22222●第一项()[]R i xp R O ϕRe 22+为照明光,即参考光; ●第二项[]o i OR ϕexp 2为物光波(成虚像);●第三项[][]o R i O i R ϕϕ-exp 2exp 2为物光波的共轭波.第五章 光的电磁性一、偏振1.2.3.布儒斯特角B θ4.e5. 波晶片,2πϕ±=-e o ,则称波晶片为4λ片.ππ2,e o ±=-,则称波晶片为2λ片.6. 椭圆偏振光.E E E y x += 其中⎪⎭⎫ ⎝⎛-=z t cos E E x x λπω20,⎪⎭⎫⎝⎛--=δλπωz t cos E E y y 20.7.电场引起双折射,BdE d n n e 202=-=λπδ8.磁致旋光.VBd =ψ二、光的吸收、色散和散射 1. 2. 色散●柯西公式:.CBA n 42λλ++=●色散率.,d dn,d dn 反常色散正常色散;00><λλ●.n r ε=,n i n n ''+'=()(),t n k zi exp z n k exp E E ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-'''-=000ωωn k ''=02α,.n cn k V '='=0ω3.瑞利散射:()().a ,f I s λλλλ<∝4第六章 光的量子性1.普朗克能量子2.光电效应3.康普顿散射4第七章 激光自发辐射:,N A dtdN 22121=受激辐射:(),N B dt N d 22121νρ='受激吸收:(),N B dtdN 11212νρ=谐振腔纵模 ,,j ,nL c j j 212==ν间隔.nLc 2=∆ν。
工程光学第二章资料PPT课件

n1rr2
f
置于其他介质中
1(n1)(11)1
f' n0 r1 r2
f
工程光学
例:一双凸透镜的两面表半径分别为r1 50mm,r2 50mm, 求该透镜位于空气中浸和没水(n0 1.33)中的焦距分别为 多少?(透镜材料折率射n 1.5) 解:位于空气中时
1(n1)(11)( 1.51)(1 1 )1
2.3理想光学系统的图解求像
工程光学
3.已知一对共轭点的位置和像方焦点的位置,求物像 方主平面的位置和物方焦点的位置。
2.4物像位置和三种放大率、两种焦距和光焦度工 程 光 学 一、理想光学系统的物像位置关系和垂轴放大率β
牛顿公式
物距x 像距x’
以焦点为原 点来确定x、 x’的值。
2.4物像位置和三种放大率、两种焦距和光焦度工 程 光 学
(2)物在2倍物方焦距处,像为等大倒立的实像
2.4物像位置和三种放大率、两种焦距和光焦度工 程 光 学 (3)物与物方焦面重合时
(4) 物与H重合
2.4物像位置和三种放大率、两种焦距和光焦度工 程 光 学
y' l'
yl
2.4物像位置和三种放大率、两种焦距和光焦度工 程 光 学 正透镜成像(图中移动的黑线为物,红线为像)
l
' F
h3
u
' 3
f
'
h1
u
' 3
工程光学
2.5光学系统的组合 各光组对总光焦度的贡献
工程光学
每个光组对总光焦度的贡献,除与自身的光焦度有关 外,还与它在系统中的位置有关。与前面得到的结论 一致。
2.5光学系统的组合
工程光学
光学公式
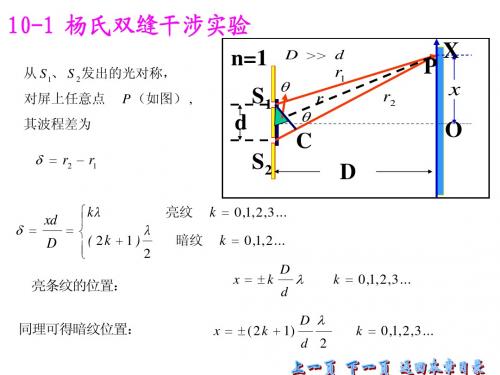
d
n2
n1 n3
相邻明纹厚度差 相邻暗纹厚度差
明纹与暗纹(相邻)之间厚度差
∆d = d k +1 − d k = 2n2 λ ∆d = 2n2 λ
4n2
λ
(2)测细丝直径(纸张的厚度) )测细丝直径(纸张的厚度)
尖劈夹角很小
θ
dk
l
dk+1 L
e
e θ ≈ sin θ ≈ tan θ = L d k +1 − d k λ 且 sin θ = =
同理可得暗纹位置:
k = 0,1,2,3...
k = 0,1,2,3...
Dλ x = ± (2k + 1) d 2
相邻亮纹(或暗纹)间距
屏上图样 S1 θ d S2
D ∆x = xk +1 − xk = λ d
等间距
D >> d
r1
P
X X
θ
C
r
r2
x
I O
D
2级明纹 级明纹 2级暗纹 级暗纹 1级明纹 级明纹 1级暗纹 级暗纹 0级明纹 级明纹 -1级暗纹 级暗纹 -1级明纹 级明纹 -2级暗纹 级暗纹 -2级明纹 级明纹
a--表示透光部分宽度 表示透光部分宽度 b--表示不透光部分宽度 表示不透光部分宽度 定义:光栅常数 定义:
d=a+b 数量级: 数量级:10-5--10-6m
(2)在衍射角θ 方向
θ
a d b
θ
B
C
从相邻单缝对应点射出的平行光依次 相差相同的光程BC或相同的相位差 或相同的相位差∆ϕ 相差相同的光程 或相同的相位差∆ϕ
a + b d L (3 ) k = ± k ' = ± k ' a a
物理光学公式

自己小结的必考物光公式:11章公式:11-22、11-23、11-24、11-25、11-26、11-28、11-29、11-30、11-35、11-36、11-37、11-38、11-45、11-60a、11-60b、11-64a、11-64b、11-65(a、b、c、d)、图11-8P278页,下什么是倏逝波,以及11-87(穿透深度)了解下。
11-126、P296页,光学拍一节看一看,群速度和相速度的概念看一下,其余不看。
P302页,11-169、什么是准单色光(公式下段末句既是)12章公式:光波干涉条件(1)频率相同、(2)振动方向相同、(3)相位差恒定得到相干光的方法:分波前法(杨氏干涉)、分振幅法(等倾干涉)P308页,这一页仔细推一遍(12-10、12-11、12-12、12-13、12-14、12-15)P310页,影响条纹可见度的因素,12-16、12-20、图12-7空间相干性(由光源宽度决定)图12-8时间相干性(由波列长度、光源宽度、光源非单色性)(12-29)(12-30)12-33、P315页,仔细推一遍,(12-34、12-36、12-37)12-38、12-39、12-40,P318页,12-40下面一段里的公式,平板厚度变化和機角αP319页,迈克耳孙干涉仪,这段详细看看12-49、12-50、12-51、12-55、12-56法布里珀罗干涉仪P327-329页仔细看看,12-57、12-58、12-59、12-64、12-6512-7513章公式:13-12,夫琅和费衍射的条件13-14,夫琅和费衍射的计算公式P344页,矩孔衍射、单缝衍射内容,(13-22、13-23、13-27、13-28、13-29、13-30、13-31)P349页,什么事艾里斑,(13-34、13-35)P351页,夫琅和费衍射的特点:(一)、(二)、(三)、(四)句话13-52、13-53、13-5513-57、13-58、13-60、13-6113-62、13-63、13-64、13-66、13-67闪耀光栅:13-77、13-78,其余的不看。
第3章工程光学

在近轴区域内,光学系统能成完善像。
E
lu l ' u ' h
A
-u -l
h O D l′
u′
A′
非理想光学系统
11
理想光学系统
12
2
3.1.1 理想光学系统的共线理论
理想光学系统理论又称之为高斯光学,其基本核心是共线成像。所谓共 线成像,就是指在理想光学系统中的一一对应关系:任一物点在像空间都 有一个和它唯一对应的像点;物空间任一条直线,则在像空间也有对应的 唯一直线;物空间任一平面,像空间也有唯一的对应平面,这种点对应点、 直线对应直线、平面对应平面的成像变换即称之共线成像,这种物像一一 对应的关系称之为共轭关系。 按照这一理论,可以得到如下推论: ① 如果一条物方光线经过物点P,则对应的像方光线必经过其共轭点P′; ② 如果物方的平面垂直于光轴,则像方的共轭平面也垂直于光轴; ③ 在任何一对共轭的垂轴平面内,垂轴放大率为一常数,即垂轴的平面物 体物像相似。
3.2.3 物方主平面与像方主平面间的关系
由符号规则确定。如果由F发出的入射光线的孔径角为U。其相应的出射 光线在物方主平面上的投射高度为h,由图2-7的三角几何关系有
f h tgU
在图中,作出一投射高度为h且平行于光轴的光线入射到理想光学系统,相应的出射光线必通
Q F H
23
过像方焦点 F’;过物方焦点 F 作一条入射光线,并且调整这条入射光线的孔径角,使得相 应出射光线的投射高度也是h。这样,两条入射光线都经过 Q点,相应的两条出射光线都经过 Q’,所以 Q 与 Q’就是一对共轭点,物方主面与像方主面是一对共轭面,而且 QH 与 Q’H’ 相等并在光轴的同一侧,所以,一对主平面的垂轴放大率为+1,即一对共轭光线在相应主面 上的投射高度相等。这一性质在用作图法追迹光线时是非常有用的。
光学元件和系统公式.

此页上的信息是对基本信息的汇总,主要是为了帮助您为特定的应用场合选择最好的光学元件和系统。
有用的公式线对的分辨率毫米:(3,000 x N.A.)/mm英寸:(75,000 x N.A.)/英寸景深毫米:.0005/N.A.²英寸:.00002/N.A.²换算系数1 英寸 = 25.4 毫米1 米 = 39.37 英寸1 微米 = 0.001 毫米术语定义景深无需重新调焦即可保持可接受的图像清晰度的距离。
焦深图像得到对焦时沿光学轴线的距离。
视野通过镜头或镜头系统的可视区域。
放大倍率目标与成像之间的外观尺寸差异的测量值。
数值孔径光线进入镜头系统的最大锥度或数量。
物象距离 (O-I)从物体到摄像机内置传感器之间的距离。
分辨率衡量镜头系统将非常靠近的点、线及物体表面作为单独图元进行成像的能力。
工作距离物体与镜头系统的最外侧表面之间的空间或距离。
它可以同时影响用户对样本进行成像和处理的能力。
与关于放大倍率的几点说明•当数值孔径增加时,景深减小,分辨率增加。
•当放大倍率增加时,视野减小。
•当放大倍率增加时,可能需要更多的光线。
•放大倍率的产生有两种方式–摄像机的不同镜头可产生不同的放大倍率,在摄像机/监视器组合中可在二者之间产生放大倍率。
摄像机的放大倍率所有的摄像机都有固定的传感器尺寸。
这就意味着无论在传感器平面上的图像有多大,摄像机只能“看到”等于传感器尺寸的那一部分。
摄像机所能“看到”的部分称为视野。
摄像机的镜头或镜头系统控制着摄像机传感器的放大倍率。
放大倍率越低,视野就越大。
监视器的放大倍率当摄像机图像显示在监视器上时,会进一步放大。
摄像机传感器的对角线扩展为监视器的对角线。
请参考如下例子:1/2”的摄像机与 13”的监视器联合使用。
摄像机的 8 毫米对角线将扩展到 13”(330.2 毫米),放大倍率为 41.3 倍。
实际应用中,摄像机图像将过度扩展,以填满监视器,并消除屏幕上的黑边。
光学公式小结重点讲义资料
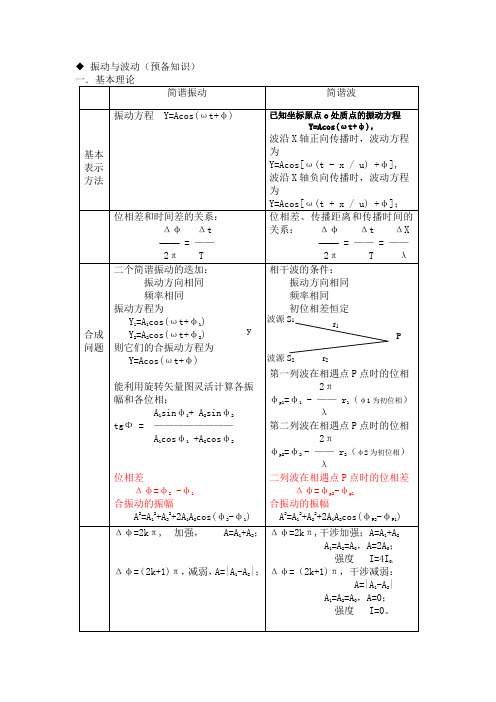
◆振动与波动(预备知识)二.电磁波的性质1.电磁波是横波。
E矢量和B(H)矢量互相垂直,且都垂直于传播方向。
E×H 的方向为波的传播方向。
2.E矢量和B(H)矢量在各自的平面上振动,位相相同。
√ε E=√μ H,B=μH3.电磁波的传播速度u=1/√εμ真空中,C =1/√ε0μ=3×108(米/秒)◆第一章和第二章(波动光学)小结一.基本概念1.光程——光在媒质走过的几何路程与媒质折射率的乘积。
2.半波损失——当光从光疏媒质入射到光密媒质时,反射光存在位相突变(改变了π),相当于多走了半个波长的光程,称为半波损失。
3.相干光的三个条件——振动方向相同、振动频率相同、初位相差恒定。
4.位相差与光程差的关系ΔΦδ——= ——,Δφ= 2kπ, δ=kλ, 加强2πλΔφ=( 2k+1)π, δ=(2k+1)λ/2,减弱5. 惠更斯--菲涅耳原理四.菲涅耳圆孔和圆屏衍射(半波带法) (p72)1. 菲涅耳圆孔衍射 理解半波带法O 为点光源,P 为观察点(p75)k 为半波带的数目Rr r R R k h 002)(λ+=如果用平行光照射圆孔,R = ∞2r R k hλ=当k 为整数(且k 不是太大时,各a k 近似相等): (P74) 当k 为偶数时,合振幅较小,可视为暗纹(合振幅A=0); 当k 为奇数时,合振幅较大,可视为明纹(合振幅A=a 1); 2. 菲涅耳圆屏衍射园屏几何影子的中心永远有光到达。
),(221-+±=偶数时取为奇数时取k aa A k k 21+=k k a A第三章几何光学第四章光学仪器1.了解光学仪器的三大本领:放大本领、聚光本领、分辨本领第五章.光的偏振1.双折射现象:光通过晶体后产生二条折射光。
2 .偏振器件的作用4.布儒斯特定律当入射光为天然光时,反射光和折射光均为部分偏振光;反射光垂直分量多于平行分量,折射光平行分量多于垂直分量。
当入射角i满足布儒斯特定律 tgi=n2/n1时,反射光成为线偏振光。
大学物理复习-光学公式

由反射干涉加强条件, k
M2
当M2移动半个波长时 光程差改变一个波长 S 视场中将看到 一条条纹移过。 当视场中看到N个 条纹移过时,M2 平移的距离为:
/2
G1
G2
L
E
M1
dN
2
A a
P5
二级明纹 二级暗纹 一级明纹 一级暗纹 中央明纹 -一级暗纹 -一级明纹 -二级暗纹 -二级明纹
马吕斯定律:强度为I0的线偏振光透过偏振片 后强度变为I=I0cos2。 (为入射的偏振光的振动方向与偏振片偏振化方 向间的夹角。)
I 0 E0 I0
2
I=I0cos2
E E// 0
E
线偏振光通 过偏振片后
1.光强改变 2.仍然为线偏振光,但振动方向 改变 α角度.
Polarization of reflection and refraction.Brewster’s law
同理可得暗纹位置:
x (2k 1) D d 2
k 0,1,2,3... k 0,1,2,3...
相邻亮纹(或暗纹)间距
屏上图样
D x xk 1 xk d
等间距
D d
S1
d
C
r1 r2
P
X X
r
x
O I
S2
D
2级明纹 2级暗纹 1级明纹 1级暗纹 0级明纹 -1级暗纹 -1级明纹 -2级暗纹 -2级明纹
讨论:
i ) d 0点, r 0,
O
2 ,中心为暗纹
ii)相邻明纹距离m=1
rk 1 rk R R rk 1 rk 2r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说明
图 示
光线任 任意、 共轴 轴球 面系统 统、 多个折 折射
共轴球面 面系统计 算的过渡公式
近轴 轴区计算公 公式
拉赫不变量对整个 系统而言是个不变 量
′ uk ′ yk ′ =J nk uk yk = nk
面。
′ n1u1 lk = ′ uk ′ lk nk
β=
′ yk = β1β 2 y1
sin I ′ ⎞ ⎛ L′ = r ⎜ 1 + ⎟ ⎝ sin U ′ ⎠
i=
l−r u r
近 近轴区光线 线,单个折 折射面。
n i′ = i n′
轴上 物点在近 近轴区 计 计算出射 角 i’ 计算 算出射孔径 径角 u’ 计 计算像方截 截距 l’ 光 光线矢高的 的性质
n′ l′ n l n′ − n 和 r
名 称
基本公式
sin I = ( L − r ) sin U r
应 应用条件 件
作 作用及意 意义
计 计算入射 射角 I
说 明
同心光 光束经折射 射后, 出射 光束不再 再是同 束。因此, ,单个 心光束
图
示
实 实际光线,单个折射 射面。适
n sin I ′ = sin I n′
f′=
hk h1 ′ = , lF ′ ′ tan nUk ta an U k
⎛1 1⎞ 1 1 = ( n − 1) ⎜ − ⎟ = − f′ f ⎝ r1 r2 ⎠
透镜焦 焦距的 计算公 公式
⎛ 1 1 ⎞ ( n − 1) d 1 1 = ( n − 1) ⎜ − ⎟ + =− f′ n 1r2 nr f ⎝ r1 r2 ⎠
用 用于已知折 折射面的半 半径 r, 以 以及介质的 的折射率 n,n’已 知 知的情况。 。
计 计算出射 角 I’ 计算 算出射孔径 径角 U’ 计 计算像方截 截距 L’ 计 计算入射 射角 i
实际光线 线的光路计 计算公式
U′ = U + I − I′
折射 球面对轴 轴上物 像是不完善 善的。 点成像
近 近似条件: :U、I、I’ I 和 U’都 很 很小。适用 用于已知折 折射面的 结 结构参数 r,n,n’。
成像是 内以 细光束成 的, 且高斯 斯面的 完善的 位置由 由 l’决定。 。
近轴光线 线的光路计 计算公式
u ′ = u + i − i′
i′ ⎞ n′lr ⎛ l ′ = r ⎜1 + ⎟ = ⎝ u ′ ⎠ n′l − n ( l − r )
2. 牛顿公式与 牛 与高斯公式 式计算的 的结果应该 该是一致的 的,解题时 时的选择根 根据坐标的形式而 而定,也可 可以应用坐 坐标转换公 公式。 3. 牛顿公式和 牛 和高斯公式 式给出的 的是整个理 理想光学系 系统的物像 像位置和物 物像大小的直接关 关系式。只 只要知道焦 焦距就可以 以求解出任 任意物平面 面所对应的相平面 面 的位 位置和放大 大率,反过 过来,也可 可以根据给定的物 物像位置确 确定系统的 的焦距。
′−1 − dk −1 lk = lk
理想光 光学系统, 且 每个光组的焦距 和焦点 点、 主点位 位置
物距 物 l 过渡 渡 物距 物 x 过渡 渡 光学间隔 隔 系统 统垂轴放大 大率
焦点 点间隔 (光 学间 间隔)Δ: 第 k 个光组 的像方焦点 到第 第 k+1 个 光组的物方 焦点 点的距离。
应用条 条件
两个共轴理 理想光学 系统, 且两 两系统位于 同一介质中 中。
作用及 及意义
求组合系 系统的焦距
说明
图 示
Φ = Φ1 + Φ 2 − d Φ1Φ 2
f ′f ′ f f f′=− 1 2 , f = 1 2 Δ Δ ′ =− xF f 2 f 2′ f f′ , xF = 1 1 Δ Δ
名 称
基本公式
β=
y′ (定义式 定 ) y
应 应用条件
作 作用及意 意义
像的大小 小与物体的 的大小之比
说 明
1. 若β β> 0,成正 正像,反 之成倒 倒像。 2. 若β β> 0, 物像虚实相 反,反 反之相同。 3. 若 β >1,成放 放大像; 反之成 成缩小像。
反射时此式的变形公式
近轴区内 内一对共轭 轭点的性 性 折 折射面。适 适用于已知 知折射面 质公式
n′u′ − nu = ( n′ − n ) h r
的 的结构参数 数 r,n,n’。
n′ n n′ − n − = l′ l r
体现了物 物方截距 l 与像方截 截 距 l’的关 关系
果均相 相同
多光组组 组成的理 想光学系 系统的过 渡公 公式
′ −1 − Δ k −1 xk = xk Δ k = dk − f k′ + f k +1
以及光组间的相 互位置 置均已知
β = β1β2 … βk
名 称
基本公式 基
1 1 1 d 1 =− = + − f f ' f1′ f 2′ f1′f 2′
dl ′ dl
α=
nl ′2 (近轴 轴区计算式 式) n′l 2
n′ 2 β(近轴 轴区关系式 式) n
α=
折 折射面。
一对共轭光 光线与光轴 轴的夹角之比 比
近轴区的 的成像放大 大率公式
γ = (定 定义式)
u′ u
γ = (近轴 轴区计算式) )
l l′
角放大率只与共轭点的位置有 光线的孔径 径角无关 关,而与光
2
求厚透镜 镜的焦距 透镜主面 面的位置公 式
− dr1 − dr2 lH ′ = , lH = n ( r2 − r1 ) + ( n − 1) d n ( r2 − r1 ) + ( n − 1) d
分析单个 个 折射面时 时 要考虑其 其 几何参数 数
(无)
⎞⎛ 1 1 ⎞ 1 ⎛n 1 = ⎜ − 1⎟⎜ − ⎟ = − f ′ ⎝ n0 ⎠ ⎝ r1 r2 ⎠ f
f 与 f’的关 关系
f′=−f
f′ n′ =− f n
f′=−f
1. 只有当知道 只 道系统的焦 焦距 f’之后,才能 能使用高斯 斯公式或牛 牛顿公式。如果只知 知道系统的结构参 参数 r、n、d,则应 应该追迹一 一条平行于 于光轴的近 近轴光线, 利用 用公式 f ′ = 几点说明
h h1 ′ = k ,即可求 求出像方焦 焦距与焦点 点位置,从 从而确定 定像方主点 点和像方主 主平面的位 位置。反过 过来,物方 方一侧也可以同理 理求出。 , lk ′ ′ uk uk
以第一系 系 统的物方 方 主点、第 第 二系统的 的 像方主点 点 为起点
′ = ta tan U k an U k +1 = tan nUk +
多光组组 组合的 计算公 公式 (正切计 计算法)
′ −1 hk = hk −1 − d k −1 tan U k 多个共轴理 理想光学 系统 投射高度 度计算公式 以最后一 一 像方焦距 距以及像方 个折射面 面 焦点位置公式 的像方主 主 点为起点 点 求薄透镜 镜的焦距 适用于求解 解位于空 气中的单透 透镜的焦 距
图
示
β = (近轴 轴区计算式)
nl ′ n′l
单个球面物 物象大小关 关系式,表明 明 了放大率仅 仅取决于共 共轭面的位置 置
α = (定 定义式)
1. 折射 射球面的轴向放大 为正。因此,当物 物点沿光 光轴做微小 小移动时, , 率恒为 点沿轴 轴向移动时,其像 光轴同向移动 动 所引起的 的像点移动 动量与物点 点 点沿光 2. 轴向 向放大率与垂轴放 大率不 不等,因此,空间 移动量之 之比 物体成 成像时要变形 形。 近 近轴区有限 限大物体 体,单个
名 称
基本 本公式
ni +1 = ni′ ui +1 = ui′ yi +1 = yi′ hi +1 = hi − diui′
n′u′ − nu n =h n′ f′
应用条件
作用及意义 作 义
折射率过渡 折 渡 孔径角过渡 孔 渡 像高过渡 渡 入射高度过 过渡
βk =
′ n1 l1′l2 ′ l1l2 nk
系统 统垂轴放大 大率 系统 统轴向放大 大率 系统角放大 大率
系统 统放大率的关 关系
α=
′ dlk = α1α 2 dl1 ′ uk = γ 1γ 2 u1
αk γk
γ=
α=
′ 2 nk n 1 β , γ = 1 , αγ = β ′ β n1 nk
l ′u ′ = lu l =h
其中, , − =
y n′l
对于单个 个折射面, 物空间与 与 β = y′ = nl ′ 合称 称为近
⎛1 1⎞ ⎛ 1 1⎞ n′ ⎜ − ⎟ = n ⎜ − ⎟ = Q ⎝ r l′ ⎠ ⎝r l⎠
像空间的阿贝不 不变量 Q 相 近 近轴区内一 一对共轭点 点,单个 轴光学 学基本公式 式, 它 随共轭点的 的位置而变 变 等, 仅随 是近轴 轴光路计 计算公 物方孔径 径角 u 与像方孔径 与 径 角 u’的关 关系 单个球面 面物象位置关系式 式, 式的简 简化形式, 建立 了物 像之间的 的直接 , 适用条件 件和结 关系,
1 1 1 − = l′ l f ′
物像大 大小(垂轴 轴放大率)
β =−
f x′ =− f′ x
x′ x
β=
β =−
fl ′ f′l
fl ′2 f ′ l2
β=
l′ l
