锐角三角函数与解直角三角形中考复习 (5)

合集下载

锐角三角函数与解直角三角形总复习

锐角三角函数直角三角形【学习目标】：1.了解锐角三角函数(sinA ，cosA ，tanA)的概念，熟记特殊的30。

，45。

，60。

角三角函数值； 2．能利用三角函数关系进行计算，理解三角函数的增减性；已知三角函数值求它对应的锐角。

知识要点： 1．锐角三角函数(1) sin α，cos α，tan α，cot α叫做锐角α的三角函数．定义：sin α＝____，cos α＝_______，tan α＝______ ，cot α＝______。

(2) 锐角A 的三角函数值的取值范围：sinA: cosA: tanA: cot A ： (3) 若∠A+∠B=90°，则B A tan tan = （4）若∠A+∠B=90°,A sin B cos ,A cos B sin ； 2．特殊角三角函数值典型例题：例1 在Rt△ABC 中，∠C=90°,a ＝5，c ＝13，求sinA ，cosA ，tanA ，cot A ．α abc例2 计算:4sin 304560︒︒︒+（-21）-2．例3 等腰△ABC 中，AB ＝AC ＝5，BC ＝8，求底角∠B 的四个三角函数值．例4 矩形ABCD 中AB ＝10，BC ＝8， E 为AD 边上一点，沿BE 将△ABE 对折，点A 正好落在DC 边上的F 处，求 tan∠DFE ．FD CBAE巩固练习题：1．在△ABC 中，∠C＝90°，BC ＝2，sinA＝23，则AC 的长是（） A．3 C ．45D 2．Rt ∆ABC 中，∠C=︒90，∠A∶∠B=1∶2，则sinA 的值（）A ．21B ．22C ．23D ．13．在△ABC 中，∠C ＝ 90°，tanA ＝13，则sin B ＝( )A ．10 B．23 C ．34D ．10 4．若3cos 4A =，则下列结论正确的为（） A ． 0°< ∠A < 30° B．30°< ∠A < 45°C ． 45°< ∠A < 60° D．60°< ∠A < 90°5．如图，在平面直角坐标系中，已知点A （3，0），点B （0，－4），则cos OAB ∠ 等于_______．6．计算：45tan 30cos 60sin -= .︒+︒30sin 130cos =____________．7.在Rt ABC △中，90C ∠=，5AC =，4BC =，则tan A = ． 8. 已知3tan 0 A =∠A =则． 9．△ABC 中，若（sinA －12）2＋－cosB|＝0，求∠C 的大小．解直角三角形及其应用学习目标：掌握直角三角形的边角关系，会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形；会用解直角三角形的有关知识解某些简单的实际运用问题。

锐角三角函数与解直角三角形试题解析

2020^^1l m锐角三角展教与鮮直角三角形武题鮮析■汤文卿摘要:锐角三角函数与解直角三角形是中考的重要和必考内容，考题形式多样、问题新颖、内涵丰富、解法灵活，很多问题常常与勾股定理、四边形、全等三角形、相似三角形、圆等知识相结合，紧密联系实际，文章对近年中考数学中的锐角三角函数与解直角三角形常见题型进行分类和解析，同时给出了相应的求解策略.关键词：初中数学；銳角三角函数；解直角三角形锐角三角函数与解直角三角形是近年各地中考数学试题的重要内容，必考知识点，考题形式多样、问题新颖、内涵丰富、解法灵活，很多问题常常与勾股定理、四边形、全等三角形、相似三角形、圆等知识相结合，紧密联系实际，本文对近年中考数学中的锐角三角函数与解直角三角形常见题型进行分类和解析，同时给出相应的求解策略.一、求锐角三角函数值这类问题的常见题型有给出特殊角求其某一个三角函数值（只要熟记特殊角的三角函数值即可），或给出某角的一种三角函数值求此角另外的三角函数值，亦或给出一个图形求其中某个角的三角函数值.例1 (2019年龙东地区）如图1，矩形/IBCD的对角线相交于点6C = 3 :2,过点B 作// A C ，过点C 作C E //D B ，B E ,C E 交于点E ，连接D E ,则 tan Z_£OC =( )(A )f (B )(C )f(D )盖解析:如图2,构作含有的直角三角形：作丄D C 交D C 的延长线于点F ，由已知可设/1S =31VICE /13k ，Jffj sin = sin 厶 BDC ，所以EFEC||，所以=2A :、/讯，所以狀“，由勾股定理得 Cf’ =所以= |~i ，所以 t an z£/)C =盖=|，故选(A )_DF9例(2018年眉山市）如图3,在边长为1的小正方形网格中，点都在这些小正方形的顶点上，X I C D 相交于点 0,则 tanZ/IOZ) = ________.A C A E C解析:如图4,连接狀交(：/)于F ,由正方形性质得BE 丄 CK ，而/_B 0F = /_A 0D , iX tanZ /100 =tanZBOF ,只需求O F 即可.因为4C //B (所以KO ： CO = B K ： AC ^ \ 3 KO ：(J 2 - OK ) = 1 ：3,所以尺0 = f ,所以O F = f (发现0是狀的中作者简介:汤文卿（1966 -),男，江苏省海门人，本科，中学高级教师,主要从事初中数学教学研究•31 .数理化学习/2点），而方厂=^■，所以 tanZ40D = t a n Z B O F =召OF = 2.例3 (2019年自贡市）如图5,在由10个完全相同的正三角形构成的网络图中，Z_a 、乙/3如图所示，则 cos( a + p ) =z ________•图5 图6解析:如图6,连接S C ,易得zl/lCS = 90°，A /tD£S A C EB ，所以 AEBC = ADEA = a ,所以 AABC = a + y 8•设小正二角形的边长为a ，则/4C = 2a ，B C = v ^a ，在 RtA/lBC 中，仙=V^"a ，所以 cos(a + 卢）=cos Z . ABCBCABy f i例4hl (2019年綿阳市）公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图” 如图7所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125，小正方形面积是25，则（sin0 - cos0)2 =()(A )+ (B )f (C )竽（D )务所以(sin 0 - cos 0)2 = ( - 士)2 =去，故选(A ).V5 5感悟:此题可由勾股定理求出a = 5,得出小直角二角形另外一直角边长为10,从而准确求出sin0、cos0 的值得出所求结果，但不必要.评析:求一个锐角的函数值，一般需将这个角置于一个直角三角形中，再运用锐角三角函数的定义求解，因此巧妙合理的构造直角三角形（所构造的直角三角形既要能含有这个角又要能够运用已知条件）是解题的关键.解题时，常常用到勾股定理、全等三角形（例4)、相似三角形（例3)、四边形（例2)、圆（见例10)、解直角三角形等知识点.另外，例3中的等角转换也是求三角函数的一种好方法.二、由三角函数值反求锐角这类题比较简单，只要牢记3个特殊角（30°、45°、 60°)的函数值，利用对应关系求解即可.例5[1] (2019年甘肃省）在A /15C 中乙C =F x90o，t a i L 4 = 了，贝i j cosB = ________.解析：R t A 仙C 中，因为tao4 = f ,所以Z/l =30。

中考复习：锐角三角函数

中考复习：锐角三角函数知识梳理一、锐角三角函数（正弦、余弦、正切）1、定义：在Rt △ABC 中，∠C ＝90°，我们把锐角A的对边与斜边的比叫做∠A 的正弦（sinc ），记作sin A ，即sin A aA c∠==的对边斜边。

把∠A 的邻边与斜边的比叫做∠A 的余弦（cosine ），记作cos A ，即；把∠A 的对边与邻边的比叫做∠A 的正切（tangent ），记作tan A ，即。

锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数（trigonometric function of acute angle ）。

当锐角A 的大小确定时，∠A 的对边与斜边的比（正弦）、∠A 的邻边与斜边的比（余弦）、∠A 的对边与邻边的比（正切）分别是确定的。

2、增减性：在0°到90°之间，正弦值、正切值随着角度的增大而增大，余弦随着角度的增大而减小。

3、取值范围：当∠A 为锐角时，三角函数的取值范围是：0＜sin A ＜1，0＜cos A ＜1，tan A ＞0。

4、互余两角的函数关系：如果两角互余，则其中一有的正弦等于另一角的余弦，即：若α是一个锐角，则sin α=cos （90°-α），cos α=sin （90°-α）。

5、正、余弦的平方关系：sin 2α+ cos 2α=1。

二、300、450、600的正弦值、余弦值和正切值如下表：三、解直角三角形bcos c A A ∠==的邻边斜边atan bA A A ∠=∠的对边＝的邻边C ∠A 的邻边b∠A 的对边a在直角三角形中，由已知元素求未知元素的过程就是解直角三角形。

1、在Rt△ABC 中，∠C＝90°，设三个内角A 、B 、C 所对的边分别为a 、b 、c （以下字母同），则解直角三角形的主要依据是：（1）边角之间的关系： sinA ＝cosB ＝a c ， cosA ＝sinB ＝bc，tanA ＝cotB ＝a b ，cotA ＝tanB ＝b a。

中考解直角三角形知识点整理复习

x tan 21°
8 3
x
；
B
D
第 19 题图
在
Rt△CEG 中， tan
CGE
CE GE
，则 GE
tan
CE CGE
x tan 37°
4 3
x
∵ EF FG EG，∴ 8 x 50 4 x ． x 37.5 ，∴ CD CE ED 37.51.5 39 （米）．
3
3
答：古塔的高度约是 39 米． ························ 6 分
a2 b2
a 由 Sin A＝c，求∠A；∠B＝90°－A，b＝
c2 - a2
∠B＝90°－A，a＝b·Sin A，c＝cosA
A bC 一
和
角一锐角
锐角，对边（如∠A，a）
∠B＝90°－A，b＝，c＝
斜边，锐角（如 c，∠A）
∠B＝90°－A，a＝c·Sin A， b＝c·cos A
2、测量物体的高度的常见模型
35º 40
CB
D
面 CD 有多长
º
(结果精确到 0.1m．参考数据：sin40º ≈，cos40º ≈，sin35º ≈，tan35º ≈
（2012）20.（8 分）
附历年真题标准答案：
（2007）19．（本小题满分 6 分）
解：过 C 作 AB 的垂线，交直线 AB 于点 D，得到 Rt△ACD 与 Rt△BCD．
数学模型
所用应测数据
工具
α β x
h1
h
皮尺
αβ a
h x
侧倾器
仰角α 俯角β 高度 a
俯角α 俯角β
高度
数量关系

(完整word版)锐角三角函数与解直角三角形复习专题教案、练习答案

锐角三角函数于解直角三角形小结1 本章概述锐角三角函数、解直角三角形，它们既是相似三角形及函数的继续,也是继续学习三角形的基础．本章知识首先从工作和生活中经常遇到的问题人手，研究直角三角形的边角关系、锐角三角函数等知识，进而学习解直角三角形,进一步解决一些简单的实际问题．只有掌握锐角三角函数和直角三角形的解法，才能继续学习任意角的三角函数和解斜三角形等知识，同时解直角三角形的知识有利于培养数形结合思想，应牢固掌握．小结2 本章学习重难点【本章重点】通过实例认识直角三角形的边角关系，即锐角三角函数(sin A ,c os A ，tan A )，知道30°，45°，60°角的三角函数值，会运用三角函数知识解决与直角三角形有关的简单的实际问题．【本章难点】综合运用直角三角形的边边关系、边角关系来解决实际问题．【学习本章应注意的问题】在本章的学习中，应正确掌握四种三角函数的定义，熟记特殊角的三角函数值，要善于运用方程思想求直角三角形的某些未知元素，会运用转化思想通过添加辅助线把不规则的图形转化为规则的图形来求解，会用数学建模思想和转化思想把一些实际问题转化为数学模型,从而提高分析问题和解决问题的能力．小结3 中考透视这一章在中考中主要考查一些特殊角的三角函数值及几个三角函数间的关系,主要题型是选择题、填空题．另外解直角三角形在实际问题中的应用也是考查的一个重点,主要题型是填空题和解答题，约占3~7分．知识网络结构图专题总结及应用一、知识性专题专题1：锐角三角函数的定义【专题解读】锐角三角函数定义的考查多以选择题、填空题为主．例1 如图28－123所示，在Rt △ABC 中,∠ACB ＝90°,BC ＝1，AB ＝2,则下列结论正确的是（） A ．sin A 3 B ．tan A ＝12 C ．cos B 3D ．tan B 3 分析 sin A ＝BC AB ＝12，tan A ＝BC AC 3，cos B ＝BCAB ＝12．故选D 。

(中考精题)解直角三角形-备战中考数学一遍过

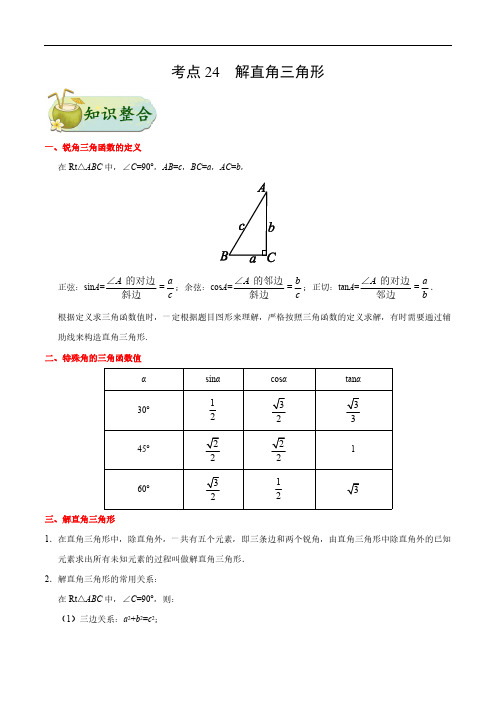
考点24 解直角三角形一、锐角三角函数的定义在Rt△ABC中，∠C=90°，AB=c，BC=a，AC=b，正弦：sin A=∠的对边=斜边A ac；余弦：cos A=∠的邻边=斜边A bc；正切：tan A=∠的对边=邻边A ab．根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.二、特殊角的三角函数值三、解直角三角形1．在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形．2．解直角三角形的常用关系：在Rt△ABC中，∠C=90°，则：（1）三边关系：a2+b2=c2；（2）两锐角关系：∠A+∠B=90°；（3）边与角关系：sin A=cos B=ac，cos A=sin B=bc，tan A=ab；（4）sin2A+cos2A=1．3．科学选择解直角三角形的方法口诀：已知斜边求直边，正弦、余弦很方便；已知直边求直边，理所当然用正切；已知两边求一边，勾股定理最方便；已知两边求一角，函数关系要记牢；已知锐角求锐角，互余关系不能少；已知直边求斜边，用除还需正余弦.四、解直角三角形的应用1．仰角和俯角仰角：在视线与水平线所成的角中，视线在水平线上方的角叫做仰角．俯角：在视线与水平线所成的角中，视线在水平线下方的角叫做俯角．2．坡度和坡角坡度：坡面的铅直高度h和水平宽度l的比叫做坡面的坡度（或坡比），记作i=hl．坡角：坡面与水平面的夹角叫做坡角，记作α，i=tanα．坡度越大，α角越大，坡面越陡．3．方向角（或方位角）指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角．4．解直角三角形中“双直角三角形”的基本模型：解题方法：这两种模型种都有一条公共的直角边，解题时，往往通过这条边为中介在两个三角形中依次求边，或通过公共边相等，列方程求解. 5．解直角三角形实际应用的一般步骤（1）弄清题中名词、术语，根据题意画出图形，建立数学模型；（2）将条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形问题；（3）选择合适的边角关系式，使运算简便、准确；（4）得出数学问题的答案并检验答案是否符合实际意义，从而得到问题的解．考向一求三角函数的值（1）分清直角三角形中的斜边与直角边.（2）正确地表示出直角三角形的三边长，常设某条直角边长为k （有时也可设为1），在求三角函数值的过程中约去k ．（3）正确应用勾股定理求第三边长．（4）应用锐角三角函数定义，求出三角函数值．典例1 的值为 ABCD ．1【答案】C 【解析】把代入原式得：原式．故选C ． 2sin 451．如图，在△ABC 中，∠C =90°．若AB =3，BC =2，则sin A 的值为A ．BCD考向二利用特殊角的三角函数值求值锐角三角函数值与三角形三边的长短无关，只与锐角的大小有关.典例2 已知∠A 为锐角，且sin A，那么∠A等于 A ．15° B ．30° C ．45° D ．60°2．已知α是锐角，sin α=cos60°，则α等于 A ．30° B ．45°C ．60°D ．不能确定考向三解直角三角形的应用解此类题的一般方法：（1）构造直角三角形；（2）理清直角三角形的边角关系；（3）利用特殊角的三角函数值解答问题.23典例3 某山的山顶B 处有一个观光塔，已知该山的山坡面与水平面的夹角∠BDC 为30°，山高BC 为100米，点E 距山脚D 处150米，在点E 处测得观光塔顶端A 的仰角为60°，则观光塔AB 的高度是A ．50米B ．100米C ．125米D ．150米【答案】A【解析】如图，作EF ⊥AC 于F ，EG ⊥DC 于G ，在Rt △DEG 中，EG =12DE =75， ∴BF =BC -CF =BC -CE =100-75=25，EF，∵∠AEF =60°， ∴∠A =30°，∴AF，∴AB =AF -BF =50（米），故观光塔AB 的高度为50米，故选A ．3．如图，某湖心岛上有一亭子A ，在亭子A 的正东方向上的湖边有一棵树B ，在这个湖心岛的湖边C 处测得亭子A 在北偏西45︒方向上，测得树B 在北偏东36︒方向上，又测得B 、C 之间的距离等于200米，求A 、B 之间的距离（结果精确到1米）．1.414≈，sin360.588︒≈，cos360.809︒≈，tan360.727︒≈，cot36 1.376︒≈）1．如图，在△ABC 中，若∠C =90°，则A ．sin A =B ．sin A =C ．cos A =D ．cos A =2的值为 A．B ．C．D ．3．在中，，，若，则的长为 A ．B ．C ．D ．4．在Rt △ABC 中，∠C =90°，，则cos A 等于 a c b c abba1sin45cos602︒-︒(112+(1121434Rt ABC △90C ∠=︒53B ∠=︒BC m =AB cos53m︒cos53m ⋅︒sin 53m ⋅︒tan 53m ⋅︒13AC AB =AB ．C ．D5．菱形ABCD 的对角线AC =10cm ，BD =6cm ，那么tan为 A ．B ．C D6．如图是边长为1的小正方形组成的网格图，其中点A ，B，C 均为格点，则sin ∠BAC 为A B CD7．在Rt △ABC 中，∠C =90°，若AB =10，sin A =，则斜边上的高等于 A ．5B．4.8C ．4.6D ．48．如图，在边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则tan∠ABC 的值为A ．B ．C D ．19．如图，某水库堤坝横截面迎水坡的坡度是，堤坝高为，则迎水坡面的是A ．10．如图，一艘海轮位于灯塔P 的北偏东55°方向，距离灯塔为2海里的点A 处．如果海轮沿正南方向航行到灯塔的正东位置B 处，海轮航行的距离AB 长是132B 5354353534AB 40m 80m B ．C 40m ．D ．A ．2海里B ．海里C ．海里D ．海里11．钓鱼是一项特别锻炼心性的运动，如图，小南在江边垂钓，河堤AB 的坡度为1∶2.4，AB 长为3.9米，钓竿AC 与水平线的夹角是60°，其长为4.5米，若钓竿AC 与钓鱼线CD 的夹角也是60°，则浮漂D 与河堤下端B≈1.732）A．1.732米B ．1.754米C ．1.766米D ．1.823米12．如图，在Rt △ABC 中，∠C =90°，BC =12，tan A =，则sinB =___________．13．在△ABC 中，AB ，AC ，tan ∠B =，则BC 的长度为__________． 14．已知相邻的两根电线杆与高度相同，且相距．小王为测量电线杆的高度，在两根电线杆之间某一处架起测角仪，如图所示，分别测得两根电线杆顶端的仰角为、，已知测角仪高，则电线杆的高度约为________．（精确到，参考数据：，，）2sin55︒2cos55︒2tan55︒12512AB CD 50m BC =E 45︒23︒EF 1.5m m 0.1m sin230.39︒≈cos230.92︒≈tan230.43︒≈15．已知：如图，在菱形ABCD 中，AE ⊥BC ，垂足为E ，对角线BD =8，tan ∠CBD =．（1）求边AB 的长；（2）求cos ∠BAE 的值．16．如图是小强洗漱时的侧面示意图，洗漱台(矩形ABCD )靠墙摆放，高AD =80cm ，宽AB =48cm ，小强的身高为166cm ，其中下半身FG =100cm ，洗漱时下半身与地面成80°角(∠FGK =80°)，身体前倾成125°角(∠EFG =125°)，脚与洗漱台的距离GC =15cm(点D ，C ，G ，K 在同一直线上)．（1）此时小强的头部点E 与地面DK 的距离是多少？（2）小强希望他的头部E 恰好在洗漱盆AB 的中点O 的正上方，他应向前或后退多少？ (sin80°≈0.98，cos80°≈0.17≈1.41，结果精确到0.1cm)121．（2019•天津）的值等于 A ．1 B． C ．D ．22．（2019•怀化）已知∠α为锐角，且sin α=，则∠α= A ．30° B ．45° C．60°D ．90°3．（2019·宜昌）如图，在5×4的正方形网格中，每个小正方形的边长都是1，△ABC 的顶点都在这些小正方形的顶点上，则sin ∠BAC 的值为A ．B ．C ．D ．A ．75 mB ．50 mC ．30 mD ．12 m5．（2019•苏州）如图，小亮为了测量校园里教学楼的高度，将测角仪竖直放置在与教学楼水平距离为的地面上，若测角仪的高度为，测得教学楼的顶部处的仰角为，则教学楼的高度是60sin 2231243343545AB CD 1.5m A 30oA ．B ．C ．D．6．（2019•广西）小菁同学在数学实践活动课中测量路灯的高度．如图，已知她的目高AB 为1.5米，她先站在A 处看路灯顶端O 的仰角为35°，再往前走3米站在C 处，看路灯顶端O 的仰角为65°，则路灯顶端O 到地面的距离约为（已知sin35°≈0.6，cos35°≈0.8，tan35°≈0.7，sin65°≈0.9，cos65°≈0.4，tan65°≈2.1）A ．3.2米B ．3.9米C ．4.7米D ．5.4米7．（2019·杭州）如图，一块矩形木板ABCD 斜靠在墙边（OC ⊥OB ，点A ，B ，C ，D ，O 在同一平面内），已知AB =a ，AD =b ，∠BCO =x ，则点A 到OC 的距离等于A ．a sin x +b sin xB ．a cos x +b cos xC ．a sin x +b cos xD ．a cos x +b sin x55.5m 54m 19.5m 18m计算这座灯塔的高度CD （结果取整数）．参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60．11．（2019•深圳）如图所示，某施工队要测量隧道长度BC ，AD =600米，AD ⊥BC ，施工队站在点D 处看向B ，测得仰角为45°，再由D 走到E 处测量，DE ∥AC ，ED =500米，测得仰角为53°，求隧道BC 长．（sin53°≈，cos53°≈，tan53°≈）．45354314．（2019•江西）图1是一台实物投影仪，图2是它的示意图，折线B–A–O表示固定支架，AO垂直水平桌面OE于点O，点B为旋转点，BC可转动，当BC绕点B顺时针旋转时，投影探头CD始终垂直于水平桌面OE，经测量：AO=6.8cm，CD=8cm，AB=30cm，BC=35cm．（结果精确到0.1）．（1）如图2，∠ABC=70°，BC∥OE．①填空：∠BAO=__________．②求投影探头的端点D到桌面OE的距离．（2）如图3，将（1）中的BC向下旋转，当投影探头的端点D到桌面OE的距离为6cm时，求∠ABC 的大小．（参考数据：sin70°≈0.94，cos20°≈0.94，sin36.8°≈0.60，cos53.2°≈0.60）15．（2019•安徽）筒车是我国古代发明的一种水利灌溉工具．如图1，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理．如图2，筒车盛水桶的运行轨迹是以轴心O为圆心的圆．已知圆心在水面上方，且圆被水面截得的弦AB 长为6米，∠OAB =41.3°，若点C 为运行轨道的最高点（C ，O 的连线垂直于AB ），求点C 到弦AB 所在直线的距离．（参考数据：sin41.3°≈0.66，cos41.3°≈0.75，tan41.3°≈0.88）16．（2019•贵阳）如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图，图中OP 为下水管道口直径，OB 为可绕转轴O 自由转动的阀门．平时阀门被管道中排出的水冲开，可排出城市污水；当河水上涨时，阀门会因河水压迫而关闭，以防河水倒灌入城中．若阀门的直径OB =OP =100cm ，OA 为检修时阀门开启的位置，且OA =OB ．（1）直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB 的取值范围；（2）为了观测水位，当下水道的水冲开阀门到达OB 位置时，在点A 处测得俯角∠CAB =67.5°，若此时点B 恰好与下水道的水平面齐平，求此时下水道内水的深度．（结果保留小数点后一位） =1.41，sin67.5°=0.92，cos67.5°=0.38，tan67.5°=2.41，sin22.5°=0.38，cos22.5°=0.92，tan22.5°=0.41）3．【解析】如图，过点C 作CH AB ⊥，垂足为点H ，由题意，得45ACH ∠=︒，36BCH ∠=︒，200BC =，在Rt △BHC 中，sin BH BCH BC ∠=，∴sin36200BH︒=， ∵sin360.588︒≈，∴117.6BH ≈，又cos HC BCH BC ∠=，∴cos36200HC︒=， ∵cos360.809︒≈，∴161.8HC ≈，在Rt △AHC 中，tan AHACH HC∠=， ∵45ACH ∠=︒，∴AH HC =，∴161.8AH ≈，又AB AH BH =+，∴279.4AB ≈，∴279AB ≈（米）．答：A 、B 之间的距离为279米．2．【答案】D【解析】原式=1–=，故选D ． 3．【答案】A 【解析】如图，∵cos53°=， ∴AB =，故选A ． 4．【答案】B【解析】如图所示：∵，∴cos A =．故选B ．5．【答案】A1122⨯1434BC AB cos53m︒13AC AB =1133ABAC AB AB ==【解析】如图，由题意得，AO ⊥BO ，AO =AC =5cm ，BO =BD =3cm ，则tan=tan ∠OBA .故选A.6．【答案】D【解析】如图所示：连接BD ，交AC于点E ，由正方形的性质可得：BD ⊥AC ，故BD ，AB则sin ∠BAC =D ． 7．【答案】B【解析】如图所示，CD ⊥AB ，CD 即为斜边上的高，在Rt △ABC 中，∠C =90°，AB =10，sin A =， ∴sin A ==，即BC =6， 12122B 53AO BO ==EB AB ==3510BC BC AB =35根据勾股定理得：AC=8，∵S △ABC =AC •BC =CD •AB ， ∴CD ==4．8，故选B ．8．【答案】B【解析】∠ABC所在的直角三角形的对边是3，邻边是4，所以，tan ∠ABC =．故选B ．9．【答案】A【解析】∵堤坝横断面迎水坡AB 的坡比是1 ∵BC =40m ，∴AC m ，∴AB ，故选A ．10．【答案】C【解析】记灯塔P 的正北方向为射线PC 的方向.根据题意可知∠APC =55°，PC ∥AB ，AP =2海里. ∵PC ∥AB ，∠APC =55°，∴∠PAB =55°. ∵在Rt △ABP 中，AP =2海里，∠PAB =55°， ∴AB =AP ·cos ∠PAB =2cos55°（海里）. 故选C. 11．【答案】C【解析】如图，延长CA 交DB 延长线与点E ，过点A 作AF ⊥BE 于点F ，12126810AC BC AB ⋅⨯=34BC AC =则∠CED =60°， ∵AB 的坡比为1∶2.4，∴，则设AF =5x ，BF =12x ， ∵AB =3.9米，∴在直角△ABF 中，由勾股定理知，3.92=25x 2+144x2．解得x =．∴AF =5x =，BF =12x =，∴EF =， ∵∠C =∠CED =60°， ∴△CDE 是等边三角形， ∵AC =4.5米，∴DE =CE =AC +AE则BD =DE ﹣EF ﹣BF≈1.766（米），答：浮漂D 与河堤下端B 之间的距离为1.766米．故选C ． 12．【答案】【解析】在Rt △ABC 中，∠C =90°，BC =12，tan A =，得，即， ∴AC =5．由勾股定理，得AB ．所以sin B =，故答案为：．13．【答案】5152.412AF BF ==31032185tan 60sin 60AF AFAE =====︒︒185513125125BC AC =12125AC =513AC AB =513【解析】如图，过点A 作AD ⊥BC 交于D ．∵，设AD =x ，则BD =2x ， ∵AB，∴在△ABD 中，由勾股定理得（2=x2+（2x）2，解得，x 1=2，x 2=﹣2（不符合，舍去），∴BD =4，同理，在△ACD 中，由勾股定理得，，∴BC =DC +BD =4+1=5，故答案为：5． 14．【答案】【解析】过点F 作AB 、CD 的垂线，垂足为点G 、H ，如图所示：设AG =x m ，则有DH =x m ， ∵，∴tan23°=，解得x ≈15.0，∴AB =x +1.5=16.5．电线杆的高度约为16.5 m ．故答案是：16.5． 15．【解析】（1）连接AC ，AC 与BD 相交于点O ，∵四边形ABCD 是菱形，∴AC ⊥BD ，BO =BD =4， 1tan 2AD B BD ∠==1DC ===16.5tan45tan23AG AG BC +=︒︒50xx-12∵Rt △BOC 中，tan ∠CBD ==，∴OC =2， ∴AB =BC（2）∵AE ⊥BC ，∴S 菱形ABCD =BC ·AE =BD·AC ， ∵AC =2OC =4，∴=×8×4，∴AE ，∴BE∴cos ∠ABE =．16．【解析】（1）如图，过点F 作FN ⊥DK 于N ，过点E 作EM ⊥FN 于M ．∵EF +FG =166，FG =100，∴EF =66， ∵∠FGK =80°，∴FN =100sin80°≈98，∵∠EFG =125°，∴∠EFM =180°–125°–10°=45°， ∴FM =66cos45°=≈46.53，∴MN =FN +FM ≈144.5， ∴此时小强头部E 点与地面DK 相距约为144.5 cm ．（2）如图，过点E 作EP ⊥AB 于点P ，延长OB 交MN 于H ． ∵AB =48，O 为AB 中点，∴AO =BO =24，∵EM =66sin45°≈46.53， ∴PH ≈46.53，∵GN =100cos80°≈17，CG =15，∴OH =24+15+17=56，OP =OH –PH =56–46.53=9.47≈9.5， ∴他应向前9.5cm ．OC OB 121212BE AB 351．【答案】B【解析】锐角三角函数计算，=2×=，故选A ． 2．【答案】A【解析】∵∠α为锐角，且sin α=，∴∠α=30°．故选A ． 3．【答案】D【解析】如图，过C 作CD ⊥AB 于D ，则∠ADC =90°，∴AC ．∴sin ∠BAC ==．故选D ．5．【答案】C【解析】过作交于，中，，，，故选C ．6．【答案】C【解析】如图，过点O 作OE ⊥AC 于点E ，延长BD 交OE 于点F ，︒60sin 223312CD AC 45D DE AB ⊥AB E DE BC ==Rt ADE △tan 30AEDE=o18(m)AE ∴==18 1.519.5(m)AB ∴=+=C7．【答案】D【解析】如图，过点A作AE⊥OC于点E，作AF⊥OB于点F，∵四边形ABCD是矩形，∴∠ABC=90°，∵∠ABC=∠AEC，∠BCO=x，∴∠EAB=x，∴∠FBA=x，∵AB=a，AD=b，∴FO=FB+BO=a•cos x+b•sin x，故选D．答：炎帝塑像DE的高度约为51m．13．【解析】如图，连接BD，作DM⊥AB于点M，∵AB=CD，AB，CD分别垂直平分踏步EF，GH，∴AB∥CD，AB=CD，∴四边形ABDC是平行四边形，∴∠C=∠ABD，AC=BD，∵∠C=65°，AC=900，∴∠ABD=65°，BD=900，∴BM=BD•cos65°=900×0.423≈381，DM=BD•sin65°=900×0.906≈815，∵381÷3=127，120＜127＜150，∴该中学楼梯踏步的高度符合规定，∵815÷3≈272，260＜272＜300，∴该中学楼梯踏步的宽度符合规定，由上可得，该中学楼梯踏步的宽度和高度都符合规定．14．【解析】（1）①过点A作AG∥BC，如图1，则∠BAG=∠ABC=70°，∵BC∥OE，∴AG∥OE，∴∠GAO=∠AOE=90°，∴∠BAO=90°+70°=160°，故答案为：160；②过点A作AF⊥BC于点F，如图2，16．【解析】（1）阀门被下水道的水冲开与被河水关闭过程中∠POB 的取值范围为：90°≤∠POB ≤0°；（2）如图，∵∠CAB =67.5°，∴∠BAO =22.5°， ∵OA =OB ，∴∠BAO =∠ABO =22.5°，∴∠BOP =45°， ∵OB =100，∴OE OB ， ∴PE =OP –OE ≈29.5cm ，答：此时下水道内水的深度约为29.5cm ．。

《中考大一轮数学复习》课件锐角三角函数与解直角三角形

1 2
3
3
夯实基本
中考大一轮复习讲义◆ 数学
知已知彼
基础知识回顾 1. 锐角三角函数定义若在 Rt△ABC 中，∠C＝90°，∠A，∠B，∠C 的对边分别为 a，b，c，则 sinA＝________，cosA ＝________，tanA＝________．温馨提示 ①锐角三角函数是在直角三角形中定义的． ②sinA，cosA，tanA 表示的是一个整体，是指两条线段的比，没有单位． ③锐角三角函数的大小仅与角的大小有关，与该角所处的直角三角形的大小无关． ④当 A 为锐角时，0<sinA<1，0<cosA<1，tanA>0. 2. 特殊角的三角函数值 α 30° 45° 60° sinα cosα tanα
1 2 3
5
夯实基本
中考大一轮复习讲义◆ 数学
知已知彼
4. 解直角三角形的应用中的相关概念 (1)仰角、俯角：如图①，在测量时，视线与水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角． (2)坡度(坡比)、坡角：如图②，坡面的高度 h 和________的比叫坡度(或坡比)，即 i＝tanα＝ h ，坡面与水平面的夹角 α 叫坡角． l
a 5 12 解析 sinA＝＝，可设 a＝5k，c＝13k，根据勾股定理得 b＝12k，所以 cosA＝ .故选 D. c 13 13
1 2
8
3
热点看台
中考大一轮复习讲义◆ 数学
快速提升
点对点训练 1. (2013·山东济南)已知直线 l1∥l2∥l3∥l4，相邻的两条平行直线间的距离均为 h，矩形 ABCD 的四个顶点分别在这四条直线上，放置方式如图所示，AB＝4，BC＝6，则 tanα的值等于( C )

初三中考数学常用知识点整理

初三中考数学常用知识点整理中考数学常用知识点1.解直角三角形1.1.锐角三角函数锐角a的正弦、余弦和正切统称∠a的三角函数。

如果∠a是Rt△ABC的一个锐角，则有1.2.锐角三角函数的计算1.3.解直角三角形在直角三角形中，由已知的一些边、角，求出另一些边、角的过程，叫做解直角三角形。

2.直线与圆的位置关系2.1.直线与圆的位置关系当直线与圆有两个公共点时，叫做直线与圆相交;当直线与圆有公共点时，叫做直线与圆相切，公共点叫做切点;当直线与圆没有公共点时，叫做直线与圆相离。

直线与圆的位置关系有以下定理：直线与圆相切的判定定理：经过半径的外端并且垂直这条半径的直线是圆的切线。

圆的切线性质：经过切点的半径垂直于圆的切线。

2.2.切线长定理从圆外一点作圆的切线，通常我们把圆外这一点到切点间的线段的长叫做切线长。

切线长定理：过圆外一点所作的圆的两条切线长相等。

2.3.三角形的内切圆与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

三角形的内心是三角形的三条角平分线的交点。

3.三视图与表面展开图3.1.投影物体在光线的照射下，在某个平面内形成的影子叫做投影。

光线叫做投影线，投影所在的平面叫做投影面。

由平行的投射线所形成的投射叫做平行投影。

可以把太阳光线、探照灯的光线看成平行光线，它们所形成的投影就是平行投影。

3.2.简单几何体的三视图物体在正投影面上的正投影叫做主视图，在水平投影面上的正投影叫做俯视图，在侧投影面上的正投影叫做左视图。

主视图、左视图和俯视图合称三视图。

产生主视图的投影线方向也叫做主视方向。

九年级中考常用数学知识点圆★重点★①圆的重要性质;②直线与圆、圆与圆的位置关系;③与圆有关的角的定理;④与圆有关的比例线段定理。

☆内容提要☆一、圆的基本性质1.圆的定义(两种)2.有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。

3.“三点定圆”定理4.垂径定理及其推论5.“等对等”定理及其推论6.与圆有关的角：⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理，与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.切线的性质(重点)2.切线的判定定理(重点)3.切线长定理三、圆换圆的位置关系1.五种位置关系及判定与性质：(重点：相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线：⑴定义⑵性质四、与圆有关的比例线段1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及计算中心角：初中数学复习提纲内角的一半：初中数学复习提纲(右图)(解Rt△OAM可求出相关元素,初中数学复习提纲、初中数学复习提纲等)六、一组计算公式1.圆周长公式2.圆面积公式3.扇形面积公式4.弧长公式5.弓形面积的计算方法6.圆柱、圆锥的侧面展开图及相关计算七、点的轨迹六条基本轨迹八、有关作图1.作三角形的外接圆、内切圆2.平分已知弧3.作已知两线段的比例中项4.等分圆周：4、8;6、3等分九、重要辅助线1.作半径2.见弦往往作弦心距3.见直径往往作直径上的圆周角4.切点圆心莫忘连5.两圆相切公切线(连心线)6.两圆相交公共弦常用中考数学知识点三角函数关系倒数关系tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)同角三角函数关系六角形记忆法构造以“上弦、中切、下割;左正、右余、中间1"的正六边形为模型。

2023年中考数学专题汇编：锐角三角函数应用、解直角三角形

2023年中考数学专题汇编：锐角三角函数应用、解直角三角形一．解答题（共60小题）1．校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于21米，在l上点D的同侧取点A、B，使∠CAD＝30°，∠CBD＝60°．（1）求AB的长（精确到0.1米，参考数据：＝1.73，＝1.41）；（2）已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由．2．如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度．如果这时气球的高度CD为90米．且点A、D、B在同一直线上，求建筑物A、B间的距离．3．如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B 处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．4．如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i＝1：，AB＝10米，AE＝15米．（i＝1：是指坡面的铅直高度BH与水平宽度AH的比）（1）求点B距水平面AE的高度BH；（2）求广告牌CD的高度．（测角器的高度忽略不计，结果精确到0.1米．参考数据： 1.414， 1.732）5．如图，某防洪指挥部发现长江边一处长500米，高10米，背水坡的坡角为45°的防洪大堤（横断面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽3米，加固后背水坡EF的坡比i＝1：．（1）求加固后坝底增加的宽度AF；（2）求完成这项工程需要土石多少立方米？（结果保留根号）6．如图所示，A、B两城市相距100km，现计划在这两座城市间修建一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P 点为圆心，50km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：≈1.732，≈1.414）7．如图，AD是△ABC的中线，tan B＝，cos C＝，AC＝．求：（1）BC的长；（2）sin∠ADC的值．8．一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）9．如图，放置在水平桌面上的台灯的灯臂AB长为40cm，灯罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠BAD＝60°．使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？（结果精确到0.1cm，参考数据：≈1.732）10．如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？11．高考英语听力测试期间，需要杜绝考点周围的噪音．如图，点A是某市一高考考点，在位于A考点南偏西15°方向距离125米的C处有一消防队．在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火．已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由．（取1.732）12．如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡角∠F AE＝30°，求大树的高度（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73）13．如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C 处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB（结果保留整数，≈1.73，≈1.41）14．某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．15．如图，在坡角为30°的山坡上有一铁塔AB，其正前方矗立着一大型广告牌，当阳光与水平线成45°角时，测得铁塔AB落在斜坡上的影子BD的长为6米，落在广告牌上的影子CD的长为4米，求铁塔AB的高（AB，CD均与水平面垂直，结果保留根号）．16．如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED＝60°，在离电线杆6米的B处安置高为1.5米的测角仪AB，在A处测得电线杆上C处的仰角为30°，求拉线CE 的长（结果保留小数点后一位，参考数据：≈1.41，≈1.73）．17．天塔是天津市的标志性建筑之一，某校数学兴趣小组要测量天塔的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB＝112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0.73，结果保留整数）．18．如图，一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处，渔船从A处沿正南方向航行一段距离后，到达位于小岛南偏东60°方向的B处．（1）求渔船从A到B的航行过程中与小岛M之间的最小距离（结果用根号表示）；（2）若渔船以20海里/小时的速度从B沿BM方向行驶，求渔船从B到达小岛M的航行时间（结果精确到0.1小时）．（参考数据：≈1.41，≈1.73，≈2.45）19．如图，已知Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与CD、CB相交于点H、E，AH＝2CH．（1）求sin B的值；（2）如果CD＝，求BE的值．20．如图，大楼AN上悬挂一条幅AB，小颖在坡面D处测得条幅顶部A的仰角为30°，沿坡面向下走到坡脚E处，然后向大楼方向继续行走10米来到C处，测得条幅的底部B的仰角为45°，此时小颖距大楼底端N处20米．已知坡面DE＝20米，山坡的坡度i＝1：（即tan∠DEM＝1：），且D、M、E、C、N、B、A在同一平面内，E、C、N在同一条直线上，求条幅的长度（结果精确到1米）（参考数据：≈1.73，≈1.41）21．如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC＝17.2米，设太阳光线与水平地面的夹角为α，当α＝60°时，测得楼房在地面上的影长AE＝10米，现有一只小猫睡在台阶的MN这层上晒太阳．（取1.73）（1）求楼房的高度约为多少米？（2）过了一会儿，当α＝45°时，问小猫能否还晒到太阳？请说明理由．22．如图，在一个18米高的楼顶上有一信号塔DC，李明同学为了测量信号塔的高度，在地面的A处测的信号塔下端D的仰角为30°，然后他正对塔的方向前进了18米到达地面的B处，又测得信号塔顶端C 的仰角为60°，CD⊥AB于点E，E、B、A在一条直线上．请你帮李明同学计算出信号塔CD的高度（结果保留整数，≈1.7，≈1.4）23．如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．（1）求小敏到旗杆的距离DF．（结果保留根号）（2）求旗杆EF的高度．（结果保留整数，参考数据：≈1.4，≈1.7）24．如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为37°，塔底B的仰角为26.6°．已知塔高BC＝80米，塔所在的山高OB＝220米，OA＝200米，图中的点O、B、C、A、P在同一平面内，求山坡的坡度．（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin37°≈0.60，tan37°≈0.75）25．我市准备在相距2千米的M，N两工厂间修一条笔直的公路，但在M地北偏东45°方向、N地北偏西60°方向的P处，有一个半径为0.6千米的住宅小区（如图），问修筑公路时，这个小区是否有居民需要搬迁？（参考数据：≈1.41，≈1.73）26．如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．（1）求点C与点A的距离（精确到1km）；（2）确定点C相对于点A的方向．（参考数据：≈1.414，≈1.732）27．一测量爱好者，在海边测量位于正东方向的小岛高度AC，如图所示，他先在点B测得山顶点A的仰角为30°，然后向正东方向前行62米，到达D点，在测得山顶点A的仰角为60°（B、C、D三点在同一水平面上，且测量仪的高度忽略不计）．求小岛高度AC（结果精确的1米，参考数值：）28．如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B 处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．29．如图，某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造．供水站M在笔直公路AD 上，测得供水站M在小区A的南偏东60°方向，在小区B的西南方向，小区A、B之间的距离为300（+1）米，求供水站M分别到小区A、B的距离．（结果可保留根号）30．如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30°，看这栋高楼底部的俯角为60°，热气球与高楼的水平距离为66m，这栋高楼有多高？（结果精确到0.1m，参考数据：≈1.73）31．阅读材料：在一个三角形中，各边和它所对角的正弦的比相等，＝＝，利用上述结论可以求解如下题目：在△ABC中，∠A、∠B、∠C的对边分别为a，b，c．若∠A＝45°，∠B＝30°，a＝6，求b．解：在△ABC中，∵＝∴b＝＝＝＝3．理解应用：如图，甲船以每小时30海里的速度向正北方向航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，且乙船从B1处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A2时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10海里．（1）判断△A1A2B2的形状，并给出证明；（2）求乙船每小时航行多少海里？32．如图，在一笔直的海岸线l上有A、B两个码头，A在B的正东方向，一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处，此时从B码头测得小船在它的北偏东45°的方向．求此时小船到B码头的距离（即BP的长）和A、B两个码头间的距离（结果都保留根号）．33．如图，防洪大堤的横截面是梯形ABCD，其中AD∥BC，α＝60°，汛期来临前对其进行了加固，改造后的背水面坡角β＝45°．若原坡长AB＝20m，求改造后的坡长AE．（结果保留根号）34．某水库大坝的横截面是如图所示的四边形ABCD，其中AB∥CD，大坝顶上有一瞭望台PC，PC正前方有两艘渔船M，N．观察员在瞭望台顶端P处观测到渔船M的俯角α为31°，渔船N的俯角β为45°．已知MN所在直线与PC所在直线垂直，垂足为E，且PE长为30米．（1）求两渔船M，N之间的距离（结果精确到1米）；（2）已知坝高24米，坝长100米，背水坡AD的坡度i＝1：0.25，为提高大坝防洪能力，请施工队将大坝的背水坡通过填筑土石方进行加固，坝底BA加宽后变为BH，加固后背水坡DH的坡度i＝1：1.75，施工队施工10天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的2倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：tan31°≈0.60，sin31°≈0.52）35．在△ABC中，AD是BC边上的高，∠C＝45°，sin B＝，AD＝1．求BC的长．36．我们把“按照某种理想化的要求（或实际可能应用的标准）来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”（我国著名数学家徐利治）．如图是一个典型的图形模式，用它可测底部可能达不到的建筑物的高度，用它可测河宽，用它可解决数学中的一些问题．等等．（1）如图，若B1B＝30米，∠B1＝22°，∠ABC＝30°，求AC（精确到1）；（参考数据：sin22°≈0.37，cos22°≈0.92，tan22°≈0.40，≈1.73）（2）如图2，若∠ABC＝30°，B1B＝AB，计算tan15°的值（保留准确值）；（3）直接写出tan7.5°的值．（注：若出现双重根式，则无需化简）37．已知：如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC＝14，AD＝12，sin B＝．求：（1）线段DC的长；（2）tan∠EDC的值．38．如图，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得点C的仰角为45°，已知OA＝100米，山坡坡度为（即tan∠P AB＝），且O，A，B在同一条直线上．求电视塔OC的高度以及此人所在位置点P的铅直高度．（测倾器的高度忽略不计，结果保留根号形式）39．如图，兰兰站在河岸上的G点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，测得小船C 的俯角是∠FDC＝30°，若兰兰的眼睛与地面的距离是1.5米，BG＝1米，BG平行于AC所在的直线，迎水坡的坡度i＝4：3，坡长AB＝10米，求小船C到岸边的距离CA的长？（参考数据：，结果保留两位有效数字）40．如图，某广场一灯柱AB被一钢缆CD固定，CD与地面成40°夹角，且CB＝5米．（1）求钢缆CD的长度；（精确到0.1米）（2）若AD＝2米，灯的顶端E距离A处1.6米，且∠EAB＝120°，则灯的顶端E距离地面多少米？（参考数据：tan40°＝0.84，sin40°＝0.64，cos40°＝）41．如图，某高速公路建设中需要确定隧道AB的长度．已知在离地面1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°，求隧道AB的长．42．如图某幢大楼顶部有广告牌CD．张老师目高MA为1.60米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进14米、站在点B处，测得广告牌顶端点C的仰角为45°．（取，计算结果保留一位小数）（1）求这幢大楼的高DH；（2）求这块广告牌CD的高度．43．图1是疫情期间测温员用“额温枪”对小红测温时的实景图，图2是其侧面示意图，其中枪柄BC与手臂MC始终在同一直线上，枪身BA与额头保持垂直．量得胳膊MN＝28cm，MB＝42cm，肘关节M与枪身端点A之间的水平宽度为25.3cm（即MP的长度），枪身BA＝8.5cm．（1）求∠ABC的度数；（2）测温时规定枪身端点A与额头距离范围为3～5cm．在图2中，若测得∠BMN＝68.6°，小红与测温员之间距离为50cm．问此时枪身端点A与小红额头的距离是否在规定范围内？并说明理由．（结果保留小数点后一位）（参考数据：sin66.4°≈0.92，cos66.4°≈0.40，sin23.6°≈0.40，≈1.414）44．图1是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角为60°时，箱盖ADE落在AD′E′的位置（如图2所示）．已知AD＝90厘米，DE＝30厘米，EC＝40厘米．（1）求点D′到BC的距离；（2）求E、E′两点的距离．45．一架无人机沿水平直线飞行进行测绘工作，在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°，面向AB方向继续飞行5米，测得该建筑物底端B的俯角为45°，已知建筑物AB的高为3米，求无人机飞行的高度（结果精确到1米，参考数据：≈1.414，≈1.732）．46．如图，在港口A处的正东方向有两个相距6km的观测点B、C．一艘轮船从A处出发，沿北偏东26°方向航行至D处，在B、C处分别测得∠ABD＝45°、∠C＝37°．求轮船航行的距离AD．（参考数据：sin26°≈0.44，cos26°≈0.90，tan26°≈0.49，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．）47．风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A处测得塔杆顶端C的仰角是55°，沿HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的顶端D（D、C、H在同一直线上）的仰角是45°．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG为10米，BG⊥HG，CH⊥AH，求塔杆CH的高．（参考数据：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）48．如图，某学校体育场看台的顶端C到地面的垂直距离CD为2m，看台所在斜坡CM的坡比i＝1：3，在点C处测得旗杆顶点A的仰角为30°，在点M处测得旗杆顶点A的仰角为60°，且B，M，D三点在同一水平线上，求旗杆AB的高度．（结果精确到0.1m，参考数据：≈1.41，＝1.73）49．如图，一艘船由A港沿北偏东65°方向航行30km至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，求（1）∠C的度数．（2）A，C两港之间的距离为多少km．50．数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度．（精确到1m．参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67，≈1.73）51．为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比）i＝1：2.4的山坡AB上发现有一棵古树CD．测得古树底端C到山脚点A的距离AC＝26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED＝48°（古树CD与山坡AB 的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为多少米？（参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）52．如图（1）是一种简易台灯，在其结构图（2）中灯座为△ABC（BC伸出部分不计），A、C、D在同一直线上．量得∠ACB＝90°，∠A＝60°，AB＝16cm，∠ADE＝135°，灯杆CD长为40cm，灯管DE长为15cm．（1）求DE与水平桌面（AB所在直线）所成的角；（2）求台灯的高（点E到桌面的距离，结果精确到0.1cm）．（参考数据：sin15°＝0.26，cos15°＝0.97，tan15°＝0.27，sin30°＝0.5，cos30°＝0.87，tan30°＝0.58．）53．如图，某中学数学活动小组在学习了“利用三角函数测高”后，选定测量小河对岸一幢建筑物BC的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为30°．且D离地面的高度DE＝5m．坡底EA ＝30m，然后在A处测得建筑物顶端B的仰角是60°，点E，A，C在同一水平线上，求建筑物BC的高．（结果用含有根号的式子表示）54．已知如图，斜坡AP的坡度为1：2.4，斜坡AP的水平长度为24米在坡顶A处的同一水平面上有一座古塔BC在斜坡底P处测得该塔的塔顶B的仰角为45°，在坡顶A处测得该塔的塔顶B的仰角为60°．求：（1）坡顶A到地面PQ的距离；（2）古塔BC的高度（结果保留根号）．55．如图，山顶有一塔AB，塔高33m．计划在塔的正下方沿直线CD开通穿山隧道EF．从与E点相距80m 的C处测得A、B的仰角分别为27°、22°，从与F点相距50m的D处测得A的仰角为45°．求隧道EF的长度．（参考数据：tan22°≈0.40，tan27°≈0.51．）56．求下列各式的值：（1）2sin30°+3cos60°﹣4tan45°；（2）tan60°﹣（4﹣π）0+2cos30°+（）﹣1．57．计算：．58．如图，港口B位于港口A的南偏东37°方向，灯塔C恰好在AB的中点处．一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行5km到达E处，测得灯塔C在北偏东45°方向上，这时，E处距离港口A有多远？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）59．王刚同学在学习了解直角三角形及其应用的知识后，尝试利用所学知识测量河对岸大树AB的高度，他在点C处测得大树顶端A的仰角为45°，再从C点出发沿斜坡走2米到达斜坡上D点，在点D处测得树顶端A的仰角为30°，若斜坡CF的坡比为i＝1：3（点E、C、B在同一水平线上）．（1）求王刚同学从点C到点D的过程中上升的高度；（2）求大树AB的高度（结果保留根号）．60．计算：（1）2sin30°+3cos60°﹣4tan45°（2）+tan260°。

2019年中考数学复习第5章图形的相似与解直角三角形第20课时锐角三角函数与解直角三角形精讲试题word版本

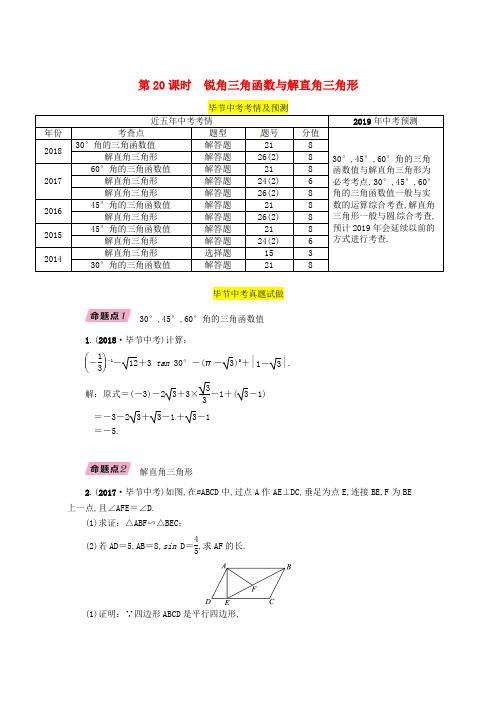
第20课时锐角三角函数与解直角三角形题号,30三角形一般与圆综合考查毕节中考真题试做30°,45°,60°角的三角函数值1.(2018·毕节中考)计算：⎝⎛⎭⎪⎫－13－1－12＋3 tan 30°－(π－3)0＋||1－3.解：原式＝(－3)－23＋3×33－1＋(3－1)＝－3－23＋3－1＋3－1＝－5.解直角三角形2.(2017·毕节中考)如图,在▱ABCD中,过点A作AE⊥DC,垂足为点E,连接BE,F为BE上一点,且∠AFE＝∠D.(1)求证：△ABF∽△BEC；(2)若AD＝5,AB＝8,sin D＝45,求AF的长.(1)证明：∵四边形ABCD是平行四边形,∴AB ∥CD,AD ∥BC,AD ＝BC. ∴∠D ＋∠C ＝180°,∠ABF ＝∠BEC. ∵∠AFB ＋∠AFE ＝180°,∠AFE ＝∠D, ∴∠C ＝∠AFB. ∴△ABF ∽△BEC ； (2)解：∵AE ⊥DC,AB ∥DC, ∴∠AED ＝∠BAE ＝90°.在Rt △ADE 中,AE ＝AD·sin D ＝5×45＝4.在Rt △ABE 中,根据勾股定理,得 BE ＝AE2＋AB2＝42＋82＝4 5. ∵△ABF ∽△BEC, ∴AF BC ＝AB BE , 即AF 5＝845,∴AF ＝2 5.毕节中考考点梳理锐角三角函数的概念特殊角的三角函数值\ 锐角α α解直角三角形1.(2018·柳州中考)如图,在Rt △ABC 中,∠C ＝90°,BC ＝4,AC ＝3,则sin B ＝ACAB ＝( A )A .35B .45C .37D .34(第1题图)(第3题图)2.若∠A＋∠B ＝90°,则下列各式成立的是( D )A .sin A ＝cos AB .tan A ＋tan B ＝1C .sin A ＝sin BD .sin A ＝cos B3.(2018·广州中考)如图,旗杆高AB ＝8 m ,某一时刻,旗杆影子长BC ＝16 m ,则tan C ＝__12__.4.(2018·滨州中考)在△ABC 中,∠C ＝90°,若tan A ＝12,则sin B ＝55.(2018·贵阳中考)如图①,在Rt △ABC 中,以下是小亮探究a sin A 与bsin B之间关系的方法：∵sin A ＝a c ,sin B ＝bc,∴c ＝a sin A ,c ＝bsin B ,∴a sin A ＝b sin B. 根据你掌握的三角函数知识.在图②的锐角△ABC 中,探究a sin A ,b sin B ,c sin C之间的关系,并写出探究过程.解：a sin A ＝b sin B ＝c sin C .证明如下：过A 作AD ⊥BC 于点D,过B 作BE ⊥AC 于点E.在Rt △ABD 中,sin B ＝ADc ,即AD ＝c si n B.在Rt △ADC 中,sin C ＝ADb ,即AD ＝b sin C.∴c sin B ＝b sin C,即b sin B ＝csin C .同理可得a sin A ＝csin C ,则a sin A ＝b sin B ＝csin C.6.(2018·遵义中考)如图,吊车在水平地面上吊起货物时,吊绳BC 与地面保持垂直,吊臂AB 与水平线的夹角为64°,吊臂底部A 距地面1.5 m .(计算结果精确到0.1 m ,参考数据sin 64°≈0.90,cos 64°≈0.44,tan 64°≈2.05)(1)当吊臂底部A 与货物的水平距离AC 为5 m 时,吊臂AB 的长为______m ； (2)如果该吊车吊臂的最大长度AD 为20 m ,那么从地面上吊起货物的最大高度是多少？(吊钩的长度与货物的高度忽略不计)解：(1)在Rt △ABC 中,∠BAC ＝64°,AC ＝5, ∴AB ＝ACcos 64°≈5÷0.44≈11.4.∴吊臂AB 的长为11.4 m .故应填：11.4； (2)过点D 作DH ⊥地面于点H,交水平线于点E.在Rt △ADE 中,AD ＝20,∠DAE ＝64°,EH ＝1.5,∴DE ＝sin 64°×AD ≈20×0.90＝18.0,即DH ＝DE ＋EH ≈18.0＋1.5＝19.5.答：从地面上吊起货物的最大高度是19.5 m .中考典题精讲精练30°,45°,60°角的三角函数值例1 (2018·广安中考)计算：⎝ ⎛⎭⎪⎫13－2＋|3－2|－12＋6 cos 30°＋(π－3.14)0.【解析】对照30°,45°,60°角的三角函数值表,然后按照实数的运算方法计算出结果.【答案】解：原式＝9＋2－3－23＋6×32＋1＝12.解直角三角形例2 (2018·潍坊中考)如图,点M 是正方形ABCD 边CD 上一点,连接AM,作DE ⊥AM 于点E,BF ⊥AM 于点F,连接BE.(1)求证：AE ＝BF ；(2)已知AF ＝2,四边形ABED 的面积为24,求∠EBF 的正弦值.【解析】(1)由正方形的性质,可得BA ＝AD,∠BAD ＝90°.由DE ⊥AM,BF ⊥AM,可得∠ABF ＝∠DAE.对于△ABF 和△DAE,可由AAS 得到△ABF ≌△DAE,结论可证；(2)设AE ＝x,由(1)中结论可得BF ＝x,DE ＝AF ＝2.利用S 四边形ABED＝S △ABE ＋S △ADE 可列方程求出x 得到EF 的长.在Rt △BFE 中利用勾股定理可求出BE 的长.最后利用正弦的定义可求结果.【答案】(1)证明：∵四边形ABCD 为正方形, ∴BA ＝AD,∠BAD ＝90°. ∵DE ⊥AM 于点E,BF ⊥AM 于点F, ∴∠AFB ＝∠DEA ＝90°,∴∠ABF ＋∠BAF ＝90°,∠DAE ＋∠BAF ＝90°, ∴∠ABF ＝∠DAE. 在△ABF 和△DAE 中, ⎩⎪⎨⎪⎧∠AFB＝∠DEA，∠ABF＝∠DAE，AB ＝DA ，∴△ABF ≌△DAE(AAS ),∴BF ＝AE ； (2)解：设AE ＝x,则BF ＝x,DE ＝AF ＝2. ∵四边形ABED 的面积为24, ∴12·x·x ＋12·x·2＝24, 解得x 1＝6,x 2＝－8(舍去),∴EF ＝x －2＝4. 在Rt △BEF 中,BE ＝42＋62＝213, ∴sin ∠EBF ＝EF BE ＝4213＝21313.解直角三角形的应用例3 (2018·烟台中考)汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40 km /h .数学实践活动小组设计了如下活动：在l 上确定A,B 两点,并在AB 路段进行区间测速.在l 外取一点P,作PC ⊥l,垂足为点C.测得PC ＝30 m ,∠APC ＝71°,∠BPC ＝35°.上午9时测得一汽车从点A 到点B 用时6 s ,请你用所学的数学知识说明该车是否超速.(参考数据：sin 35°≈0.57,cos 35°≈0.82,tan 35°≈0.70,sin 71°≈0.95,cos 71°≈0.33,tan 71°≈2.90)【解析】先根据角的正切分别得出AC ＝PC tan ∠APC,BC ＝PC tan ∠BPC,再根据线段的和与差得出AB 的长,继而根据速度＝路程时间,求得该车通过AB 路段的车速.若该车通过AB 路段的车速超过40 km /h ,则该车超速；否则,该车没有超速.【答案】解：在Rt △APC 中,AC ＝PC tan ∠APC ＝30 tan 71°≈30×2.90＝87. 在Rt △BPC 中,BC ＝PC tan ∠BPC ＝30 tan 35°≈30×0.70＝21, 则AB ＝AC －BC ＝87－21＝66, ∴该汽车的实际速度为666＝11(m /s ).又∵40 km /h ≈11.1 m /s ,11<11.1, ∴该车没有超速.1.计算：|－2|－(2 019＋2)0＋⎝ ⎛⎭⎪⎫12－1＋2 cos 30°－27.解：原式＝2－1＋2＋2×32－33＝3＋3－3 3 ＝3－2 3.2.如图,在△ABC 中,∠BAC ＝90°,AB ＝AC,点D 为边AC 的中点,DE ⊥BC 于点E,连接BD,则tan ∠DBC 的值为( A )A .13B .2－1C .2－ 3D .143.(2018·扬州中考)如图,在平行四边形ABCD 中,DB ＝DA,点F 是AB 的中点,连接DF 并延长,交CB 的延长线于点E,连接AE.(1)求证：四边形AEBD 是菱形；(2)若DC ＝10,tan ∠DCB ＝3,求菱形AEBD 的面积. (1)证明：∵四边形ABCD 是平行四边形, ∴AD ∥CE,∴∠DAF ＝∠EBF. ∵∠AFD ＝∠BFE,AF ＝FB, ∴△AFD ≌△BFE,∴AD ＝BE.∵AD ∥EB,∴四边形AEBD 是平行四边形. 又∵DB ＝DA,∴四边形AEBD 是菱形； (2)解：∵四边形ABCD 是平行四边形, ∴CD ＝AB ＝10,AB ∥CD, ∴∠ABE ＝∠DCB,∴tan ∠ABE ＝tan ∠DCB ＝3. ∵四边形AEBD 是菱形, ∴AB ⊥DE,AF ＝FB,EF ＝DF, ∴tan ∠ABE ＝EFBF ＝3.∵BF ＝102,∴EF ＝3102,∴DE ＝310. ∴S 菱形AEBD ＝12AB·D E ＝1210×310＝15.4.如图,一块三角形空地上种植草皮绿化,已知AB ＝20 m ,AC ＝30 m ,∠A ＝150°,草皮的售价为a 元/m 2,则购买草皮至少需要( C )A .450a 元B .225a 元C .150a 元D .300a 元(第4题图)(第5题图)5.一个公共房门前的台阶高出地面 1.2 m ,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( B )A .斜坡AB 的坡度是10° B .斜坡AB 的坡度是tan 10°C .AC ＝1.2 tan 10° mD.AB＝1.2cos 10°m6.(2018·重庆中考A卷)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED＝58°,升旗台底部到教学楼底部的距离DE＝7 m,升旗台坡面CD的坡度i＝1∶0.75,坡长CD＝2 m,若旗杆底部到坡面CD的水平距离BC＝1 m,则旗杆AB的高度约为(参考数据：sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.6)( B )A.12.6 mB.13.1 mC.14.7 mD.16.3 m。

中考复习-锐角三角函数和解直角三角形

探究提高在解斜三角形时，通常把斜三角形转化为直角三角形，常见的方法是作高，作高把斜三角形转化为直角三角形，再利用解直角三角形的有关知识解决问题．
知能迁移3 一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得 C在A北偏西31°的方向上，沿河岸向北前行 40m到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，求这条河的宽度．(参考 3 数值：tan 31°≈ ) 5
；
(2)角与角的关系：
(3)边与角的关系：
1 2 sinA＝cosB＝a ，cosA＝sinB＝ b ； c c
；
tanA＝b ，tanB＝ a
a
b
1．正确理解三角函数的概念书写三角函数时，若锐角用一个大写字母或者一个小写希腊字母表示的，表示它的正弦时，习惯省略角的符号，如sin A；若锐角是用三个大写字母或数字表示的，表示它的正弦时，不能省略角的符号，如sin∠ABC，余弦和正切的写法同理．由定义可以看出，锐角A的正弦、余弦、正切都是它所在直角三角形的两边的比，因此都是正数；因为锐角A 的取值范围是0<∠A<90°，则三角函数的取值范围是0<sin A<1,0<cos A<1，tan A>0；当∠A确定时，三个比值也分别有唯一确定的值与之对应．
探究提高此类问题常与仰角、俯角等知识相关，通常由视线、水平线、铅垂线构成直角三角形，再利用边与角之间存在的三角函数式，变形求得物体高度．
知能迁移2 (2011· 潜江)五月石榴红，枝头鸟儿歌．一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处．从A处看房屋 3 顶部C处的仰角为30°，看房屋底部D处的俯角为45°，石榴树与该房屋之间的水平距离为3 m，求出小鸟飞行的距离AC和房屋的高度CD.

中考专题复习解直角三角形（含答案）

中考专题复习解直⾓三⾓形（含答案）中考数学专题解直⾓三⾓形第⼀节锐⾓三⾓函数1、勾股定理：直⾓三⾓形两直⾓边、的平⽅和等于斜边的平⽅。

2、如下图，在Rt△ABC中，∠C为直⾓，则∠A的锐⾓三⾓函数为(∠A可换成∠B)：定义表达式取值范围关系正弦(∠A为锐⾓)余弦(∠A为锐⾓)正切(∠A为锐⾓)(倒数)余切(∠A为锐⾓)3、任意锐⾓的正弦值等于它的余⾓的余弦值；任意锐⾓的余弦值等于它的余⾓的正弦值。

4、任意锐⾓的正切值等于它的余⾓的余切值；任意锐⾓的余切值等于它的余⾓的正切值。

5、30°、45°、60°特殊⾓的三⾓函数值(重要)三⾓函数30°45°60°116、正弦、余弦的增减性：当0°≤≤90°时，sin随的增⼤⽽增⼤，cos随的增⼤⽽减⼩。

7、正切、余切的增减性：当0°<<90°时，tan随的增⼤⽽增⼤，cot随的增⼤⽽减⼩。

第⼆节解⾓直⾓三⾓形1、解直⾓三⾓形的定义：已知边和⾓（两个，其中必有⼀条边）→求所有未知的边和⾓。

依据：①边的关系：；②⾓的关系：∠A+∠B=90°；③边⾓关系：（见前⾯三⾓函数的定义）。

2、应⽤举例：(1)仰⾓：视线在⽔平线上⽅的⾓；俯⾓：视线在⽔平线下⽅的⾓。

(2)坡⾯的铅直⾼度和⽔平宽度的⽐叫做坡度(坡⽐)。

⽤字母表⽰，即。

坡度⼀般写成的形式，如等。

把坡⾯与⽔平⾯的夹⾓记作(叫做坡⾓)，那么。

【重点考点例析】考点⼀：锐⾓三⾓函数的概念例1 如图所⽰，△ABC的顶点是正⽅形⽹格的格点，则sinA的值为（）A．12B．55C．1010D．255对应训练1．在平⾯直⾓坐标系中，已知点A（2，1）和点B（3，0），则sin∠AOB的值等于（）A．55B．52C．32D．12考点⼆：特殊⾓的三⾓函数值例2 计算：cos245°+tan30°?sin60°=．对应训练（2012?南昌）计算：sin30°+cos30°?tan60°．考点三：化斜三⾓形为直⾓三⾓形例3 如图，在△ABC中，∠A=30°，∠B=45°，AC=23，求AB的长．对应训练3．如图，在Rt △ABC中，∠BAC=90°，点D在BC边上，且△ABD是等边三⾓形．若AB=2，求△ABC 的周长．（结果保留根号）考点四：解直⾓三⾓形的应⽤例4 黄岩岛是我国南海上的⼀个岛屿，其平⾯图如图甲所⽰，⼩明据此构造出该岛的⼀个数学模型如图⼄所⽰，其中∠B=∠D=90°，AB=BC=15千⽶，CD=32千⽶，请据此解答如下问题：（1）求该岛的周长和⾯积；（结果保留整数，参考数据2≈1.414，3≈1.73 ，6≈2.45）（2）求∠ACD的余弦值．对应训练6．超速⾏驶是引发交通事故的主要原因之⼀．上周末，⼩明和三位同学尝试⽤⾃⼰所学的知识检测车速．如图，观测点设在A 处，离益阳⼤道的距离（AC）为30⽶．这时，⼀辆⼩轿车由西向东匀速⾏驶，测得此车从B处⾏驶到C处所⽤的时间为8秒，∠BAC=75°．（1）求B、C两点的距离；（2）请判断此车是否超过了益阳⼤道60千⽶/⼩时的限制速度？（计算时距离精确到1⽶，参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732，3≈1.732，60千⽶/⼩时≈16.7⽶/秒）【聚焦中考】1．如图，在8×4的矩形⽹格中，每格⼩正⽅形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为（）A．13B．12C．22D．32．把△ABC三边的长度都扩⼤为原来的3倍，则锐⾓A的正弦函数值（）A．不变B．缩⼩为原来的13C．扩⼤为原来的3倍D．不能确定3．计算：tan45°+ 2cos45°= ．4．在△ABC中，若∠A、∠B满⾜|cosA- 12|+（sinB-22）2=0，则∠C= ．5.校车安全是近⼏年社会关注的重⼤问题，安全隐患主要是超速和超载．某中学数学活动⼩组设计了如下检测公路上⾏驶的汽车速度的实验：先在公路旁边选取⼀点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于21⽶，在l上点D的同侧取点A、B，使∠CAD=30°，∠CBD=60°．（1）求AB的长（精确到0.1⽶，参考数据：3=1.73，2=1.41）；（2）已知本路段对校车限速为40千⽶/⼩时，若测得某辆校车从A到B⽤时2秒，这辆校车是否超速？说明理由．6．如图，某校教学楼AB的后⾯有⼀建筑物CD，当光线与地⾯的夹⾓是22°时，教学楼在建筑物的墙上留下⾼2⽶的影⼦CE；⽽当光线与地⾯夹⾓是45°时，教学楼顶A在地⾯上的影⼦F与墙⾓C有13⽶的距离（B、F、C在⼀条直线上）（1）求教学楼AB的⾼度；（2）学校要在A、E之间挂⼀些彩旗，请你求出A、E之间的距离（结果保留整数）．（参考数据：sin22°≈38，cos22°≈1516，tan22°≈25）【备考真题过关】⼀、选择题1.如图，在Rt△ABC中，∠C=90°，AC=4，AB=5，则sinB的值是（）A．23B．35C．34D．452．如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tanB的值是（）A．45B．35C．34D．433．如图，在Rt △ABC中，∠C=90°，AB=6，cosB= 23，则BC的长为（）A．4 B．25C．181313D．1213134．2cos60°的值等于（）A．1 B．2C．3D．25．如图，在Rt△ABC中，∠C=90°，AB=2BC，则sinB的值为（）A．12B．22C．32D．16．如图，在Rt△ABO中，斜边AB=1．若OC∥BA，∠AOC=36°，则C( ）A．点B到AO的距离为sin54°B．点B到AO的距离为tan36°C．点A到OC的距离为sin36°sin54°D．点A到OC的距离为cos36°sin54°．7．在“测量旗杆的⾼度”的数学课题学习中，某学习⼩组测得太阳光线与⽔平⾯的夹⾓为27°，此时旗杆在⽔平地⾯上的影⼦的长度为24⽶，则旗杆的⾼度约为（）A．24⽶B．20⽶C．16⽶D．12⽶8．如图，某⽔库堤坝横断⾯迎⽔坡AB的坡⽐是1：3，堤坝⾼BC=50m，则应⽔坡⾯AB的长度是（）A．100m B．1003m C．150m D．503m1．如图，为测量某物体AB的⾼度，在D点测得A点的仰⾓为30°，朝物体AB⽅向前进20⽶，到达点C，再次测得点A的仰⾓为60°，则物体AB的⾼度为（）A．10⽶B．10⽶C．20⽶D．⽶2．⼩明想测量⼀棵树的⾼度，他发现树的影⼦恰好落在地⾯和⼀斜坡上，如图，此时测得地⾯上的影长为8⽶，坡⾯上的影长为4⽶．已知斜坡的坡⾓为30°，同⼀时刻，⼀根长为1⽶、垂直于地⾯放置的标杆在地⾯上的影长为2⽶，则树的⾼度为（）A．（6+）⽶B．12⽶C．（4﹣2）⽶D．10⽶3．如图，从热⽓球C处测得地⾯A、B两点的俯⾓分别是30°、45°，如果此时热⽓球C处的⾼度CD为100⽶，点A、D、B在同⼀直线上，则AB两点的距离是（）A．200⽶B．200⽶C．220⽶D．100（）⽶⼆、填空题9．在△ABC中∠C=90°，AB=5，BC=4，则tanA= ．10．tan60°= ．11．若∠a=60°，则∠a的余⾓为，cosa的值为．12．如图，为测量旗杆AB的⾼度，在与B距离为8⽶的C处测得旗杆顶端A的仰⾓为56°，那么旗杆的⾼度约是⽶（结果保留整数）．（参考数据：sin56°≈0.829，cos56°≈0.559，tan56°≈1.483）三、解答题13．如图，定义：在直⾓三⾓形ABC中，锐⾓α的邻边与对边的⽐叫做⾓α的余切，记作ctanα，即ctanα== ACBC，根据上述⾓的余切定义，解下列问题：（1）ctan30°= ；（2）如图，已知tanA=34，其中∠A为锐⾓，试求ctanA的值．14．⼀副直⾓三⾓板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=30°，∠A=45°，AC=122，试求CD的长．15．为促进我市经济的快速发展，加快道路建设，某⾼速公路建设⼯程中需修隧道AB，如图，在⼭外⼀点C测得BC距离为200m，∠CAB=54°，∠CBA=30°，求隧道AB的长．（参考数据：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38，3≈1.73，精确到个位）16.如图，某⾼速公路建设中需要确定隧道AB的长度.已知在离地⾯1500m，⾼度C处的飞机，测量⼈员测PABQ24.5°49°41°北东南西得正前⽅A 、B 两点处的俯⾓分别为60°和45°，求隧道AB 的长.17.如图，⾃来⽔⼚A 和村庄B 在⼩河l 的两侧，现要在A ，B 间铺设⼀知输⽔管道．为了搞好⼯程预算，需测算出A ，B 间的距离．⼀⼩船在点P 处测得A 在正北⽅向，B 位于南偏东24.5°⽅向，前⾏1200m ，到达点Q 处，测得A 位于北偏东49°⽅向，B 位于南偏西41°⽅向．（1）线段BQ 与PQ 是否相等？请说明理由；（2）求A ，B 间的距离．（参考数据cos41°＝0.75）练习作业：1. 已知在Rt △ABC 中，∠C ＝90°，根据表中的数据求其它元素的值：a b c ∠A ∠B 12 30° 4 45° 260°5 35 4 28 CD=3，AD=12，求证：AD ⊥BD ．3.计算ooo5sin 302cos60tan 45-－ oo o o2cos 45tan 30sin 45tan 60-+?4．如图所⽰，已知：在△ABC中，∠A=60°，∠B=45°，AB=443，?求△ABC的⾯积（结果可保留根号）．例5.已知：如图所⽰，在△ABC中，AD是边BC上的⾼，E?为边AC?的中点，BC=14，AD=12，sinB=45，求：（1）线段DC的长；（2）tan∠EDC的值．例6.如图，在△ABC中，∠BAC=120°，AB=10，AC=5，求sinB?sinC的值.。

中考数学总复习第15讲-锐角三角函数与解直角三角形

2016年中考数学总复习第15讲-锐角三角函数与解直角三角形-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIANb c a B C A D B C Ah l斜坡B C A b c aB C A 2016年中考数学总复习第15讲：锐角三角函数与解直角三角形【基础知识回顾】一、锐角三角函数定义：在Rt △ABC 中，∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ，在Rt △ABC 中，锐角∠A 的对边与斜边的比值叫做∠A 的正弦，记作sinA ．在Rt △ABC 中，锐角∠A 的邻边与斜边的比值叫做∠A 的余弦，记作cosA ．在Rt △ABC 中，锐角∠A 的对边与邻边的比值叫做∠A 的正切，记作tanA ．如图，则：sinA= ，∠cosA = ，tanA= ．sine[英][sa ɪn][美][sa ɪn] ；cosine[英][‵k əʊsa ɪn][美][‵ko ʊsa ɪn]；tangent[英][‵tænd ʒənt][美][‵tænd ʒənt] ．作图归纳：sinα cosα tanα3004506001、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的，要在理解的基础上结合图形进行记忆．2、三角函数可以进行变换．三、解直角三角形：1、定义：由直角三角形中除直角外的个已知元素，求出另外个未知元素的过程叫解直角三角形．2、解直角三角形的依据： Rt △ABC 中，∠C=900 ，三个角的三边对应分别为a 、b 、c ，如图： ⑴三边关系：； ⑵两锐角关系； ⑶边角之间的关系：sinA= ，cosA ，tanA ．sinB= ，cosB ，tanB ．注：1、解直角三角形中已知的两个元素应至少有一个是．2、当没有直角三角形时应注意构造直角三角形，再利用相应三角函数的边角关系解决． 3、解直角三角形应用中的有关概念：⑴仰角和俯角：如图：∠ABC 为仰角，∠DAB 为俯角．⑵坡度坡角：如图：斜坡AB 的垂直度AC 和水平宽度BC 的比叫做坡度，用i 表示，即i= ，坡面与水平面得夹角为，用字母α表示，则i=h l = ． ⑶方位角：是指南北方向线与目标方向所成的小于900的角，方位角先说南北再说东西．4、利用解直角三角形知识解决实际问题的一般步骤：⑴把实际问题抓化为数字问题（画出平面图形，转化为解直角三角形的问题）．⑵根据条件特点选取合适的锐角三角函数去解直角三角形．⑶解数学问题答案，从而得到实际问题的答案．注：在解直角三角形实际应用中，先构造符合题意的三角形，解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决．【重点考点例析】考点一：锐角三角函数的概念例1．（2012•内江）如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为（）A．12 B．55 C．1010 D．255例2．（2012•贵港）在平面直角坐标系中，已知点A（2，1）和点B（3，0），则sin∠AOB的值等于（）A．55 B．52 C．32 D．12考点二：特殊角的三角函数值例3．（2012•孝感）计算：cos245°+tan30°•sin60°=．例4．（2012•南昌）计算：sin30°+cos30°•tan60°= ．．考点三：化斜三角形为直角三角形例5．（2012•安徽）如图，在△ABC中，∠A=30°，∠B=45°，AC=23，求AB的长．例6．（2012•重庆）如图，在Rt△ABC中，∠BAC=90°，点D在BC边上，且△ABD是等边三角形．若AB=2，求△ABC的周长．（结果保留根号）考点四：解直角三角形的应用例7．（2013•益阳）如图，益阳市梓山湖中有一孤立小岛，湖边有一条笔直的观光小道AB，现决定从小岛架一座与观光小道垂直的小桥PD，小张在小道上测得如下数据：AB=80.0米，∠PAB=38.5°，∠PBA=26.5．请帮助小张求出小桥PD的长并确定小桥在小道上的位置．（以A，B为参照点，结果精确到0.1米）（参考数据：sin38.5°=0.62，cos38.5°=0.78，tan38.5°=0.80，sin26.5°=0.45，cos26.5°=0.89，tan26.5°=0.50）例8．（2013•娄底）2013年3月，某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象．已知A、B两点相距4米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C 的深度．（精确到0.1米，参考数据：）例9．（2013•呼和浩特）如图，A 、B 两地之间有一座山，汽车原来从A 地到B 地经过C 地沿折线A→C→B 行驶，现开通隧道后，汽车直接沿直线AB 行驶．已知AC=10千米，∠A=30°，∠B=45°．则隧道开通后，汽车从A 地到B 地比原来少走多少千米（结果保留根号）【综合训练】一、选择题1.（2012•哈尔滨）如图，在Rt △ABC 中，∠C=90°，AC=4，AB=5，则sinB 的值是（）A ．23B ．35C ．34D ．45 2．（2012•天津）2cos60°的值等于（） A ．1 B ．2 C ．3 D ．23．如图，某水库堤坝横断面迎水坡AB 的坡比是1：3，堤坝高BC=50m ，则应水坡面AB 的长度是（）A ．100mB ．1003mC ．150mD ．503m4．（2012•泰安）如图，为测量某物体AB 的高度，在D 点测得A 点的仰角为30°，朝物体AB 方向前进20米，到达点C ，再次测得点A 的仰角为60°，则物体AB 的高度为（）A ．310米B ．10米C ．320米D ．3320米第3题图第4题图二、填空题5．（2012•宁夏）在△ABC 中∠C=90°，AB=5，BC=4，则tanA= ．三、解答题6．（2012•遵义）为促进我市经济的快速发展，加快道路建设，某高速公路建设工程中需修隧道AB ，如图，在山外一点C测得BC距离为200m，∠CAB=54°，∠CBA=30°，求隧道AB的长．（参考数据：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38，3≈1.73，精确到个位）7．（2012•资阳）小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD=10米．求点P到AD的距离（用含根号的式子表示）．。

中考数学复习：锐角三角函数及解直角三角形

15
16
17
18
基础全练
挑战高分
中考创新练
17.(2022·四川内江)如图所示,九(1)班数学兴趣小组为了测量河对岸的古
树A,B之间的距离,他们在河边与AB平行的直线l上取相距60 m的C,D
两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°.
(1)求河的宽度;
(2)求古树A,B之间的距离.(结果保留根号)
锐角三角函数及解直角三角形
挑战高分
基础全练
中考创新练
综合模拟练
基础全练
1.(2022·广西北部湾)如图,某博物馆大厅电梯的截面图中,AB的长为12
米,AB与AC的夹角为α,则高BC是( A )
A.12sin α米
12
C.
米
sin
B.12cos α米
1
2
3
4
5
6
12
D.
米
cos
7
8
9
10

−45
22°=
≈0.4,

5
5
5
∴BF≈ (x-45),∴ x+60= (x-45),解得x=92,
2
8
2
故大楼MN的高度为92米.
14
15
16
17
18
基础全练
挑战高分
中考创新练
16.(2022·浙江舟山)小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾
的横截面是一个轴对称图形,其示意图如图2.已知AD=BE=10 cm,CD=
1
2
3
4
5
6
7
8
9
10
11

中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)

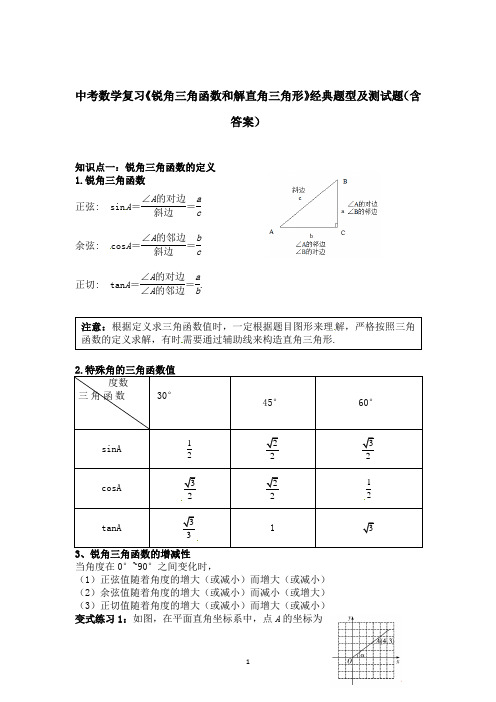
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题（含答案）知识点一：锐角三角函数的定义 1.锐角三角函数正弦: sin A ＝∠A 的对边斜边＝ac余弦: cos A ＝∠A 的邻边斜边＝bc正切: tan A ＝∠A 的对边∠A 的邻边＝ab.来源:学&科&网]2.特殊角的三角函数值[来度数三角函数[来源:Z 。

xx 。

]30°[来源:学#科#网] 45° 60°sinA1222 32 cosA32 2212tanA 331 33、锐角三角函数的增减性当角度在0°~90°之间变化时，（1）正弦值随着角度的增大（或减小）而增大（或减小）（2）余弦值随着角度的增大（或减小）而减小（或增大）（3）正切值随着角度的增大（或减小）而增大（或减小）变式练习1：如图，在平面直角坐标系中，点A 的坐标为注意：根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.[(4，3)，那么cos α的值是( ) A. 34 B. 43 C. 35 D. 45【解析】D 如解图，过点A 作AB ⊥x 轴于点B ，∵A (4，3)，∴OB ＝4，AB ＝3，∴OA ＝32＋42＝5，∴cos α＝OB OA ＝45.变式练习2：在Rt △ABC 中，∠ABC ＝90°，AB ＝3，BC ＝4，则sinA ＝________．【解析】∵在Rt △ABC 中，由勾股定理得AC ＝22AB BC +＝32＋42＝5，∴sin A ＝BC AC ＝45. 变式练习3：在Rt △ABC 中，∠C ＝90°，sin A ＝35，BC ＝6，则AB ＝( D )A ．4B ．6C ．8D ．10变式练习4：如图，若点A 的坐标为(1，3)，则sin ∠1＝__32__. ,知识点二：解直角三角形 1.解直角三角形的概念在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形． 2.解直角三角形的常用关系在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别为a ，b ，c (1)三边之间的关系：a 2＋b 2＝c 2；(2)锐角之间的关系：∠A ＋∠B ＝90°； (3)边角之间的关系：,tan ,cos ,sin ;,tan ,cos ,sin abB c a B c b B b a A c b A c a A ======（sinA＝=cosB=ac，c osA＝sinB=bc，tanA＝ab.）变式练习1：在Rt△ABC中，已知a=5,sinA=30°，则c=10,b=5.变式练习2：如图，Rt△ACB中，∠B＝30°，∠ACB＝90°，CD⊥AB交AB于D.以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E＝30°，∠DCE＝90°，再用同样的方法作Rt△FGC，∠FCG＝90°，继续用同样的方法作Rt△HIC，∠HCI ＝90°.若AC＝a，求CI的长．解：在Rt△ABC中，∠B＝30°，∠ACB＝90°，CD⊥AB，∴∠A＝60°，∵AC＝a，∴CD＝AC·sin60°＝32a，依此类推CH＝(32)3a＝338a，在Rt△CHI中，∵∠CHI＝60°，∴CI＝CH·tan60°＝338a×3＝98a.变式练习3：如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是( D )A.433B．4 C．8 3 D．4 3,灵活选择解直角三角形的方法顺口溜：已知斜边求直边，正弦、余弦很方便；已知直边求直边，理所当然用正切；已知两边求一边，勾股定理最方便；已知两边求一角，函数关系要记牢；已知锐角求锐角，互余关系不能少；已知直边求斜边，用除还需正余弦.变式练习4：如图，一山坡的坡度为i＝1∶3，小辰从山脚A出发，沿山坡向上走了200米到达点B，则小辰上升了__100__米．, ,变式练习5：一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处，沿正西方向航行3小时后到达小岛的北偏西45°的C处，则该船行驶的速度为___40＋4033___海里/小时．知识点三：解直角三角形的应用1.仰角、俯角、坡度、坡角和方向角(1)仰、俯角：视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角．（如图①）(2)坡度：坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比)，用字母i表示．坡角：坡面与水平面的夹角叫做坡角，用α表示，则有i＝tanα.（如图②）(3)方向角：平面上，通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向)，则从点O出发的视线与水平线或铅垂线所夹的角，叫做观测的方向角．（如图③）2.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语，根据题意画出图形，建立数学模型；(2)将条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形问题；(3)选择合适的边角关系式，使运算简便、准确；(4)得出数学问题的答案并检验答案是否符合实际意义，从而得到问题的解．注意：解直角三角形中“双直角三角形”的基本模型：（1）叠合式（2）背靠式解题方法：这两种模型种都有一条公共的直角边，解题时，往往通过这条边为中介在两个三角形中依次求边，或通过公共边相等，列方程求解变式练习1：如图，某数学兴趣小组想测量一棵树CD 的高度，他们先在点A 处测得树顶C 的仰角为30°，然后沿AD 方向前行10 m ，到达B 点，点B 处测得树顶C 的仰角为60°(A 、B 、D 三点在同一直线上)．请你根据他们的测量数据计算这棵树CD 的高度(结果精确到0.1 m)．(参考数据：2≈1.414，3≈ 1.732)解：如解图，由题意可知∠CAB ＝30°，∠CBD ＝60°，AB ＝10 m ，∵∠CBD ＝∠CAB ＋∠BCA ，∴∠BCA ＝∠CBD －∠CAB ＝60°－30°＝30°＝∠CAB ， ∴BC ＝AB ＝10 m ．在Rt △BCD 中，∵sin ∠CBD ＝CDBC，∴CD ＝BC ·sin ∠CBD ＝10×sin60°＝10×32＝53≈5×1.732≈8.7 m ．答：这棵树CD 的高度大约是8.7 m ．变式练习2：如图，小山岗的斜坡AC 的坡度是tan α＝34，在与山脚C 距离200米的D 处，测得山顶A 的仰角为26.6°，求小山岗的高AB (结果取整数；参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50)．解：设AB ＝x 米，在Rt △ABD 中，∠D ＝26.6°，∴BD ＝tan 26.6x≈2x ，在Rt △ABC 中，tan α＝AB BC ＝34，∴BC ＝43x ，∵BD －BC ＝CD ，CD ＝200，∴2x－43x＝200，解得x＝300.答：小山岗的高AB约为300米．变式练习3：如图，小明所在教学楼的每层高度为3.5 m，为了测量旗杆MN的高度，他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°，他在二楼窗台B 处测得M的仰角为30°，已知每层楼的窗台离该层的地面高度均为1 m，求旗杆MN的高度(结果精确到0.1 m)．(参考数据：2≈1.414，3≈1.732)解：如解图，过点M的水平线交直线AB于点H，由题意，得∠AMH＝∠MAH＝45°，∠BMH＝30°，AB＝3.5 m，设MH＝x m，则AH＝x m，BH＝x·tan30°＝33x≈0.58x m，∴AB＝AH－BH＝x－0.58x＝0.42x＝3.5 m，解得x≈8.3，则MN＝x＋1＝9.3 m.答：旗杆MN的高度约为9.3 m.变式练习4：小明去爬山，如图，在山脚看山顶的角度为30°，小明在坡比为5∶12的山坡上走了1300米，此时小明看山顶的角度为60°，则山高为( )A. (600－2505)米B. (6003－250)米C. (350＋3503)米D. 500 3 米【解析】B如解图，∵BE∶AE＝5∶12，∴设BE＝5k，AE＝12k，∴AB＝2()5K＋(12k)2＝13k，∴BE∶AE∶AB＝5∶12∶13，∵AB＝1300米，∴AE＝1200米，BE ＝500米，设EC＝FB＝x米，∵∠DBF＝60°，∴DF＝3x米，则DC＝(3x＋500)米，又∵∠DAC＝30°，∴AC＝3CD，即1200＋x＝3(3x＋500)，解得x＝600－2503，∴DF＝3x＝(6003－750)米，∴CD＝DF＋CF＝(6003－250)米，即山高CD为(6003－250)米．变式练习5：某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°.已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．(结果保留根号)解：如解图，过点A作AD⊥BC交BC于点D，过点B作BH⊥水平线交水平线于点H，由题意∠ACH＝75°，∠BCH＝30°，AB∥CH，∴∠ABC＝30°，∠ACB＝45°，∵AB＝4×8＝32米，∴CD＝AD＝AB·sin30°＝16米，BD＝AB·cos30°＝32×32＝163米，∴BC＝CD＋BD＝(16＋163)米，∴BH＝BC·sin30°＝(16＋163)×12＝(8＋83)米．答：这架无人飞机的飞行高度为(8＋83)米．变式练习6：如图，我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上，随后渔政船以80海里/小时的速度向北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在渔政船的北偏西60°的方向上，求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位，其中3≈1.732) 解：∵CD∥BE，∴∠EBC＋∠DCB＝180°.∵∠ABE＝60°，∠DCB＝30°，∴∠ABC＝90°.…………(4分)由题知，BC＝80×12＝40(海里)，∠ACB＝60°.在Rt△ABC中，AB＝BC·tan60°＝403≈40×1.732≈69.3(海里)．答：此时渔政船距钓鱼岛A的距离AB的长约为69.3海里．。

中考数学复习专题课件锐角三角函数与解直角三角形的实际应用

（D ） A．1.59 m B．2.07 m C．3.55 m D．3.66 m
6．(2021·遵义)小明用一块含有 60°(∠DAE＝60°)的直角三角尺测量校园内某棵树的高度，示意图如图所示，若小明的眼睛与地面之间的垂直高度 AB 为 1.62 m，小明与树之间的水平距离 BC 为 4 m，则这棵树的高度约为 88..55 m.(结果精确到 0.1 m，参考数据： 3≈1.73)
(1)证明：∵AB＝AC＝AD， ∴点 B，C，D 在以点 A 为圆心，BD 为直径的圆上． ∴∠BCD＝90°，即 DC⊥BC.
(2)解：过点 E 作 EF⊥BC，垂足为 F.
在 Rt△BCD 中，
BC cos B＝BD，BC＝1.8.
BC
1.8
∴BD＝cos B＝cos 55°≈3.16.
∴BE＝BD＋DE≈3.16＋2＝5.16.
13．(2022·安顺)随着我国科学技术的不断发展，5G 移动通信技术日趋完善，某市政府为了实现 5G 网络全覆盖，2021～2025 年拟建设 5G 基站 3 000 个，如图，在斜坡 CB 上有一建成的 5G 基站塔 AB，小明在坡脚 C 处测得塔顶 A 的仰角为 45°，然后他沿坡面 CB 行走了 50 m 到达 D 处，D 处离地平面的距离为 30 m 且在 D 处测得塔顶 A 的仰角 53°.(点 A，B，C，D，E 均在同一平面内， CE 为地平线，参考数据：sin 53°≈45，cos 53°≈35，tan 53°≈43) (1)求坡面 CB 的坡度； (2)求基站塔 AB 的高．
4 10＋4a ∴3＝ 4a ，解得 a＝7.5， ∴AB＝AF－BF＝10＋a＝17.5 m.
答：基站塔 AB 的高为 17.5 m.

初中数学锐角三角函数练习、解直角三角形练习及详细解答

初中三角函数练习及解答1.锐角三角函数1.比较下列各组三角函数值的大小：（1）sin19︒与cos70︒；（2）cot 65︒与cos40︒；（3）cos1︒，tan 46︒，sin88︒和cot 38︒．2.化简求值：（1）tan1tan 2tan3tan89︒⋅︒⋅︒⋅⋅︒ ；（2sin83︒；（3）2222tan sin tan sin αααα⋅-；（4cos 79sin 79-︒-︒；3.若tan 3α=求2sin sin 13sin cos αααα-+的值．4.下列四个数中哪个最大：A ．tan 48cot 48︒+︒B ．sin 48cos48︒+︒C ．tan 48cos48︒+︒D ．cot 48sin 48︒+︒5.设x 为锐角，且满足sin 3cos x x =，求sin cos x x ．6.已知sin cos αα+=，求sin cos αα的值．7．已知m 为实数，且sin α、cos α是关于x 的方程2310x mx -+=的两根．求44sin cos αα+的值．8．设A 、B 是一个直角三角形的两个锐角，满足2sin sin 2A B -=．求sin A 及sin B 的值．9．已知关于x 的一元二次方程()()22211120m x m x +--+=的两个根是一个直角三角形的两个锐角的正弦，求实数m 的值．10．已知方程2450x x k -+=的两根是直角三角形的两个锐角的正弦，求k ．11．若直角三角形中的两个锐角A 、B 的正弦是方程20x px q ++=的两个根；（1）那么，实数p 、q 应满足哪些条件？（2）如果p 、q 满足这些条件，方程20x px q ++=的两个根是否等于直角三角形的两个锐角A 、B 的正弦？12．已知方程()24210x m x m -++=的两个根恰好是一个直角三角形的两个锐角的余弦，试求m 的值．13．不查表，求15︒的四种三角函数值．14．求22.5︒角的正切值（不查表，不借助计算器）．15．求sin18︒的值．16．若x 、y 为实数，221x y +=，α为锐角，求证：sin cos x y αα+的绝对值不大于1．2解直角三角形1．如图，在直角三角形ABC 中，90C ∠=︒，AD 是A ∠的平分线，且CD =，DB =求ABC △的三边长．2．在Rt ABC △中（如图），D 、E 是斜边AB 的三等分点，已知sin CD x =，()cos 090CE x x =︒<<︒．试求AB 的长．3．如图，ABC △中，90C ∠=︒，10AB =，6AC =，AD 是BAC ∠的平分线，求点B 到直线AD 的距离BH ．4．已知ABC △是非等腰直角三角形，90BAC ∠=︒，在BC 所在直线上取两点D 、E 使DB BC CE ==，连结AD 、AE ．已知45BAD ∠=︒．求tan CAE ∠的值．5．设有一张矩形纸片ABCD （如图），3AB =，4BC =．现将纸片折叠，使C 点与A 点重合，试求折痕EF 的长．6．已知三角形两边之和是10，这两边的夹角为30︒，面积为254，求证：此三角形为等腰三角形．7．在ABC △中，90C ∠=︒，其周长为2+，且已知斜边上的中线长为1．如果BC AC >，求tan A的值．8．已知a 、b 、c 分别是ABC △中A ∠、B ∠，C ∠的对边，且a 、b 是关于x 的一元二次方程()()2 424x c c x ++=+的两个根．（1）判断ABC △的形状；（2）若3tan 4A =求a 、b 、c ．9．在Rt ABC △中，90C ∠=︒，12ABC S m =△，且两直角边长满足条件32a b m +=．（1）证明：24m ≥；（2）当m 取最小值时，求ABC △中最小内角的正切值．10．如图所示．90A BEF EBC ECD ∠=∠=∠=∠=︒，30ABF ∠=︒，45BFE ∠=︒，60ECB ∠=︒且2AB CD =．求tan CDE ∠的值．11．如图所示．在锐角ABC △中，4sin 5B =，tan 2C =，且10ABC S =△．求BC ．12．如图所示．在ACD △中，45A ∠=︒，5CB =，7CD =，3BD =．求CBD ∠及AC ．13．如图，已知ABC △中，1AB =，D 是AB 的中点，90DCA ∠=︒，45DCB ∠=︒．求BC 的长．14．如图，ABC △中，90ACB ∠=︒，CD AB ⊥于D ，DE AC ⊥于E ，DF BC ⊥于F ．求证：33AE AC BF BC =．15．如图，在ABC △中，90A ∠=︒，AB AC =，M 是AC 边的中点，AD 垂直于BM 且交BC 于D ．求证：AMB CMD ∠=∠．16．如图（a ），正方形ABCD 的边长E 、F 分别是AB 、BC 的中点，AF 分别交DE 、DB 于点M 、N ，求DMN △的面积．17．已知a 、b 、c 是ABC △三边的长，其中b a c >=，且方程20ax c +=两根的差的绝对值等．求ABC △中最大角的度数．18．如图，AB 是圆的直径，弦CD AB ∥，AC 与BD 相交于E ，已知AED θ∠=，试求:CDE ABE S S △△．19．如图所示，已知电线杆AB 直立于地面上，它的影子恰好照在土坡的坡面CD 和地面BC 上．如果CD与地面成45︒，60A ∠=︒，4m CD =，(m BC =-，求电线杆AB 的长（精确到0.1m ）．20．如图，某岛S 周围42海里内存在着大量的暗礁．现在一轮船自西向东以每小时15海里的速度航行，在、A 处测得S 在北偏东60︒，2小时后在B 处测得S 在正东北方向，试问轮船是否需要改变航行方向行驶，才能避免触礁危险，说明理由．21．如图，某污水处理站计划砌一段截面为等腰梯形的排污渠，如果渠深为h ，截面积为S ，试求当倾角θ为多少时造价最小？1.锐角三角函数（详细解答）1.比较下列各组三角函数值的大小：（1）sin19︒与cos70︒；（2）cot 65︒与cos40︒；（3）cos1︒，tan 46︒，sin88︒和cot 38︒．解析（1）利用互余角的三角函数关系式，将cos70︒化sin 20︒，再与sin19︒比大小．因为()cos70cos 9020sin 20︒=︒-︒=︒，而sin19sin 20︒<︒，所以sin19cos70︒<︒．（2）余切函数与余弦函数无法化为同名函数，但是可以利用某些特殊的三角函数值，间接比较它们的大小．32cot 60cos 4532︒=<︒=，再将cot 65︒，cos40︒分别与cot 60︒，cos45︒比大小．因为cot 65cot 60︒<︒=，cos 40cos 45︒>︒>，所以cot 60cos45︒<︒，所以cot 65cos40︒<︒．（3）tan 451︒=，显然cos1︒，sin88︒均小于1，而tan 46︒，cot 38︒均大于1．再分别比较cos1︒与sin88︒，以及tan 46︒与cot 38︒的大小即可．因为()cos38cot 9052tan52︒=︒-︒=︒，所以tan52tan 46tan 451︒>︒>︒=．因为()cos1cos 9089sin89︒=︒-︒=︒，所以sin88sin891︒<︒<，所以cot 38tan 46cos1sin88︒>︒>︒>︒．评注比较三角函数值的大小，一般分为三种类型：（1）同名的两个锐角三角函数值，可直接利用三角函数值随角变化的规律，通过比较角的大小来确定三角函数值的大小．（2）互为余函数的两锐角三角函数值，可利用互余角的三角函数关系式化为同名三角函数，比较其大小．（3）不能化为同名的两个三角函数，可通过与某些“标准量”比大小，间接判断它们的大小关系，常选择的标准量有：0，1以及其他一些特殊角如30︒，45︒，60︒的三角函数值．2.化简求值：（1）tan1tan 2tan3tan89︒⋅︒⋅︒⋅⋅︒ ；（2sin83︒；（3）2222tan sin tan sin αααα⋅-；（4cos 79sin 79-︒-︒；解析（1）原式=tan1tan 2tan3tan 44tan 45cot 44cot 43cot 3cot 2cot1︒⋅︒⋅︒⋅⋅︒⋅︒⋅︒⋅︒⋅⋅︒⋅︒⋅︒ ()()()tan1cot1tan 2cot 2tan 44cot 44tan 45=︒⋅︒⋅︒⋅︒⋅⋅︒⋅︒⋅︒ 1111=⋅⋅⋅= ．（2）原式1cos7cos71cos7=︒=⋅︒=︒．（3）原式()22442242222sin sin sin sin cos 1sin sin sin 1cos sin cos ααααααααααα⋅====--．（4）原式sin11cos11sin11cos11sin11cos110-︒-︒=︒-︒-︒-︒=．3.若tan 3α=求2sin sin 13sin cos αααα-+的值．原式2222sin cos sin sin cos sin 13sin cos sin cos 3sin cos αααααααααααα--==+++2222tan tan 336tan 13tan 313319αααα--===-++++⨯．4.下列四个数中哪个最大：A ．tan 48cot 48︒+︒B ．sin 48cos48︒+︒C ．tan 48cos48︒+︒D ．cot 48sin 48︒+︒解析显然0sin 481<︒<，0cos481<︒<0<cos48°<1．因此有：sin 48sin 48tan 48cos 48︒︒<=︒︒，cos 48cos 48cot 48sin 48︒︒<=︒︒所以A 最大．5.设x 为锐角，且满足sin 3cos x x =，求sin cos x x ．解析我们将sin 3cos x x =代入22sin cos 1x x +=，得到210cos 1x =，并且x 是锐角，因此cos x=所以sin x =．因此3sin cos 10x x =．6.已知sin cos αα+=，求sin cos αα的值．解析由sin cos αα+=两边平方得()22sin cos αα+=．又22sin cos 1αα+=，所以12sin cos 2αα+=，得1sin cos 2αα=．7．已知m 为实数，且sin α、cos α是关于x 的方程2310x mx -+=的两根．求44sin cos αα+的值．解析由根与系数的关系知1sin cos 3αα=．则有()()2244227sin cos sin cos 2sin cos 9αααααα+=+-=．8．设A 、B 是一个直角三角形的两个锐角，满足2sin sin 2A B -=．求sin A 及sin B 的值．解析由于90A B +=︒，故由互余关系得()sin sin 90cos B A A =︒-=．因此条件即为sin cos A A -=，①将上式平方，得221sin cos 2sin cos 2A A A A +-=，由正、余弦的平方关系，即有12sin cos 2A A =，所以()2223sin cos sin cos 2sin cos 12sin cos 2A A A A A A A A +=++=+=，因sin A 、cos A 均为正数，故sin cos 0A A +>．因此由上式得sin cos A A +=，②由①、②得sin A =，cos A =sin B =9．已知关于x 的一元二次方程()()22211120m x m x +--+=的两个根是一个直角三角形的两个锐角的正弦，求实数m 的值．解析设方程的两个实根1x 、2x 分别是直角三角形ABC 的锐角A 、B 的正弦．则()22222212sin sin sin cos 190x x A B A A A B +=+=+=+=︒，又122112m x x m -+=+，12122x x m =+，所以()2222111212211242122m x x x x x x m m -⎛⎫+=+-=-= ⎪++⎝⎭．化简得224230m m -+=，解得1m =或23．检验，当1m =时，()()22114820m m =--+<△；当23m =时，()()22114820m m =--+△≥．所以23m =．评注本题是三角函数与一元二次方程的综合，基本解法是利用韦达定理和22sin cos 1αα+=列方程求解．要注意最后检验方程有无实数根．10．已知方程2450x x k -+=的两根是直角三角形的两个锐角的正弦，求k ．解析根据韦达定理，有12125 , 4.4x x k x x ⎧+=-⎪⎪⎨⎪=⎪⎩并且由于其两根是直角三角形的两个锐角的正弦，所以又有22121x x +=．于是有()2222121212512244k x x x x x x ⎛⎫=+=+-=--⨯ ⎪⎝⎭．解得98k =．11．若直角三角形中的两个锐角A 、B 的正弦是方程20x px q ++=的两个根；（1）那么，实数p 、q 应满足哪些条件？（2）如果p 、q 满足这些条件，方程20x px q ++=的两个根是否等于直角三角形的两个锐角A 、B 的正弦？解析（1）设A 、B 是某个直角三角形两个锐角，sin A 、sin B 是方程20x px q ++=的两个根，则有240p q =-△≥．①由韦达定理，sin sin A B p +=-,sin sin A B q =．又sin 0A >，sin 0B >，于是0p <，0q >．由于()sin sin 90cos B A A =︒-=．所以sin cos A A p +=-，sin cos A A q =，所以()()22sin cos 1sin cos 12p A A A A q -=+=+=+，即221p q -=．由①得21240q p q -=-≥，则12q ≤．故所求条件是0p <，102p <≤，221p q -=．②（2）设条件②成立，则24120p q q -=-≥，故方程有两个实根：α==，β==．由②知p -=p <=-，所以0p p <--+，故0βα>≥．又()2222221p q αβαβαβ+=+-=-=，故01αβ<<≤．12．已知方程()24210x m x m -++=的两个根恰好是一个直角三角形的两个锐角的余弦，试求m 的值．解析设题中所述的两个锐角为A 及B ，由题设得()241160 , 1cos cos , 2cos cos .4m m m A B m A B ⎧=+-⎪⎪+⎪+=⎨⎪⎪=⎪⎩△≥因为cos sin B A =，故()2, 1cos sin , 2cos sin , 410m A A m A m m A ++==⎧=-⇒⎪⎪⎪⎨⎪⎪⎪⎩可△≥取任意实数①②①式两边平方，并利用恒等式22sin cos 1A A +=，得()()221cos sin 12sin cos 4m A A A A ++=+=．再由②得()21124m m ++=，解得m =．由cos 0A >，sin 0A >及②知0m >．所以m =．13．不查表，求15︒的四种三角函数值．解析30︒、45︒、60︒这些特殊角的三角函数值，我们可以利用含有这些特殊角的直角三角形的几何性质及勾股定理直接推出．同样，15︒角的三角函数值，也可以利用直角三角形的性质将其推出．如图所示．在ABC △中，90C ∠=︒，30ABC ∠=︒，延长CB 到D ，使BD BA =，则1152D BAD ABC ∠=∠=∠=︒．设1AC =，则2AB =，3BC =2BD =，所以 23CD CB BD =+=+所以()()())2222123843242323123162AD AC CD =++++++=+=+．所以162sin15462AC AD -︒===+，2362cos15462CD AD ++︒===+1tan152323AC CD ︒===-+cot1523CDAC︒==．评注将15︒角的三角函数求值问题，通过构造适当的三角形，将它转化为30︒角的三角函数问题，这种将新的未知问题通过一定途径转化为旧的已解决了的问题的方法，是我们研究解决新问题的重要方法．根据互余三角函数关系式，我们很容易得到75︒角的四种三角函数值．14．求22.5︒角的正切值（不查表，不借助计算器）．解析4522.52︒︒=，所以设法构造一个含22.5︒角的直角三角形，用定义求值．如图，Rt ABC △中，90C ∠=︒，45B ∠=︒，延长CB 到D ，使BD BA =，则122.52D B ∠=∠=︒．设AC b =，有222AB b b b =+=，()21DC DB BC b =+=+．故()tan 22.52121ACDCb︒==+．15．求sin18︒的值．解析构造一个顶角A 为36︒的等腰ABC △，AB AC =，如图，作内角平分线则36ABD DBC ∠=∠=︒，设1AC =，BC x =．由于36DBA DAB ∠=∠=︒，72BDC BCD ∠=∠=︒，故CB BD DA x ===，而CAB △∽CBD △（36CAB CBD ∠=∠=︒），故AC BC BC DC =，故11xx x=-，有512x -=（舍去512-）．再作AH BC ⊥于H ，则18CAH ∠=︒，514CH -=．所以1sin184-︒=．评注本题所构造的等腰三角形是圆内接正十边形的相邻顶点与圆心确定的三角形，利用它可以求出半径为R 的圆内接正十边形的边长．16．若x 、y 为实数，221x y +=，α为锐角，求证：sin cos x y αα+的绝对值不大于1．解析由221x y +=，22sin cos 1αα+=，得()()2222sin cos 1x y αα++=，即22222222sin cos cos sin 1x y x y αααα+++=，加一项减一项，得22222222sin 2sin cos cos cos 2cos sin sin 1x xy y x xy y αααααααα+++-+=．即()()2sin cos cos sin 1x y x y αααα2++-=，因为()2cos sin 0x y αα-≥，所以()2sin cos 1x y αα+≤，故sin cos 1x y αα+≤．2解直角三角形（详细解答）1．如图，在直角三角形ABC 中，90C ∠=︒，AD 是A ∠的平分线，且CD =，DB =求ABC △的三边长．解析由角平分线想到对称性，考虑过D 作DE AB ⊥，交AB 于E ，则由90C ∠=︒得CD DE ==．在直角三角形BDE 中，1sin 2DE B DB ==，则60B ∠=︒，所以3tan3AC BC B ==+⋅=，2sin ACAB AC B===，BC CD DB =+=．故ABC △的三边长分别为，．2．在Rt ABC △中（如图），D 、E 是斜边AB 的三等分点，已知sin CD x =，()cos 090CE x x =︒<<︒．试求AB 的长．解析作DF AC ⊥于F ，EG AC ⊥于G ；DP BC ⊥于P ，EQ BC ⊥于Q ．令BP PQ QC a ===，AG GF FC b ===．则2DF a =，EG a =．在Rt CDF △和Rt CEG △中，由勾股定理，得()2222sin a b x +=，及()2222cos a b x +=，两式相加得()2251a b +=，2215a b +=．所以35AB BD ===．3．如图，ABC △中，90C ∠=︒，10AB =，6AC =，AD 是BAC ∠的平分线，求点B 到直线AD 的距离BH ．解析已知Rt ABH △中，10AB =，要求BH ，可求出BAH ∠的正弦值，而BAH CAD ∠=∠，因而可先求出DC 的长．作DE AB ⊥于E ，有6AE AC ==，ED CD =．设3DC k =，由三角形内角平分线性质有106BD DC =，则5BD k =．Rt BDE △中，222DE BE BD +=，即()()()22231065k k +-=，得1k =．33CD k ==，AD ==sin10BHDAC ∠==，故BH =．4．已知ABC △是非等腰直角三角形，90BAC ∠=︒，在BC 所在直线上取两点D 、E 使DB BC CE ==，连结AD 、AE ．已知45BAD ∠=︒．求tan CAE ∠的值．解析如图，过B 、C 两点作BM AC ∥、CN AB ∥分别交AD 、AE 于M 、N ．易知2AC BM =，2AB CN =，tan BM BAD AB ∠=，tan CNCAE AC∠=，从而，1tan tan 4BAD CAE ∠∠=．因为tan 1BAD ∠=，则1tan 4CAE ∠=．5．设有一张矩形纸片ABCD （如图），3AB =，4BC =．现将纸片折叠，使C 点与A 点重合，试求折痕EF 的长．解析设O 是矩形对角线AC 的中点．连结CF ，由折叠知CF AF =，故FO AC ⊥，即EF AC ⊥．由3AB =，4BC =，得5AC =，从而1522AO AC ==．在Rt AOF △中，90AOF ∠=︒，故tan OF AO FAO =⋅∠．又由Rt ADC △得3tan tan 4DC FAO DAC AD ∠=∠==，所以5315248OF =⋅=，1524EF OF ==．7.已知三角形两边之和是10，这两边的夹角为30︒，面积为254，求证：此三角形为等腰三角形．解析由题意可设10a b +=，30α=︒，则125sin 24S ab α==△，即1125224ab ⋅=，得25ab =．于是，由10a b +=，25ab =，得a 、b 是方程210250x x -+=的两个根．而此方程有两个相等的根，所以5a b ==，即此三角形为等腰三角形．评注也可以直接由()()2240a b a b ab -=+-=，得a b =．7．在ABC △中，90C ∠=︒，其周长为2+，且已知斜边上的中线长为1．如果BC AC >，求tan A的值．解析由于斜边长是斜边上中线长的2倍，故2AB c ==．于是，由题设及勾股定理，得224. a b a b ⎧++==⎪⎨⎪⎩①②把①式两边平方，得2226a ab b ++=．再由②得1ab =．③由①、③知，a 、b 分别是二次方程210u +=的两根，解得622u ±=．因为BC AC >（即a b >），故12BC =，12AC =，所以tan 2BC A AC ===+．8．已知a 、b 、c 分别是ABC △中A ∠、B ∠，C ∠的对边，且a 、b 是关于x 的一元二次方程()()2 424x c c x ++=+的两个根．（1）判断ABC △的形状；（2）若3tan 4A =求a 、b 、c ．解析（1）根据题意，尝试从边来判断．因为4a b c +=+，()42ab c =+，所以()2222a b a b ab +=+-()()224242c c c =+-⨯+=，从而知ABC △是直角三角形，90C ∠=︒．（2）由90C ∠=︒，3tan 4A ∠=，得34a b =．令3a =，()40b k k =>，则5c k =，于是754k k =+，得2k =，从而有6a =，8b =，10c =．9．在Rt ABC △中，90C ∠=︒，12ABC S m =△，且两直角边长满足条件32a b m +=．（1）证明：24m ≥；（2）当m 取最小值时，求ABC △中最小内角的正切值．解析（1）由题设得 , 32.ab m a b m =⎧⎨+=⎩消去b ，得32m a a m -⎛⎫= ⎪⎝⎭，故实数a 满足二次方程2320x mx m -+=．①所以()224240m m m m =-=-△≥．因为0m >，所以24m ≥．10．如图所示．90A BEF EBC ECD ∠=∠=∠=∠=︒，30ABF ∠=︒，45BFE ∠=︒，60ECB ∠=︒且2AB CD =．求tan CDE ∠的值．解析因为tan CECDE CD∠=，已知2AB CD =，因此，只需求出AB 与CE 的比值即可．不妨设1CD =，则2AB =．在Rt ABF △中，90A ∠=︒，30ABF ∠=︒，所以cos30AB BF ==︒．在Rt BEF △中，90BEF ∠=︒，45BFE ∠=︒，所以2cos 452BE BF =︒==在Rt BEC △中，90EBC ∠=︒，60ECB ∠=︒，42sin 603BE CE ===︒，所以42tan 3CE CDE CD ∠==．11．如图所示．在锐角ABC △中，4sin 5B =，tan 2C =，且10ABC S =△．求BC．解析作AD BC ⊥于D ，设AD x =，在Rt ABD △中，因为4sin 5B =，所以3cos 5B ==，所以sin 4tan cos 3B B B ==，所以43AD BD =，34BD x =．在Rt ADC △中，因为tan 2AD C DC ==，所以22AD x CD ==，所以35424x BC BD CD x x =+=+=．①因为1102ABC S BC AD =⨯=△，所以151024x x ⨯⋅=，所以4x =．由①知5454BC =⨯=．评注在一般三角形中，在适当位置作高线，将其转化为直角三角形求解，这是解斜三角形常采用的方法．12．如图所示．在ACD △中，45A ∠=︒，5CB =，7CD =，3BD =．求CBD ∠及AC．解析作CE AD ⊥于E ，设CE x =，BE y =，则有()2222225 , 37. x y x y ⎧+=⎪⎨++=⎪⎩①②②-①得22697524y +=-=，所以52y =．因为2x =，所以512cos 52BE CBE CB ∠===，所以60CBE ∠=︒，18060120CBD ∠=︒-︒=︒，所以5356sin 4522CE AC ==︒．13．如图，已知ABC △中，1AB =，D 是AB 的中点，90DCA ∠=︒，45DCB ∠=︒．求BC 的长．解析作BE AC ⊥B ，交AC 的延长线于E ，设BC x =．则sin 45BE BC =⨯︒=，cos 45CE BC =⋅︒=由DC BE ∥，D 是AB 的中点，知2AE EC ==．而222AE BE AB +=，得221+=．即x =，所以BC =．评注通过构造直角三角形，使用三角函数、勾股定理等知识将边角联系起来是求线段长的常用方法．14．如图，ABC △中，90ACB ∠=︒，CD AB ⊥于D ，DE AC ⊥于E ，DF BC ⊥于F ．求证：33AE AC BF BC =．解析ADE ACD B ∠=∠=∠，而tan AE ADE DE ∠=，tan ED ACD EC ∠=，tan DFB BF=，所以tan AE ED DFB DE EC FB===，又DF EC =，所以3tan AE ED EC B DE EC BF ⋅⋅=，所以3tan AEB BF=．又tan ACB BC=，所以33AE AC BF BC =．15．如图，在ABC △中，90A ∠=︒，AB AC =，M 是AC 边的中点，AD 垂直于BM 且交BC 于D ．求证：AMB CMD ∠=∠．解析作DF AC ⊥于F ，不妨设3AB =，因AD BM ⊥，90BAM ∠=︒，所以DAF ABM ∠=∠．又112tan 2AC MA ABM AB AB ∠===．1tan 2DF DAF FA ∠==．又90BAC ∠=︒，AB AC =，45C ∠=︒，而90DFC ∠=︒，故FC FD =．由于12FC FA =，而3FC FA +=，1FC =，2FA =，而32MC =，31122FM =-=，1FD =，即1tan 212FD CMD FM ∠===，又tan 2AB AMB AM ∠==，AMB ∠，CMD ∠是锐角．因此AMB CMD ∠=∠．16．如图（a ），正方形ABCD的边长E 、F 分别是AB 、BC 的中点，AF 分别交DE 、DB 于点M 、N ，求DMN △的面积．解析记正方形ABCD 的边长为2a ．由题设易知BFN △∽DAN △，则有21AD AN DN BF NF BN ===，得2AN NF =，所以23AN AF =．在直角ABF △中，2AB a =，BF a =，则AF ==，于是cos 5AB BAF AF ∠==．由题设可知ADE △≌BAF△，所以AED AFB ∠=∠，18018090AME BAF AED BAF AFB ∠=︒-∠-∠=︒-∠-∠=︒．于是cos AM AE BAF =⋅∠=，23MN AN AM AF AM =-=-=，从而415MND AFD S MN S AF ==△△．又()()212222AFD S a a a =⋅⋅=△，所以2481515MND AFD S S a ==△△．因a =8MND S =△．17．已知a 、b 、c 是ABC △三边的长，其中b a c >=，且方程20ax c +=两根的差的绝对值等．求ABC △中最大角的度数．解析由已知条件b a c >=可知，这是一个等腰三角形，且底边b 最长，则最大角为B ∠，求出ABC △中的底角A （或C ）即可．我们可以先求角A （或C ）的三角函数值，再确定角的大小，如图所示．由图知2cos 2b AD b A AB c c===，则关键是求出b 与c 的比值．通过一元二次方程中的条件，可得到关于c 、b 的方程，则问题得到解决．因为a c =，所以方程为20cx c +=．设1x 、2x 为方程的两个根，则有122b x x c +=，121x x =．因为12x x -=，()2122x x -=，即()2121242x x x x +-=，所以2242c ⎛⎫-= ⎪ ⎪⎝⎭，c =，b c =，所以cos 22b A c ==，所以30A ∠=︒，所以1803030120B ∠=︒-︒-︒=︒．评注这是一道方程与几何知识的综合题．三角形的边是一元二次方程的系数，利用方程条件导出边的关系，由边的关系再进一步求角的大小．18．如图，AB 是圆的直径，弦CD AB ∥，AC 与BD 相交于E ，已知AED θ∠=，试求:CDE ABE S S △△．解析由AB CD ∥，得CDE △∽ABE △．所以22::CDE ABE S S DE BE =△△．连结AD ，则90ADB ∠=︒．故由Rt ADE △，有cos DE AEθ=，又AE BE =，所以2:cos CDE ABE S S θ=△△．19．如图所示，已知电线杆AB 直立于地面上，它的影子恰好照在土坡的坡面CD 和地面BC 上．如果CD 与地面成45︒，60A ∠=︒，4m CD =，(m BC =-，求电线杆AB 的长（精确到0.1m ）．解析如图，延长AD 交地面于点E ，过点D 作DF CE ⊥于点F ．因为45DCF ∠=︒，60A ∠=︒，4CD =，所以2sin 4542CF DF CD ==︒=⨯=，tan 60EF DF =︒==．因为3tan 303AB BE =︒=，所以(()8.5m 33AB BE ==++⨯=≈．20．如图，某岛S 周围42海里内存在着大量的暗礁．现在一轮船自西向东以每小时15海里的速度航行，在、A 处测得S 在北偏东60︒，2小时后在B 处测得S 在正东北方向，试问轮船是否需要改变航行方向行驶，才能避免触礁危险，说明理由．解析若设船不改变航向，与小岛S 的最近距离为SC ．则有tan 60tan 45152SC SC ︒-︒=⨯，解得1542SC =<．因此需要改变航向，以免触礁．21．如图，某污水处理站计划砌一段截面为等腰梯形的排污渠，如果渠深为h ，截面积为S ，试求当倾角θ为多少时造价最小？解析要使造价最小，只需考虑AD DC CB ++最小，故首先设法用h 、S 、θ表示AD DC CB ++．()()()1122cot cot 22S AB CD h CD h h CD h h θθ=+=+=+．有cot S CD h h θ=-，则2AD DC CB AD CD ++=+2cot sin h S h θθ⎛⎫=+- ⎪⎝⎭()2cos sin h S hθθ-=+．因S 、h 为常数，则要求AD DC CB ++的最小值，只需求2cos sin m θθ-=的最小值．设2cos sin m θθ-=，两边平方整理得()()2221cos 4cos 40m m θθ+---=，cos θ=由上式知()2230m m -≥，解得m m =时，2cos sin θθ-有最小值．当m =时，221cos 12m θ==+，从而得60θ=︒，此时排污渠造价最小．。

锐角三角函数与解直角三角形复习题

解直角三角形复习题学生版（一）锐角三角函数定义1. 如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC 的三个顶点在图中相应的格点上，则 tan ∠ACB 的值为（）.A ．1B ．13 C ．12D ． 222．已知()310cos 2=︒-α，则锐角α的度数是 °．3．如图,在平面直角坐标系中,点A 的坐标为（4,3）,那么cos α的值是A ．35B ．45C ．34D ．434．已知：2cos 10α-=，则锐角α= 45° ． 5．在Rt △ABC 中，∠C =90°，1sin 3A =，则B cos 等于 A ．13 B ．23 C ． 103 D ．2236. 在ABC ∆中，,135sin ,900==∠A C 则=A tan （） A 1312 B 135 C 125 D 12137. 如图，A 、B 、C 三点在正方形网格线的交点处.若将△ACB 绕着点A 逆时针旋转得到△''AC B ，则tan 'B 的值为( )A. 14B. 13C. 12D. 18．已知：ABC △中，︒=∠90C ，52cos =B ,15=AB ，则BC 的长是A ． 213B ．293C ．6D ． 32（二）三角函数与根式、绝对值、幂的混合运算1．计算：26tan 303sin60cos45︒-︒-︒．2．计算：︒+︒︒-60tan 45tan 60sin 12．3．计算：︒︒︒︒+⋅-60tan 45sin 45cos 30sin ．4. 计算：2cos30sin 45tan 60︒+︒-︒.5．计算： oo o o 245tan 30cos 30tan 60sin +⋅-6．计算：︒+︒-︒+︒60tan 30cos 60sin 45sin 22. （第6题）7．01)12(45cos 2260sin 3--︒-+︒- 8． ()112cos30201032-⎛⎫︒--++- ⎪⎝⎭.9．计算：2cos60tan 45sin 45sin30︒-︒+︒︒. 10．计算：182cos 45-︒-0(2010)-11()5--．11．()0114.360sin 61251--︒+--⎪⎭⎫ ⎝⎛--π．12．计算011122cos30(31)()2--︒+-- ．13. 计算201()(1)2sin 60122π-++-︒+．14． ()001201030cos 4112+⋅⎪⎭⎫⎝⎛--- 15．01)3()21(60sin 227-+-+︒--π．16． .12)21(60tan 1)2(1+-----π 17． 4145sin 21822--︒+--- 18． 30cos 1212)21(02+---+--）（． 19. 0(3)π-++︒60tan 227)31(2--.20．︒+-+-60sin 223282321． tan 452sin 304cos 45︒-︒+︒(二)解直角三角形1．如图，在ABC Rt ∆中，b a 、分别是A ∠、B ∠的对边， c 为斜边，如果已知两个元素B ∠、a ，就可以求出其余三个未知元素A c b ∠、、.⑴求解的方法有多种，请你按照下列步骤，完成一种求解过程：（第1题图）用关系式求出第一步：用关系式求出第二步：用关系式求出第三步：⑵请分别给出B ∠、a 的一个具体数值，然后按照⑴中的思路，求出A c b ∠、、的值.由条件： a 、B ∠ 由条件： a、B ∠ 由条件： a 、B ∠ 90=∠+∠B AbcACBDDCBAD CBA 2. 如图，在Rt ABC △中，90ACB CD AB =⊥，∠于点D ．已知5AC =sin ACD ∠=53。