A star算法
A-star算法

A*算法
A* [1](A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是许多其他问题的常用启发式算法。
注意——是最有效的直接搜索算法,之后涌现了很多预处理算法(如ALT,CH,HL等等),在线查询效率是A*算法的数千甚至上万倍。
公式表示为:f(n)=g(n)+h(n),
其中,f(n) 是从初始状态经由状态n到目标状态的代价估计,
g(n) 是在状态空间中从初始状态到状态n的实际代价,
h(n) 是从状态n到目标状态的最佳路径的估计代价。
(对于路径搜索问题,状态就是图中的节点,代价就是距离)
h(n)的选取
保证找到最短路径(最优解的)条件,关键在于估价函数f(n)的选取(或者说h(n)的选取)。
我们以d(n)表达状态n到目标状态的距离,那么h(n)的选取大致有如下三种情况:
1. 如果h(n)< d(n)到目标状态的实际距离,这种情况下,搜索的点数多,搜索
范围大,效率低。
但能得到最优解。
2. 如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路
径进行,此时的搜索效率是最高的。
3. 如果h(n)>d(n),搜索的点数少,搜索范围小,效率高,但不能保证得到最
优解。
[2]。
A_star算法(A算法经典译文)

GameRes游戏开发资源网 Amit's A star Page中译文译序这篇文章很适合A*算法的初学者,可惜网上没找到翻译版的。
本着好东西不敢独享的想法,也为了锻炼一下英文,本人译了这篇文章。
由于本人英文水平非常有限,六级考了两次加一块不超过370分,因此本译文难免存在问题。
不过也算是抛砖引玉,希望看到有更多的游戏开发方面的优秀译作出现,毕竟中文的优秀资料太少了,中国的游戏开发者的路不好走。
本人能力有限,译文中有小部分词句实在难以翻译,因此暂时保留英文原文放在译文中。
对于不敢确定翻译是否准确的词句,本人用圆括号保留了英文原文,读者可以对照着加以理解。
A*算法本身是很简单的,因此原文中并没有过多地讨论A*算法本身,而是花了较大的篇幅讨论了用于保存OPEN和CLOSED集的数据结构,以及A*算法的变种和扩展。
编程实现A*是简单的,读者可以用STL对本文中的伪代码加以实现(本人已花一天时间实验过基本的A*搜索)。
但是最重要的还是对A*本身的理解,这样才可以在自己的游戏中处理各种千变万化的情况。
翻译本文的想法产生于2006年5月,实际完成于2007年4月到6月,非常惭愧。
最后,本译文仅供交流和参考,对于因本译文放到网上而产生的任何问题,本人不负任何责任。
蔡鸿于南开大学软件学院2007年6月9日原文地址:/~amitp/GameProgramming/相关链接:/%7Eamitp/gameprog.html#Paths我们尝试解决的问题是把一个游戏对象(game object)从出发点移动到目的地。
路径搜索(Pathfinding)的目标是找到一条好的路径——避免障碍物、敌人,并把代价(燃料,时间,距离,装备,金钱等)最小化。
运动(Movement)的目标是找到一条路径并且沿着它行进。
把关注的焦点仅集中于其中的一种方法是可能的。
一种极端情况是,当游戏对象开始移动时,一个老练的路径搜索器(pathfinder)外加一个琐细的运动算法(movement algorithm)可以找到一条路径,游戏对象将会沿着该路径移动而忽略其它的一切。
A-STAR算法说明

序:搜索区域假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。
为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。
他们完全可以是矩形,六角形,或者其他任意形状。
节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。
我们使用这种系统,无论如何,因为它是最简单的。
开始搜索正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。
在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:1,从点A开始,并且把它作为待处理点存入一个“开启列表”。
开启列表就像一张购物清单。
尽管现在列表里只有一个元素,但以后就会多起来。
你的路径可能会通过它包含的方格,也可能不会。
基本上,这是一个待检查方格的列表。
2,寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。
也把他们加入开启列表。
为所有这些方格保存点A作为“父方格”。
当我们想描述路径的时候,父方格的资料是十分重要的。
后面会解释它的具体用途。
3,从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
在这一点,你应该形成如图的结构。
在图中,暗绿色方格是你起始方格的中心。
它被用浅蓝色描边,以表示它被加入到关闭列表中了。
所有的相邻格现在都在开启列表中,它们被用浅绿色描边。
a星算法 贝塞尔曲线平滑处理

a星算法贝塞尔曲线平滑处理
A*算法(A-star algorithm)是一种常用于图搜索和路径规划的算法。
它通过在图中沿着最有可能的路径搜索目标来找到最短路径。
贝塞尔曲线平滑处理(Bezier curve smoothing)是一种用于将曲线变得更加平滑的方法。
它使用贝塞尔曲线的特性,通过调节控制点来调整曲线的形状,从而实现平滑效果。
在路径规划中,可以将A*算法和贝塞尔曲线平滑处理结合起来,以使路径在地图中更加平滑和自然。
具体步骤如下:
1. 使用A*算法计算出起点到终点的最短路径。
2. 将最短路径的关键点作为贝塞尔曲线的控制点。
3. 通过调整控制点的位置和权重,使贝塞尔曲线与最短路径更好地拟合。
4. 使用贝塞尔曲线生成平滑路径,并将其作为最终路径。
这样做可以消除路径中的尖角和突变,使得路径更加平滑和易于理解。
同时,通过调整贝塞尔曲线的权重和控制点,还可以实现路径的进一步优化和调整,以适应具体的需求。
A-star-算法-八数码问题-C++-报告+代码+详细注释1
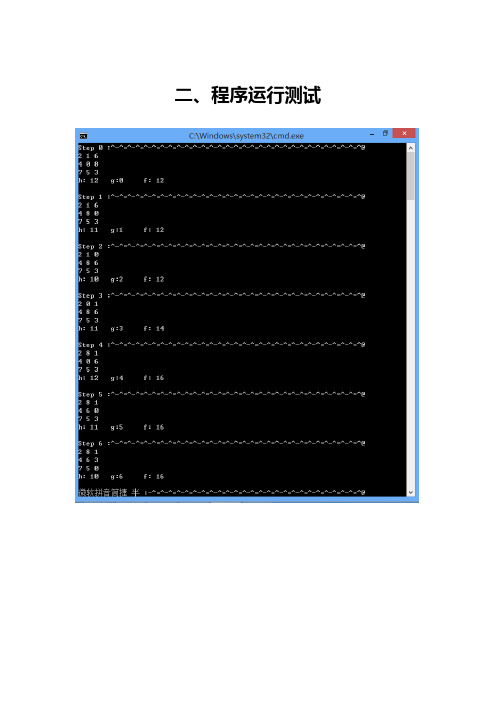
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。
距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。
距离越小, 该节点的效果越好。
某个状态所有将牌到目标位置的距离之和用“h值”表示。
2.主要函数2.1countH(state & st);countH函数功能是计算st状态的h值。
2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置(位置 = 行下标 * 3 + 列下标)。
2.3f(state * p);f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。
2.6search(state & start);在open表不为空时, 按f值由小到大对open表中元素进行排序。
调用findZero()函数找到0值元素的位置。
空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。
确定某方向可走后, 空格移动一步, 生成状态p’。
2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据;检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。
2.8重复的执行这个过程, 直到某状态的h值为零。
2.9dump_solution(state * q);在终端输出解路径。
// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等(对应位置元素相等), 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。
点到点的最短路径算法

点到点的最短路径算法
点到点的最短路径算法在计算机科学中是一个非常常见的问题,其主要用于在图中找到从一个点到另一个点的最短路径。
以下是一些常见的最短路径算法:
1. Dijkstra算法:这是一种用于在图中查找单源最短路径的算法。
其主要思想是从源点开始,每次从未访问过的节点中选择距离最短的节点,然后更新其邻居节点的距离。
这种算法不能处理负权重的边。
2. Bellman-Ford算法:这种算法可以处理带有负权重的边,并且可以找到从源点到所有其他节点的最短路径。
其主要思想是通过反复松弛所有边来找到最短路径。
如果图中存在负权重的循环,则该算法可能无法找到最短路径。
3. Floyd-Warshall算法:这是一种用于查找所有节点对之间的最短路径的算法。
其主要思想是通过逐步添加中间节点来找到最短路径。
这种算法的时间复杂度较高,为O(n^3),其中n是图中的节点数。
4. A(A-Star)算法:这是一种启发式搜索算法,用于在图中找到最短路径。
它使用启发式函数来指导搜索方向,通常可以更快地找到最短路径。
A算法的关键在于启发式函数的选择,该函数应该能够准确地估计从当前节点到目标节点的距离。
这些算法都有其各自的优点和缺点,具体选择哪种算法取决于具体的问题和场景。
A_star算法及其研究

.引言图论是计算机科学中的一个重要研究工具,它产生于欧拉(Euler)对图的连通性的研究,但直到本世纪计算机诞生以后才得最迅猛的发展。
图论中的最短路径问题在计算机中有着广泛的应用,例如网络通信中最短路由的选择,人工智能中搜索算法的研究等。
本文对几种常见最短路径的算法进行介绍,尤其是在1968年发展起来的A*算法。
二.常用算法简介为叙述的方便,本文中假定所有图均以邻接矩阵表示,并将图论中的常用符号列于下:G---------------------无向图或有向图]----------------图G的邻接矩阵表示A=[aijV(G)------------------图G的顶点数ε(G)-----------------图G的边数。
1.Floyd算法这是几种最短路径算法中最简单的一种,本文不详细介绍,仅给出算法描述。
算法:For k:=1 to n doFor i:=1 to n doFor j:=1 to n doIf A[i,j]+A[k,j]<A[i,j] thenA[i,j]=a[i,k]+a[k,j];易知该算法的复杂度为o(n3)。
执行该算法后矩阵A中aij即为点i与点j间的最短路径,若要求路径的具体行程,需在算法中以数组保存路径的改变信息,这里不再介绍。
2.Dijkstra算法这种算法是Dijkstra于1959年提出的,主要用于计算图G中的某一点u到其它点的最短距离。
算法:Step1:令l(u0)=0;l(v)=∞;v≠uS 0={u};v=0;Step2:"vÎ┑Si =V(G)-Sil(v)=min{l(v),l(uI )+ω(ui,v)}设uI+1是使l(v)取到最小值的┑Si中的点。
令Si+1=Si∪{ui+1}Step3:If i=γ(G)-1 then Stop.If i<γ(G)-1 then i=i+1,Goto Step2.该算法的复杂度为o(n2)。
a星算法资料

A星算法A星算法是一种常用的路径规划算法,它可以在很多领域得到应用,如游戏开发、机器人导航等。
本文将介绍A星算法的原理、实现过程以及应用场景。
原理A星算法是一种启发式搜索算法,用于寻找从起点到目标点的最佳路径。
它基于Dijkstra算法和最小堆叠加了启发式因子来加速搜索过程。
A星算法在搜索过程中维护两个集合:开放集合和关闭集合。
开放集合存储待探索的节点,而关闭集合存储已经探索过的节点。
算法的核心思想是维护每个节点的估价函数f值,其中f值由节点到目标点的实际代价g值和节点到目标点的启发函数h值组成。
在每一步中,算法从开放集合中选择f值最小的节点进行拓展,并更新其邻居节点的f值。
实现过程1.初始化起点,并将其加入开放集合中,设置启发函数h值为起点到目标点的估计代价。
2.重复以下步骤直到目标节点被加入关闭集合:–从开放集合中选择f值最小的节点,将其加入关闭集合。
–针对选定节点的每个邻居节点,计算其新的f值并更新。
–如果邻居节点不在开放集合中,将其加入开放集合。
3.构建路径,反向回溯从目标节点到起点的最佳路径。
应用场景•游戏开发:A星算法可以用来实现游戏中的AI寻路,使NPC角色能够智能地避开障碍物。
•机器人导航:A星算法可以帮助机器人避开障碍物,规划出最优的路径来到目标点。
•交通规划:A星算法可以用来优化城市道路的规划,减少交通拥堵,提高车辆通行效率。
•资源调度:A星算法可以帮助企业在多个资源之间寻找最佳路径,提高资源利用率。
总之,A星算法在许多领域都有着广泛的应用,它的高效性和可扩展性使其成为一种非常有力的路径规划工具。
结语A星算法是一种非常经典的路径规划算法,其优秀的性能和广泛的应用使其成为计算机科学领域的重要研究内容。
希望本文介绍的内容对读者有所帮助,让大家更加深入了解A星算法的原理和应用。
astar寻路算法原理 -回复

astar寻路算法原理-回复A*寻路算法原理及步骤一、简介A*(A-Star)寻路算法是一种常用的路径规划算法,用于找到两个点之间的最短路径。
它综合了Dijkstra算法和贪心算法的优点,既考虑了每个节点的代价,也考虑了每个节点到目标节点的预估代价。
本文将一步一步详细介绍A*寻路算法的原理和步骤。
二、原理A*算法的核心思想是使用一个估算函数来预测从起始节点到目标节点的代价,并在遍历过程中选择最小代价节点来进行扩展。
该算法综合了代价函数和启发函数的信息,以更快地找到最短路径。
其具体步骤如下:1. 初始化将起始节点添加到一个开放列表(open list)中,开放列表存放待扩展的节点。
同时,创建一个空的闭合列表(closed list),用于存放已扩展过的节点。
2. 循环操作进入循环操作,直到开放列表为空或找到目标节点。
在每次循环中,选择开放列表中代价最小的节点进行扩展。
3. 节点扩展取开放列表中代价最小的节点,将其从开放列表中删除,并加入到闭合列表中。
然后,获取该节点的相邻节点,计算它们的代价和预估代价,并更新它们的代价值和路径。
4. 判断相邻节点对于每个相邻节点,判断它们是否在开放列表或闭合列表中。
若在闭合列表,则跳过该节点;若在开放列表,比较新路径与旧路径的代价,若新路径更好,则更新代价和路径;否则,不做任何操作。
5. 添加新节点对于不在开放列表中的相邻节点,将它们添加到开放列表中,并计算它们的代价和预估代价。
6. 重复操作重复步骤2至5,直到开放列表为空或找到目标节点。
若开放列表为空,则无法找到路径;若找到目标节点,则回溯路径,回到起始节点。
三、关键要点在上述步骤中,有几个关键要点需要注意:1. 代价函数代价函数用于计算节点到起始节点的实际代价,包括走过的距离、障碍物等影响因素。
根据具体情况,可以自定义代价函数。
2. 启发函数启发函数用于估算节点到目标节点的代价,即预测代价。
常见的启发函数有曼哈顿距离、欧几里得距离等,根据实际情况选择合适的启发函数。
[Unity]A-Star(A星)寻路算法
![[Unity]A-Star(A星)寻路算法](https://img.taocdn.com/s3/m/7965322f4a35eefdc8d376eeaeaad1f3469311ef.png)
[Unity]A-Star(A星)寻路算法在游戏中,有⼀个很常见地需求,就是要让⼀个⾓⾊从A点⾛向B点,我们期望是让⾓⾊⾛最少的路。
嗯,⼤家可能会说,直线就是最短的。
没错,但⼤多数时候,A到B中间都会出现⼀些⾓⾊⽆法穿越的东西,⽐如墙、坑等障碍物。
这个时候怎么办呢?是的,我们需要有⼀个算法来解决这个问题,算法的⽬标就是计算出两点之间的最短路径,⽽且要能避开障碍物。
百度百科:A*搜寻算法俗称A星算法。
这是⼀种在图形平⾯上,有多个节点的路径,求出最低通过成本的算法。
常⽤于游戏中的NPC的移动计算,或线上游戏的BOT的移动计算上。
简化搜索区域要实现寻路,第⼀步我们要把场景简化出⼀个易于控制的搜索区域。
怎么处理要根据游戏来决定了。
例如,我们可以将搜索区域划分成像素点,但是这样的划分粒度对于⼀般的游戏来说太⾼了(没必要)。
作为代替,我们使⽤格⼦(⼀个正⽅形)作为寻路算法的单元。
其他的形状类型也是可能的(⽐如三⾓形或者六边形),但是正⽅形是最简单并且最常⽤的。
⽐如地图的长是w=2000像索,宽是h=2000像索,那么我们这个搜索区域可以是⼆维数组 map[w, h], 包含有400000个正⽅形,这实在太多了,⽽且很多时候地图还会更⼤。
现在让我们基于⽬前的区域,把区域划分成多个格⼦来代表搜索空间(在这个简单的例⼦中,20*20个格⼦ = 400 个格⼦,每个格式代表了100像索):既然我们创建了⼀个简单的搜索区域,我们来讨论下A星算法的⼯作原理吧。
我们需要两个列表 (Open和Closed列表):⼀个记录下所有被考虑来寻找最短路径的格⼦(称为open 列表)⼀个记录下不会再被考虑的格⼦(成为closed列表)⾸先在closed列表中添加当前位置(我们把这个开始点称为点 “A”)。
然后,把所有与它当前位置相邻的可通⾏格⼦添加到open列表中。
现在我们要从A出发到B点。
在寻路过程中,⾓⾊总是不停从⼀个格⼦移动到另⼀个相邻的格⼦,如果单纯从距离上讲,移动到与⾃⾝斜对⾓的格⼦⾛的距离要长⼀些,⽽移动到与⾃⾝⽔平或垂直⽅⾯平⾏的格⼦,则要近⼀些。
A-Star算法详解

B
34 30 24 20 14 30 10 40 14 50
→ → ↘ 38 40 34 30 38 40
44
44
50
↓
78
↗
58
↗
→ ← 14 50 10 60 14 70
50 64
A
↑
↙ 10 60
64
70 84
↗
70
↖
11.
第三次搜索: 1.遍历open list,找到其中F值 最小的方格。称其为选定方格。 这里会遇到两个问题: 当前open list中最小的F值为 50,但这两个方格均不经过已 经确定好的路径(红色格 子),所以需要重新选择路 径。 有两个F值为50的格子,选择 与目标点B直线距离最近的那 个。如果直线距离都相同,则 从时间角度上选择最后加入 open list 的那个格子。 综上,新选择的格子如图所示:
64 64
84 94
44 58
44
50
↓
↗
→ ← 14 50 10 60 14 70
50
64
A
↑
↙ ↖ 10 60
70
84
↗
70
↖
A*算法总结:
17.
1.把起始点加入 open list; 2.查找起始点周围所有可到达或者可通过的方格,把他们加入 open list。将 起始点设置为新加入的方格的父节点。 3.将起始点从open list中删除,加入close list中。 4.重复如下步骤: ①遍历open list,找到其中F值最小的方格。称其为选定方格。 ②对选定方格做如下操作:
↗
70
↖
15.
第n次搜索: 图中F值最小的格子为58,将其 选定,继续重复如上操作。 直至到达目标点B。 如图所示:
a star 原理

a star 原理A*算法原理引言:A*算法是一种常用于图搜索和路径规划的启发式搜索算法。
它在寻找最短路径或最优解问题中具有广泛的应用。
本文将介绍A*算法的原理及其应用。
一、A*算法的原理A*算法是一种基于图的搜索算法,它通过评估每个节点的代价函数来选择最优路径。
该算法结合了最短路径算法和贪心算法的特点,既具有较高的效率,又能够保证找到最优解。
A*算法的核心思想是维护两个列表:开放列表和关闭列表。
开放列表用于存储待扩展的节点,而关闭列表用于存储已经扩展过的节点。
算法从起始节点开始,将其加入到开放列表中,并计算该节点的代价函数值。
然后,从开放列表中选择代价函数值最小的节点进行扩展。
对于每个扩展的节点,算法计算其邻居节点的代价函数值,并将其加入到开放列表中。
重复这个过程,直到到达目标节点或者开放列表为空。
在计算节点的代价函数值时,A*算法使用了启发式函数来估计从当前节点到目标节点的代价。
这个启发式函数通常使用曼哈顿距离或欧几里得距离来计算。
通过启发式函数的引导,A*算法能够优先扩展那些距离目标节点更接近的节点,从而提高搜索效率。
二、A*算法的应用A*算法在路径规划、游戏AI等领域有着广泛的应用。
1.路径规划:在地图导航、无人驾驶等应用中,A*算法可以用于寻找最短路径。
通过将地图抽象成图的形式,可以使用A*算法找到从起点到终点的最优路径。
2.游戏AI:在游戏中,A*算法可以用于计算NPC的移动路径。
通过设置合适的启发式函数,可以让NPC根据当前情况选择最优的移动路径。
3.智能机器人:在智能机器人领域,A*算法可以用于规划机器人的移动路径。
通过结合传感器数据和环境信息,可以实现机器人的自主导航和避障。
4.迷宫求解:A*算法可以用于解决迷宫问题。
通过将迷宫抽象成图的形式,可以使用A*算法找到从起点到终点的最短路径。
三、A*算法的优缺点A*算法具有以下优点:1.可以找到最优解:A*算法通过评估代价函数来选择最优路径,因此可以找到最短路径或最优解。
人工智能(A星算法)

(A星算法)本文档介绍了中的A星算法的详细内容。
A星算法是一种常用的搜索算法,用于求解图中路径问题。
本文将从算法原理、具体步骤以及优化方案等方面进行详细介绍。
1.算法原理A星算法是一种启发式搜索算法,通过估算每个节点到目标节点的代价来确定搜索的方向。
具体而言,A星算法使用了两个评估函数:g(x)表示从起始节点到当前节点的实际代价,h(x)表示从当前节点到目标节点的预估代价。
通过综合考虑这两个代价,选择最优路径进行搜索。
2.算法步骤2.1 初始化首先,创建一个空的开放列表用于存储待搜索的节点,以及一个空的关闭列表用于存储已搜索过的节点。
将起始节点添加到开放列表中。
2.2 循环搜索2.2.1 选择最优节点从开放列表中选择具有最小f(x) = g(x) + h(x)值的节点作为当前节点。
2.2.2 扩展相邻节点对当前节点的相邻节点进行扩展,计算它们的g(x)和h(x)值,并更新它们的父节点和f(x)值。
2.2.3 判断终止条件如果目标节点属于开放列表中的节点,则搜索结束。
如果开放列表为空,表示无法找到路径,搜索也结束。
2.2.4 更新列表将当前节点从开放列表中移除,并添加到关闭列表中,表示已经搜索过。
2.3 构建路径从目标节点开始,通过追踪每个节点的父节点,直到回溯到起始节点,构建出最优路径。
3.算法优化3.1 启发函数的选择选择合适的启发函数可以极大地影响算法的效率和搜索结果。
常用的启发函数有曼哈顿距离、欧几里得距离等。
根据具体问题的特点,选择合适的启发函数进行优化。
3.2 剪枝策略在节点扩展过程中,通过对相邻节点的估价值进行快速筛选,可以减少搜索的时间和空间开销。
根据具体问题的特点,设计合理的剪枝策略,减少无效节点的扩展。
4.附件本文档没有涉及附件内容。
5.法律名词及注释A星算法:是一种常用的搜索算法,用于求解图中路径问题。
目前该算法已经广泛应用于领域。
6.结束标识。
A星算法详解范文

A星算法详解范文
一、A星算法简介
A星算法是一种在图上寻找最短路径的算法,它结合了启发式,动态
规划和图论中的最短路径算法。
A星算法合并了确定性和启发式的优点,
既去发探索有可能的解决方案,又利用估计信息避免许多无用。
A星算法
因为不依赖于模型,被广泛用于路径规划,机器人,计算机视觉等领域。
二、A星算法的估价函数
A星算法是一种非常重要的启发式算法,主要的思想是通过估计函数
f(n)来代表当前状态n,这个函数应该反映从当前状态到目标状态的距离。
在A星算法中,f(n)代表的是什么呢?
A星算法的估价函数f(n)是一种有启发性的策略,它是状态n的“总
消费成本”,其计算公式为:f(n)=g(n)+h(n),其中,g(n)表示从起点到
当前状态n的实际成本,h(n)表示从当前状态n到目标状态的估计成本,
又称为启发函数。
三、A星算法的原理
A星算法以每个节点为中心,按照代价估计f(n)从小到大查找,从起
点开始,每次新扩展出最小f值的节点,如果该节点是终点,则找到了最
短路径,否则继续进行。
A星算法的策略主要有两种:一种是开放表open。
A星算法的简单原理

A星算法的简单原理A星算法(A* algorithm)是一种常用于路径规划的算法,它能够在图形中找到最短路径。
本文将详细介绍A星算法的原理及其实现过程。
一、A星算法的原理A星算法是一种启发式算法,它通过估计离目标节点最短距离来为每个节点评分,从而决定下一步应该扩展的节点。
A星算法通常用于二维图形中,其中每个节点都有一定的代价或权重。
1. 创建一个开放列表(open list)和一个关闭列表(closedlist)。
-开放列表用于保存可能成为最佳路径的节点。
-关闭列表用于保存已经扩展过的节点。
2.将起始节点添加到开放列表中,并设置其启发式评分(也称为f值)为0。
3.重复以下步骤,直到找到目标节点或者开放列表为空。
a.从开放列表中选择一个节点,称之为当前节点。
选择当前节点的依据是当前节点的f值最低。
b.将当前节点移到关闭列表中。
c.对当前节点的邻居节点进行遍历。
d.对于每个邻居节点,判断它是否在关闭列表中,如果是则忽略。
其父节点为当前节点。
同时计算邻居节点的f值、g值和h值。
-g值是起始节点到当前节点的实际代价。
-h值是当前节点到目标节点的估计代价,也称为启发式评估。
-f值是g值和h值的和,用于排序开放列表中的节点。
4.当找到目标节点时,可以通过遍历每个节点的父节点,从而最终得到最短路径。
5.如果开放列表为空,表示找不到目标节点,路径规划失败。
二、A星算法的实现1.定义节点类:节点类包含节点的坐标、父节点、g值和h值等属性。
2.创建开放列表和关闭列表:开放列表用于保存可能成为最佳路径的节点,关闭列表用于保存已经扩展过的节点。
3.初始化起始节点和目标节点,并将起始节点添加到开放列表中。
4.重复以下步骤,直到找到目标节点或者开放列表为空。
a.从开放列表中选择一个节点,称之为当前节点。
选择当前节点的依据是当前节点的f值最低。
b.将当前节点移到关闭列表中。
c.对当前节点的邻居节点进行遍历,计算邻居节点的f值、g值和h 值。
A star算法

A*(A-Star)算法是一种静态路网中求解最短路最有A star算法在静态路网中的应用效的方法。
公式表示为:f(n)=g(n)+h(n),其中f(n) 是节点n从初始点到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
如果估价值>实际值, 搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
编辑本段估价值与实际值越接近估价函数取得就越好例如对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy-ny)*(dy-ny));这样估价函数f在g值一定的情况下,会或多或少的受估价值h的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。
明显优于Dijstra算法的毫无无方向的向四周搜索。
conditions of heuristicOptimistic (must be less than or equal to the real cost)As close to the real cost as possible编辑本段详细内容主要搜索过程伪代码如下:创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值;将起点放入OPEN表;while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X)算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE) {if( X的估价值小于CLOSE表的估价值){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
A星算法详解-通俗易懂初学者必看

t(智乐圆入门1)A*(A星)算法(一)记得好象刚知道游戏开发这一行的时候老师就提到过A星算法,当时自己基础还不行,也就没有去看这方面的资料,前几天找了一些资料,研究了一天,觉的现在网上介绍A星算法的资料都讲的不够详细(因为我下的那个资料基本算是最详细的了- -但是都有一些很重要的部分没有说清楚....),所以我自己重新写一篇讲解A星算法的资料,还是借用其他资料的一些资源.不过转载太多了,只有谢谢原作者了:)我们将以下图作为地图来进行讲解,图中对每一个方格都进行了编号,其中绿色的方格代表起点,红色的方格代表终点,蓝色的方格代表障碍,我们将用A星算法来寻找一条从起点到终点最优路径,为了方便讲解,本地图规定只能走上下左右4个方向,当你理解了A星算法,8个方向也自然明白在地图中,每一个方格最基本也要具有两个属性值,一个是方格是通畅的还是障碍,另一个就是指向他父亲方格的指针(相当于双向链表结构中的父结点指针),我们假设方格值为0时为通畅,值为1时为障碍A星算法中,有2个相当重要的元素,第一个就是指向父亲结点的指针,第二个就是一个OPEN表,第三个就是CLOSE表,这两张表的具体作用我们在后面边用边介绍,第四个就是每个结点的F值(F值相当于图结构中的权值)而F = H + G;其中H值为从网格上当前方格移动到终点的预估移动耗费。
这经常被称为启发式的,可能会让你有点迷惑。
这样叫的原因是因为它只是个猜测。
我们没办法事先知道路径的长度,因为路上可能存在各种障碍(墙,水,等等)。
虽然本文只提供了一种计算H的方法,但是你可以在网上找到很多其他的方法,我们定义H 值为终点所在行减去当前格所在行的绝对值与终点所在列减去当前格所在列的绝对值之和,而G值为从当前格的父亲格移动到当前格的预估移动耗费,在这里我们设定一个基数10,每个H和G都要乘以10,这样方便观察好了,我们开始对地图进行搜索首先,我们将起点的父亲结点设置为NULL,然后将起点的G值设置为0,再装进open 表里面,然后将起点作为父亲结点的周围4个点20,28,30,38(因为我们地图只能走4个方向,如果是8方向,则要加个点进去)都加进open列表里面,并算去每个结点的H 值,然后再将起点从open列表删除,放进close表中,我们将放进close表的所有方格都用浅蓝色线条进行框边处理,所以这次搜索以后,图片变为如下格式,其中箭头代表的是其父结点其中每个格子的左下方为G值,右下方为H值,左上方为H值,我们拿28号格子为例来讲解一写F值的算法,首先因为终点33在4行7列,而28在4行2列,则行数相差为0,列数相差为5,总和为5,再乘以我们先前定的基数10,所以H值为50,又因为从28的父结点29移动到28,长度为1格,而29号为起点,G值为0,所以在父亲结点29的基础上移动到28所消耗的G值为(0 + 1) *10 = 10,0为父亲结点的G值,1为从29到28的消耗当前OPEN表中的值: 20,28,30,38 当前CLOSE表中的值: 29现在我们开始寻找OPEN列表中F值最低的,得出结点30的F值最低,且为40,然后将结点30从OPEN表中删除,然后再加入到CLOSE表中,然后在判断结点30周围4个结点,因为结点31为障碍,结点29存在于CLOSE表中,我们将不处理这两点,只将21和39号结点加入OPEN表中,添加完后地图变为下图样式当前OPEN表中的值: 20,28,38,21,39 当前CLOSE表中的值: 29,30接着我们重复上面的过程,寻找OPEN表中F值为低的值,我们发现OPEN表中所有结点的F值都为60,我们随即取一个结点,这里我们直接取最后添加进OPEN表中的结点,这样方便访问(因为存在这样的情况,所有从一个点到另外一个点的最短路径可能不只一条),我们取结点39,将他从OPEN表中删除,并添加进CLOSE表中,然后观察39号结点周围的4个结点,因为40号结点为障碍,所以我们不管它,而30号结点已经存在与OPEN表中了,所以我们要比较下假设39号结点为30号结点的父结点,30号结点的G值会不会更小,如果更小的话我们将30结点的父结点改为39号,这里我们以39号结点为父结点,得出30号结点的新G值为20,而30号结点原来的G值为10,并不比原来的小,所以我们不对30号进行任何操作,同样的对38号结点进行上述操作后我们也不对它进行任何操作,接着我们把48号结点添加进OPEN表中,添加完后地图变为下图样式当前OPEN表中的值: 20,28,38,21,48 当前CLOSE表中的值: 29,30,39以后的过程中我们都重复这样的过程,一直到遍历到了最后终点,通过遍历父结点编号,我们能够得出一条最短路径,具体完整的推导过程我就不写出来了,因为和刚才那几步是一样的,这里我再讲出一个特例,然后基本A星算法就没问题了上面的最后一推导中,我们在观察39号结点时,发现他周围已经有结点在OPEN表中了,我说"比较下假设39号结点为30号结点的父结点,30号结点的G值会不会更小,如果更小的话我们将30结点的父结点改为39号",但是刚才没有遇到G值更小的情况,所以这里我假设出一种G值更小的情况,然后让大家知道该怎么操作,假设以39号为父结点,我们得出的30号的新G值为5(只是假设),比30号的原G值10还要小,所以我们要修改路径,改变30号的箭头,本来他是指向29号结点的,我们现在让他指向39号结点,38号结点的操作也一样好了,A星算法的大体思路就是这样了,对于8方向的地图来说,唯一的改变就是G 值方面,在上下左右,我们的G值是加10,但是在斜方向我们要加14,其他的和上面讲的一样~~~:)PS: 今天下午去天门网络面试,我竟然连简历都没带- -空着个手带了个人就去了....都不晓得我当时杂想的...汗(智乐圆入门2)终于把A*寻路算法看懂了,虽然还有点小问题,但A*寻路算法我已经略知一二,帮助还不知道的朋友进入A*算法入门阶级,应该不成问题,下面就来看看A*算法的原理(以下讲解不带入任何程序语言,因此只要你看懂了下面所有的话,那么你可以随意用在任意程序语言中)在下也是初学,写这篇文章的目的只是让新手入门,因此高手看到这就飘过吧,当然愿意给予指点的高手请继续往下看前言:在文中可能会出现一些专业术语或者是我信口雌黄的话语,未免看官不明白,前面我先加以注解,具体意思可以从文中体会到方格:一个一个的小方块障碍物:挡着去路的东西目标方格:你想到达的方格操控方格:你控制的寻路对象标记:临时为某一个方格做的标记父标记:除了操控方格所创建的临时标记,每个标记都有个父标记,但父标记不是随便乱定的,请看下文开启标记列表:当该标记还未进行过遍历,会先加入到开启标记列表中关闭标记列表:当该标记已经进行过遍历,会加入到关闭标记列表中路径评分:通过某种算法,计算当前所遍历的标记离目标方格的路径耗费估值(后面会讲一种通用的耗费算法)首先描述一个环境,在一望无际的方格中,我身处某某方格,如今我想去某某方格,接下来我开始寻路!在脑海中,先创建开启标记列表、关闭标记列表,然后把我的初始位置设置为开始标记进行遍历,同时因为开始标记已经遍历过了,因此把开始标记加入到关闭列表。
A_start路径算法

A* (路径搜索)算法导引前言:A*算法是路径搜索中的经典算法,也是公认的最优算法之一,网上找到一篇文章讲的很好,适合入门,所以翻译了一下,没有完全参照原文,主要还是意译,网上也有其他人翻译好的,个人觉得还是自己来一遍比较好,读者自斟:原文开始:搜索区域这里假设有人要从A点去往B点,另外有一面墙将两者分开。
如下图所示,绿色方块代表A点,红色方块代表B点,蓝色代表分开他们的墙。
图一首先要注意的是我们这里先将整个搜索区域网格化,以方便路径搜索。
这一方法将搜索区域简化为一个简单的2为数组。
数组的每个元素代表网格上的一片区域,并且标记为可通过或不可通过两种状态。
路径由从A点到达B点所经过的方块来表示。
这些点被称为节点。
之所以不直接叫方块是因为区域可以被划分为矩形,六边形,等。
而点也不一定是在中心,可以在边缘或其他地方。
开始搜索一旦我们如上图将搜索区域网格化,将之转化为可操作数量的节点,然后下一步就是找到一个搜索算法找出最短路径。
我们从A点出发,搜索递归周围领域,直到到达目标点开始搜索的步骤如下:1. 从A点出发并且将其放入到“候选列表”备用。
候选列表就像就像是购物清单。
现在上面只有一项在清单上,但我们会陆续添加。
其中包含一些潜在的路径点。
基本上,这个列表包含有待确认的方块。
2. 找到与起始点相邻的所有可到达方块,忽略那些墙,水等其他非法区域。
将这些点加入到“候选列表”,存入方法与先前父方块A的存入方法相同。
这些父方块会在我们进行路径跟踪回溯的时候派上用场。
3. 从“候选列表”中将A方块删除,并将其加入到“排除列表”,表明在此列表中的方块不需要再去关注。
关于这点,如下图所示,中间的方块是起始点,它周围的亮蓝色边框表明此方块一经被加入到“排除列表”。
所有在“候选列表”上的方块都需要进一步检查,他们的边框呈现亮绿色。
每一个里面都有一个箭头指向其父节点,这里是起始方框。
图2接下来,我们在选择“候选列表”中的一个领域然后大致上重复刚才的步骤,如下所述。
Unity的A-Star算法在游戏中的实现

Unity的A-Star算法在游戏中的实现Unity 的A-Star 算法在游戏中的具体实现寻路算法在游戏开发中有着广泛的应用,广泛应用的寻路算法有三种:迪杰斯特拉算法、A-Star算法、BFS。
迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。
是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。
迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止广泛应用于单源最短路径问题上。
A-Star 搜寻算法俗称A星算法。
A-Star 算法是比较流行的启发式搜索算法之一,被广泛应用于路径优化领域。
它的独特之处是检查最短路径中每个可能的节点时引入了全局信息,对当前节点距终点的距离做出估计,并作为评价该节点处于最短路线上的可能性的量度。
BFS(Bi-Directional Breadth-First-Search)双向广度优先搜索算法,数据结构的书中对此有详细的介绍。
在这三种算法中A-Star 算法在游戏开发中使用最为广泛。
这里主要介绍的就是A-Star 算法在游戏开发中的实际应用。
AStar 算法思想A* 搜索算法结合了基于广度搜索的迪杰斯特拉算法的BFS 最佳优先搜索优点的最短路径算法。
其思想是将节点的邻近节点加入带处理的队列中,通过某个评估函数,依据函数有优先级的对处理队列中的节点进行评估。
公式表示为:F(n)=G(n)+H(n)。
其中F(n) 是从初始状态经由状态n 到目标状态的代价估计,G(n) 是某个状态空间中从开始的状态到状态n 实际所要付出的代价,(n) 从状态n 到目标状态的最优路径估计的代价。
实际使用当中在地图当中找到所需的目标节点。
首先要将节点分为四类:可通过节点、不可通过节点、开始节点、目标节点。
两种队列:开启队列(open-list)、关闭队列(close-list)。
开启队列的内容:开启队列里面是一些可能构成最短路径的节点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A*(A-Star)算法是一种静态路网中求解最短路最有A star算法在静态路网中的应用效的方法。
公式表示为:f(n)=g(n)+h(n),其中f(n) 是节点n从初始点到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
如果估价值>实际值, 搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
编辑本段估价值与实际值越接近估价函数取得就越好例如对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy-ny)*(dy-ny));这样估价函数f在g值一定的情况下,会或多或少的受估价值h的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。
明显优于Dijstra算法的毫无无方向的向四周搜索。
conditions of heuristicOptimistic (must be less than or equal to the real cost)As close to the real cost as possible编辑本段详细内容主要搜索过程伪代码如下:创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值;将起点放入OPEN表;while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X)算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE) {if( X的估价值小于CLOSE表的估价值){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
}//end while(OPEN!=NULL)保存路径,即从终点开始,每个节点沿着父节点移动直至起点,这就是你的路径;编辑本段启发式搜索其实有很多的算法比如:局部择优搜索法、最好优先搜索法等等。
当然A*也是。
这些算法都使用了启发函数,但在具体的选取最佳搜索节点时的策略不同。
象局部择优搜索法,就是在搜索的过程中选取“最佳节点”后舍弃其他的兄弟节点,父亲节点,而一直得搜索下去。
这种搜索的结果很明显,由于舍弃了其他的节点,可能也把最好的节点都舍弃了,因为求解的最佳节点只是在该阶段的最佳并不一定是全局的最佳。
最好优先就聪明多了,他在搜索时,便没有舍弃节点(除非该节点是死节点),在每一步的估价中都把当前的节点和以前的节点的估价值比较得到一个“最佳的节点”。
这样可以有效的防止“最佳节点”的丢失。
那么A*算法又是一种什么样的算法呢?编辑本段其实A*算法也是一种最好优先的算法只不过要加上一些约束条件罢了。
由于在一些问题求解时,我们希望能够求解出状态空间搜索的最短路径,也就是用最快的方法求解问题,A*就是干这种事情的!我们先下个定义,如果一个估价函数可以找出最短的路径,我们称之为可采纳性。
A*算法是一个可采纳的最好优先算法。
A*算法的估价函数可表示为:f'(n) = g'(n) + h'(n)这里,f'(n)是估价函数,g'(n)是起点到节点n的最短路径值,h'(n)是n到目标的最短路经的启发值。
由于这个f'(n)其实是无法预先知道的,所以我们用前面的估价函数f(n)做近似。
g(n)代替g'(n),但g(n)>=g'(n)才可(大多数情况下都是满足的,可以不用考虑),h(n)代替h'(n),但h(n)<=h'(n)才可(这一点特别的重要)。
可以证明应用这样的估价函数是可以找到最短路径的,也就是可采纳的。
我们说应用这种估价函数的最好优先算法就是A*算法。
举一个例子,其实广度优先算法就是A*算法的特例。
其中g(n)是节点所在的层数,h(n)=0,这种h(n)肯定小于h'(n),所以由前述可知广度优先算法是一种可采纳的。
实际也是。
当然它是一种最臭的A*算法。
再说一个问题,就是有关h(n)启发函数的信息性。
h(n)的信息性通俗点说其实就是在估计一个节点的值时的约束条件,如果信息越多或约束条件越多则排除的节点就越多,估价函数越好或说这个算法越好。
这就是为什么广度优先算法的那么臭的原因了,谁叫它的h(n)=0,一点启发信息都没有。
但在游戏开发中由于实时性的问题,h(n)的信息越多,它的计算量就越大,耗费的时间就越多。
就应该适当的减小h(n)的信息,即减小约束条件。
但算法的准确性就差了,这里就有一个平衡的问题。
虽然A*(读作A星)算法对初学者来说是比较深奥难懂,但是一旦你找到门路了,它又会变得非常简单。
网上有很多解释A*算法的文章,但是大多数是写给那些有一定基础的人看的,而您看到的这一篇呢,是真正写给菜鸟的。
本篇文章并不想给这个算法题目作一些权威性论断,而是阐述它的基本原理,并为你理解更多相关资料与讨论打下基础。
文章末尾给出了一些比较好的链接,放在“进阶阅读”一节之后。
最后,本文不是编程规范,你将可能使这里讲述的东西编写成任何计算机语言。
在本文的末尾我还给出了一个例子程序包的下载链接,也许正合你意。
在这个包中有C++和Blitz Basic两个版本的程序代码,如果你只是想看看A*算法是如何运作的,该包中也有可直接执行的文件供你研究。
我们还是要超越自己的(把算法弄懂),所以,让我们从头开始吧!初步:搜索区域我们假设某个人要从A点到达B点,而一堵墙把这两个点隔开了,如下图所示,绿色部分代表起点A,红色部分代表终点B,蓝色方块部分代表之间的墙。
[图一]此主题相关图片如下:你首先会注意到我们把这一块搜索区域分成了一个一个的方格,如此这般,使搜索区域简单化,正是寻找路径的第一步。
这种方法将我们的搜索区域简化成了一个普通的二维数组。
数组中的每一个元素表示对应的一个方格,该方格的状态被标记为可通过的和不可通过的。
通过找出从A点到B点所经过的方格,就能得到AB之间的路径。
当路径找出来以后,这个人就可以从一个格子中央移动到另一个格子中央,直到抵达目的地。
这些格子的中点叫做节点。
当你在其他地方看到有关寻找路径的东西时,你会经常发现人们在讨论节点。
为什么不直接把它们称作方格呢?因为你不一定要把你的搜索区域分隔成方块,矩形、六边形或者其他任何形状都可以。
况且节点还有可能位于这些形状内的任何一处呢?在中间、靠着边,或者什么的。
我们就用这种设定,因为毕竟这是最简单的情况。
开始搜索当我们把搜索区域简化成一些很容易操作的节点后,下一步就要构造一个搜索来寻找最短路径。
在A*算法中,我们从A点开始,依次检查它的相邻节点,然后照此继续并向外扩展直到找到目的地。
我们通过以下方法来开始搜索:1. 从A点开始,将A点加入一个专门存放待检验的方格的“开放列表”中。
这个开放列表有点像一张购物清单。
当前这个列表中只有一个元素,但一会儿将会有更多。
列表中包含的方格可能会是你要途经的方格,也可能不是。
总之,这是一个包含待检验方格的列表。
2. 检查起点A相邻的所有可达的或者可通过的方格,不用管墙啊,水啊,或者其他什么无效地形,把它们也都加到开放列表中。
对于每一个相邻方格,将点A保存为它们的“父方格”。
当我们要回溯路径的时候,父方格是一个很重要的元素。
稍后我们将详细解释它。
3. 从开放列表中去掉方格A,并把A加入到一个“封闭列表”中。
封闭列表存放的是你现在不用再去考虑的方格。
此时你将得到如下图所示的样子。
在这张图中,中间深绿色的方格是你的起始方格,所有相邻方格目前都在开放列表中,并且以亮绿色描边。
每个相邻方格有一个灰色的指针指向它们的父方格,即起始方格。
[图二]此主题相关图片如下:接下来,我们在开放列表中选一个相邻方格并再重复几次如前所述的过程。
但是我们该选哪一个方格呢?具有最小F值的那个。
路径排序决定哪些方格会形成路径的关键是下面这个等式:F =G + H这里G=从起点A沿着已生成的路径到一个给定方格的移动开销。
H=从给定方格到目的方格的估计移动开销。
这种方式常叫做试探,有点困惑人吧。
其实之所以叫做试探法是因为这只是一个猜测。
在找到路径之前我们实际上并不知道实际的距离,因为任何东西都有可能出现在半路上(墙啊,水啊什么的)。
本文中给出了一种计算H值的方法,网上还有很多其他文章介绍的不同方法。
我们要的路径是通过反复遍历开放列表并选择具有最小F值的方格来生成的。
本文稍后将详细讨论这个过程。
我们先进一步看看如何计算那个等式。
如前所述,G是从起点A沿着已生成的路径到一个给定方格的移动开销,在本例中,我们指定每一个水平或者垂直移动的开销为10,对角线移动的开销为14。
因为对角线的实际距离是2的平方根(别吓到啦),或者说水平及垂直移动开销的1.414倍。
为了简单起见我们用了10和14这两个值。
比例大概对就好,我们还因此避免了平方根和小数的计算。
这倒不是因为我们笨或者说不喜欢数学,而是因为对电脑来说,计算这样的数字也要快很多。
不然的话你会发现寻找路径会非常慢。
我们要沿特定路径计算给定方格的G值,办法就是找出该方格的父方格的G值,并根据与父方格的相对位置(斜角或非斜角方向)来给这个G值加上14或者10。
在本例中这个方法将随着离起点方格越来越远计算的方格越来越多而用得越来越多。
有很多方法可以用来估计H值。
我们用的这个叫做曼哈顿(Manhattan)方法,即计算通过水平和垂直方向的平移到达目的地所经过的方格数乘以10来得到H 值。
之所以叫Manhattan方法是因为这就像计算从一个地方移动到另一个地方所经过的城市街区数一样,而通常你是不能斜着穿过街区的。
重要的是,在计算H 值时并不考虑任何障碍物。
因为这是对剩余距离的估计值而不是实际值(通常是要保证估计值不大于实际值――译者注)。
这就是为什么这个方式被叫做试探法的原因了。
想要了解更多些吗?这里还有更多式子和关于试探法的额外说明。
