高一数学限时练15

合集下载

广东省肇庆市实验中学高一数学下学期晚练15周含答案

肇庆市实验中学高一级《数学晚练》（十五周）命题人：刘志荣班姓名成绩1。

错误!sin 15°cos 15°的值等于（ )A.错误!B.错误!C.错误! D 。

错误!2．下列各式中，值为错误!的是（）A ．2sin 15°－cos 15° B．cos 215°－sin 215° C ．2sin 215°－1 D ．cos 215°＋sin 215°3．已知tan α＝错误!，则tan 2α＝__________4。

错误!·错误!＝( )A ．tan 2αB ．tan αC ．1D 。

错误!5．函数f （x ）＝sin x cos x 的最小值是（）A ．－1B ．－错误!C 。

错误!D ．16．设sin(错误!＋θ)＝错误!，则sin 2θ＝（ )A ．－79B ．－19C.错误! D 。

797。

错误!＋2错误!的化简结果是（）(提示：4表示4弧度sin 4〈0，sin 4<cos 4）A．2cos 4－4sin 4 B．2sin 4 C．2sin 4－4cos 4 D．－2sin 48．在△ABC中,已知cos 2C＝－错误!，则sin C的值为________ 9．函数f（x）＝sin(2x－错误!）－2错误!·sin2x的最小正周期是________(提示：化为）10．(1）求函数f(x）＝cos（x＋错误!π)＋2cos2错误!,x∈R的值域；（提示：化为）（2）已知tan α＝3，α∈（错误!，错误!）,求sin 2α,cos 2α，tan 2α的值．【解】(1）(2).11．（选做题）已知sin（错误!＋α)sin（错误!－α）＝错误!,且α∈(错误!,π），求sin 4α的值．【思路提示】因为（π4＋α）＋(错误!－α)＝错误!. 所以sin(错误!－α)＝cos(错误!＋α)【解】肇庆市实验中学高一级《数学晚练》（十五周）答案命题人：刘志荣班姓名成绩1. 错误!sin 15°cos 15°的值等于（ B )A.错误!B.错误!C.错误!D。

高一数学限时训练试题

高一数学必修1限时训练使用班级：高一级使用时间：10月11日班级姓名成绩一．选择题（请将答案填写在答题卡，每题5分，共50分）1．集合},{b a 的子集有（） A ．2个B ．3个C ．4个D ．5个2．设集合{}|43A x x =-<<，{}|2B x x =≤，则AB = （）A ．(4,3)-B ．(4,2]-C ．(,2]-∞D ．(,3)-∞ 3．已知()5412-+=-x x x f ，则()x f 的表达式是（）A ．x x 62+ B ．782++x x C ．322-+x x D ．1062-+x x4.函数f(x)＝x21-的定义域是（）A 、[0，＋∞）B 、（－∞，0）C 、（－∞，＋∞）D 、(]0,∞-5．下列函数中，定义域为[0，∞）的函数是（） A ．x y =B ．22x y -=C ．13+=x yD ．2)1(-=x y6.设,10<<<b a 则下列不等式正确的是（）b a b a A <. b a b b B <. a a b a C <. a b a b D <.7．指数函数y=a x 的图像经过点（2，16）则a 的值是（）A ．41 B ．21C ．2D ．4 8．若210,5100==b a，则b a +2=（）A 、0B 、1C 、2D 、3 9．已知0ab >，下面四个等式中： ①lg()lg lg ab a b =+； ②lglg lg aa b b=-； ③b ab a lg )lg(212= ； ④1lg()log 10abab =其中正确命题的个数为 ( )A ．0B ．1C ．2D ．310.定义运算a b ⊕，a b ⊕=⎩⎪⎨⎪⎧a ，a≤b，b ，a>b.例如：121⊕=，则函数12xy =⊕的值域为( )A 、(－∞，1)B 、(0,1)C 、[1，＋∞)D 、(0,1]二填空题（每空5分，共20分）11．若{}{}0,1,2,3,|3,A B x x a a A ===∈，则AB = ．12．若函数2()1x af x x bx +=++在[]1,1-上是奇函数,则a = , b = .13、函数)10()(≠>=a a a x f x且在区间]2,1[上的最大值比最小值大2a，则a =__________14 .函数 y=log (x-1)(3-x) 的定义域是。

高一数学第一学期周练15+答案

高一数学周练(15)一、选择题：（本题共12小题，每小题5分，共60分）1．tan390°的值等于（）A．B．C．﹣D．﹣2．已知M={0，1，2}，N={x|x=2a，a∈M}，则M∪N=（）A．{0}B．{0，1}C．{0，1，2}D．{0，1，2，4}3．设P是△ABC所在平面内的一点，，则（）A．P、A、C三点共线B．P、A、B三点共线C．P、B、C三点共线D．以上均不正确4．给出下列四个式子：①=x；②a3＞a2；③（log a3）2=2log a3；④log23＞log49．其中正确的有（）A．0 个B．1个C．2个D．3个5．如图，已知∠AOB=2弧度，点A1、A2、A3在OA上，点B1、B2、B3在OB上，其中每一条实线段和虚线段长度均为1个单位．一个动点M从点O出发，沿着实线段和以点O为圆心的实线圆弧匀速运动，速度为1单位/秒．则动点M到达A2处所需时间为（）秒．A．6B．8C．2+πD．2+3π6．下列四个函数中，在（0，+∞）上为增函数的是（）A．y=﹣1B．y=x2﹣3x C．y=﹣D．y=﹣|x|7．设f（x）=3x+3x﹣8，用二分法求方程3x+3x﹣8=0在x∈（1，3）内近似解的过程中取区间中点x0=2，那么下一个有根区间为（）A．（1，2）B．（2，3）C．（1，2）或（2，3）D．不能确定8．已知函数f （x ）=，若f （f （﹣1）=18，那么实数a 的值是（）A ．0B ．1C ．2D ．39．若，则sin2α的值为（）A ．B ．C ．D ．10．如图2-3-6所示，△ABC 中，若D ，E ，F 依次是AB 的四等分点，则以CB →＝e 1，CA →＝e 2为基底时，CF →＝________.A. 34e 1＋14e 2 B.C. D.11．已知函数f （x ）=Asin （wx +φ）（A ＞0，w ＞0，|φ|＜，x ∈R ）在一个周期内的图象如图所示．则y=f （x ）的图象可由函数y=cosx 的图象（纵坐标不变）（）A ．先把各点的横坐标缩短到原来的倍，再向左平移个单位B ．先把各点的横坐标缩短到原来的倍，再向右平移个单位C ．先把各点的横坐标伸长到原来的2倍，再向左平移个单位D ．先把各点的横坐标伸长到原来的2倍，再向右平移个单位12．设函数f （x ）为偶函数，且当x ≥0时，f （x ）=（）x ，又函数g （x ）=|xsinπx |，则函数h （x ）=f （x ）﹣g （x ）在[﹣，2]上的零点的个数为（）个． A ．3B ．4C ．5D ．6二、填空题（共4小题，每小题5分，满分20分）13．（5分）已知集合M={x |log 2（x ﹣3）≤0}，N={x |y=}，则集合M ∩N 为．14．（5分）函数的单调增区间为．15．（5分）甲、乙二人从A 地沿同一方向去B 地，途中都使用两种不同的速度v 1与v 2（v 1＜v 2）．甲前一半的路程使用速度v 1，后一半的路程使用速度v 2；乙前一半的时间使用速度v 1，后一半时间使用速度v 2．请在如图坐标系中画出关于甲、乙二人从A 地到达B 地的路程与时间的函数图象（其中横轴t 表示时间，纵轴s 表示路程，C 是AB 的中点，t 1是t 2的一半）．16．定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值是．三.解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（1）已知||=1，||=，若与的夹角为，求|﹣|．（2）已知=（﹣4，3），=（1，2），求（﹣3）•（2+）的值．18．已知角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点P （﹣3，4）．（1）求sinα，cosα的值；（2）的值．19．已知函数)32sin(23π+-=x y ．（1）求函数的值域；（2）求函数取最小值时x 的集合；（3）当⎥⎦⎤⎢⎣⎡-∈3,3ππx 时，求函数的最大值．20．设函数f （x ）=log a x ，x （0＜a ＜1）．（1）比较f （sin1）与f （cosl ）的大小；（2）记函数f （x ）的反函数为g （x ），若a +kg （x ﹣1）≥0在x ∈[2，+∞）上恒成立，求k 的最小值．21．已知函数2()log (21)x f x =+（1）求证：函数()f x 在(,)-∞+∞内单调递增；（2）若关于x 的方程2log (21)()x m f x -=+在[1,2]上有解，求m 的取值范围。

高一数学第15周训练题

【解答】解：由三视图可知：该几何体为一个四棱锥，如图所示，CD⊥底面PAD，BA⊥底面PAD，PA⊥AD，PA=AD=CD=2，AB=1．
PC=2 ，PB= ，BC= ．
∴S△PBC= = ．
该几何体的表面积S= + + + +
=6+ ．
故选：C．
11.
【考点】对数的运算性质；换底公式的应用．
【分析】直接利用对数的运算性质，把要求的式子化为 • ，即 • ，运算求得结果．
试卷答案
1.C
【考点】交集及其运算．
【分析】集合A和集合B的公共元素构成集合A∩B，由此利用集合A={x|2x＞1}，B={x|x2﹣3x﹣4＞0}，能求出集合A∩B．
【解答】解：∵集合A={x|2x＞1}={x|x＞0}，
B={x|x2﹣3x﹣4＞0}={x|x＜﹣1或x＞4}，
∴集合A∩B={x|x＞4}．
3.下列函数中，在区间（0，+∞）上为增函数的是（）
A． B．y=（x﹣1）2C．y=2﹣xD．y=log0.5x
4.函数的零点所在的一个区间是（）
A．（﹣1，0）B．（0，1）C．（1，2）D．（2，3）
5.设lg2=a，lg3=b，则log125=（）
A． B． C． D．
6.函数f（x）=|x﹣2|的图象为（）
对于B，函数y=（x﹣1）2在区间（﹣∞，1）上是单调减函数，（1，+∞）上是单调增函数，不满足题意；
对于C，函数y=2﹣x在定义域R上为单调减函数，不满足题意；
对于D，函数y=log0.5x在定义域（0，+∞）上为单调减函数，不满足题意．
故选：A．
4.D
【考点】函数零点的判定定理．

数的值域求法限时练习高一上学期数学

1《函数的概念》值域限时练班级: 姓名: 小组: 分数:A 卷基础过关题（6*10=60分）1. 函数2)(x x f =的定义域为}2,1,0,1{-，那么其值域是( )．A.}4,1,0,1{B.}4,1,0{C. }0|{≥y yD.}0|{>y y2.值域是(0，＋∞)的函数是( )A.y ＝x 2－x ＋1B.y ＝1xC.y ＝|x ＋1|D.y ＝1x(x ＞0) 3、函数211)(x x f +=的值域是 .A ()0,1 .B (]0,1 .C [)0,1 .D []0,14.已知函数y ＝x 2－2x ＋3在区间[0，2]上( )A.有最大值3，有最小值2B.有最大值3，无最小值C. 无最大值，有最小值2D. 无最大值，无最小值5.函数y ＝1＋2x －x 2(x ∈[0，2])的值域是( )A.[－2，2]B.[1，2]C.[0，2]D.[－2，2]6.函数y ＝2x ＋1x －3的值域为____ ____.B 卷拓展提升题（2*10=20分）7.已知函数y ＝x 2－2x ＋3在区间[0，m]上有最大值3，最小值2，则m ∈( )A.[1，＋∞)B.[0，2]C.(－∞，2]D.[1，2]8.已知函数f(x)＝x 2－2ax ＋2a ＋4的定义域为R ，值域为[1，＋∞)，则a 的值为________.C 卷能力挑战题（2*10=20分）9. 若定义域为R 的函数y ＝f(x)的值域为[a ，b]，则函数y ＝f(x ＋2)的值域为____________. 10. 求函数)0(,4)(2≠+=x xx x f 的值域（判别式法）2。

人教新课标版数学高一人教版必修1双基限时练15 待定系数法

双基限时练(十五) 待定系数法基础强化1．已知某一次函数过点(3,2)，且在x 轴、y 轴上的截距相等，则这个一次函数的解析式为( )A ．y ＝23x B ．y ＝－x ＋5C ．y ＝23x ，或y ＝－x ＋5 D ．y ＝－23x ，或y ＝x －5解析设一次函数的解析式为y ＝kx ＋b ，由题意可知⎩⎪⎨⎪⎧ 3k ＋b ＝2，－bk ＝b ，∴⎩⎪⎨⎪⎧k ＝23，b ＝0，或⎩⎨⎧k ＝－1，b ＝5，∴该一次函数的解析式为y ＝23x ，或y ＝－x ＋5. 答案 C2．若函数f (x )＝mx 4x －3(x ≠34)在定义域内恒有f [f (x )]＝x ，则m 的值为( )A ．3 B.32 C ．－32D ．－3解析 f [f (x )]＝m 2x 4x －34mx 4x －3－3＝m 2x(4m －12)x ＋9.即m 2x(4m －12)x ＋9＝x 恒成立． ∴4m －12＝0，∴m ＝3. 答案 A3．设函数f (x )＝⎩⎪⎨⎪⎧x 2＋bx ＋c ，x ≤0，2，x >0，)若f (－1)＝f (0)，f (－2)＝－2，则关于x 的方程f (x )＝x 的解的个数为( )A ．1B ．2C ．3D ．4解析由f (－1)＝f (0)，f (－2)＝－2，可得⎩⎨⎧1－b ＋c ＝c ，4－2b ＋c ＝－2，解得⎩⎨⎧b ＝1，c ＝－4，∴f (x )＝⎩⎪⎨⎪⎧x 2＋x －4，x ≤0，2，x >0.)令f (x )＝x ，得x ＝2或x ＝－2.答案 B4．若二次函数y ＝2x 2－2mx ＋2m 2－2的图象的顶点在y 轴上，则m 的值是( )A ．0B ．±1C ．±2D ．±2解析由题意可知，二次函数的对称轴为y 轴，∴m2＝0，∴m ＝0.答案 A5．抛物线y ＝ax 2＋bx ＋c (a >0)的对称轴是直线x ＝1，且经过P (3,0)，则a －b ＋c 的值为( )A ．0B ．－1C ．1D ．2解析 ∵抛物线的对称轴为x ＝1，且它经过P (3,0)， ∴抛物线也经过(－1,0)， ∴a －b ＋c ＝0. 答案 A6．已知某二次函数的图象与函数y ＝2x 2的图象形状一样，开口方向相反，且其顶点为(－1,3)，则此函数的解析式为( )A ．y ＝2(x －1)2＋3B ．y ＝2(x ＋1)2＋3C ．y ＝－2(x －1)2＋3D ．y ＝－2(x ＋1)2＋3解析设所求函数的解析式为y ＝a (x ＋h )2＋k (a ≠0)，由题意可知a ＝－2，h ＝1，k ＝3，故y ＝－2(x ＋1)2＋3.答案 D7．已知函数f (x )＝ax 2＋2x －3的图象与x 轴有且只有一个交点，则a 的值为________．解析当a ＝0时，f (x )＝2x －3，满足图象与x 轴有一个交点；当a ≠0时，Δ＝4＋12a ＝0，∴a ＝－13. 综上所述，a ＝0，或a ＝－13. 答案 0或－138．若一次函数y ＝f (x )在区间[－1,3]上的最小值为1，最大值为3，则f (x )的解析式为________．解析设f (x )＝kx ＋b (k ≠0)．当k >0时， ⎩⎨⎧k ·(－1)＋b ＝1，k ·3＋b ＝3，解得⎩⎪⎨⎪⎧ k ＝12，b ＝32.当k <0时，⎩⎨⎧k ·(－1)＋b ＝3，k ·3＋b ＝1，解得⎩⎪⎨⎪⎧k ＝－12，b ＝52.∴f (x )＝12x ＋32或f (x )＝－12x ＋52. 答案 f (x )＝12x ＋32或f (x )＝－12x ＋52能力提升9．已知二次函数当x ＝4时有最小值－3，且它的图象与x 轴两交点间的距离为6，则这个二次函数的解析式为______________________．解析由题意，知抛物线的对称轴为x ＝4，抛物线与x 轴的两交点的坐标是(1,0)与(7,0)，如图所示．设二次函数的解析式为y ＝ax 2＋bx ＋c (a ≠0)，由条件可得抛物线的顶点为(4，－3)，且过点(1,0)和(7,0)，将三个点的坐标代入，得⎩⎪⎨⎪⎧－3＝16a ＋4b ＋c ，0＝a ＋b ＋c ，0＝49a ＋7b ＋c ，解得⎩⎪⎨⎪⎧a ＝13，b ＝－83，c ＝73.∴所求二次函数的解析式为y ＝13x 2－83x ＋73. 答案 y ＝13x 2－83x ＋73 10.已知y ＝f (x )的图象如图所示． (1)求f (x )的解析式； (2)求函数的值域．解由图象可知①：当0≤x ≤2时，f (x )是一次函数．设f (x )＝kx ＋b (k ≠0)，则⎩⎨⎧f (0)＝b ＝2，f (1)＝k ＋b ＝0，即⎩⎨⎧b ＝2，k ＝－2.故f (x )＝－2x ＋2.②当2<x <3时，f (x )＝－2.③当3≤x ≤5时，f (x )是一次函数．设f (x )＝mx ＋n (m ≠0)，则⎩⎨⎧f (3)＝3m ＋n ＝－2，f (5)＝5m ＋n ＝0，解得⎩⎨⎧m ＝1，n ＝－5，此时f (x )＝x －5.综上可知，f (x )的解析式为f (x )＝⎩⎪⎪⎨⎪⎪⎧－2x ＋2，0≤x ≤2，－2，2<x <3，x －5，3≤x ≤5.)由图可知该函数的值域为[－2,2]．11．已知一次函数y ＝kx ＋b 的图象经过点(－1，－5)，且与正比例函数y ＝12x 的图象相交于点(2，a )．(1)求a 的值；(2)求一次函数的解析式．解 (1)a ＝12×2＝1.(2)⎩⎨⎧－k ＋b ＝－5，2k ＋b ＝1，∴⎩⎨⎧k ＝2，b ＝－3，∴y ＝2x －3.12．定义在[－6,6]上的奇函数f (x )，在[0,3]上为一次函数，在[3,6]上为二次函数，且x ∈[3,6]时，f (x )≤f (5)＝3，f (6)＝2，求f (x )的解析式．解当x ∈[3,6]时，∵f (x )≤f (5)＝3， ∴可设f (x )＝a (x －5)2＋3.∵f (6)＝2，∴f (6)＝a (6－5)2＋3＝2，解得a ＝－1. ∴f (x )＝－(x －5)2＋3，x ∈[3,6]，即f (x )＝－x 2＋10x －22，x ∈[3,6]． ∴f (3)＝－(3－5)2＋3＝－1.即x ∈ [0,3]和x ∈[3,6]时，f (x )均过点(3，－1)． ∵x ∈[0,3]时，f (x )为一次函数， ∴可设f (x )＝kx ＋b .∵f (x )在x ∈[－6,6]上是奇函数， ∴f (0)＝0，∴b ＝0，即f (x )＝kx ，将点(3，－1)代入，得－1＝3k ，∴k ＝－13， ∴f (x )＝－13x ，x ∈[0,3]， ∴f (x )＝⎩⎪⎨⎪⎧－13x ，x ∈[0，3]，－(x －5)2＋3，x ∈[3，6].又∵f (x )为奇函数，∴x ∈[－3,0]时，f (x )＝－f (－x )＝－13x ； x ∈[－6，－3]时，f (x )＝－f (－x )＝(－x －5)2－3＝(x ＋5)2－3. 即f (x )＝x 2＋10x ＋22，x ∈[－6，－3]．∴f (x )＝⎩⎪⎨⎪⎧x 2＋10x ＋22，x ∈[－6，－3]，－13x ，x ∈[－3，3]，－x 2＋10x －22，x ∈[3，6].品味高考13．已知一个二次函数y ＝f (x )，f (0)＝3，又知当x ＝－3或x ＝－5时，这个函数的值都为0，求其解析式．解设y ＝f (x )＝a (x ＋3)(x ＋5)(a ≠0)，由f (0)＝3，得 3＝a (0＋3)(0＋5)， ∴a ＝15.∴y ＝15(x ＋3)(x ＋5)＝15x 2＋85x ＋3. ∴f (x )＝15x 2＋85x ＋3.。

高一数学基本不等式限时训练(含答案)

高一数学基本不等式限时训练（60分钟）第I卷（选择题）一、单选题（本大题共10小题，共50.0分）1.已知t>0，则y=t2−4t+1t的最小值为()A. −2B. 12C. 1D. 22.下列说法不正确的是()A. x+1x(x>0)的最小值是22√x2+4的最小值是22√x2+2的最小值是√2D. 若x>0，则2−3x−4x的最大值是2−4√33.若mn>0，m+n=3，则1m +4n的最小值为()A. 2B. 6C. 3D. 94.若x>0，则x+9x+2有()A. 最小值6B. 最小值8C. 最大值8D. 最大值35.若a<1，则a+1a−1有()A. 最小值为3B. 最大值为3C. 最小值为−1D. 最大值为−16.已知x2−x+1x−1(x>1)，在x=t时取得最小值，则t等于()A. 1+√2B. 2C. 3D. 47.已知x>2，则函数y=4x−2+4x的最小值是()A. 6B. 8C. 12D. 168.已知0<x<35，则x(3−5x)取最大值时x的值为()A. 310B. 910C. 95D. 129.若x，y∈R+，且x+3y=5xy，则3x+4y的最小值是()A. 5B. 245C. 2√35D. 19510.若a>0，b<0，则ab +ba()A. 有最大值−2B. 有最大值2C. 有最小值−2D. 有最小值2二、多选题（本大题共2小题，共10.0分）11.(多选)若a，b∈R，且a>0，b>0，则下列不等式中恒成立的是()A. a2+b2>2abB. a+b≥2√abC. 1a +1b>2√abD. 3ba+a27b⩾2312.已知x≥1，则下列函数的最小值为2的有()A. y=2x +x2B. y=4x+1xC. y=3x−1xD. y=x−1+4x+1第II卷（非选择题）三、单空题（本大题共1小题，共5.0分）13.若a>0，b>0，3a+2b=1，则ab的最大值是．四、解答题（本大题共2小题，共24.0分）14.(1)已知x>0，y>0，xy=4，求2x +1y的最小值；(2)已知x>0，y>0，x+2y=2，求2x +1y的最小值．15.如图，某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形菜园.设菜园的长为xm，宽为ym．(1)若菜园面积为72m2，则x,y为何值时，可使所用篱笆总长最小？(2)若使用的篱笆总长度为30m，求1x +2y的最小值．答案和解析1.【答案】A【解析】【分析】本题主要考查利用基本不等式求最值，属于基础题．对原式进行化简，利用基本不等式求最值即可，注意等号取得的条件．【解答】解：t>0，则y=t2−4t+1t =t+1t−4≥2√t·1t−4=−2，当且仅当t=1t，即t=1时，等号成立，则y=t2−4t+1t的最小值为−2．故选A．2.【答案】B【解析】【分析】本题考查了基本不等式的应用，掌握利用基本不等式的条件是关键，属于中档题．对于ACD根据基本不等式和不等式性质即可判断，对于B根据基本不等式的取等号时x的不存在即可判断．【解答】解：对于A，∵x>0，∴x+1x ≥2√x⋅1x=2，当且仅当x=1时取等号，故A正确；对于B，2√x2+4=2√x2+4=√x2+4+√x2+4≥2，当且仅当x2+4=1时取等号，显然x的值不存在，故B错误；对于C，2√x2+2=√x2+2≥√2，当且仅当x=0时取等号，故C正确；对于D，∵x>0，∴2−3x−4x ≤2−2√3x⋅4x=2−4√3，当且仅当x=2√33时取等号，故D正确．故选：B．3.【答案】C【解析】【分析】本题考查了利用基本不等式求最值，属于较易题目．根据题意1m +4n=13(m+n)(1m+4n)=13(5+nm+4mn)，结合基本不等式求得最值即可．【解答】解：因为mn>0，m+n=3，所以1m +4n=13(m+n)(1m+4n)=13(5+nm+4mn)⩾13(5+2√nm⋅4mn)=3，当且仅当nm =4mn时取等号，此时{nm=4mn,m+n=3,解得{m=1n=2即1m +4n的最小值为3，故选C．4.【答案】B【解析】【分析】本题主要考查利用基本不等式求最值，属于基础题．利用基本不等式求最值即可．【解答】解：∵x>0∴x+9x +2≥2√ x·9x+2=6+2=8，当且仅当x=9x，即x=3时取等号，故最小值为8．故选B．5.【答案】D【解析】【分析】本题考查基本不等式，属于基础题．配凑，转化，再利用基本不等式求解即可．【解答】解：因为a<1，所以a−1<0，1−a>0，所以a+1a−1=a−1+1a−1+1=−(1−a+11−a)+1≤−2√(1−a)·11−a+1=−1，当且仅当1−a=11−a，即a=0时，等号成立．故答案为D．6.【答案】B【解析】【分析】本题主要考查了利用基本不等式求最值，属于基础题.由x>1得x−1>0，利用基本不等式可得x2−x+1x−1=(x−1)+1x−1+1≥2√(x−1)×1x−1+1=3，当且仅当x−1=1x−1，即x=2时取等号，由此得到t=2．【解答】解：∵x>1，∴x−1>0，∴x2−x+1x−1=(x−1)+1x−1+1≥2√(x−1)×1x−1+1=3，当且仅当x−1=1x−1，即x=2时取最小值3，∴t=2，故选B．7.【答案】D【解析】【试题解析】【分析】本题考查利用基本不等式求最值，属于基础题．因为x−2>0，4x−2>0，构造积为定值，利用基本不等式即可求解．【解答】解：已知x>2，则x−2>0，函数y=4x−2+4x=4x−2+4(x−2)+8⩾2√4x−2⋅4(x−2)+8=16，当且仅当x=3时“=”成立，故函数的最小值是16，故选D．8.【答案】A【解析】【分析】本题主要考查了基本不等式在最值求解中的应用．由x(3−5x)=15×5x(3−5x)，利用基本不等式即可得解．【解答】解：∵0<x<35，则x(3−5x)=15×5x(3−5x)≤15×(5x+3−5x2)2=920，当且仅当5x=3−5x，即x=310时取最大值，故选：A．9.【答案】A【解析】【分析】本题主要考查了利用基本不等式求解最值问题，属中档题，解题的关键是基本不等式的应用条件的配凑．将方程变形15y +35x =1，代入可得3x +4y =(3x +4y)(15y +35x )=135+3x 5y +4y5x ，然后利用基本不等式即可求解．【解答】解：∵x +3y =5xy ，x >0，y >0， ∴15y+35x=1，∴3x +4y =(3x +4y)(15y +35x )=135+3x 5y +12y 5x≥135+2√3x 5y ×12y 5x=5，当且仅当3x5y =12y 5x，即x =2y =1时取等号．故选A ．10.【答案】A【解析】【分析】本题考查了基本不等式，运用基本不等式求最值，属于基础题．根据a >0，b <0，则ab <0,ba <0，则−ab >0,−ba >0，然后结合基本不等式求最值即可．【解答】解：由题意，若a >0，b <0，则ab <0,ba <0，所以ab +ba =−[(−ab )+(−ba )] ≤−2√(−ab )·(−ba )=−2，当且仅当a =−b 时等号成立，故ab +ba 有最大值−2．故选A ．11.【答案】BD【解析】【分析】本题考查利用基本不等式求最值，属于基础题．对于A ，取a =b =2，进行验证即可；对于B ，由基本不等式可判断；对于C ，取a =2，b =2，进行判断；对于D ，利用基本不等式求最值即可．解：当a=b=2时，a2+b2=2ab，选项A不成立；当a>0，b>0时，a+b≥2√ab，当且仅当a=b时取等号，B成立；例如a=2，b=2时，，选项C不成立；由a>0，b>0可知，ba >0，由基本不等式可得，3ba+a27b⩾2√3ba·a27b=23，当且仅当a=9b时取等号，所以D正确，故选BD．12.【答案】ACD【解析】【分析】本题考查基本不等式，函数的单调性，属于基础题．由基本不等式分别对A，B，D进行验证，C选项根据函数的单调性求最值即可得答案．【解答】解：选项A，x≥1，y=2x +x2≥2√2x·x2=2，当且仅当2x=x2，即x=2时等号成立，A满足，选项B，x≥1，y=4x+1x >2√4x·1x=4，故B不满足，选项C，x≥1，y=3x−1x在[1,+∞)为增函数，所以y min=3−1=2，故C满足，选项D，x≥1，y=x−1+4x+1=x+1+4x+1−2≥2√(x+1)·4x+1−2=4−2=2,当且仅当x+1=4x+1，即x=1时等号成立，故D满足．故选ACD．13.【答案】124【解析】本题考查了基本不等式的性质，属于基础题．利用基本不等式的性质即可得出．【解答】解：a >0，b >0，3a +2b =1，所以1=3a +2b ≥2√6ab ，当且仅当a =16,b =14，时取等号，所以ab ≤124，所以ab 的最大值是124，故答案为：124．14.【答案】解：(1)∵xy =4，且x >0，y >0，∴2x +1y ≥2√2xy =2√12=√2，当且仅当x =2√2，y =√2时取等号，即2x +1y 的最小值为√2． (2)∵x >0，y >0，x +2y =2， ∴2(2x +1y )=(x +2y )(2x +1y )=4+4y x+xy≥4+2√4y x⋅xy=8，∴2x+1y ≥4，当且仅当4y x =x y ，即x =2y =1时取等号，即2x +1y 的最小值为4．【解析】本题主要考查了运用基本不等式求最值，属于中档题． (1)直接利用基本不等式求得最小值．(2)2(2x +1y )=(x +2y)(2x +1y )整理后利用基本不等式求得最小值．15.【答案】解：(1)由已知可得xy =72，篱笆总长为(x +2y)m ．又因为x +2y ≥2√2xy =24，第11页，共11页当且仅当x =2y ，即x =12，y =6时等号成立．所以当x =12，y =6时，可使所用篱笆总长最小．(2)由已知得x +2y =30，又因为(1x +2y )(x +2y)=5+2y x +2x y ≥5+2√2y x ⋅2x y =9，所以1x +2y ≥310，当且仅当x =y ，即x =10，y =10时等号成立．所以1x +2y 的最小值是310．【解析】本题考查基本不等式的实际应用和利用基本不等式求最值，属于基础题；(1)由已知可得xy =72，篱笆总长为(x +2y)m ，结合基本不等式即可得解；(2)由已知得x +2y =30，又因为(1x +2y )(x +2y)=5+2y x +2x y ，利用基本不等式即可求解．。

高一数学上学期15周周练

高一数学上学期15周周练1、假设一个圆锥的轴截面是等边三角形,,那么这个圆锥的全面积为〔〕A、3πB、C、6πD、9π2,那么球的体积比原来增加〔〕A、2倍B、4倍C、D、1)3、以下命题中：①空间四点共面,那么其中必有三点共线；②空间四点不共面,那么其中任何三点不共线；③空间四点中有三点共线,那么此四点共面；④空间四点任何三点有共线,那么此四点不共面.其中正确的选项是〔〕A、②③B、①②③C、①②D、②③④4、以下命题中正确的个数是〔〕①假设直线l上有无数个点不在平面α内,那么l//α②假设直线l平行于平面α,那么l与平面α内的任意一直线平行③两条平行线中的一条直线与一个平面平行,那么另一条也与这个平面平行④假设一直线l和平面α内一直线a平行,那么l//αA、0个B、1个C、2个D、3个-的棱BC、CD、DA的中点,那么此四面体中,与过E、F、G的截5、E、F、G分别是四面体A BCD面平行的棱的条数是〔〕A、0条B、1条C、2条D、3条⊄,那么以下结论成立的是〔〕6、假设直线m不平行于平面α,且mαA、α内的所有直线与m异面B、α内不存在与m平行的直线C、α内存在唯一的直线与m平行D、α内的直线与m都相交7、α、β是两个不重合的平面,在以下重要条件中,可判定的是〔〕A、α、β都平行于直线B、α内有三个不共线的点到β的距离相等C、l、m是α内的两条直线,且l//β,m//βD、l、m是两条异面直线,且l//α,m//α,l//β,m//β8、平面α⋂平面β=a,平面β⋂平面γ=b,平面γ⋂平面α=c,假设a//b,那么c与a、b的位置关系是〔〕A、c与a、b都异面B、c与a、b都相交C、c至少与a、b中的一条相交D、c与a、b都平行9、假设直线a //平面α,b //平面β,且,a b βα⊂⊂,那么a 、b 位置关系〔〕A 、a //bB 、a 、b 异面C 、a 、b 一定不相交D 、无法确定10、三个不重合的平面可将空间分成n 局部,那么n 的所有可能值为〔〕A 、4、6、7B 、4、7、8C 、4、6、7、8D 、4、5、6、811、假设空间四边形ABCD 两条对角线AC 、BD 的长分别是8,12,过AB 的中点E 且平行于BD 、AC 的截面四边形的周长为12、如图,正方体1111ABCD A B C D -中,O 为底面ABCD 的中央,试在图中画出平面11B C O 与平面ABCD的交线,并作适当说明13、正方体1111ABCD A B C D -中,过11,,B C D 三点的平面与底面ABCD 的交线为14、空间四边形ABCD 中,各边及对角线长为2,E 为AB 的中点,过CE 且平行于AD 的平面交BD 于F,那么CEF 的周长为 , 面积为15、//αβ,a β⊄,//a α,求证：//a β16、如图,三棱柱111ABC A B C -中,F 是11A C 中点,求证：1//BC F 1平面AB。

高一数学下册限时训练试题15

知识改变命运
第15练班级姓名
1、过点)4,3(-且在两坐标轴上的截距相等的直线方程为
2、已知数列{}n a 是等差数列，且,2,211-==d a 公差则这个数列的前n 项和n S 的最大值为
3、长方体的一个顶点上的三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积为
4、圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为π84，则圆台较小的底面的半径为
5、在ABC Rt ∆中，5,4.3===AC BC AB ,将三角形绕直角边AB 旋转一周所形成的几何体的体积为
知识改变命运
6、若三个球的表面积之比为1：2：3，则它们的体积之比为
7、已知一个正方形的直观图是有一条边长为4的平行四边形，则此正方形的面积是。

8、圆锥的轴截面是正三角形，则它的底面积与侧面积之比为
9、球内有相距cm 1的两个平行截面，截面的面积分别为2285cm cm ππ和，球心不在截面之间，求球的表面积和体积。

知识改变命运
10、P 为圆06422=-++y x y x 上一个动点，
（1）定点||),1,1(PQ Q 求-的最值；
（2）定点的最值求||),2,2(PN N -；
（3）到直线2=y 的距离最大的点P 的坐标；
（4）圆上到直线2=y 的距离为1的点有几个？薄雾浓云愁永昼，瑞脑消金兽。

佳节又重阳，玉枕纱厨，半夜凉初透。

东篱把酒黄昏后，有暗香盈袖。

莫道不消魂，帘卷西风，人比黄花瘦。

高一数学限时训练

数学限时练习(1) 一、选择题：1.已知0(x>0)f(x)=1(x=0)2x3(x<0)⎧⎪-⎨⎪-⎩，，，，则f{f[f(5)]}的值是DA. 0B.－1C.5D. －52.下列各题中两个函数表示同一函数的是C2 A.f(x)=x g(x)=，B.f(x)=x g(x)=，C.f(x)=x g(x)=，2x4D.f(x)=g(x)=x+2x2--，3.设f (x)=5，则f (x2)= CA.25C.5D.不能确定4.设2x+1f(x)=x3x+2-的定义域T，全集U=R，则C R T= CA.{x|x≤1或x≥2}B. {1，2}C. {－1，1，2}D. {x|x<1或1<x<2或x>2}5.某物体一天当中的温度T 是时间t的函数:T(t)=t3－3t+60，时间单位是小时，温度单位是0C ，t=0时，表示12:00 ，12:00之后t取值为正，则上午8时的温度是AA.8 0CB.18 0CC. 580CD. 1280C6.已知函数f (x)=3(x－2)2+5且|x1－2|>|x2－2|，则AＡ.f (x1)> f (x2)Ｂ. f (x1)= f (x2)Ｃ. f (x1)< f (x2)Ｄ.不能确定大小7.设M={x|0≤x≤2}，N={y|0≤y≤2} 给出下列四个图形，其中能表示从集合M到集合N 的函AB C D8.已知函数2x1(x0)y2x(x0)⎧+≤=⎨->⎩，，使函数值为10的x值为CA ．3或－3 B.3或－5 C.－3 D.3或－3或－5 9.若f (2x+1)的定义域为[1，4]，则f (x+3)的定义域为B A.[0, 1.5] B.[0,6] C.[0.5,1.5] D.[3, 4.5] 10.已知f (x)是奇函数，当x>0时，f(x)=x(1－x)，则当x<0时，f(x)的解析式为B A.x(x+1) B.x(x －1) C.x(1－x) D.－x(x+1)二、填空题：11.已知A=B=R ，x ∈A ，y ∈B ，对任意的x ∈A ， x→2x 2+3是从A 到B 的函数，若输出４则应输入_________.12.已知函数y=－2x 2+3，x ∈{－2，－1，0，1，2}，则它的值域为 . 13.函数3x +1y =x 1-的值域为 . 14.已知f (x+1)=x 2－3x+2，则1f ()x的解析表达式为.15．函数y =_________.数学限时练习(2)姓名_________ 班级________ 一、选择题:1.单位圆中，面积为1的扇形所对的圆心角的弧度数为A.1B.2C. 3D.4 2.下列等式中恒成立的有 A.sin(α－β)=sinαcosβ－cosαsinβ B.cos(α－β)= cosαcosβ－sinαsinβ c1sin αcos β=[sin(α+β)sin(αβ)]2⋅--D.1sin αsin β=[cos(α+β)cos(αβ)]2⋅-- 3.)函数f(x)=sinxcosx 最小值是BA.－1B.－0.5C. 0.5D.1 4. sin5850的值为A.2-B.2C.2-D. 2 5.已知函数f(x)=sin(x －π2)(x ∈R),下面结论错误．．的是 A.函数f(x)的最小正周期为2π B.函数f(x)在区间π[0]2，上是增函数 C.函数f(x)的图象关于直线x ＝0对称 D.函数f(x)是奇函数6.已知tanα=4，cotβ=13，则tan(α+β)= A.711 B.711- C.713 D.713- 7下列关系式中正确的是A.sin110<cos100<sin1680B. sin1680 <sin110<cos100C. sin110<sin1680 <cos100D. sin1680<cos100 <sin110. 8. “πα=6”是“1cos2α=2”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件9.函数2πy =2cos (x )14--是A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为π2的奇函数 D.最小正周期为π2的偶函数10.函数f(x)=(1+的最小正周期为 A.2π B.3π2 C.π D.π2二、填空题：11.化简: ① cos580sin370+sin1220sin530＝ .② cos (α－β) cos(α+β) +sin(α－β) sin(α+β)＝ .12.已知113a (,2sin ),b (cos ,)322=α=α ，a //b ，则锐角α的值为 .13.函数y=cos2x －4cosx ，x []32ππ∈-，的值域是 .14.已知偶函数f(x)=2sin(ωx+φ)(ω>0，0<φ<π)的最小正周期是π，则f(x)的单调递减区间为 . 三、解答题：15. (07安徽)已知0π<α<4，β为πf(x)=cos(2x +)8的最小正周期， 1a (tan(αβ)1)4=+- ，，b (cos α2)= ，，且a b =m ⋅ ，求22cos α+sin2(α+β)cos αsin α-的值. 数学限时练习(3)班级_______ 姓名____________ 一、选择题： 1.在△ABC 中，若sinA cosB=a b，则B 的值为 A.300 B.450 C.600 D.9002.在△ABC 中，如果(a+b+c) (b+c －a)=3bc ，那么角A 等于A.300B.600C.1200D.1500 3.在△ABC 中，根据下列条件解三角形，其中有两个解的是A. b=10，A=450，C=700B. a=60，c=48，B=600C. a=7，b=5， A=800D. a=14，b=16，A=4504.在△ABC 中，若A=600，b=16，此三角形面积S=a 的值是A. B.75 C.51 D.495.在△ABC 中，sinA ：sinB ：sinC=3：2：4，则cosC 的值为A.23 B.－23 C.14 D.－146.已知三角形的两边长分别为4，5，它们夹角的余弦是方程2x 2+3x －2=0的根，则第三边长是 A.20 B.21 C.22 D.61 7.在△ABC 中，tanAsin 2B=tanBsin 2A ，那么△ABC 一定是A.锐角三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形 8.已知锐角．．三角形三边分别为3，4，a ，则a 的取值范围为 A.1<a<5 B. 1<a<79.设A 是△ABC 中的最小角，且a 1cosA =a +1-，则实数a 的取值范围是 A.a ≥3 B.a ＞－1 C.－1＜a ≤3 D.a ＞0 10.如图：D ，C ，B 三点在地面同一直线上，DC=a ，从C ，D 两点测得A分别是β，α (α<β)，则A 点离地面的高度AB 等于 A.asin αsin βsin(βα)- B.asin αsin βcos(αβ)⋅-C.asin αcos βsin(βα)- D.acos αsin βcos(αβ)-二、填空题:11.在△ABC 中，A=60°, b=1，面积为3，则a +b +csinA +sinB +sinC= .12.在ΔABC 中，若ΔABC 1S 4=(a 2+b 2－c 2)，那么角∠C=______. 13.在ΔABC 中，A=600， c ：b=8：5，内切圆的面积为12π，则外接圆的半径为_____. 14.在ΔABC 中，a =5，b = 4，cos(A －B)=3231，则cosC=_______. 三、解答题:15.在海岸A 处，发现北偏东450方向，距离A 1n mile 的B 处有一艘走私船，在A 处北偏西750方向，距离A 为2 n mile 的C 处有一艘缉私艇奉命以的速度追截走私船，此时，走私船正以10 n mile / h 的速度从B 处向北偏东300方向逃窜，问缉私艇沿什么方向行驶才能最快追上走私船？并求出所需时间. (本题解题过程中请不要使用计算器，以保证数据的相对准确和计算的方便)北CBD三、解答题: 1.已知ΔABC 三个顶点的直角坐标分别为A(3，4)，B(0，0)，C(c ，0).(1)若AB AC =0⋅，求c 的值； (2) 若c =5，求sin ∠A 的值．2.已知△ABC 顶点的直角坐标分别为A(3，4)，B(0，0)，C(c ，0). (1)若c=5，求sin ∠A 的值； (2)若∠A 是钝角，求c 的取值范围．3.在△ABC 中，5cosA =13-，3cosB =5． (Ⅰ)求sinC 的值； (Ⅱ)设BC=5，求△ABC 的面积．4.设△ABC 的内角A ，B ，C 所对的边长分别为a ，b ，c ，且acosB=3，bsinA=4． (Ⅰ)求边长a ；(Ⅱ)若△ABC 的面积S=10，求△ABC 的周长l ．5.设△ABC 的内角A ，B ，C 所对的边长分别为a ，b ，c ，且acosB －bcosA=3c 5.(Ⅰ)求tanAcotB 的值； (Ⅱ)求tan(A －B)的最大值．6.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，tanC =(1)求cosC ； (2)若CB CA =2.5⋅，且a+b=9，求c ．7.在△ABC 中，内角A ，B ，C 对边的边长分别是a ，b ，c ，已知c=2，C=600．(Ⅰ)若△ABC a ，b ；(Ⅱ)若sinB=2sinA ，求△ABC 的面积．(Ⅲ)若sinC+sin(B －A)=2sin2A ，求△ABC 的面积．说明：本小题主要考查三角形的边角关系，三角函数公式等基础知识，考查综合应用三角函数有关知识的能力．数学限时练习(4)班级_______ 姓名____________一、选择题：1.若数列{a n }的通项公式是a n =2 (n ＋1)＋3，则此数列A.是公差为2的等差数列B.是公差为3的等差数列C.是公差为5的等差数列D.不是等差数列 2.设等差数列5，247，437…第n 项到第n+6项的和为T ，则|T|最小时，n= A. 6 B.5 C.4 D.33.在等差数列{a n }中，已知a 3=2，则前5项之和等于A. 10B.16C.20D.32 4.记等差数列{a n }的前n 项和为S n ,，若S 2n －1=(2n －1)(2n+1)，则S n = A.n (2n +1)2 B. n(2n+3) C.n(2n +3)2D. n(n+2) 5.等差数列{a n }中，若a 2+a 4+a 9+a 11=32，则a 6+a 7=A. 9B.12 C 15 D.16 6.等差数列{a n }中，已知前4项和是1，前8 项和是4，则a 17＋a 18＋a 19＋a 20=A. 7B. 8 C 9 D.10 7.已知等差数列{a n }的公差为1，且a 1+a 2+a 3+…+a 99=99，则a 3+a 6+…a 99=A. 99B. 66 C 33 D. 0 8.已知数列{a n }的通项公式为a n =2n －49，则S n 达到最小值时，n=A.23B.24 C 25 D.26 9.已知等差数列{a n }的前三项依次为a －1，a ＋1，2a ＋3，则此数列的通项 a n =A. 2n －5B.2n －3 C 2n －1 D.2n ＋1 10.已知等差数列{a n }的公差d ＝21，a 1＋a 3＋a 5＋a 7＋a 9＋…＋a 95＋a 97＋a 99=60，则前100项之和S 100=A. 120B.145 C 150 D.170 二、填空题：11.{a n }为等差数列，a 4=－20，a 16=16，则|a 1|+|a 2|+|a 3|+…+|a 20|=________.12.等差数列{a n }中，若a 1＋a 3＋a 5=－1，则a 1＋a 2＋a 3＋a 4＋a 5=___________ .13.等差数列{a n }中，若a 2+a 3+a 4+a 5=34, a 2a 5=52, 且a 4＞a 2, 则a 5=_______. 14.数列前n 项和为S n =n 2+3n, 则其通项a n 等于____________.15.等差数列{a n }中, 前4项和为26, 后4项之和为110, 且前n 项和为340, 则n 的值为___________.16.等差数列{a n }中， S 5=28， S 10=36 (S n 为前n 项和)，则S 15等于________.17.等差数列{a n }中，a 10<0， a 11>0， a 11>|a 10|，若{a n }的前n 项和S n < 0，则n 的最大值是________.18.在1与9之间插入n －1个数b 1，b 2，…b n －1，使这n+1个数成等差数列，记为A n+1，则数列{A n+1}的通项公式为_____________. 19.若数列{a n }的前n 项和S n =3 n +1，则a n = ____________.20.若数列{a n }的前n 项和S n =2n 2－n+3，则其通项公式a n =_______. 21.数列lg21250⋅, lg 32250⋅, lg 43250⋅,……中，开始出现负值的项是第_____项. 22.凸n 边形的各内角度数成等差数列，最小角为1200 ，公差为50 , 则边数n 为_______.23.给出数阵如右图，其中每行、每列均为等差数列，则数阵中所有的数的和为___________.24.设S n 是等差数列的前n 项和，已知3a 4=7a 7，且a 1>0，当S n 取得最大时，则n=________.0 1 2 (9)1 2 3 (10)2 3 4 ... 11 .................. 9 10 11 (18)。

北师大版高中数学必修一双基限时练15.docx

双基限时练(十五) 指数概念的扩充基础强化1．a－89中，字母a 不能取的值是( )A. 0B. 1C. 98D. 12答案 A2．下列各式正确的是( ) A. －x ＝(－x ) 12(x ≠0)B. x －13＝－3x (x ≠0)C. ⎝ ⎛⎭⎪⎫x y －34＝4⎝ ⎛⎭⎪⎫y x 3(x ，y ≠0) D.6y 2＝y 13(y <0)答案 C3．已知(x 2－3x ＋2)0没有意义，则x 的值为( ) A. 1B. 2C. 1或2D. －1或2解析由于00没有意义，故x 2－3x ＋2＝0，得x ＝1，或x ＝2，故答案为C.答案 C4．下列各式是分数指数幂的是( ) A. a 0 B. (m 2＋1)－3 C. 0－5D. ⎝⎛⎭⎪⎫－2332解析选项A 中a 无限制条件，不符合分数指数幂的定义；选项C 中0－5无意义，因为0的负分数指数幂无意义；选项D 不符合分数指数幂的定义，底数小于0.故选B.答案 B5．下列各式既符合分数指数幂的定义，值又相等的是( )A. (－1) 13 和(－1) 26B. 02和012C. 2 12和414D. 4－32和⎝ ⎛⎭⎪⎫12－3解析选项A 和B所给的式子(－1) 13 和(－1)23，02不符合分数指数幂定义的限制条件，故均不正确；选项D 所给的式子4－ 32和⎝ ⎛⎭⎪⎫12－3虽符合分数指数幂的定义，但值不相等，故不正确．而C 中212＝2，414 ＝422＝212＝2，故选C.答案 B6.3(－3)5＋3952等于( )A. 2335 B. －2335 C. 0 D. 1答案 C7.4(3－π)4的值为________．解析4(3－π)4＝|3－π|＝π－3.答案 π－3能力提升8．在式子(3－2x ) －12中，x 的取值范围是________．解析由于(3－2x )－12＝1(3－2x ) 12＝13－2x，因此应有3－2x >0，即x <32.答案 x <329.40.0625＋254－(π)0－3278＝________.解析40.0625＋254－(π)0－ 3278＝12＋52－1－32＝12.答案 1210．求函数y ＝(2x ＋3)－38－(6x －5)的定义域．解由题意得⎩⎪⎨⎪⎧2x ＋3>0，6x －5≠0，解得x >－32且x ≠56.∴函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >－32且x ≠56. 11．把下列是根式的化为分数指数幂，是分数指数幂的化为根式(式中字母均为正实数)．解12．已知幂函数y ＝f (x )的图像过点(9，13)．(1)求f (x )的解析式； (2)求f (25)的值；(3)若f (a )＝b (a ，b >0)，则a 用b 可表示成什么？解 (1)设f (x )＝x t ，则9t ＝13. 即32t ＝3－1，∴t ＝－12，∴f (x )＝x－12(x >0)．(2)f (25)＝25－12＝125 12＝125＝15.(3)由f (a )＝b 得a－12＝b ，∴a ＝b －2＝1b 2.考题速递13．若(4a ＋1)2＝－4a －1，则实数a 的取值范围是________．解析 ∵(4a ＋1)2＝|4a ＋1|＝－4a －1，则4a ＋1≤0，∴a ≤－14. 答案 ⎝⎛⎦⎥⎤－∞，－14。

人教A版数学必修一双基限时练15.docx

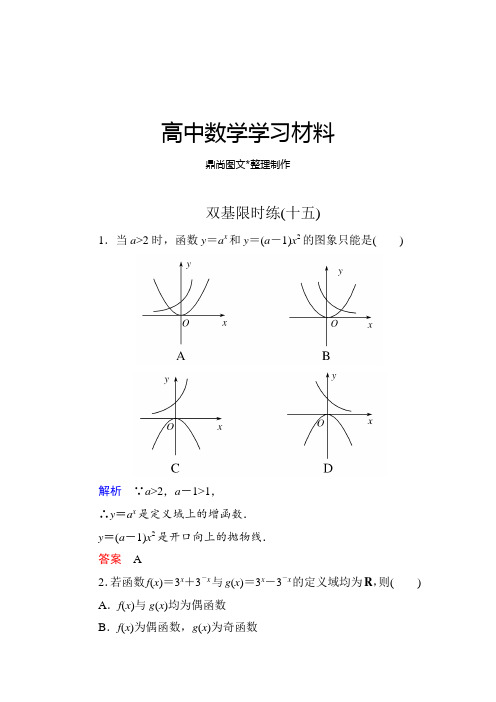
高中数学学习材料鼎尚图文*整理制作双基限时练(十五)1．当a>2时，函数y＝a x和y＝(a－1)x2的图象只能是()解析∵a>2，a－1>1，∴y＝a x是定义域上的增函数．y＝(a－1)x2是开口向上的抛物线．答案 A2．若函数f(x)＝3x＋3－x与g(x)＝3x－3－x的定义域均为R，则() A．f(x)与g(x)均为偶函数B．f(x)为偶函数，g(x)为奇函数C ．f (x )与g (x )均为奇函数D ．f (x )为奇函数，g (x )为偶函数解析因为f (－x )＝3－x ＋3－(－x )＝3－x ＋3x ＝f (x )， g (－x )＝3－x －3－(－x )＝3－x －3x ＝－g (x )，所以f (x )为偶函数，g (x )为奇函数．答案 B3．函数y ＝|2x －2|的图象是( )解析找两个特殊点，当x ＝0时，y ＝1，排除A ，C.当x ＝1时，y ＝0，排除D.故B 正确．答案 B4．a ，b 满足0<a <b <1，下列不等式中正确的是( ) A ．a a <a b B ．b a <b b C ．a a <b aD ．b b <a b解析 ∵0<a <b <1，∴a a >a b ，故A 不成立，同理B 不成立，若a a<b a，则⎝ ⎛⎭⎪⎫a b a <1，∵0<ab <1,0<a <1，∴⎝ ⎛⎭⎪⎫a b a<1成立，故C 正确．答案 C5．某厂2013年的产值为a 万元，预计产值每年以b %递增，则该厂到2025年的产值(万元)是( )A ．a (1＋b %)13B ．a (1＋b %)12C ．a (1＋b %)11D.109a (1－b %)12解析 2013年产值为a ，则2014年产值为a ＋a ·b %＝a (1＋b %)，2015年产值a (1＋b %)＋a (1＋b %)b %＝a (1＋b %)(1＋b %)＝a (1＋b %)2…所以2025年的产值为a (1＋b %)12，应选B. 答案 B6．若函数f (x )＝⎩⎨⎧a x，x >1，⎝ ⎛⎭⎪⎫4－a 2x ＋2，x ≤1是R 上的增函数，则实数a 的取值范围为( )A ．(1，＋∞)B ．(1,8)C ．(4,8)D ．[4,8)解析由题意得⎩⎪⎨⎪⎧a >1，4－a 2>0，a ≥⎝ ⎛⎭⎪⎫4－a 2·1＋2，解得4≤a <8. 答案 D7．已知a ＝0.80.7，b ＝0.80.9，c ＝1.20.8，则a ，b ，c 的大小关系为________．解析由指数函数y ＝a x 当0<a <1时为减函数知， 0．80.7>0.80.9，又1.20.8>1,0.80.7<1， ∴1.20.8>0.80.7>0.80.9，即c >a >b . 答案 c >a >b8．已知函数f (x )＝⎝ ⎛⎭⎪⎫12|x －1|，则f (x )的单调递增区间是________．解析法一：由指数函数的性质可知f (x )＝⎝ ⎛⎭⎪⎫12x在定义域上为减函数，故要求f (x )的单调递增区间，只需求y ＝|x －1|的单调递减区间．又y ＝|x －1|的单调递减区间为(－∞，1]，所以f (x )的单调递增区间(－∞，1]．法二：f (x )＝⎝ ⎛⎭⎪⎫12|x －1|＝⎩⎨⎧12x －1，x ≥1，2x－1，x <1.可画出f (x )的图象求其单调递增区间．答案 (－∞，1]9．若方程⎝ ⎛⎭⎪⎫14x ＋⎝ ⎛⎭⎪⎫12x －1＋a ＝0有正数解，则实数a 的取值范围是________．解析令⎝ ⎛⎭⎪⎫12x＝t ，∵方程有正根，∴t ∈(0,1)．方程转化为t 2＋2t ＋a ＝0， ∴a ＝1－(t ＋1)2.∵t ∈(0,1)，∴a ∈(－3,0)．答案 (－3,0)10．已知关于x 的方程⎝ ⎛⎭⎪⎫15x＝7－a 的根大于0，求a 的取值范围．解 ∵x >0，∴0<⎝ ⎛⎭⎪⎫15x<1，即0<7－a <1，∴6<a <7. ∴a 的取值范围是6<a <7.11．解不等式a 2x ＋7<a 3x －2(a >0，a ≠1)．解当a >1时，a 2x ＋7<a 3x －2等价于2x ＋7<3x －2， ∴x >9；当0<a <1时，a 2x ＋7<a 3x －2等价于2x ＋7>3x －2. ∴x <9.综上，当a >1时，不等式的解集为{x |x >9}；当0<a <1时，不等式的解集为{x |x <9}． 12．设a ∈R ，f (x )＝a －22x ＋1(x ∈R )．(1)证明对任意实数a ，f (x )为增函数； (2)试确定a 的值，使f (x )≤0恒成立．解 (1)证明：任取x 1，x 2∈R ，且x 1<x 2，则f (x 1)－f (x 2)＝⎝ ⎛⎭⎪⎫a －22x 1＋1－⎝ ⎛⎭⎪⎫a －22x 2＋1＝22x 2＋1－22x 1＋1＝2(2x 1－2x 2)(2x 1＋1)(2x 2＋1). ∵指数函数y ＝2x 在R 上是增函数，且x 1<x 2， ∴2x 1<2x 2，即2x 1－2x 2<0. 又2x >0，∴2x 1＋1>0,2x 2＋1>0. ∴f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)．故对于任意实数a ，f (x )为增函数． (2)f (x )＝a －22x ＋1≤0恒成立，只要a ≤22x ＋1恒成立，问题转化为只要a 不大于22x ＋1的最小值．∵x ∈R,2x >0恒成立，∴2x ＋1>1. ∴0<12x ＋1<1,0<22x ＋1<2，∴a ≤0.故当a ≤0时，f (x )≤0恒成立．。

高一数学限时练

高一数学限时练
1．按照如图程序运行，则输出k的值是（）
A．3B．4C．5D．6
2．执行如图所示的程序语句，输出的结果为（）
A．﹣3025B．﹣1009C．1009D．3025
第1题图第2题图
3．如图是一个算法的条件语句若使输出的y值为﹣3，则输入的x值为（）A．6B．±2C．2或6D．±2或6
4．已知有下面程序，若程序执行后输出的结果是11880，则在程序后面的“横线”处应填（）A．i≥9B．i＝8C．i≥10D．i≥8
第3 题图第4 题图
5．下面程序输出的结果为．
6．给出30个数：1，2，4，7，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依此类推．要计算这30个数的和，现已给出了该问题算法的程序框图（如图所示）：
（1）图中①处和②处应填上什么语句，使之能完成该题算法功能；
（2）根据程序框图写出程序．
7．用For语句描述计算1++++…+的值的一个程序．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高一数学限时练15
一、选择题(本大题共12小题，共60.0分)
1. 在长方体ABCD-A 1B 1C 1D 1中，M为AC与BD的交点，若, ，，则下列向量中与相等的向量是（）
A. B. C.
D.
2. 下列说法正确的是（）.
A. 方向相同或相反的向量是平行向量
B. 零向量是
C. 长度相等的向量叫做相等向量
D. 共线向量是在一条直线上的向量
3. 化简下列式子：其结果为零向量的个数是（）
① ；② ；
③ ；④
A. 1
B. 2
C. 3
D. 4
4. 如图，正六边形ABCDEF中，( )
A. 0
B.
C.
D.
5. 设
A. B. C. D.
6. 设是平行四边形的对角线的交点，为任意一点，则( )
A. B. C. D.
7. 在以下各命题中,假命题的个数为( )
①“|a|=|b|”是“a=b”的必要不充分条件
②任一非零向量的方向都是唯一的
③“a∥b”是“a=b”的充分不必要条件
④若|a|-|b|=|a|+|b|,则b=0
A. 1
B. 2
C. 3
D. 4
8. 如果, 是两个单位向量，下列结论正确的是
A. =
B. ・=1
C.
D. =
9. 设向量a＝( m，1)，b＝(2，－3)，若满足a// b，则m＝
A. B. C. D.
10.
A. B. C.
D.
11. 已知圆心为o的圆上三点A,B,C,则向量是------（）
A. 有相同起点的相等向量。

B. 长度为1的向量。

C. 模相等的向量。

D. 相等的向量。

12. 下列命题中正确的是( )
A. 两个相等的向量的起点，方向，长度必须都相同
B. 若，是两个单位向量，则 =
C. 若向量
和b 共线，则向量，的方向相同 D. 零向量的长度为0，方向是任意的
二、填空题(本大题共4小题，共20.0分)
13. 已知向量
，，，若三点共线，则实数的值为 _ ．
14. 已知
，，则的坐标为 .
15. 已知向量 =（-1,2），向量
=（3，-1），则向量的坐标为 __ __. 16. 向量 a =（n,2）与 b =（4,n ）共线，则n=________________.
三、解答题(本大题共2小题，共20分)
17.
如图所示，在△ABC 中，D 、F 分别是BC 、AC 的中点， = ， = ， = ．
(1)用、表示向量、、、、； (2)求证：B 、E 、F 三点共线．
18. 某人从A 点出发向西走了10m ，到达B 点，然后改变方向按西偏北60°走了15m 到达C 点，最后又向东走了10米到达D 点．
(1)作出向量
，， (用1cm 长的线段代表10m 长)
(2)求
．。