初三数学期中考试试卷2007
2007-2008学年度第一学期九年级数学期中考试卷(07.10)

2007—2008学年度第一学期初三数学期中考试试卷一、选择题(每题4分,共40)1.将抛物线25x y =向左平移2个单位,再向下平移3个单位,得到的抛物线是( )A .3)2(52++=x yB .3)2(52-+=x yC .3)2(52+-=x yD .3)2(52--=x y2.下列说法正确的是 ( )A .各有一个角是︒100的两个等腰三角形相似B .各有一个角是︒45的两个等腰三角形相似C .有两边对应成比例的两个等腰三角形相似D .两腰对应成比例的两个等腰三角形相似3.下列说法中,正确的是 ( )A .彩票中奖的机会是1%,买100X 一定会中奖B .天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨C .某小组有13名同学,至少有2名同学的生日在同一个月D .抛一枚圆钉,钉尖着地和钉尖朝上的概率一样大4.如图,AD 和AC 分别是⊙O 的直径和弦,且︒=∠30CAD ,OB ⊥AD 交AC 于点B , 若OB=5,则BC 为 ( )A .35B .310C .15D .55.如图,一X 矩形报纸ABCD 的长AB=a ,宽BC=b ,E 、F 分别是AB 、CD 的中点,将这X 报纸沿着直线EF 对折后,所得矩形与原矩形相似,则a ∶b 等于( )A .2∶1B .1∶2C .3∶1D .1∶3第4题 第5题6.已知正三角形边长为6,则该三角形的外接圆半径为 ( )A .32B .3C .3D .17.抛物线322-+=x x y 与x 轴交于A 、B 两点,与y 轴交于C 点,则下列叙述不正确 的是 ( )A .函数y 的最小值为-4B .抛物线开口向上C .△ABC 的面积是6D .抛物线的对称轴是1=x8.在如图的①、②两个转盘中,指针指向每一个数字的机会是均等的,当同时转动两个转盘,停止后指针所指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段不能构成三角形的概率是 ( )A .256B .259C .2512D .2516 9.如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点P 沿AB 边从点A 开始向点B 以2cm/S 的速度移动,点Q 沿DA 边从点D 开始向点A 以1cm/S 的速度移动。
山东省潍坊市2007——2008九年级数学第一学期期中考试试卷

某某省潍坊市2007——2008九年级数学第一学期期中考试试卷一、选择题(本题共12题,第1~8题每小题2分,第9~12题每小题3分,共28分)1、 下列根式a 54,32a ,b ,x 8中,最简二次根式的个数为 ( )A 、4个B 、3个C 、2个D 、1个2、方程()01=-x x 的根是 ( )A 、0B 、1C 、-1D 、0,13、实数a 、b 在数轴上的位置如图所示,那么化简|a-b|-2a 的结果是 ( )A .2a-bB .bC .-bD .-2a+b 4、用反证法证明“三角形中必有一个内角不小于60°”,应先当假设这个三角形中( )A 、有一个内角小于60°B 、每一个内角都小于60°C 、有一个内角大于60°D 、每一个内角都大于60°5、下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等的圆心角所对的弧相等其中是真命题的是 ( )A 、①②B 、②③C 、①③D 、①②③6、下列图形是轴对称图形而不是中心对称图形的是。
( )7、若两圆的的圆心距等于7,半径分别为R ,r ,且R 、 r 是关于x 的方程0652=+-x x 的两个根,则两圆的位置关系是 ( )A 、相离B 、相交C 、内切D 、外切8、当m 在可以取值X 围内取不同的值时,代数式2942+-m m 的最小值是( )A 、0B 、5C 、33D 、99、化简200320022323)()(+•-的结果为 ( ) A 、23-- B 、23- C 、23+ D 、–110、如图在等腰直角△ABC 中,∠B =90°,将△ABC 绕顶点A逆时针方向旋转60°后得到△AB ’C ’则'BAC ∠等于( )A 、60°B 、105 °C 、120°D 、135°11、关于x 的一元二次方程kx 2+2x -1=0有两个不相等的实数根, 则k 的取值X 围是 ( )A. k>-1B. k>1C. k ≠0D. k>-1且k ≠012、在△ABC 中,∠C=90º,AB=5,周长为12,那么它的内切圆的半径为( )A 、3B 、8C 、2D 、1二、填空题(本题共6小题,每小题3分,共18分)13、若最简二次根式a +1与a 24-可以合并,则a =。
2007秋期中考试九年级数学试题

2007秋期中考试九年级数学试题(试题共五大题25小题 卷面分数:120分 考试时间:120分钟)考生注意:本试卷分为两卷,解答第Ⅰ卷时,请将解答结果填写在第Ⅱ卷上指定的位置,否则答案无效,交卷只交第Ⅱ卷。
答卷时可以用计算器。
第 Ⅰ 卷一、选择题:(把正确答案的代号填在答题卡上,每题3分,共30分。
) 1、方程1432=+x x 的解是( )A 、2653±=xB 、2653±-=xC 、2233±=xD 、2233±-=x2、三角形三边上的垂直平分线相交于一点,这一点在( ) A 、三角形内 。
B 、三角形外。
C 、角形一边上。
D 、三角形内或三角形外或三角形一边上.3、用配方法解下列方程时,配方有错误的是 ( )A 、x 2-2x -99=0化为(x -1)2=100B 、x 2+8x +9=0化为(x +4)2=25C 、2t 2-7t -4=0化为1681)47(2=-tD 、3y 2-4y -2=0化为910)32(2=-y4、△ABC 中,AB=AC ,∠ABC =36︒,D 、E 是BC 上的点,∠BAD =∠DAE =∠EAC ,则图中等腰三角形的个数是 ( )A 、2个B 、3个C 、4个D 、6个 5、正方形具有而菱形不一定具有的性质是( ) A 、对角线互相平分B 、对角线相等C 、对角线平分一组对角D 、对角线互相垂直6、如图,在△ABC 中,AB=AC ,AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F.现有下列结论:(1)DE=DF ;(2)BD=CD ;(3)AD 上任意一点到AB 、AC 的距离相等;(4)AD 上任意一点到BC 两端点的距离相等,其中正确结论的个数有( ) A 、1个B 、2个C 、3个D 、4个7、平面内有三个点A 、B 、C ,其中A 、B 、C 三点不共线,再找一个点D ,使得四边形ABCD为平行四边形,则满足条件的点D 的个数有( ) A 、1个B 、2个C 、3个D 、4个8、下面是一天四个不同时刻两个建筑物的影子,将它们按时间先后顺序进行排列,则它们排列的位置是( ) A 、(C )(D )(A )(B )B 、(A )(C )(B )(D ) C 、(B )(C )(A )(D ) D 、(A )(B )(C )(D )9、在□ABCD 中,下列结论不一定正确的是( )A 、AB=CDB 、AC=BDC 、当A C ⊥BD 时。
2007教育出版社九年级数学第一册期中试题.doc

2007教育出版社九年级数学第一册期中试题时间:120分钟 满分:120分一、选择题(每小题3分,共30分)1.(2016·朝阳)方程2x 2=3x 的解为( )A .0B .32C .-32D .0,322.抛物线y =(x -1)2+2的顶点坐标是( )A .(-1,2)B .(-1,-2)C .(1,-2)D .(1,2)3.(2016·攀枝花)若x =-2是关于x 的一元二次方程x 2+32ax -a 2=0的一个根,则a的值为( )A .-1或4B .-1或-4C .1或-4D .1或44.(2016·桂林)若关于x 的一元二次方程(k -1)x 2+4x +1=0有两个不相等的实数根,则k 的取值范围是( )A .k <5B .k <5且k≠1C .k ≤5且k≠1D .k >55.某同学在用描点法画二次函数y =ax 2+bx +c 的图象时,列出了下面的表格:由于粗心,A .-11 B .-2 C .1 D .-56.若A(-6,y 1),B(-3,y 2),C(1,y 3)为二次函数y =x 2+4x -5图象上的三点,则y 1,y 2,y 3的大小关系是( )A .y 1<y 2<y 3B .y 2<y 3<y 1C .y 3<y 1<y 2D .y 2<y 1<y 37.(2016·广州)定义运算:a b =a(1-b).若a ,b 是方程x 2-x +14m =0(m <0)的两根,则b b -a a 的值为( )A .0B .1C .2D .与m 有关8.学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x 个球队参赛.根据题意,下面所列方程正确的是( )A .x 2=21B .12x(x -1)=21C .12x 2=21 D .x(x -1)=219.如图,有一块边长为6 cm 的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )A . 3 cm 2B .32 3 cm 2 C .92 3 cm 2 D .2723 cm 210.在某次足球训练中,一队员在距离球门12米处挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y =ax 2+bx +c(如图).现有四个结论:①a-b >0;②a<-160;③-160<a <0;④0<b <-12a.其中正确的结论是( )A .①③B .①④C .①②D .②④二、填空题(每小题3分,共24分)11.(2016·牡丹江)已知抛物线y =ax 2-3x +c(a≠0)经过点(-2,4),则4a +c -1=________.12.(2016·三明)若一元二次方程x 2+4x +c =0有两个不相等的实数根,则c 的值可以是________(写出一个即可).13.(2016·梅州)用一条长40 cm 的绳子围成一个面积为64 cm 2的矩形.设矩形的一边长为x cm ,则可列方程为____________________.14.将抛物线y =x 2-4x 向上平移3个单位,再向右平移4个单位得到的抛物线是____________.15.(2016·南通)设一元二次方程x 2-3x -1=0的两根分别是x 1,x 2,则x 1+x 2(x 22-3x 2)=________.16.若抛物线y =x 2+bx +c 与x 轴只有一个交点,且过点A(m ,n),B(m +6,n),则n =______.17.如图,在平面直角坐标系中,点A 在抛物线y =x 2-2x +2上运动.过点A 作AC⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连接BD ,则对角线BD 的最小值为________.18.设x 1,x 2是方程x 2-x -2 017=0的两实数根,则x 13+2 018 x 2-2 017=________.三、解答题(共66分)19.(6分)用适当的方法解下列方程. (1)(2x +3)2-16=0; (2)2x 2=3(2x +1).20.(8分)(2016·绥化)关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.(1)求m的取值范围;(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.21.(8分)已知抛物线y=-12x2-x+4.(1)用配方法确定它的顶点坐标和对称轴;(2)x取何值时,y随x的增大而减小?(3)x取何值时,抛物线在x轴上方?22.(8分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)若将这种水果每斤的售价降低x元,则每天的销售量是____________斤(用含x的代数式表示);(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?23.(8分)小区要用篱笆围成一个四边形花坛,花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米,围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.(1)请直接写出S与x之间的函数关系式;(不要求写出自变量x的取值范围)(2)当x是多少时,四边形ABCD的面积S最大?最大面积是多少?24.(8分)已知关于x的方程kx2+(2k+1)x+2=0.(1)求证:无论k取任何实数时,方程总有实数根;(2)当抛物线y=kx2+(2k+1)x+2的图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.25.(10分)近几年城市建设快速发展,对花木的需求逐年提高,某园林专业户计划投资15万元种植花卉和树木.根据市场调查与预测,种植树木的利润y1(万元)与投资量x(万元)成正比例关系:y1=2x;种植花卉的利润y2(万元)与投资量x(万元)的函数关系如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).(1)写出种植花卉的利润y2关于投资量x的函数关系式;(2)求此专业户种植花卉和树木获取的总利润W(万元)关于投入种植花卉的资金t(万元)之间的函数关系式;(3)此专业户投入种植花卉的资金为多少万元时,才能使获取的总利润最大,最大利润是多少万元?26.(10分)(2016·河池)在平面直角坐标系中,抛物线y=-x2-2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.(1)请直接写出点A,C,D的坐标;(2)如图①,在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;(3)如图②,F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.。
2007学年度第一学期九年级数学新教材期中试卷答案

2007学年度第一学期九年级数学新教材期中试卷答案一.填空题(本大题共12题,每题3分,满分36分)1.4:3; 2.34; 3.3.8; 4.3:7; 5.5:2; 6.a 25; 7.DE//BC 、∠=∠ADE B 等; 8.3:2; 9.3:1; 10.e 3-;11.︒60或︒65; 12.=DE 52BC . 二.选择题(本大题共4题,每题3分,满分12分)13. D ; 14. C ; 15. B ; 16. A .三.(本大题共4题,每题6分,满分24分)17.解:设k z y x ===432,………………………………………………………………(2分) 9432432=-+++=-+++k k k k k k z y x z y x .………………………………………………(4分) 18.作图略.…………………………………………………………………………………(6分)19.解:∵C ADE ∠=∠,A A ∠=∠,……………………………………………………(1分) ∴ADE ∆∽ACB ∆.……………………………………………………………(2分) ∴ABAE AC AD =.……………………………………………………………………(1分) ∵3=AD 厘米,5=BD 厘米,6=AC 厘米, ∴5363+=AE , 解得4=AE .…………………………………………………(1分) ∴2=-=AE AC EC 厘米.……………………………………………………(1分)20.解:∵E 是BC 边上的中点,∴BE :BC =1:2.……………………………………(1分) ∵平行四边形ABCD , ∴BC AD =,AD //BC .……………………………(1分) ∴BE :AD =1:2;…………………………………………………………………(1分) ∴FBE ∆∽FDA ∆ ………………………………………………………………(1分) ∴2)(ADBE S S FDA FBE =∆∆ .……………………………………………………………(1分) ∵32=∆FDA S , ∴8=∆FBE S . ………………………………………………(1分)四.(本大题共2题,每题8分,满分16分)21.证明:(1)∵ABD DAE ∠=∠,BDA ADE ∠=∠,∴ADE ∆∽BDA ∆.…………………………………………………………(2分) ∴ADDE BD AD =, 即DB DE AD ⋅=2.………………………………………(1分) (2)∵D 是AC 边上的中点,∴DC AD =. 由(1)知:AD DE BD AD =,即DC DE BD DC =,…………………………………(1分) 又∵BDC CDE ∠=∠.………………………………………………………(1分)∴CDE ∆∽BDC ∆.…………………………………………………………(2分)∴ACB DEC ∠=∠.…………………………………………………………(1分)22.解:画图正确.…………………………………………………………………………(2分) 过点A 作DE AH ⊥,交BC 于G .∵BC //DE ,∴ABC ∆∽△ADE .………………………………………………(2分)∴DEBC AH AG =.……………………………………………………………………(1分) ∵10010003600660=⨯⨯=DE ,30=BC ,35=GH .………………………(1分) ∴1003035=-AH AH , 解得50=AH .…………………………………………(1分) ∴小杰家到公路的距离是50米.…………………………………………………(1分)五.(本大题共1题,满分12分)23.解:(1)①过点E 作BC EH ⊥,垂足为H .∵3:2:=PC BP ,5=BC ,∴2=BP ,3=PC .∵x AE =,∴S =2+x (x >0) ………………………………………………………(2分) ②∵︒=∠=∠90GCP EHP ,∴∠EPH =90º–∠GPC =∠PGC ,∴EHP ∆∽PCG ∆.………………………………………………………………(2分) ∵x AE =,∴x HP -=2.∵EH =AB =2,∴x S EHP -=∆2 ,9924∆=-PCG S x .……………………………(1分) ∵PCG EPHEHCD S S S y ∆∆--=矩形,∴2745+=x y .……………………………(2分) 定义域为232<≤x .………………………………………………………………(1分) (2)当点G 在线段CD 上,DG DF =,DF -=23,1-=DF 不可能.………(2分) 当点G 在线段CD 的延长线上时,DG DF =,DF +=23,1=DF .此时可解得0=AE ,即当点E 与点A 重合时,DGF ∆是等腰三角形. (2)。
2007—2008学年度上期九年级期中数学试卷定稿)

2007—2008学年度上期 九年级期中数学试卷全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
学生姓名 .班级 .学号 .得分:A 卷 (共 100分)一、选择题(每小题3分,共24分)1.下列是一元二次方程的是 ( )A. 312=+xx B. 132=+x xyC. 04322=++x x D. 52222+=+x x x2.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是 ( )。
3.用配方法解方程01422=++x x ,配方后的方程是 ( )A .2)22(2-=+xB . 3)22(2-=+x C . 21)21(2=+x D . 21)1(2=+x 4.桌面上放着一个圆锥和一个长方体,其中俯视图应该是 ( ) (A)(B)(C)(D)●5 . 3. 如图,AC =AD ,BC =BD .则 ( ) A .CD 垂直平分AB B .AB 垂直平分CD C .CD 平分∠ACBD .以上结论都不正确6. 如果两点P 1(1,y 1)和P 2(2,y 2)在反比例函数xy 1=的图象上,那么y 1与y 2间的关系是 ( )A .y 2<y 1<0B .y 1<y 2<0C .y 2>y 1>0D .y 1>y 2>07.蓄电池的电压为定值,使用此电源时,电流)(A I 与电阻)(ΩR 成反比例,其函数图象如图所示,则电流I 与电阻R 之间的函 数关系式为 ( )A. R I 24=B. R I 4= C. RI 6= D. R I 10=8.对于中点四边形(顺次连接四边形各边中点的四边形),说法正确的个数是 ( ) ①任何四边形的中点四边形是平行四边形. ②中点四边形的面积是原四边形面积的一半. ③矩形的中点四边形是矩形. ④等腰梯形的中点四边形是菱形.A . 1个B . 2个C . 3个D . 4个二、填空题(每小题3分,共24分)9.方程:022=-x x的根是 .10. 四边形ABCD 中,对角线AC 、BD 交于点O, 若OA=OB=OC=OD ,则这个四边形是11. 等腰三角形的两边长为4和9,则这个等腰三角形的周长为 。
2007-2008学年第一学期九年级数学期中考试卷 华师大版

2007-2008学年第一学期初三数学期中试卷一、选择题:(共9小题,每小题3分,共27分)1. 一元二次方程2230x x --=的两个根分别为A.x l =1,x 2=3 B .x l =1,x 2=-3 C.x 1=-1,x 2=3 D.x I =-1,x 2=-3 2. 下列方程没有实数根的是A.x 2-x-1=0B. x 2-6x+5=0 C.2x 30+= D.2x 2+x+1=0 3.设—元二次方程x 2-2x -4=0的两个实根为x 1和x 2,则下列结论正确的是 A .x 1+x 2=2B .x 1+x 2=-4C .x 1·x 2=-2D .x 1·x 2=44.用换元法解分式方程2212(2)321x x x x -++=+-时,设212xy x -=+,则原方程可化为整式方程A.2320y y ++= B.2230y y ++= C.2230y y +-=D.2320y y -+=5.有两块面积相同的小麦试验田,分别收获小麦9000kg 和15000kg .已知第一块试验田每公 顷的产量比第二块少3000kg ,若设第一块试验田每公顷的产量为x kg ,根据题意,可得方程A .x x 1500030009000=+ B .3000150009000-=x x C .3000150009000+=x x D .xx 1500030009000=- 6.已知抛物线2(1)(0)y a x h a =-+≠与x 轴交于1(0)(30)A x B ,,,,则线段AB 的长度为 A.1B.2C.3D.47.一个不透明的袋中有5个红球,x 个白球,这两种球除了颜色以外没有任何其他区别.从中任取一个,恰为白球的概率为54,则x 等于 A .25 B .20 C .15 D .10 8.已知二次函数y =2 x 2+9x+34,当自变量x 取两个不同的值x 1、x 2时,函数值相等,则当自变量x 取x 1+x 2 时的函数值与A .x =1时的函数值相等B .x =0时的函数值相等C .x =41时的函数值相等D .x =-49时的函数值相等共8页(第1页)9.已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,有下列5个结论:①0>abc ;②c a b +<;③024>++c b a ;④b c 32<;⑤)(b am m b a +>+,(1≠m 的实数).其中正确的结论有 A . 2个 B .3个C .4个D .5个二.填空题:(共9小题,每小题3分,共27分)10.分式方程121+=x xx 的解是x=_________. 11.抛物线y=3(x-1)+1的顶点坐标是____________.12.已知二次函数的图象开口向上,且顶点在y 轴的负半轴上,请你写出一个满足条件的二次函数的表达式________________.13.某某市住宅是由8位数字组成,某人到电信公司申请安装一部住宅,那么该公司配送给这部的末尾数字为6的概率是_______.14.三角形的两边长分别为3和6,第三边的长是方程x 2-6x +8=0的一个根,则这个三角形的周长是_________. 15.二元二次方程组⎩⎨⎧-==+103xy y x 的解是_____________________.16.一套书共有上、中、下三册,将它们任意摆放到书架的同一层上,这三册书从左向右恰好成上、中、下顺序的概率为.17.已知a b ,是一元二次方程2430x x +-=的两个实数根,则24a ab a -+的值是______.18.“某某桥”是位于某某市中心、横跨黄河之上的一座百年老桥.如图1,桥上有五个拱形桥架紧密相联,每个桥架的内部有一个水平横梁和八个垂直于横梁的立柱,气势雄伟,素有“天下黄河第一桥”之称.如图2,一个拱形桥架可以近似看作是由等腰梯形ABD 3D 1 和其上方的抛物线D 1O D 3组成.若建立如图所示的直角坐标系,跨度AB =44米,∠A =45°,AC 1=4 米,点D 2的坐标为(-13,-1.69),则桥架的拱高OH=米.图1图2共8页(第2页)三.解答题:(共10大题,共76分)19.(10分)解方程: (1)4161222-=--x x x(2)23411x x x x ⎛⎫⎛⎫+= ⎪ ⎪--⎝⎭⎝⎭20.(5分)已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8).(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标.共8页(第3页)21.(6分)老李承包了一片荒山,在山上种植了一部分优质油桃,今年已进入第三年收获期.今年收获油桃3630千克,已知老李第一年收获的油桃重量为3000千克.试求去年和今年两年油桃产量的年平均增长率,照此增长率,预计明年油桃的产量为多少千克?22.(6分)如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,回答下列问题:(1) 抛物线y 2的顶点坐标_____________; (2) 阴影部分的面积S =___________;(3) 若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3,则抛物 线y 3的开口向__________,顶点坐标____________.23.(7分)已知关于x 的方程01)1(22=-++-k x k kx 有两个不相等的实数根, (1) 求k 的取值X 围;(2) 是否存在实数k ,使此方程的两个实数根x 1、x 2的倒数和等于0 ?若存在,求出k 的值;若不存在,说明理由.共8页(第4页)24.(6分)九年级1班将竞选出正、副班长各1名,现有甲、乙两位男生和丙、丁两位女生参加竞选.(1)男生当选正班长的概率是;(2)请用列表或画树状图的方法求出两位女生同时当选正、副班长的概率.25.(8分)某农场计划建一个养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙足够长),另外的部分用30米的竹篱笆围成,现有两种方案:①围成一个矩形(如下左图);②围成一个半圆形(如下右图).设矩形的面积为S1平方米,宽为x米,半圆形的面积为S2平方米,半径为r米,请你通过计算帮助农场主选择一个围成区域面积最大的方案(π≈3).共8页(第5页)26.(6分)阅读以下材料,并解答以下问题.“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?(3)现由于交叉点C道路施工,禁止通行.求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?共8页(第6页)27.(10分)如图,直线y=-x +3与x 轴,y 轴分别相交于点B ,点C ,经过B 、C 两点的抛物线2y ax bx c =++与x 轴的另一交点为A ,顶点为P ,且对称轴是直线2x =. (1)求A 点的坐标;(2)求该抛物线的函数表达式;(3)连结A 、C ,请问在x 轴上是否存在点Q ,使得以点P 、B 、Q 为顶点的三角形与ABC △相似,若存在,请求出点Q 的坐标;若不存在,请说明理由.x共8页(第7页)28.(12分)已知如图,矩形OABC的长OA=3,宽OC=1,将△AOC沿AC翻折得△APC.(1)填空:∠PCB=______度,P点坐标为(,);(2)若P,A两点在抛物线y=-43x2+bx+c上,求b,c的值,并说明点C在此抛物线上;(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP 的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由。
杭十五中2007年第一学期九年级数学期中考试卷 浙教版

2007学年第一学期初三年级期中数学测试卷(考试时间100分钟, 满分120分)出卷人:X小冬校对人:鲁小蓉一、仔细选一选(每小题3分,共30分)1.若比例式a2=b3=c4≠0,则a+bc的值为()(A)45(B)54(C) 2 (D)122. 收音机刻度盘的波长l和频率f分别是用米(m)和千赫兹(kHz)为单位标刻的.波长l和频率f满足关系式300000fl,这说明波长l越大,频率f就( )A、越大B、越小C、不变D、不能确定, 与l的取值X围有关3. 一个扇形的圆心角是120°,它的面积是3π,那么这个扇形的半径是( )(A)3(B) 3 (C) 6 (D)94. 把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是()(A) y=3(x+3)2 -2 (B)y=3(x+2)2+2(C)y=3(x-3)2 -2 (D)y=3(x-3)2+25.如图,A、B是两座灯塔,在弓形内有暗礁,游艇C在附近海面游弋,且∠AOB=80°,要使游艇C不驶入暗礁区,则航行中应保持∠ACB()A、小于40°B、大于40°C、小于80°D、大于80°6.下列命题中,真命题的个数为………()(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦;(3)900的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等.(5)三角形的外心是三边中垂线的交点A.、1 个B、2 个C、3 个D、4 个7. 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=()(A)35°(B)70°(C)110°(D)140°8.因受“桑美”台风影响,校园内一根电线杆AB(如图,AB垂直地面BC)的顶端A处有一条线AC被打断而挂在了地面上,有一位同学想利用这根断头线测量电线杆的长度。
2007年11月初三数学期中试题答案

(x 3)( x 1) 0
∴ x1=3,x 2=-1 ∴A(-1,0),B(3,0),C(0,3) (2) 设 CM所在直线为 y=kx+b
b3 kb 4 k1 y x3 令 y 0 x 3 D( 3,0) DA 1 ( 3) 2
……………… 4 分
又 CN ∥x 轴,且 CN=2
∴CN∥DA且 CN=DA ∴CDAN为平行四边形。 24、 1)∵∠ A=∠A,∠ ACB=90°, CD⊥AB于 D
∴∠ ADC=9°0 ∴∠ ADC=∠ACB ∴△ ADC∽△ ACB 2)∵△ ADC∽△ ACB ∴ AC AD
AB AC ∴AC2=AD·AB 又∵ AC=6,AD=18
5 ∴36=AB· 18
5 ∴AB=10
求 Rt △ABC中, BC= AB2 AC 2 100 36
AC·BC=AB·CD ∴6×8=10×CD ∴CD=24
x2 50 x 33
50
x
b 2a
3 2 ( 1)
25
3
S最大
1 (25) 2
50 2533……………… 2 分…………………… 3 分 …………………… 5 分
…………………… 2 分 …………………… 4 分 …………………… 5 分
2分
……………………… 3 分 ……………………… 5 分 ……………………… 1 分
1 3 3 1 31
2
2
93
22 6
…………………… 2 分 …………………… 4 分
23、(1)设 y a(x h)2 k, 过( 2,3)点,顶点为( 1, 4)
a(2 1) 2 4 3 a1 y 1( x 1) 2 4
x2 2x 3
2007学年上期期中初三数学

2007——2008学年上期期中检测九年级数学命题人:张睿评分数一、选择题(每小题3分,共18 分)1、下列二次根式中,是最简二次根式的是( ) A.a 8 B.22y x + C.a3D.122+-x x 2、下列图形中,既是轴对称图形又是中心对称图形的是( )3、有一段电路可以由图示的开关控制,任意闭合两个开关使电路接通的 概率是( ) A.51 B.52 C. 53 D. 54 4、已知一弧长为m 的弧所对的圆心角为120,那么它所对的弦长为( ) A.m π433 B. m π423 C. m π233 D. m π223 5、如图,已知△ABC 的内切圆⊙O 与各边相切于D 、E 、F , 那么点O 是 △DEF 的( )A .三条中线的交点 B.三条高的交点C.三条角平分线的交点D.三边垂直平分线的交点6、已知关于x 的一元二次方程x 2-(R +r )x +14 d 2=0没有实数根,其中R ,r分别为⊙O 1和⊙O 2的半径,d 为此两圆的圆心距,则⊙O 1和⊙O 2的位置关系是( )A 外离B 相切C 相交D 内含 二、填空题(每小题2分,共26分)7、已知点A (4,-a )与点B (b ,-8)关于原点对称,则ab = 。
8、有四张不透明的卡片分别写着2、722、π、2,除正面的数不同外,其余都相同,将它们背面向上洗匀后,从中随机抽取一张卡片,抽出写有无理数卡片的概率为 。
9、用反证法证明命题“三角形两边之和大于第三边”,首先应假设 。
10、已知⊙0的半径为13cm ,弦AB ∥CD ,AB =24cm ,CD =10 cm ,则AB 和CD 的距离是11、计算:=---+-+-10)12()12008()347)(347(12、如图,M 是CD 的中点,EM ⊥CD ,若CD =4cm ,EM =6cm ,则弧CED 所在圆的半径为 cm 。
13、如图,AD 和AC 分别是⊙O 的直径和弦,且∠CAD =300,OB ⊥AD ,交AC 于点B ,若OB =5,则BC = 。
2007-2008学年第一学期九年级数学期中考试卷 人教版

2007-2008学年九年级第一学期期中考试数学试卷考生注意:考试时间120分钟总分120分。
一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.方程x 2-9=0的解是……………………………………………………( ) A .x l =x 2=3 B. x l =x 2=9C .x l =3,x 2=-3 D. x l =9,x 2=-9 2.如图,已知O 的半径OA 长为5,弦AB 长为8,C 是AB 的中点,则OC 的长为 ……………………………………………………………( ) A 、3B 、6C 、9D 、103.某城市2003年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2005年底增加到363公顷.设绿化面积平均每年的增长率为x ,由题意,所列方程正确的是………………………………………………………………………………………………………………( ) A .300(1+x )=363 B .300(1+x )2=363 C .300(1+2x )=363 D .363(1-x )2=3004.如图,⊙O 的直径CD 过弦EF 的中点G ,∠EOD=40°,则∠DCF 等于……………………………………………………………………( ) ° B. 50° C. 40° D. 20° 5.如图所示,A (1x ,1y )、B (2x ,2y )、C (3x ,3y )是函数xy 1=的图象在第一象限分支上的三个点,且1x <2x <3x ,过A 、B 、C 三点分别作坐标轴的垂线,得矩形ADOH 、BEON 、CFOP ,它们的面积分别为S 1、S 2、S 3,则下列结论中正确的是……………………( )1<S 2<S 3 B. S 3 <S 2< S 1C . S 2< S 3<S 1D . S 1=S 2=S 36.如图,小正方形的边长均为l ,则下列图中的三角形(阴影部分)与△ABC 相似的是…………………( )九年级第一学期期中考试数学试卷 第1页 (共8页)7.一只封闭的圆柱形水桶(桶的厚度忽略不计),底面直径为20cm ,母线长为40cm ,盛了半桶水,现将该水桶水平放置后如图所示,则水所形成的几何体的表面积为………………………………………………( ) A .800 cm 2B.(800+400π) cm 2C .(800+500π)cm 2D .(1600+1200π)cm 28.如图,将矩形ABCD 沿对角线BD 折叠,使C 落在C '处,BC '交AD 于E ,则下列结论不一定成立的是……………………………( ) A.AD =BC ' B.∠EBD =∠EDB C.△ABE ∽△CBDD.EDAEABE =∠sin9. 如下图过矩形ABCD 的四个顶点作对角线 AC 、BD 的平行线,分别交于E 、F 、G 、H四点,则四边形EFGH 为……………………( )A.梯形B.矩形10. 如图,王虎使一长为4cm ,宽为3cm 的长方形 木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A 位置变化为12A A A →→,其中第二次翻滚被桌面上一小木块挡住, 使木板与桌面成30°角,则点A 翻滚到A 2位置时共走过的路径长……………………( ) A .10cmB .4cm πC .72cm π D .52cm 二、填空题(本大题共5个小题;每小题3分,共15分.把答案写在题中横线上)11.如图,请你补充一个你认为正确的条件,使ABC ∆∽∆12.同时抛掷两枚均匀的硬币,则两枚硬币正面都向上的概率是13.在比例尺为1:2 700 000则某某与某某的实际距离约是_________________千米。
2007学年第一学期九年级数学期中学业测试卷

2007学年第一学期九年级数学期中学业测试卷(考试时间:90分钟 满分120分)一、仔细选一选(本题共10小题,每小题3分,共30分)请选出你认为正确的一个选项填入答题卷相应的空格内。
1、若将函数y=2x 2的图象向右平移1个单位,再向上平移5个单位,可得到的抛物线解析式是( )(A)y=2(x-1)2-5 (B)y=2(x-1)2+5 (C)y=2(x+1)2-5 (D)y=2(x+1)2+52、已知圆心角∠BOC=100°,则圆周角∠BAC 的大小是( ) (A)50° (B)100° (C)130° (D)200°(第2题 3、边长为3cm 、4cm 、5cm 的三角形的外接圆半径等于( )cm(A )1.5 (B )2 (C )2.5 (D )2.4 4、下列各点中,在函数y=x2-上的是( )(A)(1,2) (B ) (0,-2) (C )(2,2-) (D )( -4, -21 ) 5、已知扇形OBC 、OAD 的半径之间的关系是OB =21OA ,则BC ︵的长是AD ︵长的( ) (A )21倍 (B )2倍 (C )41倍 (D )4倍 第5题6、下列命题是真命题的有( )个。
①过弦的中点的直线必过圆心;②相等的圆心角所对的弧相等;③弦的垂线平分弦所对的弧;④若圆的一弦长等于圆半径,则其所对的圆周角是30°;⑤三点可以确定一个圆; (A) 1个 (B )2个 (C )0个 (D )3个 7、已知函数2y ax ax =+与函数(0)ay a x=<,则它们在同一坐标系中的大致图象是 ( )第7题A BC DOO D ECB A8、人民广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1米的喷水管最大高度为3米,此时喷水水平距离为12米,在如图所示的坐标系中,这支喷泉的函数关系式是( )A.2132y x ⎛⎫=--+ ⎪⎝⎭B.21312y x ⎛⎫=-+ ⎪⎝⎭C.21832y x ⎛⎫=--+ ⎪⎝⎭D.21832y x ⎛⎫=-++ ⎪⎝⎭9、如图,P (x,y )是以坐标原点为圆心、5为半径的圆周上的点,若x,y 都是整数,则这样的点P 共有( )个(A ) 8 (B ) 10 (C ) 12 (D )16第9题10、如图,在Rt △ABC 中∠ACB =90º,AC =6,AB =10,CD 是斜边AB 上的中线,以AC 为直径作⊙O ,设线段CD 的中点为P ,则点P 与⊙O 的位置关系是( ) (A )点P 在⊙O 内 (B )点P 在⊙O 上 (C )点P 在⊙O 外 (D )无法确定第10题二、认真填一填(本题共6小题,每小题4分,共24分)要注意认真看清题目的条件和要求,把答案完整地填入相应的横线上。
2007~2008学年度九年级数学第一学期期中试卷冀教版

2007~2008学年度第一学期期中试卷九年级 数学(冀教版)考生注意:1. 考试时间120分钟,满分120分。
2. 答卷前将密封线左侧项目填写清楚。
一、单项选择题:(把正确答案的序号填在括号里,每小题2分,计20分)1.方程24x x =的解是( )A.4x =B.2x =C.4x =或0x =D.0x =2.如图,一个钢球沿坡角31o 的斜坡向上滚动了5米,此时钢球距地面的高度是( )A.5cos31米 B.5sin 31 米 C.5tan 31米 D.5tan31米 3.如图,已知等腰梯形ABCD 中,AD BC ∥,110A =∠,则C =∠( )A.90B.80C.70D.60 4. 在反比例函数3k y x-=图象的每一支曲线上,y 都随x 的增大而减小,则k 的取值X 围是 ( )A .k >3B .k >0C .k <3D . k <05.如图,将半径为2cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB 的长为( )A.2cmC.D.AD CB 3题图2题图315题图ABCDMN6题图8题图OAB6.如图,在□ABCD 中,如果M 为CD 中点,AM 与BD 相交于点 N ,那么S △DMN ∶S □ABCD为 ( )A.1∶12 ∶9 ∶8:67. 把一个小球以20 m /s 的速度竖直向上弹出,它在空中的高度h (m )与时间t (s )满足关系:2205h t t =-.当h =20 时,小球的运动时间为( )A .20 sB .2 s C.2)s D.2)s8.在图的扇形中,90AOB ∠=,面积为24πcm ,用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为( ) A .1cmB .2cmCD .4cm9..在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同.小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( ) A.6B.16C.18D.2410..如图,矩形ABCD 的周长为20cm ,两条对角线相交于O 点,过点O 作AC 的垂线EF ,分别交AD BC ,于E F ,点,连结CE ,则CDE △的周长为( ) A .5cmB .8cmC .9cmD .10cm 二、填空题: (每空2分,共16分) 11.已知tan α=125,α是锐角,则sin α=. 12.在比例尺为1︰50 000的地图上,量得甲、乙两地的距离是3cm ,则甲、乙两地的实际距离是m.AD 10题图13.某种蓄电池的电压为定值,使用此电源时,电流(A)I 与可变电阻()R Ω之间的函数关系如图所示,当用电器的电流为10A 时,用电器的可变电阻为Ω.14.图中每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖标志,则随机翻动一块木牌中奖的概率为________.15.如图是中国共产主义青年团团旗上的图案(图案本身没有字母),5个角的顶点A ,B ,C ,D ,E 把外面的圆5等分,则∠A +∠B +∠C +∠D +∠E =__________________. 16.如图所示,在等腰三角形ABC 中,12cm AB AC ==,30ABC =∠,那么底边上的高AD =cm .17. 在ABC △中,90C =∠,D 是边AB 上一点(不与点A ,B 重合),过点D 作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有条. 18.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为和2米,则学校旗杆的高度为________米. 三、基础与技能 19. (本题4分)计算:得分 评卷人2米18题图(94)P ,9O4(A)I()R Ω13题图2 3 14题图1456ADCB16题图15题图sin600tan600+sin 245020.解方程(每小题5分,共10分)(1))15(3)15(2-=-x x ; (2) 0362=+-x x .21. (本题5分)如图,在等边ABC △中,点D E ,分别在边BC AB ,上,且BD AE =,AD 与CE 交于点F . (1)求证:AD CE =; (2)求DFC ∠的度数.22. (本题6分)如图,正方形ABCD 的对角线AC BD ,交于点O OCF OBE ∠=∠,.求证:OE OF =.D 21题图DCFOE AB22题图23. (本题6分)如图,点C 、D 在线段AB 上,△PCD 是等边三角形.(1)当AC 、CD 、DB 满足怎样的关系时,△ACP ∽△PDB ? (2)当△ACP ∽△PDB 时,求∠APB 的度数.四、知识与应用24. (本题6分)将A B C D ,,,四人随机分成甲、乙两组参加羽毛球比赛,每组两人.(1)A 在甲组的概率是多少? (2)A B ,都在甲组的概率是多少?25. (本题6分)你吃过拉面吗?实际上做拉面的过程中就渗透着数学知识:一定..体积的面团做成拉面,面条总长度y (m )是面条的粗细(横截面积)s (mm 2)的反比例函数,其图象如图所示.得分 评卷人12 345 2040 60 80 100y (m)s (mm 2)(432)P ,24题图23题图(1)写出y与s的函数关系式;(2)求当面条粗1.6 mm2时,面条的总长度...是多少米?26. (本题7分)如图,在水平桌面上的两个“E”,当点P1,P2,O在一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力相同.(1)图中b1,b2,l1,l2满足怎样的关系式?(2)若b1=,b2=2cm,①号“E”的测试距离l1=8m,要使测得的视力相同,则②号“E”的测试距离l2应为多少?26题图27. (本题8分)某工程队在我市实施棚户区改造过程中承包了一项拆迁工程.原计划每天拆迁1250m2,因为准备工作不足,第一天少拆迁了20%.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了1440m2.求:(1)该工程队第一天拆迁的面积;(2)若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.28. (本题8分)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下面是水平放置的破裂管道有水部分的截面. (1)请你补全这个输水管道的圆形截面;(2)若这个输水管道有水部分的水面宽16cm AB =,水面最深地方的高度为4cm ,求这个圆形截面的半径.29.(本题8分)去年夏季山洪暴发,我市好几所学校被山体滑坡推倒教学楼,为防止滑坡,经过地质人员勘测,当坡角不超过45°时,可以确某某体不滑坡.某小学紧挨一座山坡,如图所示,已知AF BC ∥,斜坡AB 长30米,坡角60ABC ∠=°.改造后斜坡BE 与地面成45°角,求AE 至少是多少米?(精确到≈1.732)五、动手与操作30. (本题10分)如图1,将一组对边平行的纸条沿EF 折叠,点A B,27题图BD CN 28题图分别落在A B '',处,线段FB '与AD 交于点M . (1)试判断MEF △的形状,并证明你的结论.(2)如图2,将纸条的另一部分CFMD 沿MN 折叠,点C D ,分别落在C D '',处,且使MD '经过点F ,试判断四边形MNFE 的形状,并证明你的结论.(3)当BFE =∠度时,四边形MNFE 是菱形.(直接写出结果)2007-2008学年度第一学期期中试卷九年级数学答案(冀教版)一、1.C 2.B 3.C 4.A 5.C 6.A 7.B 8.A 9.B 10.D 二、11.51312.15001314.1315.180016.6 17.3 18.10 29题图1A BCD E FM A 'B ' 29题图2AB C D E F M A 'B 'C 'D ' N三、19.原式231(222=+=2. 20.(1)(5x-1)2-3(5x-1)=0, (5x-1)(5x-1-3)=0, (5x-1)(5x-4)=0 , x 1=15,x 2=45. (2)x 2-6x+9=6, (x-3)2,x 1+3,x 2+3.21.(1)证明:ABC △是等边三角形,60BAC B ∴==∠∠,AB AC = 又AE BD =(SAS)AEC BDA ∴△≌△,AD CE ∴=.(2)由(1)AEC BDA △≌△,得ACE BAD =∠∠DFC FAC ACE ∴=+∠∠∠60FAC BAD =+=∠∠.22.四边形ABCD 是正方形, AC BD ∴⊥ 即90AOB BOC ∠=∠= ,BO OC =,又OCF OBE ∠=∠,OCF OBE ∴△≌△ ,OE OF ∴=23.(1)∵ ∠ACP =∠PDB =120°,当PD AC =DB PC ,即CD AC =DBCD,也就是CD 2=AC ·DB 时,△ACP ∽△PDB . (2)由(1)得∠A =∠DPB .∴ ∠APB =∠APC +∠CPD +∠DPB =∠APC +∠A +∠CPD=∠PCD +∠CPD =120°. 24.所有可能出现的结果如下:总共有6种结果,每种结果出现的可能性相同. (1)所有的结果中,满足A 在甲组的结果有3种,所以A 在甲组的概率是12, (2)所有的结果中,满足A B ,都在甲组的结果有1种,所以A B ,都在甲组的概率是16. 25.(1)设y 与s 的函数关系式为ky s=.由图象可知,当4s =时,32y =,所以432128k =⨯=.所以y 与s 的函数关系式为128y s=. (2)当 1.6s =时,128801.6y ==,所以面条的总长度是80m . 26.(1)∵P 1D 1∥P 2D 2 ,∴△P 1D 1O ∽△P 2D 2O ,∴O D O D D P D P 212211= ,即2121l lb b =; (2)∵2121l l b b = 且b 1=3.2cm ,b 2=2cm ,l 1=8m ,∴2822.3l =,∴l 2=5m . 27. (1)1250(1-20%)=1000(m 2),所以,该工程队第一天拆迁的面积为1000 m 2. (2)设该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数是x ,则 1000(1+x )2=1440,解得x 1=0.2=20%,x 2=-2.2(舍).所以,该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数是20%. 28.(1)正确作出图形,并做答.(2)如图,过O 作OC AB ⊥于D ,交AB 于COC AB ∵⊥,11168cm 22BD AB ==⨯=∴.由题意可知,4cm CD =.设半径为cm x ,则(4)cm OD x =-.在Rt BOD△中,由勾股定理得:222OD BD OB +=222(4)8x x -+=∴.10x =∴.即这个圆形截面的半径为10cm .29.在Rt ADB △中,30AB =,60ABC ∠=°,sin 30sin 6025.9826.0AD AB ABC =∠=⨯=≈·° 15DB =, 连接BE ,过E 作EN BC ⊥于N ,AE BC ∵∥,∴四边形AEND 是矩形2NE AD =≈=,在Rt ENB △中,由已知45EBN ∠°≤,当45EBN ∠=°时,2BN EN ===AE AD BN BD ==-==∴,答:AE至少是.C27题图word11 / 11 30.(1)MEF △为等腰三角形.证明:AD BC ∥,MEF EFB ∴=∠∠. MFE EFB =∠∠,MEF MFE ∴=∠∠.ME MF ∴=,即MEF △为等腰三角形.(2)四边形MNFE 为平行四边形.证明:ME MF =,同理NF MF =, ME NF ∴=.又ME NF ∥,∴四边形MNFE 为平行四边形.(3)60.。
2007学年度第一学期九年级数学期中试卷

2007学年度第一学期九年级数学期中试卷(时间:100分钟 满分:150分)一 、填空题(本大题共12小题,每小题3分,满分36分)1.方程12=x的根是 . 2.已知2=b a ,那么=+-ba b a . 3.方程21=-x 的根是 . 4.把二次方程 0222=--y xy x 化成两个一次方程,则这两个一次方程分别是和 .5.已知点P 是线段AB 的黄金分割点,且AP <PB ,若AB =2,则PB =___________(结果保留根号). 6.在实数范围内分解因式:___________________522=--x x . 7.如果两数的和是4,积是1,那么这两个数是 .8.一种型号的数码相机,原来每台售价为5000元,经过两次降价后,现在每台售价为3200元.假设两次降价的百分率均为x ,那么可列出方程: .9.用换元法解方程312122=-+-x x xx 时,如果设21x x y -=,那么原方程可化为关于y 的整式方程,这个方程是 .10.在比例尺为1∶10000的地图上,相距5厘米的两地A 、B 的实际距离是_______千米. 11.当m = 时,解关于x 的方程222-=--x mx x 时会产生增根. 12.如图,在菱形ABCD 中,∠ABC =60°,AE ⊥AB ,交BD 于点G ,交BC 的延长线于点E ,那么GEAG= . 二、选择题(本大题共4小题,每小题4分,满分16分)〔每题列出的四个答案中,有且只有一个答案是正确的,把正确答案的代号填入括号内〕13.下列方程或方程组中,有实数解的是………………………………( ) (A ) 022=+-x x ; (B )12-=-x ; (C )x x -=+2 ; (D )11122-=-x x x . 14.下列二次三项式在实数范围内不能够分解因式的是…………………( )222232;53;76;2 2.x x x x x x x x +-++-+++(A) (B) (C) (D)15.下列方程组中,是二元二次方程组的是……………………………………( )ABCE DG(A )51x y x y +=⎧⎨-=⎩ ; (B) 210618x yx y⎧+=⎪⎪⎨⎪-=⎪⎩ ;(C )2211x y x xy y -=⎧⎨++=⎩ ; (D )312x y xy y x ⎧+=⎨=+⎩. 16.△ABC 中,直线DE 交AB 于D ,交AC 于点E ,那么能推出DE ∥BC 的条件是……………………………………( )(A) 2123==AE EC AD AB ,; (B) 3232==BC DE AB AD ,; (C)3232==AE CE DB AD ,; (D) 3434==EC AE AB AD ,.三、简答题(本大题共5小题,第17、18题每题9分,第19、20、21题每题10分,满分48分)17.解方程x =; 18.解方程 :1111132-=+--x x x ;19.解方程组:⎩⎨⎧=-=++-1201322y x x x y20.如图ABC ∆中,D 、E 分别为AB 、AC 上的点,且DE ∥BC,31=BD AD .求:(1);AB AD (2)ACEC.21.已知点A 在x 轴上,点A 与点)31(,B 的距离是5,求点A 的坐标.四、(本大题共4题,第22、23、24题每题12分,第25题14分,满分50分)22.小明与小杰同时从学校出发,骑自行车前往距离学校18千米的公园.已知小明比小杰平均每小时多行6千米,但由于小明在路上修自行车而耽搁了半个小时,结果两人同时到达公园.求小明与小杰平均每小时各行多少千米?23.已知:如图, 在△ABC 中, 点D 、E 分别在BC 、AC 上, BE 平分∠ABC, DE ∥BA .如果CE =24, AE =30, AB =45, 求DE 和CD 的长.24.若()096222=+++-b b a ,求方程组:⎩⎨⎧+==+8,3b xy a y x 的解.25.已知MN ∥EF ∥BC ,点E 、F 分别在AB 、DC 上,点A 、D 为直线MN 上的两动点,AD =a ,BC =b ,AE mBE n=. DACBE(1)当点A 、D 重合,即a =0时(如图1),试求EF .(用含,,m n b 的代数式表示)(2)请直接应用(1)的结论,当A 、D 不重合,即a ≠0, 如图二,求EF ;(结果用含,,,a b m n 的代数式表示)(3)应用(1)的结论,当A 、D 不重合,即a ≠0,如图三,求EF .(结果用含,,,a b m n 的代数式表示)(4) 指出(1)、(2)的结论与三角形中位线长公式和梯形中位线长公式是什么关系.MBCF E 图一A (D )NM CF B Ea b DNA图二图三2007学年度第一学期九年级数学期中试卷参考答案及评分标准1.22.313.54. 02,0=-=+y x y x5.15-6.()()6161+---x x 7. 32,32-+ 8.()3200150002=-x 9. 0232=+-y y 10.0.5 11.2 12. 21 13.C 14.D 15.C 16.A17.解:两边平方化简得022=--x x …………………………………………………………………3′ 解之得 2,121=-=x x …………………………………………………………3′ 检验: 把11-=x 代入原方程,左边=121=+-,右边=-1,左边≠右边,因此11-=x 是增根. …………………………………………………………1′ 把21=x 代入原方程,左边=222=+,右边=2,左边=右边,因此21=x 是原方程的根. …………………………………………………………1′所以原方程的解为2=x .…………………………………………………………1′ 18.两边同乘12-x 后,化简得0322=-+x x …………………………………………………………4′ 解之得 3,121-==x x …………………………………………………………3′ 检验: 把11=x 时,有012=-x ,因此11=x 是增根. ………………………1′ 所以原方程的解为3-=x . …………………………………………………1′ 19.解:由②得12-=x y 代入①化简得0232=+-x x ………………………………………………………4′解之得 2,121==x x …………………………………………………3′ 当11=x 时,11=y ………………………………………………………1′ 当22=x 时,32=y ……………………………………………………1′所以方程组的解为:⎩⎨⎧==⎩⎨⎧==3,21,12211y x y x .………………………………1′ 20.解:设k AD =,则k AB k BD 4,3==. ………………………………2′(1)414==k k AB AD ………………………………4′ (2)DE ∥4343===⇒k k AB BD AC EC BC ………………………………4′ 21.解:设点A 的坐标为(x ,0),则有 ………………………………1′ ()()2225301=-+-x ………………………………4′化简为 ()1612=-x ………………………………1′解之得 3,521-==x x ………………………………2′ 所以点A 的坐标为(5,0),(-3,0) ………………………………2′22.解:设小明每小时行x 千米,则小杰每小时行(x -6)千米,…………1′ 依题意有6185.018-=+x x ………………………………………………5′ 化简得 021662=--x x ………………………………………………2′解之得 12,1821-==x x (不合题意,舍去) …………………2′检验:当x =18时,()6-x x 的值不等于零,因此x =18是原方程的根,且符合题意. 又当x =18时,x-6=18-6=12. …………………1′ 答:小明与小杰平均每小时分别行18千米和12千米. …………………1′ 23.解: ∵ABC BE ∠平分,∴EBD ABE ∠=∠又∵DE ∥AB ,∴BED ABE ∠=∠,∴BED EBD ∠=∠, DE =BD. ……………………4′由DE ∥AB 20455424=⨯=⋅=⇒=⇒AB AC EC ED AC EC AB ED …………4′ 由DE ∥AB 16203024=⨯=⋅=⇒=⇒BD AE CE CD AE CE BD CD ……………4′ 24.解:由()()⎩⎨⎧-==⇒=++-3,203222b a b a ……………………3′ 所以方程组为⎩⎨⎧==+5,6xy y x ……………………3′解之得 ⎩⎨⎧==⎩⎨⎧==.1,55,12211y x y x ……………………6′ 25. 解:设,mk AE =则()k n m AB nk BE +==, ……………2′(1)由EF ∥BC ()nm mbb k n m mk BC AB AE EF AB AE BC EF +=⋅+=⋅=⇒=⇒…4′(2)过点A 作AH ∥DC 交EF 于G ,交BC 于H ,如图二.∵AH ∥DC , MN ∥EF ∥BC ,∴四边形ADFG 与四边形ADCH 均为平行四边形.∴GF=HC=AD=a,BH=b-a ……………2′ 由(1)得()n m a b m EG +-=, 所以 ()nm namb a n m a b m EF ++=++-=……………3′(3)过点A 作AH ∥DC 交EF 的延长线于G ,交BC 的延长线于H ,如图三. ∵AH ∥DC , MN ∥EF ∥BC ,∴四边形ADFG 与四边形ADCH 均为平行四边形.∴GF=HC=AD=a,BH=b+a ……………2′由(1)得()n m a b m EG ++=, 所以 ()n m namb a n m a b m EF +-=-++= ……………3′(4)当A E m B E n ==1,即m =n 时,(1)、(2)中的结论n m mb EF +=, n m na mb EF ++=分别为2b EF =和2ab EF +=,MCF BE a aH G abDNA图二M C FBE aa HG图三A ND b a MBCF E b 图一A (D )N即分别为三角形中位线长公式和梯形中位线长公式,所以它们是一般与特殊的关系.(或者说(1)(2)的结论是三角形中位线长公式和梯形中位线长公式的推广;或者说“三角形中位线长公式和梯形中位线长公式是(1)(2)的结论的特例”)……………2′。
卢湾区2007学年第一学期九年级数学期中考试卷

卢湾区2007学年第一学期初三年级期中考试数学试卷一、填空题(本大题共12题,每题3分,满分36分) 1. 在实数X 围内因式分解:228x x --=. 2. 解方程4121x x=+,可得x =. 3. 4=,可得x =.4. 用换元法解分式方程222132021x x x x --+=-,若设221x y x -=,则原方程可化为关于y 的方程是.5. 方程组3212,524x y x y⎧+=⎪⎪⎨⎪-=⎪⎩的解是.6. 在公式111u v f+=中,已知u 、v 且0u v +≠,则f =. 7. 已知线段2AB cm =,点P 是线段AB 的黄金分割点()AP BP >,则AP =cm .8. 一个直角三角形的一条直角边比斜边短2cm ,比另一条直角边长2cm ,那么这个直角三角形的斜边长是cm .9.某次校友聚会,校友见面彼此各握手一次,共握手36次,若设有x 人参加本次校友聚会,由题意可列方程.10. 若两个相似三角形的相似比是1:9,则对应中线的比是. 11. 如图,已知123l l l ∥∥,若7,4,3AB BC CD ===,则GFGE=.12. 如图,已知ABC ∆的面积是36,将ABC ∆沿直线BC 平移到'''A B C ∆,使点'B 和C 重合,连结'AC 交'AC 于点D ,则'C DC ∆的面积是. 二、选择题:(本大题共4题,每题4分,满分16分) 【下列各题的四个结论中,有且只有一个结论是正确的,把正确结论的代号写在题后的圆括号内,选对得4分;不选、错选或者多选得零分】13. 下列方程属于无理方程的是……………………………………( ) (A)210x -+=; (B=; (C2=; (D112x =-. 14. 在实数X 围内因式分解2343x x --的结果正确的是………( ) (A)(22x x --; (B)(322x x ---+;(C)3x x ⎛ ⎝⎭⎝⎭;(D)3x x ⎛ ⎝⎭⎝⎭. 15.如图,G 是ABC ∆的重心,E 在AC 边上,若GE BC ,则:AD DE 的值是( )(A ) 2; (B )3;(C ); (D )1.16.下列命题中是真命题的是………………………………………( ) (A )直角三角形都相似; (B )等腰三角形都相似;(C )两边对应成比例的直角三角形都相似; (D )等腰直角三角形都相似. 三、简答题:(本大题共5题,满分48分)(第11题)(第12题)ABDC C '(B ')A 'l 3l 2l 1ABDC EF G17. (本题满分9分)解方程:214124y y -=--.18.(本题满分92x =19. (本题满分10分)已知P 是y 轴正半轴上一点,它与点A (-9,3)之间的距离是15,求点P 的坐标.20. (本题满分10分)某种电器,原来每台售价3000元,经两次降价后现在每台售价2430元,求平均每次降价的百分率.21. (本题满分10分)如图,已知四边形ABCD 是正方形,:1:2CE DE =,线段AE 、BC 的延长线交于点F . 求ECF ∆与ABF ∆的周长比. 四、(本大题共4题,满分50分) 22. (本题满分12分)如图,已知在ABC ∆中,点D 、E 分别在AB 、AC 上,且AD AB AE AC ⋅=⋅,CD 与BE 相交于点O .(1)求证:AEB ∆∽ADC ∆; (2)求证:BO DOCO EO=.23. (本题满分12分)A 、B 两地相距45千米,甲骑车从A 地驶向B 地,(第21题)(第22题)OA B C E D1小时后,乙骑车从B 地驶向A 地,已知乙每小时比甲快5千米,甲、乙两人在距A 地24千米处相遇,求甲、乙两人的速度各是多少?24. (本题满分12分)如图,在Rt ABC ∆中,90ACB ︒∠=,CD AB ⊥,垂足为点D ,E 、F 分别是AC 、BC 边上的点,且13CE AC =,13BF BC =.(1)求证:AC CDBC BD=; (2)求EDF ∠的度数.(第24题)ABC DEF25. (本题满分14分)已知在等腰三角形ABC 中,4,6AB BC AC ===,D 是AC 的中点,E 是BC 上的动点(不与B 、C 重合),连结DE ,过点D 作射线DF ,使EDF A ∠=∠,射线DF 交射线EB 于点F ,交射线AB 于点H .(1)求证:CED ∆∽ADH ∆; (2)设,EC x BF y ==.①用含x 的代数式表示BH ;②求y 关于x 的函数解析式,并写出x 的定义域.(第25题)HABCDE FDC备用图卢湾区2007学年第一学期初三年级数学期中试卷评分参考一、填空题(本大题共12小题,每小题3分,满分共36分)1.()()24x x +-;2. 12;3. 12;4. 320y y -+=;5. 1213x y ⎧=⎪⎪⎨⎪=⎪⎩;6.uv u v +;7.1;8. 10; 9.()11362x x -=;10. 1:9;11.12;12. 18. 二、选择题:(本大题共4小题,每小题4分,共16分)13. C ;14. C ; 15. B ; 16. D.三、简答题:(本大题共5题,满分48分)17. 解:2244y y +-=-…………………………………………………3分220y y --=…………………………………………………2分()()210y y -+=…………………………………………………1分122,1y y ==-……………………………………………………2分经检验2y =是原方程的增根,1y =-是原方程的根. …………………1分 18.2x =+………………………………………………2分()22272x x x +=+……………………………………………2分2340x x +-=……………………………………………………2分 124,1x x =-=……………………………………………………2分经检验4x =-是原方程的增根,1x =是原方程的根. …………………1分 19.解:设点P 的坐标为()0,y 0y >………………………………………1分15=…………………………………2分()2813225y +-=………………………………………2分解得1215,9y y ==-…………………………………………2分经检验1215,9y y ==-都是原方程的根………………………………1分 所以点P 的坐标是(0,15). ………………………………………2分 20.解:设平均每次降价的百分率为x .………………………………1分 根据题意,得 ()2300012430x -=…………………………………4分()210.81x -=…………………………………………1分()10.90.9x ∴-=-不合题意,舍去…………………2分 0.110%x ∴==…………………………………………1分答:平均每次降价10%.…………………………………………………1分 21.解:∵四边形ABCD 是正方形∴,AB CD AB CD =…………………………………………2分∵12CE DE =,∴13CE CD =………………………………………2分 ∴13CE AB =…………………………………………………………2分 ∵AB CD ,∴ECF ∆∽ABF ∆………………………………2分∴13ECF ABF C CE C AB ∆∆==………………………………………………2分 四、(本大题共4题,满分50分) 22. 证明:(1)∵AD AB AE AC ⋅=⋅,∴AD AEAC AB=………………2分 又A A ∠=∠……………………………………………………2分 ∴AEB ∆∽ADC ∆……………………………………………1分 (2) ∵AEB ∆∽ADC ∆∴ABE ACD ∠=∠……………………………………………2分 ∵DOB EOC ∠=∠……………………………………………2分 ∴BOD ∆∽COE ∆……………………………………………1分∴BO DOCO EO=………………………………………………2分23.解:设甲每小时行x 千米. ……………………………………………1分 由题意得:()24514524x x ⎛⎫+-=-⎪⎝⎭……………………………………5分 (或24452415x x --=+) 整理得221200x x +-=……………………………………………………1分112x =-(不合题意,舍去),210x =…………………………2分经检验10x =是原方程的根. ……………………………………………1分所以乙的速度是每小时10+5=15千米……………………………………1分 答:甲的速度是每小时10千米,乙的速度是每小时15千米. ………1分 24.证明:(1)∵90ACB ︒∠=,CD AB ⊥,∴90CDB ACB ︒∠=∠=,………………………………………………1分 又B B ∠=∠…………………………………………………………………1分 ∴ACB ∆∽CDB ∆…………………………………………………………1分∴AC BCCD BD =………………………………………………………………1分 ∴AC CD BC BD=………………………………………………………………1分 (2)∵11,33CE AC BF BC ==,∴3,3AC CE BC BF ==…………………………………………………1分 ∴33CE CD CEBF BD BF==………………………………………………………2分 ∵90B BCD ECD BCD ︒∠+∠=∠+∠=,∴B ACD ∠=∠……………………………………………………………1分 ∴ECD ∆∽FBD ∆………………………………………………………1分 ∴EDC FDB ∠=∠…………………………………………………………1分∵90FDB CDF ︒∠+∠=,∴90EDF EDC CDF ︒∠=∠+∠=………………………………………1分 25.解:∵AB BC =,∴A C ∠=∠…………………………………………1分 ∵CDE EDF A H ∠+∠=∠+∠…………………………………………1分 又EDF A ∠=∠,∴CDE H ∠=∠………………………………………1分 CED ∴∆∽ADH ∆………………………………………………………1分 (2)①∵CED ∆∽ADH ∆,∴CE CDAD AH=…………………………2分 ∵D 是AC 的中点,6AC =,∴3AD CD ==,又∵,4CE x AB == ∴当H 点在线段AB 的延长线上时,334x BH =+,∴94BH x =-…………………………………………1分 当H 点在线段AB 上时, 334x BH =-,∴94BH x=-…………………………………………1分 ②过点D 作DG AB ,交BC 于点G …………………………………1分∴12DG CG CD AB BC AC ===,∴2,2DG BG ==………………………1分 ∴当H 点在线段AB 的延长线上时,∴BH BFGD GF=,∴9422y x y -=-…………………………………………1分 ∴18890924x y x x -⎛⎫=<< ⎪-⎝⎭………………………………………………1分当H 点在线段AB 上时,∴BH BF GD GF=,∴9422yx y -=+………………………………………1分 ∴81894924x y x x -⎛⎫=≤< ⎪-⎝⎭………………………………………………1分。
古城中学2007届九年级数学(上)期中试卷

古城中学 2007届九年级数学 (上 )期中试卷满分: 100 分 考试时间: 90 分钟一、选择题(每题2 分,共 20 分)1、在下列二次根式中,最简二次根式是【】A 、8aB 、5aC 、aD 、a2a 2b32、若正比例函数 y=(a-2)x 的图象过第一、三象限,化简a 12的结果是【 】A a-1B 1-aC (a-1)2D (1-a)23、两圆的圆心距为3,两圆的半径分别是方程x 2-4x+3=0 的两根, ?这两个圆的位置关系是【】A .外离B .外切C .相交D .内切4、某厂四月份生产零件 50 万个,若五六月份平均每月的增长率是20﹪,则第二季度共生产【 】A 100 万件B 160 万件C 180万件D 182 万件5x 的一元二次方程 kx 2 6 x 9 0有两个不相等的实数根,则k 的取值范围【】、若关于A 、 k < 1B、 k > 1 C 、 k < 1 且 k ≠ 0 D、 k ≠06、如图所示的几幅图中,可以旋转180°与自身重合的是【】7、 Rt △ ABC 中,∠ C=90°, AB=5,内切圆半径为 1,则三角形的周长为【 】A . 15B . 12C . 13 D. 148、如图,若将△ ABC 的绕点 C 顺时针旋转90°后得到 A B C ,则 A 点的对应点A 的坐标是【】.yA 、 ( - 3, -2)B 、 (2,2)C 、 (3,0)D 、 (2,1)43 A21B-4 -3 -2 -1 0 1 2 3 4x C -1-2 】. 9、如图,⊙ O 外接于△ ABC , AD 为⊙ O 的直径,∠ ABC=30°,则∠ CAD=【-3-4A . 30°B . 40°C .50°D . 60°10、如图 ,⊙ O 的直径为 10,圆心 O 到弦 AB 的距离 OM 的长是 3,则弦 AB 的长为【 】.A . 4B .6C . 7D . 8DCO OBAAMB二、填空(每题 2 分,共 30 分)11、当x时,25x 有意义.12、平面直角坐标系内一点P(- 2,3)关于原点对称点的坐标是.13 、一个直角三角形的两条直角边长是方程x 27x120的两个根,则此直角三角形外接圆的半径等于。
北京市海淀区2007年九年级数学第二学期期中练习卷(一模)
市海淀区2007年九年级数学第二学期期中练习卷(一模)满分120分,考试时间120分钟。
一、选择题(本题共32分,每小题4分。
)在下列各题的四个备选答案中,只有一个是正确的。
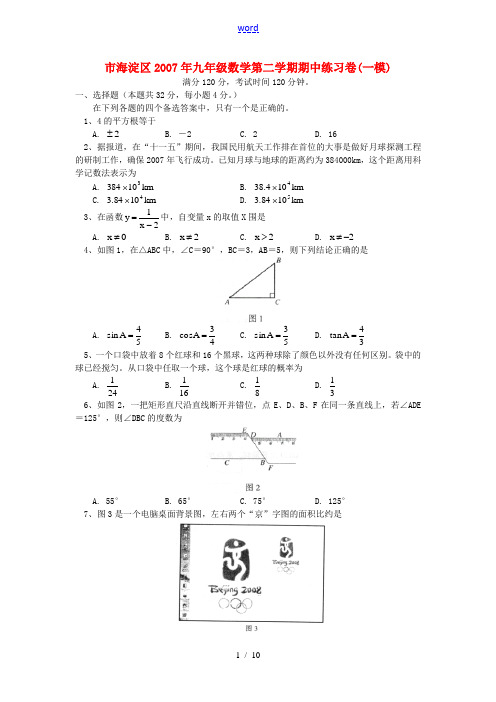
1、4的平方根等于 A. 2± B. -2 C. 2 D. 162、据报道,在“十一五”期间,我国民用航天工作排在首位的大事是做好月球探测工程的研制工作,确保2007年飞行成功。
已知月球与地球的距离约为384000km ,这个距离用科学记数法表示为 A. km 103843⨯ B. km 104.384⨯ C. km 1084.34⨯ D. km 1084.35⨯3、在函数2x 1y -=中,自变量x 的取值X 围是 A. 0x ≠ B. 2x ≠ C. 2x > D. 2x -≠ 4、如图1,在△ABC 中,∠C =90°,BC =3,AB =5,则下列结论正确的是A. 54A sin =B. 43A cos =C. 53A sin =D. 34A tan = 5、一个口袋中放着8个红球和16个黑球,这两种球除了颜色以外没有任何区别。
袋中的球已经搅匀。
从口袋中任取一个球,这个球是红球的概率为A. 241B. 161C. 81D. 316、如图2,一把矩形直尺沿直线断开并错位,点E 、D 、B 、F 在同一条直线上,若∠ADE =125°,则∠DBC 的度数为A. 55°B. 65°C. 75°D. 125° 7、图3是一个电脑桌面背景图,左右两个“京”字图的面积比约是A. 2:1B. 4:1C. 8:1D. 16:18、科技馆为某机器人编制一段程序,如果机器人在平地上按照图4中的步骤行走,那么该机器人所走的总路程为A. 6米B. 8米C. 12米D. 不能确定二、填空题(本题共16分,每小题4分。
)9、已知关于x 的方程0m x 2x 2=+-有两个不相等的实数根,则m 的取值X 围是________。
古城中学2007届九年级数学(上)期中试卷

古城中学2007届九年级数学(上)期中试卷满分:100分 考试时间:90分钟一、选择题(每题2分,共20分)1、在下列二次根式中,最简二次根式是【 】ABC D 、b a a 22+2、若正比例函数y=(a-2)x 的图象过第一、三象限,化简()1-a 2的结果是【 】A a-1B 1-aC (a-1)2D (1-a)23、两圆的圆心距为3,两圆的半径分别是方程x 2-4x+3=0的两根,•这两个圆的位置关系是【 】 A .外离 B .外切 C .相交 D .内切4、某厂四月份生产零件50万个,若五六月份平均每月的增长率是20﹪,则第二季度共生产【 】A 100万件B 160万件C 180万件D 182万件 5、若关于x 的一元二次方程0962=+-x kx 有两个不相等的实数根,则k 的取值范围【 】A 、k <1B 、k >1C 、k <1且k ≠0D 、k ≠0 6、如图所示的几幅图中,可以旋转180°与自身重合的是【 】7、Rt △ABC 中,∠C=90°,AB=5,内切圆半径为1,则三角形的周长为【 】 A .15 B .12 C .13 D .148、如图,若将△ABC 的绕点C 顺时针旋转90°后得到C B A ''∆,则A 点的对应点A '的坐标是【 】.A 、(-3,-2)B 、(2,2)C 、(3,0)D 、(2,1)9、如图,⊙O 外接于△ABC ,AD 为⊙O的直径,∠ABC=30A .30°B .40°C .50°D .60°10、如图,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长是3,则弦AB 的长为【 】. A .4 B .6 C .7 D .8二、填空(每题2分,共30分) 11、当x 时,.12、平面直角坐标系内一点P (-2,3)关于原点对称点的坐标是 .13、一个直角三角形的两条直角边长是方程01272=+-x x 的两个根,则此直角三角形外接圆的半径等于 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学上学期期中考试试卷(100分钟完成,满分150分)一、填空题(每小题3分,满分36分)1. 方程211=-x 的根是______________. 2. 方程1112+=+x x x 的根是________________. 3. 分解因式:=-+422x x _______________________. 4. 在公式21111R R R +=中,已知正数R 、R 1(1R R ≠),那么R 2= . 5. 用换元法解方程02711222=+---x x x x 时,可设y =12-x x,那么原方程可化为关于y 的整式方程是 .6. 某电子产品每件原价为800,首次降价的百分率为x ,第二次降价的百分率为2x ,那么经过两降价后每件的价格为_____________________元(用x 的代数式表示).7. 如图1,已知舞台AB 长10米,如果报幕员从点A 出发站在舞台的黄金分割点P 处,且BP AP <,则报幕员应走 米 报幕(236.25≈,结果精确到0.1米).8. 如图2,在ABC ∆中,点D 、E 分别在边AB 、AC 上,DE ∥BC ,5:2:=AC AE ,则=BC DE : .9. 已知ABC ∆与DEF ∆相似,且点A 与点E 是对应点,已知∠A =50º, ∠B =︒60,则∠F = .10. 在△ABC 中,点D 、E 分别在边AB 、AC 上,要使△ADE 与△ABC 相似,只须添加一个条件,这个条件可以是___________(只要填写一种情况) .11. 在△ABC 中,中线AD 和CE 相交于G ,则=AD AG :_________. 12. 如图3, 在△ABC 中, 点D 、E 分别在AB 、AC 上,DE//BC ,4,3==∆∆CDE ADE S S ,那么AD :DB =____________.二、选择题(每小题4分,满分16分)13. 下多项式中,在实数范围内能分解因式的是………………………………………( )(A )12+-x x ; (B )222+-x x ; (C )332+-x x ;(D )552+-x x .14. 下列方程中, 有实数根的是………………………………………………………( )(A )x x -=11; (B )11-=-xx ; 图1图2图3(C )111112--=+-x x x ; (D )11111+-=+-x x x . 15. 如果点D 、E 分别在ΔABC 的两边AB 、AC 上,下列条件中可以推出DE ∥BC 的是( )(A ) AD BD = 23 ,CE AE = 23 ; (B) AD AB = 23 ,DE BC = 23; (C )AB AD = 32 ,EC AE = 12 ; (D) AB AD =34,AE EC = 34. 16. 如图4,小正方形的边长均为l ,△ABC 与△DEF 的顶点都在小正方形的顶点上,则△DEF 与△ABC 相似的是……………………………………………………………( )(A ) (B ) (C ) (D )三、(第17、18题每小题9分,第19、20、21题每小题10分,满分48分)17.解方程:1113112=----x x x .18.方程组: ⎪⎪⎩⎪⎪⎨⎧-=---=-+-.1223,4122yx x yx x19. 函数542--=x x y 图象上一点P 的纵坐标比横坐标多1, 求这个点的坐标.20. 如图5,在△ABC 中,点D 、E 分别在边AB 、AC 上,C ADE ∠=∠,且3=AD 厘米,5=BD 厘米,6=AC 厘米,求线段EC 的长.图4A BC ED F D ED F F DE BADE 图521.已知:如图6,在四边形ABCD 中,AD //BC ,点E 在边CD 上,AE 的延长线与BC 的延长相交于点F ,FB CE CD FC ⋅=⋅.求证:∠D =∠B .四、(第22、23、24题每小题12分,第25题14分,满分50分) 22.已知:如图7,△ABC 中,点E 在中线BD 上, ABD DAE ∠=∠.求证:(1)DB DE AD ⋅=2; (2)ACB DEC ∠=∠.23.现有甲、乙两辆货车将一批货物从A 地运往B 地,每车都装满,乙车比甲车每车多运2吨, 甲车运200吨比乙车运200吨要多运5次,求甲、乙两辆货车每次各运几吨.24.如图8,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF 与长方形绿地一边的夹角为60º,且道路的出入口的边AB 、CD 、EF 、GH 的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.25. 在矩形ABCD 中,2=AB ,5=BC ,点P 在BC 上,且3:2:=PC BP ,动点E 在边AD 上,过点P 作PE PF ⊥分别交射线AD 、射线CD 于点F 、G . (1) 如图9,当点G 在线段CD 上时,设AE =x ,△EPF 与矩形ABCD 重叠义域;部分的面积为y ,求y 关于x 的函数解析式,并写出定(2) 当点E 在移动过程中,△DGF 是否可能为等腰三角形?如可能,请求出AE 的长;如不可能,请说明理由.A C E BF 图7 A BCD PF EG A BD(备用图)图9初三数学期中考试试卷参考与评分意见一、1.23=x ; 2. 1=x ; 3. );51)(51(-+++x x 4. RR RR -11; 5. ;02742=-+y y 6. )21)(1(800x x --; 7. 3.8 ; 8. 2:5 ; 9. 60º或70º; 10. 可填DE //BC 或∠AED =∠B 或ABAEAC AD =等; 11. 2:3; 12. 3:4. 二、13.D ; 14. B; 15. C; 16. B.三、17.解:11312-=+-+x x x ,(3分) ,0322=-+x x (2分)1,321=-=x x ,(2分) 经检验:3-=x 是原方程的根,1=x 是增根.(2分)所以原方程的根是3-=x .18. 解:设a x =-21,b y x =-1(1分) 则原方程组可化为⎩⎨⎧-=-=+.123,42b a b a (2分) 解此方程得⎩⎨⎧==.2,1b a (2分) ∴⎪⎪⎩⎪⎪⎨⎧=-=-.21,121y x x (1分) ∴⎪⎩⎪⎨⎧==.25,3y x (2分) 经检验:⎪⎩⎪⎨⎧==25,3y x 是原方程组的解,∴所以原方程组的解是⎪⎩⎪⎨⎧==.25,3y x (1分)19. 解:设点)1,(+x x P ,(2分) 5412--=+x x x ,(2分) 0652=--x x ,(2分)1,621-==x x ,(2分) ∴点P 的坐标为)7,6(或()0,1-.(2分) 20.解:∵C ADE ∠=∠,A A ∠=∠,(1分) ∴ADE ∆∽ACB ∆.(2分)∴AB AE AC AD =.(2分) ∵3=AD 厘米,5=BD 厘米,6=AC 厘米, ∴5363+=AE,(2分) 解得4=AE .(2分) ∴2=-=AE AC EC 厘米.(1分)21. 证明:∵FB CE CD FC ⋅=⋅,∴CD CE FB FC =.(2分)∵AD //BC ,∴.FAFECD CE =(2分) ∴FAFEFB FC =.(2分) ∴DE //BC . (2分) ∴四边形ABCD 是平行四边形.(1分) ∴∠B =∠D .(1分)四、22.证明:(1)∵ABD DAE ∠=∠,BDA ADE ∠=∠,∴ADE ∆∽BDA ∆.(2分)∴ADDEBD AD =,(2分) 即DB DE AD ⋅=2.(1分) (2)∵D 是AC 边上的中点,∴DC AD =.∵AD DEBD AD =,∴DCDE BD DC =,(2分) 又∵BDC CDE ∠=∠.(1分)∴CDE ∆∽BDC ∆.(2分)∴ACB DEC ∠=∠.(2分) 23. 解:甲货车每次各运x 吨,(1分) 则乙货车每次各运(2+x )吨.(1分)由题意得52200200=+-x x .(3分) 化简整理得 08022=-+x x .(2分) 解得10,821-==x x . (2分) 经检验10,821-==x x 都是原方程的根,但10-=x 不合题意舍去,(1分) ∴8=x ,.102=+x (1分)答:甲、乙两辆货车每次各运8吨、10吨.(1分)24.解:道路出入口的边的长度为x 米.(1分)过点F 作FM ⊥EH ,可求得EH =x 23,可得小正方形的边长为x 23米.(2分) 1374340302=-+x x x ,(3分) 054828032=+-x x ,(1分) 0)2)(2743(=--x x , (1分) 2,327421==x x .(2分) 3274=x 不符合题意,舍去.(1分)答:道路出入口的边的长度为2米.(1分) 25. 解:(1)过点E 作BC EH ⊥,垂足为H .(1分)∵3:2:=PC BP ,5=BC ,∴2=BP ,3=PC ;∵x AE =,∴x HP -=2;∵EH =AB =2, ∴x S EHP -=∆2 ,(2分)∵︒=∠=∠=∠90GCP EPF EHP ,∴∠EPH =90º–∠GPC =∠PGC ,(1分) ∴EHP ∆∽PCG ∆.(1分)∴.236,232,xCG x CG EH CP PH CG -=∴=-∴=(1分) ∴9924∆=-PCG S x .(1分) ∵PCG EPH EH CD S S S y ∆∆--=矩形,∴2745+=x y ,(2分) (232<≤x ).(1分) (2)当点G 在线段CD 上,DG DF =,DF -=23,1-=DF 不可能.(2分) 当点G 在线段CD 的延长线上时,DG DF =,DF +=23,1=DF . 此时可解得0=AE ,即当点E 与点A 重合时,DGF ∆是等腰三角形.(2分)。
