旋转体的体积PPT课件
合集下载
《旋转体的体积》课件

旋转体的性质
深入探讨了旋转体的几何性质,如旋 转体的表面积、质心和转动惯量等。
计算实例
通过具体的计算实例,演示了如何运 用旋转体的体积公式解决实际问题。
未来研究方向和展望
深入研究旋转体的性质
随着几何学的发展,旋转体的 性质将得到更深入的研究,如 探讨旋转体的对称性、稳定性 等。
扩展旋转体的应用领域
条件和范围。
计算中需要注意的事项
单位统一
在计算过程中,确保所有的长度单位都 是统一的,避免因单位不统一导致的误 差。
VS
精确度要求
根据问题的实际需求,合理选择计算方法 和工具,确保计算结果的精确度。
提高计算准确性的技巧和方法
01
02
03
多做练习
通过大量的练习,提高学 生的计算能力和对公式的 熟悉程度。
数学建模
在物理、化学和生物等学科中,旋转 体常被用来建立数学模型,以描述和 分析各种现象。
02
旋转体的体积计算公式
圆柱体的体积计算公式
总结词
圆柱体的体积计算公式是底面积乘以高。
详细描述
圆柱体的体积计算公式是底面积(πr^2)乘以高(h),即V=πr^2h,其中r是 底面圆的半径,h是高。
圆锥体的体积计算公式
随着科技的进步,旋转体在工 程、物理、生物等领域的应用 将更加广泛,如探讨旋转体在 流体动力学、机械工程和生物 学等领域的应用。
探索新的计算方法
随着数学和计算机技术的发展 ,将会有新的计算方法出现, 以更高效、精确地计算旋转体 的体积和其他几何量。
加强与其他学科的交叉研 究
旋转体作为几何学的重要分支 ,将与其他学科如物理学、化 学、生物学等产生更多的交叉 研究,以推动科学的发展。
旋转体的体积

五、求 x 2 y 2 a 2 绕 x b ( b a 0) 旋转所成旋转 体的体积 .
六、 设有一截锥体,其上,下底均为椭圆,椭圆的轴 长分别为 2 A , 2B 和2a , 2b ,高为 h ,求这截锥体 的体积 .
七、设直线 y ax b与直线x 0 ,x 1 及y 0 所围 成梯形面积等于A ,试求a , b 使这个梯形 绕 y 轴 旋转所得体积最小 .
a
a
y 2dx
a a
b2 a2
(a 2x 2)dx
O
b2 a2
[a
2x
1 3
x
3
]aa
4 3
a
b
2.
ax
类似地,如果旋转体是由连续曲线
x ( y)、直线 y c 、 y d 及y 轴所围
成的曲边梯形绕y 轴旋转一周而成的立体,
体积为
y
V d [ ( y)]2 dy c
d
x ( y)
一、旋转体的体积
旋转体就是由一个平面图形饶这平面内 一条直线旋转一周而成的立体.这直线叫做 旋转轴.
圆柱
圆锥
圆台
一般地,如果旋转体是由连续曲线 y f ( x) 、
直线x a 、x b 及x 轴所围成的曲边梯形绕
x 轴旋转一周而成的立体,体积为多少?
取积分变量为x ,
y
y f (x)
x [a,b]
a3 .
例3
计算由椭圆 x2 a2
y2 b2
1
所成的图形绕x轴旋转而成的
旋转体(旋转椭球体)的体积.
解 这个旋转椭球体也可以看作是由半个椭圆 y b a2 x2 a
及x轴围成的图形绕x轴旋转而成的立体.
体积元素为 dV y 2dx ,
旋转体的体积【创意版】.ppt

1
0
3 y 2 dy 3
5
5 y x3, x 1, x轴
绕y轴旋转一周
1
Vy
0
3 y 2 dy 2
5
y
.,
y=x3 1
y=x3
9
1
◆练习:写出下列旋转体体积的定积分表达式
绕x轴旋转一周
V 2
1
x2 1 2 dx 22
2 1
0
2 x4dx
32 2 3 2
0
1 y x3, x 1, y 0
绕x轴旋转一周
x3, y 1, x 0
绕x轴旋转一周
y=x3 x1
1
Vx
1
dx
0
1
x6dx
6
0
7
.,
y=x3
x
1
8
◆练习:写出下列旋转体体积的定积分表达式
4 y x3, y 1, y 轴
1
绕y轴旋转一周
y
Vy
d x2dy
c
d
c
g( y) 2 dy
.,
c
x=g 5(y)
◆旋转体的体积计算公式
例2 连接坐标原点 O 及点 P( h , r) 的直线,
直线 x=h及 x轴围成一个直角三角形,将它绕
x轴旋转构成一个底半径为 r,高为 h的圆锥,
计算圆锥的体积。
y P(h,r)
解 :如图所示
直线OP的方程为 y r x ,
旋转体的定义:旋转体就是由一个平面图形饶 这平面内一条直线旋转一周而成的立体.这直 线叫做旋转轴。
可选取适当坐标系,使旋转轴为x轴或y轴
最基本的情形是曲边梯形绕x轴或y轴旋转的情形。
微积分_旋转体体积共68页

55、 为 中 华 之 崛起而 读书。 ——周 恩来
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
微积分_ 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
微积分_ 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
计算旋转体体积的“柱壳法”通用课件

处理复杂边界时可能遇到困难
对于具有复杂边界的旋转体,柱壳法可能需要更精细的柱壳划分, 增加了计算的复杂度和工作量。
对计算机性能要求较高
由于柱壳法需要进行大量的数值积分和数据处理,因此对计算机的 性能要求较高,特别是内存和处理器性能。
适用场合分析
适用于各种旋转体的体积计算
柱壳法适用于各种旋转体的体积计算,如球体、圆柱体、圆锥体等。
积,最后求和得到整个旋转体的体积。
柱壳法适用于各种形状的旋转体,如圆环、圆筒、球 等,具有广泛的适用性。
掌握柱壳法对于解决实际问题、提高数学建模能力以 及理解物理现象等方面都具有重要意义。
课程目标
01
掌握柱壳法的原理和计算步骤。
02 能够运用柱壳法计算不同形状旋转体的体 积。
03
理解柱壳法在解决实际问题中的应用,提 高数学建模能力。
微分方程求解
在一些偏微分方程的求解中,柱壳法可以作为一种数值方法,用于近似求解方程的解。
几何形状的体积和表面积计算
柱壳法可以用于计算一些复杂几何形状的体积和表面积,如旋转抛物面、旋转双曲面等 。
在工程领域的应用
机械设计
在机械设计中,柱壳法可以用于分ห้องสมุดไป่ตู้旋转机械的 动态特性和稳定性,如旋转轴、轴承和齿轮等。
计算旋转体体积的“柱壳法”通用课件
目录 CONTENTS
• 引言 • “柱壳法”基本原理 • “柱壳法”应用实例 • “柱壳法”与其他方法的比较 • “柱壳法”的优缺点分析 • “柱壳法”的扩展应用
01
引言
主题介绍
柱壳法是一种计算旋转体体积的有效方法,通过将旋 转体分割成一系列柱壳,然后分别计算每个柱壳的体
流体动力学分析
在流体动力学中,柱壳法可以用 于分析流体在旋转体中的流动情 况,如离心泵和涡轮机的性能分 析。
对于具有复杂边界的旋转体,柱壳法可能需要更精细的柱壳划分, 增加了计算的复杂度和工作量。
对计算机性能要求较高
由于柱壳法需要进行大量的数值积分和数据处理,因此对计算机的 性能要求较高,特别是内存和处理器性能。
适用场合分析
适用于各种旋转体的体积计算
柱壳法适用于各种旋转体的体积计算,如球体、圆柱体、圆锥体等。
积,最后求和得到整个旋转体的体积。
柱壳法适用于各种形状的旋转体,如圆环、圆筒、球 等,具有广泛的适用性。
掌握柱壳法对于解决实际问题、提高数学建模能力以 及理解物理现象等方面都具有重要意义。
课程目标
01
掌握柱壳法的原理和计算步骤。
02 能够运用柱壳法计算不同形状旋转体的体 积。
03
理解柱壳法在解决实际问题中的应用,提 高数学建模能力。
微分方程求解
在一些偏微分方程的求解中,柱壳法可以作为一种数值方法,用于近似求解方程的解。
几何形状的体积和表面积计算
柱壳法可以用于计算一些复杂几何形状的体积和表面积,如旋转抛物面、旋转双曲面等 。
在工程领域的应用
机械设计
在机械设计中,柱壳法可以用于分ห้องสมุดไป่ตู้旋转机械的 动态特性和稳定性,如旋转轴、轴承和齿轮等。
计算旋转体体积的“柱壳法”通用课件
目录 CONTENTS
• 引言 • “柱壳法”基本原理 • “柱壳法”应用实例 • “柱壳法”与其他方法的比较 • “柱壳法”的优缺点分析 • “柱壳法”的扩展应用
01
引言
主题介绍
柱壳法是一种计算旋转体体积的有效方法,通过将旋 转体分割成一系列柱壳,然后分别计算每个柱壳的体
流体动力学分析
在流体动力学中,柱壳法可以用 于分析流体在旋转体中的流动情 况,如离心泵和涡轮机的性能分 析。
旋转体的体积计算(课堂PPT)
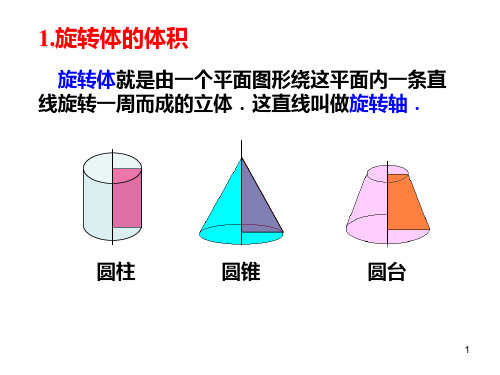
曲边梯形绕 y 轴旋转一周而成的立体,体积为
y
V d [ ( y)]2 dy c d x 2dy c
d
x ( y) c
o
x
3
例1. 求由曲线 y x ,直线x = 1及x轴所围成的平面图形
绕x轴旋转一周所生成的旋转体的体积.
解 如图, 选x为积分变量
y
y x
由旋转体的体积公式,得
1
Vx
(
0
x )2 dx
1
xdx
0
o
x
x2
1
22
0
4
例2. 求由曲线 x 2 4 y,直线y = 1及y轴所围成的图形
分别绕 x 轴, y 轴旋转一周所生成的旋转体的体积.
y
解 如图, 绕 x 轴旋转体的体积,
选x为积分变量
(2, 1)
1
Vx
12 2 2 ( x 2 )2 dx 04
b
左半圆弧方程为 x x2( y) b a2 y2 O A
Bx
体积微元
-a
D
dV
[ x1(
y)]2 dy
[ x2 (
y)]2 dy
[ x12 (
y)
x
2 2
(
y)]dy
环体体积为 V
a
(
a
x12
x22
)dy
a
[(b
a2 y2 )2 (b
a2 y2 )2 ]dy
a
a
y2
2 a 3
2
x3
3
x [a, a]
-a
o
a
x
由旋转体的体积公式,知:
V
a [ f ( x)]2dx
旋转体体积计算说课精选PPT课件
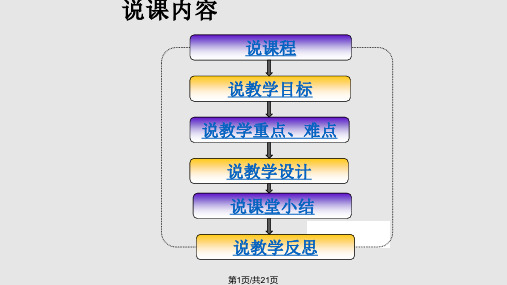
Vx
2V1 2
1
[
x2
( x3 )2
]dx
0
8
21
yx
y x3
1
第16页/共21页
课堂练习2
Find the volume of the region whose boundaries are y=x2 and x=y2 is rotated about the x-axis.
第17页/共21页
作业布置
• AP 微积分课本320页第22-26题
思考
能否通过今天所学内容,求解将曲边梯形绕y轴旋转之后形成旋转体体积。
第18页/共21页
5、小结
圆盘法
n
V Vi
i1
b[ f ( x )]2dx
a
旋转体的体积
垫圈法
V
b {[ R( x)]2 a
[r ( x)]2 }dx
第19页/共21页
求和
逼近
y
y
y
y
O
xO
xO
xO
x
S
lim
n
n i 1
ba n
f
i
b
f (x)dx
a
Back
第8页/共21页
2、问题引入,分组讨论
案例1:探究球体体积如何计算
V y2x
V r [ f ( x)]2dx r
= r y2dx r (r 2 x2 )dx
r
r
= 4r3
3
第9页/共21页
b[R(x)]2dx
a
b[r(x)]2dx
a
b{[R(x)]2 [r(x)]2}dx
a
第15页/共21页
大学高等数学ppt课件第四章2平面图形的面积 旋转体的体积计算

x
1
0
轴
A
1
3
32 3 2 x x dx 3
2
练习写出下列给定曲线所围成的图形面积的定积分表达式。
(4)
A
3
1
2x 3 x dx
2
8 3
(5)
yx ,
2
1 0
y x,
2 1
y 2x
2
A 2 x x dx
7 6
2 x x dx
例 5 求由下列给定曲线所围成的图形面积。 星形线
3 x a cos t 3 y a sin t
即
x y a
2 3
2 3
2 3
解由图形的对称性可得
A 1
A 4 A1 4 ydx
0
a
4 a sin t d a cos3 t
12a
2
0 3
3
1
绕y轴旋转一周
y
2
Vy
0
1
y
3
3 dy 5
y=x3
1
3 5 y x , x 1, x 轴
绕y轴旋转一周
Vy
0
1
y
3
2
2 dy 5
y y=x3 1
◆练习:写出下列旋转体体积的定积分表达式 2 绕y轴旋转一周
Vy
练习写出下列给定曲线所围成的图形面积的定积分表达式。
(6)
y 2x ,
2
1
yx ,
2
y 1
y 2 2 A ( y )dy (1 ) 0 2 3 2
1
0
轴
A
1
3
32 3 2 x x dx 3
2
练习写出下列给定曲线所围成的图形面积的定积分表达式。
(4)
A
3
1
2x 3 x dx
2
8 3
(5)
yx ,
2
1 0
y x,
2 1
y 2x
2
A 2 x x dx
7 6
2 x x dx
例 5 求由下列给定曲线所围成的图形面积。 星形线
3 x a cos t 3 y a sin t
即
x y a
2 3
2 3
2 3
解由图形的对称性可得
A 1
A 4 A1 4 ydx
0
a
4 a sin t d a cos3 t
12a
2
0 3
3
1
绕y轴旋转一周
y
2
Vy
0
1
y
3
3 dy 5
y=x3
1
3 5 y x , x 1, x 轴
绕y轴旋转一周
Vy
0
1
y
3
2
2 dy 5
y y=x3 1
◆练习:写出下列旋转体体积的定积分表达式 2 绕y轴旋转一周
Vy
练习写出下列给定曲线所围成的图形面积的定积分表达式。
(6)
y 2x ,
2
1
yx ,
2
y 1
y 2 2 A ( y )dy (1 ) 0 2 3 2
高等数学:第十讲 旋转体的体积

c
o
x
3. 例题
例1 连接坐标原点 O 及点 P h, r 的直线、直线 x h 及 x 轴
围成一个直角三角形.将它绕 x 轴旋转构成一个底半径为 r ,
高为 h 的圆锥体,计算圆锥体的体积。
解 直线 OP 方程为
y
y r x h
取积分变量为 x,积分区间为 o
[0, h]. 在 [0, h] 上任取小区间
P
r
x x dx h x
[x, x d x]
3. 例题
.
以d x 为底的曲边梯形绕 x轴旋转而成的圆薄片的体积用圆柱
的体积代替得体积元素为,
dV ( r x)2 d x
h
圆锥体的体积为
V
h
0
r h
x
2
d
x
r2
h2
x3 3
h 0
hr2
3yP来自rx hro
x
x
3. 例题
.
例2 求由抛物线y x 与直线y 0 ,y 1 和y 轴围成的 平面图形绕 y 轴旋转而成的旋转体的体积
旋转体的体积公式为
V
b
[
f
(
x)]2
d
x
a
2. 旋转体的体积公式
类似地,如果旋转体是由连续曲线 x y ,直线 y c、 y d
及 y 轴所围成的曲边梯形绕 y轴旋转一周而成的立体,体积元素
为
dV [( y)]2 d y
y
d
体积公式为
x ( y)
V d [( y)]2 d y c
定积分应用之 旋转体的体积
目录
01
微元法的思想
02 旋转体的体积公式
高中数学沪教版高三第一学期1旋转体体积PPT全文课件

拓展思考
你还能想到哪些旋转体? 它们的体积能否用பைடு நூலகம்暅原理构造解决?
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
课后练习
练习1:求解在 xOy 平面上,等轴双曲线x 2 y 2 1 与直线 y 1 围成的封闭图形记为D,如图所示,
4、简单的旋转体
圆柱
圆锥
球
V
S h R 2h 高中数学沪教版高三第一学期1旋转体体积PPT全文课件【完美课件】
二、圆柱体积
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
圆锥的体积
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
三、球的体积
暅原理、一个平放的圆柱和一个长方体,得出
的体积值。
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
再见: 体积。
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
小结
(1)祖暅原理解决了圆柱、圆锥、球等简单的旋转体的
体积,其主要方法是构造转化,关键在截面特性。 (2)在研究数学问题时,要遵循一种规律:未知问题转 化为已知问题来解决。
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
记D(及其内部)绕y轴旋转一周而成的几何体为,
试利用祖暅原理及已学过的几何体,求
你还能想到哪些旋转体? 它们的体积能否用பைடு நூலகம்暅原理构造解决?
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
课后练习
练习1:求解在 xOy 平面上,等轴双曲线x 2 y 2 1 与直线 y 1 围成的封闭图形记为D,如图所示,
4、简单的旋转体
圆柱
圆锥
球
V
S h R 2h 高中数学沪教版高三第一学期1旋转体体积PPT全文课件【完美课件】
二、圆柱体积
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
圆锥的体积
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
三、球的体积
暅原理、一个平放的圆柱和一个长方体,得出
的体积值。
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
再见: 体积。
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
小结
(1)祖暅原理解决了圆柱、圆锥、球等简单的旋转体的
体积,其主要方法是构造转化,关键在截面特性。 (2)在研究数学问题时,要遵循一种规律:未知问题转 化为已知问题来解决。
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
高中数学沪教版高三第一学期1旋转体 体积PP T全文 课件【 完美课 件】
记D(及其内部)绕y轴旋转一周而成的几何体为,
试利用祖暅原理及已学过的几何体,求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o
x
h
x 0, h
所求体积为 V
h 0
r h
x
2
dx
1 3
r
2h
6
例3 计算由曲线 y=x2 与 x=y2 所围成的平面 图形绕 y 轴旋转一周而成的立体的体积。
解:如图所示
Vy V1 V2 1 ydy
1
y
4dy
3
0
0
10
V1
V2
b
b
(2)a kf (x)dx k a f (x)dx
b
c
b
(3)a f (x)dx a f (x)dx c f (x)dx
4、结论
若f (x)为偶函数,则 a f (x) 2 a f (x)
-a
0
若f (x)为奇函数,则 a f (x) 0 -a
3
◆旋转体的定义
还有其他方法吗?
22
2020/1/2
23
2
11
2020/1/2
12
问题的提出
返回
13
旋转体概念
返回
14
旋转体实例圆锥
返回
15
旋转体实例圆柱
返回
16
旋转体体积推导
返回
17
体积例题 3
返回
18
体积例题 2
返回
19
体积例题 5
返回
20
基本初等函数的导数公式 1.若f (x) c f '(x) 0
2.若f (x) xn f ' (x) nxn-1(n R)
返7 回
◆练习:写出下列旋转体体积的定积分表达式
1 y x3, x 1, y 0
绕x轴旋转一周
Vx
1
x
6dx
1
0
7
2 y x3, y 1, x 0
绕x轴旋转一周
y=x3 x1
1
Vx
1
dx
0
1
x6dx
6
0
7
y=x3
x
1
8
◆练习:写出下列旋转体体积的定积分表达式
示例:圆锥、圆柱、球等的形成过程(演示)。
旋转体的定义:旋转体就是由一个平面图形饶 这平面内一条直线旋转一周而成的立体.这直 线叫做旋转轴。
可选取适当坐标系,使旋转轴为x轴或y轴
最基本的情形是曲边梯形绕x轴或y轴旋转的情形。
(演示)。
4
◆旋转体的体积计算公式
1、旋转轴为 x 轴(演示) 由x=a , x= b ,y=0, y=f (x) (f (x)>0)所围成
d x2dy
c
d g( y)2 dy
c
c
x=g5(y)
◆旋转体的体积计算公式
例2 连接坐标原点 O 及点 P( h , r) 的直线,直
线 x=h及 x轴围成一个直角三角形,将它绕 x
轴旋转构成一个底半径为 r,高为 h的圆锥,计
y
算圆锥的体积。
P(h,r)
解 :如图所示
直线OP的方程为 y r x ,
1 x ln a
8.若f (x) ln x f '(x) 1
21
x
定积分与平面图形的面积
例1 计算由 y2 2x 和 y x 4 所围
成的图形的面积。
解 A A1 A2
2 0
2x (
2x ) dx
8 2
2x (x 4) dx
18
的曲边梯形绕 x 轴旋转一周而成的旋转体的
体积为 Vx
b y2dx
a
b f (x)2 dx
a
2、旋转轴为 y 轴(演示)
y=f (x)
由y= c , y= d , x=0, x=g (y) ( g (y)>a 0)所围b 成
的曲边梯形绕 y 轴旋转一周而成的旋转体的体
d
积为 Vy
绕x轴旋转一周
V 2
1
x2 1 2 dx 22
2 1
0
2 x4dx
32 2 3 2
0
15
10
◆练习:写出下列旋转体体积的定积分表达式
2
绕y轴旋转一周
1
2
2
2
2
Vy
0
y dy 1
y 1 dy
3
定积分的应用 ----旋转体的体积
2
1
1、微积分基本定理(牛顿-莱布尼茨公式)
b a
f
(x)dx
F(x)
|ba
F (b)
F(a)
其中F(x) 是被积函数f(x)的原函数。
2、定积分的几何含义:
2
3、定积分基本性质
b
b
b
(1)a ( f (x) g(x))dx a f (x1
绕y轴旋转一周
y
Vy
1
0
3 y 2 dy 3
5
5 y x3, x 1, x轴
绕y轴旋转一周
1
Vy
0
3 y 2 dy 2
5
y
y=x3 1
y=x3
9
1
◆练习:写出下列旋转体体积的定积分表达式
3.若f (x) sin x f '(x) cos x
4.若f (x) cos x f '(x) -sin x
5.若f (x) ax f ' (x) ax ln a
6.若f (x) ex f ' (x) ex
7.若f (x) loga x
f '(x)
