基于Matlab的模糊自整定PID控制器仿真研究
基于MATLAB的模糊自整定PID参数控制器的设计与仿真

2模糊自整定PID参数控制策略与 整定原则
杨咏梅:硕士研究生
国家自然科学基金资助项目(G0501080160302001) 电话:010-62132436.62192616(T/F)
4模糊自整定PID参数控制系统仿真
0
0.5
I.0
1 5 20
25
30
(2)输出KP、KI、KD的隶属函数曲线
图2隶属函数曲线图
(3)模糊控制规则表
根据上述的PID参数整定原则及专家经验,可以
列出输出变量KP、KI、KD的控制规则如表1-3所
示。 3.2模糊控制器的编辑
在SIMULINK环境对图1所示的模糊自整定PID 参数控制系统编辑,得到如图3所示的系统仿真框 图。在系统仿真时,我们选择被控对象的传递函数为: G(s)=l/(2Sz+3s+1)。然后按SIMUL]NK仿真的正确步骤 选择计算步长、模拟示波器X/Y轴参数等进行仿真运 算。
b模糊控制器的控制规则对模糊自整定PID参数 控制系统中的参数影响较大。这将直接影响系统的调 节效果.应对模糊控制器的FIS规则语句的权值和控 制规则表作适当的修改和调整。
图4 PID控制系统响应曲线 图5模糊自整定PID参数控制系统响应曲线
c.采用Fuzzy和PID复合控制的算法,系统的响 应速度加快、调节精度提高、稳态性能变好,而且没有 超调和振荡.具有较强的鲁棒性。这是单纯的PID控 制难以实现的,它的一个显著特点就是在同样精度要 求下,系统的过渡时间变短,这在实际的过程控制中 将有重大的意义。
基于MATLAB的模糊PID控制器设计与仿真研究

35
万方数据
机 车 电 传 动 2002年
2002 年第 5期 2002 年9 月10 日
机车电传动 ELECTRIC DRIVE FOR LOCOMOTIVES
基于M A T L A B 的模糊P I D 控制器
研 究
设计与仿真研究
开
发
常满波 胡鹏飞
西南交通大学 电气工程学院 四川 成都 610031
摘 要 针对在复杂系统中实现自组织参数的 P I D 控制问题 介绍了一种基于模糊控制原 理的 P I D 参数自组织控制器的设计方案 同时利用 M A T L A B 中的 S I M U L I N K 和 F U Z Z Y 工具箱 进行了仿真研究 仿真结果表明 参数自组织模糊控制系统比参数固定的系统的控制效果好
关键词 P I D 控制器 M A T L A B 模糊控制 仿真 中图分类号 TP391.9 文献标识码 A 文章编号 1000-128X(2002)05-0034-03
5 ,2002 Sep. 10,2002
作者简介 常满波 1976- 男 西南交通大学电气工 程学院硕士研究生 主要 从事计算机应用技术的研 究
图8 G1(s)仿真结果
图9 G2(s)仿真结果
过程 G1(s)
G2(s)
表2 仿真结果分析
常规PID控制
Kp=2.81 Ki=1.64 Kd=0.41
YOS=18.7% TS=4.38 s
Kp=0.95 Ki=1.03 Kd=0.26
YOS=33.2% TS=7.33 s
设被控对象的数学模型为
图 4 Kp K i D d 的隶属函数
根据以上分析和语言变量的设定 可以总结出 Kp K i 和 K d 的自调整控制规则 见表 1
模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)2这个例子的程序百度文库里有很多版本,但我下了很多都有错误,运行不了。
以下程序我一字一字的敲出来的,已经成功运行,绝对无误。
仿真实例,被控对象为p G (s)=ss s 1047035.8752350023++ 采样时间为1ms ,采用模糊PID 控制进行阶跃响应,在第300个采样时间时控制器输出加1.0的干扰,相应的运行结果如图1~13所示。
仿真程序如下:将以下程序保存为fuzzypid.m 文件,即可得到仿真结果。
%fuzzy tunning PID controlclear all ;clear all ;a=newfis('fuzzpid');a=addvar(a,'input','e',[-3,3]); %parameter ea=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'input','ec',[-3,3]); %parameter eca=addmf(a,'input',2,'NB','zmf',[-3,-1]);a=addmf(a,'input',2,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',2,'Z','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);a=addmf(a,'input',2,'PM','trimf',[0,2,3]);a=addmf(a,'input',2,'PB','smf',[1,3]);a=addvar(a,'output','kp',[-0.3,0.3]); %parameter kpa=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);a=addmf(a,'output',1,'NM','trimf',[-0.3,-0.2,0]);a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);a=addmf(a,'output',1,'Z','trimf',[-0.2,0,0.2]);a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);a=addmf(a,'output',1,'PM','trimf',[0,0.2,0.3]);a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);a=addvar(a,'output','ki',[-0.06,0.06]); %parameter ki a=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);a=addmf(a,'output',2,'NM','trimf',[-0.06,-0.04,0]);a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]); a=addmf(a,'output',2,'Z','trimf',[-0.04,0,0.04]);a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);a=addmf(a,'output',2,'PM','trimf',[0,0.04,0.06]);a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);a=addvar(a,'output','kd',[-3,3]); %parameter kda=addmf(a,'output',3,'NB','zmf',[-3,-1]);a=addmf(a,'output',3,'NM','trimf',[-3,-2,0]);a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);a=addmf(a,'output',3,'Z','trimf',[-2,0,2]);a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);a=addmf(a,'output',3,'PM','trimf',[0,2,3]);a=addmf(a,'output',3,'PB','smf',[1,3]);rulelist=[1 1 7 1 5 1 1;1 2 7 1 3 1 1;1 3 62 1 1 1;1 4 62 1 1 1;1 5 5 3 1 1 1;1 6 4 42 1 1;1 7 4 4 5 1 1;2 1 7 1 5 1 1;2 2 7 13 1 1;2 3 6 2 1 1 1;2 4 53 2 1 1;2 5 53 2 1 1;2 6 4 43 1 1;2 734 4 1 1;3 1 6 14 1 1;3 2 6 2 3 1 1;3 3 6 3 2 1 1;3 4 5 3 2 1 1;3 54 4 3 1 1;3 6 3 5 3 1 1;3 7 3 54 1 1;4 1 6 2 4 1 1;4 2 6 2 3 1 1;4 35 3 3 1 1;4 4 4 4 3 1 1;4 5 3 5 3 1 1;4 6 2 6 3 1 1;4 7 2 6 4 1 1;35 1 5 2 4 1 1;5 2 5 3 4 1 1;5 3 4 4 4 1 1;5 4 3 5 4 1 1;5 5 3 5 4 1 1;5 6 2 6 4 1 1;5 7 2 7 4 1 1;6 1 5 47 1 1;6 2 4 4 5 1 1;6 3 3 5 5 1 1;6 4 2 5 5 1 1;6 5 2 6 5 1 1;6 6 27 5 1 1;6 7 1 7 7 1 1;7 1 4 4 7 1 1;7 2 4 4 6 1 1;7 3 2 5 6 1 1;7 4 2 6 6 1 1;7 5 2 6 5 1 1;7 6 1 7 5 1 1;7 7 1 7 7 1 1];a=addrule(a,rulelist);a=setfis(a,'DefuzzMethod','mom');writefis(a,'fuzzpid');a=readfis('fuzzpid');%PID controllerts=0.001;sys=tf(5.235e005,[1,87.35,1.047e004,0]); dsys=c2d(sys,ts,'tustin');[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0;y_1=0;y_2=0;y_3=0;x=[0,0,0]';4error_1=0;e_1=0.0;ec_1=0.0;kp0=0.40;kd0=1.0;ki0=0.0;for k=1:1:500time(k)=k*ts;rin(k)=1;%using fuzzy inference to tunning PIDk_pid=evalfis([e_1,ec_1],a);kp(k)=kp0+k_pid(1);ki(k)=ki0+k_pid(2);kd(k)=kd0+k_pid(3);u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);if k==300 %adding disturbance(1.0v at time 0.3s)u(k)=u(k)+1.0;endif u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endyout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;error(k)=rin(k)-yout(k);%%%%%%%%%%%%%%%%%%%%%%%%%return of pid parameters%%%%%%%%%%%%%%%%%%%%%%%% u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);5x(1)=error(k); %calculating Px(2)=error(k)-error_1; %calculating Dx(3)=x(3)+error(k); %calculating De_1=x(1);ec_1=x(2);error_2=error_1;error_1=error(k);endshowrule(a)figure(1);plot(time,rin,'b',time,yout,'r'); xlabel('time(s)');ylabel( 'rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel( 'error ');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel( 'u ');figure(4);plot(time,kp,'r');xlabel('time(s)');ylabel( 'kp ');figure(5);plot(time,ki,'r');xlabel('time(s)');ylabel( 'ki ');figure(6);plot(time,kd,'r');xlabel('time(s)');ylabel( 'kd ');figure(7);plotmf(a,'input',1);figure(8);plotmf(a,'input',2);figure(9);plotmf(a,'output',1);figure(10);plotmf(a,'output',2);figure(11);plotmf(a,'output',3);plotfis(a);fuzzy fuzzpid.fis6仿真运行结果:789。
基于Matlab的模糊自整定PID控制器仿真研究

基于Matlab的模糊自整定PID控制器仿真研究(1.青岛科技大学学报(自然版)编辑部, 山东青岛266061;2.中山大学数学与计算科学学院,广东广州510275)摘要:将模糊控制与PID控制结合,利用模糊推理方法实现对PID 参数的在线自整定。
使用MATLAB对系统进行仿真,结果表明系统的动态性能得到了提高。
关键词:模糊PID控制器;参数自整定;Matlab;仿真Simulation Study of Fuzzy Self-tuning PID Controller Based on MatlabJIANG Feng-hui1, CHEN Xiao-gao2(1.Editorial Office of Journal of Qingdao University of Science and Technology(Natural Science Edition), Qingdao 266061,China; 2.School of Mathematics and Computational Science Sun Yat-sen University, Guangzhou 510275,China)Abstract: Combining fuzzy control and PID control, the self-tuning of PID parameters is realized through fuzzy inference. The results of Matlab simulation indicate that the dynamic performance of system is improved.Keywords: fuzzy PID controller; parameter self-tuning; Matlab; simulationPID控制由于其算法简单、鲁棒性好和可靠性高,广泛应用于工业过程控制,尤其适用于可建立精确数学模型的确定性控制系统。
基于Matlab的模糊PID控制系统设计及仿真

me t h o d s .
Ke y wo r d s f u z z y c o n t r o l ;P I D; M a t l a b s i mu l a t i o n; b o i l e r l e v e l
P I D 控 制作 为 经典 控 制 至 今 仍 被 广 泛 应 用 , 面对
关键词 模 糊 控 制 ;P I D控 制 ;M a t l a b仿 真 ;锅 炉液 位
中图分类号
T P 2 7 3 . 4
文献标识码
A
文章编 号
1 0 0 7— 7 8 2 0 ( 2 0 1 5 ) 0 2一l 1 9— 0 4
De s i g n a n d S i mu l a t i o n o f F u z z y P I D Co n t r o l S y s t e m Ba s e d o n Ma t l a b
2 模糊 P I D控 制 器 设 计
自适 应模 糊 P I D控 制器 结 构 如 图 1所示 , 其 以常 规P I D控 制为基 础 , 采用 模糊 推理 的思 想 , 将 被 控量 的
然而模糊控制的精度受到控制规则 的限制还始终存在 静差 。模糊 P I D控 制利 用整 定 P I D参 数 的经验 来设 计模 糊 控 制 器 自动 整 定 P I D控制 器 的参 数 , 从 而 使 P I D控制 器 以变应 变 _ 3 J 。本 文采 用 基于 Ma t l a b的模糊
t r o l t h e b o i l e r l e v e 1 . Th e c o n t r o l e f f e c t s b y P I D c o n t r o l l e r ,f u z z y c o n t r o l l e r a n d f u z z y PI D c o n t r o l l e r re a c o mp re a d b y s i mu l a t i o n e x p e ime r n t .T h e e x p e ime r n t l a r e s u l t s s h o w t h a t t h e f u z z y P I D c o n t r o l l e r i s s i g n i f i c a n t l y b e t t e r t h a n o t h e r
模糊自适应PID控制控制的Matlab仿真设计研究

模糊自适应PID控制的Matlab仿真设计研究姓名:陈明学号:201208070103班级:湖南大学智能1201一、模糊控制思想、PID控制理论简介:在工业生产过程中,许多被控对象受负荷变化或干扰因素很多基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。
通过matlab 软件进行实例,仿真表明, , 提高控制系统实时性和抗干扰能力,易于实现.便于工程应用。
1.1模糊控制的思想:应用模糊数学的基本理论和方法, 控制规则的条件、操作用模糊集来表示、并把这些模糊控制规则以及有关信息, 诸如PID 控制参数等作为知识存入计算机知识库, 然后计算机根据控制系统的实际情况(系统的输入, 输出) , 运用模糊推理。
1.2PID算法:u (t) = Kp·e (t) + Ki·∫t0e (t) dt + Kd·de (t)dt= Kp e (t) + Ki Σei (t) + Kdec (t)其中, u (t) 为控制器输出量, e ( t ) 为误差信号, ec (t) 为误差变化率, Kp , Ki , Kd 分别为比例系数、积分系数、微分数。
然而,课本中,为了简化实验难度,只是考虑了kp,ki参数的整定。
1.3模糊PID控制器的原理图:二、基于Matlab的模糊控制逻辑模块的设计关于模糊逻辑的设计,主要有隶属函数的编辑,参数的选型,规则导入,生成三维图等2.1 模糊函数的编辑器的设定:打开matlab后,在命令窗口输入“fuzzy”,回车即可出现模糊函数编辑器,基本设置等。
基于课本的实验要求,我选的是二输入(e, e c)二输出(k p ,k i)。
需要注意的是,在命名输入输出函数的时候,下标字母需要借助下划线的编辑,即e_c 能够显示为e c。
2.2四个隶属函数的N, Z, P 函数设定:在隶属函数的设定中,N 选用的是基于trimf(三角形隶属函数) , Z是基于zmf (Z型隶属函数),P是基于smf(S型隶属函数)。
基于Matlab的参数模糊自整定PID控制器的设计与仿真

20 0 8年 1 2月
中原 工 学 院 学 报
J OURNAI 0F ZH0NGYUAN UNI RS TY 0F TECH N0L VE I 0GY
V0 . 9 NO 6 11 .
De ., 08 c 20
文章 编 号 : 6 1 9 6 2 0 ) 6 0 6 —0 1 7 —6 0 ( 0 8 0 — 0 8 4
2 参 数 模 糊 自整定 P D 控 制 器 设 计 I
取当前采样值
2 1 设 计 论 域 和 模 糊 规 则 表 .
I
e )r )v ( =( - 1 k k
输 入 变量 I 和 l 语 言 值 的模 糊 子 集 取 为 { l c e l 负 大, 负中 , 负小 , , 小 , 中 , 大 } 并 简 记 为 { 零 正 正 正 , NB, NM , ~S, ,P S,P ,PB} 论 域 为 { 3 3 . M , 一 , } 以 k 、 k k 、 3个参数 作 为输 出变量 , k、 模糊 量 的模 k 、 k 糊子集 取 为 { 大 , 中 , 小 , , 小 , 中 , 大 } 负 负 负 零 正 正 正 , 并 简记 为 { NB, NM , ,Z NS O,PS, M ,P , 的 P B} k 论 域 为 { . ,. }k 一0 3 0 3 , 的论 域 为 { . 6 0 0 } k 一0 0 , . 6 , 的论域 为 { , }其 中 NB、 一3 3 . PB取 S形 隶 属度 函数 ,
1 参 数 模 糊 自整 定 P D 控 制 原 理 I
参数 模糊 P D 自整 定控 制 是 以误 差 l { I 和误 差 变 e
化 lC 作 为 模 糊 P D 控 制 器 的 输 入 , 以 满 足 不 同 时 l e I 可
基于matlab的模糊PID控制仿真实验报告
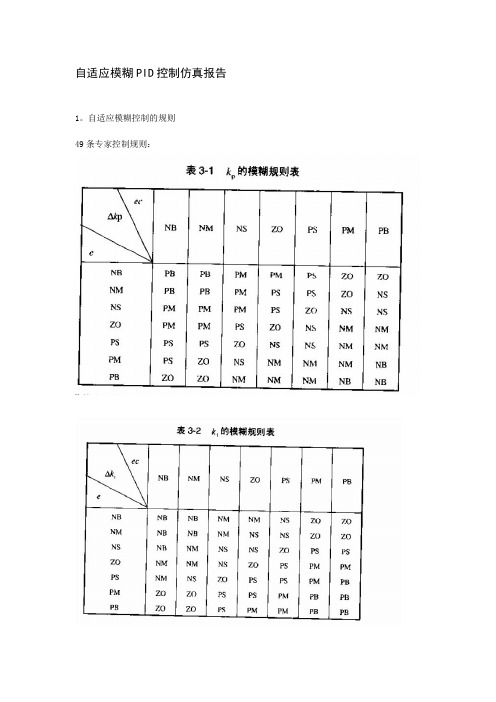
自适应模糊PID控制仿真报告
1。
自适应模糊控制的规则
49条专家控制规则:
2。
系统仿真框图
包括模糊控制器,PID控制器两部分组成。
3.模糊控制器设计
确定为双输入,三输出结构
确定每个变量的论域,其中每个变量都有一个模糊子集来表示。
这个模糊子集中有7个语言变量,分别是:NB,NM,NS,ZO,PS,PM,PB
在编辑界面中,确定好每一个语言变量的范围,以及隶属函数的类型。
如下图所示:
输入模糊控制规则:
仿真结果
PID控制器Kp参数在控制过程中的变化曲线:
Ki参数:
Kd参数:
系统闭环控制阶跃响应曲线:
传统PID控制响应曲线:(ZN整定法)
对比可以发现,自适应模糊PID控制不仅使曲线超调量小,响应过程平稳,而且动态响应时间也较短.性能优于传统PID控制器。
对比如下:(PID采用cohen-coon整定法)红色为常规PID控制器,黄色为模糊PID控制器
采用ZN法整定后对比:
而且在仿真中发现一个问题:ZN法整定存在不稳定问题,但模糊控制则非常平稳
加干扰的控制对比系统框图
对比效果:
对应的模糊PID参数变化情况: P
PI
PD。
基于MATLAB的PID参数模糊自整定控制器设计及仿真

Industry Control and Applications基于MAT LAB的PID参数模糊自整定控制器设计及仿真张 敏1,余 纯2(1.武汉化工学院电气信息学院,湖北 武汉 430074; 2.江汉大学数学与计算机学院,湖北 武汉 430056)摘要:本文针对时滞、参数时变和有干扰的控制系统,提出基于M AT LAB的PI D参数模糊自整定控制器的设计与仿真。
本文利用G UI(图形用户界面)建立模糊控制器,仿真模型为二阶延迟系统。
仿真结果表明,系统阶跃响应具有较好的动态特性和鲁棒性,表明该PI D参数模糊自整定控制器有较高的实用性。
关键词:PI D控制;模糊控制;PI D参数模糊自整定;计算机仿真中图分类号:TP23714 文献标识码:B 文章编号:100327241(2005)0720022204MAT LAB-Bas e d Desig n of A Fuzzy-Tu n nin gPID Co ntrollerZHANG Min1,YU Chun2(11Institute of In formation and Engineering,Wuhan Chemical Industry C ollege,Wuhan430074,China;21C ollege of Math1&C om puter Science,Jianghan University,Wuhan430056,China)Abstract:This paper presents the design of the fuzzy-tunning PI D controller based on M AT LAB1I t uses G UI(G raphical User Inter face)to constructa fuzzy controller and a plant of a second-order with delay1S imulation results show that the system has better dynamic character and ro2bustness1K ey w ords:PI D control;Fuzzy control;Fuzzy self-tuning PI D;C om puter simulation1 引言模糊控制器和常规的控制器(如PI D调节器)相比具有无须建立被控对象的数学模型,对被控对象的时滞、非线性和时变性具有一定的适应能力等优点,同时对噪声也具有较强的抑制能力,即鲁棒性较好。
基于Matlab的模糊自整定PID控制器设计

引言
PID控制和模糊控制广泛应用的各个系统 和领域中,其中 PID 控制中关键问题是 PID 参数的整定。单纯的模糊控制器不能消除稳 态误差,只能提高模糊控制器的精度和跟踪 性能。将 PID 控制和模糊控制结合在一起使
图 1 模糊自整定 PID 控制器结构
2 模糊控制器的设计
(1 )语言变量隶属度函数的确定 模糊控制器采用两输入三输出的形式,
c
c
PID参数自整定的要求。利用模糊规则在线对
PID 参数进行修改,便构成了自整定模糊PID
控制器,控制系统结构如图1 所示。
使其朝误差绝对值减小方向变化。 ③当 e × ec < 0 或 e=0 时,说明误差的绝
对值朝减小的方向变化,或者已达到平衡状 态。此时,可采取保持控制器输出不变。
(4)当 e × ec = 0,ec ≠ 0 时,表明系统 的曲线与理论曲线平行或一致,为使系统具有 良好的稳态性能,应采取较大 kp 和 ki 值,同 时避免设定值附近振荡,并考虑系统的抗干扰 性能,适当选取 k d 值。设
图 2 e 和 ec 隶属函数曲线 (2 )建立模糊控制器的控制规则表
根据参数 kp、ki 和 kd 对系统输出特性的 影响,可得出在不同的 e 和 ec 时,参数的自整 定原则。
①当 |e| 很大时,不论误差变化趋势如 何,都应考虑控制器的输出应按最大(或最小) 输出,以达到迅速调整误差,使误差绝对值以 最大速度减小。同时为了防止积分饱和,此时 应取较大 kp,较小的 ki 和 kd 取零。
②当 e × ec > 0 时,说明误差在朝误差 绝对值增大方向变化。此时若误差较大,可考 虑由控制器实施较强的控制作用,以达到扭转 误差绝对值朝减小方向变化,并迅速减小误差 绝对值,此时取较大的 k 、k 不能太大,取较
基于MATLAB的PID控制器参数整定及仿真

基于MATLAB的PID控制器参数整定及仿真PID控制器是一种经典的控制器,在工业自动化控制系统中广泛应用。
其主要功能是根据系统的误差信号,通过调整输出信号的比例、积分和微分部分来减小误差,并达到系统的稳定控制。
PID控制器参数整定是指确定合适的比例常数Kp、积分常数Ki和微分常数Kd的过程。
本文将介绍基于MATLAB的PID控制器参数整定及仿真的方法。
首先,在MATLAB中建立一个包含PID控制器的模型。
可以通过使用MATLAB的控制系统工具箱来实现这一过程。
在工具箱中,可以选择合适的建模方法,如直接设计模型、积分节点模型或传输函数模型。
通过这些工具,可以方便地建立控制系统的数学模型。
其次,进行PID控制器参数整定。
PID控制器参数整定的目标是通过调整比例常数Kp、积分常数Ki和微分常数Kd,使系统的响应特性达到最佳状态。
常用的PID参数整定方法有经验法、试误法、Ziegler-Nichols方法等。
1.经验法:根据系统的特性和经验,选择合适的PID参数。
这种方法常用于初步整定,但可能需要根据实际情况调整参数。
2.试误法:通过逐步试验和调整PID参数,使系统的输出响应逐渐接近期望值,从而达到最佳控制效果。
3. Ziegler-Nichols方法:该方法是一种经典的系统辨识方法,通过测试系统的临界稳定性,得到系统的传递函数参数,并据此计算出合适的PID参数。
最后,进行PID控制器参数整定的仿真。
在MATLAB中,可以通过使用PID模块进行仿真。
可以输入相应的输入信号和初始参数,观察系统的输出响应,并通过调整参数,得到最佳的控制效果。
总结起来,基于MATLAB的PID控制器参数整定及仿真的过程包括:建立控制系统模型、选择PID参数整定方法、进行PID参数整定、进行仿真实验。
PID控制器参数整定的好坏直接影响控制系统的工作性能。
通过基于MATLAB的仿真实验,可以方便地调整和优化控制系统的PID参数,提高系统的响应速度、稳定性和抗干扰性能。
基于Matlab的模糊自整定PID控制器仿真研究

2 0 , (6)4 O — 0 0 9 1 2 : 1 8 41 1 1
[] 4 基于 . T的远程教 育短信系统 的研究与 实现 [ ] 南师范 大学学 NE J. 河 报 ,0 9 3 3 )2 — 2 2 0 , ( 7 :9 3 [ ] S数据采集 软件的实现[ ]全球定位系统 ,0 8 1 :5 3 5 GP J. 2 0 ( )2 — 0
它 们 的模 糊 集 为 :
ee = N N N , P ,M,B ,模糊 集 中元 素分别代 表 ,c { B,M,SO,SP P l
负 大 、 中 、 小 、 、 小 、 中 、 大 。 根 据 k、. k 三 个 参 负 负 零 正 正 正 。k和 d 数 模 糊 规 则 表 构 造 一 个 两 输 入 ( e ) 输 出 ( 。△ k △k) e,c 三 △k 、 i d 、 的 模 糊 控 制 器 , 名 为 fz pdf 。见 图 3 取 u z i. i s 。
GF z y T ob x工 具 箱 构 造 e e u z o lo 、 c双 输 入 ,pk和 k k,. d
三 输 出 的模 糊控 制 系 统 。 利 用 上 面 分 析 的参 数 自整定 原理 和 所 建 的隶 属 函数 和 控制 规 划 在 Malb环 境 中实 现仿 真 研 究 , 过 t a 通
的论 域 。
ee =- , ,3一 , 10 12 3 4 5 , {5- 一 .2一 , , , , , ,} c 4
糊 矩 阵 表 进 行 参 数 调 整 , 方 法 实 现 简 单 、 便 易 用 , 实 际 控 该 方 对 制 有 重 要 指 导 意 义 。 能 够 发 挥 两 种 控 制 方 式 的 优 点 , 服 两 者 它 克 的 缺 点 , 高控 制质 量 。 方 面模 糊 控 制 具 有 动态 响应 快 和 超 调 提 一
基于MATLAB的参数模糊自整定PID控制器的设计与仿真研究

2 一 , , , ,) , l0 12 3 ,它 们 的 模 糊 子 集 为 : E =N E, C { B, N N ,O,S P P 1其 含 义依 次 为负 大 、 中 、 M, S Z P ,M,B , 负
推理 的方 法对 PD 的参 数 K 、 iK I p Kห้องสมุดไป่ตู้、 d进行 在线 自整 定, 以满足 不 同 E和 E C对控 制器参数 的不 同要 求 ,
从 而使 被控 对象 具有 良好 的动态 性 能和 静态 性 能 。 参数 模糊 自整定 PD控 制系统 结构框 图如 图 l I 所示
( )参数模 糊 自整定 PD控制 系统 的结构 2 I
. 弓 寓 1 I
根据 偏差 的比例 ( ) 积 分 () 微分 ( 进行 控 P、 I、 D) 制( 简称 PD控 制 ) 是控 制 系统 中应 用最 为 广泛 的 I ,
一
在 常规 PD基 础上 。 I 以被控 对象 的反馈 值 与 目 标值 的误差 E和误差 变化 率 E C作 为输 入 ,用 模糊
负小 、 、 零 正小 、 中 、 正 正大 。 规 定 输 出 变 量 K 、 、 d的 论 域 为 : p , p K K ,
建立 ]
图 3 K 。i K p K 和 d的隶 属 度 函数
在 MA L T AB命令 窗 口键人 fzy进入模 糊 推理 uz 系统 编辑 器 , 各参 数设 置 如 图 4所 示 。利用 隶 属度
维普资讯
1 廪 嚣毒
专题
270 0 . 01
蒸
蚴参数摸糊圃鳌 P n D撞 剃器蚴谈 镑 珊
基于MATLAB的模糊PID的仿真研究

基于MATLAB的模糊PID的仿真研究模糊控制技术的发展及应用概况自动控制技术通常是指,利用一些自动控制装置来代替人类驾驭机器,设备或控制生产的过程。
然而一些人们看似简单的控制问题,用传统的控制理论和方法意外的不能解决。
经典控制理论主要解决线性系统的问题,现代控制理论可以解决多输入多输出的问题,系统可以是线性的,定常的,也可以是非线性的,时变的,模糊控制就发挥了其优势,可以预料,在传统控制的难题中,将有一批难题可以应用模糊控制技术或传统控制技术与模糊控制技术结合得以解决。
模糊控制的特点模糊工程的计算方法虽然是运用模糊集理论进行的模糊算法,但最后得到的控制规律是确定的,定量的条件语句。
不需要根据机理与分析建立被控对象的数学模型,对于某些系统,要建立数学模型是很困难的,甚至是不可能的。
与传统的控制方法相比,模糊控制系统依赖于行为规则库,由于是用自然语言表达的规则,更接近于人的思维方法与习惯,因此,便于现场操作人员的理解和使用,便于人机对话,以得到更有效的控制规律。
模糊控制与计算机密切相关,从控制角度看,他实际上是一个由很多条件语句组成的软件控制器,目前,模糊控制还是应用2值逻辑的计算机来实现,模糊规律经过运算,最后还是进行确定性的控制,模糊推理硬件的研制与模糊计算机的开发,使得计算机将像人脑那样随心所欲的处理模棱两可的信息,协助人们决策和进行处理信息。
传统PID控制与模糊PID控制传统的PID控制器是过程控制中应用最广泛最基本的一种控制器,它具有简单,稳定性好,可靠性高等优点。
PID调节规律对相当多的工业控制对象,特别是对于线性定常系统控制室非常有效的。
其调节过程的品质取决于PID控制器各个参数的设定。
同时我们也注意到,考虑到模糊控制实现的简易性和快速性,通常以系统误差e和误差变化de为输入语句变量,因此它具有类似于PD控制器特性。
由经典控制理论可知,PD控制器课活动良好的系统动态特性,但无法消除系统的静态误差,为了改善模糊控制器的静态性能,提出了模糊PID控制器的思想。
基于Matlab的模糊自适应PID控制器仿真研究

模糊推理
KP KI KDrFra bibliotekt) +
e(t)
-
du / dt
c(t) PID 对象 调节器 u(t)
ec(t )
图2 自适应模糊PID控制器系统原理框图
• 如图2所示,自适应模糊PID控制器是在PID算法的基础上, 以误差e和误差变ec作为输入,利用模糊规则进行模糊推 理,查询模糊矩阵表进行参数调整,来满足不同时刻的e 和ec对PID参数自整定的要求。利用模糊规则在线对PID参 数进行修改,便构成了自适应模糊PID控制器。
比例 r(t) +
e(t)
积分 微分
+
+ u(t) c(t) 被控对象 +
图1 PID控制器系统原理框图
• 如图1,在经典PID控制中,给定值与测量值 进行比较,得出偏差e(t),并依据偏差情况, 给出控制作用u(t),然后作用于被控对象。 输出c(t)同时反馈,形成闭环系统。
T u ( k ) K p [e ( k ) TI
e(k ) e(k 1) ] e( j ) TD T j 0
k
• 模糊控制通过模糊逻辑和近似推理方法,让计算 机把人的经验形式化、模型化,根据所取得的语 言控制规则进行模糊推理,给出模糊输出判决, 并将其转化为精确量,作为馈送到被控对象(或过 程)的控制作用。 • 模糊控制表是模糊控制算法在计算机中的表达方 式,它是根据输入输出的个数、隶属函数及控制 规则等决定的。目的是把人工操作控制过程表达 成计算机能够接受,并便于计算的形式。 • 模糊控制规则一般具有如下形式: If{ e = Ai and ec = Bi}then u= Ci ,i=1,2…, 其中e,ec和u分别为误差变化和控制量的语言变 量,而Ai、Bi、Ci为其相应论域上的语言值。
基于MATLAB模糊自整定PID控制器的设计与仿真

系 统 ,它 的近 似 模 型 为 [: 4 ]
G ()= 2 0
P S PS O O O
P B
NS NS NS NS O
P s
NM NS NS NS O
P S O O O O P B P B
K 应取 小 些 。在 这 种 情 况 下 .K 的 取 侬 对 幕 统 响 应 彬 响 较 大 ,K 的取 位 要适 当 .
比,改泄仆能 挟得 世优 的舟榨性 和动、静态性及县有 良好
旧m & I m :
2模 糊 参 数 自整 定 PD 控 制 器 的设 计 I
( ]模糊托制 1 n知 l q 表, 和榄糊避辑的 则推理 为珊 l 壤础.采用讣雄 沱 机拄 制技 术构 j 的一种 具钉 厦馈通 道的闭环数 戊 ≯控制系统 雠糊控制脲理
0 O P S P M
PB
NS NS O P s
NM P M
NM NM
NS O O
O P S PM
PB
NM NM O O
NS O P S P S
图 2 建 立 模 糊 控 制 器 的规 划 编 辑 器
P B P B
3系统 仿 真
如图 2 示。 所
PB
P B
P B P B P M P M P S O O
P B P B
P B
P B
NM NS 0
P s
O
P S
PM PM
P M P S O NS NM
P M 0
NS NM
N
P S
PS O
为原先定好 的初 始 PD参数 。△ 、A 为模 糊控 I K 、A
模糊自适应PID控制的Matlab仿真设计研究_陈明201208070103

模糊自适应PID控制的Matlab仿真设计研究:明学号:201208070103班级:大学智能1201一、模糊控制思想、PID控制理论简介:在工业生产过程中,许多被控对象受负荷变化或干扰因素很多基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。
通过matlab 软件进行实例,仿真表明, , 提高控制系统实时性和抗干扰能力,易于实现.便于工程应用。
1.1模糊控制的思想:应用模糊数学的基本理论和方法, 控制规则的条件、操作用模糊集来表示、并把这些模糊控制规则以及有关信息, 诸如PID 控制参数等作为知识存入计算机知识库, 然后计算机根据控制系统的实际情况(系统的输入, 输出) , 运用模糊推理。
1.2PID算法:u (t) = Kp·e (t) + Ki·∫t0e (t) dt + Kd·de (t)dt= Kp e (t) + Ki Σei (t) + Kdec (t)其中, u (t) 为控制器输出量, e ( t ) 为误差信号, ec (t) 为误差变化率, Kp , Ki , Kd 分别为比例系数、积分系数、微分数。
然而,课本中,为了简化实验难度,只是考虑了kp,ki参数的整定。
1.3模糊PID控制器的原理图:二、基于Matlab的模糊控制逻辑模块的设计关于模糊逻辑的设计,主要有隶属函数的编辑,参数的选型,规则导入,生成三维图等2.1 模糊函数的编辑器的设定:打开matlab后,在命令窗口输入“fuzzy”,回车即可出现模糊函数编辑器,基本设置等。
基于课本的实验要求,我选的是二输入(e, )二输出()。
需要注意的是,在命名输入输出函数的时候,下标字母需要借助下划线的编辑,即e_c 能够显示为。
2.2四个隶属函数的N, Z, P 函数设定:在隶属函数的设定中,N 选用的是基于trimf(三角形隶属函数) , Z是基于zmf(Z 型隶属函数),P是基于smf(S型隶属函数)。
基于Matlab的模糊自整定PID控制器仿真研究

基于Matlab的模糊自整定PID控制器仿真研究
田海;李军
【期刊名称】《工业控制计算机》
【年(卷),期】2011(24)6
【摘要】将模糊控制与PlD控制结合,利用模糊推理方法实现对PID参数的在线自整定.利用MATLAB的模糊控制工具箱以及Simulink对其进行了仿真,结果表明设计的自整定PID模糊控制器具有控制精度高,超调小,动态性能好的特性.
【总页数】2页(P24-25)
【作者】田海;李军
【作者单位】内蒙古科技大学信息工程学院,内蒙古包头014010;山东工业职业学院电气工程系,山东淄博256414
【正文语种】中文
【相关文献】
1.基于Matlab的参数模糊自整定PID控制器的设计与仿真 [J], 蒋华勤;潘杰
2.基于MATLAB的模糊参数自整定PID控制器的仿真研究 [J], 韩宝江;张伟;康尔良
3.基于MATLAB模糊自整定PID控制器的设计与仿真 [J], 王三武;董金发
4.基于MATLAB的参数模糊自整定PID控制器的设计与仿真研究 [J], 马常举;马伯渊
5.基于Matlab的模糊自整定PID控制器仿真研究 [J], 袁静雨;虞启凯;张凡雨因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Matlab的模糊自整定PID控制器仿真研究在工程实际应用中,应用最广泛的调节器控制规律为比例、积分、微分控制,简称PID控制。
PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、鲁棒性好,工作可靠、调整方便而成为工业控制的主要技术之一。
但是对一些大惯性、非线性和时变的系统常规PID控制就无能为力了。
由于负载扰动或环境变化,受控过程参数和模型结构均发生变化,由于受到参数整定方法烦杂的困扰,常规PID控制器参数往往整定不良、性能欠佳,对运行工况的适应性差[1-2]。
针对这些问题,人们一直在寻求PID控制器参数的自动整定技术,以适应复杂的工况和高指标的控制要求。
随着计算机技术和模糊控制技术的发展,这种设想已变成了现实。
所谓模糊控制是不依赖被控对象精确的数学模型,是在总结操作经验基础上的实现自动控制的一种手段。
本文将模糊控制和PID控制结合起来,应用模糊推理的方法实现对PID参数进行在线自整定,实现PID参数的最佳调整,设计出参数模糊自整定PID控制器,并进行了Matlab/Simulink 仿真。
仿真结果表明,与常规PID控制系统相比,该设计获得了更优的鲁棒性和动、静态性及具有良好的自适应性。
1 控制系统结构模糊自整定PID控制器以被控对象的反馈值与目标值的误差e和误差变化率ec作为输入,用模糊推理的方法对PID的参数Kp,Ki,Kd进行参数自整定,可以满足不同时刻的e 和ec对PID参数自整定的要求。
利用模糊规则在线对PID参数进行修改,便构成了自整定模糊PID控制器,控制系统结构见图1。
图1 模糊自整定PID 控制器结构PID 参数模糊自整定是找出PID 三个参数与e 和ec 之间的模糊关系,在运行中通过不断检测e 和ec ,根据模糊控制原理对3个参数进行在线修改,以满足不同e 和ec 是对控制参数的不同要求,而使对象有良好的动、静态性能。
系统所使用的PID 控制器的算法为 连续情况)()()(t yout t rin t e -= (1) ⎰++=tdip dtt de T dt t e T t e k t u 0)()(1)()( (2) 式中,pk 为比例系数;iT 为积分时间常数;dT 为微分时间常数。
数字情况有位置公式(3)及增量公式(4)Tk e k e k T j e k k e k k u dkj i p )1()()()()(0--++=∑=(3)()())2()1(2)()()1()()(-+--++--=∆k e k e k e k k e k k e k e k k u d i p (4)式中,i p i T k k /=,d p d T k k /=, T 为采样周期, k 为采样序号.1 模糊控制器的设计语言变量隶属度函数的确定模糊控制器采用两输入三输出的形式,以e 和ec 为输入语言变量,pk 、ik 和dk 为输出语言变量。
输入语言变量的语言值均取为“负大”(NB)、“负中”(NM)、“负小”(NS)、“零”(ZO)、“正小”(PS)、“正中”(PM)、“正大”(PB)7种.输出语言变量的语言值均取为“零”(ZO)、“正小”(PS)、“正中”(PM)、“正大”(PB)4种.将偏差e 和偏差变化率ec 量化到(-3,3)的区域内,输出量化到(0,3)的区域内,隶属函数曲线见图2。
图2 e 和ec 隶属函数曲线建立模糊控制器的控制规则表 根据参数pk 、ik 和dk 对系统输出特性的影响,可得出在不同的e 和ec 时,参数的自整定原则。
(1)当e很大时,不论误差变化趋势如何,都应考虑控制器的输出应按最大(或最小)输出,以达到迅速调整误差,使误差绝对值以最大速度减小。
同时为了防止积分饱和,此时应取较大pk ,较小的ik 和dk 取零。
.(2)当0>⨯ec e 时,说明误差在向误差绝对值增大方向变化。
此时若误差较大,可考虑由控制器实施较强的控制作用,以达到扭转误差绝对值朝减小方向变化,并迅速减小误差绝对值,此时取较大的pk ,dk 不能太大,取较小的ik 值。
若误差绝对值较小,控制器实施一般的控制作用,只要扭转误差的变化趋势,使其朝误差绝对值减小方向变化。
(3)当0<⨯ec e 或0=e 时,说明误差的绝对值朝减小的方向变化,或者已达到平衡状态。
此时,可采取保持控制器输出不变。
(4)当0,0≠=⨯e ec e 时,表明系统的曲线与理论曲线平行或一致,为使系统具有良好的稳态性能,应采取较大pk 和ik 值,同时避免设定值附近振荡,并考虑系统的抗干扰性能,适当选取dk 值。
设⎪⎩⎪⎨⎧∆+'=∆+'=∆+'=d d di i i pp p kk k k k k k k k (5) 式(5)中pk ',i k '和dk '为系统的经典PID 参数,一般用Z-N 法来确定。
根据PID 参数的整定原则及专家经验,采用if-then 形式,可得pk ∆、ik ∆和dk ∆的整定规则如表1所示.表1 △kp.△ki.△kd 的模糊规则将系统误差e 和误差变化率ec 变化范围定义为模糊集上的论域。
}5,4,3,2,1,0,1,2,3,4,5{,-----=ec e 它们的模糊集为ec e ,={NB,NM,NS,O,PS,PM,PB},模糊集中元素分别代表负大,负中,负小,零,正小,正中,正大。
根据pk 、ik 和dk 三个参数模糊规则表构造一个两输入(ec e ,)三输出(di p k k k ∆∆∆,,)的模糊控制器,取名为fuzzpid.fis 。
见图3。
3 Matlab 仿真模糊控制器的建立在Matlab 下运行fuzzy fuzzpid.fis 可进入Matlab 动态仿真工具箱仿真环境,利用模糊逻辑工具箱建立一个fis 型文件,保存为模糊PID.fis 。
在Matlab 命令窗口键入Fuzzy,就会出现一个FIS Editor 窗口。
本文采用双入三输出模糊控制器,输入变量为系统误差e 和误差变化率ec ,输出变量为pk 、ik 和dk 。
在Edit 菜单下确定输入、输出,双击每个图标即可进行编辑。
在File 菜单下选择控制器类型为Mamdani 型,用Edit 菜单下rules 实现编辑模糊规则。
取输入量e 和误差变化率ec 的隶属函数为三角形,输出变量pk 、i k 和dk的隶属函数也为三角形。
根据控制规则表以If-then 的形式在Rule Editor 窗口输入模糊控制规则。
取与(and)的方法为min ,或(or)的方法为max ,模糊决策采用Mamdani 型推理演法。
解模糊化采用重心法(centroid)。
3.2 仿真实例设被控对象为ss s s G 1047035.87523500)(23++=采样时间为1ms ,采用模糊PID 控制进行仿真,参数的初值分别为:pk =0.4、ik =0和dk =0,在第300个采样时刻控制器输出加100%的干扰,相应响应曲线见图3到图6。
图3 模糊PID控制阶跃响应图4 模糊PID控制误差响应图5 控制器输出u 图6 kp.ki.kd的自整定过程对于3阶对象,常规PID控制很难获得理想的控制效果,特别是3个参数不易整定,当采用模糊自整定PID控制器后,取得了良好控制效果。
从系统的性能指标可看出系统具有良好的快速性和稳态精度,且抗干扰能力强,是一种良好的控制方案4 结语模糊自整定PID是在常规PID算法的基础上,通过计算当前系统误差e和误差变化率ec,利用模糊推理系统FIS,查询模糊矩阵表进行参数调整,该方法实现简单、方便易用,对实际控制有重要指导意义。
它能够发挥两种控制方式的优点,克服两者的缺点,提高控制质量。
一方面模糊控制具有控制灵活,响应快和适应性强的特点,又具有PID控制的精度高、鲁棒性强的特点。
同时,将模糊PID控制算法与Matlab结合在一起,利用模糊逻辑工具箱设计模糊控制器,能方便地修改输入输出的论域、模糊子集、隶属度函数及模糊控制规则等,突破了传统方法需要编制大量程序的做法,灵活,可视性强,用模糊推理的方法在动态过程中改变PID的参数,并可在Simulink环境中非常直观地构建各种复杂的模糊PID控制系统,观察其控制效果,为实际控制系统的设计与调试提供了理论参考依据。
参考文献:[1]王树青.西安、先进控制技术及其应用北京:化学工业出版社,20005.[2]刘金锟.先进PID控制及其Matlab仿真[M].北京:电子工业出版社,2003.[3]陶永华,尹怡欣.新型PID控制及其应用.北京:机械工业出版社,1999.作者简介:田海(1968-),男,副教授,内蒙古科技大学信息工程学院,研究方向:控制;李军(1970-),男,工程师,山东工业职业学院电气工程系。
