课时作业25直线与平面平行的判定定理
直线与平面平行的判定定理

教学设计改进稿
再来看一个问题:判别直线与直线平行的常用方法有哪些?
我们刚刚复习了:直线与平面平行,相当于直线与平面没有公共点,但是在具体证明的时候这种方法是不太好操作的,那么大家思考一下,
我们看,这个定理的关键词是什么?
BCD.
我们刚说过,关键是在平面BCD中寻找EF 的平行线,那么怎么来找呢?我们看有三角形,
分钟后,找同学板书过程。
也就是说他构造了一个中点,然后
得到了三角形的中位线,从而解决了
证明线线平行,除了利用
大家可以自己先思考思考,然后小组讨论一分钟后)找同学来说说思路。
四边形ABCD是矩形,G,
大家把这个题在学案上独立完成。
分钟时间,自己做辅助线,自己写过程,老师在下面观察大家掌握的情况,然后找一名学。
2.2.1直线与平面平行的判定

2.2.1直线与平面平行的判定知识点直线与平面平行的判定定理思考1如图,一块矩形木板ABCD的一边AB在平面α内,把这块木板绕AB转动,在转动过程中,AB的对边CD(不落在α内)和平面α有何位置关系?答案平行.思考2如图,平面α外的直线a平行于平面α内的直线b.这两条直线共面吗?直线a与平面α相交吗?答案由于直线a∥b,所以两条直线共面.直线a与平面α不相交.梳理线面平行的判定定理表示定理图形文字符号直线与平面平行的判定定理平面外一条直线与此平面内一条直线平行,则该直线与此平面平行⎭⎪⎬⎪⎫a⊄αb⊂αa∥b⇒a∥α类型一直线与平面位置关系的判定例1如果两直线a∥b,且a∥α,则b与α的位置关系是()A.相交B.b∥αC.b⊂αD.b∥α或b⊂α答案 D解析由a∥b,且a∥α,知b与α平行或b⊂α.反思与感悟用判定定理判定直线a和平面α平行时,必须具备三个条件:(1)直线a 在平面α外,即a ⊄α; (2)直线b 在平面α内,即b ⊂α;(3)两直线a 、b 平行,即a ∥b ,这三个条件缺一不可. 跟踪训练1 下列说法正确的是( )A .若直线l 平行于平面α内的无数条直线,则l ∥αB .若直线a 在平面α外,则a ∥αC .若直线a ∩b =∅,直线b ⊂α,则a ∥αD .若直线a ∥b ,b ⊂α,那么直线a 就平行于平面α内的无数条直线 答案 D解析 A 错误,直线l 还可以在平面α内;B 错误,直线a 在平面α外,包括平行和相交;C 错误,a 还可以与平面α相交或在平面α内.故选D. 类型二 直线与平面平行的证明命题角度1 以锥体为背景证明线面平行例2 如图,S 是平行四边形ABCD 所在平面外一点,M ,N 分别是SA ,BD 上的点,且AMSM =DN NB.求证:MN ∥平面SBC .证明 连接AN 并延长交BC 于P ,连接SP .因为AD ∥BC ,所以DN NB =ANNP,又因为AM SM =DN NB ,所以AM SM =ANNP ,所以MN ∥SP ,又MN ⊄平面SBC ,SP ⊂平面SBC , 所以MN ∥平面SBC . 引申探究本例中若M ,N 分别是SA ,BD 的中点,试证明,MN ∥平面SBC .证明 连接AC ,由平行四边形的性质可知AC 必过BD 的中点N ,在△SAC 中,M ,N 分别为SA ,AC 的中点,所以MN ∥SC ,又因为SC ⊂平面SBC ,MN ⊄平面SBC ,所以MN ∥平面SBC .反思与感悟 利用直线与平面平行的判定定理证线面平行的步骤上面的第一步“找”是证题的关键,其常用方法有:利用三角形、梯形中位线的性质;利用平行四边形的性质;利用平行线分线段成比例定理.跟踪训练2 如图,四边形ABCD 是平行四边形,P 是平面ABCD 外一点,M ,N 分别是AB ,PC 的中点.求证:MN ∥平面P AD .证明 如图,取PD 的中点G ,连接GA ,GN .∵G ,N 分别是△PDC 的边PD ,PC 的中点, ∴GN ∥DC ,GN =12DC .∵M 为平行四边形ABCD 的边AB 的中点, ∴AM =12DC ,AM ∥DC ,∴AM ∥GN ,∴四边形AMNG 为平行四边形,∴MN ∥AG . 又∵MN ⊄平面P AD ,AG ⊂平面P AD , ∴MN ∥平面P AD .命题角度2 以柱体为背景证明线面平行例3 如图所示,直三棱柱ABC -A 1B 1C 1中,D 是AB 的中点,证明:BC 1∥平面A 1CD .证明如图,连接AC1交A1C于点F,则F为AC1的中点.又∵D是AB的中点,连接DF,则BC1∥DF.∵DF⊂平面A1CD,BC1⊄平面A1CD,∴BC1∥平面A1CD.反思与感悟证明以柱体为背景包装的线面平行证明题,常用线面平行的判定定理,遇到题目中含有线段中点,常利用取中点去寻找平行线.跟踪训练3如图所示,已知长方体ABCD-A1B1C1D1.(1)求证:BC1∥平面AB1D1;(2)若E,F分别是D1C,BD的中点,求证:EF∥平面ADD1A1.证明(1)∵BC1⊄平面AB1D1,AD1⊂平面AB1D1,BC1∥AD1,∴BC1∥平面AB1D1.(2)∵点F为BD的中点,∴F为AC的中点,又∵点E为D1C的中点,∴EF∥AD1,∵EF⊄平面ADD1A1,AD1⊂平面ADD1A1,∴EF∥平面ADD1A1.1.如果直线a平行于平面α,则()A.平面α内有且只有一直线与a平行B.平面α内无数条直线与a平行C.平面α内不存在与a平行的直线D.平面α内的任意直线与直线a都平行答案 B2.如图,在正方体ABCD-A′B′C′D′中,E,F分别为平面ABCD和平面A′B′C′D′的中心,则正方体的六个面中与EF平行的平面有()A .1个B .2个C .3个D .4个 答案 D解析 由直线与平面平行的判定定理知.EF 与平面AB ′,平面BC ′,平面CD ′,平面AD ′均平行.故与EF 平行的平面有4个.3.如图,在正方体ABCD —A 1B 1C 1D 1中,E 是DD 1的中点,则A 1C 1与平面ACE 的位置关系为________.答案 平行解析 ∵A 1C 1∥AC ,A 1C 1⊄平面ACE ,AC ⊂平面ACE ,∴A 1C 1∥平面ACE . 4.如图,P 是平行四边形ABCD 所在平面外一点,E 、F 分别是AB 、PD 的中点.求证:AF ∥平面PCE .证明 如图,取PC 的中点M ,连接ME 、MF , 则FM ∥CD 且FM =12CD .又∵AE ∥CD 且AE =12CD ,∴FM ∥AE ,即四边形AFME 是平行四边形, ∴AF ∥ME .又∵AF ⊄平面PCE ,EM ⊂平面PCE , ∴AF ∥平面PCE .1.判断或证明线面平行的常用方法(1)定义法:证明直线与平面无公共点(不易操作). (2)判定定理法:(a ⊄α,b ⊂α,a ∥b ⇒a ∥α).(3)排除法:证明直线与平面不相交,直线也不在平面内.2.证明线线平行的常用方法(1)利用三角形、梯形中位线的性质.(2)利用平行四边形的性质.(3)利用平行线分线段成比例定理.课时作业一、选择题1.已知a,b是两条相交直线,a∥α,则b与α的位置关系是()A.b∥αB.b与α相交C.b⊂αD.b∥α或b与α相交答案 D解析由题意画出图形,当a,b所在平面与平面α平行时,b与平面α平行,当a,b所在平面与平面α相交时,b与平面α相交.2.若l是平面α外的一条直线,则下列条件中可推出l∥α的是()A.l与α内的一条直线不相交B.l与α内的两条直线不相交C.l与α内的无数条直线不相交D.l与α内的任意一条直线不相交答案 D解析根据直线与平面的位置关系易判断选项D正确.3.一条直线l上有相异三个点A、B、C到平面α的距离相等,那么直线l与平面α的位置关系是()A.l∥αB.l⊥αC.l与α相交但不垂直D.l∥α或l⊂α答案 D解析l∥α时,直线l上任意点到α的距离都相等.l⊂α时,直线l上所有的点到α的距离都是0;l⊥α时,直线l上有两个点到α的距离相等;l与α斜交时,也只能有两点到α的距4.点E,F,G,H分别是空间四面体ABCD的棱AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是()A.0 B.1 C.2 D.3答案 C解析如图,由线面平行的判定定理可知BD∥平面EFGH,AC∥平面EFGH.5.已知直线a∥平面α,P∈α,那么过点P且平行于直线a的直线()A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内答案 C解析由平行公理知过点P作与直线a平行的直线有且只有一条,又由线面平行的判定定理得,该直线一定在平面内.6.直线a,b为异面直线,过直线a与直线b平行的平面()A.有且只有一个B.有无数多个C.有且只有一个或不存在D.不存在答案 A解析在a上任取一点A,则过A与b平行的直线有且只有一条,设为b′,又∵a∩b′=A,∴a与b′确定一个平面α,即为过a与b平行的平面,可知它是唯一的.7.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出五个结论:①OM∥PD;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA;⑤OM∥平面PBC. 其中正确的个数有()A.1 B.2 C.3 D.4解析由题意知,OM是△BPD的中位线,∴OM∥PD,故①正确;PD⊂平面PCD,OM⊄平面PDC,∴OM∥平面PCD,故②正确;同理可得:OM∥平面PDA,故③正确;OM与平面PBA和平面PBC都相交,故④,⑤不正确.故共有3个结论正确.8.如图,已知三棱柱ABC—A1B1C1中,E是BC的中点,D是AA1上的动点,且ADDA1=m,若AE∥平面DB1C,则m的值为()A.12B.1 C.32D.2答案 B解析如图,取CB1的中点G,连接GE,DG,当m=1时,AD=GE=12BB1且AD∥GE,∴四边形ADGE为平行四边形,则AE∥DG,可得AE∥平面DB1C.二、填空题9.过平面外一点,与该平面平行的直线有________条,如果直线m平行于平面,那么在平面内有________条直线与直线m平行.答案无数无数10.考查下列两个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中a、b为不同的直线,α、β为不重合的平面),则此条件为________.⎭⎪⎬⎪⎫b⊂α①a∥b⇒a∥α;⎭⎪⎬⎪⎫a∥b②b∥α⇒a∥α.答案a⊄αa⊄α解析根据线面平行的判定定理知,①处横线上应填a⊄α;②处横线上应填a⊄α.11.如图所示,在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过点A,E,C 的平面的位置关系是________.答案平行解析如图,连接BD,与AC交于点O,连接OE.∵OE为△BDD1的中位线,∴BD1∥OE.又BD1⊄平面AEC,OE⊂平面AEC,∴BD1∥平面AEC.三、解答题12.如图所示,已知P是平行四边形ABCD所在平面外一点,M为PB的中点.求证:PD∥平面MAC.证明如图所示,连接BD交AC于点O,连接MO,则MO为△BDP的中位线,∴PD∥MO.∵PD⊄平面MAC,MO⊂平面MAC,∴PD∥平面MAC.13.如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.求证:BD∥平面FGH.证明如图,连接DG,CD,设CD∩GF=O,连接OH.在三棱台DEF-ABC中,AB=2DE,G为AC的中点,可得DF∥GC,所以四边形DFCG为平行四边形,则O为CD的中点,又H为BC的中点,所以OH∥BD.又OH⊂平面FGH,BD⊄平面FGH,所以BD∥平面FGH.四、探究与拓展14.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的是()A.①③B.①④C.②③D.②④答案 B解析①如图(ⅰ),连接BC,则平面ABC∥平面MNP,所以AB∥平面MNP,所以①正确.②如图(ⅱ),连接底面正方形对角线,并取其中点O,连接ON,则ON∥AB,所以AB与平面PMN相交,不平行,所以②不满足题意.③AB与平面PMN相交,不平行,所以③不满足题意.④因为AB∥NP,所以AB∥平面MNP.所以④正确.故答案为①④.第 11 页 共 11 页15.如图,四边形ABCD 为正方形,△ABE 为等腰直角三角形,AB =AE ,P 是线段CD 的中点,在直线AE 上是否存在一点M ,使得PM ∥平面BCE .若存在,指出点M 的位置,并证明你的结论.解如图,存在点M ,当点M 是线段AE 的中点时,PM ∥平面BCE .取BE 的中点N ,连接CN ,MN ,则MN ∥12AB ∥PC , 所以四边形MNCP 为平行四边形,所以PM ∥CN .因为PM ⊄平面BCE ,CN ⊂平面BCE ,所以PM ∥平面BCE .。
直线与平面平行的判定(公开课课件)

当直线不在平面内时,它与平面 平行;当直线在平面内时,它与 平面重合。
直线与平面平行的图形表示
在几何图形中,直线与平面平行通常 用平行线表示,即直线与平面内任意 一条直线不相交。
也可以通过斜线和平行四边形的形式 来表示直线与平面平行。
直线与平面平行的性质
直线与平面平行时, 直线与平面内的任意 一条直线都不相交。
已知直线$l$与平面$alpha$平行,判断 下列结论是否正确
1. 若直线$m$与直线$l$相交,则直线 $m$与平面$alpha$平行。
综合练习题
要点一
总结词
考察综合运用能力和推理能力
要点二
已知平面$beta$经过点 $P(1,2,3)$,且与…
x = -1, y = 2, z = 3$平行,求平面$beta$的方程。
在建筑设计、机械制造等领域中,可 以利用该定理进行空间位置关系的判 断,以确保结构的稳定性和安全性。
03
直线与平面平行判定定理 的证明
证明直线与平面平行的判定定理的思路
引入直线与平面平行的判定定理
如果一条直线与平面平行,那么这条直线上的任意一点到平面的距离都相等。
证明思路
通过反证法,假设直线与平面不平行,然后推导出矛盾,从而证明定理的正确 性。
应用实例三:判断某直线是否与某平面平行
总结词
根据已知直线和平面的方程,判断该 直线是否与平面平行。
详细描述
首先,确定已知直线和平面的方程, 然后通过联立方程组判断直线是否与 平面平行。如果联立方程组无解,则 直线与平面平行;如果有解,则直线 与平面相交。
05
练习题
基础练习题
总结词:考察基础概念和 性质的理解
04
直线、平面平行的判定与性质

直线、平面平行的判定知识梳理1、直线与平面平行的判定定理如果平面外一条直线与这个平面内的一条直线平行,那么这条直线和这个平面平行。
即、a⊄α,b⊂α,且a∥b⇒a∥α;例1:求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面。
已知:如图空间四边形ABCD 中,E 、F 分别是AB 、的中点。
求证:EF ∥平面BCD 证明:连结BD AE =EB⇒EF ∥BDAF =FD EF ⊄平面BCD ⇒EF ∥平面BCD BD ⊂平面BCD评析:要证EF ∥平面BCD ,关键是在平面BCD 中找到和EF 平行的直线,将证明线面平行的问题转化为证明直线的平行2.直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
a ∥α,a ⊂β∩β=l ⇒a ∥l .已知:a ∥α,a ⊂β,α∩β=b (如右图) 求证:a ∥b证明:α∩β=b ⇒b ⊂a a ⊂βa ∥α ⇒ a ∩b=φ ⇒a ∥b ⊂β评析:证明用到了“同一平面的两直线没有公共点,们平行”变式练习1、能保证直线a 与平面α平行的条件是( ) A.a ⊄α,b ⊂α,a ∥b B .b ⊂α,a ∥b C. b ⊂α,c ∥α,a ∥b,a ∥cD. b ⊂α,A ∈a,B ∈a,C ∈b ,D ∈b 且AC =BD 2、下列命题正确的是( ) A. 平行于同一平面的两条直线平行B. 若直线a ∥α,则平面α内有且仅有一条直线与a 平行C. 若直线a ∥α,则平面α内任一条直线都与a 平行D. 若直线a ∥α,则平面α内有无数条直线与a 平行E. 如果a 、b 是两条直线,且a ∥b ,那么a 平行于经过b任何平面F. 如果直线a、b和平面α满足a∥b,a∥α,b⊄α,那么b∥α3、若两直线a与b相交,且a平行于平面α,则b与α的位置关系是平面与平面平行的判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
高一年级数学 直线与平面平行的判定定理

如果平面外一条直线和这个平面内 的一条直线平行,那么这条直线和 这个平面平行
五、规律总结 直线与平面平行的判定定理:
如果平面外的一条直线与此平面内的一条直线 平行,那么这条直线与这个平面平行.
符号表示:
a
b
a
//
a // b
a
b
(2)与 AA平行的平面是_平_面_B_BC_C _平_面_C_C_DD_
(3)与AC平行的平面是___平_面__AB_C_D ___
D A
D A
C B
C B
八、定理应用
例1:如图,长方体 ABCD ABCD 中, (1)与AB平行的平面是_平_面_AB_C_D_平_面__CC_D_D
(2)与 AA平行的平面是_平_面_B_BC_C _平_面_C_C_DD_
EF / /BD
B
C
EF//平面BCD.
变式强化
小结
思考交流
作业
九、变式练习
如图,在空间四面体A-BCD中,E、F、M、N分别 为棱AB、AD、DC、BC的中点
【变式一】四边形EFMN , 是什么四边形? 平行四边形
【变式二】直线AC与平面EFMN的位置关系是什
A
么?为什么? AC与平面EFMN平行
BD1
/
/
EO
EO / /平面BCD1
D
C
O
A
B
变式强化
小结
思考交流
作业
思考交流:
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,
求证:BD1//平面AEC.
证明:连结BD交AC于O,连结EO. A1 ∵O 为矩形ABCD对角线的交点,
直线、平面平行的判定与性质课件

直线与平面平行的判定与性质
考向基础
直线与平面平行的判定与性质
文字语言
平面外一条直线与此平面内的一
图形语言
符号语言
a⊄α,b⊂α,且a∥b⇒a∥α
条直线平行,则该直线与此平面
平行.简称:线线平行,则线面平行
一条直线与一个平面平行,则过
a∥α,a⊂β,
这条直线的任一平面与此平面的
α∩β=b⇒a∥b
别平行于另一个平面内的两条相交直线,那么这两个平面平行.
3.证明两个平面都垂直于同一条直线.(客观题可用)
4.证明两个平面同时平行于第三个平面.(客观题可用)
例2 如图所示,正方体ABCD-A1B1C1D1中,
M,N分别是A1B1,A1D1的中点,E,F分别是B1C1,C1D1的中点.
(1)求证:四边形BDFE为梯形;
∴PQ∥平面BCE.
证法二:如图,在平面ABEF内,过点P作PM∥BE,交AB于点M,连接QM.
∴PM∥平面BCE,且
AP AM
=
,
PE MB
易知AE=BD,又AP=DQ,∴PE=BQ,
∴
AP DQ
AM DQ
=
,∴
=
,
PE BQ
MB QB
∴MQ∥AD,又AD∥BC,
∴MQ∥BC,
∵BC⊂平面BCE,MQ⊄平面BCE,
∴OB∥平面EFC,
∵OB∩OG=O,∴平面OBG∥平面EFC.
方法技巧
方法1
证明直线与平面平行的方法
1.利用线面平行的定义(此法一般伴随反证法证明).
2.利用线面平行的判定定理.应用此法的关键是在平面内找与已知直线
平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常
课时作业12:2.2.3 直线与平面平行的性质

2.2.3直线与平面平行的性质一、选择题1.如图,已知S为四边形ABCD外一点,点G,H分别为SB,BD上的点,若GH∥平面SCD,则()A.GH∥SAB.GH∥SDC.GH∥SCD.以上均有可能考点直线与平面平行的性质题点利用性质判定位置关系答案 B解析因为GH∥平面SCD,GH⊂平面SBD,平面SBD∩平面SCD=SD,所以GH∥SD,显然GH与SA,SC均不平行,故选B.2.直线a∥平面α,P∈α,过点P平行于a的直线()A.只有一条,不在平面α内B.有无数条,不一定在α内C.只有一条,且在平面α内D.有无数条,一定在α内考点直线与平面平行的性质题点利用性质判定位置关系答案 C解析由线面平行性质定理知过点P平行于a的直线只有一条,且在平面α内,故选C. 3.对于直线m,n和平面α,下列命题中正确的是()A.如果m⊂α,n⊄α,m,n是异面直线,那么n∥αB.如果m⊂α,n⊄α,m,n是异面直线,那么n与α相交C.如果m⊂α,n∥α,m,n共面,那么m∥nD.如果m∥α,n∥α,m,n共面,那么m∥n考点直线与平面平行的性质题点利用性质判定位置关系答案 C解析由线面平行的性质定理知C正确.4.如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是()A.平行B.相交C.异面D.平行或异面考点直线与平面平行的性质题点利用性质判定位置关系答案 A解析由长方体性质知:EF∥平面ABCD,∵EF⊂平面EFGH,平面EFGH∩平面ABCD =GH,∴EF∥GH.又∵EF∥AB,∴GH∥AB.5.在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,当BD∥平面EFGH时,下面结论正确的是()A.E,F,G,H一定是各边的中点B.G,H一定是CD,DA的中点C.BE∶EA=BF∶FC,且DH∶HA=DG∶GCD.AE∶EB=AH∶HD,且BF∶FC=DG∶GC考点直线与平面平行的性质题点利用性质判定位置关系答案 D解析由于BD∥平面EFGH,所以有BD∥EH,BD∥FG,则AE∶EB=AH∶HD,且BF∶FC =DG∶GC.6.已知正方体AC1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长为()A.22B.32C .1D. 2考点 直线与平面平行的性质 题点 与线面平行性质有关的计算 答案 A解析 如图,连接AD 1,AB 1,∵PQ ∥平面AA 1B 1B ,平面AB 1D 1∩平面AA 1B 1B =AB 1, PQ ⊂平面AB 1D 1,∴PQ ∥AB 1, ∴PQ =12AB 1=1212+12=22.7.如图,四棱锥S -ABCD 的所有的棱长都等于2,点E 是SA 的中点,过C ,D ,E 三点的平面与SB 交于点F ,则四边形DEFC 的周长为( )A .2+3B .3+ 3C .3+23D .2+2 3考点 直线与平面平行的性质 题点 与线面平行性质有关的计算 答案 C解析 ∵CD ∥AB ,CD ⊄平面SAB ,AB ⊂平面SAB , ∴CD ∥平面SAB .又平面CDEF ∩平面SAB =EF ,∴CD ∥EF , 又CD ∥AB ,∴AB ∥EF .∵SE =EA ,∴EF 为△ABS 的中位线, ∴EF =12AB =1,又DE =CF =3,∴四边形DEFC 的周长为3+2 3.二、填空题8.如图所示,ABCD —A 1B 1C 1D 1是棱长为a 的正方体,M ,N 分别是下底面的棱A 1B 1,B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =a3,过P ,M ,N 的平面交上底面于PQ ,Q 在CD 上,则PQ =________.考点 直线与平面平行的性质 题点 与线面平行性质有关的计算 答案223a 解析 ∵MN ∥平面AC ,平面PMN ∩平面AC =PQ , ∴MN ∥PQ ,易知DP =DQ =2a3,故PQ =PD 2+DQ 2=2DP =22a3.9.直线a ∥平面α,α内有n 条直线交于一点,则这n 条直线中与直线a 平行的直线有_____条.考点 直线与平面平行的性质 题点 利用性质判定位置关系 答案 0或1解析 过直线a 与交点作平面β,设平面β与α交于直线b ,则a ∥b ,若所给n 条直线中有1条是与b 重合的,则此直线与直线a 平行,若没有与b 重合的,则与直线a 平行的直线有0条.10. 如图,已知A ,B ,C ,D 四点不共面,且AB ∥α,CD ∥α,AC ∩α=E ,AD ∩α=F ,BD ∩α=H ,BC ∩α=G ,则四边形EFHG 的形状是______.考点 直线与平面平行的性质 题点 利用性质判定位置关系答案平行四边形解析∵AB∥α,平面ABC∩α=EG,∴EG∥AB.同理FH∥AB,∴EG∥FH.又CD∥α,平面BCD∩α=GH,∴GH∥CD.同理EF∥CD,∴GH∥EF,∴四边形EFHG是平行四边形.11.如图所示的正方体的棱长为4,点E,F分别为A1D1,AA1的中点,则过C1,E,F的截面的周长为________.考点直线与平面平行的性质题点与线面平行性质有关的计算答案45+6 2解析由EF∥平面BCC1B1可知平面BCC1B1与平面EFC1的交线为BC1,平面EFC1与平面ABB1A1的交线为BF,所以截面周长为EF+FB+BC1+C1E=45+6 2.三、解答题12.如图,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于点E,交DP 于点F,求证:四边形BCFE是梯形.考点直线与平面平行的性质题点利用性质证明平行问题证明∵四边形ABCD为矩形,∴BC∥AD.∵AD⊂平面P AD,BC⊄平面P AD,∴BC∥平面P AD.∵平面BCFE∩平面P AD=EF,∴BC∥EF.∵AD=BC,AD≠EF,∴BC≠EF,∴四边形BCEF是梯形.13.如图,已知E ,F 分别是菱形ABCD 中边BC ,CD 的中点,EF 与AC 交于点O ,点P 在平面ABCD 之外,M 是线段P A 上一动点,若PC ∥平面MEF ,试求PM ∶MA 的值.考点 直线与平面平行的性质 题点 与线面平行性质有关的计算解 如图,连接BD 交AC 于点O 1,连接OM .因为PC ∥平面MEF ,平面P AC ∩平面MEF =OM ,PC ⊂平面P AC , 所以PC ∥OM ,所以PM P A =OCAC.在菱形ABCD 中,因为E ,F 分别是边BC ,CD 的中点,所以OC O 1C =12.又AO 1=CO 1,所以PM P A =OC AC =14,故PM ∶MA =1∶3.四、探究与拓展14.如图,在四面体ABCD 中,截面PQMN 是正方形,则下列命题中错误的是( )A .AC ⊥BDB .AC ∥截面PQMN C .AC =BDD .异面直线PM 与BD 所成的角为45° 考点 直线与平面平行的性质 题点 利用性质判定位置关系 答案 C解析 由题意知PQ ∥AC ,QM ∥BD ,PQ ⊥QM ,则AC ⊥BD ,故A 正确;由PQ ∥AC 可得AC ∥截面PQMN ,故B 正确;异面直线PM 与BD 所成的角等于PM 与PN 所成的角,故D 正确;C 是错误的,故选C.15.如图,在三棱柱ABC -A 1B 1C 1中,点E ,F 分别是棱CC 1,BB 1上的点,点M 是线段AC 上的动点,EC =2FB =2,若MB ∥平面AEF ,试判断点M 在何位置.考点 直线与平面平行的性质 题点 利用性质证明平行问题解 若MB ∥平面AEF ,过F ,B ,M 作平面FBMN 交AE 于点N , 连接MN ,NF .因为BF ∥平面AA 1C 1C , BF ⊂平面FBMN ,平面FBMN ∩平面AA 1C 1C =MN , 所以BF ∥MN .又MB ∥平面AEF ,MB ⊂平面FBMN , 平面FBMN ∩平面AEF =FN , 所以MB ∥FN ,所以BFNM 是平行四边形, 所以MN ∥BF ,MN =BF =1. 而EC ∥FB ,EC =2FB =2, 所以MN ∥EC ,MN =12EC =1,故MN 是△ACE 的中位线. 所以当M 是AC 的中点时, MB ∥平面AEF .。
直线、平面平行的判定及性质及详细答案
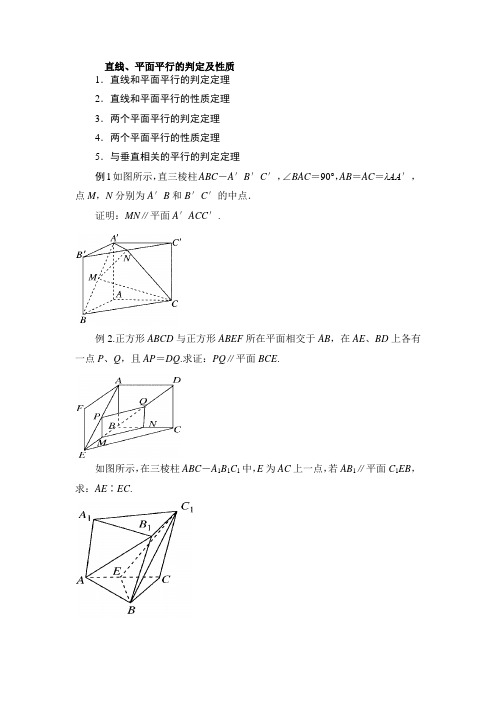
直线、平面平行的判定及性质1.直线和平面平行的判定定理2.直线和平面平行的性质定理3.两个平面平行的判定定理4.两个平面平行的性质定理5.与垂直相关的平行的判定定理例1如图所示,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点.证明:MN∥平面A′ACC′.例2.正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ∥平面BCE.如图所示,在三棱柱ABC-A1B1C1中,E为AC上一点,若AB1∥平面C1EB,求:AE∶EC.例3如图所示,正方体ABCD—A1B1C1D1中,M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点.求证:平面AMN∥平面EFDB.例4如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E、F分别在线段AB,CD上,且AE∶EB=CF∶FD.求证:EF∥β.练习题:1.(课本习题改编)给出下列四个命题:①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行;②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行;③若平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行;④若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行.其中正确命题的个数是________个.1.下列命题中正确的是________.①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.2.(2014·合肥一检)给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.1.已知两条不同直线l1和l2及平面α,则直线l1∥l2的一个充分条件是() A.l1∥α且l2∥αB.l1⊥α且l2⊥αC.l1∥α且l2⊄αD.l1∥α且l2⊂α答案 B解析l1⊥α且l2⊥α⇒l1∥l2.2.(2012·四川)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行答案 C解析若两条直线和同一平面所成的角相等,则这两条直线可平行、可异面、可相交,A项不正确;如果到一个平面距离相等的三个点在同一条直线上或在这个平面的两侧,那么经过这三个点的平面与这个平面相交,B项不正确.3.(2013·浙江)设m,n是两条不同的直线,α,β是两个不同的平面() A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β答案 C解析A项中,直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B项中,α与β也可能相交,此时直线m平行于α,β的交线;D 项中,m也可能平行于β.故选C项.4.设α,β表示平面,m,n表示直线,则m∥α的一个充分不必要条件是()A .α⊥β且m ⊥βB .α∩β=n 且m ∥nC .m ∥n 且n ∥αD .α∥β且m ⊂β答案 D解析 若两个平面平行,其中一个面内的任一直线均平行于另一个平面,故选D.5.若空间四边形ABCD 的两条对角线AC 、BD 的长分别是8、12,过AB 的中点E 且平行于BD 、AC 的截面四边形的周长为( )A .10B .20C .8D .4答案 B解析 设截面四边形为EFGH ,F 、G 、H 分别是BC 、CD 、DA 的中点,∴EF =GH =4,FG =HE =6.∴周长为2×(4+6)=20.6.在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是( )A .相交B .平行C .垂直D .不能确定答案 B解析 连接CD 1,在CD 1上取点P ,使D 1P =2a3,∴MP ∥BC ,PN ∥AD 1. ∴MP ∥面BB 1C 1C ,PN ∥面AA 1D 1D . ∴面MNP ∥面BB 1C 1C ,∴MN ∥面BB 1C 1C .7.如图所示,四个正方体图形中,A 、B 为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出AB ∥面MNP 的图形的序号是________(写出所有符合要求的图形序号).答案①③8. 棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,P A⊥底面ABCD,E为PC的中点,则BE与平面P AD的位置关系为________.答案平行解析取PD的中点F,连接EF.在△PCD中,EF綊12CD.又∵AB∥CD且CD=2AB,∴EF=12CD且CD=2AB.∴EF綊AB,∴四边形ABEF是平行四边形,∴EB∥AF.又∵EB⊄平面P AD,AF⊂平面P AD,∴BE∥平面P AD.9. 如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1、B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.答案22 3a解析 如图所示,连接AC ,易知MN ∥平面ABCD .∴MN ∥PQ .又∵MN ∥AC ,∴PQ ∥AC . 又∵AP =a 3,∴PD AD =DQ CD =PQ AC =23. ∴PQ =23AC =232a =223a .10.考查下列三个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中l 、m 为直线,α、β为平面),则此条件为________.①⎭⎬⎫m ⊂αl ∥m⇒l ∥α;②⎭⎬⎫l ∥m m ∥α⇒l ∥α;③⎭⎬⎫l ⊥βα⊥β⇒l ∥α. 答案 l ⊄α解析 ①体现的是线面平行的判定定理,缺的条件是“l 为平面α外的直线”,即“l ⊄α”,它也同样适合②③,故填l ⊄α.11.在四面体ABCD 中,M 、N 分别是面△ACD 、△BCD 的重心,则四面体的四个面中与MN 平行的是________.答案 平面ABC 和平面ABD解析 连接AM 并延长交CD 于E ,连接BN 并延长交CD 于F .由重心的性质可知,E 、F 重合为一点,且该点为CD 的中点E .由EM MA =EN NB =12,得MN ∥AB .因此MN ∥平面ABC 且MN ∥平面ABD .12.过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,其中与平面ABB 1A 1平行的直线共有________条.答案 6解析 过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,记AC ,BC ,A 1C 1,B 1C 1的中点分别为E ,F ,E 1,F 1,则直线EF ,EF 1,EE 1,FF 1,E 1F ,E 1F 1均与平面ABB1A 1平行,故符合题意的直线共6条.13. 如图所示,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E、B、F、D1四点共面;(2)求证:平面A1GH∥平面BED1F.答案(1)略(2)略解析(1)连接FG.∵AE=B1G=1,∴BG=A1E=2.∴BG綊A1E,∴A1G∥BE.又∵C1F綊B1G,∴四边形C1FGB1是平行四边形.∴FG綊C1B1綊D1A1.∴四边形A1GFD1是平行四边形.∴A1G綊D1F,∴D1F綊EB.故E、B、F、D1四点共面.(2)∵H是B1C1的中点,∴B1H=32.又B1G=1,∴B1GB1H=23.又FCBC=23,且∠FCB=∠GB1H=90°,∴△B1HG∽△CBF.∴∠B1GH=∠CFB=∠FBG,∴HG∥FB.又由(1)知,A1G∥BE,且HG∩A1G=G,FB∩BE=B,∴平面A1GH∥平面BED1F.14. 如图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:P A∥平面EFG;(2)求三棱锥P—EFG的体积.答案(1)略(2)1 6解析(1)如图所示,取AD的中点H,连接GH,FH.∵E,F分别为PC,PD的中点,∴EF∥CD.∵G,H分别是BC,AD的中点,∴GH∥CD.∴EF∥GH,∴E,F,H,G四点共面.∵F,H分别为DP,DA的中点,∴P A∥FH.∵P A⊄平面EFG,FH⊂平面EFG,∴P A∥平面EFG.(2)∵PD⊥平面ABCD,CG⊂平面ABCD,∴PD⊥CG.又∵CG⊥CD,CD∩PD=D,∴GC⊥平面PCD.∵PF =12PD =1,EF =12CD =1, ∴S △PEF =12EF ·PF =12. 又GC =12BC =1,∴V P —EFG =V G —PEF =13×12×1=16.15.一个多面体的直观图和三视图如图所示(其中M ,N 分别是AF ,BC 中点).(1)求证:MN ∥平面CDEF ; (2)求多面体A —CDEF 的体积. 答案 (1)略 (2)83解析 (1)证明 由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB =BC =BF =2,DE =CF =22,∴∠CBF =90°.取BF 中点G ,连接MG ,NG ,由M ,N 分别是AF ,BC 中点,可知:NG ∥CF ,MG ∥EF .又MG ∩NG =G ,CF ∩EF =F ,∴平面MNG ∥平面CDEF ,∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ,由于三棱柱ADE —BCF 为直三棱柱,∴AH ⊥平面CDEF ,且AH = 2.∴V A -CDEF =13S 四边形CDEF ·AH =13×2×22×2=83.16. 如图所示,三棱柱ABC -A 1B 1C 1,底面为正三角形,侧棱A 1A ⊥底面ABC ,点E 、F 分别是棱CC 1、BB 1上的点,点M 是线段AC 上的动点,EC =2FB .当点M 在何位置时,BM ∥平面AEF?答案当M为AC中点时,BM∥平面AEF.解析方法一:如图所示,取AE的中点O,连接OF,过点O作OM⊥AC 于点M.∵侧棱A1A⊥底面ABC,∴侧面A1ACC1⊥底面ABC.∴OM⊥底面ABC.又∵EC=2FB,∴OM∥FB綊12EC.∴四边形OMBF为矩形.∴BM∥OF.又∵OF⊂面AEF,BM⊄面AEF,故BM∥平面AEF,此时点M为AC的中点.方法二:如图所示,取EC的中点P,AC的中点Q,连接PQ、PB、BQ. ∴PQ∥AE.∵EC=2FB,∴PE綊BF,PB∥EF.∴PQ∥平面AEF,PB∥平面AEF.又PQ∩PB=P,∴平面PBQ ∥平面AEF .又∵BQ ⊂面PQB ,∴BQ ∥平面AEF .故点Q 即为所求的点M ,此时点M 为AC 的中点.17. (2013·福建)如图所示,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,BC =5,DC =3,AD =4,∠P AD =60°.(1)当正视方向与向量AD →的方向相同时,画出四棱锥P -ABCD 的正视图(要求标出尺寸,并写出演算过程);(2)若M 为P A 的中点,求证:DM ∥平面PBC ;(3)求三棱锥D -PBC 的体积.答案 (1)略 (2)略 (3)8 3解析 方法一:(1)在梯形ABCD 中,过点C 作CE ⊥AB ,垂足为E ,由已知得,四边形ADCE 为矩形,AE =CD =3,在Rt △BEC 中,由BC =5,CE =4,依勾股定理,得BE =3,从而AB =6.又由PD ⊥平面ABCD ,得PD ⊥AD .从而在Rt △PDA 中,由AD =4,∠P AD =60°,得PD =4 3.正视图如图所示.(2) 取PB 中点N ,连接MN ,CN .在△P AB 中,∵M 是P A 中点,∴MN ∥AB ,MN =12AB =3.又CD ∥AB ,CD =3,∴MN ∥CD ,MN =CD .∴四边形MNCD 为平行四边形.∴DM ∥CN .又DM ⊄平面PBC ,CN ⊂平面PBC ,∴DM ∥平面PBC .(3)V D -PBC =V P -DBC =13S △DBC ·PD ,又S △DBC =6,PD =43,所以V D -PBC =8 3.方法二:(1)同方法一.(2) 取AB 的中点E ,连接ME ,DE .在梯形ABCD 中,BE ∥CD ,且BE =CD ,∴四边形BCDE 为平行四边形.∴DE ∥BC .又DE ⊄平面PBC ,BC ⊂平面PBC ,∴DE∥平面PBC.又在△P AB中,ME∥PB,ME⊄平面PBC,PB⊂平面PBC,∴ME∥平面PBC.又DE∩ME=E,∴平面DME∥平面PBC.又DM⊂平面DME,∴DM∥平面PBC.(3)同方法一.。
直线、平面平行的判定及其性质

2.2 直线、平面平行的判定及其性质 第一课时 直线与平面平行的判定及性质1、直线与平面平行的定义如果一条直线与一个平面没有公共点,那么这条直线与这个平面平行。
2线面平行的判定定理 文字语言:如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行. 符号语言:,,////l m l m l ααα⊄⊂⇒.图形语言:定理的启示:要证明一条直线与一个平面平行,只要在这个平面内找出一条直线与已知直线平行即可。
简记为:线线平行,则线面平行。
说明:一条直线与一个平面平行,它可以和平面内的无数条直线平行,这无数条直线是一族平行直线,但我们不能说平面外一条直线与平面内无数条直线平行,则直线与平面平行。
所以用定理判断直线l 与平面α平行时,三个条件:,,//l m l m αα⊄⊂缺一不可。
3、 线面平行的性质定理文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行. 符号语言://,,//l l m l m αβαβ⊂=⇒ .图形语言:性质的理解:可以作为证明线线平行的方法。
简记为:线面平行,则线面平行。
问题一、空间线面平行的判定定理的理解 例1、(1)以下命题(其中a ,b 表示直线,α表示平面)①若a ∥b ,b ⊂α,则a ∥α ②若a ∥α,b ∥α,则a ∥b ③若a ∥b ,b ∥α,则a ∥α ④若a ∥α,b ⊂α,则a ∥b 其中正确命题的个数是 ( ) (A )0个 (B )1个 (C )2个 (D )3个 (2)已知a ∥α,b ∥α,则直线a ,b 的位置关系①平行;②垂直不相交;③垂直相交;④相交;⑤不垂直且不相交. 其中可能成立的有 ( ) (A )2个 (B )3个 (C )4个 (D )5个(3)如果平面α外有两点A 、B ,它们到平面α的距离都是a ,则直线AB 和平面α的位置关系一定是( ) (A )平行 (B )相交 (C )平行或相交 (D )AB ⊂αβαml(4)已知m ,n 为异面直线,m ∥平面α,n ∥平面β,α∩β=l ,则l ( ) (A )与m ,n 都相交 (B )与m ,n 中至少一条相交 (C )与m ,n 都不相交 (D )与m ,n 中一条相交 (5)下列命题中正确的命题是( )①如果一条直线与一个平面平行,那么这条直线与平面内的任意一条直线平行; ②如果一条直线与一个平面内无数条直线平行,那么这条直线与平面平行; ③过平面外一点有且只有一条直线和这个平面平行。
直线、平面平行的判定及性质

又 ME∥BC∥AD∥NF, ∴MEFN 为平行四边形, ∴NM∥EF,又∵MN⊄面 AA1B1B. ∴MN∥平面 AA1B1B.
法二
如图,连接 CN 并延长交 BA 的延长线于点 P,
连接 B1P,则 B1P⊂平面 AA1B1B.
∵△NDC∽△NBP, DN CN ∴ = .又 CM=DN, NB NP CM DN CN B1C=BD, = = , MB1 NB NP ∴MN∥B1P,∵B1P⊂平面 AA1B1B, ∴MN∥平面 AA1B1B.
教材回归
1.给出下列四个命题: ①若一条直线与一个平面内的一条直线平行,则这条 直线与这个平面平行; ②若一条直线与一个平面内的两条直线平行,则这条 直线与这个平面平行;
③若平面外的一条直线和这个平面内的一条直线平 行,那么这条直线和这个平面平行; ④若两条平行直线中的一条与一个平面平行, 则另一 条也与这个平面平行. 其中正确命题的个数是________个.
证明面面平行的方法有:
(1)面面平行的定义; (2)面面平行的判定定理:如果一个平面内有两条相 交直线都平行于另一个平面,那么这两个平面平行; (3)利用垂直于同一条直线的两个平面平行; (4)两个平面同时平行于第三个平面,那么这两个平 面平行; (5)利用“线线平行”、 “线面平行”、 “面面平行” 的相互转化.
A.m∥β 且 l1∥α C.m∥β 且 n∥β
答案 B
解析 因 m⊂α,1⊂β, α∥β, l 若 则有 m∥β 且 l1∥α, 故 α∥β 的一个必要条件是 m∥β 且 l1∥α,排除 A.因 m, n⊂α,l1,l2⊂β 且 l1 与 l2 相交,若 m∥l1 且 n∥l2,因 l1 与 l2 相交,故 m 与 n 也相交,∴α∥β;若 α∥β,则直线 m 与直线 l1 可能为异面直线,故 α∥β 的一个充分而不必 要条件是 m∥l1 且 n∥l2,应选 B.
直线与平面平行的判定及其性质答案

直线、平面平行的判定及其性质知识整理:1. 直线和平面平行的定义:直线和平面没有公共点。
2. 直线和平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行.即“线线平行,线面平行”。
符号表示为:,,////a b a b a ααα⊄⊂⇒. 图形如右图所示.3. 平面与平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.即“线面平行,面面平行”。
用符号表示为:,,////,//a b a b P a b βββααα⊂⊂=⎫⇒⎬⎭。
4. 线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.即“线面平行,线线平行”。
用符号表示为:////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭.5. 面面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行. 即“面面平行,线线平行”。
用符号表示为://,,//a b a b αβγαγβ==⇒ ,如右图。
6. 其它性质:①//,//l l αβαβ⊂⇒;②//,l l αβαβ⊥⇒⊥;③夹在平行平面间的平行线段相等。
例题解析:例1 如图所示,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 的中点。
(1)求证://MN 平面PAD ;(2)若4MN BC ==,PA =PA 与MN 所成的角的大小。
解:(1)取PD 的中点H ,连接AH ,由N 是PC 的中点,∴NH //=12DC 。
由M 是AB 的中点,∴ NH //=AM , 即AMNH 为平行四边形。
∴ //MN AH 。
由MN PAD 平面⊄,AH PAD 平面⊂,∴ //MN PAD 平面。
βaαb(2) 连接A C 并取其中点为O ,连接OM 、ON ,∴ OM //=12BC ,ON //=12PA , 所以ONM ∠就是异面直线PA 与MN 所成的角,且MO ⊥NO 。
直线、平面平行的判定与性质知识点+典型例题及答案解析

2.2直线、平面平行的判定及其性质2.2.1直线与平面平行的判定1、直线和平面的位置关系一条直线和一个平面的位置关系有且只有以下三种位置关系直线在平面内直线与平面相交直线与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a?αa ∩α=Aa||α图形表示注:直线和平面相交或平行的情况统称为直线在平面外2、直线和平面平行(1)定义:直线和平面没有公共点,则称此直线L 和平面α平行,记作L ||α。
(2)判定定理:如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
简记为:线线平行,则线面平行.符号表示:,////ab a b a 、.2.2.2平面与平面平行的判定1、定义:没有公共点的两个平面叫做平行平面。
符号表示为:平面α、平面β,若a ∩β=?,则a ∥β2、判定定理:判定文字描述如果两个平面无公共点,责成这两个平面平行一个平面内有两条相交直线与另一个平面平行,如果两个平面同时垂直于一条直线,那么这两个平面垂直。
2.2.3 直线与平面平行的性质1..性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.简记为:线面平行,则线线平行.符号表示:若//,,,//a a b a b 则.2.2.4 平面与平面平行的性质性质文字描述如果两个平行平面同时和第三平面相交,那么他们的交线平行如果两个平行平面中有一个垂直于一条直线,那么另一个平面也垂直于这条直线如果两个平面平行,那么其中一个平面内的直线平行于另一个平面图形那么这两个平面平行.图形条件=α,b ?β,α∩b =Pα∥α,b ∥α?β∥αl ⊥αl ⊥β?β∥α结论//////条件α∥ββ∩γ=bα∩γ=aα∥βl⊥αα∥βa?β结论a∥b l⊥βa∥α1.解题方法(1)证明直线与平面平行的常用方法:2.利用定义,证明直线与平面没有公共点。
一般结合反证法来证明;3.利用直线和平面平行的判定定理,注意定理成立时应满足的条件;4.利用面面平行的性质定理,把面面平行转化为线面平行;2、证明平面与平面平行的常用方法:(1)利用面面平行的定义,此法一般与反证法结合;(2)利用面面平行的判定定理;(3)利用两个平面垂直于同一直线;(4)证明两个平面同时平行于第三个平面;基础习题1.设l是直线,,β是两个不同的平面,则下列说法正确的是()A.若l∥,l∥β,则∥βB.若l∥,l⊥β,则⊥βC.若⊥β,l⊥, 则l⊥βD.若⊥β, l⊥, 则l⊥β1.【解析】 B2.下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行2.【解析】 C【例3】(2011江西)已知1,2,3是三个相互平行的平面.平面1,2之间的距离为1d ,平面2,3之间的距离为2d .直线l 与1,2,3分别相交于1P ,2P ,3P ,那么“12PP =23P P ”是“12d d ”的A.充分不必要条件B.必要不充分条件C .充分必要条件D .既不充分也不必要条件【解析】C【例4】(2011辽宁)如图,四棱锥S —ABCD 的底面为正方形,SD底面ABCD ,则下列结论中不正确...的是A .AC ⊥SB B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D .AB 与SC 所成的角等于DC 与SA 所成的角【解析】D【例5】(2012全国)设平面与平面相交于直线m ,直线a 在平面内,直线b 在平面内,且b m则“”是“ab ”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .即不充分也不必要条件【解析】A【例6】(2012河南)1l ,2l ,3l 是空间三条不同的直线,则下列命题正确的是()A .12l l ,23l l 13//l l B .12l l ,23//l l 13l l C .233////l l l 1l ,2l ,3l 共面D .1l ,2l ,3l 共点1l ,2l ,3l 共面【解析】B【例7】(2012江苏)如图,在直三棱柱111ABC A B C 中,1111AB AC ,D E ,分别是棱1BC CC ,上的点(点 D 不同于点C ),且ADDE F ,为11B C 的中点.求证:(1)平面ADE 平面11BCC B ;1A 1C (2)直线1//A F 平面ADE .1B 【解析】(1)∵三棱柱ABC ﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC ,∵AD ?平面ABC ,∴AD ⊥CC1又∵AD ⊥DE ,DE 、CC1是平面BCC1B1内的相交直线∴AD ⊥平面BCC1B1,∵AD ?平面ADE∴平面ADE ⊥平面BCC1B1;(2)∵△A1B1C1中,A1B1=A1C1,F 为B1C1的中点∴A1F ⊥B1C1,∵CC1⊥平面A1B1C1,A1F ?平面A1B1C1,∴A1F ⊥CC1又∵B1C1、CC1是平面BCC1B1内的相交直线∴A1F ⊥平面BCC1B1又∵AD ⊥平面BCC1B1,∴A1F ∥AD∵A1F ?平面ADE ,AD ?平面ADE ,∴直线A1F ∥平面ADE .【例8】(2012浙江)如图,在四棱锥P —ABCD 中,底面是边长为23的菱形,且∠BAD =120°,且PA ⊥平面FDCABEABCD,PA=26,M,N分别为PB,PD的中点.(Ⅰ)证明:MN∥平面ABCD;(Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.【解析】(Ⅰ)如图连接BD.∵M,N分别为PB,PD的中点,∴在PBD中,MN∥BD.又MN平面ABCD,∴MN∥平面ABCD;(Ⅱ) 105.【例9】(2012北京)如图1,在Rt ABC中,90C,,D E分别为,AC AB的中点,点F为线段CD上的一点,将ADE沿DE折起到1A DE的位置,使1A F CD,如图2。
直线、平面平行的判定与性质
2021年新高考数学总复习第八章《立体几何与空间向量》直线、平面平行的判定与性质1.线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(简记为“线线平行⇒线面平行”)⎭⎪⎬⎪⎫l∥aa⊂αl⊄α⇒l∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)⎭⎪⎬⎪⎫l∥αl⊂βα∩β=b⇒l∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)⎭⎪⎬⎪⎫a∥βb∥βa∩b=Pa⊂αb⊂α⇒α∥β性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行⎭⎪⎬⎪⎫α∥βα∩γ=aβ∩γ=b⇒a∥b概念方法微思考1.一条直线与一个平面平行,那么它与平面内的所有直线都平行吗?提示不都平行.该平面内的直线有两类,一类与该直线平行,一类与该直线异面.2.一个平面内的两条相交直线与另一个平面内的两条相交直线分别对应平行,那么这两个平面平行吗?提示平行.可以转化为“一个平面内的两条相交直线与另一个平面平行”,这就是面面平行的判定定理.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.(×)(2)平行于同一条直线的两个平面平行.(×)(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.(×)(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.(√)(5)若直线a与平面α内无数条直线平行,则a∥α.(×)(6)若α∥β,直线a∥α,则a∥β.(×)题组二教材改编2.平面α∥平面β的一个充分条件是()A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α答案 D解析若α∩β=l,a∥l,a⊄α,a⊄β,则a∥α,a∥β,故排除A.若α∩β=l,a⊂α,a∥l,则a∥β,故排除B.若α∩β=l,a⊂α,a∥l,b⊂β,b∥l,则a∥β,b∥α,故排除C.故选D. 3.如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与平面AEC的位置关系为________.答案平行解析连接BD,设BD∩AC=O,连接EO,在△BDD1中,E为DD1的中点,O为BD的中点,。
直线平面平行 垂直的判定及其性质知识点

一、直线、平面平行的判定及其性质知识点一、直线与平面平行的判定ⅰ.直线和平面的位置关系(一条直线和一个平面的位置关系有且只有以下三种)位置关系直线在平面内直线与平面相交直线与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a⊂αa∩α=A a||α图形表示ⅱ.思考:如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行.(a||b)直线与平面平行的判断判定文字描述直线和平面在空间平面永无交点,则直线和平面平行(定义)平面外的一条直线一次平面内的一条直线平行,则该直线与此平面平行图形条件a与α无交点结论a∥αb∥α※判定定理的证明知识点二、直线与平面平行的性质图形条件a ∥α a ∥αa ⊂βα∩β=b 结论a ∩α=∅a ∥b特别提示证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“质定理,通过“面面”平行,证得“线面”平行.知识点三、平面与平面平行的判定知识点四、平面与平面平行的性质二、直线、平面垂直的判定及其性质图形l⊥m,l⊥n,m∩n=B,m⊂α,n⊂α条件b为平面α内的任一直线,而l对这一直线总有l⊥α结论l⊥αl⊥α要点诠释:定义中“平面内的任意一条内的所有直线”,这与“无数条直线面垂直)图形条件结论知识点三、二面角Ⅰ.二面角::从一条直线出发的两个半平面所组成的图形叫二面角(dihedral angle ). 这条直线叫做二面角的棱,这两角AB αβ--. (简记P AB Q --)二面角的平面角的三个特征:ⅰ.点在棱上ⅱ. 线在面内 ⅲ.与棱垂直Ⅱ.二面角的平面角:在二面角αβ-l -的棱l 上任取一点O ,以点O 为垂足,在半平面,αβ内分别作垂直于棱l 的射成的AOB ∠叫做二面角的平面角.作用:衡量二面角的大小;范围:000180θ<<.知识点四、平面和平面垂直的定义和判定结果α∩β=l α-l-β=90o α⊥β“任何”“随意”“无数”等字眼知识点五、平面和平面垂直的性质面面垂直线面垂直(如果两个平面垂直,那么一个平面内垂直于它们交线的直线与一个面平垂直例题1.如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E BB1上异于B1的点,且EH∥A1 D1,则下列结论中不正确的是A. EH∥FGB.四边形EFGH是矩形C. Ω是棱柱D. Ω是棱台2能保证直线a与平面α平行的条件是( A )A.a⊄α,b⊂α,a∥b B .b⊂α,a∥bC. b⊂α,c∥α,a∥b,a∥cD. b⊂α,A∈a,B∈a,C∈b ,D∈b且AC=BD3下列命题正确的是( D F )A. 平行于同一平面的两条直线平行B. 若直线a∥α,则平面α内有且仅有一条直线与a平行C. 若直线a∥α,则平面α内任一条直线都与a平行D. 若直线a∥α,则平面α内有无数条直线与a平行E. 如果a、b是两条直线,且a∥b,那么a平行于经过b的任何平面F. 如果直线a、b和平面α满足a∥b,a∥α,b⊄α,那么b∥α4在空间,下列命题正确的是(A)平行直线的平行投影重合(B)平行于同一直线的两个平面平行(C)垂直于同一平面的两个平面平行(D)垂直于同一平面的两条直线平行5已知m 、n 为两条不同的直线,a 、β为两个不同的平面,则下列命题中正确的是A .,,m n αα⊂⊂m ∥β,n ∥β⇒a ∥βB .a ∥β,,m n αβ⊂⊂⇒m ∥nC .m ⊥a,m ⊥n ⇒n ∥aD .n ∥m,n ⊥a ⇒m ⊥a 6.下列命题中错误的是(A )如果平面α⊥平面β,那么平面α内一定直线平行于平面β(B )如果平面α垂直于平面β,那么平面α内一定不存在直线垂直于平面β (C )如果平面α⊥平面γ,平面β⊥平面γ,l αβ⋂=,那么l ⊥平面γ (D )如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β8.求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面. 已知:空间四边形ABCD 中,E 、F 分别是AB 、AD 的中点 求证:E F ‖平面BCD8题图 9题图9.如图,在椎体P-ABCD 中,ABCD 是边长为1的棱形,且∠DAB=60 ,,PB=2,E,F分别是BC,PC的中点.(1) 证明:AD ⊥平面DEF;(2) 求二面角P-AD-B的余弦值.课堂练习A组3.m、n是空间两条不同的直线,α、β是两个不同的平面,下面四个命题中,真命题的序号是________.①m⊥α,n∥β,α∥β⇒m⊥n;②m⊥n,α∥β,m⊥α⇒n∥β;③m⊥n,α∥β,m∥α⇒n⊥β;④m⊥α,m∥n,α∥β⇒n⊥β.4.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA1=2, E、E1、(1)证明:直线EE1//平面FCC1;CE1A1 B1C1D1D5. 在长方体ABCD—A1B1C1D1中.(1)作出过直线AC且与直线BD1平行的截面,并说明理由.(2)设E、F分别是A1B和B1C的中点,求证直线EF//平面ABCD.6. 在图中所示的一块木料中,棱BC平行于平面A’C’.(1)要经过平面内的一点P 和棱BC将木料据开,应怎样画线?(2)所画的线和平面AC 是什么位置关系?CA''。
第三节:空间直线、平面平行的判定及其性质

第三节: 空间直线、平面平行的判定及其性质知识梳理1.直线与平面平行的定义直线与平面没有公共点,叫做直线与平面平行.2.平面与平面平行的定义如果两个平面没有公共点,叫做两个平面平行.3.直线与平面平行判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简称:线线平行,则线面平行.符号语言:⎭⎪⎬⎪⎫a ⊄α,b ⊂α a ∥b ,错误!未定义书签。
⇒a ∥α. 性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.简称:线面平行,则线线平行.符号语言:⎭⎬⎫a ∥αa ⊂βα∩β=b 错误!未定义书签。
⇒a ∥b .4.平面与平面平行判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.简称:线面平行,则面面平行.符号语言:⎭⎬⎫a ⊂α,b ⊂αa ∩b =P a ∥β,b ∥β⇒α∥β.性质定理:自然语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.简称:面面平行,则线线平行.符号语言:⎭⎬⎫α∥βα∩γ=a β∩γ=b⇒ a ∥b .5.平行问题的转化关系典例剖析题型一 平行关系命题判定问题例1 空间中,下列命题正确的是( )A .若a ∥α,b ∥a ,则b ∥αB .若a ∥α,b ∥α,a ⊂β,b ⊂β,则β∥αC .若α∥β,b ∥α,则b ∥βD .若α∥β,a ⊂α,则a ∥β变式训练对于平面α和共面的直线m,n,下列命题是真命题的是()A.若m,n与α所成的角相等,则m∥n B.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n题型二线面平行的判定和性质例2如图,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点.求证:EF∥平面P AD.变式训练在空间四边形ABCD中,E、F分别为AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形解题要点对平行问题,应善于根据题意进行转化,要证线面平行,则一般需寻找线线平行。
直线与平面平面与平面平行的判定定理ppt课件

解:(1)分别连接BM,BF交AC,AD于点E,F. B 因为M,N分别为对应三角形的重心,
故E,F为相应边的中点,且有
BM:ME=2:1,BN:NF=2:1
N
∴MN//EF且MN=
2 3
EF.
A
又因为MN 平面ACD,EF 平面ACD
M E
所以 MN// 平面ACD.
F C
D
(2) 又因为在△ACD中,EF是三角形的中位线,
证明:分别取PD,AD的中点G,H ,连接GE,HF ,GH
在△PDC中,GE为三角形中位线,
所以GE//DC且 GE= 1 DC
同理,HF//AB且
2 HF=
1
AB
2
P E
G
又∵底面为正方形,∴AM//DC且 AM=DC
D
C
∴ GE//HF且 GE=HF
H
F
即HFEG为平行四边形,故EF//GH
A
2 3
FH.
25
练习
练 如图点B为△ACD所在平面外一点,M,N,G分别为△ABC, △ABD, △BCD的重心. (1)求证:平面MNG//平面ACD. (2)求 SVMNG : SVADC 的值.
B
解:(2)因为EF是△ACD的中位线,
所以,EF//CD且EF= 1 CD.
D1
N
A1
M
F
B1
C1
E
D1 M
A1
N
C1 B1
D A
C B
D
K
A
Q
C
P B
变15式
例 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F 分别为DD1,DB的中点.求证:EF//平面ABC1D1.
高一数学必修2第二单元知识点:直线、平面平行的判定及其性质

高一数学必修2第二单元知识点:直线、平面平行的判定及其性质(实用版)编制人:__审核人:__审批人:__编制单位:__编制时间:__年__月__日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用资料,如工作总结、述职报告、心得体会、工作计划、演讲稿、教案大全、作文大全、合同范文、活动方案、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of practical materials for everyone, such as work summaries, job reports, insights, work plans, speeches, lesson plans, essays, contract samples, activity plans, and other materials. If you want to learn about different data formats and writing methods, please pay attention!高一数学必修2第二单元知识点:直线、平面平行的判定及其性质数学在科学发展和现代生活生产中的应用非常广泛,本店铺准备了高一数学必修2第二单元知识点,希望你喜欢。
直线与平面平行的判定

黑龙江省实验中学课时计划、复习引入:1•异面直线: 2•空间中两条直线的位置关系有三种:3公理4:4.等角定理二、新课讲解:问题1:一支笔所在的直线与一个作业本所在的平面,可能有几种位置关系?问题2:如图,线段A B所在直线与长方体的六个面所在平面有几种位置关系?结论:直线与平面的位置关系有且只有三种:平行、相交、在面内问题3:如何用图形语言表示直线与平面的三种位置关系?all , a A, a问题5:⑴门扇的两边是平行的,当门扇绕着一边转动时,另一边与门框所在平面具有什么样的位置关系?⑵课本的对边是平行的,将课本的一边紧贴桌面,沿着这条边转动课本,课本的上边缘与桌面所在平面具有什么样的位置关系?学习过程自主探究1:如图,1 .直线a与直线b共面吗?2.直线a与平面相交吗?直线与平面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.判定定理告诉我们,判定直线与平面平行的条件有三个分别是⑴ a在平面夕卜,即卩a (面外)⑵b在平面内,即b (面内)(3)a与b平行,即a // b(平行)a符号语言: b all ,思想:线线平行线面平行all b黑龙江省实验中学学生活动与调控教师讲授与提问过程三、例题讲解: 1. 例题1 :判断下列各题对错⑴若直线a 与平面内的一条直线平行,则 all () ⑵若直线a 与平面 内无数条直线平行,则 all( ⑶若直线a 在平面 夕卜,则all( ⑷若平面 外直线a 与 内无数条直线异面,则 all () ⑸直线a 在平面 内,直线b 在 夕卜,若allb ,则all () ⑹直线a 在平面 内,直线b 在 夕卜,则a 与b 不相交()2. 求证:空间四边形相邻两边中点的连线平行于另外两边所在平面。
变式:变式训练:两个全等的正方形ABCD 和ABEF 所在平面相交于2•正方体ABCD A 1B 1C 1D 1中,E 为DD ,的中点,判断BD ,与平面AEC 的位置关系,并给出证明。
