计算方法的MATLAB实现
Matlab中常用的数值计算方法

Matlab中常用的数值计算方法数值计算是现代科学和工程领域中的一个重要问题。
Matlab是一种用于数值计算和科学计算的高级编程语言和环境,具有强大的数值计算功能。
本文将介绍Matlab中常用的数值计算方法,包括数值积分、数值解微分方程、非线性方程求解和线性方程组求解等。
一、数值积分数值积分是通过数值方法来近似计算函数的定积分。
在Matlab中,常用的数值积分函数是'quad'和'quadl'。
'quad'函数可以用于计算定积分,而'quadl'函数可以用于计算无穷积分。
下面是一个使用'quad'函数计算定积分的例子。
假设我们想计算函数f(x) = x^2在区间[0, 1]上的定积分。
我们可以使用如下的Matlab代码:```f = @(x) x^2;integral = quad(f, 0, 1);disp(integral);```运行这段代码后,我们可以得到定积分的近似值,即1/3。
二、数值解微分方程微分方程是描述自然界各种变化规律的数学方程。
在科学研究和工程应用中,常常需要求解微分方程的数值解。
在Matlab中,可以使用'ode45'函数来求解常微分方程的数值解。
'ode45'函数是采用基于Runge-Kutta方法的一种数值解法。
下面是一个使用'ode45'函数求解常微分方程的例子。
假设我们想求解一阶常微分方程dy/dx = 2*x,初始条件为y(0) = 1。
我们可以使用如下的Matlab代码:```fun = @(x, y) 2*x;[x, y] = ode45(fun, [0, 1], 1);plot(x, y);```运行这段代码后,我们可以得到微分方程的数值解,并绘制其图像。
三、非线性方程求解非线性方程是指方程中包含非线性项的方程。
在很多实际问题中,我们需要求解非线性方程的根。
MATLAB并行计算的实现方法与技巧

MATLAB并行计算的实现方法与技巧1. 引言MATLAB是一种非常强大的数值计算和科学编程工具,但在处理大规模数据以及复杂计算任务时,单个计算机资源的限制会导致计算效率低下。
为了充分利用计算资源,提高计算速度,我们可以使用并行计算技术。
本文将介绍MATLAB并行计算的实现方法与技巧,帮助读者合理利用多个计算核心,提升计算效率。
2. 并行计算概述并行计算是将一个任务划分为多个子任务,同时在多个计算核心上进行计算,以加快计算速度。
在MATLAB中,我们可以使用Parallel Computing Toolbox来实现并行计算。
其主要方式有两种:任务并行计算和数据并行计算。
3. 任务并行计算任务并行计算是指将一个大任务分解成多个子任务,每个子任务被分配到不同的计算核心上执行。
MATLAB提供了parfor循环来方便开发者实现任务并行计算。
下面是一个简单的示例,展示了如何使用parfor实现任务并行计算:```matlabparfor i = 1:100output(i) = myFunction(input(i));end```上述代码中,myFunction是一个需要计算的函数,input是输入数据,output是输出结果。
通过parfor循环,每个循环迭代都会在不同的计算核心上运行,从而提高计算速度。
需要注意的是,parfor循环中的每个迭代必须是独立的,不依赖于其他迭代的结果。
否则,parfor将无法正确处理结果的依赖关系。
4. 数据并行计算数据并行计算是指将一个大任务中的数据划分成多个部分,每个部分在不同的计算核心上进行计算。
MATLAB提供了spmd语句(single program multiple data),使得数据并行计算更容易实现。
下面是一个简单的示例,展示了如何使用spmd语句实现数据并行计算:```matlabspmddata = labindex:2:100;output = myFunction(data);end```上述代码中,labindex是一个特殊的变量,表示当前计算核心的索引。
Matlab中的并行计算方法介绍

Matlab中的并行计算方法介绍引言Matlab作为一种功能强大的科学计算工具,在各个领域的应用都不可忽视。
但是,随着数据规模的增加和计算复杂度的提升,单机计算已经无法满足研究者和工程师的需求。
这就需要使用并行计算的方法来实现更高效的计算。
本文将介绍一些常用的Matlab中的并行计算方法,包括如何使用Parallel Computing Toolbox中的函数、Parallel Computing Toolbox中的工具以及Parallel Computing Toolbox结合其他工具一起使用的方法。
一、Parallel Computing Toolbox函数的使用Parallel Computing Toolbox是Matlab中用于进行并行计算的工具箱,它提供了一系列方便易用的函数来实现并行计算。
其中主要的函数包括parfor、parpool和spmd。
1. parfor函数parfor函数是Matlab中用于实现循环并行计算的函数。
它可以将一个循环分解成多个子任务,并在多个处理器上同时执行这些子任务,从而大大提高计算效率。
使用parfor函数的方法如下所示:```matlabparfor i = 1:N% 子任务的计算过程end```在这个例子中,N表示循环的迭代次数。
使用parfor函数的时候,需要注意以下几点:- 子任务之间的计算不能相互依赖,也就是说每个子任务之间不存在数据的读取和写入操作。
- 子任务的计算过程尽量保持相对独立,避免不必要的数据交互。
2. parpool函数parpool函数用于创建一个并行计算的池子,其中包含多个工作进程。
使用这些工作进程可以实现对大规模计算任务的分布式处理。
使用parpool函数的方法如下所示:```matlabparpool('local', N)```在这个例子中,N表示要创建的工作进程的数量。
使用parpool函数的时候,需要注意以下几点:- 工作进程的数量应根据实际情况进行调整,以保证计算效率和资源的合理利用。
简单迭代法matlab例题程序

一、引言在数学建模和计算机编程中,简单迭代法是一种常用的求解方程近似解的方法。
其原理是通过不断迭代计算,逼近实际的解。
在Matlab 编程中,简单迭代法也是一种常见的应用。
本文将介绍简单迭代法的原理,并给出在Matlab中实现简单迭代法的例题程序。
二、简单迭代法原理1. 简单迭代法的基本思想是将需要求解的方程转化为迭代形式,即 x = g(x),然后通过不断迭代计算得到方程的近似解。
2. 简单迭代法的收敛条件是 |g'(x)| < 1,即迭代函数的导数的绝对值小于1时,迭代过程才能收敛。
3. 简单迭代法的收敛速度取决于迭代函数的选择,通常可以通过调整迭代函数来提高收敛速度。
三、Matlab中的简单迭代法实现在Matlab中,可以通过编写脚本文件来实现简单迭代法。
下面给出一个简单的例题:求解方程 x^2 - 3x + 2 = 0 的近似解。
4. 以下是Matlab中实现简单迭代法的脚本文件示例:```matlab定义迭代函数g = (x) 3*x - x^2;设置迭代初值和迭代次数x0 = 0.5;N = 100;迭代计算for k = 1:Nx = g(x0);fprintf('第d次迭代,近似解为:.10f\n', k, x);if abs(x - x0) < 1e-8 判断迭代是否收敛break;endx0 = x;end```5. 通过运行上述脚本文件,即可得到方程 x^2 - 3x + 2 = 0 的近似解。
四、实例分析通过上述例题程序的运行结果可以看出,简单迭代法在Matlab中的实现比较简单直观。
但是需要注意的是,迭代函数的选择和迭代初值的设定对最终的近似解都会产生影响,需要经过一定的调试和优化。
五、总结简单迭代法是一种常用的求解方程近似解的方法,在Matlab编程中也有着广泛的应用。
通过本文的介绍和示例程序,相信读者已经对简单迭代法在Matlab中的实现有了更深入的了解。
matlab牛顿迭代法算重根

一、简介Matlab是一种十分常用的科学计算软件,其功能强大,可以进行各种数值计算、数据分析和可视化操作。
而牛顿迭代法是一种用于求解方程的数值算法,可以有效地计算出函数的根。
本文将重点介绍如何使用Matlab进行牛顿迭代法来计算重根。
二、牛顿迭代法原理1. 牛顿迭代法是一种迭代逼近的方法,通过不断迭代得到更接近函数零点的近似值。
其公式如下:X_{n+1} = X_n - \frac{f(X_n)}{f'(X_n)}其中,X_{n+1}为下一次迭代的近似值,X_n为当前的近似值,f(X)为函数值,f'(X)为函数的导数值。
2. 牛顿迭代法的优点是收敛速度快,而缺点是对初始值的选择敏感,可能会产生不收敛的情况。
三、在Matlab中使用牛顿迭代法1. 在Matlab中,可以使用内置的函数`fzero`来进行牛顿迭代法的计算。
其语法如下:x = fzero(fun,x0)其中,fun为要求解的函数句柄,x0为起始点的初始值,x为函数的根。
2. 需要注意的是,在使用`fzero`函数时,需要提供函数的句柄,即在Matlab中定义要求解的函数,并使用`(x)`符号来表示函数的自变量。
另外,还需要提供初始值x0,可以根据具体问题来选择较为合适的初始值。
3. 以下是一个简单的使用牛顿迭代法求解函数根的示例代码:```matlabf = (x) x^3 - 2*x - 5;x0 = 2;x = fzero(f, x0);disp(x);```四、示例接下来,我们将通过一个具体的示例来演示如何使用Matlab的牛顿迭代法来计算重根。
1. 问题描述假设有如下方程:f(x) = x^3 - 2x^2 + 3x - 6我们希望使用牛顿迭代法来计算函数f(x)的重根。
2. 解决过程在Matlab中定义函数f(x):```matlabf = (x) x^3 - 2*x^2 + 3*x - 6;```选择初始值x0,并利用`fzero`函数进行牛顿迭代法的计算:```matlabx0 = 2;x = fzero(f, x0);disp(x);```3. 结果分析经过计算,可以得到函数f(x)的一个重根为x=2.这样,我们就成功地使用Matlab的牛顿迭代法来计算重根。
如何在MATLAB中进行数值计算

如何在MATLAB中进行数值计算1.基本数学操作:-加法、减法、乘法、除法:使用+、-、*、/操作符进行基本算术运算。
-幂运算:使用^或.^(点乘)操作符进行幂运算。
- 开平方/立方:可以使用sqrt(或power(函数进行开平方和立方运算。
2.矩阵操作:- 创建矩阵:可以使用矩阵构造函数如zeros(、ones(、rand(等创建矩阵。
- 矩阵运算:使用*操作符进行矩阵相乘,使用transpose(函数进行矩阵转置。
- 矩阵求逆和求解线性方程组:使用inv(函数求矩阵的逆,使用\操作符求解线性方程组。
3.数值积分和微分:- 数值积分:使用integral(函数进行数值积分。
可以指定积分函数、积分上下限和积分方法。
- 数值微分:使用diff(函数进行数值微分。
可以指定微分函数和微分变量。
4.解方程:- 一元方程:使用solve(函数可以解一元方程。
该函数会尝试找到方程的精确解。
- 非线性方程组:使用fsolve(函数可以求解非线性方程组。
需要提供初始值来开始求解过程。
-数值方法:可以使用牛顿法、二分法等数学方法来求解方程。
可以自定义函数来实现这些方法。
5.统计分析:- 统计函数:MATLAB提供了丰富的统计分析函数,如mean(、std(、var(等用于计算均值、标准差、方差等统计量。
- 直方图和密度估计:使用histogram(函数可以绘制直方图,并使用ksdensity(函数进行核密度估计。
- 假设检验:使用ttest(或anova(函数可以进行假设检验,用于比较多组数据之间的差异。
6.数值优化:- 非线性最小化:使用fminunc(函数可以进行非线性最小化。
需要提供目标函数和初始点。
- 线性规划:使用linprog(函数可以进行线性规划。
需要提供目标函数和限制条件。
- 整数规划:使用intlinprog(函数可以进行整数规划。
需要提供目标函数和整数约束。
7.拟合曲线:- 线性拟合:使用polyfit(函数进行线性拟合。
计算方法matlab实验报告

计算方法matlab实验报告计算方法MATLAB实验报告引言:计算方法是一门研究如何用计算机来解决数学问题的学科。
在计算方法的学习过程中,MATLAB作为一种强大的数值计算软件,被广泛应用于科学计算、工程计算、数据分析等领域。
本实验报告将介绍在计算方法课程中使用MATLAB 进行的实验内容和实验结果。
一、二分法求方程根在数值计算中,求解非线性方程是一个常见的问题。
二分法是一种简单而有效的求解非线性方程根的方法。
在MATLAB中,可以通过编写函数和使用循环结构来实现二分法求解方程根。
实验步骤:1. 编写函数f(x),表示待求解的非线性方程。
2. 设定初始区间[a, b],满足f(a) * f(b) < 0。
3. 利用二分法迭代求解方程根,直到满足精度要求或迭代次数达到预设值。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个非线性方程的根。
例如,对于方程f(x) = x^3 - 2x - 5,我们通过二分法迭代了5次,得到了方程的一个根x ≈ 2.0946。
二、高斯消元法解线性方程组线性方程组的求解是计算方法中的重要内容之一。
高斯消元法是一种常用的求解线性方程组的方法,它通过矩阵变换将线性方程组化为上三角矩阵,从而简化求解过程。
在MATLAB中,可以利用矩阵运算和循环结构来实现高斯消元法。
实验步骤:1. 构建线性方程组的系数矩阵A和常数向量b。
2. 利用高斯消元法将系数矩阵A化为上三角矩阵U,并相应地对常数向量b进行变换。
3. 利用回代法求解上三角矩阵U,得到线性方程组的解向量x。
实验结果:通过在MATLAB中编写相应的函数和脚本,我们成功求解了多个线性方程组。
例如,对于线性方程组:2x + 3y - z = 13x - 2y + 2z = -3-x + y + 3z = 7经过高斯消元法的计算,我们得到了方程组的解x = 1,y = -2,z = 3。
三、数值积分方法数值积分是计算方法中的重要内容之一,它用于计算函数在给定区间上的定积分。
最优化计算方法及其matlab程序实现

最优化计算方法及其matlab程序实现最优化计算是一种通过寻找最佳解决方案来解决问题的方法。
在许多实际问题中,我们希望找到使某个目标函数达到最大或最小值的变量取值。
最优化计算可以应用于各种领域,如工程、经济、物理等。
在最优化计算中,我们首先需要定义一个目标函数,它描述了我们要优化的问题。
目标函数可以是线性的也可以是非线性的,具体取决于问题的性质。
然后,我们需要确定变量的取值范围和约束条件。
最后,我们使用最优化算法来搜索最佳解。
常用的最优化算法包括梯度下降法、牛顿法、拟牛顿法等。
这些算法基于不同的原理和策略,在不同的问题中表现出不同的性能。
选择合适的最优化算法对于获得高效的求解结果非常重要。
接下来,我们将介绍如何使用Matlab编写程序来实现最优化计算方法。
Matlab是一种功能强大的数值计算和编程环境,它提供了丰富的工具箱和函数来支持最优化计算。
我们需要定义目标函数。
在Matlab中,我们可以使用函数句柄来表示目标函数。
例如,假设我们要最小化一个简单的二次函数f(x) = x^2,我们可以定义一个函数句柄如下:```matlabf = @(x) x^2;```然后,我们可以使用Matlab提供的最优化函数来搜索最佳解。
例如,使用fminsearch函数来实现梯度下降法:```matlabx0 = 1; % 初始值x = fminsearch(f, x0);```在上述代码中,x0是变量的初始值,fminsearch函数将根据梯度下降法来搜索最佳解,并将结果存储在变量x中。
除了梯度下降法,Matlab还提供了其他常用的最优化函数,如fminunc、fmincon等。
这些函数具有不同的功能和参数,可以根据具体的问题选择合适的函数来求解。
除了单变量最优化,Matlab还支持多变量最优化。
在多变量最优化中,目标函数和约束条件可以是多元函数。
我们可以使用Matlab 提供的向量和矩阵来表示多变量的取值和约束条件。
MATLAB计算方法与实现
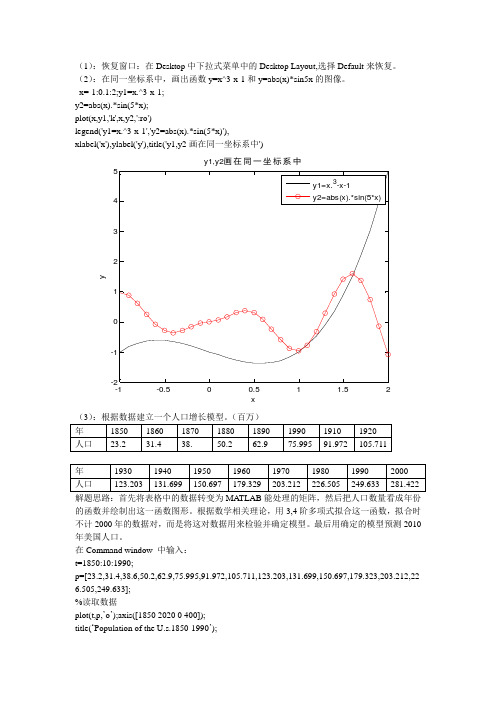
(1):恢复窗口:在Desktop 中下拉式菜单中的Desktop Layout,选择Default 来恢复。
(2):在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x 的图像。
x=-1:0.1:2;y1=x.^3-x-1; y2=abs(x).*sin(5*x); plot(x,y1,'k',x,y2,':ro')legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')-1-0.500.51 1.52xyy1,y2画在同一坐标系中(3):根据数据建立一个人口增长模型。
(百万)的函数并绘制出这一函数图形。
根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。
最后用确定的模型预测2010年美国人口。
在Command window 中输入: t=1850:10:1990;p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633]; %读取数据plot(t,p,’o ’);axis([1850 2020 0 400]); title(‘Population of the U.s.1850-1990’);ylabel(‘Millions ’);%绘制出数据的函数图形并加以修饰f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2 v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值 abs(v-251.422) %计算两个模型与2000年人口数的绝对误差。
在MATLAB中使用并行计算的方法

在MATLAB中使用并行计算的方法随着计算机的普及和性能的提高,我们可以利用并行计算的方法来加速计算任务。
MATLAB作为一种广泛使用的数值计算环境,也提供了一些并行计算的方法来提高计算效率。
在本文中,我们将介绍如何在MATLAB中使用并行计算的方法,以及一些相关技巧和注意事项。
一、什么是并行计算并行计算是指将一个大任务分解为多个小任务,并同时运行这些小任务以提高计算速度的方法。
在单核处理器时代,我们只能依次执行任务,而在多核处理器或者分布式计算环境下,我们可以同时执行多个任务,从而提高计算效率。
在MATLAB中,我们可以利用并行计算工具箱(Parallel Computing Toolbox)来实现并行计算。
这个工具箱提供了一些函数和工具,可以帮助我们将任务分解为多个小任务,并将其分配到多个处理核心或者多台计算机上进行计算。
二、使用并行计算的好处使用并行计算的好处是显而易见的。
通过将任务分解为多个小任务,并同时运行这些小任务,我们可以大幅度提高计算速度,从而节省时间和资源。
这对于需要处理大量数据或者复杂计算的任务尤为重要。
此外,使用并行计算还可以提高代码的可扩展性和灵活性。
通过将任务分解为多个小任务,我们可以更好地利用计算资源,提高代码的并行性和并行效率。
这意味着我们可以轻松地将代码应用于不同规模的问题,并随着问题规模的增大而提高计算效率。
三、在MATLAB中,我们可以使用并行计算工具箱提供的函数和工具来实现并行计算。
以下是一些常用的方法:1. 使用parfor循环:parfor循环是MATLAB中的一个特殊的循环语句,用于并行执行循环体内的代码。
parfor循环与普通的for循环类似,但是它会将循环中的迭代任务分配到多个处理核心或者多台计算机上进行并行计算。
我们可以使用parfor循环来并行处理数组、矩阵等数据结构,从而提高计算效率。
2. 使用spmd语句:spmd语句是MATLAB中的一个特殊的语句,用于并行执行任务。
利用Matlab进行精确数值计算的技术方法

利用Matlab进行精确数值计算的技术方法引言随着科技的不断发展,精确数值计算在各个领域的应用越来越广泛。
而Matlab 作为一款功能强大的数值计算软件,被广泛应用于科学研究、工程设计等领域。
本文旨在介绍利用Matlab进行精确数值计算的技术方法,包括符号计算、精确数值解、误差分析等方面。
一、符号计算符号计算是指利用数学符号进行计算和推导的方法。
Matlab提供了一系列的符号计算函数,如syms、solve等,可以在计算中保留符号的精确性。
首先,需要在Matlab中定义符号变量,可以使用syms函数。
例如,定义一个符号变量x,可以写作syms x。
然后,可以使用符号变量进行计算和推导。
例如,可以使用solve函数求解方程组,利用subs函数进行代入计算等等。
符号计算在精确数值计算中具有重要意义。
它不仅可以对数学表达式进行精确求解,还可以补充数值计算的不足之处,提高计算结果的准确度。
二、精确数值解除了符号计算,Matlab还提供了精确数值解的方法。
通过使用高精度计算库或者自定义函数,可以在Matlab中进行精确数值计算。
高精度计算库可以提供更高精度的计算结果。
在Matlab中,可以通过安装并调用高精度计算库,如Symbolic Math Toolbox等,实现高精度计算。
另外,也可以通过自定义函数的方式,实现精确数值计算。
例如,可以使用矩阵乘法、多项式插值、数值积分等方法,提高计算结果的准确性。
Matlab提供了很多数值计算函数,如matmul、interp1、integral等,可以用于精确数值计算的实现。
精确数值解方法的优势在于可以在保持数值计算效率的同时,提高计算结果的精度。
通过合理选择计算方法,并结合算法优化,可以有效解决数值计算中的精度问题。
三、误差分析在精确数值计算中,误差是不可避免的。
误差分析是对计算误差进行定量分析和控制的过程。
Matlab提供了一系列的误差分析函数,如fplot、plot等,可以用于误差分析的可视化展示。
编程MATLAB程序实现复化梯形和辛普森数值积分

编程MATLAB程序实现复化梯形和辛普森数值积分MATLAB是一种高级编程语言和计算环境,适用于各种科学和工程应用。
在MATLAB中,可以使用数值积分的方法来近似计算函数的定积分。
本文将介绍如何使用MATLAB编程实现复化梯形和辛普森数值积分。
首先,我们来介绍复化梯形法。
复化梯形法是一种基本的积分数值方法,它将定积分区间等分为若干个小的子区间,然后在每个子区间上应用梯形公式进行近似计算。
下面是复化梯形法的MATLAB代码:``` matlabh=(b-a)/N;x=a:h:b;y=f(x);I = h * (sum(y) - (y(1) + y(end)) / 2);end```在上述代码中,`f`是积分的函数,`a`和`b`是积分的上下限,`N`是子区间的数量。
首先,我们计算出每个子区间的步长`h`,然后生成一个数组`x`,其中包含了每个子区间的起始点和终止点。
接下来,根据积分函数`f`计算出在每个子区间上的函数值,并将这些函数值存储在数组`y`中。
最后,使用梯形公式计算出近似积分结果`I`。
下面是使用复化梯形法进行数值积分的示例:``` matlaba=0;b = pi;N=100;disp(I);```接下来,我们来介绍辛普森法。
辛普森法是一种更精确的数值积分方法,它将定积分区间等分为若干个小的子区间,然后在每个子区间上应用辛普森公式进行近似计算。
下面是辛普森法的MATLAB代码:``` matlabh=(b-a)/(2*N);x=a:h:b;y=f(x);I = h / 3 * (y(1) + y(end) + 4 * sum(y(2:2:end-1)) + 2 * sum(y(3:2:end-2)));end```在上述代码中,`f`是积分的函数,`a`和`b`是积分的上下限,`N`是子区间的数量。
首先,我们计算出每个子区间的步长`h`,然后生成一个数组`x`,其中包含了每个子区间的起始点和终止点。
实验一信号基本运算的MATLAB实现

实验一信号基本运算的MATLAB实现MATLAB是一种用于数值计算和数据可视化的高级编程语言和环境。
它提供了丰富的函数和工具箱来处理信号。
在MATLAB中,我们可以进行一系列信号的基本运算,包括信号的加法、乘法、平移、取反等。
下面将介绍几种常见的信号基本运算的MATLAB实现方法。
1.信号的加法:信号的加法可以使用MATLAB的"+"操作符来实现。
例如,我们有两个信号x1和x2,它们的采样点分别存储在向量x1和x2中,我们可以使用以下代码将它们相加,并将结果存储在向量y中:```matlabx1=[1,2,3];x2=[4,5,6];y=x1+x2;disp(y); % 输出结果:5 7 9```2.信号的乘法:信号的乘法可以使用MATLAB的"\*"操作符来实现。
与信号的加法类似,我们可以将要相乘的信号存储在向量中,并使用"\*"操作符进行乘法运算。
例如,两个信号x1和x2的乘积可以用以下代码实现:```matlabx1=[1,2,3];x2=[4,5,6];y=x1.*x2;disp(y); % 输出结果:4 10 18```3.信号的平移:信号的平移是将信号在时间上移动一定的步长。
在MATLAB中,我们可以使用向量索引来实现信号的平移。
例如,我们有一个信号x,要将其向右平移3个单位,可以使用以下代码实现:```matlabx=[1,2,3,4,5];shift = 3;y = [zeros(1, shift), x];disp(y); % 输出结果:0 0 0 1 2 3 4 5```在上述代码中,我们使用了`zeros`函数生成了一个长度为平移步长的零向量,并将其与信号x进行拼接。
4.信号的取反:信号的取反是将信号的每个采样点的值取相反数。
在MATLAB中,我们可以使用"-"操作符来实现信号的取反。
例如,我们有一个信号x,要将其取反,可以使用以下代码实现:```matlabx=[1,-2,3,-4,5];y=-x;disp(y); % 输出结果:-1 2 -3 4 -5```在上述代码中,我们使用了"-"操作符来实现信号的取反。
matlab function实现pi运算

matlab function实现pi运算如何用Matlab实现pi的计算在科学计算中,π(pi)是一个非常重要的数学常数。
它代表了一个圆的周长与其直径之间的比例关系。
不同的领域,如数学、物理、工程等,经常需要使用到π。
Matlab是一款功能强大的科学计算软件,我们可以利用其编程能力来实现π的计算。
本文将一步一步地介绍如何使用Matlab来编写一个计算π的函数。
步骤一:了解π的计算方法计算π的方法有很多种,其中一种著名的方法是蒙特卡洛方法。
该方法基于随机抽样,利用圆的特性进行估算。
我们首先在一个正方形内随机生成大量的点,然后计算这些点落在圆内的比例。
通过该比例乘以正方形的面积,我们就可以估算出圆的面积,从而得到π的近似值。
步骤二:编写Matlab函数首先,我们需要定义一个函数来实现π的计算。
打开Matlab编辑器,并创建一个新的函数文件pi_calculation.m。
接下来,我们将在函数内部编写代码。
步骤三:生成随机点我们可以使用Matlab的rand函数来生成随机的x和y坐标。
由于我们只需要在正方形内生成点,所以我们可以将随机数限制在[0,1]之间。
为了方便起见,我们可以一次性生成大量的点,而不是逐个生成。
matlabfunction pi_value = pi_calculation(num_points)% Generate random pointspoints = rand(num_points, 2);end步骤四:计算落在圆内的点接下来,我们需要判断这些随机生成的点是否落在圆内。
根据圆的特性,我们可以通过判断点到原点的距离是否小于半径来判断点是否在圆内。
matlab% Count points inside the circlecount_inside = sum(points(:, 1).^2 + points(:, 2).^2 < 1);步骤五:计算π的近似值通过计算落在圆内的点的个数,我们可以得到圆的面积的近似值。
matlab单个矩阵的每个元素进行计算方法

matlab单个矩阵的每个元素进行计算方法在MATLAB中,可以使用多种方法对单个矩阵的每个元素进行计算。
下面将介绍一些常见的方法。
1. 使用循环:使用for循环可以遍历矩阵的每个元素,并对其进行计算。
例如,假设我们有一个矩阵A,我们希望将其每个元素都平方,并保存到另一个矩阵B 中。
可以使用以下代码实现:```matlabA = [1 2; 3 4];B = zeros(size(A)); % 创建一个与A相同大小的全零矩阵for i = 1:size(A, 1) % 遍历行for j = 1:size(A, 2) % 遍历列B(i, j) = A(i, j)^2; % 对每个元素进行平方操作endenddisp(B);```2. 利用向量化操作:MATLAB是一种向量化操作非常高效的语言,使用向量化操作可以大大提高计算的效率。
对于单个矩阵的每个元素计算,可以直接对整个矩阵进行操作,而无需循环。
例如,我们仍然使用矩阵A,将其每个元素平方,并保存到矩阵B中,可以使用以下代码实现:```matlabA = [1 2; 3 4];B = A.^2; % 对矩阵A的每个元素进行平方操作disp(B);```3. 使用MATLAB函数:MATLAB提供了许多功能强大的函数来进行矩阵运算。
这些函数可以直接对单个矩阵的每个元素进行计算。
例如,如果我们希望计算矩阵A中每个元素的绝对值,可以使用abs函数:```matlabA = [1 -2; -3 4];B = abs(A); % 对矩阵A的每个元素取绝对值disp(B);```总结:MATLAB提供了多种方法来对单个矩阵的每个元素进行计算。
使用循环、向量化操作或利用MATLAB函数,可以根据具体的需求选择适合的方法来处理矩阵数据。
matlab的迭代法编程

matlab的迭代法编程迭代法是一种常用的解决数值计算问题的方法, 在MATLAB中也有相应的编程实现。
本文将介绍如何使用MATLAB实现迭代法来解决数值计算问题。
一、迭代法简介迭代法是通过反复迭代计算来逼近问题的解的一种方法。
它适用于无法直接求得解析解的问题,但可以通过一系列近似的计算逐步逼近真实解。
二、基本思想迭代法的基本思想是通过不断迭代,逐步逼近问题的解。
假设我们要求解一个方程 f(x)=0 的根,可以从一个初始值开始,通过迭代计算逐步逼近真实解。
三、MATLAB的迭代法编程实现在MATLAB中,可以使用循环语句结合适当的迭代公式来实现迭代法。
首先,我们需要确定迭代的终止条件。
通常可以使用误差判定条件来进行终止判断,比如当迭代结果的相对误差小于某一阈值时,可以认为迭代已经达到了足够的精度。
然后,我们可以使用循环语句(如for循环或while循环)来进行迭代计算。
在每次迭代中,根据迭代公式更新迭代结果,并进行误差判定。
最后,当满足终止条件时,迭代停止,并返回最终的迭代结果作为近似解。
下面是一个简单的例子,演示了如何使用MATLAB实现牛顿迭代法求解方程的根。
```matlabfunction x = Newton_method(f, df, x0, epsilon, max_iter)for i = 1:max_iterx = x0 - f(x0)/df(x0);if abs(f(x)) < epsilonreturn;endx0 = x;enderror('迭代次数超过上限');end```在上述代码中,函数`Newton_method`用于实现牛顿迭代法。
其中,`f`代表方程函数,`df`代表方程函数的导数,`x0`是初始点的值,`epsilon`是误差判定的阈值,`max_iter`是最大迭代次数。
四、迭代法的应用迭代法在数值计算中有广泛的应用。
它可以用于求解非线性方程的根、线性方程组的解、优化问题的最优解等等。
matlab矩阵的n次方的计算程序

文章标题:深度解析:如何编写高效的Matlab矩阵的n次方计算程序在现代科学和工程领域,矩阵的n次方计算是一个频繁出现的问题。
无论是在数学建模、信号处理、图像处理还是优化问题中,都离不开对矩阵的高效运算。
在Matlab中,作为最常用的科学计算软件之一,我们经常需要编写高效的矩阵的n次方计算程序来提高计算效率。
1. 背景介绍矩阵的n次方计算是指将一个矩阵自乘n次,即A^n。
而在Matlab 中,有多种计算矩阵的n次方的方法,包括直接计算、对角化和特征值分解等。
然而,不同的方法在不同的情况下都有其适用性和性能差异。
2. 直接计算法直接计算法是指通过循环将矩阵连乘n次来得到矩阵的n次方。
这种方法简单直接,但在n较大时计算量会很大,效率不高。
3. 对角化法对角化法是将矩阵对角化,然后计算对角矩阵的n次方,最后再将结果反变换回原矩阵。
这种方法适用于对角化后易于计算的情况,但对于一般矩阵来说,可能会增加计算复杂度。
4. 特征值分解特征值分解是将矩阵分解为特征向量和特征值的形式,然后通过特征值的幂计算矩阵的n次方。
这种方法适用于稀疏矩阵和大规模矩阵,但在实际应用中可能会受到精度问题的影响。
5. 个人观点和理解在实际编写Matlab矩阵的n次方计算程序时,我倾向于综合利用直接计算、对角化和特征值分解等方法,根据矩阵的特点和应用的情况选择最合适的计算方式。
并且,我会结合Matlab提供的优化工具和并行计算技术,提高程序的效率和性能。
总结回顾编写高效的Matlab矩阵的n次方计算程序需要综合考虑计算方法的适用性和性能,灵活选择合适的计算方式,并利用Matlab的优化和并行计算技术来提高程序的效率。
通过深入理解矩阵的特性和应用背景,我们可以更好地编写高质量的n次方计算程序,提高程序的性能和可维护性。
以上就是针对Matlab矩阵的n次方计算程序的全面解析,希望对您有所帮助。
在实际科学和工程应用中,矩阵的n次方计算是一项非常重要的任务。
如何利用Matlab进行机器学习算法实现

如何利用Matlab进行机器学习算法实现引言:机器学习在当今科技发展中占据了重要的地位,它为我们提供了解决复杂问题的有效工具。
而Matlab是一种功能强大的计算平台,它不仅为我们提供了丰富的数学函数库和数据处理工具,还集成了大量的机器学习算法。
本文将介绍如何使用Matlab实现机器学习算法,并提供一些实用的示例。
一、Matlab环境搭建在开始之前,我们需要确保已经正确安装了Matlab软件,并且熟悉Matlab的基本操作。
安装Matlab非常简单,官方网站提供了详细的安装步骤,用户可以根据自己的操作系统进行下载和安装。
安装完成后,打开Matlab,我们就可以开始进行机器学习算法的实现。
二、数据准备与探索在进行机器学习算法实现之前,我们需要准备相应的数据集,并对数据进行探索。
Matlab提供了丰富的数据导入和预处理函数,可以方便地读取和处理不同类型的数据格式,如CSV、Excel、文本文件等。
在处理数据之前,我们可以使用Matlab的数据可视化工具来直观地了解数据的分布和特征。
例如,通过绘制散点图、直方图和箱线图等,我们可以观察数据是否存在异常值、缺失值或者不平衡问题,从而采取相应的处理措施。
三、特征工程在机器学习任务中,特征工程是非常重要的一环。
通过合理的特征选择和特征提取,可以显著提高模型的性能。
Matlab提供了丰富的特征工程函数和工具箱,例如特征选择、主成分分析、离散化和标准化等。
通过这些函数和工具箱,我们可以根据数据的特点和问题的需求,灵活地进行特征处理和转换。
四、模型选择与训练在特征工程完成之后,我们需要选择合适的机器学习模型,并进行模型的训练和调优。
Matlab中集成了许多常见的机器学习算法,如线性回归、逻辑回归、支持向量机、决策树、随机森林等。
我们可以根据具体任务的要求,选择适合的模型进行训练。
在训练模型之前,我们需要将数据集划分为训练集和测试集,并采用交叉验证的方法来评估模型的性能。
matlab用牛顿柯特斯公式计算积分

牛顿-柯特斯公式是数值分析中常用的积分计算方法,特别适用于对函数在一定区间上的定积分进行近似计算。
在MATLAB中,我们可以利用牛顿-柯特斯公式来进行积分计算,从而获得函数在给定区间上的近似积分值。
让我们来理解一下牛顿-柯特斯公式的基本原理。
牛顿-柯特斯公式的核心思想是利用一系列的节点和相应的权重来逼近被积函数,从而得到积分的近似值。
在MATLAB中,我们可以通过内置的函数或自定义函数来实现牛顿-柯特斯公式的计算。
在使用MATLAB计算积分时,我们首先需要确定被积函数的表达式以及积分的区间。
我们可以选择合适的牛顿-柯特斯公式来进行计算。
MATLAB提供了多种内置的积分计算函数,例如quad和integral等,它们可以方便地实现对定积分的计算。
除了使用内置函数,我们还可以编写自定义的牛顿-柯特斯公式计算程序。
这样可以更灵活地控制节点和权重的选择,从而得到更精确的积分近似值。
编写自定义的牛顿-柯特斯公式计算程序可以加深对该方法的理解,并且在特定问题上可能获得更好的计算结果。
在实际应用中,牛顿-柯特斯公式可以广泛用于工程、科学和数学等领域。
在信号处理中,我们可以利用牛顿-柯特斯公式对信号的频谱进行积分近似计算;在物理学中,我们可以利用牛顿-柯特斯公式对连续介质的密度分布进行积分近似计算。
牛顿-柯特斯公式的灵活性和高效性使得它成为了数值分析中不可或缺的工具。
回顾本文,我们首先介绍了牛顿-柯特斯公式的基本原理,然后讨论了在MATLAB中如何利用内置函数或自定义函数来实现积分的计算。
我们还探讨了牛顿-柯特斯公式在实际应用中的广泛性和重要性。
通过本文的阐述,我们希望读者能够更深入地理解牛顿-柯特斯公式的计算方法,并且能够灵活运用于自己的问题当中。
在个人观点和理解方面,我认为牛顿-柯特斯公式作为一种数值积分计算方法,具有较高的精度和灵活性,能够有效地解决实际问题中的积分计算需求。
在MATLAB中,利用牛顿-柯特斯公式进行积分计算不仅简单方便,而且还能获得较为准确的结果。
matlab平方运算

matlab平方运算在Matlab中,平方运算可以通过使用乘法操作符或使用内置的power函数来实现。
下面是有关Matlab平方运算的参考内容。
Matlab中的平方运算可以通过使用乘法操作符“*”来实现。
例如,要计算一个数的平方,可以将该数与其自身相乘,如下所示:```matlabx = 5;y = x * x;disp(y);```这将输出25,表示5的平方。
此外,Matlab还提供了一个内置的power函数来进行平方运算。
这个函数的语法是power(base, exponent),其中base是要平方的数,exponent是要提升的幂次。
例如,要计算一个数的平方,可以像下面这样使用power函数:```matlabx = 5;y = power(x, 2);disp(y);```这将输出25,与上面使用乘法操作符的结果相同。
除了计算一个数的平方,Matlab还提供了矩阵的平方运算。
对于一个矩阵A,它的平方定义为A乘以A的转置。
在Matlab中,可以使用乘法操作符或内置的mtimes函数来实现矩阵的平方运算。
例如,假设有一个2x2的矩阵A:```matlabA = [1, 2; 3, 4];B = A * A';disp(B);```这将输出:```5 1111 25```这是矩阵A的平方。
除了上述方法,还可以使用element-wise的操作符‘.^’进行平方运算。
对于矩阵和向量,该操作符对每个元素进行平方。
例如,要计算一个向量中每个元素的平方,可以像下面这样使用element-wise的操作符:```matlabx = [1, 2, 3];y = x.^2;disp(y);```这将输出:```1 4 9```这是向量x的每个元素的平方。
在Matlab中,平方运算还可以应用于复数。
对于一个复数z=a+bi,它的平方定义为(a+bi)^2 = (a^2 - b^2) + 2abi。
Matlab 提供了一些内置函数来实现复数的平方运算,例如abs和imag。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
误差基础% ex01.mclear;digit = 3;S0 = log(6)-log(5);S0 = vpa(S0,digit);S(1) = 1 - 5*S0;S0 = vpa(S(1),digit);for n = 2 : 8S(n) = 1/n - 5*S(n-1);S(n) = vpa(S(n),digit);endS=double(S);fprintf(' S0 = %11f\n',double(S0)); for n=1:8fprintf(' S%1d = %11f\n',n,S(n)); end____________________________% ex02.mclear;digit = 3;S(8) = (1/45 + 1/54)/2;S(8) = vpa(S(8),digit);for n = 7 : -1: 1S(n) = 1/(5*(n+1)) - S(n+1)/5;S(n) = vpa(S(n),digit);endS0 = 1/5 - S(1)/5;S0 = vpa(S0,digit);S=double(S);fprintf(' S0 = %11f\n',double(S0)); for n=1:8fprintf(' S%1d = %11f\n',n,S(n)); end_________________________________________ %ex03.mclear;disp(' 用单精度计算 10^8+1');result = single(1e8 + 1);fprintf(' 10^8+1 = %f\n', result);fprintf('\n press any key to continue ... \n'); pause;disp(' 计算 1 + 2 + ... + 40 + 10^9')result = 0;for k = 1 : 40result = single(result + k);endresult = single(result+1e9);fprintf(' 1 + 2 + ... + 40 + 10^9 = %f\n', result);fprintf('\n press any key to continue ... \n'); pause;disp(' 计算 10^9 + 1 + 2 + ... + 40')result = 1e9;for k = 1 : 40result = single(result + k);endfprintf(' 10^8 + 1 + 2 + ... + 40 = %f\n', result);________________________________________________________________ lagrange插值% textbook page 35function yh = lagrange(x,y,xh)n = length(x);m = length(xh);x = reshape(x,n,1); % x = x(:);y = reshape(y,n,1); % y = y(:);xh = reshape(xh,m,1); % xh = xh(:);yh = zeros(m,1);c1 = ones(1,n-1);c2 = ones(m,1);for i=1:n,xp = x([1:i-1,i+1:n]);yh = yh + y(i) * prod((xh*c1-c2*xp')./(c2*(x(i)*c1-xp')),2); end__________________________________________% Lagrange interpolation 1function yh = mylagrange1(x,y,xh)n = length(x)-1;x = reshape(x,1,n+1);y = reshape(y,1,n+1);yh = 0;for j = 0 : nxp = x([1:j, j+2:n+1]);yh = yh + y(j+1) * prod((xh - xp)./(x(j+1) - xp));end_______________________________________% Lagrange interpolation 2function yh = mylagrange1(x,y,xh)% xh can be a vectorn = length(x)-1;m = length(xh);x = reshape(x,1,n+1);y = reshape(y,1,n+1);xh = reshape(xh,m,1);yh = zeros(m,1);for j = 0 : nxp = x([1:j, j+2:n+1]);tmp = (xh*ones(1,n)-ones(m,1)*xp)./(ones(m,1)*(x(j+1) - xp)); yh = yh + y(j+1)*prod(tmp,2);end____________________________________newton插值function [p,q] = chashang(x,y)n = length(x);x = reshape(x,n,1);p(:,1) = x;p(:,2) = reshape(y,n,1);for j = 3: n+1p(1:n+2-j,j) = diff(p(1:n+3-j,j-1)) ./ (x(j-1:n)-x(1:n+2-j)); endq = p(1,2:n+1)';____________________________________________function yh = newton(x,y,xh)[p,q] = chashang(x,y);n = length(x);m = length(xh);x = reshape(x,1,n);xh = reshape(xh,m,1);xh = xh*ones(1,n) - ones(m,1)*x;xh = xh';yh = y(1)*ones(1,m);for i = 2 : nyh = yh + q(i)*prod(xh(1:i-1,:),1);end___________________________________-三次样条插值和Matlab 插值函数介绍% textbook page 47clear;close all;clc;xh = [-5:1/4:5];yt = 1./(1+xh.^2); % true solutionplot(xh,yt,'k','linewidth',2);axis([-5 5, -0.5 2.5]);hold on;color={'r','b','g'};nn = [2 5 10];for k = 1:length(nn)n = nn(k);x = [-5:10/n:5];y = 1./(1+x.^2);yh = lagrange(x,y,xh); % Lagrange interpolationpauseplot(xh,yh,color{k},'linewidth',2);endhold off;_____________________________________________________% 比较 f(x)=1/(1+x^2) 的各种插值函数clear;close all;a = -5;b = 5; % 给定插值区间n = 10; h = (b-a)/n; % 计算步长(等距节点个数为 n+1)x = [a:(b-a)/n:b]; y = 1./(1+x.^2); % 计算节点和函数值xh = [a:(b-a)/40:b]; % 插值点% 首先画出原函数图形yh1 = 1./(1+xh.^2); % true solutionplot(xh,yh1,'k.-','linewidth',1.5);axis([a, b, -0.5 2.5]);hold on;% 10 次 Lagrnage 插值yh2 = lagrange(x,y,xh); % 由于 Lagrange 插值不稳定,系统不提供该函数plot(xh,yh2,'b+-','linewidth',1.5);% 3 次样条插值df = diff('1/(1+x^2)','x');df0 = subs(df,'x',-5); dfn = subs(df,'x',5); % 计算第一类边界条件yh3 = spline(x,[df0 y dfn], xh);plot(xh, yh3, 'ro-', 'linewidth',1.5);% 线性插值yh4 = interp1(x,y,xh);plot(xh, yh4, 'gd-', 'linewidth',1.5);legend('原函数图形','10次Lagrange插值', ...'三次样条插值','线性插值');plot(x,y,'s','linewidth',2); % 画出点 (xi,f(xi))hold off;______________________________% myspline02.mclear;a = -5;b = 5;n = 40; h = (b-a)/n;xh = [a:h:b];syms xfx = (x^2+1)^(-1);dfx = diff(fx);dfa = subs(dfx,'x',a);dfb = subs(dfx,'x',b);yh = subs(fx,'x',xh);mu = ones(1,n-1)/2;lambda = ones(1,n-1)/2;[p,q] = chashang(xh,yh);d = zeros(n+1,1);d(2:n) = 6*p(1:n-1,4);d(1) = 6*(p(1,3) - dfa)/h;d(n+1) = 6*(dfb - p(n,3))/h;A = diag(2*ones(1,n+1)) + diag([mu,1],-1) + diag([1,lambda],1); M = A\d;a3 = (M(2:n+1)-M(1:n))/(6*h);a2 = M(1:n)/2;a1 = (yh(2:n+1) - yh(1:n))'/h - h*(M(2:n+1) +2*M(1:n))/6;a0 = yh(1:n)';pp = spline(xh,[dfa yh dfb]);[breaks,coefs,npolys,ncoefs,dim] = unmkpp(pp);fprintf('\n err_a3=%f, err_a2=%f, err_a1=%f, err_a0=%f\n', ...norm(a3-coefs(:,1)), norm(a2-coefs(:,2)), ...norm(a1-coefs(:,3)), norm(a0-coefs(:,4)));% plot the figuresnp = 3;n0 = np*n; h = (b-a)/n0;xh0 = [a:h:b]; len = length(xh0);xh =xh(1:n)';for k = 1 : npindex = [k:np:len];index = index(1:n);xht = xh0(index)';yht = a3.*(xht-xh).^3 + a2.*(xht-xh).^2 + a1.*(xht-xh) + a0; yh0(index) = yht;endyh0(n0+1) = yh(n+1);yh1 = subs(fx,'x',xh0);plot(xh0,yh1,'b.-',xh0,yh0,'ro-')___________________________________________________内积和正交多项式% Legendre 多项式clear;close all;x = [-1:0.05:1];n = 6;p(1,:) = ones(1,length(x));p(2,:) = x;for k = 2 : np(k+1,:) = (2*(k-1)+1)* x .* p(k,:) - (k-1)*p(k-1,:);p(k+1,:) = p(k+1,:)/k;endplot(x,p(1,:),'b-','linewidth',2);axis([-1 1 -1 1]); box off;set(gca,'xcolor',[1,0.0,0.0],'ycolor',[1,0.0,0.0])shg; hold on; pause;for k = 2 : n+1plot(x,p(k,:),'linewidth',1.5);shg; hold on; pause;endhold off;___________________________________________________% Chebyshev 多项式clear;close all;x = [-1:0.05:1];n = 6;p(1,:) = ones(1,length(x));p(2,:) = x;for k = 2 : np(k+1,:) = 2 * x .* p(k,:) - p(k-1,:);endplot(x,p(1,:),'b-','linewidth',2);axis([-1 1 -1 1]); box off;set(gca,'xcolor',[1,0.0,0.0],'ycolor',[1,0.0,0.0])shg; hold on; pause;for k = 2 : n+1plot(x,p(k,:),'linewidth',1.5);shg; hold on; pause;endhold off;_______________________________________最佳一致逼近与切比雪夫展开% 计算最佳一次逼近多项式% 教材第 70 页clear; close all;a=0; b=1;fx = sym('sqrt(1+x^2)'); % f(x)dfx = diff(fx); % f'(x)fa = subs(fx,'x',a); % f(x)fb = subs(fx,'x',b); % f(b)a1 = (fb - fa)/(b-a);% 用 fzero 计算 f'(x)-a1 在 [a,b] 内的根。
