六年级奥数专项训练系列(一)
六年级奥数专项训练知识分享

小学六年级奥数练习(一)一、定义新运算练习1. 设)。
)(求(5101225,213**⨯-=*b a b a 2.)。
(。
求)(是两个数,规定:、设35302q p p q p q p 2∆∆⨯-+=∆3.412010M N N M N M N M -*+=*,求是两个数,规定、设。
4.=*÷*=*=*=*)(),那么(如果623644413,43312,32112 5.==⊗+++++=⊗++=⊗+=⊗x 543x ,109876565.........43232 ,2121中,在,,如果 6..8946b)-a b)a b -a 2:""b a ∆+∆⨯+=∆∆,求((定义新运算和对两个整数b a 一、定义新运算1、规定a*b=(b +a)×b ,求(2*3)*5。
2、定义运算“△”如下:对于两个自然数a 和b ,它们的最大公约数与最小公倍数的和记为a △b 。
例如: 4 △ 6=(4,6)+[4,6]=2+12=14。
根据上面定义的运算, 18△12等于几?4、对于数 a ,b ,c ,d ,规定〈a ,b ,c ,d 〉=2ab-c +d 。
已知〈1,3,5,x 〉=7,求x 的值。
5、规定: 6* 2=6+66=72,2*3=2+22+222=246,1*4=1+11+111+1111=1234。
求7*5。
6、如果a △b 表示(a-2)×b ,例如:3△4=(3-2)×4=4,那么当( a △2)△3=12时,a 等于几?7、对于任意的两个自然数a 和b ,规定新运算“*”:a*b =a(a +1)(a +2)…(a +b-1)。
如果(x*3)*2=3660,那么x 等于几?简便运算(一)75.0137341413713-⎪⎭⎫ ⎝⎛+- 125.22017687715.14-⎪⎭⎫ ⎝⎛--54211%1254115.3÷++⨯ 75.97643925.0975-⨯+⨯60125.4425529÷+⨯ 7.21111.07.09999.0⨯+⨯6.375.108.245⨯+⨯ 7786.21.1152⨯+⨯8.562.108.148⨯+⨯ 6.738.109.272⨯-⨯2.33.198.168.6⨯+⨯ 1381137138137139⨯+⨯6.53.458.574.4⨯+⨯5.465.782.435.533.355.53⨯+⨯+⨯ 3.541352.422351.12235⨯-⨯+⨯5.622.1657308373575.3⨯+⨯-⨯假设法解题练习1.兄弟俩养鸡100只。
(完整版)六年级奥数练习(阴影面积)1
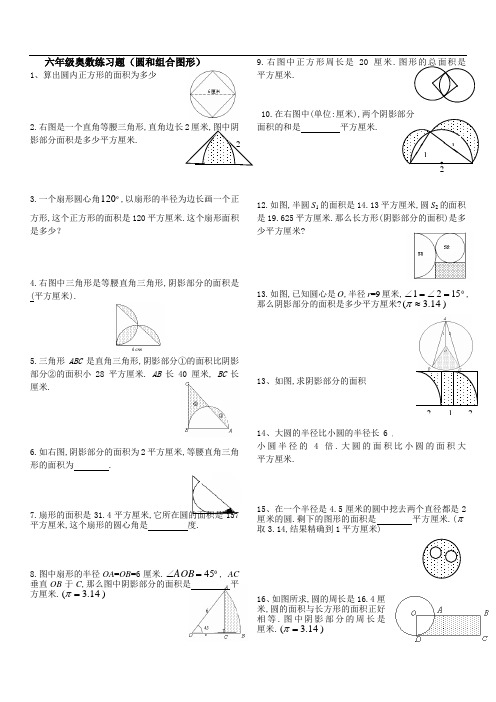
六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少 2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米. 3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少? 4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米. 10.在右图中(单位:厘米),两个阴影部分 面积的和是 平方厘米.12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π2 1 2112217.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
六年级奥数专题-转化单位“1”

六年级奥数专题-转化单位“1”转化单位“1”(一)专题简析:把不同的数量当作单位“1”,得到的分率可以在一定的条件下转化。
如果甲是乙的a b ,乙是丙的c d ,则甲是丙的ac bd ;如果甲是乙的a b ,则乙是甲的ba ;如果甲的a b 等于乙的c d ,则甲是乙的c d ÷a b =bc ad ,乙是甲的a b ÷a b =adbc 。
例题1。
乙数是甲数的23 ,丙数是乙数的45 ,丙数是甲数的几分之几?23 ×45 =815练习11. 乙数是甲数的34 ,丙数是乙数的35,丙数是甲数的几分之几?2. 一根管子,第一次截去全长的14 ,第二次截去余下的12 ,两次共截去全长的几分之几?3. 一个旅客从甲城坐火车到乙城,火车行了全程的一半时旅客睡着了。
他醒来时,发现剩下的路程是他睡着前所行路程的14 。
想一想,剩下的路程是全程的几分之几?他睡着时火车行了全程的几分之几?练1 1、 =920 2、 =58 3、 =18 =38例题2。
修一条8000米的水渠,第一周修了全长的14 ,第二周修的相当于第一周的45 ,第二周修了多少米?解一:8000×14 ×45 =1600(米)解二:8000×(14 ×45 )=1600(米)答:第二周修了1600米。
练习2用两种方法解答下面各题:1. 一堆黄沙30吨,第一次用去总数的15 ,第二次用去的是第一次的114倍,第二次用去黄沙多少吨?2. 大象可活80年,马的寿命是大象的12 ,长颈鹿的寿命是马的78,长颈鹿可活多少年?3. 仓库里有化肥30吨,第一次取出总数的15 ,第二次取出余下的13 ,第二次取出多少吨?练2 1、 =7.5(吨) 2、 =35(年) 3、 =8吨例题3。
晶晶三天看完一本书,第一天看了全书的14 ,第二天看了余下的25 ,第二天比第一天多看了15页,这本书共有多少页?解: 15÷【(1-14 )×25 - 14 】=300(页)答:这本书有300页。
六年级奥数题(一)

一、分数的巧算(一) 年级 班 姓名 得分一、填空题1.计算:=÷-⨯+⨯2582.432.02588.6 . 2.=⨯÷⎪⎭⎫ ⎝⎛++1919989898199800980019001900980980190190989898191919 . 3.1000减去它的一半,再减去余下的三分之一,再减去余下的四分之一,依此下去,直到余下的五百分之一,最后剩下 .4.计算:=⨯+⋅⋅⋅+⨯+⨯+⨯100991431321211 . 5.计算:=+++++++496124811241621311814121 . 6.计算:=+--+3121131211 . 7.计算:=⨯+⨯+⨯655161544151433141 . 8.计算:=++⋅⋅⋅+++++⋅⋅⋅+++199719953991199619943989537425313199719961995199619951994543432321 . 9.计算:=⎪⎭⎫ ⎝⎛-⨯-⎪⎭⎫ ⎝⎛+⨯+⎪⎭⎫ ⎝⎛-⨯761231537615312353123176 . 10.计算:⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛+++20115110151161121814112191613181614121 = .二、解答题11.尽可能化简427863887116690151. 12.计算:⎪⎭⎫ ⎝⎛+⋅⋅⋅+-+-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛-+914637281941322314312213211211. 13.计算:1999321132112111+⋅⋅⋅++++⋅⋅⋅++++++. 14.计算: ⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-9997319896317531643153314231.———————————————答 案—————————————————————— 1. 513. 原式()12.48.62582582.42582588.6-+=-⨯+⨯= 51351610258==⨯=. 2. 19915. 原式101191019898191000198001000119001001980100119010101981010119⨯⨯⨯÷⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯= 19981998981998199819⨯⨯⎪⎭⎫ ⎝⎛++= 19915192941998199898193==⨯⨯⨯=.3. 2 1000减去它的一半,余下⎪⎭⎫ ⎝⎛-⨯2111000,再减去余下的31, 余下⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯3112111000,再减去余下的41, 余下⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯4113112111000,…,直到减去余下的五百分之一,最后剩下: ⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯500114113112111000 5004994332211000⨯⋅⋅⋅⨯⨯⨯⨯= 2=4. 10099. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=100199199198141313121211 1009910011=-=. 5. 1615. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=124162162131131181414121211 ⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+4961248124811241 4961311311811-++-= 163131187161231187⨯+=⎪⎭⎫ ⎝⎛-⨯+=161516187=+=. 6. 542. 原式5425144758745873153116311631==⨯==-+=+--+=.7. 123. 原式655660544550433440⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛+= 123150140130=+++++=.8. 21. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=19972399219962399052842632419971199619961199551441331221=.9. 1原式=()()()532376123765315376231+⨯+-⨯--⨯ 1111=+-=. 10. 14465. 原式⎪⎭⎫ ⎝⎛+++⨯-⎪⎭⎫ ⎝⎛+++⨯+⎪⎭⎫ ⎝⎛+++⨯-⎪⎭⎫ ⎝⎛+++⨯=413121151413121141413121131413121121 ⎪⎭⎫ ⎝⎛-+-⨯⎪⎭⎫ ⎝⎛+++=514131214131211 1446560131225201611234612=⨯=⎪⎭⎫ ⎝⎛+⨯+++=.11. 分子数字之和等于30,故它可以被3整除,分母奇位上数字之和与偶位上数字之和的差为32-21=11,所以它可以被11整除,把这此因数提出,得:1131138896717338896717=⨯⨯.12.原式=⎪⎭⎫ ⎝⎛+⋅⋅⋅++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⎪⎭⎫ ⎝⎛+⋅⋅⋅++-⎪⎭⎫ ⎝⎛+⋅⋅⋅++++4642413732312822211914131211 91828173727164636261555251+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++ 9183761061265512764128731298212109+-+⨯-⨯⨯+⨯⨯-⨯⨯+⨯⨯-⨯=9183763534213281845+-+-+-+-=91837641532730+-+-+= 504533=.13.因为2)1(21+=+⋅⋅⋅++n n n ,所以 原式=200019992432322212⨯+⋅⋅⋅+⨯+⨯+⨯ ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=2000119991413131212112 100099912000112=⎥⎦⎤⎢⎣⎡-=.14.因为()()()()()()()()()11311131111312+---=+--+-=+--K K K K K K K K K ()()()()()()112211222+-+-=+--=K K K K K K K ,所以 原式()()()()()()()()()()()()()()()()()()()()198198298298197197297297151525251414242413132323+-+-⨯+-+-⨯⋅⋅⋅⨯+-+-⨯+-+-⨯+-+-= 99971009698969995647353624251⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⨯⨯⨯=97259710041=⨯=.一、分数的巧算(二) 年级 班 姓名 得分一、填空题1.计算:13471711613122374⨯+⨯+⨯= . 2.计算:⎪⎭⎫ ⎝⎛⨯+÷⨯⎪⎭⎫ ⎝⎛+-25.1522546.79428.0955= . 3.计算:25114373611125373185444.4⨯+÷+÷= . 4.计算:()()015.06.32065.022.0013.000325.0⨯÷-÷= . 5.计算:⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛+⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+9115113111011611411211= . 6.计算:222345567566345567+⨯⨯+= . 7.计算:322131433141544151655161766171⨯+⨯+⨯+⨯+⨯= . 8.计算:4513612812111511016131+++++++= . 9.计算:()()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⋅⋅⋅⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⋅⋅⋅⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++293112831133112311311312913029132912291291= . 10.计算:217665544332217665544332212⨯⎪⎭⎫ ⎝⎛++++++⎪⎭⎫ ⎝⎛+++++ ⎪⎭⎫ ⎝⎛++++⨯⎪⎭⎫ ⎝⎛++++++-76655443327665544332211= .二、问答题11.用简便方法计算:421330112091276523-+-+-.12.计算:()1999119981997199919985.19935.1995÷⨯÷-.(得数保留三位小数) 13.计算:⋅⋅⋅+++⋅⋅⋅+++++++++1999219991313233323121222111 1999119992199919981999199919991998++⋅⋅⋅++++. 14.计算:299810001299799912001312000211999111999119981199714131211++++⋅⋅⋅+++++++-+⋅⋅⋅+-+-.———————————————答 案——————————————————————1. 16 原式162874131413122374=⨯=⎪⎭⎫ ⎝⎛++⨯=.2. 90 原式⎪⎭⎫ ⎝⎛⨯+⨯⨯⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+=45522455378.0942955 ()⎪⎭⎫ ⎝⎛+⨯⨯-=522537458.08 90457210452.7=⨯=⨯⨯=.3. 9. 原式25114373625114373137825114⨯+⨯+⨯= ⎪⎭⎫ ⎝⎛++⨯=37363731378251149377525114=⨯=.4. 1 原式1100131351536325=⨯⨯⨯⨯=.5. 1.1 原式1.110119854321011674523==⨯⋅⋅⋅⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯=6. 1.原式()2223455663455663455672223451566566345567++⨯⨯+=+⨯+⨯+=1567566345566345567=+⨯⨯+=.7. 205. 原式322330433440544550655660766770⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛+= 205120130140150160=+++++++++=.8. 54 原式1092542432322⨯+⋅⋅⋅+⨯+⨯+⨯= ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=101915141413131212 54101212=⎪⎭⎫ ⎝⎛-=.9. 1. 原式2960285933423313231603059332231130⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯= 13130321605934333229283216059323130=⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯=. 10.21. 令a =+++++766554433221,则 原式⎪⎭⎫ ⎝⎛-⨯+-⨯+=21)1(212a a a a222222=⎪⎭ ⎝-+-+=a a a a .11. 原式767665655454434332322121⨯+-⨯++⨯+-⨯++⨯+-⨯+= ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=71616151514141313121211 76711=-=.12. 原式199919981200019982⨯⎪⎭⎫ ⎝⎛-⨯= 199811998199824000+⨯⎪⎭⎫ ⎝⎛-= ⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛-=199811199824000 1998199821998240004000⨯--+= 1998199821998224000⨯-++= 001.4002≈.13. 因为kk k k k k k k k k k k k k k -+⋅⋅⋅+++=+++⋅⋅⋅+-++-+⋅⋅⋅+++)321(212311321 k kk k k =-+=)1(,所以, 原式19990002200019991999321=÷⨯=+⋅⋅⋅+++=. 14. 分子⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⨯-⎪⎭⎫ ⎝⎛+++⋅⋅⋅++++=1998161412121999119981199714131211 ⎪⎭⎫ ⎝⎛+⋅⋅⋅+++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++=9991312111999131211 199911001110001+⋅⋅⋅++= 分母3998139961200412002120001++⋅⋅⋅+++=⎪⎭ ⎝+⋅⋅⋅++⨯=1999100110002 原式211999110011100012199911001110001=⎪⎭⎫ ⎝⎛+⋅⋅⋅++⨯+⋅⋅⋅++=.二、估计与估算(一)年级 班 姓名 得分 一、填空题1.有若干个小朋友,他们的年龄各不相同.将他们的年龄分别填入下式的□中,都能使不等式成立.这些小朋友最多有 个. 215<43.2.010000000009999999999100099910099109+⋅⋅⋅⋅⋅⋅+++的整数部分是 .3.10971939719297199719⨯+⋅⋅⋅+⨯+⨯+=A ,与A 最接近的整数是 .4.有24个偶数的平均数,如果保留一位小数的得数是15.9,那么保留两位小数的得数是 .5.1995003这个数,最多可以拆成 个不同的自然数相加的和.6.有一列数,第一个数是105,第二个数是85,从第三个数开始,每个数都是它前面两个数的平均数.那么第19个数的整数部分是 .7.有一长3米的线段,第一次把这条线段三等分后去掉中间一部分,第二次再把剩下的两线段中的每一段都三等分后都去掉中间一部分,第三次再把剩下的所有线段的每一段都三等分后都去掉中间一部分.继续这一过程,这样至少连续 次后,才使剩下的所有线段的长度的和小于0.4米.8.已知199711982119811198011+⋅⋅⋅+++=S ,那么S 的整数部分是 .9.1009987654321⨯⋅⋅⋅⨯⨯⨯⨯与101相比较,较大的哪个数是 .10.某工厂有三个车间,共有75人报名参加冬季长跑,其中第一车间人数最多,第三车间人数最少.如果第一车间报名人数是第三车间报名人数的212倍,那么第二车间报名人数是第三车间报名人数的 倍.二、解答题11.已知1006915681467136612651170156914681367126611⨯⨯+⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯+⨯=a ,问a 的整数部分是 .12.四个连续自然数的倒数之和等于2019,求这四个自然数的两两乘积之和.13.用四舍五入的方法计算三个分数的和,得近似值为35.1875≈++cb a ,试求c b a ,,的值.(c b a ,,是三个自然数)14.国际象棋比赛的奖金总数为10000元,发给前五名.每一名的奖金都不一样,名次在前的钱数要比名次在后的钱数多.每份奖金钱数都是100元的整数倍.现在规定,第一名的钱数是第二、第三名两人之和,第二名的钱数是第四、第五名两人之和,那么第三名最多能得多少元?———————————————答 案——————————————————————1. 3.依题意,得320326=<□<10,所以□=7,8,9.2. 9.原式>9999=+⋅⋅⋅++, 原式<10,所以原式的和的整数部分是9.3. 11.()97751010219719=+⋅⋅⋅++⨯=A ,因此与A 最接近的整数是11.4. 15.92设这24个偶数之和为S .由S >15.85×24=380.4和S <15.95×24=382.8,以及S 是偶数,推知S =382,所求数为92.1524382≈÷.5. 1997.若要拆成的不同自然数尽量多,应当从最小的自然数1开始,则2)1(321+=+⋅⋅⋅+++n n n ≤1995003. 所以 )1(+n n ≤3990006当1997=n 时,正好有)1(+n n ≤3990006, 所以最多可以拆成1997个不同自然数的和.6. 91.根据题设条件,这列数依次是105,85,95,90,92.5, 91.25, 91.875, …, 显然,从第六项起后面每个数的整数部分都是91,所以,第19个数的整数部分是91.7. 5.这一过程每进行一次,剩下所有线段的和等于上次剩下的322716323232323=⨯⨯⨯⨯>0.4, 813232323232323=⨯⨯⨯⨯⨯<0.4, 所以至少进行5次.8. 110.分母>11011819801=⨯,分母<11111819981=⨯, 所以110<S <111,即S 的整数部分等于110.9. 101.证9998765432,10099654321⨯⋅⋅⋅⨯⨯⨯=⋅⋅⋅⨯⨯⨯=B A , 则2101100110099999854433221⎪⎭⎫ ⎝⎛==⨯⨯⋅⋅⋅⨯⨯⨯⨯=⨯B A .因为A 的前49项的对应项都小于B , A 的最后一项10099<1, 所以A <B , 再由B A ⨯=⎪⎭⎫⎝⎛2101>A ×A , 推知, 101>A .10. 761或1631.设第二和第三车间报名人数分别为a 和b ,则第一车间b b 25212=⨯,依题意,得 b a b a b 272575+=++=因为b ≤a ≤b 25,所以b 29≤b a 27+≤6b ,即b 29≤75≤6b ,所以2112≤b ≤3216,又b 为偶数,所以b =14或16.(1) 当b =14时, a =26, 761=b a ;(2) 当b =16时, a =19, 1631=b a .11. 1006915661265111512111⨯⎪⎭⎫⎝⎛⨯+⋅⋅⋅+⨯+⨯+⋅⋅⋅+++=a691566126511100151001210011100⨯+⋅⋅⋅+⨯+⨯⨯+⋅⋅⋅+⨯+⨯+=6915661265113115341235111100⨯+⋅⋅⋅+⨯+⨯⨯+⋅⋅⋅+⨯+⨯++=最后一个分数小于1,所以a 的整数部分是101.12. 设这四个连续自然数分别为a ,a +1,a +2, a +3,则 20193121111=++++++a a a a ,所以 31211112019++++++=a a a a <a a a a a 41111=+++, a <1944. 易知a =1,2,4均不合题意,故a =3,这四个自然数为3,4,5,6,其两两乘积之和为:119656454635343=⨯+⨯+⨯+⨯+⨯+⨯.13. 依题意,得 1.345≤875cb a ++<1.355,所以 376.6≤56a +40b +35c <379.4又a ,b ,c 为自然数,因此, 56a +40b +35c =377 ① 或56a +40b +35c =378 ② 或56a +40b +35c =379 ③考虑不定方程①,由奇偶分析,知c 为奇数,所以40b +35c 的个位为5, 因此56a 的个位为2,a 的个位为2或7.又a <5643656379=,故a =2, 因此8b +7c =53,易知b =4, c =3.同法可知不定方程②无解,方程③的解为a =4, b =3, c =1.14. 设第i 名的奖金为100ai 元(i =1,2,3,4,5).依题意,得 1000010010010010010054321=++++a a a a a , 且542321,a a a a a a +=+=,整理 1002332=+a a ① 所以 3223100a a +=<222523a a a =+,故2a >20, 由①易知2a 必为偶数,所以2a ≥22.故 ()23310021a a -=≤()1722310021=⨯-. 即第三名最多能得1700元.二、估计与估算(二)年级 班 姓名 得分 一、填空题1. 将六个分数215,94,12011,451,83,358分成三组,使每组的两个分数的和相等,那么与451分在同一组的那个分数是 .2. 数151311197535232129171551719212321357911131÷的十分位到十万分位的数字为 .3. 满足下式的n 最小等于 . )1(1431321211+⨯+⋅⋅⋅+⨯+⨯+⨯n n >19981949.4. 已知1101011102103101102100101+⋅⋅⋅+++=A ,则A 的整数部分是 .5. 小明计算17个自然数的平均数所得的近似值是31.3,老师指出小明少取了一位有效数字,则老师要求的平均数应该是 .6.有三十个数:,302964.1,,30364.1,30264.1,30164.1,64.1+⋅⋅⋅+++如果取每个数的整数部分,并将这些整数相加,那么其和是 .7.将奇数1,3,5,7,…,由小到大按第n 组有2n -1个奇数进行分组 (1), (3,5,7), (9,11,13,15,17), … 第一组 第二组 第三组 那么1999位于第 组的第 个数.8. 22.103.823.102.824.101.8⨯+⨯+⨯的整数部分是 .9. 数222⨯⋅⋅⋅⨯⨯写成小数时的前两位小数是 .10. 有甲、乙、丙、丁四个同学去林中采蘑菇.平均每人采得的蘑菇的个数的整数部分是一个十位数为3的两位数.又知甲采的数量是乙的54,乙采的数量是丙的23倍.丁比甲多采3个蘑菇.那么,丁采蘑菇 个. 二、解答题11.两个连续自然数的平方之和等于365,又有三个连续自然数的平方之和也等于365.试找出这两个连续自然数和那三个连续自然数.12.如图所示,方格表包括A 行B 列(横向为行,纵向为列),其中依次填写了自然数1至B A ⨯ ,现知20在第3行,41在第5行,103在最后一行,试求A 和B .13.求分数1611514131211++⋅⋅⋅++++=A 的整数部分.14.甲、乙、丙三个班向希望工程捐赠图书.已知甲班1人捐6册,有2人各捐7册,其余人各捐11册;乙班有1人捐6册,3人各捐8册,其余人各捐10册;丙班有2人各捐4册,6人各捐7册,其余人各捐9册.已知甲班捐书总数比乙班多28册,乙班比丙班多101册.各班捐书总数都在400册与550册之间.问:每班各有多少人?———————————————答 案——————————————————————1.94. 注意到451是六个分数中的最小数,因此与451在同一组的分数,必须是这六个分数中的最大数(否则,六个数不能分成三组,每组的两个分数的和相等),因此所求数为94.2. 2,5,9,5,3.设题中所述式子为B A ÷,由于题中所涉及的数太大,不太可能通过直接计算来确定前五位数(否则计算量太大),下面利用估值方法来求:因为2.05313,3.05214>÷>÷<÷<÷B A B A , 所以此数的第一位数字为2.又因为259.052331357,2597.05238.135>÷>÷<÷<÷B A B A , 所以此数的第一、二、三位数字为2,5,9. 又因为,25954.0523212135792<÷<÷B A25953.0523********1>÷>÷B A , 所以此五位数字是2,5,9,5,3.3. 40.原式左端等于111+-n ,可得不等式199********>+-n ,所以19984911<+n , 解得493839>n ,故n 最小等于40.4. 67.⎪⎭⎫ ⎝⎛+⋅⋅⋅+++++⋅⋅⋅+++=11010102101011010010)11321(A⎪⎭⎫ ⎝⎛+⋅⋅⋅++++=1101010210101101001066所以 1016711100106611110106667=⨯+<<⨯+=A 因此, A 的整数部分为67.5. 31.29.设17个自然数的和为S ,由3.3117≈S ,得31.25≤35.3117<S. 所以531.25≤S <532.95,又S 为整数,所以S =532,则29.311753217≈=S6. 49.关键是判断从哪个数开始整数部分是2,因为2-1.64=0.36,我们就知⋅⋅⋅==33.0301031, 故先看3011,3011=⋅⋅⋅66.036.0>,这说明“分界点”是301164.1+,所以前11个数整数部分是1,后19个数整数部分为2,其和为4921911=⨯+.7. 32, 39.第n 组的最后一个奇数为自然数中的第2)12(531n n =-+⋅⋅⋅+++个奇数, 即122-n .设1999位于第n 组,则19991)1(22<--n ≤122-n . 由 223222047199919211312⨯=<<=-⨯1-知n=32. 所以1999在第32组第39312119992=-+个数.8. 29.当两个数的和不变时,两数越接近(即差越小)它们的积越大. 所以24.101.823.102.822.103.8⨯<⨯<⨯,从而30325.18324.101.822.103.823.102.824.101.8=⨯⨯<⨯⨯<⨯+⨯+⨯.52.2969.38)22.123.124.1(822.103.823.102.824.101.8=⨯=++⨯>⨯+⨯+⨯,所以22.103.823.102.824.101.8⨯+⨯+⨯的整数部分是29.9. 0.01注意到35327322=>=,所以6992332132,2132>>,所以01.01001961321322132561010=>=⨯=⨯> 又443818025=<=⨯,所以25132,51328844<<.所以02.0501212513225132221010==⨯<⨯<. 故数222⨯⋅⋅⋅⨯⨯写成小数时的前两位小数是0.01.10. 39.设丙采蘑菇数为x 个,则乙采x 23个,甲采x x 562354=⋅个,丁采⎪⎭⎫⎝⎛+356x 个,四人合采蘑菇数为:310493565623+=++++x x x x x . 依题意,得:30≤⎪⎭⎫⎝⎛+3104941x <40解得 4910117494323⨯=≤492324910157=⨯<x又x 1049必须为整数, x 为10的倍数,因此只能x =30, 从而丁采39356=+x (个).11. 用估值法,先求两个连续自然数,因为5.1822365=÷,所以在两个连续自然数中,一个的平方小于182.5,另一个的平方大于182.5.由132=169,142=196得到,这两个连续自然数是13和14.类似地,3365÷32121=,最接近32121的自然数的平方是112=121,所以这三个连续自然数应是10,11,12.经验证,符合题意.12. 依题意,得2B <20≤3B ,4B <41≤5B ,所以326≤B <10,518≤B <4110,故518≤B <10,因此, B =9.由103在最后一行,得9(A -1)<103≤9A ,所以, 9411≤A <9412,故A =12.13.⎪⎭⎫ ⎝⎛+⋅⋅⋅++++⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛+++=16111110191817151416131211A⎪⎭⎫ ⎝⎛+⋅⋅⋅++++⎪⎭⎫ ⎝⎛++++=16111110191817151412又因为14148171514181421=⨯<+++<⨯= 181816111110191161821=⨯<+⋅⋅⋅+++<⨯= 所以 4112212123=++<<++=A故A 的整数部分是3.14.由题目条件,甲班捐书最多,丙班最小,甲班比丙班多捐28+101=129(册). 因为丙班捐书不少于400册,所以甲班捐书在529~550册之间.甲班人数不少于11349311)776529(=+÷---(人),不多于11251311)776550(=+÷---(人),即甲班人数是50人或51人.如果甲班有50人,则甲班共捐书6+7+7+11×(50-3)=537(册),推知乙班捐书537-28=509(册),乙班有10951410)386509(=+÷⨯--(人),人数是分数,不合题意.所以甲班有51人,甲班共捐书548)351(11776=-⨯+++(册),推知乙班捐有53÷+⨯--(人),-(=548104)38628丙班有49⨯÷+-⨯-(人).-(=548)697212948三、定义新运算(一) 年级 班 姓名 得分一、填空题1.规定a ☉b =ab b a -,则2☉(5☉3)之值为 .2.规定“※”为一种运算,对任意两数a ,b ,有a ※b 32b a +=,若6※x 322=,则x =.3.设a ,b ,c ,d 是自然数,定义bc ad d c b a +>=<,,,.则<><><<,3,2,1,4,4,3,2,13, 4, 1, 2>>=<>1,4,3,2, .4.[A ]表示自然数A 的约数的个数.例如,4有1,2,4三个约数,可以表示成[4]=3.计算:]7[])22[]18([÷+= .5.规定新运算※:a ※b=3a -2b .若x ※(4※1)=7,则x= .6.两个整数a 和b ,a 除以b 的余数记为a ☆b .例如,13☆5=3,5☆13=5,12☆4=0.根据这样定义的运算,(26☆9) ☆4= .7.对于数a ,b ,c ,d 规定d c ab d c b a +->=<2,,,.如果7,5,3,1>=<x , 那么x = .8.规定:6※2=6+66=72,2※3=2+22+222=246,1※4=1+11+111+1111=1234.7※5= .9.规定:符号“△”为选择两数中较大数,“☉”为选择两数中较小数.例如:3△5=5,3☉5=3.那么,[(7☉3)△5]×[5☉(3△7)]= .10.假设式子b a a ⨯#表示经过计算后,a 的值变为原来a 与b 的值的积,而式子b a b -#表示经过计算后,b 的值为原来a 与b 的值的差.设开始时a =2,b =2,依次进行计算b a a ⨯#,b a b -#,b a a ⨯#,b a b -#,则计算结束时,a 与b 的和是 .二、解答题11.设a ,b ,c ,d 是自然数,对每两个数组(a ,b ),(c ,d ),我们定义运算※如下: (a ,b )※(c ,d )= (a+c ,b +d );又定义运算△如下: (a ,b )△(c ,d )= (ac+bd ,ad+bc ).试计算((1,2) ※(3,6))△((5,4)※(1,3)).12.羊和狼在一起时,狼要吃掉羊,所以关于羊及狼,我们规定一种运算,用符号△表示羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼.运算意思是羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了.小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示为羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼.运算意思是羊与羊在一起还是羊,狼与狼在一起还是狼,由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了.对羊或狼,可用上面规定的运算作混合运算,混合运算的法则是从左到右,括号内先算.运算的结果是羊,或是狼.求下式的结果:羊△(狼☆羊)☆羊△(狼△狼).13.22264⨯⨯=222⨯⨯⨯表示成()664=f ;33333243⨯⨯⨯⨯=表示成()5243=g .试求下列的值:(1)()=128f ; (2))()16(g f =; (3)6)27()(=+g f ;(4)如果x , y 分别表示若干个2的数的乘积,试证明:)()()(y f x f y x f +=⋅.14.两个不等的自然数a 和b ,较大的数除以较小的数,余数记为a ☉b ,比如5☉2=1,7☉25=4,6☉8=2.(1)求1991☉2000,(5☉19)☉19,(19☉5)☉5;(2)已知11☉x =2,而x 小于20,求x ;(3)已知(19☉x )☉19=5,而x 小于50,求x .———————————————答 案—————————————————————— 1. 120411. 5☉3=15165335=-,2☉(5☉3)=2☉12041112016121516151621516==-=.2. 8.依题意,6※326x x +=,因此322326=+x ,所以x=8.3. 280.;1421343,2,1,4;1032414,3,2,1=⨯+⨯>=<=⨯+⨯>=<.1443121,4,3,2;1014232,1,4,3=⨯+⨯>=<=⨯+⨯>=< 原式2801014141014,10,14,10=⨯+⨯>==<.4. 5.因为23218⨯=有6)12()11(=+⨯+个约数,所以[18]=6,同样可知[22]=4,[7]=2.原式52)46(=÷+=.5. 9.因为4※1=101243=⨯-⨯,所以x ※(4※1)= x ※10=3x -20.故3x -20=7,解得x =9.6. 0.89226+⨯=,26☆9=8,又428⨯=,故(26☆9)☆4=8☆4=0.7. 6.因为x x x +=+-⨯⨯>=<15312,5,3,1,所以71=+x ,故6=x .8. 86415.7※5=7+77+777+7777+77777=86415.9. 25.原式=[3△5]×[5☉7]=5×5=25.10. 14.第1次计算后,422=⨯=a ;第2次计算后,224=-=b ;第3次计算后,824=⨯=a ;第4次计算后,628=-=b .此时1468=+=+b a .11. (1,2)※(3,6)=(1+3,2+6)=(4,8),(5,4)※(1,3)=(5+1,4+3)=(6,7). 原式=(4,8)△(6,7)=(4×6+8×7,4×7+8×6)=(80,76).12. 原式=羊△羊☆羊△狼=羊☆羊△狼=羊△狼=狼.13. (1)()72)128(7==f f ;(2)()())81(342)16(44g g f f ====;(3)因为()())8(233636)27(633f f g g ===-=-=-,所以6)27()8(=+g f ; (4)令,2,2n m y x ==则n y f m x f ==)(,)(.()())()(222)(y f x f n m f f y x f n m n m +=+==⋅=⋅+.14. (1)1991☉2000=9;由5☉19=4,得(5☉19)☉19=4☉19=3;由19☉5=4,得(19☉5)☉5=4☉5=1.(2)我们不知道11和x 哪个大(注意,x ≠11),即哪个作除数,哪个作被除数,这样就要分两种情况讨论.1) x <11,这时x 除11余2, x 整除11-2=9.又x ≥3(因为x 应大于余数2),所以x =3或9.2) x >11,这时11除x 余2,这说明x 是11的倍数加2,但x <20,所以x =11+2=13.因此(2)的解为x =3,9,13.(3)这个方程比(2)又要复杂一些,但我们可以用同样的方法来解.用y 表示19☉x ,不管19作除数还是被除数,19☉x 都比19小,所以y 应小于19.方程y ☉19=5,说明y 除19余5,所以y 整除19-5=14,由于y ≥6,所以y =7,14.当y =7时,分两种情况解19☉x =7.1)x <19,此时x 除19余7,x 整除19-7=12.由于x ≥8,所以x =12.2) x >19,此时19除x 余7, x 是19的倍数加7,由于x <50,所以x =19+7=26或7219+⨯=x =45.当y =14时,分两种情况解19☉x =14.1) x <19,这时x 除19余14, x 整除19-14=5,但x 大于14,这是不可能的.2)x >19,此时19除x 余14,这就表明x 是19的倍数加14,因为x <50,所以x =19+14=33.总之,方程(19☉x )☉19=5有四个解,x =12,26,33,45.三、定义新运算(二) 年级 班 姓名 得分一、填空题1.规定:a ※b =(b+a )×b ,那么(2※3)※5= .2.如果a △b 表示b a ⨯-)2(,例如3△444)23(=⨯-=,那么,当a △5=30时, a= .3.定义运算“△”如下:对于两个自然数a 和b ,它们的最大公约数与最小公倍数的和记为a △b .例如:4△6=(4,6)+[4,6]=2+12=14.根据上面定义的运算,18△12= .4.已知a ,b 是任意有理数,我们规定: a ⊕b = a +b -1,2-=⊗ab b a ,那么[]=⊗⊕⊕⊗)53()86(4 .5.x 为正数,<x >表示不超过x 的质数的个数,如<5.1>=3,即不超过5.1的质数有2,3,5共3个.那么<<19>+<93>+<4>×<1>×<8>>的值是 .6.如果a ⊙b 表示b a 23-,例如4⊙5=3×4-2×5=2,那么,当x ⊙5比5⊙x 大5时, x = .7.如果1※4=1234,2※3=234,7※2=78,那么4※5= .8.我们规定:符号○表示选择两数中较大数的运算,例如:5○3=3○5=5,符号△表示选择两数中较小数的运算,例如:5△3=3△5=3.请计算:=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∙∙25.210623799343.03323625.026176.0 .9.规定一种新运算“※”: a ※b =)1()1(++⨯⋅⋅⋅⨯+⨯b a a a .如果(x ※3)※4=421200,那么x = .10.对于任意有理数x , y ,定义一种运算“※”,规定:x ※y=cxy by ax -+,其中的c b a ,,表示已知数,等式右边是通常的加、减、乘运算.又知道1※2=3,2※○ △ △ ○3=4,x ※m=x (m ≠0),则m 的数值是 .二、解答题11.设a ,b 为自然数,定义a △b ab b a -+=22.(1)计算(4△3)+(8△5)的值;(2)计算(2△3)△4;(3)计算(2△5)△(3△4).12.设a ,b 为自然数,定义a ※b 如下:如果a ≥b ,定义a ※b=a -b ,如果a <b ,则定义a ※b= b - a .(1)计算:(3※4)※9;(2)这个运算满足交换律吗?满足结合律吗?也是就是说,下面两式是否成立?①a ※b= b ※a ;②(a ※b )※c= a ※(b ※c ).13.设a ,b 是两个非零的数,定义a ※b ab b a +=. (1)计算(2※3)※4与2※(3※4).(2)如果已知a 是一个自然数,且a ※3=2,试求出a 的值.14.定义运算“⊙”如下:对于两个自然数a 和b ,它们的最大公约数与最小公倍数的差记为a ⊙b . 比如:10和14,最小公倍数为70,最大公约数为2,则10⊙14=70-2=68.(1)求12⊙21,5⊙15;(2)说明,如果c 整除a 和b ,则c 也整除a ⊙b ;如果c 整除a 和a ⊙b ,则c 也整除b ;(3)已知6⊙x =27,求x 的值.———————————————答 案——————————————————————1. 100.因为2※3=(3+2)×3=15,所以(2※3)※5=15※5=(5+15)×5=100.2. 8.依题意,得305)2(=⨯-a ,解得8=a .3. 42.18△12=(18,12)+[18,12]=6+36=42.4. 98.原式]1313[4)]253()186[(4⊕⊗=-⨯⊕-+⊗=982254254]11313[4=-⨯=⊗=-+⊗=5. 11.<19>为不超过19的质数,有2,3,5,7,11,13,17,19共8个.<93>为不超过的质数,共24个,易知<1>=0,所以原式=<<19>+<93>>=<8+24>=<32>=11.6. 6.x ⊙5-5⊙x=(3 x -2×5)-(3×5-2 x )=5 x -25,由5 x -25=5,解得x=6.7. 45678.8. 21. 因为∙6.0○322617=○322617=,0.625△853323=△853323=, ∙3.0△319934=△319934=,106237○10623725.2=○4949=, 所以,原式2149318532=++=.9. 2.令x ※3=y ,则y ※4=421200,又4212002726252413532244⨯⨯⨯=⨯⨯⨯=,所以y=24,即x ※3=24.又24=432323⨯⨯=⨯,故x =2.10. 4.由题设的等式x ※y=cxy by ax -+及x ※m=x (m ≠0),得000=⋅⋅-+⋅m c bm a ,所以bm=0,又m ≠0,故b=0.因此x ※y=ax -cxy.由1※2=3,2※3=4,得⎩⎨⎧=-=-46232c a c a 解得a =5,c =1. 所以x ※y =5x -xy ,令x =1,y=m 得5-m=1,故m =4.11. (1)原式()()62585834342222=⨯-++⨯-+=;(2)原式()323222⨯-+=△4=7△4=37474722=⨯-+;(3)原式()525222⨯-+=△()19434322=⨯-+△132831319131922=⨯-+=.12. (1)原式=(4-3)※9=1※9=9-1=8;(2)因为表示a ※b 表示较大数与较小数的差,显然a ※b= b ※a 成立,即这个运算满是交换律,但一般来说并不满足结合律,例如:(3※4)※9=8,而3※(4※9)=3※(9-4)=3※5=5-3=2.13. (1)按照定义有2※36132332=+=,3※412253443=+=. 于是(2※3)※4613=※4=3127451324241361344613=+=+. 2※(3※4)=2※60012012425252421225122521225=+=+=. (2)由已知得233=+aa ① 若a ≥6,则3a ≥2,从而233>+aa 与①矛盾.因此a ≤5,对a =1,2,3,4,5这5个可能的值,一一代入①式中检查知,只有a =3符合要求.14. (1)为求12⊙21,先求出12与21的最小公倍数和最大公约数分别为84,3,因此12⊙21=84-3=81,同样道理5⊙15=15-5=10.(2)如果c 整除a 和b ,那么c 是a 和b 的公约数,则c 整除a ,b 的最大公约数,显然c 也整除a ,b 最小公倍数,所以c 整除最小公倍数与最大公约的差,即c 整除a ⊙b .如果c 整除a 和a ⊙b ,由c 整除a 推知c 整除a ,b 的最小公倍数,再由c 整除a ⊙b 推知, c 整除a ,b 的最大公约数,而这个最大公约数整除b ,所以 c 整除b .(3)由于运算“⊙”没有直接的表达式,解这个方程有一些困难,我们设法逐步缩小探索范围.因为6与x 的最小公倍数不小于27+1=28,不大于27+6=33,而28到33之间,只有30是6的倍数,可见6和x 的最小公倍数是30,因此它们的最大公约数是30-27=3.由“两个数的最小公倍数与最大公约数的积=这两个数的积”,得到x ⨯=⨯6330.所以15=x .四、工程问题(1)年级 班 姓名 得分 一、填空题1.一项工程,甲、乙两队合作20天完成,乙丙两队合作60天完成,丙丁两队合作30完成,甲丁合作 天完成?2.甲乙两队合作一项工程,计划在24天内完成.如果甲队做6天,乙队做4天,只能做完全工程的20%,两队单独做完全工程各需要 天.3.一条公路,甲队独修24天完成,乙队独修30天完成.甲乙两队合修若干天后,乙队停工休息,甲队继续修了6天完成,乙队修了 天.4.某市举办菊展,新建一个喷水池.单开甲管1小时可将喷水池注满,单开乙管40分钟可将水注满,两管同时齐开5210分钟后,共注水314吨.喷水池能装水吨.5.一项工作,两个师傅和三个徒弟合作需922天完成,如果三个师傅2个徒弟合作需要712天完成,如果一名师傅单独做需 天完成.6.加工一批零件,甲独做需3天完成,乙独做需4天完成,两人同时加工,完成任务时,甲比乙多做24个,这批零件共有 个.7.一项建筑工程,由甲建筑队单独承建要一年半,乙建筑队单独承建要一年零三个月,现在两队合作半年,剩下的由乙队继续完成还要 个月.(假设每月实际工作天数一样)8.甲、乙、丙三人合修一围墙.甲、乙合修6天修好围墙的31,乙、丙合修2天修好余下的41,剩下的三人又合修了5天才完成.共得工资180元,按各人所完成的工作量的多少来合理分配,每人应得 元.9.原计划用24个工人挖一定数量的土方,按计划工作5天后,因为调走6人,于是剩下的工人每天比原定工作量多挖1方土才能如期完成任务,原计划每人每天挖土 方.10.一个水池,底部安有一个常开的排水管,上部安有若干个同样粗细的进水管,当打开4个进水管时,需要5小时才能注满水池,当打开2个进水管时,需要15小时才能注满水池;现在需要在2小时内将水池注满,那么至少要打开 个进水管.二、解答题11.抄一份书稿,甲每天的工作效率等于乙、丙二人每天的工作效率的和;丙每天的工作效率相当于甲、乙二人每天工作效率之和的51;如果三人合抄只需8天就完成了,那么乙一人单独抄需多少天才能完成?12.一项工程,甲独做需10天,乙独做需15天,如果两人合作,甲的工作效率就要降低,只能完成原来的54,乙只能完成原来的109,现在要8天完成这项工程,两人合作天数尽可能少,那么两人要合作多少天?13.一空水池有甲、乙两根进水管和一根排水管.单开甲管需5分钟注满水池,单开乙管需10分钟注满水池,满池水如果单开排水管需6分钟流尽.某次池中没有水,打开甲管若干分钟后,发现排水管未关上,随即关上排水管,同时打开乙管,又过了同样长的时间,水池的1/4注了水.如果继续注满水池,前后一共要花多少时间?14.有一个蓄水池装有9根水管,其中一根为进水管,其余8根为相同的出水管,进水管以均匀的速度不停地向这个蓄水池注水.后来有人想打开出水管,使池内的水全部排光(这时池内已注入一些水).如果把8根出水管全部打开,需3小时把池内的水全部排光;如果仅打开5根出水管,需6小时把池内的水全部排光.问要想在4.5小时内把池内的水全部排光,需同时打开几根出水管?———————————————答 案——————————————————————1. 156********1=⎪⎭⎫ ⎝⎛-+÷(天).2. 乙的工作效率为()()40116244%201=-÷⨯-, 甲的工作效率为601401241=-. 故甲做60天完成,乙做40天完成.3. 1030124162411=⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛⨯-(天).4. 104016015210314=⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛÷(吨)5. 一个师傅与一个徒弟工作效率之和为:()60112371219221=+÷⎪⎪⎪⎪⎭⎫⎝⎛+, 故师傅的工作效率是101601127121=⨯-,即一名师傅单独做10天完成.6. 16841311413124=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⨯⎪⎭⎫ ⎝⎛-÷(个).7. 415161511811=÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛+-(月).8. 甲分得的钱为:()3356241311541311311180=+⨯⎭⎬⎫⎩⎨⎧÷⨯⎪⎭⎫ ⎝⎛--÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛---⨯(元);丙分得的钱为:()5652631541311311180=+⨯⎭⎬⎫⎩⎨⎧÷-÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛---⨯(元);乙分得的钱为:180-33-56=91(元).9. 36)624(=÷-(方).10. 进水管一小时进水量为:()()[]15124541521=-÷⨯-⨯÷; 排水管一小时排水量为:1515120151=÷⎪⎭⎫⎝⎛-⨯.故只开一进水管、一排水管池中无水,多开进水管数为5.71521=÷,取整为8 个,至少要打开9个进水管.11. 24281511811=⎥⎦⎤⎢⎣⎡÷-⎪⎭⎫ ⎝⎛+÷÷(天).12. 设两人要合作x 天,依题意得:()15078101=+-x x ,故x =5(天).13. 设注满池中41的水需x 分钟,故有23,412615126151==⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛-x x x .继续注满池中水的43411=-需要251015143=⎪⎭⎫ ⎝⎛+÷(分), 共需时间42523=+(分).14. 将每根进水管每小时的进水量看作单位1,则每根出水管每小时的排水量为2)36()3865(=-÷⨯-⨯,而池中原有水量为186265=⨯-⨯,从而要想在4.5小时内把池中水抽干,需要打开65.4182=÷+(根)出水管.四、工程问题(2)年级 班 姓名 得分一、填空题1.一项工作,甲乙两队合作9天完成,乙丙两队合作12天完成,甲丙两队合作需18天完成,现在三队合作需 天完成.2.某工程先由甲单独做63天,再由乙单独做28天即可完成.如果由甲、乙两人合作,需48天完成.现在甲先单独做42天,然后再由乙来单独完成,那么还需要做 天.3.甲、乙两队合作20天可以完成一项工程.如果两队合作8天后,乙队再独做4天,还剩这项工程的158没有完成.甲、乙两队工作效率之比为: .4.一份稿件,甲单独打字需6小时完成,乙单独打字需10小时完成.现在甲单独打若干小时后,因有事由乙接着打完,共用了7小时,那么甲打字用了 小时.5.有批机器零件,甲单独制作需要218天,比乙单独制作多用了21天,两人合作4天后,剩下210个零件由甲单独去做,自始至终甲共制作了 零件.6.一个水池子,甲、乙两管同时开,5小时灌满,乙、丙两管同时开,4小时灌满,如果乙管先开6小时,还需要甲、丙两管同时开2小时才能注满(这时乙管关闭).那么乙管单独灌满水池需要 小时.7.一个水池,地下水从四壁渗入,每小时渗入该水池的水量是固定的.当这个水池水满时,打开A 管,8小时可将水池排空;打开B 管,10小时可将水池排空;打开C 管,12小时可将水池排空.如果打开A 、B 两管,4小时可将水池排空,那么打开B 、C 两管,将水池排空需要 小时.8.一件工作,如果单独做,甲按规定时间可提前2天完成,乙则要超过规定时间3天才完成.现在,甲乙二人合做2天后,剩下的继续由乙单独做,刚好在规定的日期内完成.若甲乙二人合做,完成这件工作需要 天.9.有一水池,装有甲、乙两个注水管,下面装有丙管放水.池空时,单开甲管5分钟可注满;单开乙管10分钟可注满.水池装满水后,单开丙管15分钟可将水放完.如果在池空时,将甲、乙、丙三管齐开,2分钟后关闭乙管,还要 分钟可以注满水池.10.放满一个水池的水,如果同时开放①、②、③号阀门,7.5小时可以完成;如果同时开放①、③、⑤号阀门,5小时可以完成;如果同时开放①③④号阀门,6小时可以完成;如果同时开放②④⑤号阀门,4小时可以完成.问同时开放这五个阀门, 小时可以放满这个水池.二、解答题11.师徒三人合作承包一项工程,4天能够全部完成.已知师傅单独做所需天数与两个徒弟合作所需天数相等;而师傅与乙徒弟合作所需天数的2倍与甲徒弟单独做完所需的天数相等.那么甲徒弟单独做,完成这项工程需要多少天?乙徒弟单独做,完成这项工程需要多少天?12.甲、乙、丙三人从三月一日开始合作一项工程,甲每天的工作量是乙每天工作量的3倍,乙每天的工作量是丙每天工作量的2倍.三人合作5天完成全工程的31后,甲休3天,乙休2天,丙没有休息,问这项工程是在几月几日完成的?13.一个蓄水池装了一根进水管和三根放水速度一样的出水管.单开一根进水管20分钟可注满空池.单开一根出水管,45分钟可以放完满池水.现有32池的水,如果四管齐开,多少分钟后池水还剩52?14.蓄水池有甲、丙两条进水管,和乙丁两条排水管.要灌满一池水,单开甲管需要3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时.现在池内有61池水.如果按甲、乙、丙、丁、甲、乙……的顺序,轮流各开一小时,多少时间后水开始溢出水池?———————————————答 案——————————————————————1. 82181121911=⎥⎦⎤⎢⎣⎡÷⎪⎭⎫ ⎝⎛++÷(天).2. 甲乙合做28天,完成任务的1274828=÷, 故甲的工作效率为()84128631271=-÷⎪⎭⎫ ⎝⎛-,乙的工作效率为1121841481=-, 于是乙还需做56112184421=÷⎪⎭⎫ ⎝⎛-(天).3. 乙的工作效率为601482011581=÷⎪⎭⎫⎝⎛⨯--,甲的工作效率为301601201=-, 甲乙工作效率之比为1:2601:301=.4. 5.41016171011=⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛⨯-(小时).5. 35702102184421218121811210=+⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⎪⎪⎪⎪⎭⎫ ⎝⎛-+-÷(个).6. 20)46(5141211=⎭⎬⎫⎩⎨⎧-÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯-÷(小时).7. B 管每小时排水量为81421=÷(池)水. 每小时渗水量为4011011081=÷⎪⎭⎫⎝⎛-⨯(池).C 管每小时排水量为1201312124011=÷⎪⎭⎫⎝⎛⨯+(池).从而B 、C 两管排一池水,需8.440112013811=⎪⎭⎫ ⎝⎛-+÷(小时).8. 甲与乙工作效率之比为3:2,甲独做要101235=⎪⎭⎫⎝⎛-÷(天),乙独做需10+5=15(天),甲乙合做要61511011=⎪⎭⎫⎝⎛+÷(天).9. 4151512151101511=⎪⎭⎫⎝⎛-÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+-(分钟).10. 434134161515.711=⎥⎦⎤⎢⎣⎡+÷⎪⎭⎫ ⎝⎛-++÷(小时).11. 243412411=⎪⎭⎫⎝⎛÷-÷÷(天).12. 甲的工作效率为4522616151=++⨯,乙的工作效率为13522612151=++⨯, 丙的工作效率为13512611151=++⨯.乙丙三天干了151313511352=⨯⎪⎭⎫ ⎝⎛+,甲丙二天干了1351421351452=⨯⎪⎭⎫ ⎝⎛+. 整个工作剩下13567135********=---.由甲乙丙合干还要9471351135245213567=⎪⎭⎫ ⎝⎛++÷(天), 完成此项工作共需9417947235=+++(天),即3月18日完成.13. 1620134515232=⎪⎭⎫ ⎝⎛-⨯÷⎪⎭⎫ ⎝⎛-(分).14. 按甲、乙、丙、丁顺序各开一小时水池中进水60761514131=-+-.这样5个周期(即20小时)后,池中有水43560761=⨯+,再开甲管注满水池需时4331431=÷⎪⎭⎫ ⎝⎛-(小时),故一共要43204320=+(小时)开始溢出.五、分数应用题(1)年级 班 姓名 得分 一、填空题1.有一个分数,它的分母比分子多4.如果把分子、分母都加上9,得到的分数约分后是97,这个分数是 .2.甲、乙两数是自然数,如果甲数的65恰好是乙数的41.那么甲、乙两数之和的最小值是 .3.商店的书包降价41后,又提价51,最后的价格是8元1角一个,那么最初是元钱一个.4.小萍今年的年龄是妈妈的31,二年前母子年龄相差24岁,四年后小萍的年龄是 .5.甲、乙、丙三人共同加工一批零件.甲比乙多加工零件20个,丙加工零件是乙加工零件的54,甲加工零件是乙丙两人加工零件总数的65.甲、乙、丙各加工零件 个.6.六一班男生的一半和女生的41共16人,女生的一半和男生的41共14人,这个班男、女生各 人.7.在4点多钟时,时钟的时针和分针在一直线上且方向相反,这时是4点 分.8.甲、乙两人各有钱若干元,已知甲的钱数是乙的4倍,当甲花去31后,又花去余下的31,如果这时甲给乙7元钱,甲、乙两人的钱数正好相等.甲原来有_____元钱.9.A 、B 、C 三根木棒插在水池中,(如图)三根捧长度和是360厘米,A 棒有43露出水面外,B 棒有4露出水面外.C 棒有2露出水面外.水池有 厘米深.。
小学六年级奥数练习(举一反三李济元A版练习)剖析

小学六年级奥数练习(举一反三李济元A版练习)剖析达标测试卷(一)第1周至第5周(定义新操作和简单操作)(本卷满分为100分,建议测试时间为80分钟)1.(10分)规定②=1*2*3,③=2*3*4,④=3*4*5……如果⑦-⑥=6a,那么a等于多少?2.(10分)指定a*b=(a+b)(a-b),49*9是多少?3.(10分)设a,b是两个数,规定a*b=,求5*10等于多少?4.(10分)如果AB=3a-4b,(157)10分是多少?5.(10分)设ab=2ab,已知(3x)2=96,求x的值?6.(10点)为两个整数a和B定义一个新的运算“#”;a#b=7.(40分)下列各题怎样算简便就怎样算。
(1)8.75-8.57+(11.25-1.43)#3#(2)0.999*0.7+0.111*3.7(3)875*0.25+8.75*76-8.75(4)72*1.09+2.4*67.3(5)4123+3412+2341+1234(6)999*375+6375(7)*2000(8)1/2+1/4+1/8+・・・+1/128(9)(10)1/99+2/99+3/99+・・・+98/99达标测试卷(二)第6周至第8周(换算单位“1”)(本卷满分为100分,建议测试时间为80分钟)1.(8分)一本书第一次看了全书的0.6,第二次看了第一次的0.6,两次一共看了多少?2.(8分)给定a=3/4b,C=2/3a,B-C=16,求a=()。
3.(8分)甲、乙、丙三位同学手机画片,甲的张数占三人总数的1/6,丙的张数是甲的3/2,乙比丙多30多张,三人一共有多少张画片?4.(8分)水果店有275公斤苹果。
梨的质量是苹果和橙子的8/21,橙子的质量是梨和苹果总质量的10/19。
梨和橙子的质量分别是多少?5.(8分)六年级学生分成甲、乙两组,如果从甲组调14人到乙组,则甲组的人数是乙组的3/5,如果从乙组调12人到甲组,则乙组人数是甲组的3/5,甲、乙两组原来分别有多少人?6.(8分)我弟弟有51块糖,我弟弟有21块糖。
六年级奥数应用题(一)

第三章 应用题(专题一)平均数问题(2课时)1、把几个不相等的数,在总和不变的条件下,通过移多补少,使它们完全相等,得到的数就是平均数。
2、牢记公式:平均数=总数量÷总份数 总数量=平均数×总份数 总份数=总数量÷平均数[例题1]有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃子平均每箱36个。
苹果和桃子平均每箱37个。
求一箱苹果多少个?举一反三1、 一次考试,甲、乙、丙三人平均分91分,乙、丙、丁三人平均分89分,甲、丁二人平均分95分,问甲、丁各得多少分?2、甲、乙、丙三个小组的同学去植树,甲、乙两组平均每组植18棵,甲、丙两组平均每组植17棵,丙、乙两组平均每组植19棵。
三个小组各植树多少棵?[例题2]一位同学在期中测验中,除了数学外,其他几门功课的平均成绩是94分,如考点归纳学习思考果数学算在内,平均每门95分。
已知他数学得了100分,问这位同学一共考了多少门功课?举一反三1、小明前几次数学测验的平均成绩是84分,这次要考100分,才能把数学平均成绩提高到86分,问这是他第几次数学测验?2、小明前五次数学测验的平均成绩是88分。
为了使平均成绩达到92.5分,小明要连续考多少次满分?[例题3] 小莉读一本小说,第一天读74页,第二天读82页,第三天读71页,第四天读63页,第五天读的页数比这5天中平均每天读的少6页,小莉第五天读了多少页?举一反三1、一个技术工人带了4个普通工人完成了一项工作,每个普通工人各得200元,这位技术工人的收入比他们5人的平均收入还多80元,问这位技术工人得多少元?2、两组工人加工零件,第一组有30人,平均每人加工60个零件。
第二组有25人,平均每人比两组工人加工的平均数多6个,两组工人平均每人加工多少个零件?[例题4]一次数学测验,全班平均分是91.2分,已知女生21人,平均分为92分,男生平均分为90.5分,求这个班的男生有多少人?举一反三1、两组同学进行跳绳比赛,平均每人跳152下。
小学六年级奥数题(1)

A (1)4.互质的两个合数。
它们的最小公倍数是702,这两个数是( , )。
A (1) 7.若(1525-口)×15+44=80,口中应是( )A (1) 10.小明前5次考试的平均成绩为90分,他暗下决心,争取尽快将平均分提高到94分以上,若他每次考试都得100分,那么他至少还要考( )次A (2)2.5、已知A ×150%=B ÷112==C ÷13,那么A 、B 、C 三个数从大到小的排列顺序是( )A 、A>B>CB 、B>A>C C 、C>B>AD 、A>C>BA (2)3.如果数a 除以数b,商是8,那么( )。
A 、a 一定能被b 整除B 、a 能被b 除尽C 、a 一定不能被b 整除D 、a 一定是b 的倍数A (2)1.甲乙两辆汽车同时从两地相向而行,甲车每小时行45千米,乙车每小时行42千米。
两车在距离中点12千米处相遇。
两车同时开出后经过多少小时相遇A (2)2.在一次数学竞赛中,有5位同学成绩分别为98分,86分,78分,89分,94分。
小明的成绩比小明在内的这6位同学的平均成绩比要高7.5分,小明的数学竞赛成绩是多少分A (2)3.一批学生,女生走了15名,这时的男生与女生的人数的比是2:1,此后,男生走了45名,余下的男生与女生的比是1:5,女生原来共有多少名A (3)计算: 1245÷45 –[667+178×(2720−214)] A (3)24.下列判断中正确的有( )个A 、0个B 、1个C 、2个D 、3个①在0.1和0.01之间的小数有9个。
② 三个连续自然数的和必定是3的倍数。
③两个面积相等的三角形,一定能拼成一个平行四边形。
④半圆的周长不等于圆周长的一半。
⑤两个小数,位数多的那个数一定较大。
A (4)4.甲乙两个两位数,甲数是乙数的75%,它们的最小公倍数是48。
小学六年级奥数练习(举一反三李济元A版练习)

达标测试卷(一)第1周~第5周(定义新运算、简便运算)(本卷满分100分,建议测试时间80分钟)1.(10分)规定②=1*2*3,③=2*3*4,④=3*4*5……如果⑦-⑥=6A,那么A等于多少?2.(10分)规定a*b=(a+b)(a-b),求49*9等于多少?3.(10分)设A,B是两个数,规定A*B= ,求5*10等于多少?4.(10分)规定a b=3a-4b,求(157)10等于多少?5.(10分)设a b=2ab,已知(3x)2=96,求x的值?6.(10分)对两个整数a和b定义新运算“#”;a#b=,求2#6+3#9.7.(40分)下列各题怎样算简便就怎样算。
(1)8.75-8.57+(11.25-1.43)(2)0.999*0.7+0.111*3.7(3)875*0.25+8.75*76-8.75 (4)72*1.09+2.4*67.3 (5)4123+3412+2341+1234 (6)999*375+6375(7)*2000(8)1/2+1/4+1/8+…+1/128(9)(10)1/99+2/99+3/99+…+98/99是达标测试卷(二)第6周~第8周(转化单位“1”)(本卷满分100分,建议测试时间80分钟)1.(8分)一本书第一次看了全书的0.6,第二次看了第一次的0.6,两次一共看了多少?2.(8分)已知a=3/4b,c=2/3a,b-c=16,求a=()。
3.(8分)甲、乙、丙三位同学手机画片,甲的张数占三人总数的1/6,丙的张数是甲的3/2,乙比丙多30多张,三人一共有多少张画片?4.(8分)水果店有275千克苹果,梨的质量是苹果和橘子的8/21,橘子的质量是梨和苹果总质量的10/19,梨和橘子的质量分别是多少?5.(8分)六年级学生分成甲、乙两组,如果从甲组调14人到乙组,则甲组的人数是乙组的3/5,如果从乙组调12人到甲组,则乙组人数是甲组的3/5,甲、乙两组原来分别有多少人?6.(8分)弟弟有51快糖,哥哥有21块糖,两人每天分别吃一块糖,多少天以后哥哥的块数是弟弟糖的块数的1/3?7.(8分)百货商场进了一批童装,按进价的50%作为利润来定价,当售出这批童装的80%以后,决定降价出售,按照定价的60%出售,这批服装全部售完后实际获利百分之几?8.(8分)阅览室里看书的同学中,男生人数占女生人数的1/2,若走出16位女生,走进16位男生,女生人数是男生的1/2,现在男、女生各有几人?9.(8分)王明参加班干部竞选,需要超过3/4的选票才能当选,在计算了总选票的1/3后,他得到的选票已达到当选票数的3/5,他还要得到剩下选票的几分之几才能当选?10.(8分)某公司女职员比总人数的3/5少18人,男职员人数是女职员的5/3,这个公司一共有职员多少人?11.(10分)有两筐苹果,一筐苹果的个数是甲筐的2/5,从甲筐取出10个苹果放入乙筐后,乙筐苹果的个数是甲筐的3/4,甲、乙两筐一共有多少苹果?12.(10分)有两根彩带,一根长8米,另一根长4米,从两根彩带上剪去同样长的一段后,短彩带剩下的长度是长彩带剩下长度的1/3,两根彩带各剪去多少米?达标测试卷(三)第9周~第11周(设数法解题、假设法解题)(本卷满分100分,建议测试时间80分钟)1.(8分)一次数学竞赛,某班全班平均分为80分,其中4/5的人及格,及格的同学平均分为88分,那么不及格的同学平均分是多少分?2.(8分)王叔叔翻越一座山,他上山的速度是每分钟100米,下山的速度是每分钟150米。
小学六年级奥数题50道题及解答(可直接打印)

练习(一)姓名1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?2、3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?3.甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?4.李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱? 得分5.甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
甲车每小时行40千米,乙车每小时行 45千米,两地相距多少千米?(交换乘客的时间略去不计)6.学校组织两个课外兴趣小组去郊外活动。
第一小组每小时走4.5千米,第二小组每小时行3.5千米。
两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组。
多长时间能追上第二小组?7.有甲乙两个仓库,每个仓库平均储存粮食32.5吨。
甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨?8.甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米。
甲、乙两队每天共修多少米? 9.学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元?10.一列火车和一列慢车,同时分别从甲乙两地相对开出。
快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米?答案:奥数题解答参考1、想:由已知条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的(10-1)倍,由此可求得一把椅子的价钱。
再根据椅子的价钱,就可求得一张桌子的价钱。
解:一把椅子的价钱:288÷(10-1)=32(元)一张桌子的价钱:32×10=320(元)答:一张桌子320元,一把椅子32元。
六年级奥数题及答案经典-(1)

六年级奥数题及答案(dáàn)经典-(1)1·由奶糖和巧克力糖混合成一堆糖,如果(rúguǒ)增加10颗奶糖后,巧克力糖占总数的60%。
再增加30颗巧克力糖后,巧克力糖占总数的75%,那么原混合糖中有奶糖多少颗?巧克力糖多少颗?答案(dá àn)加10颗奶糖,巧克力占总数的60%,说明(shuōmíng)此时奶糖占40%,巧克力是奶糖的60/40=1。
5倍再增加(zēngjiā)30颗巧克力,巧克力占75%,奶糖占25%,巧克力是奶糖的3倍增加了3-1,5=1,5倍,说明30颗占1,5倍奶糖=30/1,5=20颗巧克力=1,5*20=30颗奶糖=20-10=10颗2·小明和小亮各有一些玻璃球,小明说;“你有球的个数比我少1/4!”小亮说;“你要是能给我你的1/6,我就比你多2个了。
”小明原有玻璃球多少个?答案小明说(mínɡ shuō);“你有球的个数比我少1/4!”,则想成小明的球的个数为4份,则小亮(xiǎo liànɡ)的球的个数为3份4*1/6=2/3 (小明(xiǎo mínɡ)要给小亮2/3份玻璃球)小明(xiǎo mínɡ)还剩;4-2/3=3又1/3(份)小亮(xiǎo liànɡ)现有;3+2/3=3又2/3(份)这多出来的1/3份对应的量为2,则一份里有;3*2=6(个)小明原有4份玻璃球,又知每份玻璃球为6个,则小明原有玻璃球4*6=24(个)3·搬运一个仓库的货物,甲需要10小时,乙需要12小时,丙需要15小时,有同样的仓库A和B,甲在A仓库·乙在B 仓库同时开始搬运货物,丙开始帮助甲搬运,中途又转向帮助乙搬运,最后两个仓库货物同时搬完,问丙帮助甲·乙各多少时间?解;设搬运一个仓库的货物的工作量是1,现在相当于三人共同完成工作量2,所需时间是答;丙帮助(bāngzhù)甲搬运3小时,帮助乙搬运5小时解本题的关键,是先算出三人共同搬运(bānyùn)两个仓库的时间,本题计算当然也可以(kěyǐ)整数化,设搬运一个仓库全部工作量为 60,甲每小时(xiǎoshí)搬运 6,乙每小时搬运5,丙每小时搬运4三人共同(gòngtóng)搬完,需要60 × 2÷(6+ 5+ 4)= 8(小时)甲需丙帮助搬运(60- 6× 8)÷ 4= 3(小时)乙需丙帮助搬运(60- 5× 8)÷4= 5(小时)4·一件工作,若由甲单独做72天完成,现在甲做1天后,乙加入一起工作,合作2天后,丙也一起工作,三人再一起工作4天,完成全部工作的1/3,又过了8天,完成了全部工作的5/6,若余下的工作由丙单独完成,还需要几天?答案(dá àn)甲乙丙3人8天完成(wán chéng) :5/6-1/3=1/2甲乙丙3人每天完成(wán chéng) :1/2÷8=1/16,甲乙丙3人4天完成(wán chéng) :1/16×4=1/4则甲做一天(yī tiān)后乙做2天要做 :1/3-1/4=1/12那么乙一天做 :[1/12-1/72×3]/2=1/48则丙一天做 :1/16-1/72-1/48=1/36则余下的由丙做要 :[1-5/6]÷1/36=6天答;还需要6天5·股票交易中,每买进或卖出一种股票都必须按成交易额的1%和2%分别交纳印花税和佣金(通常所说的手续费)。
六年级奥数专题:统一单位“1”(一)

第四讲:统一单位“1”(一)对于较复杂的分数应用题,题目中出现了多个不同的单位“1”,需要统一单位“1”所有的分率都转化成占这个单位“1”的几分之几,使数量关系和对应分率明确呈现,才能顺利解题。
【例1】果园中果树比柿子树多450株,其中苹果树的53与柿子树的32株树相同,问:果园中苹果树与柿子树各有多少棵?模仿P 甲、乙两人存玉米的仓库中,甲仓比乙仓的玉米多258千克。
已知甲仓玉米的53-与乙仓玉米的76一样多。
问:甲、乙两个仓库各有玉米多少千克?模仿2 弟弟比哥哥少做10道数学题,已知哥哥做的题数的95与弟弟做的题 数的53相同,问:兄弟俩各做多少题?拓展1 某厂甲、乙两个车间共有工人1248人,如果从甲车间工人总数中调31到乙车间,这时乙车间工人总数的83正好是甲车间工人数的53,问甲、乙车间,原各有多少工人?拓展2 某校有学生1350人参加冬季体育锻炼,全校男生的60%和全校女生的52参加长跑活动,其余同学参加跳绳和其他活动,结果跳绳和其他活动的男、女生人数相等,问:该校男、女生各多少人?拓展3 某电脑公司甲、乙两个仓库共有电脑1300台,从甲仓库运走库存的43,从乙仓库运走库存的53。
剩下的电脑中,乙仓库比甲仓库多260台,问:两个仓库原各存电脑多少台?精练1 甲、乙两个养鸡房共有鸡3000只,已知甲养鸡房的115和乙养鸡房 的41合在一起是1020只。
问:甲、乙两个养鸡房各有鸡多少只?精练2 超市里有某种款式的牛仔裤共1500条,已知男裤的95与女裤的32共930条,又知女裤的进价是每条64元,是男裤进价的54。
问:商店进这批裤子的总进价是多少元?精练3 小迪有甲、乙、丙三盒卡片,她从甲盒卡片的1513中取出29张,剩下的卡片数与乙盒的张数相同;她又在乙盒卡片的74中放人40张卡片,此时乙盒卡片张数正好和丙盒的张数相同。
已知丙盒现有卡片120张,问:三盒卡片一共多少张?精练4 某梅花鹿饲养场有梅花鹿938只,其中母鹿与小鹿总数的32比雄鹿的54少20只,小鹿的52蜀母鹿的2倍相等,问:饲养场有雄鹿、母鹿、小鹿各多少只?精练5 甲、乙、丙三个车间共完成4500台电视机的组装任务,已知甲车间已完成自己任务的65,乙车间已完成自己任务的32,丙车间已完成自己任务的95,并且三个车间完成的组装台数一样多。
小学六年级奥数练习题一(精析)

一,把甲乙丙三根木棒插入水池中,三根木棒的长度和为360厘米,甲有在水外,乙有在水外,丙有在水外。
水有多深?分析:可设水深x厘米(可知三木棒在水中的部分相等,均为x厘米)。
由甲=x,乙=x,丙=x,得甲=4x,乙=x,丙=x4x+x+x =360x=45则水有45cm深。
二,小刚有若干本书,小华借走一半加一本,剩下的书小明借走一半加两本,再剩下的书小峰借走一半加三本,最后小刚还剩下两本书,那么小刚原有50本书。
分析:逆推(从问题出发,一步步向前推)问题。
小刚剩下的2本书加上3本就是小明借走后的一半,则小明借走后的书有10本;同理可以求出小华借走后的书有24本......即小峰未借前有书:(2+3)÷=10小明未借之前有:(10+2)÷=24小刚原有书:(24+1)÷=50那么乙数比甲数少几分之几?分析:设乙数是单位“1”,则甲数是(甲数=乙数×(1+))1×(1+)=乙数比甲数少:(乙数=甲数×(1-所求的数))=一,有梨和苹果若干个,梨的个数是全体的少17个,苹果的个数是全体的少31个。
那么梨和苹果的个数各有多少?分析:设总数有35x个则梨有35x·-17=21x-17个,苹果有35x·-31=20x-31个(20x-31)+(21x-17)=35xx=8则梨有21×8-17=151个,苹果有20×8-31=129个。
二,有一个分数,它的分母比分子多4,如果把分子、分母都加上9,得到的分数约分后是,这个分数是多少?分析:设分子为x9x+81=7x+91x=5x+4=9这个分数是 .三,把一根绳子分别等分折成5股和6股,如果折成5股比6股长20厘米,那么这根绳子的长度是多少厘米?分析:把绳子全长当单位1:折成5股,每股长;折成6股,每股长。
(绳长-绳长=(-)绳长=20 绳长=)绳子的长度为20÷()=600厘米一,一筐苹果,甲取一半少一个,乙取余下的一半多一个,丙取余下的一半,结果还剩下1个.这筐苹果原来有几个?分析:丙取一半,剩一个,说明丙取前是1+1=2个乙一半多一个,则乙取前是(2+1)×2=6个甲一半少一个,则甲取前时(6-1) ×2 = 10个原来有10个解:设这袋苹果原来x个甲取走苹果的个数为-1乙取走苹果的个数为(x-+1) +1=+丙取走苹果的个数(也是剩余的个数)为:总数-甲取走-乙取走,即【x-(-1)-(+)】=1-=2x=10二,小辉乘飞机参加世界少年奥林匹克数学金杯赛.机窗外是一片如画的蔚蓝大海.她看到云海占整个画面,并遮住一个海岛的,露出的海岛占整个画面的。
小学六年级奥数题集锦(1)

小学六年级奥数题集锦1、甲乙两车同时从AB两地相对开出。
甲行驶了全程的5/11,如果甲每小时行驶4.5千米,乙行了5小时。
求AB两地相距多少千米2、一辆客车和一辆货车分别从甲乙两地同时相向开出。
货车的速度是客车的五分之四,货车行了全程的四分之一后,再行28千米与客车相遇。
甲乙两地相距多少千米?3、甲乙两人绕城而行,甲每小时行8千米,乙每小时行6千米。
现在两人同时从同一地点相背出发,乙遇到甲后,再行4小时回到原出发点。
求乙绕城一周所需要的时间?4、甲乙两人同时从A地步行走向B地,当甲走了全程的1\4时,乙离B地还有640米,当甲走余下的5\6时,乙走完全程的7\10,求AB两地距离是多少米?5、甲,乙两辆汽车同时从A,B两地相对开出,相向而行。
甲车每小时行75千米,乙车行完全程需7小时。
两车开出3小时后相距15千米,A,B两地相距多少千米?6、甲,已两人要走完这条路,甲要走30分,已要走20分.现两人同时出发相向而走.走3分后,甲发现有东西没拿,拿东西耽误3分,甲再走几分钟跟已相遇7、甲,乙两辆汽车从A地出发,同向而行,甲每小时走36千米,乙每小时走48千米,若甲车比乙车早出发2小时,则乙车经过多少时间才追上甲车?8、甲乙两人分别从相距36千米的ab两地同时出发,相向而行,甲从a 地出发至1千米时,发现有物品落在a地,便立即返回,拿了物品又立即从a地向b地行进,这样甲、乙两人恰好在a,b两地的中点处相遇,又知甲每小时比乙多走0.5千米,求甲、乙两人的速度9、两列火车同时从相距400千米两地相向而行,客车每小时行60千米,货车小时行40千米,两列火车行驶几小时后,相遇有相距100千米?10、甲每小时行驶9千米,乙每小时行驶7千米。
两者在相距6千米的两地同时向背而行,几小时后相距150千米11、甲乙两车从相距600千米的两地同时相向而行已知甲车每小时行42千米,乙车每小时行58千米两车相遇时乙车行了多少千米?12、两车相向,6小时相遇,后经4小时,客车到达,货车还有188千米,问两地相距?13、甲乙两地相距600千米,客车和货车从两地相向而行,6小时相遇,已知货车的速度是客车的3分之2 ,求二车的速度?14、小兔和小猫分别从相距40千米的A、B两地同时相向而行,经过4小时候相距4千米,再经过多长时间相遇?15、甲、乙两车分别从a b两地开出甲车每小时行50千米乙车每小时行40千米甲车比乙车早1小时到两地相距多少?16、两辆车从甲乙两地同时相对开出,4时相遇。
小学数学六年级奥数《最值问题(1)》练习题(含答案)

小学数学六年级奥数《最值问题(1)》练习题(含答案)一、填空题1.一把钥匙只能开一把锁.现在有4把钥匙4把锁,但不知哪把钥匙开哪把锁,最多要试 次才能配好全部的钥匙和锁.2.用长和宽分别是4厘米和3厘米的长方形小木块,拼成一个正方形,最少要用这样的木块 块.3.一个一位小数用四舍五入法取近似值精确到万位,记作50000.在取近似值以前,这个数的最大值是 .4.100个自然数,它们的总和是10000,在这些数里,奇数的个数比偶数的个数多,那么这些数里至多有 个偶数.5.975⨯935⨯972⨯( ),要使这个连乘积的最后四个数字都是零.在括号内最小应填 .6.有三个连续自然数,它们依次是12、13、14的倍数,这三个连续自然数中(除13外)是13倍数的那个数最小是 .7.下图九个数中取出三个数来,这三个数都不在同一横行,也不在同一纵行.问:怎样取才能使这三个数之和最大,最大数是 .8.农民叔叔阿根想用20块长2米,宽1.2米的金属网建一个靠墙的长方形鸡窝.为了防止鸡飞出,所建鸡窝的高度不得低于2米,要使鸡窝面积最大,长方形的长和宽分别应是 .9.一个三角形的三条边长是三个两位的连续偶数,它们的末位数字和能被7整除,这个三角形的最大周长等于 .10.农场计划挖一个面积为432m 2的长方形养鱼池,鱼池周围两侧分别有3m 和4m 的堤堰如图所示,要想占地总面积最小,水池的长和宽应为 .二、解答题11.下图中,已知a 、b 、c 、d 、e、f 是不同的自然数,且前面标有两个箭头的每一个数恰等于箭头起点的两数的和(如b =a +d ),那么图中c 最小应为多少?a b cd ef12.唐老鸭与米老鼠进行一万米赛跑,米老鼠的速度是每分钟125米,唐老鸭的速度是每分钟100米.唐老鸭手中掌握着一种迫使米老鼠倒退的电子遥控器,通过这种遥控器发出第n 次指令,米老鼠就以原速度的n ⨯10%倒退一分钟,然后再按原来的速度继续前进,如果唐老鸭想在比赛中获胜,那么它通过遥控器发出指令的次数至少应是多少次?13.某游泳馆出售冬季学生游泳卡,每张240元,使用规定:不记名,每卡每次只限一人,每人只限一次.某班有48名学生,老师打算组织学生集体去游泳,除需购买若干张游泳卡,每次游泳还需包一辆汽车,无论乘坐多少名学生,每次的包车费均为40元.若要使每个同学游8次,每人最少交多少钱?14.某商店需要制作如图所示的工字形架100个,每个由铝合金型材长为2.3米,1.7米,1.3米各一根组装而成.市场上可购得该铝合金型材的原料长为 6.3米.问:至少要买回多少根原材料,才能满足要求(不计损耗)?———————————————答 案——————————————————————1. 6第一把钥匙最坏的情况要试3次,第二把要试2次,第三把要试1次,共计6次.2. 12因4和3的最小公倍数为12,故最少需这样的木块12块.3. 50000.44. 48一共有100个自然数,其中奇数应多于50个,因为这100个自然数的总和是偶数,所以奇数的个数是偶数,至少有52个,因而至多有48个.5. 20因975=39⨯52,935=187⨯5,972=243⨯22,要使其积为1000的倍数,至少应乘以5⨯22=20.6. 1105因为12、13、14的公倍数分别加上12、13、14后才依次是12、13、14倍数的连续自然数,故要求是13的倍数的最小自然数,只须先求12、13、14的最小公倍数为1092,再加上13得1105.7. 20第一横行取6,第二横行取7,第三横行取7.8. 12米,6米.金属网应竖着放,才能使鸡窝高度不低于2米.如图,设长方形的长和宽分别是x 米和y 米,则有x +2y =1.2⨯20=24.长方形的面积为S =xy =()y x 221⨯.因为x 与2y 的和等于24是一个定值,故它们的乘积当它们相等时最大,此时长方形的面积S 也最大,于是有:x =12,y =6.9. 264依题意,末位数字和能被7整除的只有7、14、21等三种.但三个两位的连续偶数相加其和也一定是偶数,故符合题意的只有14.这样三个最大的两位连续偶数.它们的末位数字又能被7整除的,便是90、88、86,它们的和即三角形最大周长为90+88+86=264.10. 24m ,18m如图,设水池边长为xm ,宽为ym ,则有xy =432,占地总面积S =(x +8)(y +6)m 2 于是S =xy +6x +8y +48=6x +8y +480.因6x +8y =48⨯432为定值,故当6x =8y 时,S 最小,此时x =24,y =18.11. 依题意,d 应当取最小值1,那么a 和f 只能一个为2,另一个为4.这样,根据b =a +d ,e =d +f ,b 和e 便只能一个为3,另一个为5,而c =b +e .所以c 最小应为3+5=8.12. 米老鼠跑完全程用的时间为10000÷125=80(分),唐老鸭跑完全程的时 间为10000÷100=100(分).唐老鸭第n 次发出指令浪费米老鼠的时间为n n 1.01125%101251+=⨯⨯+. 当n 次取数为1、2、3、4…13时,米老鼠浪费时间为1.1+1.2+1.3+1.4+…+2.3=22.1(分)大于20分.因为米老鼠早到100-80=20分,唐老鸭要想获胜,必须使米老鼠浪费的时间超过20分钟,因此唐老鸭通过遥控器至少要发13次指令才能在比赛中获胜.13.设一共买了x 张卡,一共游泳y 次,则共有xy =48⨯8=384(人次),总运费为:(240x +40y )元.因240x ⨯40y =240⨯40⨯384是一定值,故当240x =40y ,即y =6x 时和最小,此时可求得x =8,y =48.总用费为240⨯8+40⨯48=3840(元),平均每人最少要交3840÷48=80(元).显然④⑤⑥三种方案损耗较小. ④⑤⑥⑦方案依次切割原材料42根、14根、29根和1根共用原材料42+14+29+1=86(根).。
小学六年级奥数培优竞赛测试卷(一)及答案

小学六年级奥数培优竞赛测试卷(一)一.填空题。
(每题2分,共20分)1. 一个直角三角形的两条直角边分别是6dm 、8dm,第三条边长IOdm,这条边(斜边)上的局是()dm©2. A 和B 都是自然数,分解质因数是:A=2×5×C,B=3×5×Co 如果A 和B 的最小公倍数是60,那么C=()o3. 用短除法可得:131ab 那么:=()o23 b4 .48千克比( )千克少;,( )千克比20千克多工千克。
545 .一个四位数4AA1能被3整除,A=( )。
6 .把含盐20%的盐水60千克,制成含盐25%的盐水,需加盐()千克。
7 .六⑴班男生的一半和女生的工共16人,女生的一半和男生的工共14人,这个班有()人。
4 4 8 .有两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%,大圆的面积是()平方厘米。
9 .如图,把一张三角形的纸如图折叠,面积减少∣o 已知阴影部分的面积是50平方厘米,则这张三角形纸的面积是()平方厘米。
Nr--10 .在括号里填写出分母都小于12的异分母最简分数。
11三=()+( )=( )+( )12二.选择题。
(每题2分,共16分)11 .a 、b 、C 是三个非0自然数,且a>b,下面的结论正确的是(13.已知a 能整除19,那么a (14.甲数除以乙数的商是5,余数是3,若甲、乙两数同时扩大10倍,那么余数(aAfVl11B.- > 一 a bC.- > - C Cc cD-a >b12.有1克、2克、4克的祛码各一个, 最多能称出()种不同质量的物体。
A. 5B. 6C. 7D.8 A.只能是19B.是1或19C.是19的倍数D. 一定是3815 .甲、乙、丙、丁四人参加某次电脑技能比赛。
甲、乙两人的平均成绩为a 分,他们两人的平均成绩比丙的成绩低9分,比丁的成绩高3分,那么他们四人的平均成绩为()分。
六年级下册数学试题奥数阶段测试一全国通用

阶段测试(一)1.简算:(1)3.6×11.1+1.2×66.7(2)7.2×14.5+17×2.8计算:38252.14×7+0.65×-×14+×0.65137133.41.2×8.1+11×91+53.7×1.944.如何简易如何算.22(2)999×274+6274(1)2004-20032(3)9999+1999948贯通融会六年级(年“数学花园探秘”小高组复赛)5.2018计算:7×11×13+27×371000(年全国“数学花园探秘”比赛高年级组)6.20171)1)计算:(63-÷1-63(637.修路队俢一条公路,第一天修了这条公路的2,次日俢了余5下的1,已知这两天共俢米,这条公路全长是多少米?12038.某市有三个工厂,第一个工厂的人数占三个工厂总人数的20%,第二个工厂的人数是第三个工厂人数的2.已知第二3个工厂比第一个工厂多人,三个工厂一共有多少人?300阶段测试(一)49甲、乙两人共做了个部件,此中甲做的部件的5与乙做9.1848的部件的3共个.甲、乙两人各做了多少个部件?123410.比较222和22的大小. 1111111(秋新东方教育科技公司万人测)一件工作,甲独自完11.2017小时,乙独自达成要用小时,两人合作几小时后成要用64还剩下这项工作的1?3(“”)桌上有两堆棋子,第年数学花园探秘小高组复赛12.2018一堆棋子的枚数恰好是第二堆的一半,假如从第二堆中取走枚,那么第二堆棋子的枚数将变为第一堆的一半,那15?么两堆棋子共有多少枚50贯通融会六年级。
小学六年级奥数训练(一)及其答案

小学六年级奥数训练试卷一一、计算题:(每题5分,共10分)1、(111×66-185×8)÷37=______.2、1997+1996-1995-1994+1993+1992…-2+1=_______.二、填空题:(每题5分,共25分)1、某地区水电站规定,如果每月用电不超过24度,则每度收9分;如果超过24度,则多出度数按每度2角收费.若某月甲比乙多交了9.6角(甲、乙都是整数),则甲交了______角______分2、乒乓球单打决赛在甲、乙、丙、丁四位选手中进行,赛前,有些人预测比赛结果,A说:甲第4;B说:乙不是第2,也不是第4;C说:丙的名次在乙的前面;D说:丁将得第1.比赛结果表明,四个人中只有一人预测错了.那么,甲、乙、丙、丁四位选手的名次分别为:_______.3、41位数55…5□99…9(其中5和9各有20个)能被7整除,那么中间方格内的数字是_____.4、如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1∶3,若阴影三角形面积为1平方厘米,则原长方形面积为______平方厘米.5.字母A、B、C代表三个不同的数字,其中A比B大,B比C大,如果用数字A、B、C组成的三个三位数相加的和为777,其竖式如右,那么三位数ABC是______.三、解答题:(1~7题每题5分,8,9,10题每题10分,共65分)1.一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长是385米.坐在快车上看见慢车驶过的时间是11秒,那么坐在慢车上看见快车驶过的时间是多少秒?2.一堆苹果,2个2个地数剩1个,3个3个地数剩2个,4个4个地数剩3个,5个5个地数剩4个,6个6个地数剩5个,求这堆苹果至少有多少个?3.甲、乙、丙三人去完成植树任务,已知甲植一棵树的时间,乙可以然后丙休息了8天,乙休息了3天,甲没休息,最后一起完成任务.问:从开始植树算起,共用了多少天才完成任务?5.原计划有420块砖让若干学生搬运,每人运砖一样多,后来增加一个学生,这样每个学生就比原计划少搬2块.那么原来有学生多少人?6.六年级学生和一年级学生共120人一起给树浇水,六年级学生一人提两桶水,一年级学生两人抬一桶水,两个年级一次浇水180桶,问有一年级学生多少人?7、小红有一只手表和一只小闹钟,走时总有点差别,小闹钟走半小时,手表要多走36秒,又知在半小时的标准时间里,小闹钟少走了36秒,问:这只手表准不准?每小时差多少?8、甲、乙、丙三个小孩分别带了若干块糖,甲带的最多,乙带的较少,丙带的最少.后来进行了重新分配,第一次分配,甲分给乙、丙,各给乙、丙所有数少4块,结果乙有糖块最多;第二次分配,乙给甲、丙,各给甲、丙所有数少4块,结果丙有糖块最多;第三次分配,丙给甲、乙,各给甲、乙所有数少4块,经三次重新分配后,甲、乙、丙三个小孩各有糖块44块,问:最初甲、乙、丙三个小孩各带糖多少块?9、外表相同的18个小球中,有9克和10克的两种重量,从18个球中取出两个球放在天平左边以作比较,另外16个球分成8对,依次放在天平的右边与这两个球比较重量,发现有5对比那两个球重,有2对比那两个球轻,有一对与那两个球重量相等,这18个球的总重量是多少?10、A s shown below, the area of the parallelogram ABCD is 54 cm2, E, F trisect CA and BA, the area of the shadow is _________.小学六年级奥数训练试卷一答案一、计算题:1、(111×66-185×8)÷37=111×66÷37-185×8÷37=3×66-5×8=198-40=1582、1997+1996-1995-1994+1993+1992…-2+1=1997+(1996-1995-1994+1993)+(1992+…+(4-3-2+1)=1997二、填空题:1、甲交了27角6分解:按照这样的收费标准,如果两人在同一标准下(例如都在24度以下,或都在24度以上),那么交的钱数应该是9分或2角的倍数.甲比乙多交了9.6角,显然甲用电在24度以上,乙在24度以下。
六年级奥数《应用题(一)》练习题

第十三讲应用题(一)(必做与选做)1.三年级同学参加义务劳动,一班和二班共搬砖830块,一班比二班少搬70块,问一班、二班各搬砖多少块?A. 450 380B. 380 450C. 450 520D. 310 380解析:两班搬砖数量的总和为830块,差为70块。
因此,可以直接利用和差公式:大数=(和+差)÷2,即二班:(830+70)÷2=450(块),一班:830-450=380(块)。
所以选B。
2.米德、卡尔共有60张邮票,若米德给卡尔6张邮票后,那么两人的邮票数量相等,问米德、卡尔各有多少张邮票?A. 24 36B. 36 24C. 27 33D. 33 27解析:本题属于和差问题,两人邮票数量的和是60张,由“若米德给卡尔6张邮票后,那么两人的邮票数量相等”可知,差是(6×2)张,因此米德有邮票:(60+6×2)÷2=36(张),卡尔有邮票:60-36=24(张)。
所以选B。
3.两箱水果共重100千克,若从甲箱取12千克放到乙箱中,这时甲箱还比乙箱多4千克,求甲、乙两箱水果原来各有多少千克?A. 42 58B. 58 42C. 36 64D. 64 36解析:两箱水果重量和为100千克。
由“从甲箱取12千克放到乙箱中,这时甲箱还比乙箱多4千克”可知,甲箱水果重量比乙箱重(12×2+4)千克,即差为28千克。
因此,甲箱有水果:[100+(12×2+4)]÷2=64(千克),乙箱有水果:100-64=36(千克)。
所以选D。
4.欧拉家里养了20只兔子,其中大兔子只数是小兔子的4倍,欧拉家里养了大兔子和小兔子各几只?A. 4 16B. 16 4C. 5 15D. 15 5解析:已知一共有20只兔子,又知道大兔子的只数是小兔子的4倍,这是一个和倍问题,可直接利用和倍问题的公式解题。
把小兔子的只数看作1份,大兔子有4份,一共5份,每份:20÷5=4(只),所以小兔子有4只,大兔子有:4×4=16(只)。
【精选】小学六年级奥数精选50(附答案)一

【精选】小学六年级奥数精选50(附答案)一一、拓展提优试题1.有两辆火车,车长分别是125米和115米,车速分别是22米/秒和18米/秒,两车相向行驶,从两车车头相遇到车尾分开需要秒.2.从1开始的n个连续的自然数,如果去掉其中的一个数后,余下的各个数的平均数是,那么去掉的数是.3.如图.从楞长为10的立方体中挖去一个底面半径为2,高为10的圆柱体后,得到的几何体的表面积是,体积是.(π取3)4.(15分)王老师将200块糖分给了甲乙丙三个小朋友,甲比乙的2倍还要多,乙比丙的3倍还要多,那么甲最少有块糖,丙最多有块糖.5.若算式(□+121×3.125)÷121的值约等于3.38,则□中应填入的自然数是.6.图中每一个圆的面积都是1平方厘米,则六瓣花形阴影部分的面积是平方厘米.7.对于一个多边形,定义一种“生长”操作:如图1,将其一边AB变成向外凸的折线ACDEB,其中C和E是AB的三等分点,C,D,E三点可构成等边三角形,那么,一个边长是9的等边三角形,经过两次“生长”操作(如图2),得到的图形的周长是;经过四次“生长”操作,得到的图形的周长是.8.若质数a,b满足5a+b=2027,则a+b=.9.如图,一只玩具蚂蚁从O点出发爬行,设定第n次时,它先向右爬行n个单位,再向上爬行n个单位,达到点A n,然后从点A n出发继续爬行,若点O记为(0,0),点A1记为(1,1),点A2记为(3,3),点A3记为(6,6),…,则点A100记为.10.如图,一个长方形的长和宽的比是5:3.如果长方形的长减少5厘米,宽增加3厘米,那么这个长方形边长一个正方形.原长方形的面积是平方厘米.11.如图,一个底面直径是10厘米的圆柱形容器装满水.先将一个底面直径是8厘米的圆锥形铁块放入容器中,铁块全部浸入水中,再将铁块取出,这时水面的高度下降了3.2厘米.圆锥形铁块的高厘米.12.如图,已知AB=2,BG=3,GE=4,DE=5,△BCG和△EFG的面积和是24,△AGF和△CDG的面积和是51.那么,△ABC和△DEF的面积和是.13.甲、乙两人拥有邮票张数的比是5:4,如果甲给乙5张邮票,则甲、乙两人邮票张数的比变成4:5.两人共有邮票张.14.小丽做一份希望杯练习题,第一小时做完了全部的,第二小时做完了余下的,第三小时做完了余下的,这时,余下24道题没有做,则这份练习题共有道.15.如图,将1个大长方形分成了9个小长方形,其中位于角上的3个小长方形的面积分别为9,15和12,由第4个角上的小长方形的面积等于.【参考答案】一、拓展提优试题1.解:(125+115)÷(22+18)=240÷40=6(秒);答:从两车头相遇到车尾分开需要6秒钟.故答案为:6.2.解:设去掉的数是x,那么去掉一个数后的和是:(1+n)n÷2﹣x=×(n﹣1);显然,n﹣1是7的倍数;n=8、15、22、29、36时,x均为负数,不符合题意.n=43时,和为946,42×=912,946﹣912=34.n=50时,和为1225,49×=1064,1225﹣1064=161>50,不符合题意.答:去掉的数是34.故答案为:34.3.解:10×10×6﹣3×22×2+2×3×2×10,=600﹣24+120=696;10×10×10﹣3×22×10,=1000﹣120=880;答:得到的几何体的表面积是696,体积是880.故答案为:696,880.4.解:甲比丙的2×3=6倍多,总数就比丙的6+3+1=10倍多200÷(2×3+3+1)=20(块),丙最多:20﹣1=19(块)此时甲乙至少有:200﹣19=181(块),181÷(2+1)=60(块)…1(块),乙最多60块,甲至少:60×2+1=121(块).故答案为:121,19.5.解:令□=x,那么:(x+121×3.125)÷121,=(x+121×3.125)×,=x+121×3.125×,=x+3.125;x+3.125≈3.38,x≈0.255,0.255×121=30.855;x=30时,x=×30≈0.248;x=31时,x=×31≈0.255;当x=31时,运算的结果是3.38.故答案为:31.6.解:1×2=2(平方厘米);答:六瓣花形阴影部分的面积是2平方厘米.故答案为:2.7.解:边长是9的等边三角形的周长是9×3=27第一次“生长”,得到的图形的周长是:27×=36第二次“生长”,得到的图形的周长是:36×=48第三次“生长”,得到的图形的周长是:48×=64第四次“生长”,得到的图形的周长是:64×==85答:经过两次“生长”操作,得到的图形的周长是48,经过四次“生长”操作得到的图形的周长是85.故答案为:48,85.8.解:依题意可知:两数字和为奇数,那么一定有一个偶数.偶质数是2.当b=2时,5a+2=2027,a=405不符合题意.当a=2时,10+b=2027,b=2017符合题意,a+b=2+2017=2019.故答案为:2019.9.解:根据分析可知A100记为(1+2+3+…+100,1+2+3+…+100);因为1+2+3+…+100=(1+100)×100÷2=5050,所以A100记为(5050,5050);故答案为:A100记为(5050,5050).10.解:先求出一份的长:(5+3)÷(5﹣3)=8÷2=4(厘米)长是:4×5=20(厘米)宽是:4×3=12(厘米)原来的面积是:20×12=240(平方厘米);答:原来长方形的面积是240平方厘米.故答案为:240.11.解:圆锥形铁块的体积是:3.14×(10÷2)2×3.2=3.14×25×3.2=251.2(cm3)铁块的高是:251.2×3÷[3.14×()2]=251.2×3÷50.24=15(cm)答:铁块的高是15cm.12.解:作CM⊥AD,垂足为M,作FN⊥AD,垂足为N,设CM=x,FN=y.由题意得方程组,解方程组得,所以△ABC与△DEF的面积和是:AB•CM+DE•FN=×2×8+×5×6=8+15=23.故答案为:23.13.解:5÷()=5=45(张)答:两人共有邮票 45张.故答案为:45.14.解:24÷(1﹣)÷(1﹣)÷(1﹣)=24÷=60(道)答:这份练习题共有 60道.故答案为:60.15.解:如图,设D的面积为x,9:12=15:x9x=12×15x=x=20答:第4个角上的小长方形的面积等于20.故答案为:20.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数专项训练系列(一)第一讲 定义新运算在加.减.乘.除四则运算之外,还有其它许多种法则的运算。
在这一讲里,我们学习的新运算就是用“ #”“*”“Δ”等多种符号按照一定的关系“临时”规定的一种运算法则进行的运算。
例1:如果A*B=3A+2B ,那么7*5的值是多少?例2:如果A#B 表示3B A + 照这样的规定,6#(8#5)的结果是多少?例3:规定YX XY Y X +=∆ 求2Δ10Δ10的值。
例4:设M*N 表示M 的3倍减去N 的2倍,即M*N=3M-2N(1) 计算(14 *10)*6(2) 计算 (58*43) *(1 *21)例5:如果任何数A 和B 有A ¤B=A ×B-(A+B )求(1)10¤7(2)(5¤3)¤4(3)假设2¤X=1求X例6:设P ∞Q=5P+4Q ,当X ∞9=91时,1/5∞(X ∞ 1/4)的值是多少?例7:规定X*Y=XY Y AX +,且5*6=6*5则(3*2)*(1*10)的值是多少?例8:▽表示一种运算符号,它的意义是))((A Y A X XY Y X +++=∇11 已知3211212112=+++=∇))((A 那么20088▽2009=?巩固练习1、已知2▽3=2+22+222=246; 3▽4=3+33+333+3333=3702;按此规则类推(1) 3▽2 (2)5▽3(3)1▽X=123,求X 的值2、已知1△4=1×2×3×4;5△3=5×6×7计算(1)(4△2)+(5△3)(2)(3△5)÷(4△4)3、如果A*B=3A+2B,那么(1)7*5的值是多少?(2)(4*5)*6 (3)(1*5)*(2*4)4、如果A>B,那么{A,B}=A;如果A<B,那么{A,B}=B;试求(1){8,0.8}(2){{1.9,1.901}1.19}5、N为自然数,规定F(N)=3N-2 例如F(4)=3×4-2=10试求:F(1)+F(2)+F(3)+F(4)+F(5)+……+F(100)的值6、如果1=1!1×2=2!1×2×3=3!……1×2×3×4×……×100=100!那么1!+2!+3!+……+100!的个位数字是几?(第四届小学生“迎春杯”数学决赛试题)7、若“+、-、×、÷、=、()”的意义是通常情况,而式子中的“5”却相当于“4”。
下面四个算式(1)8×7=8(2)7×7×7=6(3)(7+8+3)×9=39(4)3×3=3那么应该是我们通常的哪四个算式?8、如果2*4=2×3×4×5 5*3=5×6×7,请按此规定计算(1)(3*4)-(5*3) (2)(4*4)÷(3*3)9、规定(25)=2+5=7 (123)=1+2+3=6 (65)=6+5=(11)=1+1=2则计算(1)(56489) (2)(92045)+(90÷5)÷(12)10、规定64=2×2×2×2×2×2表示成F (64)=6;243=3×3×3×3×3表示成G (243)=5;试求下面各题的值(1) F (128)= ( )(2) F (16)= G ( )(3) F ( )+ G( 27 )=611、如果1=1!1×2=2!1×2×3=3!……试计算(1)5! (2)X !=5040,求X12、有一种运算符号“&”使下列算式成立2&3=7 5&3=13 4&5=13 9&7=25 求995 & 9=?13、A*B=B A B A ÷+ 在X*(5*1)=6中,X 的值是多少?14、对于任意的整数X 、Y 定义新运算“¥”X ¥Y=YMX XY 26+(其中M 是一个固定的值)如果1¥2=2,那么2¥9=?第二讲 二元一次不定方程一、学习目标:掌握用奇偶性、最值和尾数特点来解答不定方程。
二、基础知识:我们知道,一般的一个方程只能解答一个未知数,而有的题目却必须设两个未知数,且列不出两个方程,类似这样的方程我们称之为二元一次不定方程。
在我们研究不定方程的解时,常常会附有其他一些限制条件,有的条件是明显的,也有隐蔽的,但它们对解题至关重要,这就需要我们在解题过程中酌情进行讨论。
三、例题解析:(一)基本方法例1、小明要买一只4元9角的钢笔,他手上有贰角和伍角的硬币各10枚,请问他可以怎样付钱?分析:本题可以用多种方法解答,这里用不定方程来解。
设小明付了X枚贰角和Y枚伍角列方程,得2X+5Y=49方法一1、利用奇偶性。
49是奇数,2X是偶数,那么5Y必定是奇数。
这样,Y只能取1,3,5,7,9这五个数。
2、利用最值:所付钱中贰角和伍角的都有,而X至多为10,那么5Y不小于49—2×19=29,这样,可得Y大于6。
方法二观察系数的特点,利用尾数(个位数)解答。
由例1可以看出,对于二元一次不定方程,尽量缩小未知数的取值范围,再求解。
不定方程常常利用奇偶性,最值和尾数来帮助解决例2、大汽车能容纳54人,小汽车能容纳36人,现有378人要乘车,问要大、小汽车各几辆才能使每个人都能上车且各车都正好坐满。
为了便于管理,要求车辆数最少,应该选择哪个方案?分析:解答不定方程时,能够把方程化简就尽量化简。
注意加了限制条件以后,答案的变化。
试一试:一个同学把他生日的月份乘以31,日期乘以12,然后加起来的和是170,你知道他出生于几月几日?例3、现有铁矿石73吨,计划用载重量分别为7吨和5吨的两种卡车一次运走,且每辆车都要装满,已知载重量7吨的卡车每台车运费65元,载重量5吨的卡车每台车运费50元,问需用两种卡车各多少台运费最省?分析:根据条件用不定方程可以求出卡车的台数,但是要注意问题求运费最省。
例4 、一个同学发现自己1991年的年龄正好等于他出生那一年的年份的各位数字之和,请问这个学生1991年时多少岁?分析与解:设他出生于19XY年,那么1991—19XY=1+9+X+Y1991—(1900+10X+Y)=10+X+Y91—10X—Y=10+X+Y(二)能力拓展例5、一辆匀速行驶的汽车,起初看路标上的数字是一个两位数xy,过了一小时路标上的数字变为yx,又行驶了一小时路标上的数字是一个三位数x0y,求每次看到的数字和汽车的速度。
分析:路标上的数字是累计数。
由于汽车是匀速行驶,因此汽车在单位时间里行驶的路程是相等的,根据这个关系可以列出方程。
试一试:一个两位数,如果把数字1放在它前面可得一个三位数,放在它后面也可得一个三位数。
已知这两个三位数之差为414,求原来的两位数。
例6、如下图,一个长方体的长、宽、高的长度都是质数,且长>宽>高,将这个长方体横切两刀,竖切两刀,得到9个长方体,这9个长方体表面积之和比原来长方体表面积之和多624平方厘米,求原来长方体的体积。
分析与解:设长方体的长、宽、高分别为a、b、c,分析可得,横切两刀,增加了4ab的面积,竖切两刀增加了4ac的面积,所以可列方程:4ab+4ac=624。
三个未知数的不定方程一般采用分解质因数的方法解答。
练习一、基本题1、求方程6x+9y=87的自然数解。
2、求方程2x+5y=24的自然数解3、大客车有48个座位,小客车有30个座位。
现在有306名旅客,要使每位旅客都有座位而且不空出座位来,需要大、小客车各几辆?4、装饼干的盒子有大、小两种,大盒每盒要11元,小盒每盒要8元,妈妈用了89元,问大小盒子各买了多少个?5、一个两位数,交换个位和十位上的数字,就得到一个新的两位数,已知新两位数比原两位数多54,求原来的两位数。
6、一个两位数,各位数字之和的6倍比原数大3,求这个两位数。
7、一个商人将弹子放进两种盒子里,每个大盒子装12个,每个小盒子装5个,恰好装完。
如果弹子数为99,盒子数大于10,问两种盒子各有多少个?二、综合题8、在一个两位质数的两个数字之间,添上数字6以后,所得的三位数比原数大870,那么原数是多少?9、会场里有两座和四座的两种长椅若干把。
现有一个班的学生(不足70人)来开会。
一部分学生一人坐一把两座的长椅,其余的同学每三人坐一把四座的长椅。
结果平均每个学生坐1.35个座位。
求有多少个学生?思考题10、有一个长方体,它的正面和上面的面积之和是209,如果它的长、宽、高都是质数,那么这个长方体的体积是多少?第三讲分数乘除法计算分数乘除法的计算方法用字母表示为:b d bd⨯=(a,c都不等于0);a c acb d bc bc÷=⨯=(a,c都不等于0)。
a c a d ad一、课前准备:1、计算下列各题:(1)35÷10÷361 (2)73+53÷157 (3)185÷79×3527(3)821÷9÷127 (4)25÷45×35 (6)52÷(41+53)2、在□或〇里填上合适的数字或符号,并说明使用了什么运算定律?(1) 25×167 ×78= ×( × ) (2) 58 ×23 ×815=( × )× (3) 229 ×(15×2931)= ×( × ) (4) 2534×4= × + × (5) 7×78= × 〇 × (6) 145×25= × 〇 × (7) 54×(89 - 56)= × 〇 ×二、例题讲解例1:计算:⑴443745⨯; ⑵152726⨯。
【分析】认真观察这两道题的数学特点:第(1)题中的4445与1只相差145,如果把写成1(1)45-的差与37相乘,再运用乘法分配律就能简化运算了。
同样,第(2)题中的27可以写成(26+1)。
练习:“挑战自己!”比一比,看一看,谁的方法最巧妙?2623 × 15 3225 ×56例2:计算:13274155⨯+⨯ 分析仔细观察因数的特点可知,1275⨯可转化为395⨯,这样就可以利用乘法的分配律进行简算了。
