19-章 程 修 正 案(改)
第19章《一次函数》 实际应用解答题培优(一)2020-2021学年人教版数学八年级下册

人教版数学八年级下册第19章《一次函数》实际应用解答题培优(一)1.甲、乙两台机器共同加工一批零件,一共用了6小时,在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工,甲机器在加工过程中工作效率保持不变,甲、乙两台机器加工零件的总数y(个)与甲加工时间x(h)之间的函数图象为折线OA﹣AB﹣BC.如图所示.(1)这批零件一共有个,甲机器每小时加工个零件;(2)在整个加工过程中,求y与x之间的函数解析式;(3)乙机器排除故障后,求甲加工多长时间时,甲与乙加工的零件个数相差10个.2.在防疫工作稳步推进的过程中,复工复产工作也在如火如荼进行.某企业计划通过扩大生产能力来消化第一季度积累的订单,决定增加一条新的生产线并招收工人.根据以往经验,一名熟练工人每小时完成的工件数量比一名普通工人每小时完成的工件数量多10个,且一名熟练工人完成160个工件与一名普通工人完成80个工件所用的时间相同.(1)求一名熟练工人和一名普通工人每小时分别能完成多少个工件?(2)新生产线的目标产能是每小时生产200个工件,计划招聘n名普通工人与m名熟练工人共同完成这项任务,请写出m与n的函数关系式(不需要写自变量n的取值范围);(3)该企业在做市场调研时发现,一名普通工人每天工资为120元,一名熟练工人每天工资为150元,而且本地区现有熟练工人不超过8人.在(2)的条件下,该企业如何招聘工人,使得工人工资的总费用最少?3.某电信公司推出如下A,B两种通话收费方式,记通话时间为x分钟,总费用为y元.根据表格内信息完成以下问题:(1)分别求出A,B两种通话收费方式对应的函数表达式;(2)在给出的坐标系中作出收费方式A对应的函数图象,并求出;①通话时间为多少分钟时,两种收费方式费用相同;②结合图象,直接写出选择哪种通话方式能节省费用?收费方式月使用费(元)包时通话(分钟)超时通话(元/分钟)A12 0 0.2B18 40 0.34.如图(1)是某手机专卖店每周收支差额y(元)(手机总利润减去运营成本)与手机台数x(台)的函数图象,由于疫情影响目前这个专卖店亏损,店家决定采取措施扭亏.方式一:改善管理,降低运营成本,以此举实现扭亏.方式二:运营成本不变,提高每台手机利润实现扭亏(假设每台手机的利润都相同).解决以下问题:(1)说明图(1)中点A和点B的实际意义;(2)若店家决定采用方式一如图(2),要使每周卖出70台时就能实现扭亏(收支平衡),求节约了多少运营成本?(3)若店家决定两种方式都采用,降低运营成本为m元,提高每台手机利润n元,当5000≤m≤7000,50≤n≤100时,求店家每周销售100台手机时可获得的收支差额范围,并在图(3)中画出取得最大收支差额时y与x的关系的大致图象,要求描出反映关键数据的点.5.如图,l A、l B分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距千米.(2)B走了一段路后,自行车发生故障,B进行修理,所用的时间是小时.(3)B第二次出发后小时与A相遇.(4)若B的自行车不发生故障,保持出发时的速度前进,则出发多长时间与A相遇?(写出过程)6.甲、乙两人相约周末登崂山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,且当乙提速后,乙的登山上升速度是甲登山上升速度的3倍,且根据图象所提供的信息解答下列问题:(1)乙在A地时距地面的高度b为米;t的值为;(2)请求出甲在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式;(3)已知AB段对应的函数关系式为y=30x﹣30,则登山多长时间时,甲、乙两人距地面的高度差为70米?(直接写出答案)7.某水果店11月份购进甲、乙两种水果共花费1800元,其中甲种水果10元/千克,乙种水果16元/千克.12月份,这两种水果的进价上调为:甲种水果13元/千克,乙种水果18元/千克.(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款400元,求该店11月份购进甲、乙两种水果分别是多少千克?(2)若12月份将这两种水果进货总量减少到130千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;(3)在(2)的条件下,若甲种水果不超过80千克,则12月份该店需要支付这两种水果的货款最少应是多少元?8.甲骑电动车,乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩,设乙行驶的时间为x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示,甲、乙两人之间的路程差y关于x的函数图象如图②所示,请你解决以下问题:(1)甲的速度是km/h,乙的速度是km/h;(2)对比图①、图②可知:a=,b=;(3)乙出发多少时间,甲、乙两人路程差为7.5km?9.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,月用电量不超过200度时,按0.55元/度计费,月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费,设每户家庭月用电量为x度时,应交电费y 元.(1)分别求出0≤x≤200和x>200时,y与x的函数解析式.(2)小明家4月份用电250度,应交电费多少元?(3)小明家6月份交纳电费117元,小明家这个月用电多少度?10.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:(1)乙队开挖到30m时,用了小时,甲队在开挖后6小时内,每小时挖m;(2)分别求出y甲、y乙与x的函数解析式,并写出自变量x的取值范围;(3)开挖2小时,甲、乙两队挖的河渠的长度相差m,开挖6小时,甲、乙两队挖的河渠的长度相差m;(4)求开挖后几小时,甲、乙两队挖的河渠的长度相差5m.11.新冠肺炎疫情爆发后,口罩成为了最紧缺的防护物资之一,比亚迪,长安,格力等企业响应国家号召,纷纷开设口罩生产线.2月1日,重庆东升公司复工,利用原有的A 生产线开始生产口罩,8天后,采用最新技术的B生产线建成投产同时,为加大口罩产能,公司耗时2天对A生产线进行技术升级,升级期间A生产线暂停生产,升级后,产能提高20%.如图反映了每条A,B生产线的口罩总产量y(万个)与时间x(天)之间的关系,根据图象,解答下列问题:(1)技术升级后,每条A生产线每天生产口罩万个;(2)每条B生产线每天生产口罩万个;(3)技术升级后,东升公司的口罩日总产量为136万个,已知公司有15条A生产线,则B生产线有条;(4)在(3)的条件下,东升公司进一步扩大产能,两生产线在原每日工作时长8小时的基础上,增加m小时(m为正整数),同时新增k条B生产线,此时公司口罩日总产量达到260万个,求正整数k的值.12.某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在A 商店,无论一次购买多少,价格均为每个50元,在B商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个(x>0).(Ⅰ)根据题意填表:5 10 15 …一次购买数量/个A商店花费/元500 …B商店花费/元600 …(Ⅱ)设在A商店花费y1元,在B商店花费y2元,分别求出y1,y2关于x的函数解析式;(Ⅲ)根据题意填空:①若小丽在A商店和在B商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为个.②若小丽在同一商店一次购买书包的数量为50个,则她在A,B两个商店中的商店购买花费少;③若小丽在同一商店一次购买书包花费了1800元,则她在A,B两个商店中商店购买数量多.13.小明和妈妈元旦假期去看望外婆,返回时,他们先搭乘顺路车到A地,约定小明爸爸驾车到A地接他们回家.一家人在A地见面,休息半小时后,小明爸爸驾车返回家中.已知小明他们与外婆家的距离s(km)和小明从外婆家出发的时间t(h)之间的函数关系如图所示.(1)小明家与外婆家的距离是km,小明爸爸驾车返回时平均速度是km/h:(2)点P的实际意义是什么?(3)求他们从A地驾车返回家的过程中,s与t之间的函数关系式.14.新冠疫情期间,口罩的需求量增大,某口罩加工厂承揽生产1600万个口罩的任务,每天生产的口罩数量相同,计划用x天(x>4)完成.(1)求每天生产口罩y(万个)与生产时间x(天)之间的函数表达式;(2)由于疫情形势严峻,卫生管理部门要求厂家提前4天交货,那么加工厂每天要多做20万个口罩才能完成任务,求实际生产时间.15.某公司销售玉米种子,价格为5元/千克,如果一次性购买10千克以上的种子,超过10千克部分的种子的价格打8折,部分表格如下:2 5 10 12 20 30 …购买种子的数量/千克10 a50 58 b130 …付款金额/元(1)直接写出表格中a,b的值;(2)设购买种子数量为x(x>10)千克,付款金额为y元,求y与x的函数关系式;(3)小李第一次购买种子35千克,第二次又购买了8千克,若两次购买种子的数量合在一起购买可省多少钱?参考答案1.解:(1)由函数图象可知,共用6小时加工完这批零件,一共有270个.AB段为甲机器单独加工,每小时加工个数为(90﹣50)÷(3﹣1)=20(个),故答案为:270,20;(2)设y OA=k1x,当x=1时,y=50,则50=k1,∴y OA=50x;设y AB=k2x+b2,,解得,∴y AB=20x+30;设y BC=k3x+b3,,解得,∴y BC=60x﹣90;综上所述,在整个加工过程中,y与x之间的函数解析式是y=;(3)乙开始的加工速度为:50÷1﹣20=30(个/小时),乙后来的加工速度为:(270﹣90)÷(6﹣3)﹣20=40(个/小时),设乙机器排除故障后,甲加工a小时时,甲与乙加工的零件个数相差10个,20a﹣[30×1+40(a﹣3)]=±10,解得a=4或a=5,答:排除故障后,甲加工4小时或5小时时,甲与乙加工个数相差10.2.解:(1)设一名普通工人每小时完成x个工件,则一名熟练工人每小时完成(x+10)个工件,,解得x=10,经检验,x=10是原分式方程的解,∴x+10=20,即一名熟练工人和一名普通工人每小时分别能完成20个工件、10个工件;(2)由题意可得,10n+20m=200,则m=﹣0.5n+10,即m与n的函数关系式是m=﹣0.5n+10;(3)设工人工资的总费用为w元,w=120n+150m=120n+150(﹣0.5m+10)=45n+1500,∴w随n的增大而增大,∵本地区现有熟练工人不超过8人,∴m≤8,即﹣0.5n+10≤8,解得n≥4,∴当n=4时,w取得最小值,此时w=1680,m=﹣0.5n+10=8,答:招聘普通工人4人,熟练工人8人时,工人工资的总费用最少.3.解:(1)由表格可得,收费方式A对应的函数表达式是y=0.2x+12,收费方式B对应的函数表达式是:当0≤x≤40时,y=18,当x>40时,y=0.3(x ﹣40)+18=0.3x+6,由上可得,收费方式A对应的函数表达式是y=0.2x+12,收费方式B对应的函数表达式是y=;(2)∵收费方式A对应的函数表达式是y=0.2x+12,∴当x=0时,y=12,当x=40时,y=20,收费方式A对应的函数图象如右图所示;①设通话时间为a分钟时,两种收费方式费用相同,0.2a+12=18或0.2a+12=0.3a+6,解得a=30或a=60,即通话时间为30分钟或60分钟时,两种收费方式费用相同;②由图象可得,当0≤x<30或x>60时,选择A种通话方式能节省费用;当x=30或x=60时,两种通话方式一样;当30<x<60时,选择B种通话方式能节省费用.4.解:(1)由图像可知A点是函数图象与x轴的交点,所以点A的实际意义表示当卖出100台手机时,该专卖店每周收支差额为0;B点是函数图象与y轴的交点,所以点B的实际意义表示当手机店一台手机都没有卖出时,该专卖店亏损20000元;(2)由图(1)可求出以前的函数为y=200x﹣20000,若店家决定采用方式一,降低运营成本,即将函数图象上下平移,所以可以设新函数为y =200x+b,∵函数图象经过点(70,0),代入可得200×70+b=0,解得:b=﹣14000,∴要使每周卖出70台时就能实现扭亏(收支平衡),运营成本为14000元,节约了6000元运营成本;(3)设新函数为y=(200+n)x﹣(20000﹣n),∵50≤n≤100,∴250≤200+n≤300,当店家每周售出100台手机,收支差额最小时y=250×100﹣7000=18000,收支差额最大时y=300×100﹣5000=25000,∴收支差额范围为18000≤y≤25000,图象为:.5.解:(1)∵当t=0时,S=10,∴B出发时与A相距10千米.故答案为:10.(2)1.5﹣0.5=1(小时).故答案为:1.(3)观察函数图象,可知:B第二次出发后1.5小时与A相遇.(4)设A行走的路程S与时间t的函数关系式为S=kt+b(k≠0),将(0,10),(3,22.5)代入S=kt+b,得:,解得:,∴A行走的路程S与时间t的函数关系式为S=x+10.设若B的自行车不发生故障,则B行走的路程S与时间t的函数关系式为S=mt.∵点(0.5,7.5)在该函数图象上,∴7.5=0.5m,解得:m=15,∴设若B的自行车不发生故障,则B行走的路程S与时间t的函数关系式为S=15t.联立两函数解析式成方程组,得:,解得:,∴若B的自行车不发生故障,保持出发时的速度前进,小时与A相遇.6.解:(1)甲登山上升的速度是:(300﹣100)÷20=10(米/分钟),乙提速后的速度为:10×3=30(米/分钟),b=15÷1×2=30;t=2+(300﹣30)÷30=11,故答案为:30;11;(2)设甲在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为y=kx+100,根据题意,得20k+100=300,解得k=10,故y=10x+100(0≤x≤20);(3)根据题意,得:当10x+100﹣(30x﹣30)=70时,解得:x=3;当30x﹣30﹣(10x+100)=70时,解得:x=10;当300﹣(10x+100)=70时,解得:x=13.答:登山3分钟、10分钟或13分钟时,甲、乙两人距地面的高度差为70米.7.解:(1)设该店11月份购进甲种水果x千克,购进乙种水果y千克,根据题意得:,解得,答:该店11月份购进甲种水果100千克,购进乙种水果50千克;(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(130﹣a)千克,根据题意得:w=10a+20(130﹣a)=﹣10a+2600;(3)根据题意得,a≤80,由(2)得,w=﹣10a+2600,∵﹣10<0,w随a的增大而减小,∴a=80时,w有最小值w最小=﹣10×80+2600=1600(元).答:12月份该店需要支付这两种水果的货款最少应是1600元.8.解:(1)由图可得,甲的速度为:25÷(1.5﹣0.5)=25÷1=25(km/h),乙的速度为:25÷2.5=10(km/h),故答案为:25,10;(2)由图可得,a=25×(1.5﹣0.5)﹣10×1.5=10,b=1.5,故答案为:10;1.5;(3)由题意可得,前0.5h,乙行驶的路程为:10×0.5=5<7.5,则甲、乙两人路程差为7.5km是在甲乙相遇之后,设乙出发xh时,甲、乙两人路程差为7.5km,25(x﹣0.5)﹣10x=7.5,解得,x=,25﹣10x=7.5,得x=;即乙出发或时,甲、乙两人路程差为7.5km.9.解:(1)当0≤x≤200时,y与x的函数解析式是y=0.55x;当x>200时,y与x的函数解析式是y=0.55×200+0.7(x﹣200),即y=0.7x﹣30;(2)小明家4月份用电250度,月用电量超过200度,所以应交电费为:0.7×250﹣30=145(元),(3)因为小明家6月份的电费超过110元,所以把y=117代入y=0.7x﹣30中,得x=210.答:小明家6月份用电210度.10.解:(1)依题意得,乙队开挖到30m时,用了2h,开挖6h时甲队比乙队多挖了60﹣50=10(m);故答案为:2;10;(2)设甲队在0≤x≤6的时段内y与x之间的函数关系式y甲=k1x,由图可知,函数图象过点(6,60),∴6k1=60,解得k1=10,∴y甲=10x,设乙队在2≤x≤6的时段内y与x之间的函数关系式为y乙=k2x+b,由图可知,函数图象过点(2,30)、(6,50),∴,解得,∴y乙=5x+20;当0≤x≤2时,设y乙与x的函数解析式为y乙=kx,可得2k=30,解得k=15,即y=15x;乙∴y乙=,(3)依题意得,开挖2小时,甲、乙两队挖的河渠的长度相差10m,开挖6小时,甲、乙两队挖的河渠的长度相差10m;故答案为:10;10;(4)当0≤x≤2时,15x﹣10x=5,解得x=1.当2<x≤4时,5x+20﹣10x=5,解得x=3,当4<x≤6时,10x﹣(5x+20)=5,解得x=5.答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.11.解:(1)由图可知,升级前A生产线的日产量为:32÷8=4(万个),∵升级后,日产能提高20%,∴技术升级后,每条A生产线每天生产口罩4×(1+20%)=4.8(万个),故答案为:4.8;(2)A生产线技术升级后,A生产线的产量由32万到56万,所用的时间为(56﹣32)÷4.8=5(天),故B生产线从第8天开始生产到第15天的产能为56万个,所以每条B生产线每天生产口罩:56÷(15﹣8)=8(万个),故答案为:8;(3)设B生产线有x条,根据题意得:15×4.8+8x=136,解得:x=8,故答案为:8;(4)A生产线升级后每小时产能为:4.8÷8=0.6(万个),B生产线的每小时产能为:8÷8=1(万个),根据题意得:0.6×(8+m)×15+(8+m)(8+k)=260,整理得:(8+m)(17+k)=260,∵m、k为正整数,∴8+m为大于8的正整数,17+k为大于17的正整数,∴(8+m)(17+k)=260=10×26=13×20,∴8+m=10,17+k=26或8+m=13,17+k=20,∴m=2,k=9或m=5,k=3,∴每日工作时长增加2小时,B生产线增加9条或每日工作时长增加5小时,B生产线增加3条即可使公司口罩日总产量达到260万个,∴正整数k的值为9或3.答:正整数k的值为9或3.12.解:(Ⅰ)在A商店,购买5个费用=5×50=250(元),购买15个费用为15×50=750(元),在B商店,购买5个费用=5×60=300(元),购买15个费用为10×60+60×0.8(15﹣10)=840(元),故答案为:250,750,300,840;(Ⅱ)由题意可得:y1=50x(x≥0),当0≤x≤10时,y2=60x,当x>10时,y2=60×10+60×0.8×(x﹣10)=48x+120(x>10),∴y2=;(Ⅲ)①由题意可得:50x=48x+120,解得x=60,故答案为:60;②∵50×50<48×50+120,∴在A商店购买花费少,故答案为:A;③若在A商店,=36(个),若在B商店,=35(个),∵36>35,∴在A商店购买的数量多,故答案为:A.13.解:(1)由图象可得小明家与外婆家的距离为300km,小明经过2小时到达点A,点A到小明外婆家的距离=(300﹣2×90)=120(km),∴小明爸爸驾车返回时平均速度==60(km/h),故答案为:300,60;(2)点P表示小明出发2小时到达A地与小明爸爸相遇;(3)设s与t之间的函数关系式为s=kt+b,且过点(2.5,180),(4.5,300),∴,解得,∴s与t之间的函数关系式为s=60t+30(2.5≤t≤4.5).14.解:(1)每天生产口罩y(万个)与生产时间x(天)之间的函数表达式为:y=(x>4);(2)由题意可得:+20=,解得:x1=20,x2=﹣16,经检验,x1=20,x2=﹣16是原分式方程的解,但x=﹣16不合题意舍去,∴20﹣4=16(天),答:实际生产时间为16天.15.解:(1)a=5×5=25,b=5×10+(20﹣10)×0.8×5=90;(2)y=5×10+5×0.8(x﹣10)=4x+10;(3)购买35千克付款金额=4×35+10=150(元),购买8千克付款金额=5×8=40(元),一起购买付款金额=4×(35+8)+10=182(元),∴150+40﹣182=8(元),答:一起购买可省8元.。
刑事诉讼法学-19 第十九章 第二审程序

第334条 第二审期间,自诉案件的当事人提出反诉 的,应当告知其另行起诉。
五、第二审案件的审判期限
同级人民法院第一审判决、裁定的抗诉,应当通过原审人
民法院提出抗诉书,并且将抗诉书抄送上一级人民检察院。
原审人民法院应当将抗诉书连同案卷、证据移送上一级人民法 院,并且将抗诉书副本送交当事人。
上级人民检察院如果认为抗诉不当,可以向同级人民法院
撤回抗诉,并且通知下级人民检察院。
2006年司考单选
36.不服地方各级法院第一审未生效判决时,哪
(1)移送上(抗)诉案件函; (2)上诉状或者抗诉书; (3)第一审判决书或者裁定书的份数; (4)全部案卷材料和证据,包括案件审结报告和其他 应当移送的材料。
☆材料齐备,收案;不齐备,通知补充。
二、全面审查原则
根据我国《刑事诉讼法》第178条和第223条规定,
第二审人民法院审判上诉、抗诉案件一律由合议庭进 行,而且合议庭的组成人员都必须为审判员,人数为 3人至5人。
关于第二审人民法院对刑事附带民事案件的处理,应当根 据上诉、抗诉的具体情况进行区分:
(1)第二审人民法院审理附带民事上诉案件,如果发现刑 事和附带民事部分均有错误需依法改判的,应当一并审理,一 并改判。
(2)第二审人民法院审理的刑事上诉、抗诉案件,附带民 事诉讼部分已经发生法律效力的,如果发现第一审判决或者裁 定中的民事部分确有错误,应当对民事部分按照审判监督程序 予以纠正。
(5)对于人民检察院抗诉的案件,经第二审人民 法院审查后,认为应当判处被告人死刑的,按照《刑 事诉讼法》第225条的规定处理,即第二审人民法院认 为原判决认定事实没有错误,但适用法律有错误,或 者量刑不当的,应当改判;认为原判决事实不清或者 证据不足的,可以在查清事实后改判或者发回重审。
人教版高中物理选修3-5教学案:第十九章 第2节 放射性元素的衰变-含解析

第2节放射性元素的衰变1.原子核衰变时电荷数和质量数都守恒。
2.α衰变:23892U→23490Th+42He3.β衰变:23490Th→23491Pa+0-1e4.放射性元素的原子核有半数发生衰变所需的时间叫做这种元素的半衰期。
一、原子核的衰变1.定义原子核放出α粒子或β粒子,则核电荷数变了,变成另一种原子核,这种变化称为原子核的衰变。
2.衰变分类(1)α衰变:放出α粒子的衰变。
(2)β衰变:放出β粒子的衰变。
3.衰变方程238U→23490Th+42He92234Th→23491Pa+0-1e。
904.衰变规律(1)原子核衰变时电荷数和质量数都守恒。
(2)当放射性物质连续衰变时,原子核中有的发生α衰变,有的发生β衰变,同时伴随着γ辐射。
这时,放射性物质发出的射线中就会同时具有α、β和γ三种射线。
二、半衰期1.定义放射性元素的原子核有半数发生衰变所需的时间。
2.决定因素放射性元素衰变的快慢是由核内部自身的因素决定的,跟原子所处的化学状态和外部条件没有关系。
不同的放射性元素,半衰期不同。
3.应用利用半衰期非常稳定这一特点,可以测量其衰变程度、推断时间。
1.自主思考——判一判(1)原子核发生α衰变时,核的质子数减少2,而质量数减少4。
(√)(2)原子核发生β衰变时,原子核的质量不变。
(×)(3)原子核发生衰变时,质量数和电荷数都守恒。
(√)(4)半衰期就是放射性元素全部衰变所用时间的一半。
(×)(5)半衰期是放射性元素的大量原子核衰变的统计规律。
(√)(6)半衰期可以通过人工进行控制。
(×)2.合作探究——议一议(1)发生β衰变时,新核的电荷数变化多少?新核在元素周期表中的位置怎样变化?提示:根据β衰变方程23490Th→23491Pa+0-1e知道,新核核电荷数增加了1个,原子序数增加1个,故在元素周期表上向后移了1位。
(2)放射性元素衰变有一定的速率。
镭226衰变为氡222的半衰期为1 620年,有人说:10 g镭226经过1 620年有一半发生衰变,镭226还有5 g,再经过1 620年另一半镭226也发生了衰变,镭226就没有了。
河南省洛阳市《行政职业能力倾向测验》事业招聘考试真题

河南省洛阳市《行政职业能力倾向测验》事业招聘考试真题《说明:本卷为历年及近期公务员(国考)考试真题》本卷共150题,考试时间90分钟,满分100分一、单选题1. “道而弗牵,强而弗抑,开而弗达”所体现的教学原则是()。
A、直观性原则B、启发性原则C、因材施教原则D、巩固性原则【参考答案】B2. 行政诉讼中由被告负举证责任,这一规定的理论基础是行政机关在做出具体行政行为时应当()。
A、先裁决,后取证B、先取证,后裁决C、边裁决,边取证D、裁决与取证在行政执法过程中没有必然的联系,只是在行政诉讼过程中才有程序的价值【参考答案】B3. 总和的或扩大的价值形式是指()。
A、一种商品的价值表现在与它相交换的一种商品上B、一系列商品的价值表现在与它相交换的一种商品上C、一种商品的价值表现在与它相交换的一系列商品上D、一系列商品的价值表现在与它相交换的一系列商品上【参考答案】C4. 下列作品与作者的对应关系,不正确的是()。
A.《梦溪笔谈》——沈括B.《水经注》——徐霞客 C.《清明上河图》——张择端 D.《步辇图》——阎立本【参考答案】B5. 应对物价上涨,可采取的措施是()。
A、降低基准利率B、扩大财政支出C、提高存款准备金率D、扩大财政赤字【参考答案】C6. 松散群体是指学生们只在空间和时间上结成群体,但成员间尚无共同活动的()。
A、目的和内容B、共同语言C、深厚友谊D、约束力量【参考答案】A7. 社会主义的根本原则是()。
A、不断发展生产,增加社会财富B、扩大改革开放,增强综合国力C、实行按劳分配,改善人民生活D、坚持公有制为主体,实现共同富裕【参考答案】D8. 邓小平理论是()。
A、马克思主义中国化第一次历史性飞跃的理论成果B、马克思列宁主义的基本原理同当代中国实际和时代特征相结合的产物C、全面建设小康社会的根本方针D、被实践证明了的关于中国革命和建设的正确的理论原则和经验总结【参考答案】B9. 冻疮是由于皮肤哪一部分受损而引起的?() A.毛囊B.汗腺C.竖毛肌D.毛细血管【参考答案】D10. 下列城市中没有被联合国教科文组织授予“音乐之都”荣誉称号的是()。
人教版八年级下册数学第十九章 一次函数含答案(有答案)
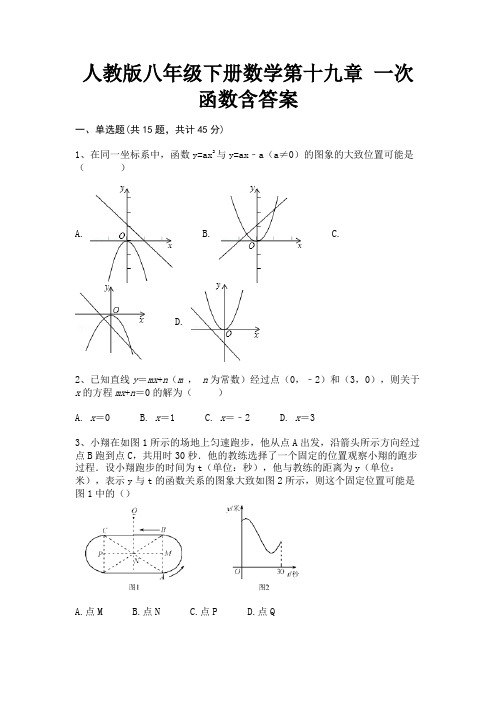
人教版八年级下册数学第十九章一次函数含答案一、单选题(共15题,共计45分)1、在同一坐标系中,函数y=ax2与y=ax﹣a(a≠0)的图象的大致位置可能是()A. B. C.D.2、已知直线y=mx+n(m,n为常数)经过点(0,﹣2)和(3,0),则关于x的方程mx+n=0的解为()A. x=0B. x=1C. x=﹣2D. x=33、小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的()A.点MB.点NC.点PD.点Q4、以下各点中,在正比例函数y=2x图象上的是()A.(2,1)B.(1,2)C.(—1,2)D.(1,—2)5、若正比例函数的图像经过点(-1,2),则这个图像必经过点()A.(1,2)B.(-1,-2)C.(2,-1)D.(1,-2)6、有一道题目:已知一次函数y=2x+b,其中b<0,…,与这段描述相符的函数图像可能是()A. B. C.D.7、y= x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为()A.没有实数根B.有一个实数根C.有两个不相等的实数根D.有两个相等的实数根8、图中两直线l1, l2的交点坐标可以看作方程组( )的解.A. B. C. D.9、汽车油箱中有油,平均耗油量为,如果不再加油,那么邮箱中的油量(单位:)与行驶路程(单位:)的函数图象为()A. B. C.D.10、二次函数的图象如图所示,反比列函数与正比列函数在同一坐标系内的大致图象是()A. B. C.D.11、在平面直角坐标系中,一次函数的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限12、如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,设第n(n是正整数)个图案是由y个基础图形组成的,则y与n之间的关系式是()A.y=4nB.y=3nC.y=6nD.y=3n+113、已知一次函数,图象与轴、轴交点、点,得出下列说法:①A ,;② 、两点的距离为5;③ 的面积是2;④当时,;其中正确的有()A.1个B.2个C.3个D.4个14、一盘蚊香长100cm,点燃时每小时缩短10cm,小明在蚊香点燃5h后将它熄灭,过了2h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y(cm)与所经过时间x(h)之间的函数关系的是()A. B. C. D.15、关于x的反比例函数y=(k为常数)的图象如图所示,则一次函数y=kx+2﹣k的图象大致是()A. B. C. D.二、填空题(共10题,共计30分)16、小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距________米.17、如图,直线交坐标轴于两点,则不等式的解是________.18、如图,一次函数y=kx+b与y=﹣x+5的图象的交点坐标为(2,3),则关于x的不等式﹣x+5>kx+b的解集为________.19、若一次函数y=kx+b(k≠0)的图象不过第四象限,且点M(﹣4,m)、N (﹣5,n)都在其图象上,则m和n的大小关系是________.20、甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B 运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为________.(并写出自变量取值范围)21、函数的图象经过的象限是________.22、如图平面直角坐标系中,直线y=kx+1与x轴交于点A点,与y轴交于B 点,P(a,b)是这条直线上一点,且a、b(a<b)是方程x2﹣6x+8=0的两根.Q是x轴上一动点,N是坐标平面内一点,以点P、B、Q、N四点为顶点的四边形恰好是矩形,则点N的坐标为________或________.23、一次函数y=(m﹣1)x+m2的图象过点(0,4),且y随x的增大而增大,则m=________.24、如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为________.25、已知平面上四点,,,,直线 y=mx-3m+2 将四边形分成面积相等的两部分,则的值为________.三、解答题(共5题,共计25分)26、一次函数y =kx+b()的图象经过点,,求一次函数的表达式.27、在直角坐标系中直接画出函数y=|x|的图象;若一次函数y=kx+b的图象分别过点A(-1,1),B(2,2),请你依据这两个函数的图象写出方程组的解.28、已知反比例函数的图象经过点,若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x 轴的交点坐标.29、如图,一次函数的图象与反比例函数(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、点=27,.D,且S△DBP(1)求点D的坐标;(2)求一次函数与反比例函数的表达式;(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值?30、已知一次函数的图象经过和(-3,3)两点,求这个一次函数的表达式并画出它的图象.试判断点P(-1,1)是否在这个一次函数的图象上.参考答案一、单选题(共15题,共计45分)1、A2、D3、D4、B5、D6、A7、A8、B9、B10、B11、C12、D13、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、23、24、三、解答题(共5题,共计25分)26、27、30、。
初中数学教材目录(全)

初中数学教材目录(全)七年级上册(61)第1章有理数(19)第2章整式的加减(8)第3章一元一次方程(18)第4章图形认识初步(16)七年级下册(62)第5章相交线与平行线(14)第6章平面直角坐标系(7)第7章三角形(8)第8章二元一次方程组(12)第9章不等式与不等式组(12)第10章数据库的收集整理与描述(9)八年级上册(62)第11章全等三角形(11)第12章轴对称(13)第13章实数(8)第14章一次函数(17)第15章整式的乘除与因式分解(13)八年级下册(61)第16章分式(14)第17章反比例函数(8)第18章勾股定理(8)第19章四边形(16)第20章数据的分析(15)九年级上册(62)第21章二次根式(9)第22章一元二次方程(13)第23章旋转(8)第24章圆(17)第25章概率初步(15)九年级下册(48)第26章二次函数(12)第27章相似(13)第28章锐角三角函数(12)第29章投影与视图(11)七年级上册第一章有理数1.1 正数和负数阅读与思考用正负数表示加工允许误差1.2 有理数1.3 有理数的加减法实验与探究填幻方阅读与思考中国人最先使用负数1.4 有理数的乘除法观察与思考翻牌游戏中的数学道理1.5 有理数的乘方数学活动小结复习题1 第二章整式的加减2.1 整式阅读与思考数字1与字母X的对话2.2 整式的加减信息技术应用电子表格与数据计算数学活动小结复习题2第三章一元一次方程3.1 从算式到方程阅读与思考“方程”史话3.2 解一元一次方程(一)——合并同类项与移项实验与探究无限循环小数化分数3.3 解一元一次方程(二)——去括号与去分母3.4 实际问题与一元一次方程数学活动小结复习题3第四章图形认识初步4.1 多姿多彩的图形阅读与思考几何学的起源4.2 直线、射线、线段阅读与思考长度的测量4.3 角4.4 课题学习设计制作长方体形状的包装纸盒数学活动小结复习题4 部分中英文词汇索引七年级下册第五章相交线与平行线5.1 相交线5.2 平行线5.3 平行线的性质5.4 平移第六章平面直角坐标系6.1 平面直角坐标系6.2 坐标方法的简单应用第七章三角形7.1 与三角形有关的线段7.2 与三角形有关的角7.3 多边形及其内角和7.4 课题学习镶嵌数学活动小结复习题7第八章二元一次方程组8.1 二元一次方程组8.2 消元8.3 再探实际问题与二元一次方程组数学活动小结复习题8第九章不等式与不等式组9.1 不等式9.2 实际问题与一元一次不等式9.3 一元一次不等式组9.4 课题学习利用不等关系分析比赛(1)第十章实数10.1 平方根10.2 立方根10.3 实数八年级上册第十一章一次函数11.1 变量与函数信息技术应用用计算机画函数图象11.2 一次函数阅读与思考科学家如何测算地球的年龄11.3 用函数观点看方程(组)与不等式第十二章数据的描述12.1 几种常见的统计图表12.2 用图表描述数据信息技术应用利用计算机画统计图阅读与思考作者可能是谁12.3 课题学习从数据谈节水第十三章全等三角形13.1 全等三角形13.2 三角形全等的条件阅读与思考为什么要证明13.3 角的平分线的性质第十四章轴对称14.1 轴对称14.2 轴对称变换信息技术应用探索轴对称的性质14.3 等腰三角形实验与探究三角形中边与角之间的不等关系第十五章整式15.1 整式的加减15.2 整式的乘法15.3 乘法公式15.4 整式的除法15.5 因式分解八年级下册第十六章分式16.1 分式16.1 分式的运算阅读与思考容器中的水能倒完吗16.1 分式方程第十七章反比例函数17.1 反比例函数17.1 实际问题与反比例函数阅读与思考生活中的反比例关系第十八章勾股定理18.1 勾股定理18.2 勾股定理的逆定理第十九章四边形19.1 平行四边形19.1 特殊的平行四边形19.1 梯形观察与猜想平面直角坐标系中的特殊四边形第二十章数据的分析20.1 数据的代表20.2 数据的波动信息技术应用用计算机求几种统计量阅读与思考数据波动的几种度量20.3 课题学习体质健康测试中的数据分析九年级上册第二十一章二次根式21.1 二次根式21.2 二次根式乘除第二十二章一元二次方程22.1 一元二次方程22.2 降次──解一元二次方程阅读与思考黄金分割数22.3 实际问题与一元二次方程观察与猜想发现一元二次方程根与系数的关系第二十三章旋转23.1 图形的旋转23.2 中心对称信息技术应用探索旋转的性质23.3 课题学习图案设计第二十四章圆24.1 圆24.2 与圆有关的位置关系24.3 正多边形和圆24.4 弧长和扇形面积实验与研究设计跑道第二十五章概率初步25.1 概率25.2 用列举法求概率阅读与思考概率与中奖25.3 利用频率估计概率阅读与思考布丰投针实验25.4 课题学习键盘上字母的排列规律九年级下册第二十六章二次函数26.1 二次函数实验与探究推测植物的生长与温度的关系26.2 用函数观点看一元二次方程信息技术应用探索二次函数的性质26.3 实际问题与二次函数第二十四章相似27.1 图形的相似27.2 相似三角形观察与猜想奇妙的分形图形27.3 位似信息技术应用探索位似的性质第二十八章锐角三角函数28.1 锐角三角函数阅读与思考一张古老的三角函数28.2 解直角三角形第二十九章投影与视图29.1 投影29.2 三视图阅读与思考视图的产生与应用29.3 课题学习制作立体模型。
人教版高中物理选修3-5教学案:第十九章 第7、8节 核聚变 粒子和宇宙含答案

第7、8节核聚变__粒子和宇宙1.两个轻核结合成质量较大的核,这样的核反应叫聚变。
2.约束核聚变材料的方法:磁约束和惯性约束。
3.粒子分为三大类,有媒介子、轻子、强子。
美国物理学家盖尔曼提出,强子是由夸克构成的。
一、核聚变1.定义两个轻核结合成质量较大的原子核的反应。
2.条件(1)轻核的距离要达到10-15_m以内。
(2)聚变可以通过高温来实现,因此又叫热核反应。
3.核反应举例(1)热核反应主要应用在核武器上,如氢弹。
(2)热核反应在宇宙中时时刻刻地进行着,太阳就是一个巨大的热核反应堆。
(3)典型的核聚变:一个氘核和一个氚核的聚变,21H+31H→42He+10n+γ该反应平均每个核子放出的能量比裂变反应平均每个核子放出的能量大3~4倍。
4.聚变与裂变相比有很多优点(1)轻核聚变产能效率高。
(2)地球上聚变燃料的储量丰富。
(3)轻核聚变更为安全、清洁。
5.实现核聚变的方法(1)难点:地球上没有任何容器能够经受几百万开尔文的高温。
(2)方案:科学家设想了两种方案,即磁约束和惯性约束,环流器是目前性能最好的一种磁约束装置。
二、粒子和宇宙1.“基本粒子”不基本(1)19世纪末,人们认为原子是组成物质的不可再分的最小微粒。
(2)后来认为光子、电子、质子和中子是组成物质的不可再分的最基本的粒子,并称为“基本粒子”。
随着科学的进一步发展,科学家们逐渐发现了数以百计的不同种类的新粒子,它们都不是由质子、中子、电子组成的,另外又发现质子、中子等本身也有自己的复杂的结构。
所以,从20世纪后半期起,就将“基本”二字去掉,统称为粒子。
2.发现新粒子与夸克模型(1)反粒子实验中发现,对应着许多粒子都存在质量、寿命、自旋等物理性质与过去已经发现的粒子相同,而电荷等其他性质相反的粒子,这些粒子叫做反粒子。
例如,电子的反粒子就是正电子。
(2)粒子的分类按照粒子与各种相互作用的不同关系,可将粒子分为三大类:①强子:参与强相互作用的粒子,质子是最早发现的强子。
公安机关办理行政案件程序规定(2019版)

公安机关办理行政案件程序规定(2012年12月19日公安部令第125号修订发布根据2014年6月29日公安部令第132号《公安部关于修改部分部门规章的决定》第一次修正根据2018年11月25日公安部令第149号《公安部关于修改〈公安机关办理行政案件程序规定〉的决定》第二次修正)目录第一章总则第二章管辖第三章回避第四章证据第五章期间与送达第六章简易程序和快速办理第一节简易程序第二节快速办理第七章调查取证第一节一般规定第二节受案第三节询问第四节勘验、检查第五节鉴定第六节辨认第七节证据保全第八节办案协作第八章听证程序第一节一般规定第二节听证人员和听证参加人第三节听证的告知、申请和受理第四节听证的举行第九章行政处理决定第一节行政处罚的适用第二节行政处理的决定第十章治安调解第十一章涉案财物的管理和处理第十二章执行第一节一般规定第二节罚款的执行第三节行政拘留的执行第四节其他处理决定的执行第十三章涉外行政案件的办理第十四章案件终结第十五章附则第一章总则第一条为了规范公安机关办理行政案件程序,保障公安机关在办理行政案件中正确履行职责,保护公民、法人和其他组织的合法权益,根据《中华人民共和国行政处罚法》《中华人民共和国行政强制法》《中华人民共和国治安管理处罚法》等有关法律、行政法规,制定本规定。
第二条本规定所称行政案件,是指公安机关依照法律、法规和规章的规定对违法行为人决定行政处罚以及强制隔离戒毒、收容教育等处理措施的案件。
本规定所称公安机关,是指县级以上公安机关、公安派出所、依法具有独立执法主体资格的公安机关业务部门以及出入境边防检查站。
第三条办理行政案件应当以事实为根据,以法律为准绳。
第四条办理行政案件应当遵循合法、公正、公开、及时的原则,尊重和保障人权,保护公民的人格尊严。
第五条办理行政案件应当坚持教育与处罚相结合的原则,教育公民、法人和其他组织自觉守法。
第六条办理未成年人的行政案件,应当根据未成年人的身心特点,保障其合法权益。
【施工方案】19--土石围堰工程安全专项施工方案(一公司)详解

姜唐湖蓄(行)洪区堤防加固工程老河口封闭堤及泵站工程土石围堰安全专项方案1编制说明、依据1。
1编制说明姜唐湖蓄(行)洪区堤防加固工程老河口封闭堤及泵站工程,共需填筑封闭堤、泵站围堰、姜家湖排涝涵围堰、淮河滩地上13#土料场挡水围堰。
填筑围堰所需土方由开挖13#、16#料场土方进行填筑围堰。
为了保障围堰施工过程中机械设备、从业人员的安全与健康,最大限度地控制危险源,尽可能地避免或减少水上施工的事故发生,认真落实“安全第一、预防为主、综合治理”的安全生产方针,特制定本方案。
1.2编制依据1。
2.1招标文件及补充说明;1。
2.2设计图纸及有关技术要求;1.2.3《堤防工程施工规范》(SL260—98);1。
2。
4《堤防工程施工质量评定与验收规程》(SL19—2001);2工程概况2。
1工程概述、特点2。
1。
1工程概述姜唐湖蓄(行)洪区堤防加固工程老河口封闭堤及泵站工程,有老河口封闭堤及泵站工程、行洪口门铲堤工程以及姜家湖排涝涵工程三部分组成。
老河口封闭堤是碾压式均质土堤,为外借土施工.泵站是封闭堤穿堤建筑物,位于老淮河口左岸滩地上,两者均需在老淮河填筑上、下游围堰。
通过初期排水、清淤、降低地下水位才能施工。
行洪口门铲堤是土堤拆除工程,不需要导流和降水。
本围堰主要是为填筑老河口封闭堤及泵站工程在河道上填筑临时围堰。
2。
1。
2特点工程填筑土方量大、水下深度约7m、水下淤泥较厚。
2。
2施工环境、地质、水文、气候等2.2。
1施工环境该工程地处姜唐湖蓄(行)洪区堤防加固工程位于淮河干流中游,地处安徽省霍邱县与颖上县交界处,施工环境复杂。
2.2。
2地质1)老河口封闭堤及泵站工程地质老河口封闭堤及泵站工程场区的河底高程一般在11m左右,两侧有少量滩地,滩地高程在18~19m左右,两岸堤距大约300m。
堤基主要由(1)、(2—3)、(3)、(5)、(6)层组成。
场地各层地基土的形成时代及成因为:全新统人工填土、全新统冲洪积沉积物、上更新统冲洪积沉积物、中更新统冲洪积沉积物.上述五个工程地质层按自上而下的顺序分别叙述如下:(1)层为新近沉积的地层,位于河床部位,由砂壤土和中粉质壤土等组成,间夹有粉砂,标贯击数在1击左右,液性指数平均值1。
管理会计模拟习题含参考答案

管理会计模拟习题含参考答案一、单选题(共52题,每题1分,共52分)1.关于财务资金对账管理,下列说法不正确的是()。
A、应坚持对账人与记账人相分离原则B、未达账项若无法清查原因,可以搁置不管C、应坚持“谁的账户,谁对账”原则D、对账时需编制存款余额调节表正确答案:B2.由于预算责任中心的业务范围小于集团整体,且算责任中心之间存在系统内往来项目。
所以在进行预算分解时应考虑()。
A、预算项目的差别性B、测算方法的适用性C、预算目标的一致性D、预算指标的适用性正确答案:A3.以下哪个属于现场绩效辅导?A、到被辅导分行举办绩效考核培训班B、对被辅导分行下发绩效提示函C、打电话提示被辅导分行绩效考核存在的问题D、向被辅导分行发送绩效跟踪评价报告正确答案:A4.以下不是未决诉讼仲裁预计负债金额中银行向对方当事人支付的款项的是()。
A、利息B、我方律师费C、本金D、违约金正确答案:B5.中间业务如收取手续费对应的剩余服务期限跨季度,应于收到手续费之日确认递延收益,并在剩余服务期内按照直线法对手续费进行摊销,按日确认中间业务手续费收入,收到款项的会计分录为借记(),贷记“××中间递延收益”。
A、借:中间业务递延收益B、借:手续费收入C、借:库存现金、××存款等D、借:××中间业务支出正确答案:C6.下列属于费用后评价主要内容之一的是()。
A、负责人考核情况B、费用是否分摊C、费用投入的预期业绩和开支效益是否实现D、费用审批流程正确答案:C7.A银行计划购置一台新型设备,设备购置价为30000元,一次性付款。
设备使用年限为6年,报废后预计净残值为3000元。
使用设备后,预计每年新增利润为5000元,每年现金净流量为()。
A、11000B、10500C、10000D、9500正确答案:D8.费用配置政策由()负责制定下达。
A、开支需求部门B、业务主管部门C、财务会计部门D、审计监察部门正确答案:C9.商业银行资产不包括以下哪一个A、应付利息B、贷款C、固定资产D、长期业务应收款正确答案:A10.A银行对下级分支机构的绩效考核方案中设置了存款付息率考核指标。
第十九章-第三节-朱熹PPT课件

因此,他倡导人们都做惟义是从的“君 子”。
2021/4/8
24
(五)论“存天理,灭人欲”
朱熹认为,由于有了人欲,使人所固有 的天理受到蔽锢,不能发挥作用。因此 倡导“存天理,灭人欲”。并提出如下 几种方案:
既然人心就是人欲,那么它就是圣人与凡 人共有的,所以它并不是一概不好的,然 而圣人是不被人心胜了道心的,圣人们所 有的人心,只是与天理和道心相符合的那 一部分。
2021/4/8
16
朱熹对人心与道心关系的观点是:
人心与道心是相去不远的,以“道心”主 宰“人心”,以道心作为人心的准则,从 而节制人心之中不合道心的那一部分,这 样的社会也就成为天理流行的社会了。
他认为人们那些为了基本生存而产生的 欲望是正常的,他说:“若是饥而欲食, 渴而欲饮,则此欲亦岂能无?”
但在此基础上,再有什么需求就是私欲 了。
2021/4/8
20
(二)论人欲对社会生活的危害
朱熹认为人欲对社会生活的危害是相当大 的。
朱熹认为,人欲必然破坏社会生活,小而 言之足以伤恩害义,大而言之则足以颠覆 社会。
2021/4/8
7
(二)论社会规范
朱熹的“理一分殊”论,具体应用于社会 伦理方面就是其“三纲五常”的学说。
三纲五常之说,起于董仲舒,完成于朱熹。 他以其作为调适人与人、人与社会、社会
与社会之间关系的准则。
2021/4/8
8
人们恪守这些封建道德及行为规范的结果 就是社会的安定和谐。
这正是朱熹“三纲五常”之说的宗旨所在。
2021/4/8
人教版八年级下册数学第十九章二次函数强化练习(附答案)

分卷I一、选择题(共9小题,每小题分,共0分)1.将抛物线y=x2平移得到抛物线y=(x+3)2,则这个平移过程正确的是()A.向左平移3个单位B.向右平移3个单位C.向上平移3个单位D.向下平移3个单位2.对于抛物线y=-(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>-1时,y随x的增大而减小,其中正确结论的个数为()A. 1B. 2C. 3D. 43.已知二次函数y=x2-2x-1的图象如图所示,根据图中提供的信息,求使得y≤2成立的x的取值范围是()A.x≤-1或x≥3B. -2≤x≤2C.x≥-2D. -1≤x≤34.已知:抛物线y=a(x+1)2的顶点为A,图象与y轴负半轴交点为B,且OB=OA,若点C(-3,b)在抛物线上,则△ABC的面积为()A. 3B. 3.5C. 4D. 4.55.超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm 的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板()平方厘米.(不计重合部分)A. 253B. 288C. 206D. 2456.已知二次函数y=a(x-2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2,若|x1-2|>|x2-2|,则下列表达式正确的是()A.y1+y2>0B.y1-y2>0C.a(y1-y2)>0D.a(y1+y2)>07.二次函数y=2x2-8x+m满足以下条件:当-2<x<-1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为()A. 8B. -10C. -42D. -248.如图,隧道的截面是抛物线,可以用y=−x2+4表示,该隧道内设双行道,限高为3m,那么每条行道宽是()A.不大于4mB.恰好4mC.不小于4mD.大于4m,小于8m9.已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是()A.y=x2-2x+3B.y=-x2-2x+3C.y=x2+2x+3D.y=-x2+2x+3分卷II二、填空题(共6小题,每小题分,共0分)10.如图,用火柴棒按如下方式摆放:设第n个图中需要y根火柴棒,请写出y与n的函数关系式:____________________.11.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为___________.12.已知点P(m,n)在抛物线y=ax2-x-a上,当m≥-1时,总有n≤1成立,则a的取值范围是_____________.13.有一个二次函数的图象,甲、乙、丙三位同学分别说出了它的特点:甲:对称轴是直线x=2;乙:与x轴两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形的面积为3.请你写出满足上述全部特点的一个二次函数解析式___________________.14.某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为____________元时,该服装店平均每天的销售利润最大.15.在平面直角坐标系中,如果把抛物线y=x2+2向上平移2个单位,那么所得抛物线的表达式为_____________.三、解答题(共6小题,每小题分,共0分)16.小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:例题:求一元二次方程x2-x-1=0的两个解.(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法).(2)解法二:利用二次函数图象与两坐标轴的交点求解.如图,把方程x2-x-1=0的解看成是二次函数y=___________的图象与x轴交点的横坐标即x1,x2就是方程的解.(3)解法三:利用两个函数图象的交点求解①把方程x2-x-1=0的解看成是二次函数y=______的图象与一个一次函数y=_________的图象交点的横坐标②画出这两个函数的图象,用x1,x2在x轴上标出方程的解.17.如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在x轴上,OA=AB=1个单位长度,把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B1.(1)求以A为顶点,且经过点B1的抛物线的解析式;(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.18.设函数y=(x-1)[(k-1)x+(k-3)](k是常数).(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;(2)根据图象,写出你发现的一条结论;(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.19.手工课上,小明准备做个形状是菱形的风筝,这个菱形两条对角线长度之和恰好为60cm,菱形的面积为S,随其中一条对角线的长x的变化而变化.①求S与x之间的函数关系式(不要求写出取值范围)②当x是多少时,菱形风筝的面积S最大?最大的面积是多少?20.如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y=x2-x+3的绳子.(1)求绳子最低点离地面的距离;(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.21.直线l过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于点P,若S△AOP=,求二次函数关系式.答案解析1.【答案】A【解析】抛物线y=x2的顶点坐标为(0,0),抛物线y=(x+3)2的顶点坐标为(-3,0),∵点(0,0)向左平移3个单位可得到(-3,0),∴将抛物线y=x2向左平移3个单位得到抛物线y=(x+3)2.2.【答案】C【解析】①∵a=-<0,∴抛物线的开口向下,正确;②对称轴为直线x=-1,故错误;③顶点坐标为(-1,3),正确;④∵x>-1时,y随x的增大而减小,∴x>1时,y随x的增大而减小一定正确;综上所述,结论正确的个数是①③④共3个.3.【答案】D【解析】由图可知,使得y≤2成立的x的取值范围是-1≤x≤3.4.【答案】A【解析】∵抛物线y=a(x+1)2的顶点为A,∴顶点A为(-1,0),∵图象与y轴负半轴交点为B,且OB=OA,∴B点坐标为(0,-1),代入y=a(x+1)2解得a=-1,∴抛物线y=-(x+1)2,∵点C (-3,b)在抛物线上,∴b=-4,如图,△ABC的面积=×(1+4)×3-×1×1-×2×4=3.5.【答案】A【解析】建立如图(2)所示的平面直角坐标系,过切点K作KH⊥OC于点H.依题意知K(x,2).易求开口向上抛物线的解析式:y=x2,所以2=x2,解得x=或x=-(舍去),∴OH=HG=,∴BC=BO+OH+HG+GC=3++ +3=6+3,∴S矩形ABCD=AB•BC=4×(6+3)=24+12(平方厘米).如图3,S矩形A′B′C′D′=6BC=6×(6+3)(平方厘米).所以,2S矩形ABCD+2S矩形A′B′C′D′+2AB•AE=2×(24+12)+2×(36+18)+2×4×6=168+60≈253(平方厘米).6.【答案】C【解析】①a>0时,二次函数图象开口向上,∵|x1-2|>|x2-2|,∴y1>y2,无法确定y1+y2的正负情况,a(y1-y2)>0,②a<0时,二次函数图象开口向下,∵|x1-2|>|x2-2|,∴y1<y2,无法确定y1+y2的正负情况,a(y1-y2)>0,综上所述,表达式正确的是a(y1-y2)>0.7.【答案】D【解析】∵抛物线y=2x2-8x+m=2(x-2)2-8+m的对称轴为直线x=2,而抛物线在-2<x<-1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方∴抛物线过点(-2,0),(6,0),把(-2,0)代入y=2x2-8x+m得8+16+m=0,解得m=-24.8.【答案】A【解析】把y=3代入y=−x2+4中得x1=4,x2=-4(舍去).∴每条行道宽应不大于4m.9.【答案】B【解析】∵抛物线开口向下,∴a<0,则A、C选项错误;∵x=1时,y=-x2-2x+3=0,y=-x2+2x+3=4,∴B选项正确,D选项错误.10.【答案】y=n2+n【解析】当n=1时,需要火柴3×1=3,当n=2时,需要火柴3×(1+2)=9;当n=3时,需要火柴3×(1+2+3)=18,…,依此类推,第n个图形共需火柴y=3×(1+2+3+…+n)==n2+n.11.【答案】15【解析】∵D是抛物线y=-x2+6x上一点,∴设D(x,-x2+6x),∵顶点C的坐标为(4,3),∴OC==5,∵四边形OABC是菱形,∴BC=OC=5,BC∥x轴,∴S△BCD=×5×(-x2+6x-3)=-(x-3)2+15,∵-<0,∴S△BCD有最大值,最大值为15.12.【答案】-≤a<0【解析】根据已知条件,画出函数图象,如图所示.由已知得,解得-≤a<0.13.【答案】y=±(x+1)(x-5)答案不唯一【解析】对称轴是直线x=2,则一次项系数与二次项系数的比是-4,因而可设函数解析式是y=ax2-4ax+ac,与y轴交点的纵坐标也是整数,因而ac是整数,y=ax2-4ax+ac=a(x2-4x+c),与x轴两个交点的横坐标都是整数,即方程x2-4x+c=0有两个整数解,设是-1和+5,则c=-5,则y=ax2-4ax+ac=a(x2-4x-5),∵以这三个交点为顶点的三角形的面积为3,∴a=±.14.【答案】22【解析】设定价为x元,根据题意得y=(x-15)[8+2(25-x)]=-2x2+88x-870∴y=-2x2+88x-870,=-2(x-22)2+98∵a=-2<0,∴抛物线开口向下,∴当x=22时,y最大值=98.15.【答案】y=x2+4【解析】原抛物线的顶点为(0,2),向上平移2个单位,那么新抛物线的顶点为(0,4);则新抛物线的解析式为y=x2+4.16.【答案】解:(1)由原方程,得(x−)2−=0,即(x−)2=;解得x1=,x2=.(2)设二次函数方程为y=ax2+bx+c(a,b,c均为实数,且a≠0).由图象得知,该函数过点(0,-1),所以该点满足方程y=ax2+bx+c,∴把(0,-1)代入方程y=ax2+bx+c,得c=-1,①二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2-x-1=0的解;∴x1•x2==-1,即c=-a;②x1+x2=−=1;③由①②③,得;∴二次函数方程为y=x2-x-1.(3)【解析】(1)用配方法解答一元二次方程;(2)二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2-x-1=0的解,所以只要求出方程x2-x-1=0的根,就可以求出二次函数方程为y=ax2+bx+c 与x轴交点;(3)由(1)(2)解得x1、x2,再根据题意画出图象.17.【答案】解:(1)由题意可知,A(1,0),A1(2,0),B1(2,1),设以A为顶点的抛物线的解析式为y=a(x-1)2;∵此抛物线过点B1(2,1),∴1=a(2-1)2,∴a=1,∴抛物线的解析式为y=(x-1)2;(2)∵当x=0时,y=(0-1)2=1,∴D点坐标为(0,1),由题意得OB在第一象限的角平分线上,故可设C(m,m),代入y=(x-1)2;得m=(m-1)2;解得m1=<1,m2=>1(舍去).故C点坐标为(,).【解析】(1)先设抛物线的解析式为y=a(x-1)2,再将B1点坐标代入抛物线的解析式即可得出答案;(2)令x=0即可求出D点坐标,再设出C点坐标C(m,m),代入抛物线解析式解方程即可求得C点坐标.18.【答案】解:(1)当k=0时,y=-(x-1)(x+3),所画函数图象如图所示:(2)①k取0和2时的函数图象关于点(0,2)中心对称.②函数y=(x-1)[(k-1)x+(k-3)](k是常数)的图象都经过(1,0)和(-1,4).(3)由题意可得y2=(x-1)[(2-1)x+(2-3)]=(x-1)2,平移后的函数y3的表达式为y3=(x-1+4)2-2=(x+3)2-2.所以当x=-3时,函数y3的最小值是-2.【解析】(1)把k=0代入函数解析式即可得到所求的函数解析式,根据函数解析式作出图象;(2)根据函数图象回答问题;(3)由“左加右减,上加下减”的规律写出函数解析式,根据函数图象的增减性来求函数y3的最小值.19.【答案】解:①根据题意可得一条对角线的长为x cm,则另一对角线长为(60-x)cm,则S=x(60-x)=-x2+30x;②由①得y=-x2+30x=-(x-30)2+450,故当x是30cm时,菱形风筝的面积S最大,最大的面积是450cm2.【解析】①首先表示出菱形对角线的长,再利用菱形面积求法得出答案;②利用配方法求出二次函数最值即可.20.【答案】解:(1)∵a=>0,∴抛物线顶点为最低点,∵y=x2-x+3=(x-4)2+,∴绳子最低点离地面的距离为m;(2)由(1)可知,BD=8,令x=0得y=3,∴A(0,3),C(8,3),由题意可得抛物线F1的顶点坐标为(2,1.8),设F1的解析式为y=a(x-2)2+1.8,将(0,3)代入得4a+1.8=3,解得a=0.3,∴抛物线F1为y=0.3(x-2)2+1.8,当x=3时,y=0.3×1+1.8=2.1,∴MN的长度为2.1m;(3)∵MN=DC=3,∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,∴抛物线F2的顶点坐标为(m+4,k),∴抛物线F2的解析式为y=(x-m-4)2+k,把C(8,3)代入得(8-m-4)2+k=3,解得k=-(4-m)2+3,∴k=-(m-8)2+3,∴k是关于m的二次函数,又∵由已知m<8,在对称轴的左侧,∴k随m的增大而增大,∴当k=2时,-(m-8)2+3=2,解得m1=4,m2=12(不符合题意,舍去),当k=2.5时,-(m-8)2+3=2.5,解得m1=8-2,m2=8+2(不符合题意,舍去),∴m的取值范围是4≤m≤8-2.【解析】(1)直接利用配方法求出二次函数最值得出答案;(2)利用顶点式求出抛物线F1的解析式,进而得出x=3时,y的值,进而得出MN的长;(3)根据题意得出抛物线F2的解析式,得出k的值,进而得出m的取值范围.21.【答案】解:设直线为y=kx+b,∵直线l过点A(4,0)和B(0,4)两点,∴4k+b=0,b=4∴y=-x+4,∵S△AOP=,∴×4×yp=,∴yp=,∴=-x+4,解得x=,把点P的坐标(,)代入y=ax2,解得a=,∴y=x2.【解析】由题意直线l过点A(4,0)和B(0,4)两点,根据待定系数法求出直线AB的解析式,再根据S△AOP=,求出点P的纵坐标,然后将它代入直线AB的解析式,求出点P的横坐标,最后把点P的坐标代入y=ax2,运用待定系数法即可求出二次函数的解析式.。
CAD第19章绘制轴类零件图

Ⅰ
3 49
4 41
3 35
170
图 19-2 阶梯轴
19.2.1 设置图层
用 AutoCAD 绘制零件图时要注意的是,各种线条要分层,这样便于管理和更改,尤其是图形复杂时。首先要建立几个常 用的图层,每个图层上的线条类型不同,或者宽度不同。
建立图层,根据图上的线条类型看,有轮廓线、中心线、剖面线,根据这几个线条类型和线宽建立图层,如错误!未找到 引用源。所示。
图 19-24 绘制直线
(2) 按“Enter”键继续执行直线命令。选择适当位置,完成绘制的效果如图 19-25 所示。
图 19-25 绘制直线
(3) 执行【绘图】面板中的 C【圆心,半径】命令图标 ,以中心线的交点为圆心,绘制直径为 50 的圆及轴的直径, 如图 19-26 所示。 (4) 执行【修改】面板中的 O【偏移】命令图标 ,输入偏移距离“7”,以水平中心线为对象,偏移出键槽宽度的两
轴按中心线形状不同可分为直轴、曲轴和挠性钢丝轴。直轴应用较多,又可分为光轴和阶梯轴,由于阶梯轴能够满足零件 的轴向定位等优点,在机械行业中被广泛使用。
阶梯轴又可分为普通阶梯轴和齿轮轴两大类。 常见的轴类零件如错误!未找到引用源。所示。
阶梯轴
2020-2021学年人教版八年级数学下册第19章一次函数应用之图像专题 (三)

2020-2021学年人教版八年级数学下册第19章一次函数应用之图像专题(三)1.小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.(1)小张在路上停留小时,他从乙地返回时骑车的速度为千米/时;(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=12x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇次;(3)请你计算第一次相遇的时间.2.某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:(1)y与x之间的函数关系式;(2)每位旅客最多可免费携带行李的千克数.3.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.(1)填空:折线OABC表示赛跑过程中(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是米.(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)乌龟用了多少分钟追上了正在睡觉的兔子?(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.4.如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶90千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的关系.请根据图象填空:(1)摩托车的速度为千米/小时;汽车的速度为千米/小时;(2)汽车比摩托车早小时到达B地.(3)在汽车出发后几小时,汽车和摩托车相遇?说明理由.5.小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:(1)小帅的骑车速度为千米/小时;点C的坐标为;(2)求线段AB对应的函数表达式;(3)当小帅到达乙地时,小泽距乙地还有多远?6.一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克西瓜出售的价格是多少?(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(4)请问这个水果贩子一共赚了多少钱?7.秋高气爽,宜登高望远,张老师从小区大门出发,匀速步行前往南山,出发8分钟,他发现手机落在了小区大门,立即原速返回,张老师出发8分钟时,邻居老朱也匀速步行,从小区大门出发沿相同路线前往南山,张老师回到起点后用了4分钟才找到手机,之后一路小跑去追赶老朱,最终两人同时到达南山,开始了愉快的爬山之旅,两人之间的距离y(米)与张老师出发所用时间x(分)之间的关系如图所示,结合图象信息解答下列问题:(1)张老师最初出发的速度为米/分,a=,老朱步行的速度为米/分;(2)b=,c=,张老师回到起点,找到手机之后的速度为米/分;(3)小区大门与南山之间的距离为多少?8.从甲地到乙地,先是一段上坡路,然后是一段平路,小冲骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小冲骑车在上坡、平路、下坡时分别保持匀速前进,已知小冲骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小冲出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.(1)求小冲在平路上骑车的平均速度以及他在乙地的休息时间;(2)分别求线段AB、EF所对应的函数关系式;(3)从甲地到乙地经过丙地,如果小冲两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.9.某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票:若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.(1)观察图象可知:a=,b=;(2)当x>10时,求y2与x之间的函数表达式;(3)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.10.李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,多宝鱼价格z(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.(1)观察图象,直接写出日销售量的最大值;(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式;(3)试比较第10天与第12天的销售金额哪天多?11.甲乙两车从A市去往B市,甲比乙早出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,如图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:(1)A、B两市的距离是千米,甲到B市后小时乙到达B市;(2)求甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式,并写出自变量t的取值范围;(3)请直接写出甲车从B市往回返后再经过几小时两车相遇.12.周末,甲、乙两人从学校出发去公园游玩,甲骑自行车出发0.5小时后到达苏果超市,在超市里休息了一段时间,再以相同的速度前往公园.乙因为一些事情耽搁了一些时间,在甲出发小时后,乙驾驶电瓶车沿相同的路线前往公园,如图,是他们离学校的路程y (km)与行走的时间x(h)的函数图象.已知乙驾驶电瓶车的速度是甲骑自行车的2倍.(1)求甲的速度和在苏果超市休息的时间;(2)乙出发后多长时间追上甲?13.如图是一辆摩托车从家里出发,离家的距离(千米)随行驶时间(分)的变化而变化的情况:(1)摩托车从出发到最后停止共经过了多少时间?离家最远的距离是多少?(2)摩托车在哪一段时间内速度最快?最快速度是多少?14.diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.15.甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:(1)货车在乙地卸货停留了多长时间?(2)货车往返速度,哪个快?返回速度是多少?16.A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.(1)求甲车行驶过程中y与x之间的函数关系式;(2)当它们行驶了7小时时,两车相遇,求乙车的速度.17.周末,小明和弟弟从家出发,步行去吉林省图书馆学习.出发2分钟后,小明发现弟弟的数学书忘记带了,弟弟继续按原速前往图书馆,小明按原路原速返回家取书,然后骑自行前往图书馆,恰好与弟弟同时到达图书馆.小明和弟弟各自距家的路程y(m)与小明步行的时间x(min)之间的函数图象如图所示.(1)求a的值.(2)求小明取回书后y与x的函数关系式.(3)直接写出小明取回书后与弟弟相距100m的时间.18.随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:(1)该市人均月生活用水不超过6吨时,求y与x的函数解析式;(2)该市人均月生活用水超过6吨时,求y与x的函数关系式;(3)若某个家庭有5人,六月份的生活用水费共75元,则该家庭这个月人均用了多少吨生活用水?19.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A的距离y(千米)与甲车行驶时间t(小时)之间的函数关系如图所示,根据图上信息回答.(1)A、B两城相距千米;乙车比甲车晚出发小时,却早到小时;(2)乙车出发后多少小时追上甲车?(3)多少小时甲、乙两车相距50千米时?20.甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A 地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:(1)图中点A表达的含义正确的是;(只填序号)①乙车出发时距离B地的路程.②甲车出发时距离A地的路程.③甲车出发时,乙车距离B地的距离.④乙车出发1小时后,距离B地的路程.(2)乙车的速度是千米/时,a=小时;甲车的速度是千米/时,t=小时.(3)在甲车到达C地之前,两车是否相遇?若相遇,求出在甲车出发后多久相遇?若没有相遇,说明理由.参考答案1.解:(1)由图象可知,小张在路上停留1小时,他从乙地返回时骑车的速度为:60÷(6﹣4)=30千米/时,故答案为:1,30;(2)如右图所示,图中虚线表示y=12x+10,由图象可知,小王与小张在途中相遇2次,故答案为:2;(3)设当2≤x≤4时,小张对应的函数解析式为y=kx+b,,得,∴当2≤x≤4时,小张对应的函数解析式为y=20x﹣20,∴,解得,,即小王与小张在途中第一次相遇的时间为小时.2.解:(1)设y与x之间的函数解析式为y=kx+b,,得,即y与x之间的函数关系式是y=x﹣6;(2)当y=0时,0=x﹣6,得x=30即每位旅客最多可免费携带行李30千克.3.解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻,∴折线OABC表示赛跑过程中兔子的路程与时间的关系;由图象可知:赛跑的全过程为1500米;故答案为:兔子,1500;(2)结合图象得出:兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).(3)700÷30=(分钟),所以乌龟用了分钟追上了正在睡觉的兔子.(4)∵兔子跑了700米停下睡觉,用了2分钟,∴剩余800米,所用的时间为:800÷400=2(分钟),∴兔子睡觉用了:50.5﹣2﹣2=46.5(分钟).所以兔子中间停下睡觉用了46.5分钟.4.解:(1)摩托车的速度为:90÷5=18千米/小时,汽车的速度为:90÷(4﹣2)=45千米/小时,故答案为:18、45;(2)5﹣4=1,即汽车比摩托车早1小时到达B地,故答案为:1;(3)解:在汽车出发后小时,汽车和摩托车相遇,理由:设在汽车出发后x小时,汽车和摩托车相遇,45x=18(x+2)解得x=∴在汽车出发后小时,汽车和摩托车相遇.5.解:(1)由图可得,小帅的骑车速度是:(24﹣8)÷(2﹣1)=16千米/小时,点C的横坐标为:1﹣8÷16=0.5,∴点C的坐标为(0.5,0),故答案为:16千米/小时,(0.5,0);(2)设线段AB对应的函数表达式为y=kx+b(k≠0),∵A(0.5,8),B(2.5,24),∴,解得:,∴线段AB对应的函数表达式为y=8x+4(0.5≤x≤2.5);(3)当x=2时,y=8×2+4=20,∴此时小泽距离乙地的距离为:24﹣20=4(千米),答:当小帅到达乙地时,小泽距乙地还有4千米.6.解:(1)由图可得农民自带的零钱为50元,答:农民自带的零钱为50元;(2)(330﹣50)÷80=280÷80=3.5元,答:降价前他每千克西瓜出售的价格是3.5元;(3)(450﹣330)÷(3.5﹣0.5)=120÷3=40(千克),80+40=120千克,答:他一共批发了120千克的西瓜;(4)450﹣120×1.8﹣50=184元,答:这个水果贩子一共赚了184元钱.7.解:(1)由函数图象可知,张老师出发8分钟行走了480米的路程,∴张老师最初出发的速度为:480÷8=60(m/min),由函数图象知,张老师出发a分钟后,与邻居老朱相距800米,此时为张老师回到起点的时候,∴a=8×2=16(min),老朱的速度为:800÷8=100(m/min),故答案为:60;16;100;(2)根据题意和图象可知,b分钟时张老师找到了手机,∴b=a+4=16+4=20(min),∵c为张老师找到手机时,两相距的路程,∴c=100×(20﹣8)=1200(m),由函数图象知,端点为(b,c)即(20,1200)和(22.5,800)的线段是张老师找到手机后两人相距的距离与张老师出发的时间的一段函数图象,∴张老师找到手机后的速度为:=260(m/min),故答案为:20;1200;260;(3)根据题意知,张老师找到手机后一路小跑去追上老朱时,所跑步的路程全是小区到南山的距离.=1950(m).答:小区大门与南山之间的距离为1950m.8.解:(1)小冲骑车上坡的速度为:(6.5﹣4.5)÷0.2=10(km/h),平路上的速度为:10+5=15(km/h);下坡的速度为:15+5=20(km/h),平路上所用的时间为:2(4.5÷15)=0.6h,下坡所用的时间为:(6.5﹣4.5)÷20=0.1h所以小冲在乙地休息了:1﹣0.1﹣0.6﹣0.2=0.1(h);(2)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:y=6.5﹣10x,即y AB=﹣10x+6.5(0≤x≤0.2).线段EF所对应的函数关系式为y EF=4.5+20(x﹣0.9).即y EF=20x﹣13.5(0.9≤x≤1);(3)由题意可知:小冲第一次经过丙地在AB段,第二次经过丙地在EF段,设小冲出发a小时第一次经过丙地,则小冲出发后(a+0.85)小时第二次经过丙地,6.5﹣10a=20(a+0.85)﹣13.5,解得:a=.×10=1(千米).答:丙地与甲地之间的距离为1千米.9.解:(1)门票定价为80元/人,那么10人应花费800元,而从图可知实际只花费480元,是打6折得到的价格,所以a=6;从图可知10人之外的另10人花费640元,而原价是800元,可以知道是打8折得到的价格,所以b=8,故答案为:6,8;(2)当x>10时,设y=kx+b.2∵图象过点(10,800),(20,1440),∴,解得,=64x+160 (x>10),∴y2(3)设甲团有m人,乙团有n人.由图象,得y=48x,1当m>10时,依题意,得,解得,答:甲团有35人,乙团有15人.10.解:(1)观察图象,发现当x=12时,y=120为最大值,∴日销售量的最大值为120千克.(2)设李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=kx+b,当0≤x≤12时,有,解得:,∴此时日销售量y与上市时间x的函数解析式为y=10x;当12<x≤20时,有,解得:,∴此时日销售量y与上市时间x的函数解析式为y=﹣15x+300.综上可知:李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=.(3)设多宝鱼价格z与上市时间x的函数解析式为z=mx+n,当5≤x≤15时,有,解得:,∴此时多宝鱼价格z与上市时间x的函数解析式为y=﹣2x+42.当x=10时,y=10×10=100,z=﹣2×10+42=22,当天的销售金额为:100×22=2200(元);当x=12时,y=10×12=120,z=﹣2×12+42=18,当天的销售金额为:120×18=2160(元).∵2200>2160,∴第10天的销售金额多.11.解:(1)3×40=120,乙车所用时间:=6,2+6﹣3=5,答:A、B两市的距离是120千米,甲到B市后5小时乙到达B市;故答案为:120,5;(2)由题意得:A(10,120),B(13,0),设甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式为:S=kt+b,把A(10,120),B(13,0)代入得:,解得:,∴甲车返回时的路程S(千米)与时间t(小时)之间的函数关系式为:S=﹣40t+520(10≤t≤13);(3)由题意得:C(8,10),120﹣(10﹣8)×20=80,∴D(10,80),设直线CD的解析式为:S=kt+b,把C(8,120)、D(10,80)代入得:,解得:,∴直线CD的解析式为:S=﹣20t+280,则:,﹣40t+520=﹣20t+280,t=12,12﹣10=2,答:甲车从B市往回返后再经过2小时两车相遇.12.解:(1)由图象得:甲骑车速度:10÷0.5=20(km/h);由函数图象得出,在苏果超市休息的时间是1﹣0.5=0.5h;(2)乙驾车速度:20×2=40(km/h)设直线OA的解析式为y=kx(k≠0),则10=0.5k,解得:k=20,故直线OA的解析式为:y=20x.∵甲走OA段与走BC段速度不变,∴OA∥BC.设直线BC解析式为y=20x+b,1=﹣10把点B(1,10)代入得b1∴y=20x﹣10,,把点D(,0),设直线DE解析式为y=40x+b2=﹣,代入得:b2∴y=40x﹣.∴,解得:x=.∴F点的横坐标为,﹣=,则乙出发小时追上甲.13.解:(1)摩托车从出发到最后停止共经过:100分钟;离家最远的距离是:40千米.(2)摩托车在20~50分钟内速度最快;最快速度是:30÷=60(千米/小时)14.解:由图象及题意,得故障前的速度为:80÷1=80海里/时,故障后的速度为:(180﹣80)÷1=100海里/时.设航行额全程有a海里,由题意,得=2+,解得:a=480,则原计划行驶的时间为:480÷80=6小时,解法二:设原计划行驶的时间为t小时,80t=80+100(t﹣2)解得:t=6,故计划准点到达的时刻为:7:00.15.解:(1)∵4.5﹣3.5=1(小时),∴货车在乙地卸货停留了1小时;(2)∵7.5﹣4.5=3<3.5,∴货车返回速度快,∵=70(千米/时),∴返回速度是70千米/时.16.解:(1)当0≤x≤6时,设甲车行驶过程中y与x之间的函数关系式为y=mx,把(6,600)代入y=mx,6m=600,解得m=100,∴y=100x;当6<x≤14时,设甲车行驶过程中y与x之间的函数关系式为y=kx+b,把(6,600)、(14,0)代入y=kx+b,得解得,∴y=﹣75x+1 050;即甲车行驶过程中y与x之间的函数关系式为:y=;(2)当x=7时,y=﹣75x+1 050解得,y=﹣75×7+1 050=525,525÷7=75(千米/时),即乙车的速度为75千米/时.17.解:(1)a=200÷2×8=800.(2)设小明取回书后y与x的函数关系式是y=kx+b.由题意,得解得(4分)∴小明取回书后y与x的函数关系式是y=200x﹣800.(3)由题意100x﹣(200x﹣800)=100,解得x=7∴7min后小明与弟弟相距100m.18.解:(1)该市人均月生活用水不超过6吨时,设y与x的函数解析式是y=kx,则9=6k,得k=1.5,即该市人均月生活用水不超过6吨时,y与x的函数解析式是y=1.5x;(2)该市人均月生活用水超过6吨时,设y与x的函数关系式是y=mx+n,则,解得,即该市人均月生活用水超过6吨时,y与x的函数关系式是y=3x﹣9;(3)由题意可得,人均月生活用水费为:75÷5=15,将y=15代入y=3x﹣9,得15=3x﹣9,解得,x=8,即该家庭这个月人均用了8吨生活用水.19.解:(1)由图可知,A、B两城相距300千米,乙车比甲车晚出发1小时,却早到1小时,故答案为:300,1,1;(2)设甲对应的函数解析式为:y=kx,300=5k解得,k=60,即甲对应的函数解析式为:y=60x,设乙对应的函数解析式为y=mx+n,解得,,即乙对应的函数解析式为y=100x﹣100,∴解得2.5﹣1=1.5,即乙车出发后1.5小时追上甲车;(3)由题意可得,当乙出发前甲、乙两车相距50千米,则50=60x,得x =,当乙出发后到乙到达终点的过程中,则60x﹣(100x﹣100)=±50,解得,x=1.25或x=3.75,当乙到达终点后甲、乙两车相距50千米,则300﹣50=60x,得x =,即小时、1.25小时、3.75小时、小时时,甲、乙两车相距50千米.20.解:(1)点A表达的含义正确的是甲车出发时,乙车距离B地的距离或乙车出发1小时后,距离B地的路程.故答案为③④.(2)乙车的速度是60千米/小时,a ==7小时,甲的速度==120千米/小时,t ==3小时.故答案为60,7,120,3.(3)相遇.设在甲车出发x小时后相遇.由题意(120+60)x=480﹣60解得x =,答:在甲车出发小时后相遇.21。
人教版数学八年级下册第19章19.2.3一次函数与方程、不等式-第1课时测试(教师版)

初中数学试卷八年级下册第十九章19.2.3一次函数与方程、不等式第1课时(测)总分:100 时间:40分钟 班级 姓名 总分一、选择题(每小题5分,共20分)1.两条直线y=11k x b +和y=22k x b +相交于点A(-2,3),则方程组1122y k x b y k x b ì=+ïí=+ïî的解是 .【答案】23x y ì=-ïí=ïî【解析】试题分析:两个一次函数的交点坐标就是以这两个一次函数为方程的二元一次方程组的解. 考点:一次函数与二元一次方程组的关系2.为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y 万个与生产时间x 天之间的函数关系如图所示,则每家企业供应的足球数量a 等于 万个.【答案】1 【解析】试题分析:结合函数图象,设乙企业每天生产足球x 万个,则甲企业每天生产足球2x 万个,根据企业供应的足球数=库存+每日产量×生产天数,得出关于x 、a 的二元一次方程组,解方程组即可得出结论. ∵(6﹣2)÷(4﹣2)=2,∴设乙企业每天生产足球x 万个,则甲企业每天生产足球2x 万个, 根据题意可得:,解得:.∴每家企业供应的足球数量a=1万个. 故答案为:1.考点:本题考查了二元一次方程组的应用,解题的关键是得出关于x 、a 的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(或方程组)是关键.3.如图,已知一次函数(0)y ax b a =+≠和(0)y kx k =≠的图象交于点P ,则二元一次方程组,0y ax b y kx -=⎧⎨-=⎩的解是 .【答案】42x y ì=-ïí=-ïî【解析】试题分析:方程组的解就是两个函数图象的交点,则42x y ì=-ïí=-ïî.考点:一次函数与方程组.4.如图,已知一次函数y=ax+b 和y=kx 的图象相交于点P ,则根据图中信息可得二元一次方程组的解是 .【答案】【解析】试题分析:直接利用已知图形结合一次函数与二元一次方程组的关系得出答案. 如图所示:根据图中信息可得二元一次方程组的解是:.故答案为:.考点:此题主要考查了一次函数与二元一次方程组的关系。
国开作业刑事诉讼法学-形考任务五(第19-20章;权重:20%)64参考(含答案)

题目:某市中级人民法院判处被告人死缓。
被告人没有上诉,检察机关没有抗诉。
该案经省高级人民法院核准后,被害人不服,提出申诉。
如果提起审判监督程序,下列哪一选项是正确的?()选项A:由市人民检察院提出抗诉选项B:由省高级人民法院院长提交本院审判委员会处理选项C:由市中级人民法院院长提交本院审判委员会处理选项D:由省人民检察院提起审判监督程序答案:由市中级人民法院院长提交本院审判委员会处理题目:人民法院受理某甲抢劫案件,开庭时,公诉人出庭公诉,没有委托辩护人,并查明某甲在案件受理后刚满18岁。
人民法院如何为某甲指定辩护人?()选项A:由于某甲在实施抢劫犯罪时尚不满18周岁,因此人民法院应当为其指定辩护人选项B:某甲在案件受理后已满18岁,但是案发时未满18岁,因此人民法院可以为其指定辩护人选项C:某甲不符合法定的应当指定的情形,人民法院可不为其指定辩护人选项D:人民法院不能为某甲指定辩护人答案:某甲不符合法定的应当指定的情形,人民法院可不为其指定辩护人题目:在刘某(15岁,涉嫌抢劫)一案的审理过程中,应当贯彻不公开审理的原则,下列做法不符合这一原则的是:()选项A:法院不准新闻记者采访报道选项B:法院允许刘某的父母到场选项C:法院宣布对于刘某涉嫌抢劫的审理过程不公开选项D:法院审理结束后,为了刘某的健康成长,决定不公开宣告判决答案:法院审理结束后,为了刘某的健康成长,决定不公开宣告判决题目:李某被甲市某区人民法院以盗窃罪判处有期徒刑3年。
在一审宣判以后,如果人民检察院认为该判决确有错误,在抗诉期间内,有权提出抗诉的人民检察院有:()选项A:甲市人民检察院选项B:省人民检察院选项C:最高人民检察院选项D:区人民检察院答案:区人民检察院题目:李某因为受贿罪,被第一审人民法院判处有期徒刑3年,被告人提起上诉,第二审人民法院改判有期徒刑2年。
随后,人民检察院按照审判监督程序提起抗诉,按照法律规定,下列哪种表述是错误的?()选项A:接受抗诉的人民法院应当组成合议庭重新审理选项B:应当在作出提审、再审决定之日起3个月之内审结,需要延长期限的,不得超过6个月选项C:接受抗诉的人民法院应当进行审查以决定是否重新审理选项D:接受抗诉的人民法院可以指定下级人民法院再审答案:接受抗诉的人民法院应当进行审查以决定是否重新审理题目:甲因犯抢劫罪被市检察院提起公诉,经一审法院审理,判处死刑缓期二年执行。
国开作业西方行政学说-第19章 本章测试19参考(含答案)

选项C:法默尔清楚地认识到,公共行政领域的后现代转向不仅仅只涉及解构,解构只是这副后现代纸牌中的一组纸牌而已。
选项A:未来文明
选项B:古罗马文明
选项C:工业文明
选项D:古代文明
答案:工业文明
题目:“想象”(imagination)这个语词曾经一度被认为是( )学界的特征,但现在成了一个被更广泛需要的特性。
选项A:物理
选项B:美
选项C:天文
选项D:化学
答案:美
题目:法默尔是西方( )公共行政理论流派的主要代表人物之一。( )
选项A:后现代
选项B:现代
选项C:当代
选项D:古代
答案:后现代
题目:以下各项中,关于法默尔基于后现代的特质对公共行政理论进行后现代探索的四个值得关注的方面之一“解构”的表述正确的是( )。
选项A:解构(deconstruction)是著名后现代主义理论家德里达(Jacques Derrida)最早探讨和倡导的一个概念。
题目:以下各项中,关于法默尔基于后现代的特质对公共行政理论进行后现代探索的四个值得关注的方面之一“想象”,表述正确的是( )。
选项A:法默尔强调,在后现代,作为诗法的想象将会比作为现代特征的逻辑中心论更有价值,“就否定的一面而言,想象是一种不依赖于制定规则和遵循程序之现代主义行为的行政精神”,而“就肯定的一面而言,想象则是一种可以为想象力的发展提供主要角色的行政精神”。作为一种创造性管理的艺术,想象将会提供现代“理性”规则导向的官僚机构所缺少的许多机会。
公司延期章程修正案范本

企业内部章程系列公司延期章程修正案范例(标准、完整、实用、可修改)编号:FS-QG-61500公司延期章程修正案范例Examples of amendments to a company's deferred bylaws说明:为规定公司的组织和活动基本准则,并通过所有股东共同一致认可,从而提升公司的经营和管理效率,特此制定。
公司延期章程修正案1股东会决议某某公司20××年10月21日股东会召开会议,应到股东5人实到5人,与会股东讨论后一致通过:公司的经营期限延长10年,从20xx年11月1日延长至20xx年11月日。
股东签字20××年10月21日某某有限公司章程修正案有限公司于____年__月__日召开股东会,决议变更公司经营期限,并决定对公司章程作如下修改:一、第条原为:“………………”。
现修改为:“………………”。
(股东盖章或签名)____年__月__日公司延期章程修正案2公司章程相当于几个出资人或者股东的协议,当时的协议是营业执照签发之日起10年,如果你们还要继续经营下去,就要重新制定公司章程,并且在营业执照期满前申请新的营业执照。
变更公司章程的程序时:法律依据:公司法:第三十八条股东会行使下列职权:(一)决定公司的经营方针和投资计划;(二)选举和更换非由职工代表担任的董事、监事,决定有关董事、监事的报酬事项;(三)审议批准董事会的报告;(四)审议批准监事会或者监事的报告;(五)审议批准公司的年度财务预算方案、决算方案;(六)审议批准公司的利润分配方案和弥补亏损方案;(七)对公司增加或者减少注册资本作出决议;(八)对发行公司债券作出决议;(九)对公司合并、分立、解散、清算或者变更公司形式作出决议;(十)修改公司章程;(十一)公司章程规定的其他职权。
对前款所列事项股东以书面形式一致表示同意的,可以不召开股东会会议,直接作出决定,并由全体股东在决定文件上签名、盖章。
