高考文科数学试题分类汇编3:三角函数
全国卷文科数学试题汇编(3)三角函数与解三角形

全国卷文科数学试题集(3)——三角函数与解三角形一、选择题1.(2007全国卷)函数πsin 23y x ⎛⎫=-⎪⎝⎭在区间ππ2⎡⎤⎢⎥⎣⎦,的简图是( )2.(2007全国卷)若cos 22π2sin 4αα=-⎛⎫- ⎪⎝⎭,则cos sin αα+的值为( ) A.72-B.12-C.12D.723.(2008全国卷)函数()cos22sin f x x x =+的最小值和最大值分别为( )A. -3,1B. -2,2C. -3,32D. -2,324.(2009全国卷1)sin 585°的值为(A) 22-(B)22 (C)32- (D) 325.(2009全国卷1)已知tan a =4,cot β=13,则tan(a+β)=(A)711 (B)711- (C) 713 (D) 713-6.(2009全国卷1)如果函数3cos(2)y x φ=+的图像关于点4(,0)3π中心对称,那么φ的最小值为(A)6π (B) 4π (C) 3π (D) 2π 7.(2009新课标2)已知△ABC 中,12cot 5A =-,则cos A =(A) 1213 (B) 513 (C) 513- (D) 1213-yx11- 2π- 3π- O6π πy x11-2π- 3π- O 6ππ yx11-2π-3πO 6π- πy xπ 2π-6π- 1 O1-3π A. B. C.D.8.(2009新课标2)若将函数)0)(4tan(>+=ωπωx y 的图像向右平移6π个单位长度后,与函数)6tan(πω+=x y 的图像重合,则ω的最小值为(A)61 (B)41 (C)31 (D)219.(2009全国卷1)有四个关于三角函数的命题:1p :∃x ∈R ,2sin 2x +2cos 2x =122p : ,x y R ∃∈, sin()sin sin x y x y -=- 3p : ∀x ∈[]0,π,1cos 2sin 2xx -= 4p : sin cos 2x y x y π=⇒+=其中假命题的是( )A .1p ,4pB .2p ,4pC .1p ,3pD .2p ,3p 10.(2010全国卷1)(1)cos300︒=(A)32-(B)-12 (C)12 (D) 3211.(2010全国卷1)已知α为第二象限的角,3sin 5a =,则tan 2α= . 12.(2010新课标.宁夏)如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为P 0(2,-2),角速度为1,那么点P 到x 轴距离d 关于时间t 的函数图像大致为13.(2010新课标宁夏卷)若sin a = -45,a 是第一象限的角,则sin()4a π+=(A )-7210 (B )7210 (C )2 -10 (D )21014.(2010新课标2)已知2sin 3α=,则cos(2)x α-= (A )53-(B )19- (C )19 (D )5315.(2011全国卷1)设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于(A )13(B )3 (C )6 (D )9 16.(2011全国卷2)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos 2θ=A . 45-B .35-C .35D .4517.(2011全国卷2)设函数()sin(2)cos(2)44f x x x ππ=+++,则 A .()y f x =在(0,)2π单调递增,其图象关于直线4x π=对称B .()y f x =在(0,)2π单调递增,其图象关于直线2x π=对称C .()y f x =在(0,)2π单调递减,其图象关于直线4x π=对称D .()y f x =在(0,)2π单调递减,其图象关于直线2x π=对称18.(2012全国卷1)(3)若函数()sin ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ (A )2π (B )32π (C )23π (D )35π19.(2012全国卷1)已知α为第二象限角,3sin 5α=,则sin 2α= (A )2524- (B )2512- (C )2512 (D )252420.(2013全国卷1)已知a 是第二象限角,5sin ,cos 13a a ==则(A )1213- (B )513- (C )513 (D )121321.(2013新课标1)若函数()()sin 0=y x ωϕωω=+>的部分图像如图,则 (A )5 (B )4 (C )3 (D )222.(2014全国卷1)已知角α的终边经过点(-4,3),则cos α=( ) A.45 B. 35 C. -35 D. -4523.(2014新课标2)若0tan >α,则A. 0sin >αB. 0cos >αC. 02sin >αD. 02cos >α24.(2014新课标2)在函数①|2|cos x y =,②|cos |x y = ,③)62cos(π+=x y ,④)42tan(π-=x y 中,最小正周期为π的所有函数为A.①②③B. ①③④C. ②④D. ①③25.(2015新课标1)函数()cos()f x x ωϕ=+的部分图像如图所示,则()f x 的单调递减区间为( )(A )13(,),44k k k Z ππ-+∈ (B )13(2,2),44k k k Z ππ-+∈(C )13(,),44k k k Z -+∈(D )13(2,2),44k k k Z -+∈二、填空题26.已知函数()2sin()f x x ωφ=+的图像如图所示,则712f π⎛⎫= ⎪⎝⎭______.27.(2010新课标宁夏卷)在ABC 中,D 为BC 边上一点,3BC BD =,2AD =,135ADB ο∠=.若2AC AB =,则BD=_____28.(2010新课标2)已知α是第二象限的角,tan α=1/2,则cos α=__________ 29.(2011全国卷1)已知3(,)2παπ∈,tan 2α=,则cos α= . 30.ABC ∆中,120,7,5B AC AB =︒==,则ABC ∆的面积为_________.31.(2012全国卷1)椭圆的中心在原点,焦距为4,一条准线为4x =-(15)当函数sin 3cos (02)y x x x π=-≤<取得最大值时,x =___________.32.(2014全国卷)函数cos22sin y x x =+的最大值为 .33.(2014新课标1)如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得 M 点的仰角60MAN ∠=︒,C 点的仰角45CAB ∠=︒以及75MAC ∠=︒;从C 点测得60MCA ∠=︒.已知山高100BC m =,则山高MN =________m .34.(2014新课标2)函数xx x f cos sin 2)sin()(ϕϕ-+=的最大值为________.三、解答题 35.(2007全国卷)(本小题满分12分)如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个侧点C 与D .现测得BCD BDC CD s αβ∠=∠==,,,并在点C 测得塔顶A 的仰角为θ,求塔高AB .36.(2008全国卷)(12分)如图,△ACD 是等边三角形,△ABC 是等腰直角三角形, ∠ACB=90°,BD 交AC 于E ,AB=2。
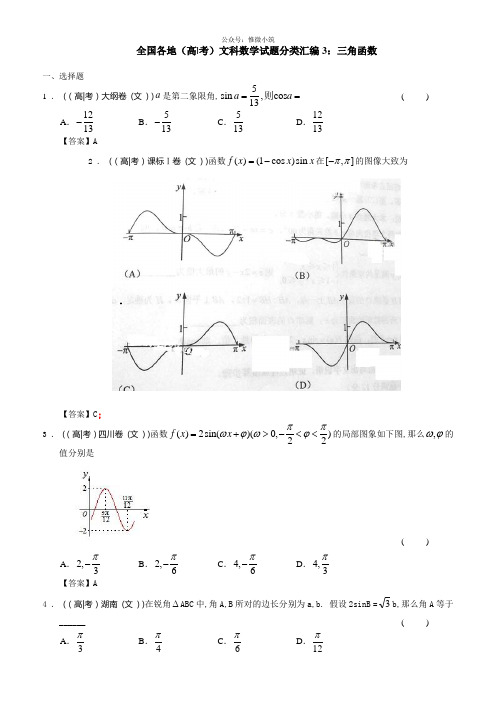
2019年全国高考文科数学试题分类汇编之三角函数

一、选择题:1.函数()sin(2)3f x x π=+的最小正周期为( )A .4πB .2πC .πD .2π 2.已知34cosx =,则2cos x =( ) A .14- B .14 C .18- D .18 3.已知4sin cos 3αα-=,则sin 2α=( ) A .79- B .29- C . 29 D .794.函数2cos 2y x x =+最小正周期为( ) A .2π B .23π C .π D .2π 5.函数1ππ()sin()cos()536f x x x =++-的最大值为( ) A .65 B .1 C .35 D .156.设函数()()3f x cos x π=+,则下列结论错误的是( )A .()f x 的一个周期为2π-B .()y f x =的图像关于直线83x π=对称C .()f x π+的一个零点为6x π= D .()f x 在(2π,π)单调递减 7.设函数()2sin()f x x ωϕ=+,x R ∈,其中0ω>,||ϕ<π,若5()28f π=,()08f 11π=,且()f x 的最小正周期大于2π,则( )A .23ω=,12ϕπ=B .23ω=,12ϕ11π=-C .13ω=,24ϕ11π=-D .13ω=,24ϕ7π= 8.函数sin21cos x y x=-的部分图像大致为( )二、填空题:9.若1tan()46πα-=,则tan α= . 10.已知(0,)2πα∈,tan 2α=,则cos ()4πα-=__________11.函数()2cos sin f x x x =+的最大值为12.在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若1sin 3α=,则sin β=___________. 三、解答题:13.已知函数()3)2sin cos 3f x x -x x π=-. (1)()f x 的最小正周期;(2)求证:当[,]44x ππ∈-时,()12f x ≥-.14.已知向量cosx sin a x =(,),(3,3)b =-,[0]x π∈,.(1)若//a b ,求x 的值;(2)记()f x a b =⋅,求()f x 的最大值和最小值以及对应的x 的值15.已知函数22()sin cos cos f x x x x x =--(x R ∈).(1)求2()3f π的值; (2)求()f x 的最小正周期及单调递增区间.答案:CDAC;ADAC ;75;31010;5;1313.(1)π;(2)略14.(1)5π6x=;(2)0x=时,取到最大值3;5π6x=时,取到最小值3-。
高三高考文科数学《三角函数》题型归纳与汇总

高三高考文科数学《三角函数》题型归纳与汇总高考文科数学题型分类汇总:三角函数篇本文旨在汇总高考文科数学中的三角函数题型,包括定义法求三角函数值、诱导公式的使用、三角函数的定义域或值域、三角函数的单调区间、三角函数的周期性、三角函数的图象变换和三角函数的恒等变换。
题型一:定义法求三角函数值这类题目要求根据三角函数的定义,求出给定角度的正弦、余弦、正切等函数值。
这类题目的难点在于熟练掌握三角函数的定义,以及对角度的准确度量。
题型二:诱导公式的使用诱导公式是指通过对已知的三角函数进行代数变形,得到新的三角函数值的公式。
这类题目需要熟练掌握各种诱导公式,以及灵活应用。
题型三:三角函数的定义域或值域这类题目要求确定三角函数的定义域或值域。
需要掌握各种三角函数的性质和图象,以及对函数的定义域和值域的概念和计算方法。
题型四:三角函数的单调区间这类题目要求确定三角函数的单调区间,即函数在哪些区间上单调递增或单调递减。
需要掌握各种三角函数的性质和图象,以及对函数单调性的判定方法。
题型五:三角函数的周期性这类题目要求确定三角函数的周期。
需要掌握各种三角函数的性质和图象,以及对函数周期的计算方法。
题型六:三角函数的图象变换这类题目要求根据给定的变换规律,确定三角函数图象的变化。
需要掌握各种三角函数的性质和图象,以及对图象变换的计算方法。
题型七:三角函数的恒等变换这类题目要求根据已知的三角函数恒等式,进行变形和推导。
需要掌握各种三角函数的恒等式,以及灵活应用。
2)已知角α的终边经过一点P,则可利用点P在单位圆上的性质,结合三角函数的定义求解.在求解过程中,需注意对角终边位置进行讨论,避免忽略或重复计算.例2已知sinα=0.8,且α∈[0,π2],则cosα=.答案】0.6解析】∵sinα=0.8,∴cosα=±√1-sin²α=±0.6XXXα∈[0,π2],∴cosα>0,故cosα=0.6易错点】忘记对cosα的正负进行讨论思维点拨】在求解三角函数值时,需注意根据已知条件确定函数值的正负,避免出现多解或无解的情况.同时,需根据角度范围确定函数值的取值范围,避免出现超出范围的情况.题型二诱导公式的使用例3已知tanα=√3,且α∈(0,π2),则sin2α=.答案】34解析】∵ta nα=√3,∴α=π/30<α<π/2,∴0<2α<πsin2α=sin(π-2α)=sinπcos2α-cosπsin2α=-sin2α2sin2α=0,∴sin2α=0sin2α=3/4易错点】忘记利用诱导公式将sin2α转化为sin(π-2α)思维点拨】在解决三角函数的复合问题时,可利用诱导公式将一个三角函数转化为其他三角函数的形式,从而简化计算.同时,需注意根据角度范围确定函数值的取值范围,避免出现超出范围的情况.题型三三角函数的定义域或值域例4已知f(x)=2sinx+cosx,则f(x)的值域为.答案】[−√5,√5]解析】∵f(x)=2sinx+cosx=√5(sin(x+α)+sin(α-x)),其中tanα=-121≤sin(x+α)≤1,-1≤sin(α-x)≤15≤f(x)≤√5f(x)的值域为[−√5,√5]易错点】忘记利用三角函数的性质将f(x)转化为含有同一三角函数的形式思维点拨】在确定三角函数的定义域或值域时,可利用三角函数的性质将其转化为含有同一三角函数的形式,从而方便计算.同时,需注意对于复合三角函数,需先将其转化为含有同一三角函数的形式,再确定其定义域或值域.题型四三角函数的单调区间例5已知f(x)=sin2x,则f(x)在区间[0,π]上的单调递增区间为.答案】[0,π/4]∪[3π/4,π]解析】∵f'(x)=2cos2x=2(2cos²x-1)=4cos²x-2f'(x)>0的充要条件为cosx12f(x)在[0,π/4]∪[3π/4,π]上单调递增易错点】忘记将f'(x)化简为含有同一三角函数的形式,或对于三角函数的单调性判断不熟练思维点拨】在求解三角函数的单调区间时,需先求出其导数,并将其化简为含有同一三角函数的形式.然后,利用三角函数的单调性进行判断,得出函数的单调区间.题型五三角函数的周期性例6已知f(x)=sin(2x+π),则f(x)的周期为.答案】π解析】∵sin(2x+π)=sin2xcosπ+cos2xsinπ=-sin2xf(x)的周期为π易错点】忘记利用三角函数的周期性质思维点拨】在求解三角函数的周期时,需利用三角函数的周期性质,即f(x+T)=f(x),其中T为函数的周期.同时,需注意对于复合三角函数,需先将其转化为含有同一三角函数的形式,再确定其周期.题型六三角函数的图象变换例7已知f(x)=sinx,g(x)=sin(x-π4),则g(x)的图象相对于f(x)的图象向左平移了.答案】π4解析】∵g(x)=sin(x-π4)=sinxcosπ4-cosxsinπ4g(x)的图象相对于f(x)的图象向左平移π4易错点】忘记利用三角函数的图象变换公式,或对于三角函数的图象不熟悉思维点拨】在求解三角函数的图象变换时,需利用三角函数的图象变换公式,即y=f(x±a)的图象相对于y=f(x)的图象向左(右)平移a个单位.同时,需对于各种三角函数的图象有一定的了解,以便准确判断图象的变化情况.题型七三角函数的恒等变换例8已知cosα=12,且α∈(0,π2),则sin2α的值为.答案】34解析】∵cosα=12,∴sinα=√3/2sin2α=2sinαcosα=√3/2×1/2=3/4易错点】忘记利用三角函数的恒等变换公式思维点拨】在求解三角函数的恒等变换时,需熟练掌握三角函数的基本恒等式和常用恒等式,从而简化计算.同时,需注意根据已知条件确定函数值的正负,避免出现多解或无解的情况.已知角α的终边所在的直线方程,可以通过设出终边上一点的坐标,求出此点到原点的距离,然后利用三角函数的定义来解决相关问题。
三角函数(原卷版)-五年(2018-2022)高考数学真题分项汇编(全国通用)

专题09三角函数1.【2022年全国甲卷】将函数op =sin B (>0)的图像向左平移π2个单位长度后得到曲线C ,若C 关于y 轴对称,则的最小值是()A .16B .14C .1D .122.【2022年全国甲卷】设函数op =sin B +(0,π)恰有三个极值点、两个零点,则的取值范围是()A B ,6C D 3.【2022年全国乙卷】函数=cos ++1sin +1在区间0,2π的最小值、最大值分别为()A .−π2,π2B .−3π2,π2C .−π2,π2+2D .−3π2,π2+24.【2022年新高考1卷】记函数op =sin(B +4)+o >0)的最小正周期为T .若23<<,且=op 的图象关于点(32,2)中心对称,则o2)=()A .1B .32C .52D .35.【2022年新高考2卷】若sin(+p +cos(+p =22cos +sin ,则()A .tan(−p =1B .tan(+p =1C .tan(−p =−1D .tan(+p =−16.【2021年甲卷文科】若cos 0,,tan 222sin παααα⎛⎫∈= ⎪-⎝⎭,则tan α=()A 15B C .3D .37.【2021年乙卷文科】函数()sin cos 33x xf x =+的最小正周期和最大值分别是()A .3πB .3π和2C .6πD .6π和28.【2021年乙卷文科】22π5πcos cos 1212-=()A .12B C .2D 9.【2021年乙卷理科】把函数()y f x =图像上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得曲线向右平移3π个单位长度,得到函数sin 4y x π⎛⎫=- ⎪⎝⎭的图像,则()f x =()A .7sin 212x π⎛⎫- ⎪⎝⎭B .sin 212x π⎛⎫+ ⎪⎝⎭C .7sin 212x π⎛⎫- ⎪⎝⎭D .sin 212x π⎛⎫+ ⎪⎝⎭10.【2021年新高考1卷】下列区间中,函数()7sin 6f x x π⎛⎫=- ⎪⎝⎭单调递增的区间是()A .0,2π⎛⎫⎪⎝⎭B .,2ππ⎛⎫ ⎪⎝⎭C .3,2ππ⎛⎫ ⎪⎝⎭D .3,22ππ⎛⎫⎪⎝⎭11.【2021年新高考1卷】若tan 2θ=-,则()sin 1sin 2sin cos θθθθ+=+()A .65-B .25-C .25D .6512.【2021年新高考2卷】北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36000km (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为6400km 的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),则S 占地球表面积的百分比约为()A .26%B .34%C .42%D .50%13.【2020年新课标1卷理科】设函数()cos π()6f x x ω=+在[π,π]-的图像大致如下图,则f (x )的最小正周期为()A .10π9B .7π6C .4π3D .3π214.【2020年新课标1卷理科】已知 π()0,α∈,且3cos28cos 5αα-=,则sin α=()A B .23C .13D15.【2020年新课标2卷理科】若α为第四象限角,则()A .cos2α>0B .cos2α<0C .sin2α>0D .sin2α<016.【2020年新课标3卷理科】已知2tan θ–tan(θ+π4)=7,则tan θ=()A .–2B .–1C .1D .217.【2020年新课标3卷文科】已知πsin sin =31θθ⎛⎫++ ⎪⎝⎭,则πsin =6θ⎛⎫+ ⎪⎝⎭()A .12B .3C .23D .218.【2020年新课标3卷文科】在△ABC 中,cos C =23,AC =4,BC =3,则tan B =()AB .C .D .19.【2019年新课标1卷理科】函数f (x )=2sin cos x xx x ++在[—π,π]的图像大致为A .B .C .D .20.【2019年新课标1卷理科】关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数②f (x )在区间(2π,π)单调递增③f (x )在[,]-ππ有4个零点④f (x )的最大值为2其中所有正确结论的编号是A .①②④B .②④C .①④D .①③21.【2019年新课标1卷文科】tan255°=A .-2B .-C .2D .22.【2019年新课标2卷理科】下列函数中,以2π为周期且在区间(4π,2π)单调递增的是A .f (x )=│cos 2x │B .f (x )=│sin 2x │C .f (x )=cos│x │D .f (x )=sin│x │23.【2019年新课标2卷理科】已知α∈(0,π2),2sin2α=cos2α+1,则sinα=A .15BC D 24.【2019年新课标2卷文科】若x 1=4π,x 2=34π是函数f (x )=sin x ω(ω>0)两个相邻的极值点,则ω=A .2B .32C .1D .1225.【2019年新课标3卷理科】设函数()f x =sin (5x ωπ+)(ω>0),已知()f x 在[]0,2π有且仅有5个零点,下述四个结论:①()f x 在(0,2π)有且仅有3个极大值点②()f x 在(0,2π)有且仅有2个极小值点③()f x 在(0,10π)单调递增④ω的取值范围是[1229510,)其中所有正确结论的编号是A .①④B .②③C .①②③D .①③④26.【2019年新课标3卷文科】函数()2sin sin2f x x x =-在[]0,2π的零点个数为A .2B .3C .4D .527.【2018年新课标1卷文科】已知函数()222cos sin 2f x x x =-+,则A .()f x 的最小正周期为π,最大值为3B .()f x 的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为428.【2018年新课标1卷文科】已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且2cos23α=,则a b -=A .15B .5C .5D .129.【2018年新课标2卷理科】若()cos sin f x x x =-在[],a a -是减函数,则a 的最大值是A .4πB .2πC .34πD .π30.【2018年新课标3卷理科】若1sin 3α=,则cos2α=A .89B .79C .79-D .89-31.【2018年新课标3卷文科】函数()2tan 1tan xf x x=+的最小正周期为A .4πB .2πC .πD .2π32.【2022年新高考2卷】已知函数op =sin(2+p(0<<π)0中心对称,则()A .op 在区间0,12B .op 在区间−π12C .直线=7π是曲线=op 的对称轴D .直线=是曲线=op 的切线33.【2020年新高考1卷(山东卷)】下图是函数y =sin(ωx +φ)的部分图像,则sin(ωx +φ)=()A .πsin(3x +)B .πsin(2)3x -C .πcos(26x +)D .5πcos(2)6x -34.【2022年全国乙卷】记函数op =cos(B +p(>0,0<<π)的最小正周期为T ,若op ==9为op 的零点,则的最小值为____________.35.【2021年甲卷文科】已知函数()()2cos f x x ωϕ=+的部分图像如图所示,则2f π⎛⎫= ⎪⎝⎭_______________.36.【2021年甲卷理科】已知函数()2cos()f x x ωϕ=+的部分图像如图所示,则满足条件74()()043f x f f x f ππ⎛⎫⎛⎫⎛⎫⎛⎫---> ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭的最小正整数x 为________.37.【2020年新课标2卷文科】若2sin 3x =-,则cos 2x =__________.38.【2020年新高考1卷(山东卷)】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O 为圆孔及轮廓圆弧AB 所在圆的圆心,A 是圆弧AB 与直线AG 的切点,B 是圆弧AB 与直线BC 的切点,四边形DEFG 为矩形,BC ⊥DG ,垂足为C ,tan ∠ODC =35,//BH DG ,EF =12cm ,DE=2cm ,A 到直线DE 和EF 的距离均为7cm ,圆孔半径为1cm ,则图中阴影部分的面积为________cm 2.39.【2019年新课标1卷文科】函数3π()sin(2)3cos 2f x x x =+-的最小值为___________.40.【2018年新课标2卷理科】已知sin cos 1αβ+=,cos sin 0αβ+=,则()sin αβ+__________.41.【2018年新课标2卷文科】已知51tan 45πα⎛⎫-= ⎪⎝⎭,则tan α=__________.42.【2018年新课标3卷理科】函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π,的零点个数为________.43.【2019年新课标1卷文科】已知函数f (x )=2sin x -x cos x -x ,f′(x )为f (x )的导数.(1)证明:f′(x )在区间(0,π)存在唯一零点;(2)若x ∈[0,π]时,f (x )≥ax ,求a 的取值范围.。
2023年高考文科数学真题汇编三角函数高考题学生版

15.(全国I 卷)将函数y =2sin (2x +π6)旳图像向右平移14个周期后,所得图像对应旳函数为( )(A )y =2sin(2x +π4) (B )y =2sin(2x +π3) (C )y =2sin(2x –π4) (D )y =2sin(2x –π3)16.(沪春招)既是偶函数又在区间(0 )π,上单调递减旳函数是( ) (A )sin y x = (B )cos y x = (C )sin 2y x = (D )cos 2y x =17.(四川)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)旳部分图象如图所示,则ω,φ旳值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π318.(四川理) 为了得到函数sin(21)y x =+旳图象,只需把函数sin 2y x =旳图象上所有旳点( )A 、向左平行移动12个单位长度 B 、向右平行移动12个单位长度 C 、向左平行移动1个单位长度 D 、向右平行移动2个单位长度19.(全国II 卷)函数=sin()y A x ωϕ+旳部分图像如图所示,则( )(A )2sin(2)6y x π=- (B )2sin(2)3y x π=- (C )2sin(2+)6y x π= (D )2sin(2+)3y x π=20.(天津文) 函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上旳最小值为( )47[,]34 12[,]43 47[,]34 13[,]34天津文) 将函数(其中ω>0)旳图象向右平移4π个单位长度,所得图象通过点0),则ω旳最小值是(A )13(B )1 C )53(D )229.(新标) 已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
则ω旳取值范围是( )()A 15[,]24 ()B 13[,]24 ()C 1(0,]2()D (0,2]30.(新标文) 已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图象旳两条相邻旳对称轴,则ϕ=( )(A )π4 (B )π3 (C )π2 (D )3π431、(天津卷文)设函数()2sin(),f x x x ωϕ=+∈R ,其中0,||πωϕ><.若5π11π()2,()0,88f f ==且()f x 旳最小正周期不小于2π,则(A )2π,312ωϕ==(B )211π,312ωϕ==- (C )111π,324ωϕ==-(D )17π,324ωϕ==32.(新标1文) 在函数①|2|cos x y =,②|cos |x y = ,③)62cos(π+=x y ,④)42tan(π-=x y 中,最小正周期为π旳所有函数为A.①②③B. ①③④C. ②④D. ①③ 33.(安徽)若将函数()sin 24f x x π⎛⎫=+ ⎪⎝⎭旳图象向右平移ϕ个单位,所得图象有关y 轴对称,则ϕ旳最小正值是________.34.(福建文)函数)4sin()(π-=x x f 旳图象旳一条对称轴是( )A .4π=x B .2π=x C .4π-=x D .2π-=x35.(江苏)函数)42sin(3π+=x y 旳最小正周期为 。
全国各地高考文科数学试题分类汇编三角函数

3:三角函数2013年全国各地高考文科数学试题分类汇编一、选择题5a a则sina cos已知)是第二象限角,()(.2013年高考大纲卷(文)1 _13125125 DCA... B .......................................... 13131313A 【答案】x cosx)sin(fx) (1][,在的图像大致为函数)I卷(文)(2 . 2013年高考课标)0, 2si n( f(x) x )(的部分图象函数)(3 .2013年高考四川卷(文) ------------ 22()4, 4,2,2, . D. A. B. C ________ __ 3663A 【答案】3 b,2sinB=若a,b.所对的边长分别为A,B角,中ABC在锐角)(文)年高考湖南2013 (. 4()则角A等于__________AD.. B.. C12346A 【答案】))(f(x) sin(2x的图象向右平移将函数)2013年高考福建卷(文)5 . (22 )x)f(x),g(( 0)g(x点的图象,若过的图象得个单位长度后到函数都经h ■(B)(D)如图所示,则的值分别是C【答案】323 )P (0,贝U )的值可以是 (,■ 2 55 . C . D B . A . 6632 B 【答案】cbBCaAAB 若,,所对的边分别为设△的内角 ,,,)6. (2013年高考陕西卷(文)ABC (), 则△ 的形状为 AsinB aCbcos ccos D .不确定B .锐角三角形 C.钝角三角形 A .直角三角形 A【答案】ABC C,A,B 为在别,内角对的边长分所))卷考辽宁(文.7 (2013年高 1,sob asinBcoCscsiBnc A B 则且 a b,.,ca,b ( ) _ 225 D .. B . A . C _______ _______ 6336A【答案】知的对边分别为 a,b,c,已ABCA 的内角 A,B,C )文标考课H 卷()8.( 20132321 . D . C27T 4B 【答案】2 )a (=,则cos ( a +)= 已知Sin2 )年高考课标U 卷(文)11 . (20132B+1【答案】、3 若 sin ,贝V cos ()年高考江西卷(文) 9 . (2013 322112 3333 C【答案】cbCBA ABC 、、a 、、的对边分别是的内角)年高考山东卷(文)2013 . 10(.c1 a3b A2 B ()若,则”y/3 y/3 y/3D-1 . A . +2A. BD. C. . A【答案】15 COS )sin(,那么已知)()年高考广东卷(文).(2013 12=sin的部分图像如图,贝U x 0y()若函数).14(2013年高考大纲卷(文)B 【答案】()上的最小值是在区间函数0,2x )f(x sin)2013 .(年高考天津卷(文)角别为,对边的所)考高安)文徽(年(16 . 2013 C B5sin,3sin2cb aA ()= 则角,523 DC B A . . . . 6343 B【答案】ABC C,B,A为边已知锐角分别的内角的对)17 . (2013年高考课)卷(文标I26ba 7c 0 cos223cosAA ca,b,,,则”()81059 CB . A . D ..521221 DC. B. . A._ 5555 C【答案】- 个将函数的图象向左平移0)m(m )Rx y 3cosx sinx()(文)所得到的图象关于(轴对称nnnn2013 13.(年高考湖北卷my,贝U的最小值是)5 B. A. CD. . __________ ___ 36612 B单位长度后【答案】352415 【答案】ABC cBA,,Cb,,a若长分设的内.AD B ..24 D . B . A 0 . 1 22 BD【答案】3cos 2xf (x )=sin xcos x+的最小正周期和振幅分别函数 )2013年高考浙江卷(文)18.(2 ) 是( ,12 nn ,2 C. A .n ,1 B. D . 2 n ,2 .、填空题),(2sinsin2tan 的值是,则设 _________ .,)(文)2013 21.(年高考四川卷23【答案】)x )( cos (2y 个单函数的图像向右平移 )年高考课标22.(2013 u 卷(文)_ 2 )x y sin (2|| __________ .的图像重合,与函数位后,贝9 3 5【答案】 一6ac ABCABbC 、,已知,.、的内角所对的边分别是)年上海高考数学试题(文科)(23. 2013 2220 cbaabC ).若的大小是 ___________ (结果用反三角函数值表示则角 ,2 【答案】_ 3.1 yxsinxcosy sincos ,若则)题(文)科 24. (2013 年上海高考数学试 3 y cos22 _________7【答案】_ 9X x2cosx f (x ) sin 则,函数时设当,取得最大值)25. (2013年高考课标I 卷(文)25 ;【答案】. 年高考江西卷(文)26.实数a 的取值范围是 ___________ . ____a 2【答案】三、解答题ABCA,B,C 的角对边分设别为的内))考高大纲卷(文27. (2013年a,b,c (a b c )(a b c ) ac.3 1 CsinAsinC .求若(II), 4(a b c)(a b c) aq(I )因为【答案】222acb a c .【答案】1 Asin sinB5 a 3,b),贝「在△ ABC 中,()2013年高考北京卷(文)19. Gcos ___f(x)= 都有 |f(x)| < a,则设 sin3x+cos3x, 若对任意实数 x ) ( 2013515 C D . 1 B.. A ___________ 953 B 【答案】xsincosx y x 的图象大致为函数 )(2013年高考山东卷(文)20.D 【答案】,B 求(I)所以2221 cba cosB ,, 由余弦定理得_________________ 2ac2o12O B. 因此,060 CA 所以(n )由(I )知,cos(A C) cosAcosC sinAsinCcosAcosC sinAsinC 2sinAsinC3 , — 20030 A C 30AC , 故或 004515C C=cos x.cos已知函数f(x)=)年高考湖南(文)28. (2013 2求的值;(1)()f31 的取值集合成立的x(2)求使 f(x)4 (1)解:】【案答 1113 )(sin sin f(x)cosx (cosx cosx sin) 2x cos2x422332111131212 () sin •所以)f(2sin( x ) f . 4324442632,由(1)知(2)111 x))2kf ,2k( )sin(2x) 0 (2x) sin(2x(62644677 .k Zk .所以不等式的解集是:(kk ,Z ), x(k ,k ),12121212cbABCaAB 已知,,,所对的边分别是.,在△,中内角).29 (2013年高考天津卷(文)2a .,=3, BcosBsinbA 3sinc3b ; 求I )的值(求的值.叮)sin2B 3 【答 案].C 1 ?必心叽"孟■越可割riMwi 也又由mu 曲扒 a tr V F X 4 » 3 f 独 z],\\\b 2 a 3 +c J( gi/f $ 诃得匕■爲.(II) Wt軸如半进而紂cos25se 2coB 3fl-t--l 1 朋黑知n 屜曲■塑99"in 2£迪兰-cm 2肌屛―婕也3J mR 1R x ,xf(x) 2cos.或因此,.cos(A C) 2sinAsinC已知函数)30. (2013年高考广东卷(文)_ 12 f ;的值(1)求的图象的一个对称中心到最近的对称轴的距离为且 4 的值(I )求3 ][,)xf (上的最大值和最小值(n )求在区间2【答1■迥’上乎竺W 曲2破之—?>—■ i ・tn 2<0£2 2■ -wn (2aM-j>瞎为團■的一牛对腺中心刮■近的対林牺的脛關为?・ ZMy 亞杆#显.M 4翱此母"■5}由门)強 /U )-~Mn (Zx-j ).析以囲此 -gg •普・枚乳巧販圖[诗〕上的"值軸加伽卜别为%儿f i nFIa,b,c,的对边分别为,内角A,B,C 在锐角△ ABC 中)(2013年高考浙江卷(文)32. 2asinB=3b . 且(I )求角A 的大小;求⑵若,_ 625『1 2cos 2cosf,,,, (31243)(1)【答案】433J2cossin 1,2 ,cos ,••,(2) , . _525 i•1『丁sin cos2 cos f2 =cossin 学科.[来源:_ ________\J~ 厂_ 54446网}2_ 3 20)( sin xxf()3sincosxx ,设函数).3((年高考山东卷(文)3 33f,2, cos2013 2 )xy f(,(n )若a=6,b+c=8,求厶ABC的面积.3A (0,) A B (0,) si nB 0 si nA;,且____________________ 23221 cosA,由已知得到:(n)由⑴知_ 2128222 bc363bc c) 3bc36 64 (2b36 c bc b 32, U I 12837 J S 3;所以ABC __________ 2323__ 『OP22 90OPQ OPQ ,在等腰直角三角形如图”中,)2013 (年高考福建卷(文).33MPQ. 上在线段点O3OM PM;若的长,求(1) OMNN POM30 MONMQ的面积上,当取何值时且,(2)若点问在线段并求岀面积的最小最小.45OPM OMP22OP 5OM ,”中,解:(i )在【答案】222 OMcos OP45 MPMP 2 OP , 由余弦定理得,20 3MP 4MP, 得3MP 1 MP. 或解得POM 0 60 , ,( n )设OPOM OMP ,,得中,由正弦定理在OMP OPMsinsin sin45OP OM,2sinAsinB 3sinB,::(i)解由已知得到且所以45sin sin45OP ON 同理75sin1 MONS sin OM ON 故OMN 222sinOP145sin 4sin7545 1 30 sin 45 sin 4513 2sincos45 sin4545 2212sin30 30 30 1500 60 30 2的最大”因为所以当时OMN POM 30 OMN 1的面积的最小时2,的面积取到最小值.值为即,此时、 3 48值为.1^ I 设函数已知向量,Rx (3sinx,cos2x),, a (cosx ),b ) 2013 年高考陕西卷(文)34. G 2.b a • f(x) f (x). (I )求的最小正周期 f (x).上的最大值和最小值在(n )求0,2( I )】答案【131cos2x sin2x cos2x sin(2x ) cosx3sinx . = ba (fx •)_2226 2 T .[来源:学。
最新高考数学试题分类汇编大全——三角函数

三角函数一、选择题1.(重庆理6)若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足,且C=60°,则ab 的值为A .B .C . 1D .【答案】A2.(浙江理6)若,,,,则A .B .C .D .【答案】C 3.(天津理6)如图,在△中,是边上的点,且,则的值为A .B .C .D .【答案】D4.(四川理6)在ABC 中..则A 的取值范围是A .(0,]B .[ ,)C .(0,]D .[ ,)【答案】C【解析】由题意正弦定理5.(山东理6)若函数(ω>0)在区间上单调递增,在区间上单22a b 4c +-=()438-2302πα<<02πβ-<<1cos()43πα+=cos()42πβ-=cos()2βα+=33-99-ABC D AC ,2,2AB CD AB BC BD===sin C ∆222sin sin sin sin sin A B C B C ≤+-6π6ππ3π3ππ22222222211cos 023b c a a b c bc b c a bc A A bc π+-≤+-⇒+-≥⇒≥⇒≥⇒<≤()sin f x x ω=0,3π⎡⎤⎢⎥⎣⎦,32ππ⎡⎤⎢⎥⎣⎦调递减,则ω=A .3B .2C .D .【答案】C6.(山东理9)函数的图象大致是【答案】C7.(全国新课标理5)已知角的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线上,则=(A )(B ) (C ) (D )【答案】B8.(全国大纲理5)设函数,将的图像向右平移个单位长度后,所得的图像与原图像重合,则的最小值等于A .B .C .D .【答案】C9.(湖北理3)已知函数,若,则x 的取值范围为A .B .C .D .【答案】B10.(辽宁理4)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,asinAsinB+bcos2A=,则32232sin 2xy x =-θ2y x =cos2θ45-35-3545()cos (0)f x x ωω=>()y f x =3πω13369()cos ,f x x x x R=-∈()1f x ≥|,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭|22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭5{|,}66x k x k k Z ππππ+≤≤+∈5{|22,}66x k x k k Z ππππ+≤≤+∈a 2=a b(A )(B)(C(D【答案】D11.(辽宁理7)设sin ,则 (A )(B )(C ) (D )【答案】A12.(福建理3)若tan =3,则的值等于A .2B .3C .4D .6【答案】D13.(全国新课标理11)设函数的最小正周期为,且则(A )在单调递减 (B )在单调递减 (C )在单调递增 (D )在单调递增 【答案】A14.(安徽理9)已知函数,其中为实数,若对恒成立,且,则的单调递增区间是(A ) (B )(C ) (D )【答案】C二、填空题15.(上海理6)在相距2千米的.两点处测量目标,若,则.两点之间的距离是 千米。
高考文科试题解析分类汇编(三角函数)

2012高考文科试题解析分类汇编:三角函数一、选择题1.【2012高考安徽文7】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象(A ) 向左平移1个单位 (B ) 向右平移1个单位(C ) 向左平移 12个单位(D ) 向右平移12个单位2.【2012高考新课标文9】已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=(A )π4 (B )π3 (C )π2 (D 3π4【命题意图】本题主要考查三角函数的图像与性质,是中档题.【解析】由题设知,πω=544ππ-,∴ω=1,∴4πϕ+=2k ππ+(k Z ∈), ∴ϕ=4k ππ+(k Z ∈),∵0ϕπ<<,∴ϕ=4π,故选A.4.【2012高考全国文3】若函数()s i n ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ(A )2π (B )32π(C )23π(D )35π【命题意图】本试题主要考查了偶函数的概念与三角函数图像性质,。
【解析】由[]()sin(0,2)3x f x ϕϕπ+=∈为偶函数可知,y 轴是函数()f x 图像的对称轴,而三角函数的对称轴是在该函数取得最值时取得,故3(0)sin 13()3322f k k k Z ϕϕπππϕπ==±⇒=+⇒=+∈,而[]0,2ϕπ∈,故0k=时,32πϕ=,故选答案C 。
5.【2012高考全国文4】已知α为第二象限角,3sin 5α=,则sin 2α=(A )2524- (B )2512-(C )2512(D )2524【命题意图】本试题主要考查了同角三角函数关系式的运用以及正弦二倍角公式的运用。
【解析】因为α为第二象限角,故cos 0α<,而3sin 5α=,故4co s 1s i n 5α==-,所以24sin 22sin cos 25ααα==-,故选答案A 。
三角函数—高考真题文科数学分项汇编(解析版)

y
f
(x)的图象.
其中所有正确结论的序号是
A.①
B.①③
【答案】B
C.②③
D.①②③
2
【解析】因为 f (x) sin(x ),所以周期T 2 2,故①正确;
3
f ( ) sin( ) sin5 1 1,故②不正确;
2
23
62
将函数 y sin x的图象上所有点向左平移 个单位长度,得到 y sin(x )的图象,
2
D.2
【答案】C
sin x
【解析】 f (x)
tan x 1 tan2 x
cos 1(sin
x sin xcos x 1sin2x,
x) 2
2
cos x
故所求的最小正周期为T 2π π,故选 C. 2
【名师点睛】函数 y Asin(x ) B(A 0, 0)的性质:
(1) ymax=B+A,ymin B A.
对应的函数为
gx.若
g
π4
2
,则
f
3π 8
A.−2
B. 2
C. 2
D.2
【答案】C
【解析】∵ f (x)为奇函数,∴ f (0) Asin 0,=kπ,k Z,k 0, 0;
∵ f x的最小正周期为π,T
2π
π,∴
2,
∴ g(x) Asin 1x Asin x,
2
又 g(π) 2,∴ A 2,
f x max
3
2
5 2
4,故选
B.
【名师点睛】该题考查的是有关化简三角函数解析式,并且通过余弦型函数的相关性质得到函数的性质, 在解题的过程中,要注意应用余弦倍角公式将式子降次升角,得到最简结果.
各省高考文科数学试题分类3三角函数

【答案】B 10.(2013 年普通高等学校招生统一考试重庆数学(理)试题(含答案))
4 cos 500 tan 400
A. 2
【答案】C
B. 2 3 2
()
C. 3
11.(2013 年高考湖南卷(理))在锐角中 ABC ,角 A, B 所对的边长分别为 a,b .若
2a sin B 3b,则角A等于
(B) 4
(C)0
5 .(2013 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))在 ABC ,内角
A, B,C 所对的边长分别为 a,b, c. a sin B cos C c sin B cos A 1 b, 且 a b ,则 B 2
A.
6
【答案】A
B.
所示,则, 的值分别是( )
(A) 2, 3
【答案】A
(B) 2, 6
(C) 4, 6
9 .(2013 年上海市春季高考数学试卷(含答案))既是偶函数又在区间 (0、 ) 上单调递减的
函数是( )
(A) y sin x (B) y cos x (C) y sin 2x (D) y cos 2x
b cosC c cos B a sin A , 则△ABC 的形状为
(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定
【答案】B
3
.(2013 年普通高等学校招生统一考试天津数学(理)试题(含答案))在△ABC 中,
ABC , AB 2, BC 3, 则 sinBAC =
4
(A) 10 (B) 10 (C) 3 10 (D) 5
【答案】C
2017--2019全国高考三角函数分类汇编(文科数学)

2017--2019全国高考三角函数分类汇编(文科数学)一、三角函数的定义【2018全国1,文11】已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1,A a ,()2,B b ,且2cos 23α=,则a b -=( )A .15B .55C .255D .1二、同角三角函数的基本关系【2016全国3,文6】若1tan 3θ=,则cos2θ=( )A. 45- B. 15- C.15 D.45【2017全国3,文4】已知4sin cos 3αα-=,则sin 2α=( )A. 79- B.29- C. 29 D.79【2016全国1,文14】已知θ是第四象限角,且3sin()45πθ+=,则tan()4πθ-= .三、同角三角函数的基本关系【2018全国1,文7】tan 255︒=( )A.23--B.23-+C.23-D.23+四、图像的性质【2017全国2,文3】函数()sin(2)3f x x π=+的最小正周期为( )A. 4πB. 2πC. πD. 2π【2019全国2,文8】若x 1=4π,x 2=43π是函数f(x)=sin x ω(ω>0)两个相邻的极值点,则ω=A .2B .32C .1D .12【2016全国2,文3】函数sin()y A x ωϕ=+的部分图象如图所示,则( )A.2sin(2)6y x π=- B. 2sin(2)3y x π=- C. 2sin(2)6y x π=+ D. 2sin(2)3y x π=+四、图像的伸缩变换【2016全国1,文6】若将函数 2sin(2)6y x π=+的图象向右平移的图像向右平移14个周期后,所得图像对应的函数为( )A.2sin(2)4y x π=+ B.2sin(2)3y x π=+C.2sin(2)4y x π=- D.2sin(2)3y x π=-【2016全国3,文14】函数sin cos y x x =-的图像可由函数2sin y x =的图像至少向右平移______个单位长度得到.五、三角恒等变换【2018全国3,文4】若1sin 3α=,则cos2α=( )A .89B .79C .79-D .89-【2018全国2,文10】若()cos sin f x x x =-在[]0,a 是减函数,则a 的最大值为( )A .π4B .π2C .3π4D .π【2017全国1,文15】已知(0,),tan 22παα∈=,则cos()4πα-= .【2017全国2,文13】函数()2cos sin f x x x =+的最大值为 【2018全国3,文6】函数()2tan 1tan xf x x =+的最小正周期为( )A .4πB .2πC .πD .2π【2017全国3,文6】函数1()sin()cos()536f x x x ππ=++-的最大值为( )A.65B.1C.35D.15【2019全国2,文11】已知a ∈(0,π2),2sin2α=cos2α+1,则sinα=A .15B C D 六、与二次函数相关【2018全国1,文8】已知函数()222cos sin 2f x x x =-+,则( )A .()f x 的最小正周期为π,最大值为3B .()f x 的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为4 【2019全国1,文15】函数3()sin(2)3cos 2f x x x π=+-的最小值为___________. 【2016全国2,文11】函数π()cos 26cos()2f x x x =+-的最大值为( )A. 4B. 5C. 6D. 【2019全国3,文5】函数()2sin sin 2f x x x =-在[0,2]π的零点个数为()A. 2B. 3C. 4D. 5。
高考文科数学真题汇编三角函数高考题学生版

x 1, x2
1 / 16
则 f 29 f 41 _______ 4 6
8、(2015 年广东文)已知 tan 2 .
1
求
tan
4
的值;
2
求
sin 2
sin 2 sin cos
cos
2
1
的值.
3、三角函数的图象和性质
16.(2013 沪春招)既是偶函数又在区间 (0, ) 上单调递减的函数是( )
(A) y sin x (B) y cos x (C) y sin 2x (D) y cos 2x
17.(2013 四川)函数 f(x)=2sin(ωx+φ)(ω>0,-2π<φ<π2)的部分图象如图所示,则 ω,φ 的值分别是(
(2)求
f
x 在区间
2
,
12
上的最大值和最小值.
y y0
O
x0
x
43.(2012
广东)已知函数
f
x
2 cos x
6
(其中
0
x
R
)的最小正周期为10
.
(Ⅰ)求
的值;(Ⅱ)设
、
0,
2
,
f
5
(A) 2 , π 3 12
(B) 2 , 11π
3
12
(C) 1 , 11π
3
24
(D) 1 , 7π 3 24
32.(2014 新标 1 文) 在函数① y cos| 2x |,② y | cosx | ,③ y cos(2x ) ,④ y tan(2x ) 中,
高考文科数学试题分类汇编三角函数

三角函数一、选择题1.【2012高考安徽】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象 (A ) 向左平移1个单位 (B ) 向右平移1个单位 (C ) 向左平移 12个单位 (D ) 向右平移12个单位2.【2012高考新课标】已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=3.【2012高考山东】函数2sin (09)63x y x ππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为(A)2 (B)0 (C)-1 (D)1--4.【2012高考全国】若函数()sin ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ (A )2π (B )32π(C )23π (D )35π5.【2012高考全国】已知α为第二象限角,3sin 5α=,则sin 2α= (A )2524- (B )2512- (C )2512 (D )25246.【2012高考重庆】sin 47sin17cos30cos17-(A )-B )12-(C )12 (D 7.【2012高考浙江】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是8.【2012高考上海】在△ABC 中,若222sin sin sin A B C +<,则△ABC 的形状是( ) A 、钝角三角形 B 、直角三角形 C 、锐角三角形 D 、不能确定 9.【2012高考四川】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )DB(1310 B 10 C 5 D 510.【2012高考辽宁】已知sin cos 2αα-=,α∈(0,π),则sin 2α= (A) -1 (B) 22- (C) 22 (D) 111.【2012高考江西】若sin cos 1sin cos 2αααα+=-,则tan2α=A. -34B. 34C. -43D. 4312.【2012高考江西】已知2()sin ()4f x x π=+若a =f (lg5),1(lg )5b f =则A.a+b=0B.a-b=0C.a+b=1D.a-b=113.【2012高考湖南】 在△ABC 中,7,BC=2,B =60°,则BC 边上的高等于A 3 33 36+ 339+14.【2012高考湖北】设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若三边的长为连续的三个正整数,且A >B >C ,3b=20acosA ,则sinA ∶sinB ∶sinC 为 A.4∶3∶2 B.5∶6∶7 C.5∶4∶3 D.6∶5∶415.【2012高考广东】在△ABC 中,若60A ∠=,45B ∠=,BC =AC =A. B. C. D.16.【2102高考福建】函数f(x)=sin(x-4π)的图像的一条对称轴是 A.x=4π B.x=2π C.x=-4π D.x=-2π17.【2012高考天津】将函数f(x)=sin x ω(其中ω>0)的图像向右平移4π个单位长度,所得图像经过点(34π,0),则ω的最小值是(A )13(B )1 C )53(D )2二、填空题18.【2012高考江苏】(5分)设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为 ▲ .19.【2102高考北京】在△ABC 中,若a =3,b=3,∠A=3π,则∠C 的大小为_________。
最新全国各地高考文科数学试题分类汇编3:三角函数
全国各地(高|考)文科数学试题分类汇编3:三角函数一、选择题1 . ((高|考)大纲卷 (文 ) )a 是第二象限角,5sin ,cos 13a a ==则 ( )A .1213-B .513-C .513 D .1213【答案】A2 . ((高|考)课标Ⅰ卷 (文 ) )函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为【答案】C ;3 . ((高|考)四川卷 (文 ) )函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的局部图象如下图,那么,ωϕ的值分别是( )A .2,3π-B .2,6π-C .4,6π-D .4,3π【答案】A4 . ((高|考)湖南 (文 ) )在锐角∆ABC 中,角A,B 所对的边长分别为a,b. 假设2sinB =3b,那么角A 等于______ ( )A .3πB .4πC .6πD .12π【答案】A5 . ((高|考)福建卷 (文 ) )将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,假设)(),(x g x f 的图象都经过点)23,0(P ,那么ϕ的值可以是 ( ) A .35π B .65π C .2πD .6π【答案】B6 . ((高|考)陕西卷 (文 ) )设△ABC 的内角A , B , C 所对的边分别为a , b , c , 假设cos cos sin b C c B a A +=,那么△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定【答案】A7 . ((高|考)辽宁卷 (文 ) )在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=,a b B >∠=且则( )A .6πB .3πC .23πD .56π【答案】A8 . ((高|考)课标Ⅱ卷 (文 ) )△ABC 的内角A,B,C 的对边分别为a,b,c,b =2,B =,C =,那么△ABC 的面积为 ( )A .2 +2B .+1C .2-2D .-1【答案】B9 . ((高|考)江西卷 (文 ) )3sincos 23αα==若,则 ( )A .23-B .13-C .13 D .23【答案】C10. ((高|考)山东卷 (文 ) )ABC ∆的内角A B C 、、的对边分别是a b c 、、,假设2B A =,1a =,3b =,那么c = ( )A .23B .2C .2D .1【答案】B11. ((高|考)课标Ⅱ卷 (文 ) )sin2α =,那么cos 2(α +) =( )A .B .C .D .【答案】A12. ((高|考)广东卷 (文 ) )51sin()25πα+=,那么cos α= ( )A .25-B .15- C .15D .25【答案】C13. ((高|考)湖北卷 (文 ) )将函数3cos sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,那么m 的最|小值是 ( )A .π12B .π6C .π3D .5π6【答案】B14. ((高|考)大纲卷 (文 ) )假设函数()()sin0=y x ωϕωω=+>的部分图像如图,则( )A .5B .4C .3D .2【答案】B15. ((高|考)天津卷 (文 ) )函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最|小值是( )A .1-B .22-C .22D .0【答案】B16. ((高|考)安徽 (文 ) )设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,假设2,3sin 5sin b c a A B +==,那么角C = ( )A .3πB .23πC .34π D .56π 【答案】B17. ((高|考)课标Ⅰ卷 (文 ) )锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,那么b =( )A .10B .9C .8D .5【答案】D18. ((高|考)浙江卷 (文 ) )函数f(x) =sin xcos x +32cos 2x 的最|小正周期和振幅分别是 ( ) A .π,1 B .π,2 C .2π,1D .2π,2【答案】A19. ((高|考)北京卷 (文 ) )在△ABC 中,3,5a b ==,1sin 3A =,那么sin B = ( )A .15B .59C .53D .1【答案】B20. ((高|考)山东卷 (文 ) )函数x x x y sin cos +=的图象大致为【答案】D 二、填空题21. ((高|考)四川卷 (文 ) )设sin 2sin αα=-,(,)2παπ∈,那么tan 2α的值是________.【答案】322. ((高|考)课标Ⅱ卷 (文 ) )函数cos(2)()y x ϕπϕπ=+-≤<的图像向右平移2π个单位后,与函数sin(2)3y x π=+的图像重合,那么||ϕ=___________.[来源:学&科&网]【答案】56π23. (上海(高|考)数学试题 (文科 ) )ABC ∆的内角A 、B 、C 所对的边分别是a ,b ,c .假设2220a ab b c ++-=,那么角C 的大小是________(结果用反三角函数值表示).[来源:学科网]【答案】23π24. (上海(高|考)数学试题 (文科 ) )假设1cos cos sin sin3x y x y +=,那么()cos 22x y -=________.【答案】79-25. ((高|考)课标Ⅰ卷 (文 ) )设当x θ=时,函数()sin 2cos f x x x =-取得最|大值,那么cos θ=______.【答案】255-; 26. ((高|考)江西卷 (文 ) )设f(x) =sin3x +cos3x,假设对任意实数x 都有|f(x)|≤a,那么实数a 的取值范围是_____._____ 【答案】2a ≥三、解答题27. ((高|考)大纲卷 (文 ) )设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=.(I)求B(II)假设31sin sin 4A C -=,求C . 【答案】(Ⅰ)因为()()a b c a b c ac ++-+=,所以222a cb ac +-=-.由余弦定理得,2221cos 22a cb B ac +-==-, 因此,0120B =.(Ⅱ)由(Ⅰ)知060A C +=,所以cos()cos cos sin sin A C A C A C -=+cos cos sin sin 2sin sin A C A C A C =-+cos()2sin sin A C A C =++ 131224-=+⨯ 32=, 故030A C -=或030A C -=-, 因此,015C =或045C =.28. ((高|考)湖南 (文 ) )函数f(x) =(1) 求2()3f π的值; (2) 求使 1()4f x <成立的x 的取值集合【答案】解: (1) 41)212cos 232(sin 21)3sin sin 3cos(cos cos )(+⋅+⋅=⋅+⋅⋅=x x x x x x f ππ41)32(.414123sin 21)32(41)62sin(21-==-=+=⇒++=ππππf f x 所以. (2)由(1)知, [来源:学|科|网Z|X|X|K])2,2()62(0)62sin(4141)62sin(21)(f ππππππk k x x x x -∈+⇒<+⇒<++=.),12,127(.),12,127(Z k k k Z k k k x ∈--∈--∈⇒ππππππππ所以不等式的解集是: 29. ((高|考)天津卷 (文 ) )在△ABC 中, 内角A , B , C 所对的边分别是a , b , c . sin 3sin b A c B =, a = 3,2cos 3B =. (Ⅰ) 求b 的值;(Ⅱ) 求sin 23B π⎛⎫- ⎪⎝⎭的值.【答案】30. ((高|考)广东卷 (文 ) )函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 假设33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【答案】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-,1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭. [来源:学科网]31. ((高|考)山东卷 (文 ) )设函数2()sin cos (0)f x x x x ωωωω=-->,且()y f x =的图象的一个对称中|心到最|近的对称轴的距离为4π, (Ⅰ)求ω的值 (Ⅱ)求()f x 在区间3[,]2ππ上的最|大值和最|小值 【答案】32. ((高|考)浙江卷 (文 ) )在锐角△ABC 中,内角A,B,C 的对边分别为a,b,c,且2asinB =3b . (Ⅰ)求角A 的大小;(Ⅱ) 假设a =6,b +c =8,求△ABC 的面积.【答案】解:(Ⅰ)由得到:2sin sin 3sin A B B =,且3(0,)sin 0sin 22B B A π∈∴≠∴=,且(0,)23A A ππ∈∴=;(Ⅱ)由(1)知1cos 2A =,由得到: 222128362()3366433623b c bc b c bc bc bc =+-⨯⇒+-=⇒-=⇒=,所以1283732323ABCS =⨯⨯=; 33. ((高|考)福建卷 (文 ) )如图,在等腰直角三角形OPQ ∆中,90OPQ ∠=,22OP =,点M 在线段PQ上.(1)假设3OM =,求PM 的长;(2)假设点N 在线段MQ 上,且30MON ∠=,问:当POM ∠取何值时,OMN ∆的面积最|小?并求出面积的最|小值.【答案】解:(Ⅰ)在OMP ∆中,45OPM∠=︒,5OM =22OP =,由余弦定理得,2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒, 得2430MP MP -+=,解得1MP =或3MP =.(Ⅱ)设POM α∠=,060α︒≤≤︒, 在OMP ∆中,由正弦定理,得sin sin OM OPOPM OMP=∠∠, 所以()sin 45sin 45OP OM α︒=︒+,同理()sin 45sin 75OP ON α︒=︒+故1sin 2OMN S OM ON MON ∆=⨯⨯⨯∠ ()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+ ()()1sin 45sin 4530αα=︒+︒++︒()()()131sin 45sin 45cos 4522ααα=⎡⎤︒+︒++︒+⎢⎥⎣⎦()()()2131sin 45sin 45cos 4522ααα=︒++︒+︒+()()1311cos 902sin 90244αα=-︒++︒+⎡⎤⎣⎦1331sin 2cos 2444αα=++()131sin 23042α=++︒因为060α︒≤≤︒,30230150α︒≤+︒≤︒,所以当30α=︒时,()sin 230α+︒的最|大值为1,此时OMN ∆30POM ∠=︒时,OMN ∆的面积的最|小值为843-.34. ((高|考)陕西卷 (文 ) )向量1(cos ,),(3sin ,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b .(Ⅰ) 求f (x)的最|小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最|大值和最|小值.【答案】(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最|小正周期ππ==22T . [来源:学 .科 .网Z .X .X .K] 所以),62sin()(π-=x x f 最|小正周期为π. [来源:学,科,网Z,X,X,K](Ⅱ) 上的图像知,在,由标准函数时,当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈. ]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f .所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最|大值和最|小值分别为21,1-.35. ((高|考)重庆卷 (文 ) )(本小题总分值13分,(Ⅰ)小问4分,(Ⅱ)小问9分)在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,且2223a b c ab =++. (Ⅰ)求A ; (Ⅱ)设3a =,S 为△ABC 的面积,求3cos cos S B C +的最|大值,并指出此时B 的值.【答案】36. ((高|考)四川卷 (文 ) )在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A c ---+=-.(Ⅰ)求sin A 的值;(Ⅱ)假设42a =,5b =,求向量BA 在BC 方向上的投影.【答案】解:(Ⅰ)由3cos()cos sin()sin()5A B B A B A c ---+=-得 53sin )sin(cos )cos(-=---B B A B B A ,那么 53)cos(-=+-B B A ,即 53cos -=A又π<<A 0,那么 54sin =A(Ⅱ)由正弦定理,有 BbA a sin sin =,所以22sin sin ==a A b B , 由题知b a >,那么 B A >,故4π=B .根据余弦定理,有 )53(525)24(222-⨯⨯-+=c c , 解得 1=c 或 7-=c (负值舍去), 向量BA 在BC 方向上的投影为=B BA cos 22[来源:学科网] 37. ((高|考)江西卷 (文 ) )在△ABC 中,角A,B,C 的对边分别为a,b,c,sinAsinB +sinBsinC +cos2B =1.[来源:学,科,网Z,X,X,K](1)求证:a,b,c 成等差数列;(2) 假设C =23π,求ab的值. 【答案】解:(1)由得sinAsinB +sinBsinC +1 -2sin 2B =1.故sinAsinB +sinBsinC =2sin 2B因为sinB 不为0,所以sinA +sinC =2sinB 再由正弦定理得a +c =2b,所以a,b,c 成等差数列 (2)由余弦定理知2222cos c a b ac C =+-得2222(2)2cos3b a a b ac π-=+-化简得35a b = 38. ((高|考)湖北卷 (文 ) )在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c . cos23cos()1A B C -+=.(Ⅰ)求角A 的大小; (Ⅱ)假设△ABC 的面积53S =,5b =,求sin sin B C 的值.【答案】(Ⅰ)由cos23cos()1A B C -+=,得22cos 3cos 20A A +-=,即(2cos 1)(cos 2)0A A -+=,解得1cos 2A = 或cos 2A =-(舍去).因为0πA <<,所以π3A =. (Ⅱ)由1133sin 53,2224S bc A bc bc ==⋅==得20bc =. 又5b =,知4c =.由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故21a =.又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.39. ((高|考)安徽 (文 ) )设函数()sin sin()3f x x x π=++.(Ⅰ)求()f x 的最|小值,并求使()f x 取得最|小值的x 的集合;(Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化得到.【答案】解:(1)3sincos 3cossin sin )(ππx x x x f ++=x x x x x cos 23sin 23cos 23sin 21sin +=++=)6sin(3)6sin()23()23(22ππ+=++=x x当1)6sin(-=+πx 时,3)(min -=x f ,此时)(,234,2236Z k k x k x ∈+=∴+=+πππππ所以,)(x f 的最|小值为3-,此时x 的集合},234|{Z k k x x ∈+=ππ.(2)x y sin =横坐标不变,纵坐标变为原来的3倍,得x y sin 3=;然后x y sin 3=向左平移6π个单位,得)6sin(3)(π+=x x f 40. ((高|考)北京卷 (文 ) )函数21(2cos 1)sin 2cos 42f x x x x =-+().(I)求f x ()的最|小正周期及最|大值;(II)假设(,)2παπ∈,且2f α=(),求α的值. 【答案】解:(I)因为21(2cos 1)sin 2cos 42f x x x x =-+() =1cos 2sin 2cos 42x x x +=1(sin 4cos 4)2x x + =)24x π+,所以()f x 的最|小正周期为2π,最|大值为2.(II)因为2f α=()所以sin(4)14πα+=. 因为(,)2παπ∈, [来源:学#科#网Z#X#X#K] 所以9174(,)444πππα+∈,所以5442ππα+=,故916πα=. 41. (上海(高|考)数学试题 (文科 ) )此题共有2个小题.第1小题总分值6分,第2小题总分值8分.函数()2sin()f x x ω=,其中常数0ω>. (1)令1ω=,判断函数()()()2F x f x f x π=++的奇偶性并说明理由;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再往上平移1个单位,得到函数()y g x =a R ∈,求()y g x =在区间[,10]a a π+上零点个数的所有可能值.【答案】法一:解:(1)()2sin 2sin()2sin 2cos )24F x x x x x x ππ=++=+=+ ()F x 是非奇函数非偶函数.∵()0,()44F F ππ-==∴()(),()()4444F F F F ππππ-≠-≠-∴函数()()()2F x f x f x π=++是既不是奇函数也不是偶函数.(2)2ω=时,()2sin 2f x x =,()2sin 2()12sin(2)163g x x x ππ=++=++,其最|小正周期T π=由2sin(2)103x π++=,得1sin(2)32x π+=-, [来源:学,科,网] ∴2(1),36k x k k Z πππ+=--⋅∈,即(1),2126k k x k Z πππ=--⋅-∈ 区间[],10a a π+的长度为10个周期,假设零点不在区间的端点,那么每个周期有2个零点;假设零点在区间的端点,那么仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点; 故当(1),2126k k a k Z πππ=--⋅-∈时,21个,否那么20个. 法二:42. ((高|考)辽宁卷 (文 ) )设向量)(),sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)假设.a b x =求的值; (II)设函数()(),.f x a b f x =求的最大值【答案】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考文科数学试题分类汇编3:三角函数一、选择题1 .(2013年高考大纲卷(文))已知a 是第二象限角,5sin ,cos 13a a ==则 ( )A .1213-B .513-C .513D .1213【答案】A2 .(2013年高考课标Ⅰ卷(文))函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为【答案】C ;3 .(2013年高考四川卷(文))函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )A .2,3π-B .2,6π-C .4,6π-D .4,3π【答案】A4 .(2013年高考湖南(文))在锐角∆ABC 中,角A,B 所对的边长分别为a,b. 若2sinB=3b,则角A 等于______( )A .3πB .4πC .6πD .12π【答案】A5 .(2013年高考福建卷(文))将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是 ( )A .35π B .65π C .2πD .6π【答案】B6 .(2013年高考陕西卷(文))设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=,则△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定【答案】A7 .(2013年高考辽宁卷(文))在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=,a b B >∠=且则( )A .6πB .3πC .23πD .56π【答案】A8 .(2013年高考课标Ⅱ卷(文))△ABC 的内角A,B,C 的对边分别为a,b,c,已知b=2,B=,C=,则△ABC 的面积为 ( )A .2+2B .+1C .2-2D .-1【答案】B9 .(2013年高考江西卷(文))sincos 2αα==若 ( )A .23-B .13-C .13 D .23【答案】C10.(2013年高考山东卷(文))ABC ∆的内角A B C 、、的对边分别是a b c 、、,若2B A =,1a =,b =,则c = ( )A .B .2C D .1【答案】B11.(2013年高考课标Ⅱ卷(文))已知sin2α=,则cos 2(α+)=( )A .B .C .D .【答案】A12.(2013年高考广东卷(文))已知51sin()25πα+=,那么cos α= ( )A .25-B .15-C .15D .25【答案】C13.(2013年高考湖北卷(文))将函数sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是 ( )A .π12B .π6C .π3D .5π6【答案】B14.(2013年高考大纲卷(文))若函数()()sin 0=y x ωϕωω=+>的部分图像如图,则 ( )A .5B .4C .3D .2【答案】B15.(2013年高考天津卷(文))函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是( )A .1-B .CD .0【答案】B16.(2013年高考安徽(文))设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2,3sin 5sin b c a A B +==,则角C = ( )A .3πB .23πC .34π D .56π 【答案】B17.(2013年高考课标Ⅰ卷(文))已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,则b =( )A .10B .9C .8D .5【答案】D18.(2013年高考浙江卷(文))函数f(x)=sin xcos x+32cos 2x 的最小正周期和振幅分别是 ( ) A .π,1 B .π,2 C .2π,1D .2π,2【答案】A19.(2013年高考北京卷(文))在△ABC 中,3,5a b ==,1sin 3A =,则sin B = ( )A .15B .59C D .1【答案】B20.(2013年高考山东卷(文))函数x x x y sin cos +=的图象大致为【答案】D 二、填空题21.(2013年高考四川卷(文))设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是________.【答案】322.(2013年高考课标Ⅱ卷(文))函数cos(2)()y x ϕπϕπ=+-≤<的图像向右平移2π个单位后,与函数sin(2)3y x π=+的图像重合,则||ϕ=___________.【答案】56π23.(2013年上海高考数学试题(文科))已知ABC ∆的内角A 、B 、C 所对的边分别是a ,b ,c .若2220a ab b c ++-=,则角C 的大小是________(结果用反三角函数值表示).【答案】23π24.(2013年上海高考数学试题(文科))若1cos cos sin sin3x y x y +=,则()cos 22x y -=________.【答案】79-25.(2013年高考课标Ⅰ卷(文))设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______.【答案】5-;26.(2013年高考江西卷(文))设f(x)=sin3x+cos3x,若对任意实数x 都有|f(x)|≤a,则实数a 的取值范围是_____._____【答案】2a ≥三、解答题27.(2013年高考大纲卷(文))设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=.(I)求B(II)若sin sin A C =,求C . 【答案】(Ⅰ)因为()()a b c a b c ac ++-+=,所以222a cb ac +-=-.由余弦定理得,2221cos 22a cb B ac +-==-, 因此,0120B =.(Ⅱ)由(Ⅰ)知060A C +=,所以cos()cos cos sin sin A C A C A C -=+cos cos sin sin 2sin sin A C A C A C =-+cos()2sin sin A C A C =++11224=+⨯=故030A C -=或030A C -=-, 因此,015C =或045C =.28.(2013年高考湖南(文))已知函数f(x(1) 求2()3f π的值; (2) 求使 1()4f x <成立的x 的取值集合【答案】解: (1) 41)212cos 232(sin 21)3sin sin 3cos(cos cos )(+⋅+⋅=⋅+⋅⋅=x x x x x x f ππ41)32(.414123sin 21)32(41)62sin(21-==-=+=⇒++=ππππf f x 所以. (2)由(1)知,)2,2()62(0)62sin(4141)62sin(21)(f ππππππk k x x x x -∈+⇒<+⇒<++=.),12,127(.),12,127(Z k k k Z k k k x ∈--∈--∈⇒ππππππππ所以不等式的解集是:29.(2013年高考天津卷(文))在△ABC 中, 内角A , B , C 所对的边分别是a , b , c . 已知sin 3sin b A c B =, a= 3, 2cos 3B =. (Ⅰ) 求b 的值;(Ⅱ) 求sin 23B π⎛⎫- ⎪⎝⎭的值.【答案】30.(2013年高考广东卷(文))已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【答案】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-, 1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭. [来源:12999数学网]31.(2013年高考山东卷(文))设函数2()sin cos (0)f x x x x ωωωω=->,且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π,(Ⅰ)求ω的值 (Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值 【答案】32.(2013年高考浙江卷(文))在锐角△ABC 中,内角A,B,C 的对边分别为a,b,c,且2asinB=3b .(Ⅰ)求角A 的大小;(Ⅱ) 若a=6,b+c=8,求△ABC 的面积.【答案】解:(Ⅰ)由已知得到:2sinsin A B B =,且(0,)sin 0sin 22B B A π∈∴≠∴=,且(0,)23A A ππ∈∴=;(Ⅱ)由(1)知1cos 2A =,由已知得到:222128362()3366433623b c bc b c bc bc bc =+-⨯⇒+-=⇒-=⇒=,所以128232ABCS =⨯⨯=33.(2013年高考福建卷(文))如图,在等腰直角三角形OPQ ∆中,90OPQ ∠=,OP =,点M 在线段PQ 上.(1)若OM =,求PM 的长;(2)若点N 在线段MQ 上,且30MON ∠= ,问:当POM ∠取何值时,OMN ∆的面积最小?并求出面积的最小值.【答案】解:(Ⅰ)在OMP ∆中,45OPM∠=︒,OM =OP =,由余弦定理得,2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒, 得2430MP MP -+=,解得1MP =或3MP =.(Ⅱ)设POM α∠=,060α︒≤≤︒, 在OMP ∆中,由正弦定理,得sin sin OM OPOPM OMP=∠∠, 所以()sin 45sin 45OP OM α︒=︒+,同理()sin 45sin 75OP ON α︒=︒+故1sin 2OMN S OM ON MON ∆=⨯⨯⨯∠ ()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+ ()()1sin 45sin 4530αα=︒+︒++︒=====因为060α︒≤≤︒,30230150α︒≤+︒≤︒,所以当30α=︒时,()sin 230α+︒的最大值为1,此时OMN ∆的面积取到最小值.即230POM ∠=︒时,OMN ∆的面积的最小值为8-.34.(2013年高考陕西卷(文))已知向量1(cos ,),,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b .(Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最小正周期ππ==22T . 所以),62sin()(π-=x x f 最小正周期为π.(Ⅱ) 上的图像知,在,由标准函数时,当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈. ]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f .所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-.35.(2013年高考重庆卷(文))(本小题满分13分,(Ⅰ)小问4分,(Ⅱ)小问9分)在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,且222a b c =+. (Ⅰ)求A ;(Ⅱ)设a =S 为△ABC 的面积,求3cos cos S B C +的最大值,并指出此时B 的值.【答案】36.(2013年高考四川卷(文))在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A c ---+=-.(Ⅰ)求sin A 的值;(Ⅱ)若a =5b =,求向量BA 在BC方向上的投影.【答案】解:(Ⅰ)由3cos()cos sin()sin()5A B B A B A c ---+=- 得53sin )sin(cos )cos(-=---B B A B B A ,则 53)cos(-=+-B B A ,即 53cos -=A又π<<A 0,则 54sin =A(Ⅱ)由正弦定理,有 Bb A a sin sin =,所以22sin sin ==a A b B , 由题知b a >,则 B A >,故4π=B .根据余弦定理,有 )53(525)24(222-⨯⨯-+=c c ,解得 1=c 或 7-=c (负值舍去),向量BA 在BC =B 22[来源:12999数学网]37.(2013年高考江西卷(文))在△ABC 中,角A,B,C 的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.(1)求证:a,b,c 成等差数列;(2) 若C=23π,求ab的值. 【答案】解:(1)由已知得sinAsinB+sinBsinC+1-2sin 2B=1.故sinAsinB+sinBsinC=2sin 2B因为sinB 不为0,所以sinA+sinC=2sinB 再由正弦定理得a+c=2b,所以a,b,c 成等差数列 (2)由余弦定理知2222cos c a b ac C =+-得2222(2)2cos3b a a b ac π-=+-化简得35a b = 38.(2013年高考湖北卷(文))在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c . 已知c o s 23c o s ()A B C -+=.(Ⅰ)求角A 的大小; (Ⅱ)若△ABC 的面积S =5b =,求sin sin B C 的值.【答案】(Ⅰ)由cos23cos()1A B C -+=,得22cos 3cos 20A A +-=,即(2cos 1)(cos 2)0A A -+=,解得1cos 2A = 或cos 2A =-(舍去). 因为0πA <<,所以π3A =.(Ⅱ)由11sin 22S bc A bc ====得20bc =. 又5b =,知4c =.由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故a =. 又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.39.(2013年高考安徽(文))设函数()sin sin()3f x x x π=++.(Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合;(Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化得到.【答案】解:(1)3sincos 3cossin sin )(ππx x x x f ++=x x x x x cos 23sin 23cos 23sin 21sin +=++=)6sin(3)6sin()23()23(22ππ+=++=x x当1)6sin(-=+πx 时,3)(min -=x f ,此时)(,234,2236Z k k x k x ∈+=∴+=+πππππ所以,)(x f 的最小值为3-,此时x 的集合},234|{Z k k x x ∈+=ππ.(2)x y sin =横坐标不变,纵坐标变为原来的3倍,得x y sin 3=; 然后x y sin 3=向左平移6π个单位,得)6sin(3)(π+=x x f 40.(2013年高考北京卷(文))已知函数21(2cos 1)sin 2cos 42f x x x x =-+().(I)求f x ()的最小正周期及最大值;(II)若(,)2παπ∈,且2f α=(),求α的值. 【答案】解:(I)因为21(2cos 1)sin 2cos 42f x x x x =-+()=1cos 2sin 2cos 42x x x +=1(sin 4cos 4)2x x +=)24x π+,所以()f x 的最小正周期为2π,最大值为2.(II)因为2f α=(),所以sin(4)14πα+=. 因为(,)2παπ∈, 所以9174(,)444πππα+∈,所以5442ππα+=,故916πα=. 41.(2013年上海高考数学试题(文科))本题共有2个小题.第1小题满分6分,第2小题满分8分.已知函数()2sin()f x x ω=,其中常数0ω>. (1)令1ω=,判断函数()()()2F x f x f x π=++的奇偶性并说明理由;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再往上平移1个单位,得到函数()y g x =的图像.对任意的a R ∈,求()y g x =在区间[,10]a a π+上零点个数的所有可能值.【答案】法一:解:(1)()2sin 2sin()2sin 2cos )24F x x x x x x ππ=++=+=+ ()F x 是非奇函数非偶函数.∵()0,()44F F ππ-==∴()(),()()4444F F F F ππππ-≠-≠-∴函数()()()2F x f x f x π=++是既不是奇函数也不是偶函数.(2)2ω=时,()2sin 2f x x =,()2sin 2()12sin(2)163g x x x ππ=++=++,其最小正周期T π=由2sin(2)103x π++=,得1sin(2)32x π+=-, ∴2(1),36k x k k Z πππ+=--⋅∈,即(1),2126k k x k Z πππ=--⋅-∈区间[],10a a π+的长度为10个周期,若零点不在区间的端点,则每个周期有2个零点;若零点在区间的端点,则仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点; 故当(1),2126k k a k Z πππ=--⋅-∈时,21个,否则20个. 法二:42.(2013年高考辽宁卷(文))设向量)(),sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)若.a b x =求的值; (II)设函数()(),.f x a b f x =求的最大值 【答案】。
