(完整)高考文科数学试题分类汇编复数,推荐文档.doc
(完整word版)高中数学(文科)复数练习题

高中数学《复数》复习作业出题:储鹏1. 设复数z a bi(a,b R),则z为纯虚数的必要不充分条件是___________________________ 。
【答案】a=02a 7a 6 22. 已知复数z ——2 ------------ (a 5a 6)i(a R),那么当a= ________________ 时,z是实数;a 1当a __________________ 时,z 是虚数;当a= ____________ 时,z是纯虚数。
【答案】a 6 a (, 1) ( 1,1) (1,6) (6, ) a23.已知x y2 6 (x y 2)i,则实数x y“宀x 1 、2亠x 1 .2【答案】或y 1 .2 y 1 24. 若复数a满足a 1 2ai 4 4i ,则复数a= _____________________ 。
【答案】1+2i2 25. 已知a R,则复数z (a2 2a 2) (6a a2 10)i必位于复平面的第__________________________ 象限。
【答案】第四6. 复数z i i2在复平面对应的点在第________________ 象限。
【答案】第二2 3 47. 设i是虚数单位,计算i i i i __________________ .【答案】08.已知向量OZ1对应的复数是5 4i,向量OZ2对应的复数是 5 4i,则0乙+0Z2对应的复数是【答案】0。
R)满足条件|z 4i| |z 2 |,则2x4y的最小值9.已知复数z x yi(x, y是。
【答案】4・.、210.计算:(5 i) (3 i) 5i |(3 2i) (4 i)|i 已知z 11 2i,则1 2i z等于3 i11. 复数z ----------- 的共轭复数是。
1 2i【答案】1 i212. 如果复数(m i)(1 mi)是实数,则实数 m __________________【答案】复数(m 2 i )(1 mi) =(m 2— m)+(1+m 3)i 是实数,•. 1+m 3=0, m= — 1xv 513.设x, v 为实数,且,则x v1 i 1 2i 1 3i【答案】丄丄0£卫v(1 2i)(X y (仝引)二1 i 1 2y 25 25 25而55(13i)1 3i101 3. i2 2所以2 土1且仝勺 2 2 53,解得 x =— 1, y = 5,所以x + y = 4。
(完整word版)人教版最新高考数学复数习题及答案Word版

咼考复习试卷(附参考答案)、选择题(每小题只有一个选项是正确的,每小题5分,共100分,在每小题给出的四个选项中,只有一项是符合题目 )2 土 i6. (2013北京东城3月)若将复数―土"表示为a + bi (a , b € R , i 是虚数单位C . 2答案:A2 土 i 解析: 千 =1— 2i ,把它表示为a + bi(a , b € R ,7. (2013北京西城4月)设i 是虚数单位,复数 z =tan45 — i s in60 ;则A.;— 3iB.4 — .3iC.4+ 3iD.4土 ,3i答案:B 解析:z = tan45 —is in 60 = 1 —当,z 2 = 4-德i ,故选 B.8. (2013黄冈中学一模)过原点和.3- i 在复平面内对应的直线的倾斜角为nn6 62 5 C. c n D. n 363 一 i(2013 山东)复数 等于I — i B . 1 — 2i 1 + 2iC . 2 + iA . 答案:C解析:汙=(3一结土- 4^ = 2 土 i.故选1 — i (1 — i)(1 土 i) 23 土 2i 3— 2i2. (2013宁夏、海南)复数 ― =2 — 3i 2 土 3iC .— 2iC.B . 2 D 3+ 2i 3— 2i (3 土 2i)(2 土 3i) (3 — 2i)(2 — 3i) 13i— 13i ..〜, c / c i 土 i 2i. 2— 3i 2+ 3i (2 — 3i)(2 土 3i) (2 — 3i)(2 土 3i) 1313z 土 23 . (2013陕西)已知z 是纯虚数,1—7是实数,那么z 等于 C . — i A . 0 答案: D . 2i 解析:A . 2i 答案:D解析:由题意得z = ai.(a € R 且0). .z ^2 (2 + ai)(1 + i) 2 — a + (a 土2)iD . - 2i1 — i (1 — i )(1 土 i ) 2则 a + 2 = 0, ••• a = — 2.有 z = — 2i ,故选 D.4. (2013武汉市高三年级 2月调研考试)若f (x ) = x 3 — x 2+ x — 1,则f (i )= A . 2i B . 0C . — 2iD . — 2答案:B解析:依题意,f (i ) = i 3— i 2+ i —1 = — i + 1 + i — 1 = 0,选择 B.2— i 4月)复数z = 1土j (i 是虚数单位)在复平面内对应的点位于 B .第二象限 D .第四象限5. (2013北京朝阳 A .第一象限C .第三象限 答案:D2 — i 1 解析:z = 1土j 3.2i , 它对应的点在第四象限,故选D.要求的。
高考数学复数习题及答案doc

一、复数选择题1.已知复数2z i =-,若i 为虚数单位,则1i z +=( ) A .3155i + B .1355i + C .113i + D .13i + 2.若()211z i =-,21z i =+,则12z z 等于( ) A .1i + B .1i -+ C .1i - D .1i --3.已知复数()123z i i +=- (其中i 是虚数单位),则z 在复平面内对应点在( ) A .第一象限 B .第二象限C .第三象限D .第四象限 4.已知复数z 满足()311z i i +=-,则复数z 对应的点在( )上A .直线12y x =-B .直线12y x =C .直线12x =-D .直线12y 5.设()2211z i i =+++,则||z =( ) AB .1C .2 D6.若复数z 满足()322i z i i -+=+,则复数z 的虚部为( ) A .35 B .35i - C .35 D .35i 7.若(1)2z i i -=,则在复平面内z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 8.设复数2i 1i z =+,则复数z 的共轭复数z 在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限9.设复数z 满足方程4z z z z ⋅+⋅=,其中z 为复数z 的共轭复数,若z,则z 为( )A .1 BC .2D .410.复数z 满足22z z i +=,则z 在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限11.复数z 对应的向量OZ 与(3,4)a =共线,对应的点在第三象限,且10z =,则z =( )A .68i +B .68i -C .68i --D .68i -+12.3( )A .i -B .iC .iD .i - 13.复数22(1)1i i -+=-( ) A .1+i B .-1+i C .1-i D .-1-i14.设复数202011i z i+=-(其中i 为虚数单位),则z 在复平面内对应的点所在象限为( )A .第四象限B .第三象限C .第二象限D .第一象限15.设复数z 满足(1)2i z -=,则z =( )A .1BCD .2二、多选题16.已知复数202011i z i+=-(i 为虚数单位),则下列说法错误的是( )A .z 的实部为2B .z 的虚部为1C .z i =D .||z =17.下面是关于复数21i z =-+的四个命题,其中真命题是( )A .||z =B .22z i =C .z 的共轭复数为1i -+D .z 的虚部为1-18.已知复数122z =-,则下列结论正确的有( )A .1z z ⋅=B .2z z =C .31z =-D .202012z =-+ 19.已知复数012z i =+(i 为虚数单位)在复平面内对应的点为0P ,复数z 满足|1|||z z i -=-,下列结论正确的是( )A .0P 点的坐标为(1,2)B .复数0z 的共轭复数对应的点与点0P 关于虚轴对称C .复数z 对应的点Z 在一条直线上D .0P 与z 对应的点Z 间的距离的最小值为220.若复数z 满足()234z i i +=+(i 为虚数单位),则下列结论正确的有( )A .z 的虚部为3B .z =C .z 的共轭复数为23i +D .z 是第三象限的点 21.下面是关于复数21iz =-+(i 为虚数单位)的命题,其中真命题为( )A .||2z =B .22z i =C .z 的共轭复数为1i +D .z 的虚部为1-22.已知复数z 满足2724z i =--,在复平面内,复数z 对应的点可能在( ) A .第一象限 B .第二象限C .第三象限D .第四象限 23.已知复数1cos 2sin 222z i ππθθθ⎛⎫=++-<< ⎪⎝⎭(其中i 为虚数单位),则( ) A .复数z 在复平面上对应的点可能落在第二象限B .z 可能为实数C .2cos z θ=D .1z 的实部为12- 24.若复数z 满足(1i)3i z +=+(其中i 是虚数单位),复数z 的共轭复数为z ,则( )A .|z |=B .z 的实部是2C .z 的虚部是1D .复数z 在复平面内对应的点在第一象限 25.已知i 为虚数单位,则下列选项中正确的是( ) A .复数34z i =+的模5z =B .若复数34z i =+,则z (即复数z 的共轭复数)在复平面内对应的点在第四象限C .若复数()()2234224m m m m +-+--i 是纯虚数,则1m =或4m =-D .对任意的复数z ,都有20z26.设i 为虚数单位,复数()(12)z a i i =++,则下列命题正确的是( )A .若z 为纯虚数,则实数a 的值为2B .若z 在复平面内对应的点在第三象限,则实数a 的取值范围是(,)122- C .实数12a =-是z z =(z 为z 的共轭复数)的充要条件 D .若||5()z z x i x R +=+∈,则实数a 的值为2 27.下面四个命题,其中错误的命题是( )A .0比i -大B .两个复数当且仅当其和为实数时互为共轭复数C .1x yi i +=+的充要条件为1x y ==D .任何纯虚数的平方都是负实数 28.以下命题正确的是( )A .0a =是z a bi =+为纯虚数的必要不充分条件B .满足210x +=的x 有且仅有iC .“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件D .已知()f x =()1878f x x '= 29.复数21i z i+=-,i 是虚数单位,则下列结论正确的是( )A .|z |=B .z 的共轭复数为3122i +C .z 的实部与虚部之和为2D .z 在复平面内的对应点位于第一象限30.设()()2225322z t t t t i =+-+++,t ∈R ,i 为虚数单位,则以下结论正确的是( )A .z 对应的点在第一象限B .z 一定不为纯虚数C .z 一定不为实数D .z 对应的点在实轴的下方【参考答案】***试卷处理标记,请不要删除一、复数选择题1.B【分析】利用复数的除法法则可化简,即可得解.【详解】,.故选:B.解析:B【分析】 利用复数的除法法则可化简1i z+,即可得解. 【详解】 2z i =-,()()()()12111313222555i i i i i i z i i i +++++∴====+--+. 故选:B.2.D【分析】由复数的运算法则计算即可.【详解】解:,.故选:D.解析:D【分析】由复数的运算法则计算即可.【详解】解:()2211122z i i i i =-=-+=-, ()()212222(1)2222111112z i i i i i i i z i i i i --⨯--+--∴=====--++--. 故选:D.3.D【分析】先由复数的运算化简复数z ,再运用复数的几何表示可得选项.【详解】由已知得,所以复数z 在复平面上所对应的点为,在第四象限,故选:D.解析:D【分析】先由复数的运算化简复数z ,再运用复数的几何表示可得选项.【详解】 由已知得()()()()312317171+21+212555i i i i z i i i i ----====--, 所以复数z 在复平面上所对应的点为17,55⎛⎫-⎪⎝⎭,在第四象限, 故选:D.4.C【分析】利用复数的乘法和除法运算求得复数z 的标准形式,得到对应点的坐标,然后验证即可.【详解】解:因为,所以复数对应的点是,所以在直线上.故选:C.【点睛】本题考查复数的乘方和除法运解析:C【分析】利用复数的乘法和除法运算求得复数z 的标准形式,得到对应点的坐标,然后验证即可.【详解】 解:因为33111(1)1(1)2(1)2i i z i i z i i --+=-⇔===-+-,所以复数z 对应的点是1,02⎛⎫- ⎪⎝⎭,所以在直线12x =-上. 故选:C.【点睛】本题考查复数的乘方和除法运算,复数的坐标表示,属基础题.注意:()()()()()3211i 12121i i i i i +=++=-+=-. 5.D 【分析】利用复数的乘除法运算法则将化简,然后求解.【详解】因为,所以,则.故选:D .【点睛】本题考查复数的运算,解答时注意复数的乘法运算符合多项式乘法的运算法则,计算复数的除法时,解析:D【分析】利用复数的乘除法运算法则将z 化简,然后求解||z .【详解】 因为()()()()2221211211211111i z i i i i i i i i i -=++=+++=-++-=+++-,所以1z i =-,则z =故选:D .【点睛】本题考查复数的运算,解答时注意复数的乘法运算符合多项式乘法的运算法则,计算复数的除法时,需要给分子分母同乘以分母的共轭复数然后化简.6.A【分析】由复数的除法法则和乘法法则计算出,再由复数的定义得结论.【详解】由题意,得,其虚部为,故选:A.解析:A【分析】由复数的除法法则和乘法法则计算出z ,再由复数的定义得结论.【详解】由题意,得()()()()()23343313343434552i i ii z i i i i i ----====-++-+, 其虚部为35, 故选:A. 7.B【分析】先求解出复数,然后根据复数的几何意义判断.【详解】因为,所以,故对应的点位于复平面内第二象限.故选:B.【点睛】本题考查复数的除法运算及复数的几何意义,属于基础题. 化简计解析:B【分析】先求解出复数z ,然后根据复数的几何意义判断.【详解】因为(1)2z i i -=,所以()212112i i i z i i +===-+-, 故z 对应的点位于复平面内第二象限.故选:B.【点睛】 本题考查复数的除法运算及复数的几何意义,属于基础题. 化简计算复数的除法时,注意分子分母同乘以分母的共轭复数.8.D【分析】先求出,再求出,直接得复数在复平面内对应的点【详解】因为,所以,在复平面内对应点,位于第四象限.故选:D解析:D【分析】先求出z ,再求出z ,直接得复数z 在复平面内对应的点【详解】因为211i z i i ==++,所以1z i -=-,z 在复平面内对应点()1,1-,位于第四象限. 故选:D9.B【分析】由题意,设复数,根据共轭复数的概念,以及题中条件,即可得出结果.【详解】因为的实部为,所以可设复数,则其共轭复数为,又,所以由,可得,即,因此.故选:B.解析:B【分析】由题意,设复数(),z yi x R y R =∈∈,根据共轭复数的概念,以及题中条件,即可得出结果.【详解】因为z ,所以可设复数(),z yi x R y R =∈∈,则其共轭复数为z yi =,又z z =,所以由4z z z z ⋅+⋅=,可得()4z z z ⋅+=,即4z ⋅=,因此z =故选:B. 10.B【分析】先设复数,根据复数模的计算公式,以及复数相等,求出,得出复数,再由复数的几何意义,即可得出结果.【详解】设复数,由得,所以,解得,因为时,不能满足,舍去;故,所以,其对应的解析:B【分析】先设复数(),z x yi x R y R =+∈∈,根据复数模的计算公式,以及复数相等,求出,x y ,得出复数,再由复数的几何意义,即可得出结果.【详解】设复数(),z x yi x R y R =+∈∈, 由22z z i +=得222x yi i +=,所以2022x y ⎧⎪+=⎨=⎪⎩,解得1x y ⎧=⎪⎨⎪=⎩,因为1x y ⎧=⎪⎨⎪=⎩时,不能满足20x =,舍去;故1x y ⎧=⎪⎨⎪=⎩3z i =-+,其对应的点3⎛⎫- ⎪ ⎪⎝⎭位于第二象限, 故选:B.11.D【分析】设,根据复数对应的向量与共线,得到,再结合求解.【详解】设,则复数对应的向量,因为向量与共线,所以,又,所以,解得或,因为复数对应的点在第三象限,所以,所以,,解析:D【分析】设(,)z a bi a R b R =+∈∈,根据复数z 对应的向量OZ 与(3,4)a =共线,得到43a b =,再结合10z =求解.【详解】设(,)z a bi a R b R =+∈∈,则复数z 对应的向量(),OZ a b =,因为向量OZ 与(3,4)a =共线,所以43a b =,又10z =,所以22100+=a b ,解得68a b =-⎧⎨=-⎩或68a b =⎧⎨=⎩, 因为复数z 对应的点在第三象限,所以68a b =-⎧⎨=-⎩, 所以68z i =--,68z i =-+,故选:D12.B【分析】首先,再利用复数的除法运算,计算结果.【详解】复数.故选:B解析:B【分析】首先3i i =-,再利用复数的除法运算,计算结果.【详解】3133i i i +====. 故选:B 13.C【分析】直接根据复数代数形式的乘除运算法则计算可得;【详解】解:故选:C解析:C【分析】直接根据复数代数形式的乘除运算法则计算可得;【详解】解:22(1)1i i-+- ()()()()2211211i i i i i +=-++-+ 12i i =+-1i =-故选:C14.A【分析】根据复数的运算,先将化简,求出,再由复数的几何意义,即可得出结果.【详解】因为,所以,其在复平面内对应的点为,位于第四象限.故选:A.解析:A【分析】根据复数的运算,先将z 化简,求出z ,再由复数的几何意义,即可得出结果.【详解】 因为()()()()4202050550512111121111111i i i z i i i i i i i ++++======+-----+, 所以1z i =-,其在复平面内对应的点为()1,1-,位于第四象限.故选:A.15.B【分析】由复数除法求得,再由模的运算求得模.【详解】由题意,∴.故选:B .解析:B【分析】由复数除法求得z ,再由模的运算求得模.【详解】由题意22(1)11(1)(1)i z i i i i +===+--+,∴z == 故选:B .二、多选题16.AC【分析】根据复数的运算及复数的概念即可求解.【详解】因为复数,所以z 的虚部为1,,故AC 错误,BD 正确.故选:AC解析:AC【分析】根据复数的运算及复数的概念即可求解.【详解】 因为复数2020450511()22(1)11112i i i z i i i i +++=====+---,所以z 的虚部为1,||z =故AC 错误,BD 正确.故选:AC17.ABCD【分析】先根据复数的除法运算计算出,再依次判断各选项.【详解】,,故A 正确;,故B 正确;的共轭复数为,故C 正确;的虚部为,故D 正确; 故选:ABCD.【点睛】本题考查复数的除法解析:ABCD【分析】先根据复数的除法运算计算出z ,再依次判断各选项.【详解】()()()2121111i z i i i i --===---+-+--,z ∴==,故A 正确;()2212z i i =--=,故B 正确;z 的共轭复数为1i -+,故C 正确;z 的虚部为1-,故D 正确;故选:ABCD.【点睛】本题考查复数的除法运算,以及对复数概念的理解,属于基础题.18.ACD【分析】分别计算各选项的值,然后判断是否正确,计算D 选项的时候注意利用复数乘方的性质.【详解】因为,所以A 正确;因为,,所以,所以B 错误;因为,所以C 正确;因为,所以,所以D 正确解析:ACD【分析】分别计算各选项的值,然后判断是否正确,计算D 选项的时候注意利用复数乘方的性质.【详解】因为11131222244z z i ⎛⎫⎛⎫-+=+= ⎪⎪ ⎪⎪⎝⎭⎭=⎝⋅,所以A 正确;因为22112222z ⎛⎫-=-- ⎪ ⎪⎝⎭=,122z =+,所以2z z ≠,所以B 错误;因为321112222z z z i ⎛⎫⎛⎫=⋅=---=- ⎪⎪ ⎪⎪⎝⎭⎝⎭,所以C 正确;因为6331z z z =⋅=,所以()2020633644311122z z z z z ⨯+⎛⎫===⋅=-⋅=-+ ⎪ ⎪⎝⎭,所以D 正确,故选:ACD.【点睛】本题考查复数乘法与乘方的计算,其中还涉及到了共轭复数的计算,难度较易.19.ACD【分析】根据复数对应的坐标,判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系,判断B 选项的正确性.设出,利用,结合复数模的运算进行化简,由此判断出点的轨迹,由此判读C 选项的正确解析:ACD【分析】根据复数对应的坐标,判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系,判断B 选项的正确性.设出z ,利用|1|||z z i -=-,结合复数模的运算进行化简,由此判断出Z 点的轨迹,由此判读C 选项的正确性.结合C 选项的分析,由点到直线的距离公式判断D 选项的正确性.【详解】复数012z i =+在复平面内对应的点为0(1,2)P ,A 正确;复数0z 的共轭复数对应的点与点0P 关于实轴对称,B 错误;设(,)z x yi x y R =+∈,代入|1|||z z i -=-,得|(1)(1)i|x yi x y -+=+-,即=y x =;即Z 点在直线y x =上,C 正确; 易知点0P 到直线y x =的垂线段的长度即为0P 、Z 之间距离的最小值,结合点到直线的距2=,故D 正确. 故选:ACD【点睛】本小题主要考查复数对应的坐标,考查共轭复数,考查复数模的运算,属于基础题. 20.BC【分析】利用复数的除法求出复数,利用复数的概念与几何意义可判断各选项的正误.【详解】,,所以,复数的虚部为,,共轭复数为,复数在复平面对应的点在第四象限. 故选:BD.【点睛】本题考解析:BC【分析】利用复数的除法求出复数z ,利用复数的概念与几何意义可判断各选项的正误.【详解】()234z i i +=+,34232i z i i+∴=-=-+,所以,复数z 的虚部为3-,z =共轭复数为23i +,复数z 在复平面对应的点在第四象限.故选:BD.【点睛】 本题考查复数的四则运算、虚部、模、共轭复数以及几何意义,考查计算能力,属于基础题.21.BD【分析】把分子分母同时乘以,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】解:,,A 错误;,B 正确;z 的共轭复数为,C 错误;z 的虚部为,D 正确.故选:BD.【点解析:BD【分析】 把21iz =-+分子分母同时乘以1i --,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】 解:22(1)11(1)(1)i z i i i i --===---+-+--,||z ∴=A 错误;22i z =,B 正确;z 的共轭复数为1i -+,C 错误;z 的虚部为1-,D 正确.故选:BD.【点睛】本题主要考查复数除法的基本运算、复数的基本概念,属于基础题.22.BD【分析】先设复数,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出,即可确定对应的点所在的象限.【详解】设复数,则,所以,则,解得或,因此或,所以对应的点为或,因此复解析:BD【分析】先设复数(),z a bi a b R =+∈,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出z ,即可确定对应的点所在的象限.【详解】设复数(),z a bi a b R =+∈,则2222724z a abi b i =+-=--,所以2222724z a abi b i =+-=--,则227224a b ab ⎧-=-⎨=-⎩,解得34a b =⎧⎨=-⎩或34a b =-⎧⎨=⎩, 因此34z i =-或34z i =-+,所以对应的点为()3,4-或()3,4-,因此复数z 对应的点可能在第二或第四象限.故选:BD.【点睛】本题主要考查判定复数对应的点所在的象限,熟记复数的运算法则,以及复数相等的条件即可,属于基础题型.23.BC【分析】由可得,得,可判断A 选项,当虚部,时,可判断B 选项,由复数的模计算和余弦的二倍角公式可判断C 选项,由复数的运算得,的实部是,可判断D 选项.【详解】因为,所以,所以,所以,所以A 选解析:BC【分析】 由22ππθ-<<可得2πθπ-<<,得01cos22θ<+≤,可判断A 选项,当虚部sin 20θ=,,22ππθ⎛⎫∈- ⎪⎝⎭时,可判断B 选项,由复数的模计算和余弦的二倍角公式可判断C 选项,由复数的运算得11cos 2sin 212cos 2i z θθθ+-=+,1z 的实部是1cos 2122cos 22θθ+=+,可判断D 选项.【详解】 因为22ππθ-<<,所以2πθπ-<<,所以1cos21θ-<≤,所以01cos22θ<+≤,所以A 选项错误;当sin 20θ=,,22ππθ⎛⎫∈- ⎪⎝⎭时,复数z 是实数,故B 选项正确;2cos z θ===,故C 选项正确:()()111cos 2sin 21cos 2sin 21cos 2sin 21cos 2sin 21cos 2sin 212cos 2i i z i i i θθθθθθθθθθθ+-+-===+++++-+,1z 的实部是1cos 2122cos 22θθ+=+,故D 不正确. 故选:BC【点睛】本题主要考查复数的概念,复数模的计算,复数的运算,以及三角恒等变换的应用,属于中档题.24.ABD【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,求出复数,根据共轭复数概念得到,即可判断.【详解】,,,故选项正确,的实部是,故选项正确,的虚部是,故选项错误,复解析:ABD【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,求出复数z ,根据共轭复数概念得到z ,即可判断.【详解】(1i)3i z +=+,()()()()3134221112i i i i z i i i i +-+-∴====-++-,z ∴==,故选项A 正确,z 的实部是2,故选项B 正确,z 的虚部是1-,故选项C 错误, 复数2z i =+在复平面内对应的点为()2,1,在第一象限,故选项D 正确.故选:ABD .【点睛】本题主要考查的是复数代数形式的乘除运算,考查了复数的代数表示及几何意义,是基础题.25.AB【分析】求解复数的模判断;由共轭复数的概念判断;由实部为0且虚部不为0求得值判断;举例说明错误.【详解】解:对于,复数的模,故正确;对于,若复数,则,在复平面内对应的点的坐标为,在第四解析:AB【分析】求解复数的模判断A ;由共轭复数的概念判断B ;由实部为0且虚部不为0求得m 值判断C ;举例说明D 错误.【详解】解:对于A ,复数34z i =+的模||5z ==,故A 正确;对于B ,若复数34z i =+,则34z i =-,在复平面内对应的点的坐标为(3,4)-,在第四象限,故B 正确;对于C ,若复数22(34)(224)m m m m i +-+--是纯虚数,则223402240m m m m ⎧+-=⎨--≠⎩,解得1m =,故C 错误; 对于D ,当z i 时,210z =-<,故D 错误.故选:AB .【点睛】本题考查复数代数形式的乘除运算,考查复数的基本概念,考查复数模的求法,属于基础题. 26.ACD【分析】首先应用复数的乘法得,再根据纯虚数概念、复数所在象限,以及与共轭复数或另一个复数相等,求参数的值或范围,进而可确定选项的正误【详解】∴选项A :为纯虚数,有可得,故正确选项B解析:ACD【分析】首先应用复数的乘法得2(12)z a a i =-++,再根据纯虚数概念、复数所在象限,以及与共轭复数或另一个复数相等,求参数的值或范围,进而可确定选项的正误【详解】()(12)2(12)z a i i a a i =++=-++∴选项A :z 为纯虚数,有20120a a -=⎧⎨+≠⎩可得2a =,故正确 选项B :z 在复平面内对应的点在第三象限,有20120a a -<⎧⎨+<⎩解得12a <-,故错误 选项C :12a =-时,52z z ==-;z z =时,120a +=即12a =-,它们互为充要条件,故正确 选项D :||5()z z x i x R +=+∈时,有125a +=,即2a =,故正确故选:ACD【点睛】本题考查了复数的运算及分类和概念,应用复数乘法运算求得复数,再根据复数的概念及性质、相等关系等确定参数的值或范围27.ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,解析:ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,A 选项错误;对于B 选项,()()123i i ++-=,但1i +与2i -不互为共轭复数,B 选项错误; 对于C 选项,由于1x yi i +=+,且x 、y 不一定是实数,若取x i =,y i =-,则1x yi i +=+,C 选项错误;对于D 选项,任取纯虚数()0,ai a a R ≠∈,则()220ai a =-<,D 选项正确. 故选:ABC.【点睛】本题考查复数相关命题真假的判断,涉及共轭复数的概念、复数相等以及复数的计算,属于基础题.28.AC【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误;解方程可判断B 选项的正误;利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误;利用基本初等函数的导数公式解析:AC【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误;解方程210x +=可判断B 选项的正误;利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误;利用基本初等函数的导数公式可判断D 选项的正误.综合可得出结论.【详解】对于A 选项,若复数z a bi =+为纯虚数,则0a =且0b ≠,所以,0a =是z a bi =+为纯虚数的必要不充分条件,A 选项正确;对于B 选项,解方程210x +=得x i =±,B 选项错误;对于C 选项,当(),x a b ∈时,若()0f x '>,则函数()f x 在区间(),a b 内单调递增, 即“在区间(),a b 内()0f x '>”⇒“()f x 在区间(),a b 内单调递增”.反之,取()3f x x =,()23f x x '=,当()1,1x ∈-时,()0f x '≥, 此时,函数()y f x =在区间()1,1-上单调递增,即“在区间(),a b 内()0f x '>”⇐/“()f x 在区间(),a b 内单调递增”.所以,“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件.C 选项正确;对于D 选项,()11172488f x x x ++===,()1878f x x -'∴=,D 选项错误. 故选:AC.【点睛】本题考查命题真假的判断,涉及充分条件与必要条件的判断、实系数方程的根以及导数的计算,考查推理能力与计算能力,属于中等题. 29.CD【分析】根据复数的四则运算,整理复数,再逐一分析选项,即得.【详解】由题得,复数,可得,则A 不正确;的共轭复数为,则B 不正确;的实部与虚部之和为,则C 正确;在复平面内的对应点为,位于第一解析:CD【分析】根据复数的四则运算,整理复数z ,再逐一分析选项,即得.【详解】由题得,复数22(2)(1)13131(1)(1)122i i i i z i i i i i ++++====+--+-,可得||2z ==,则A 不正确;z 的共轭复数为1322i -,则B 不正确;z 的实部与虚部之和为13222+=,则C 正确;z 在复平面内的对应点为13(,)22,位于第一象限,则D 正确.综上,正确结论是CD.故选:CD【点睛】本题考查复数的定义,共轭复数以及复数的模,考查知识点全面.30.CD【分析】利用配方法得出复数的实部和虚部的取值范围,结合复数的概念和几何意义可判断出各选项的正误,由此可得出结论.【详解】,,所以,复数对应的点可能在第一象限,也可能在第二象限,故A 错误 解析:CD【分析】利用配方法得出复数z 的实部和虚部的取值范围,结合复数的概念和几何意义可判断出各选项的正误,由此可得出结论.【详解】22549492532488t t t ⎛+⎫= ⎪⎝⎭+-->-,()2222110t t t ++=++>, 所以,复数z 对应的点可能在第一象限,也可能在第二象限,故A 错误;当222530220t t t t ⎧+-=⎨++≠⎩,即3t =-或12t =时,z 为纯虚数,故B 错误; 因为2220t t ++>恒成立,所以z 一定不为实数,故C 正确;由选项A 的分析知,z 对应的点在实轴的上方,所以z 对应的点在实轴的下方,故D 正确. 故选:CD.【点睛】本题考查复数的几何意义与复数的概念相关命题真假的判断,解题的关键就是求出复数虚部和实部的取值范围,考查计算能力与推理能力,属于中等题.。
最新全国各地高考文科数学试题分类汇编15:复数

全国各地(高|考)文科数学试题分类汇编15:复数一、选择题1 . ((高|考)辽宁卷 (文 ) )复数的11Z i =-模为 ( )A .12B .22C .2D .2[来源:学科网]【答案】B2 . ((高|考)课标Ⅱ卷 (文 ) )|| =( )A .2B .2C .D .1[来源:学#科#网Z#X#X#K]【答案】C3 . ((高|考)湖南 (文 ) )复数z =i·(1 +i)(i 为虚数单位)在复平面上对应的点位于___ ____ ( )A .第|一象限B .第二象限C .第三象限D .第四象限[来源:]【答案】B4 . ((高|考)四川卷 (文 ) )如图,在复平面内,点A 表示复数z ,那么图中表示z 的共轭复数的点是( )A .AB .BC .CD .D【答案】B [来源:学科网ZXXK]5 . ((高|考)课标Ⅰ卷 (文 ) )212(1)ii +=- ( )A .112i --B .112i -+C .112i +D .112i -【答案】B6 . ((高|考)北京卷 (文 ) )在复平面内,复数(2)i i -对应的点位于( )A .第|一象限B .第二象限C .第三象限D .第四象限【答案】A7 . ((高|考)山东卷 (文 ) )复数)()2(2为虚数单位i ii z -=,那么=||z ( )A .25B .41C .5D .5【答案】C8 . ((高|考)江西卷 (文 ) )复数z =i( -2 -i)(i 为虚数单位)在复平面内所对应的点在( )[来源:学科网]A .第|一象限B .第二象限C .第三象限D .第四象限【答案】D9 . ((高|考)浙江卷 (文 ) )i 是虚数单位,那么(2 +i)(3 +i) = ( )A .5 -5iB .7 -5iC .5 +5iD .7 +5i[来源:]【答案】C10. ((高|考)安徽 (文 ) )设i 是虚数单位,假设复数10()3a a R i-∈-是纯虚数,那么a 的值为 ( ) A . -3 B .-1 C .1D .3【答案】D11. ((高|考)福建卷 (文 ) )复数i z 21--=(i 为虚数单位)在复平面内对应的点位于( )A .第|一象限B .第二象限C .第三象限D .第四象限【答案】C12. ((高|考)广东卷 (文 ) )假设()34i x yi i +=+,,x y R ∈,那么复数x yi +的模是( )[来源:学#科#网Z#X#X#K] A .2 B .3 C .4 D .5【答案】D二、填空题13. (2021年(高|考)天津卷 (文 ) )i 是虚数单位. 复数(3 + i )(1 -2i ) = ______.【答案】55i - [来源:学科网ZXXK][来源:学科网ZXXK]14. ((高|考)重庆卷 (文 ) )复数12z i =+(i 是虚数单位),那么z =____________.【答案】515. (上海(高|考)数学试题 (文科 ) )设m ∈R ,()2221i m m m +-+-是纯虚数,其中i 是虚数单位,那么m =________.【答案】2m =-16. ((高|考)湖北卷 (文 ) )i 为虚数单位,设复数1z ,2z 在复平面内对应的点关于原点对称,假设123i z =-,那么2z =__________.[来源:Z_xx_]【答案】23i -+。
高考文科数学试卷复数题

1. 已知复数z满足|z-1|=|z+1|,则z在复平面上的几何意义是()A. 与实轴垂直B. 与实轴平行C. 位于实轴上D. 位于实轴的负半轴2. 设复数z=a+bi(a,b∈R),若z的辐角为θ,则下列选项中,下列正确的是()A. |z|=a^2+b^2B. cosθ=a/|z|C. sinθ=b/|z|D. tanθ=b/a3. 设复数z满足|z+1|=|z-1|,则z的取值范围是()A. (-∞,-1]∪[1,+∞)B. (-∞,-1)∪(1,+∞)C. (-∞,-1)∪[1,+∞)D. (-∞,-1]∪(1,+∞)4. 设复数z=a+bi(a,b∈R),若|z|=1,则下列选项中,下列正确的是()A. a^2+b^2=1B. |a|=|b|C. a^2+b^2=2D. a^2+b^2=05. 设复数z=a+bi(a,b∈R),若z的模为|z|=√2,则下列选项中,下列正确的是()A. a=1,b=1B. a=1,b=-1C. a=-1,b=1D. a=-1,b=-16. 设复数z=a+bi(a,b∈R),若z的辐角为θ,则下列选项中,下列正确的是()A. cosθ=a/|z|B. sinθ=b/|z|C. tanθ=b/aD. tanθ=a/b7. 设复数z=a+bi(a,b∈R),若z的实部为a,虚部为b,则下列选项中,下列正确的是()A. a^2+b^2=|z|B. a=|z|C. b=|z|D. a^2+b^2=|z|^28. 设复数z=a+bi(a,b∈R),若|z|=1,则下列选项中,下列正确的是()A. a^2+b^2=1B. |a|=1C. |b|=1D. a=1,b=19. 设复数z=a+bi(a,b∈R),若z的辐角为θ,则下列选项中,下列正确的是()A. cosθ=a/|z|B. sinθ=b/|z|C. tanθ=b/aD. tanθ=a/b10. 设复数z=a+bi(a,b∈R),若z的实部为a,虚部为b,则下列选项中,下列正确的是()A. a^2+b^2=|z|B. a=|z|C. b=|z|D. a^2+b^2=|z|^2二、填空题(本大题共5小题,每小题10分,共50分)11. 设复数z=a+bi(a,b∈R),若|z|=1,则|z|^2=__________。
高考复数专题及答案doc

一、复数选择题1.若()211z i =-,21z i =+,则12z z 等于( ) A .1i +B .1i -+C .1i -D .1i --2.复数()1z i i =⋅+在复平面上对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3.若20212zi i =+,则z =( )A .12i -+B .12i --C .12i -D .12i +4.212ii+=-( ) A .1 B .−1 C .i - D .i 5.复数z 满足12i z i ⋅=-,z 是z 的共轭复数,则z z ⋅=( )ABC .3D .56.若复数z 满足421iz i+=+,则z =( ) A .13i + B .13i -C .3i +D .3i -7.设2iz i+=,则||z =( ) ABC .2D .58.若复数2i1ia -+(a ∈R )为纯虚数,则1i a -=( ) ABC .3D .59.若复数()41i 34iz +=+,则z =( )A .45B .35C .25D.510.在复平面内,复数z 对应的点为(,)x y ,若22(2)4x y ++=,则( ) A .22z += B .22z i +=C .24z +=D .24z i +=11.复数2ii -的实部与虚部之和为( ) A .35 B .15- C .15D .3512.已知()312++=+a i i bi (,a b ∈R ,i 为虚数单位),则实数+a b 的值为( ) A .3B .5C .6D .813.复数()()212z i i =-+在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限14.已知i 是虚数单位,设11iz i,则复数2z +对应的点位于复平面( ) A .第一象限 B .第二象限C .第三象限D .第四象限15.若复数11iz i,i 是虚数单位,则z =( ) A .0B .12C .1D .2二、多选题16.i 是虚数单位,下列说法中正确的有( ) A .若复数z 满足0z z ⋅=,则0z =B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数()z a ai a R =+∈,则z 可能是纯虚数D .若复数z 满足234z i =+,则z 对应的点在第一象限或第三象限 17.若复数351iz i-=-,则( )A .z =B .z 的实部与虚部之差为3C .4z i =+D .z 在复平面内对应的点位于第四象限18.已知复数z 满足220z z +=,则z 可能为( ) A .0B .2-C .2iD .2i -19.已知复数(),z x yi x y R =+∈,则( ) A .20zB .z 的虚部是yiC .若12z i =+,则1x =,2y =D .z =20.设复数z 满足1z i z+=,则下列说法错误的是( ) A .z 为纯虚数B .z 的虚部为12i -C .在复平面内,z 对应的点位于第三象限D .2z =21.下面是关于复数21iz =-+(i 为虚数单位)的命题,其中真命题为( ) A .||2z = B .22z i =C .z 的共轭复数为1i +D .z 的虚部为1-22.复数z 满足233232iz i i+⋅+=-,则下列说法正确的是( )A .z 的实部为3-B .z 的虚部为2C .32z i =-D .||z =23.若复数z 满足()1z i i +=,则( )A .1z i =-+B .z 的实部为1C .1z i =+D .22z i =24.已知i 为虚数单位,复数322iz i+=-,则以下真命题的是( ) A .z 的共轭复数为4755i - B .z 的虚部为75i C .3z =D .z 在复平面内对应的点在第一象限25.下列结论正确的是( )A .已知相关变量(),x y 满足回归方程ˆ9.49.1yx =+,则该方程相应于点(2,29)的残差为1.1B .在两个变量y 与x 的回归模型中,用相关指数2R 刻画回归的效果,2R 的值越大,模型的拟合效果越好C .若复数1z i =+,则2z =D .若命题p :0x R ∃∈,20010x x -+<,则p ⌝:x R ∀∈,210x x -+≥26.设i 为虚数单位,复数()(12)z a i i =++,则下列命题正确的是( ) A .若z 为纯虚数,则实数a 的值为2B .若z 在复平面内对应的点在第三象限,则实数a 的取值范围是(,)122-C .实数12a =-是z z =(z 为z 的共轭复数)的充要条件 D .若||5()z z x i x R +=+∈,则实数a 的值为227.已知复数12z =-+(其中i 为虚数单位),则以下结论正确的是( )A .20zB .2z z =C .31z =D .1z =28.下面四个命题,其中错误的命题是( )A .0比i -大B .两个复数当且仅当其和为实数时互为共轭复数C .1x yi i +=+的充要条件为1x y ==D .任何纯虚数的平方都是负实数 29.复数21iz i+=-,i 是虚数单位,则下列结论正确的是( )A .|z |=B .z 的共轭复数为3122i + C .z 的实部与虚部之和为2D .z 在复平面内的对应点位于第一象限30.已知复数z ,下列结论正确的是( )A .“0z z +=”是“z 为纯虚数”的充分不必要条件B .“0z z +=”是“z 为纯虚数”的必要不充分条件C .“z z =”是“z 为实数”的充要条件D .“z z ⋅∈R ”是“z 为实数”的充分不必要条件【参考答案】***试卷处理标记,请不要删除一、复数选择题 1.D 【分析】由复数的运算法则计算即可. 【详解】 解:, . 故选:D. 解析:D 【分析】由复数的运算法则计算即可. 【详解】 解:()2211122z i i i i =-=-+=-,()()212222(1)2222111112z i i i i i i i z i i i i --⨯--+--∴=====--++--. 故选:D.2.B 【分析】先利用复数的乘法化简复数z ,再利用复数的几何意义求解. 【详解】 因为复数,所以在复数z 复平面上对应的点位于第二象限 故选:B解析:B 【分析】先利用复数的乘法化简复数z ,再利用复数的几何意义求解. 【详解】因为复数()11z i i i =⋅+=-+,所以在复数z 复平面上对应的点位于第二象限 故选:B3.C 【分析】根据复数单位的幂的周期性和复数除法的运算法则进行求解即可. 【详解】由已知可得,所以. 故选:C解析:C 【分析】根据复数单位i 的幂的周期性和复数除法的运算法则进行求解即可. 【详解】 由已知可得202150541222(2)21121i i i i i i z i i i i i i ⨯+++++⋅-======-⋅-,所以12z i =-. 故选:C4.D 【分析】利用复数的除法运算即可求解. 【详解】 , 故选:D解析:D 【分析】利用复数的除法运算即可求解. 【详解】()()()()2221222255121212145i i i i i ii i i i i +++++====--+-, 故选:D5.D 【分析】求出复数,然后由乘法法则计算. 【详解】 由题意, . 故选:D .解析:D 【分析】求出复数z ,然后由乘法法则计算z z ⋅. 【详解】 由题意12122i z i i i-==-+=--, 22(2)(2)(2)5z z i i i ⋅=---+=--=.故选:D .6.C 【分析】首先根据复数的四则运算求出,然后根据共轭复数的概念求出. 【详解】 ,故. 故选:C.解析:C 【分析】首先根据复数的四则运算求出z ,然后根据共轭复数的概念求出z . 【详解】()()()()421426231112i i i i z i i i i +-+-====-++-,故3z i =+. 故选:C.7.B 【分析】利用复数的除法运算先求出,再求出模即可. 【详解】 , .故选:B .解析:B 【分析】利用复数的除法运算先求出z ,再求出模即可. 【详解】()22212i ii z i i i++===-,∴z ==故选:B .8.B 【分析】把给出的复数化简,然后由实部等于0,虚部不等于0求解a 的值,最后代入模的公式求模. 【详解】 由复数()为纯虚数,则 ,则 所以 故选:B解析:B 【分析】把给出的复数化简,然后由实部等于0,虚部不等于0求解a 的值,最后代入模的公式求模. 【详解】由()()()()()()21i 2221112a i a a ia i i i i ----+-==++- 复数2i 1i a -+(a ∈R )为纯虚数,则202202a a -⎧=⎪⎪⎨+⎪≠⎪⎩ ,则2a =所以112ai i -=-=故选:B9.A 【分析】首先化简复数,再计算求模. 【详解】 , . 故选:A解析:A 【分析】首先化简复数z ,再计算求模. 【详解】()()()2242112434343434i i i z i i i i⎡⎤++⎣⎦====-++++ ()()()()43443412163434252525i i i i i --=-=-=-++-,45z ∴==.故选:A10.B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数对应的点为,所以 ,满足则 故选:B解析:B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数z 对应的点为(,)x y ,所以z x yi =+x ,y 满足22(2)4x y ++=则22z i +=故选:B11.C 【分析】利用复数代数形式的乘除运算化简得答案. 【详解】,的实部与虚部之和为. 故选:C 【点睛】易错点睛:复数的虚部是,不是.解析:C 【分析】利用复数代数形式的乘除运算化简得答案. 【详解】()()()2+1212222+555i i i i i i i i -+===-+--,2i i ∴-的实部与虚部之和为121555-+=. 故选:C 【点睛】易错点睛:复数z a bi =+的虚部是b ,不是bi .12.D 【分析】利用复数的乘法运算及复数相等求得a,b 值即可求解,故 则 故选:D解析:D 【分析】利用复数的乘法运算及复数相等求得a,b 值即可求解 【详解】()312++=+a i i bi ,故332a i bi -+=+ 则32,38a b a b -==∴+=故选:D13.A 【分析】利用复数的乘法化简复数,利用复数的乘法可得出结论. 【详解】 ,因此,复数在复平面内对应的点位于第一象限. 故选:A.解析:A 【分析】利用复数的乘法化简复数z ,利用复数的乘法可得出结论. 【详解】()()221223243z i i i i i =-+=+-=+,因此,复数z 在复平面内对应的点位于第一象限. 故选:A.14.A 【分析】由复数的除法求出,然后得出,由复数的几何意义得结果. 【详解】 由已知,,对应点为,在第一象限, 故选:A.解析:A 【分析】由复数的除法求出z i =-,然后得出2z +,由复数的几何意义得结果. 【详解】 由已知(1)(1)(1)(1)i i z i i i --==-+-,222z i i +=-+=+,对应点为(2,1),在第一象限,15.C 【分析】由复数除法求出,再由模计算. 【详解】 由已知, 所以. 故选:C .解析:C 【分析】由复数除法求出z ,再由模计算. 【详解】由已知21(1)21(1)(1)2i i iz i i i i ---====-++-, 所以1z i =-=. 故选:C .二、多选题 16.AD 【分析】A 选项,设出复数,根据共轭复数的相关计算,即可求出结果;B 选项,举出反例,根据复数模的计算公式,即可判断出结果;C 选项,根据纯虚数的定义,可判断出结果;D 选项,设出复数,根据题解析:AD 【分析】A 选项,设出复数,根据共轭复数的相关计算,即可求出结果;B 选项,举出反例,根据复数模的计算公式,即可判断出结果;C 选项,根据纯虚数的定义,可判断出结果;D 选项,设出复数,根据题中条件,求出复数,由几何意义,即可判断出结果. 【详解】A 选项,设(),z a bi a b R =+∈,则其共轭复数为(),z a bi a b R =-∈, 则220z z a b ⋅=+=,所以0ab ,即0z =;A 正确;B 选项,若11z =,2z i =,满足1212z z z z +=-,但12z z i =不为0;B 错;C 选项,若复数()z a ai a R =+∈表示纯虚数,需要实部为0,即0a =,但此时复数0z =表示实数,故C 错;D 选项,设(),z a bi a b R =+∈,则()2222234z a bi a abi b i =+=+-=+, 所以22324a b ab ⎧-=⎨=⎩,解得21a b =⎧⎨=⎩或21a b =-⎧⎨=-⎩,则2z i =+或2z i =--, 所以其对应的点分别为()2,1或()2,1--,所以对应点的在第一象限或第三象限;D 正确. 故选:AD.17.AD【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出.【详解】解:,,z 的实部为4,虚部为,则相差5,z 对应的坐标为,故z 在复平面内对应的点位于第四象限,所以AD 正解析:AD【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出.【详解】 解:()()()()351358241112i i i i z i i i i -+--====---+,z ∴==z 的实部为4,虚部为1-,则相差5,z 对应的坐标为()41-,,故z 在复平面内对应的点位于第四象限,所以AD 正确, 故选:AD. 18.ACD【分析】令代入已知等式,列方程组求解即可知的可能值.【详解】令代入,得:,∴,解得或或∴或或.故选:ACD【点睛】本题考查了已知等量关系求复数,属于简单题.解析:ACD【分析】令z a bi =+代入已知等式,列方程组求解即可知z 的可能值.【详解】令z a bi =+代入22||0z z +=,得:2220a b abi -+=,∴22020a b ab ⎧⎪-+=⎨=⎪⎩,解得0,0a b =⎧⎨=⎩或0,2a b =⎧⎨=⎩或0,2,a b =⎧⎨=-⎩ ∴0z =或2z i =或2z i =-.故选:ACD【点睛】本题考查了已知等量关系求复数,属于简单题.19.CD【分析】取特殊值可判断A 选项的正误;由复数的概念可判断B 、C 选项的正误;由复数模的概念可判断D 选项的正误.【详解】对于A 选项,取,则,A 选项错误;对于B 选项,复数的虚部为,B 选项错误;解析:CD【分析】取特殊值可判断A 选项的正误;由复数的概念可判断B 、C 选项的正误;由复数模的概念可判断D 选项的正误.【详解】对于A 选项,取z i ,则210z =-<,A 选项错误;对于B 选项,复数z 的虚部为y ,B 选项错误;对于C 选项,若12z i =+,则1x =,2y =,C 选项正确;对于D选项,z =D 选项正确.故选:CD.【点睛】本题考查复数相关命题真假的判断,涉及复数的计算、复数的概念以及复数的模,属于基础题. 20.AB【分析】先由复数除法运算可得,再逐一分析选项,即可得答案.【详解】由题意得:,即,所以z 不是纯虚数,故A 错误;复数z 的虚部为,故B 错误;在复平面内,对应的点为,在第三象限,故C 正确解析:AB【分析】 先由复数除法运算可得1122z i =--,再逐一分析选项,即可得答案. 【详解】 由题意得:1z zi +=,即111122z i i -==---, 所以z 不是纯虚数,故A 错误; 复数z 的虚部为12-,故B 错误; 在复平面内,z 对应的点为11(,)22--,在第三象限,故C 正确;2z ==,故D 正确. 故选:AB【点睛】本题考查复数的除法运算,纯虚数、虚部的概念,复平面内点所在象限、复数求模的运算等知识,考查计算求值的能力,属基础题.21.BD【分析】把分子分母同时乘以,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】解:,,A 错误;,B 正确;z 的共轭复数为,C 错误;z 的虚部为,D 正确.故选:BD.【点解析:BD【分析】 把21iz =-+分子分母同时乘以1i --,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】解:22(1)11(1)(1)i z i i i i --===---+-+--,||z ∴=A 错误;22i z =,B 正确;z 的共轭复数为1i -+,C 错误;z 的虚部为1-,D 正确.故选:BD.【点睛】本题主要考查复数除法的基本运算、复数的基本概念,属于基础题.22.AD【分析】由已知可求出,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】解:由知,,即,所以的实部为,A 正确;的虚部为-2,B 错误;,C 错误;,D 正确;故选:A解析:AD【分析】由已知可求出32z i =--,进而可求出实部、虚部、共轭复数、复数的模,进而可选出正确答案.【详解】解:由233232i z i i +⋅+=-知,232332i z i i +⋅=--,即()()()2233232232313i i i z i i ---=-=+ 39263213i i --==--,所以z 的实部为3-,A 正确;z 的虚部为-2,B 错误;32z i =-+,C 错误;||z ==D 正确; 故选:AD.【点睛】 本题考查了复数的除法运算,考查了复数的概念,考查了共轭复数的求解,考查了复数模的求解,属于基础题.23.BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由,得,所以z 的实部为1,,,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭 解析:BC【分析】先利用复数的运算求出复数z ,然后逐个分析判断即可【详解】解:由()1z i i +=,得2(1)2(1)11(1)(1)2i i z i i i i --====-++-, 所以z 的实部为1,1z i =+,22z i =-,故选:BC【点睛】此题考查复数的运算,考查复数的模,考查复数的有关概念,考查共轭复数,属于基础题24.AD【分析】先利用复数的除法、乘法计算出,再逐项判断后可得正确的选项.【详解】,故,故A 正确.的虚部为,故B 错,,故C 错,在复平面内对应的点为,故D 正确.故选:AD.【点睛】本题考解析:AD【分析】先利用复数的除法、乘法计算出z ,再逐项判断后可得正确的选项.【详解】()()32232474725555i i i i i z i ++++====+-,故4755i z =-,故A 正确.z 的虚部为75,故B 错,3z ==≠,故C 错, z 在复平面内对应的点为47,55⎛⎫ ⎪⎝⎭,故D 正确. 故选:AD.【点睛】本题考查复数的概念、复数的运算以及复数的几何意义,注意复数(),z a bi a b R =+∈的虚部为b ,不是bi ,另外复数的除法运算是分子分母同乘以分母的共轭复数.25.ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当时,,则该方程相应于点(2,29)的残差为,则A 正确;在两个变量解析:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当2x =时,ˆ9.429.127.9y=⨯+=,则该方程相应于点(2,29)的残差为2927.9 1.1-=,则A 正确;在两个变量y 与x 的回归模型中,2R 的值越大,模型的拟合效果越好,则B 正确;1z i =-,z ==C 错误;由否定的定义可知,D 正确;故选:ABD【点睛】本题主要考查了残差的计算,求复数的模,特称命题的否定,属于中档题. 26.ACD【分析】首先应用复数的乘法得,再根据纯虚数概念、复数所在象限,以及与共轭复数或另一个复数相等,求参数的值或范围,进而可确定选项的正误【详解】∴选项A :为纯虚数,有可得,故正确选项B解析:ACD【分析】首先应用复数的乘法得2(12)z a a i =-++,再根据纯虚数概念、复数所在象限,以及与共轭复数或另一个复数相等,求参数的值或范围,进而可确定选项的正误【详解】()(12)2(12)z a i i a a i =++=-++∴选项A :z 为纯虚数,有20120a a -=⎧⎨+≠⎩可得2a =,故正确 选项B :z 在复平面内对应的点在第三象限,有20120a a -<⎧⎨+<⎩解得12a <-,故错误 选项C :12a =-时,52z z ==-;z z =时,120a +=即12a =-,它们互为充要条件,故正确 选项D :||5()z z x i x R +=+∈时,有125a +=,即2a =,故正确故选:ACD【点睛】本题考查了复数的运算及分类和概念,应用复数乘法运算求得复数,再根据复数的概念及性质、相等关系等确定参数的值或范围27.BCD【分析】利用复数的运算法则直接求解.【详解】解:复数(其中为虚数单位),,故错误;,故正确;,故正确;.故正确.故选:.【点睛】本题考查命题真假的判断,考查复数的运算法则解析:BCD【分析】利用复数的运算法则直接求解.【详解】解:复数12z =-(其中i 为虚数单位),2131442z ∴=-=--,故A 错误; 2z z ∴=,故B 正确;31113()()12244z =--+=+=,故C 正确;||1z ==.故D 正确.故选:BCD .【点睛】本题考查命题真假的判断,考查复数的运算法则等基础知识,考查运算求解能力,属于基础题.28.ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,解析:ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,A 选项错误;对于B 选项,()()123i i ++-=,但1i +与2i -不互为共轭复数,B 选项错误; 对于C 选项,由于1x yi i +=+,且x 、y 不一定是实数,若取x i =,y i =-,则1x yi i +=+,C 选项错误;对于D 选项,任取纯虚数()0,ai a a R ≠∈,则()220ai a =-<,D 选项正确. 故选:ABC.【点睛】本题考查复数相关命题真假的判断,涉及共轭复数的概念、复数相等以及复数的计算,属于基础题.29.CD【分析】根据复数的四则运算,整理复数,再逐一分析选项,即得.【详解】由题得,复数,可得,则A 不正确;的共轭复数为,则B 不正确;的实部与虚部之和为,则C 正确;在复平面内的对应点为,位于第一解析:CD【分析】根据复数的四则运算,整理复数z ,再逐一分析选项,即得.【详解】 由题得,复数22(2)(1)13131(1)(1)122i i i i z i i i i i ++++====+--+-,可得||2z ==,则A 不正确;z 的共轭复数为1322i -,则B 不正确;z 的实部与虚部之和为13222+=,则C 正确;z 在复平面内的对应点为13(,)22,位于第一象限,则D 正确.综上,正确结论是CD.故选:CD【点睛】本题考查复数的定义,共轭复数以及复数的模,考查知识点全面.30.BC【分析】设,可得出,利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断,从而可得出结论.【详解】设,则,则,若,则,,若,则不为纯虚数,所以,“”是“为纯虚数”必要不充分解析:BC【分析】设(),z a bi a b R =+∈,可得出z a bi =-,利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断,从而可得出结论.【详解】设(),z a bi a b R =+∈,则z a bi =-, 则2z z a +=,若0z z +=,则0a =,b R ∈,若0b =,则z 不为纯虚数, 所以,“0z z +=”是“z 为纯虚数”必要不充分条件; 若z z =,即a bi a bi +=-,可得0b =,则z 为实数,“z z =”是“z 为实数”的充要条件;22z z a b ⋅=+∈R ,z ∴为虚数或实数,“z z ⋅∈R ”是“z 为实数”的必要不充分条件.故选:BC.【点睛】本题考查充分条件、必要条件的判断,同时也考查了共轭复数、复数的基本概念的应用,考查推理能力,属于基础题.。
高中数学—复数的历届高考试题解析.doc

【解析】依据虚数运算公式可知 可得 ,选D.
【答案】D
11.(2009江西卷理)若复数 为纯虚数,则实数 的值为
A. B. C. D. 或
答案:A
【解析】由 故选A
12.(2009湖北卷理)投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为
A.4+8i B.8+2i C.2+4i D.4+i
【答案】C
10.【2010·四川理数】i是虚数单位,计算i+i2+i3=( )
A.-1 B.1 C. D.
【答案】A
【解析】由复数性质知:i2=-1,故i+i2+i3=i+(-1)+(-i)=-1.
11.【2010·天津文数】i是虚数单位,复数 =( )
【答案】A
【解析】本题主要考查复数代数形式的基本运算,属于容易题。
进行复数的除法的运算需要份子、分母同时乘以分母的共轭复数,同时将i2改为-1.
13.【2010·广东理数】若复数z1=1+i,z2=3-i,则z1·z2=( )
A.4+2i B. 2+i C. 2+2i D.3
【答案】A
【解析】 .
14.【2010·福建文数】 是虚数单位, 等于 ( )
答案:D.
解析:设纯虚数 ,代入
由于其为实数,b= -2, 故选D.
19.(2009宁夏海南卷文)复数
(A) (B) (C) (D)
【答案】C
【解析】 ,故选.C。
20.(2009天津卷理)i是虚数单位, =
(A)1+2i (B)-1-2i (C)1-2i (D)-1+2i
十年真题(2010_2019)高考数学真题分类汇编专题02复数文(含解析)

专题02复数历年考题细目表题型年份考点试题位置单选题2019 复数的四则运算2019年新课标1文科01 单选题2018 复数的四则运算2018年新课标1文科02 单选题2017 复数的四则运算2017年新课标1文科03单选题2016 数系的扩充与复数的定义2016年新课标1文科02单选题2015 复数的四则运算2015年新课标1文科03 单选题2014 复数的四则运算2014年新课标1文科03 单选题2013 复数的四则运算2013年新课标1文科02 单选题2012 复数的四则运算2012年新课标1文科02 单选题2011 复数的四则运算2011年新课标1文科02 单选题2010 复数的四则运算2010年新课标1文科03历年高考真题汇编1.【2019年新课标1文科01】设z,则|z|=()A.2 B.C.D.1 【解答】解:由z,得|z|=||.故选:C.2.【2018年新课标1文科02】设z2i,则|z|=()A.0 B.C.1 D.【解答】解:z2i2i=﹣i+2i=i,则|z|=1.故选:C.3.【2017年新课标1文科03】下列各式的运算结果为纯虚数的是()A.i(1+i)2B.i2(1﹣i)C.(1+i)2D.i(1+i)【解答】解:A.i(1+i)2=i•2i=﹣2,是实数.B.i2(1﹣i)=﹣1+i,不是纯虚数.C.(1+i)2=2i为纯虚数.D.i(1+i)=i﹣1不是纯虚数.故选:C.4.【2016年新课标1文科02】设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a等于()A.﹣3 B.﹣2 C.2 D.3【解答】解:(1+2i)(a+i)=a﹣2+(2a+1)i的实部与虚部相等,可得:a﹣2=2a+1,解得a=﹣3.故选:A.5.【2015年新课标1文科03】已知复数z满足(z﹣1)i=1+i,则z=()A.﹣2﹣i B.﹣2+i C.2﹣i D.2+i【解答】解:由(z﹣1)i=1+i,得z﹣1,∴z=2﹣i.故选:C.6.【2014年新课标1文科03】设z i,则|z|=()A.B.C.D.2【解答】解:z i i.故|z|.故选:B.7.【2013年新课标1文科02】()A.﹣1i B.﹣1i C.1i D.1i【解答】解: 1i.故选:B.8.【2012年新课标1文科02】复数z的共轭复数是()A.2+i B.2﹣i C.﹣1+i D.﹣1﹣i【解答】解:复数z1+i.所以复数的共轭复数为:﹣1﹣i.故选:D.9.【2011年新课标1文科02】复数()A.2﹣i B.1﹣2i C.﹣2+i D.﹣1+2i【解答】解: 2+i故选:C.10.【2010年新课标1文科03】已知复数Z,则|z|=()A.B.C.1 D.2 【解答】解:化简得Z•••,故|z|,故选:B .考题分析与复习建议本专题考查的知识点为:复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算,与向量结合考查复数及其加法、减法的几何意义等,历年考题主要以选择题题型出现,重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算等,预测明年本考点题目会比较稳定,备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算为重点较佳. 最新高考模拟试题1.复数52iz =-在复平面上的对应点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】A 【解析】,在复平面上的对应点为()2,1,位于第一象限. 故选A.2.设i z a b =+(a ,b ∈R ,i 是虚数单位),且22i z =-,则有( ) A .1a b +=- B .1a b -=- C .0a b -= D .0a b +=【答案】D 【解析】 因为,所以220a b -=,22ab =-, 解得11a b =⎧⎨=-⎩或11a b =-⎧⎨=⎩,所以0a b +=,故选D.3.若复数1i1ia z +=+为纯虚数,则实数a 的值为( ) A .1 B .1-C .0D .2【答案】B【解析】故,解1a =-故选:B4.复数i (1+i )的虚部为( ) A .2 B .1C .0D .1-【答案】B 【解析】∵i (1+i )=-1+i , ∴i (1+i )的虚部为1. 故选:B .5.已知复数11z i =-+,复数2z 满足122z z =-,则2z = ( ) A .2 B .2C .10D .10【答案】B 【解析】 由题得,所以.故选:B6.已知复数312i z i=+,则复数z 的实部为( )A .25-B .25i -C .15-D .15i -【答案】A 【解析】 解:∵,∴复数z 的实部为25-. 故选A . 7.复数122ii-=+( ) A .1i - B .i -C .iD .1i +【答案】B 【解析】.故选B8.已知i 为虚数单位,复数z 满足:,则在复平面上复数z 对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D 【解析】 因为,所以复平面上复数z 对应的点为13(,)22-,位于第四象限, 故选D .9.设复数z a i =+,z 是其共轭复数,若3455z i z =+,则实数a =( ) A .4 B .3C .2D .1【答案】C 【解析】 解: z a i =+Qz a i ∴=-10.已知i 是虚数单位,复数z 满足,则z =( )A.2B.2 C.1 D.5【答案】A【解析】,所以,故本题选A.11.复数,其中i为虚数单位,则z的实部是()A.-1 B.1 C.2 D.3 【答案】D【解析】解:∴,∴z的实部是3故选:D.12.已知复数,则复数z=()A.2i+B.2i-C.i D.i-【答案】C【解析】由题意,复数,则,故选C. 13.已知i为虚数单位,若,则b a=()A.1 B.2C.2D.2 【答案】C【解析】i为虚数单位,若,根据复数相等得到1212a b ⎧=⎪⎪⎨⎪=⎪⎩.故答案为:C. 14.已知复数z 满足,则||z =( )A .2B .5C .52D .8【答案】C 【解析】 ∵,∴,∴.故选C .15.已知i 是虚数单位,则复数11i i -+在复平面上所对应的点的坐标为( ) A .()0,1 B .()1,0-C .()1,0D .()0,1-【答案】A 【解析】 ∵,∴该复数在复平面上对应的点的坐标为()0,1.故选A.16.若复数z 满足,则在复平面内z 的共轭复数对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A 【解析】由题得,所以1z i =+,所以在复平面内z 的共轭复数对应的点为(1,1),在第一象限. 故选:A17.已知复数z 满足12iz i =+,则z 的虚部是( ) A .1- B .i -C .2D .2i【答案】A 【解析】 因为12iz i =+ 所以所以虚部为1- 所以选A 18.已知31iz i-=-(其中i 为虚数单位),则z 的虚部为( ) A .i - B .1-C .1D .2【答案】B 【解析】 因为,所以2z i =-,故z 的虚部为1-,故选B. 19.复数的虚部为( ) A .1- B .3-C .1D .2【答案】B 【解析】所以z 的虚部为3- 故选B 项. 20.已知复数,212z i =+(i 为虚数单位),若12z z 为纯虚数,则a =( )A .2-B .2C .12-D .12【答案】C 【解析】 ∵,∴,∵12z z 为纯虚数, ∴12020a a +=⎧⎨-≠⎩,解得12a =-.故选:C . 21.设复数z 满足2ii z+=,则z =( ) A .1 B .5C .3D .5【答案】B 【解析】2ii z+=Q,,,故选B.22.已知复数1i z i=-,则2z +在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A【解析】∵,∴, ∴2z +在复平面内对应的点的坐标为211,2⎛⎫- ⎪ ⎪⎝⎭,位于第一象限. 故选:A .23.复数z 满足(1)2z i i -=,则复数z =( )A .1i -B .12i +C .1i +D .1i --【答案】D【解析】由题意得: 1z i ∴=--本题正确选项:D24.若复数是纯虚数,其中m 是实数,则1z =( )A .iB .i -C .2iD .2i -【答案】B【解析】复数z =m (m +1)+(m +1)i 是纯虚数,故m (m +1)=0且(m +1)≠0, 解得m =0,故z =i ,故i .故选:B .25.设i 为虚数单位,则复数22iz i -=+的共扼复数z =( )A .3455i + B .3455i -C .3455i -+D .3455i -- 【答案】 A 【解析】解:,故选:A .26.已知复数1z 、2z 在复平面内对应的点关于虚轴对称,113z i =+,则12z z =( )A .2B .3C .2D .1【答案】D【解析】由题意,复数1z 、2z 在复平面内对应的点关于虚轴对称,113z i =+, 则,所以,故选D.27.已知复数z 1=1+2i ,z 2=l ﹣i ,则12z z =( )A .13i 22-- B .13i 22-+ C .13i 22- D .13i 22+【答案】B【解析】∵,∴.故选:B .28.在复平面内,复数(2i)z -对应的点位于第二象限,则复数z 可取( )A .2B .-1C .iD .2i +【答案】B【解析】不妨设,则, 结合题意可知:,逐一考查所给的选项: 对于选项A :,不合题意; 对于选项B :,符合题意; 对于选项C :,不合题意; 对于选项D :,不合题意; 故选:B .29.已知i 为虚数单位,则复数3(1)i z i i +=-的虚部为( ) A .1B .2C .1-D .2- 【答案】C【解析】因为,所以z 的虚部为1-.30.已知复数(i 为虚数单位)在复平面内对应的点在直线2y x =上,则实数a 的值为( )A .0B .1-C .1D .13- 【答案】D【解析】因为,对应的点为(1,1)a a +-,因为点在直线2y x =上,所以,解得13a =-. 故选D.。
十年真题(2010-2019)高考数学(文)分类汇编专题02 复数(新课标Ⅰ卷)(原卷版)
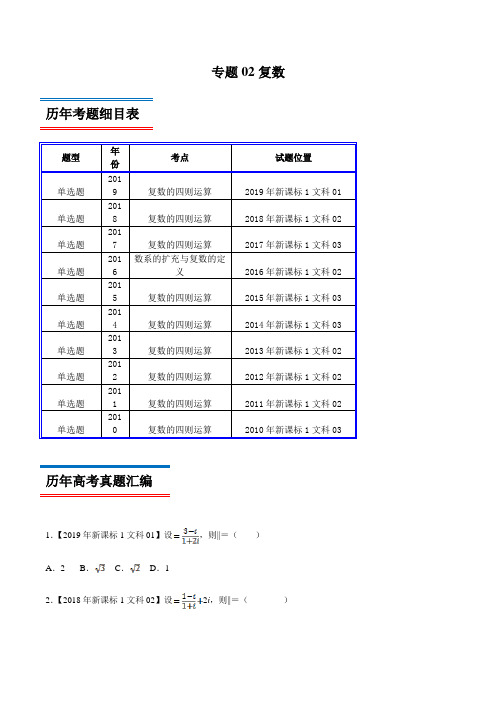
专题02复数历年考题细目表题型年份考点试题位置单选题2019 复数的四则运算2019年新课标1文科01单选题2018 复数的四则运算2018年新课标1文科02单选题2017 复数的四则运算2017年新课标1文科03单选题2016数系的扩充与复数的定义2016年新课标1文科02单选题2015 复数的四则运算2015年新课标1文科03单选题2014 复数的四则运算2014年新课标1文科03单选题2013 复数的四则运算2013年新课标1文科02单选题2012 复数的四则运算2012年新课标1文科02单选题2011 复数的四则运算2011年新课标1文科02单选题2010 复数的四则运算2010年新课标1文科03历年高考真题汇编1.【2019年新课标1文科01】设,则||=()A.2 B.C.D.12.【2018年新课标1文科02】设2i,则||=()A.0 B.C.1 D.3.【2017年新课标1文科03】下列各式的运算结果为纯虚数的是()A.i(1+i)2 B.i2(1﹣i)C.(1+i)2D.i(1+i)4.【2016年新课标1文科02】设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a等于()A.﹣3 B.﹣2 C.2 D.35.【2015年新课标1文科03】已知复数满足(﹣1)i=1+i,则=()A.﹣2﹣i B.﹣2+i C.2﹣i D.2+i6.【2014年新课标1文科03】设i,则||=()A.B.C.D.27.【2013年新课标1文科02】()A.﹣1i B.﹣1i C.1i D.1i8.【2012年新课标1文科02】复数的共轭复数是()A.2+i B.2﹣i C.﹣1+i D.﹣1﹣i9.【2011年新课标1文科02】复数()A.2﹣i B.1﹣2i C.﹣2+i D.﹣1+2i10.【2010年新课标1文科03】已知复数,则||=()A.B.C.1 D.2考题分析与复习建议本专题考查的知识点为:复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算,与向量结合考查复数及其加法、减法的几何意义等,历年考题主要以选择题题型出现,重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算等,预测明年本考点题目会比较稳定,备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算为重点较佳.最新高考模拟试题1.复数52iz =-在复平面上的对应点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.设i z a b =+(a ,b ∈R ,i 是虚数单位),且22i z =-,则有( ) A .1a b +=- B .1a b -=- C .0a b -= D .0a b +=3.若复数1i1ia z +=+为纯虚数,则实数a 的值为( ) A .1B .1-C .0D .24.复数i (1+i )的虚部为( )AB .1C .0D .1-5.已知复数11z i =-+,复数2z 满足122z z =-,则2z = ( )A .2B CD .106.已知复数312i z i=+,则复数的实部为( )A .25-B .25i -C .15-D .15i -7.复数122ii-=+( )A .1i -B .i -C .iD .1i +8.已知i 为虚数单位,复数满足:()z 12i i +=-,则在复平面上复数对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限9.设复数z a i =+,z 是其共轭复数,若3455z i z =+,则实数a =( ) A .4B .3C .2D .110.已知i 是虚数单位,复数满足2(1)1i i z-=+,则z =( )AB .2C .1D 11.复数()()21z i i =+-,其中i 为虚数单位,则的实部是( ) A .-1B .1C .2D .312.已知复数(1)1z i i -=+,则复数z =( ) A .2i +B .2i -C .iD .i -13.已知i 为虚数单位,若1(,)1a bi a b R i=+∈-,则b a =( )A .1B C D .214.已知复数满足2(1i)(3i)z +=+,则||z =( )A BC .D .815.已知i 是虚数单位,则复数11i i -+在复平面上所对应的点的坐标为( ) A .()0,1B .()1,0-C .()1,0D .()0,1-16.若复数满足(1i)|1|z +=+,则在复平面内的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限17.已知复数满足12iz i =+,则的虚部是( ) A .1-B .i -C .2D .2i18.已知31iz i-=-(其中i 为虚数单位),则z 的虚部为( ) A .i -B .1-C .1D .219.复数2(1)41i z i -+=+的虚部为( )A .1-B .3-C .1D .220.已知复数()11z ai a R =+∈,212z i =+(i 为虚数单位),若12z z 为纯虚数,则a =( )A .2-B .2C .12-D .1221.设复数满足2ii z+=,则z =( ) A .1BC .3D .522.已知复数1i z i=-,则z +在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限23.复数满足(1)2z i i -=,则复数z =( ) A .1i -B .12i +C .1i +D .1i --24.若复数2(1)z m m m i =+++是纯虚数,其中m 是实数,则1z=( ) A .iB .i -C .2iD .2i -25.设i 为虚数单位,则复数22iz i-=+的共扼复数z =( ) A .3455i + B .3455i - C .3455i -+ D .3455i -- 26.已知复数1z 、2z在复平面内对应的点关于虚轴对称,11z =,则12z z =( ) A .2BCD .127.已知复数1=1+2i ,2=l ﹣i ,则12z z =( ) A .13i 22-- B .13i 22-+ C .13i 22- D .13i 22+ 28.在复平面内,复数(2i)z -对应的点位于第二象限,则复数可取( ) A .2B .-1C .iD .2i +29.已知i 为虚数单位,则复数3(1)iz i i+=-的虚部为( )A .1B .2C .1-D .2-30.已知复数(i)(1i)z a =+-(i 为虚数单位)在复平面内对应的点在直线2y x =上,则实数a 的值为( )A .0B .1-C .1D .13-。
全国各地高考文科数学试题分类汇编复数

2013年全国各地高考文科数学试题分类汇编:复数一、选择题1 .(2013年高考辽宁卷(文))复数的11Z i =-模为( )A .12B C D .2 【答案】B2 .(2013年高考课标Ⅱ卷(文))||=( )A .2B .2C .D .1【答案】C3 .(2013年高考湖南(文))复数z=i·(1+i)(i 为虚数单位)在复平面上对应的点位于_______( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】B4 .(2013年高考四川卷(文))如图,在复平面内,点A 表示复数z ,则图中表示z 的共轭复数的点是( )A .AB .BC .CD .D【答案】B5 .(2013年高考课标Ⅰ卷(文))212(1)i i +=-( ) A .112i --B .112i -+C .112i +D .112i - 【答案】B6 .(2013年高考北京卷(文))在复平面内,复数(2)i i -对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A7 .(2013年高考山东卷(文))复数)()2(2为虚数单位i ii z -=,则=||z ( )A .25B .41C .5D .5【答案】C8 .(2013年高考江西卷(文))复数z=i(-2-i)(i 为虚数单位)在复平面内所对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】D9 .(2013年高考浙江卷(文))已知i 是虚数单位,则(2+i)(3+i)=( )A .5-5iB .7-5iC .5+5iD .7+5i【答案】C10.(2013年高考安徽(文))设i 是虚数单位,若复数10()3a a R i-∈-是纯虚数,则a 的值为( )A .-3B .-1C .1D .3【答案】D11.(2013年高考福建卷(文))复数i z 21--=(i 为虚数单位)在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】C12.(2013年高考广东卷(文))若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是( )A .2B .3C .4D .5【答案】D二、填空题13.(2013年高考天津卷(文))i 是虚数单位. 复数(3 + i )(1-2i ) = ______.【答案】55i -14.(2013年高考重庆卷(文))已知复数12z i =+(i 是虚数单位),则z =____________.15.(2013年上海高考数学试题(文科))设m ∈R ,()2221i m m m +-+-是纯虚数,其中i 是虚数单位,则m =________.【答案】2m =-16.(2013年高考湖北卷(文))i 为虚数单位,设复数1z ,2z 在复平面内对应的点关于原点对称,若123i z =-,则2z =__________.【答案】23i -+2013年全国各地数学文科高考试题分类汇编:集合一、选择题17(2013上海高考(文科))设常数a ∈R ,集合()(){}|10A x x x a =--≥,{}|1B x x a =≥-.若A B =R ,则a 的取值范围为( )A .(),2-∞B .(],2-∞C .()2,+∞D .[)2,+∞【答案】B 18 .(2013年高考重庆卷(文))已知集合{1,2,3,4}U =,集合={1,2}A ,={2,3}B ,则()U A B =ð( )A .{1,3,4}B .{3,4}C .{3}D .{4}【答案】D19 .(2013年高考浙江卷(文))设集合S={x|x>-2},T={x|-4≤x≤1},则S∩T=( )A .[-4,+∞)B .(-2, +∞)C .[-4,1]D .(-2,1]【答案】D20 .(2013年高考天津卷(文))已知集合A = {x ∈R | |x |≤2}, B = {x ∈R | x ≤1}, 则A B ⋂=( )A .(,2]-∞B .[1,2]C .[-2,2]D .[-2,1]【答案】D21 .(2013年高考四川卷(文))设集合{1,2,3}A =,集合{2,2}B =-,则A B =( )A .∅B .{2}C .{2,2}-D .{2,1,2,3}-【答案】B22 .(2013山东卷(文))已知集合B A 、均为全集}4,3,2,1{=U 的子集,且(){4}U A B =ð,{1,2}B =,则U A B =ð( )A .{3}B .{4}C .{3,4}D .∅【答案】A23 .(2013年高考辽宁卷(文))已知集合{}{}1,2,3,4,|2,A B x x A B ==<=则( )A .{}0B .{}0,1C .{}0,2D .{}0,1,2【答案】B24 .(2013年高考课标Ⅱ卷(文))已知集合M={x|-3<X<1},N={-3,-2,-1,0,1},则M ∩N=( )A .{-2,-1,0,1}B .{-3,-2,-1,0}C .{-2,-1,0}D .{-3,-2,-1 }【答案】C 25 .(2013年高考课标Ⅰ卷(文))已知集合{1,2,3,4}A =,2{|,}B x x n n A ==∈,则A B =( )A .{0}B .{-1,,0}C .{0,1}D .{-1,,0,1}【答案】A26.(2013年高考江西卷(文))若集合A ={x ∈R|ax 2+ax+1=0}其中只有一个元素,则a=( ) A .4B .2C .0D .0或4【答案】A27.(2013年高考湖北卷(文))已知全集{1,2,3,4,5}U =,集合{1,2}A =,{2,3,4}B =,则U B A =ð( )A .{2}B .{3,4}C .{1,4,5}D .{2,3,4,5}【答案】B28.(2013年高考广东卷(文))设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =( )A .{0}B .{0,2}C .{2,0}-D .{2,0,2}-【答案】A29.(2013年高考福建卷(文))若集合}4,3,1{},3,2,1{==B A ,则B A 的子集个数为( )A .2B .3C .4D .16【答案】C30.(2013年高考大纲卷(文))设集合{}{}1,2,3,4,5,1,2,u U A A ===集合则ð( )A .{}1,2B .{}3,4,5C .{}1,2,3,4,5D .∅【答案】B31.(2013年高考北京卷(文))已知集合{}1,0,1A =-,{}|11B x x =-≤<,则A B =( )A .{}0B .{}1,0-C .{}0,1D .{}1,0,1-【答案】B32.(2013年高考安徽(文))已知{}{}|10,2,1,0,1A x x B =+>=--,则()R C A B ⋂=( )A .{}2,1--B .{}2-C .{}1,0,1-D .{}0,1【答案】A二、填空题33.(2013年高考湖南(文))对于E={a 1,a 2,.a 100}的子集X={a 1,a 2,,a n },定义X 的“特征数列”为x 1,x 2,x 100,其中x 1=x 10=x n =1.其余项均为0,例如子集{a 2,a 3}的“特征数列”为0,1,0,0,,0(1) 子集{a 1,a 3,a 5}的“特征数列”的前三项和等于____ _______;(2) 若E 的子集P 的“特征数列”P 1,P 2,,P 100 满足P 1+P i+1=1, 1≤i≤99;E 的子集Q 的“特征数列” q 1,q 2,q 100 满足q 1=1,q 1+q j+1+q j+2=1,1≤j≤98,则P∩Q 的元素个数为_________.【答案】(1) 2 (2)1734.(2013湖南(文))已知集合{2,3,6,8},{2,3},{2,6,8}U A B ===,则()C A B ⋃⋂=_____【答案】}862{,,。
(完整)人教版最新高考数学复数习题及答案Word版.docx

高考复习试卷 ( 附参考答案 )一、选择题 (每小题只有一个选项是正确的,每小题5 分,共 100 分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)3- i()1. (2013 山·东 )复数 1- i 等于A .1+ 2iB . 1-2iC . 2+ iD . 2-i 答案: C3-i (3- i)(1 + i) 4+ 2i = 2+ i.故选 C.解析: 1- i = (1- i)(1 + i) =22. (2013 宁·夏、海南 )复数 3+ 2i - 3- 2i =(2- 3i 2+ 3i A .0 B . 2 C .- 2i D .2i 答案: D3+2i 3- 2i (3+ 2i)(2 + 3i) (3- 2i)(2 - 3i) 13i -13i解析: 2-3i - 2+ 3i = (2- 3i)(2 + 3i)- (2- 3i)(2 + 3i) =13 - 13 = i +i =2i.z + 2是实数,那么 z 等于() 3. (2013 陕·西 )已知 z 是纯虚数, 1- iA .2iB . iC .- iD .- 2i答案: D 解析: 由题意得 z = ai.( a ∈R 且 a ≠ 0).∴z + 2=(2 +ai)(1 + i) = 2- a + (a +2)i ,- i (1- i)(1 + i)21则 a + 2=0, ∴ a =- 2.有 z =- 2i ,故选 D.4. (2013 武·汉市高三年级 2 月调研考试 )若 f(x)= x 3- x 2+ x - 1,则 f(i) = () A .2i B . 0 C .- 2i D .- 2 答案: B 解析: 依题意, f(i) = i 3- i 2+ i -1=- i + 1+ i - 1=0,选择 B.2- i5. (2013 北·京朝阳 4 月 )复数 z = 1+ i (i 是虚数单位 )在复平面内对应的点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 答案: D解析: z =2- i = 1- 3 i ,它对应的点在第四象限,故选 D.1+ i 2 26. (2013 北·京东城 3月 )若将复数 2+i 表示为 a + bi(a , b ∈ R , i 是虚数单位 )的形式,则 i( ))ba 的值为 1 1A .- 2B .- 2C . 2 D.2答案: A解析: 2+i = 1- 2i ,把它表示为 a +bi( a , b ∈ R ,i 是虚数单位 )的形式,则 b 的值为- 2,故选 A.i a7. (2013 北·京西城 4 月 )设 i 是虚数单位,复数 z = tan45 -° i sin60· ,°则 z 2等于 ( )A. 7- 3i B.1- 3i 4 4 C. 7+ 3i D.1+ 3i 44答案: B解析: z = tan45 °-i ·sin60 °= 1-313i ,故选 B.2 i ,z 2 = -48. (2013 黄·冈中学一模 )过原点和 3- i 在复平面内对应的直线的倾斜角为()π π A. 6B .- 6 2 5 C.3πD.6π答案: D解析:3- i 对应的点为 ( 3,- 1),所求直线的斜率为-3,则倾斜角为536π,故选 D.a + bi为实数,则()9.设 a 、b 、 c 、 d ∈R ,若 c + diA .bc + ad ≠ 0B . bc - ad ≠0C . bc - ad = 0D . bc + ad = 0 答案: Ca + bi (a + bi)( c - di) ac + bd bc - adbc - ad = 0? bc - ad = 0.解析: 因为 = 2 2= 2 2 + 2 2 i ,所以由题意有 22 c + di c + d c + d c + d c + d10.已知复数 z = 1-2i ,那么 1 =()z5+ 2 55- 2 5A. 55 iB. 55 iC. 1+2iD. 1- 2i5555答案: D解析: 由 z = 1- 2i 知 z = 1+2i ,于是1 = 1 = 1- 2i = 1- 2i.故选 D.z 1+ 2i 1+ 4 5 5z 1是实数,则实数b 的值为()11.已知复数 z 1=3- bi , z 2= 1- 2i ,若 z 2 1A .6B .- 6C . 0D.6答案: A1 3-bi (3- bi)(1 + 2i)(3+ 2b)+ (6-b)i= = = 是实数,则实数 b 的值为 6,故选 A.解析: 21- 2i (1- 2i)(1 + 2i)5z12. (2013 ·东广 )设 z 是复数, α(z)表示满足 z n= 1 的最小正整数 n ,则对虚数单位 i , α(i)=( )A .2B . 4C . 6D . 8 答案: B解析: α(i)表示 i n = 1 的最小正整数 n ,因 i 4k = 1(k ∈ N * ),显然 n = 4,即 α(i)= 4.故选 B.1+ 34= a 0 4+ a 1 3+ a 2 2+ a 3 4 2等于()13.若 z =22 i ,且 (x - z)x x x x + a ,则 a A .- 1+ 3iB .- 3+ 3 3i2 2 C . 6+3 3iD .- 3-3 3i答案: Br 4- rr,解析: ∵T r + 1=C 4x(- z)由 4- r = 2 得 r = 2,221 32∴ a 2= C 4 (- z) = 6× (- 2-2 i)=- 3+ 3 3i .故选 B.14.若△ ABC 是锐角三角形,则复数 z = (cosB - sinA)+ i(sinB - cosA)对应的点位于 ()A .第一象限B .第二象限C .第三象限D .第四象限 答案: B解析: ∵△ ABC 为锐角三角形,∴ A +B > 90°, B > 90°- A , ∴ cosB < sinA , sinB > cosA , ∴ cosB - sinA < 0, sinB - cosA > 0, ∴ z 对应的点在第二象限.2- bi15.如果复数 1+ 2i (其中 i 为虚数单位, b 为实数 )的实部和虚部互为相反数,那么b 等于2 2( )A. 2B. 3C .- 3D . 2答案: C解析: 2-bi = (2- bi)(1 - 2i)1+2i 5=(2- 2b)+ (- 4-b)i55由 2- 2b =-- 4- b5得 b =- 2.531 + 3 ()16.设函数 f(x)=- x 5+5x 4- 10x 3+ 10x 2- 5x +1,则 f(2i )的值为2A .- 1 + 3iB.312 22- i2 C. 1 +3 i D .-3 12 22+ i2答案: C解析: ∵f(x)=- (x - 1)5∴ f(1+ 3i )=- (1+ 3i - 1)52 22 2=- ω5(其中 ω=- 12+ 23i)=- ω =- (-1- 31+ 32 2 i )= 2 2 i .17.若 i 是虚数单位,则满足(p +qi )2= q + pi 的实数 p , q 一共有()A .1 对B . 2 对C . 3 对D .4 对 答案: Dp 2- q 2= q ,p = 0, p = 0, 解析: 由(p + qi)2= q +pi 得(p 2- q 2)+ 2pqi =q + pi ,所以解得q = 0,或q =- 1,2pq = p.33p = 2 ,或 p =- 2 ,因此满足条件的实数p , q 一共有 4 对.或1,1,q = 2q = 2总结评述: 本题主要考查复数的基本运算,解答复数问题的基本策略是将复数问题转化为实数问题来解决,解答中要特别注意不要出现漏解现象,如由 12pq = p 应得到 p = 0 或 q = .22 - x 6 的展开式中,不含x 的项是20,那么正数 p 的值是 ()18.已知 (2)27 xpA .1B . 2C . 3D . 4答案: C解析: 由题意得:120,求得 p =3.故选 C.C 64·4·22=27px 的项,即找常数项.总结评述: 本题考查二项式定理的展开式,注意搭配展开式中不含2 x- x-1)i(x ∈ R)在复平面内对应的点位于 ()19.复数 z =- lg(x +2) -(2 + 2 A .第一象限 B .第二象限 C .第三象限 D .第四象限 答案: C解析: 本题考查复数与复平面上的点之间的关系,复数与复平面上的点是一一对应的关系,即z = a +bi ,与复平面上的点 Z( a , b)对应,由 z =- lg(x 2+2) -(2 x + 2-x -1)i(x ∈ R)知:a =- lg(x2+ 2)< 0,又 --x- 1= 1> 0;2x + 2x- 1≥ 2 2x·2∴ - (2x +2-x - 1)< 0,即 b < 0.∴(a , b)应为第三象限的点,故选 C.20.设复数 z + i(z ∈C )在映射 f 下的象为复数 z 的共轭复数与 i 的积,若复数ω 在映射 f 下的象为- 1+ 2i ,则相应的 ω为() A .2 B . 2- 2i C .- 2+ i D . 2+ i答案: A解析: 令 ω= a + bi , a , b ∈ R ,则 ω= [a + (b -1)i] + i ,∴ 映射 f 下 ω的象为 [a - (b - 1)i] ·i = (b - 1)+ai =- 1+ 2i.b - 1=- 1, b = 0,∴ 解得 a = 2. ∴ ω= 2.a = 2.第Ⅱ卷(非选择题共 50 分)二、填空题 (本大题共 5 小题,每小题 4 分,共 20 分,请将答案填在题中的横线上。
高考文科数学真题汇编复数高考题学生版

i)a(12i)(年全国I卷)设为实数,则a=的实部与虚部相等,其中a27、(20163
)2(D)B)?2(C3(A)?(i3zi)II卷)设复数z满足,则=((28、2016年全国z2i2i33()(C(B))(A)D2i2i11
222i(1+i)
(1+i)D Bi (1-i)
Ai(1+i)C....)
( (1i)(2i))32.(2017=++年新课标Ⅱ文3i
-.3 D i B.1+3i C.3+.A1-i
I201733)卷理)、(年全国设有下面四个命题(1zzppR;满足:若复数,则满足;,则:若复数2RzRzRz12zRzzpz,zp.:若复数:若复数,则;满足,则zzRzRz21321421p,p,p,p,ppppDCBA....42314132
精品文档.
欢迎来主页下载---精品文档
z3i4z=卷)III若,则29、(2016年全国|z|3443)(D(C))(A)1(B1ii5555)(卷文)复平面内表示复数z=i(–2+i)的点位于、30(2017年全国III.第四象限D C.第三象限A.第一象限B.第二象限
)(31、(2017年全国I卷文)下列各式的运算结果为纯虚数的是
精品文档.
欢迎来主页下载---精品文档
444)(D(C)(A)4(B)55
i21)2013年新ຫໍສະໝຸດ 标文)((20、2)i(11111ii11i1i1D)B)(C)()(A(2222
2i1年北京)复数201621、(=i2
))(D((A)iB)1+i(Ci1i其中i22、(2016年江苏)复数________________.z的实部是为虚数单位,则i),2i)(3z(1
山东省各地市2024年高考数学(文科)最新试题分类大汇编24:复数-推理与证明

【山东省济宁市邹城二中2024届高三其次次月考文】1.已知i 是虚数单位,=-+i i21( )A .i 5151+ B .i 5351+C .i 5153+D .i 5353-【答案】B【山东省济宁市邹城二中2024届高三其次次月考文】13.给出下列命题:命题1:点(1,1)是直线y = x 与双曲线y = x1的一个交点; 命题2:点(2,4)是直线y = 2x 与双曲线y = x8的一个交点; 命题3:点(3,9)是直线y = 3x 与双曲线y = x27的一个交点; … … .请视察上面命题,猜想出命题n (n 是正整数)为: .【答案】),(2n n ) 是直线y=nx 与双曲线yn y 3=的一个交点【山东省济宁市鱼台二中2024届高三11月月考文】6.设i z -=1(为虚数单位),则=+zz 22( )A .i --1B .i +-1C .i +1D . i -1【答案】D【山东省济宁市汶上一中2024届高三11月月考文】7、计算=+-i i13( )A 、i 21+B 、i 21-C 、i +2D 、 i -2【答案】B【山东省济南市2024届高三12月考】6.复数z 满意(12)7i z i -=+,则复数z 的共轭复数z =A.i 31+B. i 31-C. i +3D. i -3【答案】B【山东省济南市2024届高三12月考】16. )(x f 是定义在R 上恒不为0的函数,对随意x 、R ∈y 都有)()()(y x f y f x f +=,若))((,21*1N n n f a a n ∈==,则数列{}n a 的前n 项和n S 为A .12121+-=n n SB .1211+-=n n S C.n n S 211-= D .n n S 2121-=【答案】C【山东省济宁市重点中学2024届高三上学期期中文】11. 若复数3(R,12a iz a i i+=∈-是虚数单位),且z 是纯虚数,则|2|a i +等于( )A .5B .210C .25D .40 【答案】B【山东省济宁一中2024届高三第三次定时检测文】2.复数123,1z i z i =+=-,则复数12z z 在复平面内对应的点位于 ( ) A .第一象限 B .其次象限 C .第三象限 D .第四象限 【答案】A【山东省莱州一中2024届高三其次次质量检测】对于连续函数)(x f 和)(x g ,函数|)()(|x g x f -在闭区间[b a ,]上的最大值为)(x f 与)(x g 在闭区间[b a ,]上的“肯定差”,记为b x a x g x f ≤≤∆)).(),((则322221331≤≤-+∆x x)x ,x (= 【答案】103【山东省青州市2024届高三2月月考数学(文)】13.若复数312a ii-+(,a R i ∈为虚数单位)是纯虚数,则实数a 的值为 . 【答案】6【山东省青州市2024届高三2月月考数学(文)】15.在一次演讲竞赛中,10位评委对一名选手打分的茎叶图如下所示,若去掉一个最高分和一个最低分,得到一组数据(18)i x i ≤≤,在如图所示的程序框图中,x 是这8个数据中的平均数,则输出的2S 的值为_ ____【答案】15【山东省青州市2024届高三上学期期中文16.已知数列{}n a 中,11211,241n n a a a n +==+-,则n a = 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009-20XX 年高考文科数学试题分类汇编—— 复数一、选择题1.( 20XX 年广东卷文)下列 n 的取值中,使 i n= 1( i 是虚数单位)的是()(A ) n = 2 ( B ) n = 3 ( C ) n = 4 ( D ) n =52.( 2009 浙江卷文)设 z = 1+ i ( i 是虚数单位) ,则 2 + z 2=()z(A ) 1+ i ( B )- 1+ i ( C ) 1- i ( D )- 1-i3.( 2009 山东卷文)复数 3 - i等于()1- i(A ) 1+ 2i ( B )1- 2i ( C ) 2+ i ( D ) 2- i 4. ( 2009 安徽卷文) i 是虚数单位, i ( 1+ i )等于()(A ) 1+ i(B )- 1- i(C ) 1-i ( D )- 1+ i5i5.( 2009 天津卷文) i 是虚数单位, 2- i =()(A ) 1+ 2i ( B )- 1- 2i (C ) 1-2i( D )- 1+ 2i6. ( 2009 宁夏海南卷文)复数 3+ 2i2- 3i =()(A )1(B )- 1(C ) i( D )- i17. ( 2009 辽宁卷文)已知复数 z = 1- 2i ,那么 z =()(A ) 5+2 55-2 5121255 i ( B ) 55 i (C ) 5 + 5 i ( D )5 - 5 i28.( 2010 湖南文数 1)复数 1- i 等于()(A ) 1+ i ( B ) 1- i( C )- 1+ i ( D )- 1- i9.( 2010 浙江理数)对任意复数 z = x + yi ( x R , y R ), i 为虚数单位,则下列结论正确的 是()(A ) |z --z|= 2y ( B ) z 2=x 2+ y 2(C ) |z --z| ≥2x ( D ) |z| ≤|x + |y|3- i2=() 10.( 2010 全国卷 2 理数)复数( 1+ i )(A )- 3- 4i ( B )- 3+ 4i ( C ) 3- 4i (D ) 3+ 4ii11.(2010 陕西文数)复数 z = 1+ i 在复平面上对应的点位于()(A )第一象限( B )第二象限( C )第三象限( D )第四象限1+ 2i12.( 2010 辽宁理数( 2))设 a , b 为实数,若复数 a + bi = 1+ i ,则()(A ) a =31 2 , b =2 ( B )a = 3, b = 1(C ) a =132 , b =2 ( D )a = 1, b = 313.( 2010 江西理数)已知( x +i )( 1- i )= y ,则实数 x ,y 分别为()(A ) x =- 1, y = 1( B )x =- 1, y = 2(C ) x =1, y = 1(D ) x =1, y = 214.( 2010 安徽文数( 2))已知 i 2=- 1,则 i ( 1- 3 i )=()(A ) 3 - i ( B ) 3 + i ( C )- 3 - i ( D )- 3 + i 15.( 2010 浙江文数)设 i 为虚数单位,则 5- i =()1+ i (A )- 2- 3i( B )- 2+ 3i(C ) 2-3i(D ) 2+ 3i16.( 2010 山东文数)已知a +2i= b + i ( a , b R ),其中 i 为虚数单位,则 a + b =()i(A )- 1(B ) 1(C ) 2(D ) 317.( 2010 北京文数( 2))在复平面内,复数 6+ 5i ,- 2+ 3i 对应的点分别为 A , B ,若 C 为线段 AB 的中点,则点 C 对应的复数是()(A ) 4+ 8i( B ) 8+ 2i( C )2+ 4i( D ) 4+ i18.( 2010 四川理数( 1)) i 是虚数单位,计算 i + i 2+i 3=()(A )-1(B )1( C )- i ( D ) i3+i19.( 2010 天津文数) i 是虚数单位,复数 1-i =() (A ) 1+ 2i ( B ) 2+ 4i ( C )- 1- 2i (D ) 2-i 20.( 2010 天津理数) i 是虚数单位,复数-1+ 3i =()1+ 2i(A ) 1+ i ( B ) 5+ 5i ( C )- 5-5i ( D )- 1- i21.( 2010 广东理数)若复数 z 1= 1+ i ,z 2 = 3- i ,则 z 1·z 2 =()(A ) 4+ 2 i( B ) 2+ i( C ) 2+ 2 i (D )322.( 2010 福建文数) i 是虚数单位,( 1+ i ) 4等于()1- i(A ) i( B )- i(C ) 1( D )- 13+2i23.( 2010 全国卷 1 理数( 1))复数 2- 3i =() (A ) i ( B )- i ( C ) 12- 13i ( D ) 12+ 13i24.( 2010 山东理)已知 a + 2i =b + i ( a , b ∈R ),其中 i 为虚数单位,则 a + b =()i (A )-1(B ) 1(C )2(D )325.( 2010 安徽理数 1) i 是虚数单位,i=()3 + 3i(A )131 31 3 13 i4 - 12 I (B )4 + 12 i (C ) 2 + 6 i (D ) 2 - 6i - 226. ( 20XX 年北京理)复数 1+ 2i =()(A ) i( B )- i(C )- 4- 3i(D )-4+ 3i5 55 527.( 20XX 年福建理) i 是虚数单位,若集合S = { -1, 0, 1} ,则()(A ) i S ( B ) i 2S(C ) i 32S ( D ) i S28.( 2010 湖北理数)若 i 为虚数单位,图中复平面内点 Z 表示复数zZ ,则表示复数1+ i 的点是()(A )E (B )F (C )G (D )H29.( 20XX 年安徽理( 1))设 i 是虚数单位,复数 1+ ai为纯虚数,则实数 a 为() 2- i (A )2(B )- 2(C )- 1( D )12230.( 20XX 年福建文) i 是虚数单位, 1+ i 3等于()(A ) i ( B )- i ( C ) 1+ i ( D ) 1- i31.( 20XX 年广东理 1)设复数 z 满足( 1+i ) z = 2,其中 i 为虚数单位,则 Z =()(A ) 1+ i( B ) 1- i( C ) 2+ 2i( D ) 2- 2i32.( 20XX 年广东文 1)设复数 z 满足 iz = 1,其中 i 为虚数单位,则 z =() (A )- i (B ) i ( C )- 1(D ) 11+ i2011=()33.( 20XX 年湖北理 1) i 为虚数单位,则( 1- i ) (A )- i (B )- 1( C )i (D ) 134.( 20XX 年湖南理 1)若 a ,b R , i 为虚数单位,且( a + i ) i = b + i ,则() (A ) a = 1, b = 1( B ) a =- 1,b = 1(C ) a =- 1, b =- 1( D ) a = 1, b =- 135.( 20XX 年江西理 1)设 z = 1+2i ,则复数 -z =()i(A )- 2- i ( B )- 2+ i ( C ) 2- i ( D ) 2+ i36.( 20XX 年江西文 1)若( x -i ) i = y +2i , x , y R ,则复数 x +yi =()(A )- 2+ i ( B ) 2+ i ( C ) 1- 2i ( D ) 1+2i37.( 20XX 年辽宁理 1) a 为正实数, i 为虚数单位, | a + i|= 2,则 a =() i (A )2(B ) 3 (C ) 2 (D )1111 138.( 20XX 年辽宁文 2) i 为虚数单位, i + i 3 + i 5 + i 7 =() (A )0 ( B ) 2i ( C )- 2i ( D )4i2+ i39.( 20XX 年全国Ⅰ理( 1))复数 1- 2i 的共轭复数是()(A )-35i ( B )35i ( C )- i ( D ) i40.( 20XX 年全国Ⅰ文( 3))已知复数 z =3 + i,则 |z|=()(1- 3 i) 2(A )1( B )1( C )1(D )24241.( 20XX 年全国Ⅱ理( 1))复数 z = 1+ i ,-z 为 z 的共轭复数,则 z -z - z - 1=() (A )- 2i ( B )- i (C ) i ( D ) 2i2- i42.( 20XX 年山东理)复数 z = 2+ i ( i 为虚数单位)在复平面内对应的点所在象限为()(A )第一象限( B )第二象限( C )第三象限( D )第四象限43.( 20XX1=()年四川理 2)复数- i + i(A )- 2i ( B )1i ( C ) 0( D ) 2i244.( 20XX 年天津理 1) i 是虚数单位,复数 - 1+ 3i =( )1+ 2i (A ) 1+ i ( B ) 5+ 5i ( C )- 5- 5i ( D )- 1- i3+ i45.( 20XX 年天津文 1) i 是虚数单位,复数 1- i ()(A ) 1+ 2i ( B )2+ 4i ( C )- 1- 2i ( D ) 2- i46.( 20XX 年浙江文)若复数z =1+ i ,i 为虚数单位,则( 1+ i )z =()(A ) 1+ 3i ( B )3+ 3i ( C ) 3- i ( D ) 347.( 20XX 年重庆理( 1))复数 i 2+ i 3+ i 4=()1- i1 1 1 11 1 1 1 (A )- - i ( B )-+ i ( C ) - i (D ) + i2 222222 248.【 2012 安徽文 1】复数 z 满足( z - i ) i =2+ i ,则 z =() (A )- 1- i ( B )1- I ( C )- 1+ 3i ( D ) 1-2i 49.【 2012新课标文 2】复数 z =- 3+ i的共轭复数是()2+ i(A ) 2+ i ( B ) 2- i( C )- 1+ i ( D )- 1- i50.【 2012 山东文 1】若复数 z 满足 z ( 2- i )= 11+7i ( i 为虚数单位),则为()(A ) 3+ 5i(B ) 3-5i( C )- 3+5i (D )- 3- 5i3+i =()51.【 2012浙江文 2】已知 i 是虚数单位,则 1-i(A ) 1- 2i ( B ) 2- i ( C )2+ i ( D )1+ 2i52.【 2012 上海文】若 1+ 2i 是关于 x 的实系数方程 x 2+ bx +c = 0 的一个复数根,则()(A ) b = 2, c = 3( B )b = 2, c =- 1(C ) b =- 2, c =- 1( D ) b =- 2, c = 31 =( )53.【 2012 辽宁文 3】复数 1+i(A )1- 1i ( B )1+ 1i ( C )1- i ( D ) 1+ i2 22 2- 2- 2 的虚部为 54.【 2012 江西文 1】若复数 z = 1+ i ( i 为虚数单位) z 是 z 的共轭复数,则 z + z ()(A )0 (B )- 1 ( C )1 (D )- 255.【 2012 湖南文 2】复数 z = i ( i + 1)(i 为虚数单位)的共轭复数是( )(A )- 1- i ( B )- 1+i( C ) 1- i( D ) 1+ i56.【 2012 广东文 1】设 i 为虚数单位,则复数3+ 4i =( )i(A )- 4- 3i ( B )- 4+ 3i ( C ) 4+ 3i (D ) 4- 3i 57.【 2102 福建文 1】复数( 2+ i ) 2 等于( )(A ) 3+ 4i( B ) 5+ 4i(C ) 3+2i ( D ) 5+ 2i58.【 2102 北京文 2】在复平面内,复数 10i 对应的点的坐标为()3+ i(A )(1 , 3)( B )(3, 1)( C )(- 1,3)( D )( 3 ,- 1)59.【 2012 天津文科1】 i 是虚数单位,复数5+ 3i=4- i(A ) 1- i ( B)- 1+ i( C) 1+ i( D)- 1-i60.( 20XX1 模为()年辽宁卷(文))复数的 z=i-1(A )1(B)2(C) 2 (D)22 2261.( 20XX 年课标Ⅱ卷(文)) |1+i |=()(A )2 2 (B)2 (C) 2 (D)162.( 20XX 年北京卷(文))在复平面内,复数 i ( 2- i )对应的点位于()(A )第一象限( B )第二象限(C)第三象限( D )第四象限63.( 20XX 年山东卷(文))复数 z=(2-i)2( i 为虚数单位),则 |z|=()i(A )25 (B) 41 ( C) 5 (D) 51+ 2i64.( 20XX 年课标Ⅰ卷(文))(1-i) 2=()(A )- 1-1i (B)- 1+1i2 2(C) 1+1i ( D) 1-1i 2 265.( 20XX 年福建卷)复数z=- 1- 2i ( i 为虚数单位)在复平面内对应的点位于()(A )第一象限( B )第二象限( C)第三象限( D )第四象限66.( 20XX 年广东卷(文))若 i ( x+ yi )= 3+ 4i, x,y R,则复数 x+ yi 的模是()(A )2 (B)3 (C) 4 (D)567.( 20XX 年江西卷)复数z= i(- 2-i )( i 为虚数单位)在复平面内所对应的点在()(A )第一象限( B )第二象限(C)第三象限( D )第四象限68.( 20XX 年四川卷(文))如图,在复平面内,点 A 表示复数 z,则图中表示 z 的共轭复数的点是()(A )A (B)B(C) C( D) D69.( 20XX 年浙江卷(文))已知 i 是虚数单位,则(2+ i)( 3+ i )=()(A ) 5- 5i ( B) 7- 5i (C) 5+5i ( D) 7+ 5i70.(20XX10(a R)是纯虚数,则 a 的值为()年安徽)设 i 是虚数单位,若复数 a-3-i(A)-3 (B)- 1 (C)1 (D)3二、填空题71.( 2009 江苏卷)若复数z = 4+ 29i, z = 6+ 9i,其中 i 是虚数单位,则复数(z1- z2)i1 2的实部为 .72.( 2009 福建卷文)复数i2( 1+ i )的实部是.73.( 20XX 年江苏 3)设复数 i 满足 i ( z+ 1)=- 3+ 2i( i 是虚数单位),则 z 的实部是 ___2- i74.( 20XX 年浙江理 2)已知复数 z=1-i,其中 i 是虚数单位,则 |z|=.3+ bi75.【 2012 湖北文 12】若1-i = a+ bi ( a, b 为实数, i 为虚数单位),则 a+ b=____.11-7i76.【 2012 江苏 3】设 a, b 为实数, a+ bi =1-2i( i 为虚数单位),则 a+b 的值为.3- i77.【 2012 上海文 1】计算:=( i 为虚数单位)1 +i78.( 20XX 年湖南)复数z= i ·( 1+ i )( i 为虚数单位)在复平面上对应的点位于___.79.( 20XX 年天津卷(文)) i 是虚数单位 . 复数( 3+i )(1- 2i)= ______.80.( 20XX 年重庆卷(文))已知复数 z= 1+ 2i ( i 是虚数单位),则 |z|= ____________.81.(20XX 年上海卷(文科))设 m R, m2+ m- 2( m2-1)i ,是纯虚数,其中i 是虚数单位,则 m= ___.82.( 20XX 年湖北卷(文))i 为虚数单位,设复数 z1,z2在复平面内对应的点关于原点对称,若 z1= 2- 3i,则 z2= __________.三、解答题83.( 20XX 年上海理 19)已知复数z1满足( z1- 2)( 1+ i )= 1-i (i 为虚数单位),复数 z2 的虚部为2,且 z1z2是实数,求z2.。
