东诚教育集团模拟1—389
山东南山集团东海外国语学校2024年数学九上开学检测模拟试题【含答案】

山东南山集团东海外国语学校2024年数学九上开学检测模拟试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)在平面直角坐标系中,若点与点关于原点对称,则点在()A .第一象限B .第二象限C .第三象限D .第四象限2、(4分)若x =,y =,则x 2+2xy +y 2=()A .12B .8C .2D .3、(4分)矩形的对角线一定具有的性质是()A .互相垂直B .互相垂直且相等C .相等D .互相垂直平分4、(4分)下列事件中,属于随机事件的是()A .抛出的篮球往下落B .在只有白球的袋子里摸出一个红球C .购买10张彩票,中一等奖D .地球绕太阳公转5、(4分)下列各点中,在正比例函数2y x =-的图象上的点是()A .(1,1)-B .(2,1)-C .(1,2)-D .(2,2)-6、(4分)用配方法解方程x 2﹣2x ﹣5=0时,原方程应变形为()A .(x +1)2=6B .(x +2)2=9C .(x ﹣1)2=6D .(x ﹣2)2=97、(4分)有意义,则x 应满足()A .x ≥3B .x ≥﹣3C .x >3D .x >﹣38、(4分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a ,较短直角边长为b .若ab=8,大正方形的面积为25,学校________________班级____________姓名____________考场____________准考证号…………………………密…………封…………线…………内…………不…………要…………答…………题…………………………则小正方形的边长为()A .9B .6C .4D .3二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)二项方程32540x +=在实数范围内的解是_______________10、(4分)若51x =,则代数式221x x ++的值为__________.11、(4分)如图,三个正方形中,其中两个正方形的面积分别是100,36,则字母A 所代表的正方形的边长是_____.12、(4分)13123-=__.13、(4分)如图,在平面直角坐标系中,菱形OABC 的边OA 在x 轴上,AC 与OB 交于点D (4,2),反比例函数k y x =的图象经过点D .若将菱形OABC 向左平移n 个单位,使点C 落在该反比例函数图象上,则n 的值为_____________.三、解答题(本大题共5个小题,共48分)14、(12分)如图,在Rt △ABC 中,∠ACB =90°,D 是AB 上一点,BD =BC ,过点D 作AB 的垂线交AC 于点E ,连接CD ,交BE 于点F.求证:BE 垂直平分CD .15、(8分)已知某实验中学有一块四边形的空地ABCD ,如图所示,学校计划在空地上种植草坪,经测量∠A =90°,AC =3m ,BD =12m ,CB =13m ,DA =4m ,若每平方米草坪需要300元,间学校需要投入多少资金买草坪?16、(8分)如图,已知等腰Rt △ABC 中,AB =AC ,∠BAC =90,点A、B 分别在x 轴和y轴上,点C 的坐标为(6,2).(1)如图1,求A 点坐标;(2)如图2,延长CA 至点D ,使得AD =AC ,连接BD ,线段BD 交x 轴于点E ,问:在x 轴上是否存在点M ,使得△BDM 的面积等于△ABO 的面积,若存在,求点M 的坐标;若不存在,请说明理由.17、(10分)已知如图:直线AB 解析式为3=-+y x ,其图像与坐标轴x ,y 轴分别相交于A 、B 两点,点P 在线段AB 上由A 向B 点以每秒2个单位运动,点C 在线段OB 上由O 向B 点以每秒1个单位运动(其中一点先到达终点则都停止运动),过点P 与x 轴垂直的直线交直线AO 于点Q .设运动的时间为t 秒(t ≥0).(1)直接写出:A 、B 两点的坐标A (),B ().∠BAO =______________度;(2)用含t 的代数式分别表示:CB =,PQ =;(3)是否存在t 的值,使四边形PBCQ 为平行四边形?若存在,求出t 的值;若不存在,说明理由;(4)(3分)是否存在t 的值,使四边形PBCQ 为菱形?若存在,求出t 的值;若不存在,说明理由,并探究如何改变点C 的速度(匀速运动),使四边形PBCQ 在某一时刻为菱形,求点C 的速度和时间t .18、(10分)我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;平均数(分)中位数(分)众数(分)初中部85高中部85100(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)若关于x 的一元二次方程240x x a +-=有两个不相等的实数根,则a 的取值范围是________.20、(4分)如图,在平面直角坐标系中,函数2y x =和y x =-的图象分别为直线1l ,2l ,过点()1,0作x 轴的垂线交1l 于点1A ,过1A 点作y 轴的垂线交2l 于点2A ,过点2A 作x 轴的垂线交1l 于点3A ,过点3A 作y 轴的垂线交2l 于点4A ,…,依次进行下去,则点9A 的坐标为______,点2019A 的坐标为______.21、(4分)直角三角形的两边为3和4,则该三角形的第三边为__________.22、(4分)如图,已知在▱ABCD 中,∠B =60°,AB =4,BC =8,则▱ABCD 的面积=_____.23、(4分)若215x mx +-分解因式可分解为(3)()x x n ++,则m n +=______。
2024年江苏省镇江市东部教育集团数学九年级第一学期开学复习检测试题【含答案】

2024年江苏省镇江市东部教育集团数学九年级第一学期开学复习检测试题题号一二三四五总分得分批阅人A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分),0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是()A .15B .25C .35D .452、(4分)2的值是()A .B .3C .±3D .93、(4分)若A (1x ,1y )、B (2x ,2y )是一次函数y =(a -1)x +2图象上的不同的两个点,当1x >2x 时,1y <2y ,则a 的取值范围是()A .a >0B .a <0C .a >1D .a <14、(4分)如图,AB CD 中,点O 为对角线AC 、BD 的交点,下列结论错误的是()A .AC=BDB .AB//DCC .BO=DOD .∠ABC=∠CDA5、(4分)如图,在正方形ABCD 中,△BPC 是等边三角形,BP ,CP 的延长线分别交AD 于点E ,F ,连接BD ,DP ,BD 与CF 交于点H .下列结论:①BE =2AE ;②△DFP ∽△BPH ;③△PFD ∽△PDB ;④DP 2=PH •PC ,其中正确的结论是A .①②③④B .②③C .①②④D .①③④6、(4分)若a >b ,则下列式子正确的是()A .a ﹣4>b ﹣3B .12a <12b C .3+2a >3+2b D .﹣3a >﹣3b 7、(4分)如图,在菱形ABCD 中,E ,F 分别是AB ,AC 的中点,若EF =2,则菱形ABCD 的周长为()A .16B .8C .D .48、(4分)以下由两个全等的30°直角三角板拼成的图形中,属于中心对称图形的是()A .B .C .D .二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)已知直线y =kx +3经过点A (2,5)和B (m ,-2),则m =___________.10、(4分)在△ABC 中,AB =17cm ,AC =10cm ,BC 边上的高等于8cm ,则BC 的长为_____cm .11、(4分)如图,∠A=90°,∠AOB=30°,AB=2,△''A OB 可以看作由△AOB 绕点O 逆时针旋转60°得到的,则点'A 与点B 的距离为_______.12、(4分)菱形有一个内角是120°,其中一条对角线长为9,则菱形的边长为____________.13、(4分)在平面直角坐标系中,点(1,2)-在第________象限.三、解答题(本大题共5个小题,共48分)14、(12分)如图在平面直角坐标系中,O 是坐标原点,矩形OACB 的顶点A ,B 分别在x 轴、y 轴上,已知3OA =,点D 为y 轴上一点,其坐标为(0,1),若连接CD ,则5CD =,点P 从点A 出发以每秒1个单位的速度沿线段A C B --的方向运动,当点P 与点B 重合时停止运动,运动时间为t 秒(1)求B ,C 两点坐标;(2)求OPD ∆的面积S 关于t 的函数关系式;(3)当点D 关于OP 的对称点E 落在x 轴上时,请直接写出点E 的坐标,并求出此时的t 值.15、(8分)如图,四边形ABCD 是平行四边形,E 是AD 边上一点.(1)只用无刻度直尺在BC 边上作点F ,使得CF AE =,保留作图痕迹,不写作法;(2)在(1)的条件下,若2AE =,2AB FB FC ==,求四边形ABCD 的周长.16、(8分)解下列一元二次方程(1)210160x x ++=(2)23620x x +-=17、(10分)(1(2.18、(10分)为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.甲、乙射击成绩统计表平均数(环)中位数(环)方差命中10环的次数甲70乙1甲、乙射击成绩折线统计图(1)请补全上述图表(请直接在表中填空和补全折线图);(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)一个三角形的两边的长分别是3和5,要使这个三角形为直角三角形,则第三条边的长为_____.20、(4分)如图,等腰ABC ∆中,AB AC =,30A ∠=,线段AB 的垂直平分线交AB 于D ,交AC 于E ,连接BE ,则∠CBE 等于______.21、(4分)写出一个经过点()2,1-,且y 随x 的增大而减小的一次函数的关系式:______.22、(4分)如图,在平行四边形ABCD 中,∠ABC 的平分线BF 交AD 于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF 的面积为________23、(4分)如图,反比例函数y =k x (x <0)的图象经过点A (﹣2,2),过点A 作AB ⊥y 轴,垂足为B ,在y 轴的正半轴上取一点P (0,t ),过点P 作直线OA 的垂线l ,以直线l 为对称轴,点B 经轴对称变换得到的点B '在此反比例函数的图象上,则t 的值是()A .B .C .4D .二、解答题(本大题共3个小题,共30分)24、(8分)某工厂准备加工600个零件,在加工了100个零件后,采取了新技术,使每天的工作效率是原来的2倍,结果共用7天完成了任务,求该厂原来每天加工多少个零件?25、(10分)某校为了改善办公条件,计划从厂家购买A 、B 两种型号电脑。
诚成教育2022龙东地区模拟大考卷四

诚成教育2022龙东地区模拟大考卷四一、选择题(每小题3分,满分24分)1、下列现象中,由于光的反射形成的是()A、月光下的人影B、池塘的水底看起来比实际的浅C、拱桥在平静湖水中的倒影D、玻璃三棱镜分解了的太阳光2、下列物态变化中属于放热现象的是哪一组()①初春,冰封的湖面解冻②盛夏,旷野里雾的形成③深秋,路边的小草上结了一层霜④严冬,冰冻的衣服逐渐变干、A、①②B、②③C、③④D、①④3、下列说法中,正确的是()A、验电器的工作原理是同种电荷相互排斥B、宇航员在月球上无法用电磁波来通信C、只有镜面反射遵循光的反射定律D、只有凸透镜能成等大的像4、下列说法错误的是()A、并联电路的干路电流等于各支路电流之和B、使用精密仪器和改进实验方法可以避免误差C、用安培定则可判断通电螺线管的极性D、1kWh=3。
6×106J5、潜水员逐渐从水里浮出水面的过程中,他受到的浮力()A、逐渐增大B、逐渐减小C、始终不变D、先增大后不变6、能说明将电能转化为机械能的是()A、钻木取火B、水蒸气将塞子冲出C、通电导体在磁场中受力D、焦耳定律实验7、相向而行的甲、乙两物体的s﹣t图象,下列说法正确的是()A、相遇时两物体通过的路程均为100mB、0﹣30s内甲、乙均做匀速直线运动C、甲的运动速度为10m/sD、甲、乙是同时出发的8、小雅同学在做电学实验时,不小心将电压表和电流表的位置互换了,如果此时将开关闭合,则()A、两表都可能被烧坏B、两表都不会被烧坏C、电流表不会被烧坏D、电压表不会被烧坏,电流表可能被烧坏二、填空题(每小题2分,满分20分)9、人的眼睛像一架照相机,物体经晶状体成像与视网膜上,对于近视眼患者而言,远处物体成的像位于视网膜(),可配戴()透镜矫正。
10、滑冰运动员在训练中通过弯道时的情景,这一过程中她们的运动状态()(选填“改变”或“不变”);运动员穿的速滑冰鞋的冰刀表面要光滑、平整是为了()。
2023-2024学年冀教版三年级上册期中综合素质达标模拟检测数学试卷(含答案解析)

2023-2024学年冀教版三年级上册期中综合素质达标模拟检测数学试卷学校:___________姓名:___________班级:___________考号:___________一、填空题1.由5个千、6个百和6个一组成的数是(),读作()。
2.9812是由()个千、()个百、()个十和()个一组成的。
3.28的7倍是();105是5的()倍;()的6倍是432;比8的35倍多4的数是()。
4.137×8的积是()位数;426÷3的商是()位数,商的十位上是()。
5.518+483的结果大约是();489×8的结果大约是()。
6.□58÷6,要使商是三位数,□里最小能填();要使商是两位数,□里最大能填()。
7.用1、2、0、0组成不同的四位数。
(1)两个“零”都不读出来的数是()和()。
(2)只读一个“零”的数是()、()、()和()。
8.282个小朋友到儿童游乐园划船,每条船最多坐4人,他们至少需要租()条船。
二、判断题9.一个四位数中间不管有几个0,都只读一个“零”。
()10.0乘任何数都得0,0除以任何数都得0。
()11.一个三位数乘9,积一定是四位数。
()12.半圆是轴对称图形。
()13.图形通过旋转可以得到。
()三、选择题14.估一估,下列算式中积大于600的是()。
A.283×2B.198×3C.303×215.盒里有52个彩球,至少拿走()个彩球,就能正好平均分给9个小朋友了。
A.7B.3C.216.一箱牛奶有12盒,每盒9元钱。
用12×9计算一箱牛奶的价钱,去乘十位上的1(见下图)计算的是()盒牛奶的钱数。
A.10B.9C.117.把一张长方形纸对折,在如图的位置剪下两个圆,然后展开,得到的图形应该是()。
A.B.C.18.李老师在酷狗音乐下载了15首歌曲,在网易云音乐下载的歌曲数比在酷狗音乐下载的6倍少一些,他在网易云音乐可能下载了()首歌曲。
2020年中考全真模拟测试《数学试卷》含答案解析
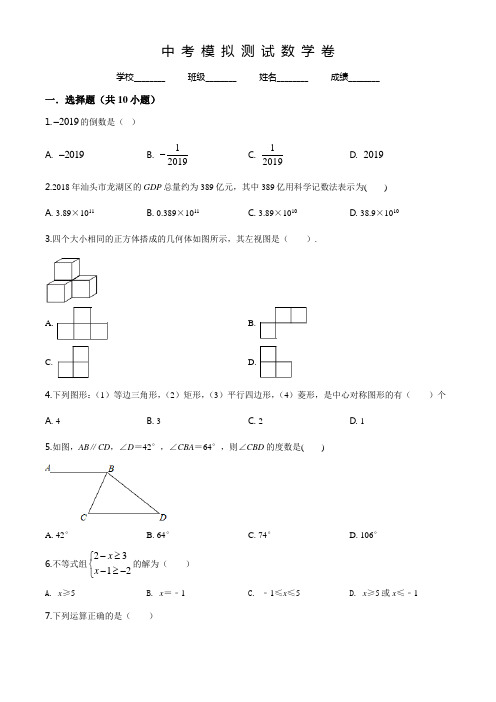
中 考 模 拟 测 试 数 学 卷学校________ 班级________ 姓名________ 成绩________一.选择题(共10小题)1.2019-的倒数是( )A. 2019-B. 12019-C. 12019 D. 20192.2018年汕头市龙湖区的GDP 总量约为389亿元,其中389亿用科学记数法表示为( )A. 3.89×1011B. 0.389×1011C. 3.89×1010D. 38.9×1010 3.四个大小相同的正方体搭成的几何体如图所示,其左视图是( ).A. B. C. D.4.下列图形:(1)等边三角形,(2)矩形,(3)平行四边形,(4)菱形,是中心对称图形的有()个A. 4B. 3C. 2D. 15.如图,AB ∥CD ,∠D =42°,∠CBA =64°,则∠CBD 的度数是( )A. 42°B. 64°C. 74°D. 106°6.不等式组2312x x -≥⎧⎨-≥-⎩的解为( )A. x ≥5B. x =﹣1C. ﹣1≤x ≤5D. x ≥5或x ≤﹣1 7.下列运算正确的是( )A. (﹣2x)3=﹣8x3B. (3x2)3=9x6C. x3•x2=x6D. x2+2x3=3x58.如图,AB为⊙O的直径,C,D为⊙O上的两点,若AB=14,BC=7.则∠BDC的度数是()A. 15°B. 30°C. 45°D. 60°9.已知一个多边形的内角和为1080°,则这个多边形是()A.九边形B. 八边形C. 七边形D. 六边形10.如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以2cm/s的速度沿AB方向运动到点B.动点Q 同时从点A出发,以1cm/s的速度沿折线AC→CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是()A. B.C. D.二.填空题(共7小题)x-中自变量x的取值范围是_____.11.函数y2312.因式分解:2x2﹣8=_____.13.已知扇形的圆心角是120°,半径为6cm,把它围成一个圆锥的侧面,则圆锥的底面半径是_____cm.14.已知|x﹣2y|+(y﹣2)2=0,则x y=_____.15.一组按规律排列的式子:9162536,,,261220--…照此规律第10个数为_____.16.如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上kyx=,则k值为_____.17.如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣13x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.三.解答题(共8小题)18.12+(π﹣2019)0﹣(﹣13)﹣2﹣4cos30°19.先化简,再求值:22242442x xx x x x--⋅-++,其中21x=.20.如图,点D在△ABC的AB边上.(1)作∠BDC平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,若直线DE与直线AC平行,则∠ACD=∠A吗?为什么?21.某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:价格/类型A型B型进价(元/只)15 35标价(元/只)25 50(1)这两种文具盒各购进多少只?(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?22.某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).(1)求本次被调查的学生人数;(2)补全条形统计图;(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?23.在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF形状,并说明理由.24.如图,在△ABC 中,∠C =90°,∠ABC 的平分线交AC 于点E ,过点E 作BE 的垂线交AB 于点F ,⊙O 是△BEF 的外接圆.(1)求证:AC 是⊙O 的切线;(2)过点E 作EH ⊥AB ,垂足为H ,求证:CD =HF ;(3)若CD =1,EH =3,求BF 及AF 长.25.已知二次函数y=ax 2+bx ﹣3a 经过点A (﹣1,0)、C (0,3),与x 轴交于另一点B ,抛物线的顶点为D ,(1)求此二次函数解析式;(2)连接DC 、BC 、DB ,求证:△BCD 是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P ,使得△PDC 为等腰三角形?若存在,求出符合条件的点P 的坐标;若不存在,请说明理由.答案与解析一.选择题(共10小题)1.2019-的倒数是( )A. 2019-B. 12019-C. 12019D. 2019【答案】B【解析】【分析】直接利用倒数的定义进而得出答案.【详解】∵2019-×(12019-)=1, ∴2019-的倒数12019-. 故选B. 【点睛】此题主要考查了倒数,正确把握倒数的定义是解题关键.2.2018年汕头市龙湖区的GDP 总量约为389亿元,其中389亿用科学记数法表示为( )A. 3.89×1011B. 0.389×1011C. 3.89×1010D. 38.9×1010【答案】C【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】389亿用科学记数法表示为89×1010. 故选C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.3.四个大小相同的正方体搭成的几何体如图所示,其左视图是( ).A. B.C. D.【答案】D【解析】【分析】根据从左边看得到的图形是左视图,可得答案.【详解】从左边看第一列是两个小正方形,第二列左边一个小正方形.故选D.【点睛】本题考查了简单组合体的三视图,从左边看得到的图形是左视图.4.下列图形:(1)等边三角形,(2)矩形,(3)平行四边形,(4)菱形,是中心对称图形的有()个A. 4B. 3C. 2D. 1【答案】B【解析】【分析】根据中心对称图形的概念判断即可.【详解】矩形,平行四边形,菱形是中心对称图形,等边三角形不是中心对称图形.故选B.【点睛】本题考查了中心对称图形的概念,判断中心对称图形的关键是要寻找对称中心,旋转180度后两部分重合.5.如图,AB∥CD,∠D=42°,∠CBA=64°,则∠CBD的度数是()A. 42°B. 64°C. 74°D. 106°【答案】C【解析】【分析】根据两直线平行,同旁内角互补可求出∠ABD的度数,再根据∠CBD=∠ABD-∠CBA即可求得答案. 【详解】∵AB∥CD,∴∠ABD+∠D=180°,∴∠ABD=180°-42°=138°,∴∠CBD=∠ABD-∠CBA=138°-64°=74°,故选C.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.6.不等式组2312xx-≥⎧⎨-≥-⎩的解为()A. x≥5B. x=﹣1C. ﹣1≤x≤5D. x≥5或x≤﹣1【答案】B【解析】【分析】先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分即可得到不等式组的解集.【详解】解:解不等式2﹣x≥3,得:x≤﹣1,解不等式x﹣1≥﹣2,得:x≥﹣1,则不等式组的解为x=﹣1.故选B.【点睛】本题考查了一元一次不等式组的解法,先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.7.下列运算正确的是()A. (﹣2x)3=﹣8x3B. (3x2)3=9x6C. x3•x2=x6D. x2+2x3=3x5【答案】A【解析】【分析】根根据整式的运算法则进行分析即可(积的乘方,幂的乘方,同底数幂相乘)【详解】解:A 、(﹣2x )3=﹣8x 3,故本选项正确;B 、应为(3x 2)3=27x 6,故本选项错误;C 、应为x 3•x 2=x 5,故本选项错误;D 、x 2与2x 3不是同类项,不能合并,故本选项错误.故选A .【点睛】考核知识点:积的乘方,幂的乘方,同底数幂相乘.掌握法则是关键.8.如图,AB 为⊙O 的直径,C ,D 为⊙O 上的两点,若AB =14,BC =7.则∠BDC 的度数是( )A. 15°B. 30°C. 45°D. 60° 【答案】B【解析】【分析】 只要证明△OCB 是等边三角形,可得∠CDB=12∠COB 即可解决问题. 【详解】如图,连接OC ,∵AB=14,BC=7,∴OB=OC=BC=7,∴△OCB 是等边三角形,∴∠COB=60°,∴∠CDB=12∠COB=30°, 故选B .【点睛】本题考查圆周角定理,等边三角形的判定等知识,解题的关键是学会利用数形结合的首先解决问题,属于中考常考题型.9.已知一个多边形的内角和为1080°,则这个多边形是()A. 九边形B. 八边形C. 七边形D. 六边形【答案】B【解析】【分析】n边形的内角和是(n﹣2)•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.【详解】根据n边形的内角和公式,得(n﹣2)•180=1080,解得n=8,∴这个多边形的边数是8,故选B.【点睛】本题考查了多边形的内角与外角,熟记内角和公式和外角和定理并列出方程是解题的关键.根据多边形的内角和定理,求边数的问题就可以转化为解方程的问题来解决.10.如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以2cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是()A. B.C. D.【答案】D【解析】【分析】在△ABC中,∠C=90°,AC=BC=3cm,可得AB=32,∠A=∠B=45°,分当0<x≤3(点Q在AC上运动,点P在AB上运动)和当3≤x≤6时(点P与点B重合,点Q在CB上运动)两种情况求出y与x的函数关系式,再结合图象即可解答.【详解】在△ABC中,∠C=90°,AC=BC=3cm,可得AB=32,∠A=∠B=45°,当0<x≤3时,点Q在AC 上运动,点P在AB上运动(如图1),由题意可得AP=2x,AQ=x,过点Q作QN⊥AB于点N,在等腰直角三角形AQN中,求得QN=22x,所以y=12AP QN⋅=21212=22x x x⨯⨯(0<x≤3),即当0<x≤3时,y随x的变化关系是二次函数关系,且当x=3时,y=4.5;当3≤x≤6时,点P与点B重合,点Q 在CB上运动(如图2),由题意可得PQ=6-x,AP=32,过点Q作QN⊥BC于点N,在等腰直角三角形PQN中,求得QN=2(6-x),所以y=12AP QN⋅=12332(6)=922x x⨯⨯--+(3≤x≤6),即当3≤x≤6时,y随x的变化关系是一次函数,且当x=6时,y=0.由此可得,只有选项D符合要求,故选D.【点睛】本题考查了动点函数图象,解决本题要正确分析动线运动过程,然后再正确计算其对应的函数解析式,由函数的解析式对应其图象,由此即可解答.二.填空题(共7小题)11.函数y23x-中自变量x的取值范围是_____.【答案】x≥3 2【解析】【详解】解:由题意得,230x -≥,解得:32x ≥. 12.因式分解:2x 2﹣8=_____.【答案】2(x +2)(x ﹣2).【解析】【分析】 观察原式,找到公因式2,提出即可得出答案.【详解】2x 2﹣8=2(x +2)(x ﹣2).故答案为:2(x +2)(x ﹣2).【点睛】此题考查提公因式法和公式法分解因式,解题关键在于掌握运算法则.13.已知扇形的圆心角是120°,半径为6cm ,把它围成一个圆锥的侧面,则圆锥的底面半径是_____cm .【答案】2【解析】【分析】利用圆锥的底面周长等于侧面展开图的扇形弧长是4π,列出方程计算.【详解】扇形的圆心角是120°,半径为6cm , 则扇形的弧长是:1206180π⋅=4π, 则圆锥的底面周长等于侧面展开图的扇形弧长是4π,设圆锥的底面半径是r ,则2πr =4π,解得:r =2.∴圆锥的底面半径是2cm .故答案为2.【点睛】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:①圆锥的母线长等于侧面展开图的扇形半径;②圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.14.已知|x ﹣2y |+(y ﹣2)2=0,则x y =_____.【答案】16;【解析】【分析】根据绝对值的定义以及平方的性质可知,x-2y=0,y-2=0,求出x,y的值,再计算x y的值即可.【详解】∵│x-2y│+(y-2)2=0,∴2020x yy⎧⎨⎩-=-=,解得x=4,y=2,则x y=42=16.故答案是16.【点睛】本题主要考查了绝对值和平方值,掌握绝对值和平方值都不能为负数是解答的关键.15.一组按规律排列的式子:9162536,,,261220--…照此规律第10个数为_____.【答案】﹣144110(或﹣7255).【解析】【分析】由分母2=1×2,6=2×3,12=3×4,20=4×5…得出第n个数的分母为(1)n n+,分子是从3开始连续自然数的平方,第n个数的分子为2(2)n+,符号为奇正偶负,由此规律求得第10个数即可.【详解】解:由式子:9162536,,,261220--…可得:第10个数为:2(102)14472101111055+-=-=-⨯,故答案为:﹣144110(或﹣7255).【点睛】此题考查了与实数运算相关的规律题,找出数字之间的运算规律,得出规律并利用规律是解题的关键.16.如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上kyx=,则k值为_____.【答案】4【解析】作DH⊥x轴于H,如图,当y=0时,-3x+3=0,解得x=1,则A (1,0),当x=0时,y=-3x+3=3,则B (0,3),∵四边形ABCD 为正方形,∴AB=AD ,∠BAD=90°,∴∠BAO+∠DAH=90°,而∠BAO+∠ABO=90°, ∴∠ABO=∠DAH ,在△ABO 和△DAH 中AOB DHA ABO DAH AB DA ∠∠⎧⎪∠∠⎨⎪⎩===∴△ABO ≌△DAH ,∴AH=OB=3,DH=OA=1,∴D 点坐标为(4,1),∵顶点D 恰好落在双曲线y=kx 上, ∴a=4×1=4.故答案是:4.17.如图,在平面直角坐标系中,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…都是等腰直角三角形,其直角顶点P 1(3,3),P 2,P 3,…均在直线y =﹣13x +4上,设△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…的面积分别为S 1,S 2,S 3,…依据图形所反映的规律,S 2019=_____.【答案】201894.【解析】【分析】分别过点P 1、P 2、P 3作x 轴的垂线段,先根据等腰直角三角形的性质求得前三个等腰直角三角形的底边和底边上的高,继而求得三角形的面积,得出面积的规律即可得出答案.【详解】解:如图,分别过点P 1、P 2、P 3作x 轴的垂线段,垂足分别为点C 、D 、E ,∵P 1(3,3),且△P 1OA 1是等腰直角三角形,∴OC =CA 1=P 1C =3,设A 1D =a ,则P 2D =a ,∴OD =6+a ,∴点P 2坐标为(6+a ,a ),将点P 2坐标代入y =﹣13x +4,得:﹣13(6+a )+4=a , 解得:a =32, ∴A 1A 2=2a =3,P 2D =32, 同理求得P 3E =34、A 2A 3=32, ∵S 1=12×6×3=9、S 2=12×3×39=24、S 3=1339=22416⨯⨯、…… ∴S 2019=201894.故答案为201894.【点睛】本题考查规律型:点的坐标、等腰直角三角形的性质,解题的关键是从特殊到一般,探究规律,利用规律解决问题.三.解答题(共8小题)18.+(π﹣2019)0﹣(﹣13)﹣2﹣4cos30° 【答案】-8.【解析】【分析】先根据二次根式的性质,零指数幂的意义,负整数指数幂的意义及特殊角的三角函数值逐项化简,再合并同类二次根式和同类项即可.【详解】解:原式=﹣9﹣8【点睛】本题考查了实数的缓和运算,熟练掌握二次根式的性质,零指数幂的意义,负整数指数幂的意义及特殊角的三角函数值是解答本题的关键.19.先化简,再求值:22242442x x x x x x--⋅-++,其中1x =.【答案】1x +1. 【解析】【分析】根据分式的运算法则先化简,再代入求值. 【详解】解:22242442x x x x x x--⋅-++ 2(2)(2)2(2)(2)x x x x x x +--=⋅-+ 1,x=当x 11=. 【点睛】考核知识点:二次根式的化简求值.掌握分式和二次根式运算法则是关键.20.如图,点D 在△ABC 的AB 边上.(1)作∠BDC 的平分线DE ,交BC 于点E (用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,若直线DE 与直线AC 平行,则∠ACD =∠A 吗?为什么?【答案】(1)见解析;(2)∠ACD=∠A,理由见解析.【解析】【分析】(1)直接利用角平分线的作法得出即可;(2)利用平行线的性质结合角平分线的性质得出答案.【详解】(1)如图所示:DE即所求;(2)∠ACD=∠A.∵直线DE与直线AC平行,理由:∴∠A=∠BDE,∠EDC=∠ACD,又∵∠BDE=∠CDE,∴∠ACD=∠A.【点睛】此题主要考查了基本作图以及角平分线的性质以及平行线的性质,熟练应用平行线的性质是解题关键.21.某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:价格/类型A型B型进价(元/只)15 35标价(元/只)25 50(1)这两种文具盒各购进多少只?(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?【答案】(1)A 型文具盒购进40只,B 型文具盒购进80只;(2)这批文具盒全部售出后,超市共获利700元.【解析】【分析】(1)设A 型文具盒购进x 只,B 型文具盒购进y 只,由该超市用3400元购进A ,B 两种文具盒共120个,可得出关于x ,y 的二元一次方程组,解之即可得出结论;(2)根据利润=销售收入-成本,即可求出销售完这批文具盒后获得的利润.【详解】解:(1)设A 型文具盒购进x 只,B 型文具盒购进y 只,依题意,得:12015353400x y x y +=⎧+=⎨⎩, 解得:{4080x y ==. 答:A 型文具盒购进40只,B 型文具盒购进80只.(2)25×0.9×40+50×0.8×80-3400=700(元).答:这批文具盒全部售出后,超市共获利700元.【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键. 22.某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出). (1)求本次被调查的学生人数;(2)补全条形统计图;(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?【答案】(1)40人(2)12人(3)1125人【解析】【分析】(1)用喜欢跳绳的人数除以其所占的百分比即可求得被调查的总人数;(2)用总人数乘以足球所占的百分比即可求得喜欢足球的人数,用总数减去其他各小组的人数即可求得喜欢跑步的人数,从而补全条形统计图;(3)用样本估计总体即可确定最喜爱篮球的人数比最喜爱足球的人数多多少.【详解】解:(1)观察条形统计图与扇形统计图知:喜欢跳绳的有10人,占25%,故总人数有10÷25%=40人;(2)喜欢足球的有40×30%=12人,喜欢跑步的有40-10-15-12=3人,故条形统计图补充:(3)全校最喜爱篮球的人数比最喜爱足球的人数多1512 300022540-⨯=人.【点睛】本题考查了扇形统计图、条形统计图及用样本估计总体的知识,解题的关键是能够读懂两种统计图并从中整理出进一步解题的有关信息,难度不大.23.在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.【答案】(1)证明见解析(2)菱形【解析】分析:(1)根据正方形的性质和全等三角形的判定证明即可;(2)四边形AECF 是菱形,根据对角线垂直的平行四边形是菱形即可判断;详证明:(1)∵四边形ABCD 是正方形,∴AB=AD ,∴∠ABD=∠ADB ,∴∠ABE=∠ADF ,在△ABE 与△ADF 中AB AD ABE ADF BE DF ⎧⎪∠∠⎨⎪⎩===,∴△ABE ≌△ADF.(2)如图,连接AC ,四边形AECF 是菱形.理由:在正方形ABCD 中,OA=OC ,OB=OD ,AC ⊥EF ,∴OB+BE=OD+DF ,即OE=OF ,∵OA=OC ,OE=OF ,∴四边形AECF 是平行四边形,∵AC ⊥EF ,∴四边形AECF 是菱形.点睛:本题考查正方形的性质、全等三角形的判定和性质、菱形的判定等知识,解题的关键是熟练掌握基本知识.24.如图,在△ABC 中,∠C =90°,∠ABC 的平分线交AC 于点E ,过点E 作BE 的垂线交AB 于点F ,⊙O 是△BEF 的外接圆.(1)求证:AC 是⊙O 的切线;(2)过点E 作EH ⊥AB ,垂足为H ,求证:CD =HF ;(3)若CD=1,EH=3,求BF及AF长.【答案】(1)证明见解析;(2)证明见解析;(3)5 4 .【解析】试题分析:(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC 是⊙O的切线;(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF;(3)由(2)中CD=HF,即可求出HF的值,先求OA和OF的长度,再由AF=OA-OF求出AF的值;试题解析:(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF证明:(1)如图,连接OE.∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠CBE,∴OE∥BC,∴∠AEO=∠C=90°,∴AC是⊙O的切线;(2)如图,连结DE.∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,∴EC=EH.∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,∴∠CDE=∠HFE .在△CDE 与△HFE 中,0{90CDE HFEC EHF EC EH∠=∠∠=∠==,∴△CDE ≌△HFE (AAS ),∴CD=HF .(3)由(2)得,CD =HF .又CD =1∴HF =1在Rt △HFE 中,EF 2231+10∵EF ⊥BE∴∠BEF =90°∴∠EHF =∠BEF =90°∵∠EFH =∠BFE∴△EHF ∽△BEF ∴EF HF BF EF =1010=∴BF =10 ∴152OE BF ==,514OH =-=, ∴在Rt △OHE 中,4cos 5EOA ∠=, ∴在Rt △EOA 中,4cos 5OE EOA OA ∠==, ∴545OA = ∴254OA = ∴255544AF =-=.25.已知二次函数y=ax 2+bx ﹣3a 经过点A (﹣1,0)、C (0,3),与x 轴交于另一点B ,抛物线的顶点为D ,(1)求此二次函数解析式;(2)连接DC 、BC 、DB ,求证:△BCD 是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P ,使得△PDC 为等腰三角形?若存在,求出符合条件的点P 的坐标;若不存在,请说明理由.【答案】(1)抛物线的解析式为y=﹣x 2+2x+3.(2)证明见解析;(3)点P 坐标为(352+,552-)或(2,3).【解析】试题分析:(1)将A (﹣1,0)、C (0,3),代入二次函数y=ax 2+bx ﹣3a ,求得a 、b 的值即可确定二次函数的解析式;(2)分别求得线段BC 、CD 、BD 的长,利用勾股定理的逆定理进行判定即可;(3)分以CD 为底和以CD 为腰两种情况讨论.运用两点间距离公式建立起P 点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解.试题解析:(1)∵二次函数y=ax 2+bx ﹣3a 经过点A (﹣1,0)、C (0,3),∴将A (﹣1,0)、C (0,3),代入,得30{33a b a a --=-=,解得12a b =-=⎧⎨⎩,∴抛物线的解析式为y=﹣x 2+2x+3;(2)如图,连接DC 、BC 、DB ,由y=﹣x 2+2x+3=﹣(x ﹣1)2+4得,D 点坐标为(1,4),22(10)(43)-+-2,2233+2,22(31)(40)-+-5∵CD 2+BC 2=2)2+(2)2=20,BD 2=(52=20,∴CD 2+BC 2=BD 2,∴△BCD 是直角三角形;(3)y=﹣x 2+2x+3对称轴为直线x=1.假设存在这样的点P ,①以CD 为底边,则P 1D=P 1C ,设P 1点坐标为(x ,y ),根据勾股定理可得P 1C 2=x 2+(3﹣y )2,P 1D 2=(x ﹣1)2+(4﹣y )2,因此x 2+(3﹣y )2=(x ﹣1)2+(4﹣y )2,即y=4﹣x .又P 1点(x ,y )在抛物线上,∴4﹣x=﹣x 2+2x+3,即x 2﹣3x+1=0,解得x 1=35+,x 2=35-<1,(不满足在对称轴右侧应舍去),∴x=352+,∴y=4﹣x=552-,即点P 1坐标为(352+,552-).②以CD 为一腰,∵点P 2在对称轴右侧的抛物线上,由抛物线对称性知,点P 2与点C 关于直线x=1对称,此时点P 2坐标为(2,3).∴符合条件的点P 坐标为(352+,552-)或(2,3).考点:1.二次函数图象性质;2.等腰三角形性质;3.直角三角形的判定.。
2021中考考前模拟考试《数学试题》含答案解析

2021年中考全真模拟测试数 学 试 题学校________ 班级________ 姓名________ 成绩________一、选择题:本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算()34-+的结果是( ) A. -7B. -1C. 1D. 72.Fitnow 遇见-中国第一个公益减肥团体,成立于2016年7月,每期40天.2018年第十三期在线打卡人数达到10045人,其中数据10045用科学计数法表示为( ) A. 10.045× 103B. 1.0045×103C. 1.0045×104D. 0.10045×1053.如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )A. B. C. D.4.下列运算,正确的是( ) A. 623a a a ÷= B. 2(2)4a a =C. 325a a a ⋅=D. 325a a a +=5.若代数式4xx -有意义,则实数x 取值范围是( )A. x =0B. x =4C. x ≠0D. x ≠46.剪纸是某市特有的民间艺术,在如图所示的四个剪纸图案中.既是轴对称图形又是中心对称图形的是( )A. B. C. D.7.在天水市汉字听写大赛中,10名学生得分情况如表 人数3421分数80859095那么这10名学生所得分数的中位数和众数分别是()A. 85和82.5B. 85.5和85C. 85和85D. 85.5和808.如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,已知AE=6,AD3DB4=,则EC的长是A. 4.5B. 8C. 10.5D. 149.关于x的二次函数y=a(x+1)(x﹣m),其图象的对称轴在y轴的右侧,则实数a、m应满足()A. a>0,m<﹣1B. a>0,m>1C. a≠0,0<m<1D. a≠0,m>110.如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )A. 3-3πB. 3-6πC. 4-3πD. 4-6π11.如图,直线y=12x与双曲线y=kx(k>0,x>0)交于点A,将直线y=12x向上平移4个单位长度后,与y轴交于点C,与双曲线y=kx(k>0,x>0)交于点B,若OA=3BC,则k的值为( )A. 3B. 6C.94D.9212.某班有20位同学参加围棋、象棋比赛,甲说:”只参加一项的人数大于14人”;乙说:”两项都参加的人数小于5人” .对于甲、乙两人的说法,有下列四个命题,其中真命题的是()A. 若甲对,则乙对B. .若乙对,则甲对C. 若乙错,则甲错D. 若甲错,则乙对二、填空题(每题4分,共24分)13.16的算术平方根是.14.分解因式:x2—4=________15.一个不透明的袋子中有2个红球、3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红色球的概率为________________________.16.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=48cm,脸盆的最低点C到AB的距离为12 cm,则该脸盆的半径为________cm.17.如图,在△ABC中,AB=2,AC=2,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.18.如图,在平面直角坐标系中,0为坐标原点,点A的坐标为(-4,0),直线BC经过点B(-4,3),C(0,3),将四边形OABC绕点O按顺时针方向旋转α度(0<α≤l80°)得到四边形OA′B′C′,此时直线OA′、直线B′C′,分别与直线BC相交于P,Q.在四边形OABC旋转过程中,若BP=12BQ则点P的坐标为__________.三、解答题(本大题共8小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(1)计算:(2017-π)0-114-⎛⎫⎪⎝⎭+|-2|;(2)化简:111a⎛⎫-⎪-⎝⎭÷2244a aa a⎛⎫-+⎪-⎝⎭.20.图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)(1)求AB的长(精确到0.01米);(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径MN的长度.(结果保留π)21.手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注:不同的分法,面积可以相等)22.我区积极开展”体育大课间”活动,引导学生坚持体育锻炼,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步.D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调査,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;(2)请把条形统计图补充完整;(3)己知该校有2000人,请根据样本估计全校最喜欢足球的人数是多少?23.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF,(1)求证:AF=DC;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.24.某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).(1)直接写出每天游客居住的房间数量y与x的函数关系式;(2)设宾馆每天的利润为W元,当每个房间定价为多少元时,宾馆每天所获利润最大,最大利润是多少;(3)某日,宾馆了解当天的住宿情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人.问:这天宾馆入住的游客人数最少有多少人.25.如图,抛物线y =x 2+bx +c 经过B (-1,0),D (-2,5)两点,与x 轴另一交点为A ,点H 是线段AB 上一动点,过点H 的直线PQ ⊥x 轴,分别交直线AD 、抛物线于点Q 、P . (1)求抛物线的解析式;(2)是否存在点P ,使∠APB =90°,若存在,求出点P 的横坐标,若不存在,说明理由;(3)连接BQ ,一动点M 从点B 出发,沿线段BQ 以每秒1个单位的速度运动到Q ,再沿线段QD以每秒2个单位的速度运动到D 后停止,当点Q 的坐标是多少时,点M 在整个运动过程中用时t 最少?26.如图1,点P 为四边形ABCD 所在平面上的点,如果∠P AD =∠PBC ,则称点P 为四边形ABCD 关于A 、B 的等角点,以点C 为坐标原点,BC 所在直线为x 轴建立平面直角坐标系,点B 的横坐标为﹣6.(1)如图2,若A 、D 两点的坐标分别为A (﹣6,4)、D (0,4),点P 在DC 边上,且点P 为四边形ABCD 关于A 、B 的等角点,则点P 的坐标为 _________ ; (2)如图3,若A 、D 两点坐标分别为A (﹣2,4)、D (0,4).①若P 在DC 边上时,则四边形ABCD 关于A 、B 的等角点P 的坐标为 _________ ;②在①的条件下,将PB 沿x 轴向右平移m 个单位长度(0<m <6)得到线段P ′B ′,连接P ′D ,B ′D ,试用含m 的式子表示P ′D 2+B ′D 2,并求出使P ′D 2+B ′D 2取得最小值时点P ′的坐标;③如图4,若点P 为四边形ABCD 关于A 、B 的等角点,且点P 坐标为(1,t ),求t 的值;④以四边形ABCD 的一边为边画四边形,所画的四边形与四边形ABCD 有公共部分,若在所画的四边形内存在一点P ,使点P 分别是各相邻两顶点的等角点,且四对等角都相等,请直接写出所有满足条件的点P的坐标.答案与解析一、选择题:本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算()34-+的结果是( ) A. -7 B. -1C. 1D. 7【答案】C 【解析】 【分析】根据异号两数相加,取绝对值较大的数的符号,再用较大的绝对值减去较小的绝对值,可得答案 【详解】解:()()34431-+=+-=. 故选C .考点:有理数的加法.2.Fitnow 遇见-中国第一个公益减肥团体,成立于2016年7月,每期40天.2018年第十三期在线打卡人数达到10045人,其中数据10045用科学计数法表示为( ) A. 10.045× 103 B. 1.0045×103 C. 1.0045×104 D. 0.10045×105 【答案】C 【解析】试题解析:10045用科学记数法表示为41.004510.⨯ 故选C.3.如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )A. B. C. D.【答案】D 【解析】【详解】解:找到从正面看所得到的图形,从几何体的正面看可得此几何体的主视图是三排,左边一排有两层,右边两排各一层.故选D .【点睛】本题考查简单组合体的三视图.4.下列运算,正确的是( ) A. 623a a a ÷= B. 2(2)4a a =C. 325a a a ⋅=D. 325a a a +=【答案】C 【解析】试题解析:A.624.a a a ÷=故错误. B.()2224.a a = 故错误. C.正确.D.不是同类项,不能合并.故错误. 故选C. 5.若代数式4xx -有意义,则实数x 的取值范围是( ) A. x =0 B. x =4C. x ≠0D. x ≠4【答案】D 【解析】由分式有意义的条件:分母不为0,即x-4≠0,解得x≠4, 故选D.6.剪纸是某市特有的民间艺术,在如图所示的四个剪纸图案中.既是轴对称图形又是中心对称图形的是( )A. B. C. D.【答案】C 【解析】A. 此图形沿一条直线对折后不能够完全重合,∴此图形不是轴对称图形,不是中心对称图形,故此选项错误;B. 此图形沿一条直线对折后能够完全重合,∴此图形是轴对称图形,不是中心对称图形,故此选项错误.C. 此图形沿一条直线对折后能够完全重合,∴此图形是轴对称图形,旋转180∘能与原图形重合,是中心对称图形,故此选项正确;D. 此图形沿一条直线对折后不能够完全重合,∴此图形不是轴对称图形,是中心对称图形,故此选项错误.故选C.7.在天水市汉字听写大赛中,10名学生得分情况如表人数 3 4 2 1分数80 85 90 95那么这10名学生所得分数的中位数和众数分别是()A. 85和82.5B. 85.5和85C. 85和85D. 85.5和80【答案】C【解析】试题分析:众数是一组数据中出现次数最多的数据,根据众数的定义可知:在这一组数据中85是出现次数最多的,故众数是85;把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数,根据中位数的定义可知:将这组数据从小到大的顺序排列80,80,80,85,85,85,85,90,90,95,处于中间位置的那个数是85,85,这组数据的中位数是=85.故答案选C.考点:中位数;众数.8.如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,已知AE=6,AD3DB4=,则EC的长是A. 4.5B. 8C. 10.5D. 14 【答案】B【解析】∵DE∥BC,∴AE ADEC DB=.又∵AE=6,AD3DB4=,∴63EC8EC4=⇒=.故选B.9.关于x的二次函数y=a(x+1)(x﹣m),其图象的对称轴在y轴的右侧,则实数a、m应满足()A. a >0,m <﹣1B. a >0,m >1C. a ≠0,0<m <1D. a ≠0,m >1【答案】D【解析】 试题解析:∵a (x +1)(x −m )=0,则x =−1或x =m ,且a ≠0,∴二次函数y =a (x +1)(x −m )的图象与x 轴的交点为(−1,0)、(m ,0), ∴二次函数的对称轴12m x ,-+= ∵函数图象的对称轴在y 轴的右侧,102m -+∴>, 解得:m >1,故选D.10.如图,在▱ABCD 中,AD =2,AB =4,∠A =30°,以点A 为圆心,AD 的长为半径画弧交AB 于点E ,连接CE ,则阴影部分的面积是( )A. 3-3πB. 3-6πC. 4-3πD. 4-6π 【答案】A【解析】过D 点作DF ⊥AB 于点F ,已知AD =2,AB =4,∠A =30°,根据在直角三角形中,30°的锐角所对的直角边等于斜边的一半可得DF =1,又因 EB=AB-AE =2,所以阴影部分的面积为AB·DF -213022360EB DF π⨯⨯⋅- =4-1-3π=3-3π ,故选A.点睛:本题涉及了平行四边形的性质,扇形面积的计算,解题的关键是理解阴影部分的面积=ABCD 的面积-扇形ADE 的面积-△BCE 的面积.11.如图,直线y =12x 与双曲线y =k x(k>0,x>0)交于点A ,将直线y =12x 向上平移4个单位长度后,与y 轴交于点C ,与双曲线y=k x (k>0,x>0)交于点B ,若OA =3BC ,则k 的值为( )A. 3B. 6C. 94D. 92【答案】D【解析】 【详解】∵将直线y=12x 向上平移4个单位长度后,与y 轴交于点C , ∴平移后直线的解析式为y=12x+4, 分别过点A 、 B 作AD ⊥x 轴,BE ⊥x 轴,CF ⊥BE 于点F,设A(3x,32x), ∵OA=3BC,BC ∥OA,CF ∥x 轴,∴△BCF ∽△AOD ,∴CF=13OD , ∵点B 在直线y=12x+4上, ∴B(x, 12x+4), ∵点A. B 在双曲线y=k x 上, ∴3x ⋅32x=x ⋅(12x+4),解得x=1, ∴k=3×1×32×1=92. 故选D.12.某班有20位同学参加围棋、象棋比赛,甲说:”只参加一项的人数大于14人” ;乙说:”两项都参加的人数小于5人” .对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )A. 若甲对,则乙对B. .若乙对,则甲对C. 若乙错,则甲错D. 若甲错,则乙对【答案】B【解析】【详解】对于选项A ,若甲对,设只参加一项的人数为15人,可知两项都参加的人数为5人,则乙错,所以选项A 不符合题意;对于选项C ,若乙错,设两项都参加的人数为5人,可知只参加一项的人数为15人,则甲对,所以选项C 不符合题意;对于选项D ,若甲错,设只参加一项的人数为14人,可知两项都参加的人数为6人,则乙错,所以选项D 不符合题意.故选B.二、填空题(每题4分,共24分)13.16的算术平方根是 .【答案】4【解析】【详解】正数的正的平方根叫算术平方根,0的算术平方根还是0;负数没有平方根也没有算术平方根 ∵2(4)16±=∴16的平方根为4和-4∴16的算术平方根为414.分解因式:x 2—4=________【答案】(x+2)(x-2)【解析】试题解析:x 2-4=(x+2)(x-2).考点:因式分解-运用公式法.15.一个不透明的袋子中有2个红球、3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红色球的概率为________________________. 【答案】29【解析】试题解析:根据题意可得:在不透明的袋子中有2个红球、3个黄球和4个蓝球,共9个,从袋子中随机摸出一个球,它是红色球的概率为29. 考点:概率公式.16.如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A ,B ,AB =48cm ,脸盆的最低点C 到AB 的距离为12 cm ,则该脸盆的半径为________cm.【答案】30【解析】试题解析:设圆心为点O ,连接OC 交AB 于点D ,连接OA ,如图所示:故24.AD BD cm ==根据题意设O 的半径为R ,则10OD R =-,所以在Rt AOD 中,根据勾股定理可得222OA OD AD =+,()2221224.R R ∴=-+解得:30.R cm =故答案为30.点睛:垂径定理:垂直于弦的直径平分弦并且平分弦所对的两条弧.17.如图,在△ABC 中,AB =2,AC 2 ,∠BAC =105°,△ABD ,△ACE ,△BCF 都是等边三角形,则四边形AEFD 的面积为__________.【答案】2【解析】∵△ABD ,△ACE 都是等边三角形,∴∠DAB=∠EAC=60°,∵∠BAC=105°∴∠DAE=135°.∵△ABD 和△FBC 都是等边三角形,∴∠DBF+∠FBA=∠ABC+∠ABF=60°,∴∠DBF=∠ABC .∴在△ABC 与△DBF 中,{BD BADBF ABC BF BC=∠=∠= ,∴△ABC ≌△DBF (SAS ),∴2 ,同理可证△ABC ≌△EFC ,∴AB=EF=AD=2,∴四边形DAEF 是平行四边形(两组对边分别相等的四边形是平行四边形).∴∠FDA=180°-∠DAE=45°,根据勾股定理可求得平行四边形DAEF 边AD 上的高为1,∴平行四边形AEFD 的面积是211⨯= .点睛:本题综合考查了全等三角形的判定与性质以及等边三角形的性质,平行四边形的判定与性质,综合性比较强,难度较大,有利于培养学生综合运用知识进行推理和计算的能力.18.如图,在平面直角坐标系中,0为坐标原点,点A 的坐标为(-4,0),直线BC 经过点B (-4,3),C (0,3),将四边形OABC 绕点O 按顺时针方向旋转α度(0<α≤l 80°)得到四边形OA ′B ′C ′,此时直线OA ′、直线B ′C ′,分别与直线BC 相交于P ,Q .在四边形OABC 旋转过程中,若BP =12BQ 则点P 的坐标为__________.【答案】93(6,3)24-或738-(,) 【解析】 试题解析:过点Q 作QH ⊥OA ′于H ,连接OQ ,则QH =OC ′=OC , 11,22POQ POQ S PQ OC S OP QH =⋅=⋅, ∴PQ =OP .设BP =x ,12BP BQ =, ∴BQ =2x ,如图1,当点P 在点B 左侧时,OP =PQ =BQ +BP =3x ,Rt △PCO 中,222(4)3(3)x x ++=,解得1213136,62424x x ==不符实际,舍去). 93624PC BC BP ∴=+=, 193(6,3).24P ∴- 如图2,当点P 在点B 右侧时,∴OP =PQ =BQ −BP =x ,PC =4−x .在Rt △PCO 中,222(4)3x x -+=,解得25.8x = 257488PC BC BP ∴=-=-=, 27(,3).8P ∴- 综上可知,点193(6,3),24P -,27(,3).8P -使12BP BQ =,故答案为93(6,3)24--或7(,3)8-.三、解答题 (本大题共8小题,共78分.解答应写出文字说明、证明过程或演算步骤.)19.(1)计算:(2017-π)0-114-⎛⎫ ⎪⎝⎭+|-2|;(2)化简:111a ⎛⎫- ⎪-⎝⎭÷2244a a a a ⎛⎫-+ ⎪-⎝⎭. 【答案】(1) -1;(2)2a a - 【解析】试题分析:()1根据实数的运算步骤进行运算即可. ()2根据分式混合运算的步骤进行运算即可.试题解析:()1原式142 1.=-+=-()2原式()()2111,112a a a a a a --⎛⎫=-⋅ ⎪--⎝⎭- ()()212,12a a a a a --=⋅-- .2a a =-20.图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON 位置运动到与地面垂直的OM 位置时的示意图.已知AC =0.66米,BD =0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)(1)求AB 的长(精确到0.01米);(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径MN的长度.(结果保留π)【答案】(1) 1.17米;(2) 2245π米【解析】【分析】(1)过B作BE⊥AC于E,求出AE,解直角三角形求出AB即可;(2)求出∠MON的度数,根据弧长公式求出即可.【详解】(1)过B作BE⊥AC于E,则AE=AC﹣BD=0.66米﹣0.26米=0.4米,∠AEB=90°,(米).(2)∠MON=90°+20°=110°,∴弧MN的长度是()米.考点:1解直角三角形;2弧长公式.21.手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注:不同的分法,面积可以相等)【答案】作图见解析;2或1cm2.【解析】【分析】(1)正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,连接HE、EF、FG、GH、HF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可;(2)正方形ABCD中,E、F分别是AB、BC的中点,O是AC、BD的交点,连接OE、OF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可;(3)正方形ABCD中,F、H分别是BC、DA的中点,O是AC、BD的交点,连接HF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可;(4)正方形ABCD中,E、F分别是AB、BC的中点,O是AC的中点,I是AO的中点,连接OE、OB、OF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可.【详解】解:根据分析,可得.(1)第一种情况下,分割后得到的最小等腰直角三角形是△AEH、△BEF、△CFG、△DHG,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2=2×2÷2=2(cm2);(2)第二种情况下,分割后得到的最小等腰直角三角形是△AEO、△BEO、△BFO、△CFO,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2=2×2÷2=2(cm2);(3)第三种情况下,分割后得到的最小等腰直角三角形是△AHO、△DHO、△BFO、△CFO,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2=2×2÷2=2(cm2);(4)第四种情况下,分割后得到的最小等腰直角三角形是△AEI、△OEI,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2÷2=2×2÷2÷2=1(cm2).【点睛】本题考查作图—应用与设计作图.22.我区积极开展”体育大课间”活动,引导学生坚持体育锻炼,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步.D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调査,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;(2)请把条形统计图补充完整;(3)己知该校有2000人,请根据样本估计全校最喜欢足球的人数是多少?【答案】(1)20%,72°;(2)补图见解析;(3)560人【解析】试题分析:(1)用整体1减去A,C、D所占的百分比,即可求出B所占的百分比,再用B所占的百分比乘以360°即可得出答案;(2)根据C所占的百分比与所给的人数,求出总人数,再用总人数乘以B所占的百分比,从而补全图形;(3)根据D所占的百分比乘以总人数即可得出全校最喜欢足球的人数.试题解析:(1)样本中最喜欢B项目的人数百分比是1-44%-28%-8%=20%,其所在扇形图中的圆心角的度数是20%×360°=72°;(2)总人数是8÷8%=100(人),B的人数是:100×20%=20(人),如图:;(3)根据题意得:2000×28%=560(人),答:全校最喜欢足球的人数是560人.考点:1.条形统计图;2.用样本估计总体;3.扇形统计图.23.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF,(1)求证:AF=DC;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.【答案】(1)见解析(2)见解析【解析】【分析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案.(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.【详解】解:(1)证明:∵AF∥BC,∴∠AFE=∠DBE.∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD.在△AFE和△DBE中,∵∠AFE=∠DBE,∠FEA=∠BED,AE=DE,∴△AFE ≌△DBE (AAS )∴AF=BD .∴AF=DC .(2)四边形ADCF 是菱形,证明如下:∵AF ∥BC ,AF=DC ,∴四边形ADCF 是平行四边形.∵AC ⊥AB ,AD 是斜边BC 的中线,∴AD=DC .∴平行四边形ADCF 是菱形24.某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x 元(x 为整数).(1)直接写出每天游客居住的房间数量y 与x 的函数关系式;(2)设宾馆每天的利润为W 元,当每个房间定价为多少元时,宾馆每天所获利润最大,最大利润是多少;(3)某日,宾馆了解当天的住宿情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人.问:这天宾馆入住的游客人数最少有多少人.【答案】(1)y =50-x ,(0≤x ≤50,且x 为整数);(2)每间房价定价为320元时,宾馆每天所获利润最大,最大利润是9000元;(3)20人.【解析】【分析】(1)根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题.(2)构建二次函数,利用二次函数的性质解决问题.(3)根据条件列出不等式组即可解决问题.【详解】解:(1)根据题意,得:y=50﹣x ,(0≤x≤50,且x 为整数);(2)W=(120+10x ﹣20)(50﹣x )=210(20)9000x --+∵a=﹣10<0,∴当x=20时,W 取得最大值,W 最大值=9000元.答:当每间房价定价为320元时,宾馆每天所获利润最大,最大利润是9000元;(3)由20)210(9000500020(50)600x x -⎧-+≥⎨-+≤⎩ 解得20≤x≤40. 当x=40时,这天宾馆入住的游客人数最少,最少人数为2y=2(﹣x+50)=20(人).【点睛】本题考查二次函数的应用;一元一次不等式组的应用;二次函数的最值;最值问题.25.如图,抛物线y =x 2+bx +c 经过B (-1,0),D (-2,5)两点,与x 轴另一交点为A ,点H 是线段AB 上一动点,过点H 的直线PQ ⊥x 轴,分别交直线AD 、抛物线于点Q 、P .(1)求抛物线的解析式;(2)是否存在点P ,使∠APB =90°,若存在,求出点P 的横坐标,若不存在,说明理由;(3)连接BQ ,一动点M 从点B 出发,沿线段BQ 以每秒1个单位的速度运动到Q ,再沿线段QD 以每秒2个单位的速度运动到D 后停止,当点Q 的坐标是多少时,点M 在整个运动过程中用时t 最少?【答案】(1)y =x 2-2x -3;(2)存在,1313;(3)(-1,4)【解析】试题分析:(1)把B (﹣1,0),D (﹣2,5)代入2y x bx c =++,得出关于b 、c 的二元一次方程组,即可求出抛物线的解析式;(2)根据抛物线解析式求出OA ,设P (m ,m 2﹣2m ﹣3),则﹣1≤m ≤3,PH =﹣(m 2﹣2m ﹣3),BH =1+m ,AH =3﹣m ,证明△AHP ∽△PHB ,得出PH 2=BH •AH ,由此得出方程[﹣(m 2﹣2m ﹣3)]2=(1+m )(3﹣m ),解方程即可;(3)由题意,动点M 运动的路径为折线BQ +QD ,运动时间:t =BQ,如备用图,作辅助线,将BQDQ 转化为BQ +QG ;再由垂线段最短,得到垂线段BH 与直线AD 的交点即为所求的Q 点. 试题解析:解:(1)把B (﹣1,0),D (﹣2,5)代入2y x bx c =++,得:10425b c b c -+=⎧⎨-+=⎩,解得:23b c =-⎧⎨=-⎩,∴抛物线的解析式为:223y x x =--; (2)存在点P ,使∠APB =90°.当y =0时,即x 2﹣2x ﹣3=0,解得:x 1=﹣1,x 2=3,∴OB =1,OA =3. 设P (m ,m 2﹣2m ﹣3),则﹣1≤m ≤3,PH =﹣(m 2﹣2m ﹣3),BH =1+m ,AH =3﹣m ,∵∠APB =90°,PH ⊥AB ,∴∠P AH =∠BPH =90°﹣∠APH ,∠AHP =∠PHB ,∴△AHP ∽△PHB ,∴PH AH BH PH=,∴PH 2=BH •AH ,∴[﹣(m 2﹣2m ﹣3)]2=(1+m )(3﹣m ),解得m 1=1+m 2=1点P 的横坐标为:11(3)如图,过点D 作DN ⊥x 轴于点N ,则DN =5,ON =2,AN =3+2=5,∴tan ∠DAB =55DN AN ==1,∴∠DAB =45°.过点D 作DK ∥x 轴,则∠KDQ =∠DAB =45°,DQ QG . 由题意,动点M 运动的路径为折线BQ +QD ,运动时间:t =BQDQ ,∴t =BQ +QG ,即运动的时间值等于折线BQ +QG 的长度值.由垂线段最短可知,折线BQ +QG 的长度的最小值为DK 与x 轴之间的垂线段.过点B 作BH ⊥DK 于点H ,则t 最小=BH ,BH 与直线AD 的交点,即为所求之Q 点.∵A (3,0),D (﹣2,5),∴直线AD 的解析式为:y =﹣x +3,∵B 点横坐标为﹣1,∴y =1+3=4,∴Q (﹣1,4).点睛:此题是二次函数综合题,主要考查了待定系数法求抛物线与直线的解析式,相似三角形的判定与性质,垂线段最短的性质,函数图象上点的坐标特征等知识.利用数形结合与方程思想是解题的关键.26.如图1,点P为四边形ABCD所在平面上的点,如果∠P AD=∠PBC,则称点P为四边形ABCD关于A、B 的等角点,以点C为坐标原点,BC所在直线为x轴建立平面直角坐标系,点B的横坐标为﹣6.(1)如图2,若A、D两点的坐标分别为A(﹣6,4)、D(0,4),点P在DC边上,且点P为四边形ABCD 关于A、B的等角点,则点P的坐标为_________ ;(2)如图3,若A、D两点的坐标分别为A(﹣2,4)、D(0,4).①若P在DC边上时,则四边形ABCD关于A、B的等角点P的坐标为_________ ;②在①的条件下,将PB沿x轴向右平移m个单位长度(0<m<6)得到线段P′B′,连接P′D,B′D,试用含m的式子表示P′D2+B′D2,并求出使P′D2+B′D2取得最小值时点P′的坐标;③如图4,若点P为四边形ABCD关于A、B的等角点,且点P坐标为(1,t),求t的值;④以四边形ABCD的一边为边画四边形,所画的四边形与四边形ABCD有公共部分,若在所画的四边形内存在一点P,使点P分别是各相邻两顶点的等角点,且四对等角都相等,请直接写出所有满足条件的点P 的坐标.【答案】(1)(0,2);(2)①(0,3);②2m 2-12m +53,(3,3);③2.8;④(-1,3),(-2,2),(-3,3),(-2,0)【解析】试题分析:(1)连结AP ,BP ,由全等三角形的性质就可以得出PD=PC 而得出结论;(2)①由△ADP ∽△BCP 就可以得出AD DP BC CP=而求出结论; ②求出代表P′D 2+B′D 2的方程式,并求最小值.③画图求证△PAM ∽△PBN ,值得注意的是本题有两个图形,容易漏掉一个答案.④由题意可知,必须是正方形才能满足题干要求.试题解析:解:(1)由B 点坐标(﹣6,0),A 点坐标(﹣6,4)、D 点坐标(0,4),可以得出四边形ABCD 为矩形,∵P 在CD 边上,且∠PAD=∠PBC ,∠ADP=∠BCP ,BC=AD ;∴△ADP ≌△BCP ,∴CP=DP ,∴P 点坐标为(0,2);(2)①∵∠DAP=∠CBP ,∠BCP=∠ADP=90°,∴△ADP ∽△BCP , ∴AD DP BC CP ==26=13, ∴CP=3DP ,∴CP=3,DP=1,∴P 点坐标为(0,3);②如图3,由题意,易得 B′(m ﹣6,0),P′(m ,3)由勾股定理得P′D 2+B′D 2=PP′2+PD 2+OD 2+B′C 2=m 2+(4﹣3)2+42+(m ﹣6)2=2m 2﹣12m+53, ∵2>0∴P′D 2+B′D 2有最小值,当m=﹣1222-⨯=3时,(在0<m <6范围内)时,P′D 2+B′D 2有最小值,此时P′坐标为(3,3); ③由题意知,点P 在直线x=1上,延长AD 交直线x=1于M ,(a )如图,当点P 在线段MN 上时,易证△PAM ∽△PBN ,∴PM AM PN BN=, 即437t t -=, 解得t=2.8(b )如图,当点P 为BA 的延长线与直线x=1的交点时,易证△PAM ∽△PBN ,∴PM AM PN BN =,即437t t -=,解得t=7, 综上可得,t=2.8或t=7;④因满足题设条件的四边形是正方形,故所求P 的坐标为(﹣1,3),(﹣2,2),(﹣3,3),(﹣2,0).考点:四边形综合题;勾股定理.。
东诚教育集团安全生产管理知识-冲刺练习题—250

东诚在工程类考试辅导领域首屈一指的地位,是无数考生在实践检验中选择的结果,优秀的学员选择了优秀的东诚,东诚的成功首先源于学员的成功,口碑是最好的广告。
正如东诚往届学员所说:“东诚如此高的命中率和上线率,使不上东诚成为一种冒险!”您是否为辛苦一年却最终可能分数不够而担忧?——东诚为您制定100%通过计划!您是否为分数不够或现场报名可能被淘汰而忧愁?——东诚为您制定100%录取计划!您是否为工作多年基础为零能否拿证而内心忐忑?——东诚为您制定零基础必胜课程!您是否为自己烦忙工作而担心不能自控学习时间?——东诚为您配备专职助教服务!您是否为自己职业生涯如何嬗变而忧愁苦恼?——东诚为您提供实现的途径和捷径!东诚隆重推出协议特训班!VIP等级服务,量身定制学习进度,全程专职高通过教学,一对一家教式辅导,保姆式跟踪督导!2009年全国注册安全工程师《安全生产管理知识》辅导资料安全生产管理知识练习题一、单项选择题1.“安全”就是_______。
A.不发生事故B.不发生伤亡事故C.不存在发生事故的危险D.所存在的发生事故的危险程度是可以承受的2.当生产和其他工作与安全发生矛盾时,要以安全为主,生产和其他工作要服从安全,这就是________原则。
A.预防B.因果关系C.偶然性D.安全第一3.安全生产管理的目标是减少、控制危害和事故,尽量避免生产过程中由于________所造成的人身伤害、财产损失及其他损失。
A.管理不善B.危险C.事故D.违章4.劳动保护是站在劳动者的立场上,强调为劳动者提供人身安全与身心健康的保障。
劳动保护的对象是________。
A.从事生产的劳动者B.从事管理的人员C.职业病人D.工伤人员5.认为新的技术发展会带来新的危险源,安全工作的目标就是控制危险源,努力把事故发生概率减到最低。
这一观点是包括在________理论中的。
A.海因里希因果连锁B.事故频发倾向C.系统安全D.能量意外释放6.根据”动态相关性原则”,下述正确的是()oA.只有掌握事故发生的规律性,才能保证安全生产系统处于安全状态。
最新山东中考全真模拟检测《数学试卷》含答案解析

山东数学中考模拟测试卷一.选择题(共12小题)1.(﹣3)2的值是( )A. ﹣9B. 9C. ﹣6D. 6 2.下面是几何体中,主视图是矩形的( ) A.B. C. D. 3.下列计算正确的是( )A. a+a=a 2B. (2a )3=6a 3C. (a-1)2=a 2-1D. a 3÷a=a 2 4.如图,一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )A .B. C.D. 5.如图,直线AB ∥CD ,则下列结论正确的是( )A. ∠1=∠2B. ∠3=∠4C. ∠1+∠3=180°D. ∠3+∠4=180° 6.分式方程1x x --1=3(1)(2)x x -+的解为( ) A. x =1B. x =-1C. 无解D. x =-2 7.不等式组372291x x +≥⎧⎨-<⎩整数解的个数是() A. 4 B. 5 C. 6 D. 78.已知直线y=ax+b(a≠0)经过第一,二,四象限,那么直线y=bx-a 一定不经过( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限9.如图,由四个直角边分别是6和8的全等直角三角形拼成的“赵爽弦图”,随机往大正方形区域内投针一次,则针扎在小正方形GHEF 部分的概率是( )A. 34B. 14C. 124D. 12510.如图,在菱形OABC 中,点A 的坐标为()10,0,对角线OB AC 、相交于点,160D OB AC ⋅=.双曲线()0k y x x=>经过点D ,交BC 的延长线于点E ,则过点E 的双曲线表达式为()A. 20y x =B. 24y x =C. 28y x =D. 32y x= 11.如图,矩形ABCD 长与宽的比为3:2,点E ,F 分别在边AB 、BC 上,tan ∠1=12,tan ∠2=13,则cos (∠1+∠2)=( )A. 3B. 2C. 23D. 112.如图,抛物线y =231544x -x +3与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,点Q 是线段OB 上一动点,连接BC ,点M 在线段BC 上,且使△BQM 为直角三角形的同时△CQM 为等腰三角形,则此时点Q 的横坐标为( )A . 209或37B. 32或207C. 32或37D. 207或209 二.填空题(共6小题)13.3月7日~3月12日,“2019槐荫区数学文化年”标志评选活动在“勾股数学”微信公众号上进行,最终该评选页面的点击量为11000次,11000用科学计数法表示为__________.14.在﹣2,1,4,﹣3,0这5个数字中,任取一个数是负数的概率是______.15.计算:()()222x y x y xy ⎡⎤+--÷=⎣⎦__________.16.如图,点A 、B 、C 都在⊙O 上,OC ⊥OB ,点A 在劣弧BC 上,且OA=AB ,则∠ABC=_____.17.如图,以正六边形ABCDEF 的中心O 为原点建立平面直角坐标系,过点A 作AP 1⊥OB 于点P 1,再过P 1作P 1P 2⊥OC 于点P 2,再过P 2作P 2P 3⊥OD 于点P 3,依次进行……若正六边形的边长为1,则点P 2019的横坐标为_____.18.如图,线段AB =4,点C 为线段AB 上任意一点(与端点不重合),分别以AC 、BC 为边在AB 的同侧作正方形ACDE 和正方形CBGF ,分别连接BF 、EG 交于点M ,连接CM ,设AC =x ,S 四边形ACME =y ,则y 与x 的函数表达式为y =_____.三.解答题(共9小题)19.分解因式:4a 2﹣9b 2.20.计算: 22142a a a ---. 21.如图,点C 是线段AB 上任意一点,分别以AC BC 、为边在AB 的同侧作等边ACD ∆和等边BCE ∆,分别连接AE BD 、.求证:AE BD =.22.有大小两种货车,3辆大货车与4辆小火车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)求1辆大货车和1辆小货车一次可以分别运多少吨;(2)现有31吨货物需要运输,货运公司拟安排大小货车共10辆把全部货物一次运完.求至少需要安排几辆大货车?23.如图,AB 是半圆O 的直径,点P 是BA 延长线上一点,PC 是⊙O 的切线,切点为C ,过点B 作BD ⊥PC 交PC 的延长线于点D ,连接BC .求证:(1)∠PBC=∠CBD ;(2)=AB•BD .24.某校为激发学生学习数学的兴趣,开设了“数独、速算、魔方、七巧板、华容道”五门校本课程,规定每位学生只能选一门.该校共有学生1600人.为了解学生的报名意向,学校随机调查了一些学生,并制成如下统计图表:校本课程报名意向统计表课程频数频率数独8 a速算m 0.2魔方27 b七巧板n 0.3华容道15 c(1)在这次活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);(2)求出扇形统计图中“速算”所对应的扇形圆心角的度数;(3)a+b+c=,m=;(答案直接填写在横线上)(4)请你估算,全校选择“数独”和“魔方”的学生共有多少人?25.如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.(1)求反比例函数的表达式和m的值;(2)求△AOB的面积;(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.26.已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC 边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.(1)如图1,当∠BOP=30°时,求点P的坐标;(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t 的式子表示m;(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.27.如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.(1)求抛物线的函数表达式以及顶点D的坐标;(2)在抛物线上取一点P(不与点C重合),并分别连接P A、PD,当△P AD的面积与△ACD的面积相等时,求点P的坐标;(3)将(1)中所求得的抛物线沿A、D所在的直线平移,平移后点A的对应点为A′,点C的对应点为C′,点D的对应点为D′,当四边形AA′C′C是菱形时,求此时平移后的抛物线的解析式.答案与解析一.选择题(共12小题)1.(﹣3)2的值是()A. ﹣9B. 9C. ﹣6D. 6【答案】B【解析】【分析】根据乘方的性质即可求解.【详解】(﹣3)2=9.故选:B.【点睛】此题考查乘方的性质,解题关键在于掌握负数的奇数次幂是负数,负数的偶数次幂是正数;-1的奇数次幂是-1,-1的偶数次幂是1.2.下面是几何体中,主视图是矩形的()A. B. C. D.【答案】A【解析】几何体的主视图是从几何体的正面看得到的平面图形,A,主视图为矩形;B主视图为圆;C主视图为三角形;D主视图为梯形.符合主视图是矩形只有选项A. 故选A.3.下列计算正确的是()A. a+a=a2 B. (2a)3=6a3 C. (a-1)2=a2-1 D. a3÷a=a2【答案】D 【解析】【详解】解:A,a+a=2a≠a2,故该选项错误;B,(2a)3=8a3≠6a3,故该选项错误C,(a-1)2=a2-2a+1≠a2-1,故该选项错误;D,a3÷a=a2,故该选项正确,故选:D.根据合并同类项运算法则和积的乘方法则、完全平方公式以及同底数幂的除法法则逐项计算即可.本题考查了并同类项运算法则和积的乘方法则、完全平方公式以及同底数幂的除法法则,解题的关键是熟记以上各种运算法则.4.如图,一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是()A. B.C. D.【答案】A【解析】【分析】根据同角的余角相等,等角的补角相等和邻补角的定义对各小题分析判断即可得解.【详解】A、图中∠α+∠β=180°﹣90°=90°,∠α与∠β互余,故本选项正确;B、图中∠α=∠β,不一定互余,故本选项错误;C、图中∠α+∠β=180°﹣45°+180°﹣45°=270°,不是互余关系,故本选项错误;D、图中∠α+∠β=180°,互为补角,故本选项错误.故选:A.【点睛】此题考查余角和补角,熟记概念与性质是解题的关键.5.如图,直线AB∥CD,则下列结论正确的是()A. ∠1=∠2B. ∠3=∠4C. ∠1+∠3=180°D. ∠3+∠4=180°【答案】D【解析】分析:依据AB ∥CD ,可得∠3+∠5=180°,再根据∠5=∠4,即可得出∠3+∠4=180°. 详解:如图,∵AB ∥CD ,∴∠3+∠5=180°, 又∵∠5=∠4,∴∠3+∠4=180°, 故选D .点睛:本题考查了平行线的性质,解题时注意:两直线平行,同旁内角互补.6.分式方程1x x --1=3(1)(2)x x -+的解为( ) A. x =1B. x =-1C. 无解D. x =-2 【答案】C【解析】解:去分母得:x (x +2)﹣(x ﹣1)(x +2)=3,整理得:2x ﹣x +2=3,解得:x =1,检验:把x =1代入(x ﹣1)(x +2)=0,所以分式方程无解.故选C .点睛:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.7.不等式组372291x x +≥⎧⎨-<⎩整数解的个数是() A. 4B. 5C. 6D. 7【答案】C【解析】【分析】先解不等式组,再求整数解. 【详解】解:372291x x +≥⎧⎨-<⎩①② 解①,得x≥-53解②,得x<5所以,不等式组的解集是-53≤x<5所以,整数解是:-1,0,1,2,3,4故选C【点睛】本题考查了一元一次不等式组,难度一般,关键是先求出不等式组的解集后再确定整数解的个数.8.已知直线y=ax+b(a≠0)经过第一,二,四象限,那么直线y=bx-a一定不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】【分析】根据直线y=ax+b(a≠0)经过第一,二,四象限,可以判断a、b的正负,从而可以判断直线y=bx-a经过哪几个象限,不经过哪个象限,本题得以解决.【详解】∵直线y=ax+b(a≠0)经过第一,二,四象限,∴a<0,b>0,∴直线y=bx-a经过第一、二、三象限,不经过第四象限,故选D.【点睛】本题考查一次函数的性质,解答本题的关键是明确题意,利用一次函数的性质解答.9.如图,由四个直角边分别是6和8的全等直角三角形拼成的“赵爽弦图”,随机往大正方形区域内投针一次,则针扎在小正方形GHEF部分的概率是()A. 34B.14C.124D.125【答案】D 【解析】【分析】求出AB,HG的边长,进而得到正方形GHEF 的面积和四个小直角三角形的面积,求出比值即可.【详解】解:∵AH=6,BH=8,勾股定理得AB=10,∴HG=8-6=2,S△AHB=24,∴S正方形GHEF =4,四个直角三角形的面积=96,∴针扎在小正方形GHEF 部分的概率是1004=125故选D.【点睛】本题考查了几何概型的实际应用,属于简单题,将概率问题转换成求图形的面积问题是解题关键. 10.如图,在菱形OABC 中,点A 的坐标为()10,0,对角线OB AC 、相交于点,160D OB AC ⋅=.双曲线()0k y x x =>经过点D ,交BC 的延长线于点E ,则过点E 的双曲线表达式为()A. 20y x =B. 24y x =C. 28y x =D. 32y x= 【答案】D【解析】【分析】 过点C 作CF ⊥x 轴于点F ,由A 点坐标可得菱形的边长,利用菱形面积可求出CF 的长,由勾股定理可求出OF 的长,即可得出C 点坐标,进而可求出AC 中点D 的坐标,代入双曲线解析式可得k 的值,根据CF 的长可得E 点纵坐标,代入双曲线解析式即可求出E 点的横坐标,即可得答案.【详解】过点C 作CF ⊥x 轴于点F ,∵OB•AC =160,A 点的坐标为(10,0),∴S 菱形OABC =OA•CF =12OB•AC =12×160=80,菱形OABC 的边长为10, ∴CF =8,在Rt △OCF 中,∵OC =10,CF =8,∴OF 22OC CF -22108-=6,∴C (6,8),∵点D 是线段AC 的中点,∴D 点坐标为(1062 ,82),即(8,4), ∵双曲线y =k x (x >0)经过D 点, ∴4=8k ,即k =32, ∴双曲线的解析式为:y =32x (x >0),故选D .【点睛】本题考查了菱形的性质、反比例函数图象上点的坐标特征以及勾股定理,结合菱形的性质以及面积公式找出点的坐标,再利用反比例函数图象上点的坐标特征求出反比例函数的解析式是关键. 11.如图,矩形ABCD 长与宽的比为3:2,点E ,F 分别在边AB 、BC 上,tan ∠1=12,tan ∠2=13,则cos (∠1+∠2)=( )A. 32B. 22C. 23D. 1【答案】B【解析】【分析】由“SAS ”可证△AED ≌△BFE ,可得DE =EF ,∠1=∠FEB ,可证∠DEF =90°,可求∠1+∠2=45°,即可求解.【详解】如图,连接EF∵矩形ABCD 长与宽的比为3:2∴设AB =CD =3a ,AD =BC =2a ,∵tan ∠1=11223AE CF tan AD DC=∠==, ∴AE=a ,CF=a ,∴BF =BC ﹣CF =a ,BE =AB ﹣AE =2a ,∴AE =BF ,AD =EB ,且∠A =∠B =90°∴△AED ≌△BFE (SAS )∴DE =EF ,∠1=∠FEB∵∠1+∠DEA =90°∴∠DEA +∠FEB =90°∴∠DEF =90°,且DE =EF∴∠EDF =45°∴∠1+∠2=45°∴cos (∠1+∠2)=22 故选:B .【点睛】此题考查了矩形的性质,全等三角形的性质和判定,锐角三角函数,证明△DAE ≌△BEF 是解题的关键.12.如图,抛物线y =231544x -x +3与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,点Q 是线段OB 上一动点,连接BC ,点M 在线段BC 上,且使△BQM 为直角三角形的同时△CQM 为等腰三角形,则此时点Q 的横坐标为( )A. 209或37B. 32或207C. 32或37D. 207或209【答案】C【解析】【分析】先求得A 、B 、C 的坐标,即可求得AB 的长,求得直线BC 的解析式,然后分两种情况分别讨论①当∠BQM=90°时,设M (a ,b ),由△MQB ∽△COB ,得BM MQ BQ BC OC OB == ,列出方程即可.②当∠QMB=90°时,设CM=MQ=m ,则BM=5-m ,由△BMQ ∽△BOC ,可得534m m-= ,解方程即可.【详解】抛物线y =231544x -x +3与x 轴交于A 、B 两点(点A 在点B的左侧),与y 轴交于点C , ∴令y =0,则231544x -x +3=0,解得x =1或4,∴A (1,0),B (4,0),令x =0,则y =3,∴C (0,3),∴OB =4,OC =3,∴BC=22OB OC +=5;①当∠BQM=90°时,如图1,设M (a ,b ),∵∠CMQ >90°,∴只能CM=MQ=b ,∵MQ ∥y 轴,∴△MQB ∽△COB ,∴BMMQBQBC OC OB == ,即 54534bba--== ,解得b=15382a =,∴点Q 的横坐标为32;②当∠QMB=90°时,如图2,∵∠CMQ=90°,∴只能CM=MQ,设CM=MQ=m,∴BM=5-m,∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,∴△BMQ∽△BOC,∴534m m-=,解得m=157,∴BM=BC-CM=5-157=207,∵∠BMQ=∠BOC=90°,∠ABM=∠OBC,∴△QMB∽△COB,∴BQ BMBC OB=,即20754BQ=,∴BQ=257,∴OQ=OB-BQ=4-257=37∴点Q的横坐标为37,综上,点Q的横坐标为32或37,故选:C.【点睛】此题考查二次函数的综合题,二次函数图象上点的坐标特征,等腰三角形的性质,相似三角形的判定和性质等,解题的关键是灵活运用所学知识解决问题,学会利用参数,构建方程解决问题.二.填空题(共6小题)13.3月7日~3月12日,“2019槐荫区数学文化年”标志评选活动在“勾股数学”微信公众号上进行,最终该评选页面的点击量为11000次,11000用科学计数法表示为__________.【答案】41.110⨯【解析】【分析】根据科学记数法的定义,科学记数法的表示形式为a×10n ,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.在确定n 的值时,看该数是大于或等于1还是小于1.当该数大于或等于1时,n 为它的整数位数减1;当该数小于1时,-n 为它第一个有效数字前0的个数(含小数点前的1个0)【详解】11000=41.110⨯故答案为41.110⨯【点睛】考核知识点:科学记数法.理解科学记数法的意义是关键.14.在﹣2,1,4,﹣3,0这5个数字中,任取一个数是负数的概率是______. 【答案】25. 【解析】【分析】一共有5个数,其中负数有2个,根据概率公式计算即可得.【详解】在﹣2,1,4,﹣3,0这5个数字中,负数有-2、-3共2个, 所以任取一个数是负数的概率是25, 故答案为25. 【点睛】本题考查了简单的概率计算,熟练掌握概率的计算公式是解题的关键.15.计算:()()222x y x y xy ⎡⎤+--÷=⎣⎦__________. 【答案】2【解析】【分析】原式中括号中利用完全平方公式展开,再利用多项式除以单项式法则计算即可得到结果.【详解】解:原式=(x 2+2xy+y 2-x 2+2xy-y 2)÷(2xy )=4xy÷(2xy )=2.故答案为2【点睛】此题考查了整式的除法,熟练掌握运算法则是解本题的关键.16.如图,点A 、B 、C 都在⊙O 上,OC ⊥OB ,点A 在劣弧BC 上,且OA=AB ,则∠ABC=_____.【答案】15°【解析】分析:根据等边三角形的判定和性质,再利用圆周角定理解答即可.详解:∵OA=OB ,OA=AB ,∴OA=OB=AB ,即△OAB 是等边三角形,∴∠AOB=60°, ∵OC ⊥OB ,∴∠COB=90°, ∴∠COA=90°-60°=30°, ∴∠ABC=15°, 故答案为15°点睛:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.17.如图,以正六边形ABCDEF 的中心O 为原点建立平面直角坐标系,过点A 作AP 1⊥OB 于点P 1,再过P 1作P 1P 2⊥OC 于点P 2,再过P 2作P 2P 3⊥OD 于点P 3,依次进行……若正六边形的边长为1,则点P 2019的横坐标为_____.【答案】202012【解析】【分析】由题意得出1213222311111111,,22222222OPOA OP OP OP OP ======⨯=,推出OP n =12n ,得出OP 2019=201912,推出OP 2019在第三象限,由点P 2019的横坐标的长为:12OP 2019即可得出结果. 【详解】解:∵正六边形ABCDEF 的中心O 为原点建立平面直角坐标系,AP 1⊥OB ,P 1P 2⊥OC ,P 2P 3⊥OD , ∴△OAB 为等边三角形,∠OAP 1=30°,∴OP 1=1122OA =, 同理:∠P 2P 1O =30°, ∴OP 2=121122OP =,∠P 3P 2O =30°, ∴OP 3=22311112222OP =⨯=,即OP n =12n , ∴OP 2019=201912,∵2019÷6=336…3, ∴OP 2019在第三象限,点P 2019的横坐标的长为:20192019111222OP ⋅=⨯=202012, ∴点P 2019的横坐标为﹣202012; 故答案为﹣202012. 【点睛】本题考查了正六边形的性质、等边三角形的性质、含30°角的直角三角形的性质以及规律型;熟练掌握正六边形的性质,找出规律是解题的关键.18.如图,线段AB =4,点C 为线段AB 上任意一点(与端点不重合),分别以AC 、BC 为边在AB 的同侧作正方形ACDE 和正方形CBGF ,分别连接BF 、EG 交于点M ,连接CM ,设AC =x ,S 四边形ACME =y ,则y 与x 的函数表达式为y =_____.【答案】2x (0<x <4)【解析】【分析】连接CE ,BE ,如图,利用正方形的性质得到∠ACE =∠CBF =45°,则可判断CE ∥BF ,根据三角形面积公式得到S △CEB =S △CEM ,则y =S △ABE =12 •x •4=2x (0<x <4). 【详解】连接CE ,BE ,如图, ∵四边形ACDE 和四边形BCFG 为正方形,∴∠ACE =∠CBF =45°,∴CE ∥BF ,∴S △CEB =S △CEM ,∴y =S △ACE +S △CEM =S △ACE +S △CEB =S △ABE =12×AE ×AB =12•x •4=2x (0<x <4). 故答案为y =2x (0<x <4). 【点睛】此题考查正方形的性质,三角形的面积的等量替换方法,判断出S △CEB =S △CEM ,是解题的关键.三.解答题(共9小题)19.分解因式:4a 2﹣9b 2.【答案】(2a +3b )(2a ﹣3b )【解析】【分析】利用平方差公式分解,即可得到结果.【详解】4a 2﹣9b 2=(2a +3b )(2a ﹣3b ).【点睛】此题考查因式分解-运用公式法,熟练掌握平方差公式是解题的关键.20.计算:22142a a a ---. 【答案】12a + 【解析】【分析】先寻找2个分式分母的最小公倍式(最小公倍是用因式分解的方法去寻找),将最小公倍式作为结果的分母;然后在进行减法计算最后进行化简【详解】解:原式=21(2)(2)2a a a a -+--= ()()22(2)(2)22a a a a a a +-+-+- = 2-(2)(2)(-2)a a a a ++ = -2(2)(-2)a a a + = 1+2a . 【点睛】本题是对分式计算的考察,正确化简是关键21.如图,点C 是线段AB 上任意一点,分别以AC BC 、为边在AB 的同侧作等边ACD ∆和等边BCE ∆,分别连接AE BD 、.求证:AE BD =.【答案】见解析【解析】【分析】根据等边三角形的性质,证ACE DCB ∆≅∆,得.AE BD =【详解】解:ACD ∆和BCE ∆是等边三角形,,,AC DC EC BC ∴== 60ACD BCE ∠=∠=ACD DCE BCE DCE ∴∠+∠=∠+∠ACE BCD ∴∠=∠ACE DCB ∴∆≅∆AE BD ∴=【点睛】考核知识点:等边三角形的性质,全等三角形判定和性质.理解性质是关键.22.有大小两种货车,3辆大货车与4辆小火车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.(1)求1辆大货车和1辆小货车一次可以分别运多少吨;(2)现有31吨货物需要运输,货运公司拟安排大小货车共10辆把全部货物一次运完.求至少需要安排几辆大货车?【答案】(1) 1辆大货车一次运货4吨,1辆小货车一次运货1.5吨;(2)7辆.【解析】【分析】(1)设1辆大货车一次运货x 吨,1辆小货车一次运货y 吨,34182617x y x y +=⎧⎨+=⎩,解方程组可得;(2)设货物公司安排大货车m 辆,则小货车需要安排()10m -辆,()4 1.51031m m +-≥,求整数解可得.【详解】解:(1)设1辆大货车一次运货x 吨,1辆小货车一次运货y 吨,34182617x y x y +=⎧⎨+=⎩ ①2⨯-②3⨯得1015y -=-1.5y ∴=把 1.5y =代入①,得4x =41.5x y =⎧∴⎨=⎩ (2)设货物公司安排大货车m 辆,则小货车需要安排()10m -辆,()4 1.51031m m +-≥解得 6.4m ≥ m 为正整数,m ∴最小可以取7答:1辆大货车一次可以运货4吨,1辆小货车一次可以运货1.5吨,该货物公司至少安排7辆大货车.【点睛】考核知识点:方程组和不等式应用.理解题意中的数量关系是关键.23.如图,AB 是半圆O 的直径,点P 是BA 延长线上一点,PC 是⊙O 的切线,切点为C ,过点B 作BD ⊥PC 交PC 的延长线于点D ,连接BC .求证:(1)∠PBC=∠CBD ;(2)=AB•BD.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】(1)连接OC,由PC为圆O的切线,利用切线的性质得到OC垂直于PC,再由BD垂直于PD,得到一对直角相等,利用同位角相等两直线平行得到OC与BD平行,进而得到一对内错角相等,再由OB=OC,利用等边对等角得到一对角相等,等量代换即可得证;(2)连接AC,由AB为圆O的直径,利用圆周角定理得到∠ACB为直角,利用两对角相等的三角形相似得到三角形ABC与三角形CBD相似,利用相似三角形对应边成比例,变形即可得证.【详解】解:(1)连接OC,∵PC与圆O相切,∴OC⊥PC,即∠OCP=90°,∵BD⊥PD,∴∠BDP=90°,∴∠OCP=∠PDB,∴OC∥BD,∴∠BCO=∠CBD,∵OB=OC,∴∠PBC=∠BCO,∴∠PBC=∠CBD;(2)连接AC,∵AB为圆O的直径,∴∠ACB=90°,∴∠ACB=∠CDB=90°,∵∠ABC=∠CBD,∴△ABC∽△CBD,∴BC ABBD BC,则2BC=AB•BD.【点睛】本题考查相似三角形的判定与性质;切线的性质.24.某校为激发学生学习数学的兴趣,开设了“数独、速算、魔方、七巧板、华容道”五门校本课程,规定每位学生只能选一门.该校共有学生1600人.为了解学生的报名意向,学校随机调查了一些学生,并制成如下统计图表:校本课程报名意向统计表课程频数频率数独8 a速算m 0.2魔方 27b 七巧板n 0.3 华容道15 c(1)在这次活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”);(2)求出扇形统计图中“速算”所对应的扇形圆心角的度数;(3)a +b +c = ,m = ;(答案直接填写在横线上)(4)请你估算,全校选择“数独”和“魔方”的学生共有多少人?【答案】(1)抽样调查;(2)72°;(3)0.5,20;(4)560.【解析】【分析】(1)利用全面调查和抽样调查的特点即可作判断.(2)根据题意列式计算即可; (3)根据统计表中的信息列式计算即可; (4)根据学生总数乘以“数独”和“魔方”的学生占总人数的百分数,即可求出答案. 【详解】(1)在这次调查活动中,根据学校的人数,即可采取的调查方式是抽样调查; 故答案为:抽样调查;(2)“速算”所对应的扇形圆心角的度数为360°×0.2=72°; (3)a +b +c =1﹣0.2﹣0.3=0.5,m =(8+27+15)÷0.5×0.2=20; 故答案为:0.5,20; (4)全校选择“数独”和“魔方”的学生共有1600×827100=560(人). 【点睛】此题考查了扇形统计图,频率分布表,解题关键在于读图时要全面细致,同时,要充分运用数形结合思想来解决由统计表的形式给出的数学实际问题.25.如图1,点A (m ,6),B (6,1)在反比例函数图象上,作直线AB ,连接OA 、OB .(1)求反比例函数的表达式和m 的值;(2)求△AOB 的面积;(3)如图2,E 是线段AB 上一点,作AD ⊥x 轴于点D ,过点E 作x 轴的垂线,交反比例函数图象于点F ,若EF =AD ,求出点E 的坐标.【答案】(1)6y=x ,m =1;(2)352;(3)E 的坐标为(2,5)或(3,4). 【解析】【分析】 (1)设反比例函数的解析式为y =k x,根据题意B 点坐标得出k 的值以及m 的值; (2)设直线AB 的解析式为y =ax +b ,求出直线AB 的解析式,再利用S △AOB =S △MON ﹣S △AOM ﹣S △BON ,求出答案即可;(3)设E 点的横坐标为m ,则E (m ,﹣m +7),F (m ,6m ),求出EF =﹣m +7﹣6m ,得出关于m 的方程,求出m 即可.【详解】解:(1)设反比例函数的解析式为y =k x, 将B (6,1)的坐标代入y =k x,得k =6. ∴反比例函数的解析式为y =6x. 将A (m ,6)的坐标代入y =6x ,得m =1. (2)如图1,设直线AB 的解析式为y =ax +b ,把A (1,6)和B (6,1)代入上式,得661a b a b +=⎧⎨+=⎩, 解得:17a b =-⎧⎨=⎩, 故直线AB 的解析式为:y =﹣x +7,∴M (0,7),N (7,0), 111222AOB MON AOM BON A B S S S S OM ON OM x ON y ∆∆∆∆∴=--=⨯-⨯-⨯ 111777171222=⨯⨯-⨯⨯-⨯⨯ 352= (3)设E 点的坐标为(m ,﹣m +7),则F (m ,6m), ∴EF =﹣m +7﹣6m. ∵EF =13AD , ∴﹣m +7﹣613m =×6. 解得m 1=2,m 2=3,经检验,m 1=2,m 2=3是分式方程的根,∴E 的坐标为(2,5)或(3,4).【点睛】本题考查了用待定系数法求出反比例函数和一次函数的解析式,正确得出直线AB 的解析式是解题关键.26.已知一个矩形纸片OACB ,将该纸片放置在平面直角坐标系中,点A (4,0),点B (0,3),点P 为BC 边上的动点(点P 不与点B 、C 重合),经过点O 、P 折叠该纸片,得点B ′和折痕OP .设BP =t . (1)如图1,当∠BOP =30°时,求点P 的坐标;(2)如图2,经过点P 再次折叠纸片,使点C 落在直线PB ′上,得点C ′和折痕PQ ,设AQ =m ,试用含有t 的式子表示m ;(3)在(2)的条件下,连接OQ ,当OQ 取得最小值时,求点Q 的坐标;(4)在(2)的条件下,点C ′能否落在边OA 上?如果能,直接写出点P 的坐标;如果不能,请说明理由.【答案】(1);(2)214333m t t =-+;(3)54,3Q ⎛⎫ ⎪⎝⎭;(4)点C ′不能落在边OA 上. 【解析】【分析】 (1)在Rt △OBP 中,∠BOP =30°,求PB ,即求P 点坐标;(2)证明OBP ∽△PCQ ,得到343t t m=--即可求解; (3)OQ 2=OA 2+AQ 2=42+AQ 2=16+AQ 2,当AQ 最短时,OQ 最短;(4)假设点C ′能落在边OA 上,在Rt △OB ′C ′中,B ′O 2+B ′C ′2=OC ′2,32+(4﹣2t )2=(4﹣t )2,△=(﹣8)2﹣4×3×9<0,该方程无实数解,点C ′不能落在边OA 上. 【详解】解:(1)∵A (4,0),B (0,3),∴OA =4,OB =3,在Rt △OBP 中,∵∠BOP =30°,∴PB==∴点P ,3),(2)由题意,得BP =t ,PC =4﹣t ,CQ =3﹣m ,由折叠可知:∠OPB =∠OPB ′,∠CPQ =∠C ′PQ ,又∵∠OPB +∠OPB ′+∠CPQ +∠C ′PQ =180°,∴∠OPB +∠CPQ =90°,又∵∠OPB +∠BOP =90°,∴∠OPB =∠CPQ ,又∵∠OBP =∠C =90°,∴△OBP ∽△PCQ , ∴OB BP PC CQ=, 343t t m∴=--, ∴m =13t 2﹣43t +3; (3)∵OQ 2=OA 2+AQ 2=42+AQ 2=16+AQ 2,∴当AQ最短时,OQ最短,∵AQ=m=13t2﹣43t+3=13(t﹣2)2+53,∴当t=2时,AQ最短,OQ最短,此时点Q(4,53),(4)点C′不能落在边OA上,理由:假设点C′能落在边OA上,由折叠可得PB=PB′=t,PC=PC′=4﹣t,OB=OB′=3,∠OPB=∠OPC′,∠OB′P=∠OBP=90°,∵BC∥OA,∴∠BPO=∠POC′,∴∠OPC′=∠POC′,∴OC′=PC′=4﹣t,∴B′C′=PC﹣PB′=(4﹣t)﹣t=4﹣2t,在Rt△OB′C′中,∵B′O2+B′C′2=OC′2,∴32+(4﹣2t)2=(4﹣t)2,整理,得3t2﹣8t+9=0,∵△=(﹣8)2﹣4×3×9<0,∴该方程无实数解,∴点C′不能落在边OA上.【点睛】本题考查一次函数图象及性质,图形的折叠,三角形的相似,最短路径问题;借助三角形相似求m与t的关系,利用二次函数求最短距离,利用勾股定理和一元二次方程根的存在性判断点的位置关系是解决本题的关键.27.如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.(1)求抛物线的函数表达式以及顶点D的坐标;(2)在抛物线上取一点P(不与点C重合),并分别连接P A、PD,当△P AD的面积与△ACD的面积相等时,求点P的坐标;(3)将(1)中所求得的抛物线沿A、D所在的直线平移,平移后点A的对应点为A′,点C的对应点为C′,点D的对应点为D′,当四边形AA′C′C是菱形时,求此时平移后的抛物线的解析式.【答案】(1)y =﹣x 2+2x +3,(1,4);(2)2,221)+或(2,221)--;(3)①当A ′在x 轴上方时,如图2,A ′2﹣1,2).②当A ′在x 轴下方时,如图3,同理可得:平移后的抛物线为y =(1+2)2422x --⋅+-【解析】【分析】(1)求得C 的坐标,然后根据A 、B 点的坐标设抛物线的函数表达式为y =a (x +1)(x ﹣3),代入c 的坐标即可求得a ,求得解析式,进而求得顶点坐标;(2)先求得直线AD 的解析式,然后求得线段AD 交y 轴于点E 点的坐标,过点C 作直线l 1∥AD ,则直线l 1的解析式为y =2x +3,求得与抛物线的交点C ,由C 的坐标即可判定在线段AD 上方的抛物线上不存在使△P AD 的面积与△ACD 的面积相等的点P ,将直线AD 沿竖直方向向下平移1个单位长度,所得的直线l 2的解析式为y =2x +1.直线l 2与抛物线交于点P ,则此时△P AD 的面积与△ACD 的面积相等,联立方程即可求得交点P 的坐标;(3)设A ′的坐标为(t ,2t +2),则得出A ′A 2=5(t +1)2.AC 2=10.由四边形AA ′C ′C 是菱形,则AC =AA ′.从而得出5(t +1)2=10.解得t 12﹣1,t 22﹣1,即可求得A ′的坐标为2﹣1,2)或2﹣1,﹣2),然后分两种情况讨论求得即可.【详解】解:(1)由抛物线y =ax 2+bx +3可知C 的坐标为(0,3),设抛物线的函数表达式为y =a (x +1)(x ﹣3),代入C (0,3)得﹣3a =3.∴a =﹣1.∴抛物线的函数表达式为y =﹣(x +1)(x ﹣3),即y =﹣x 2+2x +3,∵对称轴为直线x =132-+=1, 代入上式,得y =﹣(1+1)(1﹣3)=4.∴顶点D 的坐标为(1,4).(2)∵C (0,3),OC =3.设直线AD 的解析式为y =kx +m ,则04k m k m -+=⎧⎨+=⎩,解得22k m =⎧⎨=⎩∴直线AD 的解析式为y =2x +2,设线段AD 交y 轴于点E ,则E (0,2).∴CE =OC ﹣OE =3﹣2=1.过点C 作直线l 1∥AD ,则直线l 1的解析式为y =2x +3,如图1,由﹣x 2+2x +3=2x +3,解得x 1=x 2=0.将x =0代入y =2x +3,得y =3.∴直线l 1与抛物线只有一个交点C .∴在线段AD 上方的抛物线上不存在使△P AD 的面积与△ACD 的面积相等的点P ,将直线AD 沿竖直方向向下平移1个单位长度,所得的直线l 2的解析式为y =2x +1.直线l 2与抛物线交于点P ,则此时△P AD 的面积与△ACD 的面积相等.由﹣x 2+2x +3=2x +1,解得x 1,x 2.∴y 1=+1,y 2=﹣+1.∴点P ,+1,﹣+1).(3)设A ′的坐标为(t ,2t +2),则A ′A 2=(t +1)2+(2t +2)2=5(t +1)2.AC 2=12+32=10.∵四边形AA ′C ′C 是菱形,∴AC =AA ′.∴5(t +1)2=10.解得t 1﹣1,t 2﹣1.∴A ′﹣1,﹣1,﹣).①当A ′在x 轴上方时,如图2,A ′﹣1,).将点A 个单位长度,再向上平移个单位长度就得到点A ′,∴将点D (1,4)个单位长度,再向上平移个单位长度就得到点D ′+1+4).∴平移后的抛物线为y =﹣(x ﹣1) 2,②当A ′在x 轴下方时,如图3,同理可得:平移后的抛物线为y =﹣(x ﹣) 2+4﹣.【点睛】本题考查的是二次函数知识综合运用,涉及到待定系数法求二次函数的解析式、平移的性质,核心是通过作图确定所求点的位置,避免遗漏,本题难度较大.。
诚成教育仿真试卷龙东地区英语卷

诚成教育仿真试卷龙东地区英语卷一、单项选择。
(每小题2分,共90分)1. ________ it is today! () [单选题] *A. What fine weather(正确答案)B. What a fine weatherC. How a fine weatherD. How fine a weather2. —When shall we meet again next week?— _______ day is possible. It’s no problem with me.() [单选题] *A.EitherB. NeitherC. EveryD. Any(正确答案)3. Robert has gone to _________ city and he’ll be back in a week. () [单选题] *A. otherB. the otherC. another(正确答案)D. any other4. — A latest magazine, please.— Only one left. Would you like to have ________? ( ) [单选题] *A.it(正确答案)B. oneC. thisD. that5. —Why don’t we take a little break?—Didn’t we just have _______ ? () [单选题] *A.itB .thatC. one(正确答案)D. this6. I wonder ______ they finished so many different jobs in such a short time. () [单选题] *A. whyB. how(正确答案)C. whenD. where7. I don’t know when he _____. When he _____ here, I’ll call you in a minute. () [单选题] *A. will come; will arriveB. comes; arrivesC. will come; arrives(正确答案)D. comes; will arrive8. He turned ________ the radio a little because his father was asleep. () [单选题] *A. onC. upD. off9. —Would you like some coffee?—Yes, and please get me some milk. I prefer coffee ____ milk. ( ) [单选题] *A.with(正确答案)B.toC.ofD.on10. They each ___ a book. Each of them ___ from China. () [单选题] *A. has; areB. have; is(正确答案)C. are having; areD. is having; is11.Though it’s cloudy now, it ________ get sunny later. () [单选题] *A. canB. may(正确答案)C. mustD. need12.It is in the library, you _______ talk loudly. () [单选题] *A. may notB. can’tC. needn’t13. If anyone wants to say something in class, you ____ put up your hands first. () [单选题] *A. mustB. mayC. should(正确答案)D. can14. The pen _________ him ten yuan. () [单选题] *A. paidB. cost(正确答案)C. tookD. spent15.—Could I use your dictionary?— Yes, you _________.() [单选题] *A.needB. couldC. can(正确答案)D. should16. —Mary dances best in our school.—I agree. I’ll never forget ___ her dance for the first time. () [单选题] *A.seeB.to seeC.seeing(正确答案)D.seen17. There are many people downstairs. What do you think _________? () [单选题] *A.to happenB. happeningC. is happenedD. has happened(正确答案)18.—I hear Sam has gone to Qingdao for his holiday.—Oh, how nice! Do you know when he _______? ( )[单选题] *A.left(正确答案)B. was leavingC. has leftD. had left19.—David, look at the man in white over there. Can you tell me _______?—He is a doctor. ()[单选题] *A.who is heB. who he isC. what does he doD. what he does(正确答案)20. —I want to teach in Tibet(西藏) when I graduate from the college.—Me too. Teachers ___very much there. () [单选题] *A.needB. are needingC. are needed(正确答案)D. is needed21. —Tom, do you know if Frank __ to the shop with us this Sunday if it ____? —Sorry, I have no idea. ( ) [单选题] *A.will go, is going to be fineB. goes, is fineC.will go, is fine(正确答案)D. goes, will be fine22. I don’t have to introduce him to you ____ you know the boy. () [单选题] *A. untilB. unlessC. since(正确答案)D. but23. —This pair of shoes _______ really small for me.—Why not try another _________. ( ) [单选题] *A.is, pair(正确答案)B. are, pairC. is, oneD. are, one24. If you don’t go to the meeting tomorrow, _____? () [单选题] *A. he will, tooB. he won’t, either(正确答案)C. he does, tooD. he doesn’t, either25. I don’t think we can finish all the work before Friday, ________? () [单选题] *A. do IB. can we(正确答案)C. can’t weD. don’t we26. —Do you know _______?—I’m not sure. Maybe an artist. ( ) [单选题] *A.what the man with long hair is(正确答案)B .what is the man with long hairC.who the man with long hair isD. who is the man with long hair27. —__________? ()—Things are going very well. [单选题] *A.How soon does it goB. How often does it goC.How far is it goD. How is everything going(正确答案)28. —My parents never stop going on about(唠叨) how I should study hard __. () [单选题] *A. So my parents doB. Nor my parentsC. Nor do my parents(正确答案)D. Neither my parents do29. He never does his work _______ Mary. () [单选题] *A. as careful asB. so careful asC. as carefully as(正确答案)D. carefully as30. _________ music she is playing! () [单选题] *A. What nice(正确答案)B. How niceC. What a niceD. How nice a31. The nurse told the children the sun ______ in the east. () [单选题] *A. rises(正确答案)B. roseC. will riseD. has risen32. —Are you sure you have to? It’s been very late.— I don’t know ______ I can do it if not now. () [单选题] *A.whereB. whyC. when(正确答案)D. how33. Can you lend me the book ___ the other day? () [单选题] *A. that you talkedB. you talked about itC. which you talked toD. you talked about(正确答案)34. Jim’s father got very angry _________. () [单选题] *A. with that he had doneB. with what he had doneC. at what he had done(正确答案)D. at what had he done35. —What are on show in the museum?—Some photos _______ by the children of Yushu, Qinghai. () [单选题] *A.have been takenB. were takenC. are takenD. taken(正确答案)36. The doctor did what he could _____ the dying man. () [单选题] *A. saveB. to save(正确答案)C. savedD. saving37. —Who is singing in the next room?—_____ must be Maria. (A) [单选题] *A.It(正确答案)B. SheC. ThisD. That38. She was born _______ the evening of August 8, 2008.() [单选题] *A. inB. on(正确答案)C. atD. with39.They preferred ______ in bed rather than _____ horses. () [单选题] *A.to lie; to rideB.lying; ridingC.to lie; ride(正确答案)D.lying; ride40.Everyone except Tom and John ______ seen the film. () [单选题] *A.isB.has(正确答案)C.areD.have41. She asked me _____ I would do it or not. () [单选题] *A. ifB. whether(正确答案)C. asD. until42. —Could you tell me___________?— She has a pain in her face.( ) [单选题] *A.what is the matter with her(正确答案)B. what’s wrong with himC.what the matter is with herD. what wrong is with him43. Do you have _______ to tell me? () [单选题] *A. something importantB. important somethingC. anything important(正确答案)D. important anything44. In our country every boy and every girl ____ the right(权利) to education. () [单选题] *A. has(正确答案)B. haveC. isD. are45. Nobody but Jane and Lily ______ the secret. () [单选题] *A. knows(正确答案)B. knowC. have knowD. is known二、选出句中画线部分的同义词组。
2023-2024学年盐城市第一小学教育集团数学三下期末联考模拟试题含解析

2023-2024学年盐城市第一小学教育集团数学三下期末联考模拟试题一、认真计算。
1.直接写得数.60×2= 7.8+2.1= 50×30= 70×20=80×6= 15×30= 0.5+1.9=7.3-3.6=1 8+68=58-48= 59+29= 57-27=2.列竖式计算,带★的要验算。
14.79.8-=★2243⨯=6153÷=★8406÷=3.脱式计算。
168+32×5 840÷8×7 (334-29)÷5二、我会判断。
(对的画√,错的画×)4.把75个苹果放入箱子,每箱放9个,至少要9个箱子才能装完。
(________)5.计算26×(11-5)时应先算乘法。
(_____)6.小高的身高是1.56m,他趟过平均水深1.2m的小河,不会有任何危险.(________)7.用长是12分米的铁丝围成的正方形的面积和围成的长方形的面积相同。
(________)8.一年中没有连续两个月是小月。
(______)三、精挑细选。
(把正确答案的序号填在括号里)9.下面三道算式中,乘积最接近1000的是()A.20×59 B.29×40 C.19×4910.用小数表示1元7角等于()元.A.17 B.1.7 C.1.0711.8989÷的商是()。
A.一位数B.两位数C.三位数D.四位数12.小剧场的观众席有47排,每排24个座位。
这个小剧场能容纳的观众人数()1300人。
A.大于B.小于C.等于13.下列物体运动的现象是平移的有()。
A.摩天轮B.过山车C.船在海上航行四、快乐填空。
14.要使3□2÷3的商中间有0,且没有余数,□里应填(_____),要使商末尾有两个0,□里应填(_____).15.把1米平均分成10份,每份1分米,1分米是(____)米(填分数),也可以写成(____)米(填小数),读作(______)米。
陕西省西安市新城区东方小学教育集团2024届数学三下期末质量检测模拟试题含解析

陕西省西安市新城区东方小学教育集团2024届数学三下期末质量检测模拟试题一、用心思考,认真填写。
1.80×25积的末尾有(_________)个零.48×52积是(_______)位数,大约是(_________).2.看图填空.B在十字路口的(____)面,C在十字路口的(____)面;B在A的(____)面,B在D的(____)面,(____)在A 的东南面,(____)在C的东北面.3.最大两位数与最小两位数的2倍的积是(_____).4.在括号里填上合适的单位。
一台电脑显示屏的屏幕面积约10(________)小明的体重约30(________)小明的身高是1.35(________)一辆货车载重20(________)5.填上合适的单位名称。
小明家的住房面积约是110(______);数学课本封面的面积约是3(______);一支铅笔长15(______)。
6.小黑、小白和小灰三只兔朋友见面了,每两只小兔握一次手,三只小兔一共握了(______)次手。
7.一个长方形的长是8厘米,宽是长的一半,周长是(_________),面积是(_________),与它周长相等的正方形,边长是(__________),面积是(__________).8.381×5的积的末尾有(______)个1.9.6000米=(____)千米5吨=(____)千克2平方米=(____)平方分米800平方厘米=(____)平方分米10.把548个苹果装在6个筐里,每筐大约装(____)个.11.一个两位数乘6所得的积,等于12乘25的积,这个两位数是(______).二、仔细推敲,认真辨析。
12.1平方米比1米大.(___)13.锐角比直角小。
(______)14.一个长方形和一个正方形的周长相等,面积也一定相等。
(________)15.太阳从西方升起,从东方落下.()16.四月、六月、八月、九月、十一月,每月都有30天. (____)三、反复比较,慎重选择。
【翼教版】九年级数学上期中第一次模拟试题(含答案)

一、选择题1.有三个质地、大小一样的纸条上面分别写着三个数,其中两个正数,一个负数,任意抽取一张,记下数的符号后,放回摇匀,再重复同样的操作一次,试问两次抽到的数字之积是正数的概率为( )A .13B .49C .59D .232.如图,转盘的红、黄、蓝、紫四个扇形区域的圆心角分别记为α,β,γ,θ.自由转动转盘,则下面说法错误的是( )A .若90α>︒,则指针落在红色区域的概率大于0.25B .若αβγθ>++,则指针落在红色区域的概率大于0.5C .若αβγθ-=-,则指针落在红色或黄色区域的概率和为0.5D .若180γθ+=︒,则指针落在红色或黄色区域的概率和为0.5 3.从1,2,3,4四个数中任取一个数作为十位上的数字,再从2,3,4三个数中任取一个数作为个位上的数字,那么组成的两位数是3的倍数的概率是( )A .14B .13C .512D .234.在一个不透明的盒子中有大小均匀的黄球与白球共12个,若从盒子中随机取出一个球,若取出的球是白球的概率是13,则盒子中白球的个数是( ). A .3 B .4 C .6 D .85.一次围棋比赛,参赛的每两位棋手之间都要比赛一场,根据赛程计划共安排45场比赛,设本次比赛共有x 个参赛棋手,则可列方程为( )A .12x (x ﹣1)=45B .12x (x+1)=45 C .x (x ﹣1)=45 D .x (x+1)=456.下列关于x 的方程中,一定是一元二次方程的是( )A .221x x +B .20ax x +=C .()()121x x -+=D .223250x xy y --= 7.关于x 的一元二次方程2430x x -+=的实数根有( )A .0个B .1个C .2个D .3个8.若12,x x 是方程2420200x x --=的两个实数根,则代数式211222x x x -+的值等于( )A .2020B .2019C .2029D .20289.如图,在四边形ABCD 中,BD 平分ABC ∠,//AD BC ,90C ∠=︒,5AB =,4CD =,则四边形ABCD 的周长是( ).A .18B .20C .22D .2410.如图,在ABC 中,D 是BC 边上的中点,连结AD ,把ACD △沿AD 翻折,得到ADC ',DC '与AB 交于点E ,连结BC ',若2BD BC ='=,3AD =,则点D 到AC '的距离为( )A .33B .3217C .7D .1311.下列四个命题中真命题是( )A .对角线互相垂直平分的四边形是正方形B .对角线垂直且相等的四边形是菱形C .对角线相等且互相平分的四边形是矩形D .四边都相等的四边形是正方形 12.菱形OBCA 在平面直角坐标系中的位置如图所示,点C 的坐标是()8,0,点A 的纵坐标是2,则点B 的坐标是( )A .()4,2B .()4,2-C .()2,6-D .()2,6二、填空题13.大冶市现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为参加全市汉字听写大赛,则恰好选中一男一女两位同学参赛的概率是________________.14.如图,一枚飞镖游戏板由大小相等的小正方形格子构成向游戏板随机投掷一枚飞镖,击中黑色区域的概率是__________.15.一元二次方程260x x --=的两根分别是1x ,2x ,则1212x x x x +-的值为__________.16.α是一元二次方程2240x x --=的一个根,2αβ+=,则22ββ-的值是________.17.对于有理数a ,b ,定义{}min ,a b :当a b ≥时,{}min ,a b b =;当a b ≤时,{}min ,a b a =.若{}22min 40,12440m n m n -+--=,则n m 的值为______. 18.如图,四边形ABCD 是一个正方形,E 是BC 延长线上一点,且AC =EC ,则∠DAE 的度数为_________.19.如图,正方形AOBC 的两边分别在x 轴、y 轴上,点()4,3D -在边AC 上,以点B 为中心,把△BCD 旋转90︒,则旋转后点D 的对应点1D 的坐标是________.20.如图,四边形ABCD 中,30,120B D ∠=︒∠=︒,且,6AB AC AD CD ⊥+=,则四边形ABCD 周长的最小值是_______________________.三、解答题21.在如图所示的电路图中,有四个断开的开关A、B、C、D和一个灯泡L.(1)若任意闭合其中一个开关,则灯泡L发亮的概率为;(2)若任意闭合其中两个开关,请用列表法或画树状图法求灯泡L发亮的概率.22.“赣江”是长江主要支流之一,江西省最大的河流.其东源出自石城县武夷山,称“绵水”,流经瑞金,在会昌县与“湘水”(江西)汇合,称“贡水”;其西源出自崇义县聂都山,称“章水”.“章水"与“贡水”在赣州市八镜台汇合,是为“赣江”.小丽和小杰一起玩游戏:将“章水”、“贡水”、“绵水”、“湘水”分别写在四张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上.小丽从中随机抽取一张卡片,小杰再从剩余的卡片中随机抽取一张卡片.(1)“赣江被抽中”是______事件,“章水被抽中”是______事件(填“不可能”或“必然”或“随机”);(2)试用画树状图或列表的方法表示所有可能的结果,并求“两人抽取的河流能汇合”的概率.23.如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门.(1)所围矩形猪舍的长,宽分别为多少米时,猪舍面积为296m ?(2)能否围面积为2100m 的矩形猪舍,若能,求出长和宽;若不能,请说明理由. 24.解下列方程:(1)24830x x --=; (2)2(3)5(3)x x +=+.25.已知点(0,4)A 、(4,0)B -分别为面直角坐标中y 、x 轴上一点,将线段OA 绕O 点顺时针旋转至OC ,连接AC 、BC .(1)如图1,若60AOC ∠=︒,求ACB ∠的度数;(2)若60AOC ∠=︒,AOB ∠的平分线OD 交BC 于D ,如图2,求证:OD BD CD +=;(3)若30AOC ∠=︒,过A 作AE AC ⊥交BC 于E ,如图3,求BE 的长. 26.如图,矩形ABCD 中,AB =6,BC =8,E 为BC 上一动点.将△ABE 沿AE 翻折后得到AFE ,延长AF 交CD 所在直线于点G ,设BE =x .(1)若点G 在CD 边上,求x 的取值范围;(2)若x =5,求CG 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据题意画出树状图得出所有等可能的结果与两次抽到的数字之积是正数的情况数,然后利用概率公式求解即可.【详解】解:两个正数分别用a ,b 表示,一个负数用c 表示,画树状图如下:共有9种等情况数,其中两次抽到的数字之积是正数的有5种, 则两次抽到的数字之积是正数的概率是59; 故选:C .【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比. 2.C解析:C【分析】根据概率公式计算即可得到结论.【详解】解:A 、∵α>90°,900.25360360α∴>=,故A 正确; B 、∵α+β+γ+θ=360°,α>β+γ+θ, 1800.5360360α∴>=,故B 正确; C 、∵α-β=γ-θ,∴α+θ=β+γ,∵α+β+γ+θ=360°,∴α+θ=β+γ=180°, 1800.5360︒︒∴= ∴指针落在红色或紫色区域的概率和为0.5,故C 错误;D 、∵γ+θ=180°,∴α+β=180°,1800.5360∴=∴指针落在红色或黄色区域的概率和为0.5,故D正确;故选:C.【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.3.B解析:B【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与组成的两位数是3的倍数的情况,再利用概率公式即可求得答案.【详解】画树状图得:∵共有12种等可能的结果,组成的两位数是3的倍数的有4种情况,∴组成的两位数是3的倍数的概率是:41123=.故选:B【点睛】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.4.B解析:B【分析】根据白、黄球共有的个数乘以白球的概率即可解答.【详解】由题意得:12×13=4,即白球的个数是4.故选:B.【点睛】本题考查概率公式:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn.5.A解析:A【分析】关系式为:棋手总数×每个棋手需赛的场数÷2=45,把相关数值代入即可.【详解】解:本次比赛共有x个参赛棋手,所以可列方程为:12x(x-1)=45.故选:A.【点睛】本题考查了由实际问题抽象出一元二次方程,解决本题的关键是得到比赛总场数的等量关系,注意2队之间的比赛只有1场,最后的总场数应除以2.6.C解析:C【分析】利用一元二次方程定义进行解答即可.【详解】A.含有分式,不是一元二次方程,故此选项不符合题意;B.当a=0时,不是一元二次方程,故此选项不符合题意;C.由已知方程得到:x²+x-3=0,该方程是一元二次方程,故此选项符合题意;D.含有两个未知数,不是一元二次方程,故此选项不合题意;故选C.【点睛】本题考查了一元二次方程定义,关键是掌握一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数;②只含有一个未知数;③未知数的最高次数是2.7.C解析:C【分析】根据一元二次方程根的判别式判断即可.【详解】解:一元二次方程2430x x-+=的根的判别式为:b2-4ac=(-4)2-4×3×1=4>0,所以,方程有两个不相等的实数根,故选:C.【点睛】本题考查了一元二次方程根的判别式,求出根的判别式的值是解题关键.8.D解析:D【分析】先根据一元二次方程的解的概念和根与系数的关系得出21142020x x -=,124x x +=,代入原式计算即可.【详解】解:∵1x ,2x 是方程2420200x x --=的两个实数根,∴211420200x x --=,即21142020x x -=,由根与系数之间关系可知124x x +=,∴211222x x x -+=21112422x x x x -++=2020+122()x x +=2020+8=2028.所以选项D 正确.故答案为:D【点睛】本题主要考查了一元二次方程的解、根与系数之间的关系,本题解题的关键是将211222x x x -+进行等量变形,并代入求解.9.C解析:C【分析】过点A 做AE BC ⊥交BC 于点E ,根据角平分线和平行线性质,推导得5AD AB ==;通过判定四边形AECD 为矩形,得5EC AD ==,4AE CD ==;再根据勾股定理计算,得BE ,从而得到四边形ABCD 的周长.【详解】如图,过点A 做AE BC ⊥交BC 于点E∵BD 平分ABC ∠∴ABD CBD ∠=∠∵//AD BC∴ADB CBD ∠=∠∴ABD ADB ∠=∠∴5AD AB ==∵AE BC ⊥,90C ∠=︒∴//AE DC∴四边形AECD 为矩形∴5EC AD ==,4AE CD ==又∵AE BC ⊥,即90AEB =︒∠ ∴223BE AB AE =-=∴四边形ABCD 的周长22AB BE EC CD AD =++++=故选:C .【点睛】本题考查了平行线、角平分线、等腰三角形、矩形、勾股定理的知识;解题的关键是熟练掌握平行线、角平分线、矩形、勾股定理、等腰三角形的性质,从而完成求解. 10.B解析:B【分析】过点D 作DF ⊥BC',垂足为F ,过点A 作AG ⊥BC',交BC'的延长线于G ,则四边形ADFG 是矩形,计算AC '的长,后利用三角形ADC 'M 面积 的不同计算方法计算即可.【详解】如图,过点D 作DF ⊥BC',垂足为F ,过点A 作AG ⊥BC',交BC'的延长线于G ,∵把ACD △沿AD 翻折,得到ADC ',∴DC=DC ',∠ADC=∠A DC ',∵D 是BC 边上的中点,∴DC=BD ,∵2BD BC ='=,∴DC '=2BD BC ='=,∴BDC '是等边三角形,∴∠ADC=∠A DC '=∠B DC '=∠DC 'B=60°,∴BG ∥AD ,∵DF ⊥BC',AG ⊥BC',∴四边形ADFG 是矩形,∴BF=FC'=1,FG=AD=3,=,∴GC '=2,∴AC '=,设点D 到AC '的距离为h , ∴1122AC h AD DF '=,∴11322h =⨯,∴h=7, 故选B. 【点睛】本题考查了三角形的折叠问题,等边三角形的判定和性质,平行线的判定,矩形的判定,勾股定理,三角形的面积,熟练掌握折叠的性质,矩形的判定,三角形面积不同表示方法是解题的关键.11.C解析:C 【分析】根据正方形、菱形、矩形的判定分别判断得出即可. 【详解】A 、对角线互相垂直平分且相等的四边形是正方形,故原命题是假命题;B 、对角线垂直平分的四边形是菱形,故原命题是假命题;C 、对角线相等且互相平分的四边形是矩形,故原命题是真命题;D 、四边都相等的四边形是菱形,故原命题是假命题; 故选:C . 【点睛】本题考查了命题与定理的知识,解题的关键是了解正方形的判定定理、矩形的判定定理、菱形的判定定理.12.B解析:B 【分析】连接AB 交OC 于点D ,由菱形OACB 中,根据菱形的性质可得OD=CD=4,BD=AD=2,由此即可求得点B 的坐标. 【详解】∵连接AB 交OC 于点D ,∵四边形ABCD是菱形,∴AB⊥OC,OD=CD,AD=BD,∵点C的坐标是(8,0),点A的纵坐标是2,∴OC=8,BD=AD=2,∴OD=4,∴点B的坐标为:(4,-2).故选B.【点睛】本题考查了菱形的性质与点与坐标的关系.熟练运用菱形的性质是解决问题的关键,解题时注意数形结合思想的应用.二、填空题13.【分析】首先根据题意画出树状图可求得恰好选派一男一女两位同学参赛的有8种情况然后利用概率公式求解即可求得答案【详解】解:画树状图得:则共有12种等可能的结果恰好选派一男一女两位同学参赛的有8种情况∴解析:2 3【分析】首先根据题意画出树状图,可求得恰好选派一男一女两位同学参赛的有8种情况,然后利用概率公式求解即可求得答案.【详解】解:画树状图得:则共有12种等可能的结果,恰好选派一男一女两位同学参赛的有8种情况,∴恰好选派一男一女两位同学参赛的概率为:82123.故答案为:23.【点睛】本题考查了概率的计算问题,掌握画树状图或列表法准确求出概率是解题的关键.14.【分析】直接利用黑色区域的面积除以游戏板的面积即可;【详解】设每个小正方形格子的长度都是1∴黑色区域的面积=6游戏板的面积=16所以击中黑色区域的概率为故答案为:【点睛】本题考查了几何概率:求概率时 解析:38【分析】直接利用黑色区域的面积除以游戏板的面积即可; 【详解】设每个小正方形格子的长度都是1, ∴ 黑色区域的面积=6,游戏板的面积=16, 所以击中黑色区域的概率为63=168, 故答案为:38.【点睛】本题考查了几何概率:求概率时,已知和未知与几何有关的就是几何概率,计算方法是长度比、面积比、体积比等.15.【分析】根据一元二次方程根与系数关系即可求解【详解】解:一元二次方程的两根分别是则故答案为:7【点睛】本题考查了一元二次方程根与系数关系解题关键是知道:如果一元二次方程的两根分别是则 解析:7【分析】根据一元二次方程根与系数关系即可求解. 【详解】解:一元二次方程260x x --=的两根分别是1x ,2x , 则126x x =-,121x x =+,12121(6)7x x x x +-=--=,故答案为:7. 【点睛】本题考查了一元二次方程根与系数关系,解题关键是知道:如果一元二次方程20ax bx c ++=的两根分别是1x ,2x ,则12bx x a +=-,12c x x a=. 16.4【分析】利用根与系数的关系确定为原一元二次方程的另一个根即可求出的大小【详解】设原一元二次方程的另一个根为根据根与系数的关系可知根据题意∴为原一元二次方程的另一个根∴即故答案为:4【点睛】本题考查解析:4 【分析】利用根与系数的关系确定β为原一元二次方程的另一个根,即可求出22ββ-的大小.【详解】设原一元二次方程的另一个根为2x , 根据根与系数的关系可知22==21x α-+-, 根据题意=2αβ+, ∴β为原一元二次方程的另一个根,∴ 224=0ββ--,即22=4ββ-. 故答案为:4. 【点睛】本题考查一元二次方程根与系数的关系.掌握一元二次方程根与系数关系的公式并确定β为原一元二次方程的另一个根是解答本题的关键.17.36【分析】根据与40的大小再根据从而确定mn 的值即可得出的值【详解】解:∵∴40≤;∴∴(m+6)2+(n-2)2≤0∵(m+6)2+(n-2)20∴m+6=0n-2=0∴m=-6n=2∴故答案为解析:36 【分析】根据22124-+--m n m n 与40的大小,再根据{}22min 40,12440m n m n -+--=,从而确定m ,n 的值即可得出n m 的值. 【详解】解:∵{}22min 40,12440m n m n -+--=,∴40≤22124-+--m n m n ; ∴22412400+-≤++m n n m ∴(m+6)2+(n-2)2≤0, ∵(m+6)2+(n-2)2≥0, ∴m+6=0,n-2=0, ∴m=-6,n=2, ∴()2636=-=n m故答案为:36. 【点睛】本题考查了配方法的应用和非负数的性质.根据题意理解新定义的计算公式是解题的关键.18.5°【分析】由四边形ABCD 是一个正方形根据正方形的性质可得∠ACB=45°又由AC=EC 根据等边对等角可得∠E=∠CAE 继而根据等腰三角形的性质和三角形的内角和求得∠EAC 的度数进一步即可求得∠D解析:5° 【分析】由四边形ABCD 是一个正方形,根据正方形的性质,可得∠ACB=45°,又由AC=EC ,根据等边对等角,可得∠E=∠CAE ,继而根据等腰三角形的性质和三角形的内角和求得∠EAC 的度数,进一步即可求得∠DAE 的度数. 【详解】解:∵四边形ABCD 是正方形, ∴45ACB ∠=︒,∴18045135ACE ∠=-=︒︒︒, 又∵AC CE =, ∴()118013522.52CAE CEA ∠=∠=⨯︒-︒=︒, 则4252.52.52DAE DAC CAE ∠=∠-∠=-︒=︒︒. 故答案为:22.5° 【点睛】此题考查了正方形的性质以及等腰三角形的性质.此题比较简单,注意掌握数形结合思想的应用.19.(10)或(-18)【分析】画出旋转后的图形根据旋转的性质可知OD1的长和C2D2C2O 的长由此判断点D1的坐标【详解】如图所示:根据旋转的性质旋转前后两个图形全等如果△BCD 绕点B 逆时针旋转90°解析:(1,0)或(-1,8) 【分析】画出旋转后的图形,根据旋转的性质可知OD 1的长和C 2D 2,C 2O 的长,由此判断点D 1的坐标. 【详解】如图所示:根据旋转的性质,旋转前后两个图形全等,如果△BCD 绕点B 逆时针旋转90°后得△BOD 1, CD= OD 1,BC =BO ,∵四边形AOBC 是正方形,D(-4,3), ∴BC=4,CD =4-3=1, ∴OD 1=1 ∴D 1(1,0)如果△BCD 绕点B 顺时针旋转90°后得△BC 2D 2 C 2O=BO+BC 2=4+4=8,C 2D 2=CD=1, 点D 2的的坐标为D 2(-1,8). 故答案为:(1,0)或(-1,8). 【点睛】本题主要考查图形的旋转及旋转的性质和正方形的性质,熟练掌握旋转的性质是解题的关键.20.【分析】延长AD 至点E 使得连接CE 过点C 作证明△CDE 为等边三角形分别求出四边形ABCD 的边长判断即可;【详解】如图所示延长AD 至点E 使得连接CE 过点C 作∵∴又∵∴△CDE 为等边三角形∴设则∵∴则∴ 解析:1563+【分析】延长AD 至点E ,使得DE CD =,连接CE ,过点C 作CH AE ⊥,证明△CDE 为等边三角形,分别求出四边形ABCD 的边长判断即可; 【详解】如图所示,延长AD 至点E ,使得DE CD =,连接CE ,过点C 作CH AE ⊥,∵120ADC =∠︒,∴180********EDC ADC ∠=︒-∠=︒-︒=︒, 又∵DE CD =, ∴△CDE 为等边三角形, ∴CD DE CE ==,60E ∠=︒, 设CE x =,则CD DE x ==, ∵CH DE ⊥,∴9030ECH E ∠=︒-∠=︒, 则1122EH CE x ==, ∴=+-=+-=-11622AH AD DE EH AD CD x x , 22221342CH CE EH x x x =-=-=, ∴()⎛⎫=+=-+=-+≥ ⎪⎝⎭222221363273324AC AH CH x x x ,∴当3x =时,AC 取得最小值为33此时,3AD CD x ===,∵AB AC ⊥, ∴90BAC =︒, 又30B ∠=︒,∴12AC BC =,即2BC AC =,AB ===,∴四边形ABCD 周长AD CD AB BC=+++,()2AD CD AC =+++,))626215AC =++≥++⨯=+;∴四边形ABCD 的最小值为15+故答案是15+ 【点睛】本题主要考查了四边形综合,等边三角形的判定和性质,含30度角的直角三角形的性质,勾股定理等知识,解答本题的关键是明确题意,找出所求问题需要的条件.三、解答题21.(1)14;(2)12【分析】(1)根据概率公式直接填即可;(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率. 【详解】解:(1)有4个开关,只有D 开关一个闭合小灯发亮, 所以任意闭合其中一个开关,则小灯泡发光的概率是14; (2)根据题意,列表如下6种P ∴(灯泡L 发光)61122==. 【点睛】本题主要考查概率的求法.是跨学科综合题,综合物理学中电学知识,结合电路图,正确判断出灯泡发光的条件,掌握根据题意正确画出树状图或列表法以及概率的计算方法是解题的关键.22.(1)不可能、随机,(2)列表见解析,13.【分析】(1)根据随机事件和不可能事件的概念判断即可;(2)列举出所有情况,看所求的情况占总情况的多少即可.【详解】解:(1)“赣江被抽中”是不可能事件,“章水被抽中”是随机事件;故答案为:不可能、随机.(2)根据题意可列表如下:(A表示章水,B表示贡水,C表示绵水,D表示湘水)所以“两人抽取的河流能汇合”的概率=41 123.【点睛】本题主要考查了事件的类型,列表法求概率,列表法可以不重复不遗漏地列出所有可能的结果,适用于两步完成的事件,解题关键是注意两步实验中是否有重.23.(1)长为12m、宽为8m;(2)不能,理由见解析【分析】(1)设矩形猪舍垂直于住房墙一边长为xm,根据矩形的面积公式建立方程求出其解即可.(2)根据题意列出方程x(27-2x+1)=100,根据方程的解的情况可得结果.【详解】解:(1)设矩形猪舍垂直于住房墙一边长为xm,可以得出平行于墙的一边的长为(27-2x+1)m,由题意得x(27-2x+1)=96,解得:x1=6,x2=8,当x=6时,27-2x+1=16>15(舍去),当x=8时,27-2x+1=12.答:所围矩形猪舍的长为12m、宽为8m.(2)由题意得:x(27-2x+1)=100,化简得:-2x2+28x-100=0,△=282-4×(-2)×(-100)=-16<0, 故方程无解,∴不能围成面积为2100m 的矩形猪舍. 【点睛】本题考查了列一元二次方程解实际问题的运用,矩形的面积公式的运用及一元二次方程的解法的运用,解答时寻找题目的等量关系是关键.24.(1)121,1x x ==+;(2)123,2x x =-= 【分析】(1)根据配方法,可得答案; (2)根据因式分解法,可得答案. 【详解】解:(1)移项,得2483x x -=. 方程两边都除以4,得2324x x -=. 方程两边都加1,得232114x x -+=+. 配方,得27(1)4x -=.开平方,得12x -=±.1x ∴=+,121,1x x ∴=+=. (2)移项,得(2(3)5(3)0x x +-+=.(3)(35)0x x ∴++-=, (3)(2)0x x ∴+-=,123,2x x ∴=-=.【点睛】本题考查了解一元二次方程,熟练掌握解方程的方法是解题关键. 25.(1)45︒;(2)见解析;(3)4. 【分析】(1)将线段OA 绕O 点顺时针旋转至OC ,60AOC ∠=︒,OA=OC=4,可证△AOC 为等边三角形,由OB=OC=4,可求∠OBC=∠BCO=15°,可求∠ACB=∠ACO-∠BCO=45°即可; (2)在BC 上取点H 使45COH ∠=︒,由AOB ∠的平分线OD ,可得∠BOD=∠DOA=45°,可求∠DOH=60°,OB=OC=4,利用等边对等角∠DBO=∠HCO ,又∠BOD=∠HOC=45°,可证△BOD ≌△COH(ASA),由性质OD=OH ,BD CH =,可证△DOH 等边三角形即可退出结论 ;(3)以AE 为边作AEF ACO △≌△,连FB 由OC EF =;=4AF OA OB ==,90FAO BOA ∠=∠=︒,可得正方形AFBO ,由30AFE AOC OBE ∠=∠=∠=︒,可求60EFB EBF ∠=∠=︒可证EFB △是等边三角形即可.【详解】(1)∵将线段OA 绕O 点顺时针旋转至OC ,60AOC ∠=︒,(0,4)A ,∴OA=OC=4,∴△AOC 为等边三角形,∴∠ACO=60°,∵(4,0)B -,∴OB=OC=4,∴∠OBC=∠BCO=12(180°-90°-60°)=15°, ∴∠ACB=∠ACO-∠BCO=60°-15°=45°,∴∠ACB =45︒;(2)在BC 上取点H 使45COH ∠=︒,∵AOB ∠的平分线OD 交BC 于D ,∴∠BOD=∠DOA=45°,∵∠AOC=60°,∴∠BOC=90°+60°=150°,∴∠DOH=150°-∠BOD -∠COD=90°-45°-45°=60°,∵OB=OC=4,∴∠DBO=∠HCO ,∠BOD=∠HOC=45°,∴△BOD ≌△COH(ASA),∴OD=OH ,BD CH =,∴DOH 是等边三角形,OD DH ∴=,OD BD CD ∴+=;(3)以AE 为边作AEF ACO △≌△,连FB ,OC EF ∴=;=4AF OA OB ==,90FAO BOA ∠=∠=︒,∴正方形AFBO ,30AFE AOC OBE ∴∠=∠=∠=︒,60EFB EBF ∴∠=∠=︒,EFB ∴△是等边三角形,∴4BE BF OB ===.【点睛】本题考查旋转,等边三角形的判定与性质,等腰三角形的判定与性质,角平分线的性质,三角形全等,正方形判定与性质,掌握旋转的性质,会利用旋转和夹角60°证等边三角形,等边三角形的判定方法与性质,等腰三角形的判定方法与性质,角平分线的性质,三角形全等判断方法与性质,正方形判定与性质是解题关键.26.(1)36x ≤≤;(2)CG 的长为6815. 【分析】(1)分别求得当点G 与点C 重合和点G 与点D 重合时x 的值,即可得到x 的取值范围; (2)连接GE ,在Rt AGD 和Rt EFG 以及Rt ECG 中,利用勾股定理列式进行计算即可得解.【详解】(1)设BE x =,当点G 与点C 重合时,在Rt ABC 中,22226810AC AB BC =+=+=,由折叠的性质,得△ABE ≅△AFE ,∴AF=AB=6,BE= FE x =,在Rt CEF 中,∠CFE=90︒,CF 1064=-=,CE=8-x ,∴222EF FC EC +=,即()22248x x +=-,解得:3x =;当点G 与点D 重合时,同理,AF=AB=6,BE= FE ,∠BQF=∠B=∠AFE=90︒,∴四边形ABEF 为矩形,∴BE= AB=6,即6x =,∴点G 在CD 边上时,x 的取值范围为:36x ≤≤;(2)由(1)知,当36x ≤≤时点G 在CD 边上,连接EG ,∴当5x =时点G 在CD 边上,且点G 不与C 、D 两点不重合,设DG=y ,由折叠的性质,得△ABE ≅△AFE ,∴AF=AB=6,BE= FE 5=,在Rt AGD 中,∠D=90︒,AD 8=,DG=y ,∴22228AG AD DG y =+=+∴6FG AG AF =-=,在Rt EFG 中,222EF FG EG +=,在Rt ECG 中,222EC CG EG +=,∴2222EF FG EC CG +=+,即)()()222256856y +=-+-, ∴2215y =, ∴226861515CG =-=. 【点睛】 本题主要考查了矩形的性质,折叠的性质,全等三角形的判定和性质,勾股定理,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数,构建方程解决问题.。
【翼教版】九年级数学上期末第一次模拟试卷及答案

一、选择题1.从2020年10月12日起,金牛实验中学校开展施行“垃圾分类”主题教育,如图是生活中的四个不同的垃圾分类(A 、B 、C 、D )投放桶.小明投放了两袋垃圾.不同类的概率是( ).A .13B .23C .14D .342.下列事件是必然事件的是( )A .打开电视机,正在播放动画片B .2022年世界杯德国队一定能夺得冠军C .某彩票中奖率是1%,买100张一定会中奖D .在一只装有5个红球的袋中摸出1球,一定是红球3.现有三张正面分别标有数字1-,2,3的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m ,n ,则点()P m n ,在第二象限的概率为( )A .12B .13C .23D .294.掷一枚普通的正六面体骰子,出现的点数中,以下结果机会最大的是( ) A .点数为3的倍数B .点数为奇数C .点数不小于3D .点数不大于3 5.如图,ABC 为O 的一个内接三角形,过点B 作O 的切线PB 与OA 的延长线交于点P .已知34ACB ∠=︒,则P ∠等于( )A .17°B .27°C .32°D .22°6.如图,在半径为8的O 中,点A 是劣弧BC 的中点,点D 是优弧BC 上一点,30D ︒∠=,下列结论不正确的是( )A .OA BC ⊥B .83BC = C .四边形ABOC 是菱形D .扇形OAC 的面积为643π 7.如图,正六边形ABCDEF 内接于O ,过点O 作OM ⊥弦BC 于点M ,若O 的半径为4,则弦心距OM 的长为( )A .23B .3C .2D .22 8.如图,PA 切O 于点,A PB 切O 于点B PO ,交O 于点C ,下列结论中不一定成立的是( )A .PA PB =B .PO 平分APB ∠C .AB OP ⊥D .2PAB APO ∠=∠9.如图,将△ABC 绕点A 逆时针旋转一定角度,得到△ADE ,若∠CAE=65°,∠E=70°,且AD ⊥BC ,∠BAC 的度数为( ).A .60 °B .75°C .85°D .90°10.如图,把△ABC 绕着点A 逆时针旋转40°得到△ADE ,∠1=30°,则∠BAE =( )A .10°B .30°C .40°D .70°11.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论:①ac <0;②b <0;③4ac ﹣b 2<0;④当x >﹣1时,y 随x 的增大而减小.其中正确的有( )A .4个B .3个C .2个D .1个12.据网络统计,某品牌手机2020年一月份销售量为400万部,二月份、三月份销售量连续增长,三月份销售量达到900万部,求二月份、三月份销售量的月平均增长率?若设月平均增长率为x ,根据题意列方程为( ).A .()40012900x +=B .()40021900x ⨯+=C .()24001900x +=D .()()240040014001900x x ++++= 二、填空题13.有四张不透明卡片,分别写有实数14,﹣1-1-515,除正面的数不同外其余都相同,将它们背面朝上洗匀后,从中任取一张卡片,取到的数是无理数的可能性大小是__. 14.如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=5,BE=3,若向正方形ABCD 内随意投掷飞镖(每次均落在正方形ABCD 内,且落在正方形ABCD 内任何一点的机会均等),则恰好落在正方形EFGH 内的概率为__________.15.现有4张完全相同的卡片分别写着数字-1、1、2、3,将卡片的背面朝上并洗匀,从中任意抽取一张, 将卡片上的数字记作a ,再从余下的卡片中任意抽取一张,将卡片上的数字记作b ,则+a b 为奇数的概率为________.参考答案16.如图,点A ,B ,C 在圆O 上,54ACB ∠=︒,则ABO ∠的度数是______.17.已知O 的直径10AB =cm ,CD 是O 的弦,AE CD ⊥,垂足为点E ,BF CD ⊥,垂足为点F ,且8CD =cm ,则BF AE -的长为________cm .18.如图,把ABC ∆绕顶点C 按顺时针方向旋转得到△A B C '',当A B AC ''⊥,47A ∠=︒,128A CB ∠='︒时,B CA '∠的度数为_____.19.将二次函数 ()2213y x =-+ 的图象先向左平移2个单位,再向下平移4个单位,则所得图象的函数表达式为________.20.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积六十步,只云长阔共十六步,问长多阔几何”.意思是:一块矩形田地的面积为60平方步,只知道它的长与宽共16步,根据题意得,设长为x步,列出方程_______.三、解答题21.A、B、C、D四个队进行接力比赛,他们对比赛的四个跑道1,2,3,4进行抽签(四个跑道按1,2,3,4的先后顺序依次排列),(1)让A队先抽签,求A队抽到2跑道的概率;(2)求A、B两队抽到相邻跑道的概率.22.某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:分组49.5~59.559.5~69.569.5~79.579.5~89.589.5~100.5合计频数2a2016450频率0.040.160.400.32b1(1)频数、频率分布表中a=,b=;(2)补全频数分布直方图;(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少.23.如图,已知O的直径AB⊥弦CD于点E,且E是OB的中点,连接CO并延长交AD于点F.⊥;(1)求证:CF ADAB=,求CD的长.(2)若1224.如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△ABC的顶点均在格点上,建立如图所示的平面直角坐标系,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)画出△ABC关于原点对称的△A1B1C1,并直接写出△A1B1C1各顶点的坐标;(2)将线段AB绕点A顺时针旋转90 °后得到AB2,画出旋转后的图形,并直接写出点B2的坐标;(3)△A1B1C1的面积为.25.如图,在平面直角坐标系中,有抛物线y=ax2+bx+3,已知OA=OC=3OB,动点P在过 A、B、C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,说明理由;26.现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,我市一家“大学生自主创业”的快递公司,今年7月份与9月份完成投递的快递总件数分别是10万件和12.1万件,现假设该公司每月投递的快递总件数的增长率相同.(1)求该快递公司投递总件数的月平均增长率;(2)如果每人每月最多可投递0.6万件,那么该公司现有的22名快递业务员能否完成今年10月份的快递投递任务?请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】先利用树状图法列举出所有可能,再利用概率公式求出答案.【详解】四个不同的垃圾桶分别记为A,B,C,D表示,根据题意画图如下:由树状图知,小明投放的垃圾共有16种等可能结果,其中小明投放的两袋垃圾不同类的有12种结果,所以小明投放的两袋垃圾不同类的概率为123 164.故选:D.【点睛】此题主要考查了树状图法求概率,正确利用列举出所有可能是解题关键.2.D解析:D【分析】根据随机事件和必然事件定义一一判定即可,必然事件就是一定发生的事件,即发生的概率是1的事件.【详解】解:A. 打开电视机,正在播放动画片,可能发生,也可能不发生,是随机事件,故此项错误;B. 2022年世界杯德国队一定能夺得冠军,可能发生,也可能不发生,是随机事件,故此项错误;C. 某彩票中奖率是1%,买100张一定会中奖,可能发生,也可能不发生,是随机事件,故此项错误;D. 在一只装有5个红球的袋中摸出1球,一定是红球,一定发生,所以是必然事件.故选:D.【点睛】该题考查的是对必然事件的概念的理解;必然事件指在一定条件下一定发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.3.D【分析】画树状图展示所有9种等可能的结果数,利用第二象限内点的坐标特征确定点(,)P m n 在第二象限的结果数,然后根据概率公式求解.【详解】解:画树状图为:共有9种等可能的结果数,其中点(,)P m n 在第二象限的结果数为2,所以点(,)P m n 在第二象限的概率29. 故选:D .【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n ,再从中选出符合事件A 或B 的结果数目m ,然后利用概率公式计算事件A 或事件B 的概率.也考查了点的坐标. 4.C解析:C【分析】总共有六种情况,分别计算出所求情况的个数,比较即可得出可能性最大的.【详解】解:掷一枚普通的正六面体骰子共6种情况,A.掷一枚骰子,点数为3的倍数有2种,概率13; B.点数为奇数有3种,概率12; C.点数不小于3有四种,概率23; D.点数不大于3有3种,概率12, 故可能性最大的是点数不小于3,选C .【点睛】可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等.5.D【分析】连接OB,利用圆周角定理求得∠AOB,再根据切线性质证得∠OBP=90°,利用直角三角形的两锐角互余即可求解.【详解】解:连接OB,∵∠ACB=34°,∴∠AOB=2∠ACB=68°,∵PB为O的切线,∴OB⊥PB,即∠OBP=90°,∴∠P=90°﹣∠AOB=22°,故选:D.【点睛】本题考查了切线的性质、圆周角定理、直角三角形的两锐角互余,熟练掌握切线的性质和圆周角定理是解答的关键.6.D解析:D【分析】利用垂径定理可对A进行判断;根据圆周角定理得到∠AOC=2∠D=60°,则△OAC为等边三BC B进行判断;利用角形,根据等边三角形的性质和垂径定理可计算出83AB=AC=OA=OC=OB可对C进行判断;通过判断△AOB为等边三角形,再根据扇形的面积公式可对D进行判断.【详解】解:A.∵点A是劣弧BC的中点,∴OA⊥BC,所以A正确,不符合题意;B.∵∠AOC=2∠D=60°,OA=OC,∴△OAC为等边三角形,∴BC=2×8×sin30°=2×8×3=83B正确,不符合题意;2C. 同理可得△AOB为等边三角形,∴AB=AC=OA=OC=OB ,∴四边形ABOC 是菱形,所以C 正确,不符合题意;D.∵∠AOC=60°,OC=8∴扇形OAC 的面积为2608323603ππ⨯=,所以D 错误,符合题意. 故选:D .【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.7.A解析:A【分析】如图,连接OB 、OC .首先证明△OBC 是等边三角形,求出BC 、BM ,根据勾股定理即可求出OM .【详解】解:如图,连接OB 、OC .∵ABCDEF 是正六边形,∴∠BOC=60°,OB=OC=4,∴△OBC 是等边三角形,∴BC=OB=OC=4,∵OM ⊥BC ,∴BM=CM=2,在Rt △OBM 中,22224223OM OB BM -=-=,故选:A .【点睛】本题考查正多边形与圆、等边三角形的性质、勾股定理、弧长公式等知识,解题的关键是记住等边三角形的性质,弧长公式,属于基础题,中考常考题型.8.D解析:D【分析】利用切线长定理证明△PAG ≌△PBG 即可得出.解:连接OA,OB,AB,AB交PO于点G,由切线长定理可得:∠APO=∠BPO,PA=PB,又∵PG=PG,∴△PAG≌△PBG,从而AB⊥OP.因此A.B.C都正确.无法得出AB=PA=PB,可知:D是错误的.综上可知:只有D是错误的.故选:D.【点睛】本题考查了切线长定理、全等三角形的判定和性质,关键是利用切线长定理解答.9.C解析:C【解析】试题分析:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.如图,设AD⊥BC于点F.则∠AFB=90°,∴在Rt△ABF中,∠B=90°-∠BAD=25°,∴在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,即∠BAC的度数为85°.故选C.考点: 旋转的性质.10.D解析:D【分析】先找到旋转角,根据∠BAE=∠1+∠CAE进行计算.【详解】解:根据题意可知旋转角∠CAE=40°,所以∠BAE=30°+40°=70°.故选D.本题主要考查了旋转的性质,解题的关键是找准旋转角.11.B解析:B【分析】由抛物线的开口方向判定a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,然后根据对称轴及抛物线与x 交点情况进行推理,进而对所得结论进行判断.【详解】解:①∵由二次函数的图象可知:抛物线的开口向上,∴a >0;又∵二次函数的图象与y 轴的交点在负半轴,∴c <0;∴ac <0,即①正确;②由图象知,对称轴x =2b a=1,则b =﹣2a <0.故②正确; ③由图象知,抛物线与x 轴有2个交点,则b 2﹣4ac >0,故③正确;④由图象可知当x >1时,y 随x 的增大而增大;故④错误.综上所述,正确的结论是:①②③.故选:B .【点睛】此题考查学生掌握二次函数的图像与性质,考查了数形结合的数学思想,解本题的关键是根据图像找出抛物线的对称轴.12.C解析:C【分析】设月平均增长率为x ,根据三月及五月的销售量,即可得出关于x 的一元二次方程,此题得解.【详解】解:设月平均增长率为x ,根据题意得:400(1+x )2=900.故选:C .【点睛】本题考查了一元二次方程中增长率的知识.增长前的量×(1+年平均增长率)年数=增长后的量. 二、填空题13.【解析】四个数中无理数只有则取到的数是无理数的可能性大小是 解析:14,则取到的数是无理数的可能性大小是1 414.【分析】根据几何概型概率的求法飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比根据题意可得小正方形的面积与大正方形的面积进而可得答案【详解】解:根据题意AB2=AE2+BE2=34∴S正方形A解析:2 17【分析】根据几何概型概率的求法,飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比,根据题意,可得小正方形的面积与大正方形的面积,进而可得答案.【详解】解:根据题意,AB2=AE2+BE2=34,∴S正方形ABCD=34,∵△ABE≌△BCF,∴AE=BF=5,∵BE=3,∴EF=2,∴S正方形EFGH=4,故飞镖扎在小正方形内的概率为42 3417=.故答案为2 17.【点睛】本题考查概率、正方形的性质,用到的知识点为:概率=相应的面积与总面积之比;难点是得到正方形的边长.15.【分析】画出树状图然后由树状图求得所有等可能的结果和为奇数的结果即可求出概率【详解】解:根据题意画出树状图如下:由树状图可知共有12种等可能的结果其中为奇数的有6种∴为奇数的概率为:;故答案为:【点解析:1 2【分析】画出树状图,然后由树状图求得所有等可能的结果和+a b为奇数的结果,即可求出概率.【详解】解:根据题意,画出树状图如下:由树状图可知共有12种等可能的结果,其中+a b 为奇数的有6种,∴+a b 为奇数的概率为:61122P ==; 故答案为:12. 【点睛】本题考查了树状图法或列表法求概率,解题的关键是熟练运用树状图求出等可能的结果. 16.36°【分析】根据圆周角定理可得再利用等腰三角形的性质即可求解【详解】解:∵∴∵∴故答案为:36°【点睛】本题考查圆周角定理掌握圆周角定理是解题的关键解析:36°【分析】根据圆周角定理可得2108AOB ACB ∠=∠=︒,再利用等腰三角形的性质即可求解.【详解】解:∵54ACB ∠=︒,∴2108AOB ACB ∠=∠=︒,∵OA OB =, ∴()1180362ABO BAO AOB ∠=∠=︒-∠=︒, 故答案为:36°.【点睛】本题考查圆周角定理,掌握圆周角定理是解题的关键. 17.6【分析】如图作OH ⊥CD 于H 连接AH 延长AH 交BF 于K 连接OC 证明AE=FK 利用勾股定理求出OH 再利用三角形的中位线定理求出BK 即可解决问题【详解】解:如图作OH ⊥CD 于H 连接AH 延长AH 交BF 于解析:6【分析】如图,作OH ⊥CD 于H ,连接AH ,延长AH 交BF 于K ,连接OC .证明AE=FK ,利用勾股定理求出OH ,再利用三角形的中位线定理求出BK 即可解决问题.【详解】解:如图,作OH ⊥CD 于H ,连接AH ,延长AH 交BF 于K ,连接OC .∵OH⊥CD,∴CH=DH=4(cm),∠CHO=90°,∴2222-=-=3(cm),OC CH54∵AE⊥CD,BF⊥CD,∴AE∥OH∥BF,∵OA=OB,∴EH=FH,∵∠AEH=∠KFH=90°,∠AHE=∠FHK,∴△AEH≌△KFH(AAS),∴AH=HK,AE=FK,∵AO=OB,∴OH=1BK,2∴BK=6(cm),∴BF-AE=BF-FK=BK=6(cm).故答案为6.【点睛】本题考查了垂径定理,勾股定理,三角形的中位线定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.18.42º【分析】根据旋转的性质可知∠A′=∠A=47°则∠A′CA=90°-47°=43°由∠BCB′=∠A′CA=43°则∠B′CA=∠A′CB-∠A′CA-∠BCB′可求【详解】根据旋转的性质可知解析:42º【分析】根据旋转的性质可知∠A′=∠A=47°,则∠A′CA=90°-47°=43°,由∠BCB′=∠A′CA=43°,则∠B′CA=∠A′CB-∠A′CA-∠BCB′可求.【详解】根据旋转的性质可知∠A′=∠A=47°,∴∠A′CA=90°-47°=43°.根据旋转的性质可知旋转角相等,即∠BCB′=∠A′CA=43°,∴∠B′CA=∠A′CB-∠A′CA-∠BCB′=128°-43°-43°=42°.故答案为:42°.【点睛】本题主要考查了旋转的性质,三角形内角和定理的应用,解决这类问题要找准旋转角、以及旋转后对应的线段和角.19.y=2(x+1)2-1【分析】利用二次函数图像平移规律:上加下减左加右减可得平移后的函数解析式【详解】解:将二次函数 的图象先向左平移2个单位再向下平移4个单位则所得图象的函数表达式为:y=2(x解析:y=2(x+1)2-1【分析】利用二次函数图像平移规律:上加下减,左加右减,可得平移后的函数解析式.【详解】解:将二次函数 ()2213y x =-+ 的图象先向左平移2个单位,再向下平移4个单位,则所得图象的函数表达式为:y=2(x-1+2)2+3-4∴y=2(x+1)2-1.故答案为:y=2(x+1)2-1.【点睛】本题考查了二次函数与几何变换,正确掌握平移规律是解题关键. 20.x (16-x )=60【分析】由矩形的长与宽之间的关系可得出矩形的宽为(16-x )步再利用矩形的面积公式即可得出关于x 的一元二次方程【详解】解:矩形的长为x 步则宽为(16-x )步∴x (16-x )=60解析:x (16-x )=60【分析】由矩形的长与宽之间的关系可得出矩形的宽为(16-x )步,再利用矩形的面积公式即可得出关于x 的一元二次方程.【详解】解:矩形的长为x 步,则宽为(16-x )步,∴x (16-x )=60.故答案为:x (16-x )=60【点睛】本题考查了由实际问题抽象出一元二次方程以及数学常识,找准等量关系,正确列出一元二次方程是解题的关键.三、解答题21.(1)14;(2)12 【分析】(1)A 队先抽签,抽到2跑道的情况只有1种,即可求得概率.(2)根据题意用列表法或树状图法列举出所有情况即可求解.【详解】解:(1) 让A 队先抽签,抽到2跑道的情况只有1种,∴A 队抽到2跑道的概率为14. (2)如图共12种情形,其中相邻的有6种61(AB )=122P ∴=相邻 ∴A 、B 两队抽到相邻跑道的概率为12 【点睛】本题考查列表法或树状图法求概率,解题的关键是知道概率=所求情况数与总情况数之比.注意掌握放回试验与不放回实验的区别.22.(1)a =8,b =0.08;(2)作图见解析;(3)14. 【分析】(1)根据频数之和等于总个数,频率之和等于1求解即可;(2)直接根据(1)中的结果补全频数分布直方图即可;(3)根据89.5~100.5这一组的人数及概率公式求解即可.【详解】解:(1)由题意得a =50-2-20-16-4=8,b =1-0.04-0.16-0.40-0.32=0.08;(2)如图所示:(3)由题意得张明被选上的概率是14. 【点睛】 本题考查频数分布直方图,频数分布直方图的应用是初中数学的重点,是中考常见题,一般难度不大,要熟练掌握.23.(1)证明见解析;(2)63CD =【分析】(1)首先根据垂径定理和等腰三角形的性质得到CB=CO ,然后结合OC=OB ,得到OCB 是等边三角形根据圆周角定理和对顶角的性质,结合三角形内角和定理即可证明90AFO ∠=︒,即可证明;(2)根据题意和(1)问结论得到OE=3,在Rt OCE 中应用勾股定理求得CE ,结合垂径定理即可求得CD .【详解】(1)证明:如图,连接BC .∵AB CD ⊥,E 是OB 的中点,∴CB CO =,12BCD BCO ∠=∠. ∵OC OB =,∴OB OC BC ==, ∴OCB 是等边三角形,∴60BOC BCO ∠=∠=°,∴60AOF BOC ∠=∠=°,30BCD BAD ∠=∠=︒, ∴()180603090AFO ∠=-+=°°°°,∴CF AD ⊥.(2)∵12AB =,∴6OB =.∵E 是OB 的中点, ∴132OE OB ==. 在Rt OCE 中,22226333CE OC OE --=∵AB CD ⊥, ∴263CD CE ==.【点睛】本题考查了垂径定理,圆周角定理,等边三角形的判定和性质,勾股定理,属于圆的综合题,重点是掌握相关定理,要求考生熟记并能熟练应用,是中考的重难点.24.(1)图见解析;A 1(-1,-1),B 1(-4,-2),C 1(-3,-4);(2)B 2(2,-2);(3)3.5【分析】(1)先找到A、B、C关于原点对称的A1、B1、C1,再连线即可;(2)根据网格结构点A、B,找出将线段AB绕点A顺时针旋转90°的对应点B2,然后连接A B2,写出坐标即可;(3)△A1B1C1的面积即为三角形ABC的面积,利用“割补法”即可求得.【详解】解:(1)如图所示,△A1B1C1即为所求:A1(-1,-1),B1(-4,-2),C1(-3,-4);(2)如图所示,A1B2即为所求:B2(2,-2);(3)S△ABC=11133232113222⨯-⨯⨯-⨯⨯-⨯⨯=3.5,∴△A1B1C1的面积= S△ABC=3.5,故填:3.5.【点睛】本题考查了坐标与图形变化−旋转与对称,熟练掌握网格结构,准确找出对应点的位置是解题的关键.25.(1)2y x 2x 3=-++;(2)存在,()1,4P 或()2,5--.【分析】(1)根据A 的坐标,即可求得OA 的长,则B 、C 的坐标即可求得,然后利用待定系数法即可求得函数的解析式;(2)分点A 为直角顶点时,和C 的直角顶点两种情况讨论,根据等腰三角形的性质得到两直角边相等,即可列方程分别求解.【详解】解:(1)由题意可知:c =3∴OC =OA =3OB=3,∴点A 、B 、C 的坐标分别为:(0,3)、(﹣1,0)、(3,0),将点B 、C 代入抛物线的表达式为:09a 3303b a b =++⎧⎨=-+⎩, 解得:a 12b =-⎧⎨=⎩ ∴抛物线的表达式为:y =﹣x 2+2x+3;(2)过点A 、C 分别作直线AC 的垂线,分别交抛物线于P 1、P 2.过点P 1作P 1M ⊥ y 轴,垂足为M .∵OC =OA∴ ∠OAC=∠OCA=45º∴ ∠MAP 1=∠MP 1A=45º∴MA=MP 1设P 1点坐标(a ,﹣a 2+2a+3)则MP 1=a ,OP 1=﹣a 2+2a+3∵OA =3∴MA=﹣a 2+2a+3-3=﹣a 2+2a∴﹣a 2+2a=a解之得:a 1=0(舍去),a 2=1∴﹣a 2+2a+3=4∴P 的坐标为(1,4)过点P 2作P 2N ⊥ x 轴,垂足为N .∵OC =OA ∴ ∠OAC=∠OCA=45º∴ ∠NAP 2=∠NP 2C=45º∴CN=NP 2设P 2点坐标(a ,﹣a 2+2a+3)则NP 2=a 2-2a-3,ON=﹣a∵a 2-2a-3=3-a解之得:a 1=3(舍去), a 2=-2,∴﹣a 2+2a+3=-5∴点P 的坐标为(﹣2,﹣5)∴当点P 的坐标为(1,4)或(﹣2,﹣5)时,使得△ACP 是以AC 为直角边的直角三角形.【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求抛物线的解析式,以及等腰三角形的性质.在求有关动点问题时要注意分析题意分情况讨论结果.26.(1)该快递公司投递总件数的月平均增长率为10%;(2)不能,理由见解析【分析】(1)设该快递公司投递总件数的月平均增长率为x ,根据“今年7月份与9月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同”建立方程,解方程即可;(2)首先求出今年10月份的快递投递任务,再求出22名快递投递业务员能完成的快递投递任务,比较得出该公司不能完成今年10月份的快递投递任务.【详解】解:(1)设该快递公司投递总件数的月平均增长率为x ,根据题意得:210(1)12.1x +=,解得:10.1x =,2 2.1x =-(不合题意舍去).答:该快递公司投递总件数的月平均增长率为10%;⨯+=(万件).(2)今年10月份的快递投递任务是12.1(110%)13.31平均每人每月最多可投递0.6万件,⨯=<,22∴名快递投递员能完成的快递投递任务是:0.62213.213.31∴该公司现有的22名快递投递业务员不能完成今年10月份的快递投递任务.【点睛】此题主要考查了一元二次方程的应用,根据增长率一般公式列出方程即可解决问题.。
2022诚成教育模拟大考卷数学电子版

2022诚成教育模拟大考卷数学电子版题目1。
分式方程5x+3=2x的解是()A。
x=2B。
x=1C。
x=12D。
x=-22。
下面是四位同学解方程2x-1+x1-x=1过程中去分母的一步,其中正确的是()A。
2+x=x-1B。
2-x=1C。
2+x=1-xD。
2-x=x-13。
分式方程10020+v=6020-v的解是()A。
v=-20B。
v=5C。
v=-5D。
v=204。
甲车行驶30千米与乙车行驶40千米所用的时间相同。
已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/时,依题意列方程正确的是()A。
30x=40x-15B。
30x-15=40xC。
30x=40x+15D。
30x+15=40x5若代数式2x-1-1的值为零,则x=________。
6。
今年6月1日起,国家实施了《中央财政补贴条例》,支持高效节能电器的推广使用。
某款定速空调在条例实施后,每购买一台,客户可获财政补贴200元,若同样用1万元所购买的此款空调台数,条例实施后比条例实施前多10%,则条例实施前此款空调的售价为______________元。
7。
解方程:6x-2=xx+3-1。
8。
当x为何值时,分式3-x2-x的值比分式1x-2的值大3?9。
某工厂加工某种产品,机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件,若加工1800件这样的产品,机器加工所用的时间是手工加工所用时间的37倍,求手工每小时加工产品的数量。
2017中考数学模拟试卷B级中等题10若关于x的分式方程2x-ax-1=1的解为正数,那么字母a的取值范围是__________。
11。
若关于x的方程axx-2=4x-2+1无解,则a的值是__________。
12。
xx市某施工队负责修建1800米的绿道。
为了尽量减少施工对周边环境的影响,该队提高了施工效率,实际工作效率比原计划每天提高了20%,结果提前两天完成。
求实际平均每天修绿道的长度?13。
2019-2020学年度第二学期海城市东部教育集团网上联考(含答案)

2019-2020学年度第二学期海城市东部教育集团网上联考七年级数学试卷考试范围:第五章相交线与平行线满分:100分考试时间:60分钟注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题共24分)一、单选题(本题共8小题,每小题3分,共24分)∠+∠+∠等于()1.(3分)如图所示,三条直线交于一点,则123A.180︒B.150︒C.240︒D.120︒2.(3分)如图,直线AB,CD相交于点O,OE⊥AB于O,∠COE=53°,则∠BOD的度数是()A.33°B.47°C.37°D.53°3.(3分)如图,下列说法正确的是()A.∠1 和∠3 是对顶角B.∠1 和∠4 是同位角C.∠1 和∠2 是同旁内角D.∠2 和∠4 是同位角4.(3分)有下列说法:①在同一平面内,过一点有且只有一条直线与已知直线垂直;②两条直线被第三条直线所截,内错角相等;③垂直于同一条直线的两条直线互相平行;④平行于同一条直线的两条直线互相平行.其中正确的结论是()A.①③④B.②③C.①②③④D.①④5.(3分)如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED 的度数是()A.16°B.32°C.64°D.66°6.(3分)如图,将△ABC沿BC方向平移2个单位得到△DEF,若△ABC的周长等于7,则四边形ABFD的周长等于()A.9B.10C.11D.127.(3分)如图,直线a∥b,∠1=70°,∠2=140°,则∠3的度数为()A.100°B.105°C.110°D.115°8.(3分)如图,AB∥CD,BF,DF 分别平分∠ABE 和∠CDE,BF∥DE,∠F 与∠ABE 的和为200°,则∠F 的度数为A.30°B.36°C.38°D.40°第II卷(非选择题共76分)二、填空题(本题共8小题,每小题3分,共24分)9.(3分)若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=40°,则∠1的度数为______.10.(3分)如图,把小河里的水引到田地C处,作CD垂直于河岸,沿CD挖水沟,则水沟最短,其理论依据是___________________.11.(3分)下列命题:①过一点有且只有一条直线与这条直线平行;②相等的角是对顶角;③同位角相等;④两点之间,线段最短.其中真命题的有_______(填序号) 12.如图,图中已标明了三组互相垂直的线段,那么点C 到AB 的距离是________.点B 到AC 的距离是________,13.(3分)如图,点E 在AC 的延长线上,对于给出的四个条件:(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠D ;(4)∠D+∠ABD=180°.能判断AB ∥CD 的有______个.14.(3分)如图所示,把长方形ABCD 沿EF 折叠,若∠1=46°,则∠AEF 等于______.15.(3分)某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度均为3米的小路,则草地的实际面积______m 2.16.(3分)如图,AE ∥CF ,∠ACF 的平分线交AE 于点B ,G 是CF 上的一点,∠GBE 的平分线交CF 于点D ,且BD ⊥BC ,下列结论:①BC 平分∠ABG ;②与∠DBE 互余的角有3个;③AC ∥BG ;④若∠A =α,则∠BDC =1802α︒-.其中正确的有_____.(把你认为正确结论的序号都填上)三、解答题(本题共5小题,17题——20题每题10分,21题12分,共52分) 17.(10分)如图,∠ADE =∠DEF ,∠EFC +∠C =180°,请证明AD ∥BC 。
2024年山东省临沭县数学九年级第一学期开学复习检测模拟试题【含答案】

2024年山东省临沭县数学九年级第一学期开学复习检测模拟试题题号一二三四五总分得分批阅人A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)如图,在ABC 中,CD AB ⊥于点D ,且E 是AC 的中点,若65AD DE ==,,则CD 的长等于()A .5B .6C .7D .82、(4分)如图,函数y=2x 和y=ax+4的图象相交于A(m ,3),则不等式2x ax+4<的解集为()A .3x 2>B .x 3>C .3x 2<D .x 3<3、(4分)利用“分形”与“迭代”可以制作出很多精美的图形,以下是制作出的几个简单图形,其中是轴对称但不是中心对称的图形是()A .B .C .D .4、(4分)如图,已知点E 在正方形ABCD 内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()A .48B .60C .76D .805、(4分)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都均为8.8环,方差分别为S 甲2=0.63,S 乙2=0.51,S 丙2=0.48,S 丁2=0.42,则四人中成绩最稳定的是()A .甲B .乙C .丙D .丁6、(4分)正方形ABCD 的边长为4,点E 在对角线BD 上,且∠BAE=22.50,EF ⊥AB ,垂足为F ,则EF 的长()A .1B .4-C .2D .4-7、(4分)已知一次函数y =(1﹣a )x +1,如果y 随自变量x 的增大而增大,那么a 的取值范围为()A .a <1B .a >1C .a <﹣1D .a >﹣1.8、(4分)一组数据11、12、15、12、11,下列说法正确的是()A .中位数是15B .众数是12C .中位数是11、12D .众数是11、12二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)计算:1)+=_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
� 答案:C 37.监理文件档案的更改应由原制定部门相应责任人执行,涉及审批程序的,由 ( )审批。 信 息 p46 � � � A. 监理公司技术负责人 B.总监理工程师 C.原审批责任人
� D.档案管理责任人 � 答案:C 38.对施工单位的工程文件的形成、积累、立卷归档工作进行监督、检查是()的职责。 A.施工单位和监理单位 B.建设单位和监理单位 C.建设单位和地方城建档案管理部门 D.监理单位和地方城建档案管理部门 答案: B 39.下列监理单位用表中,可由专业监理工程师签发或签认的是 ( A.工程临时延期审批表 B.工程最终延期审批表 C.监理工作联系单 D.工程变更单 答案: C 40.当分包单位提出工程变更时,下列程序错误的是() 。信息 p50 A.由分包单位编写工程变更单报送项目监理部 B.项目监理部同意后转呈建设单位 C.需要时建设单位委托设计单位编制设计变更文件并签转项目监理部 D.施工单位收到项目监理部签署的“工程变更单”后方可实施工程变更 答案: A 41.下列表述中不属于《中华人民共和国建筑法》规定内容的是() 。
建设工程监理基本理论与相关法规模拟试卷(一) 一、单项选择题(共 50 题,每题 1 分。每题的备选项中,只有 1 个最符合题意) 1.我国的建设工程监理是由具有相应资质的工程监理企业,接受建设单位的委托,进行的 一项专业化服务活动,活动内容是代表建设单位() 。 A.对承包单位的建设行为进行监督管理 B.对建设工程参与各方的行为进行规范 C.对建设活动的工期、投资和质量进行监督控制 D.对建设工程实施全过程进行项目管理 答案: A 2.依据《建设工程监理范围和规模标准规定》 ,下列工程项目可以不实行监理的是() 。 A.总投资额为 1 亿元的体育发展项目 B.建筑面积 4 万平方米的住宅建设项目 C.总投资额为 300 万美元的世界银行援助项目 D.总投资额为 2000 万元的市话剧院项目 答案: B 3.下列效力最低的是( A.建设工程法律 B.建设工程行政法规 C.建设工程部门规章 D.宪法 答案: C 4.我国目前的建设程序与计划经济时期的建设程序相比,发生了一些关键性变化,下列不 属于建设工程管理制度体系的是() 。P31 A.项目决策咨询评估制度 B.工程招标投标制度 C.建设工程监理制度 D.合同管理制度 答案: A 5.根据《国务院关于投融资体制改革的决定》 ,对于企业不使用政府资金投资建设的项目不 再经政府审批, () 。 P27 A.无需再编制项目建议书和可行性研究报告 B.向政府提交项目申请报告进行核准 C.不需要编制项目建议书而可直接编制项目可行性研究报告 D.只向地方投资主管部门备案即可 答案: C 6.监理工程师不仅要有专业基础理论知识,还要熟悉设计、施工、管理,要有组织协调能 力,这就要求监理工程师() 。 A.执业范围广泛 B.执业内容复杂 C.执业技能全面 D.执业责任重大 答案: C 7.在工程建设程序中,建设单位进行工具、器具、备品、备件等的制造或订货是( 段的工作。 P29 )阶 )。
1
A 建设准备 B 施工安装 C 生产准备 D 竣工验收 答案: C 8.下列属于工程监理股份有限公司的特征的是() 。P46 A.公司股东的数量没有限制 B.股东拥有的权益凭证是股权证书 C.公司管理实行两权分离 D.公司发起人不得认购公司的全部股份 答案: C 9.控制流程中每个环节的控制工作有所不同,对比环节中应注意() 。P62 A.保证将质量、数量符合计划要求的资源按规定时间和地点投入到工程实施过程 B.对于可以及时解决的问题应及时采取纠偏措施,避免积重难返 C.明确目标实际值和计划值的内涵,合理选择比较的对象,建立两者的对应关系 D.根据偏差的具体情况,合理采用相应的纠偏措施 答案: C 10.下列关于目标和计划的表述中,正确的是() 。P67 A.应当根据计划来制定目标 B.计划必须保证目标的实现 C.计划是对目标的进一步论证 D.按计划对目标进行分解 答案: C 11.在建设工程实施过程中进行严格的质量控制,不仅可减少实施过程中的返工费用,而且 可减少投入使用后的维修费用,这体现了() 。 A.质量目标和投资目标之间的对立关系 B.质量目标和进度目标之间的对立关系 C.进度目标和投资目标之间的统一关系 D.质量目标和投资目标之间的统一关系 答案: D 12.建设工程质量控制的目标是实现() 。 A.建设工程质量的基本目标 B.建设工程质量的共性目标 C.建设工程的个性质量目标 D.建设工程质量的共性目标和个性目标 答案: D 13.不管是在设计阶段还是在施工阶段,监理工程师都要做的投资控制工作是() 。 A.制定建设工程投资目标划分系统 B.审核概预算 C.编制资金使用计划,进行付款控制 D.及时处理费用索赔 答案: C 解析: AB 项属于设计阶段投资控制的任务, D 项属于施工阶段投资控制任务。 14.下列属于建设工程目标控制经济措施的是() 。p87
2
A.明确目标控制人员的任务和职能分工 B.进行偏差原因分析 C.分析不同合同之间的相互联系 D.对多个技术方案进行技术经济分析 答案: B 15.关于风险的分类说法不正确的是() 。 A.纯风险重复出现的概率较大 B.投资风险存在获益的可能性 C.技术风险相对独立 D.特殊风险的影响范围大、后果严重 答案: D 16.对于业主来说,建设工程()阶段的风险主要是纯风险。 A.决策 B.实施 C.使用 D.生产运营 答案: B 17.如果数据库中的数据用于风险管理,只能得到的信息是() 。 A.各种风险综合作用的后果 B.各种风险各自作用的后果 C.既有各种风险的综合作用后果又有各自作用后果 D.建设工程存在的各种风险因素 答案: A 18. 施工现场将易发生火灾的木工加工场尽可能设在远离现场办公用房的位置, 该风险对策 是() 。 A.风险回避 B.非保险转移 C.损失控制的应急计划 D.损失控制的预防计划 答案: D 19.专门用于自留风险所造成损失的损失支付方式是() 。 A.从现金净收入中支出 B.建立非基金储备 C.自我保险 D.母公司保险 答案: C 20.在风险对策中,非保险转移的缺点是() 。 A.不能降低风险因素或风险事件发生的概率 B.不能降低风险因素或风险事件损失发生的严重性 C.增加建设单位的忧虑价值 D.转移可能因双方当事人的分歧而失败 答案: D 21.如果组织的管理层次过多,则会() 。 A.产生官僚主义
)。
)确定。P135
)。
4
P146 A.指导项目监理机构全面开展监理工作 B.指导监理企业全面开展监理工作 C.作为业主确认监理单位履行合同的依据 D.项目监理机构开展监理工作的基本方案 答案: A 29.不同的建设工程具有不同的工程特点、工程条件和运行方式,这就决定了建设工程监理 规划的内容必须() ,才能对工程实施有效监理。P149 A.统一基本构成内容 B.遵循建设工程运行规律 C.分阶段编写 D.具体内容有针对性 答案: B 30.监理规划中,属质量目标控制方法与措施的内容为 ( A.质量目标规划 B.质量目标审核 C.质量目标状况的动态分析 D.质量信息及时归档保存 答案: C 31.国际上对咨询工程师知识结构的要求比我国对监理工程师要求的更宽。下列内容中, 对 我国监理工程师执业资格考试内容未作要求的是 ( )。P169 A.企业管理知识 B.项目管理知识 C.行政管理知识 D.专业技术知识 答案: C 32.下列关于 CM 模式的表述中,正确的是() 。 P175 A.CM 单位一般在设计阶段介入,对设计单位有指令权 B. CM 单位一般在设计阶段介入,对设计单位没有指令权 C.采用 CM 模式,CM 单位只能与业主有合同关系 D.不管什么类型的 CM 模式,其 CM 合同价均为 CM 费 答案: B 解析:非代理型 CM 模式中,CM 单位与施工单位和材料、设备供应单位签订合同,且 CM 合同价包括 CM 费和工程本身的费用。 33.在采用 EPC 模式时,合同价格( )。P117 A.较低且接近于固定 B.较低但不固定 C.较高且接近于固定 D.较高但不固定 答案: C 34.下列关于 Partnering 模式的描述中,正确的是() 。P181 A.Partnering 协议是业主与施工单位双方之间的协议,采用统一、标准的格式 B.签订了 Partnering 协议,业主可以不必再签订其他工程合同 C.该模式强调共同的目标和利益,参与各方要有合作精神,共同解决问题
3
B.组织运行无序 C.信息传递慢、协调困难 D.组织缺乏活力 答案: C 解析: A 项是权大于责的结果; B 项是缺乏足够管理层次的结果; D 项是责大于权的结果。 22.建设工程监理目标是项目监理机构建立的前提,应根据( 监理机构。 A.监理实施细则 B.委托监理合同 C.监理大纲 D.监理规划 答案: B 23.有利于质量控制的建设工程组织管理模式有() 。 A.平行承发包模式和设计或施工总分包模式 B.平行承发包模式和项目总承包模式 C.项目总承包模式和项目总承包管理模式 D.设计或施工总分包模式和项目总承包模式 答案: A 解析:注意不同模式的共同优点或缺点。 24. 同时适用于平行承发包、 设计或施工总分包、 项目总承包模式的委托监理模式是业主 () 。 A.按不同合同段委托多家监理单位 B.按不同建设阶段委托监理单位 C.委托一家监理单位 D.按设计阶段和施工阶段分别委托监理单位 答案: C 25.下列工程建设监理程序中,织工程竣工验收 C.依照监理规划、监理实施细则,规范化地开展监理工作 D.向业主提交监理工作总结 答案: B 26.监理组织机构中,拥有职能部门的监理组织形式有 ( A.直线制和职能制 B.职能制和矩阵制 C.直线制和直线职能制 D.矩阵制和直线制 答案: B 27.专业监理工程师的职责由( A.承包单位负责人 B.建设单位负责人 C.监理单位负责人 D.总监理工程师 答案: D 28.从监理大纲、监理规划和监理实施细则内容的关联性来看,监理规划的作用是 ( )确定的监理目标建立项目
)。P158
5
D.无需再建立共同组织,在各自的组织关系中明确各方的职责、加强合作 答案: C 解析: Partnering 协议没有统一、标准的格式,与工程合同不同;该模式不能独立存在,在 工程合同签订后,才会签署 Partnering 协议;要建立一个由建设工程参与各方人员共同组成 的工作小组。 35.在大型建设工程的实施中,即使业主委托了建设项目管理咨询单位进行全过程、全方位 的项目管理,但重大问题仍需业主自己决策,这种情况下产生了() 。 P185 A.CM 模式 B. EPC 模式 C. Partnering 模式 D.Project Controlling 模式 答案: D 36. 项目监理机构的监理文件档案换发新版时, 应由 ( � A. 总监理工程师 � � � B.专业监理工程师 C.信息管理部门 D.监理单位档案室 )负责将原版本收回作废。 信息 p46
