2012年年第十届走美杯四年级初赛试题
小学奥数杯赛真题1312

1.小泉做一道除数是一位数的除法时,误把除数9看成6,结果算出的商是7,余数是3。
你知道正确的结果是(2012世奥(中国区)选拔赛三年级A卷)2.杨阳是班里有名的小马虎,这次在做(200×9-□)÷25+13时,又没看到题里的括号,算的结果是1788,正确的结果应该是 (2012世奥数浙江赛区四年级)。
3.袋子里有若干个球,每次拿出其中的一半又一个球,这样共操作了4次,袋中还有5个球。
袋中原有____个球(2012年第十届走美杯三年级)。
4.盒子里有若干个球。
小明每次拿出盒中的一半再放回一个球。
这样共操作了7次,袋中还有3个球。
袋中原有个球(2010年走美杯三年级)。
5.抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个球。
如此操作了2012次后, 抽屉里还剩有2个球。
那么原来抽屉里有个球(第十七届华杯赛小中组复赛)。
6.黑板上写有一个数,男同学从黑板前走过时,把他乘以3再减去14,擦去原数,换上答案,女同学从黑板前走过时,把他乘以2再减去7,擦去原数,换上答案。
全班25名男同学和15名女同学都走过后,老师把最后的数乘以5,减去5,结果是30。
那么,黑板上最初的数字是(湖北第七届创新杯)。
7.豆豆和苗苗各有一盒玻璃球,共108粒,豆豆给了苗苗10粒,豆豆剩下的玻璃比苗苗还多8粒。
原来苗苗有粒玻璃球(2010年第八届走美杯三年级)。
8.甲、乙、丙三人的平均年龄为42岁,若将甲的岁数增加7岁,乙的岁数扩大2倍,丙的岁数缩小2倍,则三人岁数相等。
丙的年龄为________岁(第四届迎春杯)。
9.甲、乙、丙、丁四人一共做了370个零件,如果把甲做的个数加上10个,乙做的个数减去20个,丙做的个数乘以2,丁做的个数除以2,四人做的零件数就正好相等。
那么乙实际做了_____ 个零件(第二届迎春杯)。
10.甲、乙、丙三所小学的学生人数的总和为1999。
已知甲校学生人数的2倍和乙校学生人数减去3人与丙校学生人数加上4人都相等。
2012年第十届走美杯初赛小学五年级(含解析)
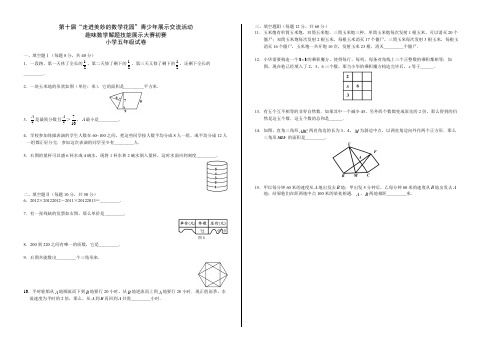
第十届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学五年级试卷一、填空题Ⅰ(每题8分,共40分)1.一段路,第一天休了全长的12,第二天修了剩下的12,第三天又修了剩下的12,还剩下全长的_________.2.一块玉米地的形状如图(单位:米).它的面积是_________平方米.3.7A 是最简分数且7A >710,A 最小是_________.4.学校参加体操表演的学生人数在60~100之间,把这些同学按人数平均分成8人一组,或平均分成12人一组都正好分完.参加这次表演的同学至少有_________人.5.右图的量杯可以盛6杯水或4碗水,现将1杯水和2碗水倒入量杯,这时水面应到刻度_________.二、填空题Ⅱ(每题10分,共50分)6.2012×20122012-2011×20122013=_________.7.有一张残缺的发票如右图,那么单价是_________.8.200到220之间有唯一的质数,它是_________.9.右图共能数出_________个三角形来.10.平时轮船从A 地顺流而下到B 地要行20小时,从B 地逆流而上到A 地要行28小时.现正值雨季,水流速度为平时的2倍,那么,从A 到B 再回到A 共需_________小时.三、填空题Ⅲ(每题12分,共60分)11.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种,单筒玉米炮每次发射1根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米每次发射3根玉米,每根玉 消灭16个僵尸,玉米炮一共开炮10次,发射玉米23根,消灭_________个僵尸.12.小华需要构造一个33 的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;如图,现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x 等于______.13.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数.这五个数的总和是______.14.如图,直角三角形ABC 两直角边的长为3、4,M 为斜边中点,以两直角边向外作两个正方形.那么三角形MEF 的面积是_________.15.甲以每分钟60米的速度从A 地出发去B 地;甲出发5分钟后,乙每分钟80米的速度从B 地出发去A 地;结果他们在距两地中点100米的某处相遇.A 、B 两地相距_________米.第十届“走进美妙的数学花园”青少年展示交流活动图3趣味数学解题技能展示大赛初赛 小学五年级试卷参考答案1 2 3 4 5 6 7 8 18 85 5 72 4 20120001 1.36 2119 10 11 12 13 14 153252.5382369312.251000或3800参考解析一、填空题Ⅰ(每题8分,共40分)1.一段路,第一天休了全长的12,第二天修了剩下的12,第三天又修了剩下的12,还剩下全长的________.【考点】分数应用题 【难度】☆ 【答案】18【解析】相当于每天将剩余的减少到12,共减少了3次,共减少到11112228⨯⨯=.2.一块玉米地的形状如图(单位:米).它的面积是_________平方米.【考点】几何 【难度】☆【答案】87【解析】分成一个三角形和一个平行四边形,其面积为6827987⨯÷+⨯=.3.7A 是最简分数且7A >710,A 最小是_________.【考点】最值问题 【难度】☆☆ 【答案】5【解析】两边乘以7得到494.910A >=,所以所求的最小值为5.4.学校参加体操表演的学生人数在60~100之间,把这些同学按人数平均分成8人一组,或平均分成12人一组都正好分完.参加这次表演的同学至少有_________人. 【考点】数论整除 【难度】☆☆【答案】72【解析】8和12的最小公倍数为24,其倍数依次为:48、72、108、……所以为72.5.右图的量杯可以盛6杯水或4碗水,现将1杯水和2碗水倒入量杯,这时水面应到刻度_________.【考点】几何【难度】☆☆☆【答案】4【解析】每杯水相当于661÷=个刻度,每碗水相当于64 1.5÷=个刻度,所以1杯水和2碗水相当于12 1.54+⨯=个刻度.二、填空题Ⅱ(每题10分,共50分)6.2012×20122012-2011×20122013=_________. 【考点】速算巧算 【难度】☆☆☆【答案】20120001【解析】原式201220120000201220122011201200002011201320120001=⨯+⨯-⨯-⨯=.7.有一张残缺的发票如右图,那么单价是_________.【考点】数论弃九法 【难度】☆☆☆【答案】1.36【解析】可观察到个位数字为7,由于72是9的倍数,可得其数字和为9的倍数,百分位为2.经检验,符合题意:97.9272 1.36÷=.8.200到220之间有唯一的质数,它是_________. 【考点】质数合数 【难度】☆☆☆【答案】211【解析】依次划去所有2、3、5、7、11的倍数可得其为211.9.右图共能数出_________个三角形来.【考点】几何计数 【难度】☆☆☆【答案】32【解析】小正三角形有6个,大正三角形有2个,以大正六边形的边为底的等腰三角形有6个,以大正六边形的两条相邻的边为腰的等腰三角形有6个,直角三角形有12个,共32个.10.平时轮船从A地顺流而下到B地要行20小时,从B地逆流而上到A地要行28小时.现正值雨季,水流速度为平时的2倍,那么,从A到B再回到A共需_________小时.【考点】行程问题【难度】☆☆☆【答案】52.5【解析】设全程为1,每小时顺水行驶的距离为1720140=,逆水行驶的距离为1528140=,则观察到水速增加后,每小时顺水行驶的距离和逆水行驶的距离分别为8140和4140,所求的时间为140140+=52.584小时.三、填空题Ⅲ(每题12分,共60分)11.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种,单筒玉米炮每次发射1根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米每次发射3根玉米,每根玉米消灭16个僵尸,玉米炮一共开炮10次,发射玉米23根,消灭_________个僵尸.【考点】鸡兔同笼【难度】☆☆☆【答案】382【解析】三种玉米炮每发射一次分别消灭20个,34个,48个僵尸,成等差数列.也就是说,无论哪种玉米炮,发射一次,消灭的僵尸数等于玉米数146⨯+.多次发射后,消灭的僵尸数应该等于总玉米数14⨯+发射次数6⨯.那么,总共发射了10次,所以消灭的僵尸数等于2314106382⨯+⨯=.12.小华需要构造一个33⨯的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;如图,现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x等于______.【考点】幻方【难度】☆☆【答案】36【解析】幻积等于中间数6的立方,所以362336x=÷÷=.13.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数.这五个数的总和是______.【考点】数论倍数约数【难度】☆☆☆【答案】93【解析】如果一开始的五个数分别是1、2、4、8、16,则将16减少15后,将其他四个数都乘以2,可以仍然得到这5个数.而45153÷=,所以原来的五个数是1、2、4、8、16的3倍,总和为313=93⨯.14.如图,直角三角形ABC两直角边的长为3、4,M为斜边中点,以两直角边向外作两个正方形.那么三角形MEF的面积是_________.【考点】几何【难度】☆☆☆【答案】12.25【解析】1(43)4142BEFS=⨯+⨯=△,1(43)310.52CBFS=⨯+⨯=△,以EF为底,则MEF△的高是BEF△和CEF△的高的平均值,所以面积也是它们的平均值,等于12.25.15.甲以每分钟60米的速度从A地出发去B地;甲出发5分钟后,乙每分钟80米的速度从B地出发去A地;结果他们在距两地中点100米的某处相遇.A、B两地相距_________米.【考点】行程问题【难度】☆☆☆【答案】1000或3800【解析】设两地相距2x米,则有10010056080x x+-=+或10010056080x x-+=+,得到500x=或1900x=,则答案为1000或3800.。
走美杯四年级试题及答案

第三届“走美杯”四年级初赛共12道题,每题10分。
1、33×34+34×35+35×36+36×37= 。
2、李东到商店买练习本,每本3角,共买9本,服务员问:“你有零钱吗?”李东说:“我带的全是5角一张的。
”服务员说:“真不巧,您没有2角一张的,我的零钱全是2角一张的,这怎么办?”你帮李东想一想,他至少应该给服务员张5角币。
3、幼儿园的老师给班里的小朋友送来40个橘子,200块饼干,120块奶糖,平均分发完毕,还剩4只橘子,20块饼干,12粒奶糖,这班里共有位小朋友。
4、有一家三口,爸爸比妈妈大3岁,他们全家今年的年龄加起来正好是58岁,而5年前他们全家人年龄加起来刚好是45岁,小孩子今年岁。
5、两个长方形如下图摆放,阴影三角形面积= 。
6、北京有一家餐馆,店号“天然居”里面有一副著名对联:客上天然居,居然天上客。
巧的很,这幅对联恰好能构成一个乘法算式(见右上图)相同的汉字代表相同的数字,不同的汉字代表不同的数字。
“天然居”表示成三位数是。
7、一个四位数给它加上小数点后比原来小2346.3,那么原四位数是。
8、用同样大小的木块堆成了如图所示的形状,这里共用了个木块。
9、下面图中有9个围棋子围成一圈,现将同色的相邻两子之间放入一个白子,在不同色的相邻两子间放入一个黑子,然后将原来的9个棋子拿掉,剩下新放入的9个棋子如右图,这算一次操作,如果继续这样操作下去,在一圈的9个子中最多有个是黑子。
10、在1999后面写一串数字,从第5个数字开始,每个数字都是它前面两个数字乘积的个位数字,这样得到1 9 8 9 2 8 6 8 4 2……,那么,这串数字中,前2005个数字的和是。
11、在下图的5×5方格表的空白处填入1~5中的数,使得每行、每列、每条对角线上的数各不相同。
2512、甲、乙二人轮流在右上图的10个方格中,甲画“○”,乙画“×”。
甲胜的情况是:最后一行有4个“○”或者其他的直线上有3个“○”;乙胜的情况是:最后一行有4个“ד或者其他的直线上有3个“×”,甲先画,他要取胜,第一步应填在标号为的方格中(至少写出2种)第四届“走美杯”四年级初赛共12题,每题10分1.计算:110+111+112+…+126=。
四年级走美自测题 教师版

四年级走美杯自测卷填空题Ⅰ(每题8分,共40分)1、2000年后为三个连续自然数乘积的第一个年份是 。
【解析】:11×12×13=1716,12×13×14=2184。
2、将正整数1,2,3,4,5,6,…,10000排成一行。
若一个数不能表示成两个合数的和,则将此数划去。
例如要划去1,但是因为8=4+4,8就不能划去。
根据上面规定划掉所有能划掉的数之后,将剩下的由小到达排列,这时从左数第2016个数是 。
【解析】:从8开始往后的偶数可以拆成两个偶合数的和;从13开始的奇数可以拆成9+2n 的形式(n 大于等于2),而1、2、3、4、5、6、7、9、11要划去,所以剩下的数列为8、10、12、13、14、15……,第2016项即为2025。
3、图中共有 个三角形。
【解析】:①由1个小三角形构成的三角形有24个;②由2个小三角形构成的三角形有20个;③由3个小三角形构成的三角形有8个;④由4个小三角形构成的三角形有8个;⑤由5个小三角形构成的三角形有4个;⑥由6个小三角形构成的三角形有4个;⑦由7个小三角形构成的三角形有4个;所以图中共有三角形24+20+8+8+4+4+4=72个。
4、四位数abcd 与cdab 的和为3636,差为396,那么四位数abcd 为 。
【解析】:100abcd ab cd =+,100cdab cd ab =+。
当ab cd >时: ()1001003636100100396ab cd cd ab ab cd cd ab ⎧+++=⎪⎨+-+=⎪⎩ 整理得36ab cd +=,4ab cd -=,所以20ab =,16cd =,2016abcd =。
同理,ab cd <时,1620abcd =。
5、A、B、C、D四个箱子中分别装有一些小球,现将A箱中的部分小球按如下要求转移到其他三个箱子中:该箱中原有几个小球,就再放入几个小球,此后,按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中,此时,四个箱子都各有16个小球,那么开始时装有小球最多的是______箱,其中装有______小球个。
相遇问题竞赛真题训练

相遇问题相遇问题竞赛真题训练竞赛真题训练真题博览:1、(第十三届小机灵杯(第十三届小机灵杯三年级三年级三年级决赛)决赛)甲、乙两地相距3千米。
明明和亮亮同时从两地出发同向而行,行了20分钟两人还未相遇且相距2900米。
已知明明每分钟行80米,亮亮每分钟行________米。
2、(第十三十三届小机灵杯三年级初赛届小机灵杯三年级初赛届小机灵杯三年级初赛))AB两地相距1000米,甲从A地出发,1小时后到达B地。
乙在甲出发后20分钟从B地出发,40分钟到达A地。
甲、乙二人相遇点距A地________米。
3、(第(第121212届届“走美杯走美杯””四年级初赛)甲、乙两市相距55千米。
小王同学从甲市出发去乙市,先骑车行了25千米,接着改乘大客车,速度提高了1倍。
到达乙市后,他发现骑车所用的时间比乘车所用的时间多了1小时。
小王同学骑车的速度是________千米/小时。
4、(2013(2013年亚太选拔赛四年级年亚太选拔赛四年级年亚太选拔赛四年级))甲、乙两地相距600千米,快车和慢车分别从甲、乙两地同时出发相向而行,10小时相遇,快车的速度是慢车的两倍。
试问:如果慢车比快车早出发3小时,当两车相遇时快车离甲乙两地中点相距多少千米?答案解析:1、【答案】85或75【解答】20分钟后,两个人的距离减少了3000-2900=100米;因此速度差每分钟100÷20=5米;因此亮亮的速度是每分钟80+5=85米或80-5=75米。
2、【答案】600米。
【解答】由乙40分钟可走1000米,得到乙的速度为1000÷40=25米/分钟;甲60分钟可走1000米,而乙60分钟可走25×60=1500米;由1000与1500的关系不难看出,相同时间内若甲走2份路程,则乙可走3份;现在甲比乙早出发20分钟,即为乙比甲晚出发20分钟;可构造一种情形:乙先向后退20分钟甲再出发,即为乙后退25×20=500米;此时甲、乙二人的实际距离为1000+500=1500米;甲、乙二人相遇点与A地的距离即为相遇时甲所走的路程;在二人的路程和1500米当中,甲所走的路程为1500÷(2+3)×2=600米;所以甲、乙二人相遇点距A地600米。
走美杯四年级试题及答案

走美杯四年级试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是正确的?A. 地球是平的B. 太阳是宇宙的中心C. 地球围绕太阳转D. 月亮是地球的卫星答案:C2. 哪个国家被称为“千岛之国”?A. 中国B. 日本C. 印度尼西亚D. 印度答案:C3. 下列哪个选项是数学中的“奇数”?A. 2B. 4C. 5D. 8答案:C4. 以下哪种动物是哺乳动物?A. 蛇B. 鳄鱼C. 鲸鱼D. 乌龟答案:C5. 世界上最高的山峰是?A. 珠穆朗玛峰B. 乞力马扎罗山C. 富士山D. 阿尔卑斯山答案:A二、填空题(每题2分,共10分)1. 一年有______个季节。
答案:四2. 地球上最大的陆地动物是______。
答案:非洲象3. 光年是长度单位,表示光在一年内通过的距离,大约是______公里。
答案:9.46万亿4. 人体最大的器官是______。
答案:皮肤5. 世界上最大的海洋是______。
答案:太平洋三、简答题(每题5分,共20分)1. 简述地球的自转和公转。
答案:地球的自转是指地球围绕自己的轴线旋转,周期约为24小时,导致了昼夜交替。
地球的公转是指地球围绕太阳的轨道运动,周期约为365.25天,导致了季节更替。
2. 请解释什么是生态系统。
答案:生态系统是由生物群落和其所在的非生物环境相互作用而形成的一个统一整体,包括了生产者、消费者和分解者等生物组成部分以及水、土壤、空气等非生物组成部分。
3. 请列举三种常见的哺乳动物。
答案:猫、狗、牛4. 描述一下水循环的过程。
答案:水循环是指地球上水分子在大气、陆地和海洋之间不断循环的过程,包括蒸发、凝结、降水和径流等环节。
四、计算题(每题10分,共20分)1. 如果一个长方形的长是8米,宽是5米,求其面积。
答案:面积 = 长× 宽 = 8米× 5米 = 40平方米2. 一个班级有40名学生,如果每名学生需要2本练习册,那么总共需要多少本练习册?答案:总练习册数 = 学生数× 每人练习册数= 40 × 2 = 80本五、阅读理解题(每题5分,共10分)阅读以下短文,回答后面的问题。
第十届走美杯

第十届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学六年级试卷一、填空题Ⅰ(每题8分,共40分) 1.712的分母增加36后,要使分数的大小不变,分子应加________.2.在“庆祝六一”征文比赛活动中,某校六年级有80人获一、二、三等奖.其中获三等奖的人数占六年级获奖人数的62.5%,获一、二等奖的人数比是1:4.六年级获二等奖共有_________人.3.把一些糖果平均分给10个小朋友,其中有两个小朋友又把他们得到的所有糖果,都分给了其余的小朋友;结果,其余的小朋友每人多了3颗糖果.一共有_________颗糖果.4. 在一个正方形里画一个最大的圆,这个圆的面积是正方形面积的_________%(π 3.14=).5.如果物价下降50%,那么原来买1件东西的钱现在就能买2件.1件变2件增加了100%,这就相当于我手中的钱增值了100%.如果物价上涨25%,相当于手中的钱贬值了_________%.二、填空题Ⅱ(每题10分,共50分) 6.计算:222221949201219492012194920121949201219492012++++1949194919501950195119511952195220112011⨯⨯⨯⨯⨯++++++…7.如图,大等边三角形中放了三个面积都是30平方厘米的小正六边形,大等边三角形的面积是_________平方厘米.8.如果1112012A B+=(A、B均为自然数),那么B最大是______.9.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数.这五个数的总和是______.10.甲、乙两车都从A地到B地.甲车比乙车提前30分钟出发,行到全程三分之一时,甲车发生了故障,修车花了15分钟,结果比乙车晚到B地15分钟.甲车修车前后速度不变,全程为300千米.那么乙车追上甲车时在距A地_______千米.三、填空题Ⅲ(每题12分,共60分)11.在一个棱长为5厘米的正方体上如图3切掉一个三棱柱.那么体积减少_______立方厘米;表面积减少______平方厘米.12.从0、2、4、6、8中挑出4个各不相同的数字能组成一个四位完全平方数,那么这个完全平方数是______.13.某网络游戏中推出圣者套装,包含圣剑、圣盔、圣甲3件装备.小强购买了4个圣装宝盒,打开每个圣装宝盒将随机获得上述3件装备之一.那么,小强打开这4个圣装宝盒后,能集齐一套完整圣者套装的可能性是______.14.一个角可以将平面分成2部分.3个角最多可以将平面分成______个部分.15.如图,将1~99依次排成第1行,对第1行相邻两数求和写成第2行,对第2行相邻两数求和写成第3行,以此类推,写到第99行时就只有1个数了.那么,第99行的这个数恰有______个约数.第十届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示大赛初赛小学六年级试卷参考答案1 2 3 4 5 6 7 8 21 24 120 78.5 20 63 135 2011 9 10 11 12 13 14 1593 150 30;22 6084 4916 300参考解析一、填空题Ⅰ(每题8分,共40分)1.712的分母增加36后,要使分数的大小不变,分子应加________.【考点】分数计算【难度】☆【答案】21【解析】分数性质:分子和分母同时增大或者缩小相同的倍数,分数的大小不变.分母12增加36变成48,即增大为原来的4倍,为了让分数大小不变,分子要乘以4,变成28,分子应加:21.2.在“庆祝六一”征文比赛活动中,某校六年级有80人获一、二、三等奖.其中获三等奖的人数占六年级获奖人数的62.5%,获一、二等奖的人数比是1:4.六年级获二等奖共有_________人.【考点】比例应用题【难度】☆☆【答案】24【解析】562.5%=8,获得一、二等奖的人数之比是1:4;所以可以知道获得一二三等奖的人数之比是::4:5a a,其中43a a+=;0.6a=;所以获得二等奖的共有:8084400.624a÷⨯=⨯=(人).3.把一些糖果平均分给10个小朋友,其中有两个小朋友又把他们得到的所有糖果,都分给了其余的小朋友;结果,其余的小朋友每人多了3颗糖果.一共有_________颗糖果.【考点】最值问题【难度】☆☆ 【答案】120【解析】一堆糖果,如果平均分给10个小朋友,每人可以得到a 颗;如果平均分给8个小朋友,每人可以得到(3)a +颗.108(3)22412a a a a =⨯+⇒=⇒=;所以一共有1210120⨯=(颗).4.在一个正方形里画一个最大的圆,这个圆的面积是正方形面积的_________%(π 3.14=).【考点】几何 【难度】☆☆ 【答案】78.5【解析】正方形的边长是2r ,面积是24r ;圆的半径是r ,面积是2πr .所以圆的面积是正方形面积的π 3.1478.5%44==.5.如果物价下降50%,那么原来买1件东西的钱现在就能买2件.1件变2件增加了100%,这就相当于我手中的钱增值了100%.如果物价上涨25%,相当于手中的钱贬值了_________%. 【考点】经济问题 【难度】☆☆☆ 【答案】20【解析】物价上涨了25%,原来1元1件,现在1.25元1件,本来5元可以买5件,现在5元只能买4件.5件变4件,相当于手中的钱贬值了(54)520%-÷=.二、填空题Ⅱ(每题10分,共50分) 6.计算:222221949201219492012194920121949201219492012++++1949194919501950195119511952195220112011⨯⨯⨯⨯⨯++++++… 【考点】速算巧算 【难度】☆☆☆ 【答案】63 【解析】原式1111=19492012(++++)19491950195019511951195220112012⨯⨯⨯⨯⨯⨯1119492012()201219496319492012=⨯⨯-=-=.7.如图,大等边三角形中放了三个面积都是30平方厘米的小正六边形,大等边三角形的面积是_________平方厘米.【考点】几何 【难度】☆☆☆ 【答案】135【解析】如图切割,然后数三角形:每个正六边形里面包含6个小三角形,面积为30,所以每个小三角形面积为5;而整个ABC △里面包含27个小三角形,所以ABC △的的面积为527135⨯=.8.如果1112012A B+=(A 、B 均为自然数),那么B 最大是______.【考点】约数倍数 【难度】☆☆☆ 【答案】211 【解析】方法一:1112012A B +=有112012B<,因为A 、B 均为自然数,所以1A 、1B 均大于0,所以11201220112012B B B<⇒<⇒≤则自然数B 最大可以取的值是2011,当2011B =时,20112012A =⨯.方法二:2012201214503=⨯=⨯.()120121*********20122012201212012201120122011201120122011B A-==-=-=-⨯-⨯⨯⨯ ∴2011B =.9.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的仍然是这五个数.这五个数的总和是______. 【考点】数论倍数约数 【难度】☆☆☆ 【答案】93【解析】如果一开始的五个数分别是1、2、4、8、16,则将16减少15后,将其他四个数都乘以2,可以仍然得到这5个数.而45153÷=,所以原来的五个数是1、2、4、8、16的3倍,总和为313=93⨯. 假设五个数:a b c d e >>>>由题意, 45a e -=,2d e =,2c d =,2b c =,∵452222a b c d e a b c d e -++++=++++ ∴45b c d e +++=代入2d e =,4c e =,8b e =得:1545e = 3e =6d =,12c =,24b =,48a =,4824126393a b c d e ++++=++++=.10.甲、乙两车都从A 地到B 地.甲车比乙车提前30分钟出发,行到全程三分之一时,甲车发生了故障,修车花了15分钟,结果比乙车晚到B 地15分钟.甲车修车前后速度不变,全程为300千米.那么乙车追上甲车时在距A 地_______千米.【考点】行程问题 【难度】☆☆☆ 【答案】150【解析】甲车比乙车早30分钟出发,甲车如果不出故障,则甲乙两车同时到达B 地.而全程长度为300千米,在跑这300千米时,乙车比甲车少用时30分钟,可以推断出如果是跑100千米,乙车比甲车少用时10分钟.现在,甲车在跑了全程13到达C地的时候发生故障,停了15分钟,本来甲乙两车到达C 的时间之差应该是20分钟.现在,甲车停了15分钟,乙车还是没有追上甲车,但是甲乙两车实际上发车的间隔变成了15分钟,所以乙车会在甲车跑了150千米之后追上甲车,乙车追上甲车是,距离A 地150千米.三、填空题Ⅲ(每题12分,共60分)11.在一个棱长为5厘米的正方体上如图3切掉一个三棱柱.那么体积减少_______立方厘米;表面积减少______平方厘米.【考点】立体几何 【难度】☆☆☆ 【答案】30,22【解析】体积减少:1345302⨯⨯⨯=(立方厘米)表面积减少:1453534255222⨯+⨯+⨯⨯⨯-⨯=(平方厘米)12.从0、2、4、6、8中挑出4个各不相同的数字能组成一个四位完全平方数,那么这个完全平方数是______. 【考点】数论 【难度】☆☆☆【答案】6048【解析】完全平方数的尾数可以是:0,1,4,5,6,9,当尾数是0时,后两个一定都是0,所以不合题意. 当尾数是6时,十位数字一定为奇数.所以不合题意当尾数是4时,0246820++++=,不用的数字如果是8,和是12是3的倍数,但不是9的倍数,如果是0或6,被3整除余2,(完全平方数被3除余数只可能是0或1)所以用的数只能是2,6084,6804,8064,8604那么6084=7878⨯.13.某网络游戏中推出圣者套装,包含圣剑、圣盔、圣甲3件装备.小强购买了4个圣装宝盒,打开每个圣装宝盒将随机获得上述3件装备之一.那么,小强打开这4个圣装宝盒后,能集齐一套完整圣者套装的可能性是______. 【考点】概率 【难度】☆☆☆ 【答案】49【解析】4个圣装宝盒有4381=种可能性,如果含有3种不同装备,则先选择一个有2件的有3种可能,选择哪两个宝盒有这个装备有4326⨯÷=种可能,剩下的两个排列有2种可能,共有36236⨯⨯=(种)可能.所求概率为364819=.14.一个角可以将平面分成2部分.3个角最多可以将平面分成______个部分.【考点】几何计数 【难度】☆☆☆☆ 【答案】16【解析】如下图,一个角分成2部分,两个角分成7部分,三个角分成16部分.1613412356789101112141515.如图,将1~99依次排成第1行,对第1行相邻两数求和写成第2行,对第2行相邻两数求和写成第3行,以此类推,写到第99行时就只有1个数了.那么,第99行的这个数恰有______个约数.【考点】约数倍数 【难度】☆☆☆【答案】300【解析】如果将原表左右对称后与原表相加,则第一行全是100,第二行全是200,……,第99行是981002⨯.因此,原表的第99行是9799100225⨯=⨯,有300个约数.。
05年第三届至13年第十一届走美杯试题答案 (1)

目录第三届“走美杯”答案 (2)第四届“走美杯”答案 (3)第五届“走美杯”答案 (4)第六届走美杯三年级初赛试题参考答案 (6)第六届走美杯三年级决赛试题参考答案 (9)第七届走美杯三年级初赛试题参考答案 (10)第八届走美杯三年级初赛试题参考答案 (11)第九届走美杯三年级A卷初赛试题参考答案 (13)第十届走美杯三年级B卷试题及答案详解 (14)第三届走美杯四年级试题参考答案 (18)第四届走美杯四年级试题参考答案 (19)第六届走美杯四年级初赛试题参考答案 (20)第六届走美杯四年级决赛试题参考答案 (24)第七届走美杯四年级初赛试题参考答案 (24)第八届走美杯四年级初赛试题参考答案 (25)第九届走美杯四年级A卷初赛参考答案 (27)第九届走美杯四年级B卷初赛参考答案 (28)第三届走美杯五年级试题参考答案 (33)第四届走美杯五年级试题参考答案 (34)第五届走美杯五年级初赛试题参考答案 (35)第六届走美杯五年级初赛试题参考答案 (39)第六届走美杯五年级决赛试题参考答案 (42)第七届走美杯五年级初赛试题参考答案 (43)第八届走美杯五年级初赛试题参考答案 (46)第九届走美杯五年级初赛试题参考答案 (48)第九届走美杯五年级B卷初赛试题参考答案 (52)第三届走美杯六年级试题参考答案 (52)第四届走美杯六年级试题参考答案 (53)第五届走美杯六年级试题参考答案 (54)第六届走美杯六年级决赛试题参考答案 (58)第七届走美杯六年级初赛试题参考答案 (59)第八届走美杯六年级初赛试题参考答案 (62)第九届走美杯六年级A卷初赛试题参考答案 (65)第十届2012走美杯六年级试题及答案详 (66)第六届走美杯三年级初赛试题参考答案1.22222.861;574;5733.604.155.4;36.90÷15=34-28=67.10;28.169.22210.3711.略12.361.【答案】100012.【答案】100003.【答案】404.【答案】11705.【答案】MT79366.【答案】2008;87.【答案】38.【答案】49.【答案】灰太狼10.【答案】711.【答案】105 ;312.【答案】7; 213.【答案】55;540 14.【答案】4或315.【答案】1、2 、4 、8 .第八届走美杯三年级初赛试题参考答案第九届走美杯三年级A卷初赛试题参考答案第十届走美杯三年级B卷试题及答案详解1、49042、73、364、35、46、9787、2607或23708、509、810、1203111、12、5,2,6 1 2 3 4 5 4 5 1 2 3 2 3 4 5 1 5 1 2 3 4 3 4 5 1 2第六届走美杯四年级初赛试题参考答案1.20082.64;15625(64×15625)3.2或54.155.906.200000077.168.1;2;2;39.5610.3011.147张,15块12.2100第七届走美杯四年级初赛试题参考答案1. 100002. 403. 丙;甲4. 3 、1 、25. 156. 2008;87. 灰太狼8. 9009. C.10. 1011. 55;54012. 413. 2614.55 ;259平方厘米15.21、555502、1043、254、445、19;5176、97、388、79、100010、126311、6412、328213、814、415、1176答案:1、2010012 2、19 3、0。
SH四年级走美杯初赛汇总

第七届走美杯四年级初赛一、填空题Ⅰ(每题8分,共40分)1、 3737263376363⨯+⨯⨯+⨯=______2、 下边的一排方格中,除9、8外,每个方格中的字都表示一个数(不同的字可以表示相同的数字),已知其中任何3个连续的方格中的数相加起来都为22,则“走”+“进”+“数”+“学”+“花”+“园”3、 “走美”商场有下列几种瓶装蜂蜜出售:甲,净重3kg ,售价33.99元;乙,净重2kg ,售价22.99元;丙,净重500g ,售价5.99元,那么,_____种蜂蜜最贵,____种蜂蜜最便宜。
4、 一个数学玩具的包装盒是正方体,其表面展开图如下。
现在每方格内都填上相应的数字。
已知将这个表面展开图沿虚线折成正方体后,相对面的两数之和为“3”,则填在A 、B 、C 内的三个数字依次是________。
5、 某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划:该球拍每只售价为人民币60元,同时购买者可获赠1张奖券,积累3张奖券可兑换1只球拍。
由此可见,1张奖券价值为________元。
二、填空题Ⅱ(第题10分,共50分)6、 A ,B 都是整数,A 大于B ,且2009A B ⨯=,那么A B -的最大值为________,最小值为________。
7、 一天,红太狼和灰太狼同时从“野猪林”出发,到“天堂镇”。
红太狼一半路程溜达,一半路程奔跑。
灰太狼一半时间溜达,一半时间奔跑。
如果它们溜达的速度相同,奔跑的速度也相同,则先到“天堂镇”是___________。
8、 柯南家2008年一年用电10200千瓦时,上半年的月平均用电比下半年的月平均用电少100千瓦时。
柯南家下半年月平均用电为___________千瓦时。
9、 某校A 、B 、C 三名同学参加“走进美妙的数学花园”,其指导教师赛前预测“A 获金牌,B 不会获金牌,C 不会获铜牌”。
结果出来后,三人之中,一人获金牌,一人获银牌,一人获铜牌,指导教师的预测只有一个人与结果相符。
2012年走美决赛试卷(四年级)

第十届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛决赛注意事项:1.考生要按要求在密封线内填好考生的有关信息.总分2.不允许使用计算器.小学四年级试卷一、填空题Ⅰ(每题8分,共32分)1.算式2012×125×25×5×8的结果未尾有个零。
2.有50个苹果分别给甲、乙、丙三人,甲分的个数是乙的2倍,丙最少,但也不少于10个,丙分到个苹果。
3.去掉20.12中的小数点,得到的整数比原来的数增加了倍.4.小刚去买牛奶,发现牛奶本周特价,每袋0.9元,买二送一.小刚有5.4元,最多可以买袋奶.二、填空题Ⅱ(每题10分,共40分)5.写有1、2、3、4、5、6、7、8的八张卡片为一组。
每人从一组中抽2张,至少人抽过,才能保证有人抽的2张卡片上的数互质。
6.王伟的语文、数学的平均分是95分,英语、数学的平均分也是95分,他这3门课的平均分95分。
(填:大于、小于、等于或不一定)7.8.自然数N的所有数字互不相同,这些数字的乘积等于240。
N的最大值是9.如图,一个长方形,长增加2厘米,宽增加3厘米后,面积增加了44平方厘米,这时恰好成为一个正方形,原长方形的面积是平方厘米。
三、填空题Ⅲ(每题12分,共48分)10.汽车和自行车分别从A、B两地同时出发相向而行,汽车每小时行60千米,自行车每小时行12千米。
两车相遇后,各自仍沿原方向行驶,汽车到达B地后立即返回追上自行车源-于-网-络-收-集时距A地还有45千米。
A、B两地间的距离是千米。
11.两个长方形如图叠放,图上已标出一些线段的长。
EF= .12.下图的六条线分别连接着九个○,其中一个○里的数是7。
请选出九个连续自然数(包括7在内)填入○内,使每条线上各数之和都是23。
13.将下图中的正方形分割成形状和大小一样的四块,并且每一块恰好都有四种不同的图案。
在图中用不同的色笔把它们区分开。
源-于-网-络-收-集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级B 卷-1
第十届“走进美妙的数学花园”中国青少年数学论坛
趣味数学解题技能展示大赛初赛
注意事项:
1. 考生要按要求在密封线内填好考生的有关信息.
2. 不允许使用计算器.
小学四年级试卷(B 卷)
一、填空题Ⅰ(每题8分,共40分)
1. 2012+2011+2010+…+1007-1006-1005-1004-…-1= 。
2. 某年7月恰有4个星期一和4个星期四,这月的15号是星期 。
3. 从正整数1~N 中去掉一个数,剩下的N-1个数的平均值是16.3;去掉的数是
4. 葛大财主请园艺师为其整修花园,要求一个月完成,3月1日开始31日结束,
每天的工钱为一钱黄金。
葛大财主是出了名的守财奴,园艺师要求每天结束时结算工钱,葛 大财主恰有一块31钱的金条。
聪明绝顶的葛大财主只做了 次切割(填最少次数),就解决了这个问题。
5. 在台球“斯诺克”比赛中,有红球15个,黄、绿、棕、蓝、粉、黑球各1个,
其中红球落袋积1分,黄、绿、棕、蓝、粉、黑球落袋分别积2、3、4、5、6、7分.比赛中,第一阶段先要将15个红球全击落袋,而每击落1个红球后必须再击落1个其它颜色的球,红球落袋不拿回,而其它颜色的球在此阶段被击落袋后再放回台面;第二阶段要按黄、绿、棕、蓝、粉、黑的顺序依次将这些球击落袋.那么,“斯诺克”比赛中最高能得 分.
二、填空题Ⅱ(每题10分,共50分)
6. 小华需要构造一个3×3的乘积魔方,使得每行、每列、每条
对角线上三个正整数的乘积都相等;现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x 等于 .
7. 十进制下的三位数TWO 和四位数FOUR 满足:TWO+TWO=FOUR, 其中不
同的字母代表不同的数字,FOUR 的最小可能的值是 .
总分 2 x 6
3
8.今年,丹丹和父亲、母亲、弟弟的年龄和是120岁.当父亲的年龄是丹丹年
龄的3倍时,母亲的年龄恰好也是弟弟年龄的3倍,当时弟弟12岁.那么丹丹今年岁.
9.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种.单筒玉米炮每炮发射
一根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米炮每次发射三根玉米,每根玉米消灭16个僵尸.玉米炮一共开炮10次,发射玉米23根,消灭个僵尸.
10.
11.有五个互不相等的非零自然数.如果其中一个减少45,另外四个数都变成原
先的2倍,那么得到的仍然是这五个数.这五个数的总和是.
三、填空题Ⅲ(每题12分,共60分)
12.如图,大正六边形的面积是24平方厘米,其中放了三个一样的小正六边形.阴
影面积是平方厘米.
13.甲、乙、丙三人同时同向骑车,各自的速度都保持不变,乙在甲、丙的正中
间.甲20分钟追上乙,又过10分钟追上丙。
再过分钟乙追上丙。
14.六位数2□012□个位上填时,万位上无论填入0~9中的哪一个数,
都不能被11整除.
15. 1 个4×4的棋盘,在每个小方格上染上黑白两色之
一,染法与国际象棋盘的染法相同.允许任意选择一个矩形(矩形的边都在格子线上),被选中的矩形中的每个小正方格改变颜色(黑变白,白变黑)。
至少需要次上述操作,才能使棋盘上的格子都同色.
16.将一个5×5×5的正方体分割成若干个3×3×3、
2×2×2和 1×1×1的小正方体.1×1×1的小
正方体最少有个.
四年级B卷-2。
