电工学第二章
电工学第2章

举例 在图中,已知直流发电机 的电动势E1=7V,内阻r1=0.2 Ω, 蓄电池组的电动势E2=6.2V,内 阻r2=0.2 Ω。负载电阻R3=3.2 Ω。 用节点电压法求各支路电流和 负载的端电压。
二、应用举例
解:负载两端的电压即为节点电压。
G1 1 1 5S r1 0.2 G2 1 1 5S r2 0.2 G3 1 1 5 S r3 3.2 16
i f u
2、非线性电阻电路的动态分析 动态分析内容:关注变化量 U S、 IQ、 UQ 动态分析工具:微变等效电路 i
+ _ us
R u
微变:(微小变化) 等效:(线性代替非线性)
i
rd
Q
在Q点附近的 电路模型
i u
u rd i
up
u
2.9 PSpice例题分析
I U
U R I
(常数)
一、非线性电阻的描述
非线性电阻: 电阻值随电压/电流的变化而变化。 非 线 性 特 性 I2 I1 I
U I
Q2
Q1 U1 U2 U
R
工作点不同 电阻不一样
Q1 : Q2 :
U1 R1 R2
I1 I2
U2
二、非线性电阻电路的电阻
1、静态电阻 2、动态电阻U R ຫໍສະໝຸດ tg Ib)有源二端网络
图4-10 二端网络的表示符号
二、无源线性二端网络的等效电阻
1. 任何一个无源线性二端网络,其端电压与端钮电 流间总是线性关系,它们的比值是一个常数。因 此,一个无源线性二端网络总可以用一个等效电 阻 Req 来代替,该等效电阻也称为网络的输入电
阻。
2.无源线性二端网络等效电阻Req的求解
电工学第二章
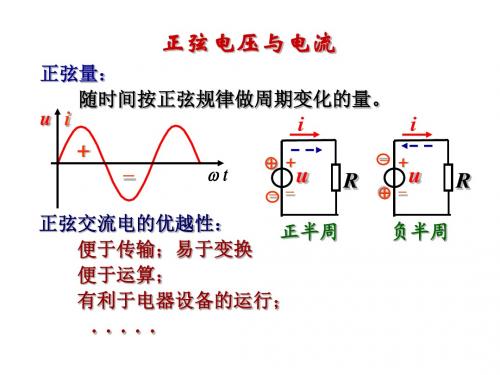
求:i i1 i2 。
i2 11 2 sin(314t 60 )A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A (16.5 - j3.18)A 16.8 10.9 A
有效值 I =16.8 A
则:
1 U I ωC
U I XC
直流: XC 交流:f
1 XC 2π f C
,电容C视为开路
XC
所以电容C具有隔直通交的作用
1 XC 2π fC
容抗XC是频率的函数 由: u
I , XC
XC
1 ωC
I U (2 π f C )
O f 2Usinω t i 2Uω C sin( ω t 90) U 0 可得相量式 U 超前 U 90 I I I I 90 jUω C
1 T
T
0
i 2 dt
注意: 交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
初相位与相位差
相位: t
ψ
i I sin( ω t ψ ) m i
ωt
反映正弦量变化的进程。 O 初相位: 表示正弦量在 t =0时的相角。
ψ (t ψ ) t 0
u i
90
(1) 频率相同 (2) I =UC ωt (3)电流超前电压90 相位差 ψ u ψ i 90
u 2Usinω t i 2Uω C sin( ω t 90)
有效值
I U ω C 或 1 1 定义: XC 容抗(Ω ) ωC 2 π f C
A a1 ja2 a cos ja sin ae
电子电工学 第二章知识点

Ia
a
Ia
a
Ra
Ib Ic
b
Rc Rb
c
Y-等效变换
Rab Ib Ic
b
Rbc
Rca
c
电阻Y形联结
电阻形联结
等效变换的条件:对应端流入或流出的电流(Ia、Ib、Ic)一一相等,对应端间的电 压(Uab、Ubc、Uca)也一一相等。经等效变换后,不影响其它部分的电压和电流。
Rab Rbc Rca Ra Rb Rb Rc Rc Ra Rc Ra Rb Rb Rc Rc Ra Ra Ra Rb Rb Rc Rc Ra Rb
二、 电阻的并联
I
+
I1
U
–
I2 R1 R 2
I
+ –
U
R
1 1 1 (3)等效电阻的倒数等于各电阻倒数之和; R R1 R2
(4)并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式:I R2 I 1 R1 R2 应用:分流、调节电流等。
I2
R1 I R1 R2
2.2 电阻星形与三角形联接的等效变换
齐性定理 只有一个电源作用的线性电路中,各支路的电压或电流和电源成正比。 若 E1 增加 n 倍,各电流也会增加 n 倍。
习题:
已知:E=120V,R1=2Ω,R2=20Ω, R3=2Ω,R4=20Ω,R5=2Ω, R6=20Ω。 求各支路电流。 设
1A I5
E 33 .02V
I5 I5
E 3.63 A E
习题:
–
+ US Uo -
线性无
IS 源网络
已知:US =1V、IS=1A 时, Uo=0V; US =10 V、IS=0A 时,Uo=1V 求:US = 0 V、IS=10A 时, Uo=? (–1V)
电工学第2章

1Ω Ω
I
I = 2 ×3 = 2A 2+1
2.3.3 电源两种模型之间的等效变换
[例题 在图中,一个理想电压源和一个理想电流源相连,试讨论 例题] 在图中,一个理想电压源和一个理想电流源相连, 例题 它们的工作状态( 和 均为正值) 它们的工作状态(U和I 均为正值) 。 I [解] (a) 电压源 电流从电压源的正端流出, 解 电流从电压源的正端流出, U和I的实际方向相反, 和 的实际方向相反, 的实际方向相反 处于电源状态; 处于电源状态; 电流从电流源的负端流出, 电流源 电流从电流源的负端流出, U和I的实际方向相同, 的实际方向相同, 和 的实际方向相同 处于负载状态; 处于负载状态; (b) 电压源 电流从电压源的负端流出, 电流从电压源的负端流出, U和I的实际方向相同, 的实际方向相同, 和 的实际方向相同 处于负载状态; 处于负载状态; 电流从电流源的正端流出, 电流源 电流从电流源的正端流出, U和I的实际方向相反, 的实际方向相反, 和 的实际方向相反 处于负载状态。 处于负载状态。
2.4 支路电流法
在图示电路中,结点数 在图示电路中,结点数n=2,支路数 ,支路数b=3,共要列出三个独立的 , 方程; 个独立的结点电流方程和2个 方程;根据基尔霍夫定律可以列出 1个独立的结点电流方程和 个 个独立的结点电流方程和 独立的回路电压方程。 独立的回路电压方程。
I1 + E1 R1 ① I3 b R3 a I2 R2 ② + E2 -
I + U I1 R1 I2 等效 + R2 U I R
G 称为电导,是电阻的倒数, 称为电导,是电阻的倒数, 电导 单位:西门子(S)。 单位:西门子 。
两个并联电阻上的电流分别为 2 1 I1 = U = RI = R I I2 = U = RI = R I R R R +R R R R +R 1 1 1 2 2 2 1 2 即并联电阻上电流的分配与电阻成反比。 即并联电阻上电流的分配与电阻成反比。
电工学第2章

返回
上一节
下一节
上一页
下一页
第 3 章
交 流 电 路
2.5 并联交流电路
KCL: I = I1 + I2
I= U + U Z2 Z1 1 1 )U U ( = Z I= Z + Z 1 2 Z = Z1∥Z2 其中:Z1= R1+ j XL
-
+
I
I1
R1
I2
R2
U
L C
Z1
Z2
并联交流电路
交 流 电 路
(2)功率关系
u,i i
a. 瞬时功率:
u
ωt
p = U I sin2ωt
o
+
i
p o
u -
u -
+
i
u
+
i
u
+
i
+ p <0
p >0
+ p <0
p >0
ωt
充电 放电 充电 放电
第 3 章
交 流 电 路
b.平均功率(有功功率): P = 0 c.无功功率: Q = U I = XC I 2 U2 = XC
Z2= R2- j XC
返回
上一节
下一节
上一页
下一页
第 3 章
交 流 电 路
2.6 交流电路的功率
一、瞬时功率
i = Imsinωt u = Umsin(ωt + ) p = u i = UmImsin(ωt + ) sinωt = U I cos + U I cos (2ωt + ) :电压超前电流的角度
电工学原理第二章

2.1.2 电阻的并联
I + I1 U – I + U – R I2 特点: (1)各电阻联接在两个公共的结点之间; (2)各电阻两端的电压相同;
R1 R2 (3)等效电阻的倒数等于各电阻倒数之和; 1 1 1 R R1 R2 (4)并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式:
据此可推出两者的关系
2.3 电压源与电流源及其等效变换
2.3.1 电压源
如果一个二端元件的电流无论为何值,其电压保持常
量US或按给定的时间函数uS(t)变化,则此二端元件称为独
立电压源,简称为电压源。电压源的符号如图(a)所示,图 中“+” , “-”号表示电压源电压的参考极性。
电压保持常量的电压源,称为恒定电压
Ia a Ra Rc
C
Ia 等效变换 Ib Ic b
a Rab RbcRca
Ib
Ic b
Rb
C
电阻Y形联结
电阻形联结
条 Ra Rb Rab //( Rca Rba )
Rb Rc Rbc //( Rab Rba ) 件 Ra Rc Rca //( Rab Rbc )
独立电流源的电压则与其连接的外电路有关。 由其电流和外电路共同确定。
例如图示电路中电阻值变化时,电流源的电压 u 和发 出功率 p 会发生变化。
R/ u/V P /W
1 2 4
2 4 8
10 20 40
20 40 80
100 200 400
0 0 0
例l-6
电路如图所示。已知uS1=10V, iS1=1A, iS2=3A,
压源实际发出功率。
P<0
也就是说,随着电压源工作状态的不同,它既
电工学B2

T
2π ω = = 2πf T
O –Im
π π 2π ω t T/2 T t T
[例 1]我国和大多数国家的电力标准频率是 50Hz, ] , 试求其周期和角频率。 试求其周期和角频率。 [解] π ω = 2π f =2 × 3.14 × 50 = 314 rad/s
1 T = = 0.02 s f
O
ωt
O
ωt
ψ
称为正弦量的相位角或相位 相位角或相位。 ω t 和(ω t + ψ)称为正弦量的相位角或相位。它表 明正弦量的进程。 明正弦量的进程。 • t = 0 时的相位角称为初相位角或初相位。 时的相位角称为初相位角或初相位 初相位角或初相位。 若所取计时时刻不同,则正弦量初相位不同 初相位不同。 若所取计时时刻不同,则正弦量初相位不同。
电工学 第二章
2.2
正弦量的相量表示法
u
正弦量具有幅值、 正弦量具有幅值、频率和 初相位三个要素, 初相位三个要素,它们可用三 角函数式和正弦波形来表示。 角函数式和正弦波形来表示。 瞬时值表达式 O
ωt
u = U m sin( ω t + ψ )
此外,还可以用相量来表示。 此外,还可以用相量来表示。 相量来表示
内蒙古工业大学 电工电子教学中心
第 2 章
正弦交流电路
本章主要介绍交流电路的一些基本概念、基本 本章主要介绍交流电路的一些基本概念、 理论和基本分析方法,为后面学习交流电机、 理论和基本分析方法,为后面学习交流电机、电器 及电子技术打下基础。 及电子技术打下基础。 本章还将讨论三相交流电路和非正弦周期电压 和电流。 和电流。
2.1.3 初相位 u i
电工学 第二章
电工学第二章

4.电容器的主要参数
(1)标称电容量 电容器的外壳上标出的电容量值称为标称电容量。
(2)允许偏差 电容器的允许偏差常用的有±2%、±5%、±10%、
用介电常数较大的物质作为电容器的电介质 可显著增大电容,而且能做成很小的极板间隔,因 而应用很广。
任何两个导体之间都存在着电容。
3. 电容器的充电和放电
(1)电容器的充电 当开关S置于A端,电源E通过电阻R 对电容器C开始充电。起初,充电电流 较大,但随着电容器C 两端电荷的不断积累,形成的电压 越来越高,它阻碍了电源 对电容器的充电,使充电电流越来越小,当电容器两端电压 达到了最大值E时,则不再变化,电流为零。故在直流稳态电 路中,电容相当于开路,这就是电容的隔直作用。
检测电感器
电感器的直流电阻很小,通常只有几欧或 几十欧,线径越细,圈数越多,电阻值越大。 一般情况下用万用表R×1电阻挡测量,只要能 测出电阻值,即可认为电感器是正常的;如果 测量结果为无穷大,说明电感器已经开路。
§2-3纯电阻、纯电感、纯电容交流电路
一、纯电阻交流电路
交流电路中如果只考虑电阻的作用,这种电 路称为纯电阻电路。
电容量也简称电容。
它只与电容器的极板正对面积、极板间距离 以及极板间电介质的特性有关;而与外加电压的 大小,电容器带电多少等外部条件无关。
C S
d
式中S、d、C的单位分别是m2、m、F,介电常 数ε的单位是F/m。
真空中的介电常数ε0≈8.86×10-12F/m ,某种介 质的介电常数ε与ε0之比,称该介质的相对介电常 数,用εr表示 。
电工学 第二章正弦交流电路

(1-2)
. 一、正弦量的三要素
二、同频率正弦量的相位差
三、正弦量的有效值
(1-3)
一、正弦量的三要素
i = Im sin (wt + j ) i
Im
j
wt Im:电流幅值(最大值)
三要素
w: 角频率(弧度/秒)
.
U Z = I
j = j u - ji
结论:Z的模为电路总电压和总电流有效值之比, 而Z的幅角则为总电压和总电流的相位差。
(1-46)
Z 和电路性质的关系
Z = R+ j (XL- XC )
阻抗角
j = ju- ji = arctg
(1-39)
以电流为 参考量时
正 误 判 断
在电阻电路中:
瞬时值
有效值
U I= R
?
U i= R
?
u ? i = R
(1-40)
正 误 判 断
在电感电路中:
u i= XL
?
U I= ωL
u i= ωL
?
?
& U = XL & I
U = jω L I
?
?
(1-41)
第四节
RLC串、并联电路及功率因数的提高 一、RLC串联的正弦交流电路
& I U=&R
& I & U
(1-25)
相量图
总结功率关系
因为:
i= Im sinwt u =Ri=R Im sinwt p=u·=R·2=u2/R i i
小写,瞬时值功率
所以:
i
u
wt
华东理工大学电工学第二章习题答案

第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征,特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数(R ,L ,C )的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值(U m ,E m ,I m )、瞬时值(u, e, i )、有效值(U ,E ,I )。
注:有效值与幅值的关系为:有效值2幅值=。
(2) 频率(f )、角频率(ω)、周期(T )。
注:三者的关系是 Tf ππω22==。
(3) 相位(ϕω+t )、初相角(ϕ)、相位差(21ϕϕ-)。
注:相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法:。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法:例如u 的波形如图2-1-1(a)所示。
(3) 相量(图)表示法:使相量的长度等于正弦量的幅值(或有效值); 使相量和横轴正方向的夹角等于正弦量的初相角; 使相量旋转的角速度等于正弦量的角速度。
注:例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解:因为同频率同性质的正弦量相加后仍为正弦量,故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1:相量图法求解如下:具体步骤为三步法(如图2-1-2所示):第一步:画出正弦量u 1、u 2的相量12U U 、(U 1=6,U 2=4)。
第二步:在相量图上进行相量的加法,得到一个新相量U。
电工学_02

不等效
§2.3 电源的两种模型及其等效变换
例2 如图所示电路中,一个理想电压源和一个理想电流源 相连,讨论它们的工作状态。
解:(a)电流从电压源 的正端流出(U和I的实 际方向相反),流进电 流源(U和I的实际方向 相同),故电压源处于 电源状态,电流源处于 负载状态。
(b)电流从电流源流出(U和I的实际方向相反),流进电流源的
§2.3 电源的两种模型及其等效变换
二.电流源
IS RS I + U _
RL
由Is和Rs组成,电流源伏安特性 Is=U/Rs+I 或 U=ISRS-IRS Rs=时,I=Is,理想电流源,称为恒流源; Rs0时, Rs分流, 输出电流减小,实际电流源Rs 越大越好; RL=0,U=0,短路,空载; RL= ,开路,U极大,不允许; 非独立电源。
则并联时 G Gi
i
分流比
§2.1 电阻串并联连接的等效变换
例1 计算图中所示电路中a、b间的等效电阻Rab。
(a) 解:
(b)
(a): Rab (8 // 8) (6 // 3) 0 6
(b): Rab [(4 // 4) (10 // 10)]// 7 3.5
R1 I3 ' R3 + R2 _ E1 B E1单独作用
§2.3 电源的两种模型及其等效变换
电压源与电阻串并联 I + R + E _ U R0 _ 电流源与电阻串并联 I + IS RS R U _ I + R U _
E R0
+ _
R
IS RS
I + U _
§2.3 电源的两种模型及其等效变换
电工学第2章正弦交流电路PPT课件

p=ui=Um sin(ωt+90°) Imsinωt
=UmIm cosωtsinωt =UIsin2ωt
电感元件的功率波形
上式表明, 电感元件的瞬时功率是一个幅值为UI 并以2ω的角频率随时间而变化的正弦量。瞬时功率 的变化曲线如右图所示。
26
当p>0时,表明电感元件吸收能量并作负载 使用,即将电能转换成磁场能量储存起来;
1. 相位角(或相位)——(ωt +ψi) 2. 初相位——t=0时的相位角,即ωt +ψi|t=0=ψi
初相位不同,正弦波的起始点不同,如下图所 示。
(a)ψi=0
(b)ψi>0
(c)ψi<0
由于正弦量是周期性变化量,其值经2π后又重复,所
以一般取主值,| ψi |≤π。
8
2.1.3 初相位
在一个正弦交流电路中, 电压u和电流i的频率是相同的, 但初相位却可以不同。设:
19
在电阻元件的交流电路中,电压u与电流i 相 位相同、频率相同。其波形图、相量图如下所示:
根据 i=Imsinωt ;u=iR=ImRsinωt
可知电压幅值: Um=Im R;
U=I R
如果用相量来表 示电压与电流的
•
•
U
•
Um
•
R
或
••
U IR
关系,则有: I I m
20
瞬时功率:p=ui= Umsinωt Imsinωt=UmImsin²ωt
③指数形式可改写为极坐标形式:
A=r
三种复数式可以互相转换。复数的加减运 算可用直角坐标式;复数的乘除运算用指数形 式或极坐标形式则比较方便。
13
e e 例如: 设A1= a1+jb1 =r1 j 1 ;A2= a2+jb2 =r2 j 2
电工学第2章习题及答案
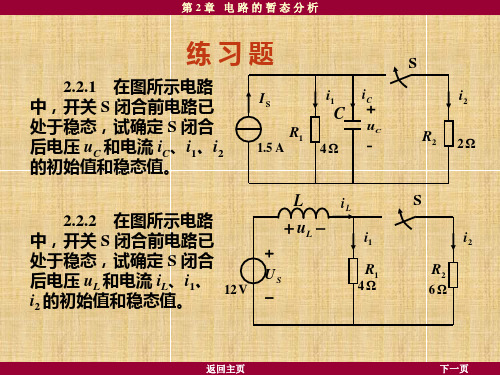
2.4.1 图所示电路原 已稳定。在 t = 0 时将开关 S 从 a 端换接到 b 端。试 求换路后的响应 iL 和 uL。24 V
2Ω
US
R2
6Ω
uL
iL L
1H
返 回
第2章 电路的暂态分析
2.4.2 图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL,并画出 其变化曲线。
i1
S
IS
R1
24 A
i2
1.5 Ω 3Ω
7Ω
R3
R2
iL L uL 0.4 H
a
S
b
R1
3Ω
2.4.3 图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL,并说明是什么 响应。
U S1
6V
US2
6V 6Ω
3Ω
R3
iL L
R2 6 i1 (0) i L ( 0) 3 A 1.8 A R1 R2 46 R1 4 i 2 ( 0) i L ( 0) 3 A 1.2 A R1 R2 46
返 回练习题题集 下一页 上一题 下一题
U S 12 uL (0) A 3A R1 4
返 回练习题题集 上一页 上一题 下一题
第2章 电路的暂态分析
2.3.3 图所示电路原已稳定,求开关 S 闭合后的响应 uC 和 i1、 i2 ,并画出其变化曲线。
S
R1
i1
20 V
4kΩ
R3 iC
R2
1.6kΩ
US
uC
iC
C 2.5F
6kΩ
电工学第2章

uC C S
uR -
R iR
L
iL
uL
iC C
uC
uR -
R iR
返回
上一节
下一节
上一页
IS
IS
下一页
第2章 电路的暂态分析
2.3 RC 电路旳暂态分析
(一) RC 电路旳零输入响应
t = 0 时换路
aS
R
b
iC
换路前,S 合在 a 端 U0
uC
C
uC(0) = U0
换路后,S 合在 b 端
L2
L L1 L2
电感并联:
i
u
L1 L2
11 1
L L1 L2
返回
上一节
下一节
上一页
下一页
第2章 电路的暂态分析
(三)换路定理
电容电压、电感电流在换路瞬间不能突变。
设:t =0 时换路 t 0 --- 换路前瞬间
t 0 --- 换路后瞬间
则:
uC (0 ) uC (0 )
注意:
iL (0 ) iL (0 )
[解] (1) 求初始值
根据换路定律,由换路
前( S 闭合时)旳电路求
得
uC (0)
iL (0)
US R
0
5 5
A
US
1A
返回
上一节
L iL
uL iC
IS
uC C
S
uR -
R iR
图 2.2.4 例2.2.1 旳电路
L
iL
uL
iC C
IS
uC
S
uR -
R
下一节
iR
上一页
电工学第二章

安阳鑫龙煤业(集团)技工学校教案(内页)授课章节教学目的第二章磁与电磁的基本知识第一节电流的磁场及其基本物理量1、了解直线电流、环形电流所产生的磁场,会用安培定则(右手定则)判断磁场的方向。
2、理解磁感应强度、磁通和磁导率的概念。
教学重点电磁感应、安培定则重点与难点教学难点磁场的主要物理量教学方法讲授法、讲练结合教学手段教学内容学时数教学过程时间分配复习提问组织教学教学过程设计引入新课讲授新课课堂小结布置作业实验思考题及作业题教后感安阳鑫龙煤业(集团)技工学校教案(附页)教学内容教法提示及备注第一节电流的磁场及其基本物理量一、电流的磁场实验表明,产生磁场的根本原因是电流。
磁的几个基本概念1、磁性:能够吸引铁、镍、钴及其合金的性质。
2、磁体:具有磁性的物体,也称磁铁。
3、磁极:磁体两端磁性最强的部分。
任何磁体都具有两个磁极,分别是北极(N)和南极( S)。
4、磁极间的相互作用力:同性磁极相互排斥,异性磁极相互吸引。
5、磁场:磁体周围空间中存在着的一种特殊物质。
磁极间的作用力就是通过磁场传递的。
6、磁感线:为了形象地描述磁场分布而画出的一些有方向的曲线。
7、磁感线的 3 个特点:①磁感线是互不交叉的闭合曲线;在磁体外部由 N极指向 S 极,在磁体内部由S 极指向 N极。
②磁感线上任一点的切线方向,就是该点的磁场方向。
第页安阳鑫龙煤业(集团)技工学校教案(附页)教学内容教法提示及备注③磁感线越密,磁场越强;磁感线越疏,磁场越弱。
通电导体周围产生磁场的现象称为电流的磁效应。
其磁场方向用右手螺旋定则(安培定则)来判断。
1、直线电流产生的磁场方向:用右手握住导线,让伸直的大拇指指向电流方向,则四指弯曲的方向就是磁感线的环绕方向。
2、环形电流(螺线管)产生的磁场方向:右手握住通电螺线管,让弯曲的四指指向电流方向,则大拇指所指的方向就是磁场的北极方向。
二、磁场的基本物理量1、磁感应强度( B)在磁场中,垂直于磁场方向的通电导线,所受电磁力 F 与电流 I 和导线长度 L 的乘积 IL 的比值称为该处的磁感应强度,用 B 表示,即 B=F/IL 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
–
U m U m0 RI m 0 R I m
电压电流同频率,同相位;数量关系满足欧姆定律; 复阻抗:无源二端元件上电压相量与电流相量之比
Z Um Im
U m u Um ( u i ) Z I m i Im
i I m sin t
u
t
有功功率
p + + – –
0
t
无功功率:瞬时功率的最大值
2 UC QC U C I I 2 X C XC
(var)
电容不消耗功率,它是储能元件。
[例]有一只47µF耐压值220V的电容器,将它接到50Hz电压有 效值110V 的交流电源上,电路电流和无功功率各是多少?;若电 压值不变,电源频率为 1000Hz ,此时电流为多少?能否直接接到 220V的交流电源上?
[解] I 1m 80 A
I 2m 690 A j 6 A
I m I 1m I 2 m 8 j 6 1036.9 A
总电流的瞬时值为: i 10sin(314t 36.9) A 相量图为:
P.59(2.1.1)
I 2m
Im
36.9°
2.1 正弦交流电的基本概念
直流电路在稳定状态下电流、电压的 大小和方向是不随时间变化的,如右上图 所示。 U/I
正弦电压和电流是按正弦规律周期性 变化的,其波形如右下图所示。
i + u – i + u –
O u i
+ O
t
R
R
t
正半周
负半周
1.正弦电量的三要素
u U m sin(t u ) e Em sin(t e ) i I m sin(t i )
u i
同相: 0
180 反相:
u 0
i
i
i
超前、滞后
t
注意
i ,u , e
2.正弦电量的相量表示
正弦量具有幅值、频率和初相位三个要素,它们除用三角 函数式和正弦波形表示外,还可以用相量来表示。 正弦量的相量表示法就是用复数来表示正弦量。 设平面有一复数 A +j 模 A
Im 2 0.707I m
T
0
i 2 dt
1 T
T
0
( I m sin(t i ))2 dt
周期 T:正弦量变化一周所需要的时间; 频率 f:正弦量每秒内变化的次数; 角频率 :
2 2f T
1 f T
[例]我国和大多数国家的电力标准频率是 50 Hz,试求其 周期和角频率。
2 2
j arctan
–
C U
–
Z e j
阻抗模 Z R2 ( X L X C )2 R 2 ( L
阻抗角 arct an
XL XC R
1 2 ) C
设电流 i = Imsint 为参考正弦量 则电压 u = Umsin( t + ) 当 XL > XC , 为正,电路中电压超前电流,电路呈电感性;
感抗
X L L 2fL 2 3.14 50 0.4 126
U L 220 1.75 A X L 126
电流有效值 I
无功功率 QL U L I L 220 1.75 var 385 var
线圈直接接到直流电源上,由于频率为零,相当于短 路元件。 P.63(2.2.1)
2.2 单一元件正弦交流电路
1.电阻元件
设在电阻元件的交流电路中,电压、电流参考方向如图所示。
i + u R
根据欧姆定律 设
u iR i I m sin t
I m I m0
U m U m0
u Ri RIm sin t U m sin t
U m RI m
u U m sin(t 90)
U m U m 90 X L I m 90
U m 90 Um 90 jX L I m 0 Im
u
波 形 图
+j
i
U 相量图
•
O
t
O
I
•
+1
电压超前电流 90; 电压与电流大小关系 电压与电流相量式
U IX L
当 XL < XC , 为负,则电压滞后电流,电路呈电容性; 当 XL = XC , = 0,则电流与电压同相,电路呈电阻性。 的大小和正负由 • • UL • UL 电路参数决定。 U
P=UI O
t
2.电感元件的正弦交流电路
设在电感元件的交流电路中,电压、电流取关联参考方向。
i
设
L
+ u
– XL
由
i I m sin t di uL 得 dt
u LI m cost U m sin(90 t ) U m sin(180 (90 t )) U m sin(t 90)
u U m sin t
i CU m cost I m sin(t 90)
i
瞬时功率 p ui
波 形 U m I m sin t sin(t 90) 图 2UI sin t cost O UI sin 2t
1 T P pdt T 0 1 T UI sin 2tdt T 0 0
I 1m
正弦电量 (时间函数)
变换 相 量 结 果
相量 (复数)
所求 正弦量
反变换
相量 运算 (复数运算)
注意
只有正弦周期量才能用相量表示; 只有同频率的正弦量才能画在同一相量图上; 相量是表示正弦交流电的复数,正弦交流电是 时间的函数,两者之间并不相等。 为什么还用相量表示?
复数在进行加减运算时应采用代数式,实部与实部相加减, 虚部与虚部相加减。 复数进行乘除运算时应采用指数式或极坐标式,模与模相 乘除,辐角与辐角相加减。
[解]电源频率为50Hz,所以有
容抗 XC 1 1 1 68 6 C 2fC 2 2.34 50 47 10
电流有效值 I
U C 110 1.62 A XC 68
QC U C I 1101.62 var 178 var
电源频率为1000Hz时,
P.65(2.2.2)
作业:(P.104) 1、 2、3
2.3 正弦交流电路的分析
1.RLC串联的交流电路
i
在 R、L、C 串联交流电路中,电流电压参考方向如图所示。
+ + uR – + u u L – + u – C –
R L C
KVL相量表示式为 U U U U R L C
容抗
XC
1 1 C 2fC
容抗与频率 f,电容 C 成反比。因 此,电容元件对高频电流所呈现的容抗 很小,而对直流所呈现的容抗趋于无穷 大,故可视为开路。
u U m sin t
U m U m 0
ZC Um Im
i CU m cost I m sin(t 90)
u Ri RIm sin t U m sin t
p ui U m I m sin 2 t 2UI sin 2 t UI (1 cos2t )
u
平均功率是指瞬时功率在一个 周期内的平均值
O p i
t
1 T P pdt T 0 1 T UI (1 cos 2t )dt T 0 2 U UI RI 2 R
a r cos
r a b
2 2
b
b r sin
b arctan a
r
O
辐角
a
+1
复数 A 可有几种式子表示 A = a + jb 代数式 三角式 指数式 极坐标式
比照复数和正弦量,正弦量可用复数来表示。复数的模即 为正弦量的幅值或有效值,复数的辐角即为正弦量的初相位角。 为与复数相区别,把表示正弦量的复数称为相量。并在大 写字母上打一“•”。
U jIXL
i I m sin t
u U m sin(t 90)
瞬时功率
p ui U m I m sin t sin(t 90) 2UI sin t cost UI sin 2t
波 形 图
u
i
有功功率
1 T P pdt T 0 1 T UI sin 2tdt T 0 0
u U m sin(t u )
的相量式为
U m U m (cos j sin ) U m e j U m
U U (cos j sin ) Ue j U
[例]已知 i1 8 sin 314tA , i2 6 sin( 314t 90) A 。试写出电 流幅值的相量式;求 i i1 i2 ;画出向量图。
[解]
= 2f = 2 3.14 50 rad/s = 314 rad/s
1 T 0.02 s f
t i 称为正弦量的相位角或相位。它表明交流电流变化 的进程。
t = 0 时的相位角称为初相位角或初相位。 同频率正弦量的相位之差或初相角之差,称为相位差,用 表示。即 (t 1 ) (t 2 ) 1 2
第 2章
正弦交流电路
• 本章将介绍交流电路的一些基本概念、基 本理论和基本分析方法,为后面学习交流 电机、电器及电子技术打下基础。 • 本章还将讨论三相交流电路和非正弦周期 电压和电流。
