2015-2016学年山西省忻州市第一中学高一下学期期末考试数学(文)试题
山西省忻州市高一下学期数学期末考试试卷

山西省忻州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2020·湖南模拟) 已知集合,集合,若只有4个子集,则的取值范围是()A .B .C .D .2. (2分) (2019高一下·梅县期末) ()A . 0B .C .D . 13. (2分) (2019高一上·新余月考) 已知定义在上的函数,若函数为偶函数,且对任意,,都有,若,则实数a的取值范围是()A .B .C .D .4. (2分) (2019高一下·安徽期中) 在△ABC中,若b=2,A=120°,三角形的面积,则三角形外接圆的半径为()A .B .C . 2D . 45. (2分)某学校高三年级一班共有60名学生,现采用系统抽样的方法从中抽取6名学生做“早餐与健康”的调查,为此将学生编号为1、2、…、60,选取的这6名学生的编号可能是()A . 1,2,3,4,5,6B . 6,16,26,36,46,56C . 1,2,4,8,16,32D . 3,9,13 ,27,36,546. (2分)若圆C1:x2+y2=1与圆C2:x2+y2﹣6x﹣8y+m=0外切,则m=()A . 21B . 19C . 9D . -117. (2分)按流程图的程序计算,若开始输入的值为,则输出的的值是()A . 6B . 21C . 156D . 2318. (2分) (2016高一下·内江期末) =()A . ﹣B . ﹣C .D .9. (2分) (2018高一下·黑龙江期末) 三棱锥中,为等边三角形,,,三棱锥的外接球的表面积为A .B .C .D .10. (2分)已知直线x=和x=是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)图象的两条相邻的对称轴,则φ的值为()A .B .C .D .11. (2分) (2019高二上·信丰月考) 某景区在开放时间内,每个整点时会有一趟观光车从景区入口发车,某人上午到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为()A .B .C .D .12. (2分)若方程的根在区间上,则k的值为()A . -1B . 1C . -1或2D . -1或1二、填空题 (共4题;共4分)13. (1分) (2019高一下·佛山期末) 若等比数列的各项均为正数,且,则等于________.14. (1分) (2018高二上·灌南月考) 空间四边形,,,则的值为________.15. (1分) (2019高三上·安顺月考) 三个同学重新随机调换座位,则恰有一个坐在自己原来的位置上的概率为________.16. (1分) (2019高二下·金山月考) 已知圆柱的底面圆的半径与球的半径相同,若圆柱与球的体积相等,则它们的表面积之比 ________.(用数值作答)三、解答题 (共6题;共50分)17. (10分) (2017高一上·安庆期末) 已知函数f(x)=sin(ωx+φ)的最小正周期为π,(1)求当f(x)为偶函数时φ的值;(2)若f(x)的图象过点(,),求f(x)的单调递增区间.18. (10分) (2017高一下·新余期末) 设关于x的一元二次方程x2+ax﹣ +1=0.(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程中有实根的概率;(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.19. (10分) (2019高二上·鸡泽月考) 如图,在四棱锥中,底面是平行四边形,,,为的中点,平面且,为的中点.(1)证明:平面;(2)求直线与平面所成角的正弦值.20. (5分)(2017·山东模拟) 已知向量 =(sin(π+ωx),2cosωx), =(2 sin(+ωx),cosωx),(ω>0),函数f(x)= • ,其图象上相邻的两个最低点之间的距离为π.(Ⅰ)求函数f(x)的对称中心;(Ⅱ)在锐角△ABC中,角A、B、C的对边分别为a、b、c,tanB= ,求f(A)的取值范围.21. (10分) (2016高二上·福州期中) 如图,平面四边形ABCD中,AB= ,AD=2 ,CD= ,∠CBD=30°,∠BCD=120°.(1)求BD的长;(2)求∠ADC的度数.22. (5分) (2016高二上·德州期中) 已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y﹣29=0相切.(Ⅰ)求圆的方程;(Ⅱ)设直线ax﹣y+5=0(a>0)与圆相交于A,B两点,求实数a的取值范围;(Ⅲ)在(Ⅱ)的条件下,是否存在实数a,使得弦AB的垂直平分线l过点P(﹣2,4),若存在,求出实数a 的值;若不存在,请说明理由.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共50分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、考点:解析:。
2015-2016年山西省忻州一中高一下学期数学期末试卷及参考答案(文科)

2015-2016学年山西省忻州一中高一(下)期末数学试卷(文科)一.选择题(本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)满足条件a=4,b=5,A=45°的△ABC的个数是()A.1 B.2 C.无数个D.不存在2.(5分)已知数列{a n}满足a1=1,a n+1=a n+2n,则a10=()A.1024 B.1023 C.2048 D.20473.(5分)若0<a<1,则不等式(x﹣a)(x﹣)>0的解集是()A.{x|a<x<}B.{x|<x<a}C.{x|x<a或x>}D.{x|x<或x >a}4.(5分)在△ABC中,sin2A≤sin2B+sin2C﹣sinBsinC,则A的取值范围是()A.(0,]B.[,π)C.(0,]D.[,π)5.(5分)在数列{a n}中,a n=﹣2n2+29n+3,则此数列最大项的值是()A.102 B. C. D.1086.(5分)在△ABC中,角A、B、C所对的边分别为a、b、c,且b2+c2=a2+bc.若sin B•sin C=sin2A,则△ABC的形状是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形7.(5分)设a=cos6°﹣sin6°,b=2sin13°cos13°,c=,则有()A.a>b>c B.a<b<c C.b<c<a D.a<c<b8.(5分)△ABC的三内角A,B,C所对边的长分别为a,b,c.设向量=(a+c,b),=(b﹣a,c﹣a),若向量∥,则角C的大小是()A.B.C.D.9.(5分)已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.设,,则()A.a<b<c B.b<a<c C.c<b<a D.c<a<b10.(5分)数列{a n}中,若S n=3n+m﹣5,数列{a n}是等比数列,则m=()A.2 B.1 C.﹣1 D.411.(5分)在区间[0,π]上随机取一个数x,则事件“sinx≥|cosx|”发生的概率为()A.B.C.D.112.(5分)设函数f(x)的定义域为R,周期为2,f(x)=,若在区间[﹣1,3]上函数g(x)=f(x)﹣mx﹣m恰有四个不同零点,则实数m 的取值范围是()A.[0,]B.[0,)C.(0,]D.(0,]二.填空题:(本大题共4小题,每小题5分,共20分)13.(5分)函数f(x)=sin2(2x﹣)的最小正周期是.14.(5分)设a>﹣38,P=﹣,Q=﹣,则P与Q的大小关系为.15.(5分)数列{a n}中,a1=1,对于所有n≥2,n∈N,都有,则a3+a5=.16.(5分)给出下列结论:①2ab是a2+b2的最小值;②设a>0,b>0,2的最大值是a+b;③+的最小值是2;④若x>0,则cosx+≥2=2;⑤若a>b>0,>>.其中正确结论的编号是.(写出所有正确的编号)三.解答题:(本大题共6小题,共70分)17.(10分)已知,求的取值范围.18.(12分)为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;(2)求频率分布表格中a,b的值,并估计800学生的平均成绩;(3)若成绩在85~95分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?19.(12分)(文科)已知{a n}是单调递增的等差数列,首项a1=3,前n项和为S n,数列{b n}是等比数列,首项b1=1,且a2b2=12,S3+b2=20.(Ⅰ)求{a n}和{b n}的通项公式.(Ⅱ)令C n=nb n(n∈N+),求{c n}的前n项和T n.20.(12分)在△ABC 中,角A、B、C所对的边分别为a、b、c,且cosA=.①求的值.②若,求△ABC的面积S的最大值.21.(12分)已知向量=(2,2),向量与向量的夹角为,且=﹣2,(1)求向量;(2)若=(1,0)且,=(cosA,2cos),其中A、C是△ABC的内角,若三角形的三内角A、B、C依次成等差数列,试求||的取值范围.22.(12分)已知二次函数f(x)满足f(x+1)﹣f(x)=2x﹣1,且f(0)=3.(1)求函数f(x)的解析式;(2)若函数y=f(log3x+m),x∈[,3]的最小值为3,求实数m的值.四.附加题:(本题每题5分,共15分)23.已知x>0,y>0,且2x+8y﹣xy=0,则x+y的最小值为.24.数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,则{a n}的前60项和为.25.已知函数f(x)=|x2﹣4x+3|,若关于x的方程f(x)﹣a=x至少有三个不相等的实数根,则实数a的取值范围是.2015-2016学年山西省忻州一中高一(下)期末数学试卷(文科)参考答案与试题解析一.选择题(本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)满足条件a=4,b=5,A=45°的△ABC的个数是()A.1 B.2 C.无数个D.不存在【解答】解:∵a=4,b=5,A=45°,∴由正弦定理可得:sinB===>1,不成立.故选:D.2.(5分)已知数列{a n}满足a1=1,a n+1=a n+2n,则a10=()A.1024 B.1023 C.2048 D.2047【解答】解:∵数列{a n}满足a1=1,a n+1=a n+2n,∴a n=a1+(a2﹣a1)+…+(a n﹣a n﹣1)=1+21+22+…+2n﹣1==2n﹣1.(n∈N*).∴a10=210﹣1=1023.故选:B.3.(5分)若0<a<1,则不等式(x﹣a)(x﹣)>0的解集是()A.{x|a<x<}B.{x|<x<a}C.{x|x<a或x>}D.{x|x<或x >a}【解答】解:∵0<a<1,∴a<,而是开口向上的二次函数,大于零的解集在两根之外∴的解集为{x|}故选:C.4.(5分)在△ABC中,sin2A≤sin2B+sin2C﹣sinBsinC,则A的取值范围是()A.(0,]B.[,π)C.(0,]D.[,π)【解答】解:由正弦定理可知a=2RsinA,b=2RsinB,c=2RsinC,∵sin2A≤sin2B+sin2C﹣sinBsinC,∴a2≤b2+c2﹣bc,∴bc≤b2+c2﹣a2∴cosA=≥∴A≤∵A>0∴A的取值范围是(0,]故选:C.5.(5分)在数列{a n}中,a n=﹣2n2+29n+3,则此数列最大项的值是()A.102 B. C. D.108【解答】解:a n=﹣2n2+29n+3对应的抛物线开口向下,对称轴为n=﹣==7,∵n是整数,∴当n=7时,数列取得最大值,此时最大项的值为a7=﹣2×72+29×7+3=108,故选:D.6.(5分)在△ABC中,角A、B、C所对的边分别为a、b、c,且b2+c2=a2+bc.若sin B•sin C=sin2A,则△ABC的形状是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形【解答】解:在△ABC中,∵b2+c2=a2+bc,∴cosA===,∵A∈(0,π),∴.∵sin B•sin C=sin2A,∴bc=a2,代入b2+c2=a2+bc,∴(b﹣c)2=0,解得b=c.∴△ABC的形状是等边三角形.故选:C.7.(5分)设a=cos6°﹣sin6°,b=2sin13°cos13°,c=,则有()A.a>b>c B.a<b<c C.b<c<a D.a<c<b【解答】解:化简可得a=cos6°﹣sin6°=sin(30°﹣6°)=sin24°;b=2sin13°cos13°=sin26°;c===sin25°,由三角函数的单调性可知a<c<b故选:D.8.(5分)△ABC的三内角A,B,C所对边的长分别为a,b,c.设向量=(a+c,b),=(b﹣a,c﹣a),若向量∥,则角C的大小是()A.B.C.D.【解答】解:∵∴(a+c)(c﹣a)=b(b﹣a)∴b2+a2﹣c2=ab2cosC=1∴C=故选:B.9.(5分)已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.设,,则()A.a<b<c B.b<a<c C.c<b<a D.c<a<b【解答】解:已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.则=﹣lg>0,=﹣lg>0,=lg<0,又lg>lg∴0<﹣lg<﹣lg∴c<a<b,故选:D.10.(5分)数列{a n}中,若S n=3n+m﹣5,数列{a n}是等比数列,则m=()A.2 B.1 C.﹣1 D.4【解答】解:∵S n=3n+m﹣5,∴a1=S1=m﹣2,a1+a2=4+m,a1+a2+a3=22+m,联立解得:a1=m﹣2,a2=6,a3=18.∵数列{a n}是等比数列,∴62=18(m﹣2),解得m=4.故选:D.11.(5分)在区间[0,π]上随机取一个数x,则事件“sinx≥|cosx|”发生的概率为()A.B.C.D.1【解答】解:∵sinx≥|cosx|,x∈[0,π],∴≤x≤,长度为∵区间[0,π]的长度为π,∴事件“sinx≥|cosx|”发生的概率为=故选:B.12.(5分)设函数f(x)的定义域为R,周期为2,f(x)=,若在区间[﹣1,3]上函数g(x)=f(x)﹣mx﹣m恰有四个不同零点,则实数m 的取值范围是()A.[0,]B.[0,)C.(0,]D.(0,]【解答】解:由g(x)=f(x)﹣mx﹣m=0得f(x)=mx+m,设g(x)=mx+m=m(x+1),则g(x)过定点(﹣1,0),作出函数f(x)和g(x)的图象如图:若g(x)=f(x)﹣mx﹣m有四个不同零点,则等价为f(x)与g(x)有四个不同的交点,由图象可知当g(x)过点(3,1)时,满足条件,可得1=3m+m,则m=,∴在区间[﹣1,3]上函数g(x)=f(x)﹣mx﹣m恰有四个不同零点时,实数m 的取值范围是(0,]故选:D.二.填空题:(本大题共4小题,每小题5分,共20分)13.(5分)函数f(x)=sin2(2x﹣)的最小正周期是.【解答】解:f(x)=sin2(2x﹣)=根据三角函数的性质知T==故答案为:14.(5分)设a>﹣38,P=﹣,Q=﹣,则P与Q的大小关系为P<Q.【解答】解:∵a>﹣38,∴>,又P=﹣=,Q=﹣=,则P<Q.故答案为:P<Q.15.(5分)数列{a n}中,a1=1,对于所有n≥2,n∈N,都有,则a3+a5=.【解答】解:∵数列{a n}中,a1=1,对于所有n≥2,n∈N,都有,∴.∴.∴=,,∴a3+a5==.故答案为.16.(5分)给出下列结论:①2ab是a2+b2的最小值;②设a>0,b>0,2的最大值是a+b;③+的最小值是2;④若x>0,则cosx+≥2=2;⑤若a>b>0,>>.其中正确结论的编号是⑤.(写出所有正确的编号)【解答】解:①中当a=b时才有最小值2ab,故错误;②中当a=b时才有最大值,故错误;③中=时,x无解,故最小值是不是2,故错误;④中需cosx为正值时成立,故错误;⑤根据均值不等式可得不等式成立,故正确.故答案为⑤.三.解答题:(本大题共6小题,共70分)17.(10分)已知,求的取值范围.【解答】解:由已知可得,(*)令,解得,因此可得:由(*)可知:1≤a≤2,2≤b≤3,由此可得,即的取值范围是.18.(12分)为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;(2)求频率分布表格中a,b的值,并估计800学生的平均成绩;(3)若成绩在85~95分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?【解答】解:(1)样本间隔为800÷50=16,则第二组第一位学生的编号为016.(2)a=50×0.16=8;90~100的频数为50﹣8﹣10﹣18=14,则b==0.28,则平均成绩约为(65×8+75×10+85×18+95×14)=82.6(3)在被抽到的学生中获二等奖的人数9+7=16(人),占样本的比例是=0.32,即获二等奖的概率为32%,所以获二等奖的人数估计为800×32%=256(人).答:获二等奖的大约有256人.19.(12分)(文科)已知{a n}是单调递增的等差数列,首项a1=3,前n项和为S n,数列{b n}是等比数列,首项b1=1,且a2b2=12,S3+b2=20.(Ⅰ)求{a n}和{b n}的通项公式.(Ⅱ)令C n=nb n(n∈N+),求{c n}的前n项和T n.【解答】解:(Ⅰ)设公差为d,公比为q,则a2b2=(3+d)q=12①S3+b2=3a2+b2=3(3+d)+q=20②联立①②可得,(3d+7)(d﹣3)=0∵{a n}是单调递增的等差数列,d>0.则d=3,q=2,∴a n=3+(n﹣1)×3=3n,b n=2n﹣1…(6分)(Ⅱ)b n=2n﹣1,c n=n•2n﹣1,∴T n=c1+c2+…+c nT n=1•20+2•21+3•22+…+n•2n﹣12T n=1•21+2•22+…+(n﹣1)•2n﹣1+n•2n…(9分)两式相减可得,﹣T n=1•20+1•21+1•22+…+1•2n﹣1﹣n•2n∴﹣T n==2n﹣1﹣n•2n∴T n=(n﹣1)•2n+1…(13分)20.(12分)在△ABC 中,角A、B、C所对的边分别为a、b、c,且cosA=.①求的值.②若,求△ABC的面积S的最大值.【解答】解:①∵cosA=,==;②,∴,,∴,,∴,.21.(12分)已知向量=(2,2),向量与向量的夹角为,且=﹣2,(1)求向量;(2)若=(1,0)且,=(cosA,2cos),其中A、C是△ABC的内角,若三角形的三内角A、B、C依次成等差数列,试求||的取值范围.【解答】解:(1)设=(x,y),则2x+2y=﹣2①又②联立解得,∴;(2)由三角形的三内角A、B、C依次成等差数列,∴,∵,∴.∴,∴=,∵,∴,22.(12分)已知二次函数f(x)满足f(x+1)﹣f(x)=2x﹣1,且f(0)=3.(1)求函数f(x)的解析式;(2)若函数y=f(log3x+m),x∈[,3]的最小值为3,求实数m的值.【解答】解:(1)设f(x)=ax2+bx+c,则f(x+1)=a(x+1)2+b(x+1)+c,∵f(x+1)﹣f(x)=2x﹣1,∴a=1,b=﹣2,c=3,则f(x)=x2﹣2x+3;(2)令t=log3x+m,则t∈[m﹣1,m+1],则y=f(log3x+m)=f(t)=t2﹣2t+3=(t﹣1)2+2,当1≤m﹣1⇔m≥2时,则f(m﹣1)=3⇒m=3,当1≥m+1⇔m≤0时,则f(m+1)=3⇒m=﹣1,当m﹣1<1<m+1⇔0<m<2时,f(1)=3不成立,综上,m=﹣1或m=3.四.附加题:(本题每题5分,共15分)23.已知x>0,y>0,且2x+8y﹣xy=0,则x+y的最小值为18.【解答】解:已知x>0,y>0,且2x+8y﹣xy=0.2x+8y=xy即:+=1.利用基本不等式:则x+y=(x+y)(+)=+10≥8+10=18,当且仅当x=2y 时成立.则x+y的最小值为18.故答案为18.24.数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,则{a n}的前60项和为1830.【解答】解:∵a n+(﹣1)n a n=2n﹣1,+1故有a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97.从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a11=2,a16+a14=56,…从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,依次取2{a n}的前60项和为15×2+(15×8+)=183025.已知函数f(x)=|x2﹣4x+3|,若关于x的方程f(x)﹣a=x至少有三个不相等的实数根,则实数a的取值范围是[﹣1,﹣] .【解答】解:令g(x)=f(x)﹣x=|x2﹣4x+3|﹣x=,其图象如下图所示:当x=1时,函数取极小值﹣1,当x=时,函数取极大值﹣,当x=3时,函数取极小值﹣3,若关于x的方程f(x)﹣a=x至少有三个不相等的实数根,则函数g(x)的图象与直线y=a至少有三个交点,故a∈[﹣1,﹣],故答案为:[﹣1,﹣]。
山西省忻州市高一下学期期末数学试卷(文科)

山西省忻州市高一下学期期末数学试卷(文科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2015高二上·太和期末) 设a>1>b>﹣1,则下列不等式中恒成立的是()A .B .C . a>b2D . a2>2b2. (2分)非常数数列{an}是等差数列,且{an}的第5、10、20项成等比数列,则此等比数列的公比为()A .B . 5C . 2D .3. (2分)(2017·云南模拟) 若x,y满足约束条件则z=ax+y的最小值为1,则正实数a的值为()A . 10B . 8C . 3D . 24. (2分)若sin()=a,则cos()=()A . ﹣aB . aC . 1﹣aD . 1+a5. (2分) (2018高一上·湖南月考) 如图,在边长为2的正方形中,,分别为,的中点,为的中点,沿,,将正方形折起,使,,重合于点,在构成的三棱锥中,下列结论错误的是()A . 平面B . 三棱锥的体积为C . 直线与平面所成角的正切值为D . 异面直线与所成角的余弦值为6. (2分)已知α是第一象限角,那么是()A . 第一象限角B . 第二象限角C . 第一或第二象限角D . 第一或第三象限角7. (2分)设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是()A . 若m∥α,n∥α,则m∥nB . 若m∥α,m∥β,则α∥βC . 若m∥n,m⊥α,则n⊥αD . 若m∥α,α⊥β,则m⊥β8. (2分) (2016高二上·桓台期中) 直线l过点A(3,4)且与点B(﹣3,2)的距离最远,那么l的方程为()A . 3x﹣y﹣13=0B . 3x﹣y+13=0C . 3x+y﹣13=0D . 3x+y+13=09. (2分)已知两个球的表面积之比为1: 9,则这两个球的半径之比为()A . 1 : 3B . 1 :C . 1 : 9D . 1 : 8110. (2分)如图,网格纸的各小格都是正方形,粗实线画出的是一个凸多面体的三视图(两个矩形,一个直角三角形),则这个几何体可能为()A . 三棱台B . 三棱柱C . 四棱柱D . 四棱锥11. (2分)若等比数列的前n项和,则a等于()A .B .C . -1D . 112. (2分) (2019高二上·靖安月考) 已知且满足 ,则的最小值为()A . 2B . 3C . 4D . 1二、填空题 (共4题;共4分)13. (1分) (2018高二上·惠来期中) 若关于的不等式对任意恒成立,则实数的取值范围是________.14. (1分) (2019高二上·寿光月考) 是上一点,和是焦点,,则面积等于________.15. (1分) (2017·上海模拟) 如图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的体积为________.16. (1分) (2017高一下·南通期中) 已知数列{an},对任意的k∈N* ,当n=3k时,an= ;当n≠3k 时,an=n,那么该数列中的第10个2是该数列的第________项.三、解答题 (共6题;共50分)17. (10分) (2017高一上·淄博期末) 求满足下列条件的直线方程:(1)求经过直线l1:x+3y﹣3=0和l2:x﹣y+1=0的交点,且平行于直线2x+y﹣3=0的直线l的方程;(2)已知直线l1:2x+y﹣6=0和点A(1,﹣1),过点A作直线l与l1相交于点B,且|AB|=5,求直线l的方程.18. (5分)已知 =(2,﹣), =(sin2( +x),cos2x).令f(x)= • ﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0,)的图象关于(﹣,0)对称.(Ⅰ)求f(x)的解析式,并求φ的值;(Ⅱ)在△ABC中sinC+cosC=1﹣,求g(B)的取值范围.19. (15分)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PA⊥PC,底面ABCD为菱形,G为PC中点,E、F 分别为AB、PB上一点,△BCE的面积为6 ,PB=4PF.(1)求证:AC⊥DF;(2)求证:EF∥平面BDG;(3)求三棱锥B﹣CEF的体积.20. (5分) (2019高一下·宁波期末) 中,角的对边分别为,且.(I)求角C的大小;(II)若,求c的最小值.21. (10分)(2017·南通模拟) 如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F 为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.(1)当∠EFP= 时,试判断四边形MNPE的形状,并求其面积;(2)若使裁剪得到的四边形MNPE面积最大,请给出裁剪方案,并说明理由.22. (5分)(2019·天津) 设是等差数列,是等比数列,公比大于0,已知,,.(Ⅰ)求和的通项公式;(Ⅱ)设数列满足求 .参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共50分)答案:17-1、答案:17-2、考点:解析:答案:18-1、考点:解析:答案:19-1、答案:19-2、答案:19-3、考点:解析:答案:20-1、考点:解析:答案:21-1、考点:解析:答案:22-1、考点:解析:。
山西省忻州市高一下学期数学期末考试试卷(普通班)

山西省忻州市高一下学期数学期末考试试卷(普通班)姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)设偶函数f(x)在[0,+∞)单调递增,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A . (,1)B . (﹣∞,)∪(1,+∞)C . (﹣,)D . (﹣∞,﹣)∪(,+∞)2. (2分) (2016高二下·黑龙江开学考) 已知函数f(x)=xlnx,则()A . f(x)在(0,+∞)上是增函数B . f(x)在上是增函数C . 当x∈(0,1)时,f(x)有最小值D . f(x)在定义域内无极值3. (2分)已知函数f(x)的定义域为R,f(﹣1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为()A . (﹣1,1)B . (﹣1,+∞)C . (﹣∞,﹣1)D . (﹣∞,+∞)4. (2分) (2019高三上·邹城期中) 已知函数的图象与轴的两个相邻交点的距离等于 ,若函数的图象上各点的纵坐标不变,先将其上各点的横坐标伸长到原来的2倍,再向左平移个单位得到函数的图象,则函数()A .B .C .D .5. (2分) (2015高三上·包头期末) 已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则的值为()A . ﹣1B . -C .D . 26. (2分) (2018高二上·湖南月考) 已知函数且则函数的图象的一条对称轴是()A .B .C .D .7. (2分)“”是“”的A . 必要不充分条件B . 充分不必要条件C . 充要条件D . 既不充分也不必要条件8. (2分)(2018·临川模拟) 设,则“ 是第一象限角”是“ ”的()A . 充分而不必要条件B . 必要而不充分条件C . 充分必要条件D . 既不充分也不必要条件9. (2分)已知函数的最大值为4,最小值为0,最小正周期为,直线是其图象的一条对称轴,则下面各式中符合条件的解析式为()A .B .C .D .10. (2分)设的内角所对的边成等比数列,则的取值范围是()A .B .C .D .11. (2分)(2018·商丘模拟) 将函数的图象向右平移个单位后,得到,为偶函数,则的最小值为()A . 1B . 2C .D .12. (2分)(2020·茂名模拟) 公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则的近似值是()(精确到).(参考数据)A . 3.14B . 3.11C . 3.10D . 3.05二、填空题 (共4题;共4分)13. (1分) (2018高二上·湖北月考) 设是的展开式中的一次项的系数,则________.14. (1分)函数的单调递减区间为________.15. (1分) (2019高一上·永嘉月考) 下面有五个命题:①终边在y轴上的角的集合是{β|β= }②设一扇形的弧长为4cm,面积为4cm2 ,则这个扇形的圆心角的弧度数是2③ 时,④函数y=x2的图像与函数y=|lgx|的图像的交点个数为2个所有正确命题的序号是________.(把你认为正确命题的序号都填上)16. (1分)(2012·福建) 已知△ABC得三边长成公比为的等比数列,则其最大角的余弦值为________三、解答题 (共6题;共60分)17. (10分) (2019高一上·哈尔滨月考) 已知函数其定义域为(1)判断函数在上的单调性,并用定义证明.(2)若求的取值范围.18. (5分) (2017高二下·彭州期中) 已知函数f(x)=ex , g(x)=mx2+ax+b,其中m,a,b∈R,e=2.71828…为自然对数的底数.(I)函数h(x)=xf (x),当a=l,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;(II)记F(x)=f(x)﹣g(x).当a=2,m=0时,若函数F(x)在[﹣1,2]上存在两个不同的零点,求b的取值范围.19. (10分)(2017·安徽模拟) 已知向量 =(sinx,﹣1),向量 =( cosx,﹣),函数f(x)=( + )• .(1)求f(x)的最小正周期T;(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=2 ,c=4,且f(A)恰是f(x)在[0,]上的最大值,求A和b.20. (15分)设复数,其中为虚数单位,当实数取何值时,复数对应的点:(1)位于虚轴上;(2)位于一、三象限;(3)位于以原点为圆心,以为半径的圆上.21. (10分)已知向量 =(1,sinx), =(cos(2x+ ),sinx),函数f(x)= • ﹣ cos2x.(1)求函数f(x)的解析式及最小正周期;(2)当x∈[0, ]时,求函数f(x)的值域.22. (10分) (2016高一下·卢龙期中) 已知向量,,且,f(x)= • ﹣2λ| |(λ为常数),求:(1)• 及| |;(2)若f(x)的最小值是,求实数λ的值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分)17-1、17-2、18-1、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、第11 页共11 页。
山西省忻州市高一下学期期末数学试卷

山西省忻州市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019高二上·长沙月考) 已知全集,集合,则()A .B .C .D .2. (2分)(2018·河北模拟) 已知数列的前项和为,,则()A .B .C .D .3. (2分) (2015高二上·承德期末) 已知在空间直角坐标系中,点A的坐标为(0,2,1),点B的坐标为(﹣2,0,3),则线段AB的中点坐标为()A . (﹣1,1,2)B . (﹣2,2,4)C . (﹣1,﹣1,1)D . (1,﹣1,2)4. (2分)圆与直线3x+4y+2=0相交于A、B两点,则线段AB的垂直平分线的方程是()A . 4x-3y-6=0B . 4x+3y+6=0C . 3x+4y+8=0D . 4x-3y-2=05. (2分)已知x,y满足条件,则x+y最大值为()A .B .C . 3D . 26. (2分)已知圆O:x2+y2-4=0,圆:x2+y2+2x-15=0,若圆O 的切线l交圆C于A,B两点,则面积的取值范围是()A .B .C .D .7. (2分)(2018·呼和浩特模拟) 设直线与直线的交点为;分别为上任意两点,点为的中点,若,则的值为()A .B .C .D .8. (2分)如图,平面四边形ABCD中, ,,,将其沿对角线BD折成四面体,使平面平面BCD,若四面体顶点在同一球面上,则该球的体积为()A .B .C .D .9. (2分) (2016高三上·黑龙江期中) 等差数列{an}的公差为d,关于x的不等式 x2+(a1﹣)x+c≥0的解集是[0,22],则使得数列{an}的前n项和大于零的最大的正整数n的值是()A . 11B . 12C . 13D . 不能确定10. (2分) (2019高二上·杭州期中) 如图所示,在正方形中,分别是的中点,现在沿把这个正方形折成一个四面体,使三点重合,重合后的点记为 .给出下列关系:① 平面;② 平面;③ ;④ 上平面 .其中关系成立的有()A . ①②B . ①③C . ②③D . ③④11. (2分) (2017高二上·湖北期末) 不同的直线a,b,c及不同的平面α,β,γ,下列命题正确的是()A . 若a⊂α,b⊂α,c⊥a,c⊥b则c⊥αB . 若b⊂α,a∥b则a∥αC . 若a∥α,α∩β=b则a∥bD . 若a⊥α,b⊥α 则a∥b12. (2分) (2018高三上·吉林期中) 在△ABC中,A=60°,AC=2,△ABC的面积为,则BC的长为()A .B .C .D . 3二、填空题 (共4题;共4分)13. (1分) (2019高三上·浙江月考) 若实数满足,且,则的最大值为________.14. (1分) (2015高一上·银川期末) 过l1:2x﹣3y+2=0与l2:3x﹣4y+2=0的交点且与直线4x+y﹣4=0平行的直线方程为________.15. (1分)(2017·衡阳模拟) 已知,数列的前n项和为Sn ,数列{bn}的通项公式为bn=n﹣8,则bnSn的最小值为________.16. (1分) (2017高二上·大连期末) 在正三棱柱ABC﹣A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为________.三、解答题 (共6题;共50分)17. (10分) (2018高二下·晋江期末) 已知平面直角坐标系xOy中,直线l的参数方程为(t 为参数,0≤α<π且),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.已知直线l与曲线C交于A、B两点,且.(1)求α的大小;(2)过A、B分别作l的垂线与x轴交于M,N两点,求|MN|.18. (10分) (2017高二上·中山月考) 在中,角,,的对边分别为,,,且满足.(1)求角的大小;(2)若,的面积为,求的周长.19. (10分) (2020高二下·海丰月考) 如图,在四棱锥中,底面,且底面是菱形.(1)证明:平面平面;(2)若,求二面角的余弦值.20. (5分) (2018高一下·攀枝花期末) 已知数列满足,.(Ⅰ)求数列的通项公式;(Ⅱ)设,求.21. (5分) (2018·宁德模拟) 设函数,若,,则对任意的实数,的最小值为.22. (10分)(2017·山西模拟) 已知函数f(x)=|x﹣1|﹣2|x+1|的最大值为k.(1)求k的值;(2)若,求证:m+2n≥2.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共50分)17-1、17-2、18-1、18-2、19-1、19-2、20-1、21-1、22-1、22-2、。
山西省忻州市第一中学2015-2016学年高一下学期期末考试语文试题 Word版含答案

姓名班级准考证号忻州一中2015—2016学年高一第二学期期末考试试题语文本试卷分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷共70分,第Ⅱ卷共80分,满分150分,考试时间为150分钟.注意事项:1.答题前,考生务必用0.5mm黑色中性笔,将姓名、班级、准考证号填写在试题和答题卡上。
2.请把答案做在答题卡上,交卷时只交答题卡,不交试题,答案写在试题上无效.第I卷阅读题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1-3题.关于重阳节的起源,一向最为人们津津乐道的,是南朝《续齐谐记》所载的东汉汝南人桓景经方士费长房指点登山辟邪躲过一劫的故事。
不过这个说法,并不可信.《齐谐》是一部志怪书,连作者自己也没有把它视作史实。
晋葛洪《神仙传》说,费长房在东汉时曾做过汝南市掾,后跟仙人壶公入山修道去了。
而桓景,在有关东汉、三国史事的文献资料中都寻觅不到影子,仅仅在《宋书·符瑞志》中提到东晋成帝时有个太守叫桓景.春秋战国时期对山神的崇拜已很普遍,并形成了一套祭祀礼仪,而这种登高祭祀活动,在人类早期是作为最直接的生存需求出现的。
原始先民依靠采集和狩猎谋生,群居穴处,辗转山林。
山林间生长着各种植物,隐栖着许多飞禽走兽,物产丰饶,早就引起人们的关注。
山上云雾弥漫,而人们又观察到云气能致雨,以为山岳为神龙居所,有降雨的能力。
而且,山峰插入云霄,高不可攀,人们以为是登天的梯子或撑天的柱子,上面是神仙的居所,并且虔诚地相信,只要登上它,就能超越芸芸众生.原始先民领略了莽莽群山千变万化的自然现象,因而滋生了“万物皆有灵”的神秘自然观念,崇拜、敬畏山岳山神,并且激发了登临神山圣境的强烈愿望。
“崇”字从“山”从“宗”,说明“崇拜”原就是专对山岳而言的.秦统一中国后,一直到汉朝,皇帝对山川祭祀都非常重视,每年都要巡狩、祭牡或封禅名山大川,各地登高的活动也随之兴起。
据史料记载,约于刘邦在中原创立汉朝之时,割据岭南的南越王赵佗就曾登临越秀山,君臣饮宴游乐。
山西省忻州市第一中学高一数学下学期期末考试试题

忻州一中2014-2015学年度第二学期期末考试高 一 数 学注意事项:1.答题前,考生务必用蓝、黑色墨水笔或圆珠笔将学校名称、姓名、班级、考号、座位号填写在试题和试卷上。
2.请把所有答案做在试卷上,交卷时只交试卷,不交试题,答案写在试题上无效。
3.满分150分+15分,考试时间120分钟。
一.选择题(本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集{1,2,3,4},{1,2},{2,3},U A B ===则A C U ∪BA.{2,3}B.{1,2,3}C.{2,3,4}D.{1,2,3,4} 2.代数式sin120cos210o o 的值为A.B. 14C.32-D. 34-3.函数41()log 4xf x x =-的零点所在的区间是 A.(10,2) B.(1,12) C.(1,2) D.(2,4)4.已知a ,b 为非零实数,且a <b ,则下列不等式成立的是A.22b a < B.ab 2<a 2b C.ba ab 2211< D.1<b a 5.已知a ρ=1,|b ρ|=2,且a ρ)(b a ρρ-⊥,则向量a ρ与向量b ρ的夹角为A.6π B.4π C. 3π D.23π 6.已知△ABC 中,内角A ,B ,C 的对边分别为,,a b c ,若222a b c bc =+-,4bc =,则△ABC 的面积为 A .12B .1 C.27.执行如右图的程序框图,若输出的48S =, 则输入k 的值可以为 A .4 B .6开始k输入1,1n s ==C .8D .108.过点(2,1)且与原点距离最大的直线的方程是 A .x+2y-5=0 B .y=12x+1C .2x+y-5=0D .3x+y-5=09. 如果实数x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,y +1≥0,x +y +1≤0,那么2x -y 的最大值为A .2B .1C .-2D .-310.已知x x g x x x f -=-=1)(,1)(,则)()(x g x f ⋅ 的最大值为 A .14 B .13 C .12 D . 22 11.在ΔABC 中,若AB →·BC → = BC →·CA → = CA →·AB →,则该三角形是A .等腰三角形B .直角三角形C .等腰直角三角形D .等边三角形12.下列4个命题,其中正确的命题序号为①|x+1x |的最小值是2; ②x 2+2x 2+1的最小值是2;③log 2x+log x 2的最小值是2; ④3x+3x的最小值是2.A .①②③B .①②④C .②③④D .①③④二.填空题(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.已知)1,(x a =,)1,2(-=b ,且∥,则|a ρ-b ρ|= ▲ .14.设S n 为等差数列{a n }的前n 项和。
山西省忻州市高一下学期数学期末考试试卷

山西省忻州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)给出下面程序:若输出的A的值为120,则输入的A的值为()A . 1B . 5C . 15D . 1202. (2分) (2016高二下·宜春期中) 吉安市高二数学竞赛中有一道难题,在30分钟内,学生甲内解决它的概率为,学生乙能解决它的概率为,两人在30分钟内独立解决该题,该题得到解决的概率为()A .B .C .D .3. (2分)有A、B、C三种零件,分别为a个、300个、200个,现采用分层抽样法抽取一个容量为45的样本,C种零件被抽取10个,则此三种零件共有()A . 900个B . 800个C . 600个D . 700个4. (2分) cos(﹣300°)=()A .B .C .D .5. (2分)将函数的图象沿x轴向左平移个单位后,得到一个偶函数的图象,则的一个可能取值为()A .B .C . 0D .6. (2分)(2017·广东模拟) 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写()A . i≤2015?B . i≤2016?C . i≤2017?D . i≤2018?7. (2分)某年级有900名学生,随机编号为001,002,…,900,现用系统抽样方法,从中抽出150人,若015号被抽到了,则下列编号也被抽到的是()A . 036B . 081C . 136D . 7388. (2分)某高三同学在七次月考考试中,数学成绩如下:90 89 90 95 93 94 93去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为()A . 92,2B . 92,2.8C . 93,2D . 93,2.89. (2分) (2018高二上·长春月考) 用秦九韶算法计算多项式在时的值时, 的值为().A . -144B . -136C . -57D . 3410. (2分)已知α∈(﹣, 0),cosα=,则tanα等于()A . -B . -C .D .11. (2分) (2016高一上·温州期末) 已知向量、不共线,若 = +2 , =﹣4 ﹣,=﹣5 ﹣3 ,则四边形ABCD是()A . 梯形B . 平行四边形C . 矩形D . 菱形12. (2分) (2016高一上·承德期中) 定义在[﹣1,1]的函数f(x)满足下列两个条件:①任意的x∈[﹣1,1],都有f(﹣x)=﹣f(x);②任意的m,n∈[0,1],当m≠n,都有<0,则不等式f(1﹣3x)<f (x﹣1)的解集是()A . [0,)B . (, ]C . [﹣1,)D . [ ,1]二、填空题 (共4题;共4分)13. (1分)从自动打包机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g):492 496 494 495 498 497 501 502 504 496497 503 506 508 507 492 496 500 501 499根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5g~501.5g之间的概率约为________14. (1分)函数y=cos2x的单调减区间为________15. (1分)如图是小王所做的六套数学附加题得分(满分40)的茎叶图则其平均得分为________.16. (1分)已知函数y=3cos(2x+φ)的图象关于点(,0)中心对称,则|φ|的最小值为________三、解答题 (共6题;共46分)17. (1分) (2016·连江模拟) 已知 =(﹣1,3), =(1,t),若(﹣2 )⊥ ,则实数t=________.18. (10分)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:X1234Y51484542这里,两株作物“相近”是指它们之间的直线距离不超过1米.(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;(2)从所种作物中随机选取一株,求它的年收获量Y的分布列.19. (10分) (2017高三上·山东开学考) 自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:产假安排(单位:周)1415161718有生育意愿家庭数48162026(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.①求两种安排方案休假周数和不低于32周的概率;②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.20. (5分)已知cosα=﹣,且α为第三象限角.求sinα的值;21. (10分)函数的图象(部分)如图.(1)求f(x)解析式(2)若,求cosα.22. (10分)如图,已知是半圆的直径,,是将半圆圆周四等分的三个分点.(1)从这5个点中任取3个点,求这3个点组成直角三角形的概率;(2)在半圆内任取一点,求的面积大于的概率.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共46分)17-1、18-1、18-2、19-1、19-2、20-1、21-1、21-2、22-1、22-2、第11 页共11 页。
山西省忻州市高一下学期期末数学试题

山西省忻州市高一下学期期末数学试题姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高一上·山西月考) 对于集合,,定义,,设,,则()A .B .C .D .2. (2分) (2016高二下·邯郸期中) 在一次测试中,测得(x,y)的四组值分别是A(1,2),B(2,3),C (3,4),D(4,5),则y与x的回归方程为()A . =x﹣1B . =2x+1C . =x+2D . =x+13. (2分)(2012·广东) 从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是()A .B .C .D .4. (2分)(2017·厦门模拟) 数列{an}满足an+1﹣an=an﹣an﹣1(n≥2,n∈N),a3=11,Sn为其前n项和,则S5=()A . 45B . 50C . 55D . 605. (2分) (2016高二上·临沂期中) 在△ABC中,A=60°,AB=2,且△ABC的面积S△ABC= ,则边BC 的长为()A .B . 3C .D . 76. (2分) (2019高一上·长春期中) 设,,,则此三个数大小关系是()A .B .C .D .7. (2分) (2016高一上·襄阳期中) 定义在R上的函数f(x)满足f(x)=﹣f(2﹣x),且当x<1时f(x)递增,若x1+x2>2,(x1﹣1)(x2﹣1)<0,则f(x1)+f(x2)的值是()A . 恒为正数B . 恒为负数C . 等于0D . 正、负都有可能8. (2分) (2018高二上·六安月考) 设点(a,b)为区域内任意一点,则使函数f(x)=在区间[ ,+ )上是增函数的概率为()A .B .C .D .9. (2分)函数y=2cos2x的一个单调增区间是()A . (-,)B . (0,)C . (,)D . (,)10. (2分) (2016高三上·集宁期中) 已知函数f(x)=log2x+ ,若x1∈(1,2),x2∈(2,+∞),则()A . f(x1)<0,f(x2)<0B . f(x1)<0,f(x2)>0C . f(x1)>0,f(x2)<0D . f(x1)>0,f(x2)>011. (2分)函数()A . 在[﹣π,π]上是增函数B . 在[0,π]上是减函数C . 在上是减函数D . 在[﹣π,0]上是减函数12. (2分)等差数列{an}的公差为2,若a2 , a4 , a8成等比数列,则{an}的前n项和Sn=()A . n(n+1)B . n(n﹣1)C .D .二、多选题 (共1题;共3分)13. (3分) (2019高一下·化州期末) 若干个人站成排,其中不是互斥事件的是()A . “甲站排头”与“乙站排头”B . “甲站排头”与“乙不站排尾”C . “甲站排头”与“乙站排尾”D . “甲不站排头”与“乙不站排尾”三、填空题 (共4题;共8分)14. (1分) (2017高一下·静海期末) 200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为________;若采用分层抽样,40﹣50岁年龄段应抽取________人.15. (5分) (2019高三上·上海期中) 若,则的最小值是________.16. (1分)如图是函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<)的一段图象,则函数的解析式为________.17. (1分)(2013·上海理) 在△ABC中,角A,B,C所对边长分别为a,b,c,若a=5,c=8,B=60°,则b=________.四、解答题 (共6题;共75分)18. (10分)(2016·四川模拟) 如图ABCD是平面四边形,∠ADB=∠BCD=90°,AB=4,BD=2.(Ⅰ)若BC=1,求AC的长;(Ⅱ)若∠ACD=30°,求tan∠BDC的值.19. (15分) (2019高三上·金华期末) 数列的前n项和为,且满足,Ⅰ 求通项公式;Ⅱ 记,求证:.20. (10分)某汽车公司有两家装配厂,生产甲、乙两种不同型的汽车,若A厂每小时可完成1辆甲型车和2辆乙型车;B厂每小时可完成3辆甲型车和1辆乙型车.今欲制造40辆甲型车和乙型车,问这两家工厂各工作几小时,才能使所费的总工作时数最小.21. (10分)(2019高二上·会宁期中) 的内角A,B,C的对边分别为,已知.(1)求;(2)若,面积为2,求.22. (15分)(2017·赤峰模拟) 某校高三特长班的一次月考数学成绩的茎叶图和频率分布直方图1都受到不同程度的损坏,但可见部分如图2,据此解答如下问题:(Ⅰ)求分数在[70,80)之间的频数,并计算频率分布直方图中[70,80)间的矩形的高;(Ⅱ)若要从分数在[50,70)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[50,60)之间的概率.23. (15分) (2018高一上·南昌月考) 已知函数f(x)是二次函数,不等式f(x)≥0的解集为{x|﹣2≤x≤3},且f(x)在区间[﹣1,1]上的最小值是4.(1)求f(x)的解析式;(2)设g(x)=x+5﹣f(x),若对任意的,均成立,求实数m的取值范围.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、多选题 (共1题;共3分)13-1、三、填空题 (共4题;共8分)14-1、15-1、16-1、17-1、四、解答题 (共6题;共75分) 18-1、19-1、20-1、21-1、21-2、22-1、23-1、23-2、。
山西省忻州市高一下学期数学期末考试试卷

山西省忻州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)若集合,则M∩P=()A .B .C .D .2. (2分)函数的最小正周期为()A .B .C .D .3. (2分) (2018高二上·武邑月考) 直线(a+2)x+(1-a)y-3=0与(a-1)x+(2a+3)y+2=0互相垂直,则a等于()A . -1B . 1C . ±1D . -4. (2分) (2016高一下·水富期中) 在△ABC中,A,B,C是其三个角,若sinA>sinB,则A与B的大小关系是()A . A≥BB . A<BC . A>BD . 不能确定5. (2分) (2019高三上·金台月考) 在等差数列中,,则的前项的和为()A .B .C .D .6. (2分)若,则z=x+2y的最小值为()A . -1B . 0C .D . 27. (2分) (2018高二上·阜阳月考) 在△ABC中,已知 ,则B等于()A . 30°B . 60°C . 30°或150°D . 60°或120°8. (2分) (2016高一下·邯郸期中) 已知点A是半径为1的⊙O外一点,且AO=2,若M,N是⊙O一条直径的两个端点,则 =()A . 1B . 2C . 3D . 49. (2分)在中,内角所对的边分别是,已知,,则()A .B .C .D .10. (2分) (2018高三上·黑龙江期中) 函数(其中)的图象如图所示,为了得到的图象,则只要将的图象()A . 向右平移个单位长度B . 向右平移个单位长度C . 向左平移个单位长度D . 向左平移个单位长度11. (2分)(2017·长春模拟) 已知向量,,(m>0,n>0),若m+n∈[1,2],则的取值范围是()A .B .C .D .12. (2分)数列{an}满足a1=3,an﹣anan+1=1,An表示{an}的前n项之积,则A2009等于()A . 2B . ﹣2C . 3D . ﹣3二、填空题 (共4题;共4分)13. (1分) (2018高一上·广东期末) 直线与直线平行,则________.14. (1分) (2016高二上·青浦期中) 已知直线y=2x+2,该直线的单位方向向量 =________15. (1分)(2017·北京) 若等差数列{an}和等比数列{bn}满足a1=b1=﹣1,a4=b4=8,则 =________.16. (1分)如图,一辆汽车在一条水平的公路上向正西行驶,到处时测得公路北侧一山顶D在西偏北的方向上,行驶600 m后到达处,测得此山顶在西偏北的方向上,仰角为,则此山的高度________ m.三、解答题 (共6题;共50分)17. (10分) (2017高二上·汕头月考) 设锐角三角形的内角、、的对边分别为、、, .(1)求角的大小.(2)若,,求 .18. (10分) (2017高三上·南通开学考) 已知向量.(1)若,求证:(2)设,若,求α,β的值.19. (10分) (2016高三上·临沂期中) 设数列{an}的前n项和为Sn ,已知S2=6,an+1=4Sn+1,n∈N* .(1)求通项an;(2)设bn=an﹣n﹣4,求数列{|bn|}的前n项和Tn.20. (5分)(2017·河北模拟) 已知在△ABC中,角A,B,C所对的边分别为a,b,c,且2sin Acos B=2sin C﹣sin B.①求角A;②若a=4 ,b+c=8,求△ABC 的面积.21. (5分)已知向量=(cos,﹣1),=(sin, cos2),设函数f(x)=•.(1)求函数f(x)的单调递增区间;(2)求函数f(x)在x∈[0,π]上的零点.22. (10分) (2016高一下·黄冈期末) 设数列{an}满足a1+3a2+32a3+…+3n﹣1an= ,n∈N* .(1)求数列{an}的通项;(2)设,求数列{bn}的前n项和Sn.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共50分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、21-1、22-1、22-2、。
山西省忻州市高一下学期数学期末考试试卷

山西省忻州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2017·宜宾模拟) 已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B=()A . {8,10}B . {8,12}C . {8,14}D . {8,10,14}2. (2分)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。
现用分层抽样的方法在这70名学生中抽样,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为()A . 6B . 10C . 8D . 93. (2分)定义在R上的函数y=f(x)满足f(-a)=-f(a),且.若当x>3时不等式成立,则的取值范围是()A .B .C .D .4. (2分) (2016高一下·郑州期中) 下列说法中正确的是()A . 数据4、6、6、7、9、4的众数是4B . 一组数据的标准差是这组数据的方差的平方C . 数据3,5,7,9的标准差是数据6、10、14、18的标准差的一半D . 频率分布直方图中各小长方形的面积等于相应各组的频数5. (2分)下列说法正确的是()A . 若a>b,c>d,则ac>bdB . 若,则a<bC . 若b>c,则|a|·b≥|a|cD . 若a>b,c>d,则a-c>b-d6. (2分)(2018·南阳模拟) 《九章算术》中的“竹九节”问题:现有一根节的竹子,自上而下各节的容积成等差数列,上面节的容积共升,下面节的容积共升,则该竹子最上面一节的容积为()A . 升B . 升C . 升D . 升7. (2分) (2018高一下·重庆期末) 中,分别是角所对应的边,,,,则()A .B .C .D .8. (2分)(2017·日照模拟) 设点(a,b)是区域内的任意一点,则使函数f(x)=ax2﹣2bx+3在区间[ ,+∞)上是增函数的概率为()A .B .C .D .9. (2分)数列前n项和为,已知,且对任意正整数,都有,若恒成立,则实数的最小值为()A .B .C .D . 410. (2分)(2018·益阳模拟) 侏罗纪蜘蛛网是一种非常有规则的蜘蛛网,如图,它是由无数个正方形环绕而成,且每一个正方形的四个顶点都恰好在它的外围一层正方形四条边的三等分点上,设外围第一个正方形的边长是,有人说,如此下去,蜘蛛网的长度也是无限的增大,那么,试问,侏罗纪蜘蛛网的长度真的是无限长的吗?设侏罗纪蜘蛛网的长度为,则()A . 无限大B .C .D . 可以取11. (2分) (2016高三上·桓台期中) 设△ABC的内角A,B,C的对边分别为a,b,c.若a=2,c=2 ,cosA= .且b<c,则b=()A . 3B . 2C . 2D .12. (2分) (2020高一下·郧县月考) 在△ABC中,角A , B , C的对边分别是a , b , c ,若A∶B∶C =1∶2∶3,则a∶b∶c等于()A . 1∶2∶3B . 2∶3∶4C . 3∶4∶5D . 1∶ ∶2二、填空题 (共4题;共4分)13. (1分)从甲,乙,丙,丁4个人中随机选取两人,甲乙两人中有且只一个被选取的概率为________.14. (1分)(2017·南京模拟) 如图是某算法流程图,则程序运行后输出的结果是________.15. (1分) (2016高二上·上海期中) 前100个正整数中,除以7余数为2的所有数的和是________.16. (1分) (2018高二下·衡阳期末) 若直线,过点,则的最小值为________.三、解答题 (共6题;共55分)17. (10分)(2017·大理模拟) 已知数列{an}满足a1=4,an+1=qan+d(q,d为常数).(1)当q=1,d=2时,求a2017的值;(2)当q=3,d=﹣2时,记,Sn=b1+b2+b3+…+bn,证明:.18. (15分) (2018高一下·蚌埠期末) 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段,,,,,进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,则得到体育成绩的折线图如下:(1)若体育成绩大于或等于70分的学生为“体育良好”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良好”的人数;(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;(3)假设甲、乙、丙三人的体育成绩分别为,且,,,当三人的体育成绩方差最小时,写出的所有可能取值(不要求证明)19. (5分)在锐角△ABC中,内角A、B、C的对边分别是a、b、c,且cos(B+C)=﹣sin2A.(1)求A;(2)设a=7,b=5,求△ABC的面积.20. (10分) (2016高一上·襄阳期中) 已知函数f(x)=xln(x+ )(a>0)为偶函数.(1)求a的值;(2)求g(x)=ax2+2x+1在区间[﹣6,3]上的值域.21. (10分) (2019高三上·广州月考) 各项均不为零的数列前n项和为,数列前n项和为,且(1)求的值;(2)求数列的通项公式.22. (5分) (2018高二上·兰州月考) 中,内角的对边分别是,已知成等比数列,且.(Ⅰ)求的值;(Ⅱ)设,求的值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分) 17-1、17-2、18-1、18-2、18-3、19-1、20-1、20-2、21-1、21-2、22-1、。
山西省忻州市受录联校高一数学文下学期期末试题含解析

山西省忻州市受录联校高一数学文下学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知∠AOB=lrad,点A l,A2,…在OA上,B1,B2,…在OB上,其中的每一个实线段和虚线段氏均为1个单位,一个动点M从O点出发,沿着实线段和以O为圆心的圆弧匀速运动,速度为l单位/秒,则质点M到达A10点处所需要的时间为( ) 秒。
A.62 B.63 C.65 D.66参考答案:C2. 已知实数x,y满足a x<a y(0<a<1),则下列关系式恒成立的是()A.>B.ln(x2+1)>ln(y2+1)C.sinx>siny D.x3>y3参考答案:D【考点】指数函数的图象与性质;对数函数的图象与性质.【分析】本题主要考查不等式的大小比较,利用函数的单调性的性质是解决本题的关键.【解答】解:∵实数x,y满足a x<a y(0<a<1),∴x>y,A.若x=1,y=﹣1时,满足x>y,但==,故>不成立.B.若x=1,y=﹣1时,满足x>y,但ln(x2+1)=ln(y2+1)=ln2,故ln(x2+1)>ln(y2+1)不成立.C.当x=π,y=0时,满足x>y,此时sinx=sinπ=0,siny=sin0=0,有sinx>siny,但sinx>siny 不成立.D.∵函数y=x3为增函数,故当x>y时,x3>y3,恒成立,故选:D.3. 已知函数f(x)=,则f[f(﹣1)]的值是()A.40 B.42 C.44 D.45参考答案:D【考点】函数的值.【分析】由已知得f(﹣1)=(﹣1)(﹣1﹣4)=5,从而f[f(﹣1)]=f(5),由此能求出结果.【解答】解:∵函数,∴f(﹣1)=(﹣1)(﹣1﹣4)=5,f[f(﹣1)]=f(5)=5(5+4)=45.故选:D.【点评】本题考查函数值的求不地,是基础题,解题时要认真审题,注意函数性质的合理运用.4. 方程的解所在的区间是()A. (0,1)B. (1,2)C. (2,3)D. (3,4)参考答案:C【分析】令,根据是上的单调递增的连续函数,,由零点的存在性定理,进而可得结论.【详解】由题意,令,则关于的方程的解所在的区间就是函数的零点所在的区间,易证是上的单调递增的连续函数,又,,所以,由零点的存在性定理知,函数的零点所在的区间为,故方程的解所在的区间为.故选:C.【点睛】本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化的数学思想,属于基础题.5. 设全集U={0,1,2,3,4},集合A={1,2,3,},B={2,3,4},则= ()A、{0}B、{1}C、{0,1} D、{01,2,3,4}参考答案:B6. 函数y=log a(x2+2x﹣3),当x=2时,y>0,则此函数的单调递减区间是()A.(﹣∞,﹣3)B.(1,+∞)C.(﹣∞,﹣1)D.(﹣1,+∞)参考答案:A【考点】4P:对数函数的单调区间.【分析】由题意可知,a的范围,以及对数函数的性质,求解即可.【解答】解:当x=2时,y=log a5>0,∴a>1.由x2+2x﹣3>0?x<﹣3或x>1,易见函数t=x2+2x﹣3在(﹣∞,﹣3)上递减,故函数y=log a(x2+2x﹣3)(其中a>1)也在(﹣∞,﹣3)上递减.故选A7. 已知f(x)=-2x+1,对任意正数,x1,x2∈R,使|f(x1)-f(x2)|< 的一个充分不必要条件是()A.|x1-x2|< B. |x1-x2|</2 C. |x1-x2|</4 D.|x1-x2|>3/4参考答案:C8. 函数(且)的图像是下列图像中的()A. B. C. D.参考答案:C【分析】将函数表示为分段函数的形式,由此确定函数图像.【详解】依题意,.由此判断出正确的选项为C.故选C.【点睛】本小题主要考查三角函数图像的识别,考查分段函数解析式的求法,考查同角三角函数的基本关系式,属于基础题.9. 若, 则的值为()A. 0B.-1 C.3 D.参考答案:B10. 已知,不等式的解集是(-1,3),若对于任意,不等式恒成立,则t的取值范围()A. (-∞,2]B. (-∞,-2]C. (-∞,-4]D. (-∞,4]参考答案:B【分析】由不等式的解集是,可得b、c的值,代入不等式f(x)+t≤4后变量分离得t≤2x2﹣4x﹣2,x∈[﹣1,0],设g(x)=2x2﹣4x﹣2,求g(x)在区间[﹣1,0]上的最小值可得答案.【详解】由不等式的解集是可知-1和3是方程的根,,解得b=4,c=6,,不等式化为,令g(x)=2x2﹣4x﹣2,,由二次函数图像的性质可知g(x)在上单调递减,则g (x)的最小值为g(0)=-2,故选:B【点睛】本题考查一元二次不等式的解法,考查不等式的恒成立问题,常用方法是变量分离,转为求函数最值问题.二、填空题:本大题共7小题,每小题4分,共28分11. 已知幂函数y=f(x)的图象经过点(2,16),则函数f(x)的解析式是。
山西省忻州市高一下学期数学期末考试试卷
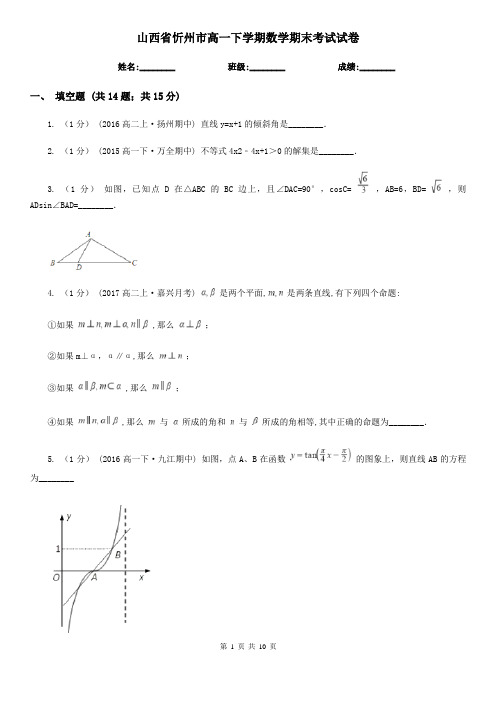
山西省忻州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共15分)1. (1分) (2016高二上·扬州期中) 直线y=x+1的倾斜角是________.2. (1分) (2015高一下·万全期中) 不等式4x2﹣4x+1>0的解集是________.3. (1分)如图,已知点D在△ABC的BC边上,且∠DAC=90°,cosC= ,AB=6,BD= ,则ADsin∠BAD=________.4. (1分) (2017高二上·嘉兴月考) 是两个平面,是两条直线,有下列四个命题:①如果 ,那么;②如果m⊥α,α∥α,那么;③如果 ,那么;④如果 ,那么与所成的角和与所成的角相等,其中正确的命题为________.5. (1分) (2016高一下·九江期中) 如图,点A、B在函数的图象上,则直线AB的方程为________6. (1分) (2016高二上·西安期中) 等比数列{an}的前n项和Sn=2n﹣1,则a12+a22+a32+…+an2=________.7. (1分)(2018·石嘴山模拟) 在中,内角的对边是,若,则等于________.8. (1分)如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面AB1C1 , AA1=1,底面△ABC是边长为2的正三角形,则三棱锥A﹣A1B1C1的体积为________.9. (2分)(2018·浙江) 若满足约束条件则的最小值是________,最大值是________.10. (1分)(2018·临川模拟) 已知圆过点,,,则圆的圆心到直线:的距离为________.11. (1分)(2016·潮州模拟) 已知三棱锥P﹣ABC中,底面△ABC是边长为3的等边三角形,侧棱长都相等,半径为的球O过三棱锥P﹣ABC的四个顶点,则点P到面ABC的距离为________.12. (1分)已知实数x,y满足x>y>0,且x+y=,则+的最小值为________13. (1分) (2019高二上·上海期中) 如图,光线从出发,经过直线反射到,该光线又在点被轴反射,若反射光线恰与直线平行,且,则实数的取值范围是________.14. (1分)(2020·上饶模拟) 一只蚂蚁从一个正四面体的顶点出发,每次从一个顶点爬行到另一个顶点,则蚂蚁爬行五次还在点的爬行方法种数是________.二、解答题 (共6题;共55分)15. (10分) (2018高二上·贺州月考) 在中,角的对边分别为且满足(1)求角的大小;(2)若,求面积的最大值.16. (15分) (2016高二上·合川期中) 如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,点M在AB上,且AM:MB=1:2,E为PB的中点.(1)求证:CE∥平面ADP;(2)求证:平面PAD⊥平面PAB;(3)棱AP上是否存在一点N,使得平面DMN⊥平面ABCD,若存在,求出的值;若不存在,请说明理由.17. (5分)已知正项数列满足4Sn=(an+1)2 .(1)求数列{an}的通项公式;(2)设bn=,求数列{bn}的前n项和Tn .18. (5分)直线l过定点P(0,1),且与直线l1:x-3y+10=0,l2:2x+y-8=0分别交于A、B两点.若线段AB的中点为P,求直线l的方程.19. (5分)物理学家和数学家牛顿曾提出了物体在常温环境下温度变化的冷却模型,如果物体的初始温度为θ1℃,空气温度为θ0℃,则tmin后物体的温度f(t)满足:f(t)=θ0+(θ1﹣θ0)•e﹣kt(其中k为正的常数,e=2.71828…为自然对数的底数),现有65℃的物体,放在15℃的空气中冷却,5min以后物体的温度是45℃.(Ⅰ)求k的值;(Ⅱ)求从开始冷却,经过多少时间物体的温度是25.8℃?(Ⅲ)运用上面的数据,作出函数f(t)的图象的草图.20. (15分) (2018高一下·四川月考) 已知数列的前项和是,满足 . (1)求数列的通项及前项和;(2)若数列满足,求数列的前项和;(3)对(2)中的,若对任意的,恒有成立,求实数的取值范围.参考答案一、填空题 (共14题;共15分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共55分)15-1、15-2、16-1、16-2、16-3、17-1、18-1、19-1、20-1、20-2、20-3、。
山西省忻州市高一下学期期末数学试卷

山西省忻州市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共14题;共28分)1. (2分) (2016高一下·华亭期中) 若,的化简结果为()A .B . ﹣C .D . ﹣2. (2分)设等差数列的前项和为,若,,则当取最小值时,()A . 6B . 7C . 8D . 93. (2分) (2018高二下·长春月考) 已知复数z满足,则的最大值为()A . 1B . 2C . 3D . 44. (2分) (2016高二下·吉林开学考) 设x,y满足约束条件,若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则的最小值为()A .B .C .D . 45. (2分)(2018高一下·长春期末) 在中,内角所对的边分别为 ,已知, , ,则()A .B .C .D .7. (2分) (2015高三上·贵阳期末) 若点A(a,b)在第一象限且在x+2y=4上移动,则log2a+log2b()A . 最大值为2B . 最小值为1C . 最大值为1D . 没有最大值和最小值8. (2分) (2017高二上·驻马店期末) 在△ABC中,S为△ABC的面积,且,则tanB+tanC ﹣2tanBtanC=()A . 1B . ﹣1C . 2D . ﹣29. (2分) (2020高三上·泸县期末) 在数列中,,则的值为()A .B .C .D .10. (2分)若a、b、c为实数,则下列命题正确的是()A . 若a>b,则ac2>bc2B . 若a<b<0,则a2>ab>b2C . 若a<b,则>D . 若a>b>0,则>11. (2分)如图所示,长为的木棒斜靠在石堤旁,木棒的一端在离堤足处的地面上,另一端在离堤足处的石堤上,石堤的倾斜角为,则坡度值等于()A .B .C .D .12. (2分) (2018高三上·河北月考) 已知函数的两个零点满足,集合,则()A . ∀m∈A ,都有f(m+3)>0B . ∀m∈A ,都有f(m+3)<0C . ∃m0∈A ,使得f(m0+3)=0D . ∃m0∈A ,使得f(m0+3)<013. (2分) (2016高一下·黑龙江期中) 在锐角△ABC中,AC=6,B=2A,则BC的取值范围为()A . (3,3 )B . (2 ,3 )C . (3 ,+∞)D . (0,3 )14. (2分)若a+b=1,则的最小值为()A . 1B . 2C .D .二、填空题 (共6题;共7分)15. (1分)已知数列{an}满足:a1=1,an+1=an+1,则数列{an}的通项公式an=________.16. (1分) (2017高二下·景德镇期末) 设变量x,y满足约束条件:,则目标函数z=x+2y 的最小值为________.17. (1分) (2017高二上·景德镇期末) 如图,数表满足:第n行首尾两数均为n;(2)表中递推关系类似杨辉三角,记第n(n>1)行第2个数为a(n).根据表中上下两行数据关系,可以求得当n≥2时,a(n)=________.18. (1分)已知sin(x+)=,则sin(x-)+sin2(-x)的值是________19. (2分)(2020·晋城模拟) 对于等差数列和等比数列,我国古代很早就有研究成果,北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”,就是关于高阶等差级数求和的问题.现有一货物堆,从上向下查,第一层有2个货物,第二层比第一层多3个,第三层比第二层多4个,以此类推,记第层货物的个数为,则数列的通项公式 ________,数列的前项和 ________.20. (1分) (2018高一下·涟水月考) 在△ABC中,BC=1,B= ,当△ABC的面积等于时,AB= ________.三、解答题 (共5题;共35分)21. (5分)已知函数f(x)=|x﹣2|.(1)解不等式:f(x+1)+f(x+2)<4;(2)已知a>2,求证:∀x∈R,f(ax)+af(x)>2恒成立.22. (10分) (2016高二下·大丰期中) 在数列{an}中,a1=1,an+1= (n=1,2,3,…),(1)计算a1,a2,a3,a4;(2)猜想an的表达式,并用数学归纳法证明你的结论.23. (10分) (2017高一上·启东期末) 已知函数f(x)= sinxcosx+sin2x﹣.(1)求f(x)的最小正周期及其对称轴方程;(2)设函数g(x)=f( + ),其中常数ω>0,|φ|<.(i)当ω=4,φ= 时,函数y=g(x)﹣4λf(x)在[ , ]上的最大值为,求λ的值;(ii)若函数g(x)的一个单调减区间内有一个零点﹣,且其图象过点A(,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式.24. (5分)已知二次函数f(x)=ax2+bx+c(a,b,c为常数,且a≠0),满足条件f(0)=0,f(1+x)=f (1﹣x)恒成立,且方程f(x)=x有两个相等的实数根.(Ⅰ)求函数f(x)的解析式;(Ⅱ)是否存在实数m,n(m<n),使f(x)的定义域和值域分别是[m,n]和[3m,3n],如果存在,求出m,n 的值;如果不存在,请说明理由.25. (5分)(2017·四川模拟) 已知数列{an}中,a2=2,其前n项和Sn满足:(n∈N*).(Ⅰ)求数列{an}的通项公式;(Ⅱ)若,求数列{bn}的前n项和Tn .参考答案一、选择题 (共14题;共28分)1-1、2-1、3-1、4-1、5-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、填空题 (共6题;共7分)15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题;共35分)21-1、22-1、22-2、23-1、23-2、24-1、25-1、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年度第二学期期末考试试题高 一 数 学(文)注意事项:1.考生务必用0.5mm 黑色中性笔答题.2.请把答案做在答题卡上,交卷时只交答题卡,不交试题,答案写在试题上无效。
3.满分150分,考试时间120分钟.一.选择题(本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的)1.满足条件a=4,b=52,A=45o 的△ABC 的个数是 ( ) A .1B .2C .无数个D .不存在2.已知数列{a n }满足a 1=1,a n +1=a n +2n ,则a 10= ( ) A .1024B .1023C .2048D .20473.若0<a <1,则不等式(x -a)(x -1a )>0的解集是 ( ) A .{x|x <a 或x >1a } B .{x|1a <x <a} C .{x|a <x <1a }D .{x|x <1a 或x >a} 4.在△ABC 中,sin 2A ≤sin 2B +sin 2C -sin Bsin C ,则A 的取值范围是 ( )A .⎝⎛⎦⎤0,π6 B .⎣⎡⎦⎤π6,πC .⎝⎛⎦⎤0,π3 D .⎣⎡⎭⎫π3,π5.在数列{a n }中,a n =-2n 2+29n +3,则此数列最大项的值是 ( ) A .102B .8658C .8178D .1086.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且b 2+c 2=a 2+bc . 若sin B ·sin C =sin 2A ,则△ABC 的形状是 ( ) A .等腰三角形 B .直角三角形 C .等边三角形D .等腰直角三角形7.设a =12cos6°-32sin6°,b =2sin13°cos13°,c =1-cos50°2,则有 ( ) A .a >b >cB .a <b <cC .b <c <aD .a <c <b8.△ABC 的三内角A 、B 、C 所对边的长分别为a ,b ,c ,设向量p →=(a +c ,b), q →=(b -a ,c -a),若p →∥q →,则角C 的大小为 ( ) A .π6B .π3C .π2D .2π39.已知f(x)是周期为2的奇函数,当0<x <1时,f(x)=lgx ,设a =f ⎝⎛⎭⎫65,b =f ⎝⎛⎭⎫32,c =f ⎝⎛⎭⎫52,则a 、b 、c 的大小关系是 ( ) A .c <a <bB .a <b <cC .b <a <cD .c <b <a10.数列{a n }中,若S n =3n +m -5,数列{a n }是等比数列,则m= ( ) A .2B .1C .-1D .411.在区间[0,π]上随机取一个数x ,则事件“sinx ≥|cosx |”发生的概率为( ) A .14B .12C .34D .112.设函数f (x )的定义域为R ,周期是2,f (x )=⎩⎪⎨⎪⎧x , 0≤x ≤1,⎝⎛⎭⎫12x -1,-1≤x <0.,若在区间[-1,3]上函数g (x )=f (x )-mx -m 恰有四个不同零点,则实数m 的取值范围是( ) A .⎣⎡⎦⎤0,12 B .⎣⎡⎭⎫0,14 C .⎝⎛⎦⎤0,12 D .⎝⎛⎦⎤0,14 二.填空题:(本大题共4小题,每小题5分,共20分)13.函数f (x )=sin 2⎝⎛⎭⎫2x -π4的最小正周期是______________. 14.设a>-38,P =a+41-a+40,Q =a+39-a+38,则P 与Q 的大小关系为 15.数列{a n }中,a 1=1,对于所有的n ≥2,n ∈N *,都有a 1·a 2·a 3·…·a n =n 2, 则a 3+a 5=______________. 16.给出下列结论:①2ab 是a 2+b 2的最小值;②设a>0,b>0,2ab 的最大值是a+b;③x 2+4 + 1x 2+4的最小值是2;④若x>0,则cosx+1cosx ≥2cosx·1cosx =2;⑤若a>b>0,a+b 2>ab>2aba+b .其中正确结论的编号是______________.(写出所有正确的编号) 三.解答题:(本大题共6小题,共70分)17.(本小题满分10分)已知1≤lg x y ≤2,2≤lg x 3y ≤3,求lg x 33y的取值范围.18.(本小题满分12分)为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)(1)000,001,002,…,799,试写出第二组第一位学生的编号;(2)求频率分布表格中a,b 的值,并估计800学生的平均成绩;(3)若成绩在85~95分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人? 19.(本小题满分12分)已知{a n }是单调递增的等差数列,首项a 1=3,前n 项和为S n ,数列{b n }是等比数列,首项b 1=1,且a 2b 2=12,S 3+b 2=20. (1)求{a n }和{b n }的通项公式;(2)设c n =1a n a n+2,求{c n }的前n 项和T n .20.(本小题满分12分)ΔABC 中,角A,B,C 所对边分别是a,b,c 且cosA =13.(1)求cos 2B +C2+cos2A 的值; (2)若a =3,求ΔABC 面积的最大值.21.(本小题满分12分)向量a →=(2,2),向量b →与向量a →的夹角为3π4,且a →·b →=-2. (1)求向量b →;(2)若t →=(1,0),且b →⊥t →,c →=⎝⎛⎭⎫cos A ,2cos 2 C 2,其中A 、B 、C 是△ABC 的内角,若△ABC的内角A 、B 、C 依次成等差数列,试求|b →+c →|的取值范围.22.(本小题满分12分)已知二次函数f(x)满足f(x+1)-f(x)=2x -1,且f(0)=3 (1)求函数f(x)的解析式;(2)若函数y =f(log 3x+m),x ∈[13,3]的最小值为3,求实数m 的值;附加题:(本题每题5分,共15分)1.已知x >0,y >0,且2x +8y -xy =0,则x +y 的最小值为 . 2.数列{a n }满足a n +1+(-1)n a n =2n -1,则{a n }的前60项和为 . 3.已知函数f (x )=|x 2-4x +3|,若关于x 的方程f (x )-a =x 至少有三个不相等的实数根,则实数a 的取值范围是 .2015-2016学年度第二学期期末考试文科数学答案一.选择题题号1 2 3 4 5 6 7 8 9 10 11 12 答案D B A C D C D B A D B D二.填空题 13. π2 14. P<Q15. 611616. ⑤三.解答题17.(本小题满分10分)已知1≤lg x y ≤2,2≤lg x 3y ≤3,求lg x 33y 的取值范围.【解析】由⎩⎪⎨⎪⎧1≤lg xy ≤2,2≤lg x 3y≤3变形,得⎩⎪⎨⎪⎧1≤lg x -lg y≤2,2≤3lg x -12lg y≤3, …………3分 ∴lg x 33y =3lg x -13lg y =m(lg x -lg y)+n(3lg x -12lg y)⇒⎩⎨⎧m=-315n=1615…………7分⎩⎨⎧-615≤-315(lg x -lg y)≤-3153215≤1615(3lg x -12lg y)≤4815⇒2615≤lg x33y ≤3,∴lg x 33y 的取值范围是⎣⎡⎦⎤2615,3.……10分18.(本小题满分12分)为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取部分学生的成绩(得分均为整数,满分为100分)(1)000,001,002,…,799,试写出第二组第一位学生的编号;(2)求频率分布表格中a,b 的值,并估计800学生的平均成绩;(3)若成绩在85~95分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人? 【解析】(1)编号为016. ………2分(2)a=8;b=0.28 ………4分平均成绩约为82.6 ………8分(3)在被抽到的学生中获二等奖的人数9+7=16(人),占样本的比例是1650=0.32,即获二等奖的概率为32%,所以获二等奖的人数估计为800×32%=256(人).答:获二等奖的大约有256人. ………12分19.(本小题满分12分)已知{a n }是单调递增的等差数列,首项a 1=3,前n 项和为S n ,数列{b n }是等比数列,首项b 1=1,且a 2b 2=12,S 3+b 2=20. (1)求{a n }和{b n }的通项公式;(2)设c n =1a n a n+2,求{c n }的前n 项和T n .【解析】(1)设数列{a n }的公差为d ,数列{b n }的公比为q ,则a 2b 2=(3+d)q =12, S 3+b 2=3a 2+b 2=3(3+d)+q =9+3d +q =20,3d +q =11,q =11-3d , 则(3+d)(11-3d)=33+2d -3d 2=12,即3d 2-2d -21=0⇒(3d +7)(d -3)=0. ………3分 ∵{a n }是单调递增的等差数列,∴d>0,∴d =3,q =2,a n =3+(n -1)×3=3n ,b n =2n-1. ………6分 (2)c n =1a n a n+2=19n(n+2)=118(1n -1n+2) ………9分T n =118(1-13)+118(12-14)+118(13-15)+……+118(1n-1-1n+1)+118(1n -1n+2)=118(1+12-1n+1-1n+2)=112-2n+318(n+1)(n+2) ………12分20.(本小题满分12分)ΔABC 中,角A,B,C 所对边分别是a,b,c 且cosA =13.(1)求cos 2B +C2+cos2A 的值; (2)若a =3,求ΔABC 面积的最大值. 【解析】(1)()22221cos 1cos cos cos 22cos 12cos 12222111142122339B C B C AA A A ++++=+-=-+-⎛⎫=-⋅+⋅-=- ⎪⎝⎭……6分 (2)由余弦定理:2222222242cos 2333a b c bc A b c bc bc bc bc ==+-=+-≥-=.∴49≤bc ,……8分当且仅当23==c b 时bc 有最大值49,()1cos ,0,,sin 3A A A π=∈===……10分∴()max 119sin 224ABC S bc A ==⋅=……12分21.(本小题满分12分)向量a →=(2,2),向量b →与向量a →的夹角为3π4,且a →·b →=-2. (1)求向量b →;(2)若t →=(1,0),且b →⊥t →,c →=⎝⎛⎭⎫cos A ,2cos 2 C 2,其中A 、B 、C 是△ABC 的内角,若△ABC的内角A 、B 、C 依次成等差数列,试求|b →+c →|的取值范围. 【解析】(1)设b →=(x ,y),则a →·b →=2x+2y=-2,且a →·b →=|a →|·|b →|·cos 3π4⇒-2=22×(-22)|b →|⇒x 2+y 2=1,得⎩⎨⎧x=-1y=0或⎩⎨⎧x=0y=-1∴b →=(-1,0)或b →=(0,-1) ……………5分 (2)∵b →⊥t →,t →=(1,0),∴b →=(0,-1) ∵A 、B 、C 依次成等差数列,∴B =π3,A+B =2π3b →+c →=(cosA,2cos 2C 2-1)=(cosA,cosC) ……………7分 ∴|b →+c →|2=cos 2A+cos 2C =1+12(cos2A+cos2C)=1+12(cos2A+cos(4π3-2A)) =1+12(cos2A-12cos2A-32sin2A)=1+12cos(2A+π3) ……………10分 ∵2A+π3∈(π3,5π3),∴-1≤cos(2A+π3)<12⇒12≤|b →+c →|2<54⇒22≤|b →+c →|2<52 ……………12分22.(本小题满分12分)已知二次函数f(x)满足f(x+1)-f(x)=2x -1,且f(0)=3 (1)求函数f(x)的解析式;(2)若函数y =f(log 3x+m),x ∈[13,3]的最小值为3,求实数m 的值; 【解析】(1)设f(x)=ax 2+bx+c ,则f(x+1)=a(x+1)2+b(x+1)+c∵f(x+1)-f(x)=2x-1,∴a=1,b= -2,c=3,即:f(x)=x 2-2x+3 ………5分 (2)令t= log 3x+m ,则t ∈[m-1,m+1],则y =f(log 3x+m)=f(t)=t 2-2t+3=(t-1)2+2 当1≤m-1⇔m ≥2时,则f(m-1)=3⇒ m =3 当1≥m+1⇔m ≤0时,则f(m+1)=3⇒ m =-1当m-1<1<m+1⇔0<m<2时,f(1)=3不成立,所以m =-1或m =3 ………12分附加题:(本题每题5分,共15分)1.已知x >0,y >0,且2x +8y -xy =0,则x +y 的最小值为 . 答案:182.数列{a n }满足a n +1+(-1)n a n =2n -1,则{a n }的前60项和为 . 答案:18303.已知函数f (x )=|x 2-4x +3|,若关于x 的方程f (x )-a =x 至少有三个不相等的实数根,则实数a 的取值范围是 . 答案[-1,-34]。
