线性方程与内插法
内插法计算方法

内插法计算方法内插法是一种常用的数值计算方法,它常用于求解函数在给定区间内的根。
内插法的基本思想是通过已知函数值构造一个插值多项式,然后利用这个多项式来近似求解函数的根。
在实际应用中,内插法通常以线性插值、拉格朗日插值和牛顿插值等形式出现。
首先,我们来介绍一下线性插值法。
线性插值法是内插法中最简单的一种,它假设函数在给定区间内是线性变化的。
设有函数f(x),在区间[a, b]上已知两个点的函数值f(a)和f(b),则可以通过线性插值的方式来近似求解函数f(x)在[a, b]上的根。
具体的计算方法是利用已知点(a, f(a))和(b, f(b))构造出一条直线,然后求出这条直线与x轴的交点,即可得到函数f(x)在区间[a, b]上的根的近似值。
接下来,我们介绍一种更为常用的插值方法——拉格朗日插值法。
拉格朗日插值法是一种基于拉格朗日插值多项式的内插法,它可以通过已知函数值构造出一个高次多项式来近似求解函数的根。
设有函数f(x),在区间[a, b]上已知n+1个点的函数值f(x0),f(x1), ..., f(xn),且这n+1个点两两不相等,那么可以构造出一个n次的拉格朗日插值多项式L(x),它满足在这n+1个点上的函数值与f(x)相等。
然后,可以通过求解这个插值多项式的根来近似求解函数f(x)在区间[a, b]上的根。
最后,我们介绍一种更为通用的插值方法——牛顿插值法。
牛顿插值法是一种基于牛顿插值多项式的内插法,它可以通过已知函数值构造出一个高次多项式来近似求解函数的根。
设有函数f(x),在区间[a, b]上已知n+1个点的函数值f(x0), f(x1), ..., f(xn),且这n+1个点两两不相等,那么可以构造出一个n次的牛顿插值多项式N(x),它满足在这n+1个点上的函数值与f(x)相等。
然后,可以通过求解这个插值多项式的根来近似求解函数f(x)在区间[a, b]上的根。
综上所述,内插法是一种常用的数值计算方法,它可以通过已知函数值构造出一个插值多项式来近似求解函数的根。
线性内插法

线性内插法具体怎么计算?内插法:就是在给定的二组数据为直线关系,在其区域之间的值,位于此直线上从而求出,在其区域之间的某一数据。
就是二者之间对应的情况下,按内插入法来求出另个数值,如二组数据:Y1,Y2 X1,X2已知:(X1,X2)一组上的某点值,求另一组(Y1,Y2)上的某点对应值。
现在要求已知:(X1,X2) )一组上的奌X,求:另一组(Y1,Y2)上的Y点对应值。
公式:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚式中:Y——所要求某区间的内插值;Y1、Y2——分别为所要求某区间之间的低值和高值;X1、X2——分别为所要求某区间之间对应的低值和高值。
图集11G101—1第53页中:锚固区的保护层厚度3d时受拉钢筋搭接长度修正系数ζa=0.8:5d时受拉钢筋搭接长度修正系数ζa=0.7。
【例1】假设,锚固区的保护层厚度为3.2d。
求受拉钢筋搭接长度修正系数ζa?公式:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚式中:Y——受拉钢筋锚固长度修正系数内插ζa取值;Y1、Y2——分别受拉钢筋锚固长度修正系数表中的低值ζa=0.7和高值ζa=0.8;X1、X2——锚固区的保护层厚度表中的低值3d和高值5d;解:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚=0.7+﹙0.8-0.7﹚÷﹙5d -3d﹚×﹙3.2d-3d﹚=0.7+0.05×0.2=0.71。
答:锚固区的保护层厚度为3.2d。
受拉钢筋锚固长度修正系数ζa=0.71。
【例2】假设,锚固区的保护层厚度为3.4d。
求受拉钢筋锚固长度修正系数ζa?解:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚=0.7+﹙0.8-0.7﹚÷﹙5d -3d﹚×﹙3.4d-3d﹚=0.7+0.05×0.4=0.72。
线性内插法[基础]
![线性内插法[基础]](https://img.taocdn.com/s3/m/0d0bb72066ec102de2bd960590c69ec3d5bbdb3c.png)
线性内插法具体怎么计算?内插法:就是在给定的二组数据为直线关系,在其区域之间的值,位于此直线上从而求出,在其区域之间的某一数据。
就是二者之间对应的情况下,按内插入法来求出另个数值,如二组数据:Y1,Y2 X1,X2已知:(X1,X2)一组上的某点值,求另一组(Y1,Y2)上的某点对应值。
现在要求已知:(X1,X2) )一组上的奌X,求:另一组(Y1,Y2)上的Y点对应值。
公式:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚式中:Y——所要求某区间的内插值;Y1、Y2——分别为所要求某区间之间的低值和高值;X1、X2——分别为所要求某区间之间对应的低值和高值。
图集11G101—1第53页中:锚固区的保护层厚度3d时受拉钢筋搭接长度修正系数ζa=0.8:5d时受拉钢筋搭接长度修正系数ζa=0.7。
【例1】假设,锚固区的保护层厚度为3.2d。
求受拉钢筋搭接长度修正系数ζa?公式:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚式中:Y——受拉钢筋锚固长度修正系数内插ζa取值;Y1、Y2——分别受拉钢筋锚固长度修正系数表中的低值ζa=0.7和高值ζa=0.8;X1、X2——锚固区的保护层厚度表中的低值3d和高值5d;解:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚=0.7+﹙0.8-0.7﹚÷﹙5d -3d﹚×﹙3.2d-3d﹚=0.7+0.05×0.2=0.71。
答:锚固区的保护层厚度为3.2d。
受拉钢筋锚固长度修正系数ζa=0.71。
【例2】假设,锚固区的保护层厚度为3.4d。
求受拉钢筋锚固长度修正系数ζa?解:Y=Y1+﹙Y2-Y1﹚÷﹙X2-X1﹚×﹙X-X1﹚=0.7+﹙0.8-0.7﹚÷﹙5d -3d﹚×﹙3.4d-3d﹚=0.7+0.05×0.4=0.72。
内插法计算公式-内插法公式

内插法计算公式-内插法公式内插法计算公式内插法公式在数学和统计学中,内插法是一种非常有用的工具,用于在已知数据点之间估计未知值。
内插法公式的应用广泛,涉及到金融、工程、科学等多个领域。
接下来,让我们深入了解一下内插法计算公式。
内插法的基本思想是假设在两个已知数据点之间存在线性关系。
也就是说,如果我们知道两个点的坐标(x1, y1)和(x2, y2),那么对于位于 x1 和 x2 之间的某个 x 值,我们可以通过线性关系来估计对应的 y 值。
内插法公式可以表示为:y = y1 +((x x1) (y2 y1))/(x2 x1)在这个公式中,x 是我们要估计 y 值的那个点的横坐标,y 是我们要估计的纵坐标。
x1 和 y1 是已知的第一个数据点的坐标,x2 和 y2 是已知的第二个数据点的坐标。
为了更好地理解这个公式,让我们通过一个具体的例子来进行说明。
假设我们有以下两个数据点:(2, 5) 和(4, 9),现在我们想要估计 x= 3 时的 y 值。
首先,我们确定 x1 = 2,y1 = 5,x2 = 4,y2 = 9。
然后,将这些值代入内插法公式:y = 5 +((3 2) (9 5))/(4 2)y = 5 +(1 4) / 2y = 5 + 2y = 7所以,当 x = 3 时,估计的 y 值为 7。
内插法不仅可以用于两个数据点之间的线性估计,还可以扩展到多个数据点的情况。
例如,在某些情况下,我们可能有一系列的数据点(x1, y1),(x2, y2),(x3, y3)等等。
如果这些数据点呈现出一定的规律,比如近似的线性关系,我们可以使用分段内插法来进行估计。
分段内插法就是将数据区间分成若干个小段,在每个小段内使用两个相邻的数据点进行内插计算。
这样可以提高估计的准确性,特别是当数据的变化趋势不是完全线性的时候。
内插法在金融领域有着重要的应用。
比如,在计算债券的收益率、股票的估值等方面,常常需要根据已知的市场数据进行内插估计。
内插法

内插法
内插法,一般是指数学上的直线内插,利用等比关系,是用一组已知的未知函数的自变量的值和与它对应的函数值来求一种未知函数其它值的近似计算方法,是一种求未知函数,数值逼近求法
数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则
(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
一、逐点内插法:
是以内插点为中心,确定一个邻域范围,用落在邻城范围内的采样点计算内插点的高程值,逐点内插本质上是局部内插,但与局部分块内插有所不同,局部内插中的分块范围一经确定,在整个内插过程中其大小、形状和位置是不变的,凡是落在该块中的内插点,都用该块的内插函数进行计算,而逐点内插法的邻域范围大小、形状、位置乃至
采样点个数随内插的位置而变动,一套数据只用来进行一个内插点的计算。
逐点内插法由于内插效率较高而成为DEM生产常采用的方法。
二、直线内插法
直线内插法是将刺激作为横坐标,以正确判断的百分数作为纵坐标,画出曲线,然后再从纵轴的50%处画出与横坐标平行的直线,与曲线相交于点a,从点a向横坐标画垂线,垂线与横轴相交处就是阈限。
三、内插法算出定点的自然标高
1、算出已知两点高差;
2、在地形图上量出已知两点平面距离或尺寸;
3,计算每米高程在两点间的平距;
4、计算内插点或任意点与已知点的平距;
5、根据平距推算需要的高差及高程。
内插法的计算原理

内插法的计算原理内插法,是数据分析中常用的一种方法,用于预测给定数据点之间的其他数据点的值。
它基于已有数据点的信息,通过利用这些点之间的关系,推导出其他点的数值。
内插法可用于大数据集的建模和分析,以及图像处理、天气预测等多个领域。
本文将详细介绍内插法的计算原理。
内插法分为两种常见的类型:线性插值和非线性插值。
线性插值是通过利用给定数据点之间的线性关系来估计其他数据点的值。
非线性插值则适用于数据点之间存在非线性关系的情况,可以使用多项式、样条函数等方法进行计算。
一、线性插值线性插值是最简单和最常用的内插法之一、它假设两个数据点之间的函数关系是线性的,即两个点之间的直线可以很好地拟合已知数据点。
设有两个已知数据点:(x0,y0)和(x1,y1),其中x0<x1、我们想要预测位于x0和x1之间的数据点(x,y)的值。
根据线性插值的原理,我们可以假设(x,y)位于(x0,y0)和(x1,y1)之间的直线上。
由于两点确定一条直线,我们可以使用斜率-截距公式将这条直线的方程表示为:y = mx + b其中m是直线的斜率,b是直线的截距。
求解斜率可以通过下式计算:m=(y1-y0)/(x1-x0)我们可以根据已知数据点的坐标和斜率,计算出直线的截距b:b = y0 - mx0有了直线的方程和坐标值,我们就可以求解位于(x0,x1)之间的数据点(x,y)的值。
二、非线性插值当给定数据点之间的关系不是线性的时候,我们可以使用非线性插值方法。
常见的非线性插值方法有多项式插值和样条插值。
1.多项式插值多项式插值是一种通过拟合多项式函数,从而对连续函数进行预测的方法。
根据给定数据点,我们可以通过构造多项式函数,使得插值函数经过这些数据点。
设有n个已知数据点:(x0, y0), (x1, y1), ..., (xn, yn)。
我们想要估计(x, y)位于两个数据点之间的值。
假设插值函数可以表示为一个n次多项式:P(x) = a0 + a1x + a2x^2 + ... + anxn为了确定多项式的系数,我们需要解决一个系数矩阵方程。
内插法的计算公式

内插法的计算公式内插法(Interpolation)是数值分析中常用的一种数值逼近方法,它通过已知数据点的函数值来估计在其它位置上的函数值。
在给定已知点的坐标和函数值的情况下,内插法用一个多项式来逼近这些已知点,并且认为这个多项式逼近函数在这些点上的函数值与实际函数值相等。
以下是几种常见的内插方法及其计算公式:1. 线性插值(Linear Interpolation)线性插值方法是用一条直线来逼近已知点,以估计其他位置上的函数值。
设已知点为(x₀,y₀)和(x₁,y₁),要估计在介于这两点之间的位置(x,y)的函数值,线性插值公式如下:y=y₀+(y₁-y₀)*(x-x₀)/(x₁-x₀)2. 拉格朗日插值(Lagrange Interpolation)拉格朗日插值方法使用拉格朗日多项式来逼近已知点,并以此估计其他位置上的函数值。
给定已知的n个点和函数值(x₀,y₀),(x₁,y₁),...,(xₙ,yₙ),拉格朗日插值公式如下:L(x) = Σ(yₙ * ℒₙ(x)), j=0 to n其中,ℒₙ(x) = Π((x - xₙ) / (xₙ - xₙ)), k ≠ j, k=0 to n 在这个公式中,ℒₙ(x)称为拉格朗日插值基函数,L(x)为拉格朗日插值多项式。
3. 牛顿插值(Newton Interpolation)牛顿插值方法使用牛顿插值多项式来逼近已知点,并以此估计其他位置上的函数值。
给定已知的n个点和函数值(x₀,y₀),(x₁,y₁),...,(xₙ,yₙ),牛顿插值公式如下:N(x) = y₀ + Σ(δₙ₋₁ * ℒₙ(x)), k=1 to n其中,ℒₙ(x)=Π(x-xₙ₋₁),δ₂=(y₁-y₀)/(x₁-x₀),δ₃=(δ₂-δ₁)/(x₂-x₀),...,δₙ=(δₙ₋₁-δₙ₋₂)/(xₙ-xₙ₋₂)以上是几种常见的内插方法及其计算公式。
根据需要,可以选择适用的方法进行内插计算。
线性方程与内插法
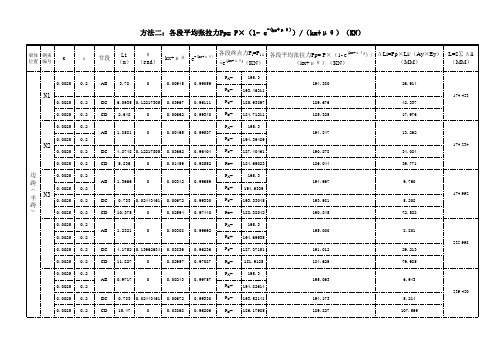
各段终点力Pi=Pi-1 各段平均张拉力Pp= P×(1- e-(kx+μθ))/ ΔLi=Pp×Li/(Ay×Ey) (MM) (kx+μθ)(KN) ×e-(kx+μθ)(KN)
L=2∑Δli (MM)
备注:节段长度均为预应力线形在水平方向的投影。
各段平均张拉力
梁体 钢束 位置 编号
×( kx+μθ)(KN) )(KN ×(1- e-(kx+μθ) ) (kx+μθ)(KN)
L=2∑Δli (MM)
K
μ
节段
Li θ (m) (rad)
kx+μθ e-(kx+μθ)
各段终点力Pi=Pi-1 各段平均张拉力Pp= P×(1- e-(kx+μθ))/ ΔLi=Pp×Li/(Ay×Ey) (MM) (kx+μθ)(KN) ×e-(kx+μθ)(KN)
N1
3 PC= PD= PA= PB= PC= PD= PA= PB= PC= PD= PA= PB= PC= PD= PA= PB= PC= PD= 184.20888 181.98337 195.3 194.908 194.51715 235.388 0.0025 0.0025 185.25237 181.96586 195.3 194.949 194.59833 235.500 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 186.29945 181.94607 195.3 194.991 194.68154 235.541 187.35436 181.9286 195.3 195.041 194.78139 238.159 193.47696 186.22412 194.128 189.827 5.212 106.269 7.599 190.995 184.628 29.210 79.498 9.062 190.419 184.114 43.683 63.786 10.281 189.847 183.604 58.070 48.154 11.470 189.275 183.094 72.368 32.608
内插法的定义及计算公式

内插法的定义及计算公式内插法(Interpolation)是一种数值计算方法,用于在已知数据点的基础上,通过适当的数学函数来估计未知数据点的值。
内插法通常在数据点之间进行估算,而不是对整个数据集进行统计分析。
内插法的目标是通过已知数据点的位置和对应的函数值来估计未知数据点的函数值。
这个过程可以看作是寻找一个函数,使得该函数在已知数据点处与实际数据点完全相符。
内插方法的计算公式取决于所使用的具体方法。
以下是几种常见的内插方法及其计算公式:1.线性插值线性插值是最简单的一种内插方法,假设已知两个数据点(x1,y1)和(x2,y2),插值函数可以表示为y=y1+((y2-y1)/(x2-x1))*(x-x1),其中x 为待估计的数据点。
这个公式基于两点之间的直线关系来进行插值。
2.拉格朗日插值拉格朗日插值法基于拉格朗日插值多项式,该多项式在已知数据点上完全满足函数值和导数值的条件。
假设已知n个数据点(x1, y1), (x2, y2), ..., (xn, yn),拉格朗日插值多项式可以表示为:L(x) = y1 *l1(x) + y2 * l2(x) + ... + yn * ln(x),其中li(x)是拉格朗日基函数,l1(x) = ((x - x2) * (x - x3) * ... * (x - xn)) / ((x1 - x2) * (x1 - x3) * ... * (x1 - xn))。
3.牛顿插值牛顿插值法基于牛顿插值多项式,该多项式是一个递推关系式。
假设已知n个数据点(x1, y1), (x2, y2), ..., (xn, yn),牛顿插值多项式可以表示为:N(x) = y1 + c1(x - x1) + c2(x - x1)(x - x2) + ... + cn(x - x1)(x - x2)...(x - xn),其中ci是递推系数,ci = f[x1,x2, ..., xi]。
内插法的计算公式

内插法的计算公式内插法是一种常用的数值计算方法,用于在已知数据点之间估计未知数据点的值。
内插法通过构造合理的插值函数,在插值区间内进行计算。
本文将介绍两种常见的内插法,分别是线性插值和拉格朗日多项式插值。
一、线性插值线性插值是一种简单且直观的内插法,适用于数据点较少的情况。
它基于线性函数的特性进行计算,公式如下:设已知数据点为 (x0, y0) 和 (x1, y1),要估计在 x0 和 x1 之间的某个点 x 的值 y,则线性插值公式为:y = y0 + (x - x0) * (y1 - y0) / (x1 - x0) (1)其中,y0 和 y1 分别是已知数据点 x0 和 x1 对应的函数值。
使用线性插值时需要注意两点:首先,x 的取值范围必须在 x0 和 x1 之间;其次,线性插值的准确性受到数据点的分布和函数曲线变化的影响。
二、拉格朗日多项式插值拉格朗日多项式插值是一种更为精确的内插方法,适用于数据点较多且分布不规则的情况。
它利用多个数据点构造一个多项式函数,并根据插值点的位置进行计算。
拉格朗日多项式插值的计算公式如下:假设已知的 n+1 个数据点为 (x0, y0),(x1, y1),...,(xn, yn),要估计在 x0 至 xn 之间某个点 x 的值 y,则拉格朗日插值多项式的计算公式为:y = L0(x)*y0 + L1(x)*y1 + ... + Ln(x)*yn (2)其中,Ln(x) 是拉格朗日基函数,由以下公式给出:Ln(x) = Π(j=0;j≠i)ⁿ (x - xj) / (xi - xj) (3)公式(3)中,i 表示基函数 Ln(x) 对应的数据点的索引。
拉格朗日多项式插值具有较高的精度和稳定性,但当数据点数量较大时,计算量会增加,同时插值函数的高次项可能引发数值计算的误差。
综上所述,线性插值和拉格朗日多项式插值是常见的两种内插法,可用于估计已知数据点之间的未知数据点的值。
最新内插法的定义及计算公式

最新内插法的定义及计算公式1.线性插值:线性插值是最简单和最常用的内插方法之一、它基于线性函数的性质,假设两个相邻数据点之间的关系是线性的。
设已知数据点为(x1,y1)和(x2,y2),要估算的未知数据点为(x,y)。
线性插值公式如下:y=y1+(x-x1)*(y2-y1)/(x2-x1)2.多项式插值:多项式插值是通过一个多项式函数来逼近已知数据点的曲线形状。
该方法假设未知数据点之间的关系可以用多项式函数来表示。
设已知数据点为(x1, y1),(x2, y2),...,(xn, yn),要估算的未知数据点为(x, y),多项式插值公式如下:y = P(x) = a0 + a1 * (x - x1) + a2 * (x - x1) * (x - x2)+ ... + an * (x - x1) * (x - x2) * ... * (x - xn-1)其中,a0, a1, a2, ..., an为多项式的系数,可以通过求解线性方程组来确定。
3.样条插值:样条插值使用分段多项式来逼近已知数据点的曲线形状。
该方法假设未知数据点之间的关系可以用不同的多项式函数段来表示。
设已知数据点为(x1, y1),(x2, y2),...,(xn, yn),要估算的未知数据点为(x, y),样条插值公式如下:y = S(x) = Si(x) = ai + bi * (x - xi) + ci * (x - xi)^2 + di * (x - xi)^3其中,Si(x)表示第i段多项式,ai, bi, ci, di为每个多项式的系数,可以通过求解线性方程组来确定。
不同的样条插值方法具有不同的限制条件,如自然边界条件、固定边界条件等,这些限制条件有助于确保插值结果的平滑和连续性。
以上是最新内插法的几种常见形式,它们在实际应用中具有广泛的适用性。
根据具体问题的特点和数据的性质,选择合适的内插方法能够提高估算的准确性和可靠性。
线性内插法公式

线性内插法公式线性内插法,也称为线性插补法,是一种广泛应用的函数拟合方法,它通过在已知数据点之间进行插补,从而拟合出未知点的函数值。
它可以用来预测数据集,预测数据收敛性,或者在一个时间点或空间点上直接预测函数值。
线性内插法具有较高的准确性,故而深受人们的喜爱,并广泛应用于工程计算中。
线性插补法比较容易理解,它是一种以常规方式实现的梯形积分的数值方法,它在某个区间上考虑函数的行为,并在每一个具体的点上求出函数的值,以求出这个点的函数行为。
线性内插法的基本原理是:给定数据点,结合数据点之间的差异,构造出经过这些数据点的线性函数,并计算出函数的值,从而拟合未知点的函数值。
其过程可以表示为:1.从数据点序列中,取出有限个点:(x_i,y_i), i=1,2,3,....,n2.根据有限点,构造出一个线性函数y=ax+b3.利用函数公式,求出每一个有限点的函数值4.求出未知点x_0处的函数值y_0从而得到线性内插法的公式:y_0=y_1+[(x_0-x_1)*(y_2-y_1)/(x_2-x_1)]在计算机中,线性内插法可以用一个循环语句、一个循环变量来完成,即:for i=1 to n doy_0=y_1+[(x_0-x_1)*(y_2-y_1)/(x_2-x_1)]end for其中,n为有限点的个数,x_1,x_2,....,x_n为有限点的横坐标,y_1,y_2,.....,y_n为有限点的函数值,y_0是未知点x_0处的函数值。
线性内插法的优点在于可以快速求出未知点的函数值,用计算机程序来实现更加方便,不需要做过多的运算量就可以实现,有效提高了计算效率。
另外,它的精度较高,可以解决较复杂的问题,能够在等分的区间内的未知点所表示函数值的精度较高。
然而,线性内插法也存在一定的不足。
首先,它不能够处理函数具有非线性特性的情况,若函数表现出非线性特性,则用线性内插法拟合可能会出现较大的错误;其次,线性内插法计算有限点处的函数值,只能从两个有限点推断函数的行为,可能会造成拟合的函数有一定偏差;再次,线性内插法计算函数值时,假设样本点服从某种分布,但有时,数据点的分布类型会受到外界因素的影响而改变,这就会对后续的线性内插法产生负面影响。
直线内插法计算公式-直线内差法计算

直线内插法计算公式-直线内差法计算直线内插法计算公式直线内差法计算在数学和统计学中,直线内插法(也称为直线内差法)是一种常用的数值计算方法。
它用于在已知两个点的坐标和对应的函数值的情况下,估算位于这两个点之间的某一未知点的函数值。
这种方法基于线性关系的假设,虽然简单,但在许多实际应用中非常有效。
直线内插法的基本思想是假设在两个已知点之间的函数值变化是线性的。
也就是说,我们可以用一条直线来近似表示这两个点之间的函数曲线。
通过这条直线的方程,我们就能够计算出中间未知点的函数值。
让我们假设已知两个点 A(x1, y1) 和 B(x2, y2),我们想要估算位于 x 处的点的函数值 y。
首先,我们需要计算出直线的斜率 k:k =(y2 y1) /(x2 x1)然后,我们可以通过点斜式来得到直线的方程:y y1 = k (x x1)将 k 的值代入上式,得到:y y1 =(y2 y1) /(x2 x1) (x x1)最后,通过移项和计算,就可以得到未知点 x 处的函数值 y:y = y1 +(y2 y1) /(x2 x1) (x x1)为了更好地理解直线内插法,让我们来看一个实际的例子。
假设我们知道在温度为 10°C 时,某种物质的溶解度为 20 克,在温度为 20°C 时,溶解度为 30 克。
现在我们想知道在温度为 15°C 时,该物质的溶解度。
首先,我们确定已知的两个点:A(10, 20) 和 B(20, 30)。
计算斜率 k:k =(30 20) /(20 10) = 1然后,将 x = 15 代入直线方程:y = 20 + 1 (15 10) = 20 + 5 = 25所以,我们估计在温度为 15°C 时,该物质的溶解度约为 25 克。
直线内插法在很多领域都有广泛的应用。
在科学实验中,如果我们只测量了有限的几个数据点,但需要了解中间未测量点的数值,就可以使用直线内插法进行估算。
内插法计算例子范文

内插法计算例子范文内插法(Interpolation)是一种在给定数据点之间估计未知数据点的方法。
在数学和统计学中,内插法被广泛应用于近似函数、构建曲线,或者从有限数量的数据点中恢复缺失的数据。
此外,内插法还可以用于数据平滑、滤波和信号处理等应用。
内插法的主要思想是根据已知数据点之间的函数关系,通过插值公式计算出未知数据点的值。
最常用的内插法包括线性内插法、拉格朗日插值法、牛顿插值法等。
下面将以线性内插法和拉格朗日插值法为例,详细介绍内插法的计算步骤和应用。
一、线性内插法线性内插法是最简单且常用的内插法之一,适用于已知两个数据点之间的线性关系。
具体步骤如下:1.给定两个已知数据点:(x1,y1)和(x2,y2),其中x1<x22.计算未知数据点x0的纵坐标y0:y0=y1+(x0-x1)*(y2-y1)/(x2-x1)线性内插法的计算过程非常简单,适用于需要快速估计未知数据点的值的情况。
然而,线性内插法对数据点之间的关系要求较高,如果数据点之间存在非线性的关系,则线性内插法的精度可能较低。
二、拉格朗日插值法拉格朗日插值法是通过构造一个多项式函数来估计未知数据点的值。
具体步骤如下:1. 给定 n+1 个已知数据点:(x0, y0),(x1, y1),...,(xn, yn)。
2.构造n次多项式函数L(x):L(x) = y0 * l0(x) + y1 * l1(x) + ... + yn * ln(x)其中 li(x) = (x - x0) * (x - x1) * ... * (x - xi-1) * (x -xi+1) * ... * (x - xn) / ((xi - x0) * (xi - x1) * ... * (xi -xi-1) * (xi - xi+1) * ... * (xi - xn))3.计算未知数据点x的纵坐标y:y=L(x)拉格朗日插值法通过构造一个满足已知数据点条件的多项式函数来进行插值计算,可以适应各种不同的数据分布和函数形态。
最简单的内插法公式和原理

最简单的内插法公式和原理
内插法又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
1内插法原理
数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则
(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
2内插法公式
求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:
A表示租赁开始日租赁资产的公平价值; R表示每期租金数额;S表示租赁资产估计残值;
n表示租期;
r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率3内插法简单计算方法
情形1:B与i同方向变化
情形2:B与i反方向变化
i1<i<i2 B1<B<B2
排列好:
i1B1
i B
i2B2
再相对应相减相除:i→B......
不用再管他谁大谁小,只要i与B对应不要错就可以了。
内插法的计算公式

内插法的计算公式在数学和金融等领域,内插法是一种常用的计算方法,它能够帮助我们在已知的数据点之间估算未知的值。
内插法的应用范围广泛,从科学研究到金融分析,都能看到它的身影。
那什么是内插法呢?简单来说,就是在已知的两个点之间,根据一定的规律和假设,推测出中间未知点的值。
为了实现这个目的,我们需要用到内插法的计算公式。
内插法的基本原理基于线性关系。
假设我们有两个已知点(x₁, y₁) 和(x₂, y₂),现在要估算一个位于 x₁和 x₂之间的 x 所对应的 y 值。
内插法的计算公式为:y = y₁+(y₂ y₁) /(x₂ x₁) ×(xx₁)我们来逐步拆解这个公式,以便更好地理解。
首先,(y₂ y₁) /(x₂ x₁) 这个部分表示的是两个已知点之间的斜率。
斜率反映了数据的变化趋势。
然后,(x x₁) 表示我们要估算的点与已知点x₁之间的水平距离。
最后,将这两个部分相乘,就得到了在这个斜率下,水平距离所对应的垂直变化量。
再加上 y₁,就得到了估算的 y 值。
为了更直观地理解内插法的计算公式,我们来看一个实际的例子。
假设某商品的价格与销售量之间存在一定的关系。
已知当价格为 10 元时,销售量为 500 件;当价格为 15 元时,销售量为 300 件。
现在我们想知道当价格为 12 元时,销售量大概是多少。
首先,x₁= 10,y₁= 500,x₂= 15,y₂= 300。
斜率=(300 500) /(15 10) =-40然后,x = 12,x₁= 10垂直变化量=-40 ×(12 10) =-80最后,y = 500 +(-80) = 420所以,当价格为 12 元时,估计销售量为 420 件。
内插法不仅在简单的线性关系中有用,在一些稍微复杂的情况中,比如曲线关系,也可以通过分段线性化等方法来应用内插法。
再比如,在金融领域,计算债券的到期收益率时,可能会用到内插法。
已知两个不同利率下债券的价格,要估算某个特定价格对应的利率,就可以借助内插法。
内插法计算投标报价

内插法计算投标报价内插法是一种用于计算投标报价的方法。
它利用已知数据点之间的关系,通过插值计算出未知数据点的值。
内插法适用于投标报价中存在一些已知的数据点,但是需要推算出其他数据点的情况。
内插法的基本原理是假设已知数据点之间存在线性关系,即数据点在直线上。
通过已知数据点的坐标(x,y)可以推算出未知数据点的坐标。
内插法有多种方法,包括线性内插法、多项式内插法等。
线性内插法是内插法中最简单的方法之一、它假设已知数据点之间的关系是线性的。
线性内插法通过已知数据点的坐标计算出直线的斜率和截距,然后根据未知数据点的横坐标计算出对应的纵坐标。
例如,假设我们需要根据已知数据点(x1,y1)和(x2,y2)计算出未知数据点(x,y)。
根据线性内插法,我们可以首先计算出直线的斜率k和截距b:k=(y2-y1)/(x2-x1)b = y1 - kx1然后根据未知数据点的横坐标x,计算出对应的纵坐标y:y = kx + b多项式内插法则假设已知数据点之间的关系是多项式的。
多项式内插法通过已知数据点的坐标计算出多项式的系数,然后根据未知数据点的横坐标计算出对应的纵坐标。
在计算投标报价中,内插法可以用于确定未知价格的值。
假设我们有一些已知价格和对应的数量,我们可以利用内插法根据给定的数量推算出对应的价格。
这对于计算投标报价是非常有用的。
通过已知的价格-数量数据点和内插法,我们可以推算出其他数量对应的价格,从而得到一个合理的投标报价。
举例来说,假设我们知道公司在过去的几次投标中的价格和对应的数量:价格A对应数量X,价格B对应数量Y。
公司现在需要根据数量Z计算出对应的价格。
我们可以使用内插法来推算出数量Z对应的价格。
根据内插法的原理,我们可以计算出价格A和价格B之间的直线方程。
然后根据数量Z计算出对应的价格。
需要注意的是,内插法只能在已知数据点之间进行插值计算,无法对超出已知数据点范围的数据进行预测。
因此,在使用内插法计算投标报价时,需要确保已知数据点覆盖了所有可能的情况,以获得准确的结果。
1.2第二章 内插法

α
3 4 4.4 5
- z 00 z10 - z 00 z 01 z =z00+ (x - x 0 ) + (y - y 0 ) x1 - x 0 y1 - y 0
37 . -46 . 9.3-4.6 Z =4.6+ (13.4-10)+ (4.4-4)=5.8 n mile 5 4 20 10
第二节 变率内插
当函数是非线性函数时,如果用比例内 插计算将会导致一定的计算误差, 为了尽量减小该误差,则引进了变率内 插。
一. 变率单内插(一元函数) 利用表中给出的函数变化率进行内插。
dy y=y0+ (x-x0) dx
例2-2-1:用y=x2造表,求x=2.3时的y?
(1) 用比例内插 y=5.5 (2) 用x=2变率内插 y=4+4(2.3-2)=5.2 (3) 用x=3变率内插 y=9+6(2.3-3)=4.8 (4) 用y=x2直接计算 y=5.29
内插分类:
a:按使用目的:
正内插-已知引数求函
数;
反内插-已知函数求引数。
b:按引数的个数:
单内插、双内插、三内插 c:按函数的性质:
线性内插、变率内插、高次内插
第一节 比例内插(线性内插)
一.比例单内插(一元函数 y=f(x) )
1.比例正内插 已知 x 求 y。 引数 函数值
x0
x1 …
(2)求α=5′,h=13.4m时的D2?
α h 3 4 5 10 6.2 4.6 3.7 13.4 20 12.3 9.3 7.4
5.0
7 .4 - 3 .7 D1-D 0 D1=D0+ (h-h0)=3.7+ 20 - 10(13.4-10)=5.0n mile h1-h0
内差法计算公式范文

内差法计算公式范文内插法是一种数值计算方法,常用于在已知一些数据点的情况下,推测其他数据点的值。
内插法有多种形式,其中最常见的是线性内插法和拉格朗日内插法。
以下是这两种内插法的计算公式。
1.线性内插法线性内插法基于一个简单的原理:如果在两个已知数据点之间存在一个未知数据点,那么未知点的值可以通过这两个已知点之间的线性关系来估计。
设已知数据点为(x₁,y₁)和(x₂,y₂),未知数据点为(x,y),线性内插公式可以表示为:y=y₁+(x-x₁)*(y₂-y₁)/(x₂-x₁)这个公式的推导是基于一条直线的方程 y = mx + b,其中 m 是斜率,b 是截距。
根据已知数据点确定的直线,线性内插法实际上就是在这条直线上求解未知数据点的纵坐标。
线性内插法的一个重要的前提条件是已知数据点是均匀分布在直线上。
如果数据点不均匀分布,那么线性内插的误差会增大。
2.拉格朗日内插法拉格朗日内插法是一种基于拉格朗日插值多项式的方法。
具体而言,拉格朗日内插法假设已知数据点为(x₀, y₀), (x₁, y₁), ..., (xn, yn),未知数据点为(x, y)。
拉格朗日插值多项式的表达式为:P(x) = Σ (yi * Li(x))其中i的取值范围是从0到n,Li(x)表示拉格朗日基函数Li(x) = Π ((x - xj) / (xi - xj))其中j的取值范围是从0到n且j≠i。
通过拉格朗日插值多项式可以求解出未知数据点的纵坐标。
拉格朗日内插法的优点是可以使用任意多个已知数据点进行插值,适用于非均匀分布的数据点。
但是它的计算复杂度较高,尤其是在数据点数目较大时。
以上是线性内插法和拉格朗日内插法的计算公式。
根据数据点的分布情况和具体的应用需求,可以选择合适的内插方法进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PC= 187.35436
PD= 181.9286
PA=
195.3
PB= 194.78139
PC= 193.47696
PD= 186.22412
194.866 189.275 183.094 194.908 189.847 183.604 194.949 190.419 184.114 194.991 190.995 184.628 195.041 194.128 189.827
AB 1.8581
0
0.00465 0.99537
BC 4.8748 0.12217305 0.03662
CD 5.836
0
0.01459
0.96404 0.98552
AB 1.3666
0
0.00342 0.99659
BC 0.733 0.02443461 0.00672
CD 10.375
0
0.02594
0.99330 0.97440
AB 1.2321
0
0.00308 0.99692
BC 4.1752 0.13962634 0.03836
CD 11.827
0
0.02957
0.96236 0.97087
AB 0.9717
0
0.00243 0.99757
BC 0.733 0.02443461 0.00672 0.99330
CD 15.47
0
0.03868 0.96206
PA=
195.3
PB= 193.46311
PC= 185.93897
PD= 184.71211
PA=
195.3
PB= 194.39489
PC= 187.40461
PD= 184.69023
PA=
195.3
PB=
194.6339
PC= 193.33045
方法二:各段平均张拉力Pp= P×(1- e-(kx+μθ))/(kx+μθ)(KN)
梁体 钢束 位置 编号
K
μ
节段
Li (m)
θ (rad)
kx+μθ
e-(kx+μθ)
各段终点力Pi=Pi-1 ×e-(kx+μθ)(KN)
各段平均张拉力Pp= P×(1- e-(kx+μθ))/ (kx+μθ)(KN)
12.695 72.368 32.608 11.470 58.070 48.154 10.281 43.683 63.786 9.062 29.210 79.498 7.599 5.212 106.269
235.343 235.388 235.500 235.541 238.159
方法二:各段平均张拉力Pp= P×(1- e-(kx+μθ))/(kx+μθ)(KN)
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
AB 1.7785
0
0.00445 0.99556
BC 10.438 0.13962634 0.05402
CD 4.862
0
0.01216
0.94741 0.98792
AB 1.6066
0
0.00402 0.99599
ΔLi=Pp×Li/(Ay×Ey) (MM)
L=2∑Δli (MM)
0.0025 0.2
N1
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
N2
0.0025 0.2
0.0025 0.2
边
0.0025 0.2
跨
( 半
0.0025
N3
0.0025
0.2 0.2
跨
)
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
AB 3.78
0
0.00945 0.99059
BC 6.0935 0.12217305 0.03967
CD 2.648
0
0.00662
0.96111 0.99340
PD= 188.38042
PA=
195.3
PB= 194.69935
PC= 187.37151
PD= 181.9125
PA=
195.3
PB= 194.82614
PC= 193.52141
PD= 186.17985
194.380 189.676 185.325 194.847 190.878 186.044 194.967 193.981 190.845 195.000 191.012 184.629 195.063 194.173 189.827
0.0025 0.2
N1
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
N2
0.0025 0.2
0.0025 0.2
中
0.0025 0.2
跨
( 半
0.0025
N3
0.0025
0.2 0.2
跨
)
0.0025 0.2
0.0025 0.2
0.0025 0.2
0.0025 0.2
26.914 42.337 17.976 13.262 34.084 39.771 9.760 5.208 72.528 8.801 29.213 79.985 6.943 5.214 107.569
174.453 174.234 174.992 235.998 239.450
方法二:各段平均张拉力Pp= P×(1- e-(kx+μθ))/(kx+μθ)(KN)
BC 8.3504 0.13962634 0.04880
CD 7.16
0
0.01790
0.95237 0.98226
AB 1.4397
0
0.00360 0.99641
BC 6.2628 0.13962634 0.04358
CD 9.458
0
0.02365
0.95735 0.97663
AB 1.2687
梁体 钢束 位置 编号
K
μ
节段
Li (m)
θ (rad)
kx+μθ
e-(kx+μθ)
各段终点力Pi=Pi-1 ×e-(kx+μθ)(KN)
各段平均张拉力Pp= P×(1- e-(kx+μθ))/ (kx+μθ)(KN)
ΔLi=Pp×Li/(Ay×Ey) (MM)
L=2∑Δli (MM)
备注:节段长度均为预应力线形在水平方向的投影。
PA=
195.3
PB= 194.43357
PC= 184.20888
PD= 181.98337
PA=
195.3
PB= 194.51715
PC= 185.25237
PD= 181.96586
PA=
195.3
PB= 194.59833
PC= 186.29945
PD= 181.94607
PA=
195.3
PB= 194.68154
梁体 钢束 位置 编号
K
μ
节段
Li (m)
θ (rad)
kx+μθ
e-(kx+μθ)
各段终点力Pi=Pi-1 ×e-(kx+μθ)(KN)
各段平均张拉力Pp= P×(1- e-(kx+μθ))/ (kx+μθ)(KN)
ΔLi=Pp×Li/(Ay×Ey) (MM)
L=2∑Δli (MM)
0.0025 0.2
0பைடு நூலகம்
0.00317 0.99683
BC 4.1752 0.13962634 0.03836
CD 11.755
0
0.02939
0.96236 0.97104
AB 1.0636
0
0.00266 0.99734
BC 0.733 0.02443461 0.00672
CD 15.283
0
0.03821
0.99330 0.96251
