2010-2011_2_随机数学期中试题及参考答案_7657_1777_20110512124257
2010~2011学年度第一学期期中考试高二数学试题及答案(理科)

2010~2011学年度第一学期期中考试高二数学试题及答案(理科)2010~2011学年度第一学期期中考试高二数学试题(理科)一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答题卡相应的位置上. 学科网 1.已知命题,则 : . 2.“ ”是“直线与圆相交”的条件。
(充分而不必要条件、必要而不充分条件、充分必要条件、既不充分也不必要条件) 3. 函数,的单调递增区间是. 4. 有下列四个命题:(1)“若,则”的逆命题;(2)“全等三角形的面积相等”的否命题;(3)“若,则有实根” 的逆命题;(4)“若,则”的逆否命题。
其中真命题的个数是________. 5.若,则等于 6.已知数列{an}的前n项和,则数列{an}成等比数列的充要条件是r=. 7.计算 8.观察下列等式:,……,根据上述规律,第五个等式为¬¬¬¬¬¬¬¬¬¬¬ ____ ________. 9.已知复数满足 =2,则的最大值为. 10.设… ,则 . 11.已知函数在处有极大值,则 = 。
12. 已知函数f(x) 在R上满足f(x)=2f(2-x)-x2+8x-8,则f’(1)= .13.已知扇形的圆心角为(定值),半径为(定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为,则按图二作出的矩形面积的最大值为 . 14.若存在过点的直线与曲线和都相切,则等于 .二、解答题 15.(本小题满分14分)已知为复数,和均为实数,其中是虚数单位.(Ⅰ)求复数;(Ⅱ)若复数在复平面上对应的点在第一象限,求实数的取值范围.16.(本小题满分14分)已知 p:,q:.⑴ 若p是q充分不必要条件,求实数的取值范围;⑵ 若“非p”是“非q”的充分不必要条件,求实数的取值范围.17. (本题满分15分) 已知a、b∈(0,+∞),且a+b=1, 求证:(1) ab≤ (2) + ≥8; (3) + ≥ . (5分+5分+5分)18. (本题满分15分)已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an (n∈N*). (1)试求出S1,S2,S3,S4,并猜想Sn的表达式; (7分) (2)用数学纳法证明你的猜想,并求出an的表达式. (8分) 19.(本小题满分16分)两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在的中点时,对城A和城B的总影响度为0.065. (1)按下列要求建立函数关系式:(i)设(rad),将表示成的函数;并写出函数的定义域. (5分) (ii)设(km),将表示成的函数;并写出函数的定义域. (5分) (2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小? (6分) 20.(本小题满分16分)已知函数的图象过点,且在点处的切线与直线垂直. (1) 求实数的值; (6分) (2) 求在(为自然对数的底数)上的最大值; (5分) (3) 对任意给定的正实数,曲线上是否存在两点,使得是以为直角顶点的直角三角形,且此三角形斜边中点在轴上? (5分) 2010~2011学年度第一学期期中考试高二数学试题(理科)参考答案一、填空题:本大题共14小题,每小题5分,共70分。
2010-2011学年第二学期七年级数学期中检测卷附答案

2010-2011学年度临沂市费县第二学期七年级期中学业水平检测数学试卷一、精心选一选(本大题共l0小题,每小题3分,共30分。
)1.下列说法中,正确的是()A.两条直线被第三条直线所截,同位角相等B.若a⊥b,b⊥c则a⊥cC.若a∥b,b∥c,则a∥cD.同旁内角相等,两直线平行2.如下图,AB∥CD,AE与CE相交于点E,∠l=25°、∠3=55°则∠2的度数是()A.90°B.80°C.100°D.50°3.直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠l=15.5°则下列结论不正确的是()A.∠2=45°B.∠1=∠3C.∠AOD与∠1互为补角D.∠l的余角等于75.5°4.横坐标是正数,纵坐标是负数的点在()A.第一象限B.第二象限C.第三象限D.第四象限5.如果点M在第二象限,且点M到Y轴的距离是4,到x轴的距离是3,则点M的坐标为()A.(4,3)B.(-4,3)C.(3,4)D.(一3,4)6.将点P(-4,3)先向左平移2个单位,再向下平移2个单位得到点P′,则点P′的坐标为()A.(-6,1)B.(-6,5)C.(-2,5)D.(一2,1)7.有两根长度分别为4cm,9cm的木棒,若想钉一个三角形木架,现有五根长度分别为3cm,6cm,11cm,12.9cm,13cm的木棒供选择,则选择的方法有()A.1种B.2种C.3种D.4种8.在四边形ABCD中,∠A,∠B;∠C,∠D的度数比为2:3:4:3,则∠D等于()A.90°B.75°C.60°D.120°9.已知等腰三角形一边长等于4,一边长等于9,它的周长是()A.17 B.22 C.17或22 D.13 10.如下图,AM是∆ABC的中线,∆ABC的面积为2a cm2,则∆AMC的面积为()A.4acm2 B.2acm2C.acm2 D.以上答案都不正确二、细心填一填(本大题共l0小题,每小题3分,共30分)把答案直接写在题中的横线上。
人教版数学八年级2010~2011学年度第一学期期中试卷(有答案)

2010~2011学年度第一学期期中试卷初 二 数 学亲爱的同学们:祝贺你完成了一个阶段的学习,现在是展示你的学习成果之时,你可以尽情地发挥,祝你成功!准备好了吗?开始吧!题号 一 二三总分19 20 21 22 23 24一、选择题(本大题有10小题,每小题3分,共30分)1.下面有4个汽车标志图案,其中是轴对称图形的是( )A .②③④B .①②③C .①②④D .①②④2、下列条件能证明两个三角形全等的是 ( )A 、有两条边对应相中等的两个三角形B 、有两个对应角相等的两个三角形C 、有三条边对应相等的两个三角形D 、有一个角和一条边对应相等的两个三角形 3、下列说法中正确的是( )A .4是16的算术平方根B .16的平方根是4C .±3是6的平方根D .—a 没有平方根4、点P (2,—3)关于y 轴的对称点的坐标是 ( )A 、(2,3 )B 、(-2,—3)C 、(—2,3)D 、(—3,2) 5、如图所示△ABC ≌△CDA ,并且AB=CD ,那么下列结论错误的是( )A 、∠1=∠2B 、CA=AC C 、∠D=∠BD 、AC=BC1221E CB AD6.如下图所示,在△ABC 中,AB=AC ,BC=6,点E 、F 是中线AD 上的两点,且AD=4,则图中阴影部分的面积为( )A .6B .12C .24D .37.如下图所示,直线ι1,ι2,ι3表示三条相互交叉公路,现要建一个货物中转站,求它到三条公路的距离相等,则可供选择的地址共有( )处.A .1B .4C .6D .78、如图,△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,则∠A 为( ) A .30° B .36° C .45° D .70°9、在△ABC 和△A 'B 'C '中有①AB =A 'B ',②BC =B 'C ',③AC =A 'C ',④∠A =∠A '⑤∠B =∠B ',⑥∠C =∠C ',则下列各组条件中不能保证△ABC ≌△A 'B 'C '的是 ( ) A .①②③ B .①②⑤ C .①②④D .②⑤⑥10、等腰三角形的一个内角为50°,则另外两个角的度数分别为( ) A . 65°,65° B . 50°,80° C .65°,65°或50°,80° D . 50°,50° 二、填空题(本大题有8小题,每小题3分,共24分)11.如图,△ABC ≌△ADE ,∠1=30°,则∠2=___________. 12.在Rt △ABC 中,∠C=90°,AB +BC=12㎝,∠A=30°,则AB= 。
2010—2011第一学期高二数学期中试题

2010——2011第一学期高二数学期中试题第I 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.已知a 、b 、c R ∈,下列命题中正确的是( ) A .22a b ac bc ⇒>>B . 22ac bc a b ⇒>>C . 3311a b a b⇒>< D . 22a b a b ⇒>> 2.若三点(3,1)A (2,)B b -,(8,11)C 在同一直线上,则实数b 等于 ( )A .2B .3|C .9D . 9-3.若,0ac bc >0<,则实数0ax by c ++=必不经过 ( )A .第一象限B .第二象限C .第三象限D .第四象限4.已知直线220x y +-=和10mx y -+=的夹角为4π,则m 的值为 ( ) A .133--或 B .133-或 C .133-或 D .133或 5.若直线(25)(2)40a x a y ++-+=与直线(2)(3)10a x a y -++-=互相垂直,则a 的值为 ( )A .2a =B .2a =-C .22a a ==-或D .2,0,2a =- 6.若(,)M x y 在直线210x y ++=上移动时, 则24x y +的最小值是 ( ) BBC. D.7.设x a ε-<,y a ε-<,则下列不等式中必成立的是 ( )A .x y ε+<B .x y ε-<C .2x y ε->D .x y ε-<2 8.直线240x y --=绕它与x 轴的交点逆时针方向旋转4π,所得直线方程为 ( )A .320x y --=B .360x y -+=C .360x y +-=D .20x y +-=9.点111(,)P x y 是直线:(,)0l f x y =上一点,直线l 外一点222(,)P x y ,则方程 1122(,)(,)(,)0f x y f x y f x y --=表示的直线是 ( )A .与l 重合B .过1P 与l 垂直C .过2P 与l 平行D .过2P 与l 相交10.若(,)P x y 在直线40x y +-=上,O 为原点,则OP 的最小值为 ( )AB.C .D .211.已知点(3,2)P 与点(1,4)Q 关于直线l 对称,则直线l 的方程为( )A .10x y -+=B .0x y -=C .10x y ++=D .0x y +=12.不等式组36020x y x y ++⎧⎨-+⎩≥<表示的平面区域是 ( )C .D .第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分)13.设0x ≠,则函数21()1y x x =+-在x = ________时,有最小值______________.14.不等式321x y -≤的解是_______________. 15.设z x y =-,式中变量x 和y 满足条件3020x y x y +-⎧⎨-⎩≥≥,则z 的最小值为 .16.光线从点(3,4)A -出发射到x 轴上,被x 反射到y 轴上,又被y 轴反射后到点(1,6)B -, 则光线所经过的路途长为 .三、解答题(本大题共6小题,共74分)17.(本小题满分12分)比较61x +与42x x +的大小,其中x R ∈.18.(本小题满分12分)已知直线l 满足下列两个条件:(1) 过直线1y x =-+和24y x =+的交点;(2) 与直线320x y -+=垂直,求直线l 的方程.19.(本小题满分12分) 解下列不等式 (1)322150x x x --> (2)22411372x x x x -+-+<20.(本小题满分12分)有两种物资(石油和粮食),可用轮船和飞机两种方式运输,每天每艘21.(本小题满分12分) 在ABC ▷中,BC 边上的高所在的直线方程为210x y -+=, A ∠的平分线所在的直线方程为0y =,若点B 的坐标为(1,2),求点A 和C 的坐标.22.(本小题满分14分) 已知等腰直角三角形的斜边所在的直线方程是320x y -+=,直角顶点142(,)55C ,求两条直角边所在的直线方程和此时三角形面积。
2010-2011学年度第二学期期中考试高二数学(文科)

2010/2011学年度第二学期期中考试高二数学(文科)出卷人: 许一鸣 审核人: 张丽本试卷分第I 卷和第II 卷两部分,共 160分,考试时间 120 分钟。
注意事项:第I 和Ⅱ卷答在答卷纸上,答题前考生务必将自己的班级、姓名、学号、考试号填写清楚。
第I 卷(共 70 分)一、填空题(每小题5 分,共70 分): 1.{}53)1(2-≤-=x x x A ,则A Z 的元素的个数2.已知A B ax x B A ⊆=-==且},01|{},2,1{,则实数a 的值为________ 3.函数12)32lg()(-++-=x x x f 的定义域是 4.已知f (x +1)=x 2+2x -1,则f (x )的解析式为5.已知命题2:,20p x R x ax a ∃∈++≤,则命题p 的否定是 6.写出“12lg <x 成立”的一个必要而不充分条件_________ 7.函数x x x f ln )(=的单调增区间为 8.下列各组函数)()(x g x f 与的图象相同的是①2)()(,)(x x g x x f == ②22)1()(,)(+==x x g x x f ③0)(,1)(x x g x f == ④⎩⎨⎧-==x x x g x x f )(|,|)( )0()0(<≥x x 9.设25abm ==,且112a b+=,则m = 10.幂函数y =(m 2-m -1)322--m m x ,当x ∈(0, +∞)时为减函数,则实数m 的值是11.若2()()x u f x e --=的最大值为m ,且f (x )为偶函数,则m +u =______12.方程223xx -+=的实数解的个数为13.已知关于x 的方程1+=ax x 有一个负根,但没有正根,则实数a 的取值范围是 14.函数f (x )=-x 2+4x -1在[t ,t +1]上的最大值为g (t ),则g (t )的最大值为_ _第II 卷(共 90 分)二、解答题(每小题 15分,共 90 分,解答应写出文字说明、证明过程或演算步骤) 15.}12|{2≤=-xxx A ,B ={}21,y y x x x R =++∈,全集为R ,密=★=ABCDMN P(1)求A ,B ;(2)求,R A B A C B ⋃⋂ 。
2010-2011下数学期中卷

2010-2011学年度第二学期初二级质量测试数学科试卷说明:本试卷满分100分,考试时间90分钟 一、选择题: (本大题共8小题, 每题3分, 共24分) 1、分式121+x 有意义,则x 的取值范围是( )A .21≠xB .21=x C .0≠xD .21-≠x2、下列命题的逆命题为真命题的是( )A .对顶角相等B .如果两个实数相等,那么它们的平方相等C .全等三角形的对应角相等D .线段垂直平分线上的点与线段的两端距离相等 3、若反比例函数22)12(--=mx m y 的图像在第二、四象限,则m 的值是( )A .1 B. -1 C. 1或-1 D.小于0.5 的任意实数4、五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )A B C D5、下列各式中正确的是( )A .1x y x y-+=-- B .x y x y 22)=( C .132--=÷a a a D .11x y x y=--+-6、在直线l 上依次摆放着七个正方形(如图所示)。
已知斜放置的三个正方形的面积 分别是1、2、3,正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4的值为( ) A .6 B .5 C .4 D .37、已知反比例函数)0(≠=k xky 的图象上有),(11y x 、),(22y x 两点,当1x <2x <0时,1y <2y ,则一次函数k kx y -=的图象不经过()A .第一象限B .第二象限C .第三象限D .第四象限8、如图是一个长4m ,宽3m ,高2m 的有盖仓库,在其内壁的A 处 (长的四等分)有一只壁虎,B 处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为( ) A .4.8 B .29 C .5 D .223+ 二、填空题(本大题共5小题, 每题3分, 共15分) 9、用科学记数法表示: 0.00002011= .10、当x _________时,分式242x x --的值是0.11、直角三角形两边长是3和4,则它的周长为 . 12、已知一次函数2+=x y 与反比例函数xky =的图象的一个交点为P (a ,b ),且P 到原点的距离是10,那么此反比例函数的解析式为 .13、如图,在x 轴的正半轴上依次截取OA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5,过点A 1、A 2、A 3、A 4、A 5分别作x 轴的垂线与反比例函数)0(2≠=x xy 的图象相交于点P 1、P 2、P 3、P 4、P 5,得直角三角形OP 1A 1、A 1P 2A 2、A 2P 3A 3、A 3P 4A 4、A 4P 5A 5,并设其面积分别为S 1、S 2、S 3、S 4、S 5,则S 5的值为 .三、解答题(每小题5分,共25分)ABl321S 4S 3S 2S 114、计算:42)13(3102+----⎪⎭⎫⎝⎛--15、先化简1121112-÷⎪⎭⎫⎝⎛+-+-+x x x x x x ,然后选取一个你喜欢的x 的值代入计算.16、解方程 :21321-=---x x x17、李先生参加了清华同方电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为1.2万元,交了首付之后每月付款y 元,x 月结清余款.y 与x 的函数关系如图所示,试根据图象提供的信息回答下列问题. (1)确定y 与x 的函数关系式,并求出首付款的数目;(2)如打算每月付款不超过500元,李先生至少几个月才能结清余款?18、“我国水资源形势非常严峻”,为了节约用水。
2010-2011学年第二学期八年级数学学科期中试卷(附答案)

(第11题图)FC DEBA 2010学年第二学期八年级数学学科期中试卷(附答案)(本试题满分100分,时间90分钟)一、填空题(本大题共14题,每题2分,满分28分)1.下列函数中:12)1(+=x y,11)2(+=xy ,xy -=)3(,是常数)、b k b kx y()4(+=,一次函数有 (填序号).2.已知直线x kx y +=是一次函数,则k 的取值范围是 . 3.直线42-=x y 的截距是 .4.已知函数1-3-x y =,y 随着x 的增大而 .5.若直线21y x =+向下平移n 个单位后,所得的直线在y 轴上的截距是3-,则n 的值是___________. 6.已知直线3+-=m x y 图像经过第一、三、四象限,则m 的取值范围是_________. 7.已知点A (a ,2),B (b ,4)在直线5-x y =上,则a 、b 的大小关系是a b .8.某市为鼓励市民节约用水和加强对节水的管理,制订了以下每月每户用水的收费标准:(1)用水量不超过83m 时,每立方米收费1元;(2)超出83m 时,在(1)的基础上,超过83m 的部分,每立方米收费2元.设某户一个月的用水量为x 3m ,应交水费y 元. 则当x >8时,y 关于x 的函数解析式是 . 9.八边形的内角和是 度.10. 已知□ABCD 中,已∠A :∠D =3:2,则∠C = 度.11.如图,AC 是□ABCD 的对角线,点E 、F 在AC 上,要使四边形BFDE 是平行 四边形,还需要增加的一个条件是 (只要填写一种情况). 12.菱形的两对角线长分别为10和24,则它的面积为 . 13.填空:CD BC AB ++ = .14.如图,正方形ABCD 中,E 在BC 上,BE =2,CE =1. 点P 在BD 上,则PE 与PC 的和的最小值为 .二、选择题(本大题共4题,每题3分,满分12分)15.已知直线3-x y =,在此直线上且位于x 轴的上方的点,它们的横坐标的取值范围是 ( )学校___________________班级_____________姓名________________学号___________请不要在装订线内答题请不要在装订线内答题请不要在装订线内答题(A )3≥x ; (B )3≤x ; (C )3>x ; (D )3<x . 16.已知一次函数的图像不经过三象限,则k 、b 的符号是 ( ) (A)k <0,b ≥0;(B)k <0,b ≤0 ;(C)k <0,b >0; (D)k <0,b <0.17.已知四边形ABCD 是平行四边形,下列结论中不正确的 ( ) (A )当AB=BC 时,它是菱形; (B )当AC ⊥BD 时,它是菱形; (C )当∠ABC =90︒时,它是矩形; (D )当AC=BD 时,它是正方形.18.如图,在矩形纸片ABCD 中,AB =3cm ,BC =4cm ,现将纸片折叠压平,使A 与C 重合,如果设折痕为EF ,那么重叠部分△AEF 的面积等于( ) (A )873; (B )875; (C )1673; (D )1675.三、解答题:(本大题共5题,每题6分,满分30分)19.已知一次函数b kx y +=的图像平行于直线x y 3-=,且经过点(2,-3). (1)求这个一次函数的解析式;(2)当y =6时,求x 的值.20.已知一次函数图像经过点A (-2,-2)、B (0,-4).(1) 求k 、b 的值;(2)求这个一次函数与两坐标轴所围成的面积.21.若直线221+=x y分别交x 轴、y 轴于A 、C 两点,点P 是该直线上在第一象限内的一点,PB ⊥x 轴,B 为垂足,且S ⊿ABC = 6.(1)求点B 和P 的坐标 .(2)过点B 画出直线BQ ∥AP ,交y 轴于点Q ,并直接写出点Q 的坐标.22.某人因需要经常去复印资料,甲复印社按A 4纸每10页2元计费,乙复印社则按A 4纸每10页1元计费,但需按月付一定数额的承包费. 两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题: (1)乙复印社要求客户每月支付的承包费是 元. (2)当每月复印 页时,两复印社实际收费相同. (3)如果每月复印页在250页左右时, 应选择哪一个复印社?请简单说明理由.23.已知:如图,在梯形A B C D 中,BC AD //,8==DC AB ,︒=∠60B ,12=BC .若F E 、分别是A B D C 、的中点,联结EF ,求线段EF 的长.装FEAB C DO (第24题图)A四、几何证明(本大题共3题, 6分+7分+7分,满分20分)24.已知:如图,矩形ABCD 的对角线AC 和BD 相交于点O , AC =2AB .求证:︒=∠120AOD .25.已知:如图,在⊿ABC 中,AB =AC ,D 、E 、F 分别是BC 、AB 、AC 边的中点.求证:四边形AEDF 是菱形.____请不要在装订线GF EDCBA(第26题图)PMDA26.已知:如图,点E 、G 在平行四边形ABCD 的边AD 上,EG =ED ,延长CE 到点F ,使得EF =EC . 求证:AF ∥BG .五、(本大题共1题,第1小题6分,第2小题4分,满分10分)27.已知:如图,矩形纸片ABCD 的边AD =3,CD =2,点P 是边CD 上的一个动点(不与点C 重合,把这张矩形纸片折叠,使点B 落在点P 的位置上,折痕交边AD 与点M ,折痕交边BC 于点N . (1)写出图中的全等三角形. 设CP =x ,AM =y ,写出y 与x 的函数关系式;(2)试判断∠BMP 是否可能等于90°. 如果可能,请求出此时CP 的长;如果不可能,请说明理由.八年级数学期中答案一、填空题(本大题共14题,每题2分,满分28分)1.(1),(3);2.1-m;>≠k;3.-4;4.减小;5.4;6.3 7.<;8.8y;9.1080°;10.108°;11.AE=CF等;=x2-12.120;13.AD;14.13.二、选择题(本大题共4题,每题3分,满分12分)15.C;16.A;17.D;18.D.三、简答题(本大题共5题,每题6分,满分30分)19.解: (1)由题意 k=-3 ………………………………………1′∴y=-3x+b 把点(2,-3)代入∴-3= -3×2+k ………………………………………1′ b=3 ………………………………………1′∴y=-3x+3 ………………………………………1′(2) 当y=6时-3x+3=6 ………………………………………1′ x =-1 ………………………………………1′ 20.解:(1)设y=kx+b(k≠0) ………………………………………1′ 把A(-2,-2),B(0,-4)代入⎩⎨⎧=-+-=-bb k 422 ………………………………………1′⎩⎨⎧-=-=41b k ………………………………1′+ 1′∴y=-x-4(2)一次函数与x 轴的交点坐标为(-4,0)一次函数与y 轴的交点坐标为(0,-4) ……………………1′ ∴S=21×4×4=8 ………………………………………1′21.解:(1)A (-4,0),C (0,2) ………………………………………1′由题意 设点P 的坐标为(221,+a a )且a >0∵PB ⊥x 轴∴B (a ,0) ∴AB=a +4 ∵S ⊿ABC =662)4(21=⨯+a ………………………………………1′∴a =2∴B(2,0),P(2,3) ……………………………………1′+1′ (2)图略; ………………………………………1′ )1,0(-Q ………………………………………1′ 22.(1) 18; ………………………………………2′(2) 150; ………………………………………2′ (3) 选择乙. ………………………………………1′ 当复印页超过150页时,乙的收费较低. …………………………1′23.解:过点D 作DE ∥AB,交BC 于点G (1)∵AD ∥BC, DE ∥AB∴四边形ABCD 为平行四边形 (平行四边形定义) ………………………1 ∴AD=BG,AB=DG (平行四边形对边相等) ………………………………1 ∵AB=DC=8 ∴DG=8 ∴DG=DC ∵∠B=60°∵∠DGC=∠B=60°∴⊿DGC 是等边三角形 ……………………………………1 ∴GC=8 ∵BC=12 ∴BG=4∴AD=4 ………………………………………1 ∵EF 分别是AB 、DC 的中点 ∴)(21BC AD EF+==8)124(21=+ (1)(梯形的中位线等于两底和的一半)24.证明:∵矩形ABCD∴︒=∠90ABC (矩形的四个角都是直角) (1)中ABC Rt ∆,AC =2AB∴︒=∠30ACB (1)∵AC =BD (矩形的对角线相等) ………………………………………1 ∴BO =BD21,CO =AC21∵AB =CD(矩形的对角线互相平分) (1)∴BO=CO ∴OCB OBC ∠=∠ …………………………………1 ∵︒=∠+∠+∠180OCB OBC BOC∴︒=∠120BOC (1)25.证明:⊿ABC 中,E 、D 分别是AB, BC 的中点∴ED =AC21(三角形的中位线等于第三边的一半) ………………1 同理 FD=AB21 (1)∵ AE=AB21,AF =AC21 (1)∴ AE=AF=ED=FD ....................................1 ∴ 四边形AEDF 是菱形 ....................................1 (四条边相等的四边形是菱形) (1)26.联结FG,FD,GC ………………………………1 ∵EG=ED,EF=EC∴四边形FGCD 是平行四边形 ………………………………1 (对角线互相平分的四边形是平行四边形)……………………………1 ∴FG ∥DC, FG = DC(平行四边形对边相等且平行) ………………………………1 同理AB ∥DC,AB=DC∴AB ∥FG,AB=FG ………………………………1 ∴四边形ABCD 是平行四边形 ………………………………1 (一组对边平行且相等的四边形是平行四边形)∴AF ∥BG (平行四边形的定义) ....................................1 27.(1) ⊿MBN ≌⊿MPN (1)∵⊿MBN ≌⊿MPN ∴MB=MP ,∴22MP MB = ∵矩形ABCD∴AD=CD (矩形的对边相等)∴∠A=∠D=90°(矩形四个内角都是直角) ………………………………1 ∵AD=3, CD=2, CP=x, AM=y∴DP=2-x, MD=3-y ………………………………1 Rt ⊿ABM 中,42222+=+=yAB AM MB同理 22222)2()3(x y PDMDMP-+-=+= (1)222)2()3(4x y y-+-=+ (1)∴6942+-=x xy (1)(3)︒=∠90BMP ………………………………1 当︒=∠90BMP 时,可证DMP ABM ∆≅∆ ………………………………1 ∴ AM=CP ,AB=DM∴1y (1)-=y3,2=∴1=xx (1)-,21=∴当CM=1时,︒BMP∠90=。
2010—2011学年度第二学期七年级数学期中试题(卷)

与很多的竞技项目不一样,高尔夫与其说是一场与他人的抗衡,更像是一次自己与自己的较量,它需要足够的耐心和专注,锻炼一个人独立思虑的能力,培育一个人踊跃进步的心态。
有人形容高尔夫的18 洞就仿佛人生,阻碍重重,崎岖不停。
但是一旦踏上了球场,你就一定集中注意力,独立面对照赛中可能出现的各样困难,而且肩负全部结果。
或许,经常还会碰到这样的状况:你刚才还在为抓到一个小鸟球而喝彩雀跃,下一刻狂风就把小白球吹跑了;或许你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而喜悦不已。
2010—2011 学年度第二学期七年级期中试题(卷)数学题号 A 卷 B 卷二三四共计29 30313233共计一得分评卷人得分A 卷(100 分)一、认真选,必定准。
(共30分,每题 3 分)1、已知同一平面内的三条直线l1,l 2, l 3,假如 l1⊥ l2, l2⊥ l 3那么 l1与 l3 的地点关系是();A 、订交B、垂直C、平行 D 、以上全不是A2、如图 1,已知 AB ⊥ CD 于 O,图中∠ 1 与∠ 2 的关系是();A 、相等B、互余C、互补 D 、没法确立EC 1D3、同一平面内的三条直线,其交点个数可能是()个;O2A、0,1B、0, 1,3 FC、 1, 2,3D、0, 1,2,3 B4、如图 2, AB ∥ CD ,AC ⊥ BC ,图中与∠ CAB 互余的角有(图 1 )个;A 、 1B 、 2C、 3 D 、 45、一辆汽车在笔挺的公路行驶,两次拐弯后,仍在本来的方向 A B上平行行驶,那么两次拐弯的角度可能是()A、先左转60 o,后右转 40oB、先左转60o,后右转 30oCDC、先左转60o,后右转 60oD、先左转60o,后右转 120o 图 26、点 P( -2, -3)在()A、第一象限B、第二象限C、第三象限D、第四象限7、把一个图形整体沿某一个方向挪动,会获得一个新图形,新图形与原图形的关系是()得分A、形状同样,大小不一样B、大小同样,形状不一样评卷人C、形状、大小都同样D、形状、大小都不一样8、一个三角形中,它的两边长分别是8和13,则第三边a的长可能是()A 、 4 B、 5 C、 20 D、 219、在△ ABC 中,∠ A=1∠B=1∠C,则△ ABC 是()2 3A 、锐角三角形B 、直角三角形 C、钝角三角形 D 、没法确立10、若一个多边形的每一个外角为20o,则这个多边形的边数是()A 、 9 B、 10 C、 17 D、 18二、专心填,我会填。
20102011学年度第二学期高二数学期中考试(理科)

2010/2011学年度第二学期期中考试高二年级数学(理科)试卷命题人:宋钢 复核人:宋钢一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题..卷.相应位置上....... 1.设i 是虚数单位,则复数32ii-+的实部为 ▲ 2. 已知11111065mA =⨯⨯⨯⨯ ,则m = ▲ .3. 6人排成一排,则甲不站在排头的排法有 ▲ 种.(用数字作答).4. 曲线1y x =-在点1(,2)2-处的切线斜率为___ ▲_____,切线方程为____ ▲______. 5.有2个红球、4个黄球,同色球不加以区分,将这6个球排成一列有__▲__种不同的方法(用数字作答).6.对,,a b R a b +∈+≥-------大前提1x x +≥ ------小前提 所以12,x x+≥ -------结 论 以上推理过程中的错误为 ▲ (1) 大前提 (2) 小前提 (3)结论 (4)无错误 7. 函数()f x 的定义域为开区间(,)a b ,导函数()f x '在(,a 的图象如图所示,则函数)(x f 在开区间),(b a8. 已知复数z 满足11z i --=,则z 的最小值是 ▲9. 已知函数()x f 的导函数为()x f ',且满足()()2'232xf x x f +=,则()=5'f ▲10. 若把英语单词“good ”的字母顺序写错了,则可能出现的错误共有 ▲ 种.(用数字作答). 11.利用数学归纳法证明“*),12(312)()2)(1(N n n n n n n n∈-⨯⋅⋅⋅⨯⨯⨯=+⋅⋅⋅++ ”时,从假设k n =推证1+=k n 成立时,左边应增乘的因式是___ ▲12. 已知函数32()39f x x x x a =-+++(a 为常数),在区间[2,2]-上有最大值20,那么此函数在区间[2,2]-上的最小值为 ▲13. )(),(x g x f 分别是定义在R 上的奇函数和偶函数,当0x >时,()()()()0f x g x f x gx ''+<且(2)0f =则不等式0)()(<x g x f 的解集为 ▲14. 已知1()sin ,[0,π]3f x x x x =-∈.01cos 3x =(0[0,π]x ∈),下面命题中真命题的序号是 ▲ . ①()f x 的最大值为0()f x ② ()f x 的最小值为0()f x ③()f x 在0[0,]x 上是减函数 ④ ()f x 在0[,π]x 上是减函数 二、解答题:本大题共6小题,共计90分.15. 已知R m ∈,复数Z=i )1m ()1m (m -+-当m 为何值时, (1)Z ∈R; (2)Z 是虚数; (3)Z 是纯虚数; 16. 已知a 为实数,))(4()(2a x x x f --=。
2010~2011学年度七年级下学期数学期中考试题
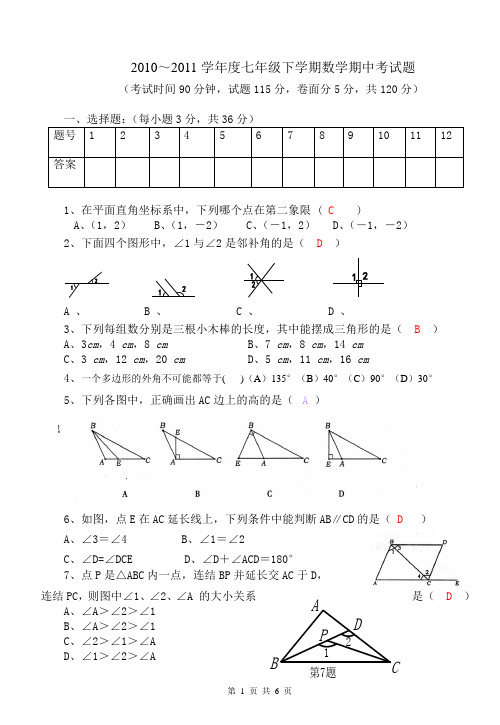
2010~2011学年度七年级下学期数学期中考试题(考试时间90分钟,试题115分,卷面分5分,共120分)一、选择题:(每小题3分,共36分) 题号 1 2 3 4 5 6 7 8 9 10 11 12答案1、在平面直角坐标系中,下列哪个点在第二象限 ( C ) A 、(1,2) B 、(1,-2) C 、(-1,2) D 、(―1,―2)2、下面四个图形中,∠1与∠2是邻补角的是( D )1221 2121A 、B 、C 、D 、3、下列每组数分别是三根小木棒的长度,其中能摆成三角形的是( B ) A 、3cm ,4 cm ,8 cm B 、7 cm ,8 cm ,14 cm C、3 cm ,12 cm ,20 cm D 、5 cm ,11 cm ,16 cm4、一个多边形的外角不可能都等于( )(A )135°(B )40°(C )90°(D )30°5、下列各图中,正确画出AC 边上的高的是( A )6、如图,点E 在AC 延长线上,下列条件中能判断AB ∥CD 的是( D ) A 、∠3=∠4B 、∠1=∠2C 、∠D=∠DCED 、∠D+∠ACD=180°7、点P 是△ABC 内一点,连结BP 并延长交AC 于D , 连结PC ,则图中∠1、∠2、∠A 的大小关系是( D )A 、∠A >∠2>∠1B 、∠A >∠2>∠1C 、∠2>∠1>∠AD 、∠1>∠2>∠AA BCDP12第7题8、在△ABC 中,∠A:∠B:∠C=1:2:3,则这个三角形是( B ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形9、只用下列正多边形地砖中的一种,能够进行平面镶嵌的是( C )A 、正十边形B 、正八边形C 、正六边形D 、正五边形 10、下列语句中,假命题的是( D )A 、如果A(a ,b)在x 轴上,那么B (b ,a )在y 轴上 B 、如果直线a 、b 、c 满足a ∥b ,b ∥c 那么a ∥cC 、两直线平行,同旁内角互补D 、相等的两个角是对顶角 11、如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( D )A、150° B、140° C、130° D、120°12、如图所示,在△ABC 中,CD 、BEBD 为角平分线,并且CD 、BE 交于点P ,若∠A=40°,则 ∠BPC 等于( C )A 、90°B 、130°C 、110°D 、150° 二、填空题:(每小题3分,共18分)13、已知点P 的坐标为(2 ,3),则点P 到y 轴的距离为___2______.14、若等腰三角形的两边长为6cm 和2cm ,则它的周长为 14 cm.15、如图是小刚画的一张脸,他对妹妹说“如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成 (2,1)1234123428EBDAO16题CDEABC15题18题_P_B_ C_A_E_ D16、如图,已知直线AB CD ,相交于点O , O E A B⊥,28EOC ∠= ,则A O D ∠= 62 度.17、在平面直角坐标系内,把点P (-5,-2)先向左平移3个单位长度,再向上平移2个单位 长度后得到的点的坐标是 _____ (-8,0)_______. 18、如图,∠A +∠B+∠C+∠D+∠E = 180 度.三、解答题:(共61分)19、(6分)如图,已知∠1=∠2,∠3=108°, 求∠4的度数. 7220、(8分)请你在右图中建立直角坐标系,使汽车站的坐标是(3,1),并用坐标 说明儿童公园、医院和学校的位置.21、(8分)如图,AF 是△ABC 的高,AD 是△ABC 的角平分线,且∠B =36°,∠C =76°,求∠DAF 的度数。
2010——2011学年度第二学期期中调研测试高二数学(文)

2010——2011学年度第二学期期中调研测试高二数学(文)时间:120分钟 分值:160分一、填空题:本大题共14小题,每小题5分,共70分.1.已知集合{}41<≤=x x A ,),(+∞=a B ,且B C A R ⊆,则实数a 的取值范围是 ▲ 2. 已知命题“若0<m ,则方程02=++m x x 有实根”,则原命题、逆命题、否命题、逆否命题、命题的否定这五个命题中,正确的个数是 ▲ 。
3. 已知一辆轿车在公路上作加速直线运动,设ts 时的速度为3)(2+=t t v )/(s m ,则s t 3=时轿车的瞬时加速度为 ▲ .4. 下列命题 :①2x x x ∀∈,≥R ;②2x x x ∃∈,≥R ; ③43≥;④“21x ≠”的充要条件是“1x ≠,或1x ≠-”. 中,其中正确命题的序号是 ▲ 5.2log 0x =的根的个数为 ▲ . 6. 函数x x x f ln )(-=的单调减区间是 ▲7. 已知f ( x ) = 2(5)0log ()f x x x x ->⎧⎨-≤⎩, 则f ( 2011 ) 等于 ▲ .8. 若372log πlog 6log 0.8a b c ===,,,则从小到大的顺序为 ▲9.若存在[]3,1∈a ,使得不等式02)2(2>--+x a ax 成立,则实数x 的取值范围是 ▲ 10. 已知f (x )是以2为周期的偶函数,且当x ∈[0,1]时,f (x )=x ,若在区间[-1,3]内,函数f (x )=kx +k +1(k ∈R 且k ≠1)有4个零点,则k 的取值范围是 ▲ .11. 给出定义:若函数()f x 在D 上可导,即()f x '存在,且导函数()f x '在D 上也可导,则称()f x 在D 上存在二阶导函数,记()()()f x f x ''''=,若()0f x ''<在D 上恒成立,则称()f x 在D 上为凸函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京交通大学 2010- 2011 学年第二学期《概率论与数理统计》期中试题答案学院 年级 学号 姓名 成绩附表:()()1.960.975, 1.6450.95Φ=Φ=,(1)0.8413,Φ=(2)0.9972Φ=.一、(6分)设1.0)(=A P ,9.0)|(=A B P ,2.0)|(=A B P ,则(|)P A B =? 解:31; (6分)二、(12分)甲、乙、丙三人独立的向同一飞行目标各射击一次,击中的概率分别为0.4,0.5,0.7。
如果只有一人击中,则目标被击落的概率为0.2;如果有两人击中,则目标被击落的概率为0.6,如果三人都击中,则目标一定被击落,求目标被击落的概率。
解:设A 表示“目标被击落”,321,,B B B 依次表示“甲、乙、丙击中目标”,i C 表示“有i 个人击中目标”,i =1,2,3。
则有题设有:7.0)(,5.0)(,4.0)(321===B P B P B P3213213211B B B B B B B B B C =)()()()(3213213211B B B P B B B P B B B P C P ++=)()()()()()()()()(321321321B P B P B P B P B P B P B P B P B P ++=36.07.05.06.03.05.06.03.05.04.0=⨯⨯+⨯⨯+⨯⨯=3213213212B B B B B B B B B C = 同理 41.0)(2=C P3213B B B C = 14.0)(3=C P由全概率公式得:∑==30)|()()(i i i C A P C P A P ………………………+2458.0114.06.041.02.036.0=⨯+⨯+⨯= …………+10三、(12分)在电报通讯中,发射端发送“点”与“划”两种信号分别占60%与40%。
由于随机干扰,接受端可能收到“点”,“划”与“不清”三种结果。
假定发射“点”时,收到“点”“划”与“不清”的概率依次是0.7, 0.1 与0.2;而发射“划”时,收到上述三种结果的概率相应为0, 0.9 与0.1。
(1)求接收端收到“点”的概率;(2)若已知接受结果为“不清”时,求发射端发出的信号为“点”的概率。
解:假设 A={接收端收到“点”},1B ={发射端发送“点”},2B ={发射端发送“划”} (1) 由全概率公式,可得∑==21)|()()(i i i B A P B P A P ……………..2分由题意可知,,4.0)(,6.0)(21==B P B P,0)|(,7.0)|(21==B A P B A P ……………..2分将这些代入上面的全概率公式知所求的概率为.42.0)(=A P ……………..2分(2) 假设C={接受结果为“不清”},则由Bayes 公式可得所求概率75.04.01.06.02.06.02.0)()|()()|()()|()|(2211111=⨯+⨯⨯=+=B P BC P B P B C P B P B C P C B P …………..3分……………3分四、(6分)已知盒子里有10张卡片,上面分别标有号码(1号~10号),从中抽取5次,每次随机地取一张,观察其上的号码后放回。
设X 表示观察到奇数号码的次数,则随机变量X 服从什么分布(指出其参数)?解:()5,0.5b ;……………6分五、(10分)设随机变量X 服从标准正态分布。
(1)写出X 的概率密度)(x f X ;(2)随机变量⎪⎩⎪⎨⎧≤<-<≤-≤≤-=其它或,32112,211,1X X X Z , 求Z 的分布律。
解:(1) 2221)(x Xe xf -=π,∞<<∞-x …………2分(2) 9972.0)2(,8413.0)1(=Φ=Φ0056.03118.06826.01}2{}1{1}3{3118.0)8413.09972.0(2)]1()2([2}21{}12{}2{6826.018413.021)1(2)1()1(}11{}1{=--==-=-===-⨯=Φ-Φ=≤<+-<≤-===-⨯=-Φ=-Φ-Φ=≤≤-==Z P Z P Z P X P X P Z P X P Z P 0056.03118.06826.0|32 1|P Z ……………8分六、(12分)设随机变量X 的分布函数()0,0,011,1x F x x x x <⎧⎪=≤<⎨⎪≥⎩。
(1)写出X 的密度函数; (2)求 2ln Y X =-的密度函数。
解:(1)X 的密度函数为()1,010,x f x <<⎧=⎨⎩其他.........(2分)(2)解一:2ln y x =- 的可取值范围是()0,+∞由 2ln y x =- 得 20y x'=-<故 2ln y x =- 在 ()0,1 上严格单减 ......(2分) 其反函数()12y x h y e-== ,且 ()1212y h y e -'=- .........(4分)所以 2ln y x =- 的密度函数11221,0()20,y y X Y f e e y f y --⎧⎛⎫->⎪ ⎪=⎨⎝⎭⎪⎩其他21,020,0yey y -⎧>⎪=⎨⎪≤⎩.........(4分)解二:先求2ln y x =- 的分布函数()Y F y 当0y ≤时, ()0Y F y =;当0y >时, ()()()2ln Y F y P Y y P X y =≤=-≤2y P X e -⎛⎫=≥ ⎪⎝⎭ ......(4分)21yP X e -⎛⎫=-≤ ⎪⎝⎭21y F e -⎛⎫=- ⎪⎝⎭......(2分)因此,2ln y x =- 的密度函数()21,0()20,0y Y Y e y f y F y y -⎧>⎪'==⎨⎪≤⎩......(4分)七、(8分) 某箱装100件产品,其中一、二和三等品分别为80,10和10件。
现从中随机取一件,定义三个随机变量123,,X X X 如下:⎩⎨⎧=其它等品抽到,0,1i X i , 1,2,3i =。
试求:(1) 随机变量1X 与2X 的联合分布律;(2)1X 与2X 的边缘分布律。
解:∵()1~1,0.8X B , ()2~1,0.1X B 则 ()12,X X 的联合分布律为……………6分写出两个边缘分布律……………2分八、(12分)设二维随机变量 (X,Y) 在 D={(x,y) | 1≤ x ≤ 3, 1≤ y≤ x } 上服从均匀分布。
(1) 求(X,Y) 的联合密度f(x,y); (2) 求Z=X+Y 密度函数。
解:(1) D 的面积m(D) = 2, 所以, (X,Y) 的联合密度f(x,y)=⎪⎩⎪⎨⎧∈.0,),(21其它D y x (2)(2) ()(),ZX f z f x z x dx +∞-∞=-⎰ -(或另一个公式)----2分非零区域131x z x x ≤≤⎧⎨≤-≤⎩131x x z x≤≤⎧⇒⎨+≤≤⎩------4分当24z ≤<时,()1212z zZ f z dx -=⎰142z =- 当46z ≤≤时,()3212z Z f z dx =⎰ 342z =-+其它,()0Zf z = -()1,24423,46420,Z z z z f z z ⎧-≤<⎪⎪⎪∴=-+≤≤⎨⎪⎪⎪⎩其它………+4九、(8分)已知随机变量X 和Y 的联合密度函数为⎩⎨⎧<≤<≤=. ,0 10,10 ,4),(其他,y x xy y x f求条件概率)21|43(=>Y X P 。
解:⎩⎨⎧<≤=. ,0 10 ,2)(其他,y y y f Y ----------2分10,2)(),()|(,0)(,10|<≤==><<x x y f y x f y x f y f y Y Y X Y -----3分,16/72)21|43(14/3===>⎰xdx Y X P ----------3分。
十、(14分)设随机向量(X,Y)的联合密度f(x, y)为⎪⎩⎪⎨⎧∞<<-∞<<+=. ,0 ,10 ,)1(),(2其他,y x y A y x f π (1) 确定常数A ;(2) 求X ,Y 的边缘密度f X (x),f Y (y),并判断X 与Y 是否相互独立;(3)计算⎪⎪⎭⎫⎝⎛>33),min(Y X P 。
解:(1).1),(2=⎰⎰dxdy y x f R.1111)1(21021=⇒==+=+⎰⎰⎰⎰∞+∞-∞+∞-A Ady y dx A dxdy y A ππππ ……………………………(+4)(2) dyy x f x f X ⎰∞∞-=),()(.0)(10.1 )1(1)(102=≥≤=+=<<⎰∞+∞-x f x x dy y x f x X X 时,或当时,当π⎩⎨⎧<<=.,0,10,1)(其他x x f X……………………………(+2)dxy x f y f Y ⎰∞∞-=),()(.,)1(1)1(1)(2102+∞<<-∞+=+=⎰y y dx y y f Y ππ ……………………………(+2)因为,..),()(),(e a y f x f y x f Y X =所以X 与Y 相互独立.……………………………(+2)(3) 因为X 与Y 相互独立,⎪⎭⎫ ⎝⎛>⎪⎭⎫ ⎝⎛>=⎪⎭⎫ ⎝⎛>>=⎪⎭⎫ ⎝⎛>333333,3333),min(Y P X P Y X P Y X P .933621331)1(1332133-=⎪⎭⎫ ⎝⎛-⋅⋅⎪⎭⎫ ⎝⎛-=+=⎰⎰∞+ππππdy y dx ……………………………(+4)。
