广东省实验中学2017届高三10月月考数学(文)试题(附答案)$749416
广东省实验中学2017届高三10月月考数学(理)试题(附答案)$749415

2016-2017学年高三级上学期10月月考理科数学2016年10月本试卷共4页,满分150分,考试时间120分钟。
注意事项:略第Ⅰ卷(选择题部分,共60分)一、选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合2{230},{ln(2)}A x x x B x y x =--≤==-,则AB =( )A .(1,3)B .(1,3]C .[1,2)-D .(1,2)- 2.若复数43(cos )(sin )55z i θθ=-+-是纯虚数(i 为虚数单位),则tan ()4πθ-的值为( )A .7-B .17- C .7D .7-或17-3.下列命题中, 是真命题的是( ) A .00,0x x R e∃∈≤B .2,2xx R x ∀∈>C .已知,a b 为实数, 则0a b +=的充要条件是1ab=- D .已知,a b 为实数, 则1,1a b >>是1ab >的充分条件4.在各项均为正数的等比数列{}n a 中,12,a =且245,2,a a a +成等差数列,记S n 是数列{a n }的前n 项和,则5S = ( )A .32B .62C .27D .81 5.已知函数()sin()(0,)2f x x πωϕωϕ=+><的最小正周期为π,且其图像向左平移3π个单位后得到函数()cos g x x ω=的图像,则函数()f x 的图像( ) A .关于直线12x π=对称 B .关于直线512x π=对称 C .关于点(,0)12π对称 D .关于点5(,0)12π对称6.甲、乙、丙、丁、戊五位同学站成一排照相留念,则在甲乙相邻的条件下,甲丙也相邻的概率为( )A .110B .23C .13D .147.已知定义在R 上的函数()f x 满足()()f x f x -=-,(1)(1)f x f x +=-,且当[0,1]x ∈ 时,2()log (1f x x =+),则(31)f = ( ) A .0 B .1 C . 1- D .2 8.若如下框图所给的程序运行结果为S =41,则图中的判断框①中应填入的是( ) A .6?i >B .6?i ≤C .5?i >D .5?i <9.设12,F F 为椭圆22195x y +=的两个焦点,点P 在椭圆上,若线段1PF 的中点在y 轴上,则21PF PF 的值为( ) A .514B .513C .49D .5910.已知变量,x y 满足48050,10x y x y y +-+--⎧⎪⎨⎪⎩≥≤≥若目标函数(0)z ax y a =+>取到最大值6,则a 的值为( )A .2B .54 C .524或 D .2- 11.如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某 多面体的三视图,则该多面体外接球的表面积为( ) A .8π B .252πC .12πD .414π12.定义在区间(0,+∞)上的函数f (x)使不等式)(3)()(2'x f x xf x f <<恒成立,其中)('x f 为f (x)的导数,则( ) A .8<(2)(1)f f <16 B .4<(2)(1)f f <8 C .3<(2)(1)f f <4 D .2<(2)(1)f f<3第Ⅱ卷(非选择题部分,共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答,第22题~第23题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.已知03sin m xdx π=⎰,则二项式(23)m a b c +-的展开式中23m ab c -的系数为 .14.在Rt △ABC 中,∠A =90°,AB =AC =2,点D 为AC 中点,点E 满足13BE BC =,则A E B D ⋅= .15.已知双曲线22221(0,0)y x a b a b-=>>的渐近线被圆22650x y x +-+=截得的弦长为2,则该双曲线的离心率为 .16.函数()|cos |(0)f x x x =≥的图象与过原点的直线恰有四个交点,设四个交点中横坐标最大值为θ,则2(1)sin 2θθθ+= .三、解答题:解答应写出文字说明,证明过程和演算步骤.17.(本小题满分12分)已知A 、B 、C 、D 为同一平面上的四个点,且满足2AB =,1BC CD DA ===,设BAD θ∠=,ABD ∆的面积为S ,BCD ∆的面积为T .(1)当3πθ=时,求T 的值;(2)当S T =时,求cos θ的值;18.(本小题满分12分)生产甲乙两种元件,其质量按检测指标划分为:指标大于或者等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:(1)试分别估计元件甲、乙为正品的概率;(2)生产一件元件甲,若是正品可盈利40元,若是次品则亏损5元;生产一件元件乙,若是正品可盈利50元,若是次品则亏损10元。
广东省广州市广东实验中学2024-2025学年高三上学期10月月考数学试卷

广东省广州市广东实验中学2024-2025学年高三上学期10月月考数学试卷一、单选题1.已知集合{}A xx a =<∣,{21}B x x =-<<∣,且R R A B ⋃=ð,则a 的取值范围是( ) A .[)1,+∞ B .()1,∞+ C .[]2,1- D .()2,-+∞2.如图,O A B '''V 是水平放置的OAB △用斜二测画法画出的直观图(图中虚线分别与x '轴和y '轴平行),26O B O D '=''=',8O C ''=,则OAB △的面积为( )A.B.C .24 D .483.设满足一元线性回归模型的两个变量的n 对样本数据为()()()1122,,,,,,n n x y x y x y L ,下列统计量中不能..刻画数据与直线y bx a =+的“整体接近程度”的是( ) A .()1ni i i y bx a =-+∑B.1ni =C .()()21ni i i y bx a =-+∑D .1ni y bx a =-+4.已知a 、b 为异面直线,则下列命题正确的是( )A .过直线a 、b 外一点P 一定可以作一条与a 、b 都平行的直线B .过直线a 、b 外一点P 一定可以作一个与a 、b 都平行的平面C .过直线a 一定可以作一个与直线b 平行的平面D .过直线a 一定可以作一个与直线b 垂直的平面 5.已知π33π5πsin ,4544x x ⎛⎫+=-<< ⎪⎝⎭,则sin 1tan x x =-( ) A .21100 B .21100-CD .6.已知椭圆C 的方程为()222210+=>>x y a b a b ,焦距为2c ,直线y=与椭圆交于A ,B两点,2AB c =,则椭圆C 的离心率为( ) A .34BCD7.已知等差数列{}n a 的前n 项和为n S ,若150S >,160S <,则21a a 的取值范围是( ) A .67,78⎛⎫ ⎪⎝⎭B .613,715⎛⎫⎪⎝⎭C .67,,78⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭UD .613,,715⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭U8.我国古代数学家李冶在其著作《测圆海镜》中系统地介绍了天元术,即利用未知数列方程的一般方法,与现代数学中列方程的方法基本一致.先“立天元一为……”,相当于“设x 为……”,再根据问题给出的条件列出两个相等的代数式,最后通过合并同类项得到方程 10110n n n n a x a x a x a --++++=L .设1011()n n n n f x a x a x a x a --=++++L若1(2)5238n f n +=⋅--,则(1)f =( ) A .2342n n+B .231142n n ++C .23542n n ++D .23742n n ++二、多选题9.设A ,B 为一个随机试验中的两个事件,且1()3P B =,5(|)6P B A =,1(|)2P B A =,则( )A .()34P A B +=B .()13P A =C .3(|)4P A B =D .()16P AB =10.已知等比数列 a n 的公比为q ,前n 项和为n S ,若11S =-且N n +∀∈,2n n a a +>,则( )A .20a >B .01q <<C .1n n a a +>D .11n S q <- 11.如图,在直三棱柱111ABC A B C -中,90ACB ∠=o ,12AC BC CC ===,E 为11B C 的中点,过AE 的截面与棱1BB 、11AC 分别交于点F 、G ,则下列说法中正确的是( )A .存在点F ,使得1A F AE ⊥B .线段1C G 长度的取值范围是 0,1C .当点F 与点B 重合时,四棱锥C AFEG -的体积为2D .设截面FEGA 、AEG △、AEF △的面积分别为1S 、2S 、3S ,则2123S S S的最小值为三、填空题12.二项式523x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为.13.设直线l 与球O 有且只有一个公共点,从直线l 出发的两个半平面α,β截球O 的两个截面圆的半径分别为1和3,二面角l αβ--的平面角为3π,则球O 的半径为. 14.已知函数()sin 1f x x x =-+,若关于x 的不等式()()e e 22x xf ax f a x +--+>的解集中有且仅有2个正整数,则实数a 的取值范围为.四、解答题15.在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c ,已知()()1tan 1tan 2A B --=,3b =,a (1)求C 的值;(2)延长AB 到D 点,使得CDB ACB ∠=∠,求BD 的长度 16.已知函数()()2f x x x c =-,R x ∈,c 是常数.(1)若()f x 在2,3⎡⎫+∞⎪⎢⎣⎭存在单调递减区间,求c 的取值范围.(2)若函数()y f x =在2x =处有极大值,求c 的值.17.如图,三棱台1111,,ABC A B C AB BC AC BB -⊥⊥,平面11ABB A ⊥平面,6ABC AB =,114,2,BC BB AC ==与1AC 相交于点,2D AE EB =u u u r u u u r,且//DE 平面11BCC B .(1)求三棱锥111C A B C -的体积;(2)平面11A B C 与平面ABC 所成角为1,CC α与平面11A B C 所成角为β,求αβ+的值. 18.已知抛物线2:4,,,W x y A B C =是W 上不同的三点,过三点的三条切线分别两两交于点,,A B C ''',则称三角形A B C '''为抛物线的外切三角形.(1)当点C 的坐标为()2,1,B 为坐标原点,且BA BC =时,求点B '的坐标;(2)设外切三角形A B C '''的垂心为H ,试判断H 是否在定直线上,若是,求出该定直线;若不是,请说明理由;(3)证明:三角形ABC 与外切三角形A B C '''的面积之比为定值.19.给定正整数3N ≥,已知项数为m 且无重复项的数对序列A :()()()1122,,,,,,m m x y x y x y ⋅⋅⋅满足如下三个性质:①{},1,2,,i i x y N ∈⋅⋅⋅,且()1,2,i i x y i m ≠=⋅⋅⋅;②()11,2,,1i i x y i m +==⋅⋅⋅-;③(),p q 与(),q p 不同时在数对序列A 中.(1)当3N =,3m =时,写出所有满足11x =的数对序列A ;(2)当6N =时,证明:13m ≤;(3)当N 为奇数时,记m 的最大值为()T N ,求()T N .。
广东省实验中学高三上学期11月月考——数学文数学文

广东省实验中学 2017届高三上学期11月月考数学(文)试题本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟.第I 卷(选择题)一、选择题:.本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若,则( )A .B .C .D . 2.若集合,,则“”是“”的( ) A .充分不必要条件. B .必要不充分条件. C .充要条件. D .既不充分也不必要条件.3.已知则的值为( )A .B .C .D .4.如图,程序框图所进行的求和运算是( ) A .12 + 14 + 16 + … + 120B .1 + 13 + 15 + … + 119C .1 + 12 + 14 + … + 118D .12 + 12 2 + 12 3 + … + 12105.如图一个空间几何体的正视图,侧视图,俯视图是全等的等腰直角三角形,且直角边的边长为1,则这个几何体体积为 ( ) A . B . C . D .6.曲线处的切线方程为在e x xxx f ==ln )(( ) A . B . C . D .7.在平面直角坐标系中, 不等式组⎩⎪⎨⎪⎧x +y≥0x -y +4≥0x≤a (a 为常数)表示的平面区域面积是9, 那么实数a 的值为( )A .32+2B .-32+2C .-5D .18.一组数据中每个数据都减去构成一组新数据,则这组新数据的平均数是,方差是,则原来一组数的方差为( ).3.24.4 4.85.69.已知5,4,120a b a b θ===与夹角,则向量在向量上的投影为( ) A . B . C . D .10.直线与平行,则的值为 ( )A .B .或C .0D .-2或011.已知双曲线的左焦点为F 1,左、右顶点为A 1、A 2,P 为双曲线上任意一点,则分别以线段PF 1,A 1A 2为直径的两个圆的位置关系为( )A .相交B .相切C .相离D .以上情况都有可能12.三位同学合作学习,对问题“已知不等式对于恒成立,求的取值范围”提出了各自的解题思路. 甲说:“可视为变量,为常量来分析”. 乙说:“寻找与的关系,再作分析”. 丙说:“把字母单独放在一边,再作分析”.参考上述思路,或自已的其它解法,可求出实数的取值范围是( )第Ⅱ卷(非选择题)二、填空题:本大题共4小题,每小题5分,满分20分.13.若函数'2'()ln (1)32,(1)f x x f x x f =-++=则 .14.等比数列中,若,,那么等于________15.设正数满足,若不等式对任意的成立,则正实数的取值范围是_____________16.在计算“1223(1)n n ⨯+⨯+⋅⋅⋅++”时,某同学学到了如下一种方法:先改写第k 项:1(1)[(1)(2)(1)(1)],3k k k k k k k k +=++--+由此得 112(123012),3⨯=⨯⨯-⨯⨯123(234123),3⨯=⨯⨯-⨯⨯…1(1)[(1)(2)(1)(1)].3n n n n n n n n +=++--+相加,得11223(1)(1)(2).3n n n n n ⨯+⨯+⋅⋅⋅++=++类比上述方法,请你计算“123234(1)(2)n n n ⨯⨯+⨯⨯+⋅⋅⋅+++”,其结果为 .三、解答题:本大题共5小题,共60分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题12分)设有关于的一元二次方程.(Ⅰ)若是从四个数中任取的一个数,是从三个数中任取的一个数,求上述方程有实根的概率. (Ⅱ)若是从区间任取的一个数,是从区间任取的一个数,求上述方程有实根的概率. 18.(本小题满分12分) 已知,.(1)若,且,求的值; (2)设,求的周期及单调减区间.19 (本小题12分)如图,矩形中,,,为上的点,且. (Ⅰ)求证:; (Ⅱ)求证;; (Ⅲ)求三棱锥的体积.20.(本小题满分12分)已知椭圆的中心在原点,焦点在轴上,直线与交于两点,,且. (Ⅰ)求椭圆的方程;(Ⅱ)若是椭圆上两点,满足,求的最小值.21.(本小题满分14分)给定实数(),设函数)ln()21(2)(a x a x x f +-+= (>,),的导数的图像为,关于直线对称的图像记为.(Ⅰ)求函数的单调区间;(Ⅱ)对于所有整数(),与是否存在纵坐标和横坐标都是整数的公共点?若存在,请求出公共点的坐标;若不若存在,请说明理由.选做题:请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4-4:坐标系与参数方程选讲在平面直角坐标系中,已知曲线的参数方程为2cos (x y θθθ=⎧⎪⎨=⎪⎩为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,直线过极坐标系内的两点和. (1)写出曲线和直线的直角坐标系中的普通方程; (2)若是曲线上任意一点,求面积的最小值.23.(本小题满分10分)选修4-5:不等式选讲已知关于的不等式的解集为.(1)求,的值; (2)若,求的最小值.2017年广东实验中学文科数学11月月考试卷本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟.第I 卷(选择题)一、选择题:.本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
2017届广东省高三上学期第一次月考文科数学试卷(解析版)

高三上学期第一次月考文科数学试卷一、单选题(共12小题)1.设全集,集合,,则()A. B. C.D.考点:集合的运算答案:B试题解析:。
故答案为:B2.已知函数,如果,且,则它的图象可以是()A.B.C.D.考点:函数图象答案:D试题解析:由a>b>c,a+b+c=0知a>0,c<0,因而图象开口向上,又f(0)=c<0,故D项符合要求.故答案为:D3.已知命题,命题q:,则下列命题是真命题的是()A.B.C.D.考点:命题及其关系答案:B试题解析:由方程x2+ax-4=0得,Δ=a2-4×(-4)=a2+16>0,所以命题p为真命题.当x=0时,20=30=1,所以命题q为假命题,所以为假命题,为真命题,为假命题,为假命题.故答案为:B4.下图是谈校长某日晨练时所走的离家距离(y)与行走时间(x)之间的函数关系的图像.若用黑点表示谈校长家的位置,则谈校长散步行走的路线可能是()A.B.C.D.考点:三角函数图像变换答案:D试题解析:因为中间有一段与家的距离不变,所以有一段路线是圆弧状,故D正确。
故答案为:D5.给出下列函数:①;②;③④则它们共同具有的性质是()A.周期性B.偶函数C.奇函数D.无最大值考点:函数综合答案:C试题解析:①②周期不同;①有最大值,②无最大值,故排除A,D。
又①②都是奇函数,故选C。
故答案为:C6.设函数定义在上,则“”是“在上存在零点”的()A.充分而不必要条件.B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件考点:零点与方程答案:D试题解析:若函数在上不连续,则若,在上不一定存在零点;反过来,若函数在上存在两个零点,则可能故“”是“在上存在零点”的既不充分也不必要条件。
故答案为:D7.设都是锐角,则下列各式中成立的是()A.B.C.D.考点:两角和与差的三角函数答案:C试题解析:取故A,B,D错。
故答案为:C8.已知函数在∈(0,+∞)上的图象恒在轴上方,则的取值范围是()A.B.C.D.考点:指数与指数函数答案:C试题解析:令t=3x,则问题转化为函数g(t)=t2-mt+m+1在t∈(1,+∞)上的图象恒在x轴的上方,即Δ=(-m)2-4(m+1)<0或解得m<2+2.故答案为:C9.函数有两个不同的零点,则实数的取值范围是()A.B.C.D.考点:零点与方程答案:B试题解析:问题等价于:在有两个交点。
2017届高三上学期10月月考数学试卷(文科) Word版含解析

2017届高三上学期10月月考试卷数学(文科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答题卷的相应位置.1.集合A={x|﹣1≤x≤2},B={x|x<1},则A∩B=()A.{x|x<1} B.{x|﹣1≤x≤2} C.{x|﹣1≤x≤1} D.{x|﹣1≤x<1}2.复数等于()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i3.若a,b∈R,且a>b,则下列不等式中恒成立的是()A.B.a2>b2C.2a>2b D.4.函数的值域是()A.[0,+∞)B.(0,+∞)C.[﹣1,+∞)D.(﹣1,+∞)5.“a>0”是“|a|>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.下列命题中的假命题是()A.∃x∈R,lgx=0 B.∃x∈R,tanx=1 C.∀x∈R,x3>0 D.∀x∈R,2x>07.某种豆类生长枝数随时间增长,前6月数据如下:则下列函数模型中能较好地反映豆类枝数在第x月的数量y与x之间的关系的是()A.y=2x B.y=x2﹣x+2 C.y=2x D.y=logx+228.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为()A.﹣1 B.0 C.1 D.无法确定9.设点P对应的复数为﹣3+3i,以原点为极点,实轴正半轴为极轴建立极坐标系,则点P的极坐标为()A.(,)B.(,) C.(3,) D.(﹣3,)10.函数f(x)=e x+x﹣2的零点所在的一个区间是()A.(﹣2,﹣1)B.(﹣1,0)C.(0,1)D.(1,2)11.给定函数①y=x,②y=log(x+1),③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是()A.①②B.②③C.③④D.①④12.已知a>0,函数f(x)=x3﹣ax在[﹣1,1]上是单调减函数,则a的最小值是()A.﹣3 B.﹣1 C.1 D.3二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.13.命题“∀x∈R,x2≥0”的否定是.14.某校有老师200人,男学生1400人,女学生1200人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为90人,则n= .15.设x>0,则的最小值是.16.设f(x)=则使f(x)=11成立的实数x的集合为.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.已知集合A={x|4≤x<8},B={x|2<x<10},C={x|x<a}.(1)求A∪B;(∁A)∩B;R(2)若A∩C≠∅,求a的取值范围.18.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?下面的临界值表供参考:(参考公式,其中n=a+b+c+d)19.已知直线l经过点P(1,1),倾斜角α=,(1)写出直线l的参数方程.(2)设l与圆x2+y2=4相交于点A、B,求点P到A、B两点的距离之积.20.设函数f(x)=|x+|+|x﹣a|(a>0).(Ⅰ)证明:f(x)≥2;(Ⅱ)若f(3)<5,求a的取值范围.21.已知函数f(x)=x3﹣3ax+b的图象在(1,f(1))处与y=2相切.(1)求a,b的值;(2)求f(x)的单调递减区间.22.设函数,a为常数,且f(3)=(1)求a值;(2)求使f(x)≥4的x值的取值范围;(3)设g(x)=﹣x+m,对于区间[3,4]上每一个x值,不等式f(x)>g(x)恒成立,求实数m的取值范围.2017届高三上学期10月月考数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答题卷的相应位置.1.集合A={x|﹣1≤x≤2},B={x|x<1},则A∩B=()A.{x|x<1} B.{x|﹣1≤x≤2} C.{x|﹣1≤x≤1} D.{x|﹣1≤x<1}【考点】交集及其运算.【分析】利用交集和数轴即可求出A∩B.【解答】解:A∩B={x|﹣1≤x≤2}∩{x|x<1}={x|﹣1≤x≤2,且x<1}={x|﹣1≤x<1}.故选D.2.复数等于()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i【考点】复数代数形式的乘除运算.【分析】利用复数的运算法则即可得出.【解答】解:原式==1+i.故选A.3.若a,b∈R,且a>b,则下列不等式中恒成立的是()A.B.a2>b2C.2a>2b D.【考点】命题的真假判断与应用.【分析】举出反例a=1,b=﹣2,可判断A,B,D均不成立,进而得到答案.【解答】解:当a=1,b=﹣2时,a>b,但,故A中不等式不恒成立,a2<b2,故B中不等式不恒成立,,故D中不等式不恒成立,而2a>2b恒成立,故选:C.4.函数的值域是()A.[0,+∞)B.(0,+∞)C.[﹣1,+∞)D.(﹣1,+∞)【考点】函数的值域.【分析】根据幂函数的值域即可求解.【解答】解:函数y=的定义域为{x|x≥0},其值域是[0,+∞),那么:函数的值域是[﹣1,+∞),故选:C.5.“a>0”是“|a|>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件.【分析】本题主要是命题关系的理解,结合|a|>0就是{a|a≠0},利用充要条件的概念与集合的关系即可判断.【解答】解:∵a>0⇒|a|>0,|a|>0⇒a>0或a<0即|a|>0不能推出a>0,∴a>0”是“|a|>0”的充分不必要条件故选A6.下列命题中的假命题是()A.∃x∈R,lgx=0 B.∃x∈R,tanx=1 C.∀x∈R,x3>0 D.∀x∈R,2x>0【考点】命题的真假判断与应用.【分析】A、B、C可通过取特殊值法来判断;D、由指数函数的值域来判断.【解答】解:A、x=1成立;B、x=成立;D、由指数函数的值域来判断.对于C选项x=﹣1时,(﹣1)3=﹣1<0,不正确.故选C7.某种豆类生长枝数随时间增长,前6月数据如下:则下列函数模型中能较好地反映豆类枝数在第x月的数量y与x之间的关系的是()x+2A.y=2x B.y=x2﹣x+2 C.y=2x D.y=log2【考点】线性回归方程.【分析】本题要选择合适的模型,从所给数据可以看出图象大约过(1,2)和(2,4),把这两个点代入所给的四个解析式发现只有y=2t最合适,再考查四个选项,找出正确选项即可.【解答】解:从所给数据可以看出图象大约过(1,2)和(2,4)把这两个点代入所给的四个解析式发现只有y=2t最合适,故选:C.8.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为()A.﹣1 B.0 C.1 D.无法确定【考点】函数奇偶性的性质.【分析】根据奇函数的性质,可得f(0)=0,代入构造关于b的方程,解得答案.【解答】解:∵f(x)为定义在R上的奇函数,∴f(0)=0,∵当x≥0时,f(x)=2x+2x+b,∴f(0)=1+b=0,解得:b=﹣1.故选:A9.设点P对应的复数为﹣3+3i,以原点为极点,实轴正半轴为极轴建立极坐标系,则点P的极坐标为()A.(,)B.(,) C.(3,) D.(﹣3,)【考点】极坐标刻画点的位置.【分析】先求出点P的直角坐标,P到原点的距离r,根据点P的位置和极角的定义求出极角,从而得到点P的极坐标.【解答】解:∵点P对应的复数为﹣3+3i,则点P的直角坐标为(﹣3,3),点P到原点的距离r=3,且点P第二象限的平分线上,故极角等于,故点P的极坐标为(,),故选 A.10.函数f(x)=e x+x﹣2的零点所在的一个区间是()A.(﹣2,﹣1)B.(﹣1,0)C.(0,1)D.(1,2)【考点】函数零点的判定定理.【分析】将选项中各区间两端点值代入f(x),满足f(a)•f(b)<0(a,b为区间两端点)的为答案.【解答】解:因为f(0)=﹣1<0,f(1)=e﹣1>0,所以零点在区间(0,1)上,故选C.11.给定函数①y=x,②y=log(x+1),③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是()A.①②B.②③C.③④D.①④【考点】函数单调性的判断与证明.【分析】根据一次函数及指数函数,对数函数的性质,判断函数的单调性,从而得出答案.【解答】解:y=x,k=1,递增,y=,底数是,递减,y=|x﹣1|=1﹣x,递减,y=2x+1,底数是2,递增,故选:B.12.已知a>0,函数f(x)=x3﹣ax在[﹣1,1]上是单调减函数,则a的最小值是()A.﹣3 B.﹣1 C.1 D.3【考点】利用导数研究函数的单调性.【分析】求出函数的导数,问题转化为a≥3x2在[﹣1,1]恒成立,根据二次函数的性质求出a的最小值即可.【解答】解:若函数f(x)=x3﹣ax在[﹣1,1]上是单调减函数,即f′(x)=3x2﹣a≤0在[﹣1,1]恒成立,即a≥3x2在[﹣1,1]恒成立,故a≥3,a的最大值是3,故选:D.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.13.命题“∀x∈R,x2≥0”的否定是∃x∈R,x2<0 .【考点】命题的否定.【分析】根据一个命题的否定定义解决.【解答】解:由命题的否定义知:要否定结论同时改变量词故答案是∃x∈R,x2<014.某校有老师200人,男学生1400人,女学生1200人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为90人,则n= 210 .【考点】分层抽样方法.【分析】先求出每个个体被抽到的概率,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,再把各层抽取的样本数相加可得样本容量 n的值.【解答】解:每个个体被抽到的概率等于=,应抽取的男学生人数为1400×=105,应抽取的老师人数为200×=15,故样本容量 n=90+105+15=210.故答案为210.15.设x>0,则的最小值是.【考点】基本不等式.【分析】依题意,利用基本不等式即可.【解答】解:∵x>0,∴y=3x+≥2(当且仅当x=时取等号).故答案为:16.设f(x)=则使f(x)=11成立的实数x的集合为{1,7,13} .【考点】函数的值.【分析】当x≥10时,f(x)=x﹣2=11;当1≤x<10时,f(x)=f(x+6),由1≤x<10,得7≤x+6<16,当7≤x+6<10时,f(x)=f(x+6)=f(x+12);当10≤x+6<16时,f(x)=f (x+6).由此能求出使f(x)=11成立的实数x的集合.【解答】解:∵f(x)=,f(x)=11,∴当x≥10时,f(x)=x﹣2=11,解得x=11;当1≤x<10时,f(x)=f(x+6),由1≤x<10,得7≤x+6<16,当7≤x+6<10时,13≤x+12<16,f(x)=f(x+6)=f(x+12)=x+12﹣2=11,解得x=1;当10≤x+6<16时,f(x)=f(x+6)=x+6﹣2=11,解得x=7.综上,使f(x)=11成立的实数x的集合为{1,7,13}.故答案为:{1,7,13}.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.已知集合A={x|4≤x<8},B={x|2<x<10},C={x|x<a}.A)∩B;(1)求A∪B;(∁R(2)若A∩C≠∅,求a的取值范围.【考点】交、并、补集的混合运算;交集及其运算.【分析】本题考查集合的交、并、补运算,对于(1)求出A的补集是关键,对于(2)利用A ∩C≠∅确定参数a的取值范围【解答】解:(1)∵集合A={x|4≤x<8},B={x|2<x<10},∴A∪B={x|2<x<10},∵CA={x|x<4或x≥8}RA)∩B={x|8≤x<10或2<x<4}∴(CR(2)∵若A∩C≠∅,A={x|4≤x<8},C={x|x<a}.∴a的取值范围是a>4∴a∈(4,+∞)18.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?下面的临界值表供参考:(参考公式,其中n=a+b+c+d)【考点】独立性检验的应用;分层抽样方法.【分析】(I)根据分层抽样的方法,在患心肺疾病的人群中抽6人,先计算了抽取比例,再根据比例即可求出男性应该抽取人数.(II)在上述抽取的6名学生中,女性的有2人,男性4人.女性2人记A,B;男性4人为c,d,e,f,列出其一切可能的结果组成的基本事件个数,通过列举得到满足条件事件数,求出概率.(III)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握认为心肺疾病与性别有关.【解答】解:(I )在患心肺疾病的人群中抽6人,则抽取比例为 =,∴男性应该抽取20×=4人….(II )在上述抽取的6名学生中,女性的有2人,男性4人.女性2人记A ,B ;男性4人为c ,d ,e ,f ,则从6名学生任取2名的所有情况为:(A ,B )、(A ,c )、(A ,d )、(A ,e )、(A ,f )、(B ,c )、(B ,d )、(B ,e )、(B ,f )、(c ,d )、(c ,e )、(c ,f )、(d ,e )、(d ,f )、(e ,f )共15种情况,其中恰有1名女生情况有:(A ,c )、(A ,d )、(A ,e )、(A ,f )、(B ,c )、(B ,d )、(B ,e )、(B ,f ),共8种情况,故上述抽取的6人中选2人,恰有一名女性的概率概率为P=.….(III )∵K 2≈8.333,且P (k 2≥7.879)=0.005=0.5%,那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.….19.已知直线l 经过点P (1,1),倾斜角α=,(1)写出直线l 的参数方程.(2)设l 与圆x 2+y 2=4相交于点A 、B ,求点P 到A 、B 两点的距离之积. 【考点】直线的参数方程.【分析】对第(1)问,由过点(x 0,y 0),且倾斜角为α的直线的参数方程可得l 的参数方程;对第(2)问,根据l 的参数方程,可设A ,B,再将l 的参数方程代入圆的方程中,得到一个关于t 的一元二次方程,由韦达定理可得点P 到A 、B 两点的距离之积.【解答】解:(1)因为过点(x 0,y 0),且倾斜角为α的直线的参数方程,由题意,将x 0=1,y 0=1,α=代入上式得直线l 的参数方程为(t 为参数).(2)因为A ,B 都在直线l 上,故可设它们对应的参数分别为t 1,t 2,则点A,B的坐标分别为A,B,将直线l的参数方程代入圆的方程x2+y2=4中,整理得,则t1,t2是此方程的两根,由韦达定理得t1t2=﹣2,所以|PA|•|PB|=|t1t2|=2.即点P到A、B两点的距离之积为2.20.设函数f(x)=|x+|+|x﹣a|(a>0).(Ⅰ)证明:f(x)≥2;(Ⅱ)若f(3)<5,求a的取值范围.【考点】绝对值不等式的解法.【分析】(Ⅰ)由a>0,f(x)=|x+|+|x﹣a|,利用绝对值三角不等式、基本不等式证得f (x)≥2成立.(Ⅱ)由f(3)=|3+|+|3﹣a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.【解答】解:(Ⅰ)证明:∵a>0,f(x)=|x+|+|x﹣a|≥|(x+)﹣(x﹣a)|=|a+|=a+≥2=2,故不等式f(x)≥2成立.(Ⅱ)∵f(3)=|3+|+|3﹣a|<5,∴当a>3时,不等式即a+<5,即a2﹣5a+1<0,解得3<a<.当0<a≤3时,不等式即 6﹣a+<5,即 a2﹣a﹣1>0,求得<a≤3.综上可得,a的取值范围(,).21.已知函数f(x)=x3﹣3ax+b的图象在(1,f(1))处与y=2相切.(1)求a,b的值;(2)求f(x)的单调递减区间.【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,根据f(1)=2,f′(1)=0,求出a,b的值即可;(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可.【解答】解:(1)f′(x)=3x2﹣3a,由题意,解得:;(2)由(1)得:f′(x)=3x2﹣3,令f′(x)<0,解得:﹣1<x<1,所以f(x)的单调递减区间为(﹣1,1).22.设函数,a为常数,且f(3)=(1)求a值;(2)求使f(x)≥4的x值的取值范围;(3)设g(x)=﹣x+m,对于区间[3,4]上每一个x值,不等式f(x)>g(x)恒成立,求实数m的取值范围.【考点】函数恒成立问题;其他不等式的解法.【分析】(1),可得,利用指数函数的单调性可得10﹣3a=1解出即可.(2)由已知,利用指数函数的单调性即可得出10﹣3x≤﹣2.(3)由题意f(x)>g(x)化为恒成立.即在[3,4]恒成立.设,上述问题等价于m<h(x)min,利用函数与在[3,4]为增函数,可得h(x)在[3,4]为增函数,即可得到h(x)的最小值.【解答】解:(1),即,∴10﹣3a=1,解得a=3.(2)由已知,∴10﹣3x≤﹣2.解得x≥4故f(x)≥4解集为{x|x≥4}.(3)依题意f(x)>g(x)化为恒成立即在[3,4]恒成立设则m<h(x)min,∵函数与在[3,4]为增函数,可得h(x)在[3,4]为增函数,∴,∴m<2.。
广东省实验中学2017届高三10月月考理科综合试题(附答案)$749414

2016-2017学年高三上学期10月月考理科综合2016年10月本试卷共14页,37小题,满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必用黑色笔迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。
2.每小题选出答案后,用2B铅笔把答题卷上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
3.作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
第一部分选择题(共132分)一、选择题:本题共13小题,每小题6分,共78分1.下列有关细胞器的叙述,错误的是( )A.精细胞变为精子后,尾部的线粒体与其运动有关B.叶绿体基质中含有核酸和参与光合作用的酶C.硅肺的病因与溶酶体缺乏某种酶有关D.合成固醇类激素的分泌细胞的内质网一般不发达2.下列有关酶的叙述正确的是( )A.酶提供了反应过程所必需的活化能从而提高了化学反应速率B.活细胞能通过转录、翻译产生酶,或通过转录产生酶C.酶是由活细胞产生的并只能在活细胞内发生作用的一类化学物质D.可以选用过氧化氢和过氧化氢酶,用以“探究温度对酶活性的影响”实验3.将蚕豆植株放在湿润的空气中光照一段时间后,取蚕豆叶下表皮制作临时装片。
先在清水中观察,然后用0.3g/mL蔗糖溶液取代清水,继续观察,结果如图所示。
下列叙述正确的是()A.蔗糖分子进入保卫细胞后,细胞渗透吸水导致气孔关闭B.只有将保卫细胞置于0.3 g/mL蔗糖溶液中时,才构成一个渗透系统C.当从清水转入0.3 g/mL蔗糖溶液中时,保卫细胞细胞液浓度将逐渐增加D.用蚕豆叶下表皮观察到的叶绿体主要存在于保卫细胞中4.夏季某晴朗的一天对一密闭蔬菜大棚中的某种气体的含量进行24小时的检测,结果如图1,图2是叶肉细胞内两种细胞器间的气体关系图解。
广东省实验中学高三上学期10月月考——数学文(数学(文
广东省实验中学2017届高三上学期10月月考数学(文)试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x|-2≤x≤3},B={x|x+1>0},则集合A∩B等于()A.{x|-2≤x≤-1} B.{x|-2≤x<-1} C.{x|-1<x≤3}D.{x|1<x≤3}2.若,则=()A.B.C.D.3.设0≤x≤2π,且x1-sin-,则()=xx cossin2A.0≤x≤πB.C.D.4.设等差数列{a n}的前n项和为S n,若a2+a4+a9=24,则S9=()A.36 B.72 C.144 D.705.已知是定义在R上周期为2的奇函数,当时,,则()A.1 B.−1 C.D.6.设a,b,c∈R,则“1,a,b,c,16为等比数列”是“b=4”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.正方体ABCD﹣A1B1C1D1中E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为()A.B.C.D.8.《庄子·天下篇》中记述了一个著名命题:“一尺之棰,日取其半,万世不竭.”反映这个命题本质的式子是( )A .21111122222n n +++⋅⋅⋅+=- B .211112222n +++⋅⋅⋅++⋅⋅⋅< C . D .21111222n ++⋅⋅⋅++⋅⋅⋅<9.如图,在△OAB 中,P 为线段AB 上的一点,且,则( ) A . B . C . D .10.已知集合A={1,2,3,4,5,6,7,8,9),在集合A 中 任取三个元素,分别作为一个三位数的个位数,十位数和百位数, 记这个三位数为a ,现将组成a 的三个数字按从小到大排成的三 位数记为I (a ),按从大到小排成的三位数记为D (a ) (例如a =219,则I (a )=129,D (a )=921),阅读如图所示的 程序框图,运行相应的程序,任意输入一个a ,则输出b 的值为( ) A .792 B .693 C .594D .49511.已知点P 为椭圆上的动点,EF 为圆N:的任一直径,求最大值和最小值是( ).A .16,B .C .19,D .20,12.设a n =1n sin n π25,S n =a 1+a 2+…+a n ,在S 1,S 2,…,S 100中,正数的个数是 ( )A .25B .50C .75D .100 二、填空题:本大题共4小题,每小题5分.13.已知正实数x ,y 满足xy =9,则x +9y 取得最小值时x = ,y = . 14.等比数列{a n }的首项a 1=1,前n 项的和为S n ,若S 6=9S 3,则a 6= . 15.如图,为了测量河对岸电视塔CD 的高度,小王在点A 处测得塔顶D 仰角为30°,塔底C 与A 的连线同河岸成15°角,小王向前走了1200m 到达 M 处,测得塔底C 与M 的连线同河岸成60°角, 则电视塔CD 的高度为 .16.设,变量在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数的最大值为,则________.三、解答题:解答应写出文字说明,证明过程或演算步骤.CDM30 60 1517.(本小题满分12分)已知数列{a n }的各项均为正数,前n 项和为S n ,且)(2)1(*N n a a S n n n ∈+= (Ⅰ)求数列{a n }的通项公式; (Ⅱ)设n n nn b b b T S b +++==21,21, 求T n . 18.(本小题满分12分)某中学共有1000名文科学生参加了该市高三第一次质量检查的考试,其中数学成绩如下表所示:(Ⅰ)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,年级将采用分层抽样的方法抽取100名同学进行问卷调查. 甲同学在本次测试中数学成绩为75分,求他被抽中的概率; (Ⅱ)年级将本次数学成绩75分以下的学生当作“数学学困生”进行辅导,请根据所提供数据估计“数学学困生”的人数;(III )请根据所提供数据估计该学校文科学生本次考试的数学平均分.19.(本小题满分12分)如图,ABC ﹣A 1B 1C 1是底面边长为2,高为的正三棱柱,经过AB 的截面与上底面相交于PQ ,设C 1P=λC 1A 1(0<λ<1). (Ⅰ)证明:PQ ∥A 1B 1;(Ⅱ)当时,在图中作出点C 在平面ABQP 内的正投影F (说明作法及理由),并求四面体CABF 的体积. 20.(本小题满分12分)已知椭圆C 的左、右焦点分别为、,且经过点 (I )求椭圆C 的方程:(II )直线y =kx (k R ,k ≠0)与椭圆C 相交于A ,B 两点,D 点为椭圆C 上的动点,且|AD|=|BD|,请问△ABD 的面积是否存在最小值?若存在,求出此时直线AB 的方程:若不存在,说明理由. 21.(本小题满分12分)设函数.ln )1(2)(2x k x k x x f --+=(Ⅰ)讨论的单调性;(Ⅱ)若k 为正数,且存在x 0使得,求k 的取值范围.A1A1B1CCBQP请考生在第22、23题中任选一题做答,做答时请写清题号. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 1的极坐标方程为ρ2cos 2θ=8,曲线C 2的极坐标方程为θ=π6,曲线C 1,C 2相交于A ,B 两点.(I)求A ,B 两点的极坐标;(II)曲线C 1与直线⎩⎨⎧x =1+32t ,y =12t(t 为参数)分别相交于M ,N 两点,求线段MN 的长度.23.(本小题满分10分)选修4-5:不等式选讲 设f (x )=|x ﹣1|﹣2|x +1|的最大值为m .(Ⅰ)求m ;(Ⅱ)若,a 2+2b 2+c 2=m ,求ab +bc 的最大值.参考答案选择题:1~12:CBCBB ACDDD CD 二、填空题:13. 9,1;14. 32;15. 600m ;16.17. 解:(Ⅰ))(2)1(*N n a a S n n n ∈+=∴①)2(21211≥+=---n a a S n n n ② 由①﹣②得:12122---+-=n n n n n a a a a a 2分 (a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0, ∵a n >0,∴ 又∵,∴a 1=1,∴n d n a a n =-+=)1(1, 5分 故a n =n . 6分(Ⅱ)2)1(2)1(+=+=n n a a S n n n 8分 111)1(1+-=+=∴n n n n b n 10分故11111113121211+=+-=+-++-+-=n n n n n T n . 12分 18.解:(Ⅰ)分层抽样中,每个个体被抽到的概率均为:,故甲同学被抽到的概率 …………………4分(Ⅱ)由题意得 1 000604003601080()0x =-+++=. ……………6分 设估计“数学学困生”人数为 .故估计该中学“数学学困生”人数为人 ……………………8分 (III )该学校本次考试的数学平均分.60608080100400120360140100107.21000x ⨯+⨯+⨯+⨯+⨯==估计该学校本次考试的数学平均分为分. ……………12分19.解:(I )∵平面ABC ∥平面A 1B 1C 1,平面ABC∩平面ABQP=AB ,平面ABQP∩平面A 1B 1C 1=QP , ∴AB ∥PQ , 2分又∵AB ∥A 1B 1,∴PQ ∥A 1B 1. 5分(Ⅱ)F 点是PQ 中点,理由如下:当,P 、Q 分别是的中点,连接CQ 和CP, 因为ABC ﹣A 1B 1C 1 是正三棱柱,所以CQ=CP ,,6分取AB 中点H ,连接FH,CH ,在等腰梯形ABQP 中,, 连接中,CF=222CH FH CF =+∴,8分⊥∴=⋂CF H FH QP , 平面ABF ,即,所以F 点是C 在平面ABQP 内的正投影。
广东省实验中学2017-2018学年高三上学期10月月考文科综合试卷 Word版含答案
2017-2018学年高三级10月月考试题文科综合2018年10月本试卷共12页,46小题,满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必用黑色笔迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。
2.每小题选出答案后,用2B铅笔把答题卷上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
3.作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
第Ⅰ卷本卷共35小题,每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
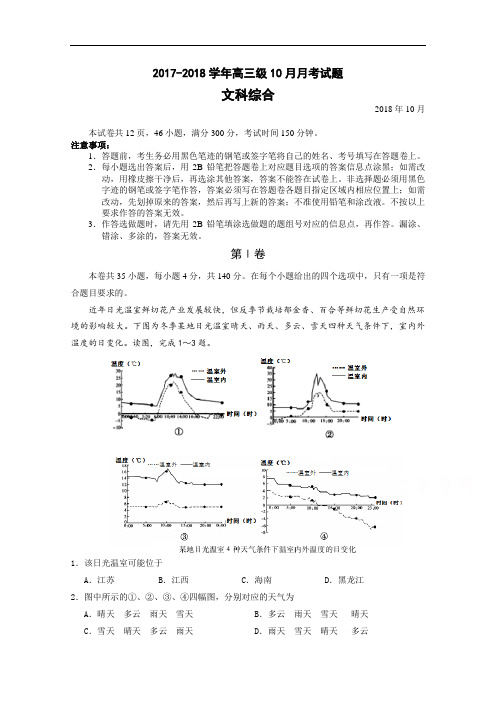
近年日光温室鲜切花产业发展较快,但反季节栽培郁金香、百合等鲜切花生产受自然环境的影响较大。
下图为冬季某地日光温室晴天、雨天、多云、雪天四种天气条件下,室内外温度的日变化。
读图,完成1~3题。
1.该日光温室可能位于A.江苏B.江西C.海南D.黑龙江2.图中所示的①、②、③、④四幅图,分别对应的天气为A.晴天多云雨天雪天B.多云雨天雪天晴天C.雪天晴天多云雨天D.雨天雪天晴天多云3.研究表明A.温度条件直接影响温室郁金香的质量和花期B.晴天和雨天温室外温度下降幅度较温室内小C.雪天融雪过程释放热量,导致室外温度不断下降D.同一天气条件下,靠近地表处地温变化幅度较大下图为世界某区域,K城海拔1048 米。
这里的人发现夏季整夜天并不完全黑下来的“白夜”现象。
冬季常出现一种神奇的气流,能使厚达10 厘米左右的积雪在一天之内融化,因此称之为“吃雪者”。
读图完成笫4~6题。
4.“吃雪者”形成的原因是A.暖流流经,增温增湿 B.反气旋控制,盛行下沉气流C.暖锋过境,气温升高 D.位于西风带背风坡,气流下沉5.该地夏天可以看到“白夜”现象的原因A.海拔高B.晴天多,光照充足 C.大气散射作用D.纬度高,有极昼现象6.当流经K 城的河流进入主汛期时,居住在K 城附近的人们最可能开展的活动是 A.东去种麦B.南下踏青 C.西山牧羊D.北山滑雪2018年春夏,由于持续的大雨和暴雨,我国不少城市出现了严重的内涝现象。
广东实验中学2017届高三数学10月月考试题 文

2016-2017学年高三级10月月考试题文科数学一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x |-2≤x ≤3},B={x |x +1>0},则集合A∩B 等于( )A .{x |-2≤x ≤-1}B .{x |-2≤x <-1}C .{x |-1<x ≤3}D .{x|1<x ≤3} 2.若i iz --=11,则z =( ) A .21 B .22C .i 2121+-D .i 2121+ 3.设0≤x ≤2π,且x x x cos sin 2sin 1-=-,则( ) A .0≤x ≤π B .474ππ≤≤x C .454ππ≤≤x D .232ππ≤≤x 4.设等差数列{a n }的前n 项和为S n ,若a 2+a 4+a 9=24,则S 9=( )A .36B .72C .144D .705.已知()f x 是定义在R 上周期为2的奇函数,当)1,0(∈x 时,14)(-=xx f , 则=)321(log 4f ( ) A .1 B .−1 C .21D .21-6.设a ,b ,c ∈R,则“1,a ,b ,c ,16为等比数列”是“b =4”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件7.正方体ABCD ﹣A 1B 1C 1D 1中E 为棱BB 1的中点(如图),用过点A ,E ,C 1的平面截去该正方体的上半部分,则剩余几何体的左视图为( )A .B .C .D .8.《庄子·天下篇》中记述了一个著名命题:“一尺之棰,日取其半,万世不竭.”反映这个命题本质的式子是( )A .21111122222n n +++⋅⋅⋅+=- B .211112222n +++⋅⋅⋅++⋅⋅⋅< C .21111222n ++⋅⋅⋅+= D .21111222n ++⋅⋅⋅++⋅⋅⋅<9.如图,在△OAB 中,P 为线段AB 上的一点,,y x +=且3=,则( )A .31,32==y xB .32,31==y x C .43,41==y x D .41,43==y x10.已知集合A={1,2,3,4,5,6,7,8,9),在集合A 中 任取三个元素,分别作为一个三位数的个位数,十位数和百位数, 记这个三位数为a ,现将组成a 的三个数字按从小到大排成的三 位数记为I (a ),按从大到小排成的三位数记为D (a ) (例如a =219,则I (a )=129,D (a )=921),阅读如图所示的 程序框图,运行相应的程序,任意输入一个a ,则输出b 的值为( ) A .792 B .693 C .594D .49511.已知点P 为椭圆1121622=+y x 上的动点,EF 为圆N:1)1(22=-+y x 的任一直径,求⋅最大值和最小值是( ).A .16,3412-B .34-13,17C .19, 3412-D .20, 3413- 12.设a n =1n sin n π25,S n =a 1+a 2+…+a n ,在S 1,S 2,…,S 100中,正数的个数是 ( )A .25B .50C .75D .100 二、填空题:本大题共4小题,每小题5分.13.已知正实数x ,y 满足xy =9,则x +9y 取得最小值时x = ,y = . 14.等比数列{a n }的首项a 1=1,前n 项的和为S n ,若S 6=9S 3,则a 6= .15.如图,为了测量河对岸电视塔CD 的高度,小王在点A 处测得塔顶D 仰角为30°,塔底C 与A 的连线同河岸成15°角,小王向前走了1200m 到达M 处,测得塔底C 与M 的连线同河岸成60°角, 则电视塔CD 的高度为 .16.设1m >,变量,x y 在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值为2,则m =________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知数列{a n }的各项均为正数,前n 项和为S n ,且)(2)1(*N n a a S n n n ∈+= (Ⅰ)求数列{a n }的通项公式; (Ⅱ)设n n nn b b b T S b +++==21,21, 求T n . 18.(本小题满分12分)某中学共有1000名文科学生参加了该市高三第一次质量检查的考试,其中数学成绩如下表所示:(Ⅰ)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,年级将采用分层抽样的方法抽取100名同学进行问卷调查. 甲同学在本次测试中数学成绩为75分,求他被抽中的概率; (Ⅱ)年级将本次数学成绩75分以下的学生当作“数学学困生”进行辅导,请根据所提供数据估计“数学学困生”的人数;(III )请根据所提供数据估计该学校文科学生本次考试的数学平均分.ACDM30 601519.(本小题满分12分)如图,ABC ﹣A 1B 1C 1是底面边长为2,高为23的正三棱柱,经过AB 的截面与上底面相交于PQ ,设C 1P=λC 1A 1(0<λ<1). (Ⅰ)证明:PQ∥A 1B 1; (Ⅱ)当21=λ时,在图中作出点C 在平面ABQP 内 的正投影F (说明作法及理由),并求四面体CABF 的体积. 20.(本小题满分12分)已知椭圆C 的左、右焦点分别为)0,3(-、)0,3(,且经过点).21,3( (I )求椭圆C 的方程:(II )直线y =kx (k ∈R ,k ≠0)与椭圆C 相交于A ,B 两点,D 点为椭圆C 上的动点,且|AD|=|BD|,请问△ABD 的面积是否存在最小值?若存在,求出此时直线AB 的方程:若不存在,说明理由. 21.(本小题满分12分)设函数.ln )1(2)(2x k x k x x f --+=(Ⅰ)讨论)(x f 的单调性;(Ⅱ)若k 为正数,且存在x 0使得2023)(k x f -<,求k 的取值范围. 请考生在第22、23题中任选一题做答,做答时请写清题号. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 1的极坐标方程为ρ2cos 2θ=8,曲线C 2的极坐标方程为θ=π6,曲线C 1,C 2相交于A ,B 两点.(I)求A ,B 两点的极坐标; (II)曲线C 1与直线⎩⎪⎨⎪⎧x =1+32t ,y =12t(t 为参数)分别相交于M ,N 两点,求线段MN 的长度.23.(本小题满分10分)选修4-5:不等式选讲 设f (x )=|x ﹣1|﹣2|x +1|的最大值为m .(Ⅰ)求m ;(Ⅱ)若),0(,,+∞∈c b a ,a 2+2b 2+c 2=m ,求ab +bc 的最大值.广东实验中学2016-2017高三10月月考试题文科数学解答及评分标准 一、选择题:1~12:CBCBB ACDDD CD二、填空题:13. 9,1;14. 32;15. 6002m ;16. 1m =17. 解:(Ⅰ))(2)1(*N n a a S n n n ∈+=∴n n n a a S +=22①)2(21211≥+=---n a a S n n n ② 由①﹣②得:12122---+-=n n n n n a a a a a 2分(a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0, ∵a n >0,∴)2(11≥=--n a a n n 又∵2)1(1111+==a a S a , ∴a 1=1,∴n d n a a n =-+=)1(1, 5分 故a n =n . 6分 (Ⅱ)2)1(2)1(+=+=n n a a S n n n8分 111)1(1+-=+=∴n n n n b n 10分故11111113121211+=+-=+-++-+-=n n n n n T n . 12分 18.解:(Ⅰ)分层抽样中,每个个体被抽到的概率均为:样本容量总体中个体总数,故甲同学被抽到的概率1P=10…………………4分 (Ⅱ)由题意得 1 000604003601080()0x =-+++=. ……………6分 设估计“数学学困生”人数为m16080804m =+⨯=. 故估计该中学“数学学困生”人数为80人 ……………………8分 (III )该学校本次考试的数学平均分.60608080100400120360140100107.21000x ⨯+⨯+⨯+⨯+⨯==估计该学校本次考试的数学平均分为107.2分. ……………12分19.解:(I )∵平面ABC∥平面A 1B 1C 1,平面ABC∩平面ABQP=AB ,平面ABQP∩平面A 1B 1C 1=QP , ∴AB∥PQ, 2分又∵AB∥A 1B 1,∴PQ∥A 1B 1. 5分(Ⅱ)F 点是PQ 中点,理由如下: 当时21=λ,P 、Q 分别是1111,B A C A 的中点,连接CQ 和CP, 因为ABC ﹣A 1B 1C 1 是正三棱柱,所以CQ=CP ,QP CF ⊥∴, 6分取AB 中点H ,连接FH,CH ,,3=CH 在等腰梯形ABQP 中,26=FH , 连接FC C F C 11,∆中,CF=,26222CH FH CF =+∴FH CF ⊥∴, 8分 ⊥∴=⋂CF H FH QP , 平面ABF ,即ABQP CF 平面⊥,所以F 点是C 在平面ABQP 内的正投影。
广东省2017届高三10月百校联考数学(文)试题 含答案

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合{|(1)(5)0}M x x x =--<,集合{|4}N x y x ==-,则MN 等于()A .(1,4]B .(1,4)C .[4,5)D .(4,5)2。
设复数z 为纯虚数,且29x=-,则复数2(1)z +的实部为( )A . -6B .6± C.-8 D .8±3.下面是2010年3月安徽省芜湖楼市商品住宅板块销售对比饼状图,由图可知,戈江区3月销售套数为( )A .350B .340C .330D . 306 4。
已知11()()122ab <<,则下列不等式成立的是( )A.22(1)(1)a b ->- B 。
ln ln a b >C 。
1a b +> a b 5.若sin cos tan 390αα+=,则sin 2α等于( )A.23-B.34- C. 23 D 。
346。
如图所示的五边形是由一个矩形截去一个角而得,且1BC =,2DE =,3AE =,4AB =,则CD 等于()A .1223AB AE + B .1223AB AE -C 。
1223AB AE -+ D .1223AB AE --7。
直线2y b =与双曲线22221(0,0)x y a b a b -=>>的左支、右支分别交于A B 、两点,O 为坐标原点,且AOB ∆为等腰直角三角形,则该双曲线的离心率为( ) A .52B .32C 。
305D .3558.某几何体的三视图如图所示,则该几何体的体积为( )A . 40B .48 C. 56 D .929.执行如图所示的程序框图,若输入的2x =,4n =,则输出的s 等于( )A .94B . 99C 。
45D .20310.飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000m ,速度为1000/km h ,飞行员先看到山顶的俯角为18,经过108s 后又看到山顶的俯角为78,则山顶的海拔高度为( )A .(15183sin18cos78)km -B .(15183sin18sin78)km -C 。
2017-2018广东省广州市海珠区高三(上)10月月考数学试卷(文科)

2017-2018学年广东省广州市海珠区高三(上)月考数学试卷(文科)(1)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)A={x|x2<x},B={x|x≥1},则A∪B=()A.R B.(0,+∞)C.{1}D.[1,+∞)【解答】解:∵A={x|x2<x}={x|0<x<1},B={x|x≥1},则A∪B={x|0<x<1}∪{x|x≥1}=(0,+∞).故选:B.【点评】本题考查并集及其运算,考查一元二次不等式的解法,是基础题.2.(5分)已知i为虚数单位,复数z=i(2﹣i)的模|z|=()A.1 B.C.D.3【解答】解:∵z=i(2﹣i)=2i+1,∴|z|=,故选:C.【点评】本题主要考查复数的有关概念的计算,比较基础.3.(5分)如图所示,该程序运行后输出的结果为()A.4 B.6 C.8 D.10【解答】解:由程序框图知:第一次循环S=0+2=2,i=6﹣1=5;第二次循环S=2+2=4,i=5﹣1=4;第三次循环S=4+2=6,i=4﹣1=3;满足条件i≤3,跳出循环,输出S=6.故选:B.【点评】本题考查了直到型循环结构的程序框图,根据框图的流程模拟运行程序是解答此类问题的常用方法.4.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为()A.2+2 B.C.2﹣2 D.﹣1【解答】解:∵b=2,B=,C=,∴由正弦定理=得:c===2,A=,∴sinA=sin(+)=cos=,则S=bcsinA=×2×2×=+1.△ABC故选B【点评】此题考查了正弦定理,三角形的面积公式,以及两角和与差的余弦函数公式,熟练掌握正弦定理是解本题的关键.5.(5分)如图是某体育比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为()A.5和1.6 B.85和1.6 C.85和0.4 D.5和0.4【解答】解:根据题意可得:评委为某选手打出的分数还剩84,84,84,86,87,所以所剩数据的平均数为=85,所剩数据的方差为[(84﹣85)2+(84﹣85)2+(86﹣85)2+(84﹣85)2+(87﹣85)2]=1.6.故选B.【点评】本题考查茎叶图、平均数和方差,对于一组数据通常要求的是这组数据的众数,中位数,平均数,方差,它们分别表示一组数据的特征,这样的问题可以出现在选择题或填空题.6.(5分)函数f(x)=(0<a<1)图象的大致形状是()A.B.C.D.【解答】解:由题意,f(﹣x)=﹣f(x),所以函数是奇函数,图象关于原点对称,排除B、D;x>0时,f(x)=log a x(0<a<1)是单调减函数,排除A.故选:C.【点评】本题考查函数的图象,考查函数的奇偶性、单调性,正确分析函数的性质是关键.7.(5分)设函数f(x)=cos(2x﹣),则下列结论错误的是()A.f(x)的一个周期为πB.y=f(x)的图象关于直线x=对称C.f(x+)的一个零点为x=﹣D.f(x)在[]上单调递减【解答】解:A.函数的周期T=,故A正确,B.f()=cos(2×﹣)=cosπ=﹣1为最小值,则y=f(x)的图象关于直线x=对称,故B正确,C.当x=﹣时,f(﹣+)=f()=cos(2×﹣)=cos0=1≠0,则f(x+)的一个零点为x=﹣错误,D.当≤x≤时,≤2x≤π,≤2x﹣≤,此时函数f(x)为减函数,故f(x)在[]上单调递减,故D正确故选:C【点评】本题主要考查三角函数的图象和性质,根据函数周期性,单调性和对称性的性质是解决本题的关键.8.(5分)点M、N分别是正方体ABCD﹣A1B1C1D1的棱A1B1、A1D1的中点,用过平面AMN和平面DNC1的两个截面截去正方体的两个角后得到的几何体如图,则该几何体的正(主)视图、侧(左)视图、俯视图依次为()A.①、②、③B.②、③、④C.①、③、④D.②、④、③【解答】解:由直观图可知,该几何体的正(主)视图、侧(左)视图、俯视图依次为②③④,故选B.【点评】三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力.9.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与圆x2+(y﹣3)2=1相切,则双曲线的离心率为()A.2 B.C.D.3【解答】解:∵双曲线﹣=1(a>0,b>0)的渐近线为bx±ay=0,依题意,直线bx±ay=0与圆x2+(y﹣2)2=1相切,设圆心(0,2)到直线bx±ay=0的距离为d,则d===1,∴双曲线离心率e==3.故选:D.【点评】本题考查双曲线的简单性质,考查点到直线间的距离,考查分析、运算能力,属于中档题.10.(5分)若函数为奇函数,,则不等式g(x)>1的解集为()A.B.(e,+∞)C.(﹣∞,0)∪(0,e)D.【解答】解:∵函数为奇函数,∴f(0)==0,即a=﹣1.∴g(x)=,当x>0时,令﹣lnx>1,解得0<x<,当x≤0时,令e﹣x>1得x<0,∴g(x)>1的解集为(﹣∞,0)∪(0,).故选A.【点评】本题考查了奇函数的性质,分段函数的应用,属于中档题.11.(5分)《九章算术》之后,人们进一步地用等差数列求和公式来解决更多的问题.《张邱建算经》卷上第22题为:今有女善织,日益功疾(注:从第2天起每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织420尺布,则第2天织的布的尺数为()A. B. C.D.【解答】解:设公差为d,由题意可得:前30项和S30=420=30×5+d,解得d=.∴第2天织的布的尺数=5+d=.故选:A.【点评】本题考查了等差数列的通项公式与求和公式、方程的解法,考查了推理能力与计算能力,属于中档题.12.(5分)已知e是自然对数的底数,函数f(x)=e x+x﹣2的零点为a,函数g(x)=lnx+x﹣2的零点为b,则下列不等式成立的是()A.f(1)<f(a)<f(b) B.f(a)<f(b)<f(1) C.f(a)<f(1)<f (b)D.f(b)<f(1)<f(a)【解答】解:易知函数f(x)=e x+x﹣2在R上是增函数,g(x)=lnx+x﹣2在(0,+∞)上也是增函数;又∵f(a)=0,f(1)=e+1﹣2>0,g(b)=0,g(1)=0+1﹣2<0,∴0<a<1<b;故f(a)<f(1)<f(b);故选C.【点评】本题考查了函数的单调性的判断与应用及函数零点的判定定理的应用,属于基础题.二、填空题:本大题共4小题,每小题5分,共20分13.(5分)已知向量,若,则等于2.【解答】解:根据题意,向量,且,则有x2=1×3=3,解可得x=±,则==2;故答案为:2.【点评】本题考查平面向量共线的坐标表示,涉及向量的模的计算,关键是求出x的值,得到的坐标.14.(5分)已知抛物线y2=2px(p>0)的焦点F与双曲线的右焦点重合,若A为抛物线上一点,且|AF|=3,则直线AF的斜率等于.【解答】解:双曲线的右焦点为(2,0),∴抛物线方程为y2=8x,p=4.∵|AF|=3,∴x A+2=3,∴x A=1代入抛物线方程可得y A=±2,∵点A在x轴上方,∴A(1,±2),∴直线AF斜率等于=.故答案为:.【点评】本题考查抛物线、双曲线的性质,考查学生的计算能力,比较基础.15.(5分)已知高为8的圆柱内接于一个直径为10的球内,则该圆柱的体积为72π.【解答】解:高为8的圆柱内接于一个直径为10的球内,如图:可得r===3,则该圆柱的体积为:π×32×8=72π.故答案为:72π.【点评】本题考查球的內接体,圆柱的体积的求法,考查空间想象能力以及计算能力.16.(5分)已知函数f(x)=5sinx﹣12cosx,当x=x0时,f(x)有最大值13,则tanx0=.【解答】解:f(x)=5sinx﹣12cosx=13sin(x﹣θ),其中sinθ=,cosθ=,当x﹣θ=+2kπ时,即x=θ++2kπ,k∈Z时,f(x)max=13,∴x0=θ++2kπ,k∈Z,∴tanx0=tan(θ++2kπ)=tan(θ+)==﹣=﹣,故答案为:﹣.【点评】本题考查了三角函数的化简和性质以及诱导公式,属于基础题三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)已知数列{a n}的首项a1=1,前n项和为S n,a n+1=2S n+1,n∈N*.(1)求数列{a n}的通项公式;(2)设b n=log3a n+1,求数列{a n+b n}的前n项和T n.=2S n+1,a n=2S n﹣1+1(n≥2)【解答】解:(1)由题意得a n+1两式相减得a n﹣a n=2(S n﹣S n﹣1)=2a n⇒a n+1=3a n(n≥2),+1所以当n≥2时,{a n}是以3为公比的等比数列.因为,所以,,{a n}是首项为1,公比为3的等比数列,所以得.(2),所以,T n=(30+1)+(31+2)+(32+3)+…+(3n﹣2+n﹣1)+(3n﹣1+n)=(30+31+32+…+3n﹣2+3n﹣1)+(1+2+3+…+(n﹣1)+n)==.【点评】本题考查数列的递推关系式的应用,数列求和,通项公式求法,考查转化思想以及计算能力.18.(12分)已知如图所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED⊥平面ABCD,.(1)求证:平面BCF∥平面AED.(注意排除重合情况)(2)若BF=BD=a,求四棱锥A﹣BDEF的体积.【解答】(1)证明:∵ABCD是菱形,∴BC∥AD,∵BC⊄面ADE,AD⊂面ADE,∴BC∥面ADE,∵BDEF是矩形,∴BF∥DE,∵BF⊄面ADE,DE⊂面ADE,∴BF∥面ADE,∵BC⊂面BCF,BF⊂面BCF,BC∩BF=B,∴面BCF∥面ADE;(2)解:连接AC,AC∩BD=O,∵ABCD是菱形,∴AC⊥BD,∵ED⊥面ABCD,AC⊂面ABCD,∴ED⊥AC,∵ED,BD⊂面BDEF,ED∩BD=D,∴AO⊥面BDEF,∴AO为四棱锥A﹣BDEF的高.由ABCD是菱形,∠BAD=,得△ABD为等边三角形,由BF=BD=a,得AD=a,AO=,∴•a2•=.【点评】本题考查线面平行、面面平行,考查四棱锥体积的求法,考查空间想象能力和思维能力,是中档题.19.(12分)小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.(Ⅰ)根据图中的数据信息,求出众数x1和中位数x2(精确到整数分钟);(Ⅱ)小明的父亲上班离家的时间y在上午7:00至7:30之间,而送报人每天在x1时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件A)的概率.【解答】解:(Ⅰ)众数最高矩形所在区间的中点,则x1=7:00由频率分布直方图可知6:50<x2<7:10即410<x2<430∴20×0.0033+20×0.0117+(x2﹣410)×0.0233=20×0.0100+20×0.0017+(430﹣x2)×0.0233解得x2=6:59,(Ⅱ)设报纸送达时间为x,则小明父亲上班前能取到报纸等价于,如图所求概率为P=1﹣=【点评】本题(Ⅰ)考查在丢失原始数据的情况下利用直方图求解一些数据,尤其是众数,中位数和平均数,要理解并记忆,(Ⅱ)概率不是古典概型就是几何概型,事件可一一列举多位古典概型,否则为几何概型,设报纸送达时间为x,关于x、y的二元一次不等式组对应平面区域,转化为几何概型,求面积之比.20.(12分)已知椭圆C的焦点在x轴上,中心在原点,离心率,直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切.(Ⅰ)求椭圆C的方程;(Ⅱ)设椭圆C的左、右顶点分别为A1,A2,点M是椭圆上异于A1,A2的任意一点,直线MA 1,MA2的斜率分别为,.证明:为定值.【解答】解:(Ⅰ)设椭圆C的方程为.∵离心率,∴a2=2c2,b2=c2.…(2分)∵直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切,∴,∴c2=2,∴a2=4.…(5分)∴椭圆C的方程为.…(6分)(Ⅱ)证明:由椭圆C的方程得A1(﹣2,0),A2(2,0),…(7分)设M点的坐标为(x0,y0),则,…(8分)∴.…(9分)∴.…(11分)∴为定值.…(12分)【点评】本题考查椭圆方程的求法,证明K MA1•K MA2为定值.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆性质,合理地进行等价转化.21.(12分)已知函数(Ⅰ)若x=2是f(x)的极值点,求f(x)的极大值;(Ⅱ)求实数a的范围,使得f(x)≥1恒成立.【解答】解:(Ⅰ)x=2是f(x)的极值点,,解得a=2.当a=2时,当(2,+∞)变化时,函数的极大值为.(Ⅱ)要使得f(x)≥1恒成立,即x>0时,x2﹣(a+1)x+alnx≥0恒成立,设g(x)=x2﹣(a+1)x+alnx,则g′(x)=x﹣(a+1)+=,(ⅰ)当a≤0时,由g′(x)<0得单减区间为(0,1),由g′(x)>0得单增区间为(1,+∞),故g(x)min=g(1)=﹣a﹣≥0,得a≤﹣;(ii)当0<a<1时,由g′(x)<0得单减区间为(a,1),由g′(x)>0得单增区间为(0,a),(1,+∞),此时g(1)=﹣a﹣<0,∴不合题意;(iii)当a=1时,f(x)在(0,+∞)上单增,此时g(1)=﹣a﹣<0,∴不合题意;(iv)当a>1时,由g′(x)<0得单减区间为(1,a),由g′(x)>0得单增区间为(0,1),(a,+∞),此时g(1)=﹣a﹣<0,∴不合题意.综上所述:a≤﹣时,f(x)≥1恒成立.【点评】本题考查利用导数研究函数的单调性及函数恒成立时所取的条件.考查考生的运算、推导、判断能力.请考生在第22~23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.直线l的参数方程为(t为参数),曲线C的极坐标方程为.(Ⅰ)求直线l的普通方程和曲线C的参数方程;(Ⅱ)设点D在C上,C在D处的切线与直线l垂直,求D的直角坐标.【解答】解:(Ⅰ)∵直线l的参数方程为(t为参数),由,得,…(1分)消去t得直线l的普通方程为.…(2分)∵曲线C的极坐标方程为=,…(3分)∴ρ2=2ρcosθ+2ρsinθ.将ρ2=x2+y2,ρcosθ=x,ρsinθ=y代入上式,得到曲线C的直角坐标方程为x2+y2=2x+2y,即(x﹣1)2+(y﹣1)2=2.…(4分)∴曲线C的直角坐标方程为(α为参数,0≤α<2π).…(5分)(Ⅱ)设曲线C上的点为,…(6分)由(1)知C是以G(1,1)为圆心,半径为的圆.…(7分)∵C在D处的切线与直线l垂直,∴直线GD与l的斜率相等,…(8分),α=60°或者α=240°,…(9分)故D的直角坐标为或.…(10分)【点评】本题考查直线的普通方程和曲线的参数方程的求法,考查点的直角坐标的求法,考查极坐标方程、参数方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.[选修4-5:不等式选讲]23.已知f(x)=|2x+3|﹣|2x﹣1|.(Ⅰ)求不等式f(x)<2的解集;(Ⅱ)若存在x∈R,使得f(x)>|3a﹣2|成立,求实数a的取值范围.【解答】解:(Ⅰ)不等式f(x)<2,等价于或或,得或,即f(x)<2的解集是(﹣∞,0);(Ⅱ)∵f(x)≤|(2x+3)﹣(2x﹣1)|=4,∴f(x)max=4,∴|3a﹣2|<4,解得实数a的取值范围是.【点评】本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.。
广东实验中学2017届高三10月月考英语试题 含解析

第I卷(满分70分)第一部分阅读理解(共两节,满分40分)第一节篇章阅读(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该题涂黑。
AI am Peter Hodes,a volunteer stem cell courier. Since March 2012,I’ve done 89 trips --—- of those, 51 have been abroad, I have 42 hours to carry stem cells (干细胞) in my little box because I've got two ice packs and that’s how long they last。
In all, from the time the stem cells are harvested from a donor to the time they can be implanted in the patient,we’ve got 72 hours at most。
So I am always conscious of time.I had one trip last year where I was caught by a hurricane in America。
I picked up the stem cells in Providence,Rhode Island, and was meant to fly to Washington then back to London. But when I arrived at the check-in desk at Providence,the lady on the desk said:“Well,I’m really sorry, I’ve got some bad news for you —-—— there are no flights from Washington." So I took my box and put it on the desk and I said: “In this box are some stem cells that are urgently needed for apatient -—-—please,please,you’ve got to get me back to the United Kingdom." She just dropped everything. She arranged for a flight on a small plane to be held for me, re—routed (改道)me through Newark and got me back to the UK even earlier than originally scheduled。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年高三级10月月考试题文科数学一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x |-2≤x ≤3},B={x |x +1>0},则集合A∩B 等于( )A .{x |-2≤x ≤-1}B .{x |-2≤x <-1}C .{x |-1<x ≤3}D .{x|1<x ≤3} 2.若i iz --=11,则z =( ) A .21 B .22C .i 2121+-D .i 2121+ 3.设0≤x ≤2π,且x x x cos sin 2sin 1-=-,则( ) A .0≤x ≤π B .474ππ≤≤x C .454ππ≤≤x D .232ππ≤≤x 4.设等差数列{a n }的前n 项和为S n ,若a 2+a 4+a 9=24,则S 9=( )A .36B .72C .144D .705.已知()f x 是定义在R 上周期为2的奇函数,当)1,0(∈x 时,14)(-=x x f , 则=)321(log 4f ( ) A .1 B .−1 C .21 D .21-6.设a ,b ,c ∈R ,则“1,a ,b ,c ,16为等比数列”是“b =4”的( ) A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 7.正方体ABCD ﹣A 1B 1C 1D 1中E 为棱BB 1的中点(如图),用过点A ,E ,C 1的平面截去该正方体的上半部分,则剩余几何体的左视图为( )A .B .C .D .8.《庄子·天下篇》中记述了一个著名命题:“一尺之棰,日取其半,万世不竭.”反映这个命题本质的式子是( )A .21111122222n n +++⋅⋅⋅+=- B .211112222n +++⋅⋅⋅++⋅⋅⋅< C .21111222n ++⋅⋅⋅+= D .21111222n ++⋅⋅⋅++⋅⋅⋅<9.如图,在△OAB 中,P 为线段AB 上的一点,,OB y OA x OP +=且3=,则( )A .31,32==y xB .32,31==y x C .43,41==y x D .41,43==y x10.已知集合A={1,2,3,4,5,6,7,8,9),在集合A 中 任取三个元素,分别作为一个三位数的个位数,十位数和百位数, 记这个三位数为a ,现将组成a 的三个数字按从小到大排成的三 位数记为I (a ),按从大到小排成的三位数记为D (a ) (例如a =219,则I (a )=129,D (a )=921),阅读如图所示的 程序框图,运行相应的程序,任意输入一个a ,则输出b 的值为( ) A .792 B .693 C .594D .49511.已知点P 为椭圆1121622=+y x 上的动点,EF 为圆N:1)1(22=-+y x 的任一直径,求⋅最大值和最小值是( ).A .16,3412-B .34-13,17C .19, 3412-D .20, 3413- 12.设a n =1n sin n π25,S n =a 1+a 2+…+a n ,在S 1,S 2,…,S 100中,正数的个数是 ( )A .25B .50C .75D .100 二、填空题:本大题共4小题,每小题5分.13.已知正实数x ,y 满足xy =9,则x +9y 取得最小值时x = ,y = . 14.等比数列{a n }的首项a 1=1,前n 项的和为S n ,若S 6=9S 3,则a 6= .15.如图,为了测量河对岸电视塔CD 的高度,小王在点A 处测得塔顶D 仰角为30°,塔底C 与A 的连线同河岸成15°角,小王向前走了1200m 到达 M 处,测得塔底C 与M 的连线同河岸成60°角, 则电视塔CD 的高度为 .16.设1m >,变量,x y 在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值为2,则m =________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知数列{a n }的各项均为正数,前n 项和为S n ,且)(2)1(*N n a a S n n n ∈+= (Ⅰ)求数列{a n }的通项公式; (Ⅱ)设n n nn b b b T S b +++==21,21, 求T n . 18.(本小题满分12分)某中学共有1000名文科学生参加了该市高三第一次质量检查的考试,其中数学成绩如下表所示:(Ⅰ)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,年级将采用分层抽样的方法抽取100名同学进行问卷调查. 甲同学在本次测试中数学成绩为75分,求他被抽中的概率;(Ⅱ)年级将本次数学成绩75分以下的学生当作“数学学困生”进行辅导,请根据所提供数据估计“数学学困生”的人数;(III )请根据所提供数据估计该学校文科学生本次考试的数学平均分.ACDM30 601519.(本小题满分12分)如图,ABC ﹣A 1B 1C 1是底面边长为2,高为23的正三棱柱,经过AB的截面与上底面相交于PQ ,设C 1P=λC 1A 1(0<λ<1). (Ⅰ)证明:PQ ∥A 1B 1; (Ⅱ)当21=λ时,在图中作出点C 在平面ABQP 内 的正投影F (说明作法及理由),并求四面体CABF 的体积. 20.(本小题满分12分)已知椭圆C 的左、右焦点分别为)0,3(-、)0,3(,且经过点).21,3( (I )求椭圆C 的方程:(II )直线y =kx (k ∈R ,k ≠0)与椭圆C 相交于A ,B 两点,D 点为椭圆C 上的动点,且|AD|=|BD|,请问△ABD 的面积是否存在最小值?若存在,求出此时直线AB 的方程:若不存在,说明理由.21.(本小题满分12分)设函数.ln )1(2)(2x k x k x x f --+=(Ⅰ)讨论)(x f 的单调性;(Ⅱ)若k 为正数,且存在x 0使得2023)(k x f -<,求k 的取值范围. 请考生在第22、23题中任选一题做答,做答时请写清题号. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 1的极坐标方程为ρ2cos 2θ=8,曲线C 2的极坐标方程为θ=π6,曲线C 1,C 2相交于A ,B 两点. (I)求A ,B 两点的极坐标;(II)曲线C 1与直线⎩⎨⎧x =1+32t ,y =12t(t 为参数)分别相交于M ,N 两点,求线段MN 的长度.23.(本小题满分10分)选修4-5:不等式选讲A1A1B1CC BQP设f (x )=|x ﹣1|﹣2|x +1|的最大值为m .(Ⅰ)求m ;(Ⅱ)若),0(,,+∞∈c b a ,a 2+2b 2+c 2=m ,求ab +bc 的最大值.广东实验中学2016-2017高三10月月考试题文科数学解答及评分标准 一、选择题:1~12:CBCBB ACDDD CD二、填空题:13. 9,1;14. 32;15. 6002m ;16. 1m =+17. 解:(Ⅰ))(2)1(*N n a a S n n n ∈+=∴n n n a a S +=22①)2(21211≥+=---n a a S n n n ② 由①﹣②得:12122---+-=n n n n n a a a a a 2分(a n +a n ﹣1)(a n ﹣a n ﹣1﹣1)=0, ∵a n >0,∴)2(11≥=--n a a n n 又∵2)1(1111+==a a S a , ∴a 1=1,∴n d n a a n =-+=)1(1, 5分 故a n =n . 6分 (Ⅱ)2)1(2)1(+=+=n n a a S n n n8分 111)1(1+-=+=∴n n n n b n 10分故11111113121211+=+-=+-++-+-=n n n n n T n . 12分 18.解:(Ⅰ)分层抽样中,每个个体被抽到的概率均为:样本容量总体中个体总数,故甲同学被抽到的概率1P=10…………………4分 (Ⅱ)由题意得 1 000604003601080()0x =-+++=. ……………6分 设估计“数学学困生”人数为m16080804m =+⨯=. 故估计该中学“数学学困生”人数为80人 ……………………8分 (III )该学校本次考试的数学平均分.60608080100400120360140100107.21000x ⨯+⨯+⨯+⨯+⨯==估计该学校本次考试的数学平均分为107.2分. ……………12分 19.解:(I )∵平面ABC ∥平面A 1B 1C 1,平面ABC∩平面ABQP=AB ,平面ABQP∩平面A 1B 1C 1=QP , ∴AB ∥PQ , 2分又∵AB ∥A 1B 1,∴PQ ∥A 1B 1. 5分(Ⅱ)F 点是PQ 中点,理由如下: 当时21=λ,P 、Q 分别是1111,B A C A 的中点,连接CQ 和CP, 因为ABC ﹣A 1B 1C 1 是正三棱柱,所以CQ=CP ,QP CF ⊥∴, 6分取AB 中点H ,连接FH,CH ,,3=CH 在等腰梯形ABQP 中,26=FH , 连接FC C F C 11,∆中,CF=,26222CH FH CF =+∴FH CF ⊥∴, 8分⊥∴=⋂CF H FH QP , 平面ABF ,即ABQP CF 平面⊥,所以F 点是C 在平面ABQP 内的正投影。
10分.21262622131=⨯⋅⋅⨯=∴-ABF C V12分20.解:(I )由题意,⎪⎪⎩⎪⎪⎨⎧=+=1413322b a c ,∴a =2,b =1, 2分 ∴椭圆C 的方程:1422=+y x 4分(II )D 在AB 的垂直平分线上,∴OD :x ky 1-= . 5分 由⎪⎩⎪⎨⎧=+=1422y x kx y ,可得(1+4k 2)x 2=4,|AB|=2|OA|=222y x +=414122++k k , 6分 同理可得|OC|=24122++k k , 7分则S △ABC =2S △OAC =|OA|×|OC|=)4)(41()1(4222+++k k k . 8分 由于2)1(5)4)(41(222k k k +≤++,10分 所以S △ABC =2S △OAC ≥58,当且仅当1+4k 2=k 2+4(k >0), 即k =1时取等号.△ABD 的面积取最小值58.直线AB 的方程为y =x . 12分21.解:(Ⅰ)f′(x )=x +1﹣k ﹣x k =xk x x x k x k x ))(1()1(2-+=--+,2分 (ⅰ)k ≤0时,f′(x )>0,f (x )在(0,+∞)上单调递增; 3分 (ⅱ)k >0时,x ∈(0,k ),f′(x )<0;x ∈(k ,+∞),f′(x )>0, ∴f (x )在(0,k )上单调递减,f (x )在(k ,+∞)上单调递增. 4分(Ⅱ)因k >0,由(Ⅰ)知f (x )+k 2﹣23的最小值为f (k )+k 2﹣23=23ln 22--+k k k k ,由题意得22k +k ﹣k ln k ﹣23<0,即2k +1﹣ln k ﹣k 23<0. 6分令g (k )=2k +1﹣ln k ﹣k 23,则g′(k )=k k 231-21+=22232kk k +->0, 8分∴g (k )在(0,+∞)上单调递增,又g (1)=0, 9分∴k ∈(0,1)时,g (k )<0,于是23ln 22--+k k k k <0;k ∈(1,+∞)时,g (k )>0,于是23ln 22--+k k k k >0. 11分故k 的取值范围为0<k <1. 12分22.解:(I)由⎩⎪⎨⎪⎧ρ2cos 2θ=8,θ=π6得ρ2cos π3=8, 2分所以ρ2=16,即ρ=±4.所以A ,B 两点的极坐标为:A ⎝⎛⎭⎫4,π6 ,B ⎝⎛⎭⎫-4,π6 或B ⎝⎛⎭⎫4,7π6 .5分(II)由曲线C 1的极坐标方程得其直角坐标方程为x 2-y 2=8, 7分将直线⎩⎨⎧x =1+32t ,y =12t代入x 2-y 2=8,整理得t 2+23t -14=0,即t 1+t 2=-23,t 1·t 2=-14, 9分 所以|MN |=172)14(4)32(2=-⨯--. 10分 23.解:(Ⅰ)当x ≤﹣1时,f (x )=3+x ≤2; 1分 当﹣1<x <1时,f (x )=﹣1﹣3x <2; 2分 当x ≥1时,f (x )=﹣x ﹣3≤﹣4. 3分 故当x =﹣1时,f (x )取得最大值m =2. 5分(Ⅱ)a 2+2b 2+c 2=(a 2+b 2)+(b 2+c 2)≥2ab +2bc =2(ab +bc ), 7分当且仅当a =b =c =22时,等号成立. 9分 此时,ab +bc 取得最大值2m=1. 10分。
