2014年深圳一模理数学试题(word版)
深圳中学2014年中考数学一模试卷(含答案)

深圳中学2014年中考第一次模拟考试数学考生须知:1.本试卷共5页。
全卷满分150分。
考试时间为120分钟。
试题包含选择题和非选择题。
考生答题全部答在答题卡上,答在本试卷上无效。
2.请将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡上。
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案。
答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡的指定位置,在其它位置答题一律无效。
一、选择题(共10小题,每小题3分,共30分.).C D.C D..C D.5.(3分)如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为().C D.7.(3分)如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的俯视图是().C D.210.(3分)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为().C D.二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上).11.(3分)因式分解:a2+2a=_________.12.(3分)某市在市中心建了一个文化广场,建成后总面积达163500平方米,成为该市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为_________平方米.13.(3分)如图,等腰梯形ABCD中,AB∥DC,BE∥AD,梯形ABCD的周长为26,DE=4,则△BEC的周长为_________.14.(3分)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且圆心距O1O2=t+2,若这两个圆相切,则t=_________.15.(3分)双曲线y1、y2在第一象限的图象如图,,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是_________.16.(3分)若a1=1﹣,a2=1﹣,a3=1﹣,…;则a2014的值为_________.(用含m的代数式表示)三、解答题(本大题共9题,满分102分.解答应写出文字说明、证明过程或演算步骤).17.(9分)解不等式组,并把解集在数轴上表示出来.18.(9分)如图,已知:在△ABC中,AB=AC,∠BAF=∠CAE,求证:BE=CF.19.(10分)化简求值:,其中x=2.20.(10分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:(1)这次抽查的家长总人数为_________;(2)请补全条形统计图和扇形统计图;(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是_________.21.(12分)某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.(1)求该市对市区绿化工程投入资金的年平均增长率;(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?22.(12分)马航事件牵动了全国甚至全世界人们的心,当得知MH370客机最后失踪地点是在印度洋南部某海域C处,“雪龙”号科考船立即从B处出发以60km/h的速度前往搜救.已知出发时在B 测得搜救指挥基地A的方位角为北偏东80°,测得失踪地点C的方位角为南偏东25°.航行10小时后到达C处,在C处测得A的方位角为北偏东20°.求C到A的距离.23.(12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD为⊙O的切线;(2)求证:∠C=2∠DBE;(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)24.(14分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.25.(14分)如图,已知抛物线的方程C1:y=﹣(x+2)(x﹣m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.(1)若抛物线C1过点M(2,2),求实数m的值;(2)在(1)的条件下,求△BCE的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标;(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m 的值;若不存在,请说明理由.深圳中学2014年中考第一次模拟试卷数学答案一、选择题(共10小题,每小题3分,共30分.).C D.C D..C D.5.(3分)如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为().C D.sinA==7.(3分)如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的俯视图是().C D.210.(3分)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为().C D.a,C=C=aa a+++l=二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上).11.(3分)因式分解:a2+2a=a(a+2).12.(3分)某市在市中心建了一个文化广场,建成后总面积达163500平方米,成为该市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为 1.635×105平方米.13.(3分)如图,等腰梯形ABCD中,AB∥DC,BE∥AD,梯形ABCD的周长为26,DE=4,则△BEC的周长为18.14.(3分)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且圆心距O1O2=t+2,若这两个圆相切,则t=2或0.15.(3分)双曲线y1、y2在第一象限的图象如图,,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是y2=.解:∵=..16.(3分)若a1=1﹣,a2=1﹣,a3=1﹣,…;则a2014的值为1﹣.(用含m的代数式表示)﹣=1=,=1=m=﹣.三、解答题(本大题共9题,满分102分.解答应写出文字说明、证明过程或演算步骤).17.(9分)解不等式组,并把解集在数轴上表示出来.18.(9分)如图,已知:在△ABC中,AB=AC,∠BAF=∠CAE,求证:BE=CF.19.(10分)化简求值:,其中x=2.20.(10分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:(1)这次抽查的家长总人数为100;(2)请补全条形统计图和扇形统计图;(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是.扇形统计图:赞成:,反对:×=.21.(12分)某市为争创全国文明卫生城,2008年市政府对市区绿化工程投入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间每年投入资金的年平均增长率相同.(1)求该市对市区绿化工程投入资金的年平均增长率;(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?22.(12分)马航事件牵动了全国甚至全世界人们的心,当得知MH370客机最后失踪地点是在印度洋南部某海域C处,“雪龙”号科考船立即从B处出发以60km/h的速度前往搜救.已知出发时在B 测得搜救指挥基地A的方位角为北偏东80°,测得失踪地点C的方位角为南偏东25°.航行10小时后到达C处,在C处测得A的方位角为北偏东20°.求C到A的距离.×=300×=100kmCA=300+100=1003)+23.(12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD为⊙O的切线;(2)求证:∠C=2∠DBE;(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)BD=2BF=2××﹣24.(14分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.25.(14分)如图,已知抛物线的方程C1:y=﹣(x+2)(x﹣m)(m>0)与x轴相交于点B、C,与y轴相交于点E,且点B在点C的左侧.(1)若抛物线C1过点M(2,2),求实数m的值;(2)在(1)的条件下,求△BCE的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标;(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m 的值;若不存在,请说明理由.((=,∴)﹣=2(•±+2∴∴((EC=。
2014年广东省深圳市龙岗区中考模拟考试数学试题及答案范文

2014年深圳市龙岗区中考模拟考试数学试题第一部分 选择题(本题共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的) 1.2014的相反数是( ) A .2014B .2014-C .20141D .20141-2.“辽宁号”航母的满载排水量为67500吨,数据67500用科学记数法表示为( ) A .210675⨯B .21075.6⨯C .41075.6⨯D .51075.6⨯3.下列图形中,既是..轴对称图形又是..中心对称图形的是( )A B C D4.下图是由八个完全相同的小正方体组成的几何体,其主视图是( )正面 A B C D 5.下列计算中,正确..的是( ) A .9132=- B .()332-=-C .326m m m =÷D .()222b a b a -=-6.已知⊙O 1与⊙O 2的半径R 、r 分别是方程01272=+-x x 的两根,且圆心距1=d ,那么⊙O 1与⊙O 2的位置关系是( ) A .外离B .外切C .相交D .内切7.已知一个多边形的每一个内角都等于135°,则这个多边形是( )A .正六边形B .正八边形C .正十边形D .正十二边形D8.下列命题中,错误..的是( ) A .平行四边形的对角线互相平分B .对角线相等的四边形是矩形C .一组对边平行,一组对角相等的四边形是平行四边形D .顺次连接等腰梯形各边中点所得的四边形为菱形9.某中学九(1)班学生为希望工程捐款,该班50名学生的捐款情况统计如图1所示,则他们捐款金额的众数和中位数分别是( ) A .16,15 B .15,16 C .20,10D .10,20图1 图210.如图2,在边长为9的等边△ABC 中,BD =3,∠ADE =60°,则AE 的长为( ) A .6B .7C .7.5D .811.如图3,菱形OABC 的顶点A 在x 轴的正半轴上,顶点C 的坐标为(3,4).反比例函数xky =(x >0)的图象经过顶点B ,则k 的值为( ) A .32 B .24C .20D .12图3 图412.如图4,在Rt ABC △中,︒=∠90C ,6=AC ,8=BC ,⊙O 为ABC △的内切圆,点D 是斜边AB 的中点,则ODA ∠tan 的值为( ) A .2 B C .34D .2第二部分 非选择题填空题(本题共4小题,每小题3分,共12分) 13.分式方程312-=x x 的解为______________. 14.如图5,已知圆锥的底面半径OA =3cm ,高SO =4cm ,则该圆锥的侧面积为 ______________cm 2.15.如图6,交警为提醒广大司机前方道路塌陷在路口设立了警示牌.已知立杆AD 的高度是3m ,从侧面B 点测得警示牌顶端C 点和底端D 点的仰角分别是60°和45°.那么警示牌CD 的高度为______________ m .16.如图7,在平面直角坐标系中,Rt △OAB 的顶点A 在x 轴的正半轴上。
深圳市2014年初中毕业考试数学模拟试卷(1)及答案解析

绝密级(解密时间2013年5月1日上午9点)2014年初中毕业考试数学模拟试卷说明:1.答题前,请将姓名、考生号、考场、试室号和座位号用规定的笔写在答题卡指定的位置上,将条形码粘贴好。
2.全卷分二部分,第一部分为选择题,第二部分为非选择题,共4页。
考试时间90分钟,满分1 00分。
3.本卷试题,考生必须在答题卡上按规定作答;凡在试卷、草稿纸上作答的,其答案一律无效。
答题卡必须保持清洁,不能折叠。
4.本卷选择题1-12,每小题选出答案后,用2B铅笔将答题卡选择题答题区内对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案;非选择题13-23,答案(含作辅助线)必须用规定的笔,按作答题目序号,写在答题卡非选择题答题区内。
5.考试结束,请将本试卷和答题卡一并交回。
第一部分选择题一、(本部分共12小题,每小题3分共36分.每小题4个选项,其中只有一个是正确的)1. -2的绝对值等于【】A.2 B.-2 C.12D.±22. 长城总长约为6700010米,用科学记数法表示是(保留两个有效数字)【】A、6.7×105米B、6.7×106米C、6.7×107米D、6.7×108米3. 下列交通标志图案是轴对称图形的是【】A.B.C.D.4. 下列计算正确的是【】A.a3a2=a6B.a2+a4=2a2C.(a3)2=a6D.(3a)2=a65. 在公式I=UR中,当电压U一定时,电流I与电阻R之间的函数关系可用图象大致表示为【】A. B.C.D.6.如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C 处的高度CD为100米,点A、D、B在同一直线上,则AB两点煌距离是【】A.200米 B.2003米 C.2203米 D.100(3+1)米7. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥HG,EH∥FG,则四边形EFGH的周长是【】A.10 B.13 C.210 D.2138. 如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差▲ km/h。
2014年深圳市中考数学全真模拟试卷含答案 (精选4套)

5、考试结束,请将本试卷和答题卡一并交回.
第一部分选择题
(4)、存在点N,做一条与BC平行的直线,平移,
当它与抛物线有一个交点时,此时以BC为底的三角形
高度最大。抛物线与该直线的交点,就是所求的N点。
易求BC的K值为 ,所以设动直线为:
,与抛物线联立:
(1分)
所以 (1分)
过N做y轴的平行线,交BC于一点,求此点坐标
BC: ,令x=4,解得y=2,∴三角形BCN面积的最大值= (1分)
A.0B.2C.-2D.0或2
7.用配方法解方程 ,配方后的方程是( )
A. B. C. D.
8.若一次函数 的函数值 随 的增大而减小,且图象与 轴的负半轴相交,那么对 和 的符号判断正确的是()
A. B. C. D.
9.如图,将△ 绕着点 顺时针旋转50°后得到△ .若∠ =40°.
∠ =110°,则∠ 的度数是()
21、(1)证明:正方形ABCD中,∠BAD=90°,AD=AB,
∵AF⊥AE,∴∠FAB+∠BAE=90°
∵∠DAE+∠BAE=90°,∴∠FAB=∠DAE -----2分
∵∠FBA=∠D=90°,∴△ABF≌△ADE
∴AE=AF -------------4分
(2)解:在Rt△ABF中,∠FBA=90°,AF=7,BF=DE=2
在Rt△BCF中,设BC=x米,则BF=2x,CF=
在Rt△BCE中,∠BEC=60°,CE=
深圳市2014年中考第一轮模拟考试(一模)数学试题

第二部分
非选择题
填空题(本题共 4 小题,每小题 3 分,共 12 分) 13.分解因式: 4 x2 9 =__________. 4 3 0 的解为 14.方程 . x x2 15.如图,三个小正方形的边长都为 1 ,则图中阴影部分面积的 和是 (结果保留 ) . 16.如图,一段抛物线: y x x 4 0 x 4 ,记为 C1 , 它与 x 轴交于点 O , A1 ; 将 C1 绕点 A1 旋转 180° 得 C2 ,交 x 轴于点 A2 ; 将 C2 绕点 A2 旋转 180° 得 C3 ,交 x 轴于点 A3 ; …… 如此进行下去,直至得 C10 .若 P 37, m 在第 10 段抛物线 C10 上,则 m =_________. 第 16 题图 第 15 题图
解答题(本题共 7 小题,其中第 17 题 5 分,第 18 题 6 分,第 19 题 7 分,第 20 题 8 分,第 21 题 8 分,第 22 题 9 分,第 23 题 9 分,共 52 分) 17. (5 分)计算: (1)3 | 3 2 | 2sin 60 4 .
2 5x2 2 x 3 6 . 18. (6 分)先化简,再求值: ,其中 x 2 x 4 x2 x2 3
19. (7 分)某学校为了解学生课外阅读的情况,对学生“平均每天课外阅读的时间”进行了随机抽样调查,下图 是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题:
第 22 题图
第 17 题图 (1)平均每天课外阅读的时间为“ 0.5 ~1 小时”部分的扇形图的圆心角为______度; (2)本次一共调查了_________名学生; (3)将条形图补充完整; (4)若该校有 1680 名学生,请估计该校有多少名学生平均每天课外阅读的时间在 0.5 小时以下. 20. (8 分)如图,已知矩形 ABCD 中, AB 4cm , AD 10cm ,点 P 在边 BC 上移动,点 E 、 F 、 G 、 H 分 别是 AB 、 AP 、 DP 、 DC 的中点. ⑴求证: EF GH 5cm ; EF ⑵求当 APD 90 时, 的值. GH
2014深圳一模
平行班 17 25 455.52 -43.97 5 殷洪岩
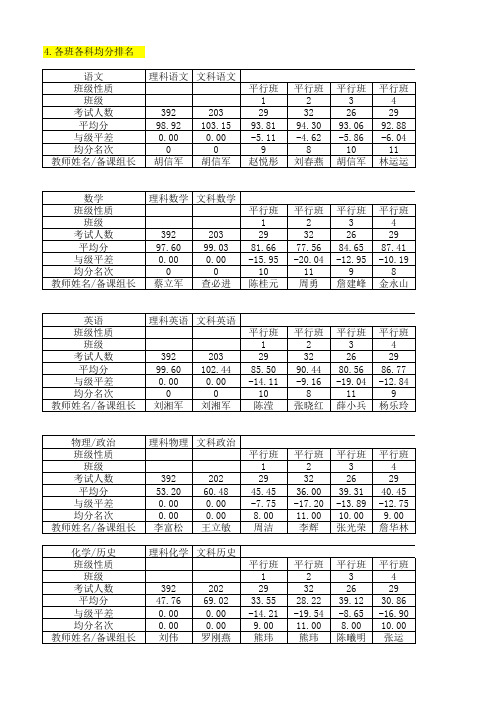
4.各班各科均分排名 语文 班级性质 班级 考试人数 平均分 与级平差 均分名次 教师姓名/备课组长 理科语文 文科语文 平行班 1 29 93.81 -5.11 9 赵悦彤 平行班 2 32 94.30 -4.62 8 刘春燕 平行班 3 26 93.06 -5.86 10 胡信军 平行班 4 29 92.88 -6.04 11 林运运
理科总分
392 456.03 0.00 0 彭元成
202 499.49 0.00 0 周洁
理科语文 实验班 实验班 实验班 5 6 7 40 37 44 101.08 100.00 100.78 2.15 1.08 1.86 3 5 4 林运运 刘春燕 彭元成
文科语文 实验班 8 44 98.36 -0.56 6 赵悦彤 实验班 9 44 98.15 -0.77 7 索玉璋 科技班 10 32 104.56 5.64 2 胡信军 科技班 11 35 106.99 8.06 1 彭元成 科技班 12 38 109.63 6.48 1 黄玲萍 科技班 13 39 106.47 3.33 2 索玉璋
理科数学 实验班 实验班 5 6 40 37 105.68 98.27 8.07 0.67 3 6 詹建峰 周勇
文科数学 实验班 7 44 98.64 1.03 5 李春明 实验班 8 44 97.18 -0.42 7 陈桂元 实验班 9 44 104.75 7.15 4 金永山 科技班 10 32 110.56 12.96 2 李春明 科技班 11 35 115.37 17.77 1 蔡立军 科技班 12 38 106.58 7.54 2 查必进 科技班 13 39 108.69 9.66 1 刘光辉
深圳市2014年中考数学全真模拟试题(针对2014版新考纲)(一)(含答案)

2014年深圳市初中毕业生学业考试模拟试题数学说明:1.全卷共4页,考试用时100分钟,满分为120分.2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓 名、试室号、座位号.用2B 铅笔把对应该号码的标号涂黑.3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交回.一、选择题(本大题共10小题,每小题3分,满分30分)1.据2013年1月2日南方都市报报道,东莞市目前汽车拥有量约为1000000辆.则1000000用科学记数法表示为( )A 、1×105B 、1×106C 、0. 1×107D 、1×1072.-0.5的倒数是( ) A 、12 B 、2 C 、-2 D 、12- 3.一个全透明的玻璃正方体,上面嵌有一根黑色的金属丝,如图,金属丝在俯视图中的形状是( )4.已知直线//a b ,且∠︒1=60,则∠2=( )A 、60︒B 、110︒C 、120︒D 、130︒5.参加一次聚会的每两个人都握一次手,所有人共握手66次,则参加聚会的人数是( ) A 、8 B 、10 C 、12 D 、14 6.如图,如果从半径为9cm 的圆形纸片剪去31圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( ) A 、6cmB、cmC 、8cmD、cm7.如图,把一个矩形纸片ABCD 沿EF 折叠后,点D 、C分别落在D ′、ABC DC ′的位置,若∠EFB=55°, 则∠AED ′等于( )A 、50°B 、60°C 、70°D 、75°8.某口袋中有20个球,其中白球x 个,绿球2x 个,其余为黑球。
2014年广东省深圳市高三一模理科数学试题及答案

广东省深圳市2014届高三2月第一次调研数学理试题2014.2本试卷共6页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生首先检查答题卡是否整洁无缺损,监考教师分发的考生信息条形码是否正确;之后务必用0.5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号,同时,将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区,请保持条形码整洁、不污损.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.不按要求填涂的,答案无效. 3.非选择题必须用0.5毫米黑色字迹的签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排;如需改动,先划掉原的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再做答.漏涂、错涂、多涂的答案无效.5.考生必须保持答题卡的整洁,考试结束后,将答题卡交回. 参考公式:如果事件A B 、互斥,那么P A B P A P B +=+()()(); 如果事件A B 、相互独立,那么P AB P A P B =()()();若锥体的底面积为S ,高为h ,则锥体的体积为13V Sh =.一、选择题:本大题共8个小题;每小题5分,共40分.在每小题给出的四个选项中,有且只有一项是符合题目要求的. 1.已知集合{2,0,1,4}A =,集合{04,R}=<≤∈B x x x ,集合C AB =.则集合C 可表示为A .{2,0,1,4}B . {1,2,3,4}C .{1,2,4}D . {04,R}x x x <≤∈2.复数z 满足(1i)1z -=(其中i 为虚数单位),则z =A .11i22- B .11i 22+ C .11i 22-+ D .11i 22-- 3.下列函数中,为奇函数的是A .122x x y =+B .{},0,1y x x =∈C .sin y x x =⋅D .1,00,01,0x y x x <⎧⎪==⎨⎪->⎩4.“1ω=”是“ 函数()cos f x x ω=在区间[]0,π上单调递减”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 5.执行如图1所示的程序框图,则输出的a 的值为 (注:“2a =”,即为“2a ←”或为“:2a =”.) A .2 B .13C .12-D .3-6.412x x -()的展开式中常数项为A .12B .12-C .32D .32-7.如图2,在矩形OABC 内:记抛物线21y x =+与直线1y x =+ 围成的区域为M (图中阴影部分).随机往矩形OABC 内投一点P ,则点P 落在区域M 内的概率是 A .118 B .112C .16 D .138.在平面直角坐标系中,定义两点11(,)P x y 与22(,)Q x y 之间的“直角距离”为1212(,)d P Q x x y y =-+-.给出下列命题:(1)若(1,2)P ,(sin ,2cos )()Q R ααα∈,则(,)d P Q 的最大值为3 (2)若,P Q 是圆221x y +=上的任意两点,则(,)d P Q 的最大值为 (3) 若(1,3)P ,点Q 为直线2y x =上的动点,则(,)d P Q 的最小值为12. 其中为真命题的是 A .(1)(2)(3) B .(1)(2) C .(1)(3) D . (2)(3)二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.本大题分为必做题和选做题两部分.(一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须作答. 9.函数f x =()的定义域为 .10.某几何体的三视图如图3所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是 . 11+图411.已知双曲线2222:1x y C a b -=与椭圆22194x y +=有相同的焦点, 且双曲线C 的渐近线方程为2y x =±,则双曲线C 的方程为 .12. 设实数,x y 满足,102,1,x y y x x ≤⎧⎪≤-⎨⎪≥⎩向量2,x y m =-()a ,1,1=-()b .若// a b ,则实数m 的最大值为 .13.在数列{}n a 中,已知24a =, 315a =,且数列{}n a n +是等比数列,则n a = . (二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计算前一题的得分. 14.(坐标系与参数方程选做题)在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.若曲线1C 的参数方程为,x t y =⎧⎪⎨⎪⎩(t 为参数),曲线2C 的极坐标方程为sin cos 1ρθρθ-=-.则曲线1C 与曲线2C 的交点个数为________个.15.(几何证明选讲选做题)如图4,已知AB 是⊙O 的直径,TA是⊙O 的切线,过A 作弦//AC BT ,若4AC =,AT =,则AB = .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数()sin(2)(0π)f x x ϕϕ=+<<的图像经过点π(,1)12. (1)求ϕ的值;(2)在ABC ∆中,A ∠、B ∠、C ∠所对的边分别为a 、b 、c ,若222a b c ab +-=,且π()2122A f +=.求sinB .17.(本小题满分12分)某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图5(1)):若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定 义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3:2.(1)试确定x ,y ,p ,q 的值,并补全频率分布直方图(如图5(2)).(2)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望.18.(本小题满分14分)如图6所示,平面ABCD⊥平面BCEF ,且四边形ABCD 为矩形,四边形BCEF 为直角梯形,//BF CE ,BC CE ⊥,4DC CE ==,2BC BF ==.(1)求证://AF 平面CDE ;(2)求平面ADE 与平面BCEF 所成锐二面角的余弦值; (3)求直线EF 与平面ADE 所成角的余弦值.19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且满足24(1)(1)(2)(N )n n n S n a n *++=+∈.图5(1) (2)AD BC FE图6(1)求1a ,2a 的值; (2)求n a ; (3)设1n n n b a +=,数列{}n b 的前n 项和为n T ,求证:34n T <.20.(本小题满分14分)如图7,直线:(0)l y x b b =+>,抛物线2:2(0)C y px p =>,已知点(2,2)P 在抛物线C 上,且抛物线C 上的点到直线l. (1)求直线l 及抛物线C 的方程;(2)过点(2,1)Q 的任一直线(不经过点P )与抛物线C 交于A 、B 两点,直线AB 与直线l 相交于点M ,记直线PA ,PB ,PM 的斜率分别为1k ,2k , 3k .问:是否存在实数λ,使得123k k k λ+=?若存在,试求出λ的值;若不存在,请说明理由.图7yMPB QxAOl21.(本小题满分14分)已知函数2901xf x a ax =>+()() .(1)求f x ()在122[,]上的最大值;(2)若直线2y x a =-+为曲线y f x =()的切线,求实数a 的值;(3)当2a =时,设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ,且121414x x x =…+++ ,若不等式1214f x f x +f x λ≤…()+()+()恒成立,求实数λ的最小值.2014年深圳市高三年级第一次调研考试数学(理科)答案及评分标准说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分数. 一、选择题:本大题每小题5分,满分40分.二、填空题:本大题每小题5分,满分30分.9. {2}x x ≥; 10. 83; 11.2214y x -=; 12.6;13.123n n -⋅-; 14.1; 15. .三、解答题16.(本小题满分12分)已知函数()sin(2)(0π)f x x ϕϕ=+<<的图像经过点π(,1)12. (1)求ϕ的值;(2)在ABC ∆中,A ∠、B ∠、C ∠所对的边分别为a 、b 、c ,若222a b c ab +-=,且π()2122A f +=.求sinB . 解:(1)由题意可得π()112f =,即πsin()16ϕ+=. ……………………………2分 0πϕ<<,ππ7π666ϕ∴<+<, ππ62ϕ∴+=, π3ϕ∴=. ……………………………………………………………5分(2)222a b c ab +-=,2221cos 22a b c C ab +-∴==, ……………………………………………………7分sin C ∴==. …………………………………………8分 由(1)知π()sin(2)3f x x =+,π(+)sin()cos 21222A f A A π∴=+==.()0,A π∈,sin A ∴==, ……………………………10分 又sin sin(π())sin()B A C A C =-+=+,1sin sin cos cos sin 2B A C A C ∴=+==12分 【说明】 本小题主要考查了三角函数)sin()(ϕω+=x A x f 的图象与性质,三角恒等变换,以及余弦定理等基础知识,考查了简单的数学运算能力. 17.(本小题满分12分)某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图5(1)):若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定 义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3:2.(1)试确定x ,y ,p ,q 的值,并补全频率分布直方图(如图5(2)).(2)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购 达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望. 解:(1)根据题意,有39151860,182.39153x y yx +++++=⎧⎪⎨=⎪+++⎩+ 解得9,6.x y =⎧⎨=⎩…………………2分0.15p ∴=,0.10q =.补全频率分布直方图如图所示. ………4分(2)用分层抽样的方法,从中选取10人,则其中“网购达人”有210=45⨯人,“非网购达人”有310=65⨯人. …………………6分故ξ的可能取值为0,1,2,3;03463101(0)6C C P C ξ=== , 12463101(1)2C C P C ξ===,21463103(2)10C C P C ξ===,30463101(3)30C C P C ξ===.…………………………10分所以ξ的分布列为:01236210305E ξ∴=⨯+⨯+⨯+⨯=. ……………………12分 )【说明】本题主要考察读图表、分层抽样、概率、随机变量分布列以及数学期望等基础知识,考查运用概率统计知识解决简单实际问题的能力,数据处理能力. 18.(本小题满分14分)如图6所示,平面ABCD⊥平面BCEF ,且四边形ABCD 为矩形,四边形BCEF 为直角梯形,//BF CE ,BC CE ⊥,4DC CE ==,2BC BF ==.(1)求证://AF 平面CDE ;(2)求平面ADE 与平面BCEF 所成锐二面角的余弦值; (3)求直线EF 与平面ADE 所成角的余弦值.解:(法一)(1)取CE 中点为G ,连接DG 、FG ,//BF CG 且BF CG =,∴四边形BFGC 为平行四边形,则//BC FG 且BC FG =. …………2分四边形ABCD 为矩形, //BC AD ∴且BC AD =,//FG AD ∴且FG AD =,∴四边形AFGD 为平行四边形,则//AF DG .DG ⊂平面CDE ,AF ⊄平面CDE ,//AF ∴平面CDE . ……………………………………………………4分(2)过点E 作CB 的平行线交BF 的延长线于P ,连接FP ,EP ,AP ,////EP BC AD ,∴A ,P ,E ,D 四点共面.四边形BCEF 为直角梯形,四边形ABCD 为矩形,∴EP CD ⊥,EP CE ⊥,又CD CE C =,EP ∴⊥平面CDE ,∴EP DE ⊥,又平面ADE平面BCEF EP =,∴DEC ∠为平面ADE 与平面BCEF 所成锐二面角的平面角.……………………7分4DC CE ==,∴cos 2CE DEC DE ∠==. 即平面ADE 与平面BCEF所成锐二面角的余弦值为2. ……………………9分 AD BCFE图6GAD BC F EP(3)过点F 作FH AP ⊥于H ,连接EH ,根据(2)知A ,P ,E ,D 四点共面,////EP BC AD ,∴BC BF ⊥,BC AB ⊥,又AB BF B =, BC ∴⊥平面ABP ,∴B C F H ⊥,则FH EP ⊥. 又FH AP ⊥, FH ∴⊥平面ADE .∴直线EF 与平面ADE 所成角为HEF ∠. ……………………………11分4DC CE ==,2BC BF ==,∴0sin 45FH FP ==EF ==HE =,∴cos HE HEF EF ∠===. 即直线EF 与平面ADE……………………………14分 (法二)(1)四边形BCEF 为直角梯形,四边形ABCD 为矩形,∴BC CE ⊥,BC CD ⊥,又平面ABCD ⊥平面BCEF ,且平面ABCD平面BCEF BC =,DC ∴⊥平面BCEF .以C 为原点,CB 所在直线为x 轴,CE 所在直线为y CD 所在直线为z 轴建立如图所示空间直角坐标系.根据题意我们可得以下点的坐标:(2,0,4)A ,(2,0,0)B ,(0,0,0)C ,(0,0,4)D ,(0,4,0)E ,(2,2,0)F , 则(0,2,4)AF =-,(2,0,0)CB =. ………………2分BC CD ⊥,BC CE ⊥, CB ∴为平面CDE 的一个法向量.又0220(4)00AF CB ⋅=⨯+⨯+-⨯=,//AF ∴平面CDE . …………………………………………………………4分(2)设平面ADE 的一个法向量为1111(,,)n x y z =,则110,0.AD n DE n ⎧⋅=⎪⎨⋅=⎪⎩(2,0,0)AD =-,(0,4,4)DE =-,∴11120440x y z -=⎧⎨-=⎩, 取11z =,得1(0,1,1)n =. ……………………………6分DC ⊥平面BCEF ,∴平面BCEF 一个法向量为(0,0,4)CD =,设平面ADE 与平面BCEF 所成锐二面角的大小为α,则11cos 24CD n CD n α⋅===⨯⋅. 因此,平面ADE 与平面BCEF . …………………9分 (3)根据(2)知平面ADE 一个法向量为1(0,1,1)n =,(2,2,0)EF =-, 1111cos ,222EF n EF n EF n ⋅∴<>===-⋅,………12分设直线EF 与平面ADE 所成角为θ,则1cos sin ,EF n θ=<>=因此,直线EF 与平面ADE 所成角的余弦值为2. ………………………14分 【说明】本题主要考察空间点、线、面位置关系,二面角及三角函数及空间坐标系等基础知识,考查空间想象能力、运算能力和推理论证能力,考查用向量方法解决数学问题的能力. 19. (本小题满分14分)已知数列{}n a 的前n 项和为n S ,且满足24(1)(1)(2)(N )n n n S n a n *++=+∈.(1)求1a ,2a 的值; (2)求n a ; (3)设1n n n b a +=,数列{}n b 的前n 项和为n T ,求证:34n T <. 解:(1)当=1n 时,有2114(11)(+1=1+2a a ⨯+)(),解得1=8a . 当=2n 时,有21224(21)(1)(22)a a a ⨯+++=+,解得2=27a .……………2分(2)(法一)当2n ≥时,有2(2)4(1)1nn n a S n ++=+, ……………①211(1)4(1)n n n a S n--++=. …………………②①—②得:221(2)(1)41n n n n a n a a n n -++=-+,即:331(1)=n n a n a n -+.…………5分 ∴1223333===1(1)(1)3n n n a a a a n n n --==+-….∴ 3=(1)n a n +(2)n ≥.………………………………………8分另解:33333121333121(1)42(1)(1)3n n n n n a a a n n a a n a a a n n ---+=⋅⋅⋅⋅=⋅⋅⋅⋅=+-. 又当=1n 时,有1=8a , ∴3=(1)n a n +.…………………………8分(法二)根据1=8a ,2=27a ,猜想:3=(1)n a n +. ………………………………3分用数学归纳法证明如下:(Ⅰ)当1n =时,有318(11)a ==+,猜想成立. (Ⅱ)假设当n k =时,猜想也成立,即:3=(1)k a k +.那么当1n k =+时,有2114(11)(1)(12)k k k S k a +++++=++,即:211(12)4(1)11k k k a S k +++++=++,………………………①又 2(2)4(1)1kk k a S k ++=+, …………………………②①-②得:22223111(3)(2)(3)(2)(1)4=2121k k k k k a k a k a k k a k k k k ++++++++=--++++,解,得33+1(2)(11)k a k k =+=++.∴当1n k =+时,猜想也成立.因此,由数学归纳法证得3=(1)n a n +成立.………………………………………8分 (3)211111=(1(11n n n b a n n n n n +=<=-+++)), ……………………………10分∴1231=n n n T b b b b b -+++++…2222211111=234(1)n n ++++++ (2)11111<22323(1)(1)n n n n +++++⨯⨯-+… 111111111=()()()()4233411n n n n +-+-++-+--+… 1113=4214n +-<+.………………………………………14分 【说明】考查了递推数列的通项公式、数列裂项求和公式、放缩法证明不等式等知识,考查了学生的运算能力,以及化归与转化的思想. 20.(本小题满分14分)如图7,直线:(0)l y x b b =+>,抛物线2:2(0)C y px p =>,已知点(2,2)P 在抛物线C 上,且抛物线C 上的点到直线l的距离的最小值为4. (1)求直线l 及抛物线C 的方程;(2)过点(2,1)Q 的任一直线(不经过点P )与抛物线C 交于A 、B 两点,直线AB 与直线l 相交于点M ,记直线PA ,PB ,PM 的斜率分别为1k ,2k , 3k .问:是否存在实数λ,使得123k k k λ+=?若存在,试求出λ的值;若不存在,请说明理由.解:(1)(法一)点(2,2)P 在抛物线C 上, 1p ∴=. ……………………2分设与直线l 平行且与抛物线C 相切的直线l '方程为y x m =+,由2,2,y x m y x =+⎧⎨=⎩ 得22(22)0x m x m +-+=, 22(22)448m m m ∆=--=-, ∴由0∆=,得12m =,则直线l '方程为12y x =+. 两直线l 、l '间的距离即为抛物线C 上的点到直线l 的最短距离,∴4=,解得2b =或1b =-(舍去).∴直线l 的方程为2y x =+,抛物线C 的方程为22y x =. …………………………6分图7yMPB QxAOl(法二)点(2,2)P 在抛物线C 上, 1p ∴=,抛物线C 的方程为22y x =.……2分设2(,))2t M t t R ∈(为抛物线C 上的任意一点,点M 到直线l的距离为d =,根据图象,有202t t b -+>,21)21]d t b ∴=-+-, t R ∈,d ∴=2b =. 因此,直线l 的方程为2y x =+,抛物线C 的方程为22y x =.…………………6分 (2)直线AB 的斜率存在,∴设直线AB 的方程为1(2)y k x -=-,即21y kx k =-+,由221,2,y kx k y x =-+⎧⎨=⎩ 得22420ky y k --+=, 设点A 、B 的坐标分别为11(,)A x y 、22(,)B x y ,则122y y k +=,1224k y y k-=, 11121112222222y y k y x y --===-+-,2222k y =+, …………………………9分121212121222+82()82242242222()4324y y k k k k k y y y y y y k k⋅+++∴+=+===-++++++⋅+.…10分 由21,2,y kx k y x =-+⎧⎨=+⎩得211M k x k +=-,411M k y k -=-,∴341221121321k k k k k k --+-==+--, ……………………………………………13分 1232k k k ∴+=.因此,存在实数λ,使得123k k k λ+=成立,且2λ=.…………………………14分 【说明】本题主要考查抛物线的方程与性质、直线方程、直线与抛物线的位置关系,切线方程,点到直线距离,最值问题等基础知识,考查学生运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想. 21. (本小题满分14分)已知函数2901xf x a ax =>+()() . (1)求f x ()在122[,]上的最大值;(2)若直线2y x a =-+为曲线y f x =()的切线,求实数a 的值;(3)当2a =时,设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ,且121414x x x =…+++ ,若不等式1214f x f x +f x λ≤…()+()+()恒成立,求实数λ的最小值.解:(1)2222229[1(1)2]9(1)()(1)(1)ax x ax ax f x ax ax ⋅+-⋅-'==++,…………………………2分令()0f x '=,解得x a=±(负值舍去),由122<<,解得144a <<. (ⅰ)当104a <≤时,由1[,2]2x ∈,得()0f x '≥,∴()f x 在1[,2]2上的最大值为18(2)41f a =+.…………………………………3分(ⅱ)当4a ≥时,由1[,2]2x ∈,得()0f x '≤,∴()f x 在1[,2]2上的最大值为118()24f a =+.……………………………………4分(ⅲ)当144a <<时,在12x <<时,()0f x '>2x <<时,()0f x '<,∴()f x 在1[,2]2上的最大值为=2f a a ).…………………………………5分(2)设切点为(,())t f t ,则()1,()2.f t f t t a '=-⎧⎨=-+⎩……………………………6分由()1f t '=-,有2229[1]1(1)at at -=-+,化简得2427100a t at -+=, 即22at =或25at =, ……………………………①由()2f t t a =-+,有2921ta t at=-+,……………②由①、②解得2a =或4a =. ……………………………………………9分(3)当2a =时,29()12xf x x =+,由(2)的结论直线4y x =-为曲线()y f x =的切线,(2)2f =,∴点(2,(2))f 在直线4y x =-上,根据图像分析,曲线()y f x =在直线4y x =-下方. …………………………10分 下面给出证明:当1[,2]2x ∈时,()4f x x ≤-.3222928104()(4)41212x x x x f x x x x x -+---=-+=++2221(2)12x x x --=+(),∴当1[,2]2x ∈时,()(4)0f x x --≤,即()4f x x ≤-.………………………12分∴12141214()()()414()f x f x f x x x x +++≤⨯-+++,121414x x x +++=, 1214()()()561442f x f x f x ∴+++≤-=.∴要使不等式1214()()()f x f x f x λ+++≤恒成立,必须42λ≥.……………13分又当12141x x x ====时,满足条件121414x x x +++=,且1214()()()42f x f x f x +++=,因此,λ的最小值为42. …………………………………………………14分【说明】本题主要考查函数的性质、导数运算法则、导数的几何意义及其应用、不等式的求解与证明、恒成立问题,考查学生的分类讨论,计算推理能力及分析问题、解决问题的能力及创新意识.。
深圳市2014年初中毕业生学业考试数学模拟试卷含答案

深圳市2014年初中毕业生学业考试数学模拟试卷说明:1.试题卷共4页,答题卡共4页。
考试时间90分钟,满分100分。
2.请在答题卡上填涂学校.班级.姓名.考生号,不得在其它地方作任何标记。
3.本卷选择题1—12,每小题选出答案后,用2B 铅笔将答题卷选择题答题区内对应题目的答案标号涂黑;非选择题的答案(含作辅助线)必须用规定的笔,写在答题卷指定的答题区内,写在本卷或其他地方无效。
第一部分 选择题一、选择题(本题共有12小题,每小题3分,共36分,每小题有四个选项,其中只有一个是正确的)1.9的算术平方根是( ) A .3 B .–3 C .±3 D .6 2.下列所给图形中,既是中心对称图形又是轴对称图形的是()3.环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为( ) A .6105.2⨯ B .5105.2-⨯ C .6105.2-⨯ D .7105.2-⨯4.一组数据3,x ,4,5,8的平均数为5,则这组数据的众数、中位数分别是( ) A .4,5 B .5,5 C .5,6 D .5,85.某商场在“庆五一”促销中推出“1元换2.5倍”活动,小红妈妈买一件标价为600元的衣服,她实际需要付款( ) A .240元 B .280元 C .480元 D .540元 6.下列运算正确的是( )A .532532a a a =+B .236a a a =÷C .623)(a a =- D .222)(y x y x +=+ 7.下列命题中错误..的是( ) A .等腰三角形的两个底角相等 B .对角线互相垂直的四边形是菱形 C .矩形的对角线相等D .圆的切线垂直于过切点的直径8.已知两圆的半径是4和5,圆心距x 满足不等式组⎪⎩⎪⎨⎧+<-+>+23245252x x x x ,则两圆的 位置关系是( ) A .相交 B . 外切 C .内切 D . 外离9.如图1,在平面直角坐标系中,点P 在第一象限,⊙P与x 轴相切于点Q ,与y 轴交于M (0,2)、N (0,8)两 点,则点P 的坐标是( ) A .(5,3) B .(3,5) C .(5,4) D .(4,5)10.已知甲车行驶35千米与乙车行驶45千米所用时间相同,且乙车每小时比甲车多行驶15千米,设甲车的速度为x 千米/小时,依据题意列方程正确的是( )A .154535-=x x B .x x 451535=+ C .x x 451535=- D .154535+=x xQP O N x yM 图1A .B .C .D .11.已知:如图2,∠MON=45º,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4……在射线ON上,点B1、B2、B3、B4……在射线OM上,……依此类推,则第6个正方形的面积S6是(A.256 B.900C.1024 D.409612.在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图3所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是()(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)A.1.2 米B.1.5米C.1.9米D.2.5米第二部分非选择题二、填空题。
深圳市2014年初中毕业考试数学模拟试卷3及答案

2014年初中毕业考试数学模拟试卷3.初中数学试卷(说明:共23题,考试时间90分钟,满分100分)第一部分(选择题 共36分)一、 选择题(本大题共12小题,每小题3分,满分36分,在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1.sin30°的值为( ▲ ) A .21 B .23 C .33 D .22 2.计算232(3)x x ⋅-的结果是( ▲ )A .56x - B .56x C .62x - D .62x3.⊙O 的半径为4,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是( ▲ ) A .相交 B .相切 C .相离 D .无法确定 4.使分式24x x -有意义的x 的取值范围是( ▲ )A .x =2B .x ≠2C .x =-2D .x ≠-2 5.不等式组2030x x ->-<⎧⎨⎩的解集是( ▲ )A .x>2B .x<3C .2<x<3D .无解 6.如图,⊙O 的直径CD 过弦EF 的中点G ,∠EOD =40°,则∠DCF 等于( ▲ ) A .80° B .50° C .40° D .20° 7.下列命题中,正确的是( ▲ )A.若0a b ⋅>,则00a b >>,B.若0a b ⋅>,则00a b <<,C.若0a b ⋅=,则0a =, 且0b =D.若0a b ⋅=,则0a =,或0b =8.右图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( ▲ )A .B .C .D .2 1 3xO yP 图29.正方形ABCD 中,E 是BC 边上一点,以E 为圆心、EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则sin EAB ∠的值为( ▲ ) A .43B .34 C .45D .3510.如图,正方形OABC ADEF ,的顶点A D C ,,在坐标轴上,点F 在AB 上,点B E,在函数1(0)y x x=>的图象上,则点E 的坐标是( ▲ )A.515122⎛⎫+- ⎪ ⎪⎝⎭, B.353522⎛⎫+- ⎪ ⎪⎝⎭, C.515122⎛⎫-+ ⎪ ⎪⎝⎭,D.353522⎛⎫-+ ⎪ ⎪⎝⎭,11.如图2,点P (3a ,a )是反比例函y = kx(k >0)与⊙O 的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为A .y =3xB .y =5xC .y =10xD .y =12x12.如图4,△ABC 与△DEF 均为等边三角形,O 为BC 、EF 的中点,则AD :BE 的值为( )A .3:1B .2:1C .5:3D .不确定第二部分(非选择题 共64分)二、填空题(本大题共4小题,每小题3分,满分12分.) 13.分解因式:4a 3-4a =______________________。
2014年高考数学深圳模拟试题

页眉内容学进辅导高三数学专题训练数列(2014-3-1)一、选择题1.(2013年高考大纲全国卷)设S n 为等差数列{a n }的前n 项和,若a 1=1,公差d =2,S k +2-S k =24,则k =( )A .8B .7C .6D .52.(2013年高考天津卷)已知{a n }为等差数列,其公差为-2,且a 7是a 3与a 9的等比中项,S n 为{a n }的前n 项和,n ∈N *,则S 10的值为( ) A .-110 B .-90 C .90 D .1103.(2013年高考四川卷)数列{a n }的首项为3,{b n }为等差数列且b n =a n +1-a n ()n ∈N *.若b 3=-2,b 10=12,则a 8=( ) A .0 B .3 C .8 D .114.(2013年高考江西卷)已知数列{a n }的前n 项和S n 满足:S n +S m =S n +m ,且a 1=1,那么a 10=( ) A .1 B .9 C .10 D .55 二、填空题5.(2013年高考湖北卷)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为__________升.6.(2013年高考重庆卷)在等差数列{a n }中,a 3+a 7=37,则a 2+a 4+a 6+a 8=__________.7.(2013年高考北京卷)在等比数列{a n }中,若a 1=12,a 4=-4,则公比q =________;|a 1|+|a 2|+…+|a n |=________.8.(2013年高考山东卷)设函数f (x )=xx +2(x >0),观察:f 1(x )=f (x )=xx +2,f 2(x )=f (f 1(x ))=x3x +4,f 3(x )=f (f 2(x ))=x7x +8,f 4(x )=f (f 3(x ))=x15x +16,…根据以上事实,由归纳推理可得:当n ∈N *且n ≥2时,f n (x )=f (f n -1(x ))=________.9.(2013年高考江苏卷)设1=a 1≤a 2≤…≤a 7,其中a 1,a 3,a 5,a 7成公比为q 的等比数列,a 2,a 4,a 6成公差为1的等差数列,则q 的最小值是________.10.(2013年高考湖南卷)设S n 是等差数列{a n }(n ∈N *)的前n 项和,且a 1=1,a 4=7,则S 5=________.11.(2013年高考陕西卷)植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返..所走的路程总和最小,这个最小值为________米. 12.(2013年高考广东卷)等差数列{a n }前9项的和等于前4项的和.若a 1=1,a k +a 4=0,则k =________.三、解答题13.(2013年高考辽宁卷)已知等差数列{a n }满足a 2=0,a 6+a 8=-10. (1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和.14.(2013年高考安徽卷)在数1和100之间插入n 个实数,使得这(n +2)个数构成递增的等比数列,将这(n +2)个数的乘积记作T n ,再令a n =lg T n ,n ≥1. 求数列{a n }的通项公式;15.(2013年高考湖北卷)已知数列{a n }的前n 项和为S n ,且满足:a 1=a ()a ≠0,a n +1=rS n ()n ∈N *,r ∈R ,r ≠-1. 求数列{a n }的通项公式;16.(2013年高考浙江卷)已知公差不为0的等差数列{a n}的首项a1为a(a∈R),设数列的前n项和为S n,且1a1,1a2,1a4成等比数列.求数列{a n}的通项公式及S n;17.(2013年高考山东卷)等比数列{a n}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.第一列第二列第三列第一行3210第二行6414第三行9818求数列{a n}的通项公式;学进辅导高二数学训练题导数的概念及其运算(2014-3-1)1.f (x )=x 3, f ′(x 0)=6,则x 0=( ) A.2 B .- 2 C .±2 D .±12.(2011年全国卷Ⅰ)设曲线y =x +1x -1在点(3,2)处的切线与直线ax +y +1=0垂直,则a=( )A .2 B.12C .-12D .-23.(文科)(2011年全国卷Ⅰ)曲线y =x 3-2x +4在点(1,3)处的切线的倾斜角为( ) A .30° B .45° C .60° D .120°4.(理科)(2011年辽宁卷)设P 为曲线C :y =x 2+2x +3上的点,且曲线C 在点P 处切线倾斜角的取值范围为⎣⎡⎦⎤0,π4,则点P 横坐标的取值范围为( ) A.⎣⎡⎦⎤-1,-12 B.[]-1,0 C.[]0,1 D.⎣⎡⎦⎤12,14.设f 0(x )=sin x ,f 1(x )=f ′0(x ),f 2(x )=f ′1(x ),…,f n +1(x )=f ′n (x )(n ∈N ),则f 2011(x )=( )A .sin xB .-sin xC .cos xD .-cos x5.(2010年厦门模拟)曲线y =e x 在点(2,e 2)处的切线与坐标轴所围三角形的面积为( ) A.94e 2 B .2e 2 C .e 2D.e 226.(2011年江苏卷)直线y =12x +b 是曲线y =ln x (x >0)的一条切线,则实数b =_________.7.(2011年江苏卷)在平面直角坐标系xOy 中,点P 在曲线C :y =x 3-10x +3上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为______.8.已知f (x )=x 2+2x ·f ′(1),则f ′(0)等于________.9.已知A ()-1,2为抛物线C :y =2x 2上的点,直线l 1过点A ,且与抛物线C 相切,直线l 2:x =a ()a <-1交抛物线C 于点B ,交直线l 1于点D .求直线l 1的方程;10.(2011年海南宁夏卷)设函数f (x )=ax -bx ,曲线y =f (x )在点(2,f (2))处的切线方程为7x -4y -12=0.求y =f (x )的解析式;学进辅导高二数学训练题利用导数研究函数的极值和最值(2014-3-1)1.(2013年株洲质检)已知函数y =f (x )的导函数y =f ′(x )的图象如下,则( ) A .函数f (x )有1个极大值点,1个极小值点 B .函数f (x )有2个极大值点,2个极小值点 C .函数f (x )有3个极大值点,1个极小值点 D .函数f (x )有1个极大值点,3个极小值点2.(2013年金山中学月考)已知二次函数f (x )=ax 2+bx +c 的导数为f ′(x ),f ′(0)>0,对于任意实数x 都有f (x )≥0,则f (1)f ′(0)的最小值为( )A .3 B.52C .2 D.323.(2012年福建卷)如果函数y =f (x )的图象如上图,那么导函数y =f ′(x )的图象可能是( )4.(2012年韶关调研)已知函数f (x )的定义域为[-2,4],且f (4)=f (-2)=1,f ′(x )为f (x )的导函数,函数y =f ′(x )的图象如上图所示.则平面区域⎩⎪⎨⎪⎧a ≥0b ≥0f (2a +b )<1所围成的面积是( )A .2B .4C .5D .85.(2013年广东实验中学月考)函数f (x )=12x -x 3在区间[-3,3]上的最小值是________. 6.(2013年厦门北师大海沧附中)已知函数f (x )=x 3-3ax 2-bx ,其中a ,b 为实数. 若f (x )在x =1处取得的极值为2,求a ,b 的值;7.(理科)设函数f (x )=ln(2x +3)+x 2. (1)讨论f (x )的单调性;(2)求f (x )在区间⎣⎡⎦⎤-34,14的最大值和最小值.专题三 数 列1.【解析】选D.∵S k +2-S k =a k +1+a k +2=a 1+kd +a 1+(k +1)d =2a 1+(2k +1)d =2×1+(2k +1)×2=4k +4=24, ∴k =5. 2.【解析】选D.∵a 3=a 1+2d =a 1-4,a 7=a 1+6d =a 1-12,a 9=a 1+8d =a 1-16,又∵a 7是a 3与a 9的等比中项,∴(a 1-12)2=(a 1-4)·(a 1-16),解得a 1=20.∴S 10=10×20+12×10×9×(-2)=110.3.【解析】选B.设数列{b n }的首项为b 1,公差为d ,由b 3=-2,b 10=12, 得⎩⎪⎨⎪⎧ b 1+2d =-2,b 1+9d =12,解得⎩⎪⎨⎪⎧b 1=-6,d =2, ∴b n =-6+2()n -1=2n -8. ∵b n =a n +1-a n ,∴a 8=()a 8-a 7+()a 7-a 6+()a 6-a 5+()a 5-a 4+()a 4-a 3+()a 3-a 2+()a 2-a 1+a 1 =b 7+b 6+b 5+…+b 1+a 1 =7×()-6+2×7-82+3=3.4.【解析】选A.∵S n +S m =S n +m ,且a 1=1, ∴S 1=1.可令m =1,得S n +1=S n +1, ∴S n +1-S n =1.即当n ≥1时,a n +1=1,∴a 10=1. 5.【解析】设所构成数列{a n }的首项为a 1,公差为d ,依题意 ⎩⎪⎨⎪⎧a 1+a 2+a 3+a 4=3,a 7+a 8+a 9=4, 即⎩⎪⎨⎪⎧4a 1+6d =3,3a 1+21d =4, 解得⎩⎨⎧a 1=1322,d =766,∴a 5=a 1+4d =1322+4×766=6766.【答案】67666.【解析】由等差数列的性质知a 2+a 4+a 6+a 8=2(a 3+a 7)=2×37=74. 【答案】747.【解析】∵{a n }为等比数列,且a 1=12,a 4=-4,∴q 3=a 4a 1=-8,∴q =-2,∴a n =12·(-2)n -1,∴|a n |=2n -2,∴|a 1|+|a 2|+|a 3|+…+|a n |=12(1-2n )1-2=12(2n -1)=2n -1-12.【答案】-2 2n -1-128.【解析】依题意,先求函数结果的分母中x 项系数所组成数列的通项公式,由1,3,7,15,…,可推知该数列的通项公式为a n =2n-1.又函数结果的分母中常数项依次为2,4,8,16,…,故其通项公式为b n =2n .所以当n ≥2时,f n (x )=f (f n -1(x ))=x(2n-1)x +2n.【答案】x(2n -1)x +2n9.【解析】由题意知a 3=q ,a 5=q 2,a 7=q 3且q ≥1,a 4=a 2+1,a 6=a 2+2且a 2≥1,那么有q 2≥2且q 3≥3.故q ≥33,即q 的最小值为33.【答案】33 10.【解析】设等差数列的公差为d .由a 1=1,a 4=7,得3d =a 4-a 1=6,故d =2,∴a 5=9,S 5=5(a 1+a 5)2=25.【答案】25 11.【解析】假设20位同学是1号到20号依次排列,使每位同学的往返所走的路程和最小,则树苗需放在第10或第11号树坑旁.此时两侧的同学所走的路程分别组成以20为首项,20为公差的等差数列,所有同学往返的总路程为S =9×20+9×82×20+10×20+10×92×20=2000(米). 【答案】2000 12.【解析】设等差数列{a n }的前n 项和为S n ,则S 9-S 4=0,即a 5+a 6+a 7+a 8+a 9=0,5a 7=0,故a 7=0.而a k +a 4=0,故k =10. 【答案】1013.【解】(1)设等差数列{a n }的公差为d ,由已知条件可得⎩⎪⎨⎪⎧ a 1+d =0,2a 1+12d =-10,解得⎩⎪⎨⎪⎧a 1=1,d =-1. 故数列{a n }的通项公式为a n =2-n .(2)设数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和为S n ,即S n =a 1+a 22+…+a n2n -1,故S 1=1,S n 2=a 12+a 24+…+a n2n .所以,当n >1时,S n2=a 1+a 2-a 12+…+a n -a n -12n -1-a n 2n =1-⎝⎛⎭⎫12+14+…+12n -1-2-n 2n=1-⎝⎛⎭⎫1-12n -1-2-n 2n =n2n .所以S n =n2n -1.综上,数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和S n =n2n -1.14.【解】设t 1,t 2,…,t n +2构成等比数列,其中t 1=1,t n +2=100, 则T n =t 1·t 2·…·t n +1·t n +2,①T n =t n +2·t n +1·…·t 2·t 1.②①×②并利用t i t n +3-i =t 1t n +2=102(1≤i ≤n +2),得T 2n =(t 1t n +2)·(t 2t n +1)·…·(t n +1t 2)·(t n +2t 1)=102(n +2).∴a n =lg T n =n +2,n ≥1. 15.【解】()1由已知a n +1=rS n , 可得a n +2=rS n +1,两式相减可得 a n +2-a n +1=r ()S n +1-S n =ra n +1, 即a n +2=()r +1a n +1. 又a 2=ra 1=ra ,所以当r =0时,数列{a n }为:a,0,…,0,…;当r ≠0,r ≠-1时,由已知a ≠0,所以a n ≠0()n ∈N *, 于是由a n +2=()r +1a n +1,可得a n +2a n +1=r +1()n ∈N *,∴a 2,a 3,…,a n ,…成等比数列,∴当n ≥2时,a n =r ()r +1n -2a .综上,数列{a n }的通项公式为a n =⎩⎨⎧a ,n =1,r ()r +1n -2a ,n ≥2.16.【解】(1)设等差数列{a n }的公差为d ,由⎝⎛⎭⎫1a 22=1a 1·1a 4, 得(a 1+d )2=a 1(a 1+3d ).因为d ≠0,所以d =a 1=a .所以a n =na ,S n =an (n +1)2.17.【解】(1)当a 1=3时,不合题意;当a 1=2时,当且仅当a 2=6,a 3=18时,符合题意; 当a 1=10时,不合题意. 因此a 1=2,a 2=6,a 3=18. 所以公比q =3.故a n =2·3n -1.导数参考答案(1)页眉内容页脚内容 1.C 2.D 3.B 4.解析:依题设切点P 的横坐标为x 0, 且y ′=2x 0+2=tan α(α为点P 处切线的倾斜角),又∵α∈[0,π4],∴0≤2x 0+2≤1,∴x 0∈⎣⎡⎦⎤-1,-12. 答案:A4.D 5.D 6.ln 2-1 7.(-2,15) 8.-49.4x +y +2=0 10.(1)f ()x =x -3x导数参考答案(2)1.A 2.C 3.A 4.B 5.-166.(1)a =43,b =-5 (2)a ≥1。
