浙江省萧山中学2012届高三上学期摸底考试题数学文
数学_2012年浙江省杭州市某校高考数学模拟试卷(2)(含答案)

2012年浙江省杭州市某校高考数学模拟试卷(2)一、选择题(8×4'=32')1. 函数y =log 3x 的定义域是( )A RB (0, +∞)C (1, +∞)D (3, +∞)2. 已知集合M ={x|x 2<4},N ={x|x 2−2x −3<0},则集合M ∩N 等于( )A {x|x <−2}B {x|x >3}C {x|−1<x <2}D {x|2<x <3}3. 已知f(x)=x 5+ax 3+bx −8,且f(−2)=10,那么f(2)等于( )A −26B −18C −10D 104. 若x 2−3x +2=0是x =1的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件5. 直线y =−2x +1在y 轴上的截距是( )A 0B 1C −1D 126. 已知命题:①过与平面α平行的直线a 有且仅有一个平面与α平行;②过与平面α垂直的直线a 有且仅有一个平面与α垂直.则( )A ①正确,②不正确B ①不正确,②正确C ①②都正确D ①②都不正确7. 函数y =3|log 3x|的图象是( ) A BC D 8. 设F 1,F 2是椭圆x 225+y 216=1的两个焦点,过F 1且平行于y 轴的直线交椭圆于A ,B 两点,则△F 2AB 的面积是( )A 245B 485C 965D 1925二、填空题(7×4'=28')9. 已知函数f(x)=ax 2+2,且f′(1)=2,则a 的值为=________.10. 等差数列{a n }中,若a l +a 4+a 7=39,a 3+a 6+a 9=27,则前9项的和S 9等于________.11. 已知x >0,则函数f(x)=2−3x −4x 的最大值是________. 12. 设数列{a n }的前n 项和为S n =n 2,则a 5=________.13. 函数f(x)=x ,求f′(2)=________.14. 已知直线3x +2y −3=0与6x +my +1=0相互平行,则它们之间的距离是________.15. 计算:(2+i)2=________.三、简答题16. 已知函数f(x)=−x3+3x2+9x+a.(1)求f(x)的单调递减区间;(2)若f(x)在区间[−2, 2]上的最大值为20,求它在该区间上的最小值.17. 如图,在底面为平行四边形的四棱锥P−ABCD中,AB⊥AC,PA⊥面ABCD,点E是PD的中点.(1)求证:AC⊥PB;(2)求证:PB // 平面AEC.18. 设函数f(x)=ax2+bx+1(a, b∈R),(1)若f(−1)=0,且对于任意的x,f(x)≥0恒成立,求f(x)的表达式;(2)在(1)的条件下,当x∈[−2, 2]时,g(x)=f(x)−kx是单调函数,求实数k的取值范围.2012年浙江省杭州市某校高考数学模拟试卷(2)答案1. B2. C3. A4. B5. B6. A7. A8. C9. 110. 9911. 2−4√312. 913. −√2814. 7√132615. 3−4i16. 解:(1)f′(x)=−3x2+6x+9.令f′(x)<0,解得x<−1或x>3,所以函数f(x)的单调递减区间为(−∞, −1),(3, +∞).(2)因为f(−2)=8+12−18+a=2+a,f(2)=−8+12+18+a=22+a,所以f(2)>f(−2).因为在(−1, 3)上f′(x)>0,所以f(x)在[−1, 2]上单调递增,又由于f(x)在[−2, −1]上单调递减,因此f(2)和f(−1)分别是f(x)在区间[−2, 2]上的最大值和最小值,于是有22+a=20,解得a=−2.故f(x)=−x3+3x2+9x−2,因此f(−1)=1+3−9−2=−7,即函数f(x)在区间[−2, 2]上的最小值为−7.17. 证明:(1)∵ PA⊥面ABCD,AC⊂面ABCD,∴ PA⊥AC又∵ AB⊥AC,PA∩AC=A,PA⊂面PAB,AB⊂面PAB∴ AC⊥面PAB∴ AC⊥PB(2)连接BD交AC于点O,并连接EO,∵ 四边形ABCD为平行四边形∴ O为BD的中点又∵ E为PD的中点∴ 在△PDB中EO为中位线,EO // PB∵ PB⊄面AEC,EO⊂面AEC∴ PB // 面AEC.18. 解:(1)由f(−1)=a−b+1=0,解得b=a+1,故函数f(x)=ax2+(a+1)x+ 1.再由f(x)≥0恒成立,可得{a>0△=(a−1)2≤0,求得a=1,可得b=2,∴ f(x)=x2+2x+1.(2)由于当x∈[−2, 2]时,g(x)=f(x)−kx=x2+(2−k)x+1是单调函数,∴ k−22≤−2,或k−22≥2.解得k≤−2,或k≥6.。
浙江省高三六校联考数学试题(文科)
2012届浙江省高三六校联考数学试题(文科)一、选择题(本大题共10小题,每小题5分,共50分。
每小题给出的四个选项,只有一项符合题目要求)1.若全集为实数集R ,集合A=}4|{2>x x ,B=}12|{>x x ,则(B A ⋂)=A .}21|{≤≥x x x 或B .}20|{≤<x xC .}20|{≤≤x xD .φ2.⎩⎨⎧≥<<-=)2()20(ln 1)(2x xx x x f 若,若2)(=m f ,则m 的值为A .eB .2C .e1D .2或e1 3.设i 为虚数单位,若i b iia +=-+1(),Rb a ∈,则b a ,的值为 A .1,0==b a B .0,1==b aC .1,1==b aD .1,21-==b a 4.一个算法的程序框图如图所示,若该程序输出的结果是45,则判断框中应填入的条件是A .5i <B .6i <C .7i <D .8i <5.若}{n a 为首项为1的等比数列,n S 为其前n 项和,已知2,,2432+a S a 三个数成等差数列,则数列}{2n a 的前5项和为A .341B .31000C .1023D .1024 6.一个袋中装有大小相同的5个球,现将这5个球分别编号为1,2,3,4,5,从袋中取出两个球,每次只取出一个球,并且取出的球不放回.求取出的两个球上编号之积为奇数的概率为A .21B .103 C .207 D .107 7.若10≠>a a 且,则“0log <b a ”是“0)1)(1(<--b a ”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件8.已知点),(y x 满足⎪⎩⎪⎨⎧≤--≥-≥+2211y x y x y x ,目标函数y ax z 2+=仅在点(1,0)处取得最小值,则a 的范围为A .)2,1(-B .)2,4(-C .)1,2(-D .)4,2(-9.]2,2[,cos )(2ππ-∈-=x x x x f 若,设21|)(|)(-=x f x g ,则函数)(x g 的零点个数为A .4B .3C .2D .110.已知点P 为双曲线)0,0(12222>>=-b a by a x 右支上一点,21,F F 分别为双曲线的左右焦点,且ab F F 221||=,I 为三角形21F PF 的内心,若2121F IF IPF IPF S S S ∆∆∆+=λ成立,则λ的值为A .2221+ B .132- C .12+ D .12-二、填空题(本大题共7小题,每小题4分,共28分)11.一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(如图),为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样的方法抽出200人作进一步调查,其中低于1500元的称为低收入者,高于3000元的称为高收入者,则应在低收入者和高收入者中抽取的人数一共是____________.12.若某多面体的三视图(单位:cm )如图所示,则此多面体的表面积是 .13.已知函数,1)(22x x x f +=则 )51()41()31()21()5()4()3()2()1(f f f f f f f f f ++++++++=_____.14.不共线的两个向量→→b a ,,且b a 2+与b a -2垂直,→→→-a b a 与垂直,a 与b 的夹角的余弦值为____.15.函数x x x f cos sin )(+=,设]3,6[ππ-∈x ,若a x f ≥)(2恒成立,则实数a 的取值范围为_______.16.如图正四面体ABCD ,E 为棱BC 上的动点,则异面直线BD 和AE 所成角的余弦值的范围为_______.17.设集合A=]1,21[),21,0[=B ,函数⎪⎩⎪⎨⎧∈-∈+=Bx x A x x x f ),2(log ,21)(2,若0x A ∈,且0[()]f f x A ∈,则0x 的取值范围是_________.三、解答题(本大题共5小题,共72分。
2012年浙江省高三名校交流模拟卷(文数)

在B选项中,过直线 一定存在平面 使得 ,故B错误
在D选项中,若直线 ,则在平面 内存在直线 使得 ,故C错误
只有C选项是正确的.应选C
B解析:由条件得 , , ,
,角A、B、C成等差数列反之也成立。应选B
6.B
解析:该几何体是以正方体的六条面对角线为边
二.填空题(本大题共7小题,每小题4分,共28分)
11.25解析:频率为 ,应抽出25人。
12.8解析:
13. 解析: ,与两两坐标轴的交点是 ,所求三角形面积为 。
14.
解析:方法一:如图所示,设双曲线的方程为 ,
两焦点分别为 , .且 关于其中一条渐近线的对称点
为 , 的中点为 .因为 为 的中点, 为
A. B. C. D.
二.填空题(本大题共7小题,每小题4分,共28分)
11.某机构就当地居民的月收入调查了1万人,并根据所得数据画出了样本频率分布直方图(如图).为了深入调查,要从这1万人中按月收入用分层抽样方法抽出100人,则月收入在 (元)段应抽出人.
12.已知函数 , 则 _____________.
故 ,
又因为 ,故 .故 的最小值为 ,当且仅当 时等号成立.此时, , 。
19.解:(1)由 及 ,得:
由 ① 得 ②
由②—①,得
即:
由于数列 各项均为正数,
即 数列 是首项为 ,公差为 的等差数列, 数列 的通项公式是
(2)∵
∴
20.证明:(1)取BD的中O点,连CO, ,∵ , ,∴ ,∴ ,∴
三.解答题(本大题共5小题,共72分.解答应写出文字说明﹑证明过程或演算过程)
数学_2012年浙江省杭州市某校高考数学模拟试卷(4)(含答案)

2012年浙江省杭州市某校高考数学模拟试卷(4)一、选择题(8×4'=32')1. 如果全集U =R ,A ={x|2<x ≤4},B ={x ∈Z|x 2−7x +10<0},则A ∩(C U B)=( )A φB (2, 4)C (2, 3)∪(3, 4]D (2, 3)∪(3, 4)2. 若a 1−i =1−bi ,其中a ,b 都是实数,i 是虚数单位,则|a +bi|=( )A √5B √2C √3D 13. 直线ax +y =1的倾斜角120∘,则a =( )A √3B −√3C √33D −√334. 下列函数是偶函数的是( )A y =(x +1)2B y =|x|⋅xC y =2x +2−xD y =x x 2+sinx5. “x =√a ⋅b”是“a ,x ,b 成等比数列”的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既非充分又非必要条件6. 数列{a n }中,a 3=2,a 7=1,且数列{1a n +1}是等差数列,则a 11等于( )A −25B 12C 23D 5 7. 设P 是双曲线x 2a 2−y 29=1上一点,双曲线的一条渐近线方程为3x −2y =O ,F 1、F 2分别是双曲线的左、右焦点,若|PF 1|=3,则|PF 2|=( )A 1或5B 6C 7D 98. 设p:f(x)=x 3+2x 2+mx +1在(−∞, +∞)内单调递增,q:m ≥2,则p 是q 的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分又不必要条件二、填空题(7×4'=28')9. 函数f(x)=−2x 2+3x −1的单调递增区间是________.10. 若正方体的棱长是1,则该正方体的外接球的表面积为________.11. 椭圆3x 2+ky 2=3焦距为2√2,则k =________.12. 已知0<a <1,log a (1−x)<log a x ,则x 的取值范围是________.13. 与直线x −y +2=0平行,且它们之间的距离是3√2的直线的方程是________.14. 已知数列{a n }中,S n 是其前项和,若a 1=1,a 2=2,a n a n+1a n+2=a n +a n+1+a n+2且a n+1a n+2≠1,则a 1+a 2+a 3=________;S 2011=________.15. 若直线y =x +a 是函数f(x)=13x 3−12x 2+x 图象的切线,则a =________.三、简答题16. 已知函数f(x)是定义在(−∞, +∞)上的奇函数,当x ∈(−∞, 0)时,f(x)=x +1,求f(x)的解析式.17. 已知f(x)=log2(2−x)−log2(2+x).(1)求f(x)的定义域;(2)试判断函数f(x)的奇偶性,并证明;(3)求不等式f(x)>1的解集.18. 已知等差数列{a n}满足a3=7,a5+a7=26,{a n}的前n项和为S n.(1)求a n及S n;(n∈N),求数列{b n}的前n项和T n.(2)令b n=1a n2−119. 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点.(1)求证:CD⊥面ADE;(2)求证:平面ABCD⊥平面ADE.2012年浙江省杭州市某校高考数学模拟试卷(4)答案1. D2. A3. A4. C5. D6. B7. C8. B]9. (−∞, 3410. 3π11. 1)12. (0, 1213. x−y+8=0或x−y−4=014. 6,402215. 0或−1616. 解:已知函数f(x)是定义在(−∞, +∞)上的奇函数,则f(0)=0,若x∈(0, +∞),则−x∈(−∞, 0),∵ x∈(−∞, 0),f(x)=x+1,∴ f(−x)=−x+1=−f(x),即f(x)=x−1,x∈(0, +∞),故f(x)={x−1,x>0 0,x=0 x+1,x<0.17. 解:(1)∵ f(x)=log2(2−x)−log2(2+x),∴ {2−x>02+x>0,解得−2<x<2;∴ f(x)的定义域是(−2, 2);(2)∵ f(−x)=log2(2+x)−log2(2−x)=−[log2(2−x)−log2(2+x)]=−f(x),∴ f(x)是定义域(−2, 2)上的奇函数;(3)∵ f(x)=log2(2−x)−log2(2+x)=log22−x2+x>1,∴ {−2<x<22−x2+x>2,解得−2<x<−23;∴ 不等式f(x)>1的解集是(−2, −23).18. 解(1)∵ a3=7,a5+a7=26.∴ a6=13,∴ d=2∴a4=9,∴ a n=2n+1s n=[3+(2n+1)]n2=n2+2n(2)由第一问可以看出a n=2n+1∴ b n=1(2n+1)2−1=14n2+4n=14×1n(n+1)∴ T n=14(11−12+12−13++1n−1n+1)=n4(n+1).19. 证明:(1)∵ 正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,∴ CD⊥AD,CD⊥AE,又AD∩AE=A,∴ CD⊥面ADE.(2)∵ AE垂直于圆O所在平面,CD在圆O所在平面上,AE⊥CD,在正方形ABCD中,CD⊥AD,AD∩AE=A,CD⊥平面ADE,CD⊂平面ABCD,∴ 平面ABCD⊥平面ADE.。
2012年萧山中学自主招生数学试卷附答案

2012年萧中自主招生推荐生文化考试数 学 试 题 卷考生须知:1.本试卷分试题卷和答题卷两部分.满分120分,考试时间100分钟.2.答题前,必须在答题卷的密封区内填写校名、班级、学号、姓名、试场号、座位号. 3.所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应. 4.考试结束后,只需上交答题卷.一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.下列计算中,结果正确的是( )A . 532)(a a =B .1120-=-C .2221=D .326a a a =÷ 2.如图,在4×4的正方形网格中,cos α=( ) A .12B .2C .552D .553. 如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的直径等于( ) A .8 B. 2 C. 10 D. 5 4.若a 、b 均为正整数,且32,7<>b a 则b a +的最小值...是( ) A. 3 B. 4 C. 5 D. 65.如图,下列四个几何体中,其各自的主视图、左视图、俯视图中有两个 相同,而另一个不同的是( )①正方体 ②球 ③圆锥 ④圆柱 A .①② B .②③ C .②④ D .③④6.杭州市某公交站每天6:30~7:30开往某学校的三辆班车票价相同,但车的舒适程度 不同.学生小杰先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适 状况,若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车, 他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,则小杰坐上优等车的 概率是( ) A.21 B. 31 C. 43D. 837.下列说法错误..的有( )个 ①无理数包括正无理数、零、负无理数;②4100.3⨯精确到千位,有2个有效数字 ③命题“若x 2= 1,则x =1”的逆命题是真命题;④若等腰三角形一腰上的高等于腰长的一半,则此等腰三角形的底角为30°和60°;⑤若两数和为6-,两数积为1-,则以这两数为根的一元二次方程的一次项系数为 6.(第2题图)A. 1B. 2C. 3D. 48.如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则 在该正方形内,这张圆形纸片“能接触到的部分”的面积是( ) A.π-4 B.π C. π+12 D. 415π+9.边长为1的正方形OABC 的顶点A 在x 正半轴上,点C 在y将正方形OABC 绕顶点O顺时针旋转75°,如图所示,使点B 恰好落 在函数)0(2<=a ax y 的图像上,则a 的值为( ) A.2-B.1-C.423-D. 32- 10.已知在⊿ABC 中,∠BAC=90°,M 是边BC 的中点,BC 的延长线上的点N 满足A M ⊥AN .⊿ABC 的内切圆与边AB 、AC 切点分别为E 、F ,延长EF 分别与AN 、BC 的延长线交于P 、Q 则QNPN =( ) A. 1 B. 5.0 C. 2 D. 5.1 二、认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案 11.分解因式:822-x = .12.甲乙两台机床生产同一种零件,并且每天产量相等,在6天中每天生产零件中的次品数依次是:甲:3、0、0、2、0、1、;乙:1、0、2、1、0、2.则甲、乙两台机床中性能较稳定的是 . 13.若二次函数)0(2≠++=a c bx ax y 图像的最低点的坐标为)1,1(-,则关于x 的一元二次方程12-=++c bx ax 的根为 . 14.如图,矩形ABCD 中,由8个面积均为1的小正方形组成的L 型模板如图放置,则矩形ABCD 的周长为 _. 15.长为1,宽为a 的矩形纸片(121<<a ),如图那样折一下, 剪下一个边长等于矩形宽度的正方形(称为第一次操作); 再把剩下的矩形如图那样折一下,剪下一个边长等于此时 矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n 此操作后,剩下的矩形为正方形,则操作终止.当n =3时,a 的值为______.16.若D 是等边三角形ABC 的内心,点E ,F 分别在AC 、BC 上,且满足CD=3,60=∠DEF ,记⊿DEF 的周长为C ,则C 的取值范围是 _. 三、 全面答一答(本题有7个小题,共66分)解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以. 17.(本题满分6分)先化简,再求值:242x x-÷)223(+--x x x x ,其中x =3-4.(第14题图 )18.(本题满分8分)如图,已知直线12y x =-经过点P (2-,a ),点P 关于y 轴的对称点P ′在反比例函数2ky x=(0≠k )的图象上. (1)求点P ′的坐标;(2)求反比例函数的解析式,并说明反比例函数的增减性; (3)直接写出当y 2<2时自变量x 的取值范围.19.(本题满分10分)一次测试九年级若干名学生1分钟跳绳次数的频数分布直方图如图.请根据这个直方图回答下面的问题:(1) 在频数分布直方图上画出频数分布折线图,并求自左至右最后一组的频率;(2)若图中自左至右各组的跳绳平均次数分别为137 次,146次,156次,164次,177次.小丽按以下方法计算参加测试学生跳绳次数的平均数是: (137+146+156+164+177)÷5=156.请你判断小丽的算式是否正确,若不正确,写出正确的算式(只列式不计算);(3)如果测试所得数据的中位数是160次,那么测试次数为160次的学生至少有多少人?20.(本题满分10分)由于受到手机更新换代的影响,某手机店经销的Iphone4手机二月售价比一月每台降价500元.如果卖出相同数量的Iphone4手机,那么一月销售额为9万元,二月销售额只有8万元.(1)一月Iphone4手机每台售价为多少元?(2)为了提高利润,该店计划三月购进Iphone4s 手机销售,已知Iphone4每台进价为3500元,Iphone4s 每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?(3)该店计划4月对Iphone4的尾货进行销售,决定在二月售价基础上每售出一台Iphone4手机再返还顾客现金a 元,而Iphone4s 按销售价4400元销售,如要使(2)中所有方案获利相同,a 应取何值? 21.(本题满分10分)定义{},,a b c 为函数2y a x b x c =++的“特征数”.如:函数223y x x =-+的“特征数”是{}1,2,3-,函数23y x =+的“特征数”是{}0,2,3,函数y x =-的“特征数”是{}0,1,0-(1)将“特征数”是⎪⎭⎪⎬⎫⎩⎨⎧1,33,0的函数图象向下平移2个单位,得到一个新函数,这个新函数的解析式是 ;(2)在(1)中,平移前后的两个函数分别与y 轴交于A 、B 两点,与直线3=x 分别交于D 、C 两点,在给出的平面直角坐标系中画出图形,判断以A 、B 、C 、D 四点为顶点的四边形形状,并说明理由;(第19题图)(次)九年级若干名学生1分钟跳绳次数频数分布直方图(3)若(2)中的四边形与“特征数”是211,2,2b b ⎧⎫-+⎨⎬⎩⎭的函数图象的有交点,试写出满足条件的实数b 的一个值.22.(本题满分10分) 如图,C 为以AB 为直径的⊙O 上一点,AD 和过点C 的切线互相垂直,垂足为点D .(1)求证:AC 平分∠BAD ;(2)过点O 作线段AC 的垂线OE ,垂足为点E (尺规作图,保留作图痕迹,不写作法);(3)若CD =4,AC =45,求垂线段OE 的长.23.(本题满分12分)已知二次函数)0(2222≠--=m m mx x y 的图像与x 轴交于A 、B 两点,它的顶点在以AB 为直径的圆上.(1)证明:A 、B 是x 轴上两个不同的交点; (2)求二次函数的解析式;(3)设以AB 为直径的圆与y 轴交于C ,D ,求弦CD 的长.A OB CD2012年萧中自主招生推荐生文化考试数学答题卷一、选择题(本题有10小题,每小题3分,共30分)二、填空题(本题有6小题,每小题4分,共24分)11. 12. 13. 14. 15.16. 三.解答题(本题有8小题,共66分) 17.(本小题满分6分)242x x -÷)223(+--x x x x ,其中x =3-418. (本小题满分8分) (1) (2) (3)19.(本小题满分10分)(1)(2)(3)20.(本小题满分10分)(1)(2)(3)(第19题图)(次) 九年级若干名学生1分钟跳绳次数频数分布直方图21.(本小题满分10分) (1)(2)(3)22. (本小题满分10分)(1)(2)(3)A O BCD23.(本小题满分12分)(1)(2)(3)2012年萧中自主招生推荐生文化考试数学评分标准一.选择题:(本大题10个小题,每小题3分,共30分)二.填空题:(本大题6个小题,每小题4分,共24分) 11、)2)(2(2-+x x 12、 乙 13、121==x x 14、58 15、5343or 16、23333+≤≤C 三.解答题(本题有8小题,共66分)17.解:原式)2)(2()4(2)2)(2(2+-+÷+-=x x x x x x x)4(2)2)(2()2)(2(2++-⋅+-=x x x x x x x ………………2分)4(1+-=x ………………2分当43-=x 时,原式=33-………………2分 18.解:(1))4,2('P ………………2分 (2)xy 8=………………2分 在每个象限内,y 随着x 的增大而减小………………1分 (3)0<x 或4>x ………………3分 19.解:(1)画出频数分布折线图………………2分24.05012=………………1分 (2)不正确………………1分501217720164815661464137⨯+⨯+⨯+⨯+⨯………………3分(3)8人………………3分20.解:(1)设今年甲型号手机每台售价为x 元,由题意得,xx 8000005090000=+.解得x =4000.经检验x =4000是方程的解.4000+500=4500 故一月Iphone4手机每台售价为4500元.………………4分(不检验扣1分) (2)设购进Iphone4手机m 台,由题意得,74000≤3500m +4000(20-m )≤76000,8≤m ≤12.因为m 只能取整数,所以m 取8、9、10、11、12,共有5种进货方案.………………3分 (3)设总获利W 元,则W =(500-a )m +400(20-m ),W =(100-a )m +8000.所以当a =100时,(2)中所有的方案获利相同.………………3分21.(1)133-=x y ………………2分 (2)图………………2分………………4分(3)26322+≤≤-b ,在这范围内给分………………2分 22. 解:(1)连接OC ,∵CD 切⊙O 于点C ,∴OC ⊥CD ;又∵AD ⊥CD ;∴OC ∥AD∴∠OCA =∠DAC ;∵OC =OA ;∴∠OCA =∠OAC ;∴∠OAC =∠DAC∴AC 平分∠DAB ………………3分 (2)解:点O 作线段AC 的垂线OE 如图所示………………2分(3)解:在Rt △ACD 中,CD =4,AC =45,∴AD =AC 2-CD 2=(45)2-42=8 ………………1分∵OE ⊥AC ,∴AE =12AC =2 5 ………………2分 ∵∠OAE =∠CAD ,∠AEO =∠ADC ,∴△AEO ∽△ADC ∴OE CD =AE AD ∴OE =AE AD ×CD =258×4=5即垂线段OE 的长为 5 ………………3分 23.(1)01284222>=+=∆m m m ,所以A 、B 是x 轴上两个不同的交点………3分(2))3,(,322m m m AB -=顶点,所以33,332±==m m m ………………4分 323322-±=x x y ………………2分 (3)因为⊿ABC 为直角三角形,由射影定理得,322=⨯=OB OA OC ,.3622==OC CD ………………3分。
浙江省杭州市萧山区高三数学上学期期中联考试题 文 新

2012学年第一学期五校联考期中卷高三数学(文) 试题卷一、选择题(本大题共12个小题,每小题5分,共50分,在每小题给出的四个选项中只有一项是符合要求的)1.已知全集U={4,3,2,1,0},集合A={3,2,1},B={4,2},则B A C U ⋃)(为 (A ){4,2,1} (B ){2,3,4} (C ){4,2,0} (D ){4,3,2,0}2.设R x ∈,则“””是“112==x x 的 (A )充分不必要条件(B )必要不充分条件(C )充要条件(D )既不充分也不必要条件 3.下列函数中,既是偶函数,又在),(∞+0上单调递增的是 (A )||ln x y = (B )x y cos = (C )2-=x y (D )3y x = 4.已知||||||-==,则与的夹角为 (A )6π(B )4π (C )3π (D )2π 5.已知等差数列}{n a 中,81,23211=++=a a a a ,则654a a a ++的值是 (A )6(B )18 (C )26 (D )546.若0lg lg =+b a (其中)1,1≠≠b a ,则函数x a x f =)(与x b x g =)(的图象(A )关于x 轴对称 (B )关于y 轴对称 (C )关于直线y x =对称 (D )关于原点对称 7.函数)sin()(ϕω+=x A x f (其中2||,0πϕ<>A )的图象如下图所示,为了得到x x g 2sin )(=的图象,则只需将)(x f 的图象 (A )右移6π个长度单位 (B )右移12π个长度单位 (C )左移6π个长度单位 (D )左移12π个长度单位8.计算=+++222222100-994-32-1K(A )-100 (B )-200 (C )-1024 (D )-50509.在ABC ∆中,C B A ∠∠∠,,所对的边分别为c b a ,,,边BC 上的高1==BC AD ,则22c b +的最小值为(A )1 (B )23 (C )2 (D )2510.已知函数x e x x f 2)1()(+=,设[]1,3--∈k ,对任意[]2,,21+∈k k x x ,则)()(21x f x f -的最大值为(A )34-e (B )e 4 (C )34-+e e (D )14+e 二、填空题(本大题共7小题,每小题4分,共28分)11.若函数⎩⎨⎧≤>=0,0,2)(2x x x x f ,则满足1)(=a f 的实数a 的值为 .12.已知等比数列{}n a 为递增数列,且8,242==a a 则=n a . 13.函数)cos (sin sin )(x x x x f -=的最小正周期为 . 14.过点)1,1(且与2)(x x f =相切的直线方程为 . 15.函数xx x f 2122)(+=的值域为 .16.已知圆O 的直径为2=AB ,C 为圆O 上任意一点,则|2|AC AB -= . 17.若函数11sin )(22+++=x x x x f 的最大值为M ,最小值为m ,则=+m M .三、解答题(本大题共5小题,共72分,解答题应写出文字说明、证明过程或演算步骤)18.(本小题满分14分)已知)),1(),-1,0(),1,-1(R m m OC OB OA ∈===(. (1)若C B A ,,三点共线,求实数m 的值;(2)证明:对任意实数m ,恒有 1≥⋅CB CA 成立. 19.(本小题满分14分)如图,点A ,B 是单位圆上的两点,A ,B 点分别在第一、二象限,点C 是圆与x 轴正半轴的交点,△AOB 是正三角形,若点A 的坐标为)54,53(,记α=∠COA .(1)求αα2cos 12sin +的值; (2)求|2|BC 的值.20.(本小题满分14分)已知k x x x f +-=2)(,若2)2(log 2=f , (1)确定k 的值;(2)求)(9)(x f x f +的最小值及对应的x 值.21.(本小题满分15分)已知n S 是数列}{n a 的前n 项和,*∈+=>N n a a S a nn n n ,2,02,(1)求证:}{n a 是等差数列;(2)若数列}{n b 满足n a n b b b n +==+2,211,求数列}{n b 的通项公式n b .22.(本小题满分15分)设函数)1,0()(≠>-=a a x a x f x(1)若e a =(e 是自然对数的底数),求)(x f 的单调区间和极值;(2)若函数)||(x f y =在全体实数R 上恰有4个零点,求实数a 的取值范围.学校 班级 姓名 学号 试场号 座位号19.(本小题满分14分)如图,点A ,B 是单位圆上的两点,A ,B 点分别在第一、二象限,点C 是圆与x 轴正半轴的交点,△AOB 是正三角形,若点A 的坐标为)54,53((1)求αα2cos 12sin +的值; (2)求2BC 的值.20.(本小题满分14分)已知k x x x f +-=2)(,若2)2(log 2=f , (1)确定k 的值;(2)求)(9)(x f x f +的最小值及对应的x 值.21.(本小题满分15分)已知n S 是数列{}n a 的前n 项和,0n a >,22n n n a a S +=,*n N ∈,(1)求证:{}n a 是等差数列;(2)若数列{}n b 满足12b =,12n an n b b +=+,求数列{}n b 的通项公式n b .22.(本小题满分15分)设函数)1,0()(≠>-=a a x a x f x(1)若e a =(e 是自然对数的底数),求)(x f 的单调区间和极值;(2)若函数)||(x f y =在全体实数R 上恰有4个零点,求实数a 的取值范围.2012学年第一学期高三期中考试 数学(文) 参考答案 2012年11月一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中只有一项是符合要求的)二、填空题(本大题共6小题,每小题3分,共18分)11.1- 12.12-n 13.π 14.012=--y x15.),1(]210+∞⋃,( 16.2 17.2三、解答题(本大题共5小题,共72分,解答题应写出文字说明、证明过程或演算步骤) 18.(本小题满分14分)(1))2,1(),1,2(-=--=m 分2ΛΛΘC B A ,,三点共线,∴2-m12-=- 分3ΛΛ ∴3-=m 分2ΛΛ (2)Θ)1,1(),1,2(m CB m CA ---=--= 分2ΛΛ∴11)1(222≥+=--=⋅m m CB CA∴恒有 1≥⋅成立. 分5ΛΛ19.(本小题满分14分) (1) Θ34tan =α 分2ΛΛ αα2cos 12sin +ααα2cos 2cos sin 2==αtan 34= 分5ΛΛ(2)53cos ,54sin ==ααΘ 分1ΛΛ10343)3cos(cos -=+=∠απBOC 分3ΛΛ 5347cos 11211||222+=∠⨯⨯-+=BOC BC 分3ΛΛ 20.(本小题满分14分)(1)Θ2)2(log 2=f 4)2(=∴f 分3ΛΛ ∴424=+-k 2=k 分3ΛΛ (2)根据(1)可知472)(2≥+-=x x x f 分3ΛΛ 692)(1)(=≥+∴x f x f 分3ΛΛ 当3)(=x f 时,即251±=x 时,取到最小值6 分3ΛΛ 21.(本小题满分15分)(1)由22n n n a a S +=,*n N ∈知:1=n 时12112a a a +=11=∴a 或01=a (舍去)分2ΛΛ22n nn a a S += )(1Λ 21121---+=n n n a a S )(2Λ (1)-(2)得:01122=-----n n n n a a a a 分2ΛΛ ∴0)1)((11=--+--n n n n a a a a 0>n a Θ ∴11=--n n a a所以{}n a 是等差数列 分3ΛΛ(2)由(1)知n n a n =⨯-+=1)1(1 分1ΛΛ12n a n n b b +=+,212=-b b 2232=-b bK K112--=-n n n b b以上各式相加得:21)21(22221121--=+++=---n n n b b Λ 分6ΛΛ n n b 2= 分1ΛΛ22.(1) x e x f x -=)(则1)('-=x e x f 分2ΛΛ 当0)('>x f 时, 解得0>x ,)(x f 在[),∞+0上单调递增, 当0)('<x f 时, 解得0<x ,)(x f 在0-,(∞]上单调递减. 分2ΛΛ所以0=x 是极小值点,1)0(==f f 极小值 分2ΛΛ(2) 函数)||(x f y =是偶函数,要使它在全体实数R 上恰有4个零点,只须)(x f y =在),0(+∞ 上有2个零点, 分2ΛΛ显然1>a ,设直线x y =与xa y =相切于点),(00y x 则有⎪⎩⎪⎨⎧==0001ln x a a a x x 分2ΛΛ e e a a e a e a e a e e e a aa a x a 1log ln 10log log ln 1ln 1=⇒=⇒=⇒=⇒=⇒=∴ 分3ΛΛ 根据图象可知),1(1e e a ∈ 分2ΛΛ 另解:要使方程x a x =在),0(+∞有2解,则有x x a ln ln =分2ΛΛ 设x x x g ln )(=,则2ln 1)(x x x g -=' 分1ΛΛ 当e x >时,0)(<'x g ,)(x g 单调递减,且ex g 1)(0<< 当e x ≤<0时,0)(>'x g ,)(x g 单调递增,且e x g 1)(≤ 分4ΛΛ 根据图象可知ea 1ln 0<<,e e a 11<<∴ 分2ΛΛ。
萧山中学2012届高三仿真考试
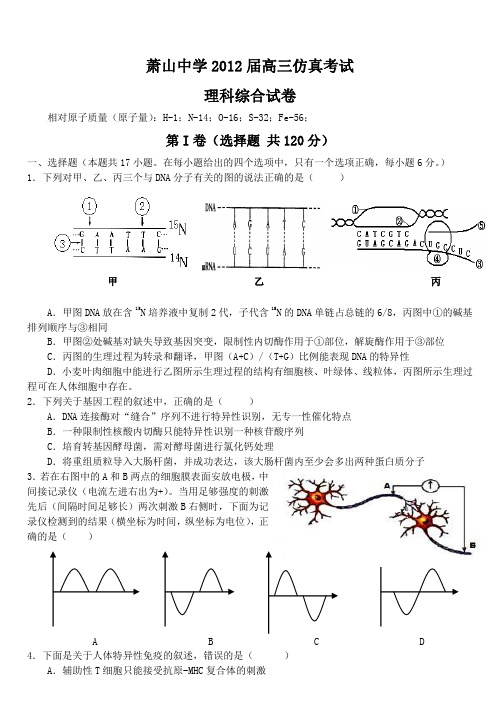
甲 乙 丙萧山中学2012届高三仿真考试理科综合试卷相对原子质量(原子量):H-1;N-14;O-16;S-32;Fe-56;第I 卷(选择题 共120分)一、选择题(本题共17小题。
在每小题给出的四个选项中,只有一个选项正确,每小题6分。
)1.下列对甲、乙、丙三个与DNA 分子有关的图的说法正确的是( )A .甲图DNA 放在含15N 培养液中复制2代,子代含15N 的DNA 单链占总链的6/8,丙图中①的碱基排列顺序与③相同B .甲图②处碱基对缺失导致基因突变,限制性内切酶作用于①部位,解旋酶作用于③部位C .丙图的生理过程为转录和翻译,甲图(A+C )/(T+G )比例能表现DNA 的特异性D .小麦叶肉细胞中能进行乙图所示生理过程的结构有细胞核、叶绿体、线粒体,丙图所示生理过程可在人体细胞中存在。
2.下列关于基因工程的叙述中,正确的是( )A .DNA 连接酶对“缝合”序列不进行特异性识别,无专一性催化特点B .一种限制性核酸内切酶只能特异性识别一种核苷酸序列C .培育转基因酵母菌,需对酵母菌进行氯化钙处理D .将重组质粒导入大肠杆菌,并成功表达,该大肠杆菌内至少会多出两种蛋白质分子3.若在右图中的A 和B 两点的细胞膜表面安放电极,中间接记录仪(电流左进右出为+)。
当用足够强度的刺激先后(间隔时间足够长)两次刺激B 右侧时,下面为记录仪检测到的结果(横坐标为时间,纵坐标为电位),正确的是( )A B C D4.下面是关于人体特异性免疫的叙述,错误的是()A.辅助性T细胞只能接受抗原-MHC复合体的刺激B.器官移植发生免疫排斥的主要原因是细胞免疫C.致敏前的B细胞不能合成抗体分子D.被动免疫时人体内抗体合成量不出现明显增加5.下列有关克隆技术的叙述正确的是()A.动物细胞培养时,保留接触抑制的连续细胞系获得不死性,但不致癌B.由于植物细胞具有全能性,水稻等在多次传代培养后,细胞全能性的表达能力不变C.从个体分离出单个组织进行培养是细胞克隆最基本要求D.若原生质体培养需要先对原生质体的活力进行检测,可以采用质壁分离的方法6.下图是某生态系统能量流动的图解,对此图解的理解有误差的是()A.b营养级的生物个体数量不一定比 a少B.a营养级固定的能量除去呼吸消耗和输入分解者,剩下为净初级生产量C.分解者细胞呼吸的产物中有CO2、H2O、酒精和乳酸等D.分解者将有机物进行分解,仍能被a营养级所利用30. (12分)红外线CO2分析仪可用于测定混合气体中CO2的浓度及其变化量。
2011―2012学年度2012届高三数学上册摸底考试题(含答案)

2011―2012学年度2012届高三数学上册摸底考试题(含答案) 2011―2012学年度高三两校联合摸底考试数学(文科)本试卷共21小题,满分150分.考试用时120分钟.第I卷(选择题)(50分)一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合M={x|x<3 ,N={x| },则M∩N=() A. B.{x|0<x<3 C.{x|1<x<3 D.{x|2<x<3 2.复数等于(). A. B. C. D. 3.“a= ”是函数y=cos2ax-sin2ax的最小正周期为“π”的( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分条件也不必要条件 4.定义在R上的函数f(x)满足f(x)= ,则f(3)的值为( ) A.-1 B. -2 C.1 D. 2 5.一个算法的程序框图如下图所示,若该程序输出的结果为,则判断框中应填入的条件是( )A. B. C. D. 6.如果一空间几何体的正视图与侧视图均为等边三角形,俯视图是半径为3的圆及其圆心,则这个几何体的体积为()A. B. C. D. 7.已知向量的夹角为,且则向量与的夹角为()A. B. C. D. 8.设斜率为2的直线过抛物线的焦点F,且和轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为 ( ). A.B. C. D. 9.已知命题p: .若命题p且q是真命题,则实数 a的取值范围为( ) A. B.a≤-2或1≤a≤2 C.a≥1 D.-2≤a≤1 10.已知O 为直角坐标系原点,P,Q坐标均满足不等式组,则使取最小值时的的大小为() A. B. C. D.第II卷(非选择题)(100分)二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11-13题) 11.设是等差数列的前项和,若,,则数列的通项为 12.若直线(,)被圆截得的弦长为4,则的最小值为 13.某企业三月中旬生产,A、B、C三种产品共3000件,根据分层抽样的结果;企业统计员制作了如下的统计表格:产品类别 A B C 产品数量(件)1300 样本容量(件) 130 由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是件。
浙江省杭州市2012届高三数学第二次教学质量检测试题(文)

求实数 t 的最大值.
2 22. (本小题满分14分)已知抛物线C: x 2 py ( p 0 ),
其 焦
5 2 点 F 到直线 x y 1 0 的距离为 8 .
(Ⅰ)求抛物线C的方程; (Ⅱ)若△ABC的三个顶点在抛物线C上,顶点B 的横 为1,且直线BA, BC的倾斜角互为补角, 过点A、 别作抛物线C 的切线,两切线相交于点D,当△ 面积等于4时,求直线BC的斜率. 坐标 C分
ADC
)
f ( x)
5.设函数
1 x x . 某程序框图如图所示,若输
2
出的结
2011 果 S 2012 ,则判断框中可以填入的关于 n 的判断
( ) B. n 2012? D. n 2012 ?
条件是
A. n 2011? C. n 2011?
6.在△ABC中,角A,B,C的对边分别为a,b,c,若△ 积
.
tan 2 x0
的值为
1 1 13.若从集合{ 3 , 4 , 3, 4 }中随机抽取一个数记为 a ,从集合{-1, 1, -2, 2}中随机抽取一个
x a 0, a 1 )的图象经过第三象限的概率是 数记为b,则函数 f ( x) a b (
.
14.设实数x,y满足不等式组
x 2 y 1 0 x 3y 6 0 x y 2 0
S 4πR 2
V Sh
球的体积公式 4 V πR 3 3 其中R表示球的半径 锥体的体积公式
1 V 体的高 台体的体积公式 1 V h S1 S1 S 2 S 2 3
其中 S1 , S2 分别表示台体的上底、下底面积,h表示
浙江省萧山中学高三上学期摸底考试题数学文.pdf

你了解他们的成功经历吗?他们的成功说明了什么?对你有何启示? 议一议: 第二部分 超越崇拜 第二层次:成功的背后 教学方案二:交流与分享 以一两位明星的成功之路为例,说一说自己对“台上一分钟,台下十年功”的理解,和同学们交流。
快乐分享: 第二部分 超越崇拜 第三层次:确立自我 成就自我 教学方案:收获背篓 收获背篓 根据同学们的学习交流,谈谈对偶像崇拜的正确认识。
说一说你会如何对待心目中的明星或偶像。
以“我与偶像”为主题撰写一篇小论文。
第七课 偶像与自我 第三单元 走自己的路 三1.1正确认识从众心理和好奇心,发展独立思考和自我控制能力,杜绝不良嗜好,养成良好行为习惯。
课标依据 教学目标情感、态度、价值观:培养理性和成熟的偶像崇拜态度,能够正确评价偶像与自我的关系,树立健康高尚的情感价值观。
能力:注意提高独立思考和自我控制能力,杜绝不良嗜好,养成良好行为习惯,能够分辨是非善恶,学会选择,能客观评价自己,形成比较清晰的自我整体形象。
知识:引导学生了解追星现象和偶像崇拜的心理原因及行为利弊,了解自我评价的重要性 。
偶像与自我 透视追星 追星利与弊 超越崇拜 (重点难点) 偶像面面观成功的背后 确立自我成就自我 教学内容分析 追星溯源 主要理论观点: 1.明星崇拜的原因 2.追星具有一定的合理性 3.对明星盲目崇拜的消极作用 4.要全面评价偶像 5.超越崇拜,走向自主 学情分析 青少年在生理上有了突飞猛进的发展,但心理上的发展却远远滞后。
由于生理上的发展,他们认为自己已经长大了,希望能够独挡一面,渴望摆脱父母的控制。
然而,他们有限的生活经验又使他们不能没有父母的帮助,这种矛盾状况使他们感到很苦恼。
因此,他们选择崇拜拥有能力、地位和独立的偶像,希望通过偶像崇拜来实现独立自主的目的,因而很容易盲目“追星”。
有的学生甚至因为迷恋偶像严重影响正常的学习和生活,影响身心健康,这是我们不能回避而且必须帮助青少年解决的问题。
2012年浙江省高三名校交流模拟卷(文数)

2012年浙江省高三名校交流模拟卷文科数学一﹑选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 集合},2{},1,0,1{A x y y B A x ∈==-=,则=⋂B A ( )A .}0{B .}1{C .}1,0{D .}1,0,1{- 2. 若复数214+=-+tz t i对应的点在第四象限,则实数t 的取值范围是( ) A .)(1-,2- B .),(∞+2 C .)(2,1- D .),(2--∞ 3. 若抛物线28y x =的焦点与椭圆221x y m+=的右焦点重合,则m 的值为( )A .5B .3C .5-D .3-4. 设a 是空间中的一条直线,α是空间中的一个平面,则下列说法正确的是 ( ) A. 过a 一定存在平面β,使得αβ// B. 过a 一定不存在平面β,使得αβ⊥ C. 在平面α内一定存在直线b ,使得b a ⊥ D. 在平面α内一定不存在直线b ,使得b a //5.在△ABC 中,sin 2cos cos cos 2sin sin A C AA C A+=-是角A 、B 、C 成等差数列的( ) A .充分非必要条件 B .充要条件C .必要非充分条件D .既不充分也不必要条件6.某几何体的三视图如图,若各视图均为边长为2的正方形.,则这个 几何体的体积是 ( ) A.34 B. 38 C. 316 D. 3207.已知函数f (x )=ax 3+bx 2+cx +d 的图象如右图所示,且|x 1|<|x 2|, 则有 ( )A .a >0,b >0,c <0,d >0B .a <0,b >0,c <0,d >0C .a <0,b >0,c >0,d >0D .a >0,b <0,c >0,d <0(第6题)正视图 侧视图俯视图0.00040.00030.00020.00018.某程序框图如图所示,则该程序运行后输出的结果是: ( ) A. 3- B .21-C .31 D. 29.设函数()(1)1xf x ax x x =+>-,若a 是从1,2,3三数中任取 一个,b 是从2,3,4,5中任取一个,那么使()f x b ≥恒成立的 概率为( )A .16 B .14 C .34 D .5610.定义在R 上的函数)(x f 满足1)4(=f ,)('x f 为)(x f 的导函数,已知)('x f y =的图像如图所示,若两个正数a 、b 满足1)2(<+b a f ,则22++a b 的取值范围是( ) A .)21,31(B .),3()21,(+∞⋃-∞C .)3,21( D .)3,(-∞二.填空题(本大题共7小题,每小题4分,共28分) 11.某机构就当地居民的月收入调查了1万人,并根据所得数据画出了样本频率分布直方图(如图).为了深入调查,要从这1万人中按月收入用分层抽样方法抽出100人,则月收入在2500 3000[,)(元)段应抽出 人.12.已知函数2(4)()(1)(4)x x f x f x x ⎧<=⎨-≥⎩, 则(5)f _____________. 13.曲线3141,33y x x ⎛⎫=+ ⎪⎝⎭在点处的切线与两坐标轴所围成的三角形面积是 。
浙江省杭州市萧山区高考模拟试卷4(数学文)

浙江省杭州市萧山区高考模拟试卷4数 学 文科参考公式:如果事件A 、B 互斥,那么 棱柱体体积公式 P (A +B )=P (A )+P (B ) V Sh =如果事件A 、B 相互,那么 其中S 表示棱锥底面积,h 表示棱锥的高 P (A ·B )=P (A )·P (B ) 棱台的体积公式 如果事件A 在一次试验中发生的概率是P , 13V Sh =那么n 次重复试验中恰好发生k 次的概率 棱台的体积公式kn k k nn P P C k P --=)1()(11221()3V Sh S S S S =++ 球的表面积公式 其中12,S S 分别表示棱台的上、下底面积, 24R S π= h 表示梭台的高球的体积公式 334R V π=球 其中R 表示球的半径卷Ⅰ客观题一、选择题:10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 设U=R ,集合{}{}04,,22≤-∈=∈==x Z x B R x y y A x,则下列结论正确的是A ()+∞=⋃,0B A B ()(]0,∞-=⋃B AC UC (){}0,1,2-=⋂B A C UD (){}2,1=⋂B A C U (2)已知a R ∈,复数122,12z ai z i =+=-,若12z z 为纯虚数,则复数12z z 的虚部为A 1B iC25D 0(3)已知函数22)(3+-=x x x f 有唯一零点,则存在零点的区间是 A ⎪⎭⎫ ⎝⎛--23,2 B ⎪⎭⎫ ⎝⎛--1,23 C ⎪⎭⎫ ⎝⎛--21,1 D ⎪⎭⎫ ⎝⎛-0,21(4) 右图的程序框图输出结果S= A 20 B 35C 40D 45开始S=0,i =0S=S+2i -1 i ≥8 i =i +2输出S否是(5) 设F 是椭圆1422=+y x 的右焦点,椭圆上的点与点F 的最大距离为M ,最小距离为N ,则椭圆上与点F 的距离等于)(21N M +的点的坐标是 A ()2,0± B ()1,0± C ⎪⎭⎫ ⎝⎛±21,3 D ⎪⎭⎫ ⎝⎛±21,0 (6) 在ABC ∆中,设命题AcC b B a p sin sin sin :==,命题ABC q ∆:是等边三角形,那么命题p 是命题q 的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分又不必要条件(7)已知等差数列{}n a 和{}n b 的前n 项和分别为n A 和n B ,且3457++=n n B A n n ,则使得nnb a 为整数的正偶数时,n 的值是 A 1 B 3或11 C 5 D 2 (8) 若对于⎪⎭⎫⎝⎛∈2,0πx ,不等式9cos sin 122≥+x p x 恒成立,则正实数p 的取值范围为 A 4>p B 4≥p C 3<p D 3≤p(9)已知m 、n 是不同的直线,α、β是不同的平面,下列命题中真命题的个数为①α//β,,m n αβ⊂⊂,则m //n ; ②αβ⊥,,m α⊥n //β,则m n ⊥;③m n ⊥,m //α,n //β,则αβ⊥;④若m 与n 异面直线,m α⊂,m //β,n //β,则α//β。
浙江萧山中学2012届高三上学期摸底考试(文数)

萧山中学2012届高三上学期摸底考试数学(文)试题一、选择题(本大题共10 小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知{}01≥+=x x A ,{}220B y y =->,全集I R =,则BC A I 为( )A .{x x x ≥≤ B .{1x x x ≥-≤或C .{1x x -≤≤D .{}1x x ≤≤-2.已知R x ∈,i 为虚数单位,若i i x i 34))(21(-=+-,则x 等于( )A .6-B .2-C .2D .63.设x 、R y ∈,则使1>+y x 成立的充分不必要条件是( )A .1≥+y xB . 21>x 或21>y C .1-<x D . 1≥x4.命题p:,03,3>+∈∀x x R x 则非p是( )A .03,3≥+∈∃xx R x B .03,3≤+∈∃xx R x C .03,3≥+∈∀xx R x D .03,3≤+∈∀xx R x5.曲线2x y x =-在点(1,-处的切线方程为( )A .2-=x yB .23+-=x yC .32-=x y ()21D y x =-+6、若,是非零向量,且≠⊥,则函数))(()(x x x f -+=是 ( ) A .一次函数且是奇函数 B .一次函数但不是奇函数 C .二次函数且是偶函数 D .二次函数但不是偶函数7、给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行; ④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是( ) A .①和② B .②和③ C .③和④ D .②和④ 8、某程序框图如图所示, 若输出的S=57,则判断框内为 A . k >4? B .k >5? C . k >6?D .k >7?9、设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近 线垂直,那么此双曲线的离心率为( ) ABCD.1210、设函数)10)(10)(10)(10()(42322212c x x c x x c x x c x x x f +-+-+-+-=-2(x x10)5c +,设集合*921},,,{}0)(|{N x x x x f x M ⊆=== ,设54321c c c c c ≥≥≥≥,则=-51c c( )A .20B .18C .16D .14二、填空题(本大题共7小题,每小题4分,共28分) 11、设等比数列{}n a 的公比12q =,前n 项和为n S ,则44S a = ;12、某个容量为N 的样本的频率分布直方图如左下图所示,已知在区间[)5,4上频数为30,则=N __ __;13、右上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 ;14、4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡 片上的数字之和为奇数的概率为 ;15、设,x y 满足约束条件:112210x y x x y ≥⎧⎪⎪≥⎨⎪+≤⎪⎩,则2z x y =-的最小值为___________.16、设yx b a b a b a R y x yx11,32,3,1,1,,+=+==>>∈则若的最大值为 ; 17、若42x ππ<<,则函数3tan 2tan y x x =的最大值为 。
数学(文)卷·2012届浙江省萧山中学高三上学期10月月考(2011.10)

浙江省萧山中学2012届高三上学期10月月考考试(数学文)一、选择题(本大题共10 小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若A 为全体正实数的集合,{}2,1,1,2B =--,则下列结论正确的是 ( ) A .}{2,1A B =--I B .()(,0)R C A B =-∞UC .(0,)A B =+∞UD .}{()2,1R C A B =--I2、函数1log 21+=x y 的单调递增区间为( )A .),1(+∞-B .)1,(--∞C .)0,1()1,(---∞YD .),1()1,(+∞---∞Y3、ο585sin 的值为( )A .2-B .2C .2-D .24、“1>x ”是“022>-+x x ”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5、给出命题:若函数()y f x =是幂函数,则函数()y f x =的图象不过第四象限。
在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是 ( ) A .3 B .2 C .1 D .06、如果若干个函数的图象经过平移后能够重合,则这些函数为“互为生成”函数,给出下列函数,其中与()sin cos f x x x =+构成“互为生成”函数的为 ( )A .2()sin f x x =B .1()f x x =C .3()cos )f x x x =+D .4()(sin cos )222x x x f x =+7、已知),1[)(3+∞-=在ax x x f 上是单调增函数,则a 的最大值是 ( ) A .0B .1C .2D .38、已知函数x x x f sin )(=的图象是下列两个图像中的一个,请你选择后再根据图象作出下面的判断:若1222,(,)x x ππ∈-,且12()()f x f x >,则( )A .21x x >B .021>+x xC .21x x <D .2221x x >9、在实数的原有运算法则中,我们补充定义新运算“⊕”如下:当a b ≥时,a b a ⊕=;当a b < 时,a b b ⊕=2.则函数[]()f x x x x x ()()()=⊕-⊕∈-1222·,(“· ”和“-”仍为通常的乘法和减法)的最大值等于 ( )A .-1B .1C .6D .1210、设x x f x2log )21()(-=,已知c b a <<<0,且0)()()(<⋅⋅c f b f a f ,若0x 是函数)(x f 的一个零点,那么下列不等式中不可能成立的是( )A .a x <0B .b x a <<0C .c x b <<0D .10>x二、填空题(本大题共7小题,每小题4分,共28分) 11、计算2225422ln lg lg loge +++= ;12、已知31)6tan(,21)6tan(-=-=++πβπβα,则)3tan(πα+=_____________; 13、某商场为迎合顾客的心理,将两件不同成本的商品价的商品捆绑在一起销售,两件商品均以216元卖出,其中一件亏损20%,但总共却盈利20%,则另一件商品的成本价应是 元;14、已知平面向量(1,3),(4,2),a b →→=-=-a b λ→→+与a r垂直,则λ= ;15、给出下列四个命题:①不等式22430x ax a -+<的解集为{|3}x a x a <<;②若函数(1)y f x =+为偶函数,则()y f x =的图象关于1x =对称; ③若不等式|4||3|x x a -+-<的解集为空集,则必有1≤a ; ④函数()y f x =的图像与直线x a =至多有一个交点。
浙江省萧山中学高三语文上学期摸底考试题【会员独享】

萧山中学2012届高三上学期摸底考试语文试题考试时间:100分钟分值:100分一、语言文字运用(共21分,其中选择题每小题3分)1.下列词语中加点的字,注音全都正确的一组是()A.庇.护(bì)漩.涡(xuán)称.心(chèn)量.体裁衣(liàng)B.脊.梁(jí)梦魇.(yǎn)下载.(zài)转弯抹.角(mò)C.刚愎.(bì)压轴.(zhóu)卓.越(zhuó)寒风朔.朔(sù)D.包扎.(zā)妊娠.(chén)唆.使(suō)曲.高和寡(qǔ)2.下列各句中,没有错别字的一项是()A.如果说竹林的连绵绿浪让人心旷神怡,江南的清浅流水世人流连忘返的话,那么面对横断山脉的峰峦起伏,我们只能用震憾磅礴来形容了。
B.土地的滥批滥用,使平畴千里、广茂辽阔的长江三角洲,现在也面临土地资源稀缺的困境。
C.一方面是大量待业人员寻工无着,一方面是沿海地区许多企业招聘不到足够的人员,“就业难”与“用工荒”折射出我国产业转型时期的“就业之觞”。
D.有资中筠先生的陪伴,陈先生并不孤独,两人既是珠联璧合的神仙眷侣,也是事业山上的山水知音,他们的豁达雍容和相敬如宾更让人羡慕不已。
3.下列各句中,加点的词语运用错误的一项是()A.入夜,月色溶溶,水天寥廓,我们或坐在桥下谈笑自若....,或坐在船上叩舷高歌,或立于小石桥上对月凝思。
B.北京大学和清华大学两所高校早前公布将自主招生时间错开进行,但两所高校却同时举行了保送生的选拔考试,这意味着考生只能忍痛割爱....,从中二选一。
C.今年夏天高温肆虐,一些户外劳动者因中暑而身亡。
为此,人们纷纷质疑,保障恶劣环境下的劳动者权益的相关规定竟成了一纸空文....?D.由于各种原因,“土地闲置满两年,依法应当无偿收回重新安排使用”这一规定在许多房地产开发商看来,往往是“雷声大,雨点小.......”,因此“囤地”现象屡禁不止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
萧山中学2012届高三上学期摸底考试数学(文)试题一、选择题(本大题共10 小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知{}01≥+=x x A ,{}220B y y =->,全集I R =,则BC A I 为( )A .{x x x ≥≤ B .{1x x x ≥-≤或C .{1x x -≤≤D .{}1x x -≤≤-2.已知R x ∈,i 为虚数单位,若i i x i 34))(21(-=+-,则x 等于( )A .6-B .2-C .2D .63.设x 、R y ∈,则使1>+y x 成立的充分不必要条件是( )A .1≥+y xB . 21>x 或21>y 高考学习网 C .1-<x D . 1≥x4.命题p:,03,3>+∈∀x x R x 则非p是( )A .03,3≥+∈∃x x R xB .03,3≤+∈∃x x R xC .03,3≥+∈∀x x R xD .03,3≤+∈∀x x R x5.曲线2x y x =-在点(1,-处的切线方程为( )A .2-=x yB .23+-=x yC .32-=x y()21D y x =-+6、若b a ,是非零向量,且≠⊥,则函数))(()(a b x b a x x f -+=是( ) A .一次函数且是奇函数B .一次函数但不是奇函数C .二次函数且是偶函数D .二次函数但不是偶函数 7、给定下列四个命题: ①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行; ④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是( ) A .①和② B .②和③ C .③和④ D .②和④ 8、某程序框图如图所示, 若输出的S=57,则判断框内为 A . k >4? B .k >5? C . k >6?D .k >7?9、设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近 线垂直,那么此双曲线的离心率为( ) ABCD10、设函数)10)(10)(10)(10()(42322212c x x c x x c x x c x x x f +-+-+-+-=-2(x x 10)5c +, 设集合*921},,,{}0)(|{N x x x x f x M ⊆=== ,设54321c c c c c ≥≥≥≥,则=-51c c( )A .20B .18C .16D .14二、填空题(本大题共7小题,每小题4分,共28分) 11、设等比数列{}n a 的公比12q =,前n 项和为n S ,则44Sa = ; 12、某个容量为N 的样本的频率分布直方图如左下图所示,已知在区间[)5,4上频数为30,则=N __ __;13、右上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 ;14、4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡 片上的数字之和为奇数的概率为 ;15、设,x y 满足约束条件:112210x y x x y ≥⎧⎪⎪≥⎨⎪+≤⎪⎩,则2z x y =-的最小值为___________.16、设yx b a b a b a R y x yx11,32,3,1,1,,+=+==>>∈则若的最大值为 ; 17、若42x ππ<<,则函数3tan 2tan y x x =的最大值为 。
三、解答题(共4题,共42分,解答应写出文字说明、证明过程或演算步骤) 18、(本小题满分10分)在锐角ABC ∆中,a 、b 、c 分别为角A 、B 、C 所对的边,且A c a sin 23=, (1)求角C 的值;(2)若1=a ,ABC ∆的面积为23,求c 的值。
19、(本小题满分10分)已知等差数列}{n a 满足:21=a ,公差0≠d , (1)若421,,a a a 成等比数列,求n a ;(2)已知05<a ,若当且仅当5=n 时,||n a 取得最小值,求d 的取值范围。
俯视图正(主)视图 侧(左)视图20、(本小题满分10分)已知函数32()23(,)f x x x mx n m n R =--+∈,若函数在点(0,(0))f 处的切线方程为12y x =-,(1)求,m n 的值;(2)求函数)(x f 在区间[,]a a -(0a >)上的最大值。
21、(本题满分12分)设直线l 与抛物线)0(22>=p px y 交于A 、B 两点,已知当直线l 经过抛物线的焦点且与x 轴垂直时,OAB ∆的面积为21(O 为坐标原点)。
(1)求抛物线的方程;(2)当直线l 经过点)0()0,(>a a P 且与x 轴不垂直时,若在x 轴上存在点C ,使得ABC∆为正三角形,求实数a 的取值范围。
(第21题)参考答案1、C2、C3、C4、 B5、D6、A7、D8、 A9、D 10、C 11、15 12、100 13、12π 14、3215、6- 16、1 17、8-18、解:(12sin c A =及正弦定理得,sinsin a A c C ==,…………………………………………………….2分 0sin ≠A 23sin =∴C , ABC ∆ 是锐角三角形,3C π∴=。
(5)(2)由面积公式得,23sin 21==C ab S , 3,1π==C a ,2=∴b , (7)由余弦定理得,C ab b a c cos 2222-+= 3212122122=⨯⨯⨯-+= 3=∴c 。
(10)19、解:由题意可设d n a n )1(2-+=,0≠d ,-------------------1分(1)若421,,a a a 成等比数列,则4122a a a ⋅=,------------------2分得)32(2)2(2d d +⋅=+, 0≠d ,2=∴d ,----------------------------4分∴n a n 2= ------------------------------------------------------5分(2) 05<a ,042<+∴d ,得21-<d ,--------------6分, 若当且仅当5=n 时,||n a 取得最小值,则⎩⎨⎧<>4540a a a ,即⎩⎨⎧+<-->+d d d 3242032,得⎪⎪⎩⎪⎪⎨⎧->->7432d d ,---------------------------9分 又21-<d ,2174-<<-∴d ,即d 的取值范围是)21,74(--。
-----------------------10分20、解:(1)由题意知,m x x x f --='66)(2,--------------------------1分函数在点(0,(0))f 处的切线方程为12y x =-,∴⎩⎨⎧-='=2)0(0)0(f f ,-----------------2分 即⎩⎨⎧-=-=120m n ,得⎩⎨⎧==012n m ----------------------3分(2)由(1)知x x x x f 1232)(23--=,)2)(1(61266)(2-+=--='x x x x x f 由0)(>'x f 得1-<x 或2>x ,由0)(<'x f 得21<<-x ,∴)(x f 在)1,(--∞内单调递增,在)2,1(-内单调递减,在),2(+∞内单调递增,----5分∴)(x f 的极大值为7)1(=-f ,由7)1()(=-=f a f 得7123223=--a a a ,07123223=---a a a0)752)(1(2=--+∴a a a ,27,0=∴>a a ,--------------------7分 结合)(x f 的图象可得:○1当10≤<a 时,)(x f 在区间[,]a a -上的最大值为=-)(a f a a a 123223+--,○2当271<<a 时,)(x f 在区间[,]a a -上的最大值为7)1(=-f , ○3当27≥a 时, )(x f 在区间[,]a a -上的最大值为=)(a f a a a 123223--。
--------------10分21、解:(1)由条件可得p AB 2||=,O 点到AB 距离为2p, …1分 ∴2212221p p p S AOB =⨯⨯=∆, …2分 0,21>=∆p S AOB得: 1=p , ∴ 抛物线的方程为x y 22=. …4分(2)设),(11y x A ,),(22y x B ,AB 的中点为),(00y x M又设)0,(t C ,直线l 的方程为a my x +=(0≠m ).由⎩⎨⎧=+=xy a m y x 22,得0222=--a m y y . ∴)2(42a m +=∆,m y y 221=+,a y y 221-=. …5分 所以m y y y =+=2210,从而a m x +=20. ∵ABC ∆为正三角形,∴AB MC ⊥,||23||AB MC =. 由AB MC ⊥,得1100-=⋅-mt x y ,所以12++=a m t . …7分 由||23||AB MC =,得2212212020)()(23)(y y x x y t x -+-⋅=+-, 即)2(4)1(23)(22222a m m m t a m +⋅+=+-+,又∵12-=-+t a m , ∴)2)(1(31222a m m m ++=+,从而2612m a -=.… 10分∵0≠m ,∴02>m ,∴610<<a . ∴a 的取值范围)61,0(. …12分(第21题)。
