最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (245)
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (129)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)如图所示,在4×4的正方形网格中,∠1,∠2,∠3的大小关系是( )A .∠1>∠2>∠3B .∠l<∠2=∠3C .∠1=∠2>∠3D .∠1=∠2=∠32.(2分)在△ABC 中,三个内角满足以下关系:∠A=12∠B=13∠C ,那么这个三角形是( )A .直角三角形B .锐角三角形C .钝角三角形D .任意三角形3.(2分)已知AD 是△ABC 的角平分线,则下列结论正确的个数有( )①BD =CD ,②BC =2CD ,③AD 平分BC ,④∠BAC =2∠DACA .一个B .二个C .三个D . 四个4.(2分)如图,△ABC 和△ADC 有公共边AC ,∠BAC =∠DAC ,在下列条件中不能..判断△ABC ≌△ADC 的是( )A .BC=DCB .AB =ADC .∠B =∠D D .∠BCA =∠DCA5.(2分)如图,CD 是Rt △ABC 斜边上的高,AC=12,BC=5,AB=13,则CD 等于( )A .1360B .1257C .313D . 4.86.(2分)如图,在ABC ∆中,AB=AC=10,AB 的垂直平分线交AC 于G ,BC=7,则GBC ∆的周长是( )A .10B .20C .17D .137.(2分)如图,AB 是ABC ∆和ABD ∆的公共边,要判定△ABC ≌△ABD 还需补充的条件不.能.是()A.∠1= ∠2,∠C= ∠D B.AC=AD,∠3= ∠4C.∠1= ∠2,∠3= ∠4 D.AC=AD,∠1= ∠28.(2分)利用基本作图,不能作出惟一三角形的是()A.已知两边及其夹角 B.已知两角及夹边C.已知两边及一边的对角 D.已知三边9.(2分)如图,AC⊥BE,∠A=∠E,不能判断△ABC≌△EDC的条件是()A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE 10.(2分)如图所示,A,B是数轴上的两点,C是AB的中点,则0C等于()A.34OB B.1()2OB OA−C.1()2OA OB+D.以上都不对11.(2分)一个三角形的两边长分别是3和6,第三边长为奇数,那么第三边长是()A 5或7 B.7或9 C.3或5 D.9评卷人得分二、填空题12.(2分)如图,长方形ABCD中(AD>AB),M为CD上一点,若沿着AM折叠,点N恰落在BC上,∠ANB+∠MNC=____________.13.(2分)如图,在△ABC中,AD是BC边上的中线,若△ABC的周长为20,BC=11,且△ABD的周长比△ACD的周长大3,则AB= ,AC= .6,314.分)如图,已知点D在AC上,点E在AB上,在△ABD和△ACE中,∠B=∠C,要判断△ABD≌△ACE,(1)根据ASA,还需条件;(2)根据AAS,还需条件 . 15.(2分)如图所示,已知AC和BD相交于0,A0=C0,∠A=∠C,说出BO=D0的理由.解:∵AC和BD相交于0,∴∠AOB= ( ).在△AOB和△COD中,∠AOB= (已证),AB= (已知),∴△AOB≌△COD( ).∴BO=D0( ).解答题16.(2分)如图所示,AB=BD,AC=CD,∠ACD=60°,则∠ACB= .17.(2分)判断正误,在括号内打“√”或“×”.(1)三角形的一条角平分线把三角形分成面积相等的两部分. ( )(2)若一个三角形的两条高在这个三角形外部,则这个三角形是钝角三角形. ( )(3)直角三角形的三条高的交点恰为直角顶点. ( )(4)三角形的中线可能在三角形的外部. ( )18.(2分)如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△= ,ABDS△AOF= .19.(2分)如图所示,四边形ABCD为正方形,它被虚线分成了9个小正方形,则△DBE 与△DEC的面积之比为.20.(2分)已知三角形的两条边的长分别是3和5,第三条边的长为a,则a的长度在和之间.21.(2分)如果三角形的三个内角都相等,那么这个三角形是三角形.评卷人得分三、解答题22.(7分)如图 ,在△ABC 中,AD 垂直平分 BC ,H 是AD 上的一点,连接BH 、CH.(1)AD 平分∠BAC 吗?为什么?(2)你能找出几对相等的角?请把它们写出来(不需写理由).23.(7分)如图,在△ABC 中,AE 是∠BAC 的角平分线,AD 是BC 边上的高,∠B=40°,∠C=60°,求∠EAD 的度数.24.(7分)如图,AC =AE ,∠BAM =∠BND =∠EAC , 图中是否存在与△ABE 全等的三角形?并说明理由.25.(7分)求各边长互不相等且都是整数、周长为24的三角形共有多少个?A D M CB EN21 E D CB A 26.(7分) 如图,已知在△ABC 中,BE 和CD 分别为∠ABC 和∠ACB 的平分线,且BD=CE ,∠1=∠2.说明BE=CD 的理由.27.(7分)画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm .28.(7分)三月三,放风筝,如图所示是小明制作的风筝,他根据DE=DF ,EH=FH ,不用度量,就知道∠DEH=∠DFH .请你运用所学知识给予说明.29.(7分)如图所示,一张三个内角都相等的三角形纸片ABC ,∠CBP=20°(图①).现将纸片沿射线BP 折叠成图②的形状,BP 交AC 于点E ,BC ′交AC 于点D .求图②中∠ADC ′,∠AEC ′的度数.30.(7分)已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.C2.A3.A4.A5.A6.C7.D8.A9.B10.C11.A评得二、填空题12.90°13.14.AB=AC ,AD=AE 或EC=BD15.∠COD ,对顶角相等,∠COD ,A0,C0,∠A ,∠C ,ASA ,全等三角形的对应边相等16.30°17.(1)× (2)√ (3)√ (4)×18.6,219.1:220.2,821.等边三、解答题22.( 1)由△ADB ≌△ADC(SAS),得∠BAD=∠CAD. (2)7对,∠BHD = ∠CHD ,∠ABD = ∠ACD ,∠HBD =∠HCD, ∠BDA=∠CDA,∠ABH=∠ACH,∠AHB=∠AHC ,∠BAD=∠CAD23.10°24.存在△ABE ≌△ADC ,理由略25.⎪⎩⎪⎨⎧===,7,8,9c b a ⎪⎩⎪⎨⎧===,6,8,10c b a ⎪⎩⎪⎨⎧===,6,7,11c b a ⎪⎩⎪⎨⎧===,5,9,10c b a ⎪⎩⎪⎨⎧===,5,8,11c b a ⎪⎩⎪⎨⎧===,4,9,11c b a ⎪⎩⎪⎨⎧===.3,10,11c b a由此知符合条件的三角形一共有7个.26.BE 和CD 分别为∠ABC 和∠ACB 的平分线,可得∠ABC=2∠1,∠ACB=2∠2, 由于∠1=∠2,∴∠ABC=∠ACB,△BCD ≌△CBE(AAS),∴BE=CD .27.略28.提示:连结DH29. ∠ADC ′=80°,∠AEC ′=20°30.∠C=90°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (243)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)已知△ABC中,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+12∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和外角∠BCE的角平分线的交点,则∠P=90°-12∠A.图1图2图3上述说法正确的有()A.0个B.1个C.2个D.3个2.(2分)下列条件能够判断△ABC≌△DEF的是()A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EFC.AB=DE,BC=EF,△ABC的周长等于△DEF的周长D.∠A=∠D,∠B=∠E,∠C=∠F3.(2分)如图,△ABC≌△DCB,AB=5cm,AC=7 cm,BC=8 cm,那么DC的长是()A.8 cm B.7 cm C.6cm D.5 cm4.(2分)如图,在ΔABC中,BC边上的垂直平分线交AC于点D, 已知AB=3,AC=7,BC=8,则ΔABD的周长为()A.10 B.11 C. 12 D. 155.(2分)有下列关于两个三角形全等的说法:①三个角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③两角与一边对应相等的两个三角形全等;④两边和一角对应相等的两个三角形全等.其中正确的个数是()A.1 B.2 C.3 D.46.(2分)如图所示,在4×4的正方形网格中,∠l,∠2,∠3的大小关系是()A.∠l>∠2>∠3 B.∠1=∠2>∠3C.∠l<∠2=∠3 D.∠l=∠2=∠3评卷人得分二、填空题7.(2分)如图,已知 AC与BD相交于点0,AO=CO,BO=DO,则AB = CD. 请说明理由.解:在△AOB和△COD中,(_____((AO COBO DO=⎧⎪⎨⎪=⎩已知)对顶角相等)已知)所以△AOB≌△COD( ).所以AB=DC( ).8.(2分)如图,AC、BD相交于点O,∠A=∠D,,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是 .9.(2分)如图,在△ABC中,AB=AC=10cm,DE是AB的中垂线,△BDC 的周长为 16 cm,则 BC 的长为 .10.(2分)如图,AB=AC ,要使ACD∆≌,应添加的条件是____________ (添加一ABE∆个条件即可)11.(2分) 如图,A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F 的度数是.12.(2分)已知BD是ΔABC的一条中线, 如果ΔABD和ΔBCD的周长分别是21,12,则AB-的长是.BC13.(2分)如图,在ΔABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2cm,BD=3cm,线段BC= .14.(2分)如图所示,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是.15.(2分)如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.16.(2分)直角三角形的两个锐角的平分线AD,BE交于点0,则∠AOB= .17.(2分)在Rt△ABC中,∠C=90°,其中∠A,∠B的平分线的交点为E,则∠AEB的度数为.18.(2分)如图,把△ABC沿虚线剪一刀,若∠A=40°,则∠l+∠2= .19.(2分)木材加工厂堆放木料的方式如图所示:依此规律可以得出第六堆木料的根数是根.20.(2分)如图所示,∠1=135°,∠2=75°,则∠3的度数是.评卷人得分三、解答题21.(7分)如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,∠B=40°,∠C=60°,求∠EAD的度数.22.(7分)在下面△ABC中,用尺规作出AB边上的高及∠B的平分线(不写作法,保留作图痕迹)21 E D CB A23.(7分)如图,直线l 表示一条公路,点A,点B 表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A ,B 的距离相等,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)24.(7分) 如图,已知在△ABC 中,BE 和CD 分别为∠ABC 和∠ACB 的平分线,且BD=CE ,∠1=∠2.说明BE=CD 的理由.25.(7分)如图所示,已知∠α,线段a ,b ,求作一个三角形,使其两边长分别为a ,a+b ,两边的夹角等于∠α.AB C26.(7分)画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm.27.(7分)三月三,放风筝,如图所示是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你运用所学知识给予说明.28.(7分)在下列图形中,分别画出△ABC的三条高.29.(7分)如图所示为由6个面积为1的小正方形组成的矩形,点A,B,C,D,E,F,G 是小正方形的顶点,以这7个点中的任意三个点为顶点,可组成多少个面积为1的三角形?请写出所有满足条件的三角形.30.(7分):如图,已知方格纸中每个小方格都是相同的正方形,∠AOB画在方格纸上,A0=B0,请在小方格的顶点上标出两个点P l,P2:,使P l,P2:落在∠AOB的平分线上.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.C2.C3.D4.A5.B6.B评卷人得分二、填空题7.∠AOB=∠COD,SAS,全等三角形的对应边相等8.AO = DO或AB = DC或BO=CO9.6cm10.B C∠=∠(答案不唯一)11.360°12.913.5cm14.三角形的稳定性15.ABE,ACD16.135°17.135°18.220°19.2820.30°三、解答题21.10°22.略23.略.24.BE和CD分别为∠ABC和∠ACB的平分线,可得∠ABC=2∠1,∠ACB=2∠2, 由于∠1=∠2,∴∠ABC=∠ACB,△BCD≌△CBE(AAS),∴BE=CD.25.略26.略27.提示:连结DH28.略29.共l4个三角形,具体表示略30.提示:P l,P2到点A,B的距离相等即可(不唯一)。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (140)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)若AD是△ABC的中线,则下列结论中,错误的是()A.AD平分∠BAC B.BD =DC C.AD平分BC D.BC =2DC2.(2分)下列说法正确的是()A.周长相等的两个三角形全等B.面积相等的两个三角形全等C.三个角对应相等的两个三角形全等D.三条边对应相等的两个三角形全等3.(2分)已知△ABC中,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+12∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和外角∠BCE的角平分线的交点,则∠P=90°-12∠A.图1图2图3上述说法正确的有()A.0个B.1个C.2个D.3个4.(2分)如图所示,0P平分∠AOB,PE⊥OB,PF⊥OA,则下列结论中正确的个数有()①OE=0F;②FP=PE;③OP⊥EF;④∠PEF=∠PFE;⑤0P平分∠FPE;⑥PQ=0QA.6个B.5个C.4个D.2个5.(2分)下列长度的三条线段,能组成三角形的是()A.6,3,3 B.4,8,8 C.3,4,8 D.8,l5,76.(2分)如图.在△ABC中,AB AC,AB的中垂线DE交AC于点D,交AB于点E,如果BC=10,△BDC的周长为22,那么△ABC的周长是()A.24 B.30 C.32 D.347.(2分)在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠8′;⑥∠C=∠C′,则下列条件中不能使△ABC≌△A′B′C′的是()A.②④⑤B.①②③C.①③⑤D.①②⑤8.(2分)如图,已知BC=BD,∠ABE=∠CBD,∠ADB=∠BCE.要说明BA=BE,则只要先说明()A.△ABE≌△DBC B.△ABD≌△EBC C.△BDG≌△BEH D.△ABG≌△BCH9.(2分)如图所示,∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()A.120°B. ll5°C.110°D.105°评卷人得分二、填空题10.(2分)如图, △ABC中,AB=AC=12,EF为AC的垂直平分线,若EC=8,则BE的长为_______.11.(2分)如图,已知ΔABC≌ΔADE,则图中与∠BAD相等的角是.12.(2分)全等三角形的对应边,对应角.13.(2分)如图,已知点D在AC上,点E在AB上,在△ABD和△ACE中,∠B=∠C,要判断△ABD≌△ACE,(1)根据ASA,还需条件;(2)根据AAS,还需条件 . 14.(2分)如图所示,直线AD交△ABC的BC边于D点,且AB=AC.(1)若已知D为BC中点,则可根据,说明△ABD≌△ACD;(2)若已知AD平分∠BAC,可以根据说明△ABD≌△ACD;(3)若AD是BC的中垂线,则可以根据,说明△ABD≌△ACD,还可以根据说明△ABD≌△ACD.15.(2分)如图所示,已知AB=AD,AE=AC,∠DAB=∠EAC,请将下列说明△ACD≌△AEB的理由的过程补充完整.解:∵∠DAB=∠EAC(已知),∴∠DAB+ =∠EAC+ ,即 = .在△ACD和△AEB中AD=AB( ),= (已证),= (已知),∴△ACD≌△AEB( ).16.(2分)如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.17.(2分)如图所示,已知AB=DE,BE=CF,AC=DF.请说明∠A=∠D的理由,并完成说理过程.解:∵BE=CF( ).∴BE+EC=CF+ ,即 = .在△ABC与△DEF中,AB=DE( ),= (已证), = (已知),∴△ABC≌△DEF( ).∴∠A=∠D( ).18.(2分)如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,则△ABC斜边上的高是,AB边上的高是,△ADB的BD边上的高是.19.(2分)直角三角形的两个锐角的平分线AD,BE交于点0,则∠AOB= .20.(2分)一个三角形最多有个钝角,最多有个直角.21.(2分)如图所示,∠1= .22.(2分)如图所示,∠1=135°,∠2=75°,则∠3的度数是.E B DC A 23.(2分)四条长度分别是2,3,4,5的线段,任选3条可以组成 个三角形.评卷人得分 三、解答题24.(7分).(1)已知△ABC ,求作:①BC 边上的中线;②BC 边上的高;③∠B 的平分线;(2)已知线段a ,c ,∠α,求作:△ABC ,使BC=a ,AB=c ,∠ABC=∠α(不必写出作法).25.(7分)如图,AD 平分∠BAC ,交BC 于点D ,∠ADB=105°,∠ACB=65°,CE 是AB 边上的高.求∠BAC ,∠BCE 的度数.26.(7分)如图.在△ABC 和△DEF中,B 、E 、C 、F 在同一直线上,下面有四个条件.请你在其中选三个作为已知条件,余下的一个作为结论,写出—个正确的结论,并说明理由.①AB =DE ;②AC =DF ;③∠ABC =∠DEF ;④BE =CF .已知:结沦:理由:27.(7分)如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.28.(7分)如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.29.(7分)在下列图形中,分别画出△ABC的三条高.30.(7分)如图所示,要测量湖中小岛E距岸边A和D的距离.作法如下:(1)任作线段AB.取串点0;(2)连结D0并延长使D0=C0;(3)连结BC;(4)用仪器测量E,O在一条线上,并交CB于点F.要测量AE,DE,只需测量BF,CF即可,为什么?【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.A2.D3.C4.B5.B6.D7.C8.B9.B评卷人得分二、填空题10.411.∠CAE12.相等,相等13.AB=AC,AD=AE或EC=BD14.(1)SSS;(2)SAS;(3)SAS,SSS15.∠BAC,∠BAC,∠DAC,∠BAE,已知,∠DAC,∠BAE,AC,AE,SAS 16.1617.已知,EC,BC,EF,已知,BC,EF,AC,DF,SSS,全等三角形对应角相等18.BD,BC,AD19.135°20.1,121.120°22.30°23.3三、解答题24.略25.80°、55°26.①③④,②,BE=CF,则BC=EF,ΔABC≌ΔDEF(SAS).27.略28.18°29.略30.略。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (423)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)如图,对任意的五角星, 结论错误的是( )A .∠1=∠C+∠EB .∠2=∠A+∠DC .∠A+∠B+∠C+∠D+∠E=360°D .∠A+∠B+∠C+∠D+∠E=180°2.(2分)在△ABC 中,三个内角满足以下关系:∠A=12∠B=13∠C ,那么这个三角形是( )A .直角三角形B .锐角三角形C .钝角三角形D .任意三角形3.(2分)在ABC △中,275A B ∠=∠=,则C ∠=( )A .30°B .135°C .105°D .67°30′4.(2分) 如果三角形的一个内角等于其他两个内角的差,那么这个三角形是( )A . 锐角三角形B .钝角三角形C .直角三角形D .无法确定5.(2分)如图,已知BE=CF ,且∠B=∠DEF, ∠A=∠D ,那么△ABC 和△DEF 是( )A .一定全等B .一定不全等C . 无法判定D .不一定全等6.(2分)在△ABC 中,若∠A =70°-∠B ,则∠C 等于( )A .35°B .70°C .110°D .140°D C B A 7.(2分)如图,△A8C ≌△BAD ,A 和B ,C 和D 是对应点,若AB=4 cm ,BD=3 cm ,AD=2 cm ,则BC 的长度为( )A .4 cmB .3 cmC .2 cmD .不能确定8.(2分)如图所示,在Rt △ADB 中,∠D=90°,C 为AD 上一点,则x 可能是( )A 10°B .20°C .30°D .40°评卷人得分 二、填空题9.(2分)如图,,已知OA=OB ,OC=OD ,D 和BC 相交于点E ,则图中全等三角形有 对.10.(2分)已知三角形的三边长为 3、1x +,4,则x 的取值范围是 .11.(2分)如图,△ABC ≌△DEF ,点B 和点E ,点A 和点D 是对应顶点,则AB= ,CB= ,∠C= ,∠CAB= .12.(2分)如图,在ABC ∆中,AD 是BC 边上的高线,︒=∠60B ,︒=∠30C ,则图中有 个直角三角形. 13.(2分)如图, △ABC 中,AB=AC=12,EF 为AC 的垂直平分线,若EC=8,则BE 的长为_______.14.(2分)如图,△ABC是不等边三角形,DE=BC,以D ,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_______个.15.(2分)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠+∠=.AOC DOB16.(2分)如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.17.(2分)如图所示,已知AB=DE,BE=CF,AC=DF.请说明∠A=∠D的理由,并完成说理过程.解:∵BE=CF( ).∴BE+EC=CF+ ,即 = .在△ABC与△DEF中,AB=DE( ),= (已证), = (已知),∴△ABC≌△DEF( ).∴∠A=∠D( ).18.(2分)如图所示,在△ABC中,AD是角平分线,已知∠B=66°,∠C=38°,那么∠ADB= ,∠ADC= .19.(2分)在Rt△ABC中,∠C=90°,其中∠A,∠B的平分线的交点为E,则∠AEB的度数为.20.(2分)三角形的三边长为3,a,7,若此三角形中有两边相等,则它的周长为.21.(2分)在△ABC中,若∠B=∠C,∠A=40°,则∠B= .22.(2分)如果三角形的三个内角都相等,那么这个三角形是三角形.23.(2分)在△ABC中,(1)∠C=85°,∠A=25°,则∠B= ;(2)∠A+∠B=90°,则∠C= ;(3)∠A=∠B=∠C,则∠A= ;(4)∠A=∠B,∠C=80°,则∠B= .评卷人得分三、解答题24.(7分)如图,AB=AD,∠BAD=∠CAE,AC=AE,试说明CB=ED.25.(7分)2008年 10月 18 日上午 10时,经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏,被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图,这是工程建设中一个山峰的平面图,施工队在施工之前需要先测量出隧道AB的长度,请你利用三角形全等的知识设计一种测量方法,并说明理由.26.(7分)如图.在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件.请你在其中选三个作为已知条件,余下的一个作为结论,写出—个正确的结论,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.已知:结沦:理由:27.(7分)如图,AC=AE,AB=AD,∠1=∠2.请说明下列结论成立的理由:(1) △ABC≌△ADE;(2)BC=DE.28.(7分)如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.29.(7分)三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.30.(7分)如图所示为由6个面积为1的小正方形组成的矩形,点A,B,C,D,E,F,G 是小正方形的顶点,以这7个点中的任意三个点为顶点,可组成多少个面积为1的三角形?请写出所有满足条件的三角形.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.C2.A3.D4.C5.A6.C7.C8.B评卷人得分二、填空题9.410.0<x<611.DE, FE,∠F, ∠FDE12.313.414.415.180°16.1617.已知,EC,BC,EF,已知,BC,EF,AC,DF,SSS,全等三角形对应角相等18.76°,l04°19.135°20.1721.70°22.等边23.(1)70°;(2)90°;(3)60°;(4)50°三、解答题24.可证△ABC≌△ADB,然后说明CB =ED25.利用全等三角形的判定(AAS,SAS,ASA)来设计完成26.①③④,②,BE=CF,则BC=EF,ΔABC≌ΔDEF(SAS).27.(1)∠1=∠2,则∠CAB=∠EAD,ΔABC≌ΔADE(SAS);(2)ΔABC≌ΔADE,则BC=DE28.略29.高线的交点可以在三角形的外部、内部及其顶点上30.共l4个三角形,具体表示略。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (669)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)若AD 是△ABC 的中线,则下列结论中,错误的是( )A .AD 平分∠BACB .BD =DC C .AD 平分BC D .BC =2DC2.(2分)下列各组长度的三条线段能组成三角形的是( )A .3cm,3cm , 6cmB .7 cm,4cm , 5cmC .3cm,4cm , 8cmD .4.2 cm, 2.8cm , 7cm3.(2分)如图,在△ABC 中,∠ABC 与∠ACB 的角平分线交于点0,且∠BOC=α,则∠A 的度数是 ( )A .180°-αB .2α-180°C .180°-2αD .12α4.(2分)下列说法正确的是( )A .周长相等的两个三角形全等B .面积相等的两个三角形全等C .三个角对应相等的两个三角形全等D .三条边对应相等的两个三角形全等 5.(2分)在ABC △中,275A B ∠=∠=o ,则C ∠=( )A .30°B .135°C .105°D .67°30′6.(2分)下面三种说法:①两个能够重合的三角形是全等三角形;②全等三角形的形状和大小相同;③全等三角形的面积相等.其中正确的个数有 ( )A .3个B .2个C .1个D .0个7.(2分)如图所示,若根据“SAS”来说明△ABC ≌△DBC ,已知BC 是公共边,需要补充的条件是 ( )A.AB=DB,∠l=∠2 B.AB=DB,∠3=∠4C.AB=DB,∠A=∠D D.∠l=∠2,∠3=∠48.(2分)如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个9.(2分)如图,AB=CD,∠l=∠2,AO=3,则AC=()A.3 B.6 C.9 D.1210.(2分)如果三角形的一个外角是锐角,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.以上三种都可能评卷人得分二、填空题11.(2分) 如图,∠B=∠DEF,AB=DE,要证明△ABC ≌△DEF,(1)若以“ASA”为依据,需添加的条件是;(2)若以“SAS”为依据,需添加的条件是 .12.(2分)如图,在Rt△ABC中,AD是BC边上的高,若∠C=36°,则∠B= ,∠DAB= .13.(2分)若a、b、c为△ABC的三边,则a b ca b c---+0(填“>”、“=”或“<”) .14.(2分)如图, △ABC中,AB=AC=12,EF为AC的垂直平分线,若EC=8,则BE的长为_______.15.(2分)如图△ABC中,D、E分别在BC上,∠BAE=∠AEB,∠CAD=∠CDA.若∠BAC=x度,则∠DAE的度数是.16.(2分)如图:请写出图中有个三角形,分别是.17.(2分)如图所示,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是.18.(2分)如图所示,四边形ABCD为正方形,它被虚线分成了9个小正方形,则△DBE 与△DEC的面积之比为.19.(2分)如图所示,共有个三角形.其中以DC为一边的三角形是.20.(2分)三角形的三边长为3,a,7,若此三角形中有两边相等,则它的周长为.评卷人得分三、解答题21.(7分)2008年 10月 18 日上午 10时,经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏,被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图,这是工程建设中一个山峰的平面图,施工队在施工之前需要先测量出隧道AB的2 1 E D CB A 长度,请你利用三角形全等的知识设计一种测量方法,并说明理由.22.(7分)看图按要求完成问题:(1)画ABC ∆边BC 的中线和B ∠的平分线;(2)分别指出直角三角形DE 和EF 边上的高线;(3)画钝角三角形OP 边上的高线.23.(7分) 如图,已知在△ABC 中,BE 和CD 分别为∠ABC 和∠ACB 的平分线,且BD=CE ,∠1=∠2.说明BE=CD 的理由.Q P O F E D C B A (2) (1) (3)24.(7分)如图,已知线段AC=8,BD=6.(1)已知线段AC⊥BD于0.设图①,图②,图③中的四边形ABCD的面积分别为S1,S2,S3,则 S1= ,S2= ,S3= ;(2)如图④,对于线段AC与线段BD垂直相交(垂足O不与A,B,C,D重合)的任意情况,请你猜想四边形ABCD的面积,并说明你的猜想是正确的;(3)当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连结点A,B,C,D,A所围成的封闭图形的面积是多少;请画出图形,并说明你的猜想是正确的.25.(7分)根据条件作图:(1)任意画一个Rt△ABC,使∠C=90°;(2)画∠CAB的平分线交对边于D;(3)画出点D到Rt△ABC的斜边的垂线段DE.26.(7分)如图所示,已知线段a,c,求作Rt△ABC,使BC=a,AB=c.27.(7分)如图所示,已知∠BAC=∠DAE,∠B=∠C,BD=CE.证明:AB=AC,AD=AE.28.(7分)三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.29.(7分)如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.30.(7分)如图所示,已知△ABC的边AB和BC边上的中线AD,请把△ABC补画完整.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.A2.B3.B4.D5.D6.A7.B8.D9.B10.B二、填空题11.∠A = ∠D ,BC=EF(或BE=CF)12.54°, 36°13.<14.415.90°-x 216.3,ΔABD 、ΔAB C 、ΔA CD17.三角形的稳定性18.1:219.7;△DBC ,△ADC20.17三、解答题21.利用全等三角形的判定(AAS ,SAS ,ASA)来设计完成22.略23.BE 和CD 分别为∠ABC 和∠ACB 的平分线,可得∠ABC=2∠1,∠ACB=2∠2, 由于∠1=∠2,∴∠ABC=∠ACB,△BCD ≌△CBE(AAS),∴BE=CD .24.(1)S 1=24,S 2=24,S 3=24;(2)面积为24,411111()8624 22222S BD AO BD CO BD AO CO BD AC=⋅+⋅=+=⋅=⨯⨯=;(3)图略,原理类似于(2),面积为2425.略26.提示:两种情况27.略28.高线的交点可以在三角形的外部、内部及其顶点上29.略30.连结BD,并延长BD到C,使DC=BD,连结AC。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (331)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,在△ABC中,∠A:∠ABC:∠ACB =3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于()A.1:2 B. 1:3 C. 2: 3 D. 1 : 42.(2分)如图,线段AC、BD交于点0,且AO=CO,BO=DO,则图中全等三角形的对数有()A.1对B. 2对C.3对D.4对3.(2分)已知在△ABC 和△A′B′C′中,AB =A′B′,∠B=∠B′,补充下面一个条件,不能说明△ABC≌△A′B′C′的是()A. BC =B′C′B.AC=A′C′C.∠C=∠C′D.∠A=∠A′4.(2分)如图,把图形沿BC对折,点A 和点D重合,那么图中共有全等三角形()A. 1对B.2对C.3对D.4对5.(2分)如图,在△ABC 中,∠ABC 与∠ACB 的角平分线交于点0,且∠BOC=α,则∠A 的度数是 ( )A .180°-αB .2α-180°C .180°-2α D.12α6.(2分)如图,点E 在BC 上,ED 丄AC 于F ,交BA 的延长线于D ,已知∠D =30°,∠C =20°,则∠B 的度数是( )A .20°B .30°C .40°D .50°7.(2分)在Rt △ABC 中,∠BAC=90度,AD 是高,则图中互余的角有 ( )A . 一对B . 二对C . 三对D .四对8.(2分)在ABC △中,275A B ∠=∠=o ,则C ∠=( )A .30°B .135°C .105°D .67°30′9.(2分)下列条件能够判断△ABC ≌△DEF 的是( ) A .AB=DE ,BC=EF ,∠A=∠DB .∠A=∠D ,∠C=∠F ,AC=EFC .AB=DE ,BC=EF ,△ABC 的周长等于△DEF 的周长D .∠A=∠D ,∠B=∠E ,∠C=∠F10.(2分)如图,点D 、E 分别在AC 、AB 上,已知AB=AC ,添加下列条件,不能说明ΔABD ≌ΔACE 的是( )A .∠B=∠CB .AD=AEC .∠BDC=∠CEBD .BD=CE11.(2分)作△ABC 的高AD ,中线AE ,角平分线AF ,三者中有可能画在△ABC 外的是( )A .中线AEB .高ADC .角平分线AFD .都有可能12.(2分) 用一副三角板画图,不能画出的角的度数是( )A .15°B .75°C .145°D .165°13.(2分)下列条件中,不能作出唯一..三角形的是( ) A .已知两边和夹角B .已知两边和其中一边的对角A B C DC.已知两角和夹边D.已知两角和其中一角的对边14.(2分)如图所示,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别是E,F,则图中与∠C(除°C外)相等的角的个数是() A.2个B.3个C.4个D.5个15.(2分)如图,△A8C≌△BAD,A和B,C和D是对应点,若AB=4 cm,BD=3 cm,AD=2 cm,则BC的长度为()A.4 cm B.3 cm C.2 cm D.不能确定评卷人得分二、填空题16.(2分) 如图,A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F 的度数是.17.(2分)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠+∠=.AOC DOB18.(2分)已知:△ABC中,∠A=100°,∠B-∠C=60°,则∠C=__________.19.(2分)如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△= ,ABDS△AOF= .20.(2分)如图所示,四边形ABCD为正方形,它被虚线分成了9个小正方形,则△DBE 与△DEC的面积之比为.21.(2分)三角形的三边长为3,a,7,若此三角形中有两边相等,则它的周长为.22.(2分)如图所示.(1)图中共有个三角形,分别是;(2)∠CDB是的内角,是的外角;(3)在AACD中,∠A是边和的夹角,边AC是的对边.评卷人得分三、解答题23.(7分)已知∠α、∠β和线段a,如图,用直尺和圆规作△ABC,使∠A=∠α,∠B =∠β,BC =a.24.(7分)如图所示,有1l ,2l ,3l 三条公路交于A ,B ,C ,现要在△ABC 内建一加油站,使它到三 条公路的距离相等,问应如何建?作出加油站的位置,并说明理由.25.(7分)如图所示,已知∠BAC=∠DAE ,∠B=∠C ,BD=CE .证明:AB=AC ,AD=AE .26.(7分)已知,如图所示,点B ,E ,C ,F 在同一条直线上,AB=DE ,AC=DF,BE=CF .试判断∠B 与∠DEC 是否相等,并说明理由.27.(7分)如图所示,在四边形ABCD 中,已知AB=AD ,CB=CD ,则在不添加其他线时,图中的哪两个角必定相等?请说明理由.28.(7分)如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.29.(7分)如图所示,在Rt △ABC中,∠ACB为直角,∠CAD的平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.30.(7分)如下表,“谢氏三角”是波兰著名数学家谢尔宾斯基在1915年~l916年期间提出的,它的作法是:第一步:取一个等边三角形(记为P1),连结各边的中点,得到完全相同的小正三角形,挖掉中间的一个;第二步:将剩下的三个小正三角形(记为P2),按上述办法各自取中点,各自分成4个小三角形,去掉各自中间的一个小正三角形;依次类推,不断划分出小的正三角形,同时去掉中间的一个小正三角形.试求P4的“黑”三角形的个数,“黑”三角形的总边数,边长,周长和面积,并将结果填入下表中.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.D2.D3.B4.C5.B6.C7.D8.D9.C10.D11.B12.C13.B14.B15.C二、填空题16.360°17.180°18.10°19.6,220.1:221.1722.(1)3;△ACD ,△BCD ,△ABC ;(2)△BDC ,△ACD ;(3)AD ,AC ,∠ADC三、解答题23.图略24.分别作∠ABC 与∠BCA 的角平分线,两条角平分线的交点即为加油站的位置,根据角平分线上的点到角两边的距离相等即可说明25.略26.∠B=∠DEC ,理由略27.∠D=∠B ,理由略28.18°29.∠E=27.5°,∠BAF=117.5°30.27,81,118a ,1818a ,12764S。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (369)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,CD是△ABC的中线,DE是△ACD的中线,BF 是△ADE 的中线,若△AEF 的面积是 1cm2,则△ABC的面积是()A. 4cm2B.5 cm2C. 6 cm2D.8 cm22.(2分)如图,已知 AE=CF,BE =DF.要证△ABE≌△CDF,还需添加的一个条件是()A.∠BAC=∠ACD B.∠ABE=∠CDF C.∠DAC=∠BCA D.∠AEB=∠CFD3.(2分)如图,已知△ABC≌△CDE,其中AB=CD,那么列结论中,不正确的是()A.AC=CE B.∠BAC=∠DCE C.∠ACB=∠ECD D.∠B=∠D4.(2分) 一个三角形的三个内角中,至少有()A.一个锐角B.两个锐角C.一个钝角D.一个直角5.(2分)如图,△ABC和△ADC有公共边AC,∠BAC=∠DAC,在下列条件中不能..判断△ABC≌△ADC的是()A.BC=DC B.AB=AD C.∠B=∠D D.∠BCA=∠DCA△),管理员从BC边上的一点D出6.(2分)一块试验田的形状是三角形(设其为ABC→→→的方向走了一圈回到D处,则管理员从出发到回到原处在发,沿DC CA AB BD途中身体()A.转过90B.转过180C.转过270D.转过3607.(2分)如图,已知直线L是线段PQ的垂直平分线,垂足为O,M、N是直线L上两点,下列结论中,错误的是()A.△MPN≌△MQN B.MO=NO C.OP=OQ D.∠MPN=∠MQN 8.(2分)下列说法中,正确的个数有()①延长直线AB;②取线段AB的中点C;③以0为圆心作弧;④已知∠α,作∠α的余角的一半.A.0个B.1个C.2个D.3个9.(2分)如图所示,0P平分∠AOB,PE⊥OB,PF⊥OA,则下列结论中正确的个数有()①OE=0F;②FP=PE;③OP⊥EF;④∠PEF=∠PFE;⑤0P平分∠FPE;⑥PQ=0QA.6个B.5个C.4个D.2个10.(2分)如图,在一块木板上均匀地钉了9颗钉子,用细绳可以像图中那样围成三角形,在这块木板上,还可以围成x个与图中三角形全等但位置不同的三角形,则x的值为()A.8 8 12 C 15 D.17评卷人得分二、填空题11.(2分)如图,AF、AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAF = .ABPO12.(2分)若a、b、c为△ABC的三边,则a b ca b c−−−+0(填“>”、“=”或“<”) . 13.(2分)在Rt△ABC中,∠C=90°,CE是△ABC的中线,若AC=2.4 cm,BC=1.5 cm,则△AE的面积为.解答题14.(2分)如图,点P在AOB∠的平分线上,若使AOP BOP△≌△,则需添加的一个条件是.(只写一个即可,不添加辅助线)15.(2分)如图,AD=AE,DB=EC,则图中一共有对全等三角形.16.(2分)如图△ABC中,D、E分别在BC上,∠BAE=∠AEB,∠CAD=∠CDA.若∠BAC=x度,则∠DAE的度数是.17.(2分)全等三角形的对应边,对应角.18.(2分)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃.最省事的办法是带去,理由是.19.(2分)如图,AD为△ABC中BC边上的中线,则S△ADB S△ADC12S△ABC(填“>”或“<”或“一”号)20.(2分)已知△ABC三边为a,b,c,且a,b满足21(3)0a b−+−=,c 为整数,则c的取值为.21.(2分)如图所示.(1)图中共有个三角形,分别是;(2)∠CDB是的内角,是的外角;(3)在AACD中,∠A是边和的夹角,边AC是的对边.评卷人得分三、解答题22.(7分)如图,DB是△ABC的高,AE是∠BAC的角平分线,∠BAE=26°,求∠BFE 的度数.23.(7分)已知:△ABC的周长为 18 cm,AB边比AC边短2 cm,BC边是AC边的一半,求△ABC三边的长.24.(7分).(1)已知△ABC,求作:①BC边上的中线;②BC边上的高;③∠B的平分线;(2)已知线段a,c,∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α(不必写出作法).EBD C A25.(7分)如图,AD 平分∠BAC ,交BC 于点D ,∠ADB=105°,∠ACB=65°,CE 是AB 边上的高.求∠BAC ,∠BCE 的度数.26.(7分)如图,AC=AE ,AB=AD,∠1=∠2.请说明下列结论成立的理由: (1) △ABC ≌△ADE ;(2)BC=DE .27.(7分)如图,直线l 表示一条公路,点A,点B 表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A ,B 的距离相等,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)28.(7分)如图所示,有1l ,2l ,3l 三条公路交于A ,B ,C ,现要在△ABC 内建一加油站,使它到三 条公路的距离相等,问应如何建?作出加油站的位置,并说明理由.29.(7分)如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.30.(7分)如图所示,△ABC中,∠A=40°,∠ABC和∠ACB的外角平分线交于P.求∠P的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.D2.D3.C4.B5.A6.D7.B8.C9.B10.C二、填空题11.20012.<13.0.9cm 214.OA =OB15.416.90°-x 217.相等,相等18.③,可根据③中的两角及夹边画出一个与之全等的三角形19.=,=20.321.(1)3;△ACD ,△BCD ,△ABC ;(2)△BDC ,△ACD ;(3)AD ,AC ,∠ADC三、解答题22.64°23.AB=6 cm ,BC=4cm ,AC=8cm24.略25.80°、55°26.(1)∠1=∠2,则∠CAB=∠EAD ,ΔABC ≌ΔADE (SAS );(2)ΔABC ≌ΔADE ,则BC=DE27.略.28.分别作∠ABC与∠BCA的角平分线,两条角平分线的交点即为加油站的位置,根据角平分线上的点到角两边的距离相等即可说明29.略30.∠P=70°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (488)
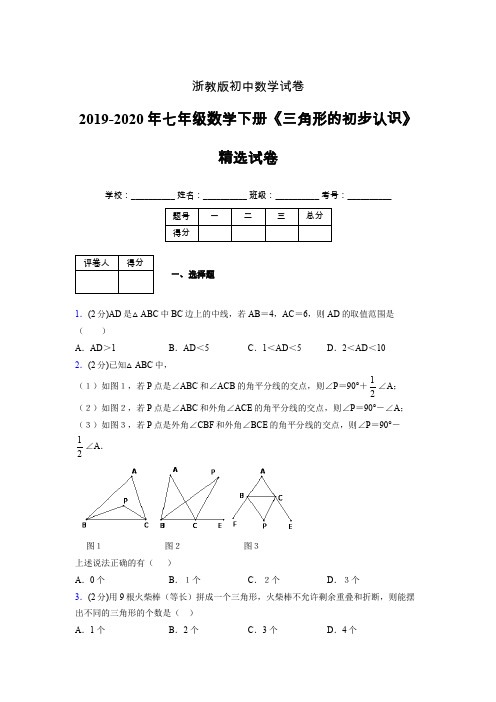
浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.(2分)AD是△ABC中BC边上的中线,若AB=4,AC=6,则AD的取值范围是()A.AD>1 B.AD<5 C.1<AD<5 D.2<AD<10 2.(2分)已知△ABC中,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+12∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和外角∠BCE的角平分线的交点,则∠P=90°-12∠A.图1图2图3上述说法正确的有()A.0个B.1个C.2个D.3个3.(2分)用9根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余重叠和折断,则能摆出不同的三角形的个数是()A.1 个B.2 个C.3 个D.4个4.(2分)如图,在△ABC 中,DE 是边AB 的垂直平分线,BC=8cm ,AC=5cm 则△ADC 的周长为( )A .14 cmB .13 cmC .11 cmD .9 cm5.(2分) 如图,O 是直线AB 上的一点,过O 点作射线OC ,已知OD 、OE 分别平分∠AOC 、∠COB .则△ODE 是( )A .钝角三角形B .锐角三角形C .直角三角形D .无法判断6.(2分)下列6组长度的线段中,可以首尾相接组成三角形的是( )①3,4,5;②1,1,3;③1,2,3;④5,5,5;⑤2,2,5;⑥3,7,4A .①②③④⑤⑥B .①④⑤C .①③④D .①②③④7.(2分)如图所示,A ,B 是数轴上的两点,C 是AB 的中点,则0C 等于( )A .34OB B .1()2OB OA - C .1()2OA OB + D .以上都不对8.(2分)如图所示,已知CD=CE ,AE=BD ,∠ADC=∠BEC=100°,∠ACD=26°,则∠BCD 的度数是 ( )A .72°B .54°C . 46°D .20°9.(2分)如图所示,把三角形纸片ABC 沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠l+∠2之间有一种数量关系始终保持不变,你认为该规律是( )A .∠A=∠l+∠2B .2∠A=∠l+∠2C .3∠A=2∠1+∠2D .3∠A=2(∠1+∠2)10.(2分)如图,在一块木板上均匀地钉了9颗钉子,用细绳可以像图中那样围成三角形,在这块木板上,还可以围成x 个与图中三角形全等但位置不同的三角形,则x 的值为( )A .8 8 12 C 15 D .1711.(2分)如图,已知BC=BD ,∠ABE=∠CBD ,∠ADB=∠BCE .要说明BA=BE ,则只要先说明 ( )A .△ABE ≌△DBCB .△ABD ≌△EBC C .△BDG ≌△BEHD .△ABG ≌△BCH12.(2分)下列条件中不能判定两个直角三角形全等的是 ( )A .两条直角边对应相等B .直角边和斜边对应相等C .两个锐角对应相等D .斜边和锐角对应相等13.(2分)如图,M 是AB 的中点,∠C=∠D ,∠1=∠2,说明AC=BD 的理由.解: M 是AB 的中点,∴ AM =在BMD AMC ∆∆和中 ∴ ≌( )∴AC=BD ( )14.(2分)一副三角板,如图所示叠放在一起,则图中α的度数是( )A .75°B .60°C .65°D .55°)(21M DC BA ()()________________________________________________________AM ⎧=⎪⎪=⎨⎪=⎪⎩二、填空题15.(2分) 如图 ,∠B=∠DEF ,AB=DE ,要证明△ABC ≌△DEF,(1)若以“ASA ”为依据,需添加的条件是 ;(2)若以“SAS ”为依据,需添加的条件是 .16.(2分)如图,已知AC=BD ,要使△ABC ≌△DCB ,只需增加的一个条件是 .17.(2分)如图,△ABC ≌△CDA ,A 与C 对应,D 与B 对应,则∠1与 是对应角.18.(2分)如图,AD=AE ,DB=EC ,则图中一共有 对全等三角形.19.(2分)在△ABC 中AB =3,BC =7则AC 的取值范围是 .4 <AC<1020.(2分)如图,OP 平分BOA ∠,PD OB ⊥于D ,PC OA ⊥于C ,写出你可以得到的结论(至少写出3个).21.(2分)如图,已知点D 在AC 上,点E 在AB 上,在△ABD 和△ACE 中,∠B=∠C ,要判断△ABD ≌△ACE ,(1)根据ASA ,还需条件 ;(2)根据AAS ,还需条件 .22.(2分)如图所示,已知AC=AD ,BC=BD ,说明△ABC ≌△ABD 的理由.解:在△ABC 和△ABD 中, ( ),BC=BD( ),( ),∴△ABC ≌△△ABD( ).23.(2分)直角三角形的两个锐角的平分线AD,BE交于点0,则∠AOB= .24.(2分)(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.三、解答题25.(7分)如图,AB=AD,∠BAD=∠CAE,AC=AE,试说明CB=ED.26.(7分)如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问:AD与BC是否相等?说明你的理由.解: AE⊥CD∴∠AED=BF⊥CD∴∠BFC=∴ =在△ADE和△BCF中,()()()⎪⎩⎪⎨⎧=∠=∠=∠_____________________________________________________________________AEAEDD∴△ADE≌△BCF( )∴AD=BC( )90 º,90 º,∠AED,∠BFC,∠C,已知,BFC,已证,BF,已知,AAS,全等三角形的对应边相等.27.(7分)如图,已知线段AC=8,BD=6.(1)已知线段AC⊥BD于0.设图①,图②,图③中的四边形ABCD的面积分别为S1,S2,S3,则 S1= ,S2= ,S3= ;(2)如图④,对于线段AC与线段BD垂直相交(垂足O不与A,B,C,D重合)的任意情况,请你猜想四边形ABCD的面积,并说明你的猜想是正确的;(3)当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连结点A,B,C,D,A所围成的封闭图形的面积是多少;请画出图形,并说明你的猜想是正确的.28.(7分)如图所示,在△ABC中,∠ABC=60°,∠ACB=72°,BD,CE分别是AC,AB上的高,BD交CE于点0.求:(1)∠A的度数;(2)∠ACE的度数;(3)∠BOC的度数.29.(7分)在下列图形中,分别画出△ABC的三条高.30.(7分)如图所示为由6个面积为1的小正方形组成的矩形,点A,B,C,D,E,F,G 是小正方形的顶点,以这7个点中的任意三个点为顶点,可组成多少个面积为1的三角形?请写出所有满足条件的三角形.【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.C3.C4.B5.C6.D7.C8.C9.B10.C11.B12.C13.BM,∠C,∠D,已知,∠1,∠2,已知,BM,ΔAMC,ΔBMD,AAS,全等三角形的对应边相等.14.A得二、填空题15.∠A = ∠D,BC=EF(或BE=CF)16.A0=D0或B0=C0或AB=CD或∠ACB=∠DBC17.∠318.419.20.略21.AB=AC,AD=AE或EC=BD22.AC=AD,已知,已知,AB=AB,公共边,SSS23.135°24.(1)三角形的稳定性;(2)5三、解答题25.可证△ABC≌△ADB,然后说明CB =ED26.27.(1)S1=24,S2=24,S3=24;(2)面积为24,411111()8624 22222S BD AO BD CO BD AO CO BD AC=⋅+⋅=+=⋅=⨯⨯=;(3)图略,原理类似于(2),面积为2428.(1)48°;(2)42°;(3)132°29.略30.共l4个三角形,具体表示略。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (450)
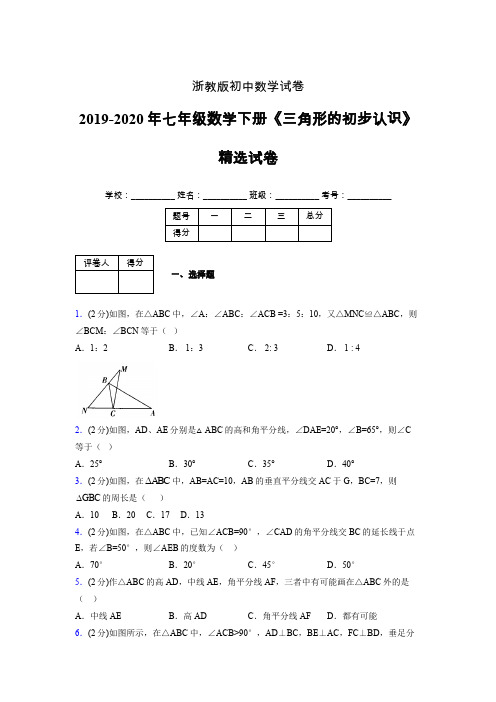
浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.(2分)如图,在△ABC中,∠A:∠ABC:∠ACB =3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于()A.1:2 B. 1:3 C. 2: 3 D. 1 : 42.(2分)如图,AD、AE分别是△ABC的高和角平分线,∠DAE=20°,∠B=65°,则∠C 等于()A.25°B.30°C.35°D.40°∆中,AB=AC=10,AB的垂直平分线交AC于G,BC=7,则3.(2分)如图,在ABC∆的周长是()GBCA.10 B.20 C.17 D.134.(2分)如图,在△ABC中,已知∠ACB=90°,∠CAD的角平分线交BC的延长线于点E,若∠B=50°,则∠AEB的度数为()A.70°B.20°C.45°D.50°5.(2分)作△ABC的高AD,中线AE,角平分线AF,三者中有可能画在△ABC外的是()A.中线AE B.高AD C.角平分线AF D.都有可能6.(2分)如图所示,在△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,FC⊥BD,垂足分别为点D,E,C,下列说法错误的是()A.AD是△ABC的高B.FC是△ABC的高C.BE是△ABC的高D.BC是△BCF的高7.(2分)三角形一边上的中线把原三角形分成两个()A.形状相同的三角形 B.面积相等的三角形C.直角三角形 D.周长相等的三角形8.(2分)下列长度的三条线段,能组成三角形的是()A.6,3,3 B.4,8,8 C.3,4,8 D.8,l5,79.(2分)如图①,在△ABC中,D,E分别是AB,AC的中点,把△ADE沿线段DE向下折叠.使点A落在BC上,记作点A′,得到图②,下列四个结论中,不一定成立的是()A.DB=DA B.∠B+∠C+∠l=180° C.BA=CA D.△ADE≌△A′DE10.(2分)一副三角板,如图所示叠放在一起,则图中α的度数是()A.75°B.60°C.65°D.55°11.(2分)如果三角形的一个外角是锐角,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.以上三种都可能二、填空题12.(2分)三角形两个外于第三个内角的 4倍,则第三个内角等于 .13.(2分)如图,在△ABC中,AD是高,E是AB上一点,AD与CE相交于点P,已知∠APE=50°,∠AEP=80°,则∠B= .14.(2分)如图,△ABC是不等边三角形,DE=BC,以D ,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_______个.15.(2分) 如图,平面镜A与B之间夹角为110°,光线经平面镜A反射到平面镜B上,再反射出去,若∠1=∠2,则∠1的度数为.16.(2分) 已知三角形的两边长分别为3cm和7cm,第三边的长为偶数,则这个三角形的周长为 .17.(2分)在△ABC中,∠A=∠B,∠C=50°,则∠A= 度.18.(2分)仔细观察下图:(1)图中的△ABC与△A′B′C′全等吗? .(2)由图中的信息,你可以得到的重要结论是:.19.(2分)如图所示,四边形ABCD为正方形,它被虚线分成了9个小正方形,则△DBE 与△DEC的面积之比为.20.(2分)如图所示,AD是△ABC的中线,AB=8.AC=6,则△ABD与△ACD的周长之差是.21.(2分)三角形的三边长为3,a,7,若此三角形中有两边相等,则它的周长为.22.(2分)如图,小明想测一块泥地AB的长度,他在AB的垂线BM上分别取C,D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这时这块泥地AB的长度就是线段的长度.23.(2分)木材加工厂堆放木料的方式如图所示:依此规律可以得出第六堆木料的根数是EB DC A C BA 根.三、解答题24.(7分)设计三种不同方案,把AABC 的面积三等分.25.(7分)如图,AD 平分∠BAC ,交BC 于点D ,∠ADB=105°,∠ACB=65°,CE 是AB 边上的高.求∠BAC ,∠BCE 的度数.26.(7分)如图,∠A :∠B :∠C=2:3:4,求△ABC 的内角的度数.27.(7分)如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的理由.(1)∠DBH=∠DAC;(2)ΔBDH≌ΔADC.28.(7分)如图,已知∠A=∠D,AB=DE.AF=DC,图中有哪几对全等三角形?并选取其中一对说明理由.29.(7分)在墙上有一个很大的圆形设计图,其中O是圆心,A,B在圆周上,如图所示.现在想测量AB两点间的距离,但墙很高,又没有梯子,不能直接测量.如果给你一根长度超过直径的竹竿和一把卷尺,你能测量AB两点之间的距离吗?说说你的方法.30.(7分)A,B是平面上的两个固定点,它们之间的距离为5 cm,请你在平面上找一点C(1)要使点C到A,B两点的距离之和等于5 cm ,则C点在什么位置?(2)要使点C到A,B两点的距离之和大于5 cm ,则点C在什么位置?(3)能使点C到A,B两点的距离之和小于5 cm吗?为什么?【参考答案】***试卷处理标记,请不要删除一、选择题1.D2.A3.C4.B5.B6.B7.B8.B9.C10.A11.B二、填空题12.60°13.40°14.415.35°16.16cm或18cm17.6518.(1)不全等;(2)有两边及其中一边的对角对应相等的两个三角形不一定全等19.1:220.221.1722.DE23.28三、解答题24.略25.80°、55°26.∠A=40°,∠B=60°,∠C=80°.27.(1)ΔABC的两条高AD、BE相交于H,则∠BDH=∠AEH=90 º,由于∠BHD=∠AHE,则∠DBH=∠DAC;(2)AD为ΔABC的高,则∠BDH=∠ADC=90 º,ΔBDH≌ΔADC(ASA)..找出下图中每个轴对称图形的对称轴,并画出来.略.28.△ABF≌△DEC,△FCB≌△CFE,△ABC≌△DEF,证明略29.能.方法:构造三角形全等(具体略)30.(1)点C在线段AB上;(2)点C在线段AB外;(3)不能,因为两点之间线段最短(为5 cm)。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (90)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,△ABC三个内角的平分线AD、BF、CE交于点O,则∠1+∠2等于()A.100°B.90°C. 95°D.不能确定2.(2分)如图,线段AC、BD交于点0,且AO=CO,BO=DO,则图中全等三角形的对数有()A.1对B. 2对C.3对D.4对3.(2分)在△ABC和△A′B′C′中,已知 AB=A′B′,∠B=∠B′,要保证△ABC ≌△A′B′C′,可补充的条件是()A.∠B+∠A=90°B. AC=A′C′C.BC=B′C′D.∠A+∠A′=90°4.(2分)如图,已知△ABC≌△CDE,其中AB=CD,那么列结论中,不正确的是()A.AC=CE B.∠BAC=∠DCE C.∠ACB=∠ECD D.∠B=∠D5.(2分)如图所示,在4×4的正方形网格中,∠1,∠2,∠3的大小关系是()A.∠1>∠2>∠3 B.∠l<∠2=∠3 C.∠1=∠2>∠3 D.∠1=∠2=∠36.(2分)如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为()A.80°B.100°C.60°D.45°△),管理员从BC边上的一点D出7.(2分)一块试验田的形状是三角形(设其为ABC→→→的方向走了一圈回到D处,则管理员从出发到回到原处在发,沿DC CA AB BD途中身体()A.转过90B.转过180C.转过270D.转过3608.(2分)如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对9.(2分)以下列各组线段的长为边,能构成三角形的是()A.4 cm,5 cm,6 cm B.2 cm,3 cm,5 cmC.4 cm,4 cm。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (110)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)若AD 是△ABC 的中线,则下列结论中,错误的是( )A .AD 平分∠BACB .BD =DC C .AD 平分BC D .BC =2DC2.(2分)如图,直线123,,l l l 表示三条相互交叉的公路,现要建造一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .两处C .三处D .四处3.(2分)如图,在ABC ∆中,AB=AC=10,AB 的垂直平分线交AC 于G ,BC=7,则GBC ∆的周长是( )A .10B .20C .17D .134.(2分)△ABC 中,AC=AB ,BC=8 cm ,且|AC -BC|=2 cm ,则AC 的长为( )A .10 cm 或6 cmB .10 cmC .6 cmD .8 cm 或6 cm5.(2分)如图所示,在直角三角形ABC 中,AC ≠AB ,AD 是斜边BC 上的高,DE ⊥AC ,DF ⊥AB ,垂足分别是E ,F ,则 图中与∠C (除°C 外)相等的角的个数是( )A .2个B .3个C .4个D .5个6.(2分)如果三条线段的比是:(1)1:4:6;(2)1:2:3;(3)3:4:5;(4)7:7:11;(5)3 : 3:6,那么其中可构成三角形的比有( )A .1种B .2种C .3种D .4种7.(2分)下列条件中不能判定两个直角三角形全等的是 ( )A .两条直角边对应相等B .直角边和斜边对应相等C .两个锐角对应相等D .斜边和锐角对应相等8.(2分)如图,△A8C ≌△BAD ,A 和B ,C 和D 是对应点,若AB=4 cm ,BD=3 cm ,AD=2 cm ,则BC 的长度为( )A .4 cmB .3 cmC .2 cmD .不能确定评卷人 得分 二、填空题9.(2分)一个三角形中最多有 个内角是钝角,最多可有 个角是锐角.10.(2分)如图,在△ABC 中,AB=AC=10cm ,DE 是AB 的中垂线,△BDC 的周长为 16 cm ,则 BC 的长为 .11.(2分)已知ABC DEF △≌△,5cm BC EF ==,△ABC 的面积是220cm ,那么△DEF 中EF 边上的高是__________cm .12.(2分)若一个三角形的三个内角这比为2:3:4,则三个内角中最小的内角为 .13.(2分)在下列条件中:①∠A+∠B=∠C ;②∠A ∶∠B ∶∠C=1∶2∶3;③∠A=900-∠B ;④∠A=∠B=12∠C 中,能确定△ABC 是直角三角形的条件有 个. 14.(2分)判断正误,对的打“√”,错的打“×”.(1)经过线段中点的直线是线段的中垂线. ( )(2)以AB 为直径可以作一个圆. ( )(3)已知两条边和一个角可以作唯一的三角形. ( )(4)已知两角一边可以作唯一的三角形. ( )15.(2分)如图所示,点B在AE上,且∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是(写一个即可):.16.(2分)判断正误,在括号内打“√”或“×”.(1)三角形的一条角平分线把三角形分成面积相等的两部分. ( )(2)若一个三角形的两条高在这个三角形外部,则这个三角形是钝角三角形. ( )(3)直角三角形的三条高的交点恰为直角顶点. ( )(4)三角形的中线可能在三角形的外部. ( )17.(2分)如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于D,则△ABC斜边上的高是,AB边上的高是,△ADB的BD边上的高是.18.(2分)如图,已知∠DBC=∠ACB,要说明△ABC≌△DCB.(1)若以“SAS”为依据,则需要添加的一个条件是;(2)若以“AAS”为依据,则需添加一个条件是;(3)若以“ASA”为依据,则需添加一个条件是.19.(2分)(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.评卷人得分三、解答题D CB A20.(7分)如图,在△ABC中,∠B=44°,∠C=72°,AD是△ABC的角平分线.(1)求∠BAC的度数;(2)求∠ADC的度数.21.(7分)如下图,已知△ABC,用尺规作△DEF,使得ABC DEF∆≅∆(不用写出作法,但要保留作图痕迹).CBA略.22.(7分)如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.23.(7分)如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠DAE的大小.24.(7分)在下列图形中,分别画出△ABC的三条高.25.(7分)如图所示,CD是△ABC的高,∠BAE=25°,∠BCD=35°.求∠AEC的度数.26.(7分)如图所示,△ABC中,∠A=40°,∠ABC和∠ACB的外角平分线交于P.求∠P的度数.27.(7分)如图所示,在△ABC中,∠A=∠ACB,CD是∠ACB的平分线,CE⊥AB于E.(1)试说明∠CDB=3∠DCB;(2)若∠DCE=48°,求∠ACB的度数.28.(7分)为测量出池塘两端点A、B的距离,小明在地面上选择三个点O、D、C,使OA=OC,OB=OD,且点A,O,C和点B,O,D都在一条直线上,小明认为只要量出DC 的距离,就能知道AB的距离,你认为小明的做法正确吗?请说明理由.29.(7分)已知三角形的周长是46 cm,其中一边比最短边长2 cm,比最长边短3 cm,求三角形三边的长.30.(7分)已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.A2.D3.C4.A5.B6.B7.C8.C二、填空题9.1,310.6cm11.812.40°13.414.(1)× (2)√ (3)× (4)×15.AC=AD或∠C=∠D等16.(1)× (2)√ (3)√ (4)×17.BD,BC,AD18.(1)AC=DB;(2)∠BAC=∠CDB;(3)∠ABC=∠DCB 19.(1)三角形的稳定性;(2)5三、解答题20.∠BAC=64°,∠ADC=108°.21.22.△ABD≌△ACD(SAS),则BD=CD.23.18°24.略25.80°26.∠P=70°27.(1)略;(2)28°28.正确.连接AB,可得△AOB≌△COD(SAS),∴AB=CD,即AB的距离等于CD 的距离29.13 cm,15 cm,18 cm30.∠C=90°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (375)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,对任意的五角星, 结论错误的是()A.∠1=∠C+∠EB.∠2=∠A+∠DC.∠A+∠B+∠C+∠D+∠E=360°D.∠A+∠B+∠C+∠D+∠E=180°2.(2分)如图,△ABC和△ADC有公共边AC,∠BAC=∠DAC,在下列条件中不能..判断△ABC≌△ADC的是()A.BC=DC B.AB=AD C.∠B=∠D D.∠BCA=∠DCA3.(2分)已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm4.(2分)如图,AC=AD,BC=BD,则图中全等三角形的对数是()A.6对 B.3对 C.2对D.1对5.(2分)任何一个三角形的三个内角中至少有()A.一个角大于60°B.两个锐角C.一个钝角D.一个直角6.(2分)如图,在ΔABC中,BC边上的垂直平分线交AC于点D, 已知AB=3,AC=7,BC=8,则ΔABD的周长为()A.10 B.11 C. 12 D. 157.(2分)如图所示,△ABC中,AB=AC,BE=CE,则由“SSS”可直接判定()A.△ABD≌△ACD B.△ABE≌△ACE C.△BED≌△CED D.以上答案都不对8.(2分)如图所示,S△ABC=l,若S△BDE=S△DEC=S△ACE,则S△ADE等于()A.15B.16C.17D.189.(2分)关于三角形的高的位置,下列判断中正确的是()A.必在三角形内B.必在三角形外C.不在三角形内,就在三角形外D.以上都不对10.(2分)三角形一边上的中线把原三角形分成两个()A.形状相同的三角形 B.面积相等的三角形C.直角三角形 D.周长相等的三角形11.(2分)一个三角形的两边长分别是3和6,第三边长为奇数,那么第三边长是()A 5或7 B.7或9 C.3或5 D.912.(2分)有下列关于两个三角形全等的说法:①三个角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③两角与一边对应相等的两个三角形全等;④两边和一角对应相等的两个三角形全等.其中正确的个数是()A.1 B.2 C.3 D.4评卷人得分二、填空题13.(2分)如图,在△ABC. 中,AB=AC=13 cm,AB的垂直平分线交AB边于点D,交AC 边于点E,若△EBG的周长为 21 cm,则BC= cm.14.(2分)如图,,已知OA=OB,OC=OD,D和BC相交于点E,则图中全等三角形有对.15.(2分)一个三角形中最多有个内角是钝角,最多可有个角是锐角.16.(2分)如果一个三角形的两个角都是80°,那么第三个角的度数是 .17.(2分)四条线段的长分别是5 cm,6 cm,8 cm,13 cm,则以其中任意三条线段为边可以构成个三角形.18.(2分)如图,∠A=80°,∠2=130°,则∠l= .19.(2分)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃.最省事的办法是带去,理由是.20.(2分)如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.21.(2分)判断下列说法是否正确,正确的打“√”,错误的打“×”.(1)面积相等的两个三角形全等. ( )(2)周长相等的两个三角形全等.’( )(3)三边对应相等的两个三角形全等. ( )2 1ED A(4)全等三角形的面积相等,周长相等. ( )22.(2分)如图所示,在△ABC中,∠B=35°,∠C=60°,AE是∠BAC的平分线,AD⊥BC于D,则∠DAE的度数为.23.(2分)如图所示.(1)AD是△ABC的角平分线,则∠BAC=2 =2 ;(2)AE是△ABC的中线,则 = 2BE=2 .24.(2分)在△ABC中,若∠B=∠C,∠A=40°,则∠B= .25.(2分)(1)自行车用脚架撑放比较稳定的原因是.(2)若AABC的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为.评卷人得分三、解答题26.(7分)如下图,已知△ABC,用尺规作△DEF,使得ABC DEF∆≅∆(不用写出作法,但要保留作图痕迹).CBA略.27.(7分) 如图,已知在△ABC中,BE和CD分别为∠ABC和∠ACB的平分线,且BD=CE,∠1=∠2.说明BE=CD的理由.28.(7分)如图,在△ABC和△DEF中,AC=DF,AE=BD,BC=EF,则∠C=∠F,请说明理由(填空).解:∵ AE=BD(已知)∴ =∴ =在△ABC和△DEF中===∴△ABC≌△DEF ( )∴∠C=∠F ( )29.(7分)如图所示,已知∠β=30°,a=3 cm.用直尺和圆规完成下列尺规作图(不写作法,保留痕迹),求作△ABC,使∠B=∠β,BC=a,AC=1.5 cm.30.(7分)如图所示,已知AB=AC,D是BC的中点,说明AD⊥BC的理由.解:∵D是BC的中点( ),∴ (中点的定义).在△和△中,= ( ),= (已证),= ( ),∴△≌△ ( ),∴∠l=∠2( )∴∠+∠2= ,∴∠l=∠2= ,即AD⊥BC.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.C2.A3.B4.B5.B6.A7.B8.B9.D10.B11.A12.B二、填空题13.814.415.1,316.20°17.218.130°19.③,可根据③中的两角及夹边画出一个与之全等的三角形20.1621.(1)× (2)× (3)√ (4)√22.12.5°23.(1)∠BAD,∠CAD;(2)BC,CE24.70°25.(1)三角形的稳定性;(2)5三、解答题26.27.BE和CD分别为∠ABC和∠ACB的平分线,可得∠ABC=2∠1,∠ACB=2∠2, 由于∠1=∠2,∴∠ABC=∠ACB,△BCD≌△CBE(AAS),∴BE=CD.28.AE-BE,BD-BE,AB,DE,AC,DF,AB,DE,BC,EF,SSS,全等三角形的角相等.29.略30.已知,BD=CD,ABD,ACD,AB,AC,已知,BD,CD,AD,AD,公共边,ABD,ACD,SSS,全等三角形对应角相等,l80°,90°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (232)
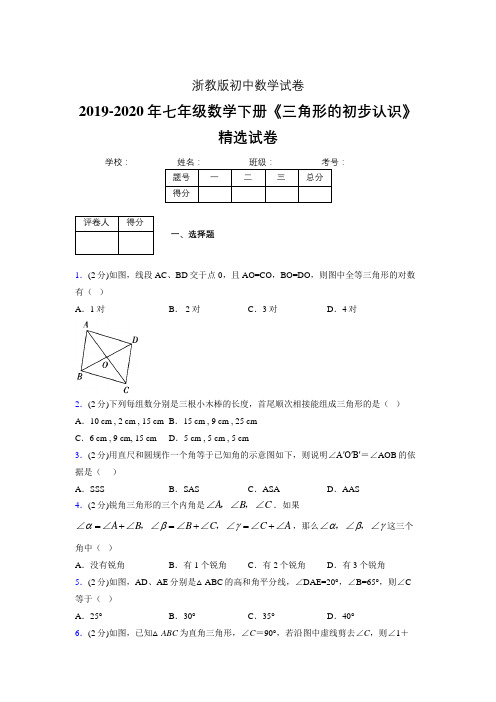
浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)如图,线段AC 、BD 交于点0,且AO=CO ,BO=DO ,则图中全等三角形的对数有( )A .1对B . 2对C .3对D .4对2.(2分)下列每组数分别是三根小木棒的长度,首尾顺次相接能组成三角形的是( )A .10 cm , 2 cm , 15 cmB .15 cm , 9 cm , 25 cmC .6 cm , 9 cm, 15 cmD .5 cm , 5 cm , 5 cm3.(2分)用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB 的依据是( )A .SSSB .SASC .ASAD .AAS4.(2分)锐角三角形的三个内角是AB C ,,∠∠∠.如果A B B C C A αβγ=+=+=+,,∠∠∠∠∠∠∠∠∠,那么αβγ,,∠∠∠这三个角中( )A .没有锐角B .有1个锐角C .有2个锐角D .有3个锐角5.(2分)如图,AD 、AE 分别是△ABC 的高和角平分线,∠DAE=20°,∠B=65°,则∠C 等于( )A .25°B .30°C .35°D .40°6.(2分)如图,已知△ABC 为直角三角形,∠C =90°,若沿图中虚线剪去∠C ,则∠1+A.315°B.270°C.180°D.135°7.(2分)下面三种说法:①两个能够重合的三角形是全等三角形;②全等三角形的形状和大小相同;③全等三角形的面积相等.其中正确的个数有()A.3个B.2个C.1个D.0个8.(2分)如图所示,BA=BD,BC=BE,根据“边角边”条件得到△ABE△DBC,则需要增加条件()A.∠A=∠D B.∠E=∠C C.∠A=∠C D.∠l=∠29.(2分)如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对10.(2分)如图所示,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠l+∠2之间有一种数量关系始终保持不变,你认为该规律是()A.∠A=∠l+∠2 B.2∠A=∠l+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)11.(2分)如果三条线段的比是:(1)1:4:6;(2)1:2:3;(3)3:4:5;(4)7:7:11;(5)3 : 3:6,那么其中可构成三角形的比有()A.1种B.2种C.3种D.4种12.(2分)下列长度的三条线段,能组成三角形的是()A.6,3,3 B.4,8,8 C.3,4,8 D.8,l5,713.(2分)在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠8′;⑥∠C=∠C′,则下列条件中不能使△ABC≌△A′A .②④⑤B .①②③C .①③⑤D .①②⑤ 评卷人 得分 二、填空题 14.(2分)如图,△ABC ≌△DEF ,点B 和点E ,点A 和点D 是对应顶点,则AB= ,CB= ,∠C= ,∠CAB= .15.(2分)如图,在△ABC 中,已知∠BAC=80°,∠B=40°,AD 是△ABC 的角平分线,那么∠ADB= .16.(2分)Rt △ABC 中,∠C =Rt ∠,∠A =30°,AB 的中垂线交AB 于D ,交AC 于E ,若△ADE 的面积是8,EC =3,BC =4,则△ABC 的面积为 .17.(2分)在ABC △中,BC 边不动,点A 竖直向上运动,A ∠越来越小,BC ∠∠,越来越大.若A ∠减少α度,B ∠增加β度,C ∠增加γ度,则αβγ,,三者之间的等量关系是 .18.(2分)如图所示,已知点C 是∠AOB 角平分线上的一点,点P ,P ′分别在边0A ,OB 上,如果要得到OP=OP ′,需添加以下条件中的某一个即可,请你写出所有可能结果的序号: .①∠0CP=∠OCP ′;②∠0PC=∠OP ′C ;③PC=P ′C ;④PP ′⊥0C ;⑤PC ⊥OA ,P ′C ⊥OB .19.(2分)如图所示.(1)AD 是△ABC 的角平分线,则∠BAC=2 =2 ;(2)AE 是△ABC 的中线,则 = 2BE=2 .20.(2分)如图,把△ABC沿虚线剪一刀,若∠A=40°,则∠l+∠2= .评卷人得分三、解答题21.(7分)如图,已知 AB=DC,AD=BC,说出下列判断成立的理由:(1)△ABC≌△ACD; (2)∠B=∠D.22.(7分)2008年 10月 18 日上午 10时,经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏,被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图,这是工程建设中一个山峰的平面图,施工队在施工之前需要先测量出隧道AB的长度,请你利用三角形全等的知识设计一种测量方法,并说明理由.23.(7分)如图,已知BE=CF,AB=CD,∠B=∠C,则AF=DE吗?请说明理由.24.(7分)如图,ΔABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由.(1)∠DBH=∠DAC;(2)ΔBDH≌ΔADC.25.(7分)如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.26.(7分)如图①所示,长方形通过剪切可以拼成直角三角形,方法如下:仿照上图,用图示的方法,解答下列问题:(1)如图②所示,已知直角三角形,设计一种方案,将它分成若干块,再拼成一个与之等面积的长方形;(2)如图③所示,对任意一个三角形,设计一种方案,把它分成若干块,再拼成一个与它等面积的长方形.27.(7分)如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.28.(7分)如图所示,已知∠BAC=∠DAE,∠B=∠C,BD=CE.证明:AB=AC,AD=AE.29.(7分)如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置关系,并说明理由.30.(7分)一根木条被9条红线均匀地分成l0等分,相邻两条红线之间的长度为l个单位长度.如果只能沿着红线把这根木条锯成3段,以这3段为边拼成三角形,有几种不同的锯法?请写出每种锯法锯成的3段木条的长度.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.D2.D3.A4.A5.A6.B7.A8.D9.C10.B11.B12.B13.C评卷人得分二、填空题14.DE, FE,∠F, ∠FDE15.100°16.2217.αβγ=+18.①②④⑤19.(1)∠BAD,∠CAD;(2)BC,CE20.220°评卷人得分三、解答题21.略22.利用全等三角形的判定(AAS,SAS,ASA)来设计完成23.利用SAS说明△ABF≌△DCE24.(1)ΔABC的两条高AD、BE相交于H,则∠BDH=∠AEH=90 º,由于∠BHD=∠AHE,则∠DBH=∠DAC;(2)AD为ΔABC的高,则∠BDH=∠ADC=90 º,ΔBDH≌ΔADC(ASA)..找出下图中每个轴对称图形的对称轴,并画出来.略.25.略26.(1)(2)27.略28.略29.CD⊥AB,理由略30.用列表尝试法得共有两种不同的锯法,三边分别为2、4、4和3、3、4。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (123)
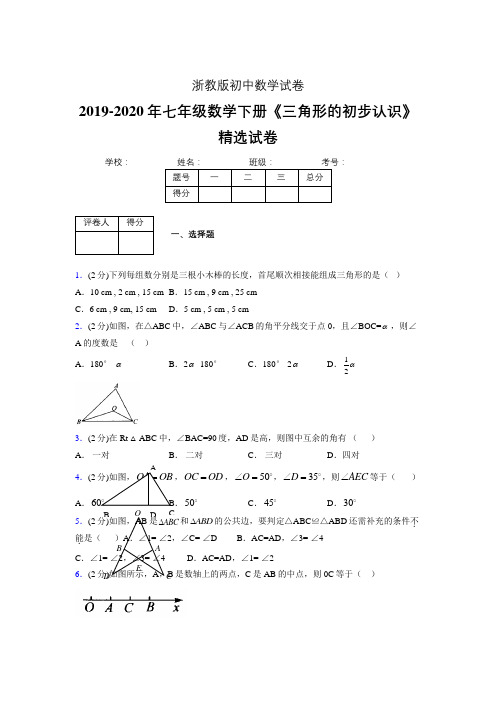
OE ABD C 浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)下列每组数分别是三根小木棒的长度,首尾顺次相接能组成三角形的是()A.10 cm , 2 cm , 15 cm B.15 cm , 9 cm , 25 cmC.6 cm , 9 cm, 15 cm D.5 cm , 5 cm , 5 cm2.(2分)如图,在△ABC中,∠ABC与∠ACB的角平分线交于点0,且∠BOC=α,则∠A的度数是()A.180°-αB.2α-180°C.180°-2αD.12α3.(2分)在Rt △ABC中,∠BAC=90度,AD是高,则图中互余的角有()A.一对B.二对C.三对D.四对4.(2分)如图,OA OB=,OC OD=,50O∠=o,35D∠=o,则AEC∠等于()A.60o B.50o C.45o D.30o5.(2分)如图,AB是ABC∆和ABD∆的公共边,要判定△ABC≌△ABD还需补充的条件不.能.是()A.∠1= ∠2,∠C= ∠D B.AC=AD,∠3= ∠4C.∠1= ∠2,∠3= ∠4 D.AC=AD,∠1= ∠26.(2分)如图所示,A,B是数轴上的两点,C是AB的中点,则0C等于()AB CDA.34OB B.1()2OB OA-C.1()2OA OB+D.以上都不对7.(2分)如图所示,0P平分∠AOB,PE⊥OB,PF⊥OA,则下列结论中正确的个数有()①OE=0F;②FP=PE;③OP⊥EF;④∠PEF=∠PFE;⑤0P平分∠FPE;⑥PQ=0QA.6个B.5个C.4个D.2个8.(2分)如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个9.(2分)下列叙述中正确的个数是()①三角形的中线、角平分线都是射线;②三角形的中线、角平分线都在三角形内部;③三角形的中线就是过一边中点的线段;④三角形三条角平分线交于一点.A.0个B.1个C.2个D.3个评卷人得分二、填空题10.(2分)如图, △ABC中,AB=AC=12,EF为AC的垂直平分线,若EC=8,则BE的长为_______.11.(2分)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则AOC DOB∠+∠=.12.(2分)如图,已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.根据上图所示,①一个四边形可以分成2个三角形,于是四边形的内角和为度;②一个五边形可以分成3个三角形,于是五边形的内角和为度;……,③按此规律,n边形可以分成个三角形,于是n边形的内角和为度.解答题13.(2分)已知△ABC中,AB=AC,①当它的两个边长分别为8 cm和3 cm时,它的周长为 cm;②如果它的周长为18 cm,一边的长为4 cm,则腰长为 cm.14.(2分)如图,∠1∶∠2∶∠3=1∶2∶3,则∠4=.72 º15.(2分)如图,已知点D在AC上,点E在AB上,在△ABD和△ACE中,∠B=∠C,要判断△ABD≌△ACE,(1)根据ASA,还需条件;(2)根据AAS,还需条件 . 16.(2分)如图所示,∠1=∠2,∠ABC=∠DCB,AC,BD相交于O,请将下列说明AB=DC的理由的过程补充完整.解:∵∠ABC=∠DCB,∠l=∠2(已知),∴∠ABC一∠l=∠DCB一∠2,即∠DBC= .在△ABC和△DCB中,= ( ),= ( ),= ( ),∴≌ ( ),∴AB=DC( ).17.(2分)如图所示,△ABC三条中线AD、BE、CF交于点0,S△ABC=l2,则S△= ,ABDS△AOF= .18.(2分)已知三角形的两条边的长分别是3和5,第三条边的长为a,则a的长度在和之间.19.(2分)一个三角形最多有 个钝角,最多有 个直角. 20.(2分)在△ABC 中,(1)∠C=85°,∠A=25°,则∠B= ;(2)∠A+∠B=90°,则∠C= ;(3)∠A=∠B=∠C ,则∠A= ;(4)∠A=∠B ,∠C=80°,则∠B= .21.(2分)已知△ABC 三边为a,b ,c ,且a ,b 满足21(3)0a b -+-=,c 为整数,则c 的取值为 .评卷人得分 三、解答题22.(7分)如图,已知:A ,F ,C ,D 四点在一条直线上,AF=CD ,∠D=∠A ,且AB=DE .请将下面说明△ABC ≌△DEF 的过程和理由补充完整.解:∵AF=CD( ),∴AF+FC=CD+ ,即AC=DF .在△ABC 和△DEF 中,____(__________(AC D AAB =⎧⎪∠=∠⎨⎪=⎩已证)()已知)(已证), ∴△ABC ≌△DEF( ).23.(7分)如图,DF ⊥AB ,∠A=430,∠D=42°,求∠ACB 的度数.E B DF C A∠ACB=89 º.24.(7分)如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.25.(7分)如图,在△ABC和△DEF中,AC=DF,AE=BD,BC=EF,则∠C=∠F,请说明理由(填空).解:∵ AE=BD(已知)∴ =∴ =在△ABC和△DEF中===∴△ABC≌△DEF ( )∴∠C=∠F ( )26.(7分)如图所示,已知点A,B,C,D在一条直线上,AB=CD.AE=DF,EC=FB,说明∠ACE=∠DBF的理由.27.(7分)如图所示,在△ABC中,AD是高,CE是角平分线,它们相交于点P.已知∠APE=55°,∠AEP=80°,求△ACB各个内角的度数.28.(7分)如图所示,在Rt△ABC中,∠A=∠B,CD是∠ACB的平分线,请判定CD与AB的位置关系,并说明理由.29.(7分)A,B是平面上的两个固定点,它们之间的距离为5 cm,请你在平面上找一点C(1)要使点C到A,B两点的距离之和等于5 cm ,则C点在什么位置?(2)要使点C到A,B两点的距离之和大于5 cm ,则点C在什么位置?(3)能使点C到A,B两点的距离之和小于5 cm吗?为什么?30.(7分)已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.D2.B3.D4.A5.D6.C7.B8.D9.C评卷人得分二、填空题10.411.180°12. 360,540,(n-2),180(n-2)13.19cm,7cm14.15.AB=AC,AD=AE或EC=BD16.∠ACB,∠ACB,∠DBC,已证,∠ABC,∠DCB,已知,BC,CB,公共边,△ABC,△DCB,AAS,全等三角形对应边相等17.6,218.2,819.1,120.(1)70°;(2)90°;(3)60°;(4)50°21.3三、解答题22.已知,FC,DF,已知,DE,SAS23.24.△ABD≌△ACD(SAS),则BD=CD.25.AE-BE,BD-BE,AB,DE,AC,DF,AB,DE,BC,EF,SSS,全等三角形的角相等.26.略27.∠B=45°,∠ACB=70°,∠BAC=6528.CD⊥AB,理由略29.(1)点C在线段AB上;(2)点C在线段AB外;(3)不能,因为两点之间线段最短(为5 cm)30.∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (414)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)若△ABC≌△DEF,AB=DE,∠A=35°,∠B=75°,则F的度数是()A. 35°B. 70°C.75°D.70°或75°2.(2分)如图,对任意的五角星, 结论错误的是()A.∠1=∠C+∠EB.∠2=∠A+∠DC.∠A+∠B+∠C+∠D+∠E=360°D.∠A+∠B+∠C+∠D+∠E=180°3.(2分)在下列条件中,不能说明△ABC≌△A′B′C′的是()A.∠A=∠A′,∠B=∠B′,AC=A′C′B.∠A=∠A′,AB=A′B′,BC=B′C′C.∠B=∠B′,BC=B′C′、AB=A′B′D.AB=A′B′,BC=B′C′,AC=A′C ′4.(2分)如图,△ABC和△ADC有公共边AC,∠BAC=∠DAC,在下列条件中不能..判断△ABC≌△ADC的是()A.BC=DC B.AB=AD C.∠B=∠D D.∠BCA=∠DCA5.(2分) 如图,O是直线AB上的一点,过O点作射线OC,已知OD、OE分别平分∠AOC、∠COB.则△ODE是()A.钝角三角形B.锐角三角形C.直角三角形D.无法判断6.(2分)如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对7.(2分)如图所示,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别是E,F,则图中与∠C(除°C外)相等的角的个数是()A.2个B.3个C.4个D.5个8.(2分)下列说法中正确的是()A.从三角形一个顶点向它对边所在直线画垂线,此垂线就是三角形的高B.三角形的角平分线是一条射线C.直角三角形只有一条高D.钝角三角形的三条高所在的直线的交点在此三角形的外部9.(2分)如图所示,∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()A.120°B. ll5°C.110°D.105°评卷人得分二、填空题10.(2分)如图,在Rt△ABC中,AD是BC边上的高,若∠C=36°,则∠B= ,∠DAB= .11.(2分)如图,△ABC≌△CDA,A与C对应,D与B对应,则∠1与是对应角.12.(2分)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有____________个.13.(2分)如图△ABC中,D、E分别在BC上,∠BAE=∠AEB,∠CAD=∠CDA.若∠BAC=x度,则∠DAE的度数是.14.(2分)已知BD是ΔABC的一条中线, 如果ΔABD和ΔBCD的周长分别是21,12,则BCAB 的长是.15.(2分) 如图,平面镜A与B之间夹角为110°,光线经平面镜A反射到平面镜B上,再反射出去,若∠1=∠2,则∠1的度数为.16.(2分)要使△ABC≌△A′B′C′,已知AB=A′B′,∠B=∠B′,如果利用“ASA”,要补充条件,如果利用“AAS”,要补充条件.17.(2分)如图所示,∠1=∠2,∠ABC=∠DCB,AC,BD相交于O,请将下列说明AB=DC的理由的过程补充完整.解:∵∠ABC=∠DCB,∠l=∠2(已知),∴∠ABC一∠l=∠DCB一∠2,即∠DBC= .在△ABC和△DCB中,= ( ),= ( ),= ( ),∴≌ ( ),∴AB=DC( ).18.(2分)判断下列说法是否正确,正确的打“√”,错误的打“×”.(1)面积相等的两个三角形全等. ( )(2)周长相等的两个三角形全等.’( )(3)三边对应相等的两个三角形全等. ( )(4)全等三角形的面积相等,周长相等. ( )19.(2分)如图所示.(1)AD是△ABC的角平分线,则∠BAC=2 =2 ;(2)AE是△ABC的中线,则 = 2BE=2 .20.(2分)如图,小明想测一块泥地AB的长度,他在AB的垂线BM上分别取C,D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这时这块泥地AB的长度就是线段的长度.21.(2分)木材加工厂堆放木料的方式如图所示:依此规律可以得出第六堆木料的根数是根.评卷人得分三、解答题22.(7分)已知∠α、∠β和线段a,如图,用直尺和圆规作△ABC,使∠A=∠α,∠B =∠β,BC =a.23.(7分)已知:△ABC的周长为 18 cm,AB边比AC边短2 cm,BC边是AC边的一半,求△ABC三边的长.24.(7分)如图,在△ABC中,∠B=44°,∠C=72°,AD是△ABC的角平分线.DCB A(1)求∠BAC的度数;(2)求∠ADC的度数.25.(7分)如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.26.(7分)如图所示,在△ABC中,a=2.7cm,b=1.7 cm,c=1.9 cm,∠B=38°,∠C=44°.请你从中选择适当的数据,画出与△ABC全等的三角形.(把你能画的三角形全部画出来,不写画法,但要在所画的三角形中标出用到的数据)27.(7分)如图所示,△ABC中,AB=AC,BE,CD分别是AC,AB的中线,说明下列各式成立的理由.(1)BE=CD;(2)∠1=∠2.28.(7分)如图所示,在四边形ABCD中,已知AB=AD,CB=CD,则在不添加其他线时,图中的哪两个角必定相等?请说明理由.29.(7分)如图所示,△ABC中,∠A=40°,∠ABC和∠ACB的外角平分线交于P.求∠P的度数.30.(7分)已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.B2.C3.B4.A5.C6.C7.B8.D9.B二、填空题10.54°, 36°11.∠312.313.90°-x 214.915.35°16.∠A=∠A ′,∠=∠C ′17.∠ACB ,∠ACB ,∠DBC ,已证,∠ABC ,∠DCB ,已知,BC ,CB ,公共边,△ABC ,△DCB ,AAS ,全等三角形对应边相等18.(1)× (2)× (3)√ (4)√19.(1)∠BAD ,∠CAD ;(2)BC ,CE20.DE21.28三、解答题22.图略23.AB=6 cm,BC=4cm,AC=8cm24.∠BAC=64°,∠ADC=108°.25.△ABD≌△ACD(SAS),则BD=CD.26.利用全等判别方法去画,图略27.略28.∠D=∠B,理由略29.∠P=70°30.∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (483)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)如图,在△ABC 中,∠ABC 与∠ACB 的角平分线交于点0,且∠BOC=α,则∠A 的度数是 ( )A .180°-αB .2α-180°C .180°-2αD .12α2.(2分)如图,123,,∠∠∠的大小关系为( ) A .213>>∠∠∠ B .132>>∠∠∠ C .321>>∠∠∠ D .123>>∠∠∠3.(2分)下列命题中正确的是( )A .三角形的角平分线、中线和高都在三角形内B .直角三角形的高只有一条C .三角形的高至少有一条在三角形内D .钝角三角形的三条高都在三角形外4.(2分)王老师的一块三角形教学用玻璃不小心打破了(如图),他想再到玻璃店划一块,为了方便他只要带哪一块就可以了( )A .①B .②C .③D .④5.(2分)如图,AC ⊥BE ,∠A =∠E ,不能判断△ABC ≌△EDC 的条件是( )A.BC=DC B.∠B=∠CDE C.AB=DE D.AC=CE6.(2分)如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对7.(2分)如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个8.(2分)一个三角形的两边长分别是3和6,第三边长为奇数,那么第三边长是()A 5或7 B.7或9 C.3或5 D.99.(2分)下列长度的三条线段,能组成三角形的是()A.6,3,3 B.4,8,8 C.3,4,8 D.8,l5,7评卷人得分二、填空题10.(2分)如图,在△ABC. 中,AB=AC=13 cm,AB的垂直平分线交AB边于点D,交AC 边于点E,若△EBG的周长为 21 cm,则BC= cm.11.(2分)如图,△ABC≌△DEF,点B和点E,点A 和点D是对应顶点,则AB= ,CB= ,∠C= ,∠CAB= .12.(2分)如图,在△ABC中,∠ACB=90°,角平分线 AD、BE交于点F,则∠AFB= .13.(2分)如图, △ABC中,AB=AC=12,EF为AC的垂直平分线,若EC=8,则BE的长为_______.14.(2分)已知BD是ΔABC的一条中线, 如果ΔABD和ΔBCD的周长分别是21,12,则AB 的长是.BC15.(2分)全等三角形的对应边,对应角.16.(2分)在ΔABC中, ∠C=90°,BD平分∠ABC,交AC于D,若AB=5,CD=2, 则ΔABD的面积是 .17.(2分)在△ABC中AB=3,BC=7则AC的取值范围是.4 <AC<1018.(2分)如图所示,已知AB=AD,AE=AC,∠DAB=∠EAC,请将下列说明△ACD≌△AEB的理由的过程补充完整.解:∵∠DAB=∠EAC(已知),∴∠DAB+ =∠EAC+ ,即 = .在△ACD和△AEB中AD=AB( ),= (已证),= (已知),∴△ACD≌△AEB( ).19.(2分)如图,已知∠DBC=∠ACB,要说明△ABC≌△DCB.(1)若以“SAS”为依据,则需要添加的一个条件是;(2)若以“AAS”为依据,则需添加一个条件是;(3)若以“ASA”为依据,则需添加一个条件是.20.(2分)如图,在△ABC中,已知AD=ED,AB=EB,∠A=75°,那么∠1+∠C的度数是.21.(2分)一个三角形最多有个钝角,最多有个直角.22.(2分)如果三角形的三个内角都相等,那么这个三角形是三角形.评卷人得分三、解答题23.(7分)如图,AB=AD,∠BAD=∠CAE,AC=AE,试说明CB=ED.24.(7分)如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问:AD与BC是否相等?说明你的理由.解:Θ AE⊥CD∴∠AED=Θ BF⊥CD∴∠BFC=∴ =在△ADE和△BCF中,()()()⎪⎩⎪⎨⎧=∠=∠=∠_____________________________________________________________________AEAEDD∴△ADE≌△BCF( )∴AD=BC( )90 º,90 º,∠AED,∠BFC,∠C,已知,BFC,已证,BF,已知,AAS,全等三角形的对应边相等.25.(7分)如图①所示,长方形通过剪切可以拼成直角三角形,方法如下:仿照上图,用图示的方法,解答下列问题:(1)如图②所示,已知直角三角形,设计一种方案,将它分成若干块,再拼成一个与之等面积的长方形;(2)如图③所示,对任意一个三角形,设计一种方案,把它分成若干块,再拼成一个与它等面积的长方形.26.(7分)如图所示,已知△ABE≌△ACE,D是BC的中点,你能说明△BDE≌△CDE吗?27.(7分)如图所示,在△ABC中,∠BAC=90°,画出BC边上的中线AM,分别量出AM,BC的长,并比较AM与12BC的大小.再画一个锐角△ABC及其中线AM,此结论还成立吗?对于钝角三角形呢?28.(7分)如图,已知∠A=∠D,AB=DE.AF=DC,图中有哪几对全等三角形?并选取其中一对说明理由.29.(7分)A,B是平面上的两个固定点,它们之间的距离为5 cm,请你在平面上找一点C(1)要使点C到A,B两点的距离之和等于5 cm ,则C点在什么位置?(2)要使点C到A,B两点的距离之和大于5 cm ,则点C在什么位置?(3)能使点C到A,B两点的距离之和小于5 cm吗?为什么?30.(7分)在△ABC中,∠A+∠C=120°,∠B+∠C=110°,求三角形各内角的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.B2.D3.C4.A5.B6.C7.D8.A9.B二、填空题10.811.DE, FE,∠F, ∠FDE12.135°13.414.915.相等,相等16.517.18.∠BAC,∠BAC,∠DAC,∠BAE,已知,∠DAC,∠BAE,AC,AE,SAS 19.(1)AC=DB;(2)∠BAC=∠CDB;(3)∠ABC=∠DCB20.75°21.1,122.等边评卷人得分三、解答题23.可证△ABC≌△ADB,然后说明CB =ED 24.25.(1)(2)26.略27.对于Rt△ABC,AM=12BC,对于其他三角形此结论不成立28.△ABF≌△DEC,△FCB≌△CFE,△ABC≌△DEF,证明略29.(1)点C在线段AB上;(2)点C在线段AB外;(3)不能,因为两点之间线段最短(为5 cm)30.∠A=70°,∠B=60°,∠C=50°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (534)
浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270°C.180°D.135°2.(2分)一个三角形的两边长分别是3和6,第三边长为奇数,那么第三边长是()A 5或7 B.7或9 C.3或5 D.93.(2分)现有两根木棒,它们的长度分别是20 cm和30 cm.如果不改变木棒的长度,要钉成一个三角形木架,那么应在下列四根木棒中选取()A.10 cm的木棒B.20 cm的木棒C.50 cm的木棒D.60 cm的木捧4.(2分)如果三条线段的比是:(1)1:4:6;(2)1:2:3;(3)3:4:5;(4)7:7:11;(5)3 : 3:6,那么其中可构成三角形的比有()A.1种B.2种C.3种D.4种5.(2分)如图所示,已知∠A=∠D,∠l=∠2,那么,要得到△ABC≌△DEF,还应给出的条件是()A.∠E=∠B B.ED=BC C.AB=EF D.AF=CD6.(2分)如图,AB=CD,∠l=∠2,AO=3,则AC=()A.3 B.6 C.9 D.127.(2分)下列条件中,不能作出唯一..三角形的是( ) A .已知两边和夹角B .已知两边和其中一边的对角C .已知两角和夹边D .已知两角和其中一角的对边8.(2分)如图,线段AC 、BD 交于点0,且AO=CO ,BO=DO ,则图中全等三角形的对数有( )A .1对B . 2对C .3对D .4对9.(2分)如图,AD 、AE 分别是△ABC 的高和角平分线,∠DAE=20°,∠B=65°,则∠C 等于( )A .25°B .30°C .35°D .40°10.(2分)锐角三角形的三个内角是AB C ,,∠∠∠.如果A B B C C A αβγ=+=+=+,,∠∠∠∠∠∠∠∠∠,那么αβγ,,∠∠∠这三个角中( )A .没有锐角B .有1个锐角C .有2个锐角D .有3个锐角11.(2分)下列说法正确的是( )A .周长相等的两个三角形全等B .面积相等的两个三角形全等C .三个角对应相等的两个三角形全等D .三条边对应相等的两个三角形全等12.(2分)如图,△ABC ≌△BAD ,A 与B ,C 与D 是对应点,若AB=4cm ,BD=4.5cm ,AD=1.5cm ,则BC 的长为( )A .4cmB .4.5cmC .1.5cmD .不能确定13.(2分)用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB 的依据是( )A .SSSB .SASC .ASAD .AAS14.(2分)已知在△ABC 和△A′B′C′中,AB =A′B′,∠B=∠B′,补充下面一个条件,不能说明△ABC≌△A′B′C′的是()A. BC =B′C′B.AC=A′C′C.∠C=∠C′D.∠A=∠A′15.(2分)如图所示,A,B是数轴上的两点,C是AB的中点,则0C等于()A.34OB B.1()2OB OA-C.1()2OA OB+D.以上都不对16.(2分)如图所示,在4×4的正方形网格中,∠l,∠2,∠3的大小关系是()A.∠l>∠2>∠3 B.∠1=∠2>∠3C.∠l<∠2=∠3 D.∠l=∠2=∠3评卷人得分二、填空题17.(2分)如图,已知ΔABC≌ΔADE,则图中与∠BAD相等的角是.18.(2分)三角形中线将三角形的平分.19.(2分) 如图,平面镜A与B之间夹角为110°,光线经平面镜A反射到平面镜B上,再反射出去,若∠1=∠2,则∠1的度数为.20.(2分)如图所示,AB=BD,AC=CD,∠ACD=60°,则∠ACB= .21.(2分)只要三角形三边的长度固定,这个三角形的和就完全确定,三角形的这个性质叫做三角形的.22.(2分)如图所示,△ABC中,D,E是BC边上的两点,且BD=DE=EC,则AD是三角形的中线,AE是三角形的中线.23.(2分)如图所示,共有个三角形.其中以DC为一边的三角形是.24.(2分)在△ABC中,(1)∠C=85°,∠A=25°,则∠B= ;(2)∠A+∠B=90°,则∠C= ;(3)∠A=∠B=∠C,则∠A= ;(4)∠A=∠B,∠C=80°,则∠B= .评卷人得分三、解答题25.(7分) 如图,把4×4的正方形方格图形分割成两个全等图形,请在下图中,沿虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.26.(7分)在下面△ABC中,用尺规作出AB边上的高及∠B的平分线(不写作法,保留作图痕迹)AB C27.(7分)如图所示,△ABC中,AB=AC,BE,CD分别是AC,AB的中线,说明下列各式成立的理由.(1)BE=CD;(2)∠1=∠2.28.(7分)如图所示,已知△ABE≌△ACE,D是BC的中点,你能说明△BDE≌△CDE吗?29.(7分)已知,如图所示,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断∠B与∠DEC是否相等,并说明理由.30.(7分)如图所示,在△ABC中,∠ABC=60°,∠ACB=72°,BD,CE分别是AC,AB上的高,BD交CE于点0.求:(1)∠A的度数;(2)∠ACE的度数;(3)∠BOC的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.B2.A3.B4.B5.D6.B7.B8.D9.A10.A11.D12.C13.A14.B15.C16.B评卷人得分二、填空题17.∠CAE18.面积19.35°20.30°21.形状,大小,稳定性22.ABE,ACD23.7;△DBC,△ADC24.(1)70°;(2)90°;(3)60°;(4)50°评卷人得分三、解答题25.26.略27.略28.略29.∠B=∠DEC,理由略30.(1)48°;(2)42°;(3)132°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (240)

O EA B D C浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)如图,OA OB =,OC OD =,50O ∠=o ,35D ∠=o ,则AEC ∠等于( )A .60oB .50oC .45oD .30o2.(2分)如图,AC=AD ,BC=BD ,则图中全等三角形的对数是( )A .6对B .3对C .2对D .1对 3.(2分)如图,在△ABC 中,已知∠ACB=90°,∠CAD 的角平分线交BC 的延长线于点E ,若∠B=50°,则∠AEB 的度数为( )A .70°B .20°C .45°D .50°4.(2分) 在△ABC 中,∠A =30°,∠B =50°,则∠C 的外角=( )A .60°B .80°C .100°D .120°5.(2分)如图,AC ⊥BE ,∠A =∠E ,不能判断△ABC ≌△EDC 的条件是( )A .BC =DCB .∠B =∠CDEC .AB =DED .AC =CE6.(2分)如图所示,BA=BD ,BC=BE ,根据“边角边”条件得到△ABE △DBC ,则需要增加条件 ( )A .∠A=∠DB .∠E=∠C C .∠A=∠CD .∠l=∠27.(2分)如图所示,已知AC=AB ,∠1=∠2,E 为AD 上一点,则图中全等三角形有( )A . 1对B .2对C .3对D .4对8.(2分)如果三角形的两边长分别为7和2,且它的周长为偶数,那么,第三边的长为()A.5 B.6 C.7 D.89.(2分)三角形的三边长都是整数,并且唯一的最长边是5,则这样的三角形共有() A 1个 B.2个 C.3个 D.4个10.(2分)在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠8′;⑥∠C=∠C′,则下列条件中不能使△ABC≌△A′B′C′的是()A.②④⑤B.①②③C.①③⑤D.①②⑤11.(2分)如图,已知BC=BD,∠ABE=∠CBD,∠ADB=∠BCE.要说明BA=BE,则只要先说明()A.△ABE≌△DBC B.△ABD≌△EBC C.△BDG≌△BEH D.△ABG≌△BCH评卷人得分二、填空题12.(2分)如果一个三角形的三条高都在三角形的内部,那么这个三角形是三角形(按角分类).13.(2分)已知ABC DEF20cm,那么△DEF △≌△,5cm==,△ABC的面积是2BC EF中EF边上的高是__________cm.14.(2分)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠+∠=.AOC DOB15.(2分)如图所示.(1)AD是△ABC的角平分线,则∠BAC=2 =2 ;(2)AE是△ABC的中线,则 = 2BE=2 .16.(2分)等腰三角形两边长分别是7cm和3 cm,则第三边长是.17.(2分)如图,把△ABC沿虚线剪一刀,若∠A=40°,则∠l+∠2= .18.(2分)如图,小明想测一块泥地AB的长度,他在AB的垂线BM上分别取C,D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A,C,E三点共线,这时这块泥地AB的长度就是线段的长度.19.(2分)如果三角形的三个内角都相等,那么这个三角形是三角形.评卷人得分三、解答题20.(7分) 如图,把4×4的正方形方格图形分割成两个全等图形,请在下图中,沿虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.21.(7分)如图,已知BE=CF,AB=CD,∠B=∠C,则AF=DE吗?请说明理由.F E DC B A 22.(7分)如图,直线l 表示一条公路,点A,点B 表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A ,B 的距离相等,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)23.(7分)如图,已知D 、E 分别在AC 、AB 上,BD 、CE 相交于点O ,且AB = AC ,∠1=∠2.(1)写出图中所有的全等三角形.(2)要说明以上各对三角形全等,应先说明哪一对?并说明这一对三角形全等的理由.24.(7分)如图,BD =CD ,∠ABD =∠ACD ,DE 、DF 分别垂直于AB 及AC 交延长线于E 、F .求证:DE =DF .A B E D O 1 225.(7分)如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.26.(7分)如图所示,在△ABC中,a=2.7cm,b=1.7 cm,c=1.9 cm,∠B=38°,∠C=44°.请你从中选择适当的数据,画出与△ABC全等的三角形.(把你能画的三角形全部画出来,不写画法,但要在所画的三角形中标出用到的数据)27.(7分)已知,如图所示,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断∠B与∠DEC是否相等,并说明理由.28.(7分)如图所示,在四边形ABCD中,已知AB=AD,CB=CD,则在不添加其他线时,图中的哪两个角必定相等?请说明理由.29.(7分)三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.30.(7分):如图,已知方格纸中每个小方格都是相同的正方形,∠AOB画在方格纸上,A0=B0,请在小方格的顶点上标出两个点P l,P2:,使P l,P2:落在∠AOB的平分线上.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.A2.B3.B4.B5.B6.D7.C8.C9.D10.C11.B评卷人得分二、填空题12.锐角13.814.180°15.(1)∠BAD,∠CAD;(2)BC,CE16.7 cm17.220°18.DE19.等边评卷人得分三、解答题20.21.利用SAS说明△ABF≌△DCE22.略.23.(1)△AEO≌△ADO,△EOB≌△DOC,△ABO≌△ACO,△ABD≌△ACE;(2)△AOB≌△AOC,理由: △AOB≌△AOC(SAS) .24.∠ABD=∠ACD,则∠E+∠BDE =∠F+∠CDF, 由于∠E=∠F,∴∠BDE =∠CDF ,∴△BED≌△CFD(AAS),∴DE=DF.25.△ABD≌△ACD(SAS),则BD=CD.26.利用全等判别方法去画,图略27.∠B=∠DEC,理由略28.∠D=∠B,理由略29.高线的交点可以在三角形的外部、内部及其顶点上30.提示:P l,P2到点A,B的距离相等即可(不唯一)。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (660)

浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________一、选择题1.(2分)已知在△ABC 和△A ′B ′C ′中,AB =A ′B ′,∠B=∠B ′,补充下面一个条件,不能说明△ABC ≌△A ′B ′C ′的是( )A . BC =B ′C ′ B .AC=A ′C ′ C .∠C=∠C ′D .∠A=∠A ′2.(2分)在△ABC 和△A ′B ′C ′中,已知 AB=A ′B ′,∠B=∠B ′,要保证△ABC ≌△A ′B ′C ′,可补充的条件是( )A .∠B+∠A=90°B . AC=A ′C ′ C .BC=B ′C ′D .∠A+∠A ′=90°3.(2分)在下列条件中,不能说明△ABC ≌△A ′B ′C ′的是( )A .∠A=∠A ′,∠B=∠B ′,AC=A ′C ′B .∠A=∠A ′,AB=A ′B ′,BC=B ′C ′C .∠B=∠B ′,BC=B ′C ′、AB=A ′B ′D .AB=A ′B ′,BC=B ′C ′,AC=A ′C ′4.(2分)如图,△ABC 和△ADC 有公共边AC ,∠BAC =∠DAC ,在下列条件中不能..判断△ABC ≌△ADC 的是( )A .BC=DCB .AB =ADC .∠B =∠D D .∠BCA =∠DCA5.(2分)下列长度的三条线段,能组成三角形的是( )A .224,,B .225,,C .236,,D .245,,6.(2分)如图△ABC 中,AB 的中垂线交AC 于D ,AB =10,AC =8,△DBC 的周长是a ,则BC 等于 ( )A . a -6B .a -8C .a -10D .10-a7.(2分)一块试验田的形状是三角形(设其为ABC △),管理员从BC 边上的一点D 出发,沿DC CA AB BD →→→的方向走了一圈回到D 处,则管理员从出发到回到原处在途中身体( )A .转过90oB .转过180oC .转过270oD .转过360o8.(2分)下列条件能够判断△ABC ≌△DEF 的是( )A .AB=DE ,BC=EF ,∠A=∠DB .∠A=∠D ,∠C=∠F ,AC=EFC .AB=DE ,BC=EF ,△ABC 的周长等于△DEF 的周长D .∠A=∠D ,∠B=∠E ,∠C=∠F9.(2分) 用一副三角板画图,不能画出的角的度数是( )A .15°B .75°C .145°D .165°10.(2分)如图.在△ABC 中,AB AC ,AB 的中垂线DE 交AC 于点D ,交AB 于点E ,如果BC=10,△BDC 的周长为22,那么△ABC 的周长是( )A .24B .30C .32D .3411.(2分)如图所示,在Rt △ADB 中,∠D=90°,C 为AD 上一点,则x 可能是( )A 10°B .20°C .30°D .40°评卷人得分 二、填空题12.(2分)如图,已知 AC 与BD 相交于点0,AO=CO ,BO=DO ,则AB = CD. 请说明理由. 解:在△AOB 和△COD 中,(_____((AO CO BO DO =⎧⎪⎨⎪=⎩已知)对顶角相等)已知) 所以△AOB ≌△COD( ).所以AB=DC( ). 13.(2分)如图,AF 、AD 分别是△ABC 的高和角平分线,且∠B=36°,∠C=76°,则∠DAF = .14.(2分)已知三角形的三边长为 3、1x +,4,则x 的取值范围是 .15.(2分)四条线段的长分别是5 cm ,6 cm ,8 cm ,13 cm ,则以其中任意三条线段为边可以构成个三角形.16.(2分)如图,AD=AE ,DB=EC ,则图中一共有 对全等三角形.17.(2分)如图,BE ,CD 是△ABC 的高,且AD =AE ,判定△ACD ≌△ABE 的依据是“______”.18.(2分)在△ABC 中,∠A=∠B ,∠C=50°,则∠A= 度.19.(2分)如图,在△ABC 中,AD 是BC 边上的中线,若△ABC 的周长为20,BC=11,且△ABD 的周长比△ACD 的周长大3,则AB= ,AC= . 6,320.(2分)如图,OP 平分∠EOF ,PA ⊥OE 于点A.已知PA =2cm ,求点P 到OF 的距离为 . 21.(2分)如图所示,∠1=135°,∠2=75°,则∠3的度数是 .22.(2分)已知△ABC 三边为a,b ,c ,且a ,b 满足21(3)0a b -+-=,c 为整数,则c 的取值为 .D AB评卷人得分三、解答题23.(7分)如图,已知:A,F,C,D四点在一条直线上,AF=CD,∠D=∠A,且AB=DE.请将下面说明△ABC≌△DEF的过程和理由补充完整.解:∵AF=CD( ),∴AF+FC=CD+ ,即AC=DF.在△ABC和△DEF中,____(__________(ACD AAB=⎧⎪∠=∠⎨⎪=⎩已证)()已知)(已证),∴△ABC≌△DEF( ).24.(7分)如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问:AD与BC是否相等?说明你的理由.解:Θ AE⊥CD∴∠AED=Θ BF⊥CD∴∠BFC=∴ =在△ADE和△BCF中,()()()⎪⎩⎪⎨⎧=∠=∠=∠_____________________________________________________________________AEAEDD∴△ADE≌△BCF( )∴AD=BC( )90 º,90 º,∠AED,∠BFC,∠C,已知,BFC,已证,BF,已知,AAS,全等三角形的对应边相等.25.(7分)如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.26.(7分)如图所示,△ABC中,AB=AC,BE,CD分别是AC,AB的中线,说明下列各式成立的理由.(1)BE=CD;(2)∠1=∠2.27.(7分)已知,如图所示,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断∠B与∠DEC是否相等,并说明理由.28.(7分)如图,已知∠A=∠D,AB=DE.AF=DC,图中有哪几对全等三角形?并选取其中一对说明理由.29.(7分)在△ABC中,∠A+∠C=120°,∠B+∠C=110°,求三角形各内角的度数.30.(7分)在△ABC中,已知∠A+∠B=70°,∠C=2∠A,求∠A,∠B,∠C的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.B2.C3.B4.A5.D6.B7.D8.C9.C10.D11.B二、填空题12.∠AOB=∠COD,SAS,全等三角形的对应边相等13.20014.0<x<615.216.417.ASA(或AAS)18.6519.20.2cm21.30°22.3三、解答题23.已知,FC,DF,已知,DE,SAS24.25.略26.略27.∠B=∠DEC,理由略28.△ABF≌△DEC,△FCB≌△CFE,△ABC≌△DEF,证明略29.∠A=70°,∠B=60°,∠C=50°30.∠A=55°,∠B=15°,∠C=110°。
最新浙教版初中数学七年级下册《三角形的初步认识》专项测试 (含答案) (250)
浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,已知 AE=CF,BE =DF.要证△ABE≌△CDF,还需添加的一个条件是()A.∠BAC=∠ACD B.∠ABE=∠CDF C.∠DAC=∠BCA D.∠AEB=∠CFD2.(2分)如图△ABC中,AB的中垂线交AC于D,AB=10,AC=8,△DBC的周长是a,则BC等于()A. a-6 B.a-8 C.a-10 D.10-a3.(2分)用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是()A.SSS B.SAS C.ASA D.AAS4.(2分)下列各条件中,不能作出惟一三角形的是()A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角D.已知三边5.(2分)下列说法正确的是()A.周长相等的两个三角形全等B.面积相等的两个三角形全等C.三个角对应相等的两个三角形全等D.三条边对应相等的两个三角形全等6.(2分)如图,已知直线L是线段PQ的垂直平分线,垂足为O,M、N是直线L上两点,下列结论中,错误的是()A.△MPN≌△MQN B.MO=NO C.OP=OQ D.∠MPN=∠MQN 7.(2分)下列说法中,正确的个数有()①延长直线AB;②取线段AB的中点C;③以0为圆心作弧;④已知∠α,作∠α的余角的一半.A.0个B.1个C.2个D.3个8.(2分)如图所示,已知AC=AB,∠1=∠2,E为AD上一点,则图中全等三角形有()A. 1对B.2对C.3对D.4对9.(2分)如图,△A8C≌△BAD,A和B,C和D是对应点,若AB=4 cm,BD=3 cm,AD=2 cm,则BC的长度为()A.4 cm B.3 cm C.2 cm D.不能确定评卷人得分二、填空题10.(2分)如图,在Rt△ABC中,AD是BC边上的高,若∠C=36°,则∠B= ,∠DAB= .11.(2分)若a、b、c为△ABC的三边,则a b ca b c−−−+0(填“>”、“=”或“<”) .12.(2分)在Rt△ABC中,∠C=90°,CE是△ABC的中线,若AC=2.4 cm,BC=1.5 cm,则△AE的面积为.解答题13.(2分)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有____________个.14.(2分)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则AOC DOB∠+∠=.∠= .15.(2分)如图,图中的116.(2分)在△ABC中,∠A=∠B,∠C=50°,则∠A= 度.17.(2分)直角三角形两锐角的平分线所成角的度数是度.13518.(2分)如图,∠1∶∠2∶∠3=1∶2∶3,则∠4=.72 º19.(2分)如图所示,直线AD交△ABC的BC边于D点,且AB=AC.(1)若已知D为BC中点,则可根据,说明△ABD≌△ACD;(2)若已知AD平分∠BAC,可以根据说明△ABD≌△ACD;(3)若AD是BC的中垂线,则可以根据,说明△ABD≌△ACD,还可以根据说明△ABD≌△ACD.20.(2分)如图所示,△ABC 中,BC=16 cm,AB,AC边上的中垂线分别交BC于E,F,则△AEF的周长是 cm.21.(2分)如图所示,已知点D,E,F分别是BC,AC,DC的中点,△EFC的面积为6 cm2,则△ABC的面积为.评卷人得分三、解答题22.(7分)如图,已知:A,F,C,D四点在一条直线上,AF=CD,∠D=∠A,且AB=DE.请将下面说明△ABC≌△DEF的过程和理由补充完整.解:∵AF=CD( ),∴AF+FC=CD+ ,即AC=DF .在△ABC 和△DEF 中,____(__________(AC D AAB =⎧⎪∠=∠⎨⎪=⎩已证)()已知)(已证), ∴△ABC ≌△DEF( ).23.(7分)如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的理由.(1)∠DBH=∠DAC ;(2)ΔBDH ≌ΔADC .24.(7分)如图,AC=AE ,AB=AD ,∠1=∠2.请说明下列结论成立的理由:(1) △ABC ≌△ADE ;(2)BC=DE .25.(7分)如图,已知D 、E 分别在AC 、AB 上,BD 、CE 相交于点O ,且AB = AC ,∠1=∠2.(1)写出图中所有的全等三角形.(2)要说明以上各对三角形全等,应先说明哪一对?并说明这一对三角形全等的理由.26.(7分)如图,AD 平分∠BAC ,AB =AC ,则BD =CD ,试说明理由.27.(7分)在墙上有一个很大的圆形设计图,其中O 是圆心,A ,B 在圆周上,如图所A B CE D O 1 2示.现在想测量AB两点间的距离,但墙很高,又没有梯子,不能直接测量.如果给你一根长度超过直径的竹竿和一把卷尺,你能测量AB两点之间的距离吗?说说你的方法.28.(7分)一个三角形有两条边相等,它的最长的边比最短的边多2,已知这个三角形的周长为8,求它的三条边长.29.(7分)已知三角形的周长是46 cm,其中一边比最短边长2 cm,比最长边短3 cm,求三角形三边的长.30.(7分)已知,如图所示,△ABC中,∠B=30°,∠C=40°,D为BC上一点,∠1=∠2,求∠BAD的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.D2.B3.A4.C5.D6.B7.C8.C9.C二、填空题10.54°, 36°11.<12.0.9cm213.314.180°15.50°16.6517.18.19.(1)SSS;(2)SAS;(3)SAS,SSS20.1621.48cm2三、解答题22.已知,FC,DF,已知,DE,SAS23.(1)ΔABC的两条高AD、BE相交于H,则∠BDH=∠AEH=90 º,由于∠BHD=∠AHE,则∠DBH=∠DAC;(2)AD为ΔABC的高,则∠BDH=∠ADC=90 º,ΔBDH≌ΔADC(ASA)..找出下图中每个轴对称图形的对称轴,并画出来.略.24.(1)∠1=∠2,则∠CAB=∠EAD,ΔABC≌ΔADE(SAS);(2)ΔABC≌ΔADE,则BC=DE25.(1)△AEO≌△ADO,△EOB≌△DOC,△ABO≌△ACO,△ABD≌△ACE;(2)△AOB≌△AOC,理由: △AOB≌△AOC(SAS) .26.△ABD≌△ACD(SAS),则BD=CD.27.能.方法:构造三角形全等(具体略)28.103,103,4329.13 cm,15 cm,18 cm30.∠l=∠2=70°,∠1=∠B+∠BAD,得∠BAD=40°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙教版初中数学试卷
2019-2020年七年级数学下册《三角形的初步认识》
精选试卷
学校:
__________
题号
一 二 三 总分 得分
评卷人
得分 一、选择题
1.(2分)如图,线段AC 、BD 交于点0,且AO=CO ,BO=DO ,则图中全等三角形的对数有( )
A .1对
B . 2对
C .3对
D .4对
2.(2分)若△ABC ≌△DEF ,AB=DE ,∠A=35°,∠B=75°,则F 的度数是( )
A . 35°
B . 70°
C .75°
D .70°或75°
3.(2分)下列每组数分别是三根小木棒的长度,首尾顺次相接能组成三角形的是( )
A .10 cm , 2 cm , 15 cm
B .15 cm , 9 cm , 25 cm
C .6 cm , 9 cm, 15 cm
D .5 cm , 5 cm , 5 cm
4.(2分)在下列长度的四根木棒中,能与4 cm ,9 cm 长的两根木棒钉成一个三角形的是( )
A .4 cm
B .5 cm
C .9cm
D .13 cm
5.(2分)在Rt △ABC 中,∠BAC=90度,AD 是高,则图中互余的角有 ( )
A . 一对
B . 二对
C . 三对
D .四对
6.(2分)下列长度的三条线段,能组成三角形的是( )
A .224,,
B .225,,
C .236,,
D .245,,
7.(2分)锐角三角形的三个内角是A B C ,,∠∠∠.如果A B B C C A αβγ=+=+=+,,∠∠∠∠∠∠∠∠∠,那么αβγ,,∠∠∠这三个
A B C
D
角中()
A.没有锐角B.有1个锐角C.有2个锐角D.有3个锐角
8.(2分) 用一副三角板画图,不能画出的角的度数是()
A.15°B.75°C.145°D.165°
9.(2分)如图所示,0P平分∠AOB,PE⊥OB,PF⊥OA,则下列结论中正确的个数有()
①OE=0F;②FP=PE;③OP⊥EF;④∠PEF=∠PFE;⑤0P平分∠FPE;⑥PQ=0Q
A.6个B.5个C.4个D.2个
10.(2分)如图所示,已知AD⊥BC,BD=CD,则①△ABD≌△ACD,②△ABD和△ACD 不全等,③AB=AC,④∠BAD=∠CAD,以上判断正确的是()
A.①B.②C.①③④D.①②③
11.(2分)下列说法中:①如果两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等;③要判断两个三角形全等,给出的条件中至少要有一对边对应相等.正确的是()
A.①和②B.②和③C.①和③D.①②③
12.(2分)如图所示,在4×4的正方形网格中,∠l,∠2,∠3的大小关系是()
A.∠l>∠2>∠3 B.∠1=∠2>∠3
C.∠l<∠2=∠3 D.∠l=∠2=∠3
评卷人得分
二、填空题
13.(2分)如图,在△ABC中,∠ACB=90°,角平分线 AD、BE交于点F,则∠
AFB= .
14.(2分)如图,在△ABC中,∠BAC=45O,现将△ABC绕点A旋转30O至△ADE的位置.则∠DAC= .
15.(2分)判断正误,对的打“√”,错的打“×”.
(1)经过线段中点的直线是线段的中垂线. ( )
(2)以AB为直径可以作一个圆. ( )
(3)已知两条边和一个角可以作唯一的三角形. ( )
(4)已知两角一边可以作唯一的三角形. ( )
16.(2分)如图所示,已知AB=DC,AD=BC,E,F是BD上两点,且BE=DF.若∠AEB=100°,∠ADB=30°,则∠BCF= .
17.(2分)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃.最省事的办法是带去,理由是.
18.(2分)仔细观察下图:
(1)图中的△ABC与△A′B′C′全等吗? .
(2)由图中的信息,你可以得到的重要结论是:.
19.(2分)如图所示,分别根据下列已知条件,再补充一个条件,使图中的△ABD≌△ACE(SAS).
①AB=AC,∠A=∠A,;
②AB=AC,∠B=∠C, ;
③AD=AE,,BD=CE.
20.(2分)如图所示,在△ABC中,∠B=35°,∠C=60°,AE是∠BAC的平分线,AD⊥BC于D,则∠DAE的度数为.
21.(2分)如果三角形的三个内角都相等,那么这个三角形是三角形.
评卷人得分
三、解答题
22.(7分)已知∠α、∠β和线段a,如图,用直尺和圆规作△ABC,使∠A=∠α,∠B =∠β,BC =a.
23.(7分)如图,在△ABC 中,AE 是∠BAC 的角平分线,AD 是BC 边上的高,∠B=40°,∠C=60°,求∠EAD 的度数.
24.(7分)如图,直线OA ,OB 表示两条相互交叉的公路.点M ,N 表示两个蔬菜基地.现要建立一个蔬菜批发市场,要求它到两个基地的距离相等,并且到公路OA ,OB
25.(7分)如图,AD ,CE 分别是△ABC 的两条高,问∠BAD 与∠BCE 相等吗?请说明理由.
26.(7分)如图所示,有1l ,2l ,3l 三条公路交于A ,B ,C ,现要在△ABC 内建一加油站,
使它到三 条公路的距离相等,问应如何建?作出加油站的位置,并说明理由.
M A
O N B
A B C
D E
27.(7分)如图所示,已知△ABE≌△ACE,D是BC的中点,你能说明△BDE≌△CDE吗?
28.(7分):如图,已知方格纸中每个小方格都是相同的正方形,∠AOB画在方格纸上,
A0=B0,请在小方格的顶点上标出两个点P l,P2:,使P l,P2:落在∠AOB的平分线上.
29.(7分)(1)为了求出四边形的内角和,你能根据图中的两种添线方法,分别求出四边形的内角和吗?
(2)请你用类似的方法求出五边形、六边形的内角和,比较一下,你发现了什么规律?
(3)利用你发现的规律,可以求得20边形的内角和为度.
30.(7分)已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.【参考答案】***试卷处理标记,请不要删除
一、选择题
1.D
2.B
3.D
4.C
5.D
6.D
7.A
8.C
9.B
10.C
11.C
12.B
二、填空题
13.135°
14.15°
15.(1)× (2)√ (3)× (4)×
16.70°
17.③,可根据③中的两角及夹边画出一个与之全等的三角形
18.(1)不全等;(2)有两边及其中一边的对角对应相等的两个三角形不一定全等
19.①AD=AE;②BD=CE;③∠ADB=∠AEC
20.12.5°
21.等边
三、解答题
22.图略
23.10°
的平分线OC和线段MN的垂直平分线DE,则射线OC与直线DE 24.分别作AOB
的交点P即为批发市场应建的地方.
25.相等,理由略
26.分别作∠ABC与∠BCA的角平分线,两条角平分线的交点即为加油站的位置,根据角平分线上的点到角两边的距离相等即可说明
27.略
28.提示:P l,P2到点A,B的距离相等即可(不唯一)
29.(1)360°;(2)规律:n边形的内角和为(n-2)·180°;(3)3240
30.∠C=90°。
