第十五章分式知识体系框架图
人教版八年级各章知识结构图
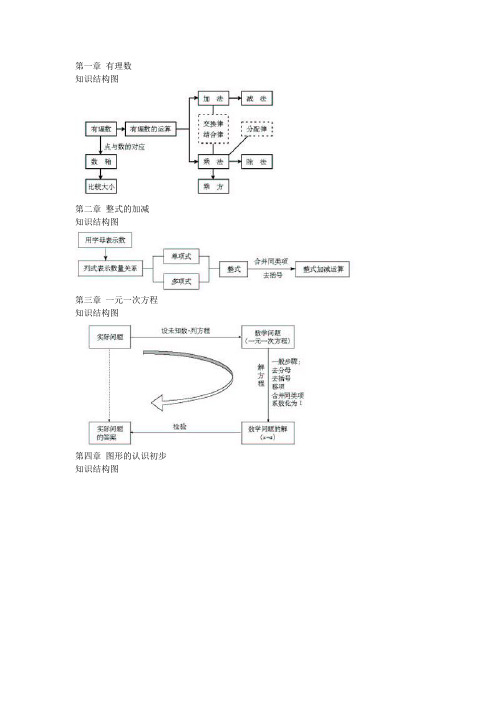
第一章有理数
知识结构图
第二章整式的加减
知识结构图
第三章一元一次方程知识结构图
第四章图形的认识初步知识结构图
第五章相交线与平行线知识结构图
第六章平面直角坐标系知识结构图
第七章三角形
知识结构图
第八章二元一次方程组
知识结构图
第九章不等式与不等式组
知识结构图
第十章数据的收集、描述与整理知识结构图
第十一章全等三角形知识结构图
第十二章轴对称
知识结构图
等十三章实数
知识结构图
第十四章一次函数知识结构图
第十五章整式的乘除与因式分解知识结构图
第十六章分式
知识结构图
第十七章反比例函数
知识结构图
第十八章勾股定理知识结构图
第十九章四边形
知识结构图
第二十章数据的分析知识结构图
第二十一章二次根式
知识结构图
第二十二章一元二次方程知识结构图
第二十三章旋转
知识结构图
第二十四章圆
知识结构图
第二十五章概率初步知识结构图
第二十六章二次函数知识结构图
第二十七章相似
知识结构图
第二十八章锐角三角函数知识结构图
第二十九章投影与视图知识结构图。
八年级数学上册第十五章分式本章整合课件新版新人教版

知识建构导图
1
2
345ຫໍສະໝຸດ 6789 10 11 12 13 14 15
1.(2017·广西桂林中考)若分式������������2+-24的值为 0,则 x 的值为(
).
A.-2
B.0
C.2
D.±2
中考聚焦体验
由题意可知 ������2-4 = 0, ������ + 2 ≠ 0,
解得 x=2.故选 C.
2019/5/25
最新中小学教学课件
20
得1
800 ������
−
118.20���0��� =6,
解得 x=50,
经检验,x=50 是原分式方程的解,
故小芳的速度是 50 m/min.
答案
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15
中考聚焦体验
15.(2017·广西河池中考)某班为满足同学们课外活动的需求,要求 购买排球和足球若干个.已知足球的单价比排球的单价多30元,用 500元购得的排球数量与用800元购得的足球数量相等. (1)排球和足球的单价各是多少元? (2)若恰好用去1 200元,有哪几种购买方案?
.
中考聚焦体验
原 =������式+������ ������=. ������������++2������������
·������
������ +2������
������ ������ + ������
关闭
关闭
解析 答案
1
2
3
4
5
6
7
人教版八年级数学上册课件:15章 分式--知识点复习(共48张PPT)
贵了8元,商家销售这种衬衫时每件定价都是100元,最后剩
下10件按8折销售,很快售完.设第一批进货单价为x元,根据
题意得到的方程是
;在这两笔生意中,商家
共盈利
元.
43
知识点六:分式方程的应用
巩固练习
分式方程的应用
4.某工厂对产品进行包装,引进了包装机器.已知台包装机的 工作效率相当于一名包装员的20倍若用这台包装机包装900件 产品要比15名包装员包装这些零件少3小时. (1)求一台包装机每小时包装产品多少个? (2)现有一项包装任务,要求不超过7小时包装完成3450个零 件.该厂调配了2台包装机和30名包装员,工作3小时后又调配 了一些包装机进行支援,则该厂至少再调配几台包装机才能
38
知识点五:分式方程及解法
合作探究
先独立完成导学案专题五,再同桌相互交流, 最后小组交流;
39
知识点六:分式方程的应用
知识回顾
分式方程的应用
请说出列分 式方程解应 用题的一般 步骤?
审找设列解 验 答
40
知识点六:分式方程的应用
巩固练习
分式方程的应用
1.“绿水青山就是金山银山”.某工程队承接了60万平方米的
知识回顾
分式的基本性质:
分式的基本性质用式子表示为: 其中A,B,C是整式.
11
知识点二:分式的基本性质
知识回顾
分式的符号法则:
分式的分子、分母与分式本身 这三处的正负号,同时改 变两处,分式的值不变 .
或
12
知识点二:分式的基本性质
巩固练习
1.写出下列分式中未知的分子或分母:
(1)
(2) 4n
3
知识点一:分式及其相关概念
八年级数学上册第十五章分式15.1分式15.1.1从分数到分式课件新版新人教版

知识点 3 分式的值为零的条件
6.在分式23������������+-1式无意义;当 y=
-12
时,分式的值为
零.
7.若分式|������������+|-11的值为零,则 x 的值是 1 . 知识点 4 分式的实际应用
8.列式表示下列各量:
( 1 )如果从一卷粗细均匀的电线上截取 1 米长的电线,称得它的
x-y
),0 中,是分式的
有
������+3 ������
,
������+������ ������-������
,
���1���(
x-y
)
,是整式的有
5+������ π
,
43(
x2+1
),0
.
知识点 2 分式有意义、无意义的条件
3.若分式���������-���4有意义,则实数 x 的取值范围是 x≠4 .
0.
17.已知分式2���������+���-������������,当 x=3 时,分式的值不存在;当 x=-1 时,分式的值等 于 0.求���������2���+-������������2的值.
解:∵当 x=3 时,分式的值不存在,∴3+n=0,解得 n=-3;
∵当 x=-1 时,分式的值等于 0,∴-2-m=0,解得 m=-2,
质量为 m 克,再称得剩余电线的质量为 n 克,那么原来这卷电线的总
长度是 ������+������
������
米.
( 2 )李老师骑自行车用了 m 小时到达离家 n 千米的商场,则李老
师 共的 汽平 车均 的速 平度 均为 速度������������ 是千������-米���0��� .2/时;千若米乘/公 时共. 汽车则可少用 0.2 小时,则公
分式知识体系框架图
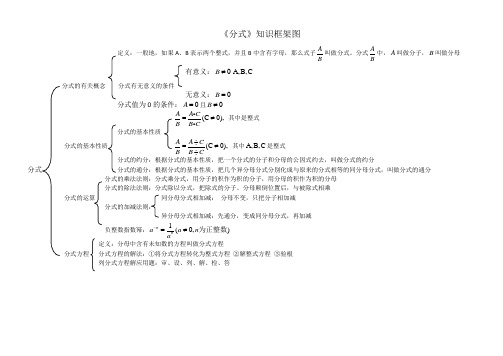
《分式》知识框架图
定义:一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子A B 叫做分式。
分式A B 中,A 叫做分子,B 叫做分母 有意义:0B ≠A,B,C
分式的有关概念 分式有无意义的条件
无意义:0B =
分式值为0的条件:0A =且0B ≠
(C 0),A A C B B C
=≠ 其中是整式 分式的基本性质
分式的基本性质 (C 0),A A C B B C
÷=≠÷ 其中A,B,C 是整式 分式的约分:根据分式的基本性质,把一个分式的分子和分母的公因式约去,叫做分式的约分
分式 分式的通分:根据分式的基本性质,把几个异分母分式分别化成与原来的分式相等的同分母分式,叫做分式的通分 分式的乘法法则:分式乘分式,用分子的积作为积的分子,用分母的积作为积的分母 分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘 分式的运算 同分母分式相加减: 分母不变,只把分子相加减 分式的加减法则:
异分母分式相加减:先通分,变成同分母分式,再加减 负整数指数幂:1(0,)n n a a n a
-=≠为正整数 定义:分母中含有未知数的方程叫做分式方程
分式方程 分式方程的解法:①将分式方程转化为整式方程 ②解整式方程 ③验根 列分式方程解应用题:审、设、列、解、检、答。
八年级数学上册第十五章分式15.1分式15.1.1从分数到分式课件新版新人教版

( 4 )因为 x 无论取什么值,x2+2>0,所以 x 取任何实数,分式������2 +2都 有意义.
������+2
知识点 3 分式的值为零的条件 6.在分式 零. 7.若分式������+1的值为零,则 x 的值是 1
|������|-1 2������+1 中,当 3������-1
y=
������ ������ ������-0.2
共汽车的平均速度是
千米/时.
1 9.在式子 ( 8
1-x
A.1 个 B.2 个 C.3 个 D.4 个 10.无论 x 取什么数时,总是有意义的分式是
2������ ������2 +1 3������ C. 3 ������ +1
4������ ������2 -������2 1 ), , , +x π-3 2 ������
( C
)
B.
12.分式
2 3
A.分式值为 0
������+������ 中,当 3������-2
x=-a 时,下列结论正确的是
( B
)
B.a≠- 时,分式的值为 0 C.分式无意义 D.当 a≠3时,分式无意义
2
13.下列关于分式的判断,错误的是 ������ A.当 x=0 时,分式������+3的值为 0 B.当 x≠-3 时,分式������+3有意义 C.无论 x 为何值,分式 D.无论 x
������ 4 的值总为正数 ������2 +3 4 为何值,分式������2 +3的值不可能为整数
( D )
14.若分式
15.某种长途电话的收费标准如下:接通电话的第 1 分钟收费 a 元,之 后的每一分钟收费 b 元.若某人打该长途电话共花费 10 元,则此人打 长途电话的时间是
人教版八年级数学上册 第十五章分式小结与复习(共26张PPT)

⑶约分: 把一个分式的分子与分母的 公因式 约去, 叫做分式的约分.
⑷通分: 把几个异分母的分式化成 同分母的分式, 注 然意 后:再叫约分做分式.分的分式子的、通分分母. 是多项式的,应先分解因式,
-A ( -B )
-A A
=
=
-B ( B )
( -A ) =
B
-A (B )
9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/82021/9/8Wednesday, September 08, 2021 10、阅读一切好书如同和过去最杰出的人谈话。2021/9/82021/9/82021/9/89/8/2021 1:33:24 AM 11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/82021/9/82021/9/8Sep-218-Sep-21 12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/82021/9/82021/9/8Wednesday, September 08, 2021
分式小结与复习
一、本章知识结构图
列式
实
分式
际
问 题 列方程
目标
类比分数
性质
分式的基本
性质
类比分数 运算
分式的运算
分式方程
去分母
目标
整式方程
解整 式方 程
实际问 题的解
分式方程的解
分式知识体系框架图
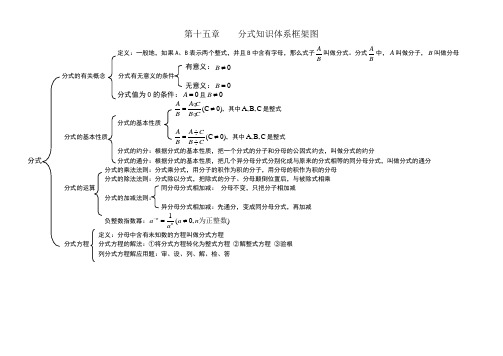
第十五章 分式知识体系框架图 定义:一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子A B 叫做分式。
分式A B 中,A 叫做分子,B 叫做分母 有意义:0B ≠
分式的有关概念 分式有无意义的条件
无意义:0B =
分式值为0的条件:0A =且0B ≠
(C 0),A A C B B C
=≠g g 其中A,B,C 是整式 分式的基本性质
分式的基本性质 (C 0),A A C B B C
÷=≠÷ 其中A,B,C 是整式 分式的约分:根据分式的基本性质,把一个分式的分子和分母的公因式约去,叫做分式的约分
分式 分式的通分:根据分式的基本性质,把几个异分母分式分别化成与原来的分式相等的同分母分式,叫做分式的通分 分式的乘法法则:分式乘分式,用分子的积作为积的分子,用分母的积作为积的分母 分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘 分式的运算 同分母分式相加减: 分母不变,只把分子相加减 分式的加减法则:
异分母分式相加减:先通分,变成同分母分式,再加减 负整数指数幂:1(0,)n n
a a n a -=≠为正整数 定义:分母中含有未知数的方程叫做分式方程
分式方程 分式方程的解法:①将分式方程转化为整式方程 ②解整式方程 ③验根 列分式方程解应用题:审、设、列、解、检、答。
名师导秋新人教版八年级数学上册第十五章分式课件图片版2

名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件) 名师导秋新人教版八年级数学上册第 十五章 分式课件-图片版,共份2(PPT优秀 课件)
分式知识框架

(1)a a a (m,n 是整数); n 归纳结论 (2) (a m) a mn(m,n 是整数); n n n ( ab ) a b (n 是整数); ( 3) m n mn a a a ( 4) (m,n 是整数); a n an ( ) n (n 是整数). ( 5) b b 例1 计算: 3 b 2 ( 1)a 2 a 5;(2)( 2 ); a 3 3 (3)(a 1b 2) ;(4)a 2b 2 (a 2b 2).
两个分式相乘, 把分子 相乘的积作为积的分子, 把分母相乘的积作为积的 分母; 两个分式相除, 把除式的 分子分母颠倒位置后,再与 被除式相乘.
(1)
7b 8a 2; 2 6 a 7b
3
(2)
3b 2ab a
3
2
;
2x y 1 4 5 5y x
2
填一填:
a a a a b b 2 ; b b
2
2
a b
4
3
a a a b b b
a ; 3 b
3
4
a a a a a a b b b b 4 ; b b
(类比分数的基本性质,得出分式的基本性质)
分式的分子与分母同乘(或除以)一个不等于 0的整式,分式的值不变。
跟踪练习 应用分式的基本性质 填空
x3 ( x 2) 3x 2 3xy x y () 1 , ; 2 xy y ( 2x ) 6x 1 ( a ) 2a b ( 2ab b 2 ) (2) , (b 0) . 2 2 2 ab ab a ab
x=5.
验证:将x=5代入原方程得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十五章 分式知识体系框架图 定义:一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子A B 叫做分式。
分式A B 中,A 叫做分子,B 叫做分母 有意义:0B ≠
分式的有关概念 分式有无意义的条件
无意义:0B =
分式值为0的条件:0A =且0B ≠
(C 0),A A C B B C =≠ 其中A,B,C 是整式 分式的基本性质
分式的基本性质 (C 0),A A C B B C
÷=≠÷ 其中A,B,C 是整式 分式的约分:根据分式的基本性质,把一个分式的分子和分母的公因式约去,叫做分式的约分
分式 分式的通分:根据分式的基本性质,把几个异分母分式分别化成与原来的分式相等的同分母分式,叫做分式的通分 分式的乘法法则:分式乘分式,用分子的积作为积的分子,用分母的积作为积的分母 分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘 分式的运算 同分母分式相加减: 分母不变,只把分子相加减 分式的加减法则:
异分母分式相加减:先通分,变成同分母分式,再加减 负整数指数幂:1(0,)n n a a n a
-=≠为正整数 定义:分母中含有未知数的方程叫做分式方程
分式方程分式方程的解法:①将分式方程转化为整式方程②解整式方程③验根列分式方程解应用题:审、设、列、解、检、答。
