2019春九年级数学下册第三章圆 3.8 圆内接正多边形课时作业 (新版)北师大版

合集下载

九年级下第三章圆8圆内接正多边形习题新版北师大版

11．由于同圆中相等的圆心角所对的弧相等，因此作相等的 __圆__心__角___就可以等分圆周，从而得到相应的正多边形．
12．利用等分圆可以作正多边形，下列只利用直尺和圆
规不能作出的正多边形是( D )
A．正三角形
B．正方形
C．正六边形
D．正七边形
13．【教材P98读一读变式】【中考·兰州】如图，已知⊙O，用尺规作⊙O的内接正四边形ABCD(写出结论，不写作法，保留作图痕迹)．
∵点P，Q同时分别从A，D两点出发，以1 cm/s的速度沿AF，DC向终点F，C运动， ∴AP＝DQ＝t cm，PF＝QC＝(6－t)cm. 在△ABP和△DEQ中， A∠BA＝＝D∠ED，， AP＝DQ， ∴△ABP≌△DEQ(SAS)．∴BP＝EQ.
同理可证PE＝QB，∴四边形PBQE为平行四边形．
5．【2021·赤峰】如图，在拧开一个边长为a的正六边形螺
帽时，扳手张开的开口b＝20 mm，则边长a＝ 20 3 ___3_____mm.
6．【中考·衢州】如图，取两根等宽的纸条折叠穿插，拉紧，
可得边长为2的正六边形，则原来的纸条宽为( C )
A．1
B. 2
C. 3
D．2
7．【2020·凉山州】如图，等边三角形ABC和正方形ADEF都内接于⊙O，则AD∶AB＝( )
解：如图，四边形ABCD即为所求．
14．【2021·上海】六个带30度角的直角三角尺拼成一个正
六边形，直角三角尺的最短边为1，则中间正六边形的面积为__3_2_3____．
15．【中考·镇江】在三角形纸片ABC(如图①)中，∠BAC
＝78°，AC＝10，小霞用5张这样的三角形纸片拼成
了一个内外都是正五边形的图形(如图②)．

精品-2019春九年级数学下册第三章圆3.8圆内接正多边形学案无答案新版北师大版

3.8 圆内接正多边形
【自主学习】
（一）复习巩固
1. 等边三角形的边、角各有什么性质？
2. 正方形的边、角各有什么性质？
（二）新知导学
1.各边，各角的多边形是正多边形.
2.正多边形的外接圆(或内切圆)的圆心叫做，外接圆的半径叫做，内切圆的半径做．
正多边形各边所对的外接圆的圆心角都．正多边形每一边所对的外接圆的圆心角叫做．正n 边形的每个中心角都等于．
3. 正多边形都是对称图形，正n边形有条对称轴；正数边形是中心对称图形，对称中心就是正多边形的，正数边形既是中心对称图形，又是轴对称图形.
【合作探究】
1.问题：用直尺和圆规作出正方形，正六边形.
【自我检测】
1．正方形ABCD的外接圆圆心O叫做正方形ABCD的______．
2．正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______．
3．若正六边形的边长为1，那么正六边形的中心角是______度，半径是______，边心距是______，它的每一个内角是______．
4．正n边形的一个外角度数与它的______角的度数相等．
5.已知三角形的两边长分别是方程的两根，第三边的长是方程的根，求这个三角形的周长. 6．如图，PA和PB分别与⊙O相切于A，B两点，作直径AC，并延长交PB于点D．连结OP，
CB．求证：OP∥CB；。

九年级数学下册第三章圆3.8圆内接正多边形练习北师大版(2021年整理)

2018-2019学年九年级数学下册第三章圆3.8 圆内接正多边形同步练习（新版）北师大版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年九年级数学下册第三章圆3.8 圆内接正多边形同步练习（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年九年级数学下册第三章圆3.8 圆内接正多边形同步练习（新版）北师大版的全部内容。

课时作业(二十八）[第三章8 圆内接正多边形]一、选择题1．2017·株洲下列圆的内接正多边形中，一条边所对的圆心角最大的图形是( )A．正三角形 B．正方形C．正五边形 D．正六边形2．2017·滨州若正方形的外接圆半径为2，则其内切圆半径为错误!（)A.错误! B．2 错误!C。

错误! D．13．2017·达州以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( ）A。

错误! B。

错误! C。

错误! D。

错误!4．若正六边形的两条平行边相距12 cm，则它的边长为(）A．6 cm B．12 3 cmC．4 错误! cm D。

错误! cm5．2017·慈溪市期末如图K－28－1，A,B，C三点在⊙O上，AB是⊙O内接正六边形的一边，BC是⊙O内接正十边形的一边，若AC是⊙O内接正n边形的一边，则n等于（)图K－28－1A．12 B．15 C．18 D．206．如图K－28－2，在⊙O中，OA＝AB,OC⊥AB,交⊙O于点C,那么下列说法错误的是（）链接听课例1归纳总结图K－28－2A．∠BAC＝30°B.错误!＝错误!C．线段OB的长等于圆内接正六边形的半径D．弦AC的长等于圆内接正十二边形的边长二、填空题7．2017·邗江区一模如图K－28－3，正六边形螺帽的边长是2 cm，这个扳手的开口a应是________.错误!图K－28－38．正六边形的面积是18 错误!，则它的外接圆与内切圆所围成的圆环面积为________．9．如图K－28－4，M，N分别是正八边形相邻的边AB，BC上的点，且AM＝BN，点O是正八边形的中心，则∠MON的度数为________．图K－28－410．2017·广东模拟为增加绿化面积，某小区将原来正方形地砖更换为如图K－28－5所示的正八边形植草砖，更换后，图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为________．图K－28－5三、解答题11．已知:如图K－28－6,△ABC是⊙O的内接三角形，AB＝AC,∠BAC＝36°，弦BD，CE 分别平分∠ABC,∠ACB.求证:五边形AEBCD是正五边形．图K－28－612．2018·平房区二模如图K－28－7，在正六边形ABCDEF中,对角线AE与BF相交于点M，BD与CE相交于点N.(1)求证:AE＝BF;(2)在不添加任何辅助线的情况下，请直接写出图中所有与△ABM全等的三角形．图K－28－713．用一个长60米的篱笆围成一个羊圈,分别计算所围羊圈是正三角形、正方形、正六边形、圆时的面积（结果精确到1平方米)．（1)比较这些面积的大小；（2)归纳出周长相等的正多边形、圆面积大小的规律（不需证明)．探究题（1）如图K－28－8①所示，M,N分别是⊙O的内接正三角形ABC的边AB，BC上的点，且BM＝CN，连接OM，ON，求∠MON的度数；(2M，N分别是⊙O的内接正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB，BC上的点，且BM＝CN，连接OM,ON，则图②中∠MON的度数是________，图③中∠MON的度数是________中，∠MON的度数是________．图K－28－8详解详析【课时作业】[课堂达标]1．［解析] A ∵正三角形一条边所对的圆心角是360°÷3＝120°,正方形一条边所对的圆心角是360°÷4＝90°，正五边形一条边所对的圆心角是360°÷5＝72°，正六边形一条边所对的圆心角是360°÷6＝60°,∴一条边所对的圆心角最大的图形是正三角形．故选A。

九年级数学下册圆内接正多边形同步测试

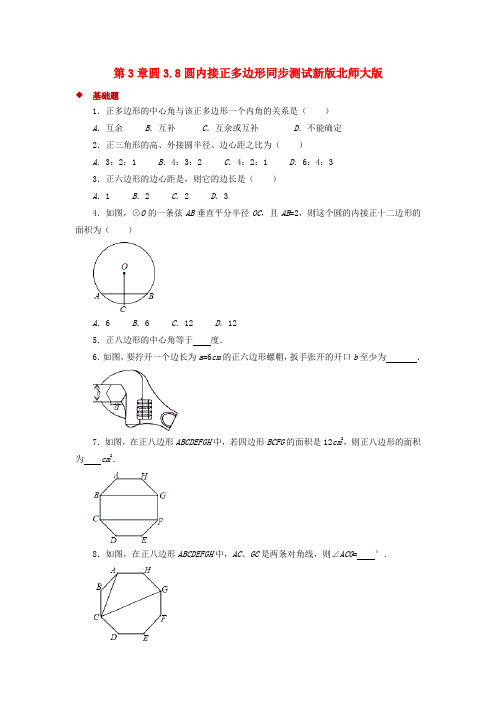
第3章圆3.8圆内接正多边形同步测试新版北师大版◆基础题1．正多边形的中心角与该正多边形一个内角的关系是（）A．互余B．互补C．互余或互补D．不能确定2．正三角形的高、外接圆半径、边心距之比为（）A．3：2：1 B．4：3：2 C．4：2：1 D．6：4：33．正六边形的边心距是，则它的边长是（）A．1 B．2 C．2 D．34．如图，⊙O的一条弦AB垂直平分半径OC，且AB=2，则这个圆的内接正十二边形的面积为（）A．6 B．6 C．12 D．125．正八边形的中心角等于度．6．如图，要拧开一个边长为a=6cm的正六边形螺帽，扳手张开的开口b至少为．7．如图，在正八边形ABCDEFGH中，若四边形BCFG的面积是12cm2，则正八边形的面积为cm2．8．如图，在正八边形ABCDEFGH中，AC、GC是两条对角线，则∠ACG= °．9．如图，正三角形ABC内接于⊙O，若AB=2cm，求⊙O的半径．10．如图，点G，H分别是正六边形ABCDEF的边BC，CD上的点，且BG=CH，AG交BH 于点P．（1）求证：△ABG≌△BCH；（2）求∠APH的度数．◆能力题1．如图，由7个形状，大小完全相同的正六边形组成的网格，正六边形的顶点称为格点，已知每个正六边形的边长为1，△ABC的顶点都在格点上，则△ABC的面积是（）A．B．2 C．D．32．若一个正多边形的中心角等于其内角，则这个正多边形的边数为（）A．3 B．4 C．5 D．63．古代数学家祖冲之和他的儿子根据刘徽的“割圆术”（用圆内接正多边形的周长代替圆周长），来计算圆周率π的近似值．他从正六边形算起，一直算到正24576边形，将圆周率精确到小数后七位，在世界上领先一千多年．根据这个办法，由圆内接正六边形算得的圆周率π的近似值是（）A．2.9 B．3 C．3.1 D．3.144．如果正n边形的中心角为2α，边长为5，那么它的边心距为．（用锐角α的三角比表示）5．如图，AB，AC分别为⊙O的内接正六边形，内接正方形的一边，BC是圆内接n边形的一边，则n等于．6．如图，P、Q分别是⊙O的内接正五边形的边AB、BC上的点，BP=CQ，则∠POQ= ．7．如图，⊙O半径为4cm，其内接正六边形ABCDEF，点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，连接PB，QE，PE，BQ．设运动时间为t（s）．（1）求证：四边形PEQB为平行四边形；（2）填空：①当t= s时，四边形PBQE为菱形；②当t= s时，四边形PBQE为矩形．8．（1）如图1，在圆内接正六边形ABCDEF中，半径OC=4，求正六边形的边长．（2）如图2，在△ABC中，AB=13，BC=10，BC边上的中线AD=12．求证：AB=AC．◆提升题1．如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，下列说法不正确的是（）A．△CDF的周长等于AD+CD B．FC平分∠BFDC．AC2+BF2=4CD2D．DE2=EF•CE2．如图，有一圆内接正八边形ABCDEFGH，若△ADE的面积为10，则正八边形ABCDEFGH 的面积为何（）A．40 B．50 C．60 D．80【答案】A3．小刚在纸上画了一个面积为6分米2的正六边形，然后连接相隔一点的两点得到如图所示的对称图案，他发现中间也出现了一个正六边形，则中间的正六边形的面积是分米2．4．阅读下面材料：对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖．对于平面图形A，如果存在两个或两个以上的圆，使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径，则称图形A被这些圆所覆盖．例如：图中①的三角形被一个圆覆盖，②中的四边形被两个圆所覆盖．已知长宽分别为2cm，1cm的矩形被两个半径都为r的圆所覆盖，则r的最小值是cm．5．如图正方形ABCD内接于⊙O，E为CD任意一点，连接DE、AE．（1）求∠AED的度数．（2）如图2，过点B作BF∥DE交⊙O于点F，连接AF，AF=1，AE=4，求DE的长度．6．教材的《课题学习》要求同学们用一张正三角形纸片折叠成正六边形，小明同学按照如下步骤折叠：请你根据小明同学的折叠方法，回答以下问题：（1）如果设正三角形ABC的边长为a，那么CO= （用含a的式子表示）；（2）根据折叠性质可以知道△CDE的形状为三角形；（3）请同学们利用（1）、（2）的结论，证明六边形KHGFED是一个六边形．答案和解析◆基础题1．【答案】B解：设正多边形的边数为n，则正多边形的中心角为，正多边形的一个外角等于，所以正多边形的中心角等于正多边形的一个外角，而正多边形的一个外角与该正多边形相邻的一个内角的互补，所以正多边形的中心角与该正多边形一个内角互补．2．【答案】A解：如图，△ABC是等边三角形，AD是高．点O是其外接圆的圆心，由等边三角形的三线合一得点O在AD上，并且点O还是它的内切圆的圆心．∵AD⊥BC，∠1=∠4=30°，∴BO=2OD，而OA=OB，∴AD=3OD，∴AD：OA：OD=3：2：1．3．【答案】B解：∵正六边形的边心距为，∴OB=，AB=OA，∵OA2=AB2+OB2，∴OA2=（OA）2+（）2，解得OA=2．4．【答案】C解：如图，连接OA；取的中点D，连接AD、CD、OD；过点D作DE⊥OC于点E；∵OF=OA，且∠OFA=90°，∴∠OAF=30°，∠AOC=60°，∠AOD=∠COD=30°；∵圆的内接正十二边形的中心角==30°，∴AD、DC为该圆的内接正十二边形的两边；∵OC⊥AB，且AB=2，∴AF=；在△AOF中，由勾股定理得：；在△ODE中，∵∠EOD=30°，∴DE=OD=1，，∴这个圆的内接正十二边形的面积为12．5．【答案】45解：正八边形的中心角等于360°÷8=45°．6．【答案】6cm解：设正多边形的中心是O，其一边是AB，∴∠AOB=∠BOC=60°，∴OA=OB=AB=OC=BC，∴四边形ABCO是菱形，∵AB=6cm，∠AOB=60°，∴cos∠BAC=，∴AM=6×=3（cm），∵OA=OC，且∠AOB=∠BOC，∴AM=MC=AC，∴AC=2AM=6（cm）．7．【答案】24解：连接HE，AD，在正八边形ABCDEFGH中，可得：HE⊥BG于点M，AD⊥BG于点N，∵正八边形每个内角为：=135°，∴∠HGM =45°，∴MH =MG ，设MH =MG =x ，则HG =AH =AB =GF =x ，∴BG ×GF =2（+1）x 2=12，∴四边形ABGH 面积=（AH +BG ）×HM =（+1）x 2=6，∴正八边形的面积为：6×2+12=24（cm 2）．8．【答案】45°解：设正八边形ABCDEFGH 的外接圆为⊙O ；∵正八边形ABCDEFGH 的各边相等，∴圆周长，∴的度数为=90°，∴圆周角∠ACG =．9．解：过点O 作OD ⊥BC 于点D ，连接BO ，∵正三角形ABC 内接于⊙O ，∴点O 即是三角形内心也是外心，∴∠OBD =30°，BD =CD =BC =AB =，∴cos 30°=，解得：BO =2，即⊙O 的半径为2cm ．10．（1）证明：∵在正六边形ABCDEF 中，AB =BC ，∠ABC =∠C =120°，在△ABG 与△BCH 中120AB BC ABC C BG CH =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABG ≌△BCH ；（2）解：由（1）知：△ABG ≌△BCH ，∴∠BAG =∠HBC ，∴∠BPG =∠ABG =120°，∴∠APH =∠BPG =120°．◆ 能力题1．【答案】B解：延长AB ，然后作出过点C 与格点所在的直线，一定交于格点E ．正六边形的边长为1，则半径是1，则CE =4，中间间隔一个顶点的两个顶点之间的距离是，则△BCE 的边EC 上的高是，△ACE 边EC 上的高是，则S △ABC =S △AEC ﹣S △BEC =×4×（﹣）=2．2．【答案】B解：360°÷n =．故这个正多边形的边数为4．3．【答案】B解：由题意n =6时，π≈=3．4．【答案】解：如图所示：∵正n 边形的中心角为2α，边长为5，∵边心距OD =．5．【答案】12解：连接AO ，BO ，CO ．∵AB 、AC 分别为⊙O 的内接正六边形、内接正方形的一边，∴∠AOB ==60°，∠AOC ==90°，∴∠BOC =30°，∴n ==12．6．【答案】72°解：连接OA 、OB 、OC ，∵五边形ABCDE 是⊙O 的内接正五边形，∴∠AOB =∠BOC =72°，∵OA =OB ，OB =OC ，∴∠OBA =∠OCB =54°，在△OBP 和△OCQ 中，OB OC OBP OCQ BP CQ =⎧⎪∠=∠⎨⎪=⎩，∴△OBP ≌△OCQ ，∴∠BOP =∠COQ ，∵∠AOB =∠AOP +∠BOP ，∠BOC =∠BOQ +∠QOC ，∴∠BOP =∠QOC ，∵∠POQ =∠BOP +∠BOQ ，∠BOC =∠BOQ +∠QOC ，∴∠POQ =∠BOC =72°．7．（1）证明：∵正六边形ABCDEF内接于⊙O，∴AB=BC=CD=DE=EF=FA，∠A=∠ABC=∠C=∠D=∠DEF=∠F，∵点P，Q同时分别从A，D两点出发，以1cm/s速度沿AF，DC向终点F，C运动，∴AP=DQ=t，PF=QC=4﹣t，在△ABP和△DEQ中，AB DE A D AP DQ=⎧⎪∠=∠⎨⎪=⎩，∴△ABP≌△DEQ（SAS），∴BP=EQ，同理可证PE=QB，∴四边形PEQB是平行四边形．（2）解：①当PA=PF，QC=QD时，四边形PBEQ是菱形时，此时t=2s．②当t=0时，∠EPF=∠PEF=30°，∴∠BPE=120°﹣30°=90°，∴此时四边形PBQE是矩形．当t=4时，同法可知∠BPE=90°，此时四边形PBQE是矩形．综上所述，t=0s或4s时，四边形PBQE是矩形．8．（1）解：连接OD，如图所示：∵六边形ABCDEF是圆O的内接正六边形，∴∠O==60°，∵OC=OD，∴△OCD是等边三角形，∴CD=OC=4，即正六边形的边长为4；（2）证明：∵AD是△ABC的中线，∴BD=CD=BC=5，∵AB=13，AD=12，∴BD2+AD2=52+122=169=132=AB2，∴△ABD是直角三角形，AD⊥BC，又∵BD=CD，∴AB=AC．◆提升题1．【答案】B解：∵五边形ABCDE是正五边形，∴AB=BC=CD=DE=AE，BA∥CE，AD∥BC，AC∥DE，AC=AD=CE，∴四边形ABCF是菱形，∴CF=AF，∴△CDF的周长等于CF+DF+CD，即△CDF的周长等于AD+CD，故A选项正确；∵四边形ABCF是菱形，∴AC⊥BF，设AC与BF交于点O，由勾股定理得OB2+OC2=BC2，∴AC2+BF2=（2OC）2+（2OB）2=4OC2+4OB2=4BC2，∴AC2+BF2=4CD2．故C选项正确；由正五边形的性质得，△ADE≌△CDE，∴∠DCE=∠EDF，∴△CDE∽△DFE，∴，∴DE2=EF •CE，故D选项正确．2．【答案】A解：取AE中点I，则点I为圆的圆心，圆内接正八边形ABCDEFGH是由8个与△IDE全等的三角形构成．易得△IDE的面积为5，则圆内接正八边形ABCDEFGH为8×5=40．3．【答案】2解：设O是原正六边形的中心，连接AO，FO，MO，设FO与AE交于点Q，AO与BE交于P，∵一个面积为6分米2的正六边形，连接相隔一点的两顶点得到如图所示的对称图案，∴∠AOF=×360°=60°，S△AOF=×6=1（分米2），∴△OAF是等边三角形，∵AB=AF，∴OA⊥BF，∴AP=OP，∴AM=OM，同理：OF⊥AE，OQ=FQ，∴OM=FM，∴点M是△AOF的外心，∴S△OAM=S△AOF=（分米2），∴S△OPM=S△OAM=（分米2），∴中间的正六边形的面积是：12×S△OPM=2（分米2）．4．【答案】解：如图：矩形ABCD中AB=1，BC=2，则覆盖ABCD的两个圆与矩形交于E、F两点，由对称性知E、F分别是AD和BC的中点，则四边形ABFE、EFCD是两个边长为1的正方形，所以圆的半径r=，两圆心距=1．5．解：（1）如图1中，连接OA、OD．∵四边形ABCD是正方形，∴∠AOD=90°，∴∠AED=∠AOD=45°．（2）如图2中，连接CF、CE、CA，作DH⊥AE于H．∵BF∥DE，AB∥CD，∴∠ABF=∠CDE，∵∠CFA=∠AEC=90°，∴∠DEC=∠AFB=135°，∵CD=AB，∴△CDE≌△ABF，∴AF=CE=1，∴AC=，∴AD=AC=，∵∠DHE=90°，∴∠HDE=∠HED=45°，∴DH=HE，设DH=EH=x，在Rt△ADH中，∵AD2=AH2+DH2，∴=（4﹣x）2+x2，解得x=或，∴DE=DH=或．6．解：（1）∵正三角形ABC的边长为a，由折叠的性质可知，点O是三角形的重心，∴CO=a；（2）△CDE为等边三角形；（3）由（2）知△CDE为等边三角形，∴CD=CE=DE=CO÷cos30°=a，∠ADE=∠BED=120°，同理可得，AH=AK=KH=a，BG=BF=GF=a，∠CKH=∠BHK=120°，∵AB=BC=AC=a，∴DE=DK=KH=HG=GF=FE=a，∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°，∴六边形KHGFED是一个正六边形．3.8圆内接正多边形一、选择题1.下列说法正确的是（） A.各边相等的多边形是正多边形 B.各角相等的多边形是正多边形C.各边相等的圆内接多边形是正多边形D.各角相等的圆内接多边形是正多边形2.（2013•天津）正六边形的边心距与边长之比为（） A ．：3 B ．：2 C ． 1：2 D ．：23.(2013山东滨州)若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为 ( )A ．6，32B ．32，3C ．6，3D ．62，324. 如图所示，正六边形ABCDEF 内接于⊙O ，则∠ADB 的度数是（）．A ．60°B ．45°C ．30°D ．22．5°5.半径相等的圆的内接正三角形，正方形，正六边形的边长的比为（） A.1:2:3 B.3:2:1C.3:2:1D.1:2:36. 圆内接正五边形ABCDE 中，对角线AC 和BD 相交于点P ，则∠APB 的度数是（）． A ．36° B ．60° C ．72° D ．108°7.（2013•自贡）如图，点O 是正六边形的对称中心，如果用一副三角板的角，借助点O （使该角的顶点落在点O 处），把这个正六边形的面积n 等分，那么n 的所有可能取值的个数是（）A.4B.5C.6D.78.如图，△PQR 是⊙O 的内接正三角形，四边形ABCD 是⊙O 的内接正方形，BC ∥QR ，则∠AOQ 的度数是（） A.60° B.65°C.72°D.75°二、填空题9.一个正n 边形的边长为a ，面积为S ，则它的边心距为__________.第4题第6题第7题第8题10.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于__________度.11.若正六边形的面积是243cm2，则这个正六边形的边长是__________.12.已知正六边形的边心距为3，则它的周长是_______.13.点M、N分别是正八边形相邻的边AB、BC上的点，且AM=BN，点O是正八边形的中心，则∠MON=_____________.14.边长为a的正三角形的边心距、半径（外接圆的半径）和高之比为_________________.15.要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形铁片的直径最小要__________cm.16.若正多边形的边心距与边长的比为1:2，则这个正多边形的边数是__________.17.一个正三角形和一个正六边形的周长相等，则它们的面积比为__________.18.(2013•徐州)如图，在正八边形ABCDEFGH中，四边形BCFG的面积为20cm2，则正八边形的面积为________cm2.三、解答题19.比较正五边形与正六边形，可以发现它们的相同点与不同点.正五边形正六边形例如它们的一个相同点：正五边形的各边相等，正六边形的各边也相等.它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形.请你再写出它们的两个相同点和不同点.相同点：（1）____________________________________________________________________;（2）___________________________________________________________________. 不同点：（1）____________________________________________________________________;（2）____________________________________________________________________.20.已知，如图，正六边形ABCDEF的边长为6cm，求这个正六边形的外接圆半径R、边心距r6、面积S6.第13题第18题第20题21.如图，⊙O 的半径为2，⊙O 的内接一个正多边形，边心距为1，求它的中心角、边长、面积.22.已知⊙O 和⊙O 上的一点A.（1）作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ；（2）在（1）题的作图中，如果点E 在弧AD 上，求证：DE 是⊙O 内接正十二边形的一边.23.如图1、图2、图3、…、图n ，M 、N 分别是⊙O 的内接正三角形ABC 、正方形ABCD 、正五边形ABCDE 、…、正n 边形ABCDE…的边AB 、BC 上的点，且BM=CN ，连结OM 、ON.(1)求图1中∠MON 的度数；(2)图2中∠MON 的度数是_________，图3中∠MON 的度数是_________； (3)试探究∠MON 的度数与正n 边形边数n 的关系(直接写出答案).第21题第22题3.8圆内接正多边形知识要点基础练知识点1正多边形与圆1.以下说法正确的是(C)A.每个内角都是120°的六边形一定是正六边形B.正n边形的对称轴不一定有n条C.正n边形的每一个外角度数等于它的中心角度数D.正多边形一定既是轴对称图形,又是中心对称图形2.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为(B)A.2 3 cmB.4 3 cmC.6 3 cmD.8 3 cm3.如图所示,正六边形ABCDEF内接于☉O,则∠ADB的度数是(C)A.60°B.45°C.30°D.22.5°知识点2正多边形的性质4.同圆的内接正三角形与内接正方形的边长的比是(A)A. 6 2B. 3 4C. 6 3D. 4 3【变式拓展】以半径为1的圆内接正三角形、正方形、正六边形的边长为三边作三角形,则(B)A.这个三角形是等腰三角形B.这个三角形是直角三角形C.这个三角形是锐角三角形D.不能构成三角形5.如图,在☉O中,OA=AB,OC⊥AB,则下列结论正确的是(D)①弦AB的长等于圆内接正六边形的边长;②弦AC的长等于圆内接正十二边形的边长;③AA=AA ;④∠BAC=30°.A.①②④B.①③④C.②③④D.①②③6.(贵阳中考)如图,正六边形ABCDEF内接于☉O,☉O的半径为6,则这个正六边形的边心距OM的长为 3 3 .7.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH.(不写作法,保留作图痕迹)解:如图所示,八边形ABCDEFGH即为所求.综合能力提升练8.正六边形的两条平行边之间的距离为1,则它的边长为(D)A. 3 6B. 3 4C. 2 3 3D. 3 39.(连云港中考)如图所示,一动点从半径为2的☉O上的A0点出发,沿着射线A0O方向运动到☉O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到☉O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到☉O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到☉O上的点A4处;…按此规律运动到点A2019处,则点A2019与点A0间的距离是(C) A.4 B.2 3C.2D.010.张萌取三个如图1所示的面积为4 cm2的钝角三角形按如图2所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为(C)A.12 cm2B.20 cm2C.24 cm2D.32 cm211.如图,正六边形ABCDEF中,AB=4,P是ED的中点,连接AP,则AP的长为 (C)A.4 3B.8C.2 13D.2 1112.(株洲中考)如图,正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM= 48°.13.如图,若干个全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需7个五边形.14.如图,已知☉O和☉O上的一点A.(1)作☉O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在AA上,求证:DE是☉O的内接正十二边形的一边.解:(1)作法:①作直径AC;②作直径BD⊥AC;③依次连接A,B,C,D四点,四边形ABCD即为☉O的内接正方形;④分别以A,C为圆心,OA长为半径作弧,交☉O于点E,H,F,G;⑤顺次连接A,E,F,C,G,H各点,六边形AEFCGH即为☉O的内接正六边形.(2)连接OE,DE.∵∠AOD= 360° 4 =90°,∠AOE= 360° 6 =60°,∴∠DOE=∠AOD-∠AOE=30°,∴DE为☉O的内接正十二边形的一边.拓展探究突破练15.如图1,2,3,4分别是☉O的内接正三角形、正四边形、正五边形、正n边形,点M,N分别从点B,C开始以相同的速度在☉O上逆时针运动.(1)求图1中∠APN的度数;(2)图2中,∠APN的度数是90°,图3中,∠APN的度数是108°;(3)试探索∠APN的度数与正多边形边数n的关系.解:(1)∵点M,N分别从点B,C开始以相同的速度在☉O上逆时针运动,∴AA=AA ,则∠BAM=∠CBN,∴∠APN=∠ABP+∠BAM=∠ABP+∠CBN=∠ABC=60°.(2)提示:在题图2中,∵点M,N分别从点B,C开始以相同的速度在☉O上逆时针运动,∴AA=AA ,∴∠BAM=∠CBN.又∵∠APN=∠ABN+∠BAM,∴∠APN=∠ABN+∠CBN,即∠APN=∠ABC.∵四边形ABCD是正四边形,∴∠ABC=90°,∴∠APN=90°.同理可得:在题图3中,∠APN=108°.(3)由(1)(2)可知,∠APN=它所在的正多边形的内角度数,由多边形内角和公式可知:正多边形的内角度数为 (A-2)×180°A (n≥3,且n为整数), ∴∠APN= (A-2)×180°A.。

九年级数学下册第三章圆3.8圆内接正多边形作业设计(新版)北师大版

九年级数学下册第三章圆3.8圆内接正多边形作业设计（新版）北师大版3.8 圆内接正多边形一、选择题1．若正六边形的边心距是，则它的边长是（）A．1 B．2 C．2 D．32．下列正多边形的中心角等于内角的是（）A．正六边形 B．正五边形 C．正方形 D．正三角形3．如图，⊙O是正五边形ABCDE的外接圆，这个正五边形的边长为a，半径为R，边心距为r，则下列关系式错误的是（）A．R2-r2=a2 B．a=2R sin 36° C．a=2r tan 36° D．r=R cos 36°4．正多边形的中心角与该正多边形一个内角的关系是（）A．互余 B．互补 C．互余或互补 D．不能确定5．利用等分圆可以作正多边形，下列只利用直尺和圆规不能作出的正多边形是（）A．正三角形 B．正方形 C．正六边形 D．正七边形6．以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）A． B． C． D．二、填空题7．若一个圆的半径为5 cm，则它的内接正六边形的边长为________．8．如图，从一个半径为10 cm的圆形纸片上裁出一个最大的正方形，则此正方形的边长为________．9．如果圆的半径为a，它的内接正方形的边长为b，该正方形的内切圆的内接正方形的边长为c，那么a，b，c之间的数量关系为______________．三、解答题10．用尺规作图（不要求写作法和证明，但要保留作图痕迹）．（1）如图①，已知正五边形ABCDE，求作它的中心O；（2）如图②，已知⊙O，求作⊙O的内接正八边形．①②11．如图①②③④，M，N分别是⊙O的内接正三角形ABC，正方形ABCD，正五边形ABCDE，…，正n边形ABCDEFG…的边AB，BC上的点，且BM=CN，连接OM，ON．（1）求图①中∠MON的度数；（2）图②中，∠MON的度数是________，图③中∠MON的度数是________；（3）试探究∠MON的度数与正n边形的边数n的关系（直接写出答案）．参考答案一、1．B 2．C 3．A 4．B 5．D 6．A二、7．5 cm 8．10 cm 9．a=c=b三、10．解：（1）如图①，点O即为所求．（2）如图②，八边形ABCDEFGH即为所求．①②11．解：（1）（方法一）如图①，连接OB，OC．∵正三角形ABC内接于⊙O，∴∠OBM=∠OCN=30°，∠BOC=120°．又∵BM=CN，OB=OC，∴△OBM≌△OCN，∴∠BOM=∠CON，∴∠MON=∠BOC=120°．（方法二）如图②，连接OA，OB．∵正三角形ABC内接于⊙O，∴AB=BC，∠OAM=∠OBN=30°，∠AOB=120°．∵BM=CN，∴AM=BN．又∵OA=OB，∴△AOM≌△BON，∴∠AOM=∠BON，∴∠MON=∠AOB=120°．（2）90°；72°．（3）∠MON=．①②。

北师大九年级下《3.8圆内接正多边形》课时练习含答案解析

北师大版数学九年级下册第3章第8节圆内接正多边形同步检测一、选择题1.正多边形的中心角是36°，那么这个正多边形的边数是（）A．10 B．8 C．6 D．5答案：A解析：解答：设这个正多边形的边数是n，∵正多边形的中心角是36°，∴360°n =36°，解得n=10．故选A．分析：设这个正多边形的边数是n，再根据正多边形的中心角是36°求出n的值即可．2.下列正多边形中，中心角等于内角的是（）A．正三角形 B．正四边形 C．正六边形 D．正八边形答案：B解析：解答：设正边形的边数是n．根据题意得：180-360360n n，解得：n=4．故选B．分析：设正边形的边数是n，根据内角根据中心角等于内角，就可以得到一个关于n的方程，解方程就可以解得n的值3.半径为8cm的圆的内接正三角形的边长为（）A．8√3cm B．4√3cm C．8cm D．4cm答案：A解析：解答：如图所示：∵半径为8cm的圆的内接正三角形，∴在Rt△BOD中，OB=8cm，∠OBD=30°，∴BD=cos30°×OB= √32×8=4√3（cm），∵BD=CD，∴BC=2BD=8√3cm．故它的内接正三角形的边长为8√3cm．故选：A．分析：欲求△ABC的边长，把△ABC中BC边当弦，作BC的垂线，在Rt△BOD中，求BD的长；根据垂径定理知：BC=2BD，从而求正三角形的边长．4.圆的内接正五边形ABCDE的边长为a，圆的半径为r．下列等式成立的是（）A．a=2rsin36° B．a=2rcos36° C．a=rsin36° D．a=2rsin72°答案：A解析：解答：作OF⊥BC．∵∠COF=72°÷2=36°，∴CF=r•sin36°，∴CB=2rsin36°．故选A．分析：作OF⊥BC，在Rt△OCF中，利用三角函数求出a的长．5.正八边形的中心角是（）A．45° B．135° C．360° D．1080°答案：A解析：解答：正八边形的中心角等于360°÷8=45°；故选A．分析：根据中心角是正多边形相邻的两个半径的夹角来解答．6.顺次连接正六边形的三个不相邻的顶点，得到如图的图形，下列说法错误的是（）A．△ACE是等边三角形B．既是轴对称图形也是中心对称图形C．连接AD，则AD分别平分∠EAC与∠EDCD．图中一共能画出3条对称轴答案：B解析：解答： A.∵多边形ABCDEF是正六边形，∴△ACE是等边三角形，故本选项正确；B.∵△ACE是等边三角形，∴是轴对称图形，不是中心对称图形，故本选项错误；C.∵△ACE是等边三角形，∴连接AD，则AD分别平分∠EAC与∠EDC，故本选项正确；D.∵△ACE是等边三角形，∴图中一共能画3条对称轴，故本选项正确．故选B．分析：根据正多边形的性质和轴对称图形与中心对称图形的定义解答．7.若正多边形的一个外角为60°，则这个正多边形的中心角的度数是（）A．30° B．60° C．90° D．120°答案：B解析：解答：∵正多边形的一个外角为60°，∴正多边形的边数为360 ÷60 =6，其中心角为360° ÷6 =60°．故选B．分析：根据正多边形的外角和是360°求出正多边形的边数，再求出其中心角．8.⊙O的半径等于3，则⊙O的内接正方形的边长等于（）A．3 B．2√2 C．3√2 D．6答案：C解析：解答：如图所示：⊙O的半径为3，∵四边形ABCD是正方形，∠B=90°，∴AC是⊙O的直径，∴AC=2×3=6，AB BC AC，AB=BC，∵222∴22AB BC=36，解得：AB=3√2，即⊙O的内接正方形的边长等于3√2，故选C．分析：根据正方形与圆的性质得出AB=BC，以及AB2+BC2=AC2，进而得出正方形的边长即可．9.如图，在一张圆形纸片上剪下一个面积最大的正六边形纸片ABCDEF，它的边长是24cm，AB的长度是（）A．6πcm B．8πcm C．36πcm D．96πcm答案：B解析：解答：连接OB、OA，∵六边形ABCDEF是正六边形，∴∠AOB=360°÷6 =60°，∵OA=OB，∴△OAB是等边三角形，∴OB=AB=24cm，∴60248 180ππ故选B分析：连接OA、OB，得出等边三角形AOB，求出OB长和∠AOB度数，根据弧长公式求出即可．A．2 B．1 C．√3 D．2√3答案：C解析：解答：已知正六边形的半径为2，则正六边形ABCDEF的外接圆半径为2，如图：连接OA，作OM⊥AB于点M，得到∠AOM=30°，则OM=OA•cos30°=√3．则正六边形的边心距是√3．故选C．分析：根据正六边形的边长与外接圆的半径相等，构建直角三角形，利用直角三角形的边角关系即可求出．11.已知圆的半径是2√3，则该圆的内接正六边形的面积是（）A．3√3 B．9√3 C．18√3 D．36√3答案：C解析：解答：连接正六边形的中心与各个顶点，得到六个等边三角形，等边三角形的边长是2√3，高为3，因而等边三角形的面积是3√3，∴正六边形的面积=18√3，故选C．分析：解题的关键要记住正六边形的特点，它被半径分成六个全等的等边三角形．12.已知某个正多边形的内切圆的半径是√3，外接圆的半径是2，则此正多边形的边数是（）A．八 B．六 C．四 D．三答案：B解析：解答：根据勾股定理得：22−(√3)2=1，∴正多边形的边长为2，∴正多边形的中心角为60°，∴此正多边形是正六边形，故选B．分析：根据正多边形的内切圆的半径，外接圆的半径，正多边形的边长的一半构成直角三角形，可得出正多边形的中心角，从而得出正多边形的边数即可．13.正三角形的外接圆半径与内切圆的半径之比是（）A．1：2 B．1：√ 3 C．√3：1 D．2：12答案：D解析：解答：如图，△ABC是等边三角形，AD是高．点O是其外接圆的圆心，由等边三角形的三线合一得点O在AD上，并且点O还是它的内切圆的圆心．∵AD⊥BC，∠1=∠4=30°，∴BO=2OD，而OA=OB，∴OA：OD=2：1．故选D．分析：先作出图形，根据等边三角形的性质确定它的内切圆和外接圆的圆心；通过特殊角进行计算，用内切圆半径来表示外接圆半径，最后求出比值即可．14、已知圆内接正三角形的边心距为1，则这个三角形的面积为（）A．23 B．33 C．43 D．63答案：B解析：解答：如图所示：作AD⊥BC与D，连接OB，则AD经过圆心O，∠ODB=90°，OD=1，∵△ABC是等边三角形，∴BD=CD，∠OBD=12∠ABC=30°，∴OA=OB=2OD=2，∴AD=3，BD3∴BC3，∴△ABC的面积=12BC•AD=12×23×3=33；故选：B．分析：作AD⊥BC与D，连接OB，则AD经过圆心O，∠ODB=90°，OD=1，由等边三角形的性质得出BD=CD，∠OBD=12∠ABC=30°，得出OA=OB=2OD，求出AD、BC，△ABC的面积=12BC•AD，即可得出结果．15.如图，以正六边形ADHGFE的一边AD为边向外作正方形ABCD，则∠BED的度数为（）A．30° B．45° C．50° D．60°答案：B解析：解答：∵正六边形ADHGFE的内角为120°，正方形ABCD的内角为90°，∴∠BAE=360°-90°-120°=150°，∵AB=AE，∴∠BEA=12×（180°-150°）=15°，∵∠DAE=120°，AD=AE，∴∠AED=(180°−120°)÷ 2 =30°，∴∠BED=15°+30°=45°．故选B分析：根据正六边形ADHGFE的内角为120°，正方形ABCD的内角为90°，求出∠BEA，∠AED，据此即可解答．二、填空题16.利用等分圆可以作正多边形，只利用直尺和圆规不能作出的多边形是 .答案：正七边形解析：解答：直接利用圆的半径即可将圆等分为6份，这样即可得出正三角形，也可以得出正六边形，作两条互相垂直的直径即可将圆4等分，可得出正方形，但是无法利用圆规与直尺7等分圆，故无法得到正七边形．故答案为：正七边形．分析：利用直尺和圆规可以将圆等分为6份、4份，这样即可得出正三角形、正方形、正六边形等，但是无法得到正七边形．17.一个正n边形的面积是240cm2，周长是60cm，则边心距是 .答案：8cm解析：解答：∵一个正n边形的面积是240cm2，周长是60cm，∴设边心距是hcm，则12×60×h=240，解得：h=8（cm），即边心距为8cm.分析：根据正n边形的面积=12周长×边心距，进而得出答案．18.若一个正多边形的一个外角为60°，则它的内切圆半径与外接圆半径之比是 . 答案：√3：2．解析：解答：∵一个正多边形的一个外角为60°，∴360°÷60°=6，∴这个正多边形是正六边形，设这个正六边形的半径是r，则外接圆的半径r，∴内切圆的半径是正六边形的边心距，即是32r，∴它的内切圆半径与外接圆半径之比是：3：2．分析：由一个正多边形的一个外角为60°，可得是正六边形，然后从内切圆的圆心和外接圆的圆心向三角形的三边引垂线，构建直角三角形，解三角形即可．19.如图所示，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接六边形的面积为答案：33 2解析：解答：连接AO，BO，过点O作OE⊥AB于点E，∵∠C=30°，∴∠AOB=60°，∵AO=BO，∴△AOB是等边三角形，∴AO=BO=AB=1，∴EO=sin60°×1=3 2，∴S△AOB=12×EO×AB=34，∴⊙O的内接六边形的面积为：6×34=332．分析：利用圆周角定理以及等边三角形的判定与性质得出△AOB的面积，进而得出答案．20.人民币1993年版的一角硬币正面图案中有一个正九边形，如果设这个正九边形的半径为R，那么它的周长是 .答案：18Rsin20°解析：解答：连接OA、OB，过O作OM⊥AB于M，则OA=OB=R，∵九边形ABCDEFGHI是正九边形，∴AB=BC=CD=DE=EF=GF=GH=HI=AI，∠AOB=360°÷9 =40°，在△AOM中，sin∠AOM=AM OA，AM=OAsin20°=Rsin20°，∵OA=OB，OM⊥AB，∴AB=2AM=2Rsin20°，即正九边形的周长是9×2Rsin20°=18Rsin20°.分析：连接OA、OB，过O作OM⊥AB于M，根据正九边形得出AB=BC=CD=DE=EF=GF=GH=HI=AI,∠AOB=40，在△AOM中求出AM=OAsin20°=Rsin20°，根据三线合一定理得出AB=2AM=2Rsin20°，即可求出正九边形的周长．三、证明、计算题21.已知，如图，△ABC内接于⊙O，AB=AC，∠BAC=36°，AB、AC的中垂线分别交⊙O 于点E、F，证明：五边形AEBCF是⊙O的内接正五边形．答案：见解析解析：解答：连接BF，CE，∵AB=AC，∴∠ABC=∠ACB，又∵∠BAC=36°，∴∠ABC=∠ACB=72°．又∵AB、AC的中垂线分别交⊙O于点E、F，∴AF=CF，AE=BE，∴∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36°，̂=AF̂=BÊ=BĈ=FĈ，∴AE∴AE=AF=BE=BC=FC，∴∠EAF=∠AFC=∠FCB=∠CBE=∠BEA．∴五边形AEBCD为正五边形．分析：要求证五边形AEBCD是正五边形，就是证明这个五边形的五条边所对的弧相等进而得出即可．22.如图，正方形EFGH的外接圆⊙O是正方形ABCD的内切圆，试求AB：EF的值．答案：√2解析：解答：如图，设大正方形的边长为1，则HF=1，则S正方形ABCD=1，S正方形EFGH=2S△HGF=2×1×（1÷2）÷2=0.5，∵正方形ABCD∽正方形EFGH，∴AB：EF=√2:1=√2．分析：设大正方形的边长为1，那么圆的直径为1，根据“正方形的面积=边长×边长”求出大正方形的面积，从而得出△HGF的面积：1×（1÷2）÷2=0.25，即可得出正方形EFGH的面积：0.25×2=0.5，再根据相似得出边之比．23.如图，点G，H分别是正六边形ABCDEF的边BC，CD上的点，且BG=CH，AG交BH 于点P．（1）求证：△ABG≌△BCH；（2）求∠APH的度数．答案：(1)略；(2)120°解析：解答：（1）证明：∵在正六边形ABCDEF中，AB=BC，∠ABC=∠C=120°，在△ABG与△BCH中AB＝BC，∠ABC＝∠C＝120°，BG＝CH，∴△ABG≌△BCH；（2）解：由（1）知：△ABG≌△BCH，∴∠BAG=∠HBC，∴∠BPG=∠ABG=120°，∴∠APH=∠BPG=120°．分析：（1）根据正六边形的性质得到AB=BC，∠ABC=∠C=120°，由三角形全等的判定定理SAS即可证出△ABG≌△BCH；（2）由△ABG≌△BCH，得到∠BAG=∠HBC，然后根据三角形的内角和和对顶角的性质即可得到结果．24.如图，要拧开一个边长为a=6cm的正六边形螺帽，扳手张开的开口b至少为多少？答案：63cm解析：解答：设正多边形的中心是O，其一边是AB，∴∠AOB=∠BOC=60°，∴OA=OB=AB=OC=BC，∴四边形ABCO是菱形，∵AB=6cm，∠AOB=60°，∴cos∠BAC=AM :AB，∴AM=6×33（cm），∵OA=OC，且∠AOB=∠BOC，∴AM=MC=12 AC，∴AC=2AM3cm）．扳手张开的开口b至少为3.分析：根据题意，即是求该正六边形的边心距的2倍．构造一个由半径、半边、边心距组成的直角三角形，且其半边所对的角是30°，再根据锐角三角函数的知识求解．25.如图，正方形ABCD的外接圆为⊙O，点P在劣弧CD上（不与C点重合）．（1）求∠BPC的度数；（2）若⊙O的半径为8，求正方形ABCD的边长．答案：(1)45°；(2)8√2解析：解答：：（1）连接OB，OC，∵四边形ABCD为正方形，∴∠BOC=90°，ssssss∴∠P=12∠BOC=45°；（2）过点O作OE⊥BC于点E，∵OB=OC，∠BOC=90°，∴∠OBE=45°，∴OE=BE，∵OE2+BE2=OB2，∴BE23242 2OB∴BC=2BE=2×4282分析：（1）连接OB，OC，由正方形的性质知，△BOC是等腰直角三角形，根据∠BOC=90°，由圆周角定理可以求出；（2）过点O作OE⊥BC于点E，由等腰直角三角形的性质可知OE=BE，由垂径定理可知BC=2BE，故可得出结论．。

九年级数学下册第3章圆3.8圆内接正多边形同步练习新版北师大版_

3.8圆内接正多边形一、夯实基础1．方形ABCD的外接圆圆心O叫做正方形ABCD的______．2．正六边形的边长为1，那么正六边形的中心角是______度，半径是______，边心距是______，它的每一个内角是______．3．正多边形都是对称图形，一个正n边形有条对称轴，每条对称轴都通过正n边形的；一个正多边形，如果有偶数条边，那么它既是，又是对称图形。

4．如图，将若干全等的正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需要五边形（）A．7个 B．8个 C．9个 D．10个5．下列图形中既是中心对称图形，又是轴对称图形的是（）A正三角形 B正五边形 C正六边形 D正七边形．二、能力提升6．用一张圆形的纸剪一个边长为4cm的正六边形，则这个圆形纸片半径最小应为__ cm7．正方形ABCD的内切圆⊙O的面积是81π，正方形ABCD的周长是______．8．要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形铁片的直径最小要____________cm．9．如图，有一个边长为3cm的正六边形，如果要在正六边形纸片中剪出一个最大的圆，则这个圆的半径是___________cm．10．如图，五个相同的圆的圆心连成一个边长为10cm的正五边形，五边形内阴影部分的面积为_____.11．已知两个正多边形的边数之比为2：1，而它们的内角和之比为8：3，求这两个正多边形的边数．三、课外拓展12．求出半径为R的圆内接正三角形的边长，边心距和面积.13．足球面是由若干个正五边形和正六边形拼接而成，已知有12块正五边形，则正六边形的块数是多少？14．将固定宽度的纸条打一个简单的结，然后系紧，使它成为一个平面的结，如图所示，求证：这个五边形是正五边形.15．图①是“口子窖”酒的一个由铁片制成的包装底盒，它是一个无盖的六棱柱形状的盒子（如图②），侧面是矩形或正方形．经测量，底面六边形有三条边的长是9cm，有三条边长是3cm，每个内角都是120，六棱柱的高为3cm．现沿它的侧棱剪开展平，得到如图③的平面展开图．（1）制作这种底盒时，可以按图④中虚线裁剪出如图③的模片．现有一块长为17.5cm、宽为16.5cm的长方形铁片，请问能否按图④的裁剪方法制作这样的无盖底盒？并请说明理由；（2）如果用一块正三角形铁皮按图⑤中虚线剪出如图③的模片，那么这个正三角形的边长至少应为________________cm．（说明：以上裁剪不计接缝处损耗）四、中考链接1．（2016·山东省德州市·4分）正六边形的每个外角是度．2．（2016·广西桂林·3分）正六边形的每个外角是度．6．（2016广西南宁3分）有3个正方形如图所示放置，阴影部分的面积依次记为S1，S2，则S1：S2等于（）。

九年级数学下册第三章圆3.8圆内接正多边形教案新北师大

3.8 圆内接正多边形1．了解圆内接正多边形的有关概念；(重点)2．理解并掌握圆内接正多边形的半径和边长、边心距、中心角之间的关系；(重点)3．掌握圆内接正多边形的画法．(难点)一、情境导入这些美丽的图案，都是在日常生活中我们经常能看到的．你能从这些图案中找出正多边形来吗？二、合作探究探究点：圆内接正多边形【类型一】圆内接正多边形的相关计算已知正六边形的边心距为3，求正六边形的内角、外角、中心角、半径、边长、周长和面积．解析：根据题意画出图形，可得△OBC是等边三角形，然后由三角函数的性质，求得OB 的长，继而求得正六边形的周长和面积．解：如图，连接OB ，OC ，过点O 作OH ⊥BC 于H ，∵六边形ABCDEF 是正六边形，∴∠BOC ＝16×360°＝60°，∴中心角是60°.∵OB ＝OC ，∴△OBC 是等边三角形，∴BC ＝OB ＝OC .∵OH ＝3，sin ∠OBC ＝OH OB ＝32，∴OB ＝BC ＝2.∴内角为180°×（6－2）6＝120°，外角为60°，周长为2×6＝12，S 正六边形ABCDEF ＝6S △OBC ＝6×12×2× 3＝63. 方法总结：圆内接正六边形是一个比较特殊的正多边形，它的半径等于边长，对于它的计算要熟练掌握．变式训练：见《学练优》本课时练习“课堂达标训练”第11题【类型二】圆内接正多边形的画法如图，已知半径为R 的⊙O ，用多种工具、多种方法作出圆内接正三角形．解析：度量法：用量角器量出圆心角是120度的角；尺规作图法：先将圆六等分，然后再每两份合并成一份，将圆三等分．解：方法一：(1)用量角器画圆心角∠AOB ＝120°，∠BOC ＝120°；(2)连接AB ，BC ，CA ，则△ABC 为圆内接正三角形．方法二：(1)用量角器画圆心角∠BOC ＝120°；(2)在⊙O 上用圆规截取AC ︵＝AB ︵；(3)连接AC ，BC ，AB ，则△ABC 为圆内接正三角形．方法三：(1)作直径AD ；(2)以D 为圆心，以OA 长为半径画弧，交⊙O 于B ，C ；(3)连接AB ，BC ，CA ，则△ABC 为圆内接正三角形．方法四：(1)作直径AE ；(2)分别以A ，E 为圆心，OA 长为半径画弧与⊙O 分别交于点D ，F ，B ，C ；(3)连接AB ，BC ，CA (或连接EF ，ED ，DF )，则△ABC (或△EFD )为圆内接正三角形．方法总结：解决正多边形的作图问题，通常可以使用的方法有两大类：度量法、尺规作图法；其中度量法可以画出任意的多边形，而尺规作图只能作出一些特殊的正多边形，如边数是3、4的整数倍的正多边形．变式训练：见《学练优》本课时练习“课后巩固提升”第5题【类型三】正多边形外接圆与内切圆的综合如图，已知正三角形的边长为2a.(1)求它的内切圆与外接圆组成的圆环的面积；(2)根据计算结果，要求圆环的面积，只需测量哪一条弦的大小就可算出圆环的面积？(3)将条件中的“正三角形”改为“正方形”、“正六边形”你能得出怎样的结论？(4)已知正n边形的边长为2a，请写出它的内切圆与外接圆组成的圆环的面积．解析：正多边形的边心距、半径、边长的一半正好构成直角三角形，根据勾股定理就可以求解．解：(1)设正三角形ABC的中心为O，BC切⊙O于点D，连接OB、OD，则OD⊥BC，BD＝DC ＝a.则S圆环＝π·OB2－π·OD2＝πOB2－OD2＝π·BD2＝πa2；(2)只需测出弦BC(或AC，AB)的长；(3)结果一样，即S圆环＝πa2；(4)S圆环＝πa2.方法总结：正多边形的计算，一般是过中心作边的垂线，连接半径，把内切圆半径、外接圆半径、边心距，中心角之间的计算转化为解直角三角形．变式训练：见《学练优》本课时练习“课后巩固提升”第4题【类型四】圆内接正多边形的实际运用如图①，有一个宝塔，它的地基边缘是周长为26m的正五边形ABCDE(如图②)，点O 为中心(下列各题结果精确到0.1m)．(1)求地基的中心到边缘的距离；(2)已知塔的墙体宽为1m ，现要在塔的底层中心建一圆形底座的塑像，并且留出最窄处为1.6m 的观光通道，问塑像底座的半径最大是多少？解析：(1)构造一个由正多边形的边心距、半边和半径组成的直角三角形．根据正五边形的性质得到半边所对的角是360°10＝36°，再根据题意中的周长求得该正五边形的半边是26÷10＝2.6，最后由该角的正切值进行求解；(2)根据(1)中的结论，塔的墙体宽为1m 和最窄处为1.6m 的观光通道，进行计算．解：(1)作OM ⊥AB 于点M ，连接OA 、OB ，则OM 为边心距，∠AOB 是中心角．由正五边形性质得∠AOB ＝360°÷5＝72°，∴∠AOM ＝36°.∵AB ＝15×26＝5.2，∴AM ＝2.6.在Rt △AMO 中，边心距OM ＝AM tan36°＝ 2.6tan36°≈3.6(m)．所以，地基的中心到边缘的距离约为3.6m ； (2)3.6－1－1.6＝1(m)．所以，塑像底座的半径最大约为1m.方法总结：解决问题关键是将实际问题转化为数学问题来解答．熟悉正多边形各个元素的算法．三、板书设计圆内接正多边形1．正多边形的有关概念2．正多边形的画法3．正多边形的有关计算本节课新概念较多，对概念的教学要注意从“形”的角度去认识和辨析，但对概念的严格定义不能要求过高．在概念教学中，要重视运用启发式教学，让学生从“形”的特征获得对几何概念的直观认识，鼓励学生用自己的语言表述有关概念，再进一步准确理解有关概念的文字表述，促进学生主动学习．所以在教学的过程中应尽量使用多媒体教学手段.。

3.8圆内接正多边形课时训练(含答案)

3.8圆内接正多边形课时训练学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知⊙O 的半径是2，一个正方形内接于⊙O ，则这个正方形的边长是（）A ．B ．2CD ．4 2．将一枚飞镖投掷到如图所示的正六边形镖盘上，飞镖落在白色区域的概率为（）A ．12B ．25C ．35D ．23 3．已知正六边形ABCDEF 内接于O ，若O 的直径为2，则该正六边形的周长是（）A ．12B ．C ．6D ．4．如图，正五边形ABCDE 内接于O ，点P 为DE 上一点（点P 与点D ，点E 不重合），连接PC ，PD ，DG PC ⊥，垂足为G ，则PDG ∠等于（）A ．72°B ．54°C ．36°D ．64° 5．一个圆的内接正六边形与内接正方形的边长之比为（）A ．3:2B ．C ．D 6．如图，有一个半径为4cm 的圆形纸片，若在该纸片上沿虚线剪一个最大正六边形纸片，则这个正六边形纸片的边心距是（）．A B．2cm C．D．4cm7．若⊙O的内接正n边形的边长与⊙O的半径相等，则n的值为（）A．4 B．5 C．6 D．78．如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧AC延弦AC翻折交AB于点D，连接CD．若∠BAC＝20度，则∠BDC＝（）A．80°B．70°C．60°D．50°9．如图，四边形ABCD为⊙O的内接正四边形，△AEF为⊙O的内接正三角形，若DF恰好是同圆的一个内接正n边形的一边，则n的值为（）A．8 B．10 C．12 D．1510．如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，点M为劣弧FG的中点．若FM＝⊙O的半径为（）A．2 B C．D．二、填空题11．一个半径为4cm的圆内接正六边形的周长等于_____cm．12．如图，已知AB 为O 直径，若CD 是O 内接正n 边形的一边，AD 是O 内接正()4n +边形的一边，BD AC =，则n =_____．13．公元263年左右，我国数学家刘徽发现当正多边形的边数无限增加时，这个正多边形面积可无限接近它的外接圆的面积，因此可以用正多边形的面积来近似估计圆的面积，如图，O 是正十二边形的外接圆，设正十二边形的半径OA 的长为1，如果用它的面积来近似估计O 的面积，那么O 的面积约是___．14．如图，在边长为4cm 的正六边形ABCDEF 中，点P 在BC 上，则PEF 的面积为________2cm ．15．如图，正五边形ABCDE 内接于O ，F 是CD 的中点，则CBF ∠的度数为________．16．如图所示的长方体材料要切割成体积最大的圆柱，则这个圆柱的体积是______．三、解答题17．如图，O 的内接四边形ABCD 两组对边的延长线分别交于点M ，N ．（1）当∠M=∠N=42°时，求∠A 的度数；（2）若DMC α∠=，BNC β∠=且αβ≠，请你用含有α、β的代数式表示∠A 的度数．18．如图，已知抛物线的顶点坐标为M （1，4），且经过点N （2，3），与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ．抛物线的对称轴与x 轴交于点E ，点P 在对称轴上．（1）求抛物线的解析式；（2）直线CM 与x 轴交于点D ，若DME APE ∠∠=，求点P 的坐标；（3）请探索：是否存在这样的点P ，使ANB 2APE ∠∠=？若存在，求出点P 的坐标；若不存在，请说明理由．19．如图，正方形ABCD 内接于O ，E 为CD 任意一点，连接DE 、AE ．（1）求AED ∠的度数．（2）如图2，过点B 作//BF DE 交O 于点F ，连接AF ，1AF =，4AE =，求DE的长度．20．如图，已知A、B、C、D四点都在⊙O上．（1）若∠ABC=120°，求∠AOC的度数；（2）在（1）的条件下，若点B是弧AC的中点，求证：四边形OABC为菱形．参考答案1．A2．A3．C4．B5．C6．C7．C8．B9．C10．C11．2412．413．314．15．18︒16．3000πcm 317．（1）∠A=48°；（2）∠A=90°2αβ+-．【详解】解：（1）在△CDM 与△CBN 中，∵∠M=∠N=42°，∠MCD=∠NCB ，∴∠CDM=∠CBN ，∴180°-∠CDM=180°-∠CBN ，即∠ADC=∠ABC ，∵四边形ABCD 内接于⊙O ，∴∠ADC+∠ABC=180°，∴∠ABC=90°；∵∠M =42°，∴∠A=90°-∠M=48°；（2）∵四边形ABCD 内接于⊙O ，∴∠ADC+∠ABC=180°，∴∠MDC+∠NBC=180°，∵∠M+∠MDC+∠MCD=180°，∠N+∠NCB+∠NBC=180°，∴∠M+∠N+∠MCD+∠NCB=180°，又DMC α∠=，BNC β∠=∴∠MCD+∠NCB=180°-（α+β），∴∠BCD+∠NCM=360°-（∠MCD+∠NCB ）=180°+（α+β），∵∠BCD=∠NCM ，∴∠BCD=90°+2αβ+，∵∠A+∠BCD=180°，∴∠A=90°-2αβ+；18．（1）y=-x 2+2x+3；（2）P （1，2）或（1，-2）；（3）P （1）或（1，）．【详解】解：（1）设抛物线为y=a （x-1）2+4.∵抛物线过点（2，3）∴3=a （2-1）2+4，解得a=-1∴抛物线的解析式为y=-（x-1）2+4，即y=-x 2+2x+3；（2）如图1，令y=0，则-（x-1）2+4=0，解得x=-1或x=3，∴A （-1,0）,B （3，0），令x=0，可得y=3∴C （0，3），∵M（1，4）∴运用待定系数法可得：直线CM的解析式为y=x+3 令y=0，则x+3=0，x=-3，∴D（-3，0）∵∠DEM=∠AEP=90°，∠DMB=∠APE.∴△DEM∽△AEP，∴DE ME AE PE=∵A（-1，0），E（1，0），D（-3，0），M（1，4）. ∴DE=4，ME=4，AE=2.∴442PE=，即PE=2∴P（1，2）或（1，-2）；（3）存在，P的坐标为（1）或（1，），理由如下：如图2，①当点P在x轴上方时，连接BP，∵PE是抛物线的对称轴，∴∠APE=∠BPE，∠APB=2∠APE∵∠ANB=2∠APE∴∠ANB=∠APB∴点A，B，N，P四点共圆，设圆心F的坐标为（1，n），即PF=AF=NF，∵A（-1，0），N（2，3）∴AF NF ==∴n 2+4=1+（3-n ）2，解得n=1∴F （1，1）,即∴，P （1）；②当点P 在x 轴下方时，由对称知，P （1，）；综上，点P 的坐标为P （1）或（1，）．19．（1）45°；（2）2【详解】（1）如图1中，连接OA 、OD ．四边形ABCD 是正方形，90AOD ∴∠=︒，1452AED AOD ∴∠=∠=︒．（2）如图2中，连接CF ，CE ，CA ，BD ，作DH AE ⊥于H ．//BF DE ，//AB CD ，BDE DBF ∴∠=∠，BDC ABD ∠=∠，ABF CDE ∴∠=∠，90CFA AEC ∠=∠=︒，135DEC AFB ∴∠=∠=︒， CD AB =，CDE ABF ∴∆≅∆，1AF CE ∴==，AC ∴==22AD AC ∴==， 90DHE ∠=︒，45HDE HED ∴∠=∠=︒， DH HE ∴=，设DH EH x ==，在Rt ADH ∆中，222AD AH DH =+， ∴2234(4)4x x =-+，解得32x =或52（舍弃），2DE ∴== 20．（1）∠AOC=120°；（2）见解析【详解】（1）∵A 、B 、C 、D 四点都在⊙O 上 ∴∠ABC+∠ADC=180°，∵∠ABC=120°，∴∠ADC=60°，∴∠AOC=2∠ADC=120°；（2）连接OB ，如图所示：∵点B是弧AC的中点，∠AOC=l20°，∴∠AOB=∠BOC=60°，又∵OA=OC=OB，∴△OAB和△OBC都是等边三角形，∴AB=OA=OC=BC，∴四边形OABC是菱形．。

北师大版九年级下册数学 3.8 圆内接正多边形同步习题

3.8 圆内接正多边形同步习题一．选择题1．如图，⊙O的周长等于4πcm，则它的内接正六边形ABCDEF的面积是（）A．B．C．D．2．如图，已知正五边形ABCDE内接于⊙O，连结BD，CE相交于点F，则∠BFC的度数是（）A．60°B．70°C．72°D．90°3．如图是半径为2的⊙O的内接正六边形ABCDEF，则圆心O到边AB的距离是（）A．2B．1C．D．4．如图，AB，AC分别为⊙O的内接正三角形和内接正四边形的一边，若BC恰好是同圆的一个内接正n边形的一边，则n的值为（）A．8B．10C．12D．155．如图，⊙O与正六边形OABCDE的边OA，OE分别交于点F，G，点M为劣弧FG的中点．若FM＝4．则点O到FM的距离是（）A．4B．C．D．6．如图，⊙O与正五边形ABCDE的边AB，DE分别相切于点B，D，则劣弧BD所对的圆心角∠BOD的大小为（）A．108°B．118°C．144°D．120°7．如图，边长为3的正六边形ABCDEF内接于⊙O，则扇形OAB（图中阴影部分）的面积为（）A．πB．C．3πD．8．边长相等的正方形与正六边形按如图方式拼接在一起，则∠ABC的度数为（）A．10°B．15°C．20°D．30°9．10个大小相同的正六边形按如图所示方式紧密排列在同一平面内，A、B、C、D、E、O均是正六边形的顶点．则点O是下列哪个三角形的外心（）A．△AED B．△ABD C．△BCD D．△ACD10．如图，以正六边形ABCDEF的对角线CF为边，再作一个正六边形CFGHMN，若AB ＝，则EG的长为（）A．2B．2C．3D．2二．填空题11．用正五边形钢板制作一个边框总长为40cm的五角星（如图），则正五边形的边长为cm（保留根号）．12．用两条宽均为2cm的纸条（假设纸条的长度足够长），折叠穿插，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正六边形ABCDEF，则折出的正六边形的边长为cm．13．同圆的内接正三边形、正四边形、正六边形的边长之比为．。

北师大版九年级数学下册3.8圆内接正多边形课时同步练习题.doc

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】3.8 圆内接正多边形1．下列边长为a 的正多边形与边长为a 的正方形组合起来，不能镶嵌成平面的是( )(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A ．(1)(2)B ．(2)(3)C ．(1)(3)D ．(1)(4) 2．以下说法正确的是A ．每个内角都是120°的六边形一定是正六边形．B ．正n 边形的对称轴不一定有n 条．C ．正n 边形的每一个外角度数等于它的中心角度数．D ．正多边形一定既是轴对称图形，又是中心对称图形．3.若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3，r 4，r 6，则r 3：r 4：r 6等于( )A ．1:2:3B ．3:2:1C ．1:2:3D ． 3:2:1 4.如图，若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆，则ABB A 11的值为（） A ．21B ．22C ．41D ．425．已知正六边形ABCDEF 内接于⊙O ，图中阴影部分的面积为312，则⊙O 的半径为______________________．第5题图第6题图6．如图，正方形ABCD 内接于⊙O ，点E 在AD 上，则∠BEC= ．7．将一块正六边形硬纸片（图1），做成一个底面仍为正六边形且高相等的无盖纸盒（侧面均垂直于底面，见图2），需在每一个顶点处剪去一个四边形，例如图中的四边形AGA /H ，那么∠GA /H 的大小是度．OB CD A EF E D C BA O8．从一个半径为10㎝的圆形纸片上裁出一个最大的正方形，则此正方形的边长为．9．如图五边形ABCDE 内接于⊙O,∠A =∠B=∠C=∠D=∠E ．求证：五边形ABCDE 是正五边形10．如图，10－1、10－2、10－3、…、10－n 分别是⊙O 的内接正三角形ABC ，正四边形ABCD 、正五边形ABCDE 、…、正n 边形ABCD …，点M 、N 分别从点B 、C 开始以相同的速度在⊙O 上逆时针运动。