2020年高考数学模拟试卷汇编:专题4 立体几何(含答案解析)
(人教版)2020年高三数学模拟试卷及参考答案

(人教版)2020年高三数学模拟试卷及参考答案一、选择题(5×10=50分)1.已知集合{10}{lg(1)}M x x N x y x =+>==-,,则M N =I ( ) A .{11}x x -<< B .{1}x x > C .{11}x x -≤< D .{1}x x ≥-2.等比数列{}n a 中,44a =,则26a a ⋅等于( ) A .4 B .8 C .16D .323.已知:1231,:(3)0p x q x x -<-<-<, 则p 是q 的什么条件( )A .必要不充分B .充分不必要C .充要D .既不充分也不必要4.若点(cos ,sin )P αα在直线2y x =-上,则sin 22cos2αα+=( ) A .145- B .75- C .2-D .455.圆0222=++x y x 和0422=-+y y x 的公共弦所在直线方程为( ) A .02=-y x B .02=+y x C .02=-y x D .02=+y x 6. 已知函数()22xf x =-,则函数()y f x =的图象可能是( )7.函数()3cos 2sin 2f x x x =-的单调减区间为( )A .2[,]63k k ππππ++,k Z ∈ B .7[,]1212k k ππππ--,k Z ∈C .7[2,2]1212k k ππππ--,k Z ∈D .5[,]1212k k ππππ-+,k Z ∈8.设11321log 2,log 3,()2a b c ===0.3,则( )A .c b a <<B .b c a <<C .a c b <<D .c a b <<9.在复平面内,复数211)i (i-+对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限10.已知某几何体的三视图如右图所示, 则该几何体的体积是( )A .21 B .61 C . 121 D . 181二、填空题(5×5=25分)11.向量b a ,的夹角为120°,|5|,3||,1||b a b a -==则= 12.不等式0)1)(3(1<+--x x x 的解集为13.已知圆C 的圆心是直线01=+-y x 与x 轴的交点,且圆C与直线03=++y x 相切.则圆C 的方程为14.已知0,0x y >>,且211x y+=,若222x y m m +>+恒成立,则实数m 的取值范围是______15.已知向量(,1)x =-a ,(3,)y =b ,其中x 随机选自集合{1,1,3}-,y 随机选自集合{1,3},那么⊥a b 的概率是_____.三、解答题(75分)16.设集合A ={x |x 2<4},B ={x |1<4x +3}(1)求集合B A I(2)若不等式022<++b ax x 的解集为B ,求a ,b 的值17.已知向量)2,(sin -=θa 与)cos ,1(θ=b 互相垂直,其中(0,)2πθ∈(1)求θsin 和θcos 的值(2)求函数x x x f sin 22cos )(+=的值域18. 将一颗均匀的四面分别标有1,2,3,4点的正四面体骰子先后抛掷2次,观察向上的点数,求:(1)两数之和为5的概率;(2)以第一次向上点数为横坐标x ,第二次向上的点数为纵坐标y 的点(),x y在区域Ω:0020x y x y >⎧⎪>⎨⎪-->⎩内的概率.19.已知数列{}n a 的前n 项和为22n n nS +=, (1)求数列{}n a 的通项公式 (2)求数列1{}n n a x -的前n 项和(其中0x >)20.如图,正三棱柱111C B A ABC -中,D AA AB ,3,21==为B C 1的中点,P 为AB 边上的动点.(1)当点P 为AB 边上的中点,证明DP //平面11A ACC (2)若,3PB AP =求三棱锥CDP B -的体积.21.若椭圆1C :)20( 14222<<=+b by x 的离心率等于23,抛物线2C :)0( 22>=p py x 的焦点在椭圆的顶点上。
2024年9-10月新高考数学名校模拟大题汇编:立体几何(解析版)

2024年9-10月新高考数学名校大题汇编:立体几何大题必备基础知识梳理【知识点一:空间向量及其加减运算】(1)空间向量在空间,我们把具有大小和方向的量叫做空间向量,向量的大小叫做向量的长度或模.空间向量也可用有向线段表示,有向线段的长度表示向量的模,若向量a 的起点是A ,终点是B ,则向量a也可以记作AB ,其模记为a或AB .(2)零向量与单位向量规定长度为0的向量叫做零向量,记作0.当有向线段的起点A 与终点B 重合时,AB=0.模为1的向量称为单位向量.(3)相等向量与相反向量方向相同且模相等的向量称为相等向量.在空间,同向且等长的有向线段表示同一向量或相等向量.空间任意两个向量都可以平移到同一个平面,成为同一平面内的两个向量.与向量a 长度相等而方向相反的向量,称为a 的相反向量,记为-a .(4)空间向量的加法和减法运算①OC=OA+OB=a +b ,BA=OA-OB=a -b.如图所示.②空间向量的加法运算满足交换律及结合律a +b =b +a ,a +b +c =a +b +c【知识点二:空间向量的数乘运算】(1)数乘运算实数λ与空间向量a 的乘积λa 称为向量的数乘运算.当λ>0时,λa 与向量a方向相同;当λ<0时,向量λa 与向量a 方向相反.λa 的长度是a的长度的λ 倍.(2)空间向量的数乘运算满足分配律及结合律λa +b =λa +λb ,λμa =λμ a .(3)共线向量与平行向量如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量,a 平行于b ,记作a ⎳b.(4)共线向量定理对空间中任意两个向量a ,b b ≠0,a ⎳b的充要条件是存在实数λ,使a =λb.(5)直线的方向向量如图8-153所示,l 为经过已知点A 且平行于已知非零向量a 的直线.对空间任意一点O ,点P 在直线l 上的充要条件是存在实数t ,使OP =OA +ta ①,其中向量a 叫做直线l 的方向向量,在l 上取AB =a ,则式①可化为OP =OA +tAB =OA +t OB -OA =1-t OA +tOB ②①和②都称为空间直线的向量表达式,当t =12,即点P 是线段AB 的中点时,OP =12OA +OB ,此式叫做线段AB 的中点公式.(6)共面向量如图8-154所示,已知平面α与向量a ,作OA=a,如果直线OA 平行于平面α或在平面α内,则说明向量a 平行于平面α.平行于同一平面的向量,叫做共面向量.(7)共面向量定理如果两个向量a ,b不共线,那么向量p 与向量a,b共面的充要条件是存在唯一的有序实数对x ,y ,使p =xa +yb.推论:①空间一点P 位于平面ABC 内的充要条件是存在有序实数对x ,y ,使AP =xAB +yAC;或对空间任意一点O ,有OP-OA=xAB+yAC,该式称为空间平面ABC 的向量表达式.②已知空间任意一点O 和不共线的三点A ,B ,C ,满足向量关系式OP =xOA +yOB +zOC (其中x +y +z =1)的点P 与点A ,B ,C 共面;反之也成立.【知识点三:空间向量的数量积运算】(1)两向量夹角已知两个非零向量a ,b ,在空间任取一点O ,作OA =a ,OB =b ,则∠AOB 叫做向量a ,b 的夹角,记作a ,b ,通常规定0≤a ,b ≤π,如果a ,b =π2,那么向量a ,b 互相垂直,记作a ⊥b .(2)数量积定义已知两个非零向量a ,b ,则a b cos a ,b 叫做a ,b 的数量积,记作a ⋅b ,即a ⋅b =a b cos a,b.零向量与任何向量的数量积为0,特别地,a ⋅a =a 2.(3)空间向量的数量积满足的运算律:λa ⋅b =λa ⋅b ,a ⋅b =b ⋅a (交换律);a ⋅b +c =a ⋅b +a ⋅c(分配律).【知识点四:空间向量的坐标运算及应用】(1)设a =a 1,a 2,a 3 ,b=b 1,b 2,b 3 ,则a +b=a 1+b 1,a 2+b 2,a 3+b 3 ;a -b=a 1-b 1,a 2-b 2,a 3-b 3 ;λa=λa 1,λa 2,λa 3 ;a ⋅b=a 1b 1+a 2b 2+a 3b 3;a ⎳b b ≠0⇒a 1=λb 1,a 2=λb 2,a 3=λb 3;a ⊥b⇒a 1b 1+a 2b 2+a 3b 3=0.(2)设A x 1,y 1,z 1 ,B x 2,y 2,z 2 ,则AB =OB -OA=x 2-x 1,y 2-y 1,z 2-z 1 .这就是说,一个向量在直角坐标系中的坐标等于表示该向量的有向线段的终点的坐标减起点的坐标.(3)两个向量的夹角及两点间的距离公式.①已知a =a 1,a 2,a 3 ,b =b 1,b 2,b 3 ,则a =a 2=a 12+a 22+a 32;b =b2=b 12+b 22+b 32;a ⋅b=a 1b 1+a 2b 2+a 3b 3;cos a ,b =a 1b 1+a 2b 2+a 3b 3a 12+a 22+a 32b 12+b 22+b 32;②已知A x 1,y 1,z 1 ,B x 2,y 2,z 2 ,则AB=x 1-x 22+y 1-y 2 2+z 1-z 2 2,或者d A ,B =AB.其中d A ,B 表示A 与B 两点间的距离,这就是空间两点的距离公式.(4)向量a 在向量b 上的投影为a cos a ,b=a ⋅b b.【知识点五:法向量的求解与简单应用】(1)平面的法向量:如果表示向量n 的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作n ⊥α,如果n⊥α,那么向量n叫做平面α的法向量.几点注意:①法向量一定是非零向量;②一个平面的所有法向量都互相平行;③向量n 是平面的法向量,向量m 是与平面平行或在平面内,则有m ⋅n =0.第一步:写出平面内两个不平行的向a=x 1,y 1,z 1 ,b=x 2,y 2,z 2 ;第二步:那么平面法向量n=x , y , z ,满足n ⋅a=0n ⋅b =0⇒xx 1+yy 1+zz 1=0xx 2+yy 2+zz 2=0.(2)判定直线、平面间的位置关系①直线与直线的位置关系:不重合的两条直线a ,b 的方向向量分别为a ,b.若a ∥b,即a =λb,则a ∥b ;若a ⊥b,即a ⋅b=0,则a ⊥b .②直线与平面的位置关系:直线l 的方向向量为a ,平面α的法向量为n ,且l ⊥α.若a ∥n ,即a =λn ,则l ⊥α;若a ⊥n ,即a ⋅n =0,则a ∥α.(3)平面与平面的位置关系平面α的法向量为n 1,平面β的法向量为n 2.若n 1∥n 2,即n 1=λn 2,则α∥β;若n 1⊥n 2,即n 1⋅n 2=0,则α⊥β.【知识点六:空间角公式】(1)异面直线所成角公式:设a ,b分别为异面直线l 1,l 2上的方向向量,θ为异面直线所成角的大小,则cos θ=cos a,b =a ⋅b a b.(2)线面角公式:设l 为平面α的斜线,a 为l 的方向向量,n为平面α的法向量,θ为l 与α所成角的大小,则sin θ=cos a ,n=a ⋅na n.(3)二面角公式:设n 1,n 2分别为平面α,β的法向量,二面角的大小为θ,则θ=n 1 ,n 2 或π-n 1 ,n 2(需要根据具体情况判断相等或互补),其中cos θ =n 1 ⋅n 2n 1 n 2.【知识点七:空间中的距离】求解空间中的距离(1)异面直线间的距离:两条异面直线间的距离也不必寻找公垂线段,只需利用向量的正射影性质直接计算.如图,设两条异面直线a ,b 的公垂线的方向向量为n ,这时分别在a ,b 上任取A ,B 两点,则向量在n上的正射影长就是两条异面直线a ,b 的距离.则d =AB ⋅n |n |=|AB ⋅n ||n|即两异面直线间的距离,等于两异面直线上分别任取两点的向量和公垂线方向向量的数量积的绝对值与公垂线的方向向量模的比值.(2)点到平面的距离A 为平面α外一点(如图),n为平面α的法向量,过A 作平面α的斜线AB 及垂线AH .|AH |=|AB |⋅sin θ=|AB |⋅|cos <AB ,n >|=|AB ||AB ⋅n |AB ⋅n =|AB ⋅n|nd =|AB ⋅n||n|【必考题型汇编】1.(湖南省长沙市2025届高三六校九月大联考解析第16题)如图,四边形ABCD 与四边形ADEF 均为等腰梯形,BC ⎳AD ,EF ⎳AD ,AD =4,AB =2,BC =EF =2,AF =11,FB ⊥平面ABCD ,M 为AD 上一点,且FM ⊥AD ,连接BD 、BE 、BM .(1)证明:BC ⊥平面BFM ;(2)求平面ABF 与平面DBE 的夹角的余弦值.方法提供与解析:(1)解析:因为FB ⊥平面ABCD ,又AD ⊂平面ABCD ,所以FB ⊥AD .又FM ⊥AD ,且FB ∩FM =F ,所以AD ⊥平面BFM .因为BC ⎳AD ,所以BC ⊥平面BFM .(2)解析:作EN ⊥AD ,垂足为N ,则FM ⎳EN .又EF ⎳AD ,所以四边形FMNE 是平行四边形,又EN ⊥AD ,所以四边形FMNE 是矩形,又四边形ADEF 为等腰梯形,且AD =4,EF =2,所以AM =1.由(1)知AD ⊥平面BFM ,所以BM ⊥AD .又AB =2,所以BM =1.在Rt △AFM 中,FM =AF 2-AM 2=10.在Rt △FMB 中,∴FB =FM 2-BM 2=3.由上可知,能以BM 、BC 、BF 所在的直线分别为x 轴、y 轴、z 轴建立如图所示空间直角坐标系.则A -1,-1,0 ,B 0,0,0 ,F 0,0,3 ,D -1,3,0 ,E 0,2,3 ,所以,AB =1,1,0 ,BF =0,0,3 ,BD =-1,3,0 ,BE=0,2,3 ,设平面ABF 的法向量为m=x 1,y 1,z 1 ,由m ⋅AB=0m ⋅BF =0,得x 1+y 1=0z 1=0 ,可取m =1,-1,0 ;设平面BDE 的法向量为n=x 2,y 2,z 2 ,由n ⋅BD=0n ⋅BE =0,得-x 2+3y 2=0-2y 2+3z 2=0 ,可取n=9,3,2 .因此,cos ‹m ,n›=m ⋅n m ⋅n=9-31+1⋅81+9+4=34747.依题意可知,平面ABF 与平面DBE 的夹角的余弦值为34747.2.(辽宁省沈阳市郊联体2024年高三上学期开学联考解析第17题)如图,已知斜三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C ⊥侧面AA 1B 1B ,侧面BB 1C 1C 是矩形,侧面AA 1B 1B 是菱形,∠BAA 1=60°,AB =2BC =2,点E ,F ,G 分别为棱AA 1,A 1C ,BB 1的中点.(1)证明:FG ⎳平面ABC ;(2)求二面角A 1-B 1C -E 的余弦值.方法提供与解析:解析:(1)证明:因为点E ,F ,G 分别为棱AA 1,A 1C ,BB 1的中点,连接EF ,EG ,则EF ⎳AC ,EG ⎳AB ,又因为EF ⊄平面ABC ,AC ⊂平面ABC ,所以EF ⎳平面ABC ,同理可得EG ⎳平面ABC ,因为EF ∩EG =E ,EF ⊂平面EFG ,EG ⊂平面EFG ,所以平面EFG ⎳平面ABC ,因为FG ⊂平面EFG ,所以FG ⎳平面ABC .(2)解:侧面BB 1C 1C 是矩形,所以BC ⊥BB 1,又因为平面BB 1C 1C ⊥平面AA 1B 1B ,平面BB 1C 1C ∩平面AA 1B 1B =BB 1,所以BC ⊥平面AA 1B 1B ,又BE ⊂平面AA 1B 1B ,因此BC ⊥BE .在菱形AA 1B 1B 中,∠BAA 1=60°,因此△AA 1B 是等边三角形,又E 是AA 1的中点,所以BE ⊥AA 1,从而得BE ⊥BB 1.如图,以B 为坐标原点,BE ,BB 1,BC 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.因为AB =2BC =2,所以BE =AB sin60°=3,因此B 10,2,0 ,A 13,1,0 ,E 3,0,0 ,C 0,0,1 ,所以B 1C =0,-2,1 ,B 1E =3,-2,0 ,B 1A 1=3,-1,0 ,设平面EB 1C 的法向量为m=x 1,y 1,z 1 ,由m⊥B 1C,得-2y 1+z 1=0 ,令y 1=1,得m =23,1,2设平面A 1B 1C 的法向量为n=x 2,y 2,z 2 ,由n ⊥B 1Cn ⊥B 1A 1,得-2y 2+z 2=03x 2-y 2=0 ,令y 2=1,得n =33,1,2 ,cos ‹m ,n ›=m ⋅n m ⋅n =23+1+4193⋅163=171976,即二面角A 1-B 1C -E 的余弦值为171976.3.如图,在四棱柱ABCD -A 1B 1C 1D 1中,AA 1⊥平面ABCD ,底面ABCD 为梯形,AD ⎳BC ,BC =4,AB =AD =DC =AA 1=2,Q 为AD 的中点.(1)在A 1D 1上是否存在点P ,使直线CQ ⎳平面AC 1P ,若存在,请确定点P 的位置并给出证明,若不存在,请说明理由;(2)若(1)中点P 存在,求平面AC 1P 与平面ABB 1A 1所成的锐二面角的余弦值.方法提供与解析:(1)解析:(几何法)存在,证明如下:在四棱柱ABCD -A 1B 1C 1D 1中,因为平面ABCD ⎳平面A 1B 1C 1D 1,所以可在平面A 1B 1C 1D 1内作C 1P ⎳CQ ,由平面几何知识可证△C 1D 1P ≅△CDQ ,所以D 1P =DQ ,可知P 是A 1D 1中点,因为C 1P ⊂平面AC 1P ,所以CQ ⎳平面AC 1P .即存在线段A 1D 1的中点,满足题设条件.满足条件的点只有一个,证明如下:当CQ ⎳平面AC 1P 时,因为CQ ⎳平面A 1B 1C 1D 1,所以过C 1作平行于CQ 的直线既在平面A 1C 1P 内,也在平面A 1B 1C 1D 1内,而在平面A 1B 1C 1D 1内过C 1只能作一条直线C 1P ⎳CQ ,故满足条件的点P 只有唯一一个.所以,有且只有A 1D 1的中点为满足条件的点P ,使直线CQ ⎳平面AC 1P .(2)解析:(坐标法)过点D 作DF ⊥BC ,垂足为F ,又因为DD 1⊥平面ABCD ,以D 为坐标原点,分别以DA ,DF ,DD 1所在直线为x 轴,y 轴,z 轴建立如图的空间直角坐标系D -xyz ,则A 2,0,0 ,P 1,0,2 ,C 1-1,3,2 ,A 12,0,2 ,B 3,3,0 ,P A =1,0,-2 ,PC 1 =-2,3,0 ,AB =1,3,0 ,AA 1=0,0,2设平面P AC 1的法向量为n=x ,y ,z ,则有n ⋅P A=0,n ⋅PC 1 =0,即x -2z =0,-2x +3y =0. 令x =23,得y =4,z =3,所以n=23,4,3 .设平面ABB 1A 1的法向量为m=x ,y ,z .则有AB ⋅m =0,AA 1 ⋅m =0,即x +3y =0,2z =0. 令x =3,得y =-1,z =0,所以m=3,-1,0 .所以cos n ,m =n ⋅m n m=6-4+0231=3131.故平面AC 1P 与平面ABB 1A 1所成的锐二面角的余弦值为3131.4.(福建泉州市2025届高中毕业班模拟检测(一)解析第16题)4:如图,在四棱锥P -ABCD 中,PD =PC =CB =BA =12AD =2,AD ⎳CB ,∠CPD =∠ABC =90°,平面PCD ⊥平面ABCD ,E 为PD 中点.(1)求证:PD ⊥平面PCA ;(2)点Q 在棱P A 上,CQ 与平面PDC 所成角的正弦值为63,求平面PCD 与平面CDQ 夹角的余弦值.方法提供与解析:(1)解析:由题意:BC =AB =2,∠ABC =90°,AC =AB 2+BC 2=22同理CD =22,又AD =4,CD 2+AC 2=AD 2,CD ⊥AC .而CD =22=PD 2+PC 2,即PC ⊥PD ,又平面PCD ⊥平面ABCD ,平面PCD ∩平面ABCD =CD ,AC ⊂平面ABCD ,AC ⊥平面PCD ,PD ⊂平面PCD ,PD ⊥AC ,又PC ⊥PD ,且PC ⊂面PCA ,AC ⊂面PCA ,PC ∩AC =C ,PD ⊥平面PCA .(2)解析:以C 为原点,建立如图所示的空间直角坐标系,则C 0,0,0 ,A 0,22,0 ,D 22,0,0 ,P 2,0,2 ,所以CD =22,0,0 ,CP =2,0,2 ,P A=-2,22,-2 ,设PQ =λP A 0<λ<1 ,有CQ =CP +λP A=21-λ ,22λ,21-λ ,取面PCD 的一个法向量m =0,1,0 ,则cos CQ ,m =22λ41-λ 2+8λ2=63,λ=12,故CQ =22,2,22.令n=x ,y ,z 是平面CDQ 的一个法向量,则n ⋅CD =0n ⋅CQ =0,即22x =022x +2y +22z =0,令y =1,有n =0,1,-2 ,则cos ‹n ,m › =n ⋅m n m=55,故平面PCD 与平面CDQ 夹角的余弦值为55.5.(长沙市雅礼中学2025届高三上学期(9月)综合自主测试解析第17题)5:如图(1),在△ABC 中,CD ⊥AB ,BD =2CD =2AD =4,点E 为AC 的中点.将△ACD 沿CD 折起到△PCD 的位置,使DE ⊥BC ,如图(2).图(1)图(2)(1)求证:PB ⊥PC ;(2)在线段BC 上是否存在点F ,使得CP ⊥DF ?若存在,求二面角P -DF -E 的余弦值;若不存在,说明理由。
2020最新高考数学模拟测试含解答(20200404103106)

平面 PAD
∴ BG ∥ 平 面 PAD
∵ EF ∥ BG ∴ EF ∥ 平 面 PAD
(7 分)
(II)∵ BG⊥平面 PDC,EF∥BG ∴EF⊥平面 PDC
2
(B) cos
1
2
1 sin
2
(D) sin
1
2
( C)
(文)已知曲线 C 与 C′ 关于直线 x y 2 0对称,若 C 的方程为
, x2 y2 4x 4y 7 0
则 C′的方程为
()
(A ) x 2 y2 8x 8y 31 0
(B) x 2 y2 8x 8y 31 0
(C) x2 y 2 8x 8 y 31 0
又 CD=2a, DP=a,
CP CD 2 DP2 5a
△ PBC 中, G 为 PC 中点,∴ BG⊥PC
易得 BG 3 a, HG 1 a, BH a
2
2
∴ △ BGH 为直角三角形,且
BG ⊥ GH ∴ GB ⊥平面 PDC
(5 分)
∴GB⊥CD 又 CD⊥HB ∴CD⊥平面 BGH ∴平面 BGH ∥
( 12 )有一位同学写了这样一个不等式: x 2 1 c 1 c ( x R) ,他发现,
x2 c
c
当 c=1 ,2 ,
3 时,不等式对一切实数 x 都成立,由此他作出如下猜测:
①当 c 为所有自然数时,不等式对一切实数 x 都成立;
②只存在有限个自然数 c,对 x R不等式都成立;
③当 c 1时,不等式对一切 x R都成立;
已 知 z1=3+4 i , z2=65 cos i sin ) (
2
5
sin(
高考数学《立体几何》练习题及答案

立体几何1.[四川省宜宾市第四中学高2020届一诊模拟考试理科数学]若某空间几何体的三视图如图所示,则该几何体的体积是A .2B .1C .D .【答案】B2.[湖南省衡阳县2020届高三12月联考数学(理)试题]【答案】D 【解析】3.[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学(理)试题] 在正方体1111ABCD A B C D -中,动点E 在棱1BB 上,动点F 在线段11A C 上,O 为底面ABCD 的中心,若1,BE x A F y ==,则四面体O AEF -的体积 A .与,x y 都有关 B .与,x y 都无关 C .与x 有关,与y 无关D .与y 有关,与x 无关【答案】B4.[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学(理)试题]5.[四川省宜宾市第四中学高2020届一诊模拟考试理科数学] 一个圆锥SC的高和底面直径相等,且这个圆锥SC和圆柱OM的底面半径及体积也都相等,则圆锥SC和圆柱OM的侧面积的比值为A.322B.23C.35D.45【答案】C6.[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【答案】D【解析】7.[广东省三校(广州真光中学、深圳市第二中学、珠海市第二中学)2020届高三上学期第一次联考数学(理)试题] 在如图直二面角ABDC中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD的中点E,将△ABE 沿BE 翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是A.BC与平面A1BE内某直线平行B.CD∥平面A1BEC.BC与平面A1BE内某直线垂直D.BC⊥A1B【答案】D8.[湖南省衡阳县2020届高三12月联考数学(理)试题]【答案】D【解析】9.[陕西省汉中市2020届高三教学质量第一次检测考试理科数学试题] 圆锥的侧面展开图是半径为R 的半圆,则该圆锥的体积为________. 【答案】33πR 10.[辽宁省本溪高级中学2020届高三一模考试数学(理)试卷]【答案】4π11.[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学(理)试题] 如图,在棱长为 1 的正方体1111ABCD A B C D -中,点M 是AD 的中点,动点P 在底面ABCD 内(不包括边界),若1B P ∥平面1A BM ,则1C P 的最小值是________.【答案】305【解析】 【分析】由面面平行找到点P 在底面ABCD 内的轨迹为线段DN ,再找出点P 的位置,使1C P 取得最小值,即1C P 垂直DN 于点O ,最后利用勾股定理求出最小值. 【详解】取BC 中点N ,连接11,,B D B N DN ,作CO DN ⊥,连接1C O ,因为平面1B DN ∥平面1A BM ,所以动点P 在底面ABCD 内的轨迹为线段DN ,当点P 与点O 重合时,1C P 取得最小值,因为11152225DN CO DC NC CO ⋅=⋅⇒==,所以221min 11130()155C P C O CO CC ==+=+=. 故1C P 的最小值是305. 【点睛】本题考查面面平行及最值问题,求解的关键在于确定点P 的位置,再通过解三角形的知识求最值.12.[四川省成都外国语学校2019-2020学年高三(上)期中数学试卷(理科)]已知某几何体的三视图如图所示,则该几何体的外接球的半径为________.21【答案】【解析】【分析】根据三视图还原几何体,设球心为O,根据外接球的性质可知,O与PAB△和正方形ABCD中心的连线分别与两个平面垂直,从而可得到四边形OGEQ 为矩形,求得OQ和PQ后,利用勾股定理可求得外接球半径.【详解】由三视图还原几何体如下图所示:设PAB△的中心为Q,正方形ABCD的中心为G,外接球球心为O,则OQ⊥平面PAB,OG⊥平面ABCD,E为AB中点,∴四边形OGEQ为矩形,112OQ GE BC ∴===,2233PQ PE ==, ∴外接球的半径:22213R GE PQ =+=. 故答案为21. 【点睛】本题考查多面体外接球半径的求解,关键是能够根据球的性质确定球心的位置,从而根据长度关系利用勾股定理求得结果. 13.[湖南省衡阳县2020届高三12月联考数学(理)试题]【答案】【解析】14.[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学(理)试题]【答案】1 315.[江苏省南通市2020届高三第一学期期末考试第一次南通名师模拟试卷数学试题]如图,在四棱锥P ABCD-中,底面ABCD是平行四边形,平面ABP⊥平面BCP,90APB=,M为CP的中点.求证:∠=︒,BP BC(1)AP//平面BDM;(2)BM ACP⊥平面.【解析】(1)设AC 与BD 交于点O ,连接OM , 因为ABCD 是平行四边形,所以O 为AC 中点, 因为M 为CP 的中点,所以AP ∥OM , 又AP ⊄平面BDM ,OM ⊂平面BDM , 所以AP ∥平面BDM .(2)平面ABP ⊥平面BCP ,交线为BP , 因为90APB ∠=︒,故AP BP ⊥,因为AP ⊂平面ABP ,所以AP ⊥平面BCP , 因为BM ⊂平面BCP ,所以AP ⊥BM . 因为BP BC =,M 为CP 的中点,所以BM CP ⊥. 因为AP CP P =I ,AP CP ⊂,平面ACP , 所以BM ⊥平面ACP .16.[河南省新乡市高三第一次模拟考试(理科数学)] 如图,在四棱锥ABCDV -中,二面角D BC V --为︒60,E 为BC 的中点. (1)证明:VE BC =;(2)已知F 为直线VA 上一点,且F 与A 不重合,若异面直线BF 与VE 所成角为︒60,求.VA VFABCDPMABCDPMO【解析】17.[四川省成都外国语学校2019-2020学年高三(上)期中数学试卷(理科)]如图,在底面是菱形的四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=60°,PA=AB=2,点E,F分别为BC,PD的中点,设直线PC与平面AEF交于点Q.(1)已知平面PAB∩平面PCD=l,求证:AB∥l.(2)求直线AQ 与平面PCD 所成角的正弦值. 【解析】 【分析】(1)证明AB ∥平面PCD ,然后利用直线与平面平行的性质定理证明AB ∥l ; (2)以点A 为原点,直线AE 、AD 、AP 分别为轴建立空间直角坐标系,求出平面PCD 的法向量和直线AQ 的方向向量,然后利用空间向量的数量积求解直线AQ 与平面PCD 所成角的正弦值即可.【详解】(1)证明:∵AB ∥CD ,AB ⊄平面PCD ,CD ⊂平面PCD . ∴AB ∥平面PCD ,∵AB ⊂平面PAB ,平面PAB ∩平面PCD =l , ∴AB ∥l ;(2)∵底面是菱形,E 为BC 的中点,且AB =2, ∴13BE AE AE BC ==⊥,,, ∴AE ⊥AD ,又PA ⊥平面ABCD ,则以点A 为原点,直线AE 、AD 、AP 分别为x 、y 、z 轴建立如图所示空间直角坐标系,则()()()()020,002,30,300D P C E,,,,,,,,,∴()0,1,1F ,()()()()3000,11310022AE AF DC DP ===-=-u u u r u u u r u u u r u u u r,,,,,,,,,,,设平面PCD 的法向量为(),,x y z =n ,有0PD ⋅=u u u r n ,0CD ⋅=u u u rn ,得()133=,,n ,设()1AQ AC AP λλ=+-u u u r u u u r u u u r,则()()321AQ λλλ=-u u u r ,,,再设(3,,)AQ mAE n m n n AF =+=u u u r u u u r u u u r,则()3321m n nλλλ⎧=⎪=⎨⎪-=⎩,解之得23m n λ===,∴2223333AQ ⎛⎫=⎪⎝⎭u u u r ,,, 设直线AQ 与平面PCD 所成角为α,则3105sin cos ,AQ AQ AQα⋅>=<==u u u r u u u r u u u r n n n ,∴直线AQ 与平面PCD 所成角的正弦值为3105. 【点睛】本题考查直线与平面平行的判定定理以及性质定理的应用,直线与平面所成角的向量求法,合理构建空间直角坐标系是解决本题的关键,属中档题.18.[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学(理)试题] 已知三棱柱111ABC A B C -中,1AB AC AA ==,侧面11ABB A ⊥底面ABC ,D 是BC 的中点,160B BA ∠=︒,1B D AB ⊥.(1)求证:ABC △为直角三角形;(2)求二面角1C AD B --的余弦值. 【解析】(1)取AB 中点O ,连接OD ,1B O ,易知1ABB △为等边三角形,从而得到1B O AB ⊥,结合1B D AB ⊥,可根据线面垂直判定定理得到AB ⊥平面1B OD ,由线面垂直的性质知AB OD ⊥,由平行关系可知AB AC ⊥,从而证得结论;(2)以O 为坐标原点可建立空间直角坐标系,根据空间向量法可求得平面1ADC 和平面ADB 的法向量的夹角的余弦值,根据所求二面角为钝二面角可得到最终结果. 【详解】(1)取AB 中点O ,连接OD ,1B O ,在1ABB △中,1AB B B =,160B BA ∠=︒,1ABB ∴△是等边三角形, 又O 为AB 中点,1B O AB ∴⊥,又1B D AB ⊥,111B O B D B =I ,11,B O B D ⊂平面1B OD ,AB ∴⊥平面1B OD ,OD ⊂Q 平面1B OD ,AB OD ∴⊥, 又OD AC ∥,AB AC ∴⊥, ∴ABC △为直角三角形.(2)以O 为坐标原点,建立如下图所示的空间直角坐标系:令12AB AC AA ===,则()1,2,0C -,()1,0,0A -,()0,1,0D ,()1,0,0B ,()10,0,3B ,()11,0,3BB ∴=-u u u v ,()0,2,0AC =u u u v ,()1,1,0AD =u u u v,()1111,2,3AC AC CC AC BB =+=+=-u u u u v u u u v u u u u v u u u v u u u v,设平面1ADC 的法向量为(),,x y z =m ,10230AD x y AC x y z ⎧⋅=+=⎪∴⎨⋅=++=⎪⎩u u u v u u u u v m m ,令1x =,则1y =-,3z =,()1,1,3∴=-m , 又平面ADB 的一个法向量为()0,0,1=n ,315cos ,5113∴<>==++m n , Q 二面角1C AD B --为钝二面角,∴二面角1C AD B --的余弦值为15-.【点睛】本题考查立体几何中垂直关系的证明、空间向量法求解二面角的问题,涉及到线面垂直判定定理和性质定理的应用;证明立体几何中线线垂直关系的常用方法是通过证明线面垂直得到线线垂直的关系.19.[江西省宜春市上高二中2020届高三上学期第三次月考数学(理)试题]20.[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学(理)试题]21.[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【解析】22.[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学(理)试题] 如图,在四棱锥P ABCD-中,底面ABCD为矩形,平面PCD⊥平面ABCD,2AB=,1BC=,2PC PD==,E为PB中点.(1)求证:PD∥平面ACE;(2)求二面角E AC D--的余弦值;(3)在棱PD上是否存在点M,使得AM⊥BD?若存在,求PMPD的值;若不存在,说明理由.【解析】(1)设BD交AC于点F,连接EF. 因为底面ABCD是矩形,所以F为BD中点 . 又因为E为PB中点,所以EF∥PD.因为PD ⊄平面,ACE EF ⊂平面ACE ,所以PD ∥平面ACE.(2)取CD 的中点O ,连接PO ,FO .因为底面ABCD 为矩形,所以BC CD ⊥.因为PC PD =,O CD 为中点,所以,PO CD OF ⊥∥BC ,所以OF CD ⊥. 又因为平面PCD ⊥平面ABCD ,PO ⊂平面,PCD 平面PCD ∩平面ABCD =CD . 所以PO ⊥平面ABCD ,如图,建立空间直角坐标系O xyz -, 则111(1,1,0)(0,1,0)(1,1,0),(0,0,1),(,,)222A C B P E -,,, 设平面ACE 的法向量为(,,)x y z =m ,131(1,2,0),(,,)222AC AE =-=-u u u r u u u r , 所以20,2,0,131.00222x y x y AC z y x y z AE -+=⎧⎧=⎧⋅=⎪⇒⇒⎨⎨⎨=--++=⋅=⎩⎩⎪⎩u u u v u u u v m m 令1y =,则2,1x z ==-,所以2,11=-(,)m .平面ACD 的法向量为(0,0,1)OP =u u u r ,则6cos ,OP OP OP⋅<>==-⋅u u u r u u u r u u u r m m |m |. 如图可知二面角E AC D --为钝角,所以二面角E AC D --的余弦值为66-. (3)在棱PD 上存在点M ,使AM BD ⊥.设([0,1]),(,,)PM M x y z PD=∈λλ,则,01,0PM PD D =-u u u u r u u u r λ(,).因为(,,1)(0,1,1)x y z -=--λ,所以(0,,1)M --λλ. (1,1,1),(1,2,0)AM BD =---=--u u u u r u u u r λλ.因为AM BD ⊥,所以0AM BD ⋅=u u u u r u u u r .所以12(1)0λ--=,解得1=[0,1]2∈λ. 所以在棱PD 上存在点M ,使AM BD ⊥,且12PM PD =。
2020高考模拟试题立体几何部分解答题汇编(含答案)
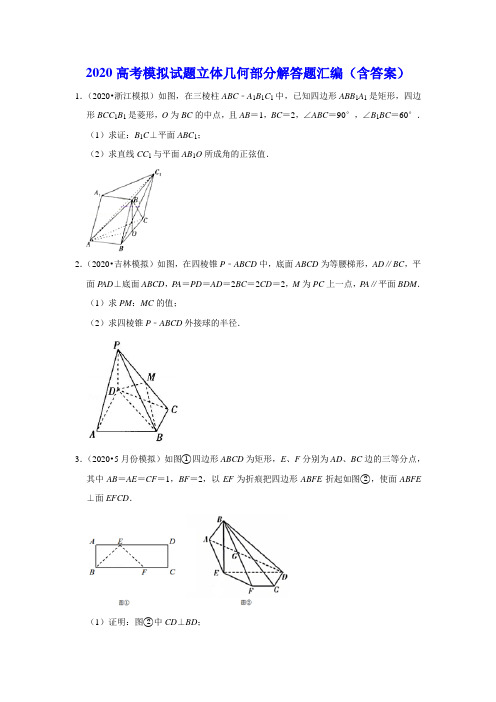
2020高考模拟试题立体几何部分解答题汇编(含答案)1.(2020•浙江模拟)如图,在三棱柱ABC﹣A1B1C1中,已知四边形ABB1A1是矩形,四边形BCC1B1是菱形,O为BC的中点,且AB=1,BC=2,∠ABC=90°,∠B1BC=60°.(1)求证:B1C⊥平面ABC1;(2)求直线CC1与平面AB1O所成角的正弦值.2.(2020•吉林模拟)如图,在四棱锥P﹣ABCD中,底面ABCD为等腰梯形,AD∥BC,平面P AD⊥底面ABCD,P A=PD=AD=2BC=2CD=2,M为PC上一点,P A∥平面BDM.(1)求PM:MC的值;(2)求四棱锥P﹣ABCD外接球的半径.3.(2020•5月份模拟)如图①四边形ABCD为矩形,E、F分别为AD、BC边的三等分点,其中AB=AE=CF=1,BF=2,以EF为折痕把四边形ABFE折起如图②,使面ABFE ⊥面EFCD.(1)证明:图②中CD⊥BD;(2)求二面角A﹣BD﹣C的余弦值.4.(2020•江西模拟)已知如图,菱形ABCD的边长为2,对角线AC=2,现将菱形ABCD 沿对角线AC翻折,使B翻折至点B'.(1)求证:AC⊥B'D;(2)若B'D=1,且点E为线段B'D的中点,求CE与平面AB'D夹角的正弦值.5.(2020•德阳模拟)如图,四棱柱ABCD﹣A1B1C1D1的侧棱与底面垂直,底面ABCD是菱形,四棱锥P﹣ABCD的顶点P在平面A1B1C1D1上的投影恰为四边形A1B1C1D1对角线的交点O1,四棱锥P﹣ABCD和四棱柱ABCD﹣A1B1C1D1的高相等.(1)证明:PB∥平面ADO1;(2)若∠BAD=,AA1=A1B1,求平面PBC与平面ABO1所成的锐二面角的余弦值.6.(2020•内江三模)如图,在直棱柱ABCD﹣A1B1C1D1中,AD∥BC,∠BAD=90°,AC ⊥BD,BC=1,AD=AA1=4.(1)证明:面ACD1⊥面BB1D;(2)求二面角B1﹣AC﹣D1的余弦值.7.(2020•天津二模)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,AB∥CD,且CD=2,AB=1,,AB⊥BC,N为PD的中点.(1)求证:AN∥平面PBC;(2)求平面P AD与平面PBC所成锐二面角的余弦值;(3)在线段PD上是否存在一点M,使得直线CM与平面PBC所成角的正弦值为,若存在,求出的值;若不存在,说明理由.8.(2020•汉阳区校级模拟)如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,P A⊥底面ABCD,P A=AB=4,E为线段PB的中点.(1)若F为线段BC上的动点,证明:平面AEF⊥平面PBC;(2)若F为线段BC的中点,求点P到平面AEF的距离.9.(2020•西湖区校级模拟)如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1=2,,∠BAC=120°,O为线段B1C1的中点,P线段CC1上一动点(异于点C、C1).Q为线段BC上一动点,且QP⊥OP;(1)求证:平面A1PQ⊥平面A1OP;(2)若BO∥PQ,求直线OP与平面A1PQ所成角的正弦值.10.(2020•高港区校级模拟)如图,在四棱锥P ABCD中,M是P A上的点,△ABD为正三角形,CB=CD,P A⊥BD.(1)求证:平面MBD⊥平面P AC;(2)若∠BCD=120°,DM∥平面BPC,求证:点M为线段P A的中点.11.(2020•柯桥区二模)如图,在四棱锥P﹣ABCD中,PD=PB=BD=AB=1,∠BAD =30°,CD=CB.(1)求证:PC⊥BD;(2)若P A=,求直线P A与平面PBD所成角的正弦值.12.(2020•三模拟)如图甲,在矩形ABCD中,E是边CD的中点,AB=2,BC=.以AE,BE为折痕将△ADE与△BCE折起,使D,C重合(仍记为D),如图乙.(1)探索:翻折后形成的几何体中直线DE的几何性质(写出一条即可,说明理由.不含DE⊥DA,DE⊥DB)(2)求翻折后的几何体E﹣ABD外接球的体积.13.(2020•运城模拟)在三棱锥P﹣ABC中,BC=2,AB=2,AP⊥PC,平面P AC⊥平面ABC,E是PB的中点.(1)求证:BC⊥P A;(2)求点B到平面ACE的距离.14.(2020•镜湖区校级模拟)如图,已知正三棱柱ABC﹣A1B1C1底面边长为1,BC1∩B1C =E,点D在AC上,使得AB1∥平面BDC1.(Ⅰ)求的值;(Ⅱ)若AB1⊥BC1,作出点D在平面BCC1B1上投影F,并求线段EF的长.15.(2020•香坊区校级一模)已知直三棱柱ABC﹣A1B1C1中,△ABC为正三角形,AB=AA1=4,F为BC的中点.点E在棱C1C上,且C1E=3EC.(Ⅰ)求证:直线B1F⊥平面AEF;(Ⅱ)求二面角B1﹣AE﹣F的余弦值.16.(2020•沙坪坝区校级模拟)如图,在正三棱柱ABC﹣A1B1C1中,D为CC1的中点,AB =2.(1)求证:平面ADB1⊥平面ABB1A1;(2)若直线AB1与平面A1B1C1所成角为60°,求二面角B1﹣AD﹣C1的余弦值.17.(2020•衡阳三模)如图,半圆弧所在平面与平面ABCD垂直,M是上异于A,B 的动点,∠BAD=∠ADC=90°,AB=AD=2DC(1)证明:MB⊥平面MAD;(2)当直线MB与平面ABCD所成的角为45°时,求二面角D﹣MA﹣C的正弦值.18.(2020•德阳模拟)如图,四棱柱ABCD﹣A1B1C1D1的侧棱与底面垂直,底面ABCD是菱形,四棱锥P﹣ABCD的顶点P在平面A1B1C1D1上的投影恰为四边形A1B1C1D1对角线的交点O1,四棱锥P﹣ABCD和四棱柱ABCD﹣A1B1C1D1的高相等.(1)证明:PB∥平面ADO1;(2)若AB=BD=BB1=2,求几何体P﹣AB1C1的体积.19.(2020•内江三模)如图,在直棱柱ABCD﹣A1B1C1D1中,AD∥BC,∠BAD=90°,AC ⊥BD,BC=1,AD=AA1=4.(1)证明:面ACD1⊥面BB1D;(2)求多面体ABC﹣A1B1C1D1的体积.20.(2020•二模拟)如图甲所示,在平面四边形ABCD中,∠ABC=∠ADC=90°,∠DCA =60°,AB=BC=,现将平面ADC沿AC向上翻折,使得DB=,M为AC的中点,如图乙.(1)证明:BM⊥DC;(2)线段DC上是否存在点Q,使得直线BQ与平面ADB所成角的正弦值为,若存在,求出线段DQ的长度;若不存在,请说明理由.21.(2020•南岗区校级模拟)如图,组合体由棱长为2的正方体ABCD﹣A1B1C1D1和四棱锥S﹣ABCD组成,SD⊥平面ABCD,SD=2,E是DD1中点,F是SB中点.(Ⅰ)求证:SB∥平面EA1C1;(Ⅱ)求证:A1C1⊥EF;(Ⅲ)求S到平面EA1C1的距离.22.(2020•河南模拟)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,BC∥AD,AB⊥BC,AB=BC=1,AD=AP=2,E为PD的中点,F为BP的中点.(1)求证:CE∥平面P AB;(2)求点D到平面PBC的距离.23.(2020•滨州三模)在如图所示的圆柱O1O2中,AB为圆O1的直径,C,D是的两个三等分点,EA,FC,GB都是圆柱O1O2的母线.(1)求证:FO1∥平面ADE;(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A﹣FB﹣C的余弦值.24.(2020•金凤区校级四模)如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在平面互相垂直,已知AB=4,EF=2.(1)求证:平面ADF⊥平面BCF;(2)若几何体F﹣BCE和几何体F﹣ABCD的体积分别为V1和V2,求V1:V2.25.(2020•韩城市模拟)如图,在Rt△AOB中,OA=OB=2,△AOC通过△AOB以直线OA为轴顺时针旋转120°得到(即∠BOC=120°),点M为线段BC上一点,且MB=.(Ⅰ)求证:OA⊥OM;(Ⅱ)若D是线段AB的中点,求四棱锥O﹣ACMD的体积.26.(2020•南岗区校级模拟)图中组合体由一个棱长为2的正方体ABCD﹣A1B1C1D1和一个四棱锥S﹣ABCD组成(SD⊥平面ABCD,S,D,D1三点共线,SD=2),E是DD1中点.(Ⅰ)求证:SB∥平面EA1C1;(Ⅱ)点F在棱SB上靠近S的三等分点,求直线EF与平面EA1C1所成角的正弦值.27.(2020•邵阳三模)如图所示,已知正方体ABCD﹣A1B1C1D1.(1)线段AC上是否存在点O,使得C1O∥平面AB1D1,若存在,求的值;若不存在,请说明理由;(2)求直线D1A与平面A1ACC1所成角的大小.28.(2020•龙潭区校级模拟)如图,在四棱锥P﹣ABCD中,AB∥DC,DC=2AB=2AD=2BC,△P AB为等边三角形,平面P AB⊥底面ABCD,E为PD的中点.(1)求证:AE∥平面PBC;(2)求二面角B﹣AE﹣P的正弦值.29.(2020•武昌区校级模拟)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,AB =2AD=4,PD=BD=AD,且PD⊥底面ABCD.(1)证明:BC⊥平面PBD;(2)若Q为PC的中点,求三棱锥A﹣PBQ的体积.30.(2020•东兴区校级模拟)如图,四棱锥E﹣ABCD中,四边形ABCD是边长为2的菱形∠DAE=∠BAE=45°,∠DAB=60°.(Ⅰ)证明:平面ADE⊥平面ABE;(Ⅱ)当平面DCE与平面ABE所成锐二面角的余弦值,求直线DE与平面ABE所成角正弦值.31.(2020•宝鸡三模)如图,DA⊥平面ABC,DA∥PC,E为PB的中点,PC=2,AC⊥BC,△ACB和△DAC是等腰三角形,AB=.(Ⅰ)求证:DE∥平面ABC;(Ⅱ)求三棱锥E﹣BCD体积.32.(2020•杜集区校级模拟)如图,将长方形OAA1O1(及其内部)绕OO1旋转一周形成圆柱,其中OA=1,OO1=2,弧的长为为⊙O的直径.(Ⅰ)在弧上是否存在点C(C,B1在平面OAA1O1的同侧),使BC⊥AB1,若存在,确定其位置;若不存在,说明理由;(Ⅱ)求A1到平面BO1B1的距离.33.(2020•靖远县模拟)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E,F分别为AD,PC的中点.(1)证明:DF∥平面PBE;(2)求直线PD与平面PBE所成角的正弦值.34.(2020•梅河口市校级模拟)如图,在四棱锥P﹣ABCD中,底面ABCD的对角线互相垂直,且BC=CD,PB=PD,P A⊥平面ABCD.(1)若Q为PD的中点,求证:OQ∥平面P AB;(2)若AB⊥BC,AB=P A=AC=1,点M在PC上,且PM=PC,求点A到平面MBD的距离.35.(2020•襄州区校级四模)如图,DA⊥平面ABC,DA∥PC,E为PB的中点,PC=4,AC⊥BC,△ACB和△DAC都是等腰三角形,.(1)求证:DE∥平面ABC;(2)求直线DE和平面BCD所成角的正弦值.36.(2020•二模拟)如图甲所示,在平面四边形ABCD中,∠ABC=∠ADC=90°,∠DCA =60°,AB=BC=,现将平面ADC沿AC向上翻折,使得DB=,M为AC的中点,如图乙.(1)证明:BM⊥DC;(2)求BM与平面ADB所成角的正弦值.37.(2020•东湖区校级三模)如图,在六棱锥P﹣ABCDEF中,底面ABCDEF是边长为4的正六边形,.(1)证明:平面P AC⊥平面PBE;(2)若,求二面角B﹣P A﹣F的余弦值.38.(2020•泸州四模)如图,在多面体ABCDEF中,侧面ADEF是平行四边形,底面ABCD是等腰梯形,AB∥CD,AB=4,BC=CD=2,顶点E在底面ABCD内的射影恰为点C.(Ⅰ)求证:BC⊥平面ACE;(Ⅱ)若CD=CE,求四面体ABEF的体积.39.(2020•福州三模)如图,在多面体P ABCD中,平面ABCD⊥平面P AD,AD∥BC,∠BAD=90°,∠P AD=120°,BC=1,AB=AD=P A=2.(1)求平面PBC与平面P AD所成二面角的正弦值;(2)若E是棱PB的中点,求证:对于棱CD上任意一点F,EF与PD都不平行.40.(2020•庐阳区校级模拟)如图,在四棱锥P﹣ABCD中,平面P AD⊥平面ABCD.平面PCD⊥平面ABCD.(1)证明:PD⊥平面ABCD;(2)若E为PC的中点,DE⊥PC,四边形ABCD为菱形,且∠BAD=60°,求二面角D﹣BE﹣C的余弦值.1.【解答】解:(1)因为,∠ABC=90°,所以AB⊥BC,因为四边形ABB1A1是矩形,所以AB⊥BB1,又BC⊂平面BCC1B1,BB1⊂平面BCC1B1,BC∩BB1=B,所以AB⊥平面BCC1B1.因为B1C⊂平面BCC1B1,所以AB⊥B1C,又四边形BCC1B1是菱形,所以BC1⊥CB1,因为AB⊂平面ABC1,B1C⊂平面ABC1,AB∩BC1=B,所以B1C⊥平面ABC1.(2)因为四边形BCC1B1是菱形,∠B1BC=60°,O为BC的中点,所以B1O⊥BC,由(l)知AB⊥平面BCC1B1,所以AB⊥B1O,又BC∩AB=B,所以B1O⊥平面ABC,又B1O⊂平面AB1O,所以平面AB1O⊥平面ABC,过点B作BH⊥AO于点H,则BH⊥平面AB1O,连接B1H,则∠BB1H即直线CC1与平面AB1O所成的角,在直角△ABO中,易得BH=,又B1B=2,所以sin,所以直线CC1与平面AB1O所成角的正弦值为.2.【解答】解:(1)如图,连接AC交BD于点N,连接MN,因为平面P AC∩平面BDM=MN,P A∥平BDM,所以P A∥MN,所以=.又因为△BCN∽△DAN,所以=2,故=2.(2)根据题意,取AD的中点O,连接PO,因为△P AD为等边三角形,所以PO⊥AD,PO=.因为平面P AD⊥底面ABCD,且平面P AD∩底面ABCD=AD,所以PO⊥平面ABCD.设△P AD的重心为G,则GO平面ABCD,AG=DG=PG=.解等腰梯形ABCD,可得O为梯形ABCD外接圆的圆心,所以OD=OA=OB=OC=1,所以GD=GA=GB=GC=,故G为四棱锥P﹣ABCD外接球球心,半径为.3.【解答】解:(1)证明:连接BE,易知,∴BE2+EF2=BF2,∴BE⊥EF,∵面ABFE⊥面EFCD,面ABFE∩面EFCD=EF,∴BE⊥面EFCD,∴BE⊥CD,∵CD⊥DE,BE∩DEE,且BE,DE都在平面BDE内,∴CD⊥面BDE,又BD⊂面BDE,∴CD⊥BD;(2)以ED,EB分别为y,z轴建立如图所示的空间直角坐标系,则,BF的中点,∵,∴,∴,设平面ABD的法向量为,则,则可取,同理可得平面BDC的法向量为,∴,∵二面角A﹣BD﹣C的平面角为钝角,∴二面角A﹣BD﹣C的余弦值为.4.【解答】(1)证明:如图所示,取AC的中点为O,连结OD,OB′,∵AB′=B′C,AD=CD,∴B′O⊥AC,DO⊥AC,又B′O∩DO=O,∴AC⊥平面B′OD,∵B′D⊂平面B′ED,∴AC⊥B′D.(2)解:以O为原点,OC为x轴,OD为y轴,过O作平面ACD的垂线为z轴,建立空间直角坐标系,在等腰△B′AC中,B′O=1,同理DO=1,∵B′D=1,A(﹣,0,0),D(0,1,0),B′(0,,),C(,0,0),E (0,,),∴=(,1,0),=(0,,﹣),=(﹣,,),设平面B′AD的一个法向量为=(x,y,z),则,即,取z=1,得=(﹣1,,1),∴cos<>===.设CE与平面AB'D夹角为θ,则sinθ=|cos<>|=.∴CE与平面AB'D夹角的正弦值为.5.【解答】(1)证明:连接BO1、PO1,由题知,PO1⊥平面A1B1C1D1且四棱柱ABCD﹣A1B1C1D1的侧棱与底面垂直,∴PO1∥BB1∥DD1,即P、B、O1、D四点共面.∵四棱锥P﹣ABCD和四棱柱ABCD﹣A1B1C1D1的高相等,∴在四边形PBO1D中,PO1与BD的交点O为BD的中点,也是PO1的中点,∴四边形PBO1D为平行四边形,∴PB∥O1D,又O1D⊂平面ADO1,PB⊄平面ADO1,∴PB∥平面ADO1.(2)解:由题意知,O1A1、O1B1、O1P三直线两两垂直,∴以O1为原点,O1A1、O1B1、O1P所在直线分别为x、y、z轴建立如图所示的空间直角坐标系,设O1B1=1,则O1A1=,AA1=2,∴O1(0,0,0),A(,0,2),B(0,1,2),P(0,0,4),C(,0,2),∴=(,0,2),=(0,1,2),设平面ABO1的法向量为=(x,y,z),则,即,令z=,则x=﹣2,y=,∴=(﹣2,,).同理可得,平面PBC的法向量=(﹣2,,).∴cos<,>===.故平面PBC与平面ABO1所成的锐二面角的余弦值为.6.【解答】解:(1)证明:由直棱柱ABCD﹣A1B1C1D1可知,BB1⊥平面ABCD,AC⊂平面ABCD,∴BB1⊥AC,又∵AC⊥BD,且BB1∩BD=B,∴AC⊥平面BB1D,又AC⊂平面ACD1,∴面ACD1⊥面BB1D;(2)易知,AB,AD,AA1两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,设AB=t,则A(0,0,0),B(t,0,0),B1(t,0,4),C(t,1,0),C1(t,1,4),D(0,4,0),D1(0,4,4),∴,∵AC⊥BD,∴,解得t=2(t=﹣2舍去),∴,设是平面ACD1的一个法向量,则,即,令x=1,可得,同理可得平面ACB1的一个法向量为,∴,∵二面角B1﹣AC﹣D1为锐二面角,∴二面角B1﹣AC﹣D1的余弦值为.7.【解答】解:过A作AE⊥CD于点E,则DE=1,以A为原点,AE、AB、AP所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,则A(0,0,0),B(0,1,0),E(,0,0),D(,﹣1,0),C(,1,0),P(0,0,1),∵N为PD的中点,∴N(,,).(1)=(,,),=(0,﹣1,1),=(,0,0).设平面PBC的法向量为=(x,y,z),则,令y=1,则x=0,z=1,∴=(0,1,1),∴•=+=0,即⊥,又AN⊄平面PBC,∴AN∥平面PBC.(2)由(1)知,=(0,0,1),=(,﹣1,0),设平面P AD的法向量为=(a,b,c),则,令a=1,则b=,c=0,∴=(1,,0),∴cos<,>===.故平面P AD与平面PBC所成锐二面角的余弦值为.(3)令=λ,λ∈[0,1],设M(x,y,z),∴(x﹣,y+1,z)=λ(,1,1),∴M(,λ﹣1,λ),∴=(,λ﹣2,λ).由(1)知,平面PBC的法向量为=(0,1,1),∵直线CM与平面PBC所成角的正弦值为,∴=||=,化简得21λ2﹣50λ+24=0,即(3λ﹣2)(7λ﹣12)=0,∵λ∈[0,1],∴λ=,故=.8.【解答】(1)证明:∵P A=AB,E为线段PB的中点,∴AE⊥PB,∵P A⊥底面ABCD,BC⊂平面ABCD,∴BC⊥P A,∵底面ABCD为正方形,∴BC⊥AB,P A∩AB=A,∴BC⊥平面P AB,∵AE⊂平面P AB,∴AE⊥BC.∵PB∩BC=B,∴AE⊥平面PBC,∵AE⊂平面AEF,∴平面AEF⊥平面PBC.(2)解:∵P A⊥底面ABCD,∴平面P AB⊥底面ABCD,∵平面P AB∩底面ABCD=AD,CD⊥AD,∴CD⊥平面P AB,∴CD⊥PD.∵,CD=AB=4∴PC=4,∵E为线段PB的中点,F为线段BC的中点,∴,点P到面AEF的距离等于点B到面AEF的距离,设为h.∵,,由(1)知AE⊥EF,∴S△AEF=2,S△ABF=4,V B﹣AEF=V E﹣ABF得即点P到面AEF的距离为.9.【解答】(1)证明:∵A1B1=A1C1=2,O为线段B1C1的中点,∴A1O⊥B1C1,∵直三棱柱ABC﹣A1B1C1中,∴CC1⊥平面A1B1C1,∴A1O⊥CC1,又CC1∩B1C1=C1,∴A1O⊥平面CBB1C1,∴QP⊥A1O.又∵QP⊥OP,A1O∩OP=O,∴QP⊥平面A1OP,又QP⊂平面A1OP,∴平面A1PQ⊥平面A1OP.(2)解:建立如图空间直角坐标系O﹣xyz,∵A1B1=A1C1=2,∠B1A1C1=∠BAC=120°,∴,OA1=1,则O(0,0,0),,,,A1(﹣1,0,0),设,,则,=(0,﹣b,a﹣2),=(0,,a).∵QP⊥OP,BO∥PQ,∴,,故,解得:,(P异于点C,C1),∴,,.设平面A1QP的法向量为,则,即,可取,设直线OP与平面A1QP所成角为θ,则.故直线OP与平面A1QP所成角的正弦值为.10.【解答】证明:(1)取BD的中点O,连结OA,OC,∵△ABD为正三角形,∴OA⊥BD.∵CB=CD,∴OC⊥BD.在平面ABCD内,过O点垂直于BD的直线有且只有一条,∴A,O,C三点共线,即AC⊥BD.∵P A⊥BD,AC,P A⊂平面P AC,AC∩P A=A,∴BD⊥平面P AC.∵BD⊂平面MBD,∴平面MBD⊥平面P AC.(2)(证法1)延长BC,AD,交于Q点,连结PQ,如图1;∵DM∥平面BPC,DM⊂平面P AQ,平面BPC∩平面P AQ=PQ,∴DM∥PQ.在△CBD中,∵CB=CD,∠BCD=120°,∴∠CBD=30°,∴∠ABC=30°+60°=90°,∴△ABO为直角三角形.∵在Rt△ABQ中,∠BAQ=60°,∴AQ=2AB=2AD,∴点D是AQ的中点,∴点M为线段P A的中点.(证法2)取AB的中点N,连结MN和DN,如图2;易算得∠ABC=90°,即AB⊥BC.∵△ABD为正三角形,∴DN⊥AB.又DN,BC,AB共面,∴DN∥CB.∵DN⊄平面BPC,CB⊂平面BPC,∴DN∥平面BPC.DM∥平面BPC,DN,DM⊂平面DMN,∴平面DMN∥平面BPC.∵MN⊂平面DMN,∴MN∥平面BPC.∵MN⊂平面P AB,平面P AB∩平面BPC=PB,∴MN∥PB.∵N是AB的中点,∴M为线段P A的中点.11.【解答】证明:(1)取BD的中点O,连接OP、OC,∵PD=PB,∴OP⊥BD,又CD=CB,∴OC⊥BD,∵OP∩OC=O,OP、OC⊂平面OPC,∴BD⊥平面OPC,∵PC⊂平面OPC,∴PC⊥BD;解:(2)∵BD=AB=1,∴AB=2,BD=1,而∠BAD=30°,由余弦定理可得:BD2=AD2+AB2﹣2AD•AB cos∠BAD,即,解得AD=,∴AD2+DB2=AB2,则AD⊥DB.取AB中点E,连接OE,则OE∥AD,∴OE⊥BD,可得OE⊂平面POC,连接PE,在平面PCE中,过O作OZ⊥CE,以O为坐标原点,分别以OB,OC,OZ所在直线为x,y,z轴建立空间直角坐标系.在△P AB中,由P A=,AB=2,PB=1,可得cos,在△P AE中,有PE==.在△POE中,有cos=.∴cos.则B(,0,0),D(﹣,0,0),P(0,,),A(,﹣,0).=(0,,),=(1,0,0),.设平面PDB的一个法向量为,由,取z=﹣1,得.设直线P A与平面PBD所成角为θ,则sinθ===.∴直线P A与平面PBD所成角的正弦值为.12.【解答】解:(1)性质:DE⊥平面ABD,证明如下:翻折前,DE⊥DA,DE⊥BC,翻折后满足,DE⊥DA,DE⊥BD且DA∩DB=D,则DE⊥平面ABD,(2)解:因为DA,DB,DE两两垂直,所以几何体E﹣ABD的外接球就是以DA,DB,DE相邻的棱的长方体的外接球,所以(2R)2=DA2+DB2+DE2=2+2+1=5,所以R=.故V==13.【解答】(1)证明:∵,∴,∵,∴AB2=AC2+BC2,∴AC⊥BC,∵平面P AC⊥平面ABC,平面P AC∩平面ABC=AC,∴BC⊥平面P AC,∴BC⊥P A.(2)解:∵E是PB的中点,∴点P,B到平面ACE的距离相等,设为d,,即,化简得S△ACE×d=1,由(1)可得BC⊥PC,∴,∵AB2=AP2+PB2,∴P A⊥PB,∴,∴,∴,∴,∴,∴点B到平面ACE的距离为.14.【解答】解:(Ⅰ)连接DE,由题意可知点E为B1C的中点,∵AB1∥平面BDC1,又平面AB1C∩平面BDC1=DE,AB1⊂平面AB1C,∴AB1∥DE,∵E为B1C的中点,∴D为AC的中点,∴.(Ⅱ)作DF⊥BC于F,则DF⊥平面B1BCC1,连接EF,则EF是ED在平面B1BCC1上的射影.∵AB1⊥BC1,由(Ⅰ)知AB1∥DE,∴DE⊥BC1,则BC1⊥EF,由已知AC=1,则,∵△ABC是正三角形,∴在Rt△DCF中,,取BC中点G,∵EB=EC,∴EG⊥BC.则在Rt△BEF中,EF2=BF•GF,又,∴,即.15.【解答】解:(Ⅰ)取B1C1中点D,连接DF,设AB=4,以F为坐标原点,的方向为x,y,z轴的正方向建立空间直角坐标系,,∴,设平面AEF的法向量为∵,∴,∴,∵,∴,∴直线B1F⊥平面AEF.(Ⅱ),设平面B1AE的法向量为∵,∴,不妨取y2=3,则x2=﹣5,z2=﹣4.∴,平面AEF的法向量为,设二面角B1﹣AE﹣F的平面角为θ,∴.16.【解答】(1)证明:取AB1中点H,连接DH.由题设条件易知:Rt△ACD与Rt△B1C1D全等,所以DA=DB1,DH⊥AB1,同理:Rt△A1C1D与Rt△BCD全等,所以DA1=DB1,DH⊥A1B,所以DH⊥平面ABB1A1⇒平面ADB1⊥平面ABB1A1.(2)解:AA1⊥平面A1B1C1⇒AB1与平面A1B1C1所成角即为∠AB1A1,∴,取A1C1中点O,连接OB1,则OB1⊥A1C1,以O为坐标原点,OB1方向为x轴,OC1方向为y轴,过O作平面A1B1C1的垂线为z轴建立如图所示空间直角坐标系,则:,设平面ADB1的法向量为,由得,易知为平面AA1C1C的法向量,设二面角B1﹣AD﹣C1的大小为θ,则,所以二面角B1﹣AD﹣C1的余弦值为.17.【解答】解:(1)证明:因为半圆弧所在平面与平面ABCD垂直,平面MAB∩平面ABCD=AB,由DA⊥AB,所以DA⊥平面MAB,又MB⊂平面MAB,则有DA⊥MB又AB为半圆弧所对的直径,所以MB⊥MA,而MA∩DA=A,所以MB⊥平面MAD.(2)法1(空间向量法):过M作AO⊥AB于O,因为平面MAB⊥平面ABCD,平面MAB∩平面ABCD=AB,所以MO⊥平面ABCD,∠MBO即MB与平面ABCD所成的角,由已知条件得∠MBA=45°,MA=MB,即O为AB中点.由∠BAD=∠ADC=90°,AB=AD=2DC,四边形AOCD为矩形,所以OC⊥AB以O为坐标原点,OB,OC,OM方向分别为x,y,z轴建立如图所示的空间直角坐标系,设AB=AD=2DC=2,所以C(0,2,0),D(﹣1,2,0),A(﹣1,0,0),M(0,0,1),B(1,0,0)由(1)知,MB⊥平面MAD,则平面MAD的一个法向量设平面MAC的法向量因为,由,得,取y=﹣1,则设二面角D﹣MA﹣C大小为θ,则所以,即二面角D﹣MA﹣C的正弦值为.法2(传统几何法):二面角D﹣MA﹣C的大小即为二面角B﹣MA﹣D的大小与二面角B ﹣MA﹣C大小的差,由(1)的证明可得,二面角B﹣MA﹣D的大小为90°,所以二面角D﹣MA﹣C的正弦值即为二面角B﹣MA﹣C的余弦值.由平面MAB⊥平面ABCD,平面MAB∩平面ABCD=AB,CO⊥AB,所以CO⊥平面MAB,又MA⊂平面MAB,则OC⊥MA,取MA中点H,连HC,由AB为半圆弧所对的直径,所以BM⊥MA,O,H分别为AB,MA的中点,所以OH∥BM,则OH⊥MA,又OH∩OC=O,所以MA⊥平面OHC则∠OHC即为二面角B﹣MA﹣C的平面角,设AB=AD=2DC=2,在Rt△COH中,,OC=2,所以,故二面角D﹣MA﹣C的正弦值为.18.【解答】(1)证明:由已知可得,PO1⊥平面A1B1C1D1,且四棱柱ABCD﹣A1B1C1D1的侧棱与底面垂直,故PO1∥BB1∥DD1,即P、B、O1、D四点共面.由四棱锥P﹣ABCD和四棱柱ABCD﹣A1B1C1D1的高相等,可知,在四边形PBO1D中,PO1与BD的交点O为PO1的中点,也是BD的中点.∴四边形PBO1D是平行四边形,故PB∥DO1,又PB⊄平面ADO1,O1D⊂ADO1,∴PB∥平面ADO1;(2)解:∵=,∵AB=BD=BB1=2,∴B1O1=1.连接PC1和AC交于点E,由△POE≌△C1CE,得OE=,则AE==.∴=.∴几何体P﹣AB1C1的体积为.19.【解答】证明:(1)∵棱柱ABCD﹣A1B1C1D1是直棱柱,∴BB1⊥底面ABCD,可得AC⊥BB1,又AC⊥BD,而BB1∩BD=B,∴直线AC⊥平面BDB1,而AC⊂面ACD1,∴面ACD1⊥面BB1D;解:(2)AB,AD,AA1两两垂直,如图所示,以A为坐标原点,AB,AD,AA1所在直线分别为x,y,z轴建立空间直角坐标系.设|AB|=t>0,A(0,0,0),B(t,0,0),C(t,1,0),D(0,4,0).又AC⊥BD,∴,即(t,1,0)•(﹣t,4,0)=﹣t2+4=0,得t=2.∴多面体ABC﹣A1B1C1D1的体积V===.20.【解答】(1)证明:连接DM,∵AB=BC=,∠ABC=90°,且M是AC的中点,∴BM⊥AC,BM=1,AC=2,∵∠ADC=90°,∠DCA=60°,M是AC得中点,∴DM=AC=1,又DB=,∴DM2+BM2=DB2,∴DM⊥BM,又DM∩AC=M,∴BM⊥平面ACD,∴BM⊥DC;(2)解:由(1)知,BM⊥平面ACD,又BM⊂平面ABC,∴平面ADC⊥平面ABC.在平面ADC内,过M作MZ⊥AC.以M为坐标原点,分别以MB、MC、MZ所在直线为x、y、z轴建立空间直角坐标系.则B(1,0,0),A(0,﹣1,0),D(0,,),C(0,1,0).,.设平面ABD的一个法向量为,由,取y=﹣1,得.假设线段DC上是否存在点Q,满足(0<λ≤1),使得直线BQ与平面ADB所成角的正弦值为,则=.由=|cos<>|==,整理得:15λ2+λ﹣2=0,解得(λ>0).∴,即|DQ|=.21.【解答】(Ⅰ)证明:连接DB1,连接D1B1交A1C1于点O,则D1O=OB1,∵D1E=ED,∴EO∥DB1,又SD∥BB1,SD=BB1,因此四边形SDB1B是平行四边形,∴SB∥DB1,故SB∥EO.又SB⊄平面EAC,EO⊂平面EA1C1,因此SB∥平面EA1C1.(Ⅱ)证明:四边形A1B1C1D1是正方形,∴A1C1⊥B1D1,又DD1⊥平面A1B1C1D1,A1C1⊂平面A1B1C1D1,A1C1⊥SD1,又SD1∩B1D1=D1,∴A1C1⊥平面SD1B1B,又EF⊂平面SD1B1B,因此A1C1⊥EF.(Ⅲ)解:设S到平面EA1C1的距离为d,==,即××3×2×2=××2××d,解得d=,∴S到平面EA1C1的距离为.22.【解答】(1)证明:如图,取AP的中点G,连接EG,BG,∵DE=PE,AG=PG,∴GE∥AD且AD=2GE.∵AD=2,∴GE=1.∵BC∥AD,BC=1,∴GE∥BC且GE=BC,∴四边形BCEG为平行四边形,∴CE∥BG.又∵BG⊂平面P AB,CE⊄平面P AB,∴CE∥平面P AB.(2)解:如图,过点A作AH⊥BP,垂足为H.∵AP⊥平面ABCD,BC⊂平面ABCD,∴AP⊥BC.∵BC⊥AB,AB∩AP=A,又AB,AP⊂平面P AB,∴BC⊥平面P AB.∵AH⊂平面P AB,∴AH⊥BC.∵AH⊥BP,BP∩BC=B,BP,BC⊂平面PBC,∴AH⊥平面PBC.在Rt△APB中,BP==,AH===.∵AD∥BC,BC⊂平面PBC,AD⊄平面PBC,∴AD∥平面PBC,∴点D到平面PBC的距离与点A到平面的距离相等,故点D到平面PBC的距离为.(注:也可利用V P﹣BCD=V D﹣PBC求解)23.【解答】(1)证明:连接O1C,O1D,因为C,D是半圆弧的两个三等分点,所以∠AO1D=∠DO1C=∠CO1B=60°,又O1A=O1B=O1C=O1D,所以△AO1D,△CO1D,△BO1C均为等边三角形,所以O1A=AD=DC=CO1,所以四边形ADCO1是平行四边形.所以CO1∥AD.因为EA,FC都是圆柱O1O2的母线,所以EA∥FC.又因为CO1、FC⊂平面FCO1,CO1∩FC=C,AD、EA⊂平面ADE,AD∩EA=A,所以平面FCO1∥平面ADE,又FO1⊂平面FCO1,所以FO1∥平面ADE.(2)解:连接AC,因为FC是圆柱O1O2的母线,所以FC⊥平面ACB,所以∠F AC为直线AF与平面ACB 所成的角,即∠F AC=30°.因为AB为圆O1的直径,所以∠ACB=90°,在Rt△ABC中,∠ABC=60°,BC=1,所以,所以在Rt△F AC中,FC=AC•tan30°=1.因为AC⊥BC,AC⊥FC,BC∩FC=C,BC、FC⊂平面FBC,所以AC⊥平面FBC,又FB⊂平面FBC,所以AC⊥FB.在△FBC内,作CH⊥FB于点H,连接AH.因为AC∩CH=C,AC、CH⊂平面ACH,所以FB⊥平面ACH,又AH⊂平面ACH,所以FB⊥AH,所以∠AHC是二面角A﹣FB﹣C的平面角.在Rt△FBC中,CH===,在Rt△ACH中,,所以,故二面角A﹣FB﹣C的余弦值为.24.【解答】(1)证明:由已知得,平面ABCD⊥平面ABEF,在矩形ABCD中,CB⊥AB,又平面ABCD∩平面ABEF=AB,CB⊂平面ABCD,∴CB⊥平面ABEF.∵AF⊂平面ABEF,∴CB⊥AF.又AB为圆O的直径,∴AF⊥BF.∵CB∩BF=B,CB⊂平面CBF,BF⊂平面CBF,∴AF⊥平面CBF.而AF⊂平面DAF,∴平面ADF⊥平面BCF;(2)解:过点F作FH⊥AB,垂足为H,∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,∴FH⊥平面ABCD,∴V1=V F﹣BCE=V C﹣BEF=.=.∴V1:V2=1:4.25.【解答】(Ⅰ)证明:由题意得OA⊥OB,OA⊥OC,∵OB∩OC=O,∴OA⊥平面COB,∵OM⊂平面COB,∴OA⊥OM;(Ⅱ)解:由已知得,.在△MOB中,由OB=2,MB=,∠OBM=30°,利用余弦定理得OM==,∴OM2+OB2==MB2,得OM⊥OB,由(Ⅰ)知OM⊥OA,且OA∩OB=O,∴MO⊥平面AOB.∵D是线段AB的中点,∴V D﹣OMB=V M﹣DOB=,∴四棱锥O﹣ACMD的体积为:V O﹣ACMD=V A﹣BOC﹣V D﹣OBM=.26.【解答】(Ⅰ)证明:连接DB1,连接D1B1交A1C1于O,则D1O=OB1.∵D1E=ED,∴EO∥DB1,又SD∥BB1,SD=BB1,∴四边形SDB1B是平行四边形,得SB∥DB1,故SB∥EO.∵SB⊄平面EA1C1,EO⊂平面EA1C1,∴SB∥平面EA1C1;(Ⅱ)解:以D1为坐标原点,分别以D1A1、D1C1、D1D所在直线为x、y、z轴建立空间直角坐标系.则A1(2,0,0),C1(0,2,0),E(0,0,1),F(,,).,,.设平面EA1C1的一个法向量为,由,取x=1,得.设直线EF与平面EA1C1所成角为θ.则sinθ=|cos<>|====.∴直线EF与平面EA1C1所成角的正弦值为.27.【解答】解:(1)假设存在O∈AC,使C1O∥平面AB1D1,设A1C1∩B1D1=O1.连结AO1,则平面A1ACC1∩平面AB1D1=AO1,∵C1O⊂平面A1ACC1,∴AO1∥C1O,∵O1为A1C1的中点,∴O必为AC的中点,故存在O为AC的中点,使C1O∥平面AB1D1,且.(2)∵ABCD﹣A1B1C1D1为正方体,∴AA1⊥平面A1B1C1D1,∵D1O1⊂平面A1B1C1D1,∴AA1⊥D1O1.又D1O1⊥A1C1,A1C1∩AA1=A1,A1C1、AA1⊂面A1ACC1,∴D1O1⊥平面A1ACC1,D1O1⊥AO1,∴∠D1AO1为直线D1A与平面A1ACC1所成的角.∵D1O1⊥AO1,且,∴∠D1AO1=30°.故直线D1A与平面A1ACC1所成的角为30°.28.【解答】(1)证明:如图1,取PC中点F,连接EF,BF,在△PDC中,E,F分别为PD,PC的中点,∴EF∥DC,,∵AB∥DC,,∴EF∥AB,EF=AB,∴四边形AEFB为平行四边形,∴AE∥BF,又AE⊄平面PBC,BF⊂平面PBC,∴AE∥平面PBC.(2)解:取AB中点O,CD中点Q,连接OP,OQ,∵△P AB为正三角形,∴OP⊥AB,在四边形ABCD中,AB∥DC,AB≠DC,AD=BC,∴四边形ABCD为等腰梯形,O,Q分别为AB,DC的中点,∴OQ⊥AB,∵平面P AB⊥底面ABCD,且平面P AB∩底面ABCD=AB,OP⊥AB,∴OP⊥底面ABCD,∴以点O为原点,以向量,,的方向为x,y,z轴正方向,建立空间直角坐标系O﹣xyz,如图2,设AB=2,在等腰梯形ABCD中,AD=2,DC=4,,在等边三角形△P AB中,,∴A(0,﹣1,0),B(0,1,0),,,∵E为PD中点,∴,∴,,.设平面BAE的法向量为,则,即,取z1=﹣1,得,设平面P AE的法向量为,则,即,取z2=﹣1,得,设二面角B﹣AE﹣P为θ,有,∴,∴二面角B﹣AE﹣P的正弦值为.29.【解答】解:(1)证明:∵PD⊥底面ABCD,BC⊂底面ABCD,∴BC⊥PD,∵底面ABCD为平行四边形,AB=2AD=4,PD=BD=AD,∴BD2+BC2=CD2,∴BC⊥BD,∵PD∩BD=D,∴BC⊥平面PBD.(2)解:以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,则A(2,0,0),P(0,0,2),B(0,2,0),C(﹣2,2,0),Q(﹣1,,),=(2,0,﹣2),=(0,2,﹣2),=(﹣1,,﹣),设平面PBQ的法向量=(x,y,z),则,取y=1,得=(0,1,1),cos<>===,sin<>==,S△PBQ==,点A到平面PBQ的距离d===,∴三棱锥A﹣PBQ的体积V A﹣PBQ===2.30.【解答】(Ⅰ)证明:过D作DO⊥AE,垂足为O,连接OB,∵AD=2,∠DAO=45°,∴OD=OA=,在△AOB中,由余弦定理可得OB2=OA2+AB2﹣2OA•AB•cos∠OAB=2+4﹣2××2×=2,∴OB=,∵AB=AD=2,∠DAB=60°,∴△ABD是等边三角形,∴BD=2.∴OD2+OB2=BD2,则OB⊥OD,又OD⊥AE,AE∩OB=O,∴OD⊥平面ABE,而OD⊂平面ADE,∴平面ADE⊥平面ABE;(Ⅱ)由(Ⅰ)知AO=OB=,AB=2,∴OA2+OB2=AB2,得OA⊥OB,∵OD⊥平面ABE,∴∠DEO为直线ED与平面ABE所成的角.以O为原点,以OB,OE,OD为坐标轴建立空间直角坐标系O﹣xyz,则A(0,﹣,0),B(,0,0),D(0,0,),设E(0,t,0)(t>0),∴=(,,0),=(0,t,﹣),设平面CDE的法向量为=(x,y,z),则,令y=1,得,∵OD⊥平面ABE,∴=(0,0,1)为平面ABE的一个法向量,由平面DCE与平面ABE所成锐二面角的余弦值,得|cos<>|===,解得t=.∴tan∠DEO=,得∠DEO=30°.故直线DE与平面ABE所成角正弦值为.31.【解答】(Ⅰ)证明:取BC的中点F,连接EF、AF,因为E、F是PB,BC的中点,所以EF∥PC且=1,又因为△ACB和△DAC是等腰三角形,AB=,所以AD=AC=BC=1,又因为DA∥PC,所以四边形ADEF是平行四边形,故DE∥AF,又因为AF⊂面ABC,DE⊄平面ABC,所以DE∥平面ABC.(Ⅱ)解:因为AC⊥BC,AC⊥PC,所以AC⊥面PBC,又因为DA∥PC,所以D到面PBC高等于|AC|,又因为S△BCE=,所以.32.【解答】解:(Ⅰ)当B1C为圆柱OO1的母线时,BC⊥AB1.证明如下:在上取点C,使B1C为圆柱的母线,连接AC,则B1C⊥BC,∵AB为圆O的直径,∴BC⊥AC,∵B1C∩AC=C,B1C⊂平面AB1C,AC⊂平面AB1C,∴BC⊥平面AB1C,∵AB1⊂平面AB1C,∴BC⊥AB1.(Ⅱ)由弧,的长为可得,AC=A1C1=1,∴,所以,∵BC==,BB1==,BO1==,∴cos∠BO1B1==﹣,∴sin∠BO1B1=,∴S==,设A1到平面BO1B1的距离为h,则V==,解得h=.∴A1到平面BO1B1的距离是.33.【解答】(1)证明:取PB的中点G,连接EG,FG,则FG∥BC,且FG=BC,∵四边形ABCD是正方形,E是AD的中点,∴DE∥BC,DE=BC,∴FG∥DE且FG=DE,∴四边形DEGF为平行四边形,∴DF∥EG,又DF⊄平面PBE,EG⊂平面PBE,∴DF∥平面PBE.(2)解:∵BD=DC=2,PD=2,∴PB==2,又AE=DE=1,AB=PD=2,∴BE=PE=,∴△PBE的边PB上的高为h==,∴S△PBE==,设D到平面PBE的距离为d,则V D﹣PBE==.又V D﹣PBE=V P﹣BDE==.∴d=.设PD与平面PBE所成角为α,则sinα==.故直线PD与平面PBE所成角的正弦值为.34.【解答】(1)证明:∵AC⊥BD,BC=CD,∴Rt△OBC≌Rt△ODC,∴OB=OD,即O为BD的中点,又Q是PD的中点,∴OQ∥PB,又PB⊂平面P AB,OQ⊄平面P AB,∴OQ∥平面P AB.(2)解:∵M是PC的中点,P A⊥平面ABCD,∴M到平面ABCD的距离为P A=,∵AB⊥BC,AB=1,AC=2,∴BC=,OB==,∴BD=2OB=,OA=,∴V M﹣ABD==,∵PB==,BC=,PC==,∴PB2+BC2=PC2,∴PB⊥BC,∴BM=PC=.同理可得DM=,又BD=,∴cos∠BMD==﹣,∴sin∠BMD=,∴S△BMD==.设A到平面BMD的距离为h,则V A﹣BMD==,解得h=.故点A到平面MBD的距离为.35.【解答】(1)证明:取BC的中点F,连接EF、AF,因为E、F分别是PB、BC的中点,所以EF∥PC且.因为AC⊥BC,△ACB和△DAC是等腰三角形,,所以DA=AC=BC=2,即DA=PC,又因为DA∥PC,所以DA∥EF,DA=EF,所以四边形ADEF是平行四边形,所以DE ∥AF因为AF⊂面ABC,DE⊄面ABC,所以DE∥平面ABC.(2)解:因为AC⊥BC,AC⊥PC,BC∩PC=C,BC、PC⊂面PBC,所以AC⊥面PBC,因为DA∥PC,所以点D到面PBC的距离为AC=2.因为DA⊥平面ABC,DA∥PC,所以PC⊥平面ABC,所以PC⊥BC,所以EF⊥BC,所以S△BCE=EF•BC=××4×2=2.因为PC⊥BC,AC⊥BC,PC∩AC=C,PC、AC⊂平面ACD,所以BC⊥平面ACD,所以BC⊥CD,所以S△BCD=BC•CD=2×=.设点E到平面BCD的距离为d,∵V E﹣BCD=V D﹣BCE,∴d•S△BCD=AC•S△BCE,即d•=2•2,解得d=,所以点E到平面BCD的距离,∵DE=AF===,设DE与平面BCD所成角为θ,则,故DE与平面BCD所成角的正弦值为.36.【解答】(1)证明:连接DM,∵AB=BC=,∠ABC=90°,且M是AC的中点,∴BM⊥AC,BM=1,AC=2,∵∠ADC=90°,∠DCA=60°,M是AC得中点,∴DM=AC=1,又DB=,∴DM2+BM2=DB2,∴DM⊥BM,又DM∩AC=M,∴BM⊥平面ACD,∴BM⊥DC.(2)解:∵AD=,AB=BD=,∴cos∠ABD==,sin∠ABD=,∴S△ABD==,设M到平面ABD的距离为h,则V M﹣ABD==h,又V M﹣ABD=V B﹣ADM=S△ADM•BM=•S△ACD•BM=××1×1=.∴h=,解得h=.设BM与平面ADB所成角为α,则sinα==,故BM与平面ADB所成角的正弦值为.37.【解答】(1)证明:设AC∩BE=O,则O为AC的中点,∵P A=PC,∴PO⊥AC.由正六边形的性质可知,AC⊥BE.∵PO∩BE=O,PO、BE⊂平面PBE,∴AC⊥平面PBE,∵AC⊂平面P AC,∴平面P AC⊥平面PBE.。
三年 (2020-2022 ) 新高考数学真题汇编 专题04立体几何

新高考专题04立体几何【2022年新高考1卷】1.南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m . 2.65)( )A .931.010m ⨯B .931.210m ⨯C .931.410m ⨯D .931.610m ⨯【答案】C 【解析】 【分析】根据题意只要求出棱台的高,即可利用棱台的体积公式求出. 【详解】依题意可知棱台的高为157.5148.59MN =-=(m),所以增加的水量即为棱台的体积V . 棱台上底面积262140.014010S ==⨯km m ,下底面积262180.018010S '==⨯km m ,∴((66119140101801033V h S S =+=⨯⨯⨯+⨯+'(()679933320109618 2.6510 1.43710 1.410(m )=⨯+⨯≈+⨯⨯=⨯≈⨯.故选:C .【2022年新高考1卷】2.已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤则该正四棱锥体积的取值范围是( )A .8118,4⎡⎤⎢⎥⎣⎦B .2781,44⎡⎤⎢⎥⎣⎦C .2764,43⎡⎤⎢⎥⎣⎦D .[18,27]【答案】C 【解析】 【分析】设正四棱锥的高为h ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围. 【详解】∴ 球的体积为36π,所以球的半径3R =,设正四棱锥的底面边长为2a ,高为h , 则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭,所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l ≤0V '<,所以当l =时,正四棱锥的体积V 取最大值,最大值为643,又3l =时,274V =,l =814V =,所以正四棱锥的体积V 的最小值为274,所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C.【2022年新高考2卷】3.已知正三棱台的高为1,上、下底面边长分别为则该球的表面积为( ) A .100π B .128π C .144π D .192π【答案】A 【解析】 【分析】根据题意可求出正三棱台上下底面所在圆面的半径12,r r ,再根据球心距,圆面半径,以及球的半径之间的关系,即可解出球的半径,从而得出球的表面积. 【详解】设正三棱台上下底面所在圆面的半径12,r r ,所以123432,260sin 60r r ==,即123,4r r ==,设球心到上下底面的距离分别为12,d d ,球的半径为R ,所以1d 2d =故121d d -=或121d d +=,1=1=,解得225R =符合题意,所以球的表面积为24π100πS R ==. 故选:A .【2021年新高考1卷】4)A .2B .C .4D .【答案】B 【解析】 【分析】设圆锥的母线长为l ,根据圆锥底面圆的周长等于扇形的弧长可求得l 的值,即为所求. 【详解】设圆锥的母线长为l ,由于圆锥底面圆的周长等于扇形的弧长,则2l ππ=解得l = 故选:B.【2021年新高考2卷】5.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )A.20+B .C .563D 【答案】D 【解析】 【分析】由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解. 【详解】作出图形,连接该正四棱台上下底面的中心,如图,因为该四棱台上下底面边长分别为2,4,侧棱长为2,所以该棱台的高h下底面面积116S =,上底面面积24S =,所以该棱台的体积((121116433V h S S =+=+ 故选:D.【2020年新高考1卷(山东卷)】6.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40°,则晷针与点A 处的水平面所成角为( )A .20°B .40°C .50°D .90°【答案】B【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图,根据面面平行的性质定理和线面垂直的定义判定有关截线的关系,根据点A 处的纬度,计算出晷针与点A 处的水平面所成角. 【详解】画出截面图如下图所示,其中CD 是赤道所在平面的截线;l 是点A 处的水平面的截线,依题意可知OA l ⊥;AB 是晷针所在直线.m 是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥.. 由于40,//AOC m CD ∠=︒,所以40OAG AOC ∠=∠=︒, 由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒,所以40BAE OAG ∠=∠=︒,也即晷针与点A 处的水平面所成角为40BAE ∠=︒. 故选:B【点睛】本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质,属于中档题.【2022年新高考1卷】7.已知正方体1111ABCD A B C D -,则( ) A .直线1BC 与1DA 所成的角为90︒ B .直线1BC 与1CA 所成的角为90︒ C .直线1BC 与平面11BB D D 所成的角为45︒ D .直线1BC 与平面ABCD 所成的角为45︒【答案】ABD【分析】数形结合,依次对所给选项进行判断即可. 【详解】如图,连接1B C 、1BC ,因为11//DA B C ,所以直线1BC 与1B C 所成的角即为直线1BC 与1DA 所成的角,因为四边形11BB C C 为正方形,则1B C ⊥1BC ,故直线1BC 与1DA 所成的角为90︒,A 正确;连接1A C ,因为11A B ⊥平面11BB C C ,1BC ⊂平面11BB C C ,则111A B BC ⊥, 因为1B C ⊥1BC ,1111A B B C B =,所以1BC ⊥平面11A B C ,又1AC ⊂平面11A B C ,所以11BC CA ⊥,故B 正确; 连接11A C ,设1111AC B D O =,连接BO ,因为1BB ⊥平面1111D C B A ,1C O ⊂平面1111D C B A ,则11C O B B ⊥, 因为111C O B D ⊥,1111B D B B B ⋂=,所以1C O ⊥平面11BB D D , 所以1C BO ∠为直线1BC 与平面11BB D D 所成的角,设正方体棱长为1,则1C O =1BC 1111sin 2C O C BO BC ∠==, 所以,直线1BC 与平面11BB D D 所成的角为30,故C 错误;因为1C C ⊥平面ABCD ,所以1C BC ∠为直线1BC 与平面ABCD 所成的角,易得145C BC ∠=,故D 正确. 故选:ABD【2022年新高考2卷】8.如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为123,,V V V ,则( )A .322V V =B .31V V =C .312V V V =+D .3123V V =【答案】CD 【解析】 【分析】直接由体积公式计算12,V V ,连接BD 交AC 于点M ,连接,EM FM ,由3A EFM C EFM V V V --=+计算出3V ,依次判断选项即可. 【详解】设22AB ED FB a ===,因为ED ⊥平面ABCD ,FB ED ,则()2311114223323ACDV ED Sa a a =⋅⋅=⋅⋅⋅=, ()232111223323ABCV FB Sa a a =⋅⋅=⋅⋅⋅=,连接BD 交AC 于点M ,连接,EM FM ,易得BD AC ⊥,又ED ⊥平面ABCD ,AC ⊂平面ABCD ,则ED AC ⊥,又ED BD D =,,ED BD ⊂平面BDEF ,则AC ⊥平面BDEF ,又12BM DM BD ==,过F 作FG DE ⊥于G ,易得四边形BDGF 为矩形,则,FG BD EG a ===,则,EM FM ==,3EF a =,222EM FM EF +=,则EM FM ⊥,212EFMS EM FM =⋅=,AC =, 则33123A EFM C EFM EFMV V V AC S a --=+=⋅=,则3123V V =,323V V =,312V V V =+,故A 、B 错误;C 、D 正确. 故选:CD.【2021年新高考1卷】9.在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中[]0,1λ∈,[]0,1μ∈,则( )A .当1λ=时,1AB P △的周长为定值B .当1μ=时,三棱锥1P A BC -的体积为定值 C .当12λ=时,有且仅有一个点P ,使得1A P BP ⊥ D .当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P 【答案】BD 【解析】 【分析】对于A ,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;对于B ,将P 点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值; 对于C ,考虑借助向量的平移将P 点轨迹确定,进而考虑建立合适的直角坐标系来求解P 点的个数;对于D ,考虑借助向量的平移将P 点轨迹确定,进而考虑建立合适的直角坐标系来求解P 点的个数.【详解】易知,点P 在矩形11BCC B 内部(含边界).对于A ,当1λ=时,11=BP BC BB BC CC μμ=++,即此时P ∈线段1CC ,1AB P △周长不是定值,故A 错误;对于B ,当1μ=时,1111=BP BC BB BB BC λλ=++,故此时P 点轨迹为线段11B C ,而11//B C BC ,11//B C 平面1A BC ,则有P 到平面1A BC 的距离为定值,所以其体积为定值,故B 正确.对于C ,当12λ=时,112BP BC BB μ=+,取BC ,11B C 中点分别为Q ,H ,则BP BQ QH μ=+,所以P 点轨迹为线段QH ,不妨建系解决,建立空间直角坐标系如图,1A ⎫⎪⎪⎝⎭,()0,0P μ,,10,,02B ⎛⎫⎪⎝⎭,则112A P μ⎛⎫=-- ⎪ ⎪⎝⎭,10,,2BP μ⎛⎫=- ⎪⎝⎭,()110A P BP μμ⋅=-=,所以0μ=或1μ=.故,H Q 均满足,故C 错误; 对于D ,当12μ=时,112BP BC BB λ=+,取1BB ,1CC 中点为,M N .BP BM MN λ=+,所以P 点轨迹为线段MN .设010,,2P y ⎛⎫ ⎪⎝⎭,因为0,0A ⎫⎪⎪⎝⎭,所以01,2AP y ⎛⎫=- ⎪ ⎪⎝⎭,11,12A B ⎛⎫=-- ⎪ ⎪⎝⎭,所以00311104222y y +-=⇒=-,此时P 与N 重合,故D 正确. 故选:BD .【点睛】本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.【2021年新高考2卷】10.如图,在正方体中,O 为底面的中心,P 为所在棱的中点,M ,N 为正方体的顶点.则满足MN OP ⊥的是( )A .B .C .D .【答案】BC 【解析】 【分析】根据线面垂直的判定定理可得BC 的正误,平移直线MN 构造所考虑的线线角后可判断AD 的正误. 【详解】设正方体的棱长为2,对于A ,如图(1)所示,连接AC ,则//MN AC , 故POC ∠(或其补角)为异面直线,OP MN 所成的角,在直角三角形OPC ,OC =1CP =,故tanPOC ∠== 故MN OP ⊥不成立,故A 错误.对于B ,如图(2)所示,取NT 的中点为Q ,连接PQ ,OQ ,则OQ NT ⊥,PQ MN ⊥, 由正方体SBCM NADT -可得SN ⊥平面ANDT ,而OQ ⊂平面ANDT , 故SN OQ ⊥,而SNMN N =,故OQ ⊥平面SNTM ,又MN ⊂平面SNTM ,OQ MN ⊥,而OQ PQ Q =,所以MN ⊥平面OPQ ,而PO ⊂平面OPQ ,故MN OP ⊥,故B 正确.对于C ,如图(3),连接BD ,则//BD MN ,由B 的判断可得OP BD ⊥, 故OP MN ⊥,故C 正确.对于D ,如图(4),取AD 的中点Q ,AB 的中点K ,连接,,,,AC PQ OQ PK OK , 则//AC MN ,因为DP PC =,故//PQ AC ,故//PQ MN ,所以QPO ∠或其补角为异面直线,PO MN 所成的角,因为正方体的棱长为2,故12PQ AC ==OQ ==PO =222QO PQ OP <+,故QPO ∠不是直角,故,PO MN 不垂直,故D 错误. 故选:BC.【2020年新高考1卷(山东卷)】11.已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∴BAD =60°.以1D 球面与侧面BCC 1B 1的交线长为________.. 【解析】 【分析】根据已知条件易得1D E =1D E ⊥侧面11B C CB ,可得侧面11B C CB 与球面的交线上的点到E 可得侧面11B C CB 与球面的交线是扇形EFG 的弧FG ,再根据弧长公式可求得结果. 【详解】 如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A B C D -的棱长均为2,所以∴111D B C 为等边三角形,所以1D E 111D E B C ⊥,又四棱柱1111ABCD A B C D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11B C CB ,设P 为侧面11B C CB 与球面的交线上的点,则1D E EP ⊥,1D E =||EP ==所以侧面11B C CB 与球面的交线上的点到E因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG , 因为114B EFC EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得2FG π==.. 【点睛】本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,属于中档题. 【2020年新高考2卷(海南卷)】12.已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,则三棱锥A -NMD 1的体积为____________ 【答案】13【解析】 【分析】利用11A NMD D AMN V V --=计算即可. 【详解】因为正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点 所以11111112323A NMD D AMN V V --==⨯⨯⨯⨯=故答案为:13【点睛】在求解三棱锥的体积时,要注意观察图形的特点,看把哪个当成顶点好计算一些. 【2022年新高考1卷】13.如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1A C 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C --的正弦值.【答案】【解析】 【分析】(1)由等体积法运算即可得解;(2)由面面垂直的性质及判定可得BC ⊥平面11ABB A ,建立空间直角坐标系,利用空间向量法即可得解. (1)在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h ,则111111112211433333A A BC A A ABC A ABC AB BC C C B V Sh h V S A A V ---=⋅===⋅==,解得h =所以点A 到平面1A BC (2)取1A B 的中点E ,连接AE ,如图,因为1AA AB =,所以1AE A B ⊥, 又平面1A BC ⊥平面11ABB A ,平面1A BC平面111ABB A A B =,且AE ⊂平面11ABB A ,所以AE ⊥平面1A BC , 在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥, 又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A ,所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE 12AA AB ==,1A B =2BC =, 则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1A C 的中点()1,1,1D , 则()1,1,1BD =,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩,可取()1,0,1m =-,设平面BDC 的一个法向量(),,n a b c =,则020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩, 可取()0,1,1n =-, 则11cos ,22m n m n m n⋅===⨯⋅,所以二面角A BD C --.【2022年新高考2卷】14.如图,PO 是三棱锥P ABC -的高,PA PB =,AB AC ⊥,E 是PB 的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B --的正弦值. 【答案】(1)证明见解析 (2)1113【解析】 【分析】(1)连接BO 并延长交AC 于点D ,连接OA 、PD ,根据三角形全等得到OA OB =,再根据直角三角形的性质得到AO DO =,即可得到O 为BD 的中点从而得到//OE PD ,即可得证; (2)建立适当的空间直角坐标系,利用空间向量法求出二面角的余弦的绝对值,再根据同角三角函数的基本关系计算可得. (1)证明:连接BO 并延长交AC 于点D ,连接OA 、PD ,因为PO 是三棱锥P ABC -的高,所以PO ⊥平面ABC ,,AO BO ⊂平面ABC , 所以PO AO ⊥、PO BO ⊥,又PA PB =,所以POA POB ≅△△,即OA OB =,所以OAB OBA ∠=∠,又AB AC ⊥,即90BAC ∠=︒,所以90OAB OAD ∠+∠=︒,90OBA ODA ∠+∠=︒, 所以ODA OAD ∠=∠所以AO DO =,即AO DO OB ==,所以O 为BD 的中点,又E 为PB 的中点,所以//OE PD , 又OE ⊄平面PAC ,PD ⊂平面PAC , 所以//OE 平面PAC(2)解:过点A 作//Az OP ,如图建立平面直角坐标系, 因为3PO =,5AP =,所以4OA ==,又30OBA OBC ∠=∠=︒,所以28BD OA ==,则4=AD,AB = 所以12AC =,所以()O,()B,()P ,()0,12,0C ,所以32E ⎛⎫ ⎪⎝⎭,则332AE ⎛⎫= ⎪⎝⎭,()4AB =,()0,12,0AC =,设平面AEB 的法向量为(),,n x y z =,则33302430n AE y z n AB ⎧⋅=++=⎪⎨⎪⋅==⎩,令2z =,则3y =-,0x =,所以()0,3,2n =-;设平面AEC 的法向量为(),,m a b c =,则33302120m AE ab c m AC b ⎧⋅=++=⎪⎨⎪⋅==⎩,令a =6c =-,0b =,所以()3,0,6m =-;所以cos ,13n m n m n m⋅-===设二面角C AE B --的大小为θ,则43cos cos ,=13n m θ=,所以11sin 13θ==,即二面角C AE B --的正弦值为1113.【2021年新高考1卷】15.如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.【答案】(1)证明见解析; 【解析】【分析】(1)由题意首先证得线面垂直,然后利用线面垂直的定义证明线线垂直即可;(2)方法二:利用几何关系找到二面角的平面角,然后结合相关的几何特征计算三棱锥的体积即可. 【详解】(1)因为AB AD =,O 是BD 中点,所以OA BD ⊥, 因为OA ⊂平面ABD ,平面ABD ⊥平面BCD , 且平面ABD ⋂平面BCD BD =,所以OA ⊥平面BCD . 因为CD ⊂平面BCD ,所以OA CD ⊥. (2)[方法一]:通性通法—坐标法如图所示,以O 为坐标原点,OA 为z 轴,OD 为y 轴,垂直OD 且过O 的直线为x 轴,建立空间直角坐标系O xyz -,则1,0),(0,1,0),(0,1,0)2C D B -,设12(0,0,),(0,,)33A m E m ,所以4233(0,,),(,,0)3322EB m BC =--=,设(),,n x y z =为平面EBC 的法向量,则由00EB n EC n ⎧⋅=⎨⋅=⎩可求得平面EBC 的一个法向量为2(3,1,)n m =--.又平面BCD 的一个法向量为()0,0,OA m =,所以cos ,n OA ==1m =. 又点C 到平面ABD112132A BCD C ABD V V --==⨯⨯⨯=, 所以三棱锥A BCD -[方法二]【最优解】:作出二面角的平面角 如图所示,作EG BD ⊥,垂足为点G .作GF BC ⊥,垂足为点F ,连结EF ,则OA EG ∥.因为OA ⊥平面BCD ,所以EG ⊥平面BCD ,EFG 为二面角E BC D --的平面角.因为45EFG ∠=︒,所以EG FG =. 由已知得1OB OD ==,故1OB OC ==.又30OBC OCB ∠=∠=︒,所以BC =因为24222,,,,133333GD GB FG CD EG OA ======,111122(11)13332A BCD BCDBOCV SO S OA A -==⨯⨯=⨯⨯⨯⨯⨯=. [方法三]:三面角公式考虑三面角B EDC -,记EBD ∠为α,EBC ∠为β,30DBC ∠=︒, 记二面角E BC D --为θ.据题意,得45θ=︒. 对β使用三面角的余弦公式,可得cos cos cos30βα=⋅︒,化简可得cos βα=.∴使用三面角的正弦公式,可得sin sin sin αβθ=,化简可得sin βα.∴ 将∴∴两式平方后相加,可得223cos 2sin 14αα+=,由此得221sin cos 4αα=,从而可得1tan 2α=±.如图可知π(0,)2α∈,即有1tan 2α=,根据三角形相似知,点G 为OD 的三等分点,即可得43BG =, 结合α的正切值,可得2,13EG OA ==从而可得三棱锥A BCD -【整体点评】(2)方法一:建立空间直角坐标系是解析几何中常用的方法,是此类题的通性通法,其好处在于将几何问题代数化,适合于复杂图形的处理;方法二:找到二面角的平面角是立体几何的基本功,在找出二面角的同时可以对几何体的几何特征有更加深刻的认识,该法为本题的最优解.方法三:三面角公式是一个优美的公式,在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速. 【2021年新高考2卷】16.在四棱锥Q ABCD -中,底面ABCD 是正方形,若2,3AD QD QA QC ====.(1)证明:平面QAD ⊥平面ABCD ; (2)求二面角B QD A --的平面角的余弦值. 【答案】(1)证明见解析;(2)23. 【解析】 【分析】(1)取AD 的中点为O ,连接,QO CO ,可证QO ⊥平面ABCD ,从而得到面QAD ⊥面ABCD . (2)在平面ABCD 内,过O 作//OT CD ,交BC 于T ,则OT AD ⊥,建如图所示的空间坐标系,求出平面QAD 、平面BQD 的法向量后可求二面角的余弦值. 【详解】(1)取AD 的中点为O ,连接,QO CO . 因为QA QD =,OA OD =,则QO ⊥AD ,而2,AD QA ==2QO ==.在正方形ABCD 中,因为2AD =,故1DO =,故CO =因为3QC =,故222QC QO OC =+,故QOC 为直角三角形且QO OC ⊥, 因为OCAD O =,故QO ⊥平面ABCD ,因为QO ⊂平面QAD ,故平面QAD ⊥平面ABCD .(2)在平面ABCD 内,过O 作//OT CD ,交BC 于T ,则OT AD ⊥, 结合(1)中的QO ⊥平面ABCD ,故可建如图所示的空间坐标系.则()()()0,1,0,0,0,2,2,1,0D Q B -,故()()2,1,2,2,2,0BQ BD =-=-.设平面QBD 的法向量(),,n x y z =,则00n BQ n BD ⎧⋅=⎨⋅=⎩即220220x y z x y -++=⎧⎨-+=⎩,取1x =,则11,2y z ==,故11,1,2n ⎛⎫= ⎪⎝⎭.而平面QAD 的法向量为()1,0,0m =,故12cos ,3312m n ==⨯.二面角B QD A --的平面角为锐角,故其余弦值为23. 【2020年新高考1卷(山东卷)】17.如图,四棱锥P -ABCD 的底面为正方形,PD ∴底面ABCD .设平面P AD 与平面PBC 的交线为l .(1)证明:l ∴平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值. 【答案】(1)证明见解析;(2. 【解析】 【分析】(1)利用线面垂直的判定定理证得AD ⊥平面PDC ,利用线面平行的判定定理以及性质定理,证得//AD l ,从而得到l ⊥平面PDC ;(2)方法一:根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点(,0,1)Q m ,之后求得平面QCD 的法向量以及向量PB 的坐标,求得cos ,n PB <>的最大值,即为直线PB 与平面QCD 所成角的正弦值的最大值. 【详解】 (1)证明:在正方形ABCD 中,//AD BC ,因为AD ⊄平面PBC ,BC ⊂平面PBC , 所以//AD 平面PBC,又因为AD ⊂平面PAD ,平面PAD 平面PBC l =,所以//AD l ,因为在四棱锥P ABCD -中,底面ABCD 是正方形,所以,,AD DC l DC ⊥∴⊥且PD ⊥平面ABCD ,所以,,AD PD l PD ⊥∴⊥ 因为CD PD D =,所以l ⊥平面PDC . (2)[方法一]【最优解】:通性通法因为,,DP DA DC 两两垂直,建立空间直角坐标系D xyz -,如图所示:因为1PD AD ==,设(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B , 设(,0,1)Q m ,则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-, 设平面QCD 的法向量为(,,)n x y z =,则00DC n DQ n ⎧⋅=⎨⋅=⎩,即00y mx z =⎧⎨+=⎩,令1x =,则z m =-,所以平面QCD 的一个法向量为(1,0,)n m =-,则 1cos ,3n PB n PB n PB⋅+<>==根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线PB 与平面QCD 所成角的正弦值等于|cos ,|n PB <>==≤,当且仅当1m =时取等号,所以直线PB 与平面QCD . [方法二]:定义法如图2,因为l ⊂平面PBC ,Q l ∈,所以Q ∈平面PBC .在平面PQC 中,设PB QC E =.在平面PAD 中,过P 点作PF QD ⊥,交QD 于F ,连接EF . 因为PD ⊥平面,ABCD DC ⊂平面ABCD ,所以DC PD ⊥. 又由,,DC AD ADPD D PD ⊥=⊂平面PAD ,AD ⊂平面PAD ,所以DC ⊥平面PAD .又PF ⊂平面PAD ,所以DC PF ⊥.又由,,PF QD QDDC D QD ⊥=⊂平面,QOC DC ⊂平面QDC ,所以PF ⊥平面QDC ,从而FEP ∠即为PB 与平面QCD 所成角.设PQ a =,在PQD △中,易求PF =由PQE 与BEC △相似,得1PE PQ a EB BC ==,可得PE =所以sin FEP ∠=≤1a =时等号成立. [方法三]:等体积法如图3,延长CB 至G ,使得BG PQ =,连接GQ ,GD ,则//PB QG ,过G 点作GM ⊥平面QDC ,交平面QDC 于M ,连接QM ,则GQM ∠即为所求.设PQ x =,在三棱锥Q DCG -中,111()(1)326Q DCG V PD CD CB BG x -=⋅⋅+=+.在三棱锥G QDC -中,111323G QDC V GM CD QD GM -=⋅⋅=由Q DCG G QDC V V --=得11(1)63x GM +=解得GM ==, 当且仅当1x =时等号成立.在Rt PDB △中,易求PB QG ==,所以直线PB 与平面QCD 所成角的正弦值的最大值为sin MQG ∠== 【整体点评】(2)方法一:根据题意建立空间直角坐标系,直线PB 与平面QCD 所成角的正弦值即为平面QCD 的法向量n 与向量PB 的夹角的余弦值的绝对值,即cos ,n PB <>,再根据基本不等式即可求出,是本题的通性通法,也是最优解;方法二:利用直线与平面所成角的定义,作出直线PB 与平面QCD 所成角,再利用解三角形以及基本不等式即可求出;方法三:巧妙利用//PB QG ,将线转移,再利用等体积法求得点面距,利用直线PB 与平面QCD 所成角的正弦值即为点面距与线段长度的比值的方法,即可求出. 【2020年新高考2卷(海南卷)】18.如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD .设平面P AD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,QB ,求PB 与平面QCD 所成角的正弦值.【答案】(1)证明见解析;(2. 【解析】 【分析】(1)利用线面平行的判定定理以及性质定理,证得//AD l ,利用线面垂直的判定定理证得AD ⊥平面PDC ,从而得到l ⊥平面PDC ;(2)根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点(,0,1)Q m ,之后求得平面QCD 的法向量以及向量PB 的坐标,求得cos ,n PB <>,即可得到直线PB 与平面QCD 所成角的正弦值.【详解】 (1)证明:在正方形ABCD 中,//AD BC , 因为AD ⊄平面PBC ,BC ⊂平面PBC , 所以//AD 平面PBC ,又因为AD ⊂平面PAD ,平面PAD 平面PBC l =, 所以//AD l ,因为在四棱锥P ABCD -中,底面ABCD 是正方形,所以,,AD DC l DC ⊥∴⊥ 且PD ⊥平面ABCD ,所以,,AD PD l PD ⊥∴⊥ 因为CD PD D = 所以l ⊥平面PDC ;(2)如图建立空间直角坐标系D xyz -,因为1PD AD ==,则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B , 设(,0,1)Q m ,则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-,因为QB 1m = 设平面QCD 的法向量为(,,)n x y z =,则00DC n DQ n ⎧⋅=⎨⋅=⎩,即00y x z =⎧⎨+=⎩,令1x =,则1z =-,所以平面QCD 的一个法向量为(1,0,1)n =-,则2cos ,1n PB n PB n PB⋅<>==== 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于6|cos ,|3n PB <>=所以直线PB 与平面QCD 【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有线面平行的判定和性质,线面垂直的判定和性质,利用空间向量求线面角,利用基本不等式求最值,属于中档题目.。
2024年高考数学立体几何复习试卷及答案解析

2024年高考数学立体几何复习试卷及答案
一、选择题
1.已知直线l和平面α,若l∥α,P∈α,则过点P且平行于l的直线()
A.只有一条,不在平面α内
B.只有一条,且在平面α内
C.有无数条,一定在平面α内
D.有无数条,不一定在平面α内
答案B
解析假设过点P且平行于l的直线有两条m与n,则m∥l且n∥l,由平行公理得m∥n,这与两条直线m与n相交与点P相矛盾,故过点P且平行于l的直线只有一条,又因为点P 在平面内,所以过点P且平行于l的直线只有一条且在平面内.故选B.
2.设m,n为两条不同的直线,α为平面,则下列结论正确的是()
A.m⊥n,m∥α⇒n⊥αB.m⊥n,m⊥α⇒n∥α
C.m∥n,m⊥α⇒n⊥αD.m∥n,m∥α⇒n∥α
答案C
解析对于A,若m⊥n,m∥α时,可能n⊂α或斜交,故错误;
对于B,m⊥n,m⊥α⇒n∥α或n⊂α,故错误;
对于C,m∥n,m⊥α⇒n⊥α,正确;
对于D,m∥n,m∥α⇒n∥α或n⊂α,故错误.
故选C.
3.已知l⊥平面α,直线m⊂平面β.有下面四个命题:
①α∥β⇒l⊥m;②α⊥β⇒l∥m;
③l∥m⇒α⊥β;④l⊥m⇒α∥β.
其中正确的命题是()
A.①②B.③④
C.②④D.①③
答案D
解析∵l⊥α,α∥β,∴l⊥β,∵m⊂β,∴l⊥m,故①正确;∵l∥m,l⊥α,∴m⊥α,又∵m⊂β,∴α⊥β,故③正确.
4.如图所示,在四面体D-ABC中,若AB=BC,AD=CD,E是AC的中点,则下列命题中正确的是()
第1页共11页。
2020年高考数学 立体几何试题分类汇编 理
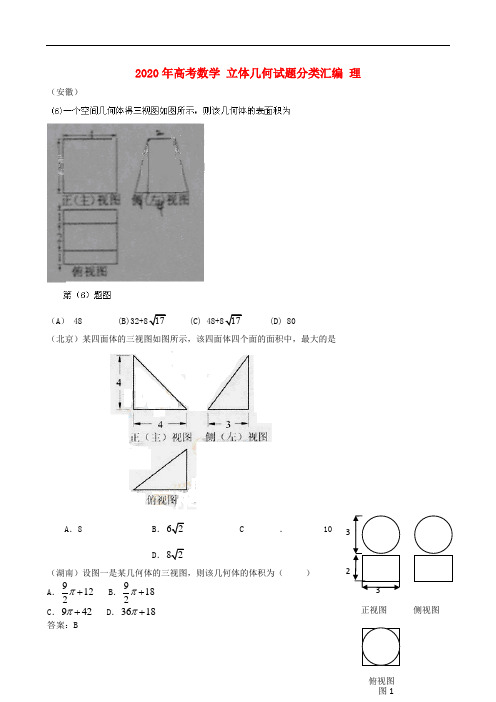
2020年高考数学 立体几何试题分类汇编 理(安徽)(A ) 48 (B)32+817 (C) 48+817 (D) 80(北京)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A .8B .62C.10D .82(湖南)设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+ C .942π+ D .3618π+答案:B3 正视图侧视图解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
(广东)如图l —3.某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为A.63B.93C.123D.183(江西)已知321,,ααα是三个相互平行的平面,平面21,αα之间的距离为1d ,平面32,αα之间的距离为2d .直线l 与321,,ααα分别交于321,,P P P .那么”“3221P P P P =是”“21d d =的 ( ) A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件答案:C解析:平面321,,ααα平行,由图可以得知:如果平面距离相等,根据两个三角形全等可知3221P P P P = 如果3221P P P P =,同样是根据两个三角形全等可知21d d =(辽宁)如图,四棱锥S —ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确...的是 A .AC ⊥SB B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角(辽宁)已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,ο30=∠=∠BSC ASC ,则棱锥S —ABC的体积为 A .33B .32C .3D .1(全国2)已知直二面角l αβ--,点,A AC l α∈⊥,C 为垂足,,,B BD l D β∈⊥为垂足.若AB=2,AC=BD=1,则D 到平面ABC 的距离等于 (A)2 (B)3 (C)6 (D) 1 【思路点拨】本题关键是找出或做出点D 到平面ABC 的距离DE ,根据面面垂直的性质不难证明AC ⊥平面β,进而β⊥平面平面ABC,所以过D 作DE BC ⊥于E ,则DE 就是要求的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年高考数学模拟试卷汇编
专题4 立体几何(含答案解析)
1.(2020·河南省实验中学高三二测(理))现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知,64DAB BAC ππ∠=
∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为
( )
A 3
B .36
C 3
D 3 2.(2020·湖南省长沙市明达中学高三二模(理)魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”,刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为π:4.若正方体的棱长为2,则“牟合方盖”的体积为( )
A .16
B .163
C .163
D .1283 3.(2020·湖南省长沙市明达中学高三二模(理)关于三个不同平面,,αβγ与直线l ,下列命题中的假命题是( )
A .若αβ⊥,则α内一定存在直线平行于β
B .若α与β不垂直,则α内一定不存在直线垂直于β
C .若αγ⊥,βγ⊥,l αβ=I ,则l γ⊥
D .若αβ⊥,则α内所有直线垂直于β
4.(2020·江西省南昌市第十中学校高三模拟(理))榫卯是我国古代工匠极为精巧的发明,
它是在两个构件上采用凹凸部位相结合的一种连接方式。
广泛用于建筑,同时也广泛用于家具。
我国的北京紫禁城,山西悬空寺,福建宁德的廊桥等建筑都用到了榫卯结构,榫卯结构
中凸出部分叫榫(或叫榫头),已知某“榫头”的三视图如图所示,则该“榫头”的体积是( )
A .36
B .45
C .54
D .63
5.(2020·江西省名高三第二次大联考(理))某几何体的三视图如图所示,则该几何体的体积为( )
A .83π3
B .4π1633
C 16343π+
D .43π1636.(2020·江西省名高三第二次大联考(理))在平面五边形ABCD
E 中,60A ∠=︒,63AB AE ==BC CD ⊥,DE CD ⊥,且6BC DE ==.将五边形ABCDE 沿对角线BE 折起,使平面ABE 与平面BCDE 所成的二面角为120︒,则沿对角线BE 折起后所得几何体的外接球的表面积为( )
A .63π
B .84π
C .252π
D .126π
7.(2020·陕西省西安中学高三三模(理))某几何体的三视图如图所示,则该几何体的表面积为( )。
