一次函数与几何问题练习题
中考数学专题《一次函数与几何综合》高分必刷原卷

(培优特训)专项19.3 一一次函数与几何综合高分必刷1.(2023春•普兰店区期中)已知△ABC中,∠C=90°,AC=3,CD=4,BD =AD.点F从点A出发,沿AC﹣CD运动,速度为1cm/s,同时点E从点B 出发,沿BD﹣DA运动,运动速度为1cm/s,一个点到达终点,另一点也停止运动.(1)求BD的长;(2)设△AEF的面积为S,点P、Q运动时间为t,求S与的函数关系式,并写出的取值范围.2.(2023春•鼓楼区期中)如图1,已知直线l1:y=ax﹣6a交x轴于点A,交轴y于点B,直线l2:y=bx﹣18a交x轴于点C,交y轴于点D,交直线l1于点E.(1)求点A的坐标;(2)若点B为线段AE的中点,求证:EC=EA;(3)如图2,已知P(0,m),将线段P A绕点P逆时针方向旋转90°至PF,连接OF,求证:点F在某条直线上运动,并求OF的最小值.3.(2023春•苍南县期中)如图,在平面直角坐标系中,▱OABC的顶点A落在x轴上,点B的坐标为(7,4),AB=2,点D是OC的中点,点E是线段AD上一动点,EF⊥BC于点F,连结DF.(1)求点A、C的坐标.(2)求直线AD的函数表达式.(3)若△DEF是等腰三角形,求CF的长.4.(2023•佳木斯一模)如图,将矩形纸片OABC放在平面直角坐标系中,O为坐标原点.点A在y轴上,点C在x轴上,OA,OB的长是x2﹣16x+60=0的两个根,P是边AB上的一点,将△OAP沿OP折叠,使点A落在OB上的点Q处.(1)求点B的坐标;(2)求直线PQ的解析式;(3)点M在直线OP上,点N在直线PQ上,是否存在点M,N,使以A,C.M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.5.(2023春•顺德区校级月考)如图,请根据图象所提供的信息解答下列问题:(1)当x时,kx+b≥mx﹣n;(2)不等式kx+b<0的解集是;(3)求两个一次函数表达式;(4)若直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.6.(2023春•北碚区校级期中)如图,在平面直角坐标系中,直线y=2x﹣2与x 轴、y轴分别交于点A、点B,与直线CD:y=kx+b(k≠0)交于点P,OC =OD=4OA.(1)求直线CD的解析式;(2)连接OP、BC,若直线AB上存在一点Q,使得S△PQC =S四边形OBCP,求点Q的坐标;(3)将直线CD向下平移1个单位长度得到直线,直线l与x轴交于点E,点N为直线l上的一点,在平面直角坐标系中,是否存在点M,使以点O,E,N,M为顶点的四边形是矩形?若存在,请直接写出点M的坐标;若不存在,请说明理由.7.(2023春•宜兴市期中)如图,在平面直角坐标系中,已知A(0,4),点B、C都在x轴上,BC=12,AD∥BC,CD所在直线的函数表达式为y=﹣x+9,E是BC的中点,点P是BC边上一个动点.(1)当PB=时,以点P、A、D、E为顶点的四边形为平行四边形;(2)点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.8.(2023春•工业园区校级期中)如图,在平面直角坐标系中,点A、点B分别在x轴与y轴上,直线AB的解析式为,以线段AB、BC为边作平行四边形ABCD.(1)如图1,若点C的坐标为(3,7),判断四边形ABCD的形状,并说明理由;(2)如图2,在(1)的条件下,P为CD边上的动点,点C关于直线BP的对称点是Q,连接PQ,BQ.①当∠CBP=°时,点Q位于线段AD的垂直平分线上;②连接AQ,DQ,设CP=x,设PQ的延长线交AD边于点E,当∠AQD=90°时,求证:QE=DE,并求出此时x的值.9.(2023•沈阳一模)如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(﹣5,0),与y轴交于点A,直线过点A,与x轴交于点C,点P 是x轴上方一个动点.(1)求直线AB的函数表达式;(2)若点P在线段AB上,且S△APC =S△AOB,求点P的坐标;(3)当S△PBC =S△AOB时,动点M从点B出发,先运动到点P,再从点P运动到点C后停止运动.点M的运动速度始终为每秒1个单位长度,运动的总时间为t(秒),请直接写出t的最小值.10.(2023春•鼓楼区期中)如图1,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.(1)求直线BC的函数解析式;(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.①若△PQB的面积为,求点M的坐标;②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.11.(2023春•顺德区校级期中)一次函数y=kx+b的图象经过点A(﹣2,0)、B(﹣1,1),且和一次函数y=﹣2x+a的图象交于点C,如图所示.(1)填空:不等式kx+b<0的解集是;(2)若不等式kx+b>﹣2x+a的解集是x>1,求点C的坐标;(3)在(2)的条件下,点P是直线y=﹣2x+a上一动点.且在点C上方,当∠P AC=15°时,求点P的坐标.12.(2023春•重庆期中)如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C,D,且点D的坐标为(1,n).(1)则k=,b=,n=;(2)求四边形AOCD的面积;(3)在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形,请求出点P的坐标.13.(2023春•崇川区校级月考)模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.(1)求证:△BEC≌△CDA;(2)模型应用:已知直线l1:y=﹣x﹣4与y轴交于A点.将直线l1绕着A 点逆时针旋转45°至l2,如图2,求l2的函数解析式.14.(2023春•崇川区校级月考)如图,在平面直角坐标系中,直线l1:y=﹣x+4分别与x轴,y轴交于点B,C.直线l2:y=x.(1)直接写出点B,C的坐标:B,C.(2)若D是直线l2上的点,且△COD的面积为6,求直线CD的函数表达式;(3)在(2)的条件下,且当点D在第一象限时,设P是射线CD上的点,在平面内存在点Q.使以O,C,P,Q为顶点的四边形是菱形,请直接求点Q的坐标.15.(2023•城固县模拟)如图,A、B两个长方体水箱放置在同一水平桌面上,开始时水箱A中没有水,水箱B盛满水,现以6dm3/min的流量从水箱B中抽水注入水箱A中,直至水箱A注满水为止.设注水时间为t(min),水箱A 的水位高度为y A(dm),水箱B中的水位高度为y B(dm).(抽水水管的体积忽略不计)(1)分别求出y A,y B与t之间的函数表达式;(2)当水箱A与水箱B中的水的体积相等时,求出此时两水箱中水位的高度差.16.(2022秋•常州期末)在平面直角坐标系中,一次函数的图象l1与x轴交于点A,一次函数y=x+6的图象l2与x轴交于点B,与l1交于点P.直线l3过点A且与x轴垂直,C是l3上的一个动点.(1)分别求出点A、P的坐标;(2)设直线PC对应的函数表达式为y=kx+b,且满足函数值y随x的增大而增大.若△PCA的面积为15,分别求出k、b的值;(3)是否存在点C,使得2∠PCA+∠P AB=90°?若存在,直接写出点C的坐标;若不存在,请说明理由.17.(2023春•靖江市期中)如图,平面直角坐标系中,已知点A(0,a)在y 轴正半轴上,点B(0,b)(a>b),点C(c,0)在x轴正半轴上,且a2﹣2ab+b2(1)如图1,求证:AB=OC;(2)如图2,当a=3,b=1时,过点B的直线与AC成45°夹角,试求该直线与AC交点的横坐标;(3)如图3,当b<0时,点D在OC的延长线上,且CD=OB,连接AD,射线BC交AD于点E.当点B在y轴负半轴上运动时,∠AEB的度数是否为定值?如果是,请求出∠AEB的度数;如果不是,请说明理由.18.(2023春•沙坪坝区校级期中)如图,在平面直角坐标系xOy中,直线AB:与直线CD:y=kx﹣2相交于点M(4,a),分别交坐标轴于点A,(1)求直线CD的解析表达式;(2)如图,点P是直线CD上的一个动点,当△PBM的面积为20时,求点P的坐标;(3)直线AB上有一点F,在平面直角坐标系内找一点N,使得以BF为一边,以点B,D,F,N为顶点的四边形是菱形,请直接写出符合条件的点N的坐标.19.(2023春•揭西县校级月考)在平面直角坐标系中,直线y1=kx+b经过点P (2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.(1)求出直线y1=kx+b的解析式;(2)当m<0时,直接写出y1<y2时自变量x的取值范围;(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△P AB是等腰三角形时,请直接写出符合条件的所有点B的坐标.20.(2023春•溧阳市校级月考)如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是2和4;(1)求直线BD的表达式;(2)求△OFH的面积;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.21.(2023春•江都区月考)如图,在平面直角坐标系中,直线y=﹣x+3与x 轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)求点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.22.(2023春•新城区校级月考)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.(1)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,求出点P的坐标;(2)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M 在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.23.(2022秋•宿豫区期末)如图,直线l分别与x轴、y轴交于点A(4,0)、B (0,5),把直线l沿y轴向下平移3个单位长度,得到直线m,且直线m分别与x轴、y轴交于点C、D.(1)求直线l对应的函数表达式;(2)求四边形ABDC的面积.24.(2022秋•临淄区期末)如图,在直角坐标系中,四边形ABCD的顶点坐标分别为A(﹣1,0),B(0,2),C(2,3),D(4,0).(1)求直线BC的表达式;(2)线段AB与BC相等吗?请说明理由;(3)求四边形ABCD的面积;(4)已知点M在x轴上,且△MBC是等腰三角形,求点M的坐标.25.(2022秋•金牛区期末)如图1,在平面直角坐标系xOy中,直线AB:y=2x+b 与x轴交于点A(﹣2,0),与y轴交于点B.(1)求直线AB的解析式;(2)若直线CD:y=﹣x+与x轴、y轴、直线AB分别交于点C、D、E,求△BDE面积;(3)如图2,在(2)的条件下,点F为线段AC上一动点,将△EFC沿直线EF翻折得到△EFN,EN交x轴于点M.当△MNF为直角三角形时,求点N 的坐标.26.(2022秋•婺城区期末)如图,直线y=x+4与x轴、y轴分别交于点A、点B,点P是射线BO上的动点,过点B作直线AP的垂线交x轴于点Q,垂足为点C,连结OC.(1)当点P在线段BO上时,①求证:△AOP≌△BOQ;②若点P为BO的中点,求△OCQ的面积.(2)在点P的运动过程中,是否存在某一位置,使得△OCQ成为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.27.(2022秋•郫都区期末)在直角坐标系xOy中,直线l1:y=﹣x+4与x轴、y 轴分别交于点A,点B.直线l2:y=mx+m(m>0)与x轴,y轴分别交于点C,点D,直线l1与l2交于点E.(1)若点E坐标为(,n).ⅰ)求m的值;ⅱ)点P在直线l2上,若S△AEP=3S△BDE,求点P的坐标;(2)点F是线段CE的中点,点G为y轴上一动点,是否存在点F使△CFG 为以FC为直角边的等腰直角三角形.若存在,求出m的值,若不存在,请说明理由.28.(2022秋•市中区期末)如图,直线y=kx+b经过点,点B(0,25),与直线交于点C,点D为直线AB上一动点,过D点作x轴的垂线交直线OC于点E.(1)求直线AB的表达式和点C的坐标;(2)当时,求△CDE的面积;(3)连接OD,当△OAD沿着OD折叠,使得点A的对应点A'落在直线OC 上,直接写出此时点D的坐标.29.(2022秋•新都区期末)如图1,在平面直角坐标系中,点A的坐标为(4,4),点B的坐标为(﹣4,0).(1)求直线AB的表达式;(2)点M是坐标轴上的一点,若以AB为直角边构造Rt△ABM,请求出满足条件的所有点M的坐标;(3)如图2,以A为直角顶点作∠CAD=90°,射线AC交x轴的正半轴于点C,射线AD交y轴的负半轴于点D,当∠CAD绕点A旋转时,求OC﹣OD 的值.30.(2022秋•皇姑区期末)如图,在平面直角坐标系中,直线AD:y=﹣x+4交y轴于点A,交x轴于点D.直线AB交x轴于点B(﹣3,0),点P为直线AB上的动点.(1)求直线AB的关系式;(2)连接PD,当线段PD⊥AB时,直线AD上有一点动M,x轴上有一动点N,直接写出△PMN周长的最小值;(3)若∠POA=∠BAO,直接写出点P的纵坐标.31.(2022秋•新都区期末)如图所示,直线l1:y=x﹣1与y轴交于点A,直线l2:y=﹣2x﹣4与x轴交于点B,直线l1与l2交于点C.(1)求点A,C的坐标;(2)点P在直线l1上运动,求出满足条件S△PBC=S△ABC且异于点A的点P的坐标;(3)点D(2,0)为x轴上一定点,当点Q在直线l1上运动时,请直接写出|DQ﹣BQ|的最大值.32.(2022秋•鸡西期末)如图,直角三角形ABC在平面直角坐标系中,直角边BC在y轴上,AB,BC的长分别是一元二次方程x2﹣14x+48=0的两个根,AB<BC,且BC=2OB,P为BC上一点,且∠BAP=∠C.(1)求点A的坐标;(2)求直线AP的解析式;(3)M为x轴上一点,在平面内是否存在点N,使以A,C,M,N为顶点的四边形为矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.33.(2022秋•锦江区校级期末)如图,直线y=kx+b与x轴、y轴分别交于点A 和点B,点C在线段AO上,将△ABC沿BC所在直线折叠后,点A恰好落在y轴上点D处,若OA=4,OD=2.(1)求直线AB的解析式.(2)求S△ABC :S△OCD的值.(3)直线CD上是否存在点P使得∠PBC=45°,若存在,请直接写出P的坐标.34.(2022秋•福田区校级期末)已知:如图,一次函数的图象分别与x 轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D.点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为:;(2)点Q为线段DE上的一个动点,连接BQ.①若直线BQ将△BDE的面积分为1:2两部分,求点Q的坐标;②点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,请直接写出点Q的坐标;若不存在,请说明理由.35.(2022秋•抚州期末)如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),与y轴交于点A(0,a),且a,p满足=0.(1)求直线AP的解析式;(2)如图1,直线x=﹣2与x轴交于点N,点M在x轴上方且在直线x=﹣2上,若△MAP的面积等于6,请求出点M的坐标;(3)如图2,已知点C(﹣2,4),若点B为射线AP上一动点,连接BC,在坐标轴上是否存在点Q,使△BCQ是以BC为底边,点Q为直角顶点的等腰直角三角形,若存在,请直接写出点Q坐标;若不存在,请说明理由.36.(2022秋•天桥区期末)如图1,在平面直角坐标系xOy中,点O是坐标原点,直线AB:y=kx+与直线AC:y=﹣2x+b交于点A,两直线与x轴分别交于点B(﹣3,0)和C(2,0).(1)求直线AB和AC的表达式.(2)点P是y轴上一点,当P A+PC最小时,求点P的坐标.(3)如图2,点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F,若△DEF为直角三角形,求点D坐标.37.(2023•桐乡市校级开学)如图,一次函数y=x+6的图象与x轴交于点A,与y轴交于点B,OC⊥AB于点C,点P在直线AB上运动,点Q在y轴的正半轴上运动.(1)求点A,B的坐标;(2)求OC的长;(3)若以O,P,Q为顶点的三角形与△OCP全等,求点Q的坐标.38.(2022秋•秦都区期末)如图,平面直角坐标系中,直线AB与x轴交于点A (﹣3,0)与y轴交于点B(0,6),点C是直线AB上的一点,它的坐标为(m,4),经过点C作直线CD∥x轴交y轴于点D.(1)求点C的坐标;(2)已知点P是直线CD上的动点,①若△POC的面积为4,求点P的坐标;②若△POC为直角三角形,请求出所有满足条件的点P的坐标.39.(2022秋•南海区期末)如图,在平面直角坐标系中,直线y=x+1分别交x 轴,y轴于点A、B.另一条直线CD与直线AB交于点C(a,6),与x轴交于点D(3,0),点P是直线CD上一点(不与点C重合).(1)求a的值.(2)当△APC的面积为18时,求点P的坐标.(3)若直线MN在平面直角坐标系内运动,且MN始终与AB平行,直线MN 交直线CD于点M,交y轴于点N,当∠BMN=90°时,求△BMN的面积.40.(2023•丰顺县校级开学)问题提出:如图,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;问题探究:如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标;问题解决:古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA﹣AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线y=﹣2x平行,请帮助施工队计算出AC和AD所在直线的解析式.41.(2022秋•碑林区校级期末)(1)模型建立:如图1,在等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,请直接写出图中相等的线段(除CA=CB);模型应用:(2)如图2,在平面直角坐标系xOy中,直线与x,y轴分别交于A、B两点,C为第一象限内的点,若△ABC是以AB为直角边的等腰直角三角形,请求出点C的坐标和直线BC的表达式;探究提升:(3)如图3,在平面直角坐标系xOy中,A(3,0),点B在y轴上运动,将AB绕点A顺时针旋转90°至AC,连接OC,求CA+OC的最小值,及此时点B坐标.42.(2023•南岸区校级开学)如图,已知直线l1:y=﹣x+b与直线l2:y=kx+3相交于y轴的B点,且分别交x轴于点A、C,已知OC=OA.(1)如图,求点C的坐标及k的值;(2)如图,若E为直线l1上一点,且E点的横坐标为,点P为y轴上一个动点,求当|PC﹣PE|最大时,点P的坐标;(3)若M为x轴上一点,当△ABM是等腰三角形时,直接写出点M的坐标.43.(2022秋•驿城区校级期末)(1)操作思考:如图1,在平面直角坐标系中,等腰直角△ACB的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点(1,2)处.则:①OA的长为;②点B的坐标为.(直接写结果)(2)感悟应用:如图2,在平面直角坐标系中,将等腰直角△ACB如图放置,直角顶点C(﹣1,0),点A(0,4),试求直线AB的函数表达式.(3)拓展研究:如图3,在直角坐标系中,点B(4,3),过点B作BA⊥y 轴,垂足为点A,作BC⊥x轴,垂足为点C,P是线段BC上的一个动点,点Q是直线y=2x﹣8上一动点,存在以点P为直角顶点的等腰直角△APQ,请直接写出点P的坐标.。
一次函数代数几何综合问题

一次函数代几综合问题一.填空题(共6小题)1.如图,直线和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是.2.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C的坐标为.3.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为.4.如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为.5.在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、A n B n C n C n﹣1按如图所示的方式放置,其中点A1、A2、A3、…、A n均在一次函数y=kx+b的图象上,点C1、C2、C3、…、C n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点A n的坐标为.6.如图,直线1:与x轴、y轴分别相交于点A、B,△AOB与△ACB关于直线l对称,则点C的坐标为.二.解答题(共24小题)7.已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y 轴的距离分别为d1、d2.(1)当P为线段AB的中点时,求d1+d2的值;(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.8.在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.(1)如图1,当CG=OD时,直接写出点D和点G的坐标,并求直线DG的函数表达式;(2)如图2,连接BF,设CG=a,△FBG的面积为S.①求S与a的函数关系式;②判断S的值能否等于等于1?若能,求此时m的值,若不能,请说明理由;(3)如图3,连接GE,当GD平分∠CGE时,m的值为.9.认真阅读材料,然后回答问题:我们知道,在数轴上,x=1表示一个点.而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方方程2x﹣y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图2;y≧2x+1也表示一个平面区域,即直线y=2x+1以及它上方的部分,如图3.回答下列问题:请你自己作一个直角坐标系,并在直角坐标系中(1)用作图象的方法求出方程组的解.(2)用阴影表示,所围成的区域.10.如图,直线l1的解析表达式为:y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求△ADC的面积;(2)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,则点P的坐标为;(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,已知直线l1和l2相交于点A,它们的解析式分别为l1:y=x,l2:y=﹣x+.直线l2与两坐标轴分别相交于点B和点C,点P在线段OB上从点O出发.以每秒1个单位的速度向点B运动,同时点Q从点B出发以每秒4个单位的速度沿B→O→C→B的方向向点B运动,过点P作直线PM⊥OB分别交l1,l2于点M,N.连接MQ.设点P,Q运动的时间是t秒(t>0)(1)求点A的坐标;(2)点Q在OC上运动时,试求t为何值时,四边形MNCQ为平行四边形;(3)试探究是否存在某一时刻t,使MQ∥OB?若存在,求出t的值;若不存在,请说明理由.12.已知,将边长为5的正方形ABCO放置在如图所示的直角坐标系中,使点A在x轴上,点C在y轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.(1)当t=1时,求直线MC的解析式;(2)设△AMN的面积为S,求S关于t的函数解析式并写出相应t的取值范围;(3)在该平面直角坐标系中,第一象限内取点P(2,y),是否存在以M、N、C、P为顶点的四边形是直角梯形?若存在,直接写出点P的坐标;若不存在,请说明理由.13.如图①,以四边形AOCD的顶点O为原点建立直角坐标系,点A、C、D的坐标分别为(0,2)、(2,0)、(2,2),点P(m,0)是x轴上一动点,m是大于0的常数,以AP为一边作正方形APQR(QR落在第一象限),连接CQ.(1)请判断四边形AOCD的形状,并说明理由:(2)连接RD,请判断△ARD的形状,并说明理由:(3)如图②,随着点P(m,0)的运动,正方形APQR的大小会发生改变,若设CQ所在直线的表达式为y=kx+b(k≠0),求k的值.14.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.(1)求点M、P的坐标;(2)求折痕AM所在直线的解析式;(3)设点H为直线AM上的点,是否存在这样的点H,使得以H、A、P为顶点的三角形为等腰三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.15.如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动.设运动了x秒.(1)点N的坐标为(,);(用含x的代数式表示)(2)当x为何值时,△AMN为等腰三角形;(3)如图②,连接ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度.16.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).(1)求AB、BD的长度,并证明△ABD是直角三角形;(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.17.如图:直线y=kx+3与x轴、y轴分别交于A、B两点,,点C(x,y)是直线y=kx+3上与A、B不重合的动点.(1)求直线y=kx+3的解析式;(2)当点C运动到什么位置时△AOC的面积是6;(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣5,1),B(﹣2,4),C(5,4),点D在第一象限.(1)写出D点的坐标;(2)求经过B、D两点的直线的解析式,并求线段BD的长;(3)将平行四边形ABCD先向右平移1个单位长度,再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.19.如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.20.已知,直线y=﹣x+1与x轴,y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90度.且点P(1,a)为坐标系中的一个动点.(1)求三角形ABC的面积S△ABC;(2)证明不论a取任何实数,三角形BOP的面积是一个常数;(3)要使得△ABC和△ABP的面积相等,求实数a的值.21.如图,在直角坐标系xoy中,一次函数的图象与x轴交于点A,与y轴交于点B.(1)已知OC⊥AB于C,求C点坐标;(2)在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.22.如图1,在正方形ABOC中,BD平分∠OBC,交OA于点D.(1)若正方形ABOC的边长为2,对角线BC与OA相交于点E.则:①BC的长为;②DE的长为;③根据已知及求得的线段OB、BC、DE的长,请找出它们的数量关系?(2)如图2,当直角∠BAC绕着其顶点A顺时针旋转时,角的两边分别与x轴正半轴、y轴正半轴交于点C1和B1,连接B1C1交OA于P.B1D平分∠OB1C1,交OA于点D,过点D作DE⊥B1C1,垂足为E,请猜想线段OB、B1C1、DE三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当B1E=6,C1E=4时,求直线B1D的解析式.23.如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°;(1)如果点P(m,)在第二象限内,试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;(2)如果△QAB是等腰三角形并且点Q在坐标轴上,请求出点Q所有可能的坐标;(3)是否存在实数a,b使一次函数和y=ax+b的图象关于直线y=x对称?若存在,求出的值;若不存在,请说明理由.24.一次函数的图象与x轴、y轴分别交于点A(8,0)和点B(0,6).(1)确定此一次函数的解析式.(2)求坐标原点O到直线AB的距离.(3)点P是线段AB上的一个动点,过点P作PM垂直于x轴于M,作PN垂直于y轴于N,记L=PM+PN,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.25.已知直线y=2x+4与x轴交于点A,与y轴交于点B,点P在坐标轴上,且PO=2AO.求△ABP的面积.26.已知A(1,5),B(3,﹣1)两点,在x轴上取一点M,使AM﹣BM取得最大值时,则M的坐标为.27.如图,在平面直角坐标系中,直线分别交于x轴,y轴于B、A两点,D、E分别是OA、OB的中点,点P从点D出沿DE方向运动,过点P作PQ⊥AB于Q,过点Q作QR∥OA交OB于R,当点Q与B点重合时,点P停止运动.(1)求A、B两点的坐标;(2)求PQ的长度;(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的点R的坐标;若不存在,请说明理由.28.如图,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.(1)填空:点C的坐标是(,),点D的坐标是(,);(2)设直线CD与AB交于点M,求线段BM的长;(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.29.已知△ABC,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC,AB所在直线为x轴,y 轴建立直角坐标系(如图).(1)在BD所在直线上找出一点P,使四边形ABCP为平行四边形,画出这个平行四边形,并简要叙述其过程;(2)求直线BD的函数关系式;(3)直线BD上是否存在点M,使△AMC为等腰三角形?若存在,求点M的坐标;若不存在,说明理由.30.如图,一次函数的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC,(1)求△ABC的面积;(2)如果在第二象限内有一点P(a,);试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;(3)在x轴上,是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.。
专题11一次函数与几何压轴问题(优选真题44道)三年(20212023)中考数学真题分项汇编【全国通
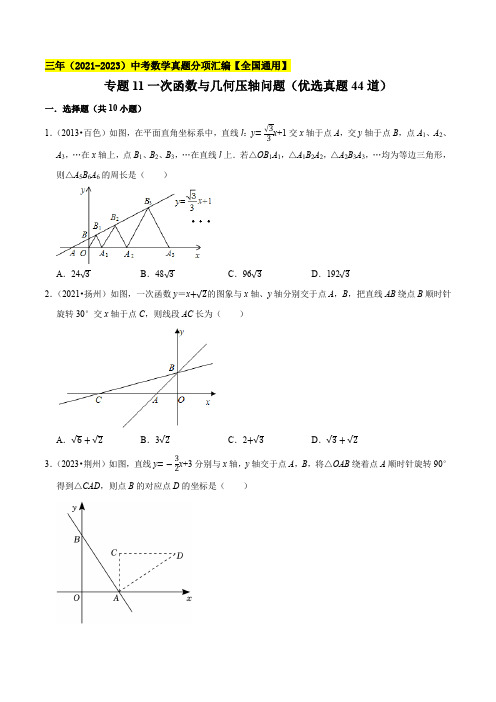
三年(2021-2023)中考数学真题分项汇编【全国通用】专题11一次函数与几何压轴问题(优选真题44道)一.选择题(共10小题)1.(2013•百色)如图,在平面直角坐标系中,直线l:y=√33x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是()A.24√3B.48√3C.96√3D.192√32.(2021•扬州)如图,一次函数y=x+√2的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为()A.√6+√2B.3√2C.2+√3D.√3+√23.(2023•荆州)如图,直线y=−32x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是()A .(2,5)B .(3,5)C .(5,2)D .(√13,2)4.(2022•聊城)如图,一次函数y =x +4的图象与x 轴,y 轴分别交于点A ,B ,点C (﹣2,0)是x 轴上一点,点E ,F 分别为直线y =x +4和y 轴上的两个动点,当△CEF 周长最小时,点E ,F 的坐标分别为( )A .E (−52,32),F (0,2)B .E (﹣2,2),F (0,2)C .E (−52,32),F (0,23)D .E (﹣2,2),F (0,23) 5.(2022•巴中)在平面直角坐标系中,直线y =−√3x +√3与x 轴交于点A ,与y 轴交于点B ,将△AOB 绕O 点逆时针旋转到如图△A ′OB ′的位置,A 的对应点A ′恰好落在直线AB 上,连接BB ′,则BB ′的长度为( )A .√32B .√3C .2D .3√326.(2022•阜新)如图,平面直角坐标系中,在直线y =x +1和x 轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在x 轴上,另一条直角边与x 轴垂直,则第100个等腰直角三角形的面积是( )A .298B .299C .2197D .21987.(2021•安顺)小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线y=k n x+b n (n=1,2,3,4,5,6,7),其中k1=k2,b3=b4=b5,则他探究这7条直线的交点个数最多是()A.17个B.18个C.19个D.21个8.(2022•鄂州)数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=13x都经过点A(3,1),当kx+b<13x时,根据图象可知,x的取值范围是()A.x>3B.x<3C.x<1D.x>19.(2022•柳州)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为()A.1B.2C.4D.610.(2021•呼和浩特)在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为()A.y=−17x+4B.y=−14x+4C.y=−12x+4D.y=4二.填空题(共16小题)11.(2023•黑龙江)如图,在平面直角坐标系中,△ABC的顶点A在直线l1:y=√33x上,顶点B在x轴上,AB垂直x轴,且OB=2√2,顶点C在直线l2:y=√3x上,BC⊥l2;过点A作直线l2的垂线,垂足为C1,交x轴于B1,过点B1作A1B1垂直x轴,交l1于点A1,连接A1C1,得到第一个△A1B1C1;过点A1作直线l2的垂线,垂足为C2,交x轴于B2,过点B2作A2B2垂直x轴,交l1于点A2,连接A2C2,得到第二个△A2B2C2;如此下去,…,则△A2023B2023C2023的面积是.12.(2023•杭州)在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于.13.(2023•眉山)如图,在平面直角坐标系xOy中,点B的坐标为(﹣8,6),过点B分别作x轴,y轴的垂线,垂足分别为点C,点A,直线y=﹣2x﹣6与AB交于点D,与y轴交于点E,动点M在线段BC 上,动点N在直线y=﹣2x﹣6上,若△AMN是以点N为直角顶点的等腰直角三角形,则点M的坐标为.14.(2023•广安)在平面直角坐标系中,点A1、A2、A3、A4…在x轴的正半轴上,点B1、B2、B3…在直线y=√33x(x≥0)上,若点A1的坐标为(2,0),且△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,则点B2023的纵坐标为.15.(2023•南充)如图,直线y=kx﹣2k+3(k为常数,k<0)与x,y轴分别交于点A,B,则2OA +3 OB的值是.16.(2022•遵义)如图,在等腰直角三角形ABC中,∠BAC=90°,点M,N分别为BC,AC上的动点,且AN=CM,AB=√2.当AM+BN的值最小时,CM的长为.17.(2022•菏泽)如图,在第一象限内的直线l:y=√3x上取点A1,使OA1=1,以OA1为边作等边△OA1B1,交x轴于点B1;过点B1作x轴的垂线交直线l于点A2,以OA2为边作等边△OA2B2,交x轴于点B2;过点B2作x轴的垂线交直线l于点A3,以OA3为边作等边△OA3B3,交x轴于点B3;……,依次类推,则点A2022的横坐标为.18.(2022•东营)如图,△AB1A1,△A1B2A2,△A2B3A3,…是等边三角形,直线y=√33x+2经过它们的顶点A,A1,A2,A3,…,点B1,B2,B3,…在x轴上,则点A2022的横坐标是.19.(2022•盐城)《庄子•天下篇》记载“一尺之棰,日取其半,万世不竭”.如图,直线l1:y=12x+1与y轴交于点A,过点A作x轴的平行线交直线l2:y=x于点O1,过点O1作y轴的平行线交直线l1于点A1,以此类推,令OA=a1,O1A1=a2,…,O n﹣1A n﹣1=a n,若a1+a2+…+a n≤S对任意大于1的整数n恒成立,则S的最小值为.20.(2022•辽宁)如图,直线y=2x+4与x轴交于点A,与y轴交于点B,点D为OB的中点,▱OCDE的顶点C在x轴上,顶点E在直线AB上,则▱OCDE的面积为.21.(2021•泰安)如图,点B1在直线l:y=12x上,点B1的横坐标为2,过点B1作B1A1⊥l,交x轴于点A1,以A1B1为边,向右作正方形A1B1B2C1,延长B2C1交x轴于点A2;以A2B2为边,向右作正方形A2B2B3C2,延长B3C2交x轴于点A3;以A3B3为边,向右作正方形A3B3B4C3,延长B4C3交x轴于点A4;…;照这个规律进行下去,则第n个正方形A n B n B n+1∁n的边长为(结果用含正整数n的代数式表示).22.(2021•贺州)如图,一次函数y=x+4与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为.23.(2021•兴安盟)如图,点B1在直线l:y=12x上,点B1的横坐标为1,过点B1作B1A1⊥x轴,垂足为A1,以A1B1为边向右作正方形A1B1C1A2,延长A2C1交直线l于点B2;以A2B2为边向右作正方形A2B2C2A3,延长A3C2交直线l于点B3;…;按照这个规律进行下去,点B2021的坐标为.24.(2021•梧州)如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4),…,A n(n+1,n),构成形如“”的图形的阴影部分面积分别表示为S1,S2,S3,…,S n,则S2021=.25.(2021•毕节市)如图,在平面直角坐标系中,点N1(1,1)在直线l:y=x上,过点N1作N1M1⊥l,交x轴于点M1;过点M1作M1N2⊥x轴,交直线于N2;过点N2作N2M2⊥l,交x轴于点M2;过点M2作M2N3⊥x轴,交直线l于点N3;…,按此作法进行下去,则点M2021的坐标为.26.(2021•广安)如图,在平面直角坐标系中,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=−34x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2也落在直线y=−34x上,以此进行下去…若点B的坐标为(0,3),则点B21的纵坐标为.三.解答题(共18小题)27.(2023•黑龙江)如图,在平面直角坐标系中,菱形AOCB的边OC在x轴上,∠AOC=60°,OC的长是一元二次方程x2﹣4x﹣12=0的根,过点C作x轴的垂线,交对角线OB于点D,直线AD分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿OD向终点D运动,动点N从点F 以每秒2个单位长度的速度沿FE向终点E运动.两点同时出发,设运动时间为t秒.(1)求直线AD的解析式;(2)连接MN,求△MDN的面积S与运动时间t的函数关系式;(3)点N在运动的过程中,在坐标平面内是否存在一点Q,使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.28.(2023•鄂州)如图1,在平面直角坐标系中,直线l⊥y轴,交y轴的正半轴于点A,且OA=2,点B 是y轴右侧直线l上的一动点,连接OB.(1)请直接写出点A的坐标;(2)如图2,若动点B满足∠ABO=30°,点C为AB的中点,D点为线段OB上一动点,连接CD.在平面内,将△BCD沿CD翻折,点B的对应点为点P,CP与OB相交于点Q,当CP⊥AB时,求线段DQ的长;(3)如图3,若动点B满足ABOA=2,EF为△OAB的中位线,将△BEF绕点B在平面内逆时针旋转,当点O、E、F三点共线时,求直线EB与x轴交点的坐标;(4)如图4,OC平分∠AOB交AB于点C,AD⊥OB于点D,交OC于点E,AF为△AEC的一条中线.设△ACF ,△ODE ,△OAC 的周长分别为C 1,C 2,C 3.试探究:在B 点的运动过程中,当2c 1+c 2c 3=118时,请直接写出点B 的坐标.29.(2023•广东)综合运用 如图1,在平面直角坐标系中,正方形OABC 的顶点A 在x 轴的正半轴上.如图2,将正方形OABC 绕点O 逆时针旋转,旋转角为α(0°<α<45°),AB 交直线y =x 于点E ,BC 交y 轴于点F .(1)当旋转角∠COF 为多少度时,OE =OF ;(直接写出结果,不要求写解答过程)(2)若点A (4,3),求FC 的长;(3)如图3,对角线AC 交y 轴于点M ,交直线y =x 于点N ,连接FN .将△OFN 与△OCF 的面积分别记为S 1与S 2.设S =S 1﹣S 2,AN =n ,求S 关于n 的函数表达式.30.(2023•河北)在平面直角坐标系中,设计了点的两种移动方式:从点(x ,y )移动到点 (x +2,y +1)称为一次甲方式;从点(x ,y )移动到点(x +1,y +2)称为一次乙方式.例点P 从原点O 出发连续移动2次:若都按甲方式,最终移动到点M (4,2);若都按乙方式,最终移动到点N (2,4);若按1次甲方式和1次乙方式,最终移动到点E (3,3).(1)设直线l 1经过上例中的点M 、N ,求l 1的解析式,并直接写出将l 1向上平移9个单位长度得到的直线l 2的解析式;(2)点P 从原点O 出发连续移动10次,每次移动按甲方式或乙方式,最终移动到点Q (x ,y ).其中,按甲方式移动了m 次.①用含m 的式子分别表示x ,y ;②请说明:无论m 怎样变化,点Q 都在一条确定的直线上.设这条直线为l 3,在图中直接画出l 3的图象;(3)在(1)和(2)中的直线l 1,l 2,l 3上分别有一个动点A ,B ,C ,横坐标依次为a ,b ,c ,若A ,B ,C 三点始终在一条直线上,直接写出此时a ,b ,c 之间的关系式.31.(2022•黑龙江)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.32.(2022•泰州)定义:对于一次函数y1=ax+b、y2=cx+d,我们称函数y=m(ax+b)+n(cx+d)(ma+nc ≠0)为函数y1、y2的“组合函数”.(1)若m=3,n=1,试判断函数y=5x+2是否为函数y1=x+1、y2=2x﹣1的“组合函数”,并说明理由;(2)设函数y1=x﹣p﹣2与y2=﹣x+3p的图象相交于点P.①若m+n>1,点P在函数y1、y2的“组合函数”图象的上方,求p的取值范围;②若p≠1,函数y1、y2的“组合函数”图象经过点P.是否存在大小确定的m值,对于不等于1的任意实数p,都有“组合函数”图象与x轴交点Q的位置不变?若存在,请求出m的值及此时点Q的坐标;若不存在,请说明理由.33.(2022•攀枝花)如图,直线y=34x+6分别与x轴、y轴交于点A、B,点C为线段AB上一动点(不与A、B重合),以C为顶点作∠OCD=∠OAB,射线CD交线段OB于点D,将射线OC绕点O顺时针旋转90°交射线CD于点E,连结BE.(1)证明:CDDB =ODDE;(用图1)(2)当△BDE为直角三角形时,求DE的长度;(用图2)(3)点A关于射线OC的对称点为F,求BF的最小值.(用图3)34.(2022•沈阳)如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B (0,9),与直线OC交于点C(8,3).(1)求直线AB的函数表达式;(2)过点C作CD⊥x轴于点D,将△ACD沿射线CB平移得到的三角形记为△A′C′D′,点A,C,D的对应点分别为A′,C′,D′,若△A′C′D′与△BOC重叠部分的面积为S,平移的距离CC′=m,当点A′与点B重合时停止运动.①若直线C′D′交直线OC于点E,则线段C′E的长为(用含有m的代数式表示);②当0<m<103时,S与m的关系式为;③当S=245时,m的值为.35.(2022•兰州)在平面直角坐标系中,P(a,b)是第一象限内一点,给出如下定义:k1=ab和k2=ba两个值中的最大值叫做点P的“倾斜系数”k.(1)求点P(6,2)的“倾斜系数”k的值;(2)①若点P(a,b)的“倾斜系数”k=2,请写出a和b的数量关系,并说明理由;②若点P(a,b)的“倾斜系数”k=2,且a+b=3,求OP的长;(3)如图,边长为2的正方形ABCD沿直线AC:y=x运动,P(a,b)是正方形ABCD上任意一点,且点P的“倾斜系数”k<√3,请直接写出a的取值范围.36.(2022•河北)如图,平面直角坐标系中,线段AB的端点为A(﹣8,19),B(6,5).(1)求AB所在直线的解析式;(2)某同学设计了一个动画:在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,使得到射线CD,其中C(c,0).当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.①若有光点P弹出,试推算m,n应满足的数量关系;②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光.求此时整数m的个数.37.(2021•遂宁)已知平面直角坐标系中,点P(x0,y0)和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式d=00√A+B来计算.例如:求点P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x﹣y+1=0,其中A=2,B=﹣1,C=1,所以点P(1,2)到直线y=2x+1的距离为:d=00√A+B =√22+(−1)2=√5=√55.根据以上材料,解答下列问题:(1)求点M(0,3)到直线y=√3x+9的距离;(2)在(1)的条件下,⊙M的半径r=4,判断⊙M与直线y=√3x+9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.38.(2021•衡阳)如图,△OAB的顶点坐标分别为O(0,0),A(3,4),B(6,0),动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作MN∥OB分别交AO、AB于点M、N,连接PM、PN.设运动时间为t(秒).(1)求点M的坐标(用含t的式子表示);(2)求四边形MNBP面积的最大值或最小值;(3)是否存在这样的直线l,总能平分四边形MNBP的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;(4)连接AP,当∠OAP=∠BPN时,求点N到OA的距离.39.(2021•黑龙江)如图,矩形ABOC在平面直角坐标系中,点A在第二象限内,点B在x轴负半轴上,点C在y轴正半轴上,OA,OB的长是关于x的一元二次方程x2﹣9x+20=0的两个根.解答下列问题:(1)求点A的坐标;(2)若直线MN分别与x轴,AB,AO,AC,y轴交于点D,M,F,N,E,S△AMN=2,tan∠AMN=1,求直线MN的解析式;(3)在(2)的条件下,点P在第二象限内,在平面内是否存在点Q,使以E,F,P,Q为顶点的四边形是正方形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.40.(2021•金华)在平面直角坐标系中,点A的坐标为(−√73,0),点B在直线l:y=38x上,过点B作AB的垂线,过原点O作直线l的垂线,两垂线相交于点C.(1)如图,点B,C分别在第三、二象限内,BC与AO相交于点D.①若BA=BO,求证:CD=CO.②若∠CBO=45°,求四边形ABOC的面积.(2)是否存在点B,使得以A,B,C为顶点的三角形与△BCO相似?若存在,求OB的长;若不存在,请说明理由.41.(2021•宁夏)如图,已知直线y=kx+3与x轴的正半轴交于点A,与y轴交于点B,sin∠OAB=3 5.(1)求k的值;(2)D、E两点同时从坐标原点O出发,其中点D以每秒1个单位长度的速度,沿O→A→B的路线运动,点E以每秒2个单位长度的速度,沿O→B→A的路线运动.当D,E两点相遇时,它们都停止运动,设运动时间为t秒.①在D、E两点运动过程中,是否存在DE∥OB?若存在,求出t的值,若不存在,请说明理由;②若设△OED的面积为S,求S关于t的函数关系式,并求出t为多少时,S的值最大?42.(2021•沈阳)如图,平面直角坐标系中,O是坐标原点,直线y=kx+15(k≠0)经过点C(3,6),与x轴交于点A,与y轴交于点B.线段CD平行于x轴,交直线y=34x于点D,连接OC,AD.(1)填空:k=,点A的坐标是(,);(2)求证:四边形OADC是平行四边形;(3)动点P从点O出发,沿对角线OD以每秒1个单位长度的速度向点D运动,直到点D为止;动点Q同时从点D出发,沿对角线DO以每秒1个单位长度的速度向点O运动,直到点O为止.设两个点的运动时间均为t秒.①当t=1时,△CPQ的面积是.②当点P,Q运动至四边形CP AQ为矩形时,请直接写出此时t的值.43.(2023•大连)如图1,在平面直角坐标系xOy中,直线y=x与直线BC相交于点A.P(t,0)为线段OB上一动点(不与点B重合),过点P作PD⊥x轴交直线BC于点D,△OAB与△DPB的重叠面积为S,S关于t的函数图象如图2所示.(1)OB的长为;△OAB的面积为;(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.44.(2023•北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.(1)求该函数的解析式及点C的坐标;(2)当x<3时,对于x的每一个值,函数y=23x+n的值大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值.。
第19章一次函数——几何变换 专项练习 2022—2023学年人教版数学八年级下册

一次函数典型例题——几何变换◆一次函数的基本性质1.已知一次函数y=(k﹣2)x﹣3k2+12.(1)k为何值时,图象经过原点;(2)k为何值时,图象与直线y=﹣2x+9的交点在y轴上;(3)k为何值时,图象平行于y=﹣2x的图象;(4)k为何值时,y随x增大而减小.2.已知一次函数y=(3m﹣7)x+m﹣1(1)当m为何值时,函数图象经过原点?(2)若图象不经过三象限,求m的取值范围.(3)不论m取何值,直线恒过一定点P,求定点P坐标.3.已知y=y1+y2,y1与x﹣2成正比例,y2﹣3与x成正比例,当x=1时,y=4;x=2时,y=7.求y与x的函数解析式.◆图形的平移、旋转、对称4.如图,直线y=2x﹣2与x轴、y轴分别相交于点A、点B.(1)求点A、点B的坐标.(2)将直线AB向上平移3个单位得直线l,若C为直线l上一点,且S△AOC=3,求点C的坐标.5.如图,在平面直角坐标系xOy中,直线y=﹣x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长;(2)求点C和点D的坐标;(3)y轴上是否存在一点P,使得S△P AB=S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.6.如图,直线y=﹣x+4与x轴交于点A,与y轴交于点C,在第一象限内将线段CA沿同一直线CG向下翻折得到线段CD,点D与点A对应且CD∥x轴,过点D作DE⊥x轴于E点,与GC交于F点.求点F的坐标.7.如图,一次函数y=(m+1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4.(1)则m=,点A的坐标为(,).(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;(3)将一次函数y=(m+1)x+4的图象绕点B顺时针旋转45°,求旋转后的对应的函数表达式.8.如图,一次函数y=2x+b的图象经过点M(1,3),且与x轴,y轴分别交于A,B两点.(1)填空:b=;(2)将该直线绕点A顺时针旋转45°至直线l,过点B作BC⊥AB交直线l于点C,求点C的坐标及直线l的函数表达式.9.直线y=2x+2与x轴,y轴分别交于A,B两点,将直线AB绕点O按逆时针方向旋转90度得到直线CD,(1)求直线CD的解析式;(2)若将直线AB绕原点按顺时针方向旋转90度得到直线EF,求直线EF的解析式.◆交点问题求范围10.在平面直角坐标系xOy中,直线y=2x+4与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.(1)求点C的坐标;(2)求直线CD的表达式;(3)若点B关于原点的对称点为点E,设过点E的直线y=kx+b,与四边形ABCD有公共点,结合函数图象,求k的取值范围.11.如图,点A的坐标为(﹣1,0),点B在直线y=2x﹣4上运动.(1)若点B的坐标是(1,﹣2),把直线AB向上平移m个单位后,与直线y=2x﹣4的交点在第一象限,求m 的取值范围;(2)当线段AB最短时,求点B的坐标.12.在平面直角坐标系xOy中,点A(﹣1,m)是直线y=﹣x+2上一点,点A向右平移4个单位长度得到点B.(1)求点A,B的坐标;(2)若直线l:y=kx﹣2(k≠0)与线段AB有公共点,结合函数的图象,求k的取值范围.练习1.如图,已知直线l:y=2x+4交x轴于A,交y轴于B.(1)直接写出直线l向右平移2个单位得到的直线l1的解析式;(2)直接写出直线l关于y=﹣x对称的直线l2的解析式;(3)点P在直线l上,若S△OAP=2S△OBP,求P点坐标.2.如图:一次函数y=x+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.(1)求点B的坐标;(2)求四边形ABCO的面积;(3)求直线CD的解析式.3.如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为B',折痕为CE,已知OC:OB'=4:3.(1)求点B'的坐标;(2)求折痕CE所在直线的解析式.4.若一次函数y=(6﹣3m)x+(2n﹣4)不经过第三象限,求m、n的取值范围.5.已知直线l1:y=2x+3与x轴、y轴的交点分别为A、B两点,将直线l1向下平移1个长度单位后得到直线l2,直线l2与x轴交于点C,与y轴交于点D,(1)求△AOB的面积;(2)直线l2的表达式;(3)求△CBD的面积.6.如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),已知直线l:y=x﹣2(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.一次函数典型例题——几何变换(解析)◆一次函数的基本性质1.已知一次函数y=(k﹣2)x﹣3k2+12.(1)k为何值时,图象经过原点;(2)k为何值时,图象与直线y=﹣2x+9的交点在y轴上;(3)k为何值时,图象平行于y=﹣2x的图象;(4)k为何值时,y随x增大而减小.【解答】解:(1)∵一次函数y=(k﹣2)x﹣3k2+12的图象经过原点,∴﹣3k2+12=0,∴,∴k=﹣2;(2)∵直线y=﹣2x+9求出此直线与y轴的交点坐标为(0,9),∴﹣3k2+12=9,∴k=1或k=﹣1;(3)∵一次函数的图象平行于y=﹣2x的图象,∴k﹣2=﹣2,∴k=0;(4)∵一次函数为减函数,∴k﹣2<0,∴k<2.2.已知一次函数y=(3m﹣7)x+m﹣1(1)当m为何值时,函数图象经过原点?(2)若图象不经过三象限,求m的取值范围.(3)不论m取何值,直线恒过一定点P,求定点P坐标.【解答】解:(1)∵函数的图象经过原点,∴m﹣1=0,解得:m=1;(2)∵图象不经过三象限,∴3m﹣7<0,m﹣1≥0,解得:1≤m<;(3)∵不论m取何值,直线恒过一定点P,∴当x=﹣时,y=﹣1=,即不论m取何值,直线恒过一定点P,定点P坐标为:(﹣,).3.已知y=y1+y2,y1与x﹣2成正比例,y2﹣3与x成正比例,当x=1时,y=4;x=2时,y=7.求y与x的函数解析式.【解答】解:∵y1与kx﹣2成正比例,y2﹣3与x成正比例,∴y1=k1(x﹣2),y2﹣3=k2x,∴y=k1(x﹣2)+k2x+3,把x=1时,y=4;x=2时,y=7代入上式解得,解得:,则y与x的解析式为y=3x+1.◆图形的平移、旋转、对称4.如图,直线y=2x﹣2与x轴、y轴分别相交于点A、点B.(1)求点A、点B的坐标.(2)将直线AB向上平移3个单位得直线l,若C为直线l上一点,且S△AOC=3,求点C的坐标.【解答】解:(1)当y=0,则2x﹣2=0,解得x=1;当x=0时,y=﹣2,∴点A的坐标为(1,0),点B的坐标为(0,﹣2);(2)将直线AB向上平移3个单位得直线l:y=2x+1,设C的坐标为(m,2m+1),∵S△AOC=3,∴|2m+1|=3,∴2m+1=±6,解得m=或﹣,∴C(,6)或(﹣,﹣6).5.如图,在平面直角坐标系xOy中,直线y=﹣x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.(1)求AB的长;(2)求点C和点D的坐标;(3)y轴上是否存在一点P,使得S△P AB=S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.【解答】解:(1)令x=0得:y=4,∴B(0,4).∴OB=4,令y=0得:0=﹣x+4,解得:x=3,∴A(3,0).∴OA=3.在Rt△OAB中,AB==5.(2)∵AC=AB=5,∴OC=OA+AC=3+5=8,∴C(8,0).设OD=x,则CD=DB=x+4.在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,解得:x=6,∴D(0,﹣6).(3)存在,理由如下:∵S△P AB=S△OCD,∴S△P AB=××6×8=12.∵点P在y轴上,S△P AB=12,∴BP•OA=12,即×3BP=12,解得:BP=8,∴P点的坐标为(0,12)或(0,﹣4).6.如图,直线y=﹣x+4与x轴交于点A,与y轴交于点C,在第一象限内将线段CA沿同一直线CG向下翻折得到线段CD,点D与点A对应且CD∥x轴,过点D作DE⊥x轴于E点,与GC交于F点.求点F的坐标.【解答】解:连接AF,直线y=﹣x+4与x轴交于点A,与y轴交于点C,令x=0,则y=4;令y=0,则x=3,∴A(3,0),C(0,4),∴OA=3,OC=4,∴AC==5,∵CD∥x轴,点D、点A关于直线CF对称,∴CD=CA=5.∠DCF=∠ACF=∠FGA,∴∠CAF=∠D=90°设EF=x,则DF=AF,DF=4﹣x,AE=2,∴(4﹣x)2﹣x2=4.解得x=.∴点F坐标为(5,).7.如图,一次函数y=(m+1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4.(1)则m=1,点A的坐标为(﹣2,0).(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;(3)将一次函数y=(m+1)x+4的图象绕点B顺时针旋转45°,求旋转后的对应的函数表达式.【解答】解:(1)由一次函数y=(m+1)x+4,令x=0,则y=4,∴B(0,4),∴OB=4,∵S△OAB=4,∴×OA×OB=4,解得OA=2,∴A(﹣2,0),把点A(﹣2,0)代入y=(m+1)x+4,得m=1,故答案为:1;﹣2,0;(2)∵OP=4OA,OA=2,∴P(8,0),设直线BP的解析式为y=kx+b,将(8,0),(0,4)代入得,解得k=﹣,b=4,∴直线BP的解析式为y=﹣x+4;(3)设直线AB绕点B顺时针旋转45°得到直线BE,如图,过点A作AF⊥AB交BE于点F,作FH⊥x轴于H.则∠AHF=∠BOA=90°,AF=BA,∠F AH=∠ABO,∴△AOB≌△FHA(AAS),∴FH=AO=2,AH=BO=4,∴HO=6,∴F(﹣6,2),设直线BE的解析式为y=mx+n,则把点F和点B的坐标代入,可得,解得,∴直线BE的解析式为y=x+4.8.如图,一次函数y=2x+b的图象经过点M(1,3),且与x轴,y轴分别交于A,B两点.(1)填空:b=1;(2)将该直线绕点A顺时针旋转45°至直线l,过点B作BC⊥AB交直线l于点C,求点C的坐标及直线l的函数表达式.【解答】解:(1)∵一次函数y=2x+b的图象经过点M(1,3),∴3=2+b,解得b=1,(2)∵一次函数y=2x+1的图象与x轴,y轴分别交于A,B两点.∴A(﹣,0),B(0,1),∴OA=,OB=1,作CD⊥y轴于D,∵∠BAC=45°,BC⊥AB,∴∠ACB=45°,∴AB=BC,∵∠ABO+∠BAO=90°=∠ABO+∠CBD,∴∠BAO=∠CBD,在△AOB和△BDC中,,∴△AOB≌△BDC(AAS),∴BD=OA=,CD=OB=1,∴OD=OB﹣BD=,∴C(1,),设直线l的解析式为y=mx+n,把A(﹣,0),C(1,)代入得,解得,∴直线l的解析式为y=x+.9.直线y=2x+2与x轴,y轴分别交于A,B两点,将直线AB绕点O按逆时针方向旋转90度得到直线CD,(1)求直线CD的解析式;(2)若将直线AB绕原点按顺时针方向旋转90度得到直线EF,求直线EF的解析式.【解答】解:∵直线y=2x+2与x轴,y轴分别交于A,B两点,当x=0时,y=2;当y=0时,x=﹣1;∴A(﹣1,0),B(0,2).(1)∵直线AB绕点O按逆时针方向旋转90度得到直线CD,∴直线CD与x轴,y轴的交点坐标(﹣2,0),(0,﹣1),设直线CD的解析式是y=k1x+b1,则,解得.故直线CD的解析式是y=﹣x﹣1;(2)∵将直线AB绕原点按顺时针方向旋转90度得到直线EF,∴直线EF与x轴,y轴的交点坐标(2,0),(0,1),设直线EF的解析式是y=k2x+b2,则,解得.故直线EF的解析式是y=﹣x+1.◆交点问题求范围10.在平面直角坐标系xOy中,直线y=2x+4与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.(1)求点C的坐标;(2)求直线CD的表达式;(3)若点B关于原点的对称点为点E,设过点E的直线y=kx+b,与四边形ABCD有公共点,结合函数图象,求k的取值范围.【解答】解:(1)直线y=2x+4与x轴,y轴分别交于点A,B,令x=0,则y=4,令y=0,则x=﹣2,∴B(0,4),A(﹣2,0),将直线AB向右平移6个单位长度,点B平移后的对应点为点C为(6,4);(2)∵A(﹣2,0),∴D(4,0),解得:k=2,b=﹣8,∴直线CD的表达式为y=2x﹣8.把C(6,4),D(4,0)代入y=kx+b中得,(3)∵点B(0,4)关于原点的对称点为点E(0,﹣4),∴设过点E的直线y=kx﹣4,把D(4,0)代入y=kx﹣4中得4k﹣4=0,∴k=1,把A(﹣2,0)代入y=kx﹣4中,∴k=﹣2∴k≥1或k≤﹣2.11.如图,点A的坐标为(﹣1,0),点B在直线y=2x﹣4上运动.(1)若点B的坐标是(1,﹣2),把直线AB向上平移m个单位后,与直线y=2x﹣4的交点在第一象限,求m 的取值范围;(2)当线段AB最短时,求点B的坐标.【解答】解:(1)设直线AB的解析式为y=kx+b.∵点A的坐标为(﹣1,0),点B的坐标是(1,﹣2),∴,解得,∴直线AB的解析式为y=﹣x﹣1,把直线AB向上平移m个单位后得y=﹣x+m﹣1.由,解得,即交点为(,).由题意,得,解得m>3;(2)AB最短时有AB⊥CD,设此时直线AB的解析式为y=﹣x+n,将A(﹣1,0)代入,得0=﹣×(﹣1)+n,解得n=﹣.即直线AB的解析式为y=﹣x﹣.由,解得,所以B点坐标为(,﹣).12.在平面直角坐标系xOy中,点A(﹣1,m)是直线y=﹣x+2上一点,点A向右平移4个单位长度得到点B.(1)求点A,B的坐标;(2)若直线l:y=kx﹣2(k≠0)与线段AB有公共点,结合函数的图象,求k的取值范围.【解答】解:(1)∵点A(﹣1,m)是直线y=﹣x+2上一点,∴m=1+2=3.∴点A的坐标为(﹣1,3).∴点(﹣1,3)向右平移4个单位长度得到点B的坐标为(3,3).(2)当直线l:y=kx﹣2过点A(﹣1,3)时,得3=﹣k﹣2,解得k=﹣5.当直线l:y=kx﹣2过点B(3,3)时,得3=3k﹣2,解得k=.如图,若直线l:y=kx﹣2(k≠0)与线段AB有公共点,则b的取值范围是k≤﹣5或k≥.练习1.如图,已知直线l:y=2x+4交x轴于A,交y轴于B.(1)直接写出直线l向右平移2个单位得到的直线l1的解析式y=2x;(2)直接写出直线l关于y=﹣x对称的直线l2的解析式y=x+2;(3)点P在直线l上,若S△OAP=2S△OBP,求P点坐标.【解答】解:(1)直线l:y=2x+4向右平移2个单位得到的直线l2的解析式为:y=2(x﹣2)+4,即y=2x,(2)∵(0,4),(﹣2,0)在直线ly=2x+4上,这两点关于y=﹣x的对称点为(﹣4,0),(0,2),设直线l1的解析式为y=kx+b,∴,解得,∴直线l1的解析式为:y=x+2,故答案为y=x+2;(3)∵直线l:y=2x+4交x轴于A,交y轴于B.∴A(﹣2,0),B(0,4),∴OA=2,OB=4,设P的坐标为(x,2x+4),∵S△OAP=2S△OBP,∴OA•|2x+4|=2×OB•|x|,即|2x+4|=4|x|,解得x=﹣或2,∴P(﹣,)或(2,8).2.如图:一次函数y=x+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.(1)求点B的坐标;(2)求四边形ABCO的面积;(3)求直线CD的解析式.【解答】解:(1)由,解得,∴B(3,3).(2)由题意A(0,2),C(2,0),∴S四边形ABCO=S△OCB+S△AOB=×2×3+×2×3=6.(3)如图,将线段BC绕点B逆时针旋转90得到C′.∵△BCC′是等腰直角三角形,∠BCD=45°,∴点C′在直线CD上,∵B(3,3),C(2,0),∴C′(6,2),设直线CD的解析式为y=kx+b,则有,解得,∴直线CD的解析式为y=x﹣1.3.如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为B',折痕为CE,已知OC:OB'=4:3.(1)求点B'的坐标;(2)求折痕CE所在直线的解析式.【解答】解:(1)∵四边形OABC是矩形,∴∠AOC=90°,∵OC:OB'=4:3,∴B′C:OB′=5:3,∵B′C=BC=10,∴OB′=6,∴B′点的坐标为:(6,0);(2)将纸片翻折后,点B恰好落在x轴上的B′点,CE为折痕,∴△CBE≌△CB′E,故BE=B′E,CB′=CB=OA,由OB′=6,OC:OB'=4:3,∴OC=8,设AE=a,则EB′=EB=8﹣a,AB′=AO﹣OB′=10﹣6=4,由勾股定理,得a2+42=(8﹣a)2,解得a=3,∴点E的坐标为(10,3),点C的坐标为(0,8),设直线CE的解析式为y=kx+b,根据题意,得,解得,∴CE所在直线的解析式为y=﹣x+8.4.若一次函数y=(6﹣3m)x+(2n﹣4)不经过第三象限,求m、n的取值范围.【解答】解:∵y=(6﹣3m)x+(2n﹣4)不经过第三象限,∴6﹣3m<0,2n﹣4≥0,故m>2,n≥2.5.已知直线l1:y=2x+3与x轴、y轴的交点分别为A、B两点,将直线l1向下平移1个长度单位后得到直线l2,直线l2与x轴交于点C,与y轴交于点D,(1)求△AOB的面积;(2)直线l2的表达式;(3)求△CBD的面积.【解答】解:(1)在y=2x+3中,令x=0,得y=3;令y=0,得x=,所以A、B的坐标分别为:A(,0),B(0,3),∴S△ABC=×|3|×=;(2)把l1:y=2x+3向下平移1个长度单位后得l2:y=2x+2;(3)直线l2:y=2x+2与x轴、y轴的交点C、D的坐标分别为:C(﹣1,0)、D(0,2),∴S△CBD=×|1|×|3﹣2|=.216.如图,在平面直角坐标系中,边长为2的正方形ABCD 在第一象限内,AB ∥x 轴,点A 的坐标为(5,3),已知直线l :y =x ﹣2(1)将直线l 向上平移m 个单位,使平移后的直线恰好经过点A ,求m 的值(2)在(1)的条件下,平移后的直线与正方形的边长BC 交于点E ,求△ABE 的面积.【解答】解:(1)设平移后的直线方程为y =x +b ,把点A 的坐标为(5,3)代入,得3=×5+b ,解得 b =.则平移后的直线方程为:y =x +.则﹣2+m =,解得 m =;(2)∵正方形ABCD 的边长为2,且点A 的坐标为(5,3),∴B (3,3).把x =3代入y =x +,得y =×3+=2,即E (3,2).∴BE =3﹣2=1,∴△ABE 的面积=×2×1=1.22。
一次函数与几何综合(垂直的函数意义)(人教版)(含答案)

一次函数与几何综合(垂直的函数意义)(人教版)一、单选题(共7道,每道14分)1.如图,直线:y=x+2与y轴交于点A,将直线绕点A旋转90°后,所得直线的表达式为( )A.y=x-2B.y=-x+2C.y=-x-2D.y=-2x-1答案:B解题思路:试题难度:三颗星知识点:一次函数与几何转化2.在平面直角坐标系中,把直线y=2x+4绕着原点O顺时针旋转90°后,所得的直线一定经过下列各点中的( )A.(2,0)B.(2,3)C.(4,2)D.(6,-1)答案:D解题思路:试题难度:三颗星知识点:一次函数与几何转化3.如图,一次函数的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,且∠BAC=90°,则AC所在直线的表达式为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数与几何综合4.如图,在平面直角坐标系中放入一张矩形纸片ABCO,已知点B的坐标为(4,-3),连接AC,作AC的垂直平分线交AB于点D,交y轴于点E.则DE所在直线的表达式为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:一次函数与几何综合5.如图,在平面直角坐标系中放入一张矩形纸片ABCO,OC=6,将纸片沿过点C的直线翻折后,点B恰好落在x轴上的点D处,折痕交AB于点E,若,则DE所在直线的解析式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与几何综合6.如图,已知长方形纸片OABC,D是OA上的一点,且OD:AD=5:3,CD=,把△OCD 沿折痕CD向上翻折,若点O恰好与AB边上的点E重合,则CD所在直线的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转7.如图,在平面直角坐标系中放入一张矩形纸片ABCO,OC=9,将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知,则折痕B′E所在直线的解析式为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与几何综合。
一次函数和几何综合题含答案

一次函数和几何综合题含答案1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共10小题)1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.(2)由△ABD由△AOP旋转得到,证明△ABD≌△AOP.AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形.利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标.(3)本题分三种情况进行讨论,设点P的坐标为(t,0):①当P在x轴正半轴上时,即t>0时,关键是求出D点的纵坐标,方法同(2),在直角三角形DBG中,可根据BD即OP的长和∠DBG的正弦函数求出DG的表达式,即可求出DH的长,根据已知的△OPD的面积可列出一个关于t的方程,即可求出t的值.②当P在x轴负半轴,但D在x轴上方时.即<t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出DG,进而求出GF的长,然后同①.③当P在x轴负半轴,D在x轴下方时,即t≤时,方法同②.综合上面三种情况即可求出符合条件的t的值.解答:解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F.由已知得:BF=OE=2,OF==,∴点B的坐标是(,2)设直线AB的解析式是y=kx+b(k≠0),则有.解得.∴直线AB的解析式是y=x+4;(2)如图2,∵△ABD由△AOP旋转得到,∴△ABD≌△AOP,∴AP=AD,∠DAB=∠PAO,∴∠DAP=∠BAO=60°,∴△ADP是等边三角形,∴DP=AP=.如图2,过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.方法(一)在Rt△BDG中,∠BGD=90°,∠DBG=60°.∴BG=BD•cos60°=×=.DG=BD•sin60°=×=.∴OH=EG=,DH=∴点D的坐标为(,)方法(二)易得∠AEB=∠BGD=90°,∠ABE=∠BDG,∴△ABE∽△BDG,∴;而AE=2,BD=OP=,BE=2,AB=4,则有,解得BG=,DG=;∴OH=,DH=;∴点D的坐标为(,).(3)假设存在点P,在它的运动过程中,使△OPD的面积等于.设点P为(t,0),下面分三种情况讨论:①当t>0时,如图,BD=OP=t,DG=t,∴DH=2+t.∵△OPD的面积等于,∴,解得,(舍去)∴点P1的坐标为(,0).②∵当D在y轴上时,根据勾股定理求出BD==OP,∴当<t≤0时,如图,BD=OP=﹣t,DG=﹣t,∴GH=BF=2﹣(﹣t)=2+t.∵△OPD的面积等于,∴,解得,,∴点P2的坐标为(,0),点P3的坐标为(,0).③当t≤时,如图3,BD=OP=﹣t,DG=﹣t,∴DH=﹣t﹣2.∵△OPD的面积等于,∴(﹣t)[﹣(2+t)]=,解得(舍去),∴点P4的坐标为(,0),综上所述,点P的坐标分别为P1(,0)、P2(,0)、P3(,0)、P4(,0).点评:本题综合考查的是一次函数的应用,包括待定系数法求解析式、旋转的性质、相似三角形的判定和性质、三角形面积公式的应用等,难度较大.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.考点:一次函数综合题.专题:压轴题.分析:(1)根据直线y=﹣x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出==,据此可以求得点P的运动速度;(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.解答:解:(1)∵直线y=﹣x+4与坐标轴分别交于点A、B,∴x=0时,y=4,y=0时,x=8,∴==,当t秒时,QO=FQ=t,则EP=t,∵EP∥BO,∴==,∴AP=2t,∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,∴点P运动的速度是每秒2个单位长度;(2)如图1,当PQ=PE时,矩形PEFQ为正方形,则∵OQ=FQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴8﹣3t=t,解得:t=2;如图2,当PQ=PE时,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8﹣2t,∴QP=t﹣(8﹣2t)=3t﹣8,∴t=3t﹣8,解得:t=4;(3)如图1,当Q在P点的左边时,∵OQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴S矩形PEFQ=QP•QF=(8﹣3t)•t=8t﹣3t2,当t=﹣=时,S矩形PEFQ的最大值为:=,如图2,当Q在P点的右边时,∵OQ=t,PA=2t,∴2t>8﹣t,∴t,∴QP=t﹣(8﹣2t)=3t﹣8,∴S矩形PEFQ=QP•QF=(3t﹣8)•t=3t2﹣8t,∵当点P、Q其中一点停止运动时,另一点也停止运动,∴<t≤4,当t=﹣=时,S矩形PEFQ的最大,∴t=4时,S矩形PEFQ的最大值为:3×42﹣8×4=16,点评:此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.考点:一次函数综合题.专题:压轴题.分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.解答:解:(1)解方程x2﹣14x+48=0得x1=6,x2=8.∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,∴OC=6,OA=8.∴C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).由(1)知,OA=8,则A(8,0).∵点A、C都在直线MN上,∴,解得,,∴直线MN的解析式为y=﹣x+6;(3)∵A(8,0),C(0,6),∴根据题意知B(8,6).∵点P在直线MNy=﹣x+6上,∴设P(a,﹣a+6)当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);②当PC=BC时,a2+(﹣a+6﹣6)2=64,解得,a=,则P2(﹣,),P3(,);③当PB=BC时,(a﹣8)2+(a﹣6+6)2=64,解得,a=,则﹣a+6=﹣,∴P4(,﹣).综上所述,符合条件的点P有:P1(4,3),P2(﹣,)P3(,),P4(,﹣).点评:本题考查了一次函数综合题.其中涉及到的知识点有:待定系数法求一次函数解析式,一次函数图象上点的坐标特征,等腰三角形的性质.解答(3)题时,要分类讨论,防止漏解.另外,解答(3)题时,还利用了“数形结合”的数学思想.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)通过解一元二次方程x2﹣(+1)x+=0,求得方程的两个根,从而得到A、B两点的坐标,再根据两点之间的距离公式可求AB的长,根据AB:AC=1:2,可求AC的长,从而得到C点的坐标;(2)分①当点M在CB边上时;②当点M在CB边的延长线上时;两种情况讨论可求S关于t的函数关系式;(3)分AQ=AB,BQ=BA,BQ=QA三种情况讨论可求Q点的坐标.解答:解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,﹣2),Q3(1,2),Q4(1,).点评:考查了一次函数综合题,涉及的知识点有:解一元二次方程,两点之间的距离公式,三角形面积的计算,函数思想,分类思想的运用,菱形的性质,综合性较强,有一定的难度.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.考点:一次函数综合题;解二元一次方程组;待定系数法求一次函数解析式;三角形的面积;角平分线的性质;勾股定理;菱形的性质.专题:计算题.分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得到方程组,求出即可;(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P 在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.解答:(1)解:∵A(﹣3,4),∴AH=3,OH=4,由勾股定理得:AO==5,答:OA的长是5.(2)解:∵菱形OABC,∴OA=OC=BC=AB=5,5﹣3=2,∴B(2,4),C(5,0),设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得:,解得:,∴直线AC的解析式为,当x=0时,y=2.5∴M(0,2.5),答:直线AC的解析式是,点M的坐标是(0,2.5).(3)①解:过M作MN⊥BC于N,∵菱形OABC,∴∠BAC=∠OCA,∵MO⊥CO,MN⊥BC,∴OM=MN,当0≤t<2.5时,P在AB上,MH=4﹣2.5=,S=×BP×MH=×(5﹣2t)×=﹣t+,∴,当t=2.5时,P与B重合,△PMB不存在;当2.5<t≤5时,P在BC上,S=×PB×MN=×(2t﹣5)×=t﹣,∴,答:S与t的函数关系式是(0≤t<2.5)或(2.5<t≤5).②解:当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是×5×=,同理在BC上时,P与C重合时,S最大是×5×=,∴S的最大值是,答:S的最大值是.点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.考点:一次函数综合题.专题:压轴题.分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.解答:(1)证明:∵∠AOG=∠ADG=90°,∴在Rt△AOG和Rt△ADG中,∵,∴△AOG≌△ADG(HL);(2)解:PG=OG+BP.由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,又∠1+∠DAG+∠DAP+∠BAP=90°,所以,2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,故∠PAG=∠DAG+∠DAP=45°,∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP;(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°,∴∠1=∠2=30°,在Rt△AOG中,AO=3,AG=2OG,AG2=AO2+OG2,∴OG=,则G点坐标为:(,0),CG=3﹣,在Rt△PCG中,PG=2CG=2(3﹣),PC==3﹣3,则P点坐标为:(3,3﹣3),设直线PE的解析式为y=kx+b,则,解得,所以,直线PE的解析式为y=x﹣3.点评:本题考查了一次函数的综合运用.关键是根据正方形的性质证明三角形全等,根据三角形全等的性质求角、边的关系,利用特殊角解直角三角形,求P、G两点坐标,确定直线解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.考点:一次函数综合题.专题:压轴题;探究型.分析:(1)△AOC和△BCP全等,则AO=BC=1,又∵AB=,t=AB﹣BC=﹣1;(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;(3)根据题意可直接得出b=1﹣t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1﹣),但t=0时,点C不在第一象限,所以不符合题意.解答:解:(1)△AOC和△BCP全等,则AO=BC=1,又AB=,所以t=AB﹣BC=﹣1;(2)OC=CP.证明:过点C作x轴的平行线,交OA与直线BP于点T、H.∵PC⊥OC,∴∠OCP=90°,∵OA=OB=1,∴∠OBA=45°,∵TH∥OB,∴∠BCH=45°,又∠CHB=90°,∴△CHB为等腰直角三角形,∴CH=BH,∵∠AOB=∠OBH=∠BHT=90°,∴四边形OBHT为矩形,∴OT=BH,∴OT=CH,∵∠TCO+∠PCH=90°,∠CPH+∠PCH=90°,∴∠TCO=∠CPH,∵HB⊥x轴,TH∥OB,∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,∴△OTC≌△CHP,∴OC=CP;(3)①∵△OTC≌△CHP,∴CT=PH,∴PH=CT=AT=AC•cos45°=t,∴BH=OT=OA﹣AT=1﹣t,∴BP=BH﹣PH=1﹣t,∴;(0<t<)②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,PB=BC,则﹣t=|1﹣t|,解得t=1或t=﹣1(舍去),∴当t=1时,△PBC为等腰三角形,即P点坐标为:P(1,1﹣).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.考点:一次函数综合题.专题:综合题;数形结合.分析:(1)①联立两个函数式,求解即可得出交点坐标,即为点C的坐标.②欲求△OAC的面积,结合图形,可知,只要得出点A和点C的坐标即可,点C的坐标已知,利用函数关系式即可求得点A的坐标,代入面积公式即可.(2)在OC上取点M,使OM=OP,连接MQ,易证△POQ≌△MOQ,可推出AQ+PQ=AQ+MQ;若想使得AQ+PQ存在最小值,即使得A、Q、M三点共线,又AB⊥OP,可得∠AEO=∠CEO,即证△AEO≌△CEO(ASA),又OC=OA=4,利用△OAC的面积为6,即可得出AM=3,AQ+PQ存在最小值,最小值为3.解答:解:(1)①由题意,(2分)解得所以C(4,4)(3分)②把y=0代入y=﹣2x+12得,x=6,所以A点坐标为(6,0),(4分)所以.(6分)(2)存在;由题意,在OC上截取OM=OP,连接MQ,∵OQ平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ,∴△POQ≌△MOQ(SAS),(7分)∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小.即AQ+PQ存在最小值.∵AB⊥ON,所以∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=4,∵△OAC的面积为6,所以AM=12÷4=3,∴AQ+PQ存在最小值,最小值为3.(9分)点评:本题主要考查一次函数的综合应用,具有一定的综合性,要求学生具备一定的数学解题能力,有一定难度.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:开放型.分析:(1)已知直线解析式,令y=0,求出x的值,可求出点A,B的坐标.联立方程组求出点P的坐标.推出AO=QO,可得出∠PAB=45°.(2)先根据CQ:AO=1:2得到m、n的关系,然后求出S△AOQ,S△PAB并都用字母m表示,根据S四边形PQOB=S△PAB ﹣S△AOQ积列式求解即可求出m的值,从而也可求出n的值,继而可推出点P的坐标以及直线PA与PB的函数表达式.(3)本题要依靠辅助线的帮助.求证相关图形为平行四边形,继而求出D1,D2,D3的坐标.解答:解:(1)在直线y=x+m中,令y=0,得x=﹣m.∴点A(﹣m,0).在直线y=﹣3x+n中,令y=0,得.∴点B(,0).由,得,∴点P(,).在直线y=x+m中,令x=0,得y=m,∴|﹣m|=|m|,即有AO=QO.又∵∠AOQ=90°,∴△AOQ是等腰直角三角形,∴∠PAB=45°.(2)∵CQ:AO=1:2,∴(n﹣m):m=1:2,整理得3m=2n,∴n=m,∴==m,而S四边形PQOB=S△PAB﹣S△AOQ=(+m)×(m)﹣×m×m=m2=,解得m=±4,∵m>0,∴m=4,∴n=m=6,∴P().∴PA的函数表达式为y=x+4,PB的函数表达式为y=﹣3x+6.(3)存在.过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点D1,过点A作BP的平行线交PM于点D2,过点A、B分别作BP、AP的平行线交于点D3.①∵PD1∥AB且BD1∥AP,∴PABD1是平行四边形.此时PD1=AB,易得;②∵PD2∥AB且AD2∥BP,∴PBAD2是平行四边形.此时PD2=AB,易得;③∵BD3∥AP且AD3∥BP,此时BPAD3是平行四边形.∵BD3∥AP且B(2,O),∴y BD3=x﹣2.同理可得y AD3=﹣3x﹣12,得,∴.点评:本题的综合性强,主要考查的知识点为一次函数的应用,平行四边形的判定以及面积的灵活计算.难度较大.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:综合题.分析:(1)先求出A、B两点的坐标,再由一个角等于30°,求出AC的长,从而计算出面积;(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.解答:解:(1)∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B,∴A(1,0),B(0,),∴AB=2,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,解得x=,S△ABC==;(2)过P作PD⊥x轴,垂足为D,S△APB=S梯形ODPB+S△AOB﹣S△APD==,﹣=,解得m=;(3)∵AB==2,∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣);当AB=BQ时,点Q4(0,+2),Q2(0,﹣2),Q2(﹣1,0);当AQ=BQ时,点Q6(0,),Q2(﹣1,0),综上可得:(0,),(0,),(﹣1,0)(3,0),(0,),(0,)点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.。
2024年中考数学复习重难点题型训练—一次函数与几何图形综合题一(含答案解析)

2024年中考数学复习重难点题型训练—一次函数与几何图形综合题二(含答案解析)类型一与三角形有关1.(2022·天津)如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x 轴,若AB=6,OA=OB=5,则点A的坐标是()A.(5,4)B.(3,4)C.(5,3)D.(4,3)【答案】D【分析】利用HL证明△ACO≌△BCO,利用勾股定理得到OC=4,即可求解.【详解】解:∵AB⊥x轴,∴∠ACO=∠BCO=90°,∵OA=OB,OC=OC,∴△ACO≌△BCO(HL),∴AC=BC=12AB=3,∵OA=5,∴=4,∴点A的坐标是(4,3),故选:D.【点睛】本题考查了坐标与图形,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用所学知识解决问题.2.(2020·宁夏中考真题)如图,直线542y x =+与x 轴、y 轴分别交于A 、B 两点,把AOB 绕点B 逆时针旋转90°后得到11AO B ,则点1A的坐标是_____.【答案】(4,125)【解析】【分析】首先根据直线AB 来求出点A 和点B 的坐标,A 1的横坐标等于OB ,而纵坐标等于OB-OA ,即可得出答案.【详解】解:在542y x =+中,令x=0得,y=4,令y=0,得5042x =+,解得x=8-5,∴A (8-5,0),B (0,4),由旋转可得△AOB ≌△A 1O 1B ,∠ABA 1=90°,∴∠ABO=∠A 1BO 1,∠BO 1A 1=∠AOB=90°,OA=O 1A 1=85,OB=O 1B=4,∴∠OBO 1=90°,∴O 1B ∥x 轴,∴点A 1的纵坐标为OB-OA 的长,即为48-5=125;横坐标为O 1B=OB=4,故点A 1的坐标是(4,125),故答案为:(4,125).【点睛】本题主要考查了旋转的性质以及一次函数与坐标轴的交点问题,利用基本性质结合图形进行推理是解题的关键.3.(2021·广西贺州市·中考真题)如图,一次函数4y x =+与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且45OPC ∠=︒,PC PO =,则点P 的标为________.【答案】(--【分析】过P 作PD ⊥OC 于D ,先求出A ,B 的坐标,得∠ABO=∠OAB=45°,再证明△PCB ≌△OPA ,从而求出BD =,OD =,进而即可求解.【详解】如图所示,过P 作PD ⊥OC 于D ,∵一次函数4y x =+与坐标轴分别交于A ,B 两点,∴A(-4,0),B(0,4),即:OA=OB ,∴∠ABO=∠OAB=45°,∴△BDP 是等腰直角三角形,∵∠PBC=∠CPO=∠OAP=45°,∴∠PCB+∠BPC=135°=∠OPA+∠BPC,∴∠PCB=∠OPA,又∵PC=OP,∴△PCB≌△OPA(AAS),∴AO=BP=4,∴Rt△BDP中,BD=PD=2=2,∴OD=OB−BD=2,∴P(2,2).故答案是:P(2,2).【点睛】本题主要考查了一次函数图象上点的坐标特征以及等腰三角形的性质,结合等腰三角形的性质,判定全等三角形是解决问题的关键.4.(2022·湖北黄冈)如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C 匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为________.【答案】252+##2+25【分析】根据函数图像可得AB=4=BC ,作∠BAC 的平分线AD ,∠B =36°可得∠B =∠DAC =36°,进而得到ADC BAC △△,由相似求出BD 的长即可.【详解】根据函数图像可得AB=4,AB+BC=8,∴BC=AB=4,∵∠B =36°,∴72BCA BAC ∠∠︒==,作∠BAC 的平分线AD ,∴∠BAD =∠DAC =36°=∠B ,∴AD=BD ,72BCA DAC ∠∠︒==,∴AD=BD=CD ,设AD BD CD x ===,∵∠DAC =∠B =36°,∴ADC BAC △△,∴AC DC BC AC =,∴x 4x 4x-=,解得:1225x =-+,225x =--,∴252AD BD CD ===,此时521AB BD t +==(s),故答案为:52.【点睛】此题考查了图形与函数图象间关系、相似三角形的判定与性质、解一元二次方程,关键是证明ADC BAC △△.5.(2020·四川内江?中考真题)如图,在平面直角坐标系中,点A (-2,0),直线33:33l y x =+与x 轴交于点B ,以AB 为边作等边1ABA ∆,过点1A 作11//A B x 轴,交直线l 于点1B ,以11A B 为边作等边112A B A ∆,过点2A 作22//A B x 轴,交直线l 于点2B ,以22A B 为边作等边223A B A ∆,以此类推……,则点2020A 的纵坐标是______________【答案】20203(21)2-【解析】【分析】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),且与x 轴夹角为30º,则有AB=1,然后根据平行线的性质、等边三角形的性质、含30º的直角三角形的性质,分别求的A 1、A 2、A 3、的纵坐标,进而得到A n 的纵坐标,据此可得A 2020的纵坐标,即可解答.【详解】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),与y 轴交于点D (0,33),∴OB=1,OD=33,∴∠DBO=30º由题意可得:∠A 1B 1B=∠A 2B 2B 1=30º,∠B 1A 1B=∠B 2A 2B 1=60º∴∠A 1BB 1=∠A 2B 1B 2=90º,∴AB=1,A 1B 1=2A 1B=21,A 2B 2=2A 2B 1=22,A 3B 3=2A 3B 2=23,…A n B n =2n∴A 1C=2AB=2×1,A 1纵坐标为32×1=13(21)2-;A 2C 1=32A 1B 1=1322⨯,A2的纵坐标为32×1+1322⨯=013(22)2+=332⨯=23(21)2-;A 3C 2=32A 2B 2=2322⨯,A 3的纵坐标为32×1+1322⨯+2322⨯=0123(222)2++=372⨯=33(21)2-;…由此规律可得:A n C n-1=1322n -⨯,A n 的纵坐标为01213(2222)2n -++++ =3(21)2n -,∴A 2020=20203(21)2-,故答案为:20203(21)2-【点睛】本题是一道点的坐标变化规律探究,涉及一次函数的图象、等边三角形的性质、含30º角的直角三角形的性质,数字型规律等知识,解答的关键是认真审题,观察图象,结合基本图形的有关性质,找到坐标变化规律.6.(2022·陕西)如图,ABC 的顶点坐标分别为(23)(30)(11)A B C ----,,,,,.将ABC 平移后得到A B C '''V ,且点A 的对应点是(23)A ',,点B 、C 的对应点分别是B C '',.(1)点A 、A '之间的距离是__________;(2)请在图中画出A B C '''V .【答案】(1)4(2)见解析【分析】(1)由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4;(2)根据题意找出平移规律,求出103-1B C ''(,),(,),进而画图即可.(1)解:由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4.故答案为:4.(2)解:由题意,得103-1B C ''(,),(,),如图,A B C '''V 即为所求.【点睛】本题考查了坐标系中两点之间的距离求解以及平移求点坐标画图,题目相对较简单,掌握平移规律是解决问题的关键.7.(2021·贵州毕节市·中考真题)如图,在平面直角坐标系中,点()11,1N 在直线:l y x =上,过点1N 作11N M l ⊥,交x 轴于点1M ;过点1M 作12M N x ⊥轴,交直线l 于点2N ;过点2N 作22N M l ⊥,交x 轴于点2M ;过点2M 作23M N x ⊥轴,交直线l 于点3N ;…;按此作法进行下去,则点2021M 的坐标为_____________.【答案】(20212,0).【分析】根据题目所给的解析式,求出对应的1M 坐标,然后根据规律求出n M 的坐标,最后根据题目要求求出最后答案即可.【详解】解:如图,过点N 作NM ⊥x 轴于M将1x =代入直线解析式y x =中得1y =∴1OM MN ==,MON ∠=45°∵1ONM =∠90°∴1ON NM =∵1ON NM ⊥∴11OM MM ==∴1M 的坐标为(2,0)同理可以求出2M 的坐标为(4,0)同理可以求出3M 的坐标为(8,0)同理可以求出n M 的坐标为(2n ,0)∴2021M 的坐标为(20212,0)故答案为:(20212,0).【点睛】本题主要考查了直线与坐标轴之间的关系,解题的关键在于能够发现规律.8.(2020·湖南湘西?中考真题)在平面直角坐标系中,O 为原点,点(6,0)A ,点B 在y 轴的正半轴上,30ABO ∠=︒.矩形CODE 的顶点D ,E ,C 分别在,,OA AB OB 上,2OD =.将矩形CODE 沿x 轴向右平移,当矩形CODE 与ABO 重叠部分的面积为时,则矩形CODE 向右平移的距离为___________.【答案】2【解析】【分析】先求出点B 的坐标(0,3),得到直线AB 的解析式为:33y =+,根据点D 的坐标求出OC 的长度,利用矩形CODE 与ABO 重叠部分的面积为63列出关系式求出3D G '=,再利用一次函数关系式求出OD '=4,即可得到平移的距离.【详解】∵(6,0)A ,∴OA=6,在Rt △AOB 中,30ABO ∠=︒,∴63tan 30OA OB ==∴B (0,63),∴直线AB 的解析式为:33y =+,当x=2时,y=43∴E (2,3,即DE=3∵四边形CODE 是矩形,∴OC=DE=43设矩形CODE 沿x 轴向右平移后得到矩形C O D E '''',D E ''交AB 于点G ,∴D E ''∥OB ,∴△AD G '∽△AOB ,∴∠AGD '=∠AOB=30°,∴∠EGE '=∠AGD '=30°,∴GE ''=,∵平移后的矩形CODE 与ABO 重叠部分的面积为,∴五边形C O D GE '''的面积为∴12O D O C EE GE ''''''⋅-⋅=,∴122EE ''⨯-⨯=,∴2EE '=,∴矩形CODE 向右平移的距离DD '=2EE '=,故答案为:2.【点睛】此题考查了锐角三角函数,求一次函数的解析式,矩形的性质,图形平移的性质,是一道综合多个知识点的综合题型,且较为基础的题型.9.(2021·浙江金华市·中考真题)在平面直角坐标系中,点A 的坐标为(,点B 在直线8:3l y x =上,过点B 作AB 的垂线,过原点O 作直线l 的垂线,两垂线相交于点C .(1)如图,点B ,C 分别在第三、二象限内,BC 与AO 相交于点D .①若BA BO =,求证:CD CO =.②若45CBO ∠=︒,求四边形ABOC 的面积.(2)是否存在点B ,使得以,,A B C 为顶点的三角形与BCO 相似?若存在,求OB 的长;若不存在,请说明理由.【答案】(1)①见解析;②552;(2)存在,44+-4,9,1【分析】(1)①等腰三角形等角对等边,则BAD AOB ∠=∠,根据等角的余角相等和对顶角相等,得到CDO COD ∠=∠,根据等角对等边,即可证明CD CO =;②添加辅助线,过点A 作AH OB ⊥于点H ,根据直线l 的解析式和角的关系,分别求出线段AB 、BC 、OB 、OC 的长,则11+22ABC CBO ABOC S S S AB BC OB OC =+=⨯⨯ 四边形;(2)分多钟情况进行讨论:①当点C 在第二象限内,ACB CBO ∠=∠时;②当点C 在第二象限内,ACB BCO ∠=∠时;③当点C 在第四象限内,ACB CBO ∠=∠时.【详解】解:(1)①证明:如图1,∵BA BO =,∴12∠=∠.∴BA BC ⊥,∴2590∠+∠=︒.而45∠=∠,∴2490∠+∠=︒.∵OB OC ⊥,∴1390∠+∠=︒.∴34∠=∠,∴CD CO =.②如图1,过点A 作AH OB ⊥于点H .由题意可知3tan 18∠=,在Rt AHO 中,3tan 18AH OH ∠==.设3m AH =,8m OH =.∵222AH OH OA +=,∴()()22238m m +=,解得1m =.∴38AH OH ==,.∵4590CBO ABC ∠=︒∠=︒,,∴45ABH ∠=︒,∴3,tan 45sin 45AH AH BH AB ====︒︒∴5OB OH BH =-=.∵45OB OC CBO ⊥∠=︒,,∴tan 455,cos 45OB OC OB BC =⨯︒===︒,∴111522ABC S AB BC =⨯=⨯= ,112555222CBO S OB OC =⨯=⨯⨯= :∴552ABC CBO ABOC S S S =+= 四边形.(2)过点A 作AH OB ⊥于点H ,则有38AH OH ==,.①如图2,当点C 在第二象限内,ACB CBO ∠=∠时,设OB t=∵ACB CBO ∠=∠,∴//AC OB .又∵AH OB OC OB ⊥⊥,,∴3AH OC ==.∵AH OB AB BC ⊥⊥,,∴12902390∠+∠=︒∠+∠=︒,,∴13∠=∠,∴AHB BOC ∽,∴AH HB BO OC=,∴383t t -=,整理得2890t t -+=,解得4t =±∴4OB =±②如图3,当点C 在第二象限内,ACB BCO ∠=∠时,延长AB CO ,交于点G ,则ACB GCB ≌,∴AB GB =.又∵AH OB OC OB ⊥⊥,,∴90AHB GOB ∠=∠=︒,而ABH GBO ∠=∠,∴ABH GBO ≌,∴142OB HB OH ===③当点C 在第四象限内,ACB CBO ∠=∠时,AC 与OB 相交于点E ,则有BE CE =.(a)如图4,点B 在第三象限内.在Rt ABC 中,1290,90ACB CAB ∠+∠=︒∠+∠=︒,∴2CAB∠=∠∴AE BE CE ==,又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒,而AEH CEO∠=∠∴AHE COE ≌,∴142HE OE OH ===∴225AE AH HE =+=,∴5BE =,∴9OB BE OE =+=(b)如图5,点B 在第一象限内.在Rt ABC 中90,90ACB CAB CBO ABE ∠+∠=︒∠+∠=︒∴CAB ABE ∠=∠,∴AE BE CE ==.又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒而AEH CEO ∠=∠,∴AHE COE≌∴142HE OE OH ===∴5AE ==,∴5BE =,∴1OB BE OE =-=综上所述,OB 的长为44+4,9,1.【点睛】本题涉及到等腰三角形、等角的余角相等、利用切割法求四边形的面积和相似三角形等知识,综合性较强.在题中已知两个三角形相似时,要分情况考虑.10.(2020·河南中考真题)小亮在学习中遇到这样一个问题:如图,点D 是弧BC 上一动点,线段8,BC cm =点A 是线段BC 的中点,过点C 作//CF BD ,交DA 的延长线于点F .当DCF ∆为等腰三角形时,求线段BD 的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:()1根据点D 在弧BC 上的不同位置,画出相应的图形,测量线段,,BD CD FD 的长度,得到下表的几组对应值.操作中发现:①"当点D 为弧BC 的中点时, 5.0BD cm =".则上中a 的值是②"线段CF 的长度无需测量即可得到".请简要说明理由;()2将线段BD 的长度作为自变量x CD ,和FD 的长度都是x 的函数,分别记为CD y 和FD y ,并在平面直角坐标系xOy 中画出了函数FD y 的图象,如图所示.请在同一坐标系中画出函数CD y 的图象;()3继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当DCF ∆为等腰三角形时,线段BD 长度的近似值.(结果保留一位小数).【答案】(1)①5.0;②见解析;(2)图象见解析;(3)图象见解析;3.5cm 或5.0cm 或6.3cm ;【解析】【分析】(1)①点D 为弧BC 的中点时,△ABD ≌△ACD ,即可得到CD=BD ;②由题意得△ACF ≌△ABD ,即可得到CF=BD ;(2)根据表格数据运用描点法即可画出函数图象;(3)画出CF y 的图象,当DCF ∆为等腰三角形时,分情况讨论,任意两边分别相等时,即任意两个函数图象相交时的交点横坐标即为BD 的近似值.【详解】解:(1)①点D 为弧BC 的中点时,由圆的性质可得:AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACD ,∴CD=BD=5.0,∴ 5.0a =;②∵//CF BD ,∴BDA CFA ∠=∠,∵BDA CFA BAD CAF AD AF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACF ≌△ABD ,∴CF=BD ,∴线段CF 的长度无需测量即可得到;(2)函数CD y的图象如图所示:(3)由(1)知=CF BD x =,画出CF y 的图象,如上图所示,当DCF ∆为等腰三角形时,①CF CD =,BD 为CF y 与CD y 函数图象的交点横坐标,即BD=5.0cm ;②CF DF =,BD 为CF y 与DF y 函数图象的交点横坐标,即BD=6.3cm ;③CD DF =,BD 为CD y 与DF y 函数图象的交点横坐标,即BD=3.5cm ;综上:当DCF ∆为等腰三角形时,线段BD 长度的近似值为3.5cm 或5.0cm 或6.3cm .【点睛】本题考查一次函数结合几何的应用,学会用描点法画出函数图象,熟练掌握一次函数的性质以及三角形全等的判定及性质是解题的关键.11.(2020·河北中考真题)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN-匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持APQ B∠=∠.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将ABC∆的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当03x≤≤及39x≤≤时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角APQ∠扫描APQ∆区域(含边界),扫描器随点P从M到B再到N共用时36秒.若94AK=,请直接..写出点K被扫描到的总时长.【答案】(1)3;(2)43MP=;(3)当03x≤≤时,24482525d x=+;当39x≤≤时,33355d x=-+;(4)23t s=【解析】【分析】(1)根据当点P在BC上时,PA⊥BC时PA最小,即可求出答案;(2)过A点向BC边作垂线,交BC于点E,证明△APQ∽△ABC,可得2APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,根据SS上下=45可得24=9APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,可得23APAB=,求出AB=5,即可解出MP;(3)先讨论当0≤x≤3时,P在BM上运动,P到AC的距离:d=PQ·sinC,求解即可,再讨论当3≤x≤9时,P在BN上运动,BP=x-3,CP=8-(x-3)=11-x,根据d=CP·sinC即可得出答案;(4)先求出移动的速度=936=14,然后先求出从Q 平移到K 耗时,再求出不能被扫描的时间段即可求出时间.【详解】(1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3;(2)过A 点向BC 边作垂线,交BC 于点E,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AP AD PQ AB AC BC==,∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,∴23AP AB =,AE=2BC ·tan 3C =,根据勾股定理可得AB=5,∴2253AP MP AB +==,解得MP=43;(3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35,∴d=35PQ ,∵AP=x+2,∴25AP x PQ AB BC+==,∴PQ=285x +⨯,∴d=23855x +⨯⨯=24482525x +,当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335,综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩;(4)AM=2<AQ=94,移动的速度=936=14,①从Q 平移到K ,耗时:92414-=1秒,②P 在BC 上时,K 与Q 重合时CQ=CK=5-94=114,∵∠APQ+∠QPC=∠B+∠BAP ,APQ B∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-,整理得y 2-8y=554-,(y-4)2=94,解得y 1=52,y 2=112,52÷14=10秒,112÷14=22秒,∴点K 被扫描到的总时长36-(22-10)-1=23秒.【点睛】本题考查了相似三角形的判定和性质,锐角三角函数,一次函数的应用,结合知识点灵活运用是解题关键.12.(2020·湖南衡阳?中考真题)如图1,平面直角坐标系xOy 中,等腰ABC ∆的底边BC 在x 轴上,8BC =,顶点A 在y 的正半轴上,2OA =,一动点E 从(3,0)出发,以每秒1个单位的速度沿CB 向左运动,到达OB 的中点停止.另一动点F 从点C 出发,以相同的速度沿CB 向左运动,到达点O 停止.已知点E 、F 同时出发,以EF 为边作正方形EFGH ,使正方形EFGH 和ABC ∆在BC 的同侧.设运动的时间为t 秒(0t ≥).(1)当点H 落在AC 边上时,求t 的值;(2)设正方形EFGH 与ABC ∆重叠面积为S ,请问是存在t 值,使得9136S =若存在,求出t 值;若不存在,请说明理由;(3)如图2,取AC 的中点D ,连结OD ,当点E 、F 开始运动时,点M 从点O 出发,以每秒OD DC CD DO ---运动,到达点O 停止运动.请问在点E 的整个运动过程中,点M 可能在正方形EFGH 内(含边界)吗?如果可能,求出点M 在正方形EFGH 内(含边界)的时长;若不可能,请说明理由.【答案】(1)t=1;(2)存在,143t =,理由见解析;(3)可能,3455t ≤≤或4533t ≤≤或35t ≤≤理由见解析【解析】【分析】(1)用待定系数法求出直线AC 的解析式,根据题意用t 表示出点H 的坐标,代入求解即可;(2)根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,用待定系数法求出直线AB 的解析式,求出点H 落在BC 边上时的t 值,求出此时重叠面积为169﹤9136,进一步求出重叠面积关于t 的表达式,代入解t 的方程即可解得t 值;(3)由已知求得点D (2,1),AC=,结合图形分情况讨论即可得出符合条件的时长.【详解】(1)由题意,A(0,2),B(-4,0),C(4,0),设直线AC 的函数解析式为y=kx+b ,将点A 、C 坐标代入,得:402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =-+,当点H 落在AC 边上时,点E(3-t ,0),点H (3-t ,1),将点H 代入122y x =-+,得:11(3)22t =--+,解得:t=1;(2)存在,143t =,使得9136S =.根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,设直线AB 的函数解析式为y=mx+n ,将点A 、B 坐标代入,得:402m n n -+=⎧⎨=⎩,解得:122m n ⎧=⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =+,当t ﹥4时,点E (3-t ,0)点H (3-t ,t-3),G(0,t-3),当点H 落在AB 边上时,将点H 代入122y x =+,得:13(3)22t t -=-+,解得:133t =;此时重叠的面积为221316(3)(3)39t -=-=,∵169﹤9136,∴133﹤t ﹤5,如图1,设GH 交AB 于S ,EH 交AB 于T,将y=t-3代入122y x =+得:1322t x -=+,解得:x=2t-10,∴点S(2t-10,t-3),将x=3-t 代入122y x =+得:11(3)2(7)22y t t =-+=-,∴点T 1(3,(7))2t t --,∴AG=5-t ,SG=10-2t ,BE=7-t ,ET=1(7)2t -,211(7)24BET S BE ET t ∆==- ,21(5)2ASG S AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-,由2527133424t t -+-=9136得:1143t =,29215t =﹥5(舍去),∴143t =;(3)可能,35≤t≤1或t=4.∵点D 为AC 的中点,且OA=2,OC=4,∴点D (2,1),AC=,易知M 点在水平方向以每秒是4个单位的速度运动;当0﹤t ﹤12时,M 在线段OD 上,H 未到达D 点,所以M 与正方形不相遇;当12﹤t ﹤1时,12+12÷(1+4)=35秒,∴t =35时M 与正方形相遇,经过1÷(1+4)=15秒后,M 点不在正方行内部,则3455t ≤≤;当t=1时,由(1)知,点F 运动到原E 点处,M 点到达C 处;当1≤t≤2时,当t=1+1÷(4-1)=43秒时,点M 追上G 点,经过1÷(4-1)=13秒,点M 都在正方形EFGH 内(含边界),4533t ≤≤当t=2时,点M 运动返回到点O 处停止运动,当t=3时,点E 运动返回到点O 处,当t=4时,点F 运动返回到点O 处,当35t ≤≤时,点M 都在正方形EFGH 内(含边界),综上,当3455t ≤≤或4533t ≤≤或35t ≤≤时,点M 可能在正方形EFGH 内(含边界).【点睛】本题考查了一次函数与几何图形的综合,涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识,解答的关键是认真审题,提取相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,进而推理、探究、发现和计算.13.(2020·黑龙江哈尔滨?中考真题)已知,在平面直角坐标系中,点O 为坐标原点,直线AB 与x 轴的正半轴交于点A ,与y 轴的负半轴交于点B ,OA OB =,过点A 作x 轴的垂线与过点O 的直线相交于点C ,直线OC 的解析式为34y x =,过点C 作CM y ⊥轴,垂足为,9M OM =.(1)如图1,求直线AB 的解析式;(2)如图2,点N 在线段MC 上,连接ON ,点P 在线段ON 上,过P 点作PD x ⊥轴,垂足为D ,交OC 于点E ,若NC OM =,求PE OD的值;(3)如图3,在(2)的条件下,点F 为线段AB 上一点,连接OF ,过点F 作OF 的垂线交线段AC 于点Q ,连接BQ ,过点F 作x 轴的平行线交BQ 于点G ,连接PF 交x 轴于点H ,连接EH ,若,DHE DPH GQ FG ∠=∠-=,求点P 的坐标.【答案】(1)12y x =-;(2)94;(3)1236(,)55P .【解析】【分析】(1)根据题意求出A ,B 的坐标即可求出直线AB 的解析式;(2)求出N (3,9),以及ON 的解析式为y=3x ,设P (a ,3a ),表达出PE 及OD 即可解答;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,先证明四边形OSRA 为矩形,再通过边角关系证明△OFS ≌△FQR ,得到SF=QR ,进而证明△BSG ≌△QRG ,得到SG=RG=6,设FR=m ,根据GQ FG -=,以及在Rt △GQR 中利用勾股定理求出m 的值,得到FS=8,AR=4,证明四边形OSFT 为矩形,得到OT=FS=8,根据∠DHE=∠DPH ,利用正切函数的定义得到DE DH DH PD=,从而得到DH=32a ,根据∠PHD=∠FHT ,得到HT=2,再根据OT=OD+DH+HT ,列出关于a 的方程即可求出a 的值,从而得到点P 的坐标.【详解】解:(1)∵CM ⊥y 轴,OM=9,∴当y=9时,394x =,解得:x=12,∴C (12,9),∵CA ⊥x 轴,则A (12,0),∴OB=OA=12,则B (0,-12),设直线AB 的解析式为y=kx+b ,∴12012k b b +=⎧⎨=-⎩,解得:112k b =⎧⎨=-⎩,∴12y x =-;(2)由题意可得,∠CMO=∠OAC=∠MOA=90°,∴四边形MOAC 为矩形,∴MC=OA=12,∵NC=OM ,∴NC=9,则MN=MC-NC=3,∴N (3,9)设直线ON 的解析式为1y k x =,将N (3,9)代入得:193k =,解得:13k =,∴y=3x ,设P (a ,3a )∵PD ⊥x 轴交OC 于点E ,交x 轴于点D ,∴3(,)4E a a ,(a,0)D ,∴PE=39344a a a -=,OD=a ,∴9944a PE OD a ==;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,∵GF ∥x 轴,∴∠OSR=∠MOA=90°,∠CAO=∠R=90°,∠BOA=∠BSG=90°,∠OAB=∠AFR ,∴∠OSR=∠R=∠AOS=∠BSG=90°,则四边形OSRA为矩形,∴OS=AR,SR=OA=12,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠FAR=90°-∠AFR=45°,∴∠FAR=∠AFR,∴FR=AR=OS,∵QF⊥OF,∴∠OFQ=90°,∴∠OFS+∠QFR=90°,∵∠SOF+∠OFS=90°,∴∠SOF=∠QFR,∴△OFS≌△FQR,∴SF=QR,∵∠SFB=∠AFR=45°,∴∠SBF=∠SFB,∴BS=SF=QR,∵∠SGB=∠RGQ,∴△BSG≌△QRG,∴SG=RG=6,设FR=m,则AR=m,∴QR=SF=12-m,∴=,-=,∵GQ FG∴66m m +-=+,∵QG 2=GR 2+QR 2,即222(6)6(12)m m +=+-,解得:m=4,∴FS=8,AR=4,∵∠OAB=∠FAR ,FT ⊥OA ,FR ⊥AR ,∴FT=FR=AR=4,∠OTF=90°,∴四边形OSFT 为矩形,∴OT=FS=8,∵∠DHE=∠DPH ,∴tan ∠DHE=tan ∠DPH ,∴DE DH DH PD=,由(2)可知,DE=34a ,PD=3a ,∴343a DH DH a=,解得:DH=32a ,∴tan ∠PHD=3232PD a DH a ==,∵∠PHD=∠FHT ,∴tan ∠FHT=2TF HT =,∴HT=2,∵OT=OD+DH+HT ,∴3282a a ++=,∴a=125,∴1236(,)55P 【点睛】本题考查了一次函数与几何综合问题,涉及了一次函数解析式的求法,矩形的判定与性质,全等三角形的判定与性质以及锐角三角函数的定义等知识点,第(3)问难度较大,解题的关键是正确做出辅助线,熟悉几何的基本知识,综合运用全等三角形以及锐角三角函数的概念进行解答.类型二与平行四边形有关14.(2022·山东泰安)如图,四边形ABCD 为平行四边形,则点B 的坐标为________.【答案】()2,1--【分析】根据平行四边形的性质以及点的平移即可得出结论.【详解】解: 四边形ABCD 为平行四边形,∴DA CB ∥,即将D 点平移到A 的过程与将C 点平移到B 的过程保持一致,将D 点平移到A 的过程是::134x --=-(向左平移4各单位长度);:220y -=(上下无平移);∴将C 点平移到B 的过程按照上述一致过程进行得到()24,1B --,即()2,1B --,故答案为:()2,1--.【点睛】本题考查平行四边形的性质及点的平移,掌握点的平移的代数表示是解决问题的关键.15.(2022·甘肃武威)如图1,在菱形ABCD 中,60A ∠=︒,动点P 从点A 出发,沿折线AD DC CB →→方向匀速运动,运动到点B 停止.设点P 的运动路程为x ,APB △的面积为y ,y 与x 的函数图象如图2所示,则AB 的长为()AB .C .D .【答案】B【分析】根据图1和图2判定三角形ABD 为等边三角形,它的面积为【详解】解:在菱形ABCD 中,∠A=60°,∴△ABD 为等边三角形,设AB=a ,由图2可知,△ABD 的面积为∴△ABD 的面积24a ==解得:a=故选B【点睛】本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此题的关键.16.(2020·黑龙江牡丹江?中考真题)如图,已知直线AB 与x 轴交于点A ,与y 轴交于点B ,线段OA 的长是方程27180x x --=的一个根,12OB OA =.请解答下列问题:(1)求点A ,B 的坐标;(2)直线EF 交x 轴负半轴于点E ,交y 轴正半轴于点F ,交直线AB 于点C .若C 是EF 的中点,6OE =,反比例函数k y x=图象的一支经过点C ,求k 的值;(3)在(2)的条件下,过点C 作CD OE ⊥,垂足为D ,点M 在直线AB 上,点N 在直线CD 上.坐标平面内是否存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形?若存在,请写出点P 的个数,并直接写出其中两个点P 的坐标;若不存在,请说明理由.【答案】(1)A (9,0),B (0,92);(2)-18;(3)存在5个,(9,12)或(9,-12)或(1,0)或(-7,4)或(-15,0).【解析】【分析】(1)解一元二次方程,得到点A 的坐标,再根据12OB OA =可得点B 坐标;(2)利用待定系数法求出直线AB 的表达式,根据点C 是EF 的中点,得到点C 横坐标,代入可得点C 坐标,根据点C 在反比例函数图像上求出k 值;(3)画出图形,可得点P 共有5个位置,分别求解即可.【详解】解:(1)∵线段OA 的长是方程27180x x --=的一个根,解得:x=9或-2(舍),而点A 在x 轴正半轴,∴A (9,0),∵12OB OA =,∴B (0,92);(2)∵6OE =,∴E (-6,0),设直线AB 的表达式为y=kx+b ,将A 和B 代入,得:0992k b b =+⎧⎪⎨=⎪⎩,解得:1292k b ⎧=-⎪⎪⎨⎪=⎪⎩,∴AB 的表达式为:1922y x =-+,∵点C 是EF 的中点,∴点C 的横坐标为-3,代入AB 中,y=6,则C (-3,6),∵反比例函数k y x=经过点C ,则k=-3×6=-18;(3)存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形,如图,共有5种情况,在四边形DM 1P 1N 1中,M 1和点A 重合,∴M 1(9,0),此时P 1(9,12);在四边形DP 3BN 3中,点B 和M 重合,可知M 在直线y=x+3上,联立:31922y x y x =+⎧⎪⎨=-+⎪⎩,解得:14x y =⎧⎨=⎩,∴M (1,4),∴P 3(1,0),同理可得:P 2(9,-12),P 4(-7,4),P 5(-15,0).故存在点P 使以D ,M ,N ,P 为顶点的四边形是正方形,点P 的坐标为P 1(9,12),P 2(9,-12),P 3(1,0),P 4(-7,4),P 5(-15,0).【点睛】本题考查了解一元二次方程,一次函数表达式,正方形的性质,反比例函数表达式,难度较大,解题的关键是根据图像画出符合条件的正方形.类型三最值问题17.(2020·江苏宿迁?中考真题)如图,在平面直角坐标系中,Q是直线y=﹣12x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为()A.455B C.523D.655【答案】B【解析】【分析】利用等腰直角三角形构造全等三角形,求出旋转后Q′的坐标,然后根据勾股定理并利用二次函数的性质即可解决问题.【详解】解:作QM⊥x轴于点M,Q′N⊥x轴于N,设Q(m,122m-+),则PM=1m﹣,QM=122m-+,∵∠PMQ=∠PNQ′=∠QPQ′=90°,∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,∴∠QPM=∠PQ′N ,在△PQM 和△Q′PN 中,'90''PMQ PNQ QPM PQ N PQ Q P ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△PQM ≌△Q′PN(AAS),∴PN=QM=122m -+,Q′N=PM=1m ﹣,∴ON=1+PN=132m -,∴Q′(132m -,1m ﹣),∴OQ′2=(132m -)2+(1m ﹣)2=54m 2﹣5m+10=54(m ﹣2)2+5,当m=2时,OQ′2有最小值为5,∴OQ′故选:B .【点睛】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形全等的判定和性质,坐标与图形的变换-旋转,二次函数的性质,勾股定理,表示出点的坐标是解题的关键18.(2020·湖南永州?中考真题)已知点()00,P x y 和直线y kx b =+,求点P 到直线y kx b =+的距离d可用公式d =C 的圆心C 的坐标为()1,1,半径为1,直线l 的表达式为26y x =-+,P 是直线l 上的动点,Q 是C 上的动点,则PQ 的最小值是()A .355B .3515-C .6515-D .2【答案】B 【解析】【分析】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,利用公式计算即可.【详解】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,如图,∵点C 到直线l 的距离()00222116355112kx y b d k -+-⨯-+==++-,C 半径为1,∴PQ 的最小值是3515-,故选:B.【点睛】此题考查公式的运用,垂线段最短的性质,正确理解公式中的各字母的含义,确定点P与点Q最小时的位置是解题的关键.A B-,在x19.(2020·辽宁鞍山?中考真题)如图,在平面直角坐标系中,已知(3,6),(2,2)CD=,线段CD在x轴上平移,当轴上取两点C,D(点C在点D左侧),且始终保持1+的值最小时,点C的坐标为________.AD BC【答案】(-1,0)【解析】【分析】作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,得到此时AD+BC的值最小,求出直线AB″,得到点D坐标,从而可得点C坐标.【详解】解:如图,作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,可知四边形B′B″DC为平行四边形,则B′C=B″D,由对称性质可得:BC=B′C,∴AD+BC=AD+B′C=AD+B″D=AB″,则此时AB″最小,即AD+BC最小,∵A(3,6),B(-2,2),∴B′(-2,-2),∴B″(-1,-2),设直线AB″的表达式为:y=kx+b,则632k bk b=+⎧⎨-=-+⎩,解得:2kb=⎧⎨=⎩,∴直线AB″的表达式为:y=2x,令y=0,解得:x=0,即点D坐标为(0,0),∴点C坐标为(-1,0),故答案为:(-1,0).【点睛】本题考查了轴对称的性质,最短路径问题,一次函数表达式,解题的关键是找到AD+BC最小时的情形20.(2020•连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=34x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为.【分析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.首先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE的面积最小.【解析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x﹣3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,﹣3),∴OD =4,OE =3,∴DE =32+42=5,∵∠MDN =∠ODE ,∠MND =∠DOE ,∴△DNM ∽△DOE ,∴MN OE=DM DE,∴MN 3=35,∴MN =95,当点C 与C′重合时,△C′DE 的面积最小,最小值=12×5×(95−1)=2,故答案为2.21.(2020·江苏连云港?中考真题)如图,在平面直角坐标系xOy 中,半径为2的O 与x 轴的正半轴交于点A ,点B 是O 上一动点,点C 为弦AB 的中点,直线334y x =-与x 轴、y 轴分别交于点D 、E ,则CDE △面积的最小值为________.【答案】2【解析】【分析】如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN ⊥DE 于N .首先证明点C 的运动轨迹是以M 为圆心,1为半径的⊙M ,设⊙M 交MN 于C′.求出MN ,当点C 与C′重合时,△C′DE的面积最小.【详解】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x-3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),∴OD=4,OE=3,∴5 DE===,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴MN DM OE DE=,∴3 35 MN=,∴95 MN=,当点C 与C′重合时,△C′DE 的面积最小,△C′DE 的面积最小值1951225⎛⎫=⨯⨯-= ⎪⎝⎭,故答案为2.【点睛】本题考查三角形的中位线定理,三角形的面积,一次函数的性质等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.22.(2020·北京中考真题)在平面直角坐标系xOy 中,⊙O 的半径为1,A ,B 为⊙O 外两点,AB=1.给出如下定义:平移线段AB ,得到⊙O 的弦A B ''(,A B ''分别为点A ,B 的对应点),线段AA '长度的最小值称为线段AB 到⊙O 的“平移距离”.(1)如图,平移线段AB 到⊙O 的长度为1的弦12PP 和34P P ,则这两条弦的位置关系是;在点1234,,,P P P P 中,连接点A 与点的线段的长度等于线段AB 到⊙O 的“平移距离”;(2)若点A ,B 都在直线y =+上,记线段AB 到⊙O 的“平移距离”为1d ,求1d 的最小值;(3)若点A 的坐标为32,2⎛⎫ ⎪⎝⎭,记线段AB 到⊙O 的“平移距离”为2d ,直接写出2d 的取值范围.【答案】(1)平行,P 3;(2)32;(3)233922d ≤≤。
一次函数几何综合题

1.如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边等边△CDE,连接BE(1)求证:AD=BE;(2)过点D作DF⊥BC于点F,连接AF,AF∥DE,AB=3,求线段CF的长度.2.如图1,在平面直角坐标系中,点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,连接BC交y轴于点M,N为AC中点,连接NO并延长至D,使OD=ON,连接BD.(1)求a,b的值;(2)求∠DBC;(3)如图2,Q为ON,BC的交点,连接AQ,AB,过点O作OP⊥OQ,交AB于P,过点O作OH⊥AB于H,交BQ于E,请探究线段EH,PH与OH之间有何数量关系?并证明你的结论.3.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣4a﹣2b+5=0.①求a、b的值;②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第一象限内以AB为斜边作等腰Rt△ABC,请用b表示S,并写出解答四边形AOBC过程.(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E 对应B)连接DO,作EF⊥DO于F,连接AF、BF.①如图2,判断AF与BF的关系并说明理由;②若BF=OA﹣OB,则∠OAF=(直接写出结果).4.如图,在平面直角坐标系中,A(8,0),点B在第一象限,△OAB为等边三角形,OC⊥AB,垂足为点C.(1)直接写出点C的横坐标;(2)作点C关于y轴的对称点D,连DA交OB于E,求OE的长;(3)P为y轴上一动点,连接PA,以PA为边在PA所在直线的下方作等边△PAH.当OH最短时,求点H的横坐标.5.四边形ABCD是由等边△ABC和顶角为120°的等腰△ABD拼成,将一个60°角顶点放在D处,将60°角绕D点旋转,该60°角两边分别交直线BC、AC 于M、N.交直线AB于E、F两点,(1)当E、F分别在边AB上时(如图1),求证:BM+AN=MN;(2)当E、F分别在边BA的延长线上时如图2,求线段BM、AN、MN之间又有怎样的数量关系;(3)在(1)的条件下,若AC=5,AE=1,求BM的长.6.如图,在平面直角坐标系中,已知两点A(m,0),B(0,n)(n>m>0),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.(1)点C的坐标为:(用含m,n的式子表示);(2)求证:BM=BN;(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.7.等腰Rt△ABC中,∠BAC=90°,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E.(1)如图1,若A(0,1),B(2,0),求C点的坐标.(2)如图2,当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE.(3)如图3,M为y轴上一点,连接CM,以CM为直角边向右作等腰Rt△CMN,其中CM=MN,连接NB,若AM=7,求五边形ACMNB的面积.8.在直角坐标系中,点A坐标为(﹣3,0),点B的坐标为(0,b),以AB 为边作等腰直角△ABC,其中点A、B、C成顺时针顺序排列,AB=BC.(1)如图1,求点C的坐标(含字母b)(2)如图2,若b=3,点D为边BC边上一动点,点T为线段BD的中点,TE ⊥BC于T,交AC于点E,DF⊥AC于点F,求EF的长(3)点G与点A关于y轴对称,连接CG,记∠OAB=α,∠BCG=β,若α、β均为锐角,当b的取值发生变化时,α与β之间可能满足什么等量关系?请直接写出你的结论.9.如图1,已知点A(a,0),点B(0,b),且a、b满足+|4﹣b|=0.(1)求A、B两点的坐标;(2)若点C是第一象限内一点,且∠OCB=45°,过点A作AD⊥OC于点F,求证:FA=FC;(3)如图2,若点D的坐标为(0,1),过点A作AE⊥AD,且AE=AD,连接BE交x轴于点G,求G点的坐标.10.已知,如图1,在平面直角坐标系内,直线l1:y=﹣x+4与坐标轴分别相交于点A、B,与直线l2:相交于点C.(1)求点C的坐标;(2)如图1,平行于y轴的直线x=1交直线l1于点E,交直线l2于点D,平行于y轴的直x=a交直线l1于点M,交直线l2于点N,若MN=2ED,求a的值;(3)如图2,点P是第四象限内一点,且∠BPO=135°,连接AP,探究AP与BP之间的位置关系,并证明你的结论.11.如图,直线y=﹣x+与y轴、x轴分别交于A,B两点,点C在x轴上,且△ABC为等边三角形.(1)写出直线AC的解析式;(2)如图1,M,N分别在BA,AC的延长线上,且AM=CN,直线MC交BN 于K,BG⊥MK于点G,求证:MC﹣KN=2GK;(3)如图2,过B作DB⊥AB,交y轴于D,将一块含30°角的三角板的60°角的顶点置于D点,角的两边分别交AC,AB于E,F.当此三角板任意旋转时,△AEF的周长是否变化?若变化,请说明理由;若不变,请证明并求出其值.12.如图1,在平面直角坐标系中,A(0,a),C(c,0),△ABC为等腰直角三角形且a、c满足.≥(1)求点B的坐标;(2)如图2,P是直线上的一个动点,是否存在点P使△PAC的面积等于△BAC的面积?若存在,求出P点坐标;若不存在,说明理由;(3)如图3,BF是△ABC内部且经过B点的任一条射线,分别过A作AM⊥BF于M,过CN⊥BF于N.当射线BF绕点B在△ABC内部旋转时,试探索下列结论:①的值不变;②的值不变.13.如图,在平面直角坐标系xoy中,直线AP交x轴于点P(p,0),交y 轴于点A(0,a),且a、b满足.(1)求直线AP的解析式;(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.14.如图,在平面直角坐标系中,直线AB 交x 轴于点A (a ,0),交y 轴于点B (0,b ),且a 、b 满足,直线y=x 交AB 于点M .(1)求直线AB 的解析式;(2)过点M 作MC ⊥AB 交y 轴于点C ,求点C 的坐标;(3)在直线y=x 上是否存在一点D ,使得S △ABD =6?若存在,求出D 点的坐标;若不存在,请说明理由.15.直线AB :y=﹣x ﹣b 分别与x 、y 轴交于A (6,0)、B 两点,过点B 的直线交x 轴负半轴于C ,且OB :OC=3:1;(1)求直线BC 的解析式;(2)直线EF :y=kx ﹣k (k ≠0)交AB 于E ,交BC 于点F ,交x 轴于D ,是否存在这样的直线EF ,使得S △EBD =S △FBD ?若存在,求出k 的值;若不存在,说明理由;(3)如图,P 为A 点右侧x 轴上的一动点,以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ,连接QA 并延长交y 轴于点K .当P 点运动时,K 点的位置是否发生变化?如果不变请求出它的坐标;如果变化,请说明理由.16.如图1,在平面直角坐标系xoy 中,直线y=x +6与x 轴交于A ,与y 轴交于B ,BC ⊥AB 交x 轴于C .①求△ABC 的面积.②如图2,D 为OA 延长线上一动点,以BD 为直角边做等腰直角三角形BDE ,连接EA .求直线EA 的解析式.③点E 是y 轴正半轴上一点,且∠OAE=30°,AF 平分∠OAE ,点M 是射线AF 上一动点,点N 是线段AO 上一动点,试判断是否存在这样的点M 、N ,使得OM +NM 的值最小?若存在,请写出其最小值,并加以说明.17.如左图:直线y=kx +4k (k ≠0)交x 轴于点A ,交y 轴于点C ,点M (2,m )为直线AC 上一点,过点M 的直线BD 交x 轴于点B ,交y 轴于点D .(1)求的值(用含有k 的式子表示.);(2)若S △BOM =3S △DOM ,且k 为方程(k +7)(k +5)﹣(k +6)(k +5)=的根,求直线BD 的解析式.(3)如右图,在(2)的条件下,P 为线段OD 之间的动点(点P 不与点O 和点D 重合),OE ⊥AP 于E ,DF ⊥AP 于F ,下列两个结论:①值不变;②值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值..18.如图1,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足.(1)求直线AB的解析式;(2)若点M为直线y=mx在第一象限上一点,且△ABM是等腰直角三角形,求m的值.(3)如图3过点A的直线y=kx﹣2k交y轴负半轴于点P,N点的横坐标为﹣1,过N点的直线交AP于点M,给出两个结论:①的值是不变;②的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值.19.如图1,在平面直角坐标系中,直线y=﹣x+m(m>0)与x轴,y轴分别交于点A,B,过点A作x轴的垂线交直线y=x于点D,C点坐标(m,0),连接CD.(1)求证:CD⊥AB;(2)连接BC交OD于点H(如图2),求证:DH=BC;(3)若m=2,E为射线AD上的一点,且AE=BE,F为EB延长线上的一点,连FA,作∠FAN交y轴于点N,且∠FAN=∠FBO(如图3),当点F在EB的延长线上运动时,NB﹣FB的值是否发生变化?若不变,请求出NB﹣FB的值;若变化,请求出其变化范围.20.如图,直线l1与x轴、y轴分别交于A、B两点,直线l2与直线l1关于x 轴对称,已知直线l1的解析式为y=x+3,(1)求直线l2的解析式;(2)过A点在△ABC的外部作一条直线l3,过点B作BE⊥l3于E,过点C作CF⊥l3于F,请画出图形并求证:BE+CF=EF;(3)△ABC沿y轴向下平移,AB边交x轴于点P,过P点的直线与AC边的延长线相交于点Q,与y轴相交于点M,且BP=CQ,在△ABC平移的过程中,①OM为定值;②MC为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.21.在平面直角坐标系中,直线y=﹣x+m交y轴于点A,交x轴于点B,点C 坐标(,0 ),作C关于AB对称点F,连BF和OF,OF交AC于点E,交AB于点M.(1)求证:OF⊥AC;(2)连接CF交AB于点H,求证:AH=CF;(3)若m=2,E为x轴负半轴上一动点,连接ME,过点M作EM的垂线交FB的延长线于点D,问EB﹣BD的值是否改变,若不变,求其值,若改变,求其取值范围.22.如图①,点A(m,0)是x轴的上一点,且|n|+=0.以OA为一边,在第四象限内作等边△OAB.C是x轴负半轴上的一动点,连接CB,在CB 的上方作等边△DCB,直线DA交y轴于E点.(1)求线段OA的长;(2)当C点在y轴的负半轴上运动时,线段AE的长度是否发生变化?若变化,请说明理由;若不变,请证明你的结论并求出AE的长.(3)如图②,F是点A关于y轴的对称点,作直线FE.P是直线FE上的E 点上方一动点,连接PA,在PA的左侧作等边△PAT,I是∠APT与∠PAT的角平分线的交点.当点P运动时,点I是否总在y轴上运动?请判断并证明你的结论.23.已知,如图:直线AB:y=﹣x+8与x轴、y轴分别相交于点B、A,过点B作直线AB的垂线交y轴于点D.(1)求BD两点确定的直线解析式;(2)若点C是x轴负半轴上的任意一点,过点C作AC的垂线与BD相交于点E,请你判断:线段AC与CE的大小关系并证明你的判断;(3)若点G为第二象限内任一点,连接EG,过点A作AF⊥FG于F,连接CF,当点C在x轴的负半轴上运动时,∠EFC的度数是否发生变化?若不变,请求出∠EFC的度数;若变化,请求出其变化范围.24.在Rt△ABC中,AC=BC,P是BC中垂线MN上一动点,连接PA,交CB 于E,F是点E关于MN的对称点,连接PF延长交AB于D,连接CD交PA 于G.(1)若P点移动到BC上时,如图点P,E,F重合,若PD=a,CD=b,则AP=(用含a,b的式子表示);(2)若点P移动到BC的上方时,如图,其它条件不变,求证:CD⊥AE;(3)若点P移动到△ABC的内时,其它条件不变,线段AE,CD,DF有什么确定的数量关系,请画出图形,并直接写出结论(不必证明).25.如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点.OA、OB的长度分别为a和b,且满足a2﹣2ab+b2=0.(1)判断△AOB的形状.(2)如图②,正比例函数y=kx(k<0)的图象与直线AB交于点Q,过A、B 两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.(3)如图③,E为AB上一动点,以AE为斜边作等腰直角△ADE,P为BE 的中点,连接PD、PO,试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明.26.如图1,在平面直角坐标系中,直线y=﹣x+4分别交x轴、y轴于A、B 两点,直线BD平分∠OBA,交x轴于D点.(1)连接AB的中点M交BD于N,求证:ON=OD.(2)如图2,过点A作AE⊥BD,垂足为E,猜想AE与BD间的数量关系,并证明你的猜想;(3)如图3,在x轴上有一个动点P(在A点的右侧),连接PB,并作等腰直角三角形BPF,其中∠BPF=90°,连接FA并延长交y轴于G点,当P点在运动时,OG的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.27.如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且AD∥OB,AB∥OD,点C为AB的中点,直线CD交x轴于点F.(1)求直线CD的函数关系式;(2)过点C作CE⊥DF且交于点E,求证:∠ADC=∠EDC;(3)求点E坐标;(4)点P是直线CE上的一个动点,求PB+PF的最小值.28.如图1,在平面直角坐标系中,点A坐标为(﹣4,4),点B的坐标为(4,0).(1)求直线AB的解析式;(2)点M是坐标轴上的一个点,若AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC﹣OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).29.如图①,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC 绕点D逆时针旋转90°至DE.(1)直接写出点B、D、E的坐标并求出直线DE的解析式.(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.30.(1)问题如图1,点A为线段BC外一动点,且AB=a,BC=b.填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)(2)应用点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值.(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.31.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣8a﹣4b+20=0.①求a、b的值;②如图1,在①的条件下,第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;(2)如图2,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.32.如图1,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,过点B作线段BC⊥AB且BC=AB,直线AC交x轴于点D.(1)求A,B两点的坐标;(2)求点C的坐标,并直接写出直线AC的函数关系式;(3)若点P是图1中直线AC上的一点,连接OP,得到图2.请在下面的A,B两题中任选一题解答,我选择.A.当点P的纵坐标为3时,求△AOP的面积;B.当点P在第二象限,且到x轴,y轴的距离相等时,求△AOP的面积;(4)若点Q是图1中坐标平面内不同于点B、点C的一点.请在下面的A,B两题中任选一题解答,我选择A.当以点B,D,Q为顶点的三角形与△BCD全等时,直接写出点Q的坐标;B.当以点C,D,Q为顶点的三角形与△BCD全等时,直接写出点Q的坐标.33.正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图1所示,直线l经过A、C两点.(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;(2)如图2,坐标系xOy内有一点D(﹣1,2),点E是直线l上的一个动点,请求出|BE+DE|的最小值和此时点E的坐标.(3)若点D关于x轴对称,对称到x轴下方,直接写出|BE﹣DE|的最大值,并写出此时点E的坐标.34.(1)问题发现:如图(1),小明在同一个平面直角坐标系中作出了两个一次函数y=x+1和y=x﹣1的图象,经测量发现:∠1∠2(填数量关系)则l1l2(填位置关系),从而二元一次方程组无解.(2)问题探究:小明发现对于一次函数y=k1x+b1与y=k2x+b2(b1≠b2),设它们的图象分别是l1和l2(如备用图1)①如果k1k2(填数量关系),那么l1l2(填位置关系);②反过来,将①中命题的结论作为条件,条件作为结论,所得命题可表述为,请判断此命题的真假或举出反例;(3)问题解决:若关于x,y的二元一次方程组(各项系数均不为0)无解,那么各项系数a1、b1、c1、a2、b2、c2应满足什么样的数量关系?请写出你的结论.35.【模型建立】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;【模型应用】(2)①已知直线l1:y=x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,﹣6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=﹣2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.36.在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.(Ⅰ)若点M的坐标为(1,﹣1),①当点F的坐标为(1,1)时,如图,求点P的坐标;②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.(Ⅱ)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.37.如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O 出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1.(1)求点C1的坐标;(2)连接CC1,求证:△AOB≌△AC1C;(3)求动点C所在图象的函数表达式.38.已知:如图1,在△AOB中,OA=AB=,BO=2,点B在x轴上,直线l1:y=kx+3(k为常数,且k≠0)过点A,且与x轴、y轴分别交于点D,C,直线l2:y=ax(a为常数,且a>0)与直线l1交于点P,且△DOP的面积为.(1)求直线l1,l2的解析式;(2)如图2,直线l3∥y轴,与直线l1,x轴分别交于点M,Q,且直线l3与线段OA或线段OP交于点N.若点Q的横坐标为m(﹣1<m<2),求△APN 的面积S关于m的函数关系式.39.如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,1),交x轴于点B,过点E(1,0)作x轴的垂线EF交AB于点D,点P从D出发,沿着射线ED的方向向上运动,设PD=n.(1)求直线AB的表达式;(2)求△ABP的面积(用含n的代数式表示);(3)若以P为直角顶点,PB为直角边在第一象限作等腰直角△BPC,请问随着点P的运动,点C是否也在同一直线上运动?若在同一直线上运动,请求出直线解析式;若不在同一直线上运动,请说明理由.40.在平面直角坐标系中,直线y=﹣x+4交x轴,y轴分别于点A,点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E,如图1:(1)求:直线CD的函数关系式;(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,如图2,①求证:∠OEF=45°;②求:点F的坐标;(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ和△DOC全等时,直接写出点P的坐标.一.解答题(共40小题)1.如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边等边△CDE,连接BE(1)求证:AD=BE;(2)过点D作DF⊥BC于点F,连接AF,AF∥DE,AB=3,求线段CF的长度.【分析】(1)根据等边三角形的性质得到AC=BC,DC=EC,∠ACB=∠DCE=60°,推出△ACD≌△BCE,根据求三角形的性质得到AD=BE;(2)根据平行线的性质得到∠BAF=∠BDE,推出∠BAF=∠BDE=∠ACD=∠BCE,证得△ABF≌△CBE,由全等三角形的性质得到BF=BE解直角三角形即可得到结论.【解答】(1)证明:∵△ABC,△CDE是等边三角形,∴AC=BC,DC=EC,∠ACB=∠DCE=60°,∴∠ACD=60°﹣∠BCD=∠BCE,在△ACD与△BCE中,,∴△ACD≌△BCE,∴AD=BE;(2)解:∵AF∥DE,∴∠BAF=∠BDE,∵∠BDC=∠BDE+CDE=∠BDE+60°=∠BAC+∠ACD,∴∠BAF=∠BDE=∠ACD=∠BCE,在△ABF与△CBE中,,∴△ABF≌△CBE,∴BF=BE,∵DF⊥BC,∠ABC=60°,∴AD=BE=BF=BD•cos∠ABC=BD,∵AB=BC,AD=BF,∴CF=BD=2BF,∴CF=BC=AB=×3=2.【点评】本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,解直角三角形,熟练掌握全等三角形的性质是解题的关键.2.如图1,在平面直角坐标系中,点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,连接BC交y轴于点M,N为AC中点,连接NO并延长至D,使OD=ON,连接BD.(1)求a,b的值;(2)求∠DBC;(3)如图2,Q为ON,BC的交点,连接AQ,AB,过点O作OP⊥OQ,交AB于P,过点O作OH⊥AB于H,交BQ于E,请探究线段EH,PH与OH之间有何数量关系?并证明你的结论.【分析】(1)把a2+b2+4a﹣4b=﹣8化成(a+2)2+(b﹣2)2=0,根据非负数的和等于0,即可求得a,b的值;(2)根据A(0,﹣2),B(2,0),C(﹣2,﹣2),对称AC∥x轴,从而求得N的坐标,根据中心对称的性质对称D的坐标,然后根据AAS证得△ACM ≌△OBM,根据SAS证得△BDE≌△MBO,即可求得∠MBO+∠OBD=90°,从而求得∠DBC=90°;(3)分别证得四边形ABOC是平行四边形,四边形AHOF是正方形,然后根据三角形中位线定理和三角形全等即可证得2EH=OH﹣PH.【解答】解:(1)∵点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,∴(a+2)2+(b﹣2)2=0,∴a+2=0,b﹣2=0,∴a=﹣2,b=2;(2)∵A(0,﹣2),B(2,0),C(﹣2,﹣2),∴AC∥x轴,∵N为AC中点,∴N(﹣1,﹣2),∴AN=1,∵OD=ON,∴D和N点关于O点对称,∴D(1,2),如图1,作DE⊥OB于E,∴DE=2,BE=1,在△ACM和△OBM中,∴△ACM≌△OBM(AAS),∴AM=OM=OA=1,在△BDE和△MBO中,∴△BDE≌△MBO(SAS),∴∠MBO=∠BDE,∵∠BDE+∠OBD=90°,∴∠MBO+∠OBD=90°,即∠DBC=90°;(3)延长AQ交OC于F,∵A(0,﹣2),B(2,0),∴OA=OB=2,∴∠OAB=∠OBA=45°,∵OH⊥AB,∴AH=BH,∴OH=AB,∵AC∥OB且AC=OB,∴四边形ABOC是平行四边形,∴OC∥AB,且OC=AB,∵ON是AC的中线,CB是OA的中线,∴AQ是OC的中线,∵AC=OA=2,∴AQ⊥OC,∴AQ⊥AB,∴四边形AHOF是正方形,∴AF=OH,∵OH=AB=AH,OC=AB,∴OF=OH,易证得△OFQ≌△OHP,∴FQ=PH,∵AH=BH,OH∥AF,∴EH=AQ,∴EH=(AF﹣FQ)=(OH﹣PH),∴2EH=OH﹣PH.【点评】本题考查了坐标和图形的性质,平行四边形的判定和性质,正方形的判定和性质,三角形全等的判定和性质以及三角形中位线定理等,熟练掌握性质定理是解题的关键.3.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣4a﹣2b+5=0.①求a、b的值;②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第,并写出解答一象限内以AB为斜边作等腰Rt△ABC,请用b表示S四边形AOBC过程.(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E 对应B)连接DO,作EF⊥DO于F,连接AF、BF.①如图2,判断AF与BF的关系并说明理由;②若BF=OA﹣OB,则∠OAF=60°(直接写出结果).【分析】(1)①化简得(a﹣2)2+(b﹣1)2=0,根据非负数的性质即可求出a、b.②利用S四边形AOBC=S△AOB+S△ABC即可解决.(2)①结论:AF=FB,AF⊥FB,作FG⊥y轴,FH⊥x轴垂足分别为G、H,先证明四边形FHOG是正方形,然后证明△FGA≌△FHB得FA=FB,∠AFG=∠BFH 所以∠AFB=∠GFH=90°.从而得证.②由△FGA≌△FHB得∠FBH=∠OAF,在Rt△FBH中,求出cos∠FBH=的值即可解决.【解答】解:(1)①∵a2+b2﹣4a﹣2b+5=0,∴(a﹣2)2+(b﹣1)2=0,∴a=2,b=1,②∵A(0,2),B(b,0),∴AB=,∵△ABC是等腰直角三角形,∴BC=AB=,∴S四边形AOBC =S△AOB+S△ABC=•AO•BO +BC2=b2+b+1,(0<b<2).(2)①结论:FA=FB,FA⊥FB,理由如下:如图,作FG⊥y轴,FH⊥x轴垂足分别为G、H.∵A(0,a)向右平移a个单位到D,∴点D坐标为(a,a),点E坐标为(a+b,0),∴∠DOE=45°,∵EF⊥OD,∴∠OFE=90°∠FOE=∠FEO=45°,∴FO=EF,∴FH=OH=HE=(a+b),∴点F 坐标(,),∴FG=FH,四边形FHOG是正方形,∴OG=FH=,∠GFH=90°,∴AG=AO﹣OG=a ﹣=,BH=OH﹣OB==,∴AG=BH,在△FGA和△FHB中,,∴△FGA≌△FHB,∴FA=FB,∠AFG=∠BFH,∴∠AFB=∠GFH=90°.AF⊥BF,AF=BF.②∵△FGA≌△FHB,∴∠FBH=∠OAF,在Rt△BFH中,∵BF=OA﹣OB=a﹣b,BH=,∴cos∠FBH==,∴∠FBH=60°,∴∠OAF=60°.故答案为60°.【点评】本题考查全等三角形的判定和性质、勾股定理、非负数的性质、三角函数等知识,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.4.如图,在平面直角坐标系中,A(8,0),点B在第一象限,△OAB为等边三角形,OC⊥AB,垂足为点C.(1)直接写出点C的横坐标6;(2)作点C关于y轴的对称点D,连DA交OB于E,求OE的长;(3)P为y轴上一动点,连接PA,以PA为边在PA所在直线的下方作等边△PAH.当OH最短时,求点H的横坐标.【分析】(1)如图1所示:过点B作BF⊥OA,垂足为F.由等腰三角形三线合一的性质可知OF=AF=4、BC=AC,由等边三角形的性质可知:∠BOF=60°,由特殊锐角三角函数值可知;FB=4,从而得到点B的坐标为(4,4),由中点坐标公式可知点C的坐标为(6,2);(2)方法1:设OB的解析式为y=kx,将点B的坐标代入得:k=,于是得到直线OB的解析式为y=.由关于y轴对称的点的坐标特点可求得点D 的坐标,然后依据待定系数法可求得直线AD的解析式为y=.将y=代入y=可求得点E的坐标为(1,).由两点间的距离公式可知:OE==2;方法2:连接CD,交OB于F.由关于y轴对称对称的点坐标坐标特点可知:CD∥OA,D(﹣6,2),从而得到DC=12,由题意可知△BCF为等边三角形,从而得到CF=4,然后可求得DF=12﹣4=8=OA,依据AAS可证明△DEF≌△AEO (AAS),由全等三角形的性质可知OE=EF,从而可求得OE=2;(3)如图3,连接PB.依据SAS可证明△HAO≌△PAB,由全等三角形的性质可知:OH=PB,由垂线段最短的性质可知:当BP⊥y轴时,PB有最小值为4,由PB⊥y轴可知∠AOH=∠ABP=120°,从而得到∠COH=60°,过点H作HC ⊥x轴于C,由OH=4,∠COH=60°,可求得OC=2.【解答】解:(1)如图1所示:过点B作BF⊥OA,垂足为F.∵OB=AB,BF⊥OA,∴OF=AF=4.∵△OAB为等边三角形,∴∠BOF=60°.∴FB=OBsin60°=8×=4.∴点B的坐标为(4,4).∵AO=OB,OC⊥AB,∴BC=AC.由中点坐标公式可知点C的坐标为(6,2).故答案为:6.(2)方法1:设OB的解析式为y=kx,将点B的坐标代入得:4k=4,解得:k=.∴直线OB的解析式为y=.∵点C与点D关于y轴对称,∴点D的坐标为(﹣6,2).设DA的解析式为y=k1x+b.将点A和点D的坐标代入得:,解得:k1=﹣,b=.∴直线DA的解析式为y=.将y=代入y=得:.解得:x=1.∴y=.∴点E的坐标为(1,).由两点间的距离公式可知:OE==2.方法2:如图2所示:连接CD,交OB于F.∵点C与点D关于y轴对称,∴CD∥OA,点D(﹣6,2).∴△BCF为等边三角形,∴CF=4,CD=12.∴DF=12﹣4=8=OA.在△DEF和△AEO中,∴△DEF≌△AEO(AAS),∴OE=EF=OF,∵BF=BC=4,∴OF=4,∴OE=2.(3)如图3,连接PB.∵∠HAO+∠PAO=∠BAP+∠PAO=60°,∴∠HAO=∠PAB,在△HAO和△PAB中,∴△HAO≌△PAB(SAS),∴OH=PB,当BP⊥y轴时,PB有最小值为4,此时,∠AOH=∠ABP=120°,∴∠COH=60°过点H作HC⊥x轴于C,∵OH=4,∠COH=60°,∴OC=2,即H点横坐标为﹣2.【点评】本题主要考查的是一次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式、全等三角形的性质和判定、特殊锐角三角函数、垂线段的性质、等边三角形的性质,证得当BP⊥y轴时,OH有最小值是解题的关键.5.四边形ABCD是由等边△ABC和顶角为120°的等腰△ABD拼成,将一个60°角顶点放在D处,将60°角绕D点旋转,该60°角两边分别交直线BC、AC 于M、N.交直线AB于E、F两点,(1)当E、F分别在边AB上时(如图1),求证:BM+AN=MN;(2)当E、F分别在边BA的延长线上时如图2,求线段BM、AN、MN之间又有怎样的数量关系MN=BM﹣AN;(3)在(1)的条件下,若AC=5,AE=1,求BM的长.【分析】(1)把△DBM绕点D逆时针旋转120°得到△DAQ,根据旋转的性质可得DM=DQ,AQ=BM,∠ADQ=∠BDM,然后求出∠QDN=∠MDN,利用“边角边”证明△MND和△QND全等,根据全等三角形对应边相等可得MN=QN,再根据AQ+AN=QN整理即可得证;(2)把△DAN绕点D顺时针旋转120°得到△DBP,根据旋转的性质可得DN=DP,AN=BP,根据∠DAN=∠DBP=90°可知点P在BM上,然后求出∠MDP=60°,然后利用“边角边”证明△MND和△MPD全等,根据全等三角形对应边相等可得MN=MP,从而得证;(3)过点M作MH∥AC交AB于G,交DN于H,可以证明△BMG是等边三角形,根据等边三角形的性质可得BM=MG=BG,根据全等三角形对应角相等可得∠QND=∠MND,再根据两直线平行,内错角相等可得∠QND=∠MHN,然后求出∠MND=∠MHN,根据等角对等边可得MN=MH,然后求出AN=GH,再利用“角角边”证明△ANE和△GHE全等,根据全等三角形对应边相等可得AE=GE,再根据BG=AB﹣AE﹣GE代入数据进行计算即可求出BG,从而得到BM的长.【解答】(1)证明:把△DBM绕点D逆时针旋转120°得到△DAQ,则DM=DQ,AQ=BM,∠ADQ=∠BDM,∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD﹣∠MDN=120°﹣60°=60°,∴∠QDN=∠MDN=60°,∵在△MND和△QND中,,∴△MND≌△QND(SAS),∴MN=QN,∵QN=AQ+AN=BM+AN,∴BM+AN=MN;(2)MN+AN=BM.理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,则DN=DP,AN=BP,∵∠DAN=∠DBP=90°,∴点P在BM上,∵∠MDP=∠ADB﹣∠ADM﹣∠BDP=120°﹣∠ADM﹣∠ADN=120°﹣∠MDN=120°﹣60°=60°,∴∠MDP=∠MDN=60°,∵在△MND和△MPD中,,∴△MND≌△MPD(SAS),∴MN=MP,∵BM=MP+BP,∴MN+AN=BM;。
人教版八年级下册知识点试题精选-一次函数图象与几何变换

一次函数图象与几何变换一.选择题(共20小题)1.把直线y=﹣x+1的图象关于x轴对称,得到的直线是()A.y=x﹣1 B.y=x+1 C.y=﹣x+1 D.y=﹣x﹣12.把直线y=﹣4x通过平移得到直线y=﹣4x﹣6,则直线y=﹣4x必须()A.向上平移6个单位B.向下平移6个单位C.向左平移6个单位D.向右平移6个单位3.直线y=2x经过平移可以得到直线y=2x﹣2的是()A.向左平移1个单位B.向左平移2个单位C.向右平移1个单位D.向上平移2个单位4.将直线y=2x向右平移1个单位后所得图象对应的函数解析式为()A.y=2x﹣1 B.y=2x﹣2 C.y=2x+1 D.y=2x+25.把直线y=﹣x﹣3向上平移2个单位后,得到的直线是()A.y=﹣x﹣1 B.y=﹣x﹣5 C.y=x﹣1 D.y=x﹣56.把直线y=﹣x﹣1向右平移2个单位后得到的直线的解析式是()A.y=﹣x+3 B.y=﹣x+2 C.y=﹣x+1 D.y=﹣x﹣37.在平面直角坐标系中,将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,则下列平移作法正确的是()A.将l1向右平移3个单位长度B.将l1向右平移6个单位长度C.将l1向上平移2个单位长度D.将l1向上平移4个单位长度8.在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(﹣,0),则直线l的函数关系式为()A.y=﹣x B.y=﹣x+6 C.y=﹣x D.y=﹣x+69.在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为()A.y=x B.y=x﹣1 C.y=x+1 D.y=﹣x+110.一次函数y=2x﹣1的图象可以由一次函数y=2x+3的图象()A.向右平移4个单位长度得到B.向左平移2个单位长度得到C.向上平移2个单位长度得到D.向下平移4个单位长度得到11.将函数y=2x的图象沿y轴向下平移2个单位得到的函数是()A.y=﹣x+2 B.y=2x﹣2 C.y=2x+2 D.y=﹣2x﹣212.要从的图象得到直线,就要将直线()A.向上平移个单位B.向下平移个单位C.向上平移2个单位D.向下平移2个单位13.直线y=2x﹣6关于y轴对称的直线的解析式为()A.y=2x+6 B.y=﹣2x+6 C.y=﹣2x﹣6 D.y=2x﹣614.将一次函数y=x的图象向左平移4个单位,平移后,若y>0,则x的取值范围是()A.x>4 B.x>﹣4 C.x>2 D.x>﹣215.如图,已知直线y=﹣x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则n的值是()A.B.1 C.D.1.516.如图,已知点A(1,1)关于直线y=kx的对称点恰好落在x轴的正半轴上,则k的值是()A.B.﹣1 C.2﹣D.17.把直线y=2x向()平移()单位得到直线y=2x+6,括号内应填()A.上2 B.下6 C.上6 D.右318.在平面直角坐标系中,把直线y=2x向左平移1个单位长度,平移后的直线解析式是()A.y=2x+1 B.y=2x﹣1 C.y=2x+2 D.y=2x﹣219.将一次函数y=x的图象向上平移2个单位,平移后,若y>0,则x的取值范围是()A.x>4 B.x>﹣4 C.x>2 D.x>﹣220.在平面直角坐标系中,把直线y=x﹣2向左平移2个单位长度后,其直线解析式为()A.y=x+1 B.y=x﹣1 C.y=x D.y=x﹣2二.填空题(共20小题)21.一次函数y=2x+1的函数图象向右平移一个单位后所得直线的解析式是.22.将直线y=﹣x沿着y轴向上平移3个单位得到直线l,那么直线l与两条坐标轴围成的三角形的周长为.23.直线y=﹣x﹣2向右平移2个单位得到直线.24.将直线y=﹣x﹣5向上平移4单位,得到直线.25.将一次函数y=x﹣2的图象平移,使其经过点(2,3),则所得直线的函数解析式是.26.已知直线y=3x+1,把其沿y轴向下平移3个单位后的直线所对应的函数解析式是.27.将函数y=﹣3x的图象沿y轴向上平移2个单位的长度后,所得图象对应的函数关系式为.28.函数y=中自变量x的取值范围是;将直线y=3x向下平移5个单位,得到直线.29.将直线y=3x向下平移2个单位长度,得到直线;将直线y=﹣x﹣5向上平移8个单位长度,得到直线.30.已知直线l与直线y=﹣2x﹣3互相垂直,且直线l经过点(﹣2,3),现将直线l先向上平移2个单位,再向右平移3个单位得到的新直线解析式为.31.把函数y=的图象向平移个单位得到函数y=.32.将直线y=3x+1向左平移2个单位并向下平移4个单位,平移后所得直线的解析式为.33.直线y=3x+1向右平移2个单位,再向下平移3个单位得到的直线的解析式为:.34.一次函数y=﹣6x+5的图象可由正比例函数的图象向上平移5个单位长度得到.35.若一次函数y=﹣6x图象沿y轴向上平移5个单位,则平移后图象的解析式为.36.如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为.37.将直线y=2x﹣3沿y轴向上平移2个单位后,所得直线的解析式是.38.将直线y=3x沿x轴正方向向右平移2个单位,所得直线的解析式为y=.39.如图,将直线y=﹣x沿y轴向下平移后的直线恰好经过点A(2,﹣4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为.40.直线y=2x﹣3沿x轴向右平移2个单位,再沿y轴向上平移5个单位,则平移后直线与y轴的交点坐标为.三.解答题(共10小题)41.(1)请你在图1中画出正比例函数y=﹣2x的图象关于x轴对称的图象,并写出此图象的函数关系式为;(2)请你探究一次函数y=kx+b(k、b为常数,k≠0)的图象关于x轴对称的图象的函数关系式为.(图2供探究用)42.已知直线y=mx+3﹣m,根据下列条件,分别求m的值.(1)直线经过点(﹣1,1);(2)将直线向右平移1个单位,再向下平移2个单位后,所得直线经过点(3,﹣4)43.已知直线y=﹣x+1,将此直线沿x轴如何平移,才能过原点.44.已知一次函数y=3x+2,求出该直线关于y=0.5x﹣1对称的直线函数解析式.45.(1)在平面直角坐标系中,将直线l:y=﹣2x+4绕坐标原点O顺时针旋转90°后得到直线l1,再将直线l1;向上平移1个单位得到直线l2,直接写出直线l1l2、的解析式.(2)在平面直角坐标系中,将直线a:y=﹣2x+m绕坐标原点O顺时针旋转90°后得到直线a1,再将直线a1向上平移k个单位得到直线a2,直接写出直线a1、a2的解析式.(3)在平面直角坐标系中,将直线b:y=nx+m绕坐标原点O顺时针旋转90°后得到直线b1,再将直线b1沿竖直方向平移k个单位得到直线b2,直接写出直线b2的解析式.46.直线y=x+2与x轴交于点A,(1)求过点A与该直线垂直的直线的解析式.(2)求过点(1,1)与该直线垂直的直线的解析式.47.求直线y=x+1关于点M(1,0)中心对称的直线的解析式.48.如图,已知正比例函数y=kx经过点P.(1)求这个正比例函数的解析式;(2)该直线向上平移3的单位,求平移后所得直线的解析式;(3)画出平移后的直线.49.已知直线l1:y=﹣3x+3交x轴于点A、交y轴于点B,将直线绕点B逆时针转45°,得到的直线为l2,求l2的解忻式.50.如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.(1)求点C的坐标和直线l1的解析式;(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l1上;(3)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.一次函数图象与几何变换参考答案与试题解析一.选择题(共20小题)1.把直线y=﹣x+1的图象关于x轴对称,得到的直线是()A.y=x﹣1 B.y=x+1 C.y=﹣x+1 D.y=﹣x﹣1【分析】欲求直线y=﹣x+1关于x轴对称的直线方程,只须将原直线方程中的y 用﹣y替换得到的新方程即为所求.【解答】解:∵直线y=f(x)关于x轴对称的直线方程为y=﹣f(x),∴直线y=﹣x+1关于x对称的直线方程为:﹣y=﹣x+1,即y=x﹣1.故选A.【点评】本题考查一次函数图象与几何变换,考查同学们对函数基础知识的把握程度以及数形结合的思维能力.2.把直线y=﹣4x通过平移得到直线y=﹣4x﹣6,则直线y=﹣4x必须()A.向上平移6个单位B.向下平移6个单位C.向左平移6个单位D.向右平移6个单位【分析】直线y=﹣4x通过原点,比较平移得到直线y=﹣4x﹣6自变量为0时的函数值,可知直线平移方向和单位.【解答】解:直线y=﹣4x通过原点,而平移得到直线y=﹣4x﹣6不通过原点,当x=0时,y=﹣6,∴直线y=﹣4x必须向下平移6个单位.故选B.【点评】本题主要考查一次函数图象与几何变换,根据已知直线的解析式求得平移后的解析式.3.直线y=2x经过平移可以得到直线y=2x﹣2的是()A.向左平移1个单位B.向左平移2个单位C.向右平移1个单位D.向上平移2个单位【分析】根据上加下减,左加右减的平移原则,即可得出答案.【解答】解:根据上加下减的平移原则,直线y=2x﹣2可以看作是由直线y=2x 向下平移2个单位得到的;根据左加右减的平移原则,直线y=2x﹣2=2(x﹣1)可以看作是由直线y=2x向右平移1个单位得到的.故选C.【点评】本题考查了一次函数图象与几何变换,属于基础题,关键是掌握上加下减,左加右减的平移原则.4.将直线y=2x向右平移1个单位后所得图象对应的函数解析式为()A.y=2x﹣1 B.y=2x﹣2 C.y=2x+1 D.y=2x+2【分析】根据函数图象平移的法则进行解答即可.【解答】解:直线y=2x向右平移1个单位后所得图象对应的函数解析式为y=2(x﹣1),即y=2x﹣2.故选B.【点评】本题考查的是一次函数的图象与几何变换,熟知“上加下减,左加右减”的原则是解答此题的关键.5.把直线y=﹣x﹣3向上平移2个单位后,得到的直线是()A.y=﹣x﹣1 B.y=﹣x﹣5 C.y=x﹣1 D.y=x﹣5【分析】利用平移时k的值不变,只有b发生变化,由上加下减得出即可.【解答】解:直线y=﹣x﹣3向上平移2个单位长度得到了新直线,那么新直线的解析式为y=﹣x﹣3+2=﹣x﹣1.故选:A.【点评】本题考查了一次函数图象与几何变换,熟记直线解析式平移的规律:“上加下减,左加右减”是解题的关键.6.把直线y=﹣x﹣1向右平移2个单位后得到的直线的解析式是()A.y=﹣x+3 B.y=﹣x+2 C.y=﹣x+1 D.y=﹣x﹣3【分析】根据“左加右减”的原则进行解答即可.【解答】解:由“左加右减”的原则可知:直线y=﹣x﹣1向右平移2个单位,得到直线的解析式为:y=﹣(x﹣2)﹣1,即y=﹣x+1.故选C.【点评】本题考查的是一次函数的图象与几何变换,熟知“左加右减”的原则是解答此题的关键.7.在平面直角坐标系中,将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,则下列平移作法正确的是()A.将l1向右平移3个单位长度B.将l1向右平移6个单位长度C.将l1向上平移2个单位长度D.将l1向上平移4个单位长度【分析】利用一次函数图象的平移规律,左加右减,上加下减,得出即可.【解答】解:∵将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,∴﹣2(x+a)﹣2=﹣2x+4,解得:a=﹣3,故将l1向右平移3个单位长度.故选:A.【点评】此题主要考查了一次函数图象与几何变换,正确把握变换规律是解题关键.8.在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(﹣,0),则直线l的函数关系式为()A.y=﹣x B.y=﹣x+6 C.y=﹣x D.y=﹣x+6【分析】首先求出直线AB的解析式进而求出AC的解析式进而利用平移的性质得出直线l的解析式.【解答】解:设直线AB的解析式为:y=kx+b,则,解得:,故AB的解析式为:y=x+3,∵直线b绕点A顺时针旋转60°后所得直线经过点B(﹣,0),∴tan∠BAO==,∴∠BAO=30°,∴直线b经过C(,0),∴设直线b的解析式为:y=mx+n,则,解得:,故直线b的解析式为:y=﹣x+3,则直线l的解析式为:y=﹣x+6.故选:B.【点评】此题主要考查了待定系数法求一次函数解析式以及一次函数的平移,得出直线b的解析式是解题关键.9.在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为()A.y=x B.y=x﹣1 C.y=x+1 D.y=﹣x+1【分析】先求直线x=0绕原点顺时针旋转45°后的解析式,然后根据“上加下减”的规律即可求得求直线a的解析式.【解答】解:∵直线x=0与x轴的夹角是90°,∴将直线x=0绕原点顺时针旋转45°后的直线与x轴的夹角为45°,∴此时的直线方程为y=x.∴再向上平移1个单位得到直线a的解析式为:y=x+1.故选C.【点评】本题考查了一次函数图象与几何变换.在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.10.一次函数y=2x﹣1的图象可以由一次函数y=2x+3的图象()A.向右平移4个单位长度得到B.向左平移2个单位长度得到C.向上平移2个单位长度得到D.向下平移4个单位长度得到【分析】根据函数图象平移的规律:“左加右减,上加下减”,可得答案.【解答】解:一次函数y=2x﹣1的图象可以由一次函数y=2x+3的图象向下平移4个单位得到,故选:D.【点评】本题考查了一次函数图象与几何变换,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.11.将函数y=2x的图象沿y轴向下平移2个单位得到的函数是()A.y=﹣x+2 B.y=2x﹣2 C.y=2x+2 D.y=﹣2x﹣2【分析】根据上下平移的原则,“上加,下减”即可得出y=2x的图象沿y轴向下平移2个单位得到的函数.【解答】解:y=2x的图象沿y轴向下平移2个单位得到的函数为:y=2x﹣2.故选B.【点评】本题考查一次函数图象及几何变换的知识,属于基础题,掌握平移的法则“上加下减,左加右减”是解答此类题目的关键.12.要从的图象得到直线,就要将直线()A.向上平移个单位B.向下平移个单位C.向上平移2个单位D.向下平移2个单位【分析】把新直线解析式整理得:y=x+,比例系数不变,只常数项改变,那么是进行了上下平移.原来直线解析式的常数项是0,从0到,是向上平移个单位.【解答】解:新直线解析式为:y=x+,∵原直线解析式为y=x,∴是向上平移个单位得到的,故选A.【点评】用到的知识点为:两个直线解析式的比例系数相同,这两条直线平行,可通过上下平移得到;上下平移直线解析式,看常数项是如何平移的即可,上加,下减.13.直线y=2x﹣6关于y轴对称的直线的解析式为()A.y=2x+6 B.y=﹣2x+6 C.y=﹣2x﹣6 D.y=2x﹣6【分析】找到原直线解析式上的关于相应的坐标轴对称的点.【解答】解:可从直线y=2x﹣6上找两点:(0,﹣6)、(3,0)这两个点关于y 轴的对称点是(0,﹣6)(﹣3,0),那么这两个点在直线y=2x﹣6关于y轴对称的直线y=kx+b上,则b=﹣6,﹣3k+b=0解得:k=﹣2.∴y=﹣2x﹣6.故选:C.【点评】本题考查了一次函数图象的几何变换,难度不大,要注意轴对称的性质.14.将一次函数y=x的图象向左平移4个单位,平移后,若y>0,则x的取值范围是()A.x>4 B.x>﹣4 C.x>2 D.x>﹣2【分析】根据函数图象向左平移加,可得函数解析式,根据函数与不等式的关系,可得答案.【解答】解:由将一次函数y=x的图象向左平移4个单位,得y=(x+4)=x+2,当y>0时,即x+2>0,解得x>﹣4,故选:B.【点评】本题考查了一次函数图象与几何变换,平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.15.如图,已知直线y=﹣x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则n的值是()A.B.1 C.D.1.5【分析】先求出A、B两点的坐标,根据勾股定理得出AB==5.再根据折叠的性质得出AB′=AB=5,B′C=BC=3﹣n.然后在直角△OB′C中,利用勾股定理列出方程(3﹣n)2=12+n2,解方程即可求出n的值.【解答】解:∵直线y=﹣x+3与x轴、y轴分别交于A、B两点,∴A(4,0),B(0,3),∴AB==5.∵把坐标平面沿直线AC折叠,使点B刚好落在x轴上,∴AB′=AB=5,B′C=BC=3﹣n.在直角△OB′C中,∵∠B′OC=90°,OB′=5﹣4=1,OC=n,B′C=3﹣n,∴(3﹣n)2=12+n2,解得n=.故选C.【点评】本题考查了一次函数图象上点的坐标特征,折叠的性质,勾股定理,利用勾股定理列出方程(3﹣n)2=12+n2是解题的关键.16.如图,已知点A(1,1)关于直线y=kx的对称点恰好落在x轴的正半轴上,则k的值是()A.B.﹣1 C.2﹣D.【分析】作辅助线,构建点与x轴和y轴的垂线,先根据点A的坐标得出OA′的长,再根据中位线定理和推论得:CF是△AA′E的中位线,所以CF=AE=,也可以求OF的长,表示出点C的坐标,代入直线y=kx中求出k的值.【解答】解:设A关于直线y=kx的对称点为A′,连接AA′,交直线y=kx于C,分别过A、C作x轴的垂线,垂足分别为E、F,则AE∥CF,∵A(1,1),∴AE=OE=1,∴OA=,∵A和A′关于直线y=kx对称,∴OC是AA′的中垂线,∴OA′=OA=,∵AE∥CF,AC=A′C,∴EF=A′F=,∴CF=AE=,∴OF=OA′﹣A′F=﹣=,∴C(,),把C(,)代入y=kx中得:=k,k=﹣1,故选B.【点评】本题考查了一次函数及轴对称的性质,要熟知对称轴是对称点连线的垂直平分线,本题还利用了中位线的性质及推论,这此知识点要熟练掌握:三角形的中位线平行于第三边且等于第三边的一半.求正比例函数的解析式,就是求直线上一点的坐标即可.17.把直线y=2x向()平移()单位得到直线y=2x+6,括号内应填()A.上2 B.下6 C.上6 D.右3【分析】直接利用一次函数的平移规律“上加下减”进而求出答案.【解答】解:把直线y=2x向(上)平移(6)单位得到直线y=2x+6,故选:C.【点评】此题主要考查了一次函数的平移,正确掌握平移规律是解题关键.18.在平面直角坐标系中,把直线y=2x向左平移1个单位长度,平移后的直线解析式是()A.y=2x+1 B.y=2x﹣1 C.y=2x+2 D.y=2x﹣2【分析】根据“左加右减”的原则进行解答即可.【解答】解:由“左加右减”的原则可知,将直线y=2x向左平移1个单位所得的直线的解析式是y=2(x+1)=2x+2.即y=2x+2,故选C【点评】本题考查的是一次函数的图象与几何变换,熟知“左加右减”的原则是解答此题的关键.19.将一次函数y=x的图象向上平移2个单位,平移后,若y>0,则x的取值范围是()A.x>4 B.x>﹣4 C.x>2 D.x>﹣2【分析】首先得出平移后解析式,进而求出函数与坐标轴交点,即可得出y>0时,x的取值范围.【解答】解:∵将一次函数y=x的图象向上平移2个单位,∴平移后解析式为:y=x+2,当y=0时,x=﹣2,所以y>0,x的取值范围是:x>﹣2.故选D.【点评】此题主要考查了一次函数图象与几何变换,正确得出平移后解析式是解题关键.20.在平面直角坐标系中,把直线y=x﹣2向左平移2个单位长度后,其直线解析式为()A.y=x+1 B.y=x﹣1 C.y=x D.y=x﹣2【分析】根据“左加右减”的原则进行解答即可.【解答】解:由“左加右减”的原则可知,在平面直角坐标系中,把直线y=x﹣2向左平移2个单位长度后,其直线解析式为y=x+2﹣2,即y=x.故选C.【点评】本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.二.填空题(共20小题)21.一次函数y=2x+1的函数图象向右平移一个单位后所得直线的解析式是y=2x ﹣1.【分析】根据根据函数图象平移的法则“横坐标左移加右移减”,就可以求出平移以后函数的解析式,【解答】解:一次函数y=2x+1的函数图象向右平移一个单位后所得直线的解析式是:y=2(x﹣1)+1=2x﹣1,故答案为:y=2x﹣1.【点评】本题考查图形的平移变换和函数解析式之间的关系,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标左移加,右移减;纵坐标上移加,下移减.平移后解析式有这样一个规律“左加右减,上加下减”.关键是要搞清楚平移前后的解析式有什么关系.22.将直线y=﹣x沿着y轴向上平移3个单位得到直线l,那么直线l与两条坐标轴围成的三角形的周长为6+3.【分析】根据题意求出平移后解析式,进而得出图象与坐标轴交点,再利用勾股定理得出斜边长,进而得出答案.【解答】解:∵直线y=﹣x沿着y轴向上平移3个单位得到直线l,∴平移后解析式为:y=﹣x+3,当x=0,则y=3,当y=0,则x=3,∴直线l与两条坐标轴围成的三角形的周长为:3+3+3=6+3.故答案为:.【点评】此题主要考查了一次函数图象与几何变换以及一次函数与坐标轴交点求法,得出各边长是解题关键.23.直线y=﹣x﹣2向右平移2个单位得到直线y=﹣x.【分析】根据“左加右减”的原则进行解答即可.【解答】解:由“左加右减”的原则可知:直线y=﹣x﹣2向右平移2个单位,得到直线的解析式为:y=﹣(x﹣2)﹣2,即y=﹣x.故答案为y=﹣x.【点评】本题考查的是一次函数的图象与几何变换,熟知“左加右减”的原则是解答此题的关键.24.将直线y=﹣x﹣5向上平移4单位,得到直线y=﹣x﹣1.【分析】根据平移的规则“上加下减”,即可得出平移后的直线的解析式.【解答】解:将直线y=﹣x﹣5向上平移4单位后得到的直线解析式为y=﹣x﹣5+4=﹣x﹣1.故答案为:y=﹣x﹣1.【点评】本题考查了一次函数图象与几何变换,解题的关键是牢记平移的规则“上加下减”.本题属于基础题,难度不大,解决该题型题目时,熟练运用“上加下减,左加右减”解决问题是关键.25.将一次函数y=x﹣2的图象平移,使其经过点(2,3),则所得直线的函数解析式是y=x+1.【分析】根据平移不改变k的值可设y=x+b,然后将点(2,3)代入即可得出直线的函数解析式.【解答】解:设y=x+b,∴3=2+b,解得:b=1.∴函数解析式为:y=x+1.故答案为:y=x+1.【点评】本题要注意利用一次函数的特点,求出未知数的值从而求得其解析式,求直线平移后的解析式时要注意平移时k的值不变.26.已知直线y=3x+1,把其沿y轴向下平移3个单位后的直线所对应的函数解析式是y=3x﹣2.【分析】利用一次函数平移规律,上加下减得出答案.【解答】解:由题意可得:y=3x+1﹣3=3x﹣2.故答案为:y=3x﹣2.【点评】此题主要考查了一次函数平移变换,正确记忆平移规律是解题关键.27.将函数y=﹣3x的图象沿y轴向上平移2个单位的长度后,所得图象对应的函数关系式为y=﹣3x+2.【分析】根据“上加下减”,即可找出平移后的函数关系式,此题得解.【解答】解:根据平移的性质可知:平移后的函数关系式为y=﹣3x+2.故答案为:y=﹣3x+2.【点评】本题考查了一次函数图象与几何变换,牢记“左加右减,上加下减”是解题的关键.28.函数y=中自变量x的取值范围是x>﹣1;将直线y=3x向下平移5个单位,得到直线y=3x﹣5.【分析】先根据“上加下减,左加右减”的原则得出将直线y=3x向下平移5个单位的直线解析式,再与y=kx+b进行比较,即可求解.【解答】解:函数y=中自变量x的取值范围是x>1,将直线y=3x向下平移5个单位,得到直线为y=3x﹣5.故答案为:x>1;y=3x﹣5.【点评】本题考查的是一次函数的图象与几何变换,熟知函数图象平移时“上加下减,左加右减”的法则是解答此题的关键.29.将直线y=3x向下平移2个单位长度,得到直线y=3x﹣2;将直线y=﹣x ﹣5向上平移8个单位长度,得到直线y=﹣x+3.【分析】上下平移时k值不变,b值是上加下减,依此求解即可.【解答】解:将直线y=3x向下平移2个单位长度,得到直线y=3x﹣2;将直线y=﹣x﹣5向上平移8个单位长度,得到直线y=﹣x﹣5+8,即y=﹣x+3.故答案为y=3x﹣2;y=﹣x+3.【点评】此题考查了一次函数图象与几何变换.要注意求直线平移后的解析式时k的值不变,只有b发生变化.30.已知直线l与直线y=﹣2x﹣3互相垂直,且直线l经过点(﹣2,3),现将直线l先向上平移2个单位,再向右平移3个单位得到的新直线解析式为y=x+.【分析】首先设直线l的解析式为y=kx+b(k≠0),根据题意求出k和b的值,进而根据平移的性质求出新直线的解析式.【解答】解:设直线l的解析式为y=kx+b(k≠0),∵直线l与直线y=﹣2x﹣3互相垂直,∴k=,∵直线l经过点(﹣2,3),∴×(﹣2)+b=3,∴b=4,∴y=x+4,∵直线l先向上平移2个单位,再向右平移3个单位,∴新直线的解析式为y=(x﹣3)+4+2=x+,故答案为y=x+【点评】本题主要考查了一次函数的图象的几何变换,解题的关键是求出直线l 的k的值,此题难度不大.31.把函数y=的图象向下平移2个单位得到函数y=.【分析】直接根据“上加下减”的原则进行解答即可.【解答】解:由“上加下减”的原则可知,函数y=向下平移2个单位得到的函数为y=.故答案为:下,2【点评】本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.32.将直线y=3x+1向左平移2个单位并向下平移4个单位,平移后所得直线的解析式为y=3x+3.【分析】直接根据“上加下减,左加右减”的平移规律求解即可.【解答】解:将直线y=3x+1向左平移2个单位并向下平移4个单位,所得直线的解析式为y=3(x+2)+1﹣4,即y=3x+3.故答案为y=3x+3.【点评】本题考查图形的平移变换和函数解析式之间的关系,在平面直角坐标系中,平移后解析式有这样一个规律“左加右减,上加下减”.33.直线y=3x+1向右平移2个单位,再向下平移3个单位得到的直线的解析式为:y=3x﹣8.【分析】平移后的直线的解析式的k不变,设出相应的直线解析式,从原直线解析式上找一个点,然后找到向右平移2个单位,再向下平移3个单位得到的点,代入设出的直线解析式,即可求得b,也就求得了所求的直线解析式.【解答】解:∵是平移得到,∴可设新直线解析式为y=3x+b,∵原直线经过点(0,1),∴向右平移2个单位,再向下平移3个单位得到的点为(2,﹣2),代入新直线解析式得:b=﹣8,∴新直线解析式为:y=3x﹣8.【点评】用到的知识点为:平移不改变直线解析式中的k,关键是得到平移后经过的一个具体点.34.一次函数y=﹣6x+5的图象可由正比例函数y=﹣6x的图象向上平移5个单位长度得到.【分析】根据平移法则上加下减可得出平移后的解析式.【解答】解:由题意得:一次函数y=﹣6x+5的图象可由正比例函数y=﹣6x的图象向上平移5个单位长度得到.故答案为:y=﹣6x.【点评】本题考查图形的平移变换和函数解析式之间的关系,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标左移加,右移减;纵坐标上移加,下移减.35.若一次函数y=﹣6x图象沿y轴向上平移5个单位,则平移后图象的解析式为y=﹣6x+5.【分析】根据“上加下减”的原则进行解答即可.【解答】解:一次函数的几何变换中,沿y轴平移常数项变换,且满足“上加下减”的规律,所以若一次函数y=﹣6x图象沿y轴向上平移5个单位,则平移后图象的解析式为y=﹣6x+5.故答案为:y=﹣6x+5.【点评】本题考查的是一次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.。
中考数学重难点专题12 一次函数与几何综合问题(学生版)

中考数学复习重难点与压轴题型专项突围训练(全国通用版)专题12一次函数与几何综合问题【典型例题】1.(2022·四川成都·九年级期末)如图,在平面直角坐标系中,点A,B分别在x轴,y轴正半轴上,AO=2BO,点C(3,0)(A点在C点的左侧),连接AB,过点A作AB的垂线,过点C作x轴的垂线,两条垂线交于点D,已知△ABO△△DAC,直线BD交x轴于点E.(1)求直线AD的解析式;(2)直线AD有一点F,设点F的横坐标为t,若△ACF与△ADE相似,求t的值;(3)如图2,在直线AD上找一点G,直线BD上找一点P,直线CD上找一点Q,使得四边形AQPG是菱形,求出G点的坐标.【专题训练】一、选择题1.(2022·山东龙口·七年级期末)对于函数y=-3x+1,下列结论正确的是()A.它的图象必经过点(1,3)B.y的值随x值的增大而增大C.当x>0时,y<0D.它的图象与x轴的交点坐标为(13,0)2.(2022·江苏溧阳·八年级期末)如图,直线122y x=-+与x轴、y轴交于A、B两点,在y轴上有一点C(0,4),动点M从A点发以每秒1个单位的速度沿x轴向左移动.当动到△COM与△AOB全等时,移的时间t是()A.2B.4C.2或4D.2或63.(2022·陕西·辋川乡初级中学八年级期末)数学课上,老师提出问题:“一次函数的图象经过点A(3,2),B(-1,-6),由此可求得哪些结论?”小明思考后求得下列4个结论:①该函数表达式为y=2x-4;②该一次函数的函数值随自变量的增大而增大:③点P(2a,4a-4)在该函数图象上;④直线AB与坐标轴围成的三角形的面积为8.其中错误的结论是()A.1个B.2个C.3个D.4个4.(2022·江苏启东·八年级期末)如图,在平面直角坐标系中,O为原点,点A,C,E的坐标分别为(0,4),(8,0),(8,2),点P,Q是OC边上的两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标为()A.(2,0)B.(3,0)C.(4,0)D.(5,0)二、填空题5.(2022·江苏滨湖·八年级期末)如图,直线y=﹣43x+8与坐标轴分别交于A、B两点,P是AB的中点,则OP的长为_____.6.(2021·山东济阳·八年级期中)如图,一次函数y =x +2的图像与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且△OPC =45°,PC =PO ,则点P 的坐标为______.7.(2021·湖北阳新·模拟预测)如图,直线AB 的解析式为y =﹣x +b 分别与x ,y 轴交于A ,B 两点,点A的坐标为(3,0),过点B 的直线交x 轴负半轴于点C ,且31OB OC ::,在x 轴上方存在点D ,使以点A ,B ,D 为顶点的三角形与△ABC 全等,则点D 的坐标为_____.8.(2022·山东龙口·七年级期末)正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示放置,点A 1,A 2,A 3,和点C 1,C 2,C 3,…,分别在直线y =kx +b (k >0)和x 轴上,已知点B 1,B 2,B 3,B 4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn 的坐标为_____三、解答题9.(2022·江苏海州·八年级期末)已知直线l 1经过点A (3,2)和点B (0,5),直线l 2:y =2x ﹣4经过点A 且与y 轴相交于点C .(1)求直线l 1的函数表达式;(2)已知点M 在直线l 1上,过点M 作MN //y 轴,交直线l 2于点N .若MN =6,请求出点M 的横坐标.10.(2022·广西·桂林市雁山中学九年级期末)如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=mx在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:(1)点A、B、C的坐标;(2)这个反比例函数的表达式;(3)这个一次函数的表达式.11.(2022·江苏溧阳·八年级期末)如图,在平面直角坐标系中长方形AOBC的顶点A、B坐标分别为(0,8)、(10,0),点D是BC上一点,将△ACD沿直线AD翻折,使得点C落在OB上的点E处,点F是直线AD 与x轴的交点,连接CF.(1)点C坐标为____________;(2)求直线AD的函数表达式_______________________;(3)点P是直线AD上的一点,当△CFP是直角三角形时,请你直接写出点P的坐标.。
(完整word版)一次函数练习题及答案(较难 实用)

初二一次函数与几何题(附答案)1、 平面直角坐标系中,点A 的坐标为(4,0),点P 在直线y=-x-m 上,且AP=OP=4,则m的值是多少?2、如图,已知点A 的坐标为(1,0),点B 在直线y=-x 上运动,当线段AB 最短时,试求点B 的坐标。
3、如图,在直角坐标系中,矩形OABC 的顶点B 的坐标为(15,6),直线y=1/3x+b 恰好将矩形OABC 分为面积相等的两部分,试求b 的值。
4、如图,在平面直角坐标系中,直线y= 2x —6与x 轴、y 轴分别相交于点A 、B ,点C在x 轴上,若△ABC 是等腰三角形,试求点C 的坐标。
5、在平面直角坐标系中,已知A (1,4)、B (3,1),P 是坐标轴上一点,(1)当P 的坐标为多少时,AP+BP 取最小值,最小值为多少? 当P 的坐标为多少时,AP-BP 取最大值,最大值为多少?A B C O x y xyA B O6、如图,已知一次函数图像交正比例函数图像于第二象限的A点,交x轴于点B(-6,0),△AOB的面积为15,且AB=AO,求正比例函数和一次函数的解析式。
7、已知一次函数的图象经过点(2,20),它与两坐标轴所围成的三角形的面积等于1,求这个一次函数的表达式。
8、已经正比例函数Y=k1x的图像与一次函数y=k2x-9的图像相交于点P(3,-6)求k1,k2的值如果一次函数y=k2x-9的图象与x轴交于点A 求点A坐标9、正方形ABCD的边长是4,将此正方形置于平面直角坐标系中,使AB在x轴负半轴上,A 点的坐标是(-1,0),(1)经过点C的直线y=-4x-16与x轴交于点E,求四边形AECD的面积;(2)若直线L经过点E且将正方形ABCD分成面积相等的两部分,求直线L的解析式。
10、在平面直角坐标系中,一次函数y=Kx+b(b 小于0)的图像分别与x 轴、y 轴和直线x=4交于A 、B 、C ,直线x=4与x 轴交于点D ,四边形OBCD 的面积为10,若A 的横坐标为-1/2,求此一次函数的关系式11、在平面直角坐标系中,一个一次函数的图像过点B(-3,4),与y 轴交于点A ,且OA=OB :求这个一次函数解析式12、如图,A 、B 分别是x 轴上位于原点左右两侧的点,点P (2,m )在第一象限,直线PA 交y 轴于点C (0,2),直线PB 交y 轴于点D ,S AOP =6.求:(1)△COP 的面积(2)求点A 的坐标及m 的值;(3)若S BOP =S DOP ,求直线BD 的解析式13、一次函数y=-33x+1的图像与x 轴、y 轴分别交于点A 、B ,以AB 为边在第一象限内做等边△ABC(1)求△ABC 的面积和点C 的坐标;(2)如果在第二象限内有一点P (a ,21),试用含a 的代数式表示四边形ABPO 的面积。
一次函数与几何图形结合的问题习题

一次函数与几何图形的综合问题类型一 一次函数与面积问题1.如图,一次函数y =- x +m 的图象和y 轴交于点B ,与正比例函数y =12x 的图象交于点P (2,n ).(1)求m 和n 的值;(2)求APOB 的面积.2.如图,把Rt △ABC 放在平面直角坐标系内,其中∠CAB =90°,BC =5,点A ,B 的坐标分别为(1,0),(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线y =2x -6上时,线段BC 扫过的面积为 .3.如图,直线y =-2x +3与x 轴相交于点A ,与y 轴相交于点B .[易错7](1)求A ,B 两点的坐标;(2)过B 点作直线BP 与x 轴相交于点P ,且使OP =2OA ,求△ABP 的面积.4.如图,直线y =-x +10与x 轴、y 轴分别交于点B ,C ,点A 的坐标为(8,0),点P (x ,y )是在第一象限内直线y =-x +10上的一个动点.(1)求△OPA 的面积S 与x 的函数解析式,并写出自变量x 的取值范围;(2)当△OPA 的面积为10时,求点P 的坐标.图类型二一次函数与几何图形的规律探究问题1. (2017●安顺中考)如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,..在直线l上,点B1,B2,B3,...在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,...依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn,顶点Bn的横坐为.2.(2016●潍坊中考)在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,.. ,正方形AnBnCnC n-1,使得点A1,A2,A3…在直线l上,点C1 ,C2,C3,...在y轴正半轴上,则点Bn的坐标是.类型三一次函数与新定义几何图形的探究1.在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2, y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q 的“相关矩形”.下图①为点P,Q的“相关矩形”的示意图.(1)已知点A的坐标为(1,0),①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;②点B在直线x=3上.若点A,B的“相关矩形”面积是4,求点B的坐标;(2)一次函数y=-2x+b的图象经过点A,交y轴于点C,若在线段AC上存在一点D,使得点D、B的对角矩形是正方形,求m的取值范围;(3)一次函数y=k x+4的图象交y轴于点C,点A、B的对角矩形且面积是12,且m>0,要使得一次函数y=k x+4的图象与该对角矩形有交点,求k的取值范围.图①。
一次函数与几何及动点综合题(含解析)
一、选择题(题型注释)1.如图反映的过程是:矩形ABCD 中,动点P 从点A 出发,依次沿对角线AC 、边CD 、边DA 运动至点A 停止,设点P 的运动路程为x , ABP S y △.则矩形ABCD 的周长是(P )D A BC61295Oy xA .6B .12C .14D .15 【答案】C 【解析】试题分析:结合图象可知,当P 点在AC 上,△ABP 的面积y 逐渐增大,当点P 在CD 上,△ABP 的面积不变,由此可得AC=5,CD=4,则由勾股定理可知AD=3,所以矩形ABCD 的周长为:2×(3+4)=14.考点:动点问题的函数图象;矩形的性质.点评:本题考查的是动点问题的函数图象,解答本题的关键是根据矩形中三角形ABP 的面积和函数图象,求出AC 和CD 的长.2.小芳步行上学,最初以某一速度匀速前进,中途遇红灯,稍作停留后加快速度跑步去上学,到校后,她请同学们画出她行进路程s (米)与行进时间t (分钟)的函数图象的示意图.你认为正确的是( )【答案】C 【解析】试题分析:运用排除法解答本题,中间的停留路程不变,可排除BD 两项,最后的加速图象应为比最初的路程增加直线增速更快的图象,C 对3.如图,已知A 1、A 2、A 3、…、A n 、A n+1是x 轴上的点,且OA 1=A 1A 2=A 2A 3=…=A n A n+1=1,分别过点A 1、A 2、A 3、…、A n 、A n+1作x 轴的垂线交直线y=2x 于点B 1、B 2、B 3、…、B n 、B n+1,连接A 1B 2、B 1A 2、B 2A 3、…、A n B n+1、B n A n+1,依次相交于点P 1、P 2、P 3、…、P n .△A 1B 1P 1、△A 2B 2P 2、△A n B n P n 的面积依次记为S 1、S 2、S 3、…、S n ,则S n 为( )A.121nn++B.31nn-C.221nn-D.221nn+【答案】D.【解析】试题分析:∵A1、A2、A3、…、A n、A n+1是x轴上的点,且OA1=A1A2=A2A3=…=A n A n+1=1,∴A1(1,0),A2(2,0),A3(3,0),…A n(n,0),A n+1(n+1,0),∵分别过点A1、A2、A3、…、A n、A n+1,作x轴的垂线交直线y=2x于点B1、B2、B3、…、B n、B n+1,∴B1的横坐标为:1,纵坐标为:2,则B1(1,2),同理可得:B2的横坐标为:2,纵坐标为:4,则B2(2,4),B3(2,6),…B n(n,2n),B n+1(n+1,2n+2),根据题意知:P n是A n B n+1与 B n A n+1的交点,设:直线A n B n+1的解析式为:y=k1x+b1,直线B n A n+1的解析式为:y=k2x+b2,∵A n(n,0),A n+1(n+1,0),B n(n,2n),B n+1(n+1,2n+2),∴直线A n B n+1的解析式为:y=(2n+2)x﹣2n2﹣2n,直线B n A n+1的解析式为:y=﹣2n x+2n2+2n,∴P n(22221n nn++,24421n nn++)∴△A n B n P n的A n B n边上的高为:22221n nnn+-+=21nn+,△A n B n P n的面积S n为:21222121n nnn n⨯⋅=++.故选D .考点:一次函数图象上点的坐标特征. 4.如图,已知直线l :x y 33,过点A (0,1)作y 轴的垂线 交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过 点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 4的坐标为 A.(0,64) B.(0,128) C.(0,256) D.(0,512)【答案】C. 【解析】试题分析:∵直线l 的解析式为;3, ∴l 与x 轴的夹角为30°, ∵AB ∥x 轴, ∴∠ABO=30°, ∵OA=1, ∴OB=2, ∴3,∵A 1B ⊥l ,∴∠ABA 1=60°, ∴A 1O=4, ∴A 1(0,4),同理可得A 2(0,16), …∴A 4纵坐标为44=256, ∴A 4(0,256). 故选C .考点:一次函数综合题.5.如图,在矩形ABCD 中,O 是对角线AC 的中点,动点P ,Q 分别从点C ,D 出发,沿线段CB ,DC 方向匀速运动,已知P ,Q 两点同时出发,并同时到达终点B ,C .连接OP ,OQ .设运动时间为t ,四边形OPCQ 的面积为S ,那么下列图象能大致刻画S 与t 之间的关系的是【答案】A . 【解析】试题分析:作OE ⊥BC 于E 点,OF ⊥CD 于F 点,如图,设BC=a ,AB=b ,点P 的速度为x ,点F 的速度为y , 则CP=xt ,DQ=yt ,所以CQ=b-yt , ∵O 是对角线AC 的中点,∴OE 、OF 分别是△ACB 、△ACD 的中位线, ∴OE=12b ,OF=12a , ∵P ,Q 两点同时出发,并同时到达终点, ∴a bx y=,即ay=bx , ∴S=S △OCQ +S △OCP =12•12a•(b-yt )+12•12b•xt=14ab-14ayt+14bxt=14ab (0<t <a x), ∴S 与t 的函数图象为常函数,且自变量的范围为0<t <ax).故选A .考点:动点问题的函数图象.6.函数321+=x y 的图象与x 、y 轴分别交于点A 、B ,点P )(y x ,为直线AB 上的一动点(0>x )过P 作PC ⊥y 轴于点C ,若使PBC ∆的面积大于AOB ∆的面积,则P的横坐标x 的取值范围是( )A 、30<<xB 、3>xC 、63<<xD 、6>x【解析】试题分析:由题意知:PC=x ,OC=132x + ∴BC=12x ∵PBC ∆的面积大于AOB ∆的面积∴x >6. 故选D.考点: 一次函数综合题.7.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为 ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( )A .3B .4C .5D .6 【答案】A 【解析】 试题分析:动点P 从直角梯形ABCD 的直角顶点B 出发,沿BC ,CD 的顺序运动,则△ABP 面积y 在BC 段随x 的增大而增大;在CD 段,△ABP 的底边不变,高不变,因而面积y 不变化.由图2可以得到:BC=2,CD=3,△BCD 的面积是12×2×3=3. 故选A .考点:动点问题的函数图象.8.如图,正方形ABCD 的边长为4,P 为正方形边上一动点,沿A →D →C →B →A 的路径匀速移动,设P 点经过的路径长为x ,△APD 的面积是y ,则下列图象能大致反映y 与x 的函数关系的是A .B .C .D .【解析】当点P 由点A 向点D 运动时,y 的值为0; 当点p 在DC 上运动时,y 随着x 的增大而增大; 当点p 在CB 上运动时,y 不变;当点P 在BA 上运动时,y 随x 的增大而减小。
一次函数与几何综合(通用版)(含答案)

一次函数与几何综合(通用版)试卷简介:一次函数与几何综合一、单选题(共10道,每道10分)1.如图,已知一条直线经过A(0,2),B(1,0)两点,将这条直线向左平移与x轴,y轴分别交于点C,点D.若DB=DC,则直线CD的函数解析式为( )A. B.C. D.答案:C解题思路:由题意可求得直线AB的解析式为y=-2x+2,AB∥CD.由DB=DC,DO⊥BC可得,OC=OB=1,∴C(-1,0).由AB∥CD可设直线CD的解析式为y=-2x+b,把C点坐标代入可得,b=-2,∴直线CD的函数解析式为y=-2x-2.试题难度:三颗星知识点:一次函数图象与几何变换2.如图,一束光线从点A(3,3)出发,经过y轴上的点C反射后经过点B(1,0),则光线从点A到点B 经过的路径长为( )A. B.C. D.5答案:D解题思路:如图,延长AC交x轴于点B′.则点B,B′关于y轴对称,CB=CB′.作AD⊥x轴于点D,则AD=3,DB′=3+1=4,AB′=5.∴AC+CB=AC+CB′=AB′=5.即光线从点A到点B经过的路径长为5.试题难度:三颗星知识点:坐标与图形性质3.如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为,则tanA的值是( )A. B.C. D.答案:B解题思路:根据三角形内心的定义可知∠ABO=∠CBO,∵C(2,0),B(0,2),∴OB=OC,∠CBO=∠ABO=45°,,∴∠ABC=90°即AB⊥BC,可求得直线AB的表达式为:,由得,,即A(-6,-4),∴,在Rt△ABC中,.试题难度:三颗星知识点:一次函数综合题4.如图,直线⊥x轴于点(1,0),直线⊥x轴于点(2,0),直线⊥x轴于点(3,0)…,直线⊥x轴于点(n,0).函数y=x的图象与直线,,,…,分别交于点,…,;函数y=2x的图象与直线,,,…,分别交于点,…,.如果△的面积为,四边形的面积为,四边形的面积为,…,四边形的面积为,那么=( )A.4025B.4023C. D.答案:C解题思路:∵函数y=x的图象与直线,,,…,分别交于点,∴∵函数y=2x的图象与直线,,,…,分别交于点∴,,…….当n=2013时,.试题难度:三颗星知识点:一次函数综合题5.如图,在平面直角坐标系中,直线经过原点O,且与x轴正半轴的夹角为30°.点M在x轴上,⊙M的半径为2,⊙M与直线相交于A,B两点.若△ABM为等腰直角三角形,则点M的坐标为( )A. B.C. D.答案:B解题思路:如图,当点M在原点右边时,过点M作MN⊥AB,垂足为N,则,∵△ABM为等腰直角三角形,∴AN=MN,∴,∵AM=2,∴,∴,∵直线与x轴正半轴的夹角为30°,∴,∴点M的坐标为,由对称性可知,点M′的坐标为.试题难度:三颗星知识点:一次函数之存在性6.已知在直角坐标系中有两条直线,直线所对应的函数解析式为y=x-2,如果将坐标纸折叠,使与重合,则点(-1,0)与点(0,-1)也重合,那么直线所对应的函数解析式为( )A.y=x-2B.y=x+2C.y=-x-2D.y=-x+2答案:B解题思路:∵折叠坐标纸可以使点(-1,0)与点(0,-1)重合,∴是沿直线y=x折叠的(也就是对称轴为直线y=x).∵y=x-2过点(0,-2),(2,0),折叠后的对应点为(-2,0),(0,2),即直线过两点(-2,0),(0,2).可以求得:y=x+2.试题难度:三颗星知识点:一次函数图象与几何变换7.如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是( )A.3<b<6B.2<b<6C.3≦b≦6D.2<b<5答案:C解题思路:题干意思是指直线与小正方形有交点时,求b的取值范围.我们知道直线是由直线向上平移b个单位得到的,若直线与小正方形有交点,可知当直线经过A(1,1)时b的值最小,此时b=3;当直线经过C(2,2)时,b最大,此时b=6.∴能够使黑色区域变白的b的取值范围为3≦b≦6.试题难度:三颗星知识点:一次函数综合题8.已知矩形ABCD中,AB=9,AD=3,将此矩形置于平面直角坐标系中,使AB在x轴正半轴上,若经过点C的直线与x轴交于点E,则四边形AECD的面积为( )A.9B.18C.6D.21答案:B解题思路:在矩形ABCD中,要求四边形AECD的面积,只需求出△EBC的面积即可,即求BE的长.∵点C的纵坐标是3,代入直线解析式可得点C(10,3),∴OB=10,∵直线与x轴交于点E,∴点E(4,0),∴OE=4,BE=6,则△EBC的面积为9,∴四边形AECD的面积为18.试题难度:三颗星知识点:一次函数综合题9.如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A,B,C三点为顶点的三角形是等腰三角形,则满足条件的点C的个数为( )A.2B.3C.4D.5答案:B解题思路:由于点A,B是固定点,要使△ABC是等腰三角形,只需根据一线两圆,判断与直线的交点即可.①作线段AB的垂直平分线,交直线于点,则是以AB为底的等腰三角形;②以点A为圆心,AB长为半径作圆,交直线于两点,,则,分别是以为底的等腰三角形;③以点B为圆心,AB长为半径作圆,我们发现该圆与直线无交点,原因在于:过点B作直线的垂线BM,垂足为M,.试题难度:三颗星知识点:一次函数之存在性10.如图,在以点O为原点的平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且,反比例函数的图象经过点C,则所有可能的k值为( )A. B.C. D.答案:C解题思路:由题意得,A(2,0),B(0,1),.显然当点为线段AB的中点时,有,此时点的坐标为,.如图,以点O为圆心,的长为半径作圆,交直线AB于另一点,则点也符合条件.过点O作OE⊥AB于点E,过点作⊥x轴于点F,则,.在中,,,则;在中,,且,则,∴点,综上:,试题难度:三颗星知识点:一次函数综合题。
一次函数与几何图形综合题10及答案

一次函数与几何图形综合题10及答案1、1) AC的解析式为y=-x-2;2) 设BP与PQ的交点为R,由相似三角形可得BP/PQ=OB/OQ,即BP/PQ=1/2,故BP=2PQ。
证明如下:设BP=x,PQ=y,则由OC=OB可得AC=-x-2,又由直线AC和BP的垂线PQ相似可得y/x=(x+2)/(y+2),解得y=2x,代入AC 的解析式可得BP=2PQ,结论得证。
3) 正确结论为①(MQ+AC)/PM的值不变。
证明如下:由(2)可得BP=2PQ,又由相似三角形可得MQ/PM=OB/OQ,即MQ/PM=1/3,代入AC的解析式可得(MQ+AC)/PM=-2/3,为定值。
而(MQ-AC)/PM=(MQ+AC)/PM-2AC/PM=-2/3-2x/(x+2),不是定值。
故正确结论为①。
2、1) 直线L的解析式为y=-x+5;2) 由相似三角形可得MN/BN=AM/AB=4/(4+3),即MN=12/7;3) 猜想PB的长为定值,其值为2.证明如下:设点B在y轴上的坐标为h,则BP=h,由△OBF和△ABE相似可得BE=BF=h/2,EF=AB-BE=5-h/2,由相似三角形可得FP/EF=BP/BE=h/(5-h/2),所以FP=5h/(5-h/2),由于P在y轴上,故FP=2h,解得h=2,即PB=2,结论得证。
3、1) 直线l2的解析式为y=-x+1;2) 画图如下,由相似三角形可得BE/BC=AB/AC,即BE/(BE+CF)=(AB+BC+AC)/AC,代入AB=1,BC=3,AC=4可得BE/(BE+CF)=5/4,即BE=5CF/3,代入△BEC的勾股定理可得CF=3/2,BE=5/2,故BE+CF=8/2=4=EF,结论得证。
3) 正确结论为①OM为定值,其值为1/2.证明如下:设△ABC沿y轴向下平移的距离为h,则BP=CQ=h,由相似三角形可得OM/AB=OC/AC,即OM/1=(h+2)/(h+4),解得OM=(2h+4)/(h+4),为定值。
中考数学《一次函数-动态几何问题》专项练习题及答案

中考数学《一次函数-动态几何问题》专项练习题及答案一、单选题1.如图,在四边形ABCD中,AB∥CD,∥B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设∥APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为()A.B.C.D.2.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形ABCD的边上沿A→B→C的方向运动到点C停止设点P的运动路程为x(cm),在下列图象中,能表示∥ADP的面积y(cm2)关于x(cm)的函数关系的图象是()A.B.C.D.3.如图,矩形ABCD中,P为CD中点,点Q为AB上的动点(不与A,B重合).过Q作QM∥PA 于M,QN∥PB于N.设AQ的长度为x,QM与QN的长度和为y.则能表示y与x之间的函数关系的图象大致是( )A.B.C.D.4.如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P与点Q的速度之比为1:2,则下列说法正确的是()A.线段PQ始终经过点(2,3)B.线段PQ始终经过点(3,2)C.线段PQ始终经过点(2,2)D.线段PQ不可能始终经过某一定点5.如图1,在四边形ABCD中,DC//AB,∠DAB=90°,点E沿着B→C→D的路径以2cm/s速度匀速运动,到达点D停止运动,EF始终与直线BC保持垂直,与AB或AD交于点F,设线段EF的长度为d(cm),运动时间为t(s),若d与t之间的关系如图2所示,则图中a的值为()A.3.8B.3.9C.4.5D.4.86.如图,在平面直角坐标系中,A(1,1),B(2,2),直线y=kx+x+3与线段AB有公共点,则k的取值范围是()A.k≥−3B.k<−32C.−3<k<−32D.−3≤k≤−3 27.如图所示,A、M、N点坐标分别为A(0,1),M(3,2),N(4,4),动点P从点A出发,沿y 轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t 秒,若点m,n分别位于l的异侧,则t的取值范围是()A.5<t<8B.4<t<7C.4≤t≤7D.4<t<88.一次函数y=−2x+4的图象与y轴交于点P,将一次函数图象绕着点P转动,转动后得到的一次函数图象与两坐标轴所围成的面积比原来增加2,则转动后得到的一次函数图象与x轴交点横坐标为()A.−3B.3C.3或−3D.6或−69.如图,在平面直角坐标系中有-个3×3的正方形网格,其左下角格点A的坐标为(1,1),右上角格点B的坐标为(4,4),若分布在直线y=k(x-1)两侧的格点数相同,则k的取值可以是()A.52B.2C.74D.3210.如图,直线AB:y=-3x+9交y轴于A,交x轴于B,x轴上一点C(-1,0),D为y轴上一动点,把线段BD绕B点逆时针旋转90°得到线段BE,连接CE,CD,则当CE长度最小时,线段CD的长为()A.√10B.√17C.5D.2√711.小颖从家出发,走了20分钟,到一个离家1000米的图书室,看了40分钟的书后,用15分钟返回到家,图(3)中表示小颖离家时间x与距离y之间的关系正确的是()A.B.C.D.12.如图,在平面直角坐标系中,线段AB的端点A(−1,−2),B(3,−1),若直线y=kx+2与线段AB有交点,则k的值可能是()A.2B.3C.−12D.-4二、填空题13.如图,在平面直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持∥ABC 是等边三角形(点A,B,C按逆时针排列),当点B运动到原点O处时,则点C的坐标是.随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的表达式是.14.在平面直角坐标系中,点A,B的坐标分别是(m,2),(2m−1,2),若直线y=4x+1与线段AB有公共点,则m的取值范围是≤m≤.15.在平面坐标系中,已知点A(2,3),B(5,8),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为.16.如图,在直角坐标系中,∥A的圆心的坐标为(﹣2,0),半径为2,点P为直线y=﹣34x+6上的动点,过点P作∥A的切线,切点为Q,则切线长PQ的最小值是17.如图,在∥ABC中,∥C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,∥BCD 的面积y,则y与x之间的函数表达式为.18.如图,点M的坐标为(3,2),点P从原点O出发,以每秒1个单位的速度沿y轴向上移动,同时过点P的直线关于直线l也随之上下平移,且直线l与直线y=−x平行,如果点M关于直线l的对称点落在坐标轴上,如果点P的移动时间为t秒,那么t的值为.三、综合题19.如图,在平面直角坐标系中,点F的坐标为(0,10).点E的坐标为(20,0),直线l1经过点F 和点E,直线l1与直线l2 、y= 34x相交于点P.(1)求直线l1的表达式和点P的坐标;(2)矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒√5个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线l1或l2上,请直接写出此时t的值;②若矩形ABCD在移动的过程中,直线CD交直线l1于点N,交直线l2于点M.当∥PMN的面积等于18时,请直接写出此时t的值.20.在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:(1)这辆汽车的往、返速度是否相同?请说明理由;(2)求返程中y与x之间的函数表达式;(3)求这辆汽车从甲地出发4h时与甲地的距离.21.如图,在平面直角坐标系中,直线y=x+2与x轴、y轴分别交A、B两点,与直线y=−12x+b相交于点C(2,m)(1)求点A、B的坐标;(2)求m和b的值;(3)若直线y=−12x+b与x轴相交于点D.动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒①若点P在线段DA上,且ΔACP的面积为10,求t的值;②是否存在t的值,使ΔACP为等腰三角形?若存在,求出t的值;若不存在,请说明理由.22.当我们将一条倾斜的直线进行上下平移时,直线的左右位置也发生着变化.下面是关于“一次函数图象平移的性质”的探究过程,请补充完整.(1)如图1,将一次函数y=x+2的图像向下平移1个单位长度,相当于将它向右平移了个单位长度;(2)将一次函数y=−2x+4的图像向下平移1个单位长度,相当于将它向(填“左”或“右”)平移了个单位长度;(3)综上,对于一次函数y=kx+b(k≠0)的图像而言,将它向下平移m(m>0)个单位长度,相当于将它向(填“左”或“右”)(k>0时)或将它向(填“左”或“右”)(k<0时)平移了n(n>0)个单位长度,且m,n,k满足等式.23.如图,在平面直角坐标系中,点A(2,a),B(a+2,a),其中a>0,直线y=kx﹣2与y轴相交于C点.(1)已知a=2①求S∥ABC;②若点A和点B在直线y=kx﹣2的两侧,求k的取值范围;(2)当k=2时,若直线y=kx﹣2与线段AB的交点为D点(不与A点、B点重合),且AD<3,求a的取值范围.24.如图所示,平面直角坐标系中,直线AB交x轴于点B(﹣3,0),交y轴于点A(0,1),直线x=﹣1交AB于点D,P是直线x=﹣1上一动点,且在点D上方,设P(﹣1,n).(1)求直线AB的解析式;(2)求∥ABP的面积(用含n的代数式表示);(3)点C是y轴上一点,当S∥ABP=2时,∥BPC是等腰三角形①满足条件的点C的个数是▲ 个(直接写出结果);②当BP为等腰三角形的底边时,求点C的坐标.参考答案1.【答案】D 2.【答案】A 3.【答案】D 4.【答案】B 5.【答案】B 6.【答案】D 7.【答案】B 8.【答案】C 9.【答案】C 10.【答案】B 11.【答案】A 12.【答案】D13.【答案】( √3 ,1);y = √3 x -2 14.【答案】14;5815.【答案】2≤k ≤3 16.【答案】4√2 17.【答案】y =-3x +24 18.【答案】2或319.【答案】(1)解:设直线l 1的表达式为y=kx+b ∵直线l 1过点F (0,10),E (20,0)∴{b =1020k +b =0解得 {k =−12b =10直线l 1的表达式为y=﹣ 12 x+10求直线l 1与直线l 2 交点,得34 x=﹣ 12 x+10解得x=8y= 34×8=6 ∴点P 坐标为(8,6)(2)解:①如图,当点D 在直线上l 2时∵AD=9∴点D 与点A 的横坐标之差为9∴将直线l1与直线l2交解析式变为x=20﹣2y,x= 43y∴43y﹣(20﹣2y)=9解得y= 8710则点A的坐标为:(135,8710)则AF= √(135)2+(10−8710)2=13√510∵点A速度为每秒√5个单位∴t= 1310如图,当点B在l2直线上时∵AB=6∴点A的纵坐标比点B的纵坐标高6个单位∴直线l1的解析式减去直线l2 的解析式得﹣12x+10﹣34x=6解得x= 165则点A坐标为(165,425)则AF= √(165)2+(10−425)2=8√55∵点A速度为每秒√5个单位∴t= 8 5故t值为1310或85②如图设直线AB交l2 于点H设点A横坐标为a,则点D横坐标为a+9由①中方法可知:MN= 54a+54此时点P到MN距离为:a+9﹣8=a+1∵∥PMN的面积等于18∴12×(54a +54)⋅(a +1)=18解得a 1= 12√55−1 ,a 2=﹣ 12√55−1 (舍去)∴AF=6﹣ √52则此时t 为 6√55−12 当t= 6√55−12 时,∥PMN 的面积等于18 20.【答案】(1)解:不同.理由如下:∵ 往、返距离相等,去时用了2小时,而返回时用了2.5小时∴ 往、返速度不同.(2)解:设返程中 y 与 x 之间的表达式为 y =kx +b则 {120=2.5k +b ,0=5k +b.解之,得 {k =−48,b =240.∴ y =−48x +240 .( 2.5x ≤x ≤5 )(3)解:当 x =4 时,汽车在返程中∴y =−48×4+240=48 .∴ 这辆汽车从甲地出发4h 时与甲地的距离为48km.21.【答案】(1)解:在 y =x +2 中当 x =0 时当 y =0 时∴A(−2,0)(2)解: ∵ 点 C(2,m) 在直线 y =x +2 上∴m =2+2=4又 ∵ 点 C(2,4) 也在直线 y =−12x +b 上 ∴ 即 4=12x +5 解得 b =5(3)解:在 y =−12x +5 中 当 x =0 时∴D(10,0)∵A(−2,0)∴AD =12①设 PD =t ,则 AP =12−t过 C 作 CE ⊥AP 于 E ,则 CE =4由 ΔACP 的面积为 10得 12(12−t)×4=10 解得 t =7②过 C 作 CE ⊥AP 于 E则 CE =4∴AC =4√2a. 当 AC =CP 时,如图①所示则 AP =2AE =8∴PD =AD −AP =4∴t =4b. 当 AP 1=AP 2=AC =4√2 时,如图②所示DP 1=t =12−4√2c. 当 CP =AP 时,如图③所示设 EP =a则 CP =√a 2+42∴√a 2+42=a +4解得 a =0∴AP =4∴PD =8∴t =8综上所述,当 t =4 或 t =12−4√2 或 t =12+4√2 或 t =8 时,ΔACP 为等腰三角形22.【答案】(1)1(2)左;12(3)右;左;m=n|k|23.【答案】(1)解:①∵a =2∴A (2,2),B (4,2)∴AB =2∵直线y =kx ﹣2与y 轴相交于C 点∴C (0,﹣2),如图∴S ∥ABC =12AB×(2+2)=12×2×4=4. ②当直线y =kx ﹣2经过点A (2,2)时2k ﹣2=2,解得k =2当直线y =kx ﹣2经过点B (4,2)时4k ﹣2=2,解得k =1∴点A 和点B 在直线y =kx ﹣2的两侧时,1<k <2;(2)解:直线AB 的解析式为:y =a当k =2时,直线y =2x ﹣2∴2x ﹣2=a ,即x =a+22∴D (a+22,a )∴2<a+22<a+2解得a >2又∵AD =a+22−2<3解得a <8所以a 的取值范围为2<a <8.24.【答案】(1)解:设直线AB 的解析式为y=kx+b ,把A(0,1),B(﹣3,0)代入,得{b =1−3k +b =0解得{b =1k =13∴y =13x +1; (2)解:当x=-1时,y =13×(−1)+1=23∵P(﹣1,n)∴PD=n−2 3∴∥ABP的面积=∥APD的面积+∥BPD的面积=12PD⋅OB=12(n−23)×3=32n−1;(3)解:①3;②设C(0,c)∵P(-1,2),B(﹣3,0)∴PC2=(−1−0)2+(2−c)2=c2−4c+5BC2=(−3−0)2+(0−c)2=c2+9当PC=BC时c2-4c+5= c2+9∴c=-1∴C(0,-1).。
一次函数与几何问题练习题

A B C O y 2y 1x yP 一次函数与几何问题一、面积问题1、如图,在平面直角坐标系xOy 中,一次函数1223y x =-+与x 轴、y 轴分别相交于点A 和点B ,直线2 (0)y kx b k =+≠经过点C (1,0)且与线段AB 交于点P ,并把△ABO 分成两部分.(1)求△ABO 的面积;(2)若△ABO 被直线CP 分成的两部分的面积相等,求点P 的坐标及直线CP 的函数表达式。
2、如图,直线1l 过点A (0,4),点D (4,0),直线2l :121+=x y 与x 轴交于点C ,两直线1l ,2l 相交于点B 。
(1)、求直线1l 的解析式和点B 的坐标; (2)、求△ABC 的面积。
3、如图,直线OC 、BC 的函数关系式分别是y 1=x 和y 2=-2x+6,动点P (x ,0)在OB 上运动(0<x<3),过点P 作直线m 与x 轴垂直.(1)求点C 的坐标,并回答当x 取何值时y 1>y 2?(2)设△COB 中位于直线m 左侧部分的面积为s ,求出s 与x 之间函数关系式. (3)当x 为何值时,直线m 平分△COB 的面积?(10分)二、平移问题4、 正方形ABCD 的边长为4,将此正方形置于平面直角坐标系中,使AB 边落在X 轴的正半轴上,且A 点的坐标是(1,0)。
①直线y=43x-83经过点C ,且与x 轴交与点E ,求四边形AECD 的面积;②若直线l 经过点E 且将正方形ABCD 分成面积相等的两部分求直线l 的解析式, ③若直线1l 经过点F ⎪⎭⎫⎝⎛-0.23且与直线y=3x 平行,将②中直线l 沿着y 轴向上平移32个单位交x 轴于点M ,交直线1l 于点N ,求NMF ∆的面积.ABCODxy1l 2l5、如图,在平面直角坐标系中,直线1l :x y 34=与直线2l :b kx y += 相交于点A ,点A 的横坐标为3,直线2l 交y 轴于点B ,且OB OA 21=。
初二下学期压轴题练习- 一次函数与几何变换(含答案)

专题09一次函数与几何变换一.选择题1.(2021春•大同期末)对于一次函数y=﹣2x+4,下列结论正确的是()A.函数的图象与y轴的交点坐标是(4,0)B.函数的图象不经过第三象限C.函数的图象向上平移4个单位长度得y=﹣2x的图象D.若A(x1,y1),B(x2,y2)两点在该函数图象上,且x1<x2,则y1<y22.(2021•扬州)如图,一次函数y=x+的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为()A.+B.3C.2+D.+3.(2020秋•天桥区期末)如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为()A.5B.4C.3D.24.(2020秋•碑林区校级期中)将直线y=﹣3x沿着x轴向右平移2个单位,所得直线的表达式为()A.y=﹣3x+6B.y=﹣3x﹣6C.y=﹣3x+2D.y=﹣3x﹣2 5.(2020•碑林区校级模拟)若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为()A.k=2、b=﹣3B.k=﹣2、b=﹣3C.k=﹣2、b=1D.k=﹣2、b=﹣1 6.(2019•嘉祥县三模)在平面直角坐标系中,将直线y1:y=2x﹣2平移后,得到直线y2:y=2x+4,则下列平移作法正确的是()A.将y1向上平移2个单位长度B.将y1向上平移4个单位长度C.将y1向左平移3个单位长度D.将y2向右平移6个单位长度7.(2018春•雨花区校级月考)如图,A(0,1),M(3,2),N(4,4).点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒,当M、N位于直线l的异侧时,t应该满足的条件是()A.3<t<6B.4<t<7C.3<t<7D.<t<7二.填空题8.(2021春•安丘市期末)在平面直角坐标系xOy中,Rt△AOB的直角顶点B在y轴上,点A的坐标为(1,),将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',过A'作A'C垂直于OA′交y轴于点C,则点C 的坐标为.9.(2021春•东台市月考)如图1,在平面直角坐标系中,将▱ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为.10.(2021•广东模拟)如图,已知一条直线经过点A(﹣1,0),B(0,﹣2),将这条直线向右平移与x 轴、y轴分别交于点C、D,若AB=AD,则直线CD的函数表达式为.11.(2020春•黄陂区期末)将直线y=2x﹣3沿y轴向上平移2个单位后,所得直线的解析式是.12.(2018秋•福田区校级期中)如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点B n的坐标为.13.(2017秋•碑林区校级期末)如图,一次函数y=,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x 轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为.14.(2018春•丰南区期末)如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为.15.(2019春•西湖区校级期中)在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=4x+1以每秒2个单位的速度向下平移,经过秒该直线可将平行四边形OABC的面积平分.16.(2019•天津二模)将函数y=3x+1的图象平移,使它经过点(1,1),则平移后的函数表达式是.17.(2019春•常州期中)如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过秒该直线可将平行四边形OABC分成面积相等的两部分.三.解答题18.(2021春•古丈县期末)如图,直线l是一次函数y=kx+b的图象.(1)求出这个一次函数的解析式;(2)将该函数的图象向下平移5个单位,求出平移后一次函数的解析式,并写出平移后的图象与x轴的交点坐标.19.(2021春•武汉月考)已知,在平面直角坐标系中,函数y1=2|x﹣a|,(1)若该函数经过点A(1,0),求该函数的解析式,并在图1中画出函数图象;(2)在(1)的条件下,将函数y2=x向上平移m个单位后与函数y1的图象相交于点B和C点,若BC =,求m;(3)如图2,设直线y3=6n与直线y4=2n分别与函数y1=2|x﹣a|相交于点E、F和M、N,点P为直线y3=6n上一点,连接PM、PN并延长交直线y5=kn于点G、H,若2EF=3GH,求k.20.(2021春•河北区期末)如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x 轴,点A的坐标为(5,4)经过点O、点C作直线l,将直线l沿y轴上下平移.(1)当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;(2)当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F,连接BE、BF,求△BEF的面积.21.(2019秋•罗湖区校级期末)如图,在平面直角坐标系中,直线l1:y=x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=OB.(1)试求直线l2的函数表达式;(2)若将直线l1沿着x轴向左平移3个单位,交y轴于点C,交直线l2于点D.试求△BCD的面积.22.(2018秋•宿迁期末)如图,一次函数y=(m+1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4.(1)则m=,点A的坐标为(,).(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;(3)将一次函数y=(m+1)x+4的图象绕点B顺时针旋转45°,求旋转后的对应的函数表达式.23.(2019•大渡口区模拟)如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AD∥y轴,点A的坐标为(5,3),已知直线l:y=x﹣2.(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值;(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.24.(2018春•沙坪坝区校级期末)如图:一次函数y=x+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.(1)求点B的坐标;(2)求四边形ABCO的面积;(3)求直线CD的解析式.25.(2017春•武昌区期末)已知一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4)(1)求直线AB的解析式;(2)将直线AB平移,使其经过原点O,则线段AB扫过的面积为.26.(2017春•安岳县期中)已知直线y=(m+1)x|m|﹣1+(2m﹣1),当x1>x2时,y1>y2,求该直线的解析式.并求该直线经过怎么的上下平移就能过点(2,5)?27.(2016春•大兴区期末)阅读材料:通过一次函数的学习,小明知道:当已知直线上两个点的坐标时,可以用待定系数法,求出这个一次函数的表达式.有这样一个问题:直线l1的表达式为y=﹣2x+4,若直线l2与直线l1关于y轴对称,求直线l2的表达式.下面是小明的解题思路,请补充完整.第一步:求出直线l1与x轴的交点A的坐标,与y轴的交点B的坐标;第二步:在平面直角坐标系中,作出直线l1;第三步:求点A关于y轴的对称点C的坐标;第四步:由点B,点C的坐标,利用待定系数法,即可求出直线l2的表达式.小明求出的直线l2的表达式是.请你参考小明的解题思路,继续解决下面的问题:(1)若直线l3与直线l1关于直线y=x对称,则直线l3的表达式是;(2)若点M(m,3)在直线l1上,将直线l1绕点M顺时针旋转90°.得到直线l4,求直线l4的表达式.28.(2016•河北模拟)如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.(1)求点C的坐标和直线l1的解析式;(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l1上;(3)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.29.(2015秋•栖霞区期末)课本P152有段文字:把函数y=2x的图象分别沿y轴向上或向下平移3个单位长度,就得到函数y=2x+3或y=2x﹣3的图象.【阅读理解】小尧阅读这段文字后有个疑问:把函数y=﹣2x的图象沿x轴向右平移3个单位长度,如何求平移后的函数表达式?老师给了以下提示:如图1,在函数y=﹣2x的图象上任意取两个点A、B,分别向右平移3个单位长度,得到A′、B′,直线A′B′就是函数y=﹣2x的图象沿x轴向右平移3个单位长度后得到的图象.请你帮助小尧解决他的困难.(1)将函数y=﹣2x的图象沿x轴向右平移3个单位长度,平移后的函数表达式为.A.y=﹣2x+3;B.y=﹣2x﹣3;C.y=﹣2x+6;D.y=﹣2x﹣6【解决问题】(2)已知一次函数的图象与直线y=﹣2x关于x轴对称,求此一次函数的表达式.【拓展探究】(3)一次函数y=﹣2x的图象绕点(2,3)逆时针方向旋转90°后得到的图象对应的函数表达式为.(直接写结果)专题09一次函数与几何变换一.选择题1.(2021春•大同期末)对于一次函数y=﹣2x+4,下列结论正确的是()A.函数的图象与y轴的交点坐标是(4,0)B.函数的图象不经过第三象限C.函数的图象向上平移4个单位长度得y=﹣2x的图象D.若A(x1,y1),B(x2,y2)两点在该函数图象上,且x1<x2,则y1<y2【思路引导】代入y=0求出与之对应的x值,即可得出A不正确;根据一次函数的系数结合一次函数的性质,即可得知B选项正确、D选项不正确,根据平移的规律求得平移后的解析式,即可判断C不正确,此题得解.【完整解答】解:A、令y=﹣2x+4中y=0,则x=2,∴一次函数的图象与x轴的交点坐标是(2,0),故本选项不符合题意;B、∵k=﹣2<0,b=4>0,∴一次函数的图象经过第一、二、四象限,即函数的图象不经过第三象限,故本选项符合题意;C、根据平移的规律,函数的图象向上平移4个单位长度得到的函数解析式为y=﹣2x+4+4,即y=﹣2x+8,故本选项不符合题意;D、∵k=﹣2<0,∴一次函数中y随x的增大而减小,∴若A(x1,y1),B(x2,y2)两点在该函数图象上,且x1<x2,则y1>y2,故本选项不符合题意.故选:B.【考察注意点】本题考查了一次函数的图象以及一次函数的性质,解题的关键是逐条分析四个选项.本题属于基础题,难度不大,解决该题时,熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键.2.(2021•扬州)如图,一次函数y=x+的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为()A.+B.3C.2+D.+【思路引导】根据一次函数表达式求出点A和点B坐标,得到△OAB为等腰直角三角形和AB的长,过点C作CD⊥AB,垂足为D,证明△ACD为等腰直角三角形,设CD=AD=x,结合旋转的度数,用两种方法表示出BD,得到关于x的方程,解之即可.【完整解答】解:∵一次函数y=x+的图像与x轴、y轴分别交于点A、B,令x=0,则y=,令y=0,则x=﹣,则A(﹣,0),B(0,),则△OAB为等腰直角三角形,∠ABO=45°,∴AB==2,过点C作CD⊥AB,垂足为D,∵∠CAD=∠OAB=45°,∴△ACD为等腰直角三角形,设CD=AD=x,∴AC==x,由旋转的性质可知∠ABC=30°,∴BC=2CD=2x,∴BD==x,又BD=AB+AD=2+x,∴2+x=x,解得:x=+1,∴AC=x=(+1)=,故选:A.【考察注意点】本题考查了一次函数与坐标轴的交点问题,等腰直角三角形的判定和性质,直角三角形的性质,勾股定理,二次根式的混合运算,知识点较多,解题的关键是作出辅助线,构造特殊三角形.3.(2020秋•天桥区期末)如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为()A.5B.4C.3D.2【思路引导】先根据△AEF为等腰直角三角形,可得直线l与直线BD平行,即直线l沿x轴的负方向平移时,同时经过B,D两点,再根据BD的长即可得到b的值.【完整解答】解:如图1,连接BD并且两端延长,直线y=x﹣3中,令y=0,得x=3;令x=0,得y =﹣3,即直线y=x﹣3与坐标轴围成的△OEF为等腰直角三角形,∴直线l与直线BD平行,即直线l沿x轴的负方向平移时,同时经过B,D两点,由图2可得,t=2时,直线l经过点A,∴AO=3﹣2×1=1,∴A(1,0),由图2可得,t=12时,直线l经过点C,∴当t=+2=7时,直线l经过B,D两点,∴AD=(7﹣2)×1=5,∴等腰Rt△ABD中,BD=5,即当a=7时,b=5.故选:A.【考察注意点】本题考查了动点问题的函数图象,一次函数图象与几何变换,用图象解决问题时,要理清图象的含义即会识图.解决问题的关键是掌握正方形的性质以及平移的性质.4.(2020秋•碑林区校级期中)将直线y=﹣3x沿着x轴向右平移2个单位,所得直线的表达式为()A.y=﹣3x+6B.y=﹣3x﹣6C.y=﹣3x+2D.y=﹣3x﹣2【思路引导】根据平移性质可由已知的解析式写出新的解析式.【完整解答】解:根据题意,得直线向右平移2个单位,即对应点的纵坐标不变,横坐标减2,所以得到的解析式是y=﹣3(x﹣2)=﹣3x+6.故选:A.【考察注意点】此题主要考查了一次函数图象与几何变换,解题时注意:y=kx左右平移|a|个单位长度的时候,即直线解析式是y=k(x±|a|);当直线y=kx上下平移|b|个单位长度的时候,则直线解析式是y =kx±|b|.5.(2020•碑林区校级模拟)若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为()A.k=2、b=﹣3B.k=﹣2、b=﹣3C.k=﹣2、b=1D.k=﹣2、b=﹣1【思路引导】先求出一次函数y=kx+3与y轴交点关于直线x=1的对称点,得到b的值,再求出一次函数y=2x+b与y轴交点关于直线x=1的对称点,代入一次函数y=kx+3,求出k的值即可.【完整解答】解:∵一次函数y=kx+3与y轴交点为(0,3),∴点(0,3)关于直线x=1的对称点为(2,3),代入直线y=2x+b,可得4+b=3,解得b=﹣1,一次函数y=2x﹣1与y轴交点为(0,﹣1),(0,﹣1)关于直线x=1的对称点为(2,﹣1),代入直线y=kx+3,可得2k+3=﹣1,解得k=﹣2.故选:D.【考察注意点】本题考查的是一次函数图象与几何变换,待定系数法求函数解析式,先根据题意得出直线与坐标轴的交点是解决问题的关键.6.(2019•嘉祥县三模)在平面直角坐标系中,将直线y1:y=2x﹣2平移后,得到直线y2:y=2x+4,则下列平移作法正确的是()A.将y1向上平移2个单位长度B.将y1向上平移4个单位长度C.将y1向左平移3个单位长度D.将y2向右平移6个单位长度【思路引导】利用一次函数图象的平移规律,左加右减,上加下减,得出即可.【完整解答】解:∵将直线y1:y=2x﹣2平移后,得到直线y2:y=2x+4,∴2(x+a)﹣2=2x+4,解得:a=3,故将y1向左平移3个单位长度.故选:C.【考察注意点】此题主要考查了一次函数图象与几何变换,正确把握变换规律是解题关键.7.(2018春•雨花区校级月考)如图,A(0,1),M(3,2),N(4,4).点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒,当M、N位于直线l的异侧时,t应该满足的条件是()A.3<t<6B.4<t<7C.3<t<7D.<t<7【思路引导】分别求出直线l经过点M、点N时的t值,即可得到t的取值范围.【完整解答】解:当直线y=﹣x+b过点M(3,2)时,2=﹣3+b,解得:b=5,5=1+t,解得t=4.当直线y=﹣x+b过点N(4,4)时,4=﹣4+b,解得:b=8,8=1+t,解得t=7.故若点M,N位于l的异侧,t的取值范围是:4<t<7.故选:B.【考察注意点】本题考查了坐标平面内一次函数的图象与性质,关键是利用一次函数图象上点的坐标特征解答.二.填空题8.(2021春•安丘市期末)在平面直角坐标系xOy中,Rt△AOB的直角顶点B在y轴上,点A的坐标为(1,),将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',过A'作A'C垂直于OA′交y轴于点C,则点C 的坐标为(0,﹣4).【思路引导】依据轴对称的性质可得OB'=OB=,A′B′=AB=1,OA′=OA=2,进而通过证得△A′OB′∽△COA′,求得OC=4,即可证得C的坐标为(0,﹣4).【完整解答】解:∵点A的坐标为(1,),∴AB=1,OB=,∴OA===2,∵将Rt△AOB沿直线y=﹣x翻折,得到Rt△A'OB',∴OB'=OB=,A′B′=AB=1,OA′=OA=2,∴A'(﹣,﹣1),∵过A'作A'C垂直于OA'交y轴于点C,∴∠A′OC+∠A′CO=90°,∵∠A′OB′+∠A′OC=90°,∴∠A′CO=∠A′OB′,∵∠A′B′O=∠OA′C=90°,∴△A′OB′∽△OCA′,∴=,即=,∴OC=4,∴C(0,﹣4),故答案是:(0,﹣4).【考察注意点】本题考查了轴对称的性质,正比例函数的性质,求得对称点的坐标是解题的关键.9.(2021春•东台市月考)如图1,在平面直角坐标系中,将▱ABCD放置在第一象限,且AB∥x轴.直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为8.【思路引导】通过图象中(4,0),(7,2),(8,2)可得直线运动到A,D,B三点时所移动距离,从而求出AB长度,再通过添加辅助线构造直角三角形求出平行四边形的高而求解.【完整解答】解:由图象可知,直线经过A时移动距离为4,经过D时移动距离为7,经过B时移动距离为8,∴AB=8﹣4=4.如图,当直线经过点D时,交AB于点E,作DF垂直于AB于点F,由图2可知DE=2,∵直线与AB夹角为45°,∴DF=EF=2,∴ABCD面积为AB•DF=4×2=8.故答案为:8.【考察注意点】本题考查一次函数图象与图形结合问题,解题关键是掌握k=﹣1时直线与x轴所夹锐角为45°.10.(2021•广东模拟)如图,已知一条直线经过点A(﹣1,0),B(0,﹣2),将这条直线向右平移与x 轴、y轴分别交于点C、D,若AB=AD,则直线CD的函数表达式为y=﹣2x+2.【思路引导】先求出直线AB的解析式,再根据平移的性质求直线CD的解析式.【完整解答】解:设直线AB的解析式为y=kx+b(k≠0),∵点A(﹣1,0)点B(0,﹣2)在直线AB上,∴,解得,∴直线AB的解析式为y=﹣2x﹣2,∵AB=AD,AO⊥BD,∴OD=OB,∴D(0,2),∴直线CD的函数解析式为:y=﹣2x+2,故答案为:y=﹣2x+2.【考察注意点】本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.11.(2020春•黄陂区期末)将直线y=2x﹣3沿y轴向上平移2个单位后,所得直线的解析式是y=2x﹣1.【思路引导】直接根据“上加下减,左加右减”的原则进行解答即可.【完整解答】解:由“上加下减”的原则可知,直线y=2x﹣3沿y轴向上平移2个单位,所得直线的函数关系式为y=2x﹣3+2,即y=2x﹣1;故答案为y=2x﹣1.【考察注意点】本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.12.(2018秋•福田区校级期中)如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点B n的坐标为(2n﹣1,2n).【思路引导】先根据题意求出A2点的坐标,再根据A2点的坐标求出B2的坐标,以此类推总结规律便可求出点B n的坐标.【完整解答】解:∵点A1坐标为(1,0),∴OA1=1,过点A1作x轴的垂线交直线于点B1,可知B1点的坐标为(1,2),∵点A2与点O关于直线A1B1对称,∴OA1=A1A2=1,∴OA2=1+1=2,∴点A2的坐标为(2,0),B2的坐标为(2,4),∵点A3与点O关于直线A2B2对称.故点A3的坐标为(4,0),B3的坐标为(4,8),依此类推便可求出点A n的坐标为(2n﹣1,0),点B n的坐标为(2n﹣1,2n).故答案为:(2n﹣1,2n).【考察注意点】本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式.也考查了轴对称的性质.13.(2017秋•碑林区校级期末)如图,一次函数y=,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为(﹣,).【思路引导】利用勾股定理和一次函数图象上点的坐标特征,列出二次函数关系式,结合二次函数最值的求法解答.【完整解答】解:由已知条件得到直线l解析式为:y=﹣2,即y=,设P(a,),所以EF2=a2+()2=a2+a+.当EF取最小值时,a=﹣=﹣,此时,=,即P(﹣,),故答案是:(﹣,).【考察注意点】考查了一次函数图象与几何变换,解题时,利用了二次函数最值的求法,熟记二次函数顶点坐标公式是解题的关键.14.(2018春•丰南区期末)如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为y=x﹣.【思路引导】设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x 轴于点C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标,再利用待定系数法可求出该直线l的解析式,再根据平移规律即可得到直线l′的函数解析式.【完整解答】解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,∵正方形的边长为1,∴OB=3,∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,∴两边分别是4,∴三角形ABO面积是5,∴OB•AB=5,∴AB=,∴OC=,由此可知直线l经过(,3),设直线l为y=kx,则3=k,k=,∴直线l解析式为y=x,∴直线l向右平移3个单位长度后所得直线l′的函数解析式为y=(x﹣3),即y=x﹣,故答案为:y=x﹣.【考察注意点】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.15.(2019春•西湖区校级期中)在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=4x+1以每秒2个单位的速度向下平移,经过6秒该直线可将平行四边形OABC的面积平分.【思路引导】首先连接AC、BO,交于点D,当y=4x+1经过D点时,该直线可将▱OABC的面积平分,然后计算出过D且平行直线y=4x+1的直线解析式,从而可得直线y=4x+1要向下平移,进而可得答案.【完整解答】解:连接AC、BO,交于点D,当y=4x+1经过D点时,该直线可将▱OABC的面积平分;∵四边形AOCB是平行四边形,∴BD=OD,∵B(6,2),点C(4,0),∴D(3,1),设DE的解析式为y=kx+b,∵平行于y=4x+1,∴k=4,∵过D(3,1),∴DE的解析式为y=4x﹣11,∴直线y=4x+1要向下平移12个单位,∴时间为6秒,故答案为:6【考察注意点】此题主要考查了平行四边形的性质,以及一次函数,关键是正确掌握经过平行四边形对角线交点的直线平分平行四边形的面积.16.(2019•天津二模)将函数y=3x+1的图象平移,使它经过点(1,1),则平移后的函数表达式是y=3x﹣2.【思路引导】根据函数图象平移的性质得出k的值,设出相应的函数解析式,再把经过的点代入即可得出答案.【完整解答】解:新直线是由一次函数y=3x+1的图象平移得到的,∴新直线的k=3,可设新直线的解析式为:y=3x+b.∵经过点(1,1),则1×3+b=1,解得b=﹣2,∴平移后图象函数的解析式为y=3x﹣2;故答案为:y=3x﹣2.【考察注意点】此题考查了一次函数图形与几何变换,求直线平移后的解析式时要注意平移时k和b的值的变化.17.(2019春•常州期中)如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过6秒该直线可将平行四边形OABC分成面积相等的两部分.【思路引导】首先连接AC、BO,交于点D,当y=2x+1经过D点时,该直线可将▱OABC的面积平分,然后计算出过D且平行直线y=2x+1的直线解析式,从而可得直线y=2x+1要向下平移6个单位,进而可得答案.【完整解答】解:连接AC、BO,交于点D,当y=2x+1经过D点时,该直线可将▱OABC的面积平分;∵四边形AOCB是平行四边形,∴BD=OD,∵B(6,2),点C(4,0),∴D(3,1),设DE的解析式为y=kx+b,∵平行于y=2x+1,∴k=2,∵过D(3,1),∴DE的解析式为y=2x﹣5,∴直线y=2x+1要向下平移6个单位,∴时间为6秒,故答案为:6.【考察注意点】此题主要考查了平行四边形的性质,以及一次函数,关键是正确掌握经过平行四边形对角线交点的直线平分平行四边形的面积.三.解答题18.(2021春•古丈县期末)如图,直线l是一次函数y=kx+b的图象.(1)求出这个一次函数的解析式;(2)将该函数的图象向下平移5个单位,求出平移后一次函数的解析式,并写出平移后的图象与x轴的交点坐标.【思路引导】(1)利用待定系数法确定该一次函数的解析式;(2)根据平移规律“上加下减”写出平移后一次函数解析式,然后根据一次函数图象上点的坐标特征求直线与x轴的交点坐标.【完整解答】解:(1)∵一次函数y=kx+b的图象经过点(﹣2,0)和点(2,2),∴.解得k=,b=1.∴一次函数的解析式为:y=x+1;(2)∵一次函数y=x+1向下平移5个单位的解析式为y=x+1﹣5=x﹣4,即y=x﹣4.∴当y=0时,x=8,∴平移后的图象与x轴的交点坐标为(8,0).【考察注意点】本题考查的是一次函数的图象与几何变换,熟知函数图象平移的性质是解答此题的关键.19.(2021春•武汉月考)已知,在平面直角坐标系中,函数y1=2|x﹣a|,(1)若该函数经过点A(1,0),求该函数的解析式,并在图1中画出函数图象;(2)在(1)的条件下,将函数y2=x向上平移m个单位后与函数y1的图象相交于点B和C点,若BC=,求m;(3)如图2,设直线y3=6n与直线y4=2n分别与函数y1=2|x﹣a|相交于点E、F和M、N,点P为直线y3=6n上一点,连接PM、PN并延长交直线y5=kn于点G、H,若2EF=3GH,求k.【思路引导】(1)把点A坐标代入函数,求出a,得到函数y1的解析式,画出图象;(2)设出函数y2的解析式,得到B、C的坐标,根据BC=列出方程,求m的值;(3)由三角形相似得出MN和GH的比例,求出k的值.【完整解答】解:(1)把点A(1,0)代入y1=2|x﹣a|,得:2|1﹣a|=0,解得:a=1,∴y1=2|x﹣1|,图象如右所示.(2)由题意得y2=x+m(m>0),x≤1时,y1=﹣2x+2,x>1时,y1=2x﹣2,由,解得:,∴B(,),由,解得:,∴C(m+2,2m+2),∵BC=,∴(m+2﹣)2+(2m+2﹣)2=128,解得:m1=5,m2=﹣7(舍),∴m=5.(3)∵直线y3=6n与直线y4=2n间的距离为4n,直线y4=2n与x轴间的距离为2n,∴EF=3MN,∵2EF=3GH,∴MN:GH=1:2,∴MN是△PGH的中位线,∴y3=6n与y4=2n间的距离和y3=6n与y5=kn间的距离相等,∴k=﹣2.【考察注意点】本题考查了分段函数图象和函数图象变换,画图的关键顺序是“列表﹣描点﹣连线”,需要注意的是连线的时候要用平滑的曲线连接.20.(2021春•河北区期末)如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x 轴,点A的坐标为(5,4)经过点O、点C作直线l,将直线l沿y轴上下平移.(1)当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;(2)当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F,连接BE、BF,求△BEF的面积.【思路引导】(1)根据题意求得正方形各顶点的坐标,然后根据待定系数法求得直线l的解析式,直线平移,斜率不变,设平移后的直线方程为y=x+b;把点B和D的坐标代入进行解答即可;(2)根据正方形是中心对称图形,当直线l经过对角线的交点时,恰好平分正方形ABCD的面积,求得交点坐标,代入y=x+b,根据待定系数法即可求得直线l此时的解析式,然后求得E、F的坐标,根据待定系数法求得直线BE的解析式,得到与y轴的交点Q的坐标,根据三角形面积公式即可求得.【完整解答】解:(1)∵长为3的正方形ABCD中,点A的坐标为(5,4),∴B(2,4),C(2,1),D(5,1),设直线l的解析式为y=kx,把C(2,1)代入得,1=2k,解得k=,∴直线l为y=,设平移后的直线方程为y=x+b,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B C O y 2y 1xyP 一次函数与几何问题一、面积问题1、如图,在平面直角坐标系xOy 中,一次函数1223y x =-+与x 轴、y 轴分别相交于点A 和点B ,直线2 (0)y kx b k =+≠经过点C (1,0)且与线段AB 交于点P ,并把△ABO 分成两部分.(1)求△ABO 的面积;(2)若△ABO 被直线CP 分成的两部分的面积相等,求点P 的坐标及直线CP 的函数表达式。
2、如图,直线1l 过点A (0,4),点D (4,0),直线2l :121+=x y 与x 轴交于点C ,两直线1l ,2l 相交于点B 。
(1)、求直线1l 的解析式和点B 的坐标; (2)、求△ABC 的面积。
3、如图,直线OC 、BC 的函数关系式分别是y 1=x 和y 2=-2x+6,动点P (x ,0)在OB 上运动(0<x<3),过点P 作直线m 与x 轴垂直.(1)求点C 的坐标,并回答当x 取何值时y 1>y 2(2)设△COB 中位于直线m 左侧部分的面积为s ,求出s 与x 之间函数关系式. (3)当x 为何值时,直线m 平分△COB 的面积(10分)二、平移问题4、 正方形ABCD 的边长为4,将此正方形置于平面直角坐标系中,使AB 边落在X 轴的正半轴上,且A 点的坐标是(1,0)。
①直线y=43x-83经过点C ,且与x 轴交与点E ,求四边形AECD 的面积;②若直线l 经过点E 且将正方形ABCD 分成面积相等的两部分求直线l 的解析式, ③若直线1l 经过点F ⎪⎭⎫⎝⎛-0.23且与直线y=3x 平行,将②中直线l 沿着y 轴向上平移32个单位交x 轴于点M ,交直线1l 于点N ,求NMF ∆的面积.5、如图,在平面直角坐标系中,直线1l :x y 34=与直线2l :b kx y += 相交于点A ,点A 的横坐标为3,直线2l 交y 轴于点B ,且OB OA 21=。
(1)试求直线2l 函数表达式。
(6分)ABCODxy1l 2l(2)若将直线1l 沿着x 轴向左平移3个单位,交 y 轴于点C ,交直线2l 于点D ;试求 △BCD 的面积。
(4分)。
三、一次函数与特殊四边形6、如图,在平面直角坐标系中,点A 、B 分别在x 轴、y 轴上,线段OA 、OB 的长(0A<OB)是方程组⎩⎨⎧=+-=632y x yx 的解,点C 是直线x y 2=与直线AB 的交点,点D 在线段OC 上,OD=52(1)求点C 的坐标; (2)求直线AD 的解析式;(3)P 是直线AD 上的点,在平面内是否存在点Q ,使以0、A 、P 、Q 为顶点的四边形是菱形若存在,请直接写出点Q 的坐标;若不存在,请说明理由.7、.如图,在平面直角坐标系xOy 中,已知直线PA 是一次函数y=x+m (m>0)的图象,直线PB 是一次函数n n x y (3+-=>m )的图象,点P 是两直线的交点,点A 、B 、C 、Q 分别是两条直线与坐标轴的交点。
(1)用m 、n 分别表示点A 、B 、P 的坐标及∠PAB 的度数;(2)若四边形PQOB 的面积是211,且CQ:AO=1:2,试求点P 的坐标,并求出直线PA 与PB 的函数表达式;(3)在(2)的条件下,是否存在一点D ,使以A 、B 、P 、D 为顶点的四边形是平行四边形若存在,求出点D 的坐标;若不存在,请说明理由。
8、如图,在Rt △OAB 中,∠A=90°,∠ABO=30°,OB=833,边AB 的垂直平分线CD 分别与AB 、x 轴、y 轴交于点C 、G 、D .(1)求点G 的坐标;(2)求直线CD 的解析式;(3)在直线CD 上和平面内是否分别存在点Q 、P ,使得以O 、D 、P 、Q 为顶点的四边形是菱形若存在,求出点Q 得坐标;若不存在,请说明理由.四、一次函数与三角形9、如图,矩形OABC 在平面直角坐标系内(O 为坐标原点),点A 在x 轴上,点C 在y 轴上,点B 的坐标为(-2,32),点E 是BC 的中点,点H 在OA 上,且AH=21,过点H 且平行于y 轴的HG 与EB 交于点G,现将矩形折叠,使顶点C 落在HG 上 ,并与HG 上的点D 重合,折痕为EF,点F 为折痕与y 轴的交点.(1)求∠CEF 的度数和点D 的坐标;(3分) (2)求折痕EF 所在直线的函数表达式;(2分)(3)若点P 在直线EF 上,当△PFD 为等腰三角形时,试问满足条件的点P 有几个,请求出点P 的坐标,并写出解答过程.(5分)xAOB PQC xOAB1l 11yL 2y10、如图,直线y=-2x+2与x 轴、y 轴分别交于A 、B 两点,将△OAB 绕点O 逆时针方向旋转90°后得到△OCD .(1)填空:点C 的坐标是( , ),点D 的坐标是( ,); (2)设直线CD 与AB 交于点M ,求线段BM 的长;(3)在y 轴上是否存在点P ,使得△BMP 是等腰三角形若存在,请求出所有满足条件的点P 的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,函数y=2x+12的图象分别交x 轴,y 轴于A ,B 两点过点A 的直线交y 轴正半轴与点M ,且点M 为线段OB 的中点. (1)求直线AM 的函数解析式.(2)试在直线AM 上找一点P ,使得S △ABP =S △AOB ,请直接写出点P 的坐标.(3)若点H 为坐标平面内任意一点,在坐标平面内是否存在这样的点H ,使以A ,B ,M ,H 为顶点的四边形是等腰梯形若存在,请直接写出点H 的坐标;若不存在,请说明理由五、重叠面积问题12、已知如图,直线343y x =-+与x 轴相交于点A ,与直线3y x =相交于点P . ①求点P 的坐标.②请判断OPA ∆的形状并说明理由.③动点E 从原点O 出发,以每秒1个单位的速度沿着O →P →A 的路线向点A 匀速运动(E 不与点O 、A 重合),过点E 分别作EF ⊥x 轴于F ,EB ⊥y 轴于B .设运动t 秒时,矩形EBOF 与△OPA 重叠部分的面积为S .求: S 与t 之间的函数关系式.13、如图,已知直线1l :2+-=x y 与直线2l :82+=x y 相交于点F ,1l 、2l 分别交x 轴于点E 、G ,矩形ABCD 顶点C 、D 分别在直线1l 、2l ,顶点A 、B 都在x 轴上,且点B 与点G 重合。
(1)、求点F 的坐标和∠GEF 的度数;(2)、求矩形ABCD 的边DC 与BC 的长; (3)、若矩形ABCD 从原地出发,沿x 轴正方向以每秒1个单位长度的速度平移,设移动时间为t ()60≤≤t 秒,矩形ABCD 与△GEF 重叠部分的面积为s ,求s 关于t 的函数关系式,并写出相应的t 的取值范围。
xy FCE B GAH O DxyF CE B GAHO DFyOAxPE B CD Fy 1l2l14、如图,过A (8,0)、B (0,83)两点的直线与直线x y 3=交于点C .平行于y 轴的直线l 从原点O出发,以每秒1个单位长度的速度沿x 轴向右平移,到C 点时停止;l 分别交线段BC 、OC 于点D 、E ,以DE 为边向左侧作等边△DEF ,设△DEF 与△BCO 重叠部分的面积为S (平方单位),直线l 的运动时间为t (秒).(1)直接写出C 点坐标和t 的取值范围; (2)求S 与t 的函数关系式;(3)设直线l 与x 轴交于点P ,是否存在这样的点P ,使得以P 、O 、F 为顶点的三角形为等腰三角形,若存在,请直接写出点P 的坐标;若不存在,请说明理由.15.如图,直线4+-=x y 与两坐标轴分别相交于点,点M 是线段AB 上任意一点(两点除外),过M 分别作MC ⊥OA 于点C ,MD ⊥OB 于D .(1)当点M 在AB 上运动时,你认为四边形OCMD 的周长是否发生变化并说明理由;(2)当点M 运动到什么位置时,四边形OCMD 的面积有最大值最大值是多少(3)当四边形OCMD 为正方形时,将四边形OCMD 沿着x 轴的正方向移动,设平移的距离为)40<<a a (,正方形OCMD 与△AOB 重叠部分的面积为S .试求S 与a 的函数关系式并画出该函数的图象.B x y MC DO A 图(1)B x yOA 图(2)B x yO A图(3)六、关系式问题16、如图,已知直线的解析式为,直线与x轴、y轴分别相交于A、B 两点,直线经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q 在直线从点C向点B移动.点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t 秒().(1)求直线的解析式.(2)设△PCQ的面积为S,请求出S关于t的函数关系式.17、已知直线y=x+4与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.(1)试确定直线BC的解析式.(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形若存在,请直接写出N点的坐标;若不存在,请说明理由.18、已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C.(1)求直线l的解析式;(2)若点P(x,0)在线段OA上运动,过点P作l的平行线交直线y=x于D,求△PCD的面积S与x的函数关系式;S有最大值吗若有,求出当S最大时x的值;(3)若点P(x,0)在x轴上运动,是否存在点P,使得△PCA成为等腰三角形若存在,请写出点P的坐标;若不存在,请说明理由.。
