梅涅劳斯定理
梅涅劳斯定理

梅涅劳斯定理如果一条直线与ABC ∆的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点, 那么1=⋅⋅EACEDC BD FB AF .等价叙述:ABC ∆的三边AB 、BC 、CA 或其延长线上有三点F 、D 、E ,则F 、D、E 三点共线的充要条件是1=⋅⋅EACEDC BD FB AF 。
三点所在直线称为三角形的梅氏线。
证法1:(平行线分线段成比例)证:如图,过A 作BC AG //交EF 延长线于G ,∵BC AG //,∴BD AG FB AF =,AGCDEA CE =, 又CDBD CD BD =则1=⋅⋅=⋅⋅CD BD AG CD BD AG CD BD EA CE FB AF ∴1=⋅⋅EACEDC BD FB AF 梅涅劳斯定理的逆定理也成立,即如果有三点F 、D 、E 分别在ABC ∆的三边AB 、BC 、CA 或其延长线上,且满足1=⋅⋅EACEDC BD FB AF ,那么F 、D 、E 三点共线。
BG利用梅涅劳斯定理的逆定理可判定三点共线。
梅涅劳斯定理的应用定理1:若ABC ∆的A ∠的外角平分线交边BC 延长线于P ,B ∠的平分线交边AC 于Q ,C ∠的平分线交边AB 于R ,则P 、Q 、R 三点共线。
证:由三角形内、外角平分线定理知,CA BA PC BP =,AB BC QA CQ =,CB CARB AR =, 则1=⋅⋅=⋅⋅ABBCCA BA CB CA QA CQ PC BP RB AR , 故P 、Q 、R 三点共线。
例题赏析:已知:过ABC ∆顶点C 的直线,与边AB 及中线AD 分别交于点F 和E .求证:FBAFED AE 2=. 证明:直线CEF 截ABD ∆, 由梅涅劳斯定理,得:1=⋅⋅EADE CD BC FB AF又CD BC 2=,∴21=⋅EA DE FB AF , 则FBAFED AE 2=BDBC。
上犹中学高中奥数教材---梅涅劳斯定理

平面几何的几个重要的定理一、梅涅劳斯定理:1=⋅⋅=⋅⋅BAA C CBC B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度,则:到直线、、分别是、、证:设注:此定理常运用求证三角形相似的过程中的线段成比例的条件;。
的交点,证明:与是的中点,是上,在点的平分线,是是斜边上的高,中,:若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠∆11PC BP R Q PAB CA BC ABC ABC l 1=⋅⋅RBARQA CQ ,则、、的延长线分别交于或它们、、的三边的顶点,并且与不经过:若直线定理∆∆CE//BF CKE FKB KEBKKC KF BEBK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FCKFEK AE DA CD F E D ACK EPCK EP BC EBC CE BH 90HCB ACE HCB HBC ACEHBC ACKEBC BH B EBC ∴≅∴=====⋅⋅=∴⊥︒=∠+∠=∠+∠∠=∠∠=∠∠∆∆∆∆∆=依分比定理有:=即:=于是依梅涅劳斯定理有:、、和三点对于,则:上的高作为等腰三角形即:则:的平分线中,作在证:111111111111D B D A :C B C A BD AD :BC AC D C B A DC B A K 1=,试证:、、、和、、、线分别交这四条直线于引四条直线,另两条直】从点【练习注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘;共线;、、证明点引的垂线的垂足,、、向是从点、、的外接圆上;位于点例111111C B A AB CA BC P C B A ABC P .2∆三点共线;、、综上可得:也重合与的延长线上时,同在与类似地可证得当矛盾=这与于是可得即这时设必定重合,不然的话,与线段上,则同在与若的延长线上;线段上,或者同在或者同在与因此,或边上的点的个数也为三点中,位于、、由于在同一直线上的=,则:又得:,于是由定理交于与直线证:设直线R Q P R R AB R R BR AR BR AR BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RBAR B R AR 1RB AR QA CQ 1BR AR QA CQ 1R AB PQ ''''''''''''''''''><-<->=⋅⋅=⋅⋅∆PC BP PC BP 三点共线;、、求证:,,这时若或边上的点的个数为三点中,位于、、三点,并且上或它们的延长线上的、、的三边分别是、、:设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RBARQA CQ =⋅⋅∆∆三点共线;、、依梅涅劳斯定理可知,=可得且将上面三条式子相乘,证:易得:111111111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBA cos PB PABcos AP BC AC PAC cos AP PCAcos CP AB CB ,PCBcos CP PBCcos BP CA BA ⋅⋅︒=∠+∠∠=∠∠=∠∠⋅∠⋅-=∠⋅∠⋅-=∠⋅∠⋅-=直线上;在同一条、、的交点与,与,与,则、、上的切点分别为、、的内切圆在三边】设不等腰【练习Z Y X AB DE CA FD BC EF F E D AB CA BC ABC 2∆三点共线;、、,试证:的交点是与线,直的交点是与,直线的交点为和,直线相交于,,】已知直线【练习222211*********C B A B C A AC A C B BC C B A AB O CC BB AA 311111111111111111111111111111111111111D B D A :C B C A BD AD :BC AC 1C BD B D A C A BD BC AC AD 1LD D B K B BK BD LD 1BKKB C B LC LC BC 1LC C A K A AK AC LC 1AK KA D A LD LD AD BLB AL A L D A AD D A //AD 1==⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅即:得:将上面四条式子相乘可可得:和别用于,则把梅涅劳斯定理分相交与点与若,结论显然成立;证:若的证明练习∆∆三点共线、、可得的边上,由定理都不在、、又得:将上面三条式子相乘可==同理可得:=代人上式可得:又可得:所截,由定理被直线证:的证明练习Z Y X 2ABC Z Y X 1ZBAZYA CY XC BX BDEAZB AZ AF DC YA CY CEFBXC BX AF AE 1FBAFEA CE XC BX 1XFE ABC 2∆∆ =⋅⋅==⋅⋅共线、、,证明:、、的交点依次为和,和,和,和,记直线、、,在另一条上取点、、】在一条直线上取点【练习N M L N M L BC EF AF CD AF CD ED AB D F B A C E 4共线由梅涅劳斯定理可知可得:将上面的三条式子相乘应用梅涅劳斯定理有:,和,和,和们边上的点:对所得的三角形和在它的交点,和,和,和分别是直线、、证:设的证明练习222222222221111221111221111211211211111111222C ,B ,A 1BA CA CB AB AC BC 1CB AB OC CC AA OA 1BA CA OB BB CC OC 1AC BC BB OB OA AA )B ,C A (OAC ),A ,C B (OBC ),C ,B A (OAB B A AB C A AC C B BC C B A 3=⋅⋅=⋅⋅=⋅⋅=⋅⋅共线点得:将上面五条式子相乘可,则有点涅劳斯定理于五组三元,应用梅,对、、的交点分别为和,和,和证:记直线的证明练习N ,M ,L ,1VNUNUM WM WL VL 1UFVFWD UD VB WB 1UE VE WC UC VA WA 1WB VBUC WC VN UN 1YM WM VF UF WA VA 1UD WD WL VL VE UE )F ,D ,B (),E ,C ,A (),N ,C ,B (),F ,M ,A (),E ,D ,L (UVW W V U CD AB AB EF CD EF 4∴=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅∆。
平面几何的几个重要的定理--梅涅劳斯定理
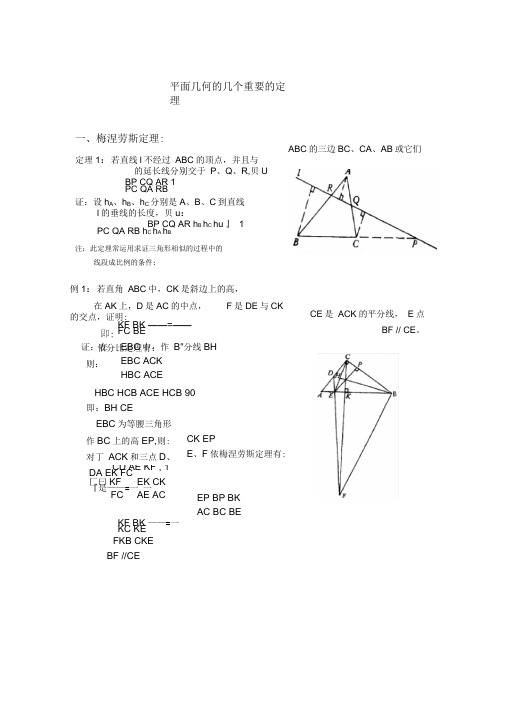
平面几何的几个重要的定理一、梅涅劳斯定理:定理1:若直线l 不经过 ABC 的顶点,并且与的延长线分别交于 P 、Q 、R,贝U BP CQ AR 1 PC QA RB证:设h A 、h B 、h C 分别是A 、B 、C 到直线l 的垂线的长度,贝u :BP CQ AR h B h C hu 』 1PC QA RB h C h A h B注:此定理常运用求证三角形相似的过程中的线段成比例的条件;例1:若直角 ABC 中,CK 是斜边上的高, 在AK 上,D 是AC 的中点, F 是DE 与CK的交点,证明:KF BK ——=—— FC BE KF BK ——=一 KC KE FKB CKE BF //CECE 是 ACK 的平分线, E 点BF // CE 。
证:在 则:EBC 中,作 B"分线BH EBC ACK HBC ACEHBC HCB ACE HCB 90即:BH CEEBC 为等腰三角形作BC 上的高EP,则:对丁 ACK 和三点D 、 CK EPE 、F 依梅涅劳斯定理有:CD AE KF , 1 DA EK FC匚曰KF EK CK 『是——=一 一FC AE ACEP BP BK AC BC BE依分比定理有: ABC 的三边BC 、CA 、AB 或它们【练习1从点K 引四条直线,另两条直 -一 一 、…AC和 A 1、B 1、C 1、D 1,试证: ------- 1 1 1BC线分别交这四条直线丁 A 、B 、C 、DAD BD定理2:设P 、Q 、R 分别是 ABC 的三边 BC 、CA 、AB 上或它们的延长线上的 P 、Q 、R 三点中,位于 ABC 边上的点的个数为 0或2,这时若 既 PC 三点,并且 CQ AR QA RB 1, 求证:P 、Q 、R 三点共线; 证:设直线PQ 与直线AB 交丁 R ', 丁是由定理 BP CQ AR _ __ ' PC QA R B乂 BP CQ AR PC QA RB 由丁在同一直线上的 _ ' ____ AR AR1,则:^―=—— R B RB P 、Q 、R '三点中,位丁 ABC 边上的点的个数也为 0或2,因此R 与R '或者同在AB 线段上,或者同在 AB 的延长线上; 若R 与R '同在AB 线段上,则R 与R '必定重合,不然的话, 设AR AR ', AR AR BR BR 这时AB AR AB AR ',即BR BR ',丁是可得 _ ____ ' 这与AR =竺 矛盾 BR BR 类似地可证得当 R 与R '同在AB 的延长线上时,综上可得:P 、Q 、R 三点共线; 注:此定理常用于证明三点共线的问题,且常需要多次使用 R 与R '也重合再相乘;例2点P 位丁 ABC 的外接圆上;A 1、B 1、C 1是从点P 向BC 、CA 、AB 引的垂线的垂足, 证明点A 1、B 1、 BA 1BP cos PBC CA 1 CP cos PCB CB 1 CP cos PCA AB 1 AP cos PAC AC 1AP cos PABBC 1 PB cos PBAC i 共线; 证:易得: 将上面三条式子相乘, 且 PAC PBC , PAB PCB , 十曰 BA 1 CB 1 AC 1可得 一111= 1 ,CA 1 AB 1 BC 1依梅涅劳斯定理可知 A 1、B 1、C 1三点共线;PCA PBA 180A 1C 1 A 1D 1B 1C ; :BD【练习2设不等腰 ABC 的内切圆在三边 BC 、CA 、AB 上的切点分别为 D 、E 、F,则EF 与BC , FD 与CA , DE与AB 的交点 X 、Y 、Z 在同一条 直线上;【练习&已知直线 AA i, BB i, CC i 相交于O,直线AB 和A 1B 1的交点为C 2,直线 BC 与B 1C 1的交点是 A 2,直 线AC 与A i C i 的交点是B 2,试证:A 2、B 2、C 2三点共线;【练习M 在一条直线上取点 E 、C 、A,在另一条上取点 B 、F 、D,记直线AB 和ED , CD 和AF ,CD 和AF , EF 和BC 的交点依次为 L 、M 、N,证明:L 、M 、N 共线练习i 的证明练习2的证明乂 AE AF 代人上式可得:BXXC FB =—— CE CY DC AZ EA同理口」彳寸: — —YA AFZB BD将上面三条式子相乘可 得:乳CY J i XC YA ZB 乂 X 、Y 、Z 都不在 ABC 的边上,由定理 2可得X 、Y 、 证: ABC 被直线XFE 所截,由定理 Z 三点共线 证:若AD // A i D^,结论显然成立;若AD 与A i D i 相交与点 AD LD LD BD LD 〔 A i K A i D i AK BK BQ B i K LDi L,则把梅涅劳斯定理分 LC AK A 。
《梅涅劳斯定理》课件

根据定理的特点,选择合适的证 明方法,如代数推导、几何证明 或构造反例等。
证明的步骤和过程
步骤详细
按照逻辑顺序,详细列出每一步的证 明过程,确保每一步都有明确的解释 和推导。
过程完整
确保证明过程完整,没有遗漏任何关 键的推导或结论,保证定理的正确性 和严密性。
证明的难点和关键点
难点解析
指出证明中的难点,并解释难点产生的原因和解决方法。
求解几何最值问题
利用梅涅劳斯定理,可以求解几何中 最值问题,例如求三角形中的最大或 最小值等。
在日常生活中的应用
建筑设计
建筑设计中经常需要使用几何学 知识,梅涅劳斯定理可以帮助设 计师更好地理解建筑物的结构, 从而设计出更加稳定和美观的建
筑。
机械制造
在机械制造中,零件的尺寸和形 状需要精确控制,梅涅劳斯定理 可以帮助工程师更好地理解零件 的几何关系,从而制造出更加精
梅涅劳斯定理在几何学中有着广泛的应用,它可以帮助我 们解决一些与三角形相关的问题,例如求三角形的边长、 角度等。
定理的意义不仅在于其应用价值,更在于它对于三角形性 质和规律的深入揭示。通过研究梅涅劳斯定理,我们可以 更深入地理解三角形的本质和特性。
02
梅涅劳斯定理的证明
证明的思路和方法
思路清晰
首先明确梅涅劳斯定理的内容和 意义,然后根据定理的表述,确 定证明的总体方向和策略。
关键点把握
明确指出证明中的关键点,并解释这些关键点在证明中的重要性和作用。
03
梅涅劳斯定理的应用
在几何学中的应用
证明三角形相似
梅涅劳斯定理可以用于证明两个 三角形相似,通过比较三角形的 边长和角度,可以推导出它们相
似的结论。
奥数定理

在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。于是AL、BM、CN三线交于一点的充要条件是λμν=1。(注意与梅涅劳斯定理相区分,那里是λμν=-1)
[编辑本段]塞瓦定理推论
1.设E是△ABD内任意一点,AE、BE、DE分别交对边于C、G、F,则(BD/BC)*(CE/AE)*(GA/DG)=1
因为(BC/CD)*(DG/GA)*(AF/FB)=1,(塞瓦定理)所以 (BD/CD)*(CE/AE)*(AF/FB)=K(K为未知参数)且(BD/BC)*(CE/AE)*(GA/DG)=K(K为未知参数)又由梅涅劳斯定理得:(BD/CD)*(CE/AE)*(AF/FB)=1
所以(BD/BC)*(CE/AE)*(GA/DG)=1
3:海伦公式
原理简介 海伦公式又译作希伦公式、海龙公式、希罗公式、海伦-秦九韶公式,传说是古代的叙拉古国王 希伦
(Heron,也称海龙)二世发现的公式,利用三角形的三条边长来求取三角形面积。但根据Morris Kline在1908年出版的著作考证,这条公式其实是阿基米德所发现,以托希伦二世的名发表(未查证)。 我国宋代的数学家秦九韶也提出了“三斜求积术”,它与海伦公式基本一样。
———————————————————————————————————————rica"(《度量论》)手抄本中用s作为半周长,所以
S=√[p(p-a)(p-b)(p-c)] 和S=√[s(s-a)(s-b)(s-c)]两种写法都是可以的,但多用p作为半周长。
证法简介
(Ⅰ)本题可利用梅涅劳斯定理证明:
∵△ADC被直线BOE所截,
梅涅劳斯(Menelaus)定理

梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 证明一:过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二:过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/E A)=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
梅涅劳斯(Menelaus)定理证明三:过ABC三点向三边引垂线AA'BB'CC',所以AD:DB=AA':BB',BE:EC=BB':CC',CF:FA=CC':AA'所以(AF/FB)×(BD/DC)×(CE/EA)=1证明四:连接BF。
(AD:DB)·(BE:EC)·(CF:FA)=(S△ADF:S△BDF)·(S△BEF:S△CEF)·(S△BCF:S△BAF)=(S△ADF:S△BDF)·(S△BDF:S△CDF)·(S△CDF:S△ADF)=1此外,用定比分点定义该定理可使其容易理解和记忆:在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
梅涅劳斯定理怎么记

梅涅劳斯定理怎么记
梅氏定理记忆:
记忆口诀:顶点到交点,交点回顶点。
1、了解这个定理的内容。
2、能熟练地证明定理。
3、在能证明定理内容的基础上,进行理解的记忆。
梅涅劳斯定理
梅涅劳斯(Menelaus)定理是由古希腊数学家梅涅劳斯首先证明的。
他指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么AF/FB×BD/DC×CE/EA=1。
证明:
过点A作AG‖BC交DF的延长线于G
AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG
三式相乘得:
AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1
它的逆定理也成立:若有三点F、D、E分别在的边AB、BC、CA或其延长
线上,且满足AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
梅涅劳斯定理公式证明

梅涅劳斯定理公式证明梅涅劳斯定理是一个在平面几何中非常有趣且实用的定理。
咱们先来说说这个定理到底是啥。
梅涅劳斯定理指出:如果一条直线与△ABC 的三边 AB、BC、CA或其延长线交于 F、D、E 点,那么 (AF/FB)×(BD/DC)×(CE/EA)=1 。
那这个定理咋证明呢?咱们一步步来。
咱们先画个三角形 ABC ,然后随便画一条直线,和三角形的三条边或者延长线相交于 F 、 D 、 E 这三个点。
假设咱们从点 A 作一条和 BC 平行的直线,交 FE 的延长线于点 G 。
因为 AG // BC ,所以就有 AF/FB = AG/BD , CE/EA = DC/AG 。
把这两个式子乘起来,就得到了 AF/FB × CE/EA = AG/BD ×DC/AG 。
两边一约分,就得到了 AF/FB × CE/EA = DC/BD 。
再把 BD/DC 乘到左边去,那不就得到了(AF/FB)×(BD/DC)×(CE/EA)=1 嘛,这就证明出来啦!我记得有一次给学生讲这个定理的时候,有个特别调皮的小家伙,怎么都理解不了。
我就又重新给他画了好几遍图,一步一步带着他推导。
这小家伙一开始还满脸的不耐烦,觉得这定理太难太复杂。
可当最后推导出来,他那眼睛一下子亮了,兴奋地说:“老师,原来这么简单啊!” 看到他那恍然大悟的样子,我心里可美了,觉得自己这功夫没白费。
梅涅劳斯定理在解决很多几何问题的时候,那可真是一把好手。
比如说,在判断三点是否共线的时候,就特别有用。
咱们就拿一个具体的题目来说。
有一个三角形 ABC , D 、 E 、 F 分别是 AB 、 BC 、 CA 上的点,已知 AF/FB = 1/2 , BD/DC = 1/3 ,CE/EA = 1/4 ,咱们来判断 D 、 E 、 F 这三个点是不是共线。
根据梅涅劳斯定理,咱们算一下 (AF/FB)×(BD/DC)×(CE/EA) =(1/2)×(1/3)×(1/4) = 1/24 ,这可不等于 1 呀,所以 D 、 E 、 F 这三个点不共线。
角元梅涅劳斯定理

角元梅涅劳斯定理
角元梅涅劳斯定理,也叫做“梅涅劳斯定理”,是一个多项式系统的几何学定理,由俄国数学家谢尔盖·角元在1850年提出。
它声明如下:如果y = f(x1,x2)是两个变量的多项式函数,那么有:
f(x1,x2)的二阶偏导数的和等于X1的二阶偏导数乘以X2的二阶偏导数,即
Ñ_Ñ_f(x1,x2)= Ñ2f/DX1DX2 + Ñ2f/DX2DX1 = Ñ2f/DX1DX2,其中Ñ是偏导符号,表示偏导,D表示微分。
角元梅涅劳斯定理提供了一种有效的方法来证明多项式系统的性质,如吗塞尔定理、Rouché-Frobenius定理和Rabinowitz定理的特殊情况。
它也可以用来证明最大化或最小化一个多项式函数的必要条件,例如边界上的点处的二阶导数必须呈现特定的性质。
角元梅涅劳斯定理也可以应用于研究多元函数的性质。
例如,可以通过使用该定理来证明Morse定理,即当函数f(x1,x2)在极值点处满足下面式子时,极值点必须是拐点:
Ñ_Ñ_f(x1,x2)= 0 , (dx1)^2*(dx2)^2f
角元梅涅劳斯定理也可以用来确定某种多项式函数在极值点处的局部极值,即当函数f(x1,x2)在极值点处满足下面三个条件时,极值点必定是局部最小值:
(1) Ñ_Ñ_f(x1,x2)> 0
(2) Ñ2f/DX1DX2 > 0
(3) Δf(x1,x2)> 0
其中Δ是二阶偏导向量的张量。
角元梅涅劳斯定理是广义梅涅劳斯定理的一种特殊情况,它可以用来验证广义梅涅劳斯定理是否成立。
梅涅劳斯定理证明

梅涅劳斯(Menelaus)定理的证明1. 梅涅劳斯定理梅涅劳斯(Menelaus )定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的,是平面几何学以及射影几何学中的一项基本定理。
它指出:任何一条直线截三角形的各边,都使得三条不相邻线段之积等于另外三条线段之积。
直线与三角形的位置关系有两种情况:1) 如图(1),三角形ABC 与直线DEF 交点其中两点在边上,另一交点在边的延长线上,则有:2) 如图(2),三角形ABC 与直线DEF 的三个交点均在边的延长线上时,仍有:AF FB ×BD DC ×CE EA =1图(1) AF FB ×BD DC ×CE EA=1图(2)AF FB =AI BJ BD DC =JD DH ,CE EA =CH AI ∴AF FB ×BD DC ×CE EA =AI BJ ×JD DH ×CH AI =CH BJ ×JD DH=12. 证明方法分析命题:设直线l 分别与△ABC 的三边所在直线相交于点D 、E 、F ,则有分析:需证明比例式,一般采用的方法为相似、正弦或余弦定理、共边共角定理等。
添加辅助线的方法多为创造平行线。
在得到比例 式后相乘得所求式子。
3. 证明方法i. 证法1(作平行线,利用平行线分线段成比例)如图(3),过点C 作直线DF 平行线,交AB 与点G 。
由平行线分线段成比例得:ii. 证法2(作高创造平行,利用比例线段)如图(4),过点ABC 作直线DF 垂线,垂足为点I 、J 、H 。
∵ BJ ⊥DF ,AI ⊥DF∴ BJ ∥AI∴ ∠3=∠4又∵∠1=∠2∴ △AFI ∼△BFJ得同理 BD DC =FB GF ,CE EA =GF AF ∴AF FB ×BD DC ×CE EA =AF FB ×FB GF ×GF AF =1图(3) 图(4) AF FB ×BD DC ×CE EA =1∴AFFB×BDDC×CEEA=ADEBDE×BDECDE×CDEADE=1AEFBFD=AF×EFFB×DF,BFDCDE=BD×DFDC×DE,CDEAEF=DE×CEEA×EF1=AF×EF×BD×DF×DE×CEFB×DF×DC×DE×EA×EF=AFFB×BDDC×CEEAAFFB×BDDC×CEEA=AF×BD×CEEA×FB×DC=Sin∠AEF×Sin∠BFD×Sin∠EDCSin∠AFE×Sin∠BDF×Sin∠ECDAFFB×BDDC×CEEA=1iii.证法3(利用共边定理)如图(5),联结BE、AD由共边定理得:iv.证法4(利用共角定理)如图(6),由共角定理得:三式相乘,得:v.证法5(利用正弦定理)同图(6),在△AEF、△BDF、△CDE中,由正弦定理得:∵∠AEF=∠ECD,∠EDC=∠FDB∠BFD+∠AFE=180°∴Sin∠AEF=Sin∠ECD,Sin∠EDC=Sin∠FDB且Sin∠BFD=Sin∠AFE∴上式右端分式化为1即图(5)图(6)图(6)。
梅涅劳斯定理

梅涅劳斯(Menelaus )定理
如果一条直线与△ABC 的三边BC 、CA 、AB 或其延长线交于D 、E 、F 点,证明:1BD CE AF DC EA FB
∙∙=。
(逆定理也成立)
例1 如图,过三角形ABC 的三个顶点A 、B 、C 做它的外接圆的切线,分别和BC 、CA 、BA 的延长线交于P 、Q 、R ,求证:P 、Q 、R 三点共线。
例2 设四边形ABCD 外切于一圆,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的切点,若直线HE 与GF 相交于M 点,则直线BD 必通过点M 。
例3 圆O 1与圆O 2和三角形的三边所在的三条直线都相切,E 、F 、G 、H 为切点,直线EG 与FH 交于点P ,求证:PA ⊥BC
例4以三角形ABC 的底边BC 为直径做半圆,分别于边AB 、AC 交于D 、E ,分别过点D ,E 做BC 的垂线,垂足分别为F 、G ,线段DG 和EF 交于点M ,求证:AM ⊥BC 。
练习:
1、证明三角形三条高线交于一点
2、P 是三角形ABC 内的一点,直线AC 、BP 交于Q ,AB ,CP 交于R 。
已知AR=RB=CP ,CQ=PQ,Q 求BRC ∠.
3、在ABC 中,∠C =90°,AD 和BE 是它的两条内角平分线,设L 、M 、N 分别为AD 、AB 、BE 的中点,X =LM ∩BE ,Y =MN ∩AD ,Z =NL ∩DE .求证:X 、Y 、Z 三点共线.(2000年江苏省数学冬令营)
A C
B Y X Z M N
L E D F G H。
梅涅劳斯定理

梅涅劳斯定理:1l ABC ABC BC CA AB BP P Q R 1PC CQ ARQA RB∆∆⋅⋅=定理:若直线不经过的顶点,并且与的三边、、或它们的延长线分别交于、、,则 1A B C C B AC A Bh h h A B C l h h h BP CQ AR PC QA RB h h h ⋅⋅=⋅⋅=证:设、、分别是、、到直线的垂线的长度,则:注:此定理常运用求证三角形相似的过程中的线段成比例的条件;1//ABC CK CE ACK E AK D AC F DE CK BF CE ∆∠例:若直角中,是斜边上的高,是的平分线,点在上,是的中点,是与的交点,证明:。
,901EBC B BH EBC ACK HBC ACE HBC HCB ACE HCB BH CE EBC BC EP CK EPCD AE KF ACK D E F DA EK FCKF EK CK EP BP BK KF BK FC AE AC AC BC BE FC BEKF BKFKB KC KE∆∠∠=∠∠=∠∠+∠=∠+∠=︒⊥∴∆=∆⋅⋅=====∴∆≅ 证:在中,作的平分线则:即:为等腰三角形作上的高,则:对于和三点、、依梅涅劳斯定理有:于是=即:=依分比定理有://CKE BF CE∆∴ 2P Q R ABC BC CA AB P Q R ABC BP 021PC P Q R CQ ARQA RB ∆∆⋅⋅=定理:设、、分别是的三边、、上或它们的延长线上的三点,并且、、三点中,位于边上的点的个数为或,这时若,求证:、、三点共线;''''''''''1BP BP 11PC PC 02,PQ AB R CQ AR CQ AR AR AR QA R B QA RB R B RBP Q R ABC R R AB AB R R AB R R AR AR ⋅⋅=⋅⋅=∆> 证:设直线与直线交于,于是由定理得:又,则:=由于在同一直线上的、、三点中,位于边上的点的个数也为或,因此与或者同在线段上,或者同在的延长线上;若与同在线段上,则与必定重合,不然的话,设'''''',,AR AR AR AR AB AR AB AR BR BR BR BR BR BR -<-<>这时即于是可得这与=矛盾''R R AB R R P Q R 类似地可证得当与同在的延长线上时,与也重合综上可得:、、三点共线;注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘;1111112.P ABC A B C P BC CA AB A B C ∆例点位于的外接圆上;、、是从点向、、引的垂线的垂足,证明点、、共线;111111111111111cos ,cos cos cos ,cos cos ,,1BA BP PBCCA CP PCB CB AC CP PCA AP PABAB AP PAC BC PB PBAPAC PBC PAB PCB PCA PBA BA CB AC A B C CA AB BC ⋅∠=-⋅∠⋅∠⋅∠=-=-⋅∠⋅∠∠=∠∠=∠∠+∠=⋅⋅ 证:易得:将上面三条式子相乘,且可得,依梅涅劳斯定理可知、、三点共线;1111111111111::K A B C DACA D AC AD ABCD BC BD B C B D =【练习】从点引四条直线,另两条直线分别交这四条直线于、、、和、、、,试证:2ABC BC CA AB DEF EF BC FD CA DE AB X Y Z ∆【练习】设不等腰的内切圆在三边、、上的切点分别为、、,则与,与,与的交点、、在同一条直线上;1111121121122223AA BB CC O AB A B C BC B C A AC A C B A B C 【练习】已知直线,,相交于,直线和的交点为,直线与的交点是,直线与的交点是,试证:、、三点共线;4E C A B F D AB ED CD AF CD AF EF BC L M N L M N 【练习】在一条直线上取点、、,在另一条上取点、、,记直线和,和,和,和的交点依次为、、,证明:、、共线11111111111111111111111111111111//11111:AD A D AD A D L A AL B BL LD A K A C LC B KAD LC AK BC LD A D AK AC A K LC LC B C BK B D LD BK BD B K LD A C B D AD BC AC BD A D B C A AC AD BC BD ∆∆⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅⋅==练习的证明证:若,结论显然成立;若与相交与点,则把梅涅劳斯定理分别用于和可得:将上面四条式子相乘可得:即:1111111:C AD B C B D21112BX CE AFABC XFE XC EA FBBX FBAE AF XC CECY DC AZ EAYA AF ZB BDBX CY AZXC YA ZBX Y Z ABC X Y Z ∆⋅⋅==⋅⋅=∆ 练习的证明证:被直线所截,由定理可得:又代人上式可得:=同理可得:==将上面三条式子相乘可得:又、、都不在的边上,由定理可得、、三点共线2221111111121121121121121121121121123(,),(,),(,)111A B C BC B C AC A C AB A B OAB A B C OBC B C A OAC A C B AA OB BC OC BB CA OA CC AB OA BB AC CC OB BA AA OC CB BC ⋅⋅=⋅⋅=⋅⋅=练习的证明证:设、、分别是直线和,和,和的交点,对所得的三角形和在它们边上的点:和,和,和,应用梅涅劳斯定理有:将上面的三条式子相乘可得:2222222221,,AB CA AC CB BA A B C ⋅⋅=由梅涅劳斯定理可知共线4(,,),(,,),(,,),(,,),(,,)11111EF CD EF AB AB CD U V W UVW L D E A M F B C N A C E B D F UE VL WD VA UF WM UN WC VBVE WL UD WA VF YM VN UC WB WA UC VE WB UD VFVA WC UE VB WD UFVL W WL ∆⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅练习的证明证:记直线和,和,和的交点分别为、、,对,应用梅涅劳斯定理于五组三元点,则有将上面五条式子相乘可得:1,,,M UNL M N UM VN⋅=∴点共线。
menelaus 定理

梅涅劳斯(Menelaus)定理,也被称为梅氏定理,最早出现在古希腊数学家梅涅劳斯的著作《球面学》(Sphaerica)中。
该定理的内容是:一条截线在三角形各边上确定出的六条线段,三条不连续线段的乘积等于剩下三条线段的乘积。
这个定理可以用初等几何或通过应用简单的三角比关系来证明。
梅涅劳斯定理不仅适用于平面三角形,还可以扩展到球面三角形。
此外,梅涅劳斯定理还有一些其他证明方法,例如通过作垂线、连接线段、应用定比分点定义等。
在实际应用中,这个定理可以用于寻找据点发射炮弹等场合。
角元梅涅劳斯定理

角元梅涅劳斯定理
角元梅涅劳斯定理(英语:Angle–Measurement Maximization of Theorem,简称AMM)是一项重要的数学定理,它对不变凸多面体有一个重要的应用。
该定理告诉我们某凸多面体的全部顶点角之和必须大于或等于2π(π=3.14159……)。
如果它等于2π,则称该多面体是完整的。
角元梅涅劳斯定理也称为三角测量最大化定理,它由19世纪俄国数学家角元·梅涅劳斯在1860年左右提出。
它与欧几里得的五边形定理和高斯的交叉定理有着密不可分的关系。
角元梅涅劳斯定理的两个主要版本是:
(1)任意凸n边形任意形状的全部n顶点角的总和必须大于或等于
2π。
(2)任意凹n边形任意形状的全部n顶点角的总和必须小于或等于
2π。
角元梅涅劳斯定理的一个重要推广,即角元梅涅劳斯-勒贝格定理,它说明了所有多面体的总角度一定大于或等于n-2π,其中n为多面体拥有的顶点数,这个定理是如此重要,以至于被列入 W.T.Tutte 所著《Graph Theory》一书中。
数学史上角元梅涅劳斯定理也有很多著名的推广,例如原子论者L.H.Euler 对定理的推广,它是关于非凹多面体的总角度的定理。
它的定理总是大于或等于当面体的顶点数减2倍2π的。
此外,许多其他学者也参与了角元梅涅劳斯定理的探究和完善,这充分证明了它非常重要的地位。
它也为其他形式几何图形研究提供了重要的理论依据。
梅涅劳斯定理和塞瓦定理

第十讲:梅涅劳斯定理和塞瓦定理一、梅涅劳斯定理定理1若直线l不经过?ABC的顶点,并且与?ABC的三边BC、CA、AB或它们的延长线分别交于P 、Q、R,则BPPC ?CQQA?ARRB=1证明:设ℎA、ℎB、ℎC分别是A、B、C到直线l的垂线的长度,则:BPPC ?CQQA?ARRB=ℎBℎC?ℎCℎA?ℎAℎB=1。
注:此定理常运用求证三角形相似的过程中的线段成比例的条件。
例1若直角?ABC中,CK是斜边上的高,CE是∠ACK的平分线,E点在AK上,D是AC的中点,F是DE与CK的交点,证明:BF∥CE。
【解析】因为在?EBC中,作∠B的平分线BH,则:∠EBC=∠ACK,∠HBC=∠ACE,∠HBC+∠HCB=∠ACK+∠HCB=90°,即BH⊥CE,所以?EBC为等腰三角形,作BC上的高EP,则:CK=EP,对于?ACK和三点D、E、F根据梅涅劳斯定理有:CDDA ?AEEK?KFFC=1,于是KFFC=EKAE=CK AC =EPAC=BPBC=BKBE,即KFFC=BKBE,根据分比定理有:KFKC=BKKE,所以?FKB??CKE,所以BF∥CE。
例2从点K引四条直线,另两条直线分别交直线与A、B、C、D和A1,B1,C1,D1,试证:AC BC :ADBD=A1C1B1C1:A1D1B1D1。
【解析】若AD∥A1D1,结论显然成立;若AD与A1D1相交于点L,则把梅涅劳斯定理分别用于?A1AL和?B1BL可得:ADLD ?LD1A1D1?A1KAK=1,LCAC?AKA1K?A1C1LC1=1,BCLC?LC1B1C1?B1KBK=1,LD BD ?BKB1K?B1D1LD1=1,将上面四个式子相乘,可得:ADAC?BCBD?A1C1A1D1?B1D1B1C1=1,即:ACBC:ADBD=A1C1 B1C1:B1D1 B1C1定理2设P、Q、R 分别是?ABC的三边BC、CA、AB上或它们延长线上的三点,并且P、Q、R三点中,位于?ABC边上的点的个数为0或2,这时若BPPC ?CQQA?ARRB=1,求证P、Q、R三点共线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梅涅劳斯定理
简介
梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1
证明一:
过点A作AG∥BC交DF的延长线于G,
则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1
证明二:
过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF
所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1
它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
梅涅劳斯(Menelaus)定理
证明三:
过ABC三点向三边引垂线AA'BB'CC',
所以AD:DB=AA':BB',BE:EC=BB':CC',CF:FA=CC':AA'
所以(AF/FB)×(BD/DC)×(CE/EA)=1
此外,用定比分点定义该定理可使其容易理解和记忆:
在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/ LC、μ=CM/MA、ν=AN/NB。
于是L、M、N三点共线的充要条件是λμν=-1。
(注意与塞瓦定理相区分,那里是λμν=1)
记忆
ABC为三个顶点,DEF为三个分点
(AF/FB)×(BD/DC)×(CE/EA)=1
(顶到分/分到顶)*(顶到分/分到顶)*(顶到分/分到顶)=1
空间感好的人可以这么记:(上1/下1)*(整/右)*(下2/上2)=1
实际应用
为了说明问题,并给大家一个深刻印象,我们假定图中的A、B、C、D、E、F 是六个旅游景点,各景点之间有公路相连。
我们乘直升机飞到这些景点的上空,然后选择其中的任意一个景点降落。
我们换乘汽车沿公路去每一个景点游玩,最后回到出发点,直升机就停在那里等待我们回去。
我们不必考虑怎样走路程最短,只要求必须“游历”了所有的景点。
只“路过”而不停留观赏的景点,不能算是“游历”。
例如直升机降落在A点,我们从A点出发,“游历”了其它五个字母所代表的景点后,最终还要回到出发点A。
另外还有一个要求,就是同一直线上的三个景点,必须连续游过之后,才能变更到其它直线上的景点。
从A点出发的旅游方案共有四种,下面逐一说明:
方案①——从A经过B(不停留)到F(停留),再返回B(停留),再到D(停留),之后经过B(不停留)到C(停留),再到E(停留),最后从E经过C(不停留)回到出发点A。
按照这个方案,可以写出关系式:
(AF:FB)*(BD:DC)*(CE:EA)=1。
现在,您知道应该怎样写“梅涅劳斯定理”的公式了吧。
从A点出发的旅游方案还有:
方案②——可以简记为:A→B→F→D→E→C→A,由此可写出以下公式:(AB:BF)*(FD:DE)*(EC:CA)=1。
从A出发还可以向“C”方向走,于是有:
方案③——A→C→E→D→F→B→A,由此可写出公式:
(AC:CE)*(ED:DF)*(FB:BA)=1。
从A出发还有最后一个方案:方案④——A→E→C→D→B→F→A,由此写出公式:
(AE:EC)*(CD:DB)*(BF:FA)=1。
我们的直升机还可以选择在B、C、D、E、F任一点降落,因此就有了图中的另外一些公式。
值得注意的是,有些公式中包含了四项因式,而不是“梅涅劳斯定理”中的三项。
当直升机降落在B点时,就会有四项因式。
而在C点和F点,既会有三项的公式,也会有四项的公式。
公式为四项时,有的景点会游览了两次。
不知道梅涅劳斯当年是否也是这样想的,只是列出了一两个典型的公式给我们看看。
还可以从逆时针来看,从第一个顶点到逆时针的第一个交点比上到下一个顶点的距离,以此类推,可得到三个比例,它们的乘积为1.。
