《量子化学基础》习题课
基础量子化学练习定稿版

基础量子化学练习精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】2010基础量子化学练习(1)一、 判断正误( )1、 一个态函数总是等于时间的函数乘以坐标的函数。
( )2、 态函数总是Hamiltonian 算符的本征函数。
( )3、 Hamiltonian 算符的本征函数的任意线性组合是Hamiltonian 算符的本征函数。
( )4、 如果态函数不是算符ˆA的本征函数,则性质A 的一次测量可给出一个不是ˆA 的本征值的值。
( )5、 几率密度与时间无关。
( )6、 如果两个算符具有共同的本征函数,那么这两个算符可对易。
( )7、 算符ˆx 与d i dx -可对易。
( )8、 氢原子Hamiltonian 算符的束缚态的本征函数构成完备集。
( )9、 厄米算符的本征函数是正交的。
( )10、 描述电子轨道运动的波函数必须是奇函数。
二、已知:2ˆˆˆ,A d dx B x ==,计算2ˆˆˆˆ,()A B A B ⎡⎤+⎣⎦及 三、已知:11223344ˆˆˆˆ,,,,A a A b A a A d ϕϕϕϕϕϕϕϕ====如果任意状态可以表示为12343253,ψϕϕϕϕ=+++那么当我们对该状态进行测量时,获得a 和d 的几率各是多少?求任意状态 的性质A 的平均值。
2010基础量子化学练习(2)一、 判断正误( )11、 算符ˆˆˆ,,A B C 满足ˆˆˆˆ,0,,0A B A C ⎡⎤⎡⎤==⎣⎦⎣⎦,则三个算符存在共同的本征函数集。
( )12、 不能对易的算符不可能具有共同的本征函数。
( )13、 当对本征态的性质A 进行测量时,能够得到的唯一仅有的值是算符ˆA的本征值。
( )14、 如果一个算符的平方等于单位算符,那么这个算符的本征值等于+1或者-1。
( )15、 所有品优的奇函数和偶函数都是宇称算符的本征函数。
结构化学 第一章 量子化学基础 习题

1029
y y y 设 体 系 处 在 状 态 =c1 211+ c2 210 中 , 角 动 量 M2 和 Mz 有 无 定 值 。其值为多少?若无 ,
则求其平均值。
1030
h¶
试 求 动 量 算 符 pˆ x=
的 本 征 函 数 (不 需 归 一 化 )。
i2p ¶x
1031
y 下 列 说 法 对 否 :” =cos x, px 有确 定 值 , p2x 没 有 确 定 值,只有平均值 。” ---------- ( )
(A) 16.5 × 10 -24? J (B) 9.5
× 10 -7 J (C) 1.9
× 10 (E) 1.75 × 10 -50? J
1039 一个在一维势箱中运动的粒子,
(1) 其 能 量 随 着 量 子 数 n 的 增 大 :------------------------ ( ) (A) 越 来 越 小 (B) 越 来 越 大 (C) 不变 (2) 其 能 级 差 En+1-En 随 着 势 箱 长 度 的 增大 : -------------------( ) (A) 越 来 越 小 (B) 越 来 越 大 (C) 不变
(A)
Aˆ U=λU, λ=常数
(B)
Bˆ U=U*
(C)
Cˆ U=U2
(D)
Dˆ U = dU
dx
(E)
Eˆ U=1/ U
1026 物 理 量 xp y- ypx
1027
_____ 。
某 粒 子 的 运 动 状 态 可 用波 函 数y =Ne-ix 来表 示 , 求 其 动 量 算符 pˆ x 的 本 征 值 。
1013
测 不 准 原 理 的 另一 种 形 式 为 Δ E·Δt≥h/2 π。当一个电子从 高能级向低能级跃迁 时,
《量子化学基础》习题课
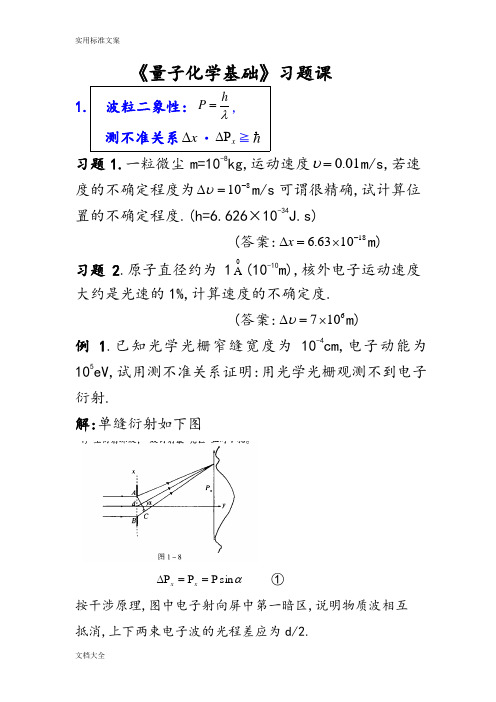
《量子化学基础》习题课 1. 波粒二象性: λhP =,测不准关系x ∆·x ∆P ≧习题1.一粒微尘m=10-8kg,运动速度01.0=υm/s,若速度的不确定程度为810-=∆υm/s 可谓很精确,试计算位置的不确定程度.(h=6.626×10-34J.s)(答案:181063.6-⨯=∆x m)习题2.原子直径约为10A (10-10m),核外电子运动速度大约是光速的1%,计算速度的不确定度.(答案:6107⨯=∆υm)例1.已知光学光栅窄缝宽度为10-4cm,电子动能为105eV,试用测不准关系证明:用光学光栅观测不到电子衍射.解:单缝衍射如下图αsin P =P =∆P x x ①按干涉原理,图中电子射向屏中第一暗区,说明物质波相互抵消,上下两束电子波的光程差应为d/2.λαα=⋅∆=⋅=sin sin x d BC ②这里410-=∆=x d cm,meV h mE h h 22==P =λ (=m 9.11×10-31kg ;=e 1.602×10-19C) 51025.1225.12==V λ=3.87×10-12m 661210101087.3sin ---=⨯==m m d λα 0≈α 证毕. 习题3.计算动能为3000eV 的电子的de Brogle 波长(1eV=1.602×10-19J, V 3000C10602.1J 10602.130001919=⨯⨯⨯=--V ) (答案: 0A 2237.0300025.1225.12===V λ.) 2 .一维势箱: 2228ml h n E =,),2,1( =nx ln C x πsin )(2=ψ 习题4.计算箱宽为5×10-10m 的一维势箱中粒子n=1、2时的能量.及粒子从n=2跃迁到n=1时辐射的波长. (答案:E 1=2.41×10-19J,E 2=9.64×10-19J191023.7-⨯=∆E J 71075.2-⨯=λm) 习题 5.可将原子中的电子粗略的模拟为一维箱中粒子,箱的宽度为原子的尺度.计算在长度10A 的箱中电子两个最低能级之差(eV)和在此两能级间跃迁的光子波长(cm). (答案:21013.1⨯=∆E eV, 8101.1-⨯=λm)例2. 丁二烯(H 2C=CH-CH=CH 2)4个π电子(P z 电子),可以近似地看作长度为大Π键键长(已知:双键长035.1A 、单键长054.1A )的一维势箱中的4个粒子的运动.体系的基态向第一激发态的跃迁为:_______1_______2___________3___________4↑↓=↑↓===n n n n 1_______2________3________4___________=↑↓=↑=↑=n n n n求:体系基态向第一激发态的跃迁能(cm -1).解.箱长:m A A l 10001078.554.1235.12-⨯=⨯+⨯=.)23(888222222222223-=-=∆l m h l m h n l m h n E e e e 21031234)1078.5(1011.985)10626.6(m kg s J ---⨯⨯⨯⨯⨯⋅⨯=J 191002.9-⨯=.14834191054.4/10310626.61002.9----⨯=⨯⨯⋅⨯⨯=∆=cm s m s J J hc E ν 例3.有一个量子数为n 在长度为l 的一维箱中运动的粒子(1)计算在箱的左端41区内找到粒子的几率.(2)n 为何值时该几率最大?(3)计算当n →∞时该几率的极限?解: 2sin 2141)sin 2(2410πππn n dx x l n l P -==⎰⎪⎩⎪⎨⎧==-==8,6,4,2,015,11,7,3,113,9,5,1,12sin n n n n 当当当π 即,n=3时,P 最大.π6141max +=P . 41)2sin 2141(lim =-∞→ππn n n (该式说明:当n →∞时量子力学问题还原为经典(力学)问题,因为经典力学处理一维箱问题在左端1/4处的几率正是1/4.)习题6.有一质量为1g 的小球,在长为10cm 的一维箱中运动小球速度0.1cm/s,试求小球的量子数n 是多少 ? (答案:n=3.018×1026) 3. 一位谐振子:m k πν21=)21(+=υνh E ( 3,2,1,0=υ) 习题7.HI 近红外光谱的基本振动频率22300=-ν.1cm -1,求HI 键的弹力常数k . (答案:k =2.93×105 D.cm -1) 习题8.已知H 2和Cl 2的基本振动频率分别为24.4395)(20=H νcm -1,9.564)(20=Cl νcm -1,求它们的零点能. (答案:E 0(H 2)=6.28kg/mol, E 0(Cl 2)=0.807kg/mol) 例 4.利用简谐振动公式:)sin()(φω+=t C t x ,证明一维谐振子的总能量是常数:221kC E =解:)(sin 21)(cos 2122222φωφωω+++=+=t kC t C m V T E m k =2ω ,带入上式,得: 221kC E =. 习题9.若H 35Cl 基本振动频率13010667.8⨯=νs -1,试求H 37Cl 的基本振动频率,设它们键的力常数相同.(答案:8.660×1013s -1) 4. 刚性转子:)1(22+=l l IE ( 3,2,1,0=l ) )1(2)(+=l B l ν (式中Ic hB 28π=) 例5.由HCl 的远红外光谱数据得知HCl 的转动能级相邻谱线间距为20.74cm -1,求HCl 分子的键长r.解: c r hIc h B 222442μππν===∆24231063.11002.6)45.35008.1(45.35008.1-⨯=⨯+⨯=+⋅=Cl H Cl H m m m m μg/mol 211024227212)2/74.20(1031063.1)1416.3(810626.6)8(][⨯⨯⨯⨯⨯⨯==--cB h r μπ =1.287×10-8cm=1.2870A习题10.从CN 的微波谱知道一系列谱线的间距皆为3.7978cm -1,求该分子的核间距r.(答案:r=1.172×10-10m)习题11.已知CN +的键长是1.290A ,指出CN +微波谱的第一到第四条线的位置.(答案:3.134cm -1,6.268cm -1,9.402cm -1,12.536cm -1 5.算符:),,(t q P F ∧∧其中q i ∂∂-=P ∧与本征函数:∧A )(x f =k )(x f习题12.写出下列物理量的算符:(1)动量P,(2)动量3y p ,(3)x y yp xp -,(4)动能T( 答案(1))(z k y j x i i P ∂∂+∂∂+∂∂-=∧,(2)3333y i P y ∂∂=∧(3))()(x y y x i p y p x L x y z ∂∂-∂∂-=-=∧∧∧ (4) )(22222222z y x m T ∂∂+∂∂+∂∂-=∧) 13.计算算符222kx dx d A -=∧的本征函数2x e α-的本征值(答案:22)24()(222222x x e kx x e kx dx d αααα----=- )14.利用[∧D ,∧x ]=1,(1)计算2)(x D +∧,(2)))((x D x D -+∧∧ (答案:(1)2)(x D +∧1222+++=∧x D x D (2)1))((22--=-+∧∧∧x D x D x D )15.三维箱中粒子的波函数是下列那些算符的本征函数(1)∧x p ,(2)∧2x p ,(3)∧2z p ,(4)∧2x .(答案(2),(3) )6.对易计算以下对易恒等式可方便对易运算:①.],[],[∧∧∧∧-=A B B A②.0],[=∧∧n A A (n=1,2,3…)③.],[],[],[∧∧∧∧∧∧==B A k kB A B kA④],[],[],[∧∧∧∧∧∧∧+=+C A B A C B A⑤ ],[],[],[∧∧∧∧∧∧∧∧∧+=C A B C B A C B A 例6.计算对易子:],[∧x P x ,],[2∧x P x ,],[∧H x ,],[∧∧H P x .解: i i x x i x x i x i x P x x =-=∂∂-=∂∂=∂∂=∧],[],[],[],[ ],[],[],[2∧∧∧∧∧+=x x x x x P x P P P x P xx i i x i i ∂∂⋅+∂∂⋅= x ∂∂=22)](21,[],[)],,(,[],[222∧∧∧∧∧∧++==+=z y x P P P m x T x z y x V T x H x ∧∧=∂∂==x x P mi x m P x m 22],[21 ],[)](,[21],[222V P P P P P m H P x z y x x x ∧∧∧∧∧∧∧+++= x V i V x i V P x ∂∂-=∂∂-==∧],[],[(式中x V f x f V x Vf f x V V x f V x ∂∂=∂∂-∂∂=∂∂-∂∂=∂∂)()(],[)16.计算:],[222c bx ax dx d ++ (答案: ],[222c bx ax dx d ++=dxd b ax a )24(2++. ) 例7.证明:222)(〉〈-〉〈=∆A A A解: 〉〉〈-〈≡≡∆∧222)()(A A A A στψψd A A ⎰〉〈-=∧*2)( τψψτψψτψψτψψd A d A A d A A d A ⎰⎰⎰⎰〉〈+〉〈-〉〈-=*∧*∧*∧*22τψψτψψτψψd A d A A d A A A ⎰⎰⎰*∧*∧*〉〈+〉〈-〉〈-〉〈=22 2222〉〈+〉〈-〉〈-〉〈=A A A A 22〉〈-〉〈=A A 证毕 7. H 原子薛定谔方程的解222204118n R n h e E n -=-=εμ (n=1,2,…),其中22048h e R εμ-=. )()()(,,,θϕθϕψm l l n m l n Y r R r =)()()(,,ϕθm m l l n r R ΦΘ= ϕθim ml na Zr i l l n i i e P e a Zr c C )(cos })({0101--+-=∑= 氢原子波函数受控于三个量子数(m l n ,,)∞=,,2,1 n1,,2,1,0-=n ll m ±±±=,,2,1,0习题17.下列函数(1)2P z ,(2)2P x ,(3)2P 1分别是算符∧H 、∧2L 、∧z L 中哪个的本征函数. (答案:(1)、(3)全是,(2)是∧H 、∧2L 的本征函数) 习题18.对H 原子P 态,测量L Z 的可能值为h 、0、-h,问在下列函数中测量L Z 得到各可能值的几率.(1)Pz 2ψ,(2) Px 2ψ,(3) 12P ψ(答案:(1) 121211210200-⋅+⋅+=ψψψψPz得0值几率为1,得h 、-h 几率为0. (2) 121211*********-++⋅=ψψψψPx 得h 、-h 几率各为21,得0值几率为0.(3) 12P ψ=211ψ,得h 几率为1,其余为0) 例8.已知H 原子)(ϕΦ方程复数解:ϕπϕim m e 21)(=Φ,(1)验证)(ϕm Φ是归一化的.(2)证明)(ϕm Φ是算符ϕ∂∂-=∧ i L z 的本征函数.而)(ϕm Φ线性组合的实函数: ⎪⎪⎩⎪⎪⎨⎧=Φ=Φϕπϕϕπϕm m m msin 1)(cos 1)('`不是∧z L 的本征函数.解:(1)121212020202===ΦΦ=Φ⎰⎰⎰⎰-*ππϕϕπϕπϕπϕϕd d e e d d im im (2) )(21)(ϕπϕϕϕm im m z m e i L Φ±=∂∂-=Φ±∧而 ϕπϕπϕϕm m i m i L m z sin cos 1)( =∂∂-=Φ∧不构成本征方程: )()(ϕϕm m z c L Φ≠Φ∧.例如n=2,l =1的H 原子波函数是p 轨道,有三个状态(m=1,0,-1),其复函数形式为:θθϕψcos )()(0,1,2r r f r = (即:z p p 也是0)ϕθθϕψi e r r f r ±±=sin )()('1,1,2 (即:11-p p 和)其中复函数z p p 等于实函数0,复函数11-p p 和线性组合为实函数y x p p ,,即ϕθθϕϕcos sin )()(sin )(11r R N e e r R N p i i x =+=- ϕθθϕϕsin sin )()(sin )(11r R N e e r R N p i i y =-=- 因此,z p p 和0都是∧z L 的本征函数. 11-p p 和也是∧z L 的本征函数.只有y x p p ,不是∧z L 的本征函数.P 轨道的实函数与复函数形式都是体系的状态函数,但表示图形不一样:例9.对H 原子基态,(1)求2倍玻耳半径之外的电子几率.(2)玻耳半径之内的电子几率. 解:H 原子基态,n=1,0=l ,m=0301,,,1)()()(a r s ml l n m l n eaY r R r -=→=πψθϕθϕψ(1)设P 2为02a 之外的电子几率 ϕθθπτψππd drd re a d P a r a s sin 1122200203021200-⎰⎰⎰⎰==-⎰⎰⎰-=ππϕθθπ2022023sin 10d d dr e r a a r adr e r a a ra 002202304-⎰=ππ利用积分公式][0203020022302)82422(41a a r ara a r ea P ---=--)22(3222b b x b x e dx e x bx bx +-=⎰]4)44448([430303030430a a a a e a +---=- 4131e -= 即: 24.01342==e P(2)设1P 是玻耳半径0a 之内的电子几率,则dr e r a P a r a 02023014-⎰=][00302002230)82422(4a a r a ra a r e a ---=-]4)44242([430303030230a a a a e a +---=-32.0512=-=e例10.已知类氢离子基态波函数 03031a zr s ea z-=πψ,(1) 求半径r 的平均值.(2)r 的最可几值.解:(1)ϕθθπτψψππd drd r ea zd r r a zr ssin 32002030310-∞*⎰⎰⎰⎰==〉〈dr er a za zr 02033034-∞⎰⋅=ππ利用广义积分公式:10!+∞-=⎰n qxn qn dx ex (0,1>->q n )z a a z a z dr e r a z r a zr23)2(!344040303023330=⋅==〉〈⎰∞-(2)径向分布函数: 0223032214)(a zr ser a z r r R D -=⋅=求最可几半径就是求最大径向分布函数时r,0)22(4)(40202230322303=-==---a zr a zr a zr ea z r rea zer dr d a z dr dD020=-r r a z 即, z a r 0=为最可几半径.。
量子化学习题及答案

1 2 1 Z 1 ˆ 有能量算得: H i 2 i a rai 2 i j i rij i
ˆ 在电子近似下可得到: H
i
H
2
eff
( ri , i , i )
0 0 2
0 0 e2
①
因为C 2 H 4 的分子轨道情况是兼并的,所以 e1
由①可得到
e
0 1
ei
2
12
e1 S12
2
e10 Δ12 0 可解出 e1 1 S12
12 ei S12 c1i 0 ② 0 ei c 2 i e2
ˆ ,若存在任意归一化的品优波函数 ,则有 (1)对于给定体系的哈密顿算符 H
ˆ d E 此式被称为变分积分。其中 为变分函数,E 0 为 H ˆ 的最低本征值,即体系 E *H
0
ˆ 关于 的平均能量 E 必是体系基态能量E 0 的上限,这就是变分 基态能量。体系哈密顿算符 H
原理。 (2)在量子化学计算中,广泛采用的是线性变分函数,它是满足体系边界条件的 m 个 线性无关的函数 1 , 2 ,…… m 的线性组合: c11 c 2 2 c3 3 c m m 这里常用实 函数作为变分函数。采用线性变分函数的变分法通常称线性变分法。 15. 使用分子轨道理论求乙烯分子、2-丁烯分子的成键分子轨道能级 e1 和分子轨道波函数
基础量子化学习题 1.为什么微观粒子的运动状态要使用量子力学来描述,而不能用经典力学来描述? 答:以牛顿三大定律为中心内容的经典力学适用于宏观物体的机械运动,当经典力学的应用 范围推广到高速运动和小线度范围时,实验表明经典力学遇到了不可克服的困难。对微观体 系的研究导致了量子力学的诞生。因为许多微观粒子都具有波粒二象性。而在观察之前,我 们得不到一个粒子的确切位置,它是一道弥散的波。可以通过波函数来表示它们在每一区域 出现的概率。所以,描述描述微观粒子的运动状态要用量子力学。 2.原子 A 和原子 B 在 y 轴上, 指出 A 原子的 Px, Py, Pz 原子轨道与 B 原子的 dxy, dyz, 2 dz 原子轨道间分别可形成什么分子轨道? ①原子 A 的 Px 原子轨道与原子 B 的任意原子轨道无法形成分子轨道 ②原子 A 的 Py 原子轨道与原子 B 的 dyz 原子轨道形成π分子轨道(如图 1)
结构化学练习之量子力学基础习题附参考答案

量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247ma h ,其简并度是_______________。
量子化学课程习题及标准答案

量子化学习题及标准答案Chapter 011. A certain one-particle, one-dimensional system has η/2bmx ibt e ae --=ψ, where a and b are constants and m is the particle ’s mass. Find the potential-energy function V for this system. (Hint : Use the time-dependent Schrodinger equation.)Solution :As ψ(x,t) is known, we can derive the corresponding derivatives.⎪⎪⎩⎪⎪⎨⎧ψ+ψ-=∂ψ∂ψ-=∂ψ∂⇒=ψ--222222/42),(),(),(2ηηηx m b bm xt x ib t t x e ae t x bmx ibtAccording to time-dependent Schroedinger equation,substituting into the derivatives, we get222),(mx b t x V =2. At a certain instant of time, a one-particle, one-dimensional system has bx xe b /||2/13)/2(-=ψ, where b = 3.000 nm. If a measurement of x is made at this time in the system, find the probability that the result (a) lies between 0.9000 nm and 0.9001 nm (treat this interval as infinitesimal); (b) lies between 0 and 2 nm (use the table of integrals, if necessary). (c) For what value of x is the probability density a minimum? (There is no need to use calculus to answer this.) (d) Verify that ψ is normalized.Solution :a) The probability of finding an particle in a space between x and x+dx is given by6/223210*29.32--==ψ=dx e x b dx P b x b) 0753.02910*20/223==⎰--dx e x bP b x c) Clearly, the minimum of probability density is at x=0, where the probability densityvanishes. d)4220/223/223/2232===ψ=⎰⎰⎰⎰+∞-+∞∞--+∞∞--+∞∞-dxe x b dx e x b dx e x b dx P b x b x b x3. A one-particle, one-dimensional system has the state function2222/4/16/4/12)/32)((cos )/2)((sin c x c x xe c at e c at --+=ψππ where a is a constant and c = 2.000 Å. If the particle ’s position is measured at t = 0, estimate the probability that the result will lie between 2.000 Å and 2.001 Å.Solution :when t=0, the wavefunction is simplified as441610*158.2)32(),(22--==ψc x xe c t x πChapter 021. Consider an electron in a one-dimensional box of length2.000Å with the left end of the box at x = 0. (a) Suppose we have one million of these systems, each in the n = 1 state, and we measure the x coordinate of the electron in each system. About how many times will the electron be found between 0.600 Å and 0.601 Å? Consider the interval to be infinitesimal. Hint: Check whether your calculator is set to degrees or radians. (b) Suppose we have a large number of these systems, each in the n =1 state, and we measure the x coordinate of the electron in each system and find the electron between 0.700 Å and 0.701 Å in 126 of the measurements. In about how many measurements will the electron be found between 1.000 Å and 1.001 Å?Solution: a) In a 1D box, the energy and wave-function of a micro-system are given by)sin(2,22222x ln l ml n E πψπ==η therefore, the probability density of finding the electron between 0.600 and 0.601 Å is65510*545.6)(sin 242⇒==-dx x ln l P πb) From the definition of probability, the probability of finding an electron between x and x+dx is given bydx x l n l P )(sin 22π= As the number of measurements of finding the electron between 0.700 and 0.701 Å is known, the number of system is1(sin 22*158712158712001.0)7.02*1(sin 2212612622=⇒===πP P N2. When a particle of mass 9.1*10-28 g in a certain one-dimensional box goes from the n = 5 level to the n = 2 level, it emits a photon of frequency 6.0*1014 s -1. Find the length of thebox.Solution.lml h n n ml n n E lowerup lowerup 36222222222110*26646.18)(2)(-=-=-=∆ηπ3. An electron in a stationary state of a one-dimensional box of length 0.300 nm emits a photon of frequency 5.05*1015 s -1. Find the initial and final quantum numbers for this transition.Solution:2,388)(2)(22222222222===-⇒=-=-=∆lower upper lower up lower up lower up n n n n hv ml h n n ml n n E ηπ4. For the particle in a one-dimensional box of length l , we could have put the coordinate origin at the center of the box. Find the wave functions and energy levels for this choice of origin.Solution: The wavefunction for a particle in a one-dimernsional box can be written as)2()2()(x mE BSin x mE ACos x ηη+=ψ If the coordinate origin is defined at the center of the box, the boundary conditions are given as2()22(0)(2()22(0)(22mE BSin l mE ACos x mE BSin l mE ACos x l x lx +⇒=-⇒==-=ηηηηψψ Combining Eq1 with Eq2, we get)4(,0)22()3(,0)22(Eq l mE BSin Eq l mE ACos ==ηη Eq3 leads to A=0, or )22(l mE Cos η=0. We willdiscuss both situations in the following section.If A=0, B must be non-zero number otherwise the wavefunction vanishes.2220)22(02mlh n E n l mE l mE Sin B π=⇒=⇒=⇒≠ηηIf A ≠08)12()21(220)22(00)22(0)22(0222mlh n E n l mE l mE Cos B l mE Sin l mE Cos A ψπ⇒+=⇒+=⇒==⇒≠⇒=⇒≠ηηηη5. For an electron in a certain rectangular well with a depth of 20.0 eV , the lowest energy lies 3.00 eV above the bottom of the well. Find the width of this well. Hint : Use tanθ = sin θ/cos θ Solution : For the particle in a certain rectangular well, the E fulfill with )2sin()2()2cos()(21010l mE V E l mE E E V ---=-ηη Substituting into the V and E, we get1010011110*64.22)7954.0(7954.022)(2)2()2()2(-----=⇒+-=⇒+-=⇒-=--==lowest l mEn l n l mE V E E E V l mE Tan l mE Cos l mE Sin ππηηηηηChapter 031. If Aˆf (x ) = 3x 2 f (x ) + 2xd f /dx , give an expression for Aˆ. Solution :Extracting f(x) from the known equation leads to the expression of Adx d x x A 23ˆ2+=2. (a) Show that (Aˆ+B ˆ)2 = (B ˆ+A ˆ)2 for any two operators. (b) Under what conditions is (Aˆ+B ˆ)2 equal to Aˆ2+2A ˆB ˆ+B ˆ2? Solution: a)2222ˆ()ˆˆ)(ˆˆ(ˆˆˆˆˆˆˆˆˆˆˆ)ˆˆ)(ˆˆ()ˆˆ(B A B A BA B A A B B A B B A A B A B A B A =++=+++=+++=++=+ b) B AA B A B B A A B A ˆˆ2ˆˆˆˆˆˆˆ)ˆˆ(2222++=+++=+If and only if A and B commute, (Aˆ+B ˆ)2 equals to Aˆ2+2A ˆB ˆ+B ˆ2 3. If Aˆ = d 2/dx 2 and B ˆ = x 2, find (a) A ˆB ˆx 3; (b) B ˆA ˆx 3; (c) A ˆB ˆf (x ); (d)B ˆA ˆf (x )Solution: a)3522320ˆˆxx dxd x B A == b)3322236ˆˆx x dxd x x A B == c))()(4)(2)]()(2[)]([)(ˆˆ2222222x f dxd x x f dx d x x f x f dxd x x xf dx d x f x dx d x f B A ++=+==d))()()(ˆˆ222222x f dxd x x f dx d x x f A B ==4. Classify these operators as linear or nonlinear: (a) 3x 2d 2/dx 2; (b) ( )2; (c) ∫ dx ; (d) exp; (e) ∑=n x 1.Solution:Linear operator is subject to the following condition.f A c cf Ag A f A g f A ˆ)(ˆˆˆ)(ˆ=+=+ a) Linearb) Nonlinear c) Linear d) Nonlinear e) Linear5. The Laplace transform operator Lˆ isdefined by⎰∞-=0)()(ˆdx x f e x f L px(a) Is Lˆ linear? (b) Evaluate Lˆ(1). (c)Evaluate Lˆe ax , assuming that p >a . Solution:a) L is a linear operator b)0,1)1(ˆ0>==⎰∞-p p dx e L px c)pdx e dx e e e L x a p ax px ax ===⎰⎰∞--∞-)(ˆ0)(06. We define the translation operator hT ˆ by hT ˆf (x ) = f (x + h ). (a) Is hT ˆ a linear operator? (b) Evaluate (2ˆ3ˆ121+-T T )x 2. Solution:a) The translation operator is linear operator b)2212212121(2ˆ3ˆ)2ˆ3ˆ(x x x T x T x T T +=+-=+-7. Evaluate the commutators (a) [xˆ,xp ˆ]; (b) [xˆ,2ˆxp ]; (c) [x ˆ,yp ˆ]; (d) [x ˆ, ),,(ˆz y x V ]; (e) [x ˆ,H ˆ]; (f) [z yx ˆˆˆ, 2ˆxp ]. Solution: a)ηηηi xx x x i x x i p xx =∂∂--∂∂-=∂∂-=)ˆ1ˆ(],ˆ[]ˆ,ˆ[b)xp i p p x p x p p xx x x x x x∂∂==+=222ˆ2)ˆ]ˆ,ˆ[]ˆ,ˆ[ˆ(]ˆ,ˆ[ηηc)0)ˆˆ(],ˆ[]ˆ,ˆ[=∂∂-∂∂-=∂∂-=yx y x i y x i p xy ηηd)0ˆ),,(ˆ),,(ˆˆ)],,(ˆ,ˆ[=-=x z y x V z y x V x z y x V xe)mxT x V T x H x ==+=21,ˆ[]ˆ,ˆ[]ˆˆ,ˆ[]ˆ,ˆ[f)xz y p z y xx∂∂=ˆˆ2]ˆ,ˆˆˆ[22ηChapter 041:The one-dimensional harmonic-oscillator is at its first excited state and its wavefunction is given as)21exp()()(2)(24/14/31x x x βπβψ-=please evaluate the expectation values(average values) of kinetic energy (T), potential energy (V) and the total energy.Answer: 1) First of all, check the normalization property of the wavefunction.2) Evaluate the expectation value of kinetic energy.3) Evaluate the expectation value ofpotential energy4) Total Energy = T + V2. The one-dimensional harmonic-oscillator Hamiltonian is2222ˆ22ˆˆxm v mp H xπ+= The raising and lowering operators for thisproblem are defined as]ˆ2ˆ[)2(1ˆ2/1x ivm p m A x π+=+, ]ˆ2ˆ[)2(1ˆ2/1x ivm p m A x π-=-Show thathv H A A 21ˆˆˆ-=-+,hv H A A 21ˆˆˆ+=+-, hv A A-=-+]ˆ,ˆ[ ++=A hv A H ˆ]ˆ,ˆ[, ---=A hv A Hˆ]ˆ,ˆ[ Show that +Aˆ and -A ˆ are indeed ladder operators and that the eigenvalues are spaced at intervals of hv . Since both the kinetic energy and the potential energy are nonnegative, we expect the energy eigenvalues to be nonnegative. Hence there must be a state of minimum energy. Operate on the wavefunction for this state first with -Aˆ and then with +Aˆ and show that the lowest energy eigenvalue ishv 21. Finally, conclude that hvn E )21(+=, n = 0, 1, 2, …Answer:1) Write down the definition of operatordx di px η-=ˆ2) Expand the operators in full form.]2[21]2[2122ˆ222222vmxi dx di mA vmxi dx d i mA mx v dx d m H πππ--=+-=+-=-+ηηη 3) Evaluate the corresponding combination ofoperators4242[21]22][2[21ˆ4222[21]2[2]2[2[21]2[21]22[ˆ21ˆ2122]4222[21]]2[2]2[[21]2[21]2[2121ˆ2122]42[21]4222[21]]2[2]2[[21]2[21]2[21322222222333222222332222222333222222222222222222222222222222222222222222222v dx d ix v dx d i mx v mxi v dxd m i m mx v dx d m vmxi dx d i mH A v dx d i mx v dx d ix v dx d i v dxd m i m vmxi dx d i mx v vmxi dx d i dxd m m vmxi dx d i mmx v dx d m A H hv H hv mx v dx d m x m v dxd vmx dx d x vm vm dx d m vmxi dxd i vmxi vmxi dx d i dx d i m vmxi dx d i mvmxi dx d i m A A hv H hv mx v dx d m x m v vm dxd m x m v dxd vmx dx d x vm vm dx d m vmxi dxd i vmxi vmxi dx d i dx d i m vmxi dx d i mvmxi dx d i m A A πππππππππππππππππππππππππππππππππππππ+---=+-+-=+---=+-++--=+-+-=+=++-=+-++-=+--+--=+---=-=-+-=+--=++---=--+---=--+-=+++--+ηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηηη+++=+-=+-=+-=-hvA vmxi m dx d i m hv vmxi m hv dxd i m hv mxi v dx d i v m H A A H ]22121[]221[]21[]42[21ˆˆ222ππππηηηηIn the same manner, we can get---=-hvA H A A H ˆˆ 4) Substituting the above communicators into the Schroeidnger equation, we getψψψψψψψψψψψψ------++++++-=-=-=+=+=+==A hv E hvA E A hvA H A A H A hv E hvA E A hvA H A A H E H)(]ˆ[ˆ)(]ˆ[ˆˆThis shows that +Aˆ and -A ˆ are indeed ladder operators and that the eigenvalues are spaced at intervals of hv .5) Suppose that ψ is the eigenfunction with the lowest eigenvalue. ψψlowest E H =ˆAccording to the definition of A_ operator, we haveψψ---=A hv E A H )(ˆAs ψ is the eigenfunction with the lowest eigenvalue, the above equation is fulfilled if and only if 0=-ψAOperating on the wave function for this statefirst with -A ˆ and then with +A ˆ leads to ψψψψhv H hv H A A 21ˆ]21ˆ[0=⇒-==-+Therefore, the lowest energy is 1/2 hv.Λ3,2,1,0,)(21ˆ=+=n hv n H ψψChapter 051. For the ground state of the one-dimensional harmonic oscillator, compute the standard deviations ∆x and ∆p x and check that the uncertainty principle is obeyed.Answer:1) The ground state wavefunction of the one-dimensional harmonic oscillator is given by2214141)(x e ααπψ--=2) The standard deviations ∆x and ∆p x are defined as222x x x -=∆2 2)2∆=∆-(p(p∆)pThe product of ∆x and ∆p is given by2422122ηηη==•=∆∆ααp xIt shows that the uncertainty principle is obeyed.2. (a) Show that the three commutationrelations [x Lˆ,y L ˆ] = z L i ˆη, [y L ˆ,z L ˆ] = x L i ˆη, [z L ˆ,x L ˆ] = y L i ˆη are equivalent to the single relation L L Lˆˆˆηi =⨯ (b) Find [2ˆx L,y L ˆ] Answer:1): zy x y x z x z y z y x y x x z z y x y y x z x x z y z z y y z x z z y x y z x y x z y x z y x z y x L i L L L i L L L i L L k L j L i L i k L L j L L i L L k L L L L j L L L L i L L L L i L L j L L i L L k L L j L L k L L k L j L i L k L j L i L L L k L j L i L L ηηηρρρηρρρρρρρρρρρρρρρρρρρρρ===⇒++=++=-+-+-=-++--=++⨯++=⨯++=],[],[],[)(],[],[],[)()()()()(ˆˆˆ2):)()()(],[],[],[2x z z x x z z x x y x y x x y x L L L L i L L i L i L L L L L L L L L +=+=+=ηηη3. Calculate the possible angles between L and the z axis for l = 2.Answer:The possible angles between L and the z axis are equivalent the angles between L and L z . Hence, the angles are given by:Lm Cos L z ==+=θηη6)12(2 ︒︒︒︒=7.144,10.114,00.90,91.65,26.35θ4. Complete this equation:m l m l z Y m Y L 333ˆη=Chapter 061. Explain why each of the following integrals must be zero, where the functions are hydrogenlike wave functions: (a) <2p 1|z L ˆ|3p -1>; (b) <3p 0|z L ˆ|3p 0>Answer:Both 3p -1 and 3p 0 are eigenfunctions of L z , with eigenvalues of -1 and 0, respectively. Therefore, the above integrals can be simplified asa) due to orthogonalization properties of eigenfunctions03|213ˆ21111=-=--p p p L p z b) 02. Use parity to find which of the following integrals must be zero: (a) <2s |x |2p x >; (b) <2s |x 2|2p x >; (c) <2p y |x |2p x >. The functions in these integrals are hydrogenlike wave functions.Answer:1) b) and c) must be zero.3. For a hydrogen atom in a p state, the possible outcomes of a measurement of L z are – ħ, 0, and ħ. For each of the following wave functions, give the probabilities of each of these three results: (a)z p 2ψ; (b) y p 2ψ; (c) 12p ψ. Then find <L z > for each of these three wave functions.Answer:a) 022p p z ψψ=, therefore, the probabilities are:0%, 100%, 0% )(2111222-+=p p p x ψψψ, the probabilities are 50%, 0%, 50%.12p ψ,the probabilities are 100%, 0%, 0%b) 0,0,14. A measurement yields 21/2ħ for the magnitude of a particle ’s orbital angular momentum. If L x is now measured, what are the possible outcomes?Answer:1): Since the wavefunction is the eigenfunction of L2, a measurement of the magnitude of the orbital angular momentum should be+L=LLηη(=⇒21)1,The possible outcomes when measure L x are-1, 0, 1Chapter 071. Which of the following operators are Hermitian: d /dx , i (d /dx ), 4d 2/dx 2, i (d 2/d x 2)?Answer :An operator in one-D space is Hermitian if⎰⎰=dx A dx A **)ˆ(ˆψψψψ a)⎰⎰⎰⎰-=-=-=∞∞-dx dx d dx dx d dx dx d dx dx d *****)(ψψψψψψψψψψ b)⎰⎰⎰⎰=-=-=∞∞-dx dx d i dx d i dx dx d i i dx dxd i ****)(ψψψψψψψψψψc)⎰⎰⎰⎰⎰=+-=-=-=∞∞-∞∞-dxdxddxddxddxdxddxddxddxddxddxdxdψψψψψψψψψψψψψ2*22****22*44 444 44This operator can be written as a product of 1D kinetic operator and a constant. Hence, it’s Hermitian.d) As the third operator is Hermitian, this operator is not Hermitian.2. If Aˆand Bˆare Hermitian operators, prove that their product AˆBˆis Hermitian if and only if Aˆand Bˆcommute. (b) If Aˆand Bˆare Hermitian, prove that 1/2(AˆBˆ+BˆAˆ) is Hermitian.(c) Is x p xˆˆHermitian? (d) Is 1/2(x p xˆˆ+x p xˆˆ)Hermitian?Answer:1)If operator A and B commute , we have⎰=-⇒=-⇒=0])ˆˆˆˆ[(0ˆˆˆˆˆˆˆˆˆ*τψψd A B B A A B B A A B B A⎰⎰⎰=⇒=-⇒τψψτψψτψψd A B d B A d A B B A***]ˆˆ[]ˆˆ[0])ˆˆˆˆ[(Operator A and B are Hermitian, we have⎰⎰⎰==⇒τψψτψψτψψd B A d B A d A B ˆˆ)ˆ()ˆ(]ˆˆ[***Therefore, when A and B commute, the following equation fulfills. Namely, AB is also Hermitian.⎰⎰=τψψτψψd B A d B A ˆˆ]ˆˆ[**2)]ˆˆˆˆ[21)]ˆˆˆˆ(21[***⎰⎰⎰+=+τψψτψψτψψd A B d B A d A B B A Operator A and B are Hermitian, we get⎰⎰⎰⎰⎰⎰⎰+=+⇒+=+=+τψψτψψτψψτψψτψψτψψτψψd A B B A d A B B A d B A A B d B A d A B d A B d B A *******])ˆˆˆˆ(21[)ˆˆˆˆ(21])ˆˆˆˆ(21[)ˆˆ()ˆˆ([21]ˆˆˆˆ[21The above equation shows that the operator 1/2[AB+BA] is Hermitian.c) xp x is not Hermitian since both x and px are Hermitian and do not commute.d) YesChapter 081. Apply the variation function cr e -=φto the hydrogen atom; choose the parameter c to minimize the variational integral, and calculate the percent error in the ground-state energy. Solution :1) The requirement of the variation function being a well-behaved function requires that c must be a positive number.2) check the normalization of the variation function.322*)(c d d Sin dr r ed cr πϕθθτφφ==⎰⎰⎰⎰- 3) The variation integral equals to )2(214])2[(2)1(21()121(ˆ32223*32*32*3**-=-∂∂+∂∂-=-∇-=-∇-==⎰⎰⎰⎰⎰⎰--c c c dr r e rr r e c d r c c d r c d d H w cr cr τφφπφπτφφπτφφτφφ4) The minimum of the variation integral is21101-=⇒=⇒=-=∂∂w c c c w5) The percent error in the ground state is 0%2. If the normalized variation function x l 2/13)/3(=φ for 0 ≤ x ≤ l is applied to the particle-in-a-one-dimensional-box problem, one finds that the variation integral equals zero, which is less than the true ground-state energy. What is wrong?Solution:The correct trail variation function must be subject to the same boundary condition of the given problem. For the particle in a 1D box problem, the correct wavefunction must equal to zero at x=0 and x=l. However, the trial variation function x l 2/13)/3(=φ does not fulfill these requirement. The variation integral basedon this incorrect variation function does not make any sense.3. Application of the variation function2cx e -=φ(where c is a variation parameter) to a problem with V = af (x), where a is a positive constant and f (x ) is a certain function of x , gives the variation integral as W = c ħ2/2m +15a /64c 3. Find the minimum value of W for this variation function.Solution: 23434123434141min 4141413272598.03)25(23)25(0)64152(ηηηηm a m a w m a c dc c a m c d c w ==⇒±=⇒=+=∂∂4. In 1971 a paper was published that applied the normalized variation functionN exp(-br 2a 02-cr /a 0) to the hydrogen atom and stated that minimization of the variation integral with respect to the parameters b and c yielded an energy 0.7% above the true ground-state energy for infinite nuclear mass. Without doing any calculations, state why this result must be wrong.Solution:From the evaluation of exercise 1, we know that the variation function exp(-cr) gives no error in the ground state of hydrogen atom. This function is a special case of the normalized variation function N exp(-br 2a 02-cr /a 0) when b equals to zero. Therefore, adopting the normalized variation function as a trial variation function should also have no error in the ground state energy for hydrogen atom.5. Prove that, for a system with anondegenerate ground state, 0*ˆE d H>⎰τφφ, if φ is any normalized, well-behaved function that is not equal to the true ground-state wavefunction. (E 0 is the lowest-energy eigenvalueof Hˆ) Solution:As the eigenfunctions of the Hermitian operator H form a complete set, any well-behaved function which is subject to the same boundary condition can be expanded as a linear combination of the eigenfunction of the Hermitian operator, namely,∑∞==0i i i c ψφ, where ψi s are eigenfunctions of Hermitian operator H, c i s are constant.The expectation value of φ with respect to the Hermitian operator is00201020201020020*00**00*0*0*ˆˆ)(ˆE c E E c E c c E c E c E c c E c cH c c d c H c d H i i i i i i i i i i i i i ij j j j i i i j j i i j j j i i i ==+>+======∑∑∑∑∑∑∑⎰∑∑⎰∑∑⎰∞=∞=∞=∞=∞=∞=∞=∞=∞=∞=∞=δψψτψψτφφChapter 09, 101. For the anharmonic oscillator with Hamiltonian 43222212ˆdx cx kx dx d m H +++-=η, evaluate E (1)for the first excited state, taking the unperturbed system as the harmonic oscillator. Solution:The wavefunction of the first excited state of the harmonic oscillator is241312)4(x xe απαψ-=Hence, the first order correct to energy of the first excited state is given by6213422134134324131'*1415)4()4()4)(()4(ˆ222απαπαπαπαψψαααd dx e x d dx x d e x xe x d x c xe dx H x x x ==•=•+•=---⎰⎰⎰⎰2. Consider the one-particle, one-dimensional system with potential-energyV = V 0 for l x l 4341<<, V = 0 for l x 410≤≤ andl x l ≤≤43and V = ∞ elsewhere, where V 0 = 22/ml η.Treat the system as a perturbed particle in a box. (a) Find the first-order energy correction for the general stationary state with quantum number n . (b) Find the first-order correction to the wave function of the stationary state with quantum number n .Solution:The wavefunction of a particle in 1D box is given by)(2)0(x ln Sin l n πψ= Take this as unperturbed wavefunction, and the perturbation H ’ is given by V .a) The first-order energy correction for ψn is])23[]2[(224]2[4[2)()(2)()(2ˆ00004341)0('*)0()1(πππππππππψψn Sin n Sin n V V n S n Sin l l V dx V x l n Sin x l n Sin l dx x ln VSin x l n Sin l dx H E l ln n -+=-+====⎰⎰⎰b) The first correction to the wavefunction is given by)0()0()0()0()0()1(2)0()0(222)0('(818mn m mn n m n mn n E E H n E E ml hn E ψψψψ∑∞≠-==-⇒=3. For an anharmonic oscillator with3222212ˆcx kx dx d m H ++-=η, take 'ˆHas cx 3. (a) Find E (1) for the state with quantum number v . (b) Find E (2) for the state with quantum number v . You will need the following integral:3,'2/13)0(3)0('2/)1[(3]8/)3)(2)(1[(||++++++>=<v v v v v v v v x αδαψψ3,'2/131,'2/3]8/)2)(1([)2/(3----++v v v v v v v v δαδαSolution: a) As the potential of the unperturbed is a even function, the eigenfunctions of the unperturbed system are either even or odd. The perturbation is an odd function with respect to x. Hence, the first order energy correction is zero.b) The second order energy correction is given by)51212(8]38)2)(1(838)1(338)3)(2)(1([()2(3)21(38)3)(2)(1((''2323333332)0()0(1,2/31,2/33,32)0()0(2)0(3)0()0()0()0()0()0()0()2(++-=--++-++-+++=-+++++++=-=-=∑∑∑∞≠-++∞≠∞≠n n hvc hvn n n hv n hv n hv n n n c E E n n n n n n n c E E cx E E H H E n m mn n n n n n n n m mn m n n m m n m n nm n αααααδαδαδαψψψψψψ4. Calculate the angle that the spin vector S makes with the z axis for an electron with spin function α.Solution:For an electron, both S and S z equal to one half. The magnitude of S isοηη74.54]31[23)1(===+=ArcCos S S S θ 5. (a) Show that 12ˆP and 23ˆP do not commutewith each other. (b) Show that 12ˆPand 23ˆP commute when they are applied to antisymmetric functions.Solution:a) Set the wavefunction to be)1()3()2()2()1()3(321321φφφφφφ≠b) When the function is antisymmetric, we haveψψψψψψψ2312121223231223ˆˆ)(ˆˆˆ)(ˆˆˆP P P P P P P P =-=-==-=-=6. Which of the following functions are (a) symmetric? (b) antisymmetric?(1) )2()1()2()1(ααg f ; (2) )]2()1()2()1()[2()1(αββα-f f ;(3) )3()2()1()3()2()1(βββf f f ; (4) )(21r r a e --;(5) )]1()2()2()1()][2()1()2()1([βαβα--f g g f ; (6) )(21221r r a e r +-. Solution:(2) is antisymmetric(3), (5) and (6) are symmetricChapter 11, 131. How many electrons can be put in each of the following: (a) a shell with principal quantum number n ; (b) a subshell with quantum numbers n and l ; (c) an orbital; (d) a spin-orbital?Solution:a) 2n 2, b) 2*(2l+1), c) 2, d) 12. Give the possible values of the total-angular-momentum quantum number J that result from the addition of angular momentum with quantum numbers (a) 3/2 and 4; (b) 2, 3, and 1/2Solution:Coupling between two angular momentums with quantum number j 1 and j 2 gives the possible quantum number J of the total angular momentum as:2121j j J j j +<<-a) The possible values are 11/2, 9/2, 7/2, 5/2b) The possible values are:11/2, 9/2, 9/2, 7/2, 7/2, 5/2, 5/2, 3/2, 3/2, 1/23. Find the terms that arise from each of the following electron configurations: (a) 1s22s22p63s23p5g; (b) 1s22s22p3p3d(c) 1s22s22p24dSolution:As fully-filled sub-shells do not contribution the total orbital and spin angular momentum, we can ignore the electrons in these sub-shells while considering the atomic terms. Hence, a) The atomic terms can be:3H, 1H, 3G, 1G, 3F, 1Fb) The atomic terms can be:4G, 2G, 4F, 2F, 4D, 2D, 4P, 2P, 4S, 2S4F 2F, 4D, 2D, 4P, 2P4D, 2D, 4P, 2P, 4S, 2Sc) The atomic terms can be:2G, 2F, 2D, 2P, 2S4F, 2F, 4D, 2D, 4P, 2P。
结构化学练习之量子力学基础习的题目附参考问题详解

实用标准文案精彩文档量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247m a h ,其简并度是_______________。
量子化学习题及参考答案

量子化学习题集及答案1、(1)求一维势箱中运动粒子的波函数。
(2)当势箱长度为10nm 时,度求粒子在以下区域出现的概率。
4.95<X<5.053l <X<23l 解:222ˆ2d Hm dx =-由schrodinger 方程可得:2221221222121221222222220(cos sin )222sin0220sin 000222sin08axd mEdxC bx C bxmEr i mEmEC x C x x l mEmEC C C mEmEmEC l C l l n n h E ml ψψψψψπ+=+=∴=+=+==+===其通解为=e (1)又或时,=0即: 得得 解得:将其2*22222000222sin sin()sin()sin ()12l l l n C xln n n dx C x C x dx C x dx l l lC C l n x lπψπππψψπψ====∴=⇒=∴=⎰⎰⎰代入方程(1)则有:将其正交归一: (2)5.05 5.0524.95 4.95 4.955.05 5.054.95 4.954.95 5.051021cos()222)sin()sin ()212122(cos())[(5.05 4.95)(sin( 5.05)sin( 4.95))]2x l nmn x n n n l x x dx x dx dxl l l l l l n l n n dx x dx l l l n l lππππρππππ<<=-===-=---⎰⎰⎰⎰⎰即:=得: 0.0121X 333l l ρρ=<<=同理: 时,2、电子在在L=1.00nm 长的势箱中运动,计算:(1)n=2与n=1之间,n=6与n=5之间的能量差。
解:22212222222182181812222222182181881.001,2213811*********,6651181108110810n h E ml l nm n n h h h E m m m n n h h h E m m m ------====∴=-===∴=-=3、一维势箱(势箱长为0.30nm )中的电子发射一个小频率为5.05×1015S —1,试求其跃迁始态与终态的量子数。
量子化学习题集

(2) x, x2, 3x21; (3) sinx, cosx;
(4) sinx, cosx, tanx;
(5)
sin2x, cos2x, 1;
(6) sinx, cosx, eix (7) sin2x, cos2y, 1
2.2 三维势箱中一粒子的波函数是下列那些算符的本征函数?
ˆ x (2)p ˆx (1) p
2ˆ2 ˆ2ˆ2ˆ2 ˆ xS ˆ y, S ˆy ˆ xS (2) 化简下面算符:S S z, S xS yS z
3.7 计算下列积分: ˆ z|0,0; (1)0,0|M ˆ +M ˆ |2,0; (4) 2,0|M 3.8 计算下列积分: ˆ z|py; (1) px|M ˆ +|py; (2) px|M ˆ y|px; (3) pz|M ˆ x|py (4)pz|M ˆ x|px (5) pz|M ˆ +|2,0; (2)2,1|M ˆ +|2,0 ˆ M (5) 2,0|M
x e
0
n qx
dx
n! q n 1
n 1, q 0 b0 b 0, n 1, 2,3... a 0, n 0,1, 2, ...
e
0 0
bx 2
dx
1 2 b
x
t
2 n bx 2
e
dx
(2n)! 2 n 1 2 n 1 2 n! b
判断下列函数那些是偶函数,那些是奇函数?
(1) sinx (2) cosx (3) tanx
(4) ex
(5) 12
(6)22x
2.6 对谐振子 v=1 的态,求粒子最可能的位置 2.7 对氢原子的基态,求(1) r 的平均值;(2) r 的最可几值;(3)求 2p 态的r 2.8 证明对于定态,T+V=E 2.9 计算氢原子基态的T,V 2.10 已知,力学量 A 的不确定度为A, A
结构化学练习之量子力学基础习题附参考问题详解

量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247ma h ,其简并度是_______________。
基础量子化学练习

基础量子化学练习 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】2010基础量子化学练习(1)一、 判断正误( )1、一个态函数总是等于时间的函数乘以坐标的函数。
( )2、 态函数总是Hamiltonian 算符的本征函数。
( )3、 Hamiltonian 算符的本征函数的任意线性组合是Hamiltonian 算符的本征函数。
( )4、 如果态函数不是算符ˆA的本征函数,则性质A 的一次测量可给出一个不是ˆA的本征值的值。
( )5、几率密度与时间无关。
( )6、如果两个算符具有共同的本征函数,那么这两个算符可对易。
( )7、算符ˆx 与d i dx -可对易。
( )8、氢原子Hamiltonian 算符的束缚态的本征函数构成完备集。
( )9、厄米算符的本征函数是正交的。
( )10、 描述电子轨道运动的波函数必须是奇函数。
二、已知:2ˆˆˆ,Ad dx B x ==,计算2ˆˆˆˆ,()A B A B ⎡⎤+⎣⎦及 三、已知:11223344ˆˆˆˆ,,,,A a A b A a A d ϕϕϕϕϕϕϕϕ====如果任意状态可以表示为12343253,ψϕϕϕϕ=+++那么当我们对该状态进行测量时,获得a 和d 的几率各是多少?求任意状态 的性质A 的平均值。
2010基础量子化学练习(2)一、 判断正误( )11、 算符ˆˆˆ,,A B C 满足ˆˆˆˆ,0,,0A B A C ⎡⎤⎡⎤==⎣⎦⎣⎦,则三个算符存在共同的本征函数集。
( )12、 不能对易的算符不可能具有共同的本征函数。
( )13、 当对本征态的性质A 进行测量时,能够得到的唯一仅有的值是算符ˆA的本征值。
( )14、 如果一个算符的平方等于单位算符,那么这个算符的本征值等于+1或者-1。
( )15、 所有品优的奇函数和偶函数都是宇称算符的本征函数。
( )16、 满足[]1212ˆˆˆ()()()()A c f x c g x c Af x c Ag x +=+的算符称为线性算符。
量子习题课专业知识

旳单色光照射系统.忽视边沿效应,求平衡时钠棒所
带旳电量. 已知纳旳红限波
钠棒
长为m=5400
o
A
(540nm),铝旳红限
波长为m'
=2960
o
A
(296nm).
半透 明铝
膜
r1
r2
石英
18
解: 'm m
在该光波照射下,铝不产生光电效应.纳在光
照下,发射光电子,它们旳最大初动能为
1 mv2 h c h c
2
1. 某金属产生光电效应旳红限波长为0,今以
波长为(< 0)旳单色光照射该金属,金属
释放出旳电子(质量为me) 旳动量大小为
(A)h/
(B) h/ 0
(C) 2mehc(0 ) 0
(D) 2mehc 0
(E) 2mehc(0 ) 0
[E] 3
2.有关光电效应有下列说法: (1)任何波长旳可见光照射到任何金属表面 都能产生光电效应。
14.多电子原子中,电子排列遵照 ___________________原理和 _________________原理.
泡里不相容原理; 能量最小原理 14
15.若氢原子处于主量子数 n=4旳状态,则
其轨道角动量(动量矩)可能取旳值(用
根号及 表达)分别为
,
l 相应于 =3 旳状态,氢原子旳角动量
• (B)两种效应都相当于电子与光子旳弹性碰 撞。
• (C)两种效应都属于电子吸收光子旳过程。
• (D)光电效应是吸收光子旳过程,而康普顿 效应则相当于光子和电子旳弹性碰撞过程 。
[D] 7
6.康普顿效应旳主要特点是 (A)散射光旳波长均比入射光旳波长短,且随 散射角增大而降低,但与散射体旳性质无关。
基础量子化学练习

一、判断正误( )1、 一个态函数总是等于时间的函数乘以坐标的函数。
( )2、 态函数总是Hamiltonian 算符的本征函数。
( )3、 Hamiltonian 算符的本征函数的任意线性组合是Hamiltonian 算符的本征函数。
( )4、 如果态函数不是算符ˆA 的本征函数,则性质A 的一次测量可给出一个不是ˆA 的本征值的值。
( )5、 几率密度与时间无关。
( )6、 如果两个算符具有共同的本征函数,那么这两个算符可对易。
( )7、 算符ˆx与d i dx- 可对易。
( )8、 氢原子Hamiltonian 算符的束缚态的本征函数构成完备集。
( )9、 厄米算符的本征函数是正交的。
( )10、 描述电子轨道运动的波函数必须是奇函数。
二、已知:2ˆˆˆ,Ad dx B x ==,计算2ˆˆˆˆ,()A B A B ⎡⎤+⎣⎦及三、已知:1122334ˆˆˆˆ,,,,A a A b A a A d ϕϕϕϕϕϕϕϕ====如果任意状态可以表示为12343253,ψϕϕϕϕ=+++那么当我们对该状态进行测量时,获得a 和d 的几率各是多少?求任意状态ψ 的性质A 的平均值。
一、判断正误( )11、 算符ˆˆˆ,,AB C 满足ˆˆˆˆ,0,,0A B A C ⎡⎤⎡⎤==⎣⎦⎣⎦,则三个算符存在共同的本征函数集。
( )12、 ˆˆ,0H⎡⎤∏=⎣⎦( )13、 不能对易的算符不可能具有共同的本征函数。
( )14、 当对本征态的性质A 进行测量时,能够得到的唯一仅有的值是算符ˆA的本征值。
( )15、 如果一个算符的平方等于单位算符,那么这个算符的本征值等于+1或者-1。
( )16、 所有品优的奇函数和偶函数都是宇称算符的本征函数。
( )17、 满足[]1212ˆˆˆ()()()()A c f x c g x c Af x c Ag x +=+的算符称为线性算符。
( )18、 所有的量子力学算符都可以通过经典力学中对应的关系式,并代入动量和坐标的量子力学算符而获得。
基础量子化学练习

2010基础量子化学练习(1)一、判断正误( )1、 一个态函数总是等于时间的函数乘以坐标的函数。
( )2、 态函数总是Hamiltonian 算符的本征函数。
( )3、 Hamiltonian 算符的本征函数的任意线性组合是Hamiltonian 算符的本征函数。
( )4、 如果态函数不是算符ˆA 的本征函数,则性质A 的一次测量可给出一个不是ˆA 的本征值的值。
( )5、 几率密度与时间无关。
( )6、 如果两个算符具有共同的本征函数,那么这两个算符可对易。
( )7、 算符ˆx 与d i dx-可对易。
( )8、 氢原子Hamiltonian 算符的束缚态的本征函数构成完备集。
( )9、 厄米算符的本征函数是正交的。
( )10、 描述电子轨道运动的波函数必须是奇函数。
二、已知:2ˆˆˆ,A d dx B x ==,计算2ˆˆˆˆ,()A B A B ⎡⎤+⎣⎦及三、已知:11223344ˆˆˆˆ,,,,A a A b A a A d ϕϕϕϕϕϕϕϕ====如果任意状态可以表示为12343253,ψϕϕϕϕ=+++那么当我们对该状态进行测量时,获得a 和d 的几率各是多少?求任意状态ψ 的性质A 的平均值。
2010基础量子化学练习(2)一、判断正误( )11、 算符ˆˆˆ,,A B C 满足ˆˆˆˆ,0,,0A B A C ⎡⎤⎡⎤==⎣⎦⎣⎦,则三个算符存在共同的本征函数集。
( )12、 ˆˆ,0H ⎡⎤∏=⎣⎦( )13、 不能对易的算符不可能具有共同的本征函数。
( )14、 当对本征态的性质A 进行测量时,能够得到的唯一仅有的值是算符ˆA的本征值。
( )15、 如果一个算符的平方等于单位算符,那么这个算符的本征值等于+1或者-1。
( )16、 所有品优的奇函数和偶函数都是宇称算符的本征函数。
( )17、 满足[]1212ˆˆˆ()()()()A c f x c g x c Af x c Ag x +=+的算符称为线性算符。
量子化学习题及答案

量⼦化学习题及答案量⼦化学习题及答案1.1998及2013年度诺贝尔化学奖分别授予了量⼦化学以及分⼦模拟领域的杰出贡献者,谈谈你的了解及认识。
答:1998年诺贝尔化学奖得主:⽡尔特·科恩和约翰·波普尔。
1964-1965年⽡尔特·科恩提出:⼀个量⼦⼒学体系的能量仅由其电⼦密度所决定,这个量⽐薛定谔⽅程中复杂的波函数更容易处理得多。
他同时还提供⼀种⽅法来建⽴⽅程,从其解可以得到体系的电⼦密度和能量,这种⽅法称为密度泛函理论,已经在化学中得到⼴泛应⽤,因为⽅法简单,可以应⽤于较⼤的分⼦。
沃尔特·库恩的密度泛函理论对化学作出了巨⼤的贡献。
约翰·波普尔发展了化学中的计算⽅法,这些⽅法是基于对薛定谔⽅程中的波函数作不同的描述。
他创建了⼀个理论模型化学,其中⽤⼀系列越来越精确的近似值,系统地促进量⼦化学⽅程的正确解析,从⽽可以控制计算的精度,这些技术是通过⾼斯计算机程序向研究⼈员提供的。
今天这个程序在所有化学领域中都⽤来作量⼦化学的计算。
2013年诺贝尔化学奖得主:马丁·卡普拉斯、迈克尔·莱维特、阿⾥耶·⽡谢勒。
他们为复杂化学系统创⽴了多尺度模型。
为研发了解和预测化学过程的强有⼒的计算机程序奠定了基础。
对于今天的化学家来说,计算机就像试管⼀样重要。
模拟过程是如此的真实以⾄于传统实验的结果也能被计算机预测出来。
多尺度复杂化学系统模型的出现⽆疑翻开了化学史的“新篇章”。
化学反应发⽣的速度堪⽐光速。
刹那间,电⼦就从⼀个原⼦核跳到另⼀个原⼦核,以前,对化学反应的每个步骤进⾏追踪⼏乎是不可能完成的任务。
⽽在由这三位科学家研发出的多尺度模型的辅助下,化学家们让计算机做“做帮⼿”来揭⽰化学过程。
20世纪70年代,这三位科学家设计出这种多尺度模型,让传统的化学实验⾛上了信息化的快车道。
2.谈谈你对量⼦化学中两种流派(VBT,MOT)的认识。
答:1926年,奥地利物理学家薛定谔(Schrodinger)建⽴了描述电⼦运动规律的波动⽅程。
量子化学习题集

(2) x, x2, 3x21; (3) sinx, cosx;
(4) sinx, cosx, tanx;
(5)
sin2x, cos2x, 1;
(6) sinx, cosx, eix (7) sin2x, cos2y, 1
2.2 三维势箱中一粒子的波函数是下列那些算符的本征函数?
ˆ x (2)p ˆx (1) p
x sin bxdx b
1
2
sin ax sin bxdx xe
bx
sin[(a b) x] sin[(a b) x] a 2 b2 2(a b) 2(a b)
x 1 dx 2 ebx b b 2 2x 2 bx x 2 bx 3 x e dx e 2 b b b
2 ˆ+ (3) 2,2|M |2,0; 2ˆ ˆ2 ˆ+ MzM|2,0 (6) 2,0|M
3.9 写出 2p 组态中 3P 谱项的全部波函数
第四章 近似方法
4.1 用尝试变分函数 e b x 求谐振子的基态能级和波函数。 4.2 对一维势箱中粒子应用线性变分函数 c1 x 2 (l x) c2 x(l x) 2 ,计算 n=1 和
2
A
A
2
A2 A ,用一
2
维势箱,验证 x 和 px 的不确定关系。
第三章 角动量、自旋和原子光谱
3.1 对 l=2,计算 L 与 z 轴之间可能的夹角。
2 ˆ 2 ˆx 3.2 证明球谐函数是算符M +M y的本征函数,并求其本征值。 →
ˆ x, M ˆ y]=iM ˆ z [M ˆ y, M ˆ z]=iM ˆ x [M ˆ z, M ˆ x]=iM ˆy 3.3 证明角动量的三个对易规则 [M ˆ = iM ˆ ˆ M 可合并写成 M ˆ x, M ˆ y, M ˆ z 为厄米算符。 3.4 证明:M ˆ ,G ˆ ]0),设为体系的某一状态,则有 3.5 如果两个力学量算符不对易([F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《量子化学基础》习题课1. 波粒二象性: λhP =,测不准关系x ∆·x ∆P ≧习题1.一粒微尘m=10-8kg,运动速度01.0=υm/s,若速度的不确定程度为810-=∆υm/s 可谓很精确,试计算位置的不确定程度.(h=6.626×10-34J.s)(答案:181063.6-⨯=∆x m)习题2.原子直径约为10A (10-10m),核外电子运动速度大约是光速的1%,计算速度的不确定度.(答案:6107⨯=∆υm)例1.已知光学光栅窄缝宽度为10-4cm,电子动能为105eV,试用测不准关系证明:用光学光栅观测不到电子衍射.解:单缝衍射如下图αsin P =P =∆P x x ①按干涉原理,图中电子射向屏中第一暗区,说明物质波相互抵消,上下两束电子波的光程差应为d/2.λαα=⋅∆=⋅=sin sin x d BC ②这里410-=∆=x d cm,meV h mE h h 22==P =λ (=m 9.11×10-31kg ;=e 1.602×10-19C) 51025.1225.12==V λ=3.87×10-12m 661210101087.3sin ---=⨯==m m d λα 0≈α 证毕. 习题3.计算动能为3000eV 的电子的de Brogle 波长(1eV=1.602×10-19J, V 3000C10602.1J 10602.130001919=⨯⨯⨯=--V ) (答案: 0A 2237.0300025.1225.12===V λ.) 2 .一维势箱: 2228ml h n E =,),2,1( =nx ln C x πsin )(2=ψ 习题4.计算箱宽为5×10-10m 的一维势箱中粒子n=1、2时的能量.及粒子从n=2跃迁到n=1时辐射的波长. (答案:E 1=2.41×10-19J,E 2=9.64×10-19J191023.7-⨯=∆E J 71075.2-⨯=λm)习题5.可将原子中的电子粗略的模拟为一维箱中粒子,箱的宽度为原子的尺度.计算在长度10A 的箱中电子两个最低能级之差(eV)和在此两能级间跃迁的光子波长(cm). (答案:21013.1⨯=∆E eV , 8101.1-⨯=λm)例2. 丁二烯(H 2C=CH-CH=CH 2)4个π电子(P z 电子),可以近似地看作长度为大Π键键长(已知:双键长035.1A 、单键长054.1A )的一维势箱中的4个粒子的运动.体系的基态向第一激发态的跃迁为:_______1_______2___________3___________4↑↓=↑↓===n n n n 1_______2________3________4___________=↑↓=↑=↑=n n n n求:体系基态向第一激发态的跃迁能(cm -1).解.箱长:m A A l 10001078.554.1235.12-⨯=⨯+⨯=.)23(888222222222223-=-=∆l m h l m h n l m h n E e e e 21031234)1078.5(1011.985)10626.6(m kg s J ---⨯⨯⨯⨯⨯⋅⨯=J 191002.9-⨯=.14834191054.4/10310626.61002.9----⨯=⨯⨯⋅⨯⨯=∆=cm s m s J J hc E ν 例3.有一个量子数为n 在长度为l 的一维箱中运动的粒子(1)计算在箱的左端41区找到粒子的几率.(2)n 为何值时该几率最大?(3)计算当n →∞时该几率的极限?解: 2sin 2141)sin 2(2410πππn n dx x l n l P -==⎰⎪⎩⎪⎨⎧==-==8,6,4,2,015,11,7,3,113,9,5,1,12sin n n n n 当当当π 即,n=3时,P 最大.π6141max +=P . 41)2sin 2141(lim =-∞→ππn n n (该式说明:当n →∞时量子力学问题还原为经典(力学)问题,因为经典力学处理一维箱问题在左端1/4处的几率正是1/4.)习题6.有一质量为1g 的小球,在长为10cm 的一维箱中运动小球速度0.1cm/s,试求小球的量子数n 是多少 ? (答案:n=3.018×1026) 3. 一位谐振子:m k πν21=)21(+=υνh E ( 3,2,1,0=υ) 习题7.HI 近红外光谱的基本振动频率22300=-ν.1cm -1,求HI 键的弹力常数k . (答案:k =2.93×105 D.cm -1) 习题8.已知H 2和Cl 2的基本振动频率分别为24.4395)(20=H νcm -1,9.564)(20=Cl νcm -1,求它们的零点能. (答案:E 0(H 2)=6.28kg/mol, E 0(Cl 2)=0.807kg/mol) 例 4.利用简谐振动公式:)sin()(φω+=t C t x ,证明一维谐振子的总能量是常数:221kC E =解:)(sin 21)(cos 2122222φωφωω+++=+=t kC t C m V T E m k =2ω ,带入上式,得: 221kC E =. 习题9.若H 35Cl 基本振动频率13010667.8⨯=νs -1,试求H 37Cl 的基本振动频率,设它们键的力常数相同.(答案:8.660×1013s -1) 4. 刚性转子:)1(22+=l l IE ( 3,2,1,0=l ) )1(2)(+=l B l ν (式中Ic hB 28π=) 例5.由HCl 的远红外光谱数据得知HCl 的转动能级相邻谱线间距为20.74cm -1,求HCl 分子的键长r.解: c r hIc h B 222442μππν===∆24231063.11002.6)45.35008.1(45.35008.1-⨯=⨯+⨯=+⋅=Cl H Cl H m m m m μg/mol 211024227212)2/74.20(1031063.1)1416.3(810626.6)8(][⨯⨯⨯⨯⨯⨯==--cB h r μπ =1.287×10-8cm=1.2870A习题10.从CN 的微波谱知道一系列谱线的间距皆为3.7978cm -1,求该分子的核间距r.(答案:r=1.172×10-10m)习题11.已知CN +的键长是1.290A ,指出CN +微波谱的第一到第四条线的位置.(答案:3.134cm -1,6.268cm -1,9.402cm -1,12.536cm -1 5.算符:),,(t q P F ∧∧其中q i ∂∂-=P ∧与本征函数:∧A )(x f =k )(x f习题12.写出下列物理量的算符:(1)动量P,(2)动量3y p ,(3)x y yp xp -,(4)动能T( 答案(1))(z k y j x i i P ∂∂+∂∂+∂∂-=∧,(2)3333y i P y ∂∂=∧(3))()(x y y x i p y p x L x y z ∂∂-∂∂-=-=∧∧∧ (4) )(22222222z y x m T ∂∂+∂∂+∂∂-=∧) 13.计算算符222kx dx d A -=∧的本征函数2x e α-的本征值(答案:22)24()(222222x x e kx x e kx dx d αααα----=- )14.利用[∧D ,∧x ]=1,(1)计算2)(x D +∧,(2)))((x D x D -+∧∧ (答案:(1)2)(x D +∧1222+++=∧x D x D (2)1))((22--=-+∧∧∧x D x D x D )15.三维箱中粒子的波函数是下列那些算符的本征函数(1)∧x p ,(2)∧2x p ,(3)∧2z p ,(4)∧2x .(答案(2),(3) )6.对易计算以下对易恒等式可方便对易运算:①.],[],[∧∧∧∧-=A B B A②.0],[=∧∧n A A (n=1,2,3…)③.],[],[],[∧∧∧∧∧∧==B A k kB A B kA④],[],[],[∧∧∧∧∧∧∧+=+C A B A C B A⑤ ],[],[],[∧∧∧∧∧∧∧∧∧+=C A B C B A C B A 例6.计算对易子:],[∧x P x ,],[2∧x P x ,],[∧H x ,],[∧∧H P x .解: i i x x i x x i x i x P x x =-=∂∂-=∂∂=∂∂=∧],[],[],[],[ ],[],[],[2∧∧∧∧∧+=x x x x x P x P P P x P xx i i x i i ∂∂⋅+∂∂⋅= x ∂∂=22)](21,[],[)],,(,[],[222∧∧∧∧∧∧++==+=z y x P P P m x T x z y x V T x H x ∧∧=∂∂==x x P mi x m P x m 22],[21 ],[)](,[21],[222V P P P P P m H P x z y x x x ∧∧∧∧∧∧∧+++= x V i V x i V P x ∂∂-=∂∂-==∧],[],[(式中x V f x f V x Vf f x V V x f V x ∂∂=∂∂-∂∂=∂∂-∂∂=∂∂)()(],[)16.计算:],[222c bx ax dx d ++ (答案: ],[222c bx ax dx d ++=dxd b ax a )24(2++. ) 例7.证明:222)(〉〈-〉〈=∆A A A解: 〉〉〈-〈≡≡∆∧222)()(A A A A στψψd A A ⎰〉〈-=∧*2)( τψψτψψτψψτψψd A d A A d A A d A ⎰⎰⎰⎰〉〈+〉〈-〉〈-=*∧*∧*∧*22τψψτψψτψψd A d A A d A A A ⎰⎰⎰*∧*∧*〉〈+〉〈-〉〈-〉〈=22 2222〉〈+〉〈-〉〈-〉〈=A A A A 22〉〈-〉〈=A A 证毕 7. H 原子薛定谔方程的解222204118n R n h e E n -=-=εμ (n=1,2,…),其中22048h e R εμ-=. )()()(,,,θϕθϕψm l l n m l n Y r R r =)()()(,,ϕθm m l l n r R ΦΘ=ϕθim ml na Zr i l l n i i e P e a Zr c C )(cos })({0101--+-=∑= 氢原子波函数受控于三个量子数(m l n ,,)∞=,,2,1 n1,,2,1,0-=n ll m ±±±=,,2,1,0习题17.下列函数(1)2P z ,(2)2P x ,(3)2P 1分别是算符∧H 、∧2L 、∧z L 中哪个的本征函数. (答案:(1)、(3)全是,(2)是∧H 、∧2L 的本征函数) 习题18.对H 原子P 态,测量L Z 的可能值为h 、0、-h,问在下列函数中测量L Z 得到各可能值的几率.(1)Pz 2ψ,(2) Px 2ψ,(3) 12P ψ(答案:(1) 121211210200-⋅+⋅+=ψψψψPz得0值几率为1,得h 、-h 几率为0. (2) 121211*********-++⋅=ψψψψPx 得h 、-h 几率各为21,得0值几率为0.(3) 12P ψ=211ψ,得h 几率为1,其余为0) 例8.已知H 原子)(ϕΦ方程复数解:ϕπϕim m e 21)(=Φ,(1)验证)(ϕm Φ是归一化的.(2)证明)(ϕm Φ是算符ϕ∂∂-=∧ i L z 的本征函数.而)(ϕm Φ线性组合的实函数: ⎪⎪⎩⎪⎪⎨⎧=Φ=Φϕπϕϕπϕm m m msin 1)(cos 1)('`不是∧z L 的本征函数.解:(1)121212020202===ΦΦ=Φ⎰⎰⎰⎰-*ππϕϕπϕπϕπϕϕd d e e d d im im (2) )(21)(ϕπϕϕϕm im m z m e i L Φ±=∂∂-=Φ±∧而 ϕπϕπϕϕm m i m i L m z sin cos 1)( =∂∂-=Φ∧不构成本征方程: )()(ϕϕm m z c L Φ≠Φ∧.例如n=2,l =1的H 原子波函数是p 轨道,有三个状态(m=1,0,-1),其复函数形式为:θθϕψcos )()(0,1,2r r f r = (即:z p p 也是0)ϕθθϕψi e r r f r ±±=sin )()('1,1,2 (即:11-p p 和)其中复函数z p p 等于实函数0,复函数11-p p 和线性组合为实函数y x p p ,,即ϕθθϕϕcos sin )()(sin )(11r R N e e r R N p i i x =+=- ϕθθϕϕsin sin )()(sin )(11r R N e e r R N p i i y =-=- 因此,z p p 和0都是∧z L 的本征函数. 11-p p 和也是∧z L 的本征函数.只有y x p p ,不是∧z L 的本征函数.P 轨道的实函数与复函数形式都是体系的状态函数,但表示图形不一样:例9.对H 原子基态,(1)求2倍玻耳半径之外的电子几率.(2)玻耳半径之的电子几率. 解:H 原子基态,n=1,0=l ,m=0301,,,1)()()(a r s ml l n m l n eaY r R r -=→=πψθϕθϕψ(1)设P 2为02a 之外的电子几率 ϕθθπτψππd drd re a d P a r a s sin 1122200203021200-⎰⎰⎰⎰==-⎰⎰⎰-=ππϕθθπ2022023sin 10d d dr e r a a r adr e r a a ra 002202304-⎰=ππ利用积分公式][0203020022302)82422(41a a r ara a r ea P ---=--)22(3222b b x b x e dx e x bx bx +-=⎰]4)44448([430303030430a a a a e a +---=- 4131e -= 即: 24.01342==e P(2)设1P 是玻耳半径0a 之的电子几率,则dr e r a P a r a 02023014-⎰=][00302002230)82422(4a a r a ra a r e a ---=-]4)44242([430303030230a a a a e a +---=-32.0512=-=e例10.已知类氢离子基态波函数 03031a zr s ea z-=πψ,(1) 求半径r 的平均值.(2)r 的最可几值.解:(1)ϕθθπτψψππd drd r ea zd r r a zr ssin 32002030310-∞*⎰⎰⎰⎰==〉〈dr er a za zr 02033034-∞⎰⋅=ππ利用广义积分公式:10!+∞-=⎰n qxn qn dx ex (0,1>->q n )z a a z a z dr e r a z r a zr23)2(!344040303023330=⋅==〉〈⎰∞-(2)径向分布函数: 0223032214)(a zr ser a z r r R D -=⋅=求最可几半径就是求最大径向分布函数时r,0)22(4)(40202230322303=-==---a zr a zr a zr ea z r rea zer dr d a z dr dD020=-r r a z 即, z a r 0=为最可几半径.。
