二次函数之二次函数中的面积问题1

合集下载

初中数学中考二轮6二次函数中的面积问题(1)

中考压轴题:二次函数中的面积问题学生姓名年级学科授课教师日期时段核心内容二次函数中求面积最值，图形平移或折叠面积问题课型一对一/一对N教学目标1.会利用函数的图象性质来研究几何图形的面积最值问题；2.掌握几种求图形面积的常见解题方法与技巧，如：割补法、平行等积变换法等。

3.掌握图形平移或折叠变换过程中找等量关系列函数解析式求图形面积问题的一般方法．重、难点割补法求三角形面积，动态问题一般解题思路。

课首沟通1、上次的作业给我看看，完成了没有？还有不会的题吗？2、在初中学习二次函数过程中，是否还存在思维障碍和知识点？3、面对二次函数图象中的图形平移得到面积问题能不能自我总结出一般法则呢？知识导图导学一：二次函数中求面积的最值知识点讲解 1：直接公式法求解图形面积S△ = a ha d (d表示已知点到直线的距离)2、割补（和差）法以动点作垂直(平行)x轴的直线，即铅垂高，再分别过点A,C作PF的高，即和为水平宽。

S△ = ×水平宽×铅垂高如下图：或S△ =3、平行线等积变换①等底等高的两个三角形面积相等．②底在同一条直线上并且相等，该底所对角的顶点是同一个点或在与底平行的直线上，这两个三角形面积相等．如图，AD∥BC中，AC与BD交点O，则S△ABC= S△DBC，S△AOB =S△COD例 1. （2015潍坊中考改编）如图，在平面直角坐标系中，抛物线y＝mx2－8mx＋4m＋2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2－x1＝4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线，直线AD的交点分别为P，Q．（1）求抛物线的解析式；（2）当0＜t≤8时，求△APC面积的最大值．【学有所获】图形面积的求法常见有三种，分别是：(1)(2)(3)[学有所获答案] (1) 直接公式求法(2) 割补法(3) 平行线等积变换法我爱展示1.（2014海珠一模）如图，已知抛物线y＝x2＋bx＋c与轴交于A，B两点（点A 在点B的左侧）与轴交于点C（0，－3），对称轴是直线x＝1，直线BC与抛物线的对称轴交于点D，点E为y轴上一动点，CE的垂直平分线交抛物线于P，Q两点（点P在第三象限）（1）求抛物线的函数表达式和直线BC的函数表达式；（2）当△CDE是直角三角形，且∠CDE＝90°时，求出点P的坐标；（3）当△PBC的面积为时，求点E的坐标．2.（2015越秀期末考试）如图，已知抛物线y＝x2＋ax＋4a与x轴交于点A，B，与y轴负半轴交于点C且OB＝OC，点P为抛物线上的一个动点，且点P位于x轴下方，点P与点C不重合．（1）求该抛物线的解析式；（2）若△PAC的面积为，求点P的坐标；（3）若以A，B，C，P为顶点的四边形面积记作S，则S取何值时，对应的点P有且只有2个?导学二：二次函数中的图形平移、折叠问题知识点讲解 1：二次函数、一次函数图象平移法则将（）的图像如何平移到的图像。

二次函数面积问题(整)

二次函数面积问题(整)1.题型一：割补法1.1 求解析式已知抛物线经过点A（4，）和点B（，2），且对称轴为直线l，顶点为C，求解析式。

由对称性可知，顶点C的横坐标为4/2=2，代入抛物线方程得2b+c=-4，又由于抛物线经过点A和B，代入方程可得2b+c=16和-b+c=2.解方程组得b=-3，c=2，代入方程y=-x^2-3x+2即可得到解析式。

1.2 求面积连接AC、BC、BD，求四边形ADBC的面积。

由于AC和BC在对称轴上，所以它们的长度相等。

设AC=BC=x，由顶点C的坐标可知，AC和BC的纵坐标分别为2和-2，因此四边形ADBC的面积为x*4+1/2*x*(-4)=2x。

2.如图，在直角坐标系中，已知直线y=x+4与y轴交于A 点，与x轴交于B点，C点坐标为（-2，），求解析式和四边形AOBM的面积。

2.1 求解析式由于抛物线经过点A、B、C，所以可以列出三个方程，分别是c=4，a+b+c=0，4a-2b+c=-2.解方程组得a=1，b=-3，c=4，因此抛物线的解析式为y=x^2-3x+4.2.2 求面积设抛物线的顶点为M，连接AM和XXX，求四边形AOBM的面积。

由于抛物线的对称轴与x轴垂直，所以顶点M的横坐标为1.5，代入抛物线方程可得纵坐标为4.25.因此，四边形AOBM的面积为1/2*2*4.25=4.25.3.已知抛物线y=3(x+1)^2-12如图所示3.1 求交点坐标抛物线与y轴的交点为(-3,-3)，因为当x=0时，y=-3.抛物线与x轴的交点为(-3±2√3,0)，因为当y=0时，x=-1±√3.3.2 求面积设顶点D的坐标为(-1,0)，连接AD和BD，求四边形ABCD的面积。

由于AD和BD在对称轴上，所以它们的长度相等。

设AD=BD=x，由顶点D的坐标可知，AD和BD的纵坐标分别为3和-3，因此四边形ABCD的面积为x*6+1/2*x*6=9x。

二次函数中的面积计算问题(包含铅垂高)

(D)二次函数中的面积计算问题【典型例子】例如，如图所示，二次函数2y x bx c =++图像x 在A 和B 两点（A 在B 的左边）与y 轴相交，在C 点与轴相交，顶点为M ，MAB ∆为直角三角形，图像的对称轴是一条直线2-=x ，该点P 是两点之间抛物线上的移动点,A C ，则PAC ∆面积的最大值为（C ）A.274 B. 112C 。

278D.3 二次函数中常见的面积问题类型：1.选择填空的简单应用2.不规则三角形的面积用S=3.使用4.使用相似的三角形5.使用分割法将不规则图形转为规则图形例 1如图 1 所示，已知正方形ABCD 的边长为 1 ， E , F , G , H 为每边的点， AE=BF=CG=DH ，设面积为小s 正方形EFGH 为, AE 为x , 那么about s 的x 函数图大致为 (乙)示例 2.回答以下问题：如图1所示，抛物线的顶点坐标为C 点( 1,4 )，与x 轴相交于A 点( 3 , 0)，与y 轴相交于B 点。

抛物线和直线AB 的解析公式；(2)求△ CA AB 和S △ CAB 的垂直高度CD ；(3)假设点P 是抛物线上（第一象限）上的一个移动点，是否存在点P ，使得S △ PA B = 89S △ CA B ，如果存在，求点P 的坐标；如果不存在，请解释原因。

思想分析这个问题是二次函数中的常见面积问题。

该方法不是唯一的。

可以使用截补法，但是有点麻烦。

如图第10题xyABCOM图1B铅垂高水平宽ha图2A xC Oy ABD 112所示，我们可以画出一种计算三角形面积的新方法：ah S ABC 21=∆即三角形的面积等于水平宽度与前导垂直乘积的一半。

掌握了这个公式之后，思路就直截了当，过程也比较简单，计算量也相对少了很多。

答：（1）据已知，抛物线的解析公式可以设为y 1 = a ( x - 1 ) 2+ 4 ( a ≠ 0 ) 。

将A (3, 0)代入解析表达式，得到a = - 1 ，∴抛物线的解析公式为y 1 = - ( x - 1 ) 2+ 4，即y 1 = - x 2+2 x +3。

二次函数与面积问题

二次函数与面积问题一、引言二次函数是高中数学中的重要内容之一，它在实际生活中有许多应用。

其中之一就是与面积问题相关联。

本文将详细讨论二次函数与面积问题的关系，并分析实际应用。

首先，我们将介绍二次函数的基本概念和公式，然后探讨如何利用二次函数解决面积问题。

二、二次函数基本概念2.1 二次函数的定义二次函数是指具有形如f(x)=ax2+bx+c的函数，其中a、b、c为实数且a≠0。

二次函数的图像通常为一个抛物线。

2.2 二次函数的图像与性质二次函数的图像可分为三种情况：开口向上、开口向下和与x轴相切。

其开口的方向由二次项的系数a决定。

二次函数还具有顶点坐标、对称轴和零点等性质，这些性质对于解决面积问题非常关键。

2.3 二次函数的标准形式和一般形式二次函数可通过变换转化为标准形式或一般形式。

标准形式为f(x)=a(x−ℎ)2+ k，其中(ℎ,k)为顶点坐标。

一般形式为f(x)=ax2+bx+c。

三、二次函数与面积问题3.1 二次函数与矩形面积问题矩形是我们生活中常见的图形之一。

假设一个矩形的长度为x，宽度为y，则它的面积A可以表示为A=xy。

现在，我们希望找到一个长度固定的矩形，使得它的面积最大。

我们可以建立一个二次函数来解决这个问题。

首先，根据矩形的面积公式A=xy，我们可以将y表示为x的函数：y=Ax。

然后，我们将该函数进行变形，得到一个二次函数的标准形式。

将x的取值范围限定为正实数，我们可以排除矩形不存在的情况。

通过对二次函数的顶点坐标求解，我们可以找到使得面积最大的矩形。

3.2 二次函数与三角形面积问题二次函数与三角形面积问题也有密切的联系。

考虑一个等腰三角形，已知其底边长为x，高为y。

我们希望找到一个底边固定的三角形，使得它的面积最大。

根据三角形的面积公式A=12xy，我们可以得到y=2Ax。

类似地，我们将其转化为二次函数的形式，并求解顶点坐标，从而找到最大面积的三角形。

3.3 二次函数与其他面积问题除了矩形和三角形，二次函数还可以应用于其他形状的面积问题，如圆形、梯形等。

二次函数中的面积最值问题最佳处理方法

因材教育二次函数中的面积最值问题从近几年的各地中考试卷来看，求面积的最值问题在压轴题中比较常见，而且通常与二次函数相结合．使解题具有一定难度，本文以一道中考题为例，介绍几种不同的解题方法，供同学们在解决这类问题时参考．如图1，抛物线y＝－x2＋bx＋c与x轴交于A(1，0)，B(－3，0)两点．(1)求该抛物线的解析式；(2)设(1)中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC 的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；(3)如图2，在(1)中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由．解答(1)抛物线解析式为y＝－x2－2x＋3；(2)Q(－1，2)；下面着重探讨求第(3)小题中面积最大值的几种方法．一、补形、割形法几何图形中常见的处理方式有分割、补形等，通过对图形的这些直观处理，一般能辅助解题，使解题过程简捷、明快．此类方法的要点在于把所求图形的面积进行适当的补或割，变成有利于表示面积的图形．方法一如图3，设P点（x，－x2－2x＋3）(－3<x<0)．方法二如图4，设P 点(x ，－x 2－2x ＋3)(－3<x<0)．（下略．）二、“铅垂高，水平宽”面积法如图5，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a)，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h)”，我们可得出一种计算三角形面积的另一种方法：S △ABC ＝12ah ，即三角形面积等于水平宽与铅垂高乘积的一半．根据上述方法，本题解答如下：解如图6，作PE ⊥x 轴于点E ，交BC 于点F ．设P 点（x ，－x 2－2x ＋3）（－3<x<0）．∴点P 坐标为（－32，154）三、切线法若要使△PBC 的面积最大，只需使BC 上的高最大．过点P 作BC 的平行线l ，当直线l 与抛物线有唯一交点(即点P)时，BC 上的高最大，此时△PBC 的面积最大，于是，得到下面的切线法．解如图7，直线BC 的解析式是y ＝x ＋3，过点P 作BC 的平行线l ，从而可设直线l 的解析式为：y ＝x ＋b ．＝278．四、三角函数法本题也可直接利用三角函数法求得．解如图8，作PE ⊥x 轴交于点E ，交BC 于点F ，怍PM ⊥BC 于点M ．设P 点（x ，－x 2－2x ＋3）（－3<x<0），则F(x ，x ＋3)．从以上四种解法可以看到，本题解题思路都是过点P 作辅助线，然后利用相关性质找出各元素之间的关系进行求解．如此深入挖掘一道题的多种解法，可使我们摆脱题海战术，提高解题能力．同时，善于总结一道题的多种解法能加快解题速度，提高解题效率，也有利于培养我们的钻研能力和创新精神．二次函数之面积问题（讲义）一、知识点睛1.二次函数之面积问题的处理思路①分析目标图形的点、线、图形特征；②依据特征、原则对图形进行割补、转化；③设计方案，求解、验证．面积问题的处理思路：公式、割补、转化．坐标系背景下问题处理原则：________________________，__________________________．2.二次函数之面积问题的常见模型①割补求面积——铅垂法：1()2APB B A S PM x x =⋅⋅-△1()2APB B A S PM x x =⋅⋅-△②转化法——借助平行线转化：若S △ABP =S △ABQ ，若S △ABP =S △ABQ ，当P ，Q 在AB 同侧时，当P ，Q 在AB 异侧时，PQ ∥AB ．AB 平分PQ ．二、精讲精练1.如图，抛物线经过A(-1，0)，B(3，0)，C(0，3)三点．（1）求抛物线的解析式．（2）点M是直线BC上方抛物线上的点（不与B，C重合），过点M作MN∥y轴交线段BC于点N，若点M的横坐标为m，请用含m 的代数式表示MN的长．（3）在（2）的条件下，连接MB，MC，是否存在点M，使四边形OBMC的面积最大？若存在，求出点M的坐标及四边形OBMC的最大面积；若不存在，请说明理由．2.如图，抛物线322++-=x x y 与直线1+=x y 交于A ，C 两点，其中C点坐标为(2，t )．（1）若P 是直线AC 上方抛物线上的一个动点，求△APC 面积的最大值．（2）在直线AC 下方的抛物线上，是否存在点G ，使得6AGC S =△？如果存在，求出点G 的坐标；如果不存在，请说明理由．3.如图，抛物线223y x x =--与x 轴交于A ，B 两点，与直线y x p =-+交于点A 和点C (2，-3).（1）若点M 在抛物线上，且以点M ，A ，C 以及另一点N 为顶点的平行四边形ACNM 的面积为12，求M ，N 两点的坐标．（2）在（1）的条件下，若点Q 是x 轴下方抛物线上的一动点，当△QMN 的面积最大时，请求出△QMN 的最大面积及此时点Q 的坐标．4.如图，抛物线223y x x =-++与x 轴交于A ，B 两点，与y 轴交于点C ，对称轴与抛物线交于点P ，与直线BC 交于点M ，连接PB ．（1）抛物线上是否存在异于点P 的一点Q ，使△QMB 与△PMB 的面积相等？若存在，求出点Q 的坐标；若不存在，请说明理由．（2）在第一象限对称轴右侧的抛物线上是否存在一点R ，使△RMP 与△RMB 的面积相等？若存在，求出点R 的坐标；若不存在，请说明理由．5.如图，已知抛物线2y x bx c =++与x 轴交于点A (1，0)和点B ，与y 轴交于点C (0，-3)．（1）求抛物线的解析式．（2）如图，已知点H (0，-1)．①在x 轴下方的抛物线上是否存在点D ，使得S △ABH =S △ABD ？若存在，求出点D 的坐标；若不存在，请说明理由．②在抛物线上是否存在点G （点G 在y 轴的左侧），使得S △GHC =S △GHA ？若存在，求出点G 的坐标；若不存在，请说明理由．【参考答案】一、知识点睛充分利用横平竖直的线段长函数特征几何特征互转二、精讲精练12。

二次函数中的面积问题

二次函数中的面积问题
二次函数中的面积问题是一个广泛应用的数学概念。通过深入研究二次函数，我们可以探索其标准式、图像、交点、对称轴以及顶点等属性，进而应用面积公式解决各种实际问题。
什么是二次函数
二次函数是一个以x的二次项为特征的函数。它的标准形式为y=ax^2+bx+c，其中a、b、c是常数。二次函数的图像通常呈现开口向上或向下的抛物线形状。
二次函数的变形及面积问题的应用
通过对二次函数进行平移、缩放和翻转等变形操作，可以解决更加复杂的面积问题，例如计算部分面积的问题。
二次函数的导数是代表函数斜率的函数，可以通过求导得到。导函数即为二次函数的一阶导数。
求二次函数的最小值及最大值
二次函数的最小值或最大值是函数的极值点。可以通过求导数和解方程得到最小值或最大值的坐标。
二次函数与勾股定理
二次函数与勾股定理有一定的联系。通过勾股定理，我们可以计算二次函数的斜边长度或直角边长。
要计算二次函数与坐标轴的交点，可以将函数等于零得到二次方程，然后使用求根公式解方程。交点包括x轴与y轴的交点。
二次函数的对称轴
对称轴是二次函数的一个重要属性，通过对称轴可以找到抛物线的对称中心。对称轴的公式为x=-b/2a。
求二次函数的顶点及最值
顶点是二次函数的极值点，可以通过求导数或通过对称轴的坐标计算得出。最值可以是极大值或极小值，具体取决于抛物线的开口方向。
二次函数与坐标系围成的面积
二次函数与坐标系围成的面积可以通过计算二次函数与x轴、y轴围成的矩形面积和差值的方式得到。
求二次函数与x轴围成的面积
要求二次函数与x轴围成的面积，可以将函数转化为标准形式，计算定积分，或通过求解二次方程得到交点坐标进而计算面积。

二次函数中的面积问题

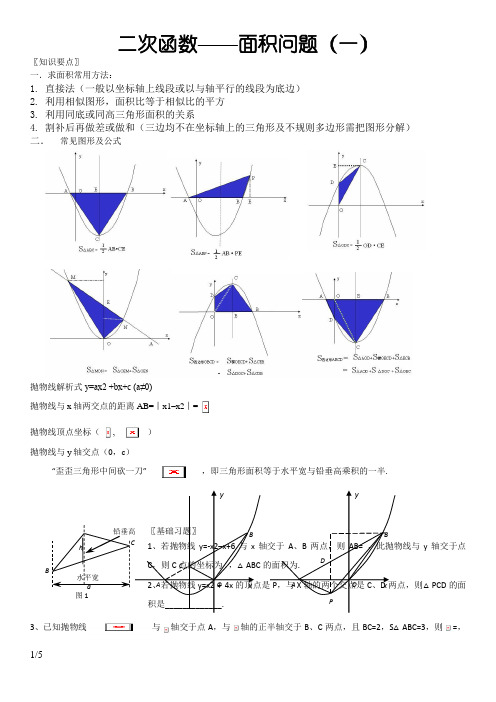
二次函数——面积问题（一）〖知识要点〗一．求面积常用方法：1. 直接法（一般以坐标轴上线段或以与轴平行的线段为底边）2. 利用相似图形，面积比等于相似比的平方3. 利用同底或同高三角形面积的关系4. 割补后再做差或做和（三边均不在坐标轴上的三角形及不规则多边形需把图形分解）二．常见图形及公式抛物线解析式y=ax2 +bx+c (a≠0)抛物线与x 轴两交点的距离AB=︱x1–x2︱=抛物线顶点坐标（-, ）抛物线与y 轴交点（0，c ）“歪歪三角形中间砍一刀”，即三角形面积等于水平宽与铅垂高乘积的一半. 〖基础习题〗 1、若抛物线y=-x2–x+6与x 轴交于A 、B 两点，则AB= ，此抛物线与y 轴交于点C ，则C 点的坐标为，△ABC 的面积为.2、若抛物线y=x2 + 4x 的顶点是P ，与X 轴的两个交点是C 、D 两点，则△PCD 的面积是_____________.3、已知抛物线与轴交于点A ，与轴的正半轴交于B 、C 两点，且BC=2，S △ABC=3，则=，B C 铅垂高水平宽ha图1 C BA O y x DB A O y x P=．〖典型例题〗● 面积最大问题1、二次函数的图像与轴交于点A （-1,0）、B （3，0），与轴交于点C ，∠ACB=90°.（1）求二次函数的解析式；（2）P 为抛物线X 轴上方一点，若使得△PAB 面积最大，求P 坐标（3）P 为抛物线X 轴上方一点，若使得四边形PABC 面积最大，求P 坐标(4) P 为抛物线上一点，若使得，求P 点坐标。

● 同高情况下，面积比=底边之比2．已知：如图，直线y=﹣x+3与x 轴、y 轴分别交于B 、C ，抛物线y=﹣x2+bx+c 经过点B 、C ，点A 是抛物线与x 轴的另一个交点．（1）求B 、C 两点的坐标和抛物线的解析式；（2）若点P 在直线BC 上，且，求点P 的坐标．3．已知：m 、n 是方程x2﹣6x+5=0的两个实数根，且m ＜n ，抛物线y=﹣x2+bx+c 的图象经过点A （m ，0）、B （0，n ）．（1）求这个抛物线的解析式；（2）设（1）中抛物线与x 轴的另一交点为C ，抛物线的顶点为D ，试求出点C 、D 的坐标和△BCD 的面积；（注：抛物线y=ax2+bx+c （a≠0）的顶点坐标为（3）P 是线段OC 上的一点，过点P 作PH ⊥x 轴，与抛物线交于H 点，若直线BC 把△PCH 分成面积之比为2：3的两部分，请求出P 点的坐标． yx B A C O三角形面积等于水平宽与铅垂高乘积的一半4．阅读材料：如图，过△ABC的三个顶点分别作出水平垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可以得出一种计算三角形面积的新方法：S△ABC=ah，即三角形面积等于水平宽与铅垂高乘积的一半．解答下列问题：如图，抛物线顶点坐标为点C（1，4）交x轴于点A，交y轴于点B（0，3）（1）求抛物线解析式和线段AB的长度；（2）点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；（3）在第一象限内抛物线上求一点P，使S△PAB=S△CAB．法一：同底情况下，面积相等转化成平行线法二：同底情况下，面积相等转化成铅垂高相等变式一：如图2，点P是抛物线（在第一象限内）上的一个动点，连结PA，PB，是否存在一点P，使S△PAB=S△CAB？若存在，求出P点的坐标；若不存在，请说明理由．变式二：抛物线上是否存在一点P，使S△PAB=S△CAB？若存在，求出P点的坐标；若不存在，请说明点动+面积5．如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm，如果点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s，连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．解答下列问题：（1）当t为何值时，PQ∥BC．（2）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在求出此时t的值；若不存在，请说明理由．（3）如图2，把△APQ沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由．形动+面积6．如图1，抛物线y=ax2+bx+3（a≠0）与x轴、y轴分别交于点A（﹣1，0）、B（3，0）、点C三点．（1）试求抛物线的解析式；（2）点D（2，m）在第一象限的抛物线上，连接BC、BD．试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由；（3）如图2，在（2）的条件下，将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，记平移后的三角形为△B′O′C′．在平移过程中，△B′O′C′与△BCD重叠的面积记为S，设平移的时间为t秒，试求S与t之间的函数关系式？。

二次函数中面积问题

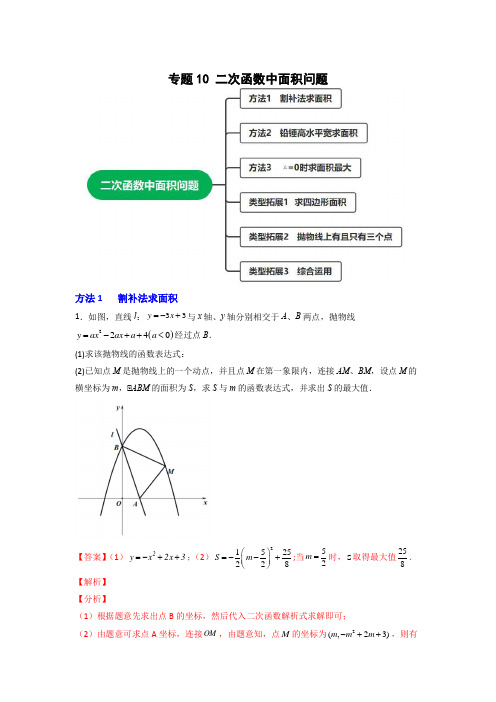
专题10 二次函数中面积问题方法1 割补法求面积1．如图，直线l ：33y x =-+与x 轴、y 轴分别相交于A 、B 两点，抛物线()2240y ax ax a a =-++<经过点B ．(1)求该抛物线的函数表达式：(2)已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM 、BM ，设点M 的横坐标为m ，△ABM 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值．【答案】（1）2y x 2x 3=-++；（2）21252528S m ⎛⎫=--+ ⎪⎝⎭;当52m =时，S 取得最大值258．【解析】【分析】（1）根据题意先求出点B 的坐标，然后代入二次函数解析式求解即可；（2）由题意可求点A 坐标，连接OM ，由题意知，点M 的坐标为2(,23)m m m -++，则有03m <<，然后根据割补法求面积即可．【详解】解：（1）把0x =代入33y x =-+得3y =， △(0,3)B ．把(0,3)B 代入224y ax ax a =-++，得34a =+，△1a =-．△抛物线的解析式为2y x 2x 3=-++；（2）令0y =，则2230x x -++=，解得1x =-或3， △抛物线与x 轴的交点横坐标分别为1-和3． △点M 在抛物线上，且在第一象限内， △03m <<．将0y =代入33y x =-+，得033x =-+，解得1x =， △(1,0)A ．如解图，连接OM ，由题意知，点M 的坐标为2(,23)m m m -++，则2111(31)2223132AOBOBMOAMAOBOAMB S S SSSSm m m =-=+-=⨯⨯+⨯-⨯-++⨯⨯四边形 2215122522528m m m ⎛⎫=-+=--+⎪⎝⎭， △102-<，且03m <<， △当52m =时，S 取得最大值258．【点睛】本题主要考查二次函数的综合，熟练掌握二次函数的性质是解题的关键．方法2 铅锤高水平宽求面积2．如图，抛物线y ＝ax 2+bx+c 经过A （0，3）、B （﹣1，0）、D （2，3），抛物线与x 轴的另一交点为E,点P 为直线AE 上方抛物线上一动点，设点P 的横坐标为t ．（1）求抛物线的表达式；（2）当t 为何值时，△PAE 的面积最大？并求出最大面积；解：（1）由题意得：4233a b ca b cc-+=⎧⎪++=⎨⎪=⎩，解得：123abc=-⎧⎪=⎨⎪=⎩，△抛物线解析式为y＝﹣x2+2x+3；（2）△A（0，3），D（2，3），△抛物线对称轴为x＝1，△E（3，0），设直线AE的解析式为y＝kx+3，△3k+3＝0，解得，k＝﹣1，△直线AE的解析式为y＝﹣x+3，如图1，作PM△y轴，交直线AE于点M，设P（t，﹣t2+2t+3），M（t，﹣t+3），△PM＝﹣t2+2t+3+t﹣3＝﹣t2+3t，△12PAE PMA PMES S S PM OE=+=⋅＝()21332t t⨯⨯-+＝23327228t⎛⎫--+⎪⎝⎭，△t＝32时，△PAE的面积最大，最大值是278．方法3 △=0时求面积最大3．如图，二次函数的图象与轴交于、两点，与轴交于点，已知点（－1，0），点C(0，－2)．（1）求抛物线的函数解析式；（2）若点是线段下方的抛物线上的一个动点，求面积的最大值以及此时点的坐标．（1）将A （－1，0）、点C(0，－2)．代入232y ax x c =-+ 求得：213222y x x =-- （2）已求得：B （4，0）、C （0，-2），可得直线BC 的解析式为：y=12x -2；设直线l△BC ，则该直线的解析式可表示为：y=12x+b ，当直线l 与抛物线只有一个交点时，可列方程：12x+b=12x 2-32x -2，即：12x 2-2x -2-b=0，且△=0； △4-4×12（-2-b ）=0，即b=-4； △直线l ：y=12x -4．所以点M 即直线l 和抛物线的唯一交点，有： 213222{142y x x y x =--=-，解得：2{3x y ==-即 M （2，-3）．过M 点作MN△x 轴于N ，S△BMC=S 梯形OCMN+S△MNB -S△OCB=12×2×（2+3）+12×2×3-12×2×4=4． △点M （2，﹣3），△MBC 面积最大值是4. 考点：二次函数综合题．类型拓展1 求四边形面积4．如图1，在平面直角坐标系中，一次函数y ＝12x ﹣2的图象与x 轴交于点B ，与y 轴交于点C ，抛物线y ＝12x 2＋bx ＋c 的图象经过B 、C 两点，且与x 轴的负半轴交于点A ．（1）求二次函数的表达式；（2）若点D 在直线BC 下方的抛物线上，如图1，连接DC 、DB ，设四边形OCDB 的面积为S ，求S 的最大值；解：（1）对于y ＝12x ﹣2，令y ＝12x ﹣2＝0，解得：x ＝4；令x ＝0，则y ＝﹣2，故点B 、C 的坐标分别为（4，0）、（0，﹣2）；将点B 、C 的坐标代入抛物线表达式得2116402c b c =-⎧⎪⎨⨯++=⎪⎩，解得：322b c ⎧=-⎪⎨⎪=-⎩，故抛物线的表达式为213222y x x =--①；（2）连接OD ，点D 的坐标为（x ，213222x x --），则S ＝S △ODC ＋S △ODB ＝12×OC ×D x ＋12×BO ×（﹣D y ）＝12×2×x ＋12×4×（213222x x -++）＝﹣x 2＋4x ＋4，△﹣1＜0，故S 有最大值，当x ＝2时，S 有最大值8；5．如图，抛物线2y x bx c =-++与x 轴交于A （-1，0），B （3，0）两点，与y 轴交于点C ，直线3y x =-+经过B ，C 两点，连接AC ．(1)求抛物线的表达式；(2)点E 为直线BC 上方的抛物线上的一动点（点E 不与点B ，C 重合），连接BE ，CE ，设四边形BECA 的面积为S ，求S 的最大值； (1)解：（1）将(1A -，0)(3B ，0)代入2y x bx c =-++，∴10930b c b c --+=⎧⎨-++=⎩，解得：23b c =⎧⎨=⎩，223y x x ∴=-++；(2)（2）过E 作EF x ⊥轴于点F ，与BC 交于点H ，(1A -，0)(3B ，0)，4AB ∴=当0x =时，3y =，(0,3)C ∴，3OC ∴=，设2(,23)F a a a -++，则(,3)H a a -+，222333EH a a a a a ∴=-+++-=-+，ABC BCE BECA S S S ∆∆=+四边形，21143(3)322S a a ∴=⨯⨯+-+⨯ 236(3)2a a =+-+23375()228a =--+，∴当32a =时，S 的最大值为758；类型拓展2 抛物线上有且只有三个点6．如图1，已知抛物线y ＝ax 2+2x +c （a ≠0），与y 轴交于点A （0，6），与x 轴交于点B （6，0）．（1）求这条抛物线的表达式及其顶点坐标；（2）设点P 是抛物线上的动点，若在此抛物线上有且只有三个P 点使得△P AB 的面积是定值S ，求这三个点的坐标及定值S ．解：(1)△抛物线y＝ax2+2x+c（a≠0），与y轴交于点A（0，6），与x轴交于点B（6，0）．△603612ca c=⎧⎨=++⎩△126 ac⎧=-⎪⎨⎪=⎩△抛物线解析式为：y＝﹣12x2+2x+6，△y＝﹣12x2+2x+6＝﹣12（x﹣2）2+8，△顶点坐标为（2，8）(2)△点A（0，6），点B（6，0），△直线AB解析式y＝﹣x+6，当x＝2时，y＝4，△点D（2，4）如图1，设AB上方的抛物线上有点P，过点P作AB的平行线交对称轴于点C，且与抛物线只有一个交点为P，设直线PC解析式为y＝﹣x+b，△﹣12x2+2x+6＝﹣x+b，且只有一个交点，△△＝9﹣4×12×（b﹣6）＝0△b ＝212， △直线PC 解析式为y ＝﹣x +212， △当x ＝2，y ＝172， △点C 坐标（2，172）， △CD ＝92，△﹣12x 2+2x +6＝﹣x +92，△x ＝3， △点P （3，152） △在此抛物线上有且只有三个P 点使得△P AB 的面积是定值S ，△另两个点所在直线与AB ，PC 都平行，且与AB 的距离等于PC 与AB 的距离， △DE ＝CD ＝92，△点E （2，﹣12），设P 'E 的解析式为y ＝﹣x +m ， △﹣12＝﹣2+m ， △m ＝32△P 'E 的解析式为y ＝﹣x +32，△﹣12x 2+2x +6＝﹣x +32，△x ＝△点P '（，﹣32﹣，P ''（3﹣，﹣32，△S ＝12×6×（152﹣3）＝272．7．如图，直线334y x =-+与 x 轴交于点 C ，与 y 轴交于点 B ，抛物线 234y ax x c =++经过 B 、C 两点．（1）求抛物线的解析式；（2）如图，点 E 是抛物线上的一动点（不与 B ，C 两点重合），△BEC 面积记为 S ，当 S 取何值时，对应的点 E 有且只有三个？【答案】（1）233384y x x =-++；（2）3【解析】【分析】（1）先利用一次函数解析式确定B （0，3），C （4，0），然后利用待定系数法求抛物线解析式；（2）由于E 点在直线BC 的下方的抛物线上时，存在两个对应的E 点满足△BEC 面积为S ，则当E 点在直线BC 的上方的抛物线上时，只能有一个对应的E 点满足△BEC 面积为S ，所以过E 点的直线与抛物线只有一个公共点，设此时直线解析式为34y x b =-+，利用方程组23433384y x b y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩只有一组解求出b 得到E 点坐标，然后计算此时S △BEC ．【详解】（1）当x=0时，y=-34x+3=3，则B （0，3），当y=0时，-34x+3=0，解得x=4，则C （4，0），把B （0，3），C （4，0）代入y=ax 2+34x+c 得383a c ⎧=-⎪⎨⎪=⎩，所以抛物线解析式为233384y x x =-++；（2）当E 点在直线BC 的下方的抛物线上时，一定有两个对应的E 点满足△BEC 面积为S ，所以当E 点在直线BC 的上方的抛物线上时，只能有一个对应的E 点满足△BEC 面积为S ，即此时过E 点的直线与抛物线只有一个公共点，设此时直线解析式为34y x b =-+，方程组23433384y x b y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩只有一组解，方程23333844x x x b -++=-+有两个相等的实数解，则△=122-4×3×（-24+8b ）=0，解得b=92，解方程得x 1=x 2=2， E 点坐标为（2，3），此时1343322BEC S ⎛⎫=⨯⨯-= ⎪⎝⎭，所以当S=1时，对应的点E 有且只有三个．【点睛】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x 轴有两个交点时，可选择设其解析式为交点式来求解．8．如图，直线4y x =-+与x 轴交于点C ，与y 轴交于点B ，抛物线223y x bx c =-++经过B 、C 两点．（1）求抛物线的解析式；（2）如图，点E 是抛物线上的一动点(不与B ，C 两点重合)，当14BEC BOC S S =△时，求点E 的坐标；（3）若点F 是抛物线上的一动点，当BFC S △为什么取值范围时，对应的点F 有且只有两个？【答案】（1）225433y x x =-++；（2）1E ⎝⎭，2E ⎝⎭，34222E ⎛-+ ⎝⎭，44222E ⎛+- ⎝⎭；（3）当163BFC S >△时，对应的点F 有且只有两个．【解析】【分析】（1）根据待定系数法，即可求解；（2）过点E 作x 轴的垂线交BC 于点N ，设点225,433E a a a ⎛⎫-++ ⎪⎝⎭，点(,4)N a a -+，根据12BEC B C S EN x x =-△，14BEC BOC S S =△，列出方程，即可求解；（3）当F 点在直线BC 的下方的抛物线上时，一定有两个对应的F 点满足BCF △面积为S ，当F 点在直线BC 的上方的抛物线上时，无F 点满足BCF △面积为S 才符合题意，故只需要求出当点F 在直线BC 的上方时，BFC S △的最大值，即可得到结论．【详解】（1）△直线4y x =-+与x 轴交于点C ，与y 轴交于点B ，△(0,4)B ，(4,0)C ，将(0,4)B ，(4,0)C 代入223y x bx c =-++，可得2424403c b c =⎧⎪⎨-⨯++=⎪⎩，解得534b c ⎧=⎪⎨⎪=⎩， △225433y x x =-++；（2）如图，过点E 作x 轴的垂线交BC 于点N ，设点225,433E a a a ⎛⎫-++ ⎪⎝⎭，则点(,4)N a a -+， △2212541624423333BEC B C S EN x x a a a a a =-=-+++-=-+△， △182BOC S BO OC =⋅=△，14BEC BOC S S =△， △2416233a a -+=，解得：1x =2x =3x =4x = 将1x ，2x ，3x ，4x代入抛物线解析式，可得：1y =，2y =3y =4y =△1E ⎝⎭，2E ⎝⎭，34222E ⎛ ⎝⎭，44222E ⎛ ⎝⎭；（3）当点F 在直线BC 上方的抛物线上时，设点225,433F m m m ⎛⎫-++ ⎪⎝⎭，由（2）同理可得：22416416(2)3333BFC S m m m =-+=--+△， △当2m =时，BFC S △的最大值为163， △当BFC S △＞163时，在直线BC 的上方的抛物线上无法找到F 点，综上所述：当163BFC S >△时，对应的点F 有且只有两个．【点睛】本题主要考查二次函数与一次函数的综合，掌握待定系数法，函数图像上的点的坐标特征以及三角形的面积=铅垂高×水平宽，是解题的关键．类型拓展3 综合运用9．综合与实践如图，二次函数234y x bx c =++的图象与x 轴交于点A 和B ，点B 的坐标是()4,0，与y 轴交于点()0,3C -，点D 在抛物线上运动．(1)求抛物线的表达式；(2)如图2，当点D 在第四象限的抛物线上运动时，连接BD ，CD ，BC ，当BCD △的面积最大时，求点D 的坐标及BCD △的最大面积；(1)解：点B ()4,0和点()0,3C -代入二次函数234y x bx c =++，得：01243b c c=++⎧⎨-=⎩ 解得943b c ⎧=-⎪⎨⎪=-⎩． △抛物线的表达式是239344y x x =--． (2) 解：如图，连接OD ，过点D 作DM x ⊥轴，作DN y ⊥轴．设点D 的坐标是239,344m m m ⎛⎫-- ⎪⎝⎭．△239344DM m m =-++，DN m =． △()4,0B ，()0,3C -，△4OB =，3OC =．△BCD OCD OBD OBC S S S S =+-△△△△111222OC DN OB DM OB OC =⋅+⋅-⋅ 2113913434322442m m m ⎛⎫=⨯+⨯-++-⨯⨯ ⎪⎝⎭ 2362m m =-+ 23(2)62m =--+． △302-<， △当2m =时，BCD △的面积最大且为6．当2m =时，2239399322344442m m --=⨯-⨯-=-． △点D 的坐标是92,2⎛⎫- ⎪⎝⎭，BCD △的最大面积是6． 10．如图，抛物线2y x bx c =-++与x 轴相交于A 、B 两点，与y 轴相交于点C ，且点B 与点C 的坐标分别为()()3,0,0,3B C ，点M 是抛物线的顶点．(1)求二次函数的关系式；(2)点P 为线段MB 上一个动点，过点P 作PD x ⊥轴于点D ，若OD m =，PCD 的面积为S ，求S 与m 的函数关系式，并求当S 取得最大值时，点P 的坐标；(1)解：将点B （3，0），C （0，3）代入y =-x 2+bx +c ，得09333b c =-++⎧⎨=⎩；解得23b c =⎧⎨=⎩， △二次函数的解析式为y =-x 2+2x +3；(2)△y =-x 2+2x +3=-（x -1）2+4，△顶点M （1，4），设直线BM 的解析式为y =kx +b ，将点B （3，0），M （1，4）代入，得304k b k b +=⎧⎨+=⎩，解得26k b =-⎧⎨=⎩， △直线BM 的解析式为y =-2x +6，△PD △x 轴且OD =m ，△P （m ，-2m +6），△S =S △PCD =12PD •OD =12m （-2m +6）=-m 2+3m ，即S =-m 2+3m ，△当点P 与点B 重合时，不存在以P 、C 、D 为顶点的三角形，△1≤m <3，△S =-m 2+3m =-（m -32）2+94， △-1＞0，△当m =32时，S 取最大值94；此时点P 的坐标为332⎛⎫ ⎪⎝⎭，. 11．如图，在平面直角坐标系中，抛物线2y ax bx c =++的对称轴为2x =，与y 轴交于点A 与x 轴交于点E 、B ，且点(0,5)A ，(5,0)B ，过点A 作AC 平行于x 轴，交抛物线于点C ，点P 为抛物线上的点，且在AC 的上方，作PD 平行于y 轴交AB 于点D ．(1)求二次函数的解析式；(2)当点P 在何位置时，四边形APCD 的面积最大？并求出最大面积；(1) 解：抛物线2y ax bx c =++的对称轴为2x =， △22b a-=， 4b a ∴=-，∴抛物线解析式为24y ax ax c =-+，点(0,5)A ，(5,0)B ，∴52550c a b c =⎧⎨-+=⎩， ∴15a c =-⎧⎨=⎩， ∴二次函数的解析式为245y x x =-++；(2)解：//AC x 轴，点(0,5)A ，当5y =时，2455x x -++=，10x ∴=，24x =，(4,5)C ∴，4AC ∴=，设直线AB 的解析式为y mx n =+，(0,5)A ，(5,0)B ，由点A 、B 的坐标得，直线AB 的解析式为5y x =-+；设2(,45)P m m m -++，,5()D m m ∴-+，224555PD m m m m m ∴=-+++-=-+，4AC =， △()221525252222APCD S AC PD m m m ⎛⎫=⋅=-+=--+ ⎪⎝⎭四边形 ∴当52m =时，四边形APCD 的面积最大， ∴即点5(2P ，35)4时，四边形APCD 的面积最大为252； 12．如图，在平面直角坐标系中，二次函数y ＝﹣x 2＋bx ＋c 的图象与坐标轴交于A ，B ，C 三点，其中点B 的坐标为（1，0），点C 的坐标为（0，4），点D 的坐标为（0，2），点P 为二次函数图象上的动点．（1）求二次函数的解析式和直线AD 的解析式；（2）当点P 位于第二象限内二次函数的图象上时，连接AD ，AP ，以AD ，AP 为邻边作平行四边形APED ，设平行四边形APED 的面积为S ，求S 的最大值．【答案】（1）y ＝－x 2－3x ＋4，122y x =+；（2）814【解析】【分析】（1）利用待定系数法将B （1，0），C （0，4）代入二次函数y ＝﹣x 2＋bx ＋c 即可求出二次函数的解析式，令y ＝0，可求出A 点坐标，然后设直线AD 的解析式为y ＝kx ＋b ，利用待定系数法将A 点坐标和D 点坐标代入y ＝kx ＋b 即可求出直线AD 的解析式；（2）连接PD ，作PG y 轴交AD 于点G ，根据题意设出点P 和点G 的坐标，然后表示出线段PG 的长度，进而根据2APD S S ∆=表示出平行四边形APED 的面积，最后根据二次函数的性质求解即可．【详解】解：（1）将B （1，0），C （0，4）代入y ＝－x 2＋bx ＋c 中，得014b c c =-++⎧⎨=⎩，解得34b c =-⎧⎨=⎩， △二次函数的解析式为y ＝－x 2－3x ＋4在y ＝－x 2－3x ＋4中，令y ＝0，即2340x x --+=，解得x 1＝－4，x 2＝1，△A （－4，0）．设直线AD 的解析式为y ＝kx ＋b'．△D （0，2），△04'2'k b b =-+⎧⎨=⎩，解得：12'2k b ⎧=⎪⎨⎪=⎩ △直线AD 的解析式为122y x =+．（2）连接PD ，作PG y 轴交AD 于点G ，如图所示．设P （t ，－t 2－3t ＋4）（－4＜t ＜0），则G （t ，122t +）， △2217342222PG t t t t t =--+--=--+， △2122||41482APD D A S S PG x x t t ∆==⨯⋅-=--+， 27814()44t =-++． △－4＜0，－4＜t ＜0，△当74t =-时，S 有最大值814．【点睛】此题考查了待定系数法求二次函数和一次函数表达式，二次函数中有关面积的综合题，解题的关键是熟练掌握待定系数法求函数表达式，根据题意设出点的坐标表示出平行四边形APED的面积．。

二次函数面积最值问题

二次函数面积最值问题1. 问题概述二次函数是代数学中的重要概念，它服从形如f(x) = ax^2 + bx + c的数学表达式，其中a、b、c为实数且a不等于零。

二次函数的图像是一个抛物线，它在平面上呈现出优美的曲线形状。

本文将探讨与二次函数相关的面积最值问题。

2. 背景知识在进一步讨论二次函数面积最值问题之前，我们需要了解一些基本的数学知识。

### 2.1 二次函数的图像特点 * 二次函数的图像是一个抛物线，可以开口向上或者向下。

* 如果a大于0，则抛物线开口向上，称为上凸函数；如果a小于0，则抛物线开口向下，称为下凸函数。

2.2 二次函数的面积计算公式对于一个给定的二次函数f(x)，在给定区间[a, b]内的曲线与x轴之间的面积可以通过积分来计算：S = ∫[a, b] |f(x)|dx3. 二次函数面积最值问题二次函数面积最值问题是指在某个给定的区间内，找到一个二次函数的图像与x轴之间的面积最大或最小的情况。

接下来，我们将探讨如何解决这个问题。

3.1 二次函数面积最大值问题对于一个上凸的二次函数，它的图像与x轴之间的面积是连续且单调递增的。

因此，我们可以通过求解二次函数f(x) = ax^2 + bx + c的顶点坐标来确定面积最大值时的x值。

3.1.1 求解顶点坐标一个二次函数的顶点坐标可以通过如下公式得出： x_v = -b / (2a) y_v = f(x_v) = f(-b / (2a))3.1.2 面积最大值计算已知二次函数的顶点坐标后，我们可以计算出它与x轴之间的面积，即面积最大值。

由于上凸二次函数对称，我们可以将区间[a, b]划分为两部分，分别计算两个子区间内的面积，并将它们相加，即得到整个区间[a, b]内的面积最大值。

3.2 二次函数面积最小值问题对于一个下凸的二次函数，它的图像与x轴之间的面积是连续且单调递减的。

因此，我们可以通过求解二次函数f(x) = ax^2 + bx + c的顶点坐标来确定面积最小值时的x值。

二次函数综合(一)——面积问题

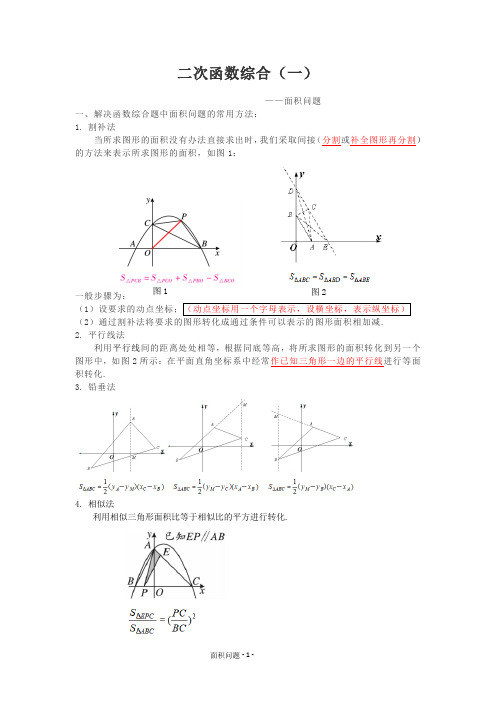
二次函数综合（一） ——面积问题
一、解决函数综合题中面积问题的常用方法：
1. 割补法
当所求图形的面积没有办法直接求出时，我们采取间接（分割或补全图形再分割）的方法来表示所求图形的面积，如图1：
4. 相似法
利用相似三角形面积比等于相似比的平方进行转化.
二、基本题型
1.如图，在平面直角坐标系中，△AOB的顶点O为原点，已知点A（3,6），B（5,2），求△AOB的面积.
2.已知二次函数的图像y=－x2+3x+4与x轴交于A、B两点（点A在点B的左端），与y轴交于点C，抛物线的顶点为D。

求△ACD的面积。

3已知二次函数的图像y=－x2+3x+4与x轴交于A、B两点（点A在点B的左端），与y轴交于点C，抛物线的顶点为D。

求△BCD的面积。

《二次函数专题提优》：二次函数有关面积问题

《二次函数提优专题》：二次函数有关面积问题2、如图，抛物线y＝x2+bx+c（b、c为常数）与x轴相交于点A（﹣1，0）、B（3，0），与y轴相交于点C，其对称轴与x轴相交于点D，作直线BC．（1）、求抛物线的解析式．（2）、设点P为抛物线对称轴上的一个动点．①、如图①，若点P为抛物线的顶点，求△PBC的面积．②、是否存在点P使△PBC的面积为6？若存在，求出点P坐标；若不存在，请说明理由．（二）、三角形面积最值：3、如图，已知抛物线c bx x y ++=2-与x 轴交于A(−1,0)、B(3,0)两点，与y 轴交于点C ，抛物线的对称轴与抛物线交于点P 、与直线BC 相交于点M ，连接PB 。

(1)、求该抛物线的解析式；(2)、在(1)中位于第一象限内的抛物线上是否存在点D ，使得BCD △的面积最大?若存在，求出D 点坐标及BCD △面积的最大值；若不存在，请说明理由。

(3)、在(1)中的抛物线上是否存在点Q ，使得QMB △与PMB △的面积相等?若存在，直接写出满足条件的所有点Q 的坐标；若不存在，请说明理由。

（三）、有关三角形面积倍数关系：4、如图，已知：m 、n 是方程x 2－6x+5=0的两个实数根，且m<n ，•抛物线y=－x 2+bx+c 的图象经过点A （m ，0），B （0，n ）．（1）、求这个抛物线的解析式；（2）、设（1）中的抛物线与x 轴的另一交点为C ，抛物线的顶点为D ，试求出点C ，D 的坐标和△BCD 的面积；（3）、P 是线段OC 上的一点，过点P 作PH ⊥x 轴，与抛物线交于H 点，若直线BC 把△PCH 分成面积之比为2：3的两部分，请求出P 点的坐标。

5、如图，在平面直角坐标系中，二次函数5-x 6-x y 2+=的图象与x 轴交于A 、B 两点，与y 轴交于点C ，其顶点为P ，连接PA 、AC 、CP ，过点C 作y 轴的垂线l 。

二次函数求面积问题解题思路

二次函数求面积问题解题思路【导语】在数学中，二次函数是非常常见的一种函数类型。

而对于二次函数求面积问题，我们可以通过一定的解题思路来解决。

本文将围绕着二次函数求面积问题展开，详细介绍解题思路，并分享个人观点和理解。

【引言】二次函数是形如y=ax^2+bx+c的函数，其中a、b、c为常数，且a 不等于零。

在二次函数中，求解其曲线所围成的面积是一道常见的数学题目。

解决这类问题需要掌握一定的数学知识和解题技巧。

下面将按照从简到繁、由浅入深的方式，分享二次函数求面积问题的解题思路。

【正文】1. 面积问题的基本思路在解决二次函数求面积问题时，我们可以使用定积分的思想。

具体来说，我们将二次函数的曲线与x轴所围成的面积，分解为无穷多个无限小的矩形，然后对这些矩形的面积进行求和。

通过计算这个和，我们就可以得到所求的面积。

2. 简单情况下的求解在一些简单的情况下，我们可以直接使用基本的几何知识来求解二次函数的面积。

当二次函数的解析式可以方便地转化为一个简单的几何形状时，我们可以直接计算这个几何形状的面积，得到答案。

3. 进阶情况下的求解在更复杂的情况下，我们需要使用定积分的方法来求解二次函数的面积。

具体而言，我们可以首先确定二次函数与x轴的交点，然后根据这些交点将整个面积分割成多个部分。

接下来，我们可以分别计算每个小矩形的面积，并对这些面积进行求和，最后得到所求的总面积。

4. 完整解题思路的展示下面，我们将通过一个具体的例子来展示完整的解题思路。

假设我们需要计算二次函数y=x^2与x轴所围成的面积。

我们可以求解出二次函数与x轴的交点，得到交点为x=0和x=1。

我们可以将整个面积分割成两部分：在0到1之间的部分和在1到正无穷之间的部分。

对于0到1之间的部分，我们可以使用定积分的方法计算出面积为∫[0,1]x^2 dx；对于1到正无穷之间的部分，我们可以使用类似的方法计算出面积为∫[1,+∞)x^2 dx。

将这两部分的面积相加，即可得到最终的结果。

二次函数求面积问题

二次函数求面积问题
在数学中，二次函数是形如f(x) = ax^2 + bx + c的函数，其中a、b和c是实数
且a不等于零。

这种类型的函数可以用来解决许多实际问题，包括求解面积问题。

想象一下，我们有一个二次函数的图像，限定在x轴上的两个点x1和x2之间。

我们需要求解这段x轴上方的面积。

首先，我们需要将x1和x2代入二次函数的方程中，计算出对应的y值，在这
两个点上方的y值都表示函数图像在该范围内的高度。

然后，我们需要找到一个近似函数或者采用数值积分的方法来计算这两个点之
间的曲线下面积。

一种常用的方法是通过定积分来计算二次函数的面积。

我们可以将二次函数表
示为f(x) = ax^2 + bx + c。

然后，我们对该函数进行积分，积分结果将是一个新的函数F(x)，即f(x)的原
函数。

在这个过程中，我们需要记住积分的不定性，并添加一个常数项。

接下来，我们在范围[x1, x2]上划定区间，在F(x)的两个端点x1和x2处的值分
别为F(x1)和F(x2)。

最后，我们通过计算这两个点的函数值之差来求得二次函数在给定范围内的面积。

简而言之，求解二次函数在给定范围内的面积可以通过以下步骤来实现：
1. 将x1和x2代入二次函数方程，计算对应的y值。

2. 采用数值积分或定积分方法，计算二次函数f(x)在这两个点之间的面积。

需要注意的是，如果x1和x2是两个实根，那么函数图像将在这两个点之间与
x轴相交，并形成一个三角形。

在这种情况下，求解面积就等于计算这个三角形的
面积。

二次函数面积最值问题

二次函数面积最值问题一、问题概述二次函数面积最值问题是指在给定的二次函数中，找到使其面积最大或最小的变量取值。

这个问题在数学中有着广泛的应用，比如在经济学、物理学、工程学等领域都有着重要的作用。

二、问题分析为了解决二次函数面积最值问题，我们需要先了解一些基本概念和公式。

下面是一些常见的数学公式：1. 二次函数的标准形式：y=ax^2+bx+c其中a,b,c都是实数，且a≠0。

2. 二次函数的顶点坐标：(h,k)其中h=-b/2a，k=f(h)，f(x)表示二次函数。

3. 二次函数的对称轴方程：x=h4. 两点之间距离公式：d=sqrt[(x2-x1)^2+(y2-y1)^2]5. 矩形面积公式：S=lw其中S表示矩形面积，l表示矩形长，w表示矩形宽。

了解了这些基本概念和公式后，我们可以开始分析如何解决二次函数面积最值问题。

三、求解方法1. 求最大值要求一个二次函数在给定区间内的最大面积，我们可以通过以下步骤来实现：步骤一：将二次函数化为标准形式。

步骤二：求出二次函数的顶点坐标。

步骤三：根据顶点坐标和区间端点，确定矩形的长和宽。

步骤四：计算矩形面积，并比较得出最大值。

具体的，可以按照以下函数来实现：```pythondef max_area(a,b,c,start,end):# 将二次函数化为标准形式f = lambda x: a*x**2+b*x+c# 求出二次函数的顶点坐标h = -b/(2*a)k = f(h)# 根据顶点坐标和区间端点，确定矩形的长和宽l = end-startw = abs(f(start)-k)*2# 计算矩形面积，并比较得出最大值S = l*wreturn S if S>0 else 0```其中，a,b,c分别表示二次函数的系数，start,end表示给定区间的端点。

这个函数会返回一个最大面积值。

2. 求最小值要求一个二次函数在给定区间内的最小面积，我们可以通过以下步骤来实现：步骤一：将二次函数化为标准形式。

二次函数面积问题

二次函数面积问题
二次函数面积是数学中一个重要内容，也是很多人亟待解决的问题。

二次函数
面积有着渊博的数学知识，涉及数学几何、初等数学、微积分等多学科交叉的知识。

在数学运算中，二次函数面积被广泛应用于极限计算、微积分、复数函数和三角函数等复杂问题的解决中。

二次函数面积的计算基本包括曲线上的点的坐标、函数的参数，面积的值取决
于曲线的参数，而参数则是二次函数的系数和截距。

我们可以把曲线上的点的坐标写成关于参数的式子，而面积的计算则取决于把这些表达式代入到一般方程中，根据方程得出面积的结果。

二次函数面积的计算还涉及到三角函数，比如求椭圆面积，我们要对函数求导，再对导数求积分，而有时候，为了方便计算，我们也可以采用其它方法，比如变量积分求解法、微分法，可以利用相关函数和变量求助于有效地求解二次函数面积。

总之，二次函数面积的计算涉及到诸多的数学知识，使用不同的方法解决二次
函数面积的计算才可以达到最优的结果。

在现实中，二次函数面积的计算往往与诸多应用紧密相关，在科研和工程中有着重要的意义，要有效求解二次函数面积的问题，需要更深入地学习和研究，无论是针对实践中的经验，还是更深入的理论分析，对于二次函数面积的深入研究都有着突出的重要价值。

二次函数综合专题一面积问题

二次函数专题一ABC的“水平宽”（a），中间的这条直线在△ABC 内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：S△ABC=ah，即三角形面积等于水平宽与铅垂高乘积的一半．解答下列问题：如图2，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．（1）求抛物线和直线AB的解析式；（2）点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；（3）是否存在抛物线上一点P，使S△PAB=S△CAB？若存在，求出P点的坐标；若不存在，请说明理由．如图，在直角坐标系中，点A的坐标为（﹣2，0），连接OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．（1）求点B的坐标；（2）求经过A、O、B三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．（注意：本题中的结果均保留根号）．2+bx+4与x轴的两个交点分别为A（﹣4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．（1）求抛物线的函数解析式，并写出顶点D的坐标；（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．题型一：面积问题变式训练1变式训练2如图已知：直线y=﹣x+3交x 轴于点A ，交y 轴于点B ，抛物线y=ax 2+bx+c 经过A 、B 、C （1，0）三点．（1）求抛物线的解析式；（2）若点D 的坐标为（﹣1，0），在直线y=﹣x+3上有一点P ，使△ABO 与△ADP 相似，求出点P 的坐标；（3）在（2）的条件下，在x 轴下方的抛物线上，是否存在点E ，使△ADE 的面积等于四边形APCE 的面积？如果存在，请求出点E 的坐标；如果不存在，请说明理由．堂堂清一．选择题（共5小题）1．如图，如果把抛物线y=x 2沿直线y=x 向上方平移2个单位后，其顶点在直线y=x 上的A 处，那么平移后的抛物线解析式是（）A ．y=（x+2）2+2B ．y=（x+2）2+2C ．y=（x ﹣2）2+2D ．y=（x ﹣2）2+22．已知抛物线c ：y=x 2+2x ﹣3，将抛物线c 平移得到抛物线c ′，如果两条抛物线，关于直线x=1对称，那么下列说法正确的是（）A ．将抛物线c 沿x 轴向右平移个单位得到抛物线c ′B ．将抛物线c 沿x 轴向右平移4个单位得到抛物线c ′C ．将抛物线c 沿x 轴向右平移个单位得到抛物线c ′D ．将抛物线c 沿x 轴向右平移6个单位得到抛物线c ′3．将抛物线y 1=x 2﹣2x ﹣3先向左平移1个单位，再向上平移4个单位后，与抛物线y 2=ax 2+bx+c 重合，现有一直线y 3=2x+3与抛物线y 2=ax 2+bx+c 相交，当y 2≤y 3时，利用图象写出此时x 的取值范围是（）A ．x ≤﹣1B ．x ≥3C ．﹣1≤x ≤3D ．x ≥04．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，有下列4个结论：①abc ＞0；②b ＜a+c ；③4a+2b+c ＞0；④b 2﹣4ac ＞0；其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个5．二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，对于下列结论：①a ＜0；②b ＜0；③c ＞0；④2a+b=0；⑤a ﹣b+c ＜0，其中正确的个数是（）A ．4个B ．3个C ．2个D ．1个二．填空题（共5小题）6．已知抛物线y=ax 2+x+c 与x 轴交点的横坐标为﹣1，则a+c= ．7．如果抛物线y=ax 2﹣2ax+c 与x 轴的一个交点为（5，0），那么与x 轴的另一个交点的坐标是．8．如果抛物线y=ax 2+5的顶点是它的最低点，那么a 的取值范围是．9．已知点（﹣1，m ）、（2，n ）在二次函数y=ax 2﹣2ax ﹣1的图象上，如果m ＞n ，那么a 0（用“＞”或“＜”连接）．10．如图，抛物线y=ax 2+bx+c （a ≠0）的对称轴为直线x=1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac ＜b 2；②方程ax 2+bx+c=0的两个根是x 1=﹣1，x 2=3；③3a+c ＞0；④当y ＞0时，x 的取值范围是﹣1≤x ＜3；⑤当x ＜0时，y 随x 增大而增大；其中结论正确有．三．解答题（共4小题）11．甲、乙两人分别站在相距6米的A、B两点练习打羽毛球，已知羽毛球飞行的路线为抛物线的一部分，甲在离地面1米的C处发出一球，乙在离地面1.5米的D处成功击球，球飞行过程中的最高点H与甲的水平距离AE为4米，现以A为原点，直线AB为x轴，建立平面直角坐标系（如图所示）．求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度．12．如图，在直角坐标系中，已知直线y=x+4与y轴交于A点，与x轴交于B点，C点坐标为（﹣2，0）．（1）求经过A，B，C三点的抛物线的解析式；（2）如果M为抛物线的顶点，联结AM、BM，求四边形AOBM的面积．13．抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（，0），且与y轴相交于点C．（1）求这条抛物线的表达式；（2）求∠ACB的度数；（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．14．如图，已知抛物线y=+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的一个动点．（1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP 的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．。

二次函数中的面积问题课后练习一及详解

学科：数学专题：二次函数中的面积问题重难点易错点解析题面：如图，二次函数y=ax2－4x＋c的图象经过坐标原点，与x轴交于点A(－4，0)．(1)求二次函数的解析式；(2)在抛物线上存在点P，满足S△AOP=8，请直接写出点P的坐标．金题精讲题面：如图，二次函数y=(x-2)2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A(1，0)及点B．(1)求二次函数与一次函数的解析式；(2)根据图象，写出满足kx+b≥(x-2)2+m的x的取值范围．满分冲刺题面：如图，抛物线32-+=bx ax y 交y 轴于点C ，直线 l 为抛物线的对称轴，点 P 在第三象限且为抛物线的顶点.P 到x 轴的距离为103，到y 轴的距离为1.点C 关于直线l 的对称点为A ，连接AC 交直线 l 于B .(1)求抛物线的表达式； (2)直线m x y +=43与抛物线在第一象限内交于点D ，与y 轴交于点F ,连接BD 交y 轴于点E ，且DE :BE =4:1.求直线m x y +=43的表达式思维拓展题面：已知，如图，在平面直角坐标系中，Rt △ABC 的斜边BC 在x 轴上，直角顶点A 在y 轴的正半轴上，A (0，2)，B (－1，0).(1)求点C 的坐标；(2)求过A 、B 、C 三点的抛物线的解析式和对称轴课后练习详解重难点易错点解析答案：(1)y = －x 2－4x ；(2)点P 的坐标是：(－2，4)、(222-+ ，－4)、(222--，－4) 详解：(1)将O (0，0)，A (－4，0)代入y =ax 2－4x ＋c 得 2(4)4(4)00a c c ⎧⨯--⨯-+=⎨=⎩，解得10a c =-⎧⎨=⎩. ∴此二次函数的解析式为y = －x 2－4x .(2)∵点A 的坐标为(－4，0)，∴AO =4.设点P 到x 轴的距离为h ，则1482AOP S h =⨯⨯=，解得h =4. ①当点P 在x 轴上方时，－x 2－4x =4，解得x = －2.∴点P 的坐标为(－2，4).②当点P 在x 轴下方时，－x 2－4x = -4，解得122222x x 22-+--==，. ∴点P 的坐标为(222-+ ，－4)或(222-- ，－4)，综上所述，点P 的坐标是：(－2，4)、(222-+ ，－4)、(222-- ，－4) 金题精讲答案：(1) 二次函数的解析式为y =(x -2)2-1，y =x -1; (2)1≤x ≤4详解：(1)将点A (1,0)代入y =(x -2)2+m 得，(1-2)2+m =0，解得m = -1.∴二次函数的解析式为y =(x -2)2-1.当x =0时，y =4-1=3，∴点C 的坐标为(0,3)∵二次函数y =(x -2)2-1的对称轴为x =2，C 和B 关于对称轴对称，∴点B 的坐标为(4,3)将A (1,0)、B (4,3)代入y =kx +b 得，043k b k b +=⎧⎨+=⎩，解得11k b =⎧⎨=-⎩∴一次函数的解析式为y =x -1.(2) ∵A (1,0)、B (4,3)∴当kx +b ≥(x -2)2+m 时，直线y =x -1的图象在二次函数y =(x -2)2-1的图象上方或相交，此时1≤x ≤4.满分冲刺答案：(1)212333y x x =+-.(2)324y x =+. 详解：(1)∵抛物线23y ax bx =+-交y 轴于点C ，∴C (0，-3)则 OC =3.∵P 到x 轴的距离为103，P 到y 轴的距离是1，且在第三象限， ∴P (-1，-103). ∵C 关于直线l 的对称点为A ，∴A (-2，-3).将点A (-2，-3)，P (-1，-103)代入23y ax bx =+-得， 42331033a b a b --=-⎧⎪⎨--=-⎪⎩，解得1323a b ⎧=⎪⎪⎨⎪=⎪⎩. ∴抛物线的表达式为212333y x x =+-. (2)过点D 做DG ⊥y 轴于G ，则∠DGE =∠BCE =90°.∵∠DEG =∠BEC ，∴△DEG ∽△BEC .∴DG DE BC BE=. ∵DE :BE =4:1，BC =1，∴DG 411=, 则DG =4. 将x =4代入212333y x x =+-，得y =5. ∴D (4,5).∵34y x m =+过点D (4,5),∴3544m =⨯+, 则m =2. ∴所求直线的表达式为 324y x =+.思维拓展答案：(1)(4，0).(2) 213222y x x =-++,抛物线的对称轴为32x =. 详解：(1)∵A (0，2)，B (－1，0)，∴OA =2，OB =1. 由Rt △ABC 知Rt △ABO ∽Rt △CAO ，∴OA OB OC OA =，即212OC =，解得OC =4. ∴点C 的坐标为(4，0).(2)设过A 、B 、C 三点的抛物线的解析式为(1)(4)y a x x =+-，将A (0，2)代入，得2(01)(04)a =+-，解得12a =-∴过A 、B 、C 三点的抛物线的解析式为1(1)(4)2y x x =-+-，即213222y x x =-++. ∵221313252()22228y x x x =-++=--+，∴抛物线的对称轴为32x =.。

二次函数之二次函数中的面积问题1

初中数学中考二轮6二次函数中的面积问题(1)

二次函数面积问题(整)

二次函数中的面积计算问题(包含铅垂高)

二次函数与面积问题

二次函数中的面积最值问题最佳处理方法

二次函数中的面积问题

二次函数中的面积问题

二次函数中面积问题

二次函数面积最值问题

二次函数综合(一)——面积问题

《二次函数专题提优》：二次函数有关面积问题

二次函数求面积问题解题思路

二次函数求面积问题

二次函数面积最值问题

二次函数面积问题

二次函数综合专题一面积问题

二次函数中的面积问题 课后练习一及详解

二次函数中的面积问题课后练习一及详解