人教版初中数学七年级下学期 第五章相交线与平行线测试卷
人教版七年级初一数学下册 第五章 相交线与平行线综合综合测试卷(含答案)

第五章《相交线与平行线》综合测试题(答题时间:90分钟 满分:120分)一、选择题:(每小题3分,共30分)1.若三条直线交于一点,则共有对顶角(平角除外)( )A.6对B.5对C.4对D.3对 2.如图1所示,∠1的邻补角是( )A.∠BOCB.∠BOE 和∠AOFC.∠AOFD.∠BOC 和∠AOF3. 如图2,点E 在BC 的延长线上,在下列四个条件中,不能判定AB ∥CD 的是( ) A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°4. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )A .第一次右拐50°,第二次左拐130°;B .第一次左拐50°,第二次右拐50°C .第一次左拐50°,第二次左拐130° ;D .第一次右拐50°,第二次右拐50° 5. 如图3,AB ∥CD ,那么∠A ,∠P ,∠C 的数量关系是( ) A.∠A+∠P+∠C=90° B.∠A+∠P+∠C=180°C.∠A+∠P+∠C=360°D.∠P+∠C=∠A6. 一个人从点A 点出发向北偏东60°方向走到B 点,再从B 点出发向南偏西15°方向走到C 点,那么∠ABC 等于( )A.75°B.105°C.45°D.135° 7.如图4所示,内错角共有( )A.4对B.6对C.8对D.10对图1F EO 1C BA D 图3DAPCBC B A D1CBA324DO FE DCBA8.如图5所示,已知∠3=∠4,若要使∠1=∠2,则需( ) A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.AB ∥CD9.下列说法正确的个数是( )①同位角相等; ②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;;④三条直线两两相交,总有三个交点; ⑤若a ∥b ,b ∥c ,则a ∥c.A.1个B.2个C.3个D.4个10. 如图6,O 是正六边形ABCDEF 的中心,下列图形:△OCD ,△ODE ,△OEF ,•△OAF ,•△OAB ,其中可由△OBC 平移得到的有( )A.1个B.2个C.3个D.4个 二、填空题(每小题3分,共30分)11.•命题“垂直于同一直线的两直线平行”的题设是•____________,•结论是__________. 12.三条直线两两相交,最少有_____个交点,最多有______个交点.13.观察图7中角的位置关系,∠1和∠2是______角,∠3和∠1是_____角,∠1•和∠4是_______角,∠3和∠4是_____角,∠3和∠5是______角.54321 4321ACDB火图7 图8 图914.如图8,已知AB ∥CD ,∠1=70°则∠2=_______,∠3=______,∠4=_______.15.如图9所示,在铁路旁边有一李庄,现要建一火车站,•为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:________________.16.如图10所示,直线AB 与直线CD 相交于点O ,EO ⊥AB ,∠EOD=25°,则∠BOD=______,图4 图5图6∠AOC=_______,∠BOC=________.AECDOB21ACDB图10 图11 图12 17.如图11所示,四边形ABCD 中,∠1=∠2,∠D=72°,则∠BCD=_______.18.我们可以把“火车在一段笔直的铁轨上行驶了一段距离”看作“火车沿铁轨方向_________”. 19. 根据图12中数据求阴影部分的面积和为_______.20. 如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是_________. 三、解答题(每小题8分,共40分)21. 已知a 、b 、c 是同一平面内的3条直线,给出下面6个命题:a ∥b , b ∥c ,a ∥c ,a ⊥b ,b ⊥c ,a ⊥c ,请从中选取3个命题(其中2个作为题设,1个作为结论)尽可能多地去组成一个真命题,并说出是运用了数学中的哪个道理。
人教版数学七年级下册第五章相交线与平行线 测试卷含答案

人教版数学七年级下册第五章相交线与平行线一、单选题1.同一平面内,三条不同直线的交点个数可能是()个.A.1或3 B.0、1或3 C.0、1或2 D.0、1、2或32.如图,在所标识的角中,互为对顶角的两个角是()A.∠1和∠2 B.∠1和∠4 C.∠2和∠3 D.∠3和∠43.已知,OA⊥OC,且∠AOB:∠AOC=2:3,则∠BOC的度数为()A.30°B.150°C.30°或150°D.90°4.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是()A.两点之间线段最短B.点到直线的距离C.两点确定一条直线D.垂线段最短5.下列图形中,线段AD的长表示点A到直线BC距离的是()A.B.C.D.6.如图,直线l与∠BAC的两边分别相交于点D、E,则图中是同旁内角的有()A.2对B.3对C.4对D.5对7.如图,直线DE截AB,AC,其中内错角有()对.A.1 B.2 C.3 D.48.下列说法正确的是()A.不相交的两条线段是平行线B.不相交的两条直线是平行线C.不相交的两条射线是平行线D.在同一平面内,不相交的两条直线是平行线9.在同一平面内两条不重合的直线的位置关系是()A.相交或垂直B.平行或垂直C.相交或平行D.以上都不对10.下列说法正确的有()①同位角相等;②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;④同一平面内两条直线的位置关系可能是平行或垂直;⑤有公共顶点并且相等的角是对顶角.A.1个B.2个C.3个D.4个二、填空题11.下列说法中,①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.不正确的是_____(填序号)12.已知直线a∥b,b∥c,则直线a、c的位置关系是_____.13.如图所示,请你填写一个适当的条件:_____,使AD∥BC.14.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为__________.(任意添加一个符合题意的条件即可)15.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是_____.16.如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E=_____度.17.如图,DF∥AC,若∠1=∠2,则DE与AH的位置关系是_____.18.已知直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是_____.19.把命题“对顶角相等”改写成“如果⋯那么⋯”的形式:_____.20.一个七边形棋盘如图所示,7个顶点顺序从0到6编号,称为七个格子.一枚棋子放在0格,现在依逆时针移动这枚棋子,第一次移动1格,第二次移动2格,…,第n次移动n 格.则不停留棋子的格子的编号有_____.三、解答题21.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.22.作图并写出结论:如图,点P是∠AOB的边OA上一点,请过点P画出OA,OB的垂线,分别交BO 的延长线于M、N,线段的长表示点P到直线BO的距离;线段的长表示点M到直线AO的距离;线段ON的长表示点O到直线的距离;点P到直线OA的距离为.23.如图,∠ACD=2∠B,CE平分∠ACD,求证:CE∥AB.24.如图1,已知AB∥CD,那么图1中∠PAB、∠APC、∠PCD之间有什么数量关系?并说明理由.如图2,已知∠BAC=80°,点D是线段AC上一点,CE∥BD,∠ABD和∠ACE的平分线交于点F,请利用(1)的结论求图2中∠F的度数.25.(1)如图,它的周长是cm.(2)已知:|a|=2,|b|=5,且a>b,求a+b的值.26.如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.(1)试求出∠E的度数;(2)若AE=9cm,DB=2cm,求出BE的长度.参考答案1.D【解析】试题分析:根据两直线平行和相交的定义作出图形即可得解.解:如图,三条直线的交点个数可能是0或1或2或3.故选D.2.D【解析】根据对顶角的定义:“有公共顶点,且两边分别互为反向延长线的两个角互为对顶角”分析可知,在图中所标示的4个角中,互为对顶角的是∠3和∠4.故选D.3.C【解析】解:∵OA⊥OC,∴∠AOC=90°.∵∠AOB:∠AOC=2:3,∴∠AOB=60°.因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.①当在∠AOC内时,∠BOC=90°﹣60°=30°;②当在∠AOC外时,∠BOC=90°+60°=150°.故选C.点睛:本题主要考查了垂线的定义:当两条直线相交所成的四个角中,有一个角是直角时,即两条直线互相垂直.同时做这类题时一定要结合图形.4.D【解析】【分析】根据垂线段的性质:垂线段最短进行解答.【详解】要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,故选D.【点睛】本题考查垂线段的性质:垂线段最短.5.B【解析】【分析】根据点到直线的距离是指垂线段的长度,即可解答.【详解】解:线段AD的长表示点A到直线BC距离的是图B故选:B.【点睛】本题考查了点到直线的距离的定义,注意是垂线段的长度,不是垂线段.6.C【解析】【分析】根据同旁内角的定义依次【详解】解:直线AC与直线AB被直线l所截形成的同旁内角有:∠ADE与∠AED、∠CDE与∠BED;直线AC与直线DE被直线AB所截形成的同旁内角有:∠DAE与∠DEA;直线AB与直线DE被直线AC所截形成的同旁内角有:∠EAD与∠EDA;故选C.【点睛】此题主要考查同旁内角的定义,解题的关键是每条直线依次判断.7.D【解析】如果两条直线被第三条直线所截,那么位于截线的两侧,在两条被截直线之间的两个角是内错角.两条直线被第三条直线所截,可形成两对内错角.解:直线DE截AB,AC,形成两对内错角;直线AB截AC,DE,形成一对内错角;直线AC截AB,DE,形成一对内错角.故共有4对内错角.故选D.8.D【解析】根据平行线的描述,易选D.9.C【解析】【分析】根据两直线的位置关系即可解答.【详解】解:在同一平面内两条不重合的直线的位置关系是平行和相交.故选:C.【点睛】此题主要考查两直线的位置关系,熟知定义是解题的关键.10.A【解析】【分析】根据相交直线的位置关系综合判定即可.【详解】解:∵同位角不一定相等,∴①错误;∵互补或互余是两个角之间的关系,∴说∠A+∠B+∠C=180°,则∠A、∠B、∠C互补错误,∴②错误;∵同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交,∴③正确;∵同一平面内两条直线的位置关系可能是平行或相交,∴④错误;∵如图,∠ABC=∠ABD,∠ABC和∠ABD有公共顶点并且相等的角,但不是对顶角,∴⑤错误;即正确的个数是1个,故选A.【点睛】此题主要考查相交线之间的关系,解题的关键是根据每项找到反例说明.11.①②④【解析】【分析】根据平行线的判定与性质即可判断.【详解】解:①在同一平面内,不相交的两条线段叫做平行线,正确;②过一点,有且只有一条直线平行于已知直线,正确;③两条平行直线被第三条直线所截,当两直线平行,同位角相等,故原命题错误;④同旁内角相等,两直线平行,正确.故答案为①②④.【点睛】此题主要考查平行线的判定与性质,解题的关键是熟知平行线的判定与性质.12.a∥c【解析】试题解析:∵在同一平面内,直线a∥b,直线b∥c,根据平行公理:平行于同一条直线的两条直线平行,∴直线c与直线a的位置关系是:a∥c.故答案为a∥c.13.∠FAD=∠FBC(答案不唯一)【解析】根据同位角相等,两直线平行,可填∠FAD=∠FBC;根据内错角相等,两直线平行,可填∠ADB=∠DBC;根据同旁内角互补,两直线平行,可填∠DAB+∠ABC=180°.14.∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE【解析】分析:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断.详解:若180A ABC ∠+∠=︒,则BC ∥AD ;若∠C +∠ADC =180°,则BC ∥AD ;若∠CBD =∠ADB ,则BC ∥AD ;若∠C =∠CDE ,则BC ∥AD ;故答案为:∠A +∠ABC =180°或∠C +∠ADC =180°或∠CBD =∠ADB 或∠C =∠CDE .(答案不唯一)点睛:本题主要考查了平行线的判定,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.15.同位角相等,两直线平行【解析】分析:由全等三角形的对应角相等判定同位角∠1=∠2,则AB ∥CD .详解:根据题意,图中的两个三角尺全等,∴∠1=∠2 ,∴AB ∥CD (同位角相等,两直线平行).16.80【解析】【详解】如图,根据角平分线的性质和平行线的性质,可知∠FMA=12∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE=2∠FMA ,即∠E=2∠F=2×40°=80°.故答案为80.17.平行【解析】【分析】先根据DF∥AC得∠2=∠G,再通过等量替换得出∠1=∠G,再利用内错角相等,两直线平行即可判断.【详解】解:∵DF∥AC,∴∠2=∠G,又∵∠1=∠2,∴∠1=∠G,∴DE∥AH,故答案为平行.【点睛】此题主要考查平行线的判定与性质,解题的关键是利用两直线平行找到一个角与目标角相等.18.3【解析】【分析】根据平行线间的距离与点到直线的距离即可求出.【详解】解:∵直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,∴点P到b的距离是5﹣2=3,故答案为3.【点睛】此题主要考查平行线之间的距离,解题的关键是正确理解点到直线的距离.19.如果两个角是对顶角,那么它们相等.【解析】【分析】先把命题分解为题设和条件,再改写成“如果⋯那么⋯”的形式,即可.【详解】题设为:对顶角,结论为:相等,故写成“如果⋯那么⋯”的形式是:如果两个角是对顶角,那么它们相等.故答案为:如果两个角是对顶角,那么它们相等.【点睛】本题主要考查把命题改写成“如果⋯那么⋯”的形式,理解命题的题设和结论是解题的关键.20.2,4,5【解析】【分析】因棋子移动了n 次后走过的总格数是1+2+3+…+n =12n (n +1),然后再根据题目中所给的第n 次依次移动n 个顶点的规则,可得到不等式最后求得解.【详解】解:因棋子移动了n 次后走过的总格数是1+2+3+…+n =12n (n +1),应停在第12n (n +1)﹣7p 格,这时p 是整数,且使0≤12n (n +1)﹣7p ≤6,分别取n =1,2,3,4,5,6,7时,12n (n +1)﹣7p =1,3,6,3,1,0,0,发现第2,4,5格没有停留棋子,若7<n ≤10,设n =7+t (t =1,2,3)代入可得,12 n (n +1)﹣7p =7m +12t (t +1),由此可知,停棋的情形与n =t 时相同,故第2,4,5格没有停留棋子.故答案为:2,4,5.【点睛】此题主要考查推理与论证,解题的关键是根据题意分析运动规则,再列出式子来解答. 21.(1)见解析;(2)见解析.【解析】本题考查了线段和垂线的性质在实际生活中的运用(1)由两点之间线段最短可知,连接AD 、BC 交于H ,则H 为蓄水池位置;(2)根据垂线段最短可知,要做一个垂直EF 的线段.⑴连结AD ,BC ,交于点H ,则H 为所求的蓄水池点.于K,沿HK开挖,可使开挖的渠最短,依据是:“点与直线的连线中,⑵过H作HK EF垂线段最短”.(如图)22.PN,PM,PN,0【解析】【分析】先根据题意画出图形,再根据点到直线的距离的定义得出即可.【详解】如图所示:线段PN的长表示点P到直线BO的距离;线段PM的长表示点M到直线AO的距离;线段ON的长表示点O到直线PN的距离;点P到直线OA的距离为0,故答案为PN,PM,PN,0.【点睛】本题考查了点到直线的距离,能熟记点到直线的距离的定义是解此题的关键.23.证明见解析【解析】试题分析:由CE为角平分线,利用角平分线的定义得到∠ACD=2∠ECD,再由∠AC D=2∠B,可得∠ECD=∠B,利用同位角相等两直线平行即可证得结论.试题解析:∵CE平分∠ACD,∴∠ACD=2∠ECD,∵∠ACD=2∠B,∴∠ECD=∠B,∴AB∥CE.24.(1)∠P=∠PCD﹣∠PAB,理由见解析;(2)∠F=40°【解析】【分析】(1)先根据两直线平行得到∠PCD=∠AHC,再根据三角形的外角定理,即可得出∠P=∠PCD﹣∠PAB;(2)如图2中,设∠ABF=∠FBD=y,∠ACF=∠FCE=x,由(1)可知:∠F=x﹣y,再根据∠BDC=∠ABD+∠A,即2x=2y+80°求得x﹣y的度数,即可求出∠F的度数.【详解】(1)结论:∠P=∠PCD﹣∠PAB.理由:如图1中,设AB交PC于H.∵AB∥CD,∴∠PCD=∠AHC,∵∠AHC=∠PAB+∠P,∴∠P=∠AHC﹣∠PAB,∴∠P=∠PCD﹣∠PAB.(2)如图2中,设∠ABF=∠FBD=y,∠ACF=∠FCE=x,由(1)可知:∠F=x﹣y,∵BD∥CE,∴∠BDC=∠DCE=2x,∵∠BDC=∠ABD+∠A,∴2x=2y+80°,∴x﹣y=40°,∴∠F=40°.【点睛】此题主要考查平行线的性质,解题的关键是熟知三角形的外角定理.25.(1)20;(2)a+b=﹣3或﹣7.【解析】【分析】(1)把图像平移为长方形即可求出周长;(2)根据绝对值的性质与a,b的大小分情况讨论即可.【详解】(1)(6+4)×2=10×2=20(cm).答:它的周长是20cm.(2)∵|a|=2,|b|=5,且a>b,∴a=2,b=﹣5;a=﹣2,b=﹣5,则a+b=﹣3或﹣7.故答案为20.【点睛】此题主要考查周长的计算及绝对值的化简,解题的关键是利用已知条件进行灵活解答. 26.(1)57°;(2)3.5cm.【解析】试题分析:(1)在Rt△ABC中,利用三角形内角和先求出∠CBA的度数,再由平移的性质得到∠E的度数;(2)由平移可得AB=DE,从而得AD=BE,由平移的距离为CF=BE=AD即可得.试题解析:(1)∵在Rt△ABC中,∠C=90°,∠A=33°,∴∠CBA=90°﹣33°=57°,由平移得,∠E=∠CBA=57°;(2)由平移得,AD=BE=CF,∵AE=9cm,DB=2cm,∴AD=BE=×(9﹣2)=3.5cm,∴CF=3.5cm.。
人教版七年级数学第五章相交线与平行线检测卷(附答案)
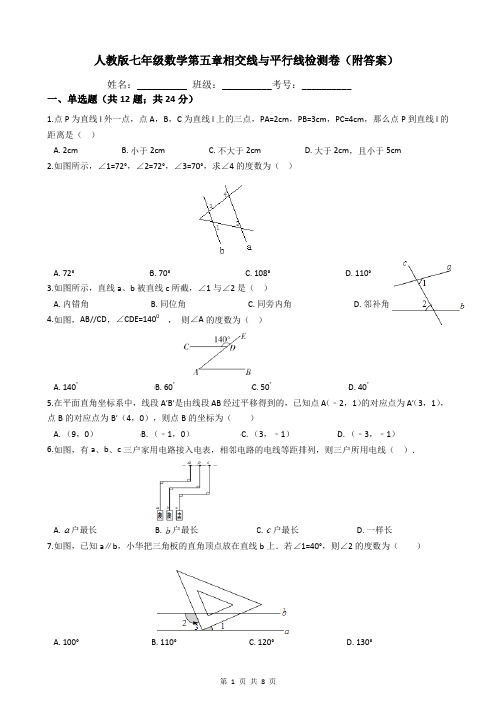
人教版七年级数学第五章相交线与平行线检测卷(附答案)姓名:__________ 班级:__________考号:__________一、单选题(共12题;共24分)1.点P为直线l外一点,点A,B,C为直线l上的三点,PA=2cm,PB=3cm,PC=4cm,那么点P到直线l的距离是()A. 2cmB. 小于2cmC. 不大于2cmD. 大于2cm,且小于5cm2.如图所示,∠1=72°,∠2=72°,∠3=70°,求∠4的度数为()A. 72°B. 70°C. 108°D. 110°3.如图所示,直线a、b被直线c所截,∠1与∠2是()A. 内错角B. 同位角C. 同旁内角D. 邻补角4.如图,AB//CD,∠CDE=1400,则∠A的度数为()A. 140°B. 60°C. 50°D. 40°5.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为()A. (9,0)B. (﹣1,0)C. (3,﹣1)D. (﹣3,﹣1)6.如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线().A. 户最长B. 户最长C. 户最长D. 一样长7.如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为()A. 100°B. 110°C. 120°D. 130°8.如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为()A. 80°B. 70°C. 90°D. 100°9.如图,∠1和∠2是对顶角的图形个数有()A. 1个B. 2个C. 3个D. 4个10.如右图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为()A. 1B. 2C. 3D. 411.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有( )A. 1个B. 2个C. 3个D. 4个12.如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是()A. ∠A+∠C+∠D+∠E=360°B. ∠A+∠D=∠C+∠EC. ∠A-∠C+∠D+∠E=180°D. ∠E-∠C+∠D-∠A=90°二、填空题(共8题;共13分)13.直线AB、CD、EF交于点O,则∠1+∠2+∠3=________度.14.如图,AB∥CD,且∠A=25°,∠C=45°,则∠E的度数是________.15.已知线段AB,点A的坐标是(3,2),点B的坐标是(2,﹣5),将线段AB平移后,得到点A的对应点A′的坐标是(5,﹣1),则点B的对应点B′的坐标为________.16.下列说法正确的有(填序号):________ .①同位角相等;②一条直线有无数条平行线;③在同一平面内,两条不相交的线段是平行线;④在同一平面内,如果a∥b,b∥c,则a∥c;⑤过一点有且只有一条直线与已知直线平行.17.如图,AH⊥BC,垂足为H,若AB=1.7cm,AC=2cm,AH=1.1cm,则点A到直线BC的距离是________cm .18.如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y= (x>0)的图象上,此时点A移动的距离为________.19.如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.证明:∵∠1+∠2﹦180(已知),∠1﹦∠4 (________),∴∠2﹢________﹦180°.∴EH∥AB (________).∴∠B﹦∠EHC(________).∵∠3﹦∠B(已知)∴∠3﹦∠EHC(________).∴DE∥BC(________).19题20题20.如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯________米.三、解答题(共3题;共30分)21.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)试证明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PEC之间会满足怎样的数量关系,证明你的结论.22.如图,有三个论断①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.23.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系四、综合题(共3题;共31分)24.如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.(1)求∠AED的度数;(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.25.如图,已知△ABC,按要求画图、填空:(1)过点A画线段BC的垂线,垂足为D;过点D画AB的平行线交AC于点E;(2)已知∠B=70°,则∠ADE=________°.26.将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°.(1)求证:∠ACE=∠BCD;(2)猜想∠ACB与∠ECD数量关系并说明理由;(3)按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.答案一、单选题1. C2. D3.A4. D5. B6. D7. D8. C9. A 10. B 11.C 12. C二、填空题13. 180 14.70°15.(4,﹣8)16.②④ 17.1.1 18.219.对顶角相等;∠4;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行20.3.8三、解答题21.(1)证明:作OM∥AB,如图1,∴∠1=∠BEO,∵AB∥CD,∴OM∥CD,∴∠2=∠DFO,∴∠1+∠2=∠BEO+∠DFO,即:∠O=∠BEO+∠DFO.(2)解:∠O+∠PFC=∠BEO+∠P.理由如下:作OM∥AB,PN∥CD,如图2,∵AB∥CD,∴OM∥PN∥AB∥CD,∴∠1=∠BEO,∠2=∠3,∠4=∠PFC,∴∠1+∠2+∠PFC=∠BEO+∠3+∠4,∴∠O+∠PFC=∠BEO+∠P.22.已知:∠B=∠D,∠A=∠C.求证:∠1=∠2.证明:∵∠A=∠C,∴AB∥CD.∴∠B=∠BFC.∵∠B=∠D,∴∠BFC=∠D.∴DE∥BF.∴∠DMN=∠BNM.∵∠1=∠DMN,∠2=∠BNM,∴∠1=∠2.23.(1)证明:过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)解:∠3=∠2﹣∠1;证明:过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)解:∠3=360°﹣∠1﹣∠2.证明:过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.(4)解:过P作PQ∥l1∥l2;①当P在C点上方时,同(2)可证:∠3=∠DFP﹣∠CEP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠DFP﹣∠CEP+∠2﹣∠1=0,即∠3=∠1﹣∠2.②当P在D点下方时,∠3=∠2﹣∠1,解法同上.综上可知:当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.四、综合题24.(1)解:∵AB∥DE,∴∠DEC=∠B= 60°(两直线平行,同位角相等),又∵BC⊥AE,∴∠AEC=90°(垂直定义),∴∠AED=90°-60°=30°;(2)解:当∠EDC=30°时,AE∥DC.由⑴得∠AED=30°,∴∠AED=∠EDC∴ AE∥DC,25.(1)解:如图:(2)20.26.(1)证明:∵∠ACD=∠ECB=90°,∴∠ACD﹣∠ECD=∠ECB﹣∠ECD,即∠ACE=∠BCD(2)解:猜想:∠ACB+∠ECD=180°.理由如下:∵∠ACB=∠ACD+∠DCB∴∠ACB+∠ECD=∠ACD+∠DCB+∠ECD又∵∠DCB+∠ECD=∠ECB,∴∠ACB+∠ECD=∠ACD+∠ECB=90°+90°=180°(3)解:当∠ACB=120°或60°时,AD∥CB.理由如下:①如图1,根据“同旁内角互补,两直线平行”:当∠A+∠ACB=180°时,AD∥BC,此时,∠ACB=180°﹣∠A=180°﹣60°=120°.②如图2,根据“内错角相等,两直线平行”:当∠ACB=∠A=60°时,AD∥BC.综上所述,当∠ACB=120°或60°时,AD∥BC.。
人教版初中数学七年级下册第五章《相交线与平行线》测试题(含答案)

第五章《相交线与平行线》检测题一、选择题(每小题只有一个正确答案)1.下列图形中,∠1与∠2是对顶角的是( )A. B. C. D.2.下列命题的逆命题不正确...的是()A. 同角的余角相等B. 等腰三角形的两个底角相等C. 两直线平行,内错角相等D. 线段中垂线上的点到线段两端的距离相等3.如图,AB∥CD,∠1=50°,∠2=110°,则∠3=()A. 60°B. 50°C. 70°D. 80°4.下列图形中线段PQ的长度表示点P到直线a的距离的是()A. B. C. D.5.如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180º;②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是()A. ①②B. ③④C. ①③④D. ①②④6.如图所示,已知∠1=∠2,那么下列结论正确的是( )A. AB∥BCB. AB∥CDC. ∠C=∠DD. ∠3=∠47.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是().B. 如图2,展开后测得12∠=∠C. 如图3,测得12∠=∠D. 如图4,展开后再沿CD 折叠,两条折痕的交点为O ,测得OA OB =, OC OD = 8.如图,01,220,=B D ∠=∠∠=∠则( )A. 20B. 22C. 30D. 459.如图,从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20°方向行走至C 处,则∠ABC 的度数是( ) .A. 80°B. 90°C. 100°D. 95°10.如图,AB∥CD∥EF,则下列各式中正确的是( )A. ∠1+∠3=180°B. ∠1+∠2=∠3C. ∠2+∠3+∠1=180°D. ∠2+∠3﹣∠1=180°11.对于命题“若22a b >,则a b >”,下面四组关于a ,b 的值中,能说明这个命题是假命题的是( ).A. 3a =, 2b =-B. 2a =-, 3b =C. 2a =, 3b =-D. 3a =-, 2b = 12.下面的每组图形中,左面的平移后可以得到右面的是( )A. B. C. D.二、填空题13.如图,DF 平分∠CDE .∠CDF =50°.∠C =80°,则________∥________.a b c d,若a∥b. a⊥c. b⊥d,则直线,c d的位置14.同一平面内有四条直线,,,关系_________.15.如图.直线a.b.且∠1.28°..2.50°.则∠ABC._______.16.下列说法:①三角形的一个外角等于它的两个内角和;②三角形的内角和等于180°,外角和等于360°.③若一个三角形的三边长分别为3.5.x,则x的取值范围是2.x.8.④角是轴对称图形,角的对称轴是角的平分线;⑤圆既是轴对称图形,也是中心对称图形,圆有无数条对称轴.其中正确的有_ __.(填序号)17.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D 在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为________.三、解答题18.将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.19.如图,已知,AB∥CD,∠1=∠2,AE与EF平行吗?为什么?20.完成下面的证明:如图.AB和CD相交于点O.∠C.∠COA.∠D.∠BOD.求证:∠A.∠B.21.如图,在6×8 方格纸中,. ABC 的三个顶点和点P .Q都在小方格的顶点上.按要求画一个三角形,使它的顶点在方格的顶点上:. 1)在图1中画. DEF,使. DEF 与. ABC 全等,且使点P在. DEF 的内部.. 2. 在图2中画. MNH,使. MNH 与. ABC 的面积相等,但不全等,且使Q在. MNH的边上.22.如图,已知射线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.(1)求∠EOB的度数;(2)若向右平移AB,其他条件都不变,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值.参考答案1.C 2.A 3.A 4.C 5.A 6.B 7.C 8.A 9.C 10.D 11.D 12.D 13. DE BC14.c ∥d 15.78° 16.②③⑤17.5.5秒或14.5秒 18.CF ∥AB 19.AE∥DF, . 20.证明:∵∠C.∠COA.∠D.∠BOD(已知). 又∵∠COA.∠BOD(__对顶角相等__). ∴∠C.__∠D__(等量代换).∴AC ∥__BD__(__内错角相等.两直线平行__). ∴∠A.∠B(__两直线平行.内错角相等__).21. 1)利用三角形平移的规律进而得出对应点位置即可; . 2)利用三角形面积公式求出符合题意的图形即可. 试题解析:解:(1)如图所示:. DEF 即为所求;.2)如图所示:.MNH 即为所求.22. (1)∵CB ∥OA ,180.C COA ∴∠+∠=︒100C OAB ∠=∠=︒Q ,80.COA ∴∠=︒ ∵OE 平分COF ∠, .COE EOF ∴∠=∠2COA COE EOF FOB AOB EOB ∠=∠+∠+∠+∠=∠Q ,40.EOB ∴∠=︒(2)这个比值不变,比值为1∶2.理由: ∵CB ∥OA ,.OBC BOA OFC FOA ∴∠=∠∠=∠,FOB BOA ∠=∠Q , 12BOA FOA ∴∠=∠,OBC OFC ∴∠=∠,:1:2.OBC OFC ∴∠∠=。
人教版数学七年级下册第五章相交线与平行线单元测试卷
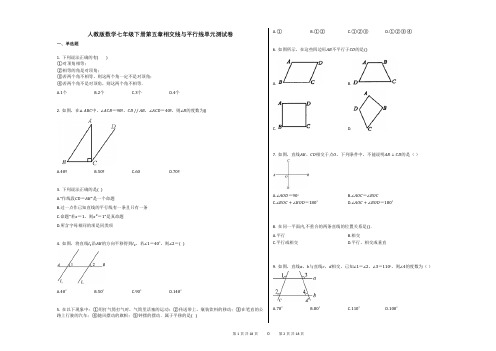
人教版数学七年级下册第五章相交线与平行线单元测试卷一、单选题1. 下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个2. 如图,在△ABC中,∠ACB=90º,CD // AB,∠ACD=40º,则∠B的度数为()A.40ºB.50ºC.60D.70º3. 下列说法正确的是()A.“作线段CD=AB”是一个命题B.过一点作已知直线的平行线有一条且只有一条C.命题“若x=1,则x2=1”是真命题D.所含字母相同的项是同类项4. 如图,将直线l1沿AB的方向平移得到l2,若∠1=40∘,则∠2=()A.40∘B.50∘C.90∘D.140∘5. 在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动.属于平移的是()A.① B.①② C.①②③ D.①②③④6. 如图所示,在这些四边形AB不平行于CD的是()A. B.C. D.7. 如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是()A.∠AOD=90∘B.∠AOC=∠BOCC.∠BOC+∠BOD=180∘D.∠AOC+∠BOD=180∘8. 在同一平面内,不重合的两条直线的位置关系是().A.平行B.相交C.平行或相交D.平行、相交或垂直9. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110∘,则∠4的度数为()A.70∘B.80∘C.110∘D.100∘10. 如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F;三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )A.0B.1C.2D.3二、填空题如图所示,AB交CD于点O,已知∠AOC=60∘,则∠AOD的度数为________.直线a同侧有A,B,C三点,若过点A,B的直线m和过点B,C的直线n都与a平行,则A,B,C三点________,原因是________.练习本中的横线格中的横线段位置关系是________,如图所示.要在台阶上铺设某种红地毯,已知这种红地毯每平方米的售价是40元,台阶宽为3米,侧面如图所示.购买这种红地毯至少需要________元.如图,直线a、b被第三条直线c所截,如果a // b,∠1=70∘,那么∠3的度数是________.三、解答题如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90∘(1)若OC平分∠AOM,求∠AOD的度数.(2)若∠1=∠BOC,求∠AOC和∠MOD.将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60∘,∠D=30∘,∠E=∠B=45∘.(1)①若∠DCE=45∘,则∠ACB的度数为________.②若∠ACB=140∘,则∠DCE的度数为________.(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<90∘且点E在直线AC的上方时,当这两块角尺有一组边互相平行时,请写出∠ACE角度所有可能的值.并说明理由.如图,点P,Q分别是∠AOB的边OA,OB上的点.(1)过点P画OB的垂线,垂足为H;(2)过点Q画OA的垂线,交OA于点C,连接PQ;(3)线段QC的长度是点Q到________的距离,________的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是________(用“<”号连接).如图,张三打算在院落里种上蔬菜,已知院落为东西长32m,南北宽20m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1m,求蔬菜的总种植面积是多少?若在运动会颁奖台上面及两侧铺上地毯(如图阴影部分),长为m,宽为n,高为ℎ,(单位为:cm).(1)用m,n,ℎ表示需要地毯的面积;(2)若m=160,n=60,ℎ=80,求地毯的面积.参考答案与试题解析人教版数学七年级下册第五章相交线与平行线单元测试卷一、单选题1.【答案】B【考点】对顶角【解析】根据对顶角的定义和性质逐题分析即可得到答案.【解答】解:①对顶角相等,故①正确;②对顶角要符合两直线相交构成的没有公共边的两个相对的角是对顶角,但相等的角不一定是对顶角,故②错误;③因为对顶角相等,所以两个角不相等,则这两个角一定不是对顶角,故③正确;④例如30∘与30∘的角不一定是对顶角,但这两个角一定相等,故④错误;正确的有①③两个.故选B.【点评】本题考查了对顶角的性质及定义,是一个需要熟记的内容.2.【答案】B【考点】平行线的判定【解析】试题分析:已知CDIIAB,∠ACD=40∘,根据平行线的性质可得∠A=∠ACD=40∘,再由直角三角形的两锐角互余可得∠B=90∘⋅∠A=90∘40∘=50∘,故答案选B.【解答】此题暂无解答【点评】平行线的性质;直角三角形的两锐角互余.3.【答案】C【考点】定义、命题、定理、推论的概念【解析】试题解析:A.不是命题.故错误.B.过直线外一点,作已知直线的平行线有一条且只有一条.故错误.C.正确.D.所含字母相同,并且相同字母的指数也相同的项叫做同类项.故错误故选C.【解答】此题暂无解答【点评】此题暂无点评4.【答案】A【考点】平移的性质平行线的性质角的计算【解析】试题分析:根据平移的性质得到平移前后的两条直线平行,然后利用平行线的性质确定答案即可.解:将直线l,沿AB的方向平移得到t2.1112∵ ∠1=40∘2=40∘故选A.【解答】此题暂无解答【点评】平移的性质.5.【答案】C【考点】一次函数的应用全面调查与抽样调查常量与变量【解析】①用打气筒打气时,气筒里活塞沿直线运动,符合平移的性质,故属平移;②传送带上,瓶装饮料的移动沿直线运动,符合平移的性质,故属平移;③在笔直的公路上行驶的汽车沿直线运动,符合平移的性质,故属平移;④随风摆动的旗帜,在运动的过程中改变图形的形状,不符合平移的性质;⑤钟摆的摆动,在运动的过程中改变图形的方向,不符合平移的性质,故选C.【解答】此题暂无解答【点评】本题考查了平移,能根据平移的特征准确识别出生活中的平移现象是解题的关键6.【答案】D【考点】平行线的概念及表示【解析】A是平行四边形,由此可以判定对边AB平行于CD;B是梯形,由此可以判定上底AB平行于下底CD;C是正方形,由此可以判定对边AB平行于CD;D是一般的四边形,AB不平行于CD.故选:D.【解答】此题暂无解答【点评】此题暂无点评7.【答案】C【考点】对顶角垂线余角和补角【解析】根据垂直的定义分析即可,两条直线相交所成的4个角中,如果有一个角等于90∘,那么这两条直线互相垂直.【解答】A.∵ ∠AOD=90∘AB⊥CD,故正确;B.∵ ∠AOC=∠BOC,∠AOC+∠BOC=180∘,2AOC=∠BOC=90∘,AB⊥CD,故正确;C.由∠BOC+∠BOO=180∘不能说明哪一个角是直角,故不正确;D.∵ ∠AOC+∠BOD=180∘,∠AOC=∠BOD,…∠AOC+∠BOD=90∘,∴AB⊥CD,故正确;故选C.【点评】本题考查了垂直的定义,对顶角相等,熟练掌握垂直的定义是解答本题的关键.8.【答案】C【考点】平行线的概念及表示相交线轴对称图形【解析】在同一平面内,不重合的两条直线的位置关系是平行或者相交.故选C【解答】此题暂无解答【点评】此题暂无点评9.【答案】A 【考点】平行线的判定与性质【解析】此题暂无解析【解答】解:∠3=∠5=10∘∠1=∠2=58∘∴ ab∠4+51180∘,∠4=70∘故选A.【点评】本题考查平行线的判定与性质.10.【答案】D【考点】平行线的判定平行线的性质【解析】如图所示:当①∠1=2,则23=2,故DBIEC,则D=±4当②∠C=2D,故∠4=±C,则DFIAC,可得:ΔA=∠F即①②可证得③;当①∠1=±2,则23=2,故DBIEC,则D=±4当③∠A=∠F,故DFIIAC,则∠4=±C,故可得:∠C=2D即①③可证得;当③∠A=∠F,故DFIAC,则∠4=±C当②2C=2D,则∠4=2D,故DBIEC,则2=23,可得:2==∠2即②③可证得①.故正确的有3个.故选D.【解答】此题暂无解答【点评】本题主要考查了平行线的判定和性质,正确掌握并熟练运用平行线的判定与性质是解题关键.二、填空题【答案】120∘【考点】角的计算余角和补角平行线的性质【解析】根据邻补角的定义即可解决问题.【解答】.AB交CD于点O,△AOC+∠AOD=180∘△AOC=60∘△AOD=180∘−60∘=120∘故答案为120∘【点评】本题考查了邻补角的定义,掌握邻补角互补是解题的关键【答案】共线;,经过直线外一点,有且只有一条直线与这条直线平行.【考点】平行公理及推论【解析】根据平行公理:经过直线外一点,有且只有一条直线与这条直线平行即可解答.【解答】直线a同侧有A,B,C三点,若过A,B的直线m和过B,C的直线n都与a平行,则经过同一点B有两条直线m 和n都与直线a平行,这与平行公理相矛盾,所以A,B,C三点共线,原因是经过直线外一点,有且只有一条直线与这条直线平行.故答案为共线;经过直线外一点,有且只有一条直线与这条直线平行.【点评】本题考查了平行公理:经过直线外一点,有且只有一条直线与这条直线平行.平行公理中要准确理解“有且只有”的含义.从作图的角度说,它是“能但只能画出一条”的意思.【答案】平行【考点】平行线的概念及表示【解析】观察可知练习本中的横线格中的横线段位置关系是平行.故答案为:平行.【解答】此题暂无解答【点评】此题暂无点评【答案】1200【考点】生活中的平移现象勾股定理的应用有理数的混合运算【解析】试题解析:利用平移线段,把楼梯的横竖向上向右平移,构成一个矩形,长宽分别为5.2米,4.8米,…地毯的长度为5.2+4.8=10米,地毯的面积为10×3=30平方米,…购买这种红地毯至少需要30×40=1200元.故答案为1200.【解答】此题暂无解答【点评】此题暂无点评【答案】70∘.【考点】平行线的判定【解析】试题分析:allb,∴2=∠1=70∘2=∠2=70∘(对顶角相等).故答案是70∘【解答】此题暂无解答【点评】平行线的性质.三、解答题【答案】(1)$${\{135}$^${\{\backslash circ \}}$; }(2)∠AOC=60∘∠MOD=150∘【考点】角平分线的定义平行线的性质角的计算【解析】(1)根据OC平分∠AOM,易得∠1=∠AOC=45∘,再由平角可求出∠AOD的度数(2)由题目中给出的∠1=14∠BOC和∴ AOM=90∘,可求出∠1的度数,进而再求出△AOC和MOD的度数.【解答】(1)△AOM=∠CON=90∘,OC平分∵ ∠AOM…∠1=∠AOC=45∘∴△AOD=180∘−∠AOC=180∘−45∘=135∘(2)∵ ∠AOM=90∘∠BOM=180∘−90∘=90∘∠1=14∠BOC∠1=13∠BOM=30∘△AOC=90∘−30∘=60∘,∠MOD=180∘−30∘=150故答案是:(1)△AOD=135∘;(2)∠AOC=60∘;∵ MOD=150∘【点评】本题主要考察角度的计算,合理分析角度之间的关系是解题的关键.【答案】135∘,40∘(2)猜想:∠ACB+∠DCE=180∘.理由如下:∵∠ACE=90∘−∠DCE,∠ACB=∠ACE+90∘,∴∠ACB=90∘−∠DCE+90∘=180∘−∠DCE,即∠ACB+∠DCE=180∘.(3)∠ACE=30∘或∠ACE=45∘.理由:①当CB//AD时,如图所示,则∠A+∠ACB=180∘.∵∠A=60∘,∠BCE=90∘,∴∠ACE=180∘−∠A−∠BCE=30∘;②当EB//AC时,如图所示,则∠ACE=∠E=45∘,综上,∠ACE=30∘或∠ACE=45∘.【考点】余角和补角平行线的性质【解析】(1)①根据直角三角板的性质结合∠DCB=45∘即可得出∠ACB的度数;②由ACB=140∘,∠ECB=90∘,可得出ACE的度数,进而得出∠DCE的度数;(2)根据①中的结论可提出猜想,再由∠ACB=∠ACD+∠DCB,∠ACB+∠DCE=90∘+∠DCB+∠DCE可得出结论;(3)分CB//AD、EB//AC两种情况进行讨论即可.【解答】解:(1)①∵∠DCE=45∘,∠ACD=90∘,∴∠ACE=∠ACD−∠DCE=45∘.∵∠BCE=90∘,∴∠ACB=∠ACE+∠BCE=45∘+90∘=135∘.②∵∠ACB=140∘,∠BCE=90∘,∴ ∠ACE=140∘−90∘=50∘,∴∠DCE=90∘−∠ACE=90∘−50∘=40∘.故答案为:135∘;40∘.(2)猜想:∠ACB+∠DCE=180∘.理由如下:∵∠ACE=90∘−∠DCE,∠ACB=∠ACE+90∘,∴∠ACB=90∘−∠DCE+90∘=180∘−∠DCE,即∠ACB+∠DCE=180∘.(3)∠ACE=30∘或∠ACE=45∘.理由:①当CB//AD时,如图所示,则∠A+∠ACB=180∘.∵∠A=60∘,∠BCE=90∘,∴∠ACE=180∘−∠A−∠BCE=30∘;②当EB//AC时,如图所示,则∠ACE=∠E=45∘,综上,∠ACE=30∘或∠ACE=45∘.【点评】本题考查了三角板的性质,直角三角形两锐角互余,角的和差,平行线的性质等知识,熟练掌握相关知识是解题的关键【答案】(1)画图见解析;(2)见解析;(3)直线OA,线段PH;PH<PQ【考点】垂线段最短【解析】(1)根据垂线的概念、结合网格特点作图即可;(2)根据垂线的概念、结合网格特点和线段的作法作图;(3)根据垂线段最短进行比较即可.【解答】(1)如图,直线PH即为所求;(2)如图,直线QC即为所求;(3)线段QC的长度是点Q到直线OA的距离,线段PH的长度是点P到直线OB的距离,根据直线外一点和直线上各点连接的所有线段中,垂线段最短可知PH<PQ故答案为直线OA,线段PH:PH<PQ【点评】本题考查了复杂作图和垂线段的性质,掌握基本尺规作图、得到复杂图形,连接垂线段最短是解题的关键.【答案】558【考点】一元二次方程的应用三角形的面积生活中的平移现象【解析】试题分析:从平移的角度考虑本题,只需要将道路平移到边上去,即可求出总面积.试题解析:如图,将三条道路都平移到边上去,则空白部分的面积(即蔬菜的总种植面积)不变,因此,蔬菜的总种植面积为:(20−2×1)(32−1)=558(m2)答:蔬菜的总种植面积是558平方米【解答】此题暂无解答【点评】此题暂无点评【答案】(1)mn+2nℎ;.(2)19200cm2【考点】列代数式一元二次方程的应用整式的加减【解析】(1)根据平移计算出地毯总长为(m+2ℎ),然后再根据长×宽可得面积;(2)把已知数据代入(1)中求出答案.【解答】(1)地毯的面积为:(m+2b)n=mn+2nℎ(2)地毯总长:80×2+160=320(cm)靠晴地能题图要判窗了独活中的平移现象、代数式求值,关键是根据平移得出地毯的总长为(m+2ℎ)【点评】此题暂无点评。
人教版数学七年级下册 第五章《相交线与平行线》测试试题(含答案)

第五章《相交线与平行线》测试题一、单选题(每小题只有一个正确答案)1.在下图中,∠1,∠2是对顶角的图形是( )A .B .C .D .2.已知1∠与2∠互为补角,1120∠=︒,则2∠的余角的度数为( )A .30°B .40︒C .60︒D .120︒3.如图,不能判断12//l l 的条件是( )A .13∠=∠B .24180∠+∠=︒C .45∠=∠D .23∠∠=4.下列图案中,可以利用平移来设计的图案是( )A .B .C .D .5.如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6旁内角;④∠5和∠2是同位角;⑤<1和∠3是同旁内角;其中正确的是( )A .①②③④B .①②③④C .①②③④⑤D .①②④⑤6.如图,点E 在AD 的延长线上,下列条件中能判断BC∥AD 的是( )A .∠3=∠4B .∠A +∠ADC =180° C .∠1=∠2D .∠A =∠57.如图,计划把河水引到水池A 中,可以先引AB ⊥CD ,垂足为B ,然后沿AB 开渠,则能使所开的渠最短,这样设计的依据是( )A .垂线段最短B .两点之间,线段最短C .两点确定一条直线D .两点之间,直线最短8.如图,已知AB CD ∥,BE 平分ABC ∠,150CDE ∠=︒,则C ∠=( )A .105︒B .120︒C .130︒D .150︒9.命题:①对顶角相等;②垂直于同一条直线的两条直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )A .1个B .2个C .3个D .4个10.如图,若∠1=∠2,则下列选项中可以判定AB ∥CD 的是( )A .B .C .D .11.将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )A .40°B .50°C .60°D .70°12.如图,若AB∥CD,CD∥EF,那么∠BCE=( )A .∠1+∠2B .∠2-∠1C .180°-∠1+∠2D .180°-∠2+∠1二、填空题13.如图,直线,AB CD 相交于点O ,OA 平分EOC ∠,:2:3EOC EOD ∠∠=,则BOD ∠=________°.14.如图,直线AB 、CD 相交于点O ,OE AB ⊥于点O ,且50COE ∠=︒,则BOD ∠=________.15.小泽在课桌上摆放了一副三角板,如图所示,得到________∥________,依据是________.16.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A 的度数为130°,第二次拐角∠B 的度数为______.三、解答题17.如图,1∠和2∠互为补角,A D ∠=∠,求证://AB CD .请根据条件进行推理,得出结论,并在括号内注明理由.证明:∵1∠和2∠互为补角(已知),∴12180∠+∠=︒(补角定义).又1CGD ∠=∠( ),∴2180CGD ∠+∠=︒(等量代换).∴//AE ( ).又∵A D ∠=∠(已知),∴D ∠=∠ .( )∴//AB CD .( ).18.如图,OA ⊥OB ,OC ⊥OD ,∠BOC =28°,求∠AOD 的度数.19.已知:如图,在△ABC 中,CD ⊥AB 于点D ,E 是AC 上一点且∠1+∠2=90°.求证:DE ∥BC .20.如图,∠ADC=∠ABC,BE 、DF 分别平分∠ABC、∠ADC、且∠1=∠2.(1)求证:AB∥CD.(2)求证:∠A=∠C.21.如图,已知,A ADE C E ∠=∠∠=∠.(1)若3,EDC C ∠=∠求C ∠的度数;(2)求证://BE CD .22.如图所示,已知//,80,140AB DE ABC CDE ︒︒∠=∠=,求BCD ∠的度数.23.如图,已知∠A = ∠C,∠E=∠F,试说明AB∥CD.参考答案1.B2.A3.D4.D5.D6.C7.A8.B9.C10.D11.D12.D13.36 14.40︒ 15.AC ∥DF 内错角相等 两直线平行 16.130°17. 证明:∵1∠和2∠互为补角(已知),∴12180∠+∠=︒(补角定义).又1CGD ∠=∠( 对顶角相等 ),∴2180CGD ∠+∠=︒(等量代换).∴//AE FD ( 同旁内角互补,两直线平行 ).又∵A D ∠=∠(已知),∴D ∠=∠ BFD .( 两直线平行,同位角相等 )∴//AB CD .( 内错角相等,量直线平行 ).18. 解:∵OC ⊥OD ,∠BOC =28°,∴∠BOD =90BOC ︒-∠=62°,∵OA ⊥OB ,∴∠AOB =90°,∴∠AOD =∠BOD +∠AOB =62°+90°=152°.19. 解:证明:∵CD ⊥AB (已知),∴∠1+∠3=90°(垂直定义).∵∠1+∠2=90°(已知),∴∠3=∠2(同角的余角相等).∴DE ∥BC (内错角相等,两直线平行).20. 证明:(1)∵BE、DF 平分∠ABC、∠ADC ∴112322ABC ADC ,∠=∠∠=∠ ∵∠ABC=∠ADC,∴∠2=∠3∵∠1=∠2,∴∠1=∠3,∴AB∥CD;(2)由(1)得AB∥CD∴∠A+∠ADC=180°,∠C+∠ABC=180°∵∠ADC=∠ABC,∴∠A=∠C.21.解:(1)A ADE∠=∠Q,∴,//ED AC∴∠+∠=︒.180EDC CQ,∠=∠EDC C3∴∠+∠=︒,3180C C∴∠=︒;45C(2)A ADE∠=∠Q,∴,//ED AC∴∠=∠.ABE E∠=∠Q,C E∴∠=∠,ABE C∴.//BE CD22.解:延长ED交BC于M.因为AB∥DE,∠ABC=80°,所以∠BMD=∠ABC=80°,因为∠CDE =140°,所以∠MDC=180°-140°=40°.在△CDM中,∠BMD=∠C+∠MDC,所以∠BCD =∠BMD-∠MDC=80°-40°=40°.23.证明:∵∠E=∠F,∴AE∥CF,∴∠A=∠ABF,∵∠A=∠C,∴∠ABF=∠C,∴AB∥CD.。
人教版七年级下册数学第五章相交线与平行线测试卷及参考答案

学校班级学号姓名第五章《相交线与平行线》检测卷温馨提示:1.本卷共三道大题,24小题,满分100分;2.考试时量:90分钟。
一、选择题(每小题3分,共30分)1.下列命题:①对顶角相等;②同位角相等;③过一点,有且只有一条直线与已知直线平行;④在同一平面内有且只有一条直线与已知直线垂直。
其中的真命题有( )A.①③B.①④C. ①②③D.①②③④2.如图,点A,B在直线l上,点C是射线AC上一点,则关于图中构成的角,说法正确的是( )A.只有同位角是3对B.只有内错角是3对C.只有同旁内角是3对D.同位角、内错角、同旁内角的对数相等。
3.如图,直线AB,CD交于点O,下列说法正确的是( )A.∠AOD=∠BODB.∠AOC=∠DOBC.∠AOC+∠BOD=180°D.以上都不对4.如图,AB∥CD,∠A=50°,则∠1的大小是( )A.50°B.120°C.130°D.150°lA BC5.如图,下列条件中,不能判定直线a ∥b 的是( ) A.∠3=∠5 B.∠2=∠6 C.∠1=∠2 D.∠4+∠6=180°6.如图所示,P 为直线m 外一点,点A ,B ,C 在直线m 上,且PB⊥m ,垂足为B ,∠APC =90°,则下列说法错误的是( ) A.线段PB 的长度叫做点P 到直线m 的距离 B .PA ,PB ,PC 三条线段中,PB 最短 C .图中的所有线段中,AC 最长 D .图中所有的线段中,AB 最短7.如图,直线AB 、CD 被EF 所截,下列结论中正确的是( ) A.∠2=∠6B.∠4=∠6C.∠4+∠5=180°D.∠5+∠6=180°8.如图,平行线AB ,CD 被直线AE 所截,∠CEF =78°,则∠A 的度数是( )A .102°B .78°C .112°D .62°9. 如图,直线l 1∥l 2,且分别与直线l 交于C ,D 两点,把一块含30º的三角尺按如图所示的位置摆放。
人教版七年级下册数学第五章相交线与平行线-测试题含答案

图中对顶角有:∠AOC 与∠BOD、∠AOD 与∠BOC,共 2 对.
故选 B.
【点睛】
本题主要考查了对顶角的定义,注意对顶角是两条直线相交而成的四个角中,没有公共边的
两个角.本题关键是分清楚已知的角是哪两条直线相交形成的,根据角的两条边,找出它的
反向延长线形成的夹角即可
8.C
【解析】
【详解】
然后由 AC∥DF,根据平行线的性质得到∠ACD=∠CDF=60°.
【详解】
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠BAC=120°,
∴∠ACD=180°-120°=60°,
∵AC∥DF,
∴∠ACD=∠CDF,
∴∠CDF=60°.
故选 A.
【点睛】
本题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.
A.120°
B.125°
C.135°
10.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=(
)
D.145°
)
第 2 页
A.60°
B.65°
C.50°
D.45°
二、填空题
11.如图, AB、CD 相交于点 O , OE 平分 AOD ,若 BOC 60 ,则 COE 的度数是
∴∠1=∠EBC=16°,
故选:C.
【点睛】
考查了平行线的性质,解题时注意:两直线平行,内错角相等.
4.D
【解析】
【分析】
直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三
条直线(截线)的同旁,则这样一对角叫做同位角,进而得出答案.
【详解】
