因式分解练习题 PPT
合集下载
整式的乘法因式分解复习课件

因式分解
1.运用前两节所学的知识填空
1).m(a+b+c)= ma+mb+你m能. c发现这 2).(a+b)(a-b)= a2-b2 两组.等式之 3).(a+b)2= a2+2ab.+b2间区的别联吗系? 和
2.试一试 填空:
1).ma+mb+mc= m•( a+b+c )
2).a2-b2=((a+b)(a-b))
A. 4X²+y² B. 4 x- (-y)²
C. -4 X²-y³ D. - X²+ y²
D. 4) -4a²+1分解因式的结果应是 (D )
A. -(4a+1)(4a-1)
B. -( 2a –1)(2a –1)
B. -(2a +1)(2a+1) D. -(2a+1) (2a-1)
整式的乘法因式分解复习课件
被除式的系数 除式的系数
底数不变, 指数相减。 整式的乘法因式分解复习课件
保留在商里 作为因式。
解: (1).(2x²y)³·(–7xy²)÷(14x4y³)
=8x6y3 ·(–7xy²)÷(14x4y³)
=-56x7y5 ÷(14x4y³) = -4x3y2 解:(2).(2a+b)4÷(2a+b)²
整式的乘法因式分解复习课件
a a a 同底数幂的乘法
m · n = m+n
幂的乘方
a a ( m )n = mn
整 式
积的乘方
( ab )n= an b n
的 乘
单项式的乘法
4a2x5 ·(-3a3bx2)
因式分解综合运用ppt课件

5
x - 4 y)(53
x + 4 y)
答案:4xy
(5)a3-ab2
(6)x4-16
答案:a(a+b)(a-b)
答案:(x2+4)(x+2)(x-2)
3. 手表表盘的外圆直径D=3.2cm,内圆直径d=2.6cm, 在外圆与内圆之间涂有黑色材料,如右图.试求涂
上材料的圆环的面积( π=3.14,结果保留两位有效 数字).怎样计算比较简便?
42
= x2 +2· x·
=
x+
5 2; 2
5 2
+
5 2
(2) 16y2-24y+9; = (4y)2 -2 ·4y ·3 + 32; = (4y-3)2 ;
(3)
x2
+
2 3
x
+
1 9
;
2
=
x2 +2·
x·
1 3
+
1 3
=
x
+
1
2;
3
(4)3x4+6x3y2+3x2y4.
因式分解综合运用
• 一、检测训练:分解因式
• (1)a-2a2+a3
(2) x2(a-1)+y2(1-a)
•
• (3)-4x2y2
• (5) (x2-3)2+(3-x2)+1 • (6) m4-2(m2-1/2) • (7) -3a(1-x)-2b(x-1)+(1-x) • (8) 8x(2x+y)3-12x2(2x+y)2
2.7
说一说
1. 平方差公式是什么样子?
x - 4 y)(53
x + 4 y)
答案:4xy
(5)a3-ab2
(6)x4-16
答案:a(a+b)(a-b)
答案:(x2+4)(x+2)(x-2)
3. 手表表盘的外圆直径D=3.2cm,内圆直径d=2.6cm, 在外圆与内圆之间涂有黑色材料,如右图.试求涂
上材料的圆环的面积( π=3.14,结果保留两位有效 数字).怎样计算比较简便?
42
= x2 +2· x·
=
x+
5 2; 2
5 2
+
5 2
(2) 16y2-24y+9; = (4y)2 -2 ·4y ·3 + 32; = (4y-3)2 ;
(3)
x2
+
2 3
x
+
1 9
;
2
=
x2 +2·
x·
1 3
+
1 3
=
x
+
1
2;
3
(4)3x4+6x3y2+3x2y4.
因式分解综合运用
• 一、检测训练:分解因式
• (1)a-2a2+a3
(2) x2(a-1)+y2(1-a)
•
• (3)-4x2y2
• (5) (x2-3)2+(3-x2)+1 • (6) m4-2(m2-1/2) • (7) -3a(1-x)-2b(x-1)+(1-x) • (8) 8x(2x+y)3-12x2(2x+y)2
2.7
说一说
1. 平方差公式是什么样子?
课件《因式分解》PPT_完美课件_人教版2

所学的解题过程,我们应用了如下关系:
x(a−b)3+y(b−a)3=(a−b)3(x+y)
因式分解与整式乘法是互逆过程.
(1)8a3b2+12ab3c (6) m2-4=(m+2)(m-2)
14.3.1 提公因式法因式分解
理解公因式的概念,会根据“三定法”确定公因式。
(7) 2πR+ 2πr= 2π(R+r)
新的多项式中若 有小括号,要化
简
即是提公因式后剩下的另一个因式.
练一练
下面的因式分解正确吗?
➢ 3x2y−9xy2=3x(xy−3y2) 3xy (x−3y) ➢ 4x2y−6xy2+2xy=2xy(2x−3y) 2xy (2x−3y+1) ➢ x(a−b)3+y(b−a)3=(a−b)3(x+y) (a−b)3(x−y)
分解因式
例1: 找 3x 2 – 6 x3y 的公因式.
因式分解与整式乘法有何关系?
提公因式并确定另一个因式:要确定另一个因式,可用原多项式除以公因式,所得的商即是提公因式后剩下的另一个因式.
所以,公因式是3x2 .
所以,公因式是3x2 . 所以,公因式是3x2 . 所以,公因式是3x2 .
第十四章 整式的乘法
(5) (a-3)(a+3)=a2-9
定系数,再确定字母,最后确定公因式字母 【名师点拨】别忘记最后核实括号内的多项式是否还有公因式。
2)(x+2)(x-2)= 这种分解因式方法叫提公因式法。
6)a2+2ab+b2= 是pa+pb+pc除以p的商
2xy (2x−3y+1)
的指数;
八年级数学下册第四章因式分解4.1因式分解典型训练ppt课件

7.一个多项式因式分解后是 3x(x+1),那么这个多项式是( C )
A.3x2+1 B.3x2+x C.3x2+3x D.4x
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
14.连一连.
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
答案如图:
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
1.把一个多项式化成_几__个__整___式__的__积__的形式,这种变形叫做因
式分解.因式分解也可称为分解因式.
2.因式分解与整式的乘法是互为_逆__运___算__的关系.
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
6.一个多项式分解因式的结果是(b3+2)(2-b3),那么这个多项
式是( B )
A.b6-4 B.4-b6 C.b6+4 D.-b6-4
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
A.3x2+1 B.3x2+x C.3x2+3x D.4x
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
14.连一连.
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
答案如图:
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
1.把一个多项式化成_几__个__整___式__的__积__的形式,这种变形叫做因
式分解.因式分解也可称为分解因式.
2.因式分解与整式的乘法是互为_逆__运___算__的关系.
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
6.一个多项式分解因式的结果是(b3+2)(2-b3),那么这个多项
式是( B )
A.b6-4 B.4-b6 C.b6+4 D.-b6-4
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
因式分解ppt(共22张PPT)

3.(随堂练习p31、2)
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式,
特征是向着积化和差的形式发展;
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式,特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式,且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止(具 体由所在的数集决定)。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2:计算
(1) 8728713 (2) 1012992
=87(87+13) =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数?
2517-532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式,
特征是向着积化和差的形式发展;
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式,特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式,且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止(具 体由所在的数集决定)。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2:计算
(1) 8728713 (2) 1012992
=87(87+13) =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数?
2517-532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法,由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
因式分解_ppt1
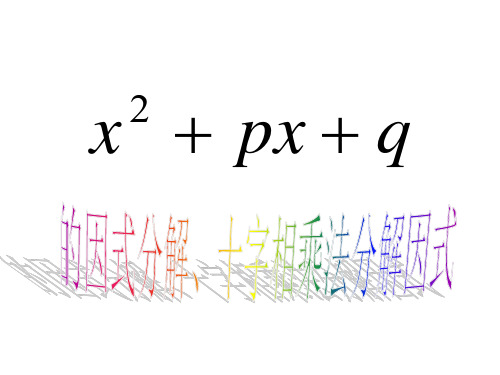
x
3
x -7
x -3
x5
因式分解_ppt1
计算:(x+2)(3x+5) =3x2+11x+10 反过来:3x2+11x+10 =(x+2)(3x+5) 我们可以发现,二次项3x2分解成 x、3x 的积; 常数项10分解成 2、5 的积;
x
2
x ·5+2 ·3x = 11x
3x
5
这个例子启发我们,如何把二次三项式
ax2+bx+c进行分解
因式分解_ppt1
因式分解_ppt1
例2、把下列各式分解因式:
(1)2x 2-7x+3
(2)6x 2-7x-5
(3)5x 2+6xy-8y2 (4)ab2+4abc+3ac 2
解:(1)原式=(x-3)(2x-1)
x
-3
2x -1
(2)原式=(2x+1)(3x-5)
2x 1 3x -5
因式分解_ppt1
x2 px q
因式分解_ppt1
1、(x+3)(x-4) =x2-x-12 2、(a-6)(a-5)=a2-11a+30 3、(y+1)(y-3) =y2-2y-3
(x a)(x b) x2 (a b)x ab
能分解x 2 5x 6吗?
(x a)(x b) x2 (a b)x ab
x2 x2 5x 6 (2) a2 2a 3 (3) x2 2x 8 (4) (x y)2 3(x y) 2
x 2 px q 分解方法
(1)找出a,b使a+b=p且ab=q (先分解q再考虑p)
(2)把q分解成两个整数的积的符号规律: q>0则a,b同号, 若p>0,a,b同正,若p<0,a,b同负; q<0则a,b异号, 若p>0,a,b中正数绝对值大, 若p<0,a,b中负数的绝对值大。
因式分解的复习PPT课件(华师大版):

因式分解的复习
一、因式分解的定义
把一个多项式化为几个整式的积的情势叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
二、因式分解与整式乘法的关系是什么﹖
整式的积
多项式
整式乘法
因式分解
练习1 下列各式中,是因式分解的,请在括号内打“√”,否则打“×”。
(1)m(x-y)=mx-my
( × )
( ×)
( √ )
(பைடு நூலகம்× )
( × )
三、因式分解的几种方法
(1)提公因式法 (2)套用公式法
(3)分组分解法 (4)十字相乘法
1、提公因式法的关键是确定公因式。
即系数取各项系数的最大公约数,字母取相同字母的 最低次幂。
2、套用公式法时要注意判断是否符合 公式要求,并熟记公式特征。
3、分组分解法的关键是适当分组,一般情况下,四项采用二二分组法或一三分组法,五项采用二三分组法。分组后还能进行继续分解。
4、十字相乘法的关键是拆常数项凑中间项。
四、例题分析
1、把下列各式分解因式
(1)3ay-3by+3y
解:原式=3y(a-b+I)
(2)-4a3b2+6a2b-2ab
解:原式= -(4a3b2-6a2b+2ab)
= -(2ab·2a2b-2ab·3a+2ab·1)
=-2ab(2a2b-3a+1)
(3)、 5(x-y)2-10(y-x)3
解:
原式=5(x-y)2+10(x-y)3
=5(x-y)2[1+2(x-y)]
=5(x-y)2(1+2x-2y)
(4)、 4x2-y2
一、因式分解的定义
把一个多项式化为几个整式的积的情势叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
二、因式分解与整式乘法的关系是什么﹖
整式的积
多项式
整式乘法
因式分解
练习1 下列各式中,是因式分解的,请在括号内打“√”,否则打“×”。
(1)m(x-y)=mx-my
( × )
( ×)
( √ )
(பைடு நூலகம்× )
( × )
三、因式分解的几种方法
(1)提公因式法 (2)套用公式法
(3)分组分解法 (4)十字相乘法
1、提公因式法的关键是确定公因式。
即系数取各项系数的最大公约数,字母取相同字母的 最低次幂。
2、套用公式法时要注意判断是否符合 公式要求,并熟记公式特征。
3、分组分解法的关键是适当分组,一般情况下,四项采用二二分组法或一三分组法,五项采用二三分组法。分组后还能进行继续分解。
4、十字相乘法的关键是拆常数项凑中间项。
四、例题分析
1、把下列各式分解因式
(1)3ay-3by+3y
解:原式=3y(a-b+I)
(2)-4a3b2+6a2b-2ab
解:原式= -(4a3b2-6a2b+2ab)
= -(2ab·2a2b-2ab·3a+2ab·1)
=-2ab(2a2b-3a+1)
(3)、 5(x-y)2-10(y-x)3
解:
原式=5(x-y)2+10(x-y)3
=5(x-y)2[1+2(x-y)]
=5(x-y)2(1+2x-2y)
(4)、 4x2-y2
湘教版初中数学七年级下册第3章因式分解 习题课件

(4) 1ax+ 1bx= 1x(a+b)等号的左侧是多项式,右侧是几个整式
3 33
的积的形式,所以该变形是因式分解. (5)4a2-8a-1=4a(a-2)-1等号的左侧是多项式,但等号的 右侧不是几个整式的积的形式,所以该变形不是因式分解.
【规律总结】 因式分解的两个要求
1.分解的结果要以积的形式表示. 2.每个因式必须是整式,且每个因式的次数都必须低于原来多项 式的次数.
m2-16
y2-6y+9
a3-a
2.根据上面的算式填空: (1)3x2-3x=________; ((23))my22--166y=+_9_=3__x__(__x__-__1__)_;__; (4)a3-a=__(_m_+_4_)_(_m_-_4_)_.
(y-3)2
a(a+1)(a-1)
【归纳】把一个多项式表示成若干个多项式_乘__积__的形式,称 为把这个多项式因式分解.
111 333
【解题探究】 (1)36a2b=3a·12ab等号的左侧是单项式,所以该变形不是因 式分解. (2)x2-2xy+y2=(x-y)2等号的左侧是多项式,右侧是几个整 式的积的形式,所以该变形是因式分解. (3)(a-1)(a+2)=a2+a-2等号的左侧是几个整式的积的形式, 不是多项式,所以该变形不是因式分解.
1
1
4
2
1.(2012·济宁中考)下列式子变形是因式分解的是( ) (A)x2-5x+6=x(x-5)+6 (B)x2-5x+6=(x-2)(x-3) (C)(x-2)(x-3)=x2-5x+6 (D)x2-5x+6=(x+2)(x+3)
