高二数学经典讲义之复数根与系数的关系-教师
根与系数的关系

根与系数的关系系数与方程根之间存在着紧密的联系,在解方程、求根等数学问题中起着重要的作用。
本文将探讨根和系数之间的关系,并探讨其在代数计算和现实生活中的应用。
一、根和系数的定义及关系根是指方程中使方程成立的未知数的值,可以是实数或复数。
而系数是方程中未知数的前面的数字或字母,用来表示未知数的倍数。
根和系数之间的关系可以用代数方程的一般形式来表达,即 a_nx^n +a_{n-1}x^{n-1} + ... + a_1x + a_0 = 0,其中 a_n, a_{n-1}, ..., a_1, a_0 是系数,x 是未知数。
二、根与系数之间的基本关系1. 根的个数与系数的关系:根的个数和方程的次数有关。
一个次数为 n 的方程最多有 n 个不同的复数根,其中包括重根。
具体而言,如果方程的系数全都是实数,则他的复数根都是成对出现的,即复数根共轭存在。
而如果方程的系数是复数,则有可能出现零个、一个或多个根。
2. 根与系数的关系及运算法则:(1)根与系数之间的关系可以由 Vieta's formulas 给出。
Vieta's formulas 断言,在一个 n 次方程的 n 个根 x_1,x_2,...,x_n 中,这些根的和等于方程的倒数第二个系数的相反数,即x_1 + x_2 + ... + x_n = -a_{n-1} / a_n。
而这些根的乘积等于最后一个系数与首项系数的比值的相反数,即x_1 * x_2 * ... * x_n = (-1)^n * a_0 / a_n。
(2)在解方程时,根与系数之间的关系也可以通过韦达定理进行推导。
韦达定理指出,对于一个 n次方程a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0 = 0,如果 x_1, x_2, ..., x_n 是方程的 n 个根,则它们满足以下关系:x_1 + x_2 + ... + x_n = -a_{n-1} / a_n,x_1 * x_2 * ... * x_n = (-1)^n * a_0 / a_n,x_1 * x_2 * ... * x_{n-1} = (-1)^{n-1} * a_1 / a_n,以此类推。
高中数学复数讲义.教师版

知识内容一、复数的概念1.虚数单位i:(1)它的平方等于,即;1-21i =-(2)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.(3)i 与-1的关系:i 就是的一个平方根,即方程的一个根,方程的另一个根是-i .1-21x =-21x =-(4)i 的周期性:, , , .41n i i +=421n i +=-43n i i +=-41n i =2.数系的扩充:复数(0)i i(0)i(0)i(0)a b a b b a a b b a b a =⎧⎪+=⎧⎨+≠⎨⎪+≠⎩⎩实数纯虚数虚数非纯虚数3.复数的定义:形如的数叫复数,叫复数的实部,叫复数的虚部.全体复数所成的集合叫做i()a b a b +∈R ,a b 复数集,用字母表示C 4.复数的代数形式:通常用字母表示,即,把复数表示成的形式,叫做复数的代数形式.z ()z a bi a b R =+∈,a bi +5.复数与实数、虚数、纯虚数及的关系:0对于复数,当且仅当时,复数是实数;当时,复数()a bi a b R +∈,0b =()a bi a b R +∈,a 0b ≠叫做虚数;当且时,叫做纯虚数;当且仅当时,就是实数z a bi =+0a =0b ≠z bi =0a b ==z 0复数h i n6.复数集与其它数集之间的关系:N Z Q R C ÜÜÜÜ7.两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.这就是说,如果,a , ,,那么,a b d ,,c d ∈R i ia b c d +=+⇔a c =b d =二、复数的几何意义1.复平面、实轴、虚轴:复数与有序实数对是一一对应关系.建立一一对应的关系.点的横i()z a b a b =+∈R ,()a b ,Z 坐标是,纵坐标是,复数可用点表示,这个建立了直角坐标系来a b i()z a b a b =+∈R ,()Z a b ,表示复数的平面叫做复平面,也叫高斯平面,轴叫做实轴,轴叫做虚轴.实轴上的点都表x y 示实数.2..对于虚轴上的点要除原点外,因为原点对应的有序实数对为,它所确定的复数是()00,表示是实数.00i 0z =+=除了原点外,虚轴上的点都表示纯虚数.3.复数复平面内的点z a bi =+←−−−→一一对应()Z a b ,这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.三、复数的四则运算1.复数与的和的定义:1z 2z 12z z +=()()i i a b c d +++=()()ia cb d +++2.复数与的差的定义:1z 2z 12z z -=()()i i a b c d +-+=()()ia cb d -+-3.复数的加法运算满足交换律:1221z z z z +=+4.复数的加法运算满足结合律:123123()()z z z z z z ++=++5.乘法运算规则:设,(、、、)是任意两个复数,1i z a b =+2i z c d =+a b c d ∈R 那么它们的积()()()()12i i izz a b c dac bd bc ad =++=-++其实就是把两个复数相乘,类似两个多项式相乘,在所得的结果中把换成,并且把实部与2i 1-虚部分别合并.两个复数的积仍然是一个复数.6.乘法运算律:(1)()()123123z z z z z z =(2)123123()()z z z z z z ⋅⋅=⋅⋅(3)()1231213z z z z z z z +=+7.复数除法定义:满足的复数(、)叫复数除以复数的商,记为:()()()i i i c d x y a b ++=+x yi +x y ∈R a bi +c di +或者()()a bi c di +÷+a bi c di++8.除法运算规则:设复数 (、),除以 (,),其商为(、),i a b +a b ∈R i c d +c d ∈R i x y +x y ∈R 即∵()(i)i i a b c d x y +÷+=+()()()()x yi c di cx dy dx cy i ++=-++∴()()i icx dy dx cy a b -++=+由复数相等定义可知解这个方程组,得cx dy a dx cy b -=⎧⎨+=⎩,2222ac bd x c d bc ad y c d +⎧=⎪⎪+⎨-⎪=⎪+⎩,于是有: ()(i)i a b c d +÷+2222ac bd bc adic d c d +-=+++②利用于是将的分母有理化得:()()22i i c d c d c d +-=+iia b c d ++原式22i (i)(i)[i (i)]()ii (i)(i)a b a b c d ac b d bc ad c d c d c d c d ++-+⋅-+-===++-+.222222()()i i ac bd bc ad ac bd bc adc d c d c d++-+-==++++∴(()(i)i a b c d +÷+=2222iac bd bc adc d c d +-+++点评:①是常规方法,②是利用初中我们学习的化简无理分式时,都是采用的分母有理化思想方法,而复数与复数,它们之积i c d +i c d --为是有理数,而是正实数.所以可以分母实数化. 把这种方法叫做分1()()22c di c di c d +-=+母实数化法.9.共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。
根与系数的关系与应用

应用场景:利用根与 系数的关系,可以解 决多种方程组问题, 特别是当方程组中存 在二次方程时。
解决步骤:首先找到 二次方程的根,然后 利用韦达定理确定其 他方程的系数,从而 解出整个方程组。
优势与它不适用于所有类 型的方程组问题。
根与系数在不等式中的应用
添加标题
添加标题
添加标题
添加标题
根的判别式
定义:根的判别式是用来判断一元二次方程实数根的个数和类型的公式。 公式:根的判别式Δ=b²-4ac。 应用:通过根的判别式可以判断一元二次方程的根的情况,进而解决实际问题。 重要性:根的判别式是数学中一元二次方程求解的重要工具,也是解决实际问题的基础。
根与系数在代数中的应用
根与系数在三 角函数中可以 用来求解三角 函数的值
根与系数在三 角函数中可以 用来判断三角 函数的单调性
根与系数在三 角函数中可以 用来研究三角 函数的周期性 和对称性
根与系数在三 角函数中可以 用来解决一些 实际问题
0
0
0
0
1
2
3
4
根与系数在实际问题中的应用
根与系数在经济问题中的应用
根与系数在金融领域的应用: 用于评估金融产品的风险和回 报,例如股票、债券等。
添加标题
根与系数的扩展应用
根与系数的复数应用
扩展定义:根与系数的关系可以扩展到复数领域 应用场景:解决复数方程的根的问题 计算方法:利用根与系数的关系,通过代数运算求出复数方程的根 实例分析:通过具体实例展示复数应用中根与系数的关系及其求解过程
根与系数的矩阵应用
定义:根与系 数的关系在矩 阵中的表现
理解遗传规律。
生态学中的应用: 根与系数可以用于 描述种群数量变化 的关系,预测种群
根与系数的关系知识点及综合应用

根与系数的关系知识点及综合应用一、一元二次方程根与系数的关系(1) 若方程02=++c bx ax (a ≠0)的两个实数根是x 1,x 2,则x 1+x 2= -a b ,x 1x 2=a c(2) 若一个方程的两个根为x 1,,x 2,那么这个一元二次方程为()[]021212=+++x x x x x x a (a ≠0) 二、根与系数的关系的应用:(1)验根:不解方程,利用根与系数的关系可以检验两个数是不是一元二次方程的两根;(2)判别一元二次方程两根的符号。
例1:不解方程,判别方程两根的符号。
分析:对于来说,往往二次项系数,一次项系数,常数项皆为已知,可据此求出根的判别式△,但△只能用于判定根的存在与否,若判定根的正负,则需要确定或的正负情况。
因此解答此题的关键是:既要求出判别式的值,又要确定 或的正负情况。
解:∵,∴△=—4×2×(—7)=65>0∴方程有两个不相等的实数根。
设方程的两个根为, ∵<0∴原方程有两个异号的实数根。
说明:判别根的符号,需要把“根的判别式”和“根与系数的关系”结合起来进行确定,另外由于本题中<0,所以可判定方程的根为一正一负;倘若>0,仍需考虑的正负,方可判别方程是两个正根还是两个负根。
(3)求根及未知数字母系数:已知方程的一个根,可利用根与系数的关系求出另一个数及未知数字母系数.例2:已知方程的一个根为2,求另一个根及的值。
分析:此题通常有两种解法:一是根据方程根的定义,把代入原方程,先求出的值,再通过解方程办法求出另一个根;二是利用一元二次方程的根与系数的关系求出另一个根及的值。
解法一:把代入原方程,得:即解得当时,原方程均可化为:,解得:∴方程的另一个根为4,的值为3或—1。
解法二:设方程的另一个根为,根据题意,利用韦达定理得:,∵,∴把代入,可得:∴把代入,可得:,即解得∴方程的另一个根为4,的值为3或—1。
说明:比较起来,解法二应用了韦达定理,解答起来较为简单。
上海(沪教版)数学高二下学期同步辅导讲义教师版:第二讲复数的方根与实系数一元二次方程

沪教版数学高二下春季班第二讲课题 复数的方根与实系数一元二次方程单元第十三章 学科数学年级十一学习 目标1.掌握待定系数法求解复数的平方根和立方根;掌握1的立方根的相关性质,并能利用其进行化简与求值2.掌握实系数一元二次方程的解法,并会结合根的情况加以讨论3.理解复数模的几何意义,熟悉常见几何图形的复数表达式 重点 1.方根的求解与化简求值;2.实系数一元二次方程的解法与根的情况分析. 难点 实系数一元二次方程的解法与根的情况分析一、复数的平方根与立方根 1.复数的平方根的定义若复数1z ,2z 满足212z z =,则称1z 是2z 的平方根.2.复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等,把复数平方根问题转化为实数方程组来求. 教学安排版块 时长1 知识梳理 302 例题解析 603 巩固训练 204 师生总结 10 5课后练习30复数的方根与实系数一元二次方程知识梳理3.复数的平方根的性质复数(0)z z ≠总有两个平方根1z ,2z ,且120z z +=(见图1). 4.复数的立方根的定义类似的,若复数1z ,2z 满足312z z =,则称1z 是2z 的立方根.5.1的立方根 设复数1322i ω=-+,则21,,ωω都是1的立方根. 6.ω的性质 ①210ωω++=, ②31ω=, ③21322i ωω==--. 可运用这些性质化简相关问题(见图2). 7.其他有用结论2(1)2i i -=-,2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式,那么(1)0∆>⇔方程有两个不相等的实根242b b aca-±-;(2)0∆=⇔方程有两个相等的实根2b a-; (3)0∆<⇔方程有两个共轭虚根242b ac b ia-±-,在(3)的情况下,方程的根与系数关系(韦达定理)仍然成立. 求解复数集上的方程的方法:(1)设(,)z x yi x y =+∈R 化归为实数方程来解决(化归思想).(2)把z 看成一个未知数(而不是实部和虚部两个未知数),用复数的性质来变形(整体思想). (3)对二次方程,直接用一元二次方程的求根公式(公式法). 图1图2三、常见几何图形的复数表达式 复数1z ,2z 为定值,且12z z ≠.(1)线段12Z Z 的中垂线方程:12||||z z z z -=-; (2)以1Z 为圆心,半径为r 的圆方程:1||z z r -=; (3)以1Z 、2Z 为焦点,长轴长为2(0)a a >的椭圆方程:12||||2z z z z a -+-=(其中12||2z z a -<); (4)以1Z 、2Z 为焦点,实轴长为2(0)a a >的双曲线方程:12||||||2z z z z a ---=(其中12||2z z a ->).1、复数的平方根与立方根 【例1】求4-及86i -的平方根.【难度】★【答案】4-的平方根为2i 或2i -;86i -的平方根为3i -或3i -+ 【例2】计算:(1)615212(13)(13)112(1)22i i i i i ---⎛⎫-+ ⎪⎝⎭;(2)50820028223(22)112313i i i i i i ⎛⎫-+++-++ ⎪ ⎪ ⎪-+-⎝⎭⎝⎭. 例题解析【注意】 (1)在复数集C 中的一元二次方程的求根公式和韦达定理仍适用,但根的判别式仅 在实数集上有效; (2)实系数一元二次方程在复数集中一定有根,若是虚根则一定成对出现; (3)齐二次实系数二次方程2211220(,,)az bz z cz a b c R ++=∈,将等式两端除以2z 后,将得到一个关于12zz 得实系数一元二次方程;(不作要求) (4)虚系数一元二次方程20(0ax bx c a a b c ++=≠,,,至少有一个为虚数)①判别式判断实根情况失效; ②虚根成对出现的性质失效; 如220x ix --=,虽然70∆=>,但该方程并无实根,不过韦达定理仍适用.【难度】★★【答案】(1)513;(2)247+【例3】记122ω=-+,求1ωω+,221ωω+. 【难度】★★ 【答案】11ωω+=-,2211ωω+=-【例4】已知等比数列123,,,,n z z z z L ,其中11z =,2z x yi =+,3z y xi =+(,,0x y x ∈>R ). (1)求,x y 的值;(2)试求使1230n z z z z ++++=L 的最小正整数n ;(3)对(2)中的正整数n ,求123n z z z z g g gL g 的值. 【难度】★★【答案】(1)12x y ⎧=⎪⎪⎨⎪=⎪⎩;(2)12n =;(3)1-.【巩固训练】1.复数34i +的平方根是 .【难度】★ 【答案】(2)i ±+2.计算:(11996= . (2)151512(1)(1)(1)i -=-+ . 【难度】★ 【答案】(1)122-;(2)03.已知ω满足等式210ωω++=.(1)计算4(1)ωω++;304050ωωω++;224(1)(1)ωωωω-+-+;(2)求证:对任意复数u ,有恒等式33233(1)()()3(1)u u u u ωω+++++=+; (3)计算:21n n ωω++,*n ∈N . 【难度】★★【答案】(1)1-;0;4;(2)略;(3)*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式:2223x x ++ 【难度】★【答案】222223244x x x x ⎛⎫⎛⎫-+-++=-- ⎪⎪ ⎪⎪⎝⎭⎝⎭2x x ⎛=+- ⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=,求()41z z ++的值 【难度】★★【答案】由210z z ++=得,211022z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1.若虚数z 满足327z =,则32315z z z +++的值为 . 【难度】★★ 【答案】332.1≠ω,13=ω,求32302ωωω+++Λ的值.【难度】★★【答案】122i ω=-+时,原式=15-;122ω=--时,原式;3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ,求方程的解.【难度】★【答案】920m ∆=-当0∆>时,即920m <时,32x ±=;当0∆=时,即920m =时,32x =;当0∆<时,即920m >时,32i x ±=.【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根,且2αβ∈R ,求βα的值.【难度】★★【答案】∵2αβ∈R ,∴2222ααβαββαβ=⇒=,即330αβ-=∴12αβ=-± 【例9】已知12,x x 是实系数方程20x x p ++=的两个根,且满足12||3x x -=,求实数p 的值. 【难度】★★ 【答案】14p ∆=-,(1)当0∆≥时,即14p ≤时,12,x x 是实根,∴12||3x x -==,即32p =⇒=-;(2)当0∆<时,即14p >时,12,x x 是共轭虚根,设1(,)x a bi a b =+∈R ,则2x a bi =-, ∴123|||2|2||32x x bi b b -===⇒=±,由1221x x a +==-,得12a =-.从而21215||2p x x x ===.综上,2p =-或52.【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根,求||||αβ+的值.【难度】★★【答案】212m ∆=-,(1)当0∆≥时,即m ≥m ≤-30αβ=>,∴||||||||m αβαβ+=+=;(2)当0∆<时,即m -<<||||2||αβα+===【例11】已知复数12,z z 满足1||2z =,2||1z =,12||2z z -=,求12z z . 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=, ∴12121z z z z ⋅+⋅=, ∴122211211z zz z z z z z ⋅⋅+⋅⋅=, ∴122141z zz z +=. 令12z t z =,则141t t+=, ∴240t t -+=,∴122t i =±,即1212z z =.【例12】(1)方程20()x px k p -+=∈R 有一个根为12i +,求实数k 的值; (2)方程240x x k -+=有一个根为12i +,求k 的值. 【难度】★【答案】(1)由题意:另一个根为12i -,∴(12)(12)5k i i =+-=; (2)由题意2(12)4(12)074i i k k i +-++=⇒=+.【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根,且一个根的模是2,求实数a 、b 的值. 【难度】★★【答案】设()t t ∈R 是方程的一实根,则2(2)()i 0t at a bt b -++-=.则220,0t at a bt b ⎧-+=⎨-=⎩.(1)当0b =时,此方程为220x ax a -+=.①有实根,0∆≥即1a ≥或0a ≤. 当根为2时,440a a -+=.得43a =.当根为2-时,440a a ++=.得45a =-. ②有一对共轭虚根即01a <<.模为2,即有4a =(舍).(2)当0b ≠时,则1t =,此时1a =.又因为模为2,所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1.下列命题在复数集中是否正确?为什么?(1)若,,a b c ∈R ,0a ≠,且240b ac -≥,则方程20ax bx c ++=有两个实数根; (2)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则12b x x a +=-,12c x x a=; (3)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则221212||()x x x x -=-;(4)若,,a b c ∈R ,0a ≠,且α是方程20ax bx c ++=的根,则α也是方程的根. 【难度】★★【答案】(1)、(2)、(4)正确,(3)不正确2.若12,x x 为方程270x x -+=的两个根,则212||x x -= .【难度】★★ 【答案】273.已知,0x y ≠且022=++y xy x ,求20092009()()x y x y x y+++的值. 【难度】★★【答案】14.关于x 的方程222(31)10x m x m --++=的两根为αβ、,且||||3αβ+=,求实数m 的值. 【难度】★★【答案】53m =-或m =5.设αβ、为方程220x x t ++=,(t ∈R )的两个根,()||||f t αβ=+,(1)求()f t 的解析式;(2)证明关于t 的方程()f t m =,当2m >时恰有两个不等的根,且两根之和为定值. 【难度】★★【答案】(1)0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩...(2)证明:函数()y f t =的图像关于直线12t =对称(证略) 当(1,)t ∈+∞时,()f t 为增函数,且()(2,)f t ∈+∞; 当(,0)t ∈-∞时,()f t 为减函数,且()(2,)f t ∈+∞.所以当2m >,方程()f t m =在区间(1,)+∞上有唯一解1t ,在区间(,0)-∞上也有唯一解2t , 则121212t t +=⨯=.4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中,1z ,2z ,m 都是复数,且21241620z z i -=+,设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值. 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=.∴2121|(4)|74m z z --=,即|(45)|7m i -+=, 这表明复数m 在以(4,5)C 为圆心,7为半径的圆周上,∴max ||7m =,min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<.【例14】已知22016220160122016(1)x x a a x a x a x ++=++++g g g ,试求0362016a a a a ++++g g g 的值。
根与系数关系及根的判别式

一元二次方程根的判别式、根与系数的关系一、根的判别式21.4022.02043.,22ac b b ac b x x a a ⎧⎪≠-∆⎪⎪∆>⎧⎪⎪⎪∆=⎨⎨⎪⎪∆<⎩⎪⎪-±--±∆⎪==⎪⎩22概念:对于一个一元二次方程ax +bx+c=0(a 0)来说,b 称为根的判别式,记为。
时,方程有个不相等的根根的判别式意义:时,方程有个相等的根时,方程没有实数根公式法:解为即为二、根与系数的关系(韦达定理):如果)0(02≠=++a c bx ax 的两个根是,,21x x 则acx x a b x x =⋅-=+2121, 以x 1和x 2为根的一元二次方程为:x 2-( x 1+x 2)x + x 1x 2=0一、选择题1. 若关于x 的方程x 2+2(k -1)x +k 2=0有实数根,则k 的取值范围是( )A. 12k <B. 12k ≤C. 12k >D. k ≥122.若t 是一元二次方程20(0)ax bx c a ++=≠的根,则判别式24b ac =-和完全平方式2(2)M at b =+的关系( )A. M =B.M >C.M <D.大小关系不能确定3.已知关于x 的一元二次方程220x x a -+=有实数根,则实数a 的取值范围是( )A.a ≤1B. a<1C. a ≤-1D. a ≥14.下列关于x 的一元二次方程中,有两个不.相等的实数根的方程是( ) A.012=+xB.0122=++x xC.0322=++x xD.0322=-+x x5.若1x 、2x 是一元二次方程0572=+-x x的两根,则2111x x +的值是( ) A.57 B.57- C.75 D.75- 6.已知x 1、x 2是方程x 2-3x +1=0的两个实数根,则1x 1+1x 2的值是()A 、3B 、-3C 、13D 、17. 不解方程,判别方程5-7x+5=0的根的情况是( ).8.已知方程x 2+(2k+1)x+k 2-2=0的两实根的平方和等于11,k 的取值是( ) A .-3或1B .-3C .1D .39.满足“两实数根之和等于3”的一个方程是( )A.0232=--x xB.02322=--x xC.0232=-+x xD.02322=-+x x 10.一元二次方程0322=--x x 的根为( )A 、3,121==x xB 、3,121=-=x xC 、3,121-=-=x xD 、3,121-==x x 11.下列方程中,没有实数根的是( )A .012=++x xB .0122=++x xC .0122=--x xD .022=--x x 12.两个不相等的实数m ,n 满足m 2-6m=4,n 2-6n=4,则mn 的值为( ) A.6 B.-6 C.4 D.-413.关于x 的一元二次方程2x 2x 40--=的两根为12x x 、,那么代数式1211x x +的值为( ) A12 B 12- C 2 D -2 14.方程x 2-5x -1=0 ( )A 、有两个相等实根B 、有两个不等实根C 、没有实根D 、无法确定 15.两个不相等的实数m ,n 满足462=-m m ,462=-n n ,则mn 的值为( )A.6B.-6C.4D.-416.已知:a +b =m ,ab =-4, 化简(a -2)(b -2)的结果是( ) A. 6 B. 2 m -8 C. 2 m D. -2 m17.方程组18ax y x by -=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,那么方程x 2+a x+b=0( )A .有两个不相等实数根B .有两个相等实数根C .没有实数根D .有两个根为2和3 18.一元二次方程0132=-+x x 的根的情况为( ) A 、有两个不相等的实数根B 、有两个相等的实数根C 、只有一个实数根D 、没有实数根二、填空题1.等腰△ABC 中,BC =8,AB 、AC 的长是关于x 的方程0102=+-m x x 的两根,则m 的值是 。
(完整版)根与系数的关系知识点及综合应用,推荐文档

根与系数的关系知识点及综合应用一、一元二次方程根与系数的关系(1)若方程 (a≠0)的两个实数根是x 1,x 2,02=++c bx ax 则x 1+x 2= -,x 1x 2=a b ac (2)若一个方程的两个根为x 1,,x 2,那么这个一元二次方程为(a≠0)()[]021212=+++x x x x x x a 二、根与系数的关系的应用:(1)验根:不解方程,利用根与系数的关系可以检验两个数是不是一元二次方程的两根;(2)判别一元二次方程两根的符号。
例1:不解方程,判别方程两根的符号。
分析:对于来说,往往二次项系数,一次项系数,常数项皆为已知,可据此求出根的判别式△,但△只能用于判定根的存在与否,若判定根的正负,则需要确定 或的正负情况。
因此解答此题的关键是:既要求出判别式的值,又要确定 或的正负情况。
解:∵,∴△=—4×2×(—7)=65>0 ∴方程有两个不相等的实数根。
设方程的两个根为, ∵<0∴原方程有两个异号的实数根。
说明:判别根的符号,需要把“根的判别式”和“根与系数的关系”结合起来进行确定,另外由于本题中<0,所以可判定方程的根为一正一负;倘若>0,仍需考虑的正负,方可判别方程是两个正根还是两个负根。
(3)求根及未知数字母系数:已知方程的一个根,可利用根与系数的关系求出另一个数及未知数字母系数.例2:已知方程的一个根为2,求另一个根及的值。
分析:此题通常有两种解法:一是根据方程根的定义,把代入原方程,先求出的值,再通过解方程办法求出另一个根;二是利用一元二次方程的根与系数的关系求出另一个根及的值。
解法一:把代入原方程,得: 即 解得 当时,原方程均可化为: , 解得: ∴方程的另一个根为4,的值为3或—1。
解法二:设方程的另一个根为,根据题意,利用韦达定理得:,∵,∴把代入,可得:∴把代入,可得:,即解得∴方程的另一个根为4,的值为3或—1。
高中数学复数讲义.教师版

复数知识内容一、复数的概念1.虚数单位 i:〔1〕它的平方等于1,即i2 1;2〕实数可以与它进行四那么运算,进行四那么运算时,原有加、乘运算律仍然成立.3〕i与-1的关系:i就是1的一个平方根,即方程21的一个根,方程21的另一个根是-i.x x〔4〕i的周期性:i4n1i,i4n21,i4n3i,i4n1.实数a(b0)2.数系的扩充:复数a bibi(b0)纯虚数bi(a0)虚数a非纯虚数a b i(a 0 )3.复数的定义:形如a bi(a,bR)的数叫复数,a叫复数的实部,b叫复数的虚部.全体复数所成的集合叫做复数集,用字母C表示4.复数的代数形式:通常用字母z表示,即z a bi(a,b R),把复数表示成abi的形式,叫做复数的代数形式.5.复数与实数、虚数、纯虚数及0的关系:对于复数abi(a,b R),当且仅当b0时,复数abi(a,b R)是实数a;当b0时,复数zabi叫做虚数;当a0且b 0时,z bi叫做纯虚数;当且仅当ab0时,z就是实数06.复数集与其它数集之间的关系:N苘ZQ苘R C7.两个复数相等的定义:如果两个复数的实部和虚局部别相等,那么我们就说这两个复数相等.这就是说,如果a,a,b,d,c,dR,那么a bi cdia c,bd二、复数的几何意义1.复平面、实轴、虚轴:复数zabi(a,bR)与有序实数对a,b是一一对应关系.建立一一对应的关系.点Z的横坐标是a,纵坐标是b,复数z abi(a,b R)可用点Za,b表示,这个建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,x轴叫做实轴,y轴叫做虚轴.实轴上的点都表示实数.2..对于虚轴上的点要除原点外,因为原点对应的有序实数对为0,0,它所确定的复数是z00i0表示是实数.除了原点外,虚轴上的点都表示纯虚数.3.复数za bi 一一对应复平面内的点Z(a,b)这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.三、复数的四那么运算1.复数z1与z2的和的定义:z1z2 a bi c di a c b di2.复数z1与z2的差的定义:z1z2abi cdi ac bdi3.复数的加法运算满足交换律:z1z2z2z14.复数的加法运算满足结合律:(z1z2)z3z1(z2z3)5.乘法运算规那么:设z1abi,z2c di(a、b、c、d R)是任意两个复数,那么它们的积z1z2abi c di ac bd bcadi其实就是把两个复数相乘,类似两个多项式相乘,在所得的结果中把i2换成1,并且把实部与虚局部别合并.两个复数的积仍然是一个复数.6.乘法运算律:〔1〕z1z2z3z1z2z3〔2〕(z1z2)z3z1(z2z3)〔3〕z1z2z3z1z2z1z37.复数除法定义:满足c di x yi a bi的复数x yi(x、y R)叫复数a bi除以复数c di的商,记为:(abi)c di或者abi c di8.除法运算规那么:设复数a bi(a、b R),除以c di(c,d R),其商为x yi〔x、y R),即(a bi)c di x yi∵x yi c di cx dy dx cy i∴cx dy dx cyi a bixac bdcx dy a c2d2,由复数相等定义可知,解这个方程组,得dx cy by bc ad c2d2于是有:(a bi)c di ac bdbc adi2222 c d c d②利用c di c di c22abi的分母有理化得:d于是将c di原式a bi(a bi)(c di)[ac bi(di)](bc ad)i c di(c di)(cdi)c2d2(ac bd)(bc ad)i ac bd bc adc2d2c2d2c2d2i.∴((a bi)c di ac bd bc ad c2d2c2d2i点评:①是常规方法,②是利用初中我们学习的化简无理分式时,都是采用的分母有理化思想方法,而复数c di与复数cdi,相当于我们初中学习的32的对偶式32,它们之积为1是有理数,而c di c di c2d2是正实数.所以可以分母实数化.把这种方法叫做分母实数化法.9.共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。
根与系数关系

根与系数的关系【教材分析】㈠教材的地位、作用和特点:“实践与探索”是新教材中一个十分新颖的教学内容,它强调“有意识、有计划地设计教学活动,引导学生体会数学之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力”。
本章的“实践与探索”内容与以往的章节相比,有了进一步的强化。
从知识上说,通过提供学生进行探究性学习的素材,学习和体会数学建模的思想和方法,拓宽一元二次方程的内容。
一方面,通过选取与生活密切相关,且具有一定思考和探索性的问题,让学生综合应用已有的知识,经过自主探索与合作交流去尝试解决,在实践中获得成功的经验。
另一方面,利用教材的弹性空间,对一元二次方程的相关知识进行拓展和探索,并以此为载体,让学生经历和体验数学发现的过程,提高学生的思维品质和进行探究性学习的能力,同时体验成功的喜悦。
本节课是第二方面的内容,主要围绕问题3展开进行探索。
在过去的教材里,这个内容是单列的,称为“一元二次方程的根与系数的关系”,教学课时也较多。
新教材把其编写成一个“实践与探索”的内容,其用意是:避免繁、难、偏、旧的模式化教学,以此为载体,创设一次探究性的学习活动,探索一元二次方程相关知识的拓展,让学生经历和体验数学发现的过程,培养学生自主学习的能力。
它强调学生的实验、观察、对比、分析、归纳,相互交流和表达自己意见;强调学生的动手,通过实验不断验证自己的发现;强调学生对解决问题策略的总结,鼓励学生自己归纳、概括并掌握基本的数学思想和方法。
㈡教学目标:根据课标要求、学生已有的知识基础和认知能力,确定以下教学目标:1.通过观察、实验、分析、归纳等数学活动,得到一元二次方程的根与系数关系的简单形式,并能简单应用。
2.参与探究性学习的过程,经历和体验数学发现的过程,培养独立思考、主动探索的习惯,培养思维的批判性、严密性,学会尝试、合作与交流,开拓思路,体验成功的喜悦。
㈢教学的重点和难点:教学重点:结合实践与探索,让学生经历和体验数学发现的过程,通过观察、实验、分析、归纳等数学思维活动,得到一元二次方程的根与系数关系的简单形式。
根与系数的关系_课件

x , x2 ,则:
1
例题讲解与练习
例1:不解方程,写出下列方程 的两根和与两根积:
(1) x 3 x 1 0 2 (2)2 x 3 x 50
1 2 ( 3) x 2 x 0 3
2
例题讲解与练习
2
(4) 2 x 6 x 3
(5) x 1 0
2
(6) x 2 x 2 0
2
⑤ x12 x2 +x1x22
⑥ x13 +x23
⑦ 2x12 7 x1 +x2
③ |x1 x2 |
④
x1 +1 x2 +1
⑧ x 3x2 +6x2
2 1 2
例3 设实数s、t分别满足 19s 99s 1 0 ,
2
t 99t 19 0 ,并且 st 1 ,
k 0 1 k 4 1 k 2
k 0 1 k 4 1 k 2
解:由题意得:
k 2 0 2 2 (2k 1) 4k 0 2k 1 x1 x2 2 0 k
2
例题讲解与练习
例2:不解方程,检验下列方程 的解是否正确?
(1) x 2 2 x 10
2
(2)2 x 3 x 80
1
2
( x 2 1, x 2 1)
1 2
7 73 5 73 (x ,x ) 4 4
2
例题讲解与练习
例3 例4
求一个方程,使它的两根分别是2和-3 已知两个数的和等于8,积等于9, 求这两个数
2
st 4t 1 求 的值. t
根与系数的关系
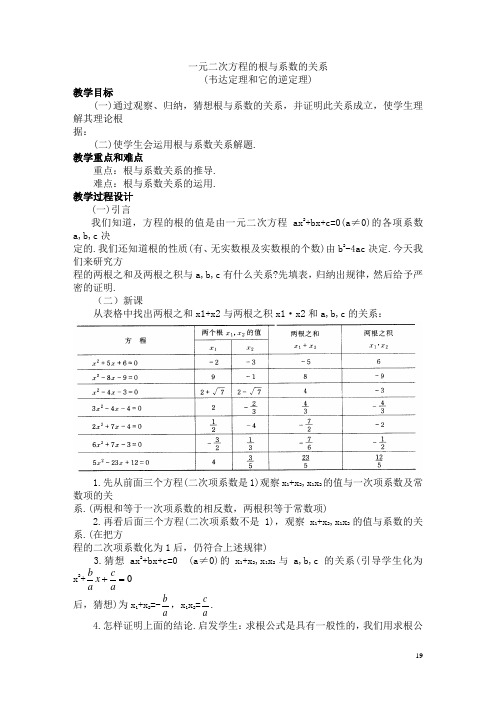
一元二次方程的根与系数的关系 (韦达定理和它的逆定理) 教学目标(一)通过观察、归纳,猜想根与系数的关系,并证明此关系成立,使学生理解其理论根 据:(二)使学生会运用根与系数关系解题. 教学重点和难点重点:根与系数关系的推导. 难点:根与系数关系的运用. 教学过程设计(一)引言我们知道,方程的根的值是由一元二次方程ax 2+bx+c=0(a ≠0)的各项系数a,b,c 决定的.我们还知道根的性质(有、无实数根及实数根的个数)由b 2-4ac 决定.今天我们来研究方程的两根之和及两根之积与a,b,c 有什么关系?先填表,归纳出规律,然后给予严密的证明.(二)新课从表格中找出两根之和x1+x2与两根之积x1·x2和a,b,c 的关系:1.先从前面三个方程(二次项系数是1)观察x 1+x 2,x 1x 2的值与一次项系数及常数项的关系.(两根和等于一次项系数的相反数,两根积等于常数项)2.再看后面三个方程(二次项系数不是1),观察x 1+x 2,x 1x 2的值与系数的关系.(在把方程的二次项系数化为1后,仍符合上述规律)3.猜想ax 2+bx+c=0 (a ≠0)的x 1+x 2,x 1x 2与a,b,c 的关系(引导学生化为x 2+0=+acx a b 后,猜想)为x 1+x 2=-a b ,x 1x 2=ac.4.怎样证明上面的结论.启发学生:求根公式是具有一般性的,我们用求根公式来证明 就可以了.证明:设ax 2+bx+c=0 (a ≠0)的两根为x 1,x 2,5.读课文以强化印象.6.为了使这个定理易于记忆,我们把二次项系数是1的方程叫做“简化的一元二次方程” .如果方程x 2+px+q=0的两根是x 1,x 2,那么x 1+x 2=-p,x 1x 2=q. 教师必须要求学生能用语言表达上述定理.“对于简化的二次方程,两根之和等于一次项系数的相反数,两根之积等于常数项”.(这个定理又叫做韦达定理)7. “对于简化的二次方程,一次项的系数等于两根之和的相反数,常数项等于两根之积”.(这是韦达定理的逆定理) 例题讲解例1 已知方程5x 2+kx-6=0的一个根是2,求它的另一个根及k 的值.解:把方程两边都除以5,化为最简二次方程例1 已知方程5x 2+kx-6=0的一个根是2,求它的另一个根及k 的值.例2 利用根与系数的关系,求一元二次方程2x 2+3x-1=0两根的(1)平方和;(2)倒数和.分析:根与系数关系告诉我们,不必解出方程,可以直接用方程的系数来表示两根之和与两根之积.如查我们所求的式子可以转化成用两根之和及两根之积表示,也就可以直接把方程的系数代入,算出结果了.例3 求一个一元二次方程,使它的两根分别是分析:“对于简化的一元二次方程,一次项的系数等于两根之和的相反数,常数项等于两根之积”.例4 已知两数的和等于8,积等于9,求:这两个数.分析:我们可以用多种方法来解决这个问题.解法1:设两个数中的一个为x,因为两数之和为8,所以另一个数为8-x.再根据“两数之积为9”,可列出方程x(8-x)=9.解法2:设两个数是x,y,可列出方程组这类方程组的解法,我们将在以后学到.解法3:因为两根和与两根积都已知,我们可以直接造出一个是简化二次方程.x2-8x+9=0.这就是方法1得到的方程.(三)课堂练习1.已知方程x2-12x+m=0的一个根是另一个根的2倍,则m= .2.已知关于x的一元二次方程(k2-1)x2-(k+1)=0的两根互为倒数,则k的取值是( ).3.已知方程x2+3x+k=0的两根之差为5,k= .答案或提示(四)小结1.应用一元二次方程的根与系数关系时,首先要把已知方程化成一般形式.2.应用一元二次方程的根与系数关系时,要特别注意,方程有实根的条件,即在初中代数里,当且仅当b2-4ac≥0时,才能应用根与系关系.3.已知方程的两根,求作一元二次方程时,要注意根与系数的正、负号.(五)作业1.设方程3x2-5x+q=0的两根为x1和x2,且6x1+x2=0,那么q的值等于( ).2.若关于x的方程3(x-1)(x-2m)=x(m-12)的两根之积等于两根之积,则此方程的两根为( ).3.已知关于x的二次方程x2+2px+2q=0有实数根,其中p,q都是奇数,那么它的根( ).(A) 一定都是奇数 (B)一定都是偶数 (C) 有可能是真分数 (D) 有可能是无理数4.(1)如果-5是方程5x2+bx-10=0的一个根,求方程的另一个根及b的值.(2)如果是方程x2+4x+c=0的一个根,求方程的另一个根及c的值.5.设x1,x2是方程2x2+4x-3=0的两个根,利用根与系数关系,求下列各式的值:6.求一个元二次方程,使它的两个根分别为7.已知两个数的和等于-6,积等于2,求这两个数.作业的答案或提示.一元二次方程的根与系数的关系练习与测试1.已知关于x 的方程)0(02>=++a c bx ax 有一个正根和一个负根,则这个方程的判别式ac b 42- 0,常数项c 0。
根与系数的关系的应用PPT课件

2.解方程组
(提示:将x,y视为x1,x2)
返回
求未知系数的取值范围
例题:已知关于x的方程9x2+(m+7)x+m-3=0.
(1)求证:无论k取何于1,另一根小于1?
分析: (1)列出△的代数式,证其恒大于零
(2)(x1-1)(x2-1)<0 解:(1)∵△=(m+7)2-4(m-3)=(m+5)2+36>0 ∴方程总有两个不相等的实数根
对于方程ax2+bx+c=0的两根x1,x2,有
对于方程x2+px+q=0的两根x1,x2,有
应用
小结
知一根(两根关系),求另一根及未知系数的值; 不解方程,求方程两根的对称式的值; 构造新方程; 求未知系数的取值范围。
返回
知一根,求另一根与未知系数的值
例题:已知关于x的方程k2x2+(2k-1)x+1=0有两个不相等的实
是方程(1)的两根的平方,则关于y的方程是__________
分析: 由y1+y2=x12+x22=(x1+x2)2-2x1x2= y1y2=x12x22=(x1x2)2= 再由知识点的第二个种情况可列出方程
练习
返回
1.已知关于x的方程2x2+5x-6=0,且关于y的方程的两根是 关于x的方程的两根的倒数,则关于y的方程是__________
返回
根与系数的关系在人教版中属于选学内容,也是高 中招生考试的重点内容之一; 在根与系数的关系的应用中,考试的热点是应用一 与应用四; 根与系数的关系常常还与三角形的有关知识相结 合一起应用.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.分类讨论是重要的思想方法。复数里也会有这样的题目,虚根、实根不同情况下,解的形式是不同的。
巩固练习
1.若 是方程 的一个解,那么 , 13
2. 是方程 的虚数根,且 ,则 _____
3.在复数集内分解因式:(1) _________
求:实数k的值。
解:
无解
, ,
, , (舍)
自我测试
1.在复数范围内解方程 ,解集是_______
2.已知 ,若方程 的一个根为 ,则 ______
3.已知一元二次方程 有实数根,则 _____
4.满足方程 的复数 有________个
5.方程 的两个根为 ,且 ,求实数 的值
6、已知:虚数(x-2)+yi(x、y )的模为 ,
3.已知复数 满足 且 ,则 ________ ,
4.方程 的解集是________
5.方程 的两根为__________
6.已知 是实系数方程 的根,则 ______
精解名题
例1.关于 的方程 的两根的模的和为 ,求实数 的值。
解:
(1)当 ,即 时,
,且
与 同号
由 得
(2)当 ,即 时, 与 为一对共轭复数,得
,
(1) ,即 ,
(2) ,
因每个方程的两根之和均为 ,故所求的和为
例4.关于 的方程 有实根,求 的取值范围。
解:设实根为 ,则 ,即
,得 ,
例5.对任意非零复数 ,定义集合 ,设 是方程
的一个根,试用例举法表示集合
解: 是 的根,则 或
当 时,
当 时,有
例6.设复数 是实系数方程 的根,又 为实数,求点 的轨迹。
(2) _____
4.已知复数 ,求实数 使 。
5.关于 的方程 有一个虚根的模为 ,求实数 并解这个方程。
6、已知复数 满足 ,求 的最大、最小值。
解:
最小 、最大
7、已知复数 满足 ,求复数 在复平面上的对应点到
点 距离的最大、最小值。
解:
,
最大距离是 最小距离最小距离
8、若关于x的方程 至少有一个模为1的根,
复数的根与系数的关系
知识精要
1.复数的平方根与立方根:
(1)利用复数相等求复数的平方根
(2)1的立方根: ( )
2.实系数一元二次方程 在复数集中恒有解.当判别式 时,方程有实数解 ;当判别式 时,方程有一对共轭虚根 .
热身练习
1. 是一元二次方程 的根,则
2.在复数范围内分解因式 ________
求: 的最大值。
解:
的最大值得是
7、已知:Z C解方程:
解:
,
又 , , ,
综上所述,得 或
例2.已知复数 满足 ( 为虚数单位), ,求一个以 为根的实系数一元二次方程。
解:
若实系数一元二次方程有虚根 ,则必有共轭虚根
,
例3.设非零复数 满足 ,并且 是虚数。
(1)求证:
(2)若 ,当 在其允许范围内变化时,求所有满足条件的虚数 的和
解:令 ,则原方程可化为 ,
解: 实系数方程的根, 也是此方程的根。
为实数( )
,即
得 ,
,所以
轨迹
例7、设复数 的虚部减去实部所得差为 ,求 。
解:
例8、已知:1+i是方程 的一个根 , 是实系数一元二次方程 的两个虚根,且 ,
求:m的值。
解:设
方法提炼
1.判别根的虚实,运用判别式,求根公式,这些方法要熟练工人
