全等三角形与角平分线经典题型
初二数学全等三角形角平分线辅助知识点-+典型题含答案

初二数学全等三角形角平分线辅助知识点-+典型题含答案一、全等三角形角平分线辅助1.已知点C 是∠MAN 平分线上一点,∠BCD 的两边CB 、CD 分别与射线AM 、AN 相交于B ,D 两点,且∠ABC +∠ADC =180°.过点C 作CE ⊥AB ,垂足为E .(1)如图1,当点E 在线段AB 上时,求证:BC =DC ;(2)如图2,当点E 在线段AB 的延长线上时,探究线段AB 、AD 与BE 之间的等量关系; (3)如图3,在(2)的条件下,若∠MAN =60°,连接BD ,作∠ABD 的平分线BF 交AD 于点F ,交AC 于点O ,连接DO 并延长交AB 于点G .若BG =1,DF =2,求线段DB 的长.2.(特例感知)(1)如图(1),ABC ∠是O 的圆周角,BC 为直径,BD 平分ABC ∠交O 于点D ,3CD =,4BD =,求点D 到直线AB 的距离.(类比迁移)(2)如图(2),ABC ∠是O 的圆周角,BC 为O 的弦,BD 平分ABC ∠交O 于点D ,过点D 作DE BC ⊥,垂足为点E ,探索线段AB ,BE ,BC 之间的数量关系,并说明理由.(问题解决)(3)如图(3),四边形ABCD 为O 的内接四边形,90ABC ∠=︒,BD 平分ABC ∠,72BD =,6AB =,求ABC 的内心与外心之间的距离.3.在平面直角坐标系中,点()5,0A -,()0,5B ,点C 为x 轴正半轴上一动点,过点A 作AD BC ⊥交y 轴于点E .(1)如图①,若点C 的坐标为(3,0),试求点E 的坐标;(2)如图②,若点C 在x 轴正半轴上运动,且5OC <,其它条件不变,连接DO ,求证:OD 平分ADC ∠(3)若点C 在x 轴正半轴上运动,当2OCB DAO ∠=∠时,试探索线段AD 、OC 、DC 的数量关系,并证明.4.在ABC 中,60A ∠=︒,BD ,CE 是ABC 的两条角平分线,且BD ,CE 交于点F .(1)如图1,用等式表示BE ,BC ,CD 这三条线段之间的数量关系,并证明你的结论;小东通过观察、实验,提出猜想:BE CD BC +=.他发现先在BC 上截取BM ,使BM BE =,连接FM ,再利用三角形全等的判定和性质证明CM CD =即可. ①下面是小东证明该猜想的部分思路,请补充完整:ⅰ)在BC 上截取BM ,使BM BE =,连接FM ,则可以证明BEF 与 全等,判定它们全等的依据是 ;ⅱ)由60A ∠=︒,BD ,CE 是ABC 的两条角平分线,可以得出EFB ∠= °; ②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想BE CD BC +=的过程. (2)如图2,若40ABC ∠=︒ ,求证:BF CA =.5.阅读资料,解决问题.人教版《数学九年级(下册)》的30页有这样一个思考问题:问题:如图,在ABC △中,DE BC ∥交AB ,AC 于点D ,E ,如果通过“相似的定义”证明ADE ABC △△∽?分析:根据“两直线平行,同位角相等”容易得出三对对应角分别相等,再根据“平行线分线段成比例”的基本事实,容易得出AD AE AB AC =,所以这个问题的核心时如何证明“DE AE BC AC =”. 证明思路:过点E 作EF AB ∥交BC 于点F ,构造平行四边形BDEF ,得到DE BF =,从而将比例式中的DE ,BC 转化为共线的两条线段BF ,BC ,同时也构造了基本图形“”,得到BF AE BC AC=,从而得证.解决问题:(1)①类比资料中的证明思路,请你证明“三角形内角平分线定理”.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.已知:如图1,ABC △中,AD 是角平分线.求证:AB BD AC DC=.②运用“三角形内角平分线定理”填空:已知:如图2,ABC △中,AD 是角平分线,7AB =,4AC =,6BC =,则BD =__________.(2)我们知道,如果两个三角形有相同的高或者相等的高,那么它们面积的比就等于底的比.请你通过研究ABD△和ACD面积的比来证明三角形内角平分线定理.已知:如图3,ABC△中,AD是角平分线.求证:AB BD AC DC.6.教材呈现:如图是华师版八年级上册数学教材第94页的部分内容.2.线段垂直平分线.我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,如图,直线MN是线段AB的垂直平分线,P是MN上任一点,连结PA、PB,将线段AB沿直线MN对称,我们发现PA与PB完全重合,由此即有:线段垂直平分线的性质定理线段垂直平分线上的点到线段的距离相等.已知:如图,MN⊥AB,垂足为点C,AC=BC,点P是直线MN上的任意一点.求证:PA=PB.分析:图中有两个直角三角形APC和BPC,只要证明这两个三角形全等,便可证明PA=PB.定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.定理应用:(1)如图②,在△ABC中,直线m、n分别是边BC、AC的垂直平分线,直线m、n的交点为O.过点O作OH⊥AB于点H.求证:AH=BH.(2)如图③,在△ABC中,AB=BC,边AB的垂直平分线l交AC于点D,边BC的垂直平分线k交AC于点E.若∠ABC=120°,AC=15,则DE的长为.7.在平面直角坐标中,等腰Rt△ABC中,AB=AC,∠CAB=90°,A(0,a),B(b,0).-+(a-2)2=0,求△ABO的面积;(1)如图1,若2a b(2)如图2,AC与x轴交于D点,BC与y轴交于E点,连接DE,AD=CD,求证:∠ADB=∠CDE;(3)如图3,在(1)的条件下,若以P(0,-6)为直角顶点,PC为腰作等腰Rt△PQC,连接BQ,求证:AP∥BQ.8.如图,已知B (-1, 0),C (1, 0),A 为y 轴正半轴上一点,AB =AC ,点D 为第二象限一动点,E 在BD 的延长线上,CD 交AB 于F ,且∠BDC =∠BAC .(1)求证:∠ABD =∠ACD ;(2)求证:AD 平分∠CDE ;(3)若在D 点运动的过程中,始终有DC =DA +DB ,在此过程中,∠BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC 的度数?9.已知:等腰直角三角形ABC中,∠ACB=90°;AC=BC;∠1=∠3;BE⊥AD。
(完整版)利用角平分线构造全等三角形

善于构造 活用性质安徽 张雷几何问题中,若出现角平分线这一条件时,可联想角平分线的特性,灵活利用角平分线的特性来解决问题.1.显“距离”, 用性质很多时候,题意中只给角平分线这个条件,图上并没有出现“距离”,而角平分线性质的运用又离不开这个“距离”,所以同学们应大胆地让“距离”现身(过角平分线上的一点向角的两边作垂线段)例:三角形的三条角平分线交于一点,你知道这是为什么吗? 分析:我们知道两条直线是交于一点的,因此可以想办法证明第三条角平分线通过前两条角平分线的交点.已知:如图,△ABC 的角平分线AD 与BE 交于点I ,求证:点I 在∠ACB 的平分线上. 证明:过点I 作IH ⊥AB 、IG ⊥AC 、IF ⊥BC ,垂足分别是点H 、G 、F . ∵点I 在∠BAC 的角平分线AD 上,且IH ⊥AB 、IG ⊥AC ∴IH=IG (角平分线上的点到角的两边距离相等) 同理 IH=IF ∴IG=IF (等量代换) 又IG ⊥AC 、IF ⊥BC∴点I 在∠ACB 的平分线上(到一个角的两边的距离相等的点,在这个角的平分线上).即:三角形的三条角平分线交于一点.【例2】已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.【分析】要证BP 为∠MBN 的平分线,只需证PD=PF ,而PA 、PC 为外角平分线,•故可过P 作PE ⊥AC 于E .根据角平分线性质定理有PD=PE ,PF=PE ,则有PD=PF ,故问题得证.【证明】过P 作PE ⊥AC 于E .∵PA 、PC 分别为∠MAC 与∠NCA 的平分线.且PD ⊥BM ,PF ⊥BN ∴PD=PE ,PF=PE,∴PD=PF又∵PD ⊥BM ,PF ⊥BN,∴点P 在∠MBN 的平分线上,D C A EHI F G2DCBA35EF14即BP是∠MBN的平分线.2.构距离,造全等有角平分线时常过角平分线上的点向角两边引垂线,根据角平分线上的点到角两边距离相等,可构造处相应的全等三角形而巧妙解决问题.例3.△ABC中,∠C=90°,AC=BC,DA平分∠CAB交BC于D点,问能否在AB•上确定一点E使△BDE的周长等于AB的长.请说明理由.解:过D作DE⊥AB,交AB于E点,则E点即可满足要求.因为∠C=90°,AC=BC,又DE⊥AB,∴DE=EB.∵AD平分∠CAB且CD⊥AC、ED⊥AB,∴CD=DE.由“HL”可证Rt△ACD≌Rt△AED.∴AC=AE.∴L△BDE=BD+DE+EB =BD+DC+EB =BC+EB=AC+EB =AE+EB =AB.例4.如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB.求证:AD=CD+AB.证明:过M作ME⊥AD,交AD于E.∵DM平分∠ADC,∠C=90°.MC=ME.根据“HL”可以证得Rt△MCD≌Rt△MED,∴CD=ED.同理可得AB=AE.∴CD+AB=ED+AE=AD.即AD=CD+AB.3.巧翻折, 造全等以角平分线为对称轴,构造两三角形全等.即在角两边截取相等的线段,构造全等三角形.例5.如图,已知△ABC中∠BAC=90°,AB=AC,CD•垂直于∠ABC•的平分线BD 于D,BD交AC于E,求证:BE=2CD.分析:要证BE=2CD,想到要构造等于2CD的线段,结合角平分线,•利用翻折的方法把△CBD沿BD翻折,使BC重叠到BA所在的直线上,即构造全等三角形(△BCD ≌△BFD),然后证明BE和CF(2CD)所在的三角形全等.证明:延长BA、CD交于点F∵BD ⊥CF (已知) ∴∠BDC=∠BDF=90° ∵BD 平分∠ABC (已知) ∴∠1=∠2 在△BCD 和△BFD 中21()()()BD BD BDC BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩已知公共边已证∴△BCD ≌△BFD (ASA ) ∴CD=FD , 即CF=2CD∵∠5=∠4=90°,∠BDF=90° ∴∠3+∠F=90°,∠1+∠F=90°。
全等三角形中角平分线问题的处理方法

【全等三角形中角平分线问题的处理方法】一、引言在初中数学中,我们学习了很多关于三角形的性质和定理,其中包括全等三角形的判定方法和性质。
而全等三角形中角平分线问题作为一个常见的题型,涉及到多个知识点的综合运用。
在本文中,我们将探讨全等三角形中角平分线的性质和处理方法,希望能够帮助大家更深入地理解这一知识点。
二、全等三角形的性质回顾在研究全等三角形中角平分线问题之前,首先我们来回顾一下全等三角形的性质。
全等三角形指的是具有相同形状和大小的三角形,它们的对应边长相等,对应角相等。
根据全等三角形的性质,我们可以得出以下结论:1. 对应角相等:如果两个三角形的三个内角分别相等,则它们是全等三角形。
2. 对应边相等:如果两个三角形的对应边分别相等,则它们是全等三角形。
3. 全等三角形的判定:SSS(边边边)、SAS(边角边)、ASA(角边角)三种情况。
三、角平分线的概念和性质角平分线是指从一个角的顶点引出,将角平分为两个相等的角的线段。
在全等三角形中,角平分线问题通常涉及到角平分线的性质和运用。
1. 角平分线的性质:角平分线将一个角平分为两个相等的角,即内角平分线和外角平分线的性质。
2. 角平分线的判定:在全等三角形中,如果两个三角形的某个角的内角平分线相等,则可以得出这两个三角形是全等的结论。
3. 角平分线的运用:在解题过程中,可以利用角平分线的性质,结合全等三角形的性质,求解各种角度的大小和线段的长度。
四、全等三角形中角平分线问题的处理方法针对全等三角形中角平分线问题,我们可以采取以下处理方法:1. 从简到繁,由浅入深:可以从单一角平分线的情况开始,逐步引入多个角平分线的情况,展示全等三角形中角平分线问题的多样性和复杂性。
2. 运用角平分线的性质:在解题过程中,可以充分利用角平分线将角分为相等部分的性质,结合全等三角形的判定方法,进行角度和线段的推导和求解。
3. 举例分析:通过具体的例题分析,展示角平分线问题的解题思路和方法,并强调在解题过程中的关键步骤和技巧。
全等三角形的判定方法50道经典题

全等三角形的判定方法50道经典题以下是全等三角形判定的50道经典题:1. 给定两个三角形的三边长,判断它们是否全等。
2. 给定两个三角形的一个角和两个侧边,判断它们是否全等。
3. 给定两个三角形的两个角和一个侧边,判断它们是否全等。
4. 给定两个三角形的一个角和两个高,判断它们是否全等。
5. 给定两个三角形的两个角和一个高,判断它们是否全等。
6. 给定两个三角形的两个角和一个中线,判断它们是否全等。
7. 给定两个三角形的一个角和两个角平分线,判断它们是否全等。
8. 给定两个三角形的两个角和一个外接圆半径,判断它们是否全等。
9. 给定两个三角形的一个角和一个内切圆半径,判断它们是否全等。
10. 给定两个三角形的一个角和一个内心到边的距离,判断它们是否全等。
11. 给定两个三角形的两个角和一个重心到边的距离,判断它们是否全等。
12. 给定两个三角形的两个角和一个垂心到边的距离,判断它们是否全等。
13. 给定两个三角形的一个角和一个外心到边的距离,判断它们是否全等。
14. 给定两个三角形的两个角和一个外心到边的距离,判断它们是否全等。
15. 给定两个三角形的两个角和一个垂足到边的距离,判断它们是否全等。
16. 给定两个三角形的两个角和一个内心到边的角平分线的距离,判断它们是否全等。
17. 给定两个三角形的一个角和一个外心到边的角平分线的距离,判断它们是否全等。
18. 给定两个三角形的两个角和一个内角平分线的夹角,判断它们是否全等。
19. 给定两个三角形的一个角和两个角平分线的夹角,判断它们是否全等。
20. 给定两个三角形的两个角和一个内心到边的角平分线的夹角,判断它们是否全等。
21. 给定两个三角形的两个角和一个内心到边的角平分线的夹角,判断它们是否全等。
22. 给定两个三角形的一个角和两个角平分线的夹角之和,判断它们是否全等。
23. 给定两个三角形的两个角和一个内心到边的角平分线的夹角之和,判断它们是否全等。
【微专题】2023学年八年级数学上册常考点提分精练(人教版) 角平分线与全等三角形结合(解析版)

角平分线与全等三角形结合1.如图 A B 两点分别在射线OM ON 上 点C 在MON ∠的内部且CA CB = CD OM ⊥ CE ON ⊥ 垂足分别为D E 且AD BE =.(1)求证:OC 平分MON ∠;(2)如果10AO = 4BO = 求OD 的长.【答案】(1)见解析(2)7【解析】【分析】(1)证明Rt △ACD ≌Rt △BCE (HL ) 得CD =CE .再由角平分线的判定即可得出结论;OC 平分∠MON ;(2)证Rt △ODC ≌Rt △OEC (HL ) 得OD =OE 设BE =AD =x .则OE =OD =4+x 再由AO =OD +AD =4+2x =10 得x =3.即可得出答案.(1)证明:∵CD OM ⊥ CE ON ⊥∴90CDA CEB ∠=∠=︒.在Rt ACD △与Rt BCE 中 CA CB AD BE =⎧⎨=⎩∴Rt ACD △≌Rt BCE (HL )∴CD CE =.又∵CD OM ⊥ CE ON ⊥∴OC 平分MON ∠.(2)解:在Rt ODC △与Rt OEC △中 CD CE OC OC =⎧⎨=⎩∴Rt ODC △≌Rt OEC △(HL )∴OD OE =设BE AD x ==.∵4BO = ∴4OE OD x ==+∵AD BE x == ∴4210AO OD AD x =+=+=∴3x = ∴437OD =+=.【点睛】本题考查了全等三角形的判定与性质、角平分线的判定等知识 证明Rt △ACD ≌Rt △BCE 和Rt △ODC ≌Rt △OEC 是解题的关键.2.已知∠MAN AC 平分∠MAN D 为AM 上一点 B 为AN 上一点.(1)如图①所示 若∠MAN =120° ∠ABC =∠ADC =90° 求证:AB +AD =AC ;(2)如图②所示 若∠MAN =120° ∠ABC +∠ADC =180° 则(1)中的结论是否仍然成立?请说明理由.【答案】(1)见解析;(2)成立 见解析【解析】【分析】(1)根据AC 平分∠MAN 可得CB =CD ∠CAB =60° 即可证明RT △ACD ≌RT △ACB 可得AD =AB 再根据AC =2AB 即可解题;(2)根据AC 平分∠MAN 可得CB =CD ∠CAB =60° 易证∠FCD =∠BCE 即可证明△CDF ≌△CBE 可得BE =DF 再根据(1)中证明AC =AE +AF 即可解题.【详解】解:(1)证明:∵AC 平分∠MAN∴CB =CD ∠CAB =60°在Rt △ACD 和Rt △AC B 中AC AC CD CB =⎧⎨=⎩∴Rt △ACD ≌Rt △ACB (HL )∴AD =AB∵∠ACB =90°﹣∠CAB =30°∴AC =2AB∴AD +AB =AC ;(2)成立 过C 作CE ⊥AN 于E CF ⊥AM 于F∵AC 平分∠MAN∴CB =CD ∠CAB =60°∵∠ABC +∠ADC =180°∴∠DCB =60°∵∠FCE =180°﹣∠BAD =60°∴∠FCE =∠BCD∵∠FCD +∠DCE =∠FCE ∠BCE +∠DCE =∠BCD∴∠FCD =∠BCE在△CDF 和△CBE 中90FCD BCE CF CE CFD CEB ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩∴△CDF ≌△CBE (ASA )∴BE =DF∴AD +AB =AD +AE +BE =AD +DF +AE =AE +AF∵AC =AE +AF∴AD +AB =A C .【点睛】本题考查了全等三角形的判定和性质 考查了全等三角形对应边相等的性质 本题中求证△CDF ≌△CBE 是解题的关键.3.如图:在直角△AB C 中 ∠ABC =90° 点D 在AB 边上 连接C D .(1)如图1 若CD 是∠ACB 的角平分线 且AD =CD 探究BC 与AC 的数量关系 说明理由; (2)如图2 若BC =BD BF ⊥AC 于点F 交CD 于点G 点E 在AB 的延长线上且AD =BE 连接GE 求证:BG +EG =A C .【答案】(1)12BC AC =理由见解析;(2)见解析 【解析】【分析】 (1)如图1 过点D 作DM AC ⊥于点M 证明()Rt CDM Rt CDB HL ≌ 由全等三角形的性质得出CM CB = 则可得出结论;(2)作DK AB ⊥交BF 的延长线于点K 证明()Rt CAB Rt BKD AAS ≌ 得出BK AC = DK AB = 证明()DKG DEG SAS ∆≅∆ 得出KG EG = 则结论可得出.【详解】解:(1)12BC AC =. 理由如下:如图1 过点D 作DM AC ⊥于点MAD CD =M ∴为AC 的中点12CM AM AC ∴== CD 平分ACB ∠DM DB ∴=在Rt CDM 和Rt CDB 中CD CD DM DB=⎧⎨=⎩ ()Rt CDM Rt CDB HL ∴≌CM CB ∴=12BC AC ∴=; (2)证明:如图2 作DK AB ⊥交BF 的延长线于点KBF AC ⊥90AFK ∴∠=︒A K ∴∠=∠又90BDK ABC ∠=∠=︒ BC BD =()Rt CAB Rt BKD AAS ∴≌BK AC ∴= DK AB =AD BE =AD BD BE BD ∴+=+即AB DE =DK DE ∴=又DB BC = 90ABC ∠=︒45CDB ∴∠=︒45KDG EDG ∴∠=∠=︒又DG DG =()DKG DEG SAS ∴∆≅∆KG EG ∴=AC BK KG BG EG BG ∴==+=+.【点睛】本题考查了全等三角形的判定与性质 角平分线的性质 等腰三角形的性质 等腰直角三角形的性质等知识 解题的关键是熟练掌握全等三角形的判定与性质.4.观察、猜想、探究:在△AB C 中 ∠ACB =2∠B .(1)如图① 当∠C =90° AD 为∠BAC 的角平分线时 过D 作AB 的垂线DE,垂足为E 可以发现AB 、AC 、CD 存在的数量关系是 ;(2)如图② 当∠C ≠90° AD 为∠BAC 的角平分线时 线段AB 、AC 、CD 是否还存(1)中的数量关系?如果存在 请给出证明.如果不存在 请说明理由;(3)如图③ 当AD 为△ABC 的外角平分线时 线段AB 、AC 、CD 又有怎样的数量关系?请写出你的猜想 并对你的猜想给予证明.【答案】(1)AB =AC +CD ;(2)存在 理由见解析;(3)AB =CD ﹣AC 理由见解析【解析】【分析】(1)根据∠ACB =90° ∠ACB =2∠B 得到∠B =45° CD ⊥AC 由线段垂直平分线的性质可得DE =CD 再证明∠B =∠EDB 得到BE =ED =CD 最后证明Rt △AED ≌Rt △ACD 得到AE =AC 即可得到结论;(2)在AB 上截取AG =AC 证明△ADG ≌△ADC 得到CD =DG ∠AGD =∠ACB 再由∠ACB =2∠B 得到∠B =∠GDB 则BG =DG =DC 即可得到AB =BG +AG =CD +AC ;(3)在AF 上截取AG =AC 由AD 为∠F AC 的平分线 得到∠GAD =∠CAD 可证△ADG ≌△ACD 得到CD =GD ∠AGD =∠ACD 即可推出∠ACB =∠FGD 再由∠ACB =2∠B 推出∠B =∠GDB 得到BG =DG =DC 则AB =BG ﹣AG =CD ﹣A C .【详解】解:(1)AB =AC +CD 理由如下:∵∠ACB =90° ∠ACB =2∠B∴∠B =45° CD ⊥AC∵DE ⊥AB AD 平分∠BAC∴DE =CD ∠DEB =∠DEA =90°∴∠EDB =180°-∠B -∠DEB =45°∴∠B =∠EDB∴BE =ED =CD在Rt △AED 和Rt △AD C 中DE DC AD AD =⎧⎨=⎩∴Rt △AED ≌Rt △ACD (HL )∴AE =AC∴AB +AE +BE =AC +CD ;(2)还存在AB =CD +AC 理由如下:在AB 上截取AG =AC 如图2所示∵AD 为∠BAC 的平分线∴∠GAD =∠CAD∵在△ADG 和△AD C 中AG AC GAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∴△ADG ≌△ADC (SAS )∴CD =DG ∠AGD =∠ACB∵∠ACB =2∠B∴∠AGD =2∠B又∵∠AGD =∠B +∠GDB∴∠B =∠GDB∴BG =DG =DC则AB =BG +AG =CD +AC ;(3)AB =CD ﹣AC 理由如下:在AF 上截取AG =AC 如图3所示∵AD 为∠F AC 的平分线∴∠GAD =∠CAD∵在△ADG 和△AC D 中AG AC GAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∴△ADG ≌△ACD (SAS )∴CD =GD ∠AGD =∠ACD∵∠FGD =180°-∠AGD ∠ACB =180°-∠ACD∴∠ACB =∠FGD∵∠ACB =2∠B∴∠FGD =2∠B又∵∠FGD =∠B +∠GDB∴∠B =∠GDB∴BG =DG =DC则AB =BG ﹣AG =CD ﹣A C .【点睛】本题主要考查了全等三角形的性质与判定 角平分线的性质与定义 三角形外角的性质 三角形内角和定理 解题的关键在于能够熟练掌握全等三角形的性质与判定条件.5.已知:如图1 在ABC 中 AD 是BAC ∠的平分线.E 是线段AD 上一点(点E 不与点A 点D 重合) 满足2∠=∠ABE ACE .(1)如图2 若18∠=︒ACE 且EA EC = 则DEC ∠=________︒ AEB ∠=_______︒. (2)求证:AB BE AC +=.(3)如图3 若BD BE = 请直接写出ABE ∠和BAC ∠的数量关系.【答案】(1)36 126;(2)见解析;(3)3180∠+∠=︒ABE BAC【解析】【分析】(1)18∠=︒ACE 且EA EC = 再结合三角形的外角定理即可求DEC ∠ 18∠=︒ACE 且EA EC = AD 是BAC ∠的平分线 2∠=∠ABE ACE 再结合三角形内角和定理即可求解AEB ∠; (2)在AC 上截取AF AB = 连接FE 可证()≌AEF AEB SAS 故EF EB = AFE ABE 从而可得FEC FCE ∠=∠ 所以EF FC =进而可证得:=+=+AC AF FC AB BE (3)由BD BE = 可得BED BDE ∠=∠ BED ABE BAE ∠=∠+∠ ∠=∠+∠BDE DAC ACD 又AD 是BAC ∠的平分线 可得ABE ACD ∠=∠ 故CE 是ACD ∠的平分线 所以BE 是ABD ∠的平分线 故∠=∠=∠ABE ACD DBE 又180ACB ABC BAC ∠+∠+∠=︒ 所以ABE ∠和BAC ∠的数量关系即可求解.【详解】(1)∵18∠=︒ACE 且EA EC =∴∠EAC =∠ACE =18°∴∠DEC =∠EAC +∠ACE =36°又∵AD 是BAC ∠的平分线∴∠BAD =∠CAD =18°∵2∠=∠ABE ACE∴∠ABE =36°∴1801836126∠=︒-︒-︒=︒AEB ;故答案为:36 126(2)在AC 上截取AF AB = 连接FE又∵AE =AE EAF EAB ∠=∠∴()≌AEF AEB SAS∴EF EB = AFE ABE∵∠AFE =∠ACE +∠FEC ∠ABE =2∠ACE∴FEC FCE ∠=∠∴EF FC =∴=+=+AC AF FC AB BE ;(3)∵BD BE =∴BED BDE ∠=∠∵BED ABE BAE ∠=∠+∠ ∠=∠+∠BDE DAC ACD∠CAD =∠BAE∴∠ACD =∠ABE∵∠ABE =2∠ACE∴∠ACD =2∠ACE∴CE 平分∠ACB∴点E 到CA 、CB 的距离相等又∵AD 是BAC ∠的平分线∴点E 到AC 、AB 的距离相等∴点E 到BA 、BC 的距离相等∴BE 是ABD ∠的平分线∴∠ABE =∠CBE∴∠=∠=∠ABE ACD DBE又∵180ACB ABC BAC ∠+∠+∠=︒∴2180∠+∠+∠=︒ABE ABE BAC即3180∠+∠=︒ABE BAC .【点睛】本题考查了三角形外角的性质、三角形的内角和定理、角平分线的性质、三角形全等的判定和性质 解题的关键是熟练掌握各知识点 准确作出辅助线 熟练运用数形结合的思想.6.已知:如图 D 为△ABC 外角∠ACP 平分线上一点 且DA =DB DM ⊥BP 于点M .(1)若AC =6 DM =2 求△ACD 的面积;(2)求证:AC =BM +CM .【答案】(1)6;(2)见解析【解析】【分析】(1)如图作DN ⊥AC 于N .根据角平分线的性质定理可得DM =DN =2 由此即可解决问题; (2)由Rt △CDM ≌Rt △CDN 推出CN =CM 由Rt △ADN ≌Rt △BDM 推出AN =BM 由此即可解决问题.【详解】(1)解:如图作DN ⊥AC 于N .∵DC 平分∠ACP DM ⊥CP DN ⊥CA∴DM =DN =2∴S △ADC =12•AC •DN =12×6×2=6.(2)∵CD =CD DM =DN∴Rt △CDM ≌Rt △CDN∴CN =CM∵AD =BD DN =DM∴Rt △ADN ≌Rt △BDM∴AN =BM∴AC =AN +CN =BM +CM .【点睛】本题考查全等三角形的判定和性质、角平分线的性质定理等知识 解题的关键是学会添加常用辅助线 构造全等三角形解决问题 属于中考常考题型.7.如图 在∠EAF 的平分线上取点B 作BC ⊥AF 于点C 在直线AC 上取一动点P .在直线AE 上取点Q 使得BQ=BP .(1)如图1 当点P 在点线段AC 上时 ∠BQA +∠BP A = °;(2)如图2 当点P 在CA 延长线上时 探究AQ 、AP 、AC 三条线段之间的数量关系 说明理由; (3)在满足(1)的结论条件下 当点P 运动到在射线AC 上时 直接写出AQ 、AP 、PC 三条线段之间的数量关系为: .【答案】(1)180;(2)2AQ AP AC -=;理由见解析;(3)2AQ AP PC -=或2AP AQ PC -=.【解析】【分析】(1)作BM ⊥AE 于点M 根据角平分线的性质得到BM =BC 证明Rt BMQ ∆Rt ()BPC HL ∆≌,继而证明BQA BPC ∠=∠解题即可;(2)作BM AE ⊥于M 先证明Rt Rt ABM ABC ∆∆≌(HL ) 继而得到ABM ABC ∠=∠ AM AC = BM BC = 再证明Rt Rt BMQ BCP ∆∆≌(HL ) 从而得到PC QM = 据此解题即可;(3)分两种情况讨论 当点P 在线段AC 上时 或当点P 在线段AC 的延长线上时 分别画出适合的图 再由QBM PBC ∆∆≌(AAS )可得QBM PBC ∠=∠ QM PC = BM BC = 再由Rt Rt ABM ABC ∆∆≌(HL )可得AM AC = 利用线段和差计算即可.【详解】(1)证明:过点B 作BM AE ⊥于M∵BA 平分EAF ∠ BC AF ⊥∴BM BC =在Rt BMQ ∆和Rt BPC ∆中BQ BP BM BC =⎧⎨=⎩∴Rt Rt BMQ BPC ∆∆≌(HL )∴BQA BPC ∠=∠又∵180BPC BPA ∠+∠=︒∴180BQA BPA ∠+∠=︒故答案为180;(2)解:2AQ AP AC -=理由如下:如图2 作BM AE ⊥于M∵AB 平分∠EAF BC AF ⊥∴BM =BC 90BMA BCA ∠=∠=︒在Rt ABM ∆和Rt ABC ∆中BM BC AB AB=⎧⎨=⎩ ∴Rt Rt ABM ABC ∆∆≌(HL )∴ABM ABC ∠=∠ AM AC =在Rt BMQ ∆和Rt BCP ∆中BQ BP BM BC =⎧⎨=⎩∴Rt Rt BMQ BCP ∆∆≌(HL )∴PC QM =∴()()2AQ AP AM QM PC AC AM AC AC -=+--=+=(3)当点P 在线段AC 上时 如图 2AQ AP PC -=理由如下:作BM AE ⊥于M∵BC ⊥AF∴90BMA BCA ∠=∠=︒∵180BQA BPA ∠+∠=︒ ∠BPC +∠BP A =180°∴∠BPC =∠BQM在QBM ∆和PBC ∆中BMQ BCP BQM BPC QB PB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴QBM PBC ∆∆≌(AAS )∴QBM PBC ∠=∠ QM PC = BM BC =在Rt ABM ∆和Rt ABC ∆中BM BC AB AB =⎧⎨=⎩∴Rt Rt ABM ABC ∆∆≌(HL )∴AM AC =∴()2AQ AP AM QM AC PC QM PC PC -=+--=+=当点P 在线段AC 的延长线上时 如图 2AP AQ PC -=理由如下:作BM AE ⊥于M∵BC ⊥AF∴90BMA BCA ∠=∠=︒∵180BQA BPA ∠+∠=︒ ∠BQM +∠BQA =180°∴∠BPC =∠BQM在QBM ∆和PBC ∆中BMQ BCPBQM BPCQB PB∠=∠⎧⎪∠=∠⎨⎪=⎩∴QBM PBC ∆∆≌(AAS )∴QBM PBC ∠=∠ QM PC = BM BC =在Rt ABM ∆和Rt ABC ∆中BM BCAB AB =⎧⎨=⎩∴Rt Rt ABM ABC ∆∆≌(HL )∴AM AC =∴()2AP AQ AC CP AM QM MQ PC PC -=+--=+=故答案为:2AQ AP PC -=或2AP AQ PC -=.【点睛】本题考查全等三角形的判定与性质 角平分线性质 分类讨论思想等知识 掌握相关知识利用辅助线画出准确图形是解题关键.8.如图 在ABC 中 BAD DAC ∠=∠ DF AB ⊥ DM AC ⊥ 10AF cm = 14AC cm = 动点E 以2/cm s 的速度从A 点向F 点运动 动点G 以1/cm s 的速度从C 点向A 点运动 当一个点到达终点时 另一个点随之停止运动 设运动时间为t .(1)CM = :AE CG = ;(2)当t 取何值时 DFE △和DMG △全等;(3)在(2)的前提下 若:119:126BD DC = 228cm AED S =△ 求BFD S .【答案】(1)4 2;(2)143;(3)293cm 2.【解析】【分析】(1)根据角平分线的性质可证Rt △AFD ≌Rt △AMD 得AF =AM 从而求出即可;(2)分两种情况进行讨论:①当0<t <4时 ②当4≤t <5时 分别根据△DFE ≌△DMG 得出EF =GM 据此列出关于t 的方程 进行求解即可.(3)利用等高三角形的面积比等于对应底的比 即可求得答案.【详解】(1)∵∠BAD =∠DAC DF ⊥AB DM ⊥AC ∴DF =DM在Rt △AFD 和Rt △AM D 中DF DMAD AD =⎧⎨=⎩∴Rt △AFD ≌Rt △AMD (HL );∴10AF AM cm ==14104CM AC AM cm ∴=-=-=2AE t = CG t = :2AE CG ∴=(2)①当0<t <4时 点G 在线段CM 上 点E 在线段AF 上.EF =10﹣2t MG =4﹣t∴10﹣2t=4﹣t∴t=6(不合题意舍去);②当4<t<5时点G在线段AM上点E在线段AF上.EF=10﹣2t MG=t﹣4∴10﹣2t=t﹣4∴t=143;综上所述当t=143时△DFE与△DMG全等;(3)∵t=14 3∴AE=2t=28 3∵DF=DM∴S△ABD:S△ACD=AB:AC=BD:CD=119:126 ∵AC=14∴AB=119 9∴BF=AB﹣AF=1199﹣10=299∵S△ADE:S△BDF=AE:BF=283:299S△AED=28cm2∴S△BDF=293cm2.【点睛】本题考查了全等三角形的判定和性质、角平分线的性质、三角形的面积公式以及动点问题解题的难点在于第二问中求运动的时间此题容易漏解和错解.9.在平面直角坐标系中A(﹣3 0)、B(0 7)、C(7 0)∠ABC+∠ADC=180° BC⊥C D.(1)如图1①求证:∠ABO=∠CAD;②AB与AD是否相等?请说明理由;(2)如图2 E为∠BCO的邻补角的平分线上的一点且∠BEO=45° OE交BC于点F求BF 的长.【答案】(1)①见解析;②AB=AD见解析;(2)7【解析】【分析】(1)根据四边形的内角和定理、直角三角形的性质证明;(2)过点A作AF⊥BC于点F作AE⊥CD的延长线于点E△ABF≌△ADE得到AB=AD(3)过点E作EH⊥BC于点H作EG⊥x轴于点G根据角平分线的性质得到EH=EG证明△ABF ≌△ADE得到EB=EO根据等腰三角形的判定定理解答.【详解】证明:①在四边形ABC D中∵∠ABC+∠ADC=180°∴∠BAD+∠BCD=180°∵BC⊥CD∴∠BCD=90°∴∠BAD=90°∴∠BAC+∠CAD=90°∵∠BAC+∠ABO=90°∴∠ABO=∠CAD;解:②AB=AD如图:过点A 作AF ⊥BC 于点F 作AE ⊥CD 的延长线于点E ∵B (0 7) C (7 0)∴OB =OC∴∠BCO =45°∵BC ⊥CD∴∠BCO =∠DCO =45°∵AF ⊥BC AE ⊥CD∴AF =AE ∠F AE =90°∴∠BAF =∠DAE在△ABF 和△ADE 中BAF DAE AF AEAFB AED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABF ≌△ADE (ASA )∴AB =AD(3)过点E 作EH ⊥BC 于点H 作EG ⊥x 轴于点G∵E 点在∠BCO 的邻补角的平分线上∴EH =EG∵∠BCO =∠BEO =45°∴∠EBC =∠EOC在△EBH 和△EOG 中EBH EOG EHB EGO EH EG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EBH ≌△EOG (AAS )∴EB =EO∵∠BEO =45°∴∠EBO =∠EOB =67.5° 又∠OBC =45°∴∠BOE =∠BFO =67.5°∴BF =BO =7.【点睛】本题考查的是全等三角形的判定和性质、角平分线的性质 掌握全等三角形的判定定理和性质定理是解题的关键.10.如图所示 直线AB 交x 轴于点A (a 0) 交y 轴于点B (0 b )且a 、b2(4)0a -= C 的坐标为(﹣1 0) 且AH ⊥BC 于点H AH 交OB 于点P .(1)如图1 写出a 、b 的值 证明△AOP ≌△BOC ;(2)如图2 连接OH 求证:∠OHP =45°;(3)如图3 若点D 为AB 的中点 点M 为y 轴正半轴上一动点 连接MD 过D 作DN ⊥DM 交x 轴于N 点 当M 点在y 轴正半轴上运动的过程中 求证:S △BDM ﹣S △ADN =4.【答案】(1)a =4 b =﹣4 见解析;(2)见解析;(3)见解析【解析】【分析】(1)先依据非负数的性质求得a 、b 的值从而可得到OA OB = 然后再90COB POA ∠=∠=︒OAP OBC ∠=∠ 最后 依据ASA 可证明OAP OBC ∆∆≌;(2)要证45OHP ∠=︒ 只需证明HO 平分CHA ∠ 过O 分别作OM CB ⊥于M 点 作ON HA ⊥于N 点 只需证到OM ON = 只需证明COM PON ∆∆≌即可;(3)连接OD 易证ODM ADN ∆∆≌ 从而有ODM ADN S S ∆∆= 由此可得12BDM ADN BDM ODM BOD AOB S S S S S S ∆∆∆∆∆∆-=-==. 【详解】(1)解:2(4)0a -=0a b ∴+= 40a -=4a ∴= 4b =-则4OA OB ==.AH BC ⊥即90AHC ∠=︒ 90COB ∠=︒90HAC ACH OBC OCB ∴∠+∠=∠+∠=︒HAC OBC ∴∠=∠.在OAP ∆与OBC ∆中90COB POA OA OBOAP OBC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()OAP OBC ASA ∴∆∆≌;(2)证明:过O 分别作OM CB ⊥于M 点 作ON HA ⊥于N 点.在四边形OMHN 中 36039090MON ∠=︒-⨯︒=︒90COM PON MOP ∴∠=∠=︒-∠.OAP OBC ∆∆≌OC OP ∴=在COM ∆与PON ∆中90COM PON OMC ONP OC OP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩()COM PON AAS ∴∆∆≌OM ON ∴=.OM CB ⊥ ON HA ⊥HO ∴平分CHA ∠1452OHP CHA ∴∠=∠=︒; (3)证明:如图:连接OD .90AOB ∠=︒ OA OB = D 为AB 的中点OD AB ∴⊥ 45BOD AOD ∠=∠=︒ OD DA BD ==45OAD ∴∠=︒ 9045135MOD ∠=︒+︒=︒135DAN MOD ∴∠=︒=∠.MD ND ⊥即90MDN ∠=︒90MDO NDA MDA ∴∠=∠=︒-∠.在ODM ∆与ADN ∆中MDO NDA DOM DAN OD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩()ODM ADN ASA ∴∆∆≌ODM ADN S S ∆∆∴=.11114442222BDM ADN BDM ODM BOD AOB S S S S S S AO BO ∆∆∆∆∆∆∴-=-===⨯⋅=⨯⨯⨯=. 【点睛】本题是一次函数综合题 考查了全等三角形的判定与性质、等腰直角三角形的性质、角平分线的判定、二次根式及完全平方式的非负性等知识 在解决第(3)小题的过程中还用到了等积变换而运用全等三角形的性质则是解决本题的关键.11.在△AB C 中 ∠BAC =90° AB =A C .(1)如图1 若A 、B 两点的坐标分别是A (0 4) B (﹣2 0) 求C 点的坐标;(2)如图2 作∠ABC 的角平分线BD 交AC 于点D 过C 点作CE ⊥BD 于点E 求证: BD =2CE【答案】(1)(4 2);(2)证明过程见解析【解析】【分析】(1)作CM ⊥OA 垂足为M 证明△ABO ≌△CAM 即可得解;(2)延长CE 、BA 相交于点F 证明△ABD ≌△ACF (ASA ) 得到BD =CF 证明△BCE ≌△BFE (ASA ) 即可得解;【详解】(1)作CM ⊥OA 垂足为M∵∠AOB =∠BAC =90°∴∠BAO +∠CAM =90° ∠BAO +∠ABO =90°∴∠ABO =∠CAM在ABO 和CAM 中AOB CMA ABO CAM AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABO ≌△CAM∴MC =AO =4 AM =BO =2 MO =AO -AM =2∴点C 坐标(4 2);(2)如图2 延长CE 、BA 相交于点F∵∠EBF+∠F =90° ∠ACF+∠F =90°∴∠EBF =∠ACF在ABD △和ACF 中ABD ACF AB ACBAD CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABD ≌△ACF (ASA )∴BD=CF在BCE 和BFE △中CBE FBE BE BEBEF BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BCE ≌△BFE (ASA )∴CE =EF∴BD =CF =2 CE .【点睛】本题主要考查了全等三角形的判定与性质 角平分线的性质 准确分析证明是解题的关键. 12.如图1 点A 、D 在y 轴正半轴上 点B 、C 分别在x 轴上 CD 平分∠ACB 与y 轴交于D 点 ∠CAO +∠BDO =90°.(1)求证:AC =BC ;(2)如图2 点C 的坐标为(6 0) 点E 为AC 上一点 且∠DEA =∠DBO 求BC +EC 的值;(3)如图3 过D 作DF ⊥AC 于F 点 点H 为FC 上一动点 点G 为OC 上一动点 当H 在FC 上移动、点G 在OC 上移动时 始终满足∠GDH =∠GDO +∠FDH .试判断FH 、GH 、OG 这三者之间的数量关系 写出你的结论并加以证明.【答案】(1)证明见解析;(2)BC +EC =12;(3)GH =FH +OG 证明见解析.【解析】【分析】(1)由题意∠CAO +∠BDO =90° 可知∠CAO =∠CBD 再结合CD 平分∠ACB 所以可由AAS 定理证明△ACD ≌△BCD 由全等三角形的性质可得AC =BC ;(2)过D 作DN ⊥AC 于N 点 可证明Rt △BDO ≌Rt △EDN 、△DOC ≌△DNC 因此 BO =EN 、OC =NC 所以 BC +EC =BO +OC +NC -NE =2OC 即可得BC +EC 的长;(3)在x 轴的负半轴上取OM =FH 可证明△DFH ≌△DOM 、△HDG ≌△MDG 因此 MG =GH 所以 GH =OM +OG =FH +OG 即可证明所得结论.【详解】(1)证明:∵x 轴⊥y 轴∴∠CBD +∠BDO =90°∵∠CAO +∠BDO =90°∴∠CAO =∠CB D .∵CD 平分∠ACB∴ACD BCD ∠=∠在△ACD 和△BC D 中ACD BCD CAO CBD CD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△BCD (AAS ).∴AC =BC AD =DE ;(2)解:由(1)知∠CAD =∠DEA =∠DBO∴BD =AD =DE过D 作DN ⊥AC 于N 点 如右图所示:∵∠ACD =∠BCD∴DO =DN在Rt △BDO 和Rt △EDN 中BD DE DO DN=⎧⎨=⎩ ∴Rt △BDO ≌Rt △EDN (HL )∴BO =EN .在△DOC 和△DN C 中90DOC DNC OCD NCD DC DC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DOC ≌△DNC (AAS )可知:OC =NC ;∴BC +EC =BO +OC +NC -NE =2OC =12;(3)GH =FH +OG .证明:由(1)知:DF =DO在x 轴的负半轴上取OM =FH 连接DM 如图所示: 在△DFH 和△DOM 中90DF DO DFH DOM OM FH ︒=⎧⎪∠=∠=⎨⎪=⎩∴△DFH ≌△DOM (SAS ).∴DH =DM ∠1=∠ODM .∴∠GDH =∠1+∠2=∠ODM +∠2=∠GDM . 在△HDG 和△MDG 中DH DMGDH GDM DG DG=⎧⎪∠=∠⎨⎪=⎩ ∴△HDG ≌△MDG (SAS ).∴MG =GH∴GH =OM +OG =FH +OG .【点睛】本题考查坐标与图形 全等三角形的性质和判定 角平分线的性质.能正确作出辅助线构造全等三角形是解题关键.。
(完整)全等三角形和角平分线专题讲解和练习题

C EODBA21C EDB A21OA全等三角形专题讲解专题一 全等三角形判别方法的应用专题概说:判定两个三角形全等的方法一般有以下4种: 1.三边对应相等的两个三角形全等(简写成“SSS ”)2.两边和它们的夹角对应相等的两个三角形全等(简写成“SAS") 3.两角和它们的夹边对应相等的两个三角形全等(简写成“ASA ”)4.两个角和其中一个角的对边对应相等的两个三角形全等(简写成“AAS")而在判别两个直角三角形全等时,除了可以应用以上4种判别方法外,还可以应用“斜边、直角边”,即斜边和一条直角边对应相等的两个直角三角形全等(简写成“HL ”).也就是说“斜边、直角边”是判别两个直角三角形全等的特有的方法,它仅适用于判别两个直角三角形全等.三角形全等是证明线段相等,角相等最基本、最常用的方法,这不仅因为全等三角形有很多重要的角相等、线段相等的特征,还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来.那么我们应该怎样应用三角形全等的判别方法呢?(1)条件充足时直接应用在证明与线段或角相等的有关问题时,常常需要先证明线段或角所在的两个三角形全等,而从近年的中考题来看,这类试题难度不大,证明两个三角形的条件比较充分.只要同学们认真观察图形,结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等.例1 已知:如图1,CE ⊥AB 于点E ,BD ⊥AC 于点D ,BD 、CE 交于点O,且AO 平分∠BAC .那么图中全等的三角形有___对.图1(2)条件不足,会增加条件用判别方法此类问题实际是指条件开放题,即指题中没有确定的已知条件或已知条件不充分,需要补充使三角形全等的条件.解这类问题的基本思路是:执果索因,逆向思维,逐步分析,探索结论成立的条件,从而得出答案.例2 如图2,已知AB=AD ,∠1=∠2,要使△ABC ≌△ADE,还需添加的条件是(只需填一个)_____. 图2(3)条件比较隐蔽时,可通过添加辅助线用判别方法在证明两个三角形全等时,当边或角的关系不明显时,可通过添加辅助线作为桥梁,沟通边或角的关系,使条件由隐变显,从而顺利运用全等三角形的判别方法证明两个三角形全等.例3 已知:如图3,AB=AC,∠1=∠2. 求证:AO 平分∠BAC .分析:要证AO 平分∠BAC ,即证∠BAO=∠BCO,要证∠BAO=∠BCO,只需证∠BAO 和∠BCO 所在的两个三角形全等.而由已知条件知,只需再证明BO=CO 即可.图3GABF DEC ODA CBFCEDBA(4)条件中没有现成的全等三角形时,会通过构造全等三角形用判别方法有些几何问题中,往往不能直接证明一对三角形全等,一般需要作辅助线来构造全等三角形.例4 已知:如图4,在Rt △ABC 中,∠ACB=90º,AC=BC ,D 为BC 的中点,CE ⊥AD 于E ,交AB 于F ,连接DF .求证:∠ADC=∠BDF .说明:常见的构造三角形全等的方法有如下三种:①涉及三角形的中线问题时,常采用延长中线一倍的方法,构造出一对全等三角形;②涉及角平分线问题时,经过角平分线上一点向两边作垂线,可以得到一对全等三角形;③证明两条线段的和等于第三条线段时,用“截长补短”法可以构造一对全等三角形.(5)会在实际问题中用全等三角形的判别方法新课标强调了数学的应用价值,注意培养同学们应用数学的意识,形成解决简单实际问题的能力﹒在近年中考出现的与全等三角形有关的实际问题,体现了这一数学理念,应当引起同学们的重视.例5 要在湖的两岸A 、B 间建一座观赏桥,由于条件 限制,无法直接度量A ,B 两点间的距离﹒请你用学过的数 学知识按以下要求设计一测量方案﹒(1)画出测量图案﹒(2)写出测量步骤(测量数据用字母表示)﹒ 图5 (3)计算A 、B 的距离(写出求解或推理过程,结果用字母表示)﹒分析:可把此题转化为证两个三角形全等.第(1)题,测量图案如图5所示.第(2)题,测量步骤:先在陆地上找到一点O ,在AO 的延长线上取一点C ,并测得OC=OA ,在BO 的延长线上取一点D ,并测得OD=OB,这时测得CD 的长为a ,则AB 的长就是a .第(3)题易证△AOB ≌△COD ,所以AB=CD ,测得CD 的长即可得AB 的长.解:(1)如图6示.(2)在陆地上找到可以直接到达A 、B 的一点O,在AO 的延长线上取一点C ,并测得OC =OA ,在BO 的延长线上取一点D ,并测得OD =OB,这时测出CD 的长为a ,则AB 的长就是a .(3)理由:由测法可得OC=OA ,OD=OB . 又∠COD=∠AOB ,∴△COD ≌△AOB .∴CD=AB=a . 图6评注:本题的背景是学生熟悉的,提供了一个学生动手操作的机会,重点考查了学生的操作能力,培养了 学生用数学的意识﹒练习:1.已知:如图7,D 是△ABC 的边AB 上一点,AB ∥FC ,DF 交AC 于点E ,DE=FE . 求证:AE=CE .C ED B AAO Q M CPBN A D C PBHF EGAD CBADCFBEA2.如图8,在△ABC 中,点E 在BC 上,点D 在AE 上,已知∠ABD=∠ACD ,∠BDE=∠CDE .求证:BD=CD .3.用有刻度的直尺能平分任意角吗?下面是一种方法:如图9所示,先在∠AOB 的两边上取OP=OQ ,再取PM=QN,连接PN 、QM,得交点C ,则射线OC 平分∠AOB .你能说明道理吗?4.如图10,△ABC 中,AB=AC,过点A 作GE ∥BC ,角平分线BD 、CF 相交于点H ,它们的延长线分别交GE 于点E 、G .试在图10中找出3对全等三角形,并对其中一对全等三角形给出证明.5.已知:如图11,点C 、D 在线段AB 上,PC=PD .请你添加一个条件,使图中存在全等三角形,并给予证明.所添条件为__________,你得到的一对全等三角形是△_____≌△_____.6.如图12,∠1=∠2,BC=EF ,那么需要补充一个直接条件_____(写出一个即可),才能使△ABC ≌△DEF .7图13,在△ABD 和△ACD 中,AB=AC,∠B=∠C .求证:△ABD ≌△ACD .AODCBAFCGBEAF DCB EOED218.如图14,直线AD与BC相交于点O,且AC=BD,AD=BC.求证:CO=DO.9.已知△ABC,AB=AC,E、F分别为AB和AC延长线上的点,且BE=CF,EF交BC于G.求证:EG=GF.10.已知:如图16,AB=AE,BC=ED,点F是CD的中点,AF⊥CD.求证:∠B=∠E.11.如图17,某同学把一把三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么最省事的办法是()﹒(A)带①和②去 (B)带①去(C)带②去(D)带③去12.有一专用三角形模具,损坏后,只剩下如图18中的阴影部分,你对图中做哪些数据度量后,就可以重新制作一块与原模具完全一样的模具,并说明其中的道理.13.如图19,将两根钢条AA’、BB’的中点O连在一起,使AA’、BB’可以绕着点O自由转动,就做成了一个测量工件,则A' B'的长等于内槽宽AB,那么判定△OAB≌△OAB的理由是( )(A)边角边(B)角边角(C)边边边(D)角角边专题二角的平分线从一个角的顶点出发,把一个角分成相等的两个角的射线,叫做这个角的平分线.角的平分线有着重要的作用,它不仅把角分成相等的两部分,而且角的平分线上的点到角两边的距离相等,到一个角的两边距离相等的点在这个角的平分线上,再加上角的平分线所在的直线是角的对称轴.因此当题目中有角的平分线时,可根据角的平分线性质证明线段或角相等,或利用角的平分线构造全等三角形或等腰三角形来寻找解题思路.(1)利用角的平分线的性质证明线段或角相等F ED CB A 21A FH DCGBEADCBE AF DC BE C E D例6 如图20,∠1=∠2,AE ⊥OB 于E , BD ⊥OA 于D ,交点为C .求证:AC=BC .说明:本题若用全等方法证明点C 到OA 、OB 距离相等,浪费时间和笔墨,不如直接应用角平分线性质证明,原因在于同学们已经习惯了用全等的方法,不善于直接应用定理,仍去找全等三角形,结果相当于重新证明了一次定理,以后再学新定理,应用时要注意全等定势的干扰,注意采用简捷证法. 例7 已知:如图21,△ABC 中, BD=CD ,∠1=∠2.求证:AD 平分∠BAC .说明:遇到有关角平分线的问题时,可引角的两边的垂线,先证明三角形全等,然后根据全等三角形的性质得出垂线段相等,再利用角的平分线性质得出两角相等.(2)利用角的平分线构造全等三角形 ①过角平分线上一点作两边的垂线段例8 如图22,AB ∥CD ,E 为AD 上一点,且BE 、CE 分别平分∠ABC 、∠BCD . 求证:AE=ED .分析:由于角平分线上一点到角的两边的距离相等,而点E 是两条角平分线的交点,因此我们自然想到过点E 分别作AB 、BC 、CD 的垂线段.②以角的平分线为对称轴构造对称图形例9 如图23,在△ABC 中,AD 平分∠BAC,∠C=2∠B .求证:AB=AC+CD .分析:由于角平分线所在的直线是这个角的对称轴,因此在AB 上截取AE=AC,连接DE ,我们就能构造出一对全等三角形,从而将线段AB 分成AE 和BE 两段,只需证明BE=CD 就可以了.③延长角平分线的垂线段,使角平分线成为垂直平分线 例10 如图24,在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E . 求证:∠ACE=∠B+∠ECD .分析:注意到AD 平分∠BAC ,CE ⊥AD ,于是可延长CE 交AB 于点F,即可构造全等三角形..(3)利用角的平分线构造等腰三角形如图25,在△ABC 中,AD 平分∠BAC ,过点D 作DE ∥AB ,DE 交AC 于点E .易证△AED 是等腰三角形. 因此,我们可以过角平分线上一点作角的一边的平行线,构造等腰三角形.CF E BADQPCBACB AD EA例11 如图26,在△ABC 中,AB=AC,BD 平分∠ABC ,DE ⊥BD 于D ,交BC 于点E .求证:CD=21BE .分析:要证CD=21BE ,可将BE 分成两条线段,然后再证明CD 与这两条线段都相等.练习:1.如图27,在△ABC 中,∠B=90º,AD 为∠BAC 的平分线,DF ⊥AC 于F,DE=DC .求证:BE=CF .2.已知:如图28,AD 是△ABC 的中线,DE ⊥AB 于E ,DF ⊥AC 于F ,且BE=CF .求证:(1)AD 是∠BAC 的平分线;(2)AB=AC .3.在△ABC 中,∠BAC=60º,∠C=40º,AP 平分∠BAC 交BC 于P,BQ 平分∠ABC 交AC 于Q . 求证:AB+BP=BQ+AQ .4.如图30,在△ABC 中,AD 平分∠BAC ,AB=AC+CD . 求证:∠C=2∠B .5.如图31,E 为△ABC 的∠A 的平分线AD 上一点,AB >AC . 求证:AB —AC >EB-EC .CB AD 4321C E BADF CE BAD CEBADCBADACBD6.如图32,在四边形ABCD 中,BC >BA ,AD=CD ,BD 平分∠ABC . 求证:∠A+∠C=180º.7.如图33所示,已知AD ∥BC ,∠1=∠2,∠3=∠4,直线DC 过点E 作交AD 于点D ,交BC 于点C .求证:AD+BC=AB .8.已知,如图34,△ABC 中,∠ABC=90º,AB=BC,AE 是∠A 的平分线,CD ⊥AE 于D .求证:CD=21AE .9.△ABC 中,AB=AC,∠A=100º,BD 是∠B 的平分线.求证:AD+BD=BC .10.如图36,∠B 和∠C 的平分线相交于点F ,过点F 作DE ∥BC 交AB 于点D ,交AC 于点E ,若BD+CE=9,则线段DE 的长为( )A .9B .8C .7D .611.如图37,△ABC 中,AD 平分∠BAC ,AD 交BC 于点D ,且D 是BC 的中点.求证:AB=AC .A CF E B M D12.已知:如图38,△ABC 中,AD 是∠BAC 的平分线,E 是BC 的中点,EF ∥AD ,交AB 于M ,交CA 的延长线于F .求证:BM=CF .。
全等三角形角平分线例题

全等三角形角平分线例题今天咱们聊聊全等三角形和角平分线,这个话题听起来可能有点枯燥,但别担心,我会把它说得轻松有趣。
先来个小故事。
想象一下,三角形ABC,A、B、C三个角像三个好朋友,他们总是一起出门,一起玩耍。
这个三角形的每一个角都很重要,就像我们生活中的朋友,每个都有自己的个性和特点。
三角形的角平分线就像是那条神奇的路,把朋友们的个性完美地分开又能团聚在一起。
我们可以把角平分线看作是三角形中的一位调解者,负责把角度平分,既不偏心,也不失公正。
好啦,咱们再深入一点,想象一下,这个角平分线就是从点A出发,像个小精灵,悄悄地走向BC边。
小精灵的目标就是让AB和AC的角度各自和谐,平等地对待。
你要知道,这个小精灵可不是随便走的,它得计算得特别精准,因为它的任务就是把大角分成两个小角。
无论是30度、60度,还是其他什么度数,只要有这条角平分线,两个小角就会是一样的。
这不就像是把一块蛋糕分成两份,两个朋友都能吃到一模一样的那份美味,心里都乐开了花。
不得不提到全等三角形。
嘿,全等三角形可是一对一的关系。
就像两只一模一样的鞋子,左脚和右脚,缺一不可。
全等三角形的意思就是它们的边长和角度都是一样的,简直就像是镜子里的倒影。
不管你怎么看,A、B、C三角形和A'、B'、C'三角形,它们就是这么巧妙地吻合在一起,任何一个角都不会落下。
想象一下,如果你把这两个全等三角形叠在一起,它们会像两只小鸟儿,翅膀轻轻一扇,正好就能飞到一起。
这个时候,角平分线又来凑热闹了!它就像个万能的钥匙,打开了这两只小鸟儿之间的秘密。
只要有了角平分线,这两个三角形的关系就更加亲密,仿佛它们有了超能力,无论怎么翻转、旋转,都能轻松找到彼此。
生活中处处都有角平分线和全等三角形的影子。
比如说,你和朋友一起买东西,恰好有个买一送一的优惠,你们俩就可以各自分一半,省钱又开心。
这种平分的精神不就是角平分线的体现吗?而全等三角形则提醒我们,朋友之间的关系要对等,互相尊重,才能长久。
全等三角形与角平分线专题

B AACA 1.如图,已知∠ACB=90°,AD 平分∠BAC 交BC 于点D ,DE ⊥AB 于E ,BD=DF 交CA 的延长线于F 点,求证:BE=AE+AF2.如图,在四边形ABCD 中,AC 平分∠BAD ,过C 作CE ⊥AB 于E ,且AE=12(AB+AD )。
求∠ABC+∠ADC 的度数3.如图,在△ABC 中,∠ABC=100°,∠ACB=20°,CE 是△ABC 的角平分线,点D 在AC 上,且∠CBD=20°,求∠CED 的度数4.如图,点P 为△AEF 外一点,PA 平分∠EAF ,PD ⊥EF 于D ,且DE=DF ,PB ⊥AE 于B 。
求证:AF-AB=BE5.如图,正方形ABOC ,A (-4,4),点M 、N 分别在AB 、AC 上(1)若∠NMO=∠MOC ,问△AMN 的周长是否变化,若不变,请求其值;(2)若点M 在AB 延长线上,点N 在CA 的延长线上,其它条件不变,问CN 、MN 、BM 三者存在怎样的关系,试证明D①B②B图1B图2图3O 7.分别以△ABC 的AB 、AC 为边向外作等边△ABD 和等边△ACE ,连接CD 、BE 交于F.求证:AF 平分∠DFE8.如图,CA=CB ,CD=CE ,∠ACB=∠DCE=α(1)当α=60°,且点D 在AC 上,连BD 、AE 相交于点G ,如图①,求∠BGA(2)若0°<α<90°,如图②,求∠BGC9.如图所示,点A 为∠MON 的角平分线上一点,过A 任作一直线分别与∠MON 的两边交于B 、C 、P 为BC 的中点,过P 作BC 的垂线交OA 于点D. (1)若∠MON=90°,如图1,则∠BDC= ;(2)若∠MON=60°,如图2,则∠BDC= ;(3)若∠MON=α,如图3,则∠BDC= ,请给予证明10.已知:如图,∠ACB 为直角,CM ⊥AB 于点M ,AT 平分∠BAC 交CM 于点D ,交BC 于点T ,过点D 作DE ∥AB 交BC 于点E.求证:CT=EB图①EB P11.如图,P 为△ABC 的BC 边垂直平分线上的一点,且∠PBC=12∠A ,BP 、CP 的延长线分别交AC 、AB 于点D 、E.求证:BE=CD12.已知:△ACB 为等腰直角三角形,点P 在BC 上,以AP 为边长作正方形APEF.(1)如图①,当点P 在BC 上时,求∠EBP ;(2)如图②,当点P 在BC 的延长线上时,求∠EBP.13.已知等腰△ABC 和等腰△ADE 的顶点公共,B 、A 、E 在同一条直线上,∠BAC=∠DAE ,PB=PD ,PC=PE.(1)如图1,若∠BAC=90°,则∠BPC+∠DPE= ;(2)如图2,若∠BAC=α,则∠BPC+∠DPE= ;(3)在图1的基础上将等腰Rt △ABC 绕点A 旋转一个角度,得到图3,则∠BPC+∠DPE= ;并证明你的结论。
(完整版)三角形角平分线、中线、高线证明题

(完整版)三角形角平分线、中线、高线证明题2.证题的思路:找夹角()性质 1、全等三角形的SAS已知两边 找直角( HL )对应角相等、对应边相找第三边( SSS等。
)2、全等三角形的若边为角的对边,则找 随意角( AAS)找已知角的另一边( )已知一边一角SAS 对应边上的 高对应相边为角的邻边 找已知边的对角()AAS等。
找夹已知边的另一角()ASA3、全等三角形的找两角的夹边()对应角均分线相等。
已知两角ASA4、全等三角形的 找随意一边()AAS对应中线相等。
5、全等三角形面积相等。
6、全等三角形 周长相等。
( 以上能够简称 : 全等三角形的对应元素相等 ) 7、三边对应相等的两个三角形全等。
( SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS) 9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和此中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)全等三角形问题中常有的协助线的作法常有协助线的作法有以下几种:1) 碰到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思想模式是全等变换中的“对折” .2) 碰到三角形的中线,倍长中线,使延伸线段与原中线长相等,结构全等三角形,利用的思想模式是全等变换中的“旋转” .3) 碰到角均分线,能够自角均分线上的某一点向角的两边作垂线,利用的思想模式是三角形全等变换中的“对折” ,所考知识点经常是角均分线的性质定理或逆定理. 4) 过图形上某一点作特定的均分线, 结构全等三角形, 利用的思想模式是全等变换中的“平移”或“翻转折叠”5) 截长法与补短法, 详细做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延伸,是之与特定线段相等,再利用三角形全等的相关性质加以说明. 这类作法,合适于证明线段的和、差、倍、分等类的题目.特别方法:在求相关三角形的定值一类的问题时, 常把某点到原三角形各极点的线段连结起来,利用三角形面积的知识解答.三角形协助线做法图中有角均分线,可向两边作垂线。
三角形全等(HL)、角平分线性质

三角形全等(HL)、角平分线性质一、选择题1.若按给定的三个条件画一个三角形,图形惟一,则所给条件不可能是( )A .两边一夹角B .两角一夹边C .三边D .三角2.在△ABC 和△DEF 中,AB =DE ,∠A =∠D ,若证△ABC ≌△DEF ,还要补充一个条件,错误的补充方法是( )A .∠B =∠E B .∠C =∠F C .BC =EFD .AC =DF3.下列说法正确的是( )A .两边一角对应相等的两个三角形全等B .两角一边对应相等的两个三角形等C .两个等边三角形一定全等D .两个等腰直角三角形一定全等4. 如图,Rt △ACB ,90C ∠=o ,AD 平分CAB ∠,DE AB ⊥于E ,则下列结论中不正确的是( )A .BD ED BC +=B .DE 平分ADB ∠C .AD 平分EDC ∠ D .ED AC AD +>5.与相交的两条直线距离相等的点在( )A .一条直线上B .两条互相垂直的直线上C .一条射线上D .两条互相垂直的射线上6.下列说法中,错误的是( )A .三角形任意两个角的平分线的交点在三角形的内部B .三角形两个角的平分线的交点到三边的距离相等C .三角形两个角的平分线的交点在第三个角的平分线上D .三角形任意两个角的平分线的交点到三个顶点的距离相等.二、填空题1.△ABC 和A B C '''∆中,若AB A B ''=,BC B C ''=,则需要补充条件________可得到ABC A B C '''∆≅∆2.如图所示,若只有AD ⊥BD 于点D 这个条件,要证△ABD ≌△ACD ,则需补充的条件是________或__________或__________.3.如图,在△ABC 中,∠BAC =60°,将△ABC A D E B绕着点A 顺时针旋转40°后得到△ADE ,则∠BAE 的度数为__________.4.如图所示,DB ⊥AB ,DC ⊥AC ,BD =DC ,∠BAC =80°,则∠BAD =________,∠ADB =_________.5.如图,Rt △ABC 中,∠C =90º,BD 是角平分线,DE ⊥AB ,垂足为E ,BC =6,CD =3, AE =4,则DE =_______,AD =_______,△ABC 的周长是_______.三、解答题1.如图,已知△ABC 中,AB=AC,D 是BC 的中点,求证:D 到AB 、AC 的距离相等.2.如图,在∠AOB 的两边O A ,OB 上分别取OM =ON ,OD =OE ,DN 和EM 相交于点C . 求证:点C 在∠AOB 的平分线上.AB DC E O M N。
全等三角形与角平分线经典题型

全等三角形与角平分线一、知识概述1、角的平分线的作法(1)在∠AOB的两边OA、OB上分别截取OD、OE,使OD=OE.(2)分别以D、E为圆心,以大于1/2DE长为半径画弧,两弧交于∠AOB 内一点C.(3)作射线OC,则OC为∠AOB的平分线(如图)指出:(1)作角的平分线的依据是三角形全等的条件——“SSS”.(2)角的平分线是一条射线,不能简单地叙述为连接.2、角平分线的性质在角的平分线上的点到角的两边的距离相等.指出:(1)这里的距离是指点到角两边垂线段的长.(2)该结论的证明是通过三角形全等得到的,它可以独立作为证明两条线段相等的依据.即不需再用老方法——全等三角形.(3)使用该结论的前提条件是有角的平分线,关键是图中有“垂直”.3、角平分线的判定到角的两边的距离相等的点在角的平分线上.指出:(1)此结论是角平分线的判定,它与角平分线的性质是互逆的.(2)此结论的条件是指在角的内部有点满足到角的两边的距离相等,那么过角的顶点和该点的射线必平分这个角.4、三角形的角平分线的性质三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等.指出:(1)该结论的证明揭示了证明三线共点的证明思路:先设其中的两线交于一点,再证明该交点在第三线上.(2)该结论多应用于几何作图,特别是涉及到实际问题的作图题. 二、典型例题剖析例1、如图所示,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC,AF⊥CD.求证:△ABE≌△ADF.例2、如图所示,BE、CF是△ABC的高,BE、CF相交于O,且OA平分∠BAC.求证:OB=OC.例3、如图,D为BC的中点,DE⊥DF,E、F分别在AB、AC边上,则BE+CF()A.大于EF B.小于EFC.等于EF D.与EF的大小无法比较例4、(12分)如图四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠D+∠B=180°,求证:AD+AB=2AE.例5、已知:如图,在四边形ABCD中,AB>BC,BD平分.求证:AD=CD.例6、如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于O 点,求证:AE+CD=AC.三、中考解析1、在△ABC,∠C=90°,BC=16cm,∠A的平分线AD交BC于D,且CD︰DB=3︰5,则D到AB的距离等于()A.6cm B.7cmC.8cm D.9cm2、如图,D是△ABC的一个外角的平分线上一点,求证:AB+AC<DB+DC.3、如图,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,求证:BF=CG.4、已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.H是BC边的中点,连结DH与BE相交于点G.(1)求证:BF=AC;(2)求证:CE=BF;(3)CE与BG的大小关系如何?试证明你的结论.5、如图,已知∠1=∠2,P为BN上一点,且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°6、如图,△ABC中,AM是BC边上的中线,求证:7、已知:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长线于E.求证:BD=2CE.。
3--全等三角形中的动点问题专题培优、角平分线题型大全
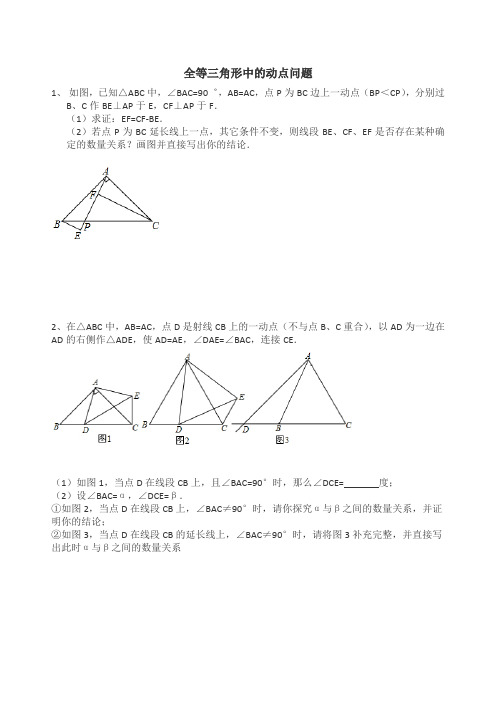
全等三角形中的动点问题1、如图,已知△ABC中,∠BAC=90゜,AB=AC,点P为BC边上一动点(BP<CP),分别过B、C作BE⊥AP于E,CF⊥AP于F.(1)求证:EF=CF-BE.(2)若点P为BC延长线上一点,其它条件不变,则线段BE、CF、EF是否存在某种确定的数量关系?画图并直接写出你的结论.2、在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;(2)设∠BAC=α,∠DCE=β.①如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;②如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时α与β之间的数量关系3、在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:(1)如图1,在爬行过程中,CD和BE始终相等吗?(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,DF始终等于EF是否正确?图1 图2 图34、如图,已知△ABC,AB=AC=10cm,BC=8cm,点D为AB的中点。
①如果点p在线段BC上以3厘米|秒的速度由B点向c点运动,同时,点Q在线段CA上由c点A点运动(1)如点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等?请说明理由(2)若点Q的运动速度与点p的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△COD全等?②如点Q以(2)中的运动速度从点C出发,点P以原来的速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?角平分线的性质与判定角平分线的性质定理:角平分线上的点到角两边的距离相等.角平分线的判定定理:角的内角到角两边距离相等的点在这个角的平分线上. 角平分线常见辅助线构造全等三角形.例1、如图,在△ABC 中,CD 平分∠ACB ,AC =5,BC =3.求ACD CBDSS ∆∆例2、如图,在△ABC 中,∠ABC =90°,BC =AC ,BE 平分∠ABC , AE ⊥BE .求证:AE =12BD例3、如图,在△ABC 中,AB >AC ,AD 是∠BAC 的平分线,P 为AC 上任意一点.求证:AB -AC>DB -DC例4、如图,在△ABC 中,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F .⑴请你判断FE 和FD 之间的数量关系,并说明理由; ⑵求证:AE +CD =AC .第4题图第2题图第5题图第3题图第1题图第5题图第3题图l 2第1题图第7题图提高练习01.如图,在Rt △ABC 中,∠C =90°,BD 平分∠ABC 交AC 于D ,若CD =n ,AB =m ,则△ABD 的面积是( )A .13mnB .12mn C . mn D .2 mn02.如图,已知AB =AC ,BE =CE ,下面四个结论:①BP =CP ;②AD ⊥BC ;③AE 平分∠BAC ;④∠PBC =∠PCB .其中正确的结论个数有( )个 A . 1 B .2 C .3 D .403.如图,在△ABC 中,P 、Q 分别是BC 、AC 上的点,作PR ⊥AB ,PS ⊥AC ,垂足分别是R 、S .若AQ =PQ ,PR =PS ,下列结论:①AS =AR ;②PQ ∥AR ;③△BRP ≌△CSP .其中正确的是( ) A . ①③ B .②③ C .①② D .①②③04.如图,△ABC 中,AB =AC ,AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,则下列四个结论中:①AD 上任意一点到B 、C 的距离相等;②AD 上任意一点到AB 、AC 的距离相等;③AD ⊥BC 且BD =CD ;④∠BDE =∠CDF .其中正确的是( ) A .②③ B .②④ C .②③④ D .①②③④05.如图,在Rt △ABC 中,∠ACB =90°,∠CAB =30°,∠ACB 的平分线与∠ABC 的外角平分线交于E 点,则∠AEB 的度数为( ) A .50° B .45° C .40° D .35°01.如图,直线l 1、l 2、l 3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )A .一处B .二处C .三处D .四处03.如图,△ABC 中,∠C =90°,AD 是△ABC 的平分线,有一个动点P 从A 向B 运动.已知:DC =3cm ,DB =4cm ,AD =8cm .DP 的长为x (cm ),那么x 的范围是__________ 05.如图,已知AB ∥CD ,O 为∠CAB 、∠ACD 的平分线的交点,OE ⊥AC ,且OE =2,则两平行线AB 、CD 间的距离等于__________07.如图,点P 是△ABC 两个外角平分线的交点,则下列说法中不正确的是( )A .点P 到△ABC 三边的距离相等B .点P 在∠ABC 的平分线上C .∠P 与∠B 的关系是:∠P +12∠B =90°D .∠P 与∠B 的关系是:∠B =12∠P如图,在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足为D一,求证;∠2=∠1+∠C二;若ED∥BC,∠ABD=28°,求∠ADE的度数如图,在△ABC中,BC=AC,∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于点E,且AE是BD的一半,求证:BD是∠ABC的角平分线.。
中考数学难点突破与经典模型精讲练全等三角形中的角平分线模型(解析版)
专题08 全等三角形中的角平分线模型【模型展示】特点利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。
利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。
结论三边对应相等的三角戏是全等三角形(SSS)、全等三角形对应角相等【模型证明】解决方案角平分线+垂直两边型角平分线性质定理:角的平分线上的点作角两边垂直段构成的两个RT三角形全等.【证明】∵ OC为∵AOB的角平分线,D为OC上一点DE∵OA,DF∵OB∵(AAS)OFD△OED△∵DE=DF角平分线+垂直角平分线型构造此模型可以利用等腰三角形的“三线合一”,也可以得到两个全等的直角三角形,进而得到对应边、对应角相等。
这个模型巧妙地把角平分线和三线合一联系了起来。
DFEOCBAOBNMBCO角平分线+平行线如图,P 是∠MON 的平分线上一点,过点 P 作 PQ∠ON ,交 OM 于点 Q 。
结论:∠POQ 是等腰三角形。
【证明】∠PQ ∥ON∴∠PON=∠OPQ又∵OP 是∠MON 的平分线∴∠POQ=∠PON∴∠POQ=∠OPQ∴△POQ 是等腰三角形【题型演练】一、单选题1.已知:如图,BD 为∠ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA ,过E 作EF∠AB ,F 为垂足,下列结论:∠∠ABD∠∠EBC∠∠BCE+∠BCD=180°∠AD=AE=EC ∠ BA+BC=2BF 其中正确的是( )A .∠∠∠B .∠∠∠C .∠∠∠D .∠∠∠∠ 【答案】D【分析】易证ABD EBC ∆∆≌,可得BCE BDA ∠=∠,AD=EC 可得∠∠正确;再根据角平分线的性质可求得DAE DCE ∠=∠ ,即∠正确,根据∠可判断∠正确;【详解】∠ BD 为∠ABC 的角平分线,∠ ∠ABD=∠CBD ,∠在∠ABD 和∠EBD 中,BD=BC ,∠ABD=∠CDB ,BE=BA ,∠∠ABD EBC ∆∆≌(SAS),故∠正确;∠ BD 平分∠ABC ,BD=BC ,BE=BA ,∠ ∠BCD=∠BDC=∠BAE=∠BEA,∠∠ABD∠∠EBC,∠∠BCE=∠BDA,∠∠BCE+∠BCD=∠BDA+∠BDC=180°,故∠正确;∠∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,∠∠DCE=∠DAE,∠∠ACE是等腰三角形,∠AE=EC,∠∠ABD∠∠EBC,∠AD=EC,∠AD=AE=EC,故∠正确;作EG∠BC,垂足为G,如图所示:∠ E是BD上的点,∠EF=EG,在∠BEG和∠BEF中BE BE EF EG=⎧⎨=⎩∠ ∠BEG∠∠BEF,∠BG=BF,在∠CEG和∠AFE中EF EG AE CE=⎧⎨=⎩∠∠CEG∠∠AFE,∠ AF=CG,∠BA+BC=BF+FA+BG-CG=BF+BG=2BF,故∠正确;故选:D.【点睛】本题考查了全等三角形的判定,全等三角形对应边、对应角相等的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应边、对应角相等的性质是解题的关键;2.如图,在菱形ABCD 中,AB=BD ,点E 、F 分别是AB 、AD 上任意的点(不与端点重合),且AE=DF ,连接BF 与DE 相交于点G ,连接CG 与BD 相交于点H .给出如下几个结论:∠∠AED∠∠DFB ;∠S 四边形BCDG 2;∠若AF=2DF ,则BG=6GF ;∠CG 与BD 一定不垂直;∠∠BGE 的大小为定值.其中正确的结论个数为( )A .4B .3C .2D .1 【答案】B【详解】试题分析:∠∠ABCD 为菱形,∠AB=AD ,∠AB=BD ,∠∠ABD 为等边三角形,∠∠A=∠BDF=60°,又∠AE=DF ,AD=BD ,∠∠AED∠∠DFB ,故本选项正确;∠∠∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD ,即∠BGD+∠BCD=180°,∠点B 、C 、D 、G 四点共圆,∠∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,∠∠BGC=∠DGC=60°,过点C 作CM∠GB 于M ,CN∠GD 于N (如图1),则∠CBM∠∠CDN (AAS ),∠S 四边形BCDG =S 四边形CMGN ,S 四边形CMGN =2S ∠CMG ,∠∠CGM=60°,∠GM=12CG ,,∠S 四边形CMGN =2S ∠CMG =2×12×122,故本选项错误; ∠过点F 作FP∠AE 于P 点(如图2),∠AF=2FD ,∠FP :AE=DF :DA=1:3,∠AE=DF ,AB=AD ,∠BE=2AE ,∠FP :BE=FP :12AE=1:6,∠FP∠AE ,∠PF∠BE ,∠FG :BG=FP :BE=1:6,即BG=6GF ,故本选项正确;∠当点E ,F 分别是AB ,AD 中点时(如图3),由(1)知,∠ABD ,∠BDC 为等边三角形,∠点E ,F 分别是AB ,AD 中点,∠∠BDE=∠DBG=30°,∠DG=BG ,在∠GDC 与∠BGC 中,∠DG=BG ,CG=CG ,CD=CB ,∠∠GDC∠∠BGC ,∠∠DCG=∠BCG ,∠CH∠BD ,即CG∠BD ,故本选项错误;∠∠∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,故本选项正确;综上所述,正确的结论有∠∠∠,共3个,故选B .考点:四边形综合题.3.如图,Rt ACB 中,90ACB ︒∠=,ABC 的角平分线AD 、BE 相交于点P ,过P 作PF AD ⊥交BC 的延长线于点F ,交AC 于点H ,则下列结论:∠135APB ︒∠=;∠PF PA =;∠AH BD AB +=;∠S 四边形23ABDE S ABP =,其中正确的个数是( )A .4B .3C .2D .1【答案】B【分析】根据三角形全等的判定和性质以及三角形内角和定理逐一分析判断即可.【详解】解:∠在∠ABC 中,∠ACB=90°,∠∠CAB+∠ABC=90°∠AD 、BE 分别平分∠BAC 、∠ABC , ∠∠BAD=12CAB ∠,∠ABE=12ABC ∠ ∠∠BAD+∠ABE=111+=()45222CAB ABC CAB ABC ∠∠∠+∠=︒ ∠∠APB=180°-(∠BAD+∠ABE )=135°,故∠正确;∠∠BPD=45°,又∠PF∠AD ,∠∠FPB=90°+45°=135°∠∠APB=∠FPB又∠∠ABP=∠FBPBP=BP∠∠ABP∠∠FBP (ASA )∠∠BAP=∠BFP ,AB=AB ,PA=PF ,故∠正确;在∠APH 与∠FPD 中∠∠APH=∠FPD=90°∠PAH=∠BAP=∠BFPPA=PF∠∠APH∠∠FPD (ASA ),∠AH=FD ,又∠AB=FB∠AB=FD+BD=AH+BD ,故∠正确;连接HD ,ED ,∠∠APH∠∠FPD ,∠ABP∠∠FBP∠APH FPD S S =,ABP FBP S S =,PH=PD ,∠∠HPD=90°,∠∠HDP=∠DHP=45°=∠BPD∠HD∠EP ,∠EPH EPD S S =∠ABP BDP AEP EPD ABDE S S SS S =+++四边形 ()ABP AEP EPH PBD S S S S =+++ABP APH PBD SS S =++ ABP FPD PBD S S S =++ABP FBP S S=+ 2ABPS = 故∠错误,∠正确的有∠∠∠,故答案为:B .【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的方法有:SSS 、SAS 、AAS 、ASA 、HL ,注意AAA 和SAS 不能判定两个三角形全等.二、填空题4.已知,∠ABC 中,∠BAC =120°,AD 平分∠BAC ,∠BDC =60°,AB =2,AC =3,则AD 的长是________.【答案】5【分析】过D 作,DE AC ⊥,DF AB ⊥交AB 延长线于F ,然后根据全等三角形的性质和30︒角直角三角形的性质即可求解.【详解】过D 作,DE AC ⊥,DF AB ⊥交AB 延长线于F ,∠AD 平分BAC ∠,DE AC ⊥,DF AB ⊥,∠DE DF =,90DEC DFB DEA ==︒=∠∠∠,∠360BAC BDC DCE DBA +++=︒∠∠∠∠,12060BAC BDC =︒=︒∠,∠,∠180DCE DBA +=︒∠∠,∠180DBF DBA +=︒∠∠,∠DCE DBF ∠=∠,在DEC 和DFB △中,DCE DBF DEC DFB DE DB ∠=∠⎧⎪∠=∠⎨⎪=⎩∠()DEC DFB AAS △≌△,∠CE BF =,在Rt DEA △和Rt DFA 中,DE DF DA DA =⎧⎨=⎩, ∠()Rt DEA DFA HL △≌△,∠AE AF =,∠,AE AC CE AF AB BF =-=+,∠AC CE AB BF -=+,∠1CE BF AC AB +=-=, ∠12CE BF ==, ∠52AF AB BF =+=, ∠AD 平分BAC ∠, ∠1602DAB BAC ==︒∠∠, ∠18030ADF DAB DFB =︒--=︒∠∠∠,∠25AD AF ==.【点睛】此题考查了全等三角形和角平分线的性质,解题的关键是作出辅助线构造全等三角形.5.如图,∠ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =50︒,∠CAP =______.【答案】40°【分析】过点P 作PF∠AB 于F ,PM∠AC 于M ,PN∠CD 于N ,根据三角形的外角性质和内角和定理,得到∠BAC 度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP ,即可得到答案.【详解】解:过点P 作PF∠AB 于F ,PM∠AC 于M ,PN∠CD 于N ,如图:设∠PCD=x ,∠CP 平分∠ACD ,∠∠ACP=∠PCD=x ,PM=PN ,∠∠ACD=2x ,∠BP 平分∠ABC ,∠∠ABP=∠PBC ,PF=PM=PN ,∠∠BPC =50°,∠∠ABP=∠PBC=50PCD BPC x ∠-∠=-︒,∠2(50)ABC x ∠=-︒,∠22(50)100BAC ACD ABC x x ∠=∠-∠=--︒=︒,∠18010080FAC ∠=︒-︒=︒,在Rt∠APF 和Rt∠APM 中,∠PF=PM ,AP 为公共边,∠Rt∠APF∠Rt∠APM (HL ),∠∠FAP=∠CAP , ∠180402CAP ∠=⨯︒=︒; 故答案为:40°;【点睛】本题考查了三角形的内角和定理,三角形的外角性质,角平分线的性质,以及全等三角形的判定和性质,解题的关键是熟练掌握所学的知识进行解题,正确求出80FAC ∠=︒是关键.6.如图所示,ABC 的外角ACD ∠的平分线CP 与ABC ∠的平分线相交于点P ,若36BPC ∠=︒,则CAP ∠=_______.【答案】54︒【分析】如图(见解析),设CBP x ∠=,从而可得2ABC x ∠=,先根据三角形的外角性质可求出72BAC =︒∠,再根据角平分线的性质可得,PM PN PM PE ==,从而可得PN PE =,然后根据直角三角形全等的判定定理与性质可得PAN PAE ∠=∠,最后根据平角的定义即可得.【详解】如图,过点P 分别作PM BD ⊥于点M ,PN BA ⊥于点N ,PE AC ⊥于点E , 设CBP x ∠=,则2ABC x ∠=,36BPC ∠=︒,36DCP BP CBP C x ∠+∴∠=∠=+︒, CP 是ACD ∠的平分线,2272ACD DCP x ∴∠=∠=+︒,272272BAC ACD ABC x x ∴∠=∠-∠=+︒-=︒, BP 是ABC ∠的平分线,PM BD ⊥,PN BA ⊥,PM PN ∴=,同理可得:PM PE =,PN PE ∴=, 在Rt ANP 和Rt AEP △中,PN PE PA PA =⎧⎨=⎩, ()Rt ANP Rt AEP HL ∴≅,PAN PAE ∴∠=∠,即PAN CAP ∠=∠,又180PAN CAP BAC ∠+∠+∠=︒,272180CAP ∴∠+︒=︒,解得54CAP ∠=︒,故答案为:54︒.【点睛】本题考查了角平分线的定义与性质、三角形的外角性质、直角三角形全等的判定定理与性质等知识点,通过作辅助线,利用角平分线的性质是解题关键.三、解答题7.如图,ABC 中,AC =BC ,∠ACB =90°,AD 平分∠BAC 交BC 于点D ,过点B 作BE ∠AD ,交AD 延长线于点E ,F 为AB 的中点,连接CF ,交AD 于点G ,连接BG .(1)线段BE 与线段AD 有何数量关系?并说明理由;(2)判断BEG 的形状,并说明理由.【答案】(1)BE =12AD ,见解析;(2)BEG 是等腰直角三角形,见解析【分析】(1)延长BE 、AC 交于点H ,先证明∠BAE ∠∠HAE ,得BE =HE =12BH ,再证明∠BCH ∠∠ACD ,得BH =AD ,则BE =12AD ;(2)先证明CF 垂直平分AB ,则AG =BG ,再证明∠CAB =∠CBA =45°,则∠GAB =∠GBA =22.5°,于是∠EGB =∠GAB +∠GBA =45°,可证明∠BEG 是等腰直角三角形.【详解】证:(1)BE =12AD ,理由如下:如图,延长BE 、AC 交于点H ,∠BE ∠AD ,∠∠AEB =∠AEH =90°,∠AD 平分∠BAC ,∠∠BAE =∠HAE ,在∠BAE 和∠HAE 中,AEB AEH AE AEBAE HAE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∠∠BAE ∠∠HAE (ASA ),∠BE =HE =12BH ,∠∠ACB =90°,∠∠BCH =180°﹣∠ACB =90°=∠ACD ,∠∠CBH =90°﹣∠H =∠CAD ,在∠BCH 和∠ACD 中,BCH ACD BC ACCBH CAD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∠∠BCH ∠∠ACD (ASA ),∠BH =AD ,∠BE =12AD .(2)∠BEG 是等腰直角三角形,理由如下:∠AC =BC ,AF =BF ,∠CF ∠AB ,∠AG =BG ,∠∠GAB =∠GBA ,∠AC =BC ,∠ACB =90°,∠∠CAB =∠CBA =45°,∠∠GAB =12∠CAB =22.5°,∠∠GAB =∠GBA =22.5°,∠∠EGB =∠GAB +∠GBA =45°,∠∠BEG =90°,∠∠EBG =∠EGB =45°,∠EG =EB ,∠∠BEG 是等腰直角三角形.【点睛】本题考查等腰直角三角形的判定与性质,全等三角形的判定与性质等,理解等腰直角三角形的基本性质,并且掌握全等三角形中常见辅助线的作法是解题关键.8.已知:如图,在四边形ABCD 中,BD 平分∠ABC ,∠A +∠C =180°,BC >BA .求证:点D 在线段AC 的垂直平分线上.【答案】见解析【分析】在BC 上截取BE =BA ,连接DE ,证明∠ABD ∠∠BED ,可得出∠C =∠DEC ,则DE =DC ,从而得出AD =CD 即可证明.【详解】证:如图,在BC 上截取BE =BA ,连接DE ,∠BD =BD ,∠ABD =∠CBD ,∠∠BAD ∠∠BED ,∠∠A =∠DEB ,AD =DE ,∠∠A +∠C =180°,∠BED +∠DEC =180°,∠∠C =∠DEC ,∠DE =DC ,∠AD =CD ,∠点D 在线段AC 的垂直平分线上.【点睛】本题考查全等三角形的判定与性质,以及垂直平分线的判定等,学会做辅助线找出全等三角形是解题的关键.9.如图所示,在四边形ABCD 中,AC 平分,DAB CD CB ∠=,求证:180B D ∠+∠=.【答案】详见解析【分析】过点C 分别作CE AB ⊥于E ,CF AD ⊥于F ,由条件可得出∠CDF∠∠CEB ,可得∠B=∠FDC ,进而可证明∠B+∠ADC=180°.【详解】证明:过点C 分别作CE AB ⊥于E ,CF AD ⊥于F ,∠AC 平分∠BAD ,CE∠AB 于E ,CF AD ⊥于F ,∠CF=CE ,在Rt∠CDF 与Rt∠CEB 中,CF=CE CD=CB ⎧⎨⎩∠CBE CDF ∆∆≌,CBE CDF ∴∠=∠,180ADC CDF ∠+∠=︒,A C 180B D ∴∠+∠=︒ .【点睛】本题考查全等三角形的判定和性质,关键是根据HL 证明∠CDF∠∠CEB 进而得出∠B=∠FDC .10.已知:如图,AC ∠BD ,AE 、BE 分别平分∠CAB 和∠ABD ,点E 在CD 上.用等式表示线段AB 、AC 、BD 三者之间的数量关系,并证明.【答案】AC +BD =AB ,理由见见解析【分析】在BA 上截取BF =BD ,连接EF ,先证得BEF BED ≌,可得到∠BFE =∠D ,再由AC ∠BD ,可得∠AFE =∠C ,从而证得AEF AEC ≌,可得AF =AC ,即可求解.【详解】解:AC +BD =AB ,证明如下:在BA 上截取BF =BD ,连接EF ,如图所示:∠AE 、BE 分别平分∠CAB 和∠ABD ,∠∠EAF =∠EAC ,∠EBF =∠EBD ,在∠BEF 和∠BED 中,BF BD EBF EBD BE BE =⎧⎪∠=∠⎨⎪=⎩,∠BEF BED ≌(SAS ),∠∠BFE =∠D ,∠AC ∠BD ,∠∠C +∠D =180°,∠∠AFE +∠BFE =180°,∠∠AFE +∠D =180°,∠∠AFE =∠C ,在∠AEF 和∠AEC 中,EAF EAC AFE C AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠AEF AEC ≌(AAS ),∠AF =AC ,∠AF +BF =AB ,∠AC +BD =AB .【点睛】本题主要考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.11.在ABC 中,BE ,CD 为ABC 的角平分线,BE ,CD 交于点F .(1)求证:1902BFC A ∠=︒+∠; (2)已知60A ∠=︒.∠如图1,若4BD =, 6.5BC =,求CE 的长;∠如图2,若BF AC =,求AEB ∠的大小.【答案】(1)证明见解析;(2)2.5;(3)100°.【分析】(1)由三角形内角和定理和角平分线得出1902FBC FCB A ∠+∠=︒-∠的度数,再由三角形内角和定理可求出BFC ∠的度数,(2)在BC 上取一点G 使BG=BD ,构造BFG BFD ≅△(SAS ),再证明()FEC FGC ASA ≅,即可得BC BD CE =+,由此求出答案;(3)延长BA 到P ,使AP=FC ,构造BFC CAP ≅△(SAS ),得PC=BC ,12P BCF ACB ∠=∠=∠,再由三角形内角和可求40ABC ∠=︒,80ACB ∠=︒,进而可得180()100AEB ABE A ∠=︒-∠+∠=︒.【详解】解:(1)BE 、CD 分别是ABC ∠与ACB ∠的角平分线,11(180)9022FBC FCB A A ∴∠+∠=︒-∠=︒-∠, 1180()180(90)2BFC FBC FCB A ∴∠=︒-∠+∠=︒-︒-∠, 1902BFC A ∴∠=︒+∠, (2)如解(2)图,在BC 上取一点G 使BG=BD ,由(1)得1902BFC A ∠=︒+∠, 60BAC ∠=︒,120BFC ∴∠=︒,∠18060BFD EFC BFC ∠=∠=︒-∠=︒,在BFG 与BFD △中,BF BF FBG FBD BD BG =⎧⎪∠=∠⎨⎪=⎩, ∠BFG BFD ≅△(SAS )∠BFD BFG ∠=∠,∠60BFD BFG ∠=∠=︒,∠12060CFG BFG ∠=︒-∠=︒,∠60CFG CFE ∠=∠=︒在FEC 与FGC △中,CFE CFG CF CFECF GCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()FEC FGC ASA ∴≅,CE CG ∴=,BC BG CG =+,BC BD CE ∴=+;∠4BD =, 6.5BC =,∠ 2.5CE =(3)如解(3)图,延长BA 到P ,使AP=FC ,60BAC ∠=︒,∠180120PAC BAC ∠=︒-∠=︒,在BFC △与CAP 中,120BF AC BFC CAP CF PA =⎧⎪∠=∠=︒⎨⎪=⎩, ∠BFC CAP ≅△(SAS )∠P BCF ∠=∠,BC PC =,∠P ABC ∠=∠,又∠12P BCF ACB ∠=∠=∠, ∠2ACB ABC ∠=∠,又∠180ACB ABC A ∠+∠+∠=︒,∠360180ABC ∠+︒=︒,∠40ABC ∠=︒,80ACB ∠=︒, ∠1202ABE ABC ∠=∠=︒,180()180(2060)100AEB ABE A ∠=︒-∠+∠=︒-︒+︒=︒ 【点睛】本题考查的是角平分线的性质、全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.12.如图,∠ABC 中,AB =AC ,∠BAC =90°,CD 平分∠ACB ,BE ∠CD ,垂足E 在CD 的延长线上.求证:BE =12CD .【答案】见解析【分析】分别延长BE 、CA 交于点F ,首先结合题意推出∠CFE ∠∠CBE ,从而得到BE =EF =12BF ,然后证明∠BF A ∠∠CDA ,得到BF =CD ,即可得出结论.【详解】证明:分别延长BE 、CA 交于点F ,∠BE ∠CD ,∠∠BEC =∠FEC =90°.∠CD 平分∠ACB ,∠∠FCE =∠BCE .在∠CFE 与∠CBE 中,∠∠BEC =∠FEC ,∠FCE =∠BCE ,CE =CE ,∠∠CFE ∠∠CBE ,∠BE =EF =12BF .在∠CFE 与∠CAD 中,∠∠F +∠FCE =∠ADC +∠ACD = 90°,∠∠F =∠ADC .在∠BF A 与∠CDA 中,∠∠F =∠ADC ,∠BAC =∠F AB ,AB =AC ,∠∠BF A ∠∠CDA ,∠BF =CD .∠BE =12CD .【点睛】本题考查全等三角形的判定与性质,理解角平分线的基本定义,熟练运用角平分线的性质构造辅助线,并且准确判定全等三角形是解题关键.13.如图,在∠ABC 中,∠C =90°,AD 是∠BAC 的角平分线,交BC 于点D ,过D 作DE ∠BA 于点E ,点F 在AC 上,且BD =DF .(1)求证:AC =AE ;(2)若AB =7.4,AF =1.4,求线段BE 的长.【答案】(1)见解析;(2)3【分析】(1)证明∠ACD ∠∠AED (AAS ),即可得出结论;(2)在AB 上截取AM =AF ,连接MD ,证∠F AD ∠∠MAD (SAS ),得FD =MD ,∠ADF =∠ADM ,再证Rt ∠MDE ∠Rt ∠BDE (HL ),得ME =BE ,求出MB =AB -AM =6,即可求解.【详解】解:(1)证明:∠AD 平分∠BAC ,∠∠DAC =∠DAE ,∠DE ∠BA ,∠∠DEA =∠DEB =90°,∠∠C =90°,∠∠C =∠DEA =90°,在∠ACD 和∠AED 中,C DEA DAC DAE AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠ACD ∠∠AED (AAS ),∠AC =AE ;(2)在AB 上截取AM =AF ,连接MD ,在∠F AD 和∠MAD 中,AF AM DAF DAM AD AD =⎧⎪∠=∠⎨⎪=⎩,∠∠F AD ∠∠MAD (SAS ),∠FD =MD ,∠ADF =∠ADM ,∠BD =DF ,∠BD =MD ,在Rt ∠MDE 和Rt ∠BDE 中,MD BD DE DE =⎧⎨=⎩, ∠Rt ∠MDE ∠Rt ∠BDE (HL ),∠ME =BE ,∠AF =AM ,且AF =1.4,∠AM =1.4,∠AB =7.4,∠MB =AB -AM =7.4-1.4=6,∠BE =12BM =3,即BE 的长为3.【点睛】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识;证明∠F AD ∠∠MAD 和Rt ∠MDE ∠Rt ∠BDE 是解题的关键.14.(1)如图1,射线OP 平分∠MON ,在射线OM ,ON 上分别截取线段OA ,OB ,使OA =OB ,在射线OP 上任取一点D ,连接AD ,BD .求证:AD =BD .(2)如图2,在Rt ∠ABC 中,∠ACB =90°,∠A =60°,CD 平分∠ACB ,求证:BC =AC +AD .(3)如图3,在四边形ABDE 中,AB =9,DE =1,BD =6,C 为BD 边中点,若AC 平分∠BAE ,EC 平分∠AED ,∠ACE =120°,求AE 的值.【答案】(1)见详解;(2)见详解;(3)AE=13【分析】(1)由题意易得∠AOD=∠BOD,然后易证∠AOD∠∠BOD,进而问题可求证;(2)在BC上截取CE=CA,连接DE,由题意易得∠ACD=∠ECD,∠B=30°,则有∠ACD∠∠ECD,然后可得∠A=∠CED=60°,则根据三角形外角的性质可得∠EDB=∠B=30°,然后可得DE=BE,进而问题可求证;(3)在AE上分别截取AF=AB,EG=ED,连接CF、CG,同理(2)可证∠ABC∠∠AFC,∠CDE∠∠CGE,则有∠ACB=∠ACF,∠DCE=∠GCE,然后可得∠ACF+∠GCE=60°,进而可得∠CFG是等边三角形,最后问题可求解.【详解】证明:(1)∠射线OP平分∠MON,∠∠AOD=∠BOD,∠OD=OD,OA=OB,∠∠AOD∠∠BOD(SAS),∠AD=BD.(2)在BC上截取CE=CA,连接DE,如图所示:∠∠ACB=90°,∠A=60°,CD平分∠ACB,∠∠ACD=∠ECD,∠B=30°,∠CD=CD,∠∠ACD∠∠ECD(SAS),∠∠A=∠CED=60°,AD=DE,∠∠B+∠EDB=∠CED,∠∠EDB=∠B=30°,∠DE=BE,∠AD=BE,∠BC=CE+BE,∠BC=AC+AD.(3)在AE上分别截取AF=AB=9,EG=ED=1,连接CF、CG,如图所示:同理(1)(2)可得:∠ABC∠∠AFC,∠CDE∠∠CGE,∠∠ACB=∠ACF,∠DCE=∠GCE,BC=CF,CD=CG,DE=GE=1,∠C为BD边中点,∠BC=CD=CF=CG=3,∠∠ACE=120°,∠∠ACB+∠DCE=60°,∠∠ACF+∠GCE=60°,∠∠FCG=60°,∠∠CFG是等边三角形,∠FG=CF=CG=3,∠AE=AF+FG+GE=9+3+1=13.【点睛】本题主要考查三角形全等的性质与判定、角平分线的定义、等腰三角形的性质与判定及等边三角形的性质与判定,解题的关键是构造辅助线证明三角形全等.15.如图,已知∠ABC中,AB=AC,∠A=108°,BD平分∠ABC.求证:BC=AB+CD.【答案】证明见解析【分析】在BC上截取点E,并使得BE=BA,连接DE,证明∠ABD∠∠EBD,得到∠DEB=∠BAD=108°,进一步计算出∠DEC=∠CDE=72°得到CD=CE即可证明.【详解】证明:在线段BC 上截取BE =BA ,连接DE ,如下图所示:∠BD 平分∠ABC ,∠∠ABD =∠EBD ,在∠ABD 和∠EBD 中:AB BE ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩, ∠∠ABD ∠∠EBD (SAS ),∠∠DEB =∠BAD =108°,∠∠DEC =180°-108°=72°,又AB =AC ,∠∠C =∠ABC =(180°-108°)÷2=36°,∠∠CDE =180°-∠C -∠DEC =180°-36°-72°=72°,∠∠DEC =∠CDE ,∠CD =CE ,∠BC =BE +CE =AB +CD .【点睛】本题考查了角平分线的定义,三角形内角和定理,全等三角形的判定与性质,等腰BC 上截取BE ,并使得BE =BA ,这是角平分线辅助线和全等三角形的应用的一种常见作法.16.如图,ABC 的外角∠DAC 的平分线交BC 边的垂直平分线于P 点,PD∠AB 于D ,PE∠AC 于E .(1)求证:BD =CE ;(2)若AB =6cm ,AC =10cm ,求AD 的长.【答案】(1)证明见解析;(2)2【分析】(1)连接BP 、CP ,根据线段垂直平分线上的点到两端点的距离相等可得BP CP =,根据角平分线上的点到角的两边距离相等可得 DP EP =,然后利用“HL ”证明Rt BDP ∆和Rt CEP 全等,根据全等三角形对应边相等证明即可;(2)利用“HL ”证明Rt ADP ∆和Rt AEP 全等,根据全等三角形对应边相等可得AD AE =,再根据AB 、AC 的长度表示出AD 、CE ,然后解方程即可.【详解】(1)证明:连接BP 、CP ,点P 在BC 的垂直平分线上,BP CP ∴=, AP 是DAC ∠的平分线,DP EP ,在Rt BDP ∆和Rt CEP 中,BPCP DP EP ,Rt BDPRt CEP(HL), BD CE ∴=;(2)解:在Rt ADP ∆和Rt AEP 中,APAP DP EP ,Rt ADPRt AEP(HL), AD AE ∴=,6AB cm =,10AC cm =,610AD AE ,即610AD AD ,解得AD 2cm =.【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,线段垂直平分线上的点到两端点的距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.17.如图,ABC ∆的外角ACD ∠的平分线CP 与内角ABC ∠的平分线BP 交于点P ,若40BPC ∠=︒,求CAP ∠的度数.【答案】50°【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP ,即可得出答案.【详解】延长BA ,作PN∠BD ,PF∠BA ,PM∠AC ,设∠PCD=x°,∠CP 平分∠ACD ,∠∠ACP=∠PCD=x°,PM=PN ,∠BP 平分∠ABC ,∠∠ABP=∠PBC ,PF=PN ,∠PF=PM ,∠∠BPC=40°,∠∠ABP=∠PBC=∠PCD -∠BPC=(x -40)°,∠∠BAC=∠ACD -∠ABC=2x°-(x°-40°)-(x°-40°)=80°,∠∠CAF=100°,在Rt∠PFA 和Rt∠PMA 中,PA PA PM PF =⎧⎨=⎩, ∠Rt∠PFA∠Rt∠PMA(HL),∠∠CAP=∠FAP ,又∠∠CAP+∠PAF=∠CAF ,∠∠CAP =50°.【点睛】本题主要考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF 是解决问题的关键.18.四边形ABCD 中,DA DC =,连接BD .(1)如图1,若BD 平分ABC ∠,求证:180A C ∠+∠=︒.(2)如图2,若BD BC =,150=︒∠BAD ,求证:2DBC ABD ∠=∠.(3)如图3,在(2)的条件下,作AE BC ⊥于点E ,连接DE ,若DA DC ⊥,2BC =,求DE 的长度.【答案】(1)见解析;(2)见解析;(3【分析】(1)过点D 分别作DF BC ⊥于点F ,DE BA ⊥交BA 的延长线于点E ,根据角平分线的性质可得ED FD =,结合已知条件HL 证明Rt DAE ≌Rt DCF △,继而可得C EAD ∠=∠,根据平角的定义以及等量代换即可证明180BAD BCD ∠+∠=︒;(2)过点D 分别作DF BC ⊥于点F ,DE BA ⊥交BA 的延长线于点E ,过点B 作BG DC ⊥,根据含30度角的直角三角形的性质可得12ED AD =,根据三线合一,可得12DG DC =,进而可得DE DG =,根据角平分线的判定定理可推出12ABD DBG DBC ∠=∠=∠,进而即可证明2DBC ABD ∠=∠;(3)先证明四边形DMEF 是矩形,证明△MAD ≌FCD ,进而证明四边形DMEF 是正方形,设ABD α∠=,根据(2)的结论以及三角形内角和定理,求得15α=︒,进而求得30DBC ∠=︒,根据含30度角的直角三角形的性质,即可求得EF ,进而在Rt DEF △中,勾股定理即可求得DE 的长.【详解】(1)如图,过点D 分别作DF BC ⊥于点F ,DE BA ⊥交BA 的延长线于点E ,BD 平分ABC ∠,ED FD ∴=DA DC =,在Rt DAE 与Rt DCF △中AD DC ED FD =⎧⎨=⎩∴Rt DAE ≌Rt DCF △(HL )C EAD ∴∠=∠180DAB EAD DAB C ∴∠+∠=∠+∠=︒即180BAD BCD ∠+∠=︒(2)如图,过点D 作DE BA ⊥交BA 的延长线于点E ,过点B 作BG DC ⊥,BD BC =11,22DG GC DC DBG CBG DBC ∴==∠=∠=∠150=︒∠BAD,18015030EAD∴∠=︒-︒=︒12ED AD∴=DA DC=ED DG∴=,ED BE DG BG⊥⊥EBD GBD∴∠=∠12ABD DBC∴∠=∠即2DBC ABD∠=∠(3)如图,过点D分别作DF BC⊥于点F,DM EA⊥交EA的延长线于点M,AE BC⊥,,DM ME DF FE⊥⊥∴四边形DMEF是矩形90MDF∴∠=︒90MDA ADF∴∠+∠=︒DA DC⊥90ADC∴∠=︒90ADF FDC∴∠+∠=︒FDC MDA∴∠=∠在△MAD与FCD中MDA FDCDMA DFCDA DC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△MAD≌FCDDM DF∴=,MDA FDC∠=∠∴四边形DMEF是正方形DF EF∴=设ABDα∠=∴22DBC ABD α∠=∠=BD BC =()11802902BDC BCD αα∴∠=∠=︒-=- 90MDA FDC BCD α∴∠=∠=︒-∠=90DAE M MDA α∴∠=∠+∠=︒+150BAD ∠=︒60BAE α∴∠=-在BAE 中9030ABE BAE α∠=︒-∠=︒+23ABE ABD DBC ααα∠=∠+∠=+=15α∴=︒230DBC α∴∠==︒2BD =112122DF BD ∴==⨯= 在Rt DEF △中,1EF DF ==DE ∴==【点睛】本题考查了三角形全等的性质与判定,角平分线的性质与判定,三角形内角和定理,三角形的外角性质,勾股定理,正方形的性质与判定,正确的添加辅助线是解题的关键.19.在∠ABC 中,AD 为∠ABC 的角平分线,点E 是直线BC 上的动点.(1)如图1,当点E 在CB 的延长线上时,连接AE ,若∠E =48°,AE =AD =DC ,则∠ABC 的度数为 .(2)如图2,AC >AB ,点P 在线段AD 延长线上,比较AC +BP 与AB +CP 之间的大小关系,并证明.(3)连接AE ,若∠DAE =90°,∠BAC =24°,且满足AB +AC =EC ,请求出∠ACB 的度数(要求:画图,写思路,求出度数).【答案】(1)108︒;(2)AC BP AB PC +>+,见解析;(3)44°或104°;详见解析.【分析】(1)根据等边对等角,可得E ADE ∠=∠,DAC C ∠=∠,再根据三角形外角的性质求出=2=48ADE DAC ∠∠︒,由此即可解题;(2)在AC 边上取一点M 使AM =AB ,构造ABP AMP ≅,根据MP MC PC +>即可得出答案;(3)画出图形,根据点E 的位置分四种情况,当点E 在射线CB 延长线上,延长CA 到G ,使AG =AB ,可得GC EC =,可得G GEC ∠=∠,设=2ACB x ∠,则=90G GEC x ∠=∠︒-;根据∠BAC =24°,AD 为∠ABC 的角平分线,可得=12BAD DAC ∠∠=︒,可证AGE ABE ≅(SAS ),得出=90ABE G x ∠=∠︒-,利用还有 242ABE x ∠=︒+,列方程90242x x ︒-=︒+;当点E 在BD 上时,∠EAD <90°,不成立;当点E 在CD 上时,∠EAD <90°,不成立;当点E 在BC 延长线上,延长CA 到G ,使AG =AB , 可得GC EC =,得出G GEC ∠=∠,设=2ACB x ∠,则G GEC x ∠=∠=;∠BAC =24°,根据AD 为∠ABC 的角平分线,得出=12BAD DAC ∠∠=︒,证明AGE ABE ≅(SAS ),得出=ABE G x ∠=∠,利用三角形内角和列方程242180x x +︒+=︒,解方程即可.【详解】解:(1)∠AE =AD =DC ,∠E ADE ∠=∠,DAC C ∠=∠,∠48E ∠=︒,=ADE DAC C ∠∠+∠,∠=2=48ADE DAC ∠∠︒,∠AD 为∠ABC 的角平分线,即=2BAC DAC ∠∠,∠48BAC ∠=︒;∠1804824108ABC ∠=︒-︒-︒=︒(2)如图2,在AC 边上取一点M 使AM =AB ,连接MP ,在ABP 和AMP 中,AB AM BAP MAP AP AP =⎧⎪∠=∠⎨⎪=⎩, ∠ABP AMP ≅(SAS ),∠BP M P =,∠MP MC PC +>,MC AC AM =-,∠AC AB BP PC -+>,∠AC BP AB PC +>+;(3)如图,点E 在射线CB 延长线上,延长CA 到G ,使AG =AB ,∠AB +AC =EC ,∠AG +AC =EC ,即GC EC =,∠G GEC ∠=∠,设=2ACB x ∠,则=90G GEC x ∠=∠︒-;又∠BAC =24°,AD 为∠ABC 的角平分线,∠=12BAD DAC ∠∠=︒,又∠90DAE ∠︒=,∠9078BAE BAD ∠︒-∠=︒=,9078GAE DAC ∠=︒-∠=︒,∠BAE GAE ∠∠=,在AGE 和ABE △中,AE AE GAE BAE AG AB =⎧⎪∠=∠⎨⎪=⎩, ∠AGE ABE ≅(SAS ),∠=90ABE G x ∠=∠︒-,又∠242ABE BAC ACB x ∠=∠+∠=︒+,∠90242x x ︒-=︒+,解得:22x =︒,∠=2=44ACB x ∠︒;当点E 在BD 上时,∠EAD <90°,不成立;当点E 在CD 上时,∠EAD <90°,不成立;如图,点E 在BC 延长线上,延长CA 到G ,使AG =AB ,∠AB +AC =EC ,∠AG +AC =EC ,即GC EC =,∠G GEC ∠=∠,设=2ACB x ∠,则G GEC x ∠=∠=又∠∠BAC =24°,AD 为∠ABC 的角平分线,∠=12BAD DAC ∠∠=︒,又∠90DAE ∠︒=,∠90102BAE BAD ∠︒+∠=︒=,90102GAE DAC ∠=︒+∠=︒,∠BAE GAE ∠∠=,在AGE 和ABE △中,AE AE GAE BAE AG AB =⎧⎪∠=∠⎨⎪=⎩, ∠AGE ABE ≅(SAS ),∠=ABE G x ∠=∠,∠242180x x +︒+=︒,解得:52x =︒,∠=2=104ACB x ∠︒.∠∠ACB 的度数为44°或104°.【点睛】本题主要考查了等腰三角形性质、全等三角形判定和性质,角平分线,三角形外角性质,三角形内角和,解一元一次方程,根据角平分线模型构造全等三角形转换线段和角的关系是解题关键.20.如图,已知在四边形ABCD 中,BD 是ABC ∠的平分线,AD CD =.2 求证:180A C ∠+∠=︒.【答案】见解析【分析】方法一,在BC 上截取BE ,使BE AB =,连接DE ,由角平分线的定义可得ABC DBC ∠=∠,根据全等三角形的判定可证ABD △和EBD △全等,再根据全等三角形的性质可得A BED ∠=∠,AD DE =,由AD =CD 等量代换可得DE DC =,继而可得C DEC ∠=∠,由于180BED DEC ∠+∠=︒,可证180A C ∠+∠=︒;方法2,延长BA 到点E ,使BE BC =,由角平分线的定义可得ABD DBC ∠=∠,根据全等三角形的判定可证EBD △和CBD △全等,继而可得E C ∠=∠,DC DE =.由AD CD =,可得DE AD =,继而求得E EAD ∠=∠,由180EAD BAD ∠+∠=︒,继而可得180BAD C ∠+∠=︒;方法3, 作DE BC ⊥于点E ,DE BA ⊥交BA 的延长线于点F ,由角平分线的定义可得,由DE BC ⊥,DE BA ⊥,可得90F DEB ∠=∠=︒,根据全等三角形的判定可证FBD 和EBD △全等,继而可得DF DE =,再根据HL 定理可得可证180BAD C ∠+∠=︒.【详解】解:方法1 截长如图,在BC 上截取BE ,使BE AB =,连接DE ,因为BD 是ABC ∠的平分线,所以ABC DBC ∠=∠.在ABD △和EBD △中,因为AB EB ABD DBC BD BD =⎧⎪∠=∠⎨⎪=⎩所以ABD EBD ≅,所以A BED ∠=∠,AD DE =.因为AD CD =,所以DE DC =,所以C DEC ∠=∠.因为180BED DEC ∠+∠=︒,所以180A C ∠+∠=︒.方法2 补短如图,延长BA 到点E ,使BE BC =.因为BD 是ABC ∠的平分线,所以ABD DBC ∠=∠在EBD △和CBD △中,因为BC BE EBD DBC BD BD =⎧⎪∠=∠⎨⎪=⎩,所以EBD CBD ≅,所以E C ∠=∠,DC DE =.因为AD CD =,所以DE AD =,所以E EAD ∠=∠.因为180EAD BAD ∠+∠=︒,所以180BAD C ∠+∠=︒.方法3 构造直角三角形全等作DE BC ⊥于点E .DE BA ⊥交BA 的延长线于点F因为BD 是ABC ∠的平分线,所以ABD DBC ∠=∠.因为DE BC ⊥,DE BA ⊥,所以90F DEB ∠=∠=︒,在FBD 和EBD △中,因为F DEB ABD DBC BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩,所以FBD EBD ≅,所以DF DE =.在Rt FAD △和Rt ECD △中,因为DF DE AD DC =⎧⎨=⎩, 所以Rt Rt FAD ECD ≅,所以FAD C ∠=∠.因为180FAD BAD ∠+∠=︒,所以180BAD C ∠+∠=︒.21.阅读下面材料:小明遇到这样一个问题:如图一,∠ABC 中,∠A=90°,AB=AC ,BD 平分∠ABC ,猜想线段AD 与DC 数量关系.小明发现可以用下面方法解决问题:作DE∠BC 交BC 于点E :(1)根据阅读材料可得AD 与DC 的数量关系为__________.(2)如图二,∠ABC 中,∠A=120°,AB=AC ,BD 平分∠ABC ,猜想线段AD 与DC 的数量关系,并证明你的猜想.(3)如图三,∠ABC 中,∠A=100°,AB=AC ,BD 平分∠ABC ,猜想线段AD 与BD 、BC 的数量关系,并证明你的猜想.【答案】(1)AD ;(2);(3)BC=AD+BD.【分析】(1)由角平分线的性质可得AD=DE ,根据∠A=90°,AB=AC ,可得∠C=45°,由DE∠BC 可得∠DEC 是等腰直角三角形,可得,进而可得答案;(2)在BC 上截取BE=AB ,连接DE ,利用SAS 可证明∠ABD∠∠EBD ,可得AD=DE ,∠BED=∠A=120°,由等腰三角形的性质可得∠C=30°,利用三角形外角性质可得∠CDE=90°,利用含30°角的直角三角形的性质即可得答案;(3)在BC 上取一点E ,使BE=BD ,作DF∠BA 于F ,DG∠BC 于G ,由角平分线的性质就可以得出DF=DG ,利用AAS 可证明∠DAF∠∠DEG ,可得 DA=DE ,利用外角性质可求出∠EDC=40°,进而可得DE=CE ,即可得出结论.【详解】(1)∠∠A=90°,BD 平分∠ABC ,DE∠BC ,∠DE=AD,∠∠A=90°,AB=AC,∠∠C=45°,∠∠CDE是等腰直角三角形,AD,故答案为(2)如图,在BC上截取BE=AB,连接DE,∠BD平分∠ABC,∠∠ABD=∠DBE,在∠ABD和∠EBD中,AB BEABD DBE BD BD=⎧⎪∠=∠⎨⎪=⎩,∠∠ABD∠∠EBD,∠DE=AD,∠BED=∠A=120°,∠AB=AC,∠∠C=∠ABC=30°,∠∠CDE=∠BED-∠C=90°,(3)如图,在BC上取一点E,是BE=BD,作DF∠BA于F,DG∠BC于G,∠∠DFA=∠DGE=90°.∠BD平分∠ABC,DF∠BA,DG∠BC,∠DF=DG.∠∠BAC=100°,AB=AC,∠∠FAD=80°,∠ABC=∠C=40°,∠∠DBC=20°,∠BE=BD,∠∠BED=∠BDE=80°,∠∠FAD=∠BED.在∠DAF和∠DEG中,DFA DGEFAD BED DF=DG∠=∠⎧⎪∠=∠⎨⎪⎩,∠∠DAF∠∠DEG(AAS),∠AD=ED.∠∠BED=∠C+∠EDC,∠80°=40+∠EDC,∠∠EDC=40°,∠∠EDC=∠C,∠DE=CE,∠AD=CE.∠BC=BE+CE,∠BC=BD+AD.【点睛】本题考查了等腰三角形的性质的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,解答时合理添加辅助线是解答本题的关键.。
利用角平分线构造全等三角形典型题

利用角平分线构造全等三角形典型题在数学的世界里,角平分线可真是个神奇的家伙。
你知道吗?它不仅仅是个线段,还能帮我们构造全等三角形,简直是数学界的“万金油”。
想象一下,有一天你在班里听到老师讲这个话题,心里可能会想:“这玩意儿跟我有什么关系?”但慢慢地,你就会发现,角平分线就像是一个聪明的小精灵,能把那些复杂的三角形问题变得简单易懂。
说到角平分线,首先得弄明白它是什么。
简单来说,角平分线就是从一个角的顶点出发,把这个角一分为二的那条线。
嘿,这可是个了不起的角色。
无论你是在解题,还是在做几何图形,角平分线总能让你变得轻松自如。
你可以把它想象成一个把复杂事物变简单的法宝,真的是一举两得。
当我们用角平分线来构造全等三角形时,别急,先来个小热身。
想象一下,两个三角形,A、B,分别有角A和角B。
我们只需要一条角平分线,把这个角平分成两个小角。
好啦,这时候就能看到两个小三角形在争先恐后地跑出来了,简直可爱得不行!这些小家伙的特征可多了:它们的边长一样,角度也相同,真是如同孪生兄弟。
想想看,这样的构造不仅好看,还特别实用。
咱们来聊聊具体的步骤。
找好一个角,拿起你的直尺,轻轻一划,就得到了那条神秘的角平分线。
然后,你可以利用这个角平分线分别连接角的两边,形成两条新的边,乖乖,这时候,你就会发现两个全等的三角形在眼前逐渐成型,简直像是魔术表演一样,令人目不暇接!这不就是数学中的“变魔术”吗?这个过程还不止于此。
我们可以用角平分线来解决很多问题,比如测量、绘图等等。
听着都觉得高大上,对吧?想象一下,今天你在做家庭作业,正遇到一道棘手的几何题,心里就像打翻了五味瓶,百感交集。
这时,突然想到用角平分线,哇,恍若拨云见日,前路明朗,简直就是“豁然开朗”啊!利用这条线,能把你的思路理顺,真是一箭双雕。
在做这些的时候,偶尔也会有些小插曲。
比如,手一抖,角平分线画得不太好,搞得自己“心烦意乱”。
这时候,你得提醒自己,慢慢来,别急。
全等三角形及角平分线难题ppt解答

1 这样的点共有_________ 个。 9、如图所示,在△ABC中,BC=5cm,BP、CP分别 是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC, 5 则△PDE的周长是_________________ cm。 10、在△ABC中,∠C=90°,BC=16cm,∠A的平分线AD交BC于D,且CD: 6cm DB=3:5,则D到AB的距离等于_________ 。
(二)填空题 6、如图所示,AB=AC,AD=AE,∠BAC=∠DAE, 55O ∠1=250,∠2=300,则∠3=________________
ห้องสมุดไป่ตู้
7、如图所示,DA⊥AB,EA⊥AC,AB=AD,AC=AE, 90O BET和CD相交于O,则∠DOE的度数是_______________. 角平分线 8、到三角形三边距离相等的点是三角形的___________ 交点,
∴△ADE≌△BCF(SAS) ∴∠E=∠F ∴DF∥BF 例2、如图所示,AD=BC,FD=EB,AB=CD,求证∠E=∠F. 证明:易证:△ADB≌△BCD(SSS) ∴ ∠ABD=∠CDB ∴ ∠BDF=∠EBD 又BE=DF,BD=BD ∴ △EDB≌△BFD(SAS)
例3、如图所示,在△ABC中,延长AC边上的中线BD到F, 使DF=BD,延长AB边上的中线CE到G,使EG=CE,求证: AF=AG. 证明:∵AE=BE,GE=CE, ∠AEG=∠CEB ∴ △ECB≌△GAE(SAS) 同理AF=BC ∴AG=AF
∴∠EDC=∠C=40O
易证△AEB≌△FEB(SAS),∴∠EFB=∠A=100O ∴ED=EF
∴BC=BD+DC=BE+AE.
例7、已知:如图所示PA、PC分别是△ABC的外角∠MAC、∠NCA的平分 线,它们交于P;PD⊥BM于D,PF⊥BN于E,则BP是∠MBN的平分线吗? 说明理由。 是。 ∵PA、PC分别是△ABC的外角∠MAC、∠NCA的平分线 又∵PD⊥BM,PF⊥BN ∴PM=PE=PF, ∴BP是∠MBN的平分线。
专题06 全等模型-角平分线模型(解析版)

专题06全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各类模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的几类全等模型作相应的总结,需学生反复掌握。
模型1.角平分线垂两边(角平分线+外垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线、CA OA ⊥于点A 时,过点C 作CA OB ⊥.结论:CA CB =、OAC ∆≌OBC ∆.图1图2常见模型1(直角三角形型)条件:如图2,在ABC ∆中,90C ∠=︒,AD 为CAB ∠的角平分线,过点D 作DE AB ⊥.结论:DC DE =、DAC ∆≌DAE ∆.(当ABC ∆是等腰直角三角形时,还有AB AC CD =+.)图3常见模型2(邻等对补型)条件:如图3,OC 是∠COB 的角平分线,AC =BC ,过点C 作CD ⊥O A 、CE ⊥OB 。
结论:①180BOA ACB ∠+∠=︒;②AD BE =;③2OA OB AD =+.例1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,∵AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,∴1DF DE ==,∴1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1.【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键.例2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =()A .40°B .45°C .50°D .60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,∴∠CAF=100°,在Rt△PFA和Rt△PMA中,{PA PA PM PF==,∴Rt△PFA≌Rt△PMA(HL),∴∠FAP=∠PAC=50°.故选C.【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF是解题的关键.例3.(2023·山东·七年级专题练习)如图,∠D=∠C=90°,点E是DC的中点,AE平分∠DAB,∠DEA =28°,求∠ABE的大小.【答案】28°【分析】过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得DE=CE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC,即可求得∠ABE的度数.【详解】如图,过点E作EF⊥AB于F,∵∠D=∠C=90°,AE平分∠DAB,∴DE=EF,∵E是DC的中点,∴DE=CE,∴CE=EF,又∵∠C=90°,∴点E在∠ABC的平分线上,∴BE平分∠ABC,又∵AD∥BC,∴∠ABC+∠BAD=180°,∴∠AEB=90°,(1)填空:角平分线的性质定理:角平分线上的点到.符号语言:∵如图1,OP 为COD ∠上的平分线,且,∴.(2)解答:已知:如图2,60AOB ∠=︒,OP 为AOB ∠的平分线,以点P 为顶点的CPD ∠与角的两边相交于点C 、D ,且120CPD ∠=︒.求证:PC PD =.(3)作图:根据以上种情况,再次寻找其它情况,点P P 为AOB ∠的平分线上的点,请你用尺规作图作PE OA ⊥于E ,作PF OB ⊥于F ,90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒,OP 平分AOB ∠,PE PF ∴=,在四边形EOFP 中,60AOB ∠=︒,90PEO PFO ∠=∠=︒,36060290120EPF ∴∠=︒-︒-⨯︒=︒,120CPD ∠=︒ ,CPD EPF ∴∠=∠,CPD EPD EPF EPD ∴∠-∠=∠-∠,CPE DPF ∴∠=∠,PEC PFD ∴≅ (ASA )PC PD ∴=;(3)证明:如图2,作射线PC ,交OA 于C ,作PCN AOB ∠=∠,反向延长NP ,交OB 于D ,则PC PD =;,(4)解:如图3,当ODP ∠和OCP ∠互补时,PC PD =,理由如下:作PE OA ⊥于E ,作PF OB ⊥于F ,90PEC PFD PEO PFO ∴∠=∠=∠=∠=︒,OP 平分AOB ∠,PE PF ∴=,在四边形EOFP 中,90PEO PFO ∠=∠=︒,360290180EPF AOB ∴∠+∠=︒-⨯︒=︒,180CPD AOB ∠+∠=︒ ,CPD EPF ∴∠=∠,CPD EPD EPF EPD ∴∠-∠=∠-∠,CPE DPF ∴∠=∠,PEC PFD ∴≅ (ASA)PC PD ∴=.【点睛】本题考查全等三角形的判定,角平分线的性质等知识,解决问题的关键是熟练掌握有关基础知识.模型2.角平分线垂中间(角平分线+内垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线,AB OC ⊥,结论:△AOC ≌△BOC ,OAB ∆是等腰三角形、OC 是三线合一等。
三角形全等角平分线模型例题及证明

三角形全等角平分线模型例题及证明好嘞,今天咱们就来聊聊三角形全等和角平分线的那些事儿。
哎,你有没有发现,三角形真的是个神奇的东西,简简单单的三个点,连起来就是个图形,偏偏它的性质可多了。
全等三角形就是那种长得一模一样的三角形,形状、大小都不差分毫,简直就是双胞胎兄弟,走到哪儿都能被认出来。
这可不是光靠眼力就能看出来的,得用几何的法则来推理推理。
你想啊,要是我把一块巧克力分成两半,照样能做出两个一模一样的巧克力,谁能不爱呢?然后咱们聊聊角平分线,听这个名字就觉得高大上,其实它就是把一个角一分为二,像是把一个大蛋糕切成两个均匀的部分。
角平分线的妙处在于,无论你这角多么刁钻,切开后左右两边总是各占一半,这就好比是把一块肉分给两只小狗,谁都不委屈。
这个东西在三角形里特别重要,尤其是当我们要证明一些三角形全等的时候,角平分线可是个好帮手。
来来,咱们用个例子来看看,想象一下一个三角形ABC,A点是个大老板,B和C 是他的两个小弟。
假如我们在A点那儿划一条角平分线,直接把这个角一分为二,结果B和C两兄弟就被各自分到了一份相等的“收益”。
这条角平分线还可以引出一些神奇的性质,比如说,平分线上的每一点到两条边的距离是相等的,就像是公园里的秋千,两边的绳子一样长。
咱们再说说证明的过程,想想看,我们要证明这条平分线把角一分为二,其实就是要把三角形的两个小部分给比出来。
用个简单的三角形来举个例子,假设你有个A点,B点和C点连起来,就是个三角形。
然后,你在A点做一个角平分线,往下拉到BC边,假设叫做D点。
这时候,ABD和ACD这两个小三角形就是咱们的主角了。
要证明它们全等,就要用到一些三角形全等的公理,比如边角边、边边边,这些可是几何的“黄金法则”。
拿到这两个小三角形,咱们就得找出相等的部分。
AD就是它们共同的边,然后,角BAD和角CAD是相等的,因为你就是那条角平分线,没跑。
BD和CD这两个小边也是相等的,因为D点就在BC边上嘛,这可太简单了。
三角形全等(全等于角平分线的综合问题)

上节课未解之谜:【例5】已知:如图,△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于E,交AC于F,连结DF 。
求证:∠ADB=∠CDF。
全等与角平分线问题四大属性:风、雷、水、火。
属性一:风!角的平分线上的点到这个角的两边的距离相等。
点评:果断!利索!够犀利!【例1】已知:如图,在四边形中,BC>AB,AD=CD,BD平分∠ABC。
求证:∠BAD+∠C=180°属性一:风!到这个角的两边的距离相等的点在角的平分线上。
【例2】已知:∠1=∠2,∠3=∠4,求证:AP平分∠BAC。
三角形全等属性二:雷!铁三角组合:角平分线、平行线、等腰三角形点评:几何里也有铁三角!?雷的我外焦内嫩呀!【例3】如图,在△ABC中,∠ABC与∠ACB的角平分线相交于点F,过F作DE∥BC ,交AB于D,交AC于E,若BD+CE=9,则线段DE之长为_____。
【例4】如图,在△ABC中,BD、CD 分别平分∠ABC和∠ACB。
ED∥AB,FD∥AC。
如果BC=6cm ,则△DEF的周长_____。
属性三:水!如图1所示,OP平分∠MON ,A为OM上一点,C为OP上一点。
连接AC,在射线ON 上截取OB=OA,连接BC(如图2),易证△AOC≌△BOC。
点评:充分利用角平分线的对称性,霸气!【例5】如图所示,在△ABC中,AC>AB,AD是内角平分线,P是AD上异于点A的任意一点,求证:PC-PB<AC-AB。
属性四:火!有垂直于角平分线的线,果断延长,就会得到一个等腰三角形。
点评:这是辅助线中相对比较高端的方法,此法必火!【例6】已知:如图,在△ABC 中,∠BAC =90°,AB =AC ,BE 平分∠ABC ,CE ⊥BE 。
求证:CE=12BD 。
本节课总结:遇到角平分线可以想到的四种作辅助线方法: 1.向两边做垂直(风) 2.“角、平、等”铁三角(雷) 3.截两边相等,构造全等(水)4.有垂直于角平分线的线,延长!(火)在线测试题温馨提示:请在线作答,以便及时反馈孩子的薄弱环节!1.如图,AD OB BC OA ⊥⊥,,垂足分别为D 、C ,AD 与BC 相交于点P ,若PA PB =,则1∠与2∠的大小是( ) A .12∠=∠ B .12∠>∠ C .12∠<∠ D .无法确定ODBPA21C2.如上右图,在△ABC 中,90C ∠=︒,AD 平分CAB ∠,8cm BC =,5cm BD =,则BE 等于( )A .3B .4C .5D .无法确定BCAD E3.如图,在△ABC 中,90A ∠=︒,AB AC BD ==,DE ⊥BC ,则AE 与DC 的关系是( ) A .大于 B .等于 C .小于 D .不确定ACBDE4.如图,在△ABC 中,AB AC =,36A ∠=︒,直线l 是线段AB 的垂直平分线,则EBC ∠=( ) A .72︒ B .40︒ C .36︒ D .24︒BAClE5.如图,△ABC 的外角FAC ∠的平分线为AE ,170∠=︒,DC ∥AE ,则ADC ∠=( ) A .40︒ B .50︒ C .60︒ D .70︒BFCEAD216.如图,在△ABC 中,B ∠,C ∠相邻的外角的平分线交于点D ,点D 一定在△ABC 中( )线的延长线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形与角平分线
一、知识概述
1、角的平分线的作法
(1)在∠AOB的两边OA、OB上分别截取OD、OE,使OD=OE.
(2)分别以D、E为圆心,以大于1/2DE长为半径画弧,两弧交于∠AOB 内一点C.
(3)作射线OC,则OC为∠AOB的平分线(如图)
指出:(1)作角的平分线的依据是三角形全等的条件——“SSS”.
(2)角的平分线是一条射线,不能简单地叙述为连接.
2、角平分线的性质
在角的平分线上的点到角的两边的距离相等.
指出:(1)这里的距离是指点到角两边垂线段的长.
(2)该结论的证明是通过三角形全等得到的,它可以独立作为证明两条线段相等的依据.即不需再用老方法——全等三角形.
(3)使用该结论的前提条件是有角的平分线,关键是图中有“垂直”.
3、角平分线的判定
到角的两边的距离相等的点在角的平分线上.
指出:(1)此结论是角平分线的判定,它与角平分线的性质是互逆的.
(2)此结论的条件是指在角的内部有点满足到角的两边的距离相等,那么
过角的顶点和该点的射线必平分这个角.
4、三角形的角平分线的性质
三角形的三条角平分线相交于一点,且这点到三角形三边的距离相等.
指出:(1)该结论的证明揭示了证明三线共点的证明思路:先设其中的两线交于一点,再证明该交点在第三线上.
(2)该结论多应用于几何作图,特别是涉及到实际问题的作图题. 二、典型例题剖析
例1、如图所示,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC,AF⊥CD.求证:△ABE≌△ADF.
例2、如图所示,BE、CF是△ABC的高,BE、CF相交于O,且OA平分∠BAC.求证:OB=OC.
例3、如图,D为BC的中点,DE⊥DF,E、F分别在AB、AC边上,则BE+CF ()
A.大于EF B.小于EF
C.等于EF D.与EF的大小无法比较
例4、(12分)如图四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠D+∠B=180°,求证:AD+AB=2AE.
例5、已知:如图,在四边形ABCD中,AB>BC,BD平分
.求证:AD=CD.
例6、如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于O 点,求证:AE+CD=AC.
三、中考解析
1、在△ABC,∠C=90°,BC=16cm,∠A的平分线AD交BC于D,且CD︰DB=3︰5,则D到AB的距离等于()
A.6cm B.7cm
C.8cm D.9cm
2、如图,D是△ABC的一个外角的平分线上一点,求证:AB+AC<DB+DC.
3、如图,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,求证:BF=CG.
4、已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且
BE⊥AC于E,与CD相交于点F.H是BC边的中点,连结DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=BF;
(3)CE与BG的大小关系如何?试证明你的结论.
5、如图,已知∠1=∠2,P为BN上一点,且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°
6、如图,△ABC中,AM是BC边上的中线,求证:
7、已知:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长线于E.
求证:BD=2CE.。
