电磁场课后习题答案
电磁学课后习题-答案

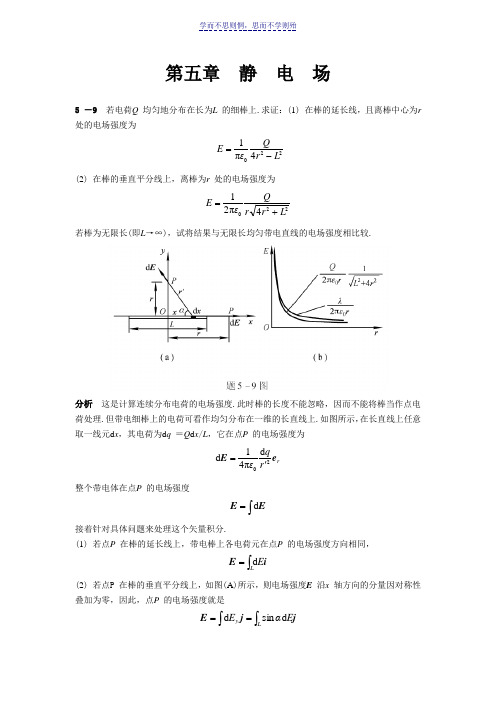
第五章 静 电 场5 -9 若电荷Q 均匀地分布在长为L 的细棒上.求证:(1) 在棒的延长线,且离棒中心为r 处的电场强度为2204π1L r QεE -=(2) 在棒的垂直平分线上,离棒为r 处的电场强度为2204π21Lr r QεE +=若棒为无限长(即L →∞),试将结果与无限长均匀带电直线的电场强度相比较.分析 这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元d x ,其电荷为d q =Q d x /L ,它在点P 的电场强度为r r q εe E 20d π41d '=整个带电体在点P 的电场强度⎰=E E d接着针对具体问题来处理这个矢量积分.(1) 若点P 在棒的延长线上,带电棒上各电荷元在点P 的电场强度方向相同,⎰=LE i E d(2) 若点P 在棒的垂直平分线上,如图(A )所示,则电场强度E 沿x 轴方向的分量因对称性叠加为零,因此,点P 的电场强度就是⎰⎰==Ly E αE j j E d sin d证 (1) 延长线上一点P 的电场强度⎰'=L r πεE 202,利用几何关系 r ′=r -x 统一积分变量,则()220022204π12/12/1π4d π41L r QεL r L r L εQ x r L x Q εE L/-L/P -=⎥⎦⎤⎢⎣⎡+--=-=⎰电场强度的方向沿x 轴.(2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为E r εqαE L d π4d sin 2⎰'=利用几何关系 sin α=r /r ′,22x r r +=' 统一积分变量,则()2203/22222041π2d π41L r r εQ rx L xrQ εE L/-L/+=+=⎰当棒长L →∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度rελL r L Q r εE l 0220π2 /41/π21lim=+=∞→此结果与无限长带电直线周围的电场强度分布相同[图(B )].这说明只要满足r 2/L 2 <<1,带电长直细棒可视为无限长带电直线.5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.分析 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=SS d s E Φ方法2:作半径为R 的平面S ′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅0d 0q εSS E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S SS E S E Φd d解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S SS E S E Φd d依照约定取闭合曲面的外法线方向为面元d S 的方向,E R πR E 22πcos π=⋅⋅-=Φ解2 取球坐标系,电场强度矢量和面元在球坐标系中可表示为①()r θθθE e e e E sin sin cos sin cos ++=r θθR e S d d sin d 2=ER θθER θθER SS2ππ2222πdsin d sin dd sin sin d ===⋅=⎰⎰⎰⎰S E Φ5 -17 设在半径为R 的球体内,其电荷为球对称分布,电荷体密度为()()R r ρkr ρ>=≤≤=0R r 0k 为一常量.试分别用高斯定理和电场叠加原理求电场强度E 与r 的函数关系.分析 通常有两种处理方法:(1) 利用高斯定理求球内外的电场分布.由题意知电荷呈球对称分布,因而电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面上电场强度大小为常量,且方向垂直于球面,因而有2S π4d r E ⋅=⋅⎰S E根据高斯定理⎰⎰=⋅V ρεd 1d 0S E ,可解得电场强度的分布. (2) 利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球壳,球壳带电荷为r r ρq ''⋅=d π4d 2,每个带电球壳在壳内激发的电场0d =E ,而在球壳外激发的电场rrεqe E 20π4d d =由电场叠加可解得带电球体内外的电场分布()()()()R r r r Rr>=≤≤=⎰⎰d R r 0d 0E E E E解1 因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定理⎰⎰=⋅V ρεd 1d 0S E 得球体内(0≤r ≤R ) ()40202πd π41π4r εk r r kr εr r E r ==⎰()r εkr r e E 024=球体外(r >R )()400202πd π41π4r εk r r kr εr r E R ==⎰ ()r εkR r e E 024=解2 将带电球分割成球壳,球壳带电r r r k V ρq '''==d π4d d 2由上述分析,球体内(0≤r ≤R )()r r rεkr r r r r k εr e e E 0222004d π4π41=''⋅'=⎰ 球体外(r >R )()r r Rr εkR r r r πr k πεr e e E 20222004d 441=''⋅'=⎰5 -20 一个内外半径分别为R 1 和R 2 的均匀带电球壳,总电荷为Q 1 ,球壳外同心罩一个半径为R 3 的均匀带电球面,球面带电荷为Q 2 .求电场分布.电场强度是否为离球心距离r 的连续函数? 试分析.分析 以球心O 为原点,球心至场点的距离r 为半径,作同心球面为高斯面.由于电荷呈球对称分布,电场强度也为球对称分布,高斯面上电场强度沿径矢方向,且大小相等.因而24d rπE ⋅=⎰S E .在确定高斯面内的电荷∑q 后,利用高斯定理∑⎰=0/d εq S E 即可求出电场强度的分布.解 取半径为r 的同心球面为高斯面,由上述分析∑=⋅02/π4εq r Er <R 1 ,该高斯面内无电荷,0=∑q ,故01=E R 1 <r <R 2 ,高斯面内电荷()31323131R R R r Q q --=∑ 故 ()()23132031312π4r R R εR r Q E --= R 2 <r <R 3 ,高斯面内电荷为Q 1 ,故2013π4r εQ E =r >R 3 ,高斯面内电荷为Q 1 +Q 2 ,故20214π4rεQ Q E +=电场强度的方向均沿径矢方向,各区域的电场强度分布曲线如图(B )所示.在带电球面的两侧,电场强度的左右极限不同,电场强度不连续,而在紧贴r =R 3 的带电球面两侧,电场强度的跃变量230234π4ΔεσR εQ E E E ==-=这一跃变是将带电球面的厚度抽象为零的必然结果,且具有普遍性.实际带电球面应是有一定厚度的球壳,壳层内外的电场强度也是连续变化的,本题中带电球壳内外的电场,在球壳的厚度变小时,E 的变化就变陡,最后当厚度趋于零时,E 的变化成为一跃变.5 -21 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 >R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL Er <R 1 ,0=∑q01=E在带电面附近,电场强度大小不连续,电场强度有一跃变 R 1 <r <R 2 ,L λq =∑rελE 02π2=r >R 2,0=∑q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变00π2π2ΔεσrL εL λr ελE ===这与5 -20 题分析讨论的结果一致.5 -22 如图所示,有三个点电荷Q 1 、Q 2 、Q 3 沿一条直线等间距分布且Q 1 =Q 3 =Q .已知其中任一点电荷所受合力均为零,求在固定Q 1 、Q 3 的情况下,将Q 2从点O 移到无穷远处外力所作的功.分析 由库仑力的定义,根据Q 1 、Q 3 所受合力为零可求得Q 2 .外力作功W ′应等于电场力作功W 的负值,即W ′=-W .求电场力作功的方法有两种:(1)根据功的定义,电场力作的功为l E d 02⎰∞=Q W其中E 是点电荷Q 1 、Q 3 产生的合电场强度. (2) 根据电场力作功与电势能差的关系,有()0202V Q V V Q W =-=∞其中V 0 是Q 1 、Q 3 在点O 产生的电势(取无穷远处为零电势). 解1 由题意Q 1 所受的合力为零()02π4π420312021=+d εQ Q d εQ Q 解得 Q Q Q 414132-=-=由点电荷电场的叠加,Q 1 、Q 3 激发的电场在y 轴上任意一点的电场强度为()22031π2yd εQ E E E yy y +=+=将Q 2 从点O 沿y 轴移到无穷远处,(沿其他路径所作的功相同,请想一想为什么?)外力所作的功为()dεQ y y d εQ Q Q W y 022/322002π8d π241d =+⋅⎥⎦⎤⎢⎣⎡--=⋅-='⎰⎰∞∞l E 解2 与解1相同,在任一点电荷所受合力均为零时Q Q 412-=,并由电势的叠加得Q 1 、Q 3 在点O 的电势dεQd εQ d εQ V 003010π2π4π4=+=将Q 2 从点O 推到无穷远处的过程中,外力作功dεQ V Q W 0202π8=-=' 比较上述两种方法,显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大,而求电势分布要简单得多. 5 -23 已知均匀带电长直线附近的电场强度近似为r rελe E 0π2=为电荷线密度.(1)求在r =r 1 和r =r 2 两点间的电势差;(2)在点电荷的电场中,我们曾取r →∞处的电势为零,求均匀带电长直线附近的电势时,能否这样取? 试说明. 解 (1) 由于电场力作功与路径无关,若沿径向积分,则有12012ln π2d 21r r ελU r r =⋅=⎰r E (2) 不能.严格地讲,电场强度r e rελE 0π2=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,r →∞处的电势应与直线上的电势相等.5 -27 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少?分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=pp V l E d 可求得电势分布.(2) 利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQV 0π4=在球面内电场强度为零,电势处处相等,等于球面的电势RεQV 0π4=其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211π4π40R r r εQ Q R r R r εQ R r r r >+=<<=<=e E e E E 由电势⎰∞⋅=rV l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r+=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞lE l E l E当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r+=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞lE l E当r ≥R 2 时,有rεQ Q V r02133π4d +=⋅=⎰∞l E(2) 两个球面间的电势差⎪⎪⎭⎫⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E 解2 (1) 由各球面电势的叠加计算电势分布.若该点位于两个球面内,即r ≤R 1 ,则2021011π4π4R εQ R εQ V +=若该点位于两个球面之间,即R 1 ≤r ≤R 2 ,则202012π4π4R εQ r εQ V +=若该点位于两个球面之外,即r ≥R 2 ,则rεQ Q V 0213π4+=(2) 两个球面间的电势差()2011012112π4π42R εQ R εQ V V U R r -=-== 第六章 静电场中的导体与电介质6 -1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定分析与解 不带电的导体B 相对无穷远处为零电势。
电磁场课后答案5

k1 sin θ B = k 2 sin θ 2
案
ε 2 k1 cosθ B = ε 1k 2 cosθ 2
cos θ 2 =
网
= 0, k z2 ε 1 − k z1 ε 2 = 0
ww w
Z 2 − Z 1 ωε 2 = k z2 Z 2 + Z1
− +
ωε 2
.k hd
k z1
对于 TM 模
ωε 1
所以
ε 1 ε 1 μ1 − ε 2 μ 2 2 μ1 ε 12 − ε 2
θ B = arccos
ε 1 ε 1 μ1 − ε 2 μ 2 2 μ1 ε 12 − ε 2
co
m
μ1 μ1ε 1 − μ 2ε 2 2 ε 1 μ12 − μ 2
当
μ1 = μ 2 ,θ B = arccos
ε1 + ε 2
2 2 μ2 k1 k 2 1 − cos θ B = 1 − 2 12 cos 2 θ B k2 μ1 k 2
两边平方,均整理后得到
cos 2 θ B =
所以
μ1 μ1ε 1 − μ 2ε 2 2 ε 1 μ12 − μ 2
θ B = arccos
k z2 ΓTM =
要使 ΓTM 即 由相位匹配条件: 由(1)
ρs
y =d
=0
案
网
ww w
(2) ∇ × E ≠ 0 ,是有旋场,不能用标量函数的负梯度表示
.k hd
aw .
co
⎞ ⎟ ⎟ ⎠
解: (1) ∇ ⋅ E =
∂E x ∂E y ∂E z + + =0 ∂x ∂y ∂z ⎛ ∂E y ∂E x ⎛ ∂E z ∂E y ⎞ ⎛ ∂E x ∂E z ⎞ ∇ × E = x0 ⎜ ⎜ ∂x − ∂y ⎜ ∂y − ∂z ⎟ ⎟ + y 0 ⎜ ∂z − ∂x ⎟ + z 0 ⎜ ⎝ ⎠ ⎝ ⎝ ⎠ π ⎛π ⎞ ⎛π ⎞ = −y 0 jkA sin⎜ y ⎟e j (ωt − kz ) − z 0 A cos⎜ y ⎟e j (ωt −kz ) d ⎝d ⎠ ⎝d ⎠
《电磁场和电磁波》课后习题解答(第一章)

第一章习题解答【习题Ll解】【习题L2解】【习题L3解】(1)要使ALR,则须散度A-B=O所以从Z∙5=T+3H8c=0可得:3b+8c=l即只要满足3b÷8c=l就可以使向量二和向量了垂直。
(2)要使4||月,则须旋度AxB=O所以从可得b=-3,c=-8【习题1・4解】A=I2以+9e y+6z,B=CIeX+be y,因为3JLA,所以应有A∙3=0g∣j(12久+9e y+e z^∙^ae x+Z?Gy)=12Q+9/?=0(I)又因为同=1;所以病存=1;(2)一4由⑴,⑵解得Q=±《,"=+W【习题1.5解】由矢量积运算规则4_B=A?C a x a2a3=(%Z-+(a3x-a x z)e y+(01y-a2x)e7xyz =8名+纥5+BZeZ取一线元:dl=e x dx+e y dy+e z dz则有dx_dy_dz则矢量线所满足的微分方程为丁二万一=Hιy xy"z或写成=常数)a2z-a3ya3x-a l za↑y-a2x求解上面三个微分方程:可以直接求解方程,也可以采用以下方法d(qx)="(/丁)二d(%z)a i a2z-a i a3ya2a3x-a l a2za l a3y-a2a i xxdx_ydy_ZdZx(a2z-a3y)y{a3x-a x z)z(a l y-a2x)由(1)(2)式可得d(a2y)=k(a2a3x-aλa2z)ydy=k(a3xy-a}yz)(4)对⑶⑷分别求和所以矢量线方程为【习题L6解】矢量场A=(αxz+x2)eχ+Sy+孙2)0+{z-z1-∖-cxz-2xyz)e z假设A是一个无源场,则应有divΛ=O即:divA=V•4=空L+空L+空■=O∂x∂y∂z因为A=axz+X2∕ξ=by+xy1A z=z-z1+cxz-2xyzx所以有divA=az+2x+b+2xy+l-2z+cχ-2xy=X(2+c)÷z(a-2)+b+l=0 得a=2,b=-1,c=-2【习题1.7解】设矢径r的方向与柱面垂直,并且矢径不到柱面的距离相等(r=a)f∙ds-[rds=a∖ds=a2πah所以,①=S JSJS【习题1.8解】φ=3X2y i A=X2yze v+3xy2e^而rot((∕A)=Vx(以)=×A÷V^×A又=巴?十3?+再等=6xye x+3jc2e y ox-oy∂z所以+9x3y2e v-lSx2y3e v+6x3y2ze z=3X2y2[(9X一X2)e x-9yeγ+4xze z]【习题1.9解】所以&CyCzrotA=VXA=———∂x∂y∂zA x A y A(-1+1)&+(4/Z-4xz)e、+(2y-2y)&=6由于场H的旋度处处等于0,所以矢量场A为无旋场。
电磁场课后答案2

0.495 0.495
=
2.96
d min1
=
ψ (0)λ
4π
+
λ 4
=
λ 4
+
0.1λ
=
0.35λ
p r = Γ 2 = 0.25 pi
2.6.下面两条传输线哪一条传输功率大?
om 传输线 1:特征阻抗Zc1=50Ω,Vmax= 100V, Vmin = 80V; c 传输线 2:特征阻抗Zc1=75Ω,Vmax= 150V, Vmin = 100V。
半轴于 B 点,B 点对应的阻抗值即为驻波系数ρ=2.9。
后 b) 离开负载第一个驻波最小点的位置dmin如图所示,dmin=0.348。
课 c) Γ = OA = 0.5 , Pr = Γ 2 = 0.25
OD
Pi
d) Vmax = 1.5, Vmin = 0.5, d min = 0.348,
dmax = 0.098, V (0) = 1 + Γ(0) = 1.2488
4 ) A 点 所 在 的 位 置 即 为 电 压 最 大 点 位 置 , 由 题 意 已 知 , Vmax = 5V , 所 以
I max
= Vmax
/ Zc
=
0.1A ,Vmin
=
PB × 5V PA
= 3.13V , I min
= Vmin
/ Zc
=
0.0627 A
注:该题也可以用公式法求解。
Owww.Ak(hC)
网 案
解:归一化负载阻抗 zL = Z L / Zc = 1.6 ,即图中的 A 点,刚好在实轴的右半轴上。
答 1) l = λ / 4 ,A 点绕等Γ圆至 B 点, zB = 1/ zL = 5 / 8,∴ Zin (B) = zB × zc = 31.25Ω 后 2) l = λ / 2 ,A 点绕等Γ圆至 C 点, zC = zL = 1.6,∴ Zin (C) = 80Ω 课 3)l = 3λ / 8 ,A 点绕等Γ圆至 D 点,zD = 0.9 + j0.43,∴ Zin (D) = zD × zc = 45 + j21.5Ω
电磁场课后习题答案

第一章 1.3 证:941(6)(6)50=0A B A B A B A B =⨯+⨯-+-⨯=∴⨯∴和相互垂直和相互平行1.11 (1)22220.50.50.522220.50.50.52272(2)(2272)124sAx Ay AzA divA x y z x x y x y zAd s Ad dz dy x x y x y z dzττ---∂∂∂∇==++∂∂∂=++=∇=++=⎰⎰⎰⎰⎰由高斯散度定理有1.18(1) 因为闭合路径在xoy 平面内, 故有:222()()8(2)(22)()2()8x y z x y x z x sA dl e x e x e y z e dx e dy xdx x dy A dl S XOY A ds e yz e x e dxdy xdxdy A ds →→→→•=+++=+∴•=∇•=+=∇•=∴⎰⎰因为在面内, 所以,定理成立。
1.21(1) 由梯度公式(2,1,3)|410410x y z x y zx y z u u uu e e e x y ze e e e e e ∂∂∂∇=++∂∂∂=++=++1方向:()(2)最小值为0, 与梯度垂直1.26证明00u A ∇⨯∇=∇∇=书上p10 1.25 第二章 2.13343sin 3sin 4qa V e wr qwr J V e aρρρπθθρπ===•=2.3''2222'30222,40=l l l dl d R Er R ez z ea a ez z ea aEr r z z a P ez z ea aE d z a ea πρραϕραϕπε===--==+-=+⎰用圆柱坐标系进行求解场点坐标为P(0,0,z).线电荷元可以视为点电荷,其到场点的距离矢量得所以点的电场强度为()2'''03222cos sin 020l zex ey ea d zE e z a πϕϕϕραε+∴=∴=+⎰()2235222023522322225052(1)4()()44()35=044()=()0351()=()0352r>b 4()8()4152()=401srs sbr b E d s r E r b r rEq b r r dr EqE d s b r r r E r b r rE r E d s r E r Eq b r r dr bEq bE r r πππεππεεππππε≤==-=--∴-==-==⎰⎰⎰⎰⎰时由高斯定理有即()时由高斯定理有250r ε222122212212221,22()2(2)121122(2r r r r r r b l Eb r l b e a e Eb Ea b e a e E Eb Ea r l Eb r l r e Eb a e Ea E επρπερρεερεεπρπερερερε∑∴=∴==∴=-=-∑∴===∴=⎰⎰0000000当r1>b 则,E=Eb-EaqEb ds=同理:r1r2r1r2对于r1<b 且在空腔外,E=Eb-EaqEb ds=,而r22211212121)(3)112,2212(12)222r r r r r r r r a e r e r b r e r e Ea r e r e E Eb Ea r e r e ερρεερρρεεε--<∑∴=∴=-=-=-⎰00000r2且在空腔内 E=Eb-Ea qE ds=,Eb=222200(1)0()cos ()sin (2)2cos r a E A a A a AA A r rA aϕϕϕϕφρεεϕ<=-∇∅=-∇∅=-∇•--+-∂==-∂2r s 时,ar>a 时 E=(r-)cos r=e e 圆柱是由导体制成的表面电荷2.20能求出边界处即z=0处的E2 根据D 的法向量分量连续12(5)103r r Z Z z E E εε⇒+=⇒=(1) 2ln22,ln ln66ln(2)62ln lne e lrbl a l rr sr s E e rbu E dl a u uE e bb r a au J E e b r aJdsI u g e ds b b uuu r a aρρρπερπεπερπδ=====∴======⎰⎰⎰设内外导体单位长度带电量分别为+和-,利用高斯定理可以求得导体介质的电场为:得到(1)=0 =000,2=00B B er arB a B J H μμ∇∴∇=≠∇=∇⨯=取圆柱坐标系,若为磁场,根据磁场连续性方程,有所以不是磁场()取直角坐标,所以是磁场。
电磁场周希朗习题答案 全

π
t
−
π 3
z
+
π 4
)
+
a
y
7.96 ×10−5 sin(108π t − π 3
z−π)A 3
m。
2-22
①
H
(t)
=
a
y
kE0 ωμ0
cos(ωt
−
kz)
;
②
S (t)
= az
kE02 2ωμ0
{1+ cos[2(ωt
− kz)]};
S
=
az
kE02 2ωμ0
;
Sav
=
az
kE02 2ωμ0
。
③
3
33 。
Wav = wav = 4.42 ×10−15 J
2-27 ①
Ey
=
Ey0
sin π x a
e− jβz ,
Hx
=
H x0
sin π x a
e− jβ z , H z
=
−
jH z0
cos π x e− jβ z ; a
②
J
=
jayε
0ω
Ey0
sin
πx a
e−
jβ
z
;
③
ρS
y=b
= − ρS
=
2 15
ρ0a3 ε0c
;
对区域④( R > c ):
E4
(R)
=
2ρ0a3 15ε 0 R 2
aR
, φ4
(R)
=
2 15
ρ0a3 ε0R
。
3-3
①
E
=
电磁学课后习题答案
第五章 静 电 场5 -9 若电荷Q 均匀地分布在长为L 的细棒上.求证:(1) 在棒的延长线,且离棒中心为r 处的电场强度为2204π1L r QεE -=(2) 在棒的垂直平分线上,离棒为r 处的电场强度为2204π21Lr r QεE +=若棒为无限长(即L →∞),试将结果与无限长均匀带电直线的电场强度相比较.分析 这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元d x ,其电荷为d q =Q d x /L ,它在点P 的电场强度为r r q εe E 20d π41d '=整个带电体在点P 的电场强度⎰=E E d接着针对具体问题来处理这个矢量积分.(1) 若点P 在棒的延长线上,带电棒上各电荷元在点P 的电场强度方向相同,⎰=LE i E d(2) 若点P 在棒的垂直平分线上,如图(A )所示,则电场强度E 沿x 轴方向的分量因对称性叠加为零,因此,点P 的电场强度就是⎰⎰==Ly E αE j j E d sin d证 (1) 延长线上一点P 的电场强度⎰'=L r πεE 202,利用几何关系 r ′=r -x 统一积分变量,则()220022204π12/12/1π4d π41L r QεL r L r L εQ x r L x Q εE L/-L/P -=⎥⎦⎤⎢⎣⎡+--=-=⎰电场强度的方向沿x 轴.(2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为E r εqαE L d π4d sin 2⎰'=利用几何关系 sin α=r /r ′,22x r r +=' 统一积分变量,则()2203/22222041π2d π41L r r εQ rx L xrQ εE L/-L/+=+=⎰当棒长L →∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度rελL r L Q r εE l 0220π2 /41/π21lim=+=∞→此结果与无限长带电直线周围的电场强度分布相同[图(B )].这说明只要满足r 2/L 2 <<1,带电长直细棒可视为无限长带电直线.5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.分析 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=SS d s E Φ方法2:作半径为R 的平面S ′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅0d 0q εSS E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S SS E S E Φd d解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S SS E S E Φd d依照约定取闭合曲面的外法线方向为面元d S 的方向,E R πR E 22πcos π=⋅⋅-=Φ解2 取球坐标系,电场强度矢量和面元在球坐标系中可表示为①()r θθθE e e e E sin sin cos sin cos ++=r θθR e S d d sin d 2=ER θθER θθER SS2ππ2222πdsin d sin dd sin sin d ===⋅=⎰⎰⎰⎰S E Φ5 -17 设在半径为R 的球体内,其电荷为球对称分布,电荷体密度为()()R r ρkr ρ>=≤≤=0R r 0k 为一常量.试分别用高斯定理和电场叠加原理求电场强度E 与r 的函数关系.分析 通常有两种处理方法:(1) 利用高斯定理求球内外的电场分布.由题意知电荷呈球对称分布,因而电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面上电场强度大小为常量,且方向垂直于球面,因而有2S π4d r E ⋅=⋅⎰S E根据高斯定理⎰⎰=⋅V ρεd 1d 0S E ,可解得电场强度的分布. (2) 利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球壳,球壳带电荷为r r ρq ''⋅=d π4d 2,每个带电球壳在壳内激发的电场0d =E ,而在球壳外激发的电场rrεqe E 20π4d d =由电场叠加可解得带电球体内外的电场分布()()()()R r r r Rr>=≤≤=⎰⎰d R r 0d 0E E E E解1 因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定理⎰⎰=⋅V ρεd 1d 0S E 得球体内(0≤r ≤R ) ()40202πd π41π4r εk r r kr εr r E r ==⎰()r εkr r e E 024=球体外(r >R )()400202πd π41π4r εk r r kr εr r E R ==⎰ ()r εkR r e E 024=解2 将带电球分割成球壳,球壳带电r r r k V ρq '''==d π4d d 2由上述分析,球体内(0≤r ≤R )()r r rεkr r r r r k εr e e E 0222004d π4π41=''⋅'=⎰ 球体外(r >R )()r r Rr εkR r r r πr k πεr e e E 20222004d 441=''⋅'=⎰5 -20 一个内外半径分别为R 1 和R 2 的均匀带电球壳,总电荷为Q 1 ,球壳外同心罩一个半径为R 3 的均匀带电球面,球面带电荷为Q 2 .求电场分布.电场强度是否为离球心距离r 的连续函数? 试分析.分析 以球心O 为原点,球心至场点的距离r 为半径,作同心球面为高斯面.由于电荷呈球对称分布,电场强度也为球对称分布,高斯面上电场强度沿径矢方向,且大小相等.因而24d rπE ⋅=⎰S E .在确定高斯面内的电荷∑q 后,利用高斯定理∑⎰=0/d εq S E 即可求出电场强度的分布.解 取半径为r 的同心球面为高斯面,由上述分析∑=⋅02/π4εq r Er <R 1 ,该高斯面内无电荷,0=∑q ,故01=E R 1 <r <R 2 ,高斯面内电荷()31323131R R R r Q q --=∑ 故 ()()23132031312π4r R R εR r Q E --= R 2 <r <R 3 ,高斯面内电荷为Q 1 ,故2013π4r εQ E =r >R 3 ,高斯面内电荷为Q 1 +Q 2 ,故20214π4rεQ Q E +=电场强度的方向均沿径矢方向,各区域的电场强度分布曲线如图(B )所示.在带电球面的两侧,电场强度的左右极限不同,电场强度不连续,而在紧贴r =R 3 的带电球面两侧,电场强度的跃变量230234π4ΔεσR εQ E E E ==-=这一跃变是将带电球面的厚度抽象为零的必然结果,且具有普遍性.实际带电球面应是有一定厚度的球壳,壳层内外的电场强度也是连续变化的,本题中带电球壳内外的电场,在球壳的厚度变小时,E 的变化就变陡,最后当厚度趋于零时,E 的变化成为一跃变.5 -21 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 >R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL Er <R 1 ,0=∑q01=E在带电面附近,电场强度大小不连续,电场强度有一跃变 R 1 <r <R 2 ,L λq =∑rελE 02π2=r >R 2,0=∑q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变00π2π2ΔεσrL εL λr ελE ===这与5 -20 题分析讨论的结果一致.5 -22 如图所示,有三个点电荷Q 1 、Q 2 、Q 3 沿一条直线等间距分布且Q 1 =Q 3 =Q .已知其中任一点电荷所受合力均为零,求在固定Q 1 、Q 3 的情况下,将Q 2从点O 移到无穷远处外力所作的功.分析 由库仑力的定义,根据Q 1 、Q 3 所受合力为零可求得Q 2 .外力作功W ′应等于电场力作功W 的负值,即W ′=-W .求电场力作功的方法有两种:(1)根据功的定义,电场力作的功为l E d 02⎰∞=Q W其中E 是点电荷Q 1 、Q 3 产生的合电场强度. (2) 根据电场力作功与电势能差的关系,有()0202V Q V V Q W =-=∞其中V 0 是Q 1 、Q 3 在点O 产生的电势(取无穷远处为零电势). 解1 由题意Q 1 所受的合力为零()02π4π420312021=+d εQ Q d εQ Q 解得 Q Q Q 414132-=-=由点电荷电场的叠加,Q 1 、Q 3 激发的电场在y 轴上任意一点的电场强度为()22031π2yd εQ E E E yy y +=+=将Q 2 从点O 沿y 轴移到无穷远处,(沿其他路径所作的功相同,请想一想为什么?)外力所作的功为()dεQ y y d εQ Q Q W y 022/322002π8d π241d =+⋅⎥⎦⎤⎢⎣⎡--=⋅-='⎰⎰∞∞l E 解2 与解1相同,在任一点电荷所受合力均为零时Q Q 412-=,并由电势的叠加得Q 1 、Q 3 在点O 的电势dεQd εQ d εQ V 003010π2π4π4=+=将Q 2 从点O 推到无穷远处的过程中,外力作功dεQ V Q W 0202π8=-=' 比较上述两种方法,显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大,而求电势分布要简单得多. 5 -23 已知均匀带电长直线附近的电场强度近似为r rελe E 0π2=为电荷线密度.(1)求在r =r 1 和r =r 2 两点间的电势差;(2)在点电荷的电场中,我们曾取r →∞处的电势为零,求均匀带电长直线附近的电势时,能否这样取? 试说明. 解 (1) 由于电场力作功与路径无关,若沿径向积分,则有12012ln π2d 21r r ελU r r =⋅=⎰r E (2) 不能.严格地讲,电场强度r e rελE 0π2=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,r →∞处的电势应与直线上的电势相等.5 -27 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少?分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=pp V l E d 可求得电势分布.(2) 利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQV 0π4=在球面内电场强度为零,电势处处相等,等于球面的电势RεQV 0π4=其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211π4π40R r r εQ Q R r R r εQ R r r r >+=<<=<=e E e E E 由电势⎰∞⋅=rV l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r+=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞lE l E l E当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r+=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞lE l E当r ≥R 2 时,有rεQ Q V r02133π4d +=⋅=⎰∞l E(2) 两个球面间的电势差⎪⎪⎭⎫⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E 解2 (1) 由各球面电势的叠加计算电势分布.若该点位于两个球面内,即r ≤R 1 ,则2021011π4π4R εQ R εQ V +=若该点位于两个球面之间,即R 1 ≤r ≤R 2 ,则202012π4π4R εQ r εQ V +=若该点位于两个球面之外,即r ≥R 2 ,则rεQ Q V 0213π4+=(2) 两个球面间的电势差()2011012112π4π42R εQ R εQ V V U R r -=-== 第六章 静电场中的导体与电介质6 -1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定分析与解 不带电的导体B 相对无穷远处为零电势。
电磁场课后答案3.

c) S W/m2
3.2 无源空间 H = zyˆ 0 + yzˆ 0 , D 随时间变化吗?
答:
∇
×
H
=
J
+
∂D ∂t
=
0,Q
J
=
0,∴
∂D ∂t
=
0
,所以
D
随时间不变化。
3.3 假定(E1,B1,H1,和D1)、(E2,B2B ,H2和D2)分别为源(J1、ρv1)、(J2、ρv2)激发的满
= 102 4π
x0 sin103 t − y 0 cos103 t
案 3.8 在一半径为 a 的无限长圆柱体中有一交变磁通通过,其变化规律为ψ = ψ 0 sin ωt ,试求 答 圆柱体内外任意点的电场强度。
后 答:由法拉第电磁感应定律:
课 ∫ ∫ E ⋅ dl = ∂ B ⋅ dS ,在半径为 r 处满足: 2πrE = S ∂ψ ' ,其中ψ ' 表示被积分环路包围
cos mπx cos nπy
a
b
com S(t) =
E(t) × H(t)
=
yˆ 0 E ym sin
mπx cos nπy cosωt × zˆ0
a
b
− ωμ0
mπE ym a
cos mπx cos nπy sin ωt
a
b
aw. =
xˆ0
−
mπE
2 ym
4aωμ0
sin
2mπx a
cos 2
nπy b
sin
2ωt
.khd <
《电磁场与电磁波》课后习题解答(全)

第一章习题解答【习题1.1解】222222222222222222222222222222222222cos cos cos cos cos cos 1xx x y z yx y z z x y z x y z x y z x y z x y z x y z x y z 矢径r 与轴正向的夹角为,则同理,矢径r 与y 轴正向的夹角为,则矢径r 与z 轴正向的夹角为,则可得从而得证a a b b g g a b g =++=++=++++=++++++++++==++【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯()()-()(9)(243)19124331514x y z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题1.3解】已知,38,x y z x y z A e be ce B e e e =++=-++ (1)要使A B ⊥,则须散度 0A B =所以从 1380A B b c =-++=可得:381b c += 即只要满足3b+8c=1就可以使向量和向量垂直。
(2)要使A B ,则须旋度 0A B ⨯= 所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=- 可得 b=-3,c=-8 【习题1.4解】已知129x y z A e e e =++,x y B ae be =+,因为B A ⊥,所以应有0A B ∙= 即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221a b +=; ⑵由⑴,⑵ 解得 34,55a b =±=【习题1.5解】由矢量积运算规则123233112()()()x y zx y z x x y y z ze e e A Ca a a a z a y e a x a z e a y a x e xyzB e B e B e B =?=-+-+-=++取一线元:x y z dl e dx e dy e dz =++则有xy z xyz e e e dlB B B dx dy dzB ?=则矢量线所满足的微分方程为 x y zd x d y d z B B B == 或写成233112()dx dy dzk a z a y a x a z a y a x==---=常数 求解上面三个微分方程:可以直接求解方程,也可以采用下列方法k xa a y a a z a d z a a x a a y a d y a a z a a x a d =-=-=-323132132231211)()()( (1)k x a y a z zdzz a x a y ydy y a z a x xdx =-=-=-)()()(211332 (2)由(1)(2)式可得)()(31211y a a x a a k x a d -=)()(21322z a a x a a k y a d -= (3) )()(32313x a a y a a k z a d -= )(32xy a xz a k xdx -=)(13yz a xy a k ydy -= (4))(21xz a yz a k zdz -=对(3)(4)分别求和0)()()(321=++z a d y a d x a d 0)(321=++z a y a x a d0=++zdz ydy xdx 0)(222=++z y x d所以矢量线方程为1321k z a y a x a =++ 2222k z y x =++【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场 ,则应有 div A =0即: div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2 【习题1.7解】设矢径 r 的方向与柱面垂直,并且矢径 r到柱面的距离相等(r =a )所以,2sssr ds rds a ds a ah πΦ===⎰⎰⎰=22a h π=【习题1.8解】已知23x y φ=,223yz A x yze xy e =+ 而 A A A A rot⨯∇+⨯∇=⨯∇=φφφφ)()(2222(6)3203xy zx y ze e e A xy x y e y e xyze x y z x yz xy ∂∂∂∇⨯==--+∂∂∂ 2223[(6)32]x y z A x y xy x y e y e xyze φ∴∇⨯=--+又y x z y xe x e xy ze y e x e 236+=∂∂+∂∂+∂∂=∇φφφφ 232233222630918603xy z x y z e e e A xyx x y e x y e x y ze x yz xy φ∇⨯==-+所以222()3[(6)32]x y z rot A A A x y xy x y e y e xyze φφφ=∇⨯+∇⨯=--+ +z y x e z y x e y x e y x 2332236189+-=]49)9[(3222z y x e xz e y e x x y x+--【习题1.9解】已知 222(2)(2)(22)x y zA y x z e x y z e x z y z e =++-+-+ 所以()()1144(22)0xyzyy x x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A 的旋度处处等于0,所以矢量场A 为无旋场。
高等电磁场理论课后习题答案

1.5Use the results obtained in Problem 1.4and show thatwhere R '=-r r .证明:223000211ˆlim lim lim 4411R 0(')4V R R V S dV d R R R R R ππδπ→→→⎛⎫⎛⎫⎛⎫∇=∇⋅=-⋅=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫∇≠-- ⎪⎝⎭⎰⎰⎰⎰⎰R S R r r 推导1又知道在处值为零,符合函数的定义。
3020(')1(')44(')14(')q qq R R q R δπεπδπδε-⎛⎫=-=∇ ⎪⎝⎭-⎛⎫∇⋅==>∇=-- ⎪⎝⎭r r E r r r r E r r 推导2点电荷产生的电场强度为1.6Consider a wire C carrying a static electric currentI .Using Equations2.1.13and 2.1.18,derive Biot –Savart ’s law given bywhere '=-R r r and d l ′points in the direction of the current flow.解:000000033d d d ()4π4π4πd d 1()()d 4π4π4πd d 4π4πV V C C C C C C V Sdl I R R RI I I R R RI I R R μμμμμμμμ'==='''=∇⨯=∇⨯=∇⨯=∇⨯'-⨯'=⨯=⎰⎰⎰⎰⎰⎰⎰⎰J J l A r l l B r A r l l l R R证明:2()()∇=∇∇⋅-∇⨯∇⨯E E E (1)()[]()(2)(3)0(4)()0(5)j j ωεωμμε∇⨯=⎧⎪∇⨯=-⎪⎨∇⋅=⎪⎪∇⋅=⎩H r E E H H r E 由(5)式可推出:[]()()()0εεε∇⋅=∇⋅+⋅∇=r E r E E r ,即:()ln ()()r r εεε⋅∇∇⋅=-=-⋅∇E E E r (6)由(2)(3)两式可得:22)()k ωμε∇⨯∇⨯==E (r E r E ,在利用性质(1)式,并将(6)的结果代入,可得22(ln ())()r k ε∇-⋅∇-∇=E E r E ,整理后为:[]22()ln ()0k r ε∇++∇⋅∇=E r E E 2.7解:222220(1)00()()0(2)j j k k k ωεωμ∇⨯=⎧⎪∇⨯=-⎪=>∇⨯∇⨯-=⎨∇⋅=⎪⎪∇⋅=⎩∇=∇∇⋅-∇⨯∇⨯=-=>∇+=H E E H E E H E E E E E E E 比如jkzz e -=E e 就是满足方程2,但不满足方程12.11解:沿z 轴放置的电偶极子的辐射远场为j j sin j e 4πsin j e 4πk r k rIlk E r Ilk H r θφηθθ--⎧=⎪⎪⎨⎪=⎪⎩通过坐标旋转,(过程略)可得沿x 轴放置的电偶极子的辐射远场为()()()()cos cos sin 4jkrr k e j Il r θφηθφφπη-⎧=⋅-⋅+⋅⎪⎪⎨⨯⎪=⎪⎩E r e e e E r H r 3.1解:由题意,镜像电流的分布如下。
大学电磁场课后答案

∫
∫
ห้องสมุดไป่ตู้
得到
(b 2 + ab − 2a 2 ) a(b − a) 6a 故两导体球壳间的电位分布为 b b σ a2 ρ a3 σ a 2 (b − r ) ρ 0 b 2 − r 2 a 3 (b − r ) ϕ (r ) = E (r ) d r = [ 2 + 0 (r − 2 )] d r = + − ] [ r r ε r 3ε 0 ε 0br br 3ε 0 2 r 0 说明 此题的要点在于导体的表面上有未知的感应电荷分布,用高斯定律求电场时,必须注意考虑 感应电荷产生的电场。 −
大学物理课后习题答案 电磁感应 电磁场

第十三章 电磁感应 电磁场 1、[D]分析:应用楞次定律为分析的根据,若要产生乙线圈中的,则乙线圈中电流产生的电感应强度是由右向左,说明甲线圈中电流产生的由右向左的电感应强度在减小,即产生该磁场的电流在减小,由此可见,将抽出甲中铁心,nI B r 0μμ=,在I 不变时,B 减小。
2、[D]依据法拉第电磁感应规律,td d φε-=在上述条件下,ε应相同。
依据欧姆定律,RI ε=因为是不同的导体电阻率不同,所以R 不同,I 也不同。
3、[B]应用楞次定律分析,在I 增长时,垂直通过线圈平面内向外的磁通量是增大,因此感应电流产生的磁感强度垂直平面向里,为顺时针方向。
4、[C]分析:当a >>r 时,有以r 为半径的圆周内各点的B可视为常矢量。
断电前通过导体环的磁通量:2012r aIBS S B ππμφ==⋅=。
断电后通过导体环的磁通量:02=φ。
对纯电阻电路有:aRIr RRq 2)(120112μφφφ==--=5、[D]θαεcos d sin d )(d l vB l B v =⋅⨯=)(B v ⨯和l d 之间夹角2πθ=,∴0d =ε 0d ==⎰εε6、[D]在t ωθθ+=,θαεcos d sin d l vB =其中θ是)(B v⨯和l d 之间夹角r r l vB d cos d sin d ωθαε-== 2OP 21d BL r r B ωωε-=-=⎰O 处为高电势 221BL ωε=7、[D]两自感线圈顺接和反接的自感系数:M L L L 221++=顺21L L KM =10≤≤KM L L L 221-+=反图(1)为反接:1111ab 2L L K L L L -+=,由于1<K ,∴0ab >L 图(2)为反接:1111ab 2L L KL L L -+=,由于1=K ,∴0ab =L8、[C]V 0.8161225.0d d 11=-⨯-=∆∆-=-=tI LtI Lε9、[C]a Ia IaIB πμπμπμ000P 22=+=10、tS B td d d d )( ⋅-=-=φεt mIa nI a nI BS BS S B mωπμπμθcos cos 2020====⋅t mIa nI mωωπμεcos 20-=11、解:Wb 1057.1)1.0(1416.310562521--⨯=⨯⨯⨯===⋅=rB BS S B πφWb 1057.1612-⨯-=-=φφC 1014.3)(1612-⨯=--=φφRq12、(1)向右移动时,垂直纸面向内的φ减小。
电磁场习题答案

1-25 已知圆球坐标系中矢量为 A = a R (2 cos ϕ R 3 ) + a θ sin θ ,求该矢量在直角坐标系中
的表达式。
3
答案: A = ax Ax + a y Ay + az Az 其中, Ax = (
2 x2 x +y
2 2
+ x3 z + xy 2 z + xz 3 ) ( x 2 + y 2 + z 2 ) 2 ;
1-9 已知一标量函数 φ = sin (πx 2) sin (πy 3) e − z ,求:① 点 p( 1, 2, 3) 处 φ 增加速率最
快的方向及大小; ② 点 p( 处向坐标原点方向 φ 增加速率 1, 2, 3) (方向导数) 的大小。 答案:① am =
-1
π 2 + 27
=
(π ay + 3 3az ), ∇u =
Ay = (
2 xy
x +y
2 2
+ x 2 yz + y 3 z + yz 3 ) ( x 2 + y 2 + z 2 ) 2 ;
Az = (
2 xz
x +y
2 2
− x4 − 2 x2 y 2 − x2 z 2 − y 2 z 2 − y 4 ) ( x2 + y 2 + z 2 )2 。
1-26 球 坐 标 系 中 的 两 个 矢 径 r1 和 r2 的 终 点 p1 和 p 2 的 坐 标 分 别 为 ( R1 ,θ 1 , ϕ 1 ) 和
1 (ax + 2a y − 3az ) ;② A − B = 53 ;③ A • B = −11 ; 14
《电磁学》第二版_课后题的答案

(参考点选在无远。)
答案:U1
=
q1 4πε 0 R1
+
q2 4πε0 2R1
∫ ∫ ∫ ∫ 〈或者:U1 =
R2 R1
E1dr
+
∞
R2
E2dr
=
2R1 q1 dr + R1 4πε 0r 2
∞ q1 + q2 dr 〉 2R1 4πε 0r 2
第一章
静电场的基本规律
1.1 判断下列说法是否正确, 说明理由。 (1)一点的场强方向就是该点的试探点电荷所受电场力的方向。 (2)场强的方向可由 E=F/q 确定,其中 q 可正可负。 (3)在以点电荷为心的球面上,由该点电荷产生的场强处处相等。
答案:(1) ×,正的试探电荷; (2) √ ;(3)× 在无外场是,球面上 E 大小相等。
力为零?
解:设 q′ 距 q 为 r,则 q′ 距 2q 为 (L − r) ,放在相距 r 处,受合力为 0,则有受力平衡条件:
k
qq′ r2
=
k
2qq′ (L − r)2
得到: r = ( 2 −1)L
1.2.4 在直角坐标系的(0m,0.1m)和(0m,-0.1m)的;两个位置上分别放有电荷 q=10-10C 的点 带电体,在(0.2m,0m )的位置上放一电荷为 Q=10-8C 的点带电体,求 Q 所受力的大小和方向。
1.2.1 真空中有两个点电荷,其中一个的量值是另一个的 4 倍。她们相距 5.0×10-2 m 时相互排斥力
为 1.6N。问: (1)她们的电荷各为多少? (2)她们相距 0.1m 时排斥力的多少?
电磁场理论基础课后答案

2-13. (教材 2-19)一个半径为 a 的导体球壳充满密度为
的电荷,已知电场分布为
求球内的电荷密度 解: ρ r ε ·E 球壳内无电场 4πa ρ ρ ρ
内 内
及球壳内外侧面上的面电荷密度 。 · Ar r ε A 3r r · r r ·3 6ε Ar
q 4πε d
q 4πε d q 4πε d q 4πε d q 4πε d
1 4π 1 4πa 1 4πa 1 4πa
1 ∂Φ R ∂n Φ · nds
Φ
∂ 1 ds ∂n R 1 4πa 1 4πa
q 4πε d Φds Φds
1 4π
1 Φ·n R
Φ
1 ds R
· Φdv · Edv
1 4πa
h h ∂f h ∂u
h h
f
1 h h h
h h ∂f h ∂u ,
1-14. (教材 1-18)证明 · 证明: ∂ ∂ ∂ x y z ·r ∂y ∂z ∂x x ∂ ∂x x y z ∂ ∂ ∂y ∂z y z
3
r
0
1-15. 在圆柱坐标系、 圆球坐标系中分别计算拉梅系数, 并写出梯度、 散度、 旋度的表达式。 解: 圆柱坐标系中, x y h h h Φ ·A ρ cos φ ρ sin φ z z cos φ sin φ 1 ρ sin φ ρ cos φ 1 ρ ∂Φ ∂ρ φ ∂Φ ρ ∂φ z ∂Φ ∂z ∂ ρA ∂z 1 ∂ ρA ρ ∂ρ 1 ∂ A ρ ∂φ ∂ A ∂z ρ
6 / 45
中国科学技术大学 电子科学与技术系 电磁场理论
Q
q
√2 2
1 4
2-6.
(教材 2-7)求半径为 a、电量为 Q 的均匀带电球面所产生的电位、电场强度和该系 统的总储能。 解: E r 0 Q E r 4πε r U r U r W a Q 4πε r Q 4πε a a Q 8πε a 的均匀带电球体相距为 d
电磁场与电磁波课后标准答案-郭辉萍版1-6章

第一章 习题解答1.2给定三个矢量A ,B ,C : A =x a +2y a -3z a B = -4y a +z aC =5x a -2za求:⑴矢量A 的单位矢量A a ; ⑵矢量A 和B 的夹角AB θ; ⑶A ·B 和A ⨯B⑷A ·(B ⨯C )和(A ⨯B )·C ;⑸A ⨯(B ⨯C )和(A ⨯B )⨯C解:⑴A a =A A=(x a +2y a -3z a ) ⑵cos AB θ=A ·B /A BAB θ=135.5o⑶A ·B =-11, A ⨯B =-10x a -y a -4z a ⑷A ·(B ⨯C )=-42(A ⨯B )·C =-42⑸A ⨯(B ⨯C )=55x a -44y a -11z a(A ⨯B )⨯C =2x a -40y a +5z a1.3有一个二维矢量场F(r)=x a (-y )+y a (x),求其矢量线方程,并定性画出该矢量场图形。
解:由dx/(-y)=dy/x,得2x +2y =c1.6求数量场ψ=ln (2x +2y +2z )通过点P (1,2,3)的等值面方程。
解:等值面方程为ln (2x +2y +2z )=c 则c=ln(1+4+9)=ln14 那么2x +2y +2z =141.9求标量场ψ(x,y,z )=62x 3y +ze 在点P (2,-1,0)的梯度。
解:由ψ∇=x a x ψ∂∂+y a y ψ∂∂+z a zψ∂∂=12x 3y x a +182x 2y y a +ze z a 得ψ∇=-24x a +72y a +z a1.10 在圆柱体2x +2y =9和平面x=0,y=0,z=0及z=2所包围的区域,设此区域的表面为S: ⑴求矢量场A 沿闭合曲面S 的通量,其中矢量场的表达式为A =x a 32x +y a (3y+z )+z a (3z -x)⑵验证散度定理。
电磁场课后答案2

1 ( R'+ jωL' )(G '+ jωC ' ) j
R '+ jωL' G '+ jωC '
课
后 答
案
网
ww w
2.5.传输线终端负载归一化阻抗zL=0.8+j1.0,计算 b. 离开负载第一个驻波最小点的位置dmin; a. 驻波系数ρ; d. 作出 V(z)~z/λ关系曲线。 c. 负载反射功率与入射功率之比;
.k hd
aw .
Z in (3λ / 8) = Z c
Z L − jZ c tan(−3kλ / 8) = 9.8 + 53.7j Z C − jZ L tan(−3kλ / 8)
aw .
co
m
1 + Γ(0) 1 + 0.5e − j108 1 − 0.1545 − j 0.4755 0.8455 − j 0.4755 ~ Z L = Zc = 50 × = 50 × = 50 × o − j 108 1 − Γ(0) 1 + 0.1545 + j 0.4755 1.1545 + j 0.4755 1 − 0.5e (0.8455 − j 0.4755)(1.1545 − j.04755) = 50 × 0.75 − j 0.951 = 50 × 1.33 + 0.226 1.556 = 50 × (0.482 − j 0.611) = 24.1 − j 30.55
电磁场课后答案4

kr =
衰减常数:
ωμσ
2
案
为 300 米。 试求电场强度的振幅为 1 微伏/米时离海面的距离, 并写出这个位置上的E, H之表示式。
=
ki =
复数波阻抗为:
网
平面电磁波在海平面处的场强表示式为: E = x 0 1000 e
2π × 10 6 × 4π × 10 −7 × 1 = 2 (弧度/米) 2
4.1 写出ω,k,f,T,λ单位。 答:ω (rad/s), k (rad/m) ,f (Hz) , T (s), λ (m) 4.2 激光器输出波长为 6.328 × 10-7m,计算它的f,T,k。 答: f =
c
λ
=
3 × 10 8 1 = 4.741 × 1014 Hz , T = = 2.11 × 10 −15 s , −7 f 6.328 × 10
ωt + 30 o = 180 o 或 ωt +
π
co
)
μ0 ,
m
解: k = ω
ε r ε 0 μ 0 = 2ω μ 0 ε 0 =
2 × 2π × 150 × 10 6 = 2π 3 × 10 8
(m )
−1
答: f = f 0 , λ = 0.5λ0 , k = 2k 0 , v = 0.5v0 。
解之得:z = 10.35(米) 距海水 10.35 米处 E、H 之表示式为:
2 z = 9 × ln 10
E = x 0 1000e −2 z e j (ωt −2 z )
= x 0 1000e − 20.7 e j (ωt −1180 )
o
= x 0 10 3 e − 20.7 e j (ωt −100 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 习题答案(第二章)2.4 由E =-∇ϕ 已知ϕ=+2ax b 得2E a =-∇ϕ=-x ax 根据高斯定理:0.E ∇=ρε得 电荷密度为:00.E ==∇-2a ρεε2.6取直角坐标系如图所示,设圆盘位于xoy 平面,圆盘中心与坐标原点重合方法1:由 '04s sds R ρϕ=πε⎰在球坐标系求电位值,取带点坐标表示源区2'''0004a sπρϕ=πε⎰⎰02s z ρ⎤=⎦ε因此,整个均匀带电圆面在轴线上P 点出产生的场强为001 z>0 21 z<02s z s z ⎧⎡⎤ρ⎪⎢ε⎪⎣=-∇ϕ=⎨⎡⎤ρ⎪+⎢⎪ε⎣⎩a E -a方法2 :(略) 2.7当r>a (球外)时,1.E ∇=ρε 221.(.)0E ∂∇==∂r r E r r10.E ∴=∇=0ρε当r<a (球内)时,2.E ∇=ρε 20231.(.)E∂∇==∂rE r E r r a00203.E ∴=∇E=aερε2.11两个点电荷-q,+q/2在空间产生的电位: 01(,,)4xy z⎡⎤ϕ=πε令(,,)0x y z ϕ= 得方程:104⎡⎤=πε方程化简得222242()33x a y z a ⎛⎫-++= ⎪⎝⎭由此可见,零电位面是以点(4 a /3,0,0)为球心,2 a /3为半径的球面。
2.20由高斯定理.sD dS q =⎰由 00r x r x D E E =εε=εεa 得 0()xqdE s x d =ε+a由0.dx U E dx =⎰ 得 0ln 2qdU s=ε 由qC U =得 0ln 2s C d ε= 2.22由于da ,球面的电荷可看作均匀分布的先计算两导体球的电位1ϕ、2ϕ: 则112...daadE dr E dr E dr ∞∞ϕ==+⎰⎰⎰112001144d a d q q q r r ∞+⎛⎫⎛⎫=-+- ⎪ ⎪πεπε⎝⎭⎝⎭ 120044q q a d=+πεπε '''212...daadE dr E dr E dr ∞∞ϕ==+⎰⎰⎰212001144d a d q q q r r ∞+⎛⎫⎛⎫=-+- ⎪ ⎪πεπε⎝⎭⎝⎭ 120044q q d a=+πεπε 得 1122014P P a ==πε,1221014P P d==πε由11221212C P P P =+-得 02ad C d a πε=-2.25方法1:设其中一个极板在yoz 平面,另一极板在x=a 位置 则电容器储能:220122e U W CU aε==当电位不变时,第二个极板移动受力:2022ea W U F aaϕ∂ε==-∂ 式中负号表示极板间作用力为吸引力方法2:设其中一个极板在yoz 平面,另一极板在x=a 位置 当电荷不变时,由0.ax U E dx =⎰ 得 x U E a =由高斯定理有0.sq E dS =ε⎰ 则0x q E =ε 得 0qaU =ε 由 20122e q aW qU ==ε 得 2202022e a q W U q F a a ∂ε=-=-=-∂ε 式中负号表示极板间作用力为吸引力二 习题答案(第三章)3. 7方法1:设流入球的电流为I ,球的半径为a , 导体球的电流分布为22==rIJ e rπ 电场强度为22r JI E e r σπσ==以无穷远处为零点电位,则导体球的电压为222∞∞===⎰⎰a a I IU Edr dr r aπσπσ 接地电阻为土壤损耗的功率为2261.5910 (W)2===⨯I P I R aπσ方法2:设半球表面的总电荷为q ,球的半径为a电场强度为22=r qE r πε以无穷远处为零点电位,则导体球的电压为2∞==⎰r a qU E dr aπε导体球的电容由静电比拟法可直接得: G=2a πσ接地电阻为 12=R aπσ土壤损耗的功率为2261.5910 (W)2===⨯I P I R aπσ3.12在圆柱坐标系计算,取导体中轴线和z 轴重合,磁场只有e φ方向分量,大小只跟r 有关,由安培环路定理:'0.2B l ==⎰Cd rB I φπμ当≤r a 时,'0=I ,0=B φ12==U R I aπσ2==qC a Uπε当<≤a r b 时,22'22-=-r a I I b a22022()2()-=-r a B I r b a φμπ当>r b 时,'=I I02=IB rφμπ 写成矢量形式2202200 () 2() 2B e e ⎧⎪≤⎪-⎪=<≤⎨-⎪⎪>⎪⎩r a r a I a r b r b a Ir b rφφμπμπ3. 21解: 球内:磁化电流体密度为得:0=∇⨯=m J M 球表面:磁化电流面密度为 因球面上 cos z a θ=22002cos sin J =⨯=⨯=msz r z M n a M a a M aφθθ3.29同轴线的内外导体之间的磁场沿φ方向 根据安培环路定理, 当r a <时,有222=I rB r aπμππ 所以 022=IB r aμπ ()r a < 当≤<a r b 时,有'02=rB I πμ所以得到'02=IB rμπ ()≤<a r b 同轴线中单位长度储存的磁场能量为2'2000112222=+⎰⎰a b m a B B W rdr rdr ππμμ2200ln 164=+I I b aμμππ (2)由212m W LI =,得到单位长度的自感为 0022ln 82==+m W bL I aμμππ补充题: 两平行无限长直线电流1I 和2I ,相距为d ,求每根导线单位长度受到的安培力m F 。
解: 方法1:设两平行无限长直线电流1I 和2I 方向相同一根无限长直导线(1l )电流的磁场 0112B =I a dϕμπ 另一根直导线(2l )的电流元22I dl 受到磁场力 2221F l B =⨯d I d01222l =⨯I I d a ϕμπ 01222=-x I Ia dl dμπ故导线2l 单位长度受力 0122222F F ==-m x I I d a dl dμπ同理,可求得导线1l 单位长度受力 01212F =m x I I a dμπ 方法2:设两平行无限长直线电流1I 和2I 方向相同一根无限长直导线(1l )电流的磁场 0112B =I a dϕμπ 另一根直导线(2l )的电流元22I dl 受到磁场力 2221F l B =⨯d I d01222l =⨯I I d a ϕμπ 01222=-x I Ia dl dμπ故导线2l 单位长度受力10122221001212120122222F l B =⨯=-==∂==-∂⎰m xm m I I I d a dI I W I I M dW I IF d dμπμπμπ同理,可求得导线1l 单位长度受力 01212F =m xI I a dμπ 三 习题答案(第五章)5.3对于海水, 传导电流为0sin c J E E t =σ=σω 位移电流为00cos d r EJ E t t∂=ε=εεωω∂ 位移电流与传导电流的幅度之比为300.2 1.1310d r r cJ f J -εεωεεπ====⨯σσd c J J 5.10应用理想导体的边界条件可以得出在0=x 处,0=y E ,0=x H )cos(0t kz H H z ω-= 在a x =处,0=y E ,0=x H )cos(0t kz H H z ω--=上述结果表明,在理想导体的表面,不存在电场的切向分量y E 和磁场的法向分量x H 。
另外,在0=x 的表面上,电流密度为00|)(|==+⨯=⨯=x z z x x x x s H e H e e H n J)cos(|00t kz H e H e e y x z z x ω--=⨯== 在a x =的表面上,电流密度则为a x z z x x x a x s H e H e e H n J ==+⨯-=⨯=|)(|0|cos()x z z x a y e e H e H kz t ==-⨯=-ω 5.13(1) ()()2Re[] a a -++-+=-j t kx j t kx x ym z zm E E eE eπωαωα()()a a ----=-j kx j kx x ym z zm E e jE e αα(2) 00()sin()cos()cos()cos()2H a a ⎛⎫=-++- ⎪⎝⎭x z a x x t H k t kz H t kz a a πππωωπ()()200Re[sin()cos()]H a a -+-⎛⎫=+ ⎪⎝⎭j t kz j t kz x z a x x H k e H e a a πωωπππ()()200sin()cos()a a -+-⎛⎫=+ ⎪⎝⎭j kz j kz x z a x x H k e H e a a ππππ(3)()0(,,,)Re[sin()sin()]a -=z j t k z z x y E x y z t E k x k y e ω0sin()sin()cos()a =-z x y z E k x k y t k z ω(4)(sin )20(,,,)Re[2sin()cos(cos )]a -+=j t kz x x E x y z t E k eπωθθθ02sin()cos(cos )cos(sin )2a =-+x x E k t kz πθθωθ02sin()cos(cos )sin(sin )a =--x x E k t kz θθωθ5.15解:(1)将E 表示为复数形式,有 a -=-jkz y m E jE e由复数形式的麦克斯韦方程,得11a a --=-∇⨯=-=jkz jkz mx m x kE H E kE e je j j ωμωμωμ磁场H 的瞬时表达式为()sin()a =--mxkE H t t kz ωωμ(2)方法1:由于是无源自由空间,根据无源自由空间的波动方程得:220020∂∇-=∂EE tμε由于E 只有y 分量,得y 分量的标量波动方程22220022220∂∂∂∂++-=∂∂∂∂y y y y E E E E xyztμε由于22∂∂y E x 、22∂∂y E y 为0,得2200220∂∂-=∂∂y y E E z t με对正弦电磁场,上方程可以写成2200()()0-=y y jk E j E μεω得==C kω方法2:由于是无源自由空间,根据无源自由空间的麦克斯韦方程得:0∇⨯=H j E ωε由于 200()=a a a --∂∇⨯=-=∂jkzjkz x m m y y y H kE k E H j jk e e z ωμωμ00a -=jkz y m j E E e ωεωε故 200a a --=jkz jkz my y mk E e E e ωεωμ得==C kω(3)坡印廷矢量的时间平均值为11Re[]Re[()(.())]22a a *-=⨯=-⨯-jkz jkz m av y m x kE S E H jE e j e ωμ201.2a =mz kE ωμ 5.20解: 由麦克斯韦方程的微分形式tEJ H ∂∂+=⨯∇ε(1) tHE ∂∂-=⨯∇μ(2) 0H ∇⋅= (3)1E ∇⋅=ρε(4)由式(1)两边取旋度,得)()(E tJ H ⨯∇∂∂+⨯∇=⨯∇⨯∇ε利用矢量恒等式,)()(2H H H ⋅∇∇+-∇=⨯∇⨯∇所以 )()(2E tJ H H ⨯∇∂∂-⨯-∇=⋅∇∇-∇ε 将式(2)和式(3)代入上式)(2tH t J H ∂∂-∂∂-⨯-∇=∇με故得J t HH ⨯-∇=∂∂-∇222εμ (5)同理可得ρεμεμ∇+∂∂=∂∂-∇1222t J t E E (6)式(5)式(6)则为所求的有源空间中E 和H 所满足的波动方程,是非齐次波动方程。
