电磁场课后答案4
《电磁场与电磁波》(第四版)课后习题解答(全)

第一章习题解答【习题1.1解】222222222222222222222222222222222222cos cos cos cos cos cos 1xx x y z yx y z z x y z x y z x y z x y z x y z x y z x y z 矢径r 与轴正向的夹角为,则同理,矢径r 与y 轴正向的夹角为,则矢径r 与z 轴正向的夹角为,则可得从而得证a a b b g g a b g =++=++=++++=++++++++++==++ 【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯()()-()(9)(243)19124331514x y z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题1.3解】已知,38,x y z x y z A e be ce B e e e =++=-++ (1)要使A B ⊥,则须散度 0A B =所以从 1380A B b c =-++=可得:381b c +=即只要满足3b+8c=1就可以使向量错误!未找到引用源。
和向量错误!未找到引用源。
垂直。
(2)要使A B ,则须旋度 0A B ⨯= 所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=-可得 b=-3,c=-8 【习题1.4解】已知129x y z A e e e =++,x y B ae be =+,因为B A ⊥,所以应有0A B ∙= 即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221=; ⑵由⑴,⑵ 解得 34,55a b =±=【习题1.5解】由矢量积运算规则123233112()()()x y zx y z x x y y z ze e e A Ca a a a z a y e a x a z e a y a x e xyzB e B e B e B =?=-+-+-=++取一线元:x y z dl e dx e dy e dz =++则有xy z xyz e e e dlB B B dx dy dzB ?=则矢量线所满足的微分方程为 x y zd x d y d z B B B == 或写成233112()dx dy dzk a z a y a x a z a y a x==---=常数 求解上面三个微分方程:可以直接求解方程,也可以采用下列方法k xa a y a a z a d z a a x a a y a d y a a z a a x a d =-=-=-323132132231211)()()( (1)k x a y a z zdzz a x a y ydy y a z a x xdx =-=-=-)()()(211332 (2)由(1)(2)式可得)()(31211y a a x a a k x a d -=)()(21322z a a x a a k y a d -= (3))()(32313x a a y a a k z a d -= )(32xy a xz a k xdx -=)(13yz a xy a k ydy -= (4))(21xz a yz a k zdz -=对(3)(4)分别求和0)()()(321=++z a d y a d x a d 0)(321=++z a y a x a d0=++zdz ydy xdx 0)(222=++z y x d所以矢量线方程为1321k z a y a x a =++ 2222k z y x =++【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场 ,则应有 div A =0即: div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2 【习题1.7解】设矢径 r的方向与柱面垂直,并且矢径 r到柱面的距离相等(r =a ) 所以,2sssr ds rds a ds a ah πΦ===⎰⎰⎰=22a h π=【习题1.8解】已知23x y φ=,223y z A x yze xy e =+而 A A A A rot⨯∇+⨯∇=⨯∇=φφφφ)()(2222(6)3203xy zx y ze e e A xy x y e y e xyze x y z x yz xy ∂∂∂∇⨯==--+∂∂∂ 2223[(6)32]x y z A x y xy x y e y e xyze φ∴∇⨯=--+又y x z y x e x e xy ze y e x e 236+=∂∂+∂∂+∂∂=∇φφφφ 232233222630918603xy z x y z e e e A xyx x y e x y e x y ze x yz xy φ∇⨯==-+所以222()3[(6)32]x y z rot A A A x y xy x y e y e xyze φφφ=∇⨯+∇⨯=--+ +z y x e z y x e y x e y x 2332236189+-=]49)9[(3222z y x e xz e y e x x y x+--【习题1.9解】已知 222(2)(2)(22)x y zA y x z e x y z e x z y z e =++-+-+ 所以()()1144(22)0xyzyy x x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A 的旋度处处等于0,所以矢量场A 为无旋场。
电磁场与电磁波课后习题及答案四章习题解答

如题图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为,求槽内的电位函数。
解根据题意,电位满足的边界条件为①②③根据条件①和②,电位的通解应取为题图由条件③,有两边同乘以,并从0到对积分,得到故得到槽内的电位分布两平行无限大导体平面,距离为,其间有一极薄的导体片由到。
上板和薄片保持电位,下板保持零电位,求板间电位的解。
设在薄片平面上,从到,电位线性变化,。
题图解应用叠加原理,设板间的电位为其中,为不存在薄片的平行无限大导体平面间(电压为)的电位,即;是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:①②③根据条件①和②,可设的通解为由条件③有两边同乘以,并从0到对积分,得到故得到求在上题的解中,除开一项外,其他所有项对电场总储能的贡献。
并按定出边缘电容。
解在导体板()上,相应于的电荷面密度则导体板上(沿方向单位长)相应的总电荷相应的电场储能为其边缘电容为如题图所示的导体槽,底面保持电位,其余两面电位为零,求槽内的电位的解。
解根据题意,电位满足的边界条件为①题图②③根据条件①和②,电位的通解应取为由条件③,有两边同乘以,并从0到对积分,得到故得到槽内的电位分布为一长、宽、高分别为、、的长方体表面保持零电位,体积内填充密度为的电荷。
求体积内的电位。
解在体积内,电位满足泊松方程(1)长方体表面上,电位满足边界条件。
由此设电位的通解为代入泊松方程(1),可得由此可得或(2)由式(2),可得故如题图所示的一对无限大接地平行导体板,板间有一与轴平行的线电荷,其位置为。
求板间的电位函数。
解由于在处有一与轴平行的线电荷,以为界将场空间分割为和两个区域,则这两个区域中的电位和都满足拉普拉斯方程。
而在的分界面上,可利用函数将线电荷表示成电荷面密度。
电位的边界条件为题图①②③由条件①和②,可设电位函数的通解为由条件③,有(1)(2)由式(1),可得(3)将式(2)两边同乘以,并从到对积分,有(4)由式(3)和(4)解得故如题图所示的矩形导体槽的电位为零,槽中有一与槽平行的线电荷。
高等电磁场理论课后习题答案

由于是远场,
e 1 e 2 e 3 e 4 e e 1 e 2 e 3 e 4 e
2
I ka sin jkr jk r1 jk r2 E E 1 E 2 E 3 E 4 e e jk r3 e jk r4 e e 4r 1 H e k E
2.7
解:
H j E E j H E k 2 E 0 H 0 E 0
比如 E e z e 2.11
jkz
(1)
2 E ( E) ( E) k 2 E 2 E k 2 E 0 (2)
代入公式,可得,
I ka sin1 jkr1 H e e x cos 1 cos 1 e y cos 1 sin 1 e z sin 1 4r1
2
I ka sin 2 jkr2 e e x cos 2 cos 2 e y cos 2 sin 2 e z sin 2 4r2
推导1 1 1 R ˆ 4 lim 2 dV lim dS lim 3 4 R 2 R V 0 R 0 R 0 R R R V S 1 1 又知道 2 在R 0处值为零,符合 (r r ')函数的定义。 4 R 推导2 点电荷q (r r ')产生的电场强度为 q 1 4 0 R 4 R q (r r ') 1 E 2 4 (r r ') 0 R E q
所以有
H 2 E1 H1 E2 E1 J 2 E2 J1 H 2 M1 H1 M 2
电磁场与电磁波第四版课后答案

答案:① aA =
1 14
(ax
+
2ay
−
3az
)
;②
A−B =
53 ;③ A • B = −11;
④
θ AB = 135.48 ; ⑤
A× C = −(4ax +13ay +10az ) ; ⑥
A •(B × C)=(A • B)× C = −42 ; ⑦
(A× B)× C = 2ax − 40ay + 5az 和
托克斯定理求解此线积分。
∫ ∫ 答案:① A •dl = π a4 ;② (∇ × A) dS = π a4 。
l
4
l
4
1-18 试在直角坐标系下证明: − 1 ∇2 (1 R)=δ(r − r′)。 4π
∫ 1-19 若矢量 A = a(R cos2 ϕ
R3 ),1 ≤ R ≤ 2 ,求
∇• AdV 。
⎡ 2 sinhξ cosη
⎢ ⎢
cosh 2ξ − cos 2η
⎢
答案:[M ] = ⎢−
2 coshξ sinη
⎢ cosh 2ξ − cos 2η
⎢
⎢
0
⎢⎢⎣
2 coshξ sinη cosh 2ξ − cos 2η
2 sinhξ cosη cosh 2ξ − cos 2η
0
⎤ 0⎥
⎥ ⎥ 0⎥ 。 ⎥ ⎥ 1⎥ ⎥⎥⎦
+ ay
y − 2x x2 + y2
。
1-22 已知 A = a a x + b a y + c a z ,写出圆柱坐标系和圆球坐标系下 A 的表达式。
答案: A = (a cosϕ + b sinϕ )ar + (b cosϕ − a sin ϕ )aϕ + caz ;
电磁学第四版课后答案详解

1.9 分别画出等值同号与等值异号的两无限大均匀带电平面的电场线图。
答案:
1.10 电场线是不
是
电电荷在电场中的运动轨迹?(设此
点电荷除电场外不受其他力)
答案:一般不是。 F = qE ; F = M a ; a = v ;只有在匀强电场中,静止点电荷运动的轨 t
迹才的电力线。
1.11 下列说法是否正确?如不正确,请举一反例加以论述。
+
r
2
)
1 2
=
0
∴ a2 = 2r2
所以该圆的半径为: r = ± 2 a 2
所得到曲线方程为:
y2
+
z2
=
⎛ ⎜⎝
a ⎞2 2 ⎟⎠
……….球面方程
1.3.1 在长为 50cm,相距为 1cm 的两个带电平行板间的电场是均匀电场(场强方向竖直向上), 将一电子从 P 点(与上下板等距离)一初速度 v0=107m/s 水平射入电场(见附图)。若电子恰在下板 由侧离开电场,求该均匀电场的大小。(忽略边缘效应,认为板外场强为零,且略去重力对电子运
(2)式代入(1)式中得:最大高度
y
=
v0
sin
300
×
v0
sin a
300
−
1 2
⎛ a⎜
⎝
v0
sin a
300
⎞2 ⎟ ⎠
=
v02
sin 2
300
(
1 a
−
1 2a
)
=
v02
sin
2
300
(
1 2a
)
=
v02
sin 2
300
1
电磁场与电磁波(第四版)课后答案__谢处方

电磁场 与电磁波(第四版) 课后答案第一章 习 题 解答1.1 给定三个矢量A 、B 和C 如下: 23x y z =+-A e e e4y z =-+B e e 52x z =-C e e求:(1)A a ;(2)-A B ;(3)A B ;(4)AB θ;(5)A 在B 上的 分量;(6)⨯A C ;(7)()⨯A B C 和()⨯A B C ;(8)()⨯⨯A B C 和()⨯⨯A B C 。
解 (1)23A x y z +-===+-e e e A a e e e A (2)-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e (3)=A B (23)x y z +-e e e (4)y z -+=e e -11 (4)由c o sAB θ=11238=A B A B ,得1c o s AB θ-=(135.5= (5)A 在B 上的分 量 B A =A c o s AB θ==A B B (6)⨯=A C 123502xyz-=-e e e 41310x y z ---e e e (7)由于⨯=B C 041502xyz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)4x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e (8)()⨯⨯=A B C 1014502xyz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点 为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
电磁场与电磁波第四课后思考题答案第四版全谢处方饶克谨高等教育出版社

电磁场与电磁波第四课后思考题答案第四版全谢处⽅饶克谨⾼等教育出版社2.1点电荷的严格定义是什么?点电荷是电荷分布的⼀种极限情况,可将它看做⼀个体积很⼩⽽电荷密度很的带电⼩球的极限。
当带电体的尺⼨远⼩于观察点⾄带电体的距离时,带电体的形状及其在的电荷分布已⽆关紧要。
就可将带电体所带电荷看成集中在带电体的中⼼上。
即将带电体抽离为⼀个⼏何点模型,称为点电荷。
2.2 研究宏观电磁场时,常⽤到哪⼏种电荷的分布模型?有哪⼏种电流分布模型?他们是如何定义的?常⽤的电荷分布模型有体电荷、⾯电荷、线电荷和点电荷;常⽤的电流分布模型有体电流模型、⾯电流模型和线电流模型,他们是根据电荷和电流的密度分布来定义的。
2,3点电荷的电场强度随距离变化的规律是什么?电偶极⼦的电场强度⼜如何呢?点电荷的电场强度与距离r 的平⽅成反⽐;电偶极⼦的电场强度与距离r 的⽴⽅成反⽐。
2.4简述和所表征的静电场特性表明空间任意⼀点电场强度的散度与该处的电荷密度有关,静电荷是静电场的通量源。
表明静电场是⽆旋场。
2.5 表述⾼斯定律,并说明在什么条件下可应⽤⾼斯定律求解给定电荷分布的电场强度。
关,即在电场(电荷)分布具有某些对称性时,可应⽤⾼斯定律求解给定电荷分布的电场强度。
2.6简述和所表征的静电场特性。
表明穿过任意闭合⾯的磁感应强度的通量等于0,磁⼒线是⽆关尾的闭合线,表明恒定磁场是有旋场,恒定电流是产⽣恒定磁场的漩涡源 2.7表述安培环路定理,并说明在什么条件下可⽤该定律求解给定的电流分布的磁感应强度。
如果电路分布存在某种对称性,则可⽤该定理求解给定电流分布的磁感应强度。
2.8简述电场与电介质相互作⽤后发⽣的现象。
在电场的作⽤下出现电介质的极化现象,⽽极化电荷⼜产⽣附加电场2.9极化强度的如何定义的?极化电荷密度与极化强度⼜什么关系?单位体积的点偶极矩的⽮量和称为极化强度,P 与极化电荷密度的关系为极化强度P 与极化电荷⾯的密度2.10电位移⽮量是如何定义的?在国际单位制中它的单位是什么电位移⽮量定义为其单位是库伦/平⽅⽶(C/m 2)2.11 简述磁场与磁介质相互作⽤的物理现象?ερ/=??E 0=??E ερ/=??E 0=??E ??V S ε00=??B JB 0µ=??0=??B JB 0µ=??CP =-p ρnsp e ?=P ρEP E D εε=+=0在磁场与磁介质相互作⽤时,外磁场使磁介质中的分⼦磁矩沿外磁场取向,磁介质被磁化,被磁化的介质要产⽣附加磁场,从⽽使原来的磁场分布发⽣变化,磁介质中的磁感应强度B 可看做真空中传导电流产⽣的磁感应强度B 0 和磁化电流产⽣的磁感应强度B ’ 的叠加,即 2.12 磁化强度是如何定义的?磁化电流密度与磁化强度⼜什么关系?单位体积内分⼦磁矩的⽮量和称为磁化强度;磁化电流体密度与磁化强度:磁化电流⾯密度与磁化强度: 2.13 磁场强度是如何定义的?在国际单位制中它的单位是什么?2,14 你理解均匀媒质与⾮均匀媒质,线性媒质与⾮线性媒质,各向同性与各向异性媒质的含义么?均匀媒质是指介电常数或磁介质磁导率处处相等,不是空间坐标的函数。
电磁场与电磁波(第4版)第4章部分习题参考解答

ω ⎡ ⎤ sin( z ) cos(ωt ) ⎥ ⎢ c ⎣ ⎦
ω G ω = −ex ( ) 2 E0 sin( z ) cos(ωt ) c c
所以
G G 1 ∂2 E ω 1 G ω ∇ E − 2 2 = −ex ( ) 2 E0 cos(ωt − x) − 2 c ∂t c c c
2
ω ⎤ ⎡ G 2 −exω E0 cos(ωt − x) ⎥ = 0 ⎢ c ⎦ ⎣ G G 1 ∂2 E G G ω 2 即矢量函数 E = ex E0 cos(ωt − x) 满足波动方程 ∇ E − 2 2 = 0 。 c ∂t c
G G G G 证:在直角坐标系中 r = ex x + ey y + ez z G G G G 设 k = ex k x + ey k y + ez k z G G G G G G G G 则 k ⋅ r = (ex k x + ey k y + ez k z ) ⋅ (ex x + ey y + ez z ) = k x x + k y y + k z z
即
G G G ∂ ∇(∇ ⋅ E ) − ∇ 2 E = − μ (∇ × H ) ∂t
将式(1)和式(4)代入式(6),得
G G G ∂2 E ∂J 1 ∇ E − με 2 = μ + ∇ρ ∂t ∂t ε
2
G 此即 E 满足的波动方程。 G G 4.6 在应用电磁位时, 如果不采用洛伦兹条件, 而采用库仑条件 ∇ ⋅ A = 0 , 导出 A 和 ϕ 所满足的微分方程。 G 解:将电磁矢量位 A 的关系式
电磁场与电磁波第四版课后思考题答案

2.1点电荷的严格定义是什么?点电荷是电荷分布的一种极限情况,可将它看做一个体积很小而电荷密度很的带电小球的极限。
当带电体的尺寸远小于观察点至带电体的距离时,带电体的形状及其在的电荷分布已无关紧要。
就可将带电体所带电荷看成集中在带电体的中心上。
即将带电体抽离为一个几何点模型,称为点电荷。
2.2 研究宏观电磁场时,常用到哪几种电荷的分布模型?有哪几种电流分布模型?他们是如何定义的? 常用的电荷分布模型有体电荷、面电荷、线电荷和点电荷;常用的电流分布模型有体电流模型、面电流模型和线电流模型,他们是根据电荷和电流的密度分布来定义的。
2,3点电荷的电场强度随距离变化的规律是什么?电偶极子的电场强度又如何呢?点电荷的电场强度与距离r 的平方成反比;电偶极子的电场强度与距离r 的立方成反比。
2.4简述 和 所表征的静电场特性 表明空间任意一点电场强度的散度与该处的电荷密度有关,静电荷是静电场的通量源。
表明静电场是无旋场。
2.5 表述高斯定律,并说明在什么条件下可应用高斯定律求解给定电荷分布的电场强度。
高斯定律:通过一个任意闭合曲面的电通量等于该面所包围的所有电量的代数和除以 与闭合面外的电荷无布的电场强度。
2.6简述 和 所表征的静电场特性。
表明穿过任意闭合面的磁感应强度的通量等于0,磁力线是无关尾的闭合线, 表明恒定磁场是有旋场,恒定电流是产生恒定磁场的漩涡源 2.7表述安培环路定理,并说明在什么条件下可用该定律求解给定的电流分布的磁感应强度。
安培环路定理:磁感应强度沿任何闭合回路的线积分等于穿过这个环路所有电流的代数和 倍,即2.8简述电场与电介质相互作用后发生的现象。
在电场的作用下出现电介质的极化现象,而极化电荷又产生附加电场 2.9极化强度的如何定义的?极化电荷密度与极化强度又什么关系?单位体积的点偶极矩的矢量和称为极化强度,P 与极化电荷密度的关系为 极化强度P 与极化电荷面的密度 2.10电位移矢量是如何定义的?在国际单位制中它的单位是什么电位移矢量定义为 其单位是库伦/平方米 (C/m 2) 2.11 简述磁场与磁介质相互作用的物理现象?在磁场与磁介质相互作用时,外磁场使磁介质中的分子磁矩沿外磁场取向,磁介质被磁化,被磁化的介质要产生附加磁场,从而使原来的磁场分布发生变化,磁介质ερ/=•∇E 0=⨯∇Eερ/=•∇E 0=⨯∇E VS0 0=⋅∇BJ Bμ=⨯∇0=⋅∇BJ Bμ=⨯∇0μCP•∇=-p ρnsp e •=P ρE P EDεε=+=0中的磁感应强度B 可看做真空中传导电流产生的磁感应强度B 0 和磁化电流产生的磁感应强度B ’ 的叠加,即2.12 磁化强度是如何定义的?磁化电流密度与磁化强度又什么关系? 单位体积内分子磁矩的矢量和称为磁化强度;磁化电流体密度与磁化强度:磁化电流面密度与磁化强度: 2.13 磁场强度是如何定义的?在国际单位制中它的单位是什么?2,14 你理解均匀媒质与非均匀媒质,线性媒质与非线性媒质,各向同性与各向异性媒质的含义么? 均匀媒质是指介电常数 或磁介质磁导率 处处相等,不是空间坐标的函数。
电磁场与电磁波答案(第四版)

第一章习题解答1.1 给定三个矢量A 、B 和C 如下: 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求:(1)A a ;(2)-A B ;(3)A B g ;(4)AB θ;(5)A 在B 上的分量;(6)⨯A C ;(7)()⨯A B C g 和()⨯A B C g ;(8)()⨯⨯A B C 和()⨯⨯A B C 。
解 (1)23A x y z +-===+e e e A a e e e A (2)-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e(3)=A B g (23)x y z +-e e e (4)y z -+=e e g -11 (4)由cos AB θ===A B A B g ,得1cos AB θ-=(135.5=o (5)A 在B 上的分量 B A =A cos ABθ==A B B g (6)⨯=A C 123502x yz-=-e e e 41310x y z ---e e e(7)由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C g (23)x y z +-e e e g (8520)42x y z ++=-e e e ()⨯=A B C g (1014)x y z ---e e e g (52)42x z -=-e e(8)()⨯⨯=A B C 1014502x yz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
(1)判断123PP P ∆是否为一直角三角形;(2)求三角形的面积。
电磁学课后答案第四章

4-2 (张方奕 PB13203055) 解: (1)相互垂直两段对 O 无电磁贡献 = 即有 =− = = ⑵代入 得B + ∙ 0. 5 4 ∙ 0. 5 4 ( − ) = 8 4
I = 20 A, a = 30 mm , b = 50 mm
4 ´ 10 -5 T
4-3 (张方奕 PB13203055) 解: 磁感 B 可分为无限长导线与圆环 O 分别贡献 由安培定理 2 =
0
4-7(张方奕 PB13203055) 解: dQ e 由电流的定义, I= = 2 p r dt ( ) v 则, B = 4p
0
*
ev 2pI = 0 2 = 12.52T r 4p r
4-8 (余阳阳 PB13203083) 解:
Q × Rd × (2p R sin )( R sin ) 2 2 Br = ò 4p R 3 2p 0 2× [( R sin ) 2 + ( R cos - x ) 2 ] 2
又由匀速圆周运动规律得
mv 2 mv = Bqv r = r Bq mv mv = v0 × 0 v× Bq B0 q v= mv0 B v0 , r = B0 q BB0
4-15 (余阳阳 PB13203083) 解: (1) 由动量定理
B
dq ldt = mdv dt
Blq = mv
又由能量守恒
0
ln
b + r 2 + b2 a+ r +b
2 2
+
a r +n
2 2
-
b r + b2
2
4-5 (张方奕 PB13203055) 解: (1).圆环两半相抵消,B=0 (2).电阻之比为
电磁场与电磁波第三版答案第四章

《电磁场与电磁波》——习题详解第四章 静态场的解4-1 一个点电荷 Q 与无穷大导体平面相距为 d ,如果把它移动到无穷远处,需要 作多少功? 解: 用镜像法, 相当于两个电荷关于 y = 0 平面向相反方向离开,当 Q 移到 y 处时,受到 的电场力为:y Qdy y xdF= Q2 4πε 0 (2 y ) 2-Q 此时移动 d y 需对电荷做功图 4-1dw = Fd y =移到无穷远处做的总功为:Q2 16πε 0 y 2dyW = dw = Fd y =d∫∫∞∫∞ dQ216πε 0 y 2dy=Q2 16πε 0 d当用外力将电荷 Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以在整个过程中,外力作的总功为Q2 8πε 0 d也可以用静电能计算,在移动以前,系统的静电能等于两个点电荷之间的相互 作用能:W=1 1 1 1 Q Q Q2 + (Q) q11 + q2 2 = Q = 2 2 2 4π ε 0 (2d ) 2 4π ε 0 (2d ) 8π ε 0 d移动点电荷到无穷远以后,系统的静电能为零.因此,在这个过程中,外力作 功等于系统静电能的增量,即外力作功为Q2 8πε 0 d.43习题四4-2 一个点电荷放在直角导体内部(如图 4-2),求出所有镜像电荷的位置和大小y-q r2 d r3O r1 r4rq ax -qq图 4-2 解:假设如图所示三个镜像电荷,则空间电荷分布为φ (r ) =v1 1 1 1 ( + ) 4πε 0 r1 r2 r3 r4q经检验:在 y = 0 平面上 φ ( r ) = 0 ,在 x = 0 平面上vφ (r ) = 0所以上述解为原问题的解.因此求得镜像电荷的位置和大小如图 4-2 所示,即vq 2 = q 位置 ( a, d ) , q3 = q 位置 ( a, d ) , q 4 = q 位置 (a, d )4-3 证明:一个点电荷 q 和一个带有电荷 Q ,半径为 R 的导体球之间的作用力为Rq Q + D q DRq F= 2 4π ε 0 D 2 (D R 2 ) 2 其中 D 是 q 到球心的距离 ( D > R ) . 证明:使用镜像法分析.由于导体球不接地,本身又带电 Q ,必须在导体球内 加上两个镜像电荷来等效导体球对外的影响.在距离球心 b = R / D 处,镜像电荷2为 q′ = Rq / D ;在球心处,镜像电荷为 q2 = Q q′ = Q + Rq / D .点电荷 q 受导 体球的作用力就等于球内两个镜像电荷对 q 的作用力,即44《电磁场与电磁波》——习题详解F= q2 q′ D 2 + ( D b) 2 4π ε 0 q Rq Rq Q + D q D = + R2 2 4π ε 0 D 2 2 (D ) D Rq Q + D DRq = 2 4π ε 0 D 2 (D R 2 ) 2 q4-4 两个点电荷 + Q 和 Q 位于一个半径为 a 的接地导体球的直径的延长线上, 分 别距离球心 D 和 D . (1) (2) 证明:镜像电荷构成一电偶极子,位于球心,偶极矩为 2a Q / D . 令 Q 和 D 分别趋于无穷,同时保持 Q / D 不变,计算球外的电场. 使用导体球面的镜像法和叠加原理分析.在球内加上两个镜像电荷:2 2 3 2解:(1)一个是 Q 在球面上的镜像电荷, 1 = aQ / D , q 距离球心 b1 = a / D ; 第二个是 Q 在球面上的镜像电荷, q2 = aQ / D ,距离球心 b2 = a / D .当距离较大时,镜像2电荷间的距离很小,等效为一个电偶极子,电偶极矩为p = q 1 (b1 b2 ) =(2) 2a 3Q D2球外任意点的电场等于四个点电荷产生的电场的叠加.设 + Q 和 Q 位于2坐标 z 轴上,当 Q 和 D 分别趋于无穷,同时保持 Q / D 不变时,由 + Q 和 Q 在空 间产生的电场相当于均匀平板电容器的电场,是一个均匀场,均匀场的大小为v 2Q / 4π ε 0 D 2 ,方向在 ez ,由镜像电荷产生的电场可以由电偶极子的公式计算.v E=p 4π ε 0 r3v v (er 2 cos θ + eθ sin θ )45习题四=4-5 2 a 3Q v v (er 2 cos θ + eθ sin θ ) 3 2 4π ε 0 r D接地无限大导体平板上有一个半径为 a 的半球形突起,在点 (0,0, d ) 处有一个 点电荷 q (如图 4-3),求导体上方的电z dq a bq2 -bq3-dq1 图 4-3位. 解:计算导体上方的电位时,要保持导 体平板部分和半球部分的电位都为零.先找平 面导体的镜像电荷 q1 = q ,位于 (0,0, d ) 处.再找球面镜像电荷 q2 = aq / d ,位于(0,0, b) 处,b = a 2 / d .当叠加这两个镜像电荷和原电荷共同产生的电位时,在导体平面上位于 (0,0,b) 处. 和球面上都不为零, 应当在球内再加上一个镜像电荷 q3 = aq / d , 这时,三个镜像电荷和原电荷共同产生的电位在导体平面和球面上都为零,而且三 个镜像电荷在要计算的区域以外. 导体上方的电位为四个点电荷电位的叠加,即=其中 q q1 q2 q3 + + + 4π ε 0 R r1 r2 r3 1R = [ x 2 + y 2 + ( z d ) 2 ]1 2 r1 = [ x 2 + y 2 + ( z + d ) 2 ]1 2 r2 = [ x 2 + y 2 + ( z b) 2 ]1 2 r3 = [ x 2 + y 2 + ( z + b) 2 ]1 24-6 求截面为矩形的无限长区域( 0 < x < a , 0 < y < b )的电位,其四壁的电位 为 ( x,0) = ( x, b) = 0 ,46《电磁场与电磁波》——习题详解 (0, y ) = 0U 0 y b , ( a, y ) = y U 0 (1 ), b 0 < y ≤ b/ 2 b/ 2 < y < b解:法一:由边界条件 ( x,0) = ( x, b) = 0 知,方程的基本解在 y 方向应该 为周期函数,且仅仅取正弦函数,即Yn = sin k n y(k n =nπ ) b在 x 方向,考虑到是有限区域,选取双曲正弦函数和双曲余弦函数,使用边界 (0, y ) = 0 条件,得出仅仅选取双曲正弦函数,即X n = sh nπ x b将基本解进行线性组合,得 = ∑ Cn shn =1∞nπ x nπ y sin b b待定常数由 x = a 处的边界条件确定,即 (a, y ) = ∑ Cn shn =1∞nπ a nπ y sin b b使用正弦函数的正交归一性质,有b nπ a C n sh = 2 b∫ (a, y) sin0bnπ y dy bb/2∫b/2 02 U0 y U b nπ y by nπ y nπ y sin d y = 0 cos sin b b b nπ b nπ b 0=U0 b b nπ b2 nπ cos sin 2 2nπ 2 nπ 2∫y nπ y U 0 1 sin dy b b/2 bb47习题四b 2 b nπ y U b nπ y by nπ y 0 = U 0 cos cos sin nπ b b / 2 b nπ b nπ b bb/2b nπ U 0 b nπ = U 0 sin + cos nπ cos 2 b nπ 2 nπ +化简以后得2U 0 b2 U b b nπ cos nπ 0 cos 2 b nπ b nπ 2b nπ a = C n sh b 2∫ (a, y) sin0bnπ y b nπ d y = 2U 0 2 2 sin b 2 nπ求出系数,代入电位表达式,得nπ 4U 2 sin nπ y sh nπ x = ∑ 2 02 nπ a b b n =1 n π sh b 4-7 一个截面如图 4-4 所示的长槽,向 y 方向无限延伸,两侧的电位是零,槽内∞siny → ∞ , → 0 ,底部的电位为 ( x,0) = U 0求槽内的电位. 解:法一:令 ( x, y ) = X ( x)Y ( y ) = 0 , 因边界条件y =0 =0 = U0 (0, y ) = (a, y ) = 0a图 4-4x所以 X(x) = Acos K x x + B sin K x xQ X ( x) = X (a) = 0求得A = 0 , Kx =nπ a( n = 1,2,3L )X ( x) = Bn sinnπ x ( n = 1,2,3L ) a48《电磁场与电磁波》——习题详解由 Kx + Ky = 0 得 所以 Y ( y ) = C n enπ y a22K y = K x K y = ± j22nπ a( n = 1,2,3L )+ Dn e nπ y a nyπ a nyπ a ( x, y ) =∑n =1 ∞∞(C n e+ Dn e )Bn sinnπ x a=∑n =1 ′ (C n enyπ a′ + Dn e nyπ a) sinnπ x a′ 由边界条件 ( x,+∞) = 0 可得 C n = 0所以 ( x, y ) =∑n =1∞′ Dn enπ y asinnπ x a再由边界条件 ( x,0) = U 0 代入可得∑n =1∞′ Dn e nπ 0 asinnπ x= a∑ D′ sinn n =1∞nπ x = U0 a再两边同乘以 sinmπ x ,并从 0 到 a 积分得 a 4U 0 2U 0 ′ Dn = (1 cos mπ ) = mπ mπ 0 所以槽内电位为∞m = 1,3,5L m = 2,4,6L ( x, y ) =4U 0 myπ mπ e a sin x mπ a m =1, 3, 5....∑=∑n =1∞( 2 n 1) yπ 4U 0 (2n 1)π a x e sin a (2n 1)π法二:由于在 x = 0 和 x = a 两个边界的电位为零,故在 x 方向选取周期解, 且仅仅取正弦函数,即X n = sin k n xnπ kn = a 49习题四在 y 方向,区域包含无穷远处,故选取指数函数,在 y → ∞ 时,电位趋于零,所以 选取Yn = e kn y由基本解的叠加构成电位的表示式为nπ x nπa y e = C n sin a n =1∑∞待定系数由 y = 0 的边界条件确定.在电位表示式中,令 y = 0 ,得U 0 = ∑ Cn sinn =1∞nπ x aCna = 2∫a0U 0 sinaU 0 nπ x dx = (1 cos nπ ) nπ a当 n 为奇数时, Cn =4U 0 ,当 n 为偶数时, Cn = 0 .最后,电位的解为 nπnπ y a=4-84U nπ x ∑,5 nπ0 sin a e n =1, 3∞若上题的底部的电位为 ( x,0) = U 0 sin重新求槽内的电位3π x a解:同上题,在 x 方向选取正弦函数,即 X n = sin k n x , k n = 向选取 Yn = e kn y nπ ,在 y 方 a .由基本解的叠加构成电位的表示式为 = ∑ Cn sinn =1∞nπ x e anπ y a将 y = 0 的电位代入,得 U 0 sinnπ x 3π x ∞ = ∑ Cn sin a a n =1其余系数 Cn = 0 , 应用正弦级数展开的惟一性, 可以得到 n = 3 时,C3 = U 0 ,50《电磁场与电磁波》——习题详解所以 = U 0 sin4-93π x e a3π y a一个矩形导体槽由两部分构成, 如图 4-5 所示, 两个导体板的电位分别是 U 0 和 零,求槽内的电位. 解: 将原问题的电位看成是两个电位的叠加. 一个电位与平行板电容器的电位相同(上板电位为 U 0 ,下板电位为零 ),另一个电位为 U ,即=U0 y +U a y = 0 ,U = 0 y = a ,U = 0 a a 2y其中,U 满足拉普拉斯方程,其边界条件为 = U0 =0x图 4-5x = 0 时, U0 U 0 a y, U0 y= U = (0, y ) U a 0 y, a a < y<a 2 a 0< y< 2x → ∞ 时,电位 U 应该趋于零. U 的形式解为 nπ y e U = ∑ Cn sin a n =1待定系数用 x = 0 的条件确定.∞ ∞ nπ x aU (0, y ) = ∑ Cn sinn =1nπ y anπ y dy aa/2a C = 2 n∫a 0U (0, y ) sin∫a/2 02 U0 y U 0 a nπ y nπ y a nπ y sin dy = y cos sin a a a nπ a nπ a 051习题四U = 0 a a 2 nπ a 2 nπ cos + sin 2 2nπ 2 nπ a∫y nπ y a nπ y U 0 1 sin d y = U 0 cos a a/2 nπ a aaa/2 aU 0 a a 2 nπ y ay nπ y cos sin a nπ a nπ nπ U0 a sin + 2 a nπ 2a/2= U 0a nπnπ cos nπ cos 2 +化简后,得到U a a U0 a2 nπ cos nπ 0 cos 2 a nπ 2 a nπ U a nπ y nπ d y = 0 cos a nπ 2a C = 2 n∫a0U (0, y ) sin只有偶数项系数不为零.将系数求出,代入电位的表达式,得=4-10∞ U0 y 2U 0 nπ nπ y + ∑ cos sin e a a 2 n = 2 , 4 ,L nπnπ x a将一个半径为 a 的无限长导体管平分成两半,两部分之间互相绝缘,上半(0 < φ < π ) 接电压 U 0 ,下半 (π < φ < 2π ) 电位为零,如图 4-6,求管内的电位. 解:圆柱坐标的通解为 (r , φ ) = ( A0φ + B0 )(C0 ln r + D0 ) + ∑ r n ( An cos nφ + Bn sin nφ )n =1∞+ ∑ r n (Cn cos nφ + Dn sin nφ )n =1∞由于柱内电位在 r = 0 点为有限值,通解中不能有 ln r 和 rn项,即有52《电磁场与电磁波》——习题详解Cn = 0 , Dn = 0 , C0 = 0 (n = 1,2, L)柱内电位是角度的周期函数, A0 = 0 .因此,该题的通 解取为 r = U0 φx (r , φ ) = B0 D0 + ∑ r ( An cos nφ + Bn sin nφ )n n =1∞ =0图 4-6各项系数用 r = a 处的边界条件来定. (a, φ ) = B0 D0 + ∑ a n ( An cos nφ + Bn sin nφ ) = n =1∞ U0, 0 < φ < π 0, π < φ < 2πB 0 D0 =a n An =U 1 2π (a, φ ) d φ = 0 2π 0 2∫1π1∫ ∫0 (a, φ ) cos nφ d φ = 02π2πa n Bn =柱内的电位为π0 (a, φ ) sin nφ d φ =U0 (1 cos nπ ) nπ2U U (r , φ ) = 0 + 0 2 π4-111r ∑5L n a sin nφ n =1, 3,∞n半径为无穷长的圆柱面上,有密度为 ρ S = ρ S 0 cos φ 的面电荷,求圆柱面内, 外的电位. 解:由于面电荷是余弦分布,所以柱内,外的电位也是角度的偶函数.柱外的电位不应有 r 项,柱内电位不应有 r 是角度的周期函数.故柱内电位选为nn项.柱内,外的电位也不应有对数项,且1 = A0 + ∑ r n An cos nφn =1∞柱外电位选为 2 = C0 + ∑ r nCn cos nφn =1∞53习题四假定无穷远处的电位为零,定出系数 C0 = 0 . 在界面 r = a 上, 1 = 2 , ε0∞ 2 + ε0 1 = ρ S 0 cos φ r r∞即A0 + ∑ a n An cos nφ = ∑ a nCn cos nφn =1 n =1 ε0 ∑ na n 1Cn cos nφ + ε0 ∑ na n 1 An cos nφ = ρ S 0 cos φn =1 n =1∞∞解之得A0 = 0 , A1 =ρS 0 a2 ρS 0 , C1 = 2ε 2ε 0(n > 1)An = 0 , Cn = 0最后的电位为 ρS0 2ε r cos φ , = 2 0 a ρ S 0 cos φ , 2ε 0 r 3-12r<a r>a将一个半径为 a 的导体球置于均匀电场 E0 中,求球外的电位,电场. 解:采用球坐标系求解,设均匀电场沿正 z 方向,并设原点为电位零点(如图v4-7) . 因 球 面 是 等 位 面 , 所 以 在 r = a 处 , = 0 ; 在 r → ∞ 处 , 电 位 应 是 = E0 r cos θ ,球坐标中电位通解具有如下形式: (r ,θ ) = ∑ ( An r n + Bn r n 1 ) Pn (cos θ )n =0∞用无穷远处的边界条件 r → ∞ 及 = E0 r cos θ ,得到 A1 = E0 ,其余An = 0 .再使用球面上 ( r = a ) 的边界条件54《电磁场与电磁波》——习题详解∞ (a,θ ) = E0 a cos θ + ∑ Bn a n 1 Pn (cos θ ) = 0n =0上式可以改写为E0 a cos θ = ∑ Bn a n 1 Pn (cos θ )n =0∞因为勒让德多项式是完备的,即将任意的函数展开成勒让德多项式的系数是 惟 一 的 , 比 较 上 式 左 右 两 边 , 并 注 意 P (cos θ ) = cos θ , 得 E0 a = B1a 12,即B1 = E0 a 3 ,其余的 Bn = 0 .故导体球外电位为 = 1 电场强度为a3 E0 r cos θ r3 rE0θz图 4-7Er = 2a 3 = E0 1 + 3 cos θ r r a = E0 1 3 sin θ r rθ 3Eθ = 4-13将半径为 a , 介电常数为 ε 的无限长介质圆柱放置于均匀电场 E0 中, E0 沿 设vvx 方向,柱的轴沿 z 轴,柱外为空气,如图 4-8,求任意点的电位,电场.解: 选取原点为电位参考点, 1 表示柱内电位, 2 表示柱外电位. r → ∞ 用 在 处,电位 2 = E0 r cos φ因几何结构和场分布关于 y = 0 平面对称, 故电位表 示式中不应有 φ 的正弦项.令rE0φε ε0图 4-8x1 = A0 + ∑ ( An r n + Bn r n ) cos nφn =1∞55习题四∞ 2 = C0 + ∑ (Cn r n + Dn r n ) cos nφn =1因在原点处电位为零,定出 A0 = 0 , Bn = 0 .用无穷远处边界条件 r → ∞ 及 2 = E0 r cos φ ,定出 C1 = E0 ,其余 Cn = 0 .这样,柱内,外电位简化为 1 = ∑ An r n cos nφn =1∞ 2 = C1r cos φ + ∑ Dn r n cos nφn =1∞再用介质柱和空气界面 ( r = a ) 的边界条件 1 = 2 及 ε 1 = ε 0 2 ,得 r r∞ ∞ n n ∑ An a cos nφ = E0 a cos φ + ∑ Dn a cos nφ n =1 n =1 ∞ ∞ ∑ εnAn a n 1 cos nφ = ε 0 E0 cos φ ∑ ε 0 nDn a n 1 cos nφ n =1 n =1 比较左右 n = 1 的系数,得A1 解之得D1 D1 = E0 , ε A1 + ε 0 2 = ε 0 E0 2 a aA1 = 2ε 0 ε ε0 E0 , D1 = E0 a 2 ε + ε0 ε + ε0比较系数方程左右 n > 1 的各项,得An Dn D = 0 , ε An + ε 0 2n = 0 2n a a n由此解出 An = Dn = 0 .最终得到圆柱内,外的电位分别是1 = E02ε 0 r cos φ , ε + ε0ε ε0 a2 2 = E0 r cos φ + E0 cos φ ε + ε0 r56《电磁场与电磁波》——习题详解电场强度分别为v v 2ε 0 v 2ε 0 E1 = 1 = er E0 cos φ eφ E0 sin φ ε + ε0 ε + ε0v v ε ε 0 a2 v ε ε 0 a2 1 + E0 cos φ eφ 1 E2 = 2 = er ε + ε r 2 E0 sin φ ε + ε0 r2 0 4-14 在均匀电场中,设置一个半径为 a 的介质球,若电场的方向沿 z 轴,求介质 球内,外的电位,电场(介质球的介电常数为 ε ,球外为空气). 解:设球内,外电位解的形式分别为1 = ∑ ( An r n + Bn r n 1 ) Pn (cos nθ ) ,n =0 ∞∞ 2 = ∑ (Cn r n + Dn r n 1 ) Pn (cos nθ )n =0在 选取球心处为电位的参考点, 则球内电位的系数中 A0 = 0 ,Bn = 0 . r → ∞ 处,电位 2 = E0 r cos θ ,则球外电位系数 Cn 中,仅仅 C1 不为零,即 C1 = E0 , 其余为零.因此,球内,外解的形式分别简化为1 = ∑ An r n Pn (cos nθ ) ,n =0∞ 2 = E0 r cos θ + ∑ Dn r n 1 Pn (cos nθ )n =0∞再用介质球面 ( r = a ) 的边界条件 1 = 2 及 ε1 = ε 0 2 ,得 r r∞ ∞ n An a Pn (cos nθ ) = E 0 a cos θ + Dn a n 1 Pn (cos nθ ) n =1 n =1 ∞ ∞ εnA a n 1 P (cos nθ ) = ε E cos θ ε 0 (n + 1) Dn a n 2 Pn (cos nθ ) n n 0 0 n =1 n =1 ∑ ∑∑∑比较上式的系数,可以知道,除了 n = 1 以外,系数 An , Dn 均为零,且A1a = E0 a + D1a 2 , ε A1 = ε 0 E0 2ε 0 D1a 357习题四由此,解出系数A1 = 3ε 0 ε ε0 E0 , D1 = E0 a 3 ε + 2ε 0 ε + 2ε 0 3ε 0 r cos θ , ε + 2ε 0最后得到电位,电场1 = E0 2 = E0 r cos θ + E0v v E1 = 1 = erε ε 0 a3 cos θ ε + 2ε 0 r 23ε 0 v 3ε 0 E0 cos θ eθ E0 sin θ ε + 2ε 0 ε + 2ε 0v ε ε 0 a3 ε ε 0 a3 v v 1 + 2 E0 cos θ eθ 1 E2 = 2 = er ε + 2ε r 3 E0 sin θ ε + 2ε 0 r 3 0 4-15 已知球面 ( r = a ) 上的电位为 = U 0 cos θ ,求球外的电位. 解:设球外电位解的形式为 = ∑ ( An r n + Bn r n 1 ) Pn (cos nθ )n =0∞在无穷远处,应该满足自然边界条件,即电位趋于零.这样确定系数 An = 0 ,球外 电位的形式解简化为 = ∑ Bn r n 1 Pn (cos nθ )n =0∞使用球面 ( r = a ) 的边界条件,有U 0 cos θ = ∑ Bn a n 1 Pn (cos nθ )n =0∞由于勒让德多项式 Pn (cos nθ ) 是线性无关的,考虑到 P (cos θ ) = cos θ ,比较上式 1 左右的系数,得到 B1 = U 0 a , Bn = 02(n = 0,2,3,L) .所以,球外的电位分布为58《电磁场与电磁波》——习题详解 = U04-16a2 cos θ r2求无限长矩形区域 (0 < x < a,0 < y < b) 第一类边值问题的格林函数(即矩形 槽的四周电位为零,槽内有一与槽平行的单位线源,求槽内电位,如图 4-9). 解:这个问题的格林函数满足的方程为 2G 2G 1 + 2 = δ( x x′) δ( y y′) 2 x y ε0格林函数的边界条件是,在矩形区域的四周为零,即 x = 0 或 x = a , G = 0 ,y = 0 或 b = 0 , G = 0 .用分离变量法求这个问题的格林函数.考虑到格林函数在x = 0 , x = a 时的边界条件,将格林函数表示为y b(x',y')G = ∑Ψ n ( y ) sinn =1∞nπ x a将其代入格林函数方程,得a x 2 nπ 2 nπ x 1 = δ( x x′) δ( y y′) Ψ n ( y ) sin 图 4-9 ∑ y 2 a ε0 a n =1 nπ x 上式左右乘以 sin , 并在 0 < x < a 区间积分, 利用正弦函数的正交性和 δ 函数 a∞的积分性质,得函数Ψ n ( y ) 满足的微分方程为2 d2 nπ x ′ 2 nπ sin δ( y y ′) Ψn ( y ) = 2 a ε 0a dy a 在确定函数Ψ n ( y ) 时,将原来的区域分为两个区域,并注意到边界条件,设nπ An sh a (b y ), Ψ n ( y) = nπ Bn sh y, a 在 y = y′ 处,电位连续,即y > y′ y < y′An shnπ nπ (b y′) = Bn sh y′ a a59习题四对于函数Ψ n ( y ) 满足的微分方程,在点源附近积分,得∫y′+ 0 y′0d2 nπ Ψn ( y ) d y 2 dy a 2∫y′+ 0 y′0Ψ0 ( y ) d y = nπ x 2 sin ε 0a a因为电位连续,故上式左边第二项的积分为零,从而有d d nπ x′ 2 sin Ψ n ( y) Ψ n ( y) = dy dy a ε 0a y = y′ y = y′ + 代入函数Ψ n ( y ) 的形式,得nπ nπ nπ nπ x′ nπ 2 (b y′) sin An ch Bn ch y′ = a a a a ε 0a a将上式与 An shnπ nπ (b y′) = Bn sh y′ 相互联立求解,得 a a nπ 2 1 An = sh y′ , nπ ε 0 sh nπ b a a nπ 2 1 Bn = sh (b y′) nπ ε 0 sh nπ b a asin最后得到矩形区域的格林函数为nπ x ′ n π x nπ nπ sin y ≤ y′ sh a (b y′) sh a y, 2 a a = G= nπ ∑ nπ nπ b ε 0π n =1 sh y′ sh (b y ), y ≥ y′ n sh a a a 4-17 推导无限长圆柱区域内(半径为 a )第一类边值问题的格林函数. 解:使用镜像法及其格林函数的定义计算.在半径为 a 的导体圆柱内部离轴 线 r ′ 处,放置一个线密度为 1 单位,与导体圆柱平行的无穷长线电荷,并且维持导∞体柱面的电位为零,求出柱内的电位,这个电位就是柱内的格林函数.当原电荷位 于 r 处,需要在 r ′ 的镜像位置 r ′′ 处,加一个线密度为 1 的线电荷.此时,圆柱内 的电位是v v G (r , r ′) =1 2π εln1 1 1 ln +C R1 2π ε R2R1 和 R2 分别是从 r ′ 和 r ′′ 到 r 的距离(如图 4-10),C 是常数.由柱面上的电位为零,60《电磁场与电磁波》——习题详解可以定出这个常数的值.最后得到柱内的格林函数为v v G (r , r ′) =1 2π εlnR2 r ′ R1 a yrR1 r'R2 r'' x =0 = U0图 4-10 4-18d图 4-11x两个无限大导体平板间距离为 d ,其间有体密度 ρ =ρ 0 x / d 的电荷,极板的电位如图 4-11 所求,用格林函数法求极板之间的电位. 解:先用直接积分法求解.电位仅仅是 x 的函数,故其满足如下方程:ρ x d2 ρ = = 0 2 dx ε0 ε 0d对以上方程积分得ρ x2 ρ x3 d = C1 0 , = C2 + C1 x 0 dx 2ε 0 d 6ε 0 d由 x = 0 及 = 0 , 可 定 出 系 数 C2 = 0 ; 由 x = d 及 = U 0 , 可 定 出 系 数C1 =U 0 ρ0d + ,从而,得到电容器内的电位为 d 6ε 0 =ρ0 x3 6ε 0 dU ρ d + 0 + 0 x d 6ε 0 再用格林函数法求解.这个问题的格林函数为 d x′ x < x′ ε d x, 0 G ( x, x′) = x′ (d x), x > x′ ε 0d 为了计算方便,将这个问题分解为两个:一个是平板电容器内有电荷,而两极板的61习题四电位为零,即奇次边界条件,记电位 1 ;另一个是无电荷分布,极板的电位维持原 来的电位,记电位 2 .用格林函数法计算奇次边界条件时的电位 1 :1 = ρ ( x ′)G ( x, x ′) d x ′0∫d= ρ ( x ′)G ( x, x ′) d x ′ + ρ ( x ′)G ( x, x ′) d x ′0 x∫x∫d=∫x 0ρ 0 x ′ x ′(d x) d x′ + d ε 0d∫d xρ 0 x ′ (d x ′) x d x′ d ε 0dρ 0 (d x) x 3 ρ 0 x 1 2 2 1 (d x )d + (d 3 x 3 ) = + 2 2 3 ε 0d 2 3 ε 0d =ρ0 3 ρ0d x + x 6ε 0 d 2 6ε 0至于电位 2 ,容易得出 2 = (U 0 / d ) x .故所求电位为 = 1 + 2 = 4-192ρ0 2 U 0 ρ0d x + d + 6ε x 6ε 0 d 0 分析复变函数 w = z 能够表示的静电场. 解: w = u + j v = z = ( x + j y ) = x y + j 2 xy2 2 2 2u = x 2 y 2 , v = 2 xy实部的等值线是双曲线 x y = C1 ;虚部的等值线也是双曲线,其方程为2 22 xy = C2 .因此,这个函数能够表示极板形状为双曲线的导体附近的静电场.如果用虚部表示电位函数,在 x = 0 或 y = 0 处,电位为零,可以表示接地的直角导体拐 角附近的静电场. 4-20 分析复变函数 w = arccos z 能够表示哪些情形的静电场.62《电磁场与电磁波》——习题详解解: z = x + j y = cos(u + j v) = cos u ch v j sin u sh vx = cos u ch v , y = sin u sh vx2 y2 x2 y2 + 2 = 1, 2 =1 ch 2 v sh v cos 2 u sin u可见,虚部的等值线是一簇椭圆,实部的等值线是一簇双曲线.当用虚部表示 电位时,能够表示两个共焦点的椭圆柱体之间的场;当用实部表示电位时,能够表 示两个共焦点的双曲线柱体之间的场. 4-21 用有限差分法求图 4-12 所示区域中各个节点的电位. 解:1 4 1 2 = (1 + 4 + 100) 4 1 3 = (1 + 4 ) 4 1 4 = ( 2 + 3 ) 41 = ( 2 + 3 + 100)解这一方程组,得到1 = 2 = 37.5 V , 3 = 4 = 12.5 V100V 1 0V 3 4 2 0V0V 图 4-1263。
电磁场与电磁波课后习题及答案--第四章习题解答
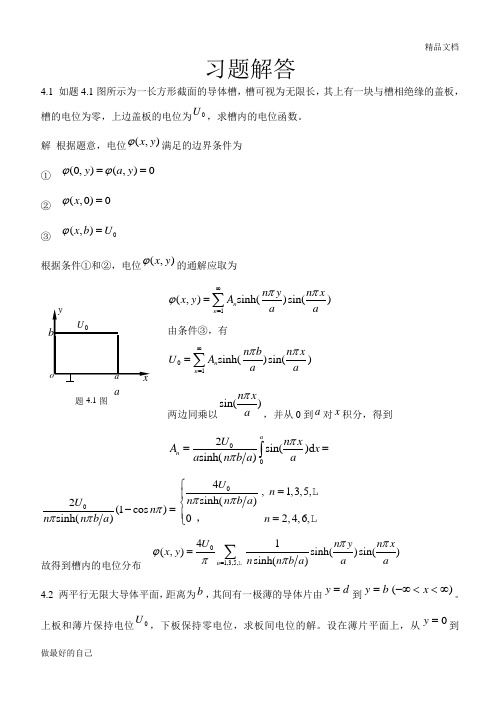
习题解答4.1 如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ=③0(,)x b U ϕ=根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑由条件③,有01sinh()sin()n n n b n x U A a a ππ∞==∑两边同乘以sin()n x a π,并从0到a 对x 积分,得到002sin()d sinh()an U n xA x a n b a a ππ==⎰02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩,故得到槽内的电位分布1,3,5,41(,)s i n h ()s i n ()s i n h ()n U n yn xx y n n b a aa ππϕππ==∑4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到a题4.1图d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为: ①22(,0)(,)0x x b ϕϕ==②2(,)0()x y x ϕ=→∞③002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b d b ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②,可设2(,)x y ϕ的通解为 21(,)sin()en x bn n n y x y A b ππϕ∞-==∑由条件③有00100(0)sin()()n n U U y y d n y b A U U b y yd y b d b π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n yb π,并从0到b 对y 积分,得到0002211(1)sin()d ()sin()d dbn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b b ππππ∞-=+∑4.3 求在上题的解中,除开0U y b 一项外,其他所有项对电场总储能的贡献。
大学电磁场课后答案

(
)
2-9 已知在半径为 a 的球体区域内外,电场强度矢量表达式为 ⎧ Ar r2 (1 − 2 )e r r < a ⎪ ⎪ 3ε a E =⎨ 2 Ba ⎪ r>a e 2 r ⎪ ⎩ε 0r
其中 A, B 均为常数。求此区域的电荷分布。 答案
ρ = A(1 −
5r 2 ), r < a , 3a 2
但可把半径为a的小圆柱面内看作同时具有体密度分别为的两种电荷分布这样在半径为b的整个圆柱体内具有体密度的均匀电荷分布而在半径为a的整个圆柱体内则具有体密度的均匀电荷分布如例36图b所示
习题二 2-3 已知真空中静电场的电位 ϕ ( x) = 解:
U x V,求电场强度的分布及电荷体密度 ρ 。 ε0 d ∂ϕ 2x U E = −∇ϕ = − e x = −( + )e x V/m ∂x ε0 d ∂E 2 ρ = ∇ ⋅ D = −ε 0 ∇ ⋅ E = −ε 0 x = −ε 0 ( ) = −2 C/m2 ε0 ∂x + x2
∫
∫
得到
(b 2 + ab − 2a 2 ) a(b − a) 6a 故两导体球壳间的电位分布为 b b σ a2 ρ a3 σ a 2 (b − r ) ρ 0 b 2 − r 2 a 3 (b − r ) ϕ (r ) = E (r ) d r = [ 2 + 0 (r − 2 )] d r = + − ] [ r r ε r 3ε 0 ε 0br br 3ε 0 2 r 0 说明 此题的要点在于导体的表面上有未知的感应电荷分布,用高斯定律求电场时,必须注意考虑 感应电荷产生的电场。 −
ρl =
∂E (a) 1 ln(b a) − 1 =− 2 =0 ∂a a ln 2 (b a)
电磁场与电磁波课后习题答案第四章

4.3若半径为a 、电流为I 的无线长圆柱导体置于空气中,已知导体的磁导率为0μ,求导体内、外的磁场强度H 和磁通密度B 。
解:(1)导体内:0≤ρ<a由安培环路定理,⎰•ll d H='I'I =22.I a πρπ=22I a ρ 所以,21.22I H a ρπρ=,122I H a ρπ=,122I H e a ϕρπ→→=,011022I B H e a ϕμρμπ→→→==(2)导体外:a ≤ρ<+∞⎰•l l d H =I, 所以2.2H I πρ=,22I H e ϕπρ→→=,022I B e ϕμπρ→→=4.5 在下面的矢量中,哪些可能是磁通密度B ?如果是,与它相应的电流密度J 为多少? (1)F a ρρ→→=解:1..()F F ρρρρ→∂∇=∂=1.2ρρ=2≠0所以F →不是磁通密度 (2)F →=-x a →y+y a →x 解:∇.F →=y x ∂-∂+xy ∂∂=0 所以F 是磁通密度 B →∇⨯=0μJ →=|x y ze e e x y zy x 0→→→∂∂∂∂∂∂-=2z e → 所以 J →=02μz e →(3)F →=x a →x —y a →y∇.F →=0F →是磁通密度B →∇⨯=0μJ →=|x y ze e e x y zx y→→→∂∂∂∂∂∂-=0所以J →=0 (4)F →=a ϕ→-r∇.F →=0所以F →是磁通密度B →∇⨯=r 2a a a r sin r sin rr 20r sin 0ϕθθθθϕθ→→→∂∂∂∂∂∂-=r a →-θcot +2a θ→=0μJ →所以J →=0cot θμ-r a →+02μa θ→ 4.6已知某电流在空间产生的磁矢位是A →=x a →2x y+y a →x 2y +z a →(2y —2z ) 求磁感应强度B →解:B →=A →∇⨯=|x y z2e e e x y z222x y xy y z →→→∂∂∂∂∂∂-=2y x e →+z e →(2y —2z )4.13已知钢在某种磁饱和情况下的磁导率为1μ=20000μ,当钢中的磁通密度为B 1=0.5×102T ,1θ= 75°时,试求此时的磁力线由钢进入自由空间一侧后,磁通密度2B 的大小与2B 与法线的夹角2θ。
电磁场与电磁波(第四版)课后答案_电科习题

3)
v C
evx
3y2 - 2x
+ evy x2 + evz 2z
问:1.哪些矢量可以由一个标量函数的梯度表示?哪些
矢量可以由一个矢量函数的旋度表示?
2.求出这些矢量的源分布。
1.28利用直角坐标,证明
v fA
vv f A Af
1.29: 矢量
在Av由 evρ=52, evzz验2=z0证和散z=度4围定成理的。圆柱形区域,
分量,根据边界条件可知,两种介质的
2
磁感应强度
uv B1
rr
uv B2
r B
er B
但磁场
强度 H1 H2
3.23一电荷量为 q 质量为 m 的小带电体,放置在无限长导体
平面下方,与平面距离h 。求 q 的值以使带电体上受到的
静电力恰好与重力相平衡(设 m 2103 kg, h 0.02m)。
对
第二章
2.1已知半径为a的导体球面上分布着电荷密度为 s s0 cos 的电荷,式中的 s0
为常数。试计算球面上的总电荷量。
2.6 一个平行板真空二极管内的电荷 体位密于度x=为0,阳 极94 板0U0位(d 于43 )xx23=,d,式极中间阴电极压板 为U0。如果U0 =40V,d=lcm,横截 面积s =10cm2。 求:
验
A
证散度定理
1.21 求矢量
v A
erx
x
ery
x2
erz
y
2
z
沿xy平面上的一个边长为2的正
形再回求路 的Av线对积此分回,路此所正包方围形的的表两面个积边分分,别验与证x斯轴托和克y轴斯相定重理合
大物电磁学课后答案4

a
|2
a
2
0I arctg a a 2x
y
a/2
dB x
Bx 0
B
B
2 x
B
2 y
By
0I arctg a
a
2x
当a 时, B 0I arctg 0I 0 j .
a
a 2 2
补充4.4 边长为a的正方形载流回路,电流为I, (1)求这回路轴
2
2
0I 2 2 R
d
0I 2R
dI
x
dB
柱面横截面图
(沿x正向)
4-15 载流长直导线弯成图中三种形状,求O点的磁感应强度B。
解:(a)分成4段
B1 B3 0
B2
0Idl 4R12
0
0I 4R12
R1d
0I 4R1
同理
B4
0I 4R 2
解: (1) eE evB v E/B 3.75103 (米/秒)
(2)E,V,B 两两垂直
4-10 已知一电量为q的粒子垂直入射到磁感应强度为B的均匀磁
场以前,经过电压为V的电场加速,粒子的初速度可以忽略不计
,进入磁场后经过半圆到达照像底片上的P点,已知粒子入口至
P点的距离为x,求该粒子质量。
解:由于BC和AD中I2方向相反,在I1的磁场中受
力,大小相等方向相反,合力为零。
I1
AB受力为
FAB
I 2lB1
I
2l
0I1 2a
(方向如图)
ab
B
C
I2 l
电磁场课后答案4

kr =
衰减常数:
ωμσ
2
案
为 300 米。 试求电场强度的振幅为 1 微伏/米时离海面的距离, 并写出这个位置上的E, H之表示式。
=
ki =
复数波阻抗为:
网
平面电磁波在海平面处的场强表示式为: E = x 0 1000 e
2π × 10 6 × 4π × 10 −7 × 1 = 2 (弧度/米) 2
4.1 写出ω,k,f,T,λ单位。 答:ω (rad/s), k (rad/m) ,f (Hz) , T (s), λ (m) 4.2 激光器输出波长为 6.328 × 10-7m,计算它的f,T,k。 答: f =
c
λ
=
3 × 10 8 1 = 4.741 × 1014 Hz , T = = 2.11 × 10 −15 s , −7 f 6.328 × 10
ωt + 30 o = 180 o 或 ωt +
π
co
)
μ0 ,
m
解: k = ω
ε r ε 0 μ 0 = 2ω μ 0 ε 0 =
2 × 2π × 150 × 10 6 = 2π 3 × 10 8
(m )
−1
答: f = f 0 , λ = 0.5λ0 , k = 2k 0 , v = 0.5v0 。
解之得:z = 10.35(米) 距海水 10.35 米处 E、H 之表示式为:
2 z = 9 × ln 10
E = x 0 1000e −2 z e j (ωt −2 z )
= x 0 1000e − 20.7 e j (ωt −1180 )
o
= x 0 10 3 e − 20.7 e j (ωt −100 )
工程电磁场 (杨宪章 邹玲 樊亚东 著) 中国电力出版社 课后答案 题ch4

习题4-16解:B 只有x 分量,从平面图可见x =0时l Id v 与r r 垂直,x ≠0时l Id v 与r r垂直 απμπμRd dl R IRdlR R R Idl dB x ===∴,443'0'2'0()()3222032220203'202424X RIR X R IR d R IR B +=+==∴∫μππμαπμπ习题4-18解:dbd Ia dr r I S d r I S d B b d d S S +==⋅=⋅=Φ∫∫∫+ln2220000πμπμαπμv v v v习题4-19解:αcos 22221ab b =a R −+ααπcos 2)cos(2222222ab b a ab b =a R ++=−−+任一点xIB πμ20=1200ln 222221R Ra I adx r I R R AB πμπμ=⋅=Φ∴∫习题4-20解:由安培环路定律10R r <<时,取单位长,22102r R I r B ππμπ=⋅,r R IB 2102πμ=21R r R <<时,I r B 02μπ=⋅,rIB πμ20=32R r R <<时,)()([])()([22223222022232220R R R r I I R R R r I I r B −−−=−−−=⋅μππμπ课后答案网ww w.kh da w .c om)()(222232230R R r R r I B −−=πμ 3R r >时,02=⋅r B π,0=B习题4-21解:任意点:j x D Ix I B v v ))(22(00−+=πμπμ习题4-22解:电流反向,则磁力线反向j x D I x I B v v )(22(00−−=πμπμ习题4-23解:I r B μωπ=⋅2,rIB πμω2=wb R R Ib dr r Ib R R 31210973.0ln 2221−×==⋅=Φ∴∫πμωπμω习题4-24解:P176例中,)(220a d d I −−=Φμ本题,wb a d d I 322109696.0))((−×=−−=Φωμ习题4-25解:B 1、B 2只有t 分量,由边界条件H 1t =H 2tT H B t 2.10024.050000111===μμμ习题4-26解:...1)2(0201122232232223223=−−∂∂=−−∂∂∂∂∂∂=×∇z z r e r R R r R r I r R R r R r I z re r e e r H v v v v v ππαα课后答案网ww w.kh da w .c om习题4-27解:0点上下的m ϕ,0=∞m ϕ 带I 圆导线线圈在轴线上产生的2/32)(2x R IR BH +==μ I l d H BAB A =⋅=−∫vv ϕϕ习题4-28解:忽略边缘效应,H 是圆线m ϕ仅与α有关,D C m +=αϕ令0=α是障碍面,且0|0==αϕm 所以0=D 由安培定律∫∫∫+==πθθπω2020Hdl Hdl I Hdl在(0,2π)中,μ->∞,H 只有法线分量,B 1n =B 2n ,知00==μμHH t 所以02=∫πθdl H t所以00||==−==∫αθαθϕϕωm m Hdl ICQ I =ω,QIC ω=αωϕQIm =0000001αωμααϕμϕμμvv v v Qr I r H B m m −=∂∂−=∇−==习题4-29解:x e z y x F v v 1222)(−++= k z y x yj z y x z z y x z y xkj iF v v v v vv 222222221222)(2)(20)(++−++=++∂∂∂∂∂∂=×∇− 课后答案网ww w.kh da w .c om习题4-30解:∫⋅=Φ∴SS d B vvr<a ,22a rIB πμ=r>a ,rIB πμ2=]2ln 21[2ln 222222202+=+=+=⋅=Φ∴∫∫∫πμπμπμπμπμr Iaa a aI a a I adr r I adr a rI S d B a a a S v v习题4-32解:H R d l L 30010*119.2ln −==πμ习题4-34解:铜:0μμ=,钢:0200μμ=(1)算每公里长自感铜e i L L L +=其中km H L i /10100010008270−×=××=πμ km H l R DL e /1027631ln 700−×=⋅=πμ km mH L L L e i /863.2=+=钢:km H L i /102000010008270−×=××=πμ km H L e /10228157−×=km mH L L L e i /286.22=+=(2)互感:根据方向判断'11Φ+Φ=Φ∴km mH l M /036.02'1'12'2'112ln 20=⋅⋅⋅=πμ习题4-35 解:r I B πμω21=,21102−×=Φdr rId πμω 2122102−×=Φ=Ψdr rId d πωμωω课后答案网ww w.kh da w .c om67ln 10210221276212−−×=×=Ψ∫πωμωπωμωI dr r IH I M 0148.067ln 102212=×=−πωμω习题4-36 解:由题意得...2)(212)2(212)2(212121322112223223020021022=−−++===∫∫∫∫∫∫R R R R R v rdr I R R r R rdr r I rdr R Ir dVH LI W πμππμππμμ...22==I WL习题4-37解:C I mW M =∂∂=|αααcos 21max 21I I M I MI W m ==ααsin 21max I I M M −=∴o 45=α,m N M ⋅×−=∴−310035.0α习题4-38解:1220022102ln 21212)2(21211R R I rdr R Ir dV H W R v πμππμμ===∫∫∫∫ l r V 2π=,l R dR dV112π= 212201212212084|R I dV dR R R R R I V W f C I mg πμπμ−=−=∂∂==测验题4-39解:将其分段考虑,与0点在一条线上的两直线段上的电流不在0点产生磁场,仅两段圆弧上的电流在0点产生磁场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
顺着 x 方向看,右旋 顺 y 方向看,椭圆极化
a ≠ b ,ϕ = π / 4
.k hd
−6
答:最小功率密度为 < S > min =
1 ε0 2 E = 8.293 × 10-7W/m3 2 μ0
aw .
4.6 商用调幅广播电台覆盖地域最低信号场强为 25mV/m。与之相联系的最小功率密度是多 少?最小磁场是多大?
ωt + 30 o = 180 o 或 ωt +
π
co
)
μ0 ,
m
解: k = ω
ε r ε 0 μ 0 = 2ω μ 0 ε 0 =
2 × 2π × 150 × 10 6 = 2π 3 × 10 8
(m )
−1
答: f = f 0 , λ = 0.5λ0 , k = 2k 0 , v = 0.5v0 + E ym +
ˆ 0 cos(ωt − kz ) + y ˆ 0 cos(ωt − kz + π / 2)] [x ˆ 0 cos(ωt − kz ) + y ˆ 0 cos(ωt − kz − π / 2)] [x
E xm − E ym 2
ˆ 0 sin φ cos(ωt − kz − 30 o ) + y ˆ 0 cos φ cos(ωt − kz − 30 o )] = 10[ x
分解为旋向相反、振幅不等的两个圆极化波。
ˆ0 E = [x
E xm + E ym 2 2 2
ˆ0 cos(ωt − kz ) + y
E xm + E ym 2 2
cos(ωt − kz + π / 2)] cos(ωt − kz + π / 2)]
ˆ0 + [x
答:
E xm − E ym
ˆ0 cos(ωt − kz ) − y
b b ˆ 0 + j sin 60 o y ˆ 0 ]e − jkz cos 60 o ) x 2 2
π
.k hd
ˆ 0 6 cos(ωt − kz − 30 o ) + y ˆ 0 8 cos(ωt − kz − 30 o ) E=x
− jkz + j 17 3 2 ˆ 0 e − jkz + jφ − ˆ0 e H= [ ∇×E = y x ] ωμ 0 4 − jωμ 0 4
1
kb
E (t ) =
17b 3b π ˆ 0 cos(ωt − kz + φ ) + ˆ 0 cos(ωt − kz + ) x y 4 2 4
aw .
π
E y = 8 cos(ωt − kz − 30 o ) ,试将它分解成振幅相等,旋向相反的两个圆极化波。
co
4.10
一 线 极 化 波 电 场 的 两 个 分 量 为 E x = 6 cos(ωt − kz − 30 o ) ,
ω = 2πf = 3π × 10 8 rad / s , k = ω μ 0 ε 0 = π ,在 z = 10 米处,t = 0.1 微秒时
H = E / η 0 = 1.86 × 10 −5 A / m ,S=0.13 微瓦/米2.
4.8 求下列场的极化性质。 (a) E=(jx0+y0)e–jkz (c) E=[(2+j)x0+(3–j)z0]e–jky 解: (a) a = b = 1, ϕ = − (b) a = b = (c) (b) E=[(1+j)y0+(1–j)z0]e–jkx (d) E=(jx0+j2y0)ejkz 顺着 z 方向看,右旋
后 答
4.11 自由空间沿z方向传播的均匀平面波E=E0e-jkz ,式中E0=Er+jEi ,且Er=2Ei=b,b为实常 数,Er在x方向,Ei与x轴夹角为 60°,试求电场强度和磁场强度瞬时值,并说明波的极化。
案
网
j j 3 ˆ0 + ˆ 0 ]e − jkz = b[(1 + ) x y 4 4 = b[
m
H (t ) =
kb
ωμ 0
[
17 3 π ˆ 0 cos(ωt − kz + φ ) − ˆ 0 cos(ωt − kz + )] y x 4 4 2
因为 φ b − φ a =
π
2
− a tan 0.25 ,所以,是椭圆极化波,且为左旋极化。
4.12 均匀平面波的频率为 10MHz。设地球的 μ = 减常数与趋肤深度。 答:
− π × 10 + 60 o ) = 0.007V / m
co
m
< S >=
1 1 1 * − jkz ˆ0 × y ˆ 0 ) = E0 H 0 z ˆ0 Re{E × H * } = E 0 e jkz H 0 e (x 2 2 2
(d)
a ≠ b ,ϕ = 0
线极化
ˆ 0 E xm cos(ωt − kz ) + y ˆ 0 E ym cos(ωt − kz + π / 2) ,试将其 4.9 设有一椭圆极化波为: E = x
kr =
衰减常数:
ωμσ
2
案
为 300 米。 试求电场强度的振幅为 1 微伏/米时离海面的距离, 并写出这个位置上的E, H之表示式。
=
ki =
复数波阻抗为:
网
平面电磁波在海平面处的场强表示式为: E = x 0 1000 e
2π × 10 6 × 4π × 10 −7 × 1 = 2 (弧度/米) 2
10 2
η
cos 2 ωt − kz + 30 o = z 0 0.398 μw/m 2
(
)
10 2 100 = = z 0 0.265 μw/m 2 2η 2 × 188.5
=π 6 5π / 6 E 达到最大, t = = 2.78 × 10 −9 s 6 2π × 150 × 10
4.4 自由空间电磁波有 f 0 、 λ 0 、 k 0 、 v0 。当它进入介质,其介电常数为 4ε 0 , μ = 求介质中电磁波的 f 、 λ 、 k 及 v 。
ww w
.k hd
}≈
π
1 ε 2 1 E 0 } = Re{ 2 μ 2
4ε 0 (1 − j
σ ) 4ωε 0
解:工作频率为 f =
由此可知,海水对该频率具有良导体性质。 相移常数为:
课
后 答
3 × 10 8 = 10 6 (赫兹) 300
σ 1 = 18 × 10 3 >> 100 = 6 −12 ωε 2π × 10 × 8.85 × 10
4.1 写出ω,k,f,T,λ单位。 答:ω (rad/s), k (rad/m) ,f (Hz) , T (s), λ (m) 4.2 激光器输出波长为 6.328 × 10-7m,计算它的f,T,k。 答: f =
c
λ
=
3 × 10 8 1 = 4.741 × 1014 Hz , T = = 2.11 × 10 −15 s , −7 f 6.328 × 10
ωμσ
2
= k r = 2 (奈贝/米)
η=
j 2π × 10 6 × 4π × 10 −7 j 4 ωμ j 4 e = e = 2.82e 4 欧 1 σ
π
aw .
− ki z
4.13 用上例数据,设地球表面电场强度为 1V/m,求地球表面功率密度。
1 w/m2 377
co
e j (ωt − k r z ) (伏/米)工作波长
− jkz + j 17 3 2 ˆ 0 e − jkz + jφ + ˆ0e x y ] , 其中 tan φ = 0.25 4 4
课
解: E = E 0 e − jkz = ( E r + jE i )e − jkz = [(b + j
ww w
ˆ 0 [sin(φ + ωt − kz − 30 o ) + sin(φ − ωt + kz + 30 o )] = 5x
π
m
趋肤深度: d p =
1 = 106.1008 m ki
在海水中传播的 E 的表示式为:
E = x01000e − k i z e j (ωt − k r z )
= x01000e − 2 z e j (ωt − 2 z )
由该表示式可求得场强振幅为 1 微伏/米时的距离,
10 −6 = 1000e − ki z = 1000e −2 z , e −2 z = 10 −9 ln e − 2 z = ln 10 −9 ,
aw .
mV/m
λ=
2π = 1m k
后 答
H (t ) = − x 0
10
η
cos ωt − kz + 30 o = − x 0
(
案
)
10 cos − 540 o + 30 o = x 0 0.046 mA/m 188.5
(
课
S(t ) = E(t ) × H(t ) = z 0 S(t ) = z 0
o
η
ˆE 0 sin kz , H = y ˆj E=x
ˆ 答: E (t ) = x ˆ H (t ) = y
1 E 0 [sin( kz + ωt ) − sin(ωt − kz )] 2
ˆ S (t ) = E (t ) × H (t ) = z
ˆ S + (t ) = z
z 2k 1 ε 2 = E 0 cos 2(ωt − kz ) ,可以得出能速为: ve = = t 2ω 8 μ
