金属薄板带应变硬化指数和厚向异性指数测定方法
金属表面硬化层的测试

显微硬度计测量金属表面镀层覆层的硬度测试方法显微硬度计测量金属表面镀层覆层的硬度测试方法金属电镀层和覆盖层:电沉积层、自催化镀层、喷涂层以及氧化复膜等。
一般覆盖层厚度比较薄,对覆盖层的硬度要求又大多比较严格,因此覆盖层硬度检测显得十分重要。
检测的几个注意事项:1、试验力的选择:对于覆盖层的硬度检测,一般选用显微硬度试验法或者努氏硬度试验法,不管采用那种试验法,对于试验力的选择尤为关键,如果试验力过大,容易造成压头击穿覆盖层,所得硬度值受基体影响较大;如试验力过小,又容易引入较大误差。
2、试验力的保持时间;通常检测试验控制在10-15s左右,但对于相对较软的覆盖层,可适当延长试验力加载时间。
3、样件的装夹:对于较小工件或者不规则工件,应当采用夹具固定或进行镶嵌制样后进行测试,尽量避免因振动、支撑力不足、表面倾斜等外在因素影响测量数据。
对于需制样的工件,切勿因制样影响覆盖层组织变化,详细请参考金相试样制备,这里不在过多阐述。
4、压痕的打压位置:a、覆盖层切面检测:压痕的角端距离覆盖层的边缘至少为压痕对角线长度的一半。
采用努氏压头时,压痕的长对角线L应当与覆盖层边缘平行。
且软金属覆盖层(金、银、铜等)的厚度不得低于400um,硬覆盖层(硬质合金等)不得低于25um。
采用维氏压头时,两个压头的距离至少为压痕长度的2.5倍以上。
b、覆盖层表面检测:维氏硬度法氏,覆盖层的厚度至少为压痕对角线长度的1.43倍,努氏硬度法时,覆盖层厚度至少为压痕长对角线L的0.33倍。
5、结果的计算:每一试样最少区5点进行测试,取平均值,结果大于100时,取整数。
结果小于100时,保留1位小数,结果小于10时,保留两位小数。
渗氮层、淬硬层、有效硬化层的硬度和厚度测试渗氮层、淬硬层、有效硬化层的硬度和厚度测试一、钢铁零件渗氮(氮化)后的硬度及厚度检测方法:随着工业的发展,渗氮处理被更多的应用到各行各业,对渗氮处理的检测要求也日益提高。
金属板材n值r值解析

金属板材的n值和r值解析在冲压领域,我们需要关注金属板材的抗拉强度、屈服强度、延伸率、加工硬化指数、各向异性指数。
本文将详细解析加工硬化指数n和各项异性指数r。
一、加工硬化指数n加工硬化指数英文为hardening index,常用字母n指代。
该指数由真实应力和真实应变定义。
计算n值的方法常用两点法,即利用拉伸试验所得的拉伸曲线,将拉伸力和伸长位移换算成真实应力和真实应变,得到真实σ-ε曲线(如下图),假设该曲线符合指数规律,即:σ = Kε^n(σ—真实应力,ε—真实应变,n —硬化指数,K —强度系数),公式两边取对数得:lnσ=lnK+nlnε,通过两点法可求出K值和n值。
硬化指数n值代表钢板在塑性变形中的硬化能力, 反映了变形均匀度、成形极限和裂纹是否产生等。
n值越大,整个成形过程中的变形越均匀。
对板材成形极限曲线具有明显的影响,n值大材料的成形极限曲线高,n值小材料的成形极限曲线低。
板材的拉胀性能在很大程度上取决于材料的n值,n值高时,拉胀性能也好。
因此,硬化指数n值是评价板材成形性能的重要指标之一。
二、塑性应变比r塑性应变比英文为plastic strain ratio,常用字母r指代,又称各项异性指数。
该指数是板材拉伸试样在试验中宽度方向应变εb和厚度方向应变εt之比。
即:b0和t0分别是试样原始宽度和厚度,b和t分别是试样在某一变形时的宽度和厚度。
板材的力学性能在轧制方向和其他方向有较大差别,故一般取为3个方位试件试验数据的平均值,用r表示:r=(r0 +2r45+r90)/4。
r0、r45、r90分别为沿板材轧制方向、与轧制方向成45°和垂直于轧制方向试件的厚向异性系数。
r值愈大,板材抵抗失稳变薄的能力愈大,愈不容易发展厚向变形;r值愈小,板材抵抗失稳变薄的能力愈弱,厚向变形愈容易。
r=1表示板材不存在厚向异性。
通俗来讲r值高,变形过程中金属在长宽上的流动优先于厚度上的流动。
金属材料 薄板和薄带 拉伸应变硬化指数(n 值)的测定-最新国标

金属材料薄板和薄带拉伸应变硬化指数(n值)的测定1范围本文件规定了金属薄板和薄带拉伸应变硬化指数(n值)的测定方法。
本方法仅适用于塑性变形范围内应力-应变曲线呈单调连续上升的部分(见8.4)。
如果材料在加工硬化阶段的应力-应变曲线呈锯齿状(如某些AlMg合金呈现出的Portevin-Le Chatelier锯齿屈服效应),为使所给出的结果具有一定的重复性,应采用自动测量方法(对真实应力-真实塑性应变的对数进行线性回归,见8.7)。
2规范性引用文件下列文件中的内容通过文中的规范性引用而构成本文件必不可少的条款。
其中,注日期的引用文件,仅该日期对应的版本适用于本文件;不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件。
GB/T228.1金属材料室温拉伸试验方法(GB/T228.1—2021,ISO6892-1:2019,MOD)GB/T16825.1静力单轴试验机的检验第一部分:拉力和(或)压力试验机测力系统的检验与校准(GB/T16825.1—2022,ISO7500-1:2018,IDT)GB/T12160 GB/T5027GB/T8170单轴试验用引伸计的标定(GB/T12160—2019,ISO9513:2012,IDT)金属材料薄板和薄带塑性应变比(r值)的测定(GB/T5027—2024,ISO10113:2020,MOD)数值修约规则与极限数值的表示和判定3术语和定义本文件未列出术语和定义。
4符号和说明4.1本文件使用的符号及说明见表1。
1表1符号和说明符号说明单位L e引伸计标距mm ΔL引伸计标距部分的瞬时延伸mm L引伸计标距部分的瞬时长度L=L e+ΔL mme p测定拉伸应变硬化指数的约定(工程)塑性应变水平(用于单应变量测算方法)%e pα-e pβ测定拉伸应变硬化指数的约定(工程)塑性应变范围(线性回归方式,e pα:塑性应变下%限,e pβ:塑性应变上限)S o试样平行长度部分的原始横截面积mm2 S真实横截面积mm2 F施加于试样上的瞬时力N R应力MPa σ真实应力MPa εp真实塑性应变-m E应力-应变曲线弹性部分的斜率MPa n拉伸应变硬化指数-C强度系数MPa N测定拉伸应变硬化指数时的测量点数目-r塑性应变比-R m抗拉强度MPaA e屈服点延伸率%A g最大力塑性延伸率% A,B,x,y采用人工方式测定n值的几个变量注:1MPa=1N/mm2。
金属材料形变硬化指数的测定
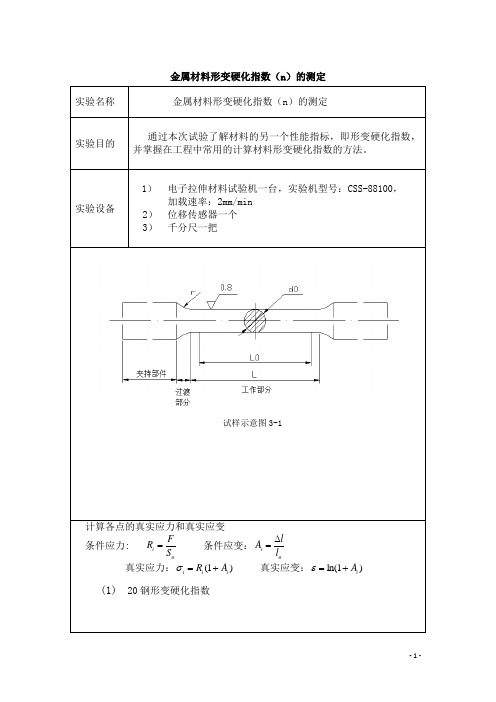
取点编号
条件应力 (MPa)
条件应变 (%)
真实应力 (MPa)
真实应变 (%)
Xi
lg
Yi
lg
1
371.71
0.0736
399.07
0.0710
-1.149
2.601
2
425.61
0.1036
469.70
0.0986
-1.006
2.672
3
466.88
0.1361
530.42
0.1276
-0.894
2)、计算直线斜率n的离散程度
标准偏差 =0.0967
3)、计算n值的变异系数V(n)
=0.220
4)、计算各测量值之间的线性相关程度Q
5)、给出n值计算结果及相关可靠度参量系列表
由 得lgσ=lgκ+nlgε
硬化指数(n)为该线性方程的斜率,拟合所得直线如下图3-3所示:
图3-3
计算结果
N
K(MPa)
0.2898
594.55
0.2545
-0.594
2.774
1)、用线性回归方法计算斜率(n)及标准偏差等参量
= 0.436
= 3.042 K=exp(b)= 20.95
2)、计算直线斜率n的离散程度
标准偏差 =0.0955
3)、计算n值的变异系数V(n)
=0.2191
4)、计算各测量值之间的线性相关程度Q
计算各点的真实应力和真实应变
条件应力: 条件应变:
真实应力: 真实应变:
(1)20钢形变硬化指数
d=9.60 72.29
代入数据可得
表3-1
取点编号
一种测量金属薄板拉伸应变硬化指数的方法

Ab s t r a c t :I n o r d e r t o r e a l i z e a p p l i c a t i o n o f t h e v i d e o e x t e n s o me t e r i n t h e s t r a i n h a r d e n i n g e x p o n e n t n v a l u e t e s t i n g p r o c e s s , t ( J ma k e u p h > r t h e me a s u r e me n t r a n g e s h o ta r g e o f t h e s h o r t s t r o k e c o n t a c t e x t e n s o me t e r . Ba s e d o n t h e r e l a t e d t e s t me t h o d o f ‘ me t a l s h e e t t e n s i l e s t r a i n h a r d e n i n g e x p o n e n t i n G B / T 5 0 2 8 -2 0 0 8 , u s i n g I NS T RON 5 9 8 5 v i d e o e x t e n s o me t e r t o me a s u r e, b ~ l 5 v a l u e ,b y me a n s o f t h e s o f t wa r e B l u e h i l l 3 a u t o ma t i c ,me a s u r e me n t a n t i ma n u a l me a s u r e n l e n t me t h o d s i n t h e s p e c i f i e d r e g r e s s i o n i n t e r v a l , a n d t h e s i mp l i i f e d f o r mu l a w a s u s e d t o v e r i f y t h e me t h o d s . T h e r e s u l t s s h o w e d t h a t t h e/ 2 5 ~ I 5 v a l u e i s 0. 1 8 , w h i c h me e t s t h e r e q u i r e me n t s o f t h e a b i l i t y c o mp a r i s o n t e s t r e s u l t s .
金属薄板成形性能试验

金属薄板成形性能试验1. 简介成形性能是指薄板对各种冲压成形的适应能力,即薄板在指定加工过程中产生塑性变形而不失效的能力。
成形性能研究的重点是成形极限的大小,也就是薄板发生破裂前能够获得的最大变形程度。
1.1 模拟成形性能指标选择或评定金属薄板冲压成形品级时,可对模拟成形性能指标提出要求。
设计或分析冲压成形工艺过程,以及设计冲压成形模具时,经常需要参考模拟成形性能指标的数据。
薄板常用模拟成形性能指标有:1、胀形性能指标:杯突值IE;2、拉深性能指标:极限拉深比LDR或载荷极限拉深比LDR(T);3、扩孔(内孔外翻)性能指标:极限扩孔率(平均极限扩孔率)λ(λ);4、弯曲性能指标:最小相对弯曲半径R min/t;5、“拉深+胀形”复合成形性能指标:锥杯值CCV;6、面内变形均匀性指标:凸耳率Z e;7、贴模(抗皱)性指标:方板对角拉伸试验皱高;8、定形性指标:张拉弯曲回弹值。
1.2 特定成形性能指标选择或评定金属薄板冲压成形品级、协议金属薄板的订货供货、设计或分析冲压成形工艺过程时,可对金属薄板的材料特性指标或工艺性能指标提出要求,或参考它们的数据,它们统称为特定成形性能指标:1、塑性应变比(r值)或平均塑性应变比(r);2、应变硬化指数(n值);3、塑性应变比平面各向异性度(r∆)。
1.3 局部成形极限评定、估测金属薄板的局部成形性能,或分析解决冲压成形破裂问题时,可使用金属薄板的成形极限图或成形极限曲线。
1.4 其他以上所列举的各种成型性能试验方法均为我国冲压生产和冶金制造行业已经使用或比较熟悉的模拟成型性能试验方法,而且也属于国际上的主流成形性能试验范畴。
除这些方法外,国际上还流行其他一些模拟成形性能试验,见图1。
图1 模拟成形性能试验方法注:整体成形极限指金属薄板在冲压过程中发生颈缩、破裂、皱曲等成形缺陷之前,某种特定的整体几何尺寸或某种几何特征的整体尺寸可以达到的极限变形程度。
局部成形极限指金属薄板在冲压过程中发生颈缩、破裂、皱曲等成形缺陷之前,局部点位或局部变形区域可以达到的极限变形程度。
金属板材n值r值解析

金属板材的n值和r值解析在冲压领域,我们需要关注金属板材的抗拉强度、屈服强度、延伸率、加工硬化指数、各向异性指数。
本文将详细解析加工硬化指数n和各项异性指数r。
一、加工硬化指数n加工硬化指数英文为hardening index,常用字母n指代。
该指数由真实应力和真实应变定义。
计算n值的方法常用两点法,即利用拉伸试验所得的拉伸曲线,将拉伸力和伸长位移换算成真实应力和真实应变,得到真实σ-ε曲线(如下图),假设该曲线符合指数规律,即:σ = Kε^n(σ—真实应力,ε—真实应变,n —硬化指数,K —强度系数),公式两边取对数得:lnσ=lnK+nlnε,通过两点法可求出K值和n值。
硬化指数n值代表钢板在塑性变形中的硬化能力, 反映了变形均匀度、成形极限和裂纹是否产生等。
n值越大,整个成形过程中的变形越均匀。
对板材成形极限曲线具有明显的影响,n值大材料的成形极限曲线高,n值小材料的成形极限曲线低。
板材的拉胀性能在很大程度上取决于材料的n值,n值高时,拉胀性能也好。
因此,硬化指数n值是评价板材成形性能的重要指标之一。
二、塑性应变比r塑性应变比英文为plastic strain ratio,常用字母r指代,又称各项异性指数。
该指数是板材拉伸试样在试验中宽度方向应变εb和厚度方向应变εt之比。
即:b0和t0分别是试样原始宽度和厚度,b和t分别是试样在某一变形时的宽度和厚度。
板材的力学性能在轧制方向和其他方向有较大差别,故一般取为3个方位试件试验数据的平均值,用r表示:r=(r0 +2r45+r90)/4。
r0、r45、r90分别为沿板材轧制方向、与轧制方向成45°和垂直于轧制方向试件的厚向异性系数。
r值愈大,板材抵抗失稳变薄的能力愈大,愈不容易发展厚向变形;r值愈小,板材抵抗失稳变薄的能力愈弱,厚向变形愈容易。
r=1表示板材不存在厚向异性。
通俗来讲r值高,变形过程中金属在长宽上的流动优先于厚度上的流动。
实验六 金属薄板拉伸试验
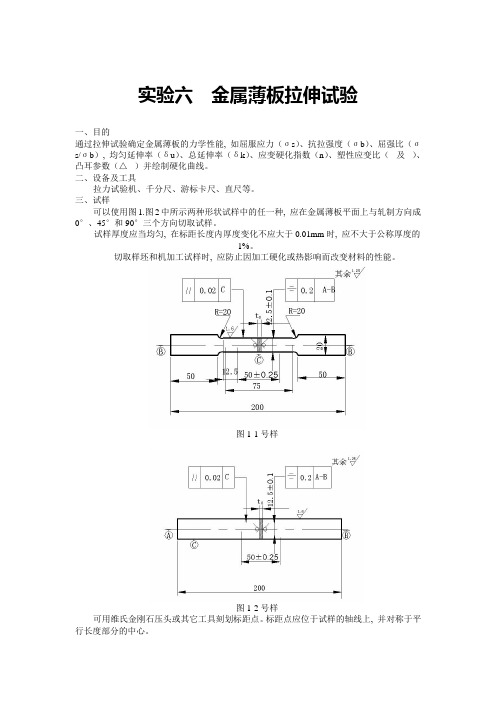
实验六金属薄板拉伸试验一、目的通过拉伸试验确定金属薄板的力学性能, 如屈服应力(σs)、抗拉强度(σb)、屈强比(σs/σb), 均匀延伸率(δu)、总延伸率(δk)、应变硬化指数(n)、塑性应变比(及)、凸耳参数(△)并绘制硬化曲线。
二、设备及工具拉力试验机、千分尺、游标卡尺、直尺等。
三、试样可以使用图1.图2中所示两种形状试样中的任一种, 应在金属薄板平面上与轧制方向成0°、45°和90°三个方向切取试样。
试样厚度应当均匀, 在标距长度内厚度变化不应大于0.01mm时, 应不大于公称厚度的1%。
切取样坯和机加工试样时, 应防止因加工硬化或热影响而改变材料的性能。
图1-1号样图1-2号样可用维氏金刚石压头或其它工具刻划标距点。
标距点应位于试样的轴线上, 并对称于平行长度部分的中心。
四、试验步骤和数据处理将试样夹紧在试验机的夹头内, 调整好测力刻度和载荷——伸长曲线记录装置。
夹头的移动速度应在0.5~20mm/min 范围内, 并应保持加载速度恒定。
记录产生屈服时的载荷Fs 和最大载荷Fmax, 并根据载荷——伸长曲线, 进行数据处理后, 便可确定板材的σs 、σb 、σs/σb 、δu 、δk1.确定板材σs 、σb 、σs/σb 、δu 、δkσs 、σb 及σs/σb 由下式确定:σs =00A F 或σ0。
2=202.0/.mm N A F (MPa ) σb =0max A F 2/,mm N (MPa )式中Fs ——屈服时的载荷 , N ;F0.2——相对伸长为0.2时的载荷, N ;Fmax ——拉伸最大载荷, N ;A0 ——试样原始横截面积, mm2。
δu 及δk 由下式确定:δu =%10000⨯-L L L uδk =%10000⨯-L L L k式中 ——试样原始标距长度, mm ;——试样产生细颈时的标距长度, mm ; ——试样断裂时的标距长度, mm 。
冷轧薄板加工硬化指数及塑性应变比的测定及分析

冷轧薄板加工硬化指数及塑性应变比的测定及分析冷轧薄板加工硬化指数及塑性应变比的测定及分析黄微涛向浪涛张丽萍(重钢股份公司钢研所)摘要:测定重钢生产的St14/SPCE的 n值、r值,对试验结果进行分析,研究n值、r值在整个应变区间的变化趋势。
关键词:深冲薄板 n值 r值 SPCE St14Measurement and Analysis of Working-hardening Indexand Plastic Strain Ratio for Deep Stamping Sheet Abstract: Measure the n and r of St14/SPCE produced by Chonggang Steel co.LTD, analysize the values, research the variation trend of n and r in the whole strain interval.Keywords: Deep stamping sheet, n, r, SPCE St14 前言,断后宽度缩减率、冲压开裂率、极限深拉比、孔径伸长率是表征材料深众多研究表明冲塑性的主要指标。
同时薄板材的加工硬化指数(n值)、塑性应变比(r值)又与以上指标有着良好的对应关系:随着r值的增加,断后宽度缩减率也明显增加,而冲压开裂率明显降低;n、r值越大,汽车专用板材的深冲性能越好,极限深拉比越高;孔径伸长率伴随着r值[1]的增加而提高。
公司冷轧薄板厂在开发SPCE、St14深冲板初期,因缺少必要的检测手段未能开展n、r值的有关研究,常出现产品冲压性能不稳定,成型性能较差,并伴随出现冲压开裂的质量异议。
为此,钢研所与薄板厂共同确定了在钢研所补充少量的检测手段,将n值、r值的测定工作开展起来,这为深冲薄板的n、r值的研究创造了必要条件。
1 试验原理1.1 塑性应变比r值对试样进行拉伸实验,测试制定塑性应变水平下长度和宽度变化,应变水平应超过屈服延伸阶段,并低于最大力时的塑性应变量。
金属材料形变硬化指数的测定
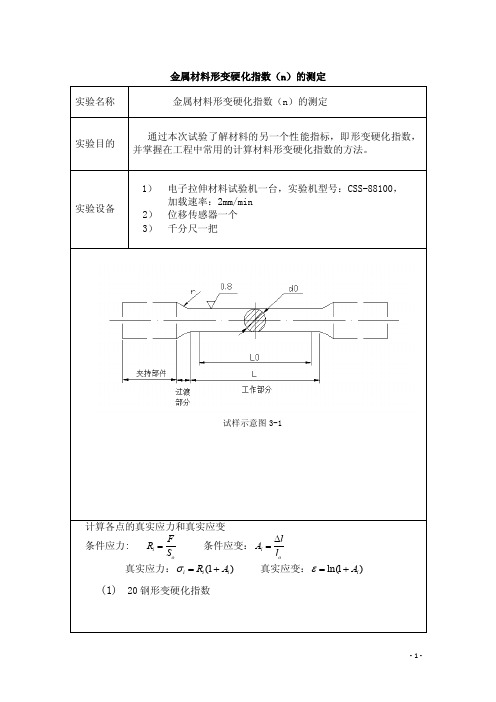
Ri (MPa) Ai (%) i (MPa) i (%)
1
331.24
0.0838
359.00
0.0804
2
383.17
0.1177
428.27
0.1113
3
419.05
0.1561
484.46
0.1451
4
442.37
0.1994
530.58
0.1818
5
454.77
0.2431
565.32
0.2176
由 σ kε2
得 lgσ =lgκ +nlgε
硬化指数(n)为该线性方程的斜率拟合曲线如下图 3-2 所示:
计算结果
N
K(MPa) V(n)
Q
6
20.95
0.219
0.995
线性方程的斜率拟合曲线 3-2:
拟合曲线图 3-2
时效铝合金的形变硬化指数
d=8.94mm
So
d 2 4
62.90 m m2
实验名称
金属材料形变硬化指数(n)的测定 金属材料形变硬化指数(n)的测定
实验目的
通过本次试验了解材料的另一个性能指标,即形变硬化指数, 并掌握在工程中常用的计算材料形变硬化指数的方法。
实验设备
1) 电子拉伸材料试验机一台,实验机型号:CSS-88100, 加载速率:2mm/min
2) 位移传感器一个 3) 千分尺一把
ΣΣ ΣΣ 标准偏差
S (n)
N
N Yi
i 1 N
N Xi
i 1
2 2
-
N
( Yi )2
i 1 N
( Xi )2
i 1
金属材料薄板和薄带塑性应变比

1金属材料薄板和薄带塑性应变比1 范围本标准规定了一种测定金属薄板和薄带塑性应变比的方法。
本标准适用于由均匀塑性变形的材料(即塑性变形范围内应力-应变曲线呈单调连续上升的部分),也适用于不均匀塑性变形的材料(即塑性变形范围内应力-应变曲线呈锯齿等不连续形状的部分)。
2 规范性引用文件下列文件对于本文件的应用是必不可少的。
凡是注日期的引用文件,仅注明日期的版本适用于本文件。
凡是不注日期的引用文件,其最新版本(包括所有修改单)适用于本文件。
GB/T 228.1-2010 金属材料 拉伸试验 第1部分:室温试验方法(ISO 6892-1:2009 , MOD ) GB/T 12160-2002 单轴试验用引伸计的标定(ISO 9513:1999,IDT )3 术语和定义下列术语和定义适用于本文件。
3.1塑性应变比 plastic strain ratior在单轴拉伸应力作用下,试样宽度方向真实塑性应变和厚度方向真实塑性应变的比ab r εε=‥‥‥‥‥‥‥‥‥‥‥‥ (1) 式中 a ε --厚度方向真实塑性应变;b ε --宽度方向真实塑性应变。
注1:以上用单应变点的表达式只适合均匀塑性应变范围的情况。
注2:因为长度的变形量比厚度的变形量测量更容易、更精确,在塑性变形伸长量不超过最大力对应的塑性伸长量g Α的范围内,由体积不变原理得到下列关系式,用于计算塑性应变比r 值⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=Lb b L b b r 000ln ln ‥‥‥‥‥‥‥‥‥‥‥‥ (2) 注3:因为r 值取决于试样与轧制方向的取向和应变水平,相关的符号用下标注明方向和应变水平,例如:r 45/20 (见表1)。
注4:对于某些会在塑性变形过程中出现相变的材料,测量段的体积不能总是假设不变。
在这种情况下,有关各方应协商测量方法。
3.2塑性应变比加权平均值 weighted average of plastic strain ratior计算不同取向试样r x/y 的加权平均值采用公式(3):4245900r r r r ++= ‥‥‥‥‥‥‥‥‥‥‥ (3)注:三个方向的r 值应在相同的应变/应变范围条件下测量,这种情况下下标变量y 可以省略。
金属材料薄板和薄带摩擦系数试验方法

YB/T ×××××-200×金属材料薄板和薄带 摩擦系数试验方法Metallic Materials Sheet and Strip Method for Coefficient of Friction编 制 说 明行业标准起草小组2011年4月金属材料薄板和薄带 摩擦系数试验方法编 制 说 明一、 任务来源根据国家工业与信息化部2010年第一批行业标准修订项目计划,《金属材料薄板和薄带摩擦系数试验方法》行业标准由武汉钢铁(集团)公司联合华中科技大学和冶金工业标准研究院共同起草。
二、 起草过程和征求意见情况摩擦广泛存在于实际生产与生活中,是固体力学的研究重点之一。
当两相互接触的物体之间有相对运动或相对运动趋势时,会在接触表面上产生阻碍相对运动的机械作用力,即为摩擦力,而相互摩擦的两物体称为摩擦副。
按摩擦副的运动状态,摩擦可分为静摩擦和动摩擦,前者是指相互接触的两物体间有相对运动趋势并处于静止临界状态时的摩擦,后者是相互接触的两物体越过静止临界状态而发生相对运动时的摩擦。
摩擦系数则是指两接触表面间的摩擦力和作用在其一表面上的垂直力比值,摩擦系数通常和接触表面的粗糙度有关,而和接触面积的大小无关。
依据运动的性质,可分为静摩擦系数和动摩擦系数。
两接触表面在相对移动开始时的最大阻力为静摩擦力,与法向力的比值即为静摩擦系数。
两接触表面以一定速度相对移动时的阻力,与法向力的比值即为动摩擦系数。
需要强调的是,摩擦系数是与一组摩擦副相对应的,与组成摩擦副的两接触物体的材质和粗糙度相关,单纯讲某种材料的摩擦系数是没有意义的。
多数学者认为摩擦力的本质是由物体接触面上的分子间内聚力引起的。
然而事实上,对于两个相互接触的物体来讲,只有在表面间的微观凸起才相互接触,而大多数地方是不接触的,因此实际接触面积远小于表观接触面积(即我们所测定的试样面积) 。
摩擦阻力与实际接触面积成正比( 不是与表观接触面积成正比),一般实际接触面积又与表面上的正压力成正比,因此摩擦力与正压力成正比。
基于压痕响应各向异性板料的硬化指数

基于压痕响应各向异性板料的硬化指数惠钰;吴建军;王明智;展学鹏;樊赫【摘要】正确识别各向异性材料力学性能中的应变硬化指数是金属成形模拟分析的重要部分.针对各向异性材料,讨论了单一方向的应变硬化指数对复杂应力问题求解的局限性,提出了一种基于扩展孔洞模型计算等效应变硬化指数的新方法.基于该方法,以TC1M钛合金板为研究对象,结合数值分析推导出载荷-接触半径曲线斜率变化比与等效应变硬化指数的关系式.通过对比和分析单一硬化指数和等效硬化指数对有限元模拟结果中材料应力应变关系的影响,验证了球形压痕法所得等效应变硬化指数对复杂应力问题的适用性.%Accurate determination of the strain hardening exponent of the anisotropic materials is the fundamental part of the numerical simulation of metal forming. For anisotropic materials, the limitations were discussed when the single orientation-dependent strain hardening exponent was used in the numerical simulation of multi-stress problems. A new approach based on the expanding cavity model was proposed to identificate the strain hardening exponent of anisotropic materials. Based on this, a new relationship between the variation of the slope ratio of load-contact radius curve and the equivalent strain hardening exponent was suggested for the TC1M titanium alloys sheet, by using the numerical and theoretical analysis. The effectiveness of this method was verified by comparing the numerical results using either the single orientation-dependent strain hardening exponent or the new indentation-based strain hardening exponent. The results show that theequivalent strain hardening exponent is more suitable for the multi-stress state problem.【期刊名称】《中国有色金属学报》【年(卷),期】2018(028)004【总页数】8页(P685-692)【关键词】各向异性板料;应变硬化指数;球形压痕;复杂应力【作者】惠钰;吴建军;王明智;展学鹏;樊赫【作者单位】西北工业大学机电学院,西安 710072;西北工业大学机电学院,西安710072;西北工业大学机电学院,西安 710072;西北工业大学机电学院,西安710072;西北工业大学机电学院,西安 710072【正文语种】中文【中图分类】TG301随着现代航空制造业的发展,各向异性板料(如钛合金板料)在飞机生产中的应用日益广泛[1−2]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
() 3 诊断功能:该功能是帮助操作者判断故 障的类型与部位, 找到排除故障的途径及方法,确 保整个光谱分析系统是否正常运行。 () 4 数据库管理及计算功能: 数据库可以存 储数百个标准样品的成千上万个标准含量,以及近 百条校准曲线, 数百个钢种的技术标准, 数千个试 样分析结果。另外如D 等,还存有数百条分析 V6 -
X一n ;I ; e 鱿 I; 一n a
在数据对的选取上, 力值最小的数据点应大于 材料的屈服点; 力值最大的数据点应尽可能接近材
料的最大强度值。 曲线拟合法测得的 n 值因采用试验数据多点
当; 时,材料宽度方向比厚度方向容易产生变 >1 形,即意味材料不易变薄或变厚。在拉深变形中加 大植 , 板料宽度方向较厚度方向易于变形, 毛坯 的变形区切向收缩而不易起皱失稳;毛坯的传力区 其厚度方向不易减薄而导致破裂失稳, 有利于提高
向异性指数r 的测定方法简介如下。 l 直
I 应变硬化指数月 值的测定 应变硬化指数 n 值的物理意义,是指材料均 匀变形的能力。n值大则意味着材料加工硬化严 重,材料的变形易于从变形区向未变形区、从大变 形区向小变形区传递, 宏观表现为材料应变分布的 均匀性好,不易进人分散失稳。n 值对伸长类变形
的数理统计、 月报表、日 报表及各种分类作表等, 还有为现场提供加料计算、产量统计、 原材料消耗 统计 、成本和利润统计等。极大的满足了用户需
要。
当然,随着信息化时代的到来, 光谱分析数据 的网络化已在很多企业应用, 给企业带来了很大效 益。只有认真的总结光谱的应用知识, 才可以使光 谱技术得到更进一步的发展。
一
了 使试验数据尽可能接近失稳点 。B B Z 和 相差较小; 另一 为了 方面 使取得的 数据不致太 靠近, 和 3 典 B 相
差较大。可以认为,阶梯试样基本是从薄板成型性 子 } 能的角度出发而设计的。其具体作法如下: 将试样拉断 也可以不拉断,而拉至出现缩 ( 0 01 . 0 . 2 0 . 3 0 . 4
(rpr i ,ubi m n m d, uzo 02 5, i ) u 70 h a Poe O c H aeAu i u L . hoh 7 y t fe l i tZ C n
S N n- e U H gm i o
1.曲 .3 线拟合法 1
曲线拟合法是在拉伸试验过程中,对应力应变 进行多点测量 ( 不得少于五点 ), 然后对各测量点 所取得的应力应变数据对采用最小二乘法进行回归 处理计算n 值。计算公式如下:
N N N N N
a i t p i e r i o ue. ns r y x r n d cd oo n d ae r t
K y rstn aptsa hr n g xh k ooy x ew d: mt leti a ei i e;i aitp i e o h e l ;rn n n tc n r n i a d d s d
先提出的。试样的工作部份分为宽度不同的 二 段,
Nln n c io 法测定n eo-W lk s 值的作法是在单向
拉伸试验过程中, 根据两个特征点,即最大载荷点
B, 凡 L 乓 几 1凡, 和 , , 分别为试样各段的 宽度 , 原始
凡a 形量为1 的载 P, 凡a P的比 x 与变 0 % 荷点 , x f o 计算 与 。
金属薄板在板金加工过程中,除具备材料必须
的使用性能: 如强度、 耐腐蚀性能等外, 还需具有 良 好的加工性能: 如焊接性能、成型性能等。材料 的加工性能和使用性能一样, 都是对材料基本的要 求。2世纪6年代以来,由于板金加工业的发展, 0 0 先进工业国家对材料的成型性能展开了大量研究并 取得很大的进展, 如汽车工业采用高强度低合金钢
总第12 2期 2 0 年第2 01 期
汀 玻冶杏
HEBEI ETALLURGY M
To a 1 2 t l 2
2 01 Nu b r 0 , m e 2
金属薄板带应变硬化指数和厚向异性指数测定方法
孙 红玫
( 华北铝业有限公司 性能室,河北 琢洲 025) 770 值和厚向异性指日 的物理意义和几种不同的测定方法,具有一定的实践指导 直 摘要 :介绍了应变硬化指数月
值后直接按RL il曲线确定n .Whe . ty 值。 ( 见图
2 )。
0 1 ‘ 工 X .已 U d
与标定长度; 1 b, L L 分别为 b, b。和 I _几 2 3 , 试 样 变形后的 度与长度。 最 段 }L 各段 宽 其中 窄 B l 和用
于测定常规的机械性能, , 3 B 两段专用于测定 和B 。
06 =l e . .7 一 -I 9 0L A /
e0 L e / 一0 6 =0 3 3 -I =1 . 7 . . A 9 0 eI=1 3 0 0/ /0 =3. . 0 3 A L . 3 两边取对数: 0 A = 3. . L I 0 I / n 3
西 一
图2 e o- n c?测定n 值 N l n s Wi ok l 去
颈) 测量。 并 下式计 值: 后, 1 和几 按 算n
n I (凡 )( Z = ( , /n , 【,叭 /ZL] [ 1 ) ( 1L] =n l 1 ) I I 1 I ) B n L n )
即
: 二/ = ,今
厚向异性指数 了 , 值越大 ,表明材料在承受拉变形 时, 宽度方向上的应变大而厚度方向上的应变小。
。(; ' 1x l (2 , i 一N , '=' ' X 一E ) E Y , ; ) i , 1 , x 一 X = N )(X 1 = Y ]
式中: N= 参加回归计算的数据对个数
影响很大, 尤其是胀形类变形。采用坐标网格法对 2 种不同n 值的材料在变形后测绘其应变分布曲线 ( 见图I ),从中可以看出, 值较大的材料应变 n
峰值较低且应变分布较均匀。
录 ) 侧 时 艘 粼
一
.叫卜 ̄
n . =02
座标网中心间距 图1 两种材料应变曲线
1 , ‘
U
一-
将 试 所获 数据( , 2 , 拉伸 验 得的 。,。)
. 、
2
C
。) 。 代人上式,即可求得n 值c
1 .N l n .2 s -Wil k 1 eo no 法 c
图3 阶梯试样
阶梯试样法是由RHHyr 0 ..ee 在2世纪6年代首 0
A s at T e yi l ai ad e l e i tn t d o sa hr n g e nad c bt c: p s a m n g s r dtmn i m h s t i a ei i x t k r h h c e n n e a e r ao e o f n d n n v r d n h i
2 厚向导性指姿 值的测定 卜 厚向异性指数r 是指单向拉伸试验时,试样宽 度方向上的应变与厚度方向上的应变之比。
曲 的 数 式 pJ . 34) 达 为: m P 1 (.n 线 函 表 a I 8 0 o 1
根据美国深压延协会 ( D R A D G)的推荐 , N ln n c法的精度可到士 . 0 eo- l k s Wio 02 0
得 ( , 2 和相对应的 ( , 2 两组条 ,,, ) £,E ) 件,
万方数据
河北冶金
20 年第2 01 期
将条件代人H lm n oo o应变关系方程 , l 得方程组 :
I J 、 e es 、
k£n I -- 口 联立求解,得: k:n 2 Z I,) I 2 I二) n= Io 一n , ( e一n , (, n 2 /n
值和二 在 2B 段宽 设计上, 面 值。 B 3 和 两 度的 一方 为
! L」
{ _二 1 目 口 !i I!::・}1{[_ 上 . } 2 生: 遏 11 .5 厂」 { 几 / 「: { 目口i { 口 口 L 下 } 口一 } 一 口 口 r 厂 };:. 一 一 i !I{ 洲 「 ! {’ 州 : 口 } } 一 :. } 「口 口 门口 { _ 卜 ! F {{ }!{}州 { i J ’ 〔 ‘ {
变形程度和成品率。
法更能确切地反映材料的应力应变关系, 但测试_ 卜 作比较烦琐, 效率较低。
1 阶梯试样法 . 2
拟合的, 故较之前述的两点法与 Nln io eo Wnc 下式计算 厂 s - lk 值:
3 几点讨论
, 值的测定方法在本文中介绍的n 值测定方法 均可使用, 具体作法无大的区别。在对试验结果的 处理上,为避免厚度测量上的误差, 可利用标定点 测量长、 宽方向上的应变, 再根据体积不变定律按
( 上接第4页) 6
根据除尘效率 q 6 % 有效驱进速度V c/ = , 9. 7 =O s l m =. / 0 ms 1 ,气体流量L9 X mh =0 0 /,可计算出集尘 1 `
极的总面积A :
尘极之间缝隙极板宽0 3m)。含尘气体实际停留 .5 7
时间:
r / 1 秒 =1 V=4 / . =1. X3 1 4 0 5 5 结束语 1= 1 -a 7 -e i 一e v
低, 宜采用电子引伸计和计算机对试验数据进行自
动采集和处理, 方可在实际_作中大量使用: _ 〔
( 下转第5页) 8
万方数据
总第12 2期
HEBEI E I Y JN
需要, 按一定的顺序、 大小、 数目、 排列组合成各 种状态填人有关表中,编辑成一个个分析组谱分析者技术 管理的需要。数据库的计算功能表现在 日 常管理中
收稿 日期:20 一0 一0 01 1 4
按照被测试样的形状 , 值的测定分为常规法 n 和阶梯试样法两类。
1 常规法 . 1
常规法测定 值,是指采用工程上惯用的等 n 截面标准拉伸试样测定 n 值。通常有如下几种:
