数学软件实验报告实验七
《数学软件》实验报告-数据处理与多项式计算

附件二:实验项目列表附件三:实验报告(七)系:专业:年级:姓名:学号:实验课程:实验室号:_ 实验设备号:实验时间:指导教师签字:成绩:1. 实验项目名称:数据处理与多项式计算2. 实验目的和要求1.掌握利数据统计和分析的方法2.掌握数值插值与曲线拟合的方法及其应用3.掌握多项式的常用运算3. 实验使用的主要仪器设备和软件方正商祺N260微机;MATLAB7. 0或以上版本4. 实验的基本理论和方法(1)rand函数(2)均值:mean(x)(3)求和:sum(x)(4)方差:std(A,flag,dim)(5)最大值函数:y=max(x),[y,k]=max(x),[Y,U]=max(A,[],dim)(6)最小值函数:y=min(x),[y,u]=min(x),[Y,U]=min(A,[],dim)(7)length函数(8)find函数(9)sort函数:[Y,I]=sort(A,dim)(10)样条插值:Y1=interp1(X,Y,X1,’spline’)(11)polyfit函数:[P,S]=polyfit(X,Y,m)(12)plot函数(13)多项式求和(14)求根函数:x=roots(A)(15)多项式求值:y=polyval(P,X), y=polyvalm(P,X)5. 实验内容与步骤(描述实验中应该做什么事情,如何做等,实验过程中记录发生的现象、中间结果、最终得到的结果,并进行分析说明)(包括:题目,写过程、答案)题目:1.利用matlab提供的rand函数生成30000个符合均匀分布的随机数,然后检验随机数的性质;(1)均值和标准方差。
(2)最大元素和最小元素。
(3)大于0.5的随机数个数占总数的百分比。
function f1x=rand(30000,1);disp('均值:');M=mean(x)disp('标准方差:');S=std(x,0,1)disp('最大元素:');MAX=max(x)disp('最小元素:');MIN=min(x)disp('百分比');a=length(find(x>0.5));X=a/30000>> f1均值:M =0.501标准方差:S =0.28946最大元素:MAX =0.99998最小元素:MIN =3.1508e-005百分比X =0.498532.将100个学生5门功课的成绩存入矩阵P中,进行如下处理。
matlab数学实验

《管理数学实验》实验报告班级姓名实验1:MATLAB的数值运算【实验目的】(1)掌握MATLAB变量的使用(2)掌握MATLAB数组的创建,(3)掌握MA TLAB数组和矩阵的运算。
(4)熟悉MATLAB多项式的运用【实验原理】矩阵运算和数组运算在MA TLAB中属于两种不同类型的运算,数组的运算是从数组元素出发,针对每个元素进行运算,矩阵的运算是从矩阵的整体出发,依照线性代数的运算规则进行。
【实验步骤】(1)使用冒号生成法和定数线性采样法生成一维数组。
(2)使用MA TLAB提供的库函数reshape,将一维数组转换为二维和三维数组。
(3)使用逐个元素输入法生成给定变量,并对变量进行指定的算术运算、关系运算、逻辑运算。
(4)使用MA TLAB绘制指定函数的曲线图,将所有输入的指令保存为M文件。
【实验内容】(1)在[0,2*pi]上产生50个等距采样数据的一维数组,用两种不同的指令实现。
0:(2*pi-0)/(50-1):2*pi 或linspace(0,2*pi,50)(2)将一维数组A=1:18,转换为2×9数组和2×3×3数组。
reshape(A,2,9)ans =Columns 1 through 71 3 5 7 9 11 132 4 6 8 10 12 14Columns 8 through 915 1716 18reshape(A,2,3,3)ans(:,:,1) =1 3 52 4 6ans(:,:,2) =7 9 118 10 12 ans(:,:,3) =13 15 17 14 16 18(3)A=[0 2 3 4 ;1 3 5 0],B=[1 0 5 3;1 5 0 5],计算数组A 、B 乘积,计算A&B,A|B,~A,A= =B,A>B 。
A.*Bans=0 0 15 121 15 0 0 A&Bans =0 0 1 11 1 0 0 A|Bans =1 1 1 11 1 1 1~Aans =1 0 0 00 0 0 1A==Bans =0 0 0 01 0 0 0A>=Bans =0 1 0 11 0 1 0(4)绘制y= 0.53t e -t*t*sin(t),t=[0,pi]并标注峰值和峰值时间,添加标题y= 0.53t e -t*t*sint ,将所有输入的指令保存为M 文件。
数学软件与数学实验报告册2013

实验报告册信计姓名:学号:钟培华编2013年3月实验一数学软件MATLAB基础知识一.实验目的1.熟悉MATLAB向量的生成及其运算;2.熟悉MATLAB矩阵的生成及其运算;3.熟悉MATLAB数组的生成及其运算;4.熟悉稀疏矩阵的生成与操作.5.熟悉MATLAB向量的生成及其运算;6.熟悉MATLAB矩阵的生成及其运算;7.熟悉MATLAB数组的生成及其运算;8.熟悉稀疏矩阵的生成与操作;9.熟悉常用快捷键和命令.二.实验准备阅读课本MTLAB7.0简介、MA TLAB7.0的安装和用户界面、基本使用方法等相关内容.阅读课本的第四数值计算功能、五章单元数组等相关内容.三.实验内容1.MATLAB的启动:双击matlab图标.2.熟悉界面四个窗口:命令窗口、命令历史窗口、当前目录窗口、工作间管理窗口、发行说明书窗口.3.在命令窗口中输入下列命令,观察运行结果,然后填空.>>dir %功能是:显示当前目录下的文件;>>clc %功能是:清除命令窗口;>>help sin %观返回的结果是.>>lookfor sin%观返回的结果是.“help”的功能是: 显示函数并解释函数的用法“lookfor +函数”的功能是: 给出与此相关的函数用法4.写出下列标点符号的功能:5. 熟悉下列常用快捷键:ctrl p Home ctrl a ctrl n End ctrl e ctrl b Esc ctrl u ctrl f Del ctrl d ctrl Backspace ctrl h ctrl ↑↓←→←键盘按钮键盘按钮功能功能和快捷键和快捷键光标置于当前(+)调用上一行(+)行开头光标置于当前(+)调用下一行(+)行结尾光标左移(+)(+)清除当前行一个字符光标右移(+)(+)删除光标处字符一个字符光标左移+(+)删除光标前字符一个单词+Alt Backspace→光标左移+恢复上一次删除一个单词6. M ATLAB 对所使用的变量有哪些规定?不要对使用的变量进行声明,不用指定类型,直接赋值即可; 变量不超过31个字符; 变量区分大小写;以字母开头,可含字母、下划线、数字,不能有标点符号。
[数学软件及应用(Lingo)实验报告范文]lingo实验报告范文心得
![[数学软件及应用(Lingo)实验报告范文]lingo实验报告范文心得](https://img.taocdn.com/s3/m/b2e98c482f3f5727a5e9856a561252d380eb20b2.png)
[数学软件及应用(Lingo)实验报告范文]lingo实验报告范文心得2022~2022学年第二学期短学期《数学软件及应用(Lingo)》实验报告班级数学131班姓名张金库学号成绩实验名称奶制品的生产与销售方案的制定完成日期:2022年9月3日实验名称:奶制品的生产与销售方案的制定二、实验目的及任务了解并掌握LINGO的使用方法、功能与应用;学会利用LINGO去解决实际中的优化问题。
三、实验内容问题一奶制品加工厂用牛奶生产,两种奶制品,1桶牛奶可以在甲类设备上用12h加工成3kg,或者在乙类设备上用8h加工成4kg。
根据市场的需求,生产,全部能售出,且每千克获利24元,每千克获利16元。
现在现在加工场每天能的到50桶牛奶的供给,每天正式工人总的劳动时间为480h,并且甲类设备每天至多能加工100kg,乙类设备的加工能力没有限制。
为增加工厂的利益,开发奶制品的深加工技术:用2h和3元加工费,可将1kg加工成0.8kg高级奶制品,也可将1kg加工成0.75kg高级奶制品,每千克能获利44元,每千克能获利32元。
试为该工厂制订一个生产销售方案,使每天的净利润最大,并讨论以下问题:假设投资30元可以增加供给1桶牛奶,投资3元可以增加1h的劳动时间,应否做这些投资?假设每天投资150,可以赚回多少?每千克高级奶制品,的获利经常有10%的波动,对制订的生产销售方案有无影响?假设每千克获利下降10%,方案应该变化吗?假设公司已经签订了每天销售10kg的合同并且必须满足,该合同对公司的利润有什么影响?问题分析要求制定生产销售方案,决策变量可以先取作每天用多少桶牛奶生产,,再添上用多少千克加工,用多少千克加工,但是问题要分析,的获利对生产销售方案的影响,所以决策变量取作,,,每天的销售量更为方便。
目标函数是工厂每天的净利润——,,,的获利之和扣除深加工费用。
根本模型决策变量:设每天销售kg,kg,kg,kg,用kg加工,用kg加工。
数学实验综合实验报告

一、实验目的:1、初步认识迭代,体会迭代思想的重要性。
2、通过在mathematica 环境下编写程序,利用迭代的方法求解方程的根、线性方程组的解、非线性方程组的解。
3、了解分形的的基本特性及利用mathematica 编程生成分形图形的基本方法, 在欣赏由mathematica 生成的美丽的分形图案的同时对分形几何这门学科有一个直观的了解。
从哲理的高度理解这门学科诞生的必然性,激发读者探寻科学真理的兴趣。
4、从一个简单的二次函数的迭代出发,利用mathematica 认识混沌现象及其所 蕴涵的规律。
5、.进一步熟悉Mathematic 软件的使用,复习总结Mathem atic 在数学作图中的应用,为便于研究数学图像问题提供方便,使我们从一个新的视角去理解数学问题以及问题的实际意义。
6、在学习和运用迭代法求解过程中,体会各种迭代方法在解决问题的收敛速度上的异同点。
二、实验的环境:学校机房,mathematica4环境三、实验的基本理论和方法:1、迭代(一)—方程求解函数的迭代法思想:给定实数域上光滑的实值函数)(x f 以及初值0x 定义数列1()n n x f x +=, ,3,2,1,0=n , (1)n x , ,3,2,1,0=n ,称为)(x f 的一个迭代序列。
(1)方程求根给定迭代函数)(x f 以及初值0x 利用(1)迭代得到数列n x , ,3,2,1,0=n .如果数列收敛到某个*x ,则有)(**x f x =. (2)即*x 是方程)(x f x =的解。
由此启发我们用如下的方法求方程0)(=x g 的近似解。
将方程0)(=x g 改写为等价的方程)(x f x =, (3) 然后选取一初值利用(1)做迭代。
迭代数列n x 收敛的极限就是方程0)(=x g 的解。
为了使得迭代序列收敛并尽快收敛到方程0)(=x g 的某一解的条件是迭代函数)(x f 在解的附近的导数将的绝对值尽量小,因此迭代方程修订成x x f x h x )1()()(λλ-+== (4) 选取λ使得|)(|x h '在解的附近尽量小. 为此, 我们可以令,01)()(=-+'='λλx f x h得)(11x f '-=λ. 于是 1)()()(-'--=x f x x f x x h . 特别地,如果取x x g x f +=)()(, 则可得到迭代公式 .,1,0,)()(1 ='-=+n x g x g x x n n n n (5) (2)线性方程组的数值解的迭代求解理论与矩阵理论给定一个n 元线性方程组⎪⎩⎪⎨⎧=++=++,,1111111n n nn n n n b x a x a b x a x a (6)或写成矩阵的形式,b Ax = (7) 其中)(ij a A =是n 阶方阵,T n x x x x ),,(21 =及T n b b b b ),,,(21 =均为n 维列向量.熟知,当矩阵A 的行列式非零时,以上的方程组有唯一解.如何有效,快速地寻求大型的线性方程组的数值解释科学工程计算中非常重要的任务.而迭代法常常是求解这些问题的有效方法之一。
数学实验报告的总结(3篇)

第1篇一、实验背景随着科技的不断发展,数学实验在各个领域中的应用越来越广泛。
数学实验作为一种以计算机为工具,通过模拟、计算和验证等方法,对数学理论进行实践探索和研究的方法,已经成为数学研究的重要手段。
本次实验旨在通过数学实验,加深对数学理论的理解,提高数学应用能力,培养创新意识和团队协作精神。
二、实验目的1. 熟悉数学实验的基本方法,掌握数学实验的基本步骤。
2. 通过实验,加深对数学理论的理解,提高数学应用能力。
3. 培养创新意识和团队协作精神,提高自身综合素质。
三、实验内容本次实验主要包括以下内容:1. 实验一:线性方程组的求解通过编写程序,实现线性方程组的直接法、迭代法等求解方法,并对比分析各种方法的优缺点。
2. 实验二:矩阵运算实现矩阵的加法、减法、乘法、转置等基本运算,以及求逆矩阵、特征值和特征向量等高级运算。
3. 实验三:数值积分通过编写程序,实现定积分、变积分、高斯积分等数值积分方法,并分析各种方法的误差和适用范围。
4. 实验四:常微分方程的数值解法实现欧拉法、龙格-库塔法等常微分方程的数值解法,并对比分析各种方法的稳定性、精度和适用范围。
四、实验过程1. 确定实验内容,明确实验目的。
2. 设计实验方案,包括实验步骤、算法选择、数据准备等。
3. 编写实验程序,实现实验方案。
4. 运行实验程序,收集实验数据。
5. 分析实验数据,得出实验结论。
6. 撰写实验报告,总结实验过程和结果。
五、实验结果与分析1. 实验一:线性方程组的求解通过实验,验证了直接法和迭代法在求解线性方程组时的有效性。
直接法在求解大规模线性方程组时具有较好的性能,而迭代法在求解稀疏线性方程组时具有较好的性能。
2. 实验二:矩阵运算实验结果表明,矩阵运算的程序实现具有较高的精度和效率。
在实际应用中,可以根据具体需求选择合适的矩阵运算方法。
3. 实验三:数值积分通过实验,验证了各种数值积分方法的有效性。
高斯积分具有较高的精度,但在求解复杂函数时,需要调整积分区间和节点。
Mathematica实验报告
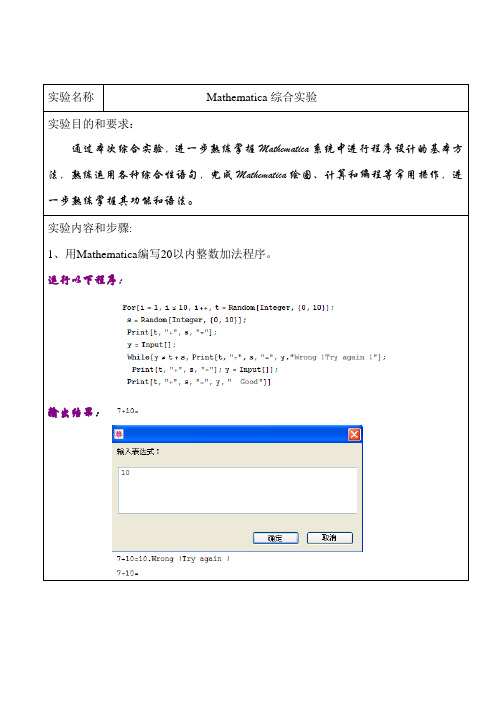
实验名称Mathematica综合实验实验目的和要求:通过本次综合实验,进一步熟练掌握Mathematica系统中进行程序设计的基本方法,熟练运用各种综合性语句,完成Mathematica绘图、计算和编程等常用操作,进一步熟练掌握其功能和语法。
实验内容和步骤:1、用Mathematica编写20以内整数加法程序。
运行以下程序:输出结果:2、编写程序,列出9*9的乘法表来。
输入程序:9*9乘法表3、编写程序,输入两个正整数,用“辗转相除法”求它们的最大公约数。
辗转相除法:(1) 以大数m作被除数,小数n做除数,相除后余数为r。
(2) 若r ≠ 0,则m ← n,n ← r,继续相除得到新的r。
若仍有r ≠ 0,则重复此过程,直到r = 0为止。
(3) 最后的n就是最大公约数。
Mathematica代码如下:运行结果4、统计一个班级某次考试个分数段的人数。
输入程序:运行结果:5、编写程序用切线法求方程的解。
Mathematica语句和运行结果如下:6、编写Mathematica程序显示二维码图像。
输入程序:二维码图像7、用0~8这九个数字,组成一个二位数和一个三位数相乘使他们的积恰好是四位数.数字不能重复。
即□□×□□□=□□□□输入以下Mathematica程序:输出结果:8、用Mathematica编写程序绘制一个围棋棋盘.输入以下程序:围棋棋牌9、假设新开辟的国家公园里没有兔子和狐狸,现引进兔子和狐狸个50只,n 个月后兔子和狐狸的数量分别记为n R 和n F ,假定有⎩⎨⎧+=-=++nn n n n n F R F F R R 6.02.02.01.111Mathematica 程序如下:运行结果如下:注释:在一段时间内,兔子和狐狸的数量均会减少,但最终均会趋于一个稳定值。
10、有一个木工、一个电工和一个油漆工,三人协商合作装修他们的房子,并达成如下协议:a.每人总共工作10天(包括给自己家干活);b.每人日工资根据市场价确定在60 80 元之间;c.每人的总支出与每人的总收入相等。
数学软件实训报告

数学软件应用实训实训报告学生姓名韩*学号13090***** 班级信计1302班成绩指导教师数学与计算机科学学院2015年12月15日实训报告评阅1特殊函数与图形问题背景与实验目的著名的Riemann函数大家都很熟悉了,但是关于它的图像你是否清楚呢?除了最上面那几点,其他都很难画吧?你想不想看看下面那些“挤在一起”的点是怎样分布的呢?还有几何中的马鞍面、单叶双曲面等是怎样由直线生成的,是不是也想目睹一下呢?这些,都离不开绘图.实际上绘图一直是数学中的一种重要手段,借助图形,往往可以化繁为简,使抽象的对象得到明白直观的体现.比如函数的基本性质,一个图形常可以使之一目了然,非常有效.它虽不能代替严格的分析与证明,但在问题的研究过程中,可以帮助研究人员节约相当一部分精力.此外,它还可以使计算、证明、建模等的结果得到更明白易懂的表现,有时,这比科学论证更有说服力.同时,数学的教学与学习过程也离不开绘图.借助直观的图形,常可以使初学者更容易接受新知识.如数学分析中有不少函数,其解析式着实让人望而生畏,即使对其性质作了详尽的分析,还是感到难明就里;但如果能看到它的图形,再配合理论分析,则问题可以迎刃而解.又如在几何的学习中,会遇到大量的曲线与曲面,也离不开图形的配合.传统的手工作图,往往费力耗时,效果也不尽理想.计算机恰恰弥补了这个不足,使你可以方便地指定各种视角、比例、明暗,从各个角度进行观察.本实验通过对函数的图形表示和几个曲面(线)图形的介绍,一方面展示它们的特点,另一方面,也将就Matlab软件的作图功能作一个简单介绍.大家将会看到,Matlab的作图功能非常强大.实验内容数学分析中,特别是积分部分,我们接触了不少有趣的函数,由于其中有的不是一一对应的,用上面的方法无法画出它们的图像,这时就只能用参数了.此外还有些图形只能用参数来画,比如空间曲线,在计算机上不接受“两个曲面的交线”这种表示,所以也只能用参数来实现.用参数方式作图的关键在于找出合适的参数表示,尤其是不能有奇点,最好也不要用到开方.所以要找的参数最好是有几何意义的.当然这也不可一概而论,需要多积累经验.实验步骤1.做出下图所示的三维图形:图9ezsurf('3*sin(u)*cos(v)','3*sin(u)*sin(v)','3*cos(u)',[0,pi,0,2*pi]);axis equalhold onezsurf('(8+2*cos(u))*cos(v)','(8+2*cos(u))*sin(v)','2*sin(u)',[0,2*pi,0,2*pi]) 2作出下图所示的墨西哥帽子及其剪裁图形:[a,b]=meshgrid(-5:.5:5);c=sqrt(a.^2+b.^2)+eps;z=sin(c)./c;mesh(a,b,z)axis square改变a、b的取值范围,可得到裁剪后的图。
《数学软件》实验指导书

《数学软件》实验指导书实验一 matlab 运算基础实验目的:熟悉matlab 编程环境,掌握建立矩阵的方法。
实验内容:1. 设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦(1) 求他们的乘积C 。
(2) 将矩阵C 的右下角3*2子矩阵赋给DclcclearA=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20;21,22,23,24,25];B=[3,0,16;17,-6,9;0,23,-4;9,7,0;4,13,11];C=A*BD=C(3:5,2:3)2. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
提示:先利用冒号表达式,再利用find和length 函数。
(2) 建立一个字符串向量,删除其中的大写字母。
提示:利用find 函数和空矩阵。
%P286 T4clcclearx=100:999;y1=find(rem(x,21)==0);length(y1)s='ABCabcD12f';l=s>'A' & s<'Z';s(l) = []实验二 选择结构程序设计实验目的:掌握建立和执行M 文件的方法,实现选择程序设计的方法。
实验内容:求下列分段的值:2226,0356,010,231,x x x x y x x x x x x x ⎧+-<≠⎪=-+≤<≠≠⎨⎪--⎩且且其它要求:(1) 用if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
提示:x 的值可以从键盘输入,可以是向量。
(2) 用逻辑表达式实现。
x=input('please enter x value:');L=( x<0 & x~=-3);Y(L)=x(L).^2+x(L)-6;L=(x>=0&x~=2&x~=3&x<10);Y(L)=x(L).^2-5*x(L)+6;y=x.^2-x-1;实验三 循环结构程序设计实验目的:掌握实现循环程序设计的方法,利用向量运算来代替循环操作的方法。
《数学实验》实验报告——用Mathematica软件解微分方程

例1
求解下列微分方程: 1)
y 2 (1 y) (2 y) 2
In[1]:= DSolve[(y[x]^2)(1-y'[x]) (2-y'[x])^2,y[x],x] Out[1]=
书中结果为: y x c 1/( x c) ,其中 c 为任意常数。 y z 2) z y In[1]:= DSolve[{y'[x] z[x],z'[x] -y[x]},{y[x],z[x]},x] Out[1]= {{y[x]C[1] Cos[x]+C[2] Sin[x],z[x]C[2] Cos[x]-C[1] Sin[x]}} 3)
中 1 2 3 为任意常数。 例 2 求常微分方程 y′= x2 + y2,满足初始条件 y(0)= 0 的数值解。 In[1]:= s1=NDSolve[{y'[x]==x^2+y[x]^2,y[0]==0},y,{x,-2,2}] Out[1]= {{yInterpolatingFunction[{{-2.,2.}},<>]}} In[2]:= y=y/.s1[[1]] Out[2]= InterpolatingFunction[{{-2.,2.}},<>] In[3]:= Plot[y[x],{x,-2,2},AspectRatioAutomatic,PlotRange{-1.5,1.5}]
例1 求解下列微分方程: 1) 2) 3)
y 2 (1 y) (2 y) 2
y z z y y 3 y 3 y y ( x 5)e x
例2 求常微分方程 y′= x2 + y2,满足初始条件 y(0)= 0 的数值解 例3 求函数 t 5 和 et sint 的拉氏变换 例 4 用拉氏变换解微分方程:
Matlab数学实验报告

实验一 Matlab基本操作1.实验课程名称数学实验2.实验项目名称Matlab基本操作3.实验目的和要求了解Matlab的基本知识,熟悉其上机环境,掌握利用Matlab进行基本运算的方法。
4.实验内容和原理内容:三角形的面积的海伦公式为:area=)s-sa--)()(s(csb其中: s=(a+b+c)/2原理:将一般数学问题转化成对应的计算机模型并进行处理的能力。
了解Matlab的基本功能,会进行简单的操作。
5.主要仪器设备计算机与Windows 2000/XP系统;Matlab等软件。
6.操作方法与实验步骤步骤:(1)在M文件编辑窗口输入以下程序,并以文件名”area_helen.m”保存:a= input(‘a=‘) ; b= input(‘b=‘) ; c= input(‘c=‘) ;s= (a+b+c)/2;area=sqrt (s* (s-a) * (s-b) * (s-c))(2)在命令窗口输入文件名“area_helen”,按回车键,即可运行上面的程序,输入三边长,立即可得三角形面积(3)第二题在命令窗口输入b=6;a=3;c=a*b,d=c-2*b(4) 按回车键,即可运行上面的程序7.实验结果与分析<1> a=3; b=4; c=5;时,aera=6 当a为3,b为4,c为5时,s=6,aera=6<2> c= 18,d=6,a为3,b为6时,c=18,d=6实验二 Matlab的数值计算1.实验课程名称数学实验2.实验项目名称Matlab的数值计算3.实验目的和要求了解一些简单的矩阵、向量、数组和多项式的构造和运算方法实例,懂得编写简单的数值计算的Matlab程序。
熟悉一些Matlab的简单程序,会用Matlab的工具箱,懂得Matlab的安装和简单的使用。
4.实验内容和原理内容:从函数表:)1(),5.0(),2( ,0x 1x 021x 1x f(x) 32-⎪⎩⎪⎨⎧≤≤<>+=f f f x x求设)1(),2( ,1211)(2-⎩⎨⎧≤>+=f f x xx x x f 求设 原理:利用矩阵、向量、数组、和多项式的构造和运算方法,用常用的几种函数进行一般的数值问题求解。
数学软件实验报告心得(3篇)

第1篇一、实验背景随着计算机技术的飞速发展,数学软件在数学研究、工程应用、科学计算等领域发挥着越来越重要的作用。
数学软件如MATLAB、Mathematica、MathCAD等,为数学工作者提供了强大的计算、图形、符号处理等功能。
本实验旨在通过使用数学软件MATLAB进行数学实验,提高我们的数学素养和实际操作能力。
二、实验目的1. 熟悉MATLAB软件的基本操作和常用命令;2. 培养运用MATLAB解决实际问题的能力;3. 提高数学建模和数学计算能力;4. 深化对数学理论知识的理解。
三、实验内容1. MATLAB基本操作:学习MATLAB的界面、命令窗口、编辑器、图形窗口等基本操作;2. 数值计算:掌握MATLAB的数值计算功能,如求和、求积、求导、积分等;3. 符号计算:学习MATLAB的符号计算功能,如代数运算、微积分运算、解方程等;4. 数据处理:掌握MATLAB的数据处理功能,如数据读取、数据存储、数据排序等;5. 图形绘制:学习MATLAB的图形绘制功能,如二维图形、三维图形、参数曲线等;6. 数学建模:运用MATLAB进行数学建模,解决实际问题。
四、实验过程1. 安装MATLAB软件,熟悉软件界面和基本操作;2. 学习MATLAB编程基础,掌握常用命令和函数;3. 阅读教材和参考书籍,了解MATLAB在数学领域的应用;4. 按照实验指导书,完成实验任务,如数值计算、符号计算、数据处理、图形绘制等;5. 分析实验结果,总结实验经验,撰写实验报告。
五、实验心得1. 熟练掌握MATLAB软件的基本操作和常用命令是进行数学实验的前提。
在本实验中,我通过不断练习,熟练掌握了MATLAB的界面操作、命令输入和图形绘制等功能。
2. MATLAB在数值计算方面具有强大的功能。
通过本实验,我学会了使用MATLAB 进行求和、求积、求导、积分等数值计算,提高了我的数学计算能力。
3. MATLAB的符号计算功能让我对数学理论知识的理解更加深刻。
数学软件与数学实验报告

《数学软件与数学实验》报告任课教师: 学号: 姓名:成绩:一、 实验内容:用Mathematica 软件求解下面各题 问题一:任意拿出黑白两种颜色的棋子共八个排成一个圆圈, 然后在两颗相同的棋子中间放一颗黑色棋子, 在两颗不同颜色的棋子中间放一颗白色棋子,放完后撤掉原来所放的棋子, 再重复上述过程, 各棋子颜色会怎样变化?同时,对棋子颜色问题进行深入探索 (对棋子数分别对4, 5, 6, 9, 16 颗) 的情况进行讨论, 将得到的结果进行拓广,并给出结论。
问题分析:由于在两颗同色棋子中放置一颗黑色棋子,两颗不同色的棋子中间放置一颗白色棋子,因此可将黑色棋子用1表示,白色棋子用-1表示。
这是因为-1-1=1⨯ ,11=1⨯ ,这代表两颗同色棋子中放一颗黑色棋子;-11=-1⨯ ,这代表两颗不同色的棋子中间放置一颗白色棋子。
设棋子数为123,,,,,n n a a a a 为初始状态,则当4n =时,有第一次操作后得到的4枚棋子颗表示为()()()()12233441,,,a a a a a a a a 第二次操作后得到的4枚棋子颗表示为()()()()()()()()1234233434414112,,,a a a a a a a a a a a a a a a a 分别化简()()()()13243142,,,a a a a a a a a 第三次操作后得到的4枚棋子颗表示为()()()()()()()()1324243131424213,,,a a a a a a a a a a a a a a a a 化简为()1234a a a a 第四次操作后得到的4枚棋子颗表示为()21234a a a a ,故这四枚棋子的颜色的赋值都是1,这表明只需操作4次即可将圆周上的棋子全变为黑色。
当n=4时,有 步数 状态(舍掉偶次项)0 1a 2a 3a 4a 1 12a a 23a a 34a a 41a a2 13a a24a a 31a a42a a 3 1234a a a a 1234a a a a1234a a a a1234a a a a4()21234a a a a()21234a a a a()21234a a a a()21234a a a a说明当n=4时,经过4部全变为黑色棋子 Mathematica 程序:我们假设开始摆放的4颗棋子为1234a a a a 。
软件算法展示实验报告(3篇)

第1篇一、实验目的1. 理解并掌握软件算法的基本概念和原理。
2. 掌握常见软件算法的设计与实现方法。
3. 通过实验,提高算法分析、设计、实现和优化能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 开发工具:PyCharm三、实验内容本次实验主要展示了以下软件算法:1. 冒泡排序2. 快速排序3. 二分查找4. 线性查找5. 简单链表操作6. 二叉树遍历四、实验步骤1. 冒泡排序(1)编写冒泡排序算法的代码实现。
(2)测试代码,验证算法的正确性。
2. 快速排序(1)编写快速排序算法的代码实现。
(2)测试代码,验证算法的正确性。
3. 二分查找(1)编写二分查找算法的代码实现。
(2)测试代码,验证算法的正确性。
4. 线性查找(1)编写线性查找算法的代码实现。
(2)测试代码,验证算法的正确性。
5. 简单链表操作(1)实现链表的创建、插入、删除和遍历等基本操作。
(2)测试代码,验证链表操作的正确性。
6. 二叉树遍历(1)实现二叉树的创建、插入、遍历等基本操作。
(2)测试代码,验证二叉树遍历的正确性。
五、实验结果与分析1. 冒泡排序实验结果:```pythondef bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]测试代码arr = [64, 34, 25, 12, 22, 11, 90]bubble_sort(arr)print("Sorted array is:", arr)```分析:冒泡排序算法是一种简单的排序算法,其基本思想是通过相邻元素的比较和交换,将待排序的序列逐步变成有序序列。
实验结果显示,冒泡排序算法能正确地将输入数组排序。
数学软件实验报告实验七

数学软件实验报告学院名称:理学院专业年级:姓名:学号:课程:数学软件实验报告日期:2014年12月6日实验七SIMULINK建模与工具箱的使用一.实验目的MATLAB 具有丰富的可用于各种专业方向的工具箱,这些工具箱已经形成了MATLAB 的系列产品。
特别是动态仿真建模工具箱,更是成为许多工具箱的基础。
本次实验的目的就是要使大家了解MA TLAB工具箱使用的基本方法,以及如何查询工具箱,主要掌握系统优化工具箱的使用和系统动态仿真建模工具箱的使用。
二.实验要求MATLAB系统的工具箱十分的丰富,并且随着版本的不断升级,其工具箱还在不断地增加。
通过本次实验,要求了解MA TLAB系统工具箱的分类与查询,会使用系统优化工具箱解决一些实际问题。
能建立系统仿真方框图,并进行系统仿真模拟。
三.实验内容最优化工具箱非线性最小化函数fgoalattain 多目标达到优化 constr 有约束最小化fminbnd 有边界最小化fminunc使用梯度法的无约束最小化fminsearch 使用简单法的无约束最小化fzero 非线性方程求解(数量情况)fsolve 非线性方程求解lsqnonlin 非线性最小二乘fminimax 最小的最大解fseminf 半无穷区间最小化2.矩阵问题的最小化linprog 线性规划quadprog 二次规划lsqnonneg 非负线性最小二乘lsqlin 约束线性最小二乘第十章10.1线性优化>> f=[-5 4 2];>> a=[6 -1 1;1 2 4];>> b=[8 10];>> 1b=[-1 0 0];>> ib=[-1 0 0];>> ub=[3 2];>> [x,fval,exitflag,output,lambda]=linprog(f,a,b,[],[],ib,ub) Optimization terminated.x =1.33330.00000.0000fval =-6.6667exitflag =1output =iterations: 7algorithm: 'large-scale: interior point'cgiterations: 0message: 'Optimization terminated.'constrviolation: 0lambda =ineqlin: [2x1 double]eqlin: [0x1 double]upper: [3x1 double]lower: [3x1 double]>> f=[-6 4];>> a=[2 3;4 2];>> b=[100 120];>> ib=[0 0];>> [x,fval]=linprog(f,a,b,[],[],ib,[]) Optimization terminated.x =30.00000.0000fval =-180.000010.2 二次优化>> h=[1 -1;-1 2];>> c=[-2;-6];>> a=[1 1;-1 2;2 1];>> b=[2;2;3];>> [x,i]=quadprog(h,c,a,b)x =0.66671.3333i =-8.2222>> h=[2 0;0 2];>> f=[-4 0];>> a=[-1 1;1 -1];>> b=[2;-1];>> [x,fval,exitflag,output,lambda]=quadprog(h,f,a,b,[],[],[0 0],[]); >> xx =0.50001.500010.3 非线性无约束优化问题π的近似值>> fminbnd('cos',3,4)ans =3.1416函数式在(0,1)范围内的最小值点>> fminbnd('(x^3+cos(x)+x*log(x))/exp(x)',0,1)ans =0.5223对第一个函数直接在命令窗中定义函数>> banana=@(x)100*(x(2)-x(1)^2)^2+(1-x(1))^2;>> [x,fval,exitflag]=fminsearch(banana,[-1.2,1])x =1.0000 1.0000fval =8.1777e-010exitflag =1对第二个函数使用函数文件的定义方法:定义M文件function f =myfun(x)f = 3*x(1)^2+2*x(1)*x(2)+x(2)^2;在命令窗口实现优化>> x0=[1,1];x =1.0e-004 *-0.0675 0.1715fval =1.9920e-01010.3.3 fminunc函数应用举例最小值求解>> fun='exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1)';>> x0=[-1 1];>> [x,fval]=fminunc(fun,x0)Warning: Gradient must be provided for trust-region algorithm;using line-search algorithm instead.> In fminunc at 347Local minimum found.Optimization completed because the size of the gradient is less than the default value of the function tolerance.<stopping criteria details>x =0.5000 -1.0000fval =3.6609e-01510.4 最小二乘优化问题非线性最小二乘问题优化调用M函数function F =myfun(x)k = 1:10;F = 2+2*k-exp(k*x(1))-exp(k*x(2));>> x0=[0.3 0.4];x =0.2578 0.2578resnorm =124.3622非负最小二乘问题优化>> C=[0.0372 0.28690.6861 0.70410.6233 0.62450.6344 0.6170];>> d=[0.85870.17810.07470.8405];>> [C\d,lsqnonneg(C,d)] %超定房乘除法即最小二乘法拟合法ans =-2.5721 03.1251 0.6947>> [norm(C*(C\d)-d),norm(C*lsqnonneg(C,d)-d)]ans =0.6638 0.911110.5非线性约束问题优化非线性约束问题优化>> x0=[-1,1];>> options=optimset('Algorithm','active-set');>> [x,fval]=fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options); >> x,fvalx =-1.5702 6.3688fval =-0.7620边界问题(使用上例在命令窗口做优化)。
《数学软件》实验报告-函数文件

附件二:实验项目列表附件三:实验报告(一)系: 专业: 年级: 姓名: 学号: 实验课程: 实验室号:_ 实验设备号: 实验时间: 指导教师签字: 成绩:1. 实验项目名称: 函数文件2. 实验目的和要求3. 实验使用的主要仪器设备和软件方正商祺N260微机;MATLAB 7. 0或以上版本 4. 实验的基本理论和方法(1) 函数M 文件:function[输出形参列表]=函数名(输入形参列表) (2) 矩阵求逆解线性方程组:X=inv(A)*B (3) find 函数 (4) rem 函数 (5) sqrt 函数 (6) fix 函数 (7) for 循环 (8) 函数调用 (9) 递归调用 5. 实验内容与步骤(描述实验中应该做什么事情,如何做等,实验过程中记录发生的现象、中间结果、最终得到的结果,并进行分析说明)(包括:题目,写过程、答案)1.一个物理系统⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----1cos 000sin 00cos 0sin 0sin cos 2111θθθθθθm m m m ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡2111N N g m a =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡g m g m 2100从键盘输入m 1,2m 和θ的值,求2121,,,N N a a 的值。
其中g=9.8,输入θ时以角度为单位。
要求:定义一个求解线性方程AX=B 的函数文件,然后在命令文件中调用该函数文件。
function [a1,a2,N1,N2]=jie(m1,m2,t) g=9.8;B=[0 m1*g 0 m2*g]';X=inv(A)*B;a1=X(1);a2=X(2);N1=X(3);N2=X(4);>> [a1,a2,N1,N2]=jie(1,2,45)a1 =3.5288a2 =1.1397N1 =9.2134N2 =28.52702.一个自然数是素数,且它的各位数字位置经过任意对换后仍为素数,则称为绝对素数。
数学软件Matlab实验报告

计算机与信息学院(数学类课程)实验报告课程名称:数学软件姓名:系:应用数学系专业:数学与应用数学年级:2010级学号:指导教师:职称:讲师2011年12月13日实验项目列表计算机与信息学院数学类实验报告(一)系:应用数学专业:数学与应用数学年级: 2010级姓名: *** 学号: 102260002051 实验课程:数学软件实验室号:_ 田C-513 实验设备号: 107 实验时间: 2011/09/25 指导教师签字:成绩:1.实验项目名称:MATLAB运算基础2.实验目的和要求:1.熟悉启动和退出MTALAB的方法。
2.熟悉MATLAB命令窗口的组成。
3.掌握建立矩阵的方法。
4.掌握MATLAB各种表达式的书写规则以及常用函数的使用。
3.实验使用的主要仪器设备和软件:联想微机;MA TLAB 6.54.实验的基本理论和方法:冒号表达式,逻辑表达式,whos,find,length,空矩阵5.实验内容与步骤:1 (1) z1=2*sin(pi*85/180)/(1+exp(2))(2) x=[2, 1+2*i; -0.45 5] ;z2=(1/2)*log(x+sqrt(1+x^2))(3) a=-3.0:0.1:3.0;z3=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2)(4) t=0:0.5:2.5;z4=t.^2.*(t>=0&t<1)+(t.^2-1).*(t>=1&t<2)+(t.^2-2*t+1).*(t>=2&t<3)2 A=[12,34,-4;34,7,87;3,65,7];B=[1,3,-1;2,0,3;3,-2,7];(1)A+6*BA-B+eye(3)(2) A*BA.*B(3) A^3A.^3(4) A/BB\A(5) [A,B][A([1,3],:);B^2]3 A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20;21,22,23,24,25];B=[3,0,16;17,-6,9;0,23,-4;9,7,0;4,13,11];C=A*BD=C(3:5,2:3)Whos4 (1) A=100:999;B=rem(A,21);C=length(find(B==0))A='IlOveMatLAb2051';a=find(A>='A'&A<='Z');A(a)=[ ]6.实验心得(质疑、建议):学会了一些Matlab的基础,并利用这些知识进行基本的数值处理。
数学应用软件综合实验

G m桶g
合力产生的加速度为:
(3)
a桶
加速度与速度关系为:
F合 m桶
(4)
a桶
所以:
dv桶 dt
dv桶 dt
(5)
G F合 f 桶 m桶
将(1) 、 (2) 、 (3) 、(4)式代入可得:
m桶 g f 浮 cv桶 m桶
由(7)计பைடு நூலகம்:
dv桶 dt
(6)
dv桶 dt m桶 g f浮 cv 桶 m桶
得: v 136.4845*(1-e 由h
t
0.0078t
)
0.0078t
vdt 17498 136.4845t 17498* e
0
再运行: function y=f2 m=24.4347;g=9.8;c=0.19; f1=213.528; t=0:0.1:15;
f=(m*g-f1)*(1-exp((-c*t)/m))/c; v=136.4845*(1-exp(-0.0078*t)); h=-17498+136.4845*t+17498*exp(-0.0078*t); plot(t,h) xlabel('时间') ylabel('高度') 可以得到圆桶下降的深度 h 随时间的变化曲线。
当 h=91.14m 时,同过数值计算: >> t=12:0.01:14; >> kk=-17498+136.4845*t+17498*exp(-0.0078*t)-91.14; >> kk 得到: t 13.32 m / s
v 13.4684m / s
由于 v 13.4684m / s 12.2m / s ,所以不应该把废料装入密封的圆桶里,然后将圆桶扔入深度为 91.14 米的海里。 四,实验结果分析或总结 通过此实验,我对 MATLAB 有了更深的了解,了解到 MATLAB 是一个功能强的软件,运用此软件可以 解决很多生活中的问题,就像试验中求最大利润和圆桶下降问题,此软件可以应用到生活的很多地 方,会对我们的生活造成极大的正面影响。在实验的同时温习了很多之前学习的知识,通过综合实 验,把很多的知识都聚集在一起,对我们的学习产生了很大的帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学软件实验报告学院名称:理学院专业年级:姓名:学号:课程:数学软件实验报告日期:2014年12月6日实验七SIMULINK建模与工具箱的使用一.实验目的MATLAB 具有丰富的可用于各种专业方向的工具箱,这些工具箱已经形成了MATLAB 的系列产品。
特别是动态仿真建模工具箱,更是成为许多工具箱的基础。
本次实验的目的就是要使大家了解MA TLAB工具箱使用的基本方法,以及如何查询工具箱,主要掌握系统优化工具箱的使用和系统动态仿真建模工具箱的使用。
二.实验要求MATLAB系统的工具箱十分的丰富,并且随着版本的不断升级,其工具箱还在不断地增加。
通过本次实验,要求了解MA TLAB系统工具箱的分类与查询,会使用系统优化工具箱解决一些实际问题。
能建立系统仿真方框图,并进行系统仿真模拟。
三.实验内容最优化工具箱非线性最小化函数fgoalattain 多目标达到优化 constr 有约束最小化fminbnd 有边界最小化fminunc使用梯度法的无约束最小化fminsearch 使用简单法的无约束最小化fzero 非线性方程求解(数量情况)fsolve 非线性方程求解lsqnonlin 非线性最小二乘fminimax 最小的最大解fseminf 半无穷区间最小化2.矩阵问题的最小化linprog 线性规划quadprog 二次规划lsqnonneg 非负线性最小二乘lsqlin 约束线性最小二乘第十章10.1线性优化>> f=[-5 4 2];>> a=[6 -1 1;1 2 4];>> b=[8 10];>> 1b=[-1 0 0];>> ib=[-1 0 0];>> ub=[3 2];>> [x,fval,exitflag,output,lambda]=linprog(f,a,b,[],[],ib,ub) Optimization terminated.x =1.33330.00000.0000fval =-6.6667exitflag =1output =iterations: 7algorithm: 'large-scale: interior point'cgiterations: 0message: 'Optimization terminated.'constrviolation: 0lambda =ineqlin: [2x1 double]eqlin: [0x1 double]upper: [3x1 double]lower: [3x1 double]>> f=[-6 4];>> a=[2 3;4 2];>> b=[100 120];>> ib=[0 0];>> [x,fval]=linprog(f,a,b,[],[],ib,[]) Optimization terminated.x =30.00000.0000fval =-180.000010.2 二次优化>> h=[1 -1;-1 2];>> c=[-2;-6];>> a=[1 1;-1 2;2 1];>> b=[2;2;3];>> [x,i]=quadprog(h,c,a,b)x =0.66671.3333i =-8.2222>> h=[2 0;0 2];>> f=[-4 0];>> a=[-1 1;1 -1];>> b=[2;-1];>> [x,fval,exitflag,output,lambda]=quadprog(h,f,a,b,[],[],[0 0],[]); >> xx =0.50001.500010.3 非线性无约束优化问题π的近似值>> fminbnd('cos',3,4)ans =3.1416函数式在(0,1)范围内的最小值点>> fminbnd('(x^3+cos(x)+x*log(x))/exp(x)',0,1)ans =0.5223对第一个函数直接在命令窗中定义函数>> banana=@(x)100*(x(2)-x(1)^2)^2+(1-x(1))^2;>> [x,fval,exitflag]=fminsearch(banana,[-1.2,1])x =1.0000 1.0000fval =8.1777e-010exitflag =1对第二个函数使用函数文件的定义方法:定义M文件function f =myfun(x)f = 3*x(1)^2+2*x(1)*x(2)+x(2)^2;在命令窗口实现优化>> x0=[1,1];x =1.0e-004 *-0.0675 0.1715fval =1.9920e-01010.3.3 fminunc函数应用举例最小值求解>> fun='exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1)';>> x0=[-1 1];>> [x,fval]=fminunc(fun,x0)Warning: Gradient must be provided for trust-region algorithm;using line-search algorithm instead.> In fminunc at 347Local minimum found.Optimization completed because the size of the gradient is less than the default value of the function tolerance.<stopping criteria details>x =0.5000 -1.0000fval =3.6609e-01510.4 最小二乘优化问题非线性最小二乘问题优化调用M函数function F =myfun(x)k = 1:10;F = 2+2*k-exp(k*x(1))-exp(k*x(2));>> x0=[0.3 0.4];x =0.2578 0.2578resnorm =124.3622非负最小二乘问题优化>> C=[0.0372 0.28690.6861 0.70410.6233 0.62450.6344 0.6170];>> d=[0.85870.17810.07470.8405];>> [C\d,lsqnonneg(C,d)] %超定房乘除法即最小二乘法拟合法ans =-2.5721 03.1251 0.6947>> [norm(C*(C\d)-d),norm(C*lsqnonneg(C,d)-d)]ans =0.6638 0.911110.5非线性约束问题优化非线性约束问题优化>> x0=[-1,1];>> options=optimset('Algorithm','active-set');>> [x,fval]=fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options); >> x,fvalx =-1.5702 6.3688fval =-0.7620边界问题(使用上例在命令窗口做优化)。
>> [x,fval]=fmincon(@objfun,x0,[],[],[],[],[0 0],[],@confun,options); Local minimum found that satisfies the constraints.Optimization completed because the objective function is non-decreasing infeasible directions, to within the default value of the function tolerance,and constraints were satisfied to within the default value of the constraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin1 1>> x,fvalx =0 1.5000fval =8.5000等式约束条件问题>> x0=[-1,1];>> [x,fval]=fmincon(@objfun,x0,[],[],[1 1],[0],[],[],@confun,options); Local minimum found that satisfies the constraints.Optimization completed because the objective function is non-decreasing infeasible directions, to within the default value of the function tolerance,and constraints were satisfied to within the default value of theconstraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-006): lower upper ineqlin ineqnonlin2>> x,fvalx =-3.1623 3.1623fval =0.5778非线性方程的优化解>> fzero('sin',3)ans =3.1416>> fsolve('cos(x)+x',0)ans =-0.7391>> cos(ans)ans =0.7391求解方程>> x0=[-5;-5];>> [x,fval]=fsolve(@myfun,x0)x =0.56710.5671fval =1.0e-006 *-0.4059-0.4059第12章1、Simulink应用举例>> sldemo_dblcart1选择命令菜单Simulation run,运行此模型,则屏幕上会出现显示双质量—弹簧系统运动状态的动画模型,下图为抓拍的静态图形。
