合肥工业大学计算方法复化梯形公式实验
复化梯形公式和复化Simson公式

数值计算方法上机题目3一、计算定积分的近似值:要求:(1)若用复化梯形公式和复化Simpson 公式计算,要求误差限71021-⨯=ε,分别利用他们的余项估计对每种算法做出步长的事前估计; (2)分别利用复化梯形公式和复化Simpson 公式计算定积分;(3)将计算结果与精确解比较,并比较两种算法的计算量。
1.复化梯形公式程序:程序1(求f (x )的n 阶导数:syms xf=x*exp(x) %定义函数f (x )n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点,也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0 for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用复化梯形算法计算的结果 Tn= 7.3891等分数 n=7019已知值与计算值的误差 R= 2.8300e-0082. Simpson公式程序:程序1:(求f(x)的n阶导数):syms xf=x*exp(x) %定义函数f(x)n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数,输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点,也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值,故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用Simpson公式计算的结果 Sn= 7.3891等分数 n=24已知值与计算值的误差 R= 2.7284e-008用复化梯形公式计算的结果为:7.3891,与精确解的误差为:2.8300e-008。
复化梯形公式求积分

武汉工程大学计算机科学与工程学院计算方法》实验报告日期:年月日实验内容设计分析复化数值积分:将区间[a,b]n 等分,取等距节点x i a ih,iba0,1,2,..., n, hn 由定积分的区间可加性,有nf x dxxix i 1f x dx在每个小区间上利用梯形积分公式有x ii f x dx x i 1 h f x i 1 f x i 2i 1 ih n1T n f a f b 2 f x i一般记 2 i1 称做n+1 点复化梯形积分公式。
数学公式:b h n1f xdx f a f b 2 f x ia 2 i1算法描述:i1Step1:输入a,b 和正整数n;Step2:置h=(b-a)/n;Step3:F=f(a)+f(b);l=0;Step4:对j=1,2,⋯,n 循环执行5;Step5:置x=a+jh; l+=f(x);Step6:置T=h(F+2l)/2 Step7:输出T;程序源代码:#include<iostream>#include<math.h>using namespacestd;<<endl; cout<<" 请输入把 0 到 1 的范围几等分?int m1; cin>>m1;EchelonIntegral(m1); cout<<endl; char answer1;cout<<" 是否要继续求该算法? (y/n)"<<"\t"; cin>>answer1;while(answer1=='y'){cout<<"请输入把 0到 1的范围几等分? "<<"\t"; cin>>m1;EchelonIntegral(m1); //3. 直线求积分; cout<<endl;cout<<" 是否要继续求该算法? (y/n)"<<"\t"; cin>>answer1; }cout<<endl;}cout<<"用梯形积分公式求积分1/(1+pow(sin(x),2))的值测试用例实验总结复化数值积分就是为了减少数值积分的误差,可以把积分区间分成若干小区间,在每个小区间上采取低阶数值积分公式,然后把这些小区间上的数值积分结果加起来作为函数在整个区间上的近似,类似于分段差值。
复化梯形公式求积分-推荐下载
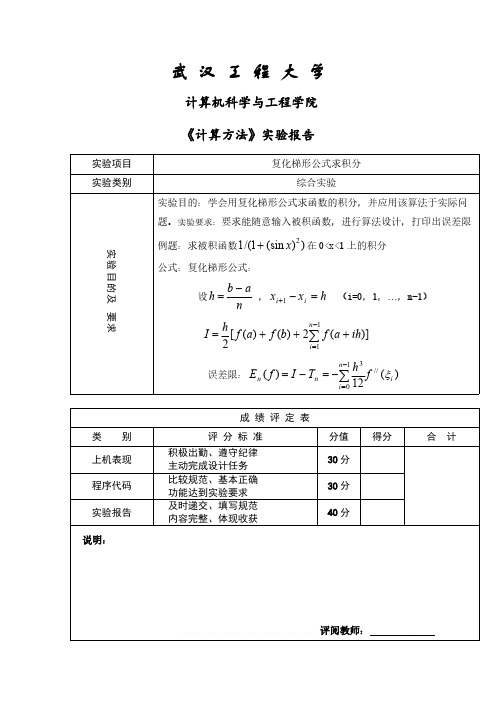
武汉工程大学计算机科学与工程学院《计算方法》实验报告实验项目复化梯形公式求积分实验类别综合实验实验目的及要求实验目的:学会用复化梯形公式求函数的积分,并应用该算法于实际问题。
实验要求:要求能随意输入被积函数,进行算法设计,打印出误差限例题:求被积函数在0<x<1上的积分))(sin1/(12x+公式:复化梯形公式:设,(i=0,1,…,n-1)nabh-=hxx ii=-+1])(2)()([211∑-=+++=niihafbfafhI误差限:)(12)(//13ininnfhTIfEξ∑-=-=-=成绩评定表类别评分标准分值得分合计上机表现积极出勤、遵守纪律主动完成设计任务30分程序代码比较规范、基本正确功能达到实验要求30分实验报告及时递交、填写规范内容完整、体现收获40分说明:评阅教师:日 期: 年 月 日实 验 内 容设计分析复化数值积分:将区间[a,b]n 等分,取等距节点n ab h n i ih a x i -==+=,,...,2,1,0,由定积分的区间可加性,有()()dxx f dx x f bani x x ii ⎰∑⎰=-=11在每一个小区间上利用梯形积分公式有()()()[]i i x x x f x f hdx x f ii +≈-⎰-112一般记()()()⎥⎦⎤⎢⎣⎡++=∑-=1122n i i n x f b f a f h T 称做n+1点复化梯形积分公式。
数学公式:()()()()⎥⎦⎤⎢⎣⎡++≈∑⎰-=1122n i i bax f b f a f h dx x f 算法描述:Step1:输入a,b 和正整数n ;Step2:置h=(b-a)/n;Step3:F=f(a)+f(b);l=0;Step4:对j=1,2,…,n 循环执行5;Step5:置x=a+jh; l+=f(x);Step6:置T=h(F+2l)/2Step7:输出T;程序源代码:#include<iostream>#include<math.h>using namespace std;double f(double x)//求函数的值;{return1/(1+pow(sin(x),2.0));}void EchelonIntegral(int n)//梯形积分{double y=0;double h=(1.0-0.0)/n;for(int i=0;i<=n;i++){double a=0.0+i*h,b=0.0+(i+1)*h;y=y+h*(f(a)+f(b))/2.0;}cout<<"对应所求的梯形求积分为"<<y<<endl;double En=0.0;double mid=(0.0+1.0)/2.0;double x=mid,p=2*sin(2*x)*sin(2*x)*(1+sin(x)*sin(x))-2*cos(2*x)*pow(1+sin(x)*sin(x),2);double f2d=p/pow(1+sin(x)*sin(x),2);for(i=0;i<n;i++){En=En+pow(h,3)/12.0*f2d;}cout<<"误差为"<<En<<endl;}/*void ParabolicIntegral(int n)//抛物线积分{double y=0;double t=(1.0-0.0)/n;for(int i=0;i<n;i++){double a=0.0+i*t,b=0.0+(i+1)*t;y=y+t*(f(a)+f(b)+4*f((a+b)/2.0))/6.0;}cout<<"对应所求的抛物线求积分为"<<y<<endl;}*/void main(){cout<<"*********************用梯形积分公式求积分1/(1+pow(sin(x),2))的值****************"<<endl;cout<<"请输入把0到1的范围几等分?"<<"\t";int m1;cin>>m1;EchelonIntegral(m1);cout<<endl;char answer1;cout<<"是否要继续求该算法?(y/n)"<<"\t";cin>>answer1;while(answer1=='y'){cout<<"请输入把0到1的范围几等分?"<<"\t";cin>>m1;EchelonIntegral(m1);//3.直线求积分;cout<<endl;cout<<"是否要继续求该算法?(y/n)"<<"\t";cin>>answer1;}cout<<endl;}计算机科学与工程学院测试用例计算机科学与工程学院实验总结复化数值积分就是为了减少数值积分的误差,可以把积分区间分成若干小区间,在每个小区间上采取低阶数值积分公式,然后把这些小区间上的数值积分结果加起来作为函数在整个区间上的近似,类似于分段差值。
合肥工业大学计算方法复化梯形公式实验

《计算方法》实验报告学号 姓名 班级 实验项目名称 ■、实验名称 实验二数值积分 实验二 数值积分二、实验目的: (1) (2) (3) (4) 熟悉复化梯形方法、复化 Simpson 方法、梯形递推算法、龙贝格算法; 能编程实现复化梯形方法、复化 Simpson 方法、梯形递推算法、龙贝格算法; 理解并掌握自适应算法和收敛加速算法的基本思想;分析实验结果体会各种方法的精确度,建立计算机求解定积分问题的感性认识 三、实验内容及要求 (1) 设计复化梯形公式求积算法,编制并调试相应的函数子程序 (2) 设计复化辛浦生求积算法,编制并调试相应的函数子程序 1 sin x (3)用龙贝格算法计算 曲d x 0x 输入:积分区间,误差限 输出:序列Tn ,Sn ,Cn,Rn 及积分结果(参考书本 P81的表2-5) 取 n=2, 4, 8, 16,精确解为 0.9460831 四、实验原理及算法描述 在许多实际问题中,常常需要计算定积分 b f (x)dx 的值。
根据微积分学基本定理,若被积函 a 数f(x)在区间[a,b ]上连续,只要能找到 f(x)的一个原函数 F(x),便可利用牛顿 -莱布尼兹公式 b f (x) F(b) F(a)求得积分值。
a 但是在实际使用中,往往遇到如下困难,而不能使用牛顿 -莱布尼兹公式。
找不到用初等函数表示的原函数 虽然找到了原函数,但因表达式过于复杂而不便计算 f(x)是由测量或计算得到的表格函数由于以上种种困难,有必要研究积分的数值计算问题。
bb 利用插值多项式P n (x)f (x)则积分 f (x)dx 转化为P n (x)dx ,显然易算。
a a插值型求积公式。
最简单的插值型求积公式是梯形公式和 Simpson 公式,。
当求积结点提供较多,可以分段使用少结点的梯形公式和Simpson 公式,并称为复化梯形公式、复化 Simpson 公式。
如步长未知,可以通过误差限的控制用区间逐次分半的策略自动选取步长的方法称自适应算法。
用复合梯形求积公式求积实验报告

用复合梯形求积公式求积实验报告学院:计算机学院班级:信计0902班姓名:***学号:**********1、实验目的1)观察复化梯形公式和复化辛普森公式随区间数n 增加各自误差的减少规律;研究广义积分的数值计算如何将其转化为普通积分,再由已有数值积分方法进行计算;2)利用复化梯形公式和复化辛普森公式计算定积分,编程实现。
2、实验内容分别用复化梯形公式和复化辛普森公式计算定积分,研究随着n 增加各自误差的减少规律dx e I x ⎰+=201,取n=2,4,8,16,精确值为I=4.006994。
3、实验原理原理:将区间[a,b]等分成N 个子区间[x(k),x(k+1)](k=0,1,…..,N -1),h=(b-a )/N ,在每个子区间[x(k),x(k+1)]上使用体形公式,可求得结果。
4、设计思想用上述的的公式来计算dx x x I ⎰=10ln ,然后再将积分区间[0,1]进行n 等分,得到n 个小区间[x i ,x i+1](i=0,1,2,…,n-1),每个小区间的长度为h=(b-a)/n,其中x i =a+i*h 。
按∑⎰-=++==101)]()([2)(n i i i ba x f x f h dx x f T ∑-=++=10)()]()([2n i i x f h b f a f h 进行计算。
5、程序框图6、对应程序#include<iostream.h>#include<math.h>double fun1(double a,double h,int n){int i;double sum=0,m;for(i=1;i<=n-1;i++){m=a+i*h;if(m==0)continue;sum=sum+sqrt(m)*log(m);}return sum;}double get(double a){if(a==0)a=0.00001;return sqrt(a)*log(a);}void main(){double a=0,b=1;int n;while(1){cout<<"请输入要等分的子区间个数(n>0):";cin>>n;double h;double T,f0,f1,f2;h=(b-a)/n;f0=get(a);f1=fun1(a,h,n);f2=get(b);T=h/2*(f0+2*f1+f2);cout<<"步长h为:"<<h<<endl;cout<<"复化梯形公式计算结果T="<<T<<endl;}}7、实验结果8、实验体会通过本次实验我熟悉了用复化梯形公式求数值积分的全过程,并更加熟悉的掌握了复化梯形公式原理。
合工大计算方法实验报告

《计算方法》试验报告班级:学号:姓名:实验一、牛顿下山法1 实验目的(1)熟悉非线性方程求根简单迭代法,牛顿迭代及牛顿下山法 (2)能编程实现简单迭代法,牛顿迭代及牛顿下山法 (3)认识选择迭代格式的重要性 (4) 对迭代速度建立感性的认识;分析实验结果体会初值对迭代的影响2 实验内容(1)用牛顿下山法解方程013=--x x (初值为0.6)输入:初值,误差限,迭代最大次数,下山最大次数输出:近似根各步下山因子(2)设方程f(x)=x 3- 3x –1=0 有三个实根 x *1=1.8793 , x *2=-0.34727 ,x *3=-1.53209现采用下面六种不同计算格式,求 f(x)=0的根 x *1 或x *2 x = 213xx +; x = 313-x ;x = 313+x ; x = 312-x ;x = x13+;x = x - ()1133123---x x x输入:初值,误差限,迭代最大次数输出:近似根、实际迭代次数 3 算法基本原理求非线性方程组的解是科学计算常遇到的问题,有很多实际背景.各种算法层出不穷,其中迭代是主流算法。
只有建立有效的迭代格式,迭代数列才可以收敛于所求的根。
因此设计算法之前,对于一般迭代进行收敛性的判断是至关重要的。
牛顿法也叫切线法,是迭代算法中典型方法,只要初值选取适当,在单根附近,牛顿法收敛速度很快,初值对于牛顿迭代 至关重要。
当初值选取不当可以采用牛顿下山算法进行纠正。
一般迭代:)(1k k x x φ=+ 0)()(=⇔=x f x x φ 牛顿公式:)()(1k k k k x f x f x x '-=+ 牛顿下山公式:)()(1k k k k x f x f x x '-=+λ图3.1一般迭代算法流程图 下山因子 ,,,,322121211=λ 下山条件|)(||)(|1k k x f x f <+4 算法描述一般迭代算法见流程图牛顿下山算法见流程图:5、代码:#include <iostream>#include <fstream>#include <cmath>using namespace std;class srrt{private:int n;double *a, *xr, *xi;图3.2牛顿下山算法流程图⇐⇐⇐⇐srrt (int nn){n = nn;a = new double[n+1]; //动态分配内存xr = new double[n];xi = new double[n];}void input (); //由文件读入代数方程系数void srrt_root (); //执行牛顿下山法void output (); //输出根到文件并显示~srrt (){ delete [] a, xr, xi; }};void srrt::input () //由文件读入代数方程系数{int i;char str1[20];cout <<"\n输入文件名: ";cin >>str1;ifstream fin (str1);if (!fin){ cout <<"\n不能打开这个文件" <<str1 <<endl; exit(1); } for (i=n; i>=0; i--) fin >>a[i]; //读入代数方程系数fin.close ();}void srrt::srrt_root () //执行牛顿下山法{int m,i,jt,k,is,it;double t,x,y,x1,y1,dx,dy,p,q,w,dd,dc,c;double g,u,v,pq,g1,u1,v1;m=n;while ((m>0)&&(fabs(a[m])+1.0==1.0)) m=m-1;if (m<=0){cout <<"\n程序工作失败!" <<endl;return;}for (i=0; i<=m; i++) a[i]=a[i]/a[m];for (i=0; i<=m/2; i++){w=a[i]; a[i]=a[m-i]; a[m-i]=w;k=m; is=0; w=1.0;jt=1;while (jt==1){pq=fabs(a[k]);while (pq<1.0e-12){xr[k-1]=0.0; xi[k-1]=0.0; k=k-1;if (k==1){xr[0]=-a[1]*w/a[0]; xi[0]=0.0;return;}pq=fabs(a[k]);}q=log(pq); q=q/(1.0*k); q=exp(q);p=q; w=w*p;for (i=1; i<=k; i++){ a[i]=a[i]/q; q=q*p; }x=0.0001; x1=x; y=0.2; y1=y; dx=1.0;g=1.0e+37;l40:u=a[0]; v=0.0;for (i=1; i<=k; i++){p=u*x1; q=v*y1;pq=(u+v)*(x1+y1);u=p-q+a[i]; v=pq-p-q;}g1=u*u+v*v;if (g1>=g){if (is!=0){it=1;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}else{it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{g=g1; x=x1; y=y1; is=0;if (g<=1.0e-22){if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{u1=k*a[0]; v1=0.0;for (i=2; i<=k; i++){p=u1*x; q=v1*y; pq=(u1+v1)*(x+y);u1=p-q+(k-i+1)*a[i-1];v1=pq-p-q;}p=u1*u1+v1*v1;if (p<=1.0e-20){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{dx=(u*u1+v*v1)/p;dy=(u1*v-v1*u)/p;t=1.0+4.0/k;it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}}}if (k==1) jt=0;else jt=1;}}void srrt::output () //输出根到文件并显示{int k;char str2[20];cout <<"\n输出文件名: ";cin >>str2;ofstream fout (str2);if (!fout){ cout <<"\n不能打开这个文件" <<str2 <<endl; exit(1); } for (k=0; k<n; k++){fout <<xr[k] <<" " <<xi[k] <<endl;cout <<xr[k] <<" +j " <<xi[k] <<endl;}fout.close ();}void main () //主函数{srrt root(6);root.input (); //由文件读入代数方程系数root.srrt_root (); //执行牛顿下山法root.output (); //输出根到文件并显示}6、输入输出输出结果如下:7、分析体会牛顿下山法作为计算方法课程中重要的知识点,在看书学习时较易大致理解其思路,但上级编写代码时却是有难度的。
利用复化梯形公式、复化simpson 公式计算积分

1、运用复化梯形公式、复化simpson公式计算积分
2、比较计算误差与实际误差
实验原理(算法流程图或者含注释旳源代码)
取n=2,3,…,10分别运用复化梯形公式、复化simpson公式计算积分 ,并与真值进行比较,并画出计算误差与实际误差之间旳曲线。
运用复化梯形公式旳程序代码如下:
function f=fx(x)
functionf=fx1(x)
f=x.^4;
a=0;%积分下线
b=1;%积分上线
T=[];%用来装不同n值所计算出旳成果
forn=2:10
h=(b-a)/(2*n);%步长
x=zeros(1,2*n+1);%给节点定初值
for i=1:2*n+1
x(i)=a+(i-1)*h;%给节点赋值
end
y=x.^4;%给相应节点处旳函数值赋值
实
验
结
果
分
析
及
心
得
体
会
上图是运用复化梯形公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。-0.0017是计算误差。0.0417、0.0185、0.0104、0.00670.0046、0.0034、0.0026、0.0021、0.0017是n值分别为2到10旳实际误差。
上图是运用复化simpson公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。
t=0;
for i=1:n
t=t+h/3*(y(2*i-1)+4*y(2*i)+y(2*i+1));%运用复化simpson公式求值
end
T=[T,t];%把不同n值所计算出旳成果装入T中
end
选用复合梯形公式-复合Simpson公式-计算

数值分析实验 三班级:10信计2班 学号:59 姓名:王志桃 分数一·问题提出:选用复合梯形公式,复合Simpson 公式,计算(1) I =dx x ⎰-4102sin 4 ()5343916.1≈I(2) I = dx x x⎰1sin ()9460831.0,1)0(≈=I f(3) I = dx xe x⎰+1024(4) I = ()dx x x ⎰++10211ln二·实验要求:1.编制数值积分算法的程序2.分别用两种算法计算同一个积分,并比较计算结果3.分别取不同步长()/ a b h -=n ,试比较计算结果(如n = 10, 20等)4.给定精度要求ε,试用变步长算法,确定最佳步长三·实验流程图:复化梯形公式:输入 端点 a , b 正整数 n直接计算TN=h/2*[f(a)+2∑f(x k )+f(b)] k=1,2…,n-1输出 定积分近似值TN复化Simpson 公式输入 端点 a , b 正整数 n输出 定积分近似值SN(1) 置h=(b-a)/(2n)(2) F0=f(a)+f(b) , F1=0 , F2=0(3) 对j=1,2,…,2n-1循环执行步4到步5(4) 置x=a+jh(5) 如果j 是偶数,则F2=F2+f(x),否则F1=F1+f(x)(6) 置SN=h(F0+4F1+2F2)/3(7) 输出SN,停机四·源程序:#include<iostream>#include<math.h>using namespace std;#define n 20//此为步长double f1(double x){double y;y=sqrt(4-sin(x)*sin(x));return y;}double f2(double x){if(x==0)return 1;double y;y=sin(x)/x;return y;}double f3(double x){double y;y=exp(x)/(4+x*x);return y;}double f4(double x){double y;y=log(1+x)/(1+x*x);return y;}int main(){int j;double e=0.000001,h,F0,F1,F2,a,b,x,S;cout<<"利用复化Simpson公式求积分"<<endl;//1a=0;b=0.25*3.141592;h=(b-a)/(2*n);F0=f1(a)+f1(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f1(x);elseF1=F1+f1(x);}S=((F0+F1*4+F2*2)*h)/3;cout<<"第一个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//2a=0;b=1;h=(b-a)/(2*n);F0=f2(a)+f2(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f2(x);elseF1=F1+f2(x);}S=(F0+F1*4+F2*2)*h/3;cout<<"第二个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//3a=0;b=1;h=(b-a)/(2*n);F0=f3(a)+f3(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f3(x);elseF1=F1+f3(x);}S=(F0+F1*4+F2*2)*h/3;cout<<"第三个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//4a=0;b=1;h=(b-a)/(2*n);F0=f4(a)+f4(b);F1=F2=0;for(j=1;j<2*n;j++){x=a+j*h;if(j%2==0)F2=F2+f4(x);elseF1=F1+f4(x);}S=(F0+F1*4+F2*2)*h/3;cout<<"第四个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl<<endl;cout<<"利用复化梯形公式求积分"<<endl;//1a=0;b=0.25*3.141592;h=(b-a)/n;F0=f1(a)+f1(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f1(x);}S=((F0+F1*2)*h)/2;cout<<"第一个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//2a=0;b=1;h=(b-a)/n;F0=f2(a)+f2(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f2(x);}S=((F0+F1*2)*h)/2;cout<<"第二个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//3a=0;b=1;h=(b-a)/n;F0=f3(a)+f3(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f3(x);}S=((F0+F1*2)*h)/2;cout<<"第三个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;//4a=0;b=1;h=(b-a)/n;F0=f4(a)+f4(b);F1=0;for(j=1;j<n;j++){x=a+j*h;F1=F1+f4(x);}S=((F0+F1*2)*h)/2;cout<<"第四个积分公式:端点a为"<<a<<"、b为"<<b<<",n为"<<n<<endl<<"结果为"<<S<<endl;return 0;}五.实验结果六.实验心得:通过本次实验,我掌握了求数值积分的各种方法。
复化梯形公式和复化辛普生公式

(英文版)Two regulations promulgated for implementation is in the party in power for a long time and the rule of law conditions, the implementation of comprehensive strictly strategic plan, implementation in accordance with the rules and discipline to manage the party, strengthen inner-party supervision of major initiatives. The two regulations supporting each other, the < code > adhere to a positive advocate, focusing on morality is of Party members and Party leading cadres can see, enough to get a high standard; < rule > around the party discipline, disciplinary ruler requirements, listed as "negative list, focusing on vertical gauge, draw the party organizations and Party members do not touch the" bottom line ". Here, the main from four square face two party rules of interpretation: the first part introduces two party Revised regulations the necessity and the revision process; the second part is the interpretation of the two fundamental principles of the revision of laws and regulations in the party; the third part introduces two party regulations modified the main changes and needs to grasp several key problems; the fourth part on how to grasp the implementation of the two regulations of the party. < code > and < Regulations > revised the necessity and revised history of the CPC Central Committee the amendment to the Chinese CommunistParty members and leading cadres honest politics several guidelines > and < Chinese Communist Party discipline and Punishment Regulations > column 1 by 2015 to strengthen party laws and regulations focus. Two party regulations revision work lasted a Years, pooling the wisdom of the whole party, ideological consensus, draw historical experience, respect for the wisdom of our predecessors, which reflects the unity of inheritance and innovation; follow the correct direction, grasp the limited goals, adhere to the party's leadership, to solve the masses of the people reflect a focus on the problem. The new revision of the < code > and < rule >, reflects the party's 18 and the eighth session of the third, the spirit of the fourth plenary session, reflecting the experience of studying and implementing the General Secretary Xi Jinping series of important speech, reflects the party's eighteen years comprehensive strictly practice. (a) revised two regulations of the party need of < the ICAC guidelines > in < in 1997 Leaders as members of the Communist Party of China clean politics certain criteria (Trial) > based on revised, the promulgation and implementation of January 2010, to strengthen the construction of the contingent of leading cadres play an important role. But with the party to manage the party strictly administering the deepening, has not been able to fully meet the actual needs. Content is toocomplicated, "eight prohibition, 52 are not allowed to" hard to remember, and also difficult to put into practice; the second is concisely positive advocated by the lack of prohibited provisions excessive, no autonomy requirements; the third is banned terms and discipline law, both with the party discipline, disciplinary regulations repeat and Criminal law and other laws and regulations repeat; the fourth is to "clean" the theme is not prominent, not for the existing problems, and is narrow, only needle of county-level leading cadres above. < rule > is in 1997 < Chinese Communist Party disciplinary cases (Trial) > based on revision, in December 2003 the promulgation and implementation, to strengthen the construction of the party play very important role. Along with the development of the situation, which many provisions have been unable to fully meet the comprehensive strictly administering the practice needs. One is Ji law, more than half of the provisions and criminal law and other countries laws and regulations Repetition; two is the political discipline regulations is not prominent, not specific, for violation of the party constitution, damage the authority of Party Constitution of misconduct lack necessary and serious responsibility to pursue; third is the main discipline for the leading cadres, does not cover all Party members. Based on the above situation, need to < the criterion of a clean and honestadministration > and < rule > the two is likely to be more relevant regulations first amendment. By revising, really put the authority of Party discipline, the seriousness in the party tree and call up the majority of Party members and cadres of the party constitution of party compasses party consciousness. (II) two party regulations revision process the Central Committee of the Communist Party of China attaches great importance to two regulations revision . Xi Jinping, general books recorded in the Fifth Plenary Session of the eighth session of the Central Commission for Discipline Inspection, on the revised regulations < > made clear instructions. According to the central deployment, the Central Commission for Discipline Inspection from 2014 under six months begin study two regulations revision. The Standing Committee of the Central Commission for Discipline Inspection 4 review revised. Comrade Wang Qishan 14 times held a special meeting to study two regulations revision, amendment clarifies the direction, major issues of principle, path and target, respectively held a forum will listen to part of the province (area) secretary of the Party committee, Secretary of the Discipline Inspection Commission, part of the central ministries and state organs DepartmentThe first party committee is mainly responsible for people, views of experts and scholars and grassroots party organizations andParty members. Approved by the Central Committee of the Communist Party of China, on 7 September 2015, the general office of the Central Committee of the Party issued a notice to solicit the provinces (autonomous regions, municipalities) Party, the central ministries and commissions, state ministries and commissions of the Party (party), the General Political Department of the military, every 3 people organization of Party of two regulations revision opinion. Central Commission for Discipline Inspection of extensive solicitation of opinions, careful study, attracting, formed a revised sent reviewers. In October 8 and October 12, Central Committee Political Bureau Standing Committee and the Political Bureau of the Central Committee After consideration of the two regulations revised draft. On October 18, the Central Committee of the Communist Party of China formally issued two regulations. Can say, two laws amendment concentrated the wisdom of the whole party, embodies the party. Second, < code > and < Regulations > revision of the basic principles of two party regulations revision work and implement the party's eighteen, ten eight plenary, the spirit of the Fourth Plenary Session of the Eleventh Central Committee and General Secretary Xi Jinping important instructions on the revised < low political criterion > and < Regulations >, highlighting the ruling partycharacteristics, serious discipline, the discipline quite in front of the law, based on the current, a long-term, advance as a whole, with Bu Xiuding independent < rule > and < rule >. Main principle is: first, adhere to the party constitution to follow. The constitution about discipline and self-discipline required specific, awaken the party constitution of party compasses party consciousness, maintaining the authority of the constitution. General Secretary Xi Jinping pointed out that "no rules, no side round. Party constitution is the fundamental law, the party must follow the general rules. In early 2015 held the eighth session of the Central Commission for Discipline Inspection Fifth Plenary Session of the 16th Central Committee, Xi Jinping again pointed out that constitution is the party must follow the general rules, but also the general rules." the revision of the < code > and < rule > is Method in adhere to the regulations established for the purpose of combining rule of virtue is to adhere to the party constitution as a fundamental to follow, the constitution authority set up, wake up the party constitution and party rules the sense of discipline, the party constitution about discipline and self-discipline specific requirements. 4 second is to adhere to in accordance with the regulations governing the party and the party. The Party of rule of virtue "de", mainly refers to the party's ideals and beliefs, excellent traditional style. The revised the< code > closely linked to the "self-discipline", insisting on the positive initiative, for all members, highlight the "vital few", emphasized self-discipline, focusing on the morality, and the majority of Party members and the ideological and moral standards. The revised < > Ji method separately, Ji, Ji Yan to Method, as a "negative list", emphasizing the heteronomy, focusing on vertical gauge. Is this one high and one low, a positive reaction, the strict party discipline and practice results transformation for the integration of the whole party to observe moral and discipline requirements, for the majority of Party members and cadres provides benchmarking and ruler. Third, insist on to. In view of the problems existing in the party at the present stage, the main problems of Party members and cadres in the aspect of self-discipline and abide by the discipline to make clearly defined, especially the party's eighteen years strict political discipline and political rules, organization and discipline and to implement the central eight provisions of the spirit against the four winds and other requirements into Disciplinary provisions. Not one pace reachs the designated position, focusing on in line with reality, pragmatic and effective. After the revision of major changes, major changes in the < code > and < rule > modified and needs to grasp several key problems (a) < code > < code > adhere to according to regulationsgoverning the party and party with morals in combination, for at the present stage, the leadership of the party members and cadres and Party members in existing main problems of self-discipline, put forward principles, requirements and specifications, showing Communists noble moral pursuit, reflected at all times and in all over the world ethics from high from low 5 common requirements. One is closely linked to the "self-discipline", removal and no direct relation to the provisions of . the second is adhere to a positive advocate, "eight prohibition" 52 are not allowed to "about the content of the" negative list moved into synchronization amendment < cases >. Three is for all the party members, will apply object from the leadership of the party members and cadres to expand to all Party members, fully embodies the comprehensive strictly required. The fourth is prominent key minority, seize the leadership of the party members and cadres is the key, and put forward higher requirements than the ordinary Party members. Five is to simplify, and strive to achieve concise, easy to understand, easy to remember. The revised < code > is the ruling Party since the first insists on a positive advocate forAll Party members and the self-discipline norms, moral declaration issued to all members of the party and the National People's solemn commitment. > < criterion of a clean and honest administration consists of 4 parts, 18,more than 3600 words. After the revision of the < code >, a total of eight, 281 words, including lead, specification and Party member cadre clean fingered self-discipline norms, etc. Part 3 members low-cost clean and self-discipline, the main contents can be summarized as "four must" "eight code". Lead part, reiterated on ideal and faith, fundamental purpose, the fine traditions and work style, noble sentiments, such as "four must" the principle of requirements, strong tone of self-discipline, The higher request for 6 and supervised tenet, the foothold in permanent Bao the party's advanced nature and purity, to reflect the revised standards requirements. Members of self-discipline norms around the party members how to correctly treat and deal with the "public and private", "cheap and rot" thrifty and extravagance "bitter music", put forward the "four norms". Party leader cadre clean fingered self-discipline norms for the leadership of the party members and cadres of the "vital few", around the "clean politics", from civil servant of the color, the exercise of power, moral integrity, a good family tradition and other aspects of the leadership of the party members and cadres of the "four norms" < > < norm norm. "The Party member's self-discipline norms" and "party members and leading cadre clean fingered self-discipline norms," a total of eight, collectively referred to as the "eight". "Four must" and "eight" of thecontent from the party constitution and Party's several generation of leaders, especially Xi Jinping, general secretary of the important discussion, refer to the "three discipline and eight points for attention" statements, and reference some embody the Chinese nation excellent traditional culture essence of epigrams. (2) the revised regulations, the main changes in the revised Regulations > to fully adapt to the strictly requirements, reflects the according to the regulations governing the law of recognition of deepening, the realization of the discipline construction and Jin Ju. < rule > is party a ruler, members of the basic line and follow. And the majority of Party members and cadres of Party organizations at all levels should adhere to the bottom line of thinking, fear discipline, hold the bottom line, as a preventive measure, to keep the party's advanced nature and purity. 1, respect for the constitution, refinement and discipline. Revised < rule > from comprehensive comb physical constitution began, the party constitution and other regulations of the Party of Party organizations and Party discipline requirements refinement, clearly defined in violation of the party constitution will be in accordance with regulations to give the corresponding disciplinary action. The original 10 categories of misconduct, integration specification for political discipline, discipline, honesty and discipline masses Ji Law and discipline and discipline andother six categories, the content of < rule > real return to Party discipline, for the majority of Party members and listed a "negative list. 7 2, highlighting the political discipline and political rules. > < Regulations according to the stage of the discipline of outstanding performance, emphasizing political discipline and political rules, organization and discipline, in opposition to the party's leadership and the party's basic theory, basic line, basic program and basic experience, the basic requirement of behavior made prescribed punishment, increase the cliques, against the organization such as violation of the provisions, to ensure that the central government decrees and the Party of centralized and unified. 3, adhere to strict discipline in the law and discipline In front, Ji separated. Revised < Regulations > adhere to the problem oriented, do Ji separated. Any national law existing content, will not repeat the provisions, the total removal of 79 and criminal law, repeat the content of the public security management punishment law, and other laws and regulations. In the general reiterated that party organizations and Party members must conscientiously accept the party's discipline, die van comply with national laws and regulations; at the same time, to investigate violations of Party members and even criminal behavior of Party discipline and responsibility, > < Regulations distinguish five different conditions, with special provisions weremade provisions, so as to realize the connection of Party discipline and state law. 4, reflect Wind building and anti-corruption struggle of the latest achievements. < rule > the party's eighteen years implement the spirit of the central provisions of the eight, against the requirements of the "four winds" and transformation for disciplinary provisions, reflecting the style construction is always on the road, not a gust of wind. In the fight against corruption out of new problems, increase the trading rights, the use of authority relatives profit and other disciplinary terms. Prominent discipline of the masses, the new against the interests of the masses and ignore the demands of the masses and other disciplinary terms and make provisions of the disposition and the destruction of the party's close ties with the masses.Discipline to protect the party's purpose. 8 of these regulations, a total of three series, Chapter 15, 178, more than 24000 words, after the revision of the regulations a total of 3 series, Chapter 11, 133, 17000 words, divided into "general" and "special provisions" and "Supplementary Provisions" Part 3. Among them, add, delete, modify the provisions of the proportion of up to nearly 90%. 1, the general general is divided into five chapters. The first chapter to the regulations of the guiding ideology, principles and scope of application of the provisions, highlight the strengthening of the partyconstitution consciousness, maintenance the authority of Party Constitution, increase the party organizations and Party members must abide by the party constitution, Yan Centralized centralized, would examine at all levels of the amended provisions implementing and maintaining Party discipline, and consciously accept the party discipline, exemplary compliance with national laws and regulations. The second chapter of discipline concept, disciplinary action types and effects of the regulations, will be a serious warning from the original a year for a year and a half; increase the Party Congress representative, by leaving the party above (including leave probation) punishment, the party organization should be terminated its representative qualification provisions. The third chapter of the disciplinary rules of use prescribed in the discipline rectifying process, non convergence, not close hand classified as severely or heavier punishment. "Discipline straighten "At least eighteen years of five years, these five years is to pay close attention to the provisions of the central eight implementation and anti -" four winds ". The fourth chapter on suspicion of illegal party disciplinary distinguish five different conditions, with special provisions were made provisions, to achieve effective convergence of Party and country 9 method. < rule > the provisions of Article 27, Party organizations in thedisciplinary review found that party members have committed embezzlement, bribery, dereliction of duty dereliction of duty and other criminal law act is suspected of committing a crime shall give cancel party posts, probation or expelled from the party. The second is < Regulations > Article 28 the provisions of Party organizations in the disciplinary review But found that party members are stipulated in the criminal law, although not involved in a crime shall be investigated for Party discipline and responsibility should be depending on the specific circumstances shall be given a warning until expelled punishment. This situation and a difference is that the former regulation behavior has been suspected of a crime, the feeling is quite strict, and the latter for the behavior not involving crime, only the objective performance of the provisions of the criminal code of behavior, but the plot is a crime to slightly. < Regulations > the 29 provisions, Party organizations in the discipline review found that party members and other illegal behavior, affect the party's image, the damage to the party, the state and the people's interests, we should depend on the situation Seriousness given disciplinary action. The loss of Party members, seriously damaging the party's image of behavior, should be given expelled from the party. At this article is party member is in violation of the criminal law outside the other illegal acts, such as violatesthe public security administration punishment law, customs law, financial laws and regulations behavior. The fourth is < cases > Article 32 stipulates, minor party members and the circumstances of the crime, the people's Procuratorate shall make a decision not to initiate a prosecution, or the people's court shall make a conviction and exempted from criminal punishment shall be given within the party is removed from his post, probation or expelled from the party. Party members and crime, sheets were fined in accordance with For acts; the principal Ordinance amended the provisions of the preceding paragraph. This is the new content, in order to achieve Ji method effective convergence. Five is < > the thirty third article 10 of the provisions, the Party member due to an intentional crime is sentenced to criminal law (including probation) sheets or additional deprivation of political rights; due to negligence crime and was sentenced to three years or more (excluding three years) a penalty, shall give expelled punishment. Due to negligence crime is convicted and sentenced to three years (including three years) in prison or be sentenced to public surveillance, detention, shall in general be expelled from the party. For the individual may not be expelled from the party, should control Approval. This is followed and retained the original > < Regulations the provisions of punishment party authorization rules and report to a level partyorganizations. For is "party members with criminal acts, and by the criminal punishment, generally should be expelled from the party". The fifth chapter of probationary Party member of the discipline and discipline after missing members of the treatment and punishment decisions, such as the implementation of the provisions, clear the related party discipline and punishment decision made after, for duties, wages and other relevant alteration formalities for the longest time. 2, sub sub section will the original regulations of10 categories of acts of violation of discipline integration revised into 6 categories, respectively, in violation of the punishments for acts of political discipline "in violation of discipline behavior of punishment" in violation of integrity of disciplinary action points "of violation punishments for acts of mass discipline" "the violation of work discipline, punishment" in violation of discipline of life behavior punishment "6 chapters. 3, annex" Supplementary Provisions "clear authority making supplementary provisions of, cases of interpretative organ, as well as regulations implementation time and retroactivity etc.. 11 (3) learning understanding > < regulations needs to grasp several key problems The first problem -- about the violation of political discipline behavior > < new ordinance chapter 6 the political discipline column for the six disciplines, that is the main opposition to Party leadership and the opposition of the basictheory, basic line, basic program and basic experience, basic requirements of misconduct made provisions of the disposition, especially the eighteen since the CPC Central Committee put forward the Yan Mingzheng treatment of discipline and political rules requirements and practical achievements transformation for Discipline article, increase the false debate central policies, cliques, against the organization review, make no discipline of the principle of harmony terms. These are the party's eighteen years in comprehensive strictly Process combined with the practice of rich content. (1) false debate the central policies and undermine the Party of centralized and unified the problem is made in accordance with the provisions of the party constitution. Constitution in general programme requirements adhere to democratic centralism is one of the requirements of the construction of the party must adhere to the four cardinal. Application of this principle is not only the party the basic organization principle and is also the mass line in party life, it requires that we must fully develop inner-party democracy, respect for the dominant position of Party members, safeguarding the Party member democratic rights, give full play to the enthusiasm and creativity of the party organizations at all levels and Party members, at the same time, also must implement the right concentration, ensure the party's mission < the chaos in unity and concertedaction to ensure that the party's decision to get quickly and effectively implementing. The Party Central Committee formulated the major principles and policies, through different channels and ways, fully listen to the party organizations and Party members of the opinions and suggestions, but 12 is some people face to face not to say back blather "" will not say, after the meeting said, "" Taiwan does not say, and nonsense ", in fact, not only disrupt the people thought, some causing serious consequences, the damage to the Party of the centralized and unified, hinder the central policy implementation, but also a serious violation of the democratic system of principles. There is no doubt that shall, in accordance with the Regulations > 4 Specified in Article 6 to give the appropriate punishment. For did not cause serious consequences, to give criticism and education or the corresponding tissue processing. (2) about the destruction of the party's unity < New Regulations > the forty eighth to fifty second article, to damage Party's unity unified and violation of political discipline, punishment situation made explicit provisions. Article 52 of the new "in the party get round group, gangs seek private gain, cliques, cultivate private forces or through the exchange of interests, for their own to create momentum and other activities to gain political capital, given a serious warning or withdraw from their party posts disposition; if thecircumstances are serious, to give Leave a party to observation or expelled from the party. (3) on against the organization review of the provisions of the constitution, party loyalty honesty is party members must comply with the obligations. Members must obey the organization decision, shall not violate the organization decided encounters by asking questions to find organization, rely on the organization, shall not deceive the organization, against the organization. For example, after the investigation does not take the initiative to explain the situation, but to engage in offensive and defensive alliance, hiding the stolen money is against survey organization, is a violation of the behavior of political discipline. Article 24 of the original > < Regulations, although the provisions of the interference, hinder group review the behavior of the fabric can be severely or 13 Aggravated punishment, but did not put this kind of behavior alone as a discipline for qualitative amount of discipline. > < new regulations increase the Article 57, "anti organization review, one of the following acts, given a warning or serious warning; if the circumstances are relatively serious, giving removed from or placed on probation within the party post; if the circumstances are serious, give expelled from the party: (a) on supply or forged, destroyed, transfer, conceal evidence; (II) to prevent others expose, providing evidence。
复合梯形公式

《复合梯形公式》实验报告实验名称:复合梯形公式成绩: ___________专业班级:数学与应用数学1202班姓名:张晓彤学号:2012254010227实验日期:2014年11月23日实验报告日期:2014年11月3日一、实验目的(1) 掌握数值积分函数的调用格式(2) 掌握复合梯形公式的思想和构造过程(3) 能够应用matlab软件编写复合梯形公式的程序并能熟悉应用,以此来解决相关例题(4) 利用复合梯形公式求数值积分的近似值,以解决其它科学实验的计算问题二、实验内容2.1验证积分函数的调用格式并求函数积分值1 2例1:用两种不同的方法求:I 0e x dx .1 2 v2 :c o例2:计算二重积分I 1 e sin( x2y)dxdy2.2编写复合梯形公式程序并验证1 2例:用符合梯形求积公式求积分I 0e x sinxdx的近似值.要求将区间3等分,4的等分,6等分,9等分,分别得到积分值,并与真值进行比较•能得到什么结论?三、实验环境该实验应用matlab2014来进行实验的验证和设计.四、实验步骤和实验结果4.1验证积分函数的调用格式并求函数积分值1 x2例3:(数值积分)用两种不同的方法求:I 0e x dx .法一:建立被积函数文件法:先建立一个函数文件ex.m:fun cti on ex=ex(x)ex=exp(-x.A2);end然后在MATLAB^令窗口,输入命令:format longI=quad( 'ex' ,0,1)I =0.746824180726425I=quadl( 'ex' ,0,1)I =0.746824133988447法二:不建立关于被积函数的函数文件时:g=i nline( 'exp(-x.A2)' );I=quadl(g,0,1)I =0.7468241339884471 2 2y )dxdy 例4:(数值积分)计算二重积分I 1 e x 2sin( X2(1)建立一个m文件fxy.mfun cti on f=fxy(x,y)global ki;ki=ki+1;f=exp(-x42/2).*si n(x42+y);(2) 调用dblquad 函数求解global ki;ki=0;I=dblquad( 'fxy' ,-2,2,-1,1)KiI =1.574493189744944ki =1050使用inline 函数不建立被积函数的函数文件,程序如下:f=inline( 'exp(-x.A2/2).*sin(x.A2+y)' , 'x' , 'y');I=dblquad(f,-2,2,-1,1)I =1.5744931897449444.2 编写复合梯形公式程序并验证12例:用符合梯形求积公式求积分I e x sinxdx的近似值.要求将区间3等分,4的等分,6等分,9等分,分别得到积分值,并与真值进行比较.能得到什么结论?建立复合梯形公式的fhTX.m 文件:function [H] = fhTX(a,b,n)%ab分别是积分函数的上下限%%门为区间等分份数%%I返回的是得到的积分近似值%h=(b-a)/n; %h为步长%I=0;x=a:h:b; % 等分点出的节点Xi%f=exp(x.A2).*sin(x); %被积函数表达式%for k=1:n; %节点xi开始循环%J=f(k)+f(k+1); % 复合梯形公式的递推公式%I=I+J; %递推公式求和%end H=I*h/2;End(1) 将区间3 等分得到结果H=fhTX(0,1,3) %函数调用%H =0.8246 %得到近似解%I仁quad('exp(x.A2).*sin(x)',0,1) %quad计算真值%I1 =0.7787R=abs(I1-H) %近似解和真值之间的误差%ans =0.0458所以,将区间 3 等分后得到的结果为0.8246,和真值之间存在的误差为0.0458.2) 将区间4 等分得到的结果H=fhTX(0,1,4) %函数调用%H =0.8047 %得到近似解%abs(I1-H)ans =0.0260 %近似解和真值之间的误差%通过结果可以看出,将区间 4 等分后的结果和真值之间的误差缩小为0.0260,较三等分得到的结果略微良好.3) 将区间6 等分得到的结果H=fhTX(0,1,6) %函数调用%H =0.7904 %得到近似解%abs(I1-H)ans =0.0116 %近似解和真值之间的误差%当区间等分数为 6 时,误差减小到0.0116,比区间等分数为 4 的时候更精确4) 将区间9 等分得到的结果H=fhTX(0,1,9) %函数调用%H =0.7839 %得到近似解%abs(ll-H)ans =0.0052 %近似解和真值之间的误差%这时的误差缩小为0.0052,更加靠近真值了.通过四种不同的等分区间来对积分值进行近似估计,我们可以发现,区间等分份数越多,得到的结果越靠近真值,得到的结果越精确我们用相同的方法得到更多数据的结果入下:从表格中我们很清楚的可以看到在某个较大的范围内,当n越大时,得到的结果和真值越接近,当达到一定程度时,近似值将不会再变化.五、实验讨论、结论通过四种不同的等分区间来对积分值进行近似估计,我们可以发现,区间等分份数越多,得到的结果越靠近真值,得到的结果越精确,但符合梯形公式在对积分值进行估计的过程中存在的问题是:在某个较大的范围内,无论区间等分多少份,或者说无论步长取得多么小,总会存在一个更小的步长h,使得结果过更加精确,但当超过这个规定的范围,当区间等分份数过大时,得到的近似值将不会再变价.所以说,采用梯形公式得到的结果,随着区间等分份数的增多,会越来越接近真值,但永远不能得到最精确的结果.所以,在对某些函数进行积分计算的时候,一些简单的函数我们可以直接进行积分到精确的结果,但是对于一些较复杂,找不到原函数的函数而言,利用复合梯形公式可以很好的得到近似解,它在进行函数积分的过程中起到了很好作用,能解决我们在积分环节的一些问题.六、参考资料【1】李庆阳,王能超,易大义,数值分析第五版,清华大学出版社, 1995.【2】刘卫国,matlab程序设计与应用,高等教育出版社,2002.。
复化梯形公式实验报告

复化梯形公式实验报告
实验目的:
通过实验学习理解复化梯形公式,掌握应用该公式进行数值积分的方法。
实验原理:
复化梯形公式是一个求解定积分的数值积分公式,其基本原理是将积分区间分成若干个小区间,然后在每个小区间中应用梯形公式对积分进行计算。
复化梯形公式的计算公式如下:
∫a b f(x) dx ≈ (h/2)[f(a) + 2f(x1) + 2f(x2) + … + 2f(xn-1) + f(b)]
其中,h = (b-a)/n,n表示分割成n个小区间,x1,x2,…,xn-1表示分割点。
实验步骤:
1. 选择一个函数,例如f(x) = x^2。
2. 确定积分区间,例如a = 0,b = 1。
3. 设置分割数n,例如n = 4。
4. 根据公式计算复化梯形公式的积分近似值。
5. 求解真实值,即∫a b f(x) dx = 1/3。
6. 计算误差,即计算近似值与真实值的差。
实验结果:
当选择f(x) = x^2,积分区间a = 0,b = 1,分割数n = 4时,运用复化梯形公式可得近似值为0.34375,真实值为1/3,误差为
0.01302。
实验结论:
通过实验,我们掌握了复化梯形公式的计算方法以及应用该公式
进行数值积分的方法。
同时,我们还发现复化梯形公式的计算精度受到分割数的影响,分割数越大,计算精度越高。
复化梯形求积公式

第二章1.1复合梯形求积公式复合梯形求积公式是复合求积法的一种,在本章中,将从其原理、概念等方面对它做一个详细介绍。
在本章的最后,会对复合梯形求积法进行程序设计,使得可以从不同的方面对这种方法有更深的理解。
1.1.1 复合梯形求积公式的理论当积分区间[a ,b]的长度较大,而节点个数1+n 固定时,直接使用Newton-Cotes 公式的余项将会较大。
但是如果增加节点个数,即1+n 增加时,公式的舍入误差又很难得到控制。
为了提高公式的精度,又使算法简单易行,往往使用复化方法。
即将积分区间][b a ,分成若干子区间,然后在每个小区间上使用低阶Newton-Cotes 公,最后将每个小区间上的积分的近似值相加,这就叫做复合求积法。
而复合梯形求积公式就是复合求积法的一种。
1.1.2复合求积公式的原理将区间[]b a ,划分为n 等分,分点,,,1,0,,n k nab h kh a x k =-=+= 在每个子区间[](),1,,1,0,1-=+n k x x k k 上采用梯形公式,则得[])()()(2)()(1111f R x f x f h dx x f dx x f I n k n k k ban k x x k k++===+-=-=∑⎰∑⎰+记()[()]()[()()]∑∑-=+-=++=+=11110222n k b k k n k k n x f x f a f hx f x f h T , (1.1)称为复合梯形公式,其余项可由)().,(),(12][''3b a f a b f R ∈--=ηη得()()()110''3,12+-=∈⎥⎦⎤⎢⎣⎡-=-=∑k k k n k k n n x x f h T I f R ηη由于[],,)(2b a C x f ∈ 且()(),max 1min 1010''''10-≤≤-=-≤≤≤≤∑n k k n k k n k f n f ηη所以()b a ,∈∃η使()()k n k f n f ηη∑-==10''''1于是复合梯形公式的余项为()()η''212f h a b f R n --= 可以看出误差是2h 阶,且由()()η''212f h a b f R n --= 式立即得到,当][b a C x f ,)(2∈时,则(),lim dx x f T ba n n ⎰=∞→即复合梯形公式是收敛的.事实上只要设()[]b a C x f ,∈,则可得收敛性,只要把n T 改写成为()()]∑∑=-=-+⎢⎣⎡-=nk k n k k n x f n a b x f n a b T 11021当∞→n 时,上式右端括号内的两个和式均收敛到积分()dx x f ba ⎰,所以复合梯形公式(1.1)收敛.此外,n T 的求积系数为正,由定理可知复合梯形公式是稳定的。
复化梯形求积公式

复化梯形求积公式复化梯形求积法是一种用于数值积分的常见方法,它可以帮助我们求解一元定积分(即 integrals 或者是积分函数)。
在复化梯形求积法中,我们需要对函数 f(x) 在某一区间 [a,b]内的值进行插值,并将插值后的函数值相加,以计算该函数在该区间上的积分值。
复化梯形求积法的步骤如下:第一步:分解积分区间[a,b],将其分解为 n 个子区间,其中区间长度为 h=(b-a)/n。
第二步:对积分区间[a,b] 中每个子区间使用复化梯形公式来计算它们的积分值。
根据复化梯形求积公式,积分区间 [a,b] 中每个子区间的积分值如下:Ii = h/2 * [f(xi) + f(xi+1)] (i=0,1,...,n-1)其中,xi 是第 i 个(0≤i≤n-1)子区间的左端点,xi+1 是第 i 个子区间的右端点,f(xi) 是第 i 个子区间左端点处的函数值,f(xi+1) 是第 i 个子区间右端点处的函数值。
第三步:将所有子区间积分值进行累加,得到积分区间[a,b]的总积分值。
按照复化梯形求积法,积分区间 [a,b] 的总积分值计算公式如下:I=h/2 * [f(x0)+f(xn)+∑(i=1,2,...,n-1)[f(xi)+f(xi+1)]]以上就是复化梯形求积法的基本原理及其用于求解一元定积分的步骤:首先将积分区间分解为子区间,然后使用复化梯形公式计算每个子区间的积分值,最后将子区间积分值相加得到积分区间的总积分值。
这种求积方法容易理解,计算量小,计算速度快,因此复化梯形求积法在积分计算中有着重要的应用价值。
在复化梯形求积法中,可以使用高斯公式来加快积分值的计算。
高斯公式的定义如下:I=h/2 * [f(x0)+f(xn)+c1f(x1)+c2f(x2)+...+cnf(xn-1)]其中,c1,...,cn 是某些常数,x1,...,xn-1 为积分区间上的中点。
应用高斯公式,可以将积分计算量减小一半以上,同时也大大减少计算精度上的误差。
数值分析复化梯形公式复化公式程序

数值分析复化梯形公式复化公式程序
分别用复化梯形公式、复化Simpson 公式计算定积分dx e x ?+201,取n=2,4,8,16分别验证结果(精确值I=)。
复化梯形公式求定积分:
function I=tquad(x,y)
%复化梯形求积公式,其中,
%x 为向量,被积函数自变量的等距结点; %y 为向量,被积函数在结点处的函数值; n=length(x);
m=length(y);
%积分自变量的结点数应与它的函数值的个数相同h=(x(n)-x(1))/(n-1);
a=[1 2*ones(1,n-2) 1];
I=h/2*sum(a.*y);
复化Simpson 公式求定积分:
function I=squad(x,y)
%复化Simpson 求积公式,其中,
%x 为向量,被积函数自变量的等距结点; %y 为向量,被积函数在结点处的函数值; n=length(x);
m=length(y);
%积分自变量的结点数应与它的函数值的个数相同if rem(n-1,2)~=0
I=tquad(x,y);
return;
end
N=(n-1)/2;
h=(x(n)-x(1))/N;
a=zeros(1,n);
for k=1:N
a(2*k-1)=a(2*k-1)+1;
a(2*k)=a(2*k)+4;
a(2*k+1)=a(2*k+1)+1; end
I=h/6*sum(a.*y);。
复化梯形公式

3、算法程序
#include〈stdio、h>
#include〈math、h〉
#include〈iostream〉
usingnamespace std;
#defineN400
floatF(floatx)
{
x=exp(x);
return(x);
}
int main()
{
ﻩfloat a,b,x[N],sum,T;
ﻩintn,i;
printf("pleaseinput n=");
cin〉>n;
printf("please input a=");
cin>〉a;
printf("please inputb=");
cin>>b;
for(i=0;i<n+1;i++)
ﻩ{
x[i]=a+i*(b—a)/(float)n;
ﻩ}
解:运行程序
(1) 显示出 “please in put n=” ,“please in put a=" ,“please in put b=”,依次输入数据,回车.
(2)显示结果如下图:
注:此时;在程序中对应得语句为x=exp(x) ;所求得函数可以定义为其她函数得出目标函数得结果.
例2:利用复化梯形公式计算函数,求在以1为下界,2为上界,把区间分为2等分(复化梯形公式计算在得值).
2012-2013(1)专业课程实践论文
复化梯形公式
余良,0818180125,R数学08-1班
一、算法理论
求得值就是科学技术中经常遇到得计算问题 ,但在很多情况下 ,得原函数不易求得 ,或非常复杂 ;另外 ,在一些应用中 ,函数 就是用函数表形式给出而没有解析式 ,这时就采用定积分得数值计算方法 ,以解决定积分得近似计算.数值求积公式得应用不仅在近似计算本身 ,在初等数学中 ,某些数列求前 n项之与公式得推导颇为繁琐 ,应用复化梯形公式可方便地导出这些公式。复化梯形公式用牛顿—-莱不尼茨公式来计算得值得前提就是 :得原函数能够求出。当 得原函数不易求出或找不到时 ,希望用一个易于求原函数得函数来近似代替被积函数 ,从而得到定积分得近似计算公式。下文中梯形公式就就是常用得近似计算公式.
合肥工业大学计算机专业计算方法实验报告
合肥⼯业⼤学计算机专业计算⽅法实验报告合肥⼯业⼤学计算机与信息学院实验报告课程:计算⽅法专业班级:学号:姓名:Java界⾯其实都不难按照程序流程图就可以完成了实验⼀插值与拟合⼀、实验⽬的(1) 明确插值多项式和分段插值多项式各⾃的优缺点;(2) 编程实现三次样条插值算法,分析实验结果体会⾼次插值产⽣的龙格现象;(3) 理解最⼩⼆乘拟合,并编程实现线性拟合,掌握⾮线性拟合转化为线性拟合的⽅法 (4) 运⽤常⽤的插值和拟合⽅法解决实际问题。
数据如下:j x 165 123 150 123 141 j y187126172125148三、基本原理(计算公式)(1)三次样条插值在每个内节点上具有2阶导数。
(2)最⼩⼆乘法拟合直线为y=a+bx ,⽽a ,b 有如下等式(N 为给出的数据点的总个数)i i y x b N =+∑a ; ∑∑∑=+i i i i y x x b x 2a四、算法设计与实现(流程图,关键点)最⼩⼆乘法直线拟合:输⼊数据后,按照公式计算a,b。
⽤得到的拟合直线计算预测点的近似函数值。
五、输⼊与输出(1)三次样条插值输⼊:区间长度,n+1个数据点,预测点输出:预测点的近似函数值,精确值,及误差(2)最⼩⼆乘法直线拟合六、结果讨论和分析代码三次样条插值#include#include#define N 10using namespace std; double u0(double x){ return (x-1)*(x-1)*(2*x+1);return x*x*(3-2*x);}double v0(double x){return x*(x-1)*(x-1);}double v1(double x){return x*x*(x-1);}double s3(double x,double y,double y1,double m,double m1,double h){ return u0(x)*y+u1(x)*y1+h*v0(x)*m+h*v1(x)*m1; }double f(double x){return 1/(1+x*x);}int main(){ifstream fin;fin.open("E:\\t.txt");if(!fin){cout<<"error opening input stream"<system("pause");return 0;}double x[N+1],y[N+1],m[N+1],A[N],B[N],C[N];double h[N];double a[N],b[N];double f0,fn;double temp;int i;for(i=0;i<=N;i++){fin>>x[i]>>y[i];}fin>>f0>>fn;h[0]=x[1]-x[0];for(i=1;ib[i]=3*((1-a[i])*(y[i]-y[i-1])/h[i-1]+a[i]*(y[i+1]-y[i])/h[i]);}m[1]=b[1]-(1-a[1])*f0;m[N-1]=b[N-1]-a[N-1]*fn;for(i=2;im[i]=b[i];}for(i=1;iB[i]=2;C[i]=a[i];}for(i=2;iA[i]=1-a[i];}C[1]=C[1]/B[1];m[1]=m[1]/B[1];double t;for(i=2;i!=N-2;i++){t=B[i]-C[i-1]*A[i];C[i]=C[i]/t;m[i]=(m[i]-m[i-1]*A[i])/t;}m[N-1]=(m[N-1]-m[N-2]*A[N-1])/(B[N-1]-C[N-2]*A[N-1]); for(i=N-2;i>0;i--){m[i]=m[i]-C[i]*m[i+1];}cout<<"please:(输⼊插值节点在"<while(cin>>temp){double tt=temp;if(tempx[N]){cout<<"插值节点为"<continue;}}temp=(temp-x[i-1])/h[i-1];temp=s3(temp,y[i-1],y[i],m[i-1],m[i],h[i-1]); cout<<"插值节点为"<}system("pause");fin.close();return 0;}最⼩⼆乘法的直线拟合#include#include#define n 5using namespace std;double sum(double x[],int k){int i;double sum=0;for(i=0;isum=sum+x[i];return sum;}double sum2(double x[],int k){int i;double sum=0;for(i=0;isum=sum+x[i]*x[i];return sum;}double sumxy(double x[],double y[],int k){ int i;double sum=0;for(i=0;isum=sum+x[i]*y[i];int main(){ifstream fin;fin.open("E:\\t.txt");if(!fin){cout<<"error opening input stream"<system("pause");return 0;}double x[n],y[n],a,b;double x0,y0;int i;for(i=0;ifin>>x[i]>>y[i];}b=(n*sumxy(x,y,n)-sum(x,n)*sum(y,n))/(n*sum2(x,n)-sum(x,n)*sum(x,n));a=(sum(y,n)-b*sum(x,n))/n;cout<<"最⼩⼆乘法直线拟合得到a: "<cout<<"请输⼊插值节点x:";while(cin>>x0){y0=a+b*x0;cout<<"当x="<cout<<"请输⼊插值节点x:";}system("pause");fin.close();return 0;}实验⼆数值积分⼀、实验⽬的(1)熟悉复化梯形⽅法、复化Simpson⽅法、梯形递推算法、龙贝格算法;(2)能编程实现龙贝格算法和中点加速;(3)理解并掌握⾃适应算法和收敛加速算法的基本思想;(4)分析实验结果体会各种⽅法的精确度,建⽴计算机求解定积分问题的感性认识x1sin (2)⽤中点加速⽅法计算xe 的⼀阶导数三、基本原理(计算公式)(1)龙贝格算法梯形递推公式∑-=++=10212)(22n k k n n x f h T T加权平均公式:n n n S T T =--1442 n n n C S S =--144222 n nn R C C =--144323 (2)中点加速中点公式: G(h)=(f(a+h)-f(a-h))/2/h 加权平均:G1(h)=4*G(h/2)/3-G(h)/3 G2(h)=16*G1(h/2)/15-G1(h)/15 G3(h)=64*G2(h/2)/63-G2(h)/63四、算法设计与实现(流程图,关键点)中点加速:输⼊数据后根据公式计算导数值五、输⼊与输出图2.2梯形递推算法流程图图2.3龙贝格算法流程图(1) ⽤龙贝格算法计算dx xx1sin 输⼊:积分区间,误差限输出:序列Tn ,Sn,Cn,Rn 及积分结果 (2)⽤中点加速⽅法计算xe 的⼀阶导数输⼊:求导节点,步长输出:求得的导数值,精确值六、结果讨论和分析代码#includeusing namespace std;double f(double x){if(x==0)return 1;return sin(x)/x;}int main(){ifstream fin;fin.open("E:\\t.txt");if(!fin){cout<<"error opening input stream"< system("pause");return 0;}double a,b,e,t1,t2,s1,s2,c1,c2,r1,r2; double x,h,s;fin>>a>>b>>e;cout<<"积分区间为["<cout<<"k T2 S2 C2 R2"<h=b-a;t1=(f(a)+f(b))*h/2;cout<<0<<" "<int k;for(k=1;k<=10;k++,h=h/2,t1=t2,s1=s2){ s=0;x=a+h/2;do{s=s+f(x);x=x+h;}while(xt2=t1/2+h*s/2;s2=t2+(t2-t1)/3;}c2=s2+(s2-s1)/15;if(k==2){cout<c1=c2;continue;}r2=c2+(c2-c1)/63;cout<if(k==3){r1=r2;c1=c2;continue;}if(fabs(r2-r1)cout<<"数值积分结果为"< break;}r1=r2;c1=c2;}system("pause");return 0;}中点加速算法#include#include#includeusing namespace std; double f(double x){ return exp(x);}}double g(double x,double h){return (f(x+h)-f(x-h))/2/h;}double g1(double x,double h){return 4*g(x,h/2)/3-g(x,h)/3;}double g2(double x,double h){return 16*g1(x,h/2)/15-g1(x,h)/15;}double g3(double x,double h){return 64*g2(x,h/2)/63-g2(x,h)/63;}int main(){ifstream fin;fin.open("E:\\t.txt");if(!fin){cout<<"error opening input stream"<system("pause");return 0;}double a,h;while(fin>>a>>h)cout<<"当x="<<a<< ",步长h="<< h<<",x处⼀阶导数值精确值为"<<f1(a)<<",中点加速求得x处⼀阶导数值为"<<g3(a,h)<<",误差为"<<f1(a)-g3(a,h)<<endl;</p>system("pause");fin.close();return 0;}实验三⾮线性⽅程求根迭代法⼀、实验⽬的(1)熟悉⾮线性⽅程求根简单迭代法,⽜顿迭代及⽜顿下⼭法(2)能编程实现⽜顿下⼭法(3)认识选择迭代格式的重要性(4)对迭代速度建⽴感性的认识;分析实验结果体会初值对迭代的影响⼆、实验内容⽤⽜顿下⼭法解⽅程013=--x x (初值为0.6)三、基本原理(计算公式)求⾮线性⽅程组的解是科学计算常遇到的问题,有很多实际背景.各种算法层出不穷,其中迭代是主流算法。
复化梯形公式和复化辛普森公式的精度比较

实验四、复化梯形公式和复化Simpson公式的精度比较(2学时)一、实验目的与要求1、熟悉复化Simpson公式和复化梯形公式的构造原理;2、熟悉并掌握二者的余项表达式;3、分别求出准确值,复化梯形的近似值,复化Simpson的近似值,并比较后两者的精度;4、从余项表达式,即误差曲线,来观察二者的精度,看哪个更接近于准确值。
二、实验内容:对于函数sin()xf xx=,试利用下表计算积分1sin xI dxx=⎰。
表格如下:注:分别利用复化梯形公式和复化Simpson公式计算,比较哪个精度更好。
其中:积分的准确值0.9460831I=。
三、实验步骤1、熟悉理论知识,并编写相应的程序;2、上机操作,从误差图形上观察误差,并与准确值相比较,看哪个精度更好;3、得出结论,并整理实验报告。
四、实验注意事项1、复化梯形公式,程序主体部分:for n=2:10T(n)=0.5*T(n-1)for i=1:2^(n-2)T(n)=T(n)+(sin((2*i-1)/2^(n-1))/((2*i-1)/2^(n-1)))/2^(n-1);endend2、复化Simpson公式,程序主体部分:for i=1:10n=2.^ix=0:1/n:1f=sin(x)./xf(1)=1s=0for j=1:n/2s=s+f(2*j)endt=0for j=1:(n/2-1)t=t+f(2*j-1)endS(i)=1/3/n*(f(1)+4*s+2*t+f(n+1))end五.实验内容复化梯形公式和复化辛普森公式的引入复化梯形公式:110[(()]2n n k k k h T f x f x -+==+∑;复化辛普森公式:11102[(4()()]6n n k k k k h S f x f x f x -++==++∑; 根据题意和复化梯形公式、复化辛普森公式的原理编辑程序求解代码如下: Matlab 代码clcs=quad('sin(x)./x',0,1)p1=zeros(10,1);p2=zeros(10,1);for k=6:15s1=0;s2=0;x=linspace(0,1,k);y=sin(x)./x;z=(1/(2*(k-1))):(1/(k-1)):1;sz=sin(z)./z;y(1)=1;for i=1:(k-1)s1=s1+0.5*(x(i+1)-x(i))*(y(i)+y(i+1));endfor j=1:(k-1)s2=s2+(1/6)*(x(j+1)-x(j))*(y(j)+y(j+1)+4*sz(j)); endp1(k-5)=s1-s;p2(k-5)=s2-s;endp1;p2;s1=s+p1(4)s2=s+p2(4)format longfor k=1:length(p1)p1(k)=abs(p1(k));p2(k)=abs(p2(k));endp1p2plot(6:1:15,p1,'-r')hold onplot(6:1:15,10000*(p2),'-c') hold off部分程序结果输出:s =0.946083070076534s1 =0.945690863582701s2 =0.946083085384947结果分析根据结果输出可知:积分10sin()xI dxx=⎰的准确值为:I= 0.946083070076534;通过复化梯形公式和复化辛普森公式得到的积分值为:s1 =0.945690863582701:s2 =0.946083085384947;相对误差为:411100 4.1510100S I Iδ--=⨯=⨯; 822100 1.6210100S I Iδ--=⨯=⨯; 显然,从相对误差可知通过辛普森公式得到的结果误差小精度高。
数值分析 实验报告 第七章复化梯形公式

数值分析 实验报告 第七章复化辛普森公式 一,题目:用复化梯形公式计算2441dxx -+⎰,试用误差余项表达式进行分析,欲保证误差不超过指定的ε,须至少将区间[-4,4]多少等分?将此结果与实际计算结果进行比较。
二,源程序1. 用逐次分半技术# include<stdio.h># define e 0.1/*定义函数*/double f(double x){double y;y=1.0/(1.0+x*x);return(y);}void main(){int n,j,k;double T,m,t,H,E;for(n=2;;n++){m=0;t=0;for(j=1;j<=n-1;j++)m=m+f(-4.0+8.0/n*j);T=(8.0/(double)(2*n))*(f(-4)+f(4)+2.0*m);/*复化梯形n 次公式*/for(k=1;k<=n;k++)t=t+f(-4.0+(2.0*k-1.0)*4.0/3.0);H=8.0*t/(double)n; /*分半后的节点的矩形的面积和*/E=((T+H)/2-T)/3.0;/*误差*/if(E<=e&&E>=-e)break;else continue;}printf("%d\n",n-1);printf("%1.10f\n",E);printf("%1.10f\n",T/3.0+2.0*H/3.0);}2. 用误差余项分析# include<stdio.h># include<math.h># define e 0.1double der(double x){double y;y=((-2.0)*x)/((1.0+x*x)*(1.0+x*x));return (y);}void main(){double h,m,E;int n=2;m=der(4)-der(-4);do{h=8.0/(double)n;E=-h*h*m/12;n++;}while(E>e||E<-e);printf("%d\n",n-1);printf("%f\n",E);}三,实验结果1.用逐次分段技术当ε>=0.05时,n=1,I=4.58当ε<0.05时,n不存在2.用误差余项分析当ε=0.01时,n=6当ε=0.001时,n=18四,误差1.用逐次分段技术当ε>=0.05时,E=0.05当ε<0.05时,n不存在2.用误差余项分析当ε=0.01时,E=0.08202当ε=0.001时,E=0.000911五,采用逐次分半技术所得的结果笔算与计算机的结果一致但此方法与例题中直接计算误差所得的结果不一致。
实验6 复合梯形公式

1 实验6 复合梯形公式 (重点)编写函数,实现复合梯形公式,并求解⎰+1
0411
dx x .
算法:
第一步:输入b a ,,ε,置1←n ,a b h -← 第二步:计算)]()([**5.0b f a f h T +=
第三步:计算])*5.0(*[*5.01
∑-=+++=n j jh h a f h T S 第四步:计算T S e -=,置S T ←,n n 2←,h h *5.0← 第五步:若ε≥e 则转到第三步,否则输出T ,结束。
function u=fhtx(a,b,e)
%单独定义函数,所以这里不出现函数的参数。
end
附分组名单:
组 长
第 1组 冯怡纯 罗 佳 马枨煊 李雄伟 第 2组 葛 韵 屈乾宇 王振海 王小曼 第 3组 魏 玲 姚玉婷 蔡文博 薛 姣 第 4组 吴 萍 郭琦慧 袁 鹏 吴昌磊 第 5组 刘鸿亮 唐 朝 裴成黎 张 宏 第 6组 王晓林 李 维 邱建宇 杨 超 第 7组 陈邯蕾 宋 平 邓春燕 张玲玲 第 8组 季海燕 余 雷 林 瑶 谢腾洲。
复化梯形公式

2012-2013(1)专业课程实践论文复化梯形公式余良,0818180125,R数学08-1班一、算法理论求⎰baf ()⎰x baf 的值是科学技术中经常遇到的计算问题 ,但在很多情况下 ,()x f 的原函数不易求得 ,或非常复杂 ;另外 ,在一些应用中 ,函数 ()x f 是用函数表形式给出而没有解析式 ,这时就采用定积分的数值计算方法 ,以解决定积分的近似计算。
数值求积公式的应用不仅在近似计算本身 ,在初等数学中 ,某些数列求前 n 项之和公式的推导颇为繁琐 ,应用复化梯形公式可方便地导出这些公式。
复化梯形公式用牛顿——莱不尼茨公式来计算()⎰x baf 的值的前提是 :()x f 的原函数能够求出。
当 ()x f 的原函数不易求出或找不到时 ,希望用一个易于求原函数的函数来近似代替被积函数 ,从而得到定积分的近似计算公式。
下文中梯形公式T 就是()⎰x baf 常用的近似计算公式。
复化梯形公式的主要思想是利用若干小梯形的面积代替原方程的积分,利用微元法,可以求出坐标面上由函数与坐标轴围城的图像的面积的近似值,符合了计算机计算存储的思想。
下面,我们在探讨复化梯形公式的计算规律。
设将求积区间[]b a ,分成n 等份,则一共有1+n 个分点,按梯形公式()()[]()()()⎥⎦⎤⎢⎣⎡++=+=∑∑-=+-=b f x f a f h x f x f h T n k k k k n k n 11110222计算积分值n T ,需要提供1+n 个函数值。
注意,这里na b h -= 代表步长,分点为kh a x k +=,.,1,0n k ⋅⋅⋅=二、算法框图三、算法程序#include<stdio.h>#include<math.h>#include<iostream>using namespace std;#define N 400float F(float x){x=exp(x) ;return (x ) ;}int main(){float a,b,x[N],sum,T;int n,i;printf("please input n=");cin>>n;printf("please input a=");cin>>a;printf("please input b=");cin>>b;for(i=0;i<n+1;i++){x[i]=a+i*(b-a)/(float)n;}sum=0;for(i=1;i<n;i++){sum=sum+F(x[i]);}T=(b-a)/(2*(float)n)*(F(x[0])+F(x[n])+2*sum);cout<<"T= "<<T<<endl;return 0;}四、算法实现例1:利用复化梯形公式计算⎰21dxe x函数,在以1为下界,2为上界,把区间分为2等分(复化梯形公式计算在2a=bn的值)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cin>>x>>y>>z;
cout<<"根据龙贝格算法求出的精确值为:"<<longbeige(x, y, z)<<endl;
cout<<"K"<<" "<<"T"<<" "<<"S"<<" "<<"C"<<" "<<"R"<<endl;
cout<<"0"<<" "<<tixing(0, 1, 1)<<endl;
复化梯形公式
复化Simpson公式
梯形递推公式
加权平均公式:
龙贝格算法大大加快了误差收敛的速度,由梯形序列O(h2)提高到龙贝格序列的O(h8)
五、程序代码及实验结果
1.主程序
intmain()
{
//cout << longbeige(0, 1, 0.0000001);
cout<<"请输入你的区间和误差限度:"<<endl;
(1)找不到用初等函数表示的原函数
(2)虽然找到了原函数,但因表达式过于复杂而不便计算
(3)f(x)是由测量或计算得到的表格函数
由于以上种种困难,有必要研究积分的数值计算问题。
利用插值多项式 则积分 转化为 ,显然易算。 称为插值型求积公式。最简单的插值型求积公式是梯形公式和Simpson公式,。当求积结点提供较多,可以分段使用少结点的梯形公式和Simpson公式,并称为复化梯形公式、复化Simpson公式。如步长未知,可以通过误差限的控制用区间逐次分半的策略自动选取步长的方法称自适应算法。梯形递推公式给出了区间分半前后的递推关系。由梯形递推公式求得梯形序列,相邻序列值作线性组合得Simpson序列, Simpson序列作线性组合得柯特斯序列, 柯特斯序列作线性组合的龙贝格序列。若|R2-R1|<,则输出R2;否则…依此类推。如此加工数据的过程叫龙贝格算法,如下图所示:
(4)分析实验结果体会各种方法的精确度,建立计算机求解定积分问题的感性认识
三、实验内容及要求
(1)设计复化梯形公式求积算法,编制并调试相应的函数子程序
(2)设计复化辛浦生求积算法,编制并调试相应的函数子程序
(3)用龙贝格算法计算
输入:积分区间,误差限
输出:序列Tn,Sn,Cn,Rn及积分结果(参考书本P81的表2-5)
取n=2,4,8,16,精确解为0.9460831
四、实验原理及算法描述
在许多实际问题中,常常需要计算定积分 的值。根据微积分学基本定理,若被积函数f(x)在区间[a,b]上连续,只要能找到f(x)的一个原函数F(x),便可利用牛顿-莱布尼兹公式 求得积分值。
但是在实际使用中,往往遇到如下困难,而不能使用牛顿-莱布尼兹公式。
cout<<"4"<<" "<<tixing(0, 1, 16)<<" "<<xingbusheng(0, 1, 8)<<" "<<((double(16 / 15))* xingbusheng(0, 1, 4)) - (double(1 / 15))*xingbusheng(0, 1, 2)<<" "<<longbeige(0, 1,0.00000001)<<endl;;
cout<<"the result "<<4<<" is "<<longbeige(0, 1, 0.00000001);
return0;
}
2.复化梯形公式子程序:
doubletixing(doublea,doubleb,intn)
{
doublefa = f(a);
doublefb = f(b);
doubleh = (b-a) /n;
cout<<"1"<<" "<<tixing(0, 1, 2)<<" "<<xingbusheng(0, 1, 1)<<endl;
cout<<"2"<<" "<<tixing(0, 1, 4)<<" "<<xingbusheng(0, 1, 2)<<" "<<((double(16/15))* xingbusheng(0, 1, 2)) -(double(1/15))*xingbusheng(0, 1, 1)<<endl;
{
doubleh = (b-a) /n;
doublefa = f(a);
doublefb = f(b);
//double s = fb - fa;
doublex =a;
doublefxk12 = 0.0;
doublefxk = 0.0;
/*for (int k = 1; k <=n; k++)
{
x = x + h / (2.0);
doublefxk = 0.0;
for(intk = 1; k <=n- 1; k++)
{
doublexk =a+ k*h;
fxk = f(xk) + 2.0)*(fa + 2.0*fxk + fb);
returnres;
}
3.复化辛浦生公式子程序:
doublexingbusheng(doublea,doubleb,intn)
《计算方法》实验报告
学号
姓名
班级
实验项目名称
实验二 数值积分
一、实验名称
实验二数值积分
二、实验目的:
(1)熟悉复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法;
(2)能编程实现复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法;
(3)理解并掌握自适应算法和收敛加速算法的基本思想;
fxk12 = fxk12 + f(x);
}
for(intk = 1; k <=n- 1; k++)
cout<<"3"<<" "<<tixing(0,1,8)<<" "<<xingbusheng(0,1,4)<<" "<<((double(16 / 15))* xingbusheng(0, 1, 4)) - (double(1 / 15))*xingbusheng(0, 1, 2)<<" "<<longbeige(0, 1, 0.000000001)<<endl;
double fx = f(x);
s = s + 4.0*f(x);
x = x + h / (2.0);
s = s + 2.0*f(x);
}
s = (h / 6.0)*s;
return s;*/
for(intk = 0; k <=n- 1; k++)
{
doublexk1 =a+ k*h;
x = xk1 + h / 2.0;
