《氢原子与碱金属原子光谱精细结构的讨论》
碱金属原子光谱的精细结构
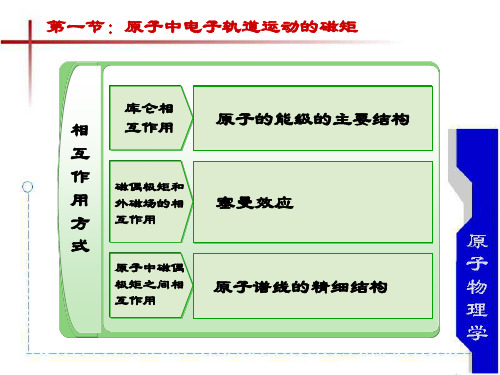
l
分量,与j垂直的分量对外的平均效 果抵消了(由于绕j转动的缘故)。
j
对外起作用的是它沿j的延线的分量, j
这就是电子的总磁矩
单电子磁矩与角动量的关系
对图示进行分析,利用三角形的余弦定理
可求出 j
lˆ l(l 1)
l
sˆ s(s 1)
ˆj
j( j 1)
1、载流闭合回路的磁矩 μ (IS)n 对应力矩: τ μ B
经典物理:封闭矩形线圈
1、载流闭合回路的磁矩 (IS)n 力矩τ μ B
2、回转运动电子的角动量与磁矩 μ e L L
2m
1、载流闭合回路的磁矩 (IS)n 力矩τ μ B
观察到两个取向;
难道是轨道角动量矢量合成?
第四章:原子的精细结构:电子的自旋
第一节 原子中电子轨道运动磁矩 第二节 史特恩—盖拉赫实验 第三节 电子自旋的假设 第四节 碱金属双线 第五节 塞曼效应 第六节 氢原子能谱研究进展
埃伦费斯特和他的学生,1924年,莱顿. 左起: 第开, 古兹密特, 汀柏根, 埃 伦费斯特, 克罗尼格, 和费米。
原子处于基态。
沿着-x方向观察:
沿X水平方向运动的氢原子束,其速度:v
3kT m
为了使进入磁场的氢原子 束受到力的作用,这个磁 场必须是不均匀的磁场区 (0.1nm的线度范围内)。
N
S
磁场沿Z 方向是变化的,即
Bz 0, Bz Bz 0
z
x y
在磁场中,磁矩在磁场中的势能:
ˆj2 lˆ2 sˆ2
ˆj2 sˆ2 lˆ2
g j gl
碱金属原子光谱的精细结构形成的原因

碱金属原子光谱的精细结构形成的原因首先,要了解碱金属原子光谱的形成原因,需要了解碱金属原子的电子结构。
碱金属原子的电子层结构是由一个核心和一系列电子壳层组成。
核心是由质子和中子组成的,在其周围围绕着一系列电子壳层,每个壳层包含一定数量的电子。
这些电子被分布在壳层的不同能级上,根据每个能级上的电子数目不同,可以产生多种谱线。
其次,光谱的形成还与量子力学的原理有关。
根据量子力学的原理,原子的能量是量子化的,即只能取离散的能级。
当原子受到激发时,电子会从低能级跃迁到高能级,吸收能量,形成吸收谱线。
当电子从高能级回到低能级时,会释放出能量,形成发射谱线。
这些发射和吸收的能量差决定了谱线所对应的波长和频率。
具体到碱金属原子的光谱,碱金属原子由于电子结构的特殊性质,光谱呈现出特定的精细结构。
碱金属原子的电子结构具有剩余电子,这些电子并非完全填满最外层的壳层,而是具有一个不完全填满的外层电子,称为价电子。
这一特点导致了碱金属原子光谱的精细结构。
具体来说,碱金属原子的光谱通常由两个部分组成:主谱线和杂谱线。
主谱线是由于电子在基态到第一激发态之间的跃迁产生的,这些跃迁是由于价电子从外层壳层跃迁到内层壳层所导致的。
杂谱线是由于电子在激发态之间的跃迁产生的,这些跃迁是由于价电子在外层壳层之间的跃迁所导致的。
这种精细结构的形成可以归因于量子力学的选择定则和电子的自旋。
量子力学的选择定则规定了电子跃迁的条件,只有符合一定的选择定则的电子跃迁才是允许的。
电子的自旋是一个量子力学的属性,具有两个可能的取值,分别为自旋向上和自旋向下。
当电子在不同能级之间跃迁时,必须满足量子力学的选择定则和自旋守恒定律。
总之,碱金属原子光谱的精细结构形成的原因主要与碱金属原子的电子结构和量子力学的选择定则和自旋守恒定律有关。
通过理解碱金属原子的电子结构和量子力学的原理,我们能够更好地解释碱金属原子光谱中的谱线形成和精细结构的特点。
最新原子物理学——碱金属原子光谱的精细结构
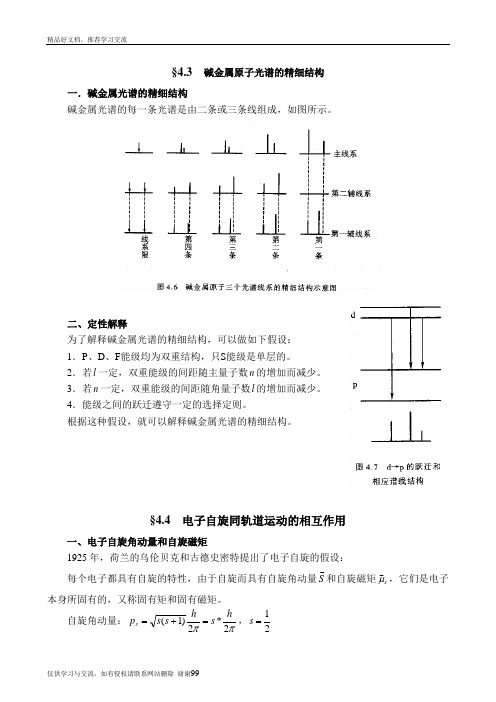
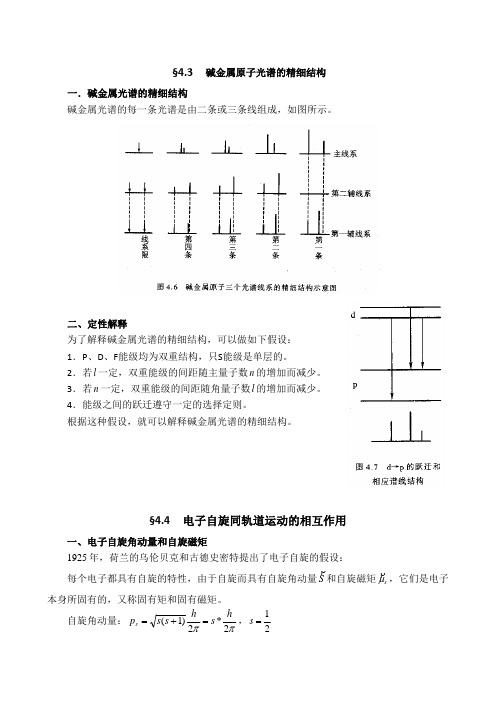
§4.3 碱金属原子光谱的精细结构一.碱金属光谱的精细结构碱金属光谱的每一条光谱是由二条或三条线组成,如图所示。
二、定性解释为了解释碱金属光谱的精细结构,可以做如下假设:1.P 、D 、F 能级均为双重结构,只S 能级是单层的。
2.若l 一定,双重能级的间距随主量子数n 的增加而减少。
3.若n 一定,双重能级的间距随角量子数l 的增加而减少。
4.能级之间的跃迁遵守一定的选择定则。
根据这种假设,就可以解释碱金属光谱的精细结构。
§4.4 电子自旋同轨道运动的相互作用一、电子自旋角动量和自旋磁矩1925年,荷兰的乌伦贝克和古德史密特提出了电子自旋的假设:每个电子都具有自旋的特性,由于自旋而具有自旋角动量S 和自旋磁矩s μ ,它们是电子本身所固有的,又称固有矩和固有磁矩。
自旋角动量:ππ2*2)1(h s h s s p s =+=,21=s外场方向投影:π2h m S s z =, 21±=s m 共2个, 自旋磁矩:s s p me -=μ Bs s h s s m e p m e μπμ32)1(-=+-=-= 外场方向投影:B z z S me μμ±=-= 共两个⇒偶数,与实验结果相符。
1928年,Dirac 从量子力学的基本方程出发,很自然地导出了电子自旋的性质,为这个假设提供了理论依据。
二、电子的总角动量电子的运动=轨道运动+自旋运动轨道角动量:ππ2*2)1(h l h l l p l =+= 12,1,0-=n l 自旋角动量:ππ2*2)1(h s h s s p s =+= 21=s 总角动量: s l j p p p += ππ2*2)1(h j h j j p j =+= s l j +=,1-+s l ,……s l -当s l >时,共12+s 个值当s l <时,共12+l 个值由于 21=s 当0=l 时,21==s j ,一个值。
21_碱金属原子光谱的精细结构.ppt

2
11 d V E p s 2 2 sp m c rd r
2
Ze 1 V r 40 r
2
1 d V 22 j j 1 1 s s 1 2 m c r d r
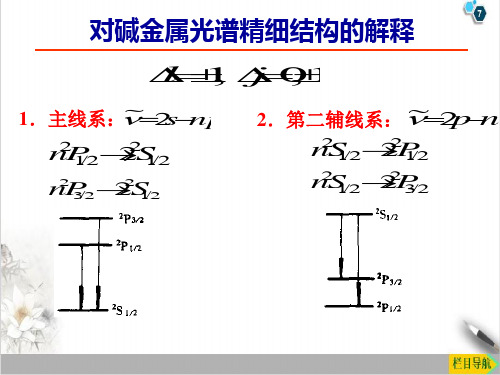
第二辅线系: ns 2p
伯格曼线系: nf 3d
Li 原子光谱的精细结构精细结构
间隔逐渐缩小
间隔不变
ns2p
因而设想 s: 单层 p: 双层
np2s 因而设想 s: 单层 p: 双层 且双层间隔随n 增加而减小
nd2p
因而设想 p、d、f: 皆为双层, 且 双层间隔随n 增加而减小
B ?
e
r
e
r
Ze
Ze
j Ze Ze
r 0 j B 3 4 r
r Ze r 0 j 0 B 3 3 4 r B 0 0 E 4 r 1 E Ze r j Ze E 2 c 4 0 r3 2 Ze 1 d V r e E F Vr 4 r d r r 0
1 2
Ze
p m s,z s
1 2
E s,zB
B
B
s,z
s,z
1 e E B s 2m
1e E B s 2m
2.2 自旋与轨道运动相互作用 能量的计算
E B s
e s ps m
2 2
给定n, l, s = ½,
第5节 氢原子光谱的精细结构

一、氢原子能级的精细结构
碱金属原子能量的主要部分:Eo
Rhc(Z )2
n2
与量子数 n、l 有关,同一个n,l 小能级低。
从量子力学得到的相对论能量的增量为:
Er
Rhc 2
n3l(l
(Z 1 )(l
s)4 1)
(
l
1 1
3 ). 4n
2
2
其中 Z s 也为有效电荷数,与 Z 不完全相同。
Rhc(Z )2
n2
Rhc(Z
n2
)2
Rhc 2(Z
n3
Rhc 2(Z
n3
s)4 ( 1 l
s)4 (1 l
1
3 ), 4n
3 ), 4n
1 jl2 jl1
2
Rhc(Z )2
n2
Rhc 2(Z
n3
s)4
(
j
1
1
3) 有关,同一个n,l 小 能级低,同一个l,j 小能级低。
两高峰波长差的理论值:0.364-0.036 =0.328cm-1, 实验值与理论值大约小了0.010cm-1。
这决不是实验的误差
胡登斯
II2-I1间隔 0.17-0.320cm-1
威廉
0.319
德林握特 0.316
理论值 0.328
三、蓝姆移动
1947年蓝姆和李瑟福用射频波谱学的方法测得22S1/2能级比 22P1/2能级高1058Mhz,即E=4.38μeV或T=0.033cm-1 =3,与 狄拉克公式结果相悖,从而导致了量子电动力学的产生。这 是因为电子除受核的静电作用、磁相互作用以及相对论效应 外,还受到因发光而产生的辐射场作用(即与其自身发出的 辐射之间的相互作用),因而在计算能级时要进行辐射修正 ,当计算到微扰的四级效应时,可得到与实验一致的结论。 理论指出,辐射场对S能级影响最大,对d、p等能级影响很 小,可以忽略不计.
高二物理竞赛对碱金属光谱精细结构的解释PPT(课件)
电子在该电场中受到的电场力 同一主量子数n下,碱金属的各轨道能级分的很开
2ep
Balmer系第一条谱线Hα Balmer系第一条谱线Hα 类氢离子体系为Li++ 4×10-4eV; n=3: ΔEr~ 6×10-5eV;
F (r) 40r3 V (r)
类氢离子体系为Li++
计算原子处于2D3/2状态的总磁矩 及投影 的可能值。
2 1/2
2 1/2
nP 2S 电 n=偶2:极Δ子Er延~ 长2. 线2上的电场
2
因此,前面精细结构3/的2讨论只是考虑Δ1E/l2s
n2S1/222P3/2
主线双重线的波数差等于22P1/2 、22P3/2两能态之间的波数差
计算原子处于2D3/2状态的总磁矩 及投影 的可能值。
12S1/2
主线双重线的波数差等于22P1/2 、22P3/2两能态之间的波数差
双E层能Rn级h3lc(间l 2Z隔1*)4 /裂n 距2 ,l 1 ,nR R3l (l21 Z0 19 4)7 3 7 2.3 91 .6cm cm 1 ,11
1 3 7 Z 3 类氢离子体系为Li++
. 原子内部磁场的估算。试估计作用在氢原子2P态电子上的磁场
32S1/2
32P3/2 32P1/2
n=3
32D5/2 32D3/2
12
56 7 3 22P3/2 4
n=2
22S1/2
22P1/2
选择定则: l1,j0,1
实际有几条谱线呢?
四个量子数小结
名称
取值
主量子数 n 1,2,
l 0,1,2,n 1
角量子数 L ll 1
§43碱金属原子光谱的精细结构21页PPT

56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
END
60、人民的ห้องสมุดไป่ตู้福是至高无个的法。— —西塞 罗
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
光谱学第三章2011

(3.3)
代入可得
1 dU (r) Ze2
r dr nl 4 0
1 r3
nl
量子力学计算结果为:
1 r3
nl
n3l (l
Z3 1)(l
1 2
)a13
于是求得
Enlj
En0l
Rhc 2Z 4
n3l(l 1)(l
1)
j *2
l *2 2
s*2
2
(3.4)
l* l(l 1) s* s(s 1) j* j( j 1)
c( j1 j2 j;m1m2m)
称为克莱布施-戈登系数或矢量耦合系数 由于磁量子数要满足m=m1+m2关系;以及j1,j2,j 满足三角条件Δ(j1j2j)时系数才不恒为零,经一定 运算后将上式改写为
j1 j2 jm c( j1 j2 j; m, m m1) j1m1 j2m2
m1m2
根据上式即可求得波函数的表达式
量子力学中磁矩的表达式与经典理论的有相同形式, 本质的区别是角动量的大小取为
lˆ l(l 1) h
2
因此,ˆl lˆ
l(l 1) h 2
l(l 1) eh
4me
l(l
1)
,
B
l 0,1,
(3.18)
B
eh
4me
称为玻尔磁子,是轨道磁矩的最小单元
磁矩μl在Z轴方向的投影为
μl,z ml B , ml 0,1,2,,l
ev
2r
r 2 nˆ
e 2me
mevrnˆ
(令lˆ mevr)
e lˆ (令 e ,旋磁比 )
2me
2me
ˆl lˆ
(3.17)
§20 碱金属光谱的精细结构
锐线系(二辅)是等距双线。
附注
(1)以上能级精细结构的公式是对类氢原子或离子算出的, 要用于碱金属原子,
公式 U
Z 有效 E0
4
2 n 3 l (l 1)
中的Z应理解为有效电荷数 Z有效 ( Z)。
(2)对碱金属原子能级的精细结构, 还应考虑相对论质量修正项U rel。但 随着原子序数的增大,相对论质量修正项相比于自旋轨道耦合项通3d
锐线系
4f
3p
漫线系
3s
2p
主线系
2s
2s
考虑自旋轨道耦合后,碱金属原子的能级除S能级外,都分裂为两个。
(2)自旋轨道相互作用:精细结构的定量考虑
原子核轨道运动引起的磁矩 1 2 i 1 2 Ze B 4 0 c2 r 4 0 c2 r 2 r / v
* l j mj
J
S
最后得到对类氢原子或离子的自旋-轨道耦合能的表达式: 1 1 Z e2 1 2 * ˆ ˆS U R R r dr L nl nl l j m l j mj d 2 2 3 3 j 2 4 π ε0 me c r r 1 Z e2 1 Z 3 [ j ( j 1) l (l 1) s ( s 1)] 1 2 2 2 3 3 2 4 π ε0 me c n l (l 1/ 2) (l 1)a1 2 1 Z e 2 ( me c)3 Z 3 [ j ( j 1) l (l 1) s ( s 1)] 4 4 π ε0 me 2 c 2 n3l (l 1/ 2)(l 1) 1 Z 4 e 2 3 me c 2 [ j ( j 1) l (l 1) s ( s 1)] 4 4 π ε0 c n3l (l 1/ 2)(l 1)
原子物理学——碱金属原子光谱的精细结构
§4.3 碱金属原子光谱的精细结构一.碱金属光谱的精细结构碱金属光谱的每一条光谱是由二条或三条线组成,如图所示。
二、定性解释1.P 、D 、F§4.4 电子自旋同轨道运动的相互作用一、电子自旋角动量和自旋磁矩1925年,荷兰的乌伦贝克和古德史密特提出了电子自旋的假设:每个电子都具有自旋的特性,由于自旋而具有自旋角动量S 和自旋磁矩s μ ,它们是电子本身所固有的,又称固有矩和固有磁矩。
自旋角动量:ππ2*2)1(h s h s s p s =+=,21=s外场方向投影:π2h m S sz =, 21±=s m 共2个, 自旋磁矩:s s p me -=μ Bs s h s s m e p m e μπμ32)1(-=+-=-= 外场方向投影:B z z S me μμ±=-= 共两个⇒偶数,与实验结果相符。
1928年,Dirac 从量子力学的基本方程出发,当s l >时,共12+s 个值当s l <时,共12+l 个值由于 21=s 当0=l 时,21==s j ,一个值。
当 3,2,1=l 时,21±=l j ,两个值。
例如:当1=l 时,23211=+=j 21211=-=j ππ222)1(h h l l p l =+= ππ2232)1(h h s s p s =+=πππ223,22152)1(h h h j j p j =+= l p 和s p 不是平行或反平行,而是有一定的夹角θcos 2222s l s l j p p p p p ++=)1()1(2)1()1()1(2cos 222+++-+-+=--=s s l l s s l l j j p p p p p s l s l j θ 当s l j +=时 0)1()1(c o s >++=s s s l l lθ,o 90<θ,称l p 和s p “平行” 当s l j -=时 0)1()1(1c o s<+++-=s s s l l l θ,o 90>θ原子的角动量=电子轨道运动的角动量+原子的磁矩=三、电子轨道运动的磁矩 电子轨道运动的闭合电流为:Te i -= “-”表示电流方向与电子运动方向相反 面积:dt r rd r dA φφ 22121=⋅= 一个周期扫过的面积: T mp dt p m dt mr m dt r dA A l T l T T 221212100202=====⎰⎰⎰⎰φφm p e iA l 2-==μ l p me 2-=μ π2)1(h l l p l += 是量子化的 B l l l mhe l l p m e μπμ)1(4)1(2+-=+-=-= 量子化的。
对碱金属光谱精细结构的解释

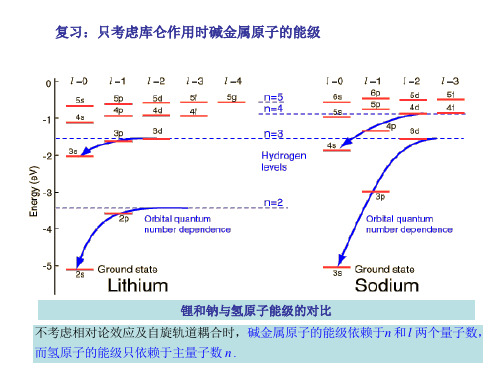
(1)主线系(the principal series): 谱线最亮,波长的分布范围最广,第一条呈红色,其 余均在紫外。
(2)第一辅线系(漫线系the diffuse series): 在可见光部分,其谱线较宽,边缘有些模糊而不清晰 ,故又称漫线系。
§4.1 碱金属原子的光谱
一、碱金属原子的光谱特点 各个碱金属原子的光谱具有相似的结构,光谱线也类似于
氢原子光谱,有如下特征:
主要特征有四条: 1.有四组谱线:—每一组的初始位置不同,即有四套初
项,四套线系。(主线系,第一辅线系(漫线系),第二辅 线系(锐线系),柏格曼线系(基线系)。)
2.有三个终端:—有三套固定项。 3.两个量子数 —主量子数n和轨道角动量量子数 l。
2
e p
2m
l(l 1) he
4 m
l(l 1)B
量子化的。
B
he
4m
9.27401023 A m2
玻尔磁子
p
z
ml
h
2
空间取向量子化
z
e 2m
p
z
ml B
4 施特恩—盖拉赫实验
实验装置
实验结果:
当 B 0 时,P上只有一条细痕,不受力的作用。 当 B均匀时,P上仍只有一条细痕,不受力的作用。
碱金属原子和氢原子中,电子轨道的异同 共同之处:最外层只有一个电子价电子 其余部分和核形成一个紧固的团体原子实 碱金属原子:带一个正电荷的原子实+一个价电子 H原子:带一个正电荷的原子核+一个电子
首先是基态不同-Li、Na、K、Rb、Cs、Fr的基态依次为 :2s、3s、4s、5s、6s、7s。
碱金属原子光谱的研究

量子力学课程设计——碱金属原子光谱的研究姓名:周尚伦氢原子是最简单的原子 ,在量子力学建立的初期 ,已对它进行了广泛深入的研究 近 1 0多年来 ,人们又对一、二维氢原子进行了研究 ,了解到它们的一些性质 所有这些研究表明 ,一、二、三维氢原子有许多不同的性质 ,置于外场中其状态及能级所发生的变化也各有其特点 ,作为量子力学中唯一可以求解的原子,氢原子为我们研究更复杂的原子光谱奠定了基础!利用玻尔的氢原子理论可以很好地解释氢原子的光谱现象及氢原子的结构问题。
但波尔理论具有很大的局限性,前面我们知道玻尔理论也适用于和氢原子有相似结构的类氢离子。
类氢离子与氢原子最大的相似之处在于原子核外都只有一个电子,但它的原子核的电荷数大于1。
下面呢,我们将要讨论另一种与氢原子类似的原子,就是碱金属。
它与氢原子的共同之处在于,最外层都只有一个电子,可以把碱金属原子去掉最外层电子之后的部分叫做“原子实”而这个原子实与氢原子核一样也只带一个正电荷。
一、碱金属原子的光谱在前面讨论氢原子光谱时,我们已知道,氢原子的光谱可表示为 222~11~n Rn m R H H -=⎥⎦⎤⎢⎣⎡-=∞υυ式中第一项为原子跃迁的终态,决定光谱所在的线系,第二项为原子跃迁的初态。
在同一线系中(m 相同)随着n 的增大,谱线的波长越来越短,且间隔越来越小,最后趋于线系限。
碱金属原子的光谱也有类似的特点,光谱线也明显地构成几个线系。
一般观察到的四个线条称为主线系、第一辅线系(又称漫线系)、第二辅线系(又称锐线系)和柏格曼线系(又称基线系)。
图4.1显示锂的这四个线系,这是按波数的均匀标尺作图的,图中也附了波长标尺。
从图中可以看到主线系的波长范围最广,第一条线是红色的,共余诸线在紫外.主线系的系限的波数是 ,相当于波长2299.7埃。
第一辅线系在可见部分.第二辅线系的第一条线在红外,其余在可见部分.这二线系有同一线系限.柏格曼线系全在红外。
其他碱金属元素也有相仿的光谱系,只是波长不同。
关于氢原子光谱的超精细结构的研究

关于氢原子光谱的超精细结构的研究摘要:本文通过介绍原子核的结构、原子核的自旋以及核磁矩,讨论了氢原子光谱的超精细结构的产生原因并介绍了相关公式推导。
关键词:光谱;氢原子;超精细结构原子核的结构1、原子核自卢瑟福提出原子的核式模型以来,原子就被分为两部分来处理:一是处于原子中心的原子核,一是绕核运动的电子。
除了原子核的质量和电荷外,原子核的其他性质对原子的影响是相当微小的,核外电子的行为对原子核的性质也几乎毫无关系。
原子和原子核是物质结构泾渭分明的两个层次。
2、原子核的结构发现中子之前,人们知道的“基本”粒子只有两种:电子和质子。
物理学家开始时有把原子核当做质子和电子的组成体的想法,但一开始就遇到了不可克服的困难。
因为假如原子核由质子和电子所组成,那么,我们将无法解释核的自旋,且推导出来的原子核内电子的能量与实验结果不符。
在查德威克发现中子之后,海森堡很快就提出了原子核由质子和中子所组成的假说。
海森堡把质子和中子统称为核子,并把中子和质子看做核子的两个不同状态。
原子核的自旋以及核磁矩1、电子自旋在乌仑贝克和古兹米特提出电子自旋之前,泡利为了解释原子光谱的超精细结构,就提出了原子核作为一个整体必须有自旋的假设。
但是,只有在查德威克发现中子之后,人们才理解自旋的起源。
实验发现,中子和质子都是费米子,具有的固有角动量(自旋)与电子一样。
既然原子核式中子和质子所组成,它的自旋就应该是中子和质子的轨道角动量和自旋之和。
我们研究的“原子核的自旋”,都是指原子核基态的自旋。
2、核磁矩除了核子的自旋磁矩外,我们还要考虑轨道磁矩。
下面给出自核自旋的核磁矩的表示式。
类似于原子磁矩的表示式,核磁矩和核自旋角动量I成正比。
μI = g IμN I在磁场中,核自旋磁矩与磁场相互作用所产生的附加能量为U = -μI •B = -g IμN Bm I因为m I有2I+1个值,所以有2I+1个不同的附加能量,于是就发生赛曼能级分裂,一条核能级在磁场中就分裂为2I+1条,相邻两条分裂能级间的能量差为上述对核自旋磁矩与磁场的相互作用的讨论是下面研究氢原子光谱的超精细结构的基础。
原子物理学 原子的精细结构:电子的自旋 (4.2.1)--施特恩-盖拉赫实验

d
e
L
进 动 角 频 率 :
frequency
2
dL dt
magnetic field
磁矩绕磁场进动示意图
d sin d
d
dt
sin ddtddt
sin
பைடு நூலகம்
d
dt
( 2 )量子表示式
l
L
L l l 1 l 0,1,2,, n 1
z d
o s1 s2
S
N
z1 a z2 x
D
通真空泵
z
S
x N
Bz x
Bz y
0
Fz
z
Bz z
原子束对应的最可几速 率:
mv 2 3kT
原子束在磁场区内的运动方程
x vt
z1
1 2
at 2
1 2
Fz m
t2
原子束经过磁场区到 达出口处时与 x 轴的偏角
a
l L ll 1
ZB
LZ
L
e
o
Y
X
L ll 1 l 0,1,2,, n 1
Lz ml
ml 0,1,2,,l
磁矩在 z 方向的投影
l,z
LZ
ml
e 2me
ml
玻尔磁子
Born magneton
e
1 2
a
( 3 )角动量取向量子
L ll 1 化
4[1].5 选择定则 4.6 氢原子光谱精细结构
![4[1].5 选择定则 4.6 氢原子光谱精细结构](https://img.taocdn.com/s3/m/cbf6773610661ed9ad51f3dc.png)
玻尔能级
n4 n3
S能级 l0
P能级 l 1
D能级 l2
F能级 l 3
1 2 1 2
3/ 2 1/ 2 3/ 2 1/ 2
3/ 2 5/ 2 3/ 2
5/ 2
5/ 2
7/2
n2
1 2
3/ 2 1/ 2
n 1
1 j 2
图4.14 氢原子能级的精细结构
五、氢原子的精细光谱
1.赖曼线系:激发能级跃迁到 n=1 能级,由选择定则知: 第一条谱线的双线结构:
对氢原子 Z-s=1。
当主量子数 n 一定时,轨道量子数 l 越小, Er 就越大, 能级就越低。对 S 能级,相对论效应尤为显著。
(2)和(3)式两者基本一致,我们采用量子力学结论
三、电子自旋与轨道的相互作用能
Rch 2 ( Z s ) 4 j 2 l 2 s 2 Esl , (4) 1 2 3 n l (l )(l 1) 2
589 .6nm
589 .0nm
课堂练习
作出锂原子的精细结构能级图,并写出其第一 辅线系第一条光谱的波数公式.
§4.6 氢原子光谱的精细结构
• • • • 1.相对论修正 2.自旋与轨道的相互作用 3.氢原子能级的狄拉克公式 4.氢原子光谱的精细结构
一、原子能量的主要部分(玻尔理论提出)
Rhc Z ) ( E0 ,() 1 2 n (Z-):原子实的有效电荷数
作业题
第四章习题:1、2、3、4、6、7
~ 4 22 P3/ 2 32 D3/ 2
六、碱金属原子能级的分裂
1 j l ,能级分裂为双层 2
当 当
1 j l 时, 2
原子物理学第四章

→
μ = −γ L
→
→
(4)
r 磁矩在外磁场 B 中将受到力矩的作用, 力矩将使得磁 r r 矩 μ 绕外磁场 B 旋进。我们将这种旋进称为拉莫尔进
动。相应的频率称为拉莫尔频率ν l 。下面我们来计算 这个频率。
由电磁学知道,在均匀外磁场中,磁矩不受力,但 受到一个力矩:
r τ = μ×B r r
引入自旋量子数后,原子的量子态需要由 n、L、S、 J 来表示: 2 S +1 J
n
L
氢原子基态为 S1/2 ,因此 L = 0,J = 1/2,S = 1/2
2
m j = ±1 / 2 3 1 0−3/4 gj = − ( )=2 2 2 3/4 m j g j = ±1
斯特恩-盖拉赫实验的解释
3 μ s = − s( s + 1) μ B = − μB 2 1 μ s , z = − ms μ B = m μ B 2
但上述表示与实验不符,为了与实验吻合,自旋磁矩 公式必须写为:
μ s = −2 s( s + 1) μ B = − 3μ B μ s , z = −2 m s μ B = m μ B
r r r r μ j = μl cos( l , j ) + μ s cos( s , j )
电子的自旋轨道耦合
r 电子绕核运动时,既有轨道角动量 L ,又有 r r 自旋角动量 S, 这时电子状态和总角动量 J 有关。 r r r J = L+S 这一角动量的合成,叫自旋轨道耦合。
由量子力学可知,J 也是量子化的, 相应的 总角动量量子数用 j 表示,且有 J = j ( j + 1) h r r l = 0 时, J = S,j = s = 1 / 2; l ≠ 0 时,j =rl +rs = l + 1 / 2,或 j = l − s = l − 1 / 2 r r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《氢原子与碱金属原子光谱精细结构的讨论》
本文旨在分析氢原子与碱金属原子光谱精细结构。
随着科学技术的不断发展,氢原子与碱金属原子光谱精细结构呈现出更加复杂的变化,引起了人们的广泛关注。
氢原子光谱的精细结构是指氢原子在不同能级、不同态间由电磁波吸收而跳转改变能量状态,这种改变最终形成一组特有的光谱线。
氢原子产生这些变化的原因是粒子占有一个被称为可视极性的定向角。
碱金属原子的光谱的精细结构是指其中的原子吸收特定的电磁波来改变其能量状态,从而形成一系列特有的光谱线,也称为精细结构。
氢原子与碱金属原子的光谱精细结构在自然界有重要的意义。
其中,氢原子的跃迁过程可以提供有关物质结构、内能改变规律等重要信息,从而帮助科学研究者探索细胞内电子运动规律。
碱金属原子的光谱精细结构可以提供有关原子结构、能量关系和化学特性的有价值信息,从而为科学研究者帮助实现原子结构及有关变化的规律。
综上所述,氢原子与碱金属原子的光谱精细结构对于促进科学的发展具有重要的意义,帮助研究者探索原子及化学特性的有价值信息,因此必须得到科学家广泛关注和研究。
