材料力学习题及答案
材料力学习题及答案
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 导电性答案:D2. 根据胡克定律,当材料受到正应力时,其应变与应力成正比,比例系数称为:A. 杨氏模量B. 剪切模量C. 泊松比D. 屈服强度答案:A3. 在材料力学中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生脆性断裂的应力答案:A4. 材料的疲劳寿命与下列哪一项无关?A. 材料的疲劳极限B. 应力循环次数C. 材料的弹性模量D. 应力循环的幅度答案:C5. 在材料力学中,下列哪一项不是材料的力学性能指标?A. 硬度B. 韧性C. 密度D. 冲击韧性答案:C二、简答题(每题5分,共10分)6. 简述材料力学中弹性模量和剪切模量的区别。
答:弹性模量,也称为杨氏模量,是描述材料在受到正应力作用时,材料的纵向应变与应力成正比的比例系数。
剪切模量,也称为刚度模量,是描述材料在受到剪切应力作用时,材料的剪切应变与剪切应力成正比的比例系数。
7. 什么是材料的疲劳寿命,它与哪些因素有关?答:材料的疲劳寿命是指材料在反复加载和卸载过程中,从开始加载到发生疲劳断裂所需的循环次数。
它与材料的疲劳极限、应力循环的幅度、材料的微观结构和环境因素等有关。
三、计算题(每题15分,共30分)8. 一根直径为20mm的圆杆,材料的杨氏模量为200GPa,当受到100N的拉力时,求圆杆的伸长量。
答:首先计算圆杆的截面积A = π * (d/2)^2 = π * (0.02/2)^2m^2 = 3.14 * 0.01 m^2。
然后根据胡克定律ΔL = F * L / (A * E),其中 L 为杆长,假设 L = 1m,代入数值得ΔL = 100 * 1 / (3.14* 0.01 * 200 * 10^9) m = 7.96 * 10^-6 m。
材料力学试题和答案解析7套

材料⼒学试题和答案解析7套材料⼒学试卷1⼀、绘制该梁的剪⼒、弯矩图。
(15分)⼆、梁的受⼒如图,截⾯为T 字型,材料的许⽤拉应⼒[σ+]=40MPa ,许⽤压应⼒[σ-]=100MPa 。
试按正应⼒强度条件校核梁的强度。
(20分)m8m 2m2M三、求图⽰单元体的主应⼒及其⽅位,画出主单元体和应⼒圆。
(15分)四、图⽰偏⼼受压柱,已知截⾯为矩形,荷载的作⽤位置在A 点,试计算截⾯上的最⼤压应⼒并标出其在截⾯上的位置,画出截⾯核⼼的形状。
(15分) 30170302002m3m1m30五、结构⽤低碳钢A 3制成,A 端固定,B 、C 为球型铰⽀,求:允许荷载[P]。
已知:E=205GPa ,σs =275MPa ,σcr=338-1.12λ,,λp =90,λs =50,强度安全系数n=2,稳定安全系数n st =3,AB 梁为N 016⼯字钢,I z =1130cm 4,W z =141cm 3,BC 杆为圆形截⾯,直径d=60mm 。
(20分)六、结构如图所⽰。
已知各杆的EI 相同,不考虑剪⼒和轴⼒的影响,试求:D 截⾯的线位移和⾓位移。
(15分)材料⼒学2⼀、回答下列各题(共4题,每题4分,共16分)1、已知低碳钢拉伸试件,标距mm l 1000=,直径mm d 10=,拉断后标距的长度变为mm l 1251=,断⼝处的直径为mm d 0.61=,试计算其延伸率和断⾯收缩率。
2、试画出图⽰截⾯弯曲中⼼的位置。
aa3、梁弯曲剪应⼒的计算公式zzQS =τ,若要计算图⽰矩形截⾯A 点的剪应⼒,试计算z S 。
4、试定性画出图⽰截⾯截⾯核⼼的形状(不⽤计算)。
4/h矩形圆形矩形截⾯中间挖掉圆形圆形截⾯中间挖掉正⽅形⼆、绘制该梁的剪⼒、弯矩图。
(15分)三、图⽰⽊梁的右端由钢拉杆⽀承。
已知梁的横截⾯为边长等于0.20m 的正⽅形,q=4OKN/m,弹性模量E 1=10GPa ;钢拉杆的横截⾯⾯积A 2=250mm 2,弹性模量E 2=210GPa 。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中,当应力达到屈服点后,材料将:A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指:A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律,下列说法正确的是:A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指:A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指:A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指:A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指:A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中,下列哪一项是衡量材料脆性程度的指标?A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中,当应力超过其极限强度时,将:A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题(每题10分,共30分)1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象,并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形,当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后,即使外力移除也无法完全恢复原状的性质。
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学的试题及答案

材料力学的试题及答案一、选择题1. 材料力学中,下列哪个选项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D2. 根据材料力学的理论,下列哪个选项是正确的?A. 材料在弹性范围内,应力与应变成正比B. 材料在塑性变形后可以完全恢复原状C. 材料的屈服强度总是高于其抗拉强度D. 材料的硬度与弹性模量无关答案:A二、填空题1. 材料力学中,应力是指_______与_______的比值。
答案:单位面积上的压力;受力面积2. 在材料力学中,材料的弹性模量E与_______成正比,与_______成反比。
答案:杨氏模量;泊松比三、简答题1. 简述材料力学中材料的三种基本变形类型。
答案:材料力学中材料的三种基本变形类型包括拉伸、压缩和剪切。
2. 描述材料的弹性模量和屈服强度的区别。
答案:弹性模量是指材料在弹性范围内应力与应变的比值,反映了材料的刚性;屈服强度是指材料开始发生永久变形时的应力值,反映了材料的韧性。
四、计算题1. 已知一材料的弹性模量E=200 GPa,杨氏模量E=210 GPa,泊松比ν=0.3,试计算该材料的剪切模量G。
答案:G = E / (2(1+ν)) = 200 / (2(1+0.3)) = 200 / 2.6 ≈ 76.92 GPa2. 某材料的抗拉强度为σt=300 MPa,若该材料承受的应力为σ=200 MPa,试判断材料是否发生永久变形。
答案:由于σ < σt,材料不会发生永久变形。
五、论述题1. 论述材料力学在工程设计中的重要性。
答案:材料力学是工程设计中的基础学科,它提供了对材料在力作用下行为的深入理解。
通过材料力学的分析,工程师可以预测材料在各种载荷下的响应,设计出既安全又经济的结构。
此外,材料力学还有助于新材料的开发和现有材料性能的优化。
2. 讨论材料的疲劳寿命与其力学性能之间的关系。
答案:材料的疲劳寿命与其力学性能密切相关。
材料的疲劳寿命是指在循环载荷作用下材料能够承受的循环次数。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,弹性模量E的单位是()。
A. N/mB. N·mC. PaD. m/N答案:C2. 材料力学中,材料的屈服强度通常用()表示。
A. σyB. σsC. σbD. E答案:A3. 根据胡克定律,当应力超过材料的弹性极限时,材料将()。
A. 保持弹性B. 发生塑性变形C. 发生断裂D. 无法预测答案:B4. 材料力学中,第一强度理论认为材料破坏的原因是()。
A. 最大正应力B. 最大剪应力C. 最大正应变D. 最大剪应变答案:A5. 下列哪种材料不属于脆性材料()。
A. 玻璃B. 铸铁C. 混凝土D. 铝答案:D6. 材料力学中,梁的弯曲应力公式为()。
A. σ = Mc/IB. σ = Mc/IbC. σ = Mc/ID. σ = Mc/Ib答案:C7. 在材料力学中,梁的剪应力公式为()。
A. τ = VQ/IB. τ = VQ/ItC. τ = VQ/ID. τ = VQ/It答案:B8. 材料力学中,梁的挠度公式为()。
A. δ = (5PL^3)/(384EI)B. δ = (5PL^3)/(384EI)C. δ = (PL^3)/(48EI)D. δ = (PL^3)/(48EI)答案:C9. 材料力学中,影响材料屈服强度的因素不包括()。
A. 材料的微观结构B. 加载速度C. 温度D. 材料的密度答案:D10. 材料力学中,影响材料疲劳强度的因素不包括()。
A. 应力集中B. 表面粗糙度C. 材料的硬度D. 材料的导热性答案:D二、填空题(每题2分,共20分)1. 材料力学中,材料在外力作用下,其形状和尺寸发生的变化称为______。
答案:变形2. 材料力学中,材料在外力作用下,其内部产生的相互作用力称为______。
答案:应力3. 材料力学中,材料在外力作用下,其内部产生的相对位移称为______。
答案:应变4. 材料力学中,材料在外力作用下,其内部产生的单位面积上的力称为______。
材料力学试题及答案全

材料力学试题一、填空题(共15分)1、 (5分)一般钢材的弹性模量E = 210 GPa ;吕材的弹性模量E = 70 GPa2、 (10分)图示实心圆锥杆受扭转外力偶作用,材料的剪切弹性模量为G ,该杆的man τ1、(5(A )各向同性材料;(B )各向异性材料; (C 正确答案是 A 。
2、(5分)边长为d 杆(1)是等截面,杆(2荷系数d k 和杆内最大动荷应力d σ论:(A )()(,)()(1max 21d d d k k σ<<(B )()(,)()(1max 21d d d k k σ><(C )()(,)()(1max 21d d d k k σ<>(D )1max 21()(,)()(d d d k k σ>>正确答案是 A 。
三、计算题(共75分) 1、(25应力相等,求:(1)直径比21/d d ; (2)扭转角比AB φ解:AC 轴的内力图:(105);(10355M Nm M BC AB ⨯=⨯= 由最大剪应力相等:8434.05/3/16/1050016/10300321323313max==⨯=⨯==d d d d W M n n ππτ 由;594.0)(23232;41221242411=••=•=⇒∴⋅=d M M M d G d G a M GI l M n n n n BC AB P n ππφφφ(2)2、(3、(15分)有一厚度为6mm 的钢板在板面的两个垂直方向受拉,拉应力分别为150Mpa 和55Mpa ,材料的E=2.1×105Mpa ,υ =0.25。
求钢板厚度的减小值。
解:钢板厚度的减小值应为横向应变所产生,该板受力后的应力状态为二向应力状态,由广义胡克定律知,其Z 向应变为:0244.010)55150(101.225.0)(69-=⨯+⨯-=+-=y x z E σσνε则 mm t Z Z 146.0-=⨯=∆ε(本资料素材和资料部分来自网络,仅供参考。
材料力学试题及答案

材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。
《材料力学》习题册附答案

F12312练习 1 绪论及基本概念1-1 是非题(1) 材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是)(3) 构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4) 应力是内力分布集度。
(是 )(5) 材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6) 若物体产生位移,则必定同时产生变形。
(非 ) (7) 各向同性假设认为,材料沿各个方向具有相同的变形。
(F ) (8) 均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9) 根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1) 根据材料的主要性质对材料作如下三个基本假设:连续性假设、均匀性假设 、各向同性假设 。
(2) 工程中的强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3) 保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性三个方面。
3(4) 图示构件中,杆 1 发生 拉伸 变形,杆 2 发生 压缩 变形,杆 3 发生 弯曲 变形。
(5) 认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6) 图示结构中,杆 1 发生 弯曲变形,构件 2发生 剪切 变形,杆件 3 发生 弯曲与轴向压缩组合。
变形。
(7) 解除外力后,能完全消失的变形称为 弹性变形,不能消失而残余的的那部分变形称为 塑性变形 。
(8) 根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
材料力学试题及答案

材料力学试题及答案一、选择题1. 材料力学中,下列哪个参数是用来描述材料在受力时抵抗变形的能力?A. 弹性模量B. 屈服强度C. 抗拉强度D. 断裂韧性答案:A2. 以下哪种材料在受力后能够完全恢复原状?A. 弹性体B. 塑性体C. 粘弹性体D. 脆性体答案:A3. 应力集中现象主要发生在哪种情况下?A. 材料表面存在缺陷B. 材料内部存在孔洞C. 材料受到均匀分布的载荷D. 材料受到单一集中载荷答案:D4. 根据胡克定律,当应力不超过比例极限时,应力与应变之间的关系是:A. 线性的B. 非线性的C. 指数的D. 对数的答案:A5. 材料的疲劳破坏是指在何种条件下发生的?A. 单次超负荷B. 长期重复载荷C. 瞬间高温D. 腐蚀环境答案:B二、填空题1. 在简单的拉伸和压缩实验中,应力(σ)是力(F)与横截面积(A)的比值,即σ=______。
答案:F/A2. 材料的韧性是指其在断裂前能够吸收的能量,通常通过______试验来测定。
答案:冲击3. 当材料在受力时发生塑性变形,且变形量随时间增加而增加,这种现象称为______。
答案:蠕变4. 剪切应力τ是剪切力(V)与剪切面积(A)的比值,即τ=______。
答案:V/A5. 材料的泊松比是指在单轴拉伸时,横向应变与纵向应变的比值,通常用希腊字母______表示。
答案:ν三、简答题1. 请简述材料弹性模量的定义及其物理意义。
答:弹性模量,又称杨氏模量,是指材料在弹性范围内抵抗形变的能力的量度。
它定义为应力与相应应变的比值。
物理意义上,弹性模量越大,表示材料在受力时越不易发生形变,即材料越硬。
2. 描述材料的屈服现象,并解释屈服强度的重要性。
答:屈服现象是指材料在受到外力作用时,由弹性状态过渡到塑性状态的过程。
在这个过程中,材料首先经历弹性变形,当应力达到某个特定值时,即使应力不再增加,材料也会继续发生显著的塑性变形。
屈服强度是衡量材料开始屈服的应力值,它对于工程设计和材料选择具有重要意义,因为它决定了结构在载荷作用下的安全性和可靠性。
材料力学练习题与答案-全

材料力学练习题与答案-全1.当T三Tp时,剪切虎克定律及剪应力互等定理。
A、虎克定律成立,互等定理不成立B、虎克定律不成立,互等定理成立(正确答案)C、均不成立D、二者均成立2.木榫接头,当受F力作用时,接头的剪切面积和挤压面积分别是A、ab,lcB、cb,lbC、lb,cb(正确答案)D、lc,ab3.在下列四种材料中,()不可以应用各向同性假设。
A、铸钢B、玻璃C、松木(正确答案)D、铸铁4.一细长压杆当轴向压力P达到临界压力Pcr时受到微小干扰后发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形。
A、有所缓和B、完全消失(正确答案)C、保持不变D、继续增大;5.矩形截面偏心受压杆件发生变形。
A、轴向压缩、平面弯曲B、轴向压缩、平面弯曲、扭转C、轴向压缩、斜弯曲(正确答案)D、轴向压缩、斜弯曲、扭转6.当杆件处于弯扭组合变形时,对于横截面的中性轴有这样的结论,正确的是:A、一定存在(正确答案)B、不一定存在C、一定不存在7.梁在某一段内作用有向下的分布载荷时,在该段内它的弯矩图为。
A、上凸曲线;(正确答案)B、下凸曲线;C、带有拐点的曲线;D、斜直线8.图示结构中,AB为钢材,BC为铝,在P力作用下()A、AB段轴力大B、BC段轴力大C、轴力一样大(正确答案)D、无法判断9.圆截面的悬臂梁在自由端受集中力的作用,若梁的长度增大一倍,其他条件不变,最大挠度是原来的倍。
图片2.pngA、2B、16C、8(正确答案)D、410.托架由横梁与杆组成。
若将杆由位于梁的下方改为位于梁的上方,其他条件不变,则此托架的承载力。
A、提高(正确答案)B、降低C、不变D、不确定11.单位长度的扭转角e与()无关A、杆的长度(正确答案)B、扭矩C、材料性质D、截面几何性质12.矩形截面拉弯组合变形时,对于横截面的中性轴有以下的结论。
正确的是:。
A、过形心B、过形心且与ZC轴有一夹角;C、不过形心,与ZC轴平行;(正确答案)D、不过形心,与ZC轴有一夹角。
大学材料力学考试题及答案

大学材料力学考试题及答案一、选择题(每题2分,共10分)1. 材料力学中,下列哪一项不是基本假设?A. 连续性假设B. 均匀性假设C. 各向同性假设D. 非线性假设答案:D2. 在拉伸试验中,弹性模量E是指:A. 屈服强度B. 抗拉强度C. 应力与应变比值D. 断后伸长率答案:C3. 根据第四强度理论,材料的脆性断裂是由于:A. 最大正应力达到临界值B. 最大切应力达到临界值C. 最大拉应力达到临界值D. 最大剪切能密度达到临界值答案:D4. 在扭转试验中,圆轴的扭转角θ与扭矩T和极惯性矩J之间的关系是:A. θ ∝ T/JB. θ ∝ TJC. θ ∝ J/TD. θ ∝ 1/(TJ)答案:A5. 下列哪一项不是影响材料疲劳寿命的因素?A. 应力幅B. 循环加载频率C. 材料的微观结构D. 环境温度答案:D二、填空题(每题2分,共10分)6. 材料在拉伸过程中,当应力达到_________时,称为屈服点。
答案:材料的屈服强度7. 根据材料力学的_________假设,材料内部各点的应力状态是相同的。
答案:均匀性8. 在纯弯曲情况下,梁的横截面上的正应力分布规律是_________。
答案:线性分布9. 剪切模量G是指材料在剪切作用下,剪切应力与剪切应变的比值,其单位是_________。
答案:帕斯卡(Pa)10. 复合应力状态下,最大剪应力τ_max与主应力σ1和σ2之间的关系是τ_max = √_________。
答案:(σ1 - σ2)^2 / 2三、简答题(每题10分,共20分)11. 简述材料力学中的强度和刚度的概念,并说明它们在工程设计中的重要性。
答案:强度是指材料在外力作用下抵抗破坏的能力,通常与材料的屈服强度或抗拉强度相关。
刚度是指材料在受力后抵抗变形的能力,与弹性模量有关。
在工程设计中,强度和刚度是确保结构安全和功能的关键参数,它们决定了结构在受力后的性能表现和耐久性。
12. 描述纯弯曲梁的正应力分布规律,并说明如何利用这一规律进行梁的设计。
材料力学习题集 (有答案)

绪 论一、 是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。
( ) 1.2 内力只能是力。
( )1.3 若物体各点均无位移,则该物体必定无变形。
( ) 1.4 截面法是分析应力的基本方法。
( ) 二、选择题1.5 构件的强度是指( ),刚度是指( ),稳定性是指( )。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设,可认为构件的( )在各点处相同。
A. 应力 B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是( ) A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力参考答案:1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1. 等截面直杆CD 位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD 两侧的摩擦力沿轴线方向均匀分布,且两侧摩擦力的集度均为q ,杆CD 的横截面面积为A ,质量密度为ρ,试问下列结论中哪一个是正确的? (A) q gA ρ=;(B) 杆内最大轴力N max F ql =; (C) 杆内各横截面上的轴力N 2gAlF ρ=;(D) 杆内各横截面上的轴力N 0F =。
2. 低碳钢试样拉伸时,横截面上的应力公式N F A σ=适用于以下哪一种情况? (A) 只适用于σ≤p σ; (B) 只适用于σ≤e σ; (C)3. 在A 和B和点B 的距离保持不变,绳索的许用拉应力为[]σ取何值时,绳索的用料最省? (A) 0; (B) 30; (C) 45; (D) 60。
4. 桁架如图示,载荷F 可在横梁(刚性杆)DE 为A ,许用应力均为[]σ(拉和压相同)。
求载荷F 的许用值。
以下四种答案中哪一种是正确的?(A)[]2A σ; (B) 2[]3Aσ;(C) []A σ; (D) 2[]A σ。
材料力学习题集 (有答案)

(C) , ;(D) , .
6.圆柱形拉伸试样直径为d,经常使用的比例试样其标距长度l是或.
7.低碳钢拉伸试验进入屈服阶段当前,发生性变形.(填“弹”、“塑”、“弹塑”)
8.低碳钢拉伸应力-应变曲线的上、下屈服极限分别为 和 ,则其屈服极限 为.
9.灰口铸铁在拉伸时,从很低的应力开始就不是直线,且没有屈服阶段、强化阶段和局部变形阶段,是以,在工程计算中,通常取总应变成 %时应力-应变曲线的割线斜率来确定其弹性模量,称为割线弹性模量.
(C)经过塑性变形,其比例极限提高,塑性降低;
(D)经过塑性变形,其弹性模量提高,泊松比减小.
4.关于材料的塑性目标有以下结论,哪个是准确的?
(A) 和 ;(B) 和ψ;(C) 和ψ;(D) 、 和ψ.
5.用标距50 mm和100 mm的两种拉伸试样,测得低碳钢的屈服极限分别为 、 ,伸长率分别为 和 .比较两试样的结果,则有以下结论,其中准确的是哪一个?
2.6δ、y值越大,说明材料的塑性越大.()
2.7研讨杆件的应力与变形时,力可按力线平移定理进行挪动.()
2.8杆件伸长后,横向会缩短,这是因为杆有横向应力存在.()
2.9线应变e的单位是长度.()
2.10轴向拉伸时,横截面上正应力与纵向线应酿成反比.()
2.11只要静不定结构才可能有温度应力和拆卸应力.()
6.横截面为三角形的直杆自在扭转时,横截面上三个角点处的切应力.
(A)必最大;(B)必最小;(C)必为零;(D)数值不定.
7.图示圆轴AB,两端固定,在横截面C处受外力偶矩 感化,若已知圆轴直径 ,材料的切变模量 ,截面 的扭转角 及长度 ,则所加的外力偶矩 ,有四种答案:
(A) ;(B) ;
材料力学考试题及答案

材料力学考试题及答案一、单项选择题(每题2分,共20分)1. 材料力学中,下列哪一项是正确的应力定义?A. 应力是物体内部单位面积上的内力B. 应力是物体内部单位体积上的内力C. 应力是物体内部单位长度上的内力D. 应力是物体内部单位质量上的内力答案:A2. 材料力学中,下列哪一项是正确的应变定义?A. 应变是物体长度的变化量与原始长度的比值B. 应变是物体长度的变化量与当前长度的比值C. 应变是物体体积的变化量与原始体积的比值D. 应变是物体体积的变化量与当前体积的比值答案:A3. 在拉伸试验中,若材料的屈服强度为300MPa,抗拉强度为400MPa,则该材料属于:A. 脆性材料B. 塑性材料C. 弹性材料D. 韧性材料答案:B4. 材料力学中,下列哪一项是正确的弹性模量定义?A. 弹性模量是材料在弹性阶段内应力与应变的比值B. 弹性模量是材料在塑性阶段内应力与应变的比值C. 弹性模量是材料在断裂阶段内应力与应变的比值D. 弹性模量是材料在任何阶段内应力与应变的比值答案:A5. 材料力学中,下列哪一项是正确的泊松比定义?A. 泊松比是材料在受力时横向应变与纵向应变的比值B. 泊松比是材料在受力时纵向应变与横向应变的比值C. 泊松比是材料在受力时体积应变与纵向应变的比值D. 泊松比是材料在受力时体积应变与横向应变的比值答案:A6. 在材料力学中,下列哪一项是正确的剪切应力定义?A. 剪切应力是材料内部单位面积上的剪切力B. 剪切应力是材料内部单位长度上的剪切力C. 剪切应力是材料内部单位体积上的剪切力D. 剪切应力是材料内部单位质量上的剪切力答案:A7. 材料力学中,下列哪一项是正确的扭矩定义?A. 扭矩是力与力臂的乘积B. 扭矩是力与力臂的比值C. 扭矩是力与力臂的商D. 扭矩是力与力臂的差值答案:A8. 在材料力学中,下列哪一项是正确的弯矩定义?A. 弯矩是力与力臂的乘积B. 弯矩是力与力臂的比值C. 弯矩是力与力臂的商D. 弯矩是力与力臂的差值答案:A9. 材料力学中,下列哪一项是正确的截面模量定义?A. 截面模量是截面面积与截面惯性矩的比值B. 截面模量是截面面积与截面惯性矩的乘积C. 截面模量是截面惯性矩与截面面积的比值D. 截面模量是截面惯性矩与截面面积的乘积答案:C10. 在材料力学中,下列哪一项是正确的应力集中定义?A. 应力集中是材料内部应力分布不均匀的现象B. 应力集中是材料内部应力分布均匀的现象C. 应力集中是材料内部应变分布不均匀的现象D. 应力集中是材料内部应变分布均匀的现象答案:A二、填空题(每题2分,共20分)11. 材料力学中,材料的弹性极限是指材料在______阶段的最大应力。
材料力学习题大全及答案
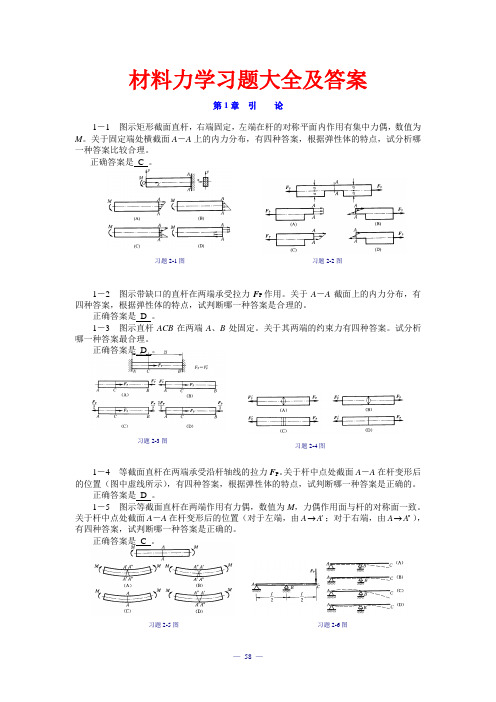
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A )d d Q x F d M(B )d d Q x F (C )d d Q x F (D )d d Q xF 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M 的力偶作用。
试问在杆件的任一横截面m-mxx存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量Mx,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-mxx,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=pcosα=120×cos10°=118.2MPaτ=psinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力FN=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩Mz=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) FNAB=F, FNBC=0, FN,max=F(b) FNAB=F, FNBC=-F, FN,max=F(c) FNAB=-2 kN, FN2BC=1 kN, FNCD=3 kN, FN,max=3 kN(d) FNAB=1 kN, FNBC=-1 kN, FN,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
如欲使BC与AB段的正应力相同,试求BC段的直径。
解:因BC与AB段的正应力相同,故2-3 图示轴向受拉等截面杆,横截面面积A=500 mm2,载荷F=50 kN。
试求图示斜截面m-m上的正应力与切应力,以及杆内的最大正应力与最大切应力。
解:2-4(2-11)图示桁架,由圆截面杆1与杆2组成,并在节点A承受载荷F=80kN作用。
杆1、杆2的直径分别为d1=30mm和d2=20mm,两杆的材料相同,屈服极限σ=320MPa,安全因数n s=2.0。
试校核桁架的强度。
s解:由A点的平衡方程可求得1、2两杆的轴力分别为由此可见,桁架满足强度条件。
2-5(2-14)图示桁架,承受载荷F作用。
试计算该载荷的许用值[F]。
设各杆的横截面面积均为A,许用应力均为[σ]。
解:由C点的平衡条件由B点的平衡条件1杆轴力为最大,由其强度条件2-6(2-17)图示圆截面杆件,承受轴向拉力F作用。
设拉杆的直径为d,端部墩头的直径为D,高度为h,试从强度方面考虑,建立三者间的合理比值。
已知许用应力[σ]=120MPa,许用切应力[τ]=90MPa,许用挤压应力[σbs]=240MPa。
解:由正应力强度条件由切应力强度条件由挤压强度条件式(1):式(3)得式(1):式(2)得故D:h:d=1.225:0.333:12-7(2-18)图示摇臂,承受载荷F1与F2作用。
试确定轴销B的直径d。
已知载荷F1=50kN,F2=35.4kN,许用切应力[τ]=100MPa,许用挤压应力[σbs]=240MPa。
解:摇臂ABC受F1、F2及B点支座反力F B三力作用,根据三力平衡汇交定理知F B的方向如图(b)所示。
由平衡条件由切应力强度条件由挤压强度条件故轴销B的直径第三章轴向拉压变形3-1 图示硬铝试样,厚度δ=2mm,试验段板宽b=20mm,标距l=70mm。
在轴向拉F=6kN的作用下,测得试验段伸长Δl=0.15mm,板宽缩短Δb=0.014mm。
试计算硬铝的弹性模量E与泊松比μ。
解:由胡克定律3-2(3-5) 图示桁架,在节点A处承受载荷F作用。
从试验中测得杆1与杆2的纵向正应变分别为ε1=4.0×10-4与ε2=2.0×10-4。
试确定载荷F及其方位角θ之值。
已知杆1与杆2的横截面面积A1=A2=200mm2,弹性模量E1=E2=200GPa。
解:杆1与杆2的轴力(拉力)分别为由A点的平衡条件(1)2+(2)2并开根,便得式(1):式(2)得3-3(3-6) 图示变宽度平板,承受轴向载荷F作用。
试计算板的轴向变形。
已知板的厚度为δ,长为l,左、右端的宽度分别为b1与b2,弹性模量为E。
解:3-4(3-11) 图示刚性横梁AB,由钢丝绳并经无摩擦滑轮所支持。
设钢丝绳的轴向刚度(即产生单位轴向变形所需之力)为k,试求当载荷F作用时端点B的铅垂位移。
解:设钢丝绳的拉力为T,则由横梁AB的平衡条件钢丝绳伸长量由图(b)可以看出,C点铅垂位移为Δl/3,D点铅垂位移为2Δl/3,则B点铅垂位移为Δl,即3-5(3-12) 试计算图示桁架节点A的水平与铅垂位移。
设各杆各截面的拉压刚度均为EA。
解:(a) 各杆轴力及伸长(缩短量)分别为因为3杆不变形,故A点水平位移为零,铅垂位移等于B点铅垂位移加2杆的伸长量,即(b) 各杆轴力及伸长分别为A点的水平与铅垂位移分别为(注意AC杆轴力虽然为零,但对A位移有约束)3-6(3-14) 图a所示桁架,材料的应力-应变关系可用方程σn=Bε表示(图b),其中n和B 为由实验测定的已知常数。
试求节点C的铅垂位移。
设各杆的横截面面积均为A。
(a) (b)解:2根杆的轴力都为2根杆的伸长量都为则节点C的铅垂位移3-7(3-16) 图示结构,梁BD为刚体,杆1、杆2与杆3的横截面面积与材料均相同。
在梁的中点C承受集中载荷F作用。
试计算该点的水平与铅垂位移。
已知载荷F=20kN,各杆的横截面面积均为A=100mm2,弹性模量E=200GPa,梁长l=1000mm。
解:各杆轴力及变形分别为梁BD作刚体平动,其上B、C、D三点位移相等3-8(3-17) 图示桁架,在节点B和C作用一对大小相等、方向相反的载荷F。
设各杆各截面的拉压刚度均为EA,试计算节点B和C间的相对位移ΔB/C。
解:根据能量守恒定律,有3-9(3-21) 由铝镁合金杆与钢质套管组成一复合杆,杆、管各载面的刚度分别为E1A1与E2A2。
复合杆承受轴向载荷F作用,试计算铝镁合金杆与钢管横载面上的正应力以及杆的轴向变形。
解:设杆、管承受的压力分别为F N1、F N2,则F N1+F N2=F(1)变形协调条件为杆、管伸长量相同,即联立求解方程(1)、(2),得杆、管横截面上的正应力分别为杆的轴向变形3-10(3-23) 图示结构,杆1与杆2的弹性模量均为E,横截面面积均为A,梁BC为刚体,载荷F=20kN,许用拉应力[σt]=160MPa,许用压应力[σc]=110MPa。
试确定各杆的横截面面积。
解:设杆1所受压力为F N1,杆2所受拉力为F N2,则由梁BC的平衡条件得变形协调条件为杆1缩短量等于杆2伸长量,即联立求解方程(1)、(2)得因为杆1、杆2的轴力相等,而许用压应力小于许用拉应力,故由杆1的压应力强度条件得3-11(3-25) 图示桁架,杆1、杆2与杆3分别用铸铁、铜和钢制成,许用应力分别为[σ1]=40MPa,[σ2]=60MPa,[σ3]=120MPa,弹性模量分别为E1=160GPa,E2=100GPa,E3=200GPa。
若载荷F=160kN,A1=A2=2A3,试确定各杆的横截面面积。
解:设杆1、杆2、杆3的轴力分别为F N1(压)、F N2(拉)、F N3(拉),则由C点的平衡条件杆1、杆2的变形图如图(b)所示,变形协调条件为C点的垂直位移等于杆3的伸长,即联立求解式(1)、(2)、(3)得由三杆的强度条件注意到条件A1=A2=2A3,取A1=A2=2A3=2448mm2。
3-12(3-30) 图示组合杆,由直径为30mm的钢杆套以外径为50mm、内径为30mm的铜管组成,二者由两个直径为10mm的铆钉连接在一起。
铆接后,温度升高40°,试计算铆钉剪切面上的切应力。
钢与铜的弹性模量分别为E s=200GPa与E c=100GPa,线膨胀系数分别为αl s=12.5×10-6℃-1与αl c=16×10-6℃-1。
解:钢杆受拉、铜管受压,其轴力相等,设为F N,变形协调条件为钢杆和铜管的伸长量相等,即铆钉剪切面上的切应力3-13(3-32) 图示桁架,三杆的横截面面积、弹性模量与许用应力均相同,并分别为A、E与[σ],试确定该桁架的许用载荷[F]。
为了提高许用载荷之值,现将杆3的设计长度l变为l+Δ。
试问当Δ为何值时许用载荷最大,其值[F max]为何。
解:静力平衡条件为变形协调条件为联立求解式(1)、(2)、(3)得杆3的轴力比杆1、杆2大,由杆3的强度条件若将杆3的设计长度l变为l+Δ,要使许用载荷最大,只有三杆的应力都达到[σ],此时变形协调条件为第四章扭转4-1(4-3) 图示空心圆截面轴,外径D=40mm,内径d=20mm,扭矩T=1kN•m。
试计算横截面上的最大、最小扭转切应力,以及A点处(ρA=15mm)的扭转切应力。
解:因为τ与ρ成正比,所以4-2(4-10) 实心圆轴与空心圆轴通过牙嵌离合器连接。
已知轴的转速n=100 r/min,传递功率P=10 kW,许用切应力[τ]=80MPa,d1/d2=0.6。
试确定实心轴的直径d,空心轴的内、外径d1和d2。
解:扭矩由实心轴的切应力强度条件由空心轴的切应力强度条件4-3(4-12) 某传动轴,转速n=300 r/min,轮1为主动轮,输入功率P1=50kW,轮2、轮3与轮4为从动轮,输出功率分别为P2=10kW,P3=P4=20kW。
(1) 试求轴内的最大扭矩;(2) 若将轮1与轮3的位置对调,试分析对轴的受力是否有利。
解:(1) 轮1、2、3、4作用在轴上扭力矩分别为轴内的最大扭矩若将轮1与轮3的位置对调,则最大扭矩变为最大扭矩变小,当然对轴的受力有利。
4-4(4-21) 图示两端固定的圆截面轴,承受扭力矩作用。
试求支反力偶矩。
设扭转刚度为已知常数。
解:(a) 由对称性可看出,M A=M B,再由平衡可看出M A=M B=M(b)显然M A=M B,变形协调条件为解得(c)(d)由静力平衡方程得变形协调条件为联立求解式(1)、(2)得4-5(4-25) 图示组合轴,由套管与芯轴并借两端刚性平板牢固地连接在一起。
