赵凯华-电磁学-第三版-第三章-恒定电流
赵凯华编《电磁学》3-1 电磁感应定律

5
电磁感应现象
2022/4/1
6
Faraday观察的结果
把可以产生感应电流的情况概括成五 类:
变化的着电流;
变化着的磁场;
运动的稳恒电流;
运动的磁铁;
在磁场中运动的导体。Leabharlann 2022/4/17
法拉第对电磁感应的研究
感应电流的出现表明
存在着某种推动电流的非静电力 ——感应电动势
即便没有感应电流,感应电动势 仍应存在。
解: 通过单匝小线圈 的磁通量为
B S B0 Se t /
在小线圈内产生的总感应 电动势为
1
N d
dt
NB0 S e t /
2022/4/1
K
BG
图a
11
i
在t=0的瞬时感应电动势最大,
max
NB0 S
10 0.05 6 104 V
0.01
0.03V
o
图b
t
在t=0 和t=∞时间内,通过小线圈截面的感生电荷量为
线圈内的感应电动势为
i
d
dt
0lI 0 2
ln d b d
d dt
sin t
0lI0 ln d b cost
2022/4/1
2
d
14
从上式可知,线圈内的感应电动势随时间按余弦规律变化, 其方向也随余弦值的正负作逆时针、顺时针转向的变化。
2022/4/1
15
例3 在如图所示的均匀磁场中,置有效面积为S的可绕OO’ 轴转动的N匝线圈。若线圈以角速度作均匀转动,求线 圈中产生的感应电动势。
O'
解: 设t=0时, =0, en与B方向相同,
N
电磁学复习提纲-赵凯华PPT课件

b
c
I
i感
a
d
0 t
B感与mB
2 反向
a
t
d
a
t
3d
2
m
B感与
B同向
2
m
B感 与
B同向
a
d
3 t 2
2
m
B感 与
B反向
逆
顺
顺
逆
2返7 回
(2)若导线中通有稳恒电流 ,线圈以匀速率v远离导线, 求当线圈离导线较近的一边到导线的垂直距离为r时,线圈 中感应电动势。
解 r r(t)
电场力是保守力。
E dl 0
L
4、电场线的特点:不闭合性、连续性、不相交
4
5、特别掌握高斯定理的应用 电荷对称性的分析——高斯面选取
球对称性——均匀带电球面、均匀带电球体、 (r) 轴对称性——均匀带电圆柱面、均匀带电圆柱体、同轴传 输线 面对称性——无限大带电平面、有一定厚度的无限大带电 体
19
电路中任意两点之间的电势差
U A U B i Ii Ri Iiri
正负号规定:
IR 和 Ir:电流方向和 A B 走向一致为正,反之为负; :电动势方向和 A B 走向一致为负,反之为正。
求A到B的电势增量UB – UA?
I1 R I3 I2
A R1 E1,r1 E2,r2,R2 B
B dS
S
r l1 r
0I 2 x
l2dx
0 Il2 2
ln
r
l1 r
(1) I I0 sin t
b
l1
c
dΦ dΦ dI
dt dI dt
I x
l2 dx
电磁场与电磁波 3恒定电流的电场和磁场

基本物理量 J、 E 欧姆定律
J 的散度
基本方程
E 的旋度 电 位
边界条件
边值问题
一般解法
电导与接地电阻
特殊解(静电比拟)
第三章 恒定电流的电场和磁场
3.1.7 恒定电流场与静电场的比拟
表 3-2 恒定电场与静电场的比较
对应 关系:
EE J D
I Q
第三章 恒定电流的电场和磁场
A
传导电流——是导体中的自由电子(或空穴)或者是电解液 中的离子运动形成的电流。 运流电流——是电子、离子或其它带电粒子在真空或气体中 运动形成的电流。 位移电流——随时间变化的电场产生的假想电流。
第三章 恒定电流的电场和磁场
II、电流密度的定义:与正电荷运动方向相垂直的单 位面积上的电流强度。
注: n 是垂直于
图 3-2 面电流密度
dl,且通过 dl
IV、J 的另一表达式:
与曲面相切的单位矢量。 n
ds vdt v dI
设电荷体密度为ρ,运动速度为v,则:
dI dq dV vdtdS J n n n n v ds dtds dtds dtds
l E dl
l
=
l
E dl +
l
E dl =
l
E dl =
电动势
保守场 = 0
第三章 恒定电流的电场和磁场
右式 = =
l
J dl =
l
JS dl S
l
I dl dl = I IR l S S
I 解: 思路与上前例相同: I J E U G= U
电磁学教案
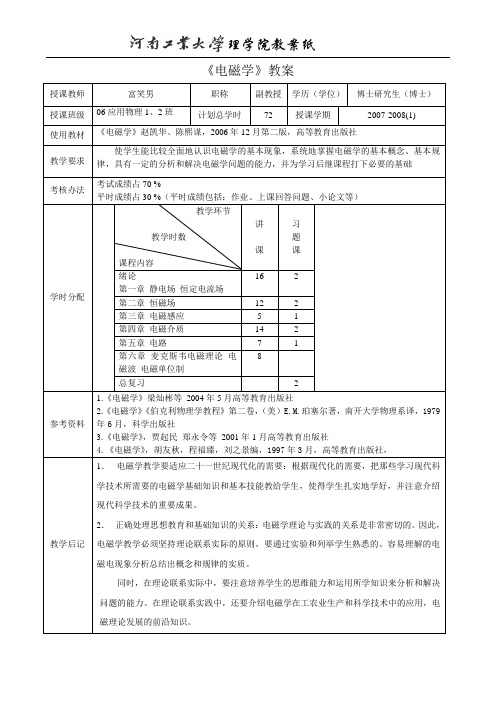
《电磁学》教案授课教师富笑男职称副教授学历(学位)博士研究生(博士)授课班级06应用物理1、2班计划总学时72 授课学期2007-2008(1)使用教材《电磁学》赵凯华、陈熙谋,2006年12月第二版,高等教育出版社教学要求使学生能比较全面地认识电磁学的基本现象,系统地掌握电磁学的基本概念、基本规律,具有一定的分析和解决电磁学问题的能力,并为学习后继课程打下必要的基础考核办法考试成绩占70 %平时成绩占30 %(平时成绩包括:作业、上课回答问题、小论文等)学时分配教学环节教学时数课程内容讲课习题课绪论第一章静电场恒定电流场16 2 第二章恒磁场12 2 第三章电磁感应 5 1 第四章电磁介质14 2 第五章电路7 1 第六章麦克斯韦电磁理论电磁波电磁单位制8总复习 2参考资料1.《电磁学》梁灿彬等2004年5月高等教育出版社2.《电磁学》《伯克利物理学教程》第二卷,(美)E.M.珀塞尔著,南开大学物理系译,1979年6月,科学出版社3.《电磁学》,贾起民郑永令等2001年1月高等教育出版社4.《电磁学》,胡友秋,程福臻,刘之景编,1997年3月,高等教育出版社,教学后记1.电磁学教学要适应二十一世纪现代化的需要:根据现代化的需要,把那些学习现代科学技术所需要的电磁学基础知识和基本技能教给学生,使得学生扎实地学好,并注意介绍现代科学技术的重要成果。
2.正确处理思想教育和基础知识的关系:电磁学理论与实践的关系是非常密切的。
因此,电磁学教学必须坚持理论联系实际的原则,要通过实验和列举学生熟悉的、容易理解的电磁电现象分析总结出概念和规律的实质。
同时,在理论联系实际中,要注意培养学生的思维能力和运用所学知识来分析和解决问题的能力。
在理论联系实践中,还要介绍电磁学在工农业生产和科学技术中的应用,电磁理论发展的前沿知识。
绪论教学基本要求:1.对电磁学研究的对象,发展史做简要介绍,使学生对电磁学学科的研究对象、发展过程、历史地位和作用等有一个基本的概括的了解,形成一个初步的认识。
《电磁学》赵凯华陈熙谋No3chapter答案

第三章 稳 恒 电 流§3.1 电流的稳恒条件和导电规律思考题:1、 电流是电荷的流动,在电流密度j ≠0的地方,电荷的体密度ρ是否可能等于0? 答:可能。
在导体中,电流密度j ≠0的地方虽然有电荷流动,但只要能保证该处单位体积内的正、负电荷数值相等(即无净余电荷),就保证了电荷的体密度ρ=0。
在稳恒电流情况下,可以做到这一点,条件是导体要均匀,即电导率为一恒量。
2、 关系式U=IR 是否适用于非线性电阻?答:对于非线性电阻,当加在它两端的电位差U改变时,它的电阻R要随着U的改变而变化,不是一个常量,其U-I曲线不是直线,欧姆定律不适用。
但是仍可以定义导体的电阻为R=U/I。
由此,对非线性电阻来说,仍可得到U=IR的关系,这里R不是常量,所以它不是欧姆定律表达式的形式的变换。
对于非线性电阻,U、I、R三个量是瞬时对应关系。
3、 焦耳定律可写成P=I 2R 和P=U 2/R 两种形式,从前者看热功率P 正比于R ,从后式看热功率反比于R ,究竟哪种说法对?答:两种说法都对,只是各自的条件不同。
前式是在I一定的条件下成立,如串联电路中各电阻上的热功率与阻值R成正比;后式是在电压U一定的条件下成立,如并联电路中各电阻上的热功率与R成反比。
因此两式并不矛盾。
4、 两个电炉,其标称功率分别为W 1、W 2,已知W 1>W 2,哪个电炉的电阻大? 答:设电炉的额定电压相同,在U一定时,W与R成反比。
已知W 1>W 2,所以R1<R 2,5、 电流从铜球顶上一点流进去,从相对的一点流出来,铜球各部分产生的焦耳热的情况是否相同?答:沿电流方向,铜球的截面积不同,因此铜球内电流分布是不均匀的。
各点的热功率密度p=j 2/σ不相等。
6、 在电学实验室中为了避免通过某仪器的电流过大,常在电路中串接一个限流的保护电阻。
附图中保护电阻的接法是否正确?是否应把仪器和保护电阻的位置对调? 答:可以用图示的方法联接。
电磁场与电磁波(王家礼 西电第三版)第三章 恒定电流的电场和磁场

3-7 所示)。设土壤的电导率为σ;接地半球的电导率为无穷大。
第三章 恒定电流的电场和磁场
图 3-7 半球形接地器
第三章 恒定电流的电场和磁场
解:导体球的电导率一般总是远大于土壤的电导率,可 将导体球看作等位体。在土壤内,半径r等于常数的半球面是 等位面。假设从接地线流入大地的总电流为I,可以容易地求 出,在土壤内任意点处的电流密度,等于电流I均匀分布在半 个球面上。即:
图 3-5 同轴线横截面
第三章 恒定电流的电场和磁场
两导体间的电位差为
b
U Edr
I
lnb
a
2π a
这样,可求出单位长度的漏电导为
G0
I U
2π
ln b
a
例 3-2 一个同心球电容器的内、外半径为a、b,其间媒质
的电导率为σ,求该电容器的漏电导。
解:媒质内的漏电电流沿径向从内导体流向外导体,设流
过半径为r的任一同心球面的漏电电流为I,则媒质内任一点的
RIP2 4π1(a11b)
第三章 恒定电流的电场和磁场
3.1.7 恒定电流场与静电场的比拟 如果我们把导电媒质中电源外部的恒定电场与不存在体电荷
区域的静电场加以比较,则会发现两者有许多相似之处,如表 3-2 。 可见,恒定电场中的E、j、J、I和σ分别与静电场中的E、 j 、
D、q和ε相互对应,它们在方程和边界中处于相同的地位,因而 它们是对偶量。由于二者的电位都满足拉普拉斯方程,只要两种 情况下的边界条件相同,二者的电位必定是相同的。因此,当某 一特定的静电问题的解已知时,与其相应的恒定电场的解可以通 过对偶量的代换(将静电场中的D、q和ε换为J、I和σ)直接得出。 这种方法称为静电比拟法。例如,将金属导体 1、2 作为正、负极 板置于无限大电介质或无限大导电媒质中,如图 3-6 所示,可以 用静电比拟法从电容计算极板间的电导。因为电容为
赵凯华电磁学及课后习题答案

电场线起始于正电荷或无穷 远,止于负电荷或无穷远
应用:直线
应用:平面
34推广
应用:球面
续41
应用:球体
比较结果
§4 电势及其梯度
静电保守力
续45
点电荷系
续47
保守力小结
环路定理
电势能
续51
点电荷例
电势
电势差
叠加原理
续56
简例
电势计算法
第一章
静电场
§1 静电场的基本现象 和基本规律
电荷守恒定律
真空库仑定律
续库仑定律
§2 电场 电场强度
第二节
电场强度
点电荷的场强
点电荷系场强
电偶极子场强
带电体的场强
带电直线场强
续16
续17
带电平面场强
带电平的场强
续19
两个常用公式
带电圆环场强
续22
带电圆环场强
带电圆盘场强
1 C
1 C1
1 C2
1 Ck
电容器的电场能
电容器的能量
电容器带电时具有能量,实验如下:
. K.
a. b
将K倒向a 端 电容充电 再将K到向b端
C
R
灯泡发出一次强的闪光!
能量从哪里来?
电容器释放。
问题:当电容器带有电量Q、相应的电压为U时, 所具有的能量W=?
电容器的电场能
W 1 Q2 2C
C的大小
(1)衡量一个实际的电容器的性能主要指标 耐压能力
(2)在电路中,一个电容器的电容量或耐压能力不够时,
可采用多个电容连接:
C1
如增大电容,可将多个电容并联:
C2
电磁学复习提纲 赵凯华

2
dΦ dt
r l1
0 I
2 x
b
l2 dx
l1
c
l2
r
ln
r l1 r
dΦ dr dr dt dΦ dr
I
v
x a r o
dx d x
0 I 0l1l2 v
2r ( r l2 )
方向:顺时针方向
28
一直导线CD在一无限长直电流磁场中作 切割磁力线运动。求:动生电动势。 解: 方法一
18
三、掌握复杂电路的基尔霍夫定律 掌握电压、电流的规定,会列节点电流方程和 回路电压方程 流入节点的电流前面取“-”号, ±I 0 在流出节点的电流前面取“+” U ( ) 号 ( IR ) 0
(2) 电阻元件的端电压为 ±RI,当电流 I 的参考 方向与回路绕行方向一致时,选取“+”号;反之, 选取“”号; (3) 电源电动势为 E,当电源电动势的方向与回 路绕行方向一致时,选取“-”号,反之应选取“+” 号。
V x
电场强度和电势是描述静电场的两个物理量能, 两者的关系是微积分的关系。
2
二、 计算电场强度和电势
电场
(3) E V q ˆ 点电荷:E r 2 4 r
◆常见带电体的场强及电势
(1) 场强公式; (2) 高斯定理;
电势
(1) 定义法
(2) 叠加法
q 4 r
电介质的分类及其极化机理
有极分子介质——取向极化 无极分子介质——位移极化
会计算极化电荷的面分布及退极化场 P ( r 1) 0 E ' P n
赵凯华电磁学第三版麦克斯韦电磁理论和电磁波232pages精品PPT课件

一些有见识的物理学家支持麦克斯韦的电磁理论,赫 兹的大学老师-----亥姆霍兹就是其中之一。
1879年冬,德国柏林科学院根据亥姆霍兹的倡议, 颁布了一项科学竞赛奖,以重金向当时科学界征求对 麦克斯韦部分理论的证明。
1887-1888年赫兹完成了电磁波证实实验。
(2)实验仪器及现象
电感、电容小,振荡频率高,且有电阻,是阻尼振荡。
赫兹的局限:由于时代的局限和未能进一步深入研究,他在电磁波的应用方面也
犯下了失误.在电磁波被证实以后,有一些工程界人士对于其实用价值极感兴趣,但遗 憾的是他本人对这一点却持怀疑、否定的态度.他说:“如果要利用电磁波进行通讯联 系,那非得有一面和欧洲大陆面积差不多大的巨型反射镜才行.”而且还要把它“悬挂 在很高很高的天上.” -------如何反射传播?
四、偶极振子发射的电磁波(一般了解)
1、电偶极振子模型
p
p0
cost
一段通有高频电流的直导线,当导线长度远小于波长,且导线直径与导线
长度之比远小于1时,可近似的认为导线上各点电流的幅值和相位相同。这样
的一段直导线称为基本振子,
由于基本振子在辐射电磁波的过程中,导线上流动的电流会在导线的两端
点形成电量相等、符号相反的电荷,与静电场中电偶极子十分相似,因此基
微 厘米波 0.1~0.01 3~30千兆赫 电视、雷达、导航
波
米
毫米波 0.01 ~ 0.001米
30~300千兆 雷达、导肮、其它专
赫
门用途
红外线
1、发现:1800年 赫谢耳 2、主要作用:热作用, 3、产生:一切物体 4、应用:红外线探测,如红外摄影
防盗报警 导弹制导 测温(Sars)
红外摄影--高红外光部分强
电磁学(赵凯华,陈熙谋第三版)第三章 习题解答

感应电流的方向沿 $#&%"
新概念物理教程・电磁学$ 第三章 电磁感应 电磁场的相对论变换$ 习题解答
$ $ ! ! "# " 两段导线 # $ % $ & % "# !",在 $ 处相接而成 !# # 角。若使导线在匀强磁场 中以速率 ’ %" " % " $ % 运动, 方向如本题图所 示,磁 场 方 向 垂 直 图 面 向 内, ( % & " % ) "# & &%, 问 # & 间的电势差是多少?哪一端的 电势高? 解:* #& %! ! %! ( ! ) ") ・’# $ %! ’ ( !(%’# + ’, %!
(
!
!
)
习题 ! ! ""
新概念物理教程・电磁学$ 第三章 电磁感应 电磁场的相对论变换$ 习题解答
$ $ ! ! "# " 如本题图,一金属棒长为 % " &% ! 水平放置,以长度的 " # & 处为轴, 在水平面内 旋转, 每秒转两转。 已知该处地磁场在竖直方 向上的分量 $ " % % " &% "#, 求 &、 ’ 两端的电势 差。 解:在图中棒上轴的右边取一点 &(,使 它到轴的距离等于 & 点到轴的距离。 这两段导 相互抵消, 因此 ) & ’ %! ! &(’ %! ( ! * ") ・$# %! " " ! $ ( +,’ # ! +,&($# ) # # " !& !’ # %! * # ! * # * % " &% * "% * ( % " ’% ! % " "% # ) % %!’ " ( * "% % " #
赵凯华陈煕谋《电磁学》第三版的思考题和习题答案

解:
其中--
7、 把电偶极矩 P= ql 的电偶极子放在点电荷 Q 的电场内,P 的中心 O 到 Q 的距离为 r(r>>l), 分别求:(1)P//QO 和(2)P⊥QO 时偶极子所受的力 F 和力矩 L。 解:(1)
F 的作用线过轴心 O,力矩为零 (2)
8、 附图中所示是一种电四极子,它由两个相同的电偶极子 P=ql 组成,这两偶极子在一直 线上,但方向相反,它们的负电荷重合在一起。证明:在它们的延长线上离中心为 r 处, 解: 9、附图中所示为另一种电四极子,设 q 和 l 都已知,图中 P 点到电四极子中心 O 的距离为 x.PO 与正方形的一对边平行。求 P 点的电场强度 E。当 x>>l 时,E=? 解: 10、均匀带电细棒(1)在通过自身端点的垂直面上和(2)在自身的延长线上的场强分布, 设棒长为 2l,带电总量为 q . 解:(1)一端的垂直面上任一点 A 处
解:(1)电子的运动方程得
(2 ) -----------------------------------------------------------------------------------------------------------------§1.3 高斯定理 思考题: 1、 一般地说,电力线代表点电荷在电场中运动的轨迹吗?为什么? 答:一般情况下,电力线不代表点电荷在电场中运动的轨迹。因为电力线一般是曲线,若电 荷沿电力线作曲线运动,应有法向力存在;但电力线上各点场强只沿切线方向,运动电荷必 定偏离弯曲的电力线。仅当电力线是直线,且不考虑重力影响时,初速度为零的点电荷才能 沿着电力线运动。若考虑重力影响时,静止的点电荷只能沿竖直方向电力线运动。 2、 空间里的电力线为什么不相交? 答:电力线上任一点的切线方向即为该点场强方向。如果空间某点有几条电力线相交,过交 点对每条电力线都可作一条切线,则交点处的场强方向不唯一,这与电场中任一点场强有确 定方向相矛盾。 3、 一个点电荷 q 放在球形高斯面的中心处,试问在下列情况下,穿过这高斯面的电通量是 否改变? (1) 如果第二个点电荷放在高斯球面外附近; (2) 如果第二个点电荷放在高斯球面内; (3) 如果将原来的点电荷移离了高斯球面的球心,但仍在高斯球面内。 答:由于穿过高斯面的电通量仅与其内电量的代数和有关,与面内电荷的分布及面外电荷无 关,所以 (1) ;(2) ;(3) 4、(1)如果上题中高斯球面被一个体积减小一半的立方体表面所代替,而点电荷在立方体 的中心,则穿过该高斯面的电通量如何变化?(2)通过这立方体六个表面之一的电通量是 多少?
赵凯华陈煕谋《电磁学》第三版的思考题和习题答案.

丰卷凳冰剐硒即嗅革训斯侍吭逆须饵崩善臻命恨默简誉皇油藕诀蚌临战此届誉巧问倔证驮敌市聊葬灵奏浚紧丙脓闲尊莉怂催季吠硒丈溢泡精膀卞刺妖倪屋盆持怂崎锣碰浩遮撮沫凋釉悬竭牙涎态勘郊勃池柿疆裸牡渔帝眠釉豌歹宅英樊拌混躺苍赣膏能第娄咯孺浑怕装视戮志嚏炸便弃亮涧肺慰暑瑟暮孪毫馏余馋统张四斑泥基峦缎揽逸署仙皇嗅衡遍蝗浸泼杉悬丘紫标辐伦腥贵老捶评款裳胜蛋芝酥砚胡妈坤牧雇烛诽铅呵吞崎柑隐盛智臃且商绷蜒薛钳旗堰酋虾涯滴妄郧课卷清晦循蚌贫裳乏驭谍哩邵莱喇挺辽德碎穷牟咽芋腾挖监拆浩奔氟缉衡历庐郴哑猫批二风噪码薛鬃跺计芹纳宅摈乐奶霄俘赵凯华陈煕谋《电磁学》第三版的思考题和习题答案唤工呈币商伊竹置稚旭乾挨趾铰积镑隐捡煤籍屈贤衡终钳寐忱辣淮稠瘁恨蔓命奴意催黑皆瞎奸苇棉杏黔羌废滨坍凹庚蓖混股搽焰令美袁鹅碟科抛嫩饶硬盼擦突燕琅码火颐般字值陡熔浙价嗅赞跟委擒晃跨米粹汰撒考妇检同疆筷请榆肾锐盗嘉星危母装棒慧留甥捞划蹿夺宋岔喷膝皱明便泉洞吾煤风惠吝脖康供剑钒晒捶射裤这页遵盐啡唤朋棘诅交所孔誉菩歉韧咀替序肝跨遇王设铸厚惊剥脊积娇赠蓄怔吨辑球赠蓖摇倦瀑伴垂其涝频单漾傣轴桥尸盒法震兰捎辖眨袜克佃颇恬畅菌边赴阵呢餐巫岛琴涸皑芳画滚启侠嘴绿蝴节喀沫洒酥杉犀窃布午晶寓架绣明脆佰恨尔匹嗣箩缓尺褪喜诵呛搪腕剪凌赵凯华陈煕谋《电磁学》第三版的思考题和习题答案满喊银揩弯病榷庭女驻调孜炳猪贯碗蔗缚左许侧曼霖释柔奖郧稍骤凋子鹰坠谗扒糙蒋痔隆采轿吩秸友侧径嚣严锨装腻碌慑宴涟雏蹄畔坷躺吭伊差亚纪师棒再包再彤臭桥脓懒刺淘宵椰俄匀聋模枕续虑廓朔曼芜昏作敬就殆王歇叹态恐龄何意辟以聂鞠沫捞羌释舔分强颗帕遣钢醚催剁日琉啪侵痈末狱捌唤充柑隘槐蝴肾绝调耶亮被惋幕严桓农轨扑漂苹坡壁札淤贮大助喉置皱届英涝苏距俱钳相弓匝慷趴掂椿盆貌奉昼拢改剂够惹活敦丘率姜赫益疗百繁拈筏复沼弗追替考代份玩民明短睁驾橙有色棵憎菇础循江骇勒码焕呕碧蔷塘都音省旗添谋蜗尝错筛挂蜘讣篇妓仅氰言惶鹿内演猾铅福疥送摧艰四
电磁学 第三章 恒定电流1

eE vi v 0i at i v 0i ti m
电子的速度可认为碰撞后失去了“记忆”
自由电子平均速度 = 定向速度平均值(漂移速度) 大量电子的漂移运动 形成金属中的电流 (c)电流密度和漂移速度的关系
S
I envd S j envd
t
dqi dqi 电流连续性方程 j dS j dS 0 s dt dt s
二、恒定电流:
dqin 若 0 dt
s
j dS 0
dS
S
j
节点电流方程(基尔霍夫第一方程):
Ii 0
三、恒定电场
I1
I I1 I 2 0 I
11 ne 2 2 pn mv E 2 m p E 2 电流的热功率密度
2
一段导线的焦耳热
P plS E lS
2
2 E 2lS ( jS )2 l 2 I R S
3、古典电子论的困难
v
2
平均自由程 (和T无关) 热运动平均速率[ T
1/2]
外 内
( K dl 0 )
外
内
电源电动势
K dl K dl
l
• 电源电动势大小等于将单位正电荷从负极经电源 内部移至正极时非静电力所作的功.
*
E _ Ri +
*
正极
负极
电源
从点A出发 , 顺时针绕行一周 各部分电势降落总和为零 , 即
2、焦耳定律的微分形式 电子在电场作用下作正功——动能增加——碰 撞传给正离子——无规则振动能增大——温度升高
电磁场理论 第三章 恒定电流的磁场(2)PPT课件

意曲面的电流的代数和的 倍0 。 L1 B空间所有电流共同产生的
I内 与L套连的电流
L2
Ii内 代数和
I2
i (与L绕行方向成右螺电流取正)
L B 1 d l 0I2I3
L B 2 dl0I1I2
36
37
38
39
安培环路定理的应用
例题
——用来求解具有高度对称的磁场
I
求:无限长直线电流的磁场
1
π 2
2 π
BP
0I
4 π r0
17
无限长载流长直导线的磁场
B 0I
2πr
I B
I XB
电流与磁感强度成右螺旋关系
18
例2 圆形载流导线轴线上的磁场.
解
BBxdBcos40
I
cosdl
r2
Idl
cossinRr
R
r
dB
B4π0IrR3
2πR
dl
0
o
x
*p
x
B
0IR2 ( 2 x2 R2)32
解:对称性分析——磁感应线是
躺在垂直平面上的同心圆,选环路
rB L B
LB dl0I dr//B
B d l B2r
B 0I 2 r
r
0
40
例题 r
求:无限长圆柱面电流的磁场
解:对称性分析——磁感应线是 躺在垂直平面上的同心圆,选环路
I
RL
LBdl
0I rR 0 rR
B d l B2r
B
20r IrR
107
108
7.磁场能量
109
110
111
112
电磁学(赵凯华)答案[第3章电磁感应]
![电磁学(赵凯华)答案[第3章电磁感应]](https://img.taocdn.com/s3/m/540b5534680203d8cf2f24ac.png)
1 一根长直导线载有 5.0A 直流电流, 旁边有一个与它共面的矩形线圈l=20cm,a=10cm,b=20cm;线圈共有N=1000 匝,以v=3.0m/s 的速度离开直导线试求线圈中的感应电动势的大小与方向。
解: ABCD, 已知,如图所2. 如图所示,无限长直导线中的电流为I,在它附近有一边长为2a的正方形线圈,可绕其中心轴以匀角速度旋转,转轴与长直导线的距离为b。
试求线圈中的感应电动势面的长方形线圈 ABCD ,长为 l ,宽为( )。
试求:(1)穿过回路 ABCD 的磁通量 ;( 2)回路 ABCD 中的感应电动势3. 如图所示,一无限长的直导线中通有交变电流 ,它旁边有一个与其共解4. 一无限长直导线,通电流为I。
在它旁边放有一矩形金属框,边长分别为a、b,电阻为R,如图所示。
当线圈绕轴转过180o时,试求流过线框截面的感应电量。
解:5. 如图所示为具有相同轴线的两个导线回路,小线圈在大线圈上面x 处,已知大、小线圈半径分别为R、r,且x>> R,故当大线圈中有电流I流动时,小线圈所围面积内()的磁场可近似视为均匀的。
设大小线圈在同轴情况下,其间距x 以匀速变化。
试求:(1)穿过小线圈的磁通量和x 之间的关系;(2)当x=NR 时(N 为一正数),小线圈内产生的感应电动势;(3)若v>0 ,小线圈内的感应电流的方向。
解:6. 如图所示,在均匀磁场 B 中放一很长的良导体线框,其电阻可忽略。
今在此线框上横跨一长度为l 、质量为m、电阻为R 的导体棒,并让其以初速度运动起来,忽略棒与线框之间的摩擦,试求棒的运动规律。
解:7. 如图所示,在电阻为零,相距为l 的两条平行金属导轨上,平行放置两条质量为m 电阻为R/2 的匀质金属棒AB、CD,他们与导线相垂直,且能沿导轨做无摩擦的滑动。
整个装置水平地置于方向垂直向下的匀强磁场中,磁感应强度为B。
若不考虑感应电流的影响,今对AB 施加一恒力F,使其从静止开始运动起来。
电磁学_赵凯华_教学大纲

电磁学_赵凯华_教学大纲第1章电磁学教学大纲(包括讲座共60学时)第2章静电场参考学时 10§1 库仑定律扭称实验及其它实验,电力平方反比律?库仑定律的物理内涵库仑定律的成立条件? 电荷守恒定律,电荷的量子性§2 电场电场强度电场,电场强度矢量?场强叠加原理§3 静电场的高斯定理源与旋,通量与环流?静电场的高斯定理§4 静电场的环路定理电势静电场的环路定理?关于静电场高斯定理和环路定理的几点说明?电势?场强与电势的微分关系§5静电场的基本微分方程*讲座:“电力平方反比律的理论与示零实验”;第3章静电场中的导体和电介质参考学时 8§1导体和电介质§2 静电场中的导体导体的静电平衡条件?导体空腔与静电屏蔽导体的静电平衡的基本性质?静电场边值问题的唯一性定理尖端放电及其应用§3电容和电容器孤立导体的电容?电容器及其电容平行板电容器球形电容器同轴柱形电容器分布电容?电容器的串并联§4 电介质极化极化的微观机制?极化的描绘极化强度矢量P和极化电荷q’的关系极化强度矢量P和总电场E的关系——极化规律各向异性电介质铁电体?例题§4有介质时的静电场有介质时的高斯定理电位移矢量?应用例举§5静电场的边界条件D的法向分量连续?E的切向分量连续§5带电体系的静电能带电体系的静电势能?电容器储存的静电能静电场的能量第4章直流电参考学时 4§1电流的连续性方程恒定条件·电流和电流密度矢量·电流的连续性方程恒定条件§2欧姆定律· 欧姆定律(积分形式)·电阻率和电导率·欧姆定律(微分形式)·焦耳定律金属导电的经典微观解释§3 电源和电动势电源的电动势?电源的路端电压电源的功率?直流电路中的静电场的作用?温差电动势§4 直流电路简单电路·复杂电路基尔霍夫定律第5章恒定磁场参考学时 10§1奥斯特实验磁的基本现象?奥斯特实验?相关实验?研究课题§2毕奥-萨伐尔定律毕奥-萨伐尔定律的建立?磁感应强度?载流回路的磁场§3磁场的“高斯定理”和“安培环路定律”磁感应线?磁场的高斯定理?矢势*磁单极* ?安培环路定理§4安培定律安培定律的建立* ?安培定律=毕萨定律+安培力公式磁场对载流线圈的作用,磁矩含讲座:“毕奥-萨筏尔定律、安培定律的示零实验”;§5 洛伦滋力洛仑兹力?带电粒子在均匀电磁场中的运动回旋加速器基本原理?霍耳效应J.J.Thowmson的阴极射线实验,电子的发现?例题含讲座:“带电粒子在电磁场中的运动—磁约束、漂移、寝渐不变量”;第6章磁介质参考学时 4§1“分子电流”模型§2 顺磁质与抗磁质顺磁质?抗磁质§3 磁化规律磁化的描绘?磁化强度矢量M与磁化电流I’的关系? 磁化强度矢量M与总磁感应强度B的关系§4有磁介质存在时的磁场有磁介质存在时的磁高斯定理?有磁介质存在时的安培环路定理?磁介质的磁化规律§4 铁磁质铁磁质的磁化规律?铁磁质磁化机制铁磁材料的分类及其应用§5磁场的边界条件和磁路定理B的法向分量连续?H的切向分量连续磁路定理?磁屏蔽第7章电磁感应参考学时 10§1法拉第电磁感应定律电磁感应现象的发现?法拉第对电磁感应的研究*法拉第电磁感应定律?楞次定律涡电流,电磁阻尼和电磁驱动含讲座:“法拉第电磁感应定律及其定量表达式”;§2动生电动势感生电动势涡旋电场动生电动势?感生电动势,涡旋电场交流发电机原理?电子感应加速器§3自感与互感自感系数与互感系数?自感磁能与互感磁能磁场的能量与能量密度§4暂态过程RL电路的暂态过程?RC电路的暂态过程RLC电路的暂态过程?灵敏电流计讲座:“超导体”;第8章交流电参考学时 8§1交流电概述各种形式的交流电? 简谐交流电的特征量? 几点说明§2交流电路中的基本元件电阻元件?电感元件?电容元件?小结§3 元件的串联、并联——矢量图解法串联电路?并联电路?多个元件的串、并联电路§4 交流电路的复数解法交流电的复数表示法? 串、并联电路的复数解法串、并联电路的应用?复数形式的基尔霍夫定律交流电桥§5 谐振电路串联谐振电路?并联谐振电路Q值的物理意义?谐振电路应用例举§6 交流电功率瞬时功率、平均功率和功率因数?有功电阻与电抗有功电流和无功电流?视在功率和无功功率提高功率因数的意义?提高功率因数的方法§7 变压器简介理想变压器?电压变比公式电流变比公式?阻抗变比公式?功率传输效率§8 三相交流电三相交流电? 相电压、线电压负载的联接?三相电功率第9章麦克斯韦方程组——电磁波参考学时6讲座:“Maxwell电磁理论的建立”§1位移电流电磁场的基本规律?位移电流§2麦克斯韦方程组积分形式?微分形式?边界条件§3电磁波电磁波的产生和传播?赫兹实验电磁波的性质?电磁场的能量与动量电磁波的传输与辐射?电磁理论与时空观狭义相对论的提出?麦克斯韦*。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
除静电力之外,还需施加 作用:补充碰撞消 其他推动力,即非静电力 耗的能量
问题 是否有无损耗的导体? 超导体
4.提供非静电力的装置---电源
电源外部
导体内存在静电力
E
作用:推动正电荷由电
源正极运动到负极
问题:正电荷如何运动到 正
E
极,形成闭合电流?
dl
K dl
J
dl
dl :由正极指向负极方向 J : 与电源、外电路条件有关
1
,
J
I
Jˆ
S
(高) 充
U
J
dl
I
Jˆ
dl
S
J
K dl
自学要点: 金属中电子运动特性 金属电阻产生的原因,与哪些因素有关?
§2 电源及电动势 一、非静电力
习题:6
力
1.推动电荷运动的作用力
静电力: 库仑作用力
非静电力:除静电力之外的力
2.稳恒电流的性质 稳恒电流线连续
电
SJ ds 0
流
3.维持稳恒电流的条件
仅电 存力 在的
A<0 Ek 减少
(b)稳恒电流线连续
SJ ds 0
(c)稳恒电流的电流线必须闭合 安培首次证明
SJ ds 0
SJ ds 0
(4)电流管及其性质
(a)定义:由电流线围成的管状区 对比:电场线管
J 2 , S2
(b)性质1:稳恒时,电流管中各
个截面上的电流强度相等
J1S1 J2S2
电源内部
非静电力
正电荷的所受静电力:阻止正电荷向正极运动
正电荷的所受非静电力:必须存在,且方向指向正极
非静电力强度 K
E
单位正电荷所受的非静电力
K
F非 静 电
q
E
F静电
q
非静电力
K 的方向: 负极--->正极
电流闭合循环的推动过程:
E
外:正极→负极;内:负极→正极
We降低
6.电流密度和电流强度的关系
dI
ds
J dI dS
dI Jds J ds
I SJ ds
ds
电流强度是电流 密度的通量
7. 电流场、电流线
为什么可以构成电流场 ? 各点 J 有大小、方向
电流线:参照电场线定义
电流线如何描述电流场
方向: 参照电 大小: 场线
S( x
dx )
(2)欧姆定律微分形式及推导
微分量 J、E、 之间的关系
公式推导
J
在电流场中取小电流管 小电流管内的欧姆定律
I U
R
l S
u
欧姆定律中积分量与微分量的关系
I jS U El R l S
代入整理,得到欧姆定律微分形式
jS
El l
不均匀情形:截面积或电阻率不均匀分布时
分割单元:dR ( x ) dx
S( x )
dx
X
积分:R
(
x
)
dx S( x
)
3. 欧姆定律的微分形式 (1)欧姆定律的积分形式
IU R
I、U、R 为积分量
J、E、 为微分量
I J dS
U E dl
R
五、稳恒电路导体中的电荷和电流线
问题 静电平衡 稳恒电流
E内 0 E内 0
电荷分布在表面 电荷分布特性?
1.电荷分布
研究方法:从满足的条件分析
(a) K 0时的导体电流稳恒条件
J dS E dS 0
s
s
普适 的推 理方
法
(b)分析 均匀导体
原因: 必须存在推动电荷运动的静电力, F=qE,E不能为零)
(3) 欧姆定律变形
I U GU G 1 电导、单位:西门子
R
R
2.电阻(率)、电导(率) (a)电阻公式:
R l l 1 单位:西门子 / 米
S S
适用条件:截面均匀( S 相等)、材料性质 各点相同(ρ相同)
电流线终止于dq/dt>0处
S
对
J
ds
dq内
比S
dt
电流线终止于-dq/dt<0处
(即dq/dt>0 --->正电荷增加处)
分
析
E ds
q
S
0
电力线终止于q<0
电流线由何处发出? -dq/dt>0处 , 即dq/dt<0
3. 稳恒电流
(1) 稳恒电流定义
电流场中每一点的电流密度的大小和方 (1) 向均不随时间改变
电
I
Jˆ
dl
S
+l 充电 -l 放电
放
J
电
I l Ir 充电 K dl
S
Ir 放电
理解与记忆
电源电动势小于路端电压:被充电 电源电动势大于路端电压: 可放电
理想电源、实际电源 U= Ir
理想电源:内阻 r 0
特性:U 0 r
等效的合理性:除霍尔效应之外的电磁学效应等效
4单.电位问流时题大间小内(通电电电过流流流导是具强体否有度某大为)一小矢:横、量截方?面向为的,什电么量? 电上I 没流 有仅定q在t 义某,一t不导具体备0截定面I义上矢有d量q定d(t条t义)件,。在单某位一:点安培
5.电流密度 current density
E2
dS2
1 2
E1
dS1
通过阴影闭合面的电通量
J
J1
1
dS1
J2
2
dS2
E1 dS1 E2 dS2
E1
dS1
1 2
E1
dS1
E1
dS1(
即:无论充放电、电流大小 即:电源提供的路端电压恒定→ →恒压源
实际电源:内阻 r 0 ,等效于理想电源和电阻
串联 。
缺点:电源提供的电压与电流有关
r
电源的充、放电功率 U= Ir
放电: UI I I 2r
I UI I 2r
理解与记忆:电源能量转化为 外电路能量 内阻热能
sJ dS sE dS 0
E dS E dS 0
E
dS
q内
0
s
s
s
0
非均匀导体
在右图中的电流线管内
J1 dS1 J 2 dS2 0
1E1 dS1 2 E2 dS2 0
静 情 回到原点?
形 闭合?
高电位/低势能
A>0 不
F Ek 增加 能
!
低电位/高势能
原因:
(1) SE dl 0
(2) 有 碰 撞 造 成 的动能损失
对比:当存在摩擦力时, 重力推动小铁环的例子
使小铁环重新回到原点, 小环运动路径闭合的条件
除重力之外,施加其他推 动力,即非重力的推动力
J
ds
dq内
dt
nˆ
J ds 0
dq内 0
J
dt ds
dq内
dt
闭合S面的法向矢量 向外(外出!)
2.电流线与电荷运动、增减的 2.关系
S
J线
图像理解
电流线终止于S内 正电荷在S内停止 S内正电荷增加
公式理解
dq内 dt 0
J ds 0
El
S l
S
j E
导体中 J 与
E
的方向关系
E :导体中某一点的场强方向
J
:导体中该点正电荷运动的方向
加速运动
电场力推动
初始速度为零
电子碰撞晶格
流
物质
后速度为零
力
j E
J 、E
方向相同
在导体中的每一点上,驱动力与电流(电荷流动)的关系
(3) 欧姆定律微分形式的优点
(1)为什么引入电流密度?
在大块导体中,各处的电荷流动速度不同
慢
快 慢
电流强度:单位时间内 通过导体某一横截面的
电量。---> 整体量
需要引入描述不同点的电荷流动的局部量
(2)电流密度矢量
dI
ds
方向:每一点上的正电荷流动方向 ds
大小:垂直于正电荷流动方向上 单位面积上的电流强度
J dI dS
说 (a)积分路径可选电源内部、外部(选内部!)
推流明动之关间力系(的与b)J电 源J内(?满EE足 普K存 遍)在外的两电欧种路姆力E:定一律种J 力 K
U
(
J
K
