梯形的面积

合集下载

计算梯形面积的公式及应用

计算梯形面积的公式及应用梯形是我们学习数学时经常遇到的一个几何形状，它具有两个平行的底边和两个不平行的侧边。

计算梯形的面积是我们学习数学的基础知识之一，它在实际生活中有着广泛的应用。

本文将介绍计算梯形面积的公式及其应用。

一、梯形的面积公式梯形的面积公式是：面积 = （上底 + 下底）×高 ÷ 2。

其中，上底和下底分别表示梯形的两个平行底边的长度，高表示梯形的高度。

例如，如果一个梯形的上底长为8cm，下底长为12cm，高为5cm，那么它的面积可以计算为：（8 + 12）× 5 ÷ 2 = 20cm²。

二、梯形面积公式的应用1. 计算图形面积梯形面积公式可以应用于计算各种图形的面积。

例如，如果一个花坛的形状是梯形，我们可以通过测量上底、下底和高来计算花坛的面积，从而确定需要多少土壤和植物。

2. 计算建筑物面积在建筑设计中，梯形的形状常常出现在屋顶或者柱子的顶部。

通过计算梯形的面积，建筑师可以确定所需的建筑材料数量，如瓦片或者涂料。

3. 计算土地面积在土地测量和规划中，梯形的形状常常用于计算土地的面积。

通过测量土地的上底、下底和高，我们可以计算出土地的面积，从而帮助农民或者房地产开发商确定土地的价值和利用规划。

4. 计算物体体积当我们需要计算一个不规则物体的体积时，可以将其分解为多个梯形，然后计算每个梯形的面积并相加。

通过这种方法，我们可以计算出物体的体积，如水箱、容器等。

三、梯形面积公式的实际应用举例举例来说，小明的家里有一个花坛，它的形状是梯形。

小明想要给花坛铺上一层新的土壤，但他不知道需要多少土壤才够。

于是，他测量了花坛的上底长为6m，下底长为8m，高为2m。

根据梯形面积公式，小明可以计算出花坛的面积为：（6 + 8）× 2 ÷ 2 = 14m²。

因此，小明需要购买14平方米的土壤来铺在花坛上。

在另一个例子中，张先生是一名房地产开发商，他购买了一块土地用于建设公寓楼。

梯形面积的公式

梯形面积的公式
梯形是只有一组对边平行的四边形。

平行的两边叫做梯形的底边：较长的一条底边叫下底，较短的一条底边叫上底；另外两边叫腰；夹在两底之间的垂线段叫梯形的高。

1梯形的面积公式
1、梯形的面积公式：(上底+下底)X高÷2,用字母表示：
S=(a+c)×h÷2
变形：h=2S÷(a+c)；变形2：a=2s÷h-c;变形3：c=2s÷h-a0
2、梯形的面积公式：中位线X高，用字母表示：1∙ho
3、对角线互相垂直的梯形面积为：对角线X对角线÷2°
2梯形性质
1、等腰梯形的两条腰相等。

2、等腰梯形在同一底上的两个底角相等。

3、等腰梯形的两条对角线相等。

4、等腰梯形是轴对称图形，对称轴是上下底中点的连线所在直线(过两底中点的直线)
判定
1、两腰相等的梯形是等腰梯形；
2、同一底上的两个角相等的梯形是等腰梯形;
3、对角线相等的梯形是等腰梯形。

梯形面积公式的换算

1、梯形的面积公式：（上底+下底）×高÷2
梯形的面积等于上下两底之和与高的乘积的一半。

如果梯形的上下两底分别用a和 b表示，高用 h表示，梯形的面积s=（a+b）×h÷2 。

2、梯形的面积公式：中位线×高
根据梯形中位线的长度等于上下两底和的一半，梯形的面积也等于中位线与高的乘积。

如果梯形的中位线用 m表示，高用 h表示，梯形的面积s=mh 。

3、对角线互相垂直的梯形面积为：对角线×对角线÷2。

扩展资料：
梯形(trapezium)是指一组对边平行而另一组对边不平行的四边形。

等腰梯形的性质：
1．等腰梯形的两条腰相等
2．等腰梯形在同一底上的两个底角相等
3．等腰梯形的两条对角线相等
4．等腰梯形是轴对称图形，对称轴是上下底中点的连线所在直线
5．等腰梯形（这个非等腰梯形同理）的中位线（两腰中点相连的线叫作中位线）等于上下底和的二分之一。

6．梯形的中位线平行于两底。

梯形的面积的公式

梯形的面积的公式
梯形的面积的公式是一个比较常见的数学表达式，也是中学数学教材上常出现的内容之一。

梯形是由两个平行线段构成的四个边的多边形，这样计算梯形面积自然就成了一件事了。

计算梯形面积的公式是：面积=（上底+下底）*高÷2，其中，上底和下底分别代表梯形的上边和下边的长度，高代表的梯形的高度，而上底和下底的和乘以梯形的高度再除以2就等于梯形的面积了。

同时，梯形的面积又可以通过面积反推的方法计算得出，即利用佐教公式，也就是梯形的面积其实等于两条对角线的积。

所以，计算梯形的面积时，可以根据这两种计算方法加以参考。

总之，梯形的面积的公式是非常简单实用的数学算法，在中学数学教学中被广泛使用和推广；计算梯形面积时可通过（上底+下底）*高÷2或者佐教公式两两计算方法来计算，十分方便快捷。

梯形的公式面积

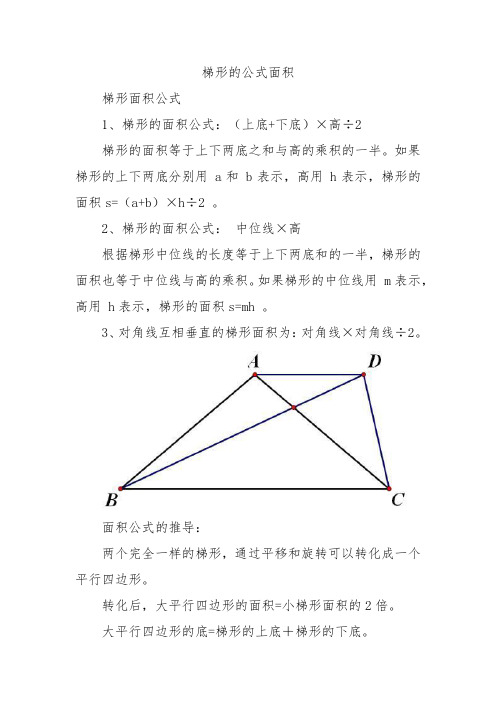
梯形的公式面积
梯形面积公式
1、梯形的面积公式：（上底+下底）×高÷2
梯形的面积等于上下两底之和与高的乘积的一半。

如果梯形的上下两底分别用 a和 b表示，高用 h表示，梯形的面积s=（a+b）×h÷2 。

2、梯形的面积公式：中位线×高
根据梯形中位线的长度等于上下两底和的一半，梯形的面积也等于中位线与高的乘积。

如果梯形的中位线用 m表示，高用 h表示，梯形的面积s=mh 。

3、对角线互相垂直的梯形面积为：对角线×对角线÷2。

面积公式的推导：
两个完全一样的梯形，通过平移和旋转可以转化成一个平行四边形。

转化后，大平行四边形的面积=小梯形面积的2倍。

大平行四边形的底=梯形的上底＋梯形的下底。

大平行四边形的高=梯形的高。

因为，平行四边形的面积=底×高，
所以，梯形的面积=（上底+下底）×高÷2。

梯形面积公式

梯形面积公式-CAL-FENGHAI.-(YICAI)-Company One1
面积公式折叠编辑本段
梯形的面积公式：（上底+下底）×高÷2，用字母表示：S=（a+b）×h÷2
变形1：h=2s÷（a+b）；变形2：a=2s÷h-b；变形3：b=2s÷h-a。

另一计算梯形的面积公式：中位线×高，用字母表示：L·h。

对角线互相垂直的梯形面积为：对角线×对角线÷2。

字母公式：（A+B)乘H除2
梯形公式折叠编辑本段
中位线×高，用字母表示：L·h
（上底+下底）×高÷2，用字母表示：S=（a+b）×h÷2
应用实例折叠编辑本段
如图，已知四边形ABCD中，AB=DC，AC=DB梯形，求证：四边形ABCD是等腰梯形。

证明：过点A作AE∥DC交BC边于点E．
∵AB=CD，AC=DB，BC=CB，
图∴△ABC≌△DCB，∴∠ABC=∠DCB
又∵AE∥DC，
∴∠AEB=∠DCB
∴∠ABC=∠AEB ，∴AB=AE，
∴四边形AECD是平行四边形．
∴AD∥BC．
又AB=DC，且AD≠BC，
∴四边形ABCD为等腰梯形．
点评：
判定一个任意四边形为等腰梯形，如果不能直接运用等腰梯形的判定定理，一般的方法是通过作辅助线，将此四边形分解为熟悉的多边形，此例就是通过作平行线，将四边形分解成为一个平行四边形和一个等腰三角形．。

梯形面积的算法公式

梯形面积的算法公式梯形是一个常见的几何图形，它的特点是有两条平行边，其余两条边不平行。

计算梯形的面积是数学中常见的问题，而梯形的面积算法公式可以帮助我们轻松解决这个问题。

梯形的面积算法公式如下：面积 = （上底 + 下底）× 高÷ 2在这个公式中，上底和下底分别表示梯形两条平行边的长度，高表示梯形两平行边之间的距离。

通过这个公式，我们可以快速计算出梯形的面积。

下面我们通过几个具体的例子来说明如何使用梯形的面积算法公式。

例子1：假设梯形的上底长度为5cm，下底长度为8cm，高为6cm。

我们可以通过公式计算梯形的面积：面积= (5 + 8) × 6 ÷ 2 = 13 × 6 ÷ 2 = 39cm²因此，这个梯形的面积为39平方厘米。

例子2：假设梯形的上底长度为12.5cm，下底长度为18.7cm，高为10cm。

我们可以通过公式计算梯形的面积：面积= (12.5 + 18.7) × 10 ÷ 2 = 31.2 × 10 ÷ 2 = 156cm²因此，这个梯形的面积为156平方厘米。

通过以上两个例子，我们可以看到，使用梯形的面积算法公式可以快速准确地计算出梯形的面积。

这个公式的原理是将梯形分解为一个矩形和两个三角形，然后分别计算出它们的面积，最后将它们的面积相加得到梯形的面积。

需要注意的是，使用这个公式计算梯形的面积时，要确保上底、下底和高的单位相同，否则计算结果将会出现错误。

另外，计算结果的单位将会是上底、下底和高的单位的平方。

除了使用梯形的面积算法公式，我们还可以通过其他方法来计算梯形的面积。

例如，我们可以将梯形分解为两个直角三角形，然后分别计算它们的面积，最后将它们的面积相加得到梯形的面积。

这种方法虽然稍微复杂一些，但同样可以准确计算出梯形的面积。

梯形的面积算法公式是一种简单高效的计算梯形面积的方法。

梯形的面积计算

梯形的面积计算
梯形是一个几何图形，由两个平行的底和连接底的两个斜边组成。

计算梯形的面积需要知道梯形的底和高的长度。

下面将介绍如何计算梯形的面积。

梯形的面积公式如下：
面积 = （上底 + 下底） ×高 ÷ 2
步骤一：测量上底和下底的长度
在计算梯形的面积之前，首先需要测量上底（较短的底）和下底（较长的底）的长度。

使用直尺或测量工具来准确测量。

步骤二：测量梯形的高
在计算梯形的面积之前，还需要测量梯形的高。

梯形的高是连接上底和下底的直线的长度。

步骤三：将测量结果代入公式计算
利用测得的上底、下底和高，将这些数值代入梯形的面积公式进行计算。

首先将上底和下底的长度相加，然后乘以高，最后除以2。

举例说明：
比如我们测得的梯形上底的长度为4cm，下底的长度为8cm，高为6cm。

代入公式计算：
面积 = (4 + 8) × 6 ÷ 2
= 12 × 6 ÷ 2
= 72 ÷ 2
= 36
所以，该梯形的面积为36平方厘米。

注意事项：
1. 在测量时，要尽量准确。

使用合适的工具并确保测量的准确性。

2. 当使用公式计算时，注意运算符的优先级。

3. 单位要保持一致，比如所有的长度用厘米或米来表示。

通过以上步骤，你可以轻松地计算任意梯形的面积。

记住，梯形的面积计算公式是一个基本的几何知识，在学习更复杂的几何图形时也会有所应用。

掌握这些基础知识是建立进一步学习的基石。

梯形形面积计算公式

梯形形面积计算公式梯形是一种常见的几何形状，它由两个平行且不等长的底边和两个等高的侧边组成。

我们可以使用梯形的面积计算公式来计算梯形的面积。

梯形的面积计算公式如下：梯形面积 = （上底 + 下底）× 高÷ 2下面我们来详细介绍一下梯形的面积计算公式及其应用。

我们来看一下梯形的定义和特点。

梯形是一个四边形，其中两条边是平行的，被称为底边；另外两条边不平行，被称为侧边。

梯形的高是两条底边之间的垂直距离，也就是侧边的长度。

底边和侧边的长度可以根据实际情况给定。

假设梯形的上底边长为a，下底边长为b，高为h。

根据梯形的定义和特点，我们可以得到梯形的面积计算公式如下：梯形面积 = （a + b）× h ÷ 2接下来，我们来看一些具体的应用例子。

例子1：假设一个梯形的上底边长为6cm，下底边长为10cm，高为4cm。

我们可以使用梯形的面积计算公式来计算该梯形的面积。

梯形面积 = （6 + 10）× 4 ÷ 2 = 16cm²所以，该梯形的面积为16平方厘米。

例子2：现在假设一个梯形的上底边长为15cm，下底边长为20cm，高为8cm。

我们可以使用梯形的面积计算公式来计算该梯形的面积。

梯形面积 = （15 + 20）× 8 ÷ 2 = 140cm²所以，该梯形的面积为140平方厘米。

通过上述例子，我们可以看到，使用梯形的面积计算公式可以方便地计算出梯形的面积。

这个公式的推导过程比较简单，只需要根据梯形的定义和特点，将梯形分解为两个三角形和一个矩形，然后分别计算它们的面积，最后将它们的面积相加即可。

除了梯形的面积计算公式，我们还可以使用其他方法来计算梯形的面积。

例如，我们可以将梯形分解为两个直角三角形和一个矩形，然后分别计算它们的面积，最后将它们的面积相加即可。

这种方法在某些情况下可能更加方便和简单。

总结起来，梯形是一个常见的几何形状，它由两个平行且不等长的底边和两个等高的侧边组成。

梯形面积公式计算公式

梯形面积公式计算公式梯形是一种四边形，它的两边是平行的，而另外两边不平行。

梯形的面积可以通过以下公式计算：面积=（上底+下底）*高/2其中，上底和下底分别是梯形的两个平行边的长度，高是两个平行边的距离。

为了更好地理解梯形面积的计算公式，我们可以从几何角度来推导。

假设梯形的两底分别为a和b，高为h。

我们先画一条连接两个底的线段，将梯形分成了一个矩形和两个直角三角形。

通过观察我们可以发现，这两个直角三角形加上矩形的面积恰好等于整个梯形的面积。

而直角三角形的面积可以通过底乘以高的一半求得，矩形的面积可以通过底乘以高求得。

因此有以下等式：梯形面积=直角三角形1的面积+矩形的面积+直角三角形2的面积直角三角形1的面积=h*a/2矩形的面积=h*(b-a)直角三角形2的面积=h*b/2将上述三个面积代入原等式中，可得：梯形面积=(h*a/2)+(h*(b-a))+(h*b/2)整理得：梯形面积=h*(a+b)/2所以，梯形的面积公式就是：面积=(上底+下底)*高/2这个公式可以很方便地用于计算梯形的面积。

例如，如果梯形的上底长为6，下底长为10，高为8，那么可以使用公式来计算面积：面积=(6+10)*8/2=16*8/2=64所以，这个梯形的面积为64平方单位。

除了使用这个公式计算梯形的面积，还可以通过其他方法进行计算。

例如，可以将梯形分割成两个直角三角形和一个矩形，然后分别计算它们的面积，最后将三个部分的面积加起来。

这种方法和上述推导的过程是一致的。

总结起来，梯形的面积计算公式为(上底+下底)*高/2，可以通过将梯形分割成直角三角形和矩形来推导得出。

这个公式可以通过代入具体数值来计算梯形的面积。

梯形面积公式计算公式

梯形面积公式计算公式梯形面积公式是计算梯形面积的数学公式。

梯形是一种四边形，它有两条平行的边，称为底边和顶边，还有两条不平行的边，称为斜边。

梯形的面积是指梯形内部的区域所占的空间。

梯形面积公式可以用以下方式表示：面积 = （底边 + 顶边）× 高÷ 2其中，底边和顶边分别代表梯形的两条平行边的长度，高代表梯形两条平行边之间的距离。

使用梯形面积公式计算梯形的面积时，首先需要知道梯形的底边和顶边的长度，以及两条平行边之间的距离。

根据这些信息，可以将这些数值代入梯形面积公式中，通过计算得出梯形的面积。

举个例子来说明梯形面积公式的使用。

假设有一个梯形，底边长为6cm，顶边长为10cm，高为4cm。

现在我们想计算这个梯形的面积。

根据梯形面积公式，将给定的数值代入公式中：面积 = （6 + 10）× 4 ÷ 2接下来进行计算：面积= 16 × 4 ÷ 2= 64 ÷ 2= 32因此，这个梯形的面积为32平方厘米。

通过梯形面积公式，我们可以快速准确地计算出梯形的面积。

这个公式简单易懂，适用于各种不同大小和形状的梯形。

除了梯形面积公式，还有其他方法可以计算梯形的面积。

例如，可以将梯形分解为一个矩形和两个三角形，然后分别计算它们的面积，并将结果相加。

这种方法也可以得到正确的答案，但相对于使用梯形面积公式，可能需要更多的计算步骤。

在实际应用中，梯形面积公式经常被使用。

例如，在建筑和工程领域，计算梯形的面积可以帮助工程师设计合适的材料和结构。

此外，在日常生活中，了解梯形面积公式也可以帮助我们更好地理解和解决一些实际问题，比如在购买地毯或者绘制地图时计算不规则房间或地区的面积。

梯形面积公式是一种用于计算梯形面积的数学公式。

通过将底边、顶边和高代入公式中，我们可以快速准确地计算出梯形的面积。

这个公式在各种实际应用中都有广泛的应用，帮助我们更好地理解和解决问题。

梯形面积计算方法

梯形面积计算方法梯形是一种特殊的四边形，它有两对平行的边，其中一对边较长，另一对边较短。

计算梯形的面积可以使用特定的公式，或者通过将梯形分解为矩形和三角形来计算。

下面将介绍两种常用的梯形面积计算方法。

方法一：使用梯形面积公式梯形的面积可以使用以下公式进行计算：面积 = （上底 + 下底）× 高÷ 2其中，上底和下底分别表示梯形的两条平行边的长度，高表示梯形的高度。

假设有一个梯形，上底长度为a，下底长度为b，高度为h，那么可以使用上述公式计算其面积。

例如，如果上底长度为5cm，下底长度为8cm，高度为4cm，则梯形的面积为：面积 = （5 + 8）× 4 ÷ 2 = 26 平方厘米方法二：分解为矩形和三角形除了使用公式计算梯形的面积外，还可以将梯形分解为矩形和三角形，分别计算它们的面积，然后将结果相加。

将梯形划分为一个矩形和两个三角形。

矩形的长度为梯形的高度，宽度为梯形上底和下底的平均值。

两个三角形的面积可以使用以下公式计算：三角形面积 = 底边长度× 高度÷ 2然后，将矩形和两个三角形的面积相加，即可得到梯形的总面积。

例如，假设有一个梯形，上底长度为6cm，下底长度为10cm，高度为3cm。

首先计算矩形的面积，矩形的长度为3cm，宽度为（6+10）÷ 2 = 8cm。

因此，矩形的面积为3cm × 8cm = 24平方厘米。

接下来，计算两个三角形的面积。

第一个三角形的底边长度为6cm，高度为3cm，面积为6cm × 3cm ÷ 2 = 9平方厘米。

第二个三角形的底边长度为10cm，高度为3cm，面积为10cm × 3cm ÷ 2 = 15平方厘米。

将矩形和两个三角形的面积相加，即可得到梯形的总面积：总面积 = 矩形面积 + 两个三角形面积 = 24 平方厘米 + 9 平方厘米 + 15 平方厘米 = 48 平方厘米梯形的面积计算方法主要有两种：使用梯形面积公式和分解为矩形和三角形。

梯形的面积与周长计算

梯形的面积与周长计算梯形是一种具有特殊形状的四边形，其两条平行边长度分别为a和b，底边长度为c，高度为h。

在本文中，我将介绍如何计算梯形的面积和周长。

一、梯形的面积计算梯形的面积可以通过以下公式来计算：面积 = （上底 + 下底） ×高度 ÷ 2也可以写成：面积 = （a + b） × h ÷ 2其中，上底和下底是指梯形的两条平行边的长度，高度则是指从上底到下底的垂直距离。

例如，如果一个梯形的上底长度为6cm，下底长度为4cm，高度为5cm，则可以按照上述公式进行计算：面积 = （6 + 4） × 5 ÷ 2 = 10 × 5 ÷ 2 = 50 ÷ 2 = 25 平方厘米所以，这个梯形的面积为25平方厘米。

二、梯形的周长计算梯形的周长可以通过以下公式来计算：周长 = 上底 + 下底 + 两个斜边的长度也可以写成：周长 = a + b + c + d其中，c和d分别代表梯形的斜边长度。

如果已知梯形的两条平行边的长度和底边的长度，可以通过勾股定理计算斜边的长度。

勾股定理表达式如下：斜边的长度= √（（上底 - 下底）^2 + 高度^2）例如，如果一个梯形的上底长度为6cm，下底长度为4cm，高度为5cm，则可以按照上述公式进行计算：斜边的长度= √（（6 - 4）^2 + 5^2）= √（2^2 + 5^2）= √（4 + 25）= √29 ≈ 5.39cm周长= 6 + 4 + 5 + 5.39 ≈ 20.39cm所以，这个梯形的周长约为20.39厘米。

总结：通过上述计算方法，我们可以准确计算出梯形的面积和周长。

根据给定的上底、下底、高度和斜边的长度，我们可以使用相应的公式来求解。

使用这些公式，我们可以更轻松地计算梯形的相关参数，而不需要进行繁琐的手算。

梯形的面积和周长计算是几何学中的常见问题，对于建筑、土木工程和日常生活中的尺寸测量都有重要的应用。

梯形的面积计算公式

梯形的面积计算公式梯形是初中数学中经常遇到的几何形状之一，它具有独特的特点和性质。

在解决与梯形相关的问题时，我们需要掌握梯形的面积计算公式，以便能够准确地计算出梯形的面积。

梯形的面积计算公式是：面积 = (上底 + 下底) ×高 ÷ 2。

这个公式可以帮助我们快速、准确地计算出梯形的面积，而不需要进行复杂的推导和计算。

为了更好地理解梯形的面积计算公式，我们来看一个具体的例子。

假设有一个梯形，上底长为6cm，下底长为10cm，高为4cm。

我们可以按照公式进行计算：面积 = (6 + 10) × 4 ÷ 2= 16 × 4 ÷ 2= 64 ÷ 2= 32所以，这个梯形的面积为32平方厘米。

通过这个例子，我们可以看到，梯形的面积计算公式非常简单明了，只需要将上底、下底和高代入公式中，按照运算规则进行计算即可。

这个公式的推导可以通过将梯形拆分为两个三角形来进行，但是在实际应用中，我们更多地使用这个简单的公式来计算梯形的面积。

梯形的面积计算公式在实际问题中具有广泛的应用。

例如，在房屋建筑中，我们需要计算梯形屋顶的面积；在农田规划中，我们需要计算梯形地块的面积；在制作手工艺品中，我们需要计算梯形图案的面积等等。

掌握了梯形的面积计算公式，我们就能够更好地解决这些实际问题，提高我们的数学应用能力。

除了梯形的面积计算公式，我们还可以通过一些特殊的性质和方法来计算梯形的面积。

例如，如果梯形的两个底边平行且等长，那么它就是一个矩形，我们可以直接使用矩形的面积计算公式来计算梯形的面积。

又或者，如果梯形可以分割为多个形状相同的小梯形，我们可以将它们的面积相加来得到整个梯形的面积。

这些方法都可以帮助我们更灵活地计算梯形的面积，提高解题的效率。

总之，梯形的面积计算公式是初中数学中的重要知识点之一。

通过掌握这个公式，我们能够准确地计算梯形的面积，解决与梯形相关的实际问题。

计算梯形面积的公式

计算梯形面积的公式梯形是一种特殊的四边形，它有两个平行的底边和两条不平行的侧边。

计算梯形的面积可以使用以下公式：面积 = (上底 + 下底) × 高÷ 2其中，上底和下底分别指梯形的两个平行底边的长度，高指梯形两个底边之间的垂直距离。

梯形面积公式的推导过程如下：假设梯形的上底为a，下底为b，高为h。

我们可以将梯形划分为两个三角形和一个矩形。

我们计算矩形的面积，即底边的平均长度乘以高，得到矩形的面积为ab×h。

然后，我们计算两个三角形的面积。

每个三角形的面积都可以表示为底边乘以高再除以2，即ah/2和bh/2。

将矩形和两个三角形的面积相加，得到梯形的总面积为(ab×h) + (ah/2) + (bh/2)。

化简上述表达式，得到梯形的总面积为(ab+ah+bh)/2，进一步化简为(a+b)×h/2。

根据以上推导，我们可以得出梯形面积的公式为(上底 + 下底) × 高÷ 2。

下面我们通过一个例子来演示如何使用梯形面积的公式进行计算。

假设某个梯形的上底长度为5 cm，下底长度为10 cm，高为8 cm。

我们可以根据公式进行计算：面积= (5 + 10) × 8 ÷ 2= 15 × 8 ÷ 2= 120 ÷ 2= 60 平方厘米因此，该梯形的面积为60平方厘米。

通过以上例子，我们可以看到使用梯形面积的公式可以快速准确地计算梯形的面积。

只需要知道梯形的上底、下底和高，就可以使用这个公式进行计算。

需要注意的是，公式中的长度单位要保持一致。

在计算过程中，如果是以厘米为单位，那么计算结果也应该以平方厘米为单位。

除了使用公式计算梯形面积，还可以通过将梯形分解为两个三角形和一个矩形来计算。

这种方法也能得出相同的结果，但相对来说计算过程稍微复杂一些。

总结起来，计算梯形面积的公式是(上底 + 下底) × 高÷ 2。

梯形面积计算公式三种

梯形面积计算公式三种作为中学数学的基本概念之一，梯形面积的计算在学习中扮演着重要的角色。

在实际生活中，无论是测量建筑面积还是计算地块大小，梯形面积计算公式都是必不可少的工具。

本文主要介绍梯形面积计算公式的三种方式，包括基本公式、高倍增法和海龙公式，旨在帮助读者更好地理解和掌握梯形面积计算技巧。

一、基本梯形面积计算公式梯形面积计算的基本公式为：面积=（上底+下底）×高÷2。

其中，上底和下底是梯形的两个相邻的并行边长度，高是梯形两个平行面之间的距离。

这个公式简单明了，容易理解，适用于所有类型的梯形面积计算。

例如，假设一个梯形上底长为10厘米，下底长为20厘米，高为5厘米，那么它的面积为（10+20）×5÷2=75平方厘米。

二、高倍增法计算公式高倍增法是一种利用梯形高倍增加面积的方法，计算公式为：面积=（上底+下底）×高倍增÷2。

具体实现方法如下：1.将上底、下底的和除以2得到平均宽度。

2.将梯形高平均分成多份，每份所占高的长度等于平均宽度。

3.将每份高的长度和平均宽度相乘，得到梯形该部分的面积。

4.将所有部分的面积累加即可得到梯形的面积。

例如，假设一个梯形上底长为10厘米，下底长为20厘米，高为5厘米，要将高倍增为10倍计算，那么它的面积为（10+20）×5×10÷2=750平方厘米。

三、海龙公式计算公式海龙公式是另一种较为复杂的梯形面积计算公式，其公式为：面积 = 根号（(p-a)×(p-b)×(p-c)×(p-d) - a×b×c×d×cos²((B+D)÷2)）。

其中，a、b、c、d分别为梯形的四个边，B表示上底与对角线夹角，D表示下底与对角线夹角，p表示半周长（即a+b+c+d÷2），cos²((B+D)÷2)表示夹角B和夹角D 的平均数的余弦值平方。