43角1PPT课件

合集下载

4.3.2 第1课时角的度量与计算

分层作业
点击进入word链接
课件目录
首页
末页
第1课时角的度量与计算
答案
点击进入答案PPT链接
点击进入答案word链接
课件目录
首页
末页
课件目录
首页
末页
第1课时角的度量与计算
解：(1)∠MON＝∠MOC＋∠CON ＝12∠AOC＋12∠COB ＝12(∠AOC＋∠COB) ＝12×(28°＋42°) ＝35°.
课件目录
首页
末页
第1课时角的度量与计算
(2)OM，ON 的位置发生变化．理由：当将 OC 绕点 O 转动时，∠AOC 的大小发生变化．∵∠AOM＝12∠AOC， ∴∠AOM 的度数也发生变化．又∵射线 OA，OB 的位置不变， ∴OM 的位置随 OC 位置的变化而变化．同理，ON 的位置随 OC 的位置变化而变化．
第1课时角的度量与计算
归类探究
类型之一角的度数的换算 (1)用度、分、秒表示 42.34°；
(2)用度表示 15°24′36″. 解： (1)先把 0.34°化为分：60′×0.34＝20.4′，再把 0.4′化为秒：60″×0.4＝24″， ∴42.34°＝42°20′24″.
课件目录
首页
课件目录
首页
末页
第1课时角的度量与计算
(3)∠MON 的大小不变，∠MON＝35°. ∠MON＝12∠AOC＋12∠COB ＝12(∠AOC＋∠COB) ＝12∠AOB ＝12×70° ＝35°.
课件目录
首页
末页
第1课时角的度量与计算
9．如图 4-3-21①，将笔记本活页的一角折过去，使角的顶点 A 落在点 A′处， BC 为折痕．

人教版二年级上册数学《角的初步认识》(课件)

谢谢观看
二年级—人教版—数学—第三单元
角的初步认识答疑
疑问1
下面图形中分别有几个角呢？
43 12
（ 4 ）个
（）个
（）个
疑问1
下面图形中分别有几个角呢？
43 12
（ 4 ）个
23
1
4
（ 4 ）个
（）个
疑问1
下面图形中分别有几个角呢？
43 12
（ 4 ）个
23
1
4
（ 4 ）个
23 1
边顶点
边
这些角有哪些相同的地方？角都有一个角顶都点有和一两个条点直和直两的条边直。直的线。
认识角
边顶点
边
辨一辨：下面的图形哪些是角，哪些不是角？
（）（×）（）（×）（×）
比角
你能用吸管折出跟这个角一样大的角吗？
比角
你能用吸管折出跟这个角一样大的角吗？
比角
你能让折出来的角变大一些吗？怎么变？
比角
角的大小与角的两边张开的大小有关，与角的两边的长短无关。
＝
画角
别忘了让我来帮助你呀！
画角
画角的方法：先画顶点，再画两边。
作品展示
同学们，今天的数学课你们有哪些收获呢？
角的组成。
小结
叠合法比较角的大小。
角的大小与角的两边张开的大小有关。
角的画法。
实践活动
下面图形中有角吗？请你折一折创作出？怎么变？
比角
角的大小角与的两大条小边与张什开么的有大关小呢有？关。
比角
比角
谁的嘴巴张开得大？
比角
谁的嘴巴张开得大？
叠合法
比角的时候要注意两个角顶点重合，一条边也重合，看另一边。

初中数学43角教案

初中数学43角教案教学目标：1. 让学生了解并掌握43角的定义和性质。

2. 培养学生运用43角解决实际问题的能力。

3. 培养学生对数学的兴趣和思维能力。

教学重点：1. 43角的定义和性质。

2. 运用43角解决实际问题。

教学难点：1. 43角的性质的理解和运用。

教学准备：1. 课件或黑板。

2. 三角板。

教学过程：一、导入（5分钟）1. 利用课件或黑板，展示一些图片，如房屋平面图、道路交叉口等，引导学生观察这些图片中的角。

2. 提问：你们对这些角有什么认识？二、探究43角的定义和性质（15分钟）1. 提问：你们知道什么是43角吗？2. 引导学生通过观察和思考，总结出43角的定义：一个角的两条边成垂直状态，这个角就是43角。

3. 提问：43角有什么特殊的性质吗？4. 引导学生通过观察和思考，总结出43角的性质：43角的度数是90度，它的两条边互相垂直，且互相垂直的直线互相平行。

三、运用43角解决实际问题（15分钟）1. 出示一些实际问题，如房屋平面图、道路交叉口等，引导学生运用43角解决这些问题。

2. 提问：你们能用43角解决这些问题吗？3. 引导学生通过观察和思考，运用43角解决这些问题。

四、总结和拓展（5分钟）1. 提问：你们今天学到了什么？2. 引导学生总结43角的定义和性质。

3. 提问：你们还能想到其他的43角的性质吗？4. 引导学生思考43角在实际生活中的应用。

教学反思：通过本节课的教学，我发现学生们对43角的定义和性质掌握得比较好，但在运用43角解决实际问题时，有些学生还有一定的困难。

在今后的教学中，我将继续加强对学生运用能力的培养，让学生更好地理解和掌握43角。

《角的初步认识》课件ppt

返回
做一做
你能用两根连接棒做一个角吗？
返回
做一做
角的两边张口越大，角越大。
返回
学习永远不晚。 JinTai College
感谢您的阅读！为了便于学习和使用，本文档下载后内容可随意修改调整及打印。
？
角的大小与边的长短无关。
返回
画一画
从一个点起，用尺子向不同的方向画两条线，就画成一个角。
返回
行业PPT模板：/hangy e/ PPT素材下载：/sucai/ PPT图表下载：/tubiao/ PPT教程： /powerpoint/ Excel教程：/excel/ P P T课件下载：/ke j ia n/ 试卷下载：/shiti/
返回
返回
返回
返回
返回
返回
边顶点
边
边顶点
边
边顶点边
返回
下面的图形，哪些是角？哪些不是
角？是角的画“√” ？不是角的画
“╳ ”？
（√ ）
（╳ ）
（√ ）（╳ ）
(╳ )
(√ ) ( √ )
( ╳ ) 返回
数数看:
下面的图形中各有几个角？
（ 3 ）个角
（ 4 ）个角
返回
张开你理想的翅膀，想一想一张正方形的纸剪去一个角，还剩几个角？看谁的剪法多。
人教版课程标准小学数学二Байду номын сангаас级上册
认识角
♠ 角各部分名称 ♠ 判断
♠ 做一做
角 ♠ 数一数
♠ 画一画
♠ 拓展廷伸
P P T模板下载：/m oba n/ 节日P P T模板：/j ie ri/ P P T背景图片：/be ij ing/ 优秀PPT下载：/xiazai/ Word教程： /word/ 资料下载：/ziliao/ 范文下载：/fanwen/ 教案下载：/j ia oa n/

43角动量角动量守恒定律

r
F
dL
M
dt dt
dt
14
物理学
第五版
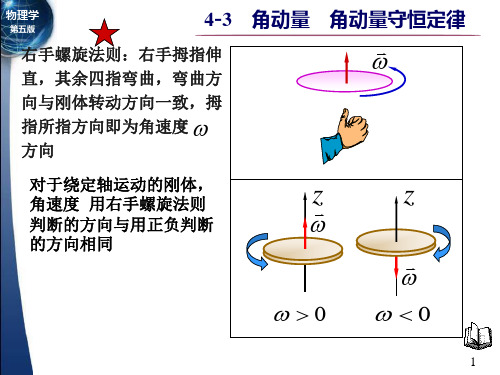
质点的合外力矩
4-3 角动量
M
dL
dt
角动量守恒定律
作用于质点的合外力对参考点 O 的力矩，等于质点对该点 O 的角动量随时间的变化率.
2 质点的角动量定理
t2 t1
Mdt
L2
L1
冲量矩
t2
M
dt
t1
3 质点的角动量守恒定律
M 0 , L 恒矢量
做匀变速转动．
与二维平面圆周运动情况相同
质点匀变速直线运动刚体绕定轴作匀变速转动
v v0 at
0 t
x
x0
v0t
1 2
at 2
0
0t
1 2
t
2
v2
v02 2a(x x0 )
2
2 0
2 (
0
)
3
物理学
第五版
4-3 角动量角动量守恒定律
三角量与线量的关系
ω d
dt
dω dt
4-3 角动量角动量守恒定律
对定轴转的刚体，受合外力矩M，从t1到t2内，角速度
M从 1变d(为J)2，积dL分可得： dt dt
t2 t1
Mdt
L2
L1
冲量矩 J2 J1
刚体的角动量定理：刚体绕定轴转动时，刚体的冲量矩等于角动量的增量
非刚体定轴转动的角动量定理
了解
t2
t1
Mdt
J 22
i
i
L J
2 M刚 i体定dd轴Lti 转动ddt的(m角ir动i2量)定理
O ri

《三角形的内角和》标准课件(人教版)1

主动建构新的认知结构，了解获取知识的途径和技巧。二、自主探究，得出结论
四年级的学生已经初步具备了动手操作的意识和能力，并形成了一定的空间观念，能够在探究问题的过程中，运用已有知识和经验，
通过交流、比较、评价寻找解决问题的途径和策略。
学法：合作交流法、动手实践法、自主探究法
这节课我设计了以“猜想一验证一归纳一运用”为主线，让学生在自主学习中“不知不觉”学习到新的知识。
在学生猜测三角形内角和是多少度的基础上，引导学生通过探究活动来验证自己的观点是否正确，激发求知的渴望和学习的热情，最后达成共识。 43 ° 小学数学人教版四年级下册第五单元直角三角形的内角和是180° 。 =40°-25° 结论不重要，重要的是让学生体会得到结论的过程，学会用转化的思想来解决生活中的问题。 3、在探索发现的过程中，培养学生大胆猜想，细心验证的数学思维。直角三角形的内角和是180° 。结论三角形的内角和是180度三角形的内角和都是180°
(一)复习引入,引发猜想三角形的内角和都是180°
三角形的内角和都是180°
(一)复习引入,引发猜想 39°
通过复习上节课三角形按角分可
以分为哪几类，从而引入学习新课三角形的内角和都是180°
在学生猜测三角形内角和是多少度的基础上，引导学生通过探究活动来验证自己的观点是否正确，激发求知的渴望和学习的热情，最
直角三角形的内角和是180° 。
两个大小一样的直角三角形
在学生猜测三角形内角和是多少度的基础上，引导学生通过探究活动来验证自己的观点是否正确，激发求知的渴望和学习的热情，最
后达成共识。
数学讲究严谨性，为了得到准确的值，学生用拼、折等多种方法得出三角形内角和是180度，验证了自己的猜想

《画角》PPT教学课文课件

重合，0°刻度线和射线重合（点重合，边重合）。 2.定点：在对应角的度数的刻度线的地方点一个点。 3.连线：以画出的射线的端点为端点，通过刚画的点，
再画一条射线。记得标出角的符号和度数。
作业1
1.教材第45页练习七第6题。
你能用三角尺画出下面的角吗？
15°
150°
165°
75°
15°
45°- 30°= 15°
（钝）角
（直）角
（平）角
（锐）角
65°
做一做（1）分别画出75。、105。的角。
。
75
。
105
可以用量角器来画。
教科书第43页“做一做” 第2（1）题
思考：怎样用三角板画出 75 °角。用三角板的 30 °＋ 45°＝ 75°。
75°
课堂检测 6.你能用三角尺画出下面的角吗？
15°
画角
学习目标
1. 经历用量角器、三角板画角并与同伴交流画角方法的过程。
2. 会用量角器画指定度数的角；会用三角板画30°、 45°、60°、90°等一些特定度数的角。
3. 激发画角的兴趣，培养认真、细心的良好品质。
65°
(1) 画一条射线，使量角器的中心和射线的端点重合，0 刻度线和射线重合。 (2)在量角器 65°刻度线的地方点一个点。
(3)以画出的射线的端点为端点，通过刚画的点，再画一条射线。 (4) 画完后在角上标上符号，写出度数。
探究新知
你会用三角尺画一个60度的角吗？
（教材P43例3）
60 °
我想画一个60°的角，你有什么好办法吗？
三、巩固练习，学以致用
（一）基础练习：课本P43做一做第1，2题。
1. 下面的角格式哪一种角？写出角的名称。

大学物理学教程马文蔚43角动量-角动量守恒定律1

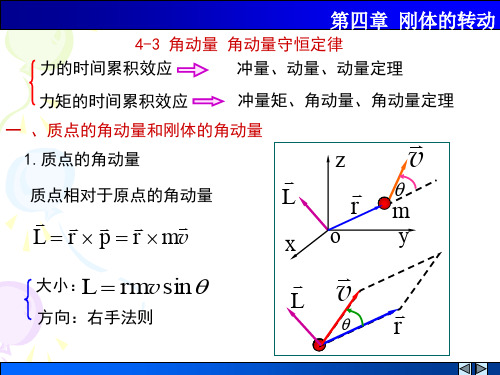
解：（1）对子弹、圆盘系统用角动量守恒定律
m00 R
(1 mR2
m020

m0
R2
)
(
1 2
m

m0
)
R
（2）先求摩擦力矩，在圆盘
上取一同轴圆环，如图，则
mOr R
dr 0
m0
dm ds 2 rdr,
m
R2
摩擦力矩
dM
dmgr
第四章刚体的转动
M
解：小虫与细杆的碰撞视为完全非弹性碰撞，碰撞前后系统角动量守恒
mv0
l 4

1 12
ml
2

m(
l 4
)2

12 v0
7l
小虫与细杆系统的外力矩为
M mgr cos
第四章刚体的转动
角速度恒定，由角动量定理
M dL d(J) dJ J 1 ml 2 mr 2
时0各反自向对滑绳行中,交点错的时角动,各量抓为住L长,为他d们的将绳绳索收一拢端为,然d 后时相,各对自旋的转速,率此
为 20 .
2
L

m0
d 2
2m0
d 2

2m
d/2 2
20
d
例8: 两只同重量的猴子,一只用力往上爬,另一只不爬,若滑轮重量忽略不计,问哪一只先到达滑轮顶端?
R
R
若 M 0 ，则 L J 恒量
讨论：(1) 守恒条件 M 0
若 J 不变，不变；若J 变，也变，但 L J 不变.
(2) 内力矩不改变系统的角动量.
第四章刚体的转动
(3)在冲击等问题中,M in M ex L C

任意角课件高一上学期数学人教A版(2019)必修第一册

S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与
整数个周角的和.
合内任意两元素的差是360 °的整数倍
名师点睛
对于集合S={β|β=α+k·360°,k∈Z}的理解应注意三点
(1)α是任意角.（一般是在0°~360°之间）
(2)“k∈Z”有三层含义:
①特殊性:每取一个整数值就对应一个具体的角.
360°+90°<475°<360°+180°,-360°<-315°<-270°,所以这四个命题都是真命
题.
探究点二坐标系中角的概念及其表示
角度1终边相同的角的求解
【例2】写出与75°角终边相同的角的集合,并求在360°~1 080°范围内与
75°角终边相同的角.
解与75°角终边相同的角的集合为
规律方法
终边落在特定位置上的角的集合
终边落在x轴的非负半轴上的角的集合为{β|β=k·360°,k∈Z};
终边落在x轴的非正半轴上的角的集合为{β|β=k·360°+180°,k∈Z};
终边落在x轴上的角的集合为{β|β=k·180°,k∈Z};
终边落在y轴的非负半轴上的角的集合为{β|β=k·360°+90°,k∈Z};
叫做互为相反角.角α的相反角记为-α.
问题角能像实数一样进行运算吗？
五、通过类比，获得概念
角的加法：设，是任意两个角．我们规定，把角的终
边旋转角，这时终边所对应的角是 + ．

+

=

角的减法：像实数减法的“减去一个数等于加上这个数的
相反数”一样，我们有 − = + (−)．这样，角的减

任意角高一数学课件(北师大版2019必修第二册)

2100
6600
-1500
特别地，当一条射线没有作任何旋转时，我们也认为这时形成了一个角，并把这个角叫做零角即零度角（0º）．此时零角的始边与终边重合。
角的记法：角α或可以简记成∠α，或简记为： α.
如∠α=-1500 ， α=00， α=6600 等等……
角的概念推广的意义：
用“旋转”定义角之后，角的范围大大地扩大了
答：第一象限的角并不都是锐角。 3、小于90°的角都是锐角吗？
答：小于90°的角并不都是锐角，它也有可能是零角或负角。
4. 下列命题：①一个角的终边在第几限，就说这个角是第几象限的角；
②1400°的角是第四象限的角； ③-300°的角与160°的角的终边相同 ④相等的角的终边一定相同； ⑤终边相同的角一定相等.其中正确命题的
• 第四象限的角表示为 {| 270 + k360<< 360 + k360，kZ}
区域角的表示
例：用集合表示顶点在坐标原点，始边重合于 x轴的非负半轴终边在阴影部分的角α的集合.
y A
450
O
x
-600
B
【解】终边落在射线OA上的角为k3600＋45°(k∈Z), 终边落在射线OB上的角为k3600＋300°(k∈Z). 所以终边落在图中阴影部分的角α的集合为{α|k3600＋ 45°≤α≤k3600＋300°,k∈Z}.
取 k 1 时， 30 1 360 330 . 故选：D
2．平面直角坐标系中，取角的顶点为坐标原点，角的始边为 x 轴的非负半轴，下列说法正确的是（） A．第一象限角一定不是负角 B．三角形的内角是第一象限角或第二象限角 C．第二象限角必大于第一象限角 D．钝角的终边在第二象限

大学物理学教程马文蔚43角动量角动量守恒定律

假定演员M落在跷板上,与跷板的碰撞是完全非弹性碰撞.问演员N 可弹起多高?
解: 碰撞前M落在A点的速度
vM (2gh)1 2
碰撞后的瞬间, M、N具有相同的线速度
N
u l
B
2
M
h
C
A
l
l/
2
M、N和跷板系统,角动量守恒
mvM
l 2
J
2mu
l 2
1 12
ml 2
1 2
ml 2
第四章刚体的转动
得
mvMl 2 ml 2 12 ml2
d
例8: 两只同重量的猴子,一只用力往上爬,另一只不爬,若滑轮重量忽略不计,问哪一只先到达滑轮顶端?
(同时到达)
第四章刚体的转动
例9: 如图，一质量为 m的均匀圆盘，半径为 R，放在一粗糙的水平面上，圆盘可绕通过其中心O 的竖直光滑轴转动，开始时，圆盘静止，有一质量为m0 的子弹以速度0 垂直打入圆盘边缘并嵌在盘边上，求(1)子弹击中圆盘后，盘获得的角速度；（2）经多
得 3m
2Ml
m
例5 已知 M , L, m, ,求
解: 子弹与杆碰撞过程,系统角动量守恒
Lm Lm 1 ML2
23
得 3m
2ML
第四章刚体的转动
O
Ml
ห้องสมุดไป่ตู้
/2
O
L
M
2
m
第四章刚体的转动
例6: 人造地球卫星绕地球作椭圆轨道运动,求远地点的速度与近
地点的速度的比值
.
m1(l1 R) m2 (l2 R)
解：小虫与细杆的碰撞视为完全非弹性碰撞，碰撞前后系统角动量守恒

同位角内错角同旁内角(共35张PPT)

截线两侧(交错)
(或反置)
同旁内角
在两条被截直线之内，在截线同侧
形如字母“U”
试一试：
请同学们分别用双手的大拇指，食指各组成一个角，两食指相对成一条线，保持在同一平面内，分别进行尝试，看可以组成哪些角。
例：如图直线DE、BC被直线AB
所截，
(1)∠1和∠2、∠1和∠3、∠1和∠4
各是什么角？ (2)如果∠1=∠4，哪么∠1和∠2相
∠1＝∠4(已知) 图中与∠1是同旁内角的角：分别在截线的左侧,在被截直线的下方例：如图直线DE、BC被直线AB所截，
内错角 3
在两条被截直线之内，在截线两侧(交错)
夹在两被截直线找出图中的同位角、内错角、同旁内角：
∠1＝∠4(已知) 一边都在截线上而且反向，另一边在截线同旁的两个角
在截线同旁,夹在两被截直线内
∠1和
(2)∵∠1=∠4（已知） ∠4＝∠2
（对顶角相等）
∴∠1＝∠2（等量代换）.
∵∠4＋∠3＝180°(邻补角定义)
∠1＝∠4(已知)
∴∠1＋∠3＝180°（等量代换）
即∠1和∠3互补.
找出图中的同位角、内错角、同旁内角：
a
b
2
5
3
67
c
找出图中的同位角、内错角、同旁内角：
b
c
2
34
a
找出图中与∠1构成同旁内角的角?
点此播放视频
两条直线CD和EF相交，能形
E
成些具有什么关系的角？
C
43 12
D
F
两条直线CD和EF相交，能形
E
成些具有什么关系的角？
具有邻补角关系的角
C