第1讲和差倍问题
高斯小学奥数含答案三年级(下)第01讲 和差倍中的隐藏条件

第一讲和差倍中的隐藏条件- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 之前我们已经学习了基础的和差倍问题,而很多时候,无法一眼看出问题中的数量关系,这时候就6需要把“隐藏”了的和差倍关系找出来,其中寻找不变量就是一个重要的手段.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1小高和墨莫玩游戏,每玩一局,输的就要给赢的一枚棋子.一开始小高有18枚棋子,墨莫则有22枚.玩了若干局之后,小高反而比墨莫多了10枚棋子.请问:此时小高有多少枚棋子?分析:在游戏过程中,两人的棋子数始终在变化.那有没有什么量是不变的?练习1有大小两个水瓶,分别装有690毫升和210毫升水.现在从大瓶中倒了一些水到小瓶后(水没有溢出),大瓶里的水量变成了小瓶的2倍.请问:从大瓶中倒了多少毫升水到小瓶?小故事阿呆和阿瓜去包子铺买包子,一共买了250个包子,阿呆看阿瓜不够吃,分了10个包子给阿瓜,阿瓜不好意思,把自己的一半拿出来给了阿呆,阿呆不高兴了,把自己的包子分成10份,挑了其中的8份给阿瓜,阿瓜执拗不过阿呆,最后给了阿呆一个包子,这么折腾下来,现在两人一共有多少个包子?从上面的故事你能得到什么样的结论?总结:___________________________________________________________________________.7例题2小高家有两根绳子,长的那根有163米,短的只有97米.他把两根绳子剪去同样多的长度,结果长绳所剩长度比短绳所剩长度的7倍还多6米.那么两根绳子都剪去了几米?分析:两条绳子同时剪短,那它们的长度和就不是不变量了.这一次,不变量又会是谁呢?练习2两只老鼠“叽叽”和“喳喳”在吃面条,“叽叽”吃的面条比较长,有40厘米;“喳喳”吃的比较短,只有25厘米.它们吃面条的速度相同,过了一段时间后,长面条的长度是短面条的2倍.那么此时短面条还剩多少厘米?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 前面2道例题都是通过寻找不变量来进行解决的,不变量主要有两种情形:“和不变”与“差不变”,在寻找不变量时,有两句小口诀可以记下:给来给去和不变,同增同减差不变.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -小判断小山羊把10捆草分给大山羊,不变量:______.两根木头,每次锯掉的部分一样长,不变量:______.小糊涂和大糊涂去炒股,最后都赚了250元,不变量:______.儿子和爸爸比年龄,无论过了几年,不变量:______.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 当然,并不是所有的题目都能有不变的“和”或“差”,这时分析倍数所对应的和或差就非常重要,我们常用的方法是画出线段图.89- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -分析:寻找题目中的倍数关系,这时的倍数关系所对应的和或差,你知道哪个?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -下面,我们来看看如何找出隐藏的“差”条件.练1:阿呆和阿瓜一样多,阿呆又买了4块,阿瓜买了29块,谁的糖多?多多少块? 练2:阿呆比阿瓜多10个,阿呆又买了4块,阿瓜吃了2块,谁的糖多?多多少块?练习画图画图举例例子:阿呆比阿瓜多18块糖,阿瓜给阿呆2块后,谁的糖多?多多少块?阿瓜 阿呆18 后 后 2222阿呆糖多,多22块.练习3阿呆和阿瓜一起一共有100元钱.阿呆花了10元买零食,阿瓜花了40元买玩具,这时阿呆的钱是阿瓜的4倍.那么后来阿呆有多少钱? 阿呆和阿瓜一共有130元钱.每包瓜子5元钱,阿呆买了两包瓜子两人分着吃,吃完后阿瓜把自己的钱两人平分,这时阿呆的钱是阿瓜的5倍.那么后来阿呆有多少钱?例题3练3:阿瓜给阿呆2块后阿呆和阿瓜一样多,之前谁的糖多?多多少块?练4:阿瓜给阿呆8块后阿瓜比阿呆多27块,之前谁的糖多?多多少块?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4有两根蜡烛,粗蜡烛比细蜡烛长15厘米.把它们同时点燃.1小时后细蜡烛缩短了20厘米,而粗蜡烛只缩短了15厘米.此时粗蜡烛长度正好是细蜡烛的3倍.请问:粗蜡烛还剩多长?分析:寻找3倍关系下粗蜡烛和细蜡烛的长度差?练习4莉娅和萱萱都在织围巾,现在两人已经织好的围巾长度相同,但萱萱织得比较快.在接下来的两个月里,萱萱可以织120厘米,而卡莉娅只能织45厘米,因此两个月后,萱萱围巾的长度将会是卡莉娅的2倍.那么现在卡莉娅的围巾有多长?例题5红、蓝两个盒子中各有一些球,红盒中的球比蓝盒多5个.如果从红盒中取出12个球,然后向蓝盒中放入19个球,那么蓝盒中的球就是红盒的3倍.求最后红盒和蓝盒中各有多少个球?分析:寻找3倍关系下蓝盒和红盒的球数差?试着画出线段图表示一下.10例题6有甲、乙两堆卡片,如果从甲堆中拿出16张放到乙堆中,则两堆卡片的张数相等;如果从乙堆卡片中拿出11张放入甲堆中,则甲堆的张数是乙堆的3倍多10.求甲、乙两堆卡片各有多少张?分析:开始时甲堆和乙堆中的卡片差几张?分析清楚倍数关系下甲乙两堆差多少张?课堂内外爱迪生与电灯爱迪生是美国人,生于1847年.他从小很喜欢问大人“为什么”,让大人无法回答.5岁时,他看见鹅在孵蛋,就把鹅赶走,自己蹲在那里,想帮母鹅孵蛋.爱迪生进小学读了3个月,老师说他是低能儿,只好回家靠妈妈的教导及自修努力学习.爱迪生13岁在火车上边卖报边做实验,一次意外实验的时候磷倒了出来,烧坏了车箱地板,他被管理员打伤右耳,从此成了半个聋子.23岁到纽约闯天下,发明了一部电报机,赚了40000美元,辞掉工作专心研究.爱迪生在1879年10月31日发明电灯.他每天工作超过18小时以上,不停的努力,不断发明有用的东西.他一生中发明1093件专利.有人认为他是天才,他认为天才是百分之一的灵感加上百分之九十九的努力,他有很大的勇气和坚强的毅力承受失败的打击,他也常常鼓励别人.他到80岁还在研究他完全不懂的植物.作业1.有大小两个水瓶,分别装有430毫升和250毫升水.现在从大瓶中倒了一些水到小瓶后(水没有溢出),大瓶里的水量和小瓶一样多.则从大瓶中倒了多少毫升水到小瓶?2.小高的积分比墨莫多30分.老师给他们每人发了100分后,小高的积分比墨莫的2倍少90分.那么墨莫后来有多少分?113.有两支粗细、材料都相同的蜡烛,长的能烧100分钟,短的能烧70分钟.同时点燃这两支蜡烛,过多少分钟后,长蜡烛长度是短蜡烛的3倍?4.小山羊和卡莉娅两人开始有一样多的饼干.小山羊比较贪吃,过了几天,小山羊已经吃了39块饼干,而卡莉娅只吃了17块.此时卡莉娅剩下的饼干数量是小山羊的3倍,那么卡莉娅原来有多少块饼干?5.红、蓝两个盒子中各有一些球,红盒中的球比蓝盒多7个.如果向红盒中放入28个球,并从蓝盒中取出5个球,此时红盒中的球是蓝盒的3倍.则后来红盒里有多少个球?1213第一讲 和差倍中的隐藏条件1.例题1 答案:25枚.详解:后来两人一共40枚棋子.小高(4010)225+÷=枚,墨莫15枚. 2.例题2 答案:87米.简答:开始两根绳子相差1639766-=米,减去同样长的两段后,还是相差66米.后来短绳子长度为()(666)7110-÷-=米.剪去了971087-=米. 3.例题3 答案:100元.简答:买完瓜子后,一共120元.后来阿瓜有()1205120÷+=元.阿呆有205100⨯=元. 4.例题4答案:30厘米.简答:点燃后,粗蜡烛比细蜡烛长15152020-+=厘米.后来细蜡烛有()203110÷-=厘米.粗蜡烛有10330⨯=厘米. 5.例题5答案:13个,39个.简答:后来红盒比蓝盒少1219526+-=个,这时红盒有()263113÷-=个.蓝盒有13339⨯=个. 6.例题6答案:65张,33张.简答:“如果从甲堆中拿出16张放到乙堆中,则两堆卡片的张数相等”说明甲比乙多32张.“从乙堆卡片中拿出11张放入甲堆中”,这时甲比乙多3211254+⨯=张,这时乙有()()54103122-÷-=张,甲有225476+=张.开始甲有761165-=张,乙有221133+=张. 7.练习1答案:90毫升.简答:后来两瓶水一共690210900+=毫升.小瓶有()90021300÷+=毫升,大瓶倒了30021090-=毫升给小瓶. 8.练习2答案:15厘米.简答:减去同样长的两段后,还是相差15厘米.后来短面条长度为()152115÷-=厘米. 9.练习3 答案:40元.简答:买完东西后,一共50元.后来阿瓜有()504110÷+=元.阿呆有10440⨯=元. 10. 练习4答案:75厘米.简答:两个月后,萱萱比卡莉娅长1204575-=厘米.这时卡莉娅有()752175÷-=厘米.1411. 作业1答案:90毫升.简答:倒完后各有()4302502340+÷=毫升,那么倒了43034090-=毫升. 12. 作业2答案:120分.简答:发完后小高还是比墨莫多30分.墨莫后来有()()309021120+÷-=分. 13. 作业3答案:55分钟.简答:能烧的时间差为30分钟,所以过()()70100703155--÷-=分钟. 14. 作业4答案:50块.简答:小山羊剩下的饼干有()()39173111-÷-=块,原来有50块. 15. 作业5答案:60个.简答:后来红盒比蓝盒多728540++=个.则后来蓝盒有()403120÷-=个,红盒有60个.。
小升初奥数知识点一(和差倍问题)

小升初奥数知识点一(和差倍问题)——10道题型及答案和差问题已知条件:几个数的和与差公式适用范围:已知两个数的和,差,倍数关系公式①(和-差)÷2=较小数较小数十差=较大数和-较小数=较大数(和十差)÷2=较大数较大数-差=较小数和-较大数=较小数和倍问题已知条件:几个数的和与倍数公式适用范围:已知两个数的和,差,倍数关系公式:和÷(倍数十1)=小数小数×倍数=大数和-小数=大数差倍问题已知条件:几个数的差与倍数公式适用范围:已知两个数的和,差,倍数关系公式差(倍数-1)=小数小数X倍数=大数小数+差=大数解题关键步骤与基本思路第一步认真理解题意,判断是和倍问题还是差倍问题。
判断“和倍问题”的一般方法是,可以抓住这么几个关键字眼:“和”、“共“谁是谁的几倍”等。
判断差倍问题,可以抓住这么几个关键字眼进行判断“比……多……”;“比……少……”“相差多少”,“谁是谁的几倍”等。
第二步确定“1倍量”,或者叫“1倍数”确定“1倍量”的常用方法是,找关键字,一般情况下是“是”、“比”、“占”、“等于”后面的那个量就是“1倍量”。
如果在一个题中,同时出现两个或者两个以上的这些字眼,那么通常我们将那个比较小的量作为“1倍量”其原因很简单,人们通常喜欢做加法,不愿意做减法,宁愿做乘法,不愿意做除法。
在划线段图的时候,一般先划“1倍量”,再划其他的量。
尽量将已知的条件都表示在线段图上面,这样更直观,便于分析和理解。
第三步通过分析,找到与“和”或者“差”相对应的倍数关系。
只有找到了一一对应关系才能解出正确的答案。
一般“和”对应的是“倍数+1”;“差”对应的是“倍数-1”。
这个很重要。
当然,具体问题要具体分析。
十道经典例题例题1:甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?分析】此题就是典型的“套用公式”应用题,用大数=(和+差)÷2求出甲班人数,用小数=(和-差)÷2求得乙班人数。
五年级奥数第1次课和差和倍问题

要有扎实的基础,我们每天进步一点点,每天熟练一道题,相信我们一定可以学好数学这门简单易懂的学科!差倍问题差÷(倍数-1)=小数小数×倍数=大数例1.暑假里,兄弟两人去池塘钓鱼,哥哥比弟弟多钓20条,哥哥钓的条数是弟弟的3倍。
哥哥与弟弟各钓了多少条鱼?例2.参加学校课外舞蹈小组的同学,女生比男生多45人,女生比男生的4倍少15人,男、女生各有多少人?例3.两堆煤重量相等,第一堆运走7吨,第二堆运走19吨以后,第一堆剩下的吨数是第二堆的3倍。
两堆煤现在各有多少吨?例4.一个畜牧场,原有山羊和绵羊的只数同样多,如果卖出山羊200只,买进绵羊350只,那么绵羊的只数是山羊的6倍还多50只。
畜牧场原有山羊、绵羊各多少只?例5.有两筐桔子,如果从第一筐拿出9个放入第二筐,则两筐桔子的个数相等;如果从第二筐拿出12个放入第一筐,则第一筐桔子的个数等于第二筐的2倍。
原来每筐桔子各有多少个?练习与思考1.暑假里,哥哥做的数学题比弟弟多180道,哥哥做的数学题是弟弟的4倍多9道。
两人各做多少数学题?2 2.甲、乙两人的钱一样多,甲给乙30元,则乙的钱是甲的5倍。
甲、乙原来各有多少元?3.甲粮仓的大米比乙粮仓多600袋,如果从乙粮仓运出300袋给甲粮仓,那么,甲粮仓的大米是乙粮仓的2倍。
两粮仓原来各有大米多少袋?4.两块同样长的花布,第一块卖出25米,第二块卖出7米,剩下的布,第二块的长度是第一块的3倍。
这两块布原来各有多少米?5.已知两个数的商是4,这两个数的差是39。
那么,这两个数中较小的一个数是多少?6.小英的故事书的本数是小娟的3倍。
如果小英借给小娟10本故事书,小娟的故事书的本数等于小英的3倍。
小英、小娟原来各有故事书多少本?7.水果店有重量相等的苹果和梨子各一筐,苹果卖出60千克,梨子又放入40千克,结果梨子的重量是苹果的3倍。
原来苹果、梨子各有多少千克?8.四(1)班和四(2)班原有图书的本数一样多。
和差倍问题

A、23
B、24
C、26
D、27
解析: 3−1=2倍,18÷2=9(只),(1倍数也就是鹅的只数),9× 3=27(只)(鸭的只数).
测验3
红、黄、蓝三个纸盒里共有彩票56张.其中红色纸盒里的彩票是黄色纸盒的2倍,蓝色纸盒里
的彩票是红色纸盒的2倍,蓝纸盒里有( )张彩票?
A、12
B、18
C、32
D、36
课堂小结
课堂小结
和差公式: 较大的数=(和+差)÷2 较小的数=(和−差)÷2 和倍公式: 一倍量(小数)=两数和÷(倍数+1) 多倍量(大数)=一倍量(小数)×倍数,或两数和−小数=大数 差倍公式: 一倍量(小数)=两数差÷(倍数−1) 多倍量(大数)=一倍量(小数)×倍数,或大数=小数+倍数差
答:小华有38本数学书。
课堂测验
测验1
果园中梨树和苹果树共有67棵,梨树比苹果树的2倍少2棵,苹果树有( )棵?
A、14
B、16
C、18
D、23
【解析】 “1”份为(67+2)÷(1+2)=23棵,苹果树有23棵.
测验2
李爷爷家养的鸭比鹅多18只,鸭的只数是鹅的3倍,你知道李爷爷家养的鸭有( )只吗?
6、有两根粗细不同但长度相同的蜡烛,把它们同时点燃,1小时后细蜡烛缩短了15厘米,而粗蜡 烛只缩短了3厘米,此时粗蜡烛长度正好是细蜡烛的3倍.请问:粗蜡烛还能燃烧( )小时? A、6 B、8 C、9 D、11
解析: 两根蜡烛的长度差12厘米相当于2份,所以1份等于12÷2=6(厘米),即细蜡烛余下6 厘米,则粗蜡烛余下6×3=18(厘米). 粗蜡烛燃烧1小时缩短3厘米,那么它余下的18厘米可以燃烧18÷3=6(时)
和差问题、和倍问题、差倍问题

一、和倍问题(一)例1 :甲班和乙班共有图书160本,甲班的图书是乙班的3倍,甲乙两班各有图书多少本?例2:果园里有梨树和桃树共165棵,桃树棵数比梨树棵数的2倍少6棵,梨树和桃树各多少棵?练习:1、小明和小强共有图书120本,小明的图书是小强的2倍,他们两人各有图书多少本?2、果园里一共有桃树和杏树340棵,其中桃树比杏树的3倍多20棵,两种树各种了多少棵?3、一个长方形的周长是是30厘米,长是宽的2倍,求长方形的长和宽分别是多少?二、差倍问题例1:一张桌子的价格是一把椅子的3倍,购买一张桌子比一把椅子贵60元。
问桌椅各多少元?例2:甲桶酒是乙桶酒重量的5倍,如从甲桶中取出20千克到入乙桶,那么两桶酒重量相等。
两桶酒原来各多少千克?作业:1、甲、乙两桶油共重100千克,从甲桶中取出5千克放入乙桶中,此时两桶油正好相等。
求两桶油原来各有多少千克?2、甲、乙两箱洗衣粉共有90袋,如果从甲箱中取出4袋放入乙箱中,则两箱中洗衣粉的袋数相等。
求原来两箱洗衣粉各有多少袋?3、刘晓每天早晨沿长和宽相差40米的操场跑步,每天跑6圈,共跑2400米,问这个操场的面积是多少平方米?4、小强今年15岁,小亮今年9岁。
几年前小强的年龄是小亮的3倍?5、有两段一样长的绳子,第一根剪去21米,第二根剪去13米后是第一根剩下的3倍,两根绳子原来有多长?6、老猫和小猫去钓雨,老猫钓的鱼是小猫的3倍,老猫比小猫多钓12条。
两只猫各钓了多少条鱼?7、学校今年参加科技兴趣小组的人数比去年多41人,今年人数比去年的3倍少35人,今年有多少人?三、和差问题:例1:有甲乙两堆煤,共重52吨,已知甲比乙多4吨,两堆煤各重多少吨?例2:两只笼子里共有15只鸡,从甲笼提出3只后,甲笼比乙笼还多2只,两只笼子原来各有多少只鸡?练习:1、两堆石子共有800吨,第一堆比第二堆多200吨,两堆石子各有多少吨?2、把长84厘米的铁丝围成一个使长比宽多6厘米的长方形。
第一讲差倍问题

第⼀讲差倍问题第⼀讲差倍问题班级姓名差÷(倍数-1)=⼩数⼩数×倍数=⼤数或差+⼩数=⼤数1、胜利⼩学开展冬季体育⽐赛,参加跳绳的⼈数是踢毽⼦⼈数的4倍,⽐踢毽⼦的多72⼈。
参加跳绳和踢毽⼦的各多少⼈?2、⽣产队利⽤⼭坡种了⼀批核桃树和红果树,核桃树的棵数是红果树的2倍多95棵,已知核桃树⽐红果树多1455棵,两种树各种了多少棵?3、有⼤、⼩两个⽔池,⼤⽔池⾥已有⽔300⽴⽅⽶,⼩⽔池⾥已有⽔70⽴⽅⽶。
现在往两个⽔池⾥注⼊同样多的⽔后,⼤⽔池⽔量是⼩⽔池⽔量的3倍。
问:每个⽔池注⼊了多少⽴⽅⽶的⽔?4、甲、⼄两⼈的存款相等,甲取出60元,⼄存⼊20元后,⼄的存款是甲的3倍,两⼈原有存款各多少元?5、⼩明所有的连环画本数是⼩华的6倍,如果两⼈各再买2本,那么⼩明所有的本数是⼩华的4倍。
两⼈原来各有连环画多少本?6、有两堆煤,甲堆94吨,⼄堆138吨,每天各⾛9吨,⼏天后⼄堆剩下的煤是甲堆剩下的煤的3倍?7、有⼤、中、⼩三筐菠萝,⼩筐装的是中筐的⼀半,中筐⽐⼤筐少装16千克,⼤筐装的是⼩筐的4倍。
⼤、中、⼩三筐各装菠萝多少千克?8、甲、⼄两根绳,甲绳长163⽶,⼄绳长97⽶,两根绳剪去同样的长度,结果甲绳所剩长度是⼄绳的7倍还多6⽶。
两绳各剪去多少⽶?9、两筐千克数相同的苹果,甲筐卖出7千克,⼄筐卖出19千克以后,甲筐余下的千克数是⼄筐的3倍,两筐苹果原来各有多少千克?10、甲的存款是⼄的5倍,如果甲取出60元,⼄存⼊60元,那么⼄的存款是甲的2倍。
甲、⼄原有的存款各多少元?11、两堆沙⼦,第⼀堆⽐第⼆堆多46吨,已知第⼀堆⽐第⼆堆的4倍还多4吨。
那么第⼀堆沙⼦多少吨?第⼆堆沙⼦多少吨?12、甲筐有梨280个,⼄筐有梨190个。
现在从两筐取出数⽬相等的梨,剩下梨的个数,甲筐恰好是⼄筐的2倍。
那么甲筐取出梨多少个?13、两袋⼤⽶重量相等,甲袋取出28千克,⼄袋装⼊14千克,这时⼄袋的重量正好是甲袋的3倍。
小学奥数知识点总结之一:和差倍问题

第一分项:和差问题练习题公式:(和-差)÷2=较小数(和+差)÷2=较大数一、单项选择题(每小题2分,共20分)1、两篮水果共重96千克,第一篮比第二篮多8千克,第二篮有多少千克? ( )A、52B、44C、53D、452、小芳今年6岁,爸爸34岁,当两人年龄和是58岁时,小芳是多少岁? ( )A、15B、16C、17D、18注:年龄差是固定值3、李明星期天上街买衣服,花85元钱买了一条裤子和一件上衣,已知上衣比裤子贵15元,李明买裤子花多少元。
( )A、15B、25C、35D、454、小兰期末考试时语文和数学平均分是96分,数学比语文多4分,问小兰数学多少分。
( )A、95B、94C、97D、98注:平均分和总分之间的关系5、A、B两船共载客623人, 若A船增加34人,B船减少57人,这时两船乘客同样多, A 船原有乘客多少人。
( )A、266B、357C、300D、350注:要搞清楚差是多少6、小娟和小芳一共擦玻璃31块,又知小娟比小芳少擦9块,小娟、小芳各擦玻璃多少块。
( )A、11,20B、10,21C、9,22D、20,117、姐姐和弟弟共有铅笔173支,把姐姐的铅笔拿走3支后,姐姐和弟弟的铅笔支数就同样多,问姐姐原来有多少支铅笔。
( )A、85B、88C、84D、868、姐姐和弟弟共有铅笔174支,把姐姐的铅笔给弟弟3支后,两人铅笔支数就同样多,问弟弟原来有多少支铅笔。
( )A、85B、88C、84D、86注:审题要仔细,“拿走”和“给对方”是不同的含义9、小强用270元买了一件外衣、一顶帽子和一双鞋子。
外衣比鞋贵140元,买外衣和鞋比帽子多花210元.小强买这双鞋花多少钱。
( )A、80B、30C、190D、50注:三个数以上的和差问题,可以把多个数看作一个整体,也就是简化为两个数;然后进行多次和差来解决10、一个减法算式里,被减数、减数与差三个数的和是388,减数比差大16,减数等于多少.()A、80B、194C、105D、89注:把已知条件转换为公式需求二、填空题(每小题3分,共30分)1、两个数的和为36,差为22,则较大的数为 ,较小的数为。
第一讲 和差倍

第一讲和差倍1、和差问题和差应用题是指已知大小两个数(或几个数)的和与它们的差,求这两个数(或几个数)各是多少的应用题,简称为和差问题。
解决和差问题的方法解答和差应用题,通常用假设的思维方法。
什么是假设法呢假设的方法有两种:一种是假设小数增加到与大数同样多,选择大数为标准数,把小数转化成与大数相等,用两数之和加上两数之差,从而得到大数的2倍,先求出大数再求小数。
另一种是假设大数减少到与小数同样多,选择小数做标准数,把大数转化成与小数相等,从两数和里减去两数差,从而得到小数的2倍,先求出小数再求大数。
和差问题的基本数量关系(和+差)÷2=大数大数-差=小数(和-大数=小数)(和-差)÷2=小数小数+差=大数(和-小数=大数)例1小明和小英共有图书45本,小英比小明少3本,两人各有图书多少本?例2、今年小刚和妈妈两人的年龄和是38岁,3年前,小刚比妈妈小26岁,问今年小刚和妈妈各多少岁?例3、甲、乙两个仓库共存大米80吨。
如果从甲仓库调15吨大米到乙仓库,两个仓库所存的大米正好相等。
求原来两个仓库各有大米多少吨?练1 、把长108厘米的铁丝围成一个长方形,使长比宽多12厘米,长和宽各是多少厘米?练2、A、B两车共有乘客160人,从甲站经乙站开往丙站,在乙站A车增加17人,B车减少23人,开往乙站时,两车乘客恰好相等,两车原有乘客多少人?练3、一个三层书架共放书108本,上层比中层多14本,下层比中层少8本,上、中、下三层各放书多少本?2、和倍问题已知两个数(或几个)数量的和,及这两个数(或几个)数量之间的倍数关系,求这两个数(或几个)数各是多少的应用题叫做和倍应用题,简称和倍问题。
解答和倍问题,关键是要找出数量和以及与其对应的倍数和,从而求出1倍数,再求出几倍数。
数量关系可以这样表示:数量和÷(倍数+1)=小数(一倍数)小数×倍数=大数(几倍数)例4、饲养小组共养黑、白兔120只,其中白兔的只数是黑兔的3倍。
和倍差倍及和差问题
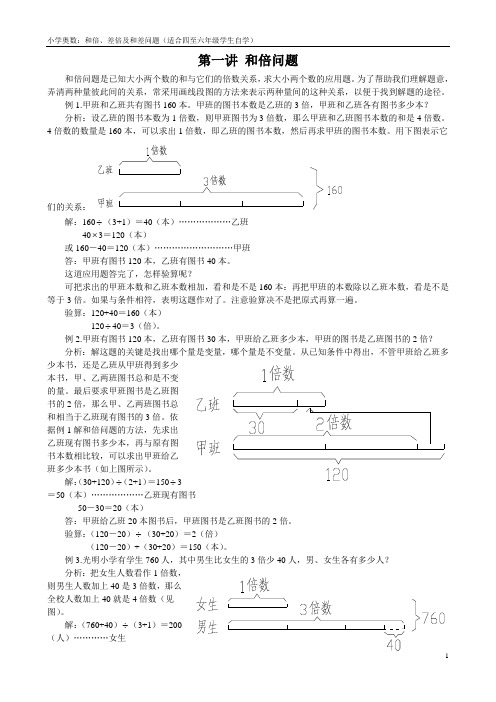
第一讲和倍问题和倍问题是已知大小两个数的和与它们的倍数关系,求大小两个数的应用题。
为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
例1.甲班和乙班共有图书160本。
甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?分析:设乙班的图书本数为1倍数,则甲班图书为3倍数,那么甲班和乙班图书本数的和是4倍数。
4倍数的数量是160本,可以求出1倍数,即乙班的图书本数,然后再求甲班的图书本数。
用下图表示它们的关系:解:160÷(3+1)=40(本)………………乙班40⨯3=120(本)或160-40=120(本)………………………甲班答:甲班有图书120本,乙班有图书40本。
这道应用题答完了,怎样验算呢?可把求出的甲班本数和乙班本数相加,看和是不是160本:再把甲班的本数除以乙班本数,看是不是等于3倍。
如果与条件相符,表明这题作对了。
注意验算决不是把原式再算一遍。
验算:120+40=160(本)120÷40=3(倍)。
例2.甲班有图书120本,乙班有图书30本,甲班给乙班多少本,甲班的图书是乙班图书的2倍?分析:解这题的关键是找出哪个量是变量,哪个量是不变量。
从已知条件中得出,不管甲班给乙班多少本书,还是乙班从甲班得到多少本书,甲、乙两班图书总和是不变的量。
最后要求甲班图书是乙班图书的2倍,那么甲、乙两班图书总和相当于乙班现有图书的3倍。
依据例1解和倍问题的方法,先求出乙班现有图书多少本,再与原有图书本数相比较,可以求出甲班给乙班多少本书(如上图所示)。
解:(30+120)÷(2+1)=150÷3=50(本)………………乙班现有图书50-30=20(本)答:甲班给乙班20本图书后,甲班图书是乙班图书的2倍。
验算:(120-20)÷(30+20)=2(倍)(120-20)+(30+20)=150(本)。
小学奥数和差倍问题一
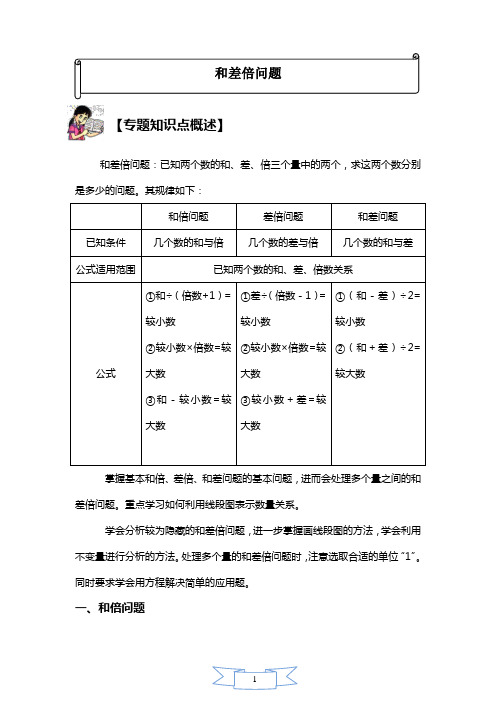
和差倍问题【专题知识点概述】和差倍问题:已知两个数的和、差、倍三个量中的两个,求这两个数分别是多少的问题。
其规律如下:和倍问题差倍问题和差问题已知条件几个数的和与倍几个数的差与倍几个数的和与差公式适用范围已知两个数的和、差、倍数关系公式①和÷(倍数+1)=较小数②较小数×倍数=较大数③和-较小数=较大数①差÷(倍数-1)=较小数②较小数×倍数=较大数③较小数+差=较大数①(和-差)÷2=较小数②(和+差)÷2=较大数掌握基本和倍、差倍、和差问题的基本问题,进而会处理多个量之间的和差倍问题。
重点学习如何利用线段图表示数量关系。
学会分析较为隐藏的和差倍问题,进一步掌握画线段图的方法,学会利用不变量进行分析的方法。
处理多个量的和差倍问题时,注意选取合适的单位“1”。
同时要求学会用方程解决简单的应用题。
一、和倍问题(1)和倍例1、纺织厂有职工480人,其中女职工人数是男职工人数的3倍。
请问:男、女职工各多少人?(★)分析:女职工人数是男职工人数的3倍,选男职工人数为“1”,用一条小线段表示,那么女职工人数就用三条小线段表示,如图:那么每一小段表示:()48031120÷+=(人)即男职工人数为120人,那么女职工人数为:1203360⨯=人例2、一个长方形,周长是300厘米,长是宽的2倍,求这个长方形的面积。
(★) 分析:周长是300厘米,那么长与宽的和为3002150÷=厘米长是宽的2倍,所以用一条小线段表示宽,那么长就用两条小线段表示,如图:那么每一小段表示:()1502150÷+=厘米即宽50厘米,那么长:502100⨯=厘米例3、甲班和乙班一共有60人。
如果从甲班调6个人到乙班,那么甲班的人数就是乙班人数的2倍。
求甲、乙两班原来的人数。
(★★)分析:现在甲班人数是乙班人数的2倍,并且两班总人数为60人,那么乙班现在的人数为:()602120÷+=人。
六年级下册数学试题-小升初强化:和差倍问题(下)(解析版)全国通用

第一讲和差倍问题(下)1、巩固解决较复杂的和差倍问题和年龄问题,并熟练运用线段图分析数量关系,复习前一讲内容;2、培养学员的读题能力,会找“隐含量”,能理清多种数量彼此对应的关系;3、培养学员解决问题的能力,提高学员的信心。
差倍问题是大数、小数、倍数以及大小数之差四者之间发生的问题,所有的问题都离不开三个基本公式:两数差÷(倍数-1)=小数(一倍数)小数×倍数=大数(几倍数)小数+两数差=大数(几倍数)同和倍问题一样,解答差倍问题一般也是先确定较小的数为标准数(或称一倍数),再根据其他数与标准数之间的倍数关系确定两数差相当于标准数的多少倍,然后利用除法求出标准数,再求出其他各数。
为了更好的弄清楚题意,同样通常采用画线段图的方法。
年龄变化基本规律:1、两人年龄差不变2、两人年龄倍数关系不是一成不变的,它会随时间改变3、随着时间推移,两人年龄的增加量相等为了过冬,小白兔和小黑兔都储藏了一些胡萝卜。
已知小白兔储藏的胡萝卜数量是小黑兔储藏数量的3倍。
它们各吃了5个胡萝卜后,小白兔剩下的胡萝卜数量是小黑兔剩下数量的4倍。
那么它们剩下的胡萝卜共有多少个?【解析】小黑兔剩下胡萝卜的数量是3×5-5=10(个),它们剩下的胡萝卜共有10+10×4=50(个)。
解答:剩下的胡萝卜共有50个。
小波问李老师今年有多少岁,李老师说:“当我像你这么大时,你才3岁;当你像我这么大时,我已经42岁了。
”你知道李老师今年多少岁吗?【解析】根据题意画线段图如下: 李老师的年龄小波的年龄42岁3岁由图可知李老师与小波的年龄差为(42-3)÷3=13(岁),那么李老师今年的年龄为42-13=29(岁)。
解答:李老师今年29岁。
讲演者:得分:讲演者:得分:有50名学生参加联欢会,第一名到会的女生同全部的男生握过手,第二名到会的女生只差1名男生没有握过手,第三名到会的女生只差2名男生没有握过手,以此类推,最后一名到会的女生同7名男生握过手。
第一讲 和倍问题(1) 许晓蕾

第一讲和倍问题(1)知识导航:解答和差问题的关键是选择适当的数作为标准(一倍量),设法把若干各不相等的数变为相等的数。
解答此类应用题时,可以用线段图表示题意,来分析数量关系,寻求解题途径。
典型例题:【例1】甲班和乙班共有图书160本,甲班的图书数是乙班的3倍,甲班和乙班各有图书多少本?【练习一】1、副食店共有白糖和红糖234千克,白糖的千克数正好是红糖的2倍,副食店有白糖、红糖各多少千克?2、兄弟俩去游乐园,他们一共带了180元。
已知哥哥带的钱数是弟弟的2倍,兄弟俩各带了多少钱?3、甲、乙两仓库共存粮264吨,甲仓库存粮是乙仓库存粮的10倍。
甲、乙两仓库各存粮多少吨?4、、徒弟加工了85个零件,师傅加工的零件数正好是徒弟的5倍。
师傅比徒弟弟加工了多少个零件?5、一个长方形,周长是30厘米,长是宽的2倍,求这个长方形的长、宽?【例2】学校图书馆有文艺书与科技书共650本,文艺书的本数比科技书的3倍多50本,图书馆有文艺书和科技书各多少本?【练习二】1、果园里共有桃树和梨树340棵,其中桃树比梨树的3倍多20棵,两种树各种了多少棵?2、光明小学有学生760人,其中男生比女生的3倍少40人,男、女生各有多少人?3、一个停车场共停大、小车27辆,其中大车比小车的2倍少3辆。
问停车场停大、小车各多少辆?4、某校四、五年级共有学生218人,五年级学生人数比四年级的2倍少22人。
问四、五年级各有学生多少人?5、徒弟加工了85个零件,师傅加工的零件数比徒弟的5倍少16个。
师傅加工了多少个零件?【例3】有两筐苹果,第一筐有73个,第二筐有77个。
问从第二筐中拿出多少个苹果放入第一筐,就能是第一筐的苹果树是第二框的2倍?【练习三】1、姐姐有画片320张,妹妹有画片180张。
问妹妹给姐姐多少张画片后,姐姐的画片比妹妹的画片多3倍?2、甲仓库有存粮54吨,乙仓库有存粮70吨,乙仓库调给甲仓库多少吨后,甲仓库存数是乙仓库的3倍?3、污水处理厂有甲乙两个水池,甲池原有水960立方米,乙池原有水90立方米。
和差倍比问题

和差倍比问题和差倍比问题是研究不同量之间的和、差、倍数、比例关系的数学应用题,是数学运算中比较简单的问题。
这类问题对计算速度和准确度要求较高,考生在平时训练中,应注意培养自己的速算能力。
按照其考查形式,和差倍比问题可以分为和倍问题、差倍问题、和差问题、比例问题等。
中公教育专家在此为考生进行详解。
一、和倍问题和倍问题是指已知两个或者两个以上的数之和,以及它们之间的倍比关系,求这两个数或这些数各是多少的问题。
例如:师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?和倍问题常用公式:和÷(倍数+1)=1倍量,1倍量×倍数=几倍量对和倍问题,可按照以下流程解题:对于上题,可以这么来解:根据题意,徒弟加工的少,可将徒弟的看成1倍量。
〔确定1倍量〕画出示意图如图:从图上可以看出,如果师傅少加工5个,两人加工的总数少5个,总数变为100个,这时是整数倍,一共有1+3=4倍。
〔确定总和相当于几倍〕1倍量=100÷4=25,即徒弟加工了25个。
〔利用公式求出1倍量〕师傅加工了105-25=80个。
〔求出其他各量〕二、差倍问题差倍问题是指已知两个数的差,以及它们之间的倍数关系,求这两个数各是多少的问题。
这类问题与和倍问题本质上没有区别,只是在求倍数的时候注意对应关系。
差倍问题常用公式:差÷(倍数-1)=1倍量,1倍量×倍数=几倍量例题1:两块同样长的花布,第一块卖出31米,第二块卖出19米后,第二块是第一块的4倍,则第一块花布原有多少米?A.48B.42C.40D.35中公解析:此题答案为D。
已知两块花布同样长,由于第一块卖出的多,第二块卖出的少,因此第一块剩下的少,第二块剩下的多。
将第一块剩下的看成1倍量,画出示意图,如下图所示。
所剩的布第二块比第一块多31-19=12米。
又知第二块所剩下的布是第一块的4倍,根据差倍公式,差÷(倍数-1)=1倍量,可知第一块所剩布的长度为12÷(4-1)=4米,则第一块布原有4+31=35米。
第1讲和差倍问题

第1讲和差倍问题典型例题:1.甲乙两个工程队合挖一条长48千米的水渠,甲队比乙队多挖了6千米,求甲、乙工程队各挖了多少千米?2.乙两个仓库共运进货物1260吨,如果从甲仓库调出120吨货物到乙仓库,则两个仓库的货物一样多,求甲乙两仓库原来运进货物各多少吨?3.甲乙两堆货物共180吨,甲堆货物运走30吨仍比乙堆货物多12吨,求甲乙两堆货物各多少吨?4.用80米长的铁丝网靠墙围一个长方形的场地(靠墙的一面不用铁丝网),对着墙的一面是长,长比宽多20米,求这块长方形场地的面积是多少?5.甲乙两个学校共有学生1245人,如果从甲校调20人去乙校后,甲校比乙校还多5人,两校原有学生多少人?6.乙两个工程队共1980人,甲队为了支援乙队,抽出285人调入乙队,这时乙队人数还比甲队少24人,求甲乙两队原有工人多少人?7.一篮苹果比一篮桔子重40千克,苹果重量是桔子的5倍,苹果、桔子各有多少千克?8.小红铅笔的支数是小明的2倍,她从中拿出15支捐给了希望工程,正好是小红小明支数的总和的一半,小红原有铅笔多少支? 9.学校图书馆有文艺书与科技书共605本,文艺书的本数比科技书的3倍多50本,图书馆有文艺书和科技书各多少本?10.禽养场今年养鸡和鸭共4600只,养的鸡比鸭的4倍还多100只,禽养场今年的鸡鸭各多少只?11.姐姐和妹妹共做了340朵小红花,后来姐姐把她做的红花送给了小明30朵,妹妹自己又做了20朵,这时姐姐做的小红花是妹妹的5倍。
问原来姐姐,妹妹各做了多少朵红花?12.甲乙两数的差及商都等于6,那么甲、乙两数的和等于多少?13.已知两个数的商是4,这两个数的差是39,那么这两个数中较小的一个数是多少?14.甲乙两数的差是9,甲数的1/6和乙数的1/4相等,甲数是多少?乙数是多少?15.已知大小两个数的差是5.49,将较大数的小数点向左移动一位,就等于较小数。
较大的数是多少?较小的数是多少?16.有两筐苹果,如果从第一筐拿出9个放到第二筐,两筐苹果个数相等;如果从第二筐拿出12个放到第一筐,则第一筐苹果的个数等于第二筐的2倍。
六年级下册数学专题-小升初数学专题之和差倍、年龄、植树问题 全国通用(含答案)

小升初数学专题第1讲典型应用题(一)和差倍、年龄、植树问题一、知识地图典型应用题2:3⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎪⎪⎪⎧⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎩和差类型,解题方法.和倍类型,解题方法.和差倍分问题差倍类型,解题方法.工具线段图关键1:年龄差不变关键年龄倍数关系变化年龄问题关键:可以转化为和差倍问题解决工具线段图植树和方阵问题─────二、基础知识(一)和差问题:已知两个数的和及两个数的差,求这两个数。
方法①:(和-差)÷2=较小数,和-较小数=较大数方法②:(和+差)÷2=较大数,和-较大数=较小数例如:两个数的和是15,差是5,求这两个数。
方法:(15-5)÷2=5,(15+5)÷2=10。
(二)和倍问题:已知两个数的和及这两个数的倍数关系,求这两个数。
方法:和÷(倍数+1)=1倍数(较小数)1倍数(较小数)×倍数=几倍数(较大数)或和-1倍数(较小数)=几倍数(较大数)例如:两个数的和为50,大数是小数的4倍,求这两个数。
方法:50÷(4+1)=10 10×4=40(三)差倍问题:已知两个数的差及两个数的倍数关系,求这两个数。
方法:差÷(倍数-1)=1倍数(较小数)1倍数(较小数)×倍数=几倍数(较大数)或和-1倍数(较小数)=几倍数(较大数)例如:两个数的差为80,大数是小数的5倍,求这两个数。
方法:80÷(5-1)=20 20×5=100(四)年龄问题关键①:年龄差不变例如:今年爸爸比儿子大30岁,明年爸爸比儿子大几岁?答:还是30岁,爸爸长1岁,儿子也长1岁。
明年父子年龄差=明年爸爸的年龄-明年儿子的年龄=(今年爸爸的年龄+1)-(今年儿子的年龄+1)=今年爸爸的年龄+1-今年儿子的年龄-1=今年爸爸的年龄-今年儿子的年龄=30(岁)关键②:年龄的倍数关系是变化的。
第一讲 和倍问题

第一讲和倍问题例1:甲班和乙班共有160本,甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?例2:某校共有学生560人,其中男生比女生的3倍少40人,男女生各有多少人?例3、果园里有桃树、梨树和杏树共350棵,梨树比桃树的两倍少14棵,杏树比桃树多24棵。
桃树、梨树和杏树各有多少棵?练习:1、哥哥和弟弟共有图书120本,哥哥的图书本数是弟弟的3倍,哥哥和弟弟各有图书多少本?2、父亲和儿子的年龄和是60岁,父亲的年龄是儿子的4倍,父亲比儿子打多少岁?3、书架上有语文、数学两类数共280本,其中数学书的本数比语文书的2倍还多7本,问数学书和语文书各多少本?4、某小学有篮球、排球、足球共105个,排球个数是篮球的2倍,足球个数是篮球的4倍,篮球、排球、足球各多少个?例4:甲班有图书120本,乙班有图书30班,甲给乙班多少本,甲班的图书是乙班的2倍?例5:549是甲、乙、丙、丁4个数的和,如果甲数加上2,乙数减少2,丙数乘以2以,丁数除以2以后,则4个数相等。
求4个数各是多少?练习:1、一个长方形,周长是30厘米,长是宽的2倍,这个长方形的面积是多少平方厘米?2、甲桶里有油470千克,乙桶里有油190千克,甲桶的油倒入乙桶多少千克,才能使甲桶油是乙桶油的2倍?3、甲、乙两粮仓共存粮320吨,后来从甲仓运出40吨,给乙仓运进20吨,这时甲仓存粮食是乙仓的2倍,两个粮仓原来各存粮多少吨?4、甲、乙、丙、丁四人共做了370个零件,如果把甲做的个数加上10个,乙做的个数减去20个,丙做的个数乘以2,丁做的个数除以2,则四个人的个数相等,那么甲、乙、丙、丁各做了多少个?第二讲差倍问题例1、哥哥有图书本数比弟弟多80本,哥哥的图书本数是弟弟的3倍,哥哥和弟弟各有图书多少本?例2、有父子二人,父亲48岁,儿子20岁,问几年以后,父亲的年龄正好是儿子的2倍?例3:甲乙两校教师的人数相等,由于工作需要,从甲校调30人到乙校去,这时乙校教师人数正好是甲校教师人数的3倍。
第课时 列一元一次方程解决和差倍分问题(共19张PPT)

解:设乙队出x人,则甲队出 x 人,丙队出2x人,三 2
队共出280人.
依题意 得
x x+=80. x =40.2x=160. 2
答:甲队出80人,乙队出40人,丙队出160人.
例4 质量为45克的某种三色冰淇淋中,咖啡色、红色和白色配料 的比为1:2:6,这种三色冰淇淋中,咖啡色、红色和白色配料分别是 多少?
练一练
小明和小东各有课外读物若干本,小明课外读物的数量是小东
的2倍,小明送给小东10本后,小东课外读物的数量是小明的3倍, 求小明和小东原来各有课外读物多少本.
解:设小东原来有课外读物x本,则小明原来有课外读物2x本, 由题意,得
3(2x-10)=x+10, 解得x=8,2x=16. 答:小明原来有课外读物16本,小东原来有课外读物8本.
我的年龄是13 岁的呢?
小敏
讲授新课
一 和差问题
合作探究
某湿地公园举行观鸟节活动,其门票价格如下:
全价票 半价票
20元/人 10元/人
该公园共售出1200张门票,得总票款20000元,问全价 票和半价票各售出多少张?
分析题意可得此题中的等量关系有:
全价票数+__半__价__票__数=1200张; _全__价__票__款_+半价票款=_____2_0_0_0.0元
设售出全价票x张,填写下表:
可不可以
分析:本问题中涉及的等量关系有:
C.5x+3(x+2)=14
D.5x+3(x-2)=14
某湿地公园举行观鸟节活动,其门票价格如下:
票数/张 小敏,我能猜出你年龄.
运用一元一次方程模型解决实际问题的步骤有哪些?
全价
x
半价 1200- x
设其他未 知量为x?
和差倍问题(一)

【加油站】 ⑴佳佳和海海的零花钱一共有100元,佳佳的零花钱比海海的3倍多4元。那么 两人各有多少元?
⑶海海和言言比赛吃樱桃,两人一共吃了200个樱桃,如果海海少吃8个,言言 多吃4个,两人吃的就一样多了。那么他们各吃了多少个樱桃? 吃的 样多 各吃 多少 桃
⑵佳佳和海海有一些巧克力。佳佳是海海的3倍,佳佳的比海海的多40块。那 么两人各有多少块巧克力?
【例2】(★★★) 佳佳、海海和言言比赛跳绳。三人一共跳了280个。其中佳佳跳的个数 是海海的2倍,言言跳的是佳佳的2倍。那么他们每人各跳了几个?
【例3】(★★★) 某校五年级比六年级人数少154人,若六年级学生再转来46人,则六年 级学生是五年级学生的3倍,问五、六年级各有多少人?
1
【例4】(★★★) 佳佳、海海两位学生原计划每天自学时间相同.若佳佳每天增加自学 时间半小时,海海每天减少自学时间半小时,则海海自学6天的时间仅 相当于佳佳自学1天的时间.问:佳佳、海海原定每天自学的时间是多 少?
加加点睛 和倍问题:1倍量=和÷(倍数+1) 差倍问题:1倍量=差÷(倍数-1) 和差问题:大数=(和+差)÷2 小数 (和-差 小数= 和 差)÷2 被 “比” “是” 的是“1倍量”
【大海招牌菜】 有2根大小相同,粗细均匀的绳子,每根从一头点燃时,燃烧 【例1】(★★) 完都是1个小时,你能想办法计量出45分钟吗? 佳佳、海海两人共加工95个零件,佳佳加工的个数比海海的3倍少5个, 佳佳和海海各加工零件多少个?
【金牌挑战】 (华杯赛中年级组复赛试题) 某班学生人数大于 20 而小于30,其中女同学的人数是男同学的2 倍。全班报 名参加“华杯赛”的人数是未报名人数的3 倍少1 人。中拿2个放到第二个盘里,那么两盘的苹果 数相同;如果从第二个盘中拿2个放到第一盘里,那么第一盘的苹果数 是第二盘的2倍。第一盘有苹果多少个?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲和差倍问题典型例题:1.甲乙两个工程队合挖一条长48千米的水渠,甲队比乙队多挖了6千米,求甲、乙工程队各挖了多少千米?2.乙两个仓库共运进货物1260吨,如果从甲仓库调出120吨货物到乙仓库,则两个仓库的货物一样多,求甲乙两仓库原来运进货物各多少吨?3.甲乙两堆货物共180吨,甲堆货物运走30吨仍比乙堆货物多12吨,求甲乙两堆货物各多少吨?4.用80米长的铁丝网靠墙围一个长方形的场地(靠墙的一面不用铁丝网),对着墙的一面是长,长比宽多20米,求这块长方形场地的面积是多少?5.甲乙两个学校共有学生1245人,如果从甲校调20人去乙校后,甲校比乙校还多5人,两校原有学生多少人?6.乙两个工程队共1980人,甲队为了支援乙队,抽出285人调入乙队,这时乙队人数还比甲队少24人,求甲乙两队原有工人多少人?7.一篮苹果比一篮桔子重40千克,苹果重量是桔子的5倍,苹果、桔子各有多少千克?8.小红铅笔的支数是小明的2倍,她从中拿出15支捐给了希望工程,正好是小红小明支数的总和的一半,小红原有铅笔多少支? 9.学校图书馆有文艺书与科技书共605本,文艺书的本数比科技书的3倍多50本,图书馆有文艺书和科技书各多少本?10.禽养场今年养鸡和鸭共4600只,养的鸡比鸭的4倍还多100只,禽养场今年的鸡鸭各多少只?11.姐姐和妹妹共做了340朵小红花,后来姐姐把她做的红花送给了小明30朵,妹妹自己又做了20朵,这时姐姐做的小红花是妹妹的5倍。
问原来姐姐,妹妹各做了多少朵红花?12.甲乙两数的差及商都等于6,那么甲、乙两数的和等于多少?13.已知两个数的商是4,这两个数的差是39,那么这两个数中较小的一个数是多少?14.甲乙两数的差是9,甲数的1/6和乙数的1/4相等,甲数是多少?乙数是多少?15.已知大小两个数的差是5.49,将较大数的小数点向左移动一位,就等于较小数。
较大的数是多少?较小的数是多少?16.有两筐苹果,如果从第一筐拿出9个放到第二筐,两筐苹果个数相等;如果从第二筐拿出12个放到第一筐,则第一筐苹果的个数等于第二筐的2倍。
原来每筐各有几个苹果?17.某车间男工人数是女工人数的两倍,若调走18个男工,那么女工数是男工人数的两倍。
这个车间的女工有多少人?18.甲乙两个学校共有学生1245人,如果从甲校调20人去乙校后,甲校比乙校还多5人,两校原有学生多少人?19.乙两个工程队共1980人,甲队为了支援乙队,抽出285人调入乙队,这时乙队人数还比甲队少24人,求甲乙两队原有工人多少人?20.山坡上有一群羊,其中有绵羊和山羊。
已知绵羊比山羊的3倍多55只,已知绵羊比山羊多345只,两种羊各有多少只?21.某小队队员提一篮苹果和梨子到敬老院去慰问,每次从篮里取出2个梨子、5个苹果送给老人,最后剩下11个苹果,梨子正好分完。
这时他们才想起原来苹果数是梨子的3倍。
问篮内原有苹果、梨子各多少个?综合检测一. 填空题1.甲、乙两个粮仓存粮320吨,后来从甲仓运出40吨,给乙仓运进20吨,这时甲仓存粮是乙仓的2倍,两个粮仓原来各存粮分别为吨和吨.2.某校共有560人,其中男生比女生的3倍少40人.则男生人,女生人.3.学校买了4个足球和2个排球,共用去了162元.每个足球比每个排球贵3元,每个足球元,每个排球元.4.南京长江大桥比美国纽约大桥长4570米,纽约大桥比我国武汉长江大桥长530米.已知三座桥长10640米,这些桥长分别是米, 米, 米.5.甲筐有梨400个,乙筐有梨240个,现在从两筐取出数目相等的梨,剩下梨的个数,甲筐恰好是乙筐的5倍,甲筐所剩的梨是个,乙筐所剩下的梨是个.6.甲、乙、丙三数之和是100,甲数除以乙数,丙数除以甲数,商都是5,余数都是1,乙数是 .7.今年哥俩的岁数加起来是55岁,曾经有一年,哥哥的岁数与今年弟弟的岁数相同,那时哥哥的岁数恰好是弟弟的2倍,哥哥今年岁.8.三块布共长220米,第二块布长是第一块的3倍,第三块布长是第二块的2倍,第一块布长米.9.有两层书架,共有书173本.从第一层拿走38本书后,第二层的书是第一层的2倍还多6本,则第二层有本书.10.小明和小强共有画200张,小明的张数比小强的张数的2倍还多20张,则小强有张画片.11.甲乙粮仓共存粮1038吨,如果把甲仓存的粮食放到乙仓9吨,两仓库的粮食就一样多了,甲粮仓原来存粮食吨,乙粮仓原来存粮食吨.12.两个数相除,商3余10,被除数,除数,商的和是163,被除数是 ,除数是 .13.小红和妈妈的年龄加在一起是40岁,妈妈年龄是小红年龄的4倍,小红有岁,妈妈有岁.14.生产队养公鸡、母鸡404只,其中公鸡是母鸡的3倍,公鸡养了只,母鸡养了只.15.小明买大单和小单线共25本,其中大单线的本数比小单线的本数的2倍多4本,大单线的本数有本,小单线的本数有本.16.师傅和徒弟共生产零件190个,师傅生产的个数比徒弟的3倍少10个;师傅、徒弟各生产个17.A、B两人同时从学校出发相背而行,2小时共行48千米,A的速度是B的2倍,A的速度是每小时千米,B的速度是每小时千米.18.一块长方形木板,长是宽的2倍,周长是54厘米.这个长方形木板的面积是平方厘米.19.甲乙两个冷藏库原来共存肉92吨,从甲库运出28吨后,乙库存肉比甲库的4倍少6吨,甲库原来存肉吨,乙库原来存肉吨.20.两个粮仓共存粮2200千克,由乙仓运出210千克,甲仓存的粮食是乙仓的2倍少380千克,甲仓库原来存粮食千克,乙仓库原来存粮食千克. 21.小红有30支铅笔,小兰有45支铅笔,小兰给小红支后,小红的支数是小兰的2倍.22.姐姐有320元钱,弟弟有180元钱,弟弟给姐姐钱后,姐姐的钱比弟弟的钱多3倍.23.小丽和小荣集邮,小丽邮票的张数是小荣的5倍,如果小丽把自己的邮票给小荣100张,她俩邮票的张数正好相等.小丽和小荣各有张、张.24.启东水泥厂有甲、乙两仓库,各有水泥若干袋,甲仓库存水泥的袋数是乙仓库的3倍,后来从甲仓库运出450袋,从乙仓库运出50袋.这时仓库剩余的袋数相等,甲仓库原有水泥袋,乙仓库原有袋.25.两筐桃的个数相等.如果第一筐卖出150个,第二筐卖出194个,那么剩下的桃第一筐是第二筐的3倍,第一筐有个,第二筐有个.26.甲、乙两人存款若干元,甲存款是乙存款的3倍,如果甲取出240元,乙取出40元,甲、乙存款数正好相等.问甲原有存款元,乙原有存款元.27.小勇和小英各有钱若干元,若小勇给小英24元,二人钱数相等.如果小英给小勇27元,则小勇的钱数就是小英钱数的2倍.问小勇原有元,小英原有元.28.如果甲数加上152等于乙数,如果乙数加上480等于甲数的3倍,问原来甲数 ,乙数 .29.有两根同样长的铅笔,第一根用去14厘米,第二根用去2厘米后,第二根的长度是第一根的3倍,问原有铅笔各厘米.30.两块同样长的布,第一块用去31米,第二块用去19米,结果所余米数,第二块是第一块的4倍,两块布原来各长米.31.哥哥的图书数比弟弟多60本,哥哥的图书本数是弟弟的3倍,则哥哥有图书本,弟弟有图书本.32.父亲现年50岁,女儿现年14岁, 年前,父亲的年龄是女儿年龄的5倍.33.小明、小红两人集邮,小明的邮票比小红多15张,小明的张数是小红的4倍,小明集邮张,小红集邮张.34.妈妈的年龄比小刚大24岁,今年妈妈的年龄正好是小刚年龄的3倍,今年妈妈岁,小刚岁.35.学农基地种的花生是白薯的16倍,现在已经知道种的花生比白薯多105棵,种花生棵,白薯棵.36.小利的科技书比故事书少16本,故事书是科技书的3倍,小利有科技书本,故事书本.37.甲、乙两个数,如果甲数加上50,就等于乙数,如果乙数加上350就等于甲数的3倍,问甲 ,乙 .38.小明、小丽做题,如果小明再做4道就和小丽做的一样多,如果小丽再做6道就是小明的3倍,小明做道题,小丽做道题.39.仓库存有面粉和大米,已知面粉比大米多4500千克,面粉的斤数比大米的3倍多700千克,大米千克,面粉千克.40.两筐重量相等的苹果,从甲筐取出7千克,乙筐加上19千克,这时乙筐的重量是甲筐重量的3倍,原来两筐各有苹果千克、千克.41.AB两人所存的钱数相等,A要买一件商品,向B借了120元,这时A的钱数正好是B的4倍,A有元,B有元.42.某班原有男生比女生多10人,如果女生转走5人,那么男生人数正好是女生人数的2倍,原有男生人.二. 解答题1.某车间共有工人77名,其中女工人数比徒工人数的2倍还多4人,男工人数比徒工和女工人数之和的2倍少7人,问:这个车间徒工,女工,男工各多少人?2.四年级甲班为筹办红领巾图书室号召同学捐送书籍,共收到科技书和故事书320笨,其中科技书是故事书的3倍,四年级甲班同学捐送的科技书和故事书各是多少本?3.甲乙丙丁四个数之和为45,若将甲数加上2,乙数减去2.,丙数乘以2,丁数除以2,则四个数恰好相等,求这四个数各是多少?4.父亲今年47岁,徐红今年11岁,问几年前父亲的年龄是徐红年龄的5倍?5.某公司为鼓励工作成绩好的职工,决定将4200元奖金分给三名优秀职工,已知第一名比第二名多得800元,第二名比第三名多得500元,三名优秀职工各得多少元奖金?6.在书架上摆放着三层书共275本,第三层比第二层的书的3倍多2本,第一层比第二层的2倍少3本,三层上个摆放着多少本书?7.一笔奖金分一等奖,二等奖和三等奖,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍。
如果评一,二,三等奖各两人,那么每个一等奖金实308元;如果凭一个一等奖,三个三等奖,两个二等奖,那么一等奖的奖金是多少元?8.把一个减法算式里的被减数,减数与差相加,得数是592,已知减数比差的2倍还大2,问减数是多少?9.甲乙丙三人的平均年龄是42岁,若将甲的岁数增加7岁,已的岁数扩大2倍,丙的岁数缩小2倍,则三人岁数相等,那么丙的年龄为多少岁?10.甲数减去878,就等于乙数;如果甲数加1142,就等于乙数的5倍。
甲乙两数各是多少?11.某中学利用暑假进行军训,晴天每日行35千米,雨天每天行22千米,13天共行403千米。
这期间雨天有多少天?12.三只木筏运木板910块,第一只木筏比第二只木筏多运30块,第三只木筏比第二只木筏少运20块。
三只木筏各运多少块?13.小明三天读完一本74页的书,第一天比第二天少读5页,第二天比第三天少读7页。
小明三天各读多少页?14.四人年龄之和是77岁,最小的10岁,他与最大的年龄之和比另外两人年龄之和大7岁。
最大的年龄是几岁?15.三个饲养场共养1600头牛,第二饲养场养牛的头数是第一饲养场的2倍,第三饲养场养的头数是第二饲养场的2倍多60头,三个饲养场各养牛多少头?16.三堆苹果共有130个,第二堆的苹果数是第一堆的3倍,第三堆的苹果数是第二堆的2倍多10个,问三堆苹果各有多少个?17.少先队一、二、三中队共植树200棵,二中队植树的棵数是一中队的2倍多5棵,三中队植树的棵数比一、二中队之和多4棵,三个中队各植树多少棵?18.甲、乙、丙三人,甲的年龄是乙的2倍还大3岁,乙的年龄是丙的2倍小2岁,三个人的年龄之和是109岁,分别求出三人的年龄.19.甲、乙、丙、丁四个人一共做了370个零件,如果把甲做的个数加2,乙做的个数减3,丙做的个数乘2,丁做的个数除以2,四个人做的零件个数正好相等,问四个人各做多少个零件?20.甲仓所存面粉是乙仓的3倍,从甲仓运走8500千克,从乙仓运走500千克后,两仓所剩的千克数相等,问两仓原有面粉多少千克?21.姐妹两人买东西,姐姐带的钱数是妹妹的2倍,姐姐用去180元,妹妹用去30元,这时二人剩下的钱数相等,问姐妹各带了多少元?22.有大小两个整千数,大数是小数的3倍,这两个数最高位上的数字的差是6,问这两个整千数各是多少.23.14.用9辆汽车和18辆大车送一批货物,每辆汽车的载重量相当于大车的3倍,结果汽车比大车一共多运18吨,汽车和大车每辆各运多少吨?24.一车间原有男工人数比女工多55人,如果调走男工5人,那么男工人数正好是女工的3倍,原有男工多少人?25.某校有排球的个数比足球多50个,如果再买40个排球,排球的个数就是足球的3倍,足球、排球各有多少个?26.小明和小丽数学作业本上的红花,小丽比小明多7朵,如果小明少得2朵,小丽再得3朵,小丽的红花数就是小明的3倍,小明小丽各得多少朵?27.甲有36本课外书,乙有24本课外书,两人捐出同样多的本数后,甲剩下的数是乙剩下本数的3倍,两人各捐出多少本书?28.一根电线长240米,把它截成三段,使第一段比第二段长20米,第三段长是第一段的2倍。
